

















































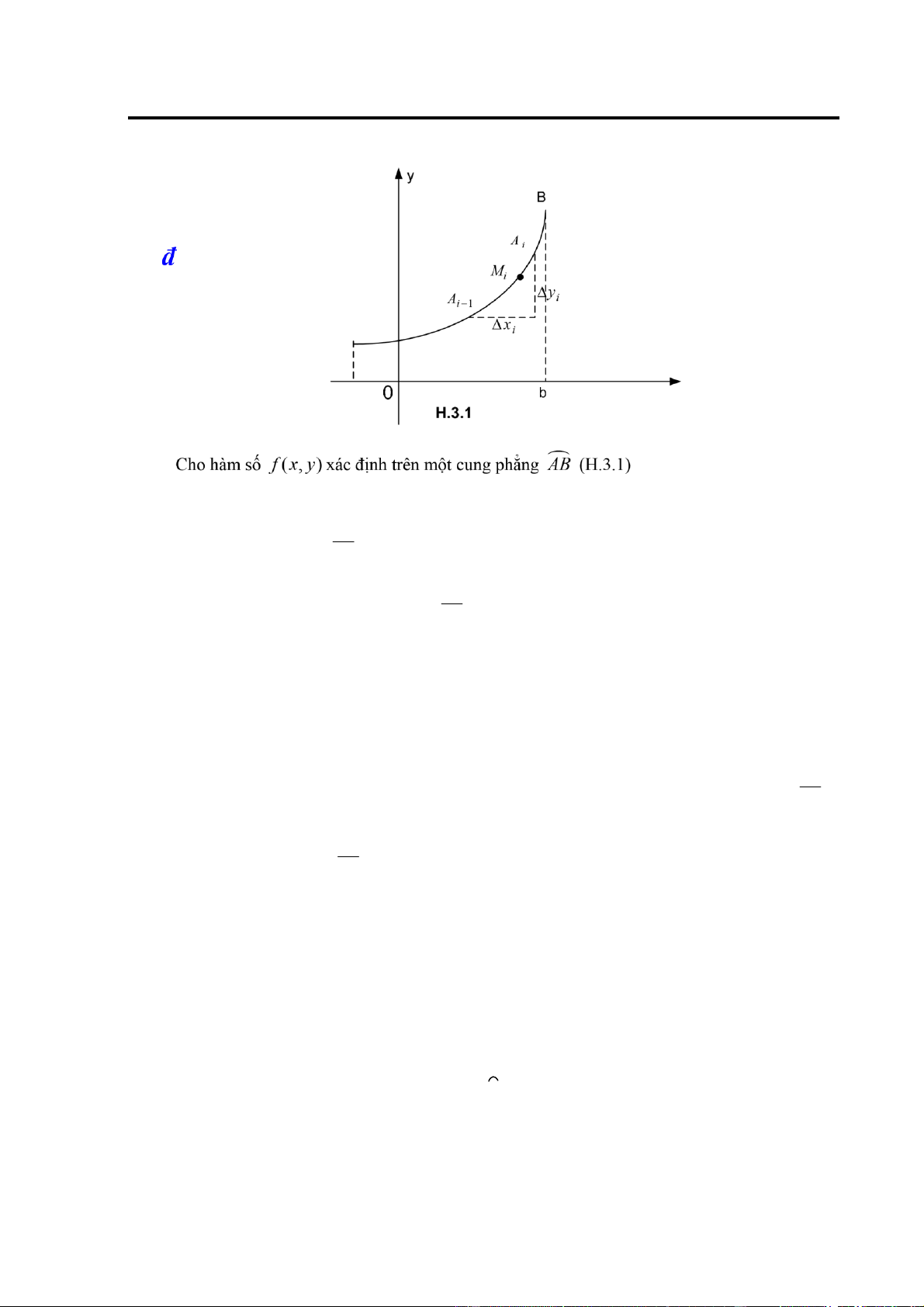


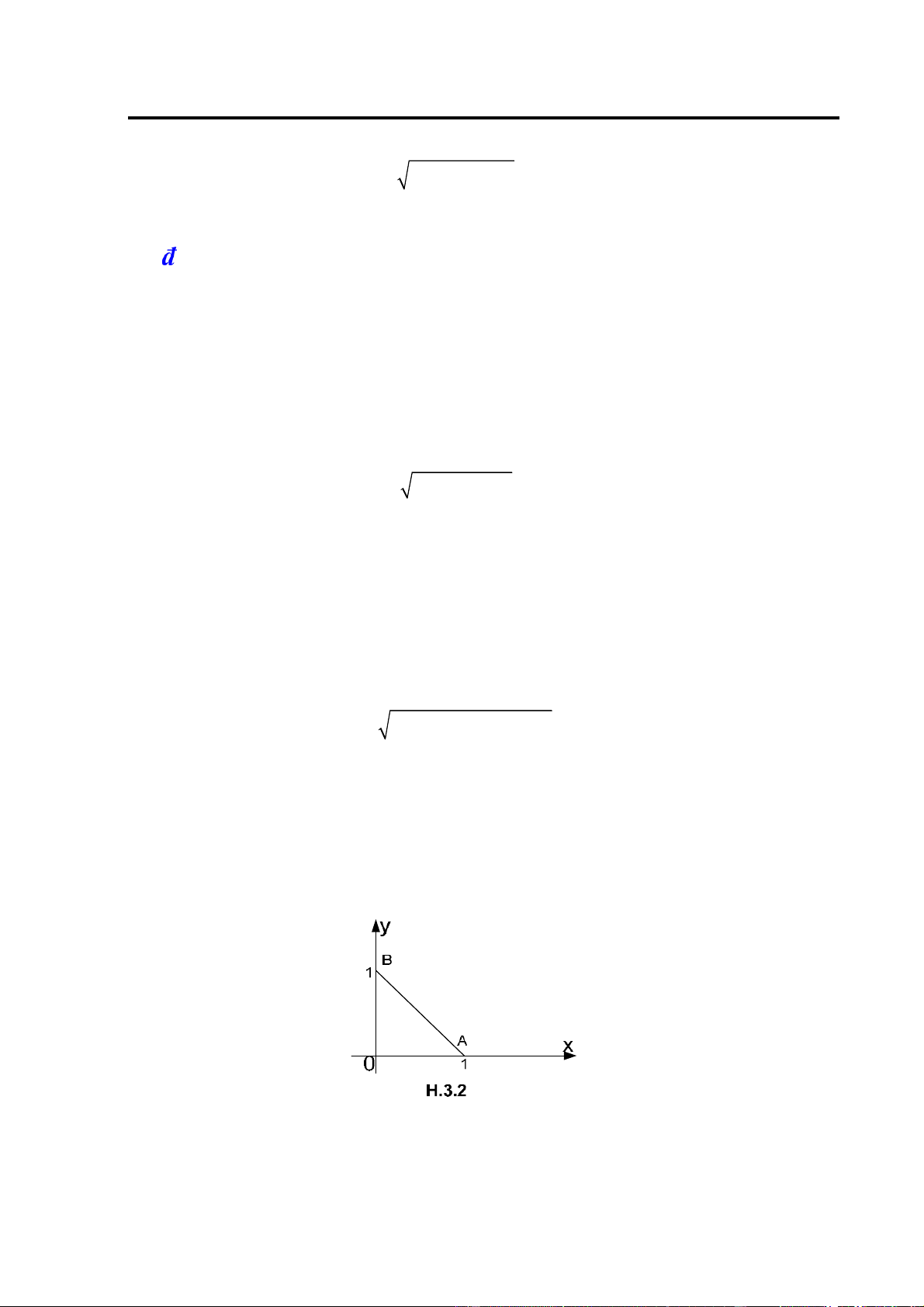
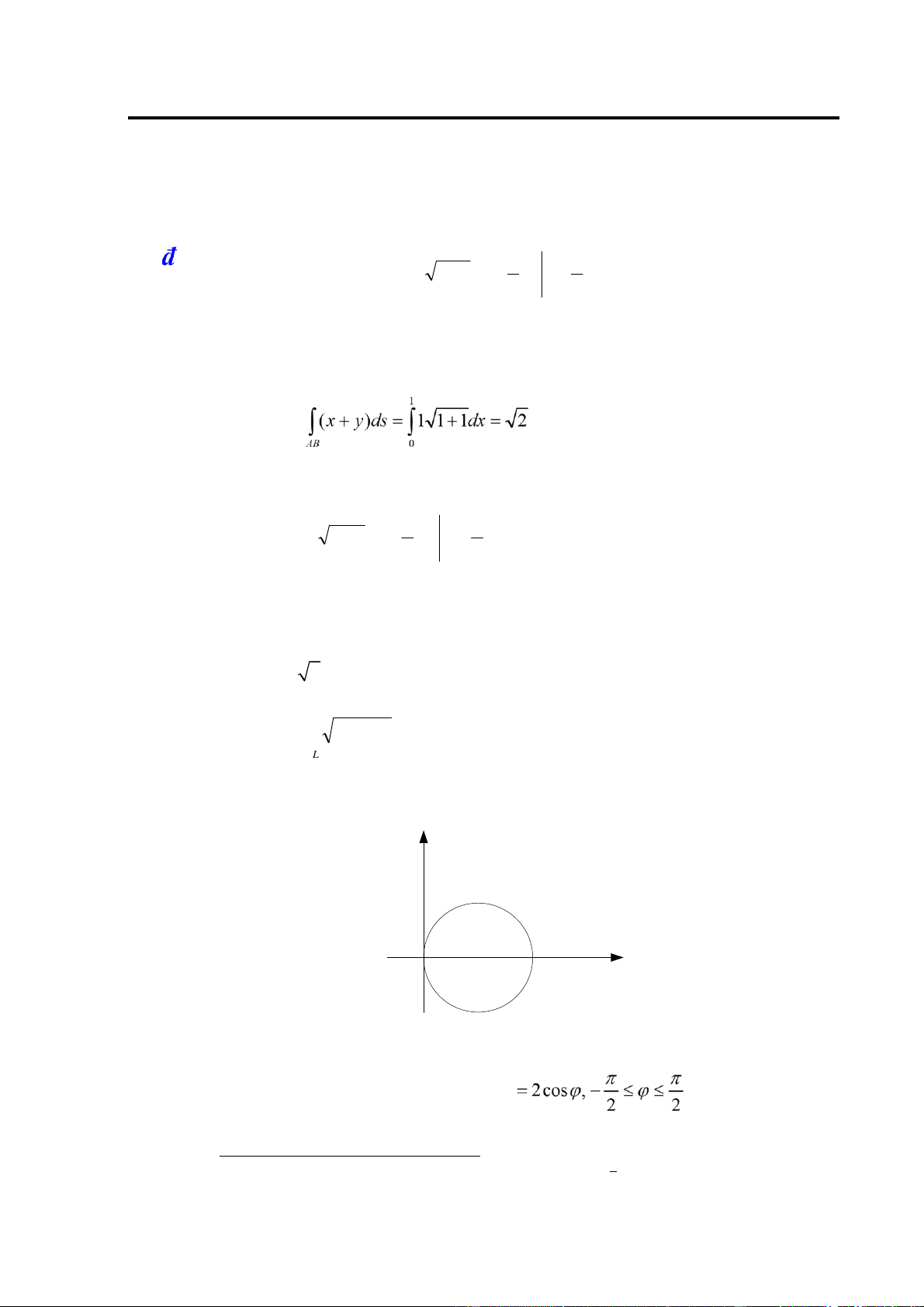
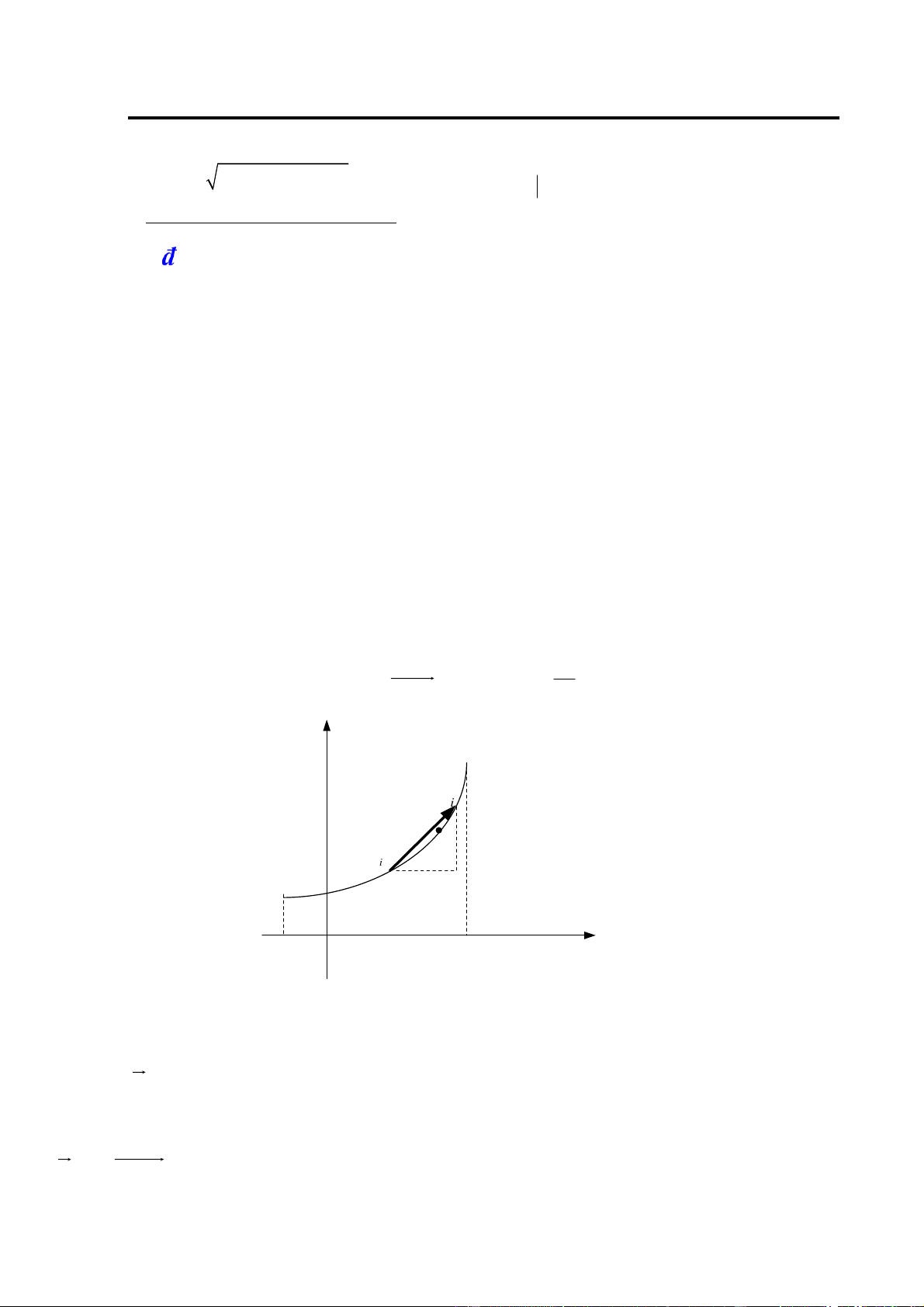
































































































Preview text:
lOMoARcPSD| 10435767
HỌC VIỆN CÔNG NGHỆ BƯU CHÍNH VIỄN THÔNG
SÁCH HƯỚNG DẪN HỌC TẬP GIẢI TÍCH 2 Lưu hành nội bộ
Downloaded by Ti?n D?ng Tr?n Lý (dungtienltr128@gmail.com) lOMoARcPSD| 10435767
SÁCH HƯỚNG DẪN HỌC TẬP GIẢI TÍCH 2 Biên soạn : Ts. VŨ GIA TÊ LỜI GIỚI THIỆU
GIAỈ TÍCH 2 (TOÁN CAO CẤP A3 ) là học phần tiếp theo các học phần GIẢI TÍCH 1,
ĐẠI SỐ ( TOÁN CAO CẤP A1, A2) dành cho sinh viên năm thứ nhất thuộc các nhóm ngành khối
kĩ thuật. Giáo trình này dùng làm tài liệu học tập cho sinh viên ại học với hình thức ào tạo từ xa.
Giáo trình ược biên soạn theo chương trình qui ịnh năm 2001 của Bộ Giáo dục- Đào tạo và theo ề
cương chương trình của Học viện Công nghệ Bưu chính Viễn thông phê duyệt năm 2006 cho hệ ào tạo chính qui.
Ở Việt nam, hình thức ào tạo từ xa tuy ã triển khai và nhân rộng từ 10 năm nay nhưng vẫn
còn khá mới mẻ. Với cách học này, òi hỏi người học phải làm việc ộc lập nhiều hơn, lấy tự học, tự
nghiên cứu là chính. Do ó tài liệu học tập, cụ thể là các giáo trình phải ược coi là phương tiện cơ
bản và quan trọng nhất. Các yếu tố trên ược chúng tôi chú ý khi viết giáo trình này, cụ thể là: Nội
dung ược trình bày ngắn gọn, chính xác. Trừ một số ịnh lí có chứng minh nhằm rèn luyện tư duy
và củng cố kiến thức, còn hầu hết các ịnh lí ưa ra ược thừa nhận với mục ích áp dụng. Tương ứng
mỗi nội dung kiến thức ều có ví dụ minh họa nhằm hướng người học hiểu sâu sắc và biết cách áp
dụng. Trong mỗi chương ều có mục ích, yêu cầu và phần tóm tắt nội dung ể người học dễ ọc, dễ
thuộc. Các câu hỏi mang tính trắc nghiệm cuối mỗi chương là cơ sở ánh giá kiến thức có ược của
người học về nội dung chương ó.
Giáo trình gồm 5 chương, tương ứng với 4 ơn vị học trình (60 tiết).
Chương 1 .Phép tính vi phân hàm số nhiều biến số.
Chương 2. Tích phân bội.
Chương 3. Tích phân ường và tích phân mặt.
Chương 4. Lý thuyết trường.
Chương 5. Phương trình vi phân.
Downloaded by Ti?n D?ng Tr?n Lý (dungtienltr128@gmail.com) lOMoARcPSD| 10435767
Mặc dù cố gắng rất nhiều, song không tránh khỏi các sơ suất về nội dung cũng như các lỗi về
ấn loát, chúng tôi rất mong ược sự góp ý kiến và rất cám ơn về iều ó.
Nhân ây, chúng tôi chân thành cám ơn Ban Giám ốc Học viện Công nghệ Bưu chính
Viễn thông, Trung tâm Đào tạo Bưu chính Viễn thông 1, ặc biệt Phòng Đào tạo Đại học từ xa và
các bạn ồng nghiệp ã tạo iều kiện, ộng viên, giúp ỡ chúng tôi hoàn thành giáo trình này. Hà Nội, 7-2006 Tác giả
Downloaded by Ti?n D?ng Tr?n Lý (dungtienltr128@gmail.com) lOMoARcPSD| 10435767
Chương 1. Phép tính vi phân hàm số nhiều biến số
CHƯƠNG 1. PHÉP TÍNH VI PHÂN HÀM SỐ NHIỀU BIẾN SỐ GIỚI THIỆU
Phép tính vi phân hàm số nhiều biến số là sự mở rộng một cách tự nhiên và cần thiết của phép
tính vi phân hàm số một biến số. Các bài toán thực tế thường xuất hiện sự phụ thuộc một biến số
vào hai biến số hoặc nhiều hơn, chẳng hạn nhiệt ộ T của một chất lỏng biến ổi theo ộ sâu z và thời
gian t theo công thức T = e z−t , nhiệt lượng toả ra trên dây dẫn phụ thuộc vào iện trở của dây, cường
ộ của dòng và thời gian dẫn iện theo công thức Q = 0,24RI t2 ,v.v…Vì vậy, khảo sát hàm số nhiều
biến số vừa mang tính tổng quát vừa mang tính thực tiễn. Để học tốt chương này, ngoài việc nắm
vững các phép tính ạo hàm của hàm một biến số, người học phải có các kiến thức về hình học không
gian (xem [2]).Trong chương này, yêu cầu người học nắm vững các nội dung chính sau:
1. Các khái niệm chung của không giann (n chiều).
Mô tả ược miền xác ịnh và ồ thị của hàm hai biến.
2. Phép tính ạo hàm riêng và vi phân toàn phần.
Nắm vững các qui tắc tính ạo hàm riêng trên cơ sở tính ạo hàm của hàm một biến. Công thức
tính ạo hàm riêng của hàm số ẩn. Công thức vi phân toàn phần và biết cách áp dụng vào phép tính gần úng.
3. Nắm vững khái niệm và cách tính ạo hàm theo hướng. Giải thích ược ạo hàm riêng theo
các biến x, y, z chính là ạo hàm theo hướng các trục Ox, Oy, Oz.
4. Bài toán tìm cực trị.
Qui tắc tìm cực trị tự do, phương pháp nhân tử Lagrange. NỘI DUNG
1.1. Các khái niệm chung
1.1.1. Không gian n chiều
* Ta ã biết mỗi iểm trong không gian 3 chiều ược ặc trưng hoàn toàn bởi bộ 3 số (x, y,
z) là 3 tọa ộ Descartes của nó: x là hoành ộ, y là tung ộ và z là cao ộ.
Tổng quát như sau: Mỗi bộ có thứ tự n số thực (x x1, 2 ,...,xn ) gọi là một iểm n chiều. Kí
hiệu M(x x1, 2 ,...,xn ) có nghĩa là iểm n chiều M có các toạ ộ x x1, 2 ,...,xn . Tập các iểm M(x x1,
2 ,...,xn ) gọi là không gian Euclide n chiều. Kí hiệu tập này là n .
* Cho M(x x1, 2,...,xn) ∈n , N(y y1, 2,..., yn)∈n . Gọi khoảng cách giữa M và N, kí hiệu d(M,
N), là số thực tính theo công thức: 3
Downloaded by Ti?n D?ng Tr?n Lý (dungtienltr128@gmail.com) lOMoARcPSD| 10435767
Chương 1. Phép tính vi phân hàm số nhiều biến số = d M N( , ) = (x − − 1
y1 )2 +......+ (xn yn )2 ∑n (x − i yi )2 i=1
Tương tự như trong , 2, 3 ta nhận ược bất ẳng thức tam giác trong n . Tức là với 3 iểm A, B, C bất kỳ trong n ta có:
d(A,C) ≤d(A,B) +d(B,C) * ChoM (x x, 0 ,...,x 0 ) . Tập gọi là
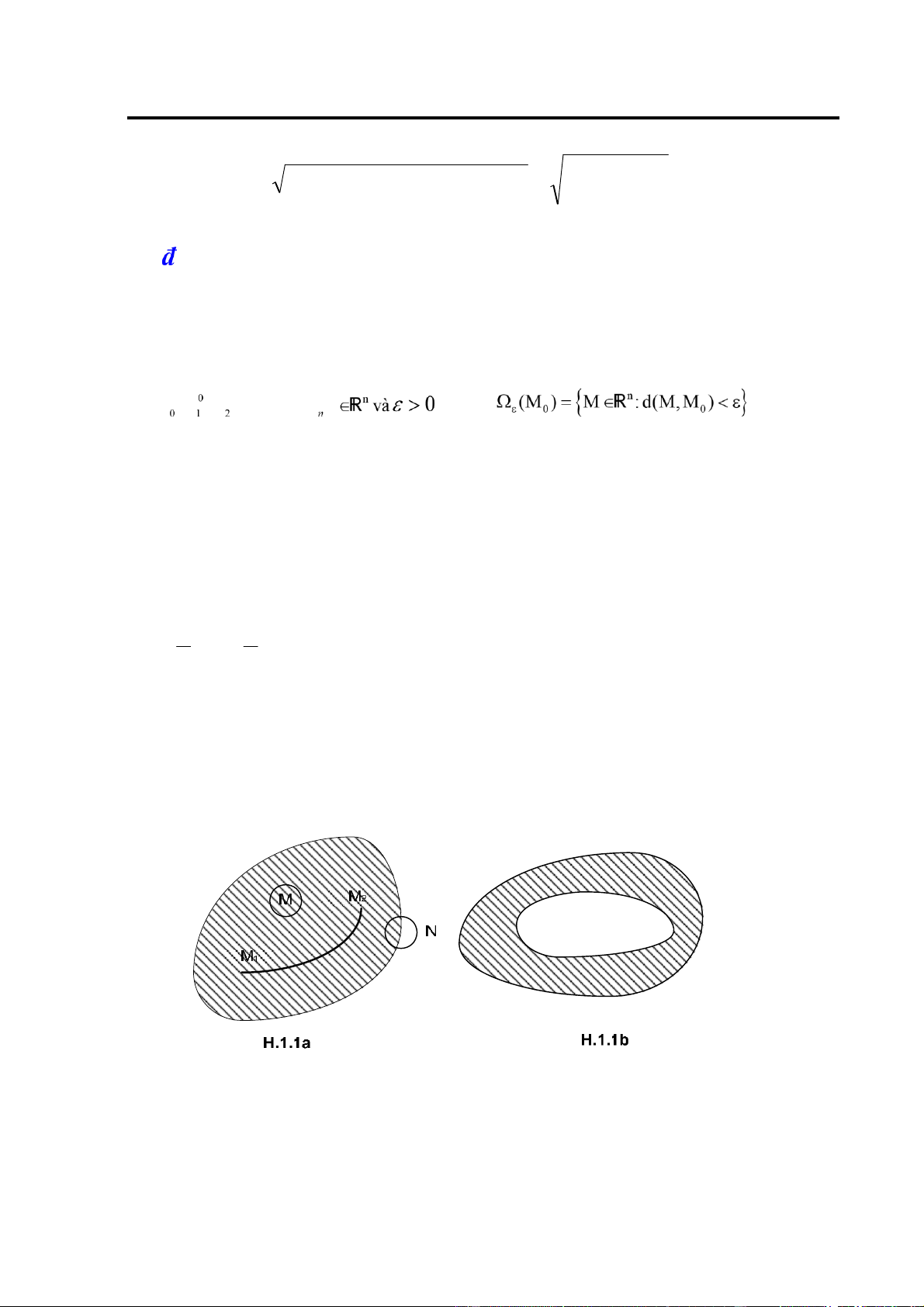
ε- lân cận hoặc lân cận bán kính ε của M0 hoặc hình cầu mở tâm M0 bán kính ε (H.1.1a).
* Cho E ⊂n . Điểm M∈E gọi là iểm trong của E nếu có Ωε(M) ⊂E(∃ε> 0).
Điểm N∈n gọi là iểm biên của E nếu bất kỳ Ωε(M) ều chứa những iểm thuộc E và iểm không thuộc
E(∀ >ε 0). Tập E gọi là mở nếu mọi iểm của nó ều là iểm trong, gọi là óng nếu nó chứa mọi iểm
biên của nó. Tập các iểm biên của E kí hiệu ∂E . Bao óng của E hay tập
E óng ký hiệu E và có E E= ∂E (H.1.1a). *
Tập E gọi là bị chặn hay giới nội nếu như tồn tại số N sao choE ⊂ ΩN (0) . *
Tập E gọi là liên thông nếu mỗi cặp iểm M1, M2 trong E ều ược nối với nhau bởi một
ường cong liên tục nào ó nằm trọn trong E. Tập liên thông E gọi là ơn liên nếu nó bị giới hạn bởi
một mặt kín (một ường cong kín trong 2 ; một mặt cong kín trong 3 ) (H.1.1a). Tập liên thông E gọi
là a liên nếu nó bị giới hạn bởi từ hai mặt kín trở lên rời nhau từng ôi một (H.1.1b).
Ví d ụ 1: Xét các t ậ p sau trong 2 . 4
Downloaded by Ti?n D?ng Tr?n Lý (dungtienltr128@gmail.com) lOMoARcPSD| 10435767
Chương 1. Phép tính vi phân hàm số nhiều biến số ={ A
(x y x, ): 2 + y 2 < 4} = B
{(1,2),( 1,0),(0,− 0)} và 2 Giải: ∂ = = A
{(x y, ) : x2 + y2 = 4} {
- ường tròn tâm O bán kính 2, A
(x y, ) : x2 + y2 ≤ 4} - hình tròn kể cả biên.
A, 2 là các tập liên thông, B không liên thông (gồm 3 iểm rời rạc).
A, B là các tập giới nội, 2 không giới nội (cả mặt phẳng 0xy).
1.1.2. Định nghĩa hàm nhiều biến số Cho D ⊂n . Gọi ánh xạ:
f : D → R Hay là M(x ,x ,....,x ) ∈ ∈ 1 2 n
D u = f(M) = f(x ,x ,....,x )1 2 n là một hàm số của n biến số xác
ịnh trên D. D gọi là miền xác ịnh của hàm số f; x x1, 2,....,xn là các biến số ộc lập, còn u gọi là biến số phụ thuộc.
1.1.3. Miền xác ịnh của hàm nhiều biến số
Người ta quy ước: Nếu cho hàm số u = f(M) mà không nói gì về miền xác ịnh D của nó thì
phải hiểu rằng miền xác ịnh D của hàm số là tập hợp các iểm M sao cho biểu thức f(M) có nghĩa.
Miền xác ịnh của hàm số thường là tập liên thông. Sau ây là một số ví dụ về miền xác ịnh của
hàm số 2 biến số, 3 biến số.
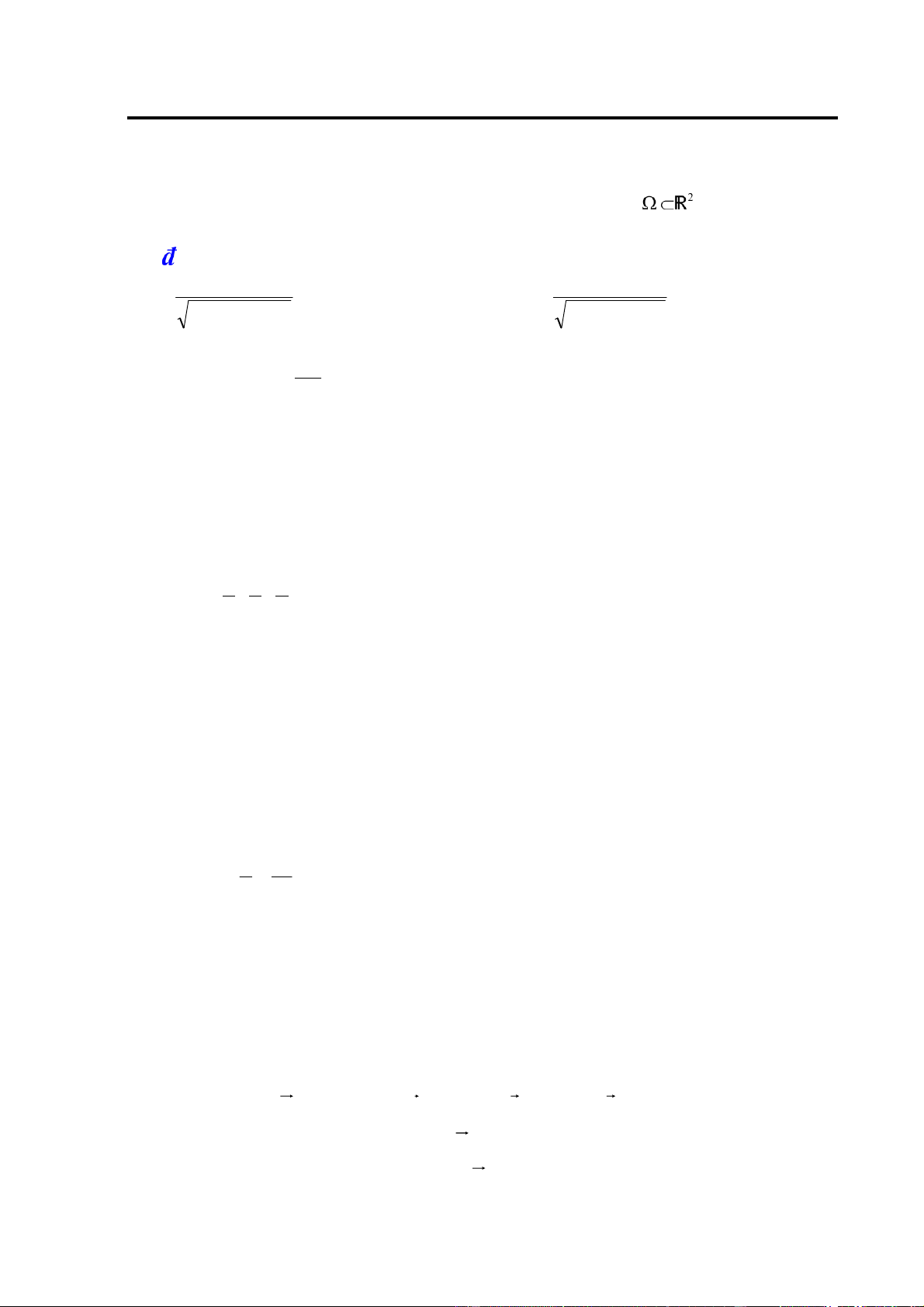
Ví dụ 2: Tìm miền xác ịnh của các hàm số sau và mô tả hình học các miền ó: = y
a) z = 1− x2 − y2 , b) z = ln(x + y) , c) u
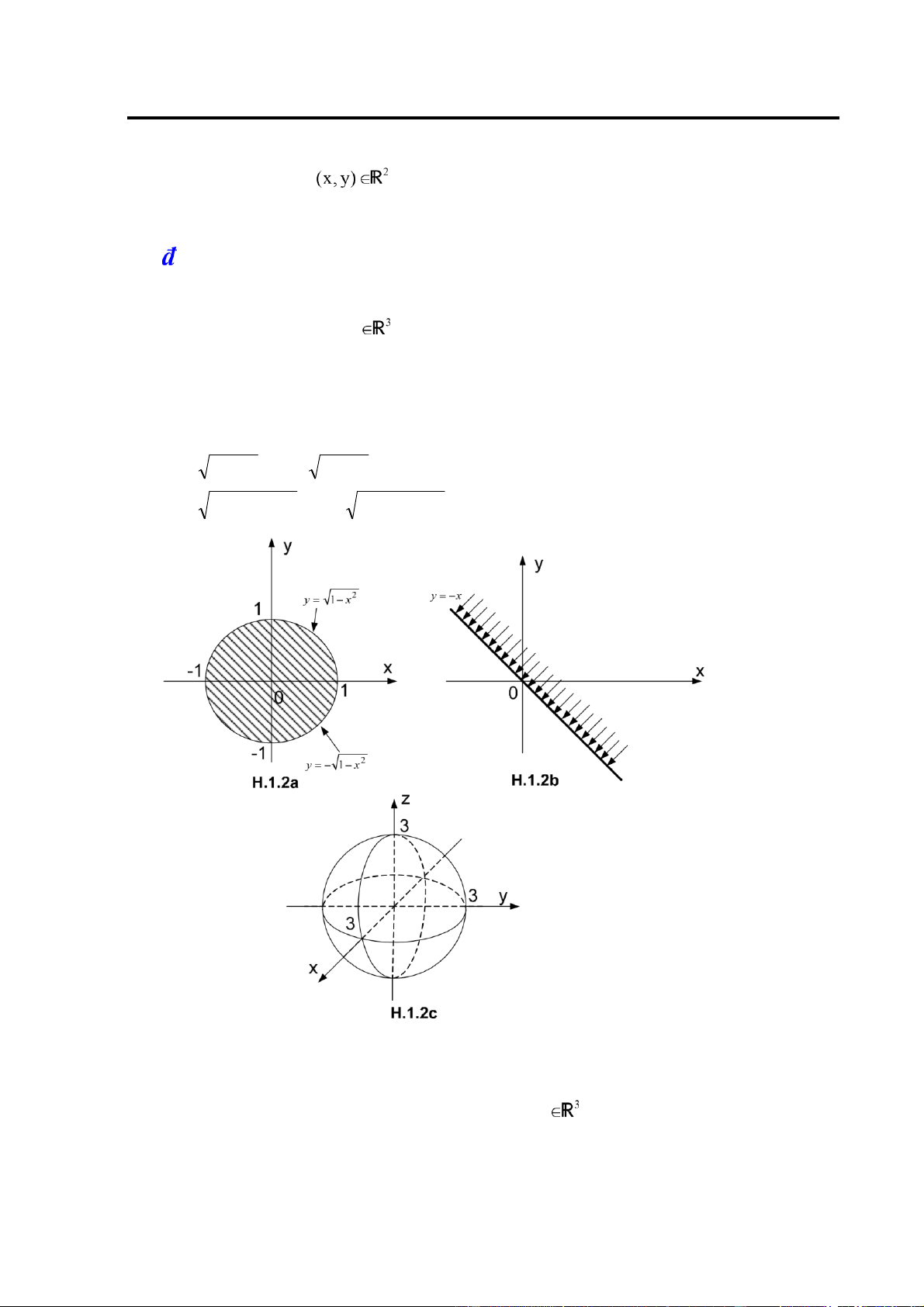
9− x2 − y2 − z2 Giải: a. Miền xác ịnh là tập
sao cho 1− x2 − y2 ≥ 0 hay x2 + y2 ≤1. Đó là hình tròn
óng tâm O bán kính bằng 1 (H.1.2a). Hình tròn óng này có thể mô tả bởi hệ bất phương trình: ⎧⎪−1≤ x ≤1
⎨⎪⎩− 1− x2 ≤ y ≤ 1− x2 5
Downloaded by Ti?n D?ng Tr?n Lý (dungtienltr128@gmail.com) lOMoARcPSD| 10435767
Chương 1. Phép tính vi phân hàm số nhiều biến số b. Miền xác ịnh là tập
thoả mãn x + y > 0 hay y > -x. Đó là nửa mặt phẳng có
biên là ường y = -x (H.1.2b). Nửa mặt phẳng này ược mô tả bởi hệ bất phương trình:
⎧−∞ < x < +∞
⎨⎩− x < y < +∞ c.
Miền xác ịnh là tập (x,y,z)
thoả mãn x2 + y2 + z2 < 9. Đó là hình cầu mở tâm O bán
kính bằng 3 (H.1.2c). Hình cầu mở này mô tả bởi hệ bất phương trình: ⎧− 3 < x < 3
⎪⎪⎨− 9 − x2 ≤ y ≤ 9 − x2 ⎪
⎪⎩− 9 − x2 − y2 ≤ z ≤ 9 − x2 − y2
1.1.4. Ý nghĩa hình học của hàm hai biến số
Cho hàm 2 biến z = f(x,y) với (x y, )∈D. Tập các iểm (x,y,z)
với z = f(x,y) gọi là ồ thị
của hàm số ã cho. Như thế ồ thị của hàm 2 biến thường là một mặt cong trong không gian 3 chiều
0xyz. Đồ thị của hàm số mô tả một cách trực quan hàm số thể hiện ược ý nghĩa hình học của hàm
số. Dưới ây ta xét các mặt cong ặc biệt và ơn giản, thông dụng trong toán học và ứng dụng. 6
Downloaded by Ti?n D?ng Tr?n Lý (dungtienltr128@gmail.com) lOMoARcPSD| 10435767
Chương 1. Phép tính vi phân hàm số nhiều biến số A. Mặt phẳng:
Mặt phẳng là ồ thị của hàm hai biến tuyến tính, nói cách khác phương trình mặt phẳng có
dạng: Ax + By + Cz + D = 0 trong ó A2 + B2 +C2 > 0. Chẳng hạn C ≠ 0 có z = − 1 (D + Ax +
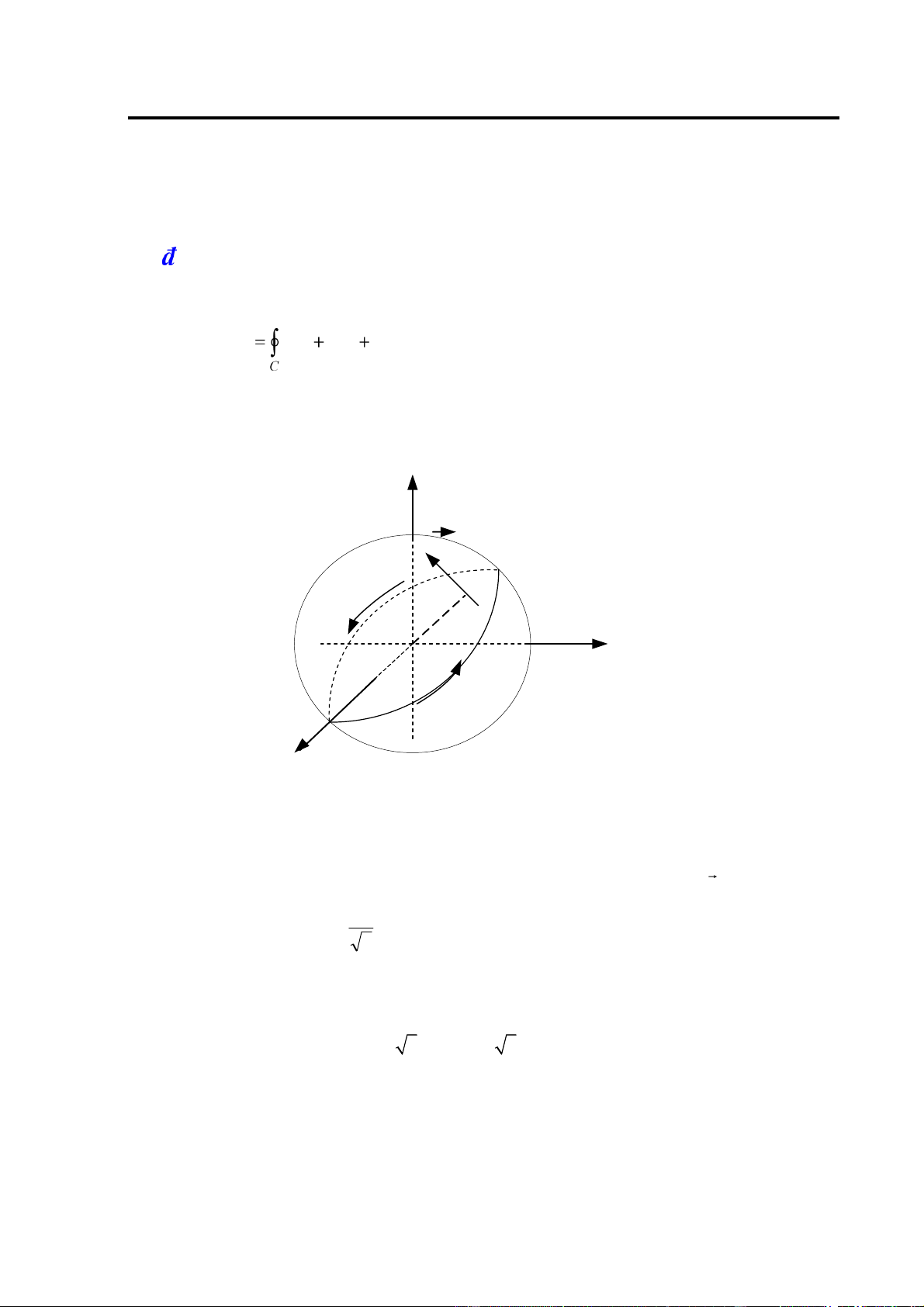
By), hàm số này xác ịnh trên 2 . C B. Ellipsoid
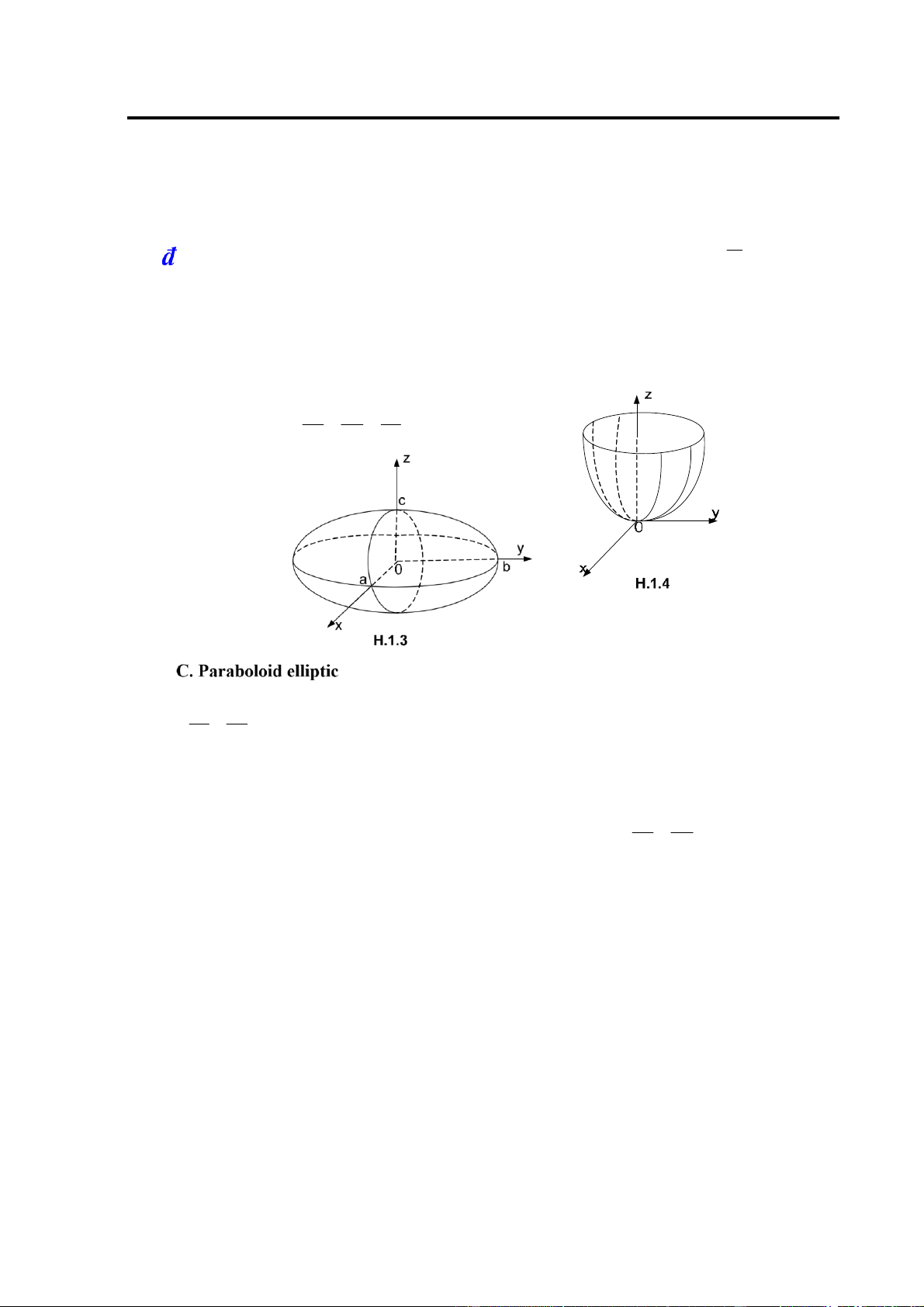
Ellipsoid là mặt cong, phương trình chính tắc của nó có dạng (H.1.3) x2 y2 z2 a + + = 2 b2 c2 1 Đây là hàm hai biến cho dưới dạng không tường minh (dạng ẩn). Hàm số là a trị. 2 2 Chẳng hạn x y coi z là biến
phụ thuộc vào x và y thì miền xác ịnh là hình ellipse có các bán trục x2 y2 + a và b: a ≤ 2 b2 1
Khi a = b = c = R ta có mặt cầu tâm gốc toạ ộ và bán kính là R: x2 + y2 + z2 = R2 +
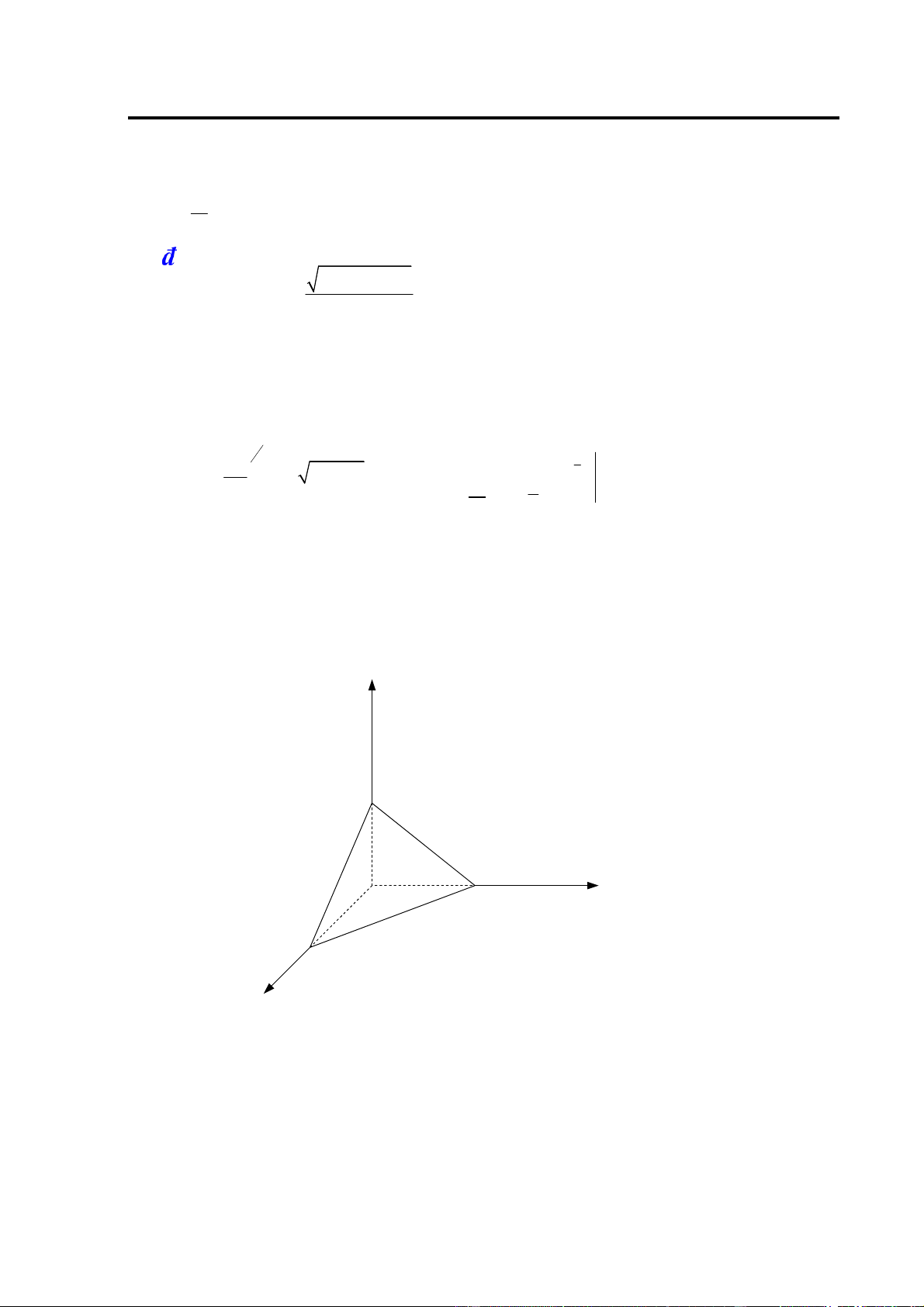
Phương trình chính tắc của paraboloid elliptic có dạng (H.1.4): a = 2 b2 z
Miền xác ịnh của hàm số trên là 2 . Khi a = b tức là phương trình có dạng: x2 + y2 = a z2
Gọi ó là paraboloid tròn xoay. 7
Downloaded by Ti?n D?ng Tr?n Lý (dungtienltr128@gmail.com) lOMoARcPSD| 10435767
Chương 1. Phép tính vi phân hàm số nhiều biến số
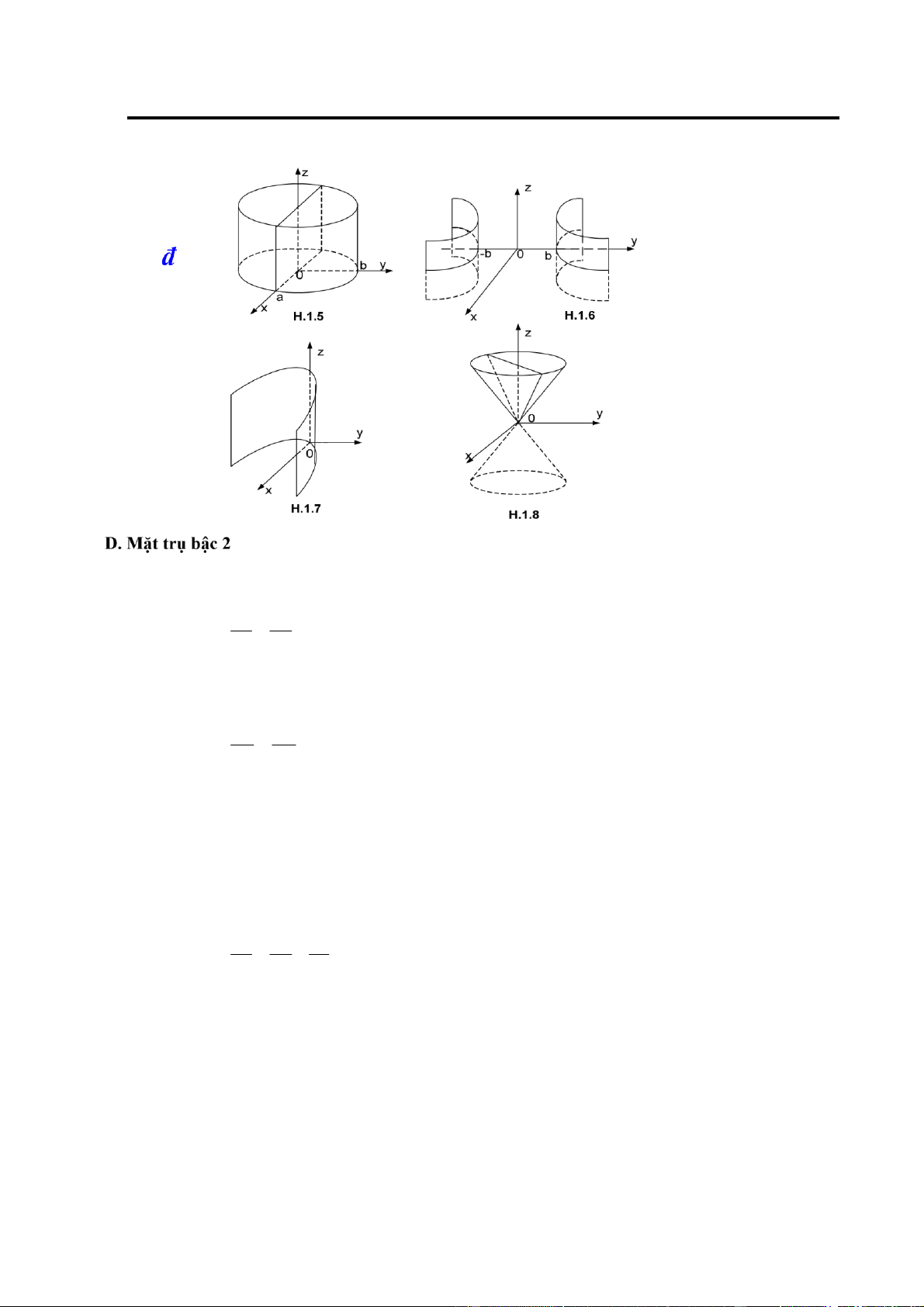
* Mặt trụ elliptic (H.1.5) có phương trình chính tắc: x2 y2 + a = 2 b2 1
* Mặt trụ hyperbolic (H.1.6) có phương trình chính tắc: x2 y 2 − = −1 a 2 b2
* Mặt trụ parabolic (H.1.7) có phương trình chính tắc: y2 = 2px E. Mặt nón bậc 2
Phương trình chính tắc của mặt nón có dạng (H.1.8) x2 y2 z2 a + − = 2 b2 c2 0
1.1.5. Giới hạn của hàm số nhiều biến số
Khái niệm giới hạn của hàm số nhiều biến số cũng ược ưa về khái niệm giới hạn của hàm một
biến số. Ở ây một biến số óng vai trò là khoảng cách d(M0, M) giữa hai iểm M0 và M trong không
gian n . Để ơn giản trong cách viết chúng ta xét trong không gian 2 chiều 2 .
* Nói rằng dãy iểm M →
n(xn, yn) dần ến iểm M0(x0, y0); kí hiệu M n
M 0 khi n → ∞ 8
Downloaded by Ti?n D?ng Tr?n Lý (dungtienltr128@gmail.com) lOMoARcPSD| 10435767
Chương 1. Phép tính vi phân hàm số nhiều biến số →∞ = 0hay là ⎧⎪⎨⎩limlim == n→∞ xynn xy00
nếu lim (d M 0 ,M n ) ⎪ n n→∞
* Cho hàm z = f(x,y) xác ịnh ở lân cận M0(x0, y0), có thể trừ iểm M0. Ta nói rằng hàm
f(M) có giới hạn là l khi M(x,y) dần ến M0(x0, y0) nếu mọi dãy iểm Mn(xn, yn) thuộc lân cận
dần ến M0 ta ều có: lim f x( n, yn ) = l n→∞
Thường kí hiệu lim f M( ) = l hay lim f (x y, ) = l M→M0
(x y, )→(x y0 0, )
Sử dụng ngôn ngữ " ,εδ" có thể ịnh nghĩa như sau: Hàm số f(M) có giới hạn l khi
M → M 0 nếu ∀ε δ> 0,∃ > 0 :0 < d M( 0,M) <δ⇒ f M( ) −l <ε
Chú ý: 1. Tất cả các khái niệm giới hạn vô hạn hoặc các ịnh lí về giới hạn: tổng, tích,
thương ều giống như hàm số một biến số.
2. Từ ịnh nghĩa ta nhận thấy: Giới hạn l của hàm số f (x y, ) khi M → M0 không
phụ thuộc ường i của M tiến ến M , vì thế nếu chỉ ra hai ường i của 0
M tiến ến M0 mà f (M) tiến
ến hai giá trị khác nhau thì hàm số không có giới hạn tại M0 .
Ví dụ 3: Tìm các giới hạn x y2 xy xy a. lim b. lim c. lim + + +
(x y, )→(0,0) x2 y2
(x y, )→(0,0) x2 y2 (x y, )→(0,0) x2 y2 Giải: x y2 2 + y2 a. Ta có x + − 2
y2 0 ≤ y, d M O( , ) = x
∀ε> 0,∃δ=ε khi 0 < x2 + y2 <δ ⇒ y <δ ⇒ x − 2x y+2 y2 0 ≤ y <δ ε= x y2 Vậy (x y, lim)→(0,0) x2 + y 2 = 0 9
Downloaded by Ti?n D?ng Tr?n Lý (dungtienltr128@gmail.com) lOMoARcPSD| 10435767
Chương 1. Phép tính vi phân hàm số nhiều biến số b. Cho
M x y( , ) →O(0,0) theo ường y = Cx, C =
const (hằng số) xy Cx2 xy C = = thì x + + 2 y2
(1+C 2 )x2 ⇒limx→0 x2 y2
1+C 2 chứng tỏ dãy giá trị hàm có giới hạn khác nhau
phụ thuộc vào C. Theo chú ý 2,.suy ra hàm không có giới hạn. xy x −0 ≤ xy 2 2 2 2 c.
. y ≤ y . Tương tự a. suy ra lim x +y x +y = 0 + (x y, )→(0,0) x2 y2
1.1.6. Sự liên tục của hàm số nhiều biến số A. Định nghĩa
* Hàm số f(M) xác ịnh trên miền D và M ∈ 0
D . Ta nói rằng hàm số f(M) liên tục tại M 0 nếu
lim→M f M( ) = f M( 0 0 ) . M
* Hàm số f(M) xác ịnh trên miền D. Nói rằng hàm số liên tục trên miền D nếu nó liên tục tại mọi iểm M ∈D .
* Hàm số f(M) liên tục trên miền óng D nếu nó liên tục trên miền D và liên tục tại mọi iểm N
∈∂D theo nghĩa lim f M( ) = f N( ),M ∈D . M→N
* Nếu ặt Δf x( +Δ +Δ
0, y0 ) = f x( 0 x y, 0
y)− f x( 0, y0 ) gọi là số gia toàn phần của hàm số tại
(x0,y0) thì hàm số f(x,y) liên tục tại (x0, y0) nếu như Δf x( 0, y0 ) → 0 khi Δ →x 0 và Δy → 0 . B. Tính chất
Hoàn toàn tương tự như hàm một biến số ta có tính chất quan trọng sau ây:
Định lý 1.1. Nếu f(x,y) liên tục trong miền óng D giới nội thì nó ạt giá trị lớn nhất và giá
trị bé nhất trong miền D tức là: ∃M ∈ ∈ 1
D M, 2 D ể có bất ẳng thức kép: f M( 1) ≤ f M( ) ≤ f M( 2 ), ∀M ∈D
1.2. Đạo hàm và vi phân
1.2.1. Đạo hàm riêng 10
Downloaded by Ti?n D?ng Tr?n Lý (dungtienltr128@gmail.com) lOMoARcPSD| 10435767
Chương 1. Phép tính vi phân hàm số nhiều biến số
Cho hàm số u = f(x,y) xác ịnh trong miền D và M 0 (x0, y0 )∈ D . Thay y = y0 vào hàm số ã
cho sẽ nhận ược hàm số một biến số u = f(x, y0). Nếu hàm số này có ạo hàm tại x0 thì ạo hàm ó ược
gọi là ạo hàm riêng của f(x, y) ối với x tại M0(x0, y0) và kí hiệu như sau: u′ ′
x (x0, y0 ) hay ∂∂ux (x0 , y0 ) hay f x (x0, y0 ) hay ∂∂fx (x0 , y0 ) Đặt Δ + Δ
x f x( 0 , y0 ) = f x( 0
x y, 0 ) − f x( 0 , y0 ) gọi ó là số gia riêng của hàm f(x, y) theo biến x tại (x0, y0) và ta có: ∂f
Δ x f x( 0 , y0 ) ∂x (x Δ
0 , y0 ) = Δ →limx 0 x
Tương tự ta có ịnh nghĩa ạo hàm riêng của hàm số ối với y tại M0(x0, y0) và ký hiệu: u′y (x ′
0 , y0 ) , ∂∂uy (x0 , y0 ), f y (x0 , y0 ), ∂∂fy (x0 , y0 )
Chú ý: Có thể chuyển toàn bộ các phép tính ạo hàm của hàm một biến số: cộng, trừ, nhân, chia,
… sang phép tính ạo hàm riêng.
Ví dụ 4: Tính ạo hàm riêng sau: a. ′
u = x y3 , u /
x (1,2), u y(1,1) .
b. u = x y (x > 0),
u′x (x y, ),
u′y (x y, ). y
c. u = x zarctg2 ,
u′x (x y z, , ),
u′y (x y z, , ),
u′z (x y z, , ) . z Giải:
a. u′x (x y, ) = 3x y2 ⇒ u′x (1, 2) = 6,
u′y (x y, ) = x3 ⇒ u′y (1,1) =1. b. u′ = = x
yx y−1, u′y x y ln x y
c. u′x (x y z, , ) = 2xzarctg , z
u′y (x y z, , ) = x z2 1z 1 2 = yx z2 2+ 2z 2 , y 11
Downloaded by Ti?n D?ng Tr?n Lý (dungtienltr128@gmail.com) lOMoARcPSD| 10435767
Chương 1. Phép tính vi phân hàm số nhiều biến số 1+ z 2
u′z (x y z, , ) = x arctg2 yz − x z2 zy2
1y 2 = x 2 (arctg yz − y 2 yz+ z 2 ) . 1+ z 2
1.2.2. Vi phân toàn phần A. Định nghĩa
* Cho hàm số u = f(x, y) xác ịnh trong miền D chứa (x0, y0). Nếu số gia toàn phần của hàm số tại
(x0, y0) ứng với số gia Δx,Δy của các ối số có dạng:
Δf x( 0, y0 ) = A.Δx + B.Δy +α.Δx +β.Δy (1.1)
trong ó A, B là những số chỉ phụ thuộc vào (x0, y0), còn α,β dần ến 0 khi M → M 0 tức là khi Δ → Δ
→x 0, y 0 thì nói rằng hàm số f(x, y) khả vi tại M0, còn biểu thức A.Δ + Δx B. y ược gọi là vi phân toàn
phần của hàm số tại M0 và kí hiệu là df(x0, y0), hay du(x0, y0). Như vậy df x( 0, y0 ) = A.Δ +x B.Δy
* Hàm số u = f(x, y) ược gọi là khả vi trong miền D nếu nó khả vi tại mọi iểm của miền D.
B. Điều kiện cần của hàm số khả vi
Định lý 1.2. Nếu f(x, y) khả vi tại (x0, y0) thì liên tục tại ó.
Từ (1.1) suy ra Δf x( 0, y0 ) → 0 khi Δx → 0, Δy → 0.
Định lý 1.3. Nếu f(x, y) khả vi tại (x0, y0) thì hàm có các ạo hàm riêng tại (x0, y0) và A = f ′ ′
x (x0, y0), B = f y (x0, y0). Chứng minh: Từ (1.1) suy ra:
Δ x f x( 0, y0 ) =
A+α, Δ y f x( 0, y0 ) = B +β Δx Δy Vậy f ′ ′
x (x0, y0 ) = A,
f y (x0, y0 ) = B chứng tỏ df x( ′ ′
0, y0 ) = fx (x0, y0 )Δ +x fy (x0, y0 )Δy (1.2)
C. Điều kiện ủ của hàm số khả vi
Định lý 1.4. Nếu hàm số u = f(x, y) có các ạo hàm riêng f ′ ′
x (x y, ), f y (x y, ) liên tục tại 12
Downloaded by Ti?n D?ng Tr?n Lý (dungtienltr128@gmail.com) lOMoARcPSD| 10435767
Chương 1. Phép tính vi phân hàm số nhiều biến số
M0(x0,y0) thì f(x, y) khả vi tại M0(x0, y0). Chứng minh: Ta có Δf x( + Δ + Δ
0, y0 ) = f x( 0 x y, 0
y) − f x( 0, y0 ) = [f x( + Δ + Δ + Δ + Δ 0 x y, 0
y) − f x( 0, y0
y)]+[f x( 0, y0
y) − f x( 0, y0 )]
Áp dụng công thức số gia hữu hạn (công thức Lagrange) cho hàm một biến số f(x, y0 + ∆y) tại
lân cận x0 và f(x0, y) ở lân cận y0 sẽ nhận ược: f x( + Δ + Δ + Δ ′ +θ Δ + Δ 0 x y, 0
y)− f x( 0, y0
y) = f x (x0 1 x y, 0
y)Δx f x( 0, y + Δ ′ +θ Δ < < 0
y)− f x( 0, y0) = f y (x0, y0 2
y)Δy Trong ó 0 <θ1 1, 0 <θ2 1
Cũng theo giả thiết f ′ ′
x (x y, ), f y (x y, ) liên tục tại (x0, y0) nên: f ′ +θ Δ + Δ ′ ′ x (x0 1 x y, 0
y) = f x (x0, y0 ) +α(Δx,Δy) f y (x0, y0 +θ Δ ′ 2
y) = f y (x0, y0 )+β(Δx,Δy) Trong ó α→ 0,β→ 0 khi Δx → 0, Δy → 0. Từ ó nhận ược: Δf x( ′ ′
0, y0) = f x (x0, y0)Δx + f y (x0, y0)Δy +αΔx +βΔy chứng tỏ hàm số khả vi tại (x0, y0).
Nếu xét các hàm số h(x, y) = x và g(x, y) = y trong 2 thì rõ ràng:
dh(x, y) = dx = 1.∆x dg(x, y) = dy = 1.∆y
Vậy vi phân toàn phần của hàm số f(x, y) tại (x0, y0) có thể viết dưới dạng: df x( ′ ′
0, y0) = f x (x0, y0)dx + f y (x0, y0)dy (1.2)’
D. Ý nghĩa của vi phân toàn phần
Nếu hàm số f(x, y) khả vi tại (x0, y0) thì rõ ràng:
Δf x( 0, y0 ) = df x( 0, y0 )+αΔx +βΔy α βΔ +x Δy Vì rằng
≤ α β+ → 0 khi Δx → 0, Δy → 0. Δx2 + Δy2
Suy ra df(x0, y0) khác số gia toàn phần ∆f(x0, y0) một vô cùng bé có bậc cao hơn vô cùng bé ρ= Δ +Δx2
y2 khi Δ →x 0, Δ →y
0. Vậy với Δx, Δy khá bé sẽ nhận ược: 13
Downloaded by Ti?n D?ng Tr?n Lý (dungtienltr128@gmail.com) lOMoARcPSD| 10435767
Chương 1. Phép tính vi phân hàm số nhiều biến số Δ ≈f df (1.3)
Công thức (1.3) thường ược sử dụng ể tính gần úng giá trị của hàm số.
Chú ý: Tính khả vi của tổng, tích, thương hai hàm cũng giống như hàm một biến số.
Ví dụ 5: Thực hiện phép tính vi phân các hàm số: ⎛ π⎞ Δx = 0,01 , Δy = 0,02.
a. Cho f(x,y) = x cos xy, tính df ⎜1, ⎟ với ⎝ 4 ⎠
b. Cho f(x,y) = xy2, (x − y e) xy2 . Tính df(x,y). Giải: π π⎞ a. f ′ ′⎛⎜ ⎟⎞ = 2 ⎛⎜ ⎟
x (x y, ) = cos xy − xysin xy , f x 1, 1− , ⎝ 4 ⎠ 2 ⎝ 4 ⎠ π⎞ f ′ ′⎛⎜ ⎟ = − 2
y (x y, ) = −x2 sin xy , f y 1, , ⎝ 4 ⎠ 2
⎛ π⎞ = 2 ⎛⎜1−π⎞⎟.0,01− 2 .0,02 = − 2 ⎛⎜1+π⎞⎟.0,01. df ⎜1, ⎟ ⎝ 4 ⎠ 2 ⎝ 4 ⎠ 2 2 ⎝ 4 ⎠ b. f ′ ′
x (x y, ) = exy2 + y2 (x − y e) xy2 , f y (x y, ) = −exy2 + 2yx x( − y e) xy2 , ]
df x y( , ) = exy {[ } 2
1+ y2 (x − y dx)
+[2xy x( − y)−1]dy . Ví dụ 6:
a. Tính gần úng arctg .
b. Một hình trụ bằng kim loại có chiều cao h = 20 cm và bán kính áy r = 4 cm. Khi nóng
lên h và r nở thêm các oạn Δh = Δr = 0,1 cm. Hãy tính gần úng thể tích hình trụ khi nóng lên. Giải: x 1,05 1+ 0,05 a. Ta viết arctg = arctg
. Xét hàm số f x y( , ) = arctg 14
Downloaded by Ti?n D?ng Tr?n Lý (dungtienltr128@gmail.com) lOMoARcPSD| 10435767
Chương 1. Phép tính vi phân hàm số nhiều biến số 0,97 1− 0,03 y Rõ ràng arctg = f x( + Δ + Δ 0 x y, 0
y), trong ó x0 = y0 = 1, Δx = 0,05 và Δy=-0,03.
Áp dụng công thức xấp xỉ (1.3) ta có: f x( + Δ + Δ ′ ′ 0 x y, 0
y) ≈ f x( 0 0, y ) + df x( 0 0, y ) = f (1,1) + fx (1,1).0,05 + fy (1,1).( 0,03)− x 1 ( , ) =− =− f ′ = + ′ +
x (x y, ) = 1y 1x2
y2 y x2 , f y x y y 2 x2 y2 x x2 1+ y2 1+ y2 f x x y y arctg
b. Ta có V =πr h V2 , ′ = ′ =π r 2πrh V, h r2
Áp dụng công thức (1.3): V r( + Δr h,
+ Δh) ≈π π πr h2+ 2 rh rΔ + r2Δh ≈π.4 .202 + 2 .4.20.0,1π +π.4 .0,12 ≈π.337,6 cm3
Chứng tỏ sai số tuyệt ối không quá 0,3πcm3 và sai số tương ối không quá .
1.2.3. Đạo hàm riêng cấp cao
Đạo hàm riêng cấp hai của một hàm là ạo hàm riêng các ạo hàm riêng cấp một của nó.
Hàm hai biến f(x,y) có 4 ạo hàm riêng cấp hai sau ây: f ′′ = ∂∂ ′′ = ∂∂ ′′ = ∂∂ ′′ = ∂∂ x 2
x ⎛⎜⎝ ∂∂fx ⎞⎟⎠,f xy
y ⎝⎜⎛ ∂∂fx ⎠⎟⎞, f yx
x ⎛⎜⎜⎝ ∂∂fy ⎞⎟⎟⎠, f y 2 y ⎜⎛⎜⎝ ∂∂fy ⎠⎟⎟⎞
∂ 2 f ∂ 2 f ∂ 2 f ∂ 2 f
hay ∂x2 , ∂ ∂x y , ∂ ∂y x , ∂y 2
Hoàn toàn tương tự ta cũng có các ịnh nghĩa ạo hàm riêng cấp cao hơn của hàm nhiều biến hơn.
Ví dụ 7: Tính các ạo hàm riêng f (3) (3) (3) x y , f , f
biết f x y z( , , ) = ex− +2y 4z . 2 xyx xyz 15
Downloaded by Ti?n D?ng Tr?n Lý (dungtienltr128@gmail.com) lOMoARcPSD| 10435767
Chương 1. Phép tính vi phân hàm số nhiều biến số Giải: f f f ′ = ′′ = = − x
ex− +2y 4z , x 2
ex− +2y 4z , x y(3)2
2ex− +2y 4z f ′′ = − = − = − xy
2ex− +2 y 4z , fxyx(3)
2ex− +2 y 4z , fxyz(3)
8ex− +2 y 4z
Nhận xét: Trong ví dụ trên có f (3) = (3) x y f . 2 xyx
Định lý 1.5(Schwarz). Nếu f(x,y) có các ạo hàm riêng hỗn hợp f ′′ ′′
xy và f yx trong lân cận Ωδ(M ′′ ′′
0 ) và liên tục tại M0(x0, y0) thì các ạo hàm hỗn hợp bằng nhau tại M0: f xy (M0) = f yx (M0).
Chứng minh: Lấy t, s ủ bé. Lập các hàm số sau ây trong lân cận M0:
g(x, y) = f(x + t, y) – f(x, y) h(x, y) = f(x, y + s) – f(x, y)
Rõ ràng g(x0, y0 + s) – g(x0, y0) = h(x0 + t, y0) – h(x0, y0) Áp
dụng ịnh lý Lagrange cho hàm g(x0, y) tại y0 nhận ược: g x( + +θ 0 , y0
s) − g x( 0 , y0 ) = s g. ′y (x0 , y0 1s) s ] = s f[ ′ + +θ ′ +θ y (x0 t y, 0
1s)− f y (x0, y0 1
Tiếp tục áp dụng ịnh lý Lagrange cho hàm f ′ +θ y (x y, 0
1s) tại x0 nhận ược: g x( + ′′ +θ +θ 0, y0
s) − g x( 0, y0) = stf yx (x0 2t y, 0 1s)
Hoàn toàn tương tự cũng có: h x( + ′′ +γ +γ 0
t y, 0 ) − h x( 0 , y0 ) = stfxy (x0 1t y, 0 2s)
Cho t s, → 0, do tính liên tục nhận ược f ′′ ′′
xy (x0, y0 ) = f yx (x0 , y0 )
Chú ý: Định lý trên cũng mở rộng cho các ạo hàm cấp cao hơn và hàm nhiều biến hơn.
1.2.4. Vi phân cấp cao
Ta nhận thấy df x y( , ) = f ′ ′
x (x y dx, ) + f y (x y dy, ) cũng là một hàm số của x, y nên có thể xét
vi phân của nó. Nếu df(x,y) khả vi thì vi phân của nó gọi là vi phân cấp hai của f(x, y), kí hiệu
d f x y2( , ) = d df x y(( , )) và nói rằng f(x, y) khả vi ến cấp 2 tại (x, y).
Tổng quát vi phân cấp n, nếu có sẽ kí hiệu: d f x yn
( , ) = d d( n−1 f
x y( , )) Công thức vi phân cấp 2 như sau: d f x y2 ( , ) = d df x y( ( 16
Downloaded by Ti?n D?ng Tr?n Lý (dungtienltr128@gmail.com) lOMoARcPSD| 10435767
Chương 1. Phép tính vi phân hàm số nhiều biến số
, )) = ∂∂x ⎜⎜⎛ ∂∂fx dx + ∂∂fy dy dx⎞⎟⎟⎠
+ ∂∂y ⎜⎛⎝⎜ ∂∂fx dx +
∂∂fy ⎟⎟⎠⎞dy ⎝ = ∂∂ +⎛⎜⎜ ∂ ∂∂ 2x2f dx2 x
y2 f + ∂ ∂∂y x2 f ⎟⎟⎠⎞dxdy +
∂∂2y 2f dy 2 ⎝
Giả sử các ạo hàm riêng hỗn hợp liên tục, theo ịnh lý Schwarz ta có: d f x y2 ( , ) = ∂ ∂ 2 f 2 f f 2 dx2 + 2 dxdy +
∂2 2 dy 2 (1.4) ∂x ∂ ∂x y ∂y
Người ta dùng kí hiệu luỹ thừa tượng trưng ể viết gọn như sau: df ∂ ∂ ⎞
x y( , ) = ⎜⎜⎛ ∂ x dx + ∂ y dy f x y⎟⎟⎠ ( , ) ⎝ n ⎛ ∂ ∂ ⎞n + ⎟⎟
Tổng quát có d f x y( , ) = ⎜⎜ ∂x dx ∂y dy ⎠ f x y( , ) (1.5) ⎝
1.2.5. Đạo hàm của hàm số hợp
Cho D ⊂n và các ánh xạ ϕ:D →m f : (D)ϕ →
Ánh xạ tích f ϕ: D → cụ thể là u = f( (M)), Mϕ
∈D, ϕ(M) ⊂m gọi là hàm số hợp.
Để cho ơn giản, sau ây ta xét n = 2, m = 2, khi ó hàm hợp f ϕ xác ịnh trên miền phẳng D
Định lý 1.6. Cho u = f(x,y) với x = x(s, t); y = y(s, t) thoả mãn: Các
biến trung gian x(s, t), y(s, t) có các ạo hàm riêng cấp 1 tại (a, b), f(x,
y) khả vi tại iểm (x0, y0) = (x(a, b), y(a, b)).
Khi ó hàm hợp u = u(s, t) có ạo hàm riêng cấp 1 tại (a, b) tính theo công thức:
∂u ∂u ∂x ∂u ∂y = +
∂s ∂x ∂s ∂y ∂s 17
Downloaded by Ti?n D?ng Tr?n Lý (dungtienltr128@gmail.com) lOMoARcPSD| 10435767
Chương 1. Phép tính vi phân hàm số nhiều biến số
∂u = ∂u ∂x + ∂u ∂y (1.6)
∂t ∂x ∂t ∂y ∂t
Công thức (1.6) có thể viết dưới dạng ma trận:
⎛ ∂x ∂x ⎞
⎝⎜⎛ ∂∂us ∂∂ut ⎠⎟⎞ = ⎝⎜⎛ ∂∂ux ∂∂uy ⎠⎟⎞⎝⎜⎜⎜⎜ ∂∂∂yss ∂∂∂ytt ⎟⎠⎟⎟⎟ ⎛∂x ∂x⎞ ⎜ ⎟ ⎜∂s ∂t
⎟ ược gọi là ma trận Jacobi của x, y ối với t, s; còn ịnh thức của ma trận này ⎜∂y ∂y⎟ ⎜ ⎟
⎝∂s ∂t ⎠
gọi là ịnh thức Jacobi của x, y ối với t, s hay Jacobian của x, y ối với t, s và ký hiệu: ∂x ∂x ∂s ∂t D x y( , ) (1.7) =
D s t( , ) ∂y ∂y ∂s ∂t
Ví dụ 8: Tính các ạo hàm riêng
u = ex ln ,y x = st, y = s2 −t 2 . Giải: ∂∂u 1 2 ⎤
s = ex ln .y t + ex.
y .2s = est ⎣⎢⎡tln(s2 −t 2 ) + s −s ⎥⎦ 2 t 2 , ∂∂u 1 2 ⎤
t = ex ln .y s + ex.
y .( 2 )− t = est ⎢⎡⎣sln(s2 −t 2 )− s −t ⎥⎦ 2 t 2 . ′ ′′ ′′
Ví dụ 9: Cho u = 1r , r = x2 + y2 + z2 . Chứng minh Δu = u ′ + + = x u u 0 . 2 y2 z2 18
Downloaded by Ti?n D?ng Tr?n Lý (dungtienltr128@gmail.com) lOMoARcPSD| 10435767
Chương 1. Phép tính vi phân hàm số nhiều biến số Giải: = ′′ Nhận xét: hàm số 1 u
r ối xứng với x, y, z. Do ó ta chỉ cần tính u x2 , sau ó thay x bởi y và z. u′ = = − x u r′ ′. x
r12 . xr = − rx3 , u′′ = − + + x2
r13 3 .x r14 . xr = − r13 3rx 2 5 , 3
3(x2 + y2 + z2 ) 3 3
Suy ra Δu = − r + = − + = 3 r5 r3 r3 0.
Chú ý: Nếu u = f(x, y), y = y(x) khi ó u là hàm số hợp của một biến x. Do vậy người ta du ∂f ∂f
′. ưa ra khái niệm ạo hàm toàn phần và công thức tính sẽ là: = + .y
dx ∂x ∂y
1.2.6. Vi phân của hàm hợp
Xét hàm hợp u = f(x, y), x = x(s, t), y = y(s, t). ∂u ∂u
Nếu hàm hợp có các ạo hàm riêng ,
liên tục thì nó khả vi và ta có: ∂s ∂t
du = ∂u ds + ∂u dt ∂s ∂t
Bây giờ ta biểu diễn du qua biến trung gian x, y theo công thức (1.6) có:
⎛ ∂u ∂x ∂u ∂y ⎞ ⎛ ∂u ∂x ∂u ∂y ⎞
du = ⎜⎜⎝ ∂x ∂s + ∂y ∂s ⎟⎠⎟ds +⎝⎜⎜ ∂x ∂t + ∂y ∂t ⎟⎠⎟dt ⎞
= ∂u ⎛⎜ ∂x ds + ∂x dt ⎟ + ∂u ⎜⎛ ∂y ds + ∂y dt⎟⎞ 19
Downloaded by Ti?n D?ng Tr?n Lý (dungtienltr128@gmail.com) lOMoARcPSD| 10435767
Chương 1. Phép tính vi phân hàm số nhiều biến số ∂x ⎝ ∂s
∂t ⎠ ∂y ⎝ ∂s ∂t ⎠
= ∂u dx + ∂u dy . ∂x ∂y
Như vậy dạng của công thức vi phân cấp 1 không ổi dù x, y là các biến ộc lập hay là hàm của các
biến s, t. Tính chất này gọi là tính chất bất biến dạng của vi phân cấp 1.
Chú ý: Cũng như hàm một biến số, vi phân cấp cao không có tính bất biến dạng.
1.2.7. Đạo hàm của hàm số ẩn
A. Hàm ẩn một biến
Cho một hệ thức giữa hai biến, x, y dạng: F(x, y) = 0 (1.8) trong
ó F(x, y) là hàm hai biến xác ịnh trong miền mở D chứa (x0, y0) và ∈ δ F(x ( −δ + )
0, y0) = 0. Giả sử rằng ∀x x0 , x0
, ∃ y x( ) sao cho ( , ( ))x y x ∈D và F(x,
y(x)) = 0. Hàm số y = y(x) gọi là hàm ẩn của x xác ịnh bởi phương trình (1.8).
Định lý 1.7. Nếu F(x, y) thoả mãn các iều kiện:
F liên tục trong lân cận Ωδ(M 0 ) và F(M0) = 0. ∂F ∂F ∂F
Các ạo hàm riêng ∂x , ∂y liên tục và ∂y (x0 , y0 ) ≠ 0 trong lân cận Ωδ(M 0 )thì phương trình
(1.8) xác ịnh một hàm ẩn y(x) khả vi liên tục trong khoảng (x −ε +ε 0 ,x0 ) và ta có: = − dx Fy ′ dy F ′ x (1.9)
Chú ý: Để nhận ược công thức (1.9) chúng ta chỉ việc lấy vi phân 2 vế của (1.8) trong ó có y =
y(x) và áp dụng tính bất biến của dạng vi phân cấp 1.
Thật vậy dF(x, y) = 0 hay F dx ′+ ′= ′ + ′ x F dyy 0 hay Fx
F yy . ′ = 0. Từ ó suy ra (1.9).
Ví dụ 10: Tính y′(1) biết xy −ex sin y =π Giải: 20
Downloaded by Ti?n D?ng Tr?n Lý (dungtienltr128@gmail.com) lOMoARcPSD| 10435767
Chương 1. Phép tính vi phân hàm số nhiều biến số
Lấy ạo hàm toàn phần (hay vi phân) và coi y là hàm của x hai vế của phương trình ã cho có:
y + xy′−ex sin y −ex cos .y y′ = 0
Thay x =1 vào phương trình hàm ẩn, nhận ược: y(1)−π= esin (1)y . Dùng phương pháp ồ
thị giải phương trình này, nhận ược nghiệm y(1) =π. Vậy π+ y′(1)−esinπ−ecos .πy′(1) = 0 π y′(1) = − . 1+ e
Ví dụ 11: Tính y y′, ′′biết x − y + arctgy = 0 Giải:
Lấy ạo hàm toàn phần hai vế coi y = y(x) ′ y 1− y′+ 1 +yy = 2⇒ 2 0 ⇒ y′ = 1 +y2
y y2 ′ = +1 y2
Lấy ạo hàm tiếp ta có 2yy′2 + y y2 ′′ = 2yy′ ⇒ y′′ =
2y′(1y− y′)⇒ y′′ = − 2(1y+5y2 ) .
B. Hàm ẩn hai biến
Định lý 1.8. Cho phương trình hàm ẩn F(x, y, z) = 0 và F(x, y, z) thoả mãn các iều kiện:
F(x, y, z) liên tục trong hình cầu mở Ωδ(M 0 ) và F(M0) = F(x0, y0, z0) = 0;
Các ạo hàm riêng F ′ ′ ′ ′
x , Fy , Fz liên tục và Fz (x0 , y0 ,z0 ) ≠ 0 trong hình cầu Ωδ(M 0 )
Khi ó phương trình hàm ẩn xác ịnh một hàm ẩn z = z (x, y) có các ạo hàm riêng liên tục trong lân
cận Ωε(x0 , y0 ) ồng thời:
∂z Fx′ , ∂z = − Fy′ (1.10) = − ∂x F ′ ∂ ′ z y Fz
Tương tự như ịnh lý 1.7. ta không chứng minh ịnh lý này.
Cũng như trong trường hợp hàm ẩn một biến, ể tính các ạo hàm riêng cũng như vi phân ∂z ∂z
của hàm ẩn ta lấy vi phân toàn phần hai vế của phương trình hàm ẩn sau ó i tìm , , dz ∂x ∂y
Ví dụ 12: Cho xyz= x + y + z. Coi z là hàm số ẩn, hãy tính z′x , z′y , dz . 21
Downloaded by Ti?n D?ng Tr?n Lý (dungtienltr128@gmail.com) lOMoARcPSD| 10435767
Chương 1. Phép tính vi phân hàm số nhiều biến số Giải:
Lấy vi phân toàn phần phương trình hàm ẩn sẽ có:
d(xyz) = d(x + y + z) yz dx + zx dy + xy dz = dx + dy + dz
(xy – 1) dz = (1- yz) dz + (1-zx) dy dz = −
1 [(yz −1)dx + (zx −1)dy] xy −1 ⇒ z′ = − = − x
yz −1, z′y
xz −1 . yx −1 xy −1
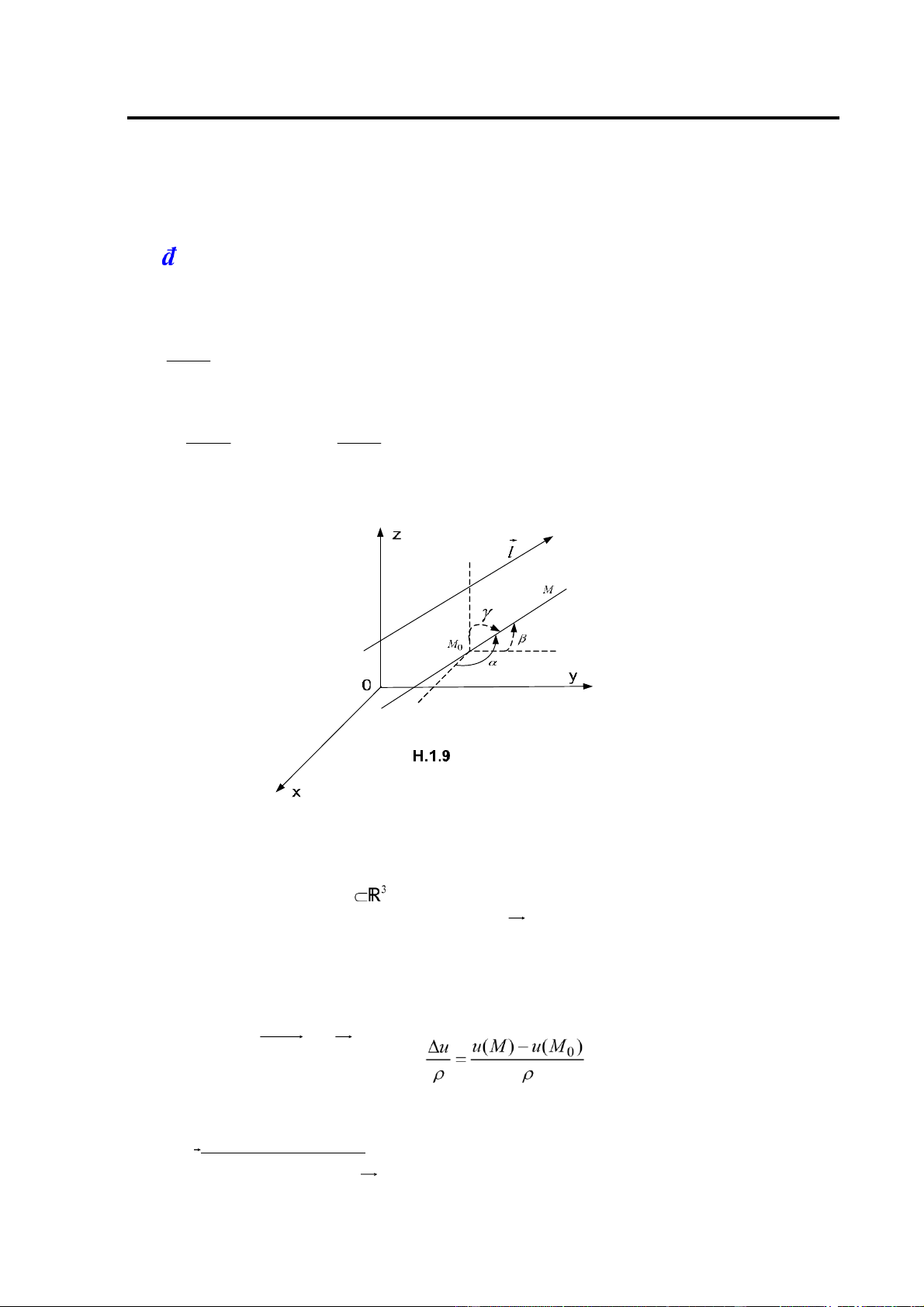
1.2.8. Đạo hàm theo hướng. Gra iên (Gradient) A. Định nghĩa:
Cho u(x, y, z) xác ịnh trên miền D
và M 0 (x0 , y0 ,z0 )∈D , một hướng ược ặc trưng bởi
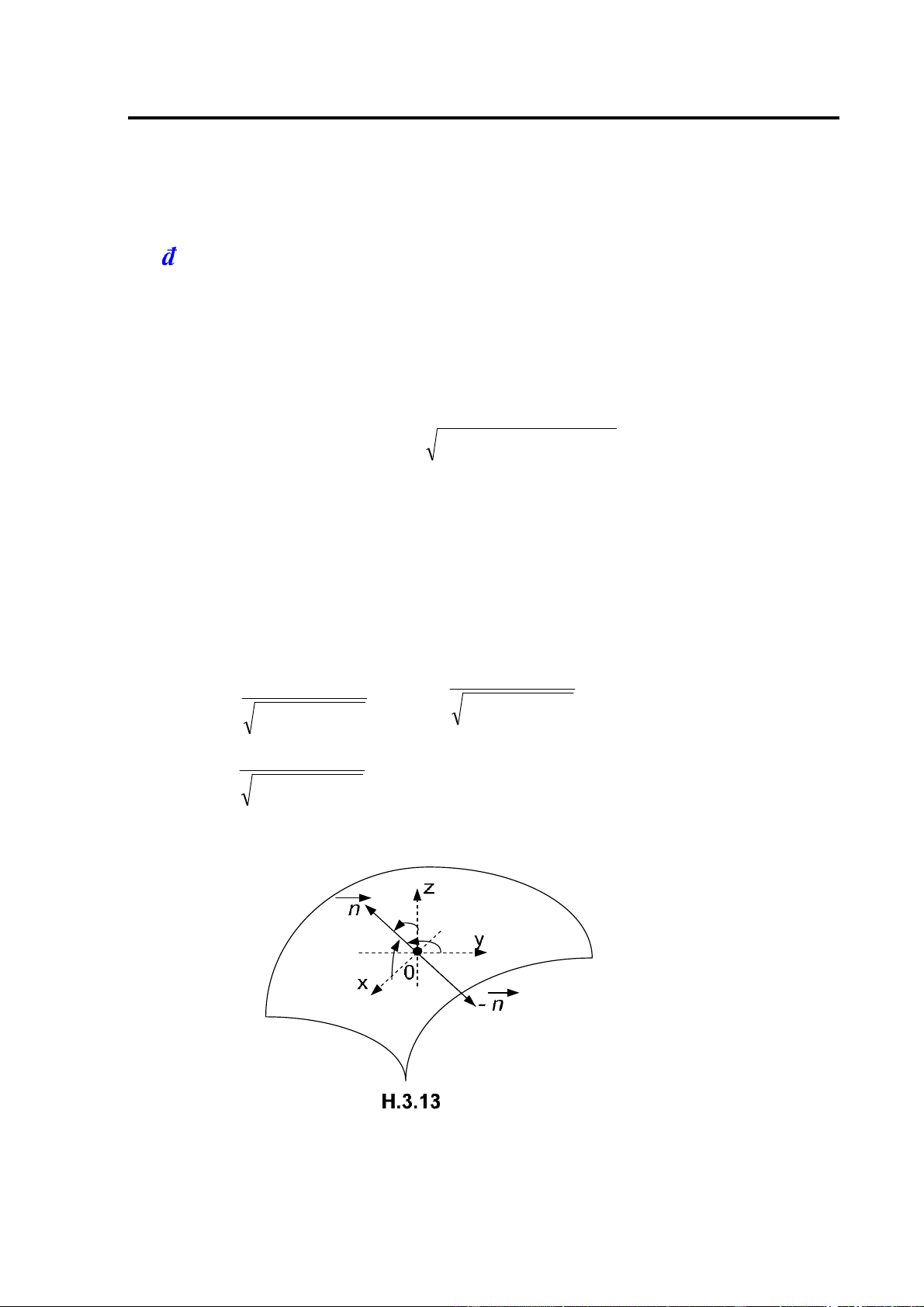
véc tơ có véc tơ ơn vị 0 (cos , cosα β γ, cos ) , tức là: α=
(Ox, ),β= (Oy, ),γ= (Oz, ) .
Người ta gọi cos , cos , cosα β γ là các côsin chỉ phương của
. Rõ ràng cos2α β γ+cos2 +cos2 =1.(H.1.9)
Lấy M ∈D sao cho M M =ρ 0 0 , lập tỉ số
Nếu tỉ số trên có giới hạn hữu hạn khi ρ→ 0 thì giới hạn ấy ược gọi là ạo hàm của hàm ∂u
u(M) theo hướng tại M0 và kí hiệu là (M 0 ) tức là: 22
Downloaded by Ti?n D?ng Tr?n Lý (dungtienltr128@gmail.com) lOMoARcPSD| 10435767
Chương 1. Phép tính vi phân hàm số nhiều biến số ∂ 0 Chú ý: 1.
Cũng giống như ý nghĩa của ạo hàm, có thể coi rằng ạo hàm theo hướng biểu thị tốc
ộ biến thiên của hàm u(M) theo hướng 2.
Nếu có hướng của trục Ox thì +ρ
0 (1,0,0). Giả sử M 0 (x0 , y0 ,z0 ) thì M x( 0 , y0 ,z0 ) khi ó: ∂∂u (M +ρ ρ 0 ) = limρ→0 u x(0 , y z0 , 0 ) −u x( 0 , y z0 ,
0 ) = ∂∂ux (M 0 ) 0
Chứng tỏ các ạo hàm riêng u′x , u′y , u′z là ạo hàm của hàm u theo hướng của các trục Ox, Oy, Oz. B. Công thức tính
Định lý 1.9. Nếu hàm số u(x, y, z) khả vi tại M0(x0, y0, z0) và bất kỳ có các côsin chỉ phương cos , cosα β, cosγ thì: ∂u ∂u ∂u ∂u
(M 0 ) = (M 0 )cosα+ (M 0 )cosβ+
(M 0 )cosγ (1.11) ∂∂x ∂y ∂z Chứng minh:
Theo ý nghĩa của hàm khả vi ta có: ′ ′ ′
Δu u M= ( ) −u M(0) = u M x(0)Δ +x u M y(0)Δ +y u M z(0)Δ +z o( )ρ
trong ó o( )ρ là VCB bậc cao hơn ρ khi ρ→ 0.
Mặt khác Δx =ρcos ,α Δ =y ρcosβ, Δz =ρcosγ suy ra: ′ ′ ′ ρ
∂ρu x( 0)cosα+ u M y( 0)cosβ+ u M z(0)cosγ+ o( )ρ . 23
Downloaded by Ti?n D?ng Tr?n Lý (dungtienltr128@gmail.com) lOMoARcPSD| 10435767
Chương 1. Phép tính vi phân hàm số nhiều biến số = u M
Chuyển qua giới hạn khi ρ→ 0 sẽ có (1.11) C. Gra iên
Cho u(x, y, z) có các ạo hàm riêng tại .
Gọi véc tơ (u′x (M 0 ), u′y (M 0 ), u′z (M 0 )) là gra iên của hàm u(x, y, z) tại M0 và kí hiệu là grad u(M0).
grad u M(0 ) = (u′x (M 0 ), u′y (M 0 ), u′z (M 0 ))
= u′x (M 0 )i+ u′y (M 0 )j + u′z (M 0 )k (1.12) trong ó i j k, , là các
véc tơ ơn vị của các trục Ox, Oy, Oz.
D. Liên hệ giữa gra iên và ạo hàm theo hướng.
Định lý 1.10. Nếu u(M) khả vi tại M0 thì tại ó có: ∂u
= ch gradu . (1.13) ∂ Chứng minh: Ta có = 0
cosαi+cosβ j +cosγk nên (1.11) có thể viết như sau:
(M 0 ) = grad u M( 0 ). grad u M( 0 )cosθ
trong ó θ là góc giữa hai véc tơ và grad u(M0), mà = 1, grad u M(
0 )cosθ= ch grad u M( 0 ) . Vậy nhận ược công thức (1.13) ∂u
Chú ý: Từ (1.13) suy ra max
(M 0 ) = grad u M( 0 ) khi cosθ= 1, tức là cùng ∂
phương với grad u(M0) chứng tỏ grad u(M0) cho ta biết phương theo nó tốc ộ biến thiên của u tại M0
có giá trị tuyệt ối cực ại.
Ví dụ 13: Cho u = x3 + y3 + z3 +3xyz , M0(1, 2, -3), (2, 1, -2). ∂u Tính grad u(M0) và (M 0 ). 24
Downloaded by Ti?n D?ng Tr?n Lý (dungtienltr128@gmail.com) lOMoARcPSD| 10435767
Chương 1. Phép tính vi phân hàm số nhiều biến số ∂ Giải: u′ = = = x
3x2 + 3yz u, ′y
3y2 + 3zx u, ′z 3z2 + 3xy
Vậy grad u(1, 2, -3) = (3 – 18, 12 – 9, 27 + 6) = (-15, 3, 33) = 3(-5, 1, 11) 1 2 1 2⎞ (2, 1, -2) ⇒ = ⎛⎜ 2 + − ⎟ = − 0
, , − 2⎞⎟ ⇒ ∂u (1,2,−3) = 3⎜⎛−5. 1. 11. 31 ⎝ 3 3 3⎠ ∂⎝ 3 3 3⎠
1.3. Cực trị của hàm nhiều biến
1.3.1. Cực trị tự do
A. Định nghĩa và iều kiện cần của cực trị Điểm
gọi là iểm cực ại (ịa phương) của hàm f(M) nếu có lân cận ủ bé
của M0 ể trong lân cận ó (trừ M0) xảy ra bất ẳng thức f(M) < f(M0)
Tương tự ta có khái niệm iểm cực tiểu (ịa phương) của hàm số f(M).
Điểm M0(x0, y0) trong các trường hợp trên gọi chung là iểm cực trị.
Tương tự như ịnh lý Fermat ối với hàm một biến số, ta có iều kiện cần của cực trị dưới ây.
Định lý 1.11. Nếu f(x, y) ạt cực trị tại M0 và có các ạo hàm riêng tại ó thì các ạo hàm riêng bằng 0.
Chứng minh: Giả sử f(x, y) ạt cực trị tại (x0, y0). Theo ịnh nghĩa suy ra hàm một biến f(x,y0) ạt
cực trị tại x0, f(x0, y) ạt cực trị tại y0. Theo ịnh lý Fermat ta có: df x y( , 0 ) = 0 hay ∂f (x )= 0 , y0 0 dx ∂ x x= 0 x df x( 0, )y = 0 hay ∂f (x ) = 0 , y0 0 dy ∂ y y= 0 y
Chú ý: Điểm mà tại ó các ạo hàm riêng bằng không gọi là iểm dừng của hàm số. Như vậy
iểm dừng chưa chắc là iểm cực trị. Chẳng hạn u = xy có iểm dừng là (0 0) nhưng trong bất kỳ lân
cận nào của gốc toạ ộ (0, 0) ều có các iểm (x y1, 1) và (x2 , y2 ) ể f x y( 1, 1) > f (0,0) và f x( 2 , y2 ) <
f (0,0) (lấy x > > < > 1 0, y1 0, x2 0, y2 0).
B. Điều kiện ủ của cực trị 25
Downloaded by Ti?n D?ng Tr?n Lý (dungtienltr128@gmail.com) lOMoARcPSD| 10435767
Chương 1. Phép tính vi phân hàm số nhiều biến số
Trong thực tế thường gặp hàm hai biến f(x, y) và ể tìm cực trị của nó, người ta thường sử
dụng ịnh lí sau ây, coi như là iều kiện ủ ể hàm ạt cực trị. Ta không chứng minh ịnh lý này.
Định lý 1.12. Giả sử f(x, y) có ạo hàm riêng cấp hai liên tục tại lân cận iểm dừng (x0, y0) và gọi: A = ∂∂x −
2 2f (x0 , y0 ),B =
∂ ∂∂x y2 f (x0 , y0 ),C =
∂∂y2 2f (x0 , y0 ) và Δ = B2 AC (1.14)
Nếu Δ > 0 thì hàm số không ạt cực trị tại (x0, y0)
Nếu Δ = 0 thì chưa kết luận gì ược về (x0, y0)
Nếu Δ < 0 thì hàm số ạt cực trị tại (x0, y0)
Cụ thể ạt cực ại nếu A < 0, ạt cực tiểu nếu A > 0. Ví
dụ 14: Xét cực trị của hàm số z = x4 + y 4 − x2 − 2xy − y 2 . Giải:
Nhận xét: Hàm số z khả vi mọi cấp trên 2 , ta có thể áp dụng ịnh lý 1.12. * Tìm iểm dừng: ⎧⎪⎪⎩zz′ = − =− − x 4x3
2x − 2y = 0 ⇒ ⎧⎪⎨x3 3 yx3
y = 0 ⇒ ⎧⎨⎩xx x(= 2y−1) = 0 ⎨ ′ = − y 4y3 2y − 2x = 0 ⎪⎩2x
Nhận ược ba iểm dừng: ⎧x = 0 ⎧x =1 ⎧x = −1 ⎨y = 0 ,
⎨⎩y =1, ⎨⎩y = −1 ⎩ * A = z′′ = x2
12x2 − 2, B = −2, C =12y 2 − 2
Δ = 4 − 4(6x2 −1) 6( y 2 −1) Δ(0,0) = 0 Nhận thấy z(0,0) = 0.
1n ⎛⎝ 1n n, 1 ⎞⎟⎠ = n2 ⎝⎜⎛ − 2 n12
2⎞⎟⎠ < 0 với n > 1 Với x = y = thì z⎜ 26
Downloaded by Ti?n D?ng Tr?n Lý (dungtienltr128@gmail.com) lOMoARcPSD| 10435767
Chương 1. Phép tính vi phân hàm số nhiều biến số Với x = , y = - thì z⎜ , 1n 1n
⎛⎝ 1n − 1n ⎞⎟⎠ = n2 > 4 0.
Như vậy trong bất kỳ lân cận nào của gốc toạ ộ ta luôn tìm ược các iểm (tìm ược n) ể hàm ổi dấu,
chứng tỏ hàm không ạt cực trị tại (0, 0)
Δ (1, 1) = Δ (-1, -1) = -96 < 0 và A (1, 1) = A(-1, -1) = 10 > 0.
Vậy hàm ạt cực tiểu tại (1,1) và (-1, -1)
Giá trị cực tiểu là z (1,1) = z(-1, -1) = -2.
1.3.2. Cực trị có iều kiện
A. Định nghĩa và iều kiện cần Điểm M
iểm cực ại của hàm số f(x, y) với ràng buộc (hoặc có iều kiện)
ϕ(x y, ) = 0 nếu thoả mãn ϕ(M 0 ) = 0 ồng thời tồn tại lân cận ủ bé của M 0 trên ường cong ràng
buộc ϕ(x y, ) = 0, trong lân cận ó có bất ẳng thức f(M)Tương tự ta có khái niệm iểm cực tiểu của hàm số với ràng buộc ϕ(x y, ) = 0
Để ơn giản bài toán tìm cực trị của hàm hai biến với iều kiện ϕ(x y, ) = 0 ược kí hiệu như sau: ⎧extf x y( , ) (1.15) ⎨ ⎩ϕ(x y, ) = 0 (1.16)
Trong ó ext là viết tắt của từ extremum nghĩa là cực trị.
Định lý 1.13. Giả sử M0(x0, y0) là iểm cực trị có iều kiện của hàm số f(x,y) với iều kiện (1.16) và thoả mãn:
Các hàm f(x, y) và ϕ(x y, ) có các ạo hàm riêng cấp 1 liên tục trong lân cận của M0(x0, y0) của
ường cong ràng buộc (1.16)
M0(x0, y0) không phải là iểm dừng của hàm ϕ(x y, ) . Khi ó tồn tại số thực λ thoả mãn hệ phương trình:
⎧ f ′x(x0 , y0 ) +λϕ′x (x0 , y0 ) = 0
⎨ f ′y(x0 , y0 ) +λϕ′y (x0 , y0 ) = 0 (1.17) ⎩
Chú ý: Hàm số L x y( , ,λ) = f x y( , ) +λϕ(x y, ) ược gọi là hàm Lagrange và λ ược gọi là nhân
tử Lagrange. Như vậy với iều kiện cho phép ta sẽ i tìm iểm dừng (x0, y0, λ0) của hàm 27
Downloaded by Ti?n D?ng Tr?n Lý (dungtienltr128@gmail.com) lOMoARcPSD| 10435767
Chương 1. Phép tính vi phân hàm số nhiều biến số
Lagrange (do iều kiện tiên quyết ϕ(x0 , y0 ) = Fλ′(x0 , y0 ,λ0 )=0), tiếp theo xem xét một số các iều
kiện của bài toán (1.15) ể có kết luận chính xác xem iểm (x0, y0) có phải là iểm cực trị có iều kiện hay không.
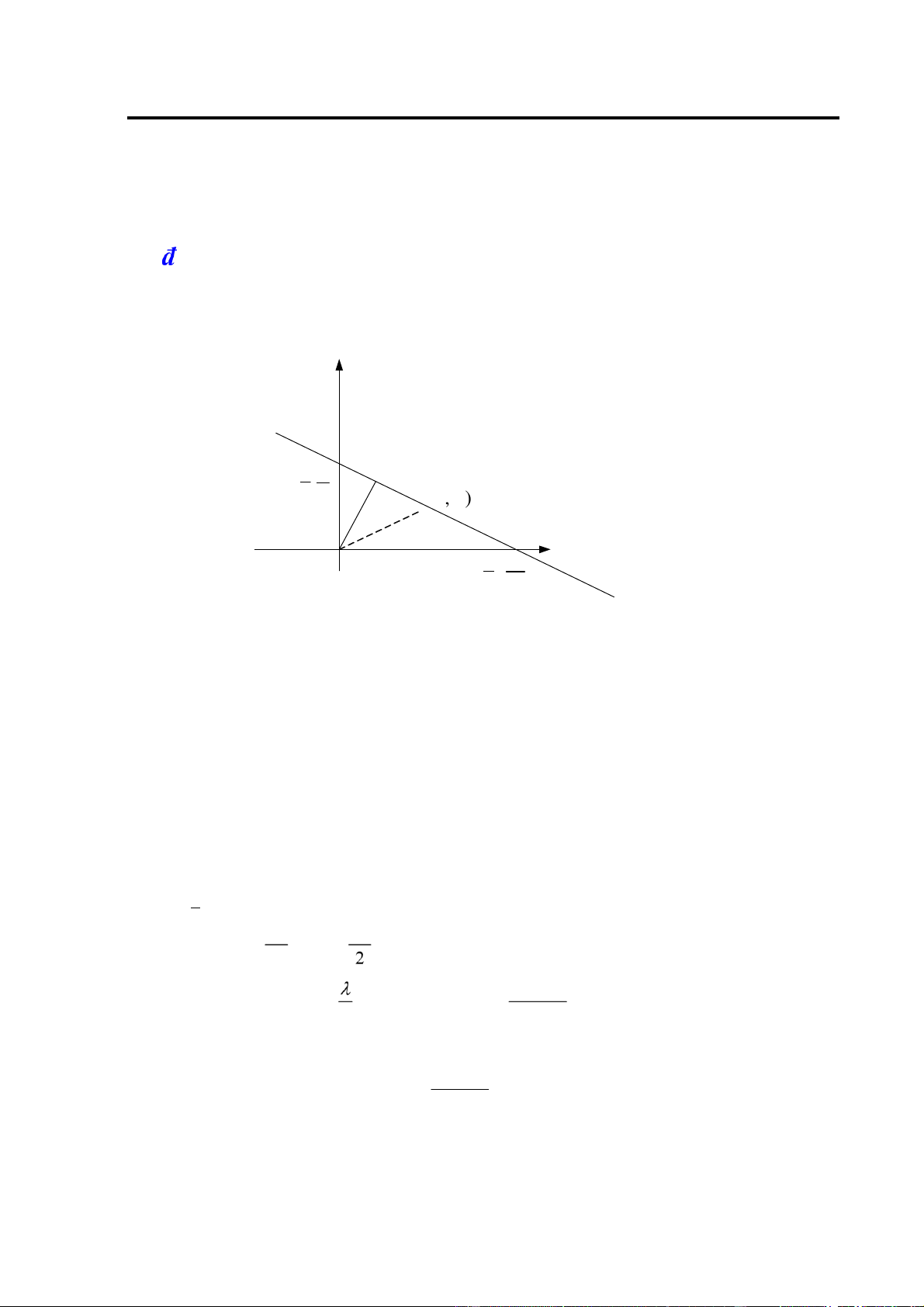
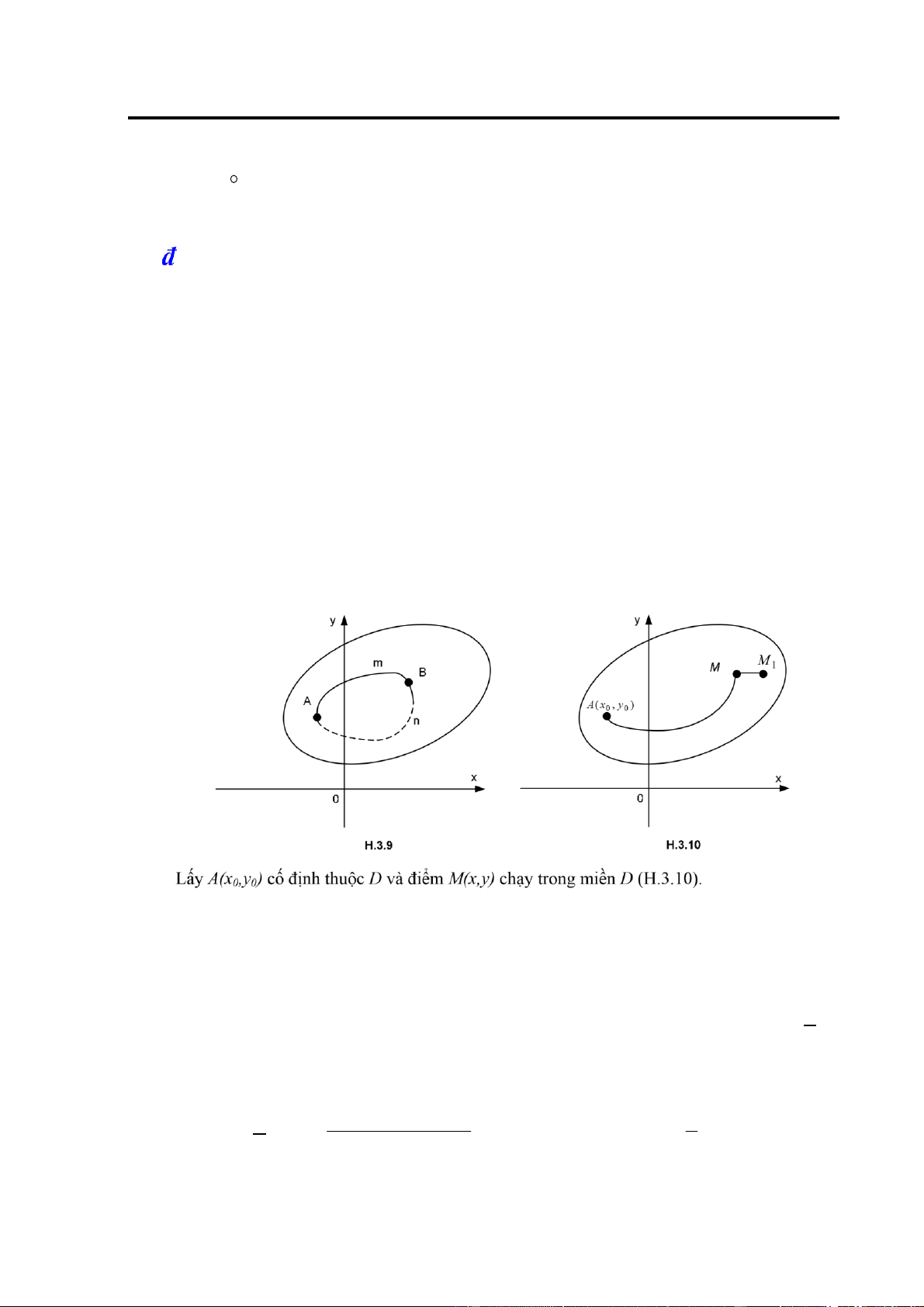
Ví dụ 15: Tìm cực trị của hàm số z = x2 + y2 với ràng buộc ax + by + c = 0, c ≠ 0, a2 + b2 > 0. Giải: y ( x , y ) c 0 0 b ( , xy ) x c 0 a H.1.10
Về hình học, ây là bài toán tìm cực trị của bình phương khoảng cách từ gốc toạ ộ ến các iểm trên
ường thẳng (H.1.10). Vậy bài toán có duy nhất cực tiểu ó là chân ường vuông góc
hạ từ O tới ường thẳng.
Lập hàm Lagrange: L = x2 + y2 + λ(ax + by + c) ⎧L ′ = x 2x +λa = 0 ⎪
Tìm iểm dừng của L: ⎨L′ = y 2y +λb = 0
⎪⎩Lλ′ = ax + by + c = 0 λa λb = − = − Thay x , y
vào phương trình cuối nhận ược: 2 2
− 2 (a 2 + b2 ) = −c, λ= a 2 +cb2 28
Downloaded by Ti?n D?ng Tr?n Lý (dungtienltr128@gmail.com) lOMoARcPSD| 10435767
Chương 1. Phép tính vi phân hàm số nhiều biến số = − ac = − bc ⇒ x a 2 + b2 , y a2 + b2 ⎛⎝− − ⎟ a ⎞ 2 ac+ b2 ,
a2bc+ b2 ⎠ là iểm cực tiểu và giá trị cực tiểu bằng
Điểm dừng duy nhất M0 ⎜ c2 + 2 b2 . a B. Điều kiện ủ
Định lý 1.14. Giả sử f(x, y) và ϕ(x y, ) có ạo hàm riêng cấp 2 liên tục ở lân cận (x0,y0) và
(x0, y0, λ) là iểm dừng của hàm Lagrange. Khi ó: λ ′′ * Nếu d L x2 ( ) = ′′ ′′ 0, y0, Lx (x (x 2
0, y0, )λdx2 + 2Lxy
0, y0, )λdxdy + L y2 (x0, y0, )λdy2 xác
ịnh dấu ối với dx, dy trong miền thoả mãn ràng buộc:
dϕ(x0 , y0 ) =ϕ′x (x0 , y0 )dx +ϕ′y (x0 , y0 )dy = 0,
dx2 + dy 2 ≠ 0
thì f(x,y) ạt cực trị có ràng buộc tại (x0, y0). Đạt cực ại nếu d2L(x0, y0,λ) >0 và ạt cực tiểu nếu d2L(x0, y0,λ) <0.
* Nếu d2L(x0, y0,λ) không xác ịnh dấu trong miền nói trên thì hàm không ạt cực trị ràng buộc tại (x0, y0).
⎧ext x( + y + z) ⎪ =1
Ví dụ 16: Giải bài toán ⎨xyz
⎪⎩x > 0, y > 0, z > 0 Giải:
* Hàm Lagrange: L(x,y,z,λ) = x + y + z + λ(xyz - 1) * Tìm iểm dừng: ⎧L/ = + x 1 λyz = 0 ⎪⎪ / = +1 λzx = 0 Ly 29
Downloaded by Ti?n D?ng Tr?n Lý (dungtienltr128@gmail.com) lOMoARcPSD| 10435767
Chương 1. Phép tính vi phân hàm số nhiều biến số ⎨ ⎪L/ = + z 1 λxy = 0 ⎪ ⎩xyz − =10
Nhân 2 vế của phương trình thứ nhất với x và ể ý ến phương trình thứ tư sẽ nhận ược λ= −1 và x = y = z = 1
* Xét dấu của d2L(1,1,1,-1) với dx, dy, dz thoả mãn d xyz() = x y z= = =1 0 và dx2 + dy2 + dz2 ≠ 0 Ta có ′′ L ′′ = = ′′ ′′ = − ′ = − ′′ = − x 0 = L L , L z, L′ x, L y 2 y2 z 2 xy yz zx
Suy ra d L2 (1,1,1,−1) = −2(dxdy + dydz + dzdx) Mặt khác d xyz() = = (1,1,1)
(yzdx + zxdy + xydz) (1,1,1)
dx + dy + dz = 0 Suy ra dz = - dx – dy
d L2 (1,1,1,−1) = −2(dxdy − (dx + dy) )2 = (dx + dy)2 + dx2 + dy 2 > 0khi dx2 + dy2+dz2> 0
Vậy hàm số ạt cực tiểu có ràng buộc tại (1,1,1) và min (x + y + z) = 3
TÓM TẮT CHƯƠNG 1.
• Giới hạn : lim f M( ) = l hay lim f x( n, yn ) = l ,d M M( , 0 ) = (x − x0
)2 + (y − y0 )2
M→M0 (x y, )→(x y0, 0 ) nếu ∀ε δ> 0,∃ > 0 :0 < d
M( 0 ,M) <δ⇒ f M( ) −l <ε
• Sự liên tục của hàm số: Hàm số f(M) xác ịnh trên miền D và M ∈ 0
D . Ta nói rằng hàm
số f(M) liên tục tại M 0 nếu Mlim→M0 f M( ) = f M( 0 )
• Đạo hàm riêng: Đặt Δ + Δ
x f x( 0 , y0 ) = f x( 0
x y, 0 )− f x( 0 , y0 ) gọi ó là số gia riêng
của hàm f(x, y) theo biến x tại (x0, y0) và ta có: ∂f Δ ′
x f x( 0 , y0 ) , fx (x0 , y0 ), ∂x (x Δ
0 , y0 ) = Δ →limx 0 x 30
Downloaded by Ti?n D?ng Tr?n Lý (dungtienltr128@gmail.com) lOMoARcPSD| 10435767
Chương 1. Phép tính vi phân hàm số nhiều biến số
Tương tự ta có ịnh nghĩa ạo hàm riêng của hàm số ối với y tại M0(x0, y0) và ký hiệu: u′y (x ′
0 , y0 ) , ∂∂uy (x0 , y0 ), f y (x0 , y0 ), ∂∂fy (x0 , y0 )
Có thể chuyển toàn bộ các phép tính ạo hàm của hàm một biến số: cộng, trừ, nhân, chia,… sang phép tính ạo hàm riêng.
• Vi phân toàn phần của hàm số f(x, y) tại (x0, y0) : df x( ′ ′
0 , y0 ) = f x (x0 , y0 )dx + f y (x0 , y0 )dy
Δf ≈ df hay f (x + Δ + Δ 0 x y, 0
y) ≈ f x( 0, y0 )+ df x( 0, y0 )
• Đạo hàm riêng cấp cao ⎛ ⎞ ⎛ f ′′ = ∂∂ ⎜⎝ ∂∂f ⎟⎠ ′′ = ∂∂
′′ = ∂∂ ⎜⎜⎝ ∂∂f ′′ = x x x ,f
y ⎝⎜⎛ ∂∂fx ⎟⎠⎞, f x y ⎟⎟⎠⎞, f 2 xy yx y 2
∂∂y ⎜⎛⎝⎜ ∂∂fy ⎟⎠⎟⎞
∂ 2 f ∂ 2 f ∂ 2 f ∂ 2 f
hay ∂x2 , ∂ ∂x y , ∂ ∂y x , ∂y 2
• Công thức Schwarz : f ′′ ′′
xy (M 0 ) = f yx (M 0 ). • Vi phân cấp cao f f d f x y2( , ) =
∂∂2x2 dx2 + 2
∂ ∂∂x y2 f dxdy + ∂∂2y2 dy 2
Người ta dùng kí hiệu luỹ thừa tượng trưng ể viết gọn như sau: ⎛ ∂ ∂ ⎞n
d f x yn ( , ) = ⎜ ∂x dx + ∂y dy⎟⎠f x y( , ) ⎝
• Đạo hàm của hàm số hợp
∂u = ∂u ∂x + ∂u ∂y , ∂u = ∂u ∂x + ∂u ∂y
∂s ∂x ∂s ∂y ∂s ∂t ∂x ∂t ∂y ∂t 31
Downloaded by Ti?n D?ng Tr?n Lý (dungtienltr128@gmail.com) lOMoARcPSD| 10435767
Chương 1. Phép tính vi phân hàm số nhiều biến số ′ ∂ ′ ∂ ′ • z z
Đạo hàm của hàm ẩn dy = − Fx , = − Fx , = − Fy dx F ′ ∂ ′ ∂ ′ y x Fz y Fz
• Đạo hàm theo hướng. Nếu hàm số u(x, y, z) khả vi tại M0(x0, y0, z0) và bất kỳ có các
côsin chỉ phương cosα, cosβ, cosγ thì: ∂u ∂u ∂u ∂u
(M 0 ) = (M 0 )cosα+ (M 0 )cosβ+ (M 0 )cosγ ∂∂x ∂y ∂z
• Gra iên: grad u M( 0) = (u′x (M0), u′y (M0), u′z (M0))
= u′x (M0)i+ u′y (M0)j + u′z (M0)k trong ó i j k, , là các véc
tơ ơn vị của các trục Ox, Oy, Oz. ∂u = ch gradu ∂ • Cực trị: Giải hệ
⎪⎩⎪⎨⎧ ff /x/ ((xx00,, yy00 )) == 00 y = f = ∂ f = ∂ f A
∂∂x2 2 (x0 , y0 ),B
∂ ∂ x y2 (x0 , y0 ),C
∂y2 2 (x0 , y0 ) GọiΔ =
B2 − AC
Nếu Δ > 0 thì hàm số không ạt cực trị tại (x0, y0)
Nếu Δ = 0 thì chưa kết luận gì ược về (x0, y0)
Nếu Δ < 0 thì hàm số ạt cực trị tại (x0, y0)
Cụ thể: ạt cực ại nếu A < 0, ạt cực tiểu nếu A > 0
•Cực trị có iều kiện. Phương pháp nhân tử Lagrange ⎧ f ′ ′
x (x , y )+λϕx (x , y ) = 0 ⎪ Tìm (x ⎨ ′
0, y0, )λ thoả mãn hệ phương trình:
fy (x , y )+λϕ′y(x , y ) = 0 ⎪⎩ϕ(x y, ) = 0 32
Downloaded by Ti?n D?ng Tr?n Lý (dungtienltr128@gmail.com) lOMoARcPSD| 10435767
Chương 1. Phép tính vi phân hàm số nhiều biến số
CÂU HỎI VÀ BÀI TẬP CHƯƠNG 1
1.1. Miền liên thông D là miền có biên chỉ là một ường cong kín. Đúng Sai
1.2. Nếu tồn tại y ylim→ 0 f (x0, )y thì tồn tại (x y, )lim→(x y0 0,) f (x y, )và chúng bằng nhau. Đúng Sai
1.3. Hàm số f(x,y) có ạo hàm riêng tại (x0, y0 )thì khả vi tại ó. Đúng Sai
1.4. Hàm số f(x,y) khả vi tại (x0, y0 )thì liên tục tại ó . Đúng Sai
1.5. Hàm số f(x,y) khả vi tại (x0, y0 )thì có các ạo hàm riêng tại ó . Đúng Sai
1.6. Tồn tại f // // // //
xy (x0, y0 ), fyx (x0, y0 )thì fxy (x0 , y0 ) = fyx (x0, y0 ) Đúng Sai
1.7. Nếu f(x,y) có ạo hàm riêng liên tục ến cấp hai và x = x t( ), y = y t( ) khả vi ến cấp hai thì
d f2 = f dx // 2 + // // 2 x 2 f dx dy . + f dy 2 xy y 2 Đúng Sai
1.8. Hàm số f(x,y) ạt cực trị và khả vi tại (x0, y0 )thì các ạo hàm riêng triệt tiêu tại ó. Đúng Sai
1.9. Các ạo hàm riêng triệt tiêu tại (x0, y0 )thì hàm số ạt cực trị tại ó Đúng Sai
1.10. Hàm số ạt giá trị lớn nhất tại (x0, y0 )∈D thì ạt cực trị tại ó Đúng Sai
1.11. Tìm miền xác ịnh của các hà m số sau: 2 2 2 2
a. z = ln xy , b. z = 9 −x − y −
x + y −1, 1 . c. z = 1 − 1 , d.
z = y − x2 x + y x − y
1.12. Tính ạo hàm riêng các hàm số sau: 33
Downloaded by Ti?n D?ng Tr?n Lý (dungtienltr128@gmail.com) lOMoARcPSD| 10435767
Chương 1. Phép tính vi phân hàm số nhiều biến số x
a. z = ln(x + x2 + y2 ), b. z = y2 sin , y y
c. z = xy3 ,x > 0 , d. z = arctg . x
1.13. Chứng minh các hệ thức sau ây với các iều kiện tương ứng a. xz / + / = x yzy
2 , với z = ln(x2 + xy + y2 ) . b. yz / + / = x xzy
0, với z = f x( 2 − y2 ),f(t) khả vi.
1.14. Tính ạo hàm của các hàm số hợp sau:
a. z = eu −2v 2
2 ,u = cosx,v= x2 + y2 .
b. z = ln(u2 +v2 ),u = xy v, = x . y
1.15. Tính vi phân toàn phần của các hàm số sau: y a. z = lntg . x
b. z = ex(cosy + xsiny).
1.16. Tính ạo hàm của các hàm số ẩn xác ịnh bởi các phương trình tương ứng
a. x y3 − y x3 = a2,a = const , tính y/ .
b. arctg x+y = y ,a = const, tính y/ . a a
c. x+ y+z = ez , tính z / / x , zy d. x + y +z = 3xyz3 3 3 , tính z / / x ,zy .
1.17. Chứng minh các hệ thức sau ây, với các iều kiện tương ứng ( x a. z z // // = // x (z
)2 , với z = xf 2 y 2 xy
y) , f(t) khả vi liên tục ến cấp hai. ∂2u ∂2u + b. ∂x = 2
∂y2 0, với u = ln 34
Downloaded by Ti?n D?ng Tr?n Lý (dungtienltr128@gmail.com) lOMoARcPSD| 10435767
Chương 1. Phép tính vi phân hàm số nhiều biến số ∂2u ∂2u 1 2 2
, r = x + y . c.. ∂x + ∂ = r 2 y2 0, với u = lnr ,r = 2 2 2 x + y .
∂2u ∂2u ∂2u + + d. ∂x = 1 2
∂y2 ∂z2 0 , với 2 2 2 u =
, r = x + y + z . r
2 3 M0 (1,2, 1),−M1(0,4,−3) . Tính ∂u M(0 ) .
1.18. Cho u = xy z , ∂M0M1 = x y z ∂u M ) 1.19. Cho u a 2 + 2 + 2 2 b 2
c 2 , r = (x y z, , ), . Tính
∂( r , r gọi là véc tơ bán kính. ∂u M( ) Khi nào = gradu ∂r 1.20. Cho u = 1 = 1
, l = (cos ,cos ,cosα β γ ∂u M( ) ).Tính ? r ∂l Khi nào
1.21. Tìm cực trị của các hàm số
a. z = ex(x + y)(x − y + 4).
b. z = x3 + y3 − 3xy .
c. z = (2ax − x2 )(2by − y 2 ), ab ≠ 0 .
d. z = x2 + xy + y 2 − 4ln x −10ln .y
e. z = x3 + y3 − x − y . 35
Downloaded by Ti?n D?ng Tr?n Lý (dungtienltr128@gmail.com) lOMoARcPSD| 10435767
Chương 1. Phép tính vi phân hàm số nhiều biến số
f. z = x4 + y 4 − 2x2 + 4xy − 2y 2 .
g. z = xy + 50 + 20 , với x > 0, y > 0 . x y
h. z = x3 + y3 − x y2 .
1.22. Tính khoảng cách từ gốc toạ ộ ến mặt phẳng x + 2y + 3z = 3. x2 y2 1.23. Cho ellipse +
=1, tìm các iểm trên ó có khoảng cách gần nhất ến ường 4 9
thẳng 3x – 4y = 0. 36
Downloaded by Ti?n D?ng Tr?n Lý (dungtienltr128@gmail.com) lOMoARcPSD| 10435767
Chương 2. Tích phân bội
CHƯƠNG 2. TÍCH PHÂN BỘI GIỚI THIỆU
Ta ã biết, ứng dụng của tích phân xác ịnh, từ hình học, cơ học ến vật lý, kỹ thuật là rất a dạng.
Tuy nhiên các ại lượng ề cập ến chỉ phụ thuộc vào một biến số, ó là sự hạn chế áng kể. Sự mở rộng
tự nhiên của hàm một biến kéo theo sự mở rộng của tích phân ơn (tích phân xác ịnh) ã làm tăng khả
năng ứng dụng, chẳng hạn tính khối lượng của vật thể hai chiều, ba chiều, từ ó có thể tính ược khối
tâm, các mô men quán tính của vật thể, v.v...Chương này cho chúng ta phương pháp tính tích phân
bội hai, bội ba và trên nguyên tắc có thể mở rộng cho tích phân bội n (n lớp). Các khái niệm về tích
phân bội cũng giống như tích phân xác ịnh, ều dựa trên sơ ồ vi phân (tính yếu tố vi phân rồi lấy
tổng). Sự tồn tại, cũng như tính chất của tích phân bội giống như tích phân xác ịnh. Chính vì thế, ể
học tốt chương này, chúng ta cần nắm vững các phương pháp tính tích phân xác ịnh và mô tả ược
miền xác ịnh của hàm nhiều biến.
Trong chương này, yêu cầu nắm vững các nội dung chính sau ây:
1. Tích phân bội hai.
Mô tả ược miền lấy tích phân bội hai bằng hình học và hệ các bất phương trình. Từ ó suy ra
các cận của các tích phân ơn. Trong một số trường hợp nên thực hiện phép ổi biến số ể tính dễ dàng
hơn, ặc biệt thường chuyển sang tọa ộ cực.
2. Tích phân bội ba.
Tương tự như tích phân bội hai, phải mô tả ược miền lấy tích phân bội ba. Trên cơ sở ó tìm
ược các cận của các tích phân ơn. Tùy từng hàm dưới dấu tích phân và miền lấy tích phân có thể
thực hiện phép ổi biến số, ặc biệt thường chuyển sang tọa ộ cầu hoặc tọa ộ trụ ể tính toán cho ơn giản. NỘI DUNG
2.1 Tích phân bội hai ( Tích phân kép)
2.1.1 Bài toán mở ầu
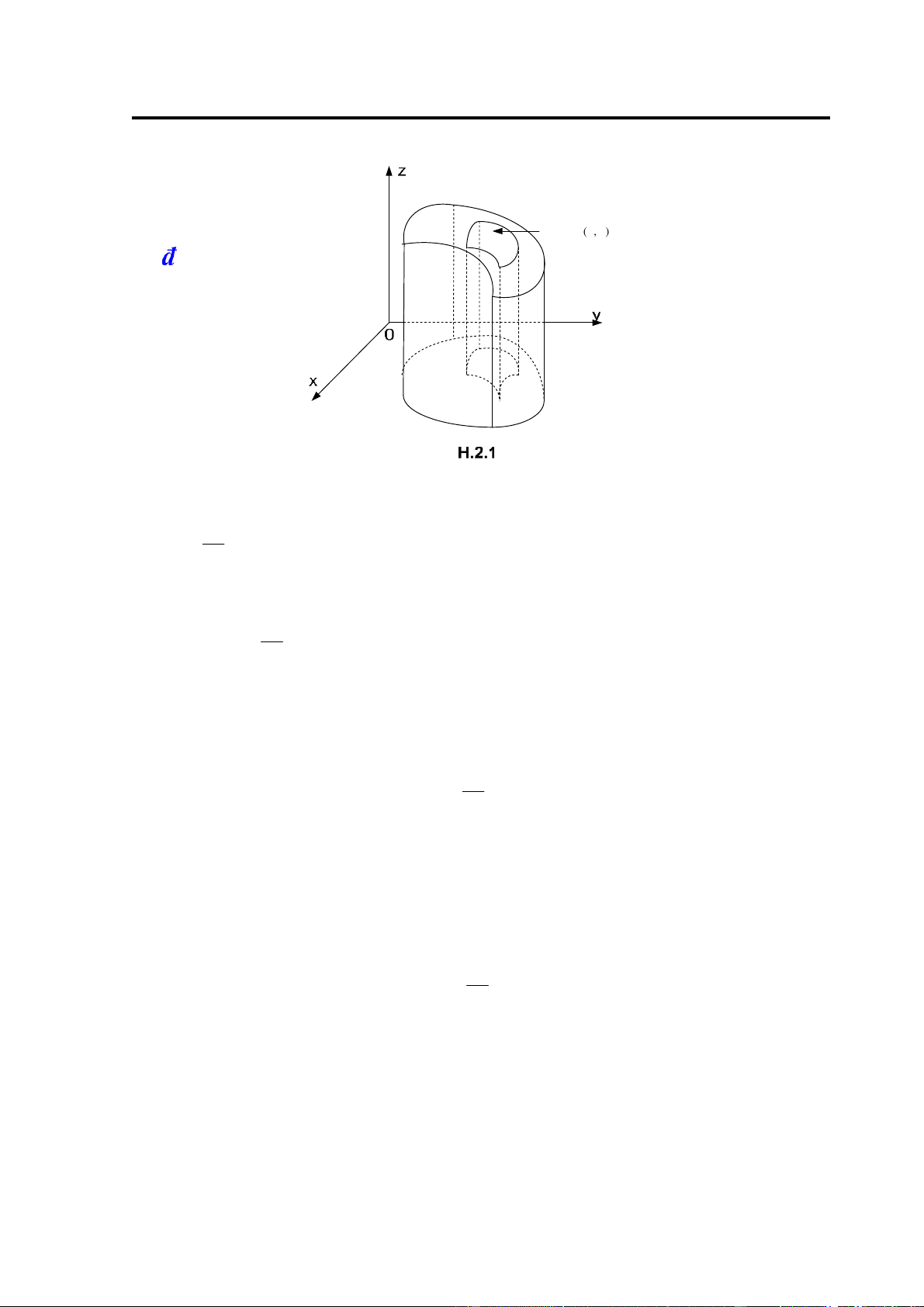
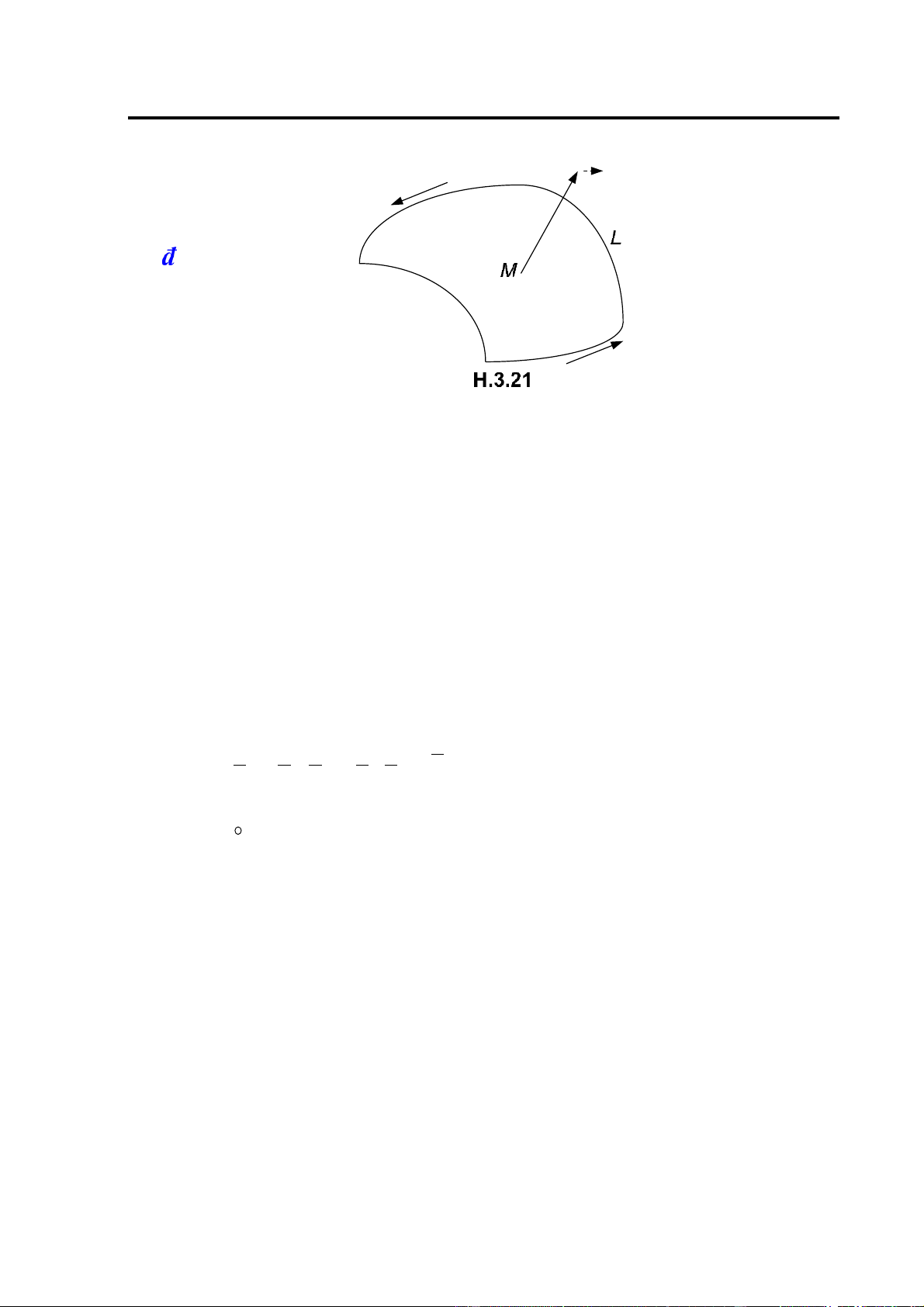
Bài toán: Cho vật thể V
giới hạn bởi các mặt sau ây: mặt phẳng Oxy, mặt trụ có ường
sinh song song với trục Oz và ường chuẩn L là biên của miền óng hữu hạn D và mặt cong cho
bởi phương trình z= f(x,y), (x y, )∈D, trong ó f(x,y) liên tục và không âm trên miền D. Hãy tính
thể tích vật thể V ( thường gọi V là hình trụ cong). Cách tính: 37
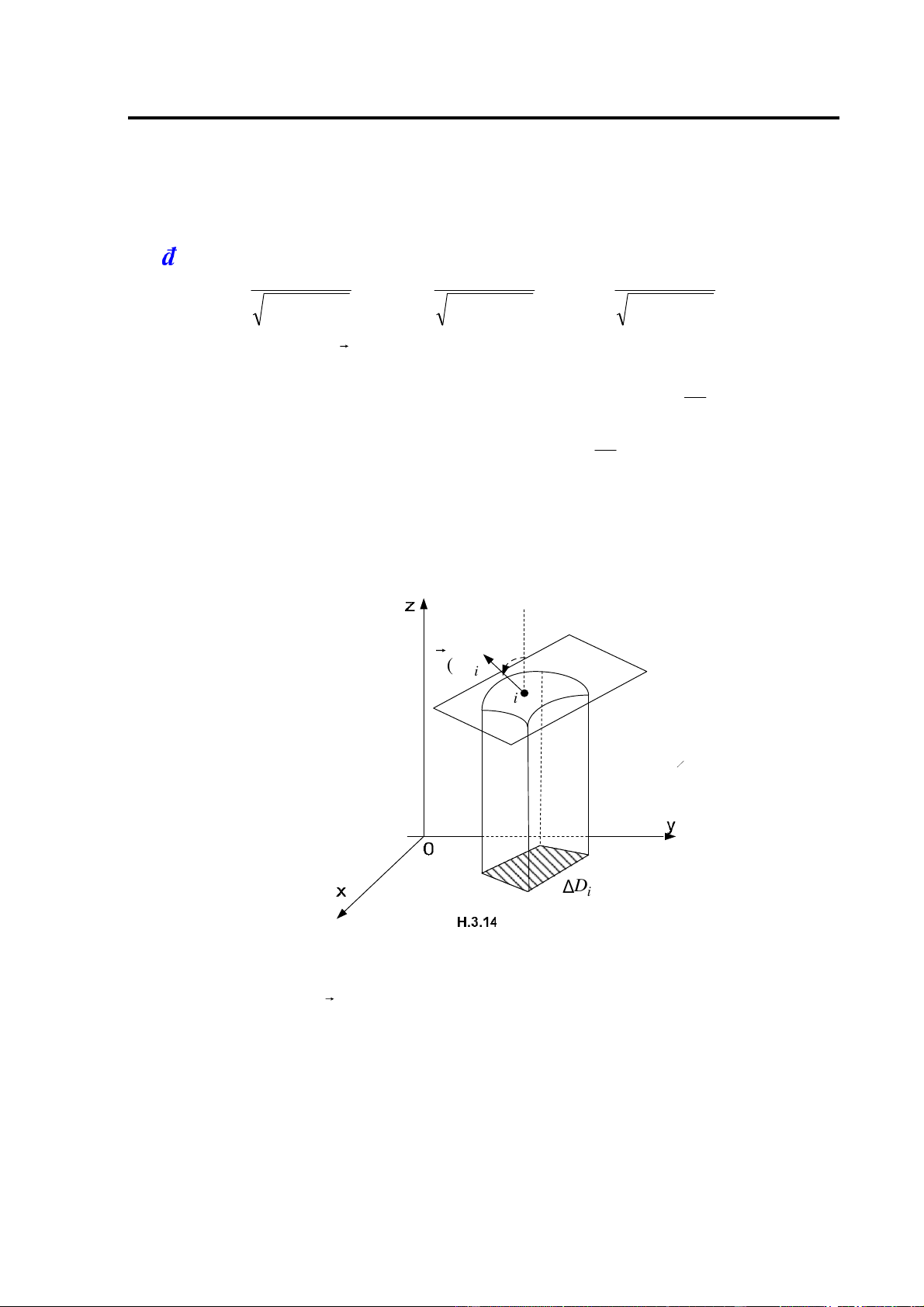
Downloaded by Ti?n D?ng Tr?n Lý (dungtienltr128@gmail.com) lOMoARcPSD| 10435767
Chương 2. Tích phân bội z = f ( xy , ) S Δ i
Chia hình tr ụ cong V thành n hình tr ụ cong b ằ ng cách chia mi ề n D thành n m ả nh không
dẫm lên nhau bởi một lưới các ường cong trong mặt phẳng Oxy. Gọi tên và diện tích các mảnh
ó là ΔSi , ( i= 1,n ) . Dựng các hình trụ cong có các áy dưới là ΔSi ; áy trên là phần của mặt phẳng
cong z= f(x,y) , ường sinh song song với trục Oz. Gọi tên và thể tích các hình trụ cong
thành phần là ΔVi ( i = 1,n). n Như vậy V= ∑ΔVi i=1
Nhận xét: Lấy tuỳ ý Mi ( xi , yi ) ∈ΔSi ( i= 1,n ). Vì miền ΔSi là nhỏ và hàm f(x,y) liên tục
nên trên miền ΔSi nên giá trị f(x,y) khác f( xi , yi ) rất ít, do ó ΔVi ≈ f x( i , yi ) ΔSi . Như n ≈ vậy V
∑ f x( i , yi ) ΔSi i=1
Gọi di là ường kính của mảnh ΔSi ( i= 1,n ) (ta gọi ường kính của miền E là số d = Sup d P
Q{ ( , )}, P∈E Q, ∈E)
Rõ ràng sự xấp xỉ theo công thức trên của V càng chính xác nếu ta chia càng nhỏ miền D .
Vậy thể tích V sẽ bằng giới hạn nếu có của tổng ở vế phải khi n → ∞ sao cho max d → i 0 . n = V lim ∑ Δ i → f(x ,y )i i Si 38
Downloaded by Ti?n D?ng Tr?n Lý (dungtienltr128@gmail.com) lOMoARcPSD| 10435767
Chương 2. Tích phân bội maxd 0 i 1=
Chú ý: Ý tưởng tính thể tích hình trụ cong hoàn toàn như tính diện tích hình thang cong , ở
ó dẫn ến khái niệm tích phân xác ịnh, còn ở ây sẽ dẫn ến khái niệm tích phân kép.
2.1.2 Định nghĩa tích phân kép.
Cho hàm z= f(x,y) xác ịnh trên miền óng D
* Chia miền D thành n miền nhỏ bởi một lưới các ường cong, gọi tên và diện tích các miền
là Δsi ( i= 1,n ) ồng thời kí hiệu di là ường kính mảnh thứ i ( i= 1,n )
* Lấy tuỳ ý Mi ( xi , yi ) ∈Δsi ( i= 1,n ) . n
* Gọi I n = ∑ f x( i , yi ) ΔSi
là tổng tích phân cuả f(x,y) trên miền D ứng với một phân i=1
hoạch và một cách chọn các iểm M →
1, M2,...,M n . Khi n→∞ sao cho maxdi 0 mà I n hội tụ
về I không phụ thuộc vào phân hoạch ΔSi và cách chọn Mi ∈ΔSi (i = 1,n ) thì số I gọi là tích phân
kép của f(x,y) trên miền D và kí hiệu là ∫∫ f x y dS( , ) . D n
Như vậy ∫∫ f x y dS( , ) =
lim ∑ f x( i , yi )ΔSi (2.1) D max d → i 0 i=1
Có ược công thức trên thì nói rằng f(x,y) khả tích trên miền D; f(x,y) là hàm dưới dấu tích
phân còn x, y là các biến tích phân, dS là yếu tố diện tích. Chú ý: a.
Vì tích phân kép không phụ thuộc vào cách chia miền D nên có thể chia D bởi một
lưới các ường thẳng song song với các trục toạ ộ Ox, Oy. Khi ó ΔS = Δ Δ i
xi yi suy ra dS = dx.dy.
Do ó là tích phân kép thường kí hiệu là: ∫∫ f x y dxdy( , ) D b.
Cũng như tích phân xác ịnh, kí hiệu biến lấy tích phân kép cũng không làm tích
phân kép thay ổi, tức là: ∫∫ f x y dxdy( , ) = ∫∫ f u v dudv( , ) D D 39
Downloaded by Ti?n D?ng Tr?n Lý (dungtienltr128@gmail.com) lOMoARcPSD| 10435767
Chương 2. Tích phân bội c.
Nếu f(x,y)≥ 0 trên D thì thể tích hình trụ cong ã xét trong phần 2.1.1 ược tính theo
công thức V=∫∫ f x y dxdy( , ) (2.2) d. Nếu f(x,y)=1 trên D thì số o diện
tích miền D tính theo công thức
S=∫∫ f x y dxdy( , ) (2.3) D
2.1.3. Điều kiện khả tích
Tương tự như tích phân xác ịnh, ta có: *
Nếu hàm số f(x,y) khả tích trên miền D thì f(x,y) bị chặn trên miền D ( iều kiện cần của hàm khả tích ). *
Nếu hàm số f(x,y) liên tục trên miền D, tổng quát hơn: nếu hàm số f(x,y) chỉ có gián oạn
loại 1 trên một số hữu hạn cung cong của miền D thì khả tích trên miền D.
2.1.4. Tính chất của tích phân kép.
Từ ịnh nghĩa của tích phân kép, tương tự như tích phân xác ịnh, suy ra ược các tính chất sau:
a. Nếu D ược chia thành 2 miền D ∩ = φ 1, D2 mà D1 D2
thì f(x,y) khả tích trên D khi và chỉ
khi nó khả tích trên D1 và D2 ồng thời. (2.4)
∫∫ f x y dxdy( , )= ∫∫ f x y dxdy( , )+ ∫∫ f x y dxdy( , ) D D1 D2
b..Nếu f(x,y) khả tích trên D và k là hằng số thì: (2.5)
∫∫k f x y dxdy. ( , )= k.∫∫ f x y dxdy( , ) D D
c.Nếu f(x,y), g(x,y) khả tích trên D thì
∫∫[f x y( , ) + g x y dxdy( , )]= ∫∫ f x y dxdy( , ) + ∫∫ g x y (2.6) dxdy( , ) D D D
d. Nếu f(x,y), g(x,y) cùng khả tích trên D và f x y( , ) ≤ g x y( , ) ( ,∀ x y)∈D thì:
∫∫ f x y dxdy( , )≤ ∫∫ g x y dxdy( , ) (2.7) 40
Downloaded by Ti?n D?ng Tr?n Lý (dungtienltr128@gmail.com) lOMoARcPSD| 10435767
Chương 2. Tích phân bội D D
e. Nếu f(x,y) khả tích thì f x y( , ) khả tích và ≤ ∫∫ f x y dxdy( , ) ∫∫ f x y dxdy( , ) (2.8) D D
f. Nếu f(x,y) khả tích trên D và thoả mãn m ≤ f x y( , ) ≤ M , ( , )∀ x y ∈D thì ≤ mS
∫∫ f x y dxdy( , )≤ MS (2.9) D
trong ó S là diện tích miền D.
2.2. Tính tích phân kép.
2.2.1. Công thức tính tích phân kép trong tọa ộ ề các (Descartes).
Định lí 2.1. Nếu hàm số f(x,y) liên tục trên miền D cho bởi hệ bất phương trình
⎧a ≤ x ≤ b ⎨
⎩ϕ1( )x ≤ y ≤ϕ2( )x b ϕ2( )x = thì
∫∫ f x y dxdy( , ) ∫dx ∫ f x y dy( , ) (2.10) D a ϕ1( )x z S(x) ϕ () ϕ () 2 x 1 x y 0 a x b x H.2.2
Chứng minh: Trước hết xét f x y( , ) ≥ 0 và liên tục trên miền D : 41
Downloaded by Ti?n D?ng Tr?n Lý (dungtienltr128@gmail.com) lOMoARcPSD| 10435767
Chương 2. Tích phân bội
⎧a ≤ x ≤ b
⎨⎩ϕ1( )x ≤ y ≤ϕ2 ( )x
Trong ó ϕ1( )x ,ϕ2 ( )x liên tục trên [a,b]. =
Theo ý nghĩa hình học ta có: V ∫∫ f x y dxdy( , ) D
Trong ó V là thể tích hình trụ cong. Mặt khác, ứng dụng tích phân xác ịnh ta lại có: b = V
∫S x dx( ) Trong ó S(x) là diện tích thiết diện của hình trụ cong do mặt phẳng vuông góc với a
trục 0x tại iểm x tạo ra. (H.2.2).Từ hình 2.2 ta thấy S(x) là diện tích hình thang cong nằm trên mặt
phẳng Oyz (bằng phép tịnh tiến) giới hạn bởi trục 0y, các ường y x y x và =
ường cong z = f(x,y), với x cố ịnh. Theo ý nghĩa tích phân xác ịnh ta có: S x( ) ∫ f x y dy( , ) ϕ1( )x ⎛ ⎞ b ϕ 2( )x
Suy ra ∫∫ f x y dxdy( , )= ∫ ∫⎜⎜f x y dy dx( , ) ⎟⎟ ⎝ ⎠ D a ϕ 1( )x
Tích phân lặp trên ược qui ước viết theo dạng: ⎛ ⎞ b ϕ2( )x b ϕ2( )x )
∫ ∫⎜⎜ f x y dy dx( ,
⎟⎟= ∫dx ∫ f x y dy( , ) ⎝ ⎠ a ϕ1( )x a ϕ1( )x
Bây giờ xét f(x,y) liên tục và có dấu bất kỳ trên miền D.
Xét các hàm số phụ sau:
⎧ f x y( , ) ( , ),∀ x yf x y( , ) ≥ 0
f1(x y, ) = ⎨⎩0 ( , ),∀ x yf x y( , ) < 0
⎧− f x y( , ) ( , ),∀ x yf x y( , ) < 0
f2 (x y, ) = ⎨⎩0 ( , ),∀ x yf x y( , ) ≥ 0
Các hàm số f1(x,y), f2(x,y) liên tục và không âm trên miền D ồng thời f x y( , ) = f1(x y, )
− f2 (x y, ) . 42
Downloaded by Ti?n D?ng Tr?n Lý (dungtienltr128@gmail.com) lOMoARcPSD| 10435767
Chương 2. Tích phân bội
Theo tính chất c. của tích phân bội và kết quả trên, ta ược:
∫∫ f x y dxdy( , )= ∫∫ f1(x y dxdy, )− ∫∫ f2 (x y dxdy, ) D D D b ϕ2( )x b ϕ2( )x
= ∫dx ∫ f1(x y dy, )− ∫dx ∫ f2 (x y dy, ) a
ϕ1( )x a ϕ1( )x b ϕ2( )x
= ∫dx ∫[f1(x y, ) − f2 (x y dy, )] a ϕ1( )x b ϕ2( )x
= ∫dx ∫ f x y dy( , ) a ϕ1( )x
Vậy ta nhận ược công thức (2.10). Như vậy, ể tính tích phân kép ta ưa về tính tích phân lặp.
Công thức (2.10) thể hiện tính tích phân theo biến y (trong khi tính coi x là hằng số) trước và theo biến x sau Chú ý: a.
Nếu miền D cho bởi hệ bất phương trình: ⎧c ≤ y ≤ d ⎨
⎩ψ1(y) ≤ x ≤ ψ2 (y) thì nhận ược công
thức tính tích phân kép tương tự là: d ψ2( y) =
∫∫ f x y dxdy( , ) ∫dy ∫ f x y dx( , ) (2.11) D c ψ1( y) b.
Công thức thay ổi thứ tự lấy tích phân hay gọi là công thức Fubini. Trong trường
hợp này, miền D có tính chất: Mỗi ường thẳng song song với các trục toạ ộ cắt miền D nhiều nhất
ở hai iểm. Khi ó tồn tại hình chữ nhật:
⎧a ≤ x ≤ b ⎨
c ≤ y ≤ d ⎩
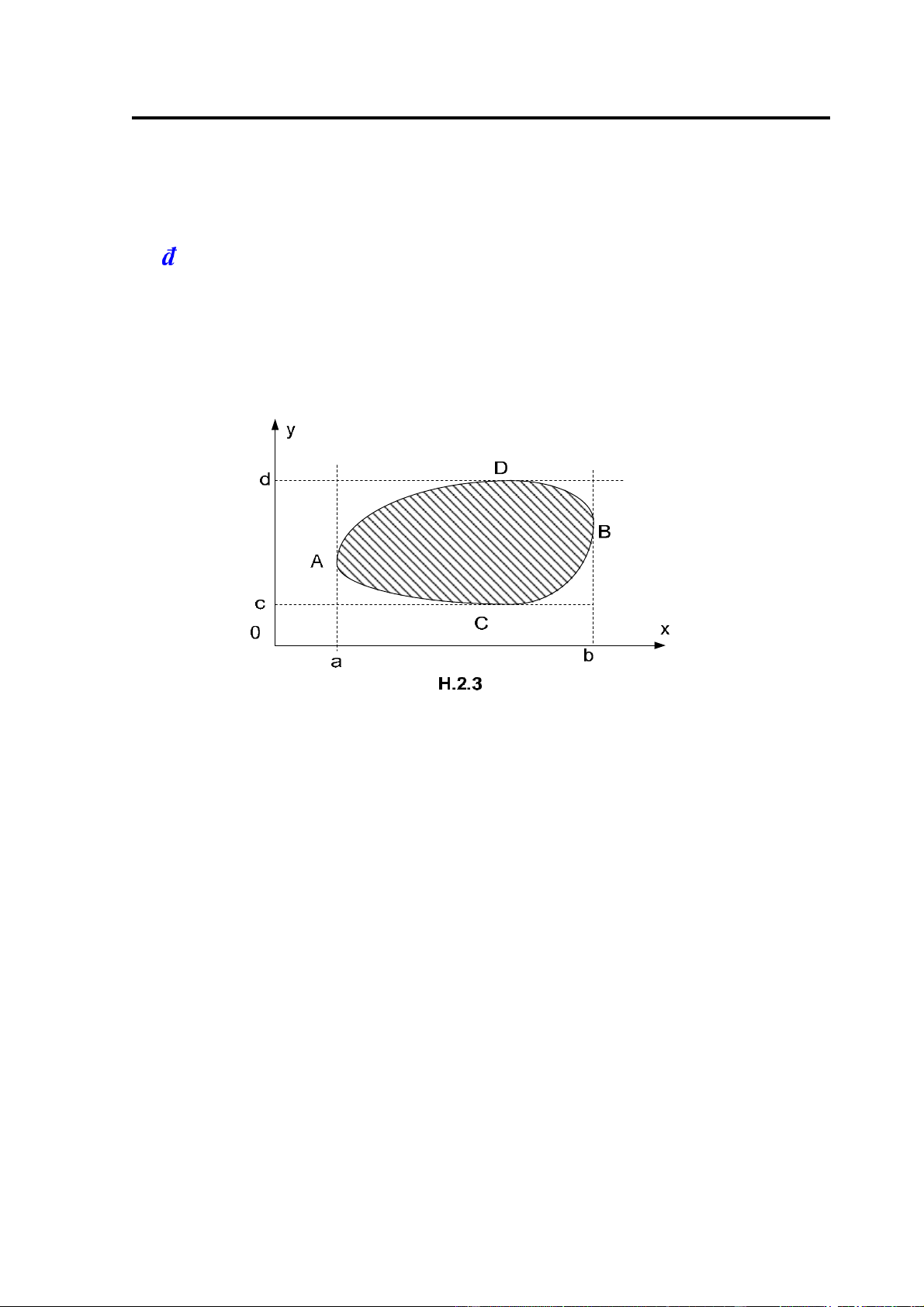
có cạnh tiếp xúc với biên của miền D (H.2.3) 43
Downloaded by Ti?n D?ng Tr?n Lý (dungtienltr128@gmail.com) lOMoARcPSD| 10435767
Chương 2. Tích phân bội
Giả sử ADB ACB, có phương trình là: y =ϕ1( )x , y =ϕ2 ( )x a, ≤ x ≤ b , CADCBD, có phương
trình là: x =ψ1( )y ,x =ψ2 ( )y c, ≤ y ≤ d
Từ công thức (2.10), (2.11) nhận ược công thức Fubini sau ây: b ϕ2( )x d ψ2( y) =
∫dx ∫ f x y dy( , ) ∫dy ∫ f x y dx( , ) (2.12) a ϕ1( )x c ψ1( y) c.
Khi miền D không có tính chất ã nêu trên thì có thể chia miền D thành một số hữu
hạn các miền D1, D2, ..., Dn có tính chất mô tả ở hình H.2.3 sau ó áp dụng tính chất a. của tích phân kép. d.
Khi miền D là hình chữ nhật a ≤ x ≤ b c, ≤ y ≤ d và hàm f x y( , ) = h1( ).x h2 ( )y
thường gọi f(x,y) là hàm có biến số phân li thì công thức (2.10) trở thành: b d =
∫∫ f x y dxdy( , ) ∫ h1 ( )x dx.∫ h2 ( )y dy D a c
Ví dụ 1: Tính tích phân sau: ∫∫ x ydxdy2 D
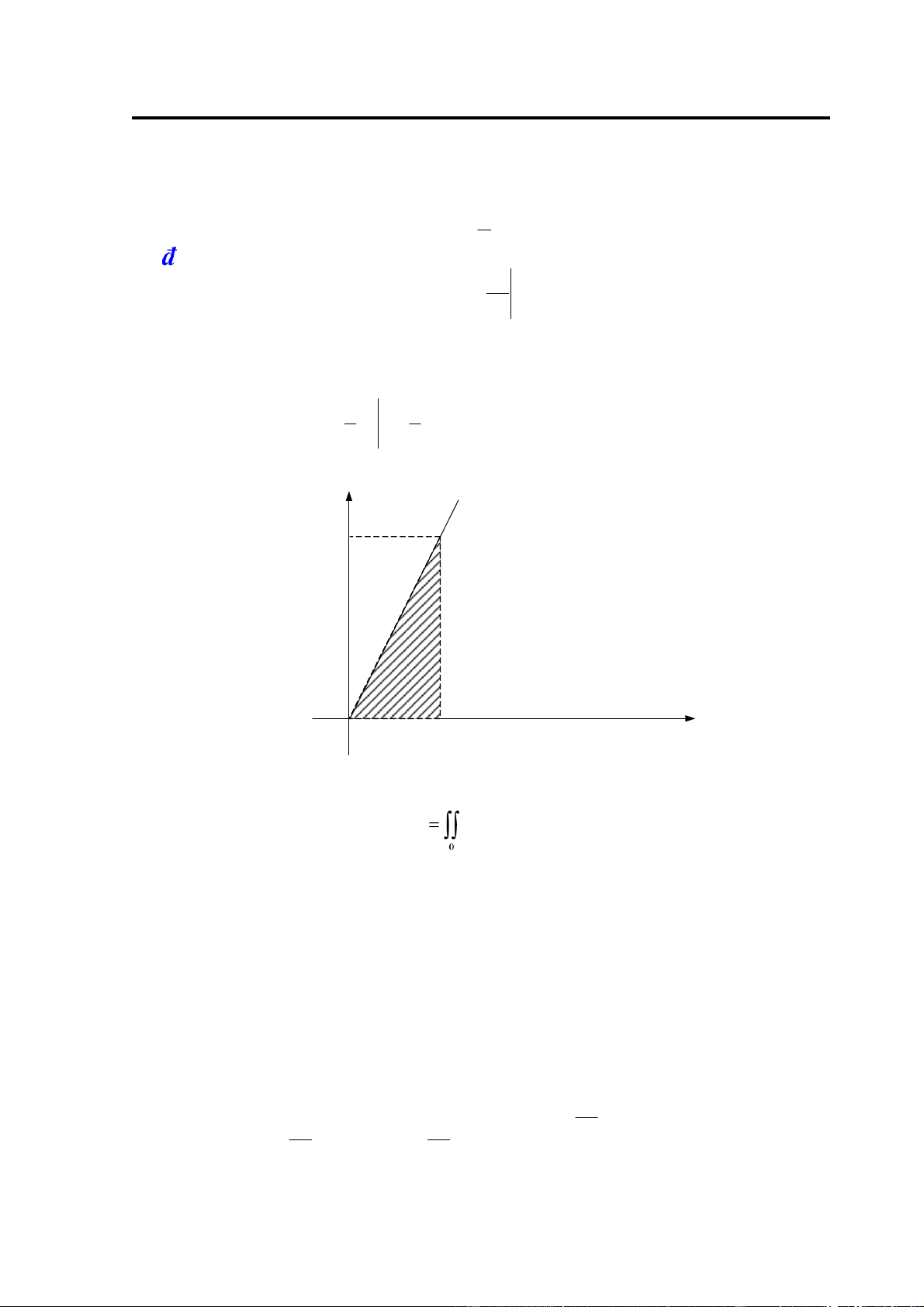
trong ó D là miền giới hạn bởi các ường y = 0, y = 2x và x = a, a>0
Giải: Để có hệ phương trình mô tả miền D trước hết phải vẽ miền D (H.2.4). 44
Downloaded by Ti?n D?ng Tr?n Lý (dungtienltr128@gmail.com) lOMoARcPSD| 10435767
Chương 2. Tích phân bội
⎧0 ≤ x ≤ a
⎧⎪0 ≤ y ≤ 2a ⎨ ⎨
Vậy D: 0 ≤ y ≤ 2x hoặc D: ⎪⎩2y ≤ x ≤ a ⎩ 2 y 2 2
∫∫ x ydxdy2= ∫ ∫ a dx2 xx ydy2
= ∫a x2xdx = 2∫a x dx4 0 D 0 0 00 a = 2 x5 = 2 a5 5 0 5 y a 2 y=2x x 0 a H.2.4
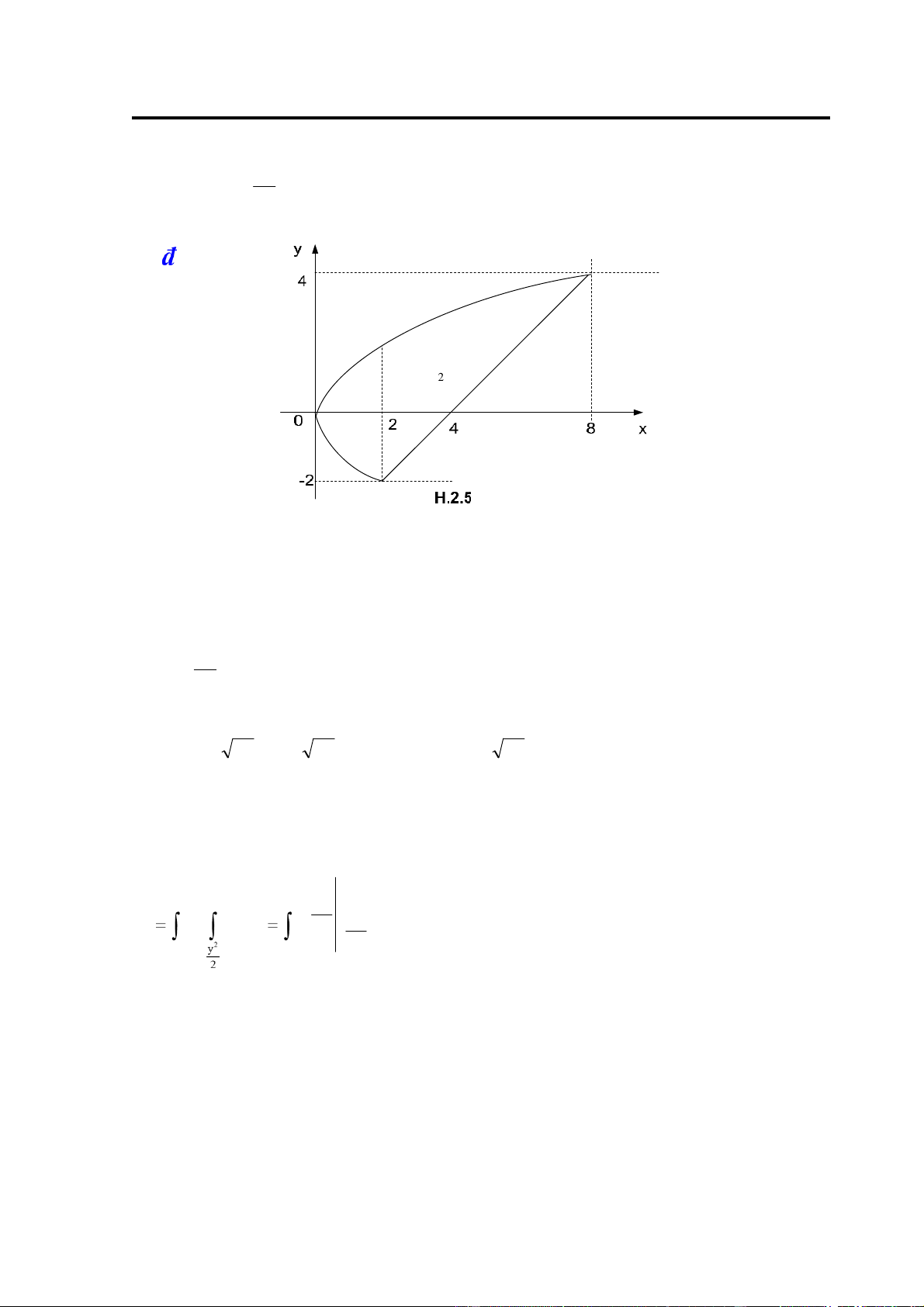
Ví dụ 2: Tính tích phân: I xydxdy
với D giới hạn bởi các ường y = x − 4 và y2 = 2x.
Giải: Vẽ miền D (H.2.5)
Để vẽ ược miền D trước hết phải tìm giao của các ường bằng cách giải hệ phương trình: ⎧y = x − 4 ⎨ 2 ⎩y = 2x
Ta suy ra: ⎧⎪⎪⎨x = y2 = ⎨⎪⎧⎪ ⇒ ⎡⎢⎢⎨⎧⎩ 22 ⇒ ⎧⎨⎪x 2 y 2 x =y y22 xy == −22 2 ⇒ 45
Downloaded by Ti?n D?ng Tr?n Lý (dungtienltr128@gmail.com) lOMoARcPSD| 10435767
Chương 2. Tích phân bội ⎩⎪y
= y2 − 4 ⎩⎪y − 2y −8 = 0
⎩⎪⎪⎡⎢⎣y = −= 42
⎢⎢⎣ ⎩⎨⎧xy ==84 ⎪
Ta mô tả miền D như sau: 2 2 xy = x = y + 2 D 4 1 D ⎧− 2 ≤ y ≤ 4 ⎪ D: ⎨ ∪ 2 hoặc D = D1 D2 y
⎪⎩ 2 ≤ x ≤ y + 4
⎧0 ≤ x ≤ 2 ⎧2 ≤ x ≤ 8
với D1 :⎨ D2 :⎨ ⎩− 2x ≤ y ≤ 2x ⎩x − 4 ≤ y ≤ 2x
Trong trường hợp này nên áp dụng công thức (2.11) tức là lấy tích phân lặp theo biến x trước và theo biến y sau: 4 y 4+ 4 x2 y + 4 I dy xydx y. y2 dx 2 −2 −2 2 46
Downloaded by Ti?n D?ng Tr?n Lý (dungtienltr128@gmail.com) lOMoARcPSD| 10435767
Chương 2. Tích phân bội y(y 8y 16 )dy = 1 1( y + + − 4 8 y3 8y2 y6 ) 4 = 90. 2 4 3 24 −2
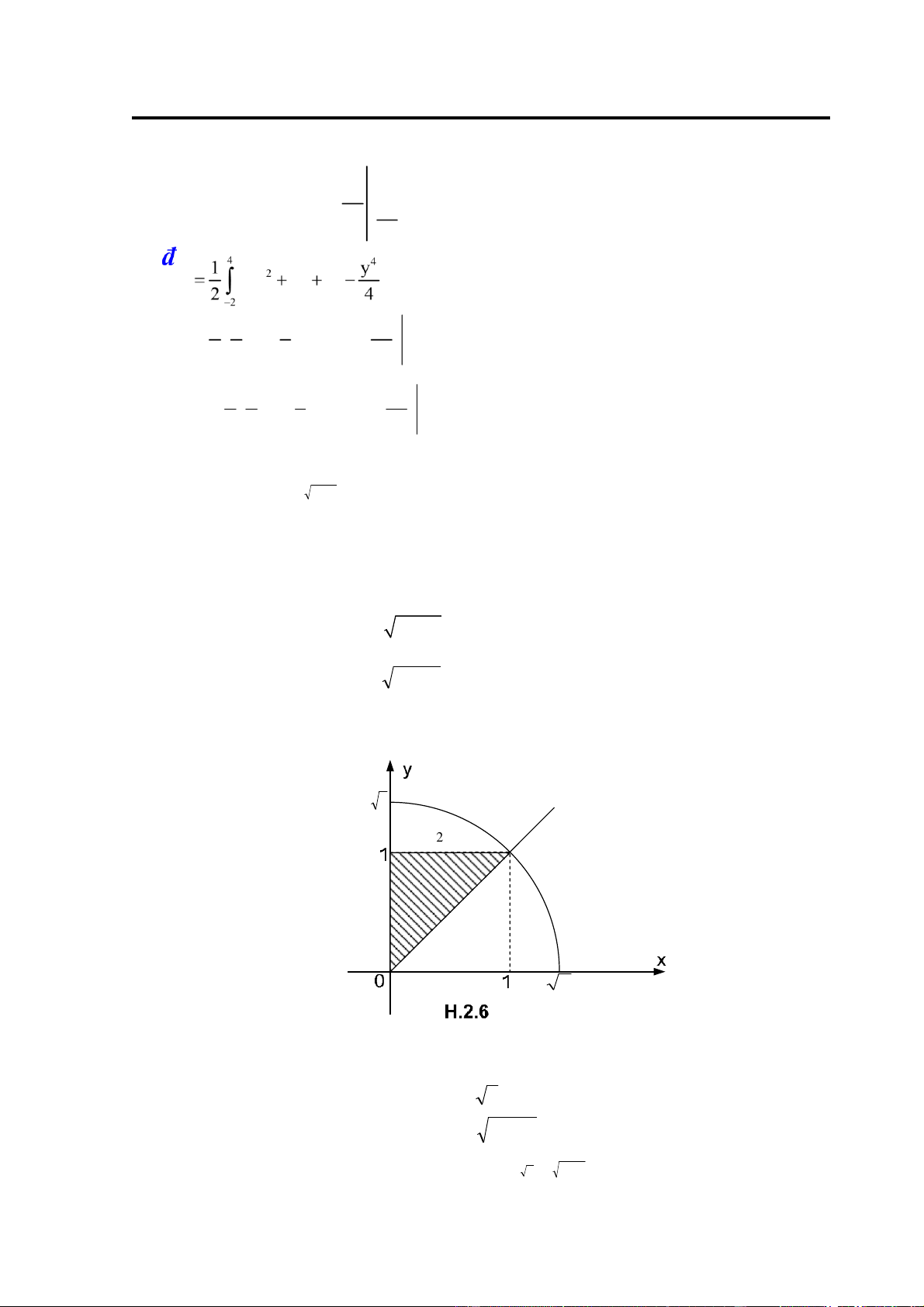
Ví dụ 3: Hãy thay ổi thứ tự lấy tích phân sau: 1 2−x2
I = ∫dx ∫ f x y dy( , ) 0 x
Giải: Vẽ miền D trên cơ sở ã biết các cận của tích phân. theo ầu bài miền D giới hạn bởi các
ường : x = 0,x =1,y = x,y = 2− x .2
2 chính là nửa ường tròn : ⎧⎨x + = 2 y 2 2
Đường có phương trình y = 2 − x ⎩y ≥ 0 2 2 D 1 D 2
Do tính không trơn của biên miền D nên ta mô tả: D = D ∪ 1 D2 ⎧0 ≤ y ≤1 ⎧⎪1≤ y ≤ 2 trong ó: D − 2 2 y
1 : ⎨⎩0 ≤ x ≤ y,D2 : ⎩⎨⎪0 ≤ x ≤ 2 − 2 2 y 47
Downloaded by Ti?n D?ng Tr?n Lý (dungtienltr128@gmail.com) lOMoARcPSD| 10435767
Chương 2. Tích phân bội 1 2−x2 1 y
Vậy I = ∫dx ∫ f x y dy( , )= ∫dy∫ f x y dx( , )+ ∫dy ∫ f x y dx( , ) 0 x 0 0 1 0
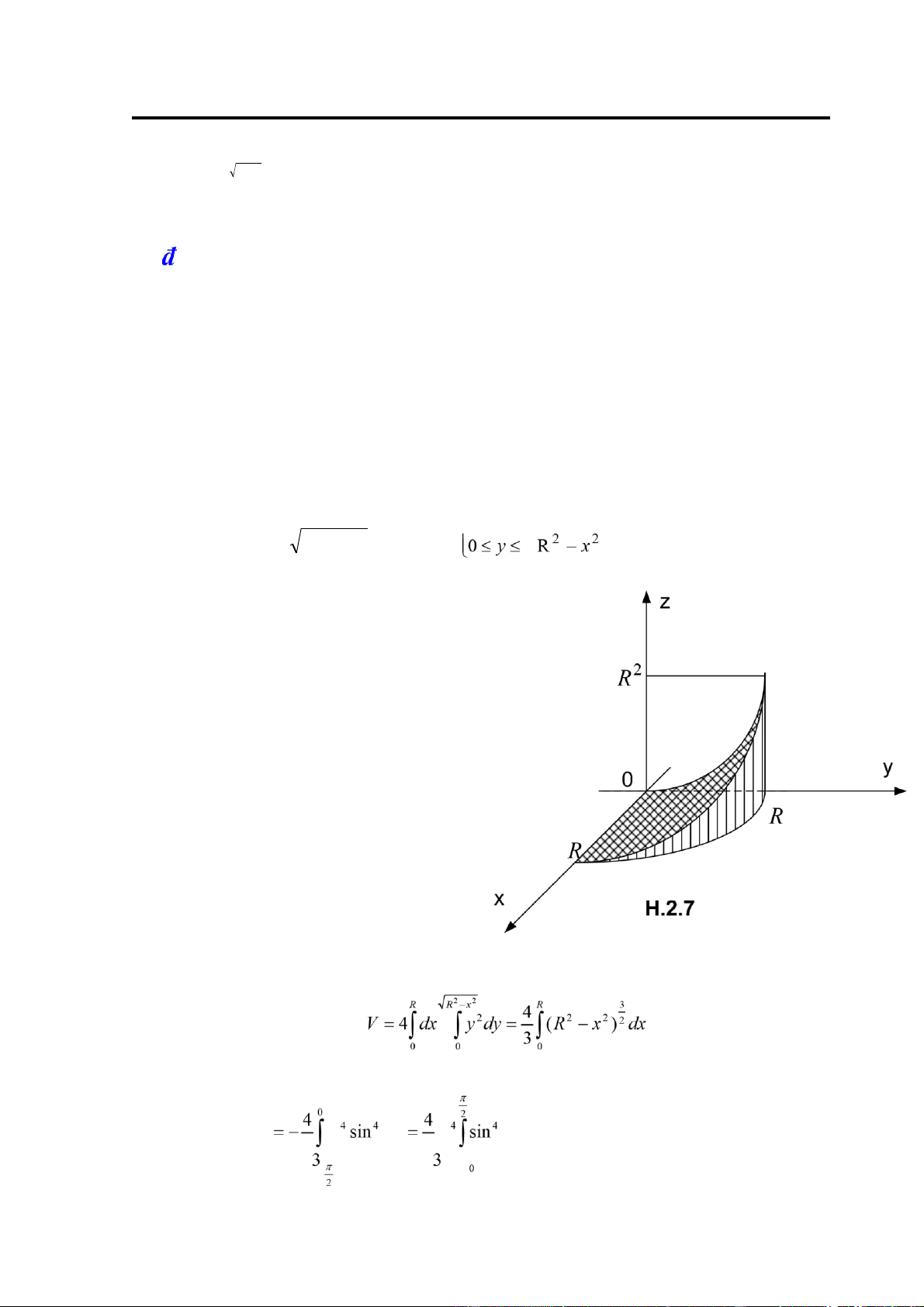
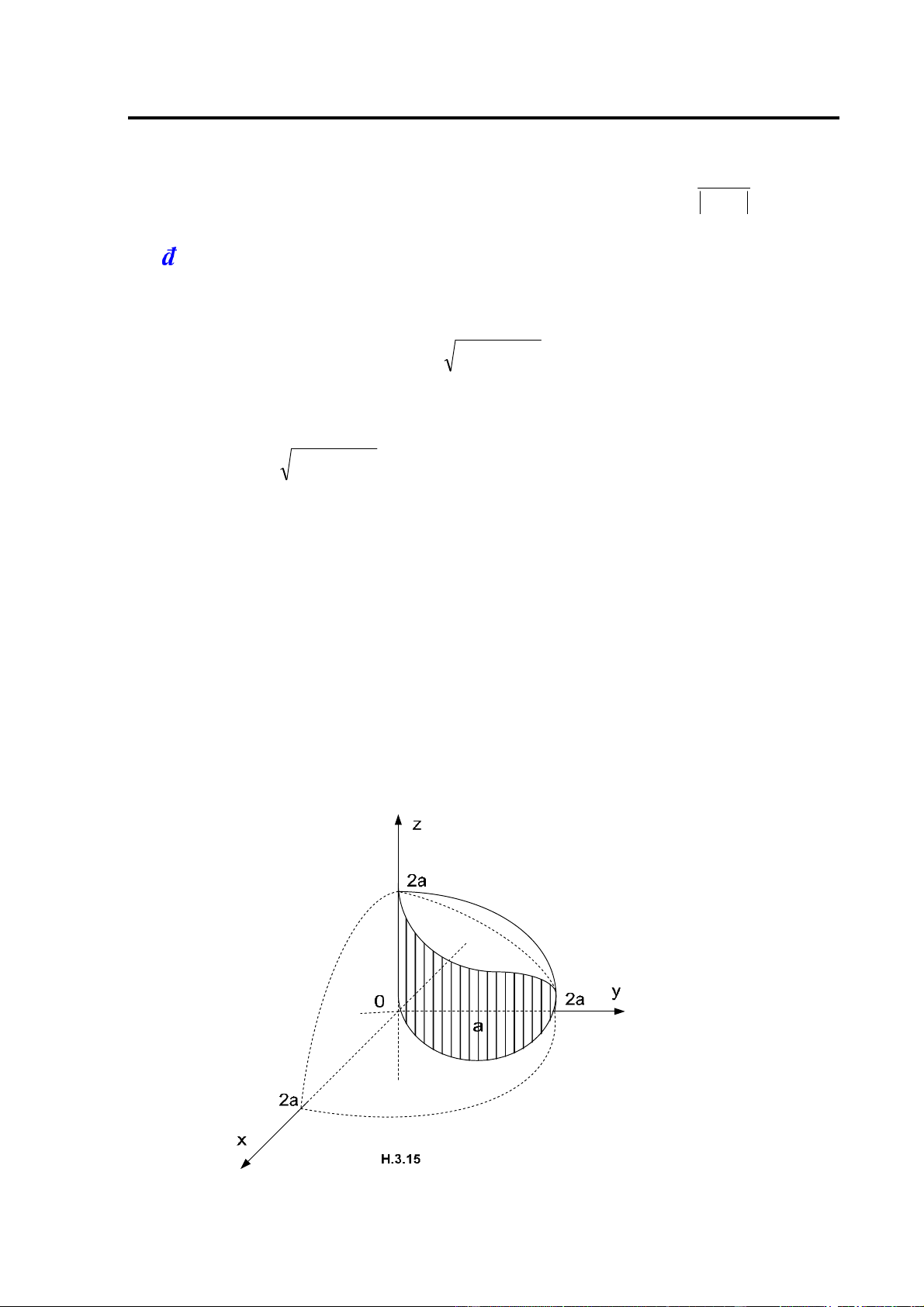
Ví dụ 4: Tính thể tích V của vật thể giới hạn bởi các mặt z = 0,x2 + y 2 = R2 ,z = y2
Giải: Vật thể ược mô tả bởi hình H.2.7. Vật thể ối xứng qua mặt tọa ộ 0xz và 0yz. ta xét phần
vật thể trong góc phần tám thứ nhất, phần vật thể này ược giới hạn bởi các mặt z = 0,x2 + y 2 = R2
,x ≥ 0, y ≥ 0 và z = y2 .
Vậy V = 4∫∫ y dxdy2 trong ó D là phần tư hình tròn x2 + y 2 = R2 ,x ≥ 0, y ≥ 0. D
⎧⎪0 ≤ x ≤ R Rõ ràng D:⎨
Đổi biến x = Rcos ,t dx = −Rsintdt V Rtdt R tdt 48
Downloaded by Ti?n D?ng Tr?n Lý (dungtienltr128@gmail.com) lOMoARcPSD| 10435767
Chương 2. Tích phân bội 4
(Xem công thức Wallis, Tr.139, Toán cao cấp A1)
2.2.2. Công thức tính tích phân kép trong toạ ộ cực
Trước khi ưa ra công thức tính tích phân kép trong toạ ộ cực, ta thừa nhận ịnh lý sau liên
quan ến phép ổi biến tích phân kép.
Định lý 2.2: Giả sử f(x,y) liên tục trên miền D ⊂ 0xy ồng thời tồn tại các hàm số
⎧x = x u v( , )
⎨y = y u v( , ) thoả mãn : ⎩
* là song ánh tử D lên Δ
* có ạo hàm riêng liên tục trong miền Δ ⊂ 0uv và ịnh thức Jacobi D x y( , ) ≠ 0 trong D u v( , ) miền
Δ ( hoặc chỉ bằng 0 ở một số iểm cô lập) khi ó:
∫∫ f x y dxdy( , )= ∫∫ f x u v[ ( , ), ( ,y u v) .] D x y( , ) dudv (2.13) D u v( , ) D Δ
a. Hệ toạ ộ cực
Để xác ịnh vị trí của các iểm trong mặt phẳng, ngoài hệ toạ ộ Descartes, người ta còn dùng
hệ toạ ộ cực ược ịnh nghĩa như sau: Chọn iểm 0 tuỳ ý gọi là cực và một trục 0x gọi là trục cực. Vị
trí của iểm M bất kỳ ược xác bởi hai số: góc ϕ giữa trục 0x và véctơ 0M gọi là góc cực và r = 0M
gọi là bán kính véctơ. Cặp (r,ϕ) gọi là toạ ộ cực của M và kí kiệu
M r( ,ϕ). Tất cả các iểm trên mặt phẳng sẽ ứng với ϕ biến thiên từ 0 ến 2πhoặc ϕbiến thiên từ -
2πến 0 và r biến thiên từ 0 ến ∞.
Nếu chọn hệ trục toạ ộ Descartes 0xy tức là 0 trùng với cực, trục hoành trùng với trục cực thì
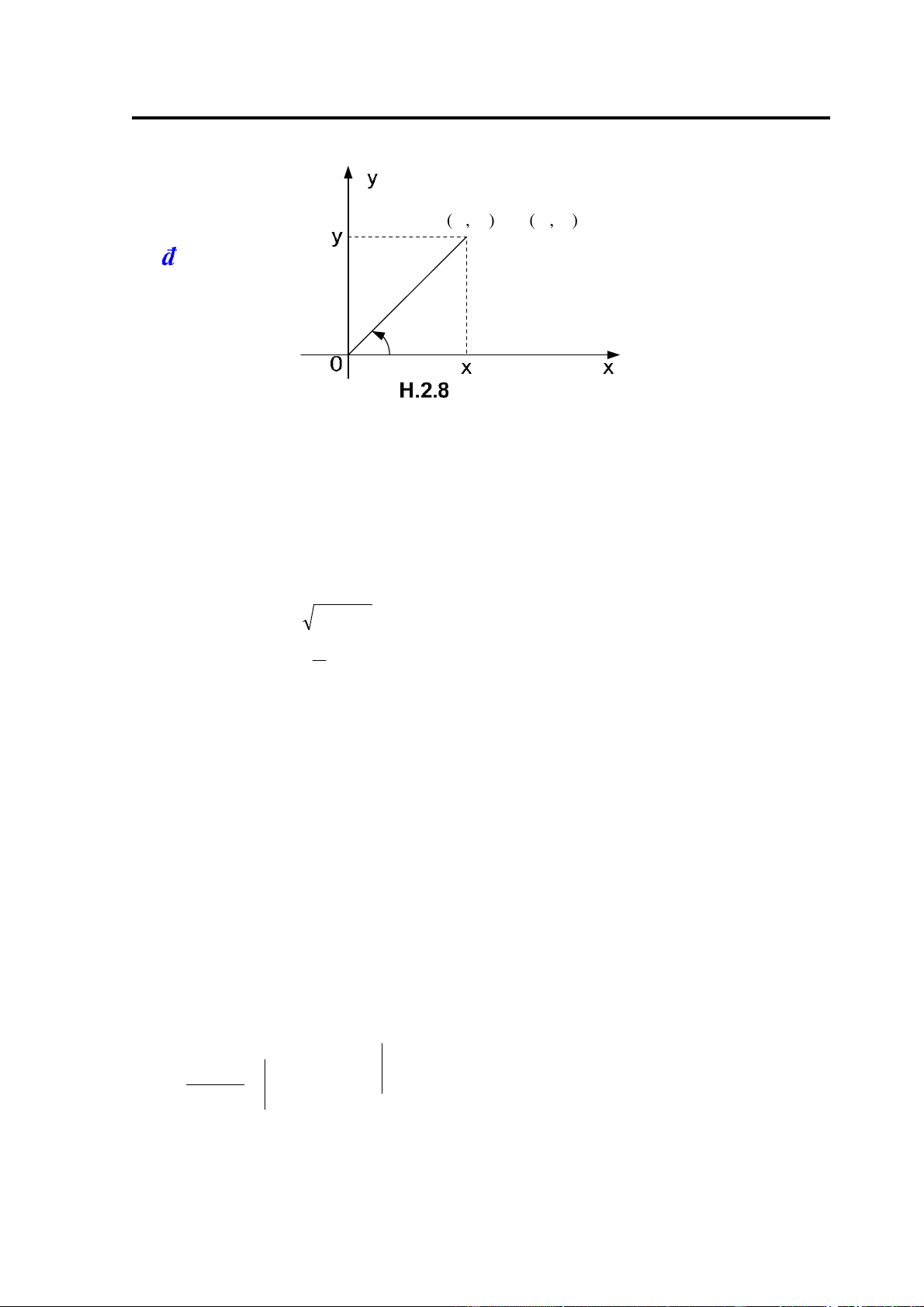
ta nhận ược liên hệ sau ây giữa các toạ ộ Descartes và toạ ộ cực của iểm M (xem H.2.8): 49
Downloaded by Ti?n D?ng Tr?n Lý (dungtienltr128@gmail.com) lOMoARcPSD| 10435767
Chương 2. Tích phân bội Mr ( , ϕ ), Mx( y , ) r ϕ ⎧ x = r c osϕ ⎨y = r sinϕ ⎩ ⎧r = 2 ⎪ x 2 + y 2
và ngược lại: ⎨ , x
cùng dấu với cosϕ hoặc y cùng dấu với sin .ϕ y x ⎪tgϕ= ⎩
b. Phương trình ường cong trong hệ toạ ộ cực
Hệ thức F r( ,ϕ) = 0 hoặc r = r( )ϕ hay ϕ=ϕ( )r gọi là phương trình ường cong trong toạ ộ
cực, chẳng hạn r = a là phương trình ường tròn bán kính bằng a và tâm ở gốc toạ ộ, ϕ=ϕ0 là phương
trình nửa ường thẳng xuất phát từ gốc toạ ộ và lập với trục cực một góc là ϕ0 .
c. Công thức tích phân kép trong toạ ộ cực Ta thực hiện phép ổi biến số: ⎧x = rcosϕ ⎨y = rsinϕ ⎩ D x y( , ) cosϕ − rsinϕ Do ó: == r D r( ,ϕ) sinϕ rcosϕ
Từ công thức (2.13) suy ra: 50
Downloaded by Ti?n D?ng Tr?n Lý (dungtienltr128@gmail.com) lOMoARcPSD| 10435767
Chương 2. Tích phân bội
∫∫ f x y dxdy( , )= ∫∫ f r( cos , sinϕ ϕ ϕr)rdrd (2.14) D Δ r () 2 ϕ r () 1 ϕ ϕ2 ϕ1
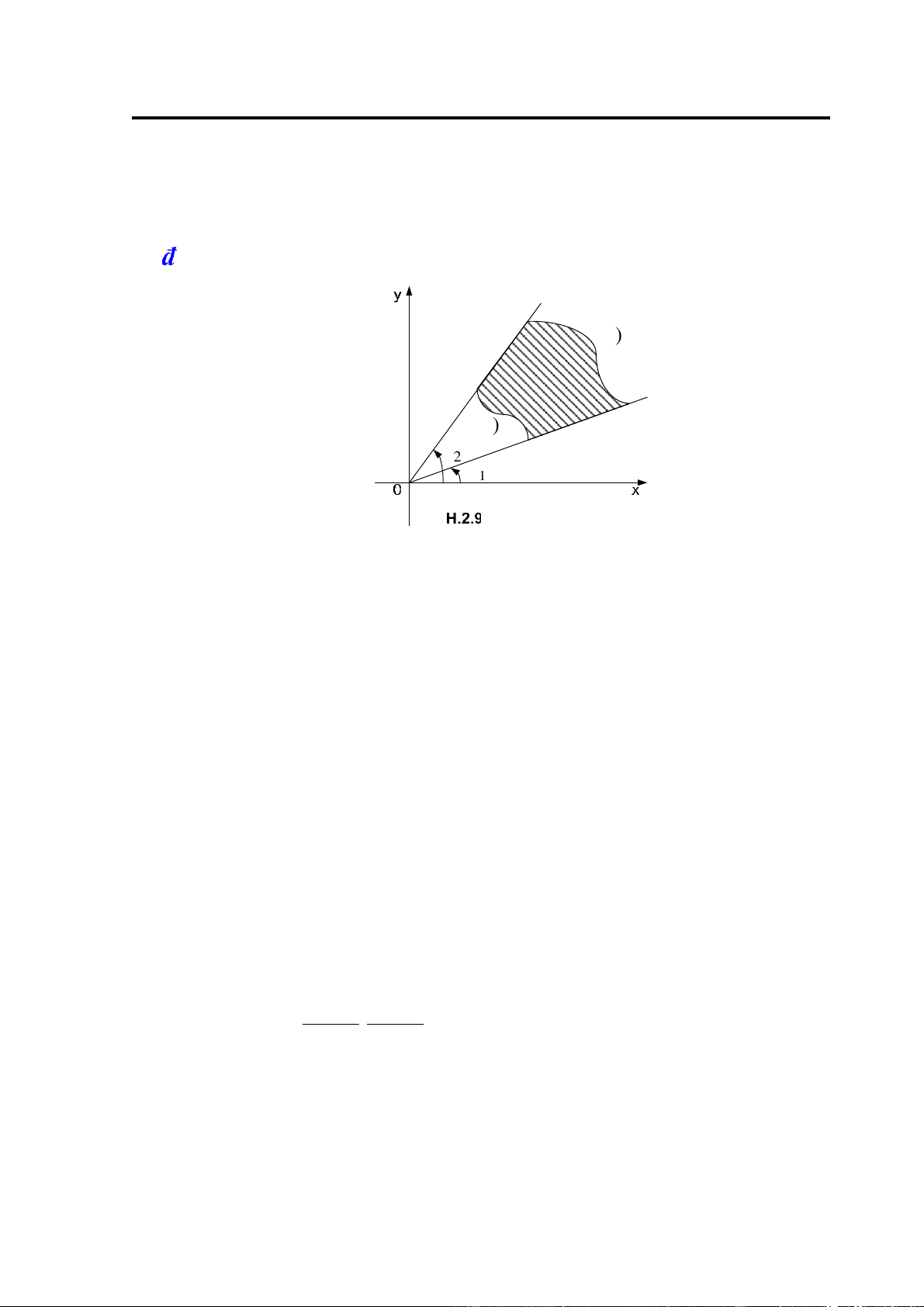
Thường gặp miền Δ ược giới hạn bởi hai tia ϕ=ϕ1,ϕ=ϕ2 và ường cong r = r1( )ϕ,r = r2( )ϕ
(H.2.9), tức là trong hệ toạ ộ cực, miền D ược mô tả bởi hệ bất phương trình: ⎧ϕ ϕ ϕ ≤ ≤ 1 2
D : ⎨⎩r1( )ϕ ≤ r ≤ r2 ( )ϕ
Khi ó công thức (2.15) sẽ có dạng: ϕ2 r2(ϕ) ϕ
∫∫ f x y dxdy( , )= ∫d ∫ f r( cos , sinϕ ϕr )rdr (2.15) D ϕ1 r1(ϕ) Chú ý: *
Mối quan hệ giữa các ịnh thức Jacôbi của phép biến ổi thoả mãn D(x,y) D(u,v) . =1 D(u,v) D(x,y) *
Nếu cực là iểm trong của miền D và mọi bán kính cực cắt biên miền D tại một iểm
có bán kính r( )ϕ thì 2π r(ϕ) ϕ
∫∫ f x y dxdy( , )= ∫d ∫ f r( cos , sinϕ ϕr )rdr 51
Downloaded by Ti?n D?ng Tr?n Lý (dungtienltr128@gmail.com) lOMoARcPSD| 10435767
Chương 2. Tích phân bội D 0 0
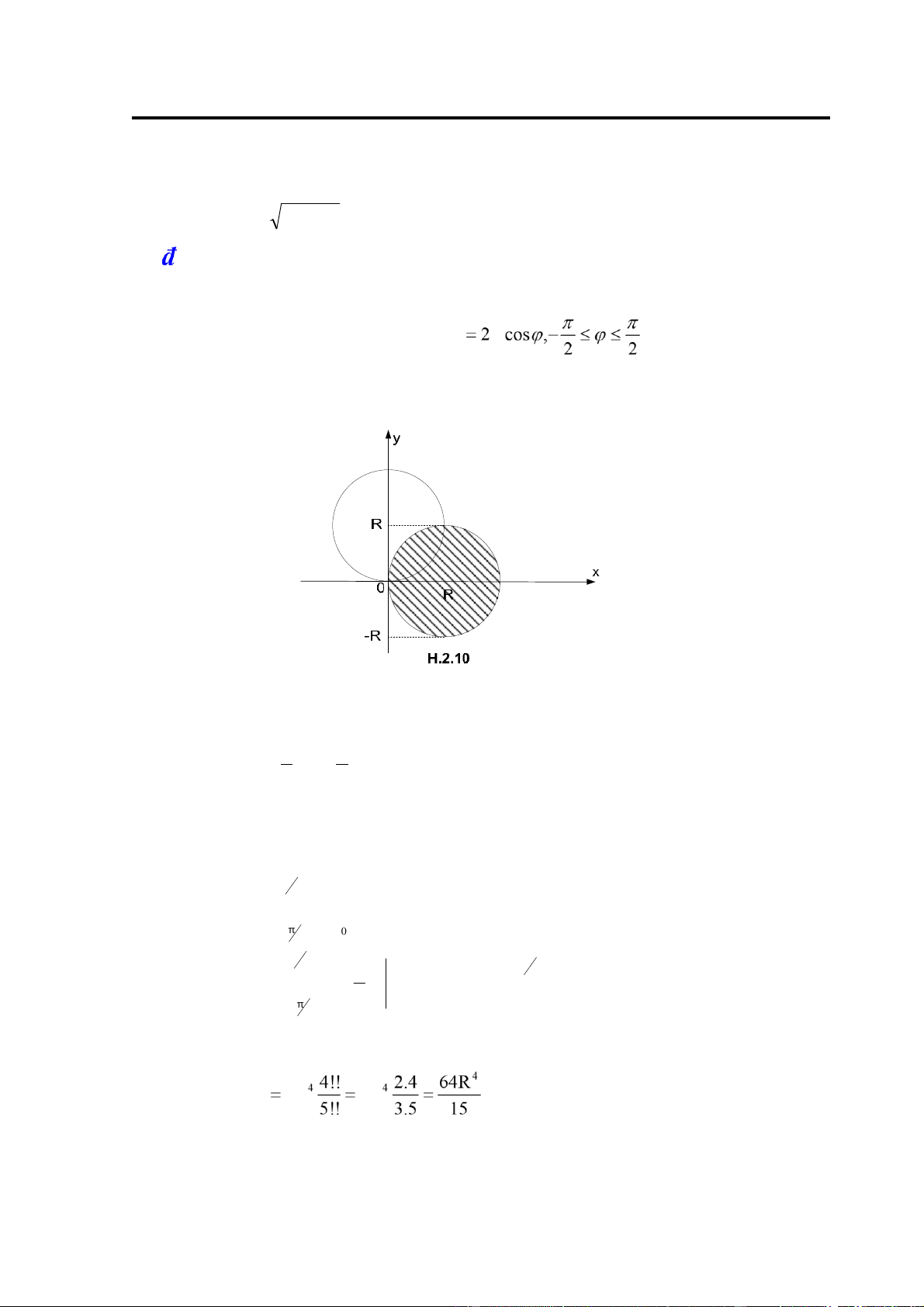
Ví dụ 5: Tính ∫∫ x x2 + y dxdy2 = I trong ó D là hình tròn (x − R)2 + y 2 ≤ R2 D
Giải: Đường tròn (x− R)2 + y 2 = R2 chuyển sang toạ ộ cực có phương trình:
(rcosϕ− R)2 + r2 sin2ϕ= R2 hay r R
Tương tự ường tròn x2 +(y − R)2 = R2 chuyển sang toạ ộ cực có phương trình r = 2Rsinϕ,0 ≤ϕ≤π (H.2.10) r =2 Rs i ϕ n r = 2 R co s ϕ
Vậy miền D trong hệ toạ ộ cực ược mô tả: ⎧⎪−π≤ϕ≤ π ⎨ 2 2
⎪⎩0 ≤ r ≤ 2Rcosϕ
Theo công thức (2.15) sẽ có: π 2 2 Rcos ϕ I = dϕ r.cos .r.rdrϕ ∫ ∫ π 0 − 2 π π 2 1 4 2R cosϕ2 cos ϕ r ∫ 4 π − =dϕ = 2 8R ∫ ϕ ϕ 4 cos5 d 0 0 8R 8R .
(Xem công thức Wallis,Tr139 Toán cao cấp A1) 52
Downloaded by Ti?n D?ng Tr?n Lý (dungtienltr128@gmail.com) lOMoARcPSD| 10435767
Chương 2. Tích phân bội =
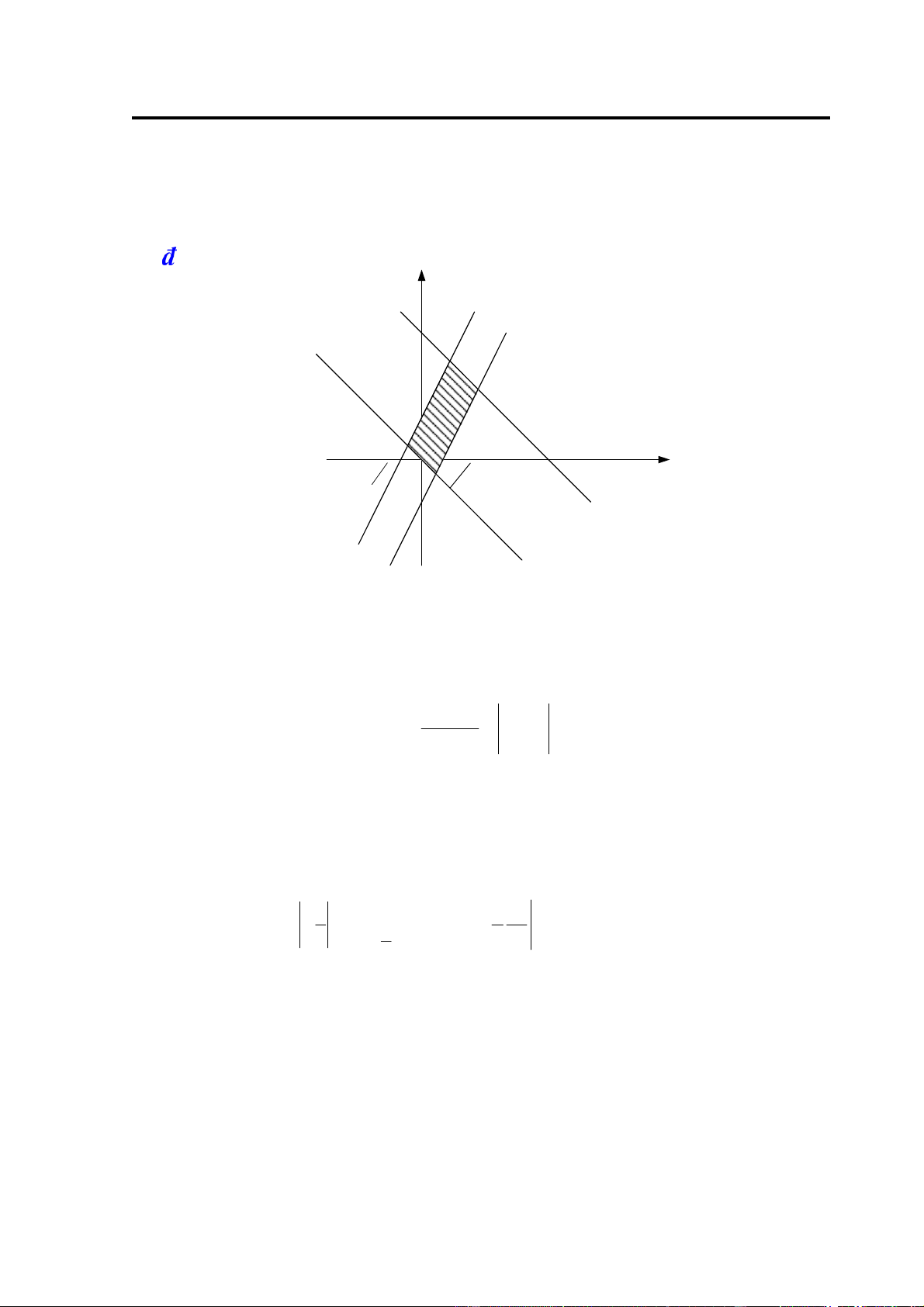
Ví dụ 6: Tính I ∫∫(x + y dxdy) trong ó D là miền giới hạn bởi các ường thẳng: D
y = −x,y = −x +3,y = 2x −1,y = 2x +1. y 3 1 1 − 2 0 1 3 x 2 - 1 H.2.11
Giải: Phương trình các ường thẳng tạo ra miền D viết lại dưới dạng:
x + y = 0, x + y = 3, 2x − y =1, 2x − y = −1 (xem H.2.11)
⎧u = x + y D u v( , ) 1 1 ⎨ =
Đổi biến ⎩v = 2x − y , khi ó D x y( , ) 2 −1= −3 ⎧0 ≤ u ≤ 3 Δ:⎨−1≤ v ≤1 ⎩ 1 1 3 1 2 u2 3
Suy ra I = ∫∫u. − dudv = ∫udu. dv∫= = 3. 3 3 3 2 0 Δ0 −1
Nhận xét: Nếu giải ví dụ trên bằng cách trực tiếp dùng công thức tính tích phân kép trong hệ
toạ ộ ề các thì phải chia miền D thành các miền thành phần rồi áp dụng tính chất a của tích phân
kép. Như vậy sẽ phức tạp hơn. Ta có thể kiểm tra lại kết quả bằng cách dùng công thức (2.10) hoặc (2.11).
2.3. Tích phân bội ba ( Tích phân 3 lớp)
2.3.1. Bài toán mở ầu: Tính khối lượng vật thể. 53
Downloaded by Ti?n D?ng Tr?n Lý (dungtienltr128@gmail.com) lOMoARcPSD| 10435767
Chương 2. Tích phân bội
Bài toán: Cho vật thể V không ồng chất, biết khối lượng riêng là
ρ= ρ(x y z, , ), ( , ,x y z)∈V
Hãy tính khối lượng của vật thể V.
Cách tính: Tương tự như tích phân bội hai, ta chia V tuỳ ý làm n phần không dẫm lên nhau
bởi một hệ thống các mặt cong. Gọi tên và thể tích các phần ó là ΔVi (i =1,n). Trong mỗi phần thứ
i lấy iểm P xi ( i , y zi , i ) tuỳ ý và gọi ường kính của phần ó là di ,(i =1,n) . Khối n n
lượng xấp xỉ của vật thể là : m = ∑ρ(P = ∑ρ i )ΔVi
(xi , yi , zi )ΔVi . i=1 i=1 n
Nếu tồn tại giới hạn
lim (xi , yi , zi )ΔVi thì ó chính là khối lượng của vật thể ã
cho. Trong thực tế nhiều bài toán dẫn ến việc tìm giới hạn hạn của tổng dạng trên. Chính vì thế cần
phải có ịnh nghĩa toán học tích phân bội ba.
2.3.2. Định nghĩa tích phân bội ba.
Cho hàm số f(x,y,z) xác ịnh trên miền V
* Chia V tuỳ ý thành n mảnh nhỏ. Gọi tên và thể tích các mảnh ó là ΔVi ,(i =1,n) , ký hiệu
ường kính mảnh ΔVi là di .
* Lấy tuỳ ý P x y zi ( i , i , i )∈ΔVi ,(i =1,n) n = * Lập tổng I ∑ n
f x( i , y zi , i )ΔVi , gọi ó là tổng tích phân bội ba của hàm f(x,y,z) lấy i=1
trên miền V ứng mới một phân hoạch và các iểm P ∈Δ i
Vi ,(i =1,n)
Khi n → ∞ sao cho maxd → i
0 mà In hội tụ về I không phụ thuộc vào phân hoạch ΔV1
và cách chọn iểm P ∈Δ i
Vi ,(i =1,n) thì số I gọi là tích phân bội ba của f(x,y,z) trên miền V, ký hiệu
là ∫∫∫ f x y z dV( , , ) . V n
Như vậy: ∫∫∫ f x y z dV( , , ) = lim ∑ → f x( i 0
i , y zi , i )ΔVi (2.16) 54
Downloaded by Ti?n D?ng Tr?n Lý (dungtienltr128@gmail.com) lOMoARcPSD| 10435767
Chương 2. Tích phân bội maxd V i=0
Tương tự, ta cũng nói rằng f(x,y,z) khả tích trên miền V. Chú ý:
* Giống như tích phân kép, yếu tố thể tích dV ược thay bằng dxdydz và khi ó thường ký hiệu
tích phân bội ba là: ∫∫∫f(x,y,z)dxdydz. V
* Tương tự như tích phân kép, tích phân bội ba không phụ thuộc vào ký hiệu biến lấy tích
phân:∫∫∫f(x,y,z)dxdydz = ∫∫∫f(u,v,ω)dudvd .ω V V
* Ý nghĩa cơ học: Nếu f x y z( , , ) ≥ 0trên miền V thì ∫∫∫ f x y z dxdydz( , , ) là khối lượng V
của vật thể V khi vật thể ó có khối lượng riêng (mật ộ hay tỉ khối) là f(x,y,z). =
* Rõ ràng thể tích V của vật thể V tính theo công thức: V
∫∫∫dxdydz (2.17) V
* Điều kiện khả tích và tính chất của tích phân bội ba tương tự như tích phân kép.
2.4. Tính tích phân bội ba
2.4.1. Công thức tính tích phân bội ba trong hệ toạ ộ ề các
Định lý 2.3: Nếu f(x,y,z) liên tục trong miền V cho bởi hệ bất phương trình:
⎧a ≤ x ≤ b ⎪
⎨y x( ) ≤ y ≤ y2 ( )x (2.18) 1
⎪⎩z x y1( , ) ≤ y ≤ z2 (x y, ) b y2( )x z2(x y, )
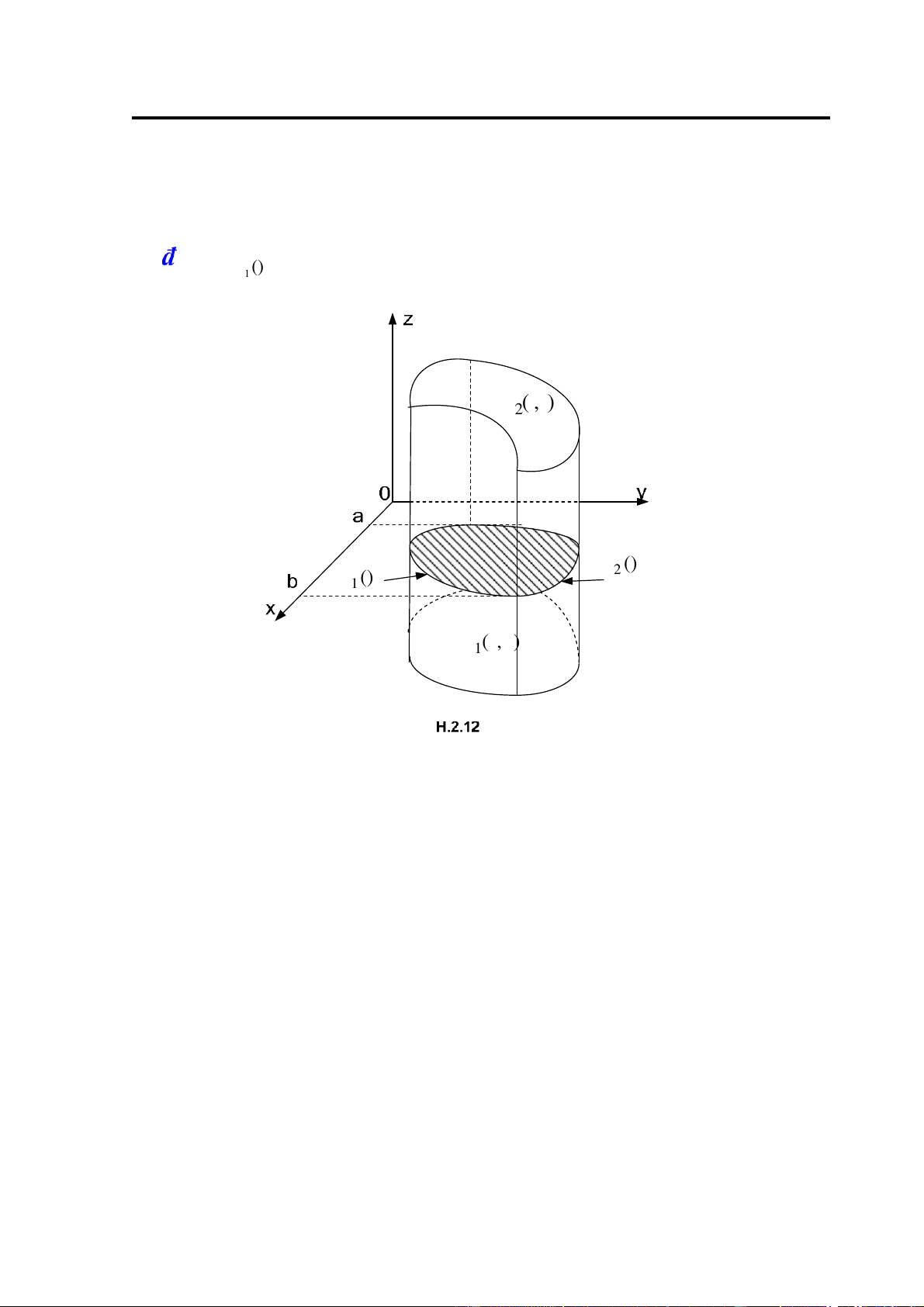
thì ∫∫∫ f x y z dxdydz( , , )= ∫dx ∫dy ∫ f x y z dz( , , ) (2.19) V a y1( )x z1(x y, )
Hệ bất phương trình (2.18) mô tả miền V là một hình trụ cong giới hạn phía
trên bởi mặt z = z (x,y),2 giới hạn phía dưới bởi mặt z = z1(x y, )và giới hạn xung
quanh bởi mặt trụ có ường sinh song song với trục 0z, ường chuẩn là biên của miền 55
Downloaded by Ti?n D?ng Tr?n Lý (dungtienltr128@gmail.com) lOMoARcPSD| 10435767
Chương 2. Tích phân bội
D (miền Dxy là hình chiếu của V trên mặt phẳng 0xy (H.2.12), cụ thể miền D cho bởi hệ bất phương trình:
⎧a ≤ x ≤ b ⎩ () 1 yx z ( , xy ) 2 () () 2 yx 1 yx ( , ) 1 zxy
Công th ứ c (2.19) ch ứ ng t ỏ ể tính tích phân b ộ i ba ta ư a v ề tính tích phân l ặ p. Khi tính tích ⎨
≤ y ≤ y2 ( )x
phân theo biến z ta coi x,y là hằng số. Khi tính tích phân theo biến y coi x là hằng số. Cuối cùng tính
tích phân theo biến x. Chú ý: a.
Từ công thức (2.10) suy ra công thức (2.119) có thể viết lại như sau: z2(x y, )
∫∫∫ f x y z dxdydz( , , )= ∫∫dzdy ∫ f x y z dz( , , ) (2.19)’ V Dxy z1(x y, ) b.
Thay ổi vai trò của các biến x,y,z ta cũng có công thức thay ổi thứ tự lấy tích phân bội ba: z2(x y, ) x2( y z, )
∫∫dxdy ∫ f x y z dz( , , )= ∫∫dydz ∫ f x y z dx( , , ) (2.19)” Dxy z1(x y, ) Dyz x1( y z, ) 56
Downloaded by Ti?n D?ng Tr?n Lý (dungtienltr128@gmail.com) lOMoARcPSD| 10435767
Chương 2. Tích phân bội
trong ó Dyz là hình chiếu của miền V lên mặt phẳng 0yz, còn x = x1(y z, ) và x = x2 (y z, ) là các mặt
cong dưới và trên theo hướng 0y ể tạo ra miền V. z2(x y, ) y2(x z, )
Tương tự: ∫∫dxdy ∫ f x y z dz( , , )= ∫∫dzdx ∫ f x y z dy( , , ) (2.19)’’’ Dxy z1(x y, ) Dzx y1(x z, )
Ví dụ 7: Tính I = ∫∫∫
(1+dxdydzx + y + z)3 trong ó miền V ược cho giới hạn bởi các mặt V
phẳng x = 0, y = 0, z = 0, x + y = 1, x + y – z = 0.
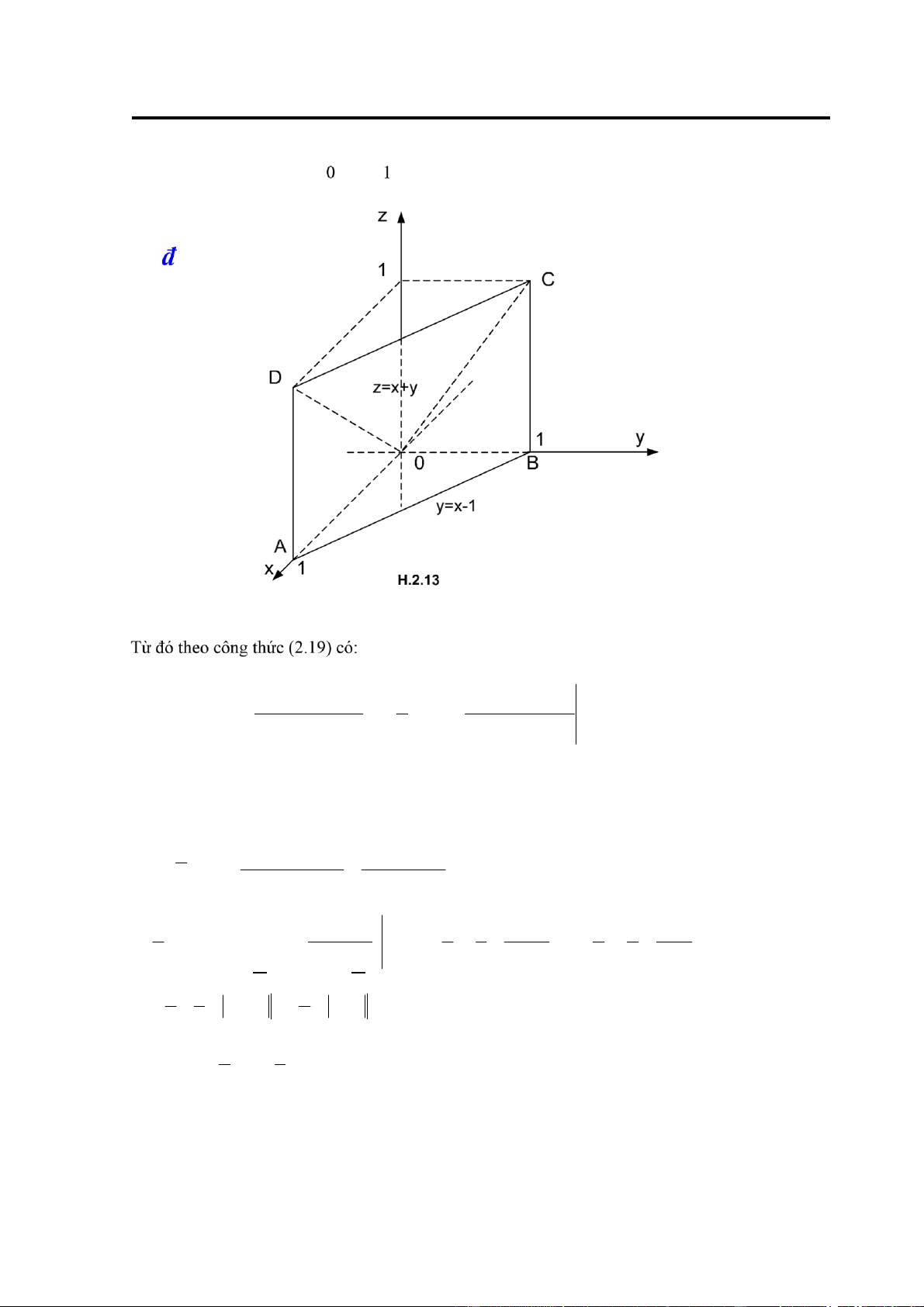
Giải: Vẽ miền V (H.2.13). V là hình chóp tứ giác có ỉnh là gốc toạ ộ, áy là hình chữ nhật
ABCD. Mặt trên của V (tam giác OCD) là mặt phẳng có phương trình z = x + y. Mặt dưới của V
(tam giác OAB ) là mặt phẳng có phương trình z = 0.
Chiếu V lên mặt phẳng Oxy ược tam giác OAB cho bởi hệ bất phương trình: ⎧0 ≤ x ≤1
⎨ ≤ y ≤1− x 57
Downloaded by Ti?n D?ng Tr?n Lý (dungtienltr128@gmail.com) lOMoARcPSD| 10435767
Chương 2. Tích phân bội ⎩ x y+ 1 1−x x y+ 1 1−x
I = ∫ dx ∫ dy ∫ dz = − 1 ∫ dx ∫ dy ( ( 0 0
0 1+ x + y + z)3 2 0
0 1+ x + y + z)2 0 1 1 1−x ⎡ 1 1 ⎤ = − 2 ∫ ⎢⎣( − ( ⎥⎦ 0 dx ∫0 1+ 2x + 2y)2
1+ x + y)2 dy 1 1−x 1 1 = 12 ∫ ⎛⎜⎝⎜ ⎛ ⎛⎜ 0
2 1( + 21x + 2y) 1+ x1+ y ⎠⎞ 01 ∫0 1 −
1 ⎟⎞dx − 1 ∫0 1 − 1 ⎟⎞dx −
⎟⎟ dx = 4 ⎜⎝ 3 1+ 2x ⎠ 2 ⎝ 2 1+ x ⎠
= − 1 − 1ln1+ 2x 1 + 1 ln1+ x 1 6 8 0 2 0 58
Downloaded by Ti?n D?ng Tr?n Lý (dungtienltr128@gmail.com) lOMoARcPSD| 10435767
Chương 2. Tích phân bội ⎛ ⎞
= 12 ⎜⎝ln2− 14 ln3− 13 ⎟⎠. =
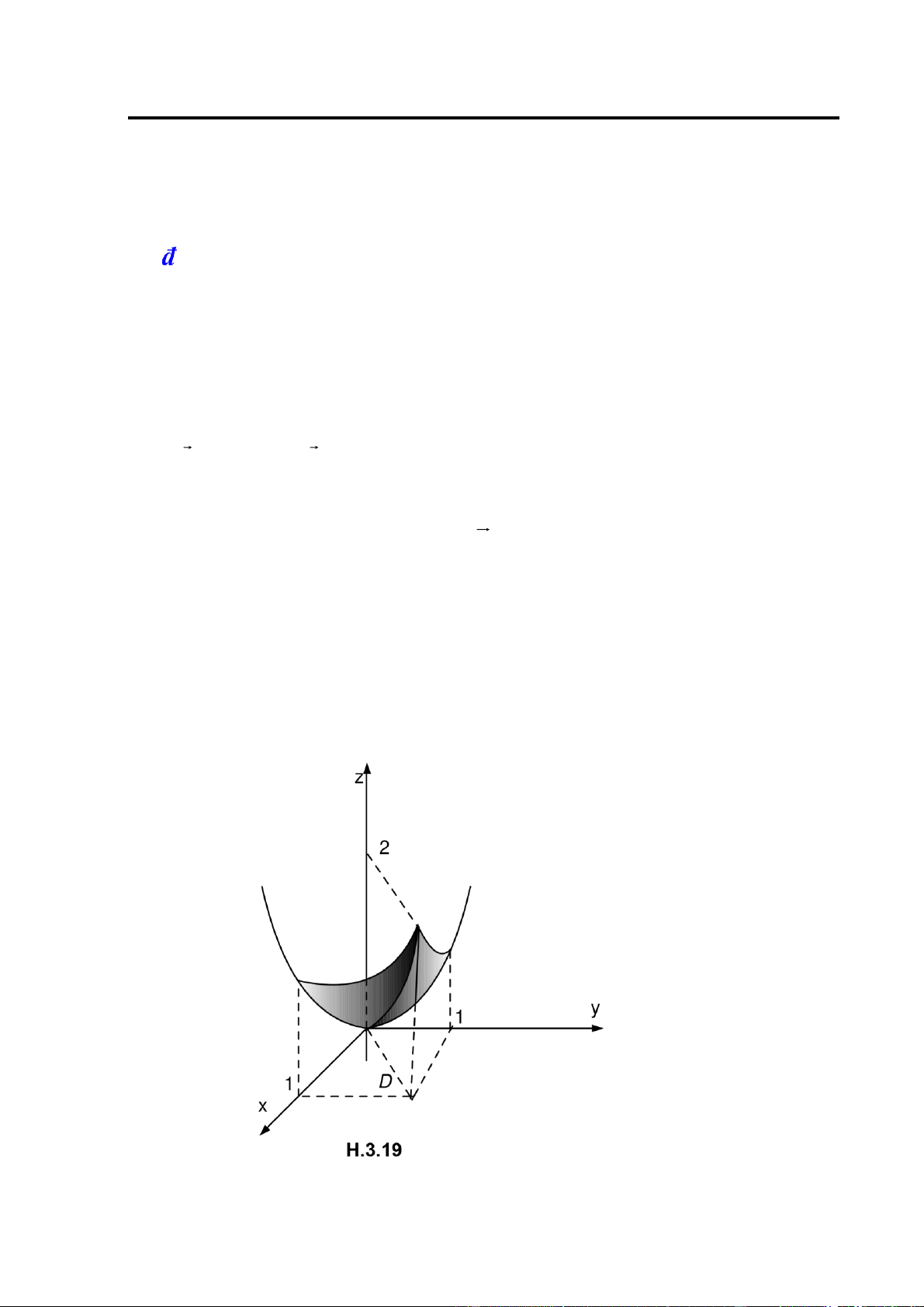
Ví dụ 8: Tính I ∫∫∫xdxdydz với V cho bởi hệ bất phương trình: V ⎧x ≥ 0 ⎪⎨y ≥ 0
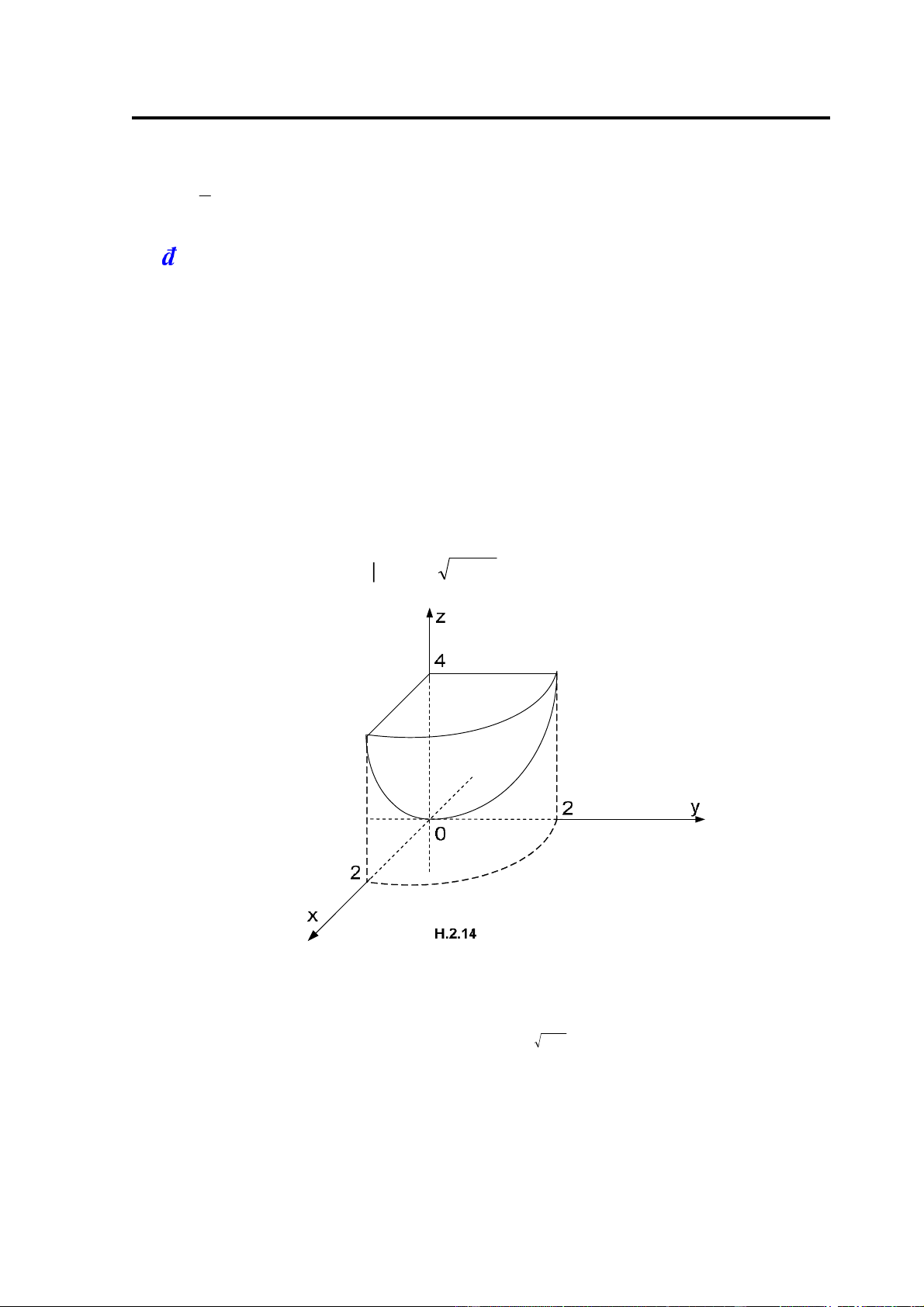
⎪⎩x2 + y 2 ≤ z ≤ 4
Giải: Miền V cho bởi H.2.14. Ta thấy mặt trên của V là z = 4 , mặt dưới là paraboloid tròn
xoay z = x2 + y 2 . Hình chiếu D của V lên mặt Oxy là phần tư hình tròn: ⎧⎪0 ≤ x ≤ 2 ⎨ ⎪ ⎩ ≤ y ≤ − 2 0 4 x Do ó: 2 4−x2 4 I = ∫
dxdy ∫ xdz = ∫
x(4 − x2 − y2 )dxdy =∫ dx ∫
x(4 − x2 − y2 )dy ∫D x2+y2 ∫D 0 0 22 2 59
Downloaded by Ti?n D?ng Tr?n Lý (dungtienltr128@gmail.com) lOMoARcPSD| 10435767
Chương 2. Tích phân bội
= ∫ x(4 − x2 ) 4 − x dx2− ∫ x y3 4−x dx 0 0 3 0 = − 1 ∫2 (4− x ) d(42 32 − x )2 = − 1 2 = 2 52 2 64. . (4− x ) 3 0 3 5 0 15
Tương tự như tích phân kép, ta cũng có công thức ổi biến số trong tích phân bội ba dưới ây.
Định lý 2.4: Cho hàm f x y z( , , ) liên tục trên miền V ⊂ Oxyz ồng thời tồn tại các hàm số: ⎧x =x(u,v,w) ⎪ ⎨y =y(u,v,w) ⎪ ⎩z = z(u,v,w) (u,v,w)∈Ω
thoả mãn các iều kiện: -
là song ánh từ V lên Ω -
có các ạo hàm riêng liên tục trong miền Ω⊂ 0uvw và ịnh thức Jacobi D x y z( , , )
≠ 0trong miền Ω (hoặc chỉ bằng 0 ở một số iểm cô lập). Khi ó: D u v w( , , )
∫∫∫f(x,y,z)dxdydz = ∫∫∫f x(u,v,w),y(u,v,w),z(u,v,w)[ ] D(x,y,z) dudvdw (2.20) D(u,v,w) V Ω
2.4.2. Công thức tính tích phân bội ba trong toạ ộ trụ
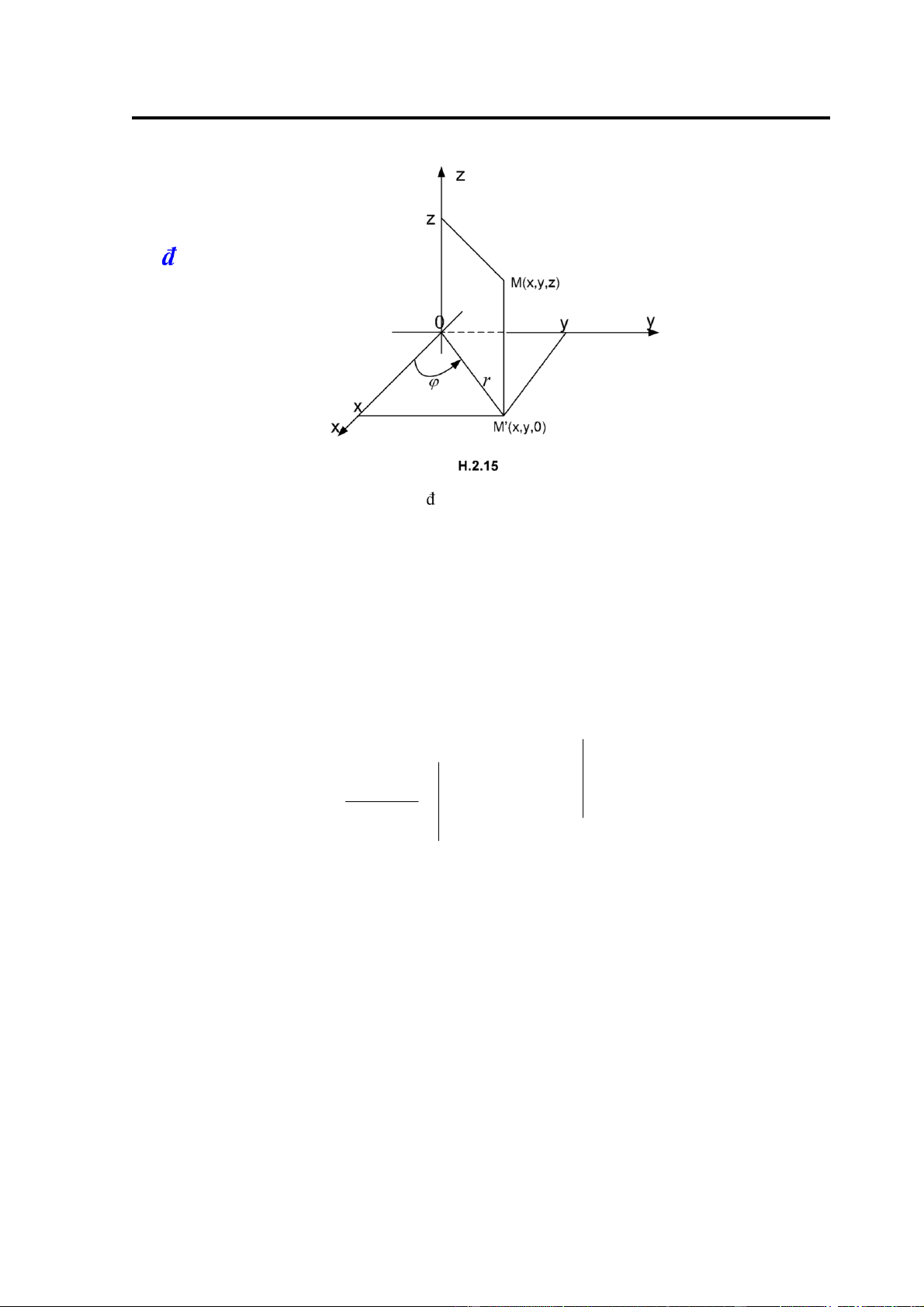
a. Toạ ộ trụ : Toạ ộ trụ của iểm M x y z( , , )∈0xyz là bộ ba số sắp thứ tự (r, ,ϕz)
trong ó (r,ϕ) là toạ ộ cực của iểm M’(x,y), hình chiếu của M lên mặt phẳng 0xy (H.2.15). Vậy với
mọi iểm của không gian, ta có: r ≥ 0,0 ≤ϕ< 2π,−∞ < z < +∞. 60
Downloaded by Ti?n D?ng Tr?n Lý (dungtienltr128@gmail.com) lOMoARcPSD| 10435767
Chương 2. Tích phân bội
Giữa toạ ộ ề các và to
ạ ộ trụ của iểm M có mối liên hệ:
⎧x = r cosϕ ⎪ = r sinϕ ⎨y ⎪⎩z = z cosϕ − rsinϕ 0 D x y z( , , ) Trong trường hợp này
= sinϕ rcosϕ 0= r (2.21) D r( , ,ϕz) 0 0 1
b. Phương trình mặt cong trong toạ ộ trụ
Hệ thức F(r,ϕ, )z = 0 hoặc giải ra ược ối với các biến số r = r(ϕ, ),z z = z r( ,ϕ) hoặc ϕ=ϕ(r
z, ) gọi là phương trình mặt cong trong toạ ộ trụ. Các trường hợp ặc biệt thường gặp sau ây:
r = r0 là phương trình mặt trụ tròn xoay bán kính là r0 và trục ối xứng là Oz (Trong hệ toạ
ộ Oxyz , mặt trụ này có phương trình x2 + y 2 = r2 ).
ϕ=ϕ0 là phương trình nửa mặt phẳng lập với mặt phẳng Ozx một góc là ϕ0 (tương ứng
trong Oxyz phương trình là y = tgϕ ≥
0.x với x.cosϕ0 0). 61
Downloaded by Ti?n D?ng Tr?n Lý (dungtienltr128@gmail.com) lOMoARcPSD| 10435767
Chương 2. Tích phân bội
z = z0 là phương trình mặt phẳng song song với mặt phẳng Oxy cắt trục Oz tại iểm có toạ ộ
z0 . Như vậy mặt cong ược mô tả trong hệ toạ ộ trụ ôi khi có phương trình rất ơn giản so với trong hệ toạ ộ Đề các.
c. Công thức tính tích phân bội ba trong toạ ộ trụ Từ công thức (2.20) và (2.21) ta nhận ược:
∫∫∫ f x y z dxdydz( , , )= ∫∫∫ f r( cos , sin ,ϕ ϕr z rdrd dz) ϕ (2.22) V Ω
Thông thường miền Ω trong toạ ộ trụ mô tả bởi hệ bất phương trình: ⎧ϕ ϕϕ ≤ ≤ 1 2
⎪ ϕ ≤ r ≤ r2( )ϕ ⎨r1( )
⎪⎩z r1( ,ϕ) ≤ z ≤ z2(r,ϕ) Khi ó (2.22) trở thành: ϕ2 r2(ϕ) z2(r,ϕ) ϕ
∫∫∫ f x y z dxdydz( , , )= ∫d ∫rdr ∫ f r( cos , sin ,ϕ ϕrz dz) (2.23) V ϕ1 r1(ϕ) z1(r,ϕ) =
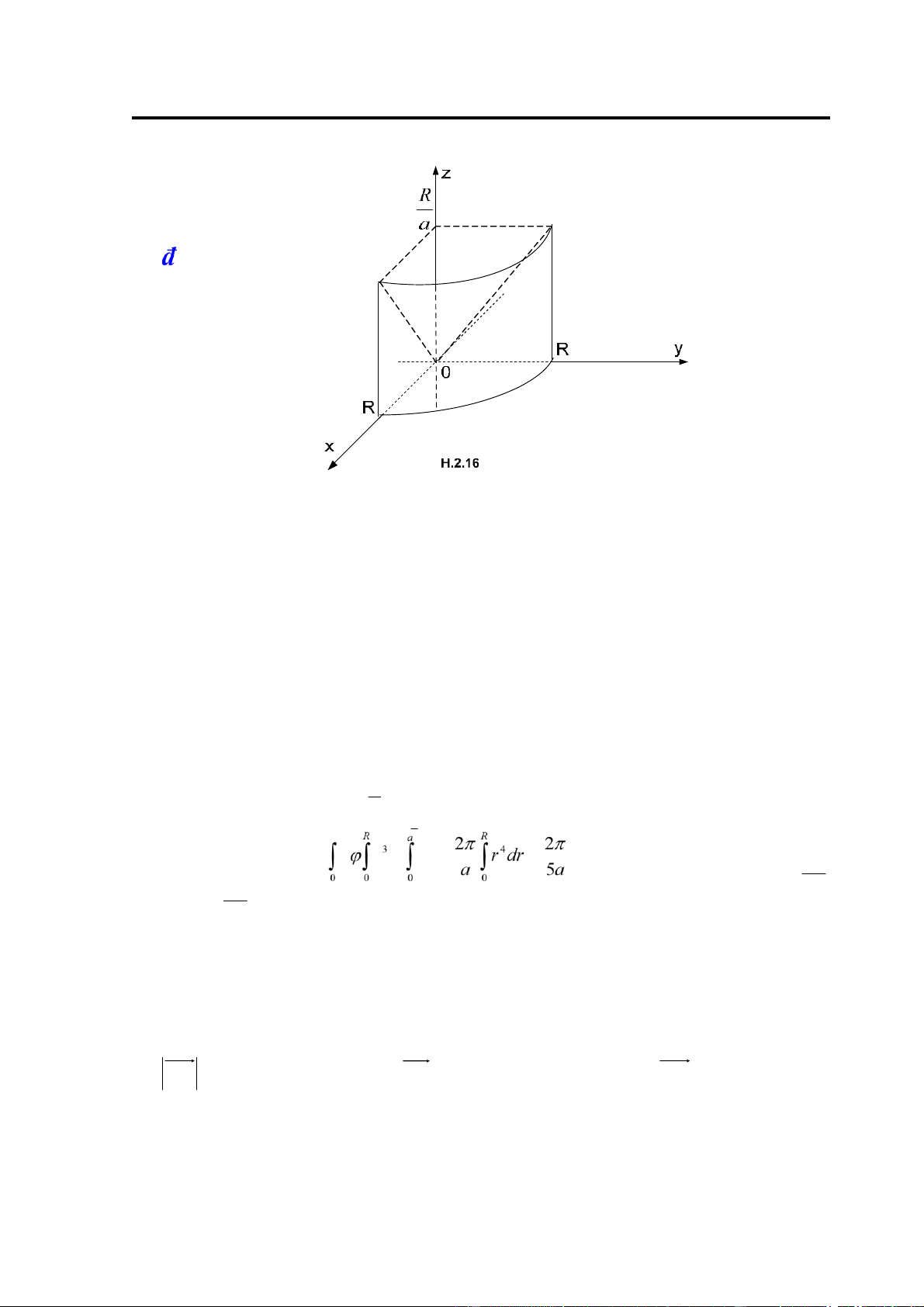
Ví dụ 9: Tính I ∫∫∫(x2 + y 2 )dxdydz trong
ó V giới hạn bởi các mặt V
z = 0,a z2 2 = x2 + y2, x2 + y2 = R2 ,z ≥ 0,a > 0. 62
Downloaded by Ti?n D?ng Tr?n Lý (dungtienltr128@gmail.com) lOMoARcPSD| 10435767
Chương 2. Tích phân bội
Giải: Miền V nằm trong góc phần tám thứ nhất ược cho trên hình H.2.16 ược giới hạn bởi
mặt 0xy, mặt nón, mặt trụ. Các mặt nón và mặt trụ có phương trình viết trong toạ ộ trụ là: az = r,r
= R (nhận ược bằng cách thay x = rcos ,ϕ y = rsinϕ vào phương trình các mặt cong ã cho).
Như vậy miền Ω cho bởi hệ bất phương trình: ⎧ ⎪0 ≤ϕ π≤ 2 ⎪
⎨0 ≤ r ≤ R ⎪ r ⎪0 ≤ z ≤ r ⎩ a 2π Suy ra I = d r dr dz = = R5
Chú ý: Khi miền V có dạng hình trụ và hàm dưới dấu tích phân chứa các biểu thức x2 + y 2
thì thường tính tích phân trong toạ ộ trụ sẽ ơn giản hơn trong toạ ộ ề các.
2.4.3. Công thức tính tích phân bội ba trong toạ ộ cầu a.
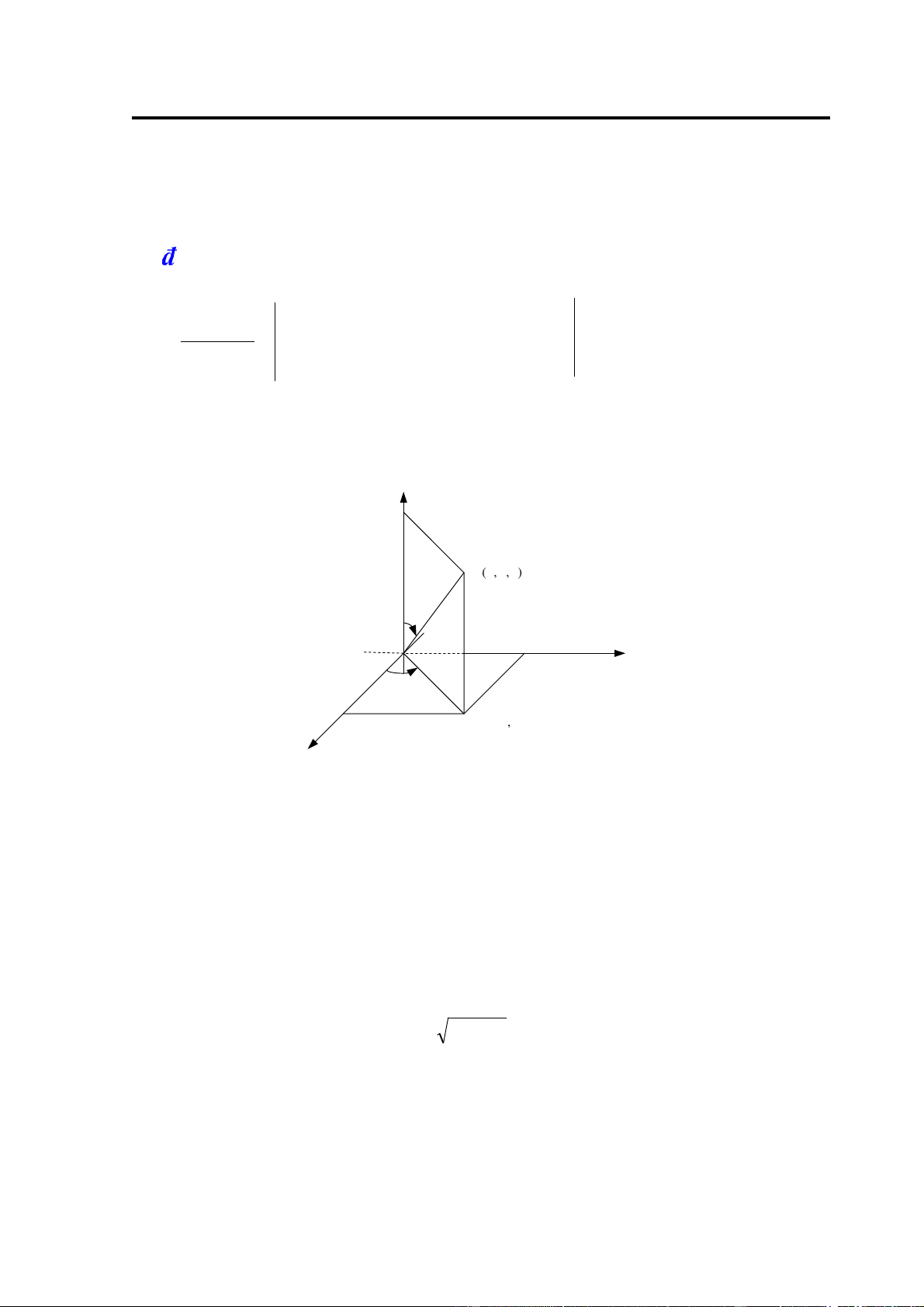
Toạ ộ cầu: Toạ ộ cầu của một iểm M x y z( , , )∈0xyz là bộ ba số (r, ,θϕ)
trong ó r = OM ,θ là góc giữa trục 0z và 0M và ϕlà góc giữa trục 0x và 0M' , ở ây M’ là
hình chiếu của M trên 0xy (H.2.17). Vậy với mọi iểm của không gian sẽ có: r ≥ 0,0 ≤ ≤θ
π,0 ≤ <ϕ 2π. Dễ thấy giữa các toạ ộ ề các và toạ ộ cầu có mối quan hệ: 63
Downloaded by Ti?n D?ng Tr?n Lý (dungtienltr128@gmail.com) lOMoARcPSD| 10435767
Chương 2. Tích phân bội
⎧x = r sinθ ϕcos ⎪
⎨y = r sinθ ϕsin
⎪⎩z = r cosθ sinθ ϕcos
r cosθ ϕcos − sinθ ϕsin D x y z( , , )2 sinθ (2.24) Và như vậy = sinθ ϕsin
r cosθ ϕ θ ϕcos rsin cos= −r D r( ,θϕ, ) θ cos −r θ sin 0 z z r (
Mx y ,z , ) θ y 0 y ϕ x M ' (, xy ,0) x H.2.17 b.
Phương trình mặt cong trong toạ ộ cầu
Hệ thức F r( , ,θϕ) = 0 hoặc giải ra ược ối với các biến số r = r(θ, );ϕθ=θ(ϕ, );r ϕ=ϕ(r,θ) gọi
là một phương trình mặt cong trong toạ ộ cầu. Các trường hợp ặc biệt thường gặp sau ây:
r = r0 mô tả mặt cầu tâm gốc toạ ộ 0 và bán kính r0 ( trong hệ toạ ộ 0xyz, mặt cầu này có
phương trình x2 + y 2 + z2 = r 2 0 ).
θ=θ0 là phương trình của mặt nón tròn xoay, ỉnh 0 và trục ối xứng là 0z có góc mở là 2θ (mặt
nón này trong hệ 0xyz có phương trình x2 + y 2 = tgθ.z). ϕ=ϕ0 là phương trình nửa mặt phẳng lập
với mặt phẳng 0xy một góc ϕ0 (nửa mặt phẳng
này trong hệ toạ ộ 0xyz có phương trình y = tgϕ ≥
0.x với xcosϕ0 0 ).
c. Công thức tính tích phân bội ba trong toạ ộ cầu Từ
công thức (2.20) và (2.24) ta nhận ược: 64
Downloaded by Ti?n D?ng Tr?n Lý (dungtienltr128@gmail.com) lOMoARcPSD| 10435767
Chương 2. Tích phân bội
∫∫∫ f x y z dxdydz( , , ) = ∫∫∫ f r( sinθ ϕ θ ϕ θ θ θϕcos , sinr sin , cos )r r2 sin drd d (2.25) V Ω
Ta hay gặp miền Ω trong toạ ộ cầu mô tả bởi hệ bất phương trình: ⎧ϕ ϕ ϕ ≤ ≤ ⎪⎨θϕ θ θϕ 1 2 1( ) ≤ ≤ 2 ( ) ⎪
⎩r1(θϕ,) < r ≤ r2 (θϕ, )
Khi ó công thức (2.25) trở thành: ϕ θ ϕ θϕ 2 2( ) r ( , )2
∫∫∫ f (x, y,z)dxdydz = ∫ dϕ ∫ sin θ θd ∫ f (r sin θcosϕ,r sin θsin ϕ,r cosθ)r dr2 (2.26) V ϕ θ ϕ 1 1( ) r ( , )θϕ =
Ví dụ 10: Tính I ∫∫∫ 1
dxdydz , trong ó V là miền giới hạn bởi hai mặt + + V x2 y 2 z2
cầu x2 + y 2 + z2 =1 và x2 + y 2 + z2 = 4
Giải: Chuyển sang toạ ộ cầu, hai mặt cầu ã cho có phương trình lần lượt là r =1,r = 2 . Gốc
toạ ộ là iểm trong của miền V nên miền Ω cho bởi hệ bất phương trình: ⎧0 ≤ϕ π≤ 2 ⎪ ⎨0 ≤θ π≤ ⎪⎩1 ≤ r ≤ 2 Do ó : 1 I = ∫ 2 π dϕ∫π sin θ θd ∫2 .r dr2 = 2π −( cosθ) π 1 r2 2 = π6 . r 0 2 1 0 0 1 =
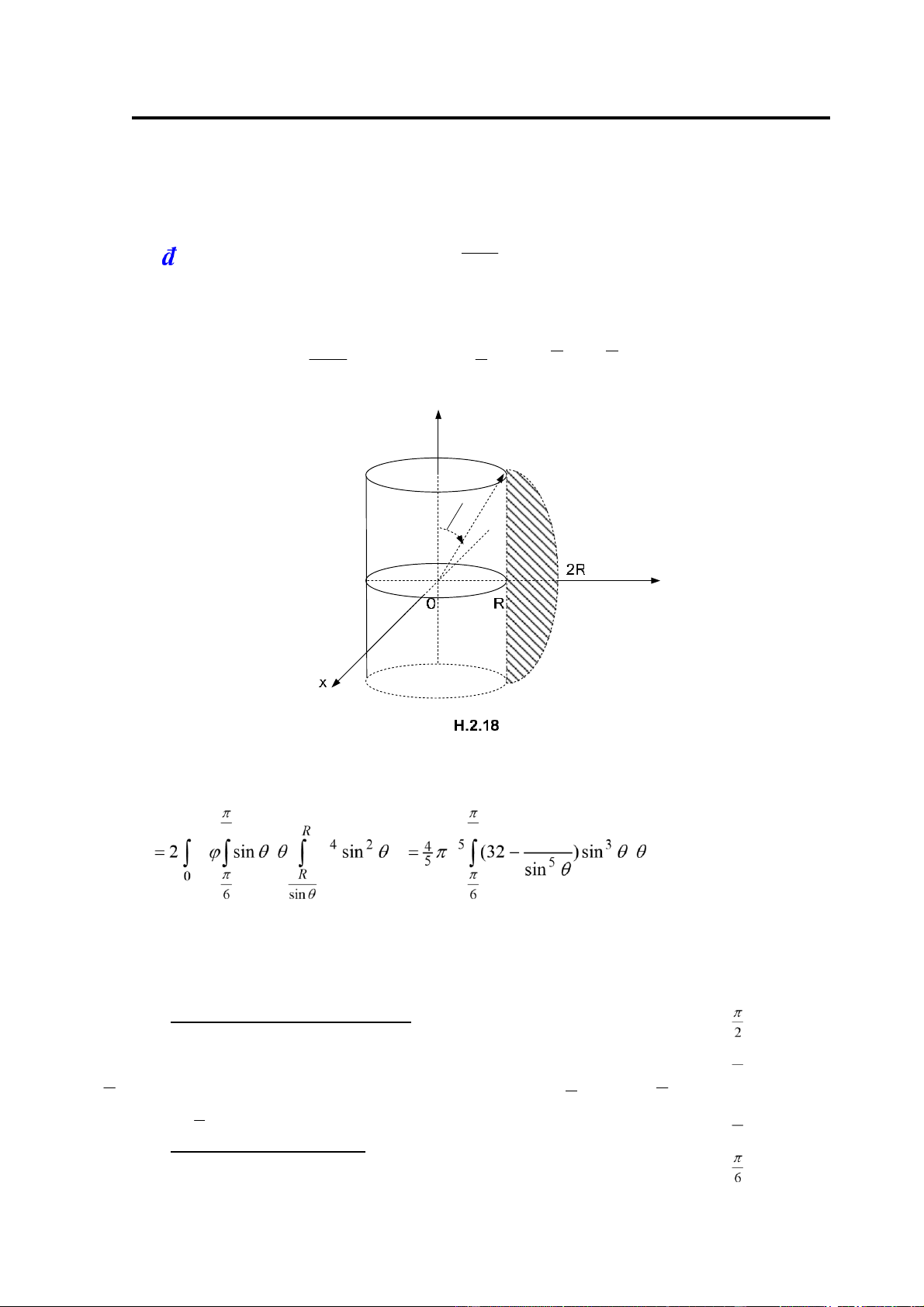
Ví dụ 11: Tính I ∫∫∫(x2 + y 2 )dxdydz trong
ó V là miền ngoài giữa hình trụ V 65
Downloaded by Ti?n D?ng Tr?n Lý (dungtienltr128@gmail.com) lOMoARcPSD| 10435767
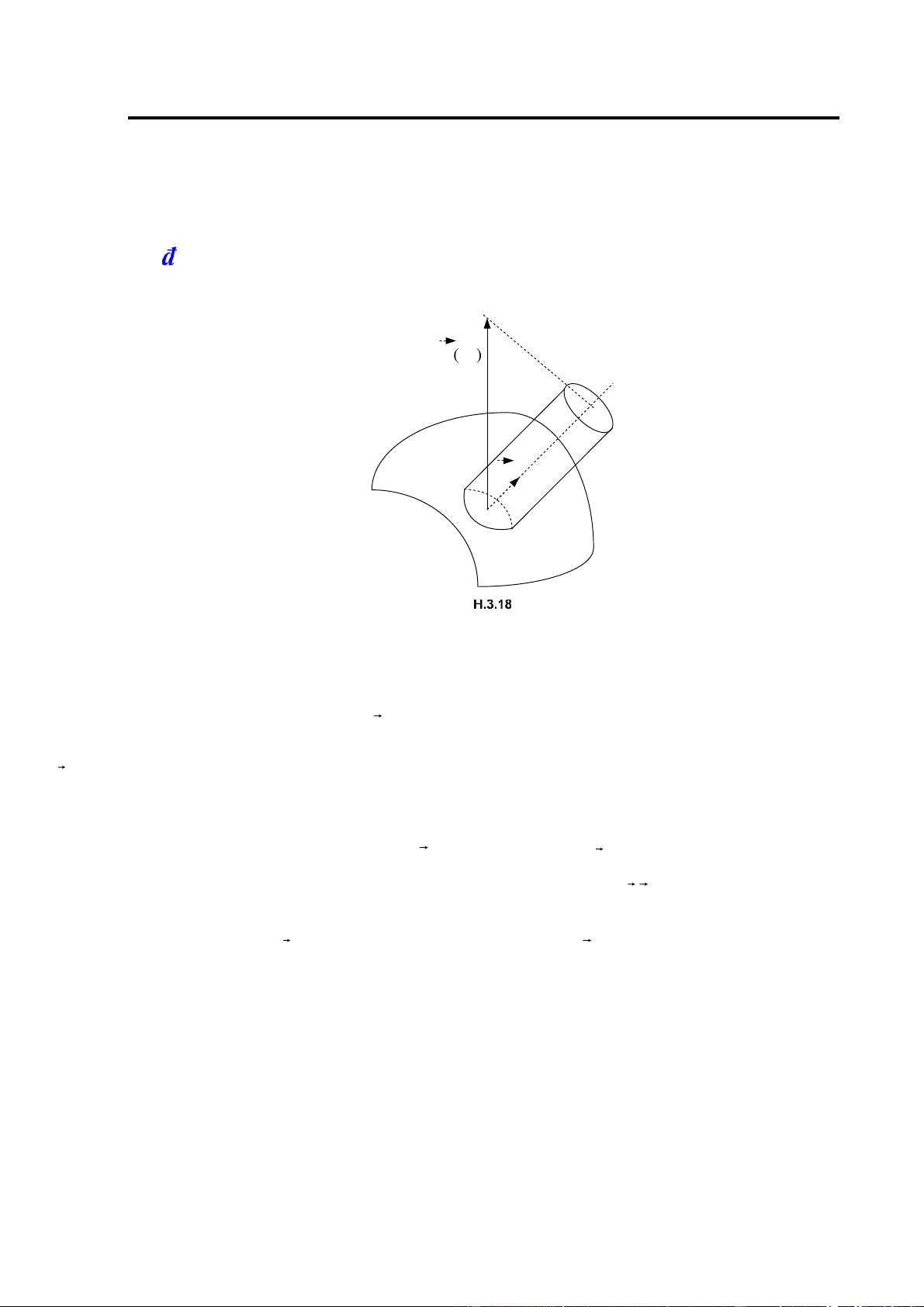
Chương 2. Tích phân bội
x2 + y2 ≤ R2 và hình cầu x2 + y2 + z2 ≤ 4R .2
Giải: Một thiết diện của miền V cho trên hình H.2.18. Xét trong hệ toạ ộ cầu, mặt cầu có
phương trình r = 2R , mặt trụ có phương trình r =
R (thay x = rsinθcos ,ϕ y = rsinθsinϕ sinθ
vào phương trình x2 + y2 = R2 sẽ nhận ược kết quả trên). Để tìm sự biến thiên của θ ta xét giao của π
mặt cầu và mặt trụ: r = 2R =
R . Suy ra sinθ= 1 ,⇒θ= ,θ= 5π sinθ 2 6 6 π 6
Vì V là vật thể tròn xoay nhận Oz làm trục ối xứng, nhận mặt phẳng Oxy làm mặt phẳng ối
xứng và hàm dưới dấu tích phân chẵn ối với x, y cho nên 2π 2 2 2 1 I d d r dr R d ⎡ π π ⎤
= 54πR5 ⎢⎢32∫2 sinθ(1− cos2θθ)d − ∫2 dθ2 ⎥⎥ = 54πR5
⎡⎢⎣32(−cosθ+ 13 cos3θ) + cot gθ⎤⎦⎥ ⎢ π πsin θ⎥ ⎢⎣ 6 6 ⎥⎦ 66
Downloaded by Ti?n D?ng Tr?n Lý (dungtienltr128@gmail.com) lOMoARcPSD| 10435767
Chương 2. Tích phân bội
Chú ý: Khi miền V có dạng hình cầu, hàm dưới dấu tích phân chứa các biểu thức dạng x2
+y2 hoặc x2 + y2 + z2 nên chuyển sang toạ ộ cầu, hoặc toạ ộ trụ ể tính toán cho ơn giản hơn.Ta có
thể kiểm tra lại kết quả của ví dụ trên bằng cách dùng toạ ộ trụ.
TÓM TẮT CHƯƠNG 2.
• Tính tích phân kép trong toạ ộ ề các Nếu
hàm số f(x,y) liên tục trên miền D cho bởi hệ bất phương trình
⎧a ≤ x ≤ b b ϕ2( )x
⎨ϕ1(x) ≤ y ≤ϕ2 (x) thì ∫∫D f x y dxdy( , ) = ∫a dxϕ ∫ 1 ( )xf x y dy( , ) ⎩
• Tính tích phân kép trong toạ ộ cực
Nếu hàm số f(x,y) liên tục trên miền Δ cho bởi hệ bất phương trình ⎧ϕ ϕϕ ≤ ≤ ∫∫ = ∫ 1 2
ϕ∫2dϕr2 (ϕ)f r( cos , sinϕ ϕr )rdr
⎨r (ϕ) ≤ r ≤ r ⎩
2 (ϕ) thì D f x y dxdy( , ) ϕ1 r1(ϕ) 1
• Thay ổi thứ tự lấy tích phân (công thức Fubini ) b ϕ2( )x d ψ2( y)
∫dx ∫ f x y dy( , )= ∫dy ∫ f x y dx( , ) a ϕ1( )x c ψ1( y)
• Tính tích phân bội ba trong toạ ộ ề các
Nếu f(x,y,z) liên tục trong miền V cho bởi hệ bất phương trình:
⎧a ≤ x ≤ b ⎪ ⎪ ⎨y x ⎩
1( ) ≤ y ≤ y2 (x)
z x y1( , ) ≤ y ≤ z2 (x y, ) b y2( )x z2(x y, )
thì ∫∫∫ f x y z dxdydz( , , )= ∫dx ∫dy ∫ f x y z dz( , , ) V a y1( )x z1(x y, )
• Tính tích phân bội ba trong toạ ộ trụ 67
Downloaded by Ti?n D?ng Tr?n Lý (dungtienltr128@gmail.com) lOMoARcPSD| 10435767
Chương 2. Tích phân bội
Nếu f(x,y,z) liên tục trong miền Ω mô tả bởi hệ bất phương trình: ⎧ϕ ϕϕ ≤ ≤ 1 2 ⎪
⎨r (ϕ) ≤ r ≤ r2 (ϕ) 1
⎪⎩z r1( ,ϕ) ≤ z ≤ z2 (r,ϕ) ϕ2 r2(ϕ) z2(r,ϕ) ϕ thì
∫∫∫ f x y z dxdydz( , , )= ∫d ∫rdr ∫ f r( cos , sin ,ϕ ϕrz dz) V ϕ1 r1(ϕ) z1(r,ϕ)
CÂU HỎI VÀ BÀI TẬP CHƯƠNG 2.
2.1. Dùng tích phân bội hai có thể xác ịnh ược diện tích hình phẳng D Đúng Sai
2.2. Khi hàm dưới dấu tích phân bội hai có dạng biến số phân ly thì tích phân bội hai sẽ là
tích của hai tích phân xác ịnh. Đúng Sai
2.3. Khi gốc toạ ộ là iểm trên biên của miền D thì chuyển sang toạ ộ cực ta có ϕ biến thiên từ 0 ến 2π. Đúng Sai
2.4. Khi gốc toạ ộ là iểm trong của miền D thì chuyển sang toạ ộ cực ta có ϕ biến thiên từ 0 ến 2π. Đúng Sai
2.5. Có thể tính khối lượng vật thể khi biết hàm mật ộ ρ nhờ vào tích phân bội 3. Đúng Sai
2.6. Có thể tính thể tích vật thể nhờ tích phân bội 3 Đúng Sai
2.7. Có thể biểu diễn tích phân bội 3 qua tích phân lặp gồm tích phân xác ịnh tích phân bội 2. Đúng Sai
2.8. Hình chiếu miền V lên mặt phẳng Oxy nhận gốc toạ ộ là iểm trong thì chuyển sang toạ ộ
trụ hoặc toạ ộ cầu sẽ có 0 ≤ϕ≤ 2π Đúng Sai
2.9. Hình chiếu miền V lên trục Oz nhận gốc toạ ộ là iểm trong thì chuyển sang toạ ộ cầu sẽ có 0 ≤ ≤θ 2π. 68
Downloaded by Ti?n D?ng Tr?n Lý (dungtienltr128@gmail.com) lOMoARcPSD| 10435767
Chương 2. Tích phân bội Đúng Sai
2.10. Đổi thứ tự tích phân các tích phân sau: 2 4
a. ∫ dx∫ f x y dy( , ) , −2 x2 3 2y
b. ∫dy∫ f x y dx( , ) , c. dx f x y dy( , ) , 2 2x x− 2
d. ∫dx ∫ f x y dy( , ) . 1 2−x
2.11. Tính các tích phân bội hai sau: ∫∫ dxdy
{(x y, ): x ≥1, y ≥1,x + y ≤ 3 .} a. (x+y)3 , D = D b.
∫∫ x + y dxdy , D ={(x y,
) : x ≤ 1, y ≤1 .} D c.
∫∫ln(x + y dxdy) ,
D là miền giới hạn bởi các ường x =1, y =1, y = +1 x. D d.
∫∫ x2 (y − x dxdy)
, D là miền giới hạn bởi các ường y = x2, x = y2. D
2.12. Tính các tích phân bội hai sau:
a. ∫∫ x2 + y dxdy2 D 69
Downloaded by Ti?n D?ng Tr?n Lý (dungtienltr128@gmail.com) lOMoARcPSD| 10435767
Chương 2. Tích phân bội
D là miền giới hạn bởi các ường tròn x2 + y2 = a2, x2 + y2 = 4a2, a > 0
b. ∫∫(x2 + y2 +1)dxdy , D là miền giới hạn bởi ường x2 + y2 − x = 0 D
c. ∫∫(x + 2y +1)dxdy , D là giao của hai hình tròn x2 + y2 ≤ 2y x, 2 + y2 ≤ 2x D
d. ∫∫ 4− x2 − y dxdy D2 ,
={(x y, ): y ≥ 0, x2 + y2 ≤ 2x}. D
2.13. Tính diện tích hình phẳng giới hạn bởi các ường:
a. x = 4y − y2, x + y = 6
b. y2 = x3, y2 = 8(6− x)3
c. y = 2x, y = − x , y = 4 2 d. y2 = x y, 2 = 5 x x, 2 = 1 y x, 2 = 2 .y 2 3
2.14. Tính thể tích vật thể giới hạn bởi các mặt:
a. z = x2 + y2, z = x + y
b. x2 + y2 + z2 = 2z x, 2 + y2 = z2.
2.15. Tính các tích phân bội ba sau: ⎫
a. ∫∫∫ zdxdydz V, = ⎧⎨(x y z, , ):0 ≤ x ≤ 1 , x ≤ y ≤ 2x, 0 ≤ z ≤
1− x2 − y2 ⎬ ⎩ V 4⎭
b. ∫∫∫(1− x − y − z dxdydz V) ,
={(x y z, , ): x ≥ 0, y ≥ 0, z ≥ 0, x + y + z ≤1} V ={
c. ∫∫∫ xyz dxdydz V, (x y z, , ):0 ≤ z ≤ a x, 2 + y2 ≤ 2z} V ⎧ + ⎫ 2 2 2 x2 y2 z2 70
Downloaded by Ti?n D?ng Tr?n Lý (dungtienltr128@gmail.com) lOMoARcPSD| 10435767
Chương 2. Tích phân bội
d. ∫∫∫(x + y + z )dxdydz V, = ⎨(x y z, , ): + ≤ 2 2 1, a > 0 .⎬ ⎩ V a 3a ⎭ 71
Downloaded by Ti?n D?ng Tr?n Lý (dungtienltr128@gmail.com) lOMoARcPSD| 10435767
Chương 3: Tích phân ường và tích phân mặt
CHƯƠNG 3. TÍCH PHÂN ĐƯỜNG VÀ TÍCH PHÂN MẶT GIỚI THIỆU
Tích phân ường và tích phân mặt là sự mở rộng của tích phân nhiều lớp trên hai phương diện:
lấy tích phân trên các cung cong thay cho trên oạn thẳng, tích phân trên mặt cong thay cho miền
phẳng, ặc biệt ể ý ến việc ịnh hướng của ường cong và mặt cong. Chính vì thế ý nghĩa thực tiễn của
tích phân ường, tích phân mặt là rất lớn. Hầu hết các bài toán kỹ thuật liên quan ến trường véctơ ều
liên quan ến tích phân ường, tích phân mặt: tính công của lực, tính thông lượng của trường. Tính
tích phân ường dẫn ến tính tích phân xác ịnh, tính tích phân mặt dẫn ến tính tích phân bội hai, vậy
một lần nữa yêu cầu người học phải có kĩ năng tính tích phân xác ịnh.
Trong chương này yêu cầu nắm vững các nội dung chính sau ây:
1. Tích phân ường loại 1
Trước hết nhớ lại công thức vi phân cung (xem công thức 4.26, mục 4.4.2,TOÁN CAO CẤP A1
) và ể ý rằng cận trên luôn luôn lớn hơn cận dưới.
2. Tích phân ường loại 2
Khi tính phải lưu ý ến hướng của ường cong tùy theo hướng ã ịnh mà tìm cận trên, cận dưới của
tích phân xác ịnh. Trường hợp ường cong kín nên vận dụng công thức Green nếu các
iều kiện của ịnh lí ược thỏa mãn, tổng quát hơn phải sử dụng công thức Xtốc.
3. Tích phân mặt loại 1
Chú ý ến công thức tính yếu tố diện tích của mặt cong cho bởi phương trình dạng tường minh
(chẳng hạn z = z (x,y)) ể từ ó ưa về tính tích phân bội hai trên hình chiếu của mặt cong lên mặt
phẳng tọa ộ tương ứng (mặt phẳng tọa ộ Oxy).
4. Tích phân mặt loại 2
Để tính tích phân mặt loại hai, trước hết phải xác ịnh các phía của mặt cong ã ịnh hướng thông
qua các côsin chỉ phương của véctơ pháp tuyến. Tiếp theo, tìm hình chiếu của mặt cong lên các mặt
phẳng tọa ộ. Khi mặt cong kín thường sử dụng công thức Ôxtrôgratxki. NỘI DUNG.
3.1. Tích phân ường loại một. 3.1.1. Định nghĩa 72
Downloaded by Ti?n D?ng Tr?n Lý (dungtienltr128@gmail.com) lOMoARcPSD| 10435767
Chương 3: Tích phân ường và tích phân mặt
* Chia cung AB là n cung nhỏ bởi các iểm chia A ≡ ≡ 0
A A, 1,..., Ai−1, Ai ,...An B gọi ộ A A
dài cung i−1 i là Δsi ,(i =1,n)
* Lấy tuỳ ý Mi(xi, yi)∈ Ai−1Ai,(i =1,n) n = * Lập tổng I ∑ n
f x( i , yi )Δsi gọi là tổng tích phân ường loại một của hàm f x y( , ) lấy i=1
trên cung AB ứng với một phân hoạch và một cách chọn tuỳ ý các iểm M ∈ i
Ai−1Ai,(i =1,n) . Nếu
khi n → ∞ sao cho maxΔs → i
0,In hội tụ về số I không phụ thuộc cách chia cung AB và cách chọn M ∈ i
Ai−1Ai,(i =1,n) thì số I gọi là tích phân ường loại một của f(x,y) dọc theo cung
AB và ký hiệu ∫ f (x y ds, ) AB n
Vậy I = lim ∑ f x( = ∫
i, yi)Δsi f x y ds( , )
(3.1) maxΔ →si 0 i=1 AB
Nếu có tích phân (3.1) thì nói rằng f(x,y) khả tích trên AB .Trong tích phân (3.1), ds ký hiệu ộ dài
yếu tố của cung AB hay vi phân của cung AB . 73
Downloaded by Ti?n D?ng Tr?n Lý (dungtienltr128@gmail.com) lOMoARcPSD| 10435767
Chương 3: Tích phân ường và tích phân mặt
Mở rộng: Nếu f(x,y,z) khả tích trên cung AB
thì tích phân ường loại một của f(x,y,z) trên cung AB ký hiệu là = I ∫ f x y z ds( , , ) (3.2) AB Chú ý:
a. Từ ịnh nghĩa trên ta thấy chiều i của cung AB không óng vai trò gì cả vì In không =
phụ thuộc vào hướng của cung AB . Vậy ∫ f (x y ds, ) ∫ f x y ds( , ) (3.3) AB BA =
b. Rõ ràng nếu gọi l là ộ dài cung AB thì l ∫ ds (3.4) AB
c. Nếu một dây vật chất có dạng cung AB và mật ộ khối lượng là ρ(x y, ) thì khối lượng =
của dây vật chất ó tính theo công thức: m ∫ ρ(x y ds, ) (3.5) AB
d. Người ta ã chứng minh ược: nếu cung AB là cung trơn (tiếp tuyến của cung biến thiên
liên tục) hoặc trơn từng khúc (chia cung AB thành hữu hạn các cung thành phần, các cung thành
phần là các cung trơn) và f(x,y) liên tục trên cung AB thì f(x,y) khả tích trên cung AB.
e. Vì ịnh nghĩa trên tương tự với tích phân xác ịnh, tích phân bội nên tích phần ường
loại một có các tính chất giống như tích phân xác ịnh.
3.1.2. Công thức tính tích phân ường loại một
Định lý 3.1. Giả sử cung AB trơn cho bởi phương trình:
y = y x( ), a ≤ x ≤ b
và hàm số f(x,y) liên tục trên cung AB . Khi ó: b
∫ f (x y ds, )= ∫ f x y x( , ( )) 1+ y' ( )2 x dx (3.6) AB a
Chứng minh: Thực hiện phép chia cung AB bởi các iểm A x yi ( i , i ),i =1,n như ịnh
nghĩa ã trình bày. Gọi Δx = − = − i xi xi−1,Δyi yi
yi−1 (i =1,n) (xem H.3.1). Với Δxi ,Δyi khá bé thì: 74
Downloaded by Ti?n D?ng Tr?n Lý (dungtienltr128@gmail.com) lOMoARcPSD| 10435767
Chương 3: Tích phân ường và tích phân mặt y Δ 2 2 i x Δ 2 +Δ = 1 + ( ). Δ i yi x i Δ x Δs ≈ i i
Theo công thức Lagrange, ta có ΔΔxyi = = i
y'(ξi ), ξ ∈i(xi 1− ,x ),ii 1,...,n Suy ra Δs ≈ ∈ i
1+ y / 2 (ξi ) Δxi ,ξi (xi−1, xi )
Sau khi thực hiện phép chia cung AB , ta chọn Mi(ξ ξi, (y i))∈ Ai−1Ai, i =1,n
Vậy tổng tích phân tương ứng sẽ là: n n I = ∑ ≈ ∑ n
f (ξ ξi , (yi ))Δsi
f (ξ ξi , (y i )) 1+ y' (2 ξi ) Δxi i=1 i=1
Cho n → ∞ sao cho maxΔx → → i 0 hay maxΔsi
0 thì do sự tồn tại của tích phân ường loại một
nên vế trái dần ến ∫ f (x y ds, ) , còn vế phải chính là tích phân xác ịnh của hàm số AB
f x y x( , ( )) 1+ y' ( )2 x trên [a,b] nghĩa là ta nhận ược công thức (3.6).
Nếu cung AB cho bởi phương trình tham số: ⎧x = x(t) ⎨y = y(t) , t ≤ 1 t ≤ t2 ⎩ thì y x'( ) =
y t'( ),dx = x t dt'( ) , 1+ y' ( )2 x = 1 x' ( )2 t
+ y' ( )2 t x t'( ) x t'( )
Vì a b≤ và t ≤ 1
t2 nên công thức (3.6) trở thành : t2 75
Downloaded by Ti?n D?ng Tr?n Lý (dungtienltr128@gmail.com) lOMoARcPSD| 10435767
Chương 3: Tích phân ường và tích phân mặt (3.7)
∫ f (x y ds, )= ∫ f x t[ ( ), ( )]y tx' ( )2 t + y' ( )2 t dt AB t1
Đặc biệt khi AB cho trong toạ ộ cực r = r( )ϕ, ϕ ≤ϕ≤ϕ 1 2 .
Ta có thể coi rằng AB cho dưới dạng tham số:
⎧x = r( )ϕ ϕcos ⎨⎩ = r( )ϕ ϕsin ϕ ϕ ϕ ≤ ≤ 1 2 y
Khi ó x′2 ( )ϕ + y′2 ( )ϕ ϕ ϕ= r2 ( ) + r′2 ( ) . Suy ra (3.6) có dạng: ϕ 2 =
∫ f(x,y)ds ∫ f r( )cos ,r( )sin[ ϕ ϕ ϕϕ] r ( )2 (3.8) ϕ + r ( )d′2 ϕ ϕ AB ϕ 1 ⎧x = x t( )
t ≤ t ≤ t ⎪ ⎪ 1 2
Tổng quát cung AB ⊂3 cho bởi phương trình tham số ⎨y = y t( ) ⎩z = z t( )
và nếu f(x,y,z) khả tích trên cung ó thì: t2
∫ f (x y z ds, , )= ∫ f x t( ( ), ( ), ( ))y t
z t x′2( )t + y′2( )t + z′2( )t dt S (3.9) AB t1
Ví dụ 1: Tính ∫(x + y ds) , C là biên tam giác với các ỉnh O (0,0), A (1,0), B (0,1). C
Giải: Đường C cho bởi H (3.2)
Theo tính chất của tích phân ta có: ∫ = ∫ + ∫ + ∫ 76
Downloaded by Ti?n D?ng Tr?n Lý (dungtienltr128@gmail.com) lOMoARcPSD| 10435767
Chương 3: Tích phân ường và tích phân mặt C OA AB BO
Đoạn OA có phương trình y = 0, 0 ≤ x ≤1
∫(x + y ds)= ∫1 x 1+ 0dx = 1 x2 1 = 1 OA 0 2 0 2
Đoạn AB có phương trình: y =1− x, 0 ≤ x ≤1
Đoạn BO có phương trình: x = 0, 0 ≤ y ≤1 1 1
∫(x + y ds) = ∫ y 1+ 0dy = 1 y 2 = 1 BO 0 2 0 2
(Sử dụng công thức (3.6) trong ó thay ổi vai trò các biến x và y cho nhau) ∫(x + y)ds = 2. +1 C ∫ 2 2 L
Ví dụ 2: Tính I =
x + y ds , L là ường tròn x2 + y2 = 2x.
Giải: Đường tròn L cho bởi H 3.3. y L 0 1 2 x H.3.3
Trong toạ ộ cực phương trình ường L có dạng r . Theo công thức (3.8) thì: π π 22 π 77
Downloaded by Ti?n D?ng Tr?n Lý (dungtienltr128@gmail.com) lOMoARcPSD| 10435767
Chương 3: Tích phân ường và tích phân mặt = ϕ I
∫ 2cosϕ 4cos2 ϕ+ 4sin2 ϕ ϕ =d8∫cos dϕ ϕ = 8sin = 02 8. π 0 − 2
Bạn ọc có thể giải ví dụ 2 bằng cách viết phương trình ường tròn x2 + y2 = 2x dưới dạng
⎧x = +1 cost tham số: ⎨y = sin t −π ≤ t ≤ π. ⎩
3.2. Tích phân ường loại hai
3.2.1. Bài toán mở ầu: Tính công của lực biến ổi
Bài toán: Một chất iểm M di chuyển dọc theo một cung phẳng AB từ iểm A ến iểm B dưới
tác dụng của lực F(M) = P M i( ) +Q M j( ) = (P Q, ), M ∈ AB . Hãy tính công W của lực ó sinh ra.
Cách tính: Chia cung AB làm n cung nhỏ bởi các iểm chia A0 , A1,..., An . Gọi Δsi là ộ A A
dài cung i−1 i và các thành phần của véc tơ Ai−1 Ai là Δxi ,Δy ii ; =1,n (H 3.4) y B i A M Δ y i i i A 1 − Δ x A i x a 0 b H.3.4
Lấy tuỳ ý Mi(xi, yi)∈ Ai−1Ai . Nếu cung Ai−1Ai khá nhỏ có thể coi nó xấp xỉ dây cung
Ai−1 Ai và F M( ) không ổi (cả chiều và ộ lớn) trên cung ó. Vì thế có thể coi rằng công của lực sinh ra
khi chất iểm di chuyển từ A A
Ai-1 ến Ai theo cung i−1 i sẽ xấp xỉ bằng F M( = +
i ).Ai−1 Ai
P M( i )Δxi
Q M( i )Δyi 78
Downloaded by Ti?n D?ng Tr?n Lý (dungtienltr128@gmail.com) lOMoARcPSD| 10435767
Chương 3: Tích phân ường và tích phân mặt
Suy ra công W của lực sinh ra sẽ xấp xỉ là: n W ≈ ∑P x( +
i , yi )Δxi
Q x( i , yi )Δyi i 1=
Như vậy giới hạn của tổng trên khi n → ∞ sao cho maxΔs → i
0 chính là công của lực: n W = lim ∑ Δ → + s P x( Q x( i0
i , yi )Δxi
i , yi )Δyi max i=1
Ý tưởng tính công của lực dẫn ến khái niệm tích phân ường loại hai. 3.2.2. Định nghĩa
Cho hai hàm số P(x,y), Q(x,y) xác ịnh trên cung L (hay cung AB )
* Chia cung L thành n cung nhỏ bởi các iểm chia: A ≡ A , ≡
0 A1,...Ai−1, Ai ,..., An B Gọi tọa ộ của vectơ A
Ai−1 Ai là Δxi ,Δyi và ộ dài cung Ai−1 i là Δs ii , =1,n .
* Lấy tuỳ ý Mi(xi, yi)∈ Ai−1A ii, =1,n. n = * Lập tổng I ∑ + n
P M( i )Δxi Q M( i )Δyi , gọi ó là tổng tích phân ường loại hai của i=1
hàm số P x y Q x y( , ), ( , )dọc theo L i từ A ến B ứng với một phân hoạch của L và một cách chọn Mi ∈ Ai−1Ai .
* Khi n → ∞ sao cho maxΔs → → → i 0hay max Δxi 0 và maxΔyi
0 mà In hội tụ về
số I không phụ thuộc cách chia cung L và cách chọn tuỳ ý M ∈ i
Ai−1Ai thì số I gọi là tích phân ường
loại hai của các hàm P(x,y),Q(x,y) dọc theo cung AB i từ A ến B và ký hiệu là ∫ P x y dx( , ) +Q x y dy( , ) . AB n * Như vậy ∫ ∑ AB P x y dx( , )
+Q x y dy( , ) = Δ →Δ →limyxii 00
i=1 P x y( i, i)Δxi
+Q x y( i, i)Δyi (3.10) 79
Downloaded by Ti?n D?ng Tr?n Lý (dungtienltr128@gmail.com) lOMoARcPSD| 10435767
Chương 3: Tích phân ường và tích phân mặt Chú ý: a.
Khác với tích phân ường loại một, ở tích phân ường loại hai, hướng lấy tích phân của
L là quan trọng. Nếu ta dọc theo cung AB i từ B ến A thì các vectơ Ai−1Ai ổi hướng, tức là
các thành phân của vectơ ó là − Δxi ,−Δyi ,(i =1,n). Vậy tổng tích phân sẽ ổi dấu, suy ra: = −
∫ P x y dx( , )+Q x y dy( , )
∫ P x y dx( , )+Q x y dy( , ) (3.11) AB BA b.
Công sinh ra do lực F = P(x,y)i +Q(x,y)j ể chất iểm dịch chuyển từ A ến B theo = cung AB sẽ là: W
∫ P(x,y)dx +Q x y dy( , ) (3.12) AB c.
Nếu AB là ường cong trong không gian có ba hàm số P(x,y,z),Q(x,y,z),R(x,y,z) xác ịnh
trên cung AB thì tích phân ường loại hai của ba hàm số ó cũng ược ký hiệu là:
∫ P x y z dx( , , )+Q x y z dy( , , )+ R x y z dz( , , ) (3.13) AB d.
Cho L là ường cong phẳng (nằm trên mặt phẳng 0xy) và kín. Người ta qui ước gọi
hướng dương của ường cong L là hướng sao cho một người i dọc L theo hướng ó thì thấy miền giới
hạn bởi L gần mình nhất ở bên trái. Tích phân lấy theo hướng dương thường ký hiệu là :
∫P x y dx( , )+Q x y dy( , ) L+
Còn tích phân lấy theo hướng ngược lại sẽ dùng dấu ∫ L− e.
Tương tự tích phân ường loại một, người ta cũng chứng minh về sự tồn tại tích phân
ường loại hai: Nếu cung AB trơn hoặc trơn từng khúc và các hàm P(x,y), Q(x,y) liên tục trên cung ó thì
tồn tại tích phân ường loại hai của hai hàm P(x,y), Q(x,y) lấy theo cung AB.
f. Tích phân ường loại hai cũng có các tính chất tương tự như tích phân xác ịnh.
3.2.2. Công thức tính tích phân ường loại hai.
Định lý 3.2. Giả sử hai hàm số P(x,y), Q(x,y) liên tục trên cung AB trơn cho bởi phương ⎧x = x t( ) 80
Downloaded by Ti?n D?ng Tr?n Lý (dungtienltr128@gmail.com) lOMoARcPSD| 10435767
Chương 3: Tích phân ường và tích phân mặt ⎨
trình tham số: ⎩y = y t( )
Điểm A ứng với giá trị tham số t = tA , B ứng với giá trị tham số tB . Khi ó: tB
∫ P x y dx( , )+Q x y dy( , )= ∫ [ ( ( ), ( )) '( )P x t
y tx t +Q x t( ( ), ( )) '( )]y t y t dt (3.14) AB tA
Chứng minh: Ta thực hiện phép chia cung AB như ã trình bày trong phần ịnh nghĩa. Khi ó oạn [t ]
A,tB tương ứng ược chia thành n oạn bởi các số ti tương ứng với các iểm A i ≡ ≡
i , =1,n tA t0 ,tB
tn và theo ịnh lý Lagrange ta có: Δx = − * i x t( )i
x t( i−1) = x t'( i )Δti Δy = − ** i y t( )i
y t( i−1) = y t'( i )Δti trong ó t * ** Δ = − i ,ti là
iểm nằm trong khoảng (ti−1, ),ti ti
ti ti−1 . Để lập tổng tích phân n ∑P x( = * = *
i , yi )Δxi , ta chọn các iểm Mi(xi, yi)∈ Ai−1Ai , sao cho xi
x t( i ), yi
y t( i ). Khi ó i=1 n ∫ P x y dx( , ) = lim ∑P x t( ( * * *
i ), y t( i ))x t'( i )Δti AB
max Δ →ti0 i=1
Vì iều kiện ủ tồn tại tích phân ã thoả mãn nên với cách chọn M i như trên ta có: tB =
∫ P x y dx( , ) ∫ P x t( ( ), ( )) '( )y t x t dt (3.15) AB tA tB =
Lý luận tương tự ta có: ∫ Q x y dy( , ) ∫ Q x t( ( ), ( )) '( )y t y t dt (3.16) AB tA
Vậy cuối cùng ta nhận ược công thức (3.14).
Trường hợp ường cong AB trong không gian 0xyz cho bởi phương trình tham số: ⎧x = x t( ) 81
Downloaded by Ti?n D?ng Tr?n Lý (dungtienltr128@gmail.com) lOMoARcPSD| 10435767
Chương 3: Tích phân ường và tích phân mặt ⎪ = y t( ) ⎨y
⎪⎩z = z t( )
Các iểm A,B tương ứng với các tham số tA,tB khì ó chứng minh hoàn toàn tương tự, ta có: : tB
∫ P x y z dx( , , )+Q x y z dy( , , )+ R x y z dz( , , )= ∫ ⎡⎣P x t( ( ), ( ), ( ))y t z t
x t/( )+Q()y/( )t + R()z/( )t ⎦⎤dt AB tA (3.17)
Khi cung AB phẳng cho bởi phương trình dạng tường minh y=y(x), A,B có hoành ộ tương ứng là
a, b thì theo công thức (3.14) , coi x là tham số, ta nhận ược: b
∫ P x y dx( , )+Q x y dy( , )= ∫[P x y x( , ( ))+Q x y x y x dx( , ( )) '( )] (3.18) AB a
hoặc nếu AB cho bởi phương trình x=x(y) , A,B có tung ộ tương ứng là c,d thì d
∫ P x y dx( , )+Q x y dy( , )= ∫[P x y( ( ), )y x y'( )+Q x y( ( ), )y dy] (3.19) AB c x2 y 2 +
Ví dụ 3: Tính công sinh bởi lực F = −yi + x j sinh ra dọc theo ellipse a = 2 b2 1và theo hướng dương của nó.
Giải: Phương trình tham số của ường ellipse ã cho là:
⎧x = acost
⎨y = bsint 0 ≤ t ≤ 2π ⎩
t tăng từ 0 ến 2πứng với hướng dương của ường ellipse. Do ó công sinh bởi lực F sẽ là: A =
xdy− ydx = (acost.bcost + bsin t.asin t)dt 82
Downloaded by Ti?n D?ng Tr?n Lý (dungtienltr128@gmail.com) lOMoARcPSD| 10435767
Chương 3: Tích phân ường và tích phân mặt L+ 0 ab dt 2 ab. =
Ví dụ 4: Tính I ∫(2xy − x2 )dx + (x + y 2 )dy trong ó L là cung của parabôn y =1− x2 L
i từ iểm A(0,+1) ến iểm B(-1,0).
Giải: y =1− x2 ⇒ dy = −2xdx −1
I = ∫ ⎡⎣2x(1− x )2 − x2 + (x + −12x2 + x )( 2x) dx4− ⎤⎦ 0 ( 2x 2x 3x )dx .
3.3. Công thức Grin (Green)
Giả sử D là miền liên thông, bị chặn có biên là L gồm một hay nhiều ường cong kín trơn hoặc
trơn từng khúc. Sau ây ta sẽ ưa ra công thức liên hệ giữa tích phân ường loại hai dọc theo L và tích
phân bội hai trên miền D có tính chất ã nêu ra.
Định lý 3.3. Cho các hàm số P(x,y), Q(x,y) liên tục cùng các ạo hàm riêng cấp một trong miền
D có biên là ường L, khi ó: dxdyPdx Qdy (3.20) ∂x ∂ D L () 2 yx () 1 yx Chứng minh: a.
Trước hết xét miền D ơn liên và ơn giản theo nghĩa nó ược mô tả bởi hệ bất phương trình: (Xem H.3.5)
⎧a ≤ x ≤ b 83
Downloaded by Ti?n D?ng Tr?n Lý (dungtienltr128@gmail.com) lOMoARcPSD| 10435767
Chương 3: Tích phân ường và tích phân mặt
⎨⎩y x1( ) ≤ y ≤ y2 ( )x
⎧c ≤ y ≤ d ⎨ hoặc
⎩x1( )y ≤ x ≤ x2 ( )y
L = AB∪ BC ∪CA
AC có phương trình : y = y x1( ), a ≤ x ≤ b
BC có phương trình x = b y b, 1( ) ≤ y ≤ y b2 ( )
AB có phương trình y = y2 ( )x , a ≤ x ≤ b
Theo công thức tính tích phân kép ta có: ∫∫ ∂P = ∫ ∫ ∂ b dx y P dy = ∫ 2 ( )x b P x
y( , )y2 ( )x dx dxdy ∂y ∂yy ( )x D a y1( )x a1 b b
= ∫ P x y( , 2 ( ))x dx − ∫ P x y( , 1( ))x dx a a
Theo công thức tính tích phân ường loại hai (3.18) và chú ý a. ta có: b b
∫P x y( , 2( ))x dx = ∫ P x y dx( , ),∫P x y x dx( , 1( ))= ∫ P x y dx( , ) ,suy ra a AB a AC dxdy P x y dx P x y dx D AB CA
Mặt khác ∫ P x y dx( , ) = 0 vì BC có phương trình x=b nên dx=0. Vậy BC ∂P
∫∫ dxdy = ∫ P x y dx( , )+ ∫ P x y dx( , )+ ∫ P x y dx( , )= ∫ P x y dx( , ) ∂y D AB BC CA L 84
Downloaded by Ti?n D?ng Tr?n Lý (dungtienltr128@gmail.com) lOMoARcPSD| 10435767
Chương 3: Tích phân ường và tích phân mặt Tương tự ta có: x D L
Từ các kết quả này suy ra công thức Green (3.20) b.
Xét D là miền ơn liên bất kỳ (H.3.6). Ta luôn có thể phân hoạch miền D thành hữu
hạn các miền ơn giản, chẳng hạn có thể chia D thành 3 miền có chung biên là oạn AB và BC. Theo
tính chất của tích phân bội hai và kết quả ã chứng mình phần trên, ta có y C D 2 p B m D 1 D n 3 x 0 b A H.3.6 ∂Q ∂P ∫∫(
− )dxdy = ∫∫ + ∫∫ + ∫∫ ∂x ∂y D D1 D2 D3 ∂Q ∂P
∫∫( − )dxdy = ∫ Pdx +Qdy + ∫ Pdx +Qdy + ∫ Pdx +Qdy ∂x ∂y D1 AB BC CmA dxdyPdx Qdy Pdx Qdy D CB BpC ∂Q ∂P
∫∫( − )dxdy = ∫ Pdx +Qdy + ∫ Pdx +Qdy ∂x ∂y D3 BA AnB
Cộng các vế với các hệ thức trên và ể ý ến chú ý a. của tích phân ường loại hai, ta nhận ược ược công thức Green (3.20). c.
Trường hợp D là miền a liên, chẳng hạn D là miền nhị liên (H.2.7), biên L gồm hai
ường L1 và L2 rời nhau. Ta có thể chia miền D thành 4 miền nhỏ. Áp dụng công thức Green cho cả
4 miền và sử dụng chú ý a, ta cũng nhận ược công thức (3.20). Trong trường hợp này cần lưu ý: 85
Downloaded by Ti?n D?ng Tr?n Lý (dungtienltr128@gmail.com) lOMoARcPSD| 10435767
Chương 3: Tích phân ường và tích phân mặt
Tích phân dọc theo L1 có hướng ngược chiều kim ồng hồ, còn tích phân dọc theo L2 có hướng thuận
chiều kim ồng hồ. Như vậy tích phân ∫Pdx + Qdy úng là lấy theo hướng dương của L+
biên L như ã qui ước ở chú ý d. y 2 L L 1 x 0 H.3.7
Chú ý: Công thức Green (3.20) cho ta công thức tính diện tích miền phẳng D nhờ vào tích phân ường loại hai như sau: ∂P ∂Q
Lấy trong (3.20) các hàm P x y( , ) = −y và Q x y( , ) = x thì = −1, = 1 ∂y ∂x = 1 Suy ra: S
∫ xdy − ydx trong ó S là diện tích miền D. (3.21) 2 L+
Ví dụ 5: Tính diện tích ellipse với các bán trục a,b. x 2 y 2 +
Giải: Có thể coi ellipse có phương trình a = 2
b2 1 hay dạng tham số
x = acost , y = bsin , 0t ≤ t ≤ 2π. Áp dụng (3.21) có S xdy ydx ab t ab t dt ab 2 L+ 2 0 =
Ví dụ 6: Tính I ∫(xarctgx + y 2 )dx + (x + 2xy + y e2 − y3 )dy L+
L là biên nửa hình tròn cho bởi bất phương trình x 2 + y 2 ≤ 2y, x ≥ 0. 86
Downloaded by Ti?n D?ng Tr?n Lý (dungtienltr128@gmail.com) lOMoARcPSD| 10435767
Chương 3: Tích phân ường và tích phân mặt 2 ⇒ ∂P = 2y
P = xarctgx + y ∂y
2 −y3 ⇒ ∂Q = 2y +1
Q = x + 2yx + y e ∂x ∂Q ∂P π
Vậy: I = ∫∫( − )dxdy = ∫∫dxdy = (nửa diện tích hình tròn bán kính là 1). ∂x ∂y 2 D D =
Ví dụ 7: Tính J ∫(xarctgx + y 2 )dx + (x + 2yx + y e2 −y3 )dy với C là nửa ường tròn C
bên phải i từ gốc toạ ộ ến A(0,2): x 2 + y 2 = 2y, x ≥ 0.
Giải: Gọi L là ường cong gồm nửa ường tròn C và oạn OA. Rõ ràng :
I = J + ∫ (xarctgx + y2)dx +(x + 2yx + y e2 −y3 )dy AO trong ó I là tích phân của ví dụ 6.
Đoạn thẳng AO có phương trình x = 0, 0 ≤ ≤ ⇒y 2 dx = 0 .
Áp dụng công thức tính tích phân ường (3.19) ta có: 87
Downloaded by Ti?n D?ng Tr?n Lý (dungtienltr128@gmail.com) lOMoARcPSD| 10435767
Chương 3: Tích phân ường và tích phân mặt = − 1 0 = 1 1 3e−y3 2 3( 8 −1). e π 1 1
Cuối cùng J = 2 + 3(1− e8 ).
Chú ý: Trong ví dụ 7 ta ã thêm một ường thẳng thích hợp ể áp dụng công thức Green, ương
nhiên sau ó phải bớt i tích phân lấy dọc theo oạn thẳng ó (hay cộng với tích phân lấy theo hướng
ngược lại). Nhiều bài toán phải làm như vậy bởi vì nếu tính trực tiếp sẽ rất khó khăn.
3.4. Định lý bốn mệnh ề tương ương
Xuất phát từ công thức Green (3.20), sau ây ta sẽ nhận ược các iều kiện ể biểu thức
P(x,y)dx +Q(x,y)dy là vi phân toàn phần của hàm u(x,y) nào ó; ể tích phân ường của một biểu thức
không phụ thuộc vào dạng ường cong lấy tích phân. Trong các trường hợp này, miền liên thông D
phải là ơn liên (biên có duy nhất một ường cong kín).
Định lý 3.4: Giả sử các hàm P(x,y), Q(x,y) liên tục cùng với các ạo hàm riêng cấp một của chúng
trong miền ơn liên D. Khi ó bốn mệnh ề sau ây tương ương với nhau: ∂P ∂Q (1).
= , ( , )∀ x y ∈ D ∂y ∂x
(2). ∫Pdx + Qdy = 0 , L là ường cong kín bất kỳ nằm trong miền D. L
(3). ∫ Pdx +Qdy , trong ó cung AB nằm trong miền D, chỉ phụ thuộc vào 2 iểm A,B AB
mà không phụ thuộc dạng cung AB .
(4). Biểu thức Pdx + Qdy là vi phân toàn phần của hàm u(x,y) nào ó trên miền D.
Chứng minh: Định lý ược chứng minh theo sơ ồ sau: (1) ⇒ (2) ⇒ (3) ⇒ (4) ⇒ (1) (1) ⇒ (2) : Gọi D ⊂
1 là miền giới hạn bởi L, L ⊂ D suy ra D1 D . Áp dụng công
thức Green (3.20) cho miền D1 ta có: Pdx +Qdy = ( − )dxdy = 0dxdy = 0 ∂ L D1 x ∂y D1 88
Downloaded by Ti?n D?ng Tr?n Lý (dungtienltr128@gmail.com) lOMoARcPSD| 10435767
Chương 3: Tích phân ường và tích phân mặt
Suy ra ∫Pdx + Qdy = 0, ∀L ⊂ D L (2)
⇒ (3) :Lấy A∈ D B, ∈ D và AmB ⊂ D AnB,
⊂ D (dạng của các cung là tuỳ ý. H.3.9)
Suy ra ường cong kín AmBnA ⊂ D. Theo (2) ta có:
∫ Pdx +Qdy = 0 hay : AmBnA
∫ Pdx +Qdy + ∫ Pdx +Qdy = 0 AmB BnA
Suy ra : ∫ Pdx +Qdy = ∫ Pdx +Qdy. AmB AnB
Chứng tỏ các tích phân không phụ thuộc vào dạng cung AB . (3)
⇒ (4) :Ta sẽ xây dựng hàm u(x,y) dưới ây sao cho: du x y( , ) = Pdx +Qdy =
Xét hàm số u x y( , )
∫ Pdx +Qdy +C với AM ⊂ D,C là hằng số tuỳ ý. (3.22) AM
Rõ ràng hàm số này phụ thuộc vào iểm M(x,y) chứ không phụ thuộc dạng cung AM và ∂u
u x( 0 , y0 ) = C . Ta sẽ chứng minh = P x y( , ). Thật vậy, theo ịnh nghĩa ạo hàm riêng tại ∂x (x,y) ta có
u x( + h y, )−u x y( , ) 1 ∂u = lim = lim
( ∫ Pdx +Qdy − ∫ Pdx +Qdy) ∂x h→0 h h→0 h 89
Downloaded by Ti?n D?ng Tr?n Lý (dungtienltr128@gmail.com) lOMoARcPSD| 10435767
Chương 3: Tích phân ường và tích phân mặt AM1 AM
trong ó M1 và M cùng có tung ộ là y, còn hoành ộ của M1 là x+h với h ủ bé ể M ∈ 1 D.
Theo (3) có thể lấy AM1 gồm cung AM và oạn thẳng nằm ngang MM1. Vậy 1 ∂u
= lim ∫ Pdx +Qdy ∂x h→0 h MM1
Đoạn MM1 vuông góc với trục Oy và hướng i từ M(x,y) ến M1(x+h,y), suy ra dy=0 1 Vậy: ∂u = lim
x h∫+ P x y dx( , ) ∂x h→0 h x
Theo ịnh lý về giá trị trung bình của tích phân xác ịnh thì: x h+
∫ P x y dx( , )= P x( * , )y h x
trong ó x* = x +θ. , 0h <θ< 1, từ ó ta có: ∂u * , )y = limP x( ∂x h→0 ∂u Do tính
liên tục của hàm P(x,y) vậy = P x y( , ). ∂x
∂u Tương tự ta chứng minh ược = Q x y( , ).
Vậy tồn tại hàm u(x,y) cho bởi (3.22) ể có ∂y du = P(x,y)dx+Q(x,y)dy ∂u
(4) ⇒ (1) : ∃u x y( , )ể du = Pdx+Qdy hay ∂u = P, = Q . Suy ra: ∂x ∂y
∂ 2u ∂P ∂ 2u ∂Q = , = 90
Downloaded by Ti?n D?ng Tr?n Lý (dungtienltr128@gmail.com) lOMoARcPSD| 10435767
Chương 3: Tích phân ường và tích phân mặt
∂ ∂x y ∂y ∂ ∂y x ∂x ∂ 2u
Do các ạo hàm riêng của P,Q liên tục trên miền D nên các ạo hàm hỗn hợp và ∂ ∂x y
∂ 2u ∂ 2u ∂ 2u
cũng liên tục trên D. Theo ịnh lý Schwarz, ta có = hay là: ∂ ∂y x
∂ ∂x y ∂ ∂y x ∂P ∂Q
= , ( , )∀ x y ∈ D ∂y ∂x
Hệ quả 1: Nếu du x y( , ) = Pdx +Qdy trong miền D thì :
∫ Pdx +Qdy = u B( )−u A( ) (3.23) AB
Chứng minh: ∫ Pdx +Qdy = ∫ du x y( , ) AB AB
Giả sử AB cho bởi phương trình y=y(x) và A(xA,yA),B(xB,yB) rõ ràng yA=y(xA),yB=y(xB). Chuyển
tích phân ường về tích phân xác ịnh theo công thức (3.18), ta có: ∫ du x y( , ) = ∫ x
B du x y x( , ( )) = u x y x( ,
( ))xB = u B( )−u A( ) AB xAxA
Hệ quả 2: Nếu Pdx + Qdy là vi phân toàn phần của hàm u(x,y) trên toàn mặt phẳng R2 thì hàm
u(x,y) cho bởi công thức: x y
u x y( , ) = ∫ P x y dx( , )+ ∫Q x( 0 , )y dy + C (3.24) x0 y0 hoặc x y
u x y( , ) = ∫ P x y( , 0 )dx + ∫Q x y dy( , ) + C (3.25) x0 y0
trong ó A x( 0 , y0 )∈ R2 ,M x y( , )∈ R2 91
Downloaded by Ti?n D?ng Tr?n Lý (dungtienltr128@gmail.com) lOMoARcPSD| 10435767
Chương 3: Tích phân ường và tích phân mặt y y0 x x 0
Ch ứ ng minh: L ậ p hàm s ố u(x,y) theo công th ứ c (3.22). Vì tích phân không ph ụ thu ộ c d ạ ng
AM vì thế có thể chọn AM là ường gấp khúc ANM hoặc ALM (H.3.11) Đoạn AL
song song với trục 0y nên dọc theo nó dx=0.
Đoạn LM song song với trục 0x nên dọc theo nó dy=0.
u x y( , ) = ∫ Pdx +Qdy +C = ∫ Pdx +Qdy + ∫ Pdx +Qdy +C AM AL LM
= ∫ Q x y dy( , )+ ∫ P x y dy( , ) +C AL LM
Áp dụng công thức (3.18) có: y x
u x y( , ) = ∫Q x( 0 , )y dy + ∫ P x y dx( , ) + C y0 x0
Tương tự, lấy tích phân theo ường ANM sẽ nhận ược công thức (3.25) Chú ý:
a. Các hàm u(x,y) nếu tồn tại sẽ sai khác nhau hằng số cộng C.
b. Thông thường lấy (x0 , y0 ) = (0,0) thì tính tích phân (3.24) hoặc (3.25) sẽ ơn giản hơn.
Ví dụ 8: Chứng minh biểu thức:
(x2 − 2xy 2 + 3)dx + (y 2 − 2x y2+ 3)dy
là vi phân toàn phần của hàm u(x,y) trên R2 và hãy tìm hàm ó. Giải: Đặt:
2 − 2xy 2 + 3⇒ ∂P = −4xy P x y( , ) = x ∂y 92
Downloaded by Ti?n D?ng Tr?n Lý (dungtienltr128@gmail.com) lOMoARcPSD| 10435767
Chương 3: Tích phân ường và tích phân mặt
2 − 2x y2 + 3⇒ ∂Q = −4xy = ∂P ,∀(x y, )∈R2 Q x y( , ) = y ∂x ∂y
Vậy có hàm số u(x,y) ể du=Pdx+Qdy. Ta có: x y
u x y( , ) = ∫ P x y dx( , )+ ∫Q(0, y dy) +C 0 0 x y
(x 2xy 3)dx (y 3)dy C x y x y x y C = − Ví dụ 9: ydx Tính I ∫ xdy2 + y 2 , (1,1),A B(2,4) x AB
a. Cung AB cho bởi phương trình: y = x2 , 1≤ x ≤ 2,
b. Cung AB bất kỳ tạo với oạn AB thành ường cong kín không bao gốc toạ ộ.
c. Cung AB bất kỳ tạo với oạn AB thành ường cong kín bao gốc toạ ộ Giải: Đặt 2 2 = P = − x2 + ⇒ y y ∂∂ 2 Py (xy +− 2 yx2 )2 93
Downloaded by Ti?n D?ng Tr?n Lý (dungtienltr128@gmail.com) lOMoARcPSD| 10435767
Chương 3: Tích phân ường và tích phân mặt x ∂ − 2 Q 2 2 Q =
x2 + y 2 ⇒ ∂x (x + y ) ∂y a.
y = x2 ⇒ dy = 2xdx ,(cung AnB) 2x − 2 2 x2 2 2dx2 π ∫ ∫ I = + 1 x2 x4 dx = 1 1
+ x2 dx = arctgx1 = arctg2 − 4 b.
Vì các hàm P, Q thoả mãn ịnh lí 4 mệnh ề tương ương trên bất kì một miền ơn liên không
chứa gốc toạ ộ ,do ó tích phân ã cho không phụ thuộc vào dạng cung AB ,sao cho cung ó tạo với oạn
AB một ường cong kín không bao gốc toạ ộ (H.3.12). Vậy I = arctg2− . c.
Khi cung AB tạo với oạn AB một ường cong kín bao gốc tạo ộ thì không thể áp dụng ịnh
lý 4 mệnh ề tương ương ược nữa do P,Q không liên tục trong miền ơn liên chứa gốc toạ ộ. Trước hết,
từ công thức Green suy ra: Tích phân không phụ thuộc dạng cung AB , miễn là cung ó tạo với oạn AB
thành ường cong kín bao gốc toạ ộ. Bây giờ ta vẽ ường tròn C tâm gốc toạ ộ, bán kính ủ bé r. Xét miền
liên thông nhị liên D có biên là C và ường cong kín. Theo công thức Green ta có: dxdy Pdx Qdy Pdx QdyPdx Qdy D x y AnB BmA C− Suy ra: π
∫ Pdx +Qdy = arctg2−
− ∫ Pdx +Qdy C+ 4 AmB
C cho bởi phương trình tham số: ⎧x = r cosϕ
⎨y = r sinϕ, 0 ≤ϕ≤ 2π ⎩
2π 2 cos 2 ϕ+ r 2 sin 2 ϕ r =
∫ Pdx + Qdy ∫ dϕ π= 2 C+ 0 r 2 Vậy I Pdx Qdy arctg2 . 94
Downloaded by Ti?n D?ng Tr?n Lý (dungtienltr128@gmail.com) lOMoARcPSD| 10435767
Chương 3: Tích phân ường và tích phân mặt
3.5. Tích phân mặt loại một 3.5.1. Định nghĩa
Cho hàm số f M( ) = f x y z( , , ) xác ịnh trên mặt cong S.
* Chia mặt cong S thành n mảnh không dẫm lên nhau, gọi tên và diện tích của mảnh thứ i là
ΔSi ,i =1,n và ký hiệu ường kính của mảnh thứ i là di ,i =1,n.
* Lấy tuỳ ý Mi (xi , yi , zi )∈ΔSi ,i =1,n n = * Lập tổng I ∑ n
f M( i )ΔSi gọi là tổng tích phân mặt loại một ứng với một cách chia i=1
mặt cong S và một cách chọn M ∈Δ i
Si ,i =1,n
Nếu khi n→∞ sao cho max d → i
0 mà In hội tụ về số I không phụ thuộc cách chia mặt
cong S và cách lấy iểm M ∈Δ i
Si ,i =1,n thì số I gọi là tích phân mặt loại một của f(M) trên mặt cong S
ký hiệu ∫∫ f x y z dS( , , ) . S n
Như vậy ∫∫ f x y z dS( , , ) = lim
∑ f x( i , yi , zi )ΔSi (3.26) max di →0 i=1 S Chú ý:
a. Từ ịnh nghĩa ta thấy công thức tính diện tích mặt cong S nhờ vào tích phân mặt loại =
một: S ∫∫dS (3.27) S
b. Nếu S là mặt cong vật chất có hàm mật ộ khối lượng là ρ(x y z, , ) thì khối lượng của
mặt cong vật chất ó sẽ là:
m = ∫∫ρ(x y z dS, , ) (3.28) S 95
Downloaded by Ti?n D?ng Tr?n Lý (dungtienltr128@gmail.com) lOMoARcPSD| 10435767
Chương 3: Tích phân ường và tích phân mặt
c. Người ta ã chứng minh ược rằng: Nếu mặt cong S trơn (mặt cong S có pháp tuyến biến
thiên liên tục) hoặc là trơn từng mảnh (chia S thành hữu hạn các mặt cong trơn) và hàm số f x y
z( , , ) liên tục hoặc liên tục từng mảnh trên mặt cong S thì tồn tại tích phân mặt loại một của hàm số ó trên S.
d. Tương tự, tích phân mặt loại một có các tính chất giống như tích phân kép.
3.5.2. Công thức tính tích phân mặt loại một
Định lý 3.5: Giả sử hàm số f(x,y,z) liên tục trên mặt cong S trơn cho bởi phương trình z = z x
y( , ),( ,x y)∈D . Khi ó:
∫∫ f x y z dS( , , )= ∫∫ f x y z x y( , , ( , )) 1+ z' ( , )2x x y + z'2y (x y dxdy, ) (3.29) S D
Chứng minh: Trước hết, ta thừa nhận các kết quả sau:
Nếu mặt cong S cho bởi phương trình F x y z( , , ) = 0 thì các côsin chỉ phương của véctơ pháp
tuyến tại M(x,y,z) ược tính theo công thức: cosα= ± Fx' ,cosβ= ± Fy'
F'2x +F'2y +F'2z
F'2x +F'2y +F'2z (3.30) cosγ= ± Fz'
F'2x +F'2y +F'2z
Trong công thức (3.30), α,β,γ là góc lập bởi véctơ pháp tuyến của mặt cong S tại
M(x,y,z) với các trục toạ ộ 0x,0y,0z (H.3.13) γ β α 96
Downloaded by Ti?n D?ng Tr?n Lý (dungtienltr128@gmail.com) lOMoARcPSD| 10435767
Chương 3: Tích phân ường và tích phân mặt
Do ó nếu mặt cong S cho bởi phương trình z = z x y( , ),( ,x y)∈D thì các côsin chỉ phương của
véctơ pháp tuyến sẽ là: cosα= ± zx' ,cosβ= ± z 'y ,cosγ= ± 1 (3.31)
1+ z'2x +z'2y
1+ z'2x +z'2y
1+ z'2x +z'2y
Khi véctơ pháp tuyến n xác ịnh thì góc α,β,γ xác ịnh và như vậy trong các công thức
trên chỉ có dấu + hoặc dấu -. Bây giờ ta chia S thành n mảnh nhỏ ΔSi ,i =1,n , tương ứng nhận
ược n hình chiếu các mảnh ó trên mặt phẳng 0xy là ΔD ii , =1,n . Nghĩa là ta ã gián tiếp chia miền D,
hình chiếu của mặt cong S trên mặt 0xy, làm n phần ΔDi (H.3.14). γ ( nM ) i ΔS i i M Δ i D
Lấy tuỳ ý Mi (xi , yi , zi )∈ΔSi và dựng tiếp diện T Mi (
i ) của mặt S tại Mi (mặt phẳng
vuông góc với pháp tuyến n tại Mi hay là mặt phẳng tiếp xúc với mặt S tại Mi).
Gọi ΔTi là mảnh của tiếp diện có hình chiếu trên 0xy trùng với mảnh ΔDi . Với ường kính 97
Downloaded by Ti?n D?ng Tr?n Lý (dungtienltr128@gmail.com) lOMoARcPSD| 10435767
Chương 3: Tích phân ường và tích phân mặt ΔDi ≈
, của ΔSi khá nhỏ thì diện tích mảnh ΔTi xấp xỉ diện tích mảnh ΔSi và rõ ràng ΔSi cosγi
theo công thức (3.31) nhận ược: n n I = ∑ ≈ ∑ + Δ n
f M( i )ΔSi
f x( i , yi , zi ) 1+ z'2x z' .2y Di i=1 i=1
Vế phải chính là tổng tích phân kép lấy trên miền D của hàm số:
f x y z x y( , , ( , )) 1 + z'2 + x z'2y
Vậy công thức tính tích phân mặt loại một khi mặt cong S cho dưới dạng hiện z = z x y( , ),( ,x
y)∈D ược cho bởi công thức (3.29). Chú ý:
a. Nếu mặt cong S cho bởi phương trình y = y z x( , ) hoặc x = x y z( , ) thì ta phải chiếu S lên
mặt phẳng 0zx hoặc 0yz ể tìm miền tính tích phân kép tương ứng.
b. Nếu mặt cong kín, ta phải chia thành hữu hạn các phần thoả mãn ịnh lý trên, sau ó áp dụng công thức (3.29).
Ví dụ 10 : Tính diện tích phần phía trên mặt cầu x2 + y2 + z2 = 4a2 nằm trong hình trụ x2 + y2 ≤ 2ay a, > 0 . Giải : Xem H.3.15 98
Downloaded by Ti?n D?ng Tr?n Lý (dungtienltr128@gmail.com) lOMoARcPSD| 10435767
Chương 3: Tích phân ường và tích phân mặt
Do tính ối xứng, ta chỉ cần tính diện tích một phần hai của phần mặt cầu trên.. Phần mặt cầu trên
có phương trình : z = 4a2 − x2 − y2 .
Hình chiếu trên mặt 0xy là nửa hình tròn D có bất phương trình :
x2 + (y − a)2 ≤ a x2, ≥ 0
Vậy S = ∫∫dS = 2∫∫ 1 + z'2 + x z'2y dxdy S D z'2x =
4a2 −xx22 − y2 , z'2y =
4a2 −yx22 − y2 S = 2∫∫ 2a dxdy D
4a 2 − x 2 − y 2
Chuyển sang toạ ộ cực ta ược : π π 2 2 asin ϕ 2a 2 sin ϕ 2 rdr d(r) − S = a 4 d ϕ 2 =− a d ϕ ∫ ∫ ∫ ∫ 2 2 2 2 − − 0 4 a r 0 4 a r 0 0 π π 2 2 a 2 sin ϕ 2 2 4 =− a a 4 −r d ϕ= 4 a (2 a-2a cos)d ϕ ϕ ∫ ∫ 0 0 0 π π π 2 2 2 =8 a ( −sin ϕ ) = a 8 ( 1). − 2 2 0
3.6. Tích phân mặt loại hai
3.6.1. Mặt ịnh hướng
Mặt cong S trơn gọi là ịnh hướng ược nếu véctơ pháp tuyến ơn vị n M( ) hoàn toàn xác ịnh tại
mọi M ∈S (có thể trừ biên của S) và biến ổi liên tục khi M chạy trên S. Tập hợp
n M( ),∀M ∈S của mặt cong có ịnh hướng xác ịnh phía dương của mặt cong, là phía mà người
ta ứng ó thì n M( ) hướng từ chân lên ầu. Vì rằng − n M( ) cũng là véctơ pháp tuyến nên mặt ịnh hướng luôn có hai phía.
Khi mặt cong S không kín ịnh hướng ược, người ta thường dùng từ phía trên và phía dưới 99
Downloaded by Ti?n D?ng Tr?n Lý (dungtienltr128@gmail.com) lOMoARcPSD| 10435767
Chương 3: Tích phân ường và tích phân mặt
ể chỉ hướng ã xác ịnh bởi n M( ) . Phía trên của mặt S là phía mà n M( ) lập với trục 0z góc nhọn, còn
phía dưới là phía mà n M( ) lập với trục 0z góc tù. n γ Phía trên Phía ngoài n − Phía trong n n −n γ n Phía d ướ i −n
Khi mặt cong S kín ịnh hướng ược, người ta dùng từ phía trong và phía ngoài ể mô tả
hướng ã xác ịnh. Phía ngoài là phía mà n M( ) hướng ra phía ngoài vật thể V bao quanh bởi mặt cong S,
phía trong là phía ngược lại. (H.3.16).
Có mặt cong không ịnh hướng ược, chẳng hạn mặt cong sau ây gọi là lá Mobius ược tạo như sau
: Lấy chữ nhật ABCD vặn cong ể hai ầu gắn nhau sao cho A trùng với C và B trùng
với D (H.3.17). Xác ịnh một véctơ n M( ) tại M nào ó của lá Mobius và cho M di chuyển theo lá
không cắt biên một vòng về lại iểm ban ầu thì n M( ) ối hướng. Chứng tỏ n M( ) không biến thiên liên
tục. Vậy lá Mobius là mặt một phía. 3.6.2. Định nghĩa 100
Downloaded by Ti?n D?ng Tr?n Lý (dungtienltr128@gmail.com) lOMoARcPSD| 10435767
Chương 3: Tích phân ường và tích phân mặt
Cho mặt cong S ã ịnh hướng theo phía trên hoặc phía dưới. Tức là véctơ pháp tuyến
n M( ) lập với trục 0z một góc nhọn (hoặc góc tù) và hàm R(x,y,z) xác ịnh trên S.
Chia mặt cong S thành n mảnh không dẫm lên nhau ΔS ii , =1, n . Ký hiệu ường kính của
mảnh thứ i là d ii , =1, n . Gọi ΔDi là hình chiếu của ΔSi lên mặt toạ ộ 0xy kèm theo dấu xác ịnh theo
quy tắc : S ịnh hướng theo phía trên thì ΔDi có dấu dương, còn S ịnh hướng theo
phía dưới thì ΔDi có dấu âm, i =1,n .
Lấy tuỳ ý Mi (xi , yi , zi )∈ΔS ii , =1, n n = Lập tổng I ∑ n
R x( i , yi , zi )ΔDi gọi là tổng tích phân mặt loại hai của hàm R x y z( , , )lấy i=1
trên mặt cong S ã ịnh hướng ứng với một cách chia và một cách chọn M ∈Δ i S ii , =1, n .
Nếu khi n→∞ sao cho max d → i
0 mà In hội tụ về số I không phụ thuộc cách chia S và cách chọn M ∈Δ i
Si thì số I gọi là tích phân mặt loại hai của biểu thức R x y z dxdy( , , ) trên mặt cong S
ã ịnh hướng và ký hiệu :
I = ∫∫R x y z dxdy( , , ) (3.32) S
Tương tự, nếu chiếu lên các mặt phẳng 0yz và 0zx và thêm các hàm P(x,y,z), Q(x,y,z) xác ịnh trên S thì ta gọi :
I = ∫∫P x y z dydz( , ,)+ Q x y z dzdx( , , )+ R x y z dxdy( , , ) (3.33) S
là tích phân mặt loại hai của các hàm P, Q, R, chính xác hơn là của biểu thức Pdydz+Qdzdx+Rdxdy
lấy trên mặt cong S ã ịnh hướng. Chú ý : a.
Theo ịnh nghĩa, nếu ổi hướng (phía ngược lại của S) thì tích phân mặt loại hai sẽ ổi dấu. → → → 101
Downloaded by Ti?n D?ng Tr?n Lý (dungtienltr128@gmail.com) lOMoARcPSD| 10435767
Chương 3: Tích phân ường và tích phân mặt b.
Công thức (3.33) mô tả thông lượng của trường véctơ F = P i + Q j + R k qua
mặt cong S ã ịnh hướng.
Φ = ∫∫Pdydz + Qdzdx + Rdxdy (3.34) S ( VM ) n M
Để thấy rõ ý nghĩa thực tế của tích phân mặt loại hai và từ ”thông lượng ” ta xét bài toán sau ây
: Giả sử có một dòng chất lỏng chảy trong miền V ⊂ R3 và trong miền V có một mặt
cong S ịnh hướng với véctơ pháp tuyến n M(
), M ∈S . Giả sử tốc ộ của dòng chất lỏng là
v M( ) (H.3.18). Hãy tính lượng chất lỏng chảy qua S trong một ơn vị thời gian.
Trước hết ta tính trong một thời gian, lượng chất lỏng chảy qua yếu tố diện tích dS của mặt
cong S. Vì mảnh dS là rất bé nên có thể coi véctơ n M( ) và véctơ vận tốc v M( ) là véctơ hằng tại mọi
iểm M ∈dS . Vậy lượng chất lỏng chảy qua dS sẽ là (cột chất lỏng) dφ= v ndS. . .
Gọi các thành phần của v là v vx, y ,vz , còn các thành phần của n là cosα,cosβ,cosγ thì :
Φ = ∫∫(vx cosα+ vy cosβ+ vz cos )γ dS S (3.35) = ∫∫v dydz + + x v dzdxy v dxdyz S
ó chính là tích phân mặt loại hai của các hàm vx ,vy ,vz trên S ã ịnh hướng. 102
Downloaded by Ti?n D?ng Tr?n Lý (dungtienltr128@gmail.com) lOMoARcPSD| 10435767
Chương 3: Tích phân ường và tích phân mặt
Công thức (3.35) ã mô tả mối liên hệ giữa tích phân mặt loại một và loại hai.
Trong trường hợp tổng quát khi có trường véctơ F P Q R( , , ) thì thông lượng của nó qua mặt
cong S ịnh hướng cho bởi công thức (3.34).
c. Người ta cũng chứng minh rằng, nếu mặt S ịnh hướng ược, trơn hoặc trơn từng mảnh
và các hàm P,Q,R liên tục trên S thì tích phân mặt loại hai (3.33) tồn tại.
d. Tích phân mặt loại hai cũng có các tính chất như tích phân ường loại hai.
3.6.3. Công thức tính
Định lý 3.6 : Giả sử R(x,y,z) liên tục trên mặt cong ịnh hướng S trơn cho bởi phương trình z = z
x y( , ),( ,x y)∈D .
Khi ó ∫∫R x y z dzdy( ,
, )= ±∫∫R x y z x y dxdy( , , ( , )) (3.36) S D
Dấu + khi lấy tích phân mặt loại hai theo phía trên của mặt S.
Dấu – khi lấy tích phân mặt loại hai theo phía dưới của S.
Chứng minh : Từ công thức (3.35) và (3.29) γ dxdy
∫∫ R x y z dxdy( , , )= ∫∫ R x y z( , , )cos .γdS = ∫∫ R x y z x y( , , ( , ))cos nếu cosγ≠ 0 S S S cosγ và ∫∫R x y z( , , ) = 0 nếu cosγ= 0 . S
Vậy khi lấy theo phía trên của mặt S tức là cosλ≥ 0 thì cosγ γ= cos . Do ó : ∫∫R x y z dxdy( ,
, )= ∫∫R x y z x y dxdy( , , ( , )) S
D còn khi lấy theo phía dưới của mặt S tức là cosγ≤ 0 thì cosγ= − cosγ . Do ó : ∫∫R x y z dxdy( ,
, )= −∫∫R x y z x y dxdy( , , ( , )) S D
Tương tự ta có : ∫∫P x y z dxdy( , , )= ±∫∫P x y z( ( , ), y z dydz, ) (3.37) 103
Downloaded by Ti?n D?ng Tr?n Lý (dungtienltr128@gmail.com) lOMoARcPSD| 10435767
Chương 3: Tích phân ường và tích phân mặt S D yz
∫∫Q x y z dxdy( , , )= ±∫∫Q x y z x( , ( , ), z dzdx) (3.38) S D zx
Trong ó Dyz là hình chiếu của S lên mặt 0yz và mặt S có phương trình : x = x
y z( , ),( ,y z)∈D
Dzx là hình chiếu của S lên mặt 0zx và mặt S có phương trình : y
= y z x( , ),( ,z x)∈D .
Chú ý : Khi lấy tích phân mặt loại hai, phải ặc biệt lưu ý ến việc ịnh hướng của mặt S,
tức là hướng của n M( ) . Tuỳ theo n M( ) lập với các trục toạ ộ góc nhọn hay tù mà xác ịnh dấu cộng
hay trừ trong các công thức (3.36), (3.37), (3.38).
Ví dụ 11 : Tìm thông lượng của trường véctơ F = (z,0, x2 ) qua phía trên của mặt z = x2 + y2
,−1≤ x ≤1,−1≤ y ≤1.
Giải : Mặt cong z = x2 + y2 là paraboloid tròn xoay .H.3.19 mô tả phần mặt cong nằm ở góc phần
tám thứ nhất. Thông lượng tính theo công công thức (3.35).
Φ = ∫∫ zdydz + x dxdy2 S 104
Downloaded by Ti?n D?ng Tr?n Lý (dungtienltr128@gmail.com) lOMoARcPSD| 10435767
Chương 3: Tích phân ường và tích phân mặt − 2x
S ược ịnh hướng lên trên nên cosγ≥ 0,cosα=. Do mặt cong S ối 4x 2 + 4y 2 +1
xứng qua các mặt toạ ộ 0yz,0zx nên ∫∫ zdydz = 0 và S S D 0 0 0 ≤ x ≤1 (D là hình vuông ) 0 ≤ y ≤1 =
Ví dụ 12 : Tính I ∫∫ zdxdy với S là phía ngoài của mặt cầu x2 + y2 + z2 = R2 S
Giải : Mặt cầu cho bởi H.3.20.
Chia mặt cầu thành nửa trên S+ và nửa dưới S− có phương trình lần lượt là : z =
R2 − x2 − y2 và z = − R2 − x2 − y2
Chiếu các nửa mặt cầu lên 0xy ta ược hình tròn :
⎧⎪x 2 + y 2 ≤ R 2 D :⎨ ⎪⎩z = 0 z R 2 2 2 z = R x −− y R - R y 0 R x 2 2 2 z =− R x −− y H.3.20
I = ∫∫ zdxdy + ∫∫ zdxdy S+ S− 105
Downloaded by Ti?n D?ng Tr?n Lý (dungtienltr128@gmail.com) lOMoARcPSD| 10435767
Chương 3: Tích phân ường và tích phân mặt
Tích phân lấy theo phía trên của S+ và tích phân lấy theo phía dưới của S .
Từ ông thức (3.36) ta có :
∫∫ zdxdy = ∫∫ R 2 − x 2 − y dxdy2 S+ D ⎞
∫∫ zdxdy = −∫∫⎛⎜−R 2 − x 2 − y 2 ⎟dxdy ⎝ ⎠ S− D
Vậy I = 2∫∫ R2 − x2 − y dxdy2 S
Chuyển sang toạ ộ cực ta có : π I = 2 ∫ ∫ 2
πdϕR 0 R 2 − r 2 . .r dr = 2 ⎜⎛⎜⎝
2 2 − r 2 ) 32 ⎟⎞⎠⎟0R = 43 R3 − (R 3 0
3.7. Công thức Stokes
Dưới ây ta sẽ có công thức mở rộng công thức Green, ó là mối liên hệ giữa tích phân ường loại
hai trong không gian với tích phân mặt loại hai.
Định lý 3.7(Stokes) : Giả sử mặt cong S ịnh hướng ược, trơn từng mảnh có biên là ường L
trơn từng khúc. Nếu các hàm số P,Q,R liên tục cùng với các ạo hàm riêng cấp một của chúng trên mặt cong S thì : ∫ ∫∫ ⎝⎛ ∂ L + S y
∂z ⎠⎟dydz + ⎛⎜⎝ ∂∂Pz − ∂∂Rx ⎠⎟⎞dzdx + ⎝⎛⎜⎜ ∂∂Qx − ∂∂Py ⎠⎞⎟⎟dxdy
(3.39) Pdx + Qdy + Rdz =
⎜⎜ ∂R − ∂Q ⎞⎟
trong ó tích phân ường ở vế trái lấy theo hướng dương quy ước như sau : Đi theo hướng dương của L
sao cho mặt cong S ở phía tay trái, khi ó mặt cong S ược ịnh hướng bởi véctơ pháp
tuyến n hướng từ chân lên ầu (H.3.21).
Gọi (3.39) là công thức Stokes. 106
Downloaded by Ti?n D?ng Tr?n Lý (dungtienltr128@gmail.com) lOMoARcPSD| 10435767
Chương 3: Tích phân ường và tích phân mặt n Chú ý:
a. Công thức Green là trường hợp riêng của công thức Stokes ( khi thay
z = 0, R x y z( , , ) = 0 vào (3.39) nhận ược công thức (3.20)). b.
Tính tích phân ường loại hai khi L ⊂ R3 thường rất khó khăn (ta mới chỉ ưa ra công
thức tính khi L cho bởi phương trình tham số, xem công thức (3.17)). Do ó công thức Stokes tỏ ra
rất hiệu lực khi mà L là biên của các mặt cong nào ó mà tích phân mặt loại hai trên nó có thể tính dễ dàng. c.
Xuất phát từ công thức Stokes, ta nhận ược ịnh lý bốn mệnh ề tương ương xét trong
không gian R3 tương tự như ịnh lý 3.4.
Định lý 3.8: Giả sử các hàm P x y z Q x y z( , , ), ( , , ),R x y z( , , ) liên tục cùng với các ạo
hàm riêng cấp một của chúng trên miền ơn liên V. Khi ó bốn mệnh ề sau ây là tương ương với nhau:
∂R ∂Q ∂P ∂R ∂Q ∂P
(1). = , = , = ,∀(x y z, , )∈V ∂y ∂z ∂z ∂x ∂x ∂y
(2). ∫Pdx + Qdy + Rdz = 0 , L là ường cong kín bất kỳ nằm trong miền V. L
(3). ∫ Pdx +Qdy + Rdz , trong ó AB ⊂V , chỉ phụ thuộc vào hai iểm A,B mà không AB
phụ thuộc dạng cung AB .
(4). Biểu thức Pdx + Qdy + Rdz là vi phân toàn phần của hàm u(x,y,z) nào ó trên miền V.
Trường hợp miền V là không gian thì hàm u(x,y,z) có thể tính theo công thức : x y z
u x y z( , , ) = ∫ P x y z dx( , , )+ ∫ Q x( o, , )y z dy + ∫ R x( 0, y0, )z dz +C (3.40) x0 y0 z0 107
Downloaded by Ti?n D?ng Tr?n Lý (dungtienltr128@gmail.com) lOMoARcPSD| 10435767
Chương 3: Tích phân ường và tích phân mặt
trong ó (x0 , y0 , z0 )∈V,( , , )x y z ∈V C, là hằng số tuỳ ý và:
∫ Pdx +Qdy + Rdz = u A( )−u B( ) (3.41) AB
trong ó AB ⊂V .
Ví dụ 13: Tính I ydx zdy
xdz , với C là ường tròn, giao của mặt cầu
x2 + y2 + z2 = R2 và mặt phẳng x + y + z = 0 và hướng của L là ngược chiều kim ồng hồ nếu
nhìn về phía z > 0 . z R n R y 0 x C H.3.22
Giải : Mặt phẳng x+ +y
z = 0 i qua tâm mặt cầu. Vậy giao tuyến là ường tròn lớn .
Xem hình H.3.22. Lấy hình tròn là mặt cong S có biên là C. Các côsin chỉ phương của n ịnh hướng theo 1
hướng của C là cosα β γ= cos = cos = 3 (Xem công thức (3.30)). Đặt P = y Q,
= z R, = x , áp dụng công thức Stokes và công thức liên hệ giữa tích phân mặt loại hai
và loại một theo công thức (3.35), ta có :
I = −∫∫dydz + dzdx + dxdy = − 3∫∫dS = −π 3R .2 S S 108
Downloaded by Ti?n D?ng Tr?n Lý (dungtienltr128@gmail.com) lOMoARcPSD| 10435767
Chương 3: Tích phân ường và tích phân mặt
3.8. Công thức Gauss – Ostrogradski
Dưới ây ta có công thức liên hệ giữa tích phân bội ba và tích phân mặt loại hai, gọi ó là công thức Gauss – Ostrogradski.
Định lý 3.9 (Gauss – Ostrogradski) : Giả sử V là miền giới nội trong R3 có biên là mặt S
trơn từng mảnh. Nếu các hàm số P,Q,R liên tục cùng với các ạo hàm riêng cấp một của chúng trong miền V thì : ⎞
∫∫S Pdydz + Qdzdx + Rdxdy = ∫∫∫V ⎜⎜⎛⎝ ∂∂Px + ∂∂Qy + ∂∂Rz ⎟⎟⎠dxdydz (3.42)
trong ó mặt lấy tích phân ịnh hướng ra phía ngoài miền V. Chú ý : a.
Nếu trong công thức (3.41) ặt P = x Q, = y R, = z thì ta nhận ược công thức tính thể
tích vật thể V nhờ vào tích phân mặt loại hai :
V = 1 ∫∫ xdydz + ydzdx + zdxdy 3 S
trong ó S ược ịnh hướng ra phái ngoài miền V. b.
Có thể coi rằng công thức Gauss – Ostrogradski là mở rộng công thức Green từ không
gian hai chiều ra ba chiều. Vì thế ôi khi tính tích phân trên mặt S không kín, ta có thể thêm mặt cong
nào ó ể áp dụng công thức Gauss –Ostrogradski. = Ví dụ 14 : q r.
Tính thông lượng của trường iện từ F
trong ó q là iện tích ặt tại gốc r 3
toạ ộ, r = xi + y j + zk , r = x2 + y2 + z2 qua phía ngoài mặt cầu : x2
+ y2 + z2 = R2 Giải : x y z Đặt P = q ,Q = q , R = q ,∀(x y z, , ) ≠
(0,0,0). r 3 r 3 r 3
Vì thế ta không thể áp dụng công thức Gauss – Ostrogradski Ta có Φ =
(xdydz + ydzdx + zdxdy). S r
Do mặt cầu ối xứng qua gốc toạ ộ và biểu thức dưới dấu tích phân ối xứng ối với x,y,z 109
Downloaded by Ti?n D?ng Tr?n Lý (dungtienltr128@gmail.com) lOMoARcPSD| 10435767
Chương 3: Tích phân ường và tích phân mặt q z
do ó : Φ=24 ∫∫ r 3 dxdy, S là phần mặt cầu góc phần tám thứ nhất ịnh hướng lên trên. S R − − 2 x2 y2 ∫∫ Φ = 24q 3 dxdy D1 R
D1 là phần tư hình tròn tâm 0, bán kính R. Chuyển sang toạ ộ cực ta có : π Φ = 24 Rq ∫ ∫ − = ⎛⎜⎝− − ⎞⎟⎠ 3 2 dϕR R2 r rdr2 24q 2Rπ 3 13(R2 r )2 23 0R = 4πq. 0 0 =
Ví dụ 15 : Tính I ∫∫ xzdydz +yxdzdx + zydxdy lấy theo phía ngoài của S là biên của hình S
chóp x ≥ 0,y ≥ 0,z ≥ 0,x + y+ z ≤1.
Giải : Hình chóp V cho trên hình H.3.23 z 1 1 y 0 1 x H.3.23
Áp dụng công thức (3.41) có : I = ∫∫∫(z + x + y dxdydz) V ⎧x + y ≤1
Chiếu V lên mặt phẳng 0xy ược tam giác : ⎨⎩x ≥ 0, y ≥ 0 110
Downloaded by Ti?n D?ng Tr?n Lý (dungtienltr128@gmail.com) lOMoARcPSD| 10435767
Chương 3: Tích phân ường và tích phân mặt 1 1−x 1− −x y
I = ∫ dx ∫ dy ∫(x + y + z dz) 0 0 0 [ ]
= ∫1 dx1−∫x 1 (x + y + z)1− x − ydy = ∫1 dx1−∫x 1 1− (x + y) 2 dy 0 0 20 0 0 2
= 1 ⎛⎜∫1 (1− x dx)− 1 ∫1 (x + y)3 1− xdx⎟⎞ = 1 − x 2 1 − 1 + 1 x 4 1 2 ⎜⎝ 0 3 00 ⎟⎠ 2 4 0 6 24 0 TÓM TẮT CHƯƠNG 3
• Cách tính tích phân ường loại một 1.
Giả sử cung AB trơn cho bởi phương trình: y = y x( ), a ≤ x ≤ b và hàm số f(x,y) liên
tục trên cung AB . Khi ó: b ∫ f (x y ds, )= ∫ f x y x( , ( )) 1+ y ' (2 x dx) AB a 2.
Nếu cung AB cho bởi phương trình tham số: ⎧x = x t( )
⎨y = y t( ) , t ≤ i t ≤ t2 : ⎩ t2
∫ f (x y ds, )= ∫ f x t[ ( ), ( )]y tx' ( )2 t + y' ( )2 t dt AB t1
• Cách tính tích phân ường loại hai
1. Giả sử hai hàm số P(x,y), Q(x,y) liên tục trên cung AB trơn cho bởi phương trình tham 111
Downloaded by Ti?n D?ng Tr?n Lý (dungtienltr128@gmail.com) lOMoARcPSD| 10435767
Chương 3: Tích phân ường và tích phân mặt ⎧x = x t( )
số: ⎨y = y t( ) Điểm A ứng với giá trị tham số t = tA , B ứng với giá trị tham số tB . Khi ó: ⎩ tB
∫ P x y dx( , )+Q x y dy( , )= ∫ [ ( ( ), ( )) '( )P x t y tx t + P x t( ( ), ( )) '( )]y t y t dt AB tA
2 .Khi cung AB phẳng cho bởi phương trình dạng tường minh y=y(x), A,B có hoành ộ tương ứng
là a, b, ta nhận ược: b ∫ P x y dx( ,
)+Q x y dy( ,)= ∫[P x y x( , ()) +Q x y x y x dx( , ( )) '( )] AB a
• . Công thức Green.. Cho các hàm số P(x,y), Q(x,y) liên tục cùng các ạo hàm riêng cấp một
trong miền D có biên là ường L, khi ó: dxdy Pdx Qdy ∂ D x ∂ L
.•. Bốn mệnh ề sau ây tương ương trong không gian R2 ∂P ∂Q (1).
= , ( , )∀ x y ∈ D ∂y ∂x
(2). ∫Pdx + Qdy = 0 , L là ường cong kín bất kỳ nằm trong miền D. L
(3). ∫ Pdx +Qdy , trong ó cung AB nằm trong miền D, chỉ phụ thuộc vào 2 iểm A,B AB
mà không phụ thuộc dạng cung AB .
(4). Biểu thức Pdx + Qdy là vi phân toàn phần của hàm u(x,y) nào ó trên miền D. x y
u x y( ,) = ∫ P x y dx( ,
) + ∫Q x( 0 , y dy) + C x0 y0 x y 112
Downloaded by Ti?n D?ng Tr?n Lý (dungtienltr128@gmail.com) lOMoARcPSD| 10435767
Chương 3: Tích phân ường và tích phân mặt = + u x y( ,) ∫ P x y( , ∫ 0 )dx Q x y dy( ,
) + C trong ó A x( 0 , y0 )∈D M x y, ( , )∈D x0 y0 •
Công thức tính tích phân mặt loại một: Hàm số f(x,y,z) liên tục trên mặt cong S trơn cho
bởi phương trình z = z x y( , ),( ,x y)∈D . Khi ó: ∫∫ f x y z dS( ,
, )= ∫∫ f x y z x y( , , ( ,
)) 1 + z'2x (x y, )
+ z'2y (x y dxdy, ) S D •
Công thức tính tích phân mặt loại hai : Hàm số R(x,y,z) liên tục trên mặt cong ịnh hướng
S trơn cho bởi phương trình z = z x y( , ),( ,x y)∈D .
Khi ó ∫∫R x y z dzdy( ,
, )= ±∫∫R x y z x y dxdy( ,, ( , )) S D
Dấu + khi lấy tích phân mặt loại hai theo phía trên của mặt S.
Dấu – khi lấy tích phân mặt loại hai theo phía dưới của S. • Công thức Stokes ∫ ∫∫ L + S ⎝⎛ ∂y
∂z ⎟⎠dydz + ⎛⎜⎝ ∂∂Pz − ∂∂Rx ⎞⎠⎟dzdx + ⎜⎜⎝⎛ ∂∂Qx − ∂∂Py
⎠⎟⎟⎞dxdy Pdx + Qdy + Rdz = ⎜⎜ ∂R − ∂Q ⎞⎟ •
Bốn mệnh ề tương ương trong không gian R3
∂R ∂Q ∂P ∂R ∂Q ∂P
(1). = , = , = ,∀(x y z, , )∈V ∂y ∂z ∂z ∂x ∂x ∂y
(2). ∫Pdx + Qdy + Rdz = 0 , L là ường cong kín bất kỳ nằm trong miền V. L
(3). ∫ Pdx +Qdy + Rdz , trong ó AB ⊂V , chỉ phụ thuộc vào hai iểm A,B mà không AB
phụ thuộc dạng cung AB
(4) Biểu thức Pdx + Qdy + Rdz là vi phân toàn phần của hàm u(x,y,z) nào ó trên x y z
u x y z( , , ) = ∫ P x y z dx( , , )+ ∫ Q x( o, , )y z dy + ∫ R x( 0, y0, )z dz +C
x0 y0 z0 trong ó (x0 , y0 , z0 )∈V,( , , )x y z ∈V C, là hằng số tuỳ ý và: 113
Downloaded by Ti?n D?ng Tr?n Lý (dungtienltr128@gmail.com) lOMoARcPSD| 10435767
Chương 3: Tích phân ường và tích phân mặt
∫ Pdx +Qdy + Rdz = u A( )−u B( ) AB • Công thức Ostrogradski ∫∫ ⎞
S Pdydz + Qdzdx + Rdxdy = ∫∫∫V ⎜⎜⎛⎝ ∂∂Px + ∂∂Qy + ∂∂Rz ⎟⎟⎠dxdydz = 1
Ứng dụng tính thể tích V
∫∫ xdydz + ydzdx + zdxdy trong ó S ược ịnh hướng ra 3 S phía ngoài miền V.
CÂU HỎI VÀ BÀI TẬP CHƯƠNG 3.
3.1. Có thể dùng tích phân ường loại 1 ể tính ộ dài một cung Đúng Sai
3.2. Tích phân ường loại 1 phụ thuộc vào hướng i của ường cong Đúng Sai
3.3. Có thể dùng tích phân ường loại 2 ể tính công của một lực. Đúng Sai
3.4. Tích phân ường loại 2 phụ thuộc vào hướng i của ường cong. Đúng Sai
3.5. Có thể dùng tích phân ường loại 2 ể tính diện tích một hình phẳng. Đúng Sai
3.6.∫ Pdx +Qdy = 0 ⇒ ∂Q = ∂P trong miền D giới hạn bởi ường cong L ∂x ∂y L Đúng Sai
3.7 Công thức Green chỉ úng cho miền ơn liên. Đúng Sai
3.8 Định lý 4 mệnh ề tương ương úng với miền liên thông. Đúng Sai
3.9 Có thể dùng tích phân mặt loại 1 ể tính diện tích mặt cong. Đúng Sai 114
Downloaded by Ti?n D?ng Tr?n Lý (dungtienltr128@gmail.com) lOMoARcPSD| 10435767
Chương 3: Tích phân ường và tích phân mặt
3.10 Tích phân mặt loại 1 không phụ thuộc vào hướng lấy tích phân mặt Đúng Sai
3.11 Dùng tích phân mặt loại 2 ể tính thông lượng của một trường véctơ. Đúng Sai
3.12 Có thể biểu diễn tích phân mặt loại 2 qua tích phân mặt loại 1 Đúng Sai
3.13 Có thể biểu diễn tích phân ường loại 2 theo ường cong kín qua tích phân mặt loại 2. Đúng Sai
3.14 Có thể biểu diễn tích phân mặt loại 2 theo phía trong của mặt cong qua tích phân bội 3. Đúng Sai
3.15 Tính tích phân mặt loại 1, mặt loại 2 phải ưa về tích phân bội 2. Đúng Sai
3.16 Tính các tích phân ường loại 1 sau:
a. ∫xyds , L là biên hình chữ nhật ABCD với A(0,0), B(4,0), C(4,2), D(0,2) L ⎧ ⎪x = t ⎪ 2
b. ∫xyzds, L cho bởi phương trình ⎪⎨y = t , 0 ≤ t ≤ 1 ⎪ ⎪ 2 L 3 ⎪ 8 t z = ⎩ 3 a ⎛⎜ea + ⎞⎟ x
e−ax ⎟, 0 ≤ x ≤ a với
3.17. Tính khối lượng của dây vật chất có phương trình y = ⎜ 2 ⎝ ⎠
khối lượng riêng ρ(x y, ) = 1 y
3.18. Tính các tích phân ường loại 2 sau: 115
Downloaded by Ti?n D?ng Tr?n Lý (dungtienltr128@gmail.com) lOMoARcPSD| 10435767
Chương 3: Tích phân ường và tích phân mặt a. y dx x y
dy , ABC là ường gấp khúc với A(0,0), B(2,2), C(4,0)
b. ∫ ydx − (y + x2 )dy , L là cung parabol y = 2x − x2 nằm ở phía trên trục 0x theo chiều L kim ồng hồ.
3.19. Tính ∫ (xy −1)dx + x ydy2 từ A(1,0) ến B(0,2) theo: L
a. ường 2x + y = 2
b. ường 4x + y 2 = 4 ⎧x = cost
c. ường ⎨y = 2sint ⎩
3.20. Tính ∫xdy và ∫ydx theo chiều dương với L là: L L
a. ường tròn x 2 + y 2 = a 2
b. biên của nửa hình tròn x 2 + y 2 ≤ a 2 , y > 0
c. tam giác có ba ỉnh O(0,0), A(a,0) và B(0,b)
3.21. Tính ∫(x 2 + y 2 )dx + (x 2 − y 2 )dy với L là biên của tam giác OAB theo chiều dương, L
biết O(0,0), A(1,0), B(0,1).
a. bằng cách tính trực tiếp b. dùng công thức Green
3.22. Tính ∫(1 − x 2 )ydx + x(1 + y 2 )dy với L là ường x 2 + y 2 = R 2 (theo chiều dương) L bằng hai cách: a. trực tiếp b. dùng công thức Green
3.23. Tính các tích phân ường sau theo chiều dương: 116
Downloaded by Ti?n D?ng Tr?n Lý (dungtienltr128@gmail.com) lOMoARcPSD| 10435767
Chương 3: Tích phân ường và tích phân mặt ∫ ⎡⎛ + x
⎞⎟dy − ⎛⎜x + y ⎞⎟dx⎤⎥ , L là biên của tam giác ABC, A(-1,0), B(1,-2), C(1,2).
a. L xy⎢⎜⎝ y 2⎠ ⎝ 2 ⎠ ⎦ ⎣ b. ∫ ⎞ ⎛
x3 ⎜⎛ y + x ⎟dy − y 3 ⎜x + y ⎞⎟dx, L là ường x 2 + y 2 = 2x ⎝ L 4 ⎠ ⎝ 4 ⎠
3.24. Tích phân ường sau ây có phụ thuộc vào ường lấy tích phân không? Tính tích phân theo AB tương ứng: a. y y y + y y ⎟⎞ ∫ ⎜⎝⎛ 2 ⎠⎟⎞ ⎝⎛ AB 1− x 2 cos x sin cos
dy với A(1,π), B(2,π), AB không cắt trục Oy. + dx ⎜ x x x ⎠ b. ∫ + ⎛⎜ AB x2
y2 3x2 x− y2 dx + 3y2y− x2 dy⎞⎟⎠với A(1,1), B⎜⎛⎝π2 ,2⎞⎟⎠ xy ⎝
⎧⎪x = t + cos2 t ≤ t ≤ π và không cắt các trục toạ ộ.
AB có phương trình ⎨ 2 , 0
⎪⎩y =1+ sin t 2
3.25. Chứng minh rằng các biểu thức Pdx + Qdy sau ây là vi phân toàn phần của hàm u(x,y) nào ó. Tìm u?
a. (x 2 − 2xy 2 + 3)dx + (y 2 − 2x y2 + 3)dy
b. ⎡⎣ex y+ +cos(x − y)⎤⎦dx + ⎡⎣ex y+ −cos(x − y)+ 2⎤⎦dy ] ]
c. e x [e y (x − y + 2) + y dx
+ e x [e y (x − y) +1 dy xdx
1− x 2 − y 2 d. + 2 2 2 2
ydy x + y x + y 1 − ydx + xdy 117
Downloaded by Ti?n D?ng Tr?n Lý (dungtienltr128@gmail.com) lOMoARcPSD| 10435767
Chương 3: Tích phân ường và tích phân mặt 3.26. Tính ∫ 2 2 với: 2πL x + y
a. L là ường x 2 + y 2 = a 2 (theo chiều ngược kim ồng hồ)
b.L là biên hình vuông với ỉnh (-1,-1), (-1,1), (1,1), (1,-1) (theo chiều thuận kim ồng hồ).
3.27. Tìm m, a, b ể các biểu thức sau là vi phân toàn phần của hàm số u nào ó và tìm hàm số ó
(x − y dx)+ (x + y dy) a. 2 2 m (x + y )
(ax 2 + 2xy + y 2 )dx − (x 2 + 2xy + by 2 )dy b. (x + 2 y 2 )2
3.28. Tính ∫∫(x 2 + y 2 )dS nếu: S
a. S là mặt nón z 2 = x 2 + y 2 , 0 ≤ z ≤1
b. S là mặt cầu x 2 + y 2 + z 2 = a 2
3.29. Tính các tích phân mặt loại một sau: ∫∫⎛ + 2x
+ 4y ⎞⎟dS , S là phần của mặt phẳng x + y + z =1 nằm trong góc phần tám a. ⎜z ⎝ 3 ⎠ 2 3 4 S thứ nhất. b.
∫∫(yz + zx + xy dS) , S là phần của mặt nón z = x2 + y2 nằm trong mặt trụ S
x2 + y2 = 2ax a, > 0 x 2 c.
∫∫ xdS , S là phần của mặt trụ parabolic z =
nằm trong góc phần tám thứ nhất của S 2
mặt trụ x 2 + y 2 =1.
3.30. Tính các tích phân mặt loại hai sau: 118
Downloaded by Ti?n D?ng Tr?n Lý (dungtienltr128@gmail.com) lOMoARcPSD| 10435767
Chương 3: Tích phân ường và tích phân mặt
a. ∫∫ xyzdxdy, S là mặt ngoài của phần hình cầu xác ịnh bởi x2 + y2 + z2 ≤1, x ≥ 0, y ≥ 0. S
b. ∫∫ xdydz +dzdx + xz dxdy2
, S là mặt ngoài của phần hình cầu xác ịnh bởi
S x 2 + y 2 + z 2 ≤1, x ≥ 0,
y ≥ 0, z ≥ 0. y z dydz dzdx dxdy x 2 2 2 ∫∫ + + c. x + y + z
, S là mặt ngoài của ellipsoid a ≤ 2 b2 c 2 1 S d. ∫∫ x y zdxdy2 2
, S là mặt trên nửa mặt cầu x 2 + y 2 + z 2 = R 2 , z ≤ 0 . S
3.31. Tính các tích phân ường sau theo hướng ngược kim ồng hồ nhìn từ phía z> 0:
∫2 3 + dy + zdz , L là ường tròn ⎧⎨x + = 2 y 2 R 2 a. x y dx ⎩ L z = 0 ⎧x + + = 2 y 2 z 2 R 2
b. ∫ydx + zdy + xdz , L là ường tròn ⎨ ⎩ L
x + y + z = 0
3.32. Tính các tích phân mặt theo phía ngoài của vật thể bao bởi mặt cong S. a.
∫∫ xzdydz + yxdzdx + zydxdy, S là biên của hình chóp x ≥ 0, y ≥ 0, z ≥ 0,x + y+ z ≤1. S b. ∫∫ x dydz3 + y dzdx3 + z dxdy3
, S là mặt cầu x2 + y2 + z2 = R .2 S c.
∫∫ x dydz2 + y dzdx2 + z dxdy2 , S là biên của hình lập phương S
0 ≤ x ≤ a, 0 ≤ y ≤ a, 0 ≤ z ≤ a. 119
Downloaded by Ti?n D?ng Tr?n Lý (dungtienltr128@gmail.com) lOMoARcPSD| 10435767
Tài liệu tham khảo 120
Downloaded by Ti?n D?ng Tr?n Lý (dungtienltr128@gmail.com) lOMoARcPSD| 10435767
Chương 4. Lý thuyết trường
CHƯƠNG 4. LÝ THUYẾT TRƯỜNG GIỚI THIỆU
Trong vật lý, ặc biệt trong kỹ thuật thường gặp khái niệm trường: Trường nhiệt ộ, từ trường,
iện trường,.... Khái niệm trường trong toán học là tổng quát hoá các trường hợp cụ thể ó. Miền
xác ịnh một trường vô hướng u(x,y,z) nếu tại mọi iểm M x y z( , , )∈Ω ều xác ịnh ại lượng
vô hướng u(M). Chẳng hạn trường nhiệt ộ là một trường vô hướng. Vậy ặc trưng của trường vô
hướng là một hàm vô hướng. Miền
xác ịnh một trường véctơ
F x y z( , , ) nếu tại mọi iểm M x y z( , , )∈Ω ều xác ịnh ại lượng véctơ:
F x y z( , , ) = P x y z i( , , ).+ Q x y z j( , , ).+ R x y z k( , , ).= (P Q R, , )
Chẳng hạn từ trường là một trường véc tơ. Vậy ặc trưng của trường véctơ là một hàm véctơ.
Một trường véctơ xác ịnh khi biết ba thành phần của véctơ ặc trưng cho trường ó: P x y z Q x y z( ,
, ), ( , , ),R x y z( , , ), tức là biết ba trường vô hướng. Từ nay về sau ta dùng các ký
hiệu: r = (x y z, , ) thay cho 0M , trong ó M có toạ ộ (x,y,z), dr= (dx dy dz, , ) dS = (dydz dzdx dxdy, , ).
Để học tốt chương này, người học cần thông thạo phép tính vi tích phân hàm nhiều biến.
Trong chương này, yêu cầu nắm vững các nội dung chính sau ây:
1. Các ặc trưng của trường vô hướng.
Mặt mức, Gra iên và ý nghĩa vật lí của các ại lượng ó.
2. Các ặc trưng của trường véctơ.
Đường dòng, thông lượng, ộ phân kì, hoàn lưu, véctơ xoáy và ý nghĩa vật lí của các ại lượng ó.
3. Các trường ặc biệt
Điều kiện nhận biết và tính chất của các trường ặc biệt: trường ống, trường iều hoà, trường thế. NỘI DUNG
4.1. Các ặc trưng của trường vô hướng 4.1.1. Mặt mức
Cho trường vô hướng u(x,y,z),(x y z, , )∈Ω . Tập các iểm (x y z, , )∈Ω thoả mãn phương
trình: u x y z( , , ) = C , C là hằng số (4.1) 121
Downloaded by Ti?n D?ng Tr?n Lý (dungtienltr128@gmail.com) lOMoARcPSD| 10435767
Chương 4. Lý thuyết trường
gọi là mặt mức của trường vô hướng ứng với giá trị C. Rõ ràng các mặt mức khác nhau (các giá trị
C khác nhau) không giao nhau và miền Ω bị phủ kín bởi các mặt mức. Nếu thì ta có khái
niệm ường mức (ường ẳng trị) cho bởi phương trình: u x y( , ) = C =
Chẳng hạn, một iện tích 1
q ặt ở gốc toạ ộ gây nên một trường iện thế u x y z( , , ) . Khi ó
mặt mức có phương trình: q = C x2 + y 2 + R 2
x2 + y 2 + z 2 = R C 2
hay x2 + y 2 + z 2 = q 2
2 . Đó là các mặt cầu ồng tâm 0.
4.1.2.Gra iên (Gradient)
Cho trường vô hướng u = u x y z( , , ),( , ,x y z)∈Ω và u x y z( , , ) khả vi trên Ω . Khi ó
⎛ ∂u ∂u ∂u ⎟⎟⎞,( , , )x y z ∈Ω . (4.2) gradu , ,
x y z( , , ) = ⎜⎜ ∂x ∂y ∂x ⎠ ⎝
(Xem mục 1.2.8,Chương 1.) Vậy một trường vô hướng u x y z( , , ) ã sinh ra một trường véctơ gradu x y z( , , ) .
Từ tính chất của phép tính ạo hàm, ta có các tính chất sau ây của Gra iên
grad(λu) =λgradu , λ là hằng số. grad u( + v) = gradu + gradv
grad u v( . ) = v gradu. + u gradv. u 1 = grad v
v2 (vgradu −ugradv), nếu v ≠ 0 gradf(u) = f '(u)gradu.
4.2. Các ặc trưng của trường véctơ
4.2.1. Đường dòng
Cho trường véctơ F M( ) = P x y z i( , , )+ Q x y z j( , , ).+ R x y z k( , , ) , (x y z, , )∈Ω .
Đường cong C ⊂ Ω gọi là ường dòng của trường véctơ F M( )nếu tại mỗi iểm M trên ường cong 122
Downloaded by Ti?n D?ng Tr?n Lý (dungtienltr128@gmail.com) lOMoARcPSD| 10435767
Chương 4. Lý thuyết trường
C, tiếp tuyến của C tại ó có cùng phương với véctơ F M( ). Chẳng hạn các ường sức trong từ trường
hoặc iện trường là các ường dòng. Nếu ường dòng có phương trình : ⎧x = x t( ) ⎪ = y t( ) ⎨y
⎪⎩z = z t( ) →
và P,Q,R là các thành phần của F thì ta có hệ thức:
x t'( ) = y t'( ) = z t'( ) (4.3)
P x y z( , , ) Q x y z( , , ) R x y z( , , )
Gọi (4.3) là hệ phương trình vi phân của họ ường dòng của trường véctơ F x y z( , , ) .
Chẳng hạn một iện tích q ặt tại gốc toạ ộ tạo ra một iện trường E , theo ịnh luật Culông thì : ⎛ ⎜ E = . qr qx qy qz =⎜ , , 3 3 3 3 r ⎜⎜ ⎝ 2 2 2 2 2 2 2 2 2 2 2 2
( x + y + z )
( x + y + z )
( x + y + z ) ⎞ ⎟ ⎟ ⎟⎟
⎠ Khi ó hệ phương trình vi phân của họ ường dòng là : dx = dy = dz x y z
Để giải hệ phương trình này, bạn ọc có thể xem trong [2],[6 .] Kết quả họ ường dòng (
trong vật lí, thường gọi là các ường sức) cho bởi phương trình : x = k t y1 , = k t z2 , = k t3 , k1,k2
,k3 là các hằng số tuỳ ý.
Đó là họ ường thẳng i qua gốc toạ ộ.
4.2.2. Thông lượng của trường véctơ
Trong mục 3.6.2 ta ã ưa ra ịnh nghĩa thông lượng của trường véctơ F x y z( , , ) qua mặt cong
ịnh hướng S xác ịnh theo công thức (3.35) : 123
Downloaded by Ti?n D?ng Tr?n Lý (dungtienltr128@gmail.com) lOMoARcPSD| 10435767
Chương 4. Lý thuyết trường
Φ = ∫∫F n dS. .= ∫∫Pdydz + Qdzdx + Rdxdy = ∫∫F dS. (4.4) S S S
Trong ó n(cosα β γ,cos
,cos ) là véctơ ơn vị của véctơ pháp tuyến của mặt S ược ịnh
hướng, P, Q, R là các thành phần của F .
4.2.3. Đive (Divergence, ộ phân kỳ)
Ta gọi ộ phân kỳ hay gọi tắt là dive của trường véctơ F x y z( , , ) tại iểm M(x,y,z) là ại
lượng vô hướng, ký hiệu divF x y z( , , ) , xác ịnh theo công thức :
divF x y z( , , ) = ∂P + ∂Q + ∂R (4.5) ∂x ∂y ∂z
Vậy một trường véctơ F ã sinh ra một trường vô hướng divF .
Nếu miền V ⊂ Ω có biên là S thì công thức Gauss –Ostrogradski (3.42) có dạng :
∫∫F n dS. .= ∫∫∫divF x y z dxdydz( , , ) (4.6) S V
Nghĩa là thông lượng của trường véctơ F qua phía ngoài mặt S bao miền V bằng tổng ộ phân
kỳ tại tất cả các iểm trong miền V của trường véctơ. Theo ý nghĩa cơ học của tích phân bội
ba, suy ra divF x y z( , , ) chính là mật ộ thông lượng tại iểm M(x,y,z) của trường. Từ ý nghĩa vật lý
của trường vận tốc ta thấy thông lượng của trường vận tốc qua mặt kín S ra phía ngoài là hiệu của
lượng vật chất từ trong chảy ra và từ ngoài vào qua S (chẳng hạn lượng nước). Nếu thông lượng
Φ>0 , từ ý nghĩa vật lý, cũng như từ tính chất của tích phân ta thấy trong miền V bao bởi S
phải có iểm nguồn. Chính vì thế ta gọi M là iểm nguồn của trường nếu divF M( ) > 0, ngược
lại nếu divF M( ) < 0 thì M là iểm hút. 4.2.4. Hoàn lưu
Cho trường véctơ F x y z( , , ) = (P Q R,
,) và một ường cong L trong trường véctơ. Ta gọi : → → 124
Downloaded by Ti?n D?ng Tr?n Lý (dungtienltr128@gmail.com) lOMoARcPSD| 10435767
Chương 4. Lý thuyết trường = = C
∫ Pdx + Qdy + Rdz ∫ F d r (4.7) L L
là hoàn lưu hay lưu số của trường F x y z( , , ) theo ường cong L. Theo ý nghĩa cơ học của tích phân
ường loại hai ta thấy nếu F x y z( , , ) là trường lực thì hoàn lưu của nó theo L là công do lực
F x y z( , , ) sinh ra khi vật di chuyển dọc theo L.
4.2.5. Rôta (Rotation,Véc tơ xoáy)
Cho trường véctơ F x y z( , , ) = (P Q R, , ), véctơ xoáy của trường, ký hiệu là rotF, xác ịnh theo công thức : rotF
= ⎛⎜⎝ ∂∂Ry − ∂∂Qz ⎞⎟⎠i+⎛⎜⎝
∂∂Pz − ∂∂Rx ⎞⎠⎟ j+⎛⎜⎝ ∂∂Qx − ∂∂Py ⎞⎟⎠k j k (4.8) ∂ ∂ = ∂y ∂z Q R
Vậy một trường véctơ F ã sinh ra một trường véctơ rotF( , , )x y z .
Giả sử có mặt cong S trong trường ược ịnh hướng và biên của nó là ường L trơn từng khúc.
Khi ó công thức Stokes (3.39) có dạng : → → ∫
F d r. =∫∫rot ndSF. . =∫∫rot dSF. (4.9) L S S
Nghĩa là hoàn lưu của trường véctơ F dọc theo chu tuyến L của mặt cong S chính bằng thông
lượng của véctơ xoáy qua mặt cong S của trường. → → 125
Downloaded by Ti?n D?ng Tr?n Lý (dungtienltr128@gmail.com) lOMoARcPSD| 10435767
Chương 4. Lý thuyết trường
Từ ý nghĩa cơ học, ta thấy ∫F d r.
là công của trường lực F x y z( , , ) khi di chuyển dọc L
theo L. Nếu L là ường cong kín thì công sinh ra thường bằng không vì công sản ra trên phần ”thuận
chiều ” của ường cong kín L cân bằng với công sản ra trên phần ”ngược chiều”, nếu
không có ”xoáy” (rotF = 0 ). Do ó, từ công thức Stokes ta thấy hoàn lưu theo chu tuyến kín L ặc
trung cho tính xoáy của trường trên mặt S có chu tuyến L, nói cách khác là tính chất ”xoáy”
của trường theo chu tuyến ó. Do ó, nếu rotF(M) ≠ 0 ta nói rằng M là iểm xoáy của trường và
rotF(M) = 0 ta nói rằng M là iểm không xoáy.
4.3. Một số trường ặc biệt.
4.3.1. Trường thế
a. Định nghĩa : Trường véctơ F M(
)gọi là trường thế nếu tồn tại một trường vô hướng u M( ) sao cho :
F M() = gradu M( ),∀M ∈V (4.10)
Khi ó hàm u M( ) ược gọi là hàm thế hay hàm thế vị của trường F M( ), còn V M( ) = −u M(
) gọi là thế năng của trường.
Giả sử F M( ) = (P Q R,
, ) là trường thế với hàm thế là u M( ) . Khi ó
P = ∂u ,Q = ∂u ,R = ∂u , tức là :
du = Pdx + Qdy + Rdz nghĩa là ∂x ∂y ∂z
Pdx + Qdy + Rdz là vi phân toàn phần của hàm u M( ) .
b. Tính chất : Xuất phát từ ịnh lý bốn mệnh ề tương ương (mục 3.4,Chương3.), suy ra : 1.
Để trường F M( )là trường thế, iều kiện cần và ủ là trường F M( ) không xoáy
(rotF(M) = 0,∀M ∈V). 126
Downloaded by Ti?n D?ng Tr?n Lý (dungtienltr128@gmail.com) lOMoARcPSD| 10435767
Chương 4. Lý thuyết trường 2.
Hoàn lưu của trường F M(
) theo mọi chu tuyến kín, trơn từng khúc trong V ều bằng 0 ⎛⎞ ⎜∫ F dr. = 0⎟ . ⎜⎟ ⎝L ⎠
Ví dụ 1 : Chứng tỏ rằng trường lực hấp dẫn tạo bởi trái ất tác ộng lên vệ tinh là trường thế và tìm hàm thế của nó.
Giải : Theo ịnh luật Newton, trường lực hấp dẫn sẽ là :
F x y z( , , ) = −γM m. r 3 r
trong ó M là khối lượng trái ất, m là khối lượng vệ tinh.γ là hệ số hấp dẫn, P(x,y,z) là vị trí của vệ
tinh, còn gốc toạ ộ coi là vị trí trái ất. Ta có : rotF 0, P(x,y,z)
\{0,0,0} (xem ví dụ 14 chương 3)
Vậy trường lực hấp dẫn là trường thế. Hàm thế tính theo công thức (3.40) : → → xdy ydy zdz+ + u P( ) = ∫ 2 +
0 Fd r u M+ (0) = −γMm ∫0 y2 + z )3 (x 2 2 MM MM ( ) ( ) ( ) trong ó các iểm P ,P0
không trùng gốc toạ ộ.
4.3.2. Trường ống
a. Định nghĩa : Trường véctơ F M(
) gọi là trường ống nếu divF M( ) = 0,∀M ∈V hay :
∂P ∂Q ∂R + + = 0 (4.11)
∂x ∂y ∂z 127
Downloaded by Ti?n D?ng Tr?n Lý (dungtienltr128@gmail.com) lOMoARcPSD| 10435767
Chương 4. Lý thuyết trường
Ta gọi ống dòng của trường véctơ là phần không gian trong V tạo bởi các ường dòng tựa trên
biên của một mặt cong S nào ó trong trường. Bản thân mặt S cũng như các thiết diện ngang của ống
gọi là thiết diện của ống dòng.
b. Tính chất : Từ công thức Gauss – Ostrogradski ta suy ra các tính chất sau ây của trường ống :
* Thông lượng của trường ống qua mặt cong kín S bất kỳ trong trường ều bằng không. Thật vậy, Φ= F dS. = divFdxdydz = 0 .
* Nếu V là ơn liên thì thông lượng của trường ống qua mặt S có biên L trong trường
chỉ phụ thuộc vào biên L mà không phụ thuộc vào mặt S. Thật vậy, giả sử S1 và S2 là hai mặt
cùng căng bởi biên L. Gọi Ω là miền giới hạn bởi hai mặt này thì :
0 = ∫∫∫divFdxdydz = ∫∫F dS.− ∫∫F dS. Ω S1 S2
Suy ra ∫∫FdS = ∫∫FdS . S1 S2
* Thông lượng qua mọi thiết diện của một ống dòng trong trường ống ều bằng không.
Thật vậy, giả sử S1 và S2 là hai thiết diện của ống dòng (H.4.1). Gọi Sxq là mặt xung quanh
của ống dòng giữa S1 và S2 và Ω là vật thể giới hạn bởi Sxq,S S1 2, . 2 n F n S2 1 n 1 S H.4.1
Theo tính chất 1, ta có : 0 =∫∫F ndS. . +∫∫F ndS. . +∫∫F ndS. . . S1 S2 Sxq
ở ây n ịnh hướng ra phía ngoài của Ω .
Theo ịnh nghĩa của ường dòng, nên trên biên Sxq thì F n. = 0 . Mặt khác, trên biên S1
thì n1 ngược hướng với n , tức là F n. = −F n. 1 . 128
Downloaded by Ti?n D?ng Tr?n Lý (dungtienltr128@gmail.com) lOMoARcPSD| 10435767
Chương 4. Lý thuyết trường
Còn trên biên S2 thì n2 cùng hướng với n . Từ ó suy ra : F n dS F n dS . S1 S2
Hay là :∫∫FdS = ∫∫FdS . S1 S2
Dễ dàng kiểm tra thấy ược trường hấp dẫn (ví dụ 1) hay iện trường (ví dụ 14 chương 3) ều là
các trường ống và trường thế trừ gốc toạ ộ. Do ó thông lượng qua mọi mặt cong kín không bao gốc toạ ộ ều bằng 0.
Ví dụ 2 : Tìm thông lượng của iện trường sinh ra bởi iện tích q ặt ở gốc toạ ộ qua phía ngoài
mặt cong kín S bất kỳ bao gốc toạ ộ. S n SR n
Giải : Từ ví dụ 14 chương 3 ta có iện trường : r E = q. r 3
và thông lượng qua mặt cầu bán kính R là 4. .πq nghĩa là không phụ thuộc bán kính R. Giả sử S là
mặt cong kín nào ó bao gốc toạ ộ. Gọi SR là mặt cầu tâm ở gốc toạ ộ và bán kính R ủ lớn sao cho SR
bao cả S (H.4.2). Gọi Ω miền giới hạn bởi S và SR. Khi ó : ∫∫∫E ndS. . =
∫∫∫divEdxdydz = 0 S∪S Ω R Suy ra E
ndSE ndS , trong ó véctơ n của S hướng vào gốc toạ ộ. Vậy thông SR S
lượng qua phía ngoài mặt cong S chính bằng thông lượng qua phía ngoài mặt cầu SR và bằng 4. .πq 129
Downloaded by Ti?n D?ng Tr?n Lý (dungtienltr128@gmail.com) lOMoARcPSD| 10435767
Chương 4. Lý thuyết trường
4.3.3. Trường iều hoà a.
Định nghĩa : Trường véctơ F M( ) gọi là trường iều hoà nếu nó vừa là trường ống
vừa là trường thế, tức là : ⎧⎪rotF = 0 ⎨ (4.12) ⎪⎩divF = 0 b.
Tính chất : Hàm thế u M( ) của trường iều hoà F M( ) là hàm iều hoà, nói cách
khác hàm thế u M( ) thoả mãn phương trình Laplace : Δu = 0
∂ 2u ∂ 2u ∂ 2u Hay + + = 0 (4.13)
∂x2 ∂y 2 ∂z 2 ∂u ∂u ∂u
Thật vậy, F M( ) là trường thế nên hàm thế u thoả mãn
= P, = Q, = R . ∂x ∂y ∂z
∂P ∂Q ∂R
Mặt khác F M( ) là trường ống nên + + = 0.
∂x ∂y ∂z
∂ 2u ∂ 2u ∂ 2u Do ó + + = 0 .
∂x2 ∂y 2 ∂z 2
Theo ịnh nghĩa thì trường hấp dẫn và iện trường là các trường iều hoà trong miền V
C1 + C2 . Trong ó C C1, 2 là các
hằng không chứa gốc toạ ộ. Hàm thế của trường ó có dạng r
số. Các ví dụ sau sẽ chỉ ra các hàm iều hoà tổng quát hơn.
Ví dụ 3. Chứng minh hàm số : u(M) = C1 +C ,r = 2 2 (x − x )0 +(y− y ) 2 + 2 là các hằng số tuỳ ý 0 (z − z ) ,0 C ,C1 2 r
là hàm iều hoà trong mọi miền V không chứa iểm M 0 (x0 , y0 ,z0 ).
Giải : Ta chứng minh hàm u M( ) thoả mãn phương trình Laplace (4.13). 130
Downloaded by Ti?n D?ng Tr?n Lý (dungtienltr128@gmail.com) lOMoARcPSD| 10435767
Chương 4. Lý thuyết trường ∂u
C r1 x' Thật vậy = − ∂x r 2 = −C x − x r 3 ∂ 2u
r 2 −3(x − x0 )2 ∂x2 = −C1 r 5 Tương tự :
∂∂y2u = −C − 1 r 2 −3(y5 y0 )2 2 r
∂∂z2u = −C − 1 r 2 −3(z5 z0 )2 2 r Do ó : Δu
= −C1 3r 2 − [ 3( x − ]
x0 )2 + (y − y0 )2 + (z − z0 )2 = 0 1 là hàm iều r
hoà trong mọi miền phẳng D không chứa iểm M 0 (x0 , y0 ) , tức là hàm u ã cho thoả mãn phương
trình Laplace trong mặt phẳng : ∂ 2u ∂ 2u
Δu = ∂x + ∂ = 2 y 2 0
4.4. Hệ tọa ộ cong trực giao
4.4.1..Định nghĩa:
Mỗi một iểm M trong không gian thực ược xác ịnh bởi một bộ 3 số sắp thứ tự 131
Downloaded by Ti?n D?ng Tr?n Lý (dungtienltr128@gmail.com) lOMoARcPSD| 10435767
Chương 4. Lý thuyết trường
(u u1, 2 ,u3 ) và ngược lại, ược kí hiệu M(u1,u2 ,u3 ) . Các số u1,u2 ,u3 gọi chung là toạ ộ cong của
iểm M. Các mặt cong lần lượt có phương trình: u = = = 1 u10 , u2 u20 , u3 u30 ,
(u10 ,u20 ,u30 là các hằng số) gọi là các mặt toạ ộ trong hệ toạ ộ cong. Giao của các mặt toạ ộ gọi
là các ường toạ ộ. Nếu các ường toạ ộ trực giao từng ôi thì hệ toạ ộ cong ược gọi là hệ toạ ộ cong
trực giao. Như vậy hệ toạ ộ ề các, hệ toạ ộ trụ (xem mục 2.4.2.), hệ toạ ộ cầu (xem mục 2.4.3.) là
các hệ toạ ộ trực giao (H.4.3, H 4.4)
4.4.2. Liên hệ giữa tọa ộ ề các và tọa ộ cong trực giao
Mối liên hệ giữa các tọa ộ ược cho bởi hệ phương trình:
⎧x = x u u( 1, 2,u3)
⎪ = y u u( 1, 2,u3) (4.14) ⎨y
⎪⎩z = z u u( 1, 2,u3)
Các ường tọa ộ l l1, 2 ,l3 cho bởi hệ phương trình:
⎧u x y zi ( , , ) = ui0 ⎨
u j (x y z, , ) = u j0 , (i j, =1,2,3.) và i ≠ j . (4.15) 132
Downloaded by Ti?n D?ng Tr?n Lý (dungtienltr128@gmail.com) lOMoARcPSD| 10435767
Chương 4. Lý thuyết trường ⎩ → → →
Các véctơ ơn vị của các ường tọa ộ tại iểm M là k k k1, 2 , 3 (H 4.5), chúng thoả mãn: → → k k = i j 0, khi i ≠ j. Đặt h = 1 i
,i =1,2,3. Người ta ã chứng minh ược những công (∂u + + i ) 2 (∂ui ) 2 (∂ui ) 2 ∂x ∂y ∂z
thức sau ây, cho mối liên hệ giữa toạ ộ ề các và toạ ộ cong. →
d r = (dx dy dz,
, ) = (h du11,h du2 2 ,h du3 3 )
→ d S = (dx dy dz, , ) = (h h du du h h du du h h du du2 3 2 3 , 3 1
3 1 , 1 2 1 2 ) (4.15) dV = dxdydz = h h h du du du1 2 3 1 2 3
Trong toạ ộ cầu (r, ,ϕθ), ta có: h = = = 1 1,h2 r h, 3 rsinθ.
Trong toạ ộ trụ (r, ,ϕz), ta có: h = = = 1 1,h2 r h, 3 1.
4.4.3.Các ặc trưng của trường trong hệ toạ ộ cong trực giao a. GradU(u ,u ,u )1 2 3 1 ∂U → 1 ∂U → 1 ∂U →
Công thức tổng quát: gradU = k + + 1 k 2 k 3 . h ∂ ∂ ∂ 1 u1 h2 u2 h3 u3
Trong toạ ộ cầu cho U r( , ,ϕθ), ta có:
∂U → 1 ∂U → 1 ∂U → gradU = k + + 1 k 2 k 3 . (4.16) ∂r r ∂θ rsinϕϕ∂
Trong toạ ộ trụ cho U r( , ,ϕz) , ta có: gradU = ∂U →k + 1 ∂U → + ∂U → 1 k 2 k 3 . (4.17) ∂r r ∂ϕ ∂z 133
Downloaded by Ti?n D?ng Tr?n Lý (dungtienltr128@gmail.com) lOMoARcPSD| 10435767
Chương 4. Lý thuyết trường → b. DivF(u ,u ,u )1 2 3 → 1 ⎡ ∂ ∂ ∂ ⎤ = ⎢ + +
Công thức tổng quát: divF ∂u ∂ ∂ 1 (F h h1 2 3) u2 (F h h2 3 1) u3 (F h h3 1 ⎥ 2 ) ⎦ h h h ⎣ 1 2 3 → Trong toạ ộ cầu 1
(r, ,ϕθ), cho F = (F θ⎡⎣∂∂
r ,Fθ ϕ,F ) , ta có: div F→ = r 2 sin r 2 ∂ ⎤⎥
sin )θ + ∂ (F rθ sin )θ + ∂ ϕ(F rϕ ) ⎦ (4.18) ⎢ (F rr ∂θ →
Trong toạ ộ trụ (r, ,ϕz), cho F = (F Fr , ϕ,Fz ), ta có: → 1 ⎡ ∂ ∂ ∂ ⎤
div F = r ⎢∂r (F rr ) + ∂ϕ(Fϕ) + ∂z (F rz )⎥⎦ (4.19) ⎣ → c. RotF(u ,u ,u )1 2 3 Công thức tổng quát: → → → k 1 k 2 k 3
h h23 h h31 h h12 → ∂ ∂ ∂ rot F = (4.20) ∂u ∂ ∂ 1 u2 u3 h F1 1h F2 2h F3 3 →
Trong toạ ộ cầu (r, ,ϕθ), cho F = (Fr,Fθ ϕ,F ) , ta có: 134
Downloaded by Ti?n D?ng Tr?n Lý (dungtienltr128@gmail.com) lOMoARcPSD| 10435767
Chương 4. Lý thuyết trường → → k ∂ ⎤ k rot F→ = 1 2 2
θ⎡⎢∂ θ(F rϕ sin )θ − ∂ϕ(F rθ ) ⎥ + rsin
θ ϕ⎣⎢⎡∂∂ (Fr θ⎤
) − ∂∂r (F rϕ sin ) ⎦⎥ + r sin ⎣ ∂ ⎦ → + ⎡⎢ ∂ − ∂ ⎤⎥
kr3 ⎣∂ r (F rθ ) ∂ θ(Fr )⎦ (4.21) →
Trong toạ ộ trụ (r, ,ϕz), cho F = (F Fr , ϕ,Fz ), ta có: → → rot
F→ = kr ⎡⎣⎢∂∂ 1
ϕ(F ) − ∂∂z (F r)⎥⎤⎦+→k ⎡ ∂ (F )
− ∂ (Fz)⎦⎥⎤ + + kr3
⎡⎢⎣∂∂r (F rϕ ) − ∂∂ϕ(Fr )⎦⎥⎤ ⎢⎣∂ ∂ z ϕ 2 z r r (4.22) d.
Biểu diễn ΔU Công thức tổng quát: ΔU =
h h h1 2 31 ⎡⎢⎣∂∂u1 (h h2 3h1 ∂∂uU1 ) + ∂u∂2 (h hh3 12
∂∂uU2 ) + ∂∂u3 (h h1 2h3 ∂∂uU3 )⎤⎦⎥ Trong toạ ộ cầu cho U r( , ,ϕθ), ta có:
∂2U 2 ∂U 1 ∂2U cosθ∂U 1 ∂2U Δ = (4.23) U
∂r2 + r ∂r +
r2 ∂θ2 + r2 ∂θ+ r2 sinθϕ∂ 2
Trong toạ ộ trụ choU r( , ,ϕz), ta có: 2 2 2 135
Downloaded by Ti?n D?ng Tr?n Lý (dungtienltr128@gmail.com) lOMoARcPSD| 10435767
Chương 4. Lý thuyết trường . (4.24) ∂r r ∂r r ∂ϕ ∂z
Ví dụ 4. Cho hàm số U = r(cosθ+ sin )θ , trong ó r là khoảng cách từ gốc toạ ộ O ến →
iểm M, còn θ là góc giữa OM và trục Oz. a. Tính gradU
b. Xác ịnh véctơ ơn vị n0 của mặt phẳng U = Const tại iểm có θ = . Giải:
a. Theo giả thiết, hàm số U có các ối số là các toạ ộ cầu.
Thay U vào công thức (4.16), ta nhận ược → →
gradU = (cosθ θ+ sin) k + 1 (cosθ θ− sin) k 2 →π
b. Ta có n o// gradU, theo trên gradU = 2,thay θ=
vào công thức trên suy ra: 3 → 1 → → n = + 0 (1+ 3)k1 (1− 3)k .2 2 2 → →
Ví dụ 5: Tìm hằng số k ể trường véctơ cho trong hệ toạ ộ cầu F = rk r có thông lượng bảo toàn (trường ống). → →
Giải: Biểu diễn F = rk r = (rk+1,0,0) , theo công thức (4.18) nhận ược: divF→ = 2 1 θ⎡ ∂ (rk+3
sinθ)⎤⎥⎦ = (k + 3)rk = 0, suy ra k = −3 . ⎢ r sin ⎣∂r → →
Ví dụ 6: Chứng minh trường véctơ cho trong hệ toạ ộ cầu F = rk r là trường thế với mọi số k. → → Giải: Biểu diễn
F = rk r = (rk+1,0,0) , theo công thức (4.21) nhận ược 136
Downloaded by Ti?n D?ng Tr?n Lý (dungtienltr128@gmail.com) lOMoARcPSD| 10435767
Chương 4. Lý thuyết trường →
→ rot F→ = r k 2
⎡⎢ ∂ k+1)⎤⎥ − kr3 ⎡⎣⎢∂∂θ(rk+1)⎤⎥⎦ = 0 , với mọi k. Vậy trường véctơ ã cho là (r sinθ ϕ⎣∂ ⎦ trường thế.
Ví dụ 7. Biết Δu = 0 và u u x= ( 2 + y2 ). Tìm dạng tổng quát của hàm u .
Giải : Rõ ràng hàm u ược cho trong toạ ộ trụ. Theo công thức (4.24), ta có d u2 1 du 1 d du Δ =u dr + 2
r dr = r dr (r dr) = 0 du dr Suy ra r
= C1,⇒ du = C1
,⇒ u = C1 lnr + C2. dr r
(C C1, 2 ,là các hằng số tuỳ ý)
Ví dụ 8. Biết Δu =0 và u = u( x2 + y 2 + z 2 ). Tìm dạng tổng quát của hàm u
Giải :Rõ ràng hàm u ược cho trong toạ ộ cầu. Theo công thức (4.23), ta có du 1 d du
Δu = d udr2 + 2 2 r
dr = r 2 dr (r 2 dr ) = 0 dr 1 Suy ra ra r 2
dudr = C1 ,⇒ du = C1 r 2 ,⇒ u = −C1 r + C2 .
(C C1 , 2 ,là các hằng số tuỳ ý) TÓM TẮT CHƯƠNG 4
• Phương trình mặt ẳng trị : u x y z( , , ) = C , C là hằng số • ∂ ∂
Gra iên tại iểm (x,y,z). gradu x y z( , , ) = ⎛⎜⎜ ∂∂ux , ∂uy , ∂ux ⎟⎟⎞⎠,( , , )x y z ∈Ω ⎝ 137
Downloaded by Ti?n D?ng Tr?n Lý (dungtienltr128@gmail.com) lOMoARcPSD| 10435767
Chương 4. Lý thuyết trường
• Phương trình ường dòng : x t'( ) =
y t'( ) = z t'( )
P x y z( , , ) Q x y z( , , ) R x y z( , , ) →
• Thông lượng của trường véc tơ F PQR( , , ) qua mặt cong S : Φ = ∫∫F n dS. .
= ∫∫Pdydz + Qdzdx +
Rdxdy = ∫∫F dS. S S S →
• Độ phân kỳ của trường véc tơ F PQR( , , )tại iểm (x,y,z):
divF x y z ( , , ) = ∂P + ∂Q + ∂R
∂x ∂y ∂z →
• Hoàn lưu của trường véc tơ F PQR( , , )dọc theo ường cong L : → →
C =∫Pdx Qdy Rdz+ +=∫F d r. L L →
• Rôta của trường véc tơ F P Q R( , , ) tại iểm (x,y,z).
rotF = ⎜⎝⎛ ∂∂Ry − ∂∂Qz ⎟⎠⎞.i+⎛⎜⎝ ∂∂Pz − ∂∂Rx ⎞⎟⎠.j+⎜⎝⎛ ∂∂Qx − ∂∂Py ⎠⎟⎞.k i j k ∂ ∂ ∂ = ∂x ∂y ∂z P Q R
• Trường thế : F M( )là trường thế nếu : 138
Downloaded by Ti?n D?ng Tr?n Lý (dungtienltr128@gmail.com) lOMoARcPSD| 10435767
Chương 4. Lý thuyết trường
∃u M( ): F M() = gradu M( ),∀M ∈V hay rotF(M) = 0,∀M ∈V .
• Trường ống : F M( )là trường ống nếu :
divF M( ) = 0,∀M ∈V
∂P ∂Q ∂R + + = 0
∂x ∂y ∂z ⎧⎪rotF = 0
• Trường iều hoà : F M(
)là trường iều hoà nếu ⎨ ⎪⎩divF = 0
• Phương trình Laplace : ∂2u2 + ∂∂y2u2 + ∂∂z2u2 = 0 ∂x
Nghiệm của phương trình Laplace gọi là hàm iều hoà.
CÂU HỎI VÀ BÀI TẬP CHƯƠNG 4.
4.1. Các mặt mức của một trường vô hướng không giao nhau. Đúng Sai
4.2. gradu x y z( , , ) là một véc tơ. Đúng Sai
4.3. divF x y z( , , ) là một véc tơ. Đúng Sai
4.4. rotF x y z( , , ) là một véc tơ. Đúng Sai
4.5. Trường thế là một trường vô hướng có gradu = 0. Đúng Sai
4.6. Trường thế là một trường không xoáy và ngược lại Đúng Sai
4.7 Trường iều hoà là trường vô hướng u mà u thoả mãn phương trình Laplace. Đúng Sai 139
Downloaded by Ti?n D?ng Tr?n Lý (dungtienltr128@gmail.com) lOMoARcPSD| 10435767
Chương 4. Lý thuyết trường
4.8. Chứng minh các công thức a. div uF(
) = gradu F. + udivF [ ] b. div G F
, = FrotG − GrotF ] c. rot uF(
) = [gradu F, + urotF x
4.9. Cho u = arcsin
. Tính góc giữa gradu tại iểm (1,1) và (3,4). x + y ⎜⎜ + 1 ⎞⎟⎟ = −16 ⎞
4.10. Cho u = ln ⎛x y
⎠. Xác ịnh iểm tại ó gradu ⎜⎛⎝1, 9 ⎠⎟ ⎝
4.11. Tìm thông lượng của các trường véc tơ sau:
a. F = xyi + yzj + zxk qua phần của mặt cầu x 2 + y 2 + z 2 = R 2 , x ≥ 0, y ≥ 0, z ≥ 0 hướng ra ngoài.
b. F = x i3 + y j3 + z k3 qua mặt cầu x 2 + y 2 + z 2 = x hướng ra ngoài.
c. F = xi + yj + zk qua mặt z =1−
x2 + y2 , z ≥ 0 hướng lên trên.
4.12. Tính lưu số của trường F = (y + z i) + (z + x j) + (x + y k) dọc theo cung tròn nhỏ
nhất của ường tròn lớn của mặt cầu x 2 + y 2 + z 2 = 25 nối các iểm M(3,4,0) và N(0,0,5).
4.13.Tính∫ 2xy zdx2+ 2x yzdy2 + (x y22 − 2 )z dz , L = L có phương trình 3 x = cos ,t y sin ,t z =sint hướng theo chiều tăng của t. 2
4.14. Chứng minh rằng các trường vectơ sau ây là những trường thế, tìm hàm thế vị của chúng. −x ⎡ 1
− ln(x + y i)⎤⎥ + xe+−xy j
a. F = e ⎢x + y ⎦ ⎣ 140
Downloaded by Ti?n D?ng Tr?n Lý (dungtienltr128@gmail.com) lOMoARcPSD| 10435767
Chương 4. Lý thuyết trường
b. F = yz(2x + y + z i) + zx(2y + z + x j)
+ xy(2z + x + y k)
c. F = (y + z i) + (z + x j) + (x + y k)
4.15. Cho u và v là các hàm iều hoà. Chứng minh trường véc tơ ugradv − vgradu là trường ống. 141
Downloaded by Ti?n D?ng Tr?n Lý (dungtienltr128@gmail.com) lOMoARcPSD| 10435767
Chương 5. Phương trình vi phân
CHƯƠNG 5. PHƯƠNG TRÌNH VI PHÂN GIỚI THIỆU
Cũng như phép tính ạo hàm và vi phân, phương trình vi phân (PTVP) có tầm quan trọng rất
lớn và có ứng dụng rộng rãi trong mọi lĩnh vực khoa học kỹ thuật và kinh tế. Cụ thể là nhiều bài
toán kinh tế, kỹ thuật iện tử, y học,... ều dẫn ến phương trình vi phân. Trong toán học, phương trình
vi phân là một chuyên ngành rất phát triển. Chương này cung cấp những kiến thức cơ bản về phương
trình vi phân thường ( gọi vắn tắt là phương trình vi phân). Để học tốt chương này, yêu cầu người
học phải nhận dạng ươc từng loại phương trình vi phân, qua ó mới có thể tích phân ược (tìm ược
nghiệm), bởi vì không có một phương pháp chung nào ể giải phương trình vi phân. Giải PTVP là
một quá trình tính tích phân, vì thế yêu cầu người học phải thông thạo phép tính tích phân và vi
phân, ó là nội dung cốt lõi của toán học cao cấp.
Một PTVP là một phương trình có dạng F x y y( , , ',..., y( )n ) = 0 hay dy d y2 d (n) y
F x y( , , , ,..., ) = 0 trong ó x là biến số ộc lập, y = y x( ) là hàm số phải tìm, dx dx2 dx(n) y y',
'',..., y( )n là các ạo hàm của hàm số phải tìm, (trong PTVP nhất thiết phải có mặt ít nhất
ạo hàm cấp k nào ó của hàm phải tìm). Cấp cao nhất của ạo hàm của hàm số y phải tìm có
mặt trong PTVP ược gọi là cấp của PTVP, chẳng hạn: y'+x = 0 (PTVP cấp 1)
y"+(y')2 = 0 (PTVP cấp 2)
Hàm số y = y x( ) là một nghiệm của PTVP nếu như nó thoả mãn phương trình tức là
thay nó vào phương trình sẽ nhận ược ồng nhất thức. Chẳng hạn với phương trình y'= x ta x 2 x2 có nghiệm y = , thậm chí y =
+ C trong ó C là hằng số tuỳ ý. 2 2
Giải hay tích phân một PTVP là tìm tất cả các nghiệm của nó. Về mặt hình học, mỗi
nghiệm của PTVP là một ường cong (ồ thị của nghiệm), vì thế người ta gọi ường cong ó là
ường cong tích phân của PTVP.
PTVP ược gọi là tuyến tính cấp n nếu hàm số F là bậc nhất ối với y y, ',..., y( )n , tức là phương trình có dạng:
y (n) + a1( )x y (n−1) +...+ an−1( )x y'+an ( )x y = f x( ) trong ó a1( )x
,...,an ( )x , f x( ) là các hàm số cho trước.
Nếu f x( ) ≡ 0 thì người ta gọi là phương trình tuyến tính cấp n thuần nhất. 126
Downloaded by Ti?n D?ng Tr?n Lý (dungtienltr128@gmail.com) lOMoARcPSD| 10435767
Chương 5. Phương trình vi phân
Nếu f x( ) ≠ 0 thì người ta gọi là phương trình tuyến tính cấp n không thuần nhất.
Trong chương này cần nắm vững các nội dung chính sau ây:
1. Các phương trình vi phân cấp một thường gặp.
Cần phân biệt ược từng dạng phương trình vi phân và phương pháp tích phân tương ứng với tùng dạng.
2. Các tính chất của PTVP tuyến tính cấp hai.
Từ các tính chất của PTVP tuyến tính có thể tích phân ược khi ã biết một nghiệm của
PTVP tuyến tính thuần nhất tương ứng, hoặc hai nghiệm riêng của phương trình không thuần
nhất ã cho, ặc biệt là khai thác nguyên lí chồng chất nghiệm.
3. Phương trình vi phân tuyến tính cấp hai có hệ số hằng số.
Bên cạnh phương pháp biến thiên hằng số Lagrange, cần nhận biết dạng hàm ặc biệt ở vế
phải ể tích phân PTVP bằng phương pháp hệ số bất ịnh.Vận dụng, có thể giải PTVP tuyến tính
có hệ số hằng số cấp n. NỘI DUNG
5.1. Phương trình vi phân cấp 1
Trước hết ta xét một bài toán hình học dẫn ến PTVP. Hãy tìm phương trình ường cong L
(y = y x( ))có tính chất: mỗi oạn của tiếp tuyến với uờng cong C nằm giữa hai trục toạ ộ ều bị tiếp
iểm chia thành hai phần bằng nhau. ( Mxy , ) L α
Giả sử M x y( , ) ∈L, khi ó hệ số góc tiếp tuyến với ường cong tại M là: 127
Downloaded by Ti?n D?ng Tr?n Lý (dungtienltr128@gmail.com) lOMoARcPSD| 10435767
Chương 5. Phương trình vi phân y x'( ) = tgα= − y (xem H.5.1) PA = − y
Do M là trung iểm của AB nên OP = PA = x , suy ra y' . x
Như vậy hàm số phải tìm thoả mãn PTVP cấp 1. Sau này chúng ta sẽ có cách giải phương =
trình trên, nhưng trước hết ta có thể thử lại rằng hàm số C y
thoả mãn phương trình với C là x
hằng số tuỳ ý. Tóm lại, họ các ường hyperbol có tính chất ã ặt ra.
5.1.1. Các khái niệm cơ bản
Dạng tổng quát của PTVP cấp 1: dy
F x y y( , , ') = 0 hay F x y( , , ) = 0 (5.1) dx
Nếu từ (5.1) giải ra ược y’ thì ta có PTVP cấp 1 ã giải ra ối với ạo hàm: y'= f x y( , ) (5.2)
A. Định lý tồn tại duy nhất nghiệm Cauchy-Peano
Cho phương trình (5.2): y'= f x y( , ) và (x0 , y0 )∈ D (5.3) Định lý 5.1. Nếu f(x,y)
liên tục trên miền D trong mặt phẳng Oxy thì tồn tại nghiệm: ∂f
y = y x( ) trong lân cận x = 0 thoả mãn y0
y x( 0 ). Ngoài ra nếu ∂y (x y, ) cũng liên tục trên miền
D thì nghiệm tìm ược là duy nhất.
Bài toán tìm nghiệm của PTVP thoả mãn iều kiện (5.3) gọi là bài toán Cauchy. Điều kiện
(5.3) gọi là iều kiện ban ầu.
B. Nghiệm tổng quát, tích phân tổng quát
Ta gọi nghiệm tổng quát của PTVP cấp 1 là hàm số
y =ϕ(x C, ) (5.4) trong
ó C là hằng số tuỳ ý, thoả mãn các iều kiện sau: a. Thoả mãn PTVP với mọi hằng số C.
b. Có thể tìm một giá trị C = C0 sao cho y =ϕ(x C,
0 ) thoả mãn iều kiện ban ầu y = 0
y x( 0 ) =ϕ(x0 ,C0 )với (x0 , y0 ) thoả mãn ịnh lý tồn tại và duy nhất nghiệm.
Nghiệm tổng quát cho dưới dạng ẩn: 128
Downloaded by Ti?n D?ng Tr?n Lý (dungtienltr128@gmail.com) lOMoARcPSD| 10435767
Chương 5. Phương trình vi phân Φ(x y C, ,) = 0 (5.5)
Hệ thức này gọi là tích phân tổng quát của PTVP cấp 1. Về mặt hình học, nghiệm tổng quát
hay tích phân tổng quát xác ịnh một họ ường cong trong mặt phẳng không cắt nhau gọi là các ường
cong tích phân của PTVP cấp 1.
C. Nghiệm riêng, tích phân riêng
Hàm số y =ϕ(x C,
0 ) gọi là một nghiệm riêng của PTVP, tức là ược suy ra từ nghiệm
tổng quát (5.4) với hằng số C xác ịnh C = C0 . Tương tự ta có một tích phân riêng của PTVP
Φ(x, ,ϕC0 ) = 0
Chú ý: PTVP còn có các nghiệm khác nữa, không thể nhận ược từ nghiệm tổng quát, ược gọi là nghiệm kỳ dị.
5.1.2. Các PTVP cấp một thường gặp
A. Phương trình với biến số phân li
a. Định nghĩa: Phương trình với biến số phân li (phương trình tách biến) là PTVP có dạng:
f1(x dx) + f2 (y dy) = 0 (5.6) x dx2 ydy Chẳng hạn: +
= 0 là phương trình với biến số phân li. 1+ x2 1+ y2
b. Phương pháp tích phân Phương trình (5.6) có dạng:
f1(x dx) = − f2 (y dy) = − f2 (y y x dx) '( )
Lấy tích phân hai vế ta có :
∫ f1( )x dx = −∫ f2 ( )y y dx,+ C = −∫ f2 ( )y dy + C + Vậy ∫ f ∫ 1( )x dx
f2( )y dy = C (5.7)
Đó là tích phân tổng quát của (5.6)
Chú ý : Phương trình dạng : M1( )x N1( )y dx + M 2 ( )x N2 ( )y dy = 0 có thể ưa về dạng
tách biến. Thật vậy, nếu M 2 ( )x ≠ 0 và N ( )1 y ≠ 0 thì chia hai về của phương trình cho M 2 ( ).x
N1( )y sẽ ược :
M1( )x dx + N2 ( )y dy = 0 M 2 ( )x N1( )y 129
Downloaded by Ti?n D?ng Tr?n Lý (dungtienltr128@gmail.com) lOMoARcPSD| 10435767
Chương 5. Phương trình vi phân
Đó là phương trình với biến số phân li.
Nếu M 2 ( )x = 0 tại x = a hoặc N1( )y = 0 tại y = b thì bằng cách thay trực tiếp nhận ược x
= a hoặc y = b là nghiệm.
Ví dụ 1 : Tìm tích phân tổng quát của phương trình :
x3(y +1)dx + (x4 −1)(y − 2)dy = 0
Giải : Với y +1≠ 0 và x4 −1≠ 0 ta có : x3 y − 2
dx + dy = 0 x4 −1 y +1
Tích phân tổng quát là :
14 ∫ d x( 44 −1) dx + ∫⎛⎜⎜1−
y3+1⎞⎟⎟⎠dy = C x −1 ⎝
lnx4 −1 + y −3ln y +1 = C
Ngoài ra y +1= 0 hay y = −1 và x4 −1= 0 hay x = ±1 ều là các nghiệm.
Ví dụ 2 : Tìm nghiệm của bài toán Cauchy
y'= cos(x + y) + cos(x − y) y(0) = 0
Giải : y'= cos(x + +y) cos(x − y) = 2cos x cos y
cos y ≠ 0 tức y k k Z Ta có : dy = 2cos xdx cos y dy
∫ = 2∫cos xdx + C cos y y π
lntg( + ) = 2sin x + C 2 4 130
Downloaded by Ti?n D?ng Tr?n Lý (dungtienltr128@gmail.com) lOMoARcPSD| 10435767
Chương 5. Phương trình vi phân π
Từ iều kiện ban ầu suy ra : lntg = C,⇒ C = 0 4 y π
Vậy nghiệm của bài toán Cauchy ã cho là lntg( + ) = 2sin x. 2 4
B.Phương trình ẳng cấp cấp một
a. Định nghĩa : Phương trình ẳng cấp cấp một là PTVP có dạng y = y y , = f ( ), hay y, = f(t), với t . (5.8) x x
b. Phương pháp tích phân
Coi t = y là hàm của x, t'= y' − y = y' − t x x x 2 x x
Thay vào phương trình sẽ có : t + xt'= f t( )
hay xt'= f t( ) − t
* Nếu f t( ) − t ≠ 0 ta có phương trình dạng (5.6) = dt dx x f t( ) − t y = y
* Nếu f t( ) − =t 0 tức là f ( )
. Vậy ta có phương trình tách biến dạng (5.6) x x dy y = dx x
* Nếu f t( )− =t
0 tại t = t0 hay y = t0.x thì bằng cách thử trực tiếp ta có nghiệm y = t x0
Ví dụ 3 : Giải phương trình
2xyy'−y2 + x2 = 0
Giải : Chia hai vế cho x 2 ta ược : 131
Downloaded by Ti?n D?ng Tr?n Lý (dungtienltr128@gmail.com) lOMoARcPSD| 10435767
Chương 5. Phương trình vi phân 2 − y' (− ) x x y y 2 +1= 0 = y Đặt t
, y = tx ⇒ y'= +t xt' vào phương trình sẽ nhận ược : x
2tt x'+ t 2 +1 = 0 2tdt = − dx dx
∫1+ t 2 = −∫ x + C1
ln(1+ t 2 ) = −ln x + C1 Hay : 1+ t 2 = C x y 2 C
Trở về biến cũ ta có :1+ = x 2 x
Hay ⎛⎜x − C ⎞⎟2 + y2 = C 2 ⎝ 2 ⎠ 4
Đó là các ường tròn có tâm nằm trên
trục Ox Ví dụ 4 : Tích phân phương trình : (y − −x 1)dx = + +(x y 2)dy Giải :
dy = y − x −1 dx x + y + 3
Đây chưa phải là dạng (5.8), tuy nhiên thực hiện phép ổi biến : 132
Downloaded by Ti?n D?ng Tr?n Lý (dungtienltr128@gmail.com) lOMoARcPSD| 10435767
Chương 5. Phương trình vi phân
⎧x = u + x0
⎨⎩y = v + y0 dy dv
có thể ưa ược về dạng (5.8). Thật vậy =
và chọn (x0 , y0 ) sao cho : dx du
⎨⎧⎩uv ++ yx00 −+ uv +− xy00 −+13==vu−+uv ⎧x − + = = − 0 y0 1 0 ⎧x0 2 Hay ⎨⎩x + + = − 0 y0 3 = 0, ⎨⎩y0 1 v dv Khi ó
= v −u = u −1 = f ( )v du v + u v +1 u u
Đặt t = v ⇒ dv = t + ut' u du dt t −1 u + t = du t +1 u
dt = t −1 −t = −t2 −1 du t +1 t +1 (t +1)dt du (t +1)dt du
2 +1 = − u ,∫ t2 +1 = −∫ u + C1 t
1 ln(t 2 +1) + arctgt = −lnu + C1 2 C arctgt = ln t 2 +1.u 133
Downloaded by Ti?n D?ng Tr?n Lý (dungtienltr128@gmail.com) lOMoARcPSD| 10435767
Chương 5. Phương trình vi phân
Trở về biến cũ sẽ có tích phân tổng quát : y +1 C
arctg = ln x + 2 y +1 (x + 2) 1+ x + 2
C. Phương trình tuyến tính cấp 1
a. Định nghĩa : PTVP có dạng sau ây ược gọi là PTVP tuyến tính cấp 1 : y'+p x y( ) = q x( ) (5.9)
với p x q x( ), ( ) liên tục trên (a,b)
Nếu q x( ) ≠ 0trên (a,b) thì gọi là PTVP tuyến tính không thuần nhất.
Nếu q x( ) ≡ 0 trên (a,b) thì gọi nó là PTVP tuyến tính thuần nhất.
b. Phương pháp tích phân
Cho phương trình không thuần nhất (5.9). Gọi phương trình vi phân sau ây là PTVP tuyến
tính thuần nhất tương ứng với (5.9) : y'+p x y( ).= 0 (5.10)
Trước hết, nhận thấy (5.10) là PTVP với biến số phân li. Nghiệm tổng quát của nó có dạng : dy = −p x dx( ) y dy
∫ y = −∫ p x dx( ) + C1 ∫ y = Ce- p(x)dx (5.11)
Bây giờ ta tìm nghiệm tổng quát của (5.9) bằng phương pháp coi hằng số C trong (5.11) là
hàm số và gọi ó là phương pháp biến thiên hằng số Lagrange. Cụ thể thay −∫ y = C x e( )
p x dx( ) (5.12) vào (5.9) ta có :
C x e'( ) −∫ p x dx(
)−C x p x e( ) ( ) −∫ p x dx( )+ C x p x e( ) ( ) −∫ p x dx( ) = q x( )
C x'( ) = q x e( ) ∫ p x dx( ) 134
Downloaded by Ti?n D?ng Tr?n Lý (dungtienltr128@gmail.com) lOMoARcPSD| 10435767
Chương 5. Phương trình vi phân ∫
C x() = ∫q x e() p x dx( )dx + C1 (5.13)
Như vậy tồn tại hàm số C(x) phụ thuộc vào một hằng số cộng C1tuỳ ý ể (5.12) là nghiệm của
PTVP (5.9). Chứng tỏ nghiệm tổng quát của (5.9) có dạng : y = Ce−∫ ( ) ( ) ∫ ( ) p x dx + e−∫ p x dx
q x e( ) ∫ p x dx dx (5.14)
Nếu trong (5.13) lấy C 0= ta ược một nghiệm riêng của (5.9). Do ó cũng có thể nói rằng
phương pháp biến thiên hằng số Lagrange là phương pháp tìm một nghiệm riêng của phương trình
không thuần nhất khi biết nghiệm tổng quát của phương trình thuần nhất tương ứng. Dạng nghiệm
(5.14) có thể mô tả tổng quát sau ây :
y = y + y* (5.15)
trong ó y là nghiệm tổng quát của PTVP thuần nhất tương ứng và y* là một nghiệm riêng của chính
phương trình không thuần nhất.
Dạng (5.15) úng cho PTVP tuyến tính có cấp bất kỳ nói riêng và úng cho các hệ tuyến tính nói chung.
Ví dụ 5 : Tích phân phương trình :
y'− y = x x = −
Giải : Đặt vào công thức (5.14) 1 trong ó p x( )
,q x( ) = x , ta có : x ∫ x x ∫ x
dx + e∫ dx xe−∫ dx dx y = Ce Xét với x >0 :
y = Celn x + eln x∫ xe. −ln xdx = Cx + x dx∫= Cx + x2 Xét với x < 0 1
y = Celn x +eln x ∫x.e−ln xdx = C x + x ∫x. dx x 135
Downloaded by Ti?n D?ng Tr?n Lý (dungtienltr128@gmail.com) lOMoARcPSD| 10435767
Chương 5. Phương trình vi phân
= −Cx − x ( 1)dx∫ −= −Cx + x .2
Vì C tuỳ ý nên ∀ ≠x 0 , nghiệm tổng quát có thể viết dưới dạng : y = Cx + x .2
D. Phương trình Bernoulli
Đây là PTVP không tuyến tính (phi tuyến) tuy nhiên có thể ưa về dạng PTVP tuyến tính bằng
cách thay ổi biến số thích hợp.
a. Định nghĩa : PTVP có dạng y'+p x y( ) = y q xα ( ) (5.16)
trong ó α∈ R và α≠ 0,α≠1, các hàm p x q x( ), ( ) cho trước, liên tục trên (a,b)
b. Phương pháp tích phân
Chia hai vế của (5.16) cho yα ta sẽ có: y' 1
α + p x( ) yα−1 = q x( ) y = 1 y'
Đặt u x() yα −1 , do ó u' = (1−α) y α . (5.17)
Thay vào phương trình trên sẽ nhận ược PTVP tuyến tính cấp 1 ối với hàm u x( ) :
u'+ −(1 α) p x u( ) = (1−α)q x( ) (5.18)
Sau khi tích phân phương trình (5.18), ta trở về biến cũ theo (5.17).
Ví dụ 6: Tích phân phương trình: x y y e 2 ' + = y
Gi ả i: Chia hai v ế cho y s ẽ có: x y' 2 + y =e y y ' yu ,' = Đặt u =
phương trình ược ưa về dạng: 2 y x u'+ u = e 2 136
Downloaded by Ti?n D?ng Tr?n Lý (dungtienltr128@gmail.com) lOMoARcPSD| 10435767
Chương 5. Phương trình vi phân 1 x − ∫ dx − dxdx 1 ∫ 2 2 u = Ce+ e ∫ e edx 2 x x − − y = Ce + e e dxx −x x y = Ce + e y C e e C
E. Phương trinh vi phân toàn phần
a. Định nghĩa: Phương trình vi phân dạng:
P x y dx( , )+ Q x y dy( , ) = 0 (5.19)
∂Q ∂ trong ó = P ,∀(x y, )∈D (5.20) ∂x ∂y
gọi là một PTVP toàn phần.
Điều kiện (5.20) chứng tỏ vế trái của phương trình (5.19) là vi phân toàn phần của hàm u x y( , ) nào ó.
b. Phương pháp tích phân
Điều kiện (5.20) chứng tỏ tồn tại hàm u x y( , ) ể du = P x y dx( , ) + Q x y dy( , ) theo công thức (3.24) thì : x y
u x y( , ) = ∫ P x y dx( , )+ ∫ Q x( 0, )y dy x0 y0
Như vậy tích phân tổng quát có dạng : u x y( , ) = C (5.21)
Ví dụ 7 : Giải PTVP
(x3 + 3xy2 )dx + (3x y2 + y3)dy = 0
Giải : Đặt P = x3 +3x y ,Q2 = 3x y2+ y3 137
Downloaded by Ti?n D?ng Tr?n Lý (dungtienltr128@gmail.com) lOMoARcPSD| 10435767
Chương 5. Phương trình vi phân
∂Q = 6xy, ∂P = 6xy ⇒ ∂Q = ∂P ,∀(x,y) ∂x ∂y ∂x ∂y
Vậy phương trình ã cho là PTVP toàn phần. x y
u x y( , ) = ∫(x3 + 3xy2 )dx + ∫ y dy3 0 0
Tích phân tổng quát : u x y( , ) = C Hay x4 +6x y2 2 + y4 = C.
c. Thừa số tích phân
Trong một số trường hợp iều kiện (5.20) không thoả mãn. Khi ó PTVP (5.19) chưa phải là
PTVP toàn phần. Nếu tồn tại hàm số α(x y, ) ể phương trình :
αPdx +αQdy = 0 (5.19) /
là PTVP toàn phần, tức là thoả mãn iều kiện : Px y D (5.22)
thì hàm số α(x y, ) gọi là thừa số tích phân của PTVP.
Người ta chứng minh ược rằng nghiệm của PTVP (5.19) / cũng là nghiệm của PTVP (5.19). Vì vậy
ể giải PTVP (5.19) không thoả mãn iều kiện (5.20) người ta có thể tìm một thừa số tích phân α(x,
y) và i tích phân PTVP toàn phần.
Ví dụ 8 : Cho phương trình :
2sin y dx2 + xycos y dy2 = 0
Chứng tỏ rằng α(x y, ) = x3 là thừa số tích phân của phương trình và giải phương trình ó.
Giải : Nhân hai vế của phương trình với x3 ta ược :
2x3 sin y dx2 + x y4 cos y dy2 = 0 Đặt ∂Q ∂P
P = 2x3 sin y2,Q = x y4 cos y2 , = 4x ycosy ,32 = 4x ycosy3 2 ⇒ ∂Q = ∂P ,∀(x,y) ∂x ∂y ∂x ∂y 138
Downloaded by Ti?n D?ng Tr?n Lý (dungtienltr128@gmail.com) lOMoARcPSD| 10435767
Chương 5. Phương trình vi phân
Chứng tỏ α(x y, ) = x3 là thừa số tích phân. Theo công thức (3.24.Chương 3), tích phân tổng quát của PTVP là x u(x,y)= C, trong ó u xy dx x y
Vậy : x4 sin y2 = C .
Trong một số trường hợp ặc biệt ta có thể kết luận về sự tồn tại thừa số tích phân phụ thuộc
vào một biến x hoặc y. Thật vậy giả sử α=α( )x là thừa số tích phân của PTVP không toàn
phần (5.19). Khi ó ∂ [α( ). ( , )x Q x y ]= ∂ [α( ). ( , )x P x y ] ∂x ∂y tức là
α α α∂P = ′Q + ∂Q ∂y ∂x
Chia hai vế cho αQvà biến ổi ta ược :
α 1 ddxα= − Q1 ⎛⎜⎜⎝ ∂∂Qx − ∂∂Py ⎟⎠⎞⎟ ⎞⎟⎟ Chứng tỏ − 1 ⎛⎜⎜ ∂ Q
∂Qx − ∂∂Py ⎠ chỉ là hàm của x và tích phân sẽ có : ⎝
dαα= − Q1 ⎜⎜⎛⎝ ∂∂Qx − ∂∂Py ⎟⎟⎠⎞
α( )x = e−∫ Q ⎜⎝ x y ⎟⎠
1 ⎛⎜ ∂∂Q −∂∂P ⎞⎟dx (5.23) ⎜⎜ ⎟
Tương tự nếu P1 ⎛ ∂∂Qx − ∂∂Py ⎟⎞⎠ chỉ là hàm của y thì sẽ tồn tại thừa số tích phân là hàm của ⎝
một biến y và công thức tìm: ∫ 1 ⎛⎜∂Q ∂ 139
Downloaded by Ti?n D?ng Tr?n Lý (dungtienltr128@gmail.com) lOMoARcPSD| 10435767
Chương 5. Phương trình vi phân
α( )y = e P⎜⎝ ∂x −∂ y ⎠ ⎟dy P ⎞⎟ (5.24)
Ví dụ 9. Tích phân PTVP :
(x 2 + y 2 )dx + (2xy + xy 2 + x3 )dy = 0 3 Giải.
Đặt P = x 2 + y 2 , Q = 2xy + xy 2 + x3 3
∂Q = 2y + y 2 + x2 , ∂P = 2y ∂x ∂y ⎛⎜⎜ ∂∂Q ⎞ 1 ∫
x − ∂∂Py ⎟⎟ P =1 Suy ra một thừa số tích phân là α( )y = e dy = e y ⎝ ⎠
Nhân hai vế của phương trình trên với ey sẽ có :
y(x2 + y 2 )dx + ey(2xy + xy 2 + x3 )dy = 0 e 3
Vế trái là vi phân toàn phần của hàm số : x y u x y e x y dx dy
u x y( , ) = ey⎛⎜⎜
x33 + y x2 ⎞⎟⎟⎠ ⎝
Vậy tích phân tổng quát của PTVP là : ⎛ ⎟ e xy ⎜⎜
x32 + y 2 ⎟⎠⎞ = C (C là hằng số tuỳ ý). ⎝
5.2 Phương trình vi phân tuyến tính cấp hai 140
Downloaded by Ti?n D?ng Tr?n Lý (dungtienltr128@gmail.com) lOMoARcPSD| 10435767
Chương 5. Phương trình vi phân
Trước hết, ta xét một bài toán dẫn ến PTVP tuyến tính cấp hai. Xét mạch RLC (hình 5.2).
Gọi u(t) là tổng iện áp trên các phần tử của mạch, vậy u(t) = 0. i(t) là cường ộ dòng iện trong ⎞
mạch. Trong kỹ thuật iện tử ã biết hiệu iện thế trên iện trở là Ri(t), trên cuộn tự cảm là di 1 ⎛ t ⎜ ⎟ L
dt và trên tụ là C ⎝⎜∫ ⎠
0 idt + q0 ⎟ trong ó q0 là iện lượng ban ầu trên tụ. Vậy ta có mối liên hệ +
sau ây: 0 = u t( ) = Ri t( ) + L dtdiC1 ⎝⎜⎛∫0t i t dt( ) + q0 ⎞⎟⎟⎠ ⎜
Lấy ạo hàm 2 vế ta sẽ có : u t′( ) = Ri′ + Li′′ + i C
Vậy nhận ược phương trình tuyến tính cấp 2 ối với hàm số i : Li′′+ Ri′+ i = 0 C
Phương trình vi phân tuyến tính cấp 2 là phương trình có dạng : 141
Downloaded by Ti?n D?ng Tr?n Lý (dungtienltr128@gmail.com) lOMoARcPSD| 10435767
Chương 5. Phương trình vi phân
y′′ + a x y1( ) ′ + a2 ( )x y = f x( ) (5.25) trong ó a x a1( ), 2 ( )x , f x( ) liên tục trên (a,b).
Nếu f x( ) ≠ 0 thì (5.25) gọi là PTVP tuyến tính không thuần nhất.
Nếu f x( ) ≡ 0 thì (5.25) gọi là PTVP tuyến tính thuần nhất.
Người ta ã chứng minh rằng với các giả thiết trên, PTVP (5.25) luôn tồn tại nghiệm và nghiệm
của bài toán Cauchy sau ây là duy nhất.
Tìm nghiệm của PTVP (5.25) thoả mãn: )
⎨⎧y xy x(′( 00 )==yy00′ (5.26) ⎩
trong ó (x0, y0, y’0) cho trước. Các iều kiện (5.26) gọi là các iều kiện ban ầu. Bài toán
trên gọi là bài toán Cauchy
Người ta gọi PTVP (giữ nguyên vế trái của (5.25))
y′′ + a x y1( ) ′ + a2 ( )x y = 0 (5.27) là PTVP tuyến tính thuần nhất
tương ứng với PTVP tuyến tính không thuần nhất (5.25).
Mọi hệ tuyến tính ều có tính chất chung nên tương tự như PTVP cấp một, nghiệm của PTVP
(5.25) có quan hệ với nghiệm của PTVP (5.27). Vì thế trước hết ta xét PTVP (5.27).
5.2.1 Tính chất nghiệm của PTVP tuyến tính thuần nhất.
Xét PTVP tuyến tính thuần nhất:
y′′ + a x y1( ) ′ + a2 ( )x y = 0 (5.28)
Định lý 5.2. Nếu y1 và y2 là nghiệm của PTVP (5.28) thì y1+y2 và Cy1 (hoặc Cy2) với C là
hằng số tuỳ ý, cũng là nghiệm của (5.28).
Chứng minh : Thật vậy thay y = y1+ y2, y = Cy1 vào PTVP (5.28) sẽ nhận thấy chúng thoả mãn PTVP ó : (Cy )″ + = ′′ + ′ + ]≡ 1
a1( )(x Cy1)′ + a2 ( )x Cy1 C y[ 1 a1( )x y1 a2 ( )x y1 0
Trước hết ta xét khái niệm hai hàm phụ tuyến tính, ộc lập tuyến tính. Các khái niệm này cũng
tương tự như các khái niệm của véc tơ trong không gian ã học trong toán cao cấp A2. 142
Downloaded by Ti?n D?ng Tr?n Lý (dungtienltr128@gmail.com) lOMoARcPSD| 10435767
Chương 5. Phương trình vi phân
Các hàm ϕ1( )x ,ϕ2 ( )x liên tục trên (a,b) gọi là phụ thuộc tuyến tính trong (a,b) nếu tồn tại 2
hằng số α1,α2 không ồng thời bằng 0 sao cho : α ϕ ϕ 1 1( )x +α2
2 ( )x ≡ 0, ∀x∈(a b, ) (5.29)
Ngược lại, tức là (5.29) chỉ xảy ra khi α =α = 1 2
0 thì nói rằng ϕ1( )x ,ϕ2 ( )x là ộc lập tuyến
tính trên (a,b). Dễ dàng chỉ ra rằng : Hai hàm số ộc lập tuyến tính khi và chỉ khi tỷ số của chúng
không phải là hằng số. Hai hàm số phụ thuộc tuyến tính khi và chỉ khi chúng tỉ lệ với nhau Chẳng
hạn : ϕ1( )x =1,ϕ2 ( )x = x,ϕ3 ( )x = x2 ϕ4 ( )x = sin ,x ϕ5 ( )x = cos ,x ϕ6 ( )x = ex,ϕ7 ( )x =
e2x là ộc lập tuyến tính từng ôi trên khoảng (a,b) bất kỳ.
Định lý 5.3. Nếu các hàm ϕ1( )x ,ϕ2 ( )x phụ thuộc tuyến tính trên (a,b) thì : ϕ ϕ W[ϕϕ ]= ϕ ϕ1 1, 2
′22′ ≡ 0, ∀ ∈x(a b, ) 1 Gọi W[ϕ ϕ ] = ϕ 1, 2 ϕ11′ ϕϕ′22 . (5.30)
là ịnh thức Wronski của hai hàm ϕ1,ϕ2 Chứng minh : Tồn tại α ϕ ϕ
1,α2 không ồng thời bằng không ể α1 1( )x +α2 2 ( )x ≡ 0 Giả sử α ≠ 2 0 , vậy suy ra : − 1ϕ α ϕ 1( )x 1 α = −α ϕ ϕ ≡ 2 1 1 1 W [ϕϕ ] = 1, 2 0. α ϕ ′ ϕ ϕ ′ ′ 1 1 ( )xα2 1 1 ϕ ′1 − α2
Định lý 5.4. Nếu các nghiệm y1, y2 của PTVP tuyến tính thuần nhất (5.28) là ộc lập tuyến
tính trên (a,b) thì W y[ ]≠ 1, y2
0, ∀x∈(a b, ) (5.31) Chứng minh :
Gỉa sử ngược lại W y[ )]=
1(x0 ), y2 (x0
0 với a < x0 < b. Xét hệ phương trình ại số với các ẩn C1, C2 : 143
Downloaded by Ti?n D?ng Tr?n Lý (dungtienltr128@gmail.com) lOMoARcPSD| 10435767
Chương 5. Phương trình vi phân
⎨⎩⎧C y xC y x11 ′1(( 00 )) ++ C yC y22 22′ ((xx00 )) == 00 1
Hệ này có nghiệm không tầm thường C ≠ 1, C2 (giả sử C2
0 ) vì ịnh thức của hệ bằng không.
Mặt khác hàm số ~y = C y + 11
C y2 2 cũng là nghiệm của (5.28) (theo ịnh lý 5,2). ~ ~
Theo trên thì y x( 0 ) = 0, y x′( 0 ) = 0. Từ tính duy nhất nghiệm suy ra ~y = 0 trên (a,b) tức là : C y + ≡ 11 C y22
0, ∀x∈(a b, ) Mà C ≠ 2
0 chứng tỏ y1, y2 phụ thuộc tuyến tính, mâu thuẫn với giả thiết.
Định lý 5.5. Nếu y1, y2 là hai nghiệm ộc lập tuyến tính của (5.28) thì nghiệm tổng quát của
PTVP (5.28) có dạng : y = C y + 11 C y22 (5.32)
trong ó C C1, 2 là các hằng số tuỳ ý Chứng minh :
Trước hết ta thấy (5.32) là nghiệm của (5.28) (theo ịnh lý 5.2) và phụ thuộc vào 2 hằng số C1, C2 tuỳ ý.
Ngoài ra với iều kiện ầu y x( ′ ′
0 ) = y0 , y1 (x0 ) = y0 thì sẽ tìm ược C1, C2 duy nhất. Thật vậy hệ phương trình :
⎧⎨⎩y xy x(′( 00))==C y xC y x11 11′(( 00))++C yC y2222′((xx00))==yy00′ có y xy x11′(( 00 ))
yy22′ ((xx00)) ≠ 0
Suy ra nghiệm (C1, C2) tồn tại duy nhất.
Định lý 5.6 Nếu biết y ≠ 1
0 là nghiệm của (5.28) thì có thể tìm ược nghiệm y2 của (5.28) ộc
lập tuyến tính với y1 dạng : ∫ 1 y ( )
2 ( )x = y1( )x
2 ( )x e−∫a x dx1 dx (5.33) y1
Chú ý : Trong tích phân trên hằng số cộng của tích phân bất ịnh luôn lấy bằng 0. 144
Downloaded by Ti?n D?ng Tr?n Lý (dungtienltr128@gmail.com) lOMoARcPSD| 10435767
Chương 5. Phương trình vi phân Chứng minh :
Trước hết ta có thể tìm nghiệm y2 trong dạng y2 ( )x = y x u x1( ) ( )
Đặt vào (5.28) sẽ nhận ược PTVP ối với hàm u(x) y ′ u ′′ + ′ ′ + ′′ + ′ + ]+ 1 2y u1 y u1 a x y u1( )[ 1 y u1 a y u2 = 1 0 y ′ u y( ′′ + ′ + ⎨⎧ ′ + ⎬⎭⎫ = 1 a y1 1 a y2 1) + y1 u′′+ ⎡⎣⎢ 2y 1
a1( )x ⎥⎦⎤u 0 ⎩
Chọn u khác hằng số thoả mãn phương trình :
⎡2y′ ⎤ ′ = 0 u′′ + ⎢⎣ y1 + a x u1( )⎥⎦ ′ ⎤ Đặt y
v = u′ có v, + ⎡⎢ 2y + ⎥⎦ = 1 a1( )x v 0 ⎣
Đây là PTVP tuyến tính cấp 1, do ó : −∫⎢⎡ 2 y′+a x( )⎤⎥dx v = Ce ⎣ y ⎦ 1 1 −2∫ y′dx
= Ce y1 .e−∫a x dx1( )
= Ce−2ln y .e−∫ 1 a x dx1( ) = C
1 .e−∫a x dx1( ) y12
Lấy C =1 do ó có thể chọn u là : u x( ) = ∫
1.e−∫a x dx1( ) dx 145
Downloaded by Ti?n D?ng Tr?n Lý (dungtienltr128@gmail.com) lOMoARcPSD| 10435767
Chương 5. Phương trình vi phân y 2 1 ( )x ∫ Vì u (x)′ = e a (x)dx1
≠ 0 nên u(x) không phải là hằng số, chứng tỏ y1, y2 ộc lập tuyến y1 tính.
Ví dụ 10 : Tìm nghiệm tổng quát của phương trình :
y′′ + 2 y′ + y = 0 biết một nghiệm riêng y = 1 sin x . x x
Giải : Tìm y2 ộc lập tuyến tính với y − 2 1 trong dạng (5.33) 2 ∫ x sin x x e. dx
sin x x e2. −2 ln x y2 = x ∫ sin2 x dx = x ∫ sin 2 x dx = sin xx ∫ sin xdx = 2 sin xx(−cotgx) = − cosxx . Vậy nghiệm tổng quát : y = 1 (C sin x + 1 C cosx . ) 2 x
Ví dụ 11 : Giải phương trình x2 (ln x −1)y′′ − xy′ + y = 0 biết rằng nó có một
nghiệm riêng dạng y = xα,α∈ R
Giải : Trước hết tìm α Đặt y = 1
xαvào phương trình sẽ có :
x2 (ln x −1) (αα−1)xα−2 −αxα α+ x = 0, ∀ ∈x (a b,
) α(ln x −1)(α−1) −α+1= 0, ∀x∈(a b, )
⎧αα( −1) = 0 suy ra ⎨⎩−α+1= 0 ⇒α=1⇒ y = 1 x Tìm y2 trong dạng (5.33) 146
Downloaded by Ti?n D?ng Tr?n Lý (dungtienltr128@gmail.com) lOMoARcPSD| 10435767
Chương 5. Phương trình vi phân
e∫ x2 (lnxdxx−1) dx ∫ y = 2 x 2 x e
∫ lnd lnx−x1 eln(ln x−1) ∫ = x∫ 2 dx = x x2 dx x = x∫
ln x2−1dx = x⎡⎢⎣− 1x (ln x −1) + ∫
dxx2 ⎦⎤⎥ = −ln x x
Nghiệm tổng quát y = C x + 1 C2 ln x
Chú ý : Để biết ược một nghiệm không tầm thường của PTVP tuyến tính thuần nhất là rất
khó khăn. Vì thế trong quá trình tích phân ta phải xem xét dạng phương trình ể suy oán ược nghiệm
hoặc tìm nghiệm theo sự gợi ý của bài toán.
5.2.2 Tính chất nghiệm của PTVP tuyến tính không thuần nhất
Xét PTVP (5.25) và PTVP thuần nhất tương ứng(5.27).
Định lý 5.7. Nghiệm tổng quát của PTVP (5.25) bằng tổng nghiệm tổng quát của PTVP
(5.27) cộng với một nghiệm riêng bất kỳ của chính phương trình (5.25)
y = y + y* (5.34)
Ở ây người ta dùng ký hiệu :
y là nghiệm tổng quát của PTVP (5.27) y*
là nghiệm riêng của PTVP (5.25)
Chứng minh : Thay y = y + y* vào (5.25) ta có:
y" + y*" + a1( )(x y ' + y*' ) + a2 ( )(xy + y* ) = f x( )
y" + a1( )x y ' + a2 ( )x y + y*" + a1( )x y*' + a2 ( )x y = f x( )
0 + f x( ) = f x( ) 147
Downloaded by Ti?n D?ng Tr?n Lý (dungtienltr128@gmail.com) lOMoARcPSD| 10435767
Chương 5. Phương trình vi phân
Chứng tỏ y = y + y* là nghiệm của (5.25). Nó phụ thuộc hai hằng số tuỳ ý C C1, 2 (có trong
biểu thức của y ) và với iều kiện ầu thì C C1, 2 sẽ tìm ược duy nhất như ã chứng minh ở ịnh lý 5.5
Định lý 5.8 (Nguyên lý chồng chất nghiệm): Nếu y * *
1 , y2 lần lượt là các nghiệm riêng của
phương trình không thuần nhất
y"+a1( )x y'+a2 ( )x y = f1( )x
y"+a1( )x y'+a2 ( )x y = f 2 ( )x thì y* = y * + * 1
y2 là nghiệm riêng của phương trình (5.25) với vế phải
f x( ) = f1( )x + f 2 ( )x
Chứng minh ịnh lý này cũng tương tự như trên bằng cách thay y* = y * + * 1 y2 vào PTVP (5.25)
sẽ nhận ược ồng nhất thức.
Ý nghĩa của nguyên lý là ở chỗ: vế phải f(x) có thể phân tích thành tổng hữu hạn các hàm số,
ứng với mỗi hàm số, nghiệm riêng thành phần có thể tìm ược dễ dàng hơn và như vậy nghiệm riêng y * sẽ tìm ược.
Định lý 5.9: Nếu biết hai nghiệm riêng của PTVP (5.25) y * * * − *
1 , y2 thì hàm số y = y1 y2
là nghiệm của PTVP (5.27).
Chứng minh ịnh lý này bằng cách thay y = y * − * * 1
y2 vào phương trình (5.27) và ể ý ến y1 , y *
2 là các nghiệm riêng của (5.25) sẽ nhận ược ồng nhất thức.
Định lý 5.10: Nếu biết hai nghiệm riêng y1, y2 ộc lập tuyến tính của (5.27) thì một nghiệm
riêng của (5.25) có thể tìm ược bằng phương pháp biến thiên hằng số Lagrange. Nghiệm ó có dạng:
y* = C1( )x y1( )x + C2 ( )x y2 ( )x (5.35) ⎧⎪C y + = 1/1 C y2/2 0 ó: ⎨ trong ⎪⎩C y + = 1/1/ C y2/2/ f(x) (5.36)
Chứng minh: Giả sử biết hai nghiệm ộc lập tuyến tính của PTVP (5.27) là y1, y2 . Khi ó
nghiệm tổng quát của (5.27) là:
y = C y11( )x + C y22 ( )x 148
Downloaded by Ti?n D?ng Tr?n Lý (dungtienltr128@gmail.com) lOMoARcPSD| 10435767
Chương 5. Phương trình vi phân
Nội dung của phương pháp biến thiên hằng số Lagrange là:
Coi y* = C1( )x y1( )x + C2 ( )x y2 ( )x là nghiệm riêng của (5.25), với sự tồn tại của C1( )x C, 2 ( )x . Thật vậy y*' = C y1' 1 + C y2' 2 + C y1 1' + C y2
2' Trước hết ặt iều kiện: C y ' + ' = , + , 1 1 C y2 2
0, khi ó y*, = C y1 1 C y22 (*)
Bây giờ thay y* vào (5.25) sẽ nhận ược:
C1(y1" + a y11' + a y21) + C2 (y2" + a y12' + a y22 ) + C y1'1' + C y2' 2' = f x( )
Để y* là nghiệm thì phải có: C y ' ' + ' ' = 1 1 C y2 2 f x( ) (**)
Các iều kiện (*) và (**) bây giờ là:
⎧⎪C y1'1 + C y2'2 = 0
⎨⎪⎩C y'' + C y2'2' = f x( ) 1 1
Hệ phương trình này hoàn toàn tìm ược ¦W y ,y C C ' ' [ ] ≠ 1 , 2 do 1 2
0 . Từ ó ó tìm ược C1( )x C, 2 ( )x .
Ví dụ 12: Tìm nghiệm tổng quát của phương trình: y"+ 2x y'= 1 . x 2 +1 x 2 +1
Giải: Phương trình thuần nhất tương ứng là: y"+ 2xy'= 0 x 2 +1
Dễ nhận thấy phương trình thuần nhất này có một nghiệm là y = 1 1 Nghiệm
thứ hai ộc lập tuyến tính tìm theo công thức (5.33) sẽ là: 149
Downloaded by Ti?n D?ng Tr?n Lý (dungtienltr128@gmail.com) lOMoARcPSD| 10435767
Chương 5. Phương trình vi phân y e dx
Nghiệm riêng của PTVP ã cho tìm trong dạng:
y* = C1( )x + C2 ( )x arctgx trong ó: ⎧⎪C ' + '= 1 C arctgx2 0
⎨⎪⎩C ' .0 + C2' .1+1x 2 = 1+1x 2 1 Giải hệ này sẽ có: C ' = = 2 1⇒ C2 x C ' = − = −∫ 1 arctgx ⇒ C1
arctgxdx = −x arctgx. +ln(1+ x 2 )
Vậy nghiệm tổng quát là:
y = ln(1+ x 2 ) + C + 1 C arctgx2
5.3. Phương trình vi phân tuyến tính cấp 2 có hệ số không ổi
5.3.1. Các dạng nghiệm của phương trình thuần nhất Cho phương trình: y"+a y a y = 1 '+ 2 0
(5.37) trong ó a a1 , 2 là các hằng số thực. Tìm nghiệm riêng của (5.37) dưới dạng
y = ekx , k = const
Vậy k thỏa mãn iều kiện:
y' = k.ekx,y"= k e2 kx,ekx(k2 +a k + = + = 1 a )2 0 ⇔ k2 + a k1 a2 0 (5.38)
Phương trình (5.38) gọi là phương trình ặc trưng của (5.37). Thông qua phương trình
này, chúng ta có thể biết ược dạng nghiệm của chính (5.37).
* Nếu (5.38) cho 2 nghiệm thực khác nhau k k1 , 2 thì có 2 nghiệm riêng của (5.37) là 150
Downloaded by Ti?n D?ng Tr?n Lý (dungtienltr128@gmail.com) lOMoARcPSD| 10435767
Chương 5. Phương trình vi phân y = = −k ) x 1 ek x1 , y2
ek x2 . Chúng ộc lập tuyến tính vì
y1 = e(k1 2 không phải là hằng số. Vậy y2
nghiệm tổng quát của (5.37) sẽ là: y = C e k x k x 1 1 + C e2 2 (5.39)
* Nếu (5.38) cho 2 nghiệm thực trùng nhau thì (5.37) có 1 nghiệm riêng, y = 1 ekx . Nghiệm riêng y =
2 ộc lập tuyến tính với y1 tìm ược theo công thức 5.33 y2
uy1 và e ukx "+ekx (a1
+ 2 )k u'= 0 vì k là nghiệm kép của (5.38) do ó a + 1
2k = 0 . Suy ra: u"= 0,u = Ax + B, lấy u = x.
Vậy nghiệm tổng quát của (5.37) : y = (C + 1 C x e2 ) kx (5.40)
* Nếu (5.38) cho 2 nghiệm phức k =α±iβ thì hai nghiệm riêng dưới dạng phức sẽ là: y1 = e
eα βx i x = eαx (cosβ βx + isin x) y = 2
e eα βx −i x = eαx (cosβ βx −isin x)
Do a a1 , 2 là các số thực, vậy các phần thực và phần ảo của y y1 , 2 cũng là nghiệm của (5.37).
Chúng ta lấy 2 nghiệm là eαx cosβx e, αx sinβx . Chúng ộc lập tuyến tính. Vậy nghiệm tổng
quát của (5.37) trong trường hợp này có dạng:
y = eαx (C1 cosβx + C2 sinβx) (5.41) Ví dụ 13:
y" 5 ' 6+ y + y = 0
Giải: Phương trình ặc trưng của nó: k 2 + 5k + 6 = 0 cho nghiệm k1 = -3,k2 = -2. Vậy : y = C e + 1 −3x
C e2 −2x Ví dụ 14: y" 2 '− y +y = 0
Giải: Phương trình ặc trưng của nó k 2 − 2k +1 = 0 có nghiệm k1=k2=1. Vậy y = ex (C + 1 C x2 )
Ví dụ 15: Tìm nghiệm của bài toán Côsi:
y" 2 ' 2+ y + y = 0, (0)y= y'(0) =1
Giải: Phương trình ặc trưng của nó: k
2 + 2k + 2 = 0,k = − ±1 i Nghiệm tổng quát: 151
Downloaded by Ti?n D?ng Tr?n Lý (dungtienltr128@gmail.com) lOMoARcPSD| 10435767
Chương 5. Phương trình vi phân y = e−x (C cosx + 1 C sin x)2 y' = e−x ((C − − + 2 C )cosx1 (C2 C )sin x ) − 1 y(0) =1= C1 y'(0) =1= C2 C1 ⇒ C = 2 2
y = e−x (cosx + 2sin x) .
5.3.2. Phương pháp tìm nghiệm riêng của phương trình không thuần nhất Cho phương trình : y"+a y a y = 1 '+ 2
f x( ) (5.42) trong ó a1,a2 là các hằng số thực.
Nhờ vào phương pháp biến thiên hằng số Lagrange và các dạng nghiệm của phương trình
thuần nhất ta có thể tìm ược nghiệm tổng quát của (5.42) với f(x) là hàm liên tục bất kỳ. ex =
Ví dụ 16: Tích phân PTVP y"−y ex +1
Giải: PTVP thuần nhất tương ứng: y"−y = 0
Phương trình ặc trưng của nó: k 2 −1= 0 ⇒ k = ±1
Nghiệm tổng quát của PTVP thuần nhất tương ứng:
y = C e −x + x 1 C e2
Bây giờ tìm nghiệm riêng của PTVP ã cho bằng phương pháp biến thiên hằng số Lagrange:
y* = C1 ( )x e−x + C2 ( )x ex ⎧⎪C e + = 1' −x C e'2x 0 = trong ó ⎩⎨⎪−C e + ' −x C e'2 x 1+exex 1 Suy ra: C' = 12 e = − x1+1,C1' 12 1e+2ex x 152
Downloaded by Ti?n D?ng Tr?n Lý (dungtienltr128@gmail.com) lOMoARcPSD| 10435767
Chương 5. Phương trình vi phân 2 C = 2 12 ∫ exdx+1
Đặt ex +1 = t , dx = dt , t −1 C ∫
2 = 12 ∫ t t( dt−1) = 12
⎛⎜⎝t −11 − 1t ⎞⎟⎠dt t −1 = 1 ln
= − 1 ln(ex +1) + 1 x 2 t 2 2 1 e2x 1 t −1
C1 = − 2 ∫ x +1dx = − 2 ∫ t dt e
= − ex +1 + 1 x +1) ln(e 2 2 Vậy nghiệm tổng quát: ] ] y =
e−x [ln(ex +1) − ex + C + ex [ 1
x − ln(ex +1) + C2 2 2
Dưới ây chúng ta xét các dạng ặc biệt của f(x) ứng với nó, nghiệm riêng của (5.42) tìm ược
mà không cần phải dùng ến phép tính tích phân.
Trường hợp 1: f x( ) = eαxP x n +
n( ) = eαx(A xn
An−1xn−1 +...+ A0) trong ó α, A ∈ ≠ 1
R i,( = 0, ),n An 0
Nếu α không phải là nghiệm của phương trình ặc trưng của phương trình thuần nhất tương ứng với (5.42) : k 2 + a k + = 1 a2
0 (5.43) thì một nghiệm riêng của (5.42) tìm dưới dạng: y* = e Qαx n +
n( )n = eαx(B xn
Bn−1xn−1 +...+ B0 ) với n+1 hệ số Bi chưa biết. 153
Downloaded by Ti?n D?ng Tr?n Lý (dungtienltr128@gmail.com) lOMoARcPSD| 10435767
Chương 5. Phương trình vi phân
Thay y* vào (5.42) thì: Q " + ' + + = n (2α+ a Q1) n (α α2 + a1 a2 )Qn Pn
Đồng nhất các hệ số của lũy thừa cùng bậc của x ta sẽ có hệ (n+1) phương trình tuyến tính
với với (n+1) ẩn số Bi (i = 0,n). Phương pháp tìm các hệ số của Qn như trên gọi là phương pháp hệ
số bất ịnh với hệ hàm số 1, ,x x2 ,...,xn,...
Nếu α là nghiệm ơn của (5.43), nghiệm riêng tìm dưới dạng: y*
= xeαxQn ( )x = xeαx (B xn n + ...+ B0 )
Nếu α là nghiệm kép của (5.43) thì:
y* = x e2 αxQ n +
n( )x = x e2 αx (B xn ...+ B0 )
Ví dụ 17: Tìm một nghiệm riêng của PTVP:
y" 2 '+ y +y = x(=
e0.xP x1 ( )) Giải: Phương trình ặc trưng của phương trình thuần nhất tương ứng:
k 2 + 2k +1= 0 có nghiệm kép k = -1 y* = B x + 1
B0 , y*/ = B1, y*" = 0 2B + + = 1 B x1 B0 x ⎧⎨⎩2BB =+ = = − = − 1 1 1 B0 0 ⇒ B0 2B1 2 y * = x − 2.
Ví dụ 18: Tìm một nghiệm riêng của PTVP: y" + 2y'−3y = e xx (= e1.xP x1(
)) Giải: Phương trình ặc trưng của PTVP thuần nhất: k2 + 2k − =3 0 có
nghiệm k = 1, k = -3 y * = x e. x(B x + 2 + 1
B0 ) = ex (B x1 B x0 )
y *' = ex(B x 2 + + 1 (B0
2B1 )x + B0 )
y *" = ex(B x 2 + + + 1 (B0
4B1 )x + 2B0 2B1 )
Thay vào phương trình sẽ có: 8B x + + = 1 2B1 4B0 x 154
Downloaded by Ti?n D?ng Tr?n Lý (dungtienltr128@gmail.com) lOMoARcPSD| 10435767
Chương 5. Phương trình vi phân ⎧⎨⎩82BB =+ = 11 14B0 0 ⇒ ⎨⎪⎧⎪⎪⎪⎩BB1 == = − 0 18− 12 B1 161 1 y* = x.ex (x − 1). 8 2
Ví dụ 19: Tìm nghiệm của bài toán Côsi:
y" 4− y ' + 4y = e 2x(x +1), (0)y= y'(0) =1
Giải: Phương trình ặc trưng của phương trình thuần nhất tương ứng k2 − 4k + =4 0 cho nghiệm k = = 1 k 2 2 .
Trước hết tìm một nghiệm riêng: y = + + *
x e2 2x (B x1 B0 ) = e 2x(B x13 B x0 2 ) ]
y *' = e 2x[2B x 3 + + 1 (2B0
3B1 )x 2 + 2B x0
y *" = e 2x(4B x 3 + + + ) 1
(4B0 12B1 )x 2 + (8B0
6B1 )x + 2B0 6B x + = 1 2B0 x +1 ⎧6B = = = 1 1 ⇒ B1 1 , B0 1 ⎨2B =1 6 2 ⎩ 0 Nghiệm tổng quát: y e (C C x) x e (x 3) 155
Downloaded by Ti?n D?ng Tr?n Lý (dungtienltr128@gmail.com) lOMoARcPSD| 10435767
Chương 5. Phương trình vi phân y' e2x (2C C C x) e2x (2x3 9x2 6x) y(0) = C1 =1 y'(0) = 2C + = 1 C2 1 C = = − 1 1,C2 1 y e (1 x) x e (x 3).
Trường hợp 2: f x( ) = eαx[Pn( )x cosβx + Qm( )x sinβx] trong ó α,β∈R P, n( )x Q,
n( )x là các a thức bậc n,m cho trước với các hệ số thực.
Nếu α± iβ không phải là nghiệm của (5.43) thì một nghiệm riêng của (5.42) ược tìm dưới dạng:
y * = eαx[Rl ( )x cosβx + Sl ( )x sinβx]
trong ó Rl ( )x ,Sl ( )x là các a thức bậc l = max( ,n m) có các hệ số ược tìm bằng phương pháp hệ
số bất ịnh với các hệ hàm: 1, ,x x 2 ,...,sinβ βx,cos x
Nếu α± iβ là nghiệm của (5.43) thì tìm nghiệm trong dạng: y*
= eαxx R[ l ( )x cosβx + Sl ( )x sinβx]
Ví dụ 20: Tìm nghiệm tổng quát: y " + y ' = xcos x
Giải: Phương trình ặc trưng tương ứng k 2 + k = 0 cho nghiệm k = 0,k = -1 156
Downloaded by Ti?n D?ng Tr?n Lý (dungtienltr128@gmail.com) lOMoARcPSD| 10435767
Chương 5. Phương trình vi phân
Nhận thấy ± i không phải là nghiệm của phương trình ặc trưng. Vậy y * = (A x + + 1
A0 )cos x + (B x1 B0 )sin x y *' = (B x + + + − 1 A1
B0 )cos x + −( A x1 B1 A0
)sin x y *" = −( A x + − − 1 2B1
A0 )cos x + −( B x1 2A − 1 B0 )sin x Vậy ( + (B − + + − ) (− + − − − ) 1 A x1 ) + A1 2B1 B0 A0 cos x (A1
B1 )x + B1 2A1 A0
B1 sin x = xcos x B − = + + − = 1 A1 1, A1 2B1 B0 A0 0 B + = + − − = 1 A1 0, −2A1 B1 B0 A0 0 B = = − = = 1 1 ,A1 1 ,A0 1,B0 1 2 2 2
Nghiệm tổng quát: y = C + −x − 1 C e2
(x − 2)cos x + (x +1)sin x
Ví dụ 21: Tìm một nghiệm riêng của phương trình:
y" 2 ' 2+ y + y = e−x (1+ sin )x
Giải: Dựa vào nguyên lý chồng chất nghiệm, ta tìm các nghiệm riêng của các phương trình sau:
y" 2 ' 2+ y + y = e−x sin x
y" 2 ' 2+ y + y = e−x
Phương trình ặc trưng tương ứng k 2 + 2k + 2 = 0 cho nghiệm k =− ±1 i y * 1
= xe−x (A0 cos x + B0 sin )x y *' = − + − − 1
e−x ((B x0 A x0 A0 )cos x + (B0 B x0 A x0 )sin x) y *" = − − − + 1
e−x ((2B0 2A0 2B x0 )cos x + −( 2B0 2A0 2A x0 )sin x)
2B0 cos x − 2A0 sin x = sin x 157
Downloaded by Ti?n D?ng Tr?n Lý (dungtienltr128@gmail.com) lOMoARcPSD| 10435767
Chương 5. Phương trình vi phân B = = − = − 0 0, A0 1 , y1*
xe−x cos x 2 2 y = = − = 2*
C e0 −x , y 2*'
C e0 −x , y2*" C e0 −x C = = 0 1, y2* e−x
Nghiệm riêng y * = y * + * = 1 y2
e−x (1− x cos )x 2
Các phương pháp trình bày trên ược áp dụng cho phương trình vi phân tuyến tính cấp cao có
hệ số hằng số, chẳng hạn xét bài toán Côsi sau:
Ví dụ 22: Giải PTVP:
y''' 2 '' 2 '− y + y −y = x 2 , (0)y= 0, 'y (0) = y"(0) = −1
Giải: Phương trình ặc trưng của PTVP thuần nhất tương ứng:
k 3 − 2k 2 + 2k −1= 0
2 − k +1) = 0,k = = 1 1,k 2,3 1 (1± i 3) (k −1)(k 2
Nghiệm tổng quát của phương trình thuần nhất tương ứng: 1 3 3 y = C e x + 1
e 2 x (C2 cos x + C3 sin
x) C1,C2,C3 là các hằng số tùy ý. 2 2
Một nghiệm riêng tìm dưới dạng: y* = A x2 2 + A x1
+ A0 y*' = 2A x2 + A1 y*" = 2A2
y*''' = 0, − A x 2 + − − − = = − 2 (4A2
A1)x + 2A1 A0 4A2 x2 A2 1 4A − = = − 2 A1 0 A1 4 2A − − = = − 1 A0 4A2 0, A0 4 Nghiệm tổng quát : 158
Downloaded by Ti?n D?ng Tr?n Lý (dungtienltr128@gmail.com) lOMoARcPSD| 10435767
Chương 5. Phương trình vi phân 1 3 3 x + C sin 2 3 x − 4x − 4 2 y = C e x + 1
e 2 (C2 cosx) − x 3 3 3) cos 3) sin 2 2 3 3 2 1
y'= C e1 x + 12 e 2 x ⎛⎜⎜⎝(C2 + C3x + (C − 3
C2x⎞⎟⎟⎠ − 2x − 4 1 y"= C e1
x + 12 e 2 x ⎛⎜⎜(C3 3 − C2 )cos 2 x − (C2 3 + C3 )sin 2 x⎞⎟⎟⎠ − 2 ⎝ ⎧ ⎪C + − 1 C2 4 = 0 ⎪ ⎪ ⎨C1 + 1 (C + 2 C3 3) − 4 = −1
Từ iều kiện ban ầu có: ⎪ 2 ⎪ ⎪⎩C + 1 1
2 (C3 3 − C2 ) − 2 = −1 C = = = 1 C2 2,C3 0 1
Vậy nghiệm của bài toán Côsi là: 3
y = 2e x + 2e 2 x cos x 2 TÓM TÁT CHƯƠNG 5.
• Phương trình có biến số phân ly. Dạng phương trình: f1( )x dx + f2 ( )y dy = 0 Tích +
phân tổng quát: ∫ f ∫ 1( )x dx
f2 ( )y dy = C
• Phương trình ẳng cấp cấp một. Dạng phương trình: y y , = f (
), hay y , = f t( ),t = y x x
Phương pháp tích phân: Coi t là hàm số của x, thay vào phương trình sẻ ưa về 159
Downloaded by Ti?n D?ng Tr?n Lý (dungtienltr128@gmail.com) lOMoARcPSD| 10435767
Chương 5. Phương trình vi phân = dt
dạng có biến số phân ly dx x f t( ) − t
• Phương trình tuyến tính cấp một. Dạng phương trình: y'+p x y( ) = q x( ) Nghiệm tổng quát: y = Ce−∫ ∫ p x dx( )
+ e−∫ p x dx() q x e( ) ∫ p x dx( ) dx
• Phương trình Bernoulli. Dạng phương trình: y'+p x y( ) = y q xα ( ) = 1
Phương pháp tích phân: Đặt u x( ) α −1 , y
Thay vào phương trình trên sẽ nhận ược PTVP tuyến tính cấp 1 ối với hàm u x( ) : u'
(1+ −α) ( )p x u = (1−α) ( )q x
• Phương trình vi phân toàn phần. Dạng phương trình: P x y dx( , ) + Q x y dy( , ) = 0 ∂Q ∂P trong ó = ,∀(x y, )∈D ∂x ∂y x y +
Tích phân tổng quát: ∫ P x y dx( , ) ∫ Q x( 0, )y dy = C x0 y0 x y
hoặc: ∫ P x y dx( , )+ ∫ Q x( 0, )y dy = C x0 y0
• Phương trình vi phân tuyến tính cấp hai thuần nhất:
y′′ + a1( )x y′ + a2 ( )x y = 0 (*)
Tính chất nghiệm: 1.
Nếu y1 và y2 là nghiệm của PTVP(*) thì y1+y2 và Cy1 (hoặc Cy2) với C là hằng số
tuỳ ý, cũng là nghiệm của(*) 2.
Nếu y1, y2 là hai nghiệm ộc lập tuyến tính của (*) thì nghiệm tổng quát nó có dạng : y = C y + 11 C y22
trong ó C1,C2 là các hằng số tuỳ ý 160
Downloaded by Ti?n D?ng Tr?n Lý (dungtienltr128@gmail.com) lOMoARcPSD| 10435767
Chương 5. Phương trình vi phân
3. Nếu biết y ≠ 1
0 là nghiệm của (*) thì có thể tìm ược nghiệm y2 của nó ộc lập tuyến tính với y1 dạng : ∫ 1 −∫a x dx ( ) 1 dx
y2 ( )x = y1( )x 2 ( )x e y1
Chú ý : Trong tích phân trên hằng số cộng của tích phân bất ịnh luôn lấy bằng 0
• Phương trình vi phân tuyến tính cấp hai không thuần nhất y′′+ a
x y1( ) ′+ a x y2( ) = f x( ) (**)
Tính chất nghiệm :
1. Nghiệm tổng quát của PTVP (**) bằng tổng nghiệm tổng quát của PTVP (*) cộng với
một nghiệm riêng bất kỳ của chính phương trình (**)
y = y + y*
Ở ây người ta dùng ký hiệu :
y là nghiệm tổng quát của PTVP
(*) y* là nghiệm riêng của PTVP (**) 2.
(Nguyên lý chồng chất nghiệm): Nếu y * *
1 , y2 lần lượt là các nghiệm riêng của
phương trình không thuần nhất
y"+a1( )x y'+a2 ( )x y = f1( )x
y"+a1( )x y'+a2 ( )x y = f 2 ( )x
thì y* = y * + * 1
y2 là nghiệm riêng của phương trình (**) với vế phải f x( ) = f1( )x + f 2 ( )x 3.
Nếu biết hai nghiệm riêng y1, y2 ộc lập tuyến tính của (*) thì một nghiệm riêng
của (**) có thể tìm ược bằng phương pháp biến thiên hằng số Lagrange. Nghiệm ó có dạng: y*
= C1( )x y1( )x + C2 ( )x y2 ( )x 161
Downloaded by Ti?n D?ng Tr?n Lý (dungtienltr128@gmail.com) lOMoARcPSD| 10435767
Chương 5. Phương trình vi phân ⎧⎪C y + 1/ 1 C y2/ = ⎨⎪⎩ 2 0 trong ó: C y/ 1/ +C y = 2/ 2/ f x( ) 1 4.
Nếu biết hai nghiệm riêng của PTVP (**) y * * * − *
1 , y2 thì hàm số y = y1 y2 là nghiệm của PTVP (*)
• Phương trình vi phân tuyến tính cấp 2 thuần nhất có hệ số không ổi y"+a y = 1 '+a y2
0, (1) a a1, 2 là các hằng số thực k2 + + =ak a1 2
0 (2) gọi là phương trình ặc trưng của (1) Dạng nghiệm tổng quát:
Nếu (2) cho 2 nghiệm thực khác nhau k1,k2 thì nghiệm tổng quát của (1) sẽ là: y = C e k x k x 1 1 + C e2 2
Nếu (2) cho 2 nghiệm thực trùng nhau thì nghiệm tổng quát của (1) sẽ là y = (C + 1 C x e2 ) kx
Nếu (2) cho 2 nghiệm phức k =α±iβ thì nghiệm tổng quát của (1) sẽ là
y = eαx (C1 cosβx + C2 sinβx)
• Phương trình vi phân tuyến tính cấp 2 không thuần nhất có hệ số không ổi y"+a y = 1 '+a y2
f x( ), (3) a1,,a2 là các hằng số thực Trường hợp 1: f x
( ) = e P x( ) = e (A x n + n
A x +...+ A ) trong ó α, A ∈ ≠ 1
R i,( = 0, ),n An 0
Nếu α không phải là nghiệm của phương trình ặc trưng của phương trình thuần nhất tương
ứng với (3) thì một nghiệm riêng của (3) tìm dưới dạng y
= e Q ( )n = e (B x n + n B x +...+ B )
Trường hợp 2: f x( ) = eαx [Pn ( )x cosβx + Qm ( )x sinβx] trong ó α,β∈R P, n ( )x
Q, n ( )x là các a thức bậc n,m cho trước với các hệ số thực.
Nếu α± iβ không phải là nghiệm của (2) thì một nghiệm riêng của (3) ược tìm dưới dạng: 162
Downloaded by Ti?n D?ng Tr?n Lý (dungtienltr128@gmail.com) lOMoARcPSD| 10435767
Chương 5. Phương trình vi phân
y* = eαx [Rl ( )x cosβx + Sl ( )x sinβx]
trong ó Rl ( )x ,Sl ( )x là các a thức bậc l = max( ,n m) có các hệ số ược tìm bằng phương
pháp hệ số bất ịnh với các hệ hàm: 1, ,x x 2 ,...,sinβ βx,cos x
Nếu α± iβ là nghiệm của (2) thì tìm nghiệm riêng trong dạng: y*
= eαxx R[ l ( )x cosβx + Sl ( )x sinβx]
CÂU HỎI VÀ BÀI TẬP CHƯƠNG 5
5.1. Nghiệm tổng quát của PTVP cấp n phụ thuộc vào n hằng số tuỳ ý. Đúng Sai
5.2. Nghiệm của bài toán Cauchy luôn duy nhất nghiệm Đúng Sai
5.3. Phương pháp biến thiên hằng số Lagrange áp dụng chỉ cho PTVP tuyến tính. Đúng Sai
5.4. Phương trình Bernoulli là PTVP tuyến tính Đúng Sai
5.5. PTVP toàn phần là phương trình vi phân tuyến tính thuần nhất. Đúng Sai
5.6. PTVP tuyến tính thuần nhất luôn luôn có nghiệm Đúng Sai
5.7. Biết 2 nghiệm y1 và y2 của PTVP tuyến tính thuần nhất thì biết ược nghiệm tổng quát của phương trình ó. Đúng Sai
5.8. Biết 2 nghiệm của PTVP tuyến tính không thuần nhất thì có thể biết ược nghiệm tổng
quát của phương trình ó. Đúng Sai
5.9. Giải PTVP tuyến tính có hệ số hằng số không cần dùng ến phép tính tích phân Đúng Sai
5.10. PTVP tuyến tính có tính chất chồng chất nghiệm. Đúng Sai
5.11. Giải các phương trình: a. y′ = 1
b. y'= x e2 x 163
Downloaded by Ti?n D?ng Tr?n Lý (dungtienltr128@gmail.com) lOMoARcPSD| 10435767
Chương 5. Phương trình vi phân 1 + x y xdy c. y'cos x = d. + ydx = 0 ln y 1− y 2 1− x 2
e. y' sin(+x + y) = sin(x − y)
f. y′ = cos(x − y)
5.12. Giải các bài toán Cauchy: a. dx + dy
= 0, y(1) =1 x y( −1) y x( + z)
b. (1+ e 2x )y dy2 = e dx yx , (0) = 0
c. sin xdy − yln ydx = 0, y(0) =1
d. (x 2 +1)y′ = y 2 + 4, y(1) = 2
5.13. Giải các phương trình:
a. xdy − ydx = x2 + y dx2
b. xyy'+x 2 − 2y 2 = 0 y (ydx + xdy)= ysin y (xdy − ydx) c. xcos x x d. (y − x dx)
+ (y + x dy) = 0
5.14. Giải các phương trình vi phân tuyến tính cấp 1:
a. x(1+ x 2 )y'−(x 2 −1)y + 2x = 0
b. y' 2+ xy = xe−x2
c. (1+ x 2 )y'−2xy = (1+ x 2 ) 2
d. 2ydx + (y 2 − 6 )x dy = 0
5.15. Giải các bài toán Cauchy: a. y'
b. (1+ x 2 )y'+xy =1, y(0) = 0 x
5.16. Chứng minh hàm số y = x e dt∫ t2
là một nghiệm của phương trình xy'−y = x e2 x2 . 1 164
Downloaded by Ti?n D?ng Tr?n Lý (dungtienltr128@gmail.com) lOMoARcPSD| 10435767
Chương 5. Phương trình vi phân
Hãy tìm nghiệm của phương trình thoả mãn iều kiện y(1)=1
5.17. Giải các phương trình:
a. y'+xy = x y3 3 dy 2 3 b.
(x y + xy) =1 dx
c. (yln x − 2)ydx = xdy
d. ydx + (x + x y dy2 ) = 0
5.18. Giải các phương trình vi phân toàn phần: ⎡ y 2 1⎤ ⎡1 x 2 ⎤
a. ⎢(x − y) − ⎥⎦ 2
x⎥⎦dx + ⎢⎣ y − (x − y) 2 dy = 0 ⎣
xdx + (2x + y dy) b. (x + y) = 2 0 x y y y x x 1 ⎟⎞
c. ⎜⎜⎝⎛ 1y sin y − x + − ⎟⎠ 2 cos x
1⎟⎟⎞⎠dx + ⎜⎝⎛⎜ 1x cos x
y 2 sin y + y 2 dy = 0 ⎞
d. 3x 2 (1+ ln y dx)
− ⎜⎜⎛⎝2y − xy3 ⎟⎟⎠dy = 0
5.19. Giải các phương trình sau ây bằng cách tìm thừa số tích phân α
a. (2y + xy dx) + 2xdy = 0,α( )x ⎛ ⎞
b. ⎜⎜2xy + x y2 +
y33 ⎟⎟⎠dx + (x 2 + y 2 )dy = 0,α( )x ⎝
c. y(1+ xy dx) − xdy = 0,α( )y
d. xdy + ydx − xy 2 ln xdx = 0,α(xy)
5.20. Giải các phương trình vi phân sau: a.
x 2 (ln x −1)y′′ − xy′ + y = 0, biết rằng nó có một nghiệm riêng dạng y = 1 xα,α∈R b.
(2x +1)y′′ + (4x − 2)y'−8y = 0, biết rằng nó có một nghiệm riêng dạng y = 1
eαx ,α∈R 165
Downloaded by Ti?n D?ng Tr?n Lý (dungtienltr128@gmail.com) lOMoARcPSD| 10435767
Chương 5. Phương trình vi phân c.
(x 2 −1)y′′ − 6y = 0 , biết rằng nó có một nghiệm riêng y1(x) có dạng a thức. d.
(2x − x 2 )y′′ + 2(x −1)y'−2y = −2 biết rằng nó có hai nghiệm riêng y = = 1 1, y2 x
5.21. Giải các phương trình sau khi biết một nghiệm riêng của phương trình thuần nhất tương ứng.
a. x y2 ′′ − 2xy' 2+ y = 2x 3 , y = 1 x b. y′′ + x y'− 1
y = x −1, y = 1 e x 1− x 1− x 1 c. y′′ + x =
2 ln x y = e x ⎜⎝⎛
2x + ln x⎠⎟⎞, y1 ln x
5.22. Giải các phương trình: a. y ′′ − = y e xe+x 1
b. y′′ + 2y'+y = 3e−x x +1
c. y′′ + y = tgx
d. y′′ + y = 1 cos2x cos2x
5.23. Giải các phương trình:
a. y′′ − 7y'+6y = sin x
b. y′′ − 3y'= 2 − 6x
c. y′′ − 2y'+3y = e−x cos x
d. y′′ + 2y'+y = 4e−x
e. y′′ − 9y'+20y = x e2 4x
f. y′′ + y = x 2 cos 2 x
5.24. Giải các bài toán Cauchy
a. y′′ − 2y'+2y = 5cos ,x y(0) =1, y′(0) = 0
b. y′′ + y = cos 3 x y, (0) = y'(0) = 0 166
Downloaded by Ti?n D?ng Tr?n Lý (dungtienltr128@gmail.com) lOMoARcPSD| 10435767
Chương 5. Phương trình vi phân 162
Downloaded by Ti?n D?ng Tr?n Lý (dungtienltr128@gmail.com) lOMoARcPSD| 10435767
Đáp số và gợi ý
ĐÁP SỐ VÀ GỢI Ý
ĐÁP SỐ VÀ GỢI Ý CHƯƠNG 1. 1.11.
a. {(x y, ), x > 0, y > 0hoặc x < 0, y < 0}
b. Vành tròn óng giới hạn bởi 2 ường tròn tâm gốc tọa ộ bán kính 1 và 3.
c. Miền mở nằm trong 2 ường y = x và y = -x, nằm bên phải trục Oy
d. Toàn mặt phẳng trừ ường parabol y = x2 1.12. 2 2 x + y a. z′ = 1 = y x , z′y x 2 2 2 2 + + + y x y x y x x −x cos b. z′ = = y y x ycos , z′y 2ysin c. z′ = = x
y x3 y3 −1 , z′y xy3 ln x d. z′ = − + = + x
x 2 y y 2 , z′y x 2 x y 2 1.14. ′ ′ a. z = − − + ( = − − + x
ecos2 x 2( x2 y2 ) sin2x + 4x), z y
ecos2 x 2( x2 y2 ).4y ( )) b. z′ = = ( − x
2x , z′y 2y y y44 +11 1.15.
a. dz = 2(xdy − ydx) x2 sin 2y x
b. dz = ex[(xcos y −sin y dy) + (sin y + cos y + xsin y dx) ] 1.16. lOMoARcPSD| 10435767
Đáp số và gợi ý
y(3x2 − y2 ) )
a. y'= x(3y2 − x2 a2 = b. y' (x + y)2 c. z'x z'y d. z′ = − x − − − − 2 yz , z′ = − y2 xz x z 2 xy y z 2 xy 1.18. 2u ∂u 1.19. = khi a = b = c ∂r r → ∂u cos( , )r 1.20. ∂ = − r 2
triệt tiêu khi ⊥ r 1.21. a.
Điểm dừng: (−2,2),(−4,2), Δ = z // 2 − // = xy zxx z //yy
4(2 − y e) 2x + 2(x 2 − y 2 + 8x + 4y +10)e2x −
Δ −( 2,2) = 4e 4 > 0, Δ −( 2,2) = −4e−8 < 0, z //yy( 4− ,2) = −2e2 < 0, Vậy z = max
z( 4− ,2) = 4e−4 b.
Điểm dừng: (0,0),(1,1), Δ(x y, ) = 9 − 36xy, Δ(0,0) = 9 > 0,
Δ(1,1) = −27 < 0, z // =
xx (1,1) = 6 > 0, vậy zmin z(1,1) = −1 c.
Có 5 iểm dừng: (0,0),(0,2 ),(2 ,0),(2 ,2 ),( , ),b a a b a b
Δ(x y, ) =16(a − x 2 )(b − y)2 − 4xy(2a − x)(2b − y), lOMoARcPSD| 10435767
Đáp số và gợi ý
Δ(0,0) = Δ(0,2 )b = Δ(2a,0) = Δ(2a,2 )b > 0,Δ(a b, ) = −4a b22 < 0 z // =
xx (a b, ) = −2b 2 < 0, Vậy zmax
z a b( , ) = a b22 . d.
Điểm dừng: (1,2), Δ(x y, ) =1− 4(1+ 2 )(1+ 5 ), Δ(1,2) = −26 < 0 x 2 y 2 z //
xx (1,2)= >60, vậy z = min z(1,2) = 7 −10ln 2 ± 1 ± 1 e. Tồn tại 4 iểm dừng: ( ,
), Δ(x y, ) =−36xy, Δ 1
( ,− 1 ) =12 > 0, Δ −( 3 3 1 1 Δ − − () = −12 < , 0, Δ( ) < 0, 3 3 1 1 ( , z //
xx ) > 0, Vậy z 3 3 lOMoARcPSD| 10435767
Đáp số và gợi ý f.
Tồn tại 3 iểm dừng: (0,0),(− 2,
Δ(x y, ) =16 −16(3x z // // xx (− 2,
2) = zxx ( 2,− 2) = 20 > 0, z
= z(− 2, 2) = z( 2,− 2) = −8.
Ngoài ra z(0,0) = 0, ( ,z x x) = 2x 4 > 0,∀ ≠x 0, ( ,z x 0) = x 4 − 2x 2 < 0,khi x ủ bé.
Vậy hàm số không ạt cực trị tai (0,0) g.
Điểm dừng: (5,2). Δ(x y, ) =1−
4000 , Δ(5,2) =−3 < 0 x y3 3 z // = xx (5,2) =
> 0 , zmin z(5,2) = 30. h.
Điểm dừng: (0,0), Δ(x y, ) = 4x 2 −12 (3y
x − y), Δ(0,0) = 0,
Nhận xét: z(0,0) = 0, ( ,z x x) = x3 , ổi dấu khi x ổi dấu, chứng tỏ hàm số không ạt cực trị. 1.22. d = 1 4 3
1.23. x = ± 5 , y = ± 5
ĐÁP SỐ VÀ GỢI Ý CHƯƠNG 2. 2.10. 2 π 2 4 1 arccos y
a. ∫dy ∫ f x y dx( , )
+ ∫dy ∫ f x y dx( , ) 0 −arccos y 2 −arccos y 2 4 y
b. ∫dy ∫ f x y dx( , ) 0 −y 2 3 6 3 lOMoARcPSD| 10435767
Đáp số và gợi ý
c. ∫ ∫dx f x y dy( , )
+ ∫ ∫dx f x y dy( , ) 0 1 2 x 2 1 1+ −1 y2
d. ∫dy ∫ f x y dx( , ) 0 2−y 2.11. a. b. c. d. 2.12. a. b. ⎞ 5⎛π−1 ⎟ c. ⎜ 2⎝ 2 ⎠ 8⎛π− 2⎞⎟ d. ⎜ 3⎝ 2 3⎠ 2.13. a. b. c. d. 2.14. lOMoARcPSD| 10435767
Đáp số và gợi ý a. b. π 2.15. a. b. a4 c. 2 4πa5 d.
(chuyển sang tọa ộ cầu hoặc tọa ộ trụ) 3
ĐÁP SỐ VÀ GỢI Ý CHƯƠNG 3. 3.16. a. 24 16 2 b. 143 3.17. 1 3.18. a. − b. 4 3.19. a. 1 b. − c. 3.20. a.
πa2 và −πa2 πa π 2 a2 b. và − 2 2
c. ab và − ab lOMoARcPSD| 10435767
Đáp số và gợi ý 2 2 3.21. 0 πR4 3.22. 2 3.23. a. 4 b. 3.24. a. 1+π (π2 +16)2 b. − 4 16π 3.25. a. x3 − x y2 2 + 3x +
y3 + 3y + C
b. ex+ y + sin(x − y) + 2y + C ]
c. ex[y + ey (x − y +1) + C 1 2 2 y2 d. ln(x + y ) − + C 2 2 3.26. a. 1 b. –1 3.27. y
a. m =1, u = 1 ln(x2 + y2 )+ arctg + C 2 x − y
b. a = b = −1,u = x + 2 2 C x + y 3.28. a. π 2 lOMoARcPSD| 10435767
Đáp số và gợi ý b. πa4 3.29. a. 4 61 b. a4 2 c. 3.30. a. b. + 4π( + + ) 2 2 b c22 c a22 c. a b abc d. − 2πR7 105 3.31. πR6 a. − 8 b. −πR2 3 3.32. a. 12πR5 b. 5 c. 3a4
ĐÁP SỐ VÀ GỢI Ý CHƯƠNG 4.
4.9. cosα≈ 0,99,α≈ 80 lOMoARcPSD| 10435767
Đáp số và gợi ý
4.10. ⎜⎛− 1 , 3⎟⎞, ⎜⎛ 7 ,− 3⎞⎟ ⎝ 3 4⎠ ⎝ 3 4⎠ 4.11. 3πR 4 a. b. c. 2π 4.12. –12
4.13. 0 (Hướng dẫn: (2xy z2 , 2x yz x y2 , 2 2 − 2 )z = grad x y z( 2 2 − z 2 ) còn L là giao của
x 2 + y 2 + z 2 =1và mặt y = 3z ) 4.14.
a. u = e−x ln(x + y) + C b. u = xyz x(
+ y + z) + C
c. u = xy + yz + +zx
C ĐÁP SỐ VÀ GỢI Ý CHƯƠNG 5. 5.11. [ ] a. y = 2
x − ln( x +1) + C
b. y = e x (x 2 − 2x + 2) + C ⎛ π⎞ c.
1 ln 2 y = lntg ⎜ x + ⎟ + C 2 ⎝ 2 4 ⎠ ( )( ) d. 1− 1− x 2
1− 1− y 2 = Cxy y
e. 2sin x + lntg = C 2 x − y f. x + cot g = C 2 5.12. lOMoARcPSD| 10435767
Đáp số và gợi ý a. x + +y
2 ln x − ln y = 2
b. y 3 = 3arctgex −
c. Mọi nghiệm ều thỏa mãn
2(x 2 −1) + 4x = d. y 2 1− x + 2x 5.13.
a. 1+ 2Cy − C x2 2 = 0
b. y = ±x 1+ C x2 2 y
c. xycos = C x
d. y 2 + 2xy − x 2 = C 2 5.14. 1
a. y = Cx + (1+ C) x ⎛
b. y = e− ⎜⎜⎝ ⎞⎟⎟⎠ x2 C + x22
c. y = (1+ x 2 )(x + C)
d. y 2 − 2x = Cy 3 (giải x theo y) 5.15.
a. y = (x +1) 2 ⎛⎜⎜ x2 + 2 x + 12⎟⎠⎞⎟ ⎝ ( ) ln x + x 2 +1 b. y = x 2 +1 5.17.
a. y 2 (x 2 +1+ Ce x2 ) =1 lOMoARcPSD| 10435767
Đáp số và gợi ý 1 b.
− 12 y2 − y 2 + 2 (giải x theo y) = Ce x 1 1 2) =1 c. y( ln x + +Cx 2 4
d. x = ( 1 ) (giải x theo y) y ln y + C 5.18.
a. ln y − xy = C x x − y
b. ln x + y − x
= C x + y y x 1 c. sin − cos + x − = C x y y
d. x 3 (1+ ln y) − y 2 = C 5.19. 1
a. α= e 2 x , x y e2 2 x = C ⎛ b. α= e ⎜⎜⎝ + ⎞⎟⎟⎠ = x, yex x 2 y32 C 1 2 x c. α= y + 2 , y x 2 = C
d. α= x y21 2 , 12 ln 2 x + xy1 = C 5.20. a. y = C x + 1 C2 ln x − + ⎡⎢ 2x C2
(2x 2+1) 2 − 2x⎤⎥⎦ b. y = C e1 ⎣ lOMoARcPSD| 10435767
Đáp số và gợi ý c. y = C x ⎡⎢ +
1 ( 3 − x) + C2 1− 23 x 2
3 (x x42 −1) .ln xx +−11⎥⎤⎦ ⎣ d. y = C x 2 + 1 C2 (x −1) +1 5.21. a. y = C x + 2 + 1 C x2 x 3 b. y = C e x + − 1 C x2 (x 2 +1)
c. y = ln x C⎛⎜⎝ + ∫ ⎞⎟⎠ 1 C2
lndx2 x + ex 5.22. ] ] a. y =
ex [x − ln(ex +1) + C − e−x [ 1
x − ln(ex +1) + C2 2 2 ⎡ 5 ⎤
b. y = e−x ⎢C + + 1 C x2 (x +1) 2 ⎥ ⎣⎦ ⎛ π⎞ c. y = C ⎜ x + ⎟
1 cos x + C2 sin x − cos xlntg ⎝ 2 4 ⎠
d. y = C1 cos x + C2 sin x − cos2x 5.23. a. y = C e + + 1 x C e2 6x
5sin x + 7cos x 74 b. y = C + 3x + 1 C e2 x 2 )
c. y = e x (C + 1 cos 2x + C2 sin 2x
e−x (5cos x − 4sin x) 41 d. y = (C + ) −x + 1 C x e2 2x e2 −x e. y = C e + − ⎛⎜ + + 1 5x C e2 4x 1 x 3 x 2 2x e⎞⎟ 4x ⎝3 ⎠ x 2 x 2 cos2x 4xsin 2x 13cos2x lOMoARcPSD| 10435767
Đáp số và gợi ý
f. y = C1 cos x + C2 sin x + −1− + + 2 6 9 27 5.24.
a. y = cos x + 2(e x −1)sin x b. y
= (cos x − cos3x)+ 3x sin x 8 lOMoARcPSD| 10435767
Đáp số và gợi ý
TÀI LIỆU THAM KHẢO
1. G. M. FICHTENGÔN, Giáo trình phép tính vi tích phân, Tập 1,2,3, Nauka, Moskva, 1969. (tiếng Nga).
2. NGUYỄN ĐÌNH TRÍ (chủ biên),Toán học cao cấp, Tập 1,2,3, NXB Giáo dục, Hà nội, 2004.
3. K. MAURIN, Analiza, Czes,c,1, PWN, Warszawa, 1976.
4. PHAN QUỐC KHÁNH, Phép tính vi tích phân, Tập 2, NXB Giáo dục, 2000.
5. JEAN-MARIE MONIER, Giáo trình toán, Tập 1,2,3,4, NXB Giáo dục, Hà nội, 1999,(dịch từ
tiếng Pháp, DUNOD, Paris, 1999).
6. V. V. STEPANOV, Giáo trình phương trình vi phân, Nhà xuất bản Quốc gia, Moskva, 1959.(tiếng Nga).




