Sách tập 1 môn Đồ họa kỹ thuật CTTT | Trường Đại học Bách Khoa Hà Nội

GVC. TS. HOÀNG LONG ĐỒ HỌA KỸ THUẬT Tập 1 HÌNH HỌC HỌA HÌNH VÀ VẼ KỸ THUẬT CƠ BẢN
NHÀ XUẤT BẢN BÁCH KHOA HÀ NỘI
Mã số: 2637-2016/CXBIPH/08-56/BKHN
Biên mục trên xuất bản phẩm của Thư viện Quốc gia Việt Nam Hoàng Long
Đồ họa kỹ thuật, tập một : Hình học họa hình và vẽ kỹ thuật cơ bản / Hoàng
Long. - H. : Bách khoa Hà Nội, 2016. - 136tr. : hình vẽ, bảng ; 27cm Thư mục: tr. 134 ISBN: 978-604-93-8982-5 1. Đồ hoạ kĩ thuật 604.2 - dc23 BKH0060p-CIP LỜI NÓI ĐẦU
Trong những năm gần đây, chương trình giảng dạy môn Hình học hoạ hình và Vẽ Kỹ
thuật (nay được tích hợp lại thành học phần có tên là Đồ hoạ Kỹ thuật – Technical Graphics)
trong Trường Đại học Bách khoa Hà Nội có nhiều thay đổi do những nguyên nhân sau: o Về
thời gian: so với những năm trước kia, chỉ còn xấp xỉ một nửa;
o Về nội dung: cần có sự phù hợp với đối tượng học nay đã được chuyên ngành hoá rất sớm;
o Về không gian: số lượng sinh viên trong một giảng đường hiện nay lớn hơn rất nhiều so với trước kia;
o Những tiến bộ của khoa học kỹ thuật, đặc biệt là công nghệ CAD/CAM.
Nhằm thích nghi với những tác nhân thay đổi nói trên và được sự giao phó của Bộ
môn Hình học Hoạ hình – Vẽ Kỹ thuật, Trường Đại học Bách khoa Hà Nội, tác giả xây dựng
cuốn sách này nhằm hướng đến mục tiêu giảng dạy và học tập chứ không có mục đích làm
cẩm nang tra cứu. Cấu trúc và nội dung của cuốn sách này phù hợp với đề cương chi tiết học
phần Đồ hoạ Kỹ thuật của Trường Đại học Bách khoa Hà Nội.
Cuốn sách được hoàn thành với cấu trúc và nội dung tối ưu, trong đó còn chứa đựng
kết quả nghiên cứu của bản thân tác giả. Đây là một quá trình lao động khổ công và tác giả
cũng coi đó là quà tặng tinh thần dành cho các em sinh viên Đại học Bách khoa Hà Nội.
Nhân dịp kỷ niệm 60 năm ngày thành lập Trường Đại học Bách khoa Hà Nội, xin chúc các
em sinh viên khoá học mới của Trường bước sang cuộc đời sinh viên với những kết quả học
tập tốt đẹp nhất và đó cũng là mục đích chính ra mắt tài liệu học tập này.
Tác giả xin được cảm ơn sự quan tâm, thúc đẩy, động viên của Nhà xuất bản Bách
khoa Hà Nội, đặc biệt là TS. Bùi Đức Hùng, TS. Phùng Lan Hương, TS. Hoàng Tuấn Bằng
và ThS. Trần Ngọc Huấn!
Để chất lượng cuốn sách ngày càng tốt hơn, tác giả mong muốn nhận được những ý
kiến xây dựng và cổ vũ của bạn đọc thông qua số điện thoại 0912369972. Xin trân trọng cảm ơn! Tác giả MỤC LỤC
LỜI NÓI ĐẦU.………………………………………………………………………. 3
Phần I. HÌNH HỌC HOẠ HÌNH
Chương 1. MỞ ĐẦU – CƠ SỞ CỦA BIỂU DIỄN………..…………………………….. 7
1.1. GIỚI THIỆU VỀ MÔN HỌC…………………………….…………..…………………. 7
1.2. PHÉP CHIẾU, PHÉP CHIẾU XUYÊN TÂM……………………………..……….…… 7
1.3. PHÉP CHIẾU SONG SONG…………………………………………….…..………….. 8
1.4. PHÉP CHIẾU VUÔNG GÓC……………………………………………..……….……. 9
1.5. TƯƠNG ỨNG CỘNG TUYẾN GIỮA HAI TRƯỜNG PHẲNG…………..…………... 9
1.6. TƯƠNG ỨNG PHỐI CẢNH GIỮA HAI TRƯỜNG PHẲNG……………….……….. 10
1.7. PHÉP BIẾN ĐỔI CỘNG TUYẾN, PHÉP THẤU XẠ……………………….………... 11
1.8. CÁC PHƯƠNG PHÁP BIỂU DIỄN……………………….…………………………... 12
Chương 2. BIỂU DIỄN, LIÊN THUỘC……………………………………………….. 13
2.1. ĐIỂM……….…………………………………………………………………………... 13
2.1.1. Tạo đồ thức điểm…………………………………………………………………... 13
2.1.2. Ví dụ áp dụng……………………………………………………………………… 15
2.2. ĐƯỜNG THẲNG……………………………………………………………………… 16
2.2.1. Biểu diễn đường thẳng…………………………………………………………….. 16
2.2.2. Điểm thuộc đường thẳng…………………………………………………………... 17
2.3. MẶT PHẲNG………………………………………………………………………….. 18
2.3.1. Biểu diễn mặt phẳng – đồ thức hai đường thẳng cắt nhau, song song……………. 18
2.3.2. Điểm, đường thẳng thuộc mặt phẳng……………………………………………… 19
2.4. MẶT (Mặt cong, Đa diện)……………………………………………………………… 21
2.4.1. Khái niệm cơ bản…………………………………………………………………... 21
2.4.2. Biểu diễn các mặt thường gặp, vẽ điểm thuộc mặt, thấy khuất……………………. 22
2.5. BIỂU DIỄN CÁC ĐỐI TƯỢNG CÓ VỊ TRÍ ĐẶC BIỆT……………………………... 28
2.5.1. Các đối tượng vuông góc với mặt phẳng hình chiếu………………………………. 28
2.5.2. Các đối tượng song song với một mặt phẳng hình chiếu (đồng mức)…………….. 29
2.5.3. Sự vuông góc với các đường đồng mức…………………………………………… 30
CÂU HỎI VÀ BÀI TẬP CHƯƠNG 2………..…………………………………………….. 32
Chương 3. BIẾN ĐỔI HÌNH CHIẾU VÀ CÁC BÀI TOÁN VỀ LƯỢNG………….. 36
3.1. MỘT SỐ BÀI TOÁN DỄ GIẢI KHI CÁC ĐỐI TƯỢNG CÓ VỊ TRÍ ĐẶC BIỆT…… 36
3.2. THAY MẶT PHẲNG HÌNH CHIẾU………………………………………………….. 38
3.2.1. Nguyên tắc cơ bản…………………………………………………………………. 38
3.2.2. Các kỹ thuật cơ bản, hiệu lực………………………………………………………... 41
3.3. PHÉP QUAY MẶT PHẲNG QUANH ĐƯỜNG ĐỒNG MỨC………………………. 46
3.3.1. Quay quanh đường bằng…………………………………………………………… 46
3.3.2. Quay quanh đường mặt……………………………………………………………. 48
CÂU HỎI VÀ BÀI TẬP CHƯƠNG 3………………….………...………………………… 49
Chương 4. GIAO CỦA CÁC ĐỐI TƯỢNG…………………………………………..... 53
4.1. MẶT PHẲNG CẮT CÁC ĐỐI TƯỢNG………………………………………………. 53
4.1.1. Trường hợp đặc biệt……………………………………………………………….. 53
4.1.2. Trường hợp tổng quát……………………………………………………………… 57
4.2. ĐƯỜNG THẲNG CẮT MẶT (Mặt cong và Đa diện)………………………………… 63
4.2.1. Trường hợp đặc biệt……………………………………………………………….. 63
4.2.2. Trường hợp tổng quát……………………………………………………………… 64
4.3. GIAO CỦA HAI ĐA DIỆN……………………………………………………………. 67
4.3.1. Trường hợp đặc biệt……………………………………………………………….. 67
4.3.2. Trường hợp tổng quát……………………………………………………………… 68
4.4. GIAO CỦA ĐA DIỆN VÀ MẶT CONG……………………………………………… 68
4.5. GIAO CỦA HAI MẶT CONG………………………………………………………… 69
4.5.1. Giao của một trụ chiếu và một mặt cong bất kỳ…………………………………… 69
4.5.2. Giao của hai mặt cong bất kỳ (phần tham khảo)………………………………………. 71
CÂU HỎI VÀ BÀI TẬP CHƯƠNG 4…………………………….………………………... 73
ĐỀ VÀ HƯỚNG DẪN LÀM BÀI THI GIỮA KỲ………………….……………………... 78
GIẢI ĐÁP CÂU HỎI VÀ HƯỚNG DẪN BÀI TẬP……………….……………………… 83
ĐÁP ÁN ĐỀ THI GIỮA KỲ SỐ 2…………………………………………………………. 88
Phần II. VẼ KỸ THUẬT CƠ BẢN
Chương 5. CÁC TIÊU CHUẨN VỀ VẼ KỸ THUẬT………………………………… 90
5.1. GIỚI THIỆU CHUNG VỀ TIÊU CHUẨN VÀ TIÊU CHUẨN QUỐC TẾ ISO…….... 90
5.2. MỘT SỐ TIÊU CHUẨN VỀ BẢN VẼ KỸ THUẬT………………………………….. 90
5.2.1. Tiêu chuẩn về khổ giấy…………………………………………………………….. 90
5.2.2. Tiêu chuẩn về khung bản vẽ, khung tên trong bản vẽ kỹ thuật……………………… 91
5.2.3. Tiêu chuẩn về tỉ lệ trong bản vẽ kỹ thuật………………………………………...... 92
5.2.4. Tiêu chuẩn về nét vẽ trên bản vẽ kỹ thuật…………………………………………. 92
5.2.5. Tiêu chuẩn về chữ viết trên bản vẽ kỹ thuật……………………………………….. 95
5.2.6. Tiêu chuẩn về ký hiệu vật liệu trên mặt cắt………………………………………... 97
5.2.7. Tiêu chuẩn về ghi kích thước trên bản vẽ kỹ thuật………………………………… 97
Chương 6. CÁC HÌNH CHIẾU CƠ BẢN VÀ HÌNH CHIẾU PHỤ………………... 101
6.1. CÁC HÌNH CHIẾU CƠ BẢN………………………………………………………… 101
6.1.1. Phương pháp chiếu góc thứ nhất (Hệ E)………………………………………….. 101
6.1.2. Phương pháp chiếu góc thứ ba (Hệ A)…………………………………………… 103
6.2. HÌNH CHIẾU PHỤ…………………………………………………………………… 104
CÂU HỎI VÀ BÀI TẬP CHƯƠNG 6…………………………………………………….. 105
Chương 7. HÌNH CHIẾU TRỤC ĐO VÀ ĐỌC HIỂU BẢN VẼ…………………… 106
7.1. TIẾP CẬN HÌNH CHIẾU TRỤC ĐO………………………………………………... 106
7.2. HÌNH CHIẾU TRỤC ĐO VUÔNG GÓC ĐỀU……………………………………… 107
7.2.1. Tích chất của hình chiếu trục đo vuông góc đều…………………………………. 107
7.2.2. Vẽ hình chiếu trục đo vuông góc đều cho một vật thể…………………………….107
7.3. HÌNH CHIẾU TRỤC ĐO XIÊN CÂN (HOẶC ĐỀU)……………………………….. 110
7.4. ĐỌC HIỂU BẢN VẼ CÁC HÌNH CHIẾU VÀ VẼ PHÁC HÌNH CHIẾU TRỤC ĐO... 111
7.4.1. Tổng quan về vấn đề đọc hiểu bản vẽ……………………………………………. 111
7.4.2. Đề xuất nguyên lý đọc hiểu bản vẽ các hình chiếu cơ bản……………………….. 113
CÂU HỎI VÀ BÀI TẬP CHƯƠNG 7…………………………………………………….. 119
Chương 8. MẶT CẮT, HÌNH CẮT…………………………………………………... 123
8.1. MẶT CẮT…………………………………………………………………………….. 123
8.1.1. Khái niệm mặt cắt………………………………………………………………… 123
8.1.2. Một số dạng trình bày mặt cắt……………………………………………………. 123
8.2. HÌNH CẮT……………………………………………………………………………. 125
8.2.1. Khái niệm hình cắt……………………………………………………………….. 125
8.2.2. Một số loại hình cắt………………………………………………………………. 125
CÂU HỎI VÀ BÀI TẬP CHƯƠNG 8…………………………………………………….. 127
GIẢI ĐÁP CÂU HỎI VÀ BÀI TẬP………………………………………………………. 130
TÀI LIỆU THAM KHẢO……………………………………………………………...137 PHẦN I HÌNH HỌC HOẠ HÌNH
Chương 1 MỞ ĐẦU – CƠ SỞ CỦA BIỂU DIỄN
1.1. GIỚI THIỆU VỀ MÔN HỌC
Hình học Hoạ hình (Descriptive Geometry) là môn học nghiên cứu để tạo ra hình biểu
diễn trên mặt phẳng của các đối tượng trong không gian (điểm, đường thẳng, mặt phẳng,...)
và sử dụng hình biểu diễn phẳng đó để giải các bài toán hình học trong không gian chỉ bằng
thước thẳng và compa. Nghiên cứu các phương pháp biểu diễn để làm sơ sở lý luận cho việc
xây dựng các bản vẽ kỹ thuật là nguồn gốc lịch sử của môn học.
Việc giảng dạy môn học này cho sinh viên nhằm hai mục đích: rèn tư duy logic và sáng
tạo của toán hình đồng thời cung cấp những kiến thức bổ trợ môn vẽ kỹ thuật cho những kỹ sư tương lai.
Hình học Hoạ hình là môn khoa học chính xác, nó không đòi hỏi năng khiếu bẩm sinh
như sự khéo tay hay khả năng hình dung không gian theo cách hiểu lầm của một số sinh viên.
Song song với phương pháp giải gần đúng dựa trên mô hình giải tích, Hình học Hoạ hình
còn góp phần tạo nên những ý tưởng để xây dựng những giải thuật trong lĩnh vực đồ hoạ
máy tính một cách hiệu quả.
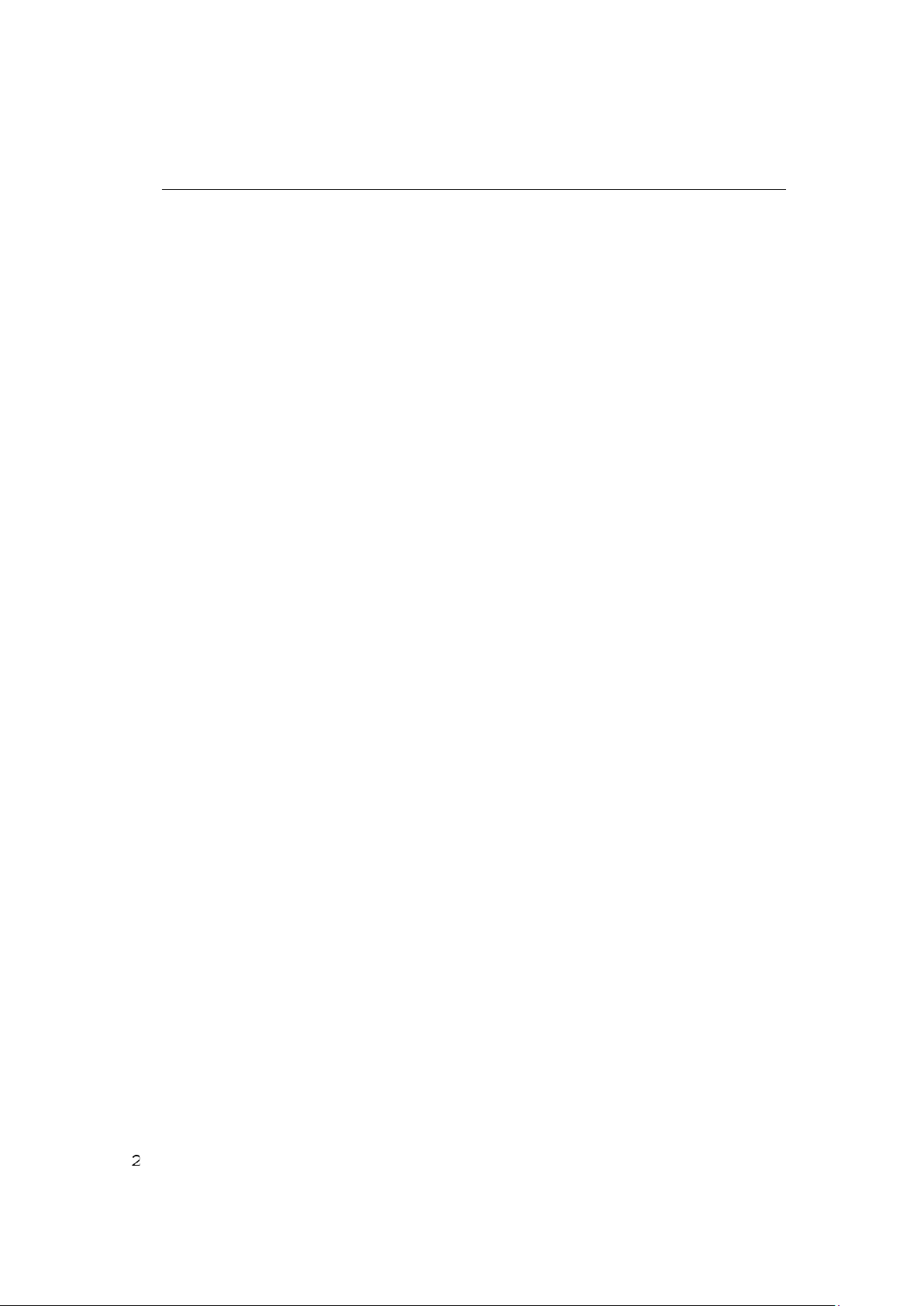
1.2. PHÉP CHIẾU, PHÉP CHIẾU XUYÊN TÂM
Công cụ để tạo ra các hình biểu diễn phẳng cho các đối tượng là phép chiếu. Phép chiếu
được thực hiện như sau (h.1.1):
Trong không gian lấy một điểm S gọi là tâm chiếu và một
mặt phẳng ’ không chứa S gọi là mặt phẳng hình chiếu.
Chiếu một điểm A bất kỳ trong không gian từ tâm S lên mặt phẳng ’ như sau:
– Vẽ tia chiếu SA. – Giao của SA với ’ là A’ gọi là hình chiếu của điểm A. Hình 1.1
Tính chất của phép chiếu: o
Phép chiếu bảo toàn tính thẳng: A, B, C nằm trên một đường thẳng d không đi qua
tâm chiếu thì hình chiếu của chúng cũng nằm trên một đường thẳng d’. Như vậy, hình
chiếu của một đường thẳng nói chung là một đường thẳng. Nói cách khác, phép chiếu bảo
toàn tính liên thuộc của điểm và đường thẳng: Một điểm B thuộc đường thẳng d (AC) thì
hình chiếu của nó là B’ cũng phải thuộc hình chiếu d’ (A’C’) của đường thẳng d.
Trường hợp đặc biệt khi đường thẳng d đi qua tâm chiếu S thì hình chiếu của nó suy biến thành một điểm. o
Phép chiếu bảo toàn tỷ số kép của bốn điểm thẳng hàng:
Nếu A, B, C, D là bốn điểm thẳng hàng và A’, B’, C’, D’ là hình chiếu của chúng thì AC AD A’C’ A’D’
: = : , viết gọn là (ABCD) = (A’B’C’D’). CB DB C’B’ D’B’
Phép chiếu như trên hình 1.1 có tâm chiếu S là một điểm hữu hạn, người ta gọi đó là
phép chiếu xuyên tâm.
1.3. PHÉP CHIẾU SONG SONG (H. 1.2) Nếu tâm chiếu S là một điểm vô tận, tức là thay
tâm chiếu hữu hạn S bằng hướng
chiếu s không song song với ’ thì
phép chiếu được gọi là phép chiếu song song.
Chiếu một điểm A bất kỳ của không
gian theo hướng s lên mặt phẳng ’ như sau:
– Vẽ tia chiếu qua A và song song với s. Hình 1.2
– Giao của tia chiếu đó với ’ là A’
Tính chất của phép chiếu song song
gọi là hình chiếu của điểm A.
Vì phép chiếu song song là một trường hợp riêng của phép chiếu nên nó có mọi tính
chất của phép chiếu và thêm những tính chất sau: o
Bảo toàn tỷ số đơn của ba điểm thẳng hàng: Nếu ba điểm A, B, M thẳng hàng thì
AM / MB = A’M’ / M’B’ thường viết gọn là (ABM) = (A’B’M’). o Nếu AB CD thì : A’B’
C’D’ và AB / CD = A’B’ / C’D’. o Nếu EF ’ thì E’F’
= EF. o Một đường thẳng song song hướng chiếu thì
hình chiếu của nó suy biến thành điểm.
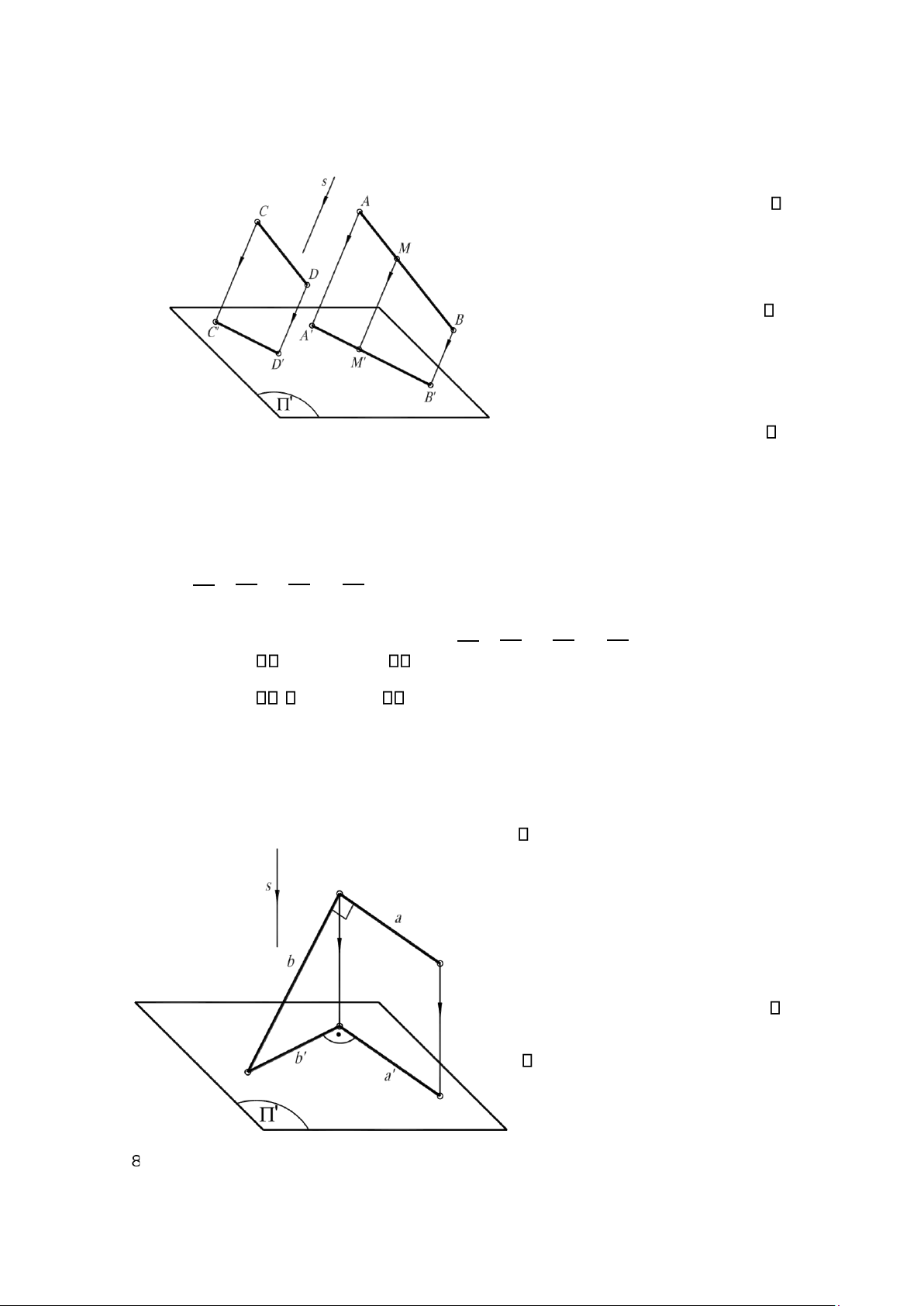
1.4. PHÉP CHIẾU VUÔNG GÓC
Phép chiếu vuông góc là một trường hợp đặc biệt của phép chiếu song song khi mà
hướng chiếu s vuông góc với mặt phẳng hình chiếu ’ (h. 1.3).
Phép chiếu vuông góc có tất cả
các tính chất của phép chiếu song song
và thoả mãn thêm định lý sau:
Xét hai đường thẳng không vuông
góc với mặt phẳng hình chiếu. Nếu
hai trong ba mệnh đề sau đây đúng thì
mệnh đề còn lại cũng đúng. Hai
đường thẳng vuông góc nhau.
Có ít nhất một trong hai đường
song song với mặt phẳng hình chiếu.
Hình chiếu của hai đường thẳng vuông góc nhau. Hình 1.3
1.5. TƯƠNG ỨNG CỘNG TUYẾN GIỮA HAI TRƯỜNG PHẲNG (THAM KHẢO) Hình 1.4
Một ánh xạ (quy luật liên hệ) một đối một giữa các điểm và đường thẳng thuộc trường
phẳng P với các điểm và đường thẳng thuộc trường phẳng P’ được gọi là tương ứng cộng
tuyến hay một phép cộng tuyến giữa hai trường phẳng đó nếu:
– Ứng với mỗi điểm A thuộc P là một điểm A’ thuộc P’.
– Ứng với mỗi đường thẳng a thuộc P là một đường thẳng a’ thuộc P’.
– Bảo toàn tính liên thuộc của điểm và đường thẳng.
Ta có thể tạo ra một phép cộng tuyến giữa hai trường phẳng bằng chuỗi các phép chiếu
vì như ta đã biết, phép chiếu bảo toàn tính liên thuộc của điểm và đường thẳng. Trên hình
1.4 là ví dụ về việc tạo ra phép cộng tuyến giữa hai trường phẳng P và P’’.
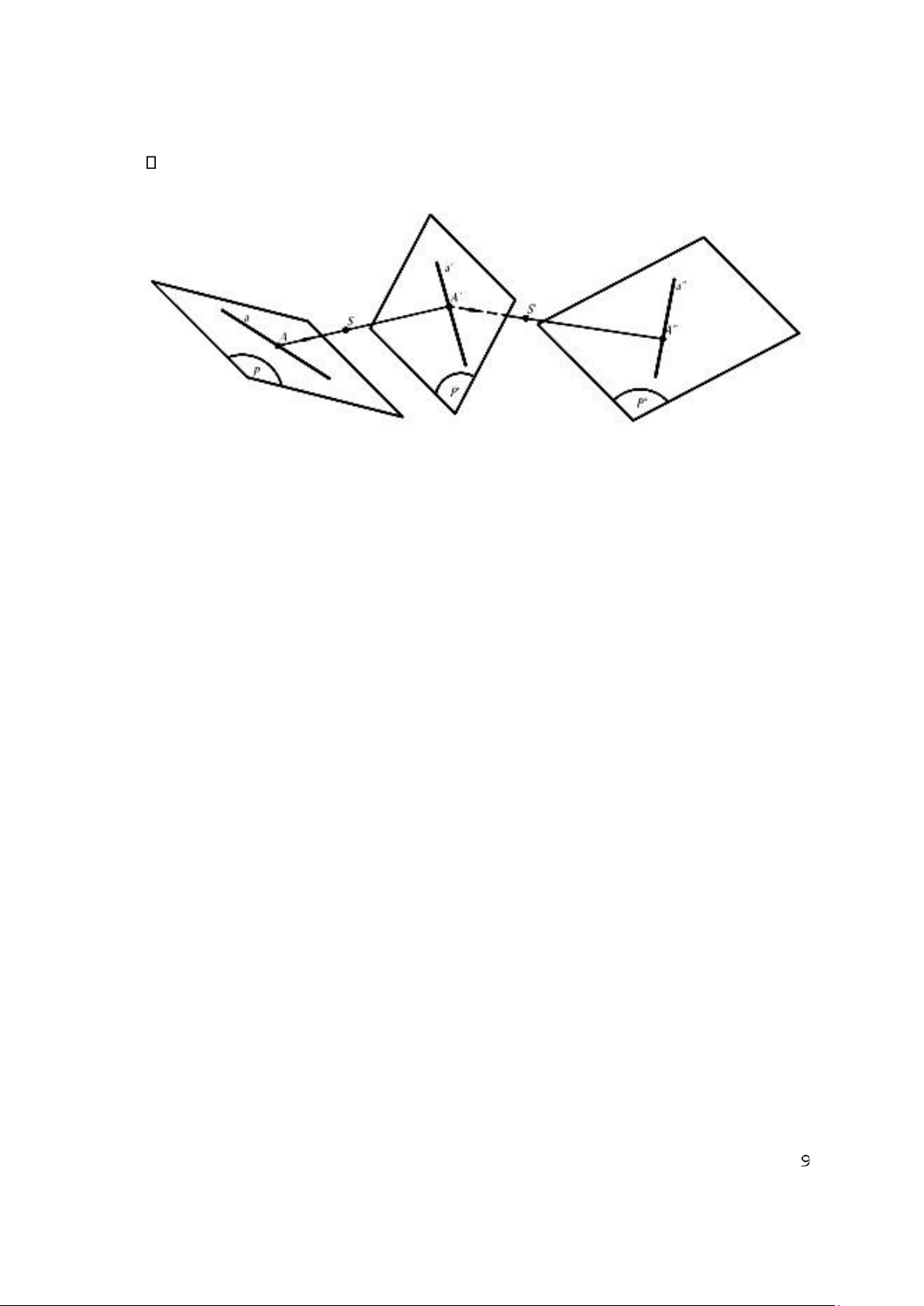
1.6. TƯƠNG ỨNG PHỐI CẢNH GIỮA HAI TRƯỜNG PHẲNG (THAM KHẢO)
Tương ứng phối cảnh giữa hai trường phẳng P và P’ là tương ứng cộng tuyến giữa hai
trường đó mà những đường thẳng nối những cặp điểm tương ứng AA’;... đều đồng quy tại một điểm.
Như vậy, phép chiếu tâm S những điểm, đường thẳng của P thành những điểm, đường
thẳng của P’ xác lập một tương ứng phối cảnh giữa P và P’ (h. 1.5).
Dễ dàng thấy rằng trong một tương ứng phối
cảnh giữa hai trường phẳng P và P’ thì mọi điểm M
thuộc giao tuyến u của hai mặt phẳng P và P’ đều
trùng với điểm tương ứng của nó, nói cách khác u
chứa những điểm kép. Ngược lại, có thể chứng
minh được rằng nếu trong một tương ứng cộng
tuyến giữa hai trường phẳng P và P’ mà các điểm
trên giao tuyến u của P và P’ đều là điểm kép thì
mọi đường thẳng nối các cặp điểm tương ứng đều
đồng quy tại một điểm S nào đấy, tức là tương ứng
cộng tuyến đó là tương ứng phối cảnh.
Điểm S và đường thẳng u gọi là tâm và
Hình 1.5 trục của tương ứng phối cảnh.
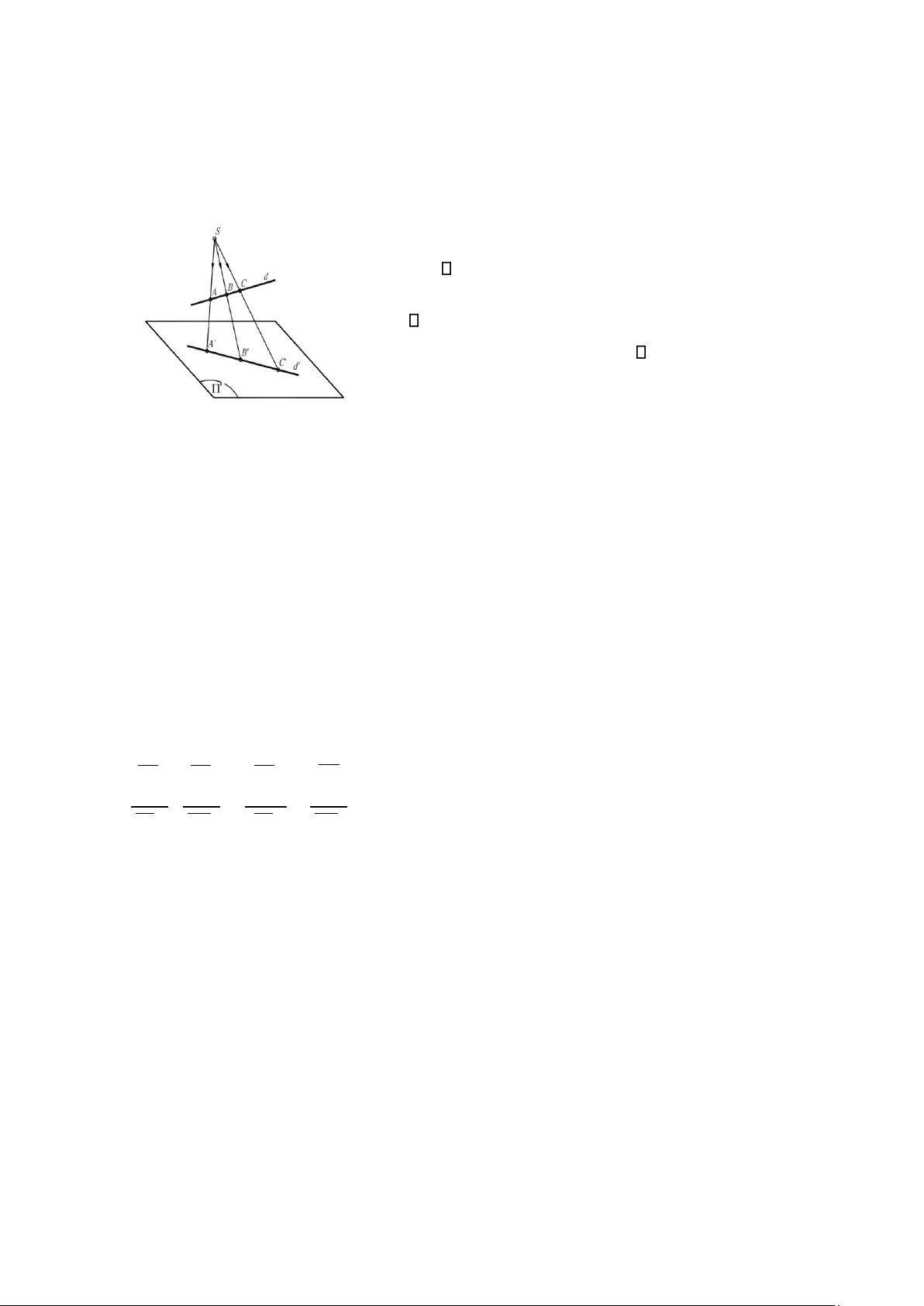
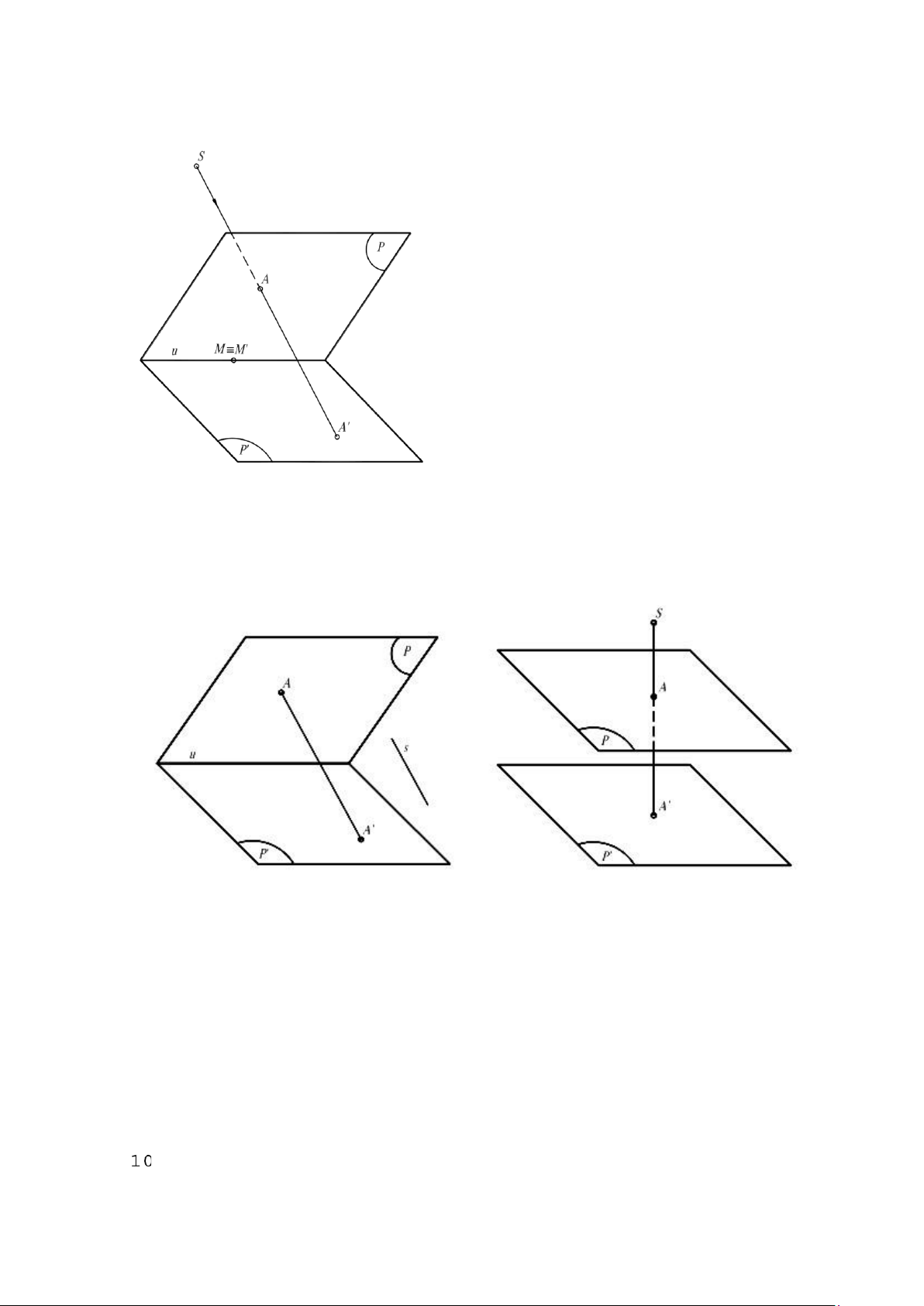
Nếu tâm phối cảnh S là một điểm vô tận (đường thẳng nối cặp điểm tương ứng song
song với s) thì tương ứng phối cảnh được gọi là tương ứng afin phối cảnh (h. 1.6).
Nếu trục phối cảnh u là một đường thẳng vô tận (P song song P’) thì tương ứng phối
cảnh được gọi là tương ứng đồng dạng phối cảnh (h. 1.7). Hình 1.6
Hình 1.7
Trong tương ứng afin phối cảnh hay đồng dạng phối cảnh thì hai đường thẳng song
song tương ứng với hai đường thẳng song song và tỷ số đơn của ba điểm thẳng hàng bằng tỷ
số đơn của ba điểm tương ứng của chúng.
1.7. PHÉP BIẾN ĐỔI CỘNG TUYẾN, PHÉP THẤU XẠ (THAM KHẢO)
Một tương ứng cộng tuyến giữa hai trường phẳng có giá trùng nhau (mặt phẳng P và
P’ trùng nhau) được gọi là phép biến đổi cộng tuyến.
Một phép biến đổi cộng tuyến trong đó có một đường thẳng u mà mọi điểm thuộc nó
đều là điểm kép hoặc một điểm O mà mọi đường thẳng nối các cặp điểm tương ứng đều đi
qua nó được gọi là phép thấu xạ. Điểm O và đường thẳng u lần lượt được gọi là tâm thấu xạ và trục thấu xạ.
Dễ dàng chứng minh được trong một phép biến đổi cộng tuyến, sự tồn tại của một
đường thẳng u mà mọi điểm thuộc nó đều là điểm kép kéo theo sự tồn tại của một điểm O
mà mọi đường thẳng nối các cặp điểm tương ứng đều đi qua nó và ngược lại.
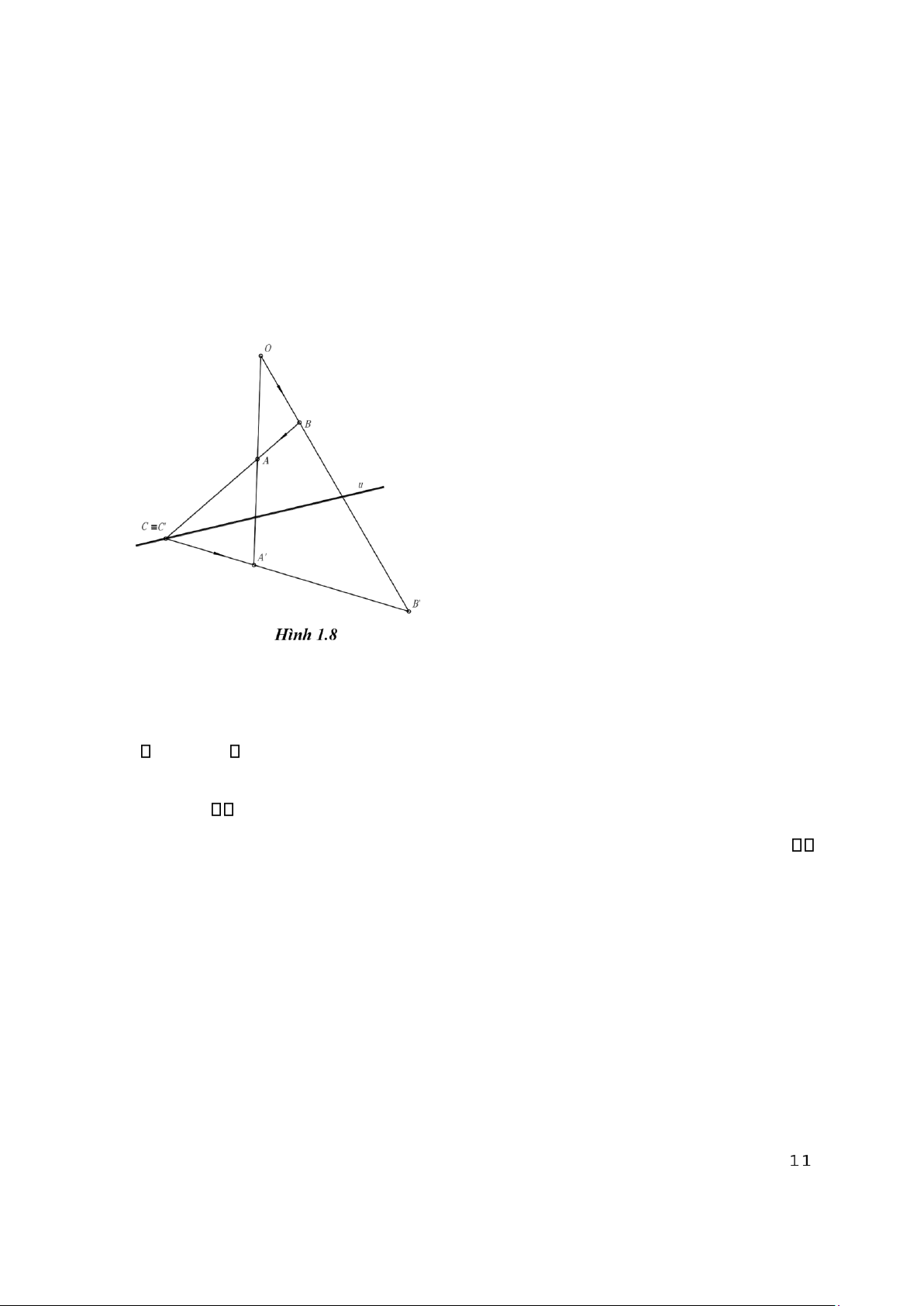
Phép thấu xạ là xác định khi cho tâm O, trục u và một cặp điểm tương ứng A, A’. Ví
dụ (h. 1.8): Cho thấu xạ (O, u, A, A’) và một điểm B. Vẽ điểm tương ứng B’ của B. Giải:
– AB cắt u tại C, ta có C’ trùng C (vì C thuộc trục thấu xạ u).
– Theo sự bảo toàn tính liên thuộc của điểm và
đường thẳng của một phép cộng tuyến thì B’ phải nằm trên C’A’.
– Trong phép thấu xạ thì B’B phải đi qua tâm thấu xạ O .
Cách vẽ B’ như hình vẽ thoả mãn những điều trên.
Phép thấu xạ cũng được xác định khi cho ba cặp điểm tương ứng (dĩ nhiên các đường
thẳng nối các cặp điểm tương ứng đó phải đồng quy tại một điểm) hoặc khi cho tâm thấu xạ
O và hai cặp đường thẳng tương ứng a, a’, b, b’ (dĩ nhiên đường thẳng nối các giao điểm I =
a b và J = a’ b’ phải đi qua O).
Phép thấu xạ có tâm ở vô tận (các đường thẳng nối các cặp điểm tương ứng song song nhau: AA’
BB’,...) gọi là phép afin phối cảnh.
Phép thấu xạ có trục ở vô tận (cặp đường thẳng tương ứng song song nhau: AB
A’B’,...) gọi là phép đồng dạng phối cảnh.
Phép thấu xạ có tâm và trục đều ở vô tận là phép tịnh tiến.
1.8. CÁC PHƯƠNG PHÁP BIỂU DIỄN
Phương tiện để biểu diễn một đối tượng trong hình học hoạ hình là phép chiếu, tuy
nhiên, dùng một hình chiếu thì không đảm bảo tính phản chuyển, nghĩa là từ một hình chiếu
đã cho của một đối tượng (hình chiếu của một đối tượng là tập hợp hình chiếu của các điểm
trên nó), ta không thể xác định duy nhất một đối tượng trong không gian. Chẳng hạn cho
trước một hình chiếu của một điểm cần tìm là A’ thì sẽ tìm được vô số những điểm A trong
không gian nằm trên tia chiếu đi qua A’ thoả mãn hình chiếu của nó là A’.
Để đảm bảo tính phản chuyển và thuận tiện trong việc khôi phục lại đối tượng cần biểu
diễn trong không gian, trong kỹ thuật người ta sử dụng những phương pháp biểu diễn sau:
o Phương pháp các hình chiếu thẳng góc (phương pháp Môngiơ). Hình biểu diễn xây
dựng bằng phương pháp này được sử dụng rộng rãi nhất trong kỹ thuật và thường là bộ
phận chính trên bản vẽ kỹ thuật. Phương pháp này sẽ được trình bày trong chương 2. o
Phương pháp hình chiếu trục đo. Hình chiếu trục đo thường dùng trong bản vẽ Cơ khí, đặt
bên cạnh những hình chiếu thẳng góc để bổ sung tính trực quan cho bản vẽ. Phương pháp
này được trình bày trong giáo trình vẽ kỹ thuật. o Phương pháp hình chiếu phối cảnh.
Dùng nhiều trong các bản vẽ xây dựng và kiến trúc.
o Phương pháp hình chiếu có số, được dùng chủ yếu để thể hiện những mặt địa hình.
Chương 2 BIỂU DIỄN, LIÊN THUỘC
Biểu diễn một đối tượng (điểm, đường thẳng, mặt phẳng, đa diện, mặt cong...) là cách
“cho” đối tượng đó: –
Trong Hình học Giải tích, các đối tượng được biểu diễn bằng toạ độ và phương trình. –
Trong Hình học Hoạ hình – một môn toán hình của kỹ sư, các đối tượng ba
chiều được biểu diễn bằng hình vẽ trên mặt phẳng.
Yêu cầu bắt buộc của việc biểu diễn là xác định được duy nhất đối tượng cần mô tả
(đảm bảo tính phản chuyển của phép biểu diễn), ngoài ra trong kỹ thuật thì phép biểu diễn
nên có tính trực quan. Trong cuốn sách này chỉ đề cập đến phép biểu diễn theo phương pháp:
các hình chiếu thẳng góc (tạo cơ sở cho môn Vẽ kỹ thuật về sau).
Trong việc biểu diễn một đối tượng, cần chỉ ra cách xác định một phần tử trên đối
tượng đó (vấn đề liên thuộc). 2.1. ĐIỂM
2.1.1 Tạo đồ thức điểm
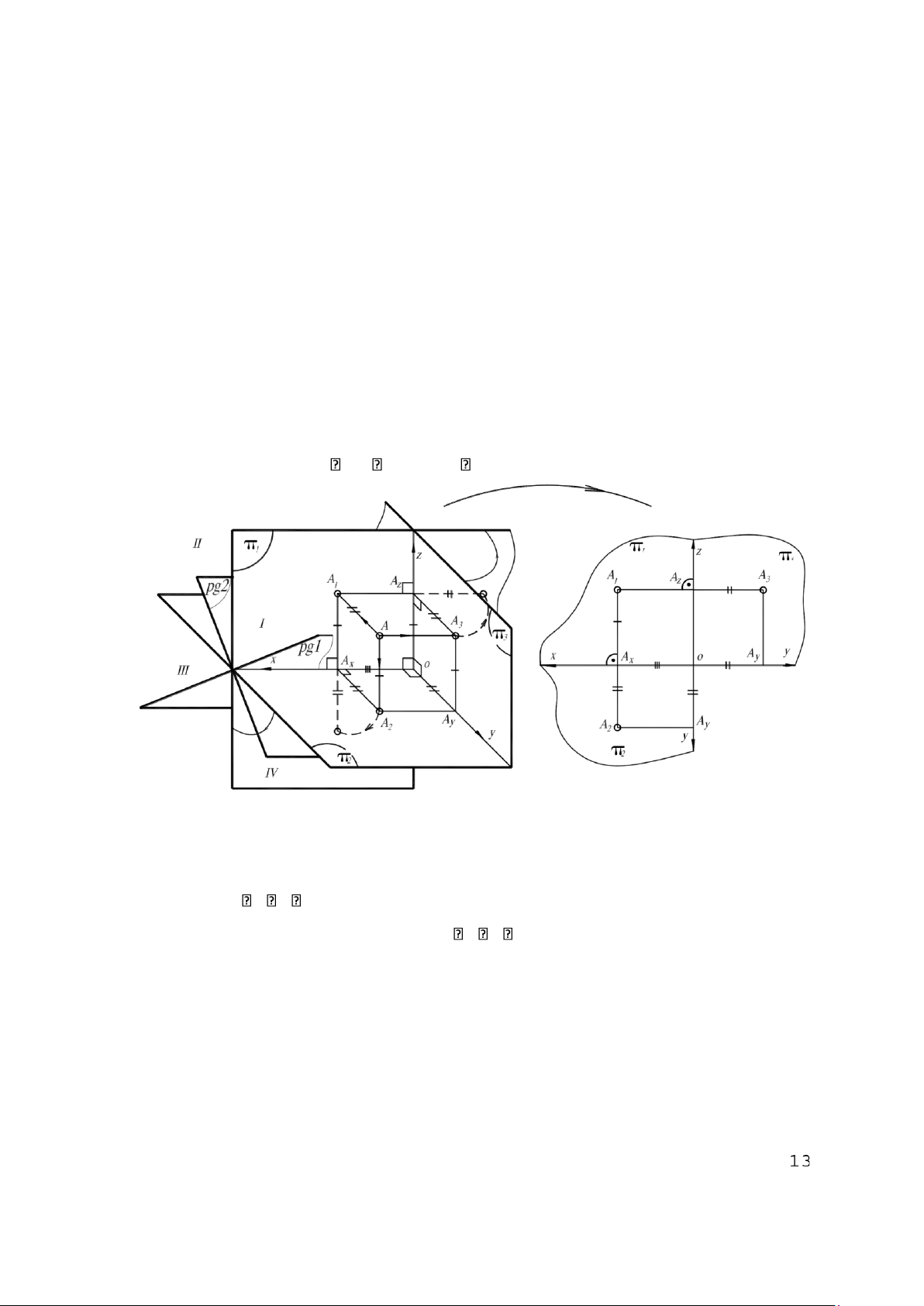
Đồ thức của một điểm được tạo ra như hình vẽ dưới đây (h. 2.1 và 2.2).
Mô hình ba chiều (3D) Biểu diễn đồ hoạ (2D) – Đồ thức
Quay 2 và 3 về trùng 1 thu được:
Hình 2.1 Hình 2.2 Các tên gọi:
– 1, 2, 3 lần lượt là mặt phẳng hình chiếu đứng, bằng, cạnh.
– Chiếu thẳng góc điểm A lên 1, 2, 3 thu được:
A1, A2, A3 lần lượt là hình chiếu đứng, bằng, cạnh của điểm A.
– | (z): Độ cao của điểm A;
|| (y): Độ xa của điểm A; |||
(x): Độ xa cạnh của điểm A.
Các “độ” ở trên chính là khoảng cách từ A đến các mặt phẳng hình chiếu tương ứng và
có dấu dương hay âm được quy định theo chiều của các trục x, y, z Tạo đồ thức:
– Đặt mặt phẳng tờ giấy vẽ trùng với 1 sẽ có A1 và các trục x, z.
– Quay 2 về trùng 1 đem theo A2 và trục y như hình 2.2.
– Quay 3 về trùng 1 đem theo A3 và trục y như hình 2.2.
Kết quả trên tờ giấy vẽ sẽ có đồ thức ba hình chiếu của điểm A như hình 2.2.
Tính chất của đồ thức:
– A1: thể hiện độ cao (z) và độ xa cạnh (x).
– A2: thể hiện độ xa (y) và độ xa cạnh (x). – A3: thể hiện độ cao (z) và độ xa (y).
A1, A2, A3 ràng buộc nhau như hình 2.2. Chú ý:
– Từ hai hình chiếu của một điểm, có thể vẽ được hình chiếu thứ ba nhờ sự ràng
buộc của các hình chiếu (xem hình 2.2). Do vậy, biểu diễn (vừa đủ) một điểm A chỉ
cần cho cặp hình chiếu thường là A1, A2 như sau:
Trong nhiều tài liệu hình hoạ, người ta chỉ nói đến đồ
thức hai hình chiếu thẳng góc, x gọi là trục hình chiếu. Cặp
hình chiếu phải nằm trên đường thẳng vuông góc với trục hình
chiếu gọi là sự liên hệ chiếu.
Mặc dù việc đưa ra đồ thức điểm bởi ba hình chiếu là
thừa nhưng nó có tác dụng xây dựng khái niệm hình chiếu Hình 2.3
cạnh sẽ được sử dụng trong nhiều trường hợp
– Việc gắn các trục x, y, z cùng với các toạ độ X, Y, Z là không cần thiết trong
hình hoạ, song nó tạo thuận lợi cho sinh viên chuyển biến dần từ mô hình giải tích sang
mô hình hình hoạ một cách chặt chẽ.
2.1.2. Ví dụ áp dụng
1 và 2 chia không gian làm bốn góc phần tư I, II, III, IV (xem lại hình 2.1). Mặt phẳng
phân giác 1 (pg1) chia đôi các góc phần tư I và III. Mặt phẳng phân giác 2 (pg2) chia đôi các góc phần tư II và IV.
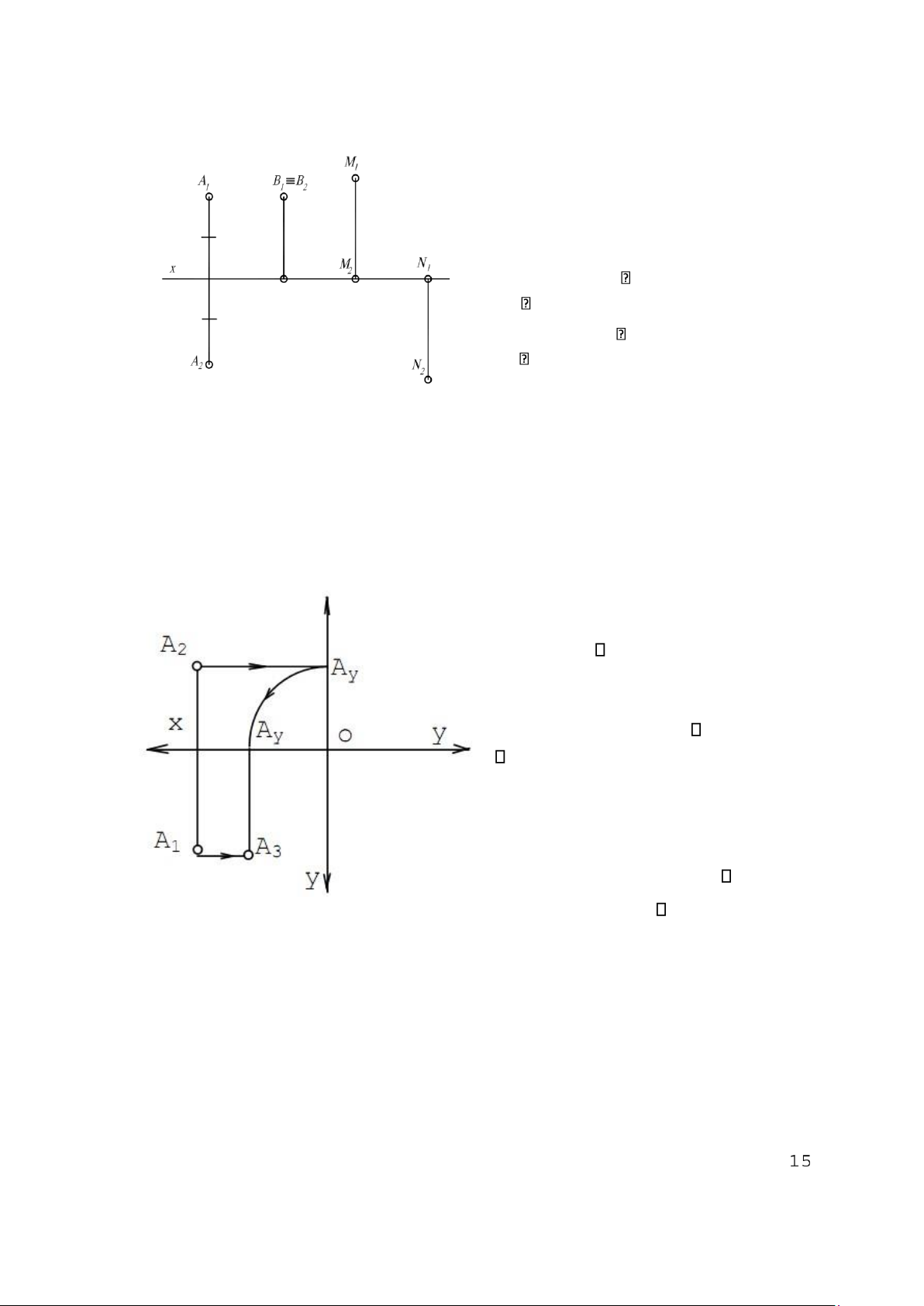
Ví dụ 1 (h. 2.4): Hãy vẽ đồ thức của các điểm A thuộc mặt phẳng phân giác 1, B thuộc
mặt phẳng phân giác 2, M thuộc 1, N thuộc 2. Giải:
Điểm A thuộc mặt phẳng pg1 nên có toạ
độ Z = Y dẫn đến hai hình chiếu đối xứng nhau qua x.
Điểm B thuộc mặt phẳng pg2 nên có toạ
độ Z = –Y dẫn đến hai hình chiếu trùng nhau.
Điểm M thuộc 1 có độ xa Y bằng không nên M2 x.
Điểm N thuộc 2 có độ cao Z bằng không nên N2 x.
Bạn đọc có thể đặt thêm trục z và y vào Hình 2.4
đồ thức cho dễ hiểu hoặc có thể nhận xét
những đặc điểm trên từ hình không gian (xem Ví dụ 2: (h. 2.5) lại h. 2.1). Cho A(A1, A2)
Vẽ A3; A thuộc góc phần tư nào?
Giải: Theo tính chất của đồ thức (xem lại h. 2.2) ta có: Z –
Quan hệ A3 và A1 là cùng độ cao Z (A1 A3 z). –
Quan hệ A3 và A2 là cùng độ xa
Y, ở đây chú ý Y âm (cần phân biệt hai trục
y trên đồ thức: một thuộc 2 và một thuộc 3).
Từ đó suy ra cách vẽ A3 như hình 2.5.
Nhìn vào A3 đã tìm được như trên, thấy A
thuộc góc phần tư III (hoặc nhận xét: A1
nằm dưới x nên A nằm dưới 2; A2 nằm
trên x nên A nằm sau 1, kết hợp lại thì A
nằm ở góc phần tư III). Hình 2.5 2.2. ĐƯỜNG THẲNG
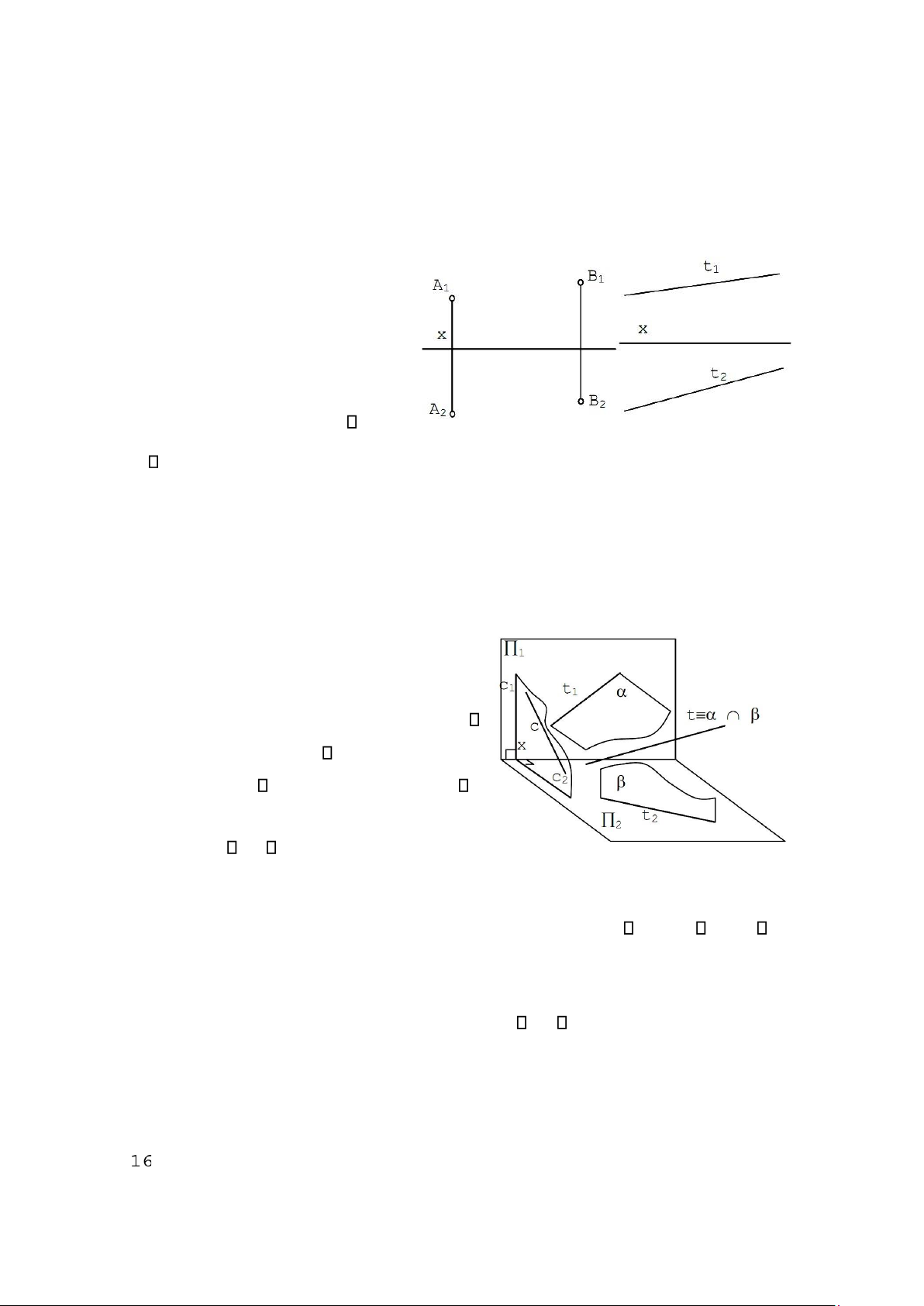
2.2.1. Biểu diễn đường thẳng
Một đường thẳng hoàn toàn được xác định khi cho hai điểm phân biệt trên nó.
Do vậy, có thể biểu diễn một đường thẳng thông qua đồ thức của hai điểm phân biệt trên nó (h. 2.6).
Cho một đường như h.2-6 về
toán là được nhưng thiếu tính trực Cho đường thẳng t (A, B) Cho đường thẳng t (t1, t2)
quan. Vì hình chiếu của một đường
thẳng là một đường thẳng chứa hình
chiếu của các điểm trên nó nên từ
hình 2.6 có thể tạo ra các hình chiếu
của đường thẳng t(A,B): t1 A1B1; t2 A2B2.
Từ phân tích trên người ta hay
biểu diễn đường thẳng thường
Hình 2.6 Hình 2.7
(không vuông góc với trục hình chiếu
x) bởi cặp hình chiếu của nó như hình 2. 7.
Chứng minh tính phản chuyển của hình
biểu diễn 2.7 (xem h. 2.8).
– Cho t1 thì t phải thuộc mặt phẳng
chứa t1 và vuông góc với 1. – Cho t2 thì t phải
thuộc mặt phẳng chứa t2 và vuông góc với 2.
Như vậy, cho t1và t2 sẽ xác định duy nhất
t là giao của và . Hình 2.8
Trường hợp c là đường thẳng vuông góc trục x (t song song 3) thì c1 c2 và x, khi
đó người ta gọi c là đường cạnh nếu c không vuông góc với các mặt phẳng hình chiếu.
Không thể biểu diễn một đường cạnh c chỉ bởi cặp hình chiếu c1, c2 vì theo cách chứng
minh tính phản chuyển như trên thì hai mặt phẳng và trùng nhau, sẽ có vô số đường c
thuộc mặt phẳng (c1, c2) thoả mãn đồ thức.
Để biểu diễn một đường cạnh c người ta có thể cho cặp hình chiếu c1 và c3 hoặc cho
hai điểm phân biệt trên nó (xem đường cạnh CD ở hình 2.10).
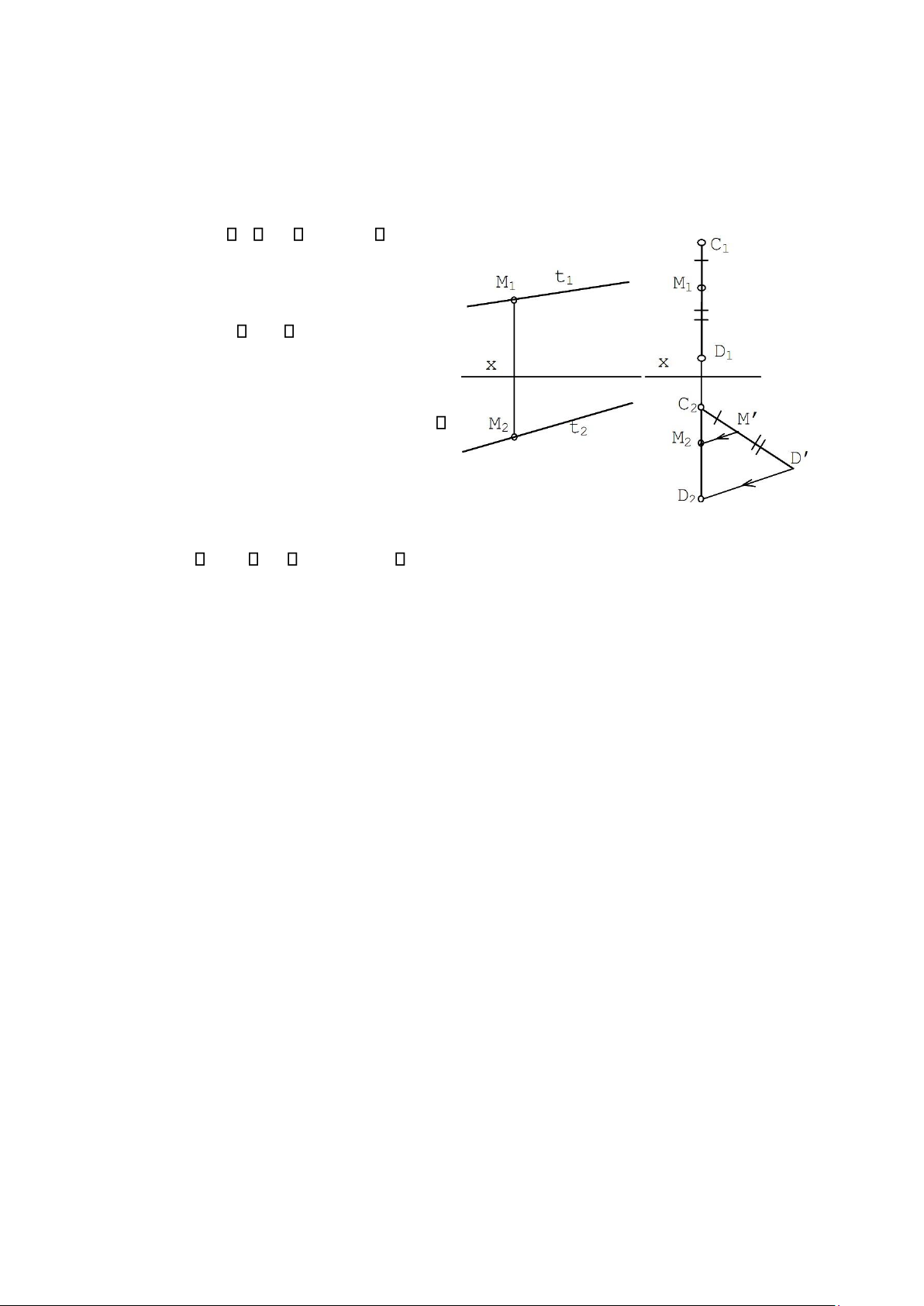
2.2.2. Điểm thuộc đường thẳng
a) Đường thẳng thường (h. 2.9) M t M1 t1 và M2 t2 (với
M1, M2 là các hình chiếu của điểm M).
b) Đường cạnh (h. 2.10) M CD (C1 M1 D1) = (C2 M2 D2).
Trên hình 2.10 chỉ ra cách vẽ
M2 khi cho trước M1 của điểm M CD.
Cũng có thể sử dụng hình chiếu cạnh: M CD M1 C1D1 và M3 C3D3 Hình 2.9 Hình 2.10
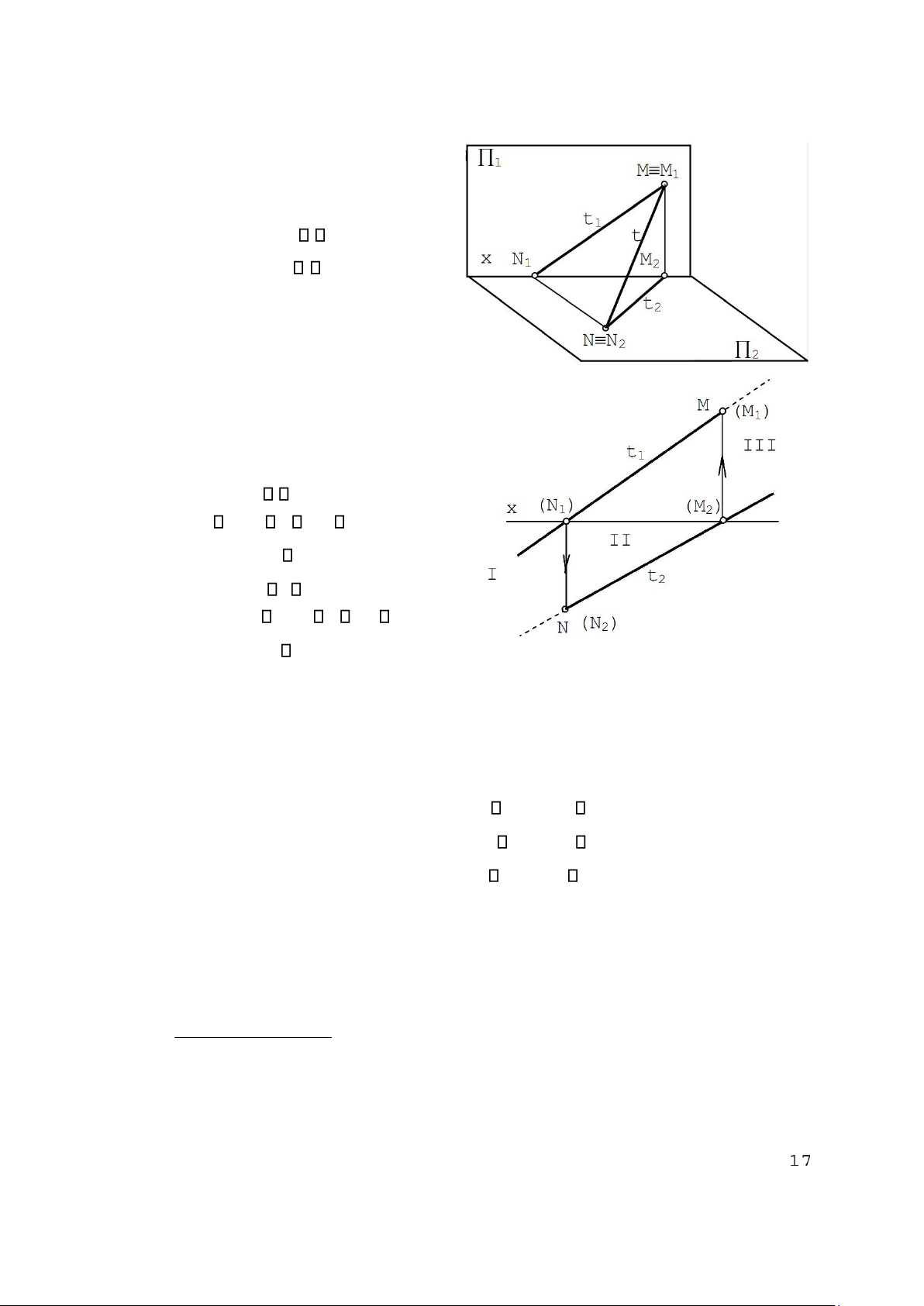
Áp dụng tìm vết của đường thẳng:
Vết của một đường thẳng là giao
điểm của đường thẳng đó với mặt phẳng hình chiếu (h.2.11). Vết đứng M = t 1 Vết bằng N = t 2
Tính chất hình chiếu của các vết như hình 2.11. Bài toán (h. 2.12):
Hình 2.11
Cho đường thẳng t(t1, t2).
Vẽ vết đứng M và vết bằng N của t; t
đi qua những góc phần tư nào? Giải: –
M 1 có độ xa bằng không nên M2 x; M t M2 t2. Do đó M2 = t2 x. – N 2 có độ cao bằng
không nên N1 x; M t N1 t1. Do đó N1 = t1 x. Hình 2.12
Trên đồ thức (h. 2.12), để cho gọn, người ta thường chỉ ghi N (thay cho N2) và M (thay
cho M1) mà không cần ghi M2, N1.
Các vết M và N chia đường thẳng t làm ba đoạn thuộc các góc phần tư khác nhau: –
Đoạn I chứa các điểm nằm trước 1 và dưới 2 nên thuộc góc phần tư IV. –
Đoạn II chứa các điểm nằm trước 1 và trên 2 nên thuộc góc phần tư I. –
Đoạn III chứa các điểm nằm sau 1 và trên 2 nên thuộc góc phần tư II.
Để thấy rõ điều trên có thể sử dụng hình chiếu cạnh. Như vậy, t đi qua các góc phần tư IV, I, II.
Trong trường hợp phải tìm vết của đường cạnh, ta sử dụng điều kiện điểm thuộc đường
cạnh để giải quyết.
Giải thích thấy khuất:
Để tăng tính trực quan, các mặt được quy định là “mờ”, nghĩa là sẽ che khuất những gì
sau nó theo hướng nhìn (người quan sát được quy định ở góc phần tư I và ở xa vô cùng trên
phương chiếu). Trên đồ thức, những đoạn khuất thể hiện bằng nét đứt.
Mặt phẳng 1 và 2 cũng được quy định là “mờ” nên: –
Những điểm nằm ở nửa trước 1 (góc phần tư I và IV) sẽ là thấy trên hình
chiếu đứng, những điểm còn lại là khuất trên hình chiếu đứng. –
Những điểm nằm ở nửa trên 2 (góc phần tư I và II) sẽ là thấy trên hình chiếu
bằng, những điểm còn lại là khuất trên hình chiếu bằng.
Đoạn I nằm trước 1 và dưới 2 nên có hình chiếu đứng là thấy và hình chiếu bằng là khuất.
Đoạn II nằm trước 1 và trên 2 nên có hình chiếu đứng là thấy và hình chiếu bằng là thấy.
Đoạn III nằm sau 1 và trên 2 nên có hình chiếu đứng là khuất và hình chiếu bằng là thấy. 2.3. MẶT PHẲNG
2.3.1. Biểu diễn mặt phẳng – đồ thức hai đường thẳng cắt nhau, song song
a) Biểu diễn mặt phẳng bởi hai đường thẳng cắt nhau (h. 2.13)
Trên hình 2.13, hai đường thẳng a và b cắt nhau tại điểm I (theo điều kiện điểm thuộc
đường thẳng đã học) sẽ xác định duy nhất mặt phẳng . Qua đây ta nhận thấy điều kiện cắt
nhau của hai đường thẳng (thường và không có hình chiếu nào trùng nhau) là:
a b (a1 b1 = I1) ( a2 b2 = I2 ) ( I1I2 x.)
b) Biểu diễn mặt phẳng bởi hai đường thẳng song song (h.2.14)
Hai đường thẳng c và d song song nhau sẽ xác định duy nhất mặt phẳng . Dễ dàng
nhận thấy điều kiện của hai đường thẳng (thường) song song nhau là: c d (c1 d1 ) ( c2 d2 ) Chú ý: