Significant Figures | Bài tập môn Vật lý đại cương 1 CTTT | Trường Đại học Bách Khoa Hà Nội

7/2/2021 Physic Experiments - I SI Units
Vietnam has accepted SI units since 1960. Measurements and Basic SI Uncertainties quantities Quantity Dimension Alternatives Root definition Vu Xuan Hien Length m m meter School of Engineering Physics Mass kg kg kilogram Add: 211- C9 Time s s second Email: hien.vuxuan@hust.edu.vn Current, electric A A ampere Measurements: Temperature K K kelvin Quantity of substance mol mol mole Every measurement has UNITS.
Luminosity | Luminous intensity cd cd candle
Every measurement has UNCERTAINTY. 1 7/2/2021 2 1 2 SI Units prefixes Physical Quantities and Units Prefix Symbol Factor Examples of usage Origin Yotta Y 1024 0.2 YW, 1.23Y [W] Greek 'octo' (eight, 10008) Quantity Definition Formula Units Dimensions Zetta Z 1021 3.33 Zs, 3.33Z [s] French 'sept' (seven, 10007) Length or Distance fundamental d m (meter) L (Length) Exa E 1018 1.23 Ekg, 1.23E [kg] Greek 'six' (10006) Time fundamental t s (second) T (Time) Peta P 1015 7.5 Ps, 7.5P [s] Greek 'five' (10005) Mass fundamental m kg (kilogram) M (Mass) Tera T 1012 0.5 Tm, 0.5T [m] Greek 'teras' = monster Area distance2 A = d2 m2 L2 Giga G 109 1.2 GΩ, 1.2G [Ω] Greek 'gigas' = giant Volume distance3 V = d3 m3 L3 Mega M 106 7 MW, 7M [W] Greek 'megas' = large Density mass / volume d = m/V kg/m3 M/L3 Kilo K, k 103 33 km, 33K [m] Greek 'kilioi' = thousand Velocity distance / time v = d/t m/s L/T M hecto h 100 Deprecated by SI Greek 'hekaton' = hundred E Acceleration velocity / time a = v/t m/s2 L/T2 Momentum mass × velocity p = mv kg·m/s ML/T deca da 10 Deprecated by SI Greek 'deka' = ten C H deci d 0.1 Deprecated by SI
Latin 'decima pars' = one tenth Force mass × acceleration F = ma A N (newton) = kg·m/s2 ML/T2 centi c 0.01 Deprecated by SI
Latin 'centesima pars' = one hundredth Weight mass × (accel. of grav.) W = mg N milli m, k 10-3 22 mm , 1.2m [m]
Latin 'millesima pars' = one thousandth I Pa (pascal) = N/m2 = C
Pressure or Stress force / area p = F/A M/LT2 micro µ, u 10-6 2.7 uJ , 2.7µ [J] Greek 'mikros' = small kg/(m·s2) A nano n 10-9 2.2 nF, 2.2n [F] Latin 'nanus' = dwarf L Energy or Work force × distance E = Fd pico p 10-12 1.5 pA, 1.5p [A]
Spanish 'pico' = minimal measure Kinetic Energy mass × velocity2 / 2 KE = mv2/2 J (joule) = N·m = kg·m2/s2 ML2/T2 femto f 10-15 4.8 fs, 4.8f [s]
Danish and Norvegian 'femten' = fifteen (10-15) Potential Energy
mass × (accel. of grav.) × height PE = mgh atto a 10-18 1.2 ag, 1.2a [g]
Danish and Norvegian 'atten' = eighteen (10-18) Power energy / time P = E/t W (watt) = J/s = kg·m2/s3 ML2/T3 zepto z 10-21 0.2 zm, 1.2z [m] French 'sept' (seven, 1000-7) Impulse force × time I = Ft N·s = kg·m/s ML/T yocto y 10-24 1 ys, 1y [s] Greek 'octo' (eight, 1000-8) energy × time A = Et Action J·s = kg·m2/s ML2/T momentum × distance A = pd 7/2/2021 3 4 7/2/2021 4 3 4 1 7/2/2021 1. UNCERTAINTY vs. DISCREPANCY 2. ORIGINS OF UNCERTAINTIES
When you report the result of a measurement of a quantity x, you should
Discrepancies between experimental values and "true" values
also give the uncertainty x: 5.0 m ± 0.1 m
I. Systematic Errors are inaccuracies due to identifiable causes and x x
can, at least in principle, be eliminated.
• The uncertainty tells you how precise you think your measurement is.
a) Theoretical - due to simplifications of the model system or
→ useful to compare your result with a "true" or accepted value
approximations in the equations describing it.
• Discrepancy is the difference between your result and accepted value
b) Instrumental - e.g., a poorly calibrated instrument.
c) Environmental - e.g., factors such as inadequately controlled temperature and pressure.
d) Observational - e.g., parallax in reading a meter scale. Result: accepted value : g g
II. Random Uncertainties are the result of small fluctuating disturbances  exp acc ]
which cause about half the measurements of any quantity to be too high and 9.75 9.81 g half to be too low. exp
The uncertainty gexp in the measurement accounts 5
nicely for the discrepancy between g 6 exp and gacc 5 6
3. CHARACTERIZING A SET OF DATA: THE NORMAL DISTRIBUTION Random vs systematic errors
- Make "many" measurements of a quantity x and plot the frequency
of occurrence N(x), → obtain a curve that approximates a Gaussian, Random errors only or normal distribution, 2 (x) N0 - True value 2 N(x) = e 2 2 Random + systematic
µ and  determine the position and width of the peak.
• A result is said to be accurate if it is relatively free from systematic error
For a set of data points xi, the mean of all values obtained for x
• A result is said to be precise if the random error is small n xi x  x    x x i1 1 2 n   n n 8 7 8 2 7/2/2021
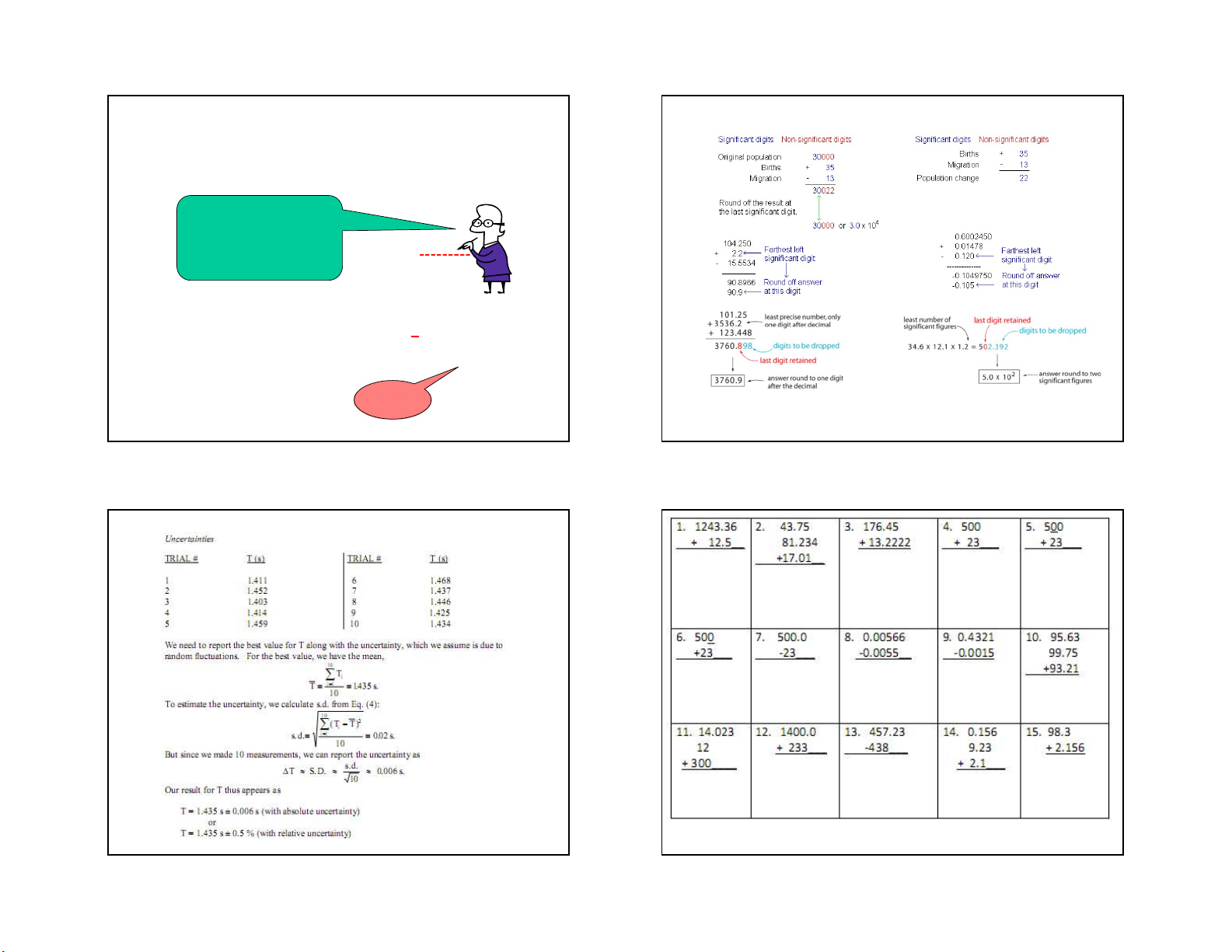
Standard deviation of a ‘single’ measurement Propagation of Uncertainties x  x 2     
Given: AA, BB and f = f(A,B) 1 x x22 ... x xN 2 s d . .  x  N
Standard deviation of Means: S. D. In general 2 2  f   f  s d . . x f   A   B S . D .    A    B   N N
Addition/ subtraction: f = A + B Report of the measurements
f   A2   B2 x  S . D .
S.D. in one or two significant figure
Multiplication/ division/ powers   f  A B 2 2  A   B  f  f       A   B  9 10 9 10
Least Squares Fit (Linear Regression)
Measurements: (x1, y1), (x2, y2),………, (xN, yN), N pairs of data. In theory:
y = mx + b; m = slope, b = y-intercept Result of Least Squares Fit: N x y   x  y m i i i i  N x2   Significant figures i  x 2i y x2  x x y b i i i i i  N x2   i  x 2i N y (mx  b i i 2 1 )  1 1  1  r i 1 r 2 2 m   m  m  N(N  ) 1 N N x r  correlati n o coefficie t n x  x  2 2 i 2 x
b  m   x ,   , x i  x x 11 N N 12 11 12 3 7/2/2021
Accuracy and Precision in Measurements Accuracy and Precision
Accuracy: how close a measurement is to the accepted value.
Precision: how close a series of
measurements are to one another or
how far out a measurement is taken.
A measurement can have high precision, but
not be as accurate as a less precise one. 13 14 13 14
Significant Figures are used to indicate the precision of a
Rules for Determining Significant Figures in a Number
measured number or to express the precision of a calculation with measured numbers.
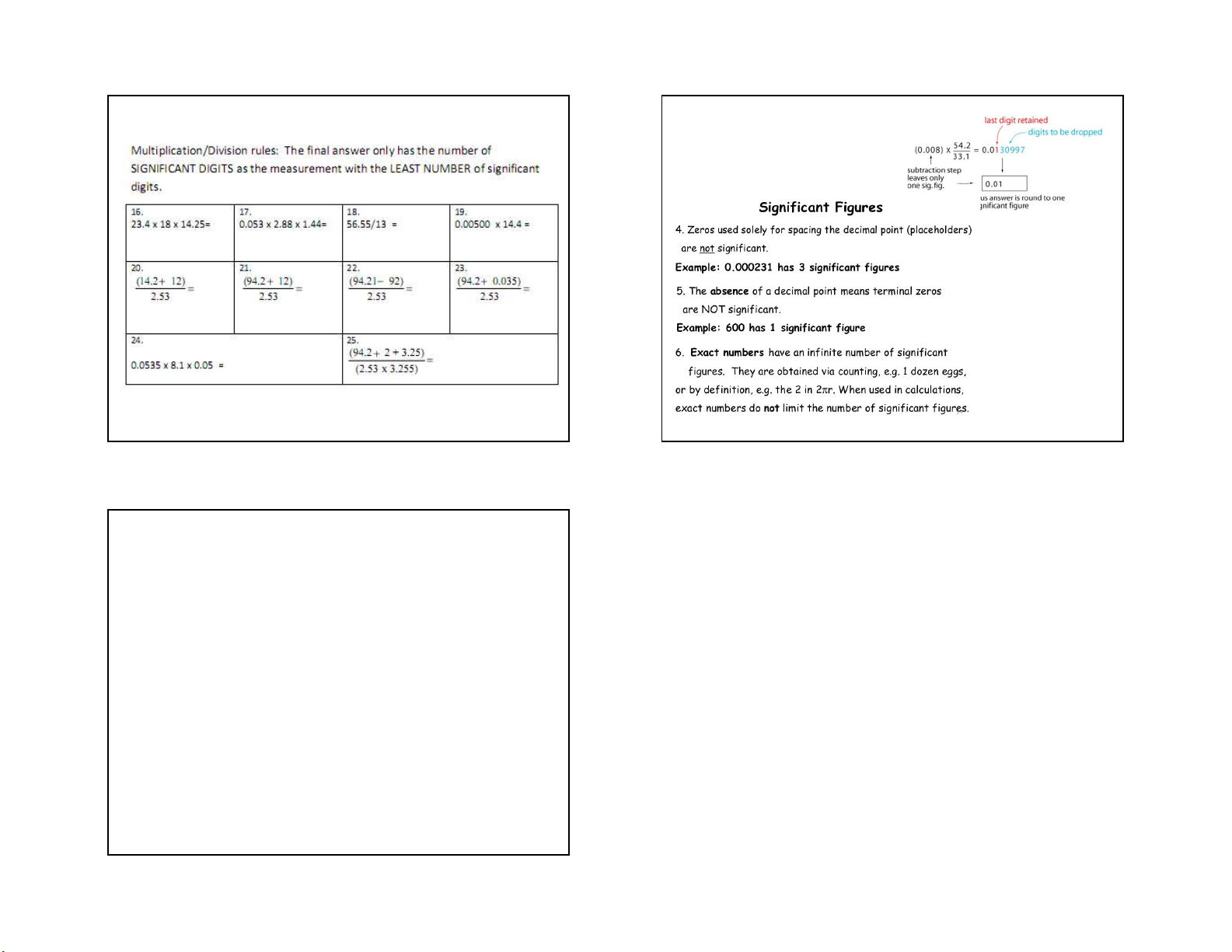
1. All non-zero numbers are significant.
2. Zeros within a number are always significant. In any measurement
3. Zeros that do nothing but set the decimal point are not the digit farthest to
significant. Both 0.000098 and 0.98 contain two significant figures. the right is
4. Zeros that aren’t needed to hold the decimal point are considered to be
significant. For example, 4.00 has three significant figures. estimated.
5. Zeros that follow a number may be significant. 0 1 2 2.0 1.3 15 16 15 16 4 7/2/2021
1. The term that is related to the reproducibility
(repeatability) of a measurement is
3. The number of significant figures in 6.0700 x 10-4… is a. accuracy. a. 3. b. precisio L ne.t’s take a “Quiz” b. 4. c. qualitative. b. precision. c. 5. c. 5. d. quantitative. d. 6. e. property. e. 7.
2. The number of significant figures in the mass
4. How many significant figures are there in the value measured as 0.010210 g is 0.003060? a. 1. a. 7 b. 2. b. 6 e. 5. c. 3. c. 5 d. 4. d. 4 d. 4 e. 5. e. 3 17 18 17 18 Calculations with sig. Figs.
Measurement Calculations with scientific notation. Addition and subtraction:
Addition/subtraction: must be placed into the same notation. Look at places! (2.3 x 103) + (3.2 x 104) = 0.23 x 104 3.63 cm +3.2 x 104 13.129 cm 3.43 x 104 = 3.4 x 104 +123.1 cm 139.859 cm = 139.9 cm significant to the 0.1 place 19 20 19 20 5 7/2/2021 Calculations with Sig. figs.
Multiplication and division (measurements): You must be able to count.
2.734 cm x 5.2 cm x 8.1294 cm = 115.5740539 cm3 4 s.f. 2 s.f. 5 s.f. written as 120 cm3 2 s.f.’s 21 22 21 22 23 24 23 24 6 7/2/2021 25 26 25 26 27 27 7