ELT3047 Computer Architecture
Lecture 6: Arithmetic processing unit implementation Hoang Gia Hung
Faculty of Electronics and Telecommunications
University of Engineering and Technology, VNU Hanoi Last lecture review
❑ Demonstration of design principles for MIPS ISA ➢ Storage model ➢ Addressing mode ➢ Instruction encoding
➢ Compiler support* (self-study) ❑ MIPS instruction set
➢ Arithmetic & logical instructions ➢ Data transfer instructions ➢ Control instructions ➢ if-then, loops ➢ Procedure call
❑ Brief introduction to compiler technology
❑ Today’s lecture: implementation of MIPS ALU
➢ First part of the MIPS datapath in incremental featurism approach. Arithmetic for Computers ❑ Operations on integers ➢ Addition and subtraction
➢ Multiplication and division ➢ Dealing with overflow ❑ Operations on real numbers ➢ Floating point operations ➢ Rounding error
❑ Arithmetic for multimedia (not covered in this course)
➢ Performing simultaneous operations on short vectors, e.g. 128-bit adder
= four 32-bit adds. Also called data-level parallelism (DLD), vector
parallelism, or Single Instruction, Multiple Data (SIMD)
➢ Saturating operations (e.g. clipping in audio, saturation in video)
Integer Addition and Subtraction
❑ Digits are added bit by bit from right to left, with carries
passed to the next digit to the left ➢ Example: 7 + 6
❑ Subtraction: the appropriate operand is simply negated before
being added, any carry-out is discarded.
➢ Example: 7 – 6 = 7 + (–6) +7: 0111 –6: 1010 +1: 1 0001 (discard carry-out) Overflow
❑ Occurs if result out of signed integer range
➢ Example: 7 - (-6) = 7 + 6 +7: 0111 +6: 0110
+13: 1101 = -8 + 4 + 1 = -3 (two’s complement)
➢ Occurs when adding operands with the same sign, or subtracting
operands with different signs.
➢ Detection: checking the MSB of two operands and the answer (3-bit
comp.) or checking Carry-in and Carry-Out from MSB’s (2-bit comp.). ❑ Dealing with Overflow.
➢ Some languages (e.g., C) ignore overflow
➢ Other languages (e.g., Ada, Fortran) require raising an exception → the
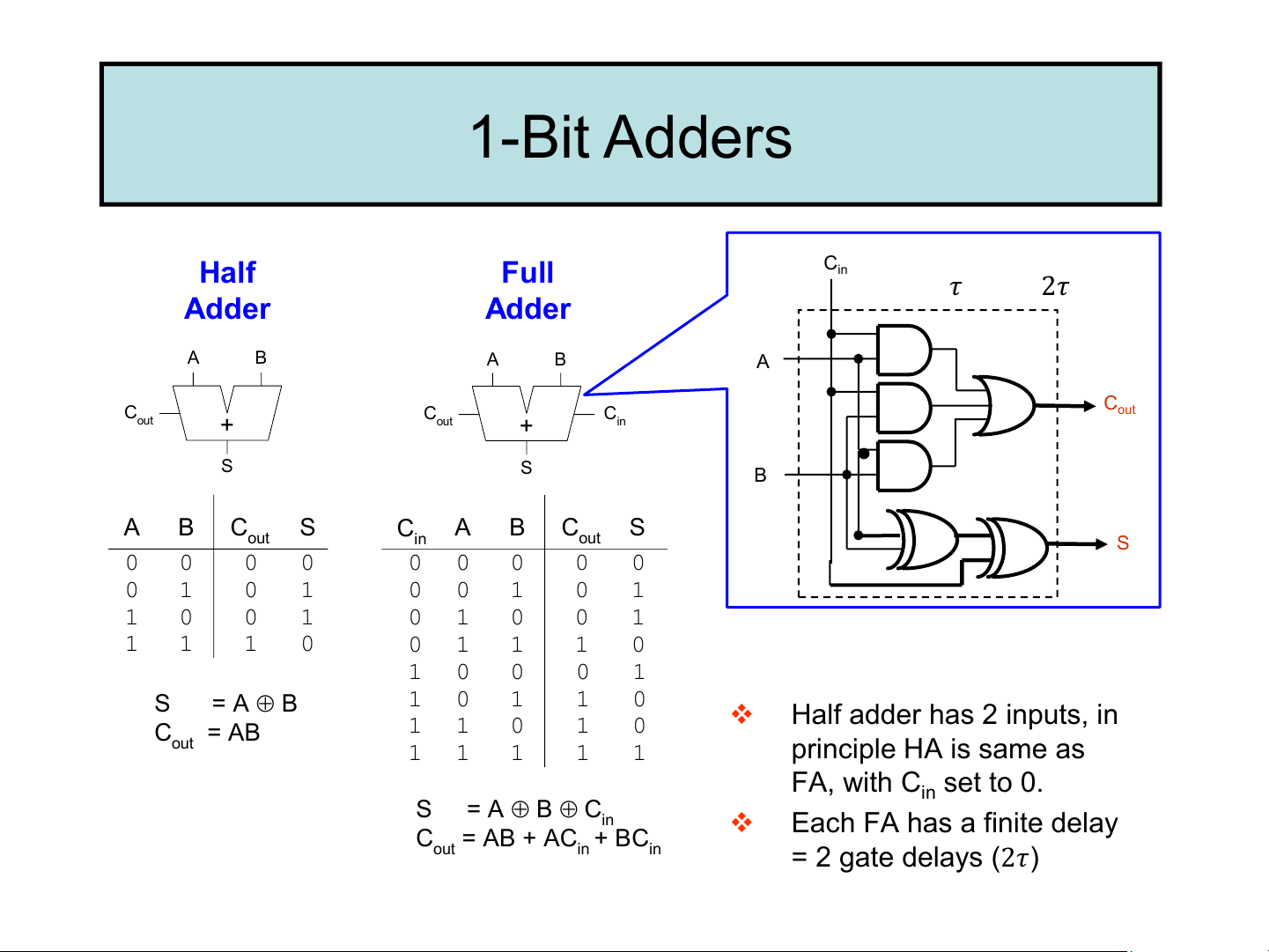
computer jumps to a predefined address to invoke the appropriate routine. 1-Bit Adders Half Full Cin 𝜏 2𝜏 Adder Adder A B A B A C C C C out out + out in + ⚫ S S B A B C S C A B C S out in out S 0 0 0 0 0 0 0 0 0 0 1 0 1 0 0 1 0 1 1 0 0 1 0 1 0 0 1 1 1 1 0 0 1 1 1 0 1 0 0 0 1 S = A  B 1 0 1 1 0 ❖ Half adder has 2 inputs, in C = AB 1 1 0 1 0 out 1 1 1 1 1 principle HA is same as FA, with C set to 0. in S = A  B  Cin ❖ Each FA has a finite delay C = AB + AC + BC out in in = 2 gate delays (2𝜏) Multibit Adders A B N N C C out in + N S
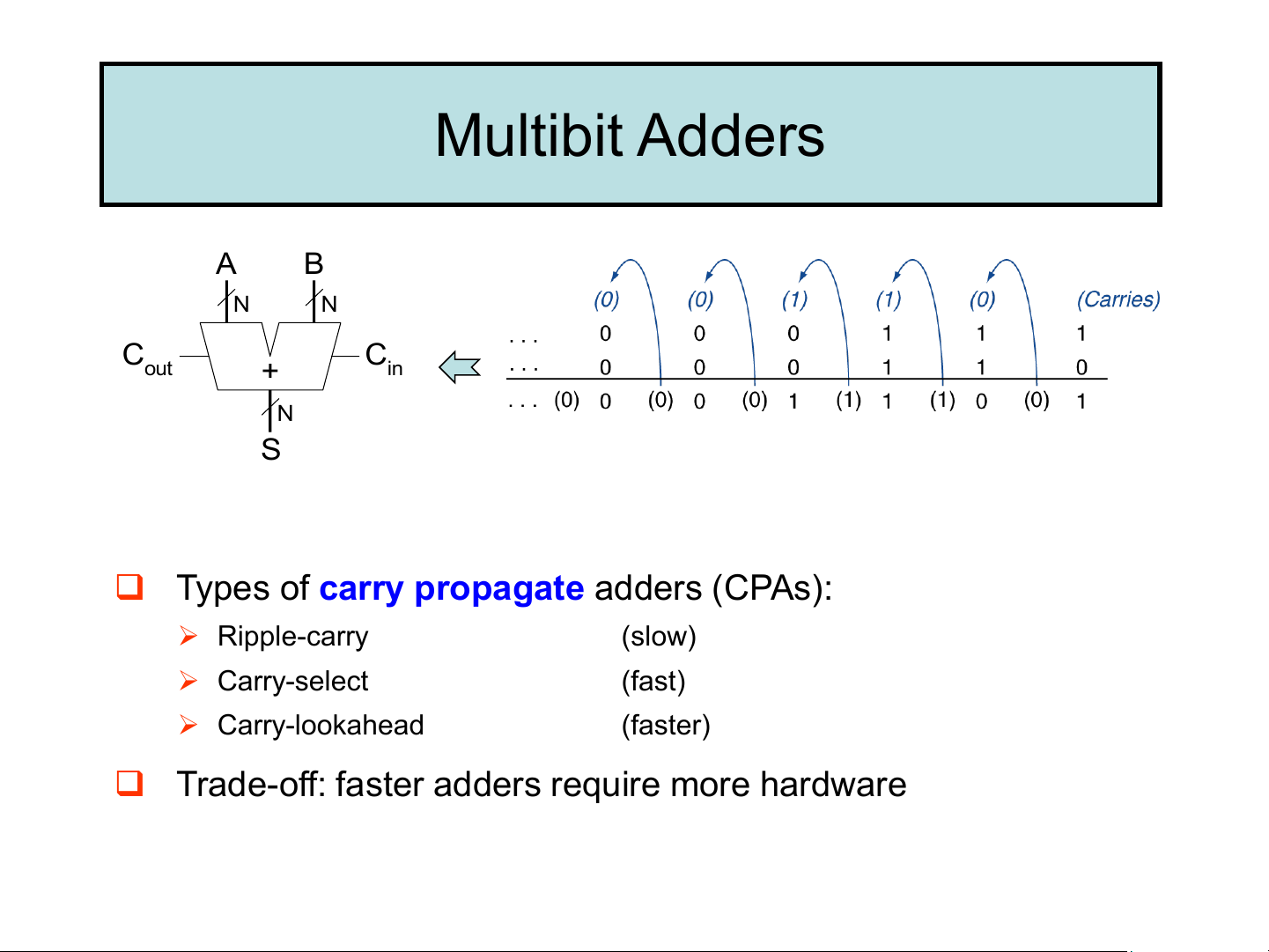
❑ Types of carry propagate adders (CPAs): ➢ Ripple-carry (slow) ➢ Carry-select (fast) ➢ Carry-lookahead (faster)
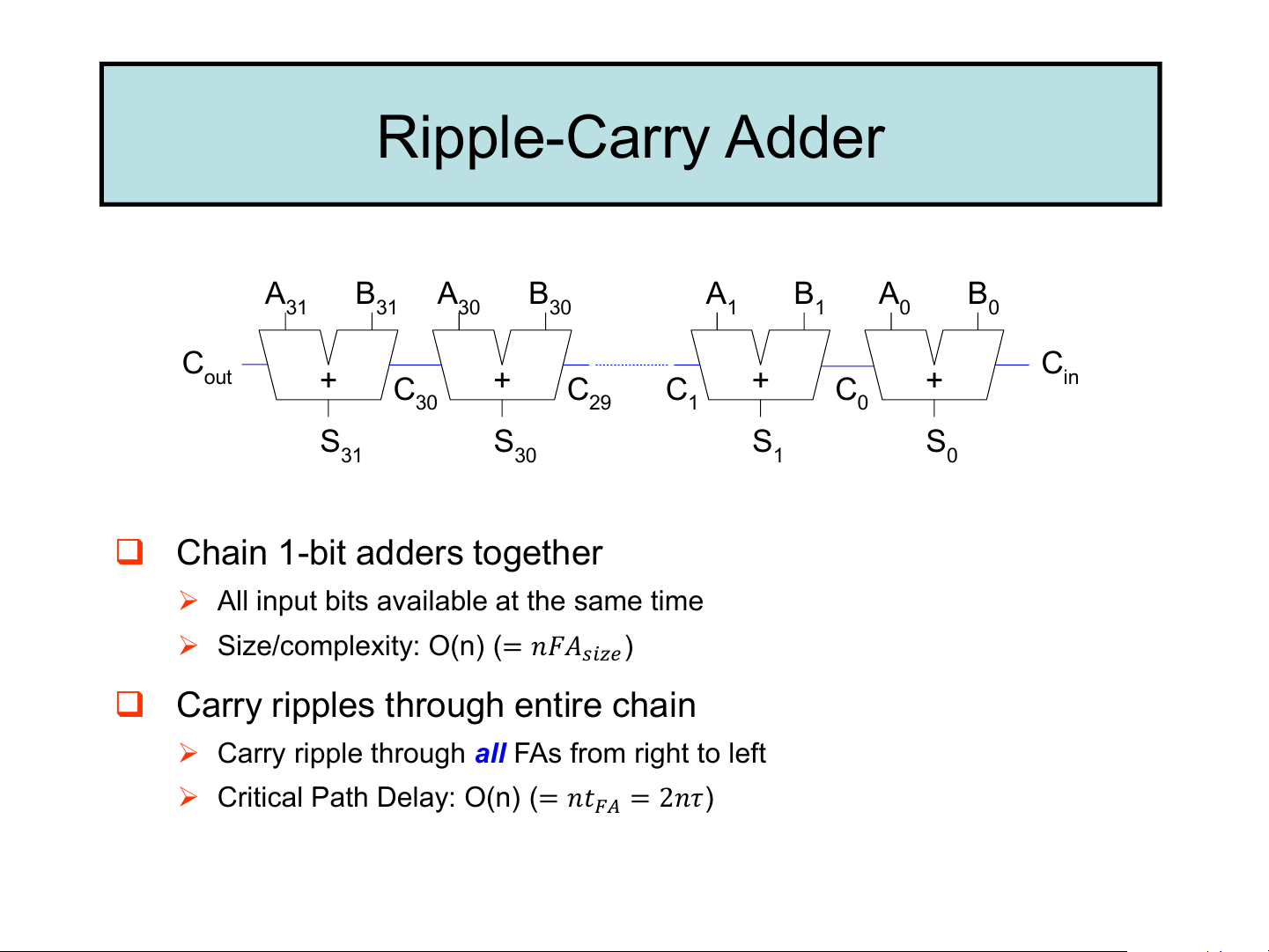
❑ Trade-off: faster adders require more hardware Ripple-Carry Adder A B A B A B A B 31 31 30 30 1 1 0 0 C C out + C + C C + C + in 30 29 1 0 S S S S 31 30 1 0
❑ Chain 1-bit adders together
➢ All input bits available at the same time
➢ Size/complexity: O(n) (= 𝑛𝐹𝐴𝑠𝑖𝑧𝑒)
❑ Carry ripples through entire chain
➢ Carry ripple through all FAs from right to left
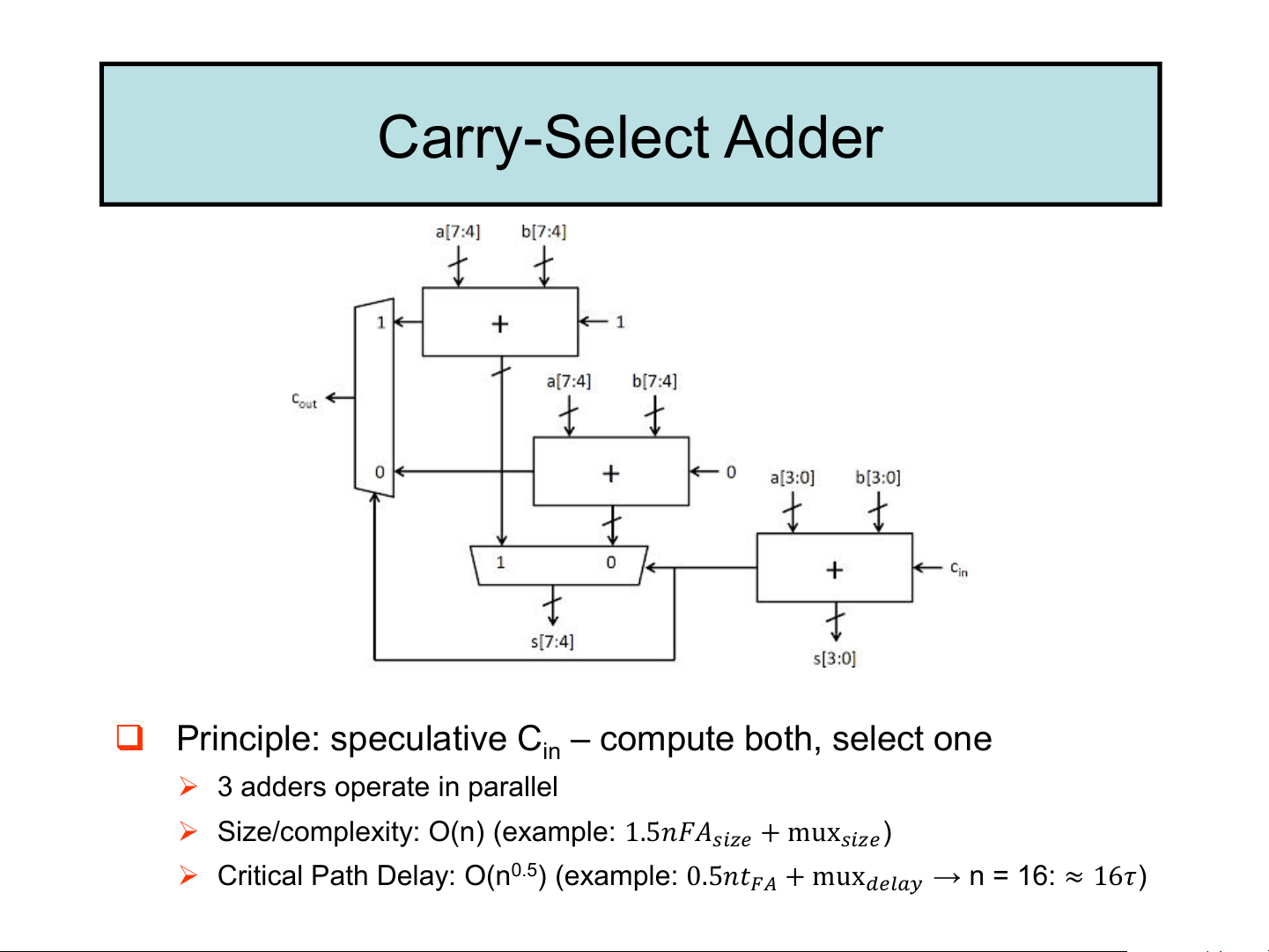
➢ Critical Path Delay: O(n) (= 𝑛𝑡𝐹𝐴 = 2𝑛𝜏) Carry-Select Adder
❑ Principle: speculative C – compute both, select one in
➢ 3 adders operate in parallel
➢ Size/complexity: O(n) (example: 1.5𝑛𝐹𝐴𝑠𝑖𝑧𝑒 + mux𝑠𝑖𝑧𝑒)
➢ Critical Path Delay: O(n0.5) (example: 0.5𝑛𝑡𝐹𝐴 + mux𝑑𝑒𝑙𝑎𝑦 → n = 16: ≈ 16𝜏) Carry Generate and Propagate ❑ Principles
➢ Generate a carry out if 𝑎 and 𝑏 are both 1, 𝐶𝑖𝑛 does not matter.
➢ Propagate a carry in to the carry out if 𝑎 or 𝑏 is 1.
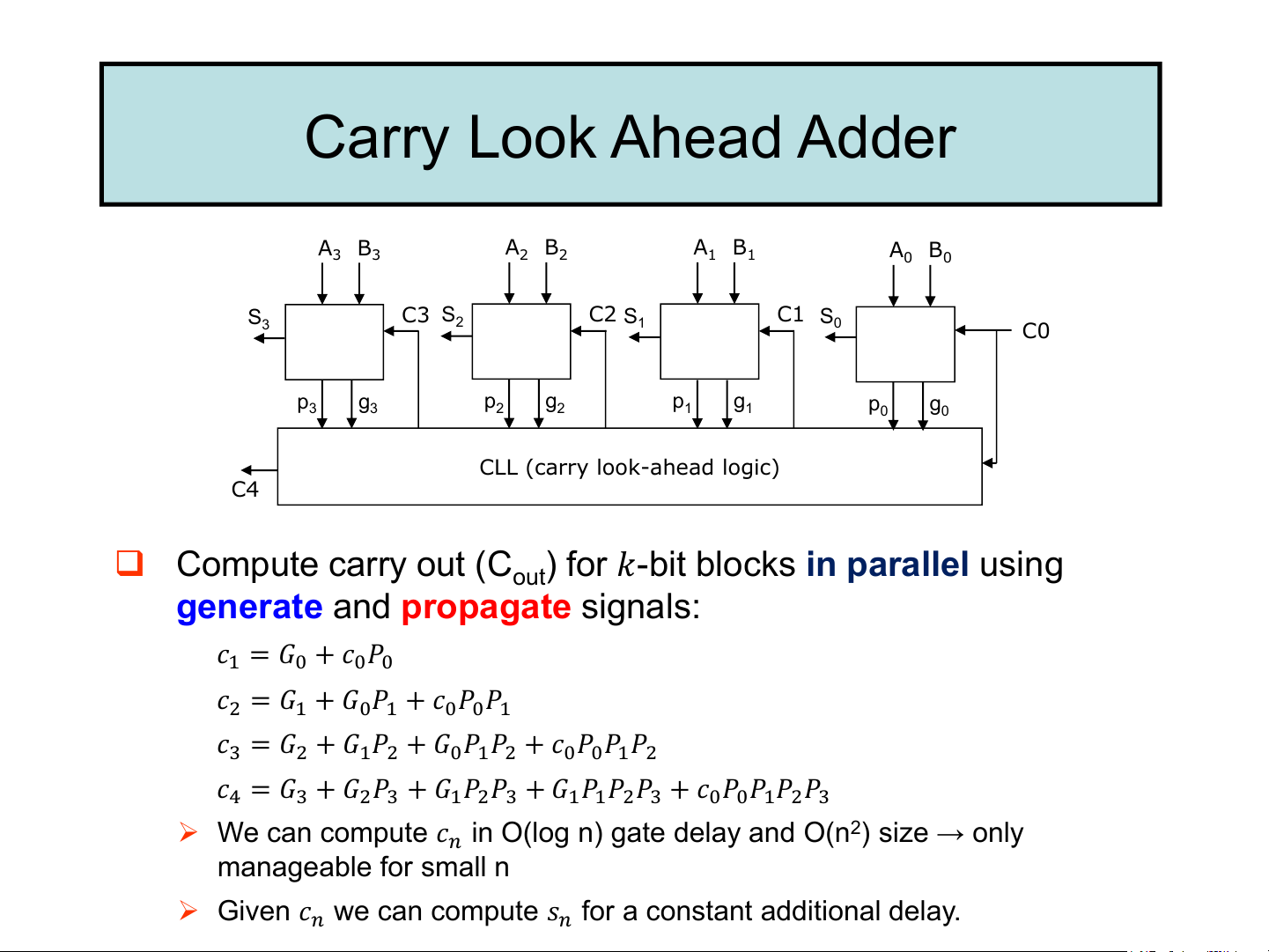
➢ Local decisions based on 𝑎 and 𝑏 only: generate 𝐺 = 𝑎𝑏, propagate 𝑃 = 𝑎 + 𝑏. Carry Look Ahead Adder A B A B A B 3 3 2 2 1 1 A B 0 0 S C3 S C2 C1 S 3 2 S1 0 C0 p g p g p g 3 3 2 2 1 1 p g 0 0 CLL (carry look-ahead logic) C4
❑ Compute carry out (C ) for 𝑘-bit blocks in parallel using out
generate and propagate signals: 𝑐1 = 𝐺0 + 𝑐0𝑃0
𝑐2 = 𝐺1 + 𝐺0𝑃1 + 𝑐0𝑃0𝑃1
𝑐3 = 𝐺2 + 𝐺1𝑃2 + 𝐺0𝑃1𝑃2 + 𝑐0𝑃0𝑃1𝑃2
𝑐4 = 𝐺3 + 𝐺2𝑃3 + 𝐺1𝑃2𝑃3 + 𝐺1𝑃1𝑃2𝑃3 + 𝑐0𝑃0𝑃1𝑃2𝑃3
➢ We can compute 𝑐𝑛 in O(log n) gate delay and O(n2) size → only manageable for small n
➢ Given 𝑐𝑛 we can compute 𝑠𝑛 for a constant additional delay.
Unsigned integer multiplication ❑ Paper and pencil example Multiplicand 1000 = 8 Multiplier x 1001 = 9 1000 Binary multiplication is easy 0000 0 x multiplicand = 0 0000
1 x multiplicand = multiplicand 1000 Product 1001000 = 72 ❑ Observations
➢ m-bit multiplicand x n-bit multiplier = (m+n)-bit product
➢ Accomplished via shifting and addition.
➢ Consume more time and more chip area than addition
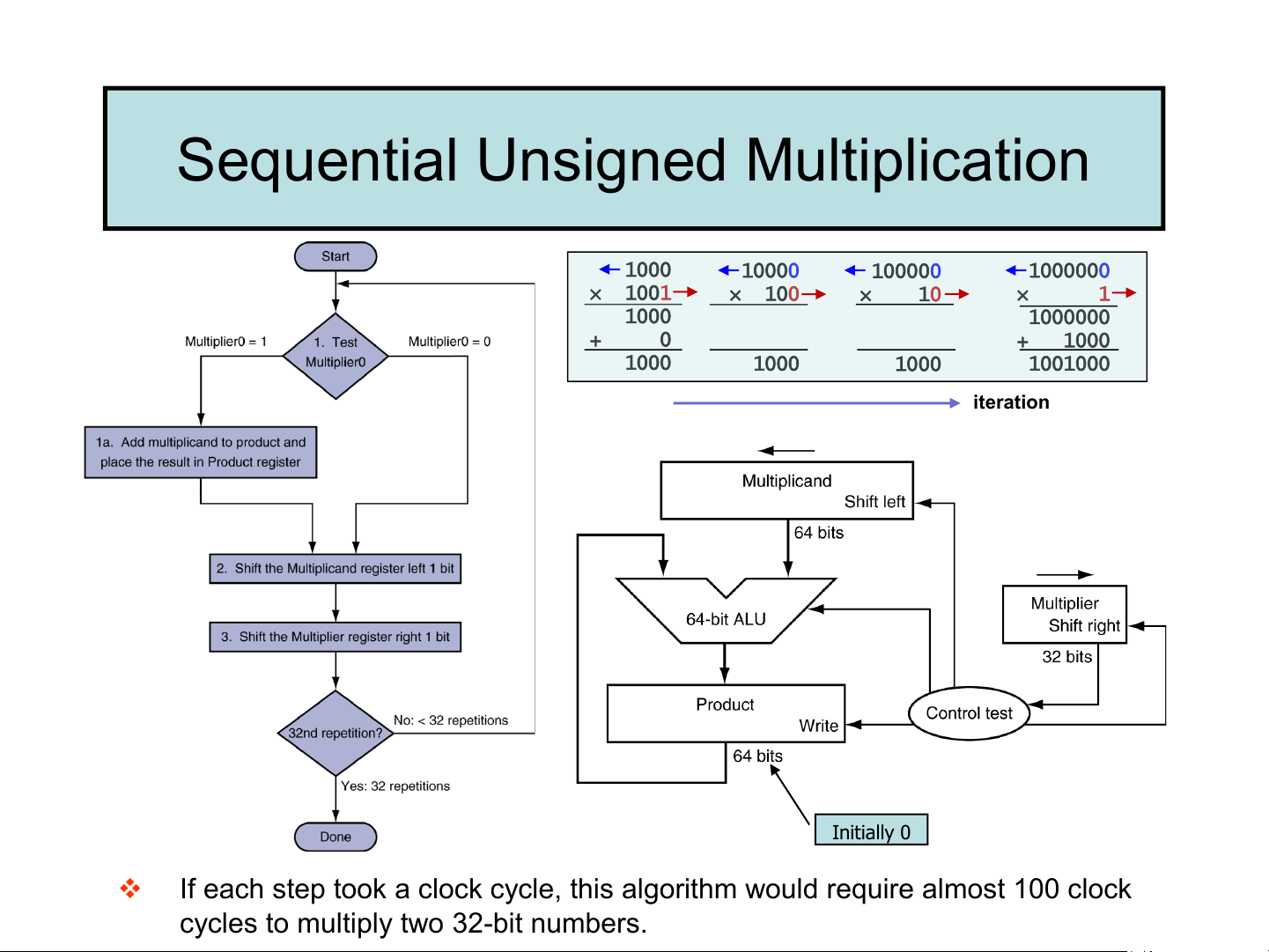
Sequential Unsigned Multiplication 1000 10000 100000 1000000 × 1001 × 100 × 10 × 1 1000 1000000 + 0 + 1000 1000 1000 1000 1001000 iteration Initially 0 ❖
If each step took a clock cycle, this algorithm would require almost 100 clock
cycles to multiply two 32-bit numbers.
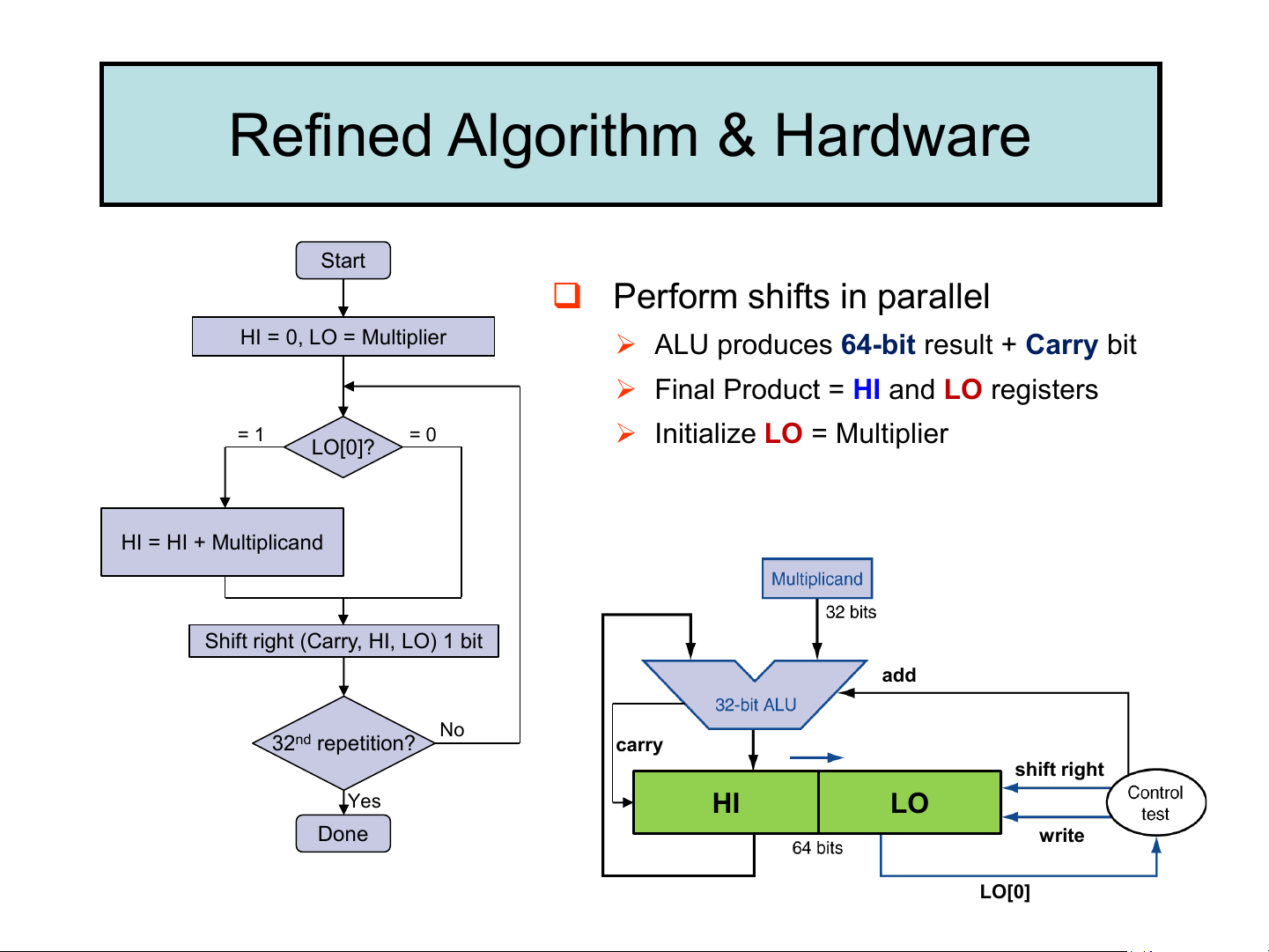
Refined Algorithm & Hardware Start ❑ Perform shifts in parallel HI = 0, LO = Multiplier
➢ ALU produces 64-bit result + Carry bit
➢ Final Product = HI and LO registers = 1 = 0
➢ Initialize LO = Multiplier LO[0]? HI = HI + Multiplicand
Shift right (Carry, HI, LO) 1 bit add No 32nd repetition? carry shift right Yes HI LO Done write LO[0] Refined algorithm: Example ❑ Consider: 1100 x 1101 2 2
➢ 4-bit multiplicand and multiplier → 4-bit adder produces a 5-bit sum (with carry) ➢ Product = 100111002
Signed Integer Multiplication (p & p)
❑ Case 1: Positive Multiplier Multiplicand 1100 = -4 Multiplier x 0101 = +5 11111100 Sign-extension 111100 Product 11101100 = -20
❑ Case 2: Negative Multiplier Multiplicand 1100 = -4 Multiplier x 1101 = -3 11111100 Sign-extension 111100 00100 (2's complement of 1100) Product 00001100 = +12
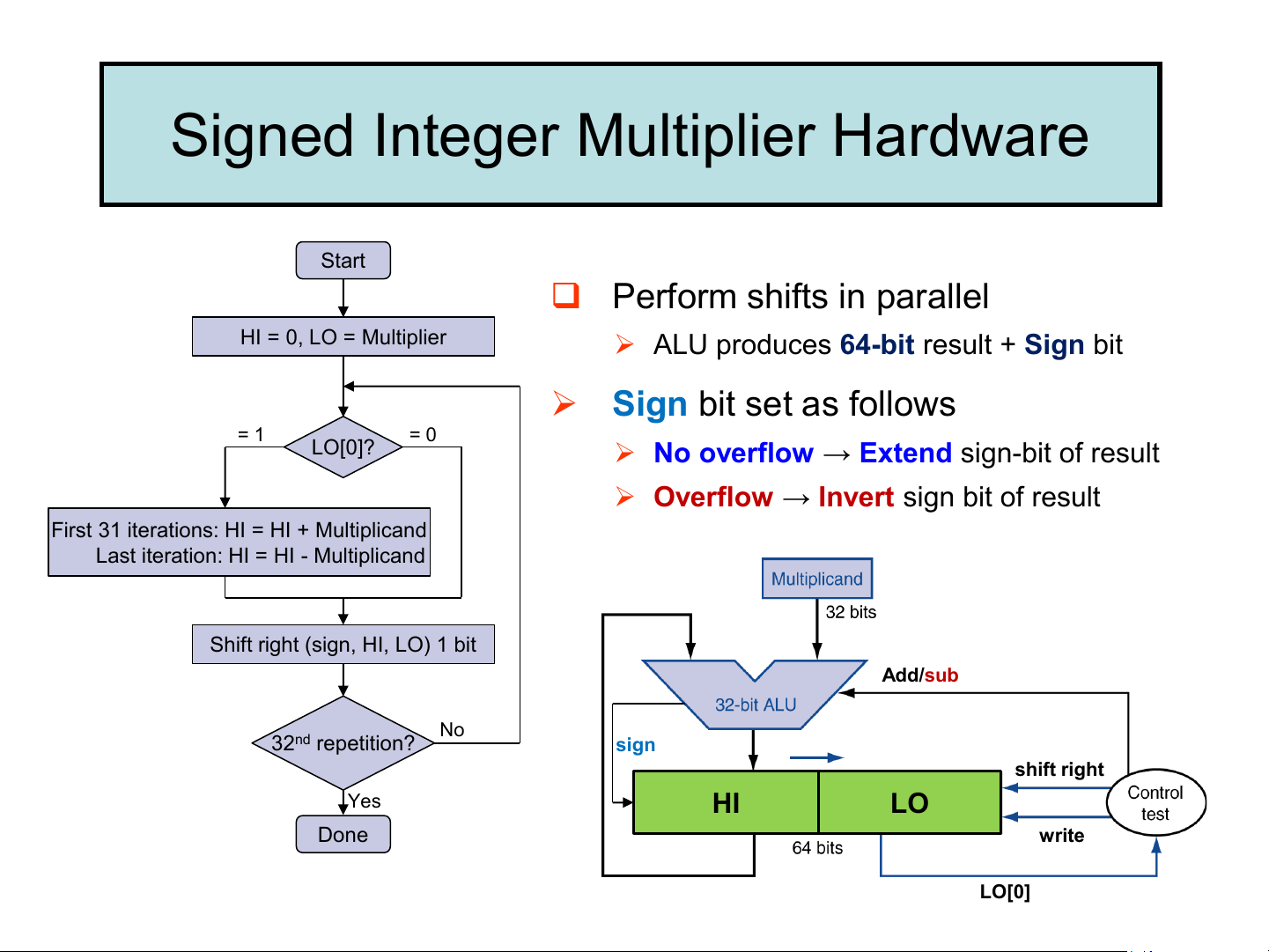
Signed Integer Multiplier Hardware Start ❑ Perform shifts in parallel HI = 0, LO = Multiplier
➢ ALU produces 64-bit result + Sign bit
➢ Sign bit set as follows = 1 = 0 LO[0]?
➢ No overflow → Extend sign-bit of result
➢ Overflow → Invert sign bit of result
First 31 iterations: HI = HI + Multiplicand
Last iteration: HI = HI - Multiplicand
Shift right (sign, HI, LO) 1 bit Add/sub No 32nd repetition? sign shift right Yes HI LO Done write LO[0] Signed Multiplication: Example ❑ Consider: 1010 x 1111 2 2
➢ Iteration 1: No overflow → Extend sign-bit (1 → 1)
➢ Iteration 2,3: Overflow → Invert sign bit (0 → 1)
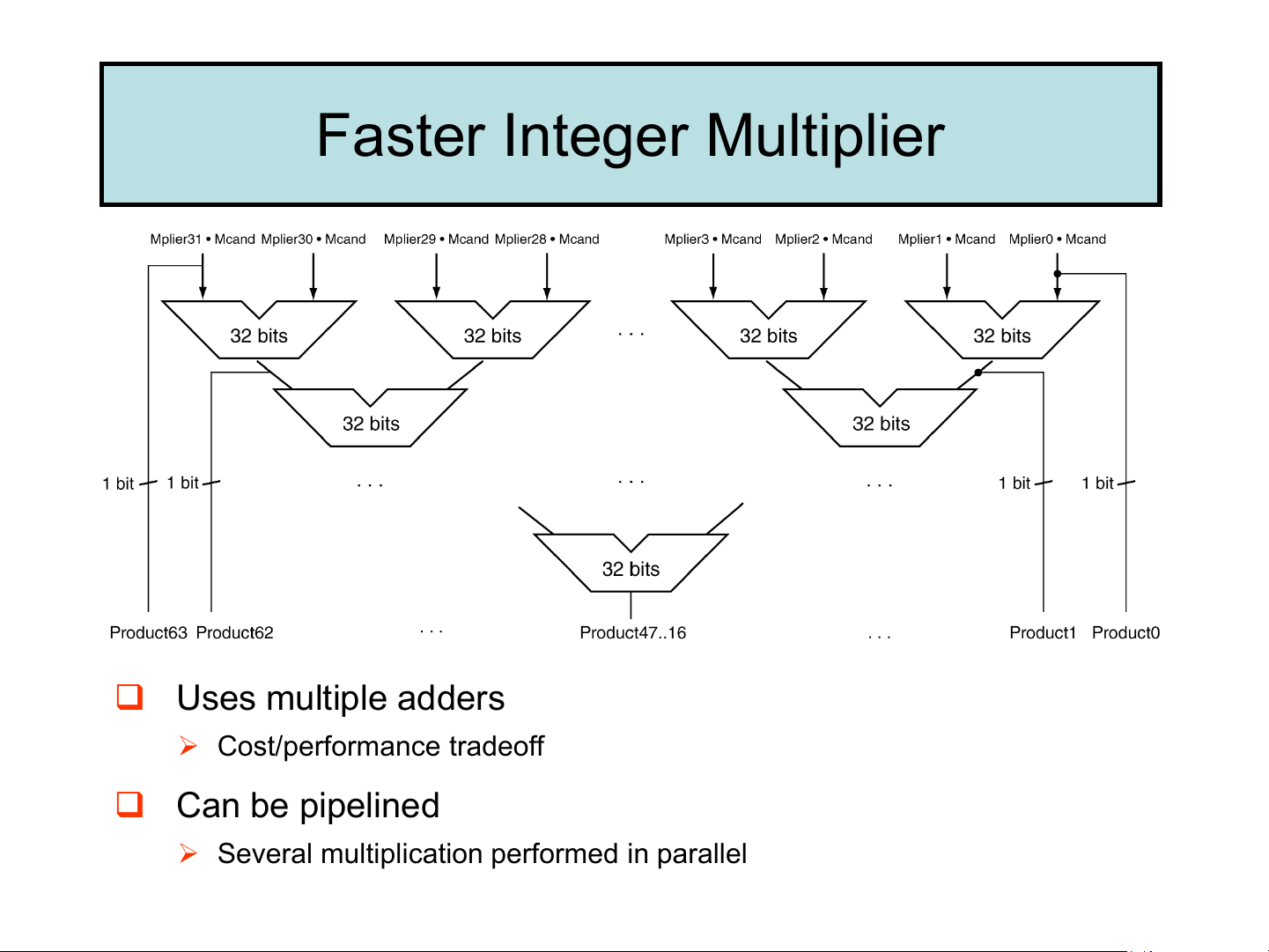
➢ Last iteration: No overflow (why?), add 2's complement of Multiplicand ➢ Product = 000011002 Faster Integer Multiplier ❑ Uses multiple adders ➢ Cost/performance tradeoff ❑ Can be pipelined
➢ Several multiplication performed in parallel MIPS multiplication
❑ Two 32-bit registers for product
➢ HI: most-significant 32 bits
➢ LO: least-significant 32-bits ❑ Instructions ➢ mult rs, rt / multu rs, rt ▪ 64-bit product in HI/LO ➢ mfhi rd / mflo rd ▪ Move from HI/LO to rd
▪ Can test HI value to see if product overflows 32 bits ➢ mul rd, rs, rt
▪ Least-significant 32 bits of product –> rd