




























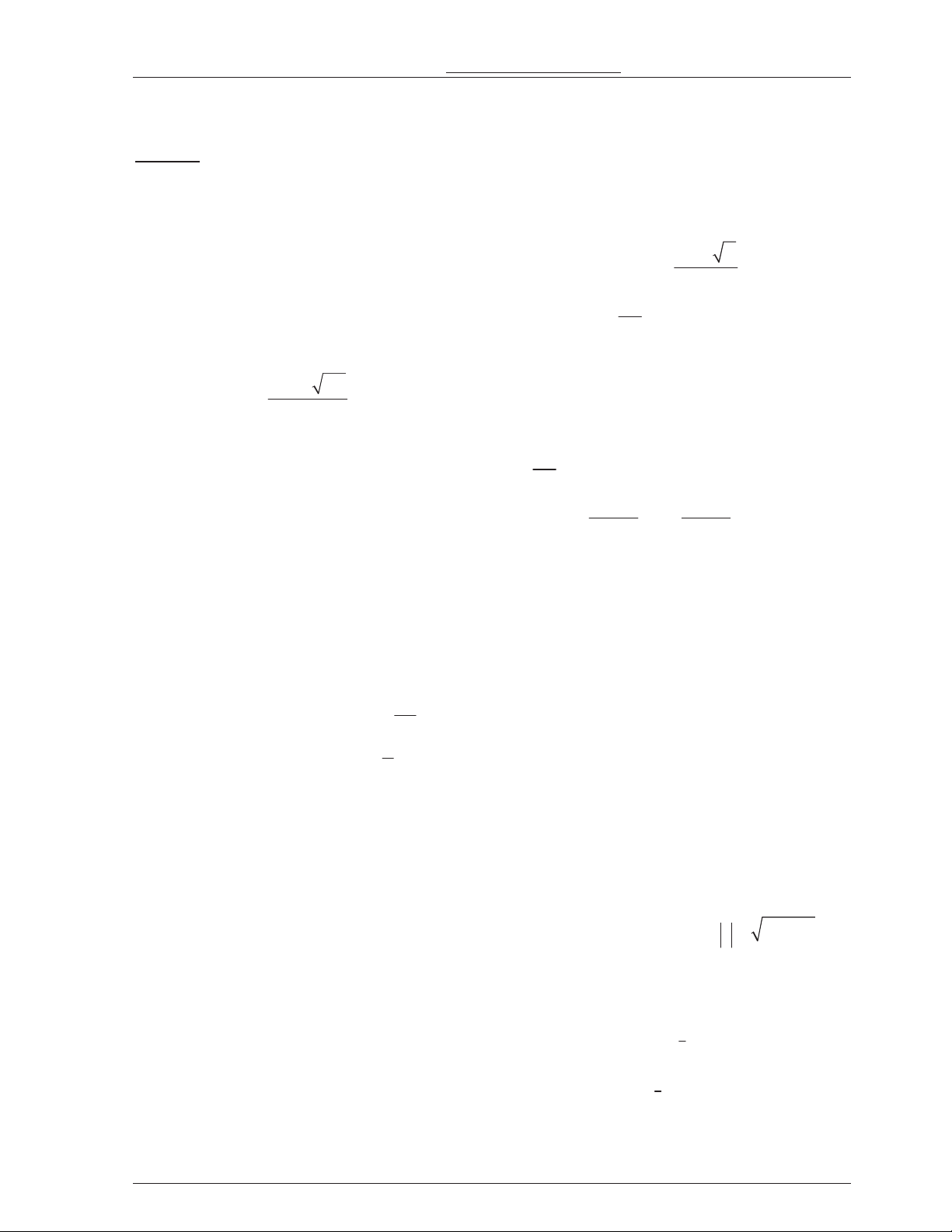
















Preview text:
Thy Nguyn c Thng
0969119789 –thangnd286@gmail.com Tr ng PTLC Vinschool S TAY GII TOÁN 12
Thy Nguyn c Thng 0969119789 –thangnd286@gmail.com Tr ng PTLC Vinschool MC LC CH TRANG A. KHO SÁT HÀM S 2
B. LU THA - M - LÔGARIT 18
C. NGUYÊN HÀM – TÍCH PHÂN VÀ NG DNG 25 D. S PHC 42 E. NÓN – TR-CU 47
F. PHNG PHÁP TO TRONG KHÔNG GIAN OXYZ 54 G. KHI A DIN 64 H. GÓC VÀ KHONG CÁCH 67 I. B SUNG MT S KIN THC 77
Trung tâm luyn thi cht lng cao Thành t – Tây M, Nam T Liêm, Hà Ni Page 1
Thy Nguyn c Thng 0969119789 –thangnd286@gmail.com Tr ng PTLC Vinschool A. KHO SÁT HÀM S 1. Tính n iu 1.1. Lí thuyt
a) nh ngha: Cho K là mt khong, on hoc na khong. Gi s f(x) là mt hàm s xác nh trên K.
- Hàm s f(x) gi là ng bin trên K nu x , x K : x x f (x ) 1 2 1 2 1 f (x2)
- Hàm s f(x) gi là nghch bin trên K nu x , x K : x x f (x ) 1 2 1 2 1 f (x2) b. i u kin cn
Gi s f có o hàm trên khong K.
- Hàm s f(x) không i trên K x K : f '(x) 0
- Nu f ng bin trên khong K thì f '(x) 0,x K
- Nu f nghch bin trên khong K thì f '(x) 0,x K c. i u kin
Gi s f có o hàm trên khong K.
- Nu f (x) 0, x I (f(x) = 0 ti mt s hu hn i!m) thì f ng bin trên K.
- Nu f (x) 0, x I (f(x) = 0 ti mt s hu hn i!m) thì f nghch bin trên K.
- Nu f(x) = 0, x I thì f không i trên K.
1. 2. M t s" v#n % khác
a) &nh lí v% d#u c(a tam th*c b-c hai: g(x) a 2
x bx c (a 0)
+ Nu < 0 thì g(x) luôn cùng d"u v#i a. b b + Nu = 0 thì (
g x) luôn cùng d"u v#i a (tr$ x g 2a ), 0 2a + Nu > 0 thì ( g x) có hai nghi%m g x 1
x , x2 và trong khong hai nghi%m thì ( ) khác d"u
v#i a, ngoài khong hai nghi%m thì (
g x) cùng d"u v#i a. 2 a 0 a 0
Chú ý: - Nu y ' ax bx c (a 0) thì: +) y ' 0, x R +) y ' 0, x R 0 0
- Nu = 0 hay g x a x 2 ( )
thì g(x) không i d u khi qua , d u ca g(x) ph thuc d u ca a.
- Nu > 0 thì g(x) i d"u khi qua x , x 1
2 ( i t$+ sang – sang +, hoc i t$ - sang + sang -)
b) So sánh các nghim 1
x , x2 c(a tam th*c b-c hai 2 (
g x) ax bx c v#i s 0: 0 0 +) 1
x x2 0 P 0 +) 0 1
x x2 P 0 +) 1
x 0 x2 P 0 S 0 S 0 c) Hàm s" b-c hai: 2
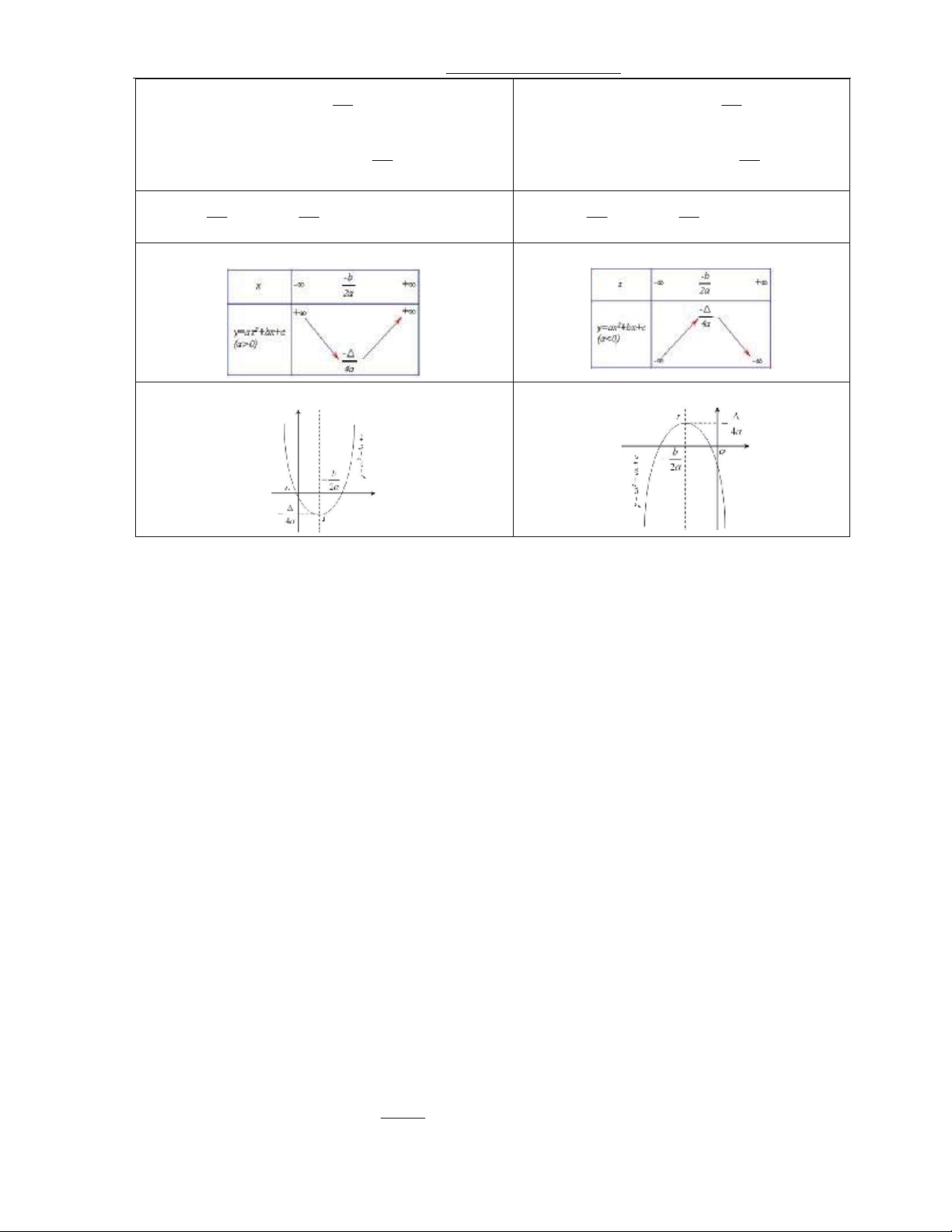
y ax bx c (a 0) a>0 a<0
th hàm s là mt parabol có &nh
th hàm s là mt parabol có &nh b b ; ; 2a 4a 2a 4a
Trung tâm luyn thi cht lng cao Thành t – Tây M, Nam T Liêm, Hà Ni Page 2 Thy Nguyn c Thng
0969119789 –thangnd286@gmail.com Tr ng PTLC Vinschool b b Hàm s ng bin trên ; 2a Hàm s nghch bin trên ; 2a b b Hàm s nghch bin trên ; 2a Hàm s ng bin trên ; 2a b b mi y n x y x 4a ti 2a max 4a ti 2a Bng bin thiên Bng bin thiên Dng th: Dng th: d) ng d.ng trong gi/i toán
Cho hàm s y=g(x) xác nh trên (a;b) và liên t(c trên [a;b]:
+) g(x) m, x ( ;
a b) max g(x) m ; a;b +) (
g x) m, x ( ; a b) min ( g x) m a;b
e) n iu trên m t kho/ng, o0n
! hàm s y f (x) ng bin trên t*p K nào ó thì tn ti khong ! f’(x)>0 cha t*p K.
! hàm s y f (x) nghch bin trên t*p K nào ó thì tn ti khong ! f’(x)<0 cha t*p K B1 tr2: - T*p (; )
a là t*p con c+a t*p (; )
b khi và ch& khi a b - T*p ( ; a ) là t*p con c+a t*p ( ; b )
khi và ch& khi b a c a - Tp ( ;
a b) là tp con ca tp ( ;
c d) khi và ch khi b d
1.3. Tính n iu ca hàm thng gp
a) Hàm s a thc bc ba 3 2
f (x) ax bx cx d (a 0) : 3 2 a 0
“iu kin hàm s f (x) ax bx cx d ng bin trên R là ; nghch bin trên 0 a 0 R là ” 0 3 2
Hàm s f (x) ax bx cx d ng bin ( nghch bin) trên K thì kho!ng mà f '(x) 0 (
f '(x) 0 ) ca hàm s ph!i cha K. ax b
b) Hàm s phân thc dng f (x)
(c 0,ad bc 0) cx d
Thy Nguyn c Thng 0969119789 –thangnd286@gmail.com Tr ng PTLC Vinschool
( ad bc 0)
iu kin hàm s ng bin (nghch bin) trên trên ; là
ad bc 0 ad bc 0 d c
iu kin hàm s ng bin (nghch bin) trên trên ; là
ad bc 0 ad bc 0 d c
+) i v"i hàm hp y f ( (
g x)) , trong ó hàm u (
g x) xác nh và có o hàm trên ;ab, ly giá tr trên kho!ng ;
c d; hàm y f ( )
u xác nh ;cdvà có o hàm trên ;cd, ly giá tr trên R.
g'(x) 0 xa;b
g'(x) 0 xa;b Nu y f g x f '(u) ho#c thì hàm s ( ( )) ng bin 0 u ;cd
f '(u) 0 u ;cd trên ; a b.
g'(x) 0 xa;b
g'(x) 0 xa;b Nu y f g x
f '(u) 0 u ho#c thì hàm s ( ( )) nghch bin ;cd
f '(u) 0 u ;cd trên ; a b. 2. C3C TR4 CA HÀM S 2.1. Lí thuyt
a) nh ngha: Gi s hàm s f (x) xác nh trên D, x0 D . - im x ; x h
0 g%i là im c&c tiu ca hàm s f(x) nu tn ti s th&c d ng h sao cho x h 0 0
cha trong D và f (x) f (x ) h
o , x x0 h; x \ 0 x 0 Khi ó:
+ Giá tr f (x0) gi là giá tr c,c ti!u c+a hàm s.
+ i!m x0; f (x0) gi là i!m c,c ti!u c+a th hàm s y=f(x).
+ Hàm s t c,c ti!u ti i!m x0 - im x x ; h x h
0 g%i là im c&c i ca hàm s f(x) nu tn ti s th&c d ng h sao cho 0 0
cha trong D và f (x) f (x ), x x ; h x 0 0 h \ o x0
Khi ó: Giá tr f (x
x ; f (x )
0 ) gi là giá tr c,c i c+a hàm s. i!m 0 0 gi là i!m c,c i c+a th hàm s y=f(x).
+ Giá tr f (x0) gi là giá tr c,c i c+a hàm s.
+ i!m x0; f (x0) gi là i!m c,c i c+a th hàm s y=f(x).
+ Hàm s t c,c i ti i!m x0
Chú ý: C,c i, c,c ti!u gi chung là c,c tr b) &nh lí:
Trung tâm luyn thi cht lng cao Thành t – Tây M, Nam T Liêm, Hà Ni Page 4
Thy Nguyn c Thng 0969119789 –thangnd286@gmail.com Tr ng PTLC Vinschool
i-u ki%n cn: Nu hàm s f(x) t c,c tr ti i!m x0 thì hoc không tn ti f '(x0 ) hoc f '(x ) 0 0
i u kin 1: Gi s tn ti ;
a b D ch x0 , hàm s y=f(x) liên t(c trên (a,b) và có o hàm trên m.i khong ;
a x0,x0;b
f '(x) 0 x ;ax0 Nu x
f '(x) 0 x
thì 0 là mt i!m c,c ti!u c+a hàm s f(x) x0;b
f '(x) 0 x ;ax0 Nu x f '(x) thì
là mt i!m c,c i c+a hàm s f(x) 0 x 0 x0;b
i u kin 2: Gi s tn ti ;
a b D ch x0 , hàm s y=f(x) liên t(c trên (a,b) và có o hàm
c"p 1 trên (a;b) và có o hàm c"p hai ti x0 . Khi ó:
f '(x ) 0 Nu 0 x f ''(x ) thì
là mt i!m c,c ti!u c+a hàm s f(x) 0 0 0
f '(x ) 0 Nu 0 x f ''(x ) thì
là mt i!m c,c i c+a hàm s f(x) 0 0 0 2.2. M t s" v#n % khác
a) Hàm s a thc bc ba 3 2
f (x) ax bx cx d (a 0) : a 0 a 0 Hàm s t c,c i ti x b 0
0 khi: f '(x) 0 hoc f ''(x c 0 ) 0 x 0 2b a 0 a 0 Hàm s t c,c ti!u ti x b 0
0 khi: f '(x) 0 hoc f ''(x c 0 ) 0 x 0 2b a 0 a 0
Hàm s không có c,c tr hoc '(x) 0 f b 0 a 0
Hàm s có c,c i, c,c ti!u '(x) 0 f
Ph ng trình ng th/ng i qua hai i!m c,c tr c+a th hàm s 3 2
y ax bx cx d a 0 2
. V#i i-u ki%n b 3ac 0 , th,c hi%n phép chia y cho y’ ta
0c y = y’(x).g(x) + Ax + B. Khi ó, ng th/ng i qua hai i!m c,c tr là y = Ax + B 4 2
b) Hàm s a thc trùng phng: f (x) ax bx c (a 0) TH1: a 0
*) Nu b 0 Hàm s ch& có 1 c,c ti!u
*) Nu b 0 Hàm s ch& có 1 c,c i
*) Nu b 0 Hàm s không có c,c tr
Trung tâm luyn thi cht lng cao Thành t – Tây M, Nam T Liêm, Hà Ni Page 5
Thy Nguyn c Thng 0969119789 –thangnd286@gmail.com Tr ng PTLC Vinschool 3 2
TH2: a 0 . Khi ó: y ' 4ax 2bx 2x 2ax b
*) Nu a.b<0 thì hàm s có ba c&c tr. C' th
a>0: Hàm s có 2 c,c ti!u, 1 c,c i
a<0: Hàm s có 2 c,c i, 1 c,c ti!u *) Nu .
a b 0 : Hàm s ch có úng mt c&c tr a>0: Hàm s có 1 c,c ti!u a<0: Hàm s có 1 c,c i 4 2
Tham kho: Tr ng h0p th hàm s: y ax bx c a 0 có ba i!m c,c tr 2 b b 2 b b
Ba i!m c,c tr là A0; c , B ; c C ; c 2a 4a và . 2a 4a 4 b 8ab 2b
Khi ó ta có AB AC và BC . 2 16a a
Dng 1. th hàm s 4 2
y ax bx c có ba im c&c tr to thành ba nh ca mt tam giác ab 0
vuông khi và ch khi 3 .
b 8a 0
Dng 2. th hàm s 4 2
y ax bx c có ba im c&c tr to thành ba nh ca mt tam giác u ab 0 khi và ch khi 3 .
b 24a 0
Dng 3. th hàm s 4 2
y ax bx c có ba im c&c tr A, B, C to thành ba nh ca mt tam ab 0
giác cân có mt góc BAC cho tr"c khi và ch khi 3 b 8a cos 3 b 8a 4 2
Dng 4. th hàm s y ax bx c có ba im c&c tr A, B, C th(a mãn iu kin BC OA ab 0
(v"i O là gc t%a ) khi và ch khi 2 .
ac 2b 0
Dng 5. th hàm s 4 2
y ax bx c có ba im c&c tr A, B, C to thành ba nh ca mt tam ab 0
giác có din tích là S cho tr"c khi và ch khi 5 b S . 3 32a
Dng 6. th hàm s 4 2
y ax bx c có ba im c&c tr A, B, C to thành ba nh ca mt tam ab 0 3
giác có bán kính )ng tròn ngoi tip là R khi và ch khi b 8a R . 8 a b
Trung tâm luyn thi cht lng cao Thành t – Tây M, Nam T Liêm, Hà Ni Page 6 Thy Nguyn c Thng
0969119789 –thangnd286@gmail.com Tr ng PTLC Vinschool 4 2
Dng 7. th hàm s y ax bx c có ba im c&c tr A, B, C to thành ba nh ca mt tam ab 0 2 b
giác có bán kính )ng tròn ni tip là r khi và ch khi 4a r . 2 1 b 1 8a
Dng 8. th hàm s 4 2
y ax bx c có ba im c&c tr A, B, C to thành ba nh ca mt tam 3
b 8a 4abc 0
giác nhn gc O là tr&c tâm khi và ch khi c 0 4 2
Dng 9. th hàm s y ax bx c có ba im c&c tr A, B, C to thành ba nh ca mt tam 3
b 8a 8abc 0
giác nhn gc O là tâm )ng tròn ngoi tip khi và ch khi c 0 ax b
c) Hàm s phân thc dng f (x)
(c 0,ad bc 0) cx không có c&c tr d 2
ax bx c
d) Hàm s" b-c 2/b-c 1 y
có c c i và c,c ti!u khi và ch& khi ph ng trình y’ = 0 có
a ' x b ' b'
hai nghi%m phân bi%t khác a' . Khi ó, ph ng trình ng th/ng i qua hai i!m c,c tr c+a 2
ax bx c 2ax b th hàm s y y
a' x b' là a' .
3. GIÁ TR4 L6N NH7T – GIÁ TR4 NH8 NH7T CA HÀM S 3.1. Lí thuyt
Gi s f xác nh trên D . Ta có
f x M x D
f x m x D
M max f x Nu
; m min f x Nu . x D x x
0 D : f x0
0 D : f x0 M x D m
3.2. Chú ý: ! tìm giá GTLN, GTNN c+a hàm s y f (x) liên t(c on ; a b , có o hàm trên
;ab và f '(x) 0 có hu hn nghi%m , ta làm nh sau:
B1 Tìm các i!m x1 , x2 , …, xm thuc khong ;
a b mà ti ó hàm s f có o hàm b1ng 0 hoc không có o hàm.
B2 Tính f x
1 , f x2 , …, f xm , f a , f b .
B3 So sánh các giá tr tìm 0c 2 b #c 2. S l#n nh"t trong các giá tr ó chính là GTLN c+a f trên on ; a b
; s nh3 nh"t trong các giá tr ó chính là GTNN c+a f trên on ; a b .
max f x maxf 1x, f x2,, f x , f a, m f b. x ; a b
min f x minf 1x, f x2,, f x , f a, m f b. x ; a b
3.3. Quy c. Khi nói n GTLN, GTNN c+a hàm s f mà không ch& rõ GTLN, GTNN trên t*p nào thì
Thy Nguyn c Thng 0969119789 –thangnd286@gmail.com Tr ng PTLC Vinschool
3.4. Chú ý: Gi! s* f(x) là mt hàm s liên t'c trên min D và tn ti min f (x) ;
m max f (x) M . Khi D D ó:
1) Ph ng trình f (x) có nghim trên D m M.
2) Bt ph ng trình f (x) có nghim trên D M .
3) Bt ph ng trình f (x) có nghim trên D m .
4) Bt ph ng trình f(x) úng v"i m%i x D m .
5) Bt ph ng trình f(x) úng v"i m%i x D M .
Trung tâm luyn thi cht lng cao Thành t – Tây M, Nam T Liêm, Hà Ni Page 8 Thy Nguyn c Thng
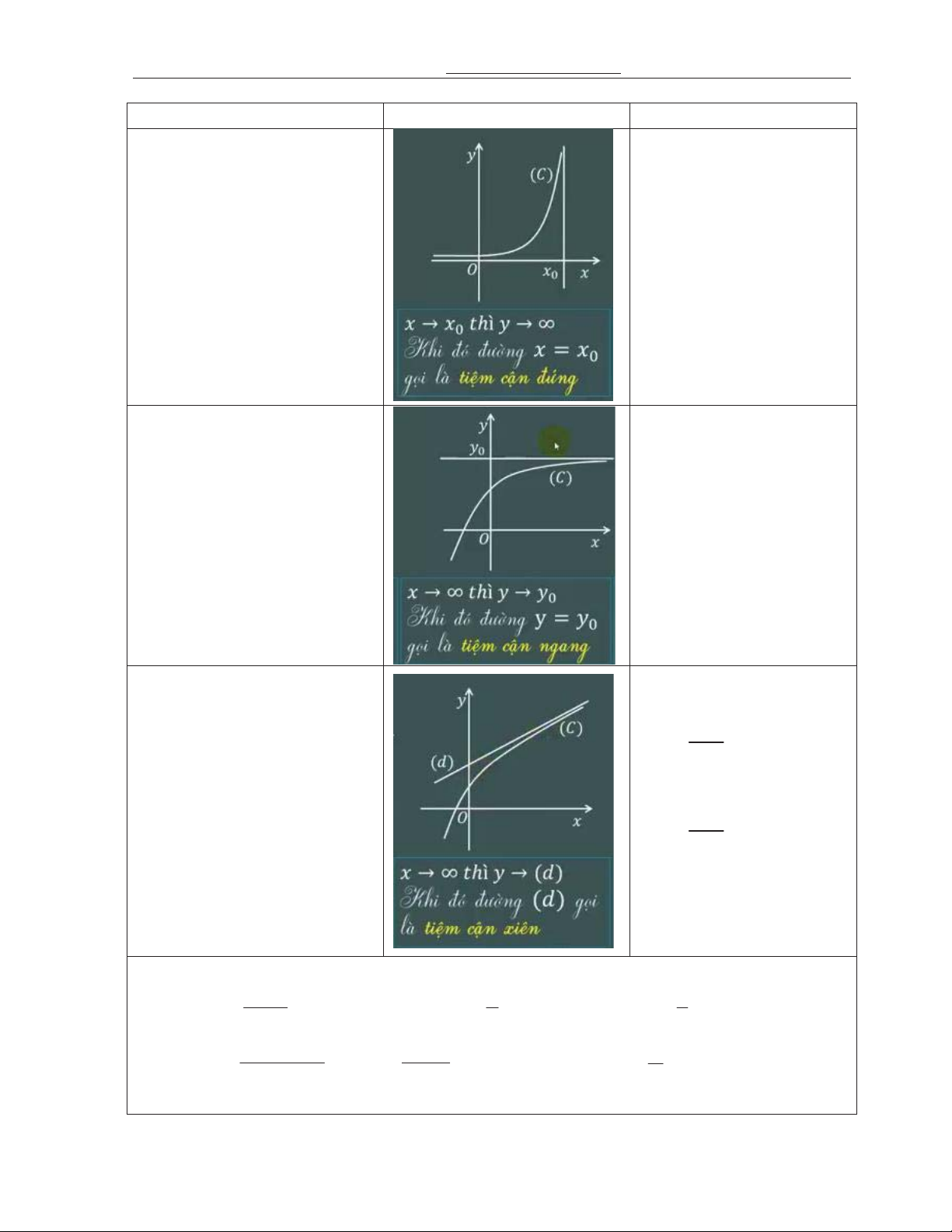
0969119789 –thangnd286@gmail.com Tr ng PTLC Vinschool 4. TIM C9N CA : TH4 HÀM S Khái nim Hình /nh minh ho0
Ph+ng pháp tìm tim c-n 1. Tim c-n *ng: B1. Tìm t*p xác nh
)ng th+ng x x0 (vuông góc
B2. Tìm các giá tr x0 mà ti
Ox) g%i là tim cn ng c+a
x0 hàm s: y=f(x) không xác
th hàm s: y=f(x) Nu có ít nh"t nh. mt trong các gi#i hn sau: B3. Tính các gi#i hn:
lim f (x) ,
lim f (x) ,
lim y & lim y xx xx 0 0 x x x x
lim f (x) ,
lim f (x) , 0 0 xx xx B4. Kt lu*n. 0 0 2. Tim c-n ngang B1. Tìm t*p xác nh
Hàm s y f (x) xác nh trên B2. Tính các gi#i hn:
mt kho!ng vô hn (có th! là lim y 0
y & lim y 0 y x x ; a, ; b , ; B3. Kt lu*n
)ng th+ng y y0 (vuông góc
Oy) g%i là tim cn ngang c+a
th hàm s: y=f(x) Nu có ít nh"t mt trong các gi#i hn sau: lim f (x) 0
y , lim f (x) 0 y x x B1. Tìm t*p xác nh 3. Tim c-n xiên B2. Tính các gi#i hn:
Hàm s y f (x) xác nh trên f (x)
mt kho!ng vô hn (có th! là lim a
x x hoc ;
a,b;,;
lim f (x) ax b x
)ng th+ng y ax b ( a 0 ) f (x)
g%i là tim cn xiên c+a th lim a x
hàm s: y=f(x) Nu có ít nh"t mt x lim trong các gi#i hn sau:
f(x)ax b x
lim f (x)
ax b 0, x B3. Kt lu*n
lim f (x)
ax b 0. x Chú ý: ax b d a 1. Hàm s: y x y cx có ti%m c*n ng là: , ti%m c*n ngang là: d c c 2 ax bx c k n 2.Hàm s: y px q x mx n
mx n có ti%m c*n ng là: m , ti%m c*n xiên là:
y px q
Thy Nguyn c Thng 0969119789 –thangnd286@gmail.com Tr ng PTLC Vinschool n n 1
a x a x ... n n a x a
n m : TCÑ &TCN 3. 1 1 0 lim m m 1 x
n m :TCÑ &TCX m b x m b 1x ... 1 b x 0 b b 4. Hàm s: 2
y f (x) ax bx c
a 0 có ti%m c*n xiên là y a x 2a 5. Hàm s: 2
y f (x) mx n p ax bx c
a 0 có ti%m c*n xiên là b
y mx n p a x 2a mx n 2 6. Hàm s: y
ch& có ti%m c*n ngang, có th! có ti%m c*n ng nu ax bx c 0 2
ax bx c có nghi%m.
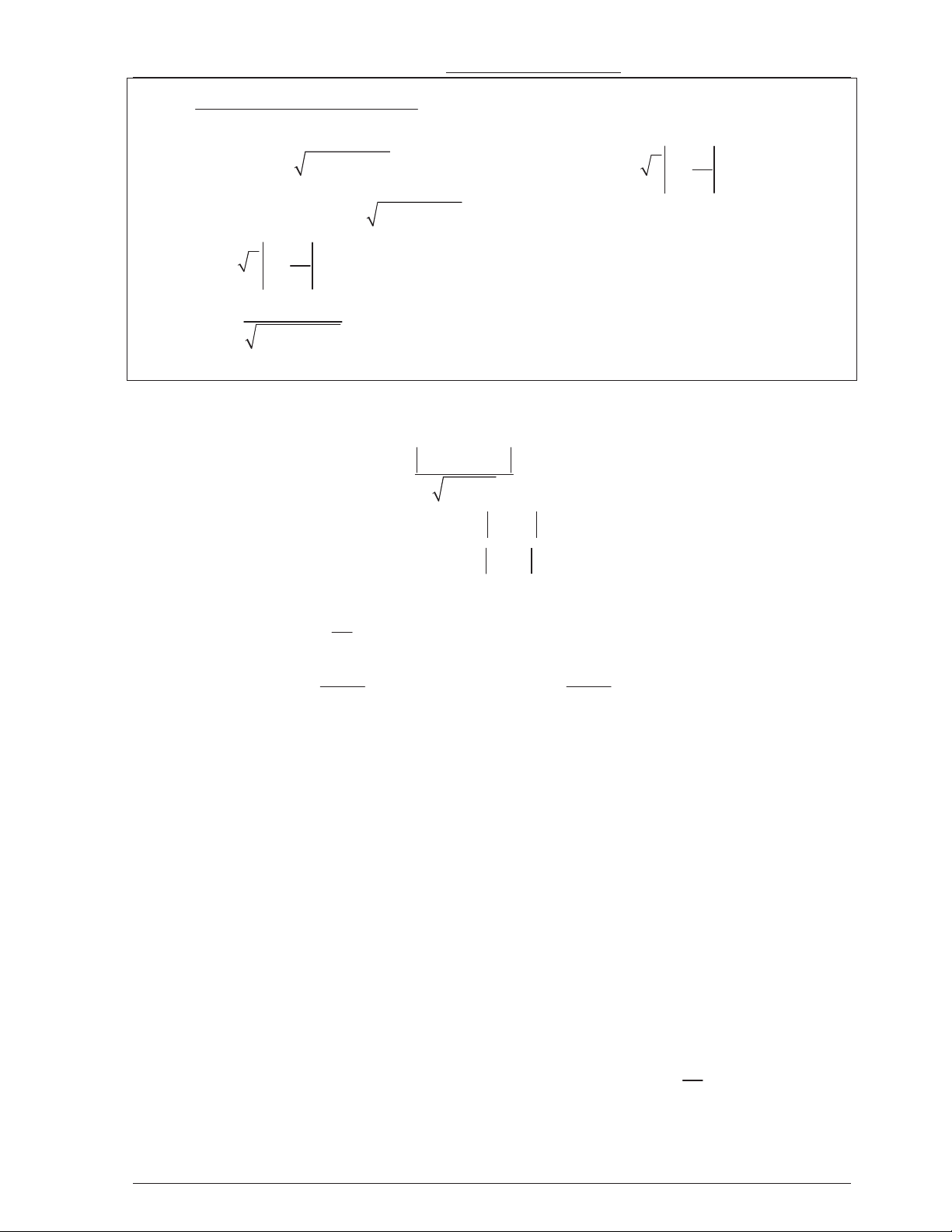
B1 sung m t s" kin th*c:
- Công thc khong cách: ng th/ng 2 2
:ax by c 0
(a b 0) và M x0; 0 y .
ax by c
Khong cách t$ M n 4 là: d M, 0 0 2 2 a b
;c bit: - ng th/ng : y m thì d M, 0 y m
- ng th/ng : x n thì d M, x0 n
- Công thc gi i hn: C n nchaün n + Gi#i hn ti vô c,c: lim
0 vôùik 0 & lim x
, lim x vôùi n N k x x n leû x x c Neáu c 0 c Neáu c 0 + Gi#i hn mt bên: lim & lim
x x x x Neáu c 0 x x x x Neáu c 0 0 0 0 0
5. TNG GIAO HAI : TH4 HÀM S 5.1. Kin thc Cho hai ng cong: 1
C :y f (x) và 2 C :y ( g x)
y f (x) +) Nu M(x M x0; 0 y
0; y0 ) là i!m chung c+a 1 C và 2 C
là nghi%m c+a h%: y (gx)
+ Hoành giao i!m c+a C
1 và C2 là nghi%m c+a ph ng trình: f (x) g(x) (*)
+) S nghi%m ph ng trình (*) b1ng s giao i!m c+a C 1 và C2
5.2 . B! sung m"t s kin thc a) Phng trình bc 2 2 0 -Ph ng trình: (
g x) ax bx c 0 a 0 có hai nghi%m phân bi%t khác x0 (gx 0 ) 0 0 2 -Ph ng trình: (
g x) ax bx c 0 a 0 có nghi%m kép khác x0 b 0 2a 2 -Ph ng trình: (
g x) ax bx c 0 a 0 vô nghi%m 0
Trung tâm luyn thi cht lng cao Thành t – Tây M, Nam T Liêm, Hà Ni Page 10
Thy Nguyn c Thng 0969119789 –thangnd286@gmail.com Tr ng PTLC Vinschool
b) Phng trình bc 3 hay tng giao # th hàm a thc bc ba và tr$c Ox 3 2
T ng giao ca th hàm bc 3 y a ' x b ' x c ' x d ' a' 0 và tr'c Ox:
Ph ng trình hoành giao im: 3 2
a' x b' x c' x d ' 0 2
Trng h%p 1: Bin ,i ph ng trình: 3 2
a' x b' x c' x d ' 0 thành x ax bx c 0 2
Ph ng trình: x ax bx c 0 có ba nghi%m phân bi%t Ph ng trình: 2
ax bx c 0 có hai nghi%m phân bi%t khác . 2
Ph ng trình: x ax bx c 0 có hai nghi%m phân bi%t Ph ng trình: 2
ax bx c 0 có nghi%m kép khác hoc có hai nghi%m phân bi%t trong ó có mt 0 g() 0 nghi%m b1ng 0 g() 0 2
Ph ng trình: x ax bx c 0 ch& có mt nghi%m Ph ng trình: 0 a 2
x bx c 0 có nghi%m kép b1ng hoc vô nghi%m g() 0 0
Tr+=ng h2p 2: Không nh5m 0c nghi%m S giao i!m c+a th hàm s 3 2
y ax bx cx d a 0 và Ox b1ng s nghi%m c+a ph ng 3 2
trình: ax bx cx d 0
Ch có mt nghim khi và ch& khi: Hàm s luôn ng bin hoc luôn nghch bin; hoc có hai y ' 0
c,c tr n1m v- cùng mt phía i v#i Ox y ' 0
trong ó: x , x là nghi%m c+a 1 2 y( 1
x ).y(x2) 0 ph ng trình: y ' 0
Ch có hai nghim khi và ch& khi hàm s có hai c,c tr, trong ó có mt c,c tr n1m trên Ox y ' 0 x , x y y(
trong ó: 1 2 là nghi%m c+a ph ng trình: ' 0 1
x ).y(x2) 0
Ch có ba nghim phân bit khi và ch& khi hàm s có hai c,c tr, trong ó có hai c,c tr n1m 0 v- hai phía c+a tr(c Ox y' x , x y(
trong ó: 1 2 là nghi%m c+a ph ng trình: 1
x ).y(x2) 0 y' 0
B1 sung: Ph ng trình ng th/ng qua hai c,c tr (nu có) là y mx n (Bi!u thc mx n là a thc d khi chia y cho y’). 2
Xét y ' 3ax 2bx c 0
Trung tâm luyn thi cht lng cao Thành t – Tây M, Nam T Liêm, Hà Ni Page 11 Thy Nguyn c Thng
0969119789 –thangnd286@gmail.com Tr ng PTLC Vinschool
c) Phng trình bc bn trùng phng hay tng giao ca # th hàm a thc bc 4 trùng phng vàc trucj Ox) 2 4 2 f (x) t x 0
ax bx c 0 a 0 . t = x2 x = t f (t) 0 S nghi%m 4 3 2 1 0 CSC P 0 0 0 P 0 P 0 S 0 P 0 0 1 t t2 i-u ki%n P 0 0 S 0 0 S 0 t 3 t S 0
S / 2 0 2 1
S / 2 0 0
M"t s kin thc hình h&c b! sung: - Cho: 1 u 1 x ; 1y, 2 u x2; 2 y 1 u . 2 u 1 x x2 1y 2 y 2 2 - Cho 1 A ( 1 x ; 1y), 2 A ( 2 x ; 2 y ) : 1 A 2
A x2 1 x ; y2 1 y ; 1 A 2
A x2 1x 2 y 1y - Cho tam giác 1 A 2 A 3 A trong ó: 1 A ( 1 x ; 1y), 2 A (x2; 2 y ), 3 A ( 3 x ; 3 y ) không th/ng hàng:
+ Tam giác
A A A .A A 0 1 A 2 A 3 A vuông ti 1 1 2 1 3 1A 2A 1 A 3 A + Tam giác 1 A 2 A 3
A -u 1 A 2 A 2 A 3 A 1 1 abc
- Di%n tích tam giác : S . h a . b csin ABC A pr
p p a p b p c 2 2 4R 6. HÀM S VÀ : TH4 6.1. # th hàm s bc 3
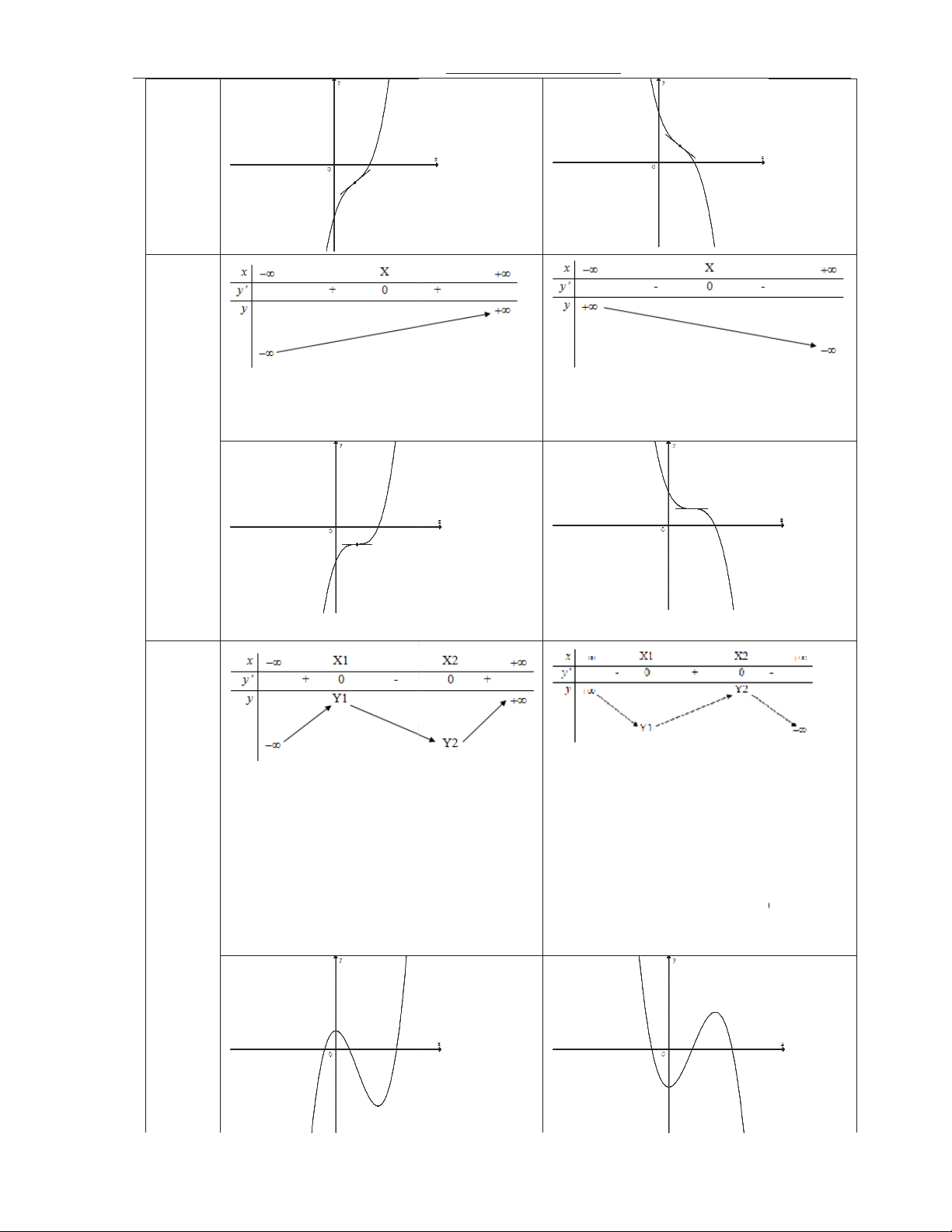
th hàm s luôn ct tr(c Ox ti ít nh"t mt i!m b b th nh*n i!m I ; f 3a là tâm i xng 3a Bng bin thiên và dng th Tr+=ng a>0 a<0 h2p y ' 0 vô nghim *) Hàm s luôn ng bin trên R
*) Hàm s luôn nghch bin trên R *) Hàm s không có c,c tr *) Hàm s không có c,c tr
Thy Nguyn c Thng 0969119789 –thangnd286@gmail.com Tr ng PTLC Vinschool *) Hàm s luôn ng bin trên R
*) Hàm s luôn nghch bin trên R *) Hàm s không có c,c tr y ' 0 *) Hàm s không có c,c tr có nghim kép *) Hàm s ng bin trên khong
*) Hàm s nghch bin trên khong ; 1
X và X2;. Hàm s nghch bin ; 1
X và X2;. Hàm s ng bin y ' 0 trên 1 X ; X2 . trên 1 X ; X2 . có hai *) Hàm s t c,c i ti nghim *) Hàm s t c,c i ti
x X ; y f (X ) phân 1 CÑ 1 . Hàm s t c,c ti!u x 1 X ; y f ( 1 X ) CT . Hàm s t c,c bit
ti x X2; y f (X2) CT .
ti!u ti x X2; y f (X2) CÑ . Thy Nguyn c Thng
0969119789 –thangnd286@gmail.com Tr ng PTLC Vinschool 4 2
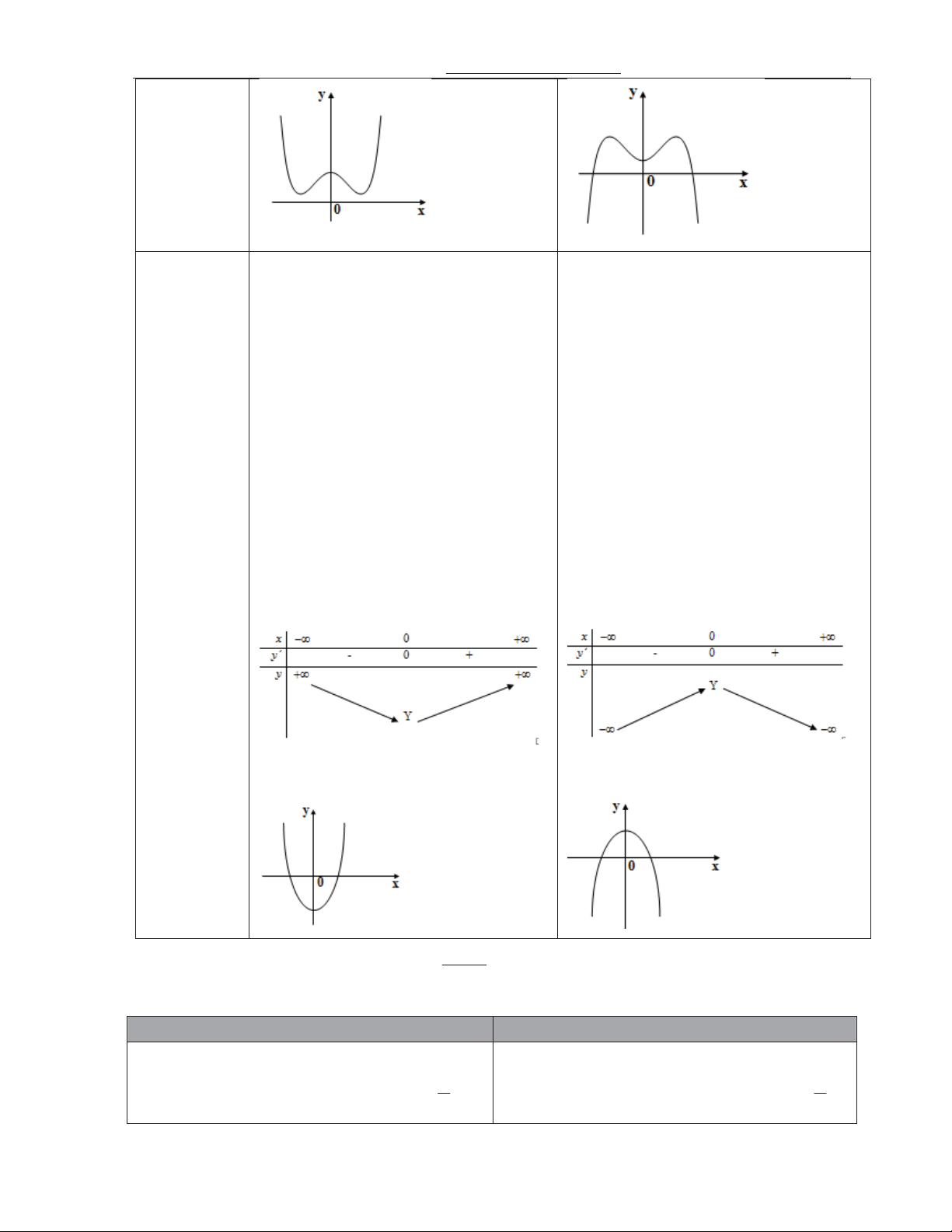
6.2. # th hàm s bc 4 trùng phng: f (x) ax bx c (a 0)
Vì hàm s là ch6n trên R nên th luôn nh*n tr(c tung làm tr(c i xng.
Hàm s luôn có c,c tr (mt c,c tr nu a.b>0 ; ba c,c tr nu a.b<0)
Có mt c,c tr luôn thuc tr(c Oy. Tr ng h0p có 3 i!m c,c tr thì ba i!m c,c tr là 3 &nh c+a tam giác cân.
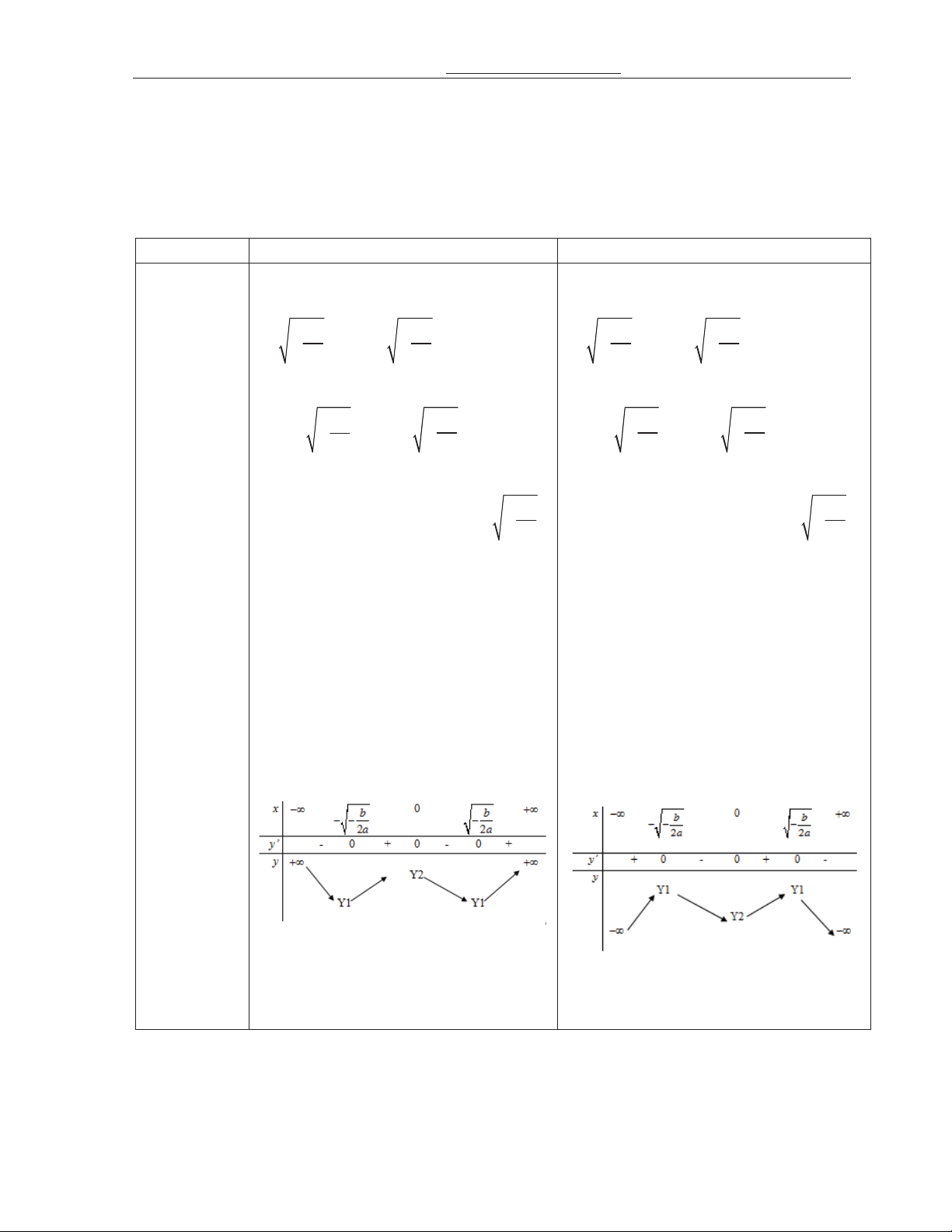
B/ng bin thiên và d0ng ? th& Các d0ng a>0 a<0 *) n iu *) n iu Hàm s ng bin trên các khong
Hàm s nghch bin trên các khong b b b b ;0 ;0 2a và ; và ; 2a 2a 2a
Hàm s nghch bin trên các khong Hàm s ng bin trên các khong b b b b ; ; 2a và 0; và 0; 2a 2a 2a * C@c tr& * C@c tr& b b
Hàm s t c,c ti!u ti : CT x x 2a
Hàm s t c,c ti!u ti : CÑ 2a y’ = 0 có 3 và y 1 Y f (x ) CT CT .Hàm s t c,c và y 1 Y f (x ) CÑ CÑ .Hàm s t c,c i nghim phân i ti 0 CÑ x và CÑ y 2 Y c . ti 0 CT x và CT y 2 Y c . bit * GiAi h0n * GiAi h0n PT (*) có Neáu a 0 Neáu a 0 hai nghim lim 4 2
ax bx c lim 4 2
ax bx c x
Neáu a 0 x
Neáu a 0 phân bit khác 0 4 2
ax bx c Neáu a 0 lim 4 2 Neáu a 0
lim ax bx c x Neáu a 0 x Neáu a 0 ab < 0 th hàm s không có ti%m c*n th hàm s không có ti%m c*n *) B/ng BT *) B/ng BT 3. ? th& 3. ? th& Thy Nguyn c Thng
0969119789 –thangnd286@gmail.com Tr ng PTLC Vinschool *) n iu *) n iu Hàm s ng bin trên các khong Hàm s ng bin trên các khong
0;. Hàm s nghch bin trên các
;0 . Hàm s nghch bin trên các khong ;0 khong 0; * C@c tr& * C@c tr& Hàm s t c,c ti!u ti 0 CT x và
Hàm s t c,c ti!u ti xCÑ 0 và CT y 2 Y c . CÑ y 2 Y c . * GiAi h0n * GiAi h0n 4 2
ax bx c Neáu a 0 lim 4 2
ax bx c Neáu a 0 lim y’ = 0 chB có x
Neáu a 0 x
Neáu a 0 1 nghim 4 2 Neáu a 0 4 2 Neáu a 0
lim ax bx c
lim ax bx c PT (*) vô x
Neáu a 0 x
Neáu a 0 nghim ho;c *) B/ng BT *) B/ng BT chB có m t nghim bDng 0 ab > 0 th hàm s không có ti%m c*n th hàm s không có ti%m c*n 3. ? th& 3. ? th& ax b
6.3.# th hàm s phân thc dng f (x)
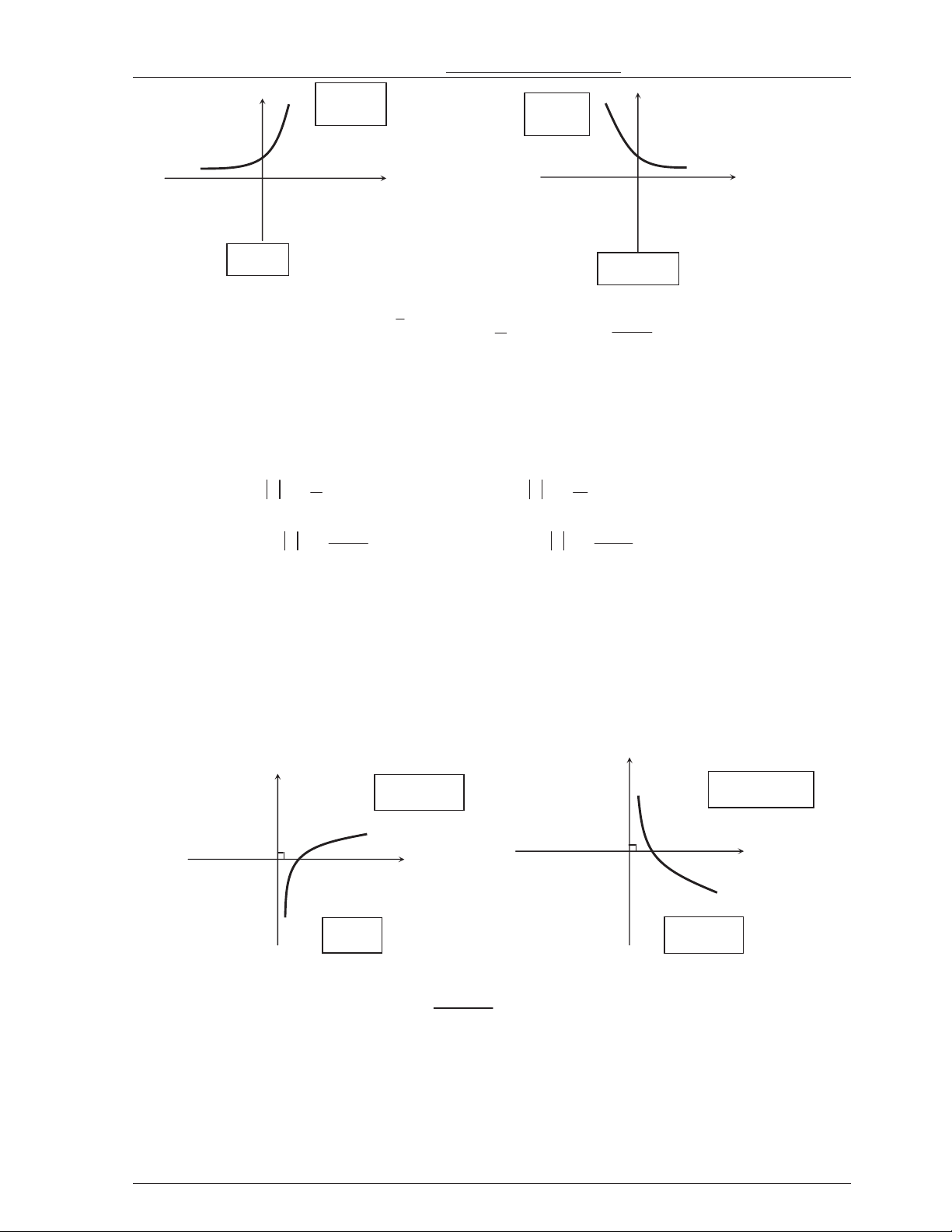
(c 0,ad bc 0) cx d Bng bin thiên và dng th ad bc 0 ad bc 0 *)n iu *)n iu Hàm s ng bin trên các khong ; d
c và Hàm s nghch bin trên các khong ; d c Thy Nguyn c Thng
0969119789 –thangnd286@gmail.com Tr ng PTLC Vinschool d d ; c và ; c *) C'c tr *) C'c tr Hàm s không có c,c tr Hàm s không có c,c tr *) Gi i hn *) Gi i hn
lim y và lim y nên ng
lim y và lim y nên ng d x d d d x x x c c c c d d th/ng x x c là ti%m c*n ng th/ng c là ti%m c*n ng lim a y a a a và lim y nên ng th/ng
lim y và lim y nên ng th/ng x c x c x c x c a y a y c là ti%m c*n ngang c là ti%m c*n ngang
*) Bng bin thiên :
*) Bng bin thiên : 3. ? th& 3. ? th& 7. BÀI TOÁN TIP TUYN
D0ng 1. Ph ng trình tip tuyn c+a ng cong (C): y f (x) ti tip i!m M x0; 0 y có dng:
d : y f ' x x y x 0 0 0
Áp d'ng trong các tr)ng hp sau: Trng h%p Cn tìm Ghí chú
1. Vit ph ng trình tip tuyn d c+a (C) t0i H% s góc : f ' 0 x i!m M x0; 0 y .
2. Vit ph ng trình tip tuyn d c+a (C) ti H% s góc : f ' 0 x
f 'x0 T$ x
i!m có hoành x x 0 f x0 0 Tung tip i!m 0
y f x0
3. Vit ph ng trình tip tuyn d c+a (C) ti Hoành tip i!m x0 Gii ph ng trình i!m có tung y 0
y f x0 0 y H% s góc : f ' 0 x Hoành tip i!m x
4. Vit ph ng trình tip tuyn d c+a (C) , 0 Gii ph ng trình
bit h% s góc k c+a tip tuyn d .
Tung tip i!m y f x f 'x 0 k
Thy Nguyn c Thng 0969119789 –thangnd286@gmail.com Tr ng PTLC Vinschool Chú ý: Gi 1
k là h% s góc c+a ng th/ng 1
d và k2 là h% s góc c+a ng th/ng d2 Nu 1
d song song v#i d2 thì 1k k2 Nu 1
d vuông góc v#i d2 thì 1k. 2 k 1
D0ng 2 (tham kh/o). Vit ph ng trình tip tuyn c+a ng cong (C) i qua i!m A 1 x ; 1y
Phng pháp: B"c 1. Vit ph ng trình ng th/ng d i qua i!m A và có h% s góc k
d : y k x 1x 1y
B"c 2. Tìm i-u ki%n ! d là tip tuyn c+a ng cong (C) :
f (x) k x 1x y d tip xúc v#i ng cong (C) 1 f ' có nghim.
x k (*)
B"c 3. Kh k , tìm x , thay x vào (*) ! tìm k , t$ ó suy ra các tip tuyn cn tìm
Trung tâm luyn thi cht lng cao Thành t – Tây M, Nam T Liêm, Hà Ni Page 17
Thy Nguyn c Thng 0969119789 –thangnd286@gmail.com Tr ng PTLC Vinschool B. M – LOGARIT
1. nh ngha và các công thc lu( th*a và m+ a) L+y th*a S" mE C s" a LuG thIa a * n N a R n a a . a ...... a a (n tha s a) 0 a 0 0 a a 1 * n 1
n( n N ) a 0
a a n a m m
(m Z,n N, n 2) a 0 n n n m
a a a (n n
a b b a) *
lim r (r Q,n N ) a 0 r n n a lim n a
2. Các phép toán: V#i a và b là nhng s th,c d ng, và là nhng s th,c tùy ý, ta có a .a a a a a a . (a ) a (a )
(ab) a .b a b b 3. So sánh:
Nu a 1 thì a a ;
Nu 0 a 1 thì a a m m m m
V#i 0 < a < b ta có: a b m 0 ;
a b m 0 b) C,n bc n: n
Khái nim : C7n b*c n c+a a là s b sao cho b a .
V#i a, b 0, m, n N*, p, q Z ta có: n n n a a p .n ab a b n m ; n (b 0) ; p n a a (a 0) n mn a a n b b p q n p m q m n Nu
thì a a (a 0) n m a a n m #c bit
- Nu n là s nguyên d ng l8 và a < b thì n n a b .
- Nu n là s nguyên d ng ch6n và 0 < a < b thì n n a b .
Chú ý: + Khi n l8, m.i s th,c a ch& có mt c7n b*c n. Kí hi%u n a .
+ Khi n ch6n, m.i s th,c d ng a có úng hai c7n b*c n là hai s i nhau, c7n có giá tr d ng ký hi%u là n a n n a khi n l a a khi n chn
2. nh ngha và các công thc lôgarit
* &nh nghJa : log
a b a b
* Phép toán : V"i a, b > 0; a 1; b1, b2 > 0; R ta có: log 1 0 log b a a b a ; log 1 a a ; log b a a b ;
Trung tâm luyn thi cht lng cao Thành t – Tây M, Nam T Liêm, Hà Ni Page 18
Thy Nguyn c Thng 0969119789 –thangnd286@gmail.com Tr ng PTLC Vinschool
* So sánh: Nu a > 1 thì log b log a
a c b c . Nu 0 < a < 1 thì log b log a
a c b c b * Phép toán: log ( 1
log log b log b 1 b 2
b ) log 1b log a a a 2 b a a 1 a 2 log b log a a b 2 b
* 1i c s" : V#i a, b, c > 0 và a, b 1, ta có: log c 1 log a 1 b c hay log .
b log c log c log b log c log c ( 0) log a b a a a a a b logb a
* Logarit th-p phân: lg b log b lo 10 g b 1 n
* Logarit t@ nhiên (logarit Nepe):
ln b loge b (v#i e lim1 2,718281......) n
3. HÀM S- L/Y TH1A
* D0ng: y x , R * T-p xác &nh: D
nguyên d ng thì TX là D = R
nguyên âm hoc b1ng 0 thì TX là D = R \ {0}.
không là s nguyên thì TX là D = (0; +). * 0o hàm : 1 (x )' .x ( x D) . 1 (u )' .u .u' v#i u là hàm h0p.
* Tính n iu : trên khong (0 ; +) hàm s ng bin nu >0 và nghch bin nu < 0 . *# th : Luôn i qua i!m (1; 1)
0 th không có ti%m c*n.
< 0 th có ti%m c*n ngang là tr(c Ox, ti%m c*n ng là tr(c Oy. 1 n
* Chú ý: Hàm s n
y x không ng nht v"i hàm s y x (n N*). n x 1 n u'
( v"i x > 0 khi n ch-n và x 0 khi n l.) u n n 1 n x n n 1 n u 4. HÀM S- M/ * D0ng: x
y a (a > 0, a 1). * T-p xác &nh: D = R. * T-p giá tr&: T = (0; +). xe x ue u x a x u a u * 0o hàm: e e .u' a .ln a
a .u'.ln a * Tính n iu:
Khi a > 1 hàm s ng bin trên R.
Khi 0 < a < 1 hàm s nghch bin trên R. * ? th&:
Luôn i qua các i!m (0; 1) ; (1 ; a)
th có ti%m c*n ngang là tr(c Ox.
Trung tâm luyn thi cht lng cao Thành t – Tây M, Nam T Liêm, Hà Ni Page 19
Thy Nguyn c Thng 0969119789 –thangnd286@gmail.com Tr ng PTLC Vinschool y y=ax y=ax y 1 1 x x a>1 01 1 x x e 1
Chú ý: Gi#i hn c bi%t: lim (1 x)x lim 1 e lim 1 x0 x x x 0 x 5. HÀM S- LÔGARIT
* D0ng: y loga x (a > 0, a 1)
* T-p xác &nh: D = (0; +).
* T-p giá tr&: T = R. u * 0o hàm: 1 ln x ln u x (x 0); u u a x 1 log log u x ln a (x0)
a ulna * Tính n iu:
Khi a > 1 hàm s ng bin trên (0; +).
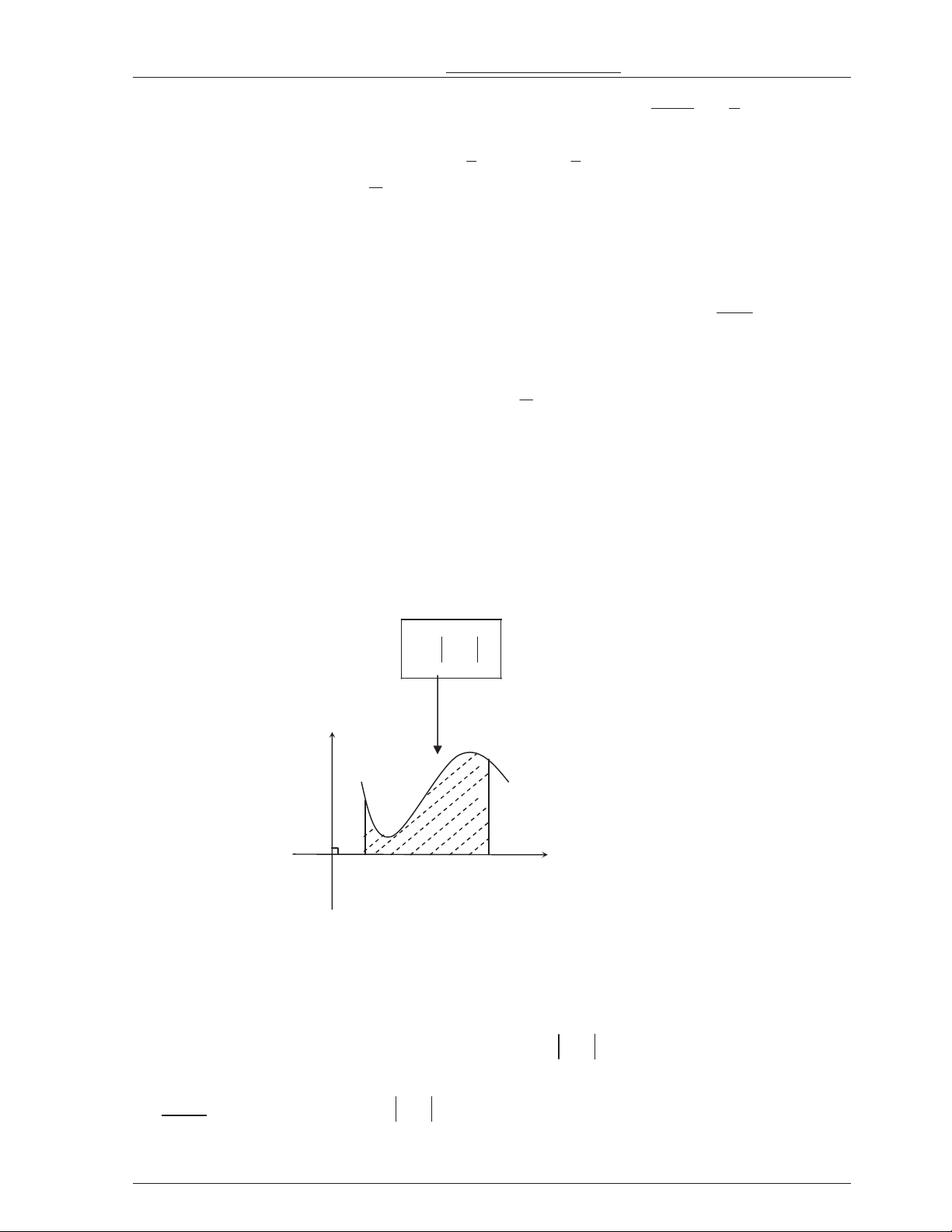
Khi 0 < a < 1 hàm s nghch bin trên (0; +). * ? th&:
Luôn i qua i!m (1; 0) và (a ; 1).
th có ti%m c*n ng là tr(c Oy. y y y=log y=logax ax 1 x x O O 1 a>1 0ln(1 x)
Chú ý : Gi#i hn c bi%t: lim 1 x0 x
6. PH23NG TRÌNH M/ x b 0
6.1. Ph+ng trình mE c b/n: V#i a > 0, a 1: a b x log a b
6.2. M t s" ph+ng pháp gi/i ph+ng trình mE f x g x
a) +a v% cùng c s": V#i a > 0, a 1: ( ) ( ) a a f (x) ( g x)
Trung tâm luyn thi cht lng cao Thành t – Tây M, Nam T Liêm, Hà Ni Page 20
Thy Nguyn c Thng 0969119789 –thangnd286@gmail.com Tr ng PTLC Vinschool M N
Chú ý: Trong tr)ng hp c s có cha /n s thì:
a a (a 1)(M N) 0 b) Logarit hoá: f (x) g(x) a b
f (x) loga b. ( g x) c) ;t Kn ph.: f (x) f x t a , t 0 Dng 1: ( ) P(a ) 0
, trong ó P(t) là a thc theo t. P(t) 0 f (x) a f x f x f x 2 f (x) Dng 2: 2 ( ) ( ) 2 ( ) a (ab) b 0 Chia 2 v cho b
, ri t 5n ph( t b f (x) f (x) f (x) f (x) 1 Dng 3: a b
m , v#i ab 1. t t a b t
d) SL d.ng tính n iu c(a hàm s" Xét ph ng trình: f(x) = g(x) (1)
oán nh*n x0 là mt nghi%m c+a (1).
D,a vào tính ng bin, nghch bin c+a f(x) và g(x) ! kt lu*n x0 là nghi%m duy nh"t:
Nu f(x) ng bin (hoc nghch bin) thì f ( )
u f (v) u v CMn nhA: x x x
+) a>1: Hàm s y a ng bin (ngh9a là: Nu 1 2 1
x x2 a a ) x x x
+) 0y a nghch bin (ngh9a là: Nu 1 2 1
x x2 a a
+) Hàm s y f x liên t(c và có o hàm trên I.
Nu f '(x) 0 thì hàm s ng bin trên I;
Nu f '(x) 0 thì hàm s nghch bin trên I.
+) Hàm s y f x liên t(c và có o hàm trên I. Nu y f (x) luôn ng bin hoc luôn nghch
bin thì f (u) f (v) u v
e) +a v% ph+ng trình các ph+ng trình ;c bit A
Ph+ng trình tích A.B = 0 0 B 0 2 2 A 0
Ph+ng trình A B 0 B 0
f) Ph+ng pháp "i l-p : Xét ph ng trình: f(x) = g(x) (1)
f (x) M
f (x) M Nu ta chng minh 0c: thì (1) ( g x) M ( g x) M
g) Ph+ng pháp phân tích thành tích: v a uv au bv ab
0 v au b 0 u b
7.B4T PH23NG TRÌNH M/
Khi gii các b"t ph ng trình m: ta cn chú ý tính n i%u c+a hàm s m:. a 1 f (x) g(x)
f (x) g(x) a a 0 a1
f (x) g(x)
Chú ý: Trong tr)ng hp c s a có cha /n s thì:
Trung tâm luyn thi cht lng cao Thành t – Tây M, Nam T Liêm, Hà Ni Page 21
Thy Nguyn c Thng 0969119789 –thangnd286@gmail.com Tr ng PTLC Vinschool M N
a a (a 1)(M N) 0
8. PH23NG TRÌNH LOGARIT:
8.1. Ph+ng trình logarit c b/n: V#i a > 0, a 1: log b
a x b x a
8.2. M t s" ph+ng pháp gi/i ph+ng trình logarit 8.3. D0ng c b/n
D0ng 1: Ph ng trình dng log f (x) log g(x); 0 a 1 a a Ph ng pháp gi!i: f (x) ( g x)
log f (x) log g(x) a a (gx) 0
D0ng 2: Ph ng trình dng : log ( ) a f x b Ph ng pháp gi!i: Ph ng trình log ( ) ( ) b a f x b f x a
D0ng 3: Ph ng trình có dng
log f (x) log g(x) (0 a,b 1) a b Ph ng pháp gi!i:
f (x) t a
+) log f (x) log ( g x) a b
g(x) t b
Kh 5n x ! a v- ph ng trình m: 5n t. a
g x f x +) log
g x a
f x
f x ; gx 0; f x 1
D0ng 4: Ph ng trình dng
t log x
+) f log x 0 0 a
1 f t a a 0
t log g x
+) f log g x 0 0 a 1 f t a a 0
8.4. M t s" ph+ng pháp gi/i ph+ng trình mE:
a) Ph+ng pháp +a v% cùng c s"
Cn nh# các công thc bin i sau: m x mn m n a n 1 n nx 1 n x 1. a a .a 2. m n a 3. a 4. n nx x a a
5. a a 6. a n a n a a nx
b) Ph+ng pháp lôgarit hoá S d(ng mt s công thc sau: x
1. log x.y log x log y x, y 0,0 a 1 a a a 2. log
log x log y x,y 0,0 a 1 a a a y 1
3. log x log x
x 0,0 a 1 a a 4. log x log x x a a 0,0 1, 0 a log b 5. log c log x log x x 0,0 a 1, 0 a b
0 a,c 1,b 0 log 6. a a c a 2n Chú ý: log x 2n log x x 0 a a
c) Ph+ng pháp ;t Kn ph.
Trung tâm luyn thi cht lng cao Thành t – Tây M, Nam T Liêm, Hà Ni Page 22
Thy Nguyn c Thng 0969119789 –thangnd286@gmail.com Tr ng PTLC Vinschool + #t /n ph' hoàn toàn: Cn nh# mt s công thc sau: log log b c b
a c b , log x
log x x 0,0 a 1, 0 a a 0 , 1, 0 log a a c t t log x a . Mt s công thc bin i
+ #t /n ph' không hoàn toàn
S d(ng bi%t thc cho tam thc b*c 2 5n t, trong ó t log x a ! phân tích thành tích
d) Ph+ng pháp sL d.ng tính n iu c(a hàm s" CMn nhA:
+) a>1: Hàm s y log x a ng bin trên R 0 x og x (ngh9a là: Nu
x1 x l 2 og l a 1 a 2 ) +) 0y log x a nghch bin trên R 0 x log x (ngh9a là: Nu
x1 x l 2 og a 1 a 2
+) Hàm s y f x liên t(c, có o hàm trên I.
- Nu f '(x) 0 thì hàm s ng bin trên I;
- Nu f '(x) 0 thì hàm s nghch bin trên I.
+) Hàm s y f x liên t(c và có o hàm trên I. Nu y f (x) luôn ng bin hoc luôn nghch
bin thì f (u) f (v) u v u +) o hàm: a u ' log ' ulna
f (x) M
e) Ph+ng pháp "i l-p: Gi s cn gii ph ng trình: f x g x ta ch& ra: (gx) M
f (x) M
khi ó: f (x) (
g x) g(x) M
f) Ph+ng pháp phân tích thành tích:
0 0 v a uv au bv ab v a u b
u b Chú ý:
Khi gi!i ph ng trình logarit c0n chú ý iu kin biu thc có ngh1a. log c log a
V"i a, b, c > 0 và a, b, c 1: b b a c
9. B4T PH23NG TRÌNH LOGARIT:
Khi gii các b"t ph ng trình logarit ta cn chú ý tính n i%u c+a hàm s logarit. a 1
f (x) g(x) 0
log f (x) log g(x) a a
0 a1
0 f (x) g(x)
Chú ý: Trong tr)ng hp c s a có cha /n s thì: log A log 0 ( 1)( 1) 0 a a B a B ;
0 (A 1)(B 1) 0 log . a B 10. MT S BÀI TOÁN TH3C T 10.1. LÃI 3N
S ti-n lãi ch& tính trên s ti-n gc mà không tính trên s ti-n lãi mà s ti-n gc sinh ra Công thc tính lãi n : 1 . n T M r n
V#i Tn : s ti-n c vn l;n lãi sau n k< hn ; M : s ti-n vn ban u.
r : Lãi su"t nh k< ( tính theo % )
Trung tâm luyn thi cht lng cao Thành t – Tây M, Nam T Liêm, Hà Ni Page 23
Thy Nguyn c Thng 0969119789 –thangnd286@gmail.com Tr ng PTLC Vinschool n : s k< hn tính lãi. 10.2. LÃI KÉP
S ti-n lãi không ch& tính trên s ti-n gc mà còn tính trên s ti-n lãi do s ti-n gc sinh ra thay i theo t$ng nh k<. n
a) Lãi kép gLi m t lMn :
Công thc tính lãi kép : n
T M 1 r
V#i Tn : s ti-n c vn l;n lãi sau n k< hn ; M : s ti-n vn ban u.
r : Lãi su"t nh k< ( tính theo % ) n : s k< hn tính lãi.
b) Lãi kép, gLi &nh kN :
*Trng h%p 1 : Tin c g*i vào cui mi tháng
Cui tháng th nht ng)i ó b3t 0u g*i tin : T1 = M M 2
Cui tháng th hai ng)ió có s tin là : M(1 + r) + M = M[(1+r) + 1] = [(1 r) 1] r M 2 M 3
Cui tháng th ba ng)ió có s tin là : [(1 r) 1] [(1 r) 1] r (1+r) + M= r M n
Cui tháng th n ng)ió có s tin là : T [(1 r) 1] n r
*Trng h%p 2 : Tin c g*i vào 0u mi tháng M n
Cui tháng th n ng)ió có s tin là : T
[(1 r) 1](1 r) n r
c) Vay tr/ góp : Vay A, lãi su"t r, s kì vay n, tr hàng kì : M M n
T A1 rn [(1 r)n 1] r
d) TOng l+ng : Kh2i i!m A, t& l% t7ng hàng kì : r, s ln t7ng l ng : n A n Tng ti-n : T [(1 r) 1] n 1 n r r
và ti-n l ng 2 kì t7ng l ng th n là n T A
Trung tâm luyn thi cht lng cao Thành t – Tây M, Nam T Liêm, Hà Ni Page 24 Thy Nguyn c Thng
0969119789 –thangnd286@gmail.com Tr ng PTLC Vinschool
C. NGUYÊN HÀM, TÍCH PHÂN VÀ NG DNG TÍCH PHÂN
I. LÍ THUYT NGUYÊN HÀM, TÍCH PHÂN 1. Nguyên hàm c b/n 1 1 1 dx ax b ax b c, 1
cosax bdx sinax b c a 1 a dx 1 1
ln ax b c
sin ax b dx
cos ax b c ax c b a a axb 1 dx axb e 1 e c
tgax bdx ln cosax b c a a axb 1 dx axb m 1 m c
cotgax bdx ln sinax b c a ln m a dx 1 dx 1
arctg x c
cotgax b c 2 2 a x a a 2
sin ax b a dx 1 dx 1
ln a x c
tgax b c 2 2 a x 2a a x 2
cos ax b a dx 2 2 ln 2
x x a c dx 1
ln a x a c 2 x a 2 2 a x x x a dx 1 ax b b c
lnax bdx
x lnax b x c
sinax b ln tg a 2 a ax ax e
a cos bx bsin bx dx 1 ax b e cos bx dx c ln tg c 2 2 a b
sinax b a 2 ax ax e
a sin bx b cos bx dx x e sin bx dx c ln tan C 2 2 a b cos x 2 4
dx ln tan x C 2 2 x 2 2 a 2 2 x a dx
x a ln x x a C sin x 2 2 2 2 2 x 2 2 a 2 2 x a dx
x a ln x x a C 2 2 2. Tích phân
Cho hàm s f liên t'c trên K và a, b K. Nu F là mt nguyên hàm ca f trên K thì: b b
F(b) – F(a) c g%i l tích phân ca f t* a n b và kí hiu là f (x)dx :
f (x)dx F(b) F(a) a a
i v"i bin s ly tích phân, ta có th ch%n bt kì mt ch4 khác thay cho x, tc là: b b b
f (x)dx f (t)dt f (u)du . . F(b) F(a) a a a
Ý ngha hình h&c:
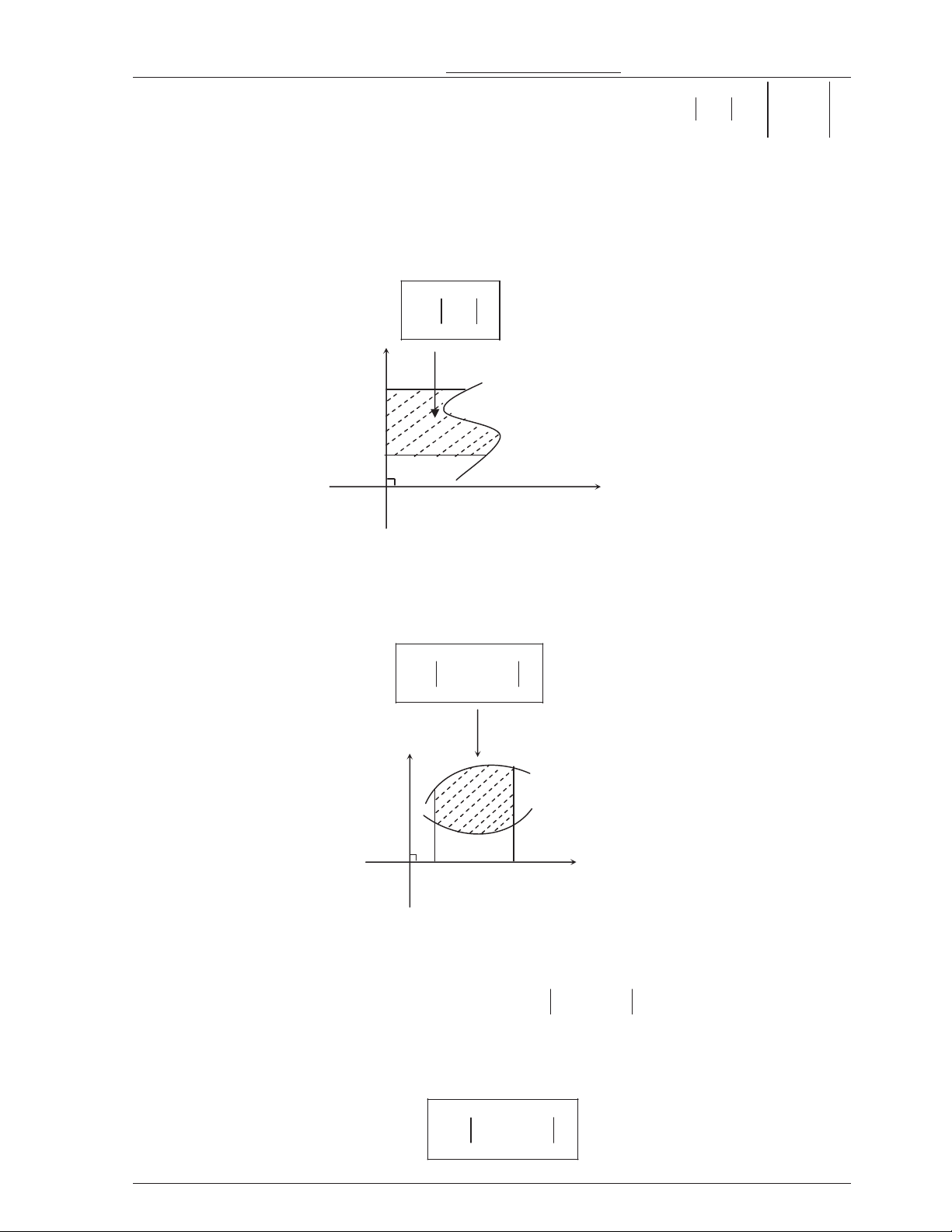
Nu hàm s y = f(x) liên t'c và không âm trên on [a; b] thì din tích S ca hình thang cong gi"i hn b
b5i th ca y = f(x), tr'c Ox và hai )ng th+ng x = a, x = b là: S f (x)dx Thy Nguyn c Thng
0969119789 –thangnd286@gmail.com Tr ng PTLC Vinschool
3. Tính ch#t c(a tích phân 0 b a b b
f (x)dx 0
f x dx f x dx
kf x dx k f x dx (k: h6ng s) ( ) ( ) ( ) ( ) 0 a b a a b b b b c b
f (x) (
g x)dx f (x)dx ( g x)dx
f (x)dx f (x)dx f (x)dx a a a a a c b b b
Nu f(x) 0 trên [a; b] thì f (x)dx 0 Nu f(x) g(x) trên [a; b] thì
f (x)dx ( g x)dx a a a b
Nu m f (x) M trên [a; b] thì m(b a) f (x)dx M (b a) a
4. Ph+ng pháp tính tích phân b u(b)
a) Phng pháp !i bin s: f (
u x).u'(x)dx f (u)du
trong ó: u = u(x) có o hàm liên t'c a u(a)
trên K, y = f(u) liên t'c và hàm hp f[u(x)] xác nh trên K, a, b K.
b) Phng pháp tích phân t*ng phn b b b
Nu u, v là hai hàm s có o hàm liên t'c trên K, a, b K thì:
udv uv vdu a a a
Chú ý: – C0n xem li các ph ng pháp tìm nguyên hàm. b b
– Trong ph ng pháp tích phân tng ph0n, ta c0n ch%n sao cho vdu d7 tính h n udv . a a b – Khi tính
f (x)dx c0n chú ý xem hàm s y = f(x) có liên t'c trên a; b không ? Nu có thì a
áp d'ng ph ng pháp ã h%c tính tích phân. Nu không kt lun tích phân không tn ti.
II. PHNG PHÁP TÍNH TÍCH PHÂN
Ph+ng pháp 1: Tính tích phân bDng ph+ng pháp 1i bin b b u(b)
Dng 1: Gi! s* c0n tính tích phân: f (x)dx
. Nu f (x) f u(x).u '(x) thì :
f (x)dx f (u)du a a u(a) b
Dng 2: Gi! s* c0n tính tích phân: f (x)dx
. Nhng tính theo dng 1 không c, lúc này ta chuyn a
v hàm lng giác. Ta th)ng g#p các dng sau: 2 2 a x dx 1 x a t x a t dx #t sin ho#c #t : cos 2 2 a x
Thy Nguyn c Thng 0969119789 –thangnd286@gmail.com Tr ng PTLC Vinschool 2 2 a x dx 1 dx
#t x a tan t
ho#c #t : x a cot t 2 2 a x 1 dx 2 2 a x 2 2 x a dx a a 1 x x dx #t sin t ho#c #t cost 2 2 x a DNG CÁCH I BIN f
ax bdx
t t ax b n 1 ( ). n f x x dx n 1 t t x dx f x . x t t x
f sin xcosxdx t t sin x
f cosxsin xdx t t cos x tan dx f x ; f tan x 2 1 tan x dx t x 2 t tan cos x cot dx f x ; f cot x 2 1 cot x dx t x 2 t cot sin x x. x f e e dx x t t e dx f ln x t x x t ln 1 1 f x 1 . x dx t x x x t x
Ph+ng pháp 2: Tính tích phân bDng ph+ng pháp tích phân tIng phMn
V"i P(x) là a thc /n x, có các dng sau: b b b b P(x). x e dx
P(x).cos xdx
P(x).sin xdx
P(x).ln xdx a a a a t u P(x) P(x) P(x) lnx t dv x e dx cos xdx sin xdx P(x)
Th t, u tiên t u trong ph ng pháp Nguyên hàm t$ng phn: sin x,cos x (Hàm lng giác)
Lôgarít a thc x e (Hàm m)
IV. TÍCH PHÂN HÀM HPU TQ
Trung tâm luyn thi cht lng cao Thành t – Tây M, Nam T Liêm, Hà Ni Page 27
Thy Nguyn c Thng 0969119789 –thangnd286@gmail.com Tr ng PTLC Vinschool
- Loi 1: Nu bc ca P(x) bc ca Q(x) thì ta th&c hin phép chia a thc.
- Loi 2: Nu bc ca P(x) < bc ca Q(x) và Q(x) có dng tích nhiu nhân t* thì ta phân tích f(x)
thành t,ng ca nhiu phân thc (b6ng ph ng pháp h s bt nh).
Các dng dùng phöông phaùp heä soá baát ñònh thng gp:
Dng 1: M;u s có nghi%m n: P(x) P(x) A B (
Q x) (x a)(x b) x a x b P(x) P(x) A B C (
Q x) (x a)(x )
b (x c) x a x b (x c)
Dng 2: M;u s có nghi%m n và b*c 2 vô nghi%m: P(x) P(x) A Bx C 2
, vôùi b 4ac 0 2 2
Q(x) (x m)(ax bx c) x m ax bx c
Dng 3: M;u s có nghi%m bi: P(x) P(x) A B
Q(x) 2 2 xa x a x a P(x) P(x) A B C
Q(x) 3 3 2 xa x a x a x a P(x) P(x) A B C D 2 2 2 2
Q(x) (x a) (x b)
x a (x a)
x b (x b) P(x) P(x) A B C D E 2 3 2 2 3
Q(x) (x a) (x b)
x a (x a)
x b (x b) (x b)
- Lo0i 3: Mt s nguyên hàm ta dùng ph ng pháp i bin hoc t$ng phn
V. TÍCH PHÂN HÀM VÔ TQ ax b ax b
+ D0ng 1: f x R x,m t: m t cx d cx d
+ D0ng 2: f x 1 R
t: t x a x b (x a)(x b) n m
+ D0ng 3: f x R x, ax b, ax b t: n.m t ax b 2 2 a x dx + D0ng 4: 1 x a t t x a t t dx #t sin , 2 2 hoaëc: cos , 0 2 2 a x 2 2 a x dx + D0ng 5: 1 x a t t x a t t dx #t tan , 2 2 hoaëc: cot , 0 2 2 a x
Trung tâm luyn thi cht lng cao Thành t – Tây M, Nam T Liêm, Hà Ni Page 28
Thy Nguyn c Thng 0969119789 –thangnd286@gmail.com Tr ng PTLC Vinschool a x dx ax + D0ng 6:
#t x a cos2t a x dx a x
+ D0ng 7: x ab xdx
#t x a b a 2 sin t
VI. TÍCH PHÂN HÀM LRNG GIÁC
sin ax.sin bxdx
D0ng 1: Các d0ng: sin ax.sin bxdx
sinax.sinbxdx 1 cos .
a cosb cos
ab cosa b 2 1
Ph+ng pháp gi/i: Dùng công thc bin ,i thành t,ng: sin .
a sin b cos
abcosa b 2 1
sin .acosb sin
absina b 2 sinn axdx D0ng 2: n N n cos axdx n n 1 n 1
+ VAi n lS : sin axdx sin ax.sin axdx sin ax.sin axdx axn 1 n 2 axdx ax 1 2 2 2 sin .sin 1 cos
.sin axdx . t : u cos x cosn axdx
. Phân tích nh trên sau ó #t: u sin x 2 1 cos2ax 2 1 cos2ax
+ VAi n chTn: S* d'ng công thc h bc: cos ax sin ax 2 ; 2 n m
D0ng 3: sin ax.cos axdx (n, m N)
+ VAi n lS hay m lS : n lS t u = cosax ; m lS t u = sinax
+ VAi n và m chTn: S d(ng công thc h b*c: 2 1 cos2ax ax cos ax 1 2 1 cos2 sin ax
sin x.cos x sin2x 2 ; 2 ; 2 1 dx ax D0ng 4: 1 cos 1 dx 1 cosax 2 ax 2 ax
S* d'ng công thc: 1 cos ax 2 cos 1 cosax 2sin 2 và 2
Trung tâm luyn thi cht lng cao Thành t – Tây M, Nam T Liêm, Hà Ni Page 29
Thy Nguyn c Thng 0969119789 –thangnd286@gmail.com Tr ng PTLC Vinschool
sin a cos a 2 sin a 4
CMn nhA: sin a cos a 2 cos a 4
sin a cosa 2 cos a 4 1 dx ax D0ng 5: sin 1 . dx cosax 1 sin ax sin ax Ph+ng pháp: dx dx dx u x 2 2 sin ax . t cos sin ax 1 cos ax 1 cosax cosax dx dx dx u x 2 2 cosax . t sin cos ax 1sin ax 1 dx n D0ng 6: sin ax nN 1 dx cosn ax Ph+ng pháp: 1 1 1 n dx 1 . dx
1 tan ax 2 2 2 .
dx ; t u tan ax . sinn ax n ax 2 sin ax sin ax 2 2 sin 2 2 1 1 1 n dx 1 . dx
1 cot ax 2 2 2 .
dx ; t u cot ax cosn ax n ax 2 cos ax cos ax 2 2 cos 2 2 tann axdx D0ng 7: n N n cot axdx 2
Ph+ng pháp: + Bin i sao cho tan ax làm th$a s chung 2 1 + Thay : tan ax 1 2 cos ax tann ax dx 2 D0ng 8: cos ax n N u ax u ax n . Ph+ng pháp: t tan hoc cot cot ax dx 2 sin ax dx D0ng 9: .s a in x .
b cos x c
Cách 1: Ph ng pháp chung:
Trung tâm luyn thi cht lng cao Thành t – Tây M, Nam T Liêm, Hà Ni Page 30
Thy Nguyn c Thng 0969119789 –thangnd286@gmail.com Tr ng PTLC Vinschool 2dt dx 2 x 1 t t : t tan 2 2 2t 1 t 2 sin ; cos ; tan t x x x 2 2 2 1 t 1 t 1-t 2 2
Cách 2: Ph ng pháp riêng: Nu c a b . 1 1 1 1 Ta có: a x . b x c c 1 cos x - . sin cos 2c 2 cos x 2 a b Trong ó : sin ; cos 2 2 2 2 a b a b 1 dx 1 x Khi ó : I tan C 2c 2 x c 2 cos 2 .s a in x . b cos x D0ng 10: dx .s
c in x d.cos x .s a in x . b cos x B( .
c cos x d.sin x)
Ph+ng pháp: Phân tích A .
c sin x d.cos x .
c sin x d.cos x
Sau ó dùng ng nh"t thc tìm A, B. . a sin x .
b cos x m D0ng 11: dx
.csinxd.cosxn Ph+ng pháp: .s a in x .
b cos x m B( .
c cos x d.sin x) C Phân tích A .
c sin x d.cos x n .s
c in x d.cos x n .s
c in x d.cos x n
Sau ó dùng ng nh"t thc tìm A, B, C. dx
D0ng 12: sinxasinxb
Ta th,c hi%n theo các b #c sau :
sina b sin x ax b
+ B #c 1: S d(ng ng nh"t thc : 1 sina b ab + B #c 2: Ta 0c : sin 1
x ax b dx dx
sinx asinx b sina b sinx asinx b 1
sinx acosx -b sinx bcosx -a dx sina b
sinx asinx b 1
cosx b
cosx a dx dx
sina b sinx b
sinx a 1 1 sinx b x b x a ln C sina b ln sin ln sin
sina b sinx a
Trung tâm luyn thi cht lng cao Thành t – Tây M, Nam T Liêm, Hà Ni Page 31
Thy Nguyn c Thng 0969119789 –thangnd286@gmail.com Tr ng PTLC Vinschool
* Chú ý: phng pháp trên c+ng %c áp d$ng cho các dng tích phân sau : dx sina b s d(ng ng nh"t thc : 1
cosx acosx b sina b dx cosa b s d(ng ng nh"t thc : 1 .
sinx acosx b cosa b dx
D0ng 13: sin x sin
* Dùng công thc tng thành tích bin i v- dng 12 ri gii bình th ng.
* Chú ý : Ph ng pháp trên c:ng áp d(ng cho các dng tích phân sau : dx dx dx m cos x ; ; 1 . cos cos x m sin x m 2 2
a sin x b sin x cos x c cos x D0ng 14: 1 1 1 dx . 2 a sin x 2 b cos x + Bin i : 2 2
a sin x b sin x cos x c cos x Asin x Bcos xa sin x b cos x C 2 2 1 1 1 2 2
sin x cos x
Asin x Bcosxa sin x b cosxC 2 2 2 2
sin x cos x + Khi ó: 2 a sin x 2 b cos x dx
A sin x B cos x C 2asinx 2b cosx cos sin C dx cos sin C ln tan x A x B x A x B x C 2 2 sin x a b 2 2 2 2 2 2 a 2 b b a Trong ó : 2 2 sin ; cos . 2 2 2 2 2 a 2 b 2 a 2 b dx D0ng 15: 2 2
asin x bsin x cos x c cos x dx dx + Bin i v- dng : 2 2 a x b x x c x
2xb xc 2 sin sin cos cos atan tan cot x 1 2 2 dt
+ t: t tan x dt
dx 1 tan x dx 1 t dx dx 2 2 cos x 1 t dx dt + Khi ó 2 2 2 .
asin x bsin x cos x ccos x
at bt c n n D0ng 16: A = sinx dx ; A cosx 1.1 1.2 dx 1. Công th*c h0 b-c 2 1 cos2x 2 1 cos2x 3
sin3x 3sin x 3 cos3x 3cos sin ; cos ; sin ; cos x x x x x 2 2 4 4
Trung tâm luyn thi cht lng cao Thành t – Tây M, Nam T Liêm, Hà Ni Page 32
Thy Nguyn c Thng 0969119789 –thangnd286@gmail.com Tr ng PTLC Vinschool 2. Ph+ng pháp
2.1. Nu n ch6n thì s d(ng công thc h b*c
2.2. Nu n 3 thì s d(ng công thc h b*c hoc bin i theo 2.3.
2.3. Nu 3 n l8 (n 2p 1) thì th,c hi%n bin i: n 2p+1 2 2 p p x xdx x d x 1.1 A = sinx dx = sinx dx sin sin 1 cos cos 0 1 2 k p C
C cos x .. 1k C 2
cos x ... 1 p k p C 2 cos x d cos x p p p p 1 1 k p k C x C x C x2k 1 1 cos cos ... cos ... p
C cos x2p 1 0 1 3 p c 3 p 2k 1 p 2p 1 p p A
= cosxn dx = cosx2p+1 dx cos 2p x cos xdx 2
1 sin x d sin x 1.2 0 1 2 k p C C
sin x ... 1 k C 2
sin x ... 1 p k p C 2 sin x d sin x p p p p 1 1 k p k C x C x C x2k 1 1 sin sin ... sin ... p
C sin x2p 1 0 1 3 p c 3 p 2k 1 p 2p 1 p D0ng 17: m n B = sin x cos x dx (m, nN) 1. Ph+ng pháp:
1.1. Trng h%p 1: m, n là các s nguyên
a. Nu m ch6n, n ch6n thì s d(ng công thc h b*c, bin i tích thành tng.
b. Nu m ch6n, n l8 (n 2p 1) thì bin i: m 2p+1 m 2p m x x xdx x 2 p B = sinx cosx dx sin cos cos sin
1 sin x d sin x k p sin xm 0 1 2 C
C sin x ... 1 k k C 2
sin x ... 1 p p C 2
sin x d sin x p p p p
sin xm 1 sin xm3 2k 1 m 2 p 1 m 0 1 C C ... k k sin x 1 C ... p p sin x 1 p C c m 1 p m 3 p 2k 1 p m
2p 1 m
c. Nu m ch6n, n l8 (n 2p 1) thì bin i: 2p+1 n n 2p n x x xdx x 2 p B = sinx cosx dx cos sin sin cos
1 cos x d cos x k p
cos xn 0 1 2 C
C cos x ... 1 k k C 2
cos x ... 1 p p C 2
cos x d cos x p p p p
cos xn 1 cos xn3 2k 1 n 2 p 1 n 0 1 C C ... k k cos x 1 C ... p p cos x 1 p C c n 1 p n 3 p 2k 1 p n
2p 1 n
d. Nu m l8, n l8 thì s d(ng bin i 1.2. hoc 1.3. cho s m: l8 bé hn.
1.2. Nu m, n là các s h6u t7 thì bin !i và t u sinx ta có: n 1 m 1 m m n 2 2 m B x xdx x x xdx u 2 u 2 sin cos sin cos cos 1 du (*)
m 1 n 1 m k
• Tích phân (*) tính 0c 1 trong 3 s ; ; 2 2 2 là s nguyên n n D0ng 18: C = tg x dx ; C = cotg x 3 .1 3 . 2 dx (nN) 1. Công th*c sL d.ng
Trung tâm luyn thi cht lng cao Thành t – Tây M, Nam T Liêm, Hà Ni Page 33
Thy Nguyn c Thng 0969119789 –thangnd286@gmail.com Tr ng PTLC Vinschool 2 dx
• 1 tg xdx d
tgx tgx c 2 cos x 2 dx
• 1 cotg xdx d
cotgx cotgx c 2 sin x sin x d cos x • tg xdx dx
ln cos x c cosx cosx cos x d sin x • cotg xdx dx
ln sin x c sinx sinx tg xm cotg xm D0ng 19: D 4.1 = dx ; D = dx cos xn 4 . 2 sin xn tg xm
1. Ph+ng pháp: Xét i di%n 4. D 1 dx cosxn
1.1. Nu n ch8n (n 2k) thì bin !i: tgxm k 1 xm 1 k dx D = dx tg
tg xm 1 tg x 1 2 d tg x 4.1 cosx2k 2 2 cos x cos x p k tg xm C C
tg x1 ... p C
tg x ... k
C tg x 1 0 1 2 2 1 2 d tg x k 1 k 1 k 1 k 1 tg xm 1 tg xm3
p tg x m 2 p 1
k tg x m 2k 1 0 1 1 Ck 1 k C 1 ... k C 1 ... C k 1 c m 1 m 3 m 2p 1 m 2k 1
1.2. Nu m l9, n l9 (m 2k 1, n 2h 1) thì bin !i: tgx2k+1 2h 2h k x x = dx
tg x2k 1 tg dx 2 tg x 1 sin D4 .1 dx cosx2h+1 2
cos x cosx
cos x cos x k 2 1 1 h 1 k 1 1 2 2 1 h d u u du u ) 2 (2 ây cos x cos x cos x cos x u C
u k C u k 1 2 0 2 1 2
p C 2 k p ... 1 u ... 1 k h p k k k k Ck du 2k2h 1 2k2h 1
2k2h2 p 1 2h 1 0 u 1 u C ... 1 p u C ... 1 k p k u Ck C c 2k 2h 1
k 2k 2h 1
k 2k 2h 2p 1 k 2h 1
1.3. Nu m ch8n, n l9 (m 2k, n 2h 1) thì s: d$ng bin !i: tg x2k
sin x2k cos x sin x2k D dx dx
d sin x ;u sinx 4.1
cos x2h 1
cos x2kh 1 2 kh 1 sin x 1 2k 2k2 u du u 1 2 1 u 2k2 2k2 u du u du 4. D 1 du kh kh kh kh 1 u 1 1u 1 1u 1 2 2 2 2 1 u
H% thc trên là h% thc truy hi, kt h0p v#i bài tích phân hàm phân thc hu t& ta có th! tính 0c D4.1.
D0ng 20: SL d.ng công th*c bin 1i tích thành t1ng 1. Ph+ng pháp:
Trung tâm luyn thi cht lng cao Thành t – Tây M, Nam T Liêm, Hà Ni Page 34
Thy Nguyn c Thng 0969119789 –thangnd286@gmail.com Tr ng PTLC Vinschool E mx nx 1 cos cos dx
cosm n x cosm n x 5.1 dx 2 E mx nx 1 sin sin dx
cosm n x cosm n x 5.2 dx 2 E mx nx 1 sin cos dx
sinm n x sinm n x 5.3 dx 2 E mx nx 1 cos sin dx
sinm n x sinm n x 5.4 dx 2
VI. TÍCH PHÂN HÀM CÓ CHA TR4 TUYT I b
D0ng 1: Gi s cn tính tích phân I f (x) dx , ta th,c hi%n các b #c sau: a
+ B+Ac 1. L*p bng xét d"u (BXD) c+a hàm s f(x) trên on [a; b], gi s f(x) có BXD: x a 1 x x b 2 f (x) 0 0 b x x 1 2 b
+ B+Ac 2. Tính I
f (x) dx f (x)dx f (x)dx f (x)dx . a a x x 1 2 b
D0ng 2: Gi s cn tính tích phân I f (x) g(x) dx , ta th,c hi%n: a b b b
Cách 1. Tách I f (x) g(x) dx
f (x) dx g(x) dx ri s d(ng dng 1 2 trên. a a a Cách 2.
B+Ac 1. L*p bng xét d"u chung c+a hàm s f(x) và g(x) trên on [a; b].
B+Ac 2. D,a vào bng xét d"u ta b3 giá tr tuy%t i c+a f(x) và g(x). b b
D0ng 3: ! tính các tích phân I max
f(x), g(x )dx và J min
f(x), g(x )dx, ta th,c hi%n a a các b #c sau:
B+Ac 1. L*p bng xét d"u hàm s (
h x) f (x) ( g x) trên on [a; b]. B+Ac 2. + Nu (
h x) 0 thì max f (x), (
g x ) f (x) và min f (x), ( g x ) ( g x) . + Nu (
h x) 0 thì maxf (x), ( g x ) (
g x) và min f (x), (
g x ) f (x).
VII. TÍCH PHÂN MT S HÀM UC BIT a
1. Cho hàm s y f (x) liên t(c và l8 trên on ; a a . Khi ó: I
f (x)dx 0 . a a a
2. Cho hàm s y f (x) liên t(c và ch6n trên on ; a a . Khi ó I
f (x)dx 2 f (x)dx . a 0
Trung tâm luyn thi cht lng cao Thành t – Tây M, Nam T Liêm, Hà Ni Page 35
Thy Nguyn c Thng 0969119789 –thangnd286@gmail.com Tr ng PTLC Vinschool f (x) 1
3. Cho hàm s y f (x) liên t(c và ch6n trên on : . Khi ó: dx f (x)dx x a 1 2 2 2
4. Cho f(x) liên t(c trên on 0;
f (sin x)dx f (cos x)dx 2 .Khi ó: . 0 0 b b
5. Hàm s f (x) liên t(c trên ; a b
Khi ó: f (x)dx f (a b x)dx a a b b a b
6. Hàm s f (x) liên t(c trên ; a b
tho mãn: f (x) f (a b x) thì xf (x)dx f (x)dx 2 a a
Nh-n xét : B1ng cách làm t ng t, ta có các công thc
*Nu f(x) liên t'c trên 0;1 thì
xf (sin x)dx
f (sin x)dx 2 2 2
*Nu f(x) liên t'c trên 0;1 thì
xf (cos x)dx
f (cos x)dx VIII. NG DNG CA TÍCH PHÂN 1. Din tích hình phVng
D0ng 1: Cho hàm s y f x liên t(c trên ; a b
. Khi ó di%n tích hình ph/ng gi#i hn b2i th
hàm s y f x , tr(c Ox ( y 0 ) và hai ng th/ng x a và x b là: b
S f (x) dx a y x b x a
(C) : y f ( ) x x a O y 0 b Phng pháp gii:
B c 1. Lp b!ng xét du hàm s y f (x) trên on ; a b . b
B c 2. D&a vào b!ng xét du tính tích phân : f (x) dx . a b
Chú ý: có 2 cách tính tích phân f (x) dx a
Trung tâm luyn thi cht lng cao Thành t – Tây M, Nam T Liêm, Hà Ni Page 36
Thy Nguyn c Thng 0969119789 –thangnd286@gmail.com Tr ng PTLC Vinschool b b
+ Cách 1: Nu trên on ; a b
hàm s f x không i d"u thì:
f (x)dx f (x)dx a a
+ Cách 2: L*p bng xét d"u hàm s f x trên on ; a b ri kh tr tuy%t i.
D0ng 2: Cho hàm s x f y liên t(c trên ; a b
. Khi ó di%n tích hình ph/ng gi#i hn b2i
th hàm s x f y , tr(c Oy ( x 0) và hai ng th/ng y a và y b là: b
S f (y) dy a y b y b x 0
(C) : x f ( y) a y a x O
2. Din tích hình phVng D n
0 g 1: Cho 2 hàm s y f x và y g x liên t(c trên ; a b
. Khi ó di%n tích c+a hình
ph/ng (H) gi#i hn b2i th hai hàm s y f x và y g x và hai ng th/ng x a và x b là: b
S f (x) ( g x) dx a y x x b a
(C ) : y f (x) 1 (H)
(C ) : y g(x) 2 x a O b Phng pháp gii:
B c 1. Lp b!ng xét du hàm s f x g x trên on ; a b . b
B c 2. D&a vào b!ng xét du tính tích phân
f (x) g(x) dx . a
D0ng 2: Cho hai hàm s y f x và y g x liên t(c trên ; a b
. Di%n tích hình ph/ng gi#i hn
b2i các ng y f x và y g x là: S
f (x) g(x) dx .
Trung tâm luyn thi cht lng cao Thành t – Tây M, Nam T Liêm, Hà Ni Page 37
Thy Nguyn c Thng 0969119789 –thangnd286@gmail.com Tr ng PTLC Vinschool
Trong ó , là nghi%m nh3 nh"t và l#n nh"t c+a ph ng trình f x g x a b Phng pháp gii:
B c 1. Gi!i ph ng trình f x g x 0 . Gi! s* ta tìm c , là nghim nh( nht
và l"n nht ca ph ng trình a b .
B c 2. Lp b!ng xét du hàm s : f x g x trên on ; .
B c 3. D&a vào b!ng xét du tính tích phân:
f (x) g(x) dx . D n
0 g 3: Cho hai hàm s x f y và x gy liên t(c trên ; a b
. Khi ó di%n tích c+a hình
ph/ng (H) gi#i hn b2i th hai hàm s x f y và x gy và hai ng th/ng y a và y b là: b
S f (y) ( g y) dy y
(C ) : x g ( y) a 2 b y b (H) a y a x O
(C ) : x f ( y) 1 Phng pháp gii:
B c 1. Lp b!ng xét du hàm s f y gy trên on ; a b . b
B c 2. D&a vào b!ng xét du tính tích phân
f (y) g(y) dy . a
D0ng 4: Cho hai hàm s x f y và x gy liên t(c trên ; a b
. Di%n tích hình ph/ng gi#i hn
b2i các ng x f y và x gy là: S 1 g (y) 2
g (y) dy .
Trong ó , là nghi%m nh3 nh"t và l#n nh"t c+a ph ng trình f y gy a b Phng pháp gii:
B c 1. Gi!i ph ng trình f y gy 0 . Gi! s* ta tìm c , là nghim nh( nht
và l"n nht ca ph ng trình a b .
B c 2. Lp b!ng xét du hàm s : f y gy trên on ; .
B c 3. D&a vào b!ng xét du tính tích phân:
f (y) g(y) dy .
Trung tâm luyn thi cht lng cao Thành t – Tây M, Nam T Liêm, Hà Ni Page 38
Thy Nguyn c Thng 0969119789 –thangnd286@gmail.com Tr ng PTLC Vinschool
D0ng 5: khi tính din tích giAi h0n 3 hàm s" trW lên thì ph+ng pháp chung là vX ? th& r?i d@a vào ? th& Y tính.
Cách tính gi i hn ca 3 hàm s: Cho 3 hàm s y f x , y g x và y h x liên t(c trên ; a b
. Khi ó di%n tích c+a hình ph/ng (H) gi#i hn b2i th 3 hàm s y f x , y g x và
y hx là: x x 2 S f
x gx 3 dx h
x gx dx x x 1 2 V#i: + f x g x 1
x là nghi%m ph ng trình: + x f x h x 2 là nghi%m ph ng trình: + x h x g x 3 là nghi%m ph ng trình: Trong ó: a 1
x x2 x3 b
Tóm l0i khi gi/i toán ta th+=ng g;p các d0ng sau:
y f (x) b
1. Din ;ch S ca mi n gi i hn: y 0
S f (x)dx
x ;ax b a
y f (x) b
2. Din ;ch S ca mi n gi i hn: y g(x) S f (x) g(x)dx
x ;ax b a
x f (y) b
3. Din ;ch S ca mi n gi i hn: x (
g y) S f (y) g(y)dy
y ;ay b a Chú ý:
1. ! tính di%n tích S ta phi tính tích phân (1) , mun v*y ta phi “phá” d"u giá tr tuy%t i . b b
Nu f (x) 0 , x a ; b thì S f (x) dx f (x)dx a a b b
Nu f (x) 0 , x a ; b thì S f (x) dx
f (x)dx a a
Mun “phá” d"u giá tr tuy%t i ta phi xét d"u c+a bi!u thc f(x) . Th ng có hai cách làm nh sau :
-Cách 1: Dùng nh lí “d"u c+a nh thc b*t nh"t” , nh lí “d"u c+a tam thc b*c hai” ! xét d"u
các bi!u thc f(x) ; ôi khi phi gii các b"t ph ng trình f(x) 8 0 , f(x) 9 0 trên on a ; b
-Cách 2: D&a vào th ca hàm s y =f(x) trên on a ; b
! suy ra d"u c+a f(x) trên on ó .
Trung tâm luyn thi cht lng cao Thành t – Tây M, Nam T Liêm, Hà Ni Page 39
Thy Nguyn c Thng 0969119789 –thangnd286@gmail.com Tr ng PTLC Vinschool
Nu trên on [a ; b] th hàm s y = f(x) n1m phía “trên” tr(c hoành thì f (x) 0 , x a ; b
Nu trên on [a ; b] th hàm s y = f(x) n1m phía “d #i” tr(c hoành thì f (x) 0 , x a ; b b b
-Cách 3 Nu f(x) không i d"u trên [a ; b] thì ta có : S
f (x) dx f (x)dx a a
2. Nu ph ng trình f(x) = 0 có k nghi%m phân bi%t x1 , x2 , …, xk thuc (a ; b) thì trên m.i khong
(a ; x1 ) , (x1 ; x2) , …, (xk ; b) bi!u thc f(x) có d"u không i . b
Khi ó ! tính tích phân S f (x) dx ta có th! tính nh sau : a b x x 1 2 b
S f (x) dx
f (x)dx
f (x)dx ... f (x)dx a a x x 1 k
2. Tính thY tích kh"i tròn xoay khi quay hình phVng quay quanh tr.c Ox, Oy D n
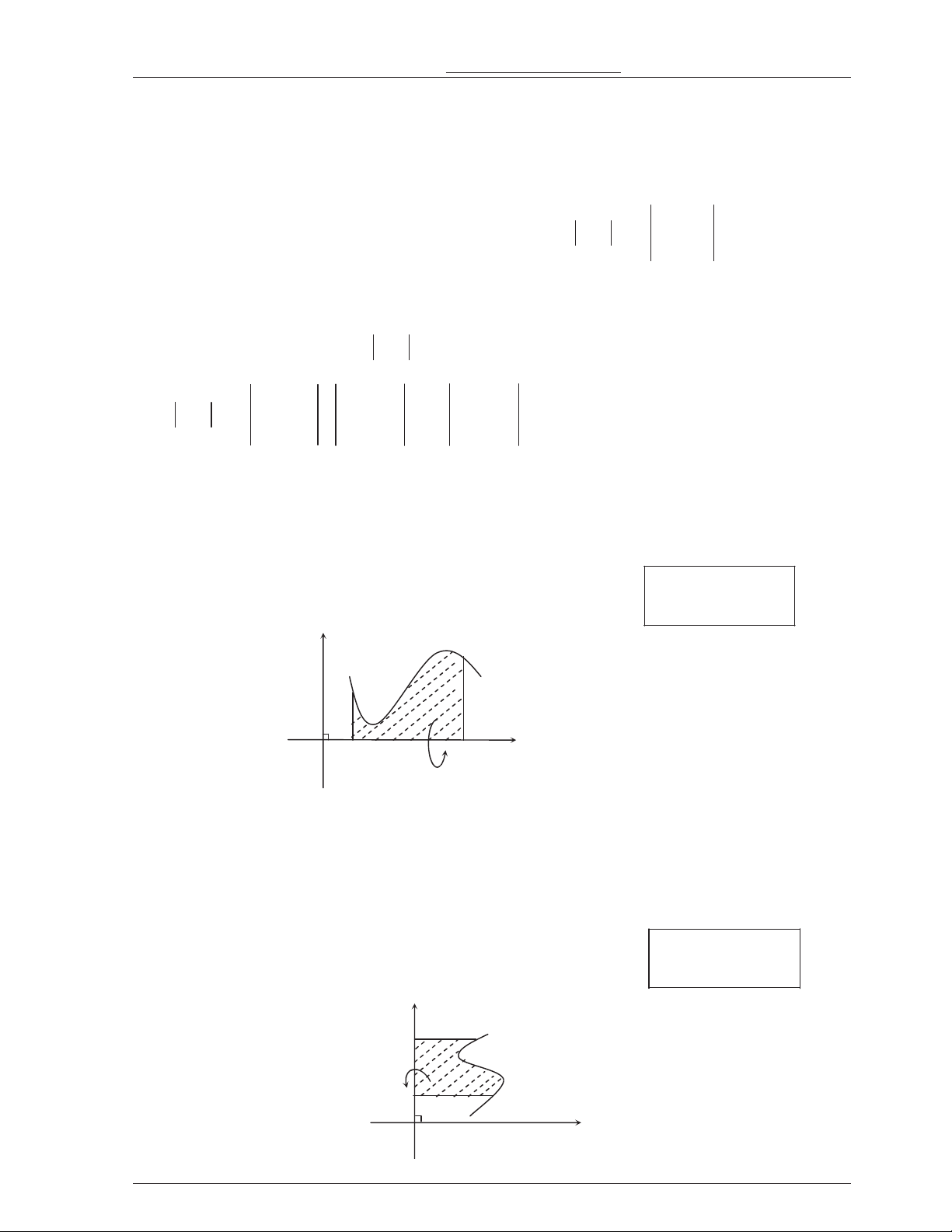
0 g 1: Th! tích c+a v*t th! tròn xoay khi cho hình ph/ng gi#i hn b2i các ng y f x , tr(c Ox b
và hai ng th/ng x a và x b a b quay xung quanh tr(c Ox là: V f x 2 Ox dx . a y x b x a
(C) : y f (x) x a O y 0 b
Chú ý: Hàm s y f x 0 x ; a b
và liên t(c trên on ; a b . D n
0 g 2: Th! tích c+a v*t th! tròn xoay khi cho hình ph/ng gi#i hn b2i các ng x f y , tr(c Oy b
và hai ng th/ng y a và y b a b quay xung quanh tr(c Oy là: V f y 2 Oy dy . a y b y b x 0
(C) : x g(y) a y a x O
Trung tâm luyn thi cht lng cao Thành t – Tây M, Nam T Liêm, Hà Ni Page 40
Thy Nguyn c Thng 0969119789 –thangnd286@gmail.com Tr ng PTLC Vinschool
Chú ý: Hàm s x f y 0 y ; a b
và liên t(c trên on ; a b .
D0ng 3: Cho hai hàm s y f x và y g x liên t(c, cùng d"u trên on ; a b . Hình ph/ng gi#i
hn b2i th c+a các hàm s trên và hai ng th/ng x a và x b a b quay xung quanh b 2 2
tr(c Ox to nên mt khi tròn xoay có th! tích là: V Ox f x g x dx a
D0ng 4: Cho hai hàm s x f y và x gy liên t(c, cùng d"u trên on ; a b . Hình ph/ng
gi#i hn b2i th c+a các hàm s trên và hai ng th/ng y a và y b a b quay xung quanh b 2 2
tr(c Ox to nên mt khi tròn xoay có th! tích là: V Oy f y g y dx a
Tóm l0i khi gi/i toán ta th+=ng g;p các d0ng sau:
y f (x)
1. Th tích ca khi tròn xoay sinh ra khi quay min gi"i hn các )ng sau: y 0 quanh Ox
x ;ax b b mt vòng là : 2 Ox V f x.dx . a
y f (x)
2. Th tích ca khi tròn xoay sinh ra khi quay min gi"i hn các )ng sau: y g(x) quanh Ox
x ;ax b b mt vòng là : 2 V f x 2 Ox
g x.dx . a
x f (y)
3. Th tích ca khi tròn xoay sinh ra khi quay min gi"i hn các )ng sau: x 0 quanh Oy
y ;ay b b mt vòng là : 2 Oy V f y.dy. a
x f (y)
4. Th tích ca khi tròn xoay sinh ra khi quay min gi"i hn các )ng sau: x ( g y) quanh Oy
y ;ay b b mt vòng là : 2 Oy V f y 2
g y.dy . a
Trung tâm luyn thi cht lng cao Thành t – Tây M, Nam T Liêm, Hà Ni Page 41
Thy Nguyn c Thng 0969119789 –thangnd286@gmail.com Tr ng PTLC Vinschool D. S PHC
1. Các &nh nghJa, công th*c, tính ch#t s" ph*c: 1.1. nh ngha s phc
M.i bi!u thc dng a bi , trong ó 2 ,
a b ,i 1 0c gi là mt s" ph*c
i v#i s phc z a bi , ta nói a là phMn th@c, b là phMn /o c+a z .
T*p h0p các s phc kí hi%u là . Chú ý:
M.i s th,c a 0c coi là mt s phc v#i phn o b1ng 0: a a 0i
Nh v*y ta có .
S phc bi v#i b 0c gi là s" thuMn /o ( hoc s" /o)
S 0 0c gi là s v$a th,c v$a o; s i 0c gi là n v& /o. 1.2. S phc b
Hai s phc là b1ng nhau nu phn th,c và phn o t ng ng c+a chúng b1ng nhau: a c
a bi c di bd
1.3. S phc i và s phc liên h%p
Cho s phc z a bi , 2
a,b ,i 1
S phc i c+a z kí hi%u là z và z a bi .
S phc liên h0p c+a z kí hi%u là z và z a bi .
1.4. Bi=u di>n hình h&c ca s phc
i!m M(a; b) trong mt h% tr(c ta vuông góc c+a mt ph/ng 0c gi là iYm biYu diZn
s" ph*c z a bi . 1.5. Môun ca s phc
Gi s s phc z a bi 0c bi!u din b2i M(a; b) trên mt ph/ng ta . dài c+a vect OM
0c gi là môun c(a s" ph*c z và kí hi%u là | z | . 2 2
V*y: | z || OM | hay | z | a b .
Nhn xét: | z || z | | z | .
2. C ng, trI, nhân, chia hai s" ph*c
2.1. Phép c"ng và phép tr*
Phép cng và phép tr$ hai s phc 0c th,c hi%n theo quy tc cng, tr$ hai a thc. Tng quát:
(a bi) (c di) (a c) (b d)i
(a bi) (c di) (a c) (b d)i 2.2. Phép nhân 2
Phép nhân hai s phc 0c th,c hi%n theo quy tc nhân a thc ri thay i 1 trong kt qu nh*n 0c.
Tng quát: (a bi).(c di) (ac bd) (ad bc) . i Chú ý:
Phép cng và phép nhân các s phc có y + các >nh ch"t c+a phép cng và phép nhân các s th,c.
Cho s phc z a bi , 2
a,b ,i 1. Ta có: z z 2a ; 2 .zz | z | .
Trung tâm luyn thi cht lng cao Thành t – Tây M, Nam T Liêm, Hà Ni Page 42
Thy Nguyn c Thng 0969119789 –thangnd286@gmail.com Tr ng PTLC Vinschool
2.3. Phép chia hai s phc c di
V#i a bi 0 , ! >nh th ng a
, ta nhân c t và m;u v#i s phc liên h0p c+a a bi bi
c di (c di)(a bi) ac bd ad bc C( th!: i 2 2 2 2
a bi (a bi)(a bi) . a b a b
2.4. Các tính ch?t cn nh
Cho s phc z a bi , 2
a,b ,i 1
Tính ch?t 1: S phc z là s th,c z z
Tính ch?t 2: S phc z là s o z z
Cho hai s phc 1z 1
a 1b ;i 2z 2 a 2 b ;i 1 a , 1b, 2 a , 2 b ta có:
Tính ch?t 3: 1z 2
z 1z 2z
Tính ch?t 4: 1z. 2
z 1z. 2z z z
Tính ch?t 5: 1 1 ; 2 z 0 2 z 2z
Tính ch?t 6: | 1z. 2
z || 1z | .| 2z | z | z |
Tính ch?t 7: 1 1 ; 2z 0 2 z | 2z |
Tính ch?t 8: | 1z 2
z || 1z | | 2z |
3. COn b-c hai c(a m t s" ph*c
Phng pháp: Cho s phc w = a + bi . Tìm c7n b*c hai c+a s phc này.
+) Nu w = 0 w có mt c7n b*c hai là 0
+) Nu w = a > 0 (a R) w có hai c7n b*c hai là a và - a
+) Nu w = a < 0 (a R) w có hai c7n b*c hai là i a và i a
+) Nu w = a + bi (b 0) 2 2
x y a
Gi s z = x +yi (x, y thuc R) là mt c7n b*c hai c+a w z2 = w (x+yi)2 = a + bi 2xy b
! tìm c7n b*c hai c+a w ta cn gii h% này ! tìm x, y. M.i cp (x, y) nghi%m úng ph ng
trình ó cho ta mt c7n b*c hai c+a w.
Chú ý: Có r"t nhi-u cách ! gii h% này, sau ây là hai cách th ng dùng ! gii.
Cách 1: S d(ng ph ng pháp th: Rút x theo y t$ ph ng trình (2) th vào pt (1) ri bin i
thành ph ng trình trùng ph ng ! gii.
Cách 2: Ta bin i h% nh sau:
x y 2 2 2 2 a 2 2
x y a 2 2
x y a 2 xy 2 2 2 2 2 2 b
x y a b 2xy b 2xy b xy b / 2
Trung tâm luyn thi cht lng cao Thành t – Tây M, Nam T Liêm, Hà Ni Page 43
Thy Nguyn c Thng 0969119789 –thangnd286@gmail.com Tr ng PTLC Vinschool
T$ h% này, ta có th! gii ra x2 và y2 mt cách d dàng, sau ó kt h0p v#i i-u ki%n xy=b/2 ! xem xét x, y cùng d"u
hay trái d"u t$ ó chn 0c nghi%m thích h0p.
Nh*n xét: M.i s phc khác 0 có hai c7n b*c hai là hai s i nhau.
4. Ph+ng trình b-c hai vAi h s" th@c
4.1.Công thc nghim ca phng trình bc hai 2 Xét ph ng trình b*c hai: 2
Az Bz C 0 ( A, B, C là các s th,c, A 0) có B 4AC B
Nu 0 thì ph ng trình có 2 nghi%m th,c phân bi%t z 2A B
Nu 0 thì ph ng trình có nghi%m kép th,c z 2A Nu 2
0 i () thì ph ng trình có 2 nghi%m phc phân bi%t B i z 2A
Chú ý : Khi A, B, C là các s phc B
0 thì ph ng trình có nghi%m kép th,c z 2A B B
0 thì ph ng trình (1) có hai nghi%m phân bi%t z1 = 2A , z2 = 2A
(trong ó là mt c7n b*c hai c+a ). 4.2. Chú ý
Ph ng trình b*c hai trên t*p h0p s phc v#i h% s th,c luôn có 2 nghi%m là 2 s phc liên h0p.
Khi b là s ch6n ta có th! >nh ' và công thc nghi%m t ng t, nh trong t*p h0p s th,c. Gi z , z
1 2 là 2 nghi%m c+a ph ng trình a 2
z bz c 0 (a 0) a, b, c là các s th,c ho7c s b 1 z 2z a phc. Khi ó ta có: c 1z. 2z a
Dng 1. Th'c hin các phép tính trên tp h%p s phc. xác nh phn th'c, phn áo và tính môun ca m"t s phc Ph+ng pháp
S* d'ng các qui t3c cng, tr, nhân, chia s phc tính toán giá tr các biu thc.
xác nh ph0n th&c, ph0n !o và môun ca s phc z thì ta ph!i s* d'ng các khái
nim liên quan n s phc và các phép toán trên tp hp s phc bin ,i s phc
z a bi(a;b )
. Khi ó: z có ph0n th&c b6ng a; ph0n !o b6ng b; z a2 b2
Trong khi tính toán v s phc ta có th s* d'ng các h6ng +ng thc áng nh" nh trong s th&c.
2. Tìm s phc th@a mãn i u kin cho tr c Ph+ng pháp
Nu trong iu kin bài ch có duy nht mt kí hiu z ho#c z thì ta quy v bài toán th&c hin phép :nh.
Nu trong iu kin bài có nhiu h n mt kí hiu z ho#c z ho#c có kí hiu môun ta
gi!i theo ph ng pháp sau: G%i z a bi , a, b .
Trung tâm luyn thi cht lng cao Thành t – Tây M, Nam T Liêm, Hà Ni Page 44
Thy Nguyn c Thng 0969119789 –thangnd286@gmail.com Tr ng PTLC Vinschool
S* d'ng gi! thit bài toán và khái nim v s lp h hai ph ng trình v"i hai /n a,b
Gi!i h ph ng trình lp c trên tp hp s th&c và kt lun.
3. Gii phng trình trên tp h%p s phc
Ph+ng pháp gi/i ph+ng trình a 2
z bz c 0 (a 0) Tính 2 b 4ac
D&a vào giá tr ca xác nh công thc nghim .
4. Bi=u di>n hình h&c s phc. tìm tp h%p i=m bi=u di>n s phc th@a mãn i u kin cho tr c Ph+ng pháp
G%i z x yi (x,y )
R M(x;y) biu di7n cho s phc z trong m#t ph+ng to .
D&a vào d4 kin bài toán, thit lp mi liên h gi4a x và y
D&a vào mi liên h ó, kt lun tp hp im trong m#t ph+ng biu di7n cho s phc z .
5. Tìm s phc có hình bi=u di>n cho tr c Ph+ng pháp
Tìm to im M (ph' thuc tham s) biu di7n cho s phc z trên m#t ph+ng to .
Cho M thuc và hình biu di7n ca z , ta tìm c giá tr ca tham s.
Kt lun s phc z c0n tìm. Chú ý: 2 2 2 2
-Ph ng trình ng tròn: 2 x a
y b R hoc x y 2ax 2by c 0 (trong ó 2 2
a b c 0 2 2
). Ph ng trình hình tròn: 2 x a y b R
- Ph ng trình ng th/ng: ax by c 0, x x0, y y0 2 2 x y 2 2 x y - Ph ng trình ng Elip:
1 . Ph ng trình ng Hypebol: 1 2 2 a b 2 2 a b
- Ph ng trình ng Parabol: 2 2
y ax bx c, x ay by c
6. Tính ch#t liên quan n hình biYu diZn c(a s" ph*c
Ph+ng pháp: ! chng minh các i!m bi!u din cho các s phc tho mãn i-u ki%n (T), thông th ng ta làm nh sau
c to các i!m bi!u din cho các s phc ã cho.
D,a vào i!u ki%n (T), ta qui 0c bài toán v- bài toán hình gii tích trong mt ph/ng. Chú ý: - Nu M , M , z , z , 1
2 M 3 l0n lt biu di7n s phc 1 2 z3 thì: M
2M1 biu di7n s phc 1 z z2 z z
OI (v"i I là trung im M1M 2 ) biu di7n s phc 1
2 . Suy ra: 2OI biu di7n s phc 2 z z M , M 1 z z2 . Do ó, 1 2
0 thì trung im I ca 1 2 trùng v"i O. z z z
OG (v"i G là tr%ng tâm M1M 2M 3 ) biu di7n s phc 1 2
3 . Suy ra: 3OG biu di7n 3 s phc z z z M M M 1 z z2 z3 . Do ó, 1 2 3
0 thì tr%ng tâm G ca tam giác 1 2 3 trùng v"i gc to O.
- Nu z (a bi) R thì im M n6m trên )ng tròn tâm I(a;b) bán kính R. - Nu z z 1 2 R thì dài M M 1 2 R
- Nu z k , s phc z tho! mãn z (a bi) R . Khi ó, im biu di7n s phc . z 0z n6m trên 0
)ng tròn I(a;b) bán kính k.R.
Trung tâm luyn thi cht lng cao Thành t – Tây M, Nam T Liêm, Hà Ni Page 45
Thy Nguyn c Thng 0969119789 –thangnd286@gmail.com Tr ng PTLC Vinschool
7. C'c tr ca s phc
Ph+ng pháp : Các bài toán qui v- bài toán tìm giá tr l#n nh"t, giá tr nh3 nh"t c+a hàm mt bin,
tìm giá tr l#n nh"t, giá tr nh3 nh"t c+a mt bi!u thc hai bin mà các bin tho mãn i-u ki%n cho tr #c
Bài toán: Trong các s phc z tho mãn i-u ki%n T. Tìm s phc z ! bi!u thc P t giá tr nh3 nh"t, l#n nh"t
T$ i-u ki%n T, bin i ! tìm cách rút 5n ri th vào bi!u thc P ! 0c hàm mt bin
Tìm giá tr l#n nh"t (hoc nh3 nh"t) tu< theo yêu cu bài toán c+a hàm s mt bin v$a tìm 0c.
S d(ng các b"t /ng thc c bn nh : B"t /ng thc liên h% gia trung bình cng và trung
bình nhân, b"t /ng thc Bunhia- Cpxki, b"t /ng thc hình hc.
B"t /ng thc liên quan n s phc:
*) 1z 2z 1z 2z *)
z z z z 1
z 2z 1z 2z *) 1 2 1 2
Chú ý: B#t Vng th*c th+=ng g;p:
a a ... a
1. B"t /ng thc Côsi: Cho a ,1 ,.. a 0 n n
a .a .. a 1 2 n , 1 2 1 2 n n D"u “=” xy ra khi
a a ...a 1 2 n 2 2 2 2 2 2 2
2. B"t /ng thc Bunhiacopski: a b a b ...a b
a a ... a
b b ... b 1 1 2 2 n n 1 2 2 1 2 n a a a D"u “=” xy ra khi: 1 2 ... n b b b 1 2 n 2 2
3. B"t /ng thc Mincopski:
a a b b 2a 2b 2a 2b 1 2 1 2 1 1 2 2 D"u “=” khi a b 1 1 0 a b 2 2
4. B"t /ng thc tam giác: Cho tam giác ABC, khi ó: AB BC AC AB BC
Trung tâm luyn thi cht lng cao Thành t – Tây M, Nam T Liêm, Hà Ni Page 46 Thy Nguyn c Thng
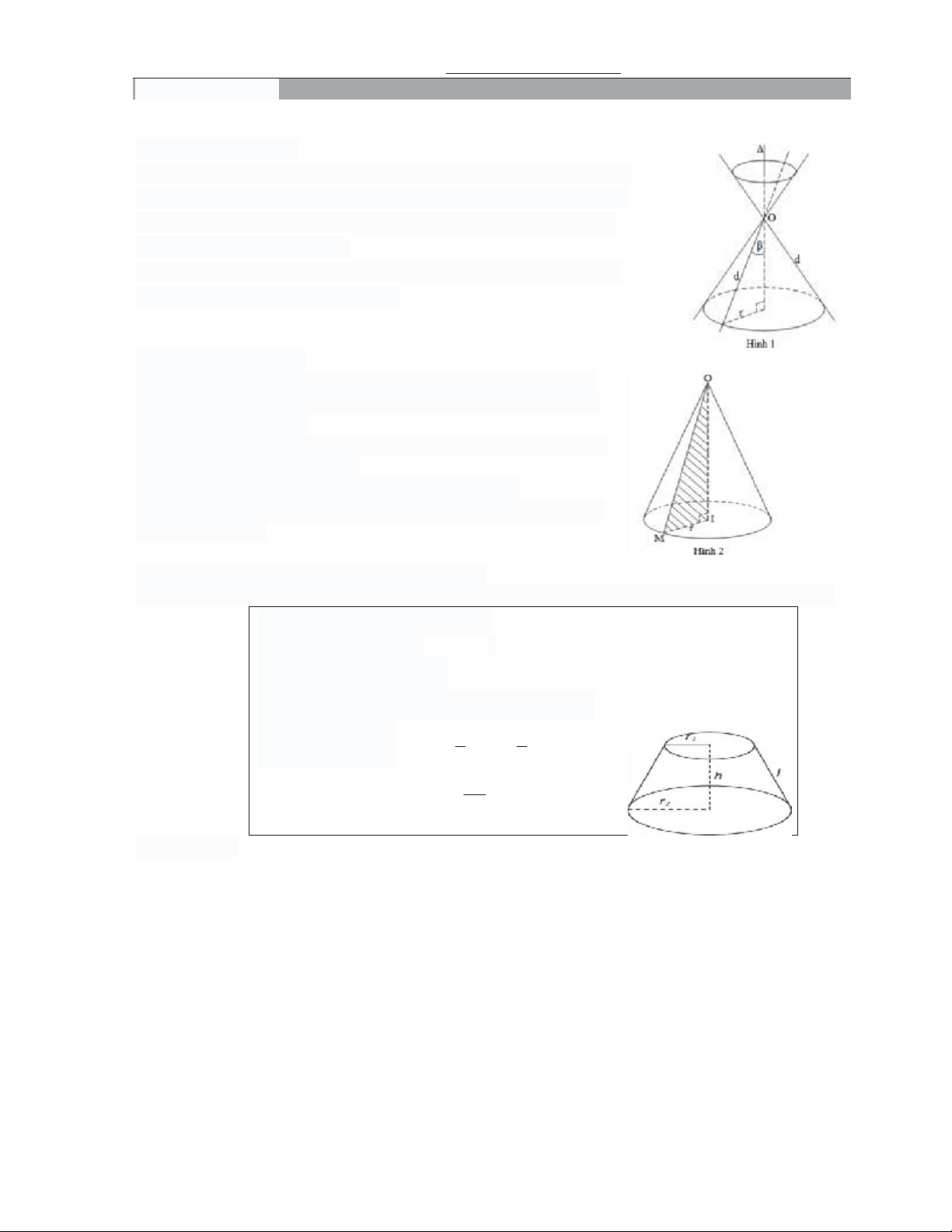
0969119789 –thangnd286@gmail.com Tr ng PTLC Vinschool E. NÓN – TR - CU 1. MUT NÓN – HÌNH NÓN 1.1 M;t nón tròn xoay
Trong mt ph/ng (P), cho 2 ng th/ng d, 4 ct nhau ti O và chúng
to thành góc B v#i 0 < B < 900. Hình tròn xoay to ra khi quay ng
th/ng d xung quanh tr(c 4 v#i góc B không thay i 0c gi là mt
nón tròn xoay &nh O (hình 1).
ng th/ng 4 gi là tr(c, ng th/ng d 0c gi là ng sinh và
góc 2B gi là góc 2 &nh c+a mt nón. 1.2. Hình nón tròn xoay
Cho 4OIM vuông ti I . Hình tròn xoay to ra khi quay ng g"p
khúc OMI quanh cnh góc vuông OI gi là hình nón tròn xoay (gi tt là hình nón) (hình 2).
+ ng th/ng OI gi là tr(c, O là &nh, OI gi là ng cao và OM gi là ng sinh c+a hình nón.
+ Hình tròn tâm I, bán kính r = IM là áy c+a hình nón.
Khi nón tròn xoay là hình to b2i mi-n tam giác OMI quay quanh cnh góc vuông OI
1.3. Công th*c din tích và thY tích c(a hình nón
Cho hình nón có chi-u cao là h, bán kính áy r và ng sinh là ?. Hc sinh cn nh# các công thc: 2 2 2
+ Mi liên h% h, r, ?: h r
+ Di%n tích xung quanh: Sxq=@.r.?
+ Di%n tích áy (hình tròn): ñ S .r2
+ Di%n tích toàn phn hình tròn: t S p S ñ Sxq 1 1 2 + Th! tích khi nón: V .h r h noùn 3 ñ S 3 h + 2 2
Th! tích khi nón c(t: V
R r .Rr 3 1.4. Tính ch#t:
* Nu ct mt nón tròn xoay b2i mt ph/ng i qua Bnh thì có các tr ng h0p sau xy ra:
+ Mt ph/ng ct mt nón theo 2 ng sinh ⇒ Thit di%n là tam giác cân.
+ Mt ph/ng Ap xúc v#i mt nón theo mt ng sinh. Trong tr ng
h0p này, ng i ta gi ó là mt ph/ng Ap di%n c+a mt nón.
* Nu ct mt nón tròn xoay b2i mt ph/ng không i qua Bnh thì có các tr ng h0p sau xy ra:
+ Nu mt ph/ng ct vuông góc v#i tr(c hình nón ⇒ giao tuyn là mt ng tròn.
+ Nu mt ph/ng ct song song v#i 2 ng sinh hình nón ⇒ giao tuyn là 2 nhánh c+a 1 hypebol.
+ Nu mt ph/ng ct song song v#i 1 ng sinh hình nón ⇒ giao tuyn là
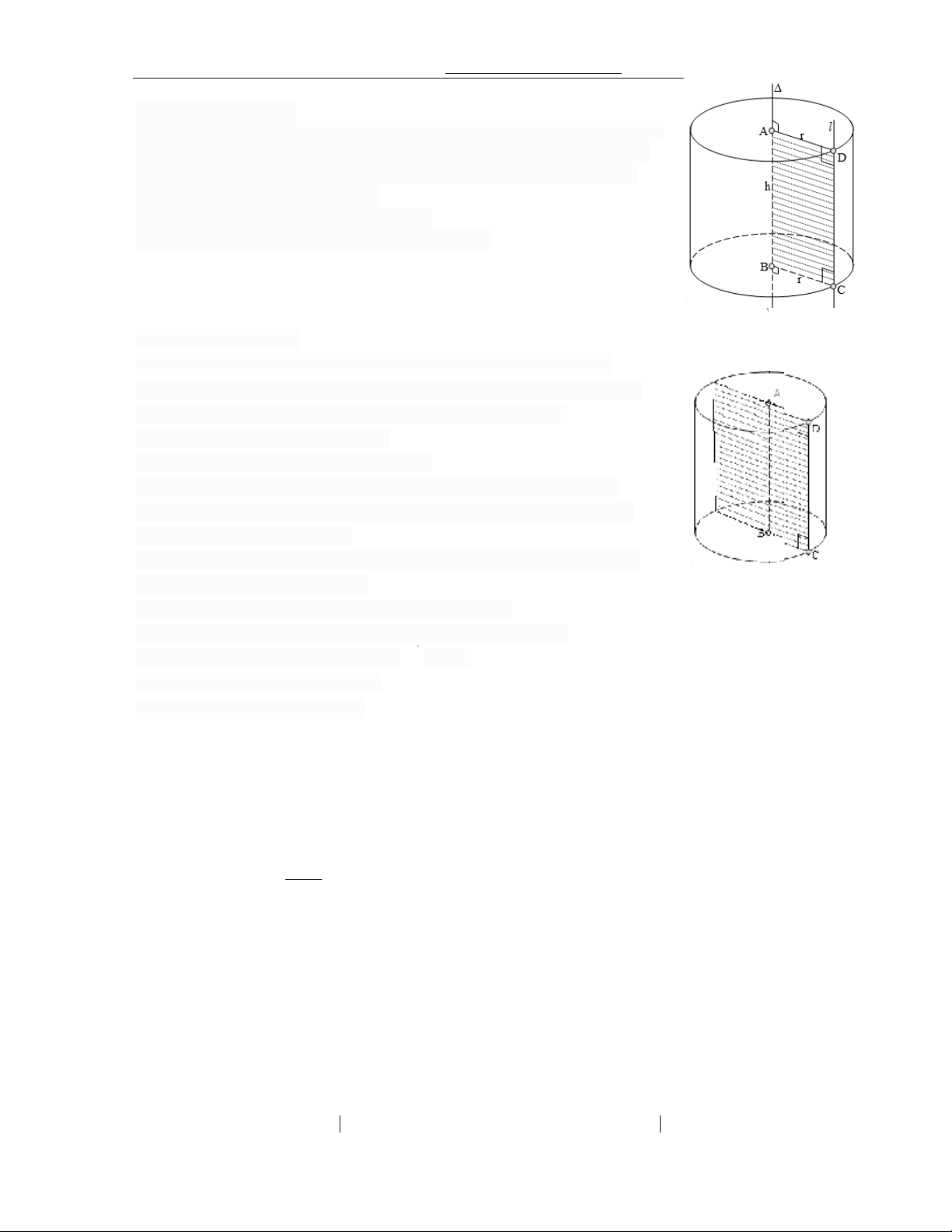
Thy Nguyn c Thng 0969119789 –thangnd286@gmail.com Tr ng PTLC Vinschool 2. HÌNH TR - KHI TR 2.1. M;t tr. tròn xoay
+ Trong mp(P) cho hai ng th/ng 4 và ? song song nhau, cách nhau mt
khong r. Khi quay mp(P) quanh tr(c c nh 4 thì ng th/ng ? sinh ra
mt mt tròn xoay 0c gi là mt tr( tròn xoay hay gi tt là mt tr(. + ng th/ng 4 0c gi là tr(c.
+ ng th/ng ? 0c gi là ng sinh.
+ Khong cách r 0c gi là bán kính c+a mt tr(. 2.2. Hình tr. tròn xoay
+ Khi quay hình ch nh*t ABCD xung quanh ng th/ng cha mt
cnh, ch/ng hn cnh AB thì ng g"p khúcABCD to thành mt hình,
hình ó 0c gi là hình tr( tròn xoay hay gi tt là hình tr(. + ng th/ng AB 0c gi là tr(c.
+ on th/ng CD 0c gi là ng sinh.
+ dài on th/ng AB = CD = h 0c g
gi là chi-u cao c+a hình tr(.
+ Hình tròn tâm A, bán kính r = AD và h hììn
nh tròn tâm B, bán kính r = BC
0c gi là 2 áy c+a hình tr(.
+ Khi tr( tròn xoay, gi tt là khi tr(, là phn không gian gi#i hn b2i
hình tr( tròn xoay k! c hình tr(.
2.3. Công th*c tính din tích và thY tích c(a hình tr.
Cho hình tr( có chi-u cao là h và bán kính áy b1ng r, khi ó:
+ Di%n tích xung quanh c+a hình tr(: Sxq = 2@rh
+ Di%n tích toàn phn c+a hình tr(: Stp=S =Sxq+S=2@rh+2@r2
+ Th! tích khi tr(: V = Bh = @r2h . 2.4. Tính ch#t
Nu ct mt tr( tròn xoay (có bán kính là r ) b2i mt mpvuông góc v#i tr(c thì ta 0c
ng tròn có tâm trên và có bán kính b1ng r v#i r c:ng chính là bán kính c+a mt tr( ó.
Nu ct mt tr( tròn xoay (có bán kính là r ) b2i mt mpkhông vuông góc v#i tr(c
nh ng ct t"t c các ng sinh, ta 0c giao tuyn là mt ng elíp có tr( nh3 b1ng 2r và 2r 0 0 tr(c l#n b1ng mp 0 90
sin , trong ó là góc gia tr(c và v#i .
Cho mpsong song v#i tr(c c+a mt tr( tròn xoay và cáchmt khong k .
Nu k r thì mp ct mt tr( theo hai ng sinh thit di%n là hình ch nh*t.
Nu k r thì mp Ap xúc v#i mt tr( theo mt ng sinh.
Nu k r thì mp không ct mt tr(. 3. MUT CU – KHI CU 3.1. M;t cMu – Kh"i cMu: &nh nghJa M;t cMu: S(O; R) M OM R Kh"i cMu: V(O;R) M OM R Thy Nguyn c Thng
0969119789 –thangnd286@gmail.com Tr ng PTLC Vinschool
3.2.V& trí t+ng "i c(a m t iYm "i vAi m;t cMu Cho mt cu S ;R
O và mt i!m A b"t kì, khi ó:
NuOA R AS ;
O R. Khi óOAgi là bán kính mt cu. Nu OA B
và OB là hai bán kính sao cho OA O
B thì on th/ng AB gi là 1 ng kính c+a mt cu. O
NuOA R A n1m trong mt cu. A A
NuOA R A n1m ngoài mt cu. Khi cu S ;R
O là t*p h0p t"t c các i!m M sao choOM R. A
3.3. V& trí t+ng "i c(a m;t phVng và m;t cMu
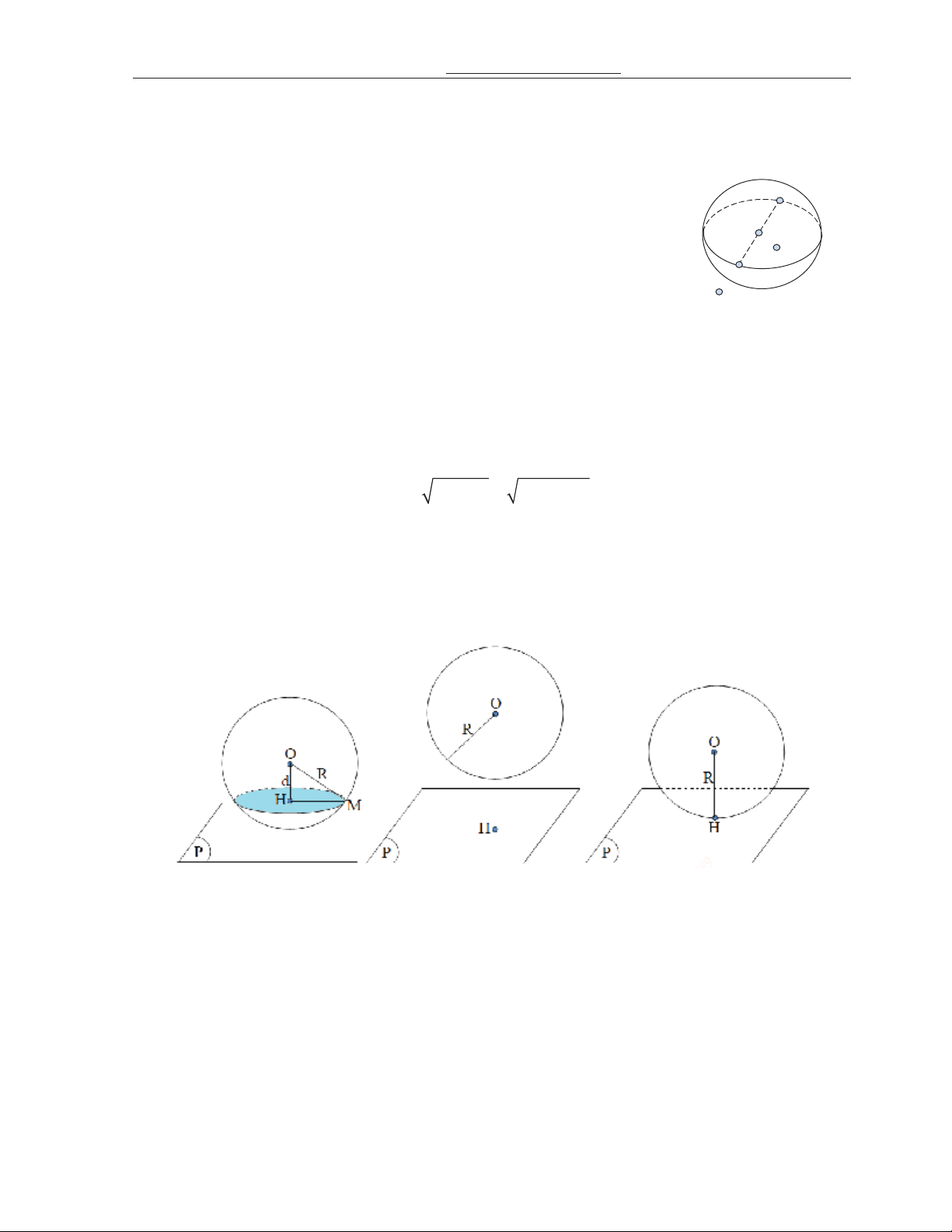
Cho mt cu S O;R và mt mpP . Gi d là khong cách t$ tâmO c+a mt cu n mpP và H là
hình chiu c+a O trên mpP d OH .
Nu d R mpPct mt cu SO;R theo giao tuyn là ng tròn n1m trên mpPcó 2 2
tâm là H và bán kính r HM R2 d2 R OH (hình a).
Nu d R mpPkhông ct mt cu SO;R (hình b)
Nu d R mpPcó mt i!m chung duy nh"t. Lúc này, ta gi mt cu SO;R Ap xúc
mpP. Do ó, i-u ki%n cn và + !mpPAp xúc v#i mt cu SO;R là
d O,mpP R (hình c). d d = Hình a Hình b Hình c
3.4. V& trí t+ng "i c(a +=ng thVng và m;t cMu Cho mt cu S ;R
O và mt ng th/ng . Gi H là hình chiu c+aOtrên ng th/ngvà
d OH là khong cách t$ tâmOc+a mt cu n ng th/ng . Khi ó:
Nu d R không ct mt cu S ;R O .
Nu d R ct mt cu S ;R
O ti hai i!m phân bi%t.
Thy Nguyn c Thng 0969119789 –thangnd286@gmail.com Tr ng PTLC Vinschool
Nu d R và mt cu Ap xúc nhau (ti mt i!m duy nh"t). Do ó: i-u ki%n cn và
+ ! ng th/ng Ap xúc v#i mt cu là d d O, R .
&nh lí: Nu i!m A n1m ngoài mt cu S ;R O thì:
Qua A có vô s Ap tuyn v#i mt cu S ;R O .
dài on th/ng ni A v#i các Ap i!m -u b1ng nhau.
T*p h0p các i!m này là mt ng tròn n1m trên mt cu S ;R O .
3.5. M;t cMu ngo0i [p kh"i a din M;t cMu ngo0i tip Hình a din
T"t c các &nh c+a hình a di%n -u n1m trên mt cu Hình tr.
Hai ng tròn áy c+a hình tr( n1m trên mt cu Hình nón
Mt cu i qua &nh và ng tròn áy c+a hình nón a/ Các khái nim c b/n
Tr.c c(a a giác áy: là ng th/ng i qua tâm ng tròn ngoi Ap c+a a giác áy và
vuông góc v#i mt ph/ng cha a giác áy.
B"t kì mt i!m nào n1m trên tr(c c+a a giác thì cách -u các &nh c+a a giác ó.
+=ng trung tr@c c(a o0n thVng: là ng th/ng i qua trung i!m c+a on th/ng và vuông góc v#i on th/ng ó.
B"t kì mt i!m nào n1m trên ng trung tr,c thì cách -u hai u mút c+a on th/ng.
M;t trung tr@c c(a o0n thVng: là mt ph/ng i qua trung i!m c+a on th/ng và vuông góc v#i on th/ng ó.
B"t kì mt i!m nào n1m trên mt trung tr,c thì cách -u hai u mút c+a on th/ng.
b/ Tâm và bán kính m;t cMu ngo0i [p hình chóp
Tâm m;t cMu ngo0i [p hình chóp: là i!m cách -u các &nh c+a hình chóp. Hay nói cách
khác, nó chính là giao i!m I c+a tr(c )ng tròn ngoi ;p m#t ph+ng áy và m#t ph+ng
trung tr&c ca mt cnh bên hình chóp.
Bán kính: là khong cách t$ I n các &nh c+a hình chóp.
c/ Cách xác &nh tâm và bán kính m;t cMu c(a m t s" hình a din c b/n
Cách 1: Nu (n – 2) &nh c+a a di%n nhìn hai &nh còn li d #i mt góc vuông thì tâm c+a
mt cu là trung i!m c+a on th/ng ni hai &nh ó.
Cách 2: ! xác nh tâm c+a mt cu ngoi tip hình chóp.
– Xác nh tr(c c+a áy ( là ng th/ng vuông góc v#i áy ti tâm
ng tròn ngoi tip a giác áy).
– Xác nh mt ph/ng trung tr,c (P) c+a mt cnh bên.
– Giao i!m c+a (P) và là tâm c+a mt cu ngoi tip hình chóp.
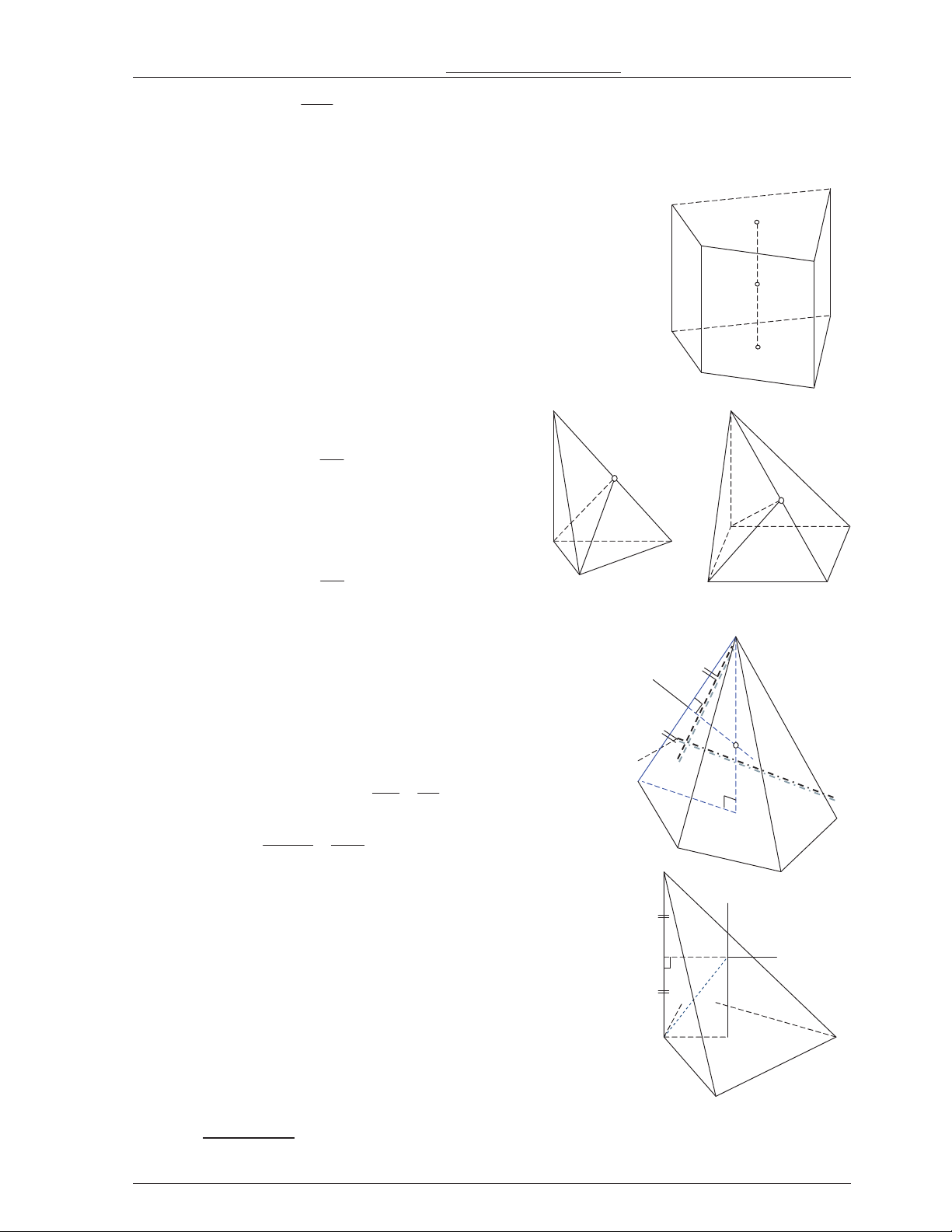
D0ng 1: Hình h p ch\ nh-t, hình l-p ph+ng.
Tâm: trùng v#i tâm i xng c+a hình hp ch A B A nh*t (hình l*p ph ng). D C
Tâm là I , là trung i!m c+a AC' . I A I
Bán kính: b1ng na dài ng chéo hình hp B’ ch nh*t (hình l*p ph ng). D C’ C’
Trung tâm luyn thi cht lng cao Thành t – Tây M, Nam T Liêm, Hà Ni Page 50
Thy Nguyn c Thng 0969119789 –thangnd286@gmail.com Tr ng PTLC Vinschool AC '
Bán kính: R 2 .
D0ng 2: Hình lOng tr. *ng có áy n i [p +=ng tròn. Xét hình l7ng tr( ng ' ' ' ' 1 A 2 A 3 A ...A . 1 A 2 A 3 A ... n n A , trong ó có 2 áy A O O' n 1 A 2 A 3 A ... n A và ' ' ' ' 1 A 2 A 3 A ... n
A ni Ap ng tròn và . Lúc A1 ó, O A2
mt cu ni Ap hình l7ng tr( ng có: A3
Tâm: I v#i I là trung i!m c+aOO'. I Bán kính: ' R 1 IA 2 IA ... n IA . A’n A’1
D0ng 3: Hình chóp có các Bnh nhìn o0n thVng n"i 2 Bnh còn l0i O A’ d+Ai 1 góc vuông. 2 A’3 0 Hình chóp .
S ABC có SAC SBC 90 . S S
+ Tâm: I là trung i!m c+a SC . SC + Bán kính: R
IA IB IC 2 . I
Hình chóp S.ABCD có I 0
SAC SBC SDC 90 . A A C
+ Tâm: I là trung i!m c+a SC . SC + Bán kính: R
IA IB IC ID 2 . B B C D0ng 4: Hình chóp %u.
Cho hình chóp -u S.ABC... S
Gi O là tâm c+a áy SO là tr(c c+a áy.
Trong mt ph/ng xác nh b2i SO và mt cnh bên, M
ch/ng hn nh mpSAO , ta vC ng trung tr,c c+a cnh SA
là ct SA ti M và ct SO ti I I là tâm c+a mt cu. I Bán kính: A SM SI
Ta có: SMI SOA Bán kính là: O D SO SA B 2 SM.SA SA R IS
IA IB IC ... C SO 2SO S
D0ng 5: Hình chóp có c0nh bên vuông góc vAi m;t phVng áy.
Cho hình chóp S.ABC...có cnh bên SA áy ABC...và áy ABC... d
ni Ap 0c trong ng tròn tâm O . Tâm và bán kính mt cu
ngoi Ap hình chóp S.ABC... 0c xác nh nh sau: M I
T$ tâm O ngoi Ap c+a ng tròn áy, ta vC ng th/ng
d vuông góc v#i mpABC ... tiO .
Trong mpd,SA , ta d,ng ng trung tr,c c+a cnh SA A O C
, ct SA ti M , ct d ti I .
I là tâm mt cu ngoi Ap hình chóp
và bán kính R IA IB IC IS ... B Tìm bán kính:
Trung tâm luyn thi cht lng cao Thành t – Tây M, Nam T Liêm, Hà Ni Page 51
Thy Nguyn c Thng 0969119789 –thangnd286@gmail.com Tr ng PTLC Vinschool 2 2 2 2 SA
Ta có: MIOB là hình ch nh*t.Xét MAI vuông ti M có: R AI MI MA AO 2 .
D0ng 6: Hình chóp khác. D,ng tr(c c+a áy.
D,ng mt ph/ng trung tr,c c+a mt cnh bên b"t kì.
I I là tâm mt cu ngoi Ap hình chóp.
Bán kính: khong cách t$ I n các &nh c+a hình chóp. Chú ý:
- i-u ki%n ! mt hình chóp ni tip mt cu là áy ni tip mt ng tròn
- ng tròn ngoi Ap mt s a giác th ng gp. Khi xác nh tâm mt cu, ta cn xác nh tr(c
c+a mt ph/ng áy, ó chính là ng th/ng vuông góc v#i mt ph/ng áy ti tâm O c+a ng
tròn ngoi Ap áy. Do ó, vi%c xác nh tâm ngoi O là yu t r"t quan trng c+a bài toán. O O O Hình vuông: O là giao i!m 2 Hình ch nh*t: O là giao i!m D -u: O là giao i!m c+a 2 ng ng chéo. c+a hai ng chéo. trung tuyn (trng tâm). O O D vuông: O là trung i!m c+a
D th ng: O là giao i!m c+a hai cnh huy-n. ng trung tr,c c+a hai cnh D.
- Hình chóp có các cnh bên -u b1ng nhau luôn ni tip mt mt cu.
- Các &nh c+a mt hình a di%n luôn nhìn mt on th/ng mt góc vuông thì hình a di%n ó ni
tip mt cu, có tâm là trung i!m on th/ng.
3.6. Din ]ch và thY ]ch m;t cMu 2 * Di%n >ch mt cu: 4 C S R . 4 * Th! >ch mt cu: 3 C V R . 3
Trung tâm luyn thi cht lng cao Thành t – Tây M, Nam T Liêm, Hà Ni Page 52 Thy Nguyn c Thng
0969119789 –thangnd286@gmail.com Tr ng PTLC Vinschool 3.6. M;t cMu n i tip M;t cMu n i tip Hình a din
T"t c các mt c+a hình a di%n -u tip xúc v#i mt cu Hình tr.
Mt cu tip xúc v#i các mt áy và mi ng sinh c+a hình tr( Hình nón
Mt cu tip xúc v#i mt áy và mi ng sinh c+a hình nón
a) nh ngha 1: mt ph/ng phân giác c+a mt góc là mt ph/ng qua gc và mi i-m n1m trên mt
ph/ng -u cách -u 2 tia c+a góc.
T ng t, ta c:ng nh ngh9a mt ph/ng phân giác c+a mt góc nh di%n là t*p h0p t"t c các i!m
trong không gian sao cho khong cách t$ i!m ó n m.i mt ph/ng c+a nh di%n là nh nhau.
b) nh ngha 2: Mt cu ni tip a di%n là mt cu tip xúc t"t c các mt c+a a di%n. Khi ó ta
c:ng nói a di%n ngoi tip mt cu. Chú ý:
T"t c các t di%n và t"t c các a di%n -u -u có mt cu ni tip và v#i a di%n -u thì
tâm c+a mt cu ni tip trùng v#i tâm c+a mt cu ngoi tip.
Mt l7ng tr( có mt cu ni tip khi và ch& khi l7ng tr( ó là l7ng tr( ng có mt áy là a
giác ngoi tip 0c ng tròn và có chi-u cao b1ng 2 ln bán kính ng tròn ni tip a giác áy.
Nu chân ng ng cao c+a hình chóp cách -u các cnh trong mt áy thì hình chóp có mt cu ni tip.
Nu hình chóp có các mt bên to v#i áy các góc b1ng nhau thì hình chóp có mt cu ni tip.
c) Cách xác &nh tâm và bán kính m;t cMu n i tip m t hình chóp * Xác &nh tâm:
- D,ng 3 mt ph/ng phân giác c+a góc to b2i hai mt ph/ng (Mt ph/ng cha ng phân giác c+a
mt góc n1m trong mt ph/ng vuông góc v#i giao tuyn c+a hai mt ó)
- Tìm i!m chung c+a 3 giao tuyn ( ba giao tuyên không song song) c+a ba mt ph/ng phân giác.
Suy ra, tâm mt cu ngoi tip hình chóp
c bit: Nu H là chân ng cao c+a hình chóp và cách -u các mt bên. Gi I là hình chiu c+a S
xung 1 cnh áy. Ta d,ng ng phân giác c+a góc SIH ct SH ti tâm mt cu ni tip hình chóp. * Xác &nh bán kính
Cách 1: Bán kính mt cu ni tip a di%n 0c tính theo công 3V thc r n
Trong ó Si là di%n là di%n tích c+a mt th i c+a iS i 1 a di%n.
Cách 2: S d(ng h% thc phân giác:
AD là phân giác trong c+a tam giác ABC. Khi ó BD BA CD CA
Thy Nguyn c Thng 0969119789 –thangnd286@gmail.com Tr ng PTLC Vinschool
F. PHNG PHÁP TO TRONG KHÔNG GIAN OXYZ I. HA TRCC TOD E
1. ng d.ng tích có h+Ang
a cùng ph ng b a,b 0
a b a.b 0
u,v, w không ng ph/ng u,v.w 0 ( ) .
u,v, w ng ph/ng u,v.w 0 ( )
(ba véc t có giá song song hoc n1m trên mt mt ph/ng).
A, B, C không th/ng hàng(3 &nh c+a mt tam giác) AB, AC 0 .
A, B, C th/ng hàng AB, AC 0 .
Bn i!m A, B, C, D ng ph/ng AB, AC.AD 0 ( ) (bn i!m n1m trên mt mt ph/ng).
Bn i!m A, B, C, D không ng ph/ng AB, AC.AD 0 ( ) (bn &nh c+a mt t di%n).
Di%n tích hình bình hành: S A , B AD ( ) ABCD 1 2 2
Di%n tích tam giác: S
AB, AC ( ) S
AB .AC A . B AC ABC 2 ; ABC 2 Th! tích khi hp: ' V
AB, AD.AA ( ) ' ' ' ' ABCD.A B C D
1 Th! tích t di%n: V
AB, AC.AD ( ) ABCD 6
2. Cho A(x ; y ; z ), B(x ; y ; z ) A A A B B B
AB (x x ; y y ;z z ) B A B A B A 2 2 2
AB (x x ) (y y ) (z z ) B A B A B A x x
y y z z
To trung i!m M c+a on th/ng AB: A B M ; A B ; A B 2 2 2
x x x
y y y z z z
To trng tâm G c+a tam giác ABC: A B C G ; A B C ; A B C 3 3 3
To trng tâm G c+a t di%n ABCD:
xA xB C
x xD y y y y z z z z G ; A B C D ; A B C C 4 4 4
ABCD là hình bình hành AB DC
Cho ABC có các chân E, F c+a các ng phân giác trong và ngoài c+a góc A c+a ABC trên AB BC. Ta có: FB .FC AC
Trung tâm luyn thi cht lng cao Thành t – Tây M, Nam T Liêm, Hà Ni Page 54
Thy Nguyn c Thng 0969119789 –thangnd286@gmail.com Tr ng PTLC Vinschool
Nu M chia on AB theo t& s k ( MA kMB ) thì ta có : xA kxB y ky z kz x ; A B y ; A B M z 1 M V#i k E 1 k 1 M k 1 k
Cho i!m M(a;b;c). Hình chiu c+a M lên Ox, Oy,Oz, (Oxy), (Oyz), (Oxz) ln l0t là: 1 M ;0 a ;0 , M2 0;b;0, 3
M 0;0;c, M4 ;ab;0, 5 M 0;b;c, 6 M a;0;c
Cho i!m M(a;b;c). i!m i xng v#i i!m M qua Ox, Oy,Oz, (Oxy),(Oyz), (Oxz) ln l0t là: 7
M ;a ;bc , 8
M ;a ;bc , 9
M ;ab;c , 10 M ;b a ; c , 11 M ;b a ;c, 12
M a; ;bc
Cho i!m M(a;b;c). i!m i xng v#i M qua O là 13
M ;a ;b c .
i!m thuc tr(c Ox, Oy, Oz ln l 0t có to : x0;0;0,0; 0
y ;0,0;0; 0z. i!m thuc
mt ph/ng (Oxy), (Oyz), (Oxz) l 0t có to là : x0;y ;0,0; 0
y ; 0z ,x0;0; o 0 z .
II. PH23NG TRÌNH MFT CGU
- M"t s v?n tr&ng tâm 2 2 2
1. Phng trình mt cu: Mt cu có tâm I(a; b; c) và bán kính R : x a y b z c R2
Ph ng trình mt cu dng khai tri!n:x2 +y2 +z2 – 2ax – 2by – 2cz + d = 0, k: a2 + b2 + c2 – d > 0 (2)
Tâm I(a; b; c) và bán kính R= a2 b2 2 c d 2. Chú ý: 2 2 2
Mt cu có tâm I và qua A thì R = IA =
xA xI yA yI zA Iz 1
Mt cu có ng kính AB thì R = AB 2 và tâm I là trung i!m AB
Mt cu qua 4 i!m A, B,C, D thì vit ph ng trình mt cu 2 dng (2) ri thay ta t$ng
i!m vào ph ng trình và gii h% ! tìm a, b, c, d. (Hoc )
3. V trí tng i ca i=m v i mt cu: 2 2 2 Cho (S) : x a y b z c 2
R và i!m M(x I a b c 0; y0; 0
z ) , Gi ( ; ; ) là tâm mc(S), R là bán kính c+a mt cu.
IM > R i!m M n1m ngoài mt cu (S)
IM < R i!m M n1m trong mt cu (S)
IM = R i!m M thuc mt cu (S) (Hay Thay ta i!m M vào PT mt cu th3a mãn)
4. V trí t ng i gi4a hai m#t c0u:
Cho hai m#t c0u S1(I1, R1) và S2(I2, R2). 1II2 1 R 2 R
(S1), (S2) trong nhau 1II2 1 R 2
R (S1), (S2) ngoài nhau 1II2 1 R 2 R
(S1), (S2) tip xúc trong 1II2 1 R 2
R (S1), (S2) tip xúc ngoài 1 R 2 R 1II2 1 R 2
R (S1), (S2) c3t nhau theo mt )ng tròn.
5. V& trí t+ng "i gi\a m;t phVng và m;t cMu
Trung tâm luyn thi cht lng cao Thành t – Tây M, Nam T Liêm, Hà Ni Page 55
Thy Nguyn c Thng 0969119789 –thangnd286@gmail.com Tr ng PTLC Vinschool 2 2 2
Cho mt ph/ng. và mt cu . 2 x a y b
z c R (S) có tâm I ; a ;
b c, ábn kính R . Gi . . .
A a B.b C.c D d d I; . 2 2 2
A B C
+ Nu d R và (S) không giao nhau.
+ Nu d R và (S) tip xúc nhau ti mt i!m H. ( gi là tip di%n c+a mt cu (S)).
+ Nu d R và (S) ct nhau theo giao tuyn là mt ng tròn (C) có bán kính 2 2
r R d và có tâm H là hình chiu vuông góc c+a I trên .
Lu ý: ! tìm ta tâm H c+a ng tròn (C) ta làm nh sau
- L*p ph ng trình ng th/ng i qua I và vuông góc v#i .
- Ta i!m H là nghi%m c+a h% gm ph ng trình c+a và ph ng trình .
6. V& trí t+ng "i gi\a +=ng thVng và m;t cMu
x x0 at 2 2 2
Cho ng th/ng th/ng : y y 2
0 bt và mt cu (S): x a y b z c R z 0 z ct , u M I
Gi d d I, 0 , trong ó M
u (a;b;c) là VTCP c+a u 0(x0; y ; 0 0 z ) ,
+ Nu d R và (S) không có i!m chung
+ Nu d R tip xúc v#i (S) ( là tip tuyn c+a mt cu (S))
+ Nu d R ct (S) tai hai i!m A, B ( gi là cát tuyn c+a mt cu (S)).
III. PH23NG TRÌNH MFT PHHNG
1. Mt ph/ng i qua i!m M (x0; y0; 0 z ) o
và có VTPT n ; A ;
B C có ph ng trình
A(x x ) B 0
(y y ) C(z z 0 0 ) 0 Chú ý:
Véc t n 0 vuông góc v#i mt ph/ng 0c gi là VTPT c+a mt ph/ng .
Véc t u 0 có giá song song hoc n1m trên mt ph/ng 0c gi là VTCP c+a mt ph/ng .
Nu u, v là hai véc t không cùng ph ng có giá song song hoc n1m trên mt ph/ng thì
u,v n
là mt VTPT c+a mt ph/ng .
Nu ba i!m A, B, C không th/ng hàng thì AB, AC n
là mt VTPT c+a mt ph/ng (ABC). Các tr)ng hp riêng
Trung tâm luyn thi cht lng cao Thành t – Tây M, Nam T Liêm, Hà Ni Page 56
Thy Nguyn c Thng 0969119789 –thangnd286@gmail.com Tr ng PTLC Vinschool Các h s"
Ph+ng trình m;t phVng ()
Tính ch#t m;t phVng () D = 0
Ax By Cz 0 () i qua gc to O A = 0
By Cz D 0 () // Ox hoc () Ox B = 0
Ax Cz D 0 () // Oy hoc () Oy C = 0
Ax By D 0 () // Oz hoc () Oz A = B = 0 Cz D 0
() // (Oxy) hoc () (Oxy)
+Nu trong ph ng trình ca () không cha /n nào thì () song song ho#c cha tr'c t ng ng. x y z
+ Ph ng trình m#t ph+ng theo on ch3n: 1 a b c
. () c3t các tr'c to ti các im (a; 0; 0), (0; b; 0), (0; 0; c)
2. V& trí t+ng "i gi\a hai m;t phVng
Cho : Ax By Cz D 0 và ' ' ' '
: A x B y C z D 0 khi ó: n n n n * , ' 0 . * , ' 0 , n MM' 0 , n MM' 0
* , ct nhau n,n' 0
Tr)ng hp #c bit: A'.B'.C'.D' 0 n kn A B C D + ' ' ' ' ' ' D kD A B C D n kn A B C D + ' ' ' ' ' ' D kD A B C D
+ và ct nhau '
n kn A B C ' ' ' : :
A : B : C ' ' ' '
+ và vuông góc v# nhau .
n n 0 AA BB CC 0
3. V& trí t+ng "i gi\a +=ng thVng và m;t phVng
x x0 at
Cho ng th/ng : y y0 bt ; M0(x0; y0; 0
z ),VTCP u ( ; a ; b c) và mt ph/ng z 0 z ct
:Ax By Cz D 0 có VTPT n ; A ; B C .
Xét ph ng trình A x0 at B 0
y btC 0z ct D 0 ( ) 5n là t , khi ó
+ ph ng trình (*) vô nghi%m .
u n 0, M0
+ ph ng trình (*) có vô s nghi%m .
u n 0, M0
+ và ct nhau ti mt i!m ph ng trình (*) có nghi%m duy nh"t . u n 0
Lu ý: u kn
Trung tâm luyn thi cht lng cao Thành t – Tây M, Nam T Liêm, Hà Ni Page 57
Thy Nguyn c Thng 0969119789 –thangnd286@gmail.com Tr ng PTLC Vinschool
4. Góc gi\a +=ng thVng và m;t phVng
ng th/ng có VTCP u ( ; a ;
b c) và mt ph/ng có VTPT n ( ; A ; B C) thì . u n
Aa Bb Cc
sin , cosu,n ; 0 0 , 0 90 2 2 2 2 2 2 u . n
A B C . a b c
5. Góc gi\a hai m;t phVng
Nu mt ph/ng có VTPT n ( ; A ;
B C) và mt ph/ng có VTPT 'n ' ' '
A ;B ;C thì ' ' ' ' . n n
AA BB CC cos , ' cosn,n ; 00 , 0 90 ' 2 2 2 '2 '2 '2 n . n
A B C . A B C
6. Kho/ng cách tI m t iYm n m;t phVng Cho i!m M
Ax By Cz D 0 (x0; y0; 0 z ) và mp : 0 thì:
Ax By Cz D d M ; 0 0 0 0 2 2 2
A B C
7. Kho/ng cách tI +=ng thVng n m;t phVng song song
Cho ng th/ng : Ax By Cz D 0 , M0(x0; y0; 0 z ) là mt i!m thuc
Ax By Cz D
d , d M ; 0 0 0 0 2 2 2
A B C
8. Kho/ng cách gi\a hai m;t phVng song song
Cho hai mt ph/ng song song : Ax By Cz D 0 và ' ' ' '
: A x B y C z D 0 , khi ó ' ' ' '
A x B y C z D
d , d M ; 0 0 0 0
. trong ó M (x ; y ; z ) là mt i!m '2 '2 '2 0 0 0 0
A B C
9. M t s" d0ng l-p ph+ng trình m;t phVng th+=ng g;p
Lp ph ng trình m#t ph+ng () ta c0n xác nh mt i=m thuc () và mt VTPT ca nó.
D0ng 1: () i qua i!m . M 0 x ; 0 y ; 0
z có VTPT n A; B;C :
(): A x x B y y C z z 0 0 0 0
D0ng 2: () i qua i!m M , n a,b 0 x ; 0 y ; 0
z có cp VTCP a b : Khi ó mt VTPT ca () là .
D0ng 3: () i qua i!m M 0 x ; 0 y ; 0
z và song song v#i mt ph/ng (): Ax + By + Cz + D = 0:
(): A x x B y y C z z 0 0 0 0
D0ng 4: () i qua 3 i!m không th/ng hàng A, B, C: Khi ó ta có th xác nh mt VTPT ca () là:
n AB, AC
D0ng 5: () i qua mt i!m M và mt ng th/ng (d) không cha M:
– Trên (d) ly im A và VTCP u.
– Mt VTPT ca () là: n AM,u
D0ng 6: () i qua mt i!m M và vuông góc v#i mt ng th/ng (d):
Trung tâm luyn thi cht lng cao Thành t – Tây M, Nam T Liêm, Hà Ni Page 58
Thy Nguyn c Thng 0969119789 –thangnd286@gmail.com Tr ng PTLC Vinschool
VTCP u ca )ng th+ng (d) là mt VTPT ca ().
D0ng 7: () i qua 2 ng th/ng ct nhau d1, d2:
– Xác nh các VTCP a, b ca các )ng th+ng d1, d2.
– Mt VTPT ca () là: n a,b . – Ly mt im M thuc d 1 ho#c d2
M ().
D0ng 8: () cha ng th/ng d1 và song song v#i ng th/ng d2 (d1, d2 chéo nhau):
– Xác nh các VTCP a, b ca các )ng th+ng d1, d2.
– Mt VTPT ca () là: n a,b .
– Ly mt im M thuc d 1
M ().
D0ng 9: () i qua i!m M và song song v#i hai ng th/ng chéo nhau d1, d2:
– Xác nh các VTCP a, b ca các )ng th+ng d1, d2.
– Mt VTPT ca () là: n a,b .
D0ng 10: () i qua mt ng th/ng (d) và vuông góc v#i mt mt ph/ng ():
– Xác nh VTCP u ca (d) và VTPT n ca ().
– Mt VTPT ca () là: n u ,n .
– Ly mt im M thuc d M ().
D0ng 11: () i qua i!m M và vuông góc v#i hai mt ph/ng ct nhau (), ():
– Xác nh các VTPT n ,n
ca () và ().
– Mt VTPT ca () là: n u ,n .
D0ng 12: () i qua ng th/ng (d) cho tr #c và cách i!m M cho tr #c mt khong k cho tr #c:
– Gi! s* () có ph ng trình: 2 2
Ax By Cz+D 0 2
A B C 0 .
– Ly 2 im A, B (d) A, B () (ta c hai ph ng trình (1), (2)).
– T iu kin kho!ng cách d(M,( )) k , ta c ph ng trình (3).
– Gi!i h ph ng trình (1), (2), (3) (b6ng cách cho giá tr mt /n, tìm các /n còn li).
D0ng 13: () là tip xúc v#i mt cu (S) ti i!m H:
– Gi! s* m#t c/u (S) có tâm I và bán kính R.
– Mt VTPT ca () là: n IH
IV. PH23NG TRÌNH 2ING THHNG
1. ng th/ng i qua i!m M (x0; y0; 0 z ) o
và có VTCP u ; a ; b c , khi ó
x x0 at
+ Ph ng trình tham s là: y y0 bt ;(t R) , t gi là tham s. z 0 z ct x x y y z z + Ph ng trình chính tc là: 0 0 0 (abc 0) a b c .
Chú ý:
Véc t u 0 có giá song song hoc trùng v#i ng th/ng 0c gi là VTCP c+a ng th/ng .
Trung tâm luyn thi cht lng cao Thành t – Tây M, Nam T Liêm, Hà Ni Page 59
Thy Nguyn c Thng 0969119789 –thangnd286@gmail.com Tr ng PTLC Vinschool
Nu hai mt ph/ng : Ax By Cz D 0 và ' ' ' '
: A x B y C z D 0 giao nhau thì
Ax By Cz D 0 h% ph ng trình: ' ' ' '
0c gi là ph ng trình tng quát c+a ng th/ng
A x B y C z D 0 trong không gian.
2. V& trí t+ng "i gi\a hai +=ng thVng
x x0 at
Cho hai ng th/ng : y y0 bt ; M0(x0; y0; 0
z ),VTCP u ( ; a ; b c) z 0 z ct ' ' '
x x0 a t ' ' ' ' ' ' ' ' ' ' ' ' ' : y 0
y b t ; M0(x0;y0; 0z) ,VTCPu (a ;b ;c ) ' ' ' z 0 z c t ' ' '
x0 at x0 a t ' ' '
Xét h% ph ng trình y0 bt y0 b t (I) , khi ó ' ' ' 0
z ct 0z c t ' ' u ku + '
, hay h% ph ng trình (I) có vô s nghi%m. M ' 0 M0 ' ' u ku ' + '
, hay u ku và h% (I) vô nghi%m. M ' 0 M0 ' '
+ và ct nhau u ku và h% ph ng trình (I) có nghi%m duy nh"t
' ' hay , u u .M 0M0 0 .
' ' ' '
+ và chéo nhau u ku và h% ph ng trình (I) vô nghi%m hay , u u .M 0M0 0
3. Góc gi\a hai +=ng thVng '
Nu ng th/ng có VTCP u ( ; a ;
b c) và ng th/ng có VTCP ' ' '
u (a ;b ;c ) thì ' u u
aa bb cc cos, ' ' ' . ' ; 00 ' , 0 90 ' 2 2 2 '2 '2 '2 u . u
a b c . a b c
4. Kho/ng cách tI m t iYm n m t +=ng thVng
Khong cách t$ i!m M x ; y ; M M M z n ng th/ng
x x0 at , u M M :
y y0 bt ; M0(x0;y0; 0
z ),VTCP u ( ; a ;
b c) ; 0c tính b2i CT: d M, 0 z u 0 z ct
5. Kho/ng cách gi\a hai +=ng thVng chéo nhau
Trung tâm luyn thi cht lng cao Thành t – Tây M, Nam T Liêm, Hà Ni Page 60
Thy Nguyn c Thng 0969119789 –thangnd286@gmail.com Tr ng PTLC Vinschool '
Nu ng th/ng i qua i!m M0(x0; y0; 0
z ) và có VTCP u ( ; a ;
b c) . ng th/ng i qua
' ' , u u .M 0M0 i!m ' ' ' ' M '
0 (x 0; y 0; z 0 ) và có ' ' ' '
VTCP u (a ;b ;c ) thì d , ' , u u
Lu ý: Khong cách gia hai ng th/ng song song b1ng khong cách t$ mt i!m n1m trên ng
' ' u , M 0M0 ' '
th/ng này n ng th/ng còn li, ngh9a là d , d M0, , M . ' 0 u
6. M t s" d0ng l-p ph+ng trình +=ng thVng th+=ng g;p
Lp ph ng trình )ng th+ng d ta c0n xác nh mt i=m thuc d và mt VTCP ca nó.
D0ng 1: d i qua i!m M (x ; y ; z )
a (a ;a ;a ) 0 0 0 0 và có VTCP 1 2 3 :
x xo a t1
(d) :y o y a t (t R) 2 z o z a t 3 D n
0 g 2: d i qua hai i!m A, B: Mt VTCP ca d là AB .
D0ng 3: d i qua i!m M (x ; y ; z ) 0 0
0 0 và song song v#i ng th/ng cho tr #c:
Vì d // nên VTCP ca c
D0ng 4: d i qua i!m M (x ; y ; z ) 0 0
0 0 và vuông góc v#i mt ph/ng (P) cho tr #c:
Vì d (P) nên VTPT ca (P) c
D0ng 5: d là giao tuyn c+a hai mt ph/ng (P), (Q):
Cách 1: Tìm mt im và mt VTCP. (P)
– Tìm to mt im A d: b6ng cách gi!i h ph ng trình (Q)
– Tìm mt VTCP ca d: a P n , Q n
Cách 2: Tìm hai im A, B thuc d, ri vit ph ng trình )ng th+ng i qua hai im ó.
D0ng 6: d i qua i!m M (x ; y ; z ) 0 0
0 0 và vuông góc v#i hai ng th/ng d1, d2: Vì d d
a a ,a
1, d d2 nên mt VTCP ca d là: d d 1 2
D0ng 7: d i qua i!m M (x ; y ; z ) 0 0
0 0 , vuông góc và ct ng th/ng . H
Cách 1: G%i H là hình chiu vuông góc ca M
0 trên )ng th+ng . M H u 0
Khi ó )ng th+ng d là )ng th+ng i qua M0, H.
Cách 2: G%i (P) là m#t ph+ng i qua A và vuông góc v"i d; (Q) là m#t ph+ng i qua A và
cha d. Khi ó d = (P) (Q)
D0ng 8: d i qua i!m M (x ; y ; z ) 0 0
0 0 và ct hai ng th/ng d1, d2: Cách 1: G%i M 1
d1, M2 d2. T iu kin M, M1, M2 th+ng hàng ta tìm c M1, M2. T
ó suy ra ph ng trình )ng th+ng d.
Trung tâm luyn thi cht lng cao Thành t – Tây M, Nam T Liêm, Hà Ni Page 61
Thy Nguyn c Thng 0969119789 –thangnd286@gmail.com Tr ng PTLC Vinschool
Cách 2: G%i (P) = (M ,d ) (M ,d ) 0 1 , (Q) = 0
2 . Khi ó d = (P) (Q). Do ó, mt VTCP ca d có
th ch%n là a P n , Q n .
D0ng 9: d n1m trong mt ph/ng (P) và ct c hai ng th/ng d1, d2:
Tìm các giao im A = d 1 (P), B = d2
(P). Khi ó d chính là )ng th+ng AB.
D0ng 10: d song song v#i và ct c hai ng th/ng d1, d2:
Vit ph ng trình m#t ph+ng (P) cha và d1, m#t ph+ng (Q) cha và d2.
Khi ó d = (P) (Q).
D0ng 11: d là ng vuông góc chung c+a hai ng th/ng d1, d2 chéo nhau: MN d
Cách 1: G%i M d1, N d2. T iu kin 1
MN d , ta tìm c M, N. 2 Khi ó, d là )ng th+ng MN. Cách 2: – Vì d d
a a ,a
1 và d d2 nên mt VTCP ca d có th là: d d . 1 2
– Lp ph ng trình m#t ph+ng (P) cha d và d1, b6ng cách: + Ly mt im A trên d1.
+ Mt VTPT ca (P) có th là: P
n a, d a . 1
– T ng t& lp ph ng trình m#t ph+ng (Q) cha d và d2.
Khi ó d = (P) (Q).
D0ng 12: d là hình chiu c+a ng th/ng lên mt ph/ng (P):
Lp ph ng trình m#t ph+ng (Q) cha và vuông góc v"i m#t ph+ng (P) b6ng cách:
– Ly M .
– Vì (Q) cha và vuông góc v"i (P) nên Q n a , P n .
Khi ó d = (P) (Q).
D0ng 13: d i qua i!m M, vuông góc v#i d1 và ct d2:
Cách 1: G%i N là giao im ca d và d2. T iu kin MN d1, ta tìm c N. Khi ó, d là )ng th+ng MN. Cách 2:
– Vit ph ng trình m#t ph+ng (P) qua M và vuông góc v"i d1.
– Vit ph ng trình m#t ph+ng (Q) cha M và d2.
Khi ó d = (P) (Q).
- M t s" d0ng toán khác
1. Xác nh hình chiu H ca m"t i=m M lên ng thJng d Cách 1:
– Vit ph ng trình m#t ph+ng (P) qua M và vuông góc v"i d.
– Khi ó: H = d (P) H d Cách 2:
im H c xác nh b5i: MH d a 3.
i=m i xng M' ca m"t i=m M qua ng thJng d Cách 1:
– Tìm im H là hình chiu ca M trên d.
– Xác nh im M sao cho H là trung im ca on MM.
Cách 2:– G%i H là trung im ca on MM. Tính to im H theo to ca M, M. MM ' a
– Khi ó to ca im M c xác nh b5i: d . H d
4.Xác nh hình chiu H ca m"t i=m M lên mt phJng (P) Cách 1:
– Vit ph ng trình )ng th+ng d qua M và vuông góc v"i (P).
– Khi ó: H = d (P)
Trung tâm luyn thi cht lng cao Thành t – Tây M, Nam T Liêm, Hà Ni Page 62
Thy Nguyn c Thng 0969119789 –thangnd286@gmail.com Tr ng PTLC Vinschool H (P) Cách 2:
im H c xác nh b5i: MH, P n cuøng phöông
5.i=m i xng M' ca m"t i=m M qua mt phJng (P) Cách 1:
– Tìm im H là hình chiu ca M trên (P).
– Xác nh im M sao cho H là trung im ca on MM. Cách 2:
– G%i H là trung im ca on MM. Tính to im H theo to ca M, M. H (P)
– Khi ó to ca im M c xác nh b5i: MH, . P n cuøng phöông
6. C@c tr& trong không gian
D0ng 1: A, B c nh. ng th/ng d thay i qua B. Khi ó. d ( A, ) l#n nh"t khi AB vuông góc v#i d.
D0ng 2: A, B c nh. Mt ph/ng (P) thay i qua B. Khi ó. d ( ,
A (P)) l#n nh"t khi AB vuông góc v#i (P).
D0ng 3: A c nh và M thay i trên mt cu (S) tâm I. Khi ó MA l#n nh"t=R+IA, MA nh3 nh"t=|R-
IA| khi và ch& khi M là giao i!m c+a IA và mt cu (S).
D0ng 4: L*p ph ng trình mt ph/ng (P) cha ng th/ng c nh, khong cách A t#i (P)
l#n nh"t khi (P) qua K và nh*n AK là vecto pháp tuyn, trong ó K là hình chiu c+a A lên .
D0ng 5: L*p ph ng trình mt ph/ng (P) cha ng th/ng c nh, to v#i mt ph/ng (Q) mt
góc nh3 nh"t khi n u .u , n P P
D0ng 6: L*p ph ng trình mt ph/ng (P) cha ng th/ng c nh, to v#i mt ph/ng d mt
góc l#n nh"t khi n u .u ,u P d
D0ng 7:L*p ph ng trình ng th/ng n1m trong (P), i qua M sao cho khong cách t$ A (P) c nh t#i d nh3 nh"t, l#n nh"t.
TH1: d (a, ) nh3 nh"t khi i qua M và hình chiu c+a A lên (P).
TH2: d (a, ) l#n nh"t khi là giao tuyn c+a (P) và mt ph/ng (Q) qua M nh*n AM là vecto phap
tuyn (hay u AM , n P
D0ng 8: Tìm M thuc mt cu (S) tâm I sao cho khong cách t$ M n (P) l#n nh"t, nh3 nh"t. Khi
ó, M là giao i!m c+a ng th/ng d (qua I vuông góc v#i (P)) và mt cu (S).
D0ng 9: Tìm M thuc mt cu (S) tâm I sao cho khong cách t$ M n l#n nh"t, nh3 nh"t. Khi ó,
M là giao i!m c+a ng th/ng d’ (d’ qua I vuông góc v#i và d’ n1m trong mp(I, ) ) và mt cu (S). B1 sung: 1. 2 2 2
MA MA ...
hoc MA MA ... t giá tr nh3 nh"t (l#n 1 1 2 2 MA MA n n 1 1 2 2 n n
nh"t) khi và ch& khi MI nh3 nh"t (l#n nh"t), trong ó K là i!m tho mãn:
MI MI ... MI 0 1 1 2 2 . n n
2. Cho A, B c nh, M thuc mt ph/ng (P) sao cho: MA MB nh3 nh"t hoc MA MB l#n nh"t
TH1: Nu A, B cùng phía so v#i (P) thì M AB (P)
TH2: Nu A, B khác phía so v#i (P) thì M AB ' (P) trong ó B’ là i!m i xng c+a B qua (P)
Trung tâm luyn thi cht lng cao Thành t – Tây M, Nam T Liêm, Hà Ni Page 63
Thy Nguyn c Thng 0969119789 –thangnd286@gmail.com Tr ng PTLC Vinschool
G. KHI A DIN VÀ TH^ TÍCH KHI A DIN 1. Lí thuyt v% kh"i a din
- Hình a di%n là hình 0c to b2i mt s hu hn các a giác tho mãn:
Hai a giác phân bi%t ch& có th!: Ch& có mt i!m chung hoc ch& có mt &nh chung, hoc ch& có mt cnh chung.
M.i cnh c+a a giác nào -u là cnh chung c+a úng hai mt.
- Khi a di%n 0c gi là li n-u v#i hai i!m b"t kì A và B thuc khi a di%n thi mi i!m thuc on AB c:ng thuc khi a di%n ó. 2. Kh"i a din %u a) nh ngh1a
Khi a di%n -u là khi a di%n li có hai tính ch"t:
Các mt là các a giác -u có cùng s cnh
M.i &nh là &nh chung c+a cùng mt s cnh (ít nh"t 3 cnh)
Ng i ta phân loi khi a di%n -u: Nu m.i mt có n cnh, m.i &nh là &nh chung c+a p cnh thì khi a di%n -u ó loi , n p .
Chú ý: Gi , C, M là s &nh, s cnh, s mt c+a mt khi da di%n -u khi ó: 4n 2np 4p
1. D-C+M=2 và 2C=nM=pD và D ; C ; M
2n 2p np
2n 2p np
2n 2p np trong ó
2n 2p np 0 và n2 p2 4, n 3, p 3,
2. Trong mt khi a di%n: C 6 , D 4 , M 4 và 2C M
3 C 6 , 2C D 3 C 6 b) Các loi khi a din u Lo0i Tên g_i S" Bnh S" c0nh S" m;t ThY tích 3, 3 T di%n -u 3 a . 2 4 6 4 V 12 4, 3 L*p ph ng 3 8 12 6 V a 3, 4 Bát di%n -u 3 a . 2 6 12 8 V 3 5, 3 M i hai mt -u 3 15 7 5 a 20 30 12 V 4 3, 5 Hai m i mt -u 3 15 5 5 a 12 30 20 V 12
c) Tâm i xng, m#t i xng ca khi a din u
* Tâm i xng: Khi l*p ph ng, khi bát di%n -u, khi m i hai mt -u, khi hai m i mt -u
* Mt i xng: T di%n -u có 6 mt i xng; Khi l*p ph ng có 9 mt i xng; Khi bát i%n
-u có 5 mt i xng; Khi m i hai mt -u có 15 mt i xng. Chú ý:
* T di%n -u: Không có tâm i xng, có 6 mt i xng, có 3 tr(c i xng;
* Hình l*p ph ng có tâm i xng, có 9 mt i xng, có 13 tr(c i xng;
* Hình bát di%n -u có tâm i xng, 9 mt i xng và 9 tr(c i xng.
* Hình có tâm i xng thì có s cnh, s mt, s &nh là s ch6n.
Trung tâm luyn thi cht lng cao Thành t – Tây M, Nam T Liêm, Hà Ni Page 64 Thy Nguyn c Thng
0969119789 –thangnd286@gmail.com Tr ng PTLC Vinschool
3. Th= tích khi a din S a) Th! tích 1
- Th tích khi chóp: V= B.h 3 C B: Di%n tích a giác áy. A h: dài ng cao. H B B’
- Th tích khi l=ng tr': V=B.h C’ A’ B: Di%n tích a giác áy. D’ h: dài ng cao. B A C H D - Th! >ch hình hp ch nh*t: V . a . b c 1 S . 2 S . 3 S 2 2 2
ng chéo: l a b c - Th! >ch khi l*p ph ng 3 V a ng chéo: a 3
- Th tích khi chóp c't: h
V B B' .BB' 3
Trong ó: B, B’ là din tích hai áy, h
là chiu cao khi chóp c't (h=OO’) S b. T> s th tích: B' C' A' * Cho khi chóp S.ABC. C A'SA, B'SB, C'SC A V . SA . SB SC S . ABC Thy Nguyn c Thng
0969119789 –thangnd286@gmail.com Tr ng PTLC Vinschool S * MSC, ta có: M C V . SA . SB SM SM S . ABM A V S . A S . B SC SC S. ABC B
4. M"t s công thc tính xác nh nhanh tâm và bán kính mt cu ngoi tip khi a din KiYu hình Tâm
Bán kính m;t cMu ngo0i tip T din u cnh a. Tâm O c+a mt cu ngoi tip A n1m trên AH và cách (BCD) a 6 mt khong OH= O 12 B a 6 D R= . H E 4 C T din OABC có OA=a, O n1m trên ng th/ng d
OB=b,OC=c và OA,OB,OC ôi vuông góc mp(ABC) ti trung mt vuông góc. c i!m H c+a AB và OH= . C 2 M O S B 2 2 2 H a b c R A 2 T di%n SABC có SA=b,SA
Ta xét hình tr( ngoi tip hình 2 2 2 .sin 4 (ABC). BC=a c nh, A thay i chóp SABC. Khi ó tâm O c+a b a R 2sin trên mt ph/ng (ABC) sao cho mt cu ngoi tip hình chóp BAC . SABC trùng v#i trung i!m on ni hai tâm c+a hình tròn áy c+a hình tr( T di%n ABCD có tính ch"t M2 rng t di%n ABCD thành 2 2 2 AB=CD=a, BC=AD=b,CA=BD=c. hình hp ch nh*t a b c R 8 B1 C AB1CC1.E1DD1B nh hình vC. D nh*n ra r1ng tâm O c+a A C1 mt cu ngoi tip t di%n ABCD chính là tâm c+a hình O D1 D hp ch nh*t AB1CC1.E1DD1B E1 B Thy Nguyn c Thng
0969119789 –thangnd286@gmail.com Tr ng PTLC Vinschool H. GÓC VÀ KHONG CÁCH
1. +=ng thVng vuông góc vAi m;t phVng Phng pháp 1
! chng minh ng th/ng d vuông góc v#i mt ph/ng () ta chng minh d vuông góc v#i hai ng th/ng ,
a b ct nhau n1m trong () . d a d a I d b b
d (P) , a b (P) .
a b I Phng pháp 2
S d(ng tính ch"t: d , mà () thì d ( ) . d I K Phng pháp 3 Nu hai mt ph/ng
( ) , () vuông góc v#i nhau và ct nhau theo giao tuyn , ng th/ng nào
n1m trong mt ph/ng ( ) mà vuông góc v#i giao tuyn thì vuông góc v#i mt ph/ng ( ) . d Phng pháp 4
Nu hai mt ph/ng phân bi%t cùng vuông góc v#i mt ph/ng th ba thì giao tuyn c+a chúng vuông góc v#i mt ph/ng th ba ó. d (P) (R) (Q) (R)
a (R). (P) Q ( ) a Thy Nguyn c Thng
0969119789 –thangnd286@gmail.com Tr ng PTLC Vinschool Phng pháp 5
Nu hai mt ph/ng song song v#i nhau, ng th/ng d vuông góc v#i mt ph/ng này thì nó vuông góc v#i mt ph/ng kia. d
2. Hai m;t phVng vuông góc Phng pháp 1
Mun chng minh hai mt ph/ng vuông góc v#i nhau ta chng minh d
mt ph/ng này cha mt ng th/ng vuông góc mt ph/ng kia.
d ()()() d () Phng pháp 2 () ( ) S d(ng tính ch"t: ( ) ( ) ( ) () . d l Phng pháp 3 S d(ng tính ch"t
( ) d , mà d () hoc d () thì () (). d
3. Hai +=ng thVng vuông góc Phng pháp 1
Mun chng minh hai ng th/ng vuông góc v#i nhau ta a
chng minh ng th/ng này vuông góc v#i mt ph/ng cha d () ng th/ng kia. d a a ( ) . Thy Nguyn c Thng
0969119789 –thangnd286@gmail.com Tr ng PTLC Vinschool Phng pháp 2
Nu ng th/ng a song song mt ph/ng () , mà ng th/ng d vuông góc mt ph/ng () , thì
d vuông góc v#i ng th/ng a . d a
d () d a a () . 4. Góc
4.1 Góc gi6a hai ng thJng Phng pháp
B #c 1: Tìm mt i!m O tùy ý (có th! l"y trên ng th/ng a hoc b ). T$ O d,ng hai tia Oa' và
Ob' ln l 0t song song v#i a và b 0c góc a 'Ob' .
B #c 2. Tính s o c+a góc b1ng các nh lý và tính ch"t c+a hình hc ph/ng hay nh lý côsin.
Chú ý: góc gia hai ng th/ng không l#n hn 900 . a a' O b' b
4.2 Góc gi\a +=ng thVng và m;t phVng Phng pháp
! xác nh góc gia ng th/ng d và mt ph/ng ( ) ta th,c hi%n nh sau:
B #c 1: Xác nh hình chiu vuông góc c+a d xung mt ph/ng ( ) là d ' .
+ Tìm giao i!m O d ( ) .
+ D,ng hình chiu vuông góc c+a A xung () là H (chn ng th/ng i qua A và vuông góc v#i () ).
B #c 2: Góc gia ng th/ng d và d ' là góc ng th/ng d và mt ph/ng () . Tính s o c+a
góc ó b1ng h% thc l 0ng trong tam giác vuông. Thy Nguyn c Thng
0969119789 –thangnd286@gmail.com Tr ng PTLC Vinschool A H O
4.3 Góc gi\a hai m;t phVng
! xác nh góc gia hai mt ph/ng () và ( ) ta làm nh sau: Phng pháp 1 Tìm hai ng th/ng ,
a b ln l 0t vuông góc v#i hai mt ph/ng () và (). Khi ó góc gia hai ng th/ng ,
a b chính là góc gia hai mt ph/ng () và (). a b a () ( , a ) b (),() b () . Phng pháp 2 Xác nh giao tuyn c+a ( ) và ().
L"y i!m I .Trong
( ) d,ng a ti I . Trong () d,ng b ti I . Khi ó góc gia hai ng th/ng ,
a b chính là góc gia hai mt ph/ng ( ) và (). b a I Phng pháp 3
Xác nh giao tuyn c+a () và ( ) .
Trong ( ) l"y i!m A . D,ng hình chiu H c+a A xung mt ph/ng () .
T$ H d,ng HI .
Khi ó góc AHI là góc gia hai mt ph/ng () và ( ) . Thy Nguyn c Thng
0969119789 –thangnd286@gmail.com Tr ng PTLC Vinschool A b a I H Phng pháp 4
Xác nh giao tuyn c+a () và ( ) . Chn mt ph/ng ( ) .
Tìm các giao tuyn a ( ) () , b ( ) ( ). Khi ó góc gia hai ng th/ng ,
a b chính là góc gia hai mt ph/ng () và (). a b
Phng pháp 5 S d(ng công thc di%n tích hình chiu S ' S cos . 5. Kho/ng cách
5.1 Kho/ng cách tI m t iYm n m t +=ng thVng
! tính khong cách t$ i!m M n ng th/ng ta cn xác nh 0c hình chiu H c+a i!m
M trên ng th/ng . i!m H th ng 0c d,ng theo hai cách sau:
- Trong mt ph/ng (M, ) vC MH . Khi ó: d(M,) MH .
- D,ng mt ph/ng () qua M và vuông góc v#i ti H . Khi ó: d(M, ) MH . M H
5.2 Kho/ng cách tI m t iYm n m t m;t phVng
Cho i!m M và mt ph/ng
( ) . Gi H là hình chiu c+a M xung
( ) . Khi ó MH 0c gi là
khong cách t$ i!m M n mt ph/ng ( ) . Phng pháp 1
B #c 1: Chn mt ph/ng ( ) qua M và vuông góc v#i ( ) .
B #c 2: Xác nh giao tuyn d () ( ) . Thy Nguyn c Thng
0969119789 –thangnd286@gmail.com Tr ng PTLC Vinschool
B #c 3: Trong mt ph/ng ( ) k8 MH d . V*y MH d(M,()) . M H d Phng pháp 2 Gi s ã bit d( ,
A ()), IM và IA .
- Nu AM ( ) thì d(M,( )) d( , A ()) .
d(M,()) IM
- Nu AM ct () ti I thì d( , A ()) IA . M M A A H K I H K
5.3 Kho/ng cách gi\a hai +=ng thVng
Khong cách gia hai ng th/ng và ' :
- Nu và ' ct nhau hoc trùng nhau thì d( , ') 0 .
- Nu và ' song song v#i nhau thì d( ,
') d(M,') d(N,) M K ' H N
5.4 Kho/ng cách gi\a +=ng thVng và m;t phVng
Khong cách gia ng th/ng và () :
- Nu ct () hoc n1m trong () thì d( , ()) 0 .
- Nu () thì d( ,
()) d(M,()). M H
5.5 Kho/ng cách gi\a hai m;t phVng Thy Nguyn c Thng
0969119789 –thangnd286@gmail.com Tr ng PTLC Vinschool
Khong cách gia hai mt ph/ng () và ( )
- Nu () ct ( ) hoc ( ) ( ) thì d((),( )) 0 .
- Nu ( ) ( ) thì d(( ),( )) d(M,( )) . M H
5.6 Kho/ng cách gi\a hai +=ng thVng chéo nhau
ng vuông góc chung c+a hai ng th/ng chéo nhau và ' là ng th/ng a ct 2 M và
ct ' 2 N ng thi vuông góc v#i c và ' .
on MN 0c gi là on vuông góc chung c+a hai ng th/ng chéo nhau và ' . M ' N Phng pháp 1 1 Chn mt ph/ng
( ) cha ng th/ng và song song v#i ' . Khi ó d(,') d(', ( )). M ' H Phng pháp 2
D,ng hai mt ph/ng song song và ln l 0t cha hai ng th/ng. Khong cách gia hai mt ph/ng ó là khong cách cn tìm. '
Phng pháp 3 D,ng on vuông góc chung và tính dài on ó.
Tr)ng hp 1: và ' v$a chéo nhau v$a vuông góc v#i nhau
B #c 1: Chn mt ph/ng () cha ' và vuông góc v#i ti I . Thy Nguyn c Thng
0969119789 –thangnd286@gmail.com Tr ng PTLC Vinschool
Khi ó IJ là on vuông góc chung và d( , ') IJ . ' I J
Tr)ng hp 2: và ' chéo nhau mà không vuông góc v#i nhau B #c 1: Chn mt ph/ng
( ) cha ' và song song v#i .
B #c 2: D,ng d là hình chiu vuông góc c+a xung
( ) b1ng cách l"y i!m M d,ng on
MN , lúc ó d là ng th/ng i qua N và song song v#i .
B #c 3: Gi H d ', d,ng HK MN
Khi ó HK là on vuông góc chung và d(, ') HK MN . K M d N H ' Hoc
B #c 1: Chn mt ph/ng () t i I .
B #c 2: Tìm hình chiu d c+a ' xung mt ph/ng ( ) . B #c 3: Trong mt ph/ng
( ) , d,ng IJ d , t$ J d,ng ng th/ng song song v#i ct ' ti
H , t$ H d,ng HM IJ .
Khi ó HM là on vuông góc chung và d(, ') HM IJ . ' M H d I J 6. Bài toán khác
DNG 1: Thit din to bKi mt phJng i qua m"t i=m và vuông góc v i m"t ng thJng d cho tr c
Cách xác nh mp( ) i qua i!m A và vuông góc v#i ng th/ng d: Cách 1:
+ K8 ng th/ng a qua A và vuông góc v#i d.
Thy Nguyn c Thng 0969119789 –thangnd286@gmail.com Tr ng PTLC Vinschool
Khi ó, mp(a,b) chính là mp( ) cn d,ng.
Cách 2: Nu có d vuông góc v#i (P). D,ng qua A và / /(P)
DNG 2: Thit din to bKi mt phJng cha m"t ng thJng và vuông góc m"t mt phJng cho tr c.
Cách xác nh mp( ) cha ng th/ng a và vuông góc v#i ng th/ng mp( ) trong ó (
a mp ):
+ Chn mt i!m A trên ng th/ng a.
+ K8 ng th/ng qua A và vuông góc v#i mp( ).
Khi ó, mp(a,b) chính là mp( ) cn d,ng. Kt qu:
+ Nu mt ng th/ng và mt mp cùng vuông góc v#i mt ng th/ng ( ng th/ng không n1m
trong mt ph/ng) thì song song.
+ Nu mt ng th/ng và mt mp cùng vuông góc v#i mt ph/ng ( ng th/ng không n1m trong mt ph/ng thì song song.
DNG 3: D'ng m"t ng thJng d qua m"t i=m A và vuông góc v i mt phJng (P)
Cách 1: Nu có a (P) : D,ng d song song v#i a. Khi ó d (P) Cách 2:
+ D,ng mt ph/ng (Q) qua i!m A và Q (P) ;
+ Tìm giao tuyn b c+a (P) và (Q);
+ T$ i!m A d,ng ng th/ng d vuông góc v#i b. Khi ó: d là ng th/ng cn d,ng
DNG 4: Ch&n m"t mt phJng qua i=m A và vuông góc v i mt phJng (P ) cho tr c
Cách 1: Nu ã có mt ng th/ng a vuông góc v#i ng th/ng b trong (P).
T$ mt i!m M nào ó trên a, k8 mt ng th/ng MH vuông góc v#i b.
Khi ó: mp(a,H) chính là mt ph/ng cn d,ng.
Cách 2: Nu bit mt ph/ng (Q) vuông góc v#i (P).
T$ i!m A k8 ln l 0t hai ng th/ng song song v#i hai ng th/ng ct nhau trong (P).
DNG 5: Tìm hình chiu H ca i=m M lên mt phJng (P) Quy tc chung:
+ i!m thuc mt ph/ng thì hình chiu c+a i!m ó lên mt ph/ng là chính nó; + i!m không thuc mt ph/ng:
- D,ng mt ng th/ng d qua i!m A và vuông góc v#i (P); - DFNG 3
- Tìm giao i!m c+aH c+a d và mt ph/ng (P). Khi ó, H chính là hình chiu c+a i!m A lên (P)
DNG 6: Tìm hình chiu ca ng thJng d ( không vuông góc v i (P)) lên mt phJng (P). Cách 1:
Chn trên d hai i!m A & B. (nu d ct (P) nên chn 1 i!m là giao c+a d và (P))
Trung tâm luyn thi cht lng cao Thành t – Tây M, Nam T Liêm, Hà Ni Page 75
Thy Nguyn c Thng 0969119789 –thangnd286@gmail.com Tr ng PTLC Vinschool
+ Tìm hình chiu A’, B’ ln l 0t c+a A, B lên (P).
+ ng th/ng d’ qua A’, B’ chính là hình chiu c+a d lên (P) Cách 2:
+ Chn mt ph/ng (Q) cha d và Q (P) ;
+ Khi ó, giao tuyn d’ c+a (P) và (Q) chính là hình chiu c+a d lên (P).
DNG 7: T7 s khong cách d( , A (P)) AM
+ Nu ng th/ng AB ct (P) ti M thì:
d(B,(P)) BM
+ Nu AB song song v#i (P) thì d( ,
A (P)) d(B,(P)).
Trung tâm luyn thi cht lng cao Thành t – Tây M, Nam T Liêm, Hà Ni Page 76
Thy Nguyn c Thng 0969119789 –thangnd286@gmail.com Tr ng PTLC Vinschool I. MT S KIN THC B SUNG
1/ Các h thc l%ng trong tam giác vuông
Cho ABC vuông ti A, AH là ng cao, AM là ng trung tuyn. Ta có: A 1 1 1 S . a h . b h . ABC c h 2 a 2 b 2 c 1 1 1 S absinC bcsin A acsin ABC B 2 2 2 abc B C S , . ABC
SABC p r H M 4R
a b c
S ABC p p a p b p c, p 2 BC AM 2
2/ Các h thc l%ng trong tam giác thng 2 2 2 a) nh lí hàm s cosin
b c a A 2 2 2
a b c 2bc cos A cos A 2bc 2 2 2
a c b c b 2 2 2
b a c 2ac cos B cos B 2ac 2 2 2 2 2 2
a b c
c a b ab C C B a C 2 cos cos 2ab b) nh lí hàm s sin A a b c c = = = 2R b sin A sin B sinC B C
(R là bán kính ng tròn ngoi tip ABC) R a
c) Công thc >nh di%n >ch c+a tam giác A 1 1 1 S a.h b.h c. ABC h 2 a 2 b 2 c c b 1 1 1 S ab sin C bc sin A ac sin ABC B 2 2 2 abc B a C S , S p. ABC r 4 ABC R p – na chu vi
a b c
S ABC p p a p b p c, p 2
r – bán kính ng tròn
d) Công thc >nh dài ng trung tuyn c+a tam giác A 2 2 2 2 2 2 2 AB AC BC K N AM BA BC AC 2 BN 2 4 . 2 4 . 2 2 2 M 2 CA CB AB B C CK 2 4 .
Trung tâm luyn thi cht lng cao Thành t – Tây M, Nam T Liêm, Hà Ni Page 77
Thy Nguyn c Thng 0969119789 –thangnd286@gmail.com Tr ng PTLC Vinschool 3/ nh lí Talet / / AM AN MN MN BC k A AB AC BC 2
SAMN AM 2 k M N S ABC AB B C
(T din tích bng t bình phng ng dng)
4/ Din ;ch ca a giác B
a/ Din :ch tam giác vuông 1 ⇒ S = AB.AC ΔABC 2
Di%n >ch tam giác vuông b1ng ½ >ch 2 cnh A C góc vuông.
b/ Din :ch tam giác u B 2 ⎧⎪ a 3 2 canh 3 S ⎪⎪ = AB Δ C ⎪ Di%n >ch tam giác -u: S ⎪ 4 4 a ⇒ ⎨ h ⎪⎪ a 3 . canh 3 h ⎪ = ⎪ ⎪⎩ 2 Chi-u cao tam giác -u: h A C 2 A B
c/ Din :ch hình vuông và hình ch4 nht 2 S ⎧⎪ = a HV ⎪ a ⎪ ⇒ O ⎨ ⎪
Di%n >ch hình vuông b1ng cnh bình ph ng.
AC = BD = a 2 ⎪ D C ⎪⎩
ng chéo hình vuông b1ng cnh nhân 2 .
Di%n >ch hình ch nh*t b1ng dài nhân rng.
d/ Din :ch hình thang A D Di%n >ch hình thang:
(AD + BC ).AH 1 ⇒ S =
SHình Thang .(áy l#n + áy bé) x chi-u cao 2 2 B H C
e/ Din :ch t giác có hai )ng chéo vuông góc B
Di%n >ch t giác có hai ng chéo vuông góc 1 A C ⇒ S = AC.BD
nhau b1ng ½ >ch hai ng chéo. H .Thoi 2
Hình thoi có hai ng chéo vuông góc nhau ti trung i!m c+a m.i ng. D
L+u ý: Trong >nh toán di%n >ch, ta có th! chia a giác thành nhng hình n gin d >nh di%n
>ch, sau ó cng các di%n >ch 0c chia này, ta 0c di%n >ch a giác.
Trung tâm luyn thi cht lng cao Thành t – Tây M, Nam T Liêm, Hà Ni Page 78
Thy Nguyn c Thng 0969119789 –thangnd286@gmail.com Tr ng PTLC Vinschool
5. M t s" phép bin 1i ? th&
1. Các phép bin 1i n gi/n. a. Hai i!m M ;
x y và M ;xy i xng v#i nhau qua tr(c hoành . b. Hai i!m M ;
x y và M ;x y i xng v#i nhau qua tr(c tung . c. Hai i!m M ;
x y và M ;xy i xng v#i nhau qua gc to O .
T$ các phép bin i n gin này ta có.
2. Các phép bin 1i ? th&.
a. th c+a hai hàm s y f x và y f x i xng v#i nhau qua tr(c hoành.
b. th c+a hai hàm s y f x và y f x i xng v#i nhau qua tr(c tung.
c. th c+a hai hàm s y f x và y f x i xng v#i nhau qua gc ta O.
H qu/ 1. th hàm s ch-n nhn tr'c tung làm tr'c i xng.
H qu/ 2. th hàm s l. nhn gc t%a O làm tâm i xng.
T$ các kt qu trên ta có các dng c bn v- th c+a hàm s có cha d"u giá tr tuy%t i. 3. Các d0ng c b/n
D0ng 1. T th (C) ca hàm s y f x , suy ra cách v@ th (G) ca hàm s y f x f x khi 0 f x
Li gii. Ta có y f x f
x khi f x 0
Suy ra G C C 1
2 v#i C1 là phn th (C) n1m phía trên tr(c hoành yC 0 , còn 2 C
là phn i xng qua tr(c hoành c+a phn th (C) n1m phía d #i tr(c hoành y 0 C
D0ng 2. T th (C) ca hàm s y f x , suy ra cách v@ th (H) ca hàm s y f x
L=i gi/i. Vì x x nên y f x là hàm s ch6n, suy ra th (H) nh*n tr(c tung làm tr(c i
xng. Vì v*y (H) 3 C 4 C v#i 3
C là phn th c+a (C) n1m bên phi tr(c tung x 0, còn C
4 là phn i xng c+a C3 qua tr(c tung.
D0ng 3. T th (C) ca hàm s y f x , suy ra cách v@ th (K) ca hàm s y f x f x khi 0 f x
Li gii. Ta có y f x f
x khi f x 0 Suy ra (K) 1
H H2 v#i 1
H là phn th c+a (H) c+a hàm s y f x n1m phía trên tr(c
hoành y 0 H H
,còn 2 làphni xngquatr(choành c+aphnth (H)2phía d #itr(c
hoành y 0 H . ux ux
D0ng 4. T th (C) ca hàm s y
, suy ra cách v@ th (L) ca hàm s y vx vx
Trung tâm luyn thi cht lng cao Thành t – Tây M, Nam T Liêm, Hà Ni Page 79
Thy Nguyn c Thng 0969119789 –thangnd286@gmail.com Tr ng PTLC Vinschool ux
ux vx khi ux 0
Li gii. y
vx u x v
x khi ux 0
Suy ra L 1 C 2 C v#i 1
C là phn c+a th (C) có hoành th3a mãn i-u ki%n ux 0 và 2
C là phn i xng qua tr(c hoành c+a phn th (C) có hoành th3a mãn ux 0. ux ux
D0ng 5. T th (C) ca hàm s y
, suy ra cách v@ th (M) ca hàm s y . vx vx ux
ux vx khi vx 0
Li gii. y vx u x v
x khi vx 0
Suy ra M 3 C 4 C v#i 3
C là phn c+a th (C) có hoành th3a mãn i-u ki%n vx 0 và 4
C là phn i xng qua tr(c hoành c+a phn th (C) có hoành th3a mãn vx 0 . ux ux
D0ng 6. T th (C) ca hàm s y
, suy ra cách v@ th (N) ca hàm s y . vx vx ux ux
ux vx khi vx 0
Li gii. y
vx u x ux v
x khi vx 0 Suy ra N y 0 C 5 C 6 C v#i 5
C là phn c+a th (C) n1m phía trên tr(c hoành và y 0 C 6
C là phn i xng qua tr(c hoành c+a phn th (C) n1m phía d #i tr(c hoành . ux u x
D0ng 7. T th (C) ca hàm s y
, suy ra cách v@ th (Q) ca hàm s y . vx v x u x
L=i gi/i. Vì x x nên y
là hàm s ch6n, suy ra th (Q) nh*n tr(c tung làm tr(c i v x xng. Vì v*y ( ) Q 7 C 8 C v#i 7
C là phn th c+a (C) n1m bên phi tr(c tung x 0, còn 8
C là phn i xng c+a 7 C qua tr(c tung. ux u x
D0ng 8. T th (C) ca hàm s y
, suy ra cách v@ th (R) ca hàm s y vx v x
Trung tâm luyn thi cht lng cao Thành t – Tây M, Nam T Liêm, Hà Ni Page 80
Thy Nguyn c Thng 0969119789 –thangnd286@gmail.com Tr ng PTLC Vinschool u x u x
u x v
x khi v x 0
Li gii. y v x u x u x v
x khi v x 0 u x
Suy ra R 1 Q 2 Q v#i 1
Q là phn th (Q) c+a hàm s y n1m phía trên tr(c v x
hoành y 0 Q , còn Q
2 là phn i xng qua tr(c hoành c+a phn th (Q) 2 phía d #i tr(c
hoành y 0 Q . 6. Công th*c 0o hàm
6.1. Các quy tLc tính o hàm (Ký hiu U=U(x), V=V(x)). U
U .V U.V
U V UV UV U V UV
{f[U(x)]} / = f ' . U 2 x V V u x sin x 1 U ' lim 1
kU k.U '
UVW ' U 'VW UV 'W UVW ' x0 x 2 U U
6.2. Các công thc tính o hàm: Tên hàm s" Công th*c 0o hàm 0o hàm c(a hàm s" h2p Các hàm s" C =0 (C là h1ng s) th+=ng g;p x ' =1, (kx)’=k (k là h1ng s ) 1 n .u' u 0 n n 1 u u n
x =n.xn-1 (nN, n 2) u 1
.u .u' 1 1 / 1 u (x 0) (u 0) 2 x x 2 u u 1 n 1 n .u' (u 0) n n 1 (x 0) x x n n 1 u u ( x) 1 u = (x>0) u / (u 0) 2 x 2 u n x' 1 (x 0) nu' 1 .u' (u 0) n n 1 n x n n 1 n u Hàm s" l+2ng
sin x/ cosx sinu/ / cos . u u giác
cosx/ sin x cosu/ / sin . u u tanx/ 1 2 1 1 tan x tanu/ / .u 2 cos x 2 cos u x/ 1 cot 1 2 1 cot x cotu/ / .u 2 sin x 2 sin u Hàm lEy thIa (xH)/= H x H -1 (uH)/= H u H -1u/
Trung tâm luyn thi cht lng cao Thành t – Tây M, Nam T Liêm, Hà Ni Page 81
Thy Nguyn c Thng 0969119789 –thangnd286@gmail.com Tr ng PTLC Vinschool Hàm s" mE (ex )’ = ex ( eu)’ = u’ .eu (ax)’ = axlna ( au)’ = u’ .au.lna Hàm logarít 1 u' (lnx )’ = x (x>0) ( lnu)’ = u (u>0) 1 u' (ln /x/ )’ = x (xE0) ( ln /u/ )’ = u (uE0) 1 u'
( loga x )’ = x lna (x>0, 0( loga u )’ = ulna (u>0, 01 u'
( loga x )’ = x lna (x>0, 0( loga u )’ = ulna (u>0, 0' (n) (n 1 )
6.3. o hàm cp cao: f (x) f (x)
T#ng các con trai, em trai, các cháu ca tôi!
Hà Ni, ngày 06 tháng 4 n=m 2017
Trung tâm luyn thi cht lng cao Thành t – Tây M, Nam T Liêm, Hà Ni Page 82




