












Preview text:
SỞ GIÁO DỤC
ĐÀO TẠO THÀNH PHỐ ĐÀ NẴNG TRƯỜNG THPT PHẠM PHÚ THỨ SỔ TAY KIẾN THỨC CHỦ ĐỀ TRONG TÂM CHƯƠNG TRÌNH MỚI ÔN THI TỐT NGHIỆP THPT QG MÔN TOÁN Đà Nẵng háng năm
SỔ TAY KIẾN THỨC TOÁN 12 dcd MỤC LỤC
CHỦ ĐỀ 0. MỘT SỐ KIẾN THỨC NỀN TẢNG ............................................... 1
CHỦ ĐỀ 1. PHƯƠNG TRÌNH VÀ BẤT PHƯƠNG TRÌNH ............................... 7
CHỦ ĐỀ 2. CẤP SỐ CỘNG VÀ CẤP SỐ NHÂN ............................................ 10
CHỦ ĐỀ 3. ĐẠO HÀM VÀ KHẢO SÁT HÀM SỐ .......................................... 11
CHỦ ĐỀ 4. NGUYÊN HÀM VÀ TÍCH PHÂN ................................................ 18
CHỦ ĐỀ 5. HÌNH HỌC KHÔNG GIAN ........................................................ 21
CHỦ ĐỀ 6. VECTƠ VÀ PHƯƠNG PHÁP TỌA ĐỘ TRONG KHÔNG GIAN ........... 25
CHỦ ĐỀ 7. MỘT SỐ YẾU TỐ VỀ THỐNG KÊ ............................................... 31
CHỦ ĐỀ 8. MỘT SỐ YẾU TỐ VỀ XÁC SUẤT ................................................ 34
TỔ TOÁN – TRƯỜNG THPT PHẠM PHÚ THỨ 1
TÀI LIỆU ÔN THI TN THPT 2025 dcd L ỜI N ÓI Đ Ầ U Các em thân mến!
Trên tay các em là cuốn “SỔ TAY KIẾN THỨC TOÁN 12” được Thầy
Cô biên soạn dựa trên 8 chủ đề thi Tốt nghiệp THPT QG môn Toán
theo chương trình mới từ năm 2025.
Năm học này là năm đầu tiên lớp 12 được học theo chương trình
GDPT mới 2018 và cũng là năm đầu tiên thi tốt nghiệp đầu ra của
chương trình này. Chương trình mới với hình thức thi hoàn toàn
mới, khi mà số lượng câu hỏi được giảm đi đáng kể, hình thức câu
hỏi cũng đa dạng hơn trước với lượng thời gian không đổi; khi đó,
các câu hỏi sẽ tập trung vào chiều sâu, cũng như bóc tỉa nhiều vấn
đề của một nội dung kiến thức, đòi hỏi các em phải nắm thật chắc
kiến thức nền tảng. Liệt kê ra các chủ đề kiến thức của bài thi TN
THPT, từ đó chinh phục từng chủ đề một là việc làm đầu tiên và
cần thiết để các em làm chủ kiến thức, tự tin hơn và từ đó chinh
phục bài thi mang tính bước ngoặc sắp đến.
Từ những yêu cầu thực tế trên, Thầy Cô đưa vào đây những kiến
thức trọng tâm nhất với các định nghĩa, định lí, tính chất và hệ quả
được trình bày đầy đủ và chi tiết, xem như là “gốc”, là “xương
sống” trong chương trình phổ thông cũng như của bài thi tốt nghiệp môn Toán.
Cuốn SỔ TAY KIẾN THỨC TOÁN 12 được Thầy Cô biên soạn dành
riêng cho các em học sinh trường THPT Phạm Phú Thứ khóa thi tốt
nghiệp THPT 2025. Hi vọng nó sẽ giúp ích phần nào trong hành
trình chinh phục môn Toán thời phổ thông của các em.
Gửi đến các em với thật nhiều sự tận tâm, trách nhiệm và đầy yêu thương!
Hòa Sơn, tháng 03 năm 2025
Tổ Toán trường THPT Phạm Phú Thứ.
TỔ TOÁN – TRƯỜNG THPT PHẠM PHÚ THỨ 2
SỔ TAY KIẾN THỨC TOÁN 12 dcd
CHỦ ĐỀ 0. MỘT SỐ KIẾN THỨC NỀN TẢNG
I. HỆ THỨC LƯỢNG TRONG TAM GIÁC. DIỆN TÍCH
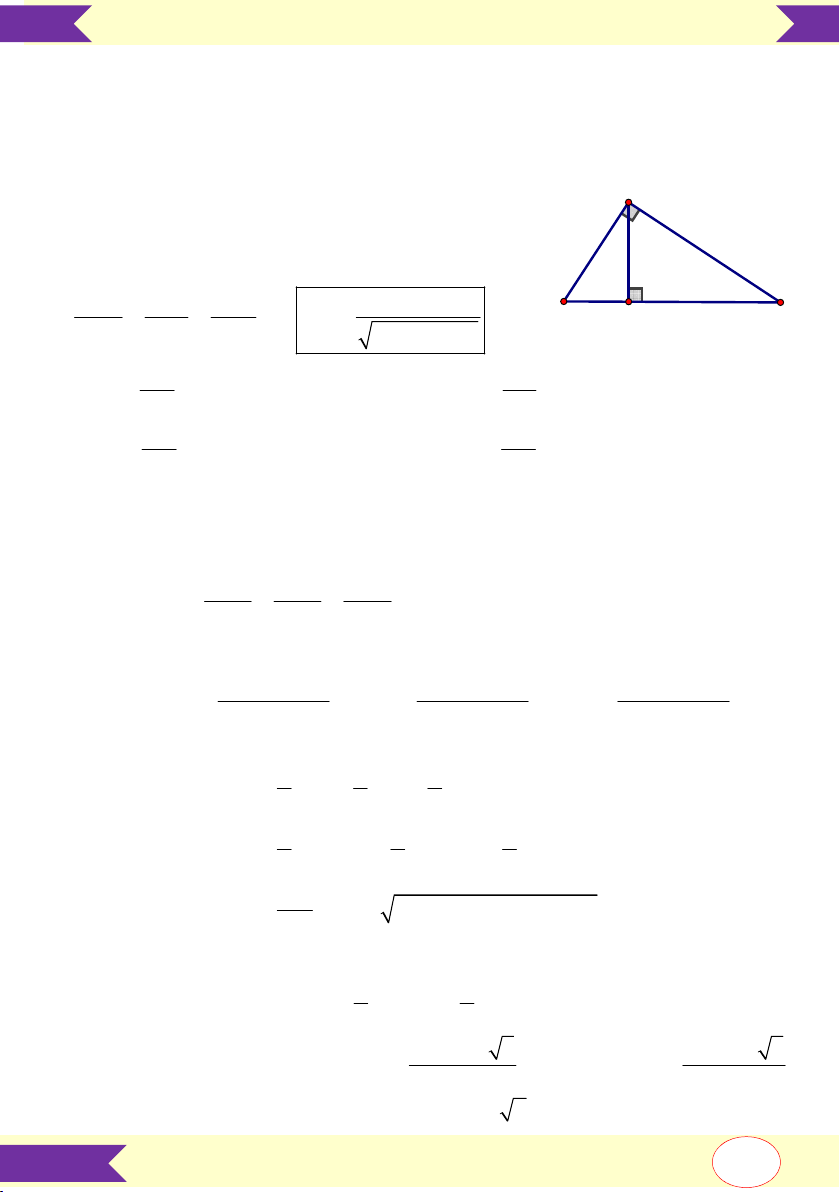
1. Hệ thức lượng trong tam giác vuông. Tỉ số lượng giác Pitago ▪ 2 2 2 AB AC BC ; A ▪ 2
AB BH .BC ; 2
AC CH .BC ; ▪ 2
AH BH .CH ; AH .BC . AB AC ; 1 1 1 A . B AC ▪ B C AH . H 2 2 2 AH AB AC 2 2 AB AC AC AB ▪ sin B (đối/huyền); ▪ cos B (kề/huyền); BC BC AC AB ▪ tan B (đối/kề) ; ▪ cot B (kề/đối). AB AC
2. Định lý sin. Định lý côsin. Diện tích tam giác
Gọi: R, r, p lần lượt là bán kính đường tròn ngoại tiếp, bán kính đường tròn nội
tiếp và nửa chu vi của một tam giác. a b c ▪ ĐL sin: 2R . sin A sin B sin C ▪ ĐL côsin: 2 2 2
a b c 2 .
bc cos A ; 2 2 2
b a c 2a .
c cos B ; 2 2 2
c a b 2a . b cos . C 2 2 2
b c a 2 2 2
a c b 2 2 2
a b c
Hệ quả: cos A ; cos B ; cos C . 2bc 2ac 2ab
(tổng bình phương hai cạnh kề trừ bình phương cạnh đối; chia 2 lần tích hai cạnh kề) 1 1 1 ▪ Diện tích: S h .a h .b h .c ; A BC 2 a 2 b 2 c 1 1 1 S a . b sin C a . c sin B b . c sin A ; A BC 2 2 2 abc S pr
p( p a)( p b)( p b) . A BC 4R
3. Công thức nhanh tính diện tích một số hình thường gặp 1 1
ABC vuông tại A : S A . B AC AH.BC . A BC 2 2 (canh) 3 2 (canh) . 3 Tam giác đều: ▪ Đường cao . ▪ Diện tích: . 2 4 Hình vuông:
▪ Đường chéo (canh) 2. ▪ Diện tích: 2 (canh) .
TỔ TOÁN – TRƯỜNG THPT PHẠM PHÚ THỨ 3
TÀI LIỆU ÔN THI TN THPT 2025 dcd
Hình chữ nhật ABCD : ▪ Đường chéo 2 2 AB AD . ▪ Diện tích: S .
AB AD (dài x rộng).
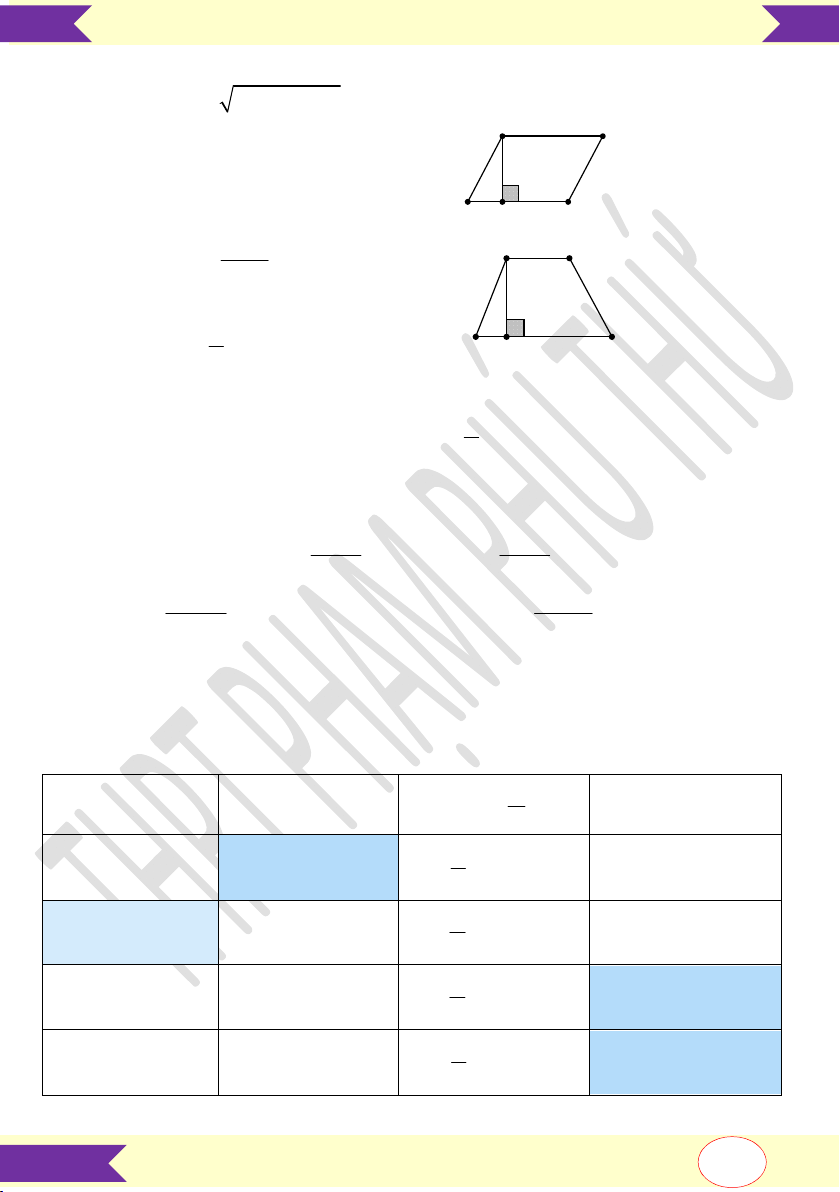
Hình bình hành: S . a h . A D
(cạnh đáy x đường cao tương ứng) h B H a C a b a
Hình thang: S .h . A D 2
(trung bình cộng hai đáy x chiều cao). h 1
Hình thoi: S
x tích 2 đường chéo. B C 2 H b
Đặc biệt: Hình thoi có một góc bằng 60 hoặc 120 được tạo bởi 2 tam giác đều. 1
Tứ giác có hai đường chéo vuông góc: S
x tích 2 đường chéo. 2
II. CÔNG THỨC LƯỢNG GIÁC
1. Các hệ thức cơ bản sin cos ▪ 2 2
sin cos 1; ▪ tan ; ▪ cot ; ▪ tan.cot 1; cos sin 1 1 ▪ 2 1 tan ; ▪ 2 1 cot . 2 cos 2 sin k 2n k 2n 1 k ▪ sin(
k ) sin ; ▪ si
n( k ) sin ; ▪ tan( k ) tan .
cos( k ) cos
cos( k ) cos
cot( k ) cot
2. Các góc lượng giác có liên quan đặc biệt
Đối: ;
Bù: ; Phụ: ;
Khác pi: ; 2 sin(
) sin sin( ) sin sin cos
sin( ) sin 2 cos(
) cos cos( ) cos cos sin
cos( ) cos 2 tan(
) tan tan( ) tan tan cot tan( ) tan 2 cot(
) cot cot( ) cot cot tan cot( ) cot 2 3. Công thức cộng
TỔ TOÁN – TRƯỜNG THPT PHẠM PHÚ THỨ 4
SỔ TAY KIẾN THỨC TOÁN 12 dcd
▪ sin(a b) sin .
a cos b cos .
a sin b ; ▪ sin(a b) sin .
a cos b cos . a sin b ;
▪ cos(a b) cos .
a cos b sin .
a sin b ; ▪ cos(a b) cos .
a cos b sin . a sin b ; tan a tan b tan a tan b
▪ tan(a b) ;
▪ tan(a b) . 1 tan . a tan b 1 tan . a tan b
4. Công thức nhân đôi. Hạ bậc
▪ sin 2 2 sin .cos ; ▪ cos 2 2 2 2 2
cos sin 2 cos 1 1 2 sin ; 2 tan ▪ tan 2 ; 2 1 tan ▪ 2 1 cos 2 sin ; ▪ 2 1 cos 2 cos ; ▪ 2 1 cos 2 tan . 2 2 1 cos 2
5. Công thức tổng thành tích a b a b a b a b
▪ cos a cos b 2 cos .cos
; ▪ sin a sin b 2 sin .cos ; 2 2 2 2 a b a b a b a b
▪ cos a cos b 2 sin .sin
; ▪ sin a sin b 2 cos .sin ; 2 2 2 2 ▪ sin cos 2 . sin 2 . cos ; 4 4 ▪ sin cos 2 sin 2 cos . 4 4
6. Công thức tích thành tổng 1 1 ▪ cos . a cos b
cos(a b) cos(a b) ; ▪ sin . a sin b
cos(a b) cos(a b) ; 2 2 1 ▪ sin . a cos b
sin(a b) sin(a b) . 2
7. Kỹ thuật làm mất dấu TRỪ
▪ sin sin(
) ; ▪ cos cos( ) ; ▪ tan tan(
) ; ▪ cot cot( ).
III. CÔNG THỨC MŨ – LOGARIT
1. Công thức lũy thừa
Cho các số dương a, b . Ta có: n 1 ▪ 0 a 1 ▪ n a . a . a ..a với * n ▪ a ▪ ( m )n mn ( n )m a a a n n thua so a m n a n a a ▪ m . n m n a a a ▪ mn a ▪ n n ( )n a b ab ▪ n a n b b n 1 1 ▪ m n m a a với * ,
m n . Đặc biệt: 2 a a ; 3 3 a a .
TỔ TOÁN – TRƯỜNG THPT PHẠM PHÚ THỨ 5
TÀI LIỆU ÔN THI TN THPT 2025 dcd
2. Công thức logarit
Cho các số a, b 0, a 1 và , m n . Ta có: log b a b
lg b log b log b
ln b log b a 10 e log 1 0 log a 1 log n a n a a a 1 n log b b log n
b n log b log n b b m log m loga a m a a a a m log b b a a b
log (bc) log b log c
log log b log c a a a a a a c log c log a b b a c log c 1 a log .
b log c log c log c log b a b a log b b a log a a b b 1 b 1 b 1
3. Hàm số mũ và hàm số logarit Hàm số mũ Hàm số logarit x Dạng
y a với 0 a 1
y log x với 0 a 1 a Tập xác định D D 0; y Tập giá trị y 0; Đạo hàm x x y a
y a ln a 1
y log x y a x ln a Sự biến thiên
a 1 thì hàm ĐB trên
a 1 : hàm ĐB trên (0; )
0 a 1 thì hàm NB trên
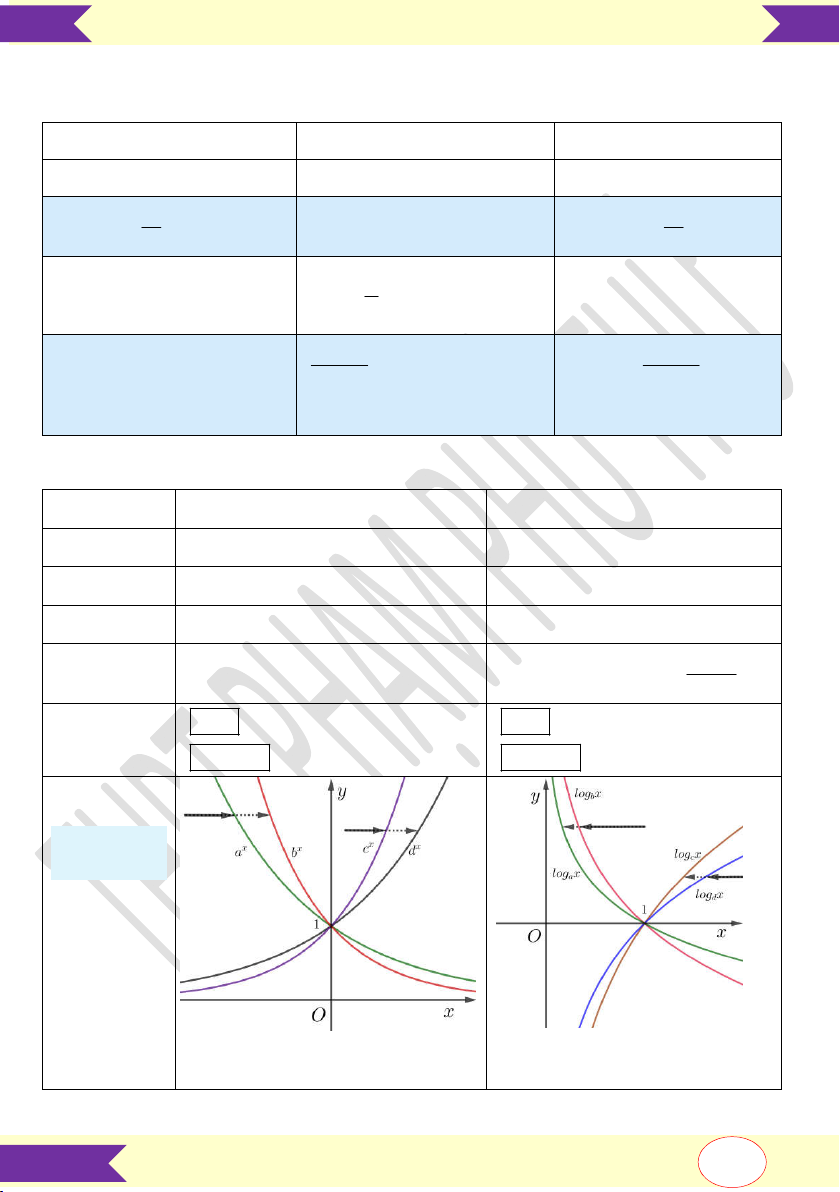
0 a 1 : hàm NB trên (0; ) Đồ thị “trên mũ; phải log” Để so sánh a, ,
b c, d ta vẽ đường Để so sánh a, , b , c d ta vẽ thẳng x 1.
đường thẳng y 1.
TỔ TOÁN – TRƯỜNG THPT PHẠM PHÚ THỨ 6
SỔ TAY KIẾN THỨC TOÁN 12 dcd
CHỦ ĐỀ 1. PHƯƠNG TRÌNH VÀ BẤT PHƯƠNG TRÌNH
I. PHƯƠNG TRÌNH LƯỢNG GIÁC
1. Phương trình lượng giác cơ bản
a) Phương trình sinx m (1)
Với m 1 , phương trình (1) vô nghiệm.
Với m 1 , gọi là số thực thuộc đoạn ; sao cho sin m. 2 2
x k 2
Khi đó, ta có: sinx m sinx sin k .
x k 2
Chú ý: Ta có một số trường hợp đặc biệt sau của phương trình sinx m
sinx 1 x
k 2 k ; 2 sinx 1 x
k 2 k ; 2
sinx 0 x k k .
Nếu x là góc lượng giác có đơn vị đo là độ thì ta có thể tìm góc lượng giác x sao cho
x a k360
sinx sina như sau: sinx sina k .
x 180 a k360
b) Phương trình cosx m (2)
Với m 1 , phương trình (2) vô nghiệm.
Với m 1 , gọi là số thực thuộc đoạn 0; sao cho cos m .
x k 2
Khi đó, ta có: cosx m cosx cos k . x k 2
Chú ý: Ta có một số trường hợp đặc biệt sau của phương trình cosx m
cosx 1 x k 2 k ; cosx 1
x k 2 k ;
cosx 0 x
k k . 2
Nếu x là góc lượng giác có đơn vị đo là độ thì ta có thể tìm góc lượng giác x sao cho
x a k360
cosx cosa như sau: cosx cosa k .
x a k360
TỔ TOÁN – TRƯỜNG THPT PHẠM PHÚ THỨ 7
TÀI LIỆU ÔN THI TN THPT 2025 dcd
c) Phương trình tanx m
Gọi là số thực thuộc khoảng ;
sao cho tan m . 2 2
Khi đó, ta có: tanx m tanx tan x k k .
Nếu x là góc lượng giác có đơn vị đo là độ thì ta có thể tìm góc lượng giác x sao
cho tanx tana như sau: tanx tana x a 1
k 80 k .
d) Phuơng trình cotx m
Gọi là số thực thuộc đoạn 0; sao cho cot m .
Khi đó, ta có: cotx m cotx cot x k k Z .
Nếu x là góc lượng giác có đơn vị đo là độ thì ta có thể tìm góc lượng giác x sao
cho cotx cota như sau: cotx cot x 180 k k .
2. Phương trình lượng giác đưa về dạng cơ bản
f x g x k2
sinf x sing x k .
f x g x k2
f x g x k2
cosf x cosg x k .
f x g x k2
Với phương trình có dạng: 2u x 2 v x 2u x 2 v x 2u x 2 sin sin , cos cos , sin
cos v x
ta có thể dùng công thức hạ bậc để đưa về phương trình dạng
cosf x cosg x .
Với một số phương trình lượng giác khác, ta có thể dùng các công thức lượng giác
và các biến đổi để đưa về phương trình dạng tích A x.B x 0 .
II. PHƯƠNG TRÌNH, BẤT PHƯƠNG TRÌNH MŨ VÀ LÔGARIT 1. Phương trình mũ Với f x
a 0, a 1 thì: a
b f x log b với b 0 ; a f x g x a a
f x g x .
TỔ TOÁN – TRƯỜNG THPT PHẠM PHÚ THỨ 8
SỔ TAY KIẾN THỨC TOÁN 12 dcd
2. Phương trình lôgarit
Vơi a 0, a 1 thì:
log f x b f x b a . a
f x 0 ho c
a g x 0
log f x log g x . a a f
x g x
3. Bất phương trình mũ
Với a 0, a 1 thì:
a) Xét bất phương trình: f x a b .
Nếu b 0 , tập nghiệm của bất phương trình là tập xác định của f x ;
Nếu b 0, a 1 thì bất phương trình đưa về: f x log b ; a
Nếu b 0, 0 a 1 thì bất phương trình đưa về: f x log b . a
b) Xét bất phương trình: f x g x a a .
Nếu a 1 thì bất phương trình đưa về: f x g x ;
Nếu 0 a 1 thì bất phương trình đưa về: f x g x .
Các bất phương trình mũ khác cùng loại được giải tương tự.
4. Bất phương trình lôgarit
Với a 0, a 1 thì:
a) Xét bất phương trình: log f x b . a
Nếu a 1 thì bất phương trình đưa về: b f x a ;
Nếu 0 a 1 thì bất phương trình đưa về: 0 b f x a .
b) Xét bất phuơng trình: log f x log g x . a a
Nếu a 1 thì bất phương trình đưa về: f x g x 0 ;
Nếu 0 a 1 thì bất phương trình đưa về: 0 f x g x .
Các bất phương trình lôgarit khác cùng loại được giải tương tự.
TỔ TOÁN – TRƯỜNG THPT PHẠM PHÚ THỨ 9
TÀI LIỆU ÔN THI TN THPT 2025 dcd
CHỦ ĐỀ 2. CẤP SỐ CỘNG VÀ CẤP SỐ NHÂN I. CẤP SỐ CỘNG 1. Định nghĩa
Dãy số u là cấp số cộng nếu u u
d với n 2, d là số không đổi. n n n 1
Số d gọi là công sai của cấp số cộng, d u u với n 2 . n n 1
Nếu d 0 thì cấp số cộng là một dãy số không đổi.
2. Số hạng tổng quát
Cấp số cộng u với số hạng đầu u và công sai d có: u u n 1 d với n 2. n 1 n 1
Chú ý: Ba số a, ,
b c theo thứ tự lập thành CSC a c 2b .
3. Tổng n số hạng đầu
Cho cấp số cộng u có số hạng đầu u và công sai d . n 1
Đặt S u u u , ta có: n 1 2 n u u n
2u n 1 d n 1 1 n S hoặc S . n 2 n 2 II. CẤP SỐ NHÂN 1. Định nghĩa
Dãy số u là cấp số nhân nếu u u .q với n 2, q là số không đổi. n n n 1
Số q gọi là công bội của cấp số nhân. u
Nếu u 0 với mọi * n thì: n q với n 2 . n un 1
Nếu q 1 thì cấp số nhân là một dãy số không đổi.
2. Số hạng tổng quát
Cấp số nhân u với số hạng đầu u và công bội q có: n 1 u u q với n 2 . n 1 n 1
Chú ý: Ba số a, ,
b c theo thứ tự lập thành CSN 2 . a c b .
3. Tổng n số hạng đầu
Cho cấp số nhân u có số hạng đầu u và công bội q q 1 . n 1 u 1 n q 1
Đặt S u u u , ta có: S . n 1 2 n n 1 q u
Cấp số nhận lùi vô hạn: 1
S u u u ... lim S với q 1. 1 2 n n n 1 q
TỔ TOÁN – TRƯỜNG THPT PHẠM PHÚ THỨ 10
SỔ TAY KIẾN THỨC TOÁN 12 dcd
CHỦ ĐỀ 3. ĐẠO HÀM VÀ KHẢO SÁT HÀM SỐ I. ĐẠO HÀM 1. Định nghĩa
Cho hàm số y f x xác định trên khoảng a;b và điểm x a;b . Nếu tồn tại 0
f x f x0 giới hạn hữu hạn lim
thì giới hạn đó được gọi là đạo hàm cúa hàm x 0 x x x0
số y f x tại x và được kí hiệu là f x hoặc y x . 0 0 0
f x f x0 f x y x lim . 0
0 x 0x x x0
b) Ý nghĩa vật lí của đạo hàm
Đạo hàm xuất hiện trong nhiều khái niệm vật lí. Chẳng hạn: Xét chuyển động thẳng
xác định bởi phương trình s s t , với s s t là một hàm số có đạo hàm. Vận tốc
tức thời của chuyển động tại thời điểm t là đạo hàm của hàm số s s t tại t : 0 0 v t s t . 0 0
c) Ý nghĩa hình học của đạo hàm
Hệ số góc của tiếp tuyến của đồ thị hàm số y f x tại điểm M x ; f x là: 0 0 0
k f x . 0
Phương trình tiếp tuyến của đồ thị hàm số y f x tại điểm M x ; f x là: 0 0 0
y f x . x x f x . 0 0 0
d) Đạo hàm của hàm hợp
Nếu hàm số u g x có đạo hàm tại x là u và hàm số y f u có đạo hàm tại x
u là y thì hàm hợp y f g x có đạo hàm tại x là u
y y u . x u x
e) Đạo hàm của một số hàm số
Đạo hàm của hàm số sơ cấp
Đạo hàm của hàm hợp
cơ bản thường gặp
(ở đây u u x )
TỔ TOÁN – TRƯỜNG THPT PHẠM PHÚ THỨ 11
TÀI LIỆU ÔN THI TN THPT 2025 dcd n x n 1 n x n u n 1
n u u 1 1 1 u 2 x x 2 u u 1 u ( x ) ( u ) 2 x 2 u
(sinx) cosx
(sinu) u cosu
(cosx) sinx
(cosu) u sinu 1 u (tanx) (tanu) 2 cos x 2 cos u 1 u (cotx) (cotu) 2 sin x 2 sin u x x e e u u e u e x x a a lna u u a
u a lna 1 u (lnx) (lnu) x u 1 u log x log u a a xlna ulna
g) Đạo hàm của tổng, hiệu, tích, thuơng
Giả sử f f x , g g x là các hàm số có đạo hàm tại điểm x thuộc khoảng xác định. Ta có:
( f g) f g ;
( f g ) f g ; f f g fg
( fg ) f g fg ;
( g g x 0 ) . 2 g g
Hệ quả: Cho f f x là hàm số có đạo hàm tại điểm x thuộc khoảng xác định. ▪ Nếu 1 f
c là một hằng số thì: (cf ) cf . ▪ f f x 0 . 2 f f
TỔ TOÁN – TRƯỜNG THPT PHẠM PHÚ THỨ 12
SỔ TAY KIẾN THỨC TOÁN 12 dcd
II. TÍNH ĐƠN ĐIỆU CỦA HÀM SỐ 1. Định lí
Cho hàm số y f x có đạo hàm trên tập K , trong đó K là một khoảng,
đoạn hoặc nửa khoảng. Nếu f x 0 (hoặc f x 0 ) với mọi x thuộc K và
f x 0 chỉ tại một số hữu hạn điểm của K thì hàm số f x đồng biến (hoặc
nghịch biến) trên K .
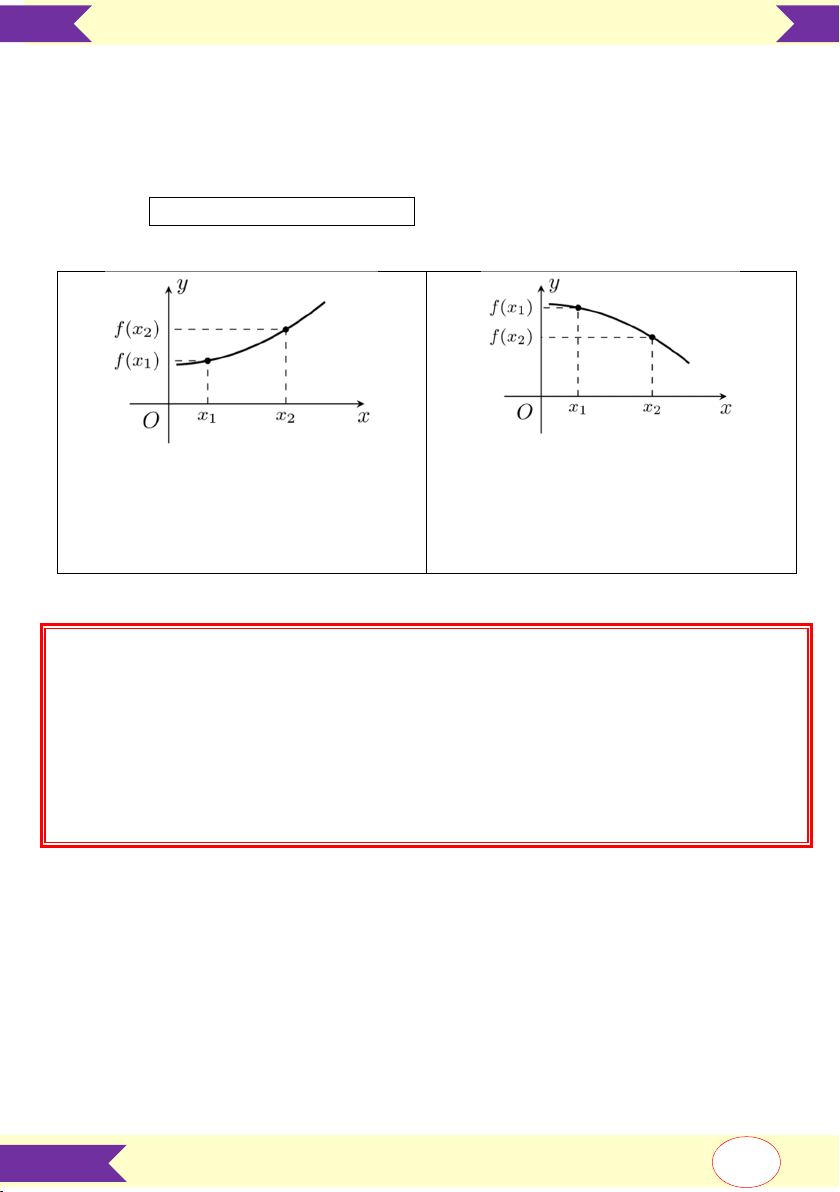
Hàm đồng biến trên K
Hàm nghịch biến trên K
f x 0 x K
f x 0 x K
đồ thị là một "đường đi lên"
đồ thị là một "đường đi xuống"
2. Các bước tìm khoảng đồng biến, nghịch biến của hàm số f x
Bước 1. Tìm tập xác định của hàm số y f x .
Bước 2. Tính đạo hàm f x . Tìm các điểm x i 1, 2,, n mà tại đó hàm số có i
đạo hàm bằng 0 hoặc không tồn tại.
Bước 3. Sắp xếp các điểm x theo thứ tự tăng dần và lập bảng biến thiên. i
Bước 4. Căn cứ vào bảng biến thiên, nêu kết luận về các khoảng đồng biến, nghịch biến của hàm số.
Chú ý: Ta cũng có thể nhận biết tính đơn điệu của hàm số bằng cách quan sát hình
dáng của đồ thị hàm số đó:
Khoảng đi lên (hàm số đồng biến trên khoảng đó);
Khoảng đi xuống (hàm số nghịch biến trên khoảng đó).
III. ĐIỂM CỰC TRỊ, GIÁ TRỊ CỰC TRỊ CỦA HÀM SỐ 1. Định nghĩa
TỔ TOÁN – TRƯỜNG THPT PHẠM PHÚ THỨ 13
TÀI LIỆU ÔN THI TN THPT 2025 dcd
Cho hàm số y f x liên tục trên tập
K R , trong đó K là một khoảng, đoạn
hoặc nửa khoảng và x K , x K . 0 1
x được gọi là một điểm cực đại của 0
hàm số đã cho nếu tồn tại một khoảng
a;b chứa điểm x sao cho a;b K 0
và f x f x với mọi x a;b và 0 x x . 0
Khi đó, f x được gọi là giá trị cực đại 0
của hàm số đã cho, kí hiệu là f CĐ
x được gọi là một điểm cực tiểu của hàm số đã cho nếu tồn tại một khoảng 1 ;
c d chứa điểm x sao cho ;
c d K và f x f x với mọi x ; c d và 1 1 x x . 1
Khi đó, f x được gọi là giá trị cực tiểu của hàm số đã cho, kí hiệu là f . 1 CT
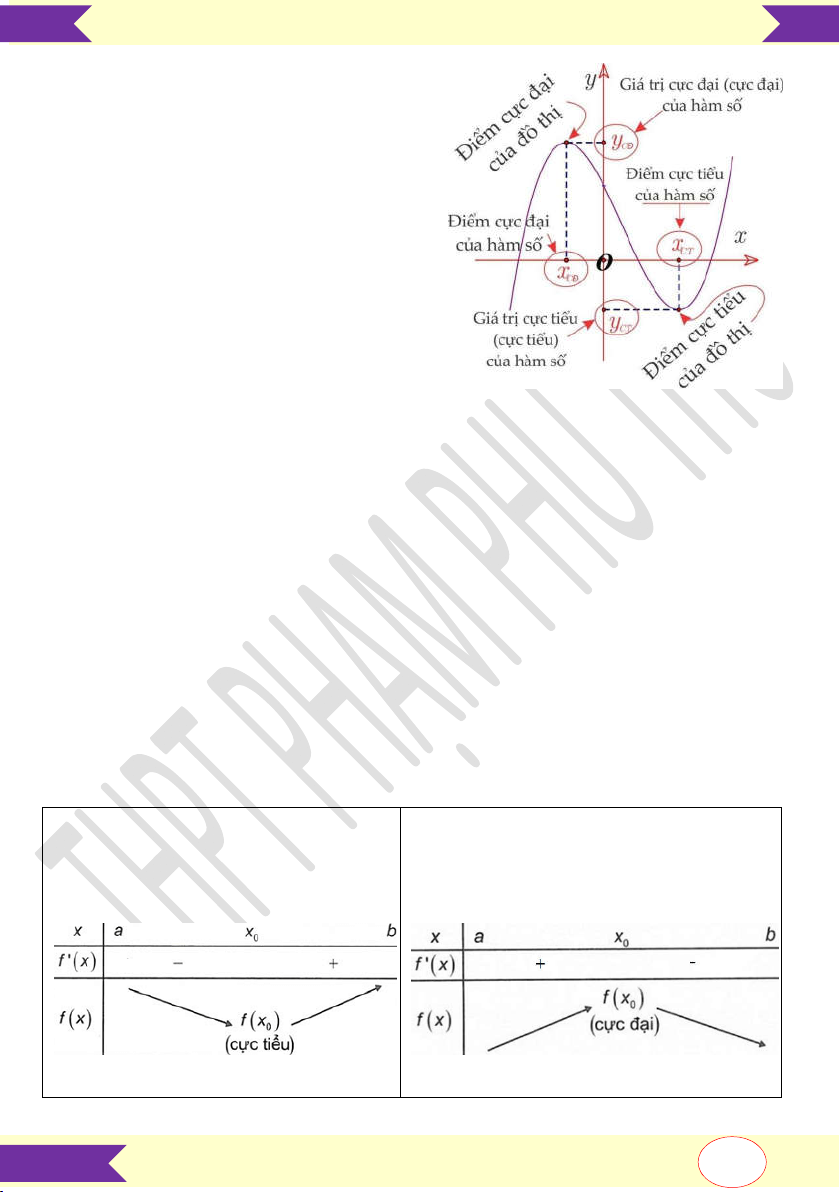
Điểm cực đại và điểm cực tiểu được gọi chung là điểm cưc trị. Giá trị cực đại và
giá trị cực tiểu được gọi chung là giá trị cực trị (hay cực trị).
Chú ý: Nếu x là một điểm cực trị của hàm số y f x thì điểm M x ; f x 0 0 0
được gọi là điểm cực trị của đồ thị hàm số y f x .
b) Dấu hiệu nhận biết cực trị của hàm số bằng đạo hàm
Giả sử hàm số f x liên tục trên khoảng a;b chứa điểm x và có đạo hàm trên 0
các khoảng a; x và x ;b . Khi đó 0 0
Nếu f x 0 với mọi x a; x và Nếu f x 0 với mọi x a; x và 0 0
f x 0 với mọi x x ;b thì hàm
f x 0 với mọi x x ;b thì hàm số 0 0
số f x đạt cực tiểu tại điểm x .
f x đạt cực đại tại điểm x . 0 0
TỔ TOÁN – TRƯỜNG THPT PHẠM PHÚ THỨ 14
SỔ TAY KIẾN THỨC TOÁN 12 dcd
c) Các Bước để tìm điểm cực trị của hàm số f x
Bước 1. Tìm tập xác định của hàm số f x .
Bước 2. Tính đạo hàm f x . Tìm các điểm x i 1, 2,, n mà tại đó hàm số có i
đạo hàm bằng 0 hoặc không tồn tại.
Bước 3. Sắp xếp các điểm x theo thứ tự tăng dần và lập bảng biến thiên. i
Bước 4. Căn cứ vào bảng biến thiên, nêu kết luận về các điểm cực trị của hàm số.
IV. GIÁ TRỊ LỚN NHẤT VÀ GIÁ TRỊ NHỎ NHẤT CỦA HÀM SỐ 1. Định nghĩa
Cho hàm số y f x xác định trên tập D .
Số M được gọi là giá trị lớn nhất của hàm số y f x trên D , kí hiệu
M max f x , nếu f x M với mọi xD và tồn tại x D sao cho 0 D
f x M . 0
Số m được gọi là giá trị nhỏ nhất của hàm số y f x trên D , kí hiệu
m min f x , nếu f x m với mọi xD và tồn tại x D sao cho 1 D
f x m . 1
2. Cách tìm giá trị lớn nhất, giá trị nhỏ nhất của hàm số bằng đạo hàm
Giả sử hàm số f x liên tục trên đoạn a;b và có đạo hàm trên khoảng a;b , có
thể trừ một số hữu hạn điểm. Nếu f x 0 chỉ tại một số hữu hạn điểm thuộc
khoảng a;b thì ta có quy tắc tìm giá trị lớn nhất và giá trị nhỏ nhất của hàm số
f x trên đoạn a;b như sau:
Bước 1. Tìm các điểm x , x ,, x thuộc khoảng a;b mà tại đó hàm số có đạo 1 2 n
hàm bằng 0 hoặc không tồn tại.
Bước 2. Tính f x , f x ,, f x , f a và f b . 1 2 n
Bước 3. So sánh các giá trị tìm được ở Bước 2.
Số lớn nhất trong các giá trị đó là giá trị lớn nhất của hàm số f x trên đoạn a;b
, số nhỏ nhất trong các giá trị đó là giá trị nhỏ nhất của hàm số f x trên đoạn a;b .
TỔ TOÁN – TRƯỜNG THPT PHẠM PHÚ THỨ 15
TÀI LIỆU ÔN THI TN THPT 2025 dcd
V. ĐƯỜNG TIỆM CẬN CỦA ĐỒ THỊ HÀM SỐ
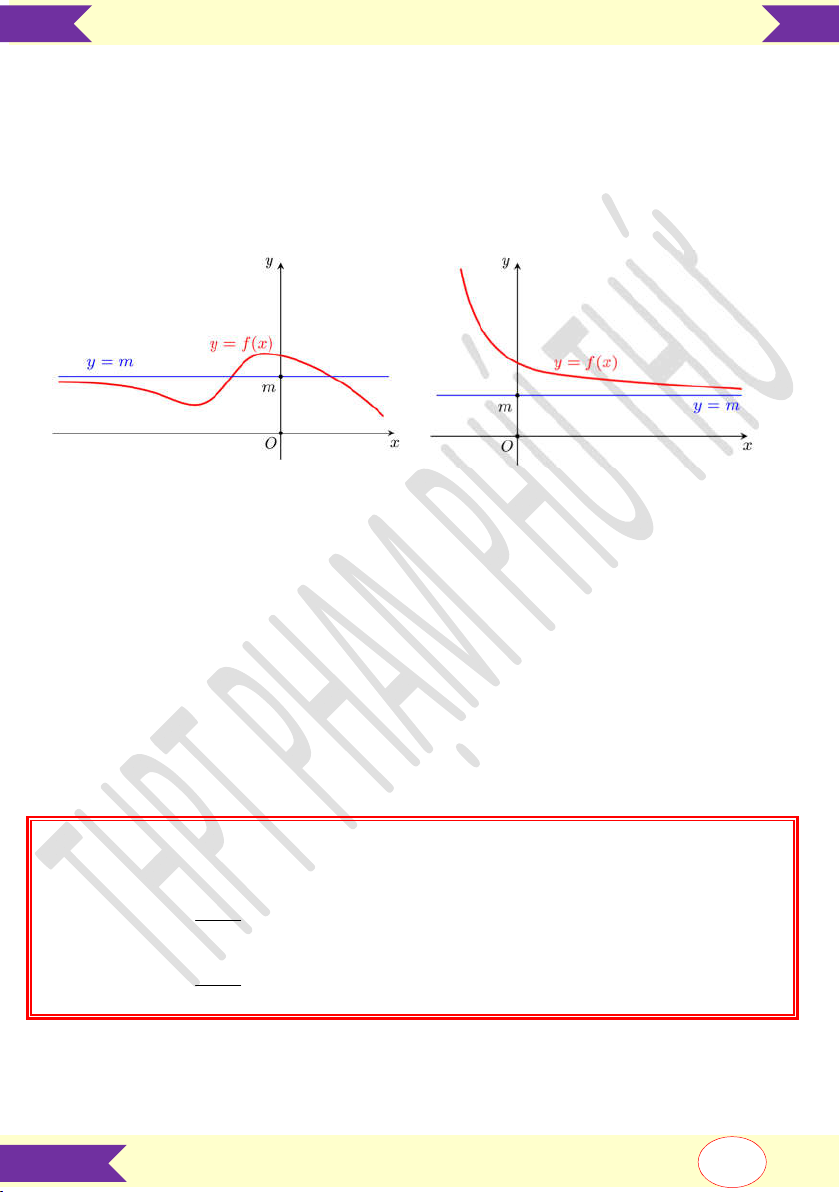
a) Đường tiệm cận ngang
Đường thẳng y m được gọi là đường tiệm cận ngang (hay tiệm cận ngang) của đồ
thị hàm số y f x nếu:
lim f x m hoặc
lim f x m x x
b) Đường tiệm cận đứng
Đường thẳng x x được gọi là đường tiệm cận đứng (hay tiệm cận đứng) của đồ 0
thị hàm số y f x nếu ít nhất một trong các điều kiện sau được thoả mãn:
lim f x
; lim f x
; lim f x
; lim f x . x x x x x x x x 0 0 0 0
c) Đường tiệm cận xiên
Đường thẳng y ax b a 0 được gọi là đường tiệm cận xiên (hay tiệm cận xiên)
của đồ thị hàm số y f x nếu:
lim f x ax b 0
hoặc lim f x ax b 0 . x x
Ta xác định hệ số a và b của tiệm cận xiên có phương trình y ax b trong 2 trường hợp sau: f (x)
1. Tính a lim
, b lim [ f (x) ax] . x x x f (x)
2. Tính a lim
, b lim [ f (x) ax] . x x x
TỔ TOÁN – TRƯỜNG THPT PHẠM PHÚ THỨ 16
SỔ TAY KIẾN THỨC TOÁN 12 dcd
VI. SƠ ĐỒ KHẢO SÁT HÀM SỐ
Bước 1. Tìm tập xác định của hàm số.
Bước 2. Xét sự biến thiên của hàm số
Tìm các giới hạn tại vô cực, giới hạn vô cực và tìm các đường tiệm cận của đồ thị (nếu có).
Lập bảng biến thiên của hàm số, bao gồm: Tính đạo hàm của hàm số, xét dấu
đạo hàm, xét chiều biến thiên và tìm cực trị của hàm số (nếu có), điền các kết quả vào bảng.
Bước 3. Vẽ đồ thị hàm số
Vẽ các đường tiệm cận (nếu có).
Xác định các điểm đặc biệt của đồ thị: cực trị, giao điểm của đồ thị với các trục
toạ độ (trong trường hợp đơn giản), ...
Nhận xét về đặc điểm của đồ thị: chỉ ra tâm đối xứng, trục đối xứng (nếu có).
TỔ TOÁN – TRƯỜNG THPT PHẠM PHÚ THỨ 17
TÀI LIỆU ÔN THI TN THPT 2025 dcd
CHỦ ĐỀ 4. NGUYÊN HÀM VÀ TÍCH PHÂN I. NGUYÊN HÀM 1. Định nghĩa
Cho K là một khoảng, đoạn hoặc nửa khoảng của tập số thực .
Cho hàm số f x xác định trên K . Hàm số F x được gọi là nguyên hàm của
hàm số f x trên K nếu F x f x với mọi x thuộc K .
Nếu F x là một nguyên hàm của hàm số f x trên K thì mọi nguyên hàm
của hàm số f x trên K đều có dạng F x C với C là một hằng số. Vì vậy:
f x dx F x C .
Mọi hàm số liên tục trên K đều có nguyên hàm trên K . Ta có:
F x dx F x C . 2. Tính chất
Cho f x , g x là hai hàm số liên tục trên K .
kf x dx k. f x dx
với k là hằng số khác 0 ;
f x g x dx f x dx g x dx ;
f x g x dx f x dx g x dx .
Nguyên hàm một số hàm số sơ cấp cơ bản 1 1 x x dx C với 1
dx ln x C 1 x 1
sinx dx cosx C
dx cotx C 2 sin x 1
cosx dx sinx C
dx tanx C 2 cos x x x a a dx C
với a 0, a 1. lna II. TÍCH PHÂN 1. Định nghĩa
Cho f x là hàm số liên tục trên a;b . Giả sử F x là một nguyên hàm của f x b
trên đoạn a;b . Khi đó
f x dx F b F a . a
TỔ TOÁN – TRƯỜNG THPT PHẠM PHÚ THỨ 18




