z 
Bài tập thủy lực đại cương c Y Ê Ê Ê Ê Ê Ê Ê Ê Ê Ê Ê Ê Ê Ê Ê Ê Ê Ê Ê Ê Ê Ê Ê Ê Ê Ê Ê Ê Ê Ê Ê 3 a Ê c Y Ê Ê c ÊÊÊ ÊÊÊÊ
Hӑ và tên: NguyӉn Thành Trung Lӟp: 53CG2 MSSV: 2461.53
Bài tұp chương 2: Thӫy tĩnh hӑc
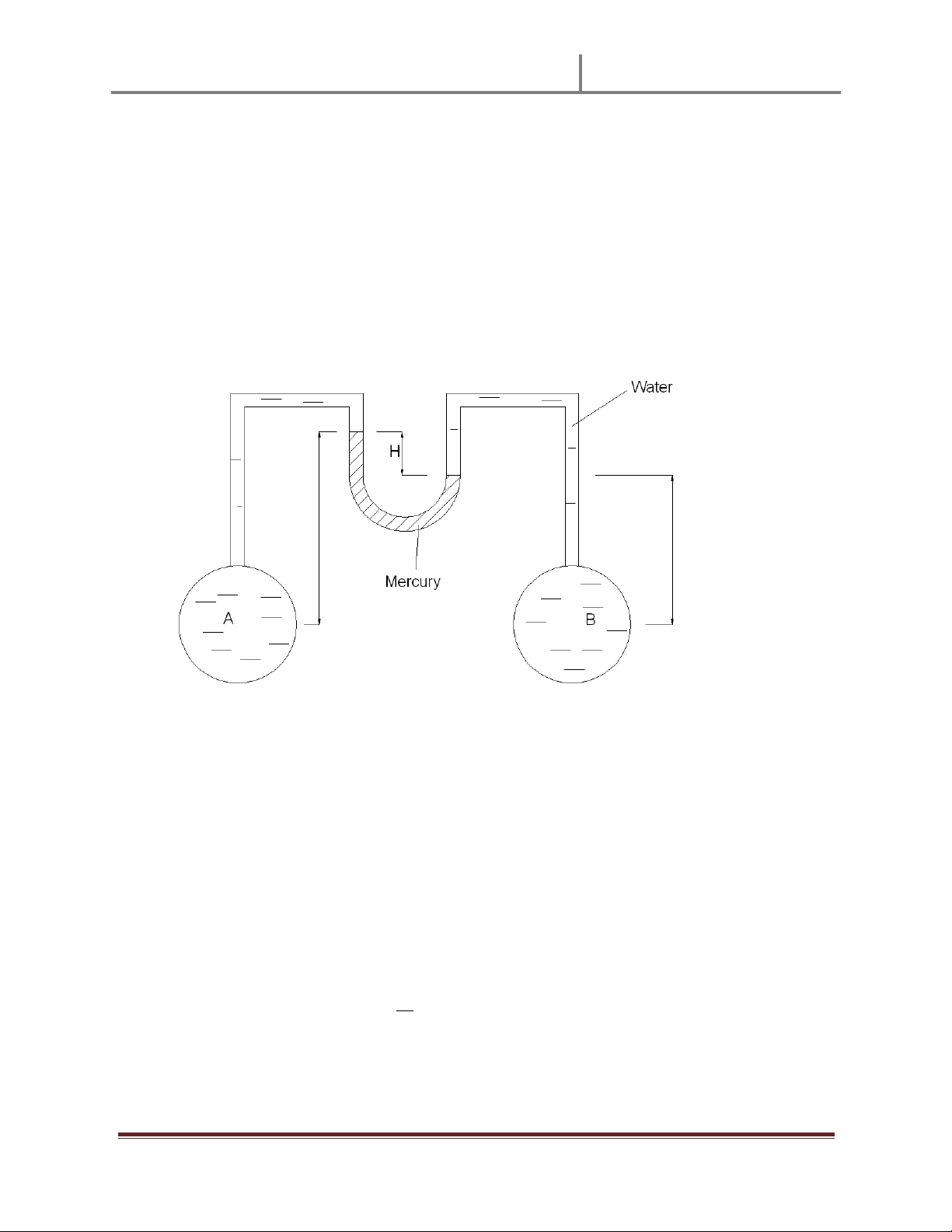
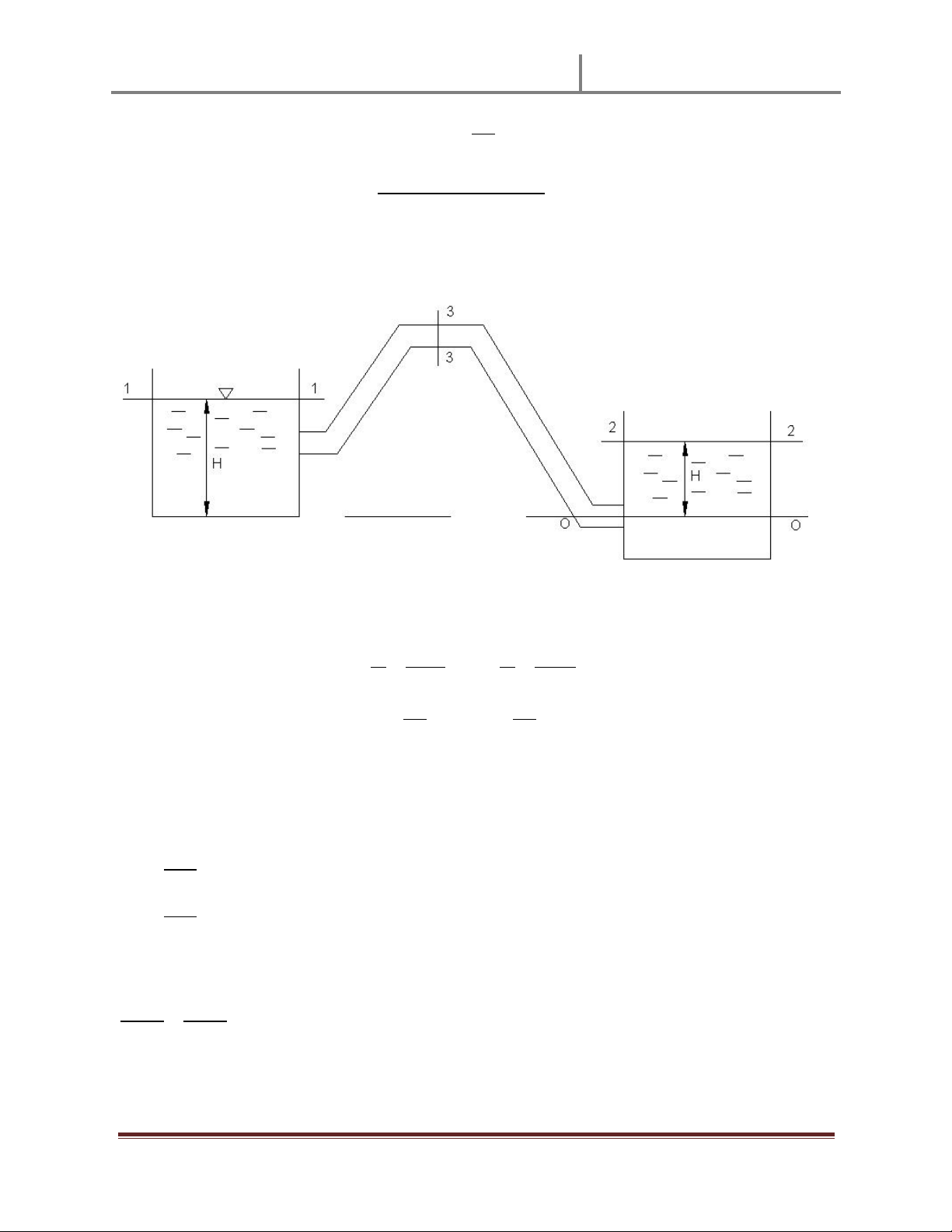
cÊÊ: Theo bài ra ta có sơ đ ӗ như hình vӁ: Ê Ê Ê Ê Ê Ê Ê Ê Ê Ê Ê Êt tҥi điӇm A là: ù ù Êt tҥi điӇm B là: ù ù
!y (1) ± (2) ta đưӧc đӝ chênh áp sut tҥi A và B ù ù ù ù
Mһt khác ta lҥi có: ù ù ; Vұy ta suy ra đưӧc: ù ù Du ³-³ nghĩa là ù ù 3 a Ê c Y Ê Ê Bài 2.11 :
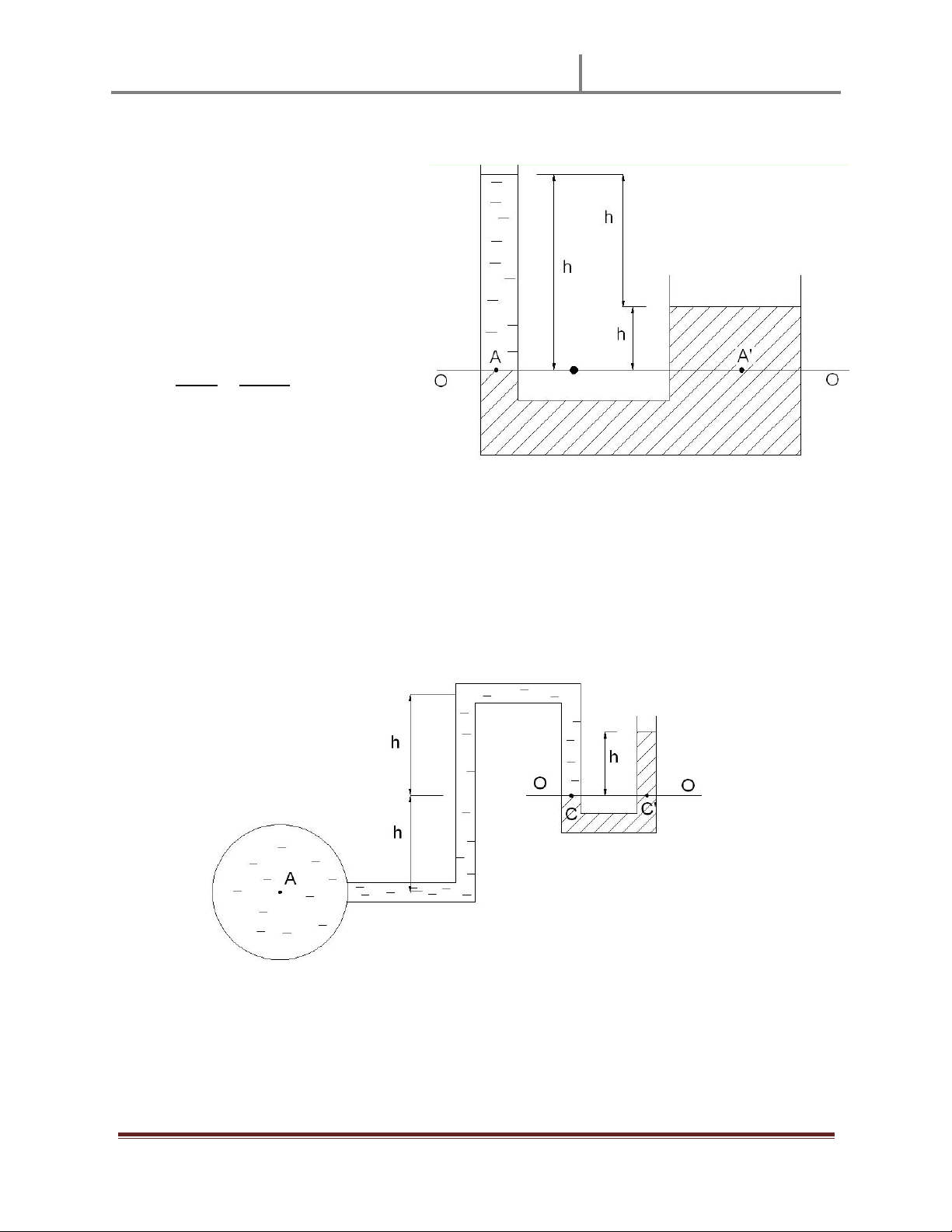
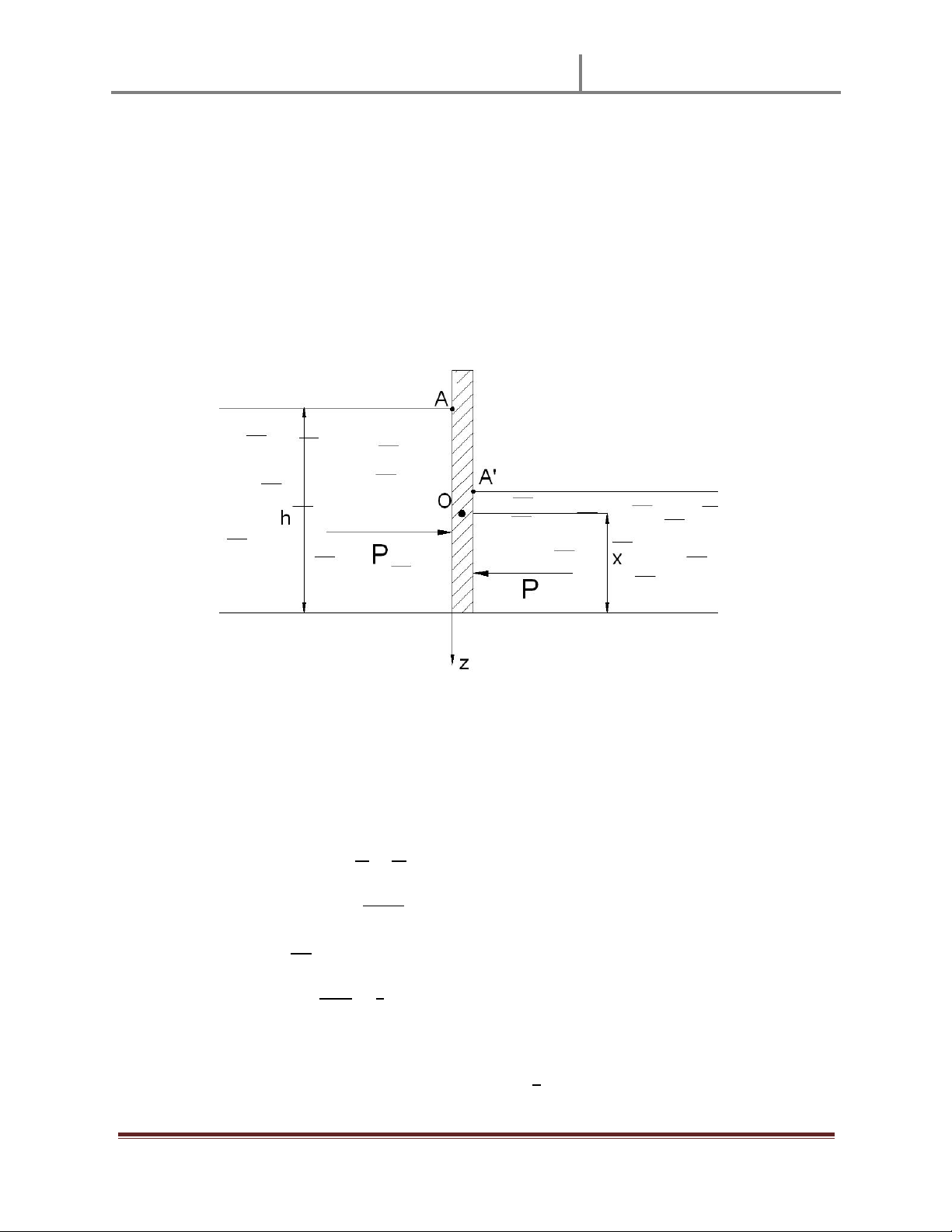
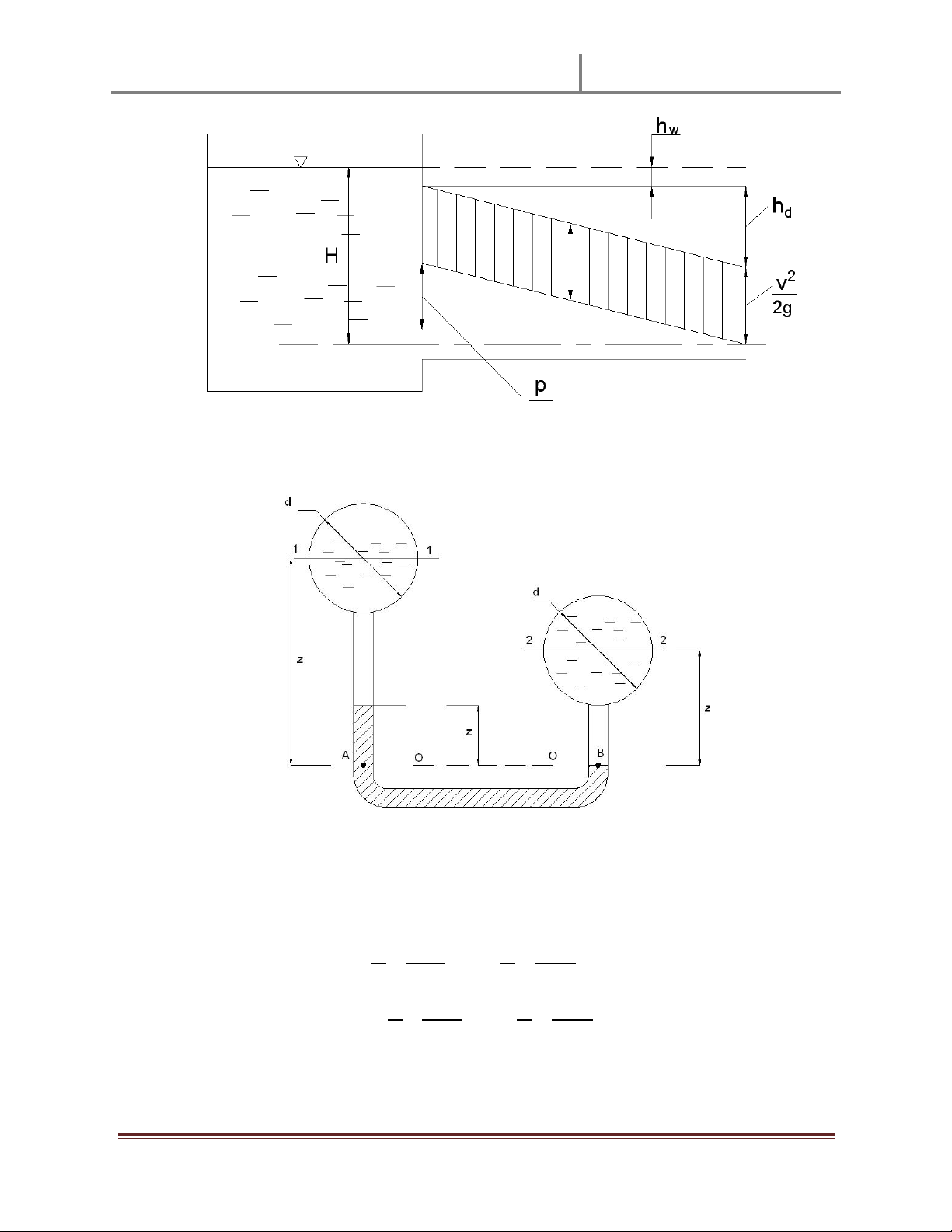
Xét áp sut dư tҥi 2 điӇm A và A¶ thuӝc cùng 1 mһt đҷng áp 0-0: Vӟi: Tӯ đó ta có !! Hay " Theo hình vӁ trên ta có: # $!! %&' $" Bài 2-12 (28)
Áp sut dư tҥi điӇm A đưӧc tính bӣi: () *
Xét áp sut dư tҥi 2 điӇm C và C¶ thuӝc cùng 1 mһt đҷng áp 0-0: + + 3 a Ê c Y Ê Ê Mà: + , () / () # $ -## .- " Hay : () #&0 Bài 2-23:
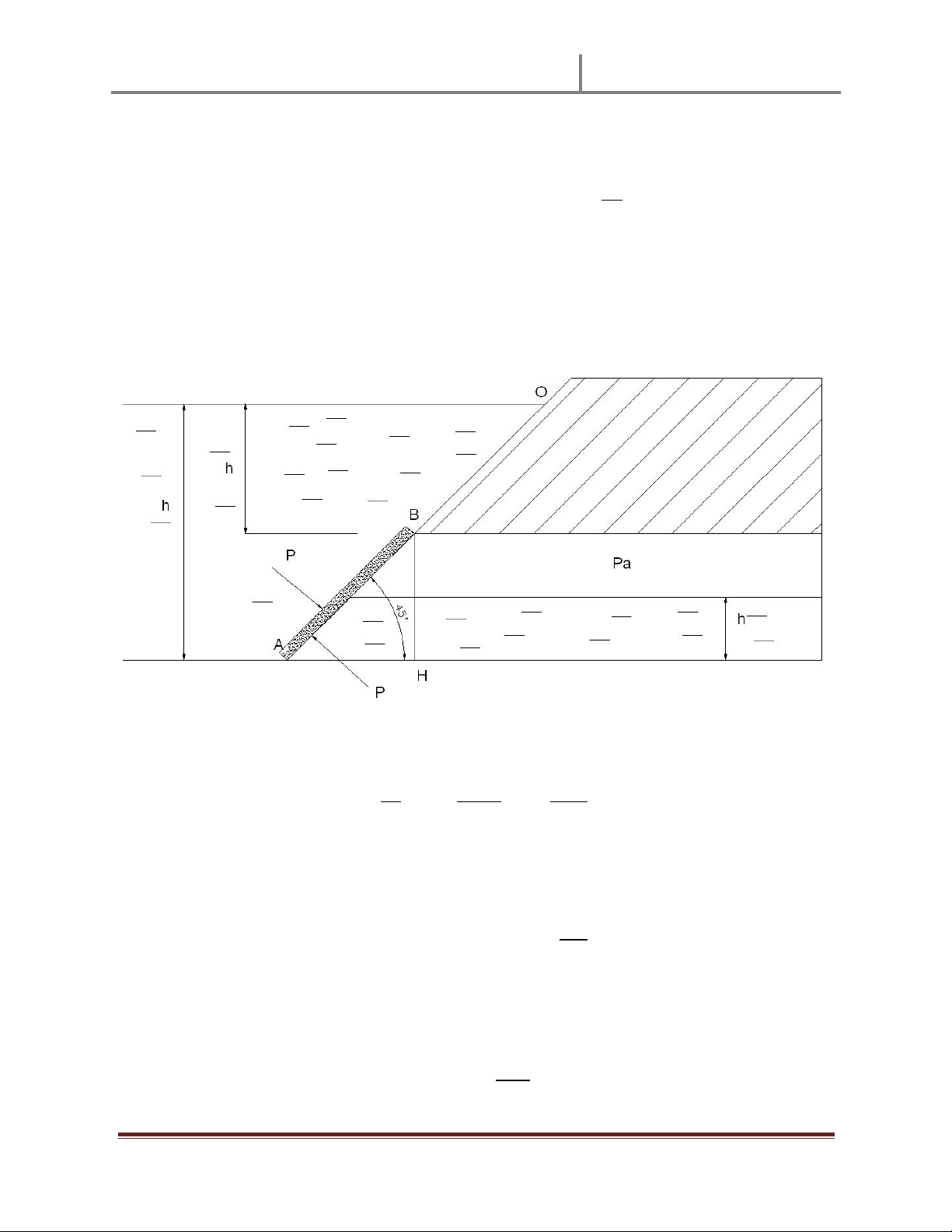
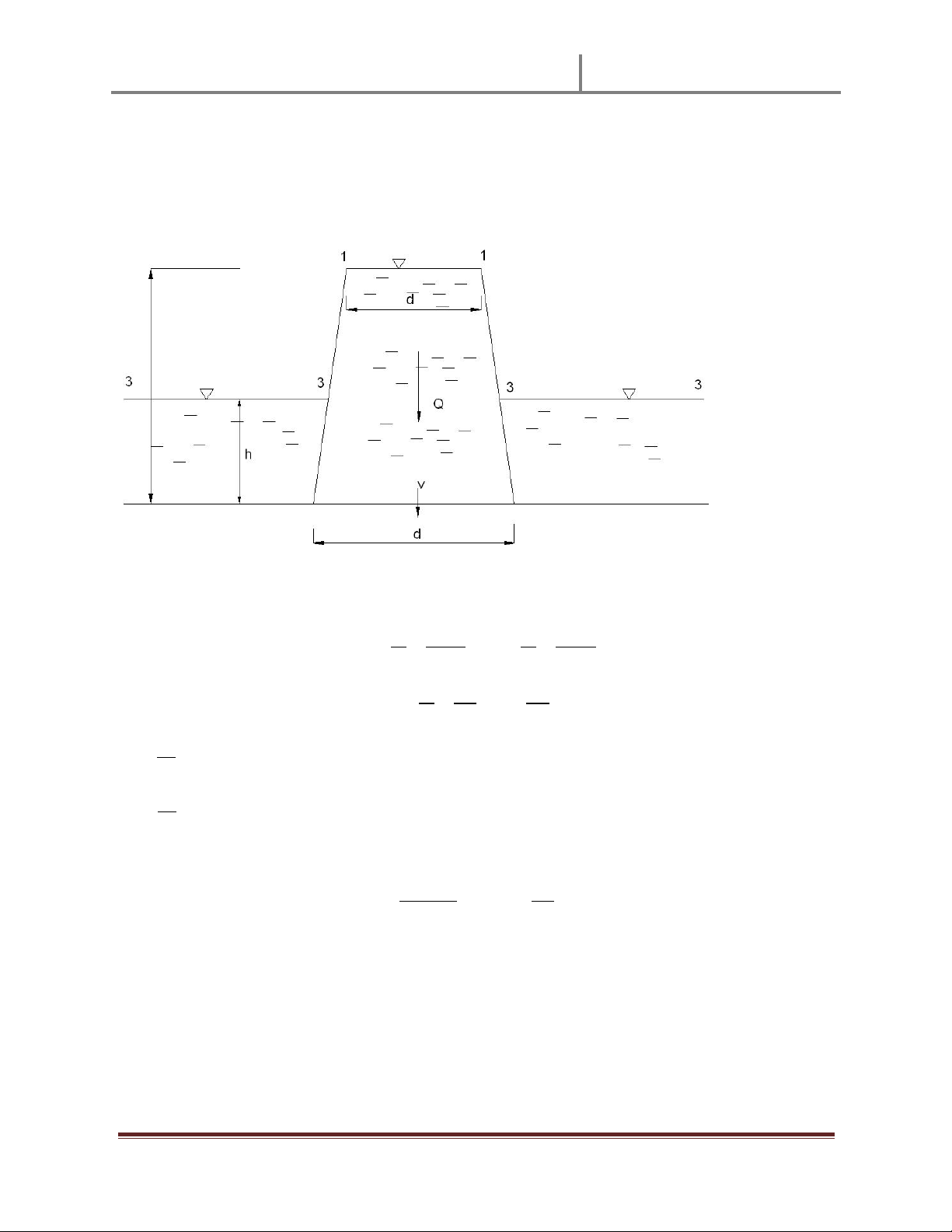
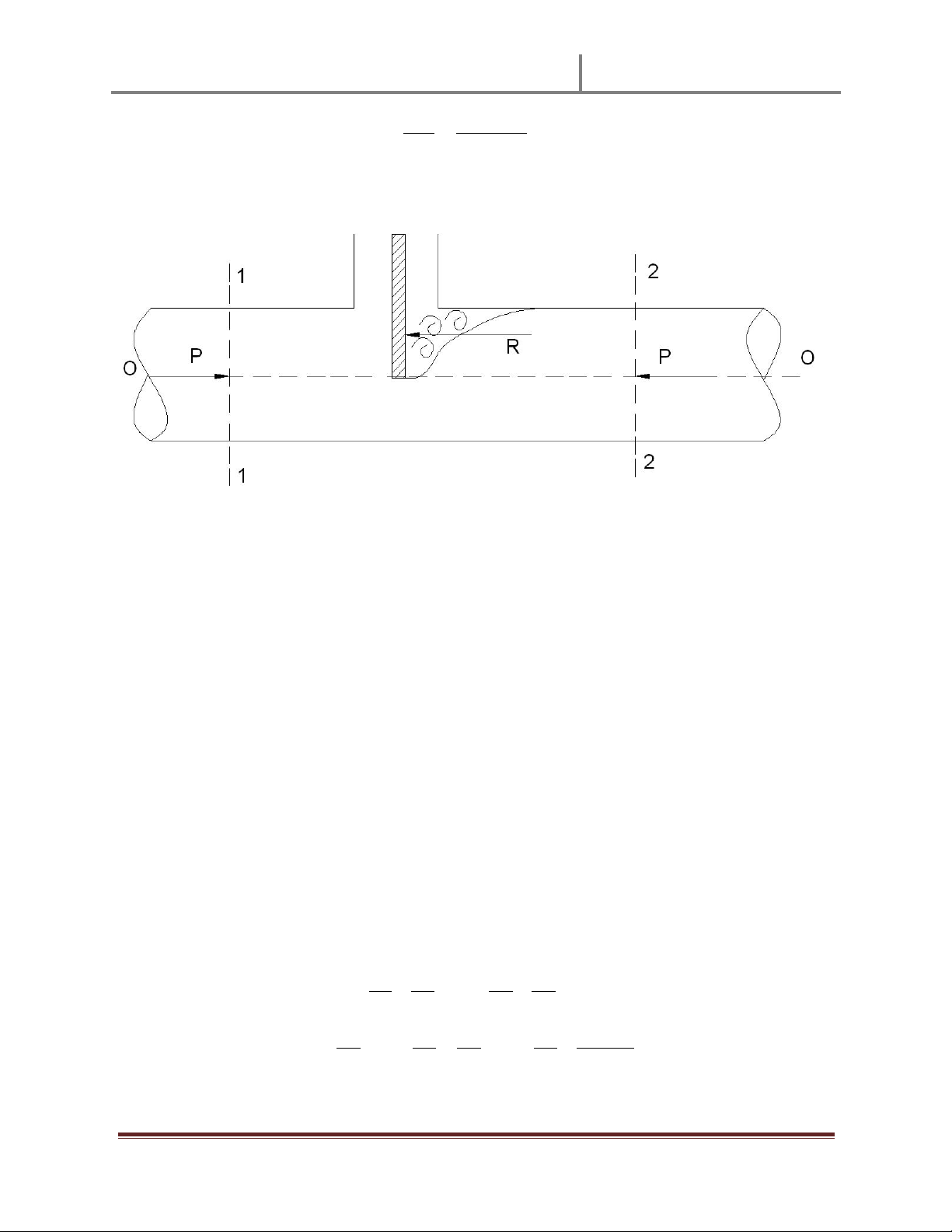
Ta tính đӝ cao trӑng tâm cӫa tiӃt diӋn cӱa van: 12 $ % * $ "
Xét áp lӵc do khӕi nưӟc có đӝ cao h1 gây ra lên cӱa van: Ta có: 89 ù *3 *456 * 7 6: ù --/
NӃu ta chӑn trөc Oz nҵm nghiêng theo m һt vӟi hưӟng như hình vӁ, điӇm O nҵm tҥi
mһt thưӧng lưu thì vӏ trí cӫa điӇm đһt lӵc P1 sӁ tính theo công th ӭc: = ; > < * 3 * 3 a Ê c Y Ê Ê Vӟi ?%@ 615@ => .$"A Tӯ đó ta có : .$ ;< ." B
Xét áp lӵc do khӕi nưӟc có đӝ cao h2 gây ra:
Đӝ cao trӑng tâm phҫn tiӃp xúc vӟi nưӟc cӫa cӱa van là: *C *D #"
DiӋn tích mһt tiӃp xúc vӟi nưӟc là: 3 9D 6 EBF 6 B ." Do đó ta có: *D 3D -## . --#./
ĐiӇm đһt lӵc là: (xét trong hӋ trөc O¶z) = ; >D < *D 3D *D #"
Trong hӋ trөc Oz thì điӇm D¶ có tӑa đӝ: ;
Vұy tӯ đó ta có đưӧc áp lӵc cӫa toàn bӝ nưӟc tác dөng lên cӫa van là: Đӝ lӟn: ù Gù ùG ##H I #JH
ĐiӇm đһt lӵc đưӧc xác đӏnh theo phương ph áp xác đӏnh điӇm đһt khi có hӧp lӵc 2 lӵc song song:
Khoҧng cách giӳa 2 điӇm đһt D và D¶ là: G;< ; "
Gӑi a là khoҧng cách tӯ D¶ đӃn điӇm đһt G cӫa hӧp lӵc
P và b là khoҧng cách tӯ D đӃn điӇm đһt G cӫa hӧp lӵc P.
Ta lұp đưӧc hӋ phương trình sau t ӯ phương trình cân b ҵng moment quanh O K 6 ! K --#. 6 -- 3 a Ê c Y Ê Ê Giҧi ra ta đưӧc: K ##-" 6 #"
Tӯ đó ta xác đinh đưӧc điӇm đһt G cӫa hӧp lӵc P cách O mӝt đoҥn: L $.. ##- $" Bài 2-24:
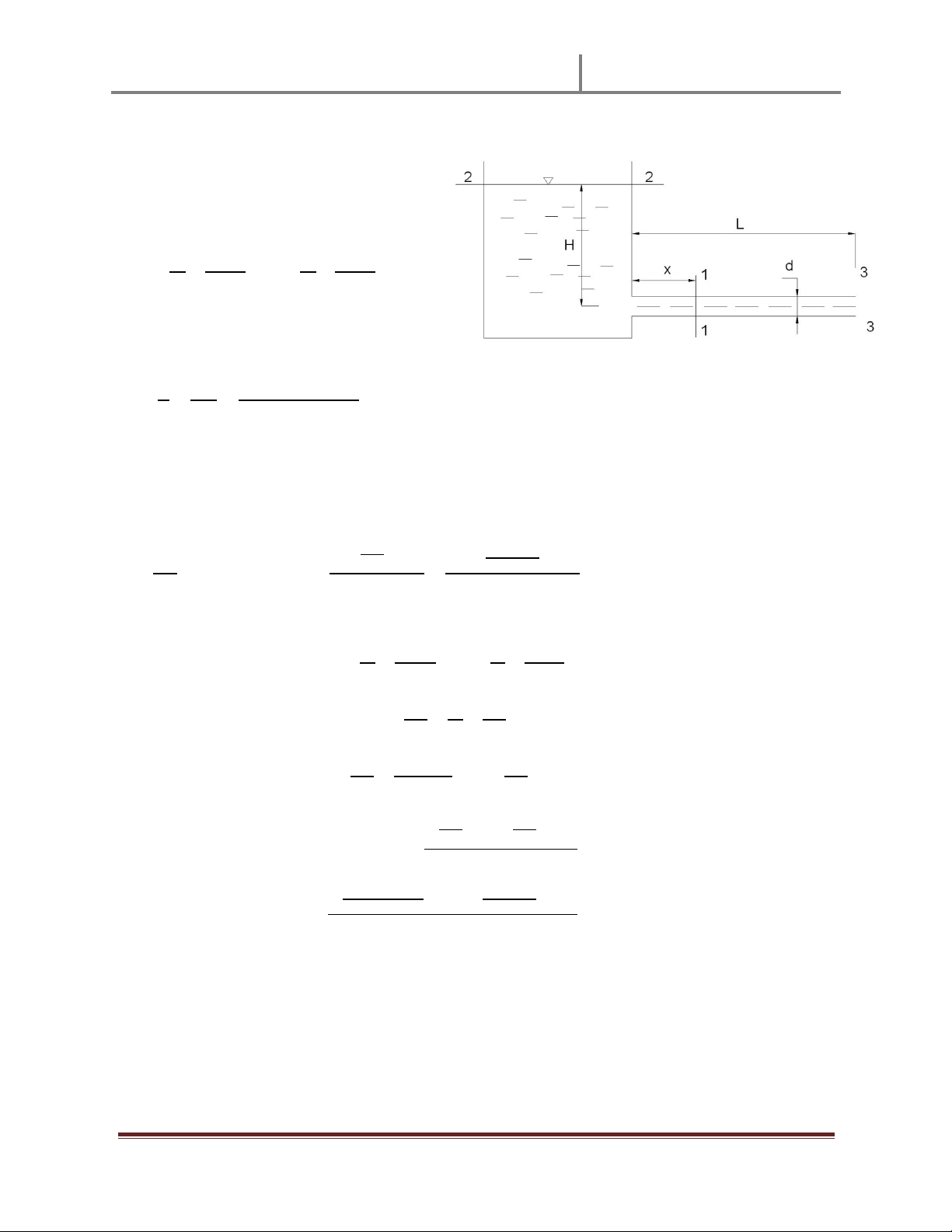
Xét áp lӵc P1 do khӕi nưӟc thưӧng lưu gây ra Chӑn trөc AZ như hình vӁ
DiӋn tích phҫn nưӟc tiӃp xúc vӟi nưӟc là:
3 6E6M 6òN7N O K6NOF
Trӑng tâm có đӝ cao: * PQ PQ Áp lӵc: ù 3 * PQRPQ ù PQ 6 ĐiӇm đһt: ; < + ST U QPV @
Tӯ đó ta suy ra khoҧng cách giӳa D và O là: W G X ;< G G XG 3 a Ê c Y Ê Ê
Xét tương tӵ cho khӕi nưӟc ӣ hҥ lưu ta có: ù 6 3 * = ; + < + 3 *
Khoҧng cách giӳa D¶ và O là: W G X ;< G Y XY
Xét điӅu kiӋn cân bҵng momen quanh O:
Van bҳt đҫu mӣ khi: ù W Z ù W P R R W Z PQ W P R R G @ XG Z PQ G @ XG [@ G # - XG @ G XG @ @
Giҧi phương trình trên ta suy đư ӧc giá trӏ cӫa X #.$-" Bài 2.27: 3 a Ê c Y Ê Ê
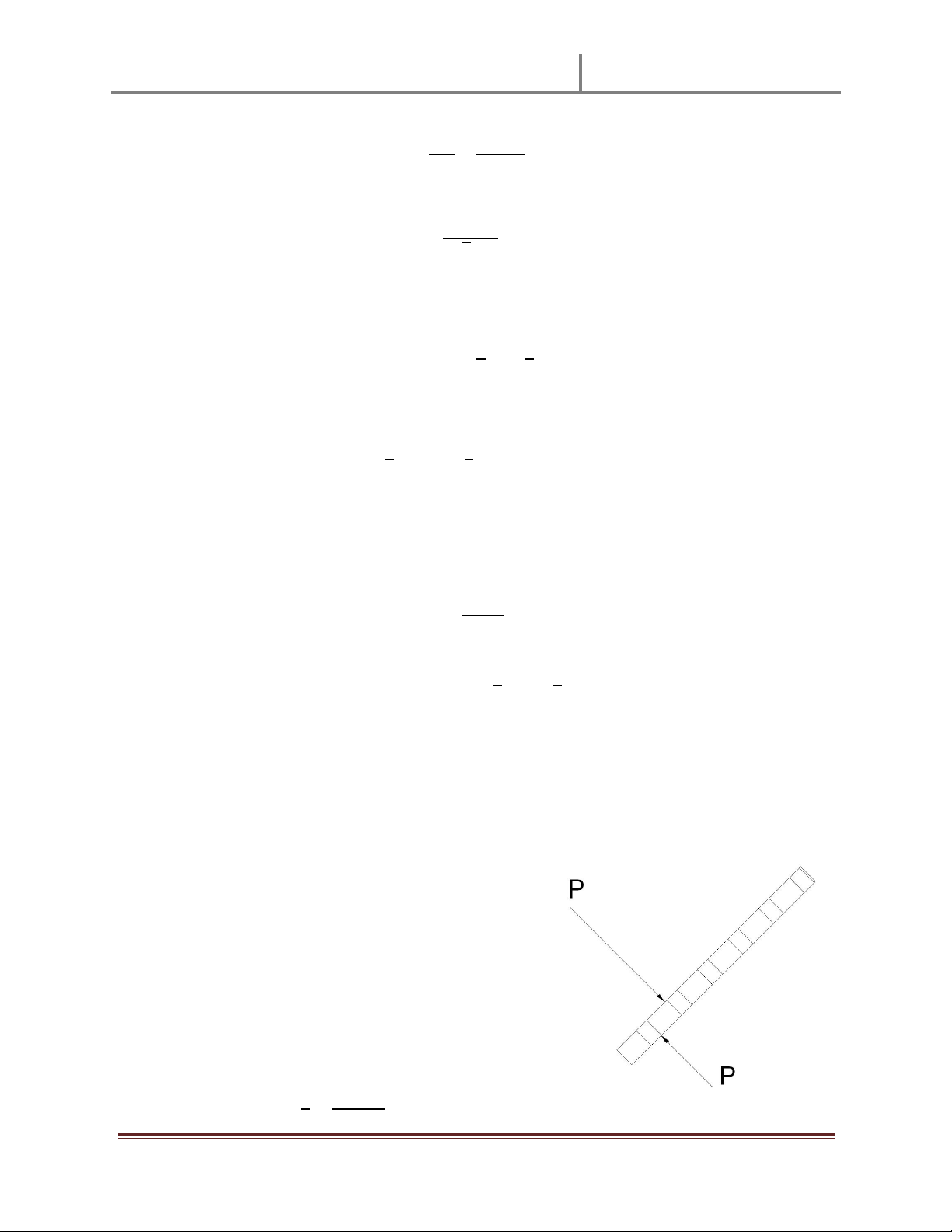
Nhìn trên hình v Ӂ ta có nhұn xét rҵng hӋ có xu hưӟng quay quanh điӇm K ( nҵm ӣ chân cӫa trө
chӕng). Do vұy đӇ hӋ cân bҵng thì lӵc P do nưӟc tác dөng vào thành van ph ҧi có phương đi qua K
hay điӇm D chính là điӇm đһt lӵc cӫa P
Chon trөc tӑa đӝ Oz như hình vӁ:
Tӑa đӝ điӇm đһt lӵc P đưӧc tính theo công th ӭc: = ; ; > + 3 ; * Vӟi:
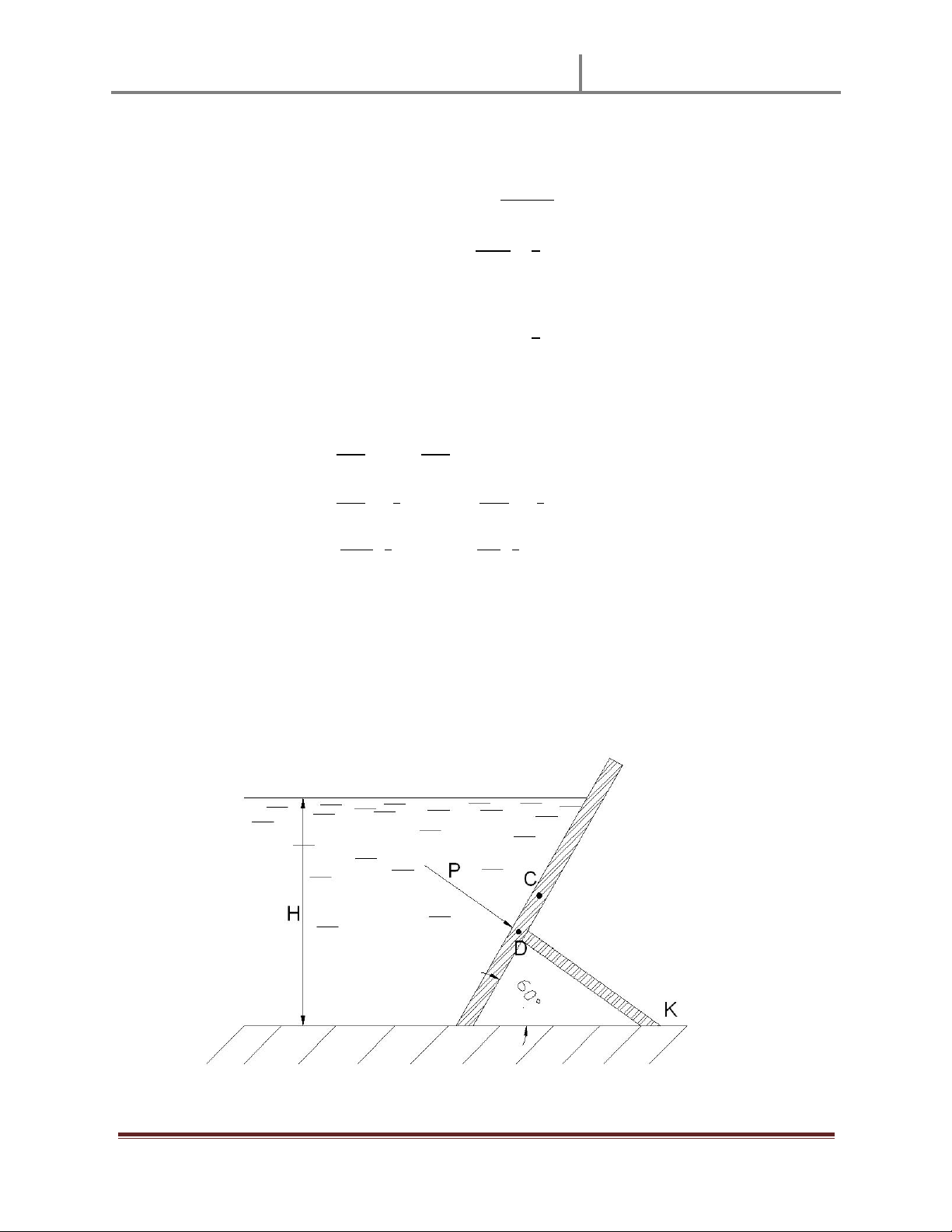
3 là phҫn diӋn tích phҫn mһt tiӃp xúc vӟi nưӟc. 9 3 4\ 6 ]^_`#a6
=> : là moment quán tính cӫa mһt tiӃt diӋn tiӃp xúc vӟi nưӟc => Rbc dec [B@
+M là đӝ cao cӫa trӑng tâm tiӃt diӋn tính tӯ mһt thoáng 9 ;+ ]^_`#a Tӯ đó ta suy ra: ; ;+ f (1) @B@
Mһt khác theo hình vӁ ta thy: ; 4] ]g 4] f ; ]g #k! hij`@a ; f # # f (2) hij@ B@
Tӯ (1) và (2) ta suy ra giá trӏ cӫa H=1,04(m)
Ta tính đưӧc đô lӟn cӫa P là: ù 3 + f 6 f hij@ P=24503,9 (N) = 24.3 (kN) Bài 2.39: 3 a Ê c Y Ê Ê cÊÊÊ Ê Bài 3-26:
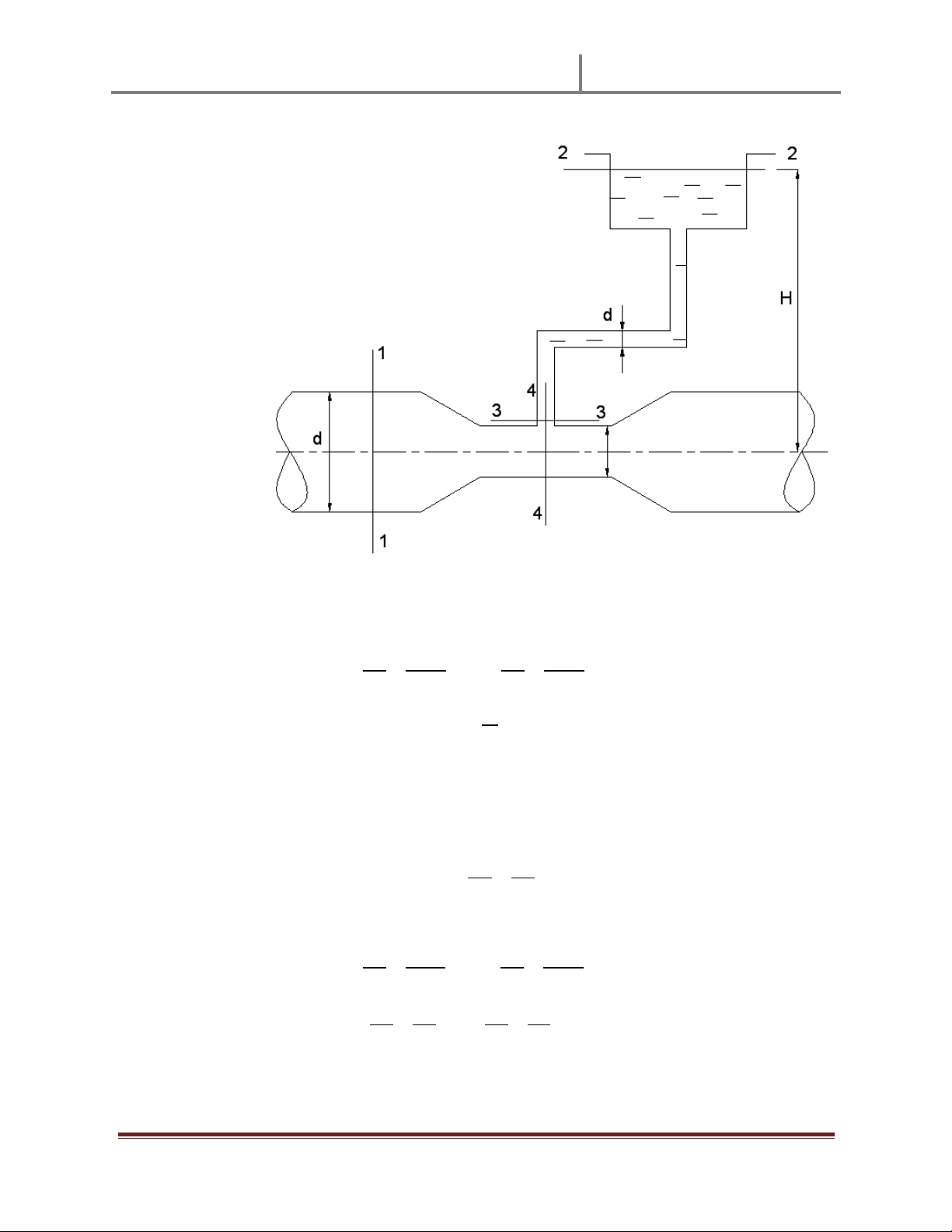
Chӑn mһt O-O là mһt phҷng chuҭn đӇ so sánh:
ViӃt phương trình Becnul i cho m һt cҳt tҥi 2-2 và 3-3 vӟi giá trӏ áp sut dư ta có: m m ; l n @l @n@ ;@ o r p p ; 9ql #qn #qm m q;@
Ta có thӇ bӓ qua giá trӏ tәn tht cӝt nưӟc s #
D2/2 rt nhӓ nên ta có thӇ bӓ qua n 9 # # @ @l
ViӃt PT đӏnh luұt Becnul i cho 1-1 và 4-4 ta có: m m ; l n Al AnA ;A o n n # l Al A # # Thay (2) vào (1): 3 a Ê c Y Ê Ê n n n 9 # @ A l n l @ t 9 u nA n v Vӟi v4 và v1 là: w # " nA 3 A x# . y z { w # " n 3 x# -y z { Ta có : n@ $"|z
Vұy lưu lưӧng nưӟc clo trong ӕng là: w@ n@ 3@ ###.$ yc{ }
2) Lưu lưӧng nưӟc Clo trong ӕng là 0.5 l/s w # $ #~@ " n@ nA 3 @ x# #$ # y z { Tӯ (*) ta có: n n n A l @ 79 : n l @ 9 u nA n n l A n@ 9 u n " nA -.y z{ w 3 i A n . ~@ " A x r . ~@ r #" 3) ni n@ vA #" " n -y z{ # v nA x# "|z Tӯ (*) ta có: 3 a Ê c Y Ê Ê n l @ 9 u nA n n n 9 l n @ A -" Bài 3.27:
Chӑn mһt chuҭn 0-0 như hình vӁ
ViӃt phương trình Becnul i cho m һt cҳt tҥi 1-1 và 2-2 vӟi giá trӏ áp tuyӋt đӕi ta có: m m ; n n ; o 9 # 9 # o s 9 9 $ "O7ôNO Mà: o l ! l #" Q ; #$÷^ҥnnòN ; ÷^ҥnnòN
Tӯ đó ta có đưӧc giá trӏ cӫa v: n n # 3 a Ê c Y Ê Ê Bài 3.35:
Chӑn mһt chuҭn 0-0 là mһt đi qua đáy dưӟi cӫa van xҧ như hình vӁ:
ViӃt phương trình Becnul i cho m һt cҳt tҥi 1-1 và 3-3 vӟi giá trӏ áp sut tuyӋt đӕi ta có: m m ; n @ @n@ ;@ n W # w n 3 $"|z w n 3 "|z Tӯ đó ta có: n W #.&0 Vұy: #.&0 3 a Ê c Y Ê Ê Bài 3.36:
ViӃt phương trình đӏnh luұt Becnul i cho mһt
cҳt 2-2 và 3-3 vӟi mһt phҷng so sánh là mһt 0-0 như hình vӁ: m m ; n @ @n@ ;@ ~@
Vӟi các giá trӏ: q ; 9q n #q ;@ #q @ q w w v v #~@ n@ 3 xr x v $# v #~@ #."|z
Tәn tht cӝt áp sӁ bҵng tәng các tәn tht dӑc đưӡng và cөc bӝ: ~@ o l
l v (do tәn tht dӑc đưӡng tӍ lӋ vӟi chiӅu dài) m m@ n 9 n@ $ #. 9 @ o v - #$ o v
ViӃt phương trình đӏnh luұt Becnul i cho mһt cҳt 2-2 và 1-1 vӟi mһt phҷng so sánh là mһt 0-0: m m ; n n ; ~ n 9 @ o v X n l @ 9 o v X l X 9 n@ o # v -## X -# $ #. v - #$ " VӁ đưӡng đo áp 3 a Ê c Y Ê Ê Bài 3.39:
Chӑn mһt O-O là mһt phҷng chuҭn đӇ so sánh:
ViӃt phương trình Becnul i cho m һt cҳt tҥi 1-1 và 2-2 vӟi giá trӏ áp tuyӋt đӕi ta có: m m ; n n ; o m m ; n n ; #
Tӯ ӕng đo áp ta có phương trình: Q Q 3 a Ê c Y Ê Ê ; ; ; ; ; ; ; ; ; ; ; ; ; ; ; ; ; u
Thay (2) vào (1) ta suy ra đư ӧc: n n ; ; n n ; ; ; u ; ; n n ; u n u n n t u n Vӟi: n $ y{ U U } ! n t u n .y _ { Lưu lưӧng nưӟc là: "@ w w n3 ##. 7 z : W w . zu 3 a Ê c Y Ê Ê Bài 3-41:
Chӑn mһt phҷng chuҭn O-O như hình vӁ
ViӃt phương trình Becnul i cho m һt cҳt 1-1 và 2-2 vӟi áp sut dư: l n l n ; ; n n # # n n 7 :
Phương trình liên t өc áp dөng cho kênh tҥi đoҥn đҫu và đoҥn thu hҽp; w n6 n6 n 6 n 6 Thay (2) vào (1) ta có: n 6 n n n 7 6 : n w n 7 : n 6 n 6 @ n 7 : 6n w #
Sau khi thay sӕ vào và giҧi ra ta đưӧc giá trӏ cӫa v2 là: " n #.$. y z{ 3 a Ê c Y Ê Ê w n 6 #.$. v -" Bài 3.46:
Phương trình đӝng lưӧng cho đoҥn dòng chҧy đưӧc giӟi hҥn bӣi 2 mһt cҳt 1-1 và 2-2 đӕi vӟi trөc
chiӃu s nҵm ngang hưӟng tӯ trái sang phҧi: À} wmi n} mi n} Coi: mi mi À} wn n Lӵc ngoài gӗm có:
Lӵc khӕi trӑng lưӧng cӫa đoҥn dòng chҧy là G tuy nhiên Gs = 0 Lӵc mһt:
Lӵc ma sát trên thành ӕng. Tuy nhiên ta chӍ xét 1 phҫn ӕng ngҳn nên coi lӵc ma sát là nhӓ nên có thӇ bӓ qua
Áp lӵc nưӟc xung quanh tác đӝng lên mһt đӭng 1-1 và 2-2: ù ù ù 3 ù 3
Phương trình đinh lu ұt Becnuli cho 2 mһt 1-1 và 2-2 vӟi mһt O-O là mһt chuҭn: n n ; l l ; ~ n n l l n ; ;
Tuy nhiên do Q và 3 là không đәi nên: n n n 3 a Ê c Y Ê Ê
ViӃt lҥi phương trình trên ta có : n n n n
Goi phҧn lӵc cӫa van tác đӝng vào dòng nưӟc là R Ta có: À} ù ù wn n 3 wn n n 3g^n n n
Giá trӏ R = giá trӏ áp lӵc tác dөng lên cӱa van: ù Vӟi: n U 3 K6
Áp dөng thay sӕ: P=112.5 (kN)
Ê! Ê"Ê#Ê$Ê%Ê&'Ê()Ê*+Ê Bài 4-14: Sӕ ¦ l
Vӟi nưӟc có nhiӋt đӝ ô #] ##k!|z Vұy ta có ¦ l @ #### # @ Vұy nưӟc chҧy rӕi
ChiӅu dày cӫa lӟp mӓng sát thành r ## , ¡¢ ¦ l ####¡¢ !! Ta thy: , L 3 a Ê c Y Ê Ê
Nên nưӟc chҧy rӕi trong khu thành trơn th ӫy lӵc Bài 4-20:
Tәn tht dӑc đưӡng hd tính theo công th ӭc Darcy: W n l £ r ."
Ta giҧ sӱ rҵng nưӟc trong ӕng chҧy ӣ khu sӭc cҧn bình phương
Ta tính C theo công th ӭc Maninh: ¤ |¥ Vӟi l $!! A A
N I ##$ (tra bҧng vӟi ӕng thưӡng)
Tӯ đó ta có : ¤ $ v #~@|¥ $#"|z Mһt khác ta có: - ¤ t£ £ O v $# ## Thay vào công thӭc hd: l ## v v ." n # y{ v¦c v[¡ }
Vӟi n #"|z ta kiӇm tra lҥi điӅu kiӋn chҧy rӕi trong khu sӭc cҧn bình phương
Ta kiӇm tra lҥi điӅu kiӋn chҧy rӕi trong khu sӭc cҧn bình phương nr ¦ $. ### O#Nòp r , ¡¢ #.!! L $"" ¦ l Vұy giҧ thiӃt đúng.
Lưu lưӧng nưӟc chҧy qua là: x$#~@ w n 3 # ##."@|z 3 a Ê