Tài liệu chương 1: ma trận và định thức - 5 điều cơ bản môn Xác suất thống kê| Trường Đại học Ngoại Thương

20:11, 27/01/2026
Tài liệu Chương 1: Ma Trận Và Định Thức - 5 Điều Cơ Bản - Studocu 1.1. Khái ni n v ma tr n 1.1.1. Ma tr n
Ma tr nlà m t b ng s x p theo dòng và theo c t. M t ma tr n có m dòng và n c t c g i là ma tr n c p . Ma tr n c p có d ng t ng . S
n m trên dòng i và c t j c a ma tr n A g i là ph n
tc a ma tr n A. Ph n t n m trên dòng i và c c kí hi u là .
vi t ng n g n ma tr n A, ta dùng kí hi u . Tp h p các ma tr n c p v i c kí hi u . Ví d 1.1. là ma tr n c p , có . 1 2 3 B là 4 ma 6 tr n3 c p , có . 5 3 7 1.1.2. Các d ng ma tr n * Ma tr n không Cho ma tr n A c p
c g i là ma tr n không n u t t các ph n t ma tr n u b ng 0, Kí hi u . * Ma tr n dòng, ma tr n c t - Ma tr n c p
g i là ma tr n c t (ma tr n có 1 c t). - Ma tr n c p
g i là ma tr n dòng (ma tr n có 1 dòng). Ví d 1.2. là ma tr n dòng. 9 20:11, 27/01/2026
Tài liệu Chương 1: Ma Trận Và Định Thức - 5 Điều Cơ Bản - Studocu là ma tr n c t. * Ma tr n chuy n v
Ma tr n chuy n v c a A là ma tr c b i dòng thành c ng
ca ma tr n A. Ma tr n chuy n v c c kí hi u là . N u A là ma tr n c p thì là ma tr n c p . Ví d 1.3. . Chú ý: . * Ma tr n vuông
Ma tr n có s dòng và s c t b
c g i là ma tr n vuông c p n. Kí hi u hay .
Tp h p t t c các ma tr n vuông c c kí hi u . Các ph n t có d ng
c g i là ph n t chéo c a ma tr n. ng th ng ch a các ph n t chéo g i là ng chéo chính c a A. Ví d 1.4.
là ma tr n vuông c p 3. Các ph n t 3, 1, 2 là ph n t chéo c a A. * Ma tr n tam giác
Cho A là ma tr n vuông c p n.
- Ma tr n A là ma tr n tam giác trên n u t t c ph n t n ng chéo u b ng 0, t c là - Ma tr n A là ma tr i n u t t c các ph n t n ng chéo u b ng 0, t c là Ví d 1.5. 10 20:11, 27/01/2026
Tài liệu Chương 1: Ma Trận Và Định Thức - 5 Điều Cơ Bản - Studocu là ma tr n tam giác trên. là ma tr i. * Ma tr n chéo Ma tr n vuông A c
c g i là ma tr n chéo n u các ph n t n ng chéo chính b ng 0, t c là . Ví d 1.6. là ma tr n chéo. * Ma tr Ma tr n
là ma tr n chéo mà các ph n t
ng chéo chính b ng 1. Kí hi u
hay (n u là ma trân vuông c p n). Ví d 1.7. là ma tr c p 3. 1.1.3. Các phép bi c p trên ma tr n Ba phép bi i là ba phép bi p trên dòng c a ma tr n - Nhân m t dòng v i m t s - C ng m t dòng b i m c nhân v i 1 s - i ch hai dòng cho nhau 11 20:11, 27/01/2026
Tài liệu Chương 1: Ma Trận Và Định Thức - 5 Điều Cơ Bản - Studocu 1.2. n trên ma tr n 1.2.1. Phép c ng hai ma tr n
Cho hai ma tr n A và B cùng c p
. T ng hai ma tr n, kí hi u A+B là ma tr n c p nh b i v i m i Ví d 1.8. . Ví d 1.9. Cho và . Ta có . Chú ý: Hai ma tr n ch c
c v i nhau khi chúng có cùng c p. 1.2.2. ng c a ma tr n v i m t s th c Tích c a ma tr n c p v i s th c , kí hi u , là ma tr n c p m n xác nh b i v i m i i,j. Ví d 1.10. . Chú ý: Khi , ta s vi t thay cho và g i là ma tr i c a A. là phép tr hai ma tr n. 1.2.3. Tích c a hai ma tr n Cho hai ma tr n
. Ta g i tích c a hai ma tr n A và B, kí hi u , là ma tr n c p . 12 20:11, 27/01/2026
Tài liệu Chương 1: Ma Trận Và Định Thức - 5 Điều Cơ Bản - Studocu Ví d 1.11. 1 3 1 2 1
1.1 2.2 ( 1).3 1.3 2.1 ( 1)( 1) 2 6 . 2 1 . 3 1 2 3.1 1.2 2.3 3.3 1.1 2.( 1) 11 8 3 1 Chú ý:
-tính tích hai ma tr n A và B thì s c t c a A ph i b ng s dòng c a B. - Ph n t
b ng t ng các tích t ng ph n t trên dòng i c a A v i ph n t ng c t j c a B. Vi m i ma tr n vuông và s t nhiên , Ta g i là lu th a b c n c a A. Ví d 1.12. Cho . Tính Ta có . . 1.2.4. Tính ch t Gi s u th c hi : i. ii. iii. iv. v. vi. vii. viii. . 1.3. nh th c 1.3.1. Hoán v 13 20:11, 27/01/2026
Tài liệu Chương 1: Ma Trận Và Định Thức - 5 Điều Cơ Bản - Studocu * Hoán v Xét t p n s t u tiên . M i các s p x p có th t c g i là m t hoán v t n s
các hoán v khác nhau t n ph n t . Mi hoán v c a t p c kí hi u là v i và . Ví d 1.13. T p có hoán v là * Ngh ch th
Trong m t hoán v , m i c p s liên ti p có s l c s bé g i là m t ngh ch
th c a hoán v . S ngh ch th c a hoán v c kí hi u là .
Ví d 1.14. V i các hoán v c a 3 ph n t trên, ta có
1.3.2. nh th c c a ma tr n vuông nh th c c p n Cho ma tr n vuông A c p n nh th c c a ma tr c kí hi u là ho c ng l y theo t t c các hoán v . nh th c c p 1 Cho ma tr n vuông c p 1, nh th c c p 2 Cho ma tr n vuông c p 2, 14 20:11, 27/01/2026
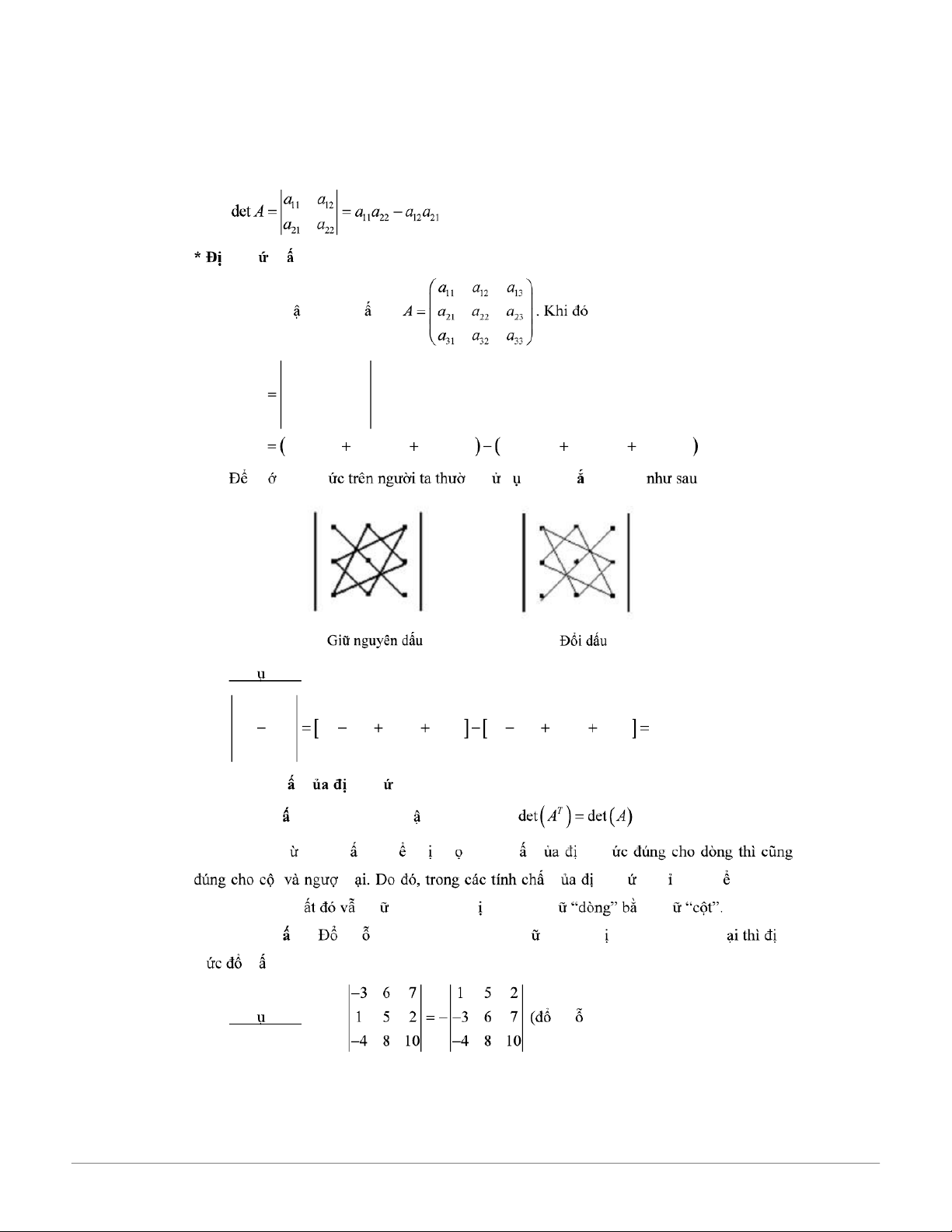
Tài liệu Chương 1: Ma Trận Và Định Thức - 5 Điều Cơ Bản - Studocu . nh th c c p 3 Cho ma tr n vuông c p 3, 1 a 1 1 a 2 a13 det A a a a 21 22 23 3 a 1a32 a33 a a a a a a a a a a a a a a a a a a . 11 22 33 12 23 31 13 21 32 11 23 32 12 21 33 13 22 31 nh công th ng s d ng quy t c Sarrus : Ví d 1.15. 2 4 8 1 1 3 2.( 1).7 4.3.5 1.8.4 8.( 1).5 2.3.4 1.4.7 66 . 5 4 7 1.3.3. Tính ch t c nh th c
Tính ch t 1: Cho A là ma tr n vuông, ta có .
Chú ý: T tính ch t chuy n v , m i tính ch t c nh th t c l t c
nh th c, ch phát bi u cho các dòng, các tính ch
n gi nguyên giá tr khi thay ch ng ch Tính ch t 2:
i ch hai dòng cho nhau và gi nguyên v trí các dòng còn l nh th i d u. Ví d 1.16. Ta có
i ch dòng 1 và dòng 2 cho nhau). 15 20:11, 27/01/2026
Tài liệu Chương 1: Ma Trận Và Định Thức - 5 Điều Cơ Bản - Studocu
Tính ch t 3: Th a s chung c a m t dòng có th nh th c.
Chú ý: Cho A là ma tr n vuông c p n và s th c , ta có .
Tính ch t 4: Cho A là ma tr n vuông c p n. Gi s dòng th i c a ma tr n A có th bi u di n v i ... ... ... ... ... ... ... ... ... ... ... ... ' ' ' ' ' ' ' ' ' ' ' ' det A a a a a a ... a a a a ..a.a a ... . i1 i1 i 2 2 i i n i n 1 2 i i 1 2i n i i i n ... ... ... ... ... ... ... ... ... ... ... ... Ví d 1.17. 3 6 7 1 ( 2) 5 1 7 0 1 5 7 2 1 0 1 5 2 1 5 2 1 5 2 1 5 2 . 4 8 10 4 8 10 4 8 10 4 8 10
Tính ch t 5: nh th c c a ma tr n A b ng 0 n u tho m u ki n sau:
- Có m t dòng mà t t c các ph n t c u b ng 0.
- Có hai dòng b ng nhau ho c t l v i nhau.
Tính ch t 6: N u ta nhân m t dòng c
nh th c v i s b t kì r i c ng vào dòng nh th i. Ví d 1.18. .
Tính ch t 7: nh th c c a ma tr n tam giác, ma tr n chéo b ng tích các ph n t n m ng chéo chính.
Tính ch t 8: N u A, B là các ma tr n vuông c p n thì . 1.3.4. M t s nh th c nh th c theo dòng ho c c t Ph i s
Cho A là ma tr n vuông c p n 16 20:11, 27/01/2026
Tài liệu Chương 1: Ma Trận Và Định Thức - 5 Điều Cơ Bản - Studocu . G i là ma tr n nh c t A b ng cách b g i là ph i s c a ph n t , kí hi u là .
nh lý Laplace (Công th c khai tri nh th c) Cho A là ma tr n vuông c - ( khai tri n theo dòng i). -(khai tri n theo c t j). Ví d 1.19. nh th c c a ma tr n . Khai tri nh th c theo dòng 1 2 1 3 det A 1 3 4 2 A 1 A 3 A . 11 12 13 2 1 2 3 4 1 4 1 1 1 2 A A ( 1) 10, ( 1) 6, 11 12 1 2 2 2 1 3 1 3 A ( 1) 7. 13 2 1 Suy ra Ví d 1.20. nh th c c a ma tr n . Khai tri nh th c theo c t th 2: 17 20:11, 27/01/2026
Tài liệu Chương 1: Ma Trận Và Định Thức - 5 Điều Cơ Bản - Studocu 1 3 2 1 2 1 3 2 0 1 3 3 det A A 3 3( 1) 1 2 1 3.( 10) 30. 12 1 0 2 1 4 3 1 4 0 3 1 nh th c v d ng tam giác Các phép bi p trên ma tr n Ba phép bi i là ba phép bi p trên dòng c a ma tr n - Nhân m t dòng v i m t s - C ng m t dòng b i m c nhân v i 1 s - i ch hai dòng cho nhau nh th c v d ng tam giác S d ng các phép bi
t) c a ma tr n và s d ng các tính ch t c nh th bi n i ma tr n c nh th c v d nh th c sau
cùng s b ng tích các ph n t ng chéo chính. Ví d 1.21. Tính Ta có 2 4 8 1 2 8 1 2 4 d d d 2 2 1 Md 1 d 1 d 3 2 1 1 3 2 0 3 1 5 3 3 1 5 4 7 5 4 7 0 6 13 1 2 4 ddd 2 2 0 3 1 2.1.( 3).( 11) 66. 3 3 2 0 0 11
1.3.5. nh th c c a ma tr n tích
N u A, B là các ma tr n vuông c p n thì c bi t, v i s t nhiên ta có . 18 20:11, 27/01/2026
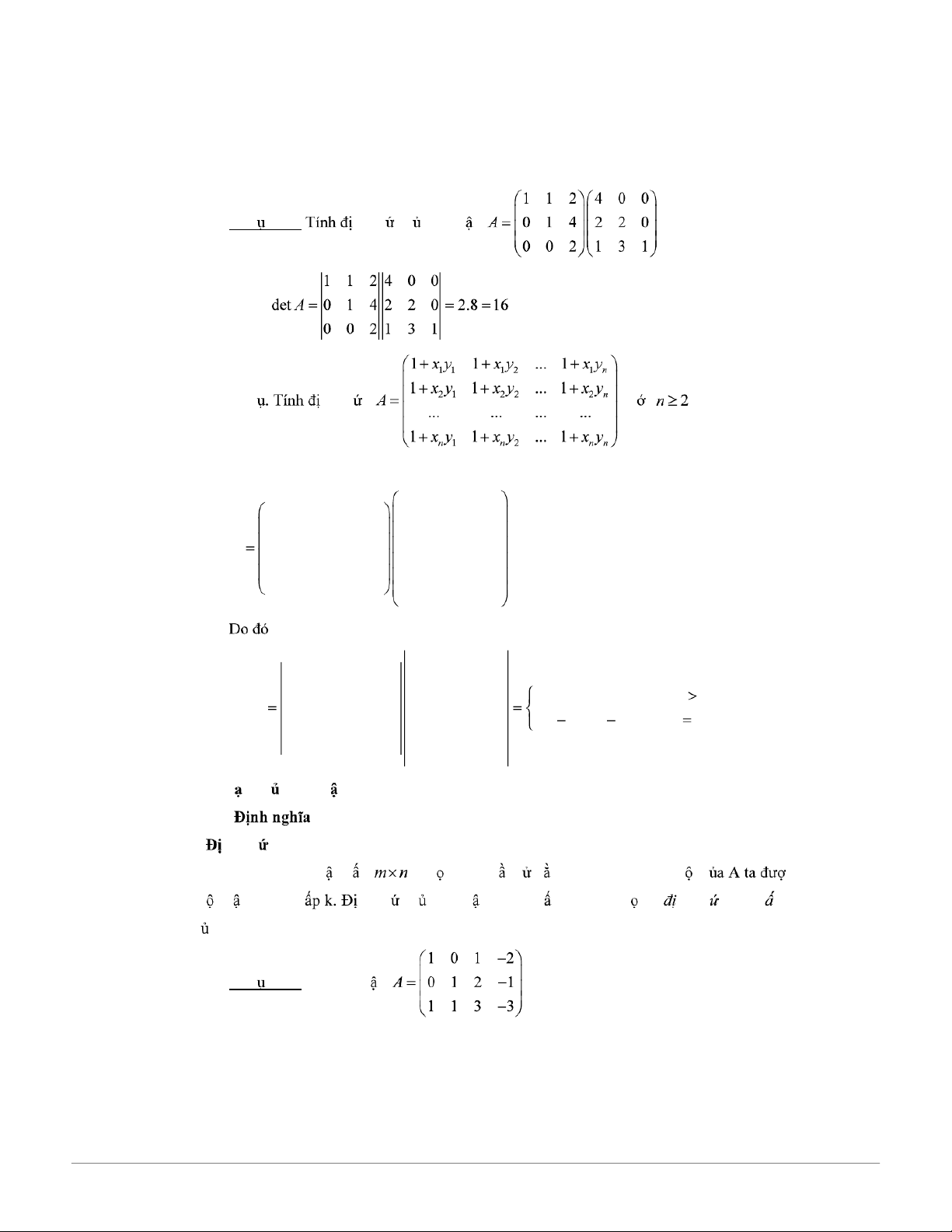
Tài liệu Chương 1: Ma Trận Và Định Thức - 5 Điều Cơ Bản - Studocu Ví d 1.22. nh th c c a ma tr n . Ta có . Ví d nh th c v i . Ta có 1 1 ... 1 1 xy 0 y ... 0 y ... 1 1 2 1 x 0 ... 0 0 0 ... 0 n 2 A
... ... ... ... ... ... ... ... ... 1 x 0 ... 0 0 0 ... 0 n 1 1 ... 1 1 1 xy 0 y ... 0 y ... 1 2 1 x n 0 ... 0 n 0 khi 2 2 det 0 Ax 0 x ... 0 y n ... ... ... ... ... ( 2 )( 1 y 2 1) khi 2 ... ... ... ... 1 x 0 ... 0 0 0 ... 0 n 1.4. H ng c a ma tr n 1.4.1. * nh th c con Cho A là ma tr n c p
. Ch n các ph n t n m trên k dòng và k c t c c mt tr n vuông c
nh th c c a ma tr n vuông c p k trên ta g i là nh th c con c p k ca A. Ví d 1.23. Cho ma tr n . 19 20:11, 27/01/2026
Tài liệu Chương 1: Ma Trận Và Định Thức - 5 Điều Cơ Bản - Studocu
Ch n các ph n t trên dòng 1 và c nh th c là m nh th c con c p 1 ca ma tr n A.
Ch n các ph n t n m trên dòng 1, dòng 3, c t 1 và c nh th c là
mnh th c con c p 2 c a ma tr n A.
Ch n các ph n t n m trên dòng 1, dòng 2, dòng 3, c t 1, c t 2 và c nh 1 0 2 th c 0 1 1 là m
nh th c con c p 3 c a ma tr n A. 1 1 3 * H ng c a ma tr n Cho A là ma tr n c p
khác 0. H ng c a ma tr n A, kí hi u hay chính là c p cao nh
nh th c con khác 0 c a ma tr n A.
Vy h ng c a A là m t s nguyên tho Tn t i ít nh t m
nh th c con c p r khác 0 c a A. M nh th c con c a A c p l u có) thì ph i b ng 0. thì . . 1 2 3 3 2 1 20 0. 0 0 5 .
1.4.2. M t s tính ch t c a h ng ma tr n Tính ch t 1: . Tính ch t 2: H ng c a ma tr i qua các phép bi i sau:
- Phép chuy n v ma tr n. T c là . - Các phép bi p dòng ho c c t. 20 20:11, 27/01/2026
Tài liệu Chương 1: Ma Trận Và Định Thức - 5 Điều Cơ Bản - Studocu - B
c các c t có t t c ph n t b ng 0. - B
c các c t là t h p tuy n tính c a các dòng hay các c t khác.
Tính ch t 3: N u A là ma tr n vuông c p n thì -
i A là ma tr n không suy bi n. - i A là ma tr n suy bi n.
Tính ch t 4: N u A, B là các ma tr n cùng c p thì .
Tính ch t 5: Cho A, B là các ma tr n sao cho ta có th th c hi n tích . 1.4.3. M t s ng ma tr n * Ma tr n b c thang
Ma tr n b c thang là ma tr n có d ng:
+ Các dòng b ng không (n u có) thì n i cùng. + Ph n t u tiên
i luôn n m bên ph i c t các ph n t khác u tiên c a dòng trên. Ph n t
u tiên này g i là các ph n t u c a ma tr n Ví d 1.25.
là ma tr n b c thang. Các s là các ph n t u.
không là ma tr n b c thang. Các s là các ph n t u. *
ng c a ma tr n b ng các phép bi p Các phép bi p trên dòng (ho c theo c i h ng c a ma
tr n tìm h ng c a ma tr n A ta dùng các phép bi n A v d ng ma tr n b c t ng c a A b ng h ng c ng s dòng khác 0 c
Ví d 1.26. Tìm h ng c a ma tr n . 21 20:11, 27/01/2026
Tài liệu Chương 1: Ma Trận Và Định Thức - 5 Điều Cơ Bản - Studocu Ta có . Vy .
Ví d 1.27. Tìm h ng c a ma tr n . Ta có 1 1 1 2 1 d d 1 d 1 1 2 1 2 2 1 2 d d d 3 3 3 1 2 3 1 4 5 0 1 1 0 3 d4 d4 1 d 3 2 3 7 4 0 1 0 1 1 1 1 2 3 1 0 2 1 1 2 1 1 1 2 1 1 1 1 2 1 3 d 3 d 2d 0 1 1 0 3 0 1 1 0 3 4 d d 4 d 22 d4 d4 3 d 0 0 1 1 4 0 0 1 1 4 0 0 1 1 4 0 0 0 0 0 Vy nh th c bao quanh nh th c bao quanh nh th c con c p c a ma tr nh th nh th c con (c p ) c a A khi và ch khi
c thành l p b ng cách b sung thêm m t dòng và m t c t c a A ngoài dòng và c l nh m c . nh lý: N u ma tr nh th c con c p mà m nh th c con c p bao quanh nó (n
u b ng 0 thì h ng c a ma tr n A b ng r. tìm h ng c a ma tr p sau: - Tìm m
nh th c con khác 0 c p s c a ma tr n A. - nh th c con c p bao quanh nó (n u có) + N u t t c nh th c con c p bao quanh u b ng 0 (ho c ma tr nh th c con c p thì h ng c a ma tr n b ng . + N u t n t nh th c con c p
bao quanh D khác không thì ta l p c trên. Sau m t s c h u h n ta s c h ng c a ma tr n. 22 20:11, 27/01/2026
Tài liệu Chương 1: Ma Trận Và Định Thức - 5 Điều Cơ Bản - Studocu
Ví d 1.28. Tìm h ng c a ma tr n . Ta có . (
nh th c con l y t dòng 1, dòng 2, c t 1 và ct 2 c a ma tr n A). Trong s nh th c bao quanh nó có Do ma tr nh th nh th c ng c a ma tr n A b ng 3. 1.5. Ma tr n ngh o 1.5.1. Cho A là ma tr n vuông c
c g i là ma tr n kh ngh ch n u t n t i ma tr n vuông B c p n sao cho , v i là ma tr c g i là ma tr n ngh o c a A, kí hi u . Ví d 1.29. Cho ma tr n và . Ta có th ki m tra c n A kh ngh ch và . 1.5.2. u ki n t n t i và duy nh t
nh lý: Cho A là ma tr n vuông c p n, ma tr n A kh ngh ch khi và ch khi (ma tr n A không suy bi a, ma tr n ngh o c a A là duy nh t. 3 m m Ví d 1.30. ma tr n Am kh ngh ch. 0 1 Ta có . A kh ngh ch khi và ch khi 1.5.3. M t s pháp tìm ma tr n ngh o * n ngh o b ng cách s d nh th c 23 20:11, 27/01/2026
Tài liệu Chương 1: Ma Trận Và Định Thức - 5 Điều Cơ Bản - Studocu
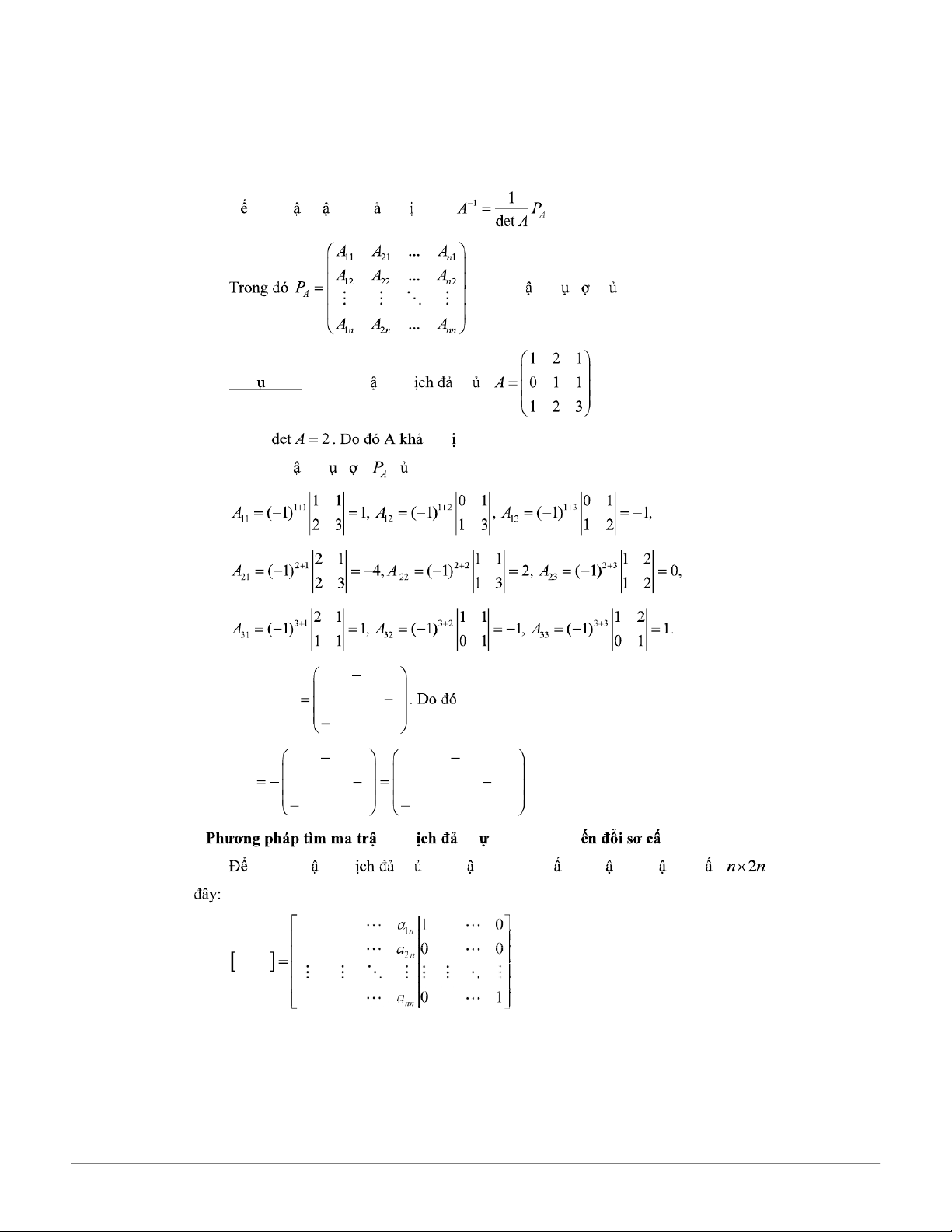
Nu ma tr n tr n A kh ngh ch thì . là ma tr n ph h p c a A. Ví d 1.31. Tìm ma tr n ngh o c a . Ta có ngh ch. Tìm ma tr n ph h p c a A. 1 4 1 Suy ra, P 1 2 1 A 1 0 1 1 4 1 1/ 2 2 1/ 2 1 1 A 1 2 1 1 / 2 1 1/ 2 . 21 0 1 1/ 2 0 1 / 2 * n ngh o d a vào phép bi p tìm ma tr n ngh
o c a ma tr n vuông A c p n ta l p ma tr n có c p sau a a 11 12 0 a a 1 21 22 | A I n a 1na2n 0 24 20:11, 27/01/2026
Tài liệu Chương 1: Ma Trận Và Định Thức - 5 Điều Cơ Bản - Studocu d ng các phép bi n v d ng n B chính là ma tr n ngh o c a ma tr n A.
Chú ý: N u trong quá trình bi
i n u kh i bên trái xu t hi n m t dòng v i t t c
ph n t b ng 0 thì ma tr n không kh ngh ch. Ví d 1.32. Tìm ma tr n ngh o (n u có) c a . L p ma tr n . Ta có Dùng các phép bi và d ng 1 1 1 1 0 0 d d d 1 1 1 1 0 0 2 2 1 d d d 3 3 1 1 2 2 0 1 0 0 1 1 1 1 0 1 2 3 0 0 1 0 1 2 1 0 1 d d d 1 0 0 2 1 0 1 0 0 2 1 0 1 1 2 d3 d3 2 d d2 d2 3 0 1 1 1 1 0 d 0 1 0 1 2 1 0 0 1 0 1 1 0 0 1 0 1 1 ngh ch và . * Dùng ma tr n ngh o gi trình ma tr n n
v i A là ma tr n vuông c p n không suy bi n. Khi . n m là . Ví d 1.33. Gi v i 1 0 2 2 A , B . 1 1 0 1 m 1 1 0 2 2 1 0 2 2 2 2 1 X A B . 1 1 0 1 1 1 0 1 2 1 25 20:11, 27/01/2026
Tài liệu Chương 1: Ma Trận Và Định Thức - 5 Điều Cơ Bản - Studocu 26 20:11, 27/01/2026
Tài liệu Chương 1: Ma Trận Và Định Thức - 5 Điều Cơ Bản - Studocu BÀI T Bài 1. b. Tính . Bài 2. và . Tính a. c. Bài 3. a. b. Bài 4. Tính và . Bài 5. Tính a. b. c. Bài 6. Cho . Tìm . Bài 7. 0 1 1 2 2 cos2 cos sin a. 101 b. c. d. 2 2 cos2 cos sin 1 1 0 2 2 cos2 cos sin 27 20:11, 27/01/2026
Tài liệu Chương 1: Ma Trận Và Định Thức - 5 Điều Cơ Bản - Studocu 1 2 3 4 2 3 4 1 e. f. g. h. 3 4 1 2 4 1 2 3 Bài 8. a. b. Bài 9. a. b. c. d. Bài 10. y z z x x y x y z a. 1 y 1z 1 z x 1 x 1 y 1 x 12 y 1 z 1 y z z x x y x y z 2 2 2 2 2 2 2 2 2 3 1 a a b. 3 1 b b (b a )( ) c (b a ) b ( a b c ) 3 1 c c Bài 11. a. b. c. d. 28