Chương 6
THUY T Đ NG H C PHÂN T CÁC CH T KHÍ
6.1 Các đ nh lu t thực nghiệm và phương trình trạng thái ch t khí
6.1.1 M t số khái niệm
a. Thông số trạng thái và phương trình trạng thái
Khi nghiên c u một vật nếu thấy tính chất c a nó thay đổi ta nói rằng trạng thái
c a vật đã thay đổi. Như vậy các tính chất c a vật biểu hiện trạng thái c a vật đó và ta
có thể dùng một tập hợp các tính chất để xác định tính chất c a một vật. Mỗi tính chất
thư ng được đặc trưng b i một đại lượng vật lí và như vậy trạng thái c a một vật được
xác định b i một tập hợp xác định các đại lượng vật lí. Các đại lượng vật lý này gọi là
các thông số trạng thái.
Những hệ th c giữa các thông số trạng thái c a một vật được gọi là phương trình trạng thái c a vật đó.
Để biểu diễn trạng thái c a một khối khí nhất định, ngư i ta thư ng dùng ba
thông số trạng thái: thể tích V; áp suất p và nhiệt độ T c a khối khí.
Thực nghiệm ch ng tỏ rằng trong 3 thông số đó chỉ có hai thông số độc lập,
nghĩa là giữa ba thông số có mối liên hệ được biểu diễn bằng một phương trình trạng
thái có dạng tổng quát như sau: f(p,V,T) = 0
Việc khảo sát dạng cụ thể c a phương trình trạng thái là một trong những vấn đề cơ bản c a nhiệt học. b. Áp suất
Áp suất là một đại lượng vật lí có giá trị bằng lực nén vuông góc lên một đơn vị
diện tích. Nếu kí hiệu F là lực nén vuông góc lên ΔS thì áp suất p được xác định: F p = ΔS
Trong hệ SI đơn vị c a áp suất là N/m2 (hay Pa). Ngoài ra để đo áp suất, ngư i ta còn dùng các đơn vị sau:
- atmôtphe kỹ thuật (gọi tắt là atmôtphe).
- milimét th y ngân (viết tắt là mmHg, còn gọi là tor) bằng áp suất tạo b i trọng
lượng c a cột th y ngân cao 1mm.
Mối liên hệ giữa các đơn vị áp suất:
1at = 736 mmHg = 9,81.104 N/m2 61 c. Nhiệt độ
Nhiệt độ là đại lượng vật lí đặc trưng cho m c độ chuyển động hỗn loạn c a các
phân tử cấu tạo nên vật. Trong
hệ SI đơn vị c a nhiệt độ là Kelvin (thang nhiệt độ tuyệt đối), kí hiệu là K.
Ngoài ra để đo nhiệt độ, ngư i ta thư ng dùng đơn vị 0C (thang nhiệt độ bách phân).
Mối liên hệ giữa các đơn vị nhiệt độ: T = t + 273,16
Trong tính toán ngư i ta thư ng lấy: T = t + 273
T: là nhiệt độ trong thang tuyệt đối, t là nhiệt độ trong thang bách phân.
6.1.2 Đ nh lu t Boyle-Mariotte
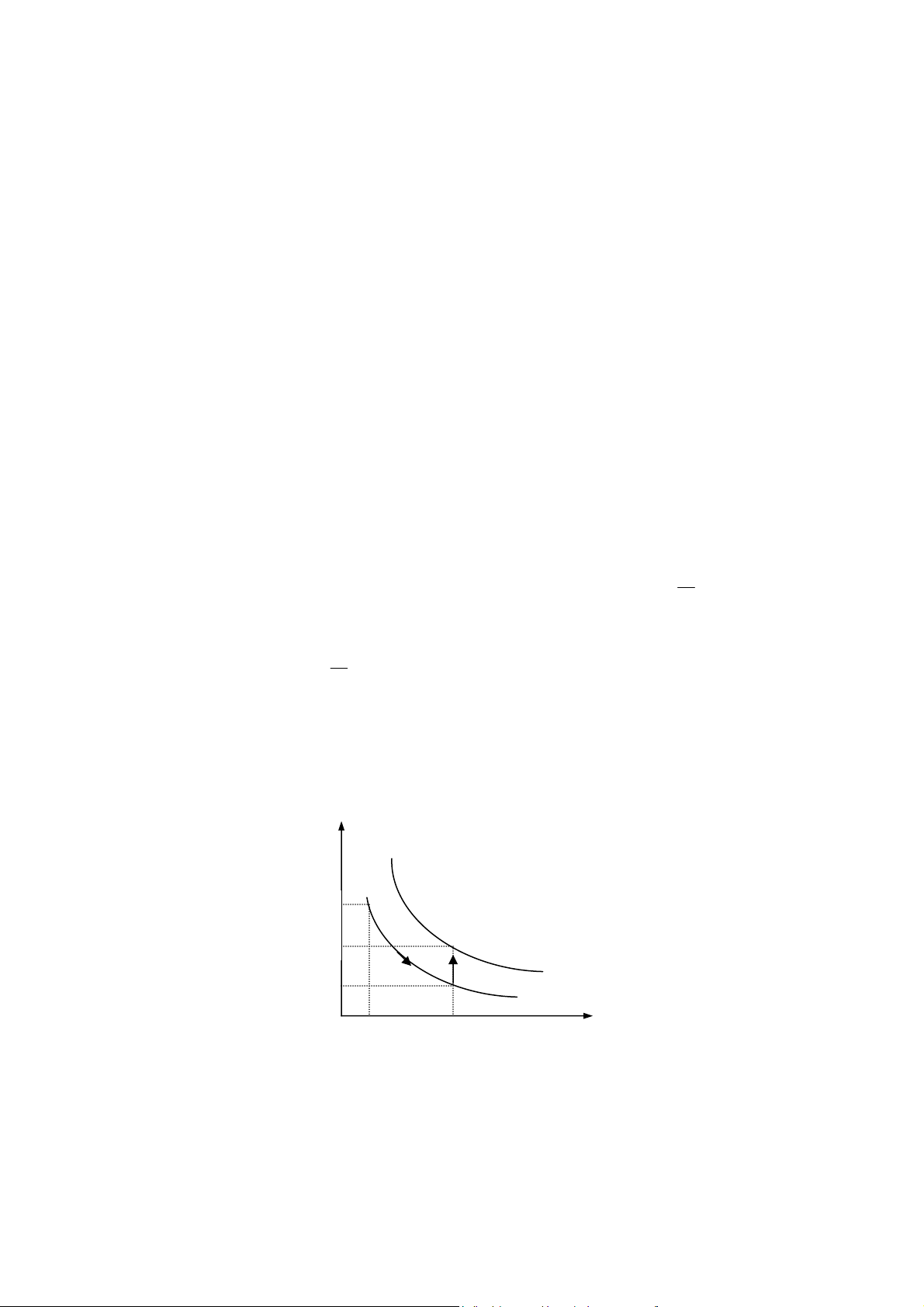
Trong quá trình đẳng nhiệt của một khối khí, thể tích tỉ lệ nghịch với áp suất. pV = const (6-1) p T 1 2 3 T3 T2 T1 V O Hình 6-1
Đư ng đẳng nhiệt là đư ng hypebol. ng với nhiệt độ khác nhau ta có các đư ng
đẳng nhiệt khác nhau (hình 6-1). Nhiệt độ càng cao, đư ng đẳng nhiệt càng xa gốc tọa
độ. Tập hợp các đư ng đẳng nhiệt gọi là họ đư ng đẳng nhiệt.
6.1.3 Các đ nh lu t GayLussac
a. Trong quá trình đẳng tích của một khối khí, áp suất tỉ lệ với nhiệt độ tuyệt đối. p = const (6-2) T
b. Trong quá trình đẳng áp của một khối khí, thể tích tỉ lệ với nhiệt độ tuyệt đối. V = const (6-3) T
(6-2) và (6-3) còn có thể viết: p p V V 0 = (V = const) và 0 = (p = const) T T T T 0 0 1
Thông thư ng ta chọn T0 = 273K = , khi đó: α 62 p = p 0 .α.T (V = const) (6-4) V = V0.α.T (p = const) (6-5)
α: hệ số giãn n nhiệt c a chất khí.
6.1.3 Giới hạn áp dụng của các đ nh lu t Boyle-Mariotte và GayLussac
Khi nghiên c u các định luật trên đây, Boyle-Mariotte và GayLussac đã nghiên
c u các chất khí nhiệt độ và áp suất thông thư ng c a phòng thí nghiệm. Vì vậy các
định luật này chỉ đúng trong điều kiện chất khí có nhiệt độ không quá thấp và áp suất không quá lớn.
6.1.4 Phương trình trạng thái của khí lý tưởng
Khí lý tư ng là chất khí tuân theo hoàn toàn chính xác 2 định luật Boyle-Mariotte và GayLussac.
Đối với 1 kmol khí (ch a N = 6,23.1026 phân tử) Clapeyron và Menđêlêev đã tìm ra phương trình sau: pv = RT (6-6)
R là hằng số c a khí lý tư ng. μ
Với một khối khí có khối lượng m và thể tích là V thì V = v (μ (kg) là khối m
lượng c a 1kilômol). Từ (6-6) suy ra: m pV = RT (6-7) μ
a. Thiết lập phương trình trạng thái của khí lý tưởng
Giả sử 1kmol khí lúc đầu có trạng thái xác định b i các thông số p1,V1,T1. Sau
khi biến đổi sang trạng thái p2,V2,T2. Trên đồ thị hình 6-2 trạng thái đầu và cuối được
biểu diễn bằng hai điểm M1và M2 trên hai đư ng đẳng nhiệt T1 và T2. p M1 p1 p2 M2 p' T 1 M'1 2 T1 V O Hình 6-2
Để tìm mối liên hệ giữa các thông số, ta giả sử rằng sự biến đổi từ trạng thái đầu
sang trạng thái cuối theo hai giai đoạn:
- Giai đoạn đầu nhiệt độ khí T1 được giữ nguyên và khí biến đổi sang trạng thái
trung gian M'1, có các thông số: p’1,V1, T1.Theo định luật Boyle-Mariotte: 63 p1V1 = p'1V2 (*)
- Giai đoạn sau khối khí giữ nguyên thể tích và khí biến đổi sang trạng thái trung
gian M'2. Theo định luật GayLussac: p' = p aT ⎫ 1 0 1 ⎬ p = p aT ⎭ 2 0 2 T →p' 1 = p (**) 1 T 2 2
Thay (**) vào (*) ta được: p V p V 1 1 2 2 = (6-8) T T 1 2 pV
Từ (6-8) đối với 1 kmol khí đã cho
=const và bằng R, nghĩa là: T pV = RT
b. Giá trị của hằng số R
Theo định luật Avogadro, nhiệt độ và thể tích giống nhau: 1kmol các
chất khác nhau đều chiếm cùng một thể tích. Khi T0=273,16K (00C);
p0=1,033at =1,013.106 N/m2 thì 1 kmol khí chiếm thể tích là V0= 22,41m3, trạng thái
này chung cho mọi chất khí, gọi là trạng thái tiêu chuẩn. Ta có: p V 0 0 = R =8,31.103 J/kmol.K T0
Nếu p đo bằng atmôtphe thì R = 0,0848 m3.at/kmol.K
c. Khối lượng riêng của khí lý tưởng
Thay m = ρ (ρ là khối lượng riêng c a khí lý tư ng) và V = 1 thì ta tính được
khối lượng riêng c a khí lý tư ng: μp m ρ = = (6-9) RT V
Ví dụ 1: Có 10kg khí đựng trong một bình áp suất 107N/m2. Ngư i ta lấy bình ra một
lượng khí cho tới khi áp suất c a khí còn lại trong bình bằng 2,5.106N/m2. Coi nhiệt độ
c a khí không đổi. Tìm khối lượng c a khí đã lấy ra. Giải
Từ phương trình trạng thái c a khí lý tư ng: m pV = RT μ
Vì quá trình là đẳng nhiệt (T1=T2=T) và thể tích bình không đổi (V1=V2=V) nên ta có: m Δ pV Δ = RT μ 64 ΔpμV Suy ra: Δm = (*) RT
Áp dụng phương trình trạng thái c a khí lý tư ng cho khối khí trạng thái đầu: m p V = RT 1 1 1 μ V μ m Suy ra: 1 = (**) T R p 1 1 Từ (*) và (**) suy ra m. p Δ 10 10 .( 7 − 10 . 5 , 2 6 ) Δm = = =7,5(kg) p 107 1
Ví dụ 2: Có 10g khí ôxy nhiệt độ 10oC, áp suất 3at. Sau khi hơ nóng đẳng áp, khối
khí chiếm thể tích 10l. Tìm:
a. Thể tích khối khí trước khi giãn n .
b. Nhiệt độ c a khối khí sau khi giãn n .
c. Khối lượng riêng c a khối khí trước khi giãn n .
d. Khối lượng riêng c a khối khí sau khi giãn n . Giải
Phương trình trạng thái c a khối khí trước khi hơ nóng: m p V = RT (*) 1 1 1 μ m Sau khi hơ nóng: p V = RT (**) 2 2 2 μ
Quá trình hơ nóng là đẳng áp (p1=p2=p) nên từ (*) và (**) ta tìm được các kết quả sau: m 10 283 31 , 8 . a. V = RT = . = , 2 10 . 4 −3 ( 3 m ) 1 μp 1 32 10 . 81 , 9 . 3 4 μpV 32 10 . 81 , 9 . 3 4 10 . 2 − b. T 2 = = . = ( 1170 K ) 2 mR 10 31 , 8 3 − 4 μp 32.10 .3.9,81.10 c. 3 ρ = = =4,14(kg / m ) 1 3 RT 8, 31.10 .283 1 2 − 4 μp μV p 32. 10 .3.9,81.10 d. 2 3 ρ = = = . =1,0(kg / m ) 2 3 RT mR 10 8,31.10 2
Ví dụ 3: Có hai bình cầu được nối với nhau bằng một ống có khóa, đựng cùng một chất
khí. Áp suất bình th nhất là 2.105N/m2, bình th hai là 106N/m2. M khóa nhẹ
nhàng để hai bình thông với nhau sao cho nhiệt độ khí vẫn không thay đổi. Khi đã cân
bằng, áp suất hai bình là 4.105N/m2. Tìm thể tích c a bình cầu th hai, nếu biết thể
tích c a bình cầu th nhất là 15dm3. Giải 65
Quá trình xảy ra là đẳng nhiệt. Khi m khóa cho hai bình thông nhau ta có
phương trình trạng thái: m +m 1 2 p(V + V ) = RT (1) 1 2 μ Ta tìm m1và m2:
Từ phương trình trạng thái c a khối khí bình 1: m p V 1 = RT 1 1 μ μp V suy ra: 1 1 m = (2) 1 RT m và bình 2: p V 2 = RT 2 2 μ μp V suy ra: 2 2 m = (3) 2 RT
Thay (2) và (3) vào (1) ta được: (p -p)V 1 1 -3 3 V = RT = 5.10 (m ) 2 p-p2
6.2 Thuy t đ ng h c phân t của ch t khí - n i năng của khí lý tưởng
6.2.1 Thuy t đ ng h c phân t
Thuyết động học phân tử bao gồm các luận điểm cơ bản sau:
- Tất cả các vật đều gồm các phân tử và nguyên tử.
- Các phân tử và nguyên tử luôn luôn chuyển động (gọi là chuyển động nhiệt).
- Các tính chất c a các vật thể vĩ mô được giải thích bằng tương tác c a các phân
tử đã tạo thành chúng.
Chuyển động nhiệt c a các phân tử được đặc trưng b i động năng trung bình Wđn
c a một phân tử, còn tương tác giữa các phân tử được giải thích bằng thế năng tương tác Wtn c a các phân tử.
Tuy nhiên, đối với các chất khí, đặc biệt khi chất khí các áp suất thấp, do các
khoảng cách giữa các phân tử lớn nê ta có thể bỏ qua thế năng tương tác Wtn c a các
phân tử. Rõ ràng rằng với giả thiết đó đối với tất cả các chất khí đ loãng, ngư i ta
phải tìm được những định luật tổng quát cho các chất khí.
6.2.2 N i năng của khí lý tưởng
Ta biết rằng vật chất luôn luôn vận động và năng lượng c a một hệ là đại lượng
xác định m c độ vận động c a vật chất trong hệ đó. mỗi trạng thái, hệ có các dạng
vận động xác định và do đó, có một năng lượng xác định. Khi trạng thái c a hệ thay
đổi thì năng lượng c a hệ có thể thay đổi và thực nghiệm xác nhận rằng: độ biến thiên
năng lượng c a hệ trong một quá trình biến đổi chỉ phụ thuộc vào trạng thái đầu và 66
trạng thái cuối mà không phụ thuộc vào quá trình biến đổi. Như vậy năng lượng chỉ
phụ thuộc vào trạng thái c a hệ. Ta nói rằng: năng lượng là một hàm trạng thái.
Năng lượng c a hệ gồm động năng ng với chuyển động có hướng (chuyển động
cơ) c a cả hệ, thế năng c a hệ trong trư ng lực và phần năng lượng ng với vận động
bên trong hệ t c là nội năng c a hệ: W = Wđ + Wt + U
Tùy theo tính chất c a chuyển động và tương tác, ta có thể chia nội năng theo các phần sau đây:
a. Động năng chuyển động hỗn loạn c a các phân tử (tịnh tiến và quay);
b. Thế năng gây b i các lực tương tác phân tử;
c. Động năng và thế năng chuyển động dao động c a các nguyên tử trong phân tử;
d. Năng lượng các vỏ điện tử c a các nguyên tử và ion, năng lượng trong hạt nhân nguyên tử;
Đối với khí lý tưởng nội năng là tổng đông năng chuyển động nhiệt của các phân
tử cấu tạo nên hệ.
Ngư i ta đã xác định được công th c tính nội năng khí lý tư ng như sau:
- Nội năng c a 1mol khí lý tư ng là: i U = RT (6-10) 2
- Với 1 khối khí lý tư ng khối lượng m, nội năng được xác định b i: m i U = RT (6-11) μ 2
trong đó i là số bậc tự do.
Số bậc tự do i là các biến độc lập cần thiết để xác định vị trí c a vật trong không gian.
Chất điểm có 3 bậc tự do, vì vị trí c a nó trong không gian được xác định b i 3 tọa độ c a nó.
Hai chất điểm cách nhau một đọan không đổi có 5 bậc tự do.
Ba hay nhiều hơn 3 điểm cách nhau những đoạn không đổi có 6 bậc tự do, vì
trong 9 tọa độ c a 3 điểm, 3 tọa độ không phải là độc lập, mà được biểu diễn qua các tọa độ còn lại. Như vậy:
- Phân tử khí gồm 1 nguyên tử thì i = 3
- Phân tử khí gồm 2 nguyên tử thì i = 5
- Phân tử khí từ 3 nguyên tử trở lên thì i = 6 67 BÀI T P
6.1 Có 40g khí ôxy chiếm thể tích 3 lít, áp suất 10at
a. Tính nhiệt độ c a khối khí.
b. Cho khối khí giãn n đẳng áp đến thể tích 4 lít. Tìm nhiệt độ c a khối khí sau khi giãn n .
Đáp số: a/ T1= 283,3K b/ T2= 377,73K
6.2 Có 10g khí hyđrô áp suất 8,2at đựng trong một bình, nhiệt độ c a khối khí là 300C.
a. Tính thể tích c a khối khí.
b. Hơ nóng đẳng tích khối khí này đến khi áp suất c a nó lên tới 9at. Tìm nhiệt độ
c a khối khí sau khi hơ nóng.
Đáp số: a/ V= 15,65.10-3m3 b/ T2= 332,6K
6.3 Một khối khí 00C có áp suất là 5at, ngư i ta đun nóng đẳng tích cho đến khi nhiệt
độ lên tới 2730C. Tìm áp suất c a khối khí. Đáp số: P= 20at
6.4 Có 10kg khí đựng trong một bình áp suất 107N/m2, ngư i ta lấy ra bình một lượng
khí cho đến khi áp suất c a khí còn lại trong bình bằng 2,5.106N/m2. Tìm lượng khí
đã lấy ra. Coi nhiệt độ c a khối khí trong quá trình là không đổi. Đáp số: m= 2,5kg
6.5 Một quả bóng có dung tích V = 8 dm3. Ngư i ta dùng bơm để bơm không khí vào
quả bóng để áp suất không khí trong quả bóng là P = 6.105 N/m2. Xi lanh c a bơm
có chiều cao h = 0,5 m và đư ng kính d = 6cm. Hỏi phải bơm trong th i gian bao
lâu? Biết th i gian mỗi lần bơm là t=4s và áp suất ban đầu c a không khí trong
quả bóng là P0 =105N/m2. Coi nhiệt độ không khí là không đổi trong quá trình bơm. Đáp số: t= 113s
6.6 Một phòng có thể tích 160m3. Ban đầu không khí trong phòng điều kiện tiêu
chuẩn, sau đó ngư i ta cho nhiệt độ c a không khí trong phòng tăng lên 100C
trong khi áp suất là 780mmHg. Tính thể tích c a lượng không khí đã ra khỏi
phòng và khối lượng không khí còn lại trong phòng. Cho
biết khối lượng riêng c a không khí điều kiện tiêu chuẩn là D0=1,293kg/m3.
Đáp số: V = 1,6(m3); m ≈ 204,84 kg 68