Tài liệu học tập HK2 Toán 12 – Huỳnh Phú Sĩ

Tài liệu học tập HK2 Toán 12 – Huỳnh Phú Sĩ được sưu tầm và soạn thảo dưới dạng file PDF để gửi tới các bạn học sinh cùng tham khảo, ôn tập đầy đủ kiến thức, chuẩn bị cho các buổi học thật tốt. Mời bạn đọc đón xem!

32 16 lượt tải Tải xuống
Chia sẻ Báo cáo tài liệu

Chủ đề: Đề HK2 Toán 12

Môn: Toán 12

Thông tin:

61 trang 8 tháng trước

Tác giả:

Profile Mai Nguyệt
TÀILIỆU
HỌCTẬP
HK2
TOÁN 12
TrườngTHCS&THPTMỹThuận
VĩnhLong
KẾ HOẠCH TUẦN
L TUẦN 19
L TUẦN 20
L TUẦN 21
L TUẦN 22
L TUẦN 23
L TUẦN 24
L TUẦN 25
L TUẦN 26
L TUẦN 27
L TUẦN 28
L TUẦN 29
L TUẦN 30
L TUẦN 31
L TUẦN 32
L TUẦN 33
L TUẦN 34
L TUẦN 35
MỤCLỤC TOÁN12
MỤC LỤC
PHẦN I GIẢI TÍCH 5
Chương 3. Nguyên hàm - Tích phân và ứng dụng. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 6
§1. Nguyên hàm . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 6
1. Nguyênhàmvàtínhchất................................................................... 6
2. Phươngpháptìmnguyênhàm.............................................................. 8
3. Thựchành................................................................................. 9
§2. Tích phân . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 13
1. Kháiniệmtíchphân....................................................................... 13
2. Tínhchấtcủatíchphân..................................................................... 14
3. Phươngpháptínhtíchphân................................................................ 14
4. Thựchành................................................................................. 15
§3. Ứng dụng của tích phân trong hình học . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 19
1. Hìnhphẳnggiớihạnbởimộtđườngcongvàtrụchoành...................................... 19
2. Hìnhphẳnggiớihạnbởihaiđườngcong.................................................... 19
3. Tínhthểtích............................................................................... 20
4. Thểtíchkhốitrònxoay..................................................................... 21
5. Thựchành................................................................................. 21
Chương 4. Số phức . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 25
§1. Số phức . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 25
1. Địnhnghĩasốphức........................................................................ 25
2. Sốphứcbằngnhau......................................................................... 25
3. Biểudiễnhìnhhọcvàmôđuncủasốphức................................................... 26
4. Thựchành................................................................................. 26
§2. Cộng, trừ và nhân số phức . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 28
1. Phépvộngvàphéptrừ..................................................................... 28
2. Phépnhân................................................................................. 28
3. Thựchành................................................................................. 28
§3. Phép chia số phức . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 30
1. Tổngvàtíchcủahaisốphứcliênhợp....................................................... 30
2. Phépchiahaisốphức...................................................................... 30
3. Thựchành................................................................................. 30
§4. Phương trình bậc hai với hệ số thực. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 32
1. Cănbậchaicủasốthựcâm................................................................. 32
2. Phươngtrìnhbậchaivớihệsốthực......................................................... 32
3. Thựchành................................................................................. 32
PHẦN II HÌNH HỌC 34
Chương 3. Phương pháp tọa độ trong không gian. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 35
§1. Hệ tọa độ trong không gian . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 35
1. Tọađộcủađiểmvàcủavectơ............................................................... 35
2. Biểuthứctọađộcủacácphéptoánvectơ.................................................... 36
3. Tíchvôhướng............................................................................. 36
4. Phươngtrìnhmặtcầu...................................................................... 37
5. Thựchành................................................................................. 37
§2. Phương trình mặt phẳng . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 40
1. Vectơpháptuyếncủamặtphẳng............................................................. 40
2. Phươngtrìnhtổngquátcủamặtphẳng...................................................... 41
3. Điềukiệnđểhaimặtphẳngsongsong,vuônggóc........................................... 41
4. Khoảngcáchtừmộtđiểmđếnmộtmặtphẳng............................................... 42
5. Thựchành................................................................................. 42
§3. Phương trình đường thẳng . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 46
1. Phươngtrìnhthamsốcủađườngthẳng...................................................... 46
2. Haiđườngthẳngsongsong,cắtnhau,chéonhau............................................. 47
3. Thựchành................................................................................. 48
Soạn:HuỳnhPhúSĩ 4 TrườngTHCS-THPTMỹThuận
PHẦNI
GIẢI TÍCH
Chương 3. Nguyên hàm - Tích phân và ứng dụng. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 6
§1. Nguyên hàm . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 6
§2. Tích phân . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 13
§3. Ứng dụng của tích phân trong hình học . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 19
Chương 4. Số phức . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 25
§1. Số phức . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 25
§2. Cộng, trừ và nhân số phức . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 28
§3. Phép chia số phức . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 30
§4. Phương trình bậc hai với hệ số thực. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 32
Soạn:HuỳnhPhúSĩ 5 TrườngTHCS-THPTMỹThuận
Chương3.Nguyênhàm-Tíchphânvàứngdụng TOÁN12
Chương3.
NGUYÊN HÀM - TÍCH PHÂN VÀ ỨNG DỤNG
§1.NGUYÊN HÀM
Đặt vấn đề
1) Bổsungthôngtinthíchhợpvàocácôtrốngdướiđây:
STT f(x) f
0
(x)
1 n · x
n−1
2 0
3 −
1
x
2
4
1
2
√
x
STT f(x) f
0
(x)
5 a
x
·lna
6 e
x
7
1
x
8
1
x · lna
STT f(x) f
0
(x)
9 cosx
10 −sinx
11
1
cos
2
x
12
1
sin
2
x
2) Tìmhàmsốf(x) biếtrằng
a.f
0
(x)=3x
2
b.f
0
(x)=x
2
1 NGUYÊN HÀM VÀ TÍNH CHẤT
1 Nguyên hàm
Định nghĩa − £ é
Chohàmsốf(x) xácđịnhtrênK.
HàmsốF(x) đượcgọilànguyên hàm củahàmsốf(x) trênK nếu............ với
mọix ∈ K.
Ví dụ 1.
•HàmsốF(x)=......... làmộtnguyênhàmcủahàmsốf(x)=3x
2
.
•HàmsốF(x)=......... làmộtnguyênhàmcủahàmsốf(x)=cosx.
Ví dụ 2. Hàmsốnàosauđâykhôngphảilànguyênhàmcủahàmsốy =
1
cos
2
x
?
A. F
1
(x)=tanx. B. F
2
(x)=tanx +2020.
C. F
3
(x)=tanx +2021. D. F
4
(x)=2020tanx.
Định lí 1 − £ é
NếuF(x)làmộtnguyênhàmcủahàmsốf(x) trênK thìvớimỗihằng số C,hàm
sốG(x)=............ cũnglàmộtnguyênhàmcủaf(x) trênK.
Định lí 2 − £ é
NếuF(x) làmộtnguyênhàmcủahàmsốf(x) trênK thìmọinguyênhàmcủaf(x)
trênK đềucódạng............,vớiC làmột.............
Z
f(x)dx =............
•F(x) làmột............ củaf(x)
•F(x)+C là...... tấtcảcácnguyên
hàmcủaf(x)
•f(x)dx =F
0
(x)dx làvi phân của...
Ví dụ 3. Tìmcácnguyênhàmsau:
Soạn:HuỳnhPhúSĩ 6 TrườngTHCS-THPTMỹThuận
§1.Nguyênhàm TOÁN12
a)
Z
x
2
dx =
b)
Z
dx
2
√
x
=
c)
Z
e
x
dx =
2 Tính chất của nguyên hàm
Chohàmsốy =f(x) cóđạohàmtrênK.
!
Tínhchất1.
Z
f
0
(x)dx =..................
Tínhchất2.
Z
k · f(x)dx =............ (k làhằngsố)
Tínhchất3.
Z
f(x)± g(x)
dx =.....................
Ví dụ 4. Tìmnguyênhàmcủahàmsốf(x)=3sinx +
2
x
trênkhoảng(0;+∞).
Ví dụ 5. Chohàmsốf(x)xácđịnhtrênkhoảng(0;+∞)thỏamãnf
0
(x)·
√
x =
1
2
và
f(4)=5.Tìmf(x).
3 Sự tồn tại của nguyên hàm
Mọihàmsố............ trênK đềucónguyênhàmtrênK.
Bảng nguyên hàm của một số hàm số thường gặp
•
Z
0dx =...............
•
Z
dx =...............
•
Z
x
n
dx =............... (n 6=−1)
•
Z
1
x
dx =...............
•
Z
e
x
dx =...............
•
Z
a
x
dx =............... (a > 0,a 6=1)
•
Z
cosx dx =...............
•
Z
sinxdx =...............
•
Z
1
cos
2
x
dx =...............
•
Z
1
sin
2
x
dx =...............
Chú ý − £ é
Từ đây, yêu cầu tìm
nguyênhàmcủamộthàm
sốđượchiểulàtìmnguyên
hàmtrêntừngkhoảngxác
địnhcủanó.
Ví dụ 6. Tìmcácnguyênhàmsau:
a)
Z
3x
2
+
1
x
2
dx
b)
Z
1+tan
2
x
dx
Soạn:HuỳnhPhúSĩ 7 TrườngTHCS-THPTMỹThuận
§1.Nguyênhàm TOÁN12
2 PHƯƠNG PHÁP TÌM NGUYÊN HÀM
1 Phương pháp đổi biến số
Ví dụ 7. Tìm
Z
(x − 2)
2021
dx.
Định lí 3 − £ é
Nếu
Z
f(u)dx =F(u)+C vàu =u(x) làhàmsốcóđạohàmliêntụcthì
Z
f
(
u(x)
)
·u
0
(x)dx =............
Ví dụ 8. Tìm
Z
(3x − 2)
2021
dx.
Chú ý − £ é
Nếutínhnguyênhàmtheo
biếnmớiu =u(x) thìsau
khi tính nguyên hàm, ta
phảitrởlạibiếnx banđầu
bằngcáchthayu bởiu(x).
Hệ quả. Vớiu =ax +b (a 6=0)thì
Z
f
(
ax +b
)
dx =............
Ví dụ 9.
Z
cos(5x +7)dx =............
Ví dụ 10. XétnguyênhàmI =
Z
x
√
x +2dx.Nếuđặtt =
√
x +2 thìtađược
A. I =
Z
4t
4
−2t
2
dt. B. I =
Z
t
4
−2t
2
dt.
C. I =
Z
2t
4
−4t
2
dt. D. I =
Z
2t
4
−t
2
dt.
2 Phương pháp nguyên hàm từng phần
Định lí 4 − £ é
Nếuhaihàmsốu =u(x) vàv =v(x) cóđạohàmliêntụctrênK thì
Z
u(x)· v
0
(x)dx =........................
Ví dụ 11. Tìmcácnguyênhàmsau:
a)
Z
(x +1)lnx dx
b)
Z
(x +1)cosxdx
c)
Z
(x +1)e
x
dx
d)
Z
e
x
cosx dx
Soạn:HuỳnhPhúSĩ 8 TrườngTHCS-THPTMỹThuận
§1.Nguyênhàm TOÁN12
Tips − £ é
Thứtựưutiênđặtu(x) là
I)Logarit
II)Đa thức
III)Lượng giác
IV)Mũ
3 THỰC HÀNH
Í TRẮC NGHIỆM
Câu 1. Trongcáckhẳngđịnhsau,khẳngđịnhnàolàđúng?
A.
Z
f(x)· g(x)
dx =
Z
f(x)dx ·
Z
g(x)dx.
B.
Z
0dx =0.
C.
Z
f(x)dx =f
0
(x)+C.
D.
Z
f
0
(x)dx =f(x)+C.
Câu 2. Chof(x), g(x) làcáchàmsốxácđịnhvàliêntụctrênR.Trongcácmệnh
đềsau,mệnhđềnàosai?
A.
Z
2f(x)+3g(x)
dx =2
Z
f(x)dx +3
Z
g(x)dx.
B.
Z
f(x)− g(x)
dx =
Z
f(x)dx −
Z
g(x)dx.
C.
Z
2f(x)dx =2
Z
f(x)dx.
D.
Z
f(x)· g(x)dx =
Z
f(x)dx ·
Z
g(x)dx.
Câu 3. Cặpsốnàosauđâycótínhchất"Cómộthàmsốlànguyênhàmcủahàm
sốcònlại"?
A. tanx
2
và
1
cos
2
x
2
. B. sin2x vàsin
2
x.
C. e
x
vàe
−x
. D. sin2x vàcos
2
x.
Câu 4. Khẳngđịnhnàosauđâylàkhẳngđịnhsai?
A.
Z
cosx dx =sinx +C.
B.
Z
1
x
2
dx =−
1
x
+C.
C.
Z
1
2
√
x
dx =
√
x +C.
D.
Z
a
x
dx =a
x
·lna +C (a > 0, a 6=1).
Câu 5. Họtấtcảcácnguyênhàmcủahàmsốf(x)=cosx +6x là
A. sinx +3x
2
+C. B. −sinx +3x
2
+C.
C. sinx +6x
2
+C. D. −sinx +C.
Soạn:HuỳnhPhúSĩ 9 TrườngTHCS-THPTMỹThuận
§1.Nguyênhàm TOÁN12
Câu 6. Xácđịnhf(x) biết
Z
f(x)dx =
1
x
+e
x
+C.
A. f(x)=ln|x| +e
x
. B. f(x)=
1
x
2
+e
x
.
C. f(x)=−
1
x
2
+e
x
. D. f(x)=lnx +e
x
.
Câu 7. HàmsốF(x)= 2sinx − 3cosx làmộtnguyênhàmcủahàmsốnàosau
đây?
A. f(x)=−2cosx − 3sinx. B. f(x)=−2cosx +3sinx.
C. f(x)=2cosx +3sinx. D. f(x)=2cosx − 3sinx.
Câu 8. Tìmm đểhàmsốF(x)=mx
3
+(3m+2)x
2
−4x +3 làmộtnguyênhàm
củahàmsốf(x)=3x
2
+10x − 4.
A. m =3. B. m =1. C. m =2. D. m =0.
Câu 9. Họnguyênhàmcủahàmsốf(x)=2x
1+3x
3
là
A. x
2
1+3x
2
+C. B. 2x
x +x
3
+C.
C. x
2
x +x
3
+C. D. x
2
1+
6x
3
5
+C.
Câu 10. Tìmhọnguyênhàmcủahàmsốf(x)=
2x
2
+x − 1
x
2
.
A.
Z
2x
2
+x − 1
x
2
dx =2+
1
x
−
1
x
2
+C.
B.
Z
2x
2
+x − 1
x
2
dx =2x +
1
x
+ln|x| +C.
C.
Z
2x
2
+x − 1
x
2
dx =x
2
+ln|x| +
1
x
+C.
D.
Z
2x
2
+x − 1
x
2
dx =x
2
−
1
x
+ln|x| +C.
Câu 11. Hàmsốnàosauđâykhông phải làmộtnguyênhàmcủahàmsốf(x)=
(2x − 3)
3
?
A. F(x)=
(2x − 3)
4
8
+8. B. F(x)=
(2x − 3)
4
8
−3.
C. F(x)=
(2x − 3)
4
8
. D. F(x)=
(2x − 3)
4
4
.
Câu 12. Hàmsốnàodướiđâylànguyênhàmcủahàmsốf(x)=
1
1− x
?
A. F(x)=−
1
4
ln|4− 4x|+3. B. F(x)=−ln|1− x|+4.
C. F(x)=ln|1− x| +2. D. F(x)=
1
2
ln
x
2
−2x +1
+5.
Câu 13. Chohàmsốf(x) = x
3
− x
2
+2x − 1.GọiF(x)làmộtnguyênhàmcủa
f(x).BiếtrằngF(1)=4.TìmF(x).
A. F(x)=
x
4
4
−
x
3
3
+x
2
−x. B. F(x)=
x
4
4
−
x
3
3
+x
2
−x +1.
C. F(x)=
x
4
4
−
x
3
3
+x
2
−x +2. D. F(x)=
x
4
4
−
x
3
3
+x
2
−x +
49
12
.
Câu 14. BiếtF(x)lànguyênhàmcủahàmsốf(x) =
1
x − 1
vàF(2)= 1.Khiđó
F(3) bằngbaonhiêu?
A. ln
3
2
. B. ln2+1. C. ln2. D.
1
2
.
Câu 15. Họtấtcảcácnguyênhàmcủahàmsốf
(
x
)
=
x +2
x − 1
trênkhoảng
(
1;+∞
)
là
A. x +3ln
(
x − 1
)
+C. B. x −3ln
(
x − 1
)
+C.
C. x −
3
(
x − 1
)
2
+C. D. x −
3
(
x − 1
)
2
+C.
Câu 16. Tìmnguyênhàmcủahàmsốf(x)=
x
3
x
4
+1
.
A.
Z
f(x)dx =
3x
4
2x
4
+6
+C. B.
Z
f(x)dx =ln
x
4
+1
+C.
C.
Z
f(x)dx =x
3
ln
x
4
+1
+C. D.
Z
f(x)dx =
1
4
ln
x
4
+1
+C.
Soạn:HuỳnhPhúSĩ 10 TrườngTHCS-THPTMỹThuận
§1.Nguyênhàm TOÁN12
Câu 17. Tìmnguyênhàmcủahàmsốf(x)=
√
5− 3x.
A.
Z
f(x)dx =−
2
9
(5− 3x)
√
5− 3x +C.
B.
Z
f(x)dx =−
2
3
(5− 3x)
√
5− 3x +C.
C.
Z
f(x)dx =
2
9
(5− 3x)
√
5− 3x +C.
D.
Z
f(x)dx =−
2
3
√
5− 3x +C.
Câu 18. Tìmnguyênhàmcủahàmsốf(x)=xe
x
.
A.
Z
f(x)dx =(x +1)e
x
+C. B.
Z
f(x)dx =(x − 1)e
x
+C.
C.
Z
f(x)dx =xe
x
+C. D.
Z
f(x)dx =x
2
e
x
+C.
Câu 19. Biết
Z
(x +3)· e
−3x+1
dx = −
1
m
e
−3x+1
(3x +n)+C vớim, n làcácsố
nguyên.TínhtổngS =m +n.
A. 10. B. 1. C. 9. D. 19.
Câu 20. Mộtvậtchuyểnđộngvớivậntốca(t)=
3
t +1
(m/s
2
).Biếtrằngvậntốc
banđầucủavậtđólà6 (m/s),hãytínhvậntốccủavậtđótạigiâythứ10.
A. 10m/s. B. 15,2m/s. C. 13,2m/s. D. 12m/s.
L TỰ LUẬN
Câu 1 (SGK GT12). Trongcáccặphàmsốdướiđây,hàmsốnàolàmộtnguyênhàmcủahàmsốcònlại?
a)e
−x
và−e
−x
b)sin2x vàsin
2
x
c)
1−
2
x
2
e
x
và
1−
4
x
2
e
x
Câu 2. Tìmnguyênhàmcủacáchàmsốsau:
a)f(x)=e
3−2x
b)f(x)=tan
2
x c)f(x)=sin5x ·cos3x
d)f(x)=
1
(1+x)(1−2x)
Câu 3. Sửdụngphươngphápđổibiếnsố,hãytính:
a)
Z
(1− x)
9
dx (đặtu =1− x) b)
Z
cos
3
xsinx dx (đặtu =cosx)
Câu 4. Sửdụngphươngpháptínhnguyênhàmtừngphần,hãytính:
a)
Z
xln(1+x)dx b)
Z
x
2
+2x − 1
e
x
dx c)
Z
xsin(2x +1)dx d)
Z
(1− x)cosx dx
Soạn:HuỳnhPhúSĩ 11 TrườngTHCS-THPTMỹThuận
§1.Nguyênhàm TOÁN12
Vocabulary − £ é
derivative đạohàm
antiderivative nguyênhàm
differential viphân
method phươngpháp
change of variable đổibiếnsố
antiderivative by parts nguyênhàmtừngphần
Soạn:HuỳnhPhúSĩ 12 TrườngTHCS-THPTMỹThuận
§2.Tíchphân TOÁN12
§2.TÍCH PHÂN
Đặt vấn đề
Nhờtíchphân,tacóthểtínhđộdàicủamộtđườngcong,diệntíchcủamộthìnhphẳng,thểtíchcủamộtkhốitròn
xoayhaycácbàitoánvềquãngđường,vậntốc...
x
y
O
x =a
x =b
y =f(x)
c
O
x
y
3 6
9
9
2
y =x
2
y =
x
2
8
y =
27
x
1 KHÁI NIỆM TÍCH PHÂN
1 Diện tích hình thang cong
Chohàmsốy =f(x) liêntục,không............ trênđoạn[a;b].
Hình ......... giởi hạn bởi đồ thị của hàm số y = f(x), trục ......... và hai đường
thẳng x =a, x =b được gọi là hình thang cong.
GiảsửF(x)làmộtnguyênhàmcủaf(x).Ngườitachứngmìnhđượcrằnghìnhthang
congnêutrêncódiệntíchlà
S =F(b)−F(a)
2 Định nghĩa tích phân
Chohàmsốy = f(x) liêntụctrênđoạn[a;b].GiảsửF(x) làmộtnguyênhàmcủaf(x)
trênđoạn[a;b].
Tíchphântừa đếnb củahàmsốf(x) làhiệuF(b)− F(a).
b
Z
a
f(x)dx =F(x)
b
a
=F(b)− F(a)
Tagọia làcậndưới,b làcậntrên.
!
Quy ước:
•
a
Z
a
f(x)dx =......
•
a
Z
b
f(x)dx =......
Ví dụ 1. Tínhcáctíchphânsau:
a)
2
Z
1
x
3
+3
x
dx
b)
e
Z
−1
1
x
−
1
x
2
dx
Soạn:HuỳnhPhúSĩ 13 TrườngTHCS-THPTMỹThuận
§2.Tíchphân TOÁN12
2 TÍNH CHẤT CỦA TÍCH PHÂN
!
Tínhchất1.
b
Z
a
k · f(x)dx =............... (k làhằngsố)
Tínhchất2.
b
Z
a
f(x)± g(x)
dx =...........................
Tínhchất3.
c
Z
a
f(x)dx +
b
Z
c
f(x)dx =............ (a < c < b)
Ví dụ 2. Tính
1
Z
0
|x − 1| dx.
3 PHƯƠNG PHÁP TÍNH TÍCH PHÂN
1 Phương pháp đổi biến số
Ví dụ 3. Đểtínhtíchphân
2
Z
1
(
2x − 1
)
3
dx,babạnTrường,MỹvàThuậnđưaracách
giảinhưsau:
Trường
2
Z
1
(
2x − 1
)
3
dx =
2
Z
1
8x
3
−3· 4x
2
+3· 2x −1
dx
=
2
Z
1
8x
3
−12x
2
+6x − 1
dx
=
8·
x
4
4
−12·
x
3
3
+6·
x
2
2
−x
2
1
=
2x
4
−4x
3
+3x
2
−x
2
1
=10.
Mỹ
Đặtu =2x − 1Ñ du =2dx.
Đổicận:
(
x =1Ñ u =2· 1− 1=1
x =2Ñ u =2· 2− 1=3
Khiđó
2
Z
1
(
2x − 1
)
3
dx =
3
Z
1
u
3
du
2
=
1
2
·
u
4
4
3
1
=10.
Thuận
2
Z
1
(
2x − 1
)
3
dx =
1
2
·
(2x − 1)
4
4
2
1
=10.
Hãysosánhbalờigiảitrên.
Ví dụ 4. Tính
a)
π
2
Z
0
cos
2
xsinx dx
b)
2
Z
−2
dx
√
4− x
2
Soạn:HuỳnhPhúSĩ 14 TrườngTHCS-THPTMỹThuận
§2.Tíchphân TOÁN12
2 Phương pháp tính tích phân từng phần
Định lí − £ é
Nếuhaihàmsốu =u(x) vàv =v(x) cóđạohàmliêntụctrênK thì
b
Z
a
u(x)· v
0
(x)dx =........................
Ví dụ 5. Tìmcácnguyênhàmsau:
a)
e
Z
1
(x +1)lnx dx
b)
π
2
Z
0
(x +1)cosxdx
c)
1
Z
0
(x +1)e
x
dx
d)
π
2
Z
0
e
x
cosx dx
4 THỰC HÀNH
Í TRẮC NGHIỆM
Câu 1. ChoF(x) làmộtnguyênhàmcủahàmsốf(x).KhiđóhiệusốF(0)−F(1)
bằng
A.
1
Z
0
−F(x)dx. B.
1
Z
0
F(x)dx. C. −
1
Z
0
f(x)dx. D.
1
Z
0
f(x)dx.
Câu 2. Chohàmsốf(x), g(x)liêntụctrên[a;b].Khẳngđịnhnàosauđâysai?
A.
b
Z
a
f(x)+g(x)
dx =
b
Z
a
f(x)dx +
b
Z
a
g(x)dx.
B.
b
Z
a
f(x)dx =
a
Z
b
f(x)dx.
C.
b
Z
a
f(x)dx =
b
Z
a
f(t)dt.
D.
b
Z
a
f(x)dx =
b
Z
c
f(x)dx +
c
Z
a
f(x)dx.
Soạn:HuỳnhPhúSĩ 15 TrườngTHCS-THPTMỹThuận
§2.Tíchphân TOÁN12
Câu 3. BiếtF(x)làmộtnguyênhàmcủaf(x)trênđoạn[−2;3],
3
Z
−2
f(x)dx =12 và
F(3)=7.TínhF(−2).
A. F(−2)=19. B. F(−2)=2. C. F(−2)=5. D. F(−2)=−5.
Câu 4. Cho
b
Z
a
f(x)dx =−3và
b
Z
a
g(x)dx =4.TínhI =
b
Z
a
[4f(x)−3g(x)]dx.
A. I =25. B. I =−24. C. I =24. D. I =0.
Câu 5. Giảsửcácbiểuthứctrongdấunguyênhàm,tíchphânđềucónghĩa,trong
cáckhẳngđịnhsau,khẳngđịnhnàolàsai?
A.
Z
f
0
(x)dx =f(x)+C.
B.
Z
kf(x)dx =k
Z
f(x)dx, ∀k ∈ R.
C.
b
Z
a
u(x)v
0
(x)dx =u(x)v(x)
b
a
−
b
Z
a
u
0
(x)v(x)dx.
D.
b
Z
a
kf(x)dx =k
b
Z
a
f(x)dx, ∀k ∈ R.
Câu 6. Chohàmsốf(x) cóđạohàmliêntụctrênđoạn[1;4],f(1) = 15,f(4) = 8.
Tính
4
Z
1
f
0
(x)dx.
A.
4
Z
1
f
0
(x)dx =7. B.
4
Z
1
f
0
(x)dx =3.
C.
4
Z
1
f
0
(x)dx =23. D.
4
Z
1
f
0
(x)dx =−7.
Câu 7. Chobiết
5
Z
2
f(x)dx =3,
5
Z
2
g(t)dt =9.Tính
5
Z
2
f(x)− 2g(x)
dx.
A. −6. B. −15. C. 12. D. 21.
Câu 8. Chocáchàmsốf(x),g(x)liêntụctrênR thỏamãn
5
Z
−1
2f(x)+3g(x)
dx =
−5;
5
Z
−1
3f(x)− 5g(x)
dx =21.Tính
5
Z
−1
f(x)+g(x)
dx.
A. −5. B. 1. C. 5. D. −1.
Câu 9. Nếu
2
Z
1
f(x)dx =−2 và
3
Z
2
f(x)dx =1 thì
3
Z
1
f(x)dx bằng
A. −3. B. −1. C. 1. D. 3.
Câu 10. Chohàmsốf(x)thỏamãn
Z
3
1
f(x)dx = 5và
Z
3
−1
f(x)dx = 1.Tínhtích
phânI =
Z
1
−1
f(x)dx.
A. I =−6. B. I =6. C. I =4. D. I =−4.
Câu 11. Cho
2
Z
−1
f(x)dx =2,
7
Z
−1
f(t)dt =9.Giátrịcủa
7
Z
2
f(z)dz là
A. 7. B. 3. C. 11. D. 5.
Câu 12. Cho
2
Z
−2
f(x)dx =1,
4
Z
−2
f(t)dt =−4.TínhI =
4
Z
2
f(y)dy.
A. I =5. B. I =3. C. I =−3. D. I =−5.
Soạn:HuỳnhPhúSĩ 16 TrườngTHCS-THPTMỹThuận
§2.Tíchphân TOÁN12
Câu 13. TínhI =
2
Z
0
(2x − x
3
)dx.
A. I =0. B. I =10. C. I =−4. D. I =−10.
Câu 14. ChoI =
π
2
Z
0
sin2xdx,J =
π
2
Z
0
sinxdx.Trongcácmệnhđềsau,mệnhđề
nàođúng?
A. I > J. B. I =J. C. I < J. D. I =2J.
Câu 15. Tíchphân
1
Z
0
3
2x+1
dx bằng
A.
27
ln9
. B.
9
ln9
. C.
4
ln3
. D.
12
ln3
.
Câu 16. Tíchphân
2
Z
1
dx
2x +1
bằng
A. log
5
3
. B.
2
15
. C.
1
2
ln
5
3
. D.
16
225
.
Câu 17. TínhI =
e
2
Z
e
(
1− lnx
)
2
x
dx đượckếtquảlà
A.
4
3
. B.
5
3
. C.
1
3
. D.
13
3
.
Câu 18. Biếtrằng
7
Z
2
xdx
x
2
+1
=aln2− bln5vớia, b ∈ Q.Giátrịcủa2a +b
bằng
A.
3
2
. B.
1
2
. C. 1. D. 2.
Câu 19. Biết
ln5
Z
ln2
(x + 1)e
x
dx = aln5 + bln2,vớia, b làcácsốnguyên.Tính
T =3a −2b.
A. T =19. B. T =−4. C. T =11. D. T =−16.
Câu 20. Giátrịcủatíchphân
π
4
Z
0
xsinx dx bằng
A.
4+π
4
√
2
. B.
4− π
4
√
2
. C.
2− π
2
√
2
. D.
2+π
2
√
2
.
Câu 21. Tìmgiátrịcủab để
b
Z
1
(2x − 6)dx =0.
A. b =0 hoặcb =1. B. b =0 hoặcb =3.
C. b =1 hoặcb =5. D. b =5 hoặcb =0.
Câu 22. Biết
3
Z
1
x +2
x
dx =a +blnc vớia,b,c ∈ Z,c < 9.TínhtổngS =
a +b +c.
A. S =6. B. S =7. C. S =5. D. S =8.
Câu 23. TíchphânI =
1
Z
0
2x
2
+3x − 6
2x +1
dx cógiátrịlà
A.
3
2
−
7
2
ln3. B.
3
2
+
7
2
ln3. C. 5ln3. D. −2ln3.
Câu 24. Cho
1
Z
0
dx
x
2
+3x +2
=aln2+bln3vớia,b làcácsốnguyên.Mệnhđề
nàosauđâyđúng?
A. a +2b =0. B. a −2b =0. C. a +b =−2. D. a +b =2.
Soạn:HuỳnhPhúSĩ 17 TrườngTHCS-THPTMỹThuận
§2.Tíchphân TOÁN12
Câu 25. TínhtíchphânI =
1
Z
0
dx
x
2
−9
.
A. I =
1
6
ln
1
2
. B. I =−
1
6
ln
1
2
. C. I =
1
6
ln2. D. I =ln
6
√
2.
Câu 26. Biết
3
Z
2
5x +12
x
2
+5x +6
dx =aln2+bln5+cln6.TínhS =3a+2b+c.
A. −11. B. −14. C. −2. D. 3.
Câu 27. Biết
1
Z
0
dx
√
x +1+
√
x
=
2
3
√
a − b
vớia, b làcácsốnguyêndương.
TínhT =a +b.
A. T =7. B. T =10. C. T =6. D. T =8.
Câu 28. Biết
3
Z
1
dx
√
x +1−
√
x
=a
√
3+b
√
2+c vớia,b,c làcácsốhữutỷ.Tính
P =a +b +c.
A. P =
13
2
. B. P =
16
3
. C. P =5. D. P =
2
3
.
Câu 29. Chohàmsốy =f(x)liêntục,nhậngiátrịdươngtrên(0;+∞)vàthỏa
mãnf(1)=1,f(x)=f
0
(x)
√
3x +1,vớimọix > 0.Mệnhđềnàosauđâyđúng?
A. 4< f(5)< 5. B. 3< f(5)< 4. C. 1< f(5)< 2. D. 2< f(5)< 3.
Câu 30. Chohàmsốf(x)liêntụctrênR,biết
π
4
Z
0
f
(
tanx
)
dx =4và
1
Z
0
x
2
·f(x)
x
2
+1
dx =
2.TínhI =
1
Z
0
f(x)dx.
A. 6. B. 1. C. 0. D. 2.
L TỰ LUẬN
Câu 1 (SGK GT12). Tínhcáctíchphânsau:
a)
π
2
Z
0
sin
π
4
−x
dx
b)
2
Z
1
2
1
x(x +1)
dx c)
2
Z
0
(x +1)
2
dx
Câu 2 (SGK GT12). Tínhcáctíchphânsau:
a)
π
2
Z
0
sin
2
xdx
b)
1
2
Z
0
x
3
−1
x
2
−1
dx
c)
1
Z
0
ln(1+x)dx
Soạn:HuỳnhPhúSĩ 18 TrườngTHCS-THPTMỹThuận
§3.Ứngdụngcủatíchphântronghìnhhọc TOÁN12
§3.ỨNG DỤNG CỦA TÍCH PHÂN TRONG
HÌNH HỌC
Đặt vấn đề
Trongbài§2.Tíchphân,tađãbiếttíchphân
b
Z
a
f(x)dx làdiệntíchcủahìnhthangconggiớihạnbởiđồthịcủahàm
sốf(x) (khôngâm),trụcOx vàhaiđườngthẳngx =a,x =b.Mờicácemtínhdiệntíchcủacáchìnhthangdướiđây:
x
y
O 1 3
y =x
3
−3
x
+3
S
S =..................
x
y
O
1 3
y =−x
3
+3
x
−3
S
S =..................
1 HÌNH PHẲNG GIỚI HẠN BỞI MỘT ĐƯỜNG CONG VÀ TRỤC HOÀNH
x
y
O
a
c
b
y =f(x)
Chohàmsốy =f(x) liêntụctrênđoạn[a;b].
Diện tích S của hình phẳng giởi hạn bởi đồ thị của hàm số y =f(x), trục ......... và
hai đường thẳng x =a, x =b được tính theo công thức
S =
b
Z
a
...... dx =
c
Z
a
...... dx +
b
Z
c
...... dx
Ví dụ 1. Tínhdiệntíchhìnhphẳngđượcgiớihạnbởiđườngcongy =x
2
−4x +3,trục
hoành,trụctungvàđườngthẳngx =5.
2 HÌNH PHẲNG GIỚI HẠN BỞI HAI ĐƯỜNG CONG
x
y
O
a
b
y =f(x)
y =g(x)
Chohaihàmsốy =f(x) vày =g(x) liêntụctrênđoạn[a;b].
Diện tích S của hình phẳng giởi hạn bởi đồ thị của hai hàm số y = f(x), y =g(x) và
hai đường thẳng x =a, x =b được tính theo công thức
S =
b
Z
a
............... dx
Ví dụ 2. Tínhdiệntíchhìnhphẳngđượcgiớihạnbởihaiparaboly =x
2
− 2x − 2và
y =2− x
2
.
Soạn:HuỳnhPhúSĩ 19 TrườngTHCS-THPTMỹThuận
§3.Ứngdụngcủatíchphântronghìnhhọc TOÁN12
3 TÍNH THỂ TÍCH
1 Thể tích của vật thể
CắtmộtvậtthểV bởihaimặtphẳng(P)và(Q)vuônggócvớitrụcOx lầnlượttạix =a,
x =b (a < b).CắtV bởimộtmặtphẳngtùyývuônggócvớiOx tạidiểmx ∈ [a;b]theo
thiếtdiệncódiệntíchS(x).
GiảsửS(x) liêntụctrênđoạn[a;b],khiđóvậtthểV cóthểtíchlà
V =
b
Z
a
............ dx
Ví dụ 3. ViếtcôngthứctínhthểtíchV củavậtthểnằmgiữahaimặtphẳngx =0và
x =ln4,bịcắtbởimộtmặtphẳngvuônggócvớitrụchoànhtạiđiểmcóhoànhđộ
x ∈ (0;ln4),cóthiếtdiệnlàmộthìnhvuôngcạnh
√
xe
x
.
A. V =π
ln4
Z
0
xe
x
dx. B. V =
ln4
Z
0
√
xe
x
dx.
C. V =
ln4
Z
0
xe
x
dx. D. V =π
ln4
Z
0
[xe
x
]
2
dx.
2 Thể tích khối chóp và khối chóp cụt
a)Chokhốichópcóchiềucaoh vàdiệntíchđáyB.
Chọnhệtrụctọađộnhưhình,khiđóhìnhchópđãchocóthểtíchlà
V =
h
Z
0
S(x)dx =
h
Z
0
...... dx =.........
b)ChokhốichópcụttạobởikhốichópđỉnhS códiệntíchhaiđáylầnlượtlàB, B
0
và
chiềucaobằngh.
Khiđókhốichópcụtđãchocóthểtíchbằng
V =...............
Soạn:HuỳnhPhúSĩ 20 TrườngTHCS-THPTMỹThuận
§3.Ứngdụngcủatíchphântronghìnhhọc TOÁN12
4 THỂ TÍCH KHỐI TRÒN XOAY
Quayhìnhthangconggiớihạnbởiđồthịhàmsốy =f(x),trụchoànhvàhaiđường
thẳngx =a,x =b quanhtrục...... tạothànhmộtkhối............ cóthểtíchlà
V =...
b
Z
a
......... dx
Ví dụ 4. Tínhthểtíchkhốitrònxoaythuđượckhiquayhìnhphẳnggiớihạnbởiđường
congy =cosx,trụchoànhvàhaiđườngthẳngx =0,x =π quanhtrụchoành.
5 THỰC HÀNH
Í TRẮC NGHIỆM
Câu 1. Nếuhàmsốy =f(x)liêntụctrênđoạn[a;b]thìdiệntíchS củahình
phẳnggiớihạnbởiđồthịhàmsốy =f(x),trụchoànhvàhaiđườngthẳngx =a,
x =b là
A.
b
Z
a
|f(x)− g(x)| dx. B.
a
Z
b
|f(x)| dx.
C.
b
Z
a
f(x)dx. D.
b
Z
a
|f(x)| dx.
x
y
O−1
y =f(x)
−2 2
Câu 2. ChohìnhphẳngH giớihạnbởiđồthịhàmsốy =f(x) trụcOx vàđường
thẳngx = −1(phầngạchsọcnhưhìnhbên).GọiS làdiệntíchcủahìnhphẳng
H.Mệnhđềnàodướiđâyđúng?
A. S =
0
Z
−1
|f(x)|dx −
2
Z
0
|f(x)|dx. B. S =
2
Z
−1
f(x)dx.
C. S =
0
Z
−1
f(x)dx −
2
Z
0
f(x)dx. D. S =
0
Z
−1
f(x)dx +
2
Z
0
f(x)dx.
x
y
O
x =a
x =b
y =f(x)
c
Câu 3. Diệntíchhìnhphẳng(H)giớihạnbởiđồthịcủahàmsốy =f(x),trục
hoànhvàhaiđườngthẳngx =a,x =b (a < b vàf(x)liêntụctrên[a;b])(phần
gạchsọctronghìnhvẽ)tínhtheocôngthức
A. S =−
c
Z
a
f(x)dx +
b
Z
c
f(x)dx. B. S =
b
Z
a
f(x)dx.
C. S =
b
Z
a
f(x)dx
. D. S =
c
Z
a
f(x)dx +
b
Z
c
f(x)dx.
Câu 4. ChohìnhphẳngD giớihạnbởiđồthịhaihàmsốy =f(x), y =g(x) liên
tụctrênđoạn[a;b] vàhaiđườngthẳngx =a, x =b.DiệntíchS củahìnhphẳng
D là
A. S =
b
Z
a
[f(x)+g(x)]dx. B. S =
b
Z
a
|f(x)− g(x)|dx.
C. S =
b
Z
a
[f(x)−g(x)]dx. D. S =
b
Z
a
[g(x)− f(x)]dx.
Soạn:HuỳnhPhúSĩ 21 TrườngTHCS-THPTMỹThuận
§3.Ứngdụngcủatíchphântronghìnhhọc TOÁN12
x
y
O
−1
2
y =x
2
−2x − 2
y =−x
2
+2
Câu 5. Diệntíchphầnhìnhphẳngđượcgạchchéotronghìnhbênbằng
A.
2
Z
−1
−2x
2
+2x +4
dx. B.
2
Z
−1
2x
2
−2x − 4
dx.
C.
2
Z
−1
−2x
2
−2x +4
dx. D.
2
Z
−1
2x
2
+2x − 4
dx.
Câu 6. TínhdiệntíchS củahìnhphẳnggiớihạnbởiđồthịhàmsốy = 3
x
,trục
Ox vàhaiđườngthẳngx =−1,x =2.
A. S =
26
3
. B. S =12. C. S =
12
ln3
. D. S =
26
3ln3
.
Câu 7. DiệntíchS củahìnhphẳnggiớihạnbởiđườngcongy =−x
3
+3x
2
− 2,
trụchoànhvàhaiđườngthẳngx =0,x =2 là
A. S =
5
2
. B. S =
3
2
. C. S =
7
2
. D. S =4.
Câu 8. TínhdiệntíchS củahìnhphẳnggiớihạnbởiđồthịhàmsốy = x
2
+x
vàđườngthẳngy =−x +3.
A. S =−
32
3
. B. S =
16
3
. C. S =16. D. S =
32
3
.
Câu 9. Tínhdiệntíchhìnhphẳnggiớihạnbởi
(
C
)
:y =x
4
− 2x
2
+1vàtrục
hoành.
A.
8
15
. B. −
15
16
. C.
15
8
. D.
16
15
.
Câu 10. Diệntíchhìnhphẳngđượcgiớihạnbởiđồthịhàmsốy =
x +1
x +2
,trục
hoànhvàđườngthẳngx =2 là
A. 3+ln2. B. 3− ln2. C. 3+2ln2. D. 3− 2ln2.
Câu 11.
Tính diện tích S của hình phẳng
(phầngạchsọc)tronghìnhbên.
A. S =
8
3
. B. S =
10
3
.
C. S =
11
3
. D. S =
7
3
.
x
y
y =x −2
y =
√
x
O 2 4
x
y
O
1 2
1
2
Câu 12. Cho(H) làhìnhphẳnggiớihạnbởiđồthịcủacáchàmsốy =
√
x,y =0,
y =2− x.Diệntíchcủa(H) là
A.
4
√
2− 1
3
. B.
8
√
2+3
6
. C.
7
6
. D.
5
6
.
Câu 13. Tínhdiệntíchhìnhphẳnggiớihạnbởicácđườngy = x
2
,y =
x
2
8
,
y =
27
x
.
A.
63
8
. B. 27ln2−
63
8
. C. 27ln2. D. 27ln2−
63
4
.
Câu 14. TínhdiệntíchS củahìnhphẳnggiớihạnbởielip(E)cóphươngtrình
x
2
a
2
+
y
2
b
2
=1,vớia, b > 0.
A. S =π
1
a
+
1
b
2
. B. S =π(a +b)
2
.
C. S =πab. D. S =
πa
2
b
2
a +b
.
Câu 15. Trêncánhđồngcỏcóhaiconbòđượccộtvàohaicâycọckhácnhau.
Biếtkhoảngcáchgiữahaicọclà4mcònhaisợidâycộthaiconbòdài3mvà2m.
Tínhphầndiệntíchmặtcỏlớnnhấtmàhaiconbòcóthểănchung(lấygiátrị
gầnđúngnhất).
A. 1,574m
2
. B. 1,034m
2
. C. 1,989m
2
. D. c.
Soạn:HuỳnhPhúSĩ 22 TrườngTHCS-THPTMỹThuận
§3.Ứngdụngcủatíchphântronghìnhhọc TOÁN12
Câu 16. Chohàmsốf(x)liêntụctrênđoạn[a;b].Gọi(H) làhìnhphẳnggiớihạn
bởiđồthịhàmsốy =f(x),trụchoànhvàhaiđườngthẳngx =a,x =b;V làthể
tíchcủakhốitrònxoayđượcthànhkhiquay(H) quanhtrụcOx.Khẳngđịnhnào
sauđâylàđúng?
A. V =π
b
Z
a
|f(x)| dx. B. V =
b
Z
a
f
2
(x)dx.
C. V =π
b
Z
a
f
2
(x)dx. D. V =
b
Z
a
|f(x)| dx.
Câu 17. ThểtíchcủakhốitrònxoaytạothànhkhiquayhìnhphẳngD giớihạn
bởicácđườngy =
√
x − 1,trụchoành,x =2 vàx =5 quanhtrụcOx bằng
A.
5
Z
2
(x − 1)dx. B.
5
Z
2
√
x − 1dx.
C. π
5
Z
2
(x − 1)dx. D. π
2
5
Z
2
(x − 1)dx.
x
y
O
a
b
y =f(x)
y =g(x)
Câu 18. Chohìnhphẳngtronghìnhvẽbên(phầntôđậm)quayquanhtrụchoành.
Thểtíchkhốitrònxoaytạothànhđượctínhtheocôngthứcnàotrongcáccông
thứcsauđây?
A. V =π
b
Z
a
g
2
(x)− f
2
(x)
dx. B. V =π
b
Z
a
f(x)− g(x)
2
dx.
C. V =π
b
Z
a
f(x)− g(x)
dx. D. V =π
b
Z
a
f
2
(x)− g
2
(x)
dx.
Câu 19. Tìmcôngthứctínhthểtíchcủakhốitrònxoaykhichohìnhphẳnggiới
hạnbởiparabol(P): y =x
2
vàđườngthẳngd: y =2x quayquanhtrụcOx.
A. π
2
Z
0
x
2
−2x
2
dx. B. π
2
Z
0
4x
2
dx − π
2
Z
0
x
4
dx.
C. π
2
Z
0
4x
2
dx +π
2
Z
0
x
4
dx. D. π
2
Z
0
2x − x
2
dx.
Câu 20. Chohìnhphẳng(D)giớihạnbởiđồthịhàmsốy =
√
x,haiđườngthẳng
x = 1,x = 2 vàtrụchoành.Tínhthểtíchkhốitrònxoaytạothànhkhiquay(D)
quanhtrụchoành.
A. 3π. B.
3
2
. C.
3π
2
. D.
2π
3
.
Câu 21. Thểtíchkhốitrònxoaysinhrakhiquayhìnhphẳnggiớihạnbởiđồthị
cáchàmsốy =x
2
−2x,y =0,x =−1,x =2 quanhtrụcOx bằng
A.
16π
5
. B.
17π
5
. C.
18π
5
. D.
5π
18
.
Câu 22. ChohìnhphẳngD giớihạnbởiđườngcongy =
√
2+cosx,trụchoành
vàcácđườngthẳngx = 0,x =
π
2
.TínhthểtíchV củakhốitrònxoaytạothành
khiquayD quanhtrụchoành.
A. V =π − 1. B. V =π +1. C. V =π(π −1). D. V =π(π +1).
Câu 23. ChohìnhphẳngD giớihạnbởiđườngcongy =e
x
,trụchoànhvàcác
đườngthẳngx =0,x =1.KhốitrònxoaytạothànhkhiquayD quanhtrụchoành
cóthểtíchV bằng
A. V =
e
2
−1
2
. B. V =
π
e
2
+1
2
.
C. V =
π
e
2
−1
2
. D. V =
πe
2
2
.
Câu 24. Thểtíchcủakhốitrònxoaysinhrakhichohìnhphẳnggiớihạnbởi
parabol(P): y =x
2
vàđườngthẳngd: y =x xoayquanhtrụcOx bằng
A. π
1
Z
0
x
2
dx − π
1
Z
0
x
4
dx. B. π
1
Z
0
x
2
dx +π
1
Z
0
x
4
dx.
Soạn:HuỳnhPhúSĩ 23 TrườngTHCS-THPTMỹThuận
§3.Ứngdụngcủatíchphântronghìnhhọc TOÁN12
C. π
1
Z
0
x
2
−x
2
dx. D. π
1
Z
0
x
2
−x
dx.
Câu 25. Gọi(H)làhìnhphẳnggiớihạnbởiđồthị(C):y =
4
x
vàđườngthẳng
(d): y = 5− x.TínhthểtíchV củakhốitrònxoaytạothànhkhiquayhình(H)
xungquanhtrụchoành.
A. V =51π. B. V =33π. C. V =9π. D. V =18π.
Câu 26.
Chohình phẳnggiới hạnbởi đồthị các hàmsố
y =
√
x,đườngthẳngy = 2 − x vàtrụchoành
(phầngạchchéotronghìnhvẽ).Thểtíchcủakhối
trònxoaysinhbởihìnhphẳngtrênkhiquayquanh
trụcOx bằng
A.
5π
4
. B.
4π
3
. C.
7π
6
. D.
5π
6
.
x
y
O
1 2
1
2
Câu 27. TínhthểtíchV củavậttrònxoaytạothànhkhiquayhìnhphẳng(H)giới
hạnbởicácđườngy =x
2
vày =
√
x quanhtrụcOx.
A. V =
3π
10
. B. V =
π
10
. C. V =
7π
10
. D. V =
9π
10
.
Câu 28. Ngườitalàmmộtchiếcphaobơinhưhìnhvẽ(vớibềmặtcóđượcbằng
cáchquayđườngtrònC quanhtrụcd).BiếtrằngOI = 30cm,R =5cm.Tínhthể
tíchV củachiếcphao.
d O
I
R
C
A. V =1500π
2
cm
3
. B. V =9000π
2
cm
3
.
C. V =1500πcm
3
. D. V =9000πcm
3
.
Câu 29. Mộtôtôđangchạyvớitốcđộ36 km/hthìngườiláixeđạpphanh,từthời
điểmđó,ôtôchuyểnđộngchậmdầnđềuvớivậntốcv(t) = −5t +10 m/s,trong
đót làkhoảngthờigiantínhbằnggiây,kểtừlúcbắtđầuđạpphanh.Hỏitừlúc
đạpphanhđếnlúcdừnghẳn,ôtôcòndichuyểnbaonhiêumét?
A. 10 m. B. 20 m. C. 2 m. D. 0,2 m.
Câu 30. Mộtchiếcxeđangchạyđềuvớivậntốc20m/sthìgiảmphanhvớivận
tốcv(t) =20− 2t m/sđếnkhidừnghẳn.Quãngđườngxeđiđượctừlúcbắtđầu
giảmphanhđếnkhidừnghẳnlà
A. 98m. B. 94 m. C. 100 m. D. 96 m.
L TỰ LUẬN
Câu 1 (SGK GT12). Tínhdiệntíchhìnhphẳnggiớihạnbởicácđường:
a)y =x
2
,y =x +2 b)y =(x −6)
2
,y =6x − x
2
Câu 2 (SGK GT12). Tínhthểtíchkhốitrònxoaydohìnhphẳnggiớihạnbởicácđườngsau
a)y =1− x
2
,y =0
b)y =tanx,y =0,x =0,x =
π
4
Soạn:HuỳnhPhúSĩ 24 TrườngTHCS-THPTMỹThuận
Chương4.Sốphức TOÁN12
Chương4.
SỐ PHỨC
§1.SỐ PHỨC
Đặt vấn đề
Sốphứcchophépgiảimộtphươngtrìnhnhấtđịnhmà
khônggiảiđượctrongtrườngsốthực.Vídụ,phươngtrình
(
x +1
)
2
=−9 khôngcónghiệmthực,vìbìnhphươngcủa
mộtsốthựckhôngthểâm.Cácsốphứcchophépgiải
phươngtrìnhnày.Ýtưởnglàmởrộngtrườngsốthựcsang
đơnvịảoi vớii
2
=−1,vìvậyphươngtrìnhtrênđượcgiải.
Sốphứcđượcsửdụngtrongnhiềulĩnhvựckhoahọc,như
khoahọckỹthuật,điệntừhọc,cơhọclượngtử,toánhọc
ứngdụngchẳnghạnnhưtronglýthuyếthỗnloạn.Nhà
toánhọcngườiÝGerolamoCardanolàngườiđầutiênđưa
rasốphức.Ôngsửdụngsốphứcđểgiảicácphươngtrình
bậcbatrongthếkỉ16.
1 ĐỊNH NGHĨA SỐ PHỨC
Mỗibiểuthứcdạng......... trongđóa, b ∈ ... vài
2
= ... đượcgọilàmộtsố
phức.
•Đốivớisốphứcz =a +bi,tanóia là............,b là............ củaz.
•Sối đượcgọilà............
•Tậphợpcácsốphứckíhiệulà...... (ThesetofComplexnumbers).
Ví dụ 1. Tìmphầnthựcvàphầnảocủacácsốphức−3+5i,4− i
√
2,−3i,2021.
!
•Mỗisốthựca đềulàmộtsốphứcvới
phần ảo bằng...
•Sốphứcbi cóphần thực bằng...
đượcgọilàsố.........
2 SỐ PHỨC BẰNG NHAU
Haisốphứcđượcgọilàbằngnhaunếu............ và............ củachúngtương
ứngbằngnhau.
a
1
+b
1
i =a
2
+b
2
i ⇔
(
a
1
=...
b
1
=...
Ví dụ 2. Tìmx, y đểhaisốphứcz =x +2+(y +4)i vàw =2x +1+(3y −2)i bằng
nhau
Soạn:HuỳnhPhúSĩ 25 TrườngTHCS-THPTMỹThuận
§1.Sốphức TOÁN12
3 BIỂU DIỄN HÌNH HỌC VÀ MÔĐUN CỦA SỐ PHỨC
1 Biểu diễn hình học của số phức
x
y
3
N(3;2)
2
O
ON =5
ĐiểmM(...;...)tronghệtrụctọađộOxy đượcgọilàđiểm............ củasốphức
z =a +bi.
Ví dụ 3. Tronghìnhbên,điểmN biểudiễnsốphứcnào?
2 Môđun của số phức
Chosốphứcz =a +bi cóđiểmbiểudiễnlàM(a;b).
......... củavectơ
−−Ï
OM đượcgọilàmôđuncủasốphứcz,kíhiệulà......
|z| =.........
Ví dụ 4. Tínhmôđuncủacácsốphứcz
1
=4− 3i,z
2
=2021,z
3
=i
√
7.
3 Số phức liên hợp
x
y
3
N(3;2)
2
O
ON =5
M(3;−2)
−2
O
OM =5
Chosốphứcz =a +bi.Tagọi......... làsố phức liên hợp củaz,kíhiệulà....
Ví dụ 5. Ghépnốicáccặpsốphứcliênhợpdướiđây:
a)3+2i
b)4− 3i
c)i
√
5
•4+3i
•−i
√
5
•−3+2i
!
•TrênmặtphẳngOxy,cácđiểmbiểudiễncủaz vàz đốixứngvớinhauqua
............
•|z| =...... vàz =......
4 THỰC HÀNH
Í TRẮC NGHIỆM
Câu 1. Chosốphứcz =a +bi.Môđuncủaz là
A. |z| =
√
a
2
+b
2
. B. |z| =
√
a
2
−b
2
.
C. |z| =a
2
+b
2
. D. |z| =2
√
a
2
+b
2
.
Câu 2. Chosốphứcz =a +bi.Khẳngđịnhnàosauđâysai?
A. z =a − bi. B. z =a +bi.
C. |z| =
√
a
2
+b
2
. D. |z| =
√
a
2
−b
2
.
Câu 3. Tìmphầnthựcvàphầnảocủasốphứcz =2−3i.
A. Phầnthựclà2 vàphầnảolà3. B. Phầnthựclà2 vàphầnảolà−3.
C. Phầnthựclà2 vàphầnảolà3i. D. Phầnthựclà2 vàphầnảolà−3i.
Câu 4. Sốphứccóphầnthựcbằng3 vàphầnảobằng4 là
A. 3+4i. B. 4−3i. C. 3− 4i. D. 4+3i.
Câu 5. Gọia, b lầnlượtlàphầnthựcvàphầnảocủasốphứcz =−3+2i.Giátrị
củaa +2b bằng
A. 1. B. −1. C. −4. D. −7.
Câu 6. Chosốphứcz =a +bi.Sốphứcliênhợpcủaz là
A.
z =a − bi. B. z =a − bi. C. z =bi. D. z =−a −bi.
Câu 7. Tínhmôđuncủasốphứcz =4− 3i.
A. |z| =5. B. |z| =
√
7. C. |z| =7. D. |z| =25.
Soạn:HuỳnhPhúSĩ 26 TrườngTHCS-THPTMỹThuận
§1.Sốphức TOÁN12
Câu 8. Trongcácsốphứcsau,sốnàocómôđunnhỏnhất?
A. z
1
=1+2i. B. z
2
=2− i. C. z
3
=2. D. z
4
=1+i.
Câu 9. Trongcácsốphứcsau,sốnàocómôđunlớnnhất?
A. z
1
=1+2i. B. z
2
=2− i. C. z
3
=3i. D. z
4
=1+i.
Câu 10. Chohaisốphứcz
1
=−1+2ivàz
2
=−1− 2i.Giátrịcủabiểuthức
|z
1
|
2
+|z
2
|
2
bằng
A.
√
10. B. 10. C. −6. D. 4.
Câu 11. Trongcácsốphứcz
1
= −2i,z
2
= 2− i,z
3
= 5i,z
4
= 4 cóbaonhiêusố
thuầnảo?
A. 4. B. 1. C. 3. D. 2.
Câu 12. Chosốphứcz =(2m−1)+(m
2
−4)i, m ∈ R.Tìmm đểsốphứcz làsố
thuầnảo.
A. m =2, m =−2. B. m =2.
C. m =−
1
2
. D. m =
1
2
.
Câu 13. Choa, b làhaisốthựcthỏamãn2a+(b−3)i=4−5i vớiilàđơnvịảo.
Giátrịcủaa, b bằng
A. a =1, b =8. B. a =8, b =8.
C. a =2, b =−2. D. a =−2, b =2.
Câu 14. Tìmcácsốthựca, b thỏamãn(a − 2b)+(a +b +4)i =(2a +b)+2bi
vớii làđơnvịảo.
A. a =−3, b =1. B. a =3, b =−1.
C. a =−3, b =−1. D. a =3, b =1.
Câu 15. Tìmcácsốthựcx, y thỏamãn(2x +5y)+(4x +3y)i=5+2i.
A. x =
5
14
, y =−
8
7
. B. x =
8
7
, y =−
5
14
.
C. x =−
5
14
, y =
8
7
. D. x =−
5
14
, y =−
8
7
.
x
y
3
M
−4
O
Câu 16. ĐiểmM tronghìnhvẽbênbiểudiễnsốphứcz.Tìmphầnthựcvàphần
ảocủaz.
A. −4 và3. B. 3 và−4i. C. 3 và−4. D. −4 và3i.
Câu 17. Trênmặtphẳngtọađộ,tìmtọađộcủađiểmM biểudiễnsốphứcz =
5− i.
A. M(5;0). B. M(5;−1). C. M(0;−5). D. M(5;1).
O
x
y
−2
A
1
1
B3
Câu 18. TrongmặtphẳngOxy,chocácđiểmA, B nhưhìnhvẽbên.Trungđiểm
củađoạnthẳngAB biểudiễnsốphức
A. −
1
2
+2i. B. 2−
1
2
i. C. −1+2i. D. 2−i.
Câu 19. GọiA, B lầnlượtbiểudiễncácsốphứcz
1
=2+3i vàz
2
=2−3i.Khẳng
địnhnàosauđâyđúng?
A. A, B đốixứngnhauquagốctọađộ.
B. A, B đốixứngnhauquatrụchoành.
C. A, B đốixứngnhauquatrụctung.
D. A, B đốixứngnhauquađiểmI(1;0).
Câu 20. Chocácsốphứcz
1
= 3i,z
2
= −1− 3i vàz
3
= m − 2i.Tậpgiátrịcủa
thamsốm đểsốphứcz
3
cómôđunnhỏnhấttrong3 sốphứcđãcholà
A.
h
−
√
5;
√
5
i
. B.
−
√
5;
√
5
.
C.
n
−
√
5;
√
5
o
. D.
−∞;
√
5
∪
√
5;+∞
.
L TỰ LUẬN
Câu 1 (SGK GT12). Trênmặtphẳngtọađộ,tìmtậphợpđiểmbiểudiễncácsốphứcz thỏamãnđiềukiện:
a)|z| =1 b)|z| ≤ 1
Soạn:HuỳnhPhúSĩ 27 TrườngTHCS-THPTMỹThuận
§2.Cộng,trừvànhânsốphức TOÁN12
§2.CỘNG, TRỪ VÀ NHÂN SỐ PHỨC
1 PHÉP VỘNG VÀ PHÉP TRỪ
Chohaisốphứcz
1
=a
1
+b
1
i vàz
2
=a
2
+b
2
i,khiđó:
•z
1
+z
2
=...............
•z
1
−z
2
=...............
Ví dụ 1. Thựchiệncácphéptínhsau:
a)(3− 5i)+(2+4i)
b)(−2− 3i)+(−1− 7i)
c)(4+3i)− (5− 7i)
d)(2− 3i)− (5− 4i)
2 PHÉP NHÂN
Vìi
2
=...... nêntacó:
(a +bi)(c +di)=.....................
Ví dụ 2. Thựchiệncácphéptínhsau:
a)(−1+i)(3+7i) b)(3+4i)(3− 4i) c) (2+3i)
2
3 THỰC HÀNH
Câu 1. Chohaisốphứcz
1
=2−2i,z
2
=−3+3i.Khiđósốphứcz
1
−z
2
là
A. −1+i. B. −5+5i. C. 5−5i. D. −5i.
Câu 2.
Tronghìnhvẽ,điểmP biểudiễnsốphứcz
1
,điểm
Q biểudiễnsốphứcz
2
.Tìmsốphứcz =z
1
+
z
2
.
A. z =1+3i. B. z =−3+i.
C. z =−1+2i. D. z =2+i.
0
x
y
−1
P
2
1
Q
2
Câu 3. Choz
1
=1+2i,z
2
=2− 3i.Khiđów =z
1
−2z
2
bằng
A. 5+8i. B. −3+8i. C. 3− i. D. −3− 4i.
Câu 4. Chosốphứcz =−
1
2
+
√
3
2
i.Tìmsốphứcw =1+z +z
2
.
A. w =−
1
2
+
√
3
2
i. B. w =0.
C. w =1. D. w =2−
√
3i.
Câu 5. Chosốphứcz,khiđóz +z là
A. Sốthực. B. Sốảo. C. 0. D. 2.
Câu 6. Chosốphứcz =2+bi.Tínhz · z.
A. z · z =
√
4+b
2
. B. z ·z =4−b
2
.
C. z ·z =−b. D. z·z =4+b
2
.
Soạn:HuỳnhPhúSĩ 28 TrườngTHCS-THPTMỹThuận
§2.Cộng,trừvànhânsốphức TOÁN12
Câu 7. Giátrịcủabiểuthứcz =(1+i)
2
là
A. 2i. B. −i. C. −2i. D. i.
Câu 8. Chohaisốphứcz
1
=3+2i vàz
2
=1−5i.Tìmphầnthựcvàphầnảocủa
sốphứcz
1
+z
2
.
A. Phầnthựclà4 vàphầnảolà3. B. Phầnthựclà4 vàphầnảolà−3i.
C. Phầnthựclà4 vàphầnảolà3i. D. Phầnthựclà4 vàphầnảolà−3.
Câu 9. Chohaisốphứcz
1
=
1
2
− 2i vàz
2
=4− i.Tínhmôđuncủasốphức
z =z
1
·z
2
.
A. |z| =
√
34
2
. B. |z| =
289
4
. C. |z| =
17
2
. D. |z| =−
17
2
.
Câu 10. Chohaisốphứcz
1
=2+3i vàz
2
=1+i.Tính|z
1
+3z
2
|.
A. |z
1
+3z
2
| =
√
11. B. |z
1
+3z
2
| =11.
C. |z
1
+3z
2
| =
√
61. D. |z
1
+3z
2
| =61.
Câu 11. Tìmsốphứcliênhợpcủasốphứcz =(11− 3i)+(5+2i)(1− i).
A. z =14+6i. B. z =18+6i. C. z =18− 6i. D. z =14−6i.
Câu 12. Chosốphứcz thỏamãn(3+2i)z +(2− i)
2
= 4+i.Hiệuphầnthựcvà
phầnảocủaz là
A. 2. B. 3. C. 1. D. 0.
Câu 13. Tìmhaisốthựcx, y thỏamãn(2x − 3yi)+(1− 3i) =−1+6i,vớiilà
đơnvịảo.
A.
(
x =1
y =−3
. B.
(
x =−1
y =−3
. C.
(
x =−1
y =−1
. D.
(
x =1
y =−1
.
Câu 14. Chosốphứcz thỏamãnz +2z =6−3i cóphầnảobằng
A. −3. B. 3. C. 3i. D. 2i.
Câu 15. Tìmsốphứcz thỏamãnz −1+4i =2iz.
A. z =
9
5
−
2
5
i. B. z =−
9
5
+
2
5
i. C. z =
7
3
+
2
3
i. D. z =−
7
3
−
2
3
i.
Câu 16. Chox, y làcácsốthực.Sốphứcz =i
(
1+xi +y +2i
)
bằng0 khi
A. x =−1; y =−2. B. x =0; y =0.
C. x =−2; y =−1. D. x =2; y =1.
Câu 17. Chosốphứcz thỏamãn|z| =2và
z
2
+1
=4.Tính|z +z|+|z −z|.
A. 3+
√
7. B. 3+2
√
2. C. 7+
√
3. D. 16.
Câu 18. Trênmặtphẳngtọađộ,tìmtậphợpđiểmbiểudiễncácsốphứcz thỏa
mãnđiềukiện|z − 2+3i| =4.
A. ĐườngtròntâmI(2;−3) vàbánkínhR =4.
B. ĐườngtròntâmI(−2;3) vàbánkínhR =16.
C. ĐườngtròntâmI(−2;3) vàbánkínhR =4.
D. ĐườngtròntâmI(2;−3) vàbánkínhR =16.
Câu 19. Chosốphứcz thỏamãn|z +2−i| =3.Tìmtậphợpcácđiểmtrongmặt
phẳngOxy biểudiễnsốphứcw =1+z.
A. ĐườngtròntâmI(−2;1) bánkínhR =3.
B. ĐườngtròntâmI(2;−1) bánkínhR =3.
C. ĐườngtròntâmI(−1;−1) bánkínhR =9.
D. ĐườngtròntâmI(−1;−1) bánkínhR =3.
Câu 20. Chosốphứcz thỏamãn|z − 1| = |z − i|.Tìmmôđunnhỏnhấtcủasố
phứcw =2z +2− i.
A. 3
√
2. B.
3
2
√
2
. C.
3
√
2
2
. D.
3
2
.
Soạn:HuỳnhPhúSĩ 29 TrườngTHCS-THPTMỹThuận
§3.Phépchiasốphức TOÁN12
§3.PHÉP CHIA SỐ PHỨC
1 TỔNG VÀ TÍCH CỦA HAI SỐ PHỨC LIÊN HỢP
Chosốphứcz =a +bi.Khiđó:
!
•z +z =...... •z ·z =......
Chú ý: Tổngvàtíchcủamộtsốphứcvớisốphứcliênhợpcủanólàmộtsố......
Ví dụ 1. Chosốphứcz =3− 4i.Tínhz +z vàz ·z.
2 PHÉP CHIA HAI SỐ PHỨC
Chohaisốphứcz
1
= a +bi vàz
2
= c +di.Khiđó,đểtính
z
1
z
2
,tanhâncảtửvàmẫu
choz
2
,tứclà
z
1
z
2
=
z
1
·z
2
z
2
·z
2
=.....................
Ví dụ 2. Tính
2+i
3− 2i
và
5− 2i
i
.
Ví dụ 3. Tìmnghịchđảocủasốphứcz,biếtz =
√
2− 3i.
Ví dụ 4. Tìmsốphứcz thỏamãn
z
4− 3i
+2− 3i =5− 2i.
3 THỰC HÀNH
Í TRẮC NGHIỆM
Câu 1. Chosốphứcz =1+i.Sốphứcnghịchđảocủaz là
A. 1− i. B.
1− i
2
. C.
1− i
√
2
. D.
−1+i
2
.
Câu 2. Chosốphứcz =2+3i.Tính
z
z
.
A.
−5+12i
13
. B.
5− 6i
11
. C.
5− 12i
13
. D.
−5− 12i
13
.
Câu 3. Tínhmôđuncủasốphứcz =
(
−2− 3i
)
(
−1+2i
)
2+i
.
A. |z| =
√
13. B. |z| =
√
5. C. |z| =13. D. |z| =5.
Câu 4. Tìmphầnthựcvàphầnảocủasốphứcz =
6− 3i
2+5i
.
A. Phầnthựclà−
3
29
vàphầnảolà−
36
29
.
B. Phầnthựclà−
3
29
vàphầnảolà−
36
29
i.
C. Phầnthựclà
1
7
vàphầnảolà
12
7
.
D. Phầnthựclà
1
7
vàphầnảolà
12
7
i.
Soạn:HuỳnhPhúSĩ 30 TrườngTHCS-THPTMỹThuận
§3.Phépchiasốphức TOÁN12
Câu 5. Chosốphứcz thỏamãn
z +i
z − 1
=2−i.Tìmsốphứcw =1+z+z
2
.
A. w =5− 2i. B. 5+2i. C. w =
9
2
+2i. D. w =
9
2
−2i.
Câu 6. Tínhmôđuncủasốphứcz thỏamãnz(2−i)+13i =1.
A. |z| =
√
34. B. |z| =34. C. |z| =
5
√
34
3
. D. |z| =
√
34
3
.
Câu 7. Sốphứcz thỏamãnđiềukiện(3+i)z +(1− 2i)
2
= 8− 17i.Khiđóhiệu
củaphầnthựcvàphầnảocủaz là
A. 7. B. −3. C. 3. D. −7.
Câu 8. Chosốphứcz thỏamãn(1− 2i)z +(1+3i)
2
= 5i.Khiđóđiểmnàosau
đâybiểudiễnsốphứcz?
A. M(2;−3). B. N(2;3). C. P(−2;3). D. Q(−2;−3).
Câu 9. Chosốphứcz thỏamãnz =
4(−3+i)
1− 2i
+
(3− i)
2
−i
.Môđuncủasốphức
w =z − iz +1 là
A. |w| =
√
85. B. |w| =4
√
5. C. |w| =6
√
3. D. |w| =
√
48.
Câu 10. Giátrịcủathamsốthựcm bằngbaonhiêuđểbìnhphươngsốphức
z =
(m +9i)(1+i)
2
làsốthực?
A. Khôngcógiátrịm thỏa. B. m =−9.
C. m =9. D. m =±9.
L TỰ LUẬN
Câu 1 (SGK GT12). Thựchiệncácphéptínhsau:
a)
5i
2− 3i
b)
(1+i)
2
(2i)
3
i − 2
c)4− 3i +
5+4i
3+6i
Câu 2 (SGK GT12). Tìmnghịchđảo
1
z
củasốphứcz,biết:
a)z =1+2i b)z =i c)z =5+i
√
3
Câu 3 (SGK GT12). Giảicácphươngtrìnhsau:
a)(3− 2i)z +(4+5i)=7+3i b)(1+3i)z − (2+5i)=(2+i)z
Soạn:HuỳnhPhúSĩ 31 TrườngTHCS-THPTMỹThuận
§4.Phươngtrìnhbậchaivớihệsốthực TOÁN12
§4.PHƯƠNG TRÌNH BẬC HAI VỚI HỆ SỐ
THỰC
Đặt vấn đề
1.Cănbậchaicủa9 là.........
2.Cănbậchaicủa−9 là.........
1 CĂN BẬC HAI CỦA SỐ THỰC ÂM
Cănbậchaicủasốthựca < 0 là.........
Ví dụ 1. Tìmcănbậchaicủa−1,−4,−9.
2 PHƯƠNG TRÌNH BẬC HAI VỚI HỆ SỐ THỰC
Trêntậphợpsốphức,mọiphươngtrìnhbậcn (n ≥ 1)đềucóđúng...... nghiệm(không
nhấtthiếtphânbiệt).
Ví dụ 2. Giảiphươngtrìnhx
2
−2x +5=0.
3 THỰC HÀNH
Í TRẮC NGHIỆM
Câu 1. Kíhiệuz
1
, z
2
làhainghiệmphứccủaphươngtrìnhz
2
− 3z +5 =0.Giá
trịcủa|z
1
|+|z
2
| bằng
A. 2
√
5. B. 3. C.
√
5. D. 10.
Câu 2. Gọiz
1
, z
2
làhainghiệmcủaphươngtrìnhz
2
−2z +2018=0.Khiđógiá
trịcủabiểuthứcA =|z
1
+z
2
−z
1
z
2
| bằng
A. 2017. B. 2019. C. 2018. D. 2016.
Câu 3. Trongtậpsốphức,phươngtrìnhz
2
−2z +5=0 cónghiệmlà
A. z =−1± 2i. B. z =2±2i. C. z =−2±2i. D. z =1± 2i.
Câu 4. GọiS làtậpnghiệmcủaphươngtrìnhz
2
+z +1=0 trêntậpsốphức.Số
tậpconcủaS là
A. 2. B. 1. C. 0. D. 4.
Câu 5. Tìmnghiệmphứccóphầnảoâmcủaphươngtrìnhz
2
−4z+13=0.
A. z =−2− 3i. B. z =2− 3i. C. z =−2+3i. D. z =2+3i.
Câu 6. Biếtphươngtrìnhz
2
+az+b =0 (a, b ∈ R)cónghiệmz =−2+i.Tính
a +b.
A. 4. B. 9. C. −1. D. 1.
Câu 7. Kíhiệuz
0
lànghiệmphứccóphầnảodươngcủaphươngtrình2z
2
−6z+
15=0.Trênmặtphẳngtọađộ,tìmtọađộcủađiểmM biểudiễnsốphứcz
0
.
A. M
−
3
2
;
√
21
2
i
!
. B. M
−
3
2
;
√
21
2
!
.
C. M
3
2
;
√
21
2
!
. D. M
3
2
;
√
21
2
i
!
.
Soạn:HuỳnhPhúSĩ 32 TrườngTHCS-THPTMỹThuận
§4.Phươngtrìnhbậchaivớihệsốthực TOÁN12
Câu 8. TìmtậpnghiệmS củaphươngtrìnhz
4
−7z
2
−18=0trêntậpsốphức.
A. S ={−2;9}. B. S =
n
−
√
2;
√
2;−3i;3i
o
.
C. S ={−4i;4i;−81;81}. D. S =
n
−3;3;−
√
2i;
√
2i
o
.
Câu 9. Tìmmộtcănbậchaicủa−8.
A. −2
√
2i. B. −2
√
2. C. 2
√
2. D. 2
√
−2i.
Câu 10. Tìmcáccănbậchaicủa−6.
A. −
√
6i. B. ±
√
6i. C. ±6i. D.
√
6i.
L TỰ LUẬN
Câu 1 (SGK GT12). Tìmcáccănbậchaiphứccủacácsốsau:−7,−8,−12,−20,−121.
Câu 2 (SGK GT12). Giảicácphươngtrìnhsautrêntậpsốphức:
a)−3z
2
+2z − 1=0 b)5z
2
−7z +11=0 c)z
4
+7z
2
+10=0
Soạn:HuỳnhPhúSĩ 33 TrườngTHCS-THPTMỹThuận
PHẦNII
HÌNH HỌC
Chương 3. Phương pháp tọa độ trong không gian. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 35
§1. Hệ tọa độ trong không gian . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 35
§2. Phương trình mặt phẳng . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 40
§3. Phương trình đường thẳng . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 46
Soạn:HuỳnhPhúSĩ 34 TrườngTHCS-THPTMỹThuận
Chương3.Phươngpháptọađộtrongkhônggian TOÁN12
Chương3.
PHƯƠNG PHÁP TỌA ĐỘ TRONG KHÔNG
GIAN
§1.HỆ TỌA ĐỘ TRONG KHÔNG GIAN
Nhắc lại về Hệ tọa độ trong mặt phẳng
HỆ TRỤC TỌA ĐỘ Oxy
x
y
O
−Ï
i
−Ï
j
•Hệ trục tọa độ Oxy gồm trục ...... Ox và trục
...... Oy,vuônggócvàcắtnhautại............
O(...;...).
•Vectơ
−Ï
u =
(
u
1
;u
2
)
nếu
−Ï
u =u
1
...+u
2
...
•ĐiểmM
(
x
0
;y
0
)
nếu
−−Ï
OM =x
0
...+y
0
...
•
−Ï
AB =
(
x
B
...x
A
;y
B
...y
A
)
•TrungđiểmcủađoạnAB:I
x
A
+x
B
...
;
......
2
•Trọngtâmcủa4ABC:G
x
A
+x
B
+x
C
...
;
.........
3
CÁC PHÉP TOÁN VECTƠ
Chohaivectơ
−Ï
a =
(
a
1
;a
1
)
và
−Ï
b =
(
b
1
;b
1
)
vàsốk ∈ R.
•
−Ï
a =
−Ï
b ⇔
(
a
1
=......
a
2
=......
•
−Ï
a ±
−Ï
b =
(
a
1
...b
1
;a
2
...b
2
)
•k ·
−Ï
a =
(
...a
1
;...a
2
)
•
−Ï
a ·
−Ï
b =...............
•
−Ï
a
=
q
a
2
1
+......
•cos
−Ï
a ,
−Ï
b
=
−Ï
a ...
−Ï
b
−Ï
a
...
−Ï
b
•
−Ï
a và
−Ï
b cùngphương⇔ ∃k ∈ R saocho.........
PHƯƠNG TRÌNH ĐƯỜNG TRÒN
ĐườngtròntâmI(a;b) bánkínhR cóphươngtrìnhlà
(x − ...)
2
+(y − ...)
2
=......
hoặccóthểviếtdướidạng
x
2
+y
2
−......x − ......y +c =0
trongđóR =
√
a
2
+b
2
−... (a
2
+b
2
−... > ...)
1 TỌA ĐỘ CỦA ĐIỂM VÀ CỦA VECTƠ
1 Hệ tọa độ
x
y
z
O
−Ï
i
−Ï
j
−Ï
k
Trongkhônggian,hệtrụctọađộOxyz baogồm... trụcOx,Oy,Oz đôimột............
•Cácvectơ
−Ï
i ,
−Ï
j ,
−Ï
k lầnlượtlàcácvectơ......... trêncáctrụcOx,Oy,Oz.
•ĐiểmO(...;...;...) đượcgọilà............
•Cácmặtphẳng......,......,...... đôimộtvuônggócvớinhau,đượcgọilàcác
mặtphẳngtọađộ.
•KhônggianvớihệtọađộOxyz cònđượcgọilàkhônggian......
2 Tọa độ của một điểm và của vectơ
ĐiểmM
(
x
0
;y
0
;z
0
)
nếu
−−Ï
OM =...............
Ví dụ 1. TrongkhônggianOxyz,vectơ
−Ï
a =2
−Ï
i −3
−Ï
j +
−Ï
k ,với
−Ï
i ,
−Ï
j ,
−Ï
k làcácvectơ
đơnvị.Tọađộcủavectơ
−Ï
a là
A. (1;2;−3). B. (2;−3;1). C. (2;3;1). D. (1;−3;2).
Soạn:HuỳnhPhúSĩ 35 TrườngTHCS-THPTMỹThuận
§1.Hệtọađộtrongkhônggian TOÁN12
2 BIỂU THỨC TỌA ĐỘ CỦA CÁC PHÉP TOÁN VECTƠ
Định lí − £ é
TrongkhônggianOxyz,chohaivectơ
−Ï
a =
(
a
1
;a
2
;a
3
)
và
−Ï
b =
(
b
1
;b
2
;b
3
)
.Tacó:
•
−Ï
a +
−Ï
b =...............
•
−Ï
a −
−Ï
b =...............
•k ·
−Ï
a =...............
Ví dụ 2. TrongkhônggianOxyz,cho~a =(2;1;3),
~
b =(4;−3;5),~c =(−2;4;6).Tìmtọa
độcủavectơ~u = ~a+2
~
b −~c.
A. (10;9;6). B. (12;−9;7). C. (10;−9;6). D. (12;−9;6).
!
•
−Ï
a =
−Ï
b ⇔
a
1
=...
a
2
=...
a
3
=...
•
−Ï
0 =.........
•Với vectơ
−Ï
b 6=
−Ï
0 thì
−Ï
a và
−Ï
b
cùngphươngkhivàchỉkhi∃k ∈ R
saochoa
1
= ......,a
2
= ......,
a
3
=......
•
−Ï
AB =...............
•TrungđiểmcủađoạnthẳngAB làM
x
A
+x
B
...
;
......
2
;
......
...
•TrọngtâmcủatamgiácABC làG
x
A
+x
B
+x
C
...
;
.........
3
;
.........
...
Ví dụ 3. ChobađiểmA(1;−1;1),B(0;1;2),C(1;0;1).TìmtọađộtrọngtâmG củatam
giácABC.
Câu 1. TrongkhônggianOxyz,chohìnhbìnhhànhABCD.BiếtA(1;0;1),B(2;1;2)và
D(1;−1;1).TọađộđiểmC là
A. C(2;0;2). B. C(2;2;2). C. C(2;−2;2). D. C(0;−2;0).
3 TÍCH VÔ HƯỚNG
1 Biểu thức tọa độ của tích vô hướng
TrongkhônggianOxyz,tíchvôhướngcủahaivectơ
−Ï
a =
(
a
1
;a
2
;a
3
)
và
−Ï
b =
(
b
1
;b
2
;b
3
)
đượcxácđịnhbởicôngthức
−Ï
a ·
−Ï
b =...............
Ví dụ 4. TrongkhônggianvớihệtọađộOxyz,chobavectơ
−Ï
a = (1;2;−2),
−Ï
b =
(−4;0;1) và
−Ï
c =(0;3;3).Tính
−Ï
a +
−Ï
b
·
−Ï
c .
A.
−Ï
a +
−Ï
b
·
−Ï
c =3. B.
−Ï
a +
−Ï
b
·
−Ï
c =9.
C.
−Ï
a +
−Ï
b
·
−Ï
c =0. D.
−Ï
a +
−Ï
b
·
−Ï
c =−10.
Soạn:HuỳnhPhúSĩ 36 TrườngTHCS-THPTMỹThuận
§1.Hệtọađộtrongkhônggian TOÁN12
2 Ứng dụng của tích vô hướng
Độ dài của một vectơ − £ é
Chovectơ
−Ï
a =
(
a
1
;a
2
;a
3
)
.Khiđó
−Ï
a
=
q
a
2
1
+.........
Ví dụ 5. TínhchuvicủatamgiácABC,biếtrằngA(1;−1;1),B(0;1;2) vàC(1;0;1).
Góc giữa hai vectơ − £ é
Gócgiữahaivectơ
−Ï
a =
(
a
1
;a
2
;a
3
)
và
−Ï
b =
(
b
1
;b
2
;b
3
)
đượctínhbởicôngthức
cos
−Ï
a ,
−Ï
b
=
−Ï
a ...
−Ï
b
−Ï
a
...
−Ï
b
=.....................
Ví dụ 6. TrongkhônggianOxyz,chohaivectơ~u =(−1;1;0), ~v =(0;0;−1).Gócgiữa~u
và~v cósốđobằng
A. 120
◦
. B. 45
◦
. C. 90
◦
. D. 60
◦
.
Hệ quả:
−Ï
a ⊥
−Ï
b ⇔ ...............
4 PHƯƠNG TRÌNH MẶT CẦU
I(a;b;c)
M(x;y;z)
Định lí − £ é
TrongkhônggianOxyz,mặtcầu(S) tâmI(a;b;c) bánkínhR cóphươngtrìnhlà
(x − ...)
2
+(y ......)
2
=......
Ví dụ 7. Lậpphươngtrìnhmặtcầutrongcáctrườnghợpsauđây:
a)CótâmC(3;−3;1) vàđiquađiểmA(5;−2;1)
b)CóđườngkínhAB vớiA(4;−3;7) vàB(2;1;3)
Nhận xét: Phươngtrìnhmặtcầunóitrêncóthểviếtdướidạng
x
2
+y
2
+z
2
−......x − ......y −......z +d =0
trongđóR =
√
a
2
+b
2
+c
2
−... (a
2
+b
2
+c
2
−... > ...)
Ví dụ 8. Tìmtâmvàbánkínhcủamặtcầucóphươngtrình
x
2
+y
2
+z
2
−8x − 2y +1=0
5 THỰC HÀNH
Í TRẮC NGHIỆM
Câu 2. TrongkhônggianvớihệtọađộOxyz,chovectơ~a = −
~
i +2
~
j − 3
~
k.Tìm
tọađộcủa~a.
A. (2;−3;−1). B. (−3;2;−1). C. (−1;2;−3). D. (2;−1;−3).
Soạn:HuỳnhPhúSĩ 37 TrườngTHCS-THPTMỹThuận
§1.Hệtọađộtrongkhônggian TOÁN12
Câu 3. TrongkhônggianOxyz,chohaiđiểmA
(
1;1;−2
)
vàB
(
2;2;1
)
.Vectơ
−Ï
AB
cótọađộlà
A.
(
3;3;−1
)
. B.
(
3;1;1
)
. C.
(
−1;−1;−3
)
. D.
(
1;1;3
)
.
Câu 4. TrongkhônggianOxyz,chohaiđiểmA(1;2;3)vàB(3;0;−5).Tọađộtrung
điểmI củađoạnthẳngAB là
A. I(2;1;−1). B. I(2;2;−2). C. I(4;2;−2). D. I(−1;1;4).
Câu 5. TrongkhônggianOxyz,chotamgiácABC vớiA(1;3;4),B(2;−1;0),C(3;1;2).
TìmtọađộtrọngtâmG củatamgiácABC.
A. G(2;1;2). B. G(6;3;6). C. G
3;
3
2
;3
. D. G(2;−1;2).
Câu 6. TrongkhônggianOxyz,chotứdiệnABCD cóA(1;0;2),B(−2;1;3),C(3;2;4)
vàD(6;9;−5).Tọađộtrọngtâmcủatứdiệnlà
A. (2;3;1). B. (2;3;−1). C. (−2;3;1). D. (2;−3;1).
Câu 7. TrongkhônggianOxyz,cho~a =(2;−3;3),
~
b =(0;2;−1),~c =(3;−1;5).
Tìmtọađộcủavectơ~u =2~a +3
~
b − 2~c.
A. (10;−2;13). B. (−2;2;−7). C. (−2;−2;7). D. (−2;2;7).
Câu 8. TrongkhônggianOxyz,chobađiểmA(1;2;−1),B(2;−1;3),C(−3;5;1).
TìmtọađộđiểmD saochotứgiácABCD làhìnhbìnhhành.
A. D(−4;8;−5). B. D(−4;8;−3).
C. D(−2;8;−3). D. Khôngtồntại.
Câu 9. TrongkhônggianOxyz chobađiểmA(2;−1;5),B(5;−5;7),M(x;y;1).Với
giátrịnàocủax, y thìA, B, M thẳnghàng?
A. x =4; y =7. B. x =4; y =−7.
C. x =−4; y =7. D. x =−4; y =−7.
Câu 10. TrongkhônggianOxyz,chohaiđiểmA(0;1;−2) vàB(3;−1;1).Tìmtọa
độđiểmM saocho
−−Ï
AM =3
−Ï
AB.
A. M(9;−5;7). B. M(9;5;7). C. M(−9;5;−7). D. M(9;−5;−5).
Câu 11. TrongkhônggianOxyz,điểmnàodướiđâythuộctrụcOy?
A. N(2;0;0). B. Q(0;3;2). C. P(2;0;3). D. M(0;−3;0).
Câu 12. TrongkhônggianOxyz,hìnhchiếucủađiểmM
(
2;−2;1
)
trênmặtphẳng
(Oxy) cótọađộlà
A.
(
2;0;1
)
. B.
(
2;−2;0
)
. C.
(
0;−2;1
)
. D.
(
0;0;1
)
.
Câu 13. TrongkhônggianOxyz,tìmtọađộđiểmH làhìnhchiếuvuônggóccủa
điểmA(2;1;−1) lêntrụctung.
A. H(2;0;−1). B. H(0;1;0). C. H(0;1;−1). D. H(2;0;0).
Câu 14. TrongkhônggianOxyz,chocácvectơ~a =
(
1;0;3
)
và
~
b =
(
−2;2;5
)
.Tích
vôhướng~a ·
~a +
~
b
bằng
A. 25. B. 23. C. 27. D. 29.
Câu 15. TrongkhônggianOxyz,chohaiđiểmA(2;−1;4)vàB(−2;2;−6).Tính
độdàiđoạnthẳngAB.
A. AB =5
√
5. B. AB =
√
21+
√
44.
C. AB =
√
65. D. AB =
√
5.
Câu 16. TrongkhônggianOxyz,chohaivectơ~u = (−1;1;0), ~v =(0;−1;0).Góc
giữa~u và~v cósốđobằng
A. 120
◦
. B. 45
◦
. C. 135
◦
. D. 60
◦
.
Câu 17. TrongkhônggianvớihệtọađộOxyz,chomặtcầu(S): (x − 7)
2
+(y +
3)
2
+z
2
=16.TìmtọađộtâmI vàbánkínhR củamặtcầu(S).
A. I(−7;3;0) vàR =4. B. I(7;−3;0) vàR =4.
C. I(−7;3;0) vàR =16. D. I(7;−3;0) vàR =16.
Câu 18. TrongkhônggianOxyz,mặtcầu(S): x
2
+y
2
+z
2
+4x−2y+2z−3=0
cótâmvàbánkínhlà
A. I(2;−1;1), R =9. B. I(2;−1;1), R =3.
C. I(−2;1;−1), R =3. D. I(−2;1;−1), R =9.
Câu 19. TrongkhônggianOxyz,choA(−1;0;0),B(0;0;2),C(0;−3;0).Tínhbán
kínhmặtcầungoạitiếptứdiệnOABC.
A. R =
√
14
4
. B. R =
√
14. C. R =
√
14
3
. D. R =
√
14
2
.
Soạn:HuỳnhPhúSĩ 38 TrườngTHCS-THPTMỹThuận
§1.Hệtọađộtrongkhônggian TOÁN12
Câu 20. TrongkhônggianOxyz,chomặtcầu
(
S
)
cótâmlàđiểmI
(
0;0;−3
)
vàđi
quađiểmM
(
4;0;0
)
.Phươngtrìnhcủa
(
S
)
là
A. x
2
+y
2
+
(
z +3
)
2
=25. B. x
2
+y
2
+
(
z +3
)
2
=5.
C. x
2
+y
2
+
(
z − 3
)
2
=25. D. x
2
+y
2
+
(
z − 3
)
2
=5.
Câu 21. TrongkhônggianOxyz,chohaiđiểmA(1;−2;3)vàB(5;4;7).Phương
trìnhmặtcầunhậnAB làmđườngkínhlà
A. (x − 6)
2
+(y − 2)
2
+(z − 10)
2
=17.
B. (x −1)
2
+(y +2)
2
+(z − 3)
2
=17.
C. (x − 3)
2
+(y − 1)
2
+(z − 5)
2
=17.
D. (x −5)
2
+(y − 4)
2
+(z − 7)
2
=17.
Câu 22. TrongkhônggiantọađộOxyz,chođiểmA
(
1;−2;3
)
.Gọi
(
S
)
làmặtcầu
chứaA cótâmI thuộctiaOx vàbánkínhbằng7.Phươngtrìnhmặtcầu
(
S
)
là
A.
(
x − 7
)
2
+y
2
+z
2
=49. B.
(
x +7
)
2
+y
2
+z
2
=49.
C.
(
x +5
)
2
+y
2
+z
2
=49. D.
(
x − 3
)
2
+y
2
+z
2
=49.
L TỰ LUẬN
Câu 1 (SGK HH12). ChohìnhhộpABCD.A
0
B
0
C
0
D
0
biếtA(1;0;1),B(2;1;2),D(1;−1;1),C
0
(4;5;−5).Tínhtọađộcácđỉnhcòn
lạicủahìnhhộp.
Câu 2 (SGK HH12). Tính
−Ï
a ·
−Ï
b biết
a)
−Ï
a =(3;0;−6) và
−Ï
b =(2;−4;0) b)
−Ï
a =(1;−5;2) và
−Ï
b =(4;3;−5)
Vocabulary − £ é
space khônggian
plane mặtphẳng
coordinates tọađộ
point điểm
coplanar đồngphẳng
midpoint trungđiểm
centroid trọngtâm
parallel cùngphương
scalar product tíchvôhướng
length độdài
sphere mặtcầu
radius bánkính
Soạn:HuỳnhPhúSĩ 39 TrườngTHCS-THPTMỹThuận
§2.Phươngtrìnhmặtphẳng TOÁN12
§2.PHƯƠNG TRÌNH MẶT PHẲNG
Nhắc lại về Phương trình tổng quát của đường thẳng trong mặt phẳng
VECTƠ PHÁP TUYẾN CỦA ĐƯỜNG THẲNG
Chođườngthẳng∆vàvectơ
−Ï
n 6=
−Ï
0.Nếu...... của
−Ï
n
vuônggócvới∆ thìtanói
−Ï
n làvectơ............ của∆.
∆
−Ï
n
•Mỗiđườngthẳngcó......... vectơpháptuyến.
•Nếu
−Ï
n làvectơpháptuyếncủa∆thìk ·
−Ï
n cũnglà
............... của∆.
PHƯƠNG TRÌNH TỔNG QUÁT CỦA ĐƯỜNG THẲNG
Chođườngthẳng∆điquađiểmM
(
x
0
;y
0
)
vàcóvectơpháp
tuyến
−Ï
n =(a;b).Khiđó
∆: ...
(
x − ...
)
+...
(
y − ...
)
=0
VỊ TRÍ TƯƠNG ĐỐI VÀ GÓC GIỮA HAI ĐƯỜNG THẲNG
Chohaiđườngthẳng∆
1
: a
1
x+b
1
y+c
1
=0 và∆
2
: a
2
x+
b
2
y +c
2
=0.
•Nếu
a
1
a
2
6=
b
1
b
2
thì∆
1
và∆
2
...............
•Nếu
a
1
a
2
=
b
1
b
2
6=
c
1
c
2
thì∆
1
và∆
2
...............
•Nếu
a
1
a
2
=
b
1
b
2
=
c
1
c
2
thì∆
1
và∆
2
...............
Gócgiữahaiđườngthẳnglàmộtgóc...... đượcxácđịnh
bởicôngthức
cos
(
∆
1
,∆
2
)
=
|a
1
·a
2
+......|
q
a
2
1
+b
2
1
·............
KHOẢNG CÁCH TỪ MỘT ĐIỂM ĐẾN MỘT ĐƯỜNG
THẲNG
KhoảngcáchtừđiểmM
(
x
0
;y
0
)
đếnđườngthẳng∆: ax +
by +c =0 bằng
d
(
M,∆
)
=
a... +b... +c
√
...
2
+...
2
1 VECTƠ PHÁP TUYẾN CỦA MẶT PHẲNG
1 Tích có hướng
Trongkhônggian,chohaivectơ
−Ï
a =
(
a
1
;a
2
;a
3
)
và
−Ï
b =
(
b
1
;b
2
;b
3
)
.Tích có hướng của
haivectơ
−Ï
a và
−Ï
b làmột...... ............ vớicả
−Ï
a và
−Ï
b .
h
−Ï
a ,
−Ï
b
i
=
(
............;............;............
)
Ví dụ 1. Tínhtíchcóhướngcủahaivectơ
−Ï
u =(2;1;−2) và
−Ï
v =(−12;6;0).
2 Vectơ pháp tuyến của mặt phẳng
Định nghĩa − £ é
Chomặtphẳng
(
α
)
.Nếuvectơ
−Ï
n 6=
−Ï
0 vàcó...... vuônggócvớimặtphẳng
(
α
)
thì
−Ï
n đượcgọilàvectơ............ của
(
α
)
.
•Mỗimặtphẳngcó......... vectơpháptuyến.
•Nếu
−Ï
n làvectơpháptuyếncủa
(
α
)
thìk ·
−Ï
n cũnglà............... của
(
α
)
.
Ví dụ 2. TrongkhônggianOxyz chobađiểmA(2;−1;3),B(4;0;1),C(−10;5;3).Hãytìm
tọađộmộtvectơpháptuyếncủamặtphẳng(ABC).
Soạn:HuỳnhPhúSĩ 40 TrườngTHCS-THPTMỹThuận
§2.Phươngtrìnhmặtphẳng TOÁN12
2 PHƯƠNG TRÌNH TỔNG QUÁT CỦA MẶT PHẲNG
1 Định nghĩa
TrongkhônggianOxyz,chomặtphẳng
(
α
)
điquađiểmM
(
x
0
;y
0
;z
0
)
vàcóvectơpháp
tuyến
−Ï
n =(a;b;c).Khiđó
a
(
x −...
)
+...
(
y...y
0
)
+c
(
...−z
0
)
=...
I Mặtphẳng
(
α
)
: Ax +By +Cz +D =0 cómộtvectơpháptuyến
−Ï
m =
(
...;...;...
)
.
Ví dụ 3. Mặtphẳng
(
α
)
: 4x − 2y − 6z +7=0 cómộtvectơpháptuyếnlà............
Ví dụ 4. Trong khônggian Oxyz choba điểmA(2;−1;3), B(4;0;1), C(−10;5;3). Lập
phươngtrìnhtổngquátcủamặtphẳng(ABC).
2 Các trường hợp riêng
TrongkhônggianOxyz,chomặtphẳng
(
α
)
: Ax +By +Cz +D =0.
!
A =0:
(
α
)
songsonghoặctrùngvớitrục......
B =0:
(
α
)
songsonghoặctrùngvớitrục......
C =0:
(
α
)
songsonghoặctrùngvớitrục......
D =0:
(
α
)
điquađiểm.........
A =B =0:
(
α
)
songsonghoặctrùngvớimặtphẳng......
A =C =0:
(
α
)
songsonghoặctrùngvớimặtphẳng......
B =C =0:
(
α
)
songsonghoặctrùngvớimặtphẳng......
Ví dụ 5. Mặtphẳng
(
β
)
songsongvớimặtphẳngOxz vàcắttrụctungtạiđiểmcótung
độbằng3.Viếtphươngtrìnhmặtphẳng
(
β
)
.
Phương trình mặt phẳng theo đoạn chắn − £ é
Nếumặtphẳng
(
α
)
cắtcáctrụcOx,Oy,Oz lầnlượttạiA(a;0;0),B(0;b;0)vàC(0;0;c)
thì
(
α
)
:
x
a
+
y
b
+
z
c
=...
Ví dụ 6. Viếtphươngtrìnhmặtphẳng(HKT),biếtH(2;0;0),K(0;0;5),T(0;−3;0).
3 ĐIỀU KIỆN ĐỂ HAI MẶT PHẲNG SONG SONG, VUÔNG GÓC
TrongkhônggianOxyz chohaimặtphẳng
(
α
)
: A
1
x+B
1
y+C
1
z+D
1
=0và
(
β
)
: A
2
x+
B
2
y +C
2
z +D
2
=0.Khiđó:
!
•
(
α
)
∥
(
β
)
⇔
(
(
A
1
;B
1
;C
1
)
...k
(
A
2
;B
2
;C
2
)
D
1
...kD
2
•
(
α
)
≡
(
β
)
⇔
(
(
A
1
;B
1
;C
1
)
...k
(
A
2
;B
2
;C
2
)
D
1
...kD
2
•
(
α
)
⊥
(
β
)
⇔ ............
Ví dụ 7. TrongkhônggianOxyz,chomặtphẳng(Q): 2x − y +5z − 15=0vàđiểm
E(1;2;−3).Mặtphẳng(P) quaE vàsongsongvới(Q) cóphươngtrìnhlà
A. x +2y −3z +15=0. B. x +2y −3z − 15=0.
C. 2x −y +5z +15=0. D. 2x − y +5z −15=0.
Soạn:HuỳnhPhúSĩ 41 TrườngTHCS-THPTMỹThuận
§2.Phươngtrìnhmặtphẳng TOÁN12
4 KHOẢNG CÁCH TỪ MỘT ĐIỂM ĐẾN MỘT MẶT PHẲNG
Trong không gian Oxyz, khoảng cách từ điểm M
(
x
0
;y
0
;z
0
)
đến mặt phẳng
(
α
)
: Ax +By +Cz +D =0 đượctínhbằng
d
(
M,
(
α
))
=
A...+B... +C... +D
√
...
2
+...
2
+...
2
Ví dụ 8. TínhkhoảngcáchtừđiểmQ(1;0;−3) đếnmặtphẳng
(
γ
)
: x −2y +2z−5=0.
Ví dụ 9. Tínhkhoảngcáchgiữahaimặtphẳng
(
λ
)
: x − 2y +2z +5=0và
(
γ
)
: x −
2y +2z − 5=0.
5 THỰC HÀNH
Í TRẮC NGHIỆM
Câu 1. TrongkhônggianOxyz,chobavectơ~a =(3;−1;−2),
~
b =(1;2;m)và
~c =(5;1;7).Tìmgiátrịcủam để
h
~a,
~
b
i
=~c.
A. m =−1. B. m =0. C. m =1. D. m =2.
Câu 2. TrongkhônggianvớihệtọađộOxyz,chomặtphẳng(P): 2x−5y−8=0.
Tìmtọađộmộtvectơpháptuyếncủamặtphẳng(P).
A.
−Ï
n =(2;−5;−8). B.
−Ï
n =(2;−5;0).
C.
−Ï
n =(2;0;−5). D.
−Ï
n =(−1;−2;0).
Câu 3. Trongkhônggian vớihệ tọa độOxyz, phươngtrình nào dướiđây là
phươngtrìnhcủamặtphẳngđiquađiểmM(5;2;−1) vàcóvectơpháptuyến
−Ï
n =
(1;1;−2)?
A. x +y −2z +9=0. B. x +y −2z − 9=0.
C. 5x +2y − z +9=0. D. 5x +2y −z − 9=0.
Câu 4. TrongkhônggianvớihệtọađộOxyz,chobađiểmA(2;1;−1),B(−1;0;4)
vàC(0;−2;−1).Phươngtrìnhnàodướiđâylàphươngtrìnhcủamặtphẳngđiqua
điểmA vàvuônggócvớiđườngthẳngBC?
A. x − 2y −5z − 5=0. B. x − 2y − 5z +5=0.
C. x −2y − 5z − 2=0. D. 2x +y − z −5=0.
Câu 5. Trongkhônggian vớihệ tọa độOxyz, phươngtrình nào dướiđây là
phươngtrìnhcủamặtphẳngđiquađiểmM(1;−2;0) vàsongsongvớimặtphẳng
(P): x −y +3z − 6=0?
A. x − y +3z − 1=0. B. x −y +3z +1=0.
C. x −y +3z − 3=0. D. x − y +3z +3=0.
Câu 6. TrongkhônggianOxyz,choA(2;−3;0)vàmặtphẳng(α): x+2y−z+3=0.
Tìmphươngtrìnhmặtphẳng(P)điquaA saocho(P)vuônggócvới(α)và(P)
songsongvớitrụcOz?
A. 2x +y −1=0. B. y +2z +3=0.
C. 2x −y − 7=0. D. x +2y − z +4=0.
Câu 7. TrongkhônggianOxyz,chọncâuđúngtrongcáccâusau:
A. Mặtphẳngtọađộ(Oxy) cóphươngtrìnhz =0.
Soạn:HuỳnhPhúSĩ 42 TrườngTHCS-THPTMỹThuận
§2.Phươngtrìnhmặtphẳng TOÁN12
B. Mặtphẳngtọađộ(Ozx) cóphươngtrìnhx =0.
C. Mặtphẳngtọađộ(Oyz) cóphươngtrìnhy +z =0.
D. Mặtphẳngtọađộ(Oxy) cóphươngtrìnhx +y =0.
Câu 8. Mặtphẳng(P) tiếpxúcvớimặtcầu(S): (x − 1)
2
+(y +3)
2
+(z − 2)
2
=49
tạiđiểmM(7;−1;5) cóphươngtrìnhlà
A. 6x +2y +3z − 55=0. B. 6x +2y +3z +55=0.
C. 3x +y +z − 22=0. D. 3x +y +z +22=0.
Câu 9. Trongkhông gian Oxyz, cho tứ diện ABCD có A(3;−2;1), B(−4;0;3),
C(1;4;−3),D(2;3;5).PhươngtrìnhmặtphẳngchứaAC vàsongsongvớiBD là
A. 12x − 10y +21z − 35=0. B. 12x +10y − 21z +35=0.
C. 12x +10y +21z +35=0. D. 12x − 10y −21z − 35=0.
Câu 10. TrongkhônggianOxyz,mặtphẳngđiquađiểmM
(
1;1;−1
)
vàvuông
gócvớiđườngthẳng∆:
x +1
2
=
y − 2
2
=
z − 1
1
cóphươngtrìnhlà
A. 2x +2y +z +3=0. B. x − 2y − z =0.
C. 2x +2y +z −3=0. D. x − 2y −z − 2=0.
Câu 11. TrongkhônggianOxyz,chohaiđiểmA(4;1;−2)vàB(5;9;3).Phương
trìnhmặtphẳngtrungtrựccủađoạnAB là
A. 2x +6y −5z +40=0. B. x +8y − 5z −41=0.
C. x −8y −5z − 35=0. D. x +8y +5z −47=0.
Câu 12. TrongkhônggianOxyz,chomặtphẳng(P)chứađiểmH(1;2;2)vàcắt
cáctrụcOx,Oy,Oz lầnlượttạiA, B, C saochoH làtrựctâmcủatamgiácABC.
Phươngtrìnhmặtphẳng(P) là
A. x +2y −2z − 9=0. B. 2x +y +z −6=0.
C. 2x +y +z − 2=0. D. x +2y +2z − 9=0.
Câu 13. TrongkhônggianOxyz,chobađiểmA(−2;0;0),B(0;0;7),C(0;3;0).Phương
trìnhmặtphẳng(ABC) là
A.
x
−2
+
y
7
+
z
3
=1. B.
x
−2
+
y
3
+
z
7
=0.
C.
x
−2
+
y
3
+
z
7
=1. D.
x
−2
+
y
3
+
z
7
+1=0.
Câu 14. TrongkhônggianOxyz,chođiểmG(1;2;3).Gọi(P): px+qy+rz+1=0
(p, q, r ∈ R)làmặtphẳngquaG vàcắtcáctrụcOx, Oy, Oz tạiA, B, C saocho
G làtrọngtâmcủatamgiácABC.TínhT =p +q +r.
A. T =−
11
18
. B. T =
11
18
. C. T =18. D. T =−18.
Câu 15. TrongkhôngOxyz,gọiA, B, C lầnlượtlàhìnhchiếuvuônggóccủa
điểmM(1;2;3) lêncáctrụctọađộ.Mặtphẳng(ABC) cóphươngtrìnhlà
A.
1
x
+
2
y
+
3
z
=1. B.
x
1
+
y
2
+
z
3
=1.
C.
1
x
+
2
y
+
3
z
=0. D.
x
1
+
y
2
+
z
3
=0.
Câu 16. TrongkhôngOxyz,gọiM, N, K lầnlượtlàhìnhchiếuvuônggóccủa
điểmA(2;−3;1)lêncácmặtphẳngtọađộ.Phươngtrìnhmặtphẳng(MNK)là
A.
x
2
+
y
3
+
z
1
=1. B. 3x − 2y +6z =6.
C.
x
2
−
y
3
+
z
1
=0. D. 3x − 2y +6z − 12=0.
Câu 17. TrongkhônggianOxyz,chohaimặtphẳng(P): x − 3y +2z −1=0 và
(Q): x − z +2 =0.Mặtphẳng(α) vuônggócvớicả(P)và(Q),đồngthờicắttrục
Ox tạiđiểmcóhoànhđộbằng3.Phươngtrìnhcủa(α) là
A. x +y +z − 3=0. B. x +y +z +3=0.
C. −2x +z +6=0. D. −2x +z −6=0.
Câu 18. TrongkhônggianOxyz,chođiểmM(2;1;−2) vàhaimặtphẳng(α):x+
y − 2z − 4= 0,(β): 2x − y +3z +1 =0.Viếtphươngtrìnhmặtphẳng(P) điqua
M đồngthờivuônggócvớigiaotuyếncủa(α) và(β).
A. x − 7y +3z +11=0. B. x − 7y −3z − 1=0.
C. x −y +3z +5=0. D. x +y −3z − 9=0.
Câu 19. TrongkhônggianOxyz,chobađiểmA(3;−1;2),B(4;−1;−1)vàC(2;0;2).
MặtphẳngđiquabađiểmA, B, C cóphươngtrìnhlà
A. 3x − 3y +z − 14=0. B. 3x +3y +z − 8=0.
C. 3x −2y +z − 8=0. D. 2x +3y − z +8=0.
Soạn:HuỳnhPhúSĩ 43 TrườngTHCS-THPTMỹThuận
§2.Phươngtrìnhmặtphẳng TOÁN12
Câu 20. TrongkhônggianOxyz,điểmM(a;b;c)thuộcmặtphẳng(P): x +y +
z − 6=0.Tổnga +b +c bằng
A. 6. B. −6. C. 0. D. 5.
Câu 21. TrongkhônggianOxyz,mặtphẳng(P): x −3y +1=0 điquađiểmnào
sauđây?
A. A(3;1;1). B. B(1;−3;1). C. C(−1;0;0). D. D(1;0;0).
Câu 22. TrongkhônggianOxyz,chohaimặtphẳng(P): 2x − y − z − 3 =0và
(Q): x −z − 2=0.Tínhsốđogócgiữahaimặtphẳng(P) và(Q).
A.
(
(P),(Q)
)
=30
◦
. B.
(
(P),(Q)
)
=45
◦
.
C.
(
(P),(Q)
)
=60
◦
. D.
(
(P),(Q)
)
=90
◦
.
Câu 23. TrongkhônggianOxyz,chotứdiệnABCD cóA(0;2;0),B(2;0;0),C
0;0;
√
2
vàD(0;−2;0).Tínhsốđogóccủahaimặtphẳng(ABC) và(ACD).
A. 30
◦
. B. 45
◦
. C. 60
◦
. D. 90
◦
.
Câu 24. KhoảngcáchtừM
(
1;4;−7
)
đếnmặtphẳng
(
P
)
:2x − y +2z − 9=0
là
A. 5. B. 12. C.
25
3
. D. 7.
Câu 25. Khoảngcáchgiữamặtphẳng(P): 2x − y +3z +5 =0 và(Q): 2x − y +
3z +1=0 bằng
A. 4. B.
6
√
14
. C. 6. D.
4
√
14
.
Câu 26. TrongkhônggianvớihệtọađộOxyz,phươngtrìnhnàodướiđâylà
phươngtrìnhcủamặtcầucótâmI(3;−1;0)vàtiếpxúcvớimặtphẳng(P): x +
2y − 2z − 10=0?
A. (x − 3)
2
+(y +1)
2
+z
2
=9. B. (x − 3)
2
+(y +1)
2
+z
2
=
1
9
.
C. (x +3)
2
+(y − 1)
2
+z
2
=9. D. (x +3)
2
+(y − 1)
2
+z
2
=
1
9
.
Câu 27. TrongkhônggianOxyz,chohaimặtphẳng(P): 2x − 3y +4z +20 =0
và(Q): 4x −13y − 6z +40=0.Vịtrítươngđốicủa(P) và(Q) là
A. Songsong.
B. Trùngnhau.
C. Cắtnhaunhưngkhôngvuônggóc.
D. Vuônggóc.
Câu 28. Trong không gian Oxyz, cặp mặt phẳng nào sau đây song song với
nhau?
A. (P): 2x − y +z − 5=0 và(Q): − 3x +2y −2z +10.
B. (R): x −y +z − 3=0 và(S): 2x −2y +2z +6=0.
C. (T): x −y +z =0 và(U):
x
2
−
y
2
+
z
2
=0.
D. (X): 3x − y +2z − 3=0 và(Y): 6z − 2y − 6=0.
Câu 29. TrongkhônggianOxyz,chođiểmA(−1;2;1)vàhaimặtphẳng(P): 2x+
4y − 6z − 5=0,(Q): x +2y − 3z =0.Mệnhđềnàosauđâylàđúng?
A. Mặtphẳng(Q) điquaA vàsongsongvới(P).
B. Mặtphẳng(Q) khôngđiquaA vàsongsongvới(P).
C. Mặtphẳng(Q) điquaA vàkhôngsongsongvới(P).
D. Mặtphẳng(Q) khôngđiquaA vàkhôngsongsongvới(P).
Câu 30. TrongkhônggianOxyz,chohaimặtphẳng(P): x − 3y +2z +1=0 và
(Q): (2m − 1)x +m(1− 2m)y +(2m − 4)z +14 = 0.Tìmm để(P)và(Q)vuông
gócvớinhau.
A. m =1 hoặcm =−
3
2
. B. m =−1 hoặcm =−
3
2
.
C. m =2. D. m =
3
2
.
Soạn:HuỳnhPhúSĩ 44 TrườngTHCS-THPTMỹThuận
§2.Phươngtrìnhmặtphẳng TOÁN12
L TỰ LUẬN
Câu 1 (SGK HH12). Viếtphươngtrìnhcủamặtphẳng
a)ĐiquađiểmM(1;−2;4) vànhận
−Ï
n =(2;3;5) làmvectơpháptuyến;
b)ĐiquađiểmA(0;−1;2) vàsongsongvớigiácủamỗivectơ
−Ï
u =(3;2;1) và
−Ï
v =(−3;0;1);
c)ĐiquabađiểmA(−3;0;0),B(0;−2;0) vàC(0;0;−1);
d)ĐiquađiểmM(2;−1;2) vàsongsongvớimặtphẳng
(
β
)
: 2x − y +3z +4=0;
e)ĐiquahaiđiểmA(1;0;1),B(5;2;3) vàvuônggócvớimặtphẳng
(
β
)
: 2x − y +z −7=0;
f)TrungtrựccủađoạnthẳngAB vớiA(2;3;7) vàB(4;1;3).
Câu 2 (SGK HH12). Xácđịnhcácgiátrịcủam vàn đểmỗicặpmặtphẳngsauđâylàmộtcặpmặtphẳngsongsongvới
nhau:
a)2x +my +3z −5=0 vànx − 8y −6z +2=0 b) 3x − 5y +mz − 3=0 và2x +ny −3z +1=0
Soạn:HuỳnhPhúSĩ 45 TrườngTHCS-THPTMỹThuận
§3.Phươngtrìnhđườngthẳng TOÁN12
§3.PHƯƠNG TRÌNH ĐƯỜNG THẲNG
Nhắc lại về Phương trình tham số của đường thẳng trong mặt phẳng
VECTƠ CHỈ PHƯƠNG CỦA ĐƯỜNG THẲNG
Chođườngthẳng∆vàvectơ
−Ï
u 6=
−Ï
0.Nếugiá của
−Ï
n
............ hoặc ...... với ∆ thì ta nói
−Ï
u là vectơ
............ của∆.
∆
−Ï
u
•Mỗiđườngthẳngcó......... vectơchỉphương.
•Nếu
−Ï
u làvectơchỉphươngcủa∆thìk ·
−Ï
u cũnglà
............... của∆.
PHƯƠNG TRÌNH THAM SỐ CỦA ĐƯỜNG THẲNG
Chođườngthẳng∆ điquađiểmM
(
x
0
;y
0
)
vàcóvectơchỉ
phương
−Ï
u =
(
u
1
;u
2
)
.Khiđó
∆:
(
x =...... +......t
y =...... +......t
Chú ý: Nếuu
1
, u
2
6=0thìphươngtrìnhtrêncóthểviết
dướidạngchính tắc nhưsau:
x − ...
...
=
y − ...
...
1 PHƯƠNG TRÌNH THAM SỐ CỦA ĐƯỜNG THẲNG
Định nghĩa − £ é
TrongkhônggianOxyz chođườngthẳng∆điquađiểmM
(
x
0
;y
0
;z
0
)
vànhận
−Ï
u =
(
u
1
;u
2
;u
3
)
làmvectơchỉphương.Khiđóphươngtrìnhthamsốcủa∆ códạng
∆:
x =...... +......t
y =...... +......t
z =......+......t
(1)
trongđót là............
Ví dụ 1. Viếtphươngtrìnhthamsốcủađườngthẳng∆điquađiểmA(1;−2;3)vàcó
vectơchỉphương
−Ï
v =(1;4;5).
!
Nếuu
1
, u
2
, u
3
6=0 thìphươngtrình(1)cóthểviếtdướidạngchính tắc nhưsau:
x − ...
...
=
y − ...
...
=
y − ...
...
Ví dụ 2. ViếtphươngtrìnhchínhtắccủađườngthẳngAB vớiA(1;−2;3) vàB(3;0;0).
Ví dụ 3. Chođườngthẳng∆:
x − 1
1
=
y − 2
2
=
z
3
.Mặtphẳngnàosauđâychứađường
thẳng∆?
A.
(
α
)
: 2x +4y +6z +9=0. B.
(
β
)
: x +y − z +3=0.
C.
(
λ
)
: x +y − z −3=0. D.
(
γ
)
: x +2y − z +3=0.
Soạn:HuỳnhPhúSĩ 46 TrườngTHCS-THPTMỹThuận
§3.Phươngtrìnhđườngthẳng TOÁN12
2 HAI ĐƯỜNG THẲNG SONG SONG, CẮT NHAU, CHÉO NHAU
∆
2
∆
1
−Ï
u
−Ï
v
M
Điều kiện để hai đường thẳng song song
Gọi
−Ï
u,
−Ï
v lầnlượtlàvectơchỉphươngcủahaiđườngthẳng∆
1
, ∆
2
vàđiểmM ∈ ∆
1
.
•∆
1
∥ ∆
2
⇔
(
−Ï
u =k......
M ......∆
2
•∆
1
≡ ∆
2
⇔
(
−Ï
u =k......
M ......∆
2
Ví dụ 4. Cặpđườngthẳngnàodướiđâysongsong,trùngnhau?
a)d:
x =3− t
y =4+t
z =5−2t
vàd
0
:
x =2− 3t
0
y =5+3t
0
z =3−6t
0
b)d:
x =1+t
y =2t
z =3−t
vàd
0
:
x =2+2t
0
y =3+4t
0
z =5−2t
0
Điều kiện để hai đường thẳng cắt nhau
Haiđườngthẳngd:
x =x
0
+u
1
t
y =y
0
+u
2
t
z =z
0
+u
3
t
vàd
0
:
x =x
0
0
+v
1
t
0
y =y
0
0
+v
2
t
0
z =z
0
0
+v
3
t
0
cắtnhaukhivàchỉ
khihệphươngtrình
x
0
+u
1
t =x
0
0
+v
1
t
0
y
0
+u
2
t =y
0
0
+v
2
t
0
z
0
+u
3
t =z
0
0
+v
3
t
0
cóđúng...... nghiệm.
Ví dụ 5. Tìmgiaođiểmcủahaiđườngthẳngd
1
:
x =3− t
y =2− 3t
z =t
vàd
2
:
x =1+2t
0
y =3− t
0
z =3−3t
0
.
Điều kiện để hai đường thẳng chéo nhau
Haiđườngthẳngd:
x =x
0
+u
1
t
y =y
0
+u
2
t
z =z
0
+u
3
t
vàd
0
:
x =x
0
0
+v
1
t
0
y =y
0
0
+v
2
t
0
z =z
0
0
+v
3
t
0
chéonhaukhivà
chỉkhihaivectơ
−Ï
u,
−Ï
v ............ phươngvàhệphươngtrình
x
0
+u
1
t =x
0
0
+v
1
t
0
y
0
+u
2
t =y
0
0
+v
2
t
0
z
0
+u
3
t =z
0
0
+v
3
t
0
...... nghiệm.
Soạn:HuỳnhPhúSĩ 47 TrườngTHCS-THPTMỹThuận
§3.Phươngtrìnhđườngthẳng TOÁN12
Ví dụ 6. Xétvịtrítươngđốicủahaiđườngthẳngd
1
:
x =5− t
y =2− 3t
z =4+t
vàd
2
:
x =1+2t
0
y =3− t
0
z =−3t
0
.
!
Đểtìmgiaođiểmcủađườngthẳng∆:
x =x
0
+u
1
t
y =y
0
+u
2
t
z =z
0
+u
3
t
vàmặtphẳng
(
α
)
: Ax +
By +Cz +D =0,taxétphươngtrình
A
(
x
0
+u
1
t
)
+B
(
y
0
+u
2
t
)
+C
(
z
0
+u
3
t
)
+D =0(1)
•Nếu(1)vônghiệmthì∆.........
(
α
)
•Nếu(1)vôsốnghiệmthì∆.........
(
α
)
•Nếu(1)cóđúngmộtnghiệmthì∆.........
(
α
)
Ví dụ 7. Tìmgiaođiểmcủamặtphẳng
(
α
)
: x +y +z −3=0 vớicácđườngthẳngsau:
a)d
1
:
x =2+t
y =3− t
z =1
b)d
2
:
x =1+2t
y =1− t
z =1−t
c)d
3
:
x =1+5t
y =1− 4t
z =1+3t
3 THỰC HÀNH
Í TRẮC NGHIỆM
Câu 1. TrongkhônggianOxyz,điểmnàọdướiđâythuộcđườngthẳngd:
x +1
−1
=
y − 2
3
=
z − 1
3
?
A. P
(
−1;2;1
)
. B. Q
(
1;−2;−1
)
. C. N
(
−1;3;2
)
. D. M
(
1;2;1
)
.
Câu 2. TrongkhônggianvớihệtọađộOxyz,chođườngthẳng∆:
x =3
y =2+2t
z =1−3t
.
TìmtọađộđiểmM thuộcđườngthẳng∆.
A. M(0;2;−3). B. M(3;2;2). C. M(3;4;2). D. M(3;0;4).
Soạn:HuỳnhPhúSĩ 48 TrườngTHCS-THPTMỹThuận
§3.Phươngtrìnhđườngthẳng TOÁN12
Câu 3. TrongkhônggianvớihệtọađộOxyz,chođườngthẳng∆:
x =2+t
y =3− t
z =1
.
Tìmtọađộmộtvectơchỉphươngcủa∆.
A.
−Ï
u =(1;−1;0). B.
−Ï
u =(1;−1;1).
C.
−Ï
u =(2;3;1). D.
−Ï
u =(2;3;0).
Câu 4. TrongkhônggianOxyz,vectơnàodướiđâylàmộtvectơchỉphươngcủa
đườngthẳngđiquahaiđiểmM
(
2;3;−1
)
vàN
(
4;5;3
)
?
A.
−Ï
u
4
=
(
1;1;1
)
. B.
−Ï
u
3
=
(
1;1;2
)
. C.
−Ï
u
1
=
(
3;4;1
)
. D.
−Ï
u
2
=
(
3;4;2
)
.
Câu 5. TrongkhônggianOxyz,đườngthẳngd:
x − 1
2
=
y − 3
−4
=
z − 7
1
nhận
vectơnàodướiđâylàmộtvectơchỉphương?
A. ~a =(−2;−4;1). B.
~
b =(2;4;1).
C. ~c =(1;−4;2). D.
~
d =(2;−4;1).
Câu 6. Trongkhônggian vớihệ tọa độOxyz, phươngtrình nào dướiđây là
phươngtrìnhcủađườngthẳngđiquađiểmM(2;−2;2)vàcóvectơchỉphương
−Ï
u =(3;1;1)?
A.
x =1+3t
y =−1+t
z =1+t
. B.
x =2+3t
y =−2+t
z =2+t
.
C.
x =3+t
y =1− t
z =1+t
. D.
x =3+2t
y =1− 2t
z =1+2t
.
Câu 7. TrongkhônggianvớihệtọađộOxyz,phươngtrìnhnàodướiđâylàphương
trìnhcủađườngthẳngđiquahaiđiểmA(1;1;2) vàB(6;11;−3)?
A.
x − 5
1
=
y − 10
2
=
z +5
2
. B.
x +5
1
=
y +10
2
=
z − 5
2
.
C.
x − 1
1
=
y − 1
2
=
z − 2
−1
. D.
x +1
1
=
y +1
2
=
z +2
−1
.
Câu 8. Trongkhônggian vớihệ tọa độOxyz, phươngtrình nào dướiđây là
phươngtrìnhcủađườngthẳngđiquađiểmM(0;4;1) vàvuônggócvớimặtphẳng
(P): 2x −2y − z =0?
A.
x =−2
y =2+4t
z =1+t
. B.
x =2
y =−2+4t
z =−1+t
.
C.
x =t
y =4− t
z =1−2t
. D.
x =2t
y =4− 2t
z =1−t
.
Câu 9. Phươngtrìnhđườngthẳng∆ điquađiểmA(3;2;1) vàsongsongvớiđường
thẳng
x
2
=
y
4
=
z +3
1
là
A.
x =3− 2t
y =2− 4t
z =1−t
. B.
x =2+3t
y =4+2t
z =1+t
.
C.
x =2t
y =4t
z =3+t
. D.
x =3+2t
y =2− 4t
z =1+t
.
Câu 10. TrongkhônggianOxyz,chođiểmA(3;5;3)vàhaimặtphẳng(P):2x +
y +2z − 8 =0,(Q): x − 4y +z − 4 =0.Viếtphươngtrìnhđườngthẳngd điqua
A vàsongsongvớicảhaimặtphẳng(P),(Q).
A. d:
x =3+t
y =5− t
z =3
. B. d:
x =3+t
y =5
z =3−t
.
C. d:
x =3+t
y =5
z =3+t
. D. d:
x =3
y =5+t
z =3−t
.
Soạn:HuỳnhPhúSĩ 49 TrườngTHCS-THPTMỹThuận
§3.Phươngtrìnhđườngthẳng TOÁN12
Câu 11. TrongkhônggianOxyz,chođiểmM(1;−3;4),đườngthẳngd:
x +3
2
=
y − 5
−5
=
z − 2
−1
vàmặtphẳng(P): 2x +z − 2=0.Viếtphươngtrìnhđườngthẳng
∆ điquaM,vuônggócvớid vàsongsongvới(P).
A. ∆:
x − 1
1
=
y +3
−1
=
z − 4
−2
. B. ∆:
x − 1
−1
=
y +3
−1
=
z − 4
−2
.
C. ∆:
x − 1
1
=
y +3
1
=
z − 4
−2
. D. ∆:
x − 1
1
=
y +3
−1
=
z − 4
2
.
Câu 12. TrongkhônggianOxyz,chođườngthẳngd:
x − 1
2
=
y +5
−1
=
z − 3
4
.
Phươngtrìnhnàodướiđâylàhìnhchiếuvuônggóccủađườngthẳngd trênmặt
phẳng(P): x +3=0?
A.
x =−3
y =−5− t
z =−3+4t
. B.
x =−3
y =−5+t
z =3+4t
.
C.
x =−3
y =−5+2t
z =3−t
. D.
x =−3
y =−6− t
z =7+4t
.
Câu 13. TrongkhônggianOxyz,chođườngthẳngd:
x − 1
2
=
y − 3
−1
=
z − 1
1
cắt
mặtphẳng(P): 2x−3y +z−2=0 tạiđiểmI(a;b;c).Khiđóa+b+c bằng
A. 7. B. 3. C. 9. D. 5.
Câu 14. TrongkhônggianOxyz,hìnhchiếuvuônggóccủađiểmA(−1;1;6) trên
đườngthẳng∆:
x =2+t
y =1− 2t
z =2t
là
A. M(3;−1;2). B. H(11;−17;18).
C. K(2;1;0). D. N(1;3;−2).
Câu 15. TrongkhônggianOxyz,tọađộhìnhchiếuvuônggóccủađiểmA(3;2;−1)
lênmặtphẳng(α): x +y +z =0 là
A. (−2;1;1). B.
5
3
;
2
3
;−
7
3
. C. (1;1;−2). D.
1
2
;
1
4
;
1
4
.
Câu 16. TrongkhônggianvớihệtọađộOxyz,chohaiđườngthẳng∆:
x
1
=
y +2
2
=
z − 3
−1
và∆
0
:
x =5− t
y =−2t
z =3+t
.Mệnhđềnàodướiđâyđúng?
A. ∆ songsongvới∆
0
. B. ∆ trùngvới∆
0
.
C. ∆ vuônggócvới∆
0
. D. ∆và∆
0
chéonhau.
Câu 17. TrongkhônggianvớihệtọađộOxyz,chođườngthẳng∆:
x +4
2
=
y +2
1
=
z − 3
3
vàmặtphẳng(P): 4x +2y +(m −1)z +13=0.Tìmgiátrịcủam
để(P) vuônggócvới∆.
A. m =−7. B. m =7. C. m =−
7
3
. D. m =
7
3
.
Câu 18. TrongkhônggianOxyz,chođườngthẳngd:
x =1
y =1+t
z =−1+t
vàhaimặt
phẳng(P): x − y +z +1 = 0,(Q): 2x +y − z − 4 = 0.Khẳngđịnhnàosauđây
đúng?
A. d∥ (P). B. d∥ (Q). C. (P)∩ (Q)=d. D. d⊥(P).
Câu 19. TrongkhônggianOxyz,chođiểmM(1;0;3) vàđườngthẳng∆:
x − 2
1
=
y +1
2
=
z − 2
−2
.TínhkhoảngcáchtừđiểmM đếnđườngthẳng∆.
A.
√
34
3
. B.
√
26
3
. C.
√
10
3
. D.
√
2.
Câu 20. TrongkhônggianOxyz,chomặtcầu(S): (x−2)
2
+(y−3)
2
+(z−5)
2
=100
vàđiểmM(−3;3;−3) nằmtrênmặtphẳng(α): 2x −2y +z+15=0.Đườngthẳng
Soạn:HuỳnhPhúSĩ 50 TrườngTHCS-THPTMỹThuận
§3.Phươngtrìnhđườngthẳng TOÁN12
∆ nằmtrênmặtphẳng(α),điquaM vàcắtmặtcầu(S) tạihaiđiểmA, B saocho
đoạnthẳngAB cóđộdàilớnnhất.Viếtphươngtrìnhđườngthẳng∆.
A.
x +3
1
=
y − 3
1
=
z +3
3
. B.
x +3
16
=
y − 3
11
=
z +3
−10
.
C.
x +3
5
=
y − 3
1
=
z +3
8
. D.
x +3
1
=
y − 3
4
=
z +3
6
.
L TỰ LUẬN
Câu 1 (SGK HH12). Viếtphươngtrìnhthamsốcủađườngthẳngd trongmỗitrườnghợpsau:
a)d điquađiểmM(5;4;1) vàcóvectơchỉphương
−Ï
a =(2;−3;1);
b)d điquađiểmA(2;−1;3) vàvuônggócvớimặtphẳng
(
α
)
: x +y − z +5=0;
c)d điquađiểmB(2;0;−3) vàsongsongvớiđườngthẳng∆:
x =1+2t
y =−3+3t
z +4t
;
d)d điquahaiđiểmP(1;2;3) vàQ(5;4;4);
Câu 2 (SGK HH12). Xétvịtrítươngđốicủacáccặpđườngthẳngd vàd
0
chobởicácphươngtrìnhsau:
a)d:
x =−3+2t
y =−2+3t
z =6+4t
vàd
0
:
x =5+t
0
y =−1− 4t
0
z =20+t
0
b)d:
x =1+t
y =2+t
z =3−t
vàd
0
:
x =1+2t
0
y =−1+2t
0
z =2−2t
0
Câu 3 (SGK HH12). Tínhkhoảngcáchgiữađườngthẳng∆:
x =−3+2t
y =−1+3t
z =−1+2t
vàmặtphẳng
(
α
)
: 2x − 2y +z +3=0.
Soạn:HuỳnhPhúSĩ 51 TrườngTHCS-THPTMỹThuận
Phụlục TOÁN12
PHỤ LỤC
SỞ GIÁO DỤC VÀ ĐÀO TẠO
VĨNHLONG
(Đề có 05 trang)
ĐỀ KIỂM TRA HỌC KÌ II NĂM HỌC 2018-2019
MÔN: TOÁN 12 THPT
Thời gian làm bài 90 phút (bao gồm trắc nghiệm và tự luận)
Họ và tên học sinh: ........................................................................................ Mã đề 101
I. PHẦN TRẮC NGHIỆM (40 câu, 8.0 điểm)
Câu 1. Cặpsốnàosauđâycótínhchất"Cómộthàmsốlànguyênhàmcủahàmsốcònlại"?
A. tanx
2
và
1
cos
2
x
2
. B. sin2x vàsin
2
x. C. e
x
vàe
−x
. D. sin2x vàcos
2
x.
Câu 2. Phátbiểunàosauđâylàđúng?
A.
Z
xsinx dx =xcosx +sinx +C. B.
Z
xsinx dx =−xcosx +sinx +C.
C.
Z
xsinx dx =−xcosx − sinx +C. D.
Z
xsinx dx =xcosx − sinx +C.
Câu 3. BiếtF(x) lànguyênhàmcủahàmsốf(x)=
1
x − 1
vàF(2)=1.KhiđóF(3) bằngbaonhiêu?
A. ln
3
2
. B. ln2+1. C. ln2. D.
1
2
.
Câu 4. Biết
Z
(x +3)· e
−3x+1
dx =−
1
m
e
−3x+1
(3x +n)+C vớim, n làcácsốnguyên.TínhtổngS =m +n.
A. 10. B. 1. C. 9. D. 19.
Câu 5. Chohàmsốy =f(x) cóđạohàmtrênđoạn[−2;1] vàf(−2)=3,f(1)=7.TínhI =
1
Z
−2
f
0
(x)dx.
A. I =
7
3
. B. I =−4. C. I =10. D. I =4.
Câu 6. Chohàmsốy =f(x) liêntụctrênđoạn[a;b].Mệnhđềnàodướiđâysai?
A.
b
Z
a
f(x)dx =−
a
Z
b
f(x)dx. B.
b
Z
a
kdx =k(a −b), ∀k ∈ R.
C.
b
Z
a
f(x)dx =
c
Z
a
f(x)dx +
b
Z
c
f(x)dx, ∀c ∈ (a;b). D.
b
Z
a
f(x)dx =
b
Z
a
f(t)dt.
Câu 7. Nếu
3
Z
0
x
1+
√
1+x
dx =
2
Z
1
f(t)dt,vớit =
√
1+x thìf(t) làhàmsốnàotrongcáchàmsốdướiđây?
A. f(t)=t
2
−1. B. f(t)=2t
2
+2t. C. f(t)=t
2
+t. D. f(t)=2t
2
−2t.
Câu 8. TínhtíchphânI =
2
Z
0
(x +2)
3
dx.
A. I =60. B. I =240. C. I =56. D. I =120.
Câu 9. TínhI =
e
2
Z
e
(
1− lnx
)
2
x
dx đượckếtquảlà
A.
4
3
. B.
5
3
. C.
1
3
. D.
13
3
.
Câu 10. Biếtrằng
5
Z
1
1
2x − 1
dx =lna.Giátrịcủaa là
A. 81. B. 27. C. 3. D. 9.
Câu 11. Cho
π
2
Z
0
cosx
(
sinx
)
2
−5sinx +6
dx =aln
4
c
+b,vớia, b làcácsốhữutỉ,c > 0.TínhtổngS =a +b +c.
A. S =3. B. S =4. C. S =0. D. S =1.
Soạn:HuỳnhPhúSĩ 52 TrườngTHCS-THPTMỹThuận
Phụlục TOÁN12
Câu 12. Giảsử
5
Z
3
dx
x
2
−x
=aln5+bln3+cln2.TínhgiátrịbiểuthứcS =−2a +b +3c
2
.
A. S =3. B. S =6. C. S =−2. D. S =0.
Câu 13. Chohàmsốf(x) liêntụctrênR,biết
π
4
Z
0
f
(
tanx
)
dx =4 và
1
Z
0
x
2
·f(x)
x
2
+1
dx =2.TínhI =
1
Z
0
f(x)dx.
A. 6. B. 1. C. 0. D. 2.
Câu 14. Diệntíchhìnhphẳngđượcgiớihạnbởiđườngcongy =
1
2
x
2
vàđườngthẳngy =x đượctínhtheocôngthứcnào
sauđây?
A. S =
2
Z
0
x
2
−2x
dx. B. S =
2
Z
0
1
2
x
2
−x
dx. C. S =
2
Z
0
1
2
x
2
−x
2
dx. D. S =
2
Z
0
1
2
x
2
−x
dx.
Câu 15. Tínhdiệntíchhìnhphẳnggiớihạnbởicácđườngy =−x
2
+4x − 3,x =0,x =3,Ox.
A. −
8
3
. B. −
4
3
. C.
4
3
. D.
8
3
.
Câu 16. Tínhdiệntíchhìnhphẳnggiớihạnbởi
(
C
)
: y =x
4
−2x
2
+1 vàtrụchoành.
A.
8
15
. B. −
15
16
. C.
15
8
. D.
16
15
.
Câu 17.
Cho(H)làhìnhphẳnggiớihạnbởiđồthịcủacáchàmsốy =
√
x,y =0,y =2− x.
Diệntíchcủa(H) là
A.
4
√
2− 1
3
. B.
8
√
2+3
6
. C.
7
6
. D.
5
6
.
x
y
O
1 2
1
2
Câu 18. GọiV làthểtíchcủakhốitrònxoaydohìnhphẳnggiớihạnbởicácđườngsauquayquanhtrụchoành:y =sinx,
y =0,x =0,x =12π.Mệnhđềnàodướiđâyđúng?
A. V =π
12π
Z
0
(
sinx
)
2
dx. B. V =π
12π
Z
0
sinxdx. C. V =π
2
12π
Z
0
(
sinx
)
2
dx. D. V =π
2
12π
Z
0
sinxdx.
Câu 19.
Chohàmbậchaiy =f(x)cóđồthịnhưhìnhbên.Tínhthểtíchkhốitrònxoaytạo
thànhkhiquayhìnhphẳnggiớihạnbởiđồthịhàmsốy =f(x)vàOx quanhOx.
A.
4π
3
. B. −
12π
15
. C.
16π
15
. D.
16π
5
.
x
y
O
1 2 3
1
Câu 20. Mộtôtôđangchạyvớivậntốc54 km/hthìtăngtốcchuyểnđộngnhanhdầnđềuvớigiatốca(t)=3t − 8(m/s
2
)
trongđót làkhoảngthờigiantínhbằnggiây.Quãngđườngmàôtôđiđượcsau10 skểtừlúctăngtốclà
A. 540 m. B. 150 m. C. 250 m. D. 246 m.
Câu 21. Chohaisốphứcz =x − yi vàw =2i +3x,(x, y ∈ R).Biếtz =w.Giátrịcủax vày lầnlượtlà
A. 2 và−3. B. −2 và0. C. 0 và2. D. 0 và−2.
Câu 22. TrênmặtphẳngtọađộOxy,chohaiđiểmA(4;0),B(0;−3) vàđiểmC thỏamãnđiềukiện
−Ï
OC =
−Ï
OA+
−Ï
OB.Khiđó
sốphứcđượcbiểudiễnbởiđiểmC là
A. z =−3− 4i. B. z =4+3i. C. z =4−3i. D. z =−3+4i.
Câu 23. Chosốphứcz =6+7i.ĐiểmM biểudiễnchosốphứcz trênmặtphẳngOxy là
A. M(−6;−7). B. M(6;−7). C. M(6;7i). D. M(6;7).
Câu 24. Chox, y làcácsốthực.Sốphứcz =i
(
1+xi +y +2i
)
bằng0 khi
A. x =−1; y =−2. B. x =0; y =0. C. x =−2; y =−1. D. x =2; y =1.
Câu 25. Chosốphứcz thỏamãn|z| =2 và
z
2
+1
=4.Tính|z +z|+|z −z|.
A. 3+
√
7. B. 3+2
√
2. C. 7+
√
3. D. 16.
Soạn:HuỳnhPhúSĩ 53 TrườngTHCS-THPTMỹThuận
Phụlục TOÁN12
Câu 26. Chosốphứcz =x + yi (x, y ∈ R)cómôđunnhỏnhấtthỏamãnđiềukiện|z − 4− 2i| = |z − 2|.Tính
P =x
2
+y
2
.
A. 10. B. 16. C. 8. D. 32.
Câu 27. Tìmcáccănbậchaicủa−6.
A. −
√
6i. B. ±
√
6i. C. ±6i. D.
√
6i.
Câu 28. Trongtậpsốphức,phươngtrìnhz
2
−2z +5=0 cónghiệmlà
A. z =−1± 2i. B. z =2± 2i. C. z =−2±2i. D. z =1± 2i.
Câu 29. Cho ~m =(1;0;−1),~n =(0;1;1).Kếtluậnnàosai?
A. Góccủa ~m và~n là30
◦
. B. [~m, ~n]=(1;−1;1).
C. ~m · ~n =−1. D. ~m và~n khôngcùngphương.
Câu 30. TrongkhônggianvớihệtrụctọađộOxyz,chobađiểmA(0;−2;−1),B(−2;−4;3),C(1;3;−1).TìmđiểmM ∈ (Oxy)
saocho
−−Ï
MA +
−−Ï
MB +3
−−Ï
MC
đạtgiátrịnhỏnhất.
A.
−
1
5
;
3
5
;0
. B.
1
5
;
3
5
;0
. C.
3
5
;
4
5
;0
. D.
1
5
;−
3
5
;0
.
Câu 31. TrongkhônggianOxyz,chomặtcầu(S): x
2
+y
2
+z
2
+6x −4y +2z − 2=0.TọađộtâmI vàbánkínhR của
(S) là
A. I(−3;2;−1) vàR =4. B. I(−3;2;−1) vàR =16. C. I(3;−2;1) vàR =4. D. I(3;−2;1) vàR =16.
Câu 32. Mặtphẳng(P)tiếpxúcvớimặtcầu(S):(x − 1)
2
+(y +3)
2
+(z − 2)
2
= 49tạiđiểmM(7;−1;5)cóphươngtrình
là
A. 6x +2y +3z − 55=0. B. 6x +2y +3z +55=0. C. 3x +y +z −22=0. D. 3x +y +z +22=0.
Câu 33. TrongkhônggianOxyz,chotứdiệnABCD cóA(3;−2;1),B(−4;0;3),C(1;4;−3),D(2;3;5).Phươngtrìnhmặtphẳng
chứaAC vàsongsongvớiBD là
A. 12x − 10y +21z − 35=0. B. 12x +10y −21z +35=0.
C. 12x +10y +21z +35=0. D. 12x −10y − 21z −35=0.
Câu 34. TrongkhônggianOxyz,chođiểmM(1;2;0)vàmặtphẳng(α): x +2y −2z +1 = 0.KhoảngcáchtừM đến(α)
là
A. 1. B. 3. C. 2. D. 4.
Câu 35. TrongkhônggianOxyz,phươngtrìnhmặtcầu(S) tiếpxúcvớihaimặtphẳngsongsong(P): x −2y +2z +6=0
và(Q): x −2y +2z −10=0 cótâmI trêntrụcOy là
A. x
2
+y
2
+z
2
+2y −
55
9
=0. B. x
2
+y
2
+z
2
+2y − 60=0.
C. x
2
+y
2
+z
2
−2y +55=0. D. x
2
+y
2
+z
2
−2y −
55
9
.
Câu 36. TrongkhônggianvớihệtọađộOxyz,chomặtcầu(S): x
2
+y
2
+z
2
+4x − 2y +6z − 11=0vàmặtphẳng
(P): x −2y +2z +1=0.Gọi(C) làđườngtròngiaotuyếncủa(P) và(S).Tínhchuviđườngtròn(C).
A. 10π. B. 4π. C. 6π. D. 8π.
Câu 37. Vịtrítươngđốicủahaimặtphẳng(α): 3x +2y − z +1=0 và
(
α
0
)
: 3x +y +11z −1=0 là
A. Vuônggócvớinhau. B. Trùngnhau.
C. Cắtnhaunhưngkhôngvuônggócvớinhau. D. Songsongvớinhau.
Câu 38. TrongkhônggianOxyz,chođườngthẳng∆điquaM(0;2;−3)vàcóvectơchỉphương~a =(4;−3;1).Phươngtrình
thamsốcủađườngthẳng∆ là
A.
x =4t
y =−2− 3t
z =3+t
. B.
x =4t
y =−2− 3t
z =−3−t
. C.
x =−4t
y =2+3t
z =−3−t
. D.
x =4
y =−3+2t
z =1−3t
.
Câu 39. Phươngtrìnhđườngthẳng∆ điquađiểmA(3;2;1) vàsongsongvớiđườngthẳng
x
2
=
y
4
=
z +3
1
là
A.
x =3− 2t
y =2− 4t
z =1−t
. B.
x =2+3t
y =4+2t
z =1+t
. C.
x =2t
y =4t
z =3+t
. D.
x =3+2t
y =2− 4t
z =1+t
.
Câu 40. TrongkhônggianOxyz,chomặtphẳng(P): x +2y +z − 4= 0 vàđườngthẳngd:
x +1
2
=
y
1
=
z +2
3
.Đường
thẳng∆ nằmtrongmặtphẳng(P) đồngthờicắtvàvuônggócvớiđườngthẳngd cóphươngtrìnhlà
A. ∆:
x − 1
5
=
y − 1
−1
=
z − 1
3
. B. ∆:
x − 1
5
=
y +1
−1
=
z − 1
2
.
C. ∆:
x − 1
5
=
y +1
−1
=
z − 1
−3
. D. ∆:
x − 1
5
=
y − 1
−1
=
z − 1
−3
.
II. PHẦN TỰ LUẬN (2.0 điểm)
Soạn:HuỳnhPhúSĩ 54 TrườngTHCS-THPTMỹThuận
Phụlục TOÁN12
Câu 41. Tínhtíchphân
1
Z
0
(2x +1)
5
dx.
Câu 42. Tìmphầnthực,phầnảo,sốphứcliênhợpvàtínhmôđuncủasốphức
z =
(
2− 4i
)
(
5+2i
)
+
4− 5i
2+i
.
Câu 43. TrongkhônggianOxyz,chotamgiácABC vớiA(1;−3;4),B(−2;−5;−7),C(6;−3;−1).Viếtphươngtrìnhđường
trungtuyếnAM củatamgiácABC.
Soạn:HuỳnhPhúSĩ 55 TrườngTHCS-THPTMỹThuận
Phụlục TOÁN12
BỘ GIÁO DỤC VÀ ĐÀO TẠO
ĐỀTHICHÍNHTHỨC
(Đề có 05 trang)
KÌ THI TỐT NGHIỆP THPT QUỐC GIA NĂM 2019
Bài thi: TOÁN
Thời gian làm bài: 90 phút, không kể thời gian phát đề
Họ và tên thí sinh: ..........................................................................................
Số báo danh: ...................................................................................................... Mã đề 101
Câu 1. TrongkhônggianOxyz,chomặtphẳng(P): 2x −y +3z +1=0.Vectơnàodướiđâylàmộtvectơpháptuyếncủa
(P)?
A.
−Ï
n
1
=(2;−1;−3). B.
−Ï
n
2
=(2;−1;3). C.
−Ï
n
3
=(2;3;1). D.
−Ï
n
4
=(2;1;3).
Câu 2. Chocấpsốcộng
(
u
n
)
vớiu
1
=2 vàu
2
=8.Côngsaicủacấpsốcộngđãchobằng
A. 4. B. 10. C. −6. D. 6.
Câu 3.
Đồthịcủahàmsốnàodướiđâycódạngnhưđườngcongtronghìnhvẽbên?
A. y =x
3
−3x +1. B. y =x
4
−2x
2
+1.
C. y =−x
3
+3x +1. D. y =−x
4
+2x
2
+1.
x
y
−2
−1
1
2
−1
1
3
Câu 4. TrongkhônggianOxyz,chođườngthẳngd:
x − 1
2
=
y − 3
−5
=
z +2
3
.Vectơnàodướiđâylàmộtvectơchỉphương
củad?
A.
−Ï
u
4
=(2;−5;3). B.
−Ï
u
1
=(2;5;3). C.
−Ï
u
3
=(1;3;−2). D.
−Ï
u
2
=(1;3;2).
Câu 5. Thểtíchcủakhốinóncóchiềucaoh vàbánkínhđáyr là
A.
4
3
πr
2
h. B. πr
2
h. C.
1
3
πr
2
h. D. 2πr
2
h.
Câu 6. Vớia làsốthựcdươngtùyý,log
5
a
3
bằng
A. 3log
5
a. B.
1
3
+log
5
a. C. 3+log
5
a. D.
1
3
log
5
a.
Câu 7. Chohàmsốf(x) cóbảngbiếnthiênnhưsau:
x
f
0
(x)
f(x)
−∞
1 3
+∞
−
0
+
0
−
+∞
−2
2
−∞
Hàmsốđãchođạtcựcđạitại
A. x =1. B. x =3. C. x =2. D. x =−2.
Câu 8. Sốphứcliênhợpcủasốphức5− 3i là
A. −5+3i. B. 5+3i. C. −3+5i. D. −5− 3i.
Câu 9. Họtấtcảcácnguyênhàmcủahàmsốf(x)=2x +6 là
A. 2x
2
+6x +C. B. x
2
+6x +C. C. 2x
2
+C. D. x
2
+C.
Câu 10. Biết
1
Z
0
f(x)dx =3 và
1
Z
0
g(x)dx =−4,khiđó
1
Z
0
f(x)+g(x)
dx bằng
A. −7. B. 7. C. −1. D. 1.
Câu 11. Nghiệmcủaphươngtrình3
2x+1
=27 là
A. x =1. B. x =5. C. x =4. D. x =2.
Câu 12. TrongkhônggianOxyz,hìnhchiếuvuônggóccủađiểmM(3;−1;1) trêntrụcOz cótọađộlà
A. (3;0;0). B. (3;−1;0). C. (0;−1;0). D. (0;0;1).
Câu 13. Sốcáchchọn2 họcsinhtừ5 họcsinhlà
A. C
2
5
. B. 5
2
. C. A
2
5
. D. 2
5
.
Câu 14. ThểtíchcủakhốilăngtrụcódiệntíchđáyB vàchiềucaoh là
A. 3Bh. B.
1
3
Bh. C.
4
3
Bh. D. Bh.
Câu 15. Chohàmsốf
(
x
)
cóbảngbiếnthiênsau:
Soạn:HuỳnhPhúSĩ 56 TrườngTHCS-THPTMỹThuận
Phụlục TOÁN12
x
f
0
(x)
f(x)
−∞
−2
0 2
+∞
−
0
+
0
−
0
+
+∞
1
3
1
+∞
Hàmsốđãchođồngbiếntrênkhoảngnàodướiđây?
A.
(
0;+∞
)
. B.
(
0;2
)
. C.
(
−∞;−2
)
. D.
(
−2;0
)
.
Câu 16.
Chohàmsốf
(
x
)
liêntụctrênR.GọiS làdiệntíchhìnhphẳnggiớihạnbởicác
đườngy =f
(
x
)
,y =0,x =−1 vàx =5 (nhưhìnhvẽbên).Mệnhđềnàodưới
đâylàđúng?
A. S =−
1
Z
−1
f
(
x
)
dx −
5
Z
1
f
(
x
)
dx. B. S =
1
Z
−1
f
(
x
)
dx −
5
Z
1
f
(
x
)
dx.
C. S =
1
Z
−1
f
(
x
)
dx +
5
Z
1
f
(
x
)
dx. D. S =−
1
Z
−1
f
(
x
)
dx +
5
Z
1
f
(
x
)
dx.
x
y
−1
1
5
1
−3
Câu 17. Chohàmsốf
(
x
)
cóbảngbiếnthiênnhưsau:
x
f
0
(x)
f(x)
−∞
−2
0 2
+∞
−
0
+
0
−
0
+
+∞
−1
2
−1
+∞
Sốnghiệmthựccủaphươngtrình3f
(
x
)
−5=0 là
A. 4. B. 2. C. 0. D. 3.
Câu 18. TrongkhônggianOxyz,chohaiđiểmA
(
−1;2;0
)
, B
(
3;0;2
)
.Phươngtrìnhmặtphẳngtrungtrựccủađoạnthẳng
AB là
A. x +y +z − 3=0. B. 2x −y +z −2=0. C. 2x +y +z − 4=0. D. 2x −y +z +2=0.
Câu 19. Mộtcơsởsảnxuấtcóhaibểnướchìnhtrụcóchiềucaobằngnhau,bánkínhđáylầnlượtbằng1mvà1,4m.Chủ
cơsởdựđịnhlàmmộtbểnướcmớihìnhtrụ,cócùngchiềucaovàcóthểtíchbằngtổngthểtíchcủahaibểnướctrên.Bán
kínhđáycủabểnướcdựđịnhlàmgầnnhấtvớikếtquảnàodướiđây?
A. 1,5m. B. 1,7m. C. 2,4m. D. 1,9m.
Câu 20. TrongkhônggianOxyz,chomặtcầu
(
S
)
: x
2
+y
2
+z
2
−2x+2y−7=0.Bánkínhcủamặtcầuđãchobằng
A.
√
7. B.
√
15. C. 3. D. 9.
Câu 21. Gọiz
1
,z
2
làhainghiệmphứccủaphươngtrìnhz
2
−6z +14=0.Giátrịcủaz
2
1
+z
2
2
bằng
A. 28. B. 36. C. 8. D. 18.
Câu 22. Choa vàb làhaisốthựcdươngthoảmãna
3
b
3
=32.Giátrịcủa3log
2
a +2log
2
b bằng
A. 4. B. 32. C. 2. D. 5.
Câu 23.
ChokhốilăngtrụđứngABC.A
0
B
0
C
0
cóđáylàtamgiácđềucạnhbằnga vàAA
0
=2a (minh
họanhưhìnhvẽbên).Thểtíchcủakhốilăngtrụđãchobằng
A.
√
3a
3
3
. B.
√
3a
3
2
. C.
√
3a
3
6
. D.
√
3a
3
.
a
2a
A
B
C
A
0
B
0
C
0
Câu 24. ChohìnhchópS.ABC cóSA vuônggócvớimặtphẳng(ABC),SA =2a,tamgiácABC vuôngtạiB,AB =a,
BC =a
√
3.GócgiữađườngthẳngSC vàmặtphẳng(ABC) bằng
A. 30
◦
. B. 90
◦
. C. 45
◦
. D. 60
◦
.
Soạn:HuỳnhPhúSĩ 57 TrườngTHCS-THPTMỹThuận
Phụlục TOÁN12
Câu 25. Nghiệmcủaphươngtrìnhlog
2
(
x +1
)
=1+log
2
(
x − 1
)
là
A. x =−2. B. x =3. C. x =2. D. x =1.
Câu 26. Chohaisốphứcz
1
=−2+i vàz
2
=1+i.TrênmặtphẳngtọađộOxy,điểmbiểudiễnsốphức2z
1
+z
2
cótọa
độlà
A.
(
−3;2
)
. B.
(
2;−3
)
. C.
(
−3;3
)
. D.
(
3;−3
)
.
Câu 27. Giátrịnhỏnhấtcủahàmsốf
(
x
)
=x
3
−3x +2 trên[−3;3] bằng
A. 4. B. 0. C. 20. D. −16.
Câu 28. Chohàmsốy =f
(
x
)
cóbảngbiếnthiênnhưsau:
x
y
0
y
−∞
0 2
+∞
− −
0
+
0
−∞
2
−2
+∞
Tổngsốtiệmcậnđứngvàtiệmcậnngangcủađồthịhàmsốđãcholà
A. 1. B. 3. C. 4. D. 2.
Câu 29. Chohàmsốf(x) cóđạohàmf
0
(x)=x(x −2)
2
,∀x ∈ R.Sốđiểmcựctrịcủahàmsốđãcholà
A. 0. B. 3. C. 1. D. 2.
Câu 30. Hàmsốy =3
x
2
−3x
cóđạohàmlà
A.
(
2x − 3
)
·3
x
2
−3x
·ln3. B. 3
x
2
−3x
·ln3. C.
x
2
−3x
·3
x
2
−3x−1
. D.
(
2x − 3
)
·3
x
2
−3x
.
Câu 31. Chosốphứcz thỏamãn3
(
z − i
)
−
(
2+3i
)
z =7−16i.Môđuncủasốphứcz bằng
A. 5. B. 3. C.
√
5. D.
√
3.
Câu 32. Họtấtcảcácnguyênhàmcủahàmsốf
(
x
)
=
3x − 1
(
x − 1
)
2
trênkhoảng
(
1;+∞
)
là
A. 3ln
(
x − 1
)
+
1
x − 1
+C. B. 3ln
(
x − 1
)
+
2
x − 1
+C.
C. 3ln
(
x − 1
)
−
1
x − 1
+C. D. 3ln
(
x − 1
)
−
2
x − 1
+C.
Câu 33. Chohàmsốf
(
x
)
.Biếtf
(
0
)
=4 vàf
0
(
x
)
=2cos
2
x +3,∀x ∈ R,khiđó
π
4
Z
0
f
(
x
)
dx bằng
A.
π
2
+2
8
. B.
π
2
+8π +2
8
. C.
π
2
+6π +8
8
. D.
π
2
+8π +8
8
.
Câu 34. TrongkhônggianOxyz,chocácđiểmA
(
1;0;2
)
, B
(
1;2;1
)
, C
(
3;2;0
)
vàD
(
1;1;3
)
.ĐườngthẳngđiquaA vàvuông
gócvớimặtphẳng
(
BCD
)
cóphươngtrìnhlà
A.
x =1− t
y =2− 4t
z =2−2t
. B.
x =1− t
y =4t
z =2+2t
. C.
x =1+t
y =4
z =2+2t
. D.
x =2+t
y =4+4t
z =4+2t
.
Câu 35. Chohàmsốf
(
x
)
,bảngxétdấuf
0
(
x
)
nhưsau:
x
f
0
(x)
−∞
−3 −1
1
+∞
−
0
+
0
−
0
+
Hàmsốy =f
(
5− 2x
)
nghịchbiếntrênkhoảngnàodướiđây?
A.
(
5;+∞
)
. B.
(
2;3
)
. C.
(
0;2
)
. D.
(
3;5
)
.
Câu 36. Chophươngtrìnhlog
9
x
2
− log
3
(
6x − 1
)
=−log
3
m (m làthamsốthực).Cótấtcảbaonhiêugiátrịnguyêncủa
m đểphươngtrìnhđãchocónghiệm?
A. Vôsố. B. 5. C. 7. D. 6.
Câu 37.
Chohàmsốf
(
x
)
,hàmsốy = f
0
(
x
)
liêntụctrênR vàcóđồthịnhưhìnhvẽbên.Bất
phươngtrìnhf
(
x
)
> x +m (m làthamsốthực)nghiệmđúngvớimọix ∈
(
0;2
)
khivà
chỉkhi
A. m ≤ f
(
0
)
. B. m < f
(
2
)
−2. C. m < f
(
0
)
. D. m ≤ f
(
2
)
−2.
x
y
2
1
Soạn:HuỳnhPhúSĩ 58 TrườngTHCS-THPTMỹThuận
Phụlục TOÁN12
Câu 38. Chọnngẫunhiênhaisốkhácnhautừ27 sốnguyêndươngđầutiên.Xácsuấtđểchọnđượchaisốcótổnglàmột
sốchẵnbằng
A.
13
27
. B.
365
729
. C.
1
2
. D.
14
27
.
Câu 39.
ChohìnhchópS.ABCD cóđáylàhìnhvuôngcạnha,mặtbênSAB làtamgiácđềuvà
nằmtrongmặtphẳngvuônggócvớimặtphẳngđáy(minhhọanhưhìnhvẽbên).Khoảng
cáchtừC đếnmặtphẳng
(
SBD
)
bằng
A.
√
21a
7
. B.
√
21a
28
. C.
√
2a
2
. D.
√
21a
14
.
A
C
D
S
B
Câu 40. Chohìnhtrụcóchiềucaobằng4
√
2.Cắthìnhtrụđãchobởimặtphẳngsongsongvớitrụcvàcáchtrụcmột
khoảngbằng
√
2,thiếtdiệnthuđượccódiệntíchbằng16.Diệntíchxungquanhcủahìnhtrụđãchobằng
A. 8
√
2π. B. 24
√
2π. C. 16
√
2π. D. 12
√
2π.
Câu 41.
Chođườngthẳngy =
3
4
x vàparaboly =
1
2
x
2
+a (a làthamsốthựcdương).Gọi
S
1
vàS
2
lầnlượtlàdiệntíchcủahaihìnhphẳngđượcgạchchéotronghìnhbên.
KhiS
1
=S
2
thìa thuộckhoảngnàodướiđây?
A.
3
16
;
7
32
. B.
7
32
;
1
4
. C.
1
4
;
9
32
. D.
0;
3
16
.
x
y
y =
1
2
x
2
+a
y =
3
4
x
O
S
1
S
2
Câu 42. Xétsốphứcz thỏamãn|z| =
√
2.TrênmặtphẳngtọađộOxy,tậphợpđiểmbiểudiễncácsốphứcw =
3+iz
1+z
là
mộtđườngtròncóbánkínhbằng
A. 12. B. 2
√
3. C. 2
√
5. D. 20.
Câu 43. TrongkhônggianOxyz,chođiểmA(0;4;−3).Xétđườngthăngd thayđổi,songsongvớitrụcOz vàcáchtrụcOz
mộtkhoảngbằng3.KhikhoảngcáchtừA đếnd lớnnhất,d điquađiểmnàodướiđây?
A. P(−3;0;−3). B. M(0;−3;−5). C. Q(0;11;−3). D. N(0;3;−5).
Câu 44. Chohàmsốf(x) cóđạohàmliêntụctrênR.Biếtf(5)=1 và
1
Z
0
xf(5x)dx =1,khiđó
5
Z
0
x
2
f
0
(x)dx bằng
A. −25. B. 15. C.
123
5
. D. 23.
Câu 45.
Chohàmsốbậcbay = f(x)cóđồthịnhưhìnhvẽbên.Sốnghiệmthựccủaphương
trình
f(x
3
−3x)
=
1
2
là
A. 3. B. 12. C. 6. D. 10.
x
y
−2
2
−1
2
Câu 46. Chohaihàmsốy =
x
x +1
+
x +1
x +2
+
x +2
x +3
+
x +3
x +4
vày =|x +1| − x +m (m làthamsốthực)cóđồthịlần
lượtlà
(
C
1
)
và
(
C
2
)
.Tậphợpcácgiátrịcủam để
(
C
1
)
và
(
C
2
)
cắtnhautạiđúngbốnđiểmphânbiệtlà
A. [3;+∞). B. (−∞;3]. C. (−∞;3). D. (3;+∞).
Câu 47. Chophươngtrình
2log
2
2
x − 3log
2
x − 2
√
3
x
−m = 0(m làthamsốthực)cótấtcảbaonhiêugiátrịnguyên
dươngcủam đểphươngtrìnhđãchocóhainghiệmphânbiệt?
A. 80. B. 81. C. 79. D. Vôsố.
Câu 48. TrongkhônggianOxyz,chomặtcầu(S): x
2
+y
2
+(z −
√
2)
2
=3.CótấtcảbaonhiêuđiểmA(a;b;c) (a,b,c là
cácsốnguyên)thuộcmặtphẳng(Oxy) saochocóítnhấthaitiếptuyếncủa(S) điquaA vàhaitiếptuyếnđóvuônggócvới
nhau?
A. 12. B. 4. C. 16. D. 8.
Soạn:HuỳnhPhúSĩ 59 TrườngTHCS-THPTMỹThuận
Phụlục TOÁN12
Câu 49. Chohàmsốf(x),bảngbiếnthiêncủahàmsốf
0
(x) nhưsau:
x
f
0
(x)
−∞
−1
0 1
+∞
+∞
−3
2
−1
+∞
Sốđiểmcựctrịcủahàmsốy =f
x
2
+2x
là
A. 7. B. 5. C. 3. D. 9.
Câu 50. CholăngtrụABC.A
0
B
0
C
0
cóchiềucaobằng8 vàđáylàtamgiácđềucạnhbằng4.GọiM,N vàP lầnlượtlàtâm
cácmặtbênABB
0
A
0
,ACC
0
A
0
vàBCC
0
B
0
.ThểtíchcủakhốiđadiệnlồicócácđỉnhlàcácđiểmA, B, C, M, N, P bằng
A.
40
√
3
3
. B.
28
√
3
3
. C. 16
√
3. D. 12
√
3.
Soạn:HuỳnhPhúSĩ 60 TrườngTHCS-THPTMỹThuận
| 1/61
| | Tải xuống

Có thể bạn quan tâm:

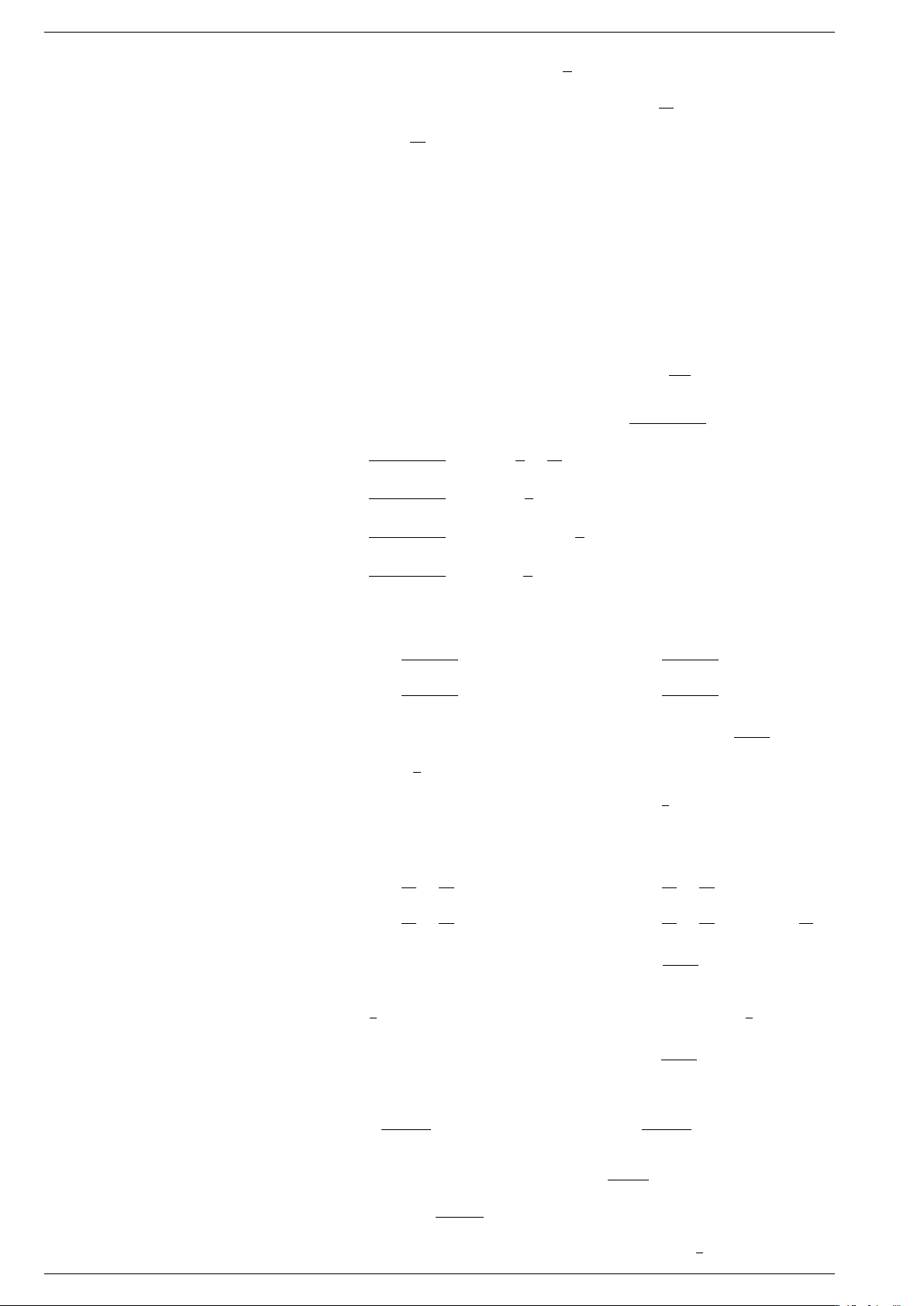
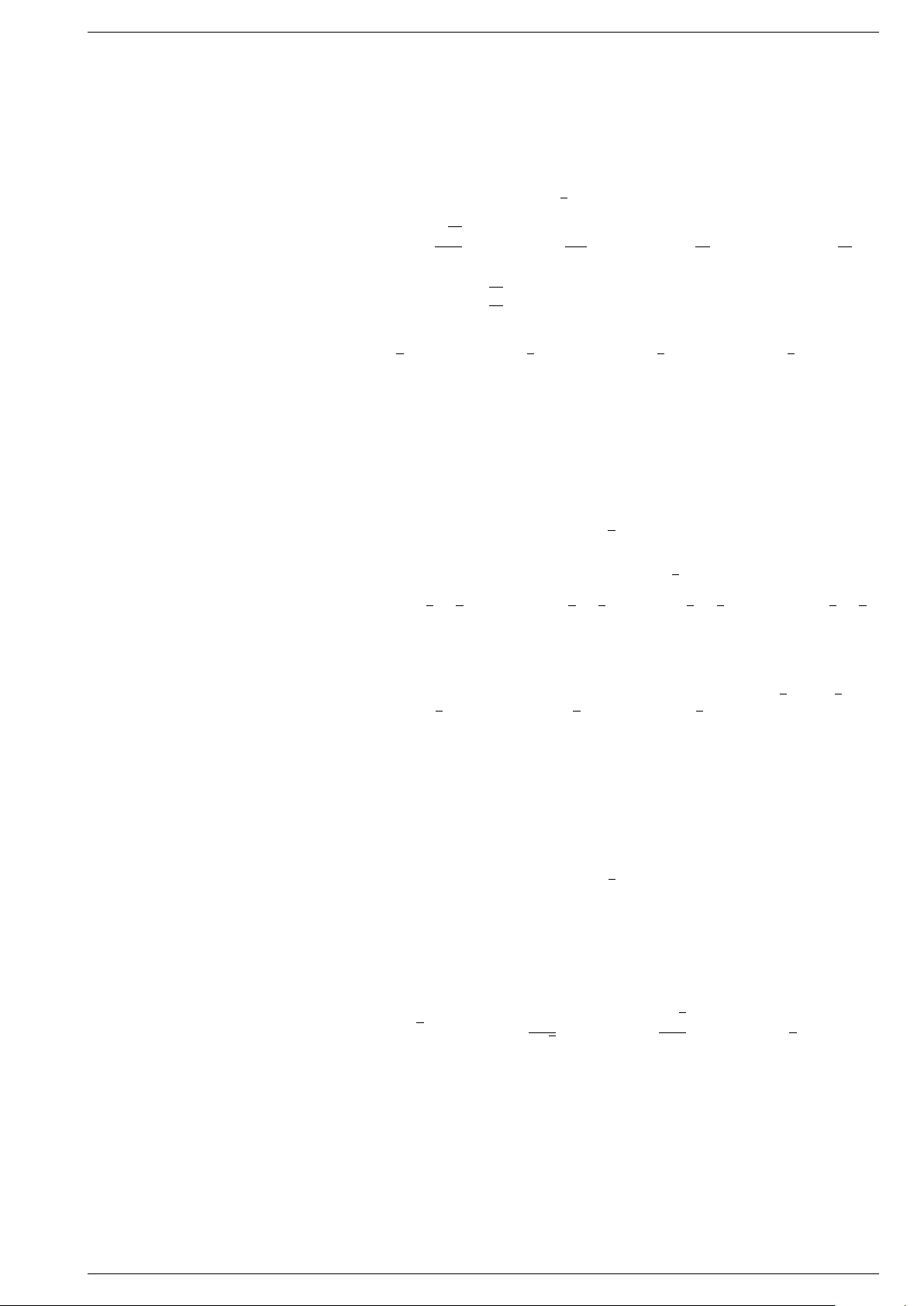
Preview text:

TÀI LIỆU HỌC TẬP HK2 TOÁN 12
Trường THCS&THPT Mỹ Thuận Vĩnh Long KẾ HOẠCH TUẦN L TUẦN 22 L TUẦN 19 L TUẦN 20 L TUẦN 23 L TUẦN 21 L TUẦN 24 L TUẦN 25 L TUẦN 28 L TUẦN 29 L TUẦN 26 L TUẦN 27 L TUẦN 30 L TUẦN 31 L TUẦN 34 L TUẦN 32 L TUẦN 35 L TUẦN 33 MỤC LỤC TOÁN 12 MỤC LỤC PHẦN I GIẢI TÍCH 5
Chương 3. Nguyên hàm - Tích phân và ứng dụng . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 6
§1. Nguyên hàm . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 6 1.
Nguyên hàm và tính chất . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 6 2.
Phương pháp tìm nguyên hàm . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 8 3.
Thực hành . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 9
§2. Tích phân . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 13 1.
Khái niệm tích phân . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 13 2.
Tính chất của tích phân . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 14 3.
Phương pháp tính tích phân . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 14 4.
Thực hành . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 15
§3. Ứng dụng của tích phân trong hình học . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 19 1.
Hình phẳng giới hạn bởi một đường cong và trục hoành . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 19 2.
Hình phẳng giới hạn bởi hai đường cong . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 19 3.
Tính thể tích . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 20 4.
Thể tích khối tròn xoay . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 21 5.
Thực hành . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 21
Chương 4. Số phức . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 25
§1. Số phức . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 25 1.
Định nghĩa số phức . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 25 2.
Số phức bằng nhau . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 25 3.
Biểu diễn hình học và môđun của số phức . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 26 4.
Thực hành . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 26
§2. Cộng, trừ và nhân số phức . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 28 1.
Phép vộng và phép trừ . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 28 2.
Phép nhân . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 28 3.
Thực hành . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 28
§3. Phép chia số phức . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 30 1.
Tổng và tích của hai số phức liên hợp . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 30 2.
Phép chia hai số phức . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 30 3.
Thực hành . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 30
§4. Phương trình bậc hai với hệ số thực. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 32 1.
Căn bậc hai của số thực âm . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 32 2.
Phương trình bậc hai với hệ số thực . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 32 3.
Thực hành . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 32 PHẦN II HÌNH HỌC 34
Chương 3. Phương pháp tọa độ trong không gian. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 35
§1. Hệ tọa độ trong không gian . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 35 1.
Tọa độ của điểm và của vectơ . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 35 2.
Biểu thức tọa độ của các phép toán vectơ . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 36 3.
Tích vô hướng . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 36 4.
Phương trình mặt cầu . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 37 5.
Thực hành . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 37
§2. Phương trình mặt phẳng . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 40 1.
Vectơ pháp tuyến của mặt phẳng . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 40 2.
Phương trình tổng quát của mặt phẳng . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 41 3.
Điều kiện để hai mặt phẳng song song, vuông góc . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 41 4.
Khoảng cách từ một điểm đến một mặt phẳng . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 42 5.
Thực hành . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 42
§3. Phương trình đường thẳng . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 46 1.
Phương trình tham số của đường thẳng . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 46 2.
Hai đường thẳng song song, cắt nhau, chéo nhau . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 47 3.
Thực hành . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 48 Soạn: Huỳnh Phú Sĩ 4
Trường THCS-THPT Mỹ Thuận PHẦN I GIẢI TÍCH
Chương 3. Nguyên hàm - Tích phân và ứng dụng . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 6
§1. Nguyên hàm . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 6
§2. Tích phân . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 13
§3. Ứng dụng của tích phân trong hình học . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 19
Chương 4. Số phức . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 25
§1. Số phức . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 25
§2. Cộng, trừ và nhân số phức . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 28
§3. Phép chia số phức . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 30
§4. Phương trình bậc hai với hệ số thực. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 32 Soạn: Huỳnh Phú Sĩ 5
Trường THCS-THPT Mỹ Thuận
Chương 3. Nguyên hàm - Tích phân và ứng dụng TOÁN 12 Chương 3.
NGUYÊN HÀM - TÍCH PHÂN VÀ ỨNG DỤNG §1.NGUYÊN HÀM Đặt vấn đề
1) Bổ sung thông tin thích hợp vào các ô trống dưới đây: f x f 0 x f x f 0 x f x f 0 x STT ( ) ( ) STT ( ) ( ) STT ( ) ( ) n · xn−1 ax · a x 1 5 ln 9 cos x − x 2 0 6 e 10 sin − 1 1 1 3 x 7 11 2 x 2 x cos 1 √ 1 1 4 x 8 x · a 12 2 x 2 ln sin 2) f x Tìm hàm số ( ) biết rằng f 0 x x2 f 0 x x2 a. ( ) = 3 b. ( ) = 1 NGUYÊN HÀM VÀ TÍNH CHẤT 1 Nguyên hàm Định nghĩa − £ é f x K Cho hàm số ( ) xác định trên . F x nguyên hàm f x K . . . . . . . . . . . . Hàm số ( ) được gọi là của hàm số ( ) trên nếu với x ∈ K mọi . Ví dụ 1. F x . . . . . . . . . f x x2 • Hàm số ( ) =
là một nguyên hàm của hàm số ( ) = 3 . F x . . . . . . . . . f x x • Hàm số ( ) =
là một nguyên hàm của hàm số ( ) = cos . Ví dụ 2. y 1
Hàm số nào sau đây không phải là nguyên hàm của hàm số = 2 x ? cos A F x x B F x x . 1 ( ) = tan . . 2 ( ) = tan + 2020. C F x x D F x x . 3 ( ) = tan + 2021. . 4 ( ) = 2020 tan . Định lí 1 − £ é F x f x K hằng số C Nếu (
) là một nguyên hàm của hàm số ( ) trên thì với mỗi , hàm G x . . . . . . . . . . . . f x K số ( ) =
cũng là một nguyên hàm của ( ) trên . Định lí 2 − £ é F x f x K f x Nếu (
) là một nguyên hàm của hàm số ( ) trên thì mọi nguyên hàm của ( ) K . . . . . . . . . . . . C . . . . . . . . . . . . trên đều có dạng , với là một . F x . . . . . . . . . . . . f x Z • ( ) là một của ( ) f x x . . . . . . . . . . . . ( ) d = F x C . . . . . . • ( ) + là tất cả các nguyên f x hàm của ( ) f x x F 0 x x vi phân . . . • ( ) d = ( ) d là của
Ví dụ 3. Tìm các nguyên hàm sau: Soạn: Huỳnh Phú Sĩ 6
Trường THCS-THPT Mỹ Thuận §1. Nguyên hàm TOÁN 12 Z Z x Z x d x 2 x √ x a) d = b) x = c) e d = 2
2 Tính chất của nguyên hàm y f x K Cho hàm số = ( ) có đạo hàm trên . Z f 0 x x
. . . . . . . . . . . . . . . . . . Tính chất 1. ( ) d = ! Z k · f x x
. . . . . . . . . . . . k Tính chất 2. ( ) d = ( là hằng số) Z f x ± g x x
. . . . . . . . . . . . . . . . . . . . . Tính chất 3. ( ) ( ) d = Ví dụ 4. f x x 2 ∞
Tìm nguyên hàm của hàm số ( ) = 3 sin
+ x trên khoảng (0; + ). √ Ví dụ 5. f x ∞ f 0 x · x 1 Cho hàm số (
) xác định trên khoảng (0; + ) thỏa mãn ( ) = và 2 f f x (4) = 5. Tìm ( ).
3 Sự tồn tại của nguyên hàm . . . . . . . . . . . . K K Mọi hàm số trên đều có nguyên hàm trên .
Bảng nguyên hàm của một số hàm số thường gặp Z Z x
. . . . . . . . . . . . . . . ax x
. . . . . . . . . . . . . . . a > a 6 • 0 d = • d = ( 0, = 1) Z Z x
. . . . . . . . . . . . . . . x x
. . . . . . . . . . . . . . . • d = • cos d = Z Z xn x
. . . . . . . . . . . . . . . n 6 − x x
. . . . . . . . . . . . . . . • d = ( = 1) • sin d = Z Z 1 x
. . . . . . . . . . . . . . . 1 x
. . . . . . . . . . . . . . . • x d = • = 2 x d cos Z Z x x
. . . . . . . . . . . . . . . 1 x
. . . . . . . . . . . . . . . • e d = • = 2 x d sin Chú ý Ví dụ 6. − £ é Tìm các nguyên hàm sau: Z Z Từ đây, yêu cầu tìm x 1 2 x 2 x x a) 3 + d b) 1 + tan d nguyên hàm của một hàm x2
số được hiểu là tìm nguyên
hàm trên từng khoảng xác định của nó. Soạn: Huỳnh Phú Sĩ 7
Trường THCS-THPT Mỹ Thuận §1. Nguyên hàm TOÁN 12 2
PHƯƠNG PHÁP TÌM NGUYÊN HÀM
1 Phương pháp đổi biến số Z Ví dụ 7. x − 2021 x Tìm ( 2) d . Định lí 3 − £ é Z f u x F u C u u x Nếu ( ) d = ( ) + và = (
) là hàm số có đạo hàm liên tục thì Z f u x · u0 x x . . . . . . . . . . . . ( ( )) ( ) d = Z Ví dụ 8. x − 2021 x Tìm (3 2) d . Chú ý − £ é Nếu tính nguyên hàm theo u u x biến mới = ( ) thì sau khi tính nguyên hàm, ta x phải trở lại biến ban đầu u u x bằng cách thay bởi ( ). Hệ quả. u ax b a 6 Với = + ( = 0) thì Z f ax b x . . . . . . . . . . . . ( + ) d = Z Ví dụ 9. x x . . . . . . . . . . . . cos(5 + 7) d = Z √ √ Ví dụ 10. I x x x t x Xét nguyên hàm = + 2 d . Nếu đặt = + 2 thì ta được Z Z A I t 4 − t2 t B I t4 − t2 t . = 4 2 d . . = 2 d . Z Z C I t 4 − t2 t D I t4 − t2 t . = 2 4 d . . = 2 d .
2 Phương pháp nguyên hàm từng phần Định lí 4 − £ é u u x v v x K Nếu hai hàm số = ( ) và = (
) có đạo hàm liên tục trên thì Z u x · v0 x x
. . . . . . . . . . . . . . . . . . . . . . . . ( ) ( ) d =
Ví dụ 11. Tìm các nguyên hàm sau: Z Z x x x x x x a) ( + 1) ln d c) ( + 1)e d Z Z x x x x x x b) ( + 1) cos d d) e cos d Soạn: Huỳnh Phú Sĩ 8
Trường THCS-THPT Mỹ Thuận §1. Nguyên hàm TOÁN 12 Tips − £ é u x Thứ tự ưu tiên đặt ( ) là Log I) arit Đa II) thức Lượng III) giác Mũ IV) 3 THỰC HÀNH Í TRẮC NGHIỆM
Câu 1. Trong các khẳng định sau, khẳng định nào là đúng? Z Z Z A f x · g x x f x x · g x x . ( ) ( ) d = ( ) d ( ) d . Z B x . 0 d = 0. Z C f x x f 0 x C . ( ) d = ( ) + . Z D f 0 x x f x C . ( ) d = ( ) + . Câu 2. f x , g x R Cho ( ) (
) là các hàm số xác định và liên tục trên . Trong các mệnh sai đề sau, mệnh đề nào ? Z Z Z A f x g x x f x x g x x . 2 ( ) + 3 ( ) d = 2 ( ) d + 3 ( ) d . Z Z Z B f x − g x x f x x − g x x . ( ) ( ) d = ( ) d ( ) d . Z Z C f x x f x x . 2 ( ) d = 2 ( ) d . Z Z Z D f x · g x x f x x · g x x . ( ) ( ) d = ( ) d ( ) d .
Câu 3. Cặp số nào sau đây có tính chất "Có một hàm số là nguyên hàm của hàm số còn lại"? A x 1 2 B x 2 x . tan và . . sin 2 và sin . 2 x 2 cos C x −x D x 2 x . e và e . . sin 2 và cos . Câu 4. sai
Khẳng định nào sau đây là khẳng định ? Z A x x x C . cos d = sin + . Z B 1 x − 1 C . x d = . 2 x + Z √ C 1 √ x x C . x d = + . 2 Z D ax x ax · a C a > , a 6 . d = ln + ( 0 = 1). Câu 5. f x x x
Họ tất cả các nguyên hàm của hàm số ( ) = cos + 6 là A x x2 C B − x x2 C . sin + 3 + . . sin + 3 + . C x x2 C D − x C . sin + 6 + . . sin + . Soạn: Huỳnh Phú Sĩ 9
Trường THCS-THPT Mỹ Thuận §1. Nguyên hàm TOÁN 12 Z Câu 6. f x f x x 1 x C Xác định ( ) biết ( ) d = x + e + . A f x |x| x B f x 1 x . ( ) = ln + e . . ( ) = x + e . 2 C f x − 1 x D f x x x . ( ) = x + e . . ( ) = ln + e . 2 Câu 7. F x x − x Hàm số ( ) = 2 sin 3 cos
là một nguyên hàm của hàm số nào sau đây? A f x − x − x B f x − x x . ( ) = 2 cos 3 sin . . ( ) = 2 cos + 3 sin . C f x x x D f x x − x . ( ) = 2 cos + 3 sin . . ( ) = 2 cos 3 sin . Câu 8. m F x mx3 m x2 − x Tìm để hàm số ( ) = + (3 + 2) 4 + 3 là một nguyên hàm f x x2 x − của hàm số ( ) = 3 + 10 4. A m B m C m D m . = 3. . = 1. . = 2. . = 0. Câu 9. f x x x 3
Họ nguyên hàm của hàm số ( ) = 2 1 + 3 là A x 2 x2 C B x x x3 C . 1 + 3 + . . 2 + + . C x3 x 6 2 x x3 C D x2 C . + + . . 1 + + . 5 Câu 10. x2 x − f x 2 + 1
Tìm họ nguyên hàm của hàm số ( ) = x . 2 Z A x2 x − 2 + 1 x 1 − 1 . x d = 2 + + C. 2 x x2 Z B x2 x − 2 + 1 x x 1 |x| . x d = 2 + + C. 2 x + ln Z C x2 x − 2 + 1 x x 1 2 |x| . x d = + ln + 2 x + C. Z D x2 x − 2 + 1 x x2 − 1 |x| . x d = + C. 2 x + ln Câu 11. không phải f x Hàm số nào sau đây
là một nguyên hàm của hàm số ( ) = x − 3 (2 3) ? A x − 4 x − 4 F x (2 3) B F x (2 3) − . ( ) = + 8. . ( ) = 3. 8 8 C x − 4 x − 4 F x (2 3) D F x (2 3) . ( ) = . . ( ) = . 8 4 Câu 12. f x 1
Hàm số nào dưới đây là nguyên hàm của hàm số ( ) = − x ? 1 A F x − 1 | − x| B F x − | − x| . ( ) = ln 4 4 + 3. . ( ) = ln 1 + 4. 4 C F x | − x| D F x 1 x 2 − x . ( ) = ln 1 + 2. . ( ) = ln 2 + 1 + 5. 2 Câu 13. f x x3 − x2 x − F x Cho hàm số ( ) = + 2 1. Gọi ( ) là một nguyên hàm của f x F F x ( ). Biết rằng (1) = 4. Tìm ( ). A x4 x3 x4 x3 F x − x2 − x B F x − x2 − x . ( ) = + . . ( ) = + + 1. 4 3 4 3 C x4 x3 x4 x3 F x − x 49 2 − x D F x − x2 − x . ( ) = + + 2. . ( ) = + + . 4 3 4 3 12 Câu 14. F x f x 1 F Biết (
) là nguyên hàm của hàm số ( ) = x − và (2) = 1. Khi đó 1
F (3) bằng bao nhiêu? A 3 B C D 1 . ln . . ln 2 + 1. . ln 2. . . 2 2 Câu 15. x f x + 2 ∞
Họ tất cả các nguyên hàm của hàm số ( ) = x − trên khoảng (1; + ) 1 là A x x − C B x − x − C . + 3 ln ( 1) + . . 3 ln ( 1) + . C x − 3 C D x − 3 C . x − + . . + . 2 x − 2 ( 1) ( 1) Câu 16. x3 f x
Tìm nguyên hàm của hàm số ( ) = x . 4 + 1 Z Z A x4 f x x 3 C B f x x x 4 C . ( ) d = x + . . ( ) d = ln + 1 + . 4 2 + 6 Z Z C f x x x 1 3 x4 C D f x x x4 C . ( ) d = ln + 1 + . . ( ) d = ln + 1 + . 4 Soạn: Huỳnh Phú Sĩ 10
Trường THCS-THPT Mỹ Thuận §1. Nguyên hàm TOÁN 12 √ Câu 17. f x − x
Tìm nguyên hàm của hàm số ( ) = 5 3 . Z √ A f x x − 2 − x − x C . ( ) d = (5 3 ) 5 3 + . 9 Z √ B f x x − 2 − x − x C . ( ) d = (5 3 ) 5 3 + . 3 Z √ C f x x 2 − x − x C . ( ) d = (5 3 ) 5 3 + . 9 Z √ D f x x − 2 − x C . ( ) d = 5 3 + . 3 Câu 18. f x x x
Tìm nguyên hàm của hàm số ( ) = e . Z Z A f x x x x C B f x x x − x C . ( ) d = ( + 1)e + . . ( ) d = ( 1)e + . Z Z C f x x x x C D f x x x x 2 C . ( ) d = e + . . ( ) d = e + . Z Câu 19. x · − x − x 3 +1 x − 1 3 +1 x n C m, n Biết ( + 3) e d = m e (3 + ) + với là các số S m n nguyên. Tính tổng = + . A B C D . 10. . 1. . 9. . 19. Câu 20. a t 3 m/s2
Một vật chuyển động với vận tốc ( ) = t ( ). Biết rằng vận tốc + 1 m/s
ban đầu của vật đó là 6 (
), hãy tính vận tốc của vật đó tại giây thứ 10. A m/s B , m/s C , m/s D m/s . 10 . . 15 2 . . 13 2 . . 12 . L TỰ LUẬN
Câu 1 (SGK GT12). Trong các cặp hàm số dưới đây, hàm số nào là một nguyên hàm của hàm số còn lại? −x − −x x 2 x 2 2 a) e và e b) sin 2 và sin − 2 x − 4 x c) 1 x e và 1 x e
Câu 2. Tìm nguyên hàm của các hàm số sau: f x − x 3 2 f x 2 x f x x · x 1 a) ( ) = e b) ( ) = tan c) ( ) = sin 5 cos 3 f x d) ( ) = x − x (1 + )(1 2 )
Câu 3. Sử dụng phương pháp đổi biến số, hãy tính: Z Z − x 9 x u − x 3 x x x u x a) (1 ) d (đặt = 1 ) b) cos sin d (đặt = cos )
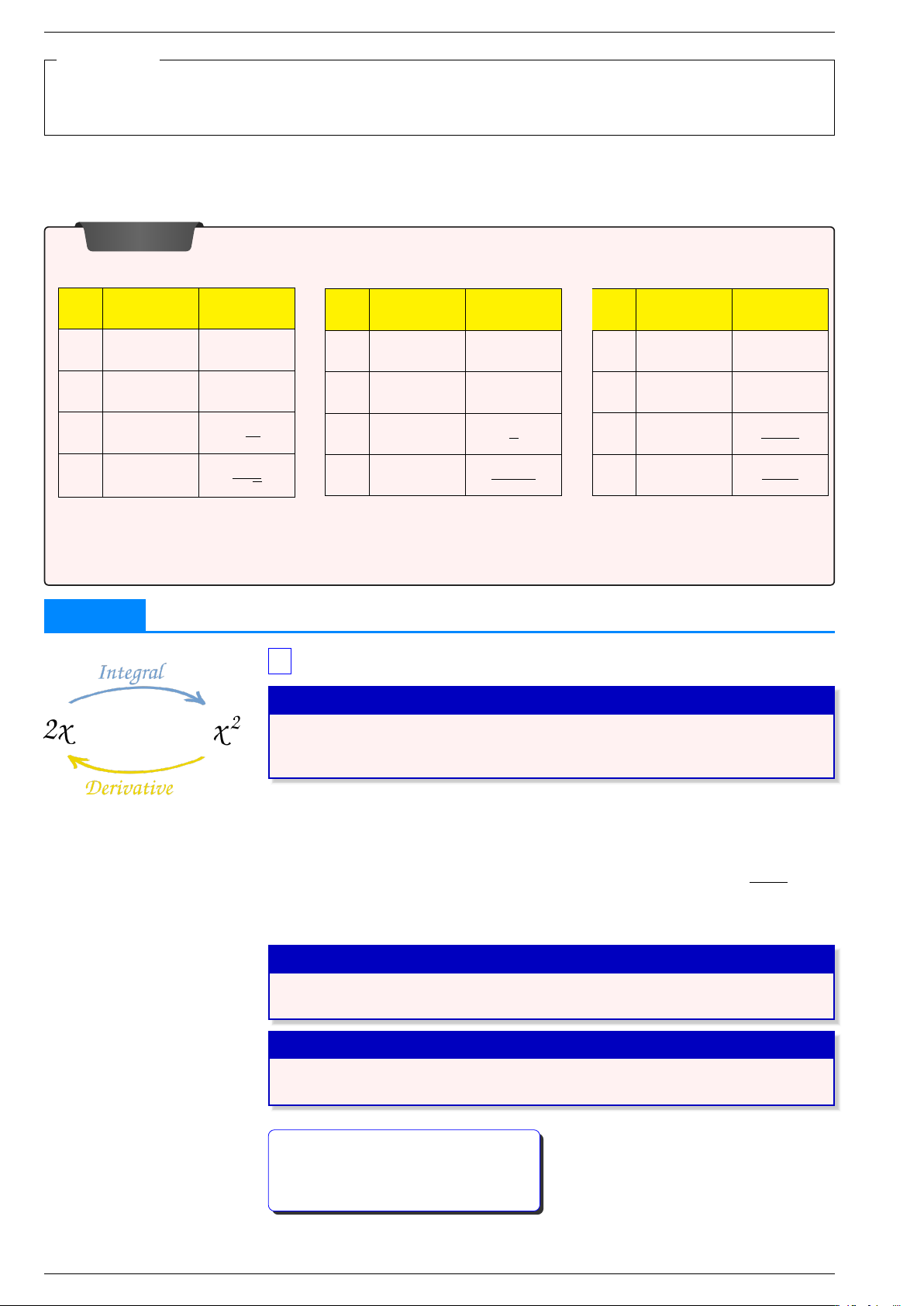
Câu 4. Sử dụng phương pháp tính nguyên hàm từng phần, hãy tính: Z Z Z Z x x x x x 2 x − x x x x − x x x a) ln(1 + ) d b) + 2 1 e d c) sin(2 + 1) d d) (1 ) cos d Soạn: Huỳnh Phú Sĩ 11
Trường THCS-THPT Mỹ Thuận §1. Nguyên hàm TOÁN 12 Vocabulary − £ é derivative method đạo hàm phương pháp antiderivative change of variable nguyên hàm đổi biến số differential antiderivative by parts vi phân nguyên hàm từng phần Soạn: Huỳnh Phú Sĩ 12
Trường THCS-THPT Mỹ Thuận §2. Tích phân TOÁN 12 §2.TÍCH PHÂN Đặt vấn đề
Nhờ tích phân, ta có thể tính độ dài của một đường cong, diện tích của một hình phẳng, thể tích của một khối tròn
xoay hay các bài toán về quãng đường, vận tốc... y y x b 9 = y f x = ( ) c x O y 27 = x y x2 = 9 x a 2 = x2 y = 8 O x 3 6 1 KHÁI NIỆM TÍCH PHÂN
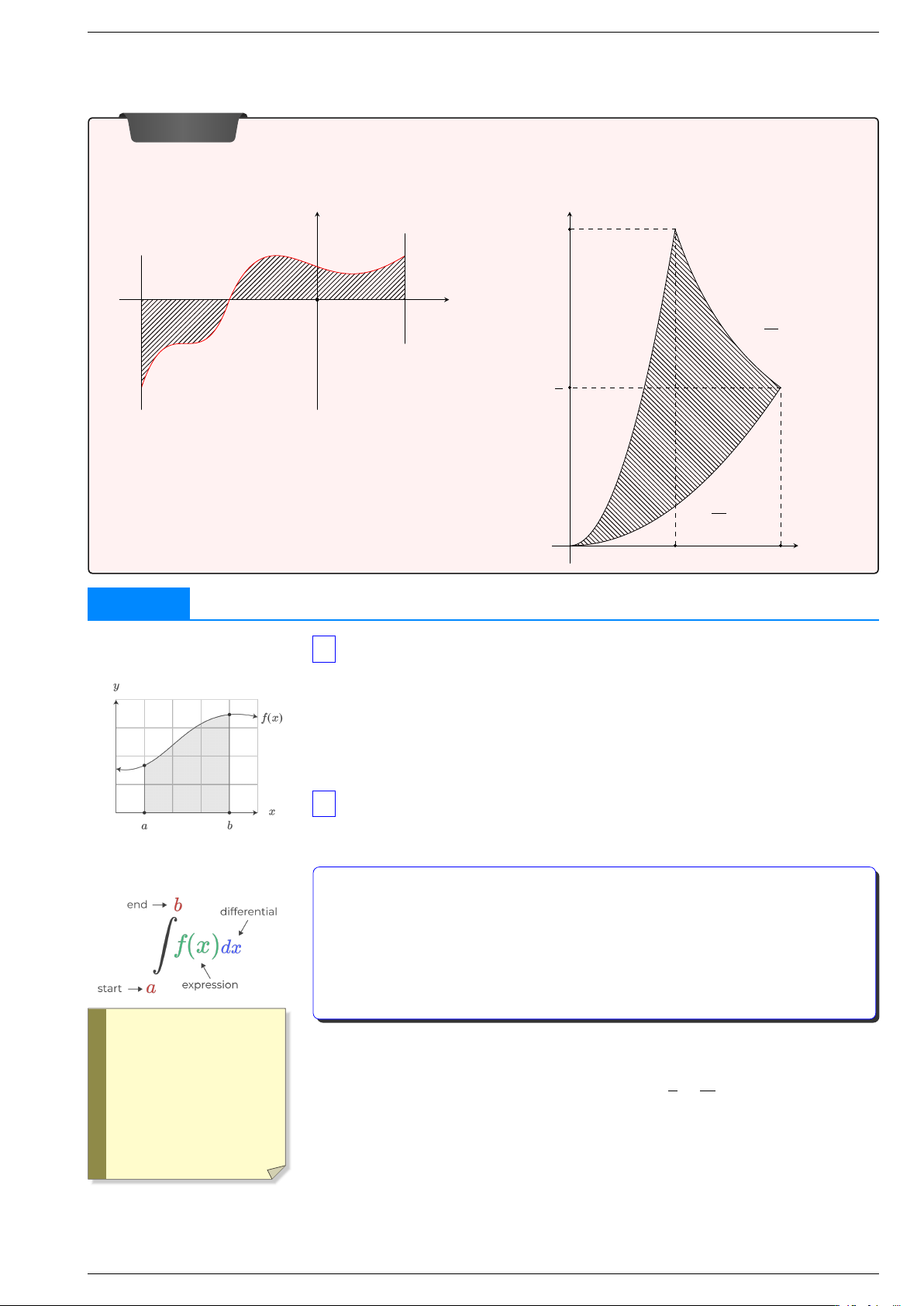
1 Diện tích hình thang cong y f x . . . . . . . . . . . . a b Cho hàm số = ( ) liên tục, không trên đoạn [ ; ].
Hình . . . . . . . . . giởi hạn bởi đồ thị của hàm số y
f x , trục . . . . . . . . . và hai đường = ( ) thẳng x a, x
b được gọi là hình thang cong = = . F x f x Giả sử ( ) là một nguyên hàm của (
). Người ta chứng mình được rằng hình thang
cong nêu trên có diện tích là S F b − F a = ( ) ( )
2 Định nghĩa tích phân y f x a b F x f x Cho hàm số = ( ) liên tục trên đoạn [ ; ]. Giả sử ( ) là một nguyên hàm của ( ) a b trên đoạn [ ; ]. a b f x F b − F a Tích phân từ đến của hàm số ( ) là hiệu ( ) ( ). b Z b f x x F x F b − F a ( ) d = ( ) = ( ) ( ) a a a b Ta gọi là cận dưới, là cận trên. Quy ước: Ví dụ 1. a Tính các tích phân sau: Z ! f x x . . . . . . e 2 • ( ) d = Z Z x 1 − 1 x a x3 x a) + 3 d b) x x d 2 a −1 1 Z f x x . . . . . . • ( ) d = b Soạn: Huỳnh Phú Sĩ 13
Trường THCS-THPT Mỹ Thuận §2. Tích phân TOÁN 12 2 TÍNH CHẤT CỦA TÍCH PHÂN b Z k · f x x
. . . . . . . . . . . . . . . k Tính chất 1. ( ) d = ( là hằng số) a ! b Z f x ± g x x
. . . . . . . . . . . . . . . . . . . . . . . . . . . Tính chất 2. ( ) ( ) d = a c b Z Z f x x f x x
. . . . . . . . . . . . a < c < b Tính chất 3. ( ) d + ( ) d = ( ) a c 1 Z Ví dụ 2. |x − | x Tính 1 d . 0 3
PHƯƠNG PHÁP TÍNH TÍCH PHÂN
1 Phương pháp đổi biến số 2 Z Ví dụ 3. x − 3 x Để tính tích phân (2 1) d
, ba bạn Trường, Mỹ và Thuận đưa ra cách 1 giải như sau: Trường Mỹ u x − Ñ u x 2 2 Z Z Đặt = 2 1 d = 2d . ( x − 3 x x3 − · x2 · x − x x Ñ u · − (2 1) d = 8 3 4 + 3 2 1 d = 1 = 2 1 1 = 1 Đổi cận: x Ñ u · − = 2 = 2 2 1 = 3 1 1 2 3 2 Z Z Z u u4 3 x d 1 3 3 − x2 x − x x − x u3 · = 8 12 + 6 1 d Khi đó (2 1) d = = = 10. 2 2 4 1 1 1 1 x 4 x3 x2 2 · − · · − x = 8 12 + 6 Thuận 4 3 2 1 2 x 2 4 − x3 x2 − x Z 2 = 2 4 + 3 x − 4 x − 1 1) 3 x · (2 1 (2 1) d = = 10. . 2 4 1 = 10 1
Hãy so sánh ba lời giải trên. Ví dụ 4. Tính π 2 Z 2 x Z d √ 2 x x x b) a) cos sin d − x2 − 4 2 0 Soạn: Huỳnh Phú Sĩ 14
Trường THCS-THPT Mỹ Thuận §2. Tích phân TOÁN 12
2 Phương pháp tính tích phân từng phần Định lí − £ é u u x v v x K Nếu hai hàm số = ( ) và = (
) có đạo hàm liên tục trên thì b Z u x · v0 x x
. . . . . . . . . . . . . . . . . . . . . . . . ( ) ( ) d = a
Ví dụ 5. Tìm các nguyên hàm sau: e Z 1 Z x x x x x x a) ( + 1) ln d c) ( + 1)e d 1 0 π π 2 Z 2 Z x x x x x x b) ( + 1) cos d d) e cos d 0 0 4 THỰC HÀNH Í TRẮC NGHIỆM Câu 1. F x f x F − F Cho (
) là một nguyên hàm của hàm số ( ). Khi đó hiệu số (0) (1) bằng 1 1 1 1 Z Z Z Z A −F x x B F x x C − f x x D f x x . ( ) d . . ( ) d . . ( ) d . . ( ) d . 0 0 0 0 Câu 2. f x , g x a b sai Cho hàm số ( ) ( ) liên tục trên [ ;
]. Khẳng định nào sau đây ? b b b Z Z Z A f x g x x f x x g x x . ( ) + ( ) d = ( ) d + ( ) d . a a a b a Z Z B f x x f x x . ( ) d = ( ) d . a b b b Z Z C f x x f t t . ( ) d = ( ) d . a a b b c Z Z Z D f x x f x x f x x . ( ) d = ( ) d + ( ) d . a c a Soạn: Huỳnh Phú Sĩ 15
Trường THCS-THPT Mỹ Thuận §2. Tích phân TOÁN 12 3 Z Câu 3. F x f x − f x x Biết ( ) là một nguyên hàm của ( ) trên đoạn [ 2; 3], ( ) d = 12 và −2 F F − (3) = 7. Tính ( 2). A F − B F − C F − D F − − . ( 2) = 19. . ( 2) = 2. . ( 2) = 5. . ( 2) = 5. b b b Z Z Z Câu 4. f x x − g x x I f x − g x x Cho ( ) d = 3 và ( ) d = 4. Tính = [4 ( ) 3 ( )] d . a a a A I B I − C I D I . = 25. . = 24. . = 24. . = 0.
Câu 5. Giả sử các biểu thức trong dấu nguyên hàm, tích phân đều có nghĩa, trong sai
các khẳng định sau, khẳng định nào là ? Z A f 0 x x f x C . ( ) d = ( ) + . Z Z B kf x x k f x x, ∀k ∈ R . ( ) d = ( ) d . b b Z b Z C u x v0 x x u x v x − u0 x v x x . ( ) ( ) d = ( ) ( ) ( ) ( ) d . a a a b b Z Z D kf x x k f x x, ∀k ∈ R . ( ) d = ( ) d . a a Câu 6. f x f f Cho hàm số (
) có đạo hàm liên tục trên đoạn [1; 4], (1) = 15, (4) = 8. 4 Z f 0 x x Tính ( ) d . 1 4 4 Z Z A f 0 x x B f 0 x x . ( ) d = 7. . ( ) d = 3. 1 1 4 4 Z Z C f 0 x x D f 0 x x − . ( ) d = 23. . ( ) d = 7. 1 1 5 5 5 Z Z Z Câu 7. f x x g t t f x − g x x Cho biết ( ) d = 3, ( ) d = 9. Tính ( ) 2 ( ) d . 2 2 2 A − B − C D . 6. . 15. . 12. . 21. 5 Z Câu 8. f x g x R f x g x x Cho các hàm số ( ), ( ) liên tục trên thỏa mãn 2 ( ) + 3 ( ) d = −1 5 5 Z Z − f x − g x x f x g x x 5; 3 ( ) 5 ( ) d = 21. Tính ( ) + ( ) d . − − 1 1 A − B C D − . 5. . 1. . 5. . 1. 2 3 3 Z Z Z Câu 9. f x x − f x x f x x Nếu ( ) d = 2 và ( ) d = 1 thì ( ) d bằng 1 2 1 A − B − C D . 3. . 1. . 1. . 3. Z Z 3 3 Câu 10. f x f x x f x x Cho hàm số ( ) thỏa mãn ( ) d = 5 và ( ) d = 1. Tính tích − 1 1 Z 1 I f x x phân = ( ) d . −1 A I − B I C I D I − . = 6. . = 6. . = 4. . = 4. 2 7 7 Z Z Z Câu 11. f x x f t t f z z Cho ( ) d = 2, ( ) d = 9. Giá trị của ( ) d là − − 1 1 2 A B C D . 7. . 3. . 11. . 5. 2 4 4 Z Z Z Câu 12. f x x f t t − I f y y Cho ( ) d = 1, ( ) d = 4. Tính = ( ) d . − − 2 2 2 A I B I C I − D I − . = 5. . = 3. . = 3. . = 5. Soạn: Huỳnh Phú Sĩ 16
Trường THCS-THPT Mỹ Thuận §2. Tích phân TOÁN 12 2 Z Câu 13. I x − x3 x Tính = (2 ) d . 0 A I B I C I − D I − . = 0. . = 10. . = 4. . = 10. π π 2 Z 2 Z Câu 14. I x x J x x Cho = sin 2 d , = sin d
. Trong các mệnh đề sau, mệnh đề 0 0 nào đúng? A I > J B I J C I < J D I J . . . = . . . . = 2 . 1 Z Câu 15. x 2 +1 x Tích phân 3 d bằng 0 A 27 B 9 C 4 D 12 . . . . . . . . ln 9 ln 9 ln 3 ln 3 2 Z Câu 16. x d Tích phân x bằng 2 + 1 1 A 5 B 2 C 1 5 D 16 . log . . . . ln . . . 3 15 2 3 225 2 e Z 2 Câu 17. − x I (1 ln ) x Tính = x d được kết quả là e A 4 B 5 C 1 D 13 . . . . . . . . 3 3 3 3 7 Z Câu 18. x x d a − b a, b ∈ Q a b Biết rằng x = ln 2 ln 5 với . Giá trị của 2 + 2 + 1 2 bằng A 3 B 1 C D . . . . . 1. . 2. 2 2 ln 5 Z Câu 19. x x x a b a, b Biết ( + 1)e d = ln 5 + ln 2, với là các số nguyên. Tính ln 2 T a − b = 3 2 . A T B T − C T D T − . = 19. . = 4. . = 11. . = 16. π 4 Z Câu 20. x x x Giá trị của tích phân sin d bằng 0 A π − π − π π 4 + √ B 4 √ C 2 √ D 2 + √ . . . . . . . . 4 2 4 2 2 2 2 2 b Z Câu 21. b x − x Tìm giá trị của để (2 6) d = 0. 1 A b b B b b . = 0 hoặc = 1. . = 0 hoặc = 3. C b b D b b . = 1 hoặc = 5. . = 5 hoặc = 0. 3 Z Câu 22. x + 2 x a b c
a b c ∈ Z c < S Biết x d = + ln với , , , 9. Tính tổng = 1 a b c + + . A S B S C S D S . = 6. . = 7. . = 5. . = 8. 1 Z Câu 23. x2 x − I 2 + 3 6 x Tích phân = x d có giá trị là 2 + 1 0 A 3 − 7 B 3 7 C D − . ln 3. . + ln 3. . 5 ln 3. . 2 ln 3. 2 2 2 2 1 Z Câu 24. x d a b a b Cho x = ln 2 + ln 3 với ,
là các số nguyên. Mệnh đề 2 x + 3 + 2 0 nào sau đây đúng? A a b B a − b C a b − D a b . + 2 = 0. . 2 = 0. . + = 2. . + = 2. Soạn: Huỳnh Phú Sĩ 17
Trường THCS-THPT Mỹ Thuận §2. Tích phân TOÁN 12 1 Z Câu 25. x I d Tính tích phân = x . 2 − 9 0 √ A I 1 1 B I − 1 1 C I 1 D I 6 . = ln . . = ln . . = ln 2. . = ln 2. 6 2 6 2 6 3 Z Câu 26. x 5 + 12 x a b c S a b c Biết x d = ln 2 + ln 5 + ln 6. Tính = 3 + 2 + . 2 x + 5 + 6 2 A − B − C − D . 11. . 14. . 2. . 3. 1 Z √ Câu 27. dx √ √ 2 a − b a, b Biết x x = với là các số nguyên dương. + 1 + 3 0 T a b Tính = + . A T B T C T D T . = 7. . = 10. . = 6. . = 8. 3 Z √ √ Câu 28. x d √ √ a b c a b c Biết x − x = 3 + 2 + với , ,
là các số hữu tỷ. Tính + 1 1 P a b c = + + . A P 13 B P 16 C P D P 2 . = . . = . . = 5. . = . 2 3 3 Câu 29. y f x ∞ Cho hàm số =
√ ( ) liên tục, nhận giá trị dương trên (0; + ) và thỏa f f x f 0 x x x > mãn (1) = 1, ( ) = ( ) 3 + 1, với mọi
0. Mệnh đề nào sau đây đúng? A < f < B < f < C < f < D < f < . 4 (5) 5. . 3 (5) 4. . 1 (5) 2. . 2 (5) 3. π 4 1 Z Z Câu 30. x2 · f x f x ( ) R f x x x Cho hàm số ( ) liên tục trên , biết (tan ) d = 4 và x d = 2 + 1 0 0 1 Z I f x x 2. Tính = ( ) d . 0 A B C D . 6. . 1. . 0. . 2. L TỰ LUẬN
Câu 1 (SGK GT12). Tính các tích phân sau: π 2 2 Z Z 2 Z π 1 x x 2 x − x x b) x x d c) ( + 1) d a) sin d ( + 1) 4 1 0 0 2
Câu 2 (SGK GT12). Tính các tích phân sau: π 1 1 Z 2 Z 2 Z x3 − x x 2 x x 1 x c) ln(1 + ) d a) sin d b) x d 2 − 1 0 0 0 Soạn: Huỳnh Phú Sĩ 18
Trường THCS-THPT Mỹ Thuận
§3. Ứng dụng của tích phân trong hình học TOÁN 12
§3.ỨNG DỤNG CỦA TÍCH PHÂN TRONG HÌNH HỌC Đặt vấn đề b Z § f x x Trong bài
2. Tích phân, ta đã biết tích phân ( ) d
là diện tích của hình thang cong giới hạn bởi đồ thị của hàm a f x Ox x a x b số ( ) (không âm), trục và hai đường thẳng = , =
. Mời các em tính diện tích của các hình thang dưới đây: y y y −x x 3 − = + 3 3 1 3 x O S S x O 1 3 y x x 3 − = 3 + 3 S
. . . . . . . . . . . . . . . . . . S
. . . . . . . . . . . . . . . . . . = = 1
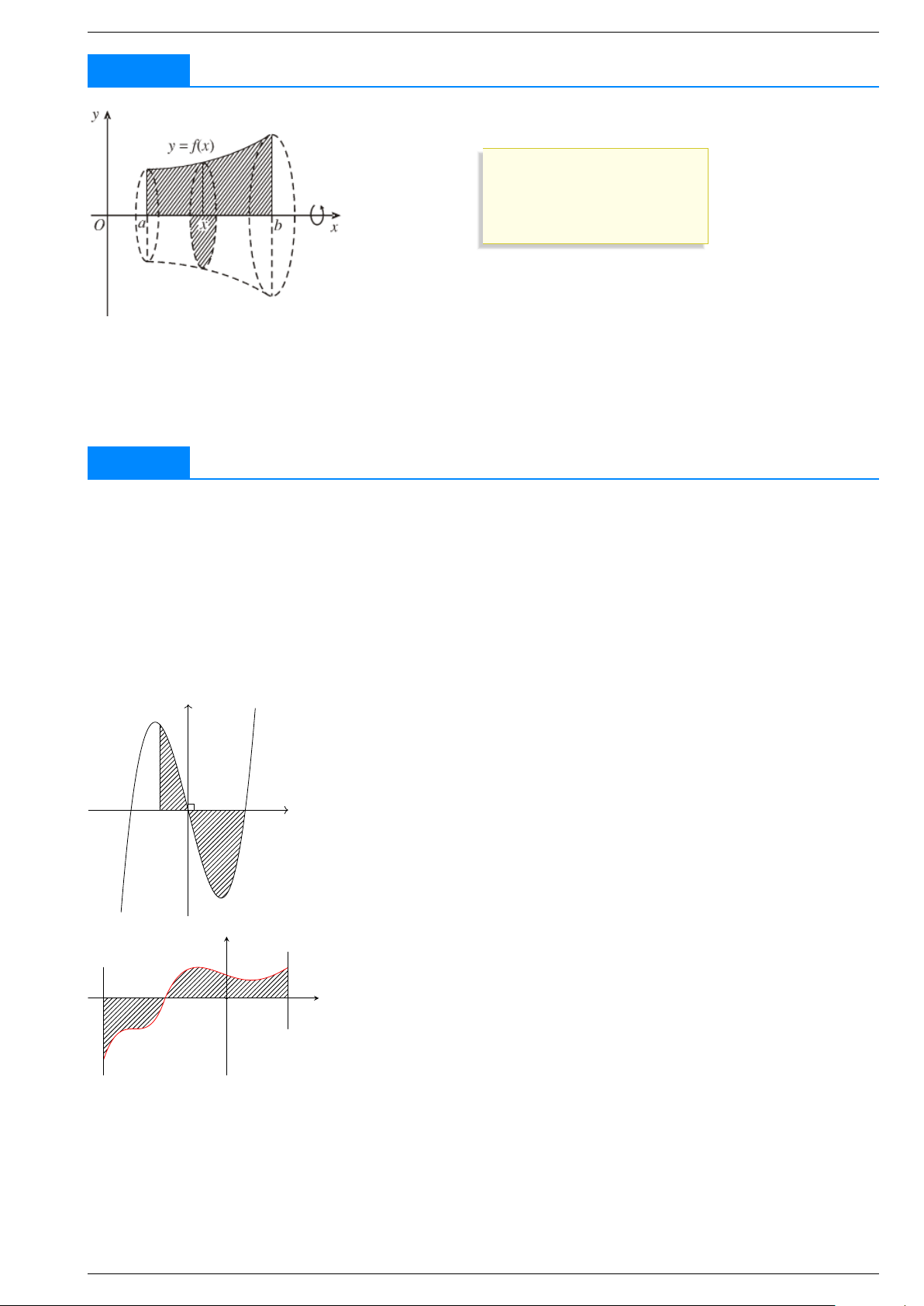
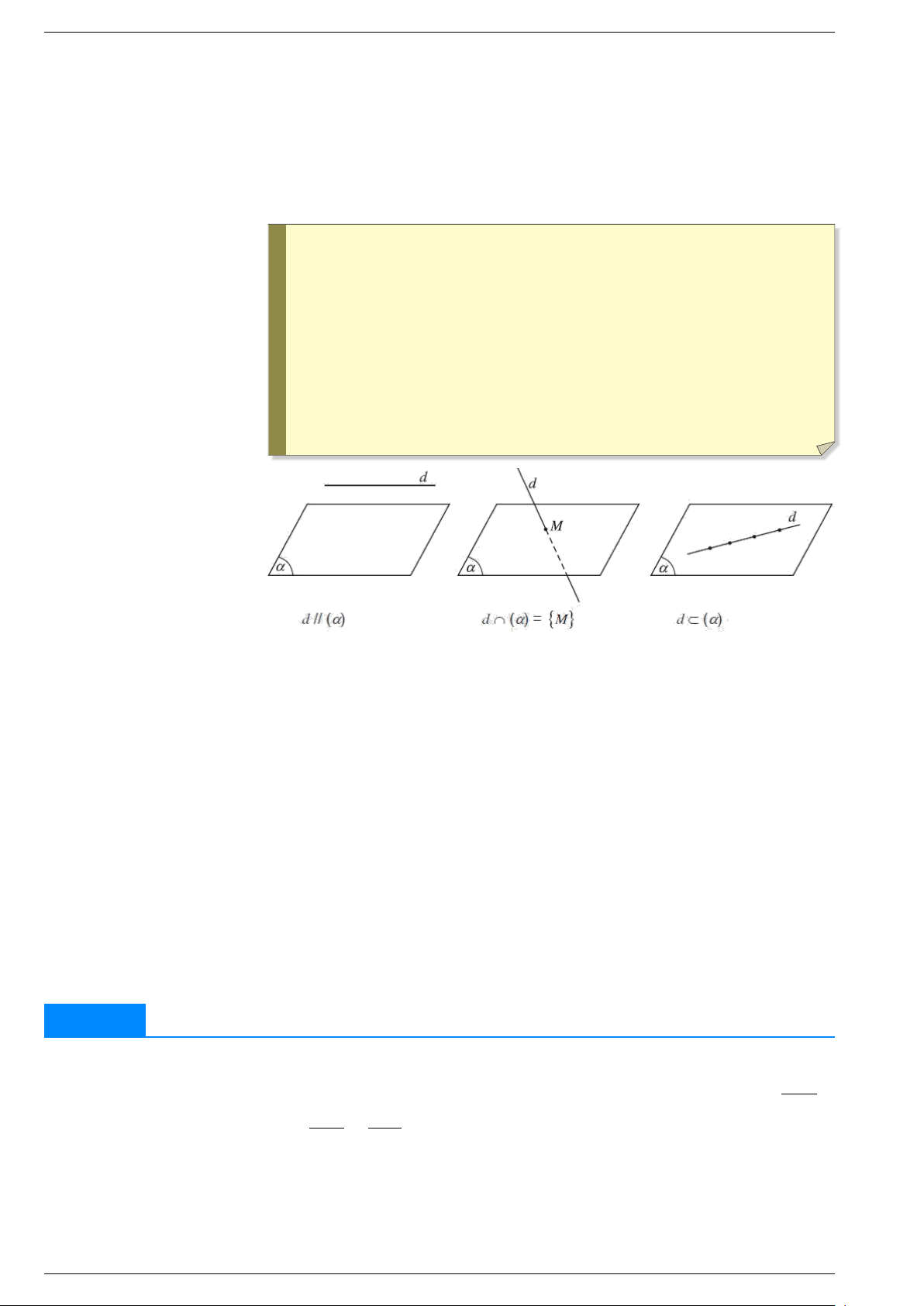
HÌNH PHẲNG GIỚI HẠN BỞI MỘT ĐƯỜNG CONG VÀ TRỤC HOÀNH y f x a b y Cho hàm số = ( ) liên tục trên đoạn [ ; ].
Diện tích S của hình phẳng giởi hạn bởi đồ thị của hàm số y
f x , trục . . . . . . . . . và = ( ) hai đường thẳng x a, x
b được tính theo công thức = = a b c b Z Z Z c x O b S . . . . . . x . . . . . . x . . . . . . x = d = d + d y f x a a c = ( ) Ví dụ 1. y x2 − x
Tính diện tích hình phẳng được giới hạn bởi đường cong = 4 + 3, trục x
hoành, trục tung và đường thẳng = 5. 2
HÌNH PHẲNG GIỚI HẠN BỞI HAI ĐƯỜNG CONG y y f x y g x a b Cho hai hàm số = ( ) và = ( ) liên tục trên đoạn [ ; ].
Diện tích S của hình phẳng giởi hạn bởi đồ thị của hai hàm số y f x , y g x và = ( ) = ( ) y f x hai đường thẳng x a, x
b được tính theo công thức = ( ) = = b b Z a x O S
. . . . . . . . . . . . . . . x = d a Ví dụ 2. y x2 − x − y g x
Tính diện tích hình phẳng được giới hạn bởi hai parabol = 2 2 và = ( ) y − x2 = 2 . Soạn: Huỳnh Phú Sĩ 19
Trường THCS-THPT Mỹ Thuận
§3. Ứng dụng của tích phân trong hình học TOÁN 12 3 TÍNH THỂ TÍCH
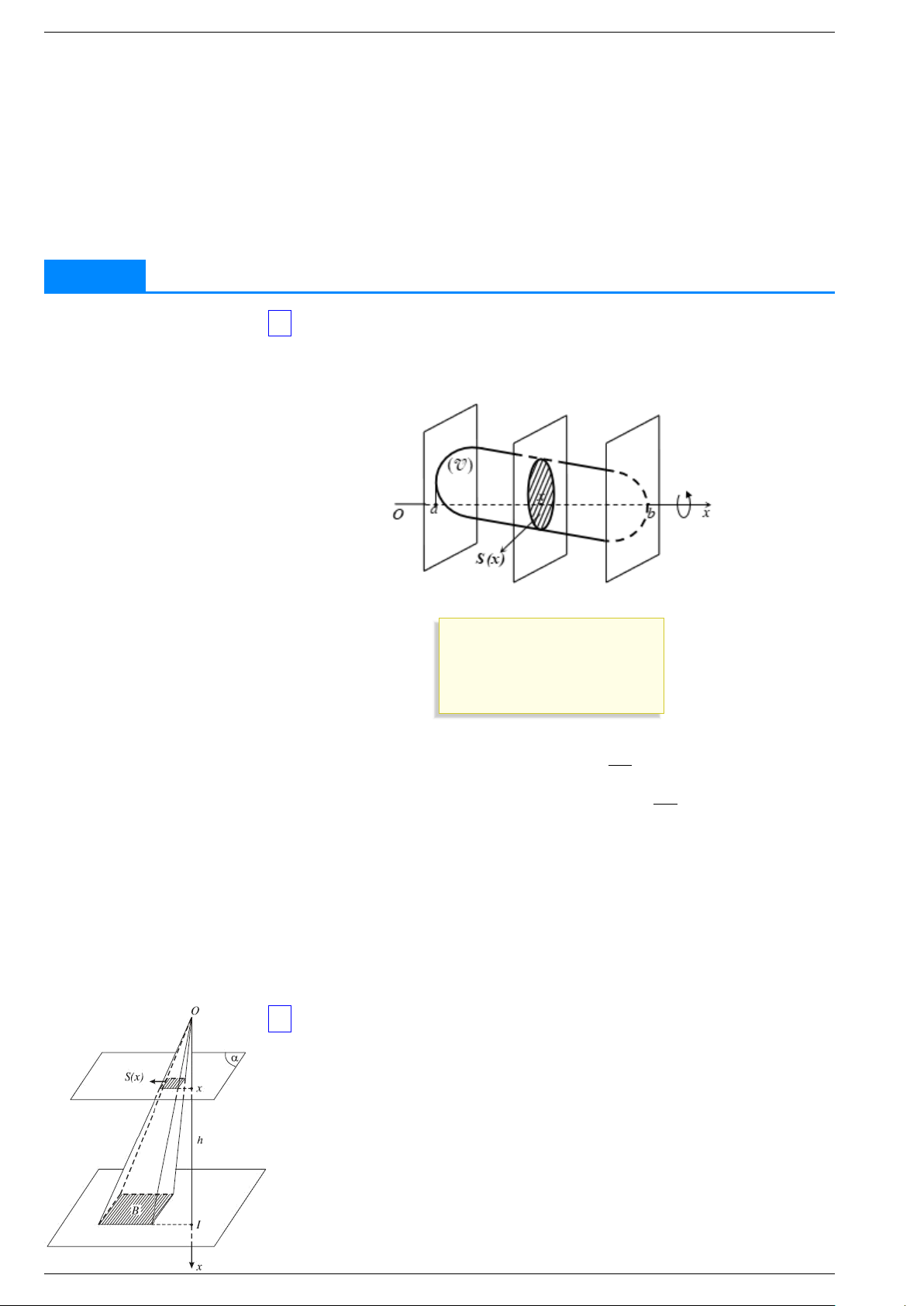
1 Thể tích của vật thể V P Q Ox x a Cắt một vật thể bởi hai mặt phẳng ( ) và ( ) vuông góc với trục lần lượt tại = , x b a < b V Ox x ∈ a b = ( ). Cắt
bởi một mặt phẳng tùy ý vuông góc với tại diểm [ ; ] theo S x
thiết diện có diện tích ( ). S x a b V Giả sử ( ) liên tục trên đoạn [ ; ], khi đó vật thể có thể tích là b Z V
. . . . . . . . . . . . x = d a Ví dụ 3. V x
Viết công thức tính thể tích
của vật thể nằm giữa hai mặt phẳng = 0 và
x = ln 4, bị cắt bởi một mặt phẳng vuông góc với trục hoành tại điểm có hoành độ √ x ∈ x x
(0; ln 4), có thiết diện là một hình vuông cạnh e . ln 4 ln 4 Z Z √ A V π x x x B V x x x . = e d . . = e d . 0 0 ln 4 ln 4 Z Z C V x x x D V π x x 2 x . = e d . . = [ e ] d . 0 0
2 Thể tích khối chóp và khối chóp cụt h B
a) Cho khối chóp có chiều cao và diện tích đáy .
Chọn hệ trục tọa độ như hình, khi đó hình chóp đã cho có thể tích là h h Z Z V S x x . . . . . . x . . . . . . . . . = ( ) d = d = 0 0 S B, B0
b) Cho khối chóp cụt tạo bởi khối chóp đỉnh
có diện tích hai đáy lần lượt là và h chiều cao bằng .
Khi đó khối chóp cụt đã cho có thể tích bằng V
. . . . . . . . . . . . . . . = Soạn: Huỳnh Phú Sĩ 20
Trường THCS-THPT Mỹ Thuận
§3. Ứng dụng của tích phân trong hình học TOÁN 12 4 THỂ TÍCH KHỐI TRÒN XOAY y f x
Quay hình thang cong giới hạn bởi đồ thị hàm số = (
), trục hoành và hai đường x a x b . . . . . . . . . . . . . . . . . . thẳng = , = quanh trục tạo thành một khối có thể tích là b Z V . . . . . . . . . . . . x = d a
Ví dụ 4. Tính thể tích khối tròn xoay thu được khi quay hình phẳng giới hạn bởi đường y x x x π cong = cos
, trục hoành và hai đường thẳng = 0, = quanh trục hoành. 5 THỰC HÀNH Í TRẮC NGHIỆM Câu 1. y f x a b S Nếu hàm số = ( ) liên tục trên đoạn [ ; ] thì diện tích của hình y f x x a
phẳng giới hạn bởi đồ thị hàm số = (
), trục hoành và hai đường thẳng = , x b = làb a Z Z A |f x − g x | x B |f x | x . ( ) ( ) d . . ( ) d . a b b b Z Z C f x x D |f x | x . ( ) d . . ( ) d . a a y Câu 2. H y f x Ox Cho hình phẳng
giới hạn bởi đồ thị hàm số = ( ) trục và đường y f x x − S = ( ) thẳng =
1 (phần gạch sọc như hình bên). Gọi
là diện tích của hình phẳng
H. Mệnh đề nào dưới đây đúng? 0 2 2 Z Z Z A S |f x | x − |f x | x B S f x x . = ( ) d ( ) d . . = ( ) d . − − O x − − 2 1 2 1 0 1 0 2 0 2 Z Z Z Z C S f x x − f x x D S f x x f x x . = ( ) d ( ) d . . = ( ) d + ( ) d . − − 1 0 1 0 Câu 3. y H y f x Diện tích hình phẳng (
) giới hạn bởi đồ thị của hàm số = ( ), trục x a x b a < b f x a b y f x x b
hoành và hai đường thẳng = , = ( và ( ) liên tục trên [ ; ]) (phần = ( ) =
gạch sọc trong hình vẽ) tính theo công thức c b b Z Z Z c x A B O S − f x x f x x S f x x . = ( ) d + ( ) d . . = ( ) d . a c a b c b Z Z Z C S D f x x S f x x f x x x a . = ( ) d . . = ( ) d + ( ) d . = a a c Câu 4. D y f x , y g x Cho hình phẳng
giới hạn bởi đồ thị hai hàm số = ( ) = ( ) liên a b x a, x b S tục trên đoạn [ ; ] và hai đường thẳng = = . Diện tích của hình phẳng D là b b Z Z A S f x g x x B S |f x − g x | x . = [ ( ) + ( )] d . . = ( ) ( ) d . a a b b Z Z C S f x − g x x D S g x − f x x . = [ ( ) ( )] d . . = [ ( ) ( )] d . a a Soạn: Huỳnh Phú Sĩ 21
Trường THCS-THPT Mỹ Thuận
§3. Ứng dụng của tích phân trong hình học TOÁN 12 y
Câu 5. Diện tích phần hình phẳng được gạch chéo trong hình bên bằng 2 2 Z Z y x A B 2 − x − − x2 x x x2 − x − x = 2 2 . 2 + 2 + 4 d . . 2 2 4 d . − − 1 1 2 2 Z Z 2 x − O C − x2 − x x D x2 x − x 1 . 2 2 + 4 d . . 2 + 2 4 d . − − 1 1 Câu 6. S y x Tính diện tích
của hình phẳng giới hạn bởi đồ thị hàm số = 3 , trục Ox x − x và hai đường thẳng = 1, = 2. y −x2 26 12 26 = + 2 A S B S C S D S . = . . = 12. . = . . = . 3 ln 3 3 ln 3 Câu 7. S y −x3 x2 − Diện tích
của hình phẳng giới hạn bởi đường cong = + 3 2, x x
trục hoành và hai đường thẳng = 0, = 2 là A S 5 B S 3 C S 7 D S . = . . = . . = . . = 4. 2 2 2 Câu 8. S y x2 x Tính diện tích
của hình phẳng giới hạn bởi đồ thị hàm số = + y −x và đường thẳng = + 3. A S − 32 B S 16 C S D S 32 . = . . = . . = 16. . = . 3 3 3 Câu 9. C y x4 − x2
Tính diện tích hình phẳng giới hạn bởi ( ) : = 2 + 1 và trục hoành. A 8 B −15 C 15 D 16 . . . . . . . . 15 16 8 15 Câu 10. x y + 1
Diện tích hình phẳng được giới hạn bởi đồ thị hàm số = x , trục + 2 x hoành và đường thẳng = 2 là A B − C D − . 3 + ln 2. . 3 ln 2. . 3 + 2 ln 2. . 3 2 ln 2. Câu 11. S Tính diện tích của hình phẳng y y x − = 2
(phần gạch sọc) trong hình bên. √ A S 8 B S 10 y x . = . . = . = 3 3 C S 11 D S 7 . = . . = . 3 3 x O 2 4 y √ Câu 12. H y x y Cho (
) là hình phẳng giới hạn bởi đồ thị của các hàm số = , = 0, y − x H = 2 . Diện tích của ( ) là √ √ 2 A − 4 2 1 B 8 2 + 3 C 7 D 5 . . . . . . . . 3 6 6 6 1 Câu 13. x2 y x2 y Tính diện tích hình phẳng giới hạn bởi các đường = , = , 8 x O y 27 1 2 = x . A 63 B − 63 C D − 63 . . . 27 ln 2 . . 27 ln 2. . 27 ln 2 . 8 8 4 Câu 14. S E Tính diện tích
của hình phẳng giới hạn bởi elip ( ) có phương trình x2 y2 a, b > a + = 1, với 0. 2 b2 2 A S π 1 1 B S π a b 2 . = a + b . . = ( + ) . C πa2b2 S πab D S . = . . = a b . +
Câu 15. Trên cánh đồng cỏ có hai con bò được cột vào hai cây cọc khác nhau.
Biết khoảng cách giữa hai cọc là 4m còn hai sợi dây cột hai con bò dài 3m và 2m.
Tính phần diện tích mặt cỏ lớn nhất mà hai con bò có thể ăn chung (lấy giá trị gần đúng nhất). A , 2 B , 2 C , 2 D c . 1 574m . . 1 034m . . 1 989m . . . Soạn: Huỳnh Phú Sĩ 22
Trường THCS-THPT Mỹ Thuận
§3. Ứng dụng của tích phân trong hình học TOÁN 12 Câu 16. f x a b H Cho hàm số ( ) liên tục trên đoạn [ ; ]. Gọi (
) là hình phẳng giới hạn y f x x a x b V bởi đồ thị hàm số = (
), trục hoành và hai đường thẳng = , = ; là thể H Ox
tích của khối tròn xoay được thành khi quay ( ) quanh trục . Khẳng định nào sau đây là đúng? b b Z Z A V π |f x | x B V f 2 x x . = ( ) d . . = ( ) d . a a b b Z Z C V π f 2 x x D V |f x | x . = ( ) d . . = ( ) d . a a Câu 17. D Thể tích của
√ khối tròn xoay tạo thành khi quay hình phẳng giới hạn y x − x x Ox bởi các đường = 1, trục hoành, = 2 và = 5 quanh trục bằng 5 5 Z Z √ A x − x B x − x . ( 1) d . . 1 d . 2 2 5 5 Z Z C π x − x D π2 x − x . ( 1) d . . ( 1) d . 2 2 y
Câu 18. Cho hình phẳng trong hình vẽ bên (phần tô đậm) quay quanh trục hoành. y f x
Thể tích khối tròn xoay tạo thành được tính theo công thức nào trong các công = ( ) thức sau đây? b b Z Z A V π g 2 2 x − f 2 x x B V π f x − g x x . = ( ) ( ) d . . = ( ) ( ) d . a a b b y g x Z Z = ( ) C V π f x − g x x D V π f 2 x − g2 x x . = ( ) ( ) d . . = ( ) ( ) d . a x b O a a
Câu 19. Tìm công thức tính thể tích của khối tròn xoay khi cho hình phẳng giới P y x2 d y x Ox hạn bởi parabol ( ) : = và đường thẳng : = 2 quay quanh trục . 2 2 2 Z Z Z A π
x2 − x2 x B π x2 x − π x4 x . 2 d . . 4 d d . 0 0 0 2 2 2 Z Z Z C π x 2 x π x4 x D π x − x2 x . 4 d + d . . 2 d . 0 0 0 √ Câu 20. D y x Cho hình phẳng (
) giới hạn bởi đồ thị hàm số = , hai đường thẳng x x D = 1,
= 2 và trục hoành. Tính thể tích khối tròn xoay tạo thành khi quay ( ) quanh trục hoành. A π π π B 3 C 3 D 2 . 3 . . . . . . . 2 2 3
Câu 21. Thể tích khối tròn xoay sinh ra khi quay hình phẳng giới hạn bởi đồ thị y x2 − x y x − x Ox các hàm số = 2 , = 0, = 1, = 2 quanh trục bằng A π π π π 16 B 17 C 18 D 5 . . . . . . . . 5 5 5 18 √ Câu 22. D y x Cho hình phẳng
giới hạn bởi đường cong = 2 + cos , trục hoành π x x V và các đường thẳng = 0, = . Tính thể tích
của khối tròn xoay tạo thành 2 D khi quay quanh trục hoành. A V π − B V π C V π π − D V π π . = 1. . = + 1. . = ( 1). . = ( + 1). Câu 23. D y x Cho hình phẳng
giới hạn bởi đường cong = e , trục hoành và các x x D đường thẳng = 0,
= 1. Khối tròn xoay tạo thành khi quay quanh trục hoành V có thể tích bằng π 2 A 2 − V e 1 B V e + 1 . = . . = . 2 2 π 2 − C π 2 V e 1 D V e . = . . = . 2 2
Câu 24. Thể tích của khối tròn xoay sinh ra khi cho hình phẳng giới hạn bởi P y x2 d y x Ox parabol ( ) : = và đường thẳng : = xoay quanh trục bằng 1 1 1 1 Z Z Z Z A π x2 x − π x4 x B π x2 x π x4 x . d d . . d + d . 0 0 0 0 Soạn: Huỳnh Phú Sĩ 23
Trường THCS-THPT Mỹ Thuận
§3. Ứng dụng của tích phân trong hình học TOÁN 12 1 1 Z Z C π
x2 − x2 x D π
x2 − x x . d . . d . 0 0 Câu 25. H C y 4 Gọi (
) là hình phẳng giới hạn bởi đồ thị ( ) : = x và đường thẳng d y − x V H ( ) : = 5 . Tính thể tích
của khối tròn xoay tạo thành khi quay hình ( ) xung quanh trục hoành. A V π B V π C V π D V π . = 51 . . = 33 . . = 9 . . = 18 . Câu 26. y Cho hình phẳng giới hạn bởi đồ thị các hàm số √ y x y − x = , đường thẳng = 2 và trục hoành 2
(phần gạch chéo trong hình vẽ). Thể tích của khối
tròn xoay sinh bởi hình phẳng trên khi quay quanh Ox trục bằng 1 A π π π π 5 B 4 C 7 D 5 . . . . . . . . 4 3 6 6 x O 1 2 Câu 27. V H Tính thể tích
của vật tròn xoay tạo thành khi quay hình phẳng ( ) giới √ y x2 y x Ox hạn bởi các đường = và = quanh trục . A π π π π V 3 B V C V 7 D V 9 . = . . = . . = . . = . 10 10 10 10
Câu 28. Người ta làm một chiếc phao bơi như hình vẽ (với bề mặt có được bằng C d OI R cách quay đường tròn quanh trục ). Biết rằng = 30cm, = 5cm. Tính thể V tích của chiếc phao. R I C d O A V π2 3 B V π2 3 . = 1500 cm . . = 9000 cm . C V π 3 D V π 3 . = 1500 cm . . = 9000 cm .
Câu 29. Một ô tô đang chạy với tốc độ 36 km/h thì người lái xe đạp phanh, từ thời v t − t
điểm đó, ô tô chuyển động chậm dần đều với vận tốc ( ) = 5 + 10 m/s, trong t đó
là khoảng thời gian tính bằng giây, kể từ lúc bắt đầu đạp phanh. Hỏi từ lúc
đạp phanh đến lúc dừng hẳn, ô tô còn di chuyển bao nhiêu mét? A B C D , . 10 m. . 20 m. . 2 m. . 0 2 m.
Câu 30. Một chiếc xe đang chạy đều với vận tốc 20 m/s thì giảm phanh với vận v t − t tốc ( ) = 20 2
m/s đến khi dừng hẳn. Quãng đường xe đi được từ lúc bắt đầu
giảm phanh đến khi dừng hẳn là A B C D . 98 m. . 94 m. . 100 m. . 96 m. L TỰ LUẬN
Câu 1 (SGK GT12). Tính diện tích hình phẳng giới hạn bởi các đường: y x2 y x y x − 2 y x − x2 a) = , = + 2 b) = ( 6) , = 6
Câu 2 (SGK GT12). Tính thể tích khối tròn xoay do hình phẳng giới hạn bởi các đường sau π y − x2 y y x y x x a) = 1 , = 0 b) = tan , = 0, = 0, = 4 Soạn: Huỳnh Phú Sĩ 24
Trường THCS-THPT Mỹ Thuận Chương 4. Số phức TOÁN 12 Chương 4. SỐ PHỨC §1.SỐ PHỨC Đặt vấn đề Số phức cho phép giải một phương trình nhất định mà
Số phức được sử dụng trong nhiều lĩnh vực khoa học, như
không giải được trong trường số thực. Ví dụ, phương trình
khoa học kỹ thuật, điện từ học, cơ học lượng tử, toán học x 2 − ( + 1) =
9 không có nghiệm thực, vì bình phương của
ứng dụng chẳng hạn như trong lý thuyết hỗn loạn. Nhà một số thực không thể âm. Các số phức cho phép giải
toán học người Ý Gerolamo Cardano là người đầu tiên đưa
phương trình này. Ý tưởng là mở rộng trường số thực sang
ra số phức. Ông sử dụng số phức để giải các phương trình i i2 − đơn vị ảo với =
1, vì vậy phương trình trên được giải. bậc ba trong thế kỉ 16. 1 ĐỊNH NGHĨA SỐ PHỨC . . . . . . . . . a, b ∈ . . . i2 . . . số Mỗi biểu thức dạng trong đó và = được gọi là một phức. z a bi a
. . . . . . . . . . . . b . . . . . . . . . . . . z • Đối với số phức = + , ta nói là , là của . i . . . . . . . . . . . . • Số được gọi là . . . . . . •
Tập hợp các số phức kí hiệu là (The set of Complex numbers). √ Ví dụ 1. − i − i − i
Tìm phần thực và phần ảo của các số phức 3 + 5 , 4 2, 3 , 2021. ! a bi phần thực . . . • Mỗi số thực
đều là một số phức với • Số phức có bằng phần ảo . . . . . . . . . . . . bằng được gọi là số 2 SỐ PHỨC BẰNG NHAU . . . . . . . . . . . . . . . . . . . . . . . .
Hai số phức được gọi là bằng nhau nếu và của chúng tương ứng bằng nhau. (a . . . a b i a b i ⇔ 1 = 1 + 1 = 2 + 2 b . . . 1 = Ví dụ 2. x, y z x y i w x y − i Tìm để hai số phức = + 2 + ( + 4) và = 2 + 1 + (3 2) bằng nhau Soạn: Huỳnh Phú Sĩ 25
Trường THCS-THPT Mỹ Thuận §1. Số phức TOÁN 12 3
BIỂU DIỄN HÌNH HỌC VÀ MÔĐUN CỦA SỐ PHỨC
1 Biểu diễn hình học của số phức M . . . . . . Oxy . . . . . . . . . . . . Điểm ( ;
) trong hệ trục tọa độ được gọi là điểm của số phức z a bi y = + . Ví dụ 3. N N Trong hình bên, điểm
biểu diễn số phức nào? (3; 2) 2
2 Môđun của số phức 5 ON = z a bi M a b Cho số phức = + có điểm biểu diễn là ( ; ). −−Ï . . . . . . . . . OM z . . . . . . của vectơ
được gọi là môđun của số phức , kí hiệu là x O 3 |z| . . . . . . . . . = √ Ví dụ 4. z − i z z i
Tính môđun của các số phức 1 = 4 3 , 2 = 2021, 3 = 7.
3 Số phức liên hợp y N z a bi . . . . . . . . . số phức liên hợp z . . . Cho số phức = + . Ta gọi là của , kí hiệu là . (3; 2) Ví dụ 5. 2
Ghép nối các cặp số phức liên hợp dưới đây: 5 ON = i i a) 3 + 2 • 4 + 3 √ − i −i b) 4 3 √ • 5 x O i − i O 3 M c) 5 • 3 + 2 = 5 Oxy z z
, các điểm biểu diễn của và đối xứng với nhau qua − ! • Trên mặt phẳng . . . . . . . . . . . . 2 M − (3; 2) |z| . . . . . . z . . . . . . • = và = 4 THỰC HÀNH Í TRẮC NGHIỆM Câu 1. z a b z Cho số √ phức = + i. Môđun của là √ A |z| a2 b2 B |z| a2 − b2 . = + . . = . √ C |z| a2 b2 D |z| a2 b2 . = + . . = 2 + . Câu 2. z a b sai Cho số phức = +
i. Khẳng định nào sau đây ? A z a − b √ B z a b . = i. . = + √ i. C |z| a2 b2 D |z| a2 − b2 . = + . . = . Câu 3. z − i
Tìm phần thực và phần ảo của số phức = 2 3 . A B − .
Phần thực là 2 và phần ảo là 3. .
Phần thực là 2 và phần ảo là 3. C i D − i .
Phần thực là 2 và phần ảo là 3 . .
Phần thực là 2 và phần ảo là 3 .
Câu 4. Số phức có phần thực bằng 3 và phần ảo bằng 4 là A B − C − D . 3 + 4i. . 4 3i. . 3 4i. . 4 + 3i. Câu 5. a, b z − Gọi
lần lượt là phần thực và phần ảo của số phức = 3 + 2i. Giá trị a b của + 2 bằng A B − C − D − . 1. . 1. . 4. . 7. Câu 6. z a b z Cho số phức = +
i. Số phức liên hợp của là A z a − b B z a − b C z b D z −a − b . = i. . = i. . = i. . = i. Câu 7. z − i
Tính môđun của số phức√ = 4 3 . A |z| B |z| C |z| D |z| . = 5. . = 7. . = 7. . = 25. Soạn: Huỳnh Phú Sĩ 26
Trường THCS-THPT Mỹ Thuận §1. Số phức TOÁN 12
Câu 8. Trong các số phức sau, số nào có môđun nhỏ nhất? A z B z − C z D z . 1 = 1 + 2i. . 2 = 2 i. . 3 = 2. . 4 = 1 + i.
Câu 9. Trong các số phức sau, số nào có môđun lớn nhất? A z B z − C z D z . 1 = 1 + 2i. . 2 = 2 i. . 3 = 3i. . 4 = 1 + i. Câu 10. z − z − − Cho hai số phức 1 = 1 + 2i và 2 = 1
2i. Giá trị của biểu thức |z |2 |z |2 √ 1 + 2 bằng A B C − D . 10. . 10. . 6. . 4. Câu 11. z − z − z z Trong các số phức 1 = 2i, 2 = 2 i, 3 = 5i, 4 = 4 có bao nhiêu số thuần ảo? A B C D . 4. . 1. . 3. . 2. Câu 12. z m − m2 − i, m ∈ R m z Cho số phức = (2 1) + ( 4) . Tìm để số phức là số thuần ảo. A m , m − B m . = 2 = 2. . = 2. C m − 1 D m 1 . = . . = . 2 2 Câu 13. a, b a b − − Cho
là hai số thực thỏa mãn 2 + ( 3)i = 4
5i với i là đơn vị ảo. a, b Giá trị của bằng A a , b B a , b . = 1 = 8. . = 8 = 8. C a , b − D a − , b . = 2 = 2. . = 2 = 2. Câu 14. a, b a − b a b a b b Tìm các số thực thỏa mãn ( 2 ) + ( + + 4)i = (2 + ) + 2 i với i là đơn vị ảo. A a − , b B a , b − . = 3 = 1. . = 3 = 1. C a − , b − D a , b . = 3 = 1. . = 3 = 1. Câu 15. x, y x y x y Tìm các số thực thỏa mãn (2 + 5 ) + (4 + 3 )i = 5 + 2i. A x 5 , y − 8 B x 8 , y − 5 . = = . . = = . 14 7 7 14 y C x − 5 , y 8 D x − 5 , y − 8 . = = . . = = . 14 7 14 7 3 x O Câu 16. M z Điểm
trong hình vẽ bên biểu diễn số phức
. Tìm phần thực và phần z ảo của . A − B − C − D − . 4 và 3. . 3 và 4i. . 3 và 4. . 4 và 3i. Câu 17. M z
Trên mặt phẳng tọa độ, tìm tọa độ của điểm biểu diễn số phức = − i 5 . A M B M − C M − D M . (5; 0). . (5; 1). . (0; 5). . (5; 1). − M 4 y Câu 18. Oxy A, B Trong mặt phẳng , cho các điểm
như hình vẽ bên. Trung điểm AB của đoạn thẳng biểu diễn số phức B A −1 i B − 1 i C − i D − i 3 . + 2 . . 2 . . 1 + 2 . . 2 . 2 2 Câu 19. A, B z z − Gọi
lần lượt biểu diễn các số phức 1 = 2 + 3i và 2 = 2 3i. Khẳng định nào sau đây đúng? A A A, B .
đối xứng nhau qua gốc tọa độ. 1 B A, B .
đối xứng nhau qua trục hoành. C A, B .
đối xứng nhau qua trục tung. − O x D A, B I 2 1 . đối xứng nhau qua điểm (1; 0). Câu 20. z i z − − i z m − i Cho các số phức 1 = 3 , 2 = 1 3 và 3 = 2 . Tập giá trị của m z tham số để số phức 3
có môđun nhỏ nhất trong 3 số phức đã cho là √ √ √ √ A h i − B − . 5; 5 . . 5; 5 . √ √ √ C n o √ − D −∞ ∪ ∞ . 5; 5 . . ; 5 5; + . L TỰ LUẬN Câu 1 (SGK GT12). z
Trên mặt phẳng tọa độ, tìm tập hợp điểm biểu diễn các số phức thỏa mãn điều kiện: |z| |z| ≤ a) = 1 b) 1 Soạn: Huỳnh Phú Sĩ 27
Trường THCS-THPT Mỹ Thuận
§2. Cộng, trừ và nhân số phức TOÁN 12
§2.CỘNG, TRỪ VÀ NHÂN SỐ PHỨC 1 PHÉP VỘNG VÀ PHÉP TRỪ z a b i z a b i Cho hai số phức 1 = 1 + 1 và 2 = 2 + 2 , khi đó: z z
. . . . . . . . . . . . . . . • 1 + 2 = z − z
. . . . . . . . . . . . . . . • 1 2 =
Ví dụ 1. Thực hiện các phép tính sau: − i i i − − i a) (3 5 ) + (2 + 4 ) c) (4 + 3 ) (5 7 ) − − i − − i − i − − i b) ( 2 3 ) + ( 1 7 ) d) (2 3 ) (5 4 ) 2 PHÉP NHÂN i2 . . . . . . Vì = nên ta có: a bi c di
. . . . . . . . . . . . . . . . . . . . . ( + )( + ) =
Ví dụ 2. Thực hiện các phép tính sau: − i i i − i i 2 a) ( 1 + )(3 + 7 ) b) (3 + 4 )(3 4 ) c) (2 + 3 ) 3 THỰC HÀNH Câu 1. z − i z − i z − z Cho hai số phức 1 = 2 2 , 2 = 3 + 3 . Khi đó số phức 1 2 là A − i B − i C − i D − i . 1 + . . 5 + 5 . . 5 5 . . 5 . Câu 2. P z y Trong hình vẽ, điểm biểu diễn số phức 1 , điểm Q z z z biểu diễn số phức 2 . Tìm số phức = 1 + z P 2 . A z B z − 2 . = 1 + 3i. . = 3 + i. C z − D z . = 1 + 2i. . = 2 + i. Q 1 x −1 0 2 Câu 3. z z − w z − z Cho 1 = 1 + 2i, 2 = 2 3i. Khi đó = 1 2 2 bằng A B − C − D − − . 5 + 8i. . 3 + 8i. . 3 i. . 3 4i. √ Câu 4. z − 1 3 w z z2 Cho số phức = + i. Tìm số phức = 1 + + . √ 2 2 A w − 1 3 B w . = + i. . = 0. √ 2 2 C w D w − . = 1. . = 2 3i. Câu 5. z z z Cho số phức , khi đó + là A B C D . Số thực. . Số ảo. . 0. . 2. Câu 6. z b z · z Cho số phức √ = 2 + i. Tính . A z · z b2 B z · z − b2 . = 4 + . . = 4 . C z · z −b D z · z b2 . = . . = 4 + . Soạn: Huỳnh Phú Sĩ 28
Trường THCS-THPT Mỹ Thuận
§2. Cộng, trừ và nhân số phức TOÁN 12 Câu 7. z 2 Giá trị của biểu thức = (1 + i) là A B − C − D . 2i. . i. . 2i. . i. Câu 8. z i z − i Cho hai số phức 1 = 3 + 2 và 2 = 1
5 . Tìm phần thực và phần ảo của z z số phức 1 + 2 . A B − i .
Phần thực là 4 và phần ảo là 3. .
Phần thực là 4 và phần ảo là 3 . C i D − .
Phần thực là 4 và phần ảo là 3 . .
Phần thực là 4 và phần ảo là 3. Câu 9. z 1 − i z − i Cho hai số phức 1 = 2 và 2 = 4
. Tính môđun của số phức 2 z z · z = √ 1 2 . A |z| 34 B |z| 289 C |z| 17 D |z| − 17 . = . . = . . = . . = . 2 4 2 2 Câu 10. z z |z z | Cho hai số phức √ 1 = 2 + 3i và 2 = 1 + i. Tính 1 + 3 2 . A |z z | B |z z | . √ 1 + 3 2 = 11. . 1 + 3 2 = 11. C |z z | D |z z | . 1 + 3 2 = 61. . 1 + 3 2 = 61. Câu 11. z − i i − i
Tìm số phức liên hợp của số phức = (11 3 ) + (5 + 2 )(1 ). A z i B z i C z − i D z − i . = 14 + 6 . . = 18 + 6 . . = 18 6 . . = 14 6 . Câu 12. z z − 2 Cho số phức thỏa mãn (3 + 2i) + (2 i)
= 4 + i. Hiệu phần thực và z phần ảo của là A B C D . 2. . 3. . 1. . 0. Câu 13. x, y x − y − − Tìm hai số thực thỏa mãn (2 3 i) + (1 3i) = 1 + 6i, với i là đơn vị ảo. ( ( ( ( A x x − x − x = 1 B = 1 C = 1 D = 1 . y − . . y − . . y − . . y − . = 3 = 3 = 1 = 1 Câu 14. z z z − i Cho số phức thỏa mãn + 2 = 6 3 có phần ảo bằng A − B C i D i . 3. . 3. . 3 . . 2 . Câu 15. z z − i iz Tìm số phức thỏa mãn 1 + 4 = 2 . A z 9 − 2 i B z − 9 2 i C z 7 2 i D z
− 7 − 2 i . = . . = + . . = + . . = . 5 5 5 5 3 3 3 3 Câu 16. x, y z i xi y i Cho
là các số thực. Số phức = (1 + + + 2 ) bằng 0 khi A x − y − B x y . = 1; = 2. . = 0; = 0. C x − y − D x y . = 2; = 1. . = 2; = 1. Câu 17. z |z| z2 |z z| |z − z| Cho số phức thỏa mãn = 2 và + 1 = 4. Tính + + . √ √ √ A B C D . 3 + 7. . 3 + 2 2. . 7 + 3. . 16. Câu 18. z
Trên mặt phẳng tọa độ, tìm tập hợp điểm biểu diễn các số phức thỏa |z − i| mãn điều kiện 2 + 3 = 4. A I − R . Đường tròn tâm (2; 3) và bán kính = 4. B I − R . Đường tròn tâm ( 2; 3) và bán kính = 16. C I − R . Đường tròn tâm ( 2; 3) và bán kính = 4. D I − R . Đường tròn tâm (2; 3) và bán kính = 16. Câu 19. z |z − | Cho số phức thỏa mãn + 2 i
= 3. Tìm tập hợp các điểm trong mặt Oxy w z phẳng biểu diễn số phức = 1 + . A I − R . Đường tròn tâm ( 2; 1) bán kính = 3. B I − R . Đường tròn tâm (2; 1) bán kính = 3. C I − − R . Đường tròn tâm ( 1; 1) bán kính = 9. D I − − R . Đường tròn tâm ( 1; 1) bán kính = 3. Câu 20. z |z − | |z − i| Cho số phức thỏa mãn 1 =
. Tìm môđun nhỏ nhất của số w z − i phức = 2 + 2 . √ √ A B 3 √ C 3 2 D 3 . 3 2. . . . . . . 2 2 2 2 Soạn: Huỳnh Phú Sĩ 29
Trường THCS-THPT Mỹ Thuận §3. Phép chia số phức TOÁN 12 §3.PHÉP CHIA SỐ PHỨC 1
TỔNG VÀ TÍCH CỦA HAI SỐ PHỨC LIÊN HỢP z a bi Cho số phức = + . Khi đó: ! z z ...... z · z . . . . . . • + = • = Chú ý: . . . . . .
Tổng và tích của một số phức với số phức liên hợp của nó là một số Ví dụ 1. z − i z z z · z Cho số phức = 3 4 . Tính + và . 2 PHÉP CHIA HAI SỐ PHỨC z z a bi z c di 1 Cho hai số phức 1 = + và 2 = + . Khi đó, để tính
z , ta nhân cả tử và mẫu 2 z cho 2 , tức là z z · z 1 1 2
. . . . . . . . . . . . . . . . . . . . . z = z · z = 2 2 2 Ví dụ 2. i − i 2 + 5 2 Tính − i và i . 3 2 √ Ví dụ 3. z z − i
Tìm nghịch đảo của số phức , biết = 2 3 . Ví dụ 4. z z − i − i Tìm số phức thỏa mãn − i + 2 3 = 5 2 . 4 3 3 THỰC HÀNH Í TRẮC NGHIỆM Câu 1. z i z Cho số phức = 1 +
. Số phức nghịch đảo của là A − i − i − i − i B 1 C 1√ D 1 + . 1 . . . . . . . 2 2 2 Câu 2. z z Cho số phức = 2 + 3i. Tính z . A − − − − − 5 + 12i B 5 6i C 5 12i D 5 12i . . . . . . . . 13 11 13 13 Câu 3. − − i − i z ( 2 3 ) ( 1 + 2 )
Tính môđun của số phức = i . √ √ 2 + A |z| B |z| C |z| D |z| . = 13. . = 5. . = 13. . = 5. Câu 4. − i z 6 3
Tìm phần thực và phần ảo của số phức = i . 2 + 5 A − 3 − 36 . Phần thực là và phần ảo là . 29 29 B − 3 − 36 i . Phần thực là và phần ảo là . 29 29 C 1 12 . Phần thực là và phần ảo là . 7 7 D 1 12 i . Phần thực là và phần ảo là . 7 7 Soạn: Huỳnh Phú Sĩ 30
Trường THCS-THPT Mỹ Thuận §3. Phép chia số phức TOÁN 12 Câu 5. z i z + − i w z z2 Cho số phức thỏa mãn z − = 2 . Tìm số phức = 1 + + . 1 A w − i B i C w 9 i D w 9 − i . = 5 2 . . 5 + 2 . . = + 2 . . = 2 . 2 2 Câu 6. z z − i i
Tính môđun của số phức thỏa mãn (2 ) + 13 = 1. √ √ √ A |z| B |z| C |z| 5 34 D |z| 34 . = 34. . = 34. . = . . = . 3 3 Câu 7. z i z − i 2 − i Số phức
thỏa mãn điều kiện (3 + ) + (1 2 ) = 8 17 . Khi đó hiệu z
của phần thực và phần ảo của là A B − C D − . 7. . 3. . 3. . 7. Câu 8. z − i z i 2 i Cho số phức thỏa mãn (1 2 ) + (1 + 3 )
= 5 . Khi đó điểm nào sau z
đây biểu diễn số phức ? A M − B N C P − D Q − − . (2; 3). . (2; 3). . ( 2; 3). . ( 2; 3). Câu 9. − i − i 2 z z 4( 3 + ) (3 ) Cho số phức thỏa mãn = − i + −i . Môđun của số phức 1 2 w z − iz = + 1 √ là √ √ √ A |w| B |w| C |w| D |w| . = 85. . = 4 5. . = 6 3. . = 48. Câu 10. m Giá trị của tham số thực bằng bao nhiêu để bình phương số phức m i i z ( + 9 )(1 + ) = là số thực? 2 A m B m − . Không có giá trị thỏa. . = 9. C m D m ± . = 9. . = 9. L TỰ LUẬN
Câu 1 (SGK GT12). Thực hiện các phép tính sau: i i i 2 i 3 5 (1 + ) (2 ) − i 5 + 4 a) − i b) i − c) 4 3 + i 2 3 2 3 + 6 Câu 2 (SGK GT12). 1 z Tìm nghịch đảo
z của số phức , biết: √ z i z i z i a) = 1 + 2 b) = c) = 5 + 3
Câu 3 (SGK GT12). Giải các phương trình sau: − i z i i i z − i i z a) (3 2 ) + (4 + 5 ) = 7 + 3 b) (1 + 3 ) (2 + 5 ) = (2 + ) Soạn: Huỳnh Phú Sĩ 31
Trường THCS-THPT Mỹ Thuận
§4. Phương trình bậc hai với hệ số thực TOÁN 12
§4.PHƯƠNG TRÌNH BẬC HAI VỚI HỆ SỐ THỰC Đặt vấn đề . . . . . . . . . 1. Căn bậc hai của 9 là − . . . . . . . . . 2. Căn bậc hai của 9 là 1
CĂN BẬC HAI CỦA SỐ THỰC ÂM a < . . . . . . . . .
Căn bậc hai của số thực 0 là Ví dụ 1. − − − Tìm căn bậc hai của 1, 4, 9. 2
PHƯƠNG TRÌNH BẬC HAI VỚI HỆ SỐ THỰC n n ≥ . . . . . .
Trên tập hợp số phức, mọi phương trình bậc ( 1) đều có đúng nghiệm (không nhất thiết phân biệt). Ví dụ 2. x2 − x Giải phương trình 2 + 5 = 0. 3 THỰC HÀNH Í TRẮC NGHIỆM Câu 1. z , z z2 − z Kí hiệu 1 2
là hai nghiệm phức của phương trình 3 + 5 = 0. Giá |z | |z | trị của 1 + √ 2 bằng √ A B C D . 2 5. . 3. . 5. . 10. Câu 2. z , z z2 − z Gọi 1 2
là hai nghiệm của phương trình 2 + 2018 = 0. Khi đó giá A |z z − z z | trị của biểu thức = 1 + 2 1 2 bằng A B C D . 2017. . 2019. . 2018. . 2016. Câu 3. z2 − z
Trong tập số phức, phương trình 2 + 5 = 0 có nghiệm là A z − ± i B z ± i C z − ± i D z ± i . = 1 2 . . = 2 2 . . = 2 2 . . = 1 2 . Câu 4. S z2 z Gọi
là tập nghiệm của phương trình +
+ 1 = 0 trên tập số phức. Số S tập con của là A B C D . 2. . 1. . 0. . 4. Câu 5. z2 − z
Tìm nghiệm phức có phần ảo âm của phương trình 4 + 13 = 0. A z − − i B z − i C z − i D z i . = 2 3 . . = 2 3 . . = 2 + 3 . . = 2 + 3 . Câu 6. z2 az b a, b ∈ R z − i Biết phương trình + + = 0 ( ) có nghiệm = 2 + . Tính a b + . A B C − D . 4. . 9. . 1. . 1. Câu 7. z z2 − z Kí hiệu 0
là nghiệm phức có phần ảo dương của phương trình 2 6 + M z
15 = 0. Trên mặt phẳng tọa độ, tìm tọa độ của điểm biểu diễn số phức 0 . √ √ ! ! A M −3 21 i B M −3 21 . ; . . ; . 2 2 2 2 √ √ ! ! C M 3 21 D M 3 21 i . ; . . ; . 2 2 2 2 Soạn: Huỳnh Phú Sĩ 32
Trường THCS-THPT Mỹ Thuận
§4. Phương trình bậc hai với hệ số thực TOÁN 12 Câu 8. S
z4 − z2 − Tìm tập nghiệm của phương trình 7
18 = 0 trên tập số phức. √ √ A n o S {− } B S − − i i . = 2; 9 . . = 2; 2; 3 ; 3 . √ √ C n o S {− i i − } D S − − i i . = 4 ; 4 ; 81; 81 . . = 3; 3; 2 ; 2 . Câu 9. − Tìm
√ một căn bậc hai của √ 8. √ √ A − i B − C D − i . 2 2 . . 2 2. . 2 2. . 2 2 . Câu 10. − Tìm √ các căn bậc hai của √ 6. √ A − i B ± i C ± i D i . 6 . . 6 . . 6 . . 6 . L TỰ LUẬN Câu 1 (SGK GT12). − − − − −
Tìm các căn bậc hai phức của các số sau: 7, 8, 12, 20, 121.
Câu 2 (SGK GT12). Giải các phương trình sau trên tập số phức: − z2 z − z2 − z z4 z2 a) 3 + 2 1 = 0 b) 5 7 + 11 = 0 c) + 7 + 10 = 0 Soạn: Huỳnh Phú Sĩ 33
Trường THCS-THPT Mỹ Thuận PHẦN II HÌNH HỌC
Chương 3. Phương pháp tọa độ trong không gian. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 35
§1. Hệ tọa độ trong không gian . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 35
§2. Phương trình mặt phẳng . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 40
§3. Phương trình đường thẳng . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 46 Soạn: Huỳnh Phú Sĩ 34
Trường THCS-THPT Mỹ Thuận
Chương 3. Phương pháp tọa độ trong không gian TOÁN 12 Chương 3.
PHƯƠNG PHÁP TỌA ĐỘ TRONG KHÔNG GIAN
§1.HỆ TỌA ĐỘ TRONG KHÔNG GIAN
Nhắc lại về Hệ tọa độ trong mặt phẳng HỆ TRỤC TỌA ĐỘ Oxy CÁC PHÉP TOÁN VECTƠ − Ï − Ï a a a b b b k ∈ R Cho hai vectơ = ( 1 ; 1 ) và = ( 1 ; 1 ) và số . y ( − Ï − Ï a . . . . . . a b ⇔ 1 = • = a . . . . . . 2 = − Ï − Ï a ± b a . . . b a . . . b • = ( 1 1 ; 2 2 ) − Ï − Ï j k · a . . . a . . . a • = ( 1 ; 2 ) x − Ï − Ï a · b
. . . . . . . . . . . . . . . O − Ï • = i q − Ï a a2 . . . . . . • = + 1 − Ï − Ï − Ï − Ï a . . . b a , b • cos = − Ï − Ï a . . . b Oxy . . . . . . Ox • Hệ trục tọa độ gồm trục và trục . . . . . . Oy . . . . . . . . . . . . − Ï , vuông góc và cắt nhau tại − Ï a b ⇔ ∃k ∈ . . . . . . . . . O . . . . . . R • và cùng phương sao cho ( ; ). − Ï − Ï
PHƯƠNG TRÌNH ĐƯỜNG TRÒN u u u u u . . . u . . . • Vectơ = ( 1 ; 2 ) nếu = 1 + 2 I a b R −−Ï Đường tròn tâm ( ; ) bán kính có phương trình là M x y OM x . . . y . . . • Điểm ( 0 ; 0 ) nếu = 0 + 0 x − . . . 2 y − . . . 2 . . . . . . − Ï ( ) + ( ) = AB x y • = B . . . xA B . . . yA ( ; )
hoặc có thể viết dưới dạng x x . . . . . . AB I A + B • Trung điểm của đoạn : . . . ; x2
y2 − . . . . . . x − . . . . . . y c 2 + + = 0 x x x . . . . . . . . . √ 4ABC G A + B + C R a b a2
b2 − . . . > . . . • Trọng tâm của : . . . ; 2 2 − . . . trong đó = + ( + ) 3 1
TỌA ĐỘ CỦA ĐIỂM VÀ CỦA VECTƠ 1 Hệ tọa độ z Oxyz . . . Ox Oy Oz . . . . . . . . . . . .
Trong không gian, hệ trục tọa độ bao gồm trục , , đôi một − Ï − Ï − Ï i j k . . . . . . . . . Ox Oy Oz • Các vectơ , , lần lượt là các vectơ trên các trục , , . O . . . . . . . . . . . . . . . . . . . . . • Điểm ( ; ; ) được gọi là − Ï
. . . . . . . . . . . . . . . . . . k • Các mặt phẳng , ,
đôi một vuông góc với nhau, được gọi là các O x mặt phẳng tọa độ. − Ï Oxyz . . . . . . i •
Không gian với hệ tọa độ
còn được gọi là không gian − Ï
2 Tọa độ của một điểm và của vectơ j y −−Ï M x y z OM
. . . . . . . . . . . . . . . Điểm ( 0 ; 0 ; 0 ) nếu = − Ï − Ï − Ï − Ï − Ï − Ï Ví dụ 1. − Ï Oxyz a i − j k i , j , k Trong không gian , vectơ = 2 3 + , với là các vectơ − Ï a
đơn vị. Tọa độ của vectơ là A − B − C D − . (1; 2; 3). . (2; 3; 1). . (2; 3; 1). . (1; 3; 2). Soạn: Huỳnh Phú Sĩ 35
Trường THCS-THPT Mỹ Thuận
§1. Hệ tọa độ trong không gian TOÁN 12 2
BIỂU THỨC TỌA ĐỘ CỦA CÁC PHÉP TOÁN VECTƠ Định lí − £ é − Ï − Ï Oxyz a a a a b b b b Trong không gian , cho hai vectơ = ( 1 ; 2 ; 3 ) và = ( 1 ; 2 ; 3 ). Ta có: − Ï − Ï − Ï a b
. . . . . . . . . . . . . . . k · a
. . . . . . . . . . . . . . . • + = • = − Ï − Ï a − b
. . . . . . . . . . . . . . . • = Ví dụ 2. Oxyz ~ a ~ b − ~ c − Trong không gian , cho = (2; 1; 3), = (4; 3; 5), = ( 2; 4; 6). Tìm tọa ~ u ~ a ~ b − ~ c độ của vectơ = + 2 . A B − C − D − . (10; 9; 6). . (12; 9; 7). . (10; 9; 6). . (12; 9; 6).  − Ï − Ï − Ï a . . . − Ï b 6 a b− Ï − Ï  1 = • Với vectơ = 0 thì và a b ⇔ a . . . ∃k ∈ R • =
cùng phương khi và chỉ khi 2 =  a . . . . . . a . . . . . .a . . . sao cho 1 = , 2 = , 3 = a . . . . . . 3 = ! −Ï − Ï . . . . . . . . . AB
. . . . . . . . . . . . . . . • 0 = • = x x
. . . . . . . . . . . . AB M A + B •
Trung điểm của đoạn thẳng là . . . ; ; . . . 2 x x x
. . . . . . . . . . . . . . . . . . ABC G A + B + C • Trọng tâm của tam giác là . . . ; ; . . . 3 Ví dụ 3. A − B C G Cho ba điểm (1; 1; 1), (0; 1; 2),
(1; 0; 1). Tìm tọa độ trọng tâm của tam ABC giác . Câu 1. Oxyz ABCD A B Trong không gian , cho hình bình hành . Biết (1; 0; 1), (2; 1; 2) và D − C (1; 1; 1). Tọa độ điểm là A C B C C C − D C − . (2; 0; 2). . (2; 2; 2). . (2; 2; 2). . (0; 2; 0). 3 TÍCH VÔ HƯỚNG
1 Biểu thức tọa độ của tích vô hướng − Ï − Ï Oxyz a a a a b b b b Trong không gian
, tích vô hướng của hai vectơ = ( 1 ; 2 ; 3 ) và = ( 1 ; 2 ; 3 )
được xác định bởi công thức − Ï − Ï a · b
. . . . . . . . . . . . . . . = − Ï Ví dụ 4. − Ï Oxyz a − b Trong không gian với hệ tọa độ , cho ba vectơ = (1; 2; 2), = − Ï − Ï − Ï − Ï − c a b · c ( 4; 0; 1) và = (0; 3; 3). Tính + . − Ï − Ï A − Ï − Ï − Ï − Ï a b · c B a b · c . + = 3. . + = 9. − Ï − Ï C − Ï − Ï − Ï − Ï a b · c D a b · c − . + = 0. . + = 10. Soạn: Huỳnh Phú Sĩ 36
Trường THCS-THPT Mỹ Thuận
§1. Hệ tọa độ trong không gian TOÁN 12
2 Ứng dụng của tích vô hướng Độ dài của một vectơ − £ é − Ï a a a a Cho vectơ = ( 1 ; 2 ; 3 ). Khi đó q − Ï a a2 . . . . . . . . . = + 1 Ví dụ 5. ABC A − B C Tính chu vi của tam giác , biết rằng (1; 1; 1), (0; 1; 2) và (1; 0; 1). Góc giữa hai vectơ − £ é − Ï − Ï a a a a b b b b Góc giữa hai vectơ = ( 1 ; 2 ; 3 ) và = ( 1 ; 2 ; 3 )
được tính bởi công thức − Ï − Ï − Ï − Ï a . . . b a , b
. . . . . . . . . . . . . . . . . . . . . cos = − Ï − Ï = a . . . b Ví dụ 6. Oxyz ~ u − , ~ v − ~ u Trong không gian , cho hai vectơ = ( 1; 1; 0) = (0; 0; 1). Góc giữa ~ v và có số đo bằng A ◦ B ◦ C ◦ D ◦ . 120 . . 45 . . 90 . . 60 . − Ï Hệ quả: − Ï
a ⊥ b ⇔ . . . . . . . . . . . . . . . 4 PHƯƠNG TRÌNH MẶT CẦU Định lí − £ é Oxyz S I a b c R Trong không gian , mặt cầu ( ) tâm ( ; ; ) bán kính có phương trình là M x y z x − . . . 2 y . . . . . . 2 . . . . . . I a b c ( ; ; ) ( ) + ( ) = ( ; ; )
Ví dụ 7. Lập phương trình mặt cầu trong các trường hợp sau đây: C − A − a) Có tâm (3; 3; 1) và đi qua điểm (5; 2; 1) AB A − B b) Có đường kính với (4; 3; 7) và (2; 1; 3)
Nhận xét: Phương trình mặt cầu nói trên có thể viết dưới dạng x2 y2
z2 − . . . . . . x − . . . . . . y − . . . . . . z d + + + = 0 √ R a2 b2 c2 − . . . a2 b2
c2 − . . . > . . . trong đó = + + ( + + )
Ví dụ 8. Tìm tâm và bán kính của mặt cầu có phương trình x2 y2 z2 − x − y + + 8 2 + 1 = 0 5 THỰC HÀNH Í TRẮC NGHIỆM Câu 2. Oxyz ~ a −~i ~j − ~k
Trong không gian với hệ tọa độ , cho vectơ = + 2 3 . Tìm ~ a tọa độ của . A − − B − − C − − D − − . (2; 3; 1). . ( 3; 2; 1). . ( 1; 2; 3). . (2; 1; 3). Soạn: Huỳnh Phú Sĩ 37
Trường THCS-THPT Mỹ Thuận
§1. Hệ tọa độ trong không gian TOÁN 12 − Ï Câu 3. Oxyz A − B AB Trong không gian , cho hai điểm (1; 1; 2) và (2; 2; 1). Vectơ có tọa độ là A − B C − − − D . (3; 3; 1). . (3; 1; 1). . ( 1; 1; 3). . (1; 1; 3). Câu 4. Oxyz A B − Trong không gian , cho hai điểm (1; 2; 3) và (3; 0; 5). Tọa độ trung I AB điểm của đoạn thẳng là A I − B I − C I − D I − . (2; 1; 1). . (2; 2; 2). . (4; 2; 2). . ( 1; 1; 4). Câu 5. Oxyz ABC A B − C Trong không gian , cho tam giác với (1; 3; 4), (2; 1; 0), (3; 1; 2). G ABC Tìm tọa độ trọng tâm của tam giác . A G B G C G 3 D G − . (2; 1; 2). . (6; 3; 6). . 3; ; 3 . . (2; 1; 2). 2 Câu 6. Oxyz ABCD A B − C Trong không gian , cho tứ diện có (1; 0; 2), ( 2; 1; 3), (3; 2; 4) D − và (6; 9;
5). Tọa độ trọng tâm của tứ diện là A B − C − D − . (2; 3; 1). . (2; 3; 1). . ( 2; 3; 1). . (2; 3; 1). Câu 7. Oxyz ~ a − ~ b − ~ c − Trong không gian , cho = (2; 3; 3), = (0; 2; 1), = (3; 1; 5). ~ u ~ a ~ b − ~ c Tìm tọa độ của vectơ = 2 + 3 2 . A − B − − C − − D − . (10; 2; 13). . ( 2; 2; 7). . ( 2; 2; 7). . ( 2; 2; 7). Câu 8. Oxyz A − B − C − Trong không gian , cho ba điểm (1; 2; 1), (2; 1; 3), ( 3; 5; 1). D ABCD Tìm tọa độ điểm sao cho tứ giác là hình bình hành. A D − − B D − − . ( 4; 8; 5). . ( 4; 8; 3). C D − − D . ( 2; 8; 3). . Không tồn tại. Câu 9. Oxyz A − B − M x y Trong không gian cho ba điểm (2; 1; 5), (5; 5; 7), ( ; ; 1). Với x, y A, B, M giá trị nào của thì thẳng hàng? A x y B x y − . = 4; = 7. . = 4; = 7. C x − y D x − y − . = 4; = 7. . = 4; = 7. Câu 10. Oxyz A − B − Trong không gian , cho hai điểm (0; 1; 2) và (3; 1; 1). Tìm tọa − − Ï − Ï M AM AB độ điểm sao cho = 3 . A M − B M C M − − D M − − . (9; 5; 7). . (9; 5; 7). . ( 9; 5; 7). . (9; 5; 5). Câu 11. Oxyz Oy Trong không gian
, điểm nào dưới đây thuộc trục ? A N B Q C P D M − . (2; 0; 0). . (0; 3; 2). . (2; 0; 3). . (0; 3; 0). Câu 12. Oxyz M − Trong không gian , hình chiếu của điểm (2; 2; 1) trên mặt phẳng Oxy ( ) có tọa độ là A B − C − D . (2; 0; 1). . (2; 2; 0). . (0; 2; 1). . (0; 0; 1). Câu 13. Oxyz H Trong không gian , tìm tọa độ điểm
là hình chiếu vuông góc của A − điểm (2; 1; 1) lên trục tung. A H − B H C H − D H . (2; 0; 1). . (0; 1; 0). . (0; 1; 1). . (2; 0; 0). Câu 14. Oxyz ~ a ~ b − Trong không gian , cho các vectơ = (1; 0; 3) và = ( 2; 2; 5). Tích ~ a · ~ a ~ b vô hướng + bằng A B C D . 25. . 23. . 27. . 29. Câu 15. Oxyz A − B − − Trong không gian , cho hai điểm (2; 1; 4) và ( 2; 2; 6). Tính AB độ dài đoạn thẳng . √ √ √ A AB B AB . = 5 √ 5. . = √21 + 44. C AB D AB . = 65. . = 5. Câu 16. Oxyz ~ u − , ~ v − Trong không gian , cho hai vectơ = ( 1; 1; 0) = (0; 1; 0). Góc ~ u ~ v giữa và có số đo bằng A ◦ B ◦ C ◦ D ◦ . 120 . . 45 . . 135 . . 60 . Câu 17. Oxyz S x − 2 y
Trong không gian với hệ tọa độ , cho mặt cầu ( ) : ( 7) + ( + 2 z2 I R S 3) + = 16. Tìm tọa độ tâm và bán kính của mặt cầu ( ). A I − R B I − R . ( 7; 3; 0) và = 4. . (7; 3; 0) và = 4. C I − R D I − R . ( 7; 3; 0) và = 16. . (7; 3; 0) và = 16. Câu 18. Oxyz S x2 y2 z2 x − y z − Trong không gian , mặt cầu ( ) : + + + 4 2 + 2 3 = 0 có tâm và bán kính là A I − , R B I − , R . (2; 1; 1) = 9. . (2; 1; 1) = 3. C I − − , R D I − − , R . ( 2; 1; 1) = 3. . ( 2; 1; 1) = 9. Câu 19. Oxyz A − B C − Trong không gian , cho ( 1; 0; 0), (0; 0; 2), (0; 3; 0). Tính bán OABC
kính mặt cầu ngoại tiếp tứ diện . √ √ √ √ A R 14 B R C R 14 D R 14 . = . . = 14. . = . . = . 4 3 2 Soạn: Huỳnh Phú Sĩ 38
Trường THCS-THPT Mỹ Thuận
§1. Hệ tọa độ trong không gian TOÁN 12 Câu 20. Oxyz S I − Trong không gian , cho mặt cầu ( ) có tâm là điểm (0; 0; 3) và đi M S qua điểm
(4; 0; 0). Phương trình của ( ) là A x2 y2 z 2 B x2 y2 z 2 . + + ( + 3) = 25. . + + ( + 3) = 5. C x2 y2 z − 2 D x2 y2 z − 2 . + + ( 3) = 25. . + + ( 3) = 5. Câu 21. Oxyz A − B Trong không gian , cho hai điểm (1; 2; 3) và (5; 4; 7). Phương AB trình mặt cầu nhận làm đường kính là A x − 2 y − 2 z − 2 . ( 6) + ( 2) + ( 10) = 17. B x − 2 y 2 z − 2 . ( 1) + ( + 2) + ( 3) = 17. C x − 2 y − 2 z − 2 . ( 3) + ( 1) + ( 5) = 17. D x − 2 y − 2 z − 2 . ( 5) + ( 4) + ( 7) = 17. Câu 22. Oxyz A − S Trong không gian tọa độ , cho điểm (1; 2; 3). Gọi ( ) là mặt cầu A I Ox S chứa có tâm thuộc tia
và bán kính bằng 7. Phương trình mặt cầu ( ) là
A x − 2 y2 z2 B x 2 y2 z2 . ( 7) + + = 49. . ( + 7) + + = 49. C x 2 y2 z2
D x − 2 y2 z2 . ( + 5) + + = 49. . ( 3) + + = 49. L TỰ LUẬN Câu 1 (SGK HH12). ABCD.A0B0C0D0 A B D − C0 − Cho hình hộp biết (1; 0; 1), (2; 1; 2), (1; 1; 1), (4; 5;
5). Tính tọa độ các đỉnh còn lại của hình hộp. − Ï Câu 2 (SGK HH12). − Ï a · b Tính biết − Ï − Ï − Ï − Ï a − b − a − b − a) = (3; 0; 6) và = (2; 4; 0) b) = (1; 5; 2) và = (4; 3; 5) Vocabulary − £ é space coplanar scalar product không gian đồng phẳng tích vô hướng plane midpoint length mặt phẳng trung điểm độ dài coordinates centroid sphere tọa độ trọng tâm mặt cầu point parallel radius điểm cùng phương bán kính Soạn: Huỳnh Phú Sĩ 39
Trường THCS-THPT Mỹ Thuận
§2. Phương trình mặt phẳng TOÁN 12
§2.PHƯƠNG TRÌNH MẶT PHẲNG
Nhắc lại về Phương trình tổng quát của đường thẳng trong mặt phẳng
VECTƠ PHÁP TUYẾN CỦA ĐƯỜNG THẲNG a b 1 1 − Ï − Ï − Ï 6
. . . . . . . . . . . . . . . n 6 . . . . . . n • Nếu
a = b thì ∆1 và ∆2
Cho đường thẳng ∆ và vectơ = 0 . Nếu của − Ï 2 2 n . . . . . . . . . . . .
vuông góc với ∆ thì ta nói là vectơ của ∆. a b c 1 1 6 1
. . . . . . . . . . . . . . . • Nếu
a = b = c thì ∆1 và ∆2 − Ï 2 2 2 n a b c 1 1 1
. . . . . . . . . . . . . . . • Nếu
a = b = c thì ∆1 và ∆2 2 2 2 ∆ . . . . . .
Góc giữa hai đường thẳng là một góc được xác định . . . . . . . . . bởi công thức • Mỗi đường thẳng có vectơ pháp tuyến. − Ï − Ï n k · n |a · a . . . . . .| • Nếu
là vectơ pháp tuyến của ∆ thì cũng là 1 2 +
. . . . . . . . . . . . . . . , cos (∆1 ∆2 ) = q của ∆. a2
b2 · . . . . . . . . . . . . +
PHƯƠNG TRÌNH TỔNG QUÁT CỦA ĐƯỜNG THẲNG 1 1 M x y
Cho đường thẳng ∆ đi qua điểm ( 0 ; 0 ) và có vectơ pháp − Ï
KHOẢNG CÁCH TỪ MỘT ĐIỂM ĐẾN MỘT ĐƯỜNG n a b tuyến = ( ; ). Khi đó THẲNG . . . x − . . . . . . y − . . . M x y ax ∆ : ( ) + ( ) = 0 Khoảng cách từ điểm ( 0 ; 0 ) đến đường thẳng ∆ : + by c
VỊ TRÍ TƯƠNG ĐỐI VÀ GÓC GIỮA HAI ĐƯỜNG THẲNG + = 0 bằng a x b y c a x a . . . b . . . c
Cho hai đường thẳng ∆1 : 1 + 1 + 1 = 0 và ∆2 : 2 + + + √ b y c M, d ( ∆) = 2 + 2 = 0. . . .2 . . .2 + 1
VECTƠ PHÁP TUYẾN CỦA MẶT PHẲNG 1 Tích có hướng − Ï − Ï a a a a b b b b Tích có hướng
Trong không gian, cho hai vectơ = ( 1 ; 2 ; 3 ) và = ( 1 ; 2 ; 3 ). của − Ï − Ï − Ï − Ï a b
. . . . . . . . . . . . . . . . . . a b hai vectơ và là một với cả và . h− Ï − Ïi a , b
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . = ( ; ; ) Ví dụ 1. − Ï − Ï u − v −
Tính tích có hướng của hai vectơ = (2; 1; 2) và = ( 12; 6; 0).
2 Vectơ pháp tuyến của mặt phẳng Định nghĩa − £ é − Ï − Ï α n 6 . . . . . . α Cho mặt phẳng ( ). Nếu vectơ = 0 và có
vuông góc với mặt phẳng ( ) thì − Ï n . . . . . . . . . . . . α được gọi là vectơ của ( ). . . . . . . . . . • Mỗi mặt phẳng có vectơ pháp tuyến. − Ï − Ï n α k · n
. . . . . . . . . . . . . . . α • Nếu
là vectơ pháp tuyến của ( ) thì cũng là của ( ). Ví dụ 2. Oxyz A − B C − Trong không gian cho ba điểm (2; 1; 3), (4; 0; 1), ( 10; 5; 3). Hãy tìm ABC
tọa độ một vectơ pháp tuyến của mặt phẳng ( ). Soạn: Huỳnh Phú Sĩ 40
Trường THCS-THPT Mỹ Thuận
§2. Phương trình mặt phẳng TOÁN 12 2
PHƯƠNG TRÌNH TỔNG QUÁT CỦA MẶT PHẲNG 1 Định nghĩa Oxyz α M x y z Trong không gian , cho mặt phẳng ( ) đi qua điểm ( 0 ; 0 ; 0 ) và có vectơ pháp − Ï n a b c tuyến = ( ; ; ). Khi đó a x − . . . . . . y . . . y c . . . − z . . . ( ) + ( 0 ) + ( 0 ) = − Ï I α Ax By Cz D m . . . . . . . . . Mặt phẳng ( ) : + + +
= 0 có một vectơ pháp tuyến = ( ; ; ). Ví dụ 3. α x − y − z . . . . . . . . . . . . Mặt phẳng ( ) : 4 2 6
+ 7 = 0 có một vectơ pháp tuyến là Ví dụ 4. Oxyz A − B C − Trong không gian cho ba điểm (2; 1; 3), (4; 0; 1), ( 10; 5; 3). Lập ABC
phương trình tổng quát của mặt phẳng ( ).
2 Các trường hợp riêng Oxyz α Ax By Cz D Trong không gian , cho mặt phẳng ( ) : + + + = 0. A α . . . . . . = 0: (
) song song hoặc trùng với trục B α . . . . . . = 0: (
) song song hoặc trùng với trục C α . . . . . . = 0: (
) song song hoặc trùng với trục ! D α . . . . . . . . . = 0: ( ) đi qua điểm A B α . . . . . . = = 0: (
) song song hoặc trùng với mặt phẳng A C α . . . . . . = = 0: (
) song song hoặc trùng với mặt phẳng B C α . . . . . . = = 0: (
) song song hoặc trùng với mặt phẳng Ví dụ 5. β Oxz Mặt phẳng (
) song song với mặt phẳng
và cắt trục tung tại điểm có tung β
độ bằng 3. Viết phương trình mặt phẳng ( ).
Phương trình mặt phẳng theo đoạn chắn − £ é α Ox Oy Oz A a B b C c Nếu mặt phẳng ( ) cắt các trục , , lần lượt tại ( ; 0; 0), (0; ; 0) và (0; 0; ) thì x y z α . . . ( ) :
a + b + c = Ví dụ 6. HKT H K T −
Viết phương trình mặt phẳng ( ), biết (2; 0; 0), (0; 0; 5), (0; 3; 0). 3
ĐIỀU KIỆN ĐỂ HAI MẶT PHẲNG SONG SONG, VUÔNG GÓC Oxyz α A x B y C z D β A x Trong không gian cho hai mặt phẳng ( ) : 1 + 1 + 1 + 1 = 0 và ( ) : 2 + B y C z D 2 + 2 + 2 = 0. Khi đó: ( ( A B C . . . k A B C A B C . . . k A B C ! α ( ( ( ( ∥ β ⇔ 1 ; 1 ; 1 ) 2 ; 2 ; 2 ) α ≡ β ⇔ 1 ; 1 ; 1 ) 2 ; 2 ; 2 ) • ( ) ( ) D . . . kD • ( ) ( ) D . . . kD 1 2 1 2
α ⊥ β ⇔ . . . . . . . . . . . . • ( ) ( ) Ví dụ 7. Oxyz Q x − y z − Trong không gian , cho mặt phẳng ( ) : 2 + 5 15 = 0 và điểm E − P E Q (1; 2; 3). Mặt phẳng ( ) qua và song song với ( ) có phương trình là A x y − z B x y − z − . + 2 3 + 15 = 0. . + 2 3 15 = 0. C x − y z D x − y z − . 2 + 5 + 15 = 0. . 2 + 5 15 = 0. Soạn: Huỳnh Phú Sĩ 41
Trường THCS-THPT Mỹ Thuận
§2. Phương trình mặt phẳng TOÁN 12 4
KHOẢNG CÁCH TỪ MỘT ĐIỂM ĐẾN MỘT MẶT PHẲNG Oxyz M x y z Trong không gian , khoảng cách từ điểm ( 0 ; 0 ; 0 ) đến mặt phẳng α Ax By Cz D ( ) : + + + = 0 được tính bằng A . . . B . . . C . . . D M, α + + + √ d ( ( )) = . . .2 . . .2 . . .2 + + Ví dụ 8. Q − γ x − y z −
Tính khoảng cách từ điểm (1; 0; 3) đến mặt phẳng ( ) : 2 + 2 5 = 0. Ví dụ 9. λ x − y z γ x −
Tính khoảng cách giữa hai mặt phẳng ( ) : 2 + 2 + 5 = 0 và ( ) : y z − 2 + 2 5 = 0. 5 THỰC HÀNH Í TRẮC NGHIỆM Câu 1. Oxyz ~ a − − ~ b m Trong không gian , cho ba vectơ = (3; 1; 2), = (1; 2; ) và h i ~ c m ~ a, ~ b ~ c
= (5; 1; 7). Tìm giá trị của để = . A m − B m C m D m . = 1. . = 0. . = 1. . = 2. Câu 2. Oxyz P x − y −
Trong không gian với hệ tọa độ , cho mặt phẳng ( ) : 2 5 8 = 0. P
Tìm tọa độ một vectơ pháp tuyến của mặt phẳng ( ). A − Ï − Ï n − − B n − . = (2; 5; 8). . = (2; 5; 0). C − Ï − Ï n − D n − − . = (2; 0; 5). . = ( 1; 2; 0). Câu 3. Oxyz Trong không gian với hệ tọa độ , phương trình nào dưới đây là − Ï M − n
phương trình của mặt phẳng đi qua điểm (5; 2;
1) và có vectơ pháp tuyến = − (1; 1; 2)? A x y − z B x y − z − . + 2 + 9 = 0. . + 2 9 = 0. C x y − z D x y − z − . 5 + 2 + 9 = 0. . 5 + 2 9 = 0. Câu 4. Oxyz A − , B −
Trong không gian với hệ tọa độ , cho ba điểm (2; 1; 1) ( 1; 0; 4) C − − và (0; 2;
1). Phương trình nào dưới đây là phương trình của mặt phẳng đi qua A BC điểm
và vuông góc với đường thẳng ? A x − y − z − B x − y − z . 2 5 5 = 0. . 2 5 + 5 = 0. C x − y − z − D x y − z − . 2 5 2 = 0. . 2 + 5 = 0. Câu 5. Oxyz Trong không gian với hệ tọa độ , phương trình nào dưới đây là M −
phương trình của mặt phẳng đi qua điểm (1;
2; 0) và song song với mặt phẳng P x − y z − ( ) : + 3 6 = 0? A x − y z − B x − y z . + 3 1 = 0. . + 3 + 1 = 0. C x − y z − D x − y z . + 3 3 = 0. . + 3 + 3 = 0. Câu 6. Oxyz A − α x y−z Trong không gian , cho (2; 3; 0) và mặt phẳng ( ) : +2 +3 = 0. P A P α P
Tìm phương trình mặt phẳng ( ) đi qua sao cho ( ) vuông góc với ( ) và ( ) Oz song song với trục ? A x y − B y z . 2 + 1 = 0. . + 2 + 3 = 0. C x − y − D x y − z . 2 7 = 0. . + 2 + 4 = 0. Câu 7. Oxyz Trong không gian
, chọn câu đúng trong các câu sau: A Oxy z . Mặt phẳng tọa độ ( ) có phương trình = 0. Soạn: Huỳnh Phú Sĩ 42
Trường THCS-THPT Mỹ Thuận
§2. Phương trình mặt phẳng TOÁN 12 B Ozx x . Mặt phẳng tọa độ ( ) có phương trình = 0. C Oyz y z . Mặt phẳng tọa độ ( ) có phương trình + = 0. D Oxy x y . Mặt phẳng tọa độ ( ) có phương trình + = 0. Câu 8. P S x − 2 y 2 z − 2 Mặt phẳng (
) tiếp xúc với mặt cầu ( ) : ( 1) + ( + 3) + ( 2) = 49 M − tại điểm (7; 1; 5) có phương trình là A x y z − B x y z . 6 + 2 + 3 55 = 0. . 6 + 2 + 3 + 55 = 0. C x y z − D x y z . 3 + + 22 = 0. . 3 + + + 22 = 0. Câu 9. Oxyz ABCD A − B − Trong không gian , cho tứ diện có (3; 2; 1), ( 4; 0; 3), C − D AC BD (1; 4; 3),
(2; 3; 5). Phương trình mặt phẳng chứa và song song với là A x − y z − B x y − z . 12 10 + 21 35 = 0. . 12 + 10 21 + 35 = 0. C x y z D x − y − z − . 12 + 10 + 21 + 35 = 0. . 12 10 21 35 = 0. Câu 10. Oxyz M − Trong không gian
, mặt phẳng đi qua điểm (1; 1; 1) và vuông x y − z − + 1 2 1
góc với đường thẳng ∆ : = = có phương trình là 2 2 1 A x y z B x − y − z . 2 + 2 + + 3 = 0. . 2 = 0. C x y z − D x − y − z − . 2 + 2 + 3 = 0. . 2 2 = 0. Câu 11. Oxyz A − B Trong không gian , cho hai điểm (4; 1; 2) và (5; 9; 3). Phương AB
trình mặt phẳng trung trực của đoạn là A x y − z B x y − z − . 2 + 6 5 + 40 = 0. . + 8 5 41 = 0. C x − y − z − D x y z − . 8 5 35 = 0. . + 8 + 5 47 = 0. Câu 12. Oxyz P H Trong không gian , cho mặt phẳng ( ) chứa điểm (1; 2; 2) và cắt Ox Oy Oz A, B, C H ABC các trục , , lần lượt tại sao cho
là trực tâm của tam giác . P
Phương trình mặt phẳng ( ) là A x y − z − B x y z − . + 2 2 9 = 0. . 2 + + 6 = 0. C x y z − D x y z − . 2 + + 2 = 0. . + 2 + 2 9 = 0. Câu 13. Oxyz A − B C Trong không gian , cho ba điểm ( 2; 0; 0), (0; 0; 7), (0; 3; 0). Phương ABC trình mặt phẳng ( ) là A x y z B x y z . − + + = 1. . − + + = 0. 2 7 3 2 3 7 C x y z D x y z . − + + = 1. . − + + + 1 = 0. 2 3 7 2 3 7 Câu 14. Oxyz G P px qy rz Trong không gian , cho điểm (1; 2; 3). Gọi ( ) : + + + 1 = 0 p, q, r ∈ R G Ox, Oy, Oz A, B, C ( ) là mặt phẳng qua và cắt các trục tại sao cho G ABC T p q r
là trọng tâm của tam giác . Tính = + + . A T − 11 B T 11 C T D T − . = . . = . . = 18. . = 18. 18 18 Câu 15. Oxyz A, B, C Trong không , gọi
lần lượt là hình chiếu vuông góc của M ABC điểm
(1; 2; 3) lên các trục tọa độ. Mặt phẳng ( ) có phương trình là A x y z 1 2 3 B .
x + y + z = 1. . + + = 1. 1 2 3 C x y z 1 2 3 D .
x + y + z = 0. . + + = 0. 1 2 3 Câu 16. Oxyz M, N, K Trong không , gọi
lần lượt là hình chiếu vuông góc của A − MNK điểm (2;
3; 1) lên các mặt phẳng tọa độ. Phương trình mặt phẳng ( ) là A x y z B x − y z . + + = 1. . 3 2 + 6 = 6. 2 3 1 C x y z − D x − y z − . + = 0. . 3 2 + 6 12 = 0. 2 3 1 Câu 17. Oxyz P x − y z − Trong không gian , cho hai mặt phẳng ( ) : 3 + 2 1 = 0 và Q x − z α P Q ( ) : + 2 = 0. Mặt phẳng ( ) vuông góc với cả ( ) và ( ), đồng thời cắt trục Ox α
tại điểm có hoành độ bằng 3. Phương trình của ( ) là A x y z − B x y z . + + 3 = 0. . + + + 3 = 0. C − x z D − x z − . 2 + + 6 = 0. . 2 + 6 = 0. Câu 18. Oxyz M − α x Trong không gian , cho điểm (2; 1; 2) và hai mặt phẳng ( ) : + y − z − β x − y z P 2 4 = 0, ( ) : 2 + 3
+ 1 = 0. Viết phương trình mặt phẳng ( ) đi qua M α β
đồng thời vuông góc với giao tuyến của ( ) và ( ). A x − y z B x − y − z − . 7 + 3 + 11 = 0. . 7 3 1 = 0. C x − y z D x y − z − . + 3 + 5 = 0. . + 3 9 = 0. Câu 19. Oxyz A − B − − C Trong không gian , cho ba điểm (3; 1; 2), (4; 1; 1) và (2; 0; 2). A, B, C
Mặt phẳng đi qua ba điểm có phương trình là A x − y z − B x y z − . 3 3 + 14 = 0. . 3 + 3 + 8 = 0. C x − y z − D x y − z . 3 2 + 8 = 0. . 2 + 3 + 8 = 0. Soạn: Huỳnh Phú Sĩ 43
Trường THCS-THPT Mỹ Thuận
§2. Phương trình mặt phẳng TOÁN 12 Câu 20. Oxyz M a b c P x y Trong không gian , điểm ( ; ; ) thuộc mặt phẳng ( ) : + + z − a b c 6 = 0. Tổng + + bằng A B − C D . 6. . 6. . 0. . 5. Câu 21. Oxyz P x − y Trong không gian , mặt phẳng ( ) : 3 + 1 = 0 đi qua điểm nào sau đây? A A B B − C C − D D . (3; 1; 1). . (1; 3; 1). . ( 1; 0; 0). . (1; 0; 0). Câu 22. Oxyz P x − y − z − Trong không gian , cho hai mặt phẳng ( ) : 2 3 = 0 và Q x − z − P Q ( ) :
2 = 0. Tính số đo góc giữa hai mặt phẳng ( ) và ( ). A P , Q ◦ B P , Q ◦ . (( ) ( )) = 30 . . (( ) ( )) = 45 . C P , Q ◦ D P , Q ◦ . (( ) ( )) = 60 . . (( ) ( )) = 90 . √ Câu 23. Oxyz ABCD A B C Trong không gian , cho tứ diện có (0; 2; 0), (2; 0; 0), 0; 0; 2 D − ABC ACD và (0;
2; 0). Tính số đo góc của hai mặt phẳng ( ) và ( ). A ◦ B ◦ C ◦ D ◦ . 30 . . 45 . . 60 . . 90 . Câu 24. M − P x − y z − Khoảng cách từ (1; 4; 7) đến mặt phẳng ( ) : 2 + 2 9 = 0 là A B C 25 D . 5. . 12. . . . 7. 3 Câu 25. P x − y z Q x − y
Khoảng cách giữa mặt phẳng ( ) : 2 + 3 + 5 = 0 và ( ) : 2 + z 3 + 1 = 0 bằng A B 6 √ C D 4 √ . 4. . . . 6. . . 14 14 Câu 26. Oxyz Trong không gian với hệ tọa độ , phương trình nào dưới đây là I − P x
phương trình của mặt cầu có tâm (3;
1; 0) và tiếp xúc với mặt phẳng ( ) : + y − z − 2 2 10 = 0? A x − 1 2 y 2 z2 B x − 2 y 2 z2 . ( 3) + ( + 1) + = 9. . ( 3) + ( + 1) + = . 9 C x 1 2 y − 2 z2 D x 2 y − 2 z2 . ( + 3) + ( 1) + = 9. . ( + 3) + ( 1) + = . 9 Câu 27. Oxyz P x − y z Trong không gian , cho hai mặt phẳng ( ) : 2 3 + 4 + 20 = 0 Q x − y − z P Q và ( ) : 4 13 6
+ 40 = 0. Vị trí tương đối của ( ) và ( ) là A. Song song. B. Trùng nhau.
C. Cắt nhau nhưng không vuông góc. D. Vuông góc. Câu 28. Oxyz Trong không gian , cặp mặt phẳng nào sau đây song song với nhau? A P x − y z − Q − x y − z . ( ) : 2 + 5 = 0 và ( ) : 3 + 2 2 + 10. B R x − y z − S x − y z . ( ) : + 3 = 0 và ( ) : 2 2 + 2 + 6 = 0. C x y z T x − y z U − . ( ) : + = 0 và ( ) : + = 0. 2 2 2 D X x − y z − Y z − y − . ( ) : 3 + 2 3 = 0 và ( ) : 6 2 6 = 0. Câu 29. Oxyz A − P x Trong không gian , cho điểm (
1; 2; 1) và hai mặt phẳng ( ) : 2 + y − z − Q x y − z 4 6 5 = 0, ( ) : + 2 3
= 0. Mệnh đề nào sau đây là đúng? A Q A P . Mặt phẳng ( ) đi qua và song song với ( ). B Q A P . Mặt phẳng ( ) không đi qua và song song với ( ). C Q A P . Mặt phẳng ( ) đi qua và không song song với ( ). D Q A P . Mặt phẳng ( ) không đi qua và không song song với ( ). Câu 30. Oxyz P x − y z Trong không gian , cho hai mặt phẳng ( ) : 3 + 2 + 1 = 0 và Q m − x m − m y m − z m P Q ( ) : (2 1) + (1 2 ) + (2 4) + 14 = 0. Tìm để ( ) và ( ) vuông góc với nhau. A m m − 3 B m − m − 3 . = 1 hoặc = . . = 1 hoặc = . 2 2 C m D m 3 . = 2. . = . 2 Soạn: Huỳnh Phú Sĩ 44
Trường THCS-THPT Mỹ Thuận
§2. Phương trình mặt phẳng TOÁN 12 L TỰ LUẬN
Câu 1 (SGK HH12). Viết phương trình của mặt phẳng − Ï M − n a) Đi qua điểm (1; 2; 4) và nhận
= (2; 3; 5) làm vectơ pháp tuyến; − Ï − Ï A − u v − b) Đi qua điểm (0;
1; 2) và song song với giá của mỗi vectơ = (3; 2; 1) và = ( 3; 0; 1); A − B − C − c) Đi qua ba điểm ( 3; 0; 0), (0; 2; 0) và (0; 0; 1); M − β x − y z d) Đi qua điểm (2;
1; 2) và song song với mặt phẳng ( ) : 2 + 3 + 4 = 0; A B β x − y z − e) Đi qua hai điểm (1; 0; 1),
(5; 2; 3) và vuông góc với mặt phẳng ( ) : 2 + 7 = 0; AB A B f)
Trung trực của đoạn thẳng với (2; 3; 7) và (4; 1; 3). Câu 2 (SGK HH12). m n
Xác định các giá trị của và
để mỗi cặp mặt phẳng sau đây là một cặp mặt phẳng song song với nhau: x my z − nx − y − z x − y mz − x ny − z a) 2 + + 3 5 = 0 và 8 6 + 2 = 0 b) 3 5 + 3 = 0 và 2 + 3 + 1 = 0 Soạn: Huỳnh Phú Sĩ 45
Trường THCS-THPT Mỹ Thuận
§3. Phương trình đường thẳng TOÁN 12
§3.PHƯƠNG TRÌNH ĐƯỜNG THẲNG
Nhắc lại về Phương trình tham số của đường thẳng trong mặt phẳng
VECTƠ CHỈ PHƯƠNG CỦA ĐƯỜNG THẲNG
PHƯƠNG TRÌNH THAM SỐ CỦA ĐƯỜNG THẲNG − Ï − Ï − Ï u 6 giá n M x y Cho đường thẳng ∆ và vectơ = 0 . Nếu của − Ï
Cho đường thẳng ∆ đi qua điểm ( 0 ; 0 ) và có vectơ chỉ − Ï . . . . . . . . . . . . . . . . . . u u u u hoặc với ∆ thì ta nói là vectơ phương = ( 1 ; 2 ). Khi đó
. . . . . . . . . . . . của ∆. − Ï u (x . . . . . . . . . . . . t = + ∆ : y . . . . . . . . . . . . t = + ∆ Chú ý: u , u 6 Nếu 1 2
= 0 thì phương trình trên có thể viết . . . . . . . . . chính tắc dưới dạng như sau: • Mỗi đường thẳng có vectơ chỉ phương. − Ï − Ï u k · u • Nếu
là vectơ chỉ phương của ∆ thì cũng là x − . . . y − . . .
. . . . . . . . . . . . . . . của ∆. . . . = . . . 1
PHƯƠNG TRÌNH THAM SỐ CỦA ĐƯỜNG THẲNG Định nghĩa − £ é Oxyz M x y z Trong không gian cho đường thẳng ∆ đi qua điểm ( 0 ; 0 ; 0 ) và nhận − Ï u u u u = ( 1 ; 2 ; 3 )
làm vectơ chỉ phương. Khi đó phương trình tham số của ∆ có dạng x . . . . . . . . . . . . t  = +  y . . . . . . . . . . . . t ∆ : = + (1)  z . . . . . . . . . . . . t = + t . . . . . . . . . . . . trong đó là Ví dụ 1. A −
Viết phương trình tham số của đường thẳng ∆ đi qua điểm (1; 2; 3) và có − Ï v vectơ chỉ phương = (1; 4; 5). ! u , u , u 6 chính tắc Nếu 1 2 3
= 0 thì phương trình (1) có thể viết dưới dạng như sau: x − . . . y − . . . y − . . . . . . = . . . = . . . Ví dụ 2. AB A − B
Viết phương trình chính tắc của đường thẳng với (1; 2; 3) và (3; 0; 0). Ví dụ 3. x − y − z 1 2 Cho đường thẳng ∆ : = =
. Mặt phẳng nào sau đây chứa đường 1 2 3 thẳng ∆? A α x y z B β x y − z . ( ) : 2 + 4 + 6 + 9 = 0. . ( ) : + + 3 = 0. C λ x y − z − D γ x y − z . ( ) : + 3 = 0. . ( ) : + 2 + 3 = 0. Soạn: Huỳnh Phú Sĩ 46
Trường THCS-THPT Mỹ Thuận
§3. Phương trình đường thẳng TOÁN 12 2
HAI ĐƯỜNG THẲNG SONG SONG, CẮT NHAU, CHÉO NHAU
Điều kiện để hai đường thẳng song song − Ï − Ï − Ï u , v M, u M ∈ Gọi
lần lượt là vectơ chỉ phương của hai đường thẳng ∆ ∆ ∆ ∆ 1 1 2 và điểm 1 . (− Ï (− Ï u k . . . . . . u k . . . . . . = = ∥ ⇔ ≡ ⇔ • ∆1 ∆2 M . . . . . . • ∆1 ∆2 M . . . . . . ∆ − Ï 2 v ∆2 ∆2
Ví dụ 4. Cặp đường thẳng nào dưới đây song song, trùng nhau?   x − t x − t0  = 3  = 2 3   d y t d0 y t0 a) : = 4 + và : = 5 + 3   z − tz − t0 = 5 2 = 3 6   x t x t0  = 1 +  = 2 + 2   d y t d0 y t0 b) : = 2 và : = 3 + 4   z − tz − t0 = 3 = 5 2
Điều kiện để hai đường thẳng cắt nhau   x x u t x x0 v t0  =  = +  0 + 1  0 1 d y y u t d0 y y0 v t0 Hai đường thẳng : = 0 + 2 và : = + cắt nhau khi và chỉ 0 2   z z u tz z0 v t0 = 0 + 3 = + 0 3 khi hệ phương trình x u t x0 v t0  = +  0 + 1 0 1 y u t y0 v t0 0 + 2 = + 0 2  z u t z0 v t0 0 + 3 = + 0 3 . . . . . . có đúng nghiệm.   x − t x t0  = 3  = 1 + 2   Ví dụ 5. d y − t d y − t0
Tìm giao điểm của hai đường thẳng 1 : = 2 3 và 2 : = 3 .   z tz − t0 = = 3 3
Điều kiện để hai đường thẳng chéo nhau   x x u t x x0 v t0  =  = +  0 + 1  0 1 d y y u t d0 y y0 v t0 Hai đường thẳng : = 0 + 2 và : = + chéo nhau khi và 0 2   z z u tz z0 v t0 = 0 + 3 = + 0 3 − Ï − Ï
u , v . . . . . . . . . . . . chỉ khi hai vectơ
phương và hệ phương trình x u t x0 v t0  = +  0 + 1 0 1 y u t y0 v t0 0 + 2 = + 0 2  z u t z0 v t0 0 + 3 = + 0 3 . . . . . . nghiệm. Soạn: Huỳnh Phú Sĩ 47
Trường THCS-THPT Mỹ Thuận
§3. Phương trình đường thẳng TOÁN 12   x − t x t0  = 5  = 1 + 2   Ví dụ 6. d y − t d y − t0
Xét vị trí tương đối của hai đường thẳng 1 : = 2 3 và 2 : = 3 .   z tz − t0 = 4 + = 3 x x u t  =  0 + 1 y y u t α Ax
Để tìm giao điểm của đường thẳng ∆ : = 0 + 2 và mặt phẳng ( ) : +  z z u t = 0 + 3 By Cz D + + = 0, ta xét phương trình ! A x u t B y u t C z u t D ( 0 + 1 ) + ( 0 + 2 ) + ( 0 + 3 ) + = 0 (1) . . . . . . . . . α •
Nếu (1) vô nghiệm thì ∆ ( ) . . . . . . . . . α •
Nếu (1) vô số nghiệm thì ∆ ( ) . . . . . . . . . α •
Nếu (1) có đúng một nghiệm thì ∆ ( ) Ví dụ 7. α x y z −
Tìm giao điểm của mặt phẳng ( ) : + +
3 = 0 với các đường thẳng sau:    x t x t x t  = 2 +  = 1 + 2  = 1 + 5    d y − t d y − t d y − t a) 1 : = 3 b) 2 : = 1 c) 3 : = 1 4    zz − tz t = 1 = 1 = 1 + 3 3 THỰC HÀNH Í TRẮC NGHIỆM Câu 1. x Oxyz d + 1 Trong không gian
, điểm nàọ dưới đây thuộc đường thẳng : − = 1 y − z − 2 1 = ? 3 3 A P − B Q − − C N − D M . ( 1; 2; 1). . (1; 2; 1). . ( 1; 3; 2). . (1; 2; 1). x  = 3  Câu 2. Oxyz y t
Trong không gian với hệ tọa độ , cho đường thẳng ∆ : = 2 + 2 .  z − t = 1 3 M Tìm tọa độ điểm thuộc đường thẳng ∆. A M − B M C M D M . (0; 2; 3). . (3; 2; 2). . (3; 4; 2). . (3; 0; 4). Soạn: Huỳnh Phú Sĩ 48
Trường THCS-THPT Mỹ Thuận
§3. Phương trình đường thẳng TOÁN 12 x t  = 2 +  Câu 3. Oxyz y − t
Trong không gian với hệ tọa độ , cho đường thẳng ∆ : = 3 .  z = 1
Tìm tọa độ một vectơ chỉ phương của ∆. A − Ï − Ï u − B u − . = (1; 1; 0). . = (1; 1; 1). C − Ï − Ï u D u . = (2; 3; 1). . = (2; 3; 0). Câu 4. Oxyz Trong không gian
, vectơ nào dưới đây là một vectơ chỉ phương của M − N
đường thẳng đi qua hai điểm (2; 3; 1) và (4; 5; 3)? A − Ï − Ï − Ï − Ï u B u C u D u . 4 = (1; 1; 1). . 3 = (1; 1; 2). . 1 = (3; 4; 1). . 2 = (3; 4; 2). Câu 5. x − y − z − Oxyz d 1 3 7 Trong không gian , đường thẳng : = − = nhận 2 4 1
vectơ nào dưới đây là một vectơ chỉ phương? A ~a − − B ~b . = ( 2; 4; 1). . = (2; 4; 1). C ~c − D ~d − . = (1; 4; 2). . = (2; 4; 1). Câu 6. Oxyz Trong không gian với hệ tọa độ , phương trình nào dưới đây là M − phương trình của đường thẳng đi qua điểm (2; 2; 2) và có vectơ chỉ phương − Ï u = (3; 1; 1)?   x t x t  = 1 + 3  = 2 + 3   A y − t B y − t . = 1 + . . = 2 + .   z tz t = 1 + = 2 +   x t x t  = 3 +  = 3 + 2   C y − t D y − t . = 1 . . = 1 2 .   z tz t = 1 + = 1 + 2 Câu 7. Oxyz
Trong không gian với hệ tọa độ
, phương trình nào dưới đây là phương A B −
trình của đường thẳng đi qua hai điểm (1; 1; 2) và (6; 11; 3)? A x − y − z x y z − 5 10 + 5 B + 5 + 10 5 . = = . . = = . 1 2 2 1 2 2 C x − y − z − x y z 1 1 2 D + 1 + 1 + 2 . = = − . . = = − . 1 2 1 1 2 1 Câu 8. Oxyz Trong không gian với hệ tọa độ , phương trình nào dưới đây là M
phương trình của đường thẳng đi qua điểm
(0; 4; 1) và vuông góc với mặt phẳng P x − y − z ( ) : 2 2 = 0?   x − x  = 2  = 2   A y t B y − t . = 2 + 4 . . = 2 + 4 .   z tz − t = 1 + = 1 +   x t x t  =  = 2   C y − t D y − t . = 4 . . = 4 2 .   z − tz − t = 1 2 = 1 Câu 9. A
Phương trình đường thẳng ∆ đi qua điểm
(3; 2; 1) và song song với đường x y z + 3 thẳng = = là 2 4 1   x − t x t  = 3 2  = 2 + 3   A y − t B y t . = 2 4 . . = 4 + 2 .   z − tz t = 1 = 1 +   x t x t  = 2  = 3 + 2   C y t D y − t . = 4 . . = 2 4 .   z tz t = 3 + = 1 + Câu 10. Oxyz A P x Trong không gian , cho điểm
(3; 5; 3) và hai mặt phẳng ( ) : 2 + y z − Q x − y z − d + 2 8 = 0, ( ) : 4 +
4 = 0. Viết phương trình đường thẳng đi qua A P Q
và song song với cả hai mặt phẳng ( ), ( ).   x t x t  = 3 +  = 3 +   A d y − t B d y . : = 5 . . : = 5 .   zz − t = 3 = 3   x t x  = 3 +  = 3   C d y D d y t . : = 5 . . : = 5 + .   z tz − t = 3 + = 3 Soạn: Huỳnh Phú Sĩ 49
Trường THCS-THPT Mỹ Thuận
§3. Phương trình đường thẳng TOÁN 12 Câu 11. x Oxyz M − d + 3 Trong không gian , cho điểm (1; 3; 4), đường thẳng : = 2 y − z − 5 2 P x z − − = − và mặt phẳng ( ) : 2 +
2 = 0. Viết phương trình đường thẳng 5 1 M d P ∆ đi qua , vuông góc với và song song với ( ). A x − y z − x − y z − 1 + 3 4 B 1 + 3 4 . ∆ : = − = − . . ∆ : − = − = − . 1 1 2 1 1 2 C x − y z − x − y z − 1 + 3 4 D 1 + 3 4 . ∆ : = = − . . ∆ : = − = . 1 1 2 1 1 2 Câu 12. x − y z − Oxyz d 1 + 5 3 Trong không gian , cho đường thẳng : = − = . 2 1 4 d
Phương trình nào dưới đây là hình chiếu vuông góc của đường thẳng trên mặt P x phẳng ( ) : + 3 = 0?   x − x −  = 3  = 3   A y − − t B y − t . = 5 . . = 5 + .   z − tz t = 3 + 4 = 3 + 4   x − x −  = 3  = 3   C y − t D y − − t . = 5 + 2 . . = 6 .   z − tz t = 3 = 7 + 4 Câu 13. x − y − z − Oxyz d 1 3 1 Trong không gian , cho đường thẳng : = − = cắt 2 1 1 P x − y z − I a b c a b c mặt phẳng ( ) : 2 3 + 2 = 0 tại điểm ( ; ; ). Khi đó + + bằng A B C D . 7. . 3. . 9. . 5. Câu 14. Oxyz A − Trong không gian
, hình chiếu vuông góc của điểm ( 1; 1; 6) trên x t  = 2 +  y − t đường thẳng ∆ : = 1 2 là  z t = 2 A M − B H − . (3; 1; 2). . (11; 17; 18). C K D N − . (2; 1; 0). . (1; 3; 2). Câu 15. Oxyz A − Trong không gian
, tọa độ hình chiếu vuông góc của điểm (3; 2; 1) α x y z lên mặt phẳng ( ) : + + = 0 là A − B 5 2 − 7 C − D 1 1 1 . ( 2; 1; 1). . ; ; . . (1; 1; 2). . ; ; . 3 3 3 2 4 4 Câu 16. x Oxyz Trong không gian với hệ tọa độ , cho hai đường thẳng ∆ : = 1 x − t y z −  = 5  + 2 3 0 y − t = − và ∆ : = 2
. Mệnh đề nào dưới đây đúng? 2 1  z t = 3 + A 0 B 0 . ∆ song song với ∆ . . ∆ trùng với ∆ . C 0 D 0 . ∆ vuông góc với ∆ . . ∆ và ∆ chéo nhau. Câu 17. x Oxyz + 4 Trong không gian với hệ tọa độ , cho đường thẳng ∆ : = 2 y z − + 2 3 P x y m − z m = và mặt phẳng ( ) : 4 + 2 + ( 1)
+ 13 = 0. Tìm giá trị của 1 3 P để ( ) vuông góc với ∆. A m − B m C m − 7 D m 7 . = 7. . = 7. . = . . = . 3 3 x  = 1  Câu 18. Oxyz d y t Trong không gian , cho đường thẳng : = 1 + và hai mặt  z − t = 1 + P x − y z Q x y − z − phẳng ( ) : + + 1 = 0, ( ) : 2 +
4 = 0. Khẳng định nào sau đây đúng? A d ∥ P B d ∥ Q C P ∩ Q d D d⊥ P . ( ). . ( ). . ( ) ( ) = . . ( ). Câu 19. x − Oxyz M 2 Trong không gian , cho điểm
(1; 0; 3) và đường thẳng ∆ : = 1 y z − + 1 2 M = −
. Tính khoảng cách từ điểm đến đường thẳng ∆. 2 √ 2 √ √ √ A 34 B 26 C 10 D . . . . . . . 2. 3 3 3 Câu 20. Oxyz S x − 2 y − 2 z− 2 Trong không gian , cho mặt cầu ( ) : ( 2) + ( 3) + ( 5) = 100 M − − α x − y z và điểm ( 3; 3; 3) nằm trên mặt phẳng ( ) : 2 2 + + 15 = 0. Đường thẳng Soạn: Huỳnh Phú Sĩ 50
Trường THCS-THPT Mỹ Thuận
§3. Phương trình đường thẳng TOÁN 12 α M S A, B
∆ nằm trên mặt phẳng ( ), đi qua và cắt mặt cầu ( ) tại hai điểm sao cho AB đoạn thẳng
có độ dài lớn nhất. Viết phương trình đường thẳng ∆. A x y − z x y − z + 3 3 + 3 B + 3 3 + 3 . = = . . = = − . 1 1 3 16 11 10 C x y − z x y − z + 3 3 + 3 D + 3 3 + 3 . = = . . = = . 5 1 8 1 4 6 L TỰ LUẬN Câu 1 (SGK HH12). d
Viết phương trình tham số của đường thẳng
trong mỗi trường hợp sau: − Ï d M a − a) đi qua điểm
(5; 4; 1) và có vectơ chỉ phương = (2; 3; 1); d A − α x y − z b) đi qua điểm (2;
1; 3) và vuông góc với mặt phẳng ( ) : + + 5 = 0; x t  = 1 + 2  d B − y − t c) đi qua điểm (2; 0;
3) và song song với đường thẳng ∆ : = 3 + 3 ;  z t + 4 d P Q d) đi qua hai điểm (1; 2; 3) và (5; 4; 4); Câu 2 (SGK HH12). d d0
Xét vị trí tương đối của các cặp đường thẳng và
cho bởi các phương trình sau:     x − t x t0 x t x t0  = 3 + 2  = 5 +  = 1 +  = 1 + 2     d y − t d0 y − − t0 d y t d0 y − t0 a) : = 2 + 3 và : = 1 4 b) : = 2 + và : = 1 + 2     z tz t0z − tz − t0 = 6 + 4 = 20 + = 3 = 2 2 x − t  = 3 + 2  Câu 3 (SGK HH12). y − t α x − y z
Tính khoảng cách giữa đường thẳng ∆ : = 1 + 3 và mặt phẳng ( ) : 2 2 + + 3 = 0.  z − t = 1 + 2 Soạn: Huỳnh Phú Sĩ 51
Trường THCS-THPT Mỹ Thuận Phụ lục TOÁN 12 PHỤ LỤC
SỞ GIÁO DỤC VÀ ĐÀO TẠO
ĐỀ KIỂM TRA HỌC KÌ II NĂM HỌC 2018-2019 MÔN: TOÁN 12 THPT VĨNH LONG Đề có 05 trang
Thời gian làm bài 90 phút (bao gồm trắc nghiệm và tự luận) ( ) Họ và tên học sinh: Mã đề 101
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
I. PHẦN TRẮC NGHIỆM (40 câu, 8.0 điểm)
Câu 1. Cặp số nào sau đây có tính chất "Có một hàm số là nguyên hàm của hàm số còn lại"? A x 1 x −x 2 B x 2 x C D x 2 x . tan và . . sin 2 và sin . . e và e . . sin 2 và cos . 2 x 2 cos
Câu 2. Phát biểu nào sau đây là đúng? Z Z A x x x x x x C B x x x −x x x C . sin d = cos + sin + . . sin d = cos + sin + . Z Z C x x x −x x − x C D x x x x x − x C . sin d = cos sin + . . sin d = cos sin + . Câu 3. F x f x 1 F F Biết (
) là nguyên hàm của hàm số ( ) = x − và (2) = 1. Khi đó (3) bằng bao nhiêu? 1 A 3 B C D 1 . ln . . ln 2 + 1. . ln 2. . . 2 2 Z Câu 4. x · − x − x 3 +1 x − 1 3 +1 x n C m, n S m n Biết ( + 3) e d = m e (3 + ) + với
là các số nguyên. Tính tổng = + . A B C D . 10. . 1. . 9. . 19. 1 Z Câu 5. y f x − f − f I f 0 x x Cho hàm số = (
) có đạo hàm trên đoạn [ 2; 1] và ( 2) = 3, (1) = 7. Tính = ( ) d . −2 A I 7 B I − C I D I . = . . = 4. . = 10. . = 4. 3 Câu 6. y f x a b sai Cho hàm số = ( ) liên tục trên đoạn [ ;
]. Mệnh đề nào dưới đây ? b a b Z Z Z A f x x − f x x B k x k a − b , ∀k ∈ R . ( ) d = ( ) d . . d = ( ) . a b a b c b b b Z Z Z Z Z C f x x f x x f x x, ∀c ∈ a b D f x x f t t . ( ) d = ( ) d + ( ) d ( ; ). . ( ) d = ( ) d . a a c a a 3 2 Z Z √ Câu 7. x √ x f t t t x f t Nếu x d = ( ) d , với = 1 + thì
( ) là hàm số nào trong các hàm số dưới đây? 1 + 1 + 0 1 A f t t2 − B f t t2 t C f t t2 t D f t t2 − t . ( ) = 1. . ( ) = 2 + 2 . . ( ) = + . . ( ) = 2 2 . 2 Z Câu 8. I x 3 x Tính tích phân = ( + 2) d . 0 A I B I C I D I . = 60. . = 240. . = 56. . = 120. 2 e Z 2 Câu 9. − x I (1 ln ) x Tính = x d được kết quả là e A 4 B 5 C 1 D 13 . . . . . . . . 3 3 3 3 5 Z Câu 10. 1 x a a Biết rằng x − d = ln . Giá trị của là 2 1 1 A B C D . 81. . 27. . 3. . 9. π 2 Z Câu 11. x cos x a 4 b a, b c > S a b c Cho x d = ln , với là các số hữu tỉ, 0. Tính tổng = + + . 2 − x c + (sin ) 5 sin + 6 0 A S B S C S D S . = 3. . = 4. . = 0. . = 1. Soạn: Huỳnh Phú Sĩ 52
Trường THCS-THPT Mỹ Thuận Phụ lục TOÁN 12 5 Z Câu 12. x d a b c S − a b c2 Giả sử x ln 5 + ln 3 +
ln 2. Tính giá trị biểu thức = 2 + + 3 . 2 − x = 3 A S B S C S − D S . = 3. . = 6. . = 2. . = 0. π 4 1 1 Z Z Z Câu 13. x2 · f x f x ( ) R f x x x I f x x Cho hàm số ( ) liên tục trên , biết (tan ) d = 4 và x d = 2. Tính = ( ) d . 2 + 1 0 0 0 A B C D . 6. . 1. . 0. . 2. Câu 14. y 1 x2 y x
Diện tích hình phẳng được giới hạn bởi đường cong = và đường thẳng =
được tính theo công thức nào 2 sau đây? 2 2 2 2 Z Z Z 2 Z A S B 1 C 1 D 1 x 2 − x x S
x2 − x x S x2 − x x S x2 − x x . = 2 d . . = d . . = d . . = d . 2 2 2 0 0 0 0 Câu 15. y −x2 x − x x Ox
Tính diện tích hình phẳng giới hạn bởi các đường = + 4 3, = 0, = 3, . A −8 B −4 C 4 D 8 . . . . . . . . 3 3 3 3 Câu 16. C y x4 − x2
Tính diện tích hình phẳng giới hạn bởi ( ) : = 2 + 1 và trục hoành. A 8 B −15 C 15 D 16 . . . . . . . . 15 16 8 15 Câu 17. √ H y x y y − x y Cho (
) là hình phẳng giới hạn bởi đồ thị của các hàm số = , = 0, = 2 . H Diện tích của ( ) là √ √ A − 4 2 1 B 8 2 + 3 C 7 D 5 . . . . . . . . 2 3 6 6 6 1 x O 1 2 Câu 18. V y x Gọi
là thể tích của khối tròn xoay do hình phẳng giới hạn bởi các đường sau quay quanh trục hoành: = sin , y x x π = 0, = 0, = 12
. Mệnh đề nào dưới đây đúng? π π π π 12 12 12 12 Z Z Z Z A V π x 2 x B V π x x C V π2 x 2 x D V π2 x x . = (sin ) d . . = sin d . . = (sin ) d . . = sin d . 0 0 0 0 Câu 19. y f x y Cho hàm bậc hai = (
) có đồ thị như hình bên. Tính thể tích khối tròn xoay tạo y f x Ox Ox
thành khi quay hình phẳng giới hạn bởi đồ thị hàm số = ( ) và quanh . A π π π π 4 B −12 C 16 D 16 1 . . . . . . . . 3 15 15 5 x O 1 2 3 Câu 20. a t t − 2
Một ô tô đang chạy với vận tốc 54 km/h thì tăng tốc chuyển động nhanh dần đều với gia tốc ( ) = 3 8 (m/s ) t trong đó
là khoảng thời gian tính bằng giây. Quãng đường mà ô tô đi được sau 10 s kể từ lúc tăng tốc là A B C D . 540 m. . 150 m. . 250 m. . 246 m. Câu 21. z x − yi w i x x, y ∈ R z w x y Cho hai số phức = và = 2 + 3 , ( ). Biết = . Giá trị của và lần lượt là A − B − C D − . 2 và 3. . 2 và 0. . 0 và 2. . 0 và 2. −Ï −Ï −Ï Câu 22. Oxy A B − C OC OA OB
Trên mặt phẳng tọa độ , cho hai điểm (4; 0), (0; 3) và điểm thỏa mãn điều kiện = + . Khi đó C
số phức được biểu diễn bởi điểm là A z − − i B z i C z − i D z − i . = 3 4 . . = 4 + 3 . . = 4 3 . . = 3 + 4 . Câu 23. z i M z Oxy Cho số phức = 6 + 7 . Điểm biểu diễn cho số phức trên mặt phẳng là A M − − B M − C M i D M . ( 6; 7). . (6; 7). . (6; 7 ). . (6; 7). Câu 24. x, y z i xi y i Cho
là các số thực. Số phức = (1 + + + 2 ) bằng 0 khi A x − y − B x y C x − y − D x y . = 1; = 2. . = 0; = 0. . = 2; = 1. . = 2; = 1. Câu 25. z |z| z2 |z z| |z − z| Cho số phức thỏa mãn = 2 và + 1 = 4. Tính + + . √ √ √ A B C D . 3 + 7. . 3 + 2 2. . 7 + 3. . 16. Soạn: Huỳnh Phú Sĩ 53
Trường THCS-THPT Mỹ Thuận Phụ lục TOÁN 12 Câu 26. z x yi x, y ∈ R |z − − i| |z − | Cho số phức = + ( ) có môđun nhỏ nhất thỏa mãn điều kiện 4 2 = 2 . Tính P x2 y2 = + . A B C D . 10. . 16. . 8. . 32. Câu 27. − Tìm các căn bậc hai của 6. √ √ √ A − i B ± i C ± i D i . 6 . . 6 . . 6 . . 6 . Câu 28. z2 − z
Trong tập số phức, phương trình 2 + 5 = 0 có nghiệm là A z − ± i B z ± i C z − ± i D z ± i . = 1 2 . . = 2 2 . . = 2 2 . . = 1 2 . Câu 29. ~ m − ~ n sai Cho = (1; 0; 1), = (0; 1; 1). Kết luận nào ? A ~ m ~ n ◦ B ~ m, ~ n − . Góc của và là 30 . . [ ] = (1; 1; 1). C ~ m · ~ n − D ~ m ~ n . = 1. . và không cùng phương. Câu 30. Oxyz A − − B − − C − M ∈ Oxy
Trong không gian với hệ trục tọa độ , cho ba điểm (0; 2; 1), ( 2; 4; 3), (1; 3; 1). Tìm điểm ( ) − − Ï − − Ï −−Ï M A MB MC sao cho + + 3
đạt giá trị nhỏ nhất. A − 1 3 B 1 3 C 3 4 D 1 − 3 . ; ; 0 . . ; ; 0 . . ; ; 0 . . ; ; 0 . 5 5 5 5 5 5 5 5 Câu 31. Oxyz S x2 y2 z2 x − y z − I R Trong không gian , cho mặt cầu ( ) : + + + 6 4 + 2 2 = 0. Tọa độ tâm và bán kính của S ( ) là A I − − R B I − − R C I − R D I − R . ( 3; 2; 1) và = 4. . ( 3; 2; 1) và = 16. . (3; 2; 1) và = 4. . (3; 2; 1) và = 16. Câu 32. P S x − 2 y 2 z − 2 M − Mặt phẳng (
) tiếp xúc với mặt cầu ( ) : ( 1) + ( + 3) + ( 2) = 49 tại điểm (7; 1; 5) có phương trình là A x y z − B x y z C x y z − D x y z . 6 + 2 + 3 55 = 0. . 6 + 2 + 3 + 55 = 0. . 3 + + 22 = 0. . 3 + + + 22 = 0. Câu 33. Oxyz ABCD A − B − C − D Trong không gian , cho tứ diện có (3; 2; 1), ( 4; 0; 3), (1; 4; 3),
(2; 3; 5). Phương trình mặt phẳng AC BD chứa và song song với là A x − y z − B x y − z . 12 10 + 21 35 = 0. . 12 + 10 21 + 35 = 0. C x y z D x − y − z − . 12 + 10 + 21 + 35 = 0. . 12 10 21 35 = 0. Câu 34. Oxyz M α x y − z M α Trong không gian , cho điểm (1; 2; 0) và mặt phẳng ( ) : + 2 2 + 1 = 0. Khoảng cách từ đến ( ) là A B C D . 1. . 3. . 2. . 4. Câu 35. Oxyz S P x − y z Trong không gian
, phương trình mặt cầu (
) tiếp xúc với hai mặt phẳng song song ( ) : 2 + 2 + 6 = 0 Q x − y z − I Oy và ( ) : 2 + 2 10 = 0 có tâm trên trục là
A x2 y2 z2 y − 55
B x2 y2 z2 y − . + + + 2 = 0. . + + + 2 60 = 0. 9
C x2 y2 z2 − y
D x2 y2 z2 − y − 55 . + + 2 + 55 = 0. . + + 2 . 9 Câu 36. Oxyz S x2 y2 z2 x − y z −
Trong không gian với hệ tọa độ , cho mặt cầu ( ) : + + + 4 2 + 6 11 = 0 và mặt phẳng P x − y z C P S C ( ) : 2 + 2 + 1 = 0. Gọi (
) là đường tròn giao tuyến của ( ) và (
). Tính chu vi đường tròn ( ). A π B π C π D π . 10 . . 4 . . 6 . . 8 . Câu 37. α x y − z α0 x y z −
Vị trí tương đối của hai mặt phẳng ( ) : 3 + 2 + 1 = 0 và ( ) : 3 + + 11 1 = 0 là A B . Vuông góc với nhau. . Trùng nhau. C D .
Cắt nhau nhưng không vuông góc với nhau. . Song song với nhau. Câu 38. Oxyz M − ~ a − Trong không gian
, cho đường thẳng ∆ đi qua (0; 2;
3) và có vectơ chỉ phương = (4; 3; 1). Phương trình
tham số của đường thẳng ∆ là     x t x t x − t x  = 4  = 4  = 4  = 4     A y − − t B y − − t C y t D y − t . = 2 3 . . = 2 3 . . = 2 + 3 . . = 3 + 2 .     z tz − − tz − − tz − t = 3 + = 3 = 3 = 1 3 Câu 39. x y z A + 3
Phương trình đường thẳng ∆ đi qua điểm
(3; 2; 1) và song song với đường thẳng = = là 2 4 1     x − t x t x t x t  = 3 2  = 2 + 3  = 2  = 3 + 2     A y − t B y t C y t D y − t . = 2 4 . . = 4 + 2 . . = 4 . . = 2 4 .     z − tz tz tz t = 1 = 1 + = 3 + = 1 + Câu 40. x y z Oxyz P x y z − d + 1 + 2 Trong không gian , cho mặt phẳng ( ) : + 2 + 4 = 0 và đường thẳng : = = . Đường 2 1 3 P d
thẳng ∆ nằm trong mặt phẳng (
) đồng thời cắt và vuông góc với đường thẳng có phương trình là A x − y − z − x − y z − 1 1 1 B 1 + 1 1 . ∆ : = − = . . ∆ : = − = . 5 1 3 5 1 2 C x − y z − x − y − z − 1 + 1 1 D 1 1 1 . ∆ : = − = − . . ∆ : = − = − . 5 1 3 5 1 3
II. PHẦN TỰ LUẬN (2.0 điểm) Soạn: Huỳnh Phú Sĩ 54
Trường THCS-THPT Mỹ Thuận Phụ lục TOÁN 12 1 Z Câu 41. x 5 x Tính tích phân (2 + 1) d . 0
Câu 42. Tìm phần thực, phần ảo, số phức liên hợp và tính môđun của số phức − i z − i i 4 5 . = (2 4 ) (5 + 2 ) + i 2 + Câu 43. Oxyz ABC A − B − − − C − − Trong không gian , cho tam giác với (1; 3; 4), ( 2; 5; 7), (6; 3;
1). Viết phương trình đường AM ABC trung tuyến của tam giác . Soạn: Huỳnh Phú Sĩ 55
Trường THCS-THPT Mỹ Thuận Phụ lục TOÁN 12
BỘ GIÁO DỤC VÀ ĐÀO TẠO
KÌ THI TỐT NGHIỆP THPT QUỐC GIA NĂM 2019 Bài thi: TOÁN ĐỀ THI CHÍNH THỨC Đề có 05 trang
Thời gian làm bài: 90 phút, không kể thời gian phát đề ( )
Họ và tên thí sinh: .......................................................................................... Số báo danh: Mã đề 101
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . Câu 1. Oxyz P x − y z Trong không gian , cho mặt phẳng ( ) : 2 + 3
+ 1 = 0. Vectơ nào dưới đây là một vectơ pháp tuyến của P ( )? A − Ï − Ï − Ï − Ï n − − B n − C n D n . 1 = (2; 1; 3). . 2 = (2; 1; 3). . 3 = (2; 3; 1). . 4 = (2; 1; 3). Câu 2. u u u Cho cấp số cộng n ( ) với 1 = 2 và 2
= 8. Công sai của cấp số cộng đã cho bằng A B C − D . 4. . 10. . 6. . 6. Câu 3.
Đồ thị của hàm số nào dưới đây có dạng như đường cong trong hình vẽ bên? y A y x3 − x B y x4 − x2 . = 3 + 1. . = 2 + 1. 3 C y −x3 x D y −x4 x2 . = + 3 + 1. . = + 2 + 1. 1 −1 2 −2 1 x −1 Câu 4. x − y − z Oxyz d 1 3 + 2 Trong không gian , cho đường thẳng : = − =
. Vectơ nào dưới đây là một vectơ chỉ phương 2 5 3 d của ? A − Ï − Ï − Ï − Ï u − B u C u − D u . 4 = (2; 5; 3). . 1 = (2; 5; 3). . 3 = (1; 3; 2). . 2 = (1; 3; 2). Câu 5. h r
Thể tích của khối nón có chiều cao và bán kính đáy là A 4πr 1 2 h B πr2h C πr2h D πr2h . . . . . . . 2 . 3 3 Câu 6. a a3 Với
là số thực dương tùy ý, log bằng 5 A a B 1 a C a D 1 a . 3 log . . + log . . 3 + log . . log . 5 5 5 5 3 3 Câu 7. f x Cho hàm số (
) có bảng biến thiên như sau: x −∞ ∞ 1 3 + f 0 x − − ( ) 0 + 0 ∞ + 2 f x ( ) −2 −∞
Hàm số đã cho đạt cực đại tại A x B x C x D x − . = 1. . = 3. . = 2. . = 2. Câu 8. − i
Số phức liên hợp của số phức 5 3 là A − i B i C − i D − − i . 5 + 3 . . 5 + 3 . . 3 + 5 . . 5 3 . Câu 9. f x x
Họ tất cả các nguyên hàm của hàm số ( ) = 2 + 6 là A x2 x C B x2 x C C x2 C D x2 C . 2 + 6 + . . + 6 + . . 2 + . . + . 1 1 1 Z Z Z Câu 10. f x x g x x − f x g x x Biết ( )d = 3 và ( )d = 4, khi đó ( ) + ( ) d bằng 0 0 0 A − B C − D . 7. . 7. . 1. . 1. Câu 11. x 2 +1
Nghiệm của phương trình 3 = 27 là A x B x C x D x . = 1. . = 5. . = 4. . = 2. Câu 12. Oxyz M − Oz Trong không gian
, hình chiếu vuông góc của điểm (3; 1; 1) trên trục có tọa độ là A B − C − D . (3; 0; 0). . (3; 1; 0). . (0; 1; 0). . (0; 0; 1).
Câu 13. Số cách chọn 2 học sinh từ 5 học sinh là A 2 B 2 C 2 D 5 . C . . 5 . . A . . 2 . 5 5 Câu 14. B h
Thể tích của khối lăng trụ có diện tích đáy và chiều cao là A Bh B 1Bh C 4Bh D Bh . 3 . . . . . . . 3 3 Câu 15. f x Cho hàm số (
) có bảng biến thiên sau: Soạn: Huỳnh Phú Sĩ 56
Trường THCS-THPT Mỹ Thuận Phụ lục TOÁN 12 x −∞ − ∞ 2 0 2 + f 0 x − − ( ) 0 + 0 0 + ∞ ∞ + + f x 3 ( ) 1 1
Hàm số đã cho đồng biến trên khoảng nào dưới đây? A ∞ B C −∞ − D − . (0; + ). . (0; 2). . ( ; 2). . ( 2; 0). Câu 16. f x R S Cho hàm số y ( ) liên tục trên . Gọi
là diện tích hình phẳng giới hạn bởi các y f x y x − x đường = ( ), = 0, = 1 và
= 5 (như hình vẽ bên). Mệnh đề nào dưới 1 đây là đúng? −1 1 5 1 5 1 5 Z Z Z Z A x S − f x x − f x x B S f x x − f x dx . = ( ) d ( ) d . . = ( ) d ( ) . − − 1 1 1 1 1 5 1 5 Z Z Z Z C S f x x f x x D S − f x x f x x . = ( ) d + ( ) d . . = ( ) d + ( ) d . −3 − − 1 1 1 1 Câu 17. f x Cho hàm số (
) có bảng biến thiên như sau: x −∞ − ∞ 2 0 2 + f 0 x − − ( ) 0 + 0 0 + ∞ ∞ + + f x 2 ( ) − − 1 1 f x −
Số nghiệm thực của phương trình 3 ( ) 5 = 0 là A B C D . 4. . 2. . 0. . 3. Câu 18. Oxyz A − , B Trong không gian , cho hai điểm ( 1; 2; 0)
(3; 0; 2). Phương trình mặt phẳng trung trực của đoạn thẳng AB là A x y z − B x − y z − C x y z − D x − y z . + + 3 = 0. . 2 + 2 = 0. . 2 + + 4 = 0. . 2 + + 2 = 0. Câu 19. ,
Một cơ sở sản xuất có hai bể nước hình trụ có chiều cao bằng nhau, bán kính đáy lần lượt bằng 1m và 1 4m. Chủ
cơ sở dự định làm một bể nước mới hình trụ, có cùng chiều cao và có thể tích bằng tổng thể tích của hai bể nước trên. Bán
kính đáy của bể nước dự định làm gần nhất với kết quả nào dưới đây? A , B , C , D , . 1 5 m. . 1 7 m. . 2 4 m. . 1 9 m. Câu 20. Oxyz S x2 y2 z2 − x y − Trong √ không gian , cho mặ √ t cầu ( ) : + + 2 + 2
7 = 0. Bán kính của mặt cầu đã cho bằng A B C D . 7. . 15. . 3. . 9. Câu 21. z z z2 − z z2 z2 Gọi 1 , 2
là hai nghiệm phức của phương trình 6 + 14 = 0. Giá trị của + bằng 1 2 A B C D . 28. . 36. . 8. . 18. Câu 22. a b a3b3 a b Cho và
là hai số thực dương thoả mãn = 32. Giá trị của 3 log + 2 log bằng 2 2 A B C D . 4. . 32. . 2. . 5. Câu 23. ABC.A0B0C0 a AA0 a Cho khối lăng trụ đứng
có đáy là tam giác đều cạnh bằng và = 2 (minh A0 C0
họa như hình vẽ bên). Thể tích của khối lăng trụ đã cho bằng √ √ √ √ A a3 a3 a3 3 B 3 C 3 D a3 . . . . . . . 3 . B0 3 2 6 a 2 A a C B Câu 24. S.ABC SA ABC SA a ABC B AB a Cho √ hình chóp có
vuông góc với mặt phẳng ( ), = 2 , tam giác vuông tại , = , BC a SC ABC =
3. Góc giữa đường thẳng và mặt phẳng ( ) bằng A ◦ B ◦ C ◦ D ◦ . 30 . . 90 . . 45 . . 60 . Soạn: Huỳnh Phú Sĩ 57
Trường THCS-THPT Mỹ Thuận Phụ lục TOÁN 12 Câu 25. x x −
Nghiệm của phương trình log + 1) = 1 + log 1) là 2 ( 2 ( A x − B x C x D x . = 2. . = 3. . = 2. . = 1. Câu 26. z − i z i Oxy z z Cho hai số phức 1 = 2 + và 2 = 1 +
. Trên mặt phẳng tọa độ
, điểm biểu diễn số phức 2 1 + 2 có tọa độ là A − B − C − D − . ( 3; 2). . (2; 3). . ( 3; 3). . (3; 3). Câu 27. f x x3 − x −
Giá trị nhỏ nhất của hàm số ( ) = 3 + 2 trên [ 3; 3] bằng A B C D − . 4. . 0. . 20. . 16. Câu 28. y f x Cho hàm số = (
) có bảng biến thiên như sau: x −∞ ∞ 0 2 + y0 − − 0 + ∞ + 2 y 0 −2 −∞
Tổng số tiệm cận đứng và tiệm cận ngang của đồ thị hàm số đã cho là A B C D . 1. . 3. . 4. . 2. Câu 29. f x f 0 x x x − 2 ∀x ∈ R Cho hàm số ( ) có đạo hàm ( ) = ( 2) ,
. Số điểm cực trị của hàm số đã cho là A B C D . 0. . 3. . 1. . 2. Câu 30. y x2− x 3 Hàm số = 3 có đạo hàm là A x − · x2− x x2− x x2− x− x2− x 3 · B 3 · C
x2 − x · 3 1 D x − · 3 . (2 3) 3 ln 3. . 3 ln 3. . 3 3 . . (2 3) 3 . Câu 31. z z − i − i z − i z Cho số phức thỏa mãn 3 ( ) (2 + 3 ) = 7 16 . Môđun √ của số phức bằng √ A B C D . 5. . 3. . 5. . 3. Câu 32. x − f x 3 1 ∞
Họ tất cả các nguyên hàm của hàm số ( ) = x − trên khoảng (1; + ) là 2 ( 1) A x − 1 C B x − 2 C . 3 ln ( 1) + x − + . . 3 ln ( 1) + x − + . 1 1 C x − − 1 C D x − − 2 C . 3 ln ( 1) x − + . . 3 ln ( 1) x − + . 1 1 π 4 Z Câu 33. f x f f 0 x 2 x , ∀x ∈ R f x x Cho hàm số ( ). Biết (0) = 4 và ( ) = 2 cos + 3 , khi đó ( ) d bằng 0 A π2 π2 π π2 π π2 π + 2 B + 8 + 2 C + 6 + 8 D + 8 + 8 . . . . . . . . 8 8 8 8 Câu 34. Oxyz A , B , C D A Trong không gian , cho các điểm (1; 0; 2) (1; 2; 1) (3; 2; 0) và
(1; 1; 3). Đường thẳng đi qua và vuông BCD góc với mặt phẳng ( ) có phương trình là     x − t x − t x t x t  = 1  = 1  = 1 +  = 2 +     A y − t B y t C y D y t . = 2 4 . . = 4 . . = 4 . . = 4 + 4 .     z − tz tz tz t = 2 2 = 2 + 2 = 2 + 2 = 4 + 2 Câu 35. f x f 0 x Cho hàm số ( ), bảng xét dấu ( ) như sau: x −∞ − − ∞ 3 1 1 + f 0 x − − ( ) 0 + 0 0 + y f − x Hàm số = (5 2
) nghịch biến trên khoảng nào dưới đây? A ∞ B C D . (5; + ). . (2; 3). . (0; 2). . (3; 5). Câu 36. x2 − x − − m m Cho phương trình log log 1) = log (
là tham số thực). Có tất cả bao nhiêu giá trị nguyên của 9 3 (6 3
m để phương trình đã cho có nghiệm? A B C D . Vô số. . 5. . 7. . 6. Câu 37. f x y f 0 x R Cho hàm số y ( ), hàm số = ( ) liên tục trên
và có đồ thị như hình vẽ bên. Bất f x > x m m x ∈ phương trình ( ) + (
là tham số thực) nghiệm đúng với mọi (0; 2) khi và chỉ khi 1 A m ≤ f B m < f − C m < f D m ≤ f − . (0). . (2) 2. . (0). . (2) 2. 2 x Soạn: Huỳnh Phú Sĩ 58
Trường THCS-THPT Mỹ Thuận Phụ lục TOÁN 12
Câu 38. Chọn ngẫu nhiên hai số khác nhau từ 27 số nguyên dương đầu tiên. Xác suất để chọn được hai số có tổng là một số chẵn bằng A 13 B 365 C 1 D 14 . . . . . . . . 27 729 2 27 Câu 39. S.ABCD a SAB Cho hình chóp
có đáy là hình vuông cạnh , mặt bên là tam giác đều và S
nằm trong mặt phẳng vuông góc với mặt phẳng đáy (minh họa như hình vẽ bên). Khoảng C SBD cách từ đến mặt phẳng √ ( ) bằng √ √ √ A a a a a 21 B 21 C 2 D 21 . . . . . . . . 7 28 2 14 A D B C √ Câu 40. Cho hình √ trụ có chiều cao bằng 4
2. Cắt hình trụ đã cho bởi mặt phẳng song song với trục và cách trục một khoảng bằng √
2, thiết diện thu được có diện √
tích bằng 16. Diện tích xung √
quanh của hình trụ đã cho √bằng A π B π C π D π . 8 2 . . 24 2 . . 16 2 . . 12 2 . Câu 41. y 3 x y 1 x2 a a Cho đường thẳng = và parabol = + (
là tham số thực dương). Gọi y 1 4 2 y x2 a S S = + 1 và 2
lần lượt là diện tích của hai hình phẳng được gạch chéo trong hình bên. 2 S S a y 3 x Khi 1 = 2 thì
thuộc khoảng nào dưới đây? = A 3 7 B 7 1 C 1 9 D 3 4 . ; . . ; . . ; . . 0; . 16 32 32 4 4 32 16 S2 S1 x O √ Câu 42. iz z |z| Oxy w 3 + Xét số phức thỏa mãn =
2. Trên mặt phẳng tọa độ
, tập hợp điểm biểu diễn các số phức = z là 1 +
một đường tròn có bán kính bằng √ √ A B C D . 12. . 2 3. . 2 5. . 20. Câu 43. Oxyz A − d Oz Oz Trong không gian , cho điểm (0; 4; 3). Xét đường thăng
thay đổi, song song với trục và cách trục A d d
một khoảng bằng 3. Khi khoảng cách từ đến lớn nhất,
đi qua điểm nào dưới đây? A P − − B M − − C Q − D N − . ( 3; 0; 3). . (0; 3; 5). . (0; 11; 3). . (0; 3; 5). 1 5 Z Z Câu 44. f x R f xf x x x2f 0 x x Cho hàm số (
) có đạo hàm liên tục trên . Biết (5) = 1 và (5 )d = 1, khi đó ( )d bằng 0 0 A − B C 123 D . 25. . 15. . . . 23. 5 Câu 45. y f x Cho hàm số bậc ba = (
) có đồ thị như hình vẽ bên. Số nghiệm thực của phương y 1 f x 3 − x trình ( 3 ) = là 2 A B C D . 3. . 12. . 6. . 10. 2 −2 2 x −1 Câu 46. x x x x y + 1 + 2 + 3 y |x | − x m m Cho hai hàm số = x + x + x + x và = + 1 + (
là tham số thực) có đồ thị lần + 1 + 2 + 3 + 4 C C m C C lượt là ( 1 ) và ( 2 ).
Tập hợp các giá trị của để ( 1 ) và ( 2 )
cắt nhau tại đúng bốn điểm phân biệt là A ∞ B −∞ C −∞ D ∞ . [3; + ). . ( ; 3]. . ( ; 3). . (3; + ). Câu 47. √ x 2 x − x − − m m Cho phương trình 2 log 3 log 2 3 = 0 (
là tham số thực) có tất cả bao nhiêu giá trị nguyên 2 2 m dương của
để phương trình đã cho có hai nghiệm phân biệt? A B C D . 80. . 81. . 79. . Vô số. √ Câu 48. Oxyz S x2 y2 z − 2 A a b c a b c Trong không gian , cho mặt cầu ( ) : + + ( 2)
= 3. Có tất cả bao nhiêu điểm ( ; ; ) ( , , là Oxy S A
các số nguyên) thuộc mặt phẳng (
) sao cho có ít nhất hai tiếp tuyến của ( ) đi qua
và hai tiếp tuyến đó vuông góc với nhau? A B C D . 12. . 4. . 16. . 8. Soạn: Huỳnh Phú Sĩ 59
Trường THCS-THPT Mỹ Thuận Phụ lục TOÁN 12 Câu 49. f x f 0 x Cho hàm số (
), bảng biến thiên của hàm số ( ) như sau: x −∞ − ∞ 1 0 1 + ∞ ∞ + + f 0 x 2 ( ) − − 1 3 y f x2 x
Số điểm cực trị của hàm số = + 2 là A B C D . 7. . 5. . 3. . 9. Câu 50. ABC.A0B0C0 M N P Cho lăng trụ
có chiều cao bằng 8 và đáy là tam giác đều cạnh bằng 4. Gọi , và lần lượt là tâm ABB0A0 ACC0A0 BCC0B0 A, B, C, M, N, P các mặt bên √ , và . Thể √
tích của khối đa diện lồi có các đỉnh là các điểm bằng √ √ A 40 3 B 28 3 C D . . . . . 16 3. . 12 3. 3 3 Soạn: Huỳnh Phú Sĩ 60
Trường THCS-THPT Mỹ Thuận