






Preview text:
CÔNG TY TNHH GIÁO DỤC THIÊN AN
HỌC VIỆN PARIS - 134 THỐNG NHẤT, TÂN THÀNH, TÂN PHÚ SĨ TOÁN GIẢ ẠC I T H Í T CH F MATHEMA MA MA TIC THEMA MA THEMA MA AL TIC THEMA TIC THEMA AL TIC F AL F ANALYSIS F F F giaoducthienan.vn N F F G N U Y IÊ Ễ K N HỮU CHUNG
TÀI LIỆU HỌC TẬP CHUẨN CẤU TRÚC MỚI TOÁN12
HỌC KÌ 1 − NĂM HỌC 2025 − 2026
• Tóm tắt chi tiết lí thuyết theo bài
• Phân chia dạng toán theo bài
• Bài tập từng bài chuẩn cấu trúc mới của BGD
• Đề ôn tập từng chương ax2 + bx + c y y = dx + e 3 b · 1 O a x −3 p ≥b+ 2a ¡ −5 a2 + b2¢ · ¡c2 + R d2¢ ≥ (a · c + b · d)2
TÀI LIỆU LƯU HÀNH NỘI ĐỊA Mục lục 5 3, Phần I
MỘT SỐ YẾU TỐ GIẢI TÍCH THỨ Chương 1.
ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ KIÊN 7 TỐI
Bài 1. Sự đồng biến, nghịch biến của hàm số 7 A
Tóm tắt lý thuyết. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .7 LỚP B
Các dạng toán thường gặp . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 8
| Dạng 1. Xét tính đơn điệu của hàm số cho bởi công thức ............................... 8
| Dạng 2. Xét tính đơn điệu dựa vào bảng biến thiên, đồ thị............................12 2026. | −
Dạng 3. Tìm điều kiện của tham số để hàm số đồng biến, nghịch biến trên một
khoảng . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 20
| Dạng 4. Ứng dụng sự biến thiên của hàm số để giải phương trình, bất phương 2025
trình. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .CHUNG
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 24
| Dạng 5. Toán thực tế sử dụng tính đồng biến, nghịch biến............................29
| Dạng 6. Tính đơn điệu của hàm hợp ............................................................. 37 HỌC
Bài 2. Cực trị của hàm số 47 A
Tóm tắt lý thuyết . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 47 NĂM B
Các dạng toán thường gặp . . .HỮU
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 48 HKI
| Dạng 1. Tìm cực trị của hàm số cho bởi công thức ....................................... 48 −
| Dạng 2. Tìm cực trị hàm số dựa vào bảng biến thiên hoặc đồ thị..................53
| Dạng 3. Tìm tham số để hàm số đạt cực trị tại một điểm ............................. 61 12
| Dạng 4. Tìm tham số để hàm số bậc ba có cực trị thỏa mãn điều kiện cho trước ÁN 65
| Dạng 5. Tìm tham số để hàm trùng phương có cực trị thỏa mãn điều kiện cho TO
trước . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 72
| Dạng 6. Tìm điều kiện của tham số để hàm bậc hai trên bậc nhất có cực trị thỏa TẬP
mãn điều kiện cho trước . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 77
| Dạng 7. Cực trị một số hàm số khác.............................................................83 HỌC | NGUYỄN
Dạng 8. Xét tính đơn điệu và cực trị của hàm số khi biết hàm số hoặc bảng biến
thiên hoặc đồ thị hàm số y = f 0 (x) . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 89
| Dạng 9. Cực trị của hàm hợp y = f (u).........................................................98 LIỆU
| Dạng 10. Ứng dụng cực trị trong thực tế.....................................................118 TÀI ThS:
Bài 3. Giá trị lớn nhất, giá trị nhỏ nhất của hàm số 126 Trang 2 Mục lục A
Tóm tắt lý thuyết . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 126 B
Các dạng toán thường gặp . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 126
| Dạng 1. Giá trị lớn nhất và giá trị nhỏ nhất của hàm số trên đoạn .............. 126 HCM
| Dạng 2. Giá trị lớn nhất, giá trị nhỏ nhất của hàm số trên khoảng .............. 131 TP
| Dạng 3. Giá trị lớn nhất, giá trị nhỏ nhất dựa vào đồ thị, bảng KIÊN biến thiên . . . 135
| Dạng 4. Ứng dụng GTLN, GTNN tìm điều kiện của tham số m để phương trình PHÚ,
có nghiệm . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 143
| Dạng 5. Ứng dụng GTLN, GTNN tìm điều kiện của tham số m để bất phương TÂN
trình có nghiệm đúng với mọi x thuộc (a; b), [a; b]. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .149
| Dạng 6. Ứng dụng GTLN, GTNN để tìm điều kiện bất phương trình có nghiệm
trên một khoảng, đoạn . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 155
| Dạng 7. Tìm GTLN, GTNN của hàm hợp, giá trị tuyệt đối và một số hàm số THÀNH,
khác . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 161
| Dạng 8. Toán thực tế ứng dụng khái niệm GTLN, GTNN của hàm số ......... 178 TÂN
Bài 4. Đường tiệm cận của đồ thị hàm số CHUNG 191 T, A
Tóm tắt lý thuyết . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 191 B
Các dạng toán thường gặp . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 192 NHẤ
| Dạng 1. Tìm tiệm cận của đồ thị hàm phân thức, hàm căn thức ................. 192 G
| Dạng 2. Tìm tiệm cận của
hàm ẩn. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .HỮU
đồ thị hàm mũ, hàm logarit . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 197
| Dạng 3. Tìm tiệm cận của đồ thị hàm số dựa vào BBT hoặc đồ thị, tiệm cận THỐN
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 202
| Dạng 4. Tiệm cận của đồ thị hàm số chứa tham số.....................................224 134
| Dạng 5. Bài toán tiệm cận liên quan đến tính toán tọa độ giao điểm...........234 −
| Dạng 6. Ứng dụng khái niệm tiệm cận vào bài toán thực tế ........................ 238 AN
Bài 5. Đồ thị của hàm số 242 A
Tóm tắt lý thuyết . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 242 B
Các dạng toán thường gặp . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 242 THIÊN
| Dạng 1. Đồ thị hàm số bậc ba .................................................................... 242
| Dạng 2. Đồ thị hàm bậc nhất trên bậc nhất ................................................ 252 TÂM | NGUYỄN
Dạng 3. Đồ thị hàm số bậc hai trên bậc nhất . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 266 G
| Dạng 4. Biến đổi đồ thị, đồ thị hàm số chứa dấu giá trị tuyệt đối................271 UN
| Dạng 5. Tương giao khi đề cho bảng biến thiên hoặc đồ thị ........................ 288 TR
| Dạng 6. Tương giao của hai đồ thị (liên quan đến tọa độ giao điểm)...........297
ThS:|Dạng7.Đồthịcủađạohàm.......................................................................302
ThS NGUYỄN HỮU CHUNG KIÊN − Ó 0987192212
Website www.thaykientoan.io.vn
TÀI LIỆU HỌC TẬP HKI TOÁN 12, NĂM HỌC 2024 − 2025 CHUẨN FORM MỚI Trang 3
| Dạng 8. Tiếp tuyến của đồ thị.....................................................................317
| Dạng 9. Điểm đặc biệt của đồ thị................................................................321 5
| Dạng 10. Bài toán thực tế ứng dụng đồ thị hàm số ..................................... 3, 326
Bài 6. Đề ôn tập cuối chương I 337 THỨ A
Đề ôn tập số 1 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . KIÊN
. . . . . . . . . . . . . . . . . . . . . . 337 B
Đề ôn tập số 2 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 341 TỐI C
Đề ôn tập số 3 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 344 D
Đề ôn tập số 4 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 350 LỚP E
Đề ôn tập số 5 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 354 2026. Phần II
HÌNH HỌC VÀ ĐO LƯỜNG − Chương 2.
VECTTƠ VÀ HỆ TỌA ĐỘ TRONG KHÔNG GIAN 361
Bài 1. Vectơ và các phép toán trong không gian 361 2025 A
Tóm tắt lý thuyết . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .CHUNG
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 361 B
Các dạng toán thường gặp . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 363 HỌC
| Dạng 1. Câu hỏi lý thuyết ........................................................................... 363
| Dạng 2. Đẳng thức vectơ ............................................................................ 368 NĂM
| Dạng 3. Phân tích (biểu HỮU
diễn) vectơ theo các vectơ cho trước, ba vectơ đồng
phẳng . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 373 HKI
| Dạng 4. Góc giữa hai vectơ ......................................................................... 384 −
| Dạng 5. Tích vô hướng và ứng dụng ........................................................... 391
Bài 2. Tọa độ của vectơ trong không gian 397 12 A
Tóm tắt lý thuyết . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 397 ÁN B
Các dạng toán thường gặp . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 398 TO
| Dạng 1. Tìm tọa độ vectơ trong không gian Oxyz ....................................... 398
| Dạng 2. Tìm tọa độ hình chiếu của điểm trên trục tọa độ, các mặt phẳng tọa TẬP
độ . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 403
| Dạng 3. Tọa độ các điểm, đỉnh đặc biệt của tam giác, tứ giác, lăng trụ ... .. 409
Bài 3. Biểu thức toạ độ của các phép toán vectơ 417 HỌC NGUYỄN A
Tóm tắt lý thuyết . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 417 LIỆU B
Các dạng toán thường gặp . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 418
| Dạng 1. Tìm vectơ tổng, hiệu, tích với một số ............................................ 418 TÀI
ThS:|Dạng2.Biểuthứctọađộcủatíchvôhướngvàápdụngtínhgóc,độdài....422
ThS NGUYỄN HỮU CHUNG KIÊN − Ó 0987192212
Website www.thaykientoan.io.vn Trang 4 Mục lục
| Dạng 3. Tìm tọa độ các điểm đặc biệt trong tam giác, tứ giác, hình hộp.....426
| Dạng 4. Vận dụng tọa độ của vectơ trong một số bài toán có liên quan đến thực
tiễn . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 437 HCM
Bài 4. Đề ôn tập cuối chương II 447 TP A
Đề ôn tập số 1 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . KIÊN
. . . . . . . . . . . . . . . . . . 447 B
Đề ôn tập số 2 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 449 PHÚ, C
Đề ôn tập số 3 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 452 D
Đề ôn tập số 4 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 454 TÂN E
Đề ôn tập số 5 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 457 Phần III
THỐNG KÊ VÀ XÁC SUẤT
THÀNH,Chương 3. CÁC SỐ ĐẶC TRƯNG ĐO MỨC ĐỘ PHÂN TÁN CHO MẪU SỐ LIỆU GHÉP NHÓM 463 TÂN
Bài 1. Khoảng biến thiên, khoảng tứ phân vị CHUNG
của mẫu số liệu ghép nhóm 463 T, A
Tóm tắt lý thuyết . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 463 NHẤ B
Các dạng toán thường gặp . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 464 | G
Dạng 1. Khoảng biến thiên. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .464
| Dạng 2. Khoảng tứ phân vị HỮU
trong mẫu số liệu ghép nhóm . . . . . . . . . . . . . . . . . . . . . . . . . . . 473
Bài 2. Phương sai, độ lệch chuẩn của mẫu số liệu ghép nhóm 481 THỐN A
Tóm tắt lý thuyết . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 481 134 B
Các dạng toán thường gặp . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 482 −
| Dạng 1. Tính phương sai và độ lệch chuẩn của mẫu số liệu ......................... 482
| Dạng 2. Giá trị ngoại lệ...............................................................................493 AN
Bài 3. Đề ôn tập cuối chương III 497 A
Đề ôn tập số 1 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 497 THIÊN B
Đề ôn tập số 2 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 502 C
Đề ôn tập số 3 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 506 TÂM D Đề ôn E Đề ônNGUYỄN
tập số 4 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 512 G
tập số 5 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 519 UN TR ThS:
ThS NGUYỄN HỮU CHUNG KIÊN − Ó 0987192212
Website www.thaykientoan.io.vn 5 3, THỨ KIÊN TỐI LỚP I PHẦN 2026. − 2025 CHUNG MỘT SỐ YẾUHỌC NĂM HỮU HKI − TỐ GIẢI TÍCH12 ÁN TO TẬP HỌC NGUYỄN LIỆU TÀI ThS: HCM TP KIÊN PHÚ, TÂN THÀNH, TÂN CHUNG T, NHẤ G HỮU THỐN 134 − AN THIÊN TÂM NGUYỄN G UN TR ThS:
TÀI LIỆU HỌC TẬP HKI TOÁN 12, NĂM HỌC 2024 − 2025 CHUẨN FORM MỚI Trang 7
CÁC DẠNG BÀI TẬP TOÁN 12 5
ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM Chương 1 3, 12 ỨNG SỐ
DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ THỨ KIÊN TỐI THẦY KIÊN TOÁN:
DẠY THẬT - HỌC THẬT - GIÁ TRỊ THẬT K12 – CHƯƠNG 1
§1. SỰ ĐỒNG BIẾN, NGHỊCH BIẾN CỦA HÀM SỐ LỚP
A. TÓM TẮT LÝ THUYẾT 2026. − A1
Nhắc lại về tính đồng biến, nghịch biến của hàm số
Kí hiệu K là khoảng hoặc đoạn hoặc nửa khoảng. Giả sử hàm số y = f (x) xác định trên K.
Hàm số y = f (x) gọi là đồng biến (tăng) trên K nếu với mọi x1, x2 thuộc K mà x1 < x2 thì f (x1) < 2025 f (x2). CHUNG
Hàm số y = f (x) gọi là nghịch biến (giảm) trên K nếu với mọi x1, x2 thuộc K mà x1 < x2 thì f (x1) > f (x2). HỌC
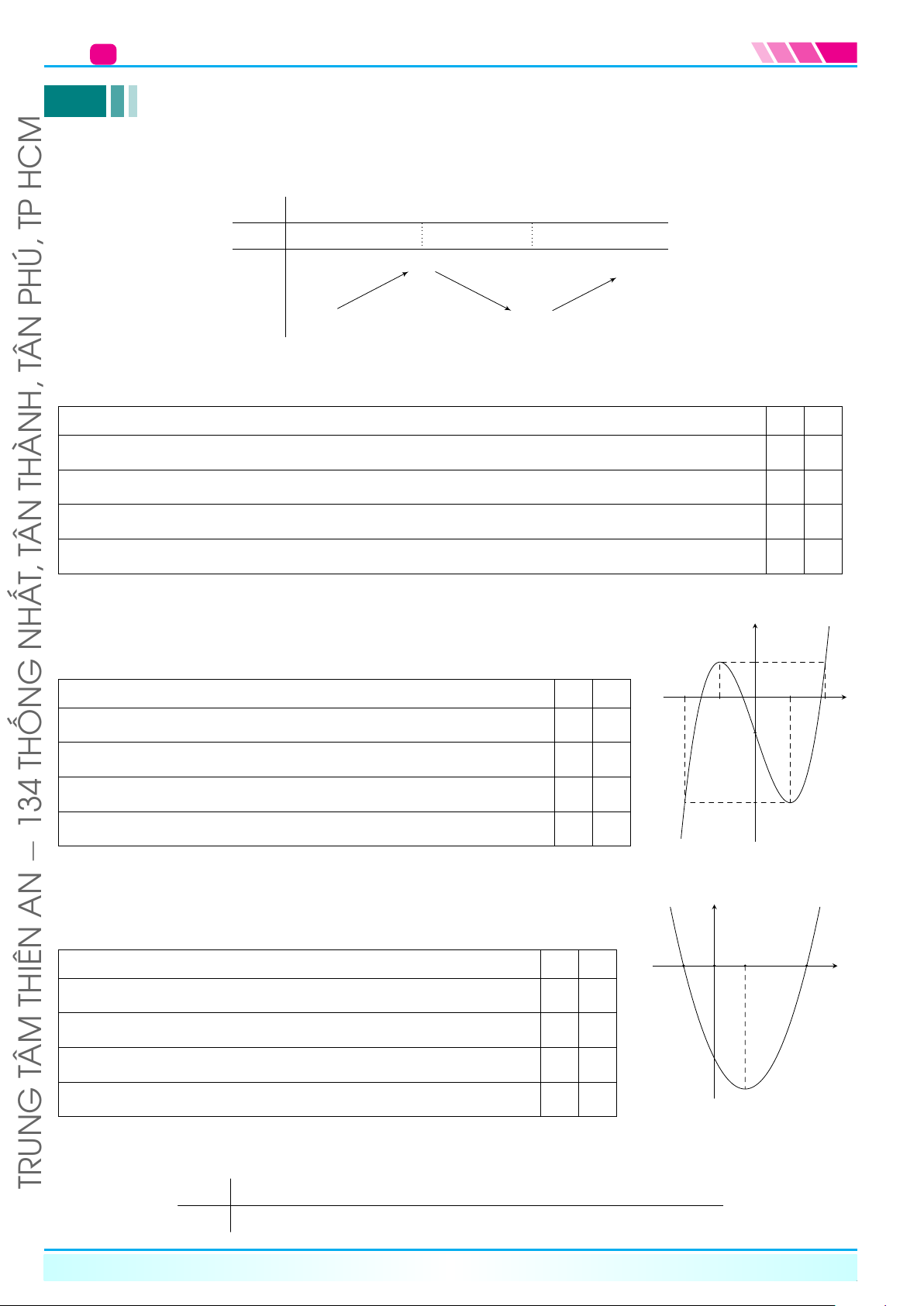
Nếu hàm số y = f (x) đồng biến trên K thì đồ thị của nó đi lên từ trái sang phải (Hình 1a).
Nếu hàm số y = f (x) nghịch biến trên K thì đồ thị của nó đi xuống từ trái sang phải (Hình 1b). y y NĂM HỮU y = f (x) HKI − y = f (x) 12 x O K x O K ÁN a) b) TO Hình 1
Hàm số đồng biến hoặc nghịch biến trên K được gọi chung là đơn điệu trên K. TẬP A2
Tính đơn điệu của hàm số HỌC
Định lí 1 Cho hàm số NGUYỄN
y = f (x) có đạo hàm trên K.
Nếu f 0(x) > 0 với mọi x thuộc K thì hàm số y = f (x) đồng biến trên K.
Nếu f 0(x) < 0 với mọi x thuộc K thì hàm số y = f (x) nghịch biến trên K. LIỆU
Nhận xét. Khi xét tính đơn điệu của hàm số mà chưa cho khoảng K, ta hiểu xét tính đơn điệu
của hàm số đó trên tập xác định của nó. TÀI Từ kết quả ThS:
trên, để xét tính đơn điệu của hàm số y = f (x), ta thực hiện các bước sau:
Bước 1. Tìm tập xác định D của hàm số.
ThS NGUYỄN HỮU CHUNG KIÊN − Ó 0987192212
Website www.thaykientoan.io.vn Trang 8
1. Sự đồng biến, nghịch biến của hàm số
Bước 2. Tính đạo hàm f 0(x) của hàm số. Tìm các điểm x1; x2;. . . ; xn thuộc D mà tại đó đạo hàm f 0(x)
bằng 0 hoặc không tồn tại.
Bước 3. Sắp xếp các điểm x1; x2;. . . ; xn theo thứ tự tăng dần, xét dấu f 0(x) và lập bảng biến thiên.
Bước 4. Nêu kết luận về các khoảng đồng biến, nghịch biến của hàm số. HCM TP Định lí 2
a) Nếu hàm số y = f (x) có đạo hàm trên K, f 0(x) ≥ 0 với mọi x ∈ K và f 0(x) = 0 KIÊN chỉ tại một số
hữu hạn điểm thì hàm số đồng biến trên K. PHÚ,
b) Nếu hàm số y = f (x) có đạo hàm trên K, f 0(x) ≤ 0 với mọi x ∈ K và f 0(x) = 0 chỉ tại một số
hữu hạn điểm thì hàm số nghịch biến trên K. TÂN
B. CÁC DẠNG TOÁN THƯỜNG GẶP DẠNG 1
Xét tính đơn điệu của hàm số cho bởi công thức
THÀNH, Bước 1. Tìm tập xác định D của hàm số.
Bước 2. Tính đạo hàm f 0(x) của hàm số. Tìm các điểm x1; x2;. . . ; xn thuộc D mà tại đó đạo hàm
f 0(x) bằng 0 hoặc không tồn tại.
TÂN Bước 3. Sắp xếp các điểm x1; x2;. . . ; xn theo thứ tự tăng dần, CHUNG
xét dấu f 0(x) và lập bảng biến thiên.
Bước 4. Nêu kết luận về các khoảng đồng biến, nghịch biến của hàm số. T, A1 Ví dụ mẫu
NHẤVí dụ 1 (Mức độ 2). Tìm khoảng đồng biến, nghịch biến của hàm số y = −2x2 + 4x + 3.
GVí dụ 2 (Mức độ 2). Tìm các khoảng đơn điệu của HỮU
hàm số y = x3 − 3x2 − 9x + 1. 1
Ví dụ 3 (Mức độ 2). Tìm các khoảng đơn điệu của hàm số y = − x3 + x2 − x + 5. 3 THỐN x2 + 4
Ví dụ 4 (Mức độ 2). Tìm các khoảng đơn điệu của hàm số y = . x
134Ví dụ 5 (Mức độ 2). Tìm các khoảng đơn điệu của hàm số y = −x4 + 4x2 − 3.√
−Ví dụ 6 (Mức độ 2). Tìm các khoảng đồng biến, nghịch biến của hàm số y = x2 − 1.√ Ä ä
Ví dụ 7 (Mức độ 2). Tìm các khoảng đồng biến, nghịch biến của hàm số y = ln x + 9 + x2 . AN x
Ví dụ 8 (Mức độ 2). Chứng minh rằng hàm số g(x) =
nghịch biến trên khoảng (1; +∞). x − 1
Ví dụ 9 (Mức độ 2). Chứng minh rằng hàm số f (x) = 3x − sin x đồng biến trên R. THIÊN x − 1
Ví dụ 10 (Mức độ 3). Cho hàm số y = f (x) =
. Mỗi khẳng định sau đúng hay sai? x − 4 TÂM −2 a) y0 = . NGUYỄN Phát biểu Đ S G (x − 4)2
UN b) Hàm số nghịch biến trên (−∞; 4) ∪ (4; +∞).
TR c) Tiếp tuyến của đồ thị hàm số tại giao điểm của đồ thị với trục hoành là x+3y−1 = 0. π d) Hàm số y ThS:
= f (sin x) đồng biến trên khoảng ; π . 2
ThS NGUYỄN HỮU CHUNG KIÊN − Ó 0987192212
Website www.thaykientoan.io.vn
TÀI LIỆU HỌC TẬP HKI TOÁN 12, NĂM HỌC 2024 − 2025 CHUẨN FORM MỚI Trang 9
Ví dụ 11 (Mức độ 3). Cho hàm số y = xex. Mỗi khẳng định sau đúng hay sai? 5 Phát biểu Đ S 3, a) y0 = ex.
b) Hàm số đồng biến trên khoảng (−1; +∞). THỨ c) y + y0 = y00. d) y (22023) < y (22024). KIÊN TỐI
Ví dụ 12 (Mức độ 3). Cho hàm số y = f (x) có đạo hàm f 0(x) = (1 − x)x. Hỏi khoảng nghịch biến của LỚP
hàm số y = f (3 − 2x) có độ dài lớn nhắt bằng bao nhiêu? KQ: A2 Bài tập tự luận 2026.
Bài 1. Tìm các khoảng đơn điệu của hàm số y = −x3 + 6x2 − 9x + 4. −
Bài 2. Tìm các khoảng đơn điệu của hàm số y = x4 − 6x2 + 8x + 1. 3 − 2x
Bài 3. Tìm các khoảng đơn điệu của hàm số y = . x + 7 2025 x2 − x + 1 CHUNG
Bài 4. Tìm các khoảng đơn điệu của hàm số y = . x − 1 √
Bài 5. Tìm các khoảng đồng biến, nghịch biến của hàm số y = x + 16 − x2. HỌC A3
Bài tập trắc nghiệm bốn phương án lựa chọn NĂM
Câu 1. Cho hàm số y = −x3 + 3x2 − 3x + 2. HỮU
Khẳng định nào sau đây là khẳng định đúng?
A. Hàm số đồng biến trên R. HKI
B. Hàm số nghịch biến trên R. −
C. Hàm số đồng biến trên khoảng (−∞; 1) và nghịch biến trên khoảng (1; +∞).
D. Hàm số nghịch biến trên khoảng (−∞; 1) và đồng biến trên khoảng (1; +∞). 12
Câu 2. Các khoảng đồng biến của hàm số y = x4 − 8x2 − 4 là
A. (−∞; −2) và (0; 2).
B. (−2; 0) và (0; +∞). ÁN
C. (−2; 0) và (2; +∞).
D. (−∞; −2) và (2; +∞). TO 3 − x
Câu 3. Cho hàm số y =
. Mệnh đề nào sau đây đúng? x + 1 TẬP
A. Hàm số nghịch biến trên khoảng (−∞; −1).
B. Hàm số nghịch biến trên R.
C. Hàm số đồng biến trên khoảng (−∞; −1).
D. Hàm số đồng biến trên R. 1
Câu 4. Cho hàm số y = x +
. Mệnh đề nào sau đây đúng? HỌC NGUYỄN x
A. Hàm số nghịch biến trên khoảng (−∞; −1).
B. Hàm số nghịch biến trên khoảng (−1; 1).
C. Hàm số đồng biến trên khoảng (−1; +∞).
D. Hàm số nghịch biến trên khoảng (−1; 0). LIỆU
Câu 5. Cho hàm số y = x − ln x. Mệnh đề nào sau đây đúng? TÀI A. Hàm số ThS:
đồng biến trên khoảng (0; +∞).
B. Hàm số đồng biến trên R.
C. Hàm số đồng biến trên khoảng (1; +∞).
D. Hàm số nghịch biến trên khoảng (−∞; 1).
ThS NGUYỄN HỮU CHUNG KIÊN − Ó 0987192212
Website www.thaykientoan.io.vn Trang 10
1. Sự đồng biến, nghịch biến của hàm số
Câu 6. Hàm số nào sau đây đồng biến trên R? x − 1 A. y = x3 + x. B. y = . C. y = x4 + x2 + 1. D. y = x3 + 3x2 + 1. x + 2 √
HCMCâu 7. Cho hàm số y = f(x) = 3x − x2. Hàm số đồng biến trên khoảng nào? Å 3 ã Å 3 ã Å 3 ã TP A. 0; . B. (0; 3). C. ; 3 . D. −∞; . 2 2
Câu 8. Hàm số nào sau đây đồng biến trên R? 2x − 1 KIÊN 2
PHÚ, A. y = 2x − cos 2x − 5. B. y = . x + 1 √ C. y = x2 − 2x. D. y = x.
TÂNCâu 9. Cho hàm số y = f(x) có f0(x) = (x + 1)2(x − 1)3(2 − x), ∀x ∈ R. Hàm số y = f(x) đồng biến
trên khoảng nào dưới đây? A. (1; 2). B. (−∞; −1). C. (−1; 1). D. (2; +∞).
Câu 10. Cho hàm số y = f (x) có đạo hàm f 0(x) = x2(x2 − 1), ∀x ∈ R. Hàm số y = 2f (−x) đồng biến THÀNH,trên khoảng A. (2; +∞). B. (−∞; −1). C. (0; 2). D. (−1; 1). TÂN A4
Bài tập trắc nghiệm đúng sai CHUNG
T,Câu11. Cho hàm số y = ln(1+x). Xét tính đúng sai của mỗi mệnh đề sau NHẤ Phát biểu Đ S
G a) Hàm số có tập xác định là R.
b) Hàm số đồng biến trên tập xác định.
c) Tiếp tuyến của đồ thị vuông góc với đường HỮU
phân giác góc phần tư thứ hai cắt hai THỐN
trục toạ độ tại hai điểm phân biệt. 1 1 1 1 d) + + + . . . + = 2025 · 2026. 134 y0(0) y0(1) y0(2) y0(2024) √
−Câu 12. Cho hàm số y = x + 4 − x2. Xét tính đúng sai của mỗi mệnh đề sau Phát biểu Đ S
AN a) Hàm số có tập xác định là D = [−2;2]. x b) y0 = 1 + √ . 4 − x2
THIÊN c) Khoảng đồng biến trên khoảng (−2; 2). √ d) Phương trình x +
4 − x2 = 3 có hai nghiệm phân biệt. TÂM −x2 + x − 1
Câu 13. Cho hàm số y = NGUYỄN
. Xét tính đúng sai của mỗi mệnh đề sau G x − 1 UN Phát biểu Đ S
TR a) Hàm số có tập xác định là D = R. −x2 + 2x b) y0 = . (x − ThS: 1)2
ThS NGUYỄN HỮU CHUNG KIÊN − Ó 0987192212
Website www.thaykientoan.io.vn
TÀI LIỆU HỌC TẬP HKI TOÁN 12, NĂM HỌC 2024 − 2025 CHUẨN FORM MỚI Trang 11 Phát biểu Đ S
c) Hàm số đồng biến trên khoảng (2; 3). 5
d) f (−52023) < f (52024). 3,
Câu 14. Cho hàm số f (x) = x − ex. Xét tính đúng sai của mỗi mệnh đề sau THỨ Phát biểu KIÊN Đ S
a) Tập xác định D = (0; +∞). TỐI b) f 0(x) = 1 − ex. LỚP
c) Hàm số đồng biến trên khoảng (0; +∞).
d) Với hai số a > b > 1 thì f (ln a) < f (ln b).
Câu 15. Cho hàm số f (x) = x3 − 3x. Xét tính đúng sai của mỗi mệnh đề sau 2026. − Phát biểu Đ S
a) Phương trình f 0(x) = 0 có hai nghiệm đối nhau.
b) Hàm số đồng biến trên khoảng (0; +∞). 2025 π
c) Với hai số 0 < a < b < thì f (sin a) < f (sin b). CHUNG 2
d) Bất phương trình cos3 x − 3 cos x ≥ −2 có đúng 10 nghiệm x ∈ [−10π; 10π]. HỌC A5
Bài tập trắc nghiệm trả lời ngắn NĂM x3 x2 3
Câu 16. Cho hàm số f (x) = −
− 6x + . Số giá trị x nguyên thuộc khoảng nghịch biến là bao 3 2 4 HỮU nhiêu? KQ: HKI
Câu 17. Hàm số y = x4 + 4x2 + 3. Có bao nhiêu giá trị x nguyên thuộc khoảng đồng biến của hàm số − và x ∈ [−10; 10]? KQ: 12 −x2 + 2x − 1
Câu 18. Cho hàm số y =
. Tổng tất cả các giá trị x nguyên âm thuộc các khoảng đồng x + 2 ÁN
biến của hàm số bằng bao nhiêu? KQ: √ TO
Câu 19. Cho hàm số y = x 3 − x. Khoảng nghịch biến của hàm số bằng có độ dài lớn nhất bao nhiêu? KQ: TẬP
Câu 20. Cho hàm số y = f (x) có đạo hàm f 0(x) = (x − 1)(x − 2). Biết hàm số y = f (x − x2) nghịch a a
biến trên khoảng có dạng ; +∞ với
là tối giản và b > 0. Giá trị của biểu thức a2 + b2 bằng bao b b HỌC nhiêu? NGUYỄN KQ: LIỆU TÀI ThS:
ThS NGUYỄN HỮU CHUNG KIÊN − Ó 0987192212
Website www.thaykientoan.io.vn Trang 12
1. Sự đồng biến, nghịch biến của hàm số DẠNG 2
Xét tính đơn điệu dựa vào bảng biến thiên, đồ thị
Nếu trên khoảng (a; b) đồ thị “đi lên” từ trái qua phải thì hàm số đồng biến trên khoảng (a; b).
Nếu trên khoảng (a; b) đồ thị “đi xuống” từ trái qua phải thì hàm số nghịch biến trên khoảng (a; b). HCM TP A1 Ví dụ mẫu
Ví dụ 13 (Mức độ 1). KIÊN
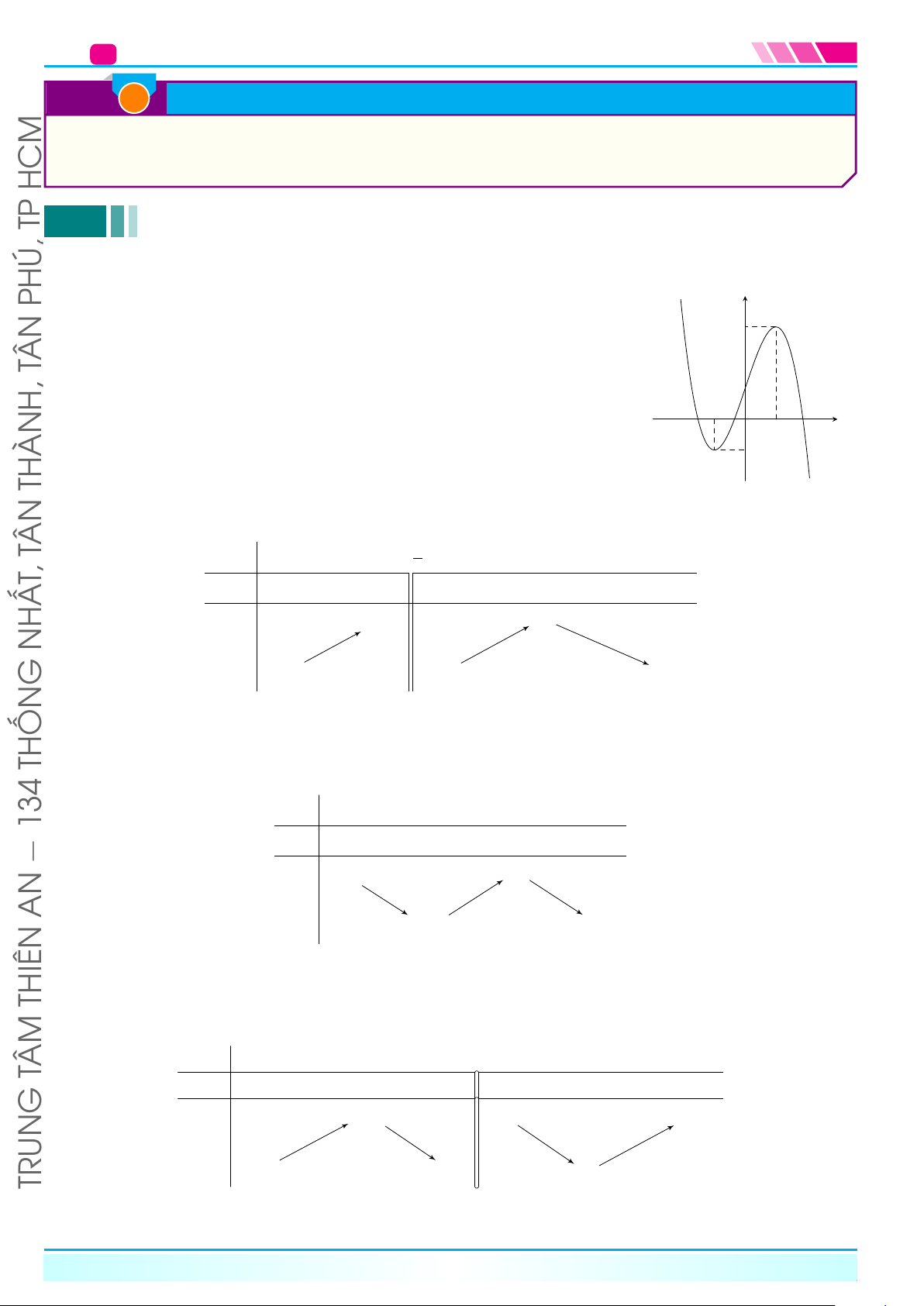
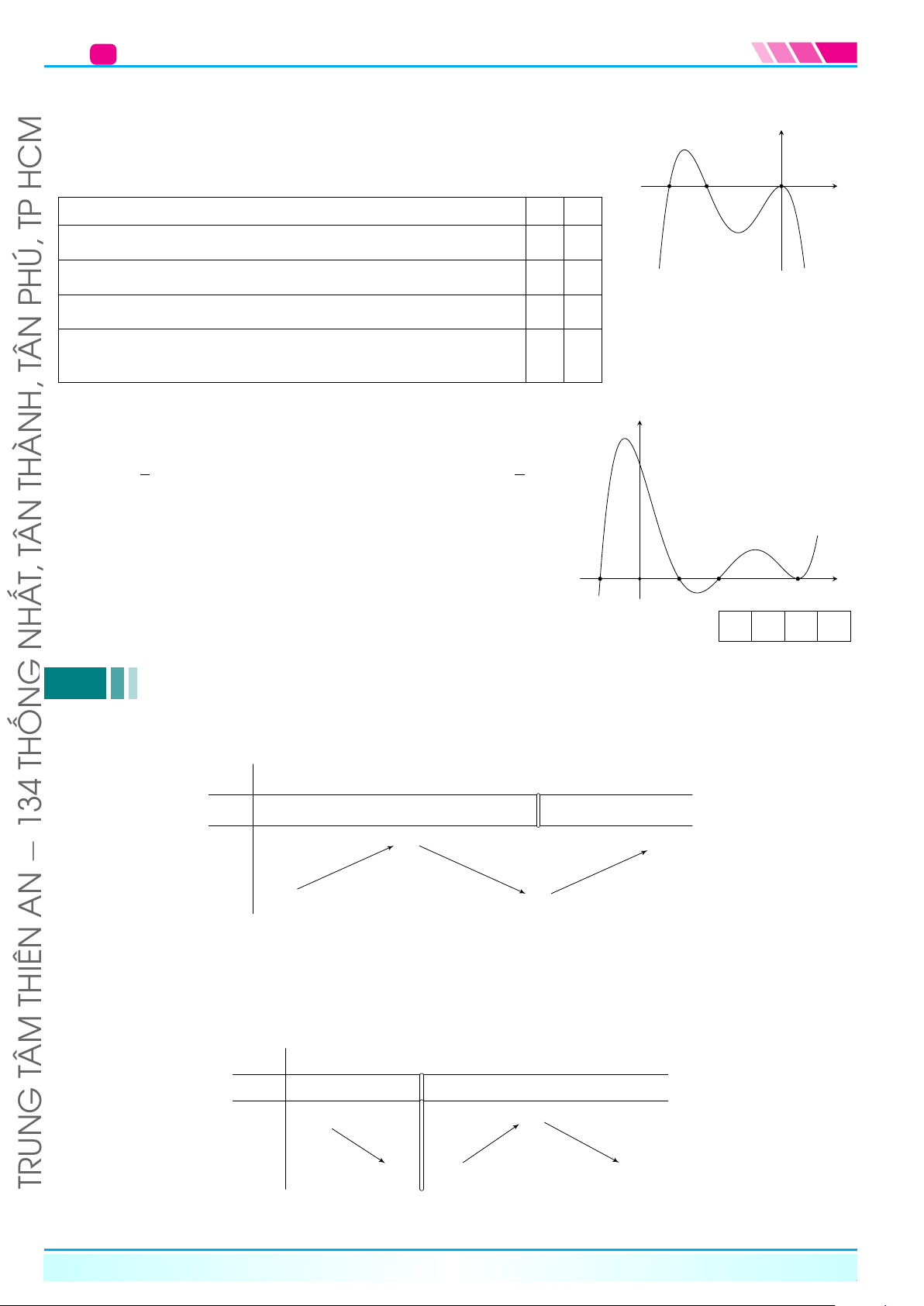
PHÚ,Cho hàm số y = f(x) liên tục trên R, có đồ thị như hình bên. Tìm khoảng y
đồng biến, khoảng nghịch biến của hàm số? 3 TÂN 1 −1 x O 1 −1
THÀNH,Ví dụ 14 (Mức độ 1). Cho hàm số y = f(x) có bảng biến thiên như hình dưới đây TÂN 1 x −∞ − 3 +∞ 2 CHUNG T, y0 + + 0 − +∞ 4 NHẤ y G −∞ −∞ −∞
Tìm các khoảng đồng biến, nghịch biến của hàm số? HỮU
THỐNVí dụ 15 (Mức độ 1). Cho hàm số y = f(x) có bảng biến thiên như sau. 134 x −∞ −3 4 +∞ − y0 − 0 + 0 − +∞ + 2 AN y −1 −∞
Tìm các khoảng đồng biến, nghịch biến của hàm số.
THIÊNVí dụ 16 (Mức độ 2). Cho hàm số y = f(x) có bảng biến thiên như hình dưới đây TÂM x −∞ 0 2 4 +∞ y0 NGUYỄN + 0 − − 0 + G −2 +∞ +∞ UN y TR −∞ −∞ 6 Tìm các khoảng ThS:
đồng biến, nghịch biến của hàm số.
ThS NGUYỄN HỮU CHUNG KIÊN − Ó 0987192212
Website www.thaykientoan.io.vn
TÀI LIỆU HỌC TẬP HKI TOÁN 12, NĂM HỌC 2024 − 2025 CHUẨN FORM MỚI Trang 13
Ví dụ 17 (Mức độ 2). −x2 + 3x − 3 5
Tìm khoảng đồng biến nghịch biến của hàm số y = y 2(x − 1) 3,
có đồ thị như hình vẽ bên? 3 2 THỨ O 1 1 KIÊN 2 TỐI x − 2 LỚP
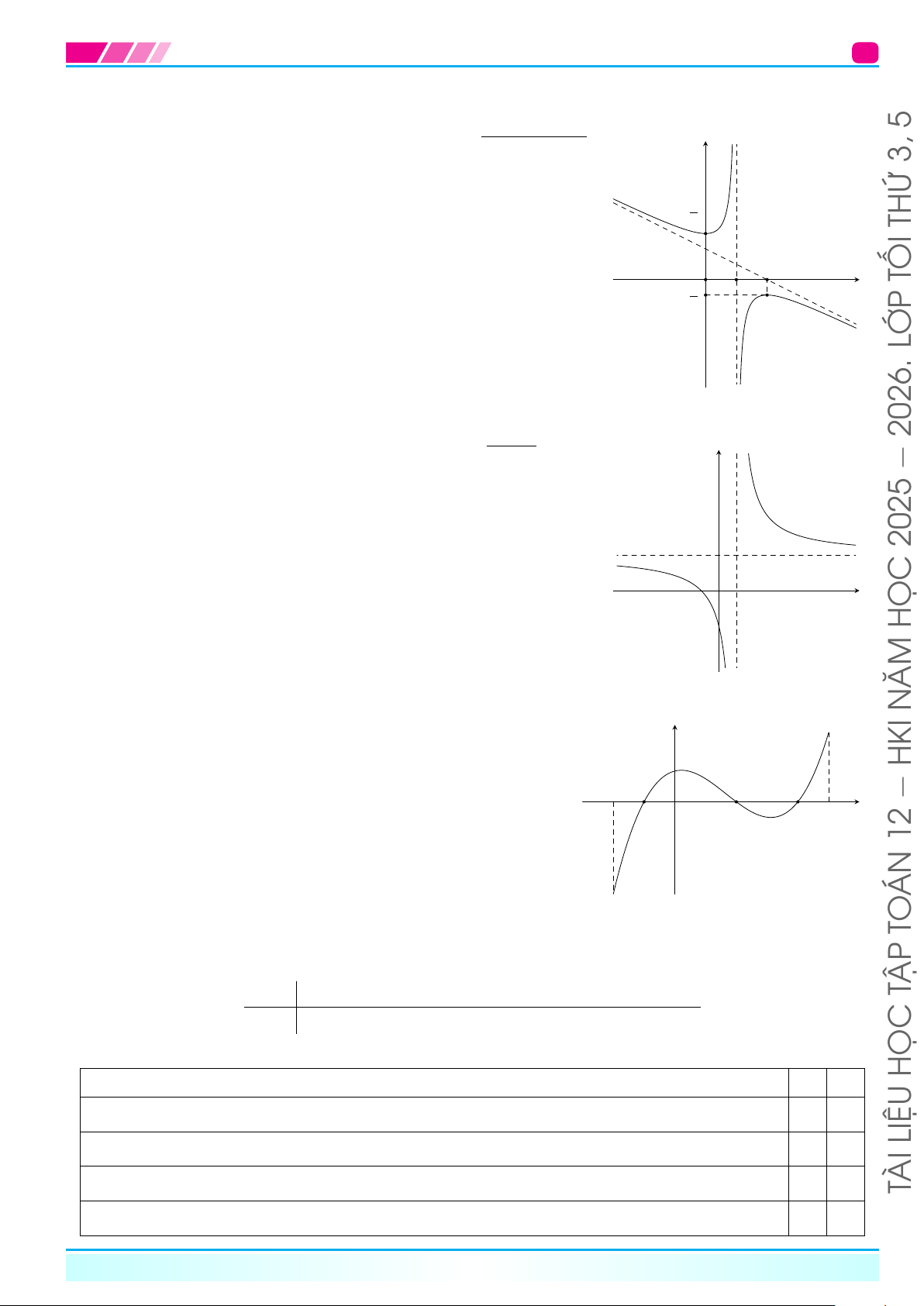
Ví dụ 18 (Mức độ 2). ax + b 2026.
Đường cong trong hình bên là đồ thị của hàm số y = , với a, y cx + d −
b, c, d là các số thực. Tìm các khoảng đồng biến, nghịch biến của hàm số. 2025 CHUNG3O 2 x HỌC
Ví dụ 19 (Mức độ 2). NĂM
Đạo hàm f 0(x) của hàm số y = f (x) trên khoảng ( HỮU −2; 5) có đồ y
thị như hình vẽ bên. Xét tính đơn điệu của hàm số y = f (x) y = f 0(x) trên khoảng (−2; 5). HKI − x −2 −1 O 2 4 5 12 ÁN TO
Ví dụ 20 (Mức độ 3). Cho hàm số f (x), có bảng xét dấu f 0(x) như sau x −∞ −3 −1 1 +∞ TẬP f 0(x) − 0 + 0 − 0 + HỌC NGUYỄN Phát biểu Đ S
a) Phương trình f 0(x) = 0 có ba nghiệm. LIỆU
b) Hàm số f (x) đồng biến trên khoảng (0; 2).
c) Hàm số f (3 − 2x) có đạo hàm là y0 = f 0(3 − 2x). TÀI d) Hàm sốThS:
y = f (3 − 2x) đồng biến trên khoảng (3; +∞).
ThS NGUYỄN HỮU CHUNG KIÊN − Ó 0987192212
Website www.thaykientoan.io.vn Trang 14
1. Sự đồng biến, nghịch biến của hàm số
Ví dụ 21 (Mức độ 3).
Cho hàm số y = f (x) xác định, liên tục trên R và có đồ thị của hàm y
số y = f 0(x) là đường cong như hình vẽ bên. Xét tính đúng sai của các HCMmệnh đề sau O x −3 −2 TP Phát biểu Đ S
a) Phương trình f 0(x) = 0 có ba nghiệm.
b) Hàm số f (x) đồng biến trên khoảng (−∞; −3). KIÊN
PHÚ, c) Hàm số f(x − 1) đồng biến trên khoảng (−2;−1).
d) Khoảng nghịch biến của hàm số y = f (1 − ln x) chứa TÂN 34 số nguyên.
Ví dụ 22 (Mức độ 3). y
Cho hàm số y = f (x) có đồ thị y = f 0(x) như hình bên. Biết hàm Å 1 ãf(5−2x) a THÀNH,số g(x) =
nghịch biến trên khoảng có dạng − ; c , e b
a, b, c là các số nguyên dương. Tổng a + b + c bằng bao nhiêu? TÂN CHUNG T, −1 x O 1 2 4 KQ: NHẤ G A2 Bài tập tự luận
Bài 6. Cho hàm số y = f (x) có bảng biến thiên như HỮU hình vẽ. THỐN x −∞ 1 2 +∞ 134 y0 + 0 − + − 3 +∞ y AN −∞ 0
Tìm các khoảng đồng biến, nghịch biến của hàm số?
THIÊNBài 7. Cho hàm số y = f(x) có bảng biến thiên như hình vẽ dưới đây. Tìm khoảng đồng biến, nghịch biến của hàm số. TÂM x −∞ 0 1 +∞ y0 NGUYỄN − + 0 − G +∞ 2 UN y TR −1 −∞ −∞ Bài 8. ThS:
ThS NGUYỄN HỮU CHUNG KIÊN − Ó 0987192212
Website www.thaykientoan.io.vn
TÀI LIỆU HỌC TẬP HKI TOÁN 12, NĂM HỌC 2024 − 2025 CHUẨN FORM MỚI Trang 15
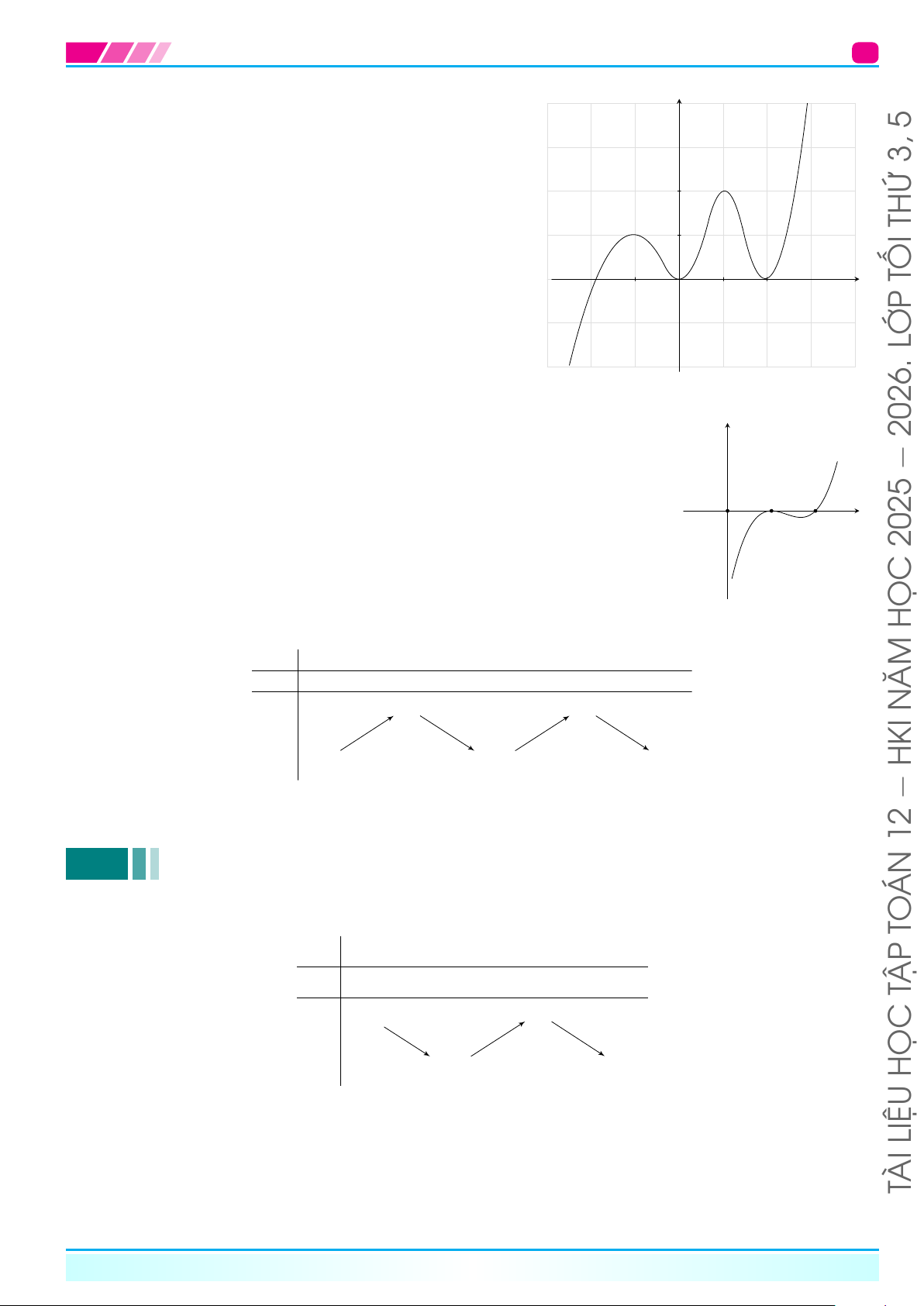
Cho hàm số y = f (x) xác định trên R có đồ thị như hình y
bên. Tìm các khoảng đồng biến, nghịch biến hàm số. 5 3, 2 y = f (x) THỨ 1 KIÊN TỐI x −1 O 1 2 LỚP Bài 9.
Cho hàm số y = f (x) xác định trên R có đồ thị của hàm số f 0(x) như hình y 2026.
vẽ. Tìm khoảng đồng biến, nghịch biến của hàm số y = f (x)? − O x 1 2 2025 CHUNG
Bài 10. Cho hàm số y = f (x) có bảng biến thiên như hình vẽ. HỌC x −∞ −2 0 2 +∞ f 0(x) + 0 − 0 + 0 − 3 3 NĂM f (x) HỮU −∞ −1 − −∞ HKI −
Tìm khoảng đồng biến của hàm số y = f (x2 − 2)? 12 A3
Bài tập trắc nghiệm bốn phương án lựa chọn ÁN
Câu 21. Cho hàm số y = f (x) có bảng biến thiên như sau. TO x −∞ −3 4 +∞ y0 − 0 + 0 − TẬP +∞ + 2 y −1 − −∞ HỌC NGUYỄN
Mệnh đề nào dưới đây sai? LIỆU
A. Hàm số y = f (x) nghịch biến trên khoảng (−∞; −4).
B. Hàm số y = f (x) đồng biến trên khoảng (−2; 2). TÀI C. Hàm số ThS:
y = f (x) đồng biến trên khoảng (−4; 1).
D. Hàm số y = f (x) nghịch biến trên khoảng (5; +∞).
ThS NGUYỄN HỮU CHUNG KIÊN − Ó 0987192212
Website www.thaykientoan.io.vn Trang 16
1. Sự đồng biến, nghịch biến của hàm số
Câu 22. Cho hàm số y = f (x) có bảng biến thiên như hình bên dưới x −∞ 0 1 +∞ HCM y0 − − 0 + +∞ +∞ +∞ TP y −∞ −2 KIÊN
PHÚ,Khẳng định nào sau đây là sai?
TÂN A. Hàm số nghịch biến trên khoảng (−∞; −1).
B. Hàm số nghịch biến trên khoảng (0; 1).
C. Hàm số đồng biến trên khoảng (2; +∞).
D. Hàm số đồng biến trên khoảng (−2; +∞).
Câu 23. Cho hàm số có bảng biến thiên như hình dưới đây x −∞ −2 0 2 +∞ THÀNH, y0 + 0 − − 0 + TÂN y CHUNG T,
NHẤKhẳng định nào sau đây là đúng
G A. Hàm số nghịch biến trên khoảng (−∞; −2).
B. Hàm số nghịch biến trên khoảng (−2; 2).
C. Hàm số đồng biến trên khoảng (−2; +∞). HỮU
D. Hàm số nghịch biến trên khoảng (−2; 0). Câu 24.
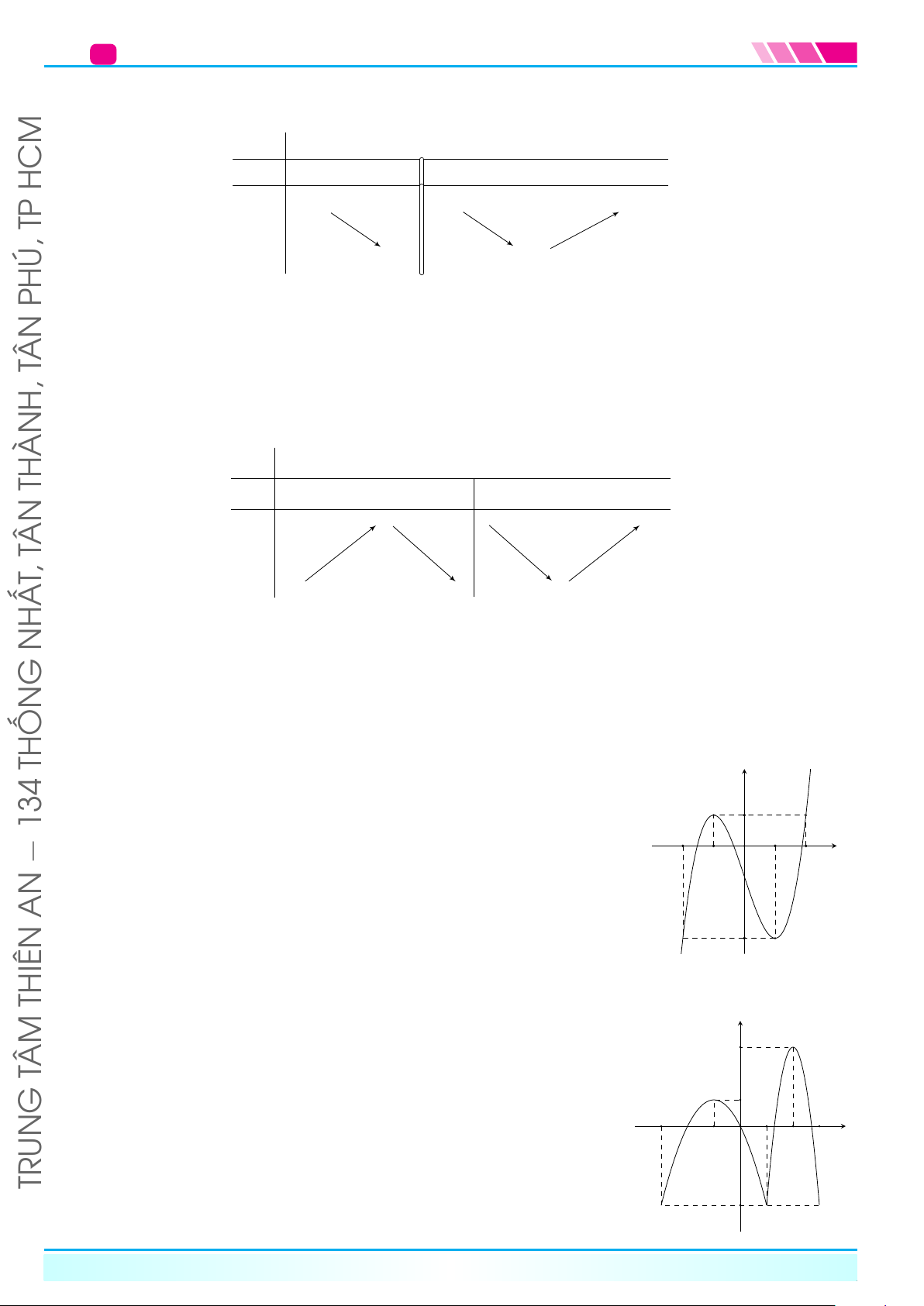
THỐNCho hàm số y = f(x) có đồ thị như hình bên. Hàm số đã cho đồng biến y
trên khoảng nào trong các khoảng dưới đây? 1 134 A. (0; 2). B. (1; +∞). C. (−∞; 1). D. (−2; 1). −2 1 − x −1 O 2 AN −3 Câu 25.
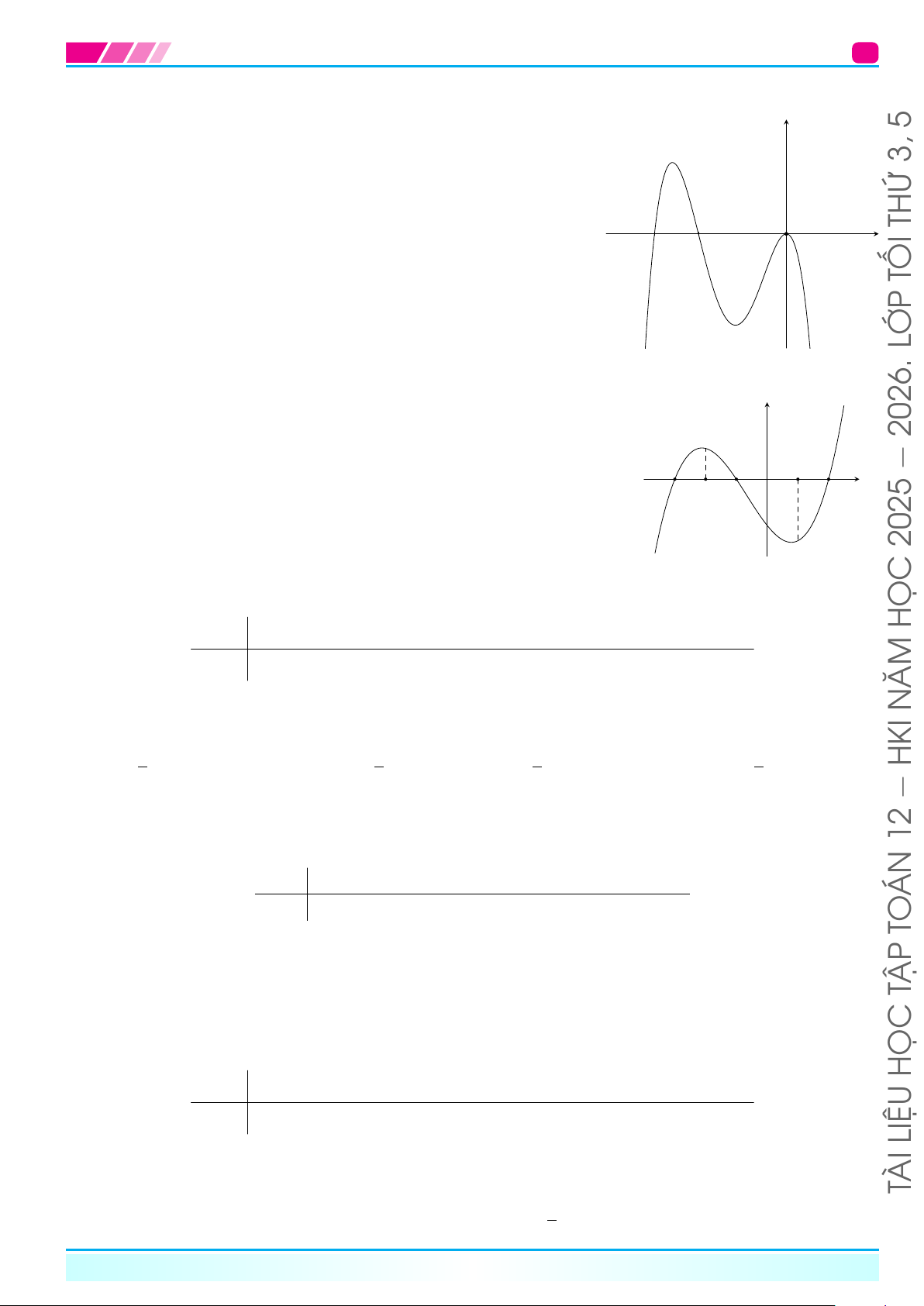
THIÊNCho hàm số y = f(x) có đồ thị như hình vẽ bên. Hàm số đã cho nghịch y biến trên khoảng A. (−3; −1). B. (2; 3). C. (−2; 0). D. (0; 2). 3 TÂM NGUYỄN 1 G −3 O 1 3 UN −1 2 x TR −3 ThS:
ThS NGUYỄN HỮU CHUNG KIÊN − Ó 0987192212
Website www.thaykientoan.io.vn
TÀI LIỆU HỌC TẬP HKI TOÁN 12, NĂM HỌC 2024 − 2025 CHUẨN FORM MỚI Trang 17 Câu 26.
Cho hàm số y = f (x) xác định, liên tục trên R và có đạo hàm y 5
f 0(x). Biết rằng f 0(x) có đồ thị như hình vẽ bên. Mệnh đề nào sau 3, đây đúng?
A. Hàm số y = f (x) nghịch biến trên khoảng (0; +∞).
B. Hàm số y = f (x) nghịch biến trên khoảng (−3; −2). O THỨ
C. Hàm số y = f (x) đồng biến trên khoảng (−∞; 3). x −3 −2
D. Hàm số y = f (x) đồng biến trên khoảng (−2; 0). KIÊN TỐI LỚP Câu 27.
Cho hàm số y = f (x) có đạo hàm f 0(x) xác định, liên tục trên R và có y
đồ thị hàm số y = f 0(x) như hình vẽ. Mệnh đề nào sau đây là mệnh y = f 0(x) 2026. đề sai?
A. Hàm số nghịch biến trên khoảng (0; 1). −3 O 1 −
B. Hàm số đồng biến trên khoảng (1; 2). x −2 2
C. Hàm số đồng biến trên khoảng (−2; −1).
D. Hàm số nghịch biến trên khoảng (−1; 2). 2025 CHUNG
Câu 28. Cho hàm số f (x) có bảng xét dấu đạo hàm như hình bên dưới. HỌC x −∞ −3 −2 0 1 3 +∞ f 0(x) − 0 + 0 − 0 − 0 + 0 − NĂM
Hàm số y = f (1 − 2x) đồng biến trên khoảng Å 1 ã Å 1 ã HỮU Å 3 ã Å 3 ã A. − ; 1 . B. −2; − . C. ; 3 . D. 0; . HKI 2 2 2 2 −
Câu 29. Cho hàm số y = f (x) có đạo hàm f 0(x) xác định, liên tục trên R và có bảng xét dấu f 0(x) như sau 12 x −∞ −1 2 +∞ ÁN f 0(x) − 0 + 0 − TO
Hàm số g(x) = f (x2 − 2) nghịch biến trên khoảng nào dưới đây? TẬP A. (1; 2). B. (−∞; −1). C. (−1; 0). D. (0; 1).
Câu 30. Cho hàm số f (x) có bảng xét dấu đạo hàm như hình bên dưới. HỌC x NGUYỄN −∞ −3 −2 0 1 3 +∞ f 0(x) − 0 + 0 − 0 − 0 + 0 − LIỆU
Hàm số y = f (3x) đồng biến trên khoảng TÀI Å 2 ã A. (−3; − ThS: 2). B. (1; 3). C. − ; −1 . D. (0; 1). 3
ThS NGUYỄN HỮU CHUNG KIÊN − Ó 0987192212
Website www.thaykientoan.io.vn Trang 18
1. Sự đồng biến, nghịch biến của hàm số A4
Bài tập trắc nghiệm đúng sai
Câu 31. Cho hàm số y = f (x) xác định và liên tục trên khoảng (−∞; +∞), có bảng biến thiên như hình sau HCM TP x −∞ −1 1 +∞ y0 + 0 − 0 + 2 +∞ + KIÊN PHÚ, y −∞ −1
TÂNXét tính đúng sai của mỗi khẳng định sau Phát biểu Đ S
a) Hàm số đồng biến trên khoảng (−∞; −3).
THÀNH, b) Hàm số nghịch biến trên khoảng (1; +∞).
c) Hàm số đồng biến trên khoảng (−1; +∞).
TÂN d) Hàm số nghịch biến trên khoảng (−∞; 1). CHUNG T, Câu 32.
NHẤCho hàm số y = ax3 + bx2 + cx + d (a, b, c, d ∈ R) có đồ thị như hình bên. y
Mỗi khẳng định sau đúng hay sai? 1 G Phát biểu HỮUĐ S −2 1 x −1 O 2 a) d = −1. −1 THỐN b) a < 0.
c) Hàm số đồng biến trên khoảng (1; 2). −3 134 d) y0(2) < 0. −Câu 33.
ANCho hàm số y = f(x) có đồ thị f0(x) là parabol như hình vẽ bên. Xét tính y
đúng sai của mỗi khẳng định sau 1 x Phát biểu Đ S −1 O 3 THIÊN a) f0(−1) = 0.
b) Hàm số đồng biến trên (1; +∞).
TÂM c) Hàm số nghịch biến NGUYỄN trên khoảng (−1; 3).
G d) Hàm số nghịch biến trên (−∞; −1).
UNCâu 34. Cho hàm số f(x) có bảng xét dấu f0(x) như sau TR x −∞ −3 −1 1 +∞ ThS: f 0(x) − 0 + 0 − 0 +
ThS NGUYỄN HỮU CHUNG KIÊN − Ó 0987192212
Website www.thaykientoan.io.vn

