Tài liệu ôn thi Chuyên đề 1 Nhóm môn Cấu trúc đại số | Đại học Sư phạm Hà Nội

lOMoAR cPSD| 57855709
TÀI LIỆU ÔN THI CẤU TRÚC ĐẠI SỐ NH Ó M
Chuyên đề 1 I. Phép toán hai ngôi:
Định nghĩa: Cho X là một tập hợp .
Một phép toán hai ngôi trên X là một ánh xạ kí hiệu :
X X → X (x y, ) x y
(hiểu đơn giản ở đây là: với hai phần tử x y,
X , thì qua phép toán x y vẫn thuộc tập X )
Một số thuật ngữ:
+) Phép toán ( ) có tính chất kết hợp nếu (x y ) z x=
(y z ), x y z X, , .
+) Phép toán ( ) có tính chất giao hoán nếu x y y x x y X = , , .
+) Có phần tử trung lập e nếu e x = x e = x, x X.
+) Phần tử x X có phần tử đối xứng x' nếu x x x x e = =' ' .
Ví dụ 1: Phép trừ trong tập không là một phép toán 2 ngôi vì 1 2− , nhưng là một phép toán 2
ngôi trên . Bởi a b, thì a−b (hiển nhiên)
Ví dụ 2: Sn là tập các phép thế bậc n .
Tích hợp thành 2 phép thế (2 ánh xạ) cũng là 1 phép thế Sn.
tích hợp thành là một phép toán 2 ngôi trên Sn.
* Nhắc lại khái niệm nhóm Sn :
Cho A ={1,2,...,n}. Ta kí hiệu Sn là tập các song ánh từ A vào chính nó. Với mỗi Sn , kí hiệu 1 2 ... n (1)(2) ... ( )n
Với (1), (2),..., ( )n là hoán vị của 1,2,...,n hoặc chính nó.
Ví dụ với nhóm S3 gồm 6 phần tử, chính là lOMoAR cPSD| 57855709
TÀI LIỆU ÔN THI CẤU TRÚC ĐẠI SỐ
S3 = {id, 1 = (12), 2 = (23), 3 = (13), 4 = (123), 5 = (132)} Ở đó 1 2 3 1 2 3 1 2 3 1 2 3 1 2 3 1 2 3 e = id = 1 23 , 1 = 213 , 2 = 13 2 , 3 = 3 2 1 , 4 = 2 3 1 , 5 = 3 1 2
hiểu là id = e (giữ nguyên, 1 vẫn là 1, 2 vẫn là 2, 3 vẫn là 3), 1 = (12) (1 biến thành 2, 2 biến
thành 1, 3 vẫn là 3), 2 = (23) (2 biến thành 3, 3 biến thành 2, 1 vẫn là 1), 3 = (13) (1 biến thành
3, 3 biến thành 1, 2 vẫn là 2), 4 = (123) (1 biến thành 2, 2 biến thành 3, 3 biến thành 1), 5 =
(132) (1 biến thành 3, 3 biến thành 2, 2 biến thành 1).
Phép toán giữa 6 phần tử này với nhau là phép toán hợp ánh xạ. Ví dụ:
- id 1 = 1 (do giữ nguyên) - 1 2 = (12)(23)
(với phép hợp ánh xạ, ta thực hiện theo thứ tự từ phải qua trái, có nghĩa là
2 biến thành 3 ở 2 trước, rồi 3 vẫn là 3 ở 1 →2 3
3 biến thành 2 ở 2 trước, rồi 2 biến thành 1 ở 1 →3 1
1 vẫn là 1 ở 2 , rồi 1 biến thành 2 ở 1 →1 2
Vậy ta được kết quả của phép hợp 2 3 1 2 = (12)(23) = 12 3 1 = (123) = 4 )
Với phép toán như trên, có thể thấy đúng thật sự rằng dù cho hợp như nào thì vẫn ra kết quả là
phần tử thuộc nhóm S3 .
Chú ý: Từ nay về sau, chúng ta sẽ sử dụng nhiều đến nhóm phép thế S3 . Một số tài liệu có quy ước
các phần tử của nhóm S3 khác ở đây, cụ thể như sau: 1 2 3 1 2 3 1 2 3 1 2 3 e = id = 1 2 3 , = = = 1 (23) = 1 3 2 , 2 (13) = 3 2 1 , 3 (12) = 2 1 3 ,
Vũ Hải Sơn – K68C HNUE Trang 2
Downloaded by My L? (mymylu9x@gmail.com) lOMoAR cPSD| 57855709
TÀI LIỆU ÔN THI CẤU TRÚC ĐẠI SỐ 1 2 3 1 2 3 = = 4 (123) = 2 3 1 , 5 (132) = 3 1 2
Nhưng đó chỉ là quy ước khác đi, chứ không ảnh hưởng đến việc chứng minh. Ví dụ 3: = n
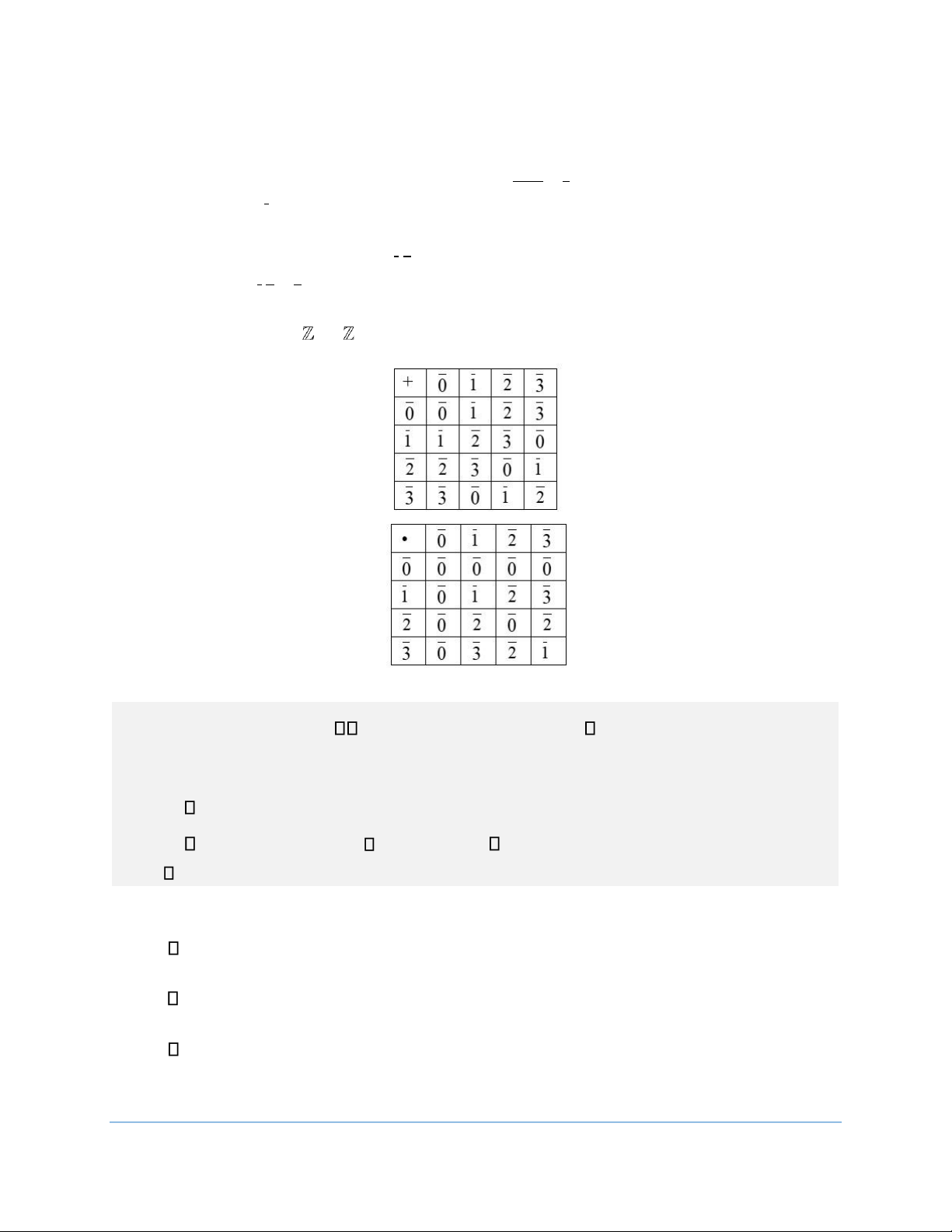
{0;1;2;...;n−1} là tập các lớp thặng dư mod n.
● Xét phép (+) được xác định như sau: a+ = +b a b
là một phép toán 2 ngôi trên n
+) Có tính chất kết hợp
(a +b) +c = a +b+c = (a +b) +c = a + (b+c) (do phép cộng trong có tính chất kết hợp)
= +a (b+c)
+) Có tính chất giao hoán a+ = +b b a
+) Có phần tử trung lập là 0 do a+ = + = + = + =0 a 0 0 a 0 a a.
+) a n có phần tử đối xứng là − = −a n a.
● Xét phép nhân được xác định ab. = ab là một phép toán 2 ngôi trên
n có tính chất giao hoán, 1 n
kết hợp, có phần tử đơn
vị 1, nhưng không có phần tử đối xứng do a a n thì chưa chắc . ● Hiểu đơn giản
n là tập các số dư có thể xảy ra khi chia một số nguyên cho n . Cụ thể chẳng
hạn ở đây là Z4 ={0;1;2;3} tức bốn loại số dư: 0, 1, 2, 3 khi chia cho 4. Và 0 ở đây là lớp đại diện
các số chia cho 4 dư 0, tương tự cho 1,2,3.
Hiển nhiên khi cộng hai lớp thặng dư, ví dụ 1+ 2 tương đương với việc xét tổng của hai số mà 1 lOMoAR cPSD| 57855709
TÀI LIỆU ÔN THI CẤU TRÚC ĐẠI SỐ
số chia 4 dư 1, 1 số chia 4 dư 2. Khi đó tổng của chúng chia 4 dư 3, tức 1+ =2 3. Ta thấy phép
cộng hiển nhiên thỏa mãn tính chất kết hợp, giao hoán, phần tử trung lập. Còn về phần tử đối
xứng, lấy ví dụ cho 1, thì phần tử đối xứng của nó là 4 1− = 3.
Còn khi nhân hai lớp thặng dư, ví dụ 1.2 , lập luận tương tự như trên ta cũng ra được tích là một
s ố chia 4 d ư 2 , t ứ c 1.2 2 = .
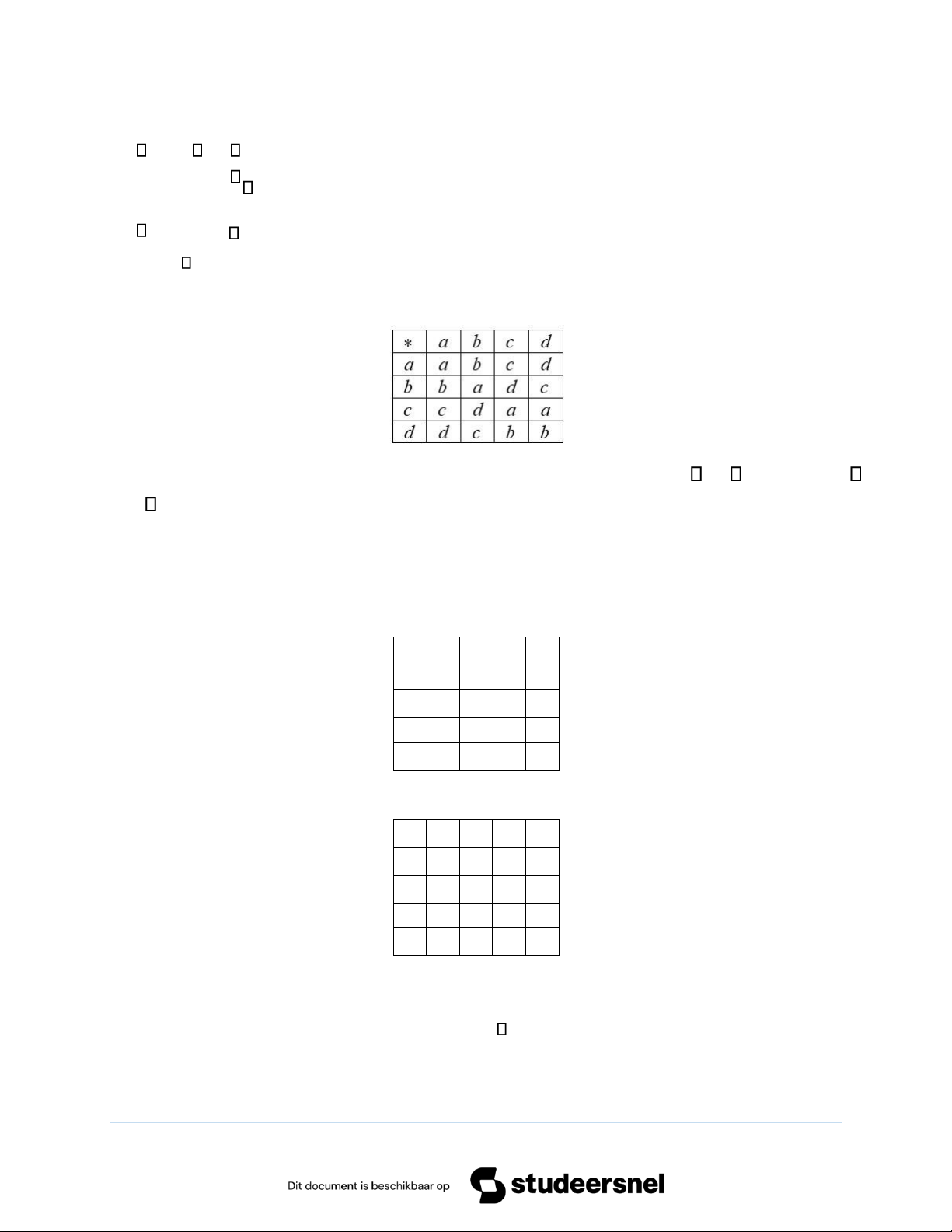
Đ ể d ễ minh h ọ a, ta ch ọ n n = 4 . Khi đó các phép toán c ộ ng và nhân đư ợ c xác đ ị nh như sau: II. Nhóm:
Định nghĩa: Cho G là 1 tập
cùng với phép toán hai ngôi ( ). Khi đó G được gọi là 1 nhóm nếu i)
( ) có tính chất kết hợp. ii)
( ) có phần tử trung lập G. iii) Mọi x G có phần tử đối xứng G. Lưu ý:
- Nếu ( ) chỉ thỏa mãn tính chất i, thì G được gọi là nửa nhóm.
- Nếu ( ) chỉ thỏa mãn tính chất i, ii, thì G được gọi là vị nhóm.
- Nếu ( ) có thêm tính chất giao hoán thì G được gọi là nhóm giao hoán hay nhóm Abel.
Vũ Hải Sơn – K68C HNUE Trang 4
Downloaded by My L? (mymylu9x@gmail.com) lOMoAR cPSD| 57855709
TÀI LIỆU ÔN THI CẤU TRÚC ĐẠI SỐ
- Từ nay khi gặp các bài toán chứng minh nhóm, ta chỉ cần chứng minh thỏa mãn 3 tính chất như
trên định nghĩa, nhiều khi không nhất thiết phải chứng minh phép toán hai ngôi.
Ví dụ 4: Từ định nghĩa, ta dễ dàng suy ra được một số ví dụ sau.
(i) ( ,+),( ,+),( ,+),( ,+) đều là nhóm giao hoán. Có thể kiểm chứng dễ dàng điều này. Chẳng hạn
lấy a b c, , thì (a b+ ) +c a= + (b c+ ) (kết hợp) a+ = + =0 0 a a (phần tử trung lập là 0)
a + −( a) = −( a) + a = 0 (phần tử đối xứng là (−a) )
Hơn nữa phép cộng trong còn giao hoán vì a b b a+ = + . Suy ra ( ,+) là một nhóm giao hoán.
Tương tự cho các tập còn lại.
(ii) ( n,+) cũng là nhóm giao hoán (đã chứng minh ở phần trước).
(iii) ( *, ),( *, ),( *, ) đều là nhóm giao hoán. Nhưng ( *, ) không phải là nhóm vì không phải lúc nào * *
cũng có phần tử đối xứng (phản chứng là 5 nhưng )
(iv) Tập các số hữu tỉ với phép nhân không thành nhóm vì số 0 không có phần tử đối xứng.
Tuy nhiên tập các số hữu tỉ dương + *
hay tập các số hữu tỉ khác không
(như trên) với phép nhân
sẽ lập thành một nhóm.
(v) Tập các ma trận vuông cấp n không suy biến trên trường thực , kí hiệu là GLn( ) , lập
thành một nhóm với phép nhân ma trận. Cụ thể như sau, lấy 3 ma trận không suy biến (tức
det 0) là A B C,, GLn( ) , khi đó theo tính chất ma trận ta có:
( . ).AB C = A BC.( . ) (kết hợp)
AI. = I A. = A ( I là ma trận đơn vị)
A A. −1 = A−1.A= I (do A là ma trận vuông không suy biến nên A khả nghịch, tức là có tồn tại A−1 )
(vi) Sn lập thành một nhóm với phép nhân ánh xạ và gọi là nhóm các phép thế bậc n , còn mỗi Sn
được gọi là một phép thế bậc n. Bài tập.
Câu 1.Hãy kiểm tra rằng các tập hợp sau cùng với phép toán tương ứng có cấu trúc nhóm. Mỗi
nhóm đó có là nhóm Abel không?
(i) Các tập hợp và phép toán trong các ví dụ trên. lOMoAR cPSD| 57855709
TÀI LIỆU ÔN THI CẤU TRÚC ĐẠI SỐ (ii)
Tập các căn phức bậc n của 1 cùng với phép nhân thông thường. (iii) Tập A
={1,2,...,n} với phép toán định nghĩa như sau:
a b = (a +b)modn
(iv) Tập tất cả các hàm bậc nhất trên cùng với phép hợp thành ánh xạ:
G = f : → ,x
ax+b a b| , ,a 0
Nhận xét: Đây là bài toán kiểm tra có phải là một nhóm hay không, tức vẫn có thể không phải là
nhóm. Vì thế ta cần kiểm tra đầy đủ từ phép toán hai ngôi cho đến 3 tính chất nhóm ở định nghĩa bên trên. Giải:
(i) Ta đã chứng minh đây là các nhóm ở các ví dụ bên trên, giờ ta chỉ cần xét nốt tính giao hoán để
xem nó có là nhóm Abel hay không.
( ,+),( ,+),( ,+),( ,+) là nhóm Abel.
( *, ),( *, ),( *, ) là nhóm Abel.
( n,+) là nhóm Abel (do tính chất giao hoán trong phép cộng của )
(GLn ( ), ) không là nhóm Abel (do không có tính chất giao hoán trong phép nhân ma trận, nghĩa
là với hai ma trận A B, GLn( ) thì AB. B A. )
(Sn, ) không là nhóm Abel (do không có tính chất giao hoán trong phép nhân các phép thế, chẳng
hạn xét nhóm S3 thì 1 2 = 4 2 1 = 5 )
(ii) A = z | zn =1
+) Kiểm tra phép toán hai ngôi:
Xét phép nhân: Lấy z,
=A z z. , ta cũng cần chứng minh z.
A để nó là phép toán hai ngôi.
Mà ( .z )n = zn. n = =1.1 1 A, vậy phép nhân đây là phép toán hai ngôi trên A
Lấy z, ,x A: +) (z
) x = ( . ).z x = z.( . ) x = z ( x) (kết hợp)
Vũ Hải Sơn – K68C HNUE Trang 6
Downloaded by My L? (mymylu9x@gmail.com) lOMoAR cPSD| 57855709
TÀI LIỆU ÔN THI CẤU TRÚC ĐẠI SỐ +) z = =1 1 z
z.1=1.z = z với 1 A (1 là phần tử trung hòa) +) z = =1 1 z
z. 1 = 1 .z = 1 và 1 n = 1 = =1 1 1 A (tồn tại phần tử đối xứng) z z z z z zn 1 z
(A, ) là một nhóm. Hơn nữa z = z, z,
A (A, ) cũng là nhóm Abel.
(iii) Chọn a =1,b = n−1 A
=a b 0modn nhưng 0 A đây không là phép toán hai ngôi nên không thể là một nhóm.
(iv) G = f : → ,x
ax+b a b| , ,a 0
+) Kiểm tra phép toán hai ngôi: Ta lấy f : → , f G x ax +b , ,a b ,a 0 g : → ,g G x cx+d , ,c d ,c 0 Khi đó f g x:
a cx( +d)+ =b acx+ad +b
Do a c, , ,a c 0 ac ,ac 0 và a d b, , ad +b Suy ra f
g G đây là phép toán hai ngôi.
- Lấy f g h, , G , trong đó f → g : → h : → : x ax b + x cx d + x ex f +
g) h f ( gh ) = ?
+) Kiểm tra tính kết hợp: ( f lOMoAR cPSD| 57855709
TÀI LIỆU ÔN THI CẤU TRÚC ĐẠI SỐ Thật vậy, ta có
f g = acx + ad +b
g h = cex +cf + d Từ đó suy ra ( f
g) h = ac ex( + f )+adb = acex+acf +ad +b f
(g h) = a cex( +cf +d)+ =b acex+acf +ad +b
( f g) h = f (g h) +) Xét ánh xạ → x x id :
,id G với a =1,b = 0
f id = id f = f (id G là phần tử trung hòa) +) Lấy ánh xạ f ': →
f ' G là phần tử đối 1
b , r õ r à ng f ' G (hi ể n nhi ê n) xứng. x x a − a
Suy ra (G, ) là 1 nhóm. 1 b Nhưng do dof f ' a x b x id = a −a +==
f f ' f ' f id = = 1 b f ' f = ( ax b + ) x id a −a ==
f g = acx+ad +b g g
g f = acx+bc+d f
f nên không có tính giao
hoán, từ đó (G, ) không là nhóm Abel.
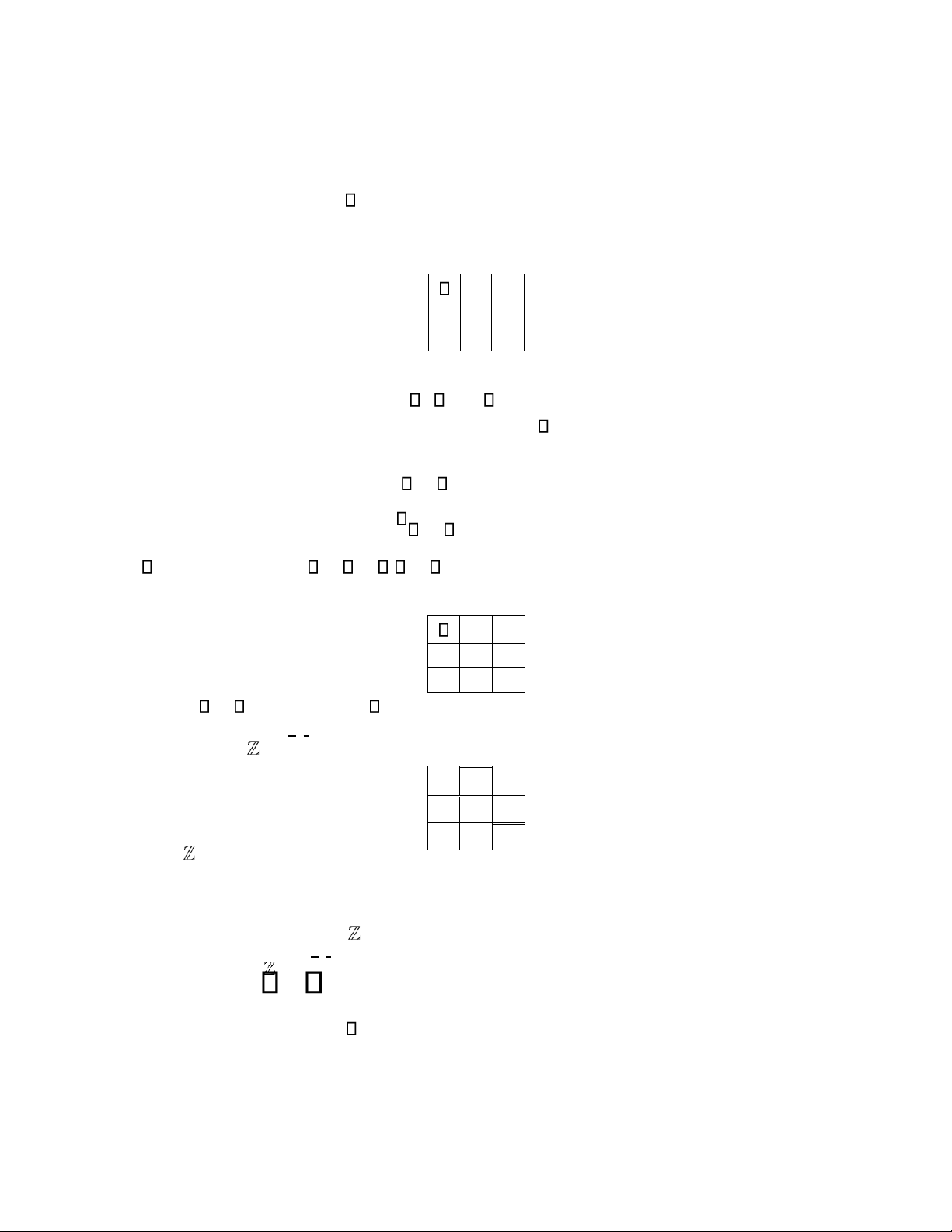
Câu 2.Hãy xây dựng tất cả các phép toán có thể có trên tập X sao cho X là một nhóm, trong đó (a) X ={a b, }
(b) X ={a b c, , }
Vũ Hải Sơn – K68C HNUE Trang 8
Downloaded by My L? (mymylu9x@gmail.com) lOMoAR cPSD| 57855709
TÀI LIỆU ÔN THI CẤU TRÚC ĐẠI SỐ
(c) X ={a b c d, , , } Giải:
a) Cách 1: Muốn cho là nhóm X ={e a, } (bởi trong một nhóm luôn phải tồn tại phần tử trung hòa) Ta có bảng sau: e a e a
Từ bảng trên, ta phải thực hiện các phép tính sau: = =e a a e a e e = e a a = a L( ) a a = e TM( )
(a a = a loại bởi a = a a = = = e a a e a e VL ) Từ đó ta sẽ có e a e e a a a e
Rõ ràng e a = =a ea nên (X , ) là nhóm Abel.
Cách 2: Coi X = 2={0,1} và xét (X, )+ , ta có bảng sau: + 0 1 0 0 1 1 1 0
Ta thấy ( 2,+) là nhóm Abel.
Nhận xét: Ở cách 1, ta thử nghiệm các kết quả của phép tính mang yếu tố mò mẫm, thay vì vậy,
ở cách 2, ta lợi dụng tính chất ( n,+) luôn là nhóm Abel để gán luôn cho tập X gồm 2 phần tử, cụ
thể ở đây là X = 2 = 0,1 .
b) Cách 1: Muốn cho là nhóm X ={e a b, , } (bởi trong một nhóm luôn phải tồn tại phần tử trung hòa) lOMoAR cPSD| 57855709
TÀI LIỆU ÔN THI CẤU TRÚC ĐẠI SỐ Ta có bảng sau: e a b e a b
Từ bảng trên, ta phải thực hiện các phép tính sau:
e a = a e = a
e b = b e = b e e = e a b = a L( ) a b = b L( ) a b = e TM( ) a a = a L( ) a a = e L( ) a a = b TM( )
(a b = a loại bởi a = a b = = = e aa e b e VL
Tương tự a b =b cũng loại
a a = a loại bởi a = a a = = = e a a e a e VL
a a e = loại bởi e = a a = = a b a b VL )
a b = =e b a e doa( = b−1) b b = b L( ) b b = e L( ) b b = a TM( )
Vũ Hải Sơn – K68C HNUE Trang 10
Downloaded by My L? (mymylu9x@gmail.com) lOMoAR cPSD| 57855709
TÀI LIỆU ÔN THI CẤU TRÚC ĐẠI SỐ
(b b =b loại bởi b =b b = = = e b b e b e VL
b b = e loại bởi e =b b = = a b a b VL) Từ đó ta sẽ có e a b
e e a b
a a b e
b b e a Ta thấy a b = =b ae e a = =a e a e b = =b e b
nên (X , ) là nhóm Abel.
Cách 2: Coi X = 3={0,1,2} và xét (X, )+ , ta có bảng sau: + 0 1 2 0 0 1 2 1 1 2 0 2 2 0 1
Ta thấy ( 2,+) là nhóm Abel.
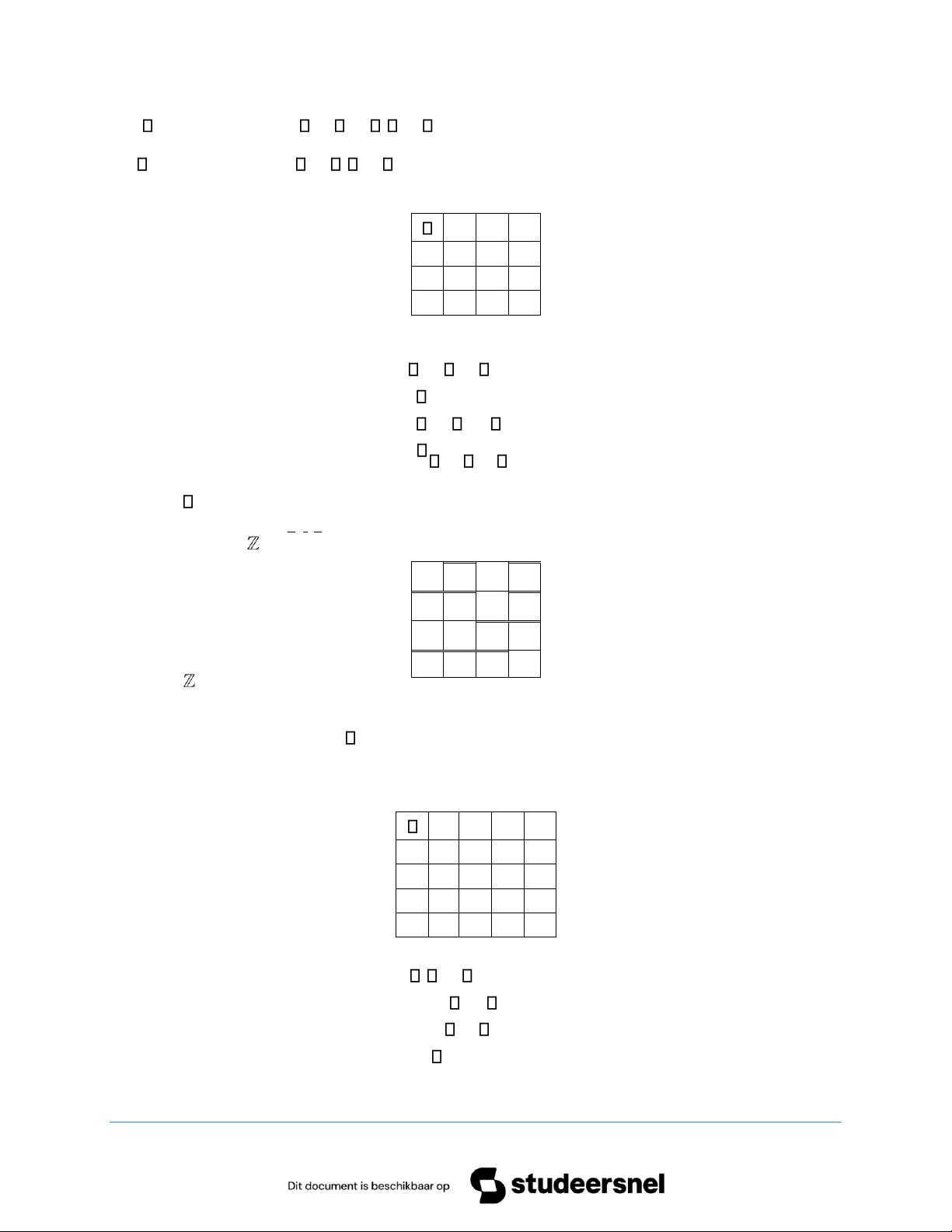
c) Cách 1: Muốn cho là nhóm X ={e a b c, , , } (bởi trong một nhóm luôn phải tồn tại phần tử trung hòa) Ta có bảng sau:
e a b c e a b c
Từ bảng trên, ta phải thực hiện các phép tính sau: = =e a a e a e b = =b e b e c = =c e c e e = e
Vũ Hải Sơn – K68C HNUE Trang 11 Downloaded by My L? (mymylu9x@gmail.com) lOMoAR cPSD| 57855709
TÀI LIỆU ÔN THI CẤU TRÚC ĐẠI SỐ a b = a L( ) a b = b L( ) a b = e a b = c
(a b = a loại bởi a = a b = = = e a a e b e VL. Tương tự a b =b cũng loại)
TH1: Nếu a b = e thì
a b = =e b a e doa( = b−1) a =aa L( ) a =ae L( ) a =a b(1) a =a c(2)
(a a = a loại bởi a = a a = = = e a a e a e VL
a a e = loại bởi e = a a = = a b a b VL ) - Từ (1) ta suy ra a c = a L( ) a c = c L( ) a a = b a c = e L( ) a c = b L( ) Vậy loại (1). - Từ (2) ta suy ra a c = a L( )
Vũ Hải Sơn – K68C HNUE Trang 12
Downloaded by My L? (mymylu9x@gmail.com) lOMoAR cPSD| 57855709
TÀI LIỆU ÔN THI CẤU TRÚC ĐẠI SỐ a c = c L( ) a a = c =a c b a c = e L( ) a c = b b b = e L( ) b b = b L( ) b c = b L( ) b b = a
b c = c L( ) L b c = e L( ) b c = a L( ) b c = b L( ) b c = c L( )
b b = c =b c a b c = e L( ) b c = a c a = e L( ) c a = c L( ) =c a b c a = a L( ) c a = b
Tương tự c b = a c c, = e. Vậy ta có bảng sau
e a b c
e e a b c
a a c e b
Vũ Hải Sơn – K68C HNUE Trang 13 Downloaded by My L? (mymylu9x@gmail.com) lOMoAR cPSD| 57855709
TÀI LIỆU ÔN THI CẤU TRÚC ĐẠI SỐ
b b e c a
c c b a e a b = =b a e a c = =c a b b c = =c ba X là nhóm Abel. = =a e a e a e b = =b e b e c = =c ec
TH2: Nếu a b = c thì a a = a L( ) a a = c L( ) a a = b(1) a a = e(2) - Từ (1) ta suy ra a c = a L( ) a a = b
a c = c L( ) = =c a a c e doa( = c−1) a c = b L( ) a c = e b a = a L( ) b a = b L( ) =b a c b a = e L( )
Vũ Hải Sơn – K68C HNUE Trang 14
Downloaded by My L? (mymylu9x@gmail.com) lOMoAR cPSD| 57855709
TÀI LIỆU ÔN THI CẤU TRÚC ĐẠI SỐ b a = c b b = b L( ) b b = c L( ) =b b e
b b = = = a b c e a c L( ) b b = e = =c b
a b ca c c, = = =b a a a c VL( ) Vậy loại (1). - Từ (2) ta suy ra a b = a L( ) a b = b L( ) a a = e = =a b c a c b a b = e L( ) a b = c b a = b L( ) b a = a L( ) = =b a c c a b b a = e L( ) b a = c b b = b L( ) b b = c L( ) b b = = =a b c
ec be dob(= c−1) = = =c c ab b c b VL( )
Vũ Hải Sơn – K68C HNUE Trang 15 Downloaded by My L? (mymylu9x@gmail.com) lOMoAR cPSD| 57855709
TÀI LIỆU ÔN THI CẤU TRÚC ĐẠI SỐ b b = = =e b c a c b a c c, = e Vậy ta có bảng sau
e a b c
e e a b c
a a e c b
b b c e a
c c b a e a b = =b a c a c = =c a b b c = =c ba X là nhóm Abel. = =a e a e a e b = =b e b e c = =c ec
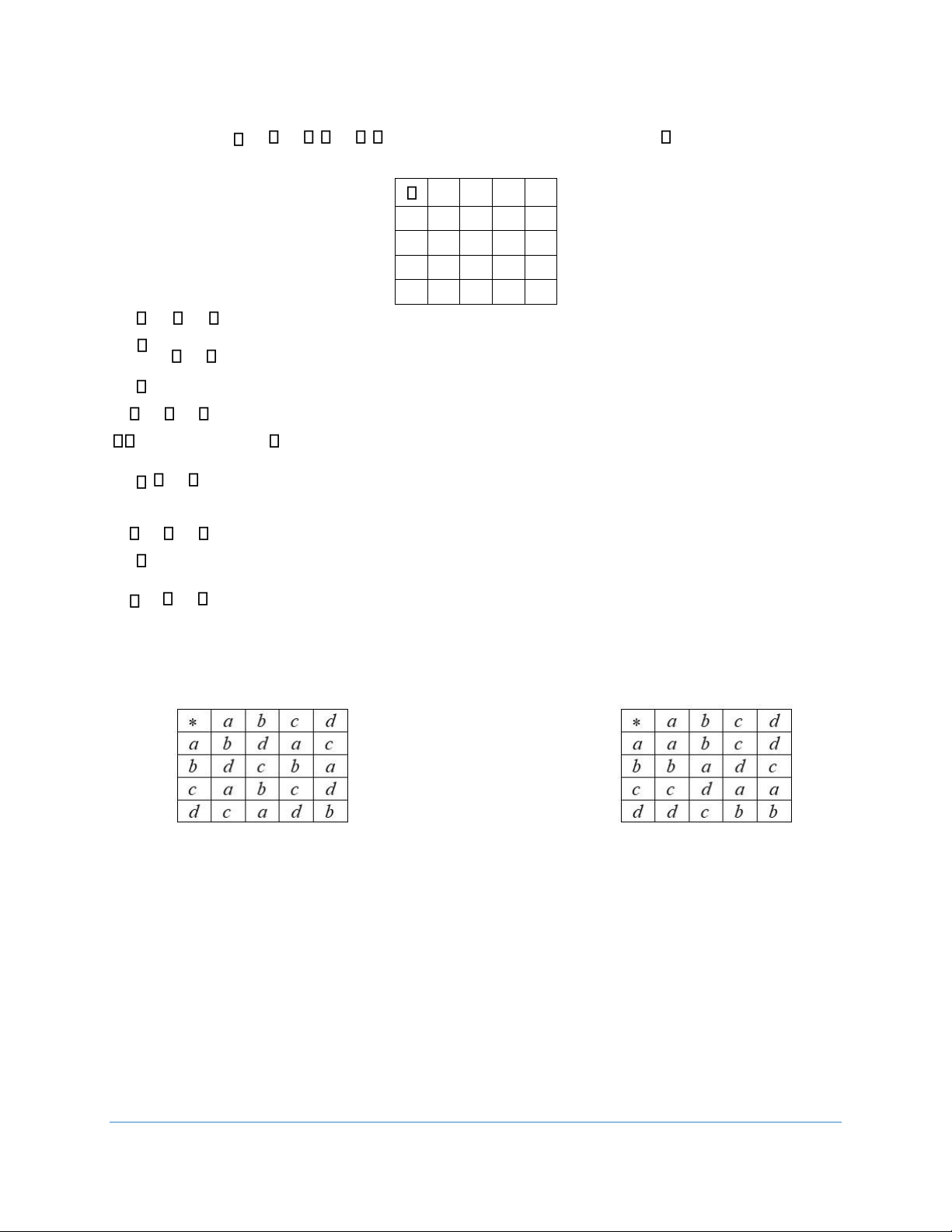
Câu 3. Tập {a b c d, , , } có là một nhóm hay không nếu phép toán trên đó được cho bởi mỗi bảng sau:
Giải: Cách 1: Ta dựa vào bài toán bên trên, nếu 1 tập hợp có 4 phần tử thì nó chỉ có thể có 2 khả
năng như bài toán trên mới tạo thành một nhóm. Đối chiếu với 2 bảng ở đề bài để so sánh đâu là e a b c, , ,
ở bên trên, và nhận thấy bảng 1 là nhóm, còn bảng 2 không là nhóm.
Cách 2: Sử dụng phép thử tính kết hợp của Light: - Ta xét bảng 1:
Vũ Hải Sơn – K68C HNUE Trang 16
Downloaded by My L? (mymylu9x@gmail.com) lOMoAR cPSD| 57855709
TÀI LIỆU ÔN THI CẤU TRÚC ĐẠI SỐ
Phép thử tính kết hợp của Light:
Bước 1: Xác định tập sinh của tập X
- Cụ thể, ở bảng 1, ta thấy tập X ={a b c d, , , } có tập sinh là {a d, } do b = a a = d d và
c = a d = d a.
Bước 2: Viết lại bảng phép toán theo các phần tử của tập sinh bằng cách viết dòng tương ứng
với phần tử đó trong bảng lên đầu của bảng mới, cột tương ứng với phần tử đó trong bảng
sang bên trái ngoài cùng của bảng mới, rồi từ trái qua phải lần lượt viết các cột tương ứng với
Vũ Hải Sơn – K68C HNUE Trang 17 Downloaded by My L? (mymylu9x@gmail.com) lOMoAR cPSD| 57855709
TÀI LIỆU ÔN THI CẤU TRÚC ĐẠI SỐ
từng phần tử. Khi đó nếu các dòng của bảng mới trùng với các dòng tương ứng của bảng ban
đầu thì thỏa mãn. Tương tự cho các bảng phần tử sinh khác, nếu tất cả các bảng đều thỏa mãn
thì phép toán này thỏa mãn tính chất kết hợp.
- Cụ thể, ta sẽ phải lập bảng theo a :
Ta thấy ở bảng 1 ban đầu, dòng tương ứng với phần tử a là (b d a c, , , ) , ta sẽ cho dòng
này lên đầu của bảng a . Cột tương ứng với phần tử a ở bảng 1 là (b d a c, , , ) , ta sẽ cho
dòng này ra bên trái ngoài cùng của bảng a .
a b d a c b d a c
Viết các cột của các phần tử {a b c d, , ,
} trong bảng a tương ứng với các cột của các phần
tử này trong bảng 1 ban đầu. Khi đó ta được
a b d a c
b d c b a
d c a d b
a b d a c
c a b c d
Ta thấy các dòng của các phần tử {a b c d, , ,
} của bảng a cũng trùng với các dòng của
các phần tử trong bảng 1 ban đầu. Vậy bảng a thỏa mãn.
- Tương tự ta cũng có bảng theo d , và bảng này cũng thỏa mãn:
d c a d b
c a b c d
a b d a c
d c a d b
b d c b a
Vậy phép toán này có tính kết hợp.
Vậy phép toán ở bảng 1 có tính kết hợp. Ta sẽ kiểm tra nốt hai tính chất còn lại, là phần tử đơn vị và phần tử đối xứng: Ta thấy
a c = c a = a b c = c b = b c c = c
c là phần tử đơn vị. d c = c d = d
Vũ Hải Sơn – K68C HNUE Trang 18
Downloaded by My L? (mymylu9x@gmail.com) lOMoAR cPSD| 57855709
TÀI LIỆU ÔN THI CẤU TRÚC ĐẠI SỐ Và
d a = a d = c
có phần tử đối xứng. b b = c
Vậy (X, ) là 1 nhóm.
- Tương tự với bảng 2:
- Cụ thể, ở bảng 2, ta thấy tập X ={a b c d, , , } có tập sinh là {b,c} do a =b b = c c và d =b c = c b.
- Cụ thể, ta sẽ phải lập bảng theo c :
Ta thấy ở bảng 2 ban đầu, dòng tương ứng với phần tử c là (c d a a, , , ), ta sẽ cho dòng
này lên đầu của bảng c . Cột tương ứng với phần tử c ở bảng 2 là (c d a b, , , ) , ta sẽ
cho dòng này ra bên trái ngoài cùng của bảng c .
c c d a a c d a b
Viết các cột của các phần tử {a b c d, , ,
} trong bảng a tương ứng với các cột của các phần tử
này trong bảng 2 ban đầu. Khi đó ta được
c c d a a
c c d a a
d d c b b
a a a c c
b b b d d
Ta thấy các dòng của các phần tử {a b c d, , , } của bảng c không trùng với các dòng của các phần
tử trong bảng 2 ban đầu. Vậy bảng c không thỏa mãn.
Vậy phép toán này không có tính kết hợp. Tức (X, ) không là 1 nhóm.
Vũ Hải Sơn – K68C HNUE Trang 19 Downloaded by My L? (mymylu9x@gmail.com) lOMoAR cPSD| 57855709
TÀI LIỆU ÔN THI CẤU TRÚC ĐẠI SỐ
Câu 4. Cho (G, ) là một nhóm với đơn vị e . Chứng minh rằng nếu x2 =e mọi x G thì G là một nhóm Abel.
Giải: Ta có x2 = e x y2. 2 = =ee.e (y G )
( . ).( . )xx y y = e x x y y e.( . ).
= (tính chất kết hợp của nhóm) (1)
Do xy G nên ( . ).( . )x y x y = e x yx y e.( . ). = (tính chất kết hợp của nhóm) (2)
Từ (1), (2) x y. = y x.
G là một nhóm Abel.
Quy ước: Để tạo trực quan, người ta thường kí hiệu phép toán trong nhóm bởi dấu cộng “+”
hay dấu nhân "" thông thường. Quy ước (G,+ =) nhóm (G, ) = nhóm
Tên gọi của phần tử trung Phần tử trung hòa Kí Phần tử đơn vị Kí lập hiệu: 0 hiệu: e
Tên gọi phần tử đối xứng Phần tử đối Kí
Phần tử nghịch đảo Kí của a hiệu: −a hiệu: a−1
Nếu không nói gì cụ thể thì ta sẽ kí hiệu phép toán theo lối nhân ( )
. Định lí: Cho (G, ) là một nhóm. Khi đó: (i) Luật giản ước:
(ii) Phương trình ẩn x có dạng ax b= (hoặc xa =b ) có nghiệm duy nhất là x = a b x−1 ( =
ba−1) (iii) Tồn tại duy nhất phần tử đơn vị e và phần tử nghịch đảo x−1 của x .
(iv) (x−1 )−1 = x, x G .
(v) (xy)−1 =y x− −1 1, x y G, .
Định nghĩa: Cho G là một nhóm, số phần tử của G được gọi là cấp của G , kí hiệu là | G |.
- Nếu | G |= G được gọi là nhóm vô hạn. - Nếu | G n|=
G được gọi là nhóm hữu hạn. Ví dụ 5:
(i) Nhóm phép thế S3 là một nhóm cấp 6 vì nó có 6 phần tử:
Vũ Hải Sơn – K68C HNUE Trang 20
Downloaded by My L? (mymylu9x@gmail.com)