Tài liệu ôn thi Giải tích 12 học kỳ 2 – Trần Thông

Tài liệu ôn thi Giải tích 12 học kỳ 2 – Trần Thông được sưu tầm và soạn thảo dưới dạng file PDF để gửi tới các bạn học sinh cùng tham khảo, ôn tập đầy đủ kiến thức, chuẩn bị cho các buổi học thật tốt. Mời bạn đọc đón xem!

90 45 lượt tải Tải xuống
Chia sẻ Báo cáo tài liệu

Chủ đề: Đề HK2 Toán 12

Môn: Toán 12

Thông tin:

80 trang 8 tháng trước

Tác giả:

Profile Mai Nguyệt
Tài liệu ôn tập giải tích 12 học kỳ II
Trần Thông sưu tầm và biên soạn Facebook: Hội Toán Bắc Nam
TÀI LIỆU ÔN TẬP HỌC KỲ II
LỚP 12- NĂM HỌC 2016-2017
MÔN: GIẢI TÍCH
Quảng Nam, tháng 2 năm 2017
Tài liệu ôn tập giải tích 12 học kỳ II
Trần Thông sưu tầm và biên soạn Facebook: Hội Toán Bắc Nam
A. TÍCH PHÂN
PHẦN 1: TÓM TẮT LÝ THUYẾT
I.Nguyên hàm
1.Định nghĩa. Cho hàm số
()fx
xác định trên K (K là đoạn, khoảng, nửa khoảng). Hàm số
()Fx
được gọi là nguyên hàm của hàm số
()fx
trên K, nếu
'( ) ( )F x f x
, với mọi
xK
.
Định lý. Giả sử
()Fx
là một nguyên hàm của hàm số
()fx
trên khoảng K. Khi đó
a. Với mỗi hằng số C, hàm số
( ) ( )G x F x C
cũng là một nguyên hàm của
()fx
.
b. Ngược lại, nếu G(x) là một nguyên hàm của
()fx
thì tồn tại hằng số C sao cho G(x)
= F(x) + C.
c. Họ tất cả các nguyên hàm của
()fx
là
( ) ( )f x dx F x C
, trong đó
()Fx
là một
nguyên hàm của
()fx
, C là hằng số bất kỳ.
d. Bảng các nguyên hàm cơ bản.
Nguyên hàm của một số hàm số thƣờng gặp
Nguyên hàm các hàm số sơ cấp thƣờng gặp
Nguyên hàm của hàm số hợp
()u u x
,kdx kx C k R
,kdu ku C k R
1
1
. ( 1)
1
x dx x C

1
1
. ( 1)
1
u du u C

ln
dx
xC
x

0x
ln
du
uC
u

(
0x
)
2
dx
xC
x

2
du
uC
u

xx
e dx e C
uu
e du e C
(0 1).
ln
x
x
a
a dx C a
a
(0 1).
ln
u
u
a
a du C a
a
cos sinxdx x C
cos sinudu u C
sin cosxdx x C
sin cosudu u C
2
tan
cos
dx
xC
x

2
cot
sin
dx
xC
x
2
tan
cos
du
uC
u

;
2
cot
sin
du
uC
u
Tài liệu ôn tập giải tích 12 học kỳ II
Trần Thông sưu tầm và biên soạn Facebook: Hội Toán Bắc Nam
Ngoài ra còn một số công thức thƣờng gặp là.
1
1 ) 1 1
( ) ,( 0, 1); ln , 0.
1
11
; ( ) sin( )
1
sin( ) ( )
ax ax
(ax
ax ax
ax
os ax ax
ax os ax
k
k
bb
b
b dx C a k dx b C a
a k b a
e dx e C c b dx b C
aa
b dx c b C
a




2. Một số tính chất của nguyên hàm
Định lý. Nếu
( ), ( )F x G x
tương ứng là một nguyên hàm của
( ), ( )f x g x
thì
a.
'( ) ( )f x dx f x C
b.
[ ( ) ( )] ( ) ( ) ( ) ( )f x g x dx f x dx g x dx F x G x C
;
c.
( ) ( ) ( 0)a.f(x)dx aFa f x dx x C a

.
3. Một số phƣơng pháp đổi nguyên hàm
a. Phƣơng pháp đổi biến số
Cơ sở của phương pháp đổi biến số là định lý sau: Cho hàm số
()u u x
có đạo hàm
liên tục trên K và hàm số
(u)yf
liên tục sao cho
[ ( )]f u x
xác định trên K. Khi đó
nếu F là một nguyên hàm của f, tức là
( ) ( )f u du F u C
thì
[ ( )]dx=F[ ( )]+Cf u x u x
.
b. Phƣơng pháp tích phân từng phần
Một số dạng thƣờng gặp:
Dạng 1.
ax
( ). , ( )sin(ax ) , ( )cos(ax )
b
P x e dx P x b dx P x b dx

Cách giải: Đặt
ax
( ), ( sin( ) , cos( ) )
b
u P x dv e dx dv ax b dx dv ax b dx
Dạng 2.
( )ln(a )P x x b dx
Cách giải: Đặt
ln( ), ( ) .axu b dv P x dx
II. Tích phân
1.Định nghĩa Cho hàm
()fx
liên tục trên khoảng K và a, b là hai số bất kỳ thuộc K. Nếu
()Fx
là một nguyên hàm của
()fx
thì hiệu số
( ) ( )F b F a
được gọi là tích phân của
()fx
từ a đến b
và ký hiệu là
()
b
a
f x dx
. Trong trường hợp
ab
thì
()
b
a
f x dx
là tích phân của f trên
;ab
.
2.Tính chất Cho các hàm số
( ), ( )f x g x
liên tục trên K và
,,abc
là ba số thuộc K.
Tài liệu ôn tập giải tích 12 học kỳ II
Trần Thông sưu tầm và biên soạn Facebook: Hội Toán Bắc Nam
( ) 0 ( ) ( )
( ) ( ) ( ) . ( ) ( )
[ ( ) ( )] ( ) ( )
a b a
a a b
b c b b b
a a c a a
b b b
a a a
f x dx f x dx f x dx
f x dx f x dx f x dx k f x dx k f x dx
f x g x dx f x dx g x dx
3.Một số phƣơng pháp tính tích phân
Phƣơng pháp đổi biến số: Công thức đổi biến số
()
()
[ ( )] '( ) ( )
ub
b
a u a
f u x u x dx f u du

. Trong
đó
()fx
là hàm số liên tục và
()ux
có đạo hàm liên tục trên khoảng J sao cho hàm hợp
[ ( )]f u x
xác định trên J;
,a b J
.
Phƣơng pháp đổi biến số thƣờng áp dụng theo hai cách
Cách 1. Đặt ẩn phụ
()u u x
(
u
là một hàm của x)
Cách 2. Đặt ẩn phụ
()x x t
(
x
là một hàm số của t).
Đối với nguyên hàm nói chung và tích phân nói riêng cần chú ý một số dấu hiệu dẫn tới việc
lựa chọn ẩn phụ như sau:
Dấu hiệu
Có thể chọn
Hàm số có mẫu
Đặt t là mẫu
Hàm
( , ( ))f x x
Đặt
()tx
Hàm
( , ( ), ( ))
nm
f x x x

Đặt
()
mn
tx
Hàm
sin cos
()
sin cos
a x b x
fx
c x d x e

Đặt
tan
2
x
t
Hàm lẻ với sinx
Đặt
costx
Hàm lẻ với cosx
Đặt
sinxt
Hàm chẵn với sinx và cosx
t =tanx
22
ax
| |sin ,
22
| | ,0os
x a t t
x a c t t

Tài liệu ôn tập giải tích 12 học kỳ II
Trần Thông sưu tầm và biên soạn Facebook: Hội Toán Bắc Nam
22
xa
||
, ; 0
sin 2 2
||
,0 ;
2os
a
x t t
t
a
x t t
ct

22
xa
| | tan ,
22
| | ,0ot
x a t t
x a c t t

ax
ax
hoặc
ax
ax
Đặt
cos2x a t
( )( )x a b x
Đặt
2
( )sinx a b a t
Phƣơng pháp tích phân từng phần.
Định lý. Nếu
( ), ( )u x v x
là hai hàm số có đạo hàm liên tục trên khoảng K và
,ab
là hai số
thuộc K thì
( ) '( ) ( ) ( ) ( ) '( )
bb
b
a
aa
u x v x dx u x v x v x u x dx

4. Ứng dụng của tích phân
Tính diện tích hình phẳng
Nếu hàm số
()y f x
liên tục trên
;ab
thì diện tích S của hình phẳng giới hạn bởi đồ
thị hàm số
()y f x
, trục hoành và hai đường thẳng
,x a x b
là
()
b
a
S f x dx
.
Diện tích hình phẳng giới hạn bởi các đồ thị hàm số
()y f x
,
()y g x
và hai đường
thẳng
,x a x b
là
( ) ( )
b
a
S f x g x dx
Để tính diện tích S ta phải tính tích phân (1) , muốn vậy ta phải “phá” dấu giá trị tuyệt đối .
Nếu
b ; a x , 0)( xf
thì
b
a
b
a
dxxfdxxfS )()(
Nếu
b ; a x , 0)( xf
thì
b
a
b
a
dxxfdxxfS )()(
Chú ý Muốn “phá” dấu giá trị tuyệt đối ta phải xét dấu của biểu thức f(x) . Thường có hai
cách làm như sau :
-Cách 1: Dùng định lí “dấu của nhị thức bật nhất” , định lí “dấu của tam thức bậc hai” để xét
dấu các biểu thức f(x) ; đôi khi phải giải các bất phương trình f(x) ≥ 0 , f(x) ≤ 0 trên đoạn
b ; a
Tài liệu ôn tập giải tích 12 học kỳ II
Trần Thông sưu tầm và biên soạn Facebook: Hội Toán Bắc Nam
-Cách 2: Dựa vào đồ thị của hàm số y =f(x) trên đoạn
b ; a
để suy ra dấu của f(x)
trên đoạn đó .
Nếu trên đoạn [a ; b] đồ thị hàm số y = f(x) nằm phía “trên” trục hoành thì
b ; a x , 0)( xf
Nếu trên đoạn [a ; b] đồ thị hàm số y = f(x) nằm phía “dưới” trục hoành thì
b ; a x , 0)( xf
-Cách 3 Nếu f(x) không đổi dấu trên [a ; b] thì ta có :
b
a
b
a
dxxfdxxfS )()(
Tính thể tích vật thể. Thể tích vật thể B giới hạn bởi hai mặt phẳng vuông góc với trục
Ox tại các điểm
,ab
là
()
b
a
V S x dx
. Trong đó S(x) là diện tích thiết diện của vật thể bị
cắt bởi mặt phẳng vuông góc với trục Ox tại điểm có hoành độ là
;x a b
và S(x) là
một hàm liên tục.
Tính thể tích khối tròn xoay.
Hàm số
()y f x
liên tục và không âm trên
;ab
. Hình phẳng giới hạn bởi đồ thị hàm
số
()y f x
, trục hoành và hai đường thẳng
,x a x b
quay quanh trục hoành tạo nên
một khối tròn xoay. Thể tích V được tính bởi công thức
2
()
b
a
V f x dx
.
Hình phẳng giới hạn bởi đồ thị hàm số
()x g y
, trục tung và hai đường thẳng
,y c y d
quay quanh trục tung tạo nên một khối tròn xoay. Thể tích V được tính bởi
công thức
2
()
d
c
V g y dy
.
PHẦN 2: BÀI TẬP MINH HỌA
Dạng 1: Tích phân hàm hữu tỷ
Bài 1: Tính tích phân
x
I dx
xx
2
2
2
1
7 12

Hƣớng dẫn:
I dx
xx
2
1
16 9
1
43




=
x x x
2
1
16ln 4 9ln 3
=
1 25ln2 16ln3
.
Bài 2: Tính tích phân
dx
I
xx
2
53
1
Hƣớng dẫn: Ta có:
x
x
x x x x
3 2 3 2
1 1 1
( 1) 1

I x x
x
2
2
2
1 1 3 1 3
ln ln( 1) ln2 ln5
2 2 2 8
1
2



Tài liệu ôn tập giải tích 12 học kỳ II
Trần Thông sưu tầm và biên soạn Facebook: Hội Toán Bắc Nam
Bài 3: Tính tích phân
xdx
I
x
1
03
( 1)
Hƣớng dẫn:
Ta có:
xx
xx
xx
23
33
11
( 1) ( 1)
( 1) ( 1)



I x x dx
1
23
0
1
( 1) ( 1)
8



Bài 4: Tính nguyên hàm
x
I dx
x
2
4
( 1)
(2 1)
Hƣớng dẫn: Ta có:
xx
fx
xx
2
1 1 1
( ) . .
3 2 1 2 1


x
IC
x
3
11
9 2 1




.
Bài 5: Tính tích phân
x
I dx
x
1
7
25
0
(1 )
Hƣớng dẫn: Đặt
t x dt xdx
2
12
t
I dt
t
2
3
55
1
1 ( 1) 1 1
.
24
2

Bài 6: Tính tích phân
I x x dx
1
5 3 6
0
(1 )
Hƣớng dẫn: Đặt
dt t t
t x dt x dx dx I t t dt
x
1
78
3 2 6
2
0
1 1 1
1 3 (1 )
3 3 7 8 168
3



.
Bài 7: Tính tích phân
I x x dx
1
5 3 6
0
(1 )
Hƣớng dẫn: Đặt
dt t t
t x dt x dx dx I t t dt
x
1
78
3 2 6
2
0
1 1 1
1 3 (1 )
3 3 7 8 168
3



.
Bài 8: Tính tích phân
x
I dx
x
2
2001
2 1002
1
.
(1 )
Hƣớng dẫn: Ta có:
x xdx
I
xx
1
2000
2 2000 2 2
0
1 .2
2
(1 ) (1 )

. Đặt
t x dt xdx
2
12
t
I dt d
tt
tt
1000
22
1000
1000 2 1001
11
1 ( 1) 1 1 1 1
11
22
2002.2

Bài 9: Tính tích phân
x
I dx
xx
15
2
2
42
1
1
1

Tài liệu ôn tập giải tích 12 học kỳ II
Trần Thông sưu tầm và biên soạn Facebook: Hội Toán Bắc Nam
Hƣớng dẫn: Ta có:
x
x
xx
x
x
2
2
42
2
2
1
1
1
1
1
1


. Đặt
t x dt dx
x
x
2
11
1



dt
I
t
1
2
0
1
. Đặt
du
t u dt
u
2
tan
cos
I du
4
0
4

Dạng 2: Tích phân hàm vô tỷ
Bài 1: Tính nguyên hàm
x
I dx
xx
2
3 9 1

Hƣớng dẫn: Ta có
x
I dx x x x dx x dx x x dx
xx
2 2 2
2
(3 9 1) 3 9 1
3 9 1

Lại có
I x dx x C
23
11
3
I x x dx
2
2
91
x d x x C
3
2 2 2
2
2
11
9 1 (9 1) (9 1)
18 27
I x x C
3
23
2
1
(9 1)
27
Bài 2: Tính nguyên hàm
xx
I dx
xx
2
1
Hƣớng dẫn: Ta có
xx
dx
xx
2
1
xx
dx dx
x x x x
2
11



.
Lại có
x
I dx
xx
2
1
1
.
Đặt t=
x x t x x
2
11
xt
3 2 2
( 1)
x dx t t dt
22
4
( 1)
3
t dt t t C
23
4 4 4
( 1)
3 9 3
=
x x x x C
3
1
44
11
93
Đối với
x
I dx
xx
2
1
=
d x x
xx
2 (1 )
3
1
=
x x C
2
4
1
3

Vậy:
I x x C
3
4
1
9
Bài 3: Tính tích phân
x
I dx
xx
3
0
3
3 1 3
Tài liệu ôn tập giải tích 12 học kỳ II
Trần Thông sưu tầm và biên soạn Facebook: Hội Toán Bắc Nam
Hƣớng dẫn:
Đặt
t x tdu dx12
tt
I dt t dt dt
t
tt
2 2 2
3
2
1 1 1
2 8 1
(2 6) 6
1
32

3
3 6ln
2
Bài 4: Tính tích phân
xx
I dx
x
3
2
0
21
1

Hƣớng dẫn: Đặt
x t x t
2
11
dx tdt2
t t t
I tdt t t dt t
t
2
22
2 2 2 5
4 2 3
1
11
2( 1) ( 1) 1 4 54
2 2 (2 3 ) 2
55




Bài 5: Tính tích phân
x
I dx
xx
5
2
1
1
31
Hƣớng dẫn: Đặt
tdt
t x dx
2
31
3
t
tdt
I
t
t
2
2
4
2
2
1
1
3
2
.
3
1
.
3




t
tt
t
3
44
2 1 1 100 9
ln ln .
9 3 1 27 5
22



Bài 5: Tính tích phân
x
I dx
xx
5
2
1
1
31
Hƣớng dẫn: Đặt
tdt
t x dx
2
31
3
t
tdt
I
t
t
2
2
4
2
2
1
1
3
2
.
3
1
.
3




t
tt
t
3
44
2 1 1 100 9
ln ln .
9 3 1 27 5
22



Bài 6: Tính tích phân
I x x x dx
1
32
0
( 1) 2
Hƣớng dẫn:
I x x x dx x x x x x dx
11
3 2 2 2
00
( 1) 2 ( 2 1) 2 ( 1)

. Đặt
t x x
2
2
I
2
15

.
Bài 7: Tính tích phân
x x x
I dx
xx
2
32
2
0
23
1


Tài liệu ôn tập giải tích 12 học kỳ II
Trần Thông sưu tầm và biên soạn Facebook: Hội Toán Bắc Nam
Hƣớng dẫn:
Ta có
x x x x
I dx dx
x
xx
11
22
22
11
1 1 1 1
2
(1 ) (1 )



x
dx dx
xx
11
2
11
1 1 1
1
22





+
I dx x x
x
1
1
11
1
1 1 1
1 ln | 1
22





+
x
I dx
x
1
2
2
1
1
2
. Đặt
t x t x tdt xdx
2 2 2
1 1 2 2
I
2
=
t dt
t
2
2
2
2
0
2( 1)
Vậy:
I 1
.
Bài 8: Tính tích phân
x
I dx
x
2
2
1
4
Hƣớng dẫn: Ta có Ta có:
x
I xdx
x
2
2
2
1
4
. Đặt t =
x t x tdt xdx
2 2 2
44
I =
t tdt t t
dt dt t
t
t t t
0
0 0 0
2
2 2 2
3
3 3 3
( ) 4 2
(1 ) ln
2
4 4 4




=
23
3 ln
23





.
Bài 9: Tính tích phân
x
I dx
xx
3
2
22
0
(1 1 ) (2 1 )
Hƣớng dẫn: Đặt
xt21
I t dt
t
t
4
2
3
42 36 4
2 16 12 42ln
3



Bài 10: Tính tích phân
dx
I
xx
1
3
33
0
(1 ). 1

Hƣớng dẫn: Đặt
tx
3
3
1
t dt
I dt
t t t t
33
22
2
22
11
4 3 2 3
33
.( 1) .( 1)



dt dt
t
dt
t
t
tt
t
t
3 3 3
2
3
2 2 2
3
2 2 4
1 1 1
33
4
23
3
3
1
1
1
1
1
.1










Tài liệu ôn tập giải tích 12 học kỳ II
Trần Thông sưu tầm và biên soạn Facebook: Hội Toán Bắc Nam
Đặt
dt
u du
tt
34
13
1
uu
I du u du u
1
1
11
21
2
21
2
22
33
33
3
00
0
0
1 1 1
1
3 3 3
2
3







Bài 11: Tính tích phân
x
I dx
xx
x
22
4
2
3
1
1




Hƣớng dẫn: Đặt
tx
2
1
t
I dt
t
3
22
2
2
( 1)
2
=
tt
dt t dt dt
tt
3 3 3
42
2
22
2 2 2
2 1 1 19 2 4 2
ln
34
42
22





Bài 12: Tính tích phân
x
I dx
xx
27
3
2
1
2
Hƣớng dẫn:
Đặt
tx
6
tt
I dt dt
t
t t t t
33
3
2 2 2
11
2 2 2 1
5 5 1
( 1) 1 1




25
5 3 1 ln
3 12



Bài 13: Tính tích phân
I x x x dx
2
5 2 2
2
( ) 4
Hƣớng dẫn: I =
x x x dx
2
5 2 2
2
( ) 4

=
x x dx
2
52
2
4
+
x x dx
2
22
2
4
= A + B.
+ Tính A =
x x dx
2
52
2
4
. Đặt
tx
. Tính được: A = 0.
+ Tính B =
x x dx
2
22
2
4
. Đặt
xt2sin
. Tính được: B =
2
.
Vậy:
I 2
.
Bài 14: Tính tích phân
x dx
I
x
2
2
4
1
34
2

Hƣớng dẫn:
x
I dx dx
xx
22
2
44
11
34
22


.
+ Tính
I
1
=
dx
x
2
4
1
3
2
=
x dx
2
4
1
37
2 16
.
+ Tính
x
I dx
x
2
2
2
4
1
4
2
. Đặt
x t dx tdt2sin 2cos
.
Tài liệu ôn tập giải tích 12 học kỳ II
Trần Thông sưu tầm và biên soạn Facebook: Hội Toán Bắc Nam
tdt
I t dt t d t
tt
2
2 2 2
22
2
42
6 6 6
1 cos 1 1 1 3
cot cot . (cot )
8 8 8 8
sin sin



Vậy:
I
1
7 2 3
16

Bài 15: Tính tích phân
I x dx
3
2
2
1
Hƣớng dẫn: Đặt
x
du dx
ux
x
dv dx
vx
2
2
1
1



x
I x x x dx x dx
xx
33
22
22
22
3
1
1 . 5 2 1
2
11






dx
x dx
x
33
2
2
22
5 2 1
1

I x x
23
2
5 2 ln 1
I
5 2 1
ln 2 1 ln2
24
Dạng 3: Tích phân hàm lƣợng giác
Bài 1: Tính nguyên hàm
xx
I dx
xx
2
8cos sin2 3
sin cos

Hƣớng dẫn:
x x x
I dx x x x x dx
xx
2
(sin cos ) 4cos2
sin cos 4(sin cos
sin cos




x x C3cos 5sin
.
Bài 2: Tính nguyên hàm
x x x
I dx
x
cot tan 2tan2
sin4

Hƣớng dẫn:
x x x x
I dx dx dx C
x x x
x
2
2cot2 2tan2 2cot4 cos4 1
2
sin4 sin4 2sin4
sin 4
Bài 3: Tính nguyên hàm
x
I dx
xx
2
cos
8
sin2 cos2 2




Hƣớng dẫn:
x
I dx
x
1 cos 2
1
4
22
1 sin 2
4








Tài liệu ôn tập giải tích 12 học kỳ II
Trần Thông sưu tầm và biên soạn Facebook: Hội Toán Bắc Nam
x
dx
dx
x
xx
2
cos 2
1
4
22
1 sin 2
sin cos
4
88













x
dx
dx
xx
2
cos 2
11
4
2
3
22
1 sin 2 sin
48










x x C
13
ln 1 sin 2 cot
48
42





Bài 4: Tính tích phân
dx
I
xx
3
2 3sin cos

Hƣớng dẫn:
dx
I
x
3
1
2
1 cos
3




=
dx
I
x
2
3
1
4
2sin
26



=
1
43
.
Bài 5: Tính tích phân
I dx
x
6
0
1
2sin 3
Hƣớng dẫn:
I dx dx
xx
66
00
1
11
2
2
sin sin sin sin
33





xx
dx dx
xx
x
66
00
cos
cos
2 6 2 6
3
sin sin
2cos .sin
3
2 6 2 6









xx
dx dx
xx
66
00
cos sin
2 6 2 6
11
22
sin cos
2 6 2 6







xx
66
00
ln sin ln cos .....
2 6 2 6


Bài 6: Tính tích phân
I x x x dx
2
44
0
cos2 (sin cos )

Tài liệu ôn tập giải tích 12 học kỳ II
Trần Thông sưu tầm và biên soạn Facebook: Hội Toán Bắc Nam
Hƣớng dẫn:
I x x dx x d x
22
22
00
1 1 1
cos2 1 sin 2 1 sin 2 (sin2 ) 0
2 2 2


Bài 7: Tính tích phân
x
I dx
x
3
2
0
4sin
1 cos
Hƣớng dẫn:
Ta có
x x x
x x x x x
x
x
33
2
4sin 4sin (1 cos )
4sin 4sin cos 4sin 2sin2
1 cos
sin
I x x dx
2
0
(4sin 2sin2 ) 2
Bài 8: Tính tích phân
I xdx
2
0
1 sin

Hƣớng dẫn:
x x x x
I dx dx
2
22
00
sin cos sin cos
2 2 2 2





x
dx
2
0
2 sin
24




xx
dx dx
3
2
2
3
0
2
2 sin sin
2 4 2 4








42
Bài 9: Tính nguyên hàm
xdx
I
xx
sin2
3 4sin cos2

Hƣớng dẫn: Ta có:
xx
I dx
xx
2
2sin cos
2sin 4sin 2

. Đặt
txsin
I x C
x
1
ln sin 1
sin 1
Bài 10: Tính nguyên hàm
dx
I
xx
35
sin .cos
Hƣớng dẫn:
xx
dx
xxx
dx
I
23233
cos.2sin
8
cos.cos.sin
Đặt
txtan
.
I t t t dt x x x C
t
x
3 3 4 2
2
3 1 3 1
3 tan tan 3ln tan
42
2tan



Bài 11: Tính nguyên hàm
xx
I xdx
x
2011
2011 2009
5
sin sin
cot
sin
Hƣớng dẫn:
Ta có:
x
x
I xdx xdx
xx
2011
2011
2
2
44
1
1
cot
sin
cot cot
sin sin


Tài liệu ôn tập giải tích 12 học kỳ II
Trần Thông sưu tầm và biên soạn Facebook: Hội Toán Bắc Nam
Đặt
txcot
I t tdt t t C
2 4024 8046
2
2011 2011 2011
2011 2011
t (1 )
4024 8046
=
x x C
4024 8046
2011 2011
2011 2011
cot cot
4024 8046

Bài 12: Tính tích phân
I x x dx
2
2
sin (2 1 cos2 )
Hƣớng dẫn:
Ta có:
I xdx x xdx H K
22
22
2sin sin 1 cos2



+
H xdx x dx
2
22
2sin (1 cos2 )
22




+
K x x x xdx
2 2 2
22
sin 2cos 2 sin cos



xd x
2
2
2
2 sin (sin )
3
I
2
23
Bài 13: Tính tích phân
2
2
0
sin2
2 sin
x
I dx
x
Hƣớng dẫn:
x x x
I dx dx
xx
22
22
00
sin2 sin cos
2
(2 sin ) (2 sin )




.
Đặt
tx2 sin
.
t
I dt dt t
tt
tt
3
33
22
22
2
2 1 2 2
2 2 2 ln

32
2ln
23

Bài 14: Tính tích phân
x
I dx
xx
4
66
0
sin4
sin cos
Hƣớng dẫn:
x
I dx
x
4
2
0
sin4
3
1 sin 2
4
. Đặt
tx
2
3
1 sin 2
4

I =
dt
t
1
4
1
21
3



=
t
1
1
4
42
33
Tài liệu ôn tập giải tích 12 học kỳ II
Trần Thông sưu tầm và biên soạn Facebook: Hội Toán Bắc Nam
Bài 15: Tính tích phân
xx
I dx
x
2
4
2
3
sin 1 cos
cos
Hƣớng dẫn:
xx
I x dx x dx
xx
44
2
22
33
sin sin
1 cos . sin
cos cos




xx
x dx x dx
xx
0
4
22
0
3
sin sin
sin sin
cos cos


=
xx
dx dx
xx
0
22
4
22
0
3
sin sin
cos cos


7
31
12
Bài 16: Tính tích phân
xx
I dx
xx
2
3
0
3sin 2cos
(sin cos )
Hƣớng dẫn:
Đặt
x t dx dt
2
t t x x
I dt dx
t t x x
22
33
00
3cos 2sin 3cos 2sin
(cos sin ) (cos sin )





x x x x
I I I dx dx dx
x x x x x x
2 2 2
3 3 2
0 0 0
3sin 2cos 3cos 2sin 1
21
(sin cos ) (cos sin ) (sin cos )

I
1
2
Bài 17: Tính tích phân
xx
I dx
x
2
0
sin
1 cos
Hƣớng dẫn:
Đặt
t t t
x t dx dt I dt dt I
tt
22
00
( )sin sin
1 cos 1 cos




t d t
I dt I
tt
2
22
00
sin (cos )
2
4 4 8
1 cos 1 cos






Bài 18: Tính tích phân
x
I dx
xx
3
2
0
sin
cos 3 sin
Hƣớng dẫn:
Đặt
tx
2
3 sin
=
x
2
4 cos
. Ta có:
xt
22
cos 4
và
xx
dt dx
x
2
sin cos
3 sin
.
Tài liệu ôn tập giải tích 12 học kỳ II
Trần Thông sưu tầm và biên soạn Facebook: Hội Toán Bắc Nam
I =
x
dx
xx
3
2
0
sin
.
cos 3 sin
=
xx
dx
xx
3
22
0
sin .cos
cos 3 sin
=
dt
t
15
2
2
3
4
=
dt
tt
15
2
3
1 1 1
4 2 2




=
t
t
15
2
3
12
ln
42
=
1 15 4 3 2
ln ln
4
15 4 3 2






=
1
ln 15 4 ln 3 2
2
Bài 19: Tính tích phân
x
I dx
xx
4
2
6
tan
cos 1 cos
Hƣớng dẫn:
Ta có:
xx
I dx dx
xx
x
x
44
22
2
2
66
tan tan
1
cos tan 2
cos 1
cos




Đặt
u x du dx
x
2
1
tan
cos
u
I dx
u
1
2
1
3
2
. Đặt
u
t u dt du
u
2
2
2
2
.
I dt t
3
3
7
7
3
3
7 3 7
3.
33
Bài 20: Tính tích phân
xx
I dx
x
3
2
3
sin
cos
Hƣớng dẫn: Sử dụng công thức tích phân từng phần ta có:
x dx
I xd J
x x x
33
3
3
33
14
,
cos cos cos 3







với
dx
J
x
3
3
cos
Để tính J ta đặt
txsin .
Khi đó
dx dt t
J
xt
t
3
3
3
2
2
2
3
3
2
3
2
1 1 2 3
ln ln
cos 2 1
23
1


Vậy
I
4 2 3
ln .
3
23

Tài liệu ôn tập giải tích 12 học kỳ II
Trần Thông sưu tầm và biên soạn Facebook: Hội Toán Bắc Nam
Bài 21: Tính tích phân
x
x
I e dx
x
2
0
1 sin
.
1 cos



Hƣớng dẫn: Ta có:
xx
xx
xx
x
22
1 2sin cos
1 sin 1
22
tan
1 cos 2
2cos 2cos
22
x
x
e dx x
I e dx
x
22
2
00
tan
2
2cos
2



=
e
2
Dạng 3: Tích phân hàm mũ logarit
Bài 1: Tính nguyên hàm
x
x
e
I dx
e
2
1
Hƣớng dẫn: Đặt
x x x
t e e t e dx tdt
2
2
.
t
I dt
t
3
2
1
t t t t C
32
2
2 2ln 1
3
x x x x x
e e e e e C
2
2 2ln 1
3
Bài 2: Tính nguyên hàm
x
x
x x e
I dx
xe
2
()
Hƣớng dẫn:
x
x
x x e
I dx
xe
2
()
=
xx
x
xe x e
dx
xe
.( 1)
1
. Đặt
x
t x e.1
xx
I xe xe C1 ln 1
.
Bài 3: Tính nguyên hàm
x
x
xx
I dx
ex e
2
2
21
ln(1 ) 2011
ln ( )



Hƣớng dẫn:
xx
I dx
xx
2
22
ln( 1) 2011
( 1) ln( 1) 1





. Đặt
tx
2
ln( 1) 1
t
I dt
t
1 2010
2
t t C
1
1005ln
2
=
x x C
22
11
ln( 1) 1005ln(ln( 1) 1)
22
Bài 4: Tính tích phân
e
x
x
xe
J dx
x e x
1
1
( ln )
Hƣớng dẫn:
e
xe
e
x
x
d e x e
J e x
e
ex
1
1
( ln ) 1
ln ln ln
ln

Bài 5: Tính tích phân
xx
x x x
ee
I dx
e e e
ln2
32
32
0
21
1

Tài liệu ôn tập giải tích 12 học kỳ II
Trần Thông sưu tầm và biên soạn Facebook: Hội Toán Bắc Nam
Hƣớng dẫn:
x x x x x x
x x x
e e e e e e
I dx
e e e
ln2
3 2 3 2
32
0
3 2 ( 1)
1
=
x x x
x x x
e e e
dx
e e e
ln2
32
32
0
32
1
1





=
x x x
e e e x
32
ln2 ln2
ln( – 1)
00
= ln11 – ln4 =
14
ln
4
Bài 6: Tính tích phân
x
dx
I
e
3ln2
2
3
0
2
Hƣớng dẫn:
x
x
x
e dx
I
ee
3ln2
3
2
0
3
3
2
. Đặt
xx
t e dt e dx
33
1
3
I
3 3 1
ln
4 2 6




Bài 7: Tính tích phân
xx
x x x x
e e dx
I
e e e e
ln15
2
3ln2
24
1 5 3 1 15
Hƣớng dẫn:
Ta có
x x x
x x x x x
x
x
33
2
4sin 4sin (1 cos )
4sin 4sin cos 4sin 2sin2
1 cos
sin
I x x dx
2
0
(4sin 2sin2 ) 2
Bài 8: Tính tích phân
I xdx
2
0
1 sin

Hƣớng dẫn: Đặt
xx
t e t e
2
11
x
e dx tdt2
.
t t dt
I dt t t t
tt
t
44
2
4
2
3
33
(2 10 ) 3 7
2 2 3ln 2 7ln 2
22
4





2 3ln2 7ln6 7ln5
Bài 9: Tính tích phân
ln3
2
ln2
12
x
xx
e dx
I
ee
Hƣớng dẫn: Đặt t =
x
e 2
x
e dx tdt
2
2
I = 2
t tdt
tt
1
2
2
0
( 2)
1

= 2
t
t dt
tt
1
2
0
21
1
1





=
t dt
1
0
2 ( 1)
+
d t t
tt
1
2
2
0
( 1)
2
1


=
tt
1
2
0
( 2 )
+
tt
1
2
0
2ln( 1)
=
2ln3 1
.
Bài 10: Tính tích phân
xx
xx
ee
I dx
ee
ln3
32
0
2
4 3 1

Hƣớng dẫn:
Đặt
x x x x x x
t e e t e e tdt e e dx
3 2 2 3 2 3 2
4 3 4 3 2 (12 6 )
xx
tdt
e e dx
32
(2 )
3
Tài liệu ôn tập giải tích 12 học kỳ II
Trần Thông sưu tầm và biên soạn Facebook: Hội Toán Bắc Nam
tdt
I dt
tt
99
11
1 1 1
(1 )
3 1 3 1


tt
9
1
1 8 ln5
( ln 1) .
33
Bài 11: Tính tích phân
x
x
e
I dx
e
ln5
2
ln2
1
Hƣớng dẫn: Đặt
xx
x
tdt t
t e t e dx I t d t
e
2
2
3
22
1
1
2 20
1 1 2 ( 1) 2
33



Bài 12: Tính tích phân
xx
xx
I dx
2
1
22
4 4 2

Hƣớng dẫn: Đặt
xx
t 22

x x x x 2
4 4 2 (2 2 ) 4

1 81
ln
4ln2 25
I
Bài 13: Tính tích phân
1
0
6
9 3.6 2.4

x
x x x
dx
I
Hƣớng dẫn:
x
xx
dx
I
1
2
0
3
2
33
32
22




. Đăt
x
t
3
2



.
dt
I
tt
3
2
2
1
1
ln3 ln2
32

ln15 ln14
ln3 ln2
Bài 14: Tính tích phân
e
xx
I dx
x
3
2
1
ln 2 ln
Hướng dẫn Đặt
tx
2
2 ln
x
dt dx
x
2ln
I tdt
3
3
2
1
2
3
3
44
3
32
8

Bài 15: Tính tích phân
e
e
dx
I
x x ex
2
ln .ln
Hƣớng dẫn:
ee
ee
dx d x
I
x x x x x
22
(ln )
ln (1 ln ) ln (1 ln )



=
e
e
dx
xx
2
11
(ln )
ln 1 ln



= 2ln2 – ln3
Bài 16: Tính tích phân
e
x
I dx
xx
3
2
2
1
log
1 3ln
Hƣớng dẫn:
e e e
x
x
x xdx
I dx dx
x
x x x x x
3
3
2
2
3
2 2 2
1 1 1
ln
log
ln2
1 ln . ln
.
ln 2
1 3ln 1 3ln 1 3ln




Đặt
dx
x t x t x tdt
x
2 2 2
11
1 3ln ln ( 1) ln .
33
.
Tài liệu ôn tập giải tích 12 học kỳ II
Trần Thông sưu tầm và biên soạn Facebook: Hội Toán Bắc Nam
Suy ra
I t t
2
3
33
1
1 1 4
3
9ln 2 27ln 2



Bài 17: Tính tích phân
e
x x x
I dx
xx
1
( 2)ln
(1 ln )

Hƣớng dẫn:
ee
x
dx dx
xx
11
ln
2
(1 ln )

=
e
x
e dx
xx
1
ln
12
(1 ln )

Tính J =
e
x
dx
xx
1
ln
(1 ln )
. Đặt
tx1 ln
t
J dt
t
2
1
1
1 ln2
.
Vậy:
Ie3 2ln2
.
Bài 18: Tính tích phân
e
e
x x x x
I dx
xx
3
2
22
2 ln ln 3
(1 ln )

Hƣớng dẫn:
ee
ee
I dx xdx
xx
33
22
1
3 2 ln
(1 ln )


ee
32
3ln2 4 2
Bài 19: Tính tích phân
5
2
ln( 1 1)
11

x
I dx
xx
Hƣớng dẫn: Đặt
txln 1 1
dx
dt
xx
2
11
I dt
ln3
22
ln2
2 ln 3 ln 2
.
Bài 20: Tính tích phân
3
3
1
ln
1 ln
e
x
I dx
xx
Hƣớng dẫn: Đặt
dx
t x x t tdt
x
2
1 ln 1 ln 2
và
xt
3 2 3
ln ( 1)
t t t t
I dt = dt t t t dt
t t t
2 2 2
2 3 6 4 2
53
1 1 1
( 1) 3 3 1 1
( 3 3 )
15
ln2
4

Bài 21: Tính tích phân
inx
I e xdx
2
s
0
.sin2
Hƣớng dẫn:
inx
I e x xdx
2
s
0
2 .sin cos
. Đặt
xx
u x du xdx
dv e xdx v e
sin sin
sin cos
cos





x x x
I xe e xdx e e
2
sin sin sin
22
00
0
2sin .cos 2 2 2

Tài liệu ôn tập giải tích 12 học kỳ II
Trần Thông sưu tầm và biên soạn Facebook: Hội Toán Bắc Nam
Bài 22: Tính tích phân
I x x x dx
1
2
0
ln( 1)
Hƣớng dẫn: Đặt
x
du dx
u x x
xx
dv xdx
x
v
2
2
2
21
ln( 1)
1
2


x x x
I x x dx
xx
1
1
2 3 2
2
2
0
0
12
ln( 1)
22
1

x dx
x dx dx
x x x x
1 1 1
22
0 0 0
1 1 1 2 1 3
ln3 (2 1)
2 2 4 4
11
33
ln3
4 12

Bài 23: Tính tích phân
x
I dx
x
8
3
ln
1
Hƣớng dẫn:
Đặt
ux
dx
du
dx
x
dv
vx
x
ln
21
1




x
I x x dx J
x
8
8
3
3
1
2 1.ln 2 6ln8 4ln3 2
+ Tính
x
J dx
x
8
3
1
.
Đặt
tt
t x J tdt dt dt
tt
tt
3 3 3
2
22
2 2 2
11
1 .2 2 2
11
11





t
t
t
8
3
1
2 ln 2 ln3 ln2
1



Từ đó
I 20ln2 6ln3 4
.
Bài 24: Tính tích phân
x
I = dx
x
2
2
1
ln( 1)
Hƣớng dẫn: Đặt
dx
ux
du
dx
x
dx
Ix
dv
x x x
v
x
x
2
2
1
ln( 1)
13
2
1
ln( 1) 3ln2 ln3
11
( 1) 2




Bài 25: Tính tích phân
x
I x dx
x
1
2
0
1
ln
1



Tài liệu ôn tập giải tích 12 học kỳ II
Trần Thông sưu tầm và biên soạn Facebook: Hội Toán Bắc Nam
Hƣớng dẫn: Đặt
du dx
x
u
x
x
x
dv xdx
v
2
2
2
1
ln
(1 )
1
2



x
I x x dx
x
x
1
2
22
2
0
1
1 1 2
ln
2
21
1
0







x
dx dx
xx
x
11
2
22
2
00
ln3 ln3 1 ln3 1 1 2
1 ln
8 8 ( 1)( 1) 8 2 2 3
1





Bài 26: Tính tích phân
22
1
ln ( ln )
.
1

e
xx
x
x e e x
I dx
e
Hƣớng dẫn: Ta có:
ee
x
x
e
I x dx dx H K
e
2
2
11
ln .
1

+
e
H x dx
2
1
ln .
. Đặt:
ux
dv dx
2
ln
e
H e x dx e
1
2ln . 2
+
e
x
x
e
K dx
e
2
1
1
. Đặt
x
te 1
e
e
e
e
e
te
I dt e e
t
e
1
2
1
11
ln
1

Vậy:
e
e
e
Ie
e
1
–2 ln
1

Bài 27: Tính tích phân
4
2
0
ln( 9 )
I x x dx
Hƣớng dẫn: Đặt
u x x
dv dx
2
ln 9
x
I x x x dx
x
4
4
2
2
0
0
ln 9 2
9
Dạng 4: Tích phân tổng hợp nhiều loại hàm số
Bài 1: Tính tích phân
x
x
I x e dx
x
3
1
4
2
0
1





Hƣớng dẫn:
x
x
I x e dx dx
x
3
11
4
2
00
1


.
+ Tính
x
I x e dx
3
1
2
1
0
. Đặt
tx
3
tt
I e dt e e
1
1
1
0
0
1 1 1 1
3 3 3 3
.
+ Tính
x
I dx
x
1
4
2
0
1
. Đặt
tx
4
t
I dt
t
1
4
2
2
0
2
44
34
1



Vậy:
Ie
1
3
3
Tài liệu ôn tập giải tích 12 học kỳ II
Trần Thông sưu tầm và biên soạn Facebook: Hội Toán Bắc Nam
Bài 2: Tính tích phân
x
x
I e x x dx
x
1
2 2 2
2
0
. 4 .
4
Hƣớng dẫn:
x
x
I x e dx dx I I
x
11
3
2
12
2
00
4

+ Tính
x
e
I x e dx
1
2
2
1
0
1
4

+ Tính
x
I dx
x
1
3
2
2
0
4
. Đặt
tx
2
4
I
2
16
33
3
e
I
2
61
33
4 12
Bài 3: Tính tích phân
x
x
I e dx
x
1
2
2
0
1
( 1)
Hƣớng dẫn:
Đặt
t x dx dt1
tt
tt
I e dt e dt
t
tt
22
2
11
22
11
2 2 2 2
1






=
e
ee
e
2
2
11
2




Bài 4: Tính tích phân
x
x e dx
I
x
2
3
31
2
0
.
1
Hƣớng dẫn: Đặt
t x dx tdt
2
1
t
I t e dt
2
2
1
( 1)
tt
t e dt e J e e
2
22
1
2
()
1
+
t t t t t t t
J t e dt t e te dt e e te e dt e e te e
2 2 2
2 2 2 2
1 1 1
2 2 2
2 4 2 4 2( )
1 1 1




Vậy:
Ie
2
Bài 5: Tính tích phân
x x x
I dx
x
23
2
ln( 1)
1

Hƣớng dẫn: Ta có:
x x x x x x x x
f x x
x x x x
2 2 2
2 2 2 2
ln( 1) ( 1) ln( 1)
()
1 1 1 1
F x f x dx x d x xdx d x
2 2 2
11
( ) ( ) ln( 1) ( 1) ln( 1)
22
=
x x x C
2 2 2 2
1 1 1
ln ( 1) ln( 1)
4 2 2
.
Tài liệu ôn tập giải tích 12 học kỳ II
Trần Thông sưu tầm và biên soạn Facebook: Hội Toán Bắc Nam
Bài 6: Tính tích phân
x x x
I dx
x
4
23
2
0
ln 9 3
9
Hƣớng dẫn:
x x x x x x
I dx dx dx I I
x x x
4 4 4
2 3 2 3
12
2 2 2
0 0 0
ln 9 3 ln 9
33
9 9 9
+ Tính
xx
I dx
x
4
2
1
2
0
ln 9
9

. Đặt
x x u
2
ln 9
du dx
x
2
1
9
u
I udu
ln9
2 2 2
1
ln3
ln 9 ln 3
ln9
ln3
22
+ Tính
x
I dx
x
4
3
2
2
0
9
. Đặt
xv
2
9
x
dv dx x v
x
22
2
,9
9
u
I u du u
5
3
2
2
3
44
5
( 9) ( 9 )
3
33
Vậy
x x x
I dx I I
x
4
2 3 2 2
12
2
0
ln 9 3 ln 9 ln 3
3 44
2
9
Bài 7: Tính tích phân
e
x x x
I dx
xx
32
1
( 1)ln 2 1
2 ln
Hƣớng dẫn:
ee
x
I x dx dx
xx
2
11
1 ln
2 ln


. +
e
e
xe
x dx
33
2
1
1
1
33

+
ee
e
x d x x
dx x x
x x x x
1
11
1 ln (2 ln )
ln 2 ln
2 ln 2 ln



e 2
ln
2
. Vậy:
ee
I
3
12
ln
32


Bài 8: Tính tích phân
4
3
2
1
ln(5 ) . 5
x x x
I dx
x
Hƣớng dẫn: Ta có:
44
2
11
ln(5 )
5.

x
I dx x x dx K H
x
.
+
x
K dx
x
4
2
1
ln(5 )
. Đặt
ux
dx
dv
x
2
ln(5 )

K
3
ln4
5
+ H=
x x dx
4
1
5.
. Đặt
tx5
H
164
15
Vậy:
I
3 164
ln4
5 15

Tài liệu ôn tập giải tích 12 học kỳ II
Trần Thông sưu tầm và biên soạn Facebook: Hội Toán Bắc Nam
Bài 9: Tính tích phân
8
ln
1
3
x
I dx
x
Hƣớng dẫn: Đặt
ux
dx
du
dx
x
dv
vx
x
ln
21
1




x
I x x dx
x
8
8
3
3
1
2 1ln 2
+ Tính
x
J dx
x
8
3
1
. Đặt
tx1
t dt
J dt
tt
33
2
22
22
21
2 1 2 ln3 ln2
11





I 6ln8 4ln3 2(2 ln3 ln2) 20ln2 6ln3 4
Bài 10: Tính tích phân
x x x x
I dx
x
3
2
0
(cos cos sin )
1 cos

Hƣớng dẫn:
Ta có:
x x x x x
I x dx x x dx dx J K
xx
2
22
0 0 0
cos (1 cos ) sin .sin
.cos .
1 cos 1 cos






+ Tính
J x x dx
0
.cos .
. Đặt
ux
dv xdxcos
J x x x dx x
00
0
( .sin ) sin . 0 cos 2

+ Tính
xx
K dx
x
2
0
.sin
1 cos
. Đặt
x t dx dt
t t t t x x
K dt dt dx
t t x
2 2 2
0 0 0
( ).sin( ) ( ).sin ( ).sin
1 cos ( ) 1 cos 1 cos
x x x x dx x dx
K dx K
x x x
2 2 2
0 0 0
( ).sin sin . sin .
2
2
1 cos 1 cos 1 cos


Đặt
t x dt x dxcos sin .
dt
K
t
1
2
1
2
1

, đặt
t u dt u du
2
tan (1 tan )
u du
K du u
u
22
44
4
2
4
44
(1 tan )
.
2 2 2 4
1 tan




Vậy
I
2
2
4

Bài 11: Tính tích phân
x x x x
I dx
xx
2
3
2
3
( sin )sin
(1 sin )sin

Tài liệu ôn tập giải tích 12 học kỳ II
Trần Thông sưu tầm và biên soạn Facebook: Hội Toán Bắc Nam
Hƣớng dẫn:
x x x x dx
I dx dx H K
x
x x x
2 2 2
2
3 3 3
22
3 3 3
(1 sin ) sin
1 sin
(1 sin )sin sin

+
x
H dx
x
2
3
2
3
sin
. Đặt
ux
du dx
dx
dv
vx
x
2
cot
sin


H
3
+
dx dx dx
K
x
x
x
2 2 2
3 3 3
2
3 3 3
32
1 sin
1 cos 2cos
2 4 2

Vậy
I 32
3
Bài 12: Tính tích phân
I x dx
4
0
ln(1 tan )

Hƣớng dẫn: Đặt
tx
4

I t dt
4
0
ln 1 tan
4






=
t
dt
t
4
0
1 tan
ln 1
1 tan



=
dt
t
4
0
2
ln
1 tan
=
dt t dt
44
00
ln2 ln(1 tan )



=
tI
4
0
.ln2
I2 ln2
4
I ln2
8
.
Bài 13: Tính tích phân
I x x dx
2
0
sin ln(1 sin )

Hƣớng dẫn: Đặt
x
ux
du dx
x
dv xdx
vx
1 cos
ln(1 sin )
1 sin
sin
cos



xx
I x x x dx dx x dx
xx
2
2 2 2
0 0 0
cos 1 sin
cos .ln(1 sin ) cos . 0 (1 sin ) 1
2
1 sin 1 sin 2
0

PHẦN 3: BÀI TẬP TRẮC NGHIỆM LUYỆN THI
CHƢƠNG 1: NGUYÊN HÀM TÍCH PHÂN
Tài liệu ôn tập giải tích 12 học kỳ II
Trần Thông sưu tầm và biên soạn Facebook: Hội Toán Bắc Nam
Câu 1. Cho biết
2
0
cos( ).
fx
t dt x x
Tính
(4)f
.
A.
(4) 2 3f
B.
(4) 1f 
C.
1
(4)
2
f
D.
3
(4) 12f
Câu 2. Cho biết
3
1
.
x
t
x
t
F x dt
e
Tính
(0).
F
A.
(0) 2 3
f
B.
(0) 2
f
C.
(0) 2 3
f
D.
(0) 1
f
Câu 3. Cho
fx
là hàm liên tục trên và
2
2
0
4,
xf x dx
3
2
2,
f t dt
16
9
6.
ft
dt
t
Tính tích phân
4
0
.
I f x dx
A. 1 B. 10 C. 12 D. 9
Câu 4. Cho m>0. Tìm điểu kiện của tham số m để tich phân
1
0
1
1
2
dx
xm
.
A.
1
4
m
B.
0m
C.
1
0
4
m
D.
1
4
m
Câu 5. Tìm đạo hàm của hàm số
1
sin
x
t
F x dt
t
.
A.
sin
x
Fx
x
B.
sin
F x x
C.
2
sin
x
Fx
x
D.
sin
F x x x
Câu 6. Cho hàm số
1
x
t
t
F x dt
e
. Mệnh đề nào dưới đây là đúng.
A. Giá trị của hàm số tại 1 là
11F
B. Hàm số
Fx
đạt cực tiểu tại
0x
C. Hàm số
Fx
đồng biến trên
D. Hàm số
Fx
có đạo hàm là
x
F x xe
Câu 7. Cho
fx
là hàm số liên tục trên đoạn
,ab
và
Fx
là một nguyên hàm của
fx
trên
,ab
. Khi đó khẳng định nào sau đây đúng?
A. Diện tích S của hình phẳng giới hạn bởi đồ thị hàm số
y f x
, trục hoành và hai đường
thẳng
,x a x b
được tính theo công thức
S F b F a
.
B.
a
b
f x dx F b F a
C.
0
b
a
b
f Ax B dx F Ax B A
a


Tài liệu ôn tập giải tích 12 học kỳ II
Trần Thông sưu tầm và biên soạn Facebook: Hội Toán Bắc Nam
D.
b
a
kf x dx k F b F a


(k là hằng số)
Câu 8. Kết quả tích phân
2
2
11
ln ln
e
e
dx
xx



được viết dưới dạng
a
e
e
b
. Tính giá trị biểu thức
a b ab
..
A.3 B.
2
C.
4
D.
8
Câu 9. Tính tích phân
4
2
0
4 4 1 .I x x dx
A.
31
B.
35
C.
38
D.
40
Câu 10. Cho
fx
là hàm số liên tục trên . Mệnh đề nào dưới đây là đúng.
A.
11
00
22f x f x

B.
1
2
00
sin
2
f x dx f x dx

C.
12
00
2 2 2f x dx f x dx

D.
22f x dx f x dx

Câu 11. Giả sử
8
63
ln 1 6 ln3.
2
a
x xdx
Tìm giá trị của
.a
A.
0
B.
2
C.
3
D.
4
Câu 12. Tính tích phân
2
1
1
sin2 .
x
I e x x dx



A.
1
B.
0
C.
1
D.
2
Câu 13. Với
1a
, kết quả tích phân
2
0
32
a
x x dx
đạt giá trị lớn nhất khi giá trị của a là:
A.
3
B.
2
C.
5
2
D.
1
Câu 14. Tính nguyên hàm
.
x
xe
I e dx
A.

x
e
I e c
B.
1

x
e
I e c
C.

x
I e c
D.
1

x
I e c
Câu 15. Đặt
1
2
0
1
x
x
a dx
e
. Kết quả tích phân
1
2
0
1
x
x
dx
e
là:
A.
1 a
B.
1 a
C.
1
2
a
D.
1
3
a
Câu 16. Xét tích phân
1
2
0
1
I x dx
và phép đổi biến
sin .xt
Mệnh đề nào dưới đây là sai.
A.
1 sin
.
2 2 2




I

B.
1
0
cos sin .
I t tdt
Tài liệu ôn tập giải tích 12 học kỳ II
Trần Thông sưu tầm và biên soạn Facebook: Hội Toán Bắc Nam
C.
2
2
0
cos .
I tdt
D.
2
0
1 sin2
.
22




t
It
Câu 17 Trong các mệnh đề sau,có bao nhiêu mệnh đề đúng?
3
2
sin
(1): sin d
3

x
x x C
2
2
42
(2): d 2ln 3
3

x
x x x C
xx
6
(3): 3 2 3 d
ln6
x
x x x
x x C
(1 )(4): d


x x x
xeexe C
32
2 sin( 6 cos5):
dxx x x x C
(6): dtan tan
x x x C
A.
3
B.
4
C.
5
D.
6
Câu 18. Giả sử
2
0

x
f t dt x x
. Tìm hàm dưới dấu tích phân.
A.
21f t t
B.
2
f t t t
C.
21f t t
D.
2
f t t t
Câu 19. Với
( ), ( )f x g x
là 2 hàm số liên tục trên
K
và
0k
thì mệnh đề nào sau đây là sai.
A.
( ) ( ) .f x dx f x C
B.
( ) ( ) .k f x dx k f x dx

C.
1
(4)
2
f
D.

( ). ( ) ( ) . ( ) .f x g x dx f x dx g x dx
Câu 20. Tìm nguyên hàm

41
.
2 1 2
x
I dx
x
A.
2 1 5ln 2 1 2 .I x x C
B.
2 1 4 2 1 5ln 2 1 2 .I x x x C
C.
2 1 4 2 1 5ln 2 1 2 .I x x x C
D.
2 1 4 2 1 5ln 2 1 2 .I x x x C
Câu 21. Cho
1
0
2 ( ) ( ) 5f x g x dx
và
1
0
3 ( ) ( ) 10f x g x dx
. Tính
1
0
()f x dx
A.
3
B.
5
C.
15
D.
10
Câu 22. Tìm nguyên hàm sau
2
()
x
f x x e
A.
2
( 2 2)
x
x x e C
B.
2
( 2 2)
x
x x e C
C.
2
( 2 2)
x
x x e C
D.
2
( 2 2)
x
x x e C
Câu 23. Với giá trị nào của số dương b thì
2
0
(6 3 )
b
x x dx
có giá trị lớn nhất
A.
2
B.
4
C.
6
D.
8
Câu 24. Tìm giá trị của
a
thỏa mãn các điều kiện
3
;
22
a
và
2
0
cos sin
a
x a dx a
A.
B.
C.
2
D.
2
Câu 25. Gọi S là tập hợp tất cả các số nguyên dương
k
thỏa mãn điều kiện
1
ln 2
e
k
dx e
x
.
Tìm số phần tử của S .
Tài liệu ôn tập giải tích 12 học kỳ II
Trần Thông sưu tầm và biên soạn Facebook: Hội Toán Bắc Nam
A.
3
B.
1
C.
2
D.
0
Câu 26. Tìm hàm số
()y f x
nếu biết
15
'( )
14
x
fx
,
'(1) 4f
và
(1) 4f
A.
3
5 23
()
77
x
fx
B.
3
23
()
77
x
fx
C.
3
53
()
77
x
fx
D.
3
8 23
()
77
x
fx
Câu 27. Tính tích phân sau
*
0
1;
a
n
I x dx n
(a là số thực)
A.
11
n
a
n

B.
1
11
1
n
a
n

C.
1
11
1
n
a
n

D.
1
11
1
n
a
n

Câu 28. Cho tích phân
2
0
sin . 8 cos .I x xdx

Với phép đổi biến
8 cosux
thì kết quả nào
sau đây đúng ?
A.
9
8
2.I udu
B.
8
9
1
.
2
I udu
C.
8
9
.I udu
D.
9
8
.I udu
Câu 29. Tính
2
3
0
.sin
x
I e xdx
A.
3
2
11
22
Ie

B.
3
2
11
22
Ie

C.
3
2
1Ie

D.
3
2
1Ie

Câu 30. Cho hàm số
3
( ) .
(x 1)
x
a
f x b xe
. Biết rằng
'(0) 22f 
và
1
0
( ) 5f x dx
. Tính tổng
ab
.
A.
146
13
B.
26
11
C.
26
11
D.
146
13
Câu 31. Hàm số nào sau đây là một nguyên hàm của hàm số
2
()f x x k
với
0?k
A.
22
( ) ln
22
xk
f x x k x x k
B.
22
1
( ) ln
22
x
f x x k x x k
C.
2
( ) ln
2
k
f x x x k
D.
2
1
()fx
xk
Câu 32. Cho
2
( ) ( ) 2 -1f x ax bx c x
là một nguyên hàm của hàm số
2
10 -7 2
()
2 -1
xx
gx
x
trên khoảng
1
;
2
.Tính tổng
abc
A.
0
B.
2
C.
3
D.
4
Tài liệu ôn tập giải tích 12 học kỳ II
Trần Thông sưu tầm và biên soạn Facebook: Hội Toán Bắc Nam
Câu 33. Xác định a, b, c sao cho
2
( ) ( ) 2 -3g x ax bx c x
là một nguyên hàm của hàm số
2
20 -30 7
()
2 -3
xx
fx
x
trong khoảng
3
;
2
A.
4, 2, 2 abc
B.
1, 2, 4 a b c
C.
2, 1, 4 a b c
D.
4, 2, 1 a b c
Câu 34. Tìm một nguyên hàm của hàm số:
2
( ) sin 1f x x x
A.
2 2 2
( ) 1 cos 1 sin 1 F x x x x
B.
2 2 2
( ) 1 cos 1 sin 1 F x x x x
C.
2 2 2
( ) 1 cos 1 sin 1 F x x x x
D.
2 2 2
( ) 1 cos 1 sin 1 F x x x x
Câu 35. Trong các hàm số sau:
(I)
2
( ) 1f x x
(II)
2
( ) 1 5f x x
III)
2
1
()
1
fx
x
(IV)
2
1
( ) -2
1
fx
x
Hàm số nào có một nguyên hàm là hàm số
2
( ) ln 1F x x x
A. Chỉ (I) B. Chỉ (III) C. Chỉ (II) D. Chỉ (III) và
(IV) Câu 36. Tìm nguyên hàm của hàm số: y =
2
x
x
e
A.
2 ln 2
x
x
e
C
B.
(1 ln 2)2
x
x
e
C
C.
.2
x
x
e
C
x
D.
ln 2
2
x
x
e
C
Câu 37. Với phép biến đổi
1tx
tích phân
3
0
11
x
dx
x
trở thành
2
1
f t dt
,. Khi đó
ft
là hàm nào trong các hàm số sau.
A.
2
22f t t t
B.
2
f t t t
C.
2
f t t t
D.
2
22f t t t
Câu 38. Cho
2
0
3f x dx
.Tính tích phân
2
0
43f x dx


.
A.
2
B.
4
C.
6
D.
8
Câu 39.Cho tích phân
dx
x
x
I
1
0
3
và
dx
x
x
J
2
0
12sin3
cos
, phát biểu nào sau đây đúng
A.
JI
B.
2I
C.
5ln
3
1
J
D.
5ln
3
1
J
Câu 40. Tính tích phân I =
3
2
2
ln[2 x(x 3)]dx
.
A.
4ln2 3
B.
5ln5 4ln2 3
C.
5ln5 4ln2 3
D.
5ln5 4ln2 3
Tài liệu ôn tập giải tích 12 học kỳ II
Trần Thông sưu tầm và biên soạn Facebook: Hội Toán Bắc Nam
Câu 41. Cho
143
23
xxxxf
và
132
23
xxxxg
. Tích phân
dxxgxf
2
1
bằng với tích phân nào dưới đây.
A.
2
1
23
22 dxxxx
B.
1
1
23
22 dxxxx
2
1
23
22 dxxxx
C.
2
32
1
x 2x x 2 dx
D.
1
1
23
22 dxxxx
2
1
23
22 dxxxx
Câu 42. Tìm nguyên hàm
ln ln
.
x
I dx
x
A.
ln .ln lnx x C
B.
ln .ln ln lnx x x C
C.
ln .ln ln lnx x x C
D.
ln ln lnx x C
Câu 43. Tính tích phân
3
4
2
6
1 sin x
dx
sin x
A.
32
2
B.
3 2 2
2

C.
32
2
D.
3 2 2 2
2

Câu 44. Tích phân
1
2
0
ln
ln 2
x
I dx
xx
có kết quả dạng
ln2I a b
với
,ab
. Khẳng định
nào sau đây đúng ?
A.
21ab
B.
22
4ab
C.
1ab
D.
2ab
Câu 45. Nếu đặt
2
3ln 1tx
thì tích phân
2
1
ln
3ln 1
e
x
I dx
xx
trở thành tích phân nào dưới
đây?
A.
2
1
1
3
I dt
B.
4
1
11
2
I dt
t
C.
2
1
2
3
e
I tdt
D.
1
11
4
e
t
I dt
t
Câu 46. Tính tích phân
4
2
0
cos
x
I dx
x
.
A.
ln 2
4
I

B.
ln 2
4
I

C.
2
ln
42
I

D.
2
ln
42
I

Câu 47. Tìm nguyên hàm của hàm số: y =
22
cos2
sin .cos
x
xx
A.
tan cot x x C
B.
tan cot x x C
C.
tan cot x x C
D.
tan xC
Câu 48. Tìm môt nguyên hàm của hàm số: y =
3
2
2
x
y
x
Tài liệu ôn tập giải tích 12 học kỳ II
Trần Thông sưu tầm và biên soạn Facebook: Hội Toán Bắc Nam
A.
2
( ) 2F x x x
B.
22
1
42
3
xx
C.
22
1
42
3
xx
D.
22
1
2
3
xx
Câu 49. Tính tích phân
1
3
0
( 1)
xdx
J
x
A.
1
8
J
B.
1
4
J
C. J =2 D. J =1
Câu 50. Tính tích phân
2
1
6
94
x
xx
K dx
A.
11
ln
3
13
2ln
2
K
B.
1 12
ln
3
25
2ln
2
K
C.
1
ln13
3
2ln
2
K
D.
1 25
ln
3
13
2ln
2
K
Câu 51. Tính tích phân
2
1
ln
e
x
K dx
x
A.
1
2K
e

B.
1
K
e
C.
1
K
e

D.
2
1K
e

Câu 52. Tìm nguyên hàm
cos2 .ln(sin cos )I x x x dx
A.
11
1 sin2 ln 1 sin2 sin2
24
F x x x x C
B.
11
1 sin2 ln 1 sin2 sin2
42
F x x x x C
C.
11
1 sin2 ln 1 sin2 sin2
44
F x x x x C
D.
11
1 sin2 ln 1 sin2 sin2
44
F x x x x C
Câu 53. Tìm nguyên hàm
3
1.I x x dx
A.
4 3 2
2 5 6 2
1 1 1 1 1
9 7 5 3



F x x x x x x C
B.
4 3 2
2 6 6 2
1 1 1 1 1
9 7 5 3



F x x x x x x C
C.
432
2 6 6 2
1 1 1 1 1
9 7 7 3



F x x x x x x C
D.
4 3 2
2 6 6 1
1 1 1 1 1
9 7 5 3



F x x x x x x C
Tài liệu ôn tập giải tích 12 học kỳ II
Trần Thông sưu tầm và biên soạn Facebook: Hội Toán Bắc Nam
Câu 54. Cho F(x) là một nguyên hàm của
( ) 2 1f x x
trên . Biết hàm số
()y F x
đạt giá trị
nhỏ nhất bằng
39
4
. Đồ thị của hàm số
()y F x
cắt trục tung tại điểm có tung độ là bao nhiêu?
A.
37
4
B.
39
4
C. J =11 D. J =10
Câu 55. Chọn khẳng định sai trong các khẳng đinh sau.
A.
11
00
sin(1 ) sinx dx xdx

B.
2
00
sin 2 sin
2
x
dx xdx

C.
1
0
3
(1 )
2
x
x dx
D.
1
2007
1
2
(1 )
2009
x x dx

Câu 56.Giả sử tích phân
3
2
0
cos

x
dx a b
x
. Tìm phần nguyên của tổng
ab
A. 1 B. -1 C. 0 D. -2
Câu 57. Cho tích phân
3
2
2
1
1
.
x
I dx
x
Với phép đổi biến
2
1
x
t
x
thì kết quả nào sau đây
đúng ?
A.
2
3
2
2
2
1

t
I dt
t
B.
3
2
2
2
1
t
I dt
t
C.
3
2
2
2
1

t
I dt
t
D.
2
3
2
2
2
1
t
I dt
t
Câu 58. Tính tích phân
1
2
0
2
1
x
I x e dx
x




.
A.
1 ln2I
B.
1 ln2I
C.
3 ln2I
D.
3 ln2I
Câu 59. Giả sử tích phân
23
1
(x ln ) . .
e
I x x dx a b e c e
.Đẳng thức nào sau đây đúng.
A.
b c a
B.
b c a
C.
b c a
D.
b c a
Câu 60. Tính tích phân
2
3
0
sin2I x x x dx

.
A.
4
64 4


I
B.
4
64 2


I
C.
4
64 2


I
D.
4
64 4


I
Câu 61. Tính tích phân
3
2
0
( sin )
cos
x x dx
I
x
.
A.
3
1 ln2
3
I
B.
3
1 ln2
3
I
C.
3
ln2
3

I
D.
3
3
I
Tài liệu ôn tập giải tích 12 học kỳ II
Trần Thông sưu tầm và biên soạn Facebook: Hội Toán Bắc Nam
Câu 62. Tính tích phân
1
1 ln
e
dx
x
x
I
.
A.
1
8
I
B.
1
2
I
C.
1
4
I
D.
3
2
I
Câu 63. Giả sử tích phân
6
1
31
.ln
2


x
dx a b c
x
. Đẳng thức nào sau đây đúng.
A.
abc
B.
abc
C.
abc
D.
a b c
Câu 64. Tính tích phân
1
23
0
(2 1)
x
I dx
x
.
A.
1
9
I
B.
1
9
I
C.
8
9
I
D.
8
9
I
Câu 65. Giả sử tích phân
10
32
5
3 4 63 3
.ln .
2 2 2





xx
a
x
Tìm giá trị của a.
A.
4a
B.
5a
C. a=2 D. a=1
Câu 66. Tính tích phân
1
0
1.
x
I x e dx
.
A.
1Ie
B.
1Ie
C.
Ie
D.
Ie
Câu 67. Xét các tích phân
7
3
0
.1
I x x dx
và
8
0
.1
J x x dx
. Nhận xét nào dưới đây là
đúng.
A.
1
8
JI
B.
1
4
IJ
C.
IJ
D.
IJ
Câu 68. Tính tích phân
1
0
3 1 2I x dx
.
A.
4
9
I
B.
4
9
I
C. I =2 D. I =1
Câu 69. Tính tích phân
2
23 9 6 3
1
ln 1 . . . 
e
a e b e c ex x x
Đẳng thức nào dưới đây là
đúng.
A.
0 abc
B.
20 a b c
C.
0 a b c
D.
20 a b c
Câu 70. Tính tích phân .
1
0
(2 )
x
I x e dx
A.
1
2
I
B.
1
4
I
C. I=2 D. I=1
Tài liệu ôn tập giải tích 12 học kỳ II
Trần Thông sưu tầm và biên soạn Facebook: Hội Toán Bắc Nam
Câu 71. Tính tích phân
2
2
0
( sin )cos .I x x xdx
A.
2
32
I
B.
2
32

I
C.
1
34
I
D.
1
34

I
Câu 72. Tính tích phân
3
2
3
1
ln( 1)x
I dx
x
.
A.
11
ln2 ln3
32
I
B.
11
ln2 ln3
32
I
C.
11
ln2 ln3
32
I
D.
12
ln
33
I
Câu 73. Tính tích phân
2
0
2cos sin
J x x xdx
.
A.
1
8
J
B.
1
4
J
C. J =2 D. J =1
Câu 74. Tính tích phân
1
2
2
0
ln( 1)
1
xx
I dx
x
.
A.
1
ln2
2
I
B.
2
1
ln2
2
I
C.
1
ln4
2
I
D.
1
ln2
4
I
Câu 75. Tính tích phân
1
3
0
2
x
J x xe dx
.
A.
9
8
J
B.
9
4
J
C. J =2 D. J =-1
Câu 76. Tính tích phân
1
2
0
3 2 ln(2 1)x x x dx


.
A.
1 ln2 I
B.
3
1 ln3
2
I
C.
3
1 ln2
2
I
D.
3
1 ln3
2
I
Câu 77. Tính tích phân .
A.
2
2
Ie
B.
2
2
Ie
C.
2 Ie
D.
2

Ie
Câu 78. Biểu thức nào sau đây bằng với tích phân
a
a
I f x dx
A.
a
0
f(x) f( x) dx
B.
a
0
f(x) f(a x) dx
C.
a
0
f(x a) f( x) dx
D.
a
0
f(x a) f(a x) dx
2
sin
0
.cos
x
I e x xdx

Tài liệu ôn tập giải tích 12 học kỳ II
Trần Thông sưu tầm và biên soạn Facebook: Hội Toán Bắc Nam
Câu 79. Cho
4
0
2I x dx
. Khẳng định nào sau đây là sai ?
A.
4
0
2I x dx
B.
14
01
22I x dx x dx

C.
0
4
I dx
D.
24
02
22I x dx x dx

Câu 80. Cho
12
2
0
1
sin 2
4




x
ab
, với a, b là các số nguyên dương. Tính
6
2.sin



a
.
A.
2
B.
2
C.
22
D. 0
Câu 81. Cho các tích phân
2
0
1
1
1 cos2 , 9 6 1
2
0
I xdx J x x dx
.Khẳng định nào
sau đây đúng
A.
2IJ
B.
3IJ
C.
25IJ
D.
5 12IJ
Câu 82. Cho
( ) 3 5sinf x x
và
(0) 10f
. Trong các khẳng định sau khẳng định nào đúng?
A.
3f
B.
3 5cosf x x x
C.
3
22
f
D.
( ) 3 5cos 2f x x x
Câu 83. Biết
a
dxx
0
4
0)
2
3
sin4(
và
);0(
a
Tìm giá trị a.
A.
4
a
B.
8
a
C.
2
a
D.
3
a
Câu 84. Ký hiệu K là khoảng hoặc đoạn hoặc nửa khoảng của . Cho hàm số
()fx
xác định
trên K. Khi nào
()Fx
được gọi là nguyên hàm của hàm số
()fx
trên K
A.
'
( ) ( )F x f x
B.
'
( ) ( )F x f x C
, C là hằng số tuỳ ý.
C.
'
( ) ( )F x f x C
, C là hằng số tuỳ ý. D.
'
( ) ( )F x f x
Câu 85. Cho
2
3
1
( ) 2f x x
x

xác định trên khoảng
( ;0)
. Biến đổi nào sau đây là sai ?
A.
22
33
11
2 2 .x dx x dx dx
xx



B.
1
22
3
3
1
2 2 .x dx x dx x dx
x



C.
1
22
3
3
1
2 2 .x dx x dx x dx
x



D.
23
33
1 2 1
2
3
x dx x dx C
xx




Câu 86. Cho đường cong
2
yx
. Với mỗi
[0 1] ;x
, gọi
()Sx
là diện tích của phần hình thang
cong đã cho nằm giữa hai đường vuông góc với trục Ox tại
điểm có hoành độ 0 và
x
(xem hình vẽ). Khi đó, khẳng
định nào sau đây đúng.
Tài liệu ôn tập giải tích 12 học kỳ II
Trần Thông sưu tầm và biên soạn Facebook: Hội Toán Bắc Nam
A.
2
()S x x
B.
'2
()S x x
C.
2
()
2
x
Sx
D.
'
( ) 2S x x
Câu 87. Tìm hàm số
()y f x
biết
43
35sin cosdy x xdx
và
( ) 2
2
f

A.
57
( ) 5sin 7sin 2f x x x
B.
57
( ) 5sin 7sin 2f x x x
C.
57
( ) 7sin 5sin 2f x x x
D.
57
( ) 7sin 5sin 2f x x x
Câu 88. Cho
()fx
là hàm số chẵn và liên tục trên thỏa mãn
1
1
( ) 2f x dx
. Tính giá trị tích
phân
1
0
()f x dx
A.
1
2
B.
1
4
C. 1 D. 2
Câu 89. Hàm số
CxexF
x
tan)(
là nguyên hàm của hàm số f(x) nào dưới đây.
A.
x
exf
x
2
sin
1
)(
B.
x
exf
x
2
sin
1
)(
C.
x
e
exf
x
x
2
cos
1)(
D.
x
2
1
f(x) e 1
sin x
Câu 90. Tính tích phân
2
2
1xI x d

A.
3
33
4
B.
3
43
4
C.
4
43
3
D.
3
33
4
Câu 91. Giả sử
3
0
00
7 cos x ( )sinx 2 sin xdxI x xd f x x


.Tìm hàm số f(x)
A.
2
6x
B.
4
2
x
C.
4
2
x
D.
3
2x
Câu 92. Giả sử
Fx
là một nguyên hàm của hàm số
sin x
fx
x
.Tính tích phân
3
1
sin 2x
I
x
A.
31I F F
B.
62I F F
C.
42I F F
D.
32I F F
Câu 93. Tính tích phân
1
0
3 1 2x x dx
A.
1
6
B.
7
6
C.
11
6
D. 0
Tài liệu ôn tập giải tích 12 học kỳ II
Trần Thông sưu tầm và biên soạn Facebook: Hội Toán Bắc Nam
Câu 94. Tính tích phân sau
1
2 3 *
0
1;
n
I x x dx n
A.
1
21
31
n
n
B.
21
31
n
n
C.
1
21
1
n
n
D.
1
21
31
n
n
Câu 95. Tính tích phân
1
2
0
( ) 2I m x x mdx
với
0m
(m là tham số)
A.
2
3
m
B.
1
3
m
C.
2
3
m
D.
2
3
m
Câu 96. Mệnh đề nào sai trong các mệnh đề sau.
A.
10
3 2 2 3
01
x x dx x x dx

B.
1 2 1
3 2 3 2 3 2
0 0 2
x x dx x x dx x x dx
C.
1 2 1
3 2 3 2 3 2
0 0 2
x x dx x x dx x x dx
D.
1 1 1
3 2 3 2
0 0 0
x x dx x dx x dx
Câu 97. Tìm giá trị K thỏa
0
2
2
42
x
e dx K e



A. 9 B. 10 C. 11 D. 12,5
Câu 98. Biết
22
22
sin cos 3
' , , .
6 2 3
sin cos
a x x b
F x F F
xx
Tìm hàm số
.Fx
A.
tan cot .
12
3
F x x x x
B.
tan cot .
3
F x x x x
C.
9 2 .F x x
D.
tan cot .
6
3
F x x x x
Câu 99. Tìm nguyên hàm của hàm số: y =
x
x
x x e
dx
xe
2
()
A.
xx
xe xe C1 ln 1
B.
xx
e xe C1 ln 1
C.
xx
xe xe C1 ln 1
D.
xx
xe xe C1 ln 1
Câu 100. Biết
sin3x axcos3x sin3x
x dx b C
.Tính giá trị a+6b
A. -21 B. -1 C. -5 D. -7
Câu 101. Biết
22
xx
x e dx x mx n e C
Tìm giá trị của tích m.n
Tài liệu ôn tập giải tích 12 học kỳ II
Trần Thông sưu tầm và biên soạn Facebook: Hội Toán Bắc Nam
A. 0 B. 4 C. 6 D. -4
Câu 102. . Biết
2
2
tan(3x-1)
cos (3 1)

a
dx C
xb
Tổng a+b có thể nhận giá trị nào dưới đây?
A. -5 B. -1 C. 5 D. 7
Câu 103. Biết
6
3 ( 1) ( 1)
x x x k
a
e e dx e C
b
Tổng a+b+2k có thể nhận giá trị nào dưới đây?
A. 33 B. 32 C. 24 D. 28
Câu 104. Biết
2
(2 3ln ) 1
(2 3lnx)
b
x
dx C
xa
Tìm giá trị của tích a.b
A.
1
3
B. 1 C. 2 D.
1
2
Câu 105. Biết
2 2 2
2 ( 2) 2
a
x x dx x x C
b
, tính tổng a+b biết a và b là hai số nguyên tố
cùng nhau.
A. 3 B. 5 C. 1 D. 4
Câu 106. Biết
2
1
ln 1 tan3x
cos 3 (1 3 )
a
dx C
b
x tan x
, tính tổng 2a+b biết a và b là hai số
nguyên tố cùng nhau.
A. 5 B. 10 C. 7 D. 4
Câu 107. Biết
sin axcos sin
3 3 3
x x x
x dx b C
, tính tổng a+b .
A. 9 B. 2 C. 6 D. 12
Câu 108. Biết
2
2
11
ln(1 ) ln(1 ) ln 1 1
x
x x dx x x x C
m n k
, tính giá trị biểu thức
2a+ b+n.
A. 2 B. 12 C. 9 D. 6
Câu 109. Biết
1
sin cos2 sin 2
a
x xdx x x x C
bn
, tính tổng 2a+b biết a và b là hai số nguyên
tố cùng nhau
A. 4 B. 10 C. 2 D. 6
Câu 110. Biết
22
1
( 3) e 2

xx
x e dx x n C
m
, tính giá trị biểu thức
22
mn
A. 5 B. 10 C. 41 D. 65
Câu 111. Cho I=
3
2
x
x e dx
và phép đổi biến
3
ux
. Đẳng thức nào dưới đây là đúng.
A.
u
I 3 e du
B.
u
I e du
C.
u
1
I e du
3
D.
u
I ue du
Câu 112. Cho I=
52
15
x x dx
và phép đổi biến
2
u x 15
. Đẳng thức nào dưới đây là đúng.
A.
6 4 2
I (u 30u 225u )du
B.
42
I (u 15u )du
C.
6 2 2
I (u 30u 225u )du
D.
53
I (u 15u )du
Tài liệu ôn tập giải tích 12 học kỳ II
Trần Thông sưu tầm và biên soạn Facebook: Hội Toán Bắc Nam
Câu 113. Biết
2
0
dx 1
lnb
3x 1 a
, tính giá trị biểu thức a
2
+ b
A. 2 B. 10 C. 14 D. 12
Câu 114. Biết
3
2
0
x 8 b
dx 3lna 4ln
x 5x 4 a



(a,b nguyên tố cùng nhau) tính giá trị biểu thức
2
b
a



A.
7
4
B.
16
49
C.
49
16
D.
1
16
Câu 115. Biết
2
2
1
dx 1 1
4x 4x 1 a b


thì a và b là nghiệm của phương trình nào sau đây?
A.
2
x 5x 6 0
B.
2
x 9 0
C.
2
2x x 1 0
D.
2
x 4x 12 0
Câu 116. Cho
π
2
3
2
π
0
6
dx 2
I dt
x x 1 a



. Chọn khẳng định đúng.
A. a = 3 B.
2
a3
C.
a3
D.
1
a
3
Câu 117. Biết
4
2
1
dx
I a lnb
x x 1
. Chọn đáp án đúng.
A.
a b 0
B.
2a b 4
C.
1
a b 1
2

D. ab=4
PHẦN 2: ỨNG DỤNG CỦA TÍCH PHÂN
Câu 1. Tính thể tích của khối tròn xoay được giới hạn bởi các đường
1
3
2 1 , 0, 3y x x y
quay quanh trục Oy
A.
50
7
V
B.
480
7
V
C.
480
9
V
D.
48
7
V
Câu 2. Tính diện tích hình phẳng được giới hạn bởi các đường
1 , 1
x
y e x y e x
A.
2
2

e
S
B.
1
2

e
S
C.
1
2

e
S
D.
1
3

e
S
Câu 3. Tính thể tích của khối tròn xoay được giới hạn bởi các đường
2
cos sin , 0, , 0.
2
y x x x y y x
quay quanh trục Ox.
A.
34
4

V
B.
34
4

V
C.
54
4

V
D.
34
5

V
Câu 4. Tính diện tích hình phẳng được giới hạn bởi các đường
sin2 , cos , 0, .
2
y x y x x x
Tài liệu ôn tập giải tích 12 học kỳ II
Trần Thông sưu tầm và biên soạn Facebook: Hội Toán Bắc Nam
A.
1
4
S
B.
1
4
S
C.
1
6
S
D.
3
2
S
Câu 5. Tính diện tích hình phẳng được giới hạn bởi các đường
2
sin , 0 .y x x y x x
A.
S
B.
2
S
C.
2
S
D.
3
S
Câu 6. Tính diện tích hình phẳng được giới hạn bởi các đường
2
2 , .y x x y x
A.
0S
B.
9
2
S
C.
7
2
S
D.
9
2
S
Câu 7. Tính thể tích của khối tròn xoay được giới hạn bởi các đường
ln , , 0.y x x e y
quay
quanh trục Ox
A.
Ve
B.
1
Ve
C.
1
Ve
D.
2
Ve
Câu 8. Tính thể tích của khối tròn xoay được giới hạn bởi các đường
ln , 1, 0, 2.y x x y x
quay quanh trục Ox
A.
2
2 ln2 1
V
B.
2
2 ln2 1
V
C.
2
2 2ln2 1
V
D.
2
2 2ln2 1
V
Câu 9. Tính thể tích của khối tròn xoay được giới hạn bởi các đường
3
, 3, 8y x x y
quay
quanh trục Ox
A.
Ve
B.
1
Ve
C.
1
Ve
D.
2
Ve
Câu 10. Tính diện tích hình phẳng được giới hạn bởi các đường
3
3
2
, 0,xy y x
A.
65
64
S
B.
81
64
S
C.
4S
D.
81
4
S
Câu 11. Tính diện tích hình phẳng được giới hạn bởi các đường
2, 0, 0,
x
ey y x x
A.
4Se
B.
2
1Se
C.
2
2 S e e
D.
2
3
2

e
S
Câu 12. Cho hình phẳng (H) được giới hạn bởi đường cong
21
1
x
x
y
, trục Ox và trục Oy. Tính
thể tích của khối tròn xoay khi cho hình (H) quay quanh trục Ox
A.
4 3ln2
V
B.
4 ln2
V
C.
3 4ln2
V
D.
3
V
Câu 13. Tính diện tích hình phẳng được giới hạn bởi các đường

3
2 ,0xxyy
A.
4
3
S
B.
5
3
S
C.
11
12
S
D.
68
3
S
Câu 14. Tính diện tích hình phẳng được giới hạn bởi các đường

2
,xyyx
A.
1
2
S
B.
1
3
S
C.
1
4
S
D.
1
5
S
Câu 15. Quay hình phẳng giới hạn bởi đường cong
2
xy
và đường thẳng
4y
quay một
vòng quanh trục Ox. Tính thể tích khối tròn xoay được sinh ra.
Tài liệu ôn tập giải tích 12 học kỳ II
Trần Thông sưu tầm và biên soạn Facebook: Hội Toán Bắc Nam
A.
64
5
V
B.
128
5
V
C.
256
5
V
D.
152
5
V
Câu 16. Tính diện tích hình phẳng được giới hạn bởi các đường
sin ; cos ; 0; y x y x x x
A.
2S
B.
3S
C.
22S
D.
32S
Câu 17. Tính thể tích của khối tròn xoay được giới hạn bởi các đường
ln , , 0.y x x e y
quay
quanh trục Ox
A.
Ve
B.
1
Ve
C.
1
Ve
D.
2
Ve
Câu 18. Cho hình phẳng (H) được giới hạn bởi đường cong
sinyx
, trục Ox và các đường
thẳng
0; xx
. Tính thể tích của khối tròn xoay khi cho hình (H) quay quanh trục Ox
A.
2
V
B.
3
V
C.
3
2
V
D.
2
3
V
Câu 19. Tính diện tích hình phẳng được giới hạn bởi các đường
3
2
;
1
x
y y x
x

A.
1S
B.
1 ln2S
C.
1 ln2S
D.
2 ln2S
Câu 20. Gọi
H
là hình phẳng giới hạn bởi các đường:
2
3y x x
và trục
Ox
. Tính thể tích
khối tròn xoay thu được khi quay
H
xung quanh trục
Ox
.
A.
81
11
V
B.
83
11
V
C.
81
10
V
D.
83
10
V
Câu 21. Tính diện tích hình phẳng được giới hạn bởi các đường
2
: 2 ; 2C y x x y x
A.
11
2
S
B.
5
2
S
C.
9
2
S
D.
7
2
S
Câu 22. Tính diện tích hình phẳng được giới hạn bởi các đường
1
: ; : 2 3C y d y x
x
A.
3
ln2
4
S
B.
3
ln2
4
S
C.
1
24
S
D.
1
24
S
Câu 23. Gọi
H
là hình phẳng giới hạn bởi các đường:
1; 0; 4 y x y x
. Quay
H
xung quanh trục
Ox
ta được khối tròn xoay có thể tích là bao nhiêu?
A.
7
6
V
B.
5
6
V
C.
2
7
6
V
D.
2
5
6
V
Câu 24. Gọi
H
là hình phẳng giới hạn bởi các đường:
3 ; ; 1y x y x x
. Quay
H
xung quanh trục
Ox
ta được khối tròn xoay có thể tích là bao nhiêu?
A.
8
3
B.
2
8
3
C.
2
8
D.
8
Câu 25. Tính diện tích hình phẳng được giới hạn bởi các đường
2yx
;
8
y
x
;
3x
A.
5 8ln6S
B.
2
5 8ln
3
S
C.
26S
D.
14
3
S
Câu 26. Diện tích hình phẳng giới hạn bởi các đường
cosy mx x
;
Ox
;
0;xx

bằng
3
.
Khi đó, tìm giá trị của
m
Tài liệu ôn tập giải tích 12 học kỳ II
Trần Thông sưu tầm và biên soạn Facebook: Hội Toán Bắc Nam
A.
3m 
B.
3m
C.
4m 
D.
3m 
Câu 27. Tính diện tích hình phẳng được giới hạn bởi các đường
: ; : 2;C y x d y x Ox
A.
10
3
B.
16
3
C.
122
3
D.
128
3
Câu 28. Tính diện tích hình phẳng được giới hạn bởi các đường
2
1; 5 y x y x
A.
1S
B.
73
3
S
C.
7
3
S
D.
23S
Câu 29. Tính diện tích hình phẳng được giới hạn bởi các đường
3
22
4 ; 4 y x y x
A.
128
15
S
B.
128 2
15
S
C.
128 2
30
S
D.
2
15
S
Câu 30. Tính diện tích hình phẳng được giới hạn bởi các đường
2 2 2 2
y 4; 2 0. x x y x
A.
1S
B.
1 ln2S
C.
1 ln2S
D.
2 ln2S
Câu 31. Tính diện tích hình phẳng được giới hạn bởi các đường
3
2
;
1
x
y y x
x

A.
3
S
B.
3
2
S
C.
S
D.
2
S
Câu 32.Giả sử hình phẳng được giới hạn bởi các đường
22
44
23
;
11


x ax a a ax
yy
aa
diện tích
lớn nhất. Tìm giá trị của a biết a là số thực dương.
A.
4
3a
B.
3
5a
C.
4
5a
D.
3
4a
Câu 33. Trên parabol
2
: P y x
ta lấy hai điểm A,B sao cho AB=2. Tìm vị trí của A và B để
diện tích hình phẳng giới hạn bởi đường thẳng AB và
P
lớn nhất.
A.
1,1 , 2,4AB
B.
1,1 , 1,1AB
C.
1,1 , 2,4AB
D.
1,1 , 2,4AB
Câu 34. Trên parabol
2
: P y x
ta lấy hai điểm
1,1 , 2,4AB
. Tìm trên cung AB điểm M
sao cho diện tích tam giác MAB lớn nhất.
A.
0,0M
B.
1,1M
C.
11
,
24



M
D.
11
,
24



M
Câu 35. Đường thẳng
:2d y mx
giao với parabol
2
:1P y x
tạo thành hình phẳng có
diện tích nhỏ nhất. Tìm m.
A.
1m
B.
0m
C.
1m
D.
2m
Câu 36. Tính thể tích của khối tròn xoay thu được khi quay hình giới hạn bởi các đường
3
ln 1 ,y 0, 1y x x x
quay quanh trục Ox
A.
2ln2 1
3
V
B.
2ln2 1
3
V
C.
2ln2 1
4
V
D.
.ln2
3
V
Câu 37. Gọi
H
là hình phẳng giới hạn bởi các đường:
2
1
1
y
x
và các đường thẳng
1, 0xy
x=0. Tính thể tích khối tròn xoay thu được khi quay
H
xung quanh trục
Oy
Tài liệu ôn tập giải tích 12 học kỳ II
Trần Thông sưu tầm và biên soạn Facebook: Hội Toán Bắc Nam
A.
V
B.
ln2
V
C.
ln4
V
D.
2
V
Câu 38. Tính thể tích của khối tròn xoay thu được khi quay hình tròn
2
2
34xy
quanh trục
Ox
A.
4
V
B.
2
4
V
C.
8
V
D.
2
8
V
Câu 39. Tính thể tích của khối tròn xoay thu được khi quay hình tròn
2
2
34xy
quanh trục
Oy
A.
32
3
V
B.
2
32
3
V
C.
8
V
D.
2
8
V
Câu 40. Tính thể tích của khối tròn xoay thu được khi quay elip

2
2
4
1
4 16
x
y
quanh trục Ox
A.
4
V
B.
2
4
V
C.
128
3
V
D.
2
128
3
V
Câu 41. Tính thể tích của khối tròn xoay thu được khi quay elip

2
2
4
1
4 16
x
y
quanh trục Oy
A.
64V
B.
2
4
V
C.
128
3
V
D.
2
128
3
V
Câu 42. Tính thể tích của khối tròn xoay được giới hạn bởi các đường
xxyy
2
2 ,0
quay
quanh trục Oy
A.
8
3
V
B.
3
8
V
C.
16
15
V
D.
15
16
V
Câu 43. Tính thể tích của khối tròn xoay được giới hạn bởi các đường
xy y y x
2
, 1, 3 10
quay quanh trục Oy
A.
61
5
V
B.
2
61
5
V
C.
101
54
V
D.
2
101
54
V
Câu 44. Tính thể tích của khối tròn xoay được giới hạn bởi các đường
x
x
x
y y y
2
2
27
27
,,
quay quanh trục Ox
A.
583
3
V
B.
583
3
V
C.
81 27ln3V
D.
81 27ln3V
Câu 45. Tính thể tích của khối tròn xoay được giới hạn bởi các đường
x
x
x
y y y
2
2
27
27
,,
quay quanh trục Ox
A.
583
3
V
B.
583
3
V
C.
81 27ln3V
D.
81 27ln3V
Câu 46. Tính thể tích của khối tròn xoay được giới hạn bởi các đường
x
x
x
y y y
2
2
27
27
,,
quay quanh trục Oy
A.
583
3
V
B.
583
3
V
C.
81 27ln3V
D.
81 27ln3V
Tài liệu ôn tập giải tích 12 học kỳ II
Trần Thông sưu tầm và biên soạn Facebook: Hội Toán Bắc Nam
Câu 47. Tính thể tích của khối tròn xoay được giới hạn bởi các đường
xy y y x
2
, 1, 3 10
quay quanh trục Oy
A.
61
5
V
B.
2
61
5
V
C.
101
54
V
D.
2
101
54
V
Câu 48. Tính thể tích của khối tròn xoay được giới hạn bởi các đường
xyy
2
2 ,4
quay
quanh trục Ox
A.
128
3
V
B.
2
256
5
V
C.
256
5
V
D.
2
101
54
V
Câu 49. Tính thể tích của khối tròn xoay được giới hạn bởi các đường
xyy
2
2 ,4
quay
quanh trục Oy
A.
128
3
V
B.
2
256
5
V
C.
256
5
V
D.
2
101
54
V
Câu 50. Tính thể tích của khối tròn xoay được giới hạn bởi các đường

x
xyy
3
2
3
,
quay
quanh trục Ox
A.
486
35
V
B.
2
256
35
V
C.
256
5
V
D.
2
35
486
V
PHẦN 3: ỨNG DỤNG TÍCH PHÂN TRONG THỰC TẾ
Câu 1. Giả sử sau t năm,dự án đầu tư thứ nhất sẽ phát sinh lợi nhuận với tốc độ
2
1
( ) 50P t t
trăm đô la/năm,trong khi đó dự án đầu tư thứ hai phát sinh lợi nhuận với tốc độ
2
( ) 200 5P t t
trăm đô la/năm.Tính lợi nhuận vượt thực tế cho khoảng thời gian để tốc độ sinh lợi nhuận của dự
án đầu tư thứ hai vượt bằng dự án đầu tư thứ nhất ?
A.
1690
trăm đô B.
1695
trăm đô C.
1687,5
trăm đô D.
1685
trăm đô
Câu 2. Một vật đang chuyển động với vận tốc 10m/s thì tăng tốc với gia tốc
a(t) = 3t +t
2
(m / s
2
)
. Hỏi quảng đường vật đi được trong khoảng thời gian 10 giây kể từ lúc bắt đầu tăng tốc ?
A. 11100 m B.
6800
3
m
C.
5800
3
m
D.
4300
3
m
Câu 3. Gọi
()h t cm
là mức nước ở bồn chứa sau khi bơm nước được
t
giây. Biết rằng
3
1
'8
5
h t t
và lúc đầu bồn không chứa nước. Tìm mức nước ở bồn sau khi bơm được
6
giây
(làm tròn kết quả đến hàng phần trăm)
A. 2.64 B. 2,65 C. 2,66 D. 2,67
Câu 4. Một vật chuyển động chậm dần với vận tốc
160 10 /v t t m s
. Hỏi rằng trong 3s
trước khi dừng hẳn vật di chuyển được bao nhiêu mét ?
A.16 B.
130
C.
45
D.
170
Câu 5. Một vật chuyển động với vận tốc v(t) (m/s) có gia tốc
2
3
'(t) (m/s )
1
v
t
.Vận tốc ban
đầu của vật là 6m/s. Hỏi vận tốc của vậy sau 10 giây gần bằng với giá trị nào nhất.
A.
10m
B.
11m
C.
12m
D.
13m
Tài liệu ôn tập giải tích 12 học kỳ II
Trần Thông sưu tầm và biên soạn Facebook: Hội Toán Bắc Nam
Câu 6. Một đám vi trùng tại ngày thứ t có số lượng là N(t). Biết rằng
'
8000
()
1 0,5
Nt
t
và lúc đầu
đám vi trùng có 350.000 con. Hỏi sau 10 ngày số lượng vi trùng là bao nhiêu con? (lấy xấp xỉ
hàng đơn vị).
A. 378668 B. 378688 C. 376668 D. 388668
Câu 7. Học sinh lần đầu thử nghiệm „„tên lửa tự chế ‟‟ phóng từ mặt đất theo phương thẳng đứng
với vận tốc 15m/s. Hỏi sau 2,5s tên lửa lên đến độ cao bao nhiêu ? (giả sử bỏ qua sức cản gió,
tên lửa chỉ chịu tác động của trọng lực
2
9,8 /g m s
)
A. 68,125(m) B.
6,875(m) C. 30,625(m) D.
61,25(m)
Câu 8. Một khối cầu có bán kính 5dm, người ta cắt bỏ 2 phần bằng 2 mặt phẳng vuông góc bán
kính và cách tâm 3dm để làm một chiếc lu đựng. Tính thể tích mà chiếc lu chứa được.
A.
132
(dm
3
) B.
41
(dm
3
) C.
100
3
(dm
3
) D.
43
(dm
3
)
Câu 9. Một vật di chuyển với gia tốc
2
20 1 2a t t
2
/ms
. Khi
0t
thì vận tốc của vật
là
30 /ms
. Tính quảng đường vật đó di chuyển sau 2 giây (làm tròn kết quả đến chữ số hàng đơn
vị).
A.
106Sm
B.
107Sm
C.
108Sm
D.
109Sm
Câu 10. Trên sân bay một máy bay cất cánh trên đường băng d (từ trái sang phải) và bắt đầu rời
mặt đất tại điểm O. Gọi (P) là mặt phẳng vuông góc với mặt đất và cắt mặt đất theo giao tuyến là
đường băng d của máy bay. Dọc theo đường băng d cách vị trí máy bay cất cánh O một khoảng
300(m) về phía bên phải có 1 người quan sát A. Biết máy bay chuyền động trong mặt phẳng (P)
và độ cao y của máy bay xác định bởi phương trình (với x là độ dời của máy bay dọc theo
đường thẳng d và tính từ O). Tìm khoảng cách ngắn nhất từ người A (đứng cố định) đến máy
bay.
A. B. C. D.
Câu 11.
Một ô tô chạy với vận tốc 20m/s thì người lái xe đạp phanh còn được gọi là “thắng”.
Sau khi đạp phanh, ô tô chuyển động chậm dần đều với vận tốc Trong đó
t là khoảng thời gian tính bằng giây kể từ lúc bắt đầu đạp phanh . Quãng đường ô tô di chuyển từ
lúc đạp phanh đến khi dừng hẳn là bao nhiêu mét?
A.2 B.
5
C.
3
D.
4
Câu 12.
Một ô tô xuất phát với vận tốc sau khi đi được một khoảng thời
gian t
1
thì bất ngờ gặp chướng ngại vật nên tài xế phanh gấp với vận tốc
và
đi thêm một khoảng thời gian t
2
nữa thì dừng lại. Biết tổng thời gian từ lúc xuất phát đến lúc
dừng lại là 4 (s). Hỏi xe đã đi được quãng đường bao nhiêu mét.
A.
47
B.
50
C.
57
D.
64
Câu 13. Thành phố định xây cây cầu bắc ngang con sông dài 500m, biết rằng người ta định xây
cầu có 10 nhịp cầu hình dạng parabol,mỗi nhịp cách nhau 40m,biết 2 bên đầu cầu và giữa mối
nhịp nối người ta xây 1 chân trụ rộng 5m. Bề dày nhịp cầu không đổi là 20cm. Biết 1 nhịp cầu
như hình vẽ. Hỏi lượng bê tông để xây các nhịp cầu là bao nhiêu (bỏ qua diện tích cốt sắt trong
mỗi nhịp cầu)
2
yx
300( )m
100. 5( )m
200( )m
100 3( )m
( ) 40 20( / ).v t t m s
1
2 10 /v t t m s
2
20 4 /v t t m s
Tài liệu ôn tập giải tích 12 học kỳ II
Trần Thông sưu tầm và biên soạn Facebook: Hội Toán Bắc Nam
A.
3
20m
B.
3
40m
C.
3
50m
D.
3
100m
Câu 14. Một ô tô đang chuyển động với vận tốc
/a m s
thì người lái đạp phanh. Sau khi đạp
phanh ô tô chuyển động chậm dần đều với vận tốc
40 /v t a t m s
(t là khỏang thời gian
tính bằng s kể từ lúc đạp phanh). Kể từ lúc đạp phanh đến khi dừng hẳn ô tô đi được quảng
đường dài 3m.Tìm giá trị của a.
A.
10a
B.
15a
C.
20a
D.
40a
Câu 15. Một người lái xe ô tô đang chạy với vận tốc 20 m/s thì nhìn thấy biển giới hạn tốc độ,
người lái đạp phanh; từ thời điểm đó, ôtô chuyển động chậm dần đều với vận tốc
4 20 /v t t m s
trong đó t là khoảng thời gian tính bằng giây, kể từ lúc bắt đầu đạp phanh.
Hỏi sau khi đạp phanh, từ lúc vận tốc còn 15m/s đến khi vận tốc của người còn 10 m/s thì ô tô đã
di chuyển được quãng đường bao nhiêu mét?
A. 37,5 B. 150 C. 15,625 D. 21,875
Câu 16. Một lực có độ lớn 40 N (newton) cần thiết để kéo căng một chiếc lò xo có độ dài tự
nhiên 10 cm lên 15 cm. Biết rằng theo định luật trong Vật lý, khi một chiếc lò xo bị kéo căng
thêm (đơn vị độ dài) so với độ dài tự nhiên của lò xo thì lò xo trì lại (chống lại) với một lực cho
bởi công thức , trong đó là hệ số đàn hồi (hoặc độ cứng) của lò xo. Hãy tìm công sinh ra khi kéo
lò xo có độ dài từ 15 cm đến 18 cm ? (kí hiệu là đơn vị của công).
A.
1,56 j
B.
0,94j
C.
1,78j
D.
3,96 j
Câu 17 Một xe máy đang chuyển động với vận tốc 10m/s thì lái xe bất ngờ tăng tốc sau 15s xe
máy đạt vận tốc
15 /ms
. Hỏi quảng đường vật đi được trong khoảng thời gian 30 giây kể từ
lúc bắt đầu tăng tốc ?
A. 270 m B.
450m
C.
360m
D.
540m
Câu 18. Khi một chiếc lò xo có độ dài tự nhiên 0,15m bị kéo căng thêm x(m) thì chiếc lò xo
chống trì lại với một lực là
800f x x
. Biết rằng theo định luật trong Vật lý, khi một chiếc lò xo
bị kéo căng thêm (đơn vị độ dài) so với độ dài tự nhiên của lò xo thì lò xo trì lại (chống lại) với
một lực cho bởi công thức , trong đó là hệ số đàn hồi (hoặc độ cứng) của lò xo. Hãy tìm công
sinh ra khi kéo lò xo có độ dài từ 15 cm đến 18 cm ? (kí hiệu là đơn vị của công).
A.
0,36j
B.
0,72 j
C.
36 j
D.
72 j
Câu 19. Một vật chuyển động với vận tốc
2
4
1,2 /
3

t
v t m s
t
. Hỏi rằng trong 20s đầu
tiên vật di chuyển được bao nhiêu mét ?
Tài liệu ôn tập giải tích 12 học kỳ II
Trần Thông sưu tầm và biên soạn Facebook: Hội Toán Bắc Nam
A.
189
B.
190
C.
191
D.
192
Câu 20. Một bác thợ xây đang bơm nước vào bể chứa. Gọi
()h t cm
là mức nước ở bồn chứa sau
khi bơm nước được
t
giây. Biết rằng
2
'3h t at bt
và lúc đầu bồn không chứa nước. Sau 5s
thể tích nước trong bể là
3
150m
, sau 10s thể tích nước trong bể là
3
1100m
.Tìm mức nước ở bồn
sau khi bơm được
20
giây (làm tròn kết quả đến hàng phần trăm)
A.
3
8400m
B.
3
2200m
C.
3
4200m
D.
3
600m
Câu 21. Người ta cần đúc một chiếc chuông cao
4m
và bán kính miệng chuông là
22m
. Giả sử
khi cắt chuông bằng một mặt phẳng qua trục của nó người ta thu được thiết diện có đường viền
là một phần parabol. Tính thể tích quả chuông cần đúc.
A.
6
B.
12
C.
3
2
D.
16
Câu 22. Dòng điện xoay chiều hình sin chạy qua một đoạn mạch LC có biểu thức có biểu thức
cường độ là . Biết
'iq
với
q
là điện tích tức thời ở tụ điện. Tính từ lúc t =
0, điện lượng chuyển qua tiết diện thẳng của dây dẫn của đoạn mạch đó trong thời gian bằng
là bao nhiêu?
A. B. C.0 D.
Câu 23. Trong kinh tế học, thặng dư tiêu dùng của hàng hóa được tính bằng công thức

0
( ) . .
a
I p x P dx
Với
()px
là hàm biểu thị biểu thị giá mà một công ty đưa ra để bán được x
đơn vị hàng hóa. a là số lượng sản phẩm đã bán ra,
()P p a
là mức giá bán ra ứng với số lượng
sản phẩm là a. Cho
2
1200 0,2 0,0001p x x
, (đơn vị tính là USD) Tìm thặng dư tiêu dùng
khi số lượng sản phẩm bán là 500
A. 33333,3 USD B. 1108333,3 USD C. 570833,3 USD D.5000 USD
Câu 24. Một chất điểm A từ trạng thái nghỉ chuyển động với vận tốc nhanh dần đều. 8 giây sau
nó đạt đến vận tốc 6m/s. Từ thời điểm đó nó chuyển động đều. Một chất điểm B khác xuất phát
từ cùng vị trí với A nhưng chậm hơn nó 12 giây với vận tốc nhanh dần đều và đuổi kịp A sau 8
giây (kể từ lúc B xuất phát). Tìm vận tốc của B tại thời điểm đó.
A. 4m/s B. 20m/s C. 24m/s D. 30m/s
Câu 25. Một Bác thợ gốm làm một cái lọ có dạng khối tròn xoay được tạo thành khi quay hình
phẳng giới hạn bởi các đường
1yx
và trục
Ox
quay quanh trục
Ox
biết đáy lọ và miệng lọ
có đường kính lần lượt là 2dm và 4dm. Tính thể tích cái lọ.
A.
2
8 dm
B.
3
15
2
dm
C.
2
14
3
dm
D.
2
15
2
dm
Câu 26. Một tên lửa A xuất phát từ vị trí T, chuyển động thẳng nhanh dần đều; sau 8 giây nó đạt
vận tốc 6km/s. Từ thời điểm đó nó chuyển động thẳng đều. Sau 12 giây kể từ lúc tên lửa A được
bắn đi người ta bắn tên lửa B cho nó chuyển động thẳng nhanh dần đều. Sau 8 giây kể từ khi
xuất phát tên lửa B đuổi kịp tên lửa A. Tìm vận tốc tên lửa B tại thời điểm đuổi kịp tên lửa A.
A. 24000m/s B. 16000m/s C. 24km/s D. 8km/s
Câu 27. Mật độ dân số cách trung tâm thành phố X một khoảng r km là
0,1
5000.
r
D r e
. Hỏi
có khoảng bao nhiêu người sống cách trung tâm thành phố 3 km.
o
i I cos( t )A
2
o
2I
.
o
I
.
2
o
2I
.
Tài liệu ôn tập giải tích 12 học kỳ II
Trần Thông sưu tầm và biên soạn Facebook: Hội Toán Bắc Nam
A. 116038 B. 117000 C. 117 D. 116,038
Câu 28. Một Bác thợ gốm làm một cái lọ có dạng khối tròn xoay được tạo thành khi quay hình
phẳng giới hạn bởi các đường
1yx
và trục
Ox
quay quanh trục
Ox
biết đáy lọ và miệng lọ
có đường kính lần lượt là 2dm và 4dm. Tính thể tích cái lọ.
A.
2
8 dm
B.
3
15
2
dm
C.
2
14
3
dm
D.
2
15
2
dm
Câu 29. Một Bác thợ gốm làm một cái lọ có dạng khối tròn xoay được tạo thành khi quay hình
phẳng giới hạn bởi các đường
1yx
và trục
Ox
quay quanh trục
Ox
biết đáy lọ và miệng lọ
có đường kính lần lượt là 2dm và 4dm. Tính thể tích cái lọ.
A.
2
8 dm
B.
3
15
2
dm
C.
2
14
3
dm
D.
2
15
2
dm
Câu 30. Một Bác thợ gốm làm một cái lọ có dạng khối tròn xoay được tạo thành khi quay hình
phẳng giới hạn bởi các đường
1yx
và trục
Ox
quay quanh trục
Ox
biết đáy lọ và miệng lọ
có đường kính lần lượt là 2dm và 4dm. Tính thể tích cái lọ.
A.
2
8 dm
B.
3
15
2
dm
C.
2
14
3
dm
D.
2
15
2
dm
B. SỐ PHỨC
PHẦN 1: TÓM TẮT LÝ THUYẾT
1.Đơn vị ảo.
Số i mà
2
1i 
gọi là đơn vị ảo.
2.Định nghĩa số phức
Số phức (dạng đại số):
(,z a bi a b
, i là đơn vị ảo); a được gọi là phần thực và b là phần
ảo của số phức z.
z là số thực khi và chỉ khi phần ảo b = 0;
z là số phức khi và chỉ khi phần thực a = 0.
Hai số phức bằng nhau:
'
' ' ( , , ', ' )
'
aa
a bi a b i a b a b
bb
Biểu diễn hình học: Số phức
( , )z a bi a b
được biểu diễn bởi điểm
( ; )M a b
hoặc
( ; )u a b
trong mặt phẳng tọa độ Oxy (mặt phẳng phức)
3.Số phức liên hợp
Số phức
( , )z a bi a b
. Ta gọi số phức
z a bi
là số phức liên hợp của z.
Chú ý:
; ' 'z z z z z z
;
''zz zz
; z là số thực
zz
; z là số ảo
zz
Nhận xét:
+ Số phức liên hợp của
z
lại là
z
, tức là
zz
. Do đó ta còn nói
z
và
z
là hai số phức liên
Tài liệu ôn tập giải tích 12 học kỳ II
Trần Thông sưu tầm và biên soạn Facebook: Hội Toán Bắc Nam
hợp với nhau.
+ Hai số phức là liên hợp với nhau khi và chỉ khi các điểm biểu diễn của chúng đối xứng nhau
qua trục Ox.
Tính chất:
i, Với mọi
12
,zz
ta có:
1 2 1 2
z z z z
;
1 2 1 2
..z z z z
ii,
z
,
z a bi
(
,ab
), số
.zz
luôn là một số thực và
22
.z z a b
4.Phép cộng và trừ hai số phức
Phép cộng và trừ hai số phức được thực hiện theo quy tắc cộng, trừ hai đa thức.Tổng của hai số
phức
1 1 1
z a bi
,
2 2 2
z a b i
(
1 1 2 2
, , ,a b a b
) là số phức
1 2 1 2 1 2
( ) ( )z z a a b b i
.
Tính chất của phép cộng số phức:
i,
1 2 3 1 2 3
( ) ( )z z z z z z
với mọi
1 2 3
,,z z z
ii,
1 2 2 1
z z z z
với mọi
12
,zz
iii,
00z z z
với mọi
z
iv, Với mỗi số phức
z a bi
(
,ab
), nếu kí hiệu số phức
a bi
là
z
thì ta có:
( ) 0z z z z
. Số
z
được gọi là số đối của số phức
z
.
Hiệu của hai số phức
1 1 1
z a bi
,
2 2 2
z a b i
(
1 1 2 2
, , ,a b a b
) là tổng của hai số phức
1
z
và
2
z
, tức là:
1 2 1 2 1 2 1 2
( ) ( ) ( )z z z z a a b b i
.
Ý nghĩa hình học của phép cộng và phép trừ số phức:
Mỗi số phức
z a bi
(
,ab
) được biểu diễn bởi
( ; )M a b
cũng có nghĩa là véc tơ
OM
.
Khi đó nếu
12
,uu
theo thứ tự biểu diễn số phức
12
,zz
thì:
+
12
uu
biểu diễn số phức
12
zz
+
12
uu
biểu diễn số phức
12
zz
5.Phép nhân hai số phức
Phép nhân hai số phức được thực hiện theo quy tắc nhân hai đa thức, ở đây chú ý i là đơn vị ảo.
Tích của hai số phức
1 1 1
z a bi
,
2 2 2
z a b i
(
1 1 2 2
, , ,a b a b
) là số phức:
1 2 1 2 1 2 1 2 2 1
. ( )z z a a bb a b a b i
.
Nhận xét: + Với mọi số thực k và mọi số phức
z a bi
(
,ab
), ta có:
()kz k a bi ka kbi
+
0. .0 0zz
với mọi
z
.
*Tính chất của phép nhân số phức:
i,
1 2 2 1
z z z z
với mọi
12
,zz
ii,
.1 1.z z z
với mọi
z
Tài liệu ôn tập giải tích 12 học kỳ II
Trần Thông sưu tầm và biên soạn Facebook: Hội Toán Bắc Nam
iii,
1 2 3 1 2 3
( ). .( )z z z z z z
với mọi
1 2 3
,,z z z
iv,
1 2 3 1 2 1 3
.( )z z z z z z z
với mọi
1 2 3
,,z z z
6.Môđun của số phức
Môđun của số phức
( , )z a bi a b
là một số ký hiệu là
22
||z a b
||zz OM
+
| | 0z
với mọi z thuộc C và
| | 0 0zz
.
+
| '| | || '|; | '| | | | '|zz z z z z z z
với mọi số phức z, z’.
7.Phép chia hai số phức
Số phức nghịch đảo của z (z khác 0):
1
2
1
||
zz
z
.
Thương của z cho z’ ( z khác 0):
1
2
' ' '
'
||
z z z z z
zz
zz
zz
Với z khác 0,
'
'ww
z
zz
z
,
''zz
z
z



,
' | '|
||
zz
zz
8.Căn bậc hai của số phức
z là một căn bậc hai của số phức w khi và chỉ khi
2
w z
.
( , )z x yi x y
là căn bậc hai của số phức
( , )w a bi a b
22
2
x y a
xy b

.
Số 0 có đúng một căn bậc hai là 0.
Số phức khác 0 có hai căn bậc hai là hai số đối nhau.
Hai căn bậc hai của số thực a dương là
a
.
Hai căn bậc hai của số thực âm là
ia
9.Phƣơng trình bậc hai của số phức
Phương trình bậc hai
2
0Az Bz C
(A, B, C là các số phức cho trước, A khác 0):
2
4B AC
+ Nếu
0
phương trình có hai nghiệm phân biệt:
1,2
2
B
z
A

với
là một căn bậc hai của
.
+Nếu
0
: phương trình có một nghiệm kép là
2
B
z
A
.
10.Dạng lƣợng giác của số phức
Tài liệu ôn tập giải tích 12 học kỳ II
Trần Thông sưu tầm và biên soạn Facebook: Hội Toán Bắc Nam
Cho số phức
( , )z a bi a b
, z khác 0. Số có dạng:
( sin )os irc

(r > 0) là dạng lượng
giác của z khi và chỉ khi
22
, ,sin .os
ab
r a b c
rr

là một acgumen của z,
( , )Ox OM
Nhân chia số phức dƣới dạng lƣợng giác
Nếu
( sin ), ' '( ' sin ')os i os iz r c z r c
thì
' ' ( ') sin( ')
( ') sin( ')
''
os i
os i
zz rr c
zr
c
zr
Công thức Moa-vrơ: Với n là số nguyên dương, thì
( sin ) (cos sin )os i i
n
n
r c r n n
Căn bậc hai của số phức dƣới dạng lƣợng giác.
Các căn bậc hai của số phức z có dạng lượng giác
( sin )os irc

là
( sin ),
22
os irc

và
( sin ) 2 ) sin( )
2 2 2 2
os i [ os( i ]r c c

PHẦN 2: BÀI TẬP MINH HỌA
Dạng 1: Thực hiện các phép toán
Bài 1: Cho số phức
31
22
zi
. Tìm các số phức sau:
3
22
; ; ;1z z z z z
Hƣớng dẫn:
3 1 3 1
2 2 2 2
z i z i
2
22
3 1 3 1 3 1 3
2 2 4 4 2 2 2
z i i i i



3 3 2
23
3
3 1 3 3 1 3 1 1
33
2 2 2 2 2 2 2 2
z i i i i i
2
3 3 1 3
1
22
z z i

Bài 2: Tính giá trị của các biểu thức
4 3 1
1 4 3



ii
A
ii
Hƣớng dẫn:
4 3 1 1 4 3
1 7 1 7 27 161
1 1 4 3 4 3 2 25 50 50
i i i i
ii
Ai
i i i i

Bài 3: Tìm phần thực, phần ảo và tính mô đun của số phức
z
biết:
Tài liệu ôn tập giải tích 12 học kỳ II
Trần Thông sưu tầm và biên soạn Facebook: Hội Toán Bắc Nam
11 8
12
11
ii
iz
ii


Hƣớng dẫn:
11 8
8
11
12
1 16
11
16
1 16 1 16
ii
i i i
ii
i
z i z i
i

Vậy
z
có phần thực bằng
1
; phần ảo bằng 16;
22
( 1) 16 257z
Bài 4: Tính giá trị của các biểu thức
5
10
10
13
13


ii
A
i
Hƣớng dẫn: Ta có:
5
10 2 5
4.
5 3 2
2 3 2
1 1 2 32 . 32
3 3 3
3 3 9 3 3 3 2 3
8 2 2 3 16 3 16
i i i i i i
i i i
i i i i i
i i i
3
10 10 3
3
1 3 1 3 1 3 1 3 8 1 3i i i i i
Thay vào biểu thức A ta có
3
32 .16 . 1 3
1
8 1 3


i i i
A
i
.
Bài 5: Tìm các số thực x, y thoả mãn:
7
2
1
(3 ) ( 2)( ) 19 23
1
i
x y y x i i
i



Hƣớng dẫn: Đặt
t x dt xdx
2
12
t
I dt
t
2
3
55
1
1 ( 1) 1 1
.
24
2

Bài 6: Chứng minh rằng số phức
52 2013 52 2013
(3 1)(79 7 ) 10(23 10 )
ii
z
ii


là số thuần ảo
Hƣớng dẫn:
Đặt
dt t t
t x dt x dx dx I t t dt
x
1
78
3 2 6
2
0
1 1 1
1 3 (1 )
3 3 7 8 168
3



.
Dạng 2: Xác định số phức
Tài liệu ôn tập giải tích 12 học kỳ II
Trần Thông sưu tầm và biên soạn Facebook: Hội Toán Bắc Nam
Bài 1: Tìm số phức z biết:
2(1 2 )
(2 ). 7 8
1
i
i z i
i
Hƣớng dẫn: ta có
2(1 )(1 )
(2 ). 7 8
2

ii
i z i
(2 ). 4 7i z i
4 7 (4 7 )(2 )
32
25
i i i
z z z i
i
Bài 2: Tìm số phức z biết:
( 1).(2 ) 3
2
2
z i i
zi
Hƣớng dẫn: Điều kiện
2zi
. Khi đó
(1) 2( 1)(2 ) (3 )( 2 )z i i z i
2
( 1)(4 2 ) 3 6 2z i z i iz i
(1 3 ) 2 4i z i
2 4 (2 4)(1 3 ) 1 7
1 3 10 5 5
i i i
zi
i
17
55
zi
(thỏa mãn điều kiện).
Bài 3: Tìm số phức z biết:
| | 5z
và
2
()zi
là số ảo.
Hƣớng dẫn:
Gọi số phức z cần tìm dạng:
z a bi , a, b
22
||z a b
. Từ giả thiết ta có:
22
| | 5 5 (1)z a b
2 2 2 2
( ) ( ) ( 1) 2 ( 1)z i a bi i a b a b i
Để
2
()zi
là số ảo thì
22
( 1) 0 (2)ab
Từ (1) và (2) ta có hệ phương trình:
22
22
5
( 1)
ab
ab


22
5
21
;
1
12
2
ab
aa
b
bb
b





Vậy số phức cần tìm là:
2 ; 1 2z i z i
.
Bài 4: Tìm số phức z biết
2 1 2z i z i
và
1 10
10
z
Hƣớng dẫn: Ta có:
Tài liệu ôn tập giải tích 12 học kỳ II
Trần Thông sưu tầm và biên soạn Facebook: Hội Toán Bắc Nam
5
10 2 5
4.
5 3 2
2 3 2
1 1 2 32 . 32
3 3 3
3 3 9 3 3 3 2 3
8 2 2 3 16 3 16
i i i i i i
i i i
i i i i i
i i i
3
10 10 3
3
1 3 1 3 1 3 1 3 8 1 3i i i i i
Thay vào biểu thức A ta có
3
32 .16 . 1 3
1
8 1 3


i i i
A
i
.
Bài 5: Tìm số phức z biết:
31z i iz
và
9
z
z
là số thuần ảo
Hƣớng dẫn: Đặt
t x dt xdx
2
12
t
I dt
t
2
3
55
1
1 ( 1) 1 1
.
24
2

Dạng 3: Giải phƣơng trình trên tập số phức
Bài 1: Giải các phương trình
2
2 5 0 zz
trên tập hợp số phức
Hƣớng dẫn: Ta có
'2
4 4 1 2i z i
Bài 2: Giải các phương trình
2
(1 3 ) 2(1 ) 0 z i z i
trên tập hợp số phức
Hƣớng dẫn: Ta có
22
(1 3 ) 8(1 ) 2 (1 )i i i i
nên phương trình có nghiệm là:
3 1 1
2
2
3 1 1 1
2
ii
z
zi
i i z i
z
Bài 3: Giải các phương trình
3
80z
trên tập hợp số phức.
Hƣớng dẫn:
32
8 0 ( 2)( 2 4) 0 z z z z
2
13
13
z
zi
zi


Bài 4: Giải các phương trình
44
( 3) ( 5) 2 zz
trên tập hợp số phức
Hƣớng dẫn: Đặt
t4z
, khi đó phương trình trở thành:
4 4 4 2
( 1) ( 1) 2 6 0t t t t
Tài liệu ôn tập giải tích 12 học kỳ II
Trần Thông sưu tầm và biên soạn Facebook: Hội Toán Bắc Nam
2
2
0
0
6
60
t
t
ti
t



+) Với
t 0 4z
+) Với
t 6 4 6i z i
+) Với
t - 6 4 6i z i
Bài 5: Giải các phương trình
2
1



zi
zi
trên tập hợp số phức
Hƣớng dẫn: Điều kiện:
zi
, khi đó phương trình tương đương với:
2
4
2
2
1
11
1
1
zi
z i z i
zi
zi
z i z i
z i z i
zi
zi
ii
z i z i
zi














0
1
()
1
()
z i z i
z
z i i z
z
z i z i i
z
z i z i i

(thỏa mãn điều kiện)
Dạng 4: Tìm tập hợp điểm biểu diễn
Bài 1: Trên mặt phẳng toạ độ, tìm tập hợp điểm biểu diễn số phức z thoả mãn
3
z
zi
Hƣớng dẫn:
Gọi
( , )z x yi x y R
( ; )M x y
biểu diễn cho số phức
z
trong mặt phẳng toạ độ.
Ta có
2 2 2 2
3 3 ( 1) 9 9( 1)
z
x yi x y i x y x y
zi
22
2 2 2
93
8 8 18 9 0
88
x y y x y
Vậy tập hợp các điểm M là đường tròn tâm
9
0;
8
I



và bán kính
3
8
R
Bài 2: Trên mặt phẳng toạ độ, tìm tập hợp điểm biểu diễn số phức
z
thoả mãn
2 4 2z i z i
Hƣớng dẫn:
Gọi
( , )z x yi x y R
( ; )M x y
biểu diễn cho số phức
z
trong mặt phẳng toạ độ.
Ta có
2 4 2 (*) ( 2) ( 4) ( 2)z i z i x y i x y i
2 2 2 2
( 2) (4 ) ( 2) 4x y x y y x
Tập hợp M là đường thẳng có phương trình
4yx
Tài liệu ôn tập giải tích 12 học kỳ II
Trần Thông sưu tầm và biên soạn Facebook: Hội Toán Bắc Nam
Bài 3: Trên mặt phẳng toạ độ, tìm tập hợp điểm biểu diễn số phức z thoả mãn
22z i z z i
.
Hƣớng dẫn:
Đặt:
( , )z x yi x y R
z
có điểm biểu diễn trên mặt phẳng phức là
M x; y .
Ta có
2
2 2 2 ( 1) (1 )
4
x
z i z z i x y i y i y
Vậy tập hợp điểm M là đường parabol (P) có phương trình
2
4
x
y
.
Bài 4: Trên mặt phẳng toạ độ, tìm tập hợp điểm biểu diễn số phức z thoả mãn
4z i z i
Hƣớng dẫn:
Đặt:
( , )z x yi x y R
z
có điểm biểu diễn trên mặt phẳng phức là
M x; y .
Ta có
2 2 2 2
4 ( 1) ( 1) 4 (*)z i z i x y x y
Đặt
12
(0; 1) ; (0;1)FF
1 2 1 2
(*) 4 2MF MF FF
Suy ra tập hợp M là elíp (E) có 2 tiêu điểm là
12
,FF
.
Gọi (E) có phương trình
22
2 2 2
22
1 (0 ; )
xy
a b b a c
ab
Ta có
12
2 2 2
12
2
2
5
21
MF MF a
a
b a c
F F c c



Vậy (E) có phương trình
22
1
45
xy

Bài 5: Trên mặt phẳng toạ độ, tìm tập hợp điểm biểu diễn số phức z thoả mãn
22
( ) 4zz
Hƣớng dẫn:
Đặt:
( , )z x yi x y R
z
có điểm biểu diễn trên mặt phẳng phức là
M x; y .
Ta có
22
1
( ) 4 4 4 4 4 1
1
y
x
z z xyi xy xy
y
x

Vậy tập hợp điểm M là đường hybebol (H) có phương trình là
1
y
x
và
1
y
x

Dạng 5: Bài toán cực trị
Tài liệu ôn tập giải tích 12 học kỳ II
Trần Thông sưu tầm và biên soạn Facebook: Hội Toán Bắc Nam
Bài 1: Trong các số phức
z
thoả mãn điều kiện
1 5 3z i z i
, tìm số phức có môđun
nhỏ nhất
Hƣớng dẫn:
Gọi
;z x yi x y
2 2 2 2
1 5 3 ( 1) ( 5) ( 3) ( 1)z i z i x y x y
3 4 0 4 3x y x y
2
2 2 2 2 2
6 8 2 10
(4 3 ) 10 24 16 10
5 5 5
z x y y y y y y



Đẳng thức xảy ra khi
62
55
yx
Vậy
z
đạt giá trị nhỏ nhất bằng
2 10
5
khi
26
55
zi
Vậy
26
55
zi
là số phức cần tìm
Bài 2: Trong các số phức
z
có phần thực, phần ảo không âm và thoả mãn:
3
1
12
z
zi

. Tìm số phức
z
sao cho biểu thức sau đạt giá trị lớn nhất, nhỏ nhất.
2 2 2 2
. . (1 ) (1 )P z z z z i z i z i
Hƣớng dẫn:
Điều kiện:
12zi
Gọi
*
;z x yi x y
3
3
1 1 3 1 2
1 2 1 2
z
z
z z i
z i z i
2 2 2 2
( 3) ( 1) ( 2) 1x y x y x y
(luôn thoả mãn điều kiện vì
1; 2xy
không thoả mãn phương trình)
2 2 2 2
4 . 4z x yi z z xyi z z xy
(vì
;xy
không âm)
2 2 2 2
. 4 4z z i xy z z xy
(1 ) (1 ) 2 2z i z i x y
Do đó
2 2 2 2
16 4 .(2 2 ) 16 8P x y xy x y x y xy
Đặt
2
1
0
24
xy
t xy t



, ta có
2
1
16 8 ; 0;
4
P t t t



Xét hàm số
2
( ) 16 8f t t t
liên tục trên
1
0;
4



Tài liệu ôn tập giải tích 12 học kỳ II
Trần Thông sưu tầm và biên soạn Facebook: Hội Toán Bắc Nam
1
'( ) 32 8 ; '( ) 0 0
4
f t t t f t t t
(loại)
1
1
0;
0;
4
4
1 33 33 1
(0) 0; max ( ) ;min ( ) 0 0
4 16 16 4
f f f t t f t t









Khi
0; 1
11
; Khi 0
1; 0
22
xy
t x y t
xy


Vậy P đạt giá trị lớn nhất bằng
33 1 1
khi
16 2 2
zi
P đạt giá trị nhỏ nhất bằng
0 khi 1 0zz
Bài 3: Trong các số phức
z
thoả mãn
3 4 4zi
. Tìm giá trị lớn nhất, giá trị nhỏ nhất của
z
.
Hƣớng dẫn:
Gọi
;z x yi x y
( ; )M x y
biểu diễn cho số phức
z
trong hệ toạ độ Oxy
2 2 2 2
3 4 4 ( 3) ( 4) 4 ( 3) ( 4) 16z i x y x y
Vậy điểm M biểu diễn cho số phức z thuộc đường tròn (T) có tâm
(3; 4)I
, bán kính R = 4.
22
z x y OM
;
5OI R
nên O nằm ngoài đường tròn (T)
z
lớn nhất , nhỏ nhất khi OM lớn nhất, nhỏ nhất khi M di dộng trên (T)
Với điểm M bất kì trên (T), ta có:
AM IM IA IB IA AB
. Đẳng thức xảy ra khi
MB
AM AI IM AI IC AC
. Đẳng thức xảy ra khi
MC
Đường thẳng OI cắt đường tròn (T) tại hai điểm phân biệt
3 4 27 36
; ; ; 1; 9
5 5 5 5
A B OA OB
Với M di động trên (T), ta có:
19OA OM OB OM
19z
OM nhỏ nhất khi M trùng với A; OM lớn nhất khi M trùng với B
Vậy
z
nhỏ nhất bằng 1 khi
34
55
zi
;
z
lớn nhất bằng 9 khi
27 36
55
zi
Bên cạnh đó bạn đọc có thể tham khảo thêm cách giải sau:
Gọi
;z x yi x y
( ; )M x y
biểu diễn cho số phức z trong hệ toạ độ Oxy
34i
(3; 4)A
biểu diễn cho số phức
; 5;z OM OA z AM

;
3 4 4 4 4z i z AM
Ta có:
4 4 4 4 1 9OM OA AM OM OA OA OM OA OM
19z
;
1z
khi
34
55
zi
;
9z
27 36
55
zi
Tài liệu ôn tập giải tích 12 học kỳ II
Trần Thông sưu tầm và biên soạn Facebook: Hội Toán Bắc Nam
Vậy
z
nhỏ nhất bằng 1 khi
34
55
zi
;
z
lớn nhất bằng 9 khi
27 36
55
zi
Bài 4: Trong các số phức
z
thoả mãn điều kiện
( 2 4 )z z i
là một số ảo, tìm số phức
z
sao
cho
1zi
có môđun lớn nhất.
Hƣớng dẫn:
Gọi
;z x yi x y
( ; )M x y
biểu diễn cho số phức z trong hệ toạ độ Oxy
( 2 4 ) ( ) ( 2) ( 4) ( 2) ( 4) ( 4) ( 2)z z i x yi x y i x x y y x y y x i
( 2 4 )z z i
là một số ảo
2 2 2 2
( 2) ( 4) 0 2 4 0 ( 1) ( 2) 5x x y y x y x y x y
M biểu diễn cho
z
thuộc đường tròn (T) có tâm
( 1;2)I
, bán kính
5R
22
1 ( 1) ( 1) ( 1) ( 1)z i x y i x y AM
với
(1;1)A
5 ( )IA A T
Vì M là điểm di động trên (T) nên AM lớn nhất
AM là đường kính của (T)
M đối xứng với A qua I
I là trung diểm của AM
( 3;3) 3 3 4 2M z i i
Vậy
lớn nhất bằng
25
khi
33zi
Bài 5: Cho các số phức
12
;zz
thoả mãn:
1 2 2
1; (1 ) 6 2z z z i i
là một số thực. Tìm số
phức
12
;zz
sao cho
2
2 1 2 1 2
P z z z z z
đạt giá trị nhỏ nhất.
Hƣớng dẫn:
Gọi
12
; ; ; ; ;z a bi z c di a b c d
( ; ), ( ; )M a b N c d
lần lượt biểu diễn cho
12
;zz
trong hệ toạ độ Oxy
2 2 2 2
1
1 1 1z a b a b
M thuộc đường tròn
()T
có tâm O, bán kính R = 1
2
;
1 6 2 ( 1) ( 1) 2 6
( 1) ( 1) 2 ( 1) ( 1) 6
z c di
z z i i c di c d i i
c c d d c d d c i



là số thực
( 1) ( 1) 6 0 6 0c d d c c d
N thuộc đường thẳng
: 6 0xy
Ta có
( ; ) 1dO
nên
và
()T
không có điểm chung
1 2 1 2 1 2 1 2
( ) ; ( ) 2( )z z ac bd bc ad i z z ac bd bc ad i z z z z ac bd
2 2 2 2 2
2( ) ( ) ( ) 1 1P c d ac bd c a b d MN
(vì
22
1ab
)
Gọi H là hình chiếu vuông góc của O trên
: 6 0 (3;3)x y H
Đoạn OH cắt đường tròn
()T
tại
22
;
22
I



Tài liệu ôn tập giải tích 12 học kỳ II
Trần Thông sưu tầm và biên soạn Facebook: Hội Toán Bắc Nam
Với N thuộc đường thẳng
, M thuộc đường tròn
()T
, ta có:
3 2 1MN ON OM OH OI IH
. Đẳng thức xảy ra khi
;M I N H
2
3 2 1 1 18 6 2P
. Đẳng thức xảy ra khi
12
22
; 3 3
22
z i z i
Vậy P đạt giá trị nhỏ nhất bằng
18 3 2
khi
12
22
; 3 3
22
z i z i
PHẦN 3: BÀI TẬP TRẮC NGHIỆM
Câu 1. Cho số phức
z a bi
. Tìm mệnh đề đúng trong các mệnh đề sau.
A.
2 z z bi
B.
2 z z a
C.
22
. z z a b
D.
2
2
zz
Câu 2. Tìm số phức liên hợp của số phức
z a a b i
A.
z a b a i
B.
z a bi
C.
z a a b i
D.
z a bi
Câu 3. Cho số phức
z a bi
. Tìm phần thực của số phức
2
z
.
A.
22
ab
B.
22
ab
C.
ab
D.
ab
Câu 4. Tìm số phức liên hợp của số phức:
13zi
A.
3zi
B.
13zi
C.
13zi
D.
13zi
Câu 5. Tìm mô đun của số phức:
23zi
A.
13
B.
5
C. 5 D. 2
Câu 6. Tìm mệnh đề sai trong các mệnh đề sau.
A. Số phức z = a + bi được biểu diễn bằng điểm M(a; b) trong mặt phẳng phức Oxy
B. Số phức z = a + bi có môđun là
22
ab
C. Số phức z = a + bi = 0
0
0
a
b
D. Số phức z = a + bi có số phức đối z‟ = a - bi
Câu 7. Tìm điểm biểu diễn số phức
12zi
trên mặt phẳng Oxy
A.
1; 2
B.
1; 2
C.
2; 1
D.
2;1
Câu 8. Với giá trị nào của x,y để 2 số phức sau bằng nhau:
23x i yi
A.
2; 3xy
B.
2; 3xy
C.
3; 2xy
D.
3; 2xy
Câu 9. Với giá trị nào của x,y thì
2 3 6x y x y i i
A.
1; 4xy
B.
1; 4xy
C.
4; 1xy
D.
4; 1xy
Câu 10. Cho hai số phức
z a bi
và
' ' 'z a b i
. Tìm phần thực số phức
z'z
A.
'aa
B.
'aa
C.
''aa bb
D.
2'bb
Câu 11. Cho số phức
2016 2017zi
. Tìm điểm biểu diễn của số phức đối của
z
A.
2016; 2017
B.
2016; 2017
C.
2016; 2017
D.
2016; 2017
Câu 12. Cho số phức
2
23zi
. Tìm phần thực và phần ảo của số phức
z
.
A. Phần thực bằng
7
, Phần ảo bằng
62i
B. Phần thực bằng
7
, Phần ảo bằng
62
Tài liệu ôn tập giải tích 12 học kỳ II
Trần Thông sưu tầm và biên soạn Facebook: Hội Toán Bắc Nam
C. Phần thực bằng
7
và Phần ảo bằng
62
D. Phần thực bằng
7
và Phần ảo bằng
62i
Câu 13. Cho số phức
23zi
. Tìm phần thực và phần ảo của số phức
3
z
.
A. Phần thực bằng
46
và Phần ảo bằng
9i
B. Phần thực bằng
46
và Phần ảo bằng
9i
C. Phần thực bằng
46
và Phần ảo bằng
9i
D. Phần thực bằng
46
và Phần ảo bằng
9
Câu 14. Tính môdun của số phức
3
1zi
A.
22z
B.
2z
C.
0z
D.
22z
Câu 15. Cho số phức
13
22
zi
. Tìm số phức
2
z
A.
13
22
i
B.
13
22
i
C.
13i
D.
3 i
Câu 16. Cho hai số phức
23zi
và
' 1 2zi
. Tính môđun của số phức
'zz
.
A.
' 10zz
B.
' 2 2zz
C.
'2zz
D.
' 2 10zz
Câu 17. Cho hai số phức
34zi
và
' 4 2zi
. Tính môđun của số phức
'zz
A.
'3zz
B.
'5zz
C.
'1zz
D.
'5zz
Câu 18. Tìm số phức
z
thỏa mãn điều kiện
2 2 5z iz i
.
A.
34zi
B.
34zi
C.
43zi
D.
43zi
Câu 19. Cho số phức z thỏa mãn điều kiện
2 3 1 1 9z i z i
. Tìm môđun của z.
A.
13
B.
82
C.
13zi
D.
13zi
Câu 20. Tìm mô đun của số phức:
23zi
A.
13
B.
5
C.
5
D. 13
Câu 21. Tìm mệnh đề sai trong các mệnh đề sau.
A. Số phức z = a + bi được biểu diễn bằng điểm M(a; b) trong mặt phẳng phức Oxy
B. Số phức z = a + bi có môđun là
22
ab
C. Số phức z = a + bi = 0
0
0
a
b
D. Số phức z = a + bi có số phức đối z‟ = a - bi
Câu 22. Tìm số phức nghịch đảo của số phức
13zi
A.
1
z
=
13
22
i
B.
1
z
=
13
44
i
C.
1
z
= 1 +
3i
D.
1
z
= -1 +
3i
Câu 23. Tìm tập hợp các điểm biểu diễn hình học của các số phức
z a ai
A.
yx
B.
2yx
C.
yx
D.
2yx
Câu 24. Tìm tập hợp các điểm biểu diễn hình học của các số phức
7z bi
với
b
A.
7x
B.
7y
C.
yx
D.
7yx
Câu 25. Cho số phức
2
z a a i
với
a
. Tìm tập hợp điểm biểu diễn của số phức liên hợp
của
z
Tài liệu ôn tập giải tích 12 học kỳ II
Trần Thông sưu tầm và biên soạn Facebook: Hội Toán Bắc Nam
A. Đường thẳng
2yx
B. Đường thẳng
1yx
C. Parabol
2
yx
D. Parabol
2
yx
Câu 26. Tập hợp các điểm trong mặt phẳng biểu diễn cho số phức
z
thỏa mãn điều kiện
1zi
có hình dạng như thế nào?
A. Đường thẳng B. Đường tròn C. Đoạn thẳng D. Hình vuông
Câu 27. Tập hợp các điểm trong mặt phẳng biểu diễn cho số phức
z
thỏa mãn điều kiện
1 2 4zi
có hình dạng như thế nào?
A. Đường thẳng B. Đường tròn C. Đoạn thẳng D. Hình vuông
Câu 28. Cho hai số phức
z a bi
và
' ' 'z a b i
. Tìm điều kiện giữa
, , ', 'a b a b
để
'zz
là
một số thực
A.
,'
'0
aa
bb

B.
'0
,'
aa
bb

C.
'0
'
aa
bb

D.
'0
'0
aa
bb


Câu 29. Cho hai số phức
z a bi
và
' ' 'z a b i
. Tìm điều kiện giữa
, , ', 'a b a b
để
'zz
là
một số thuần ảo.
A.
,'
'0
aa
bb

B.
'0
,'
aa
bb

C.
'0
'
aa
bb

D.
'0
'0
aa
bb


Câu 30. Cho hai số phức
z a bi
và
' ' 'z a b i
. Tìm điều kiện giữa
, , ', 'a b a b
để
.'zz
là
một số thực
A.
' ' 0aa bb
B.
' ' 0aa bb
C.
' ' 0ab a b
D.
' ' 0ab a b
Câu 31. Cho hai số phức
z a bi
và
' ' 'z a b i
. Tìm điều kiện giữa
, , ', 'a b a b
để
.'zz
là
một số thực
A.
' ' 0aa bb
B.
' ' 0aa bb
C.
' ' 0ab a b
D.
' ' 0ab a b
Câu 32. Cho hai số phức
z a bi
và
' ' 'z a b i
. Tìm điều kiện giữa
, , ', 'a b a b
để
.'zz
là
một số thuần ảo
A.
''aa bb
B.
''aa bb
C.
' ' 'a a b b
D.
' ' 0aa
Câu 33. Cho
2
2x i yi
,xy
. Tìm giá trị của
x
và
y
A.
2x
và
8y
hoặc
2x 
và
8y 
B.
3x
và
12y
hoặc
3x 
và
12y 
C.
1x
và
4y
hoặc
1x 
và
4y 
D.
4x
và
16y
hoặc
4x
và
16y
Câu 34. Cho
2
23 x i x yi
,xy
. Tìm giá trị của
x
và
y
A.
1x
và
2y
hoặc
1x 
và
2y 
B.
1x 
và
4y 
hoặc
4x
và
16y
Tài liệu ôn tập giải tích 12 học kỳ II
Trần Thông sưu tầm và biên soạn Facebook: Hội Toán Bắc Nam
C.
2x
và
5y
hoặc
3x
và
4y 
D.
6x
và
1y
hoặc
0x
và
4y
Câu 35. Tìm số phức z, biết:
(3 ) (2 5 ) 10 3i z i z i
.
A.
23zi
B.
23zi
C.
23zi
D.
23zi
Câu 36. Tìm số phức z, biết:
(2 ) (5 3 ) 17 16i z i z i
A.
34zi
B.
34zi
C.
34zi
D.
34zi
Câu 37. Tìm số phức z biết
5z
và phần thực lớn hơn phần ảo một đơn vị.
A.
1
43zi
,
2
34zi
B.
1
43zi
,
2
34zi
C.
1
43zi
,
2
34zi
D.
1
43zi
,
2
34zi
Câu 38. Tìm số phức z biết
20z
và phần thực gấp đôi phần ảo.
A.
1
2zi
,
2
2zi
B.
1
2zi
,
2
2zi
C.
1
2zi
,
2
2zi
D.
1
42zi
,
2
42zi
Câu 39. Tìm tập hợp các điểm trong mặt phẳng biểu diễn số phức
z
thỏa mãn điều kiện
2
z
là
một số thực âm
A. Trục hoành (trừ gốc tọa độ O)
B. Đường thẳng
yx
(trừ gốc tọa độ O)
C. Trục tung (trừ gốc tọa độ O) D. Đường thẳng
yx
(trừ gốc tọa độ O)
Câu 40. Cho số phức z thõa mãn:
50z 
. Tìm môđun của z.
A.
26
B.
5
C.0 D. 5
Câu 41. Tìm mô đun của số phức
4 (2 3 )(1 )z i i i
.
A.
2
B.
1
C.0 D. -2
Câu 42. Cho x, y là các số thực. Hai số phức
3zi
và
( 2 ) yz x y i
bằng nhau khi nào ?
A.
5, 1xy
B.
1, 1xy
C.
3, 0xy
D.
2, 1xy
Câu 43. Cho x, y là các số thực. Số phức:
12z xi y i
bằng 0 khi nào ?
A.
2, 1xy
B.
2, 1xy
C.
0, 0xy
D.
1, 2xy
Câu 44. Cho x số thực. Số phức:
(2 )z x i
có mô đun bằng
5
khi nào ?
A.
0x
B.
2x
C.
1x 
D.
1
2
x 
Câu 45. Cho số phức:
2 . 3zi
. Tính giá trị biểu thức
.zz
.
A.
1
B.
2
C.3 D. 5
Câu 46. Cho hai số phức:
1
12zi
,
2
2zi
Tính giá trị biểu thức
12
.zz
.
Tài liệu ôn tập giải tích 12 học kỳ II
Trần Thông sưu tầm và biên soạn Facebook: Hội Toán Bắc Nam
A. 5
B.
25
C.25 D. 0
Câu 47. Cho số phức z có phần ảo gấp hai phần thực và
25
1
5
z 
. Tính mô đun của z.
A.
26
B.
5
C.0 D. 5
Câu 48. Cho z có phần thực là số nguyên và
2z 7 3z i z
.Tính môđun của số phức:
2
w1zz
.
A.
w 37
B.
w 457
C.
w 425
D.
w 445
Câu 49. Cho z có phần thực là số nguyên và
3z 11 6z i z
. Tính môđun của số phức:
2
w1zz
..
A.
w 23
B.
w5
C.
w 443
D.
w 445
Câu 50. Giả sử M(z) là điểm trên mặt phẳng phức biểu diễn số phức z. Biết tập hợp các điểm
M(z) thoả mãn điều kiện sau đây:
1zi
=2 là một đường tròn. Tìm tâm và bán kính đường
tròn đó.
A. Có tâm
1; 1
và bán kính là 2
B. Có tâm
1; 1
và bán kính là
2
C. Có tâm
1;1
và bán kính là 2 D. Có tâm
1; 1
và bán kính là 2
Câu 51. Giả sử M(z) là điểm trên mặt phẳng phức biểu diễn số phức z. Biết rằng tập hợp các
điểm M(z) thoả mãn điều kiện sau đây:
21zi
là một đường thẳng. Viết phương trình
đường thẳng đó.
A.
4x 2 3 0y
B.
4x 2 3 0y
C.
4x 2 3 0y
D.
2x 2 0y
Câu 52. Giả sử M(z) là điểm trên mặt phẳng phức biểu diễn số phức z. Biết rằng tập hợp các
điểm M(z) thoả mãn điều kiện sau đây: |z +
z
+3|=4 là hai đường thẳng. Viết phương trình
những đường thẳng đó.
A.
1
2
x
và
7
2
x
B.
1
2
x 
và
7
2
x 
C.
1
2
x
và
7
2
x 
D.
1
2
x 
và
7
2
x
Câu 53. Giả sử M(z) là điểm trên mặt phẳng phức biểu diễn số phức z. Biết rằng tập hợp các
điểm M(z) thoả mãn điều kiện sau đây: |z +
z
+ 1 - i| = 2 là hai đường thẳng. Viết phương trình
những đường thẳng đó.
Tài liệu ôn tập giải tích 12 học kỳ II
Trần Thông sưu tầm và biên soạn Facebook: Hội Toán Bắc Nam
A.
13
2
y
và
13
2
y
B.
13
2
y

và
13
2
y
C.
13
2
y
và
13
2
y

D.
13
2
y

và
13
2

y
Câu 54. Tìm số phức z thỏa mãn:
2 10zi
và
. 25zz
.
A.
34zi
hoặc
5z
B.
34zi
hoặc
5z 
C.
34zi
hoặc
5z
D.
45zi
hoặc
3z
Câu 55.
G
ọi
1
z
và
2
z
là các nghiệm của phương trình
2
2 5 0zz
. Tính
44
12
P z z
A.
14P
B.
14P
C.
14Pi
D.
14Pi
Câu 56.
G
ọi
1
z
là nghiệm phức có phần ảo âm của pt:
2
2 3 0zz
. Tìm tọa độ điểm M biểu
diễn số phức
1
z
A.
( 1;2)M
B.
( 1; 2)M 
C.
( 1; 2)M 
D.
( 1; 2 )Mi
Câu 57. Cho số phức z có phần ảo âm và thỏa mãn
2
3 5 0zz
. Tìm mô đun của số phức:
2 3 14z
A. 4
B.
17
C.
24
D.
5
Câu 58.
G
ọi
1
z
và
2
z
lần lượt là nghiệm của phươngtrình:
2
2 5 0zz
. Tính
12
zz
A.
10
B.
3
C.
6
D.
25
Câu 59. Cho
s
ố phức z thỏa mãn:
2
(3 2 ) (2 ) 4 .i z i i
Tính hiệu phần thực và phần ảo của
s
ố phức z.
A.
0
B.
1
C.
4
D.
6
Câu 60. Cho số phức
11
11
ii
z
ii



. Trong các kết luận sau kết luận nào đúng?
A.
z
B.
z
là số thuần ảo.
C.
Mô đun của
z
bằng 1 D.
z
có phần thực và phần ảo đều bằng 0
Câu 61. Biểu diễn về dạng
z a bi
của số phức
2016
2
(1 2 )
i
z
i
là số phức nào?
A.
34
25 25
i
B.
34
25 25
i
C.
34
25 25
i
D.
34
25 25
i
Câu 62. Tìm điểm biểu diễn số phức
(2 3 )(4 )
32
ii
z
i

Tài liệu ôn tập giải tích 12 học kỳ II
Trần Thông sưu tầm và biên soạn Facebook: Hội Toán Bắc Nam
A. (1;-4)
B. (-1;-4) C.
(1;4) D. (-1;4)
Câu 63. Tìm nghiệm của phương trình
. 2017 0i z i
.
A.
1 2017 i
B.
1 2017 i
C.
1 2017 i
D.
2017i
Câu 64. Cho số phức
1 z x yi
(x, y R). Tìm phần ảo của số phức
1
1
z
z
.
A.
2
2
2
1
x
xy

B.
2
2
2
1
y
xy

C.
2
2
1
xy
xy
D.
2
2
1
xy
xy

Câu 65. Trong C, giải phương trình
4
1
1
i
z

.
A.
2zi
B.
32zi
C.
53zi
D.
12zi
Câu 66. Cho phương trình z
2
+ bz + c = 0. Giả sử phương trình có nghiệm z = 1 + i .Tìm các giá
trị b và c bằng (b, c là số thực).
A. b = 3, c = 5
B. b = 1, c = 3 C.
b = 4, c = 3 D. b = -2, c = 2
Câu 67. Cho phương trình z
3
+ az
2
+ bz + c = 0. Giả sử z = 1 + i và z = 2 là hai nghiệm. Tìm các
giá trị a, b, c bằng (a,b,c là số thực):.
A.
4
6
4
a
b
c


B.
2
1
4
a
b
c
C.
4
5
1
a
b
c
D.
0
1
2
a
b
c

Câu 68. Số phức nào sau đây là số thực.
A.
1 2 1 2
3 4 3 4
ii
z
ii



B.
1 2 1 2
3 4 3 4
ii
z
ii



C.
1 2 1 2
3 4 3 4
ii
z
ii



D.
1 2 1 2
3 4 3 4
ii
z
ii



Câu 69.
G
ọi
1
z
và
2
z
là các nghiệm của phương trình
2
4 9 0zz
. Gọi M, N là các điểm biểu
diễn của
1
z
và
2
z
trên mặt phẳng phức. Tính độ dài của MN.
A.
4MN
B.
5MN
C.
25MN 
D.
25MN
Câu 70.
G
ọi
1
z
và
2
z
là các nghiệm của phương trình
2
4 9 0zz
. Gọi M, N, P lần lượt là
các điểm biểu diễn của
1
z
,
2
z
và số phức
k x iy
trên mặt phẳng phức. Tìm tập hợp điểm P
trên mặt phẳng phức để tam giác MNP vuông tại P.
A. Đường thẳng có phương trình
5yx
B. Đường tròn có phương trình
22
2 8 0x x y
C.
Đường tròn có phương trình
22
2 8 0x x y
, nhưng không chứa M, N.
D. Đường tròn có phương trình
22
2 1 0x x y
, nhưng không chứa M, N.
Tài liệu ôn tập giải tích 12 học kỳ II
Trần Thông sưu tầm và biên soạn Facebook: Hội Toán Bắc Nam
Câu 71.
G
ọi
1
z
và
2
z
là các nghiệm của phương trình
1
1z
z
. Tính giá trị của
33
12
P z z
.
A.
0P
B.
1P
C.
2P
D.
3P
Câu 72. Biết số phức z thỏa phương trình
1
1z
z

. Tính giá trị của
2016
2016
1
Pz
z

.
A.
0P
B.
1P
C.
2P
D.
3P
Câu 73.
G
ọi
1
z
và
2
z
là các nghiệm của phương trình
2
2 10 0zz
. Gọi M, N, P lần lượt là
các điểm biểu diễn của
1
z
,
2
z
và số phức
k x iy
trên mặt phẳng phức. Tìm số phức k để tam
giác MNP đều.
A.
1 27 1 27k hay k
B.
1 27 1 27k i hay k i
C.
27 27k i hay k i
D. Một đáp số khác.
Câu 74. Tìm phần thực và phần ảo của
2008 2009 2010 2011 2012
2013 2014 2015 2016 2017
i i i i i
z
i i i i i
.
A. 0; -1
B. 1; 0 C.
-1; 0 D. 0; 1
Câu 75.
G
ọi
1
z
và
2
z
là các nghiệm của phương trình
2
4 9 0zz
. Gọi M, N là các điểm biểu
diễn của
1
z
và
2
z
trên mặt phẳng phức. Tính độ dài của MN.
A.
4MN
B.
5MN
C.
25MN 
D.
25MN
Câu 76.
G
ọi
1
z
và
2
z
là các nghiệm của phương trình
2
4 9 0zz
. Gọi M, N là các điểm biểu
diễn của
1
z
và
2
z
trên mặt phẳng phức. Tính độ dài của MN.
A.
4MN
B.
5MN
C.
25MN 
D.
25MN
Câu 77. Gọi
1 2 3
,,z z z
là ba nghiệm của phương trình
3
80z 
. Tính
222
1 2 3
M z z z
..
A.
4M
B.
0M
C.
6M
D.
8M
Câu 78. Tìm số phức z sao cho
(3 4 ) 5zi
và biểu thức
22
2P z z i
đạt giá trị lớn
nhất.
A.
2 i
B.
22i
C.
55 i
D.
43i
Câu 79. Cho số phức
z
có tập nghiệm biểu diễn là trục hoành . Nếu
'1
'1
z
z
z
thì tập điểm biểu
diễn
'z
là một phần của hình nào dưới đây.
A. Trục tung
B. Đường tròn C.
Trục hoành D. Hình tròn
Tài liệu ôn tập giải tích 12 học kỳ II
Trần Thông sưu tầm và biên soạn Facebook: Hội Toán Bắc Nam
Câu 80. Cho hình vuông ABCD có tâm H và A,B,C,D,H lần lượt là điểm biểu diễn cho các số
phức a,b,c,d,h. Tính môđun của số phức b biết
;a i h i 2 1 3
và số phức b có phần ảo
dương .
A.
22
B.
26
C.
42
D.
5
Câu 81. Tìm mô đun của số phức z thỏa mãn:
(1 2 )( ) 4 ( 1) 7 21 i z i i i i
.
A.
9z
B.
23z
C.
5z
D.
37z
Câu 82. Trong mặt phẳng phức Oxy , tập hợp các điểm biểu diễn số phức Z thỏa mãn
5zz
là
đường tròn có tâm
I
. Tìm I
A.
0,0I
B.
1,0I
C.
1,1I
D.
0,1I
Câu 83. Gọi
12
,zz
là hai nghiệm của phương trình
2
2 4 0z iz
. Tính môđun của số phức
12
( 2)( 2)w z z
..
A.
6w
B.
5w
C.
4w
D.
7w
Câu 84 Cho số phức z = x + yi ; x, y
thỏa mãn z
3
= 18 + 26i. Tìm giá trị của biểu thức
2021 2012
T (z 2) (4 z)
.
A.
1007
2
B.
1007
2
C.
1007
3
D.
1006
2
Câu 85. Cho số phức
34zi
.Xác định căn bậc 2 của số phức
z
.
A.
2 , 2ii
B.
2 i
C.
2 , 2ii
D.
32i
Câu 86. Cho số phức z thỏa mãn phương
(1 2 ). 1 2 .i z i
Tìm phần ảo của số phức
2 (1 2 ).iz i z
.
A.
2
5
B.
3
5
C.
1
5
D.
1
5
Câu 87. Cho số phức z thỏa mãn
3
zz
. Khẳng định nào đúng?.
A. Phần thực của z lớn hơn 1.
B. z có thể nhận giá trị là số thực hoặc số thuần ảo
C.
Chỉ có duy nhất một số phức thuần ảo z thỏa
3
zz
.
D.
1z
Câu 88. Cho
5
1
1
i
z
i



, tính
5 6 7 8
z z z z
.
Tài liệu ôn tập giải tích 12 học kỳ II
Trần Thông sưu tầm và biên soạn Facebook: Hội Toán Bắc Nam
A.0
B.
1
C.
4
D.
3
Câu 89. Cho số phức tùy ý
1z
. Xét các số phức
2005
22
()
1
ii
zz
z
và
3
2
()
1
zz
zz
z
. Mệnh đề nào dưới đây là đúng.
A.
là số thực,
là số thực
B.
là số ảo,
là số thực
C.
là số thực,
là số ảo
D.
là số ảo,
là số ảo
Câu 90. Kí hiệu
1 2 3 4
, , ,z z z z
là bốn nghiệm phức của phương trình
42
2 8 0zz
.Tính
tổng
1 2 3 4
T z z z z
.
A.
4
B.
42
C.
4 2 2
D.
2 2 2
Câu 91. Điểm M là điểm biểu diễn của số phức z thỏa mãn phương trình
3( 1) 4 .(7 ).z z i i
Tìm tọa độ điểm M.
A.
2,1M
B.
2, 1M 
C.
2,1M
D.
1,2M
Câu 92. Tính môđun của số phức
2
,zz
với
1
(2 ). 5
1
i
i z i
i
.
A.
52
B.
42
C.
22
D.
32
Câu 93. Tìm tập hợp các điểm trong mặt phẳng phức biểu diễn các số phức z thỏa mãn
22z i z z i
.
A. Đường tròn tâm
0;1I
, bán kính
1R
. B. Parabol
2
4
x
y
C.
Đường tròn tâm
3;0I
, bán kính
3R
.
D. Parabol
2
4
y
x
Câu 94. Cho số phức z thỏa mãn :
z 4 3i 3.
Tìm số phức z có mođun nhỏ nhất.
A.
z 2 3i
B.
46
zi
55

C.
5
z 3 i
2

D.
z 1 4i
Câu 95. Giải phương trình
2
3 2 2 3 2 0zz
.
A.
6
(1 )
6
i
B.
3
(1 )
6
i
C.
6
(1 )
3
i
D.
6
(1 )
5
i
Câu 96. Cho các số phức z thoả mãn
z2
, biết rằng tập hợp các điểm biểu diễn số phức
w 2 i z 2 1
là một đường tròn. Tính chu vi đường tròn đó.
Tài liệu ôn tập giải tích 12 học kỳ II
Trần Thông sưu tầm và biên soạn Facebook: Hội Toán Bắc Nam
A.
25
B.
35
C.
65
D.
45
Câu 97. Trong mặt phẳng phức, gọi
,,A B C
lần lượt là ba điểm biểu diễn các số phức
1 2 3
,,z z z
. Biết
1 2 3
z z z
, trong các khẳng định sau đây, khẳng định nào là đúng .
A. Trọng tâm của tam giác
ABC
là điểm biểu diễn số phức
1 2 3
z z z
.
B. Tam giác
ABC
có tâm đường tròn ngoại tiếp là gốc tọa độ
O
.
C.
Tam giác
ABC
có trọng tâm là gốc tọa độ
O
D. Tam giác
ABC
là tam giác đều
Câu 98. Cho các số phức w, z, u có biểu diễn hình học thỏa mãn: w nằm ở góc phần tư thứ (I), z
nằm ở góc phần tư thứ (II), và u nằm trên chiều âm của trục thực.
Khẳng định nào sau đây có thể đúng?.
A.
u z.w; u z w
B.
z u.w; u z w
C.
u z.w; u z w
D.
z u.w; u z w
Câu 99. Cho số phức
z
thỏa
12z i z i
. Tìm giá trị nhỏ nhất của
z
.
A.
2
B.
1
2
C.
1
4
D. 1
Câu 100. Cho hai số phức
w
và
z
thỏa mãn
1 2 .w i z
Biết tập hợp các điểm biểu diễn của
số phức
z
là đường tròn tâm
2;3I
, bán kính
3.r
Tìm tập hợp các điểm biểu diễn của số
phức
w
..
A. Đường tròn, tọa độ tâm
3;5
bán kính bằng
3.
B. Đường thẳng song song trục tung
C.
Đường thẳng song song trục hoành
D. Đường tròn, tọa độ tâm
1;1
bán kính bằng 3
Câu 101. Tìm tập hợp điểm biễu diễn số phức z thỏa mãn:
1 3 4zi
.
A. Đường tròn tâm I(1;3), bán kính R=4
B. Đường tròn tâm I(-1;3), bán kính R=2
Tài liệu ôn tập giải tích 12 học kỳ II
Trần Thông sưu tầm và biên soạn Facebook: Hội Toán Bắc Nam
C.
Hình tròn tâm I(-1;3), bán kính R=4
D. Hình tròn tâm I(-1;3), bán kính R=2
Câu 102. Tìm phần thực của số phức z biết:
2
||
10
z
z
z

.
A. 10
B.
10
C.
5
D. -5
Câu 103. Cho 3 số phức
;;z i z i z i
1 2 3
1 2 3 4
. Đặt số phức
,z z z z a bi
1 2 3
( , )a b R
. Tính tổng
ab
.
A. -10
B. 10 C.
-40
D. 40
Câu 104. Tìm số phức
12
2. . ,zz
biết
3
3
12
2 4 2(1 )
4 3 (1 ) ;
1
ii
z i i z
i
.
A.
18 74. .i
B.
18 75. .i
C.
18 74. .i
D.
18 75. .i
Câu 105. Hình vẽ sau biểu diễn dạng hình học của các số phức z và w. Ở đây z nằm trong góc
phần tư thứ (I) và w nằm trong góc phần tư thứ (II). Số phức nào trong các số phức sau nằm
trong góc phần tư thứ (III)?
.
A.
wz
B.
z
C.
2iz.
D.
w
Câu 106. Gọi A, B, C lần lượt là các điểm biểu diễn của 3 số phức :
26
1 2i; (1 )(1 2 );
3
i
ii
i
. Tính diện tích của tam giác ABC.
A.
1
4
B.
1
2
C.
5
5
D.
5
2
Câu 107. Cho số phức z thoả mãn điều kiện
2 3 3zi
. Tìm giá trị nhỏ nhất của
z
.
A.
13 3
B. 2 C.
13 2
D.
2
Câu 108. Tìm số phức z có mô đun lớn nhất và thỏa mãn điều kiện
13
1 3 2
2
z i i
.
Tài liệu ôn tập giải tích 12 học kỳ II
Trần Thông sưu tầm và biên soạn Facebook: Hội Toán Bắc Nam
A.
13zi
B.
21
22
zi
C.
31
22
zi
D.
3 15
44
zi
Câu 109. Cho số phức
0z
thỏa mãn
2z
. Tìm tổng giá trị lớn nhất và giá trị nhỏ nhất của
biểu thức
zi
P
z
.
A.
4
B.
1
C.
2
D.
3
Câu 110. Trên tập hợp số phức cho phương trình (*). Gọi là nghiệm của
phương trình (*). Tìm môđun của số phức .
A.
4
B.
6
C.
1
D.
2
Câu 111. Cho số phức
z
thỏa mãn:
13
1 2 2
1
i
i z i
i
. Tìm số phức
1
2
wz
zi

.
A.
71
w
10 10
i
B.
71
w
10 10
i
C.
71
w
55
i
D.
17
w
55
i
Câu 112. Tìm số phức z thỏa mãn
1
(3 )
12
z
zi
i
.
A.
4zi
B.
4zi
C.
14zi
D.
3z
Câu 113. Cho số phức z thỏa mãn:
1 2 2 3 2 2i z i z i
. Tính môđun của z.
A.
1z
B.
2z
C.
2z
D.
0z
Câu 114. Gọi
1
z
và
2
z
là hai nghiệm phức của phương trình
2
2 1 4 2 5 3 0i z i z i
Tính
22
12
T z z
.
A.
17
2
T
B.
1
2
T
C.
9T
D.
1T
Câu 115. Trên mặt phẳng tọa độ Oxy, tìm tập hợp điểm biểu diễn các số phức z thỏa mãn điều kiện
22 izi
A. Đường tròn tâm
2,1I
bán kính
2
B. Đường tròn tâm
2,1I
bán kính
4
C.
Đường tròn tâm
1, 2I
bán kính
2
D. Đường tròn tâm
1, 2I
bán kính
4
Câu 116. Trên mặt phẳng tọa độ Oxy, tìm tập hợp điểm biểu diễn các số phức z thỏa mãn điều kiện
2 ( 1) 5iz
.
2
3 1 0 zz
1, 2
zz
12
4 2 4
,
nn
zz
w n N
ii
Tài liệu ôn tập giải tích 12 học kỳ II
Trần Thông sưu tầm và biên soạn Facebook: Hội Toán Bắc Nam
A. Đường tròn tâm bán kính 25
B. Đường tròn tâm bán kính 25
C.
Đường tròn tâm bán kính 25
D. Đường tròn tâm bán kính 5
Câu 117. Tìm modul của số phức z , biết
6
13
(1 )(2 ) 8
1
i
z i i i
i



.
A.
61z
B.
61z
C.
36z
D.
25z
Câu 118. Cho số phức
2
2 3 7
(1 2 )(4 3 ) 2 8
34
ii
z i i i
i

. Xác định phần thực, phần ảo
của số phức z
A. Phần thực của số phức z là 10, phần ảo của số phức z là 4
B. Phần thực của số phức z là -10, phần ảo của số phức z là 4
C.
Phần thực của số phức z là 4, phần ảo của số phức z là -10
D. Phần thực của số phức z là 4, phần ảo của số phức z là 10
Câu 119. Tìm tập hợp các điểm biểu diễn số phức z trên mặt phẳng tọa độ thỏa mãn điều kiện:
2
5 5 0z z z
.
A. Đường tròn tâm
5,0I
bán kính 25
B. Đường tròn tâm
0,5I
bán kính 25
C.
Đường tròn tâm
5,0I
bán kính 5
D. Đường tròn tâm
0,5I
bán kính 5
Câu 120. Tìm phần thực, phần ảo của số phức
z
biết:
2016
z 2 3 3 3 1i i i
.
A. Phần thực của số phức z là
1008
29
, phần ảo của số phức z là
3
B. Phần thực của số phức z là
1008
29
, phần ảo của số phức z là
3i
C.
Phần thực của số phức z là
1008
29
, phần ảo của số phức z là
3i
D. Phần thực của số phức z là
1008
29
, phần ảo của số phức z là
3
Câu 121. Cho số phức
z
thỏa mãn:
1 2 2 3 2 2i z i z i
. Tính môđun của
z iz
.
A.
w5
B.
w 5 2
C.
w4
D.
w 4 2
Câu 122. Cho số phức
z
thỏa mãn:
11 8
12
11
ii
iz
ii


. Tìm phần thực, phần ảo của
w z iz
.
2,1I
2,1I
1, 2I
1, 2I
Tài liệu ôn tập giải tích 12 học kỳ II
Trần Thông sưu tầm và biên soạn Facebook: Hội Toán Bắc Nam
A. Phần thực của số phức z là
15
, phần ảo của số phức z là
17
B. Phần thực của số phức z là
15
, phần ảo của số phức z là
17
C.
Phần thực của số phức z là
15
, phần ảo của số phức z là
17i
D. Phần thực của số phức z là
15
, phần ảo của số phức z là
17
Câu 123. Cho số phức
z
thỏa mãn:
12iz
là số thực và
1
2z 2 5
2
z
Tìm số phức liên
hợp của z.
A.
4
B.
6
C.
1
D.
2
Câu 124. Cho số phức
z
thỏa mãn:
24
30zz
và
2 z 13z 
Tìm modul của số phức z.
A.
z5
B.
z5
C.
z 2 2
D.
z2
Câu 125. Gọi
12
,zz
là hai số phức thỏa mãn
2 3 6ziz i
và
12
1
3
zz
. Hãy tính giá
trị của biểu thức
12
A z z
.
A.
4
B.
6
C.
1
D.
2
Câu 126. Cho số phức
z
thỏa mãn:
2
12
z
z
i

. Tìm phần thực, phần ảo của
2
2w z z i
A. Phần thực của số phức z là
65
49
, phần ảo của số phức z là
128
49
B. Phần thực của số phức z là
65
49
, phần ảo của số phức z là
128
49
i
C.
Phần thực của số phức z là
65
49
, phần ảo của số phức z là
65
49
D. Phần thực của số phức z là
65
49
, phần ảo của số phức z là
128
49
i
Câu 127. Cho số phức
z
thỏa mãn:
2
2
11z z i iz
. Tìm modul của
4
1
wz
z

A.
4
B.
6
C.
1
D.
2
Câu 128. Tìm số phức
w 1 3iz
có modul lớn nhất. Biết z là số phức sao cho
12zi
A.
84zi
B.
84zi
C.
84
55
zi
D.
84
55
zi
Tài liệu ôn tập giải tích 12 học kỳ II
Trần Thông sưu tầm và biên soạn Facebook: Hội Toán Bắc Nam
Câu 129. Cho số phức
z
thỏa mãn:
2016z
. Tìm modul của
w
biết
1 1 1
wwzz

A.
w1
B.
w0
C.
w 2016
D.
w5
Câu 130. Gọi
1 2 3
,,z z z
là hai số phức thỏa mãn
1 2 3
1z z z
và
1 2 3
1z z z
. Hãy
tính giá trị của biểu thức
333
1 2 3
A z z z
.
A.
4
B.5 C.
1
D.
2
Câu 131. Gọi A,B là hai điểm biểu diển của các số phức
12
,zz
thỏa mãn
12
2z 1 3iz
và
1
1z
. Tính diện tích tam giác OAB.
A.
3
2
S
B.
3
4
S
C.
1
2
S
D.
3S
Câu 132. Trên mặt phẳng tọa độ Oxy, tìm tập hợp điểm biểu diễn các số phức
w 3z 1 i
biết z là
số phức thỏa mãn điều kiện có hình dạng như thế nào?
A.Hình tròn
B.Đường thẳng C.Đường tròn D.Parabol
Câu 133. Cho tập hợp số phức
z
thỏa mãn:
4
12zz
. Tìm giá trị nhỏ nhất, lớn nhất của
modul z.
A. Giá trị nhỏ nhất của modul z là
51
, giá trị lớn nhất của modul z là
51
.
B. Giá trị nhỏ nhất của modul z là
5
, giá trị lớn nhất của modul z là
51
.
C.
Giá trị nhỏ nhất của modul z là
2
, giá trị lớn nhất của modul z là
51
.
D. Giá trị nhỏ nhất của modul z là
2
, giá trị lớn nhất của modul z là
51
.
Câu 134. Cho các số phức
12
,zz
thỏa mãn
1 2 1 2
zzzz
Hãy tính
44
12
21
zz
P
zz

A.
1P
B.
2P
C.
1P 
D.
2P 
Câu 135. Cho số phức
z
thỏa mãn
1z
. Tìm giá trị nhỏ nhất, lớn nhất của modul
2
11z z z
.
A. Giá trị nhỏ nhất của modul z là
31
, giá trị lớn nhất của modul z là
13
4
.
2 3 3 1z i z
Tài liệu ôn tập giải tích 12 học kỳ II
Trần Thông sưu tầm và biên soạn Facebook: Hội Toán Bắc Nam
B. Giá trị nhỏ nhất của modul z là
3
, giá trị lớn nhất của modul z là
13
4
.
C.
Giá trị nhỏ nhất của modul z là
13
4
, giá trị lớn nhất của modul z là
31
.
D. Giá trị nhỏ nhất của modul z là
31
, giá trị lớn nhất của modul z là
51
.
Câu 136. Cho số phức
z
thỏa mãn
1z
. Tìm giá trị nhỏ nhất, lớn nhất của modul
3
1z
.
A. Giá trị nhỏ nhất của modul z là
1
, giá trị lớn nhất của modul z là
4
.
B. Giá trị nhỏ nhất của modul z là
0
, giá trị lớn nhất của modul z là
4
.
C.
Giá trị nhỏ nhất của modul z là
4
, giá trị lớn nhất của modul z là
5
.
D. Giá trị nhỏ nhất của modul z là
1
, giá trị lớn nhất của modul z là
5
.
Câu 137. Cho tập hợp số phức
z
thỏa mãn:
2
2
1
zi
zi


. Tìm giá trị nhỏ nhất, lớn nhất của
modul z.
A. Giá trị nhỏ nhất của modul z là
21
, giá trị lớn nhất của modul z là
21
.
B. Giá trị nhỏ nhất của modul z là
2
, giá trị lớn nhất của modul z là
21
.
C.
Giá trị nhỏ nhất của modul z là
2
, giá trị lớn nhất của modul z là
21
.
D. Giá trị nhỏ nhất của modul z là
2
, giá trị lớn nhất của modul z là
21
.
Câu 138. Tìm tập hợp các điểm biểu diễn số phức z trên mặt phẳng tọa độ sao cho
có hình dạng như thế nào?
A.Một phần hình tròn
B. Một phần hypebol
C.
Một phần đường thẳng
D. Một phần đường tròn
Câu 139. Tìm tập hợp các điểm biểu diễn số phức
w1iz
trên mặt phẳng tọa độ sao cho :
3
2 1 8zi
A. Đường tròn tâm
1,1I
bán kính 2
B. Đường tròn tâm
1,1I
bán kính 2
C.
Đường tròn tâm
1,1I
bán kính 4
D. Đường tròn tâm
1,1I
bán kính 4
Câu 140. Cho số phức
\z
thỏa mãn
2
2
1
1
zz
zz


là số thực. Tìm modul của z.
A.
B.
2z
C.
2z
D.
3z
1z i i z
1z
Tài liệu ôn tập giải tích 12 học kỳ II
Trần Thông sưu tầm và biên soạn Facebook: Hội Toán Bắc Nam
| 1/80
| | Tải xuống

Có thể bạn quan tâm:

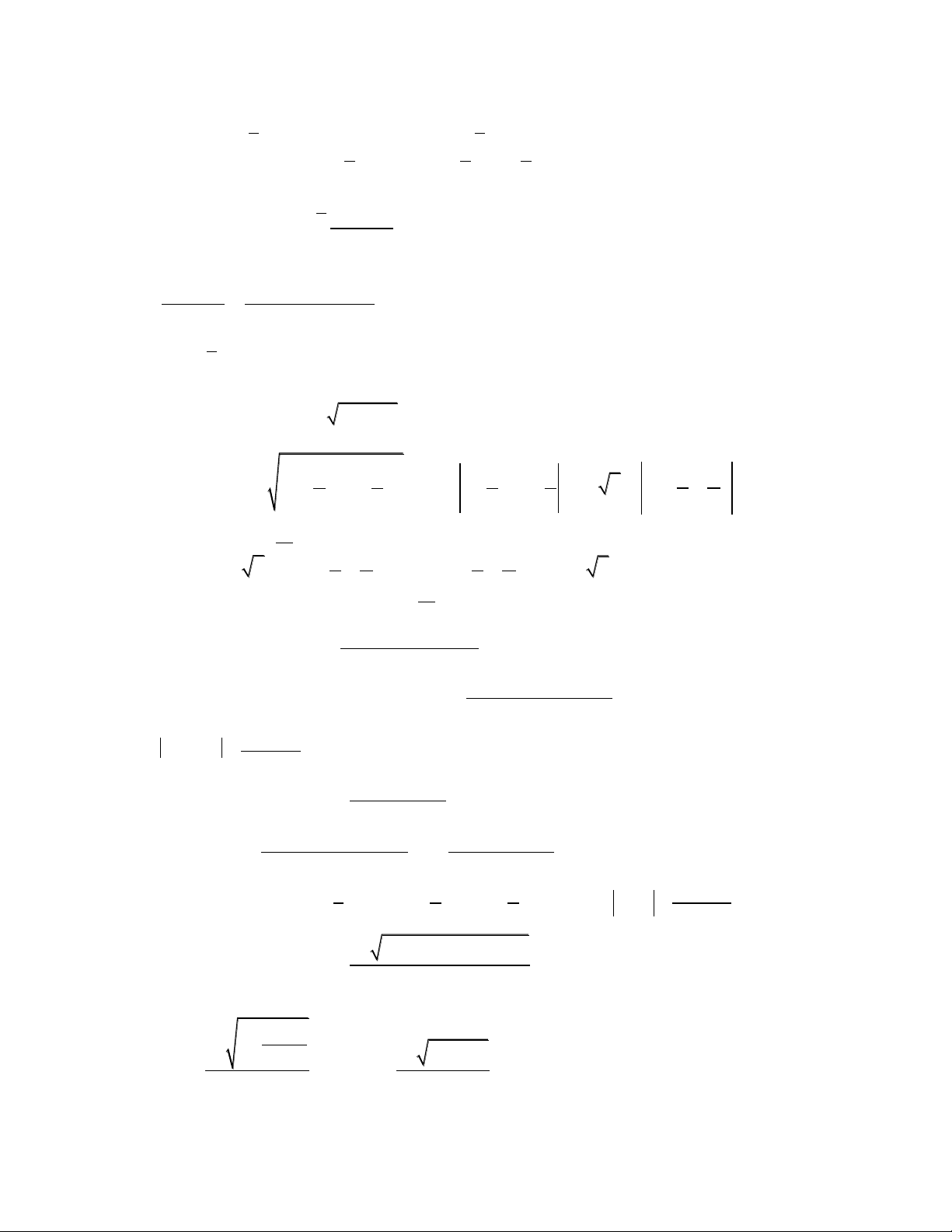
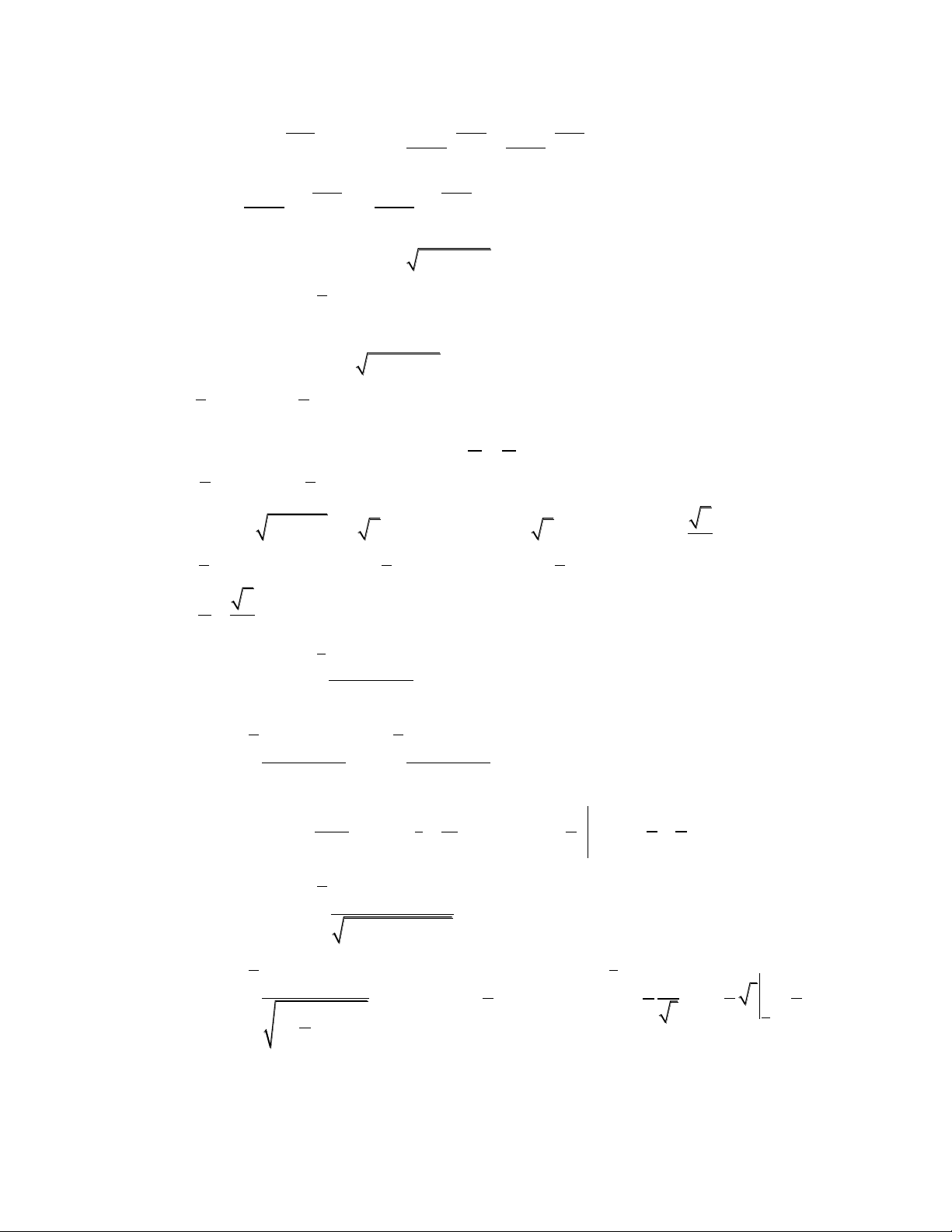
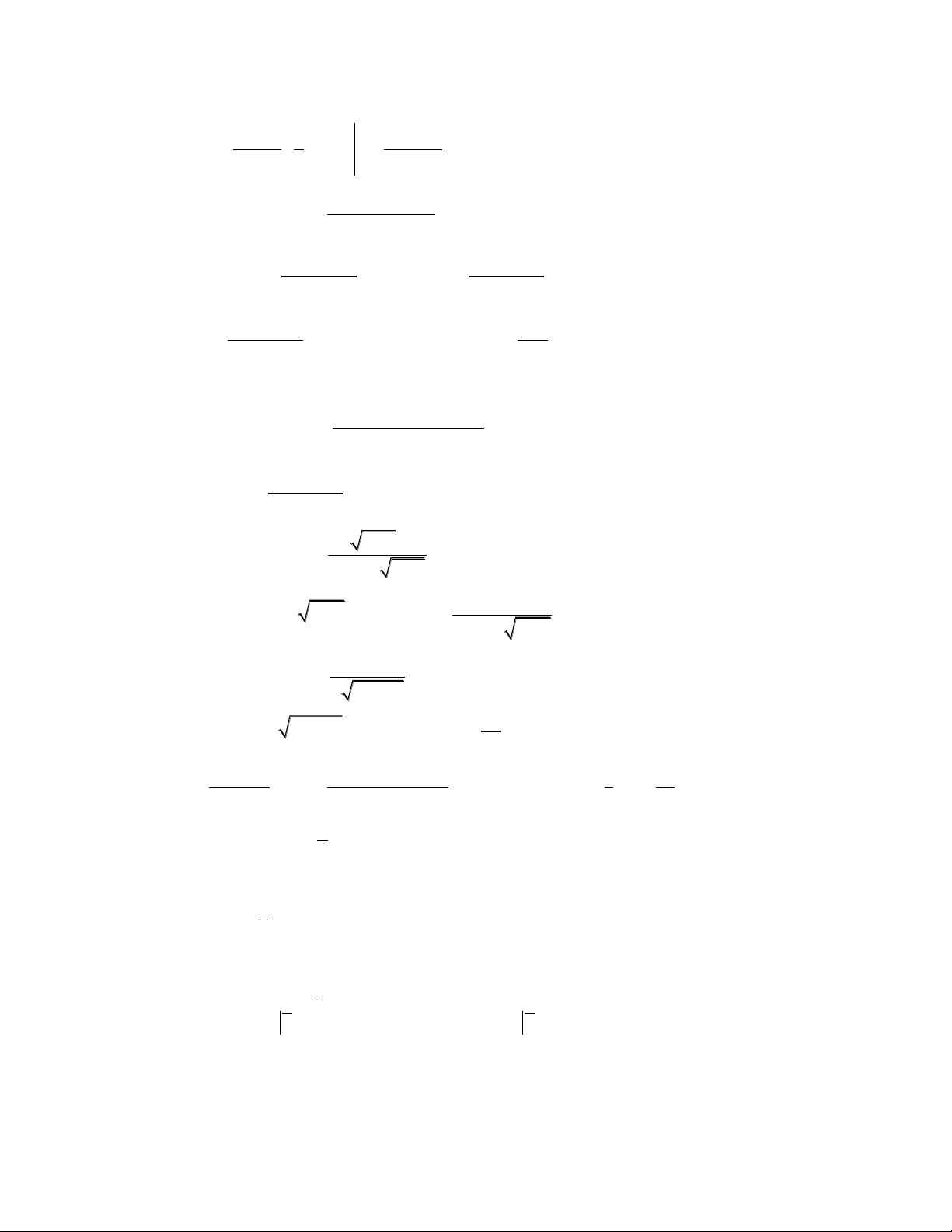
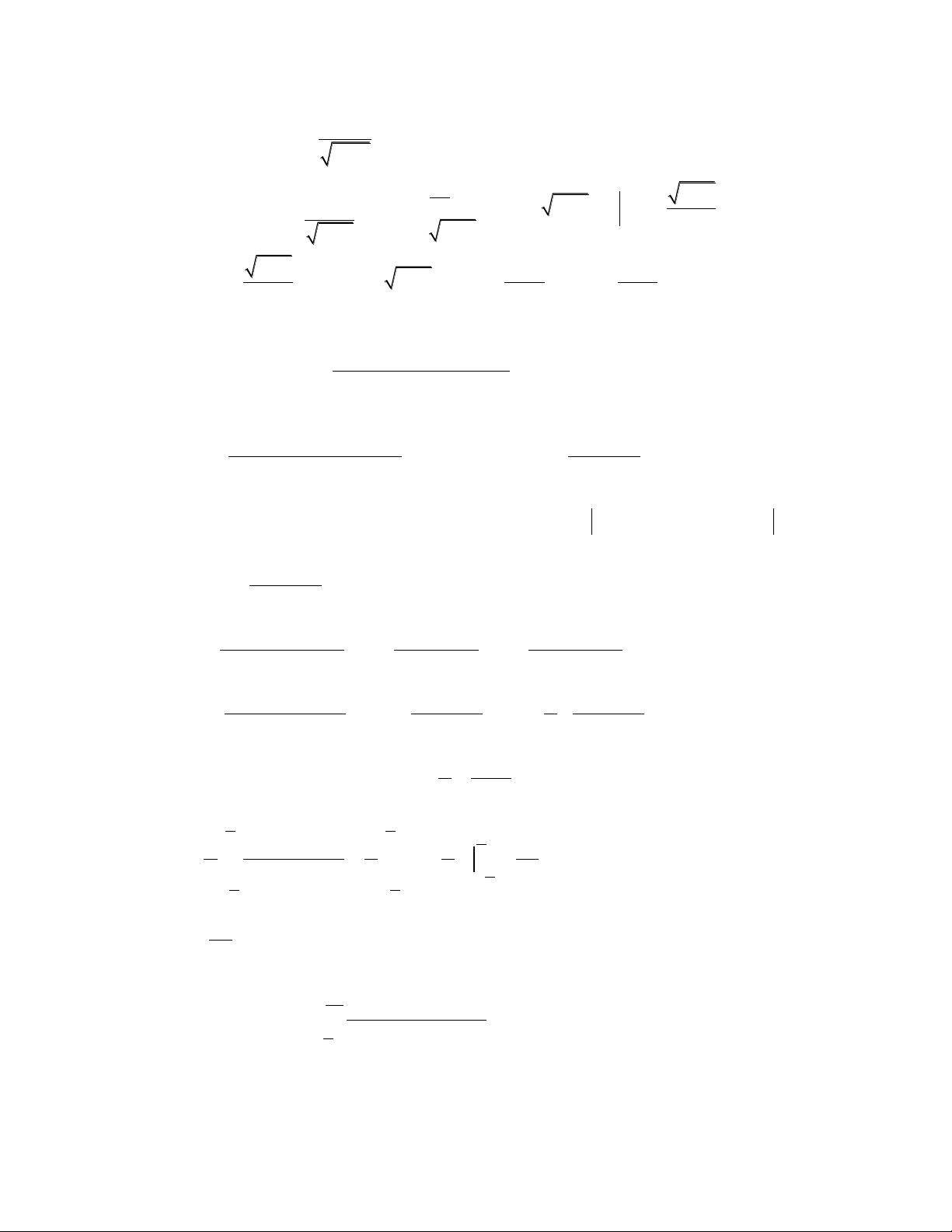
Preview text:

Tài liệu ôn tập giải tích 12 học kỳ II
TÀI LIỆU ÔN TẬP HỌC KỲ II
LỚP 12- NĂM HỌC 2016-2017
MÔN: GIẢI TÍCH
Quảng Nam, tháng 2 năm 2017
Trần Thông sưu tầm và biên soạn
Facebook: Hội Toán Bắc Nam
Tài liệu ôn tập giải tích 12 học kỳ II A. TÍCH PHÂN
PHẦN 1: TÓM TẮT LÝ THUYẾT I.Nguyên hàm
1.Định nghĩa. Cho hàm số f (x) xác định trên K (K là đoạn, khoảng, nửa khoảng). Hàm số
F (x) được gọi là nguyên hàm của hàm số f (x) trên K, nếu F '(x)  f (x) , với mọi x K .
Định lý. Giả sử F(x) là một nguyên hàm của hàm số f (x) trên khoảng K. Khi đó
a. Với mỗi hằng số C, hàm số G(x)  F(x)  C cũng là một nguyên hàm của f (x) .
b. Ngược lại, nếu G(x) là một nguyên hàm của f (x) thì tồn tại hằng số C sao cho G(x) = F(x) + C.
c. Họ tất cả các nguyên hàm của f (x) là
f (x)dx F(x)  C
, trong đó F(x) là một
nguyên hàm của f (x) , C là hằng số bất kỳ.
d. Bảng các nguyên hàm cơ bản.
Nguyên hàm của một số hàm số thƣờng gặp
Nguyên hàm các hàm số sơ cấp thƣờng gặp
Nguyên hàm của hàm số hợp u u(x)
kdx kx C, k R
kdu ku C, k R  1   1 1  x dx .x    C (  1  )  1 u du .u    C (  1  )  1  1  dx du ln x C
( x  0 )  ln u C
( x  0 ) x u dx du 2 x C  2 u C x u x x
e dx e C u u
e du e C x a u a x a dx
C (0  a  1).  u a du
C (0  a  1).  ln a ln a
cos xdx  sin x C
cos udu  sin u C
sin xdx   cos x C
sin udu   cos u C dxdx du du tan x C;
 cot x C.  tan u C;
 cot u C 2 cos x 2 sin x 2 cos u 2 sin u
Trần Thông sưu tầm và biên soạn
Facebook: Hội Toán Bắc Nam
Tài liệu ôn tập giải tích 12 học kỳ II
Ngoài ra còn một số công thức thƣờng gặp là. k 1  b k 1 (ax ) 1 1
(ax  b) dx
C ,(a  0, k  1  ); dx
ln ax  b C, a  0.   a k 1 ax  b a axb 1 axb 1 e dx eC ; o c (
s ax  b)dx
sin(ax  b)  C   a a 1
sin(ax  b)dx   o c (
s ax  b)  Ca
2. Một số tính chất của nguyên hàm
Định lý. Nếu F(x),G(x) tương ứng là một nguyên hàm của f (x), g(x) thì a.
f '(x)dx f (x)  C
b. [ f (x)  g(x)]dx
f (x)dx g(x)dx F(x)  G(x)  C    ;
c. a.f(x)dx  a f (x)dx  a (
F x)  C (a  0)   .
3. Một số phƣơng pháp đổi nguyên hàm
a. Phƣơng pháp đổi biến số
Cơ sở của phương pháp đổi biến số là định lý sau: Cho hàm số u u(x) có đạo hàm
liên tục trên K và hàm số y f (u) liên tục sao cho f [u(x)] xác định trên K. Khi đó
nếu F là một nguyên hàm của f, tức là
f (u)du F (u)  C  thì
f [u(x)]dx=F[u(x)]+C  .
b. Phƣơng pháp tích phân từng phần
Một số dạng thƣờng gặp: Dạng 1. ax ( ). b P x e dx , P(x)sin(ax  )
b dx , P(x) cos(ax  ) b dx    Cách giải: Đặt ax  ( ), b u P x dv e
dx (dv  sin(ax  ) b d ,
x dv  cos(ax  ) b dx)
Dạng 2. P(x)ln(ax  ) b dx
Cách giải: Đặt u  ln(ax  ) b , dv  ( P x)d . x II. Tích phân
1.Định nghĩa Cho hàm f (x) liên tục trên khoảng K và a, b là hai số bất kỳ thuộc K. Nếu F(x)
là một nguyên hàm của f (x) thì hiệu số F( )
b F(a) được gọi là tích phân của f (x) từ a đến b b b
và ký hiệu là f (x)dx
. Trong trường hợp a b thì f (x)dx
là tích phân của f trên  ; a b . a a
2.Tính chất Cho các hàm số f (x), g(x) liên tục trên K và a, ,
b c là ba số thuộc K.
Trần Thông sưu tầm và biên soạn
Facebook: Hội Toán Bắc Nam
Tài liệu ôn tập giải tích 12 học kỳ II a b a
f (x)dx  0
f (x)dx   f (x)dx    a a b b c b b b
f (x)dx f (x)dx f (x)dx
k. f (x)dx k f (x)dx      a a c a a b b b
 [ f (x)  g(x)]dx f (x)dx g(x)dx    a a a
3.Một số phƣơng pháp tính tích phân b u (b)
Phƣơng pháp đổi biến số: Công thức đổi biến số f [u(x)]u '(x)dx f (u)du   . Trong a u (a)
đó f (x) là hàm số liên tục và u(x) có đạo hàm liên tục trên khoảng J sao cho hàm hợp
f [u(x)] xác định trên J; ,
a b J .
Phƣơng pháp đổi biến số thƣờng áp dụng theo hai cách
Cách 1. Đặt ẩn phụ u u(x) ( u là một hàm của x)
Cách 2. Đặt ẩn phụ x x(t) ( x là một hàm số của t).
Đối với nguyên hàm nói chung và tích phân nói riêng cần chú ý một số dấu hiệu dẫn tới việc
lựa chọn ẩn phụ như sau: Dấu hiệu Có thể chọn Hàm số có mẫu Đặt t là mẫu Hàm f ( , x (x))
Đặt t  (x)
Hàm ( , n ( ), m f x x (x)) Đặt mn t  (x)
asin x b cos x x Hàm f (x)  Đặt t  tan
c sin x d cos x e 2 Hàm lẻ với sinx
Đặt t  cos x Hàm lẻ với cosx Đặt t  sin x
Hàm chẵn với sinx và cosx t =tanx 2 2    a x x |
a | sin t,  t   2 2  x |  a | os
c t, 0  t  
Trần Thông sưu tầm và biên soạn
Facebook: Hội Toán Bắc Nam
Tài liệu ôn tập giải tích 12 học kỳ II 2 2 x a    | a | x  , 
t  ;t  0  sin t 2 2  | a |  x
, 0  t   ;t   os c t 2 2 2    x a x |
a | tan t,  t   2 2  x |  a | ot
c t, 0  t   a x
Đặt x a cos 2t hoặc a x a x a x
(x a)(b x) Đặt 2
x a  (b a)sin t
Phƣơng pháp tích phân từng phần.
Định lý. Nếu u(x),v(x) là hai hàm số có đạo hàm liên tục trên khoảng K và a,b là hai số b b
thuộc K thì u(x)v '(x)dx u(x)v(x) b v(x)u '(x)dx   a a a
4. Ứng dụng của tích phân
Tính diện tích hình phẳng
Nếu hàm số y f (x) liên tục trên  ;
a b thì diện tích S của hình phẳng giới hạn bởi đồ b
thị hàm số y f (x) , trục hoành và hai đường thẳng x  ,
a x b là S f (x) dx  . a
Diện tích hình phẳng giới hạn bởi các đồ thị hàm số y f (x) , y g(x) và hai đường b thẳng x  ,
a x b là S
f (x)  g(x) dxa
Để tính diện tích S ta phải tính tích phân (1) , muốn vậy ta phải “phá” dấu giá trị tuyệt đối . b b
 Nếu f (x)  , 0 x   b ; a
 thì S   f (x)dx   f (x)dx a a b b
 Nếu f (x)  , 0 x   b ; a
 thì S f (x)dx   f (x)   dx a a
Chú ý Muốn “phá” dấu giá trị tuyệt đối ta phải xét dấu của biểu thức f(x) . Thường có hai cách làm như sau :
-Cách 1: Dùng định lí “dấu của nhị thức bật nhất” , định lí “dấu của tam thức bậc hai” để xét
dấu các biểu thức f(x) ; đôi khi phải giải các bất phương trình f(x) ≥ 0 , f(x) ≤ 0 trên đoạn  b ; a
Trần Thông sưu tầm và biên soạn
Facebook: Hội Toán Bắc Nam
Tài liệu ôn tập giải tích 12 học kỳ II
-Cách 2: Dựa vào đồ thị của hàm số y =f(x) trên đoạn  b ; a
 để suy ra dấu của f(x) trên đoạn đó .
Nếu trên đoạn [a ; b] đồ thị hàm số y = f(x) nằm phía “trên” trục hoành thì f (x)  , 0 x   b ; a 
Nếu trên đoạn [a ; b] đồ thị hàm số y = f(x) nằm phía “dưới” trục hoành thì f (x)  , 0 x   b ; a  b b
-Cách 3 Nếu f(x) không đổi dấu trên [a ; b] thì ta có : S   f (x) dx   f (x)dx a a
Tính thể tích vật thể. Thể tích vật thể B giới hạn bởi hai mặt phẳng vuông góc với trục b
Ox tại các điểm a,b là V S(x)dx
. Trong đó S(x) là diện tích thiết diện của vật thể bị a
cắt bởi mặt phẳng vuông góc với trục Ox tại điểm có hoành độ là x  ; a b và S(x) là
một hàm liên tục.
Tính thể tích khối tròn xoay.
 Hàm số y f (x) liên tục và không âm trên  ;
a b . Hình phẳng giới hạn bởi đồ thị hàm
số y f (x) , trục hoành và hai đường thẳng x  ,
a x b quay quanh trục hoành tạo nên b
một khối tròn xoay. Thể tích V được tính bởi công thức 2 V   f (x)dx  . a
 Hình phẳng giới hạn bởi đồ thị hàm số x g(y) , trục tung và hai đường thẳng y  ,
c y d quay quanh trục tung tạo nên một khối tròn xoay. Thể tích V được tính bởi d công thức 2
V   g ( y)dy  . c
PHẦN 2: BÀI TẬP MINH HỌA
Dạng 1: Tích phân hàm hữu tỷ 2 x2
Bài 1: Tính tích phân I dxx2 1  7x 12 2  16 9  2
Hƣớng dẫn: I  1  d
x =  x 16ln x  4  9ln x 3  = 1 25ln2 16ln3.  x  4 x  3 1 1  2 dx
Bài 2: Tính tích phân I   x5  x3 1 1 1 1 x
Hƣớng dẫn: Ta có:     x3(x2 1) x x3 x2 1  1 1 2  2 3 1 3
I  ln x   ln(x 1)   ln2  ln5     2x2 2  1 2 2 8
Trần Thông sưu tầm và biên soạn
Facebook: Hội Toán Bắc Nam
Tài liệu ôn tập giải tích 12 học kỳ II 1 xdx
Bài 3: Tính tích phân I  0  x 3 ( 1) Hƣớng dẫn: x x 11 2  3  1 2  3  1 Ta có:
 (x 1)  (x 1) I  (x 1) (x 1) d        x  (x 3 1) (x 3 1) 0 8 (x 2 1)
Bài 4: Tính nguyên hàm I dx  (2x 4 1) x 2 1 1 x 1       x 3 1 1 
Hƣớng dẫn: Ta có: f (x)  . . I   C 3     .  2x 1    2x 1    9  2x 1 1 x7
Bài 5: Tính tích phân I dx   x2 5 0 (1 ) 2 1 t 3 ( 1) 1 1 Hƣớng dẫn: 2
Đặt t  1 x dt  2xdx I dt  . 2  t5 5 4 1 2 1 5 3 6
Bài 6: Tính tích phân I x (1  x ) dx  0   3 2 dt 1 1 6 1 t7 t8 1
Hƣớng dẫn: Đặt t  1 x dt  3
x dx dx   I t (1 t d ) t       . 3x2 3 3  7 8  168 0 1 5 3 6
Bài 7: Tính tích phân I x (1  x ) dx  0   3 2 dt 1 1 6 1 t7 t8 1
Hƣớng dẫn: Đặt t  1 x dt  3
x dx dx   I t (1 t d ) t       . 3x2 3 3  7 8  168 0 2 x2001
Bài 8: Tính tích phân I d . x  (1 x2 1002 1 ) 1 1 x2000.2xdx Hƣớng dẫn: 2 Ta có: I  1   2 2  . Đặt t x dt xdx (1 x2 2000 ) (1 x2 2 0 ) 2 1 t 1000 2 1000 ( 1) 1  1  1 1 I dt  1 d 1  2      t1000t2 2  t   t 1001 1 1  2002.2 1 5 2 x2 1
Bài 9: Tính tích phân I dxx4  x2 1 1
Trần Thông sưu tầm và biên soạn
Facebook: Hội Toán Bắc Nam
Tài liệu ôn tập giải tích 12 học kỳ II 1 1 x2 1 2 1  1  Hƣớng dẫn: x Ta có:
. Đặt t x   dt  1 dx  
x4  x2 1 x2 1  1 xx2  x2  1 dt du 4  I  
. Đặt t  tan u dt I du   t2 2 4 0 1 cos u 0
Dạng 2: Tích phân hàm vô tỷ x
Bài 1: Tính nguyên hàm I dx x x2 3 9 1 x Hƣớng dẫn: 2 2 2 Ta có I
dx x(3x  9x 1 d
) x  3x dx x 9x d 1 x     3x  9x2 1 2 3
Lại có I  3x dx x C 1  1 3 2 1 2 2 1 2 I x x dx 2 2 9 1  
9x 1d(9x 1)  (9x 1)  C  2 18 27 3 1 2 2 3 I
(9x 1)  x C 27 x2  x
Bài 2: Tính nguyên hàm I dx 1 x x x2  x x2 x
Hƣớng dẫn: Ta có  dx dx dx   . 1 x x 1 x x 1 x x x2 Lại có I dx 1  . 1 x x 4 Đặt 2 3 2 2 2 2
t= 1 x x t 1  x x x t
( 1) x dx t t ( 1 d ) t 3 4 3 2 4 3 4 4  1 x x  4 t ( 1 d
) t t t C   1 x x C 3 9 3 = 1 9 3 x 2 d(1 x x) 4 Đối với I dx 2  = =
1 x x C2 1 x x 3 1 x x 3 3 4
Vậy: I   1 x x   C 9 3 x  3
Bài 3: Tính tích phân I dx
0 3 x  1  x  3
Trần Thông sưu tầm và biên soạn
Facebook: Hội Toán Bắc Nam
Tài liệu ôn tập giải tích 12 học kỳ II Hƣớng dẫn: 2 t3 2  t 2 2 8 1 Đặt t x 1  t
2 du dx I dt  ( t 2  6 d ) t  6 dt    3  3   6ln t2  3  2 1 2 1 t t 1 1 3 2x2  x 1
Bài 4: Tính tích phân I dx 0 x 1
Hƣớng dẫn: Đặt x   t x t2 1
1 dx t 2 dt 2 2 2 t2 2 ( 1) t2 2 ( 1) 1  t5      4 2 4 3 54 I t 2 dt  2 ( t 2  t 3 d ) t    t 2    t   5  5 1 1 1 5 x2 1
Bài 5: Tính tích phân I dx 1 x 3x  1 tdt
Hƣớng dẫn: Đặt t x   dx 2 3 1  3 2  t2 1    1 4  3  4 4 2  1 3  t    2tdt 1 100 9 I  .  t t  ln   ln .   t2 1 3 9  3  t 1 27 5 2 t. 2 2 3 5 x2 1
Bài 5: Tính tích phân I dx 1 x 3x  1 tdt
Hƣớng dẫn: Đặt t x   dx 2 3 1  3 2  t2 1    1 4  3  4 4 2  1 3  t 1 100 9    2tdt I  .  t t  ln   ln .   t2 1 3 9  3  t 1 27 5 2 t. 2 2 3 1 3 2
Bài 6: Tính tích phân I  (x 1) 2x x dx 0 1 1 Hƣớng dẫn: 3 2 2 2 I  (x 1)
2x x dx  (x  2x 1) 2x x (x 1 d ) x   . Đặt t x x2 2 0 0  I 2  15.
2 2x3 3x2  x
Bài 7: Tính tích phân I dx x2 0  x 1
Trần Thông sưu tầm và biên soạn
Facebook: Hội Toán Bắc Nam
Tài liệu ôn tập giải tích 12 học kỳ II Hƣớng dẫn:
1 1 x  1 x2
1 1 x  1 x2 1 1 1  1  1 x2 Ta có I dx dx    1 dx dx 2   x     2x  (1 )  (1 ) 2 1 x 2 x2 x 1  1  1  1 1  1  1 1 + I
1 dx  ln x x 1 |  1 2   x    1  2  1  1 1 x2 2 2 2 2 2 t dt + I dx 2   1  1  2  2   0 2x . Đặt t x t x tdt xdx I2=  2 1  2(t 2 1) Vậy: I  1. 2 4  x2
Bài 8: Tính tích phân I dxx 1 2 4  x2 Hƣớng dẫn: 2 2 2 Ta có Ta có: I xdx
. Đặt t = 4  x t  4  x tdt  xdx x2 1 0 0 t( tdt 0 ) t2 0 4  t  2   2 3   I = dt  (1 d ) t     t  ln  =  3  ln  . 4  t2 t2  4 t2  4 t  2  2  3  3 3 3   3   3 x2
Bài 9: Tính tích phân I dx   x 2   x 2 0 (1 1 ) (2 1 ) 4  42 36  4
Hƣớng dẫn: Đặt 2  1 x t I t 2 16   dt  1  2  42ln  t t2  3 3 1 dx
Bài 10: Tính tích phân I   x3 3  x3 0 (1 ). 1 3 t 3 2 2 2 dt Hƣớng dẫn: 3 3
Đặt t  1 x I dt   2  2 1 t t 1 4 3 3  t2 t3 3 .( 1) .( 1) 2 1    3 3 2 1 dt 3 2 dt 3 2    t3     dt  2  2  t4 1 1 1   1 3  1 3 t2.t3 1 t4 1       t3   t3 
Trần Thông sưu tầm và biên soạn
Facebook: Hội Toán Bắc Nam
Tài liệu ôn tập giải tích 12 học kỳ II 1 1 2 1 1  1  2  1 dt 3 2 u 2 3 2 1  1  u 1 2 3  1 Đặt u  1  du I du u 3du       u3  t3 t4 3 3 3 3 1 0 0   2   0  3  0 2 2 x4
Bài 11: Tính tích phân I dx x 1   x2 3 1  x   
Hƣớng dẫn: Đặt t x2 1 3 t2 2 ( 1) 3 t4 t2 3 3 2 1     2 1 19 2 4  2 I dt  = dt t dt dt   ln     t2 2 2  2  2 3 4   2  2 2 t 2 2 t 4  2   27 x  2
Bài 12: Tính tích phân I dx x 3  x2 1 Hƣớng dẫn: 3 t3 3  2  2 t 2 1     Đặt t 6
x I  5 dt  5 1   dt   2 5    5 3 1 ln   t t2 ( 1)  t t2 1 t2  3  12 1 1 1 2 5 2 2
Bài 13: Tính tích phân I
(x x ) 4  x dx 2  2 2 2 Hƣớng dẫn: 5 2 2 5 2 2 2 I =
(x x ) 4  x dx = x 4  x dx + x 4  x dx = A + B. 2  2  2  2 5 2 + Tính A = x 4  x dx
. Đặt t  x . Tính được: A = 0. 2  2 2 2 + Tính B = x 4  x dx
. Đặt x  2sint . Tính được: B = 2 . 2 
Vậy: I  2 .
2 3 4  x2 dx
Bài 14: Tính tích phân I   2x4 1 2 2 3 4  x2
Hƣớng dẫn: I dx dx   . 2x4 2x4 1 1 2 3 2 3 4  7 + Tính I1 = dx= x dx   . 2x4 2 16 1 1 2 4  x2 + Tính I dx  2sin   2cos 2  . Đặt x t dx tdt . 2x4 1
Trần Thông sưu tầm và biên soạn
Facebook: Hội Toán Bắc Nam
Tài liệu ôn tập giải tích 12 học kỳ II    2 2 1 cos tdt 2 2 1 2  1  1 2 3 I   cot t dt   cot t d . (cot t 2 )   4 8      sin t 2 8   sin t  8 8  6 6 6 Vậy: I 1  72 3 16 3 2
Bài 15: Tính tích phân I x d 1 x 2  x  2 du dx Hƣớng dẫn: u x 1 Đặt    x2 dv dx 1 v x 3 3 x 3   2 2 1
I x x 1  x. dx  5 2   x 1   dx   2 x2 1  x2 2 2 1 3 3 2 dx  5 2  x d 1 x   
 5 2  I  ln x x2 3 1 x2 2 2 2 1 I 5 2   ln 2   1 1  ln2 2 4
Dạng 3: Tích phân hàm lƣợng giác 2
8cos x  sin2x  3
Bài 1: Tính nguyên hàm I dx  sinx cosx Hƣớng dẫn: x x 2 (sin cos )  4cos2x I dx   
sinx cosx 4(sinx  cosxd
x  3cos 5sin  sin x cos x   x x C .
cot x  tan x  2tan2x
Bài 2: Tính nguyên hàm I dx  sin 4x
2cot 2x  2tan2x 2cot 4x cos4x 1
Hƣớng dẫn: I dx dx  2 dx    C  sin4x  sin4x  2 sin 4x 2sin4x 2 cos  x     8   
Bài 3: Tính nguyên hàm I dx
sin2x  cos2x  2 Hƣớng dẫn: 1 cos2x      I 1  4   dx
2 2 1 sin2x     4   
Trần Thông sưu tầm và biên soạn
Facebook: Hội Toán Bắc Nam
Tài liệu ôn tập giải tích 12 học kỳ II    cos2x    1   4    dx dx     2 2 2 
 1 sin2x             sin x
   cos x   4     8   8          cos2x  1  4  1 dx      dx     2 2     2 1 sin  2x 2 
sin  x 3        4   8     1      3  
 ln 1 sin2x    cot x    C 4 2   4   8      dx
Bài 4: Tính tích phân I  
 2  3 sin x  cos x 3 1  dx 1  dx 1
Hƣớng dẫn: I I  2  = 4  = .  1 cos  2  x   4 3  x      2sin    3  3  3  2 6   6 1
Bài 5: Tính tích phân I dx 0 2sin x  3   1 6 6 1 1 Hƣớng dẫn: 2 I dx dx 2     0 sin x  sin 0 sin x  sin 3 3  
 x    x  cos       6 cos 6   2 6     2 6  3  dx dx    x    x  0 sin x  sin 0 2cos  .sin   3  2 6   2 6        x     x cos sin     6   6 1 2 6 1  2 6              dx dx  ln sin   ln cos   ..... 2   x x 6 6 x   2  x    0   0  2 6   2 6 0 0 sin  cos     2 6   2 6       2 4 4
Bài 6: Tính tích phân I
cos2x(sin x  cos x d ) x 0
Trần Thông sưu tầm và biên soạn
Facebook: Hội Toán Bắc Nam
Tài liệu ôn tập giải tích 12 học kỳ II   2 2  1  1  1  Hƣớng dẫn: 2 2 I
cos2x 1 sin 2x dx
1 sin 2x d(sin2x)  0     2   2  2  0 0   3 4sin x
Bài 7: Tính tích phân I 2  dx 0  1cosx Hƣớng dẫn: 3 4sin x 3
4sin x(1 cos x) Ta có
 4sin x  4sin x cos x  4sin x  2sin2x 1  cos x 2 sin x I 2 
(4sin x  2sin2x d ) x  2 0  2
Bài 8: Tính tích phân I  1 sin xdx 0 2 x x 2 2   x x 2  x  
Hƣớng dẫn: I   sin  cos  dx  sin  cos dx   2 sin    dx  2 2  2 2  2 4  0 0 0 3   2  x 2    x     2  sin    dx  sin 
   dx  4 2  2 4   2 4   0 3   2  sin2xdx
Bài 9: Tính nguyên hàm I   3 4sin x  cos2x 2sinxcosx Hƣớng dẫn: Ta có: I dx. Đặt t  sin x 2
2sin x  4sin x  2 I x 1 ln sin 1   C sin x 1 dx
Bài 10: Tính nguyên hàm I   3 x 5 sin .cos x Hƣớng dẫn: dx dx I    8 3 3 2 
sin x.cos x.cos x 3 sin 2x 2 .cos x  3   1 3 1
Đặt t  tan x 3 3 4 2
. I  t t
3   t dt  tan x  tan x  3ln tan x   C t 2  4 2 2tan x 2011 2011 sin x 2009  sin x
Bài 11: Tính nguyên hàm I  cot xdx  5 sin x Hƣớng dẫn: 1 20111 2 sin x 2011 2  cot x Ta có: I  cot xdx  cot xdx  4  sin x 4 sin x
Trần Thông sưu tầm và biên soạn
Facebook: Hội Toán Bắc Nam
Tài liệu ôn tập giải tích 12 học kỳ II 2 4024 8046 2011 2011
Đặt t  cot x 2011 2 I  t (1 t t)dt t 2011  t2011  C  4024 8046 4024 8046 2011 2011 = 2011 cot x 2011  cot x C 4024 8046  2
Bài 12: Tính tích phân I
sin x(2  1 cos2x)dx  2 Hƣớng dẫn:   2 2 Ta có: I
2sin xdx  sin x 1 cos2xdx H K     2 2   2   + H
2sin xdx  (1 cos2x d ) x       2 2   2 2    2 2 2 2 2 + K
sin x 2cos x   2 sin x cos xdx  
  2 sin xd(sin x)   3    2 2 2  I 2   2 3  2 sin 2x
Bài 13: Tính tích phân I    dx 2  sin x2 0   2 sin2x 2 sin x cos x
Hƣớng dẫn: I dx  2 dx   . (2  sin x 2 ) (2  sin x 2 0 0 ) 3 3 t 3  2 1 2   2  3 2
Đặt t  2  sin x . I  2 dt  2  dt  2 lnt        2ln  2 3 2 t2  t 2 t2   t  2  4 sin 4x
Bài 14: Tính tích phân I dx 6 sin x 6 0  cos x  1 4 sin 4x 3 4  2 1  1 4 2 Hƣớng dẫn: 2 I dx
. Đặt t  1 sin 2x   4  I = dt   3  = t 1 3 3 0 3 2 1 1  t  sin 2x  4 4
Trần Thông sưu tầm và biên soạn
Facebook: Hội Toán Bắc Nam
Tài liệu ôn tập giải tích 12 học kỳ II  4 sin x 2 1 cos x
Bài 15: Tính tích phân I dx  2  cos x  3 Hƣớng dẫn:    4 sin x 4 0 4 2 sin x I sin x sin x  1 cos x d . x  sin x dx   sin x dx  sin x dx 2   2  2  cos x 2  cos x  cos x 0  cos x    3 3 3  0 2 sin x 4 2 sin x 7 = dx dx    3 1 2  12  cos x 2 0 cos x  3 
2 3sin x  2cos x
Bài 16: Tính tích phân I dx
(sin x  cos x 3 0 ) Hƣớng dẫn:   
2 3cost  2sint
2 3cos x  2sin x Đặt x
t dx  dt I dt dx 2   (cost  sint 3 )
(cos x  sin x 3 0 0 )   
2 3sin x  2cos x
2 3cos x  2sin x 2 1
2I I I dx dx dx  1    I 1 
(sin x  cos x 3 )
(cos x  sin x 3 )
(sin x  cos x 2 2 0 0 0 )  x sin x
Bài 17: Tính tích phân I dx  2 0 1 cos x Hƣớng dẫn:  (  t)sint   sint
Đặt x    t dx  dt I dt   dt I  2  1 cos t 2 0 0 1 cos t  sintd(cost 2 )    2I dt                I  2 1 cos t 2 1 cos  4 4  8 0 0 t  3 sin x
Bài 18: Tính tích phân I dx cos x 2 0 3  sin x Hƣớng dẫn: sin x cos x Đặt t 2  3  sin x 2 2 2
= 4  cos x . Ta có: cos x  4  t và dt dx . 2 3  sin x
Trần Thông sưu tầm và biên soạn
Facebook: Hội Toán Bắc Nam
Tài liệu ôn tập giải tích 12 học kỳ II   15 15 3 sin x 3 sin x.cos x 2 dt 2 1  1 1  I = dx .  = dx= =    dt cos x 2 2 4
t  2 t  2 0 3  sin x 2 cos x 2 0 3  sin x t  3 4  3 15 1 t  2 2 1  15 4 3 2   
1 ln 15 4ln 3 2 = ln  ln  ln  4 t = =  2 4   2 3 15  4 3  2    4 tan x
Bài 19: Tính tích phân I dx  cos x 2 1 cos x 6 Hƣớng dẫn:   4 tan x 4 tan x Ta có: I dx dx   2  1  cos x 2 2 tan x x  2 cos 1 6 2 cos x 6 1 1 u 2 u
Đặt u  tan x du dx I dx
t u  2  dt du 2 . Đặt . cos x u2 1  2 u2  2 3 3 3 7 3  7 I dt t  3   .  7 7 3 3 3 3  3 xsin x
Bài 20: Tính tích phân I dx  2   cos x 3
Hƣớng dẫn: Sử dụng công thức tích phân từng phần ta có:     3  1  x 3 3 dx 4 3 dx I xd     J,   J  cos x   với   cos x  cos x 3 cos x      3   3 3 3  3 3 3 dx 2 dt 1 t 1 2 2  3
Để tính J ta đặt t  sin x. Khi đó J     ln   ln  cosx  1 t2 2 t 1 3 3 2  3    2 3 2   Vậy I 4 2 3   ln . 3 2  3
Trần Thông sưu tầm và biên soạn
Facebook: Hội Toán Bắc Nam
Tài liệu ôn tập giải tích 12 học kỳ II
2  1 sin x x
Bài 21: Tính tích phân I e . dx   1 cos x   0  x xx 1 2sin cos 1 sin 1 x Hƣớng dẫn: 2 2 Ta có:    tan 1 cos x 2 x 2 x 2 2cos 2cos 2 2   2 x e dx 2  x x I   e tan dx   = e 2 2 x 2 0 2 cos 0 2
Dạng 3: Tích phân hàm mũ logarit 2x e
Bài 1: Tính nguyên hàm I dx x 1 e Hƣớng dẫn: 2 Đặt x x x
t e e t e dx t 2 dt . t3 2 3 2 2 x x x x x I  2 dt     2  2ln 1 
e e e  2 e  2ln e 1  C 1 t t t t t C 3 3 2 x (x x e )
Bài 2: Tính nguyên hàm I dx x x e Hƣớng dẫn: 2 x (x x e x x I )
xe .(x 1 e )  dxx x = dx
I xe 1 ln xe 1  C .x. Đặt x t x e . 1 x e x xe 1 2 x
ln(1 x )  201 x 1
Bài 3: Tính nguyên hàm I dx  2 x ln  ex ( e 2 1 )    
x ln(x2 1) 2011   Hƣớng dẫn: I dx. Đặt t x2 ln( 1) 1
(x2 1)ln(x2 1) 1     1 t  2010 1 1 2 1 2 I dt  1005ln 
ln( 1)  1005ln(ln( 1) 1)  2  t t t C 2 = x x C 2 2 e x xe 1
Bài 4: Tính tích phân J dxx 1 x e (  ln x) e x e e d e (  ln x) e 1 Hƣớng dẫn: x J
 ln e  ln x  ln  x 1 e  ln x 1 e ln2 3x 2x e 2  e 1
Bài 5: Tính tích phân I dx  3x 2x x 0 ee e 1
Trần Thông sưu tầm và biên soạn
Facebook: Hội Toán Bắc Nam
Tài liệu ôn tập giải tích 12 học kỳ II ln2 3x 2x x 3x 2x x e 3  e 2  e e (
e e 1) ln2  3x 2x x e 3 e 2 e   
Hƣớng dẫn: I dx   1 dx  3x 2x x
=   3x 2x x  0
e e e 1 0
e e e 1   3x 2x x ln2 ln2 14 = ln e (
e – e 1)  x ln 0 0 = ln11 – ln4 = 4 3ln2 dx
Bài 6: Tính tích phân I   0  2 3 x e  2 x 3ln2 e3dx x x 1  
Hƣớng dẫn: I  
t e3  dt e3dx   x . Đặt I 3 3 1 ln   2 3 4  2 6 0  e  3 3 x e  2 ln15  2x x e e 24 dx
Bài 7: Tính tích phân I   x x x x 3ln2 e e 1  e 5  3 e 1 15 Hƣớng dẫn: 3 4sin x 3
4sin x(1 cos x) Ta có
 4sin x  4sin x cos x  4sin x  2sin2x 1  cos x 2 sin x I 2 
(4sin x  2sin2x d ) x  2 0  2
Bài 8: Tính tích phân I  1 sin xdx 0 Hƣớng dẫn: 2 x Đặt x x
t e 1  t 1  e e dx t 2 dt . 4 ( t2 2 1 t 0 d ) t 4  4 3 7 I   2   dt   t
2  3ln t  2  7ln t  2     t2  4  t  2 t  2 3 3 3 
 2 3ln2  7ln6  7ln5 ln 3 2 x e dx
Bài 9: Tính tích phân I   x x    ln 2 e 1 e 2 Hƣớng dẫn: 2x Đặt t = x
e  2 e dx t 2 dt 1 t2 (  t 2) dt 1  t 2 1  1 1 d t2 (  t 1) I = 2 = 2 t 1 dt 
= 2 (t 1)dt + 2 t2 2 2 0  t 1 0  t t 1 0 0 t t  1 1 2 1 2 = t (  t
2 ) 0 + 2ln t(  t 1)0 = 2ln31. ln3 3x 2x e 2  e
Bài 10: Tính tích phân I dx x x 0 e e 4  3 1 Hƣớng dẫn: Đặt 3x 2x 2 3x 2x 3x 2x t e 4  e 3  t e 4  e 3  t 2 dt  (1 e 2  e 6 d ) x 3x 2x tdt  ( e 2  e d ) x  3
Trần Thông sưu tầm và biên soạn
Facebook: Hội Toán Bắc Nam
Tài liệu ôn tập giải tích 12 học kỳ II 9 1 tdt 9 1 1 1 8  ln5 I   (1 d
) t  (  ln 1)  . 3  t t t 9 1 3 t 1 1 3 3 1 1 ln5 2x e
Bài 11: Tính tích phân I dx x ln2 e 1 2   2 t 2 dt 2 2 t3 20
Hƣớng dẫn: Đặt x x
t e 1  t e 1 dx   I  2 t ( 1 d
)  2  t   xe  3  3 1 1 2 xx 2  2
Bài 12: Tính tích phân I dxx x 1 4  4  2 Hƣớng dẫn: xx xx 2 1 81 Đặt x x t 2 2   4  4
 2  (2  2 )  4 I  ln 4 ln 2 25 1 6x dx
Bài 13: Tính tích phân I  
9x  3.6x  2.4x 0 x  3  dx 3 1  x  2    2 1 dt ln15  ln14 Hƣớng dẫn: I   t 3  I   2x x . Đăt .  2  2 ln3  ln2 ln3  ln2 0  3   3  1 t t 3  2 3    2  2   2      e ln x3 2 2  ln x
Bài 14: Tính tích phân I dxx 1 2ln x 3 1 3   3 4 3 4 3  2  Hướng dẫn 2 3
Đặt t  2  ln x dt dxx I tdt 2  8 2 e2 dx
Bài 15: Tính tích phân I   xln x.lnex e e2 e dx 2 d(ln x) e2  1 1 
Hƣớng dẫn: I     d(ln x) x ln x(1  = = 2ln2 – ln3  ln x) ln x(1 ln x) 
 ln x 1 ln x   e e ee 3 log x
Bài 16: Tính tích phân I 2  dx x 2 1 1 3ln x Hƣớng dẫn:  ln x 3  e 3 e   e log x 2  ln2  1 ln x. ln xdx I 2  dx dx  .   3  2 2 2 1 3ln 1 3ln ln 2 x 1 x x 1 x x 1 1 3ln x 2 2 1 2 dx 1
Đặt 1 3ln x t  ln x t ( 1)  ln x.  tdt 3 x 3 .
Trần Thông sưu tầm và biên soạn
Facebook: Hội Toán Bắc Nam
Tài liệu ôn tập giải tích 12 học kỳ II 2 1  1 3  4 Suy ra I t t  3   3 9ln 2  3 1 27ln 2
e x  (x  2)ln x
Bài 17: Tính tích phân I dxx(1  ln x) 1 e e ln x e ln x
Hƣớng dẫn: dx  2 dx   e 1 2 dx x(1 =  ln x) x(1 ln x) 1 1 1 e ln x 2 t 1 Tính J = dx
. Đặt t  1 ln x J dt  1 ln2 x(1 .  ln x) t 1 1
Vậy: I e  3 2ln2 .
e3 x 2 x x x2 2 ln ln  3
Bài 18: Tính tích phân I dx  (1  ln ) 2 x x e e3 e3 1 Hƣớng dẫ 3 2 n: I  3 dx  2 ln xdx   3  ln2  4  2 (1  e e  ln ) 2 x x e e2 5 ln( 1 1)
Bài 19: Tính tích phân   x I dx x 1 x 1 2 dx ln3
Hƣớng dẫn: Đặt t  ln x 1   2 2
1  2dt
I  2 dt  ln 3  ln 2  . x 1 x 1 ln2 3 e 3 ln x
Bài 20: Tính tích phân I dx x 1 ln x 1 2 dx Hƣớng dẫn: 3 2 3
Đặt t  1 ln x  1 ln x t   t 2 dt ln  ( 1) x và x t 2 t2 3 2 ( 1) t6  t4 3  t2 2 3 1 5 3 1 I dt =
dt t(  t 3  t 3  d ) t    tt  15 ln2 t 4 1 1 1  2 sinx
Bài 21: Tính tích phân I e .sin2xdx 0  2 u   sin x
du  cos xdx Hƣớng dẫn: sinx I  2 e .sin x cos xdx. Đặt  sin x   sin x dv e cos xdxv e 0   2  sin x 2 sin x sin x
I  2sin xee .cos xdx e 2  e 2 0 2  0  2 0
Trần Thông sưu tầm và biên soạn
Facebook: Hội Toán Bắc Nam
Tài liệu ôn tập giải tích 12 học kỳ II 1 2
Bài 22: Tính tích phân I x ln(x x  1 d ) x 0  2x du 1  dx 2   2     Hƣớng dẫn: u ln(x x 1) x x 1 Đặt   dv xdx   x2 v   2 1 x2 1 1 2x3  x2 2 I
ln(x x 1)  dx 2 2  x2 0 0  x 1 1 1 1 1 1 2x 1 1 3 dx   ln3  (2x 1 d ) x dx    2 2  4   3 3 ln3 x2  x 1 4 x2 4 12 0 0 0  x 1 8 ln x
Bài 23: Tính tích phân I dx 3 x  1 Hƣớng dẫn: u  ln xdx  du  8 8 1 Đặt dx   x
I  2 x 1.ln xx dv  2
dx  6ln8  4ln3  2J  3  xx 1
v  2 x 1 3 8 x 1 + Tính J dxx . 3 3 t 3 t2 3  1 1  Đặt t x 1  J t .2 dt  2 dt  2   dt     1 1  1 1 2 t2 2 t2 t t 2   t 1  8   t 2  ln   2  ln3  ln2 t 3 1  
Từ đó I  20ln2  6ln3  4 . 2 ln(x 1)
Bài 24: Tính tích phân I = dx x2 1  dx
u  ln(x 1) du  2   1 1 2 dx 3 Hƣớng dẫn: x Đặt dx  
I   ln(x dv 1)   3ln2  ln3  1 x 1  (x 1)x  2 v 2  x   1  x 1 2 1 x
Bài 25: Tính tích phân I x ln dx    1 x   0 
Trần Thông sưu tầm và biên soạn
Facebook: Hội Toán Bắc Nam
Tài liệu ôn tập giải tích 12 học kỳ II  2  1   1 x du dx 1 u  2   1   2 1 x 2   2  Hƣớng dẫn: ln (1 x) 2 Đặt  1 x   I  x ln  2  x dx     2   1 x 2    x2 dv xdx  0 1 x   v  0  2     1 1 2 ln3 x2 2 ln3  1  ln3 1 1 2   dx   1 dx    ln 8   1 8   ( 1)( 1)    8 2 2 3 0 x2 x x 0 e 2 x x 2
ln x e (e  ln x)
Bài 26: Tính tích phân I  .  dx 1 x e 1 e e 2x 2 e
Hƣớng dẫn: Ta có: I  ln x d . x
dx H K   x 1 1 e  1 e e 2 u 2  ln x + H  ln x d . x. Đặt:
H e  2 ln x d . x e  2  dv dx 1 1 e 2x e e e 1  x t 1 e e 1 + K dx
. Đặt t e 1  I
dt e e  ln x 2  e t 1 e  1 e 1  e 1 e 1 Vậy: e
I e –2  ln e e 1 4
Bài 27: Tính tích phân 2
I  ln( x  9  x)  dx 0  4 4 u   x2 ln  9  xHƣớng dẫn:
I x ln x2  9  xx Đặt   dx  2  dv dx x2 0 0  9
Dạng 4: Tích phân tổng hợp nhiều loại hàm số 1  4  2 x3 x
Bài 1: Tính tích phân I   x e  dx   0  1 x  1 1 4 3 Hƣớng dẫn: 2 x x I x e dx dx   . 0 0 1 x 1 1 2 x3 1 t 1 t 1 1 1
+ Tính I x e dx 1  . Đặt t x3  I
e dt e e 1  3  3 3 3 . 0 0 0 1 4 x 1 4 4 t  2   + Tính I dx 2 
. Đặt t x I  4 dt 2  4     2  1  3 4 0 1 x 0 t  1
Vậy: I e    3 3
Trần Thông sưu tầm và biên soạn
Facebook: Hội Toán Bắc Nam
Tài liệu ôn tập giải tích 12 học kỳ II 1 x I   2x
e . 4  x2  x2 
Bài 2: Tính tích phân dx.  4  x2 0 Hƣớng dẫn: 1 1 3 2x x I x e dx
dx I I   1 2 x2 0 0 4 1 2 2x e 1
+ Tính I x e dx 1   4 0 1 x3 16 + Tính I dx 2  . Đặt t   x2 4 I2  3  3  x2 3 0 4 e2 61 I   3 3  4 12 1 x2 1 x
Bài 3: Tính tích phân I e dx (x 2 0 1) Hƣớng dẫn: 2 t2  t 2 2  2  2    2 2  2 e
Đặt t x 1 dx dt t 1 t I e dt  1  e d 1 t    = e 1    e  1 e  2  1 t2 1  t2 t    x x e 2 3 3 1 .  dx
Bài 4: Tính tích phân I   1 x2 0 2 2 2 Hƣớng dẫn: 2 2 t 2 2
Đặt t  1 x dx tdt I t( 1 e ) dtt tt e dt eJ e (  e)  1 1 1 2 2  2  2 t 2 t 2 t 2 t 2 t 2 t t 2
+ J t e dt t et 2 e dt e
4  e  2te
e dt   e
4  e  2 t(e e )      1 1 1 1  1 1  Vậy: I e2 
x ln(x2 1)  x3
Bài 5: Tính tích phân I dx x2 1
x ln(x2 1) x(x2 1)  x x ln(x2 1) x
Hƣớng dẫn: Ta có: f (x)     x x2 1 x2 1 x2 1 x2 1 1 2 2 1 2
F(x)  f (x d ) x  ln(x 1 d
) (x 1)  xdx d ln(x 1)  2   2  1 2 2 1 2 1 2 =
ln (x 1)  x  ln(x 1)  C 4 2 2 .
Trần Thông sưu tầm và biên soạn
Facebook: Hội Toán Bắc Nam
Tài liệu ôn tập giải tích 12 học kỳ II
4 lnx x2  9 3x3
Bài 6: Tính tích phân I dx x2 0  9
4 lnx x2  9 3x3
4 lnx x2  9 4 x3
Hƣớng dẫn: I dx dx  3
dx I I    1 3 2 x2  9 x2  9 x2 0 0 0  9
4 lnx x2  9 2 1 + Tính I dx 1 
. Đặt ln x x  9   u du dx x2 0  9 x2  9 ln9 u2 2 2 ln9 ln 9  ln 3 I udu 1    2 ln3 2 ln3 4 x3 2 x 2 2 + Tính I dx 2 
. Đặt x  9  v dv
dx, x v 9  x2 0  9 x2  9 5 u3 2 5 44 I u (  9 d ) u  (  u 2 9 )   3 3 3 3
4 lnx x2  9 3x3 2 2 ln 9  ln 3 Vậy I
dx I I  1 3 2   44 x2 2 0  9
e (x3 1)ln x  2x2 1
Bài 7: Tính tích phân I dx  2  x ln x 1 Hƣớng dẫn: e e e e 3 3 2 1 ln x I 2 x e 1  x dx dx   x dx  
2  x ln x . +  3 3 1 1 1 1 e e 1 ln x
d(2  x ln x) e e  2 e3 1 e  2 + dx
 ln 2  x ln x   ln I   ln 2   x ln x 2  x ln x 1 2 . Vậy: 3 2 1 1 4 3 ln(5  )  . 5 
Bài 8: Tính tích phân   x x x I dx 2 x 1 4 4  Hƣớng dẫn: ln(5 x) Ta có: I
dx x 5  x.dx K    H . 2 x 1 1 4 ln(5
u  ln(5  xx) )  + K dx. Đặt dx K 3  ln 4 x2 dv  5 1  x2 4
+ H= x 5  x d . x
. Đặt t  5  x H 164  15 1 Vậy: I 3 164  ln 4  5 15
Trần Thông sưu tầm và biên soạn
Facebook: Hội Toán Bắc Nam
Tài liệu ôn tập giải tích 12 học kỳ II 8 ln x
Bài 9: Tính tích phân I   dx 3 x 1 u  ln xdx  du  8 8 x 1
Hƣớng dẫn: Đặt dx   x dv
I 2 x 1ln x 2      dx    3 xx 1
v  2 x 1 3 8 x 1 3 t2 2 dt 3  1  + Tính J dx
. Đặt t x 1 J   2 1
dt  2  ln3  ln2 x  2  2  3 2 t 1 2  t 1
I  6ln8 4ln3 2(2  ln3 ln2) 20ln2  6ln3 4 x 3
(cos x  cos x  sin x)
Bài 10: Tính tích phân I dx  2 0 1 cos x Hƣớng dẫn:  cos x 2 (1 cos x) sin x       x.sin x
Ta có: I x
dx x.cos x d . x
dx J K   2   1 cos x  2 0   0 0 1 cos x  u x   
+ Tính J x.cos x d . x. Đặt
J  (x.sin x)  sin x d
. x  0  cos x  2  
dv  cos xdx 0 0 0 0  x.sin x + Tính K dx        2 . Đặt x t dx dt 0 1 cos x
 (  t).sin(  t)
 (  t).sint    
(  x).sin x K dt dt dx  2   1 cos (  t 2 ) 1 cos t 2 0 0 0 1 cos x
 (x   x).sin x  sin x d.x    sin x d . x  2K dx    K   2   1 cos x 2 1 cos x 2 2 0 0 0 1 cos x 1  dt 2
Đặt t  cos x dt  sin x d . x K   tan   (1 tan ) 2  , đặt t u dt u du  1 t2 1   4 2  (1 tan u d ) u 4  2    K   du  .u 4   2 2   1 tan u 2 2   4    4 4 4 2  Vậy I   2 4
2 x (x sin x)sin x
Bài 11: Tính tích phân I 3  dx   (1 sin x 2 )sin x 3
Trần Thông sưu tầm và biên soạn
Facebook: Hội Toán Bắc Nam
Tài liệu ôn tập giải tích 12 học kỳ II
2 x(1sin x)sin x 2 x 2 2  dx
Hƣớng dẫn: I 3  dx 3  dx 3   H K     (1 sin x 2 )sin x  2 sin x  1 sin x 3 3 3 2 u x x  du dx + H 3  dxdx      2 . Đặt H sin x dv  
v  cot x 3 3 2  sin x 2 dx 2 dx 2 dx + K 3 3 3     3  2   1    sin x      2   x  3 3 1 cos  x 3 2 cos   2   4 2       Vậy I   3  2 3  4
Bài 12: Tính tích phân I  ln(1 tan x d ) x 0    4     4  1 tant
Hƣớng dẫn: Đặt t   x   ln  1 tan  ln  1 dt 4 I t dt = =   4   1 tant 0  0   4 2 ln dt  1  tan t 0   4 4 
= ln 2dt  ln(1 tan t d ) t   = t 4 .ln2  I 0 0 0  
2I  ln2  4 I ln2 8 .  2
Bài 13: Tính tích phân I
sin x ln(1 sin x d ) x 0  1 cos x
u  ln(1 sin x) du dx
Hƣớng dẫn: Đặt    1 sin x
dv  sin xdx
v  cosx     2 cos x 2 2 1 sin x 2 
I  cos x.ln(1 sin x) 2  cos x. dx  0 
dx  (1 sin x)dx  1  1    sin x 1 sin x 2 0 0 0 0
PHẦN 3: BÀI TẬP TRẮC NGHIỆM LUYỆN THI
CHƢƠNG 1: NGUYÊN HÀM TÍCH PHÂN
Trần Thông sưu tầm và biên soạn
Facebook: Hội Toán Bắc Nam
Tài liệu ôn tập giải tích 12 học kỳ II f xCâu 1. Cho biết 2
t dt x cos( x).  Tính f (4) . 0 1
A. f (4)  2 3 B. f (4)  1  C. f (4)  D. 3 f (4)  12 2 3x t 1
Câu 2. Cho biết F x  dt.  Tính F (0  ). t e x A. f (0  )  2 3 B. f (0  )  2 C. f (0  )  2  3 D. f (0  ) 1 2 3 16 f t
Câu 3. Cho f x là hàm liên tục trên và  xf  2
x dx  4,  f tdt  2, dt  6.  t 0 2 9 4
Tính tích phân I   f xd . x 0 A. 1 B. 10 C. 12 D. 9 1 1
Câu 4. Cho m>0. Tìm điểu kiện của tham số m để tich phân 1  dx . 2x m 0 1 1 1 A. m B. m 0 C. 0 m D. m 4 4 4 x sin t
Câu 5. Tìm đạo hàm của hàm số F x   dt . t 1 sin A.   sin   x F x
B. F x  sin x C.    x F x
D. F x  x sin x x 2 x x t
Câu 6. Cho hàm số F x  dt
. Mệnh đề nào dưới đây là đúng. t e 1
A. Giá trị của hàm số tại 1 là F   1  1
B. Hàm số F x đạt cực tiểu tại x  0
C. Hàm số F x đồng biến trên
D. Hàm số F x có đạo hàm là   x F x xe
Câu 7. Cho f x là hàm số liên tục trên đoạn a,b và F x là một nguyên hàm của f x
trên a,b . Khi đó khẳng định nào sau đây đúng?
A. Diện tích S của hình phẳng giới hạn bởi đồ thị hàm số y f x , trục hoành và hai đường thẳng x  ,
a x b được tính theo công thức S F b  F a . a B. f
 xdx F b F ab b b C. f
 AxBdx  F AxB   A  0 a a
Trần Thông sưu tầm và biên soạn
Facebook: Hội Toán Bắc Nam
Tài liệu ôn tập giải tích 12 học kỳ II b D. kf
 xdx k F b F a 
(k là hằng số) a 2 e  1 1  a e
Câu 8. Kết quả tích phân  dx  
được viết dưới dạng e
. Tính giá trị biểu thức 2
 ln x ln x b e
a b ab .. A.3 B. 2 C. 4 D. 8 4
Câu 9. Tính tích phân 2 I
x  4x  4 1 d . x  0 A. 31 B. 35 C. 38 D. 40
Câu 10. Cho f x là hàm số liên tục trên
. Mệnh đề nào dưới đây là đúng.  1 1 2 1  A. f
 2x  2 f  xB. f
 sin xdx f  xdx 2 0 0 0 0 1 2
C.  f x  2dx  2  f  2xdx D. f
 x2dx  2 f  xdx 0 0 a 63 Câu 11. Giả sử
x ln 1 xdx  6  ln 3.  Tìm giá trị của . a 2 8  A. 0 B. 2 C. 3 D. 4 1 2
Câu 12. Tính tích phân x I  e
x sin2xd .x   1  A. 1  B. 0 C. 1 D. 2 a
Câu 13. Với a  1
 , kết quả tích phân  2x 3x  2dxđạt giá trị lớn nhất khi giá trị của a là: 0 5 A. 3  B. 2  C. D. 1  2 
Câu 14. Tính nguyên hàm  .  x x e I e dx x x A. e I e c B. e 1  I ec C. x I e c D. x 1  I ec 1 2 x 1 2 x
Câu 15. Đặt a  
dx . Kết quả tích phân  dx là: 1   x e 1 x e 0 0 1 1 A. 1 a B. 1 a C. a D. a 2 3 1
Câu 16. Xét tích phân 2 I  1 
x dx và phép đổi biến x  sin t.Mệnh đề nào dưới đây là sai. 0 1   sin   1 A. I  .   
B. I  cos t sin tdt.  2  2 2  0
Trần Thông sưu tầm và biên soạn
Facebook: Hội Toán Bắc Nam
Tài liệu ôn tập giải tích 12 học kỳ II   2 2 1  sin 2t C. 2 I  cos tdt.  D. I t  .   2  2  0 0
Câu 17 Trong các mệnh đề sau,có bao nhiêu mệnh đề đúng? 3 sin  2 4 2 (1) : sin d    x x x C (2) : d  2 ln  x x
 2x x3 C 2  3 x x  3  x x x   x  6 (3) : 3 2 3 dx   x   C (4) : e (1   e ) d   e x   x x x x C ln 6 (5) :  3 x x 2 2 sin
dx  6x  cos x C (6) : tan d  tan   x x x C A. 3 B. 4 C. 5 D. 6 x Câu 18. Giả sử f t  2 dt x  
x . Tìm hàm dưới dấu tích phân. 0 A. f t 2t 1 B. 2 f t t t C. f t 2t 1 D. 2 f t t t
Câu 19. Với f ( ) x , ( g )
x là 2 hàm số liên tục trên K và k  0 thì mệnh đề nào sau đây là sai. A. f (  ) x dx f ( ) x  . C
B. k f ( )
x dx k f ( ) x d . x   1 C. f (4)  D. f ( ) x . ( g ) x dx   
f( )xdx . (g )xd .x 2 x
Câu 20. Tìm nguyên hàm I   4 1 d . x 2x  1  2
A. I  2x  1  5ln 2x  1  2  . C
B. I  2x  1  4 2x  1  5ln 2x  1  2  . C
C. I  2x  1  4 2x  1  5ln 2x  1  2  .
C D. I  2x  1  4 2x  1  5ln 2x  1  2  . C 1 1 1 Câu 21. Cho
2f (x) g(x) dx 5 và 3f (x) g(x) dx 10 . Tính f (x)dx 0 0 0 A. 3 B. 5 C. 15 D. 10
Câu 22. Tìm nguyên hàm sau 2 ( ) x f x x e A. 2 (  2  2) x x x e C B. 2 (  2  2) x x x e C C. 2 (  2  2) x x x e C D. 2 (  2  2) x x x e C b
Câu 23. Với giá trị nào của số dương b thì 2
(6x  3x )dx  có giá trị lớn nhất 0 A. 2 B. 4 C. 6 D. 8 3 a
Câu 24. Tìm giá trị của a thỏa mãn các điều kiện a ; và 2 cos x a dx sina 2 2 0 A. B. C. 2  D. 2 e k
Câu 25. Gọi S là tập hợp tất cả các số nguyên dương k thỏa mãn điều kiện ln dx e 2 . x 1
Tìm số phần tử của S .
Trần Thông sưu tầm và biên soạn
Facebook: Hội Toán Bắc Nam
Tài liệu ôn tập giải tích 12 học kỳ II A. 3 B. 1 C. 2 D. 0 x
Câu 26. Tìm hàm số y f (x) nếu biết 15 f '(x) 
, f '(1)  4 và f (1)  4 14 3 5 x 23 3 x 23
A. f (x)  
B. f (x)   7 7 7 7 3 5 x 3 3 8 x 23
C. f (x)  
D. f (x)   7 7 7 7 a n
Câu 27. Tính tích phân sau I  1 x * d ; x n   (a là số thực) 0   n nnna 1 1 a   1 1 1 a   1 1 1 a   1 1 1 A. B. C. D. n n 1 n 1 n 1  2
Câu 28. Cho tích phân I  sin . x 8  cos xd . x
Với phép đổi biến u  8  cos x thì kết quả nào 0 sau đây đúng ? 9 8 8 9 1 A. I  2 ud . uB. I ud . uC. I ud . uD. I ud . u  2 8 9 9 8  2 Câu 29. Tính 3x
I e .sin xdx  0 3    1 1 3 1 1 3 3 A. 2 I   e B. 2 I   e C. 2 I  1 e D. 2 I  1 e 2 2 2 2 a 1
Câu 30. Cho hàm số f (x)   . x
b xe . Biết rằng f '(0)  2
 2 và f (x)dx  5  . Tính tổng 3 (x1) 0 a b . 146 26 26 146 A. B. C. D. 13 11 11 13
Câu 31. Hàm số nào sau đây là một nguyên hàm của hàm số 2 f (x) x k với k 0? x k 1 x A. 2 2 f (x) x k ln x x k B. 2 2 f (x) x k ln x x k 2 2 2 2 k 1 C. 2 f (x) ln x x k D. f (x) 2 2 x k 2 10x - 7x 2 Câu 32. Cho 2 f (x) (ax bx
c) 2x -1 là một nguyên hàm của hàm số g(x) 2x -1 trên khoảng 1 ; .Tính tổng a b c 2 A. 0 B. 2 C. 3 D. 4
Trần Thông sưu tầm và biên soạn
Facebook: Hội Toán Bắc Nam
Tài liệu ôn tập giải tích 12 học kỳ II
Câu 33. Xác định a, b, c sao cho 2 g(x) (ax bx
c) 2x - 3 là một nguyên hàm của hàm số 2 20x - 30x 7 f (x) trong khoảng 3 ; 2x - 3 2
A. a  4,b  2, c  2
B. a  1,b  2  ,c  4 C. a  2
 ,b 1,c  4
D. a  4,b  2  ,c 1
Câu 34. Tìm một nguyên hàm của hàm số: 2
f (x)  x sin 1  x A. 2 2 2
F(x)   1 x cos 1  x  sin 1  x B. 2 2 2
F(x)   1 x cos 1  x  sin 1  x C. 2 2 2
F(x)  1 x cos 1  x  sin 1  x D. 2 2 2
F(x)  1  x cos 1  x  sin 1  x
Câu 35. Trong các hàm số sau: (I) 2 f (x) x 1 (II) 2 f (x) x 1 5 1 1
III) f (x)
(IV) f (x) - 2 2 x 1 2 x 1
Hàm số nào có một nguyên hàm là hàm số 2 F(x) ln x x 1 A. Chỉ (I) B. Chỉ (III) C. Chỉ (II) D. Chỉ (III) và x e
(IV) Câu 36. Tìm nguyên hàm của hàm số: y = 2x x e x e x e x e ln 2 A. C B. C C. C D. C 2x ln 2 (1  ln 2)2x x.2x 2x 3 x 2
Câu 37. Với phép biến đổi t  1 x tích phân dx  trở thành
f t dt
,. Khi đó f t 1 1 x 0 1
là hàm nào trong các hàm số sau.
A. f t  2  2t  2t B.   2
f t t t C.   2
f t t t
D. f t  2  2t  2t 2 2 Câu 38. Cho f
 xdx  3.Tính tích phân 4 f
 x3dx  . 0 0 A. 2 B. 4 C. 6 D. 8  1 x 2 cos x
Câu 39.Cho tích phân I dx  và J dx
, phát biểu nào sau đây đúng x  3 3sin x  12 0 0 1 1
A. I J B. I  2 C. J  ln 5 D. J  ln 5 3 3 3
Câu 40. Tính tích phân I = 2 ln[2  x(x  3)]dx  . 2 A. 4  ln 2 3
B. 5ln 5  4ln 2  3
C. 5ln 5  4ln 2  3
D. 5ln 5  4ln 2  3
Trần Thông sưu tầm và biên soạn
Facebook: Hội Toán Bắc Nam
Tài liệu ôn tập giải tích 12 học kỳ II 2
Câu 41. Cho f x  3 3 2
x x  4x 1 và gx  2 3 2
x x  3x 1. Tích phân
f x  gxdx 1
bằng với tích phân nào dưới đây. 2 1 2 A.   3 x  2
2x x  2dx B.   3 x  2
2x x  2dx    3 x  2
2x x  2dx 1 1 1 2 1 2 C.   3 2  3 2  3x  2
2x x  2
x  2x  x  2dx D.  x  2x x  2dx dx 1  1 1  x
Câu 42. Tìm nguyên hàm I   ln ln d .x x
A. ln x.ln ln x C
B. ln x.ln ln x ln x C
C. ln x.ln ln x ln x C D. ln ln x ln x C  4 3 1 sin x
Câu 43. Tính tích phân dx  2  sin x 6 3  2 3  2  2 3  2 3  2 2  2 A. B. C. D. 2 2 2 2 1 ln x
Câu 44. Tích phân I     
dx có kết quả dạng I
a ln 2 b với , a b  . Khẳng định x ln x  22 0 nào sau đây đúng ?
A. 2a b  1 B. 2 2 a b  4
C. a b  1 D. ab  2 e ln x Câu 45. Nếu đặt 2
t  3ln x 1 thì tích phân I dx
trở thành tích phân nào dưới 2  1 x 3ln x 1 đây? 2 2 e 1 4 1 1 2 1 e t 1 A. I dtB. I dtC. I tdtD. I dt  3 2 t 3 4 t 1 1 1 1  4 x
Câu 46. Tính tích phân I dx  . 2 cos x 0    2  2 A. I   ln 2 B. I   ln 2 C. I   ln D. I   ln 4 4 4 2 4 2 cos 2x
Câu 47. Tìm nguyên hàm của hàm số: y = 2 2 sin . x cos x
A. tan x cot x
C B. tan x cot x
C C. tan x cot x
C D. tan x C 3 x
Câu 48. Tìm môt nguyên hàm của hàm số: y = y  2 2  x
Trần Thông sưu tầm và biên soạn
Facebook: Hội Toán Bắc Nam
Tài liệu ôn tập giải tích 12 học kỳ II 1 1 1 A. 2
F(x)  x 2  x B.   2 x  4 2
2  x C.   2 x  4 2 2  x D. 2 2  x 2  x 3 3 3 1 xdx
Câu 49. Tính tích phân J   3 (x  1) 0 1 1 A. J B. J C. J =2 D. J =1 8 4 2 6x
Câu 50. Tính tích phân K dx  9x  4x 1 1 1 1 12 A. K  ln B. K  ln 3 13 3 25 2 ln 2 ln 2 2 1 1 25 C. K  ln13 D. K  ln 3 3 13 2 ln 2 ln 2 2 e ln x
Câu 51. Tính tích phân K dx  2 x 1 1 1 1 2 A. K   2 B. K C. K   D. K  1  e e e e
Câu 52. Tìm nguyên hàm I  cos 2 .
x ln(sin x  cos x)dx  1 1
A. F x  1 sin 2xln 1 sin 2x  sin 2x C 2 4 1 1
B. F x  1 sin 2xln 1 sin 2x  sin 2x C 4 2 1 1
C. F x  1 sin 2xln 1 sin 2x  sin 2x C 4 4 1 1
D. F x  1 sin 2xln 1 sin 2x  sin 2x C 4 4
Câu 53. Tìm nguyên hàm 3 I x x 1d . x  2 4 5 3 6 2 2 
A. F x  x   1  x   1  x   1  x   1 x 1    C 9 7 5 3  2 4 6 3 6 2 2 
B. F x  x   1  x   1  x   1  x   1 x 1    C 9 7 5 3  2 4 6 3 6 2 2 
C. F x  x   1  x   1  x   1  x   1 x 1    C 9 7 7 3  2 4 6 3 6 2 1 
D. F x  x   1  x   1  x   1   x   1 x 1    C 9 7 5 3 
Trần Thông sưu tầm và biên soạn
Facebook: Hội Toán Bắc Nam
Tài liệu ôn tập giải tích 12 học kỳ II
Câu 54. Cho F(x) là một nguyên hàm của f (x)  2x 1 trên
. Biết hàm số y F(x) đạt giá trị
nhỏ nhất bằng 39 . Đồ thị của hàm số y F(x) cắt trục tung tại điểm có tung độ là bao nhiêu? 4 37 39 A. B. C. J =11 D. J =10 4 4
Câu 55. Chọn khẳng định sai trong các khẳng đinh sau.  1 1  2 x
A. sin(1 x)dx  sin xdx   B. sin dx  2 sin xdx   2 0 0 0 0 1 1 2 x 3
C. (1 x) dx   D. 2007 x (1 x)dx   2 2009 0 1   3 x
Câu 56.Giả sử tích phân dx   a  
b . Tìm phần nguyên của tổng a b 2 cos x 0 A. 1 B. -1 C. 0 D. -2 3 2 1 2 1
Câu 57. Cho tích phân  .  x I
dx Với phép đổi biến  x t
thì kết quả nào sau đây 2 x x 1 đúng ? 2 2 3 2 3 2 3 2 3 2 A.    t I dt B.   t I dt C.   t I dt D.   t I dt 2 t 1 2 t 1 2 t 1 2 t 1 2 2 2 2 1  2 
Câu 58. Tính tích phân x I xe dx    . 2 1 x  0
A. I  1 ln 2
B. I  1 ln 2
C. I  3  ln 2
D. I  3  ln 2 e
Câu 59. Giả sử tích phân 2 3
I x(x ln x)dx a  . b e  . 
c e .Đẳng thức nào sau đây đúng. 1
A. b c a
B. b c  a
C. b c a
D. b c  a  2
Câu 60. Tính tích phân I   3
x x sin 2xdx . 0 4   4   4   4   A. I   B. I   C. I   D. I   64 4 64 2 64 2 64 4 
3 (x  sinx)dx
Câu 61. Tính tích phân I   . 2 cos x 0 3 3 3 3 A. I  1
  ln 2 B. I 1
  ln 2 C. I    ln 2 D. I   3 3 3 3
Trần Thông sưu tầm và biên soạn
Facebook: Hội Toán Bắc Nam
Tài liệu ôn tập giải tích 12 học kỳ II e 1 ln x
Câu 62. Tính tích phân I dx  . x 1 1 1 1 3 A. I B. I C. I D. I  8 2 4 2 6  3 1
Câu 63. Giả sử tích phân   .ln  x dx a b
c . Đẳng thức nào sau đây đúng. x  2 1
A. a b c
B. a b c
C. a b c
D. a b c 1 x
Câu 64. Tính tích phân I dx  . 2 3 (2x 1) 0 1 1 8 8 A. I   B. I C. I D. I   9 9 9 9 10 3 2  3  4 63  3 
Câu 65. Giả sử tích phân   .ln .  x x a
  Tìm giá trị của a. x  2 2  2  5 A. a  4 B. a  5 C. a=2 D. a=1 1
Câu 66. Tính tích phân      1 . x I x e dx . 0
A. I  1 e
B. I  1 e
C. I  e
D. I e 7 8
Câu 67. Xét các tích phân 3 I  . x x 1  dx và J  . x x 1 
dx . Nhận xét nào dưới đây là 0 0 đúng. 1 1 A. J I B. I J
C. I J
D. I J 8 4 1
Câu 68. Tính tích phân I   3x 1  2dx . 0 4 4 A. I B. I   C. I =2 D. I =1 9 9 e 2
Câu 69. Tính tích phân 2
x ln x  3x  1  9 6 3  . a e  . b e  .
c e Đẳng thức nào dưới đây là 1 đúng.
A. a b c  0
B. a b  2c  0
C. a b c  0
D. a b  2c  0 1
Câu 70. Tính tích phân .  (2 x I xe )dx  0 1 1 A. I B. I C. I=2 D. I=1 2 4
Trần Thông sưu tầm và biên soạn
Facebook: Hội Toán Bắc Nam
Tài liệu ôn tập giải tích 12 học kỳ II  2
Câu 71. Tính tích phân 2
I  (x  sin x) cos xd . x  0 2  2  1  1  A. I    B. I   C. I    D. I   3 2 3 2 3 4 3 4 3 2 ln(x 1)
Câu 72. Tính tích phân I dx  . 3 x 1 1 1 1 1 1 1 1 2 A. I  ln 2  ln 3
B. I   ln 2  ln 3 C. I  ln 2  ln 3 D. I  ln 3 2 3 2 3 2 3 3  2
Câu 73. Tính tích phân J  x  2cos xsin xdx . 0 1 1 A. J B. J C. J =2 D. J =1 8 4 1 2 x ln(x 1)
Câu 74. Tính tích phân I dx  . 2 x 1 0 1 1 1 1 A. I  ln 2 B. I  ln 22 C. I  ln 4 D. I  ln 2 2 2 2 4 1
Câu 75. Tính tích phân   3 2    x J x xe dx . 0 9 9 A. J B. J C. J =2 D. J =-1 8 4 1
Câu 76. Tính tích phân 2
3x  2x  ln(2x 1) dx   . 0 3 3 3 A. I  1   ln 2 B. I  1   ln 3 C. I  1   ln 2 D. I  1 ln 3 2 2 2  2
Câu 77. Tính tích phân    sinx I e
x.cos xdx . 0    A. I  2   e B. I  2   e C. I  2   e
D. I e  2 2 2 a
Câu 78. Biểu thức nào sau đây bằng với tích phân I   f xdxa a a
A.  f (x) f (x)dx
B.  f (x) f (a  x)dx 0 0 a a
C.  f (x a)  f (x)dx
D.  f (x a) f (a  x)dx 0 0
Trần Thông sưu tầm và biên soạn
Facebook: Hội Toán Bắc Nam
Tài liệu ôn tập giải tích 12 học kỳ II 4
Câu 79. Cho I  2  x dx
. Khẳng định nào sau đây là sai ? 0 4 1 4 A. I x  2 dxB. I  2  x dx  2  x dx   0 0 1 0 2 4
C. I dxD. I  2  x dx x  2 dx   4 0 2  12     1  6  Câu 80. Cho 2 sin 2x      
, với a, b là các số nguyên dương. Tính 2.sin   .  4  a ba  0 A. 2 B. 2 C. 2 2 D. 0 1 1
Câu 81. Cho các tích phân 2 I 1 cos 2xdx, J 9x
6x 1dx .Khẳng định nào 2 0 0 sau đây đúng A. I 2J B. I 3J C. I 2J 5 D. 5I 12J
Câu 82. Cho f (x)
3 5sin x và f (0) 10 . Trong các khẳng định sau khẳng định nào đúng? A. f 3 B. f x 3x 5cos x 3 C. f D. f (x) 3x 5cos x 2 2 2 a 3 Câu 83. Biết  4
(4sin x  )dx  0 và a  ; 0 (  ) Tìm giá trị a. 2 0     A. a B. a C. a D. a  4 8 2 3
Câu 84. Ký hiệu K là khoảng hoặc đoạn hoặc nửa khoảng của
. Cho hàm số f (x) xác định
trên K. Khi nào F (x) được gọi là nguyên hàm của hàm số f (x) trên K A. '
F(x)  f (x) B. '
F(x)  f (x)  C , C là hằng số tuỳ ý. C. '
F (x)  f (x)  C , C là hằng số tuỳ ý. D. '
F (x)  f (x) 1 Câu 85. Cho 2
f (x)  2x  xác định trên khoảng ( ;
 0). Biến đổi nào sau đây là sai ? 3 x  1  1 1    A. 2 2 2x dx  2x dx d . x     B. 2x
dx  2 x dx x d . x     3   1 2 2 3 3 3  x xx  1   1   1  2 1 C. 2 2 3 2x
dx  2 x dx x d . x     D. 2 3 2x dx x dx C    3  x  3 3  x  3 x
Câu 86. Cho đường cong 2
y x . Với mỗi x [0 1
; ], gọi S(x) là diện tích của phần hình thang
cong đã cho nằm giữa hai đường vuông góc với trục Ox tại
điểm có hoành độ 0 và x (xem hình vẽ). Khi đó, khẳng
định nào sau đây đúng.
Trần Thông sưu tầm và biên soạn
Facebook: Hội Toán Bắc Nam
Tài liệu ôn tập giải tích 12 học kỳ II A. 2
S(x)  x B. ' 2
S (x)  x 2 x
C. S(x)  D. '
S (x)  2x 2 
Câu 87. Tìm hàm số y f (x) biết 4 3
dy  35sin x cos xdx và f ( )  2  2 A. 5 7
f (x)  5sin x  7sin x  2 B. 5 7
f (x)  5sin x  7sin x  2 C. 5 7
f (x)  7sin x  5sin x  2 D. 5 7
f (x)  7sin x  5sin x  2 1
Câu 88. Cho f (x) là hàm số chẵn và liên tục trên thỏa mãn
f (x)dx  2  . Tính giá trị tích 1  1
phân f (x)dx  0 1 1 A. B. C. 1 D. 2 2 4
Câu 89. Hàm số F(x)  ex  tan x C là nguyên hàm của hàm số f(x) nào dưới đây. 1 1
A. f (x)  e x
B. f (x)  e x  2 sin x 2 sin x   x e x  1
C. f (x)  e 1 D. x f (x)  e  1 2   cos x  2 sin x 2
Câu 90. Tính tích phân I  1 x x d  2  3 3 4 3 A. 3 3  B. 4 3  C. 4 3  D. 3 3  4 4 3 4    Câu 91. Giả sử 3
I  7x cos x x
d f (x) s inx  2x sin xdx   .Tìm hàm số f(x) 0 0 0 4 x 4 x A. 2 6x B. C. D. 3 2x 2 2 sin x
Câu 92. Giả sử F x là một nguyên hàm của hàm số f x .Tính tích phân x 3 sin 2x I x 1 A. I F 3 F 1 B. I F 6 F 2 C. I F 4 F 2 D. I F 3 F 2 1
Câu 93. Tính tích phân 3x 1 2 x dx 0 1 7 11 A. B. C. D. 0 6 6 6
Trần Thông sưu tầm và biên soạn
Facebook: Hội Toán Bắc Nam
Tài liệu ôn tập giải tích 12 học kỳ II 1 n
Câu 94. Tính tích phân sau 2 I x  3 1 x  * d ; x n   0 n 1  2  1 2n 1 n 1 2 1 n 1 2  1 A. B. C. D. 3n   1 3n   1 n 1 3n   1 1
Câu 95. Tính tích phân 2 I ( ) m
x  2x m dx
với m  0 (m là tham số) 0 2 1 2 2 A.   m B. m C. m D. m 3 3 3 3
Câu 96. Mệnh đề nào sai trong các mệnh đề sau. 1 0 A.  3 2
x x dx  2 3
x x dx 0 1 1 2 1 B.  3 2
x x dx  3 2
x x dx   3 2
x x dx 0 0 2 1 2 1 C.  3 2
x x dx  3 2
x x dx   3 2
x x dx 0 0 2 1 1 1 D.  3 2 x x  3 2
dx x dx x dx   0 0 0 0 x   
Câu 97. Tìm giá trị K thỏa 2
 4e dx K 2e   2  A. 9 B. 10 C. 11 D. 12,5 2 2
a sin x cos x b 3
Câu 98. Biết F ' x , F , F . Tìm hàm số F x . 2 2 sin x cos x 6 2 3 A. F x x tan x cotx . B. F x x tan x cotx . 3 12 3 C. F x 9x 2 . D. F x x tan x cotx . 3 6 x2 (  x x e )
Câu 99. Tìm nguyên hàm của hàm số: y =  dx x x e x x x x
A. xe  1 ln xe  1  C
B. e  1 ln xe  1  C xx x x
C. xe  1  ln xe 1  C
D. xe  1 ln xe  1  C
Câu 100. Biết sin 3x  axcos3x sin3x x dx b
C .Tính giá trị a+6b A. -21 B. -1 C. -5 D. -7
Câu 101. Biết 2   2      x x x e dx x mx n e
C Tìm giá trị của tích m.n
Trần Thông sưu tầm và biên soạn
Facebook: Hội Toán Bắc Nam
Tài liệu ôn tập giải tích 12 học kỳ II A. 0 B. 4 C. 6 D. -4 2
Câu 102. . Biết  tan(3x-1)   a dx
C Tổng a+b có thể nhận giá trị nào dưới đây? 2 cos (3x 1) b A. -5 B. -1 C. 5 D. 7 a Câu 103. Biết x x e e dx x e k   6 3 ( 1) ( 1)
C Tổng a+b+2k có thể nhận giá trị nào dưới đây? b A. 33 B. 32 C. 24 D. 28  2 (2 3ln x) 1 Câu 104. Biết dx  (2  3lnx)b  
C Tìm giá trị của tích a.b x a 1 1 A. 3 B. 1 C. 2 D. 2
Câu 105. Biết 2 2 2  2  (  2)  2   a x x dx x x
C , tính tổng a+b biết a và b là hai số nguyên tố b cùng nhau. A. 3 B. 5 C. 1 D. 4 1 a
Câu 106. Biết dx  ln 1 tan 3x  
C , tính tổng 2a+b biết a và b là hai số 2 cos 3x(1 ta 3 n x) b nguyên tố cùng nhau. A. 5 B. 10 C. 7 D. 4
Câu 107. Biết sin  ax cos  sin   x x x x dx b C , tính tổng a+b . 3 3 3 A. 9 B. 2 C. 6 D. 12 2 1 1
Câu 108. Biết ln(1 )  ln(1 ) 
ln 1   1 2   x x x dx x x x
C , tính giá trị biểu thức m n k 2a+ b+n. A. 2 B. 12 C. 9 D. 6 a
Câu 109. Biết x xdx x x x   1 sin cos 2 sin 2
C , tính tổng 2a+b biết a và b là hai số nguyên b n tố cùng nhau A. 4 B. 10 C. 2 D. 6  1
Câu 110. Biết 2 2 ( 3) e    2     x x x e dx x n
C , tính giá trị biểu thức 2 2 m  n m A. 5 B. 10 C. 41 D. 65 3 Câu 111. Cho I= 2  x
x e dx và phép đổi biến 3
u  x . Đẳng thức nào dưới đây là đúng. 1 u A. u I  3 e du  B. u I  e du  C. I  e du  3  D. u I ue du  Câu 112. Cho I= 5 2 15 x x
dx và phép đổi biến 2
u  x 15 . Đẳng thức nào dưới đây là đúng. A. 6 4 2 I  (u 30u  225u )du  B. 4 2 I  (u 15u )du  C. 6 2 2 I  (u 30u  225u )du  D. 5 3 I  (u 15u )du 
Trần Thông sưu tầm và biên soạn
Facebook: Hội Toán Bắc Nam
Tài liệu ôn tập giải tích 12 học kỳ II 2 dx 1
Câu 113. Biết  ln b 
, tính giá trị biểu thức a2 + b 3x 1 a 0 A. 2 B. 10 C. 14 D. 12 3 x 8 b
Câu 114. Biết dx  3lna 4 ln 
(a,b nguyên tố cùng nhau) tính giá trị biểu thức 2 x  5x  4 a 0 2  b     a  7 16 49 1 A. B. C. D. 4 49 16 16 2 dx 1 1
Câu 115. Biết   
thì a và b là nghiệm của phương trình nào sau đây? 2 4x  4x 1 a b 1 A. 2 x  5x  6  0 B. 2 x  9  0 C. 2 2x  x 1  0 D. 2 x  4x 12  0 π 2 3 dx 2 Câu 116. Cho I   dt  
. Chọn khẳng định đúng. 2 x  x 1  a 0 π 6 1 A. a = 3 B. 2 a  3 C. a   3 D. a  3 4 dx
Câu 117. Biết I   a  ln b  . Chọn đáp án đúng. 2 x x 1 1   1 A. a  b  0 B. 2a  b  4 C. a  b  1 D. ab=4 2
PHẦN 2: ỨNG DỤNG CỦA TÍCH PHÂN 1
Câu 1. Tính thể tích của khối tròn xoay được giới hạn bởi các đường y  2x  
1 3 ,x  0,y  3 quay quanh trục Oy 50 480 480 48 A. V B. V C. V D. V  7 7 9 7 x
Câu 2. Tính diện tích hình phẳng được giới hạn bởi các đường y  e  
1 x,y  1e x e e e e A. S   2 B. S  1 C. S  1 D. S  1 2 2 2 3
Câu 3. Tính thể tích của khối tròn xoay được giới hạn bởi các đường 2 
y x cos x  sin x,y  0,y  ,x  0. 2 quay quanh trục Ox.  3  4  3  4  5  4  3  4 A. V B. V C. V D. V  4 4 4 5
Câu 4. Tính diện tích hình phẳng được giới hạn bởi các đường y x y
x x x   sin2 , cos , 0, . 2
Trần Thông sưu tầm và biên soạn
Facebook: Hội Toán Bắc Nam
Tài liệu ôn tập giải tích 12 học kỳ II 1 1 1 3 A. S B. S C. S D. S  4 4 6 2 2
Câu 5. Tính diện tích hình phẳng được giới hạn bởi các đường y  sin x x,y x 0  x   .   A. S   B. S C. S  2 D. S  2 3 2
Câu 6. Tính diện tích hình phẳng được giới hạn bởi các đường y  2x x ,y  . x 9 7 9 A. S  0 B. S C. S D. S   2 2 2
Câu 7. Tính thể tích của khối tròn xoay được giới hạn bởi các đường y  ln x, x  , e y  0. quay quanh trục Ox
A. V   e
B. V   e  
1 C. V   e   1
D. V   e  2
Câu 8. Tính thể tích của khối tròn xoay được giới hạn bởi các đường y  ln x, x 1,y  0, x  2. quay quanh trục Ox A. V     2 2
ln 2 1 B. V     2 2
ln 2 1 C. V     2 2
2 ln 2 1 D. V     2 2 2 ln 2 1 3
Câu 9. Tính thể tích của khối tròn xoay được giới hạn bởi các đường y x , x  3,y  8 quay quanh trục Ox
A. V   e
B. V   e  
1 C. V   e   1
D. V   e  2 3 3
Câu 10. Tính diện tích hình phẳng được giới hạn bởi các đường y x , y  0, x  2 65 81 81 A. S B. S C. S  4 D. S 64 64 4 x
Câu 11. Tính diện tích hình phẳng được giới hạn bởi các đường y e ,y  0, x  0, x  2 2 e
A. S  4  e B. 2 S e 1 C. 2
S e e  2 D. S   3 2 x
Câu 12. Cho hình phẳng (H) được giới hạn bởi đường cong y  2
1 , trục Ox và trục Oy. Tính x 1
thể tích của khối tròn xoay khi cho hình (H) quay quanh trục Ox
A. V  4  3ln 2 B. V  4 ln 2 C. V  3  4ln 2 D. V  3 3
Câu 13. Tính diện tích hình phẳng được giới hạn bởi các đường y x  2x,y  0 4 5 11 68 A. S B. S C. S D. S  3 3 12 3 2
Câu 14. Tính diện tích hình phẳng được giới hạn bởi các đường y x ,y x 1 1 1 1 A. S B. S C. S D. S  2 3 4 5
Câu 15. Quay hình phẳng giới hạn bởi đường cong y  2
x và đường thẳng y 4 quay một
vòng quanh trục Ox. Tính thể tích khối tròn xoay được sinh ra.
Trần Thông sưu tầm và biên soạn
Facebook: Hội Toán Bắc Nam
Tài liệu ôn tập giải tích 12 học kỳ II 64 128 256 152 A. V B. V C. V D. V  5 5 5 5
Câu 16. Tính diện tích hình phẳng được giới hạn bởi các đường y  sin ; x y  cos ;
x x  0; x   A. S  2
B. S  3 C. S  2 2 D. S  3 2
Câu 17. Tính thể tích của khối tròn xoay được giới hạn bởi các đường y  ln x, x  , e y  0. quay quanh trục Ox
A. V   e
B. V   e  
1 C. V   e   1
D. V   e  2
Câu 18. Cho hình phẳng (H) được giới hạn bởi đường cong y  sin x , trục Ox và các đường
thẳng x  0; x   . Tính thể tích của khối tròn xoay khi cho hình (H) quay quanh trục Ox 3 2 A. V  2 B. V  3 C. V   D. V   2 3 3 x
Câu 19. Tính diện tích hình phẳng được giới hạn bởi các đường y
; y x 2 1 x A. S  1
B. S  1 ln 2 C. S  1 ln 2
D. S  2  ln 2
Câu 20. Gọi  H  là hình phẳng giới hạn bởi các đường: 2
y  3x x và trục Ox . Tính thể tích
khối tròn xoay thu được khi quay  H  xung quanh trục Ox . 81 83 81 83 A. V   B. V   C. V   D. V   11 11 10 10
Câu 21. Tính diện tích hình phẳng được giới hạn bởi các đường C 2
: y x  2x; y x  2 11 5 9 7 A. S B. S C. S D. S  2 2 2 2
Câu 22. Tính diện tích hình phẳng được giới hạn bởi các đường C 1 : y  ; d : y  2  x  3 x 3 3 1 1 A. S   ln 2
B. S  ln 2  C. S D. S  4 4 24 24
Câu 23. Gọi  H  là hình phẳng giới hạn bởi các đường: y x 1; y  0; x  4 . Quay  H
xung quanh trục Ox ta được khối tròn xoay có thể tích là bao nhiêu? 7 5 7 5 A. V
B. V   C. 2 V   D. 2 V   6 6 6 6
Câu 24. Gọi  H  là hình phẳng giới hạn bởi các đường: y  3x; y x ; x 1. Quay  H
xung quanh trục Ox ta được khối tròn xoay có thể tích là bao nhiêu? 8 2 8 A. B. C. 2 8 D. 8 3 3 8
Câu 25. Tính diện tích hình phẳng được giới hạn bởi các đường y  2x ; y  ; x  3 x 2 14
A. S  5  8ln 6
B. S  5  8ln C. S  26 D. S  3 3
Câu 26. Diện tích hình phẳng giới hạn bởi các đường y mx cos x ; Ox ; x  0; x   bằng 3 .
Khi đó, tìm giá trị của m
Trần Thông sưu tầm và biên soạn
Facebook: Hội Toán Bắc Nam
Tài liệu ôn tập giải tích 12 học kỳ II A. m  3  B. m  3 C. m  4  D. m  3 
Câu 27. Tính diện tích hình phẳng được giới hạn bởi các đường C : y x;d  : y x  2;Ox A. 10 B. 16 C. 122 D. 128 3 3 3 3
Câu 28. Tính diện tích hình phẳng được giới hạn bởi các đường 2
y x 1 ; y x  5 73 7 A. S  1 B. S C. S D. S  23 3 3
Câu 29. Tính diện tích hình phẳng được giới hạn bởi các đường y x y    x3 2 2 4 ; 4 128 128 2 128 2 2 A. S B. S C. S D. S  15 15 30 15
Câu 30. Tính diện tích hình phẳng được giới hạn bởi các đường 2 2 2 2
x  y  4; x y  2x  0. A. S  1
B. S  1 ln 2 C. S  1 ln 2
D. S  2  ln 2 3 x
Câu 31. Tính diện tích hình phẳng được giới hạn bởi các đường y
; y x 2 1 x 3  A. S  3 B. S C. S   D. S  2 2 2 2
x  2ax  3a a ax
Câu 32.Giả sử hình phẳng được giới hạn bởi các đường y  ; y  diện tích 4 4 1 a 1 a
lớn nhất. Tìm giá trị của a biết a là số thực dương. A. 4 a  3 B. 3 a  5 C. 4 a  5 D. 3 a  4
Câu 33. Trên parabol  P 2
: y x ta lấy hai điểm A,B sao cho AB=2. Tìm vị trí của A và B để
diện tích hình phẳng giới hạn bởi đường thẳng AB và P lớn nhất. A. A 1  , 
1 , B 2, 4 B. A 1  ,  1 , B 1,  1 C. A 1  , 
1 , B 2, 4 D. A1,  1 , B 2, 4
Câu 34. Trên parabol  P 2
: y x ta lấy hai điểm A 1  , 
1 , B 2, 4 . Tìm trên cung AB điểm M
sao cho diện tích tam giác MAB lớn nhất.  1 1   1 1 
A. M 0,0 B. M 1,  1 C. M ,   D. M  ,    2 4   2 4 
Câu 35. Đường thẳng d  : y mx  2 giao với parabol  P 2
: y x 1 tạo thành hình phẳng có
diện tích nhỏ nhất. Tìm m. A. m  1 B. m  0 C. m  1  D. m  2 
Câu 36. Tính thể tích của khối tròn xoay thu được khi quay hình giới hạn bởi các đường y x   3
ln 1 x ,y  0,x 1 quay quanh trục Ox  2ln 2   1  2ln 2   1  2ln 2   1 .ln 2 A. V B. V C. V D. V  3 3 4 3 1
Câu 37. Gọi  H  là hình phẳng giới hạn bởi các đường: y  và các đường thẳng 2 x  1
x 1, y  0 x=0. Tính thể tích khối tròn xoay thu được khi quay  H  xung quanh trục Oy
Trần Thông sưu tầm và biên soạn
Facebook: Hội Toán Bắc Nam
Tài liệu ôn tập giải tích 12 học kỳ II A. V  
B. V   ln 2
C. V   ln 4 D. V  2 2 2
Câu 38. Tính thể tích của khối tròn xoay thu được khi quay hình tròn x  y  3  4 quanh trục Ox A. V  4 B. 2 V  4 C. V  8 D. 2 V  8 2 2
Câu 39. Tính thể tích của khối tròn xoay thu được khi quay hình tròn x  y  3  4 quanh trục Oy 32 32 A. V   B. 2 V   C. V  8 D. 2 V  8 3 3 x  2 2 4 y
Câu 40. Tính thể tích của khối tròn xoay thu được khi quay elip  1quanh trục Ox 4 16 128 128 A. V  4 B. 2 V  4 C. V   D. 2 V   3 3 x  2 2 4 y
Câu 41. Tính thể tích của khối tròn xoay thu được khi quay elip  1quanh trục Oy 4 16 128 128
A. V  64 B. 2 V  4 C. V   D. 2 V   3 3 2
Câu 42. Tính thể tích của khối tròn xoay được giới hạn bởi các đường y  2x x ,y  0 quay quanh trục Oy 8 3 16 15 A. V B. V C. V   D. V   3 8 15 16 2
Câu 43. Tính thể tích của khối tròn xoay được giới hạn bởi các đường y x ,y 1,y  3x 10 quay quanh trục Oy 61 61 101 101 A. V B. 2 V   C. V   D. 2 V   5 5 54 54 x2 2 27
Câu 44. Tính thể tích của khối tròn xoay được giới hạn bởi các đường y x , y  ,y  27 x quay quanh trục Ox 583 583 A. V B. V  
C. V  81 27 ln 3
D. V  81 27 ln 3 3 3 x2 2 27
Câu 45. Tính thể tích của khối tròn xoay được giới hạn bởi các đường y x , y  ,y  27 x quay quanh trục Ox 583 583 A. V B. V  
C. V  81 27 ln 3
D. V  81 27 ln 3 3 3 x2 2 27
Câu 46. Tính thể tích của khối tròn xoay được giới hạn bởi các đường y x , y  ,y  27 x quay quanh trục Oy 583 583 A. V B. V  
C. V  81 27 ln 3
D. V  81 27 ln 3 3 3
Trần Thông sưu tầm và biên soạn
Facebook: Hội Toán Bắc Nam
Tài liệu ôn tập giải tích 12 học kỳ II 2
Câu 47. Tính thể tích của khối tròn xoay được giới hạn bởi các đường y x ,y 1,y  3x 10 quay quanh trục Oy 61 61 101 101 A. V B. 2 V   C. V   D. 2 V   5 5 54 54 2
Câu 48. Tính thể tích của khối tròn xoay được giới hạn bởi các đường y  x  2 ,y  4 quay quanh trục Ox 128 256 256 101 A. V B. 2 V   C. V   D. 2 V   3 5 5 54 2
Câu 49. Tính thể tích của khối tròn xoay được giới hạn bởi các đường y  x  2 ,y  4 quay quanh trục Oy 128 256 256 101 A. V B. 2 V   C. V   D. 2 V   3 5 5 54 3 2
Câu 50. Tính thể tích của khối tròn xoay được giới hạn bởi các đường y  ,y x x 3 quay quanh trục Ox 486 256 256 35 A. V B. 2 V   C. V   D. 2 V   35 35 5 486
PHẦN 3: ỨNG DỤNG TÍCH PHÂN TRONG THỰC TẾ
Câu 1. Giả sử sau t năm,dự án đầu tư thứ nhất sẽ phát sinh lợi nhuận với tốc độ 2
P (t)  t  50 1
trăm đô la/năm,trong khi đó dự án đầu tư thứ hai phát sinh lợi nhuận với tốc độ P (t)  200  5t 2
trăm đô la/năm.Tính lợi nhuận vượt thực tế cho khoảng thời gian để tốc độ sinh lợi nhuận của dự
án đầu tư thứ hai vượt bằng dự án đầu tư thứ nhất ? A. 1690 trăm đô B. 1695 trăm đô C. 1687,5 trăm đô D. 1685 trăm đô
Câu 2. Một vật đang chuyển động với vận tốc 10m/s thì tăng tốc với gia tốc a(t) = 3t + t2(m / s2 )
. Hỏi quảng đường vật đi được trong khoảng thời gian 10 giây kể từ lúc bắt đầu tăng tốc ? 6800 5800 4300 A. 11100 m B. m C. m D. m 3 3 3
Câu 3. Gọi h t (
cm) là mức nước ở bồn chứa sau khi bơm nước được t giây. Biết rằng 1 3 h ' t t
8 và lúc đầu bồn không chứa nước. Tìm mức nước ở bồn sau khi bơm được 6 giây 5
(làm tròn kết quả đến hàng phần trăm) A. 2.64 B. 2,65 C. 2,66 D. 2,67
Câu 4. Một vật chuyển động chậm dần với vận tốc v t  160 10tm / s . Hỏi rằng trong 3s
trước khi dừng hẳn vật di chuyển được bao nhiêu mét ? A.16 B. 130 C. 45 D. 170 3
Câu 5. Một vật chuyển động với vận tốc v(t) (m/s) có gia tốc 2 v '(t)  (m/ s ) .Vận tốc ban t 1
đầu của vật là 6m/s. Hỏi vận tốc của vậy sau 10 giây gần bằng với giá trị nào nhất. A. 10m B. 11m C. 12m D. 13m
Trần Thông sưu tầm và biên soạn
Facebook: Hội Toán Bắc Nam
Tài liệu ôn tập giải tích 12 học kỳ II 8000
Câu 6. Một đám vi trùng tại ngày thứ t có số lượng là N(t). Biết rằng ' N (t)  và lúc đầu 1 0,5t
đám vi trùng có 350.000 con. Hỏi sau 10 ngày số lượng vi trùng là bao nhiêu con? (lấy xấp xỉ hàng đơn vị). A. 378668 B. 378688 C. 376668 D. 388668
Câu 7. Học sinh lần đầu thử nghiệm „„tên lửa tự chế ‟‟ phóng từ mặt đất theo phương thẳng đứng
với vận tốc 15m/s. Hỏi sau 2,5s tên lửa lên đến độ cao bao nhiêu ? (giả sử bỏ qua sức cản gió,
tên lửa chỉ chịu tác động của trọng lực 2
g  9,8m / s ) A. 68,125(m)
B. 6,875(m) C. 30,625(m) D. 61,25(m)
Câu 8. Một khối cầu có bán
kính 5dm, người ta cắt bỏ 2 phần bằng 2 mặt phẳ ng vuông góc bán
kính và cách tâm 3dm để làm một chiếc lu đựng. Tính thể tích mà chiếc lu chứa được. 100 A. 132 (dm3) B. 41 (dm3) C.  (dm3)
D. 43 (dm3) 3 
Câu 9. Một vật di chuyển với gia tốc a t      t 2 20 1 2  2
m / s  . Khi t  0 thì vận tốc của vật
là 30m / s . Tính quảng đường vật đó di chuyển sau 2 giây (làm tròn kết quả đến chữ số hàng đơn vị).
A. S  106m
B. S  107m
C. S  108m
D. S  109m
Câu 10. Trên sân bay một máy bay cất cánh trên đường băng d (từ trái sang phải) và bắt đầu rời
mặt đất tại điểm O. Gọi (P) là mặt phẳng vuông góc với mặt đất và cắt mặt đất theo giao tuyến là
đường băng d của máy bay. Dọc theo đường băng d cách vị trí máy bay cất cánh O một khoảng
300(m) về phía bên phải có 1 người quan sát A. Biết máy bay chuyền động trong mặt phẳng (P)
và độ cao y của máy bay xác định bởi phương trình 2
y x (với x là độ dời của máy bay dọc theo
đường thẳng d và tính từ O). Tìm khoảng cách ngắn nhất từ người A (đứng cố định) đến máy bay. A. 300( ) m B. 100. 5( ) m C. 200( ) m D. 100 3( ) m
Câu 11. Một ô tô chạy với vận tốc 20m/s thì người lái xe đạp phanh còn được gọi là “thắng”.
Sau khi đạp phanh, ô tô chuyển động chậm dần đều với vận tốc v(t)  4
 0t  20(m / s). Trong đó
t là khoảng thời gian tính bằng giây kể từ lúc bắt đầu đạp phanh . Quãng đường ô tô di chuyển từ
lúc đạp phanh đến khi dừng hẳn là bao nhiêu mét? A.2 B. 5 C. 3 D. 4
Câu 12. Một ô tô xuất phát với vận tốc v t 2t 10 m / s 1
sau khi đi được một khoảng thời gian t v t 20 4t m / s
1 thì bất ngờ gặp chướng ngại vật nên tài xế phanh gấp với vận tốc 2 và
đi thêm một khoảng thời gian t2 nữa thì dừng lại. Biết tổng thời gian từ lúc xuất phát đến lúc
dừng lại là 4 (s). Hỏi xe đã đi được quãng đường bao nhiêu mét. A. 47 B. 50 C. 57 D. 64
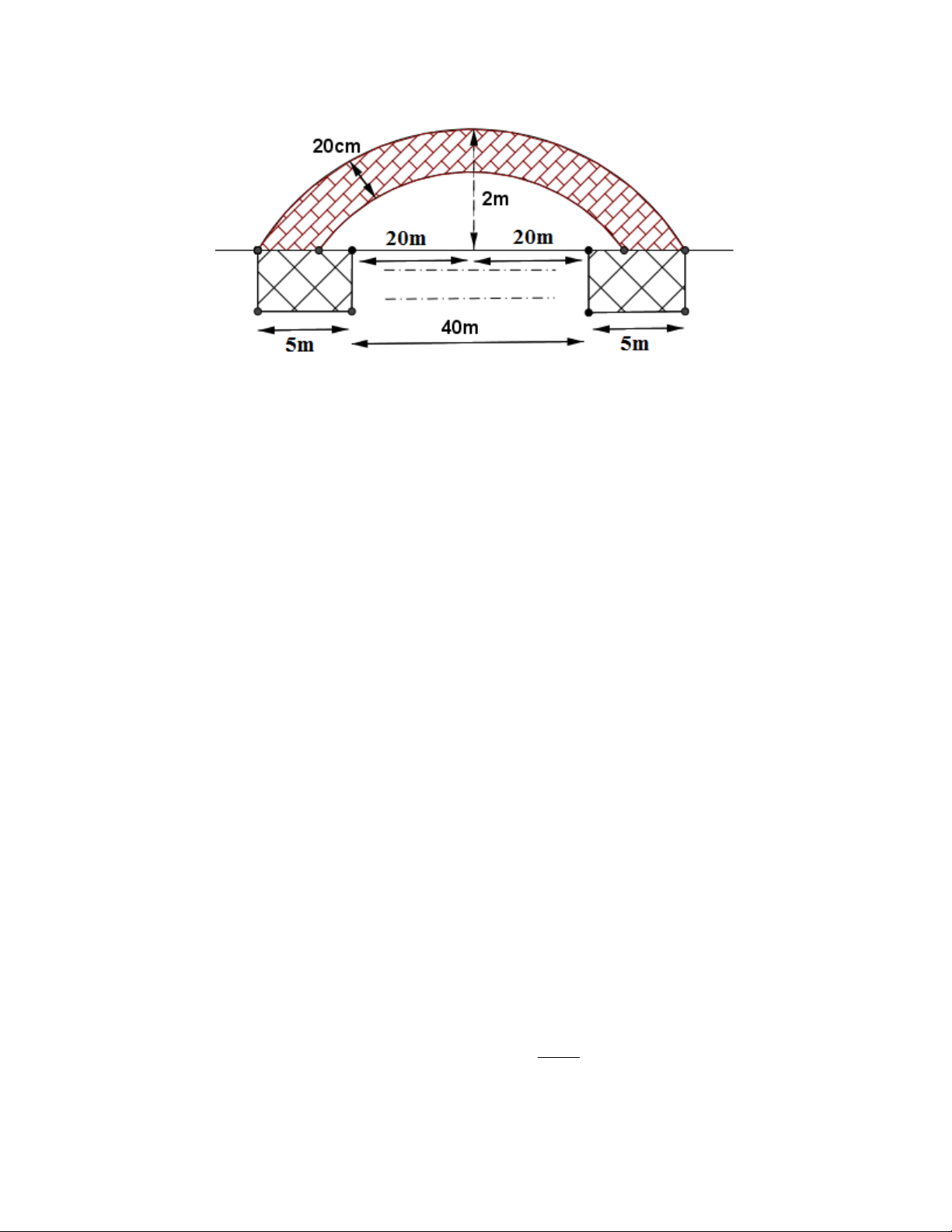
Câu 13. Thành phố định xây cây cầu bắc ngang con sông dài 500m, biết rằng người ta định xây
cầu có 10 nhịp cầu hình dạng parabol,mỗi nhịp cách nhau 40m,biết 2 bên đầu cầu và giữa mối
nhịp nối người ta xây 1 chân trụ rộng 5m. Bề dày nhịp cầu không đổi là 20cm. Biết 1 nhịp cầu
như hình vẽ. Hỏi lượng bê tông để xây các nhịp cầu là bao nhiêu (bỏ qua diện tích cốt sắt trong mỗi nhịp cầu)
Trần Thông sưu tầm và biên soạn
Facebook: Hội Toán Bắc Nam
Tài liệu ôn tập giải tích 12 học kỳ II A. 3 20m B. 3 40m C. 3 50m D. 3 100m
Câu 14. Một ô tô đang chuyển động với vận tốc am / s thì người lái đạp phanh. Sau khi đạp
phanh ô tô chuyển động chậm dần đều với vận tốc vt  a  40tm / s (t là khỏang thời gian
tính bằng s kể từ lúc đạp phanh). Kể từ lúc đạp phanh đến khi dừng hẳn ô tô đi được quảng
đường dài 3m.Tìm giá trị của a. A. a  10 B. a  15 C. a  20 D. a  40
Câu 15. Một người lái xe ô tô đang chạy với vận tốc 20 m/s thì nhìn thấy biển giới hạn tốc độ,
người lái đạp phanh; từ thời điểm đó, ôtô chuyển động chậm dần đều với vận tốc v t   4
t  20m / s trong đó t là khoảng thời gian tính bằng giây, kể từ lúc bắt đầu đạp phanh.
Hỏi sau khi đạp phanh, từ lúc vận tốc còn 15m/s đến khi vận tốc của người còn 10 m/s thì ô tô đã
di chuyển được quãng đường bao nhiêu mét? A. 37,5 B. 150 C. 15,625 D. 21,875
Câu 16. Một lực có độ lớn 40 N (newton) cần thiết để kéo căng một chiếc lò xo có độ dài tự
nhiên 10 cm lên 15 cm. Biết rằng theo định luật trong Vật lý, khi một chiếc lò xo bị kéo căng
thêm (đơn vị độ dài) so với độ dài tự nhiên của lò xo thì lò xo trì lại (chống lại) với một lực cho
bởi công thức , trong đó là hệ số đàn hồi (hoặc độ cứng) của lò xo. Hãy tìm công sinh ra khi kéo
lò xo có độ dài từ 15 cm đến 18 cm ? (kí hiệu là đơn vị của công). A. 1,56 j B. 0,94 j C. 1, 78 j D. 3,96 j
Câu 17 Một xe máy đang chuyển động với vận tốc 10m/s thì lái xe bất ngờ tăng tốc sau 15s xe
máy đạt vận tốc 15m / s  . Hỏi quảng đường vật đi được trong khoảng thời gian 30 giây kể từ
lúc bắt đầu tăng tốc ? A. 270 m B. 450m C. 360m D. 540m
Câu 18. Khi một chiếc lò xo có độ dài tự nhiên 0,15m bị kéo căng thêm x(m) thì chiếc lò xo
chống trì lại với một lực là f x  800x . Biết rằng theo định luật trong Vật lý, khi một chiếc lò xo
bị kéo căng thêm (đơn vị độ dài) so với độ dài tự nhiên của lò xo thì lò xo trì lại (chống lại) với
một lực cho bởi công thức , trong đó là hệ số đàn hồi (hoặc độ cứng) của lò xo. Hãy tìm công
sinh ra khi kéo lò xo có độ dài từ 15 cm đến 18 cm ? (kí hiệu là đơn vị của công). A. 0,36 j B. 0, 72 j C. 36 j D. 72 j 2 t  4
Câu 19. Một vật chuyển động với vận tốc v t   1, 2 
m / s . Hỏi rằng trong 20s đầu 3  t
tiên vật di chuyển được bao nhiêu mét ?
Trần Thông sưu tầm và biên soạn
Facebook: Hội Toán Bắc Nam
Tài liệu ôn tập giải tích 12 học kỳ II A. 189 B. 190 C. 191 D. 192
Câu 20. Một bác thợ xây đang bơm nước vào bể chứa. Gọi h t (
cm) là mức nước ở bồn chứa sau
khi bơm nước được t giây. Biết rằng 2 h' t 3at
bt và lúc đầu bồn không chứa nước. Sau 5s
thể tích nước trong bể là 3
150m , sau 10s thể tích nước trong bể là 3
1100m .Tìm mức nước ở bồn
sau khi bơm được 20 giây (làm tròn kết quả đến hàng phần trăm) A. 3 8400m B. 3 2200m C. 3 4200m D. 3 600m
Câu 21. Người ta cần đúc một chiếc chuông cao 4m và bán kính miệng chuông là 2 2m . Giả sử
khi cắt chuông bằng một mặt phẳng qua trục của nó người ta thu được thiết diện có đường viền
là một phần parabol. Tính thể tích quả chuông cần đúc. A. 6 B. 12 C. 3 2 D. 16
Câu 22. Dòng điện xoay chiều hình sin chạy qua một đoạn mạch LC có biểu thức có biểu thức 
cường độ là i  I cos( t   )A o
. Biết i q ' với q là điện tích tức thời ở tụ điện. Tính từ lúc t = 2 
0, điện lượng chuyển qua tiết diện thẳng của dây dẫn của đoạn mạch đó trong thời gian bằng  là bao nhiêu?  2I I  2Io A. o . B. o . C.0 D. .   2 
Câu 23. Trong kinh tế học, thặng dư tiêu dùng của hàng hóa được tính bằng công thức a I   ( p x)  P  .d .
x Với p(x) là hàm biểu thị biểu thị giá mà một công ty đưa ra để bán được x 0
đơn vị hàng hóa. a là số lượng sản phẩm đã bán ra, P p(a) là mức giá bán ra ứng với số lượng sản phẩm là a. Cho 2
p  1200  0, 2x  0, 0001x , (đơn vị tính là USD) Tìm thặng dư tiêu dùng
khi số lượng sản phẩm bán là 500 A. 33333,3 USD B. 1108333,3 USD C. 570833,3 USD D.5000 USD
Câu 24. Một chất điểm A từ trạng thái nghỉ chuyển động với vận tốc nhanh dần đều. 8 giây sau
nó đạt đến vận tốc 6m/s. Từ thời điểm đó nó chuyển động đều. Một chất điểm B khác xuất phát
từ cùng vị trí với A nhưng chậm hơn nó 12 giây với vận tốc nhanh dần đều và đuổi kịp A sau 8
giây (kể từ lúc B xuất phát). Tìm vận tốc của B tại thời điểm đó. A. 4m/s B. 20m/s C. 24m/s D. 30m/s
Câu 25. Một Bác thợ gốm làm một cái lọ có dạng khối tròn xoay được tạo thành khi quay hình
phẳng giới hạn bởi các đường y x 1và trục Ox quay quanh trục Ox biết đáy lọ và miệng lọ
có đường kính lần lượt là 2dm và 4dm. Tính thể tích cái lọ. 15 14 15 A. 2 8 dm B. 3  dm C. 2  dm D. 2 dm 2 3 2
Câu 26. Một tên lửa A xuất phát từ vị trí T, chuyển động thẳng nhanh dần đều; sau 8 giây nó đạt
vận tốc 6km/s. Từ thời điểm đó nó chuyển động thẳng đều. Sau 12 giây kể từ lúc tên lửa A được
bắn đi người ta bắn tên lửa B cho nó chuyển động thẳng nhanh dần đều. Sau 8 giây kể từ khi
xuất phát tên lửa B đuổi kịp tên lửa A. Tìm vận tốc tên lửa B tại thời điểm đuổi kịp tên lửa A. A. 24000m/s B. 16000m/s C. 24km/s D. 8km/s
Câu 27. Mật độ dân số cách trung tâm thành phố X một khoảng r km là   0,1 5000.   r D r e . Hỏi
có khoảng bao nhiêu người sống cách trung tâm thành phố 3 km.
Trần Thông sưu tầm và biên soạn
Facebook: Hội Toán Bắc Nam
Tài liệu ôn tập giải tích 12 học kỳ II A. 116038 B. 117000 C. 117 D. 116,038
Câu 28. Một Bác thợ gốm làm một cái lọ có dạng khối tròn xoay được tạo thành khi quay hình
phẳng giới hạn bởi các đường y x 1và trục Ox quay quanh trục Ox biết đáy lọ và miệng lọ
có đường kính lần lượt là 2dm và 4dm. Tính thể tích cái lọ. 15 14 15 A. 2 8 dm B. 3  dm C. 2  dm D. 2 dm 2 3 2
Câu 29. Một Bác thợ gốm làm một cái lọ có dạng khối tròn xoay được tạo thành khi quay hình
phẳng giới hạn bởi các đường y x 1và trục Ox quay quanh trục Ox biết đáy lọ và miệng lọ
có đường kính lần lượt là 2dm và 4dm. Tính thể tích cái lọ. 15 14 15 A. 2 8 dm B. 3  dm C. 2  dm D. 2 dm 2 3 2
Câu 30. Một Bác thợ gốm làm một cái lọ có dạng khối tròn xoay được tạo thành khi quay hình
phẳng giới hạn bởi các đường y x 1và trục Ox quay quanh trục Ox biết đáy lọ và miệng lọ
có đường kính lần lượt là 2dm và 4dm. Tính thể tích cái lọ. 15 14 15 A. 2 8 dm B. 3  dm C. 2  dm D. 2 dm 2 3 2 B. SỐ PHỨC
PHẦN 1: TÓM TẮT LÝ THUYẾT 1.Đơn vị ảo. Số i mà 2 i  1
 gọi là đơn vị ảo.
2.Định nghĩa số phức
Số phức (dạng đại số): z a bi ( , a b
, i là đơn vị ảo); a được gọi là phần thực và b là phần
ảo của số phức z.
z là số thực khi và chỉ khi phần ảo b = 0;
z là số phức khi và chỉ khi phần thực a = 0. a a '
Hai số phức bằng nhau: a bi a ' b 'i (a, ,
b a ',b ' )   b   b'
Biểu diễn hình học: Số phức z a bi ( ,
a b  ) được biểu diễn bởi điểm M ( ; a ) b hoặc u( ; a b)
trong mặt phẳng tọa độ Oxy (mặt phẳng phức)
3.Số phức liên hợp
Số phức z a bi ( ,
a b  ) . Ta gọi số phức z a bi là số phức liên hợp của z.
Chú ý: z z; z z '  z z ' ; zz '  z z ' ; z là số thực  z z ; z là số ảo  z  z Nhận xét:
+ Số phức liên hợp của z lại là z , tức là z z . Do đó ta còn nói z và z là hai số phức liên
Trần Thông sưu tầm và biên soạn
Facebook: Hội Toán Bắc Nam
Tài liệu ôn tập giải tích 12 học kỳ II hợp với nhau.
+ Hai số phức là liên hợp với nhau khi và chỉ khi các điểm biểu diễn của chúng đối xứng nhau qua trục Ox. Tính chất:
i, Với mọi z , z
ta có: z z z z ; z .z z .z 1 2 1 2 1 2 1 2 1 2 ii, z
  , z a bi ( , a b
), số z.z luôn là một số thực và 2 2 .
z z a b
4.Phép cộng và trừ hai số phức
Phép cộng và trừ hai số phức được thực hiện theo quy tắc cộng, trừ hai đa thức.Tổng của hai số
phức z a b i , z a b i ( a ,b , a ,b
) là số phức z z  (a a )  (b b )i . 1 1 1 2 2 2 1 1 2 2 1 2 1 2 1 2
Tính chất của phép cộng số phức:
i, (z z )  z z  (z z ) với mọi z , z , z  1 2 3 1 2 3 1 2 3
ii, z z z z với mọi z , z  1 2 2 1 1 2
iii, z  0  0  z z với mọi z
iv, Với mỗi số phức z a bi ( , a b
), nếu kí hiệu số phức a bi là z thì ta có:
z  (z)  z z  0 . Số z được gọi là số đối của số phức z .
Hiệu của hai số phức z a b i , z a b i ( a ,b , a ,b
) là tổng của hai số phức z 1 1 1 2 2 2 1 1 2 2 1
và z , tức là: z  (z )  z z  (a a )  (b b )i . 2 1 2 1 2 1 2 1 2
Ý nghĩa hình học của phép cộng và phép trừ số phức:
Mỗi số phức z a bi ( , a b
) được biểu diễn bởi M ( ; a )
b cũng có nghĩa là véc tơ OM .
Khi đó nếu u ,u theo thứ tự biểu diễn số phức z , z thì: 1 2 1 2
+ u u biểu diễn số phức z z 1 2 1 2
+ u u biểu diễn số phức z z 1 2 1 2
5.Phép nhân hai số phức
Phép nhân hai số phức được thực hiện theo quy tắc nhân hai đa thức, ở đây chú ý i là đơn vị ảo.
Tích của hai số phức z a b i , z a b i ( a ,b , a ,b  ) là số phức: 1 1 1 2 2 2 1 1 2 2
z .z a a b b  (a b a b )i . 1 2 1 2 1 2 1 2 2 1
Nhận xét: + Với mọi số thực k và mọi số phức z a bi ( , a b  ), ta có:
kz k(a bi)  ka kbi + 0.z  .
z 0  0 với mọi z  .
*Tính chất của phép nhân số phức:
i, z z z z với mọi z , z  ii, .
z 1 1.z z với mọi z  1 2 2 1 1 2
Trần Thông sưu tầm và biên soạn
Facebook: Hội Toán Bắc Nam
Tài liệu ôn tập giải tích 12 học kỳ II
iii, (z z ).z z .(z z ) với mọi z , z , z  1 2 3 1 2 3 1 2 3
iv, z .(z z )  z z z z với mọi z , z , z  1 2 3 1 2 1 3 1 2 3
6.Môđun của số phức
Môđun của số phức z a bi ( ,
a b  ) là một số ký hiệu là 2 2
| z | a b z z |  OM |
+| z | 0 với mọi z thuộc C và | z | 0  z  0 . +| zz ' | |
z || z ' |; | z z ' | |
z |  | z ' | với mọi số phức z, z’.
7.Phép chia hai số phức
Số phức nghịch đảo của  1 z (z khác 0): 1 zz . 2 | z | Thương của z '  z ' z z' z
z cho z’ ( z khác 0): 1  z ' z   2 z | z | z z   Với z ' z ' z ' z ' | z ' | z khác 0,
 w  z '  wz ,    ,  zz z z | z |
8.Căn bậc hai của số phức
z là một căn bậc hai của số phức w khi và chỉ khi 2 w  z . 2 2
x y a
z x yi ( ,
x y  ) là căn bậc hai của số phức w  a bi ( , a b  )   . 2xy b
Số 0 có đúng một căn bậc hai là 0.
Số phức khác 0 có hai căn bậc hai là hai số đối nhau.
Hai căn bậc hai của số thực a dương là  a .
Hai căn bậc hai của số thực âm là i a
9.Phƣơng trình bậc hai của số phức Phương trình bậc hai 2
Az Bz C  0 (A, B, C là các số phức cho trước, A khác 0): 2
  B  4AC   + Nếu   B
0 phương trình có hai nghiệm phân biệt: z
với  là một căn bậc hai của 1,2 2A  .  +Nếu   B
0 : phương trình có một nghiệm kép là z  . 2 A
10.Dạng lƣợng giác của số phức
Trần Thông sưu tầm và biên soạn
Facebook: Hội Toán Bắc Nam
Tài liệu ôn tập giải tích 12 học kỳ II
Cho số phức z a bi ( ,
a b  ) , z khác 0. Số có dạng: r( o
c s  i sin) (r > 0) là dạng lượng giác của a b z khi và chỉ khi 2 2 r a b , os c
  ,sin  .  là một acgumen của z, r r   ( , Ox OM )
Nhân chia số phức dƣới dạng lƣợng giác
Nếu z r( o
c s  i sin), z '  r '( o
c s ' i sin ') thì
zz '  rr ' o c (
s    ')  i sin(   ') z r   o c (
s   ')  i sin(  ') z ' r '
Công thức Moa-vrơ: Với n là số nguyên dương, thì n ( os  i sin) n r c
r (cos n  i sin n)
Căn bậc hai của số phức dƣới dạng lƣợng giác.  
Các căn bậc hai của số phức z có dạng lượng giác r( o
c s  i sin) là r ( o c s  i sin ), và 2 2      r ( o c s  i sin )  2[ o c s(  )  i sin(  )] 2 2 2 2
PHẦN 2: BÀI TẬP MINH HỌA
Dạng 1: Thực hiện các phép toán 3 1
Bài 1: Cho số phức z
i . Tìm các số phức sau: z z z3 2 2 ; ; ; 1 z z 2 2 Hƣớng dẫn: 3 1 3 1 z   i z   i 2 2 2 2 2  3 1  3 1 3 1 3 2 2 z  
i    i i   i 2 2 4 4 2 2 2   3 3 2              z  2 3 3 3 1 3 3 1 3 1 1    i      3  i  3 iii        2 2 2 2        2  2  2   2  3  3 1 3 2 1 z z   i 2 2 4  3i 1 i
Bài 2: Tính giá trị của các biểu thức A   1 i 4  3i
43i1i 1i43i 1 7i 17i 27 161
Hƣớng dẫn: A        i
1 i1 i 43i4 3i 2 25 50 50
Bài 3: Tìm phần thực, phần ảo và tính mô đun của số phức z biết:
Trần Thông sưu tầm và biên soạn
Facebook: Hội Toán Bắc Nam
Tài liệu ôn tập giải tích 12 học kỳ II 11 8 1 i   2i i z       1 i  1 i Hƣớng dẫn: 11 8 1 i   2i    i      1 i8 11  16  i 1 i  1 i  16  iz   1
 16i z  1  16i i
Vậy z có phần thực bằng 1  ; phần ảo bằng 16; 2 2 z  ( 1  ) 16  257
1i  3 i5 10
Bài 4: Tính giá trị của các biểu thức A   1   i 310
Hƣớng dẫn: Ta có:
1i  1i 5 10 2   2  i5 4.  32  i .i  32  i
 3i5  3i3 3i2   2 3
3 3  9i  3 3i i  2
3  2 3i i
 8i2  2i 3  16  3 16i
 i   i   i  3 10 10 3
 i  3 1 3 1 3 1 3 1 3 8 1 i 3 3
 2 .i16 .i1 i 3
Thay vào biểu thức A ta có A     . 8   1 3 1 i 3 7 1i  2
Bài 5: Tìm các số thực x, y thoả mãn: (3x y)
 (y  2)(x i)  1  9  23i   1 i  2 1 t 3 ( 1) 1 1 Hƣớng dẫn: 2
Đặt t  1 x dt  2xdx I dt  . 2  t5 5 4 1 2 52  2013i 52  2013i
Bài 6: Chứng minh rằng số phức z   (3 1)(79  7i) 10(23  là số thuần ảo 10i) Hƣớng dẫn:   3 2 dt 1 1 6 1 t7 t8 1
Đặt t  1 x dt  3
x dx dx   I t (1 t d ) t       . 3x2 3 3  7 8  168 0
Dạng 2: Xác định số phức
Trần Thông sưu tầm và biên soạn
Facebook: Hội Toán Bắc Nam
Tài liệu ôn tập giải tích 12 học kỳ II 2(1 2i)
Bài 1: Tìm số phức z biết: (2  i).z   7  8i 1 i
2(1 i)(1 i)
Hƣớng dẫn: ta có (2  i).z   7  8i 2   iii
(2  i).z  4  4 7 (4 7 )(2 ) 7i z   z
z  3 2i 2  i 5
(z 1).(2  i) 3  i
Bài 2: Tìm số phức z biết:  z  2i 2
Hƣớng dẫn: Điều kiện z  2  i . Khi đó
(1)  2(z 1)(2  i)  (3  i)(z  2i) 2
 (z 1)(4  2i)  3z  6i iz  2i
 (1 3i)z  2i  4 2i  4
(2i  4)(1 3i) 1  7  z     i 1 3i 10 5 5 1  7  z
i (thỏa mãn điều kiện). 5 5
Bài 3: Tìm số phức z biết: | z | 5 và 2
(z i) là số ảo. Hƣớng dẫn:
Gọi số phức z cần tìm dạng: z  a  bi , a, b   2 2 | z |
a b . Từ giả thiết ta có: 2 2
| z | 5  a b  5 (1) 2 2 2 2
(z i)  (a bi i)  a  (b 1)  2a(b 1)i Để 2
(z i) là số ảo thì 2 2
a  (b 1)  0 (2)
Từ (1) và (2) ta có hệ phương trình: 2 2 a  5  b 2 2
a b  5  a  2  a  1    b 1   ;  2 2
a  (b 1) b   1 b   2  b  2 
Vậy số phức cần tìm là: z  2   ;i z  1   2i . 1 10
Bài 4: Tìm số phức z biết z  2  i z 1 2i và  z 10
Hƣớng dẫn: Ta có:
Trần Thông sưu tầm và biên soạn
Facebook: Hội Toán Bắc Nam
Tài liệu ôn tập giải tích 12 học kỳ II
1i  1i 5 10 2   2  i5 4.  32  i .i  32  i
 3i5  3i3 3i2   2 3
3 3  9i  3 3i i  2
3  2 3i i
 8i2  2i 3  16  3 16i
 i   i   i  3 10 10 3
 i  3 1 3 1 3 1 3 1 3 8 1 i 3 3
 2 .i16 .i1 i 3
Thay vào biểu thức A ta có A     . 8   1 3 1 i 3 9
Bài 5: Tìm số phức z biết: z  3i  1 i z và z  là số thuần ảo z 2 1 t 3 ( 1) 1 1 Hƣớng dẫn: 2
Đặt t  1 x dt  2xdx I dt  . 2  t5 5 4 1 2
Dạng 3: Giải phƣơng trình trên tập số phức
Bài 1: Giải các phương trình 2
z  2z  5  0 trên tập hợp số phức
Hƣớng dẫn: Ta có ' 2
  4  4i z  1   2i
Bài 2: Giải các phương trình 2
z  (1 3i)z  2(1 i)  0 trên tập hợp số phức
Hƣớng dẫn: Ta có 2 2
  (1 3i)  8(1 i)  2i  (1 i) nên phương trình có nghiệm là:  3i 11 i z   z  2 2 i    3i 11 i  z i 1 z   2
Bài 3: Giải các phương trình 3
z  8  0 trên tập hợp số phức. z  2   Hƣớng dẫn: 3 2
z  8  0  (z  2)(z  2z  4)  0  z  1 3i  z 1 3i
Bài 4: Giải các phương trình 4 4
(z  3)  (z  5)  2 trên tập hợp số phức
Hƣớng dẫn: Đặt t  z  4 , khi đó phương trình trở thành: 4 4 4 2
(t 1)  (t 1)  2  t  6t  0
Trần Thông sưu tầm và biên soạn
Facebook: Hội Toán Bắc Nam
Tài liệu ôn tập giải tích 12 học kỳ II 2 t  0 t  0     2 t  6  0 t   6i
+) Với t  0  z  4 
+) Với t  6i z  4   6i
+) Với t  - 6i z  4   6i 2  z i
Bài 5: Giải các phương trình  1  
trên tập hợp số phức  z i
Hƣớng dẫn: Điều kiện: z i , khi đó phương trình tương đương với: 2
 z i   z i z i   1       4 1 1  z i   z i     2 z i z i  1         2 z i z i z iz i     1  i   i      z i z i
 z i
z i z i  z  0
z i i z   
z  1 (thỏa mãn điều kiện) 
z i  (z i)i   z  1  
z i  (z i)i
Dạng 4: Tìm tập hợp điểm biểu diễn z
Bài 1: Trên mặt phẳng toạ độ, tìm tập hợp điểm biểu diễn số phức z thoả mãn  3 z i Hƣớng dẫn:
Gọi z x yi ( ,
x y R)  M ( ;
x y) biểu diễn cho số phức z trong mặt phẳng toạ độ. z Ta có 2 2 2 2
 3  x yi  3 x  (y 1)i x y  9x  9(y 1) z i 2 2  9   3  2 2 2
 8x  8y 18y  9  0  x y        8   8   9  3
Vậy tập hợp các điểm M là đường tròn tâm I 0; 
 và bán kính R   8  8
Bài 2: Trên mặt phẳng toạ độ, tìm tập hợp điểm biểu diễn số phức z thoả mãn
z  2  4i z  2i Hƣớng dẫn:
Gọi z x yi ( ,
x y R)  M ( ;
x y) biểu diễn cho số phức z trong mặt phẳng toạ độ.
Ta có z  2  4i z  2i
(*)  (x  2)  ( y  4)i x  ( y  2)i 2 2 2 2
 (x  2)  (4  y)  x  (y  2)  y  x  4
Tập hợp M là đường thẳng có phương trình y  x  4
Trần Thông sưu tầm và biên soạn
Facebook: Hội Toán Bắc Nam
Tài liệu ôn tập giải tích 12 học kỳ II
Bài 3: Trên mặt phẳng toạ độ, tìm tập hợp điểm biểu diễn số phức z thoả mãn
2 z i z z  2i . Hƣớng dẫn:
Đặt: z x yi ( ,
x y R)  z có điểm biểu diễn trên mặt phẳng phức là Mx; y. 2 x
Ta có 2 z i z z  2i  2 x  ( y 1)i  (1 y)i y  4 2 x
Vậy tập hợp điểm M là đường parabol (P) có phương trình y  . 4
Bài 4: Trên mặt phẳng toạ độ, tìm tập hợp điểm biểu diễn số phức z thoả mãn
z i z i  4 Hƣớng dẫn:
Đặt: z x yi ( ,
x y R)  z có điểm biểu diễn trên mặt phẳng phức là Mx; y. Ta có 2 2 2 2
z i z i  4 
x  ( y 1) 
x  ( y 1)  4 (*) Đặt F (0; 1  ) ;F (0;1) 1 2
(*)  MF MF  4  F F  2 1 2 1 2
Suy ra tập hợp M là elíp (E) có 2 tiêu điểm là F , F . 1 2 2 2 x y Gọi (E) có phương trình 2 2 2  1 (0  a  ;
b b a c ) 2 2 a b
MF MF  2aa  2 Ta có 1 2 2 2 2   
b a c  5 F F  2c c   1 1 2 2 2 x y Vậy (E) có phương trình  1 4 5
Bài 5: Trên mặt phẳng toạ độ, tìm tập hợp điểm biểu diễn số phức z thoả mãn 2 2
z  (z )  4 Hƣớng dẫn:
Đặt: z x yi ( ,
x y R)  z có điểm biểu diễn trên mặt phẳng phức là Mx; y.  1 y   x Ta có 2 2
z  (z )  4  4xyi  4  4 xy  4  xy  1   1  y    x 1 1
Vậy tập hợp điểm M là đường hybebol (H) có phương trình là y  và y   x x
Dạng 5: Bài toán cực trị
Trần Thông sưu tầm và biên soạn
Facebook: Hội Toán Bắc Nam
Tài liệu ôn tập giải tích 12 học kỳ II
Bài 1: Trong các số phức z thoả mãn điều kiện z 1 5i z  3  i , tìm số phức có môđun nhỏ nhất Hƣớng dẫn:
Gọi z x yi  ;x y  2 2 2 2
z 1 5i z  3  i  (x 1)  ( y  5)  (x  3)  ( y 1)
x  3y  4  0  x  4  3y 2  6  8 2 10 2 2 2 2 2 z
x y  (4  3y)  y  10 y  24 y 16  10 y       5  5 5 6 2
Đẳng thức xảy ra khi y   x  5 5 2 10 2 6
Vậy z đạt giá trị nhỏ nhất bằng khi z   i 5 5 5 2 6 Vậy z
i là số phức cần tìm 5 5
Bài 2: Trong các số phức z có phần thực, phần ảo không âm và thoả mãn: z  3
 1. Tìm số phức z sao cho biểu thức sau đạt giá trị lớn nhất, nhỏ nhất. z 1 2i 2 2
P z z   2 2
z z .i
. z(1 i)  z (1 i) Hƣớng dẫn:
Điều kiện: z  1 2i
Gọi z x yi  * ; x y    z  3 z  3 1 
1  z  3  z 1 2i z 1 2i z 1 2i 2 2 2 2
(x  3)  y  (x 1)  ( y  2)  x y  1
(luôn thoả mãn điều kiện vì x 1; y  2
 không thoả mãn phương trình) 2 2 2 2
z x yi z z  4x .
y i z z  4xy (vì ; x y không âm)  2 2 z z  2 2
.i   4xy z z  4xy
z(1 i)  z (1 i)  2x  2y Do đó 2 2 2 2
P  16x y  4x .
y (2x  2y)  16x y  8xy 2  x y  1  1
Đặt t xy  0  t     , ta có 2
P  16t  8t;t  0;    2  4  4  1  Xét hàm số 2
f (t)  16t  8t liên tục trên 0;    4
Trần Thông sưu tầm và biên soạn
Facebook: Hội Toán Bắc Nam
Tài liệu ôn tập giải tích 12 học kỳ II 1
f '(t)  32t  8t; f '(t)  0  t  0  t   (loại) 4  1  33 33 1 f (0)  0; f
 max f (t) 
t  ;min f (t)  0  t  0    1  1  4  16  0; 16 4 0;      4  4 1 1
x  0; y 1 Khi t
x y  ; Khit  0   2 2
x 1; y  0 33 1 1
Vậy P đạt giá trị lớn nhất bằng khi z   i 16 2 2
P đạt giá trị nhỏ nhất bằng 0 khi z  1 z  0
Bài 3: Trong các số phức z thoả mãn z  3  4i  4 . Tìm giá trị lớn nhất, giá trị nhỏ nhất của z . Hƣớng dẫn:
Gọi z x yi  ;
x y    M ( ;
x y) biểu diễn cho số phức z trong hệ toạ độ Oxy 2 2 2 2
z  3  4i  4  (x  3)  ( y  4)  4  (x  3)  ( y  4)  16
Vậy điểm M biểu diễn cho số phức z thuộc đường tròn (T) có tâm I (3; 4  ) , bán kính R = 4. 2 2 z
x y OM ; OI  5  R nên O nằm ngoài đường tròn (T)
z lớn nhất , nhỏ nhất khi OM lớn nhất, nhỏ nhất khi M di dộng trên (T)
Với điểm M bất kì trên (T), ta có:
AM IM IA IB IA AB . Đẳng thức xảy ra khi M B
AM AI IM AI IC AC . Đẳng thức xảy ra khi M C
Đường thẳng OI cắt đường tròn (T) tại hai điểm phân biệt  3 4   27 36  A ;  ; B ; 
OA 1;OB  9      5 5   5 5 
Với M di động trên (T), ta có: OA OM OB 1 OM  9 1  z  9
 OM nhỏ nhất khi M trùng với A; OM lớn nhất khi M trùng với B 3 4 27 36
Vậy z nhỏ nhất bằng 1 khi z   i ; z lớn nhất bằng 9 khi z   i 5 5 5 5
Bên cạnh đó bạn đọc có thể tham khảo thêm cách giải sau:
Gọi z x yi  ;
x y    M ( ;
x y) biểu diễn cho số phức z trong hệ toạ độ Oxy   3 4i  ( A 3; 4
 ) biểu diễn cho số phức 
z OM ;   OA  5; z    AM ; z  3  4i  4  z    4  AM  4
Ta có: OM OA AM  4
  OM OA  4  4
  OA OM  4  OA 1 OM  9  3 4 27 36
1  z  9 ; z  1 khi z
i ; z  9 z   i 5 5 5 5
Trần Thông sưu tầm và biên soạn
Facebook: Hội Toán Bắc Nam
Tài liệu ôn tập giải tích 12 học kỳ II 3 4 27 36
Vậy z nhỏ nhất bằng 1 khi z   i ; z lớn nhất bằng 9 khi z   i 5 5 5 5
Bài 4: Trong các số phức z thoả mãn điều kiện z (z  2  4i) là một số ảo, tìm số phức z sao
cho  z 1 i có môđun lớn nhất. Hƣớng dẫn:
Gọi z x yi  ;
x y    M ( ;
x y) biểu diễn cho số phức z trong hệ toạ độ Oxy
z (z  2  4i)  (x yi)(x  2)  (y  4)i  (
x x  2)  y( y  4)   (
x y  4)  y(x  2)i
z (z  2  4i) là một số ảo 2 2 2 2
x(x  2)  y(y  4)  0  x y  2x  4y  0  (x 1)  (y  2)  5
M biểu diễn cho z thuộc đường tròn (T) có tâm I( 1
 ;2) , bán kính R  5 2 2
  z 1 i  (x 1)  (y 1)i  (x 1)  (y 1)  AM với ( A 1;1)
IA  5  A (T )
Vì M là điểm di động trên (T) nên AM lớn nhất  AM là đường kính của (T)
 M đối xứng với A qua I  I là trung diểm của AM  M( 3  ;3)  z  3
  3i    4   2i
Vậy  lớn nhất bằng 2 5 khi z  3   3i
Bài 5: Cho các số phức z ; z thoả mãn: z 1
 ; z z  (1 i)  6  2i là một số thực. Tìm số 1 2  2  1 2 phức 2
z ; z sao cho P z
z z z z đạt giá trị nhỏ nhất. 2  1 2 1 2 1 2 Hƣớng dẫn:
Gọi z a bi; z c di ; ; a ; b ; c d   M ( ; a ) b , N( ;
c d) lần lượt biểu diễn cho z ; z 1 2   1 2 trong hệ toạ độ Oxy 2 2 2 2 z  1 
a b  1  a b  1 1
M thuộc đường tròn (T ) có tâm O, bán kính R = 1
z c d ; i 2
  z z  
1i  6 2i  
c di(c 1)  (d 1)i 26i
c(c 1)  d(d 1)  2  c(d 1)  d(c 1)  6i
 là số thực  c(d 1)  d(c 1)  6  0  c d  6  0
N thuộc đường thẳng  : x y  6  0 Ta có d ( ;
O )  1 nên  và (T ) không có điểm chung
z z ac bd  (bc ad ) ;
i z z ac bd  ( b
c ad)i z z z z  2(ac bd) 1 2 1 2 1 2 1 2 2 2 2 2 2
P c d  2(ac bd)  (c a)  (b d) 1  MN 1 (vì 2 2 a b  1)
Gọi H là hình chiếu vuông góc của O trên  : x y  6  0  H(3;3)  2 2 
Đoạn OH cắt đường tròn (T ) tại I  ;  2 2  
Trần Thông sưu tầm và biên soạn
Facebook: Hội Toán Bắc Nam
Tài liệu ôn tập giải tích 12 học kỳ II
Với N thuộc đường thẳng  , M thuộc đường tròn (T ) , ta có:
MN ON OM OH OI IH  3 2 1. Đẳng thức xảy ra khi M I; N H  2 2 P    2
3 2 1 1  18  6 2 . Đẳng thức xảy ra khi z   ;
i z  3  3i 1 2 2 2 2 2
Vậy P đạt giá trị nhỏ nhất bằng 18  3 2 khi z   ;
i z  3  3i 1 2 2 2
PHẦN 3: BÀI TẬP TRẮC NGHIỆM
Câu 1. Cho số phức z a bi . Tìm mệnh đề đúng trong các mệnh đề sau. 2
A. zz  2bi
B. zz  2a C. 2 2
z .z a b D. 2 z z
Câu 2. Tìm số phức liên hợp của số phức za  a bi
A. za  b ai
B. za bi
C. z a  a bi
D. za bi
Câu 3. Cho số phức z a bi . Tìm phần thực của số phức 2 z . A. 2 2 a b B. 2 2 a b
C. a b
D. a b
Câu 4. Tìm số phức liên hợp của số phức: z  1 3i
A. z  3  i B. z  1   3i
C. z  1 3i D. z  1  3i
Câu 5. Tìm mô đun của số phức: z  2  3i A. 13 B. 5 C. 5 D. 2
Câu 6. Tìm mệnh đề sai trong các mệnh đề sau.
A. Số phức z = a + bi được biểu diễn bằng điểm M(a; b) trong mặt phẳng phức Oxy
B. Số phức z = a + bi có môđun là 2 2 a b a  0
C. Số phức z = a + bi = 0   b   0
D. Số phức z = a + bi có số phức đối z‟ = a - bi
Câu 7. Tìm điểm biểu diễn số phức z  1 2i trên mặt phẳng Oxy A. 1; 2   B.  1  ; 2   C. 2;  1  D. 2  ;1
Câu 8. Với giá trị nào của x,y để 2 số phức sau bằng nhau: x  2i  3  yi A.           x 2; y 3 B. x 2; y 3 C. x 3; y 2 D. x 3; y 2
Câu 9. Với giá trị nào của x,y thì  x y  2x yi  3 6i A. x  1  ; y  4 B. x  1  ; y  4 
C. x  4; y  1 
D. x  4; y  1
Câu 10. Cho hai số phức z a bi và z '  a ' b 'i . Tìm phần thực số phức z z '
A. a a ' B. aa '
C. aa ' bb ' D. 2bb '
Câu 11. Cho số phức z  2016  2017i . Tìm điểm biểu diễn của số phức đối của z A. 2016; 2017 B.  2  016;  2017 C.  2
 016; 2017D. 2016;  2017
Câu 12. Cho số phức z    i2 2 3
. Tìm phần thực và phần ảo của số phức z .
A. Phần thực bằng 7
 , Phần ảo bằng 6 2i
B. Phần thực bằng 7 , Phần ảo bằng 6 2
Trần Thông sưu tầm và biên soạn
Facebook: Hội Toán Bắc Nam
Tài liệu ôn tập giải tích 12 học kỳ II
C. Phần thực bằng 7
 và Phần ảo bằng 6 2
D. Phần thực bằng 7 và Phần ảo bằng 6 2i
Câu 13. Cho số phức z  2  3i . Tìm phần thực và phần ảo của số phức 3 z .
A. Phần thực bằng 46 và Phần ảo bằng 9
i B. Phần thực bằng 46  và Phần ảo bằng 9  i
C. Phần thực bằng 46 và Phần ảo bằng 9
i D. Phần thực bằng 46  và Phần ảo bằng 9 
Câu 14. Tính môdun của số phức z    i3 1 A. z  2 2 B. z  2 C. z  0 D. z  2  2 1 3
Câu 15. Cho số phức z   
i . Tìm số phức  2 z 2 2 1 3 1 3 A.   i B.   i C. 1 3i D. 3  i 2 2 2 2
Câu 16. Cho hai số phức z  2  3i và z '  1 2i . Tính môđun của số phức z z ' .
A. z z '  10
B. z z '  2 2
C. z z '  2
D. z z '  2 10
Câu 17. Cho hai số phức z  3  4i và z '  4  2i . Tính môđun của số phức z z '
A. z z '  3
B. z z '  5
C. z z '  1
D. z z '  5
Câu 18. Tìm số phức z thỏa mãn điều kiện 2z iz  2  5i .
A. z  3  4i
B. z  3  4i
C. z  4  3i
D. z  4  3i
Câu 19. Cho số phức z thỏa mãn điều kiện 2z  31 iz 1 9i . Tìm môđun của z. A. 13 B. 82
C. z  1 3i D. z  1  3i
Câu 20. Tìm mô đun của số phức: z  2  3i A. 13 B. 5 C. 5 D. 13
Câu 21. Tìm mệnh đề sai trong các mệnh đề sau.
A. Số phức z = a + bi được biểu diễn bằng điểm M(a; b) trong mặt phẳng phức Oxy
B. Số phức z = a + bi có môđun là 2 2 a b a  0
C. Số phức z = a + bi = 0   b   0
D. Số phức z = a + bi có số phức đối z‟ = a - bi
Câu 22. Tìm số phức nghịch đảo của số phức z  1 3i 1 3 1 3 A. 1     z =  i B. 1 z =  i C. 1
z = 1 + 3i D. 1
z = -1 + 3i 2 2 4 4
Câu 23. Tìm tập hợp các điểm biểu diễn hình học của các số phức z a ai A.       y x B. y 2x C. y x D. y 2x
Câu 24. Tìm tập hợp các điểm biểu diễn hình học của các số phức z  7  bi với b A. x  7 B. y  7
C. y x
D. y x  7
Câu 25. Cho số phức 2
z a a i với a
. Tìm tập hợp điểm biểu diễn của số phức liên hợp của z
Trần Thông sưu tầm và biên soạn
Facebook: Hội Toán Bắc Nam
Tài liệu ôn tập giải tích 12 học kỳ II
A. Đường thẳng y  2x
B. Đường thẳng y  x 1 C. Parabol 2 y x D. Parabol 2 y  x
Câu 26. Tập hợp các điểm trong mặt phẳng biểu diễn cho số phức z thỏa mãn điều kiện
z i  1 có hình dạng như thế nào? A. Đường thẳng B. Đường tròn
C. Đoạn thẳng D. Hình vuông
Câu 27. Tập hợp các điểm trong mặt phẳng biểu diễn cho số phức z thỏa mãn điều kiện
z 1 2i  4 có hình dạng như thế nào? A. Đường thẳng B. Đường tròn
C. Đoạn thẳng D. Hình vuông
Câu 28. Cho hai số phức z a bi và z '  a ' b 'i . Tìm điều kiện giữa , a ,
b a ', b ' để z z ' là một số thực a, a '
a a '  0
a a '  0
a a '  0 A. B. C. D. b   b'  0  , b b ' b   b' b   b'  0
Câu 29. Cho hai số phức z a bi và z '  a ' b 'i . Tìm điều kiện giữa , a ,
b a ', b ' để z z ' là một số thuần ảo. a, a '
a a '  0
a a '  0
a a '  0 A. B. C. D. b   b'  0  , b b ' b   b' b   b'  0
Câu 30. Cho hai số phức z a bi và z '  a ' b 'i . Tìm điều kiện giữa , a ,
b a ', b ' để . z z ' là một số thực
A. aa ' bb '  0
B. aa ' bb '  0
C. ab ' a 'b  0
D. ab ' a 'b  0
Câu 31. Cho hai số phức z a bi và z '  a ' b 'i . Tìm điều kiện giữa , a ,
b a ', b ' để . z z ' là một số thực
A. aa ' bb '  0
B. aa ' bb '  0
C. ab ' a 'b  0
D. ab ' a 'b  0
Câu 32. Cho hai số phức z a bi và z '  a ' b 'i . Tìm điều kiện giữa , a ,
b a ', b ' để . z z ' là một số thuần ảo
A. aa '  bb '
B. aa '  bb'
C. a ' a '  b b '
D. a ' a '  0
Câu 33. Cho  x i2 2  yi  ,
x y   . Tìm giá trị của x và y
A. x  2 và y  8 hoặc x  2  và y  8 
B. x  3 và y  12 hoặc x  3  và y  12 
C. x  1 và y  4 hoặc x  1  và y  4 
D. x  4 và y  16 hoặc x  4 và y  16 
Câu 34. Cho  x i2 2
 3x yi  ,
x y   . Tìm giá trị của x và y
A. x  1 và y  2 hoặc x  1  và y  2  B. x  1  và y  4
 hoặc x  4 và y 16
Trần Thông sưu tầm và biên soạn
Facebook: Hội Toán Bắc Nam
Tài liệu ôn tập giải tích 12 học kỳ II
C. x  2 và y  5 hoặc x  3 và y  4 
D. x  6 và y  1 hoặc x  0 và y  4
Câu 35. Tìm số phức z, biết: (3  i)z  (2  5i)z  1  0  3i .
A. z  2  3i
B. z  2  3i C. z  2   3i D. z  2  3i
Câu 36. Tìm số phức z, biết: (2  i)z  (5  3i)z  1  7 16i
A. z  3  4i
B. z  3  4i C. z  3   4i D. z  3   4i
Câu 37. Tìm số phức z biết z  5 và phần thực lớn hơn phần ảo một đơn vị.
A. z  4  3i , z  3  4i B. z  4
 3i , z  3   4i 1 2 1 2
C. z  4  3i , z  3   4i D. z  4
 3i , z  3 4i 1 2 1 2
Câu 38. Tìm số phức z biết z  20 và phần thực gấp đôi phần ảo.
A. z  2  i , z  2  i
B. z  2  i , z  2   i 1 2 1 2 C. z  2
  i , z  2  i
D. z  4  2i , z  4   2i 1 2 1 2
Câu 39. Tìm tập hợp các điểm trong mặt phẳng biểu diễn số phức z thỏa mãn điều kiện 2 z là một số thực âm
A. Trục hoành (trừ gốc tọa độ O)
B. Đường thẳng y x (trừ gốc tọa độ O)
C. Trục tung (trừ gốc tọa độ O)
D. Đường thẳng y  x (trừ gốc tọa độ O)
Câu 40. Cho số phức z thõa mãn: z  5  0. Tìm môđun của z. A. 26 B. 5 C.0 D. 5
Câu 41. Tìm mô đun của số phức z  4  i  (2  3i)(1 i) . A. 2 B. 1 C.0 D. -2
Câu 42. Cho x, y là các số thực. Hai số phức z  3  i và z  (x  2y)  yi bằng nhau khi nào ?
A. x  5, y  1 
B. x  1, y  1 C.      x 3, y 0 D. x 2, y 1
Câu 43. Cho x, y là các số thực. Số phức: z  1 xi y  2i bằng 0 khi nào ?
A. x  2, y  1 B. x  2  , y  1  C.       x 0, y 0 D. x 1, y 2
Câu 44. Cho x số thực. Số phức: z x(2  i) có mô đun bằng 5 khi nào ? 1 A. x  0 B. x  2 C. x  1  D. x   2
Câu 45. Cho số phức: z  2  .
i 3 . Tính giá trị biểu thức z.z . A. 1 B. 2 C.3 D. 5
Câu 46. Cho hai số phức: z  1 2i , z  2
 i Tính giá trị biểu thức z .z . 1 2 1 2
Trần Thông sưu tầm và biên soạn
Facebook: Hội Toán Bắc Nam
Tài liệu ôn tập giải tích 12 học kỳ II A. 5 B. 2 5 C.25 D. 0 2 5
Câu 47. Cho số phức z có phần ảo gấp hai phần thực và z 1  . Tính mô đun của z. 5 A. 26 B. 5 C.0 D. 5
Câu 48. Cho z có phần thực là số nguyên và z  2z  7
  3i z .Tính môđun của số phức: 2
w  1 z z . A. w  37 B. w  457 C. w  425 D. w  445
Câu 49. Cho z có phần thực là số nguyên và z  3z  1
 1 6i z . Tính môđun của số phức: 2
w  1 z z .. A. w  23 B. w  5 C. w  443 D. w  445
Câu 50. Giả sử M(z) là điểm trên mặt phẳng phức biểu diễn số phức z. Biết tập hợp các điểm
M(z) thoả mãn điều kiện sau đây: z 1 i =2 là một đường tròn. Tìm tâm và bán kính đường tròn đó. A. Có tâm  1  ;   1 và bán kính là 2
B. Có tâm 1;   1 và bán kính là 2 C. Có tâm  1  ;  1 và bán kính là 2
D. Có tâm 1;   1 và bán kính là 2
Câu 51. Giả sử M(z) là điểm trên mặt phẳng phức biểu diễn số phức z. Biết rằng tập hợp các
điểm M(z) thoả mãn điều kiện sau đây: 2  z  1 i là một đường thẳng. Viết phương trình đường thẳng đó. A. 4
 x  2y  3  0
B. 4x  2y  3  0
C. 4x  2y  3  0 D. 2x  y  2  0
Câu 52. Giả sử M(z) là điểm trên mặt phẳng phức biểu diễn số phức z. Biết rằng tập hợp các
điểm M(z) thoả mãn điều kiện sau đây: |z + z +3|=4 là hai đường thẳng. Viết phương trình
những đường thẳng đó. 1 7 1 7 A. x  và x B. x   và x   2 2 2 2 1 7 1 7 C. x  và x   D. x   và x  2 2 2 2
Câu 53. Giả sử M(z) là điểm trên mặt phẳng phức biểu diễn số phức z. Biết rằng tập hợp các
điểm M(z) thoả mãn điều kiện sau đây: |z + z + 1 - i| = 2 là hai đường thẳng. Viết phương trình
những đường thẳng đó.
Trần Thông sưu tầm và biên soạn
Facebook: Hội Toán Bắc Nam
Tài liệu ôn tập giải tích 12 học kỳ II 1 3 1 3 1   3 1 3 A. y  và y B. y  và y  2 2 2 2 1 3 1 3 1   3 1   3 C. y  và y   D. y  và y  2 2 2 2
Câu 54. Tìm số phức z thỏa mãn: z  2  i  10 và . z z  25 .
A. z  3  4i hoặc z  5 B. z  3
  4i hoặc z  5 
C. z  3  4i hoặc z  5
D. z  4  5i hoặc z  3
Câu 55. Gọi z và z là các nghiệm của phương trình 2
z  2z  5  0 . Tính 4 4
P z z 1 2 1 2 A. P  14 B. P  14 
C. P  14i D. P  14  i
Câu 56. Gọi z là nghiệm phức có phần ảo âm của pt: 2
z  2z  3  0 . Tìm tọa độ điểm M biểu 1 diễn số phức z 1 A. M ( 1  ;2) B. M ( 1  ; 2  ) C. M ( 1  ; 2) D. M ( 1  ; 2i)
Câu 57. Cho số phức z có phần ảo âm và thỏa mãn 2
z  3z  5  0 . Tìm mô đun của số phức:   2z 3 14 A. 4 B. 17 C. 24 D. 5
Câu 58. Gọi z và z lần lượt là nghiệm của phươngtrình: 2
z  2z  5  0 . Tính  z z 1 2 1 2 A. 10 B. 3 C. 6 D. 2 5
Câu 59. Cho số phức z thỏa mãn: 2
(3  2i)z  (2  i)  4  .
i Tính hiệu phần thực và phần ảo của số phức z. A. 0 B. 1 C. 4 D. 6 1 i 1 i
Câu 60. Cho số phức z  
. Trong các kết luận sau kết luận nào đúng? 1 i 1 i A. z
B. z là số thuần ảo.
C. Mô đun của z bằng 1
D. z có phần thực và phần ảo đều bằng 0 2016 i
Câu 61. Biểu diễn về dạng z a bi của số phức z  là số phức nào? 2 (1 2i) 3 4 3  4 3 4 3  4 A. i B. i C.i D. i 25 25 25 25 25 25 25 25 (2  3i)(4  ) i
Câu 62. Tìm điểm biểu diễn số phức z  3  2i
Trần Thông sưu tầm và biên soạn
Facebook: Hội Toán Bắc Nam
Tài liệu ôn tập giải tích 12 học kỳ II A. (1;-4) B. (-1;-4) C. (1;4) D. (-1;4) Câu 63. Tìm n ghiệ m của phương trình .
i z  2017  i  0 . A. 1 2017i B. 1 2017i C. 1   2017i D. 2017   i z 1
Câu 64. Cho số phức z x yi  1 (x, y  R). Tìm phần ảo của số phức . z 1 2  x 2  y xy x y A. B. C. D. x  2 2 1  yx  2 2  x  2 2  x  2 2  1 y 1 y 1 y
Câu 65. Trong C, giải phương trình 4  1 i . z 1
A. z  2  i
B. z  3  2i
C. z  5  3i
D. z  1 2i Câu 66. C ho phương
trình z2 + bz + c = 0. Giả sử phương trình có nghiệm z = 1 + i .Tì m các giá
trị b và c bằng (b, c là số thực). A. b = 3, c = 5 B. b = 1, c = 3 C. b = 4, c = 3 D. b = -2, c = 2 Câu 67. Cho phương
trình z3 + az2 + bz + c = 0. Giả sử z = 1 + i và z = 2 là hai nghiệ m. Tìm các
giá trị a, b, c bằng (a,b,c là số thực):. a  4 a  2 a  4 a  0     A. b   6 B. b  1 C. b  5 D. b  1     c  4  c  4  c  1  c  2 
Câu 68. Số phức nào sau đây là số thực. 1 2i 1 2i 1 2i 1 2i 1 2i 1 2i 1 2i 1 2i A. z   B. z   C. z   D. z   3  4i 3  4i 3  4i 3  4i 3  4i 3  4i 3  4i 3  4i
Câu 69. Gọi z và z là các nghiệm của phương trình 2
z  4z  9  0 . Gọi M, N là các điểm biểu 1 2
diễn của z và z trên mặt phẳng phức. Tính độ dài của MN. 1 2 A. MN  4 B. MN  5 C. MN  2  5 D. MN  2 5
Câu 70. Gọi z và z là các nghiệm của phương trình 2
z  4z  9  0 . Gọi M, N, P lần lượt là 1 2
các điểm biểu diễn của z , z và số phức k x iy trên mặt phẳng phức. Tìm tập hợp điểm P 1 2
trên mặt phẳng phức để tam giác MNP vuông tại P.
A. Đường thẳng có phương trình y x  5
B. Đường tròn có phương trình 2 2
x  2x y  8  0
C. Đường tròn có phương trình 2 2
x  2x y  8  0 , nhưng không chứa M, N.
D. Đường tròn có phương trình 2 2
x  2x y 1  0 , nhưng không chứa M, N.
Trần Thông sưu tầm và biên soạn
Facebook: Hội Toán Bắc Nam
Tài liệu ôn tập giải tích 12 học kỳ II 1
Câu 71. Gọi z và z là các nghiệm của phương trình z   1  . Tính giá trị của 3 3
P z z . 1 2 1 2 z A. P  0 B. P  1 C. P  2 D. P  3 1
Câu 72. Biết số phức z thỏa phương trình 1 z  1. Tính giá trị của 2016 P z  . z 2016 z A. P  0 B. P  1 C. P  2 D. P  3
Câu 73. Gọi z và z là các nghiệm của phương trình 2
z  2z 10  0 . Gọi M, N, P lần lượt là 1 2
các điểm biểu diễn của z , z và số phức k x iy trên mặt phẳng phức. Tìm số phức k để tam 1 2 giác MNP đều.
A. k  1 27 hay k  1 27
B. k  1 27i hay k  1 27i
C. k  27  i hay k  27  i
D. Một đáp số khác. 2008 2009 2010 2011 2012 iiiii
Câu 74. Tìm phần thực và phần ảo của z  . 2013 2014 2015 2016 2017 iiiii A. 0; -1 B. 1; 0 C. -1; 0 D. 0; 1
Câu 75. Gọi z và z là các nghiệm của phương trình 2
z  4z  9  0 . Gọi M, N là các điểm biểu 1 2
diễn của z và z trên mặt phẳng phức. Tính độ dài của MN. 1 2 A. MN  4 B. MN  5 C. MN  2  5 D. MN  2 5
Câu 76. Gọi z và z là các nghiệm của phương trình 2
z  4z  9  0 . Gọi M, N là các điểm biểu 1 2
diễn của z và z trên mặt phẳng phức. Tính độ dài của MN. 1 2 A. MN  4 B. MN  5 C. MN  2  5 D. MN  2 5
Câu 77. Gọi z , z , z là ba nghiệm của phương trình 3 z  8  0 . Tính 2 2 2
M z z z .. 1 2 3 1 2 3 A. M  4 B. M  0 C. M  6 D. M  8
Câu 78. Tìm số phức z sao cho z  (3  4i)  5 và biểu thức 2 2
P z  2  z i đạt giá trị lớn nhất. A. 2  i B. 2  2i C. 5  5i D. 4  3i z
Câu 79. Cho số phức z có tập nghiệm biểu diễn là trục hoành . Nếu ' 1 z  thì tập điểm biểu z '1
diễn z ' là một phần của hình nào dưới đây. A. Trục tung
B. Đường tròn C. Trục hoành D. Hình tròn
Trần Thông sưu tầm và biên soạn
Facebook: Hội Toán Bắc Nam
Tài liệu ôn tập giải tích 12 học kỳ II
Câu 80. Cho hình vuông ABCD có tâm H và A,B,C,D,H lần lượt là điểm biểu diễn cho các số
phức a,b,c,d,h. Tính môđun của số phức b biết a  2  ; i h  1 i
3 và số phức b có phần ảo dương . A. 2 2 B. 26 C. 4 2 D. 5 Câu 81. Tìm m
ô đun của số phức z thỏa mãn: (1 2i)(z i)  4i(i 1)  7  21i . A. z  9 B. z  2 3 C. z  5 z D. 3 7
Câu 82. Trong mặt phẳng phức Oxy , tập hợp các điểm biểu diễn số phức Z thỏa mãn z z  5 là
đường tròn có tâm I . Tìm I A. I 0,0 B. I 1,0 C. I  1  ,  1 I 0,1 D.  
Câu 83. Gọi z , z là hai nghiệm của phương trình 2
z  2iz  4  0 . Tính môđun của số phức 1 2
w  (z  2)(z  2).. 1 2 A. w  6 B. w  5 C. w  4 w D. 7
Câu 84 Cho số phức z = x + yi ; x, y 
thỏa mãn z3 = 18 + 26i. Tìm giá trị của biểu thức 2021 2012 T  (z  2)  (4  z) . A. 1007 2 B. 1007 2  C. 1007 3 D. 1006 2  Câu 85. C
ho s ố phức z  3  4i .Xác định căn bậc 2 của số phức z . A. 2  i, 2   i B. 2  i C. 2   i, 2  iD. 3 2i
Câu 86. Cho số phức z thỏa mãn phương (1  2i).z  1  2 .
i Tìm phần ảo của số phức
  2iz  (1 2i).z . 2 3 1 1 A. B. C. D. 5 5 5 5
Câu 87. Cho số phức z thỏa mãn 3
z z . Khẳng định nào đúng?.
A. Phần thực của z lớn hơn 1.
B. z có thể nhận giá trị là số thực hoặc số thuần ảo
C. Chỉ có duy nhất một số phức thuần ảo z thỏa 3 z z . D. z  1 5 1 i
Câu 88. Cho z    , tính 5 6 7 8
z z z z . 1 i
Trần Thông sưu tầm và biên soạn
Facebook: Hội Toán Bắc Nam
Tài liệu ôn tập giải tích 12 học kỳ II A.0 B. 1 C. 4 D. 3 2005 i i
Câu 89. Cho số phức tùy ý z  1. Xét các số phức 2 2   
z  (z ) và z  1 3 z z 2   
 (z )  z . Mệnh đề nào dưới đây là đúng. z  1
A.  là số thực,  là số thực
B.  là số ảo,  là số thực
C.  là số thực,  là số ảo
D.  là số ảo,  là số ảo 4 2
Câu 90. Kí hiệu z , z , z , z là bốn nghiệm phức của phương trình z  2z 8  0 .Tính 1 2 3 4
tổng T z z z z . 1 2 3 4 A. 4 B. 4  2 C. 4  2 2  D. 2 2 2
Câu 91. Điểm M là điểm biểu diễn của số phức z thỏa mãn phương trình 3(z  1)  4z  . i (7  i). Tìm tọa độ điểm M. A. M  2  ,  1 B. M  2  ,  1 C. M 2,  1 M 1, 2 D.   1  i
Câu 92. Tính môđun của số phức 2
  z z , với (2  i).z   5  i . 1  i A. 5 2 B. 4 2 C. 2 2 D. 3 2 Câu 93. Tìm t ậ
p hợp các điểm trong mặt phẳng phức biểu diễn các số phức z thỏa mãn 2 z i z z 2i . 2 x
A. Đường tròn tâm I 0;1 , bán kính R 1. B. Parabol y 4 2 y
C. Đường tròn tâm I 3;0 , bán kính R 3 . x D. Parabol 4
Câu 94. Cho số phức z thỏa mãn : z  4  3i  3. Tìm số phức z có mođun nhỏ nhất. 4 6 5 A. z  2  3i B. z   i C. z  3  i   D. z 1 4i 5 5 2
Câu 95. Giải phương trình 2
3 2z  2 3z  2  0 . 6 3 6 6 A. (1 i) B. (1 i) C. (1 i) D. (1 i) 6 6 3 5
Câu 96. Cho các số phức z thoả mãn z  2 , biết rằng tập hợp các điểm biểu diễn số phức
w  2  iz  2 1 là một đường tròn. Tính chu vi đường tròn đó.
Trần Thông sưu tầm và biên soạn
Facebook: Hội Toán Bắc Nam
Tài liệu ôn tập giải tích 12 học kỳ II A. 2 5 B. 3 5 C. 6 5 D. 4 5
Câu 97. Trong mặt phẳng phức, gọi , A ,
B C lần lượt là ba điểm biểu diễn các số phức z , z , z 1 2 3
. Biết z z z , trong các khẳng định sau đây, khẳng định nào là đúng . 1 2 3
A. Trọng tâm của tam giác ABC là điểm biểu diễn số phức z z z . 1 2 3
B. Tam giác ABC có tâm đường tròn ngoại tiếp là gốc tọa độ O .
C. Tam giác ABC có trọng tâm là gốc tọa độ O
D. Tam giác ABC là tam giác đều
Câu 98. Cho các số phức w, z, u có biểu diễn hình học thỏa mãn: w nằm ở góc phần tư thứ (I), z
nằm ở góc phần tư thứ (II), và u nằm trên chiều âm của trục thực.
Khẳng định nào sau đây có thể đúng?.
A. u  z.w; u  z  w B. z  u.w; u  z  w C. u  z.w; u  z  w    D. z u.w; u z w
Câu 99. Cho số phức z thỏa z i 1  z  2i . Tìm giá trị nhỏ nhất của z . 1 1 A. 2 B. C. D. 1 2 4
Câu 100. Cho hai số phức w và z thỏa mãn w 1 2i  .
z Biết tập hợp các điểm biểu diễn của
số phức z là đường tròn tâm I  2
 ;3, bán kính r  3. Tìm tập hợp các điểm biểu diễn của số phức w ..
A. Đường tròn, tọa độ tâm  3  ;5 bán kính bằng 3.
B. Đường thẳng song song trục tung
C. Đường thẳng song song trục hoành
D. Đường tròn, tọa độ tâm  1   ;1 bán kính bằng 3
Câu 101. Tìm tập hợp điểm biễu diễn số phức z thỏa mãn: z 1 3i  4 .
A. Đường tròn tâm I(1;3), bán kính R=4
B. Đường tròn tâm I(-1;3), bán kính R=2
Trần Thông sưu tầm và biên soạn
Facebook: Hội Toán Bắc Nam
Tài liệu ôn tập giải tích 12 học kỳ II
C. Hình tròn tâm I(-1;3), bán kính R=4
D. Hình tròn tâm I(-1;3), bán kính R=2 2 | z |
Câu 102. Tìm phần thực của số phức z biết: z  10 . z A. 10 B. 10 C. 5 D. -5
Câu 103. Cho 3 số phức z  1 2 ; i z  3  ;
i z  4  i . Đặt số phức    1 2 3 z z z z a bi, 1 2 3 ( ,
a b R) . Tính tổng a b . A. -10 B. 10 C. -40 D. 40 3
2  4i  2(1  i)
Câu 104. Tìm số phức   2.z .z , biết 3
z  4  3i  (1  i) ; z   . 1 2 1 2 1  i A.   18  74. . i B.   18  75. . i C.   18  74. . i 18 75. . i D.    Câu 105. Hình vẽ
sau biểu diễn dạng hình học của các số phức z và w. Ở đây z nằm trong góc
phần tư thứ (I) và w nằm trong góc phần tư thứ (II). Số phức nào trong các số phức sau nằm
trong góc phần tư thứ (III)? . A. w  z B. z C. 2iz.  D. w Câu 106. Gọi A, B
, C lần lượt là các điểm biểu diễn của 3 số phức : 2     6 1 2i; (1 )(1 2 ); i i i
3i . Tính diện tích của tam giác ABC. 1 1 5 5 A. B. C. D. 4 2 5 2
Câu 107. Cho số phức z thoả mãn điều kiện z  2  3i  3 . Tìm giá trị nhỏ nhất của z . A. 13  3 B. 2 C. 13  2 D. 2
Câu 108. Tìm số phức z có mô đun lớn nhất và thỏa mãn điều kiện z   i 13 1  3  2i  . 2
Trần Thông sưu tầm và biên soạn
Facebook: Hội Toán Bắc Nam
Tài liệu ôn tập giải tích 12 học kỳ II 2 1 3 1 3 15
A. z  1 3i B. z   i C. z   i D. z   i 2 2 2 2 4 4
Câu 109. Cho số phức z  0 thỏa mãn z  2 . Tìm tổng giá trị lớn nhất và giá trị nhỏ nhất của  biểu thức z i P  . z A. 4 B. 1 C. 2 D. 3
Câu 110. Trên tập hợp số phức cho phương trình 2
z  3z 1  0 (*). Gọi z z là nghiệm của 1, 2 phương trình (*). z z
Tìm môđun của số phức 1 2 w   , n N . 4n2 4n i i A. 4 B. 6 C. 1 D. 2  i 1
Câu 111. Cho số phức       z thỏa mãn:  i 1 3 1 2 z
2 i . Tìm số phức w z 1 i z  . 2i 7 1 7 1 7 1 1 7 A. w   i B. w   i C. w   i D. w   i 10 10 10 10 5 5 5 5 z 1
Câu 112. Tìm số phức z thỏa mãn
z  (3 i) 1 . i 2
A. z  4  i
B. z  4  i
C. z  1 4i z D. 3
Câu 113. Cho số phức z thỏa mãn: 1 2iz  2  3iz  2
  2i . Tính môđun của z. A. z  1 B. z  2 C. z  2 z D. 0
Câu 114. Gọi z z
1 và 2 là hai nghiệm phức của phương trình  i 2 2 1
z  42  iz  5  3i  0 2 2 Tính T zz . 1 2 17 1 A. T B. T C. T  9 D. T  1 2 2
Câu 115. Trên mặt phẳng tọa độ Oxy, tìm tập hợp điểm biểu diễn các số phức z thỏa mãn điều kiện
zi  2  i  2
A. Đường tròn tâm I 2,  1 bán kính 2
B. Đường tròn tâm I 2,  1 bán kính 4
C. Đường tròn tâm I 1, 2   bán kính 2 I 1, 2  bán kính 4
D. Đường tròn tâm  
Câu 116. Trên mặt phẳng tọa độ Oxy, tìm tập hợp điểm biểu diễn các số phức z thỏa mãn điều kiện 2
  i(z 1)  5.
Trần Thông sưu tầm và biên soạn
Facebook: Hội Toán Bắc Nam
Tài liệu ôn tập giải tích 12 học kỳ II
A. Đường tròn tâm I 2,  1 bán kính 25
B. Đường tròn tâm I 2,  1 bán kính 25
C. Đường tròn tâm I 1, 2   bán kính 25 I 1, 2  
D. Đường tròn tâm bán kính 5 6 1 i 3 
Câu 117. Tìm modul của số phức z , biết z  (1 i)(2  i)  8  i    . 1 i   A. z  61 B. z  61 C. z  36 z D. 25   i2 2 3  7i
Câu 118. Cho số phức z  (1  2i)(4  3i)  2  8i
. Xác định phần thực, phần ảo 3  4i của số phức z
A. Phần thực của số phức z là 10, phần ảo của số phức z là 4
B. Phần thực của số phức z là -10, phần ảo của số phức z là 4
C. Phần thực của số phức z là 4, phần ảo của số phức z là -10
D. Phần thực của số phức z là 4, phần ảo của số phức z là 10
Câu 119. Tìm tập hợp các điểm biểu diễn số phức z trên mặt phẳng tọa độ thỏa mãn điều kiện: 2
z  5z  5z  0 .
A. Đường tròn tâm I 5,0 bán kính 25
B. Đường tròn tâm I 0,5 bán kính 25
C. Đường tròn tâm I 5,0 bán kính 5 I 0,5 bán kính 5
D. Đường tròn tâm  
Câu 120. Tìm phần thực, phần ảo của số phức z biết:    i  i i2016 z 2 3 3 3 1 .
A. Phần thực của số phức z là 1008 2
 9 , phần ảo của số phức z là  3
B. Phần thực của số phức z là 1008 2
 9 , phần ảo của số phức z là  3i
C. Phần thực của số phức z là 1008 2
 9, phần ảo của số phức z là  3i
D. Phần thực của số phức z là 1008 2
 9, phần ảo của số phức z là  3
Câu 121. Cho số phức 
z thỏa mãn: 1 2iz  2  3iz  2
  2i . Tính môđun của z iz . A. w  5 B. w  5 2 C. w  4  D. w 4 2 11 8 1 i   2i
Câu 122. Cho số phức  
z thỏa mãn: iz   
 . Tìm phần thực, phần ảo của 1 i  1 i
w z iz .
Trần Thông sưu tầm và biên soạn
Facebook: Hội Toán Bắc Nam
Tài liệu ôn tập giải tích 12 học kỳ II
A. Phần thực của số phức z là 15 , phần ảo của số phức z là 17
B. Phần thực của số phức z là 15 , phần ảo của số phức z là 17 
C. Phần thực của số phức z là 15 , phần ảo của số phức z là 17  i
D. Phần thực của số phức z là 15
 , phần ảo của số phức z là 17 
Câu 123. Cho số phức z thỏa mãn: 1 2iz là số thực và 1 z  2z 
 2 5 Tìm số phức liên 2 hợp của z. A. 4 B. 6 C. 1 D. 2
Câu 124. Cho số phức  z thỏa mãn: 2 4
z z  30 và 2z  z
13 Tìm modul của số phức z. A. z  5 B. z  5 C. z  2 2  D. z 2 1
Câu 125. Gọi z , ziz   i z z  1
2 là hai số phức thỏa mãn 2 3 6z và . Hãy tính giá 1 2 3
trị của biểu thức A z z . 1 2 A. 4 B. 6 C. 1 D. 2 z
Câu 126. Cho số phức   2 z thỏa mãn: z
2 . Tìm phần thực, phần ảo của w z  2 z i 1 2i 65 128
A. Phần thực của số phức z là 
, phần ảo của số phức z là  49 49 65 128
B. Phần thực của số phức z là 
, phần ảo của số phức z là  i 49 49 65 65
C. Phần thực của số phức z là 
, phần ảo của số phức z là  49 49 65 128
D. Phần thực của số phức z là 
, phần ảo của số phức z là i 49 49 2 2 4
Câu 127. Cho số phức        z thỏa mãn:1 z z i
iz 1 . Tìm modul của w z z 1 A. 4 B. 6 C. 1 D. 2
Câu 128. Tìm số phức w  1 3i z có modul lớn nhất. Biết z là số phức sao cho z 1 i  2 8 4 8 4
A. z  8  4i
B. z  8  4i C. z   i z   i D. 5 5 5 5
Trần Thông sưu tầm và biên soạn
Facebook: Hội Toán Bắc Nam
Tài liệu ôn tập giải tích 12 học kỳ II 1 1 1
Câu 129. Cho số phức  
z thỏa mãn: z  2016 . Tìm modul của w biết z w z  w A. w  1 B. w  0 C. w  2016  D. w 5
Câu 130. Gọi z , z , z
z z z  1
z z z  1 1 2
3 là hai số phức thỏa mãn 1 2 3 và . Hãy 1 2 3
tính giá trị của biểu thức 3 3 3
A z z z . 1 2 3 A. 4 B.5 C. 1 D. 2 2z  1 3i z 1  
Câu 131. Gọi A,B là hai điểm biểu diển của các số phức z , z thỏa mãn 1 2 2 và
z  1. Tính diện tích tam giác OAB. 1 3 3 1 A. S B. S C. S D. S  2 4 2 3
Câu 132. Trên mặt phẳng tọa độ Oxy, tìm tập hợp điểm biểu diễn các số phức w  3z 1 i biết z là
số phức thỏa mãn điều kiện z  2  3i  3 1 z có hình dạng như thế nào? A.Hình tròn B.Đường thẳng C.Đường tròn D.Parabol
Câu 133. Cho tập hợp số phức z thỏa mãn: 4
z 1  2 z . Tìm giá trị nhỏ nhất, lớn nhất của modul z.
A. Giá trị nhỏ nhất của modul z là 5 1 , giá trị lớn nhất của modul z là 5 1 .
B. Giá trị nhỏ nhất của modul z là 5 , giá trị lớn nhất của modul z là 5 1 .
C. Giá trị nhỏ nhất của modul z là 2 , giá trị lớn nhất của modul z là 5 1 .
D. Giá trị nhỏ nhất của modul z là 2 , giá trị lớn nhất của modul z là 5 1 . 4 4  z   z
Câu 134. Cho các số phức z , z thỏa mãn z  z  z  z 1 2     1 2 Hãy tính P 1 2 1 2   z z  2   1  A. P  1 B. P  2 C. P  1  P   D. 2
Câu 135. Cho số phức z thỏa mãn z  1. Tìm giá trị nhỏ nhất, lớn nhất của modul 2
z 1  z z 1 .
A. Giá trị nhỏ nhất của modul z là 3 1 , giá trị lớn nhất của modul z là 13 . 4
Trần Thông sưu tầm và biên soạn
Facebook: Hội Toán Bắc Nam
Tài liệu ôn tập giải tích 12 học kỳ II
B. Giá trị nhỏ nhất của modul z là 3 , giá trị lớn nhất của modul z là 13 . 4
C. Giá trị nhỏ nhất của modul z là 13 , giá trị lớn nhất của modul z là 3 1. 4
D. Giá trị nhỏ nhất của modul z là 3 1, giá trị lớn nhất của modul z là 5 1 .
Câu 136. Cho số phức z thỏa mãn z  1. Tìm giá trị nhỏ nhất, lớn nhất của modul 3 z 1 .
A. Giá trị nhỏ nhất của modul z là 1 , giá trị lớn nhất của modul z là 4 .
B. Giá trị nhỏ nhất của modul z là 0 , giá trị lớn nhất của modul z là 4 .
C. Giá trị nhỏ nhất của modul z là 4 , giá trị lớn nhất của modul z là 5 .
D. Giá trị nhỏ nhất của modul z là 1, giá trị lớn nhất của modul z là 5 . z   i
Câu 137. Cho tập hợp số phức z thỏa mãn: 2
 2 . Tìm giá trị nhỏ nhất, lớn nhất của z 1 i modul z.
A. Giá trị nhỏ nhất của modul z là 2 1 , giá trị lớn nhất của modul z là 2 1.
B. Giá trị nhỏ nhất của modul z là 2 , giá trị lớn nhất của modul z là 2 1.
C. Giá trị nhỏ nhất của modul z là 2 , giá trị lớn nhất của modul z là 2 1.
D. Giá trị nhỏ nhất của modul z là 2 , giá trị lớn nhất của modul z là 2 1.
Câu 138. Tìm tập hợp các điểm biểu diễn số phức z trên mặt phẳng tọa độ sao cho
z i  i  
1 z có hình dạng như thế nào?
A.Một phần hình tròn
B. Một phần hypebol
C. Một phần đường thẳng
D. Một phần đường tròn
Câu 139. Tìm tập hợp các
điểm biểu diễn số phức w  iz 1 trê
n mặt phẳng tọa độ sao cho :
zi 3 2 1  8
A. Đường tròn tâm I  1  ,  1 bán kính 2
B. Đường tròn tâm I 1,  1 bán kính 2
C. Đường tròn tâm I  1  ,  1 bán kính 4 I 1,1 bán kính 4
D. Đường tròn tâm   2 z z 1
Câu 140. Cho số phức z  \ thỏa mãn
là số thực. Tìm modul của z. 2 z z 1 A. z  1 B. z  2 C. z  2 z D. 3
Trần Thông sưu tầm và biên soạn
Facebook: Hội Toán Bắc Nam
Tài liệu ôn tập giải tích 12 học kỳ II
Trần Thông sưu tầm và biên soạn
Facebook: Hội Toán Bắc Nam