


Preview text:
VÕ CÔNG TRƯỜNG 0983 900 570 sin y tang t 3 - 3 π 3 - 3 -1 3 2 3 1 3 B s 2π π 1 3 cotang 3 3 3π 2 2 π 4 2 4 1 3 5π π 2 3 6 6 - 2 2 π -1 1 0 (rad) x 2 2 A' - 3 -1 1 O 3 A cosin 2 2 2 2 -1 - 3 7π 2 3 11π - 2 6 6 5π 2 - 3 7π 4 2 4 4π -1 5π -1 3π 3 B' 3 2 - 3 2024-2025 Võ Công Trường
Tài liệu ôn thi Tốt nghiệp THPT theo chuong trình mới 2018 Môn Toán MỤC LỤC
CHƯƠNG TRÌNH TOÁN LỚP 12 ............................................................................................................................................... 3
PHẦN MỘT SỐ YẾU TỐ GIẢI TÍCH .......................................................................................................................................... 3
CHƯƠNG ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ ............................................................................................... 3
BÀI 1. TÍNH ĐƠN ĐIỆU VÀ CỰC TRỊ CỦA HÀM SỐ .............................................................................................................. 3
BÀI 2. GIÁ TRỊ LỚN NHẤT – GIÁ TRỊ NHỎ NHẤT CỦA HÀM SỐ ......................................................................................10
BÀI 3. ĐƯỜNG TIỆM CẬN .........................................................................................................................................................12
SƠ ĐỒ TÌM ĐƯỜNG TIỆM CẬN ............................................................................................................................................. 13
BÀI 4. ĐỒ THỊ HÀM SỐ ..............................................................................................................................................................16
BỔ SUNG KIẾN THỨC: SỰ TƯƠNG GIAO GIỮA HAI ĐỒ THỊ .......................................................................................... 20
CHƯƠNG NGUYÊN HÀM. TÍCH PHÂN..................................................................................................................................22
BÀI 1. NGUYÊN HÀM ...............................................................................................................................................................22
BÀI 2. TÍCH PHÂN .....................................................................................................................................................................25
BÀI 3. .ỨNG DỤNG HÌNH HỌC CỦA TÍCH PHÂN..................................................................................................................29
PHẦN HÌNH HỌC VÀ ĐO LƯỜNG ...........................................................................................................................................33
CHƯƠNG VECTƠ VÀ HỆ TOẠ ĐỘ TRONG KHÔNG GIAN .................................................................................................33
BÀI 1: VECTO VÀ CÁC PHÉP TOÁN TRONG KHÔNG GIAN ...............................................................................................33
BÀI 2: TOẠ ĐỘ CỦA VECTO TRONG KHÔNG GIAN ............................................................................................................36
BÀI 3: BIỂU THỨC TOẠ ĐỘ CỦA CÁC PHÉP TOÁN VECTƠ ...............................................................................................37
CHƯƠNG PHƯƠNG TRÌNH MẶT PHẲNG, ĐƯỜNG THẲNG, MẶT CẦU ..........................................................................39
BÀI 1. PHƯƠNG TRÌNH MẶT PHẲNG .....................................................................................................................................39
BÀI 2. PHƯƠNG TRÌNH ĐƯỜNG THẲNG TRONG KHÔNG GIAN ......................................................................................45
BÀI 3. PHƯƠNG TRÌNH MẶT CẦU ..........................................................................................................................................53
PHẦN THỐNG KÊ VÀ XÁC SUẤT ...........................................................................................................................................56
CHƯƠNG CÁC SỐ ĐẶC TRƯNG ĐO MỨC ĐỘ PHÂN TÁN CỦA MẪU SỐ LIỆU GHÉP NHÓM ....................................56
BÀI 1. KHOẢNG BIẾN THIÊN KHOẢNG TỨ PHÂN VỊ CỦA MẪU SỐ LIỆU GHÉP NHÓM .............................................56
BÀI 2. PHƯƠNG SAI VÀ ĐỘ LỆCH CHUẨN CỦA MẪU SỐ LIỆU GHÉP NHÓM ...............................................................60
CHƯƠNG XÁC SUẤT CÓ ĐIỀU KIỆN ....................................................................................................................................62
BÀI 1. XÁC SUẤT CÓ ĐIỀU KIỆN ............................................................................................................................................62
BÀI 2. CÔNG THỨC XÁC SUẤT TOÀN PHẦN VÀ CÔNG THỨC BAYES ...........................................................................64
PHỤ LỤC CHƯƠNG TRÌNH TOÁN LỚP 10 VÀ 11 ................................................................................................................66
PHẦN ĐẠI SỐ VÀ MỘT SỐ YẾU TỐ GIẢI TÍCH ...................................................................................................................66 I.
ĐẠI SỐ TỔ HỢP ........................................................................................................................................................................66 II.
HÀM SỐ LƯỢNG GIÁC VÀ PHƯƠNG TRÌNH LƯỢNG GIÁC ..........................................................................................68 III.
DÃY SỐ – CẤP SỐ CỘNG – CẤP SỐ NHÂN .......................................................................................................................71 IV.
GIỚI HẠN, HÀM SỐ LIÊN TỤC ..........................................................................................................................................71
V. HÀM SỐ MŨ VÀ HÀM SỐ LÔGARIT .......................................................................................................................................72 VI.
ĐẠO HÀM ............................................................................................................................................................................74
PHẦN HÌNH HỌC VÀ ĐO LƯỜNG ..........................................................................................................................................76 VII.
HÌNH HỌC PHẲNG .............................................................................................................................................................76 VIII.
PHƯƠNG PHÁP TỌA ĐỘ TRONG MẶT PHẲNG ..............................................................................................................77 IX.
ĐƯƠNG THẲNG VÀ MẶT PHẲNG. QUAN HỆ SONG SONG KHÔNG GIAN ..................................................................79
X. QUAN HỆ VUÔNG GÓC TRONG KHÔNG GIAN ...................................................................................................................81
PHẦN THỐNG KÊ VÀ XÁC SUẤT ..........................................................................................................................................90 0983.900.570 1 2024-2025 Võ Công Trường
Tài liệu ôn thi Tốt nghiệp THPT theo chuong trình mới 2018 Môn Toán XI.
CÁC SỐ ĐẶC TRƯNG ĐO XU THẾ TRUNG TÂM CỦA MẪU SỐ LIỆU ...........................................................................90 XII.
CÁC SỐ ĐẶC TRƯNG ĐO MỨC ĐỘ PHÂN TÁN CỦA MẪU SỐ LIỆU ............................................................................91 XIII.
CÁC SỐ ĐẶC TRƯNG ĐO XU THẾ TRUNG TÂM CHO MẪU SỐ LIỆU GHÉP NHÓM ..................................................93 XIV.
XÁC SUẤT ............................................................................................................................................................................95 0983.900.570 2 2024-2025 Võ Công Trường
Tài liệu ôn thi Tốt nghiệp THPT theo chuong trình mới 2018 Môn Toán
CHƯƠNG TRÌNH TOÁN LỚP 12
PHẦN MỘT SỐ YẾU TỐ GIẢI TÍCH
CHƯƠNG ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ
BÀI 1. TÍNH ĐƠN ĐIỆU VÀ CỰC TRỊ CỦA HÀM SỐ
Bảng công thức đạo hàm Hàm sơ cấp Hàm hợp Phép toán
Quy tắc đạo hào của hàm hợp (1) (C) = 0
(25) (u v) = u v f
(u) = f (u) .u (2) (x) =1 (26) ( .
u v) = u .v + . u v (3) ( x ) 1 = .x − − (14) ( u ) 1
= .u − .u u u .v v .u (27) = 2 v v u (4) ( x) 1 = (15) ( u ) = 2. x = 2. u (28) (k.u)
k.u , ( k là hằng số) 1 1 − − k −k.v (5) = 1 u (16) = (29) = 2 x x 2 u u 2 v v Đặ (6) (sin x) = cos x c biệt
(17) (sin u) = u .cos u − 1 = (7)
(cos x) = −sin x u (30) (18) (tan u) = 1 + 2 x x cos u 1 (8) (tan x) = a b 2 cos x (19) (cos u) = u − .sin u ax + b c d ad − bc 1 − − (31) = = (9) ( u cot x) = 2 2 (20) (cot u) = cx + d (cx + d ) (cx + d ) 2 sin x 2 sin u 2 2
ax + bx + c
adx + 2aex + (be − cd ) (10) ( x ) x a = a .ln a (21) ( u ) u a = a .ln . a u (32) = dx + e (dx + e)2 (11) ( x ) x e = e (22) ( u ) u e = e .u u (12) ( x = = a ) 1 log (23) (log u a ) . x ln a . u ln a (13) ( ) 1 u ln x = (24) (ln u) = x u
1. Tính đơn điệu của hàm số Định nghĩa
Kí hiệu K là khoảng; đoạn; nửa khoảng. Giả sử hàm số y = f ( x) xác định trên K .
Hàm số y = f ( x)
Gọi là đồng biến trên K nếu x
, x K mà x x thì f (x f x . 1 ) ( 2) 1 2 1 2
Gọi là nghịch biến trên K nếu x
, x K mà x x thì f (x f x . 1 ) ( 2) 1 2 1 2 Định lý
Nếu f '(x) 0, x
K thì hàm số y = f (x) đồng biến trên K
Nếu f '(x) 0, x
K thì hàm số y = f (x) nghịch biến trên K 0983.900.570 3 2024-2025 Võ Công Trường
Tài liệu ôn thi Tốt nghiệp THPT theo chuong trình mới 2018 Môn Toán Chú ý (1) Trên K ,
Nếu f (x) = 0 thì hàm số y = f (x) không đổi
Nếu f (x) 0 và f (x) = 0 tại hữu hạn điểm thì hàm số y = f (x) đồng biến
Nếu f (x) 0 và f (x) = 0 tại hữu hạn điểm thì hàm số y = f (x) nghịch biến
(2) Hàm số y = f ( x) đồng biến trên K thì đồ thị đi lên từ trái sang phải (Hình trái).
Hàm số y = f ( x) nghịch biến trên K thì đồ thị đi xuống từ trái sang phải (Hình phải).
2. Cực trị của hàm số Khái niệm
Cho hàm số y = f ( x) xác định và liên tục trên khoảng ( ;
a b) ( a có thể là −, b có thể là + ) và điểm x ; a b . 0 ( )
h 0 sao cho f ( x) f ( x với mọi x(x − ; h x + h ;
a b và x x thì ta nói hàm số f ( x) đạt cực 0 0 ) ( ) 0 ) 0
đại tại x . 0
h 0 sao cho f ( x) f ( x với mọi x(x − ; h x + h ;
a b và x x thì ta nói hàm số f ( x) đạt 0 0 ) ( ) 0 ) 0
cực tiểu tại x . 0 Chú ý
(1) x : Điểm Cực đại (Cực tiểu) của hàm số → Gọi chung là điểm 0
Cực trị của hàm số (2) y
: Giá trị Cực đại; y : Giá trị Cực tiểu của HS; Gọi chung CD CT
là Giá trị Cực trị; Gọi gọn là Cực trị.
(3) ( x ; y
: Điểm Cực đại, (x ; y
: Điểm Cực tiểu của đồ thị 0 CT ) 0 CD ) hàm số.
Điều kiện đủ để hàm số đạt cực trị tại một điểm
Giả sử hàm số y = f ( x) liên tục trên khoảng ( ;
a b) chứa điểm x và có đạo hàm trên các khoảng (a; x và 0 ) 0
(x ;b . Khi đó: 0 )
Nếu f (x) 0 với mọi x( ; a x
và f ( x) 0 với mọi x ( x ;b thì x là một điểm cực tiểu của hàm số 0 ) 0 ) 0 f ( x) .
Nếu f (x) 0 với mọi x( ; a x
và f ( x) 0 với mọi x ( x ;b thì x là một điểm cực đại của hàm số 0 ) 0 ) 0 f ( x) . 0983.900.570 4 2024-2025 Võ Công Trường
Tài liệu ôn thi Tốt nghiệp THPT theo chuong trình mới 2018 Môn Toán Nhận xét
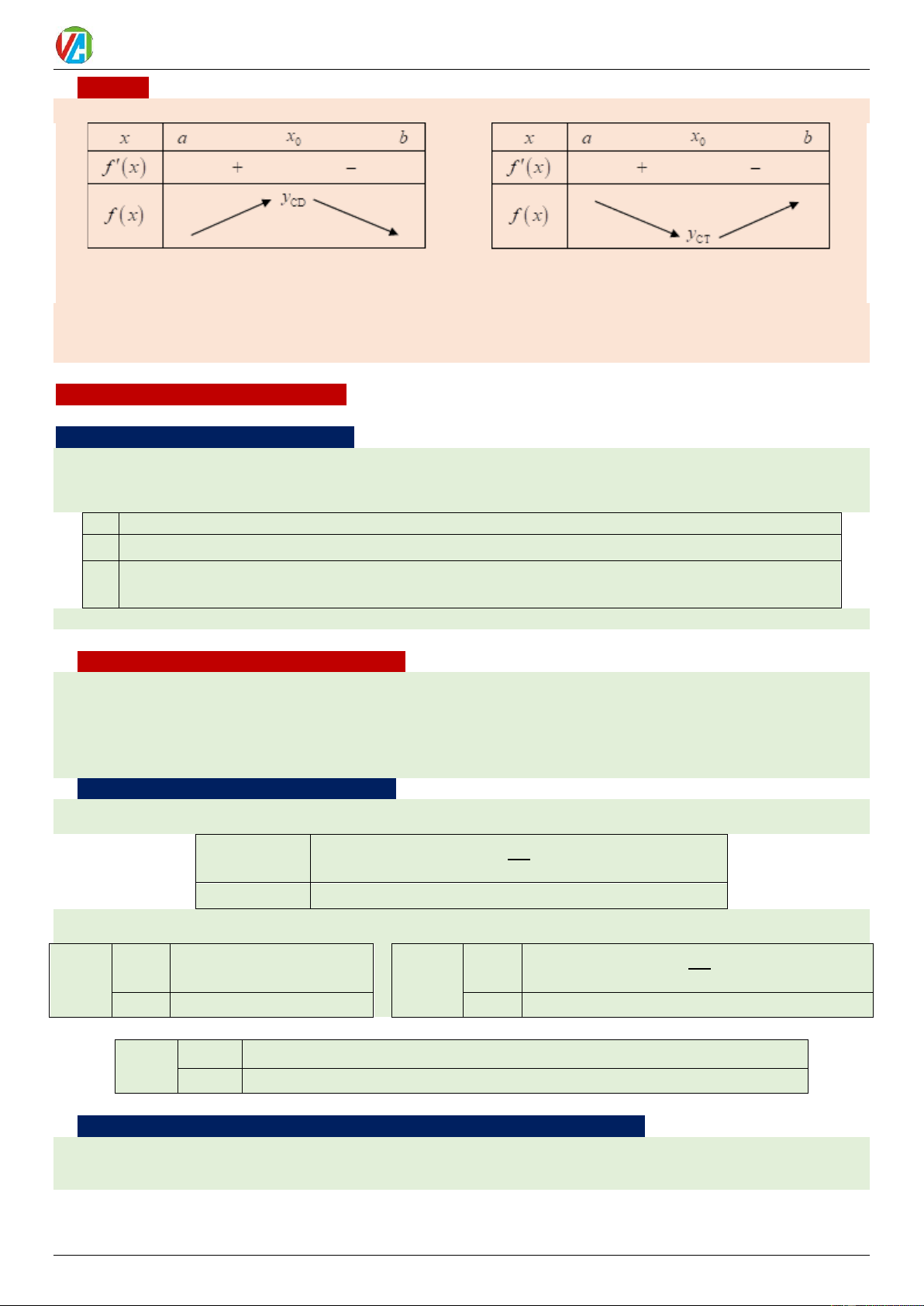
(1) Định lí trên được thể hiện bằng bảng biến thiên
Nếu đạo hàm đổi dấu từ (+) sang (–) khi x qua
Nếu đạo hàm đổi dấu từ (–) sang (+) khi x qua
điểm x xác định thì hàm số đạt cực đại tại x
điểm x xác định thì hàm số đạt cực tiểu tại x 0 0 0 0
(2) Nếu f ( x = 0 nhưng f ( x) không đổi dấu khi x qua điểm x thì hàm số không đạt cực trị tại x . 0 ) 0 0
(3) Số điểm cực trị của hàm số bằng số lần đổi dấu của đạo hàm tại các điểm xác định của hàm số.
CÁC DẠNG TOÁN THƯỜNG GẶP
1. XÉT SỰ BIẾN THIÊN CỦA HÀM SỐ
Bước 1. Tìm tập xác định
Bước 2. Tìm đạo hàm. Tìm nghiệm của đạo hàm và điểm không xác định của đạo hàm.
Bước 3. Lập bảng biến thiên: x
Điền TXĐ; nghiệm của đạo hàm và điểm không xác định của đạo hàm (theo thứ tự tăng dần). y
Xét dấu đạo hàm y
Vẽ chiều biến thiên (mũi tên chéo lên khi y 0 , chéo xuống khi y 0 ); y
Điền Giới hạn hàm số, Giá trị hàm số tại các điểm x tương ứng vào đầu, cuối các mũi tên
Bước 4. Dựa vào bảng biến thiến, kết luận chiều biến thiên trên từng khoảng.
PHƯƠNG PHÁP XÉT DẤU BIỂU THỨC
Xét dấu biểu thúc f ( x)
Bước 1. Tìm tập xác định (Nếu cần)
Bước 2. Tìm nghiệm của f (x) .
Bước 3. Lập bảng xét dấu
Cách 1. Xét dấu bằng các quy tắc đã biết:
(1) Dấu của Nhị thức bậc nhất f ( x) = ax + b (a 0) −b x − + a f (x) Trái dấu a 0 Cùng dấu a
(2) Dấu của Tam thức bậc hai f ( x) 2 = ax + bx + ,
c (a 0) , 2 = b − 4ac −b x − + x − + 0 = 0 2a f (x) Cùng dấu a f (x) Cùng dấu a 0 Cùng dấu a x − x x + 0 1 2 f (x) Cùng dấu a 0 Trái dấu a 0 Cùng dấu a
Cách 2. Xét dấu bằng cách tính giá trị biểu thức (Dùng máy tính cầm tay)
Các nghiệm chia tập xác định thành nhiều khoảng, mỗi khoảng chọn một điểm đại diện và tính giá trị của
f ( x) tại các điểm đó, xác định dấu và điền dấu vào bảng xét dấu 0983.900.570 5 2024-2025 Võ Công Trường
Tài liệu ôn thi Tốt nghiệp THPT theo chuong trình mới 2018 Môn Toán x = x1
Ví dụ 1: Giả sử f ( x) = 0 x = x
x x x . 2 ( 1 2 3) x = x 3 x a x b x c x d 1 2 3 f ( x) + 0 – 0 – 0 + f (a) 0 f (b) 0 f (c) 0 f (d ) 0
Cách 3. Xét dấu bằng quy tắc xét dấu khoảng
Quy tắc: Hai khoảng liền kề nghiệm đơn (bội lẻ) khác dấu; Hai khoảng liền kề nghiệm kép (bội chẵn) cùng dấu
1.Xác định loại nghiệm của f ( x) (nếu được): nghiệm nào là nghiệm đơn (bội lẻ), nghiệm kép (bội chẵn)
2.Xác định dấu của f ( x) trên một khoảng nào đó, từ đó lần lượt suy ra dấu của các khoảng còn lại. x = x1
Ví dụ 2: Giả sử f ( x) = 0 x = x
x x x . Trong đó: x , x là nghiệm đơn; x là nghiệm kép 2 ( 1 2 3) 1 3 2 x = x 3 x x x x 1 2 3 f ( x) + 0 – 0 – 0 +
Cách 4. Xét dấu bằng đồ thị Chú ý
Hoành độ giao điểm của đồ thị hàm số y = f (x) và y = g ( x) là nghiệm của phương trình f (x) = g (x)
Hoành độ giao điểm của đồ thị hàm số y = f (x) và trục hoành là nghiệm của phương trình f ( x) = 0
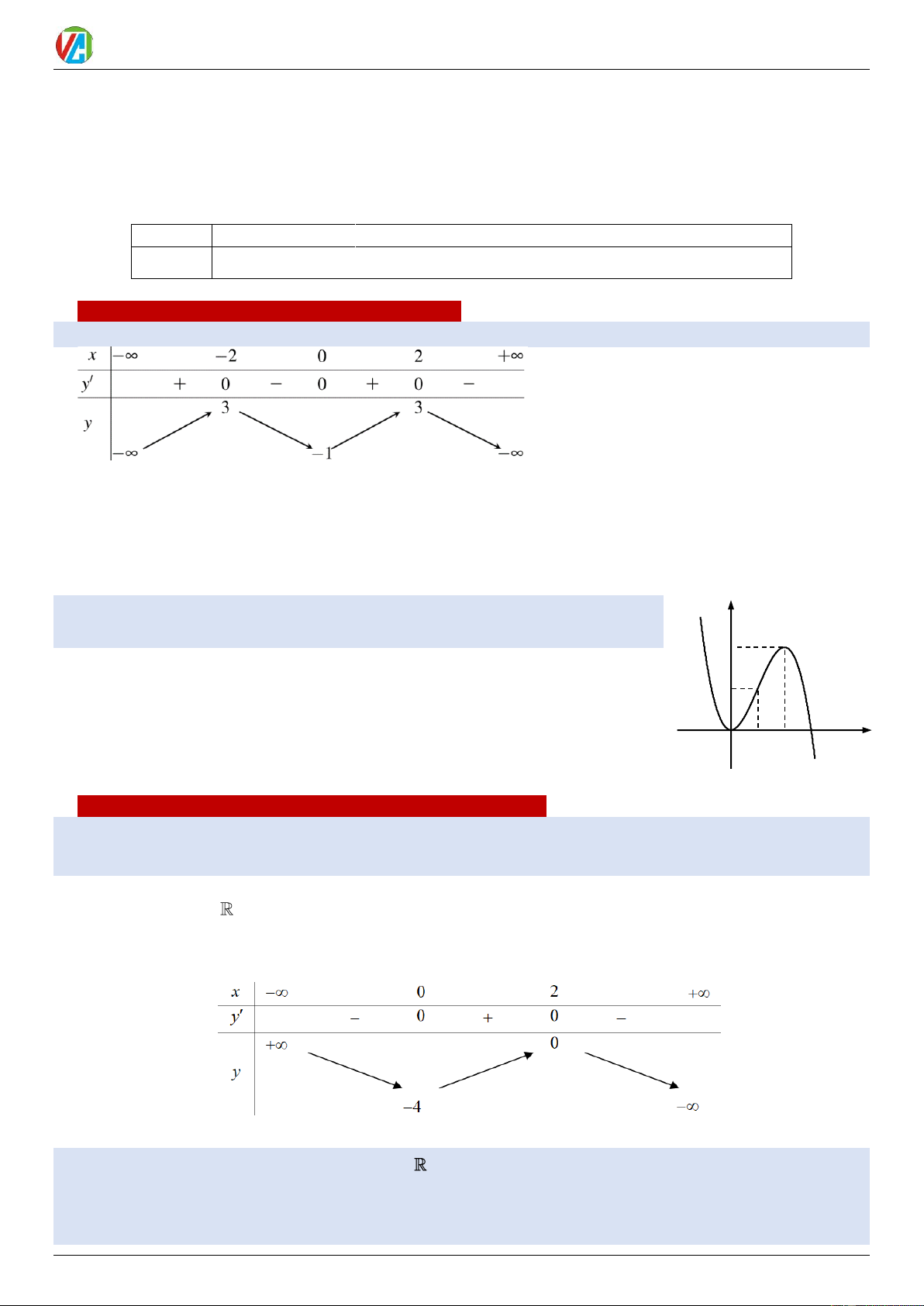
Ví dụ 3: Cho hàm số y = f (x) xác định trên và có đồ thị như hình vẽ. y Lời giải
Đồ thị và trục hoành có 2 điểm chung tại hoành độ x = 0, x = 3 , nên ta có: 4 = f ( x) x 0 = 0 x = 3 2 Trên ( ;
− 0), (0;3) đồ thị nằm trên trục hoành nên f (x) có giá trị dương; O 1 2 3 x
trên (3; +) đồ thị nằm dưới trục hoành nên f ( x) có giá trị âm. Bảng xét dấu x − 0 3 + f ( x) + 0 + 0 –
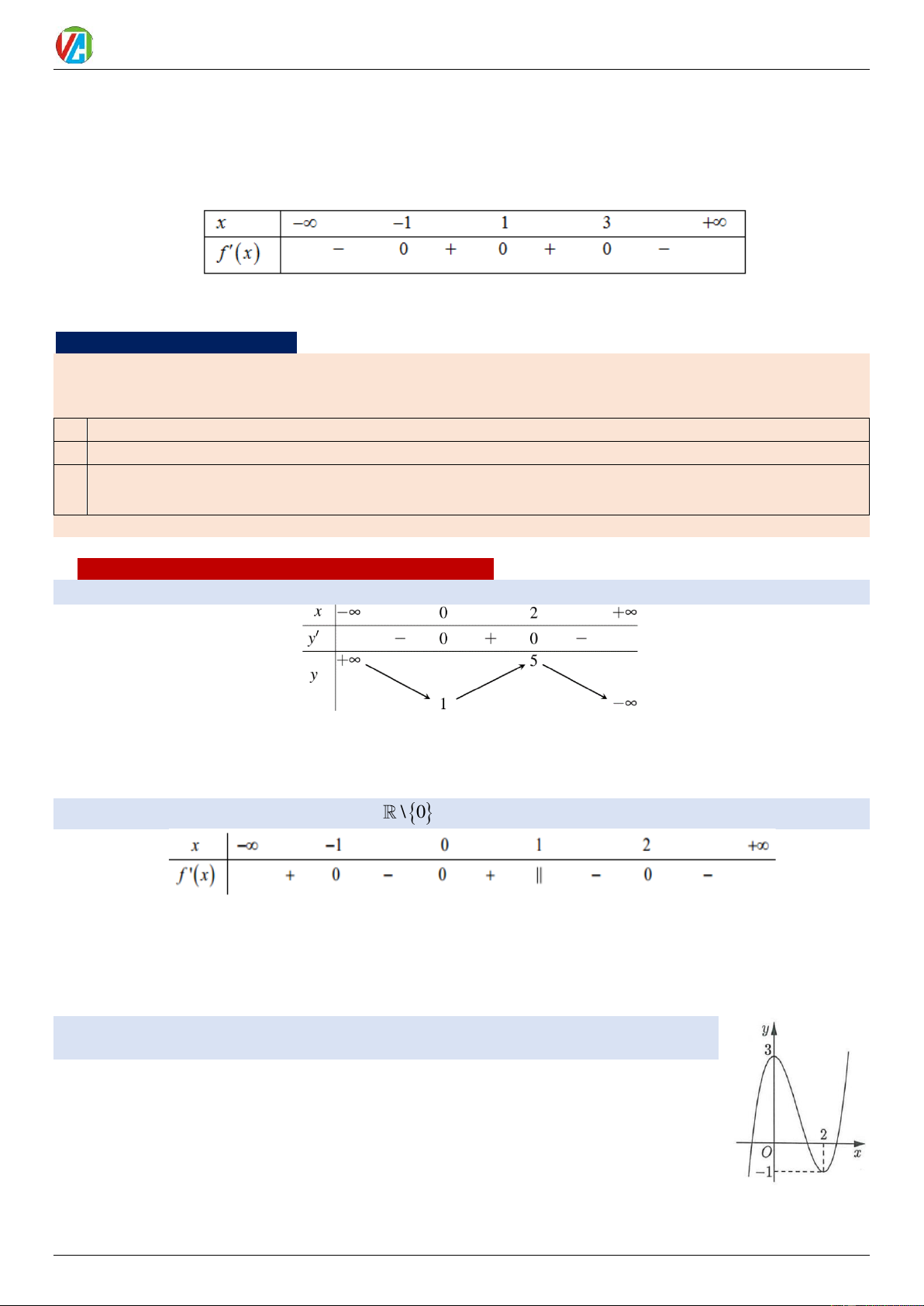
Ví dụ 4: Cho hàm số y = f (x) = g (x) − h(x) xác định trên
với y = g ( x), y = h( x) lần lượt có đồ thị là đường
cong và đường thẳng như hình vẽ. Lời giải
Đồ thị 2 hàm số y = g (x), y = h(x) có 3 điểm chung
tại hoành độ x = 2
− , x = 0, x = 4 , nên ta có: x = 2 −
f ( x) = 0 g ( x) − h ( x) = 0 g ( x) = h ( x) x = 0 x = 4 0983.900.570 6 2024-2025 Võ Công Trường
Tài liệu ôn thi Tốt nghiệp THPT theo chuong trình mới 2018 Môn Toán Trên (− ; 2
− ), (0;4), đồ thị hàm số y = g (x) nằm dưới y = h(x) nên g (x) h(x) g (x) − h(x) 0
hay f ( x) có giá trị âm; Trên ( 2
− ;0), (4;+), đồ thị hàm số y = g (x) nằm trên y = h(x) nên g (x) h(x) g (x) − h(x) 0
hay f ( x) có giá trị dương. Bảng xét dấu x − –2 0 4 + f ( x) – 0 + 0 – 0 +
Dạng 1.1. Hàm số cho bởi bảng biến thiên, đồ thị.
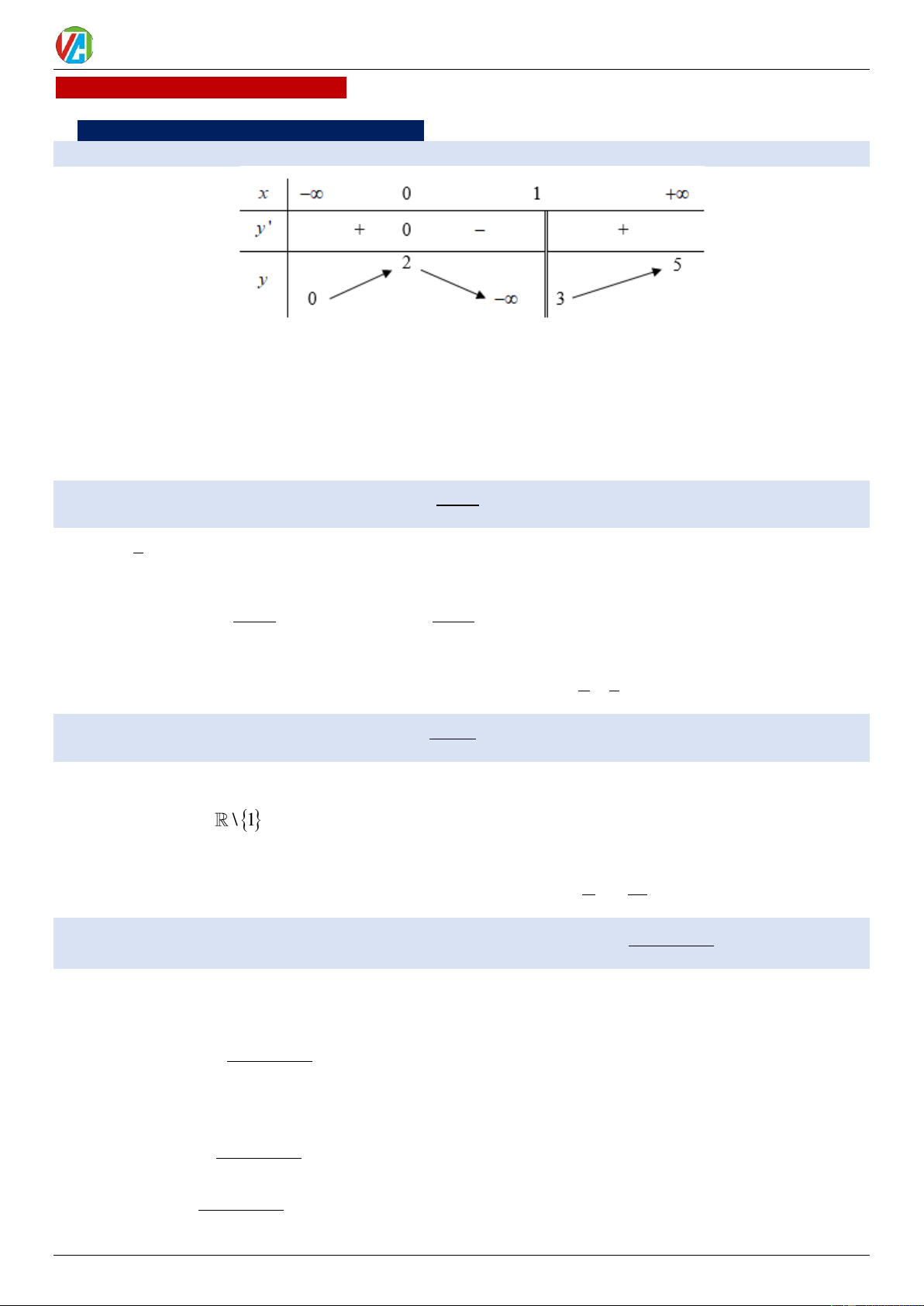
Ví dụ 5: Cho hàm số y = f (x) có bảng biến thiên như sau
Hàm số y = f (x) nghịch biến trên khoảng nào dưới đây A. ( 2 − ;0) . B. (− ; 2 − ) . C. (0; 2) . D. (0; ) + .
Lời giải
Dựa vào bảng biến thiên, ta có: y 0 trên các khoảng ( 2 − ;0), (2;+).
Vậy hàm số nghịch biến trên các khoảng ( 2
− ;0), (2;+). Chọn đáp án A Ví dụ 6: y
Cho hàm số y = f ( x) có đồ thị như hình vẽ. Hàm số đã cho đồng biến trên khoảng nào? 4 A. (−;0) . B. (1;3) . C. (0; 2) . D. (0; + ) . 2
Lời giải
Dựa vào đồ thị, ta thấy đồ thị đi lên trên các khoảng ( x 2 − ;0) . O 1 2 3
Vậy hàm số đồng biến trên các khoảng ( 2
− ;0) . Chọn đáp án C
Dạng 1.2. Hàm số cho bởi biểu thức hoặc biểu thức đạo hàm Ví dụ 7: Hàm số 3 2
y = −x + 3x − 4 đồng biến trên khoảng nào? A. (2; + ) . B. (0; 2) . C. ( 4 − ;0) . D. (−;0) .
Lời giải Tập xác định: D = x = 0 Ta có: 2 y = 3
− x + 6x ; y = 0 . x = 2
Dựa vào bảng biến thiên thì hàm số đã cho đồng biến trên khoảng (0; 2) . Chọn đáp án B Ví dụ 8: 2 3
Cho hàm số y = f ( x) liên tục trên
và có đạo hàm f ( x) = (1− x) ( x + ) 1 (3− x) . Hàm số
y = f ( x) đồng biến trên khoảng nào dưới đây? A. ( ) ;1 − . B. (− ; − ) 1 . C. (1;3) . D. (3; + ) . 0983.900.570 7 2024-2025 Võ Công Trường
Tài liệu ôn thi Tốt nghiệp THPT theo chuong trình mới 2018 Môn Toán
Lời giải x =1 2 3
Ta có: f ( x) = 0 (1− x) ( x + )
1 (3 − x) = 0 x = 1 − . x = 3 Bảng xét dấu:
Hàm số đồng biến trên các khoảng (−1;3) . Chọn đáp án C
2. TÌM CỰC TRỊ CỦA HÀM SỐ
Bước 1. Tìm tập xác định
Bước 2. Tìm đạo hàm. Tìm nghiệm của đạo hàm và điểm không xác định của đạo hàm.
Bước 3. Lập bảng biến thiên: x
Điền TXĐ; nghiệm của đạo hàm và điểm không xác định của đạo hàm (theo thứ tự tăng dần). y'
Xét dấu đạo hàm y’
Vẽ chiều biến thiên (mũi tên chéo lên khi y 0 , chéo xuống khi y 0 ); y
Điền Giới hạn hàm số, Giá trị hàm số tại các điểm x tương ứng vào đầu, cuối các mũi tên
Bước 4. Dựa vào bảng biến thiến và định lí, kết luận cực trị.
Dạng 2.1. Hàm số cho bởi bảng biến thiên hoặc đồ thị
Ví dụ 9: Cho hàm số y = f (x) có bảng biến thiên như sau
Hàm số đạt cực đại tại điểm A. x = 1 .
B. x = 0 .
C. x = 5 . D. x = 2 .
Lời giải
Dựa vào bảng biến thiên, dễ dàng thấy đáp án A
Ví dụ 10: Cho hàm số f (x) liên tục trên \
0 và có bảng xét dấu của f ( x) như sau:
Số điểm cực trị của hàm số đã cho là A. 4 . B. 1. C. 2 . D. 3 .
Lời giải
Dựa vào bảng biến thiên, ta thấy đạo hàm f ( x) đổi dấu 3 lần khi x qua các điểm x = 1
− , x = 0, x =1 ,
nhưng x = 0 là điểm không xác định nên hàm số chỉ có điểm cực trị. Chọn đáp án C
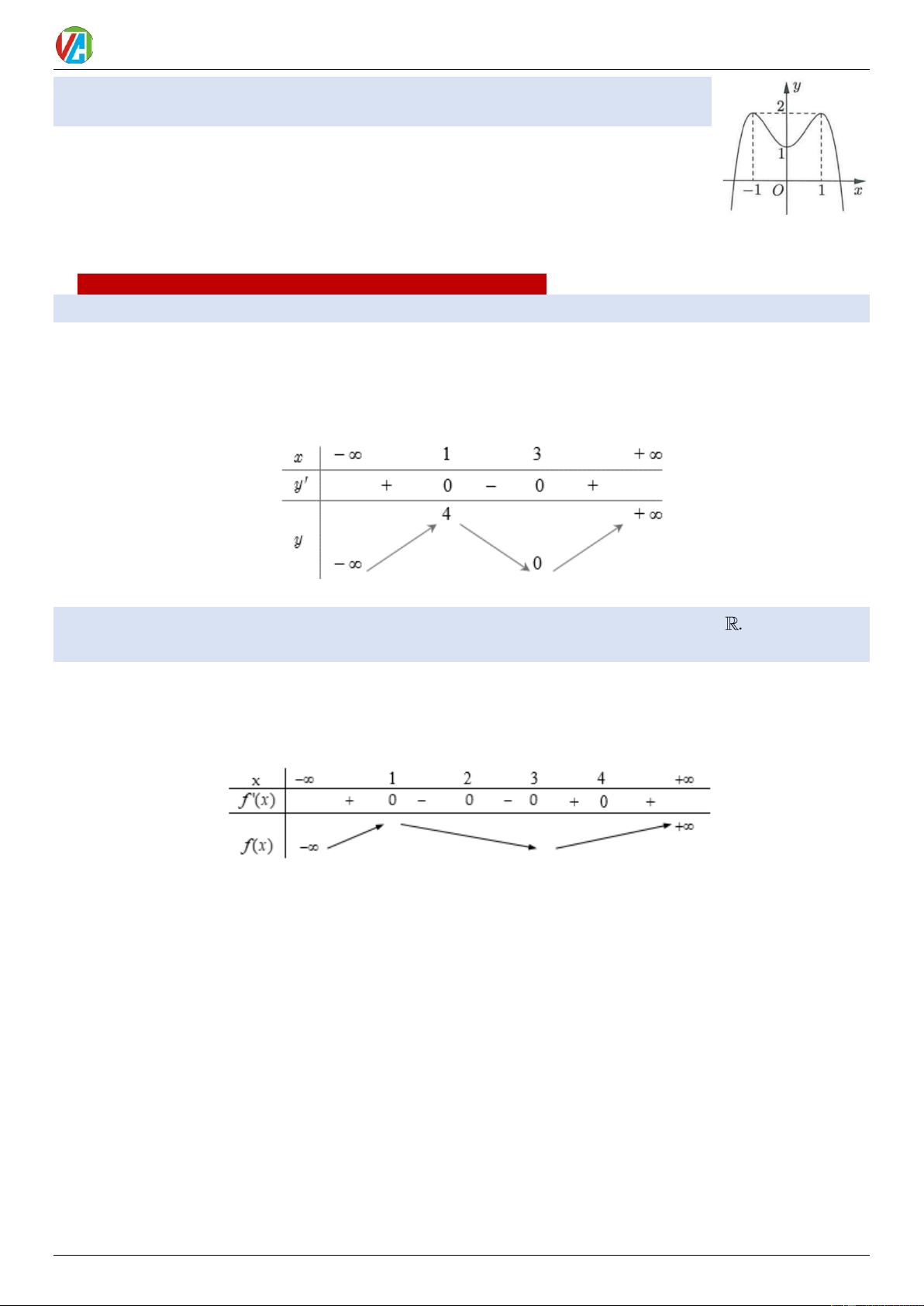
Ví dụ 11: Cho hàm số bậc ba 𝑦 = 𝑓(𝑥) có đồ thị là đường cong trong hình bên. Giá trị
cực đại của hàm số đã cho là A. −1. B. 3 . C. 2 . D. 0 .
Lời giải
Dựa và đồ thị, ta thấy đồ thị hàm số có điểm cực đại là (0;3) , điểm cực tiểu là (2; ) 1 − . Chọn đáp án B 0983.900.570 8 2024-2025 Võ Công Trường
Tài liệu ôn thi Tốt nghiệp THPT theo chuong trình mới 2018 Môn Toán
Ví dụ 12: Cho hàm số 4 2
y = ax + bx + c có đồ thị là đường cong trong hình bên. Điểm
cực tiểu của đồ thị hàm số đã cho có tọa độ là A. ( 1 − ;2) . B. (0; ) 1 . C. (1; 2) . D. (1;0) .
Lời giải
Dựa và đồ thị, ta thấy đồ thị hàm số có 2 điểm cực đại là ( 1
− ;2), (1;2) và 1 điểm cực tiểu là (0; ) 1 . Chọn đáp án B
Dạng 2.2. Hàm số cho bởi biểu thức hoặc biểu thức đạo hàm
Ví dụ 13: Điểm cực đại của đồ thị hàm số 3 2
y = x − 6x + 9x có tổng hoành độ và tung độ bằng A. 5 . B. 1. C. 3 . D. −1.
Lời giải x =1 Ta có: 2
y ' = 3x −12x + 9 = 0 x = 3 Bảng biến thiên
Khi đó: x =1 y = 4 x + y = 5. Chọn đáp án A CD CD CD CD Ví dụ 14: 2 3 4
Cho hàm số f ( x) có đạo hàm f ( x) = ( x − )
1 ( x − 2) ( x − ) 3 ( x − 4) , x
. Số điểm cực trị
của hàm số đã cho là A. 3 B. 5 C. 2 D. 4
Lời giải
f ( x) = 0 x 1;2;3; 4 Bảng biến thiên:
Dựa vào bảng biến thiên: Số điểm cực trị của hàm số đã cho là 2. Chọn đáp án C 0983.900.570 9 2024-2025 Võ Công Trường
Tài liệu ôn thi Tốt nghiệp THPT theo chuong trình mới 2018 Môn Toán
BÀI 2. GIÁ TRỊ LỚN NHẤT – GIÁ TRỊ NHỎ NHẤT CỦA HÀM SỐ 1. Định nghĩa:
Cho hàm số y = f ( x) xác định trên D
Số M được gọi là giá trị lớn nhất (GTLN) của hàm số y = f (x) trên D nếu f (x) M; x D và x
D : f x = M . 0 ( 0)
Kí hiệu M = max f ( x) hoặc M = max f ( x) . x D D
Số m được gọi là giá trị nhỏ nhất (GTNN) của hàm số y = f (x) trên D nếu f (x) ; m x D và x
D : f x = m 0 ( 0)
Kí hiệu m = min f ( x) hoặc m = min f ( x). x D D Tóm tắt f
(x) M , x D f (x) , m x D
max f (x) = M
min f (x) = m x D : D f x = M x D : D f x = m 0 ( 0) 0 ( 0) Chú ý :
(1) Nếu hàm số chỉ có 1 cực đại trên K thì max y = y
. Nếu hàm số chỉ có 1 cực tiểu trên K thì min y = y CD CT K K
(2) Nếu hàm số đồng biến trên đoạn ;
a b thì min y = y (a), max y = y (b) a;b a;b
Nếu hàm số nghịch biến trên đoạn ;
a b thì min y = y (b), max y = y (a) a;b a;b
2. Tìm giá trị lớn nhất, giá trị nhỏ nhất của hàm số trên một đoạn
Tìm giá trị lớn nhất, giá trị nhỏ nhất của hàm số y = f ( x) trên đoạn ; a b
Bước 1: Tìm đạo hàm f ( x) , Tìm các điểm x , x ,..., x trên khoảng ( ;
a b) , tại đó f ( x) = 0 hoặc f ( x) 1 2 n
không xác định. (Tìm các nghiệm và các điểm không xác định của đạo hàm f ( x) trên khoảng ( ; a b) )
Bước 2: Tính f (a), f (b), f (x , f x ,..., f x 1 ) ( 2) ( n )
Bước 3: Kết luận: max f ( x) = max f (a), f (b), f (x , f x ,..., f x . (Giá trị lớn nhất ở Bước 2) 1 ) ( 2 ) ( n ) a,b
min f ( x) = min f (a), f (b), f ( x , f x ,..., f x
. (Giá trị nhỏ nhất ở Bước 2) 1 ) ( 2) ( n ) a,b
3. Tìm giá trị lớn nhất, giá trị nhỏ nhất của hàm số trên khoảng (hay nửa khoảng) K
Bước 1. Lập bảng biến thiên → Đặt K vào vị trí thích hợp;
Bước 2. Dựa vào bảng biến thiên, nhận xét và kết luận GTLN-GTNN
Chú ý: Trên một khoảng hàm số có thể không có hay chỉ có GTLN hoặc GTNN.
CÁC DẠNG TOÁN THƯỜNG GẶP
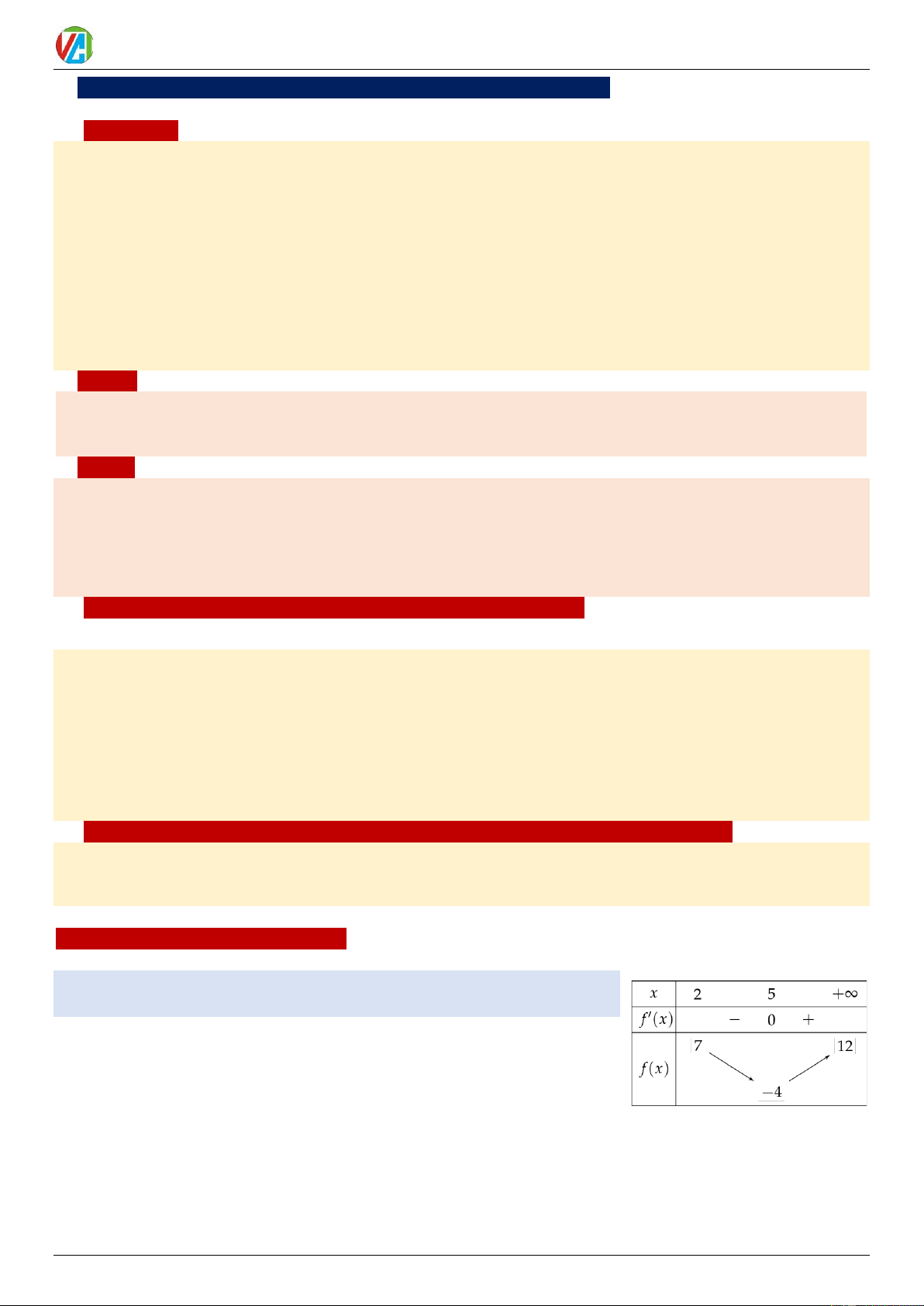
Ví dụ 15: Hàm số y = f (x) xác định, liên tục trên khoảng (2; +) và có
bảng biến thiên như sau. Chọn mệnh đề đúng.
A. min f (x) = 5.
B. min f (x) = 4 − . (2;+) (2;+)
C. max f (x) = 12 .
D. max f (x) = 7 . (2;+) (2;+)
Lời giải
Dựa vào hàng giá trị f ( x) ta thấy, giá trị −4 là giá trị nhỏ nhất của hàm số trên khonagr (2; +) . Chọn B 0983.900.570 10 2024-2025 Võ Công Trường
Tài liệu ôn thi Tốt nghiệp THPT theo chuong trình mới 2018 Môn Toán
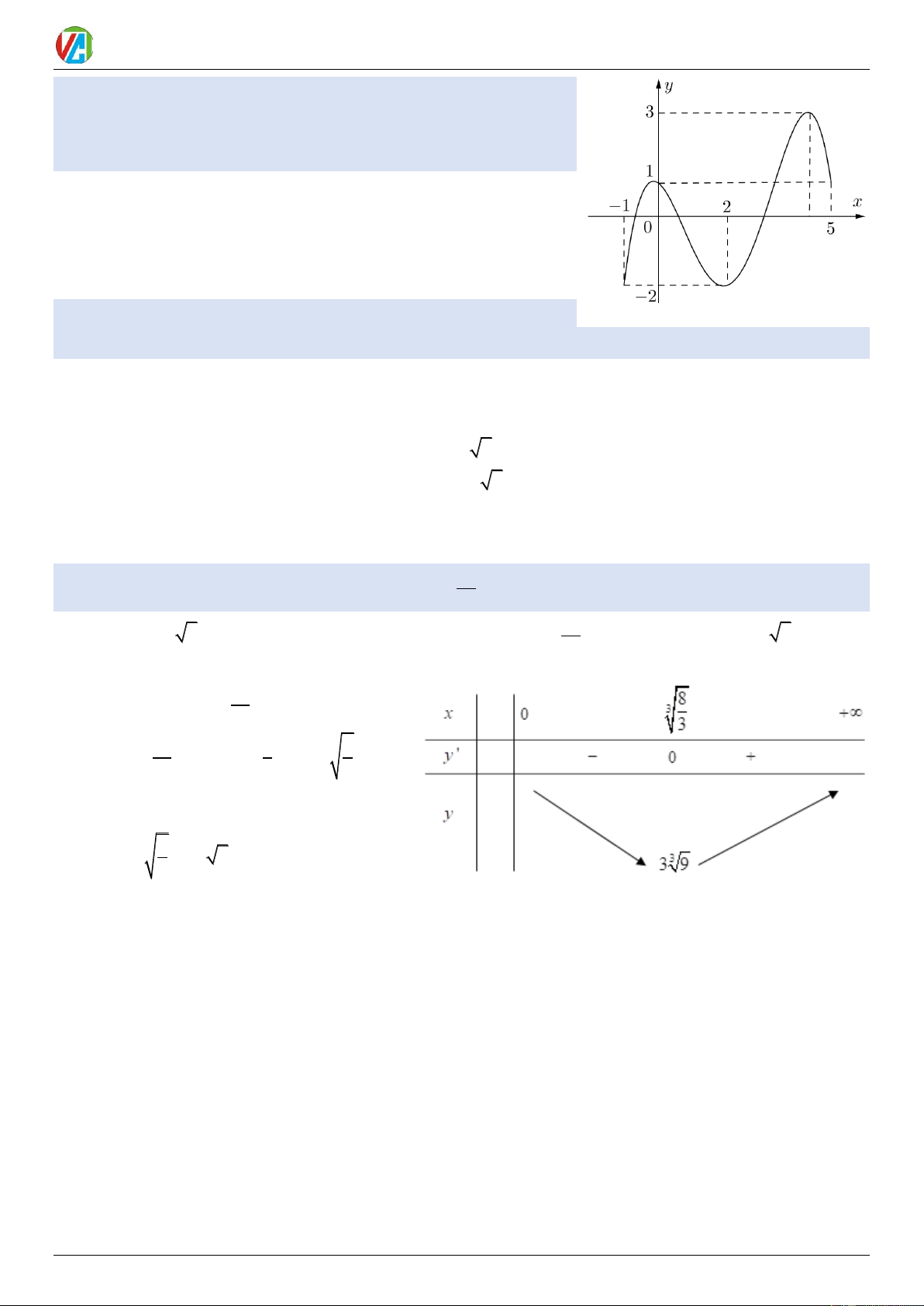
Ví dụ 16: Cho hàm số f (x) liên tục trên 1 − ; 5 và có đồ thị trên đoạn 1 − ;
5 như hình vẽ bên dưới. Tổng giá trị lớn nhất và giá trị nhỏ
nhất của hàm số f ( x) trên đoạn 1 − ; 5 bằng A. −1 B. 4 C. 1 D. 2
Lời giải
Dựa vào đồ thị ta thấy, Điểm cao nhất của đồ thị là điểm có tung độ
bằng 3, điểm thấp nhất của đồ thị có tung độ bằng −2
Vậy giá trị lớn nhất là 3 và giá trị nhỏ nhất là −2 . Chọn C
Ví dụ 17: Giá trị lớn nhất của hàm số 4 2 f ( )
x = −x +12x +1 trên đoạn 1 − ;2bằng A. 1. B. 37 . C. 33 . D. 12 .
Lời giải x = 0 1 − ;2 • Đạo hàm: 3 2 f '( ) x = 4
− x + 24x ; f (x) = 0 x = 6 1 − ;2 x = − 6 1 − ;2 • f ( 1
− ) =12, f (2) = 33, f (0) =1
Vậy, max f ( x) = 33 1 − ,2 Ví dụ 18: 4
Tính giá trị nhỏ nhất của hàm số y = 3x +
trên khoảng (0; +). 2 x 33 A. 3 min y = 3 9..
B. min y = 7. . C. min y = . . D. 3 min y = 2 9. . (0;+) (0;+) (0;+) 5 (0;+)
Lời giải • 8
Đạo hàm: y ' = 3 − ; 3 x 8 8 8 3 3 y ' = 0
= 3 x = x = 3 x 3 3 • Bảng biến thiên:
Dựa vào bảng biến thiên, ta có: 8 3 3 min y = y = 3 9 ( 0;+) 3 0983.900.570 11 2024-2025 Võ Công Trường
Tài liệu ôn thi Tốt nghiệp THPT theo chuong trình mới 2018 Môn Toán
BÀI 3. ĐƯỜNG TIỆM CẬN
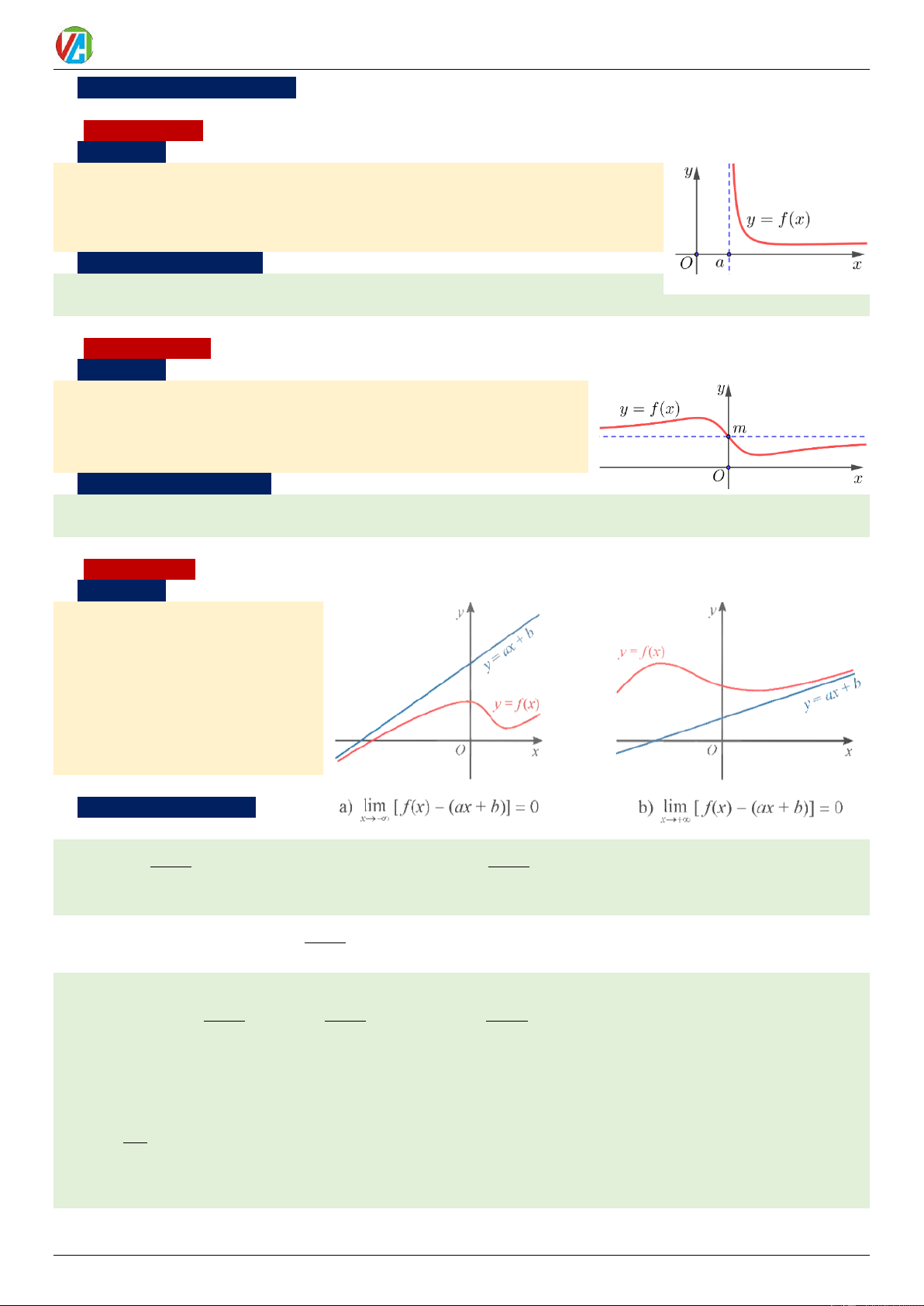
1. Tiệm cận đứng Định nghĩa
Đường thẳng x = a được gọi là một đuờng tiệm cận đứng (hay tiệm cận đúng)
của đồ thị hàm số y = f ( x) nếu ít nhất một trong các điều kiện sau thoả mãn:
lim f ( x) = + , lim f ( x) = − , lim f ( x) = + , lim f ( x) = − − − + + x a → x→a x a → x→a
Cách tìm tiệm cận đứng
Để tìm tiệm cận đứng của đồ thị hàm số thì ta tính giới hạn của hàm số tại các
nghiệm của mẫu. Dựa vào định nghĩa ta kết luận tiệm cận đứng. (Xem sơ đồ ở trang sau) 2. Tiệm cận ngang Định nghĩa
Đường thẳng y = m được gọi là một đường tiệm cận ngang (hay tiệm
cận ngang) của đồ thị hàm số y = f ( x) nếu
lim f ( x) = m hoặc lim f ( x) = m x→− x→+
Cách tìm tiệm cận ngang
Để tìm tiệm cận ngang của đồ thị hàm số thì ta tính giới hạn của hàm số tại 2 đầu vô cực. Dựa vào định
nghĩa ta kết luận tiệm cận đứng. (Xem sơ đồ ở trang sau) 3. Tiệm cận xiên Định nghĩa Đường thẳng y = ax + , b a 0 ,
được gọi là đuờng tiệm cận xiên
(hay tiệm cận xiên) của đồ thị hàm
số y = f ( x) nếu lim f
( x) − (ax + b) = 0 hoặc x→− lim f
( x) − (ax + b) = 0 x→+
Cách tìm tiệm cận xiên
Trường hợp tổng quát: f ( x) f ( x) Nếu lim
= a và lim f
( x) − ax = b hoặc lim
= a và lim f
( x) − ax = b thì đường thẳng x→+ x x→+ x→− x x→−
y = ax + b là tiệm cận xiên P x
Trường hợp hàm số y = f ( x) ( ) =
, với bậc của P ( x) lớn hơn bậc của Q( x) một đơn vị Q ( x)
Cách 1. Chia đa thức P x R ( x) R ( x)
Nếu y = f ( x) ( ) = ( ) = ax+b+ , a 0 và lim
= 0 thì đường thẳng y = ax + b là tiệm cận Q x Q ( x)
x→ Q ( x) xiên Cách 2.
Tính hệ số a, b của tiệm cận xiên y = ax + b theo công thức: a T a =
là thương của 2 hệ số của lũy thừa bậc cao nhất của tử và mẫu; aM
b = lim f ( x) − ax
hay b = lim f ( x) − ax x→+ x→− 0983.900.570 12 2024-2025 Võ Công Trường
Tài liệu ôn thi Tốt nghiệp THPT theo chuong trình mới 2018 Môn Toán
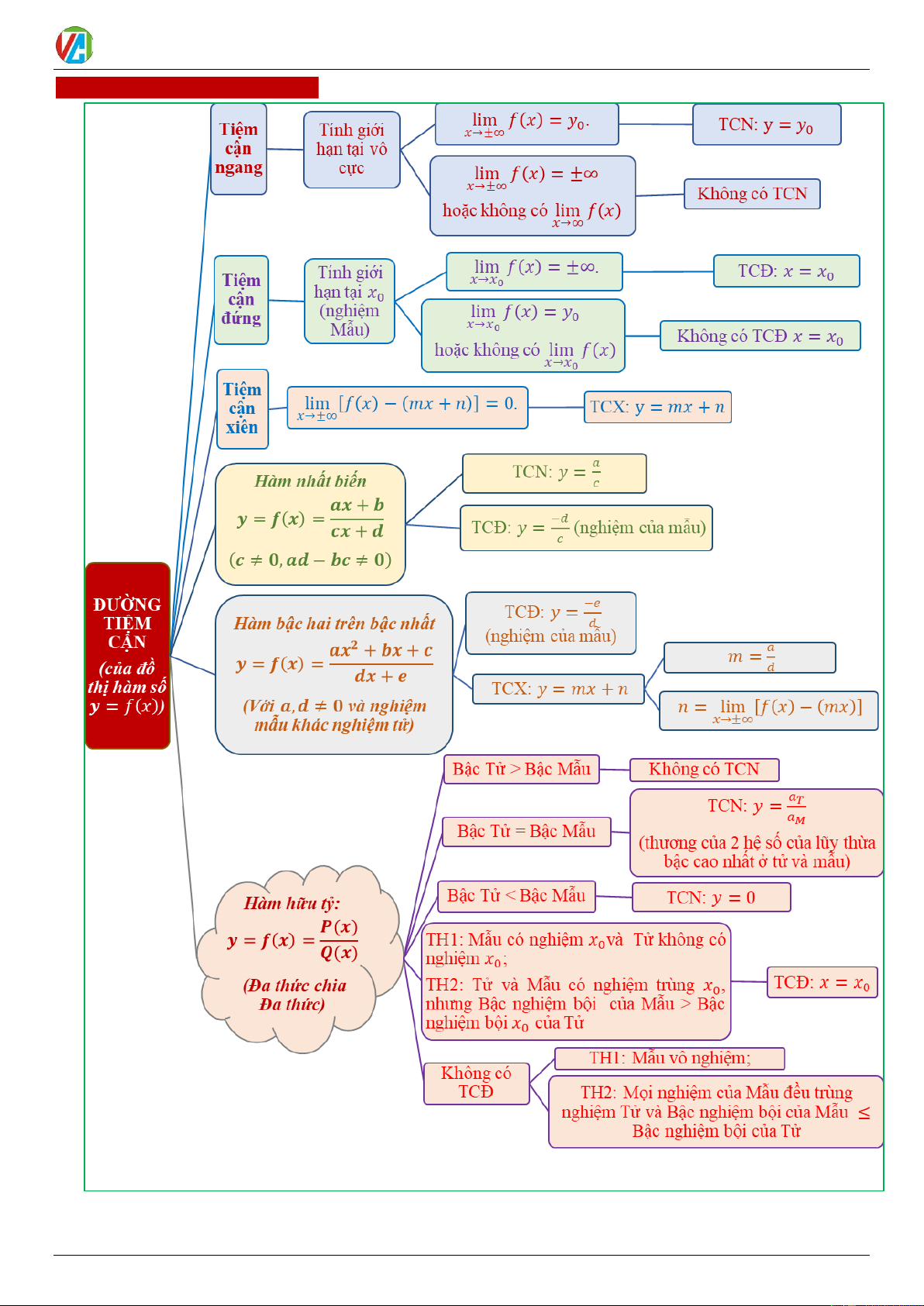
SƠ ĐỒ TÌM ĐƯỜNG TIỆM CẬN 0983.900.570 13 2024-2025 Võ Công Trường
Tài liệu ôn thi Tốt nghiệp THPT theo chuong trình mới 2018 Môn Toán
CÁC DẠNG TOÁN THƯỜNG GẶP
1. TÌM ĐƯỜNG TIỆM CẬN NGANG, ĐỨNG.
Ví dụ 19: Cho hàm số f (x) có bảng biến thiên như sau
Tổng số tiệm cận ngang và tiệm cận đứng của đồ thị hàm số đã cho là A. 4 . B. 1. C. 3 . D. 2 .
Lời giải
Dựa vào bảng biến thiên, ta có :
lim f ( x) = 0 và lim f ( x) = 5 nên tiệm cận ngang của đồ thị hàm số là 2 đường thẳng y = 0, y = 5. x→− x→+
lim f ( x) = − nên tiệm cận đứng của đồ thị hàm số là đường thẳng x = 1 . Chọn C − x 1 → + Ví dụ 20: 3x 1
Tiệm cận ngang của đồ thị hàm số y = là x −1 1 A. y = .
B. y = 3 . C. y = 1 − . D. y = 1. 3
Lời giải 3x +1 3x +1 Ta có : lim y = lim = 3 và lim y = lim
= 3 nên y = 3 là tiệm cận ngang của đồ thị hàm số. x→+ x→+ x −1 x→−
x→− x −1 Chọn B a 3
Hay ta có thể dùng công thức: Phương trình tiệm cận ngang là y = = = 3 c 1 + Ví dụ 21: 2x 2
Tiệm cận đứng của đồ thị hàm số y = là x −1
A. x = 2 .
B. x = −2 .
C. x = 1. D. x = −1 .
Lời giải Tập xác định D = \ 1 .
Ta có lim y = −; lim y = + , suy ra đồ thị có tiệm cận đứng là x = 1 . Chọn C − + x 1 → x 1 → d 1 −
Hay ta có thể dùng công thức: Phương trình tiệm cận đứng là x = − = − =1 c 1 2 − − Ví dụ 22: 5x 4x 1
Tổng số tiệm cận đứng và tiệm cận ngang của đồ thị hàm số y = là 2 x −1 A. 0. B. 1. C. 2. D. 3.
Lời giải Tiệm cận ngang: 2 − − Ta có: 5x 4x 1 lim y = lim
= 5 nên đồ thị hàm số có một tiệm cận ngang y = 5 . 2 x→ x→ x −1 Tiệm cận đứng: Cho 2 x = 1 x = 1 2 5x − 4x −1 Ta có: lim y = lim
= 3 nên x = 1không là tiệm cận đứng. 2 x 1 → x 1 → x −1 2 5x − 4x −1 lim y = lim
= − nên đồ thị hàm số có một tiệm cận đứng x = −1. + + x ( → − ) x ( → − ) 2 1 1 x −1 0983.900.570 14 2024-2025 Võ Công Trường
Tài liệu ôn thi Tốt nghiệp THPT theo chuong trình mới 2018 Môn Toán
Tổng cộng đồ thị hàm số có 2 tiệm cận. Chọn C + − + Ví dụ 23: 5x 1 x 1
Đồ thị hàm số y =
có tất cả bao nhiêu đường tiệm cận đứng và ngang? 2 x − 2x A. 0 . B. 1. C. 2 . D. 3 .
Lời giải
Tập xác định của hàm số là D = 1 − ;0)(2;+) . 9 Ta có: lim y = −
; lim y = + ; lim y = 0 . − + x→0 4 x 2 → x→+
Vậy đồ thị của hàm số có đường tiệm cận đứng x = 2 và tiệm cận ngang y = 0 . Chọn C
2. TÌM ĐƯỜNG TIỆM CẬN XIÊN. 2 − + Ví dụ 24: x 3x 1
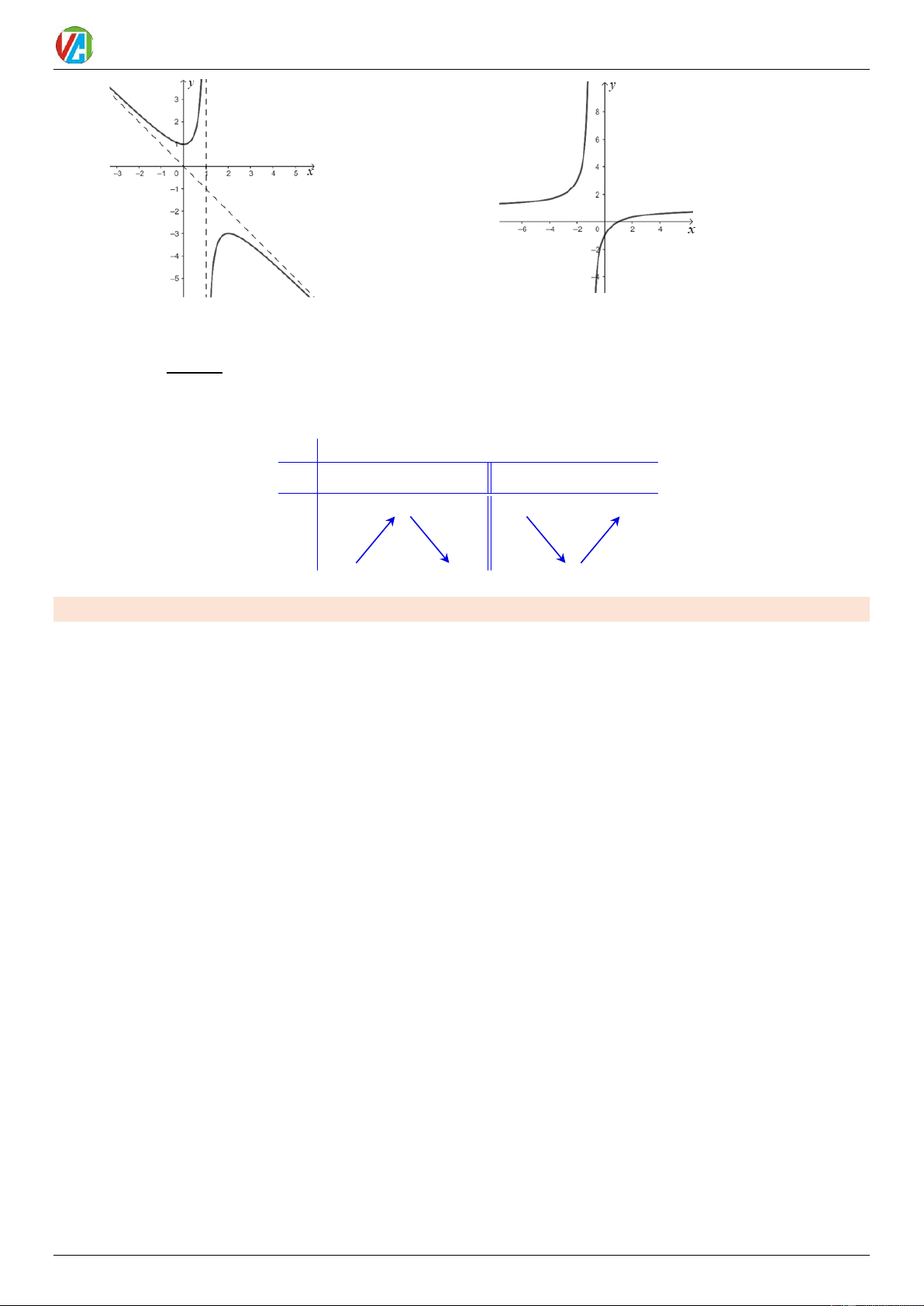
Tìm tiệm cận xiên của đồ thị hàm số y = f (x) = . x − 2
Lời giải Tập xác định: D = \{2}. 2 f (x) x − 3x +1 2 x −3x +1 −x +1 Ta có: a = lim = lim
= ; b = lim[ f (x) − ax] = lim − x = lim = 1 − . x→+ x x →+ ( x − ) 1 2 .x x→+ x→+ x − 2 x→+ x − 2 Ta cũng có f (x) lim
=1, lim[ f (x) − x] = 1 − . x→− x x →−
Do đó, đồ thị hàm số có tiệm cận xiên là đường thẳng y = x −1. Chú ý a 1 Hệ số T a = = =1 a 1 M 2 − + Đồ x 3x 1 thị hàm số y = x =
và tiệm cận xiên y = x −1 của nó được thể x −
cùng với tiệm cận đứng 2 2 hiện trong Hình 10. 0983.900.570 15 2024-2025 Võ Công Trường
Tài liệu ôn thi Tốt nghiệp THPT theo chuong trình mới 2018 Môn Toán
BÀI 4. ĐỒ THỊ HÀM SỐ
1. Sơ đồ khảo sát và vẽ đồ thị hàm số:
Bước 1. Tìm tập xác định
Bước 2. Sự biến thiên:
+ Tìm đạo hàm. Tìm nghiệm của đạo hàm và điểm không xác định của đạo hàm.
+ Tính giới hạn của hàm số tại các “đầu ngoặc tròn” của TXĐ. Suy ra các đường tiệm cận (nếu có) + Lập bảng biến thiên: x
Điền TXĐ; nghiệm của đạo hàm và điểm không xác định của đạo hàm (theo thứ tự tăng dần). y Xét dấu đạo hàm
Vẽ chiều biến thiên (mũi tên chéo lên khi y 0 , chéo xuống khi y 0 ); y
Điền Giới hạn hàm số, Giá trị hàm số tại các điểm x tương ứng vào đầu, cuối các mũi tên
Bước 3. Vẽ đồ thị: Lập bảng giá trị (hay điểm đặc biệt), vẽ đồ thị và nhận xét về đồ thị
2. Các dạng đồ thị hàm số thường gặp
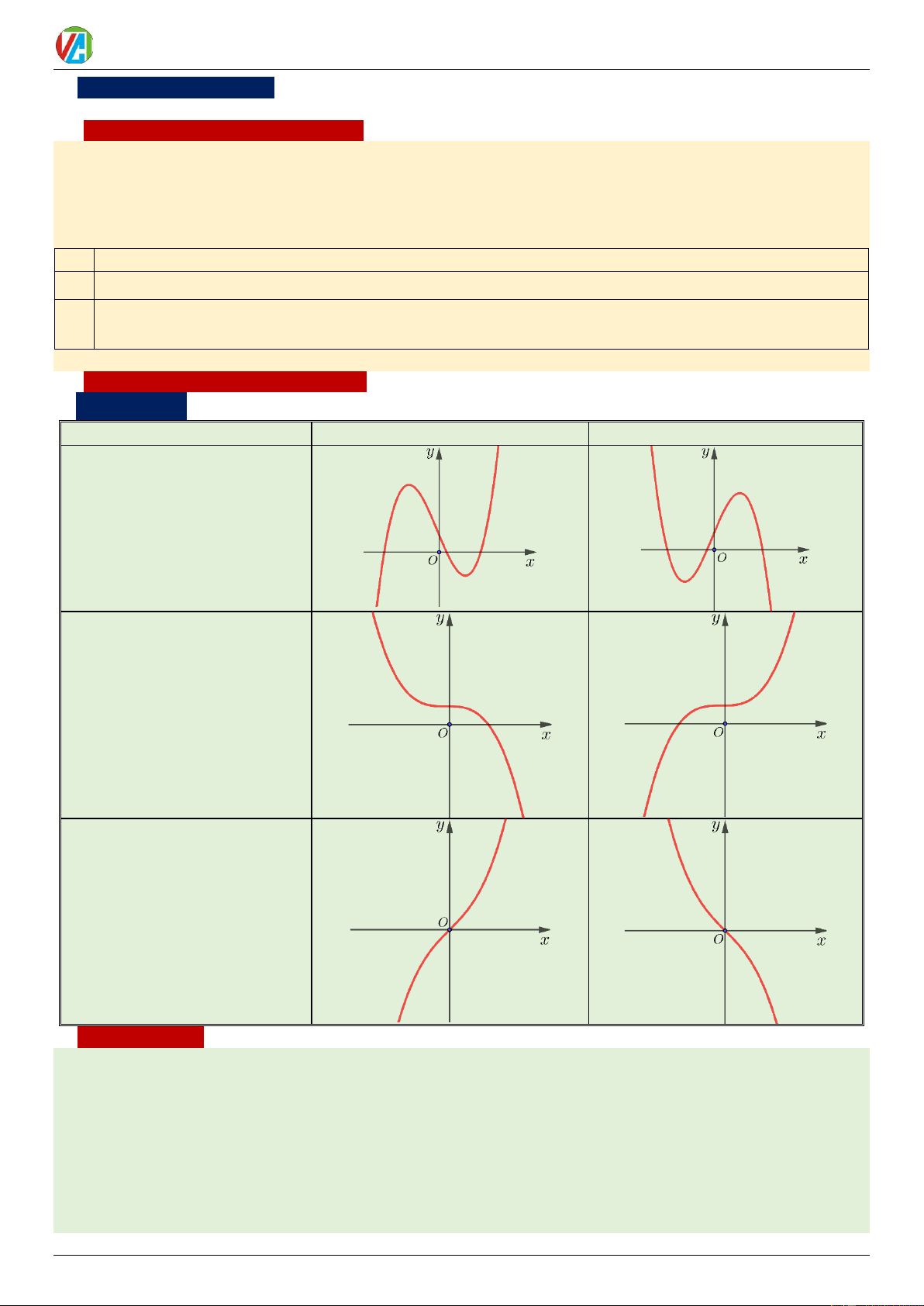
a) Hàm số bậc 3: 3 2
y = ax + bx + cx + d (a 0) a 0 a 0
Phương trình y = 0
có hai nghiệm phân biệt.
Phương trình y = 0 có nghiệm kép.
Phương trình y = 0 vô nghiệm.
Nhận xét đồ thị:
(1) Hai đầu đồ thị: ĐTHS bậc 3 (bậc lẻ nói chung) luôn có một đầu đi lên và một đầu đi xuống.
Đầu bên phải: Đi lên → a 0 ; Đi xuống → a 0 .
(2) Giao điểm với trục Oy: Nằm phía trên trục hoành → d 0 ; Nằm phía dưới trục hoành → d 0
Qua O d = 0
(3) Điểm cực trị: Hai điểm cực trị nằm:
Khác phía so với trục Oy → a.c 0 ;
Cùng phía bên phải Oy → a, c trái dấu với b ;
Cùng phía bên trái Oy → a, , b c cùng dấu.
Có điểm cực trị thuộc Oy → c = 0 0983.900.570 16 2024-2025 Võ Công Trường
Tài liệu ôn thi Tốt nghiệp THPT theo chuong trình mới 2018 Môn Toán b −
(4) Tâm đối xứng: điểm I ( x ; y , với x =
(là nghiệm PT y ' = 0 ) và y = f x 0 ( 0) 0 0 ) 0 3a
Tâm đối xứng cũng là trung điểm của đoạn thẳng nối 2 điểm cực trị.
Tâm đối xứng nằm bên phải trục Oy → a, b trái dấu; bên trái trục Oy → a, b cùng dấu. ax + b
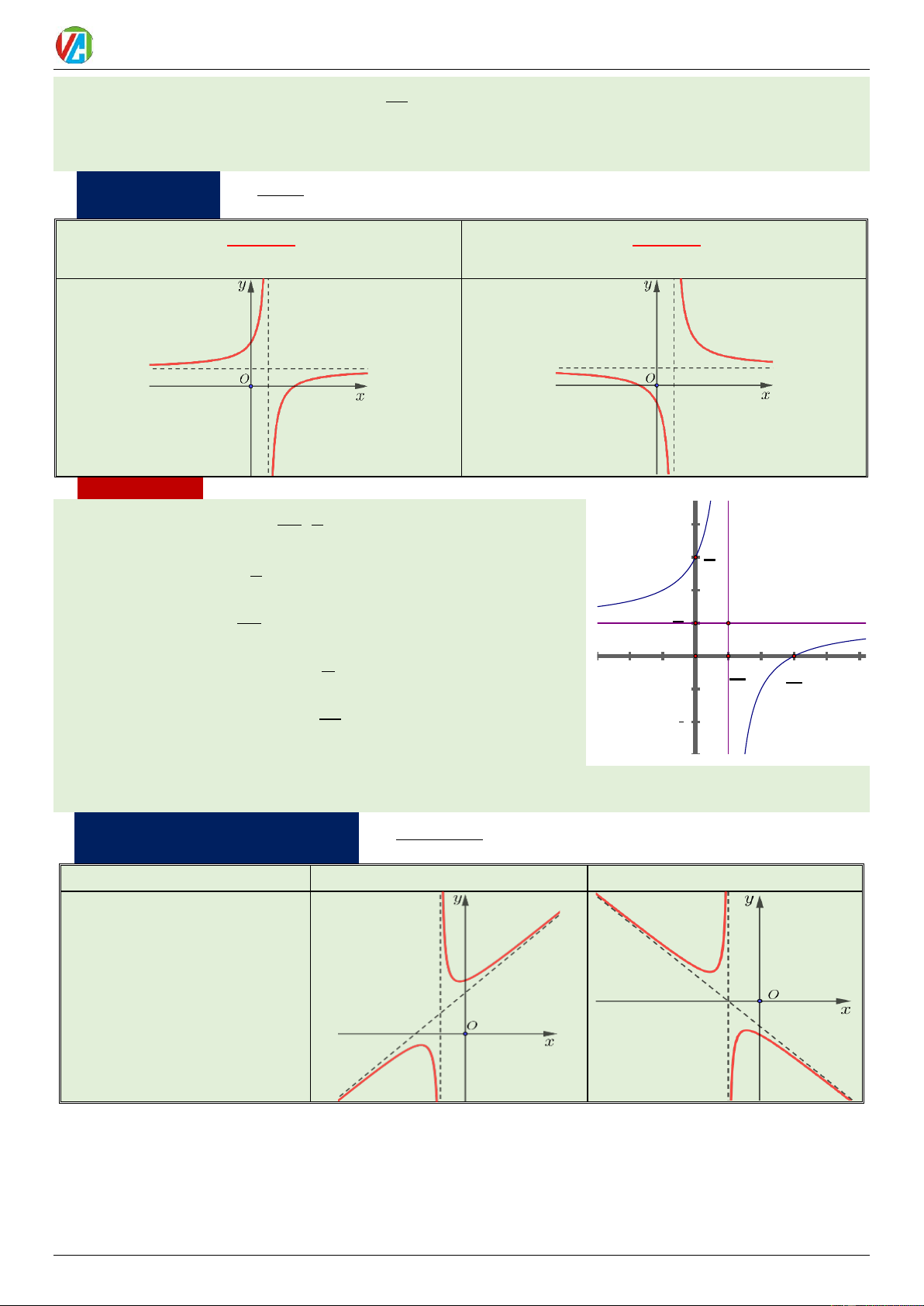
b) Hàm số nhất biến: y =
(ad − bc 0) cx + d ad – bc ad – bc y = = ( y 0 cx + d ) 0 2 (cx + d )2 8 6
Nhận xét đồ thị: −d a
(1) Tâm đối xứng là điểm I ;
(là giao điểm 2 đường tiệm cận). 4 c c b a
(2) Tiệm cận ngang: y = ; d c 2 −d a
Tiệm cận đứng: x = (nghiệm của mẫu). c TCN c b
(3) Giao điểm với Oy
15 : x = 0 y = ; 10 5 -d 5 10 15 -b O d c − a Giao điể b
m với Ox: y = 0 x = (nghiệm của tử). 2 a TCĐ
Qua O b = 0
(4) Hàm số đồng biến ad − bc 0 ; 4
Hàm số nghịch biến ad − bc 0 2
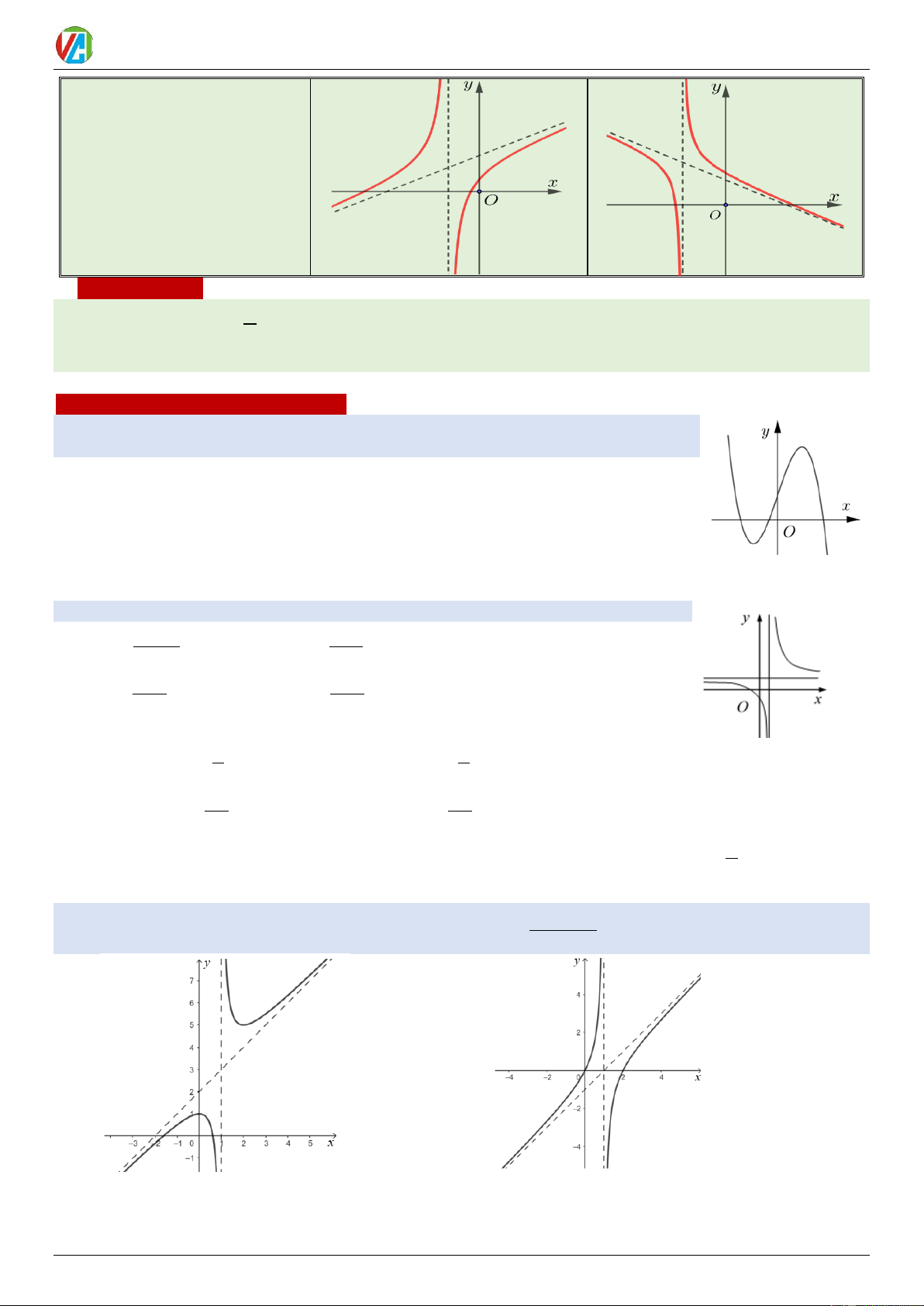
ax + bx + c
c) Hàm số hữu tỷ bậc hai chia bậc một: y = a dx + ( 0) e 6
a, d cùng dấu
a, d trái dấu
Phương trình y = 0 có hai
nghiệm phân biệt. 0983.900.570 17 2024-2025 Võ Công Trường
Tài liệu ôn thi Tốt nghiệp THPT theo chuong trình mới 2018 Môn Toán
Phương trình y = 0 vô nghiệm.
Nhận xét đồ thị: e
(1) Tiệm cận đứng x = −
(Nghiệm của mẫu) d
(2) Tiệm cận xiên: Đi lên nếu a, d cùng dấu và đi xuống nếu a, d trái dấu.
CÁC DẠNG TOÁN THƯỜNG GẶP
Ví dụ 25: Đồ thị của hàm số nào dưới đây có dạng như đường cong trong hình vẽ bên? A. 4 2
y = −x + 2x +1. B. 3
y = −x + 3x +1. C. 3
y = x − 3x +1. D. 3 2
y = −x − 2x −1.
Lời giải
Đồ thị có đầu bên trái đi lên, đầu bên phải đi xuống nên hàm số bậc lẻ và a 0 , do đó loại câu A, C
Giao điểm của đồ thị và trục tung nằm phái trên trục hoành nên d 0 . Do đó chọn B
Ví dụ 26: Đồ thị sau là đồ thị của hàm số nào sau? 2x − 3 −x A. y = . B. y = . 2x − 2 x −1 x −1 x +1 C. y = . D. y = . x +1 x −1
Lời giải a a Tiệm cận ngang y =
nằm phía trên trục hoành nên
0 , do đó loại câu B. c c −d −d
Tiệm cận đứng x =
nằm bên phải trục tung nên
0 (nghiệm của mẫu là số dương), do đó loại câu C. c c Giao điể b
m của đồ thị và trục tung nằm phía dưới trục hoành nên tung độ giao điểm y = 0 . Do đó chon d câu D 2 + − Ví dụ 27: x x 1
Đường cong nào dưới đây là đồ thị của hàm số y = x − 1 A. . B. . 0983.900.570 18 2024-2025 Võ Công Trường
Tài liệu ôn thi Tốt nghiệp THPT theo chuong trình mới 2018 Môn Toán C. . D. .
Lời giải
Câu D không đúng dạng đồ thị nên loại. 2 x − 2x x = 0 Ta có: y = = ( , y 0 x − )2 1 x = 2 Bẳng biến thiên x – ∞ 0 1 2 + ∞ y' + 0 – – 0 + 1 + ∞ + ∞ y – ∞ – ∞ 5 Vậy chọn A
Chú ý. Có thể nhận xét, do đạo hàm có 2 nghiệm và hệ số a, d cùng dấu nên đồ thị có dạng câu A 0983.900.570 19 2024-2025




