















































































Preview text:
Giáo Viên Trườn g THPT Tuy Phong HÌNH HOÏC 10 PHƯƠNG PHÁP TỌA ĐỘ TRONG MẶT PHẲNG LỜI NÓI ĐẦU
Quý đọc giả, quý thầy cô và các em học sinh thân mến!
Nhằm giúp các em học sinh có tài liệu tự học môn Toán,
tôi biên soạn cuốn giải toán trọng tâm của lớp 10.
Nội dung của cuốn tài liệu bám sát chương trình chuẩn và
chương trình nâng cao về môn Toán đã được Bộ Giáo dục và Đào tạo quy định. Nội dung gồm 3 phần
Phần 1. Kiến thức cần nắm
Phần 2. Dạng bài tập có hướng dẫn giải và bài tập đề nghị
Phần 3. Phần bài tập trắc nghiệm.
Cuốn tài liệu được xây dựng sẽ còn có những khiếm
khuyết. Rất mong nhận được sự góp ý, đóng góp của quý
đồng nghiệp và các em học sinh.
Mọi góp ý xin gọi về số 0355.334.679 – 0916.620.899 Email: lsp02071980@gmail.com Chân thành cảm ơn. Lư Sĩ Pháp
Gv_Trường THPT Tuy Phong – Bình Thuận MỤC LỤC CHƯƠNG III
PHƯƠNG PHÁP TỌA ĐỘ TRONG MẶT PHẲNG
§1. Phương trình đường thẳng ................................. 01 – 23
§2. Phương trình đường tròn .................................... 24 – 39
§3. Elip ......................................................................... 40 – 52
Ôn tập chương III ...................................................... 53 – 87
Tài liệu học tập Toán 10 GV. Lư Sĩ Pháp CHƯƠNG III
PHƯƠNG PHÁP TỌA ĐỘ TRONG MẶT PHẲNG
ÔN TẬP TỌA ĐỘ TRONG MẶT PHẲNG
1. Hệ trục toạ độ Oxy gồm hai trục Ox, Oy đôi một vuông góc với nhau với hai vectơ đơn vị i , j
(i = j = )1. Gọi là hệ trục tọa độ (O,i, j) hay gọi mặt phẳng (Oxy)
2. Tọa độ của vectơ và của điểm: a = (a ;a a a i a j ; = + 1 2 ) ⇔ = 1 + 2
M(x;y) ⇔ OM xi y j
3. Biểu thức tọa độ của vectơ: Cho u = ( ;
x y), v = (x '; y ')
a. u = v ⇔ (x = x '; y = y ')
b. u ± v = (x ± x';y ± y')
c. ku = (kx;ky) d. .
u v = xx '+ yy '
e. u ⊥ v ⇔ xx '+ yy ' = 0 f. 2 2
u = x + y . u v x.x ' . y y ' g. cos(u,v) + = = . 2 u . v x + 2 2 y . x ' + 2 y '
4. Liên hệ giữa tọa độ điểm và vectơ : Cho A(xA; yA), B(xB; yB) 2 2
a. AB = (x − x ;y − y
b. AB = AB = (x − x y y B A ) + ( − B A ) B A B A ) x + x + x y + y + y
c. G là trọng tâm tam giác ABC ta có: A B C x = ; A B C y = G 3 G 3 x − kx y − ky
d. M chia AB theo tỉ số k: A B x = ; A B y = M 1 M − k 1− k x + x y + y
Đặc biệt: M là trung điểm của AB: A B x = ; A B y = . M 2 M 2
§1. PHƯƠNG TRÌNH ĐƯỜNG THẲNG
A. KIẾN THỨC CẦN NẮM
I. Vectơ chỉ phương và vectơ pháp tuyến của đường thẳng
1. Vectơ chỉ phương của đường thẳng (VTCP) y
a. Định nghĩa: Vectơ u được gọi là vectơ chỉ phương của đường
thẳng ∆ nếu u ≠ 0 và giá của u song song hoặc trùng với ∆ . M α b. Nhận xét
- Nếu u là một VTCP của đường thẳng ∆ thì ku (k ≠ 0)cũng là M0
một VTCP của ∆ . Do đó một đường thẳng có vô số VTCP. α
- Một đường thẳng hoàn toàn được xác định nếu biết một điểm và O x
một VTCP của đường thẳng đó.
2. Vectơ pháp tuyến của đường thẳng (VTPT)
a. Định nghĩa: Vectơ n được gọi là VTPT của đường thẳng ∆ nếu n ≠ 0 và n vuông góc với VTCP của ∆ . b. Nhận xét
- Nếu n là một VTPT của đường thẳng ∆ thì kn (k ≠ 0) cũng là một VTPT của ∆ . Do đó một đường thẳng có vô số VTPT.
- Một đường thẳng hoàn toàn được xác định nếu biết một điểm và một VTPT của đường thẳng đó.
3. Mối liên hệ giữa tọa độ VTCP và VTPT của đường thẳng Gọi u = ( ; a b) và n = ( ;
A B) lần lượt là VTCP và VTPT của đường thẳng ∆ Ta có:
u ⊥ n ⇔ u.n = 0 ⇔ aA + bB = 0 1
Chương III. Phương pháp tọa độ trong
mặt phẳng. 0916620899-0355334679
Tài liệu học tập Toán 10 GV. Lư Sĩ Pháp VTCP u = ( ;
a b) suy ra VTPT n = ( ;
b −a) hoặc n = (− ; b a) VTPT n = ( ;
A B) suy ra VTCP u = ( ;
B −A) hoặc u = (− ; B A) b
Đường thẳng ∆ có VTCP u = ( ;
a b) với a ≠ 0 thì ∆ có hệ số góc k = tanα = . a
Đường thẳng ∆ có hệ số góc k thì ∆ có VTCP u = (1;k)
II. Phương trình đường thẳng
1. Phương trình tham số của đường thẳng (Ptts)
qua M (x ; y )
x = x + at Đường thẳng 0 0 0 ∆ :
. Ptts của đường thẳng ∆ : 0 ,t ∈ℝ. V
TCP u = ( ; a b)
y = y + bt 0
Lưu ý: Cho t một giá trị cụ thể thì ta xác định được một điểm trên đường thẳng ∆
x = x + at
Nếu đường thẳng ∆ có phương trình 0
,t ∈ℝ. Suy ra đường thẳng ∆ đi qua điểm
y = y + bt 0
M (x ; y ) và có một VTCP là u = ( ; a b) . 0 0 0
2. Phương trình tổng quát của đường thẳng (Pttq)
qua M (x ; y ) Đường thẳng 0 0 0 ∆ : . 2 2 V
TPT n = ( ;
A B), A + B ≠ 0
Pttq của đường thẳng ∆ : A(x − x + B y − y = 0 ⇔ Ax + By +C = 0 ( với C = −Ax − By ) 0 ) ( 0) 0 0
Lưu ý: Đường thẳng ∆ : Ax + By + C = 0 thì ∆ có VTPT n = ( ; A B)
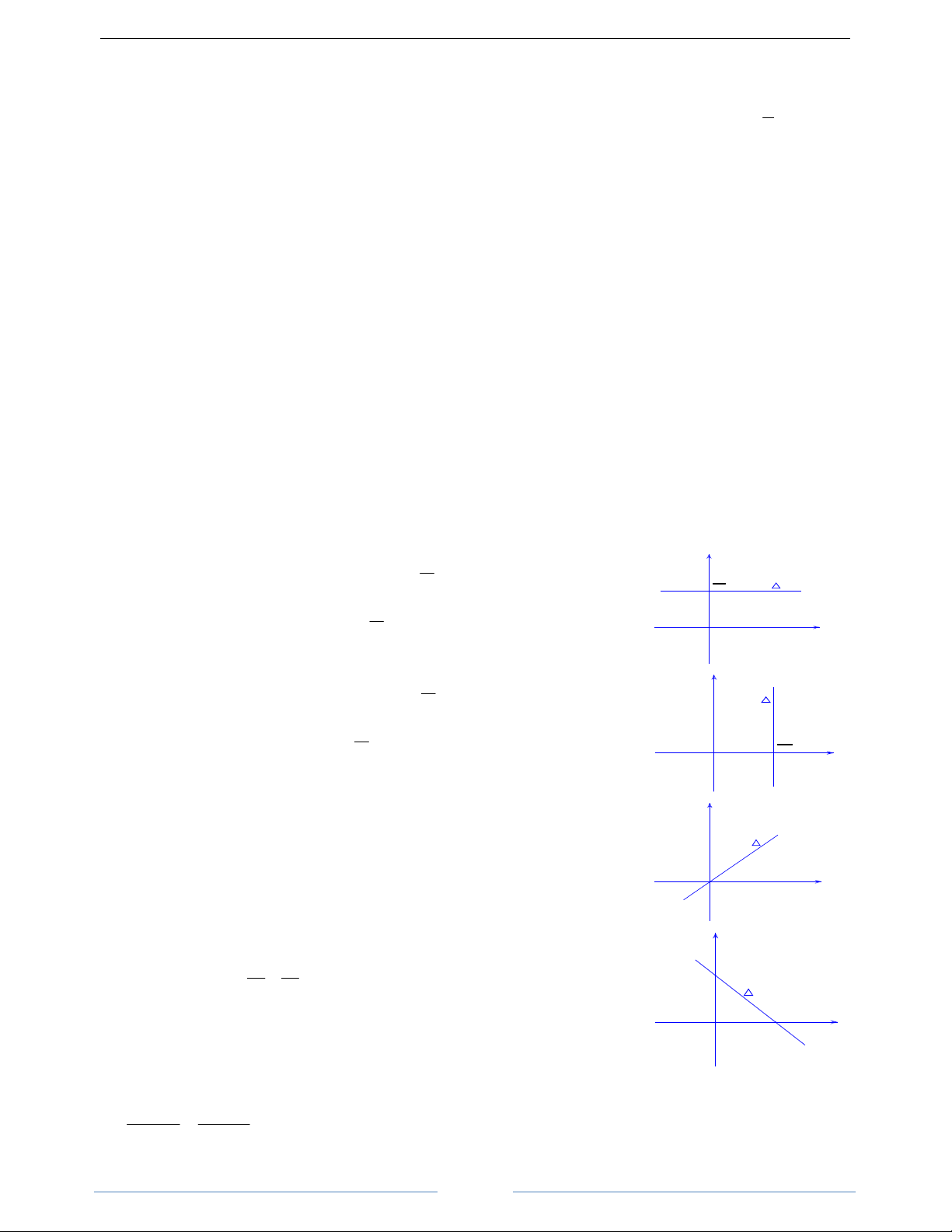
3. Các trường hợp đặc biệt
Cho đường thẳng ∆ có phương trình tổng quát Ax + By + C = 0 (1) y
A = 0 , pt(1) trở thành: + = 0 C By C
⇔ y = − . Khi đó đường thẳng ∆ B -C B
vuông góc với trục Oy tại điểm 0; C − O B x y
B = 0 , pt(1) trở thành: + = 0 C Ax C
⇔ x = − . Khi đó đường thẳng ∆ A C
vuông góc với trục Ox tại điểm − ;0 -C A O A x
C = 0 , pt(1) trở thành: Ax + By = 0 . Khi đó đường thẳng ∆ đi qua gốc y tọa độ . O O x
Đường thẳng ∆ cắt các trục tọa độ tại M(a ;0), N(0;b ). Phương trình y 0 0 x y đoạn chắn của ∆ là + = 1. b a b 0 0 0 O a0 x
Đường thẳng ∆ đi qua A(x ; y ), B(x ; y ). Phương trình chính tắc của đường thẳng A A B B − − ∆ : x x y y A A =
. Khi x − x = 0 hoặc y − y = 0 thì đường thẳng không có phương trình chình x − x y − y B A B A B A B A tắc. 2
Chương III. Phương pháp tọa độ trong
mặt phẳng. 0916620899-0355334679
Tài liệu học tập Toán 10 GV. Lư Sĩ Pháp
Đường thẳng ∆ đi qua M (x ; y ) và có hệ số góc k có phương trình: y − y = k(x − x ) 0 0 0 0 0
Đường thẳng ∆ đi qua M (x ; y ) song song với đường thẳng ∆ : A x + B y + C = 0 0 0 0 1 1 1 1
+ ∆ / /∆ ⇒ ∆ : A x + B y + m = 0,(m ≠ C ) 1 1 1 1
+ Do M (x ; y )∈ ∆ nên A x + B y + m = 0 ⇒ m = ? và kết luận. 0 0 0 1 0 1 0
Đường thẳng ∆ đi qua M (x ; y ) vuông góc với đường thẳng ∆ : A x + B y + C = 0 0 0 0 1 1 1 1
+ ∆ ⊥ ∆ ⇒ ∆ : B x − A y + m = 0 hay −B x + A y + m = 0 1 1 1 1 1
+ Do M (x ; y )∈ ∆ nên B x − A y + m = 0 ⇒ m = ? và kết luận. 0 0 0 1 0 1 0
III. Vị trí tương đối giữa hai đường thẳng
Cho hai đường thẳng ∆ : A x + B y + C = 0 và ∆ : A x + B y + C = 0 1 1 1 1 2 2 2 2
A x + B y = C − Xét hệ phương trình 1 1 1 (*)
A x + B y = C − 2 2 2
Hệ (*) có một nghiệm (x ; y ) , khi đó ∆ cắt ∆ tại điểm M (x ; y ) 0 0 1 2 0 0 0
Hệ (*) có vô số nghiệm, khi đó ∆ trùng với ∆ 1 2
Hệ (*) có vô nghiệm, khi đó ∆ ∩ ∆ = ∅ hay ∆ song song với ∆ 1 2 1 2
Lưu ý: Nếu A B C ≠ 0 thì: 2 2 2 A B ∆ cắt ∆ 1 1 ⇔ ≠ 1 2 A B 2 2 1 1 1 ∆ / / A B C ∆ ⇔ = ≠ 1 2 A B C 2 2 2 A B C 1 1 1 ∆ ≡ ∆ ⇔ = = 1 2 A B C 2 2 2
IV. Góc giữa hai đường thẳng
Cho hai đường thẳng ∆ : A x + B y + C = 0 và ∆ : A x + B y + C = 0. Đặt ϕ = (∆ ,∆ 1 2 ) 1 1 1 1 2 2 2 2
∆ ⊥ ∆ ⇒ ϕ = (∆ ,∆ ) 0 = 90 1 2 1 2
∆ ⊥ ∆ . + Xác định hai VTPT n ,n (hay VTCP) của hai đường thẳng ∆ ,∆ 1 2 1 2 1 2 n .n + Tính 1 2
cosϕ = cos(n ,n ) = . Suy ra góc ϕ = ? 1 2 n . n 1 2 + 0 0 0 ≤ ϕ ≤ 90 .
Chú ý: Nếu ∆ và ∆ có phương trình y = k x + m và y = k x + m thì 1 2 1 1 2 2
∆ / /∆ ⇒ k = k
∆ ⊥ ∆ ⇒ k .k = 1 − 1 2 1 2 1 2 1 2
V. Khoảng cách từ một điểm đến một đường thẳng
Cho đường thẳng ∆ : Ax + By + C = 0 và điểm M (x ; y ) . Khoảng cách từ điểm M đền đường thẳng ∆ , 0 0 0 0
Ax + By + C
kí hiệu là d(M ,∆) và được tính bởi công thức: 0 0 d(M , ∆) = 0 0 2 2 A + B
VI. Phương trình hai đường phân giác của các góc tạo bởi : ∆ : A x + B y + C = 0 ; 1 1 1 1 + + + + ∆ : A x B y C A x B y C
A x + B y + C = 0 là: 1 1 1 2 2 2 = ± 2 2 2 2 2 2 2 2 A + B A + B 1 1 2 2
Lưu ý: Dấu ± tương ứng với một đường phân giác của góc nhọn và một đường phân giác góc tù. Để
phân biệt được dấu nào là của đường phân giác góc nhọn và dấu nào là đường phân giác góc tù thì cần nhớ quy tắc sau: 3
Chương III. Phương pháp tọa độ trong
mặt phẳng. 0916620899-0355334679
Tài liệu học tập Toán 10 GV. Lư Sĩ Pháp
Đường phân giác góc nhọn luôn nghịch dấu với tích hai pháp véctơ, đường phân giác góc tù mang dấu còn lại.
VII. Cho hai điểm M (x ;y ),N (x ;y và đường thẳng ∆ : Ax + By +C = 0 . Khi đó: M M N N )
M và N nằm cùng phía đối với ∆ ⇔ ( Ax + By +C)( Ax + By +C) > 0 M M N N
M và N nằm khác phía đối với ∆ ⇔ ( Ax + By +C)( Ax + By +C) < 0 M M N N B. BÀI TẬP
Các bài tập dưới đây, xét trong mặt phẳng Oxy.
ấn đề 1. Viết phương trình đường thẳng V
qua M (x ; y )
x = x + at 1. Đường thẳng 0 0 0 ∆ :
. Ptts của đường thẳng ∆ : 0 ,t ∈ℝ. V
TCP u = ( ; a b)
y = y + bt 0
qua M (x ; y ) 2. Đường thẳng 0 0 0 ∆ : . 2 2 V
TPT n = ( ;
A B), A + B ≠ 0
Pttq của đường thẳng ∆ : A(x − x + B y − y = 0 ⇔ Ax + By +C = 0 ( với C = −Ax − By ) 0 ) ( 0) 0 0
3. Đường thẳng ∆ cắt các trục tọa độ tại M(a ;0), N(0;b ). Phương trình đoạn chắn của ∆ là 0 0 x y + = 1. a b 0 0
4. Đường thẳng ∆ đi qua A(x ; y ), B(x ; y ). Phương trình chính tắc của đường thẳng A A B B − − ∆ : x x y y A A =
. Khi x − x = 0 hoặc y − y = 0 thì đường thẳng không có phương trình chình x − x y − y B A B A B A B A tắc.
5. Đường thẳng ∆ đi qua M (x ; y ) và có hệ số góc
y − y = k(x − x ) 0 0 0
k có phương trình: 0 0
Lưu ý: Đường thẳng ∆ có hệ số góc k thì ∆ có VTCP u = (1; k)
6. Đường thẳng ∆ đi qua M (x ; y ) song song với đường thẳng ∆ : A x + B y + C = 0 0 0 0 1 1 1 1
+ ∆ / /∆ ⇒ ∆ : A x + B y + m = 0,(m ≠ C ) 1 1 1 1
+ Do M (x ; y )∈ ∆ nên A x + B y + m = 0 ⇒ m = ? và kết luận. 0 0 0 1 0 1 0
7. Đường thẳng ∆ đi qua M (x ; y ) vuông góc với đường thẳng ∆ : A x + B y + C = 0 0 0 0 1 1 1 1
+ ∆ ⊥ ∆ ⇒ ∆ : B x − A y + m = 0 hay −B x + A y + m = 0 1 1 1 1 1
+ Do M (x ; y )∈ ∆ nên B x − A y + m = 0 ⇒ m = ? và kết luận. 0 0 0 1 0 1 0
Bài 1.1. Lập phương trình tham số của đường thẳng ∆ trong mỗi trường hợp sau:
a. ∆ đi qua điểm M(2;1)và có VTCP u = (3;4) . b. ∆ đi qua điểm P(5; 2
− ) và có VTPT n = (4;−3).
c. ∆ đi qua điểm Q(5;1) và có hệ số góc k = 3. d. ∆ đi qua hai điểm A(3;4) và B(4;2) . HD Giải ñi qua M(2;1) x = 2 + 3t
a. Ta có đường thẳng ∆ : . Ptts của ∆ : ,t ∈ . ℝ
coù VTCP u = (3; 4) y = 1+ 4t ñi qua P(5; 2 − ) x = 5 + 3t
b. Ta có đường thẳng ∆ : . Ptts của ∆ : ,t ∈ . ℝ
coù VTPT n = (4; −3) ⇒ VTCP u = (3; 4) y = −2 + 4t ñi qua Q(5;1) x = 5 + t
c. Ta có đường thẳng ∆ : . Ptts của ∆ : ,t ∈ . ℝ
coù heä soá goùc k = 3 ⇒ VTCP u = (1;3) y = 1+ 3t ñi qua A(3;4) x = 3 + t
d. Ta có đường thẳng ∆ : . Ptts của ∆ : ,t ∈ℝ. V
TCP AB = (1; 2 − ) y = 4 − 2t
Bài 1.2. Lập phương trình tổng quát của đường thẳng ∆ trong mỗi trường hợp sau:
a. ∆ đi qua điểm M(3;4) và có VTPT n = (1;2). b. ∆ đi qua điểm P(3; 2
− ) và có VTCP u = (4;3) 4
Chương III. Phương pháp tọa độ trong
mặt phẳng. 0916620899-0355334679
Tài liệu học tập Toán 10 GV. Lư Sĩ Pháp
c. ∆ đi qua điểm Q(−5;−8) và có hệ số góc k = 3
− . d. ∆ đi qua hai điểm A(2;1) và B(−4;5). e. ∆ qua C( 1
− ;1) và vuông góc với đường thẳng có phương trình ∆ : 2x − 3y +1 = 0. 1
f. ∆ qua D(2;0) và song song với đường thẳng có phương trình ∆ : 2x + y − 5 = 0. 2 HD Giải ñi qua M(3;4)
a. Ta có đường thẳng ∆ :
. Pttq của ∆ :1(x − 3) + 2(y − 4) = 0 ⇔ x + 2y −11 = 0
coù VTPT n = (1;2) ñi qua P(3;−2)
b. Ta có đường thẳng ∆ : .
coù VTCP u = (4;3) ⇒ VTPT n = (3; 4 − )
Pttq của ∆ : 3(x − 3) − 4(y + 2) = 0 ⇔ 3x − 4y −17 = 0. ñi qua Q(−5; 8 − )
c. Ta có đường thẳng ∆ : .
coù heä soá goùc k = −3 ⇒ VTCP u = (1; −3) ⇒ VTPT n = (3;1)
Pttq của ∆ : 3(x + 5) + y + 8 = 0 ⇔ 3x + y + 23 = 0 ñi qua Q(−5; 8 − )
Chú ý: Ta có đường thẳng ∆ :
. Pttq của ∆ : y + 8 = −3(x + 5) ⇔ 3x + y + 23 = 0
coù heä soá goùc k = −3 ñi qua Q(−5; 8 − ) x = 5 − + t
Ta có đường thẳng ∆ : . Ptts của ∆ : ,t ∈ℝ.
coù heä soá goùc k = −3 ⇒ VTCP u = (1; 3 − ) y = 8 − − 3t x + 5 y + 8
Từ đó, ta có phương trình: =
⇔ 3x + y + 23 = 0. 1 3 − ñi qua ( A 2;1)
d. Ta có đường thẳng ∆ : . V
TCP AB = ( 6
− ;4) ⇒ VTPT n = (4;6)
Pttq của ∆ : 4(x − 2) + 6(y −1) = 0 ⇔ 4x + 6y −14 = 0 hay 2x + 3y − 7 = 0 x − 2 y −1
Chú ý: Ta có ∆ đi qua hai điểm A(2;1) và B(−4;5) có pt: =
⇔ 2x + 3y − 7 = 0 4 − − 2 5−1
e. Ta có ∆ ⊥ ∆ ⇒ ∆ : 3x + 2y + m = 0. 1
Do C(−1;1)∈ ∆ nên 3(−1) + 2.1+ m = 0 ⇔ m = 1. Vậy pt của ∆ : 3x + 2y +1 = 0.
f. Ta có ∆ / /∆ ⇒ ∆ : 2x + y + m = 0,(m ≠ −5). 2
Do D(2; 0)∈ ∆ nên 2.2 +1.0 + m = 0 ⇔ m = −4 . Vậy pt của ∆ : 2x + y − 4 = 0.
Bài 1.3. Cho tam giác ABC, biết A(1;4),B(3; 1 − ) và C(6;2).
a. Lập phương trình các cạnh của tam giác ABC.
b. Lập phương trình đường cao AH và đường trung tuyến AM. HD Giải
Áp dụng: Đường thẳng ∆ đi qua A(x ; y ), B(x ; y ). Phương trình A A B B A x − x y − y
chính tắc của đường thẳng ∆ : A A = . x − x y − y B A B A x −1 y − 4
a. Phương trình đường thẳng AB : =
⇔ 5x + 2y −13 = 0 C 3 −1 −1− 4 B H M x −1 y − 4
Phương trình đường thẳng AC : =
⇔ 2x + 5y − 22 = 0 6 −1 2 − 4 x − 3 y +1
Phương trình đường thẳng BC : =
⇔ x − y − 4 = 0 6 −3 2 −( 1 − )
b. Phương trình đường cao AH .
Ta có AH ⊥ BC ⇒ AH : x + y + m = 0 . Do A ∈ AH nên: 1+ 4 + m = 0 ⇔ m = −5
Vậy: AH : x + y − 5 = 0 5
Chương III. Phương pháp tọa độ trong
mặt phẳng. 0916620899-0355334679
Tài liệu học tập Toán 10 GV. Lư Sĩ Pháp 9 1
Phương trình đường trung tuyến AM. M là trung điểm của BC ⇒ M ; 2 2 x −1 y − 4
Phương trình đường trung tuyến AM : =
⇔ x + y − 5 = 0. 9 1 −1 − 4 2 2
Nhận xét: Phương trình đường đường cao AH và đường trung tuyến AM trùng nhau, suy ra tam giác ABC cân tại . A
Bài 1.4. Lập phương trình ba đường trung trực của một tam giác có trung điểm các cạnh lần lượt là M( 1
− ;0),N(4;1),P(2;4). HD Giải
Gọi ∆ ,∆ ,∆ lần lượt là các đường trung trực đi qua M, N,P 1 2 3 ∆1 A ñi qua M( 1 ∆ − ;0) 3 ∆2 Ta có: ∆ : N P 1
⊥ NP (doNP / / BC) ⇒ VTPT n = NP = ( 2 − ;3) 1 ∆ C B M Vậy: ∆ : 2
− (x +1) + 3y = 0 ⇔ 2x − 3y + 2 = 0 1
Tương tự: ∆ : 3x + 4y −16 = 0
∆ : 5x + y −14 = 0 2 3
Bài 1.5. Cho tam giác ABC , biết phương trình đường thẳng AB : x − 3y +11 = 0, đường cao
AH : 3x + 7y −15 = 0 , đường cao BH : 3x − 5y +13 = 0 . Tìm phương trình hai đường thẳng chứa hai cạnh còn lại của tam giác. HD Giải
Theo đề bài, tọa độ điểm A thỏa mãn hệ phương trình: A
x − 3y = −11 x = −2 ⇔ ⇒ A( 2 − ;3) 3 x + 7y = 15 y = 3 H
Đường thẳng AC ⊥ BH ⇒ AC : 5x + 3y + m = 0 C
A ∈ AC ⇔ 5( 2
− ) + 3.3 + m = 0 ⇔ m = 1. Vậy AC : 5x + 3y +1 = 0 B qua (4;5)
Tương tư: B = AB ∩ BH ⇒ B(4;5) . Đường thẳng : B BC
có phương trình: 7x − 3y −13 = 0. ⊥ AH
Bài 1.6. Cho tam giác ABC có A( 2
− ;3)và hai đường trung tuyến có phương trình: 2x − y +1 = 0;
x + y − 4 = 0. Hãy viết phương trình ba đường thẳng chứa ba cạnh của tam giác. HD Giải
Nhận thấy điểm A thuộc hai đường trung tuyến. Do đó đường trung A
tuyến của tam giác là BM : 2x − y +1 = 0,CN : x + y − 4 = 0
x − 2 y + 3
Gọi B(x; y) và N là trung điểm A . B Ta có N N M ; 2 2
2x − y +1 = 0 C B ∈ BM x = 2 B Do
⇔ x − 2 y + 3 ⇔ ⇒ B(2;5) N ∈CN + − 4 = 0 y = 5 2 3
Vậy đường thẳng chứa cạnh AB đi qua A và B có phương trình là: x − 2y + 8 = 0
Tương tự: Phương trình đườn thẳng chứa cạnh AC là 2x + 5y −11 = 0
Phương trình đườn thẳng chứa cạnh BC là 4x + y −13 = 0
ấn đề 2. Vị trí tương đối giữa hai đường thẳng
V1. Cho hai đường thẳng ∆ :Ax+By+C =0 và ∆ :A x+B y+C =0 1 1 1 1 2 2 2 2
A x + B y = C − Xét hệ phương trình 1 1 1 (*)
A x + B y = C − 2 2 2
Hệ (*) có một nghiệm (x ; y ) , khi đó ∆ cắt ∆ tại điểm M (x ; y ) 0 0 1 2 0 0 0 6
Chương III. Phương pháp tọa độ trong
mặt phẳng. 0916620899-0355334679
Tài liệu học tập Toán 10 GV. Lư Sĩ Pháp
Hệ (*) có vô số nghiệm, khi đó ∆ trùng với ∆ 1 2
Hệ (*) có vô nghiệm, khi đó ∆ ∩ ∆ = ∅ hay ∆ song song với ∆ 1 2 1 2
Lưu ý: Nếu A B C ≠ 0 thì: 2 2 2 A B A B C ∆ cắt ∆ 1 1 ⇔ ≠ 1 1 1 ∆ / / A B C ∆ ⇔ = ≠ 1 1 1 ∆ ≡ ∆ ⇔ = = 1 2 A B 1 2 A B C 1 2 A B C 2 2 2 2 2 2 2 2 n .n A A + B B
2. Góc giữa hai đường thẳng ∆ và ∆ là 1 2 1 2 1 2
cosϕ = cos(n ,n ) = = 1 2 1 2 2 2 2 2 n . n 1 2 A + B A + B 1 1 2 2
Bài 1.7. Xét vị trí tương đối của các cặp đường thẳng sau:
a. ∆ : 4x −10y +1 = 0 và ∆ : x + y + 2 = 0
b. ∆ :12x − 6y +10 = 0 và ∆ : 2x − y + 5 = 0 1 2 1 2 x = 6 − + 5t x = 1 − − 5t x = 6 − + 5t
c. ∆ : 8x +10y −12 = 0 và ∆ : d. ∆ : và ∆ : 1 2 1 2 y = 6 − 4t y = 2 + 4t y = 2 − 4t HD Giải 4 −10 12 −6 10 a. Ta có : ≠ . Vậy ∆ cắt ∆ . b. Ta có : = ≠ . Vậy ∆ // ∆ . 1 1 1 2 2 1 − 5 1 2 8 10 1 − 2
c. Ta có Pttq của ∆ : 4x + 5y − 6 = 0 . Nhận thấy: = = . Vậy ∆ ≡ ∆ . 2 4 5 −6 1 2
d. Ta có Pttq: ∆ : 4x + 5y − 6 = 0 và ∆ : 4x + 5y +14 = 0 . Vậy ∆ // ∆ . 1 2 1 2
Bài 1.8. Với giá trị nào của tham số m thì hai đường thẳng dưới đây vuông góc: ∆ : mx + y + q = 0 và 1
∆ : x − y + m = 0 2 HD Giải
Đường thẳng ∆ ,∆ lần lượt có VTPT là n = ( ;
m 1), n = (1; −1) 1 2 1 2
Ta có : ∆ ⊥ ∆ ⇔ n .n = 0 ⇔ m −1 = 0 ⇔ m = 1. 1 2 1 2
Bài 1.9. Cho hai đường thẳng d : x − 2y + 5 = 0 và d : 3x − y = 0. 1 2
a. Tìm giao điểm của d và d .
b. Tính góc giữa d và d . 1 2 1 2 HD Giải
x − 2y + 5 = 0 x = 1
a. Gọi M = d ∩ d . Tọa độ điểm M là nghiệm của hệ phương trình : ⇔ . 1 2 3 x − y = 0. y = 3 Vậy M(1;3)
b. Gọi ϕ = (d ,d ) . Đường thẳng d ,d lần lượt có VTPT là n = (1; 2 − ),n = (3;−1) 1 2 1 2 1 2 n .n 3 + 2 1 Ta có : 1 2 0 cosϕ = = = ⇒ ϕ = 45 . Vậy 0 (d ,d ) = 45 n . n 1 2 1 2 1+ 4. 9 +1 2
ấn đề 3. Khoảng cách từ một điểm đến một đường thẳng
V1. Áp dụng : Cho đường thẳng ∆:Ax+By+C=0 và điểm M (x ;y ). Khoảng cách từ điểm M 0 0 0 0
Ax + By + C
đền đường thẳng ∆ là 0 0 d(M , ∆) = 0 2 2 A + B
2. Cho hai đường thẳng song song ∆ : Ax + By + C = 0 và ∆ : Ax + By + D = 0 . 1 2
a. d(∆ ,∆ ) = d(M ,∆ ), M ∈ ∆ hoặc d(∆ ,∆ ) = d(M ,∆ ), M ∈ ∆ 1 2 2 1 2 2 1 2 1 2 1 1 C − D
Vận dụng nhanh công thức d(∆ ,∆ ) = 1 2 2 2 A + B C + D
b. Phương trình đường thẳng ∆ song song và cách đều ∆ và ∆ có dạng: Ax + By + = 0 3 1 2 2 7
Chương III. Phương pháp tọa độ trong
mặt phẳng. 0916620899-0355334679
Tài liệu học tập Toán 10 GV. Lư Sĩ Pháp
Bài 1.10. Tính khoảng cách từ điểm đến đường thẳng được cho tương ứng như sau :
a. A(3; 4) và ∆ : 4x + 3y +1 = 0
b. B(1;2) và ∆ : 3x − 4y +1 = 0 1 HD Giải 4.3 + 3.4 +1 3.1− 4.2 +1 4 a. d(A,∆) = = 5 b. d(B,∆) = = 2 2 4 + 3 2 2 5 3 + (−4) x = 2 + 2t
Bài 1.11. Cho đường thẳng d :
. Tìm tọa độ điểm M thuộc d và cách điểm A(0;1) một y = 3 + t khoảng bằng 5. HD Giải Ta có : M( ;
x y)∈ d ⇒ M(2 + 2 ;
t 3 + t) và theo giả thiết AM = 5 . t = 1
Ta lại có: AM = (2 + 2 ;t2 + t) . Như vậy: 2 2 2 AM 25 (2 2t) (2 t) 25 = ⇔ + + + = ⇔ 17 t = − 5 24 2
Vậy: M(4; 4) hoặc M − ;− thì thỏa YCBT. 5 5
Bài 1.12. Cho đường thẳng ∆ : x − y + 2 = 0 và hai điểm O(0;0), ( A 2;0).
a. Chứng tỏ rằng hai điểm A và O nằm về cùng một phía đối với đường thẳng ∆ .
b. Tìm điểm O′ đối xứng với O qua ∆ .
c. Tìm điểm M thuộc ∆ sao cho độ dài của đoạn gấp khúc OMA ngắn nhất. HD Giải
a. Từ đường thẳng ∆ : x − y + 2 = 0 ⇒ y = x + 2 . Ta có: y(A).y(O) = 4.2 = 8 > 0 .
Vậy A và O nằm về cùng một phía đối với đường thẳng ∆ .
b. Nhận thấy: O ∉ .
∆ Gọi d là đường thẳng qua O và vuông góc với ∆ tại H . O qua O x = t Ta có: d : ⇒ Ptts d :
. H ∈ d ⇒ H( ;t−t). V
TCP u = n = (1; 1 − ) y = −t ∆ H
Mặt khác: H ∈ ∆ ⇒ t − (−t) + 2 = 0 ⇔ t = 1 − ⇒ H(−1;1)
Ta có: H là trung điểm của OO′. Suy ra: x = 2x = −2; y = 2y = 2 Vậy: O (′ 2 − ;2) O' O′ H O′ H
c. Theo câu a. ta có: A và O nằm về cùng một phía đối với đường thẳng ∆ . O A
Ta có: OM + MA = O M
′ + MA ≥ AM ⇔ O ,′M, A thẳng hàng ⇔ O A ′ ∆ cắt tại M
Phương trình đường thẳng O A
′ : x + 2y − 2 = 0. Tọa độ điểm M là nghiệm của hệ 2 H M − + 2 = 0 x = − x y 2 4 phương trình: 3 ⇔
. Vậy M − ; . O'
x + 2y − 2 = 0 4 3 3 y = 3
Bài 1.13. Trong mặt phẳng với hệ tọa độ Oxy, cho điểm A(2;1) và đường thẳng d : 2x + 3y + 4 = 0 . Lập
phương trình đường thẳng ∆ đi qua A và tạo với đường thẳng d một góc 0 45 . HD Giải
Phương trình đường thẳng (∆) có dạng: (
a x – 2) + b(y −1) = 0 ⇔ ax + by –(2a + b) = 0 2 2 (a + b ≠ 0). 2a + 3b a = 5b Ta có: 0 cos45 = ⇔ 2 2
5a − 24ab − 5b = 0 ⇔ 2 2 13. a + b 5a = −b
Với a = 5b . Chọn a = 5,b = 1 ⇒ Phương trình ∆ : 5x + y −11 = 0 .
Với 5a = −b . Chọn a = 1,b = −5 ⇒ Phương trình ∆ : x − 5y + 3 = 0 .
Bài 1.14. Trong mặt phẳng với hệ toạ độ Oxy, cho 2 đường thẳng d : x − 7y +17 = 0, d : x + y − 5 = 0 . 1 2
Viết phương trình đường thẳng (d) qua điểm M(0;1) tạo với d ,d một tam giác cân tại giao điểm của 1 2 d , d . 1 2 8
Chương III. Phương pháp tọa độ trong
mặt phẳng. 0916620899-0355334679
Tài liệu học tập Toán 10 GV. Lư Sĩ Pháp HD Giải
Phương trình đường phân giác góc tạo bởi d ,d là: 1 2 x − 7y +17 x + y − 5
x + 3y −13 = 0 (∆ ) 1 = ⇔ 2 2 2 2 1 + (−7) 1 +1
3x − y − 4 = 0 (∆ ) 2
Đường thẳng cần tìm đi qua M(0;1) và song song với ∆ hoặc ∆ . 1 2
Vậy: x + 3y − 3 = 0 và 3x − y +1 = 0
Bài 1.15. Trong mặt phẳng với hệ trục tọa độ Oxy cho tam giác ABC với B(1; 2 − ) đường cao
AH : x − y + 3 = 0 . Tìm tọa độ các đỉnh A, C của tam giác ABC biết C thuộc đường thẳng d :2x + y −1 = 0
và diện tích tam giác ABC bằng 1. HD Giải
Phương trình BC : x + y +1 = 0 . C = BC ∩ d ⇒ C(2; 3 − ). x + y +
Gọi A(x ; y )∈ AH ⇒ x − y 0 0 0 0 + 3 = 0 (1); BC = AH = d A BC 0 0 1 2, ( , ) = 2 1 1 x + y 0 0 + 1
x + y +1 = 2 (2) S = AH B . C 0 0 = 1 ⇔ . . 2 = 1 ⇔ A ∆ BC 2 2 x + y 2 0 0 + 1 = 2 − (3) x = 1 − x = 3 − Từ (1) và (2) 0 ⇒ ⇒ A(−1;2) . Từ (1) và (3) 0 ⇒ ⇒ A( 3 − ;0) y 0 = 2 y 0 = 0
Bài 1.16. Trong mặt phẳng tọa độ Oxy, cho điểm A(1; 1) và đường thẳng ∆: 2x + 3y + 4 = 0 . Tìm điểm B
thuộc đường thẳng ∆ sao cho đường thẳng AB và ∆ hợp với nhau góc 0 45 . HD Giải
Ta có: ∆ có VTPT n = (2;3) ⇒ VTCP u(−3;2) . Giả sử B(1−3t;−2 + 2t)∈∆ . 15 1 t = A . B u 1 0 ( 13
AB,∆) = 45 ⇒ cos(A ; B u) = ⇔ = 2
⇔ 169t −156t − 45 = 0 ⇔ 2 AB. u 2 3 t = − 13 32 4 22 32 . Vậy : B − ; hoặc B ;− 13 13 13 13
Bài 1.17. Trong mặt phẳng toạ độ Oxy, cho đường thẳng d : 2x − y + 3 = 0 và 2 điểm A(1;0), B(2;1) . Tìm
điểm M trên d sao cho MA + MB nhỏ nhất. HD Giải
Ta có: (2x − y + 3).(2x − y + 3) = 30 > 0 ⇒ A, B nằm cùng phía đối với d. A A B B
Gọi A′ là điểm đối xứng của A qua d ⇒ A (′ 3
− ;2) ⇒ Phương trình A B
′ : x + 5y − 7 = 0 .
Với mọi điểm M ∈ d, ta có: MA + MB = MA′ + MB ≥ A B ′ . 8 17
Mà MA′ + MB nhỏ nhất ⇔ A′, M, B thẳng hàng ⇔ M là giao điểm của A′B và d. Vậy: M − ; . 11 11
Bài 1.18. Trong mặt phẳng với hệ toạ độ Oxy, viết phương trình đường thẳng ∆ đi qua điểm M(3;1) và cắt
các trục Ox, Oy lần lượt tại B và C sao cho tam giác ABC cân tại A với A(2;–2). HD Giải
Đường thẳng d đi qua M(3;1) và cắt các trục Ox, Oy lần lượt tại B, C khác O, nên B( ;
a 0);C(0; b) với 3 1 . x y
a b ≠ 0 ⇒ Phương trình của d có dạng +
= 1. Vì d qua M nên + = 1(1) a b a b 2 2
Tam giác ABC cân tại A nên có: AB = AC ⇔ (a − 2) + 4 = 4 + (b + 2) (2)
Giải hệ (1) và (2). Vậy d : x + 3y − 6 = 0 hoặc x − y − 2 = 0 . 9
Chương III. Phương pháp tọa độ trong
mặt phẳng. 0916620899-0355334679
Tài liệu học tập Toán 10 GV. Lư Sĩ Pháp
Bài 1.19. Trong mặt phẳng với hệ toạ độ Oxy, cho ∆ABC biết: B(2; –1), đường cao qua A có phương trình d 3 – 4 + 27 = 0 + 2 –5 = 0 1: x y
, phân giác trong góc C có phương trình d2: x y
. Tìm toạ độ điểm A. HD Giải x − 2 y + 1 Phương trình BC: =
⇒ Toạ độ điểm C(−1;3) 3 4 −
Gọi B’ là điểm đối xứng của B qua d2, I là giao điểm của BB’ và d2. x − 2 y + 1 Phương trình BB’: =
⇔ 2x − y − 5 = 0 1 2 2 − − 5 = 0 = 3
Toạ độ điểm I là nghiệm của hệ: x y x ⇔ ⇒ I(3;1)
x + 2y − 5 = 0 y = 1
x = 2x − x = 4
Vì I là trung điểm BB’ nên: B' I B ⇒ B′(4;3) y = 2y − y = 3 B ' I B
Đường AC qua C và B’ nên có phương trình: y –3 = 0. − 3 = 0 = 5 Toạ độ điểm −
A là nghiệm của hệ: y x ⇔ ⇒ A( 5 − ;3) 3
x − 4y + 27 = 0 y = 3
Bài 1.20. Trong mặt phẳng toạ độ Oxy, cho điểm A(0;2) và đường thẳng d : x − 2y + 2 = 0 . Tìm trên
đường thẳng d hai điểm B, C sao cho tam giác ABC vuông ở B và AB = 2BC . HD Giải
Ta có B,C ∈ d nên B(2b − 2;b),C(2c − 2;c) 2 6 2 5 5
Vì ∆ABC vuông ở B nên AB ⊥ d ⇔ AB u
. = 0 ⇒ B ; ⇒ AB = ⇒ BC = d 5 5 5 5
c = 1 ⇒ C(0;1) 1 2 5 BC =
125c − 300c +180 = ⇒ 7 4 7 5 5
c = ⇒ C ; 5 5 5 3
Bài 1.21. Trong mặt phẳng với hệ toạ độ Oxy, cho tam giác ABC có diện tích bằng ,
2 A(2;–3), B(3;–2).
Tìm toạ độ điểm C, biết điểm C nằm trên đường thẳng (d): 3x – y – 4 = 0 . HD Giải
Phương trình tham số của = d: x t
. Giả sử C(t; –4 + 3t) ∈ d. y = 4 − + t 3 2 1 1 3 = 2 −
S = AB.AC.sin A =
AB2.AC2 − ( AB.AC ) = ⇔ t2
4 + 4t +1 = 3 ⇔ t 2 2 2 t =1
Vậy: C(–2; –10) hoặc C(1;–1).
Bài 1.22. Trong mặt phẳng với hệ trục toạ độ Oxy, cho cho hai đường thẳng d : 2x − y + 5 = 0 . 1
d : 3x + 6y – 7 = 0 . Lập phương trình đường thẳng đi qua điểm 2
P(2; –1) sao cho đường thẳng đó cắt hai
đường thẳng d và d tạo ra một tam giác cân có đỉnh là giao điểm của hai đường thẳng d ,d . 1 2 1 2 HD Giải
Đường thẳng d có VTPT n = (2;−1) ; d có VTPT n = (3;6) 1 1 2 2
Ta có: n .n = 2.3 −1.6 = 0 nên d ⊥ d và d cắt d tại một điểm 1 2 1 2 1 2
I khác P. Gọi d là đường thẳng đi qua
P( 2; –1) có phương trình: d : A(x − 2) + B(y +1) = 0 ⇔ Ax + By − 2A + B = 0
d cắt d ,d tạo ra một tam giác cân có đỉnh
d ( hoặc d ) một góc 0 45 1 2
I ⇔ khi d tạo với 1 2 2A − B A = 3B 0 2 2 ⇔
= cos45 ⇔ 3A − 8AB − 3B = 0 ⇔ 2 2 2 2 + 2 + (−1) B = 3 − A A B
Nếu A = 3B ta có đường thẳng d : 3x + y − 5 = 0 10
Chương III. Phương pháp tọa độ trong
mặt phẳng. 0916620899-0355334679
Tài liệu học tập Toán 10 GV. Lư Sĩ Pháp
Nếu B = –3A ta có đường thẳng d : x − 3y − 5 = 0
Vậy có hai đường thẳng thoả mãn yêu cầu bài toán. d : 3x + y − 5 = 0 ; d : x − 3y − 5 = 0 .
Bài 1.23. Trong mặt phẳng Oxy, cho hai đường thẳng d : 3x + y + 5 = 0 , d : 3x + y +1 = 0 và điểm 1 2
I (1; −2) . Viết phương trình đường thẳng ∆ đi qua I và cắt d ,d lần lượt tại . 1 2
A và B sao cho AB = 2 2 HD Giải
Ta có: A ∈ d ⇒ A( ;
a −3a − 5); B ∈ d ⇒ B( ; b 3
− b −1); IA = (a −1; 3
− a − 3); IB = (b −1; 3 − b +1) 1 2
b −1 = k(a −1)
Khi đó: I, A, B thẳng hàng ⇒ IB = kIA ⇔
−3b +1 = k( 3 − a − 3)
Nếu a = 1 thì b = 1 ⇒ AB = 4 (không thoả). b −1
Nếu a ≠ 1 thì −3b +1 = ( 3
− a −3) ⇔ a = 3b − 2 a −1 2 2 2 2
AB = (b − a) + 3(a
− b) + 4 = 2 2 ⇔ t + (3t + 4) = 8 (với t = a − b). 2 2
⇔ 5t +12t + 4 = 0 ⇔ t = −2 hoặc t = − 5 Với t = 2
− ⇒ a − b = 2
− ⇒ b = 0,a = −2 ⇒ ∆ : x + y +1 = 0 2 − −2 4 2 Với t = ⇒ a − b =
⇒ b = ,a = ⇒ ∆ : 7x − y − 9 = 0 5 5 5 5
Bài 1.24. Trong mặt phẳng với hệ trục toạ độ Oxy, cho hai đường thẳng d : x + y +1 = 0 , 1
d : 2x – y –1 = 0 . Lập phương trình đường thẳng
d , d tương ứng tại 2
d đi qua M(1;–1) cắt 1 2 A và B sao
cho 2MA + MB = 0 . HD Giải
Ta có: A ∈ d ⇒ A( ;
a −a −1); B ∈ d ⇒ B( ; b 2b −1) 1 2
Từ điều kiện 2MA + MB = 0 tìm được A(1; –2), B(1;1).
Vậy d : x −1 = 0
Bài 1.25. Trong mặt phẳng với hệ tọa độ Oxy, cho điểm M(1; 0). Lập phương trình đường thẳng d đi qua
M và cắt hai đường thẳng d : x + y +1 = 0, d : x – 2y + 2 = 0 lần lượt tại 1 2
A, B sao cho MB = 3MA. HD Giải A ∈(d ) A( ; a −1− a)
MA = (a −1; 1 − − a) Ta có: 1 ⇔ ⇒ . B ∈(d )
B(2b − 2; b) 2
MB = (2b − 3;b)
Từ A, B, M thẳng hàng và MB = 3MA ⇒ MB = 3MA (1) hoặc MB = 3 − MA (2) 2 1 A − ; − A(0;− ) 1 (1) ⇒ 3 3 ⇒
(d) : x − 5y −1 = 0 hoặc (2) ⇒
⇒ (d) : x − y −1 = 0 B(4;3) B(−4; −1)
Bài 1.26. Trong mặt phẳng với hệ tọa độ Oxy, cho điểm M(1; 1). Lập phương trình đường thẳng (d) đi
qua M và cắt hai đường thẳng d : 3x − y − 5 = 0, d : x + y − 4 = 0 lần lượt tại 1 2 A, B sao cho
2MA –3MB = 0 . HD Giải Ta có: A( ;
a 3a − 5)∈ d , B( ;
b 4 − b)∈ d . 1 2 2MA = 3MB (1)
Vì A, B, M thẳng hàng và 2MA = 3MB nên 2MA = 3 − MB (2) 11
Chương III. Phương pháp tọa độ trong
mặt phẳng. 0916620899-0355334679
Tài liệu học tập Toán 10 GV. Lư Sĩ Pháp 5
2(a −1) = 3(b −1) a = 5 5 (1) ⇔ ⇔
2 ⇒ A ; ,B(2;2) . Suy ra d : x − y = 0.
2(3a − 6) = 3(3 − b) 2 2 b = 2 2(a −1) = 3 − (b −1) a = 1 (2) ⇔ ⇔ ⇒ A(1; 2
− ),B(1;3) . Suy ra d : x −1 = 0. 2(3a − 6) = 3 − (3− b) b = 1
Vậy có d : x − y = 0 hoặc d : x −1 = 0 .
Bài 1.27. Trong mặt phẳng với hệ toạ độ Oxy, cho điểm M(3; 1). Viết phương trình đường thẳng d đi qua
M cắt các tia Ox, Oy tại A và B sao cho (OA + 3OB) nhỏ nhất. HD Giải x y
Phương trình đường thẳng d cắt tia Ox tại A(a;0), tia Oy tại B(0;b): + = 1 (a, b > 0) a b 3 1 Coâsi 3 1
Do M(3; 1) ∈ d nên ta có: 1 = + ≥ 2 . ⇒ ab ≥12. a b a b a = 3b a = 6
Mà OA + 3OB = a + 3b ≥ 2 3ab = 12 ⇒ (OA + 3OB) = 12 ⇔ ⇔ min 3 1 1 = = b = 2 a b 2 x y
Phương trình đường thẳng d là: + = 1 ⇔ x + 3y − 6 = 0 6 2
Bài 1.28. Trong mặt phẳng với hệ toạ độ Oxy, viết phương trình đường thẳng ∆ đi qua điểm M(4;1) và cắt
các tia Ox, Oy lần lượt tại A và B sao cho giá trị của tồng OA + OB nhỏ nhất. HD Giải
Giải tương tự bài 7. Vậy d : x + 2y − 6 = 0
Bài 1.29. Trong mặt phẳng với hệ toạ độ Oxy, viết phương trình đường thẳng d đi qua điểm M(1; 2) và cắt 9 4
các trục Ox, Oy lần lượt tại A, B khác O sao cho + nhỏ nhất. 2 2 OA OB HD Giải
Đường thẳng d đi qua M(1;2) và cắt các trục Ox, Oy lần lượt tại A, B khác O, nên A( ;
a 0); B(0; b) với . x y
a b ≠ 0 ⇒ Phương trình của d có dạng + = 1. a b 1 2
Vì d qua M nên + = 1. Áp dụng bất đẳng thức Bunhiacôpski ta có : a b 2 2 1 2 1 3 2 1 9 4 9 4 9 9 4 9
1 = + = . +1. ≤ +1 + ⇔ + ≥ ⇔ + ≥ . 2 2 a b 3 a b 9 a b 2 2 a b 10 2 2 OA OB 10 1 3 2 1 2 20
Dấu bằng xảy ra khi : = 1: và + = 1 ⇔ a = 10, b = 3 a b a b 9
Vậy d : 2x + 9y − 20 = 0 .
Bài 1.30. Trong mặt phẳng với hệ tọa độ Oxy. Lập phương trình đường thẳng d qua M(2;1) và tạo với
các trục tọa độ một tam giác có diện tích bằng S = 4 . HD Giải x y Gọi A( ;
a 0), B(0; b) ( ,
a b ≠ 0) là giao điểm của d với Ox, Oy, suy ra: d : + = 1 . a b 2 1 + = 1
2b + a = ab
Theo giả thiết, ta có: a b ⇔ . ab = 8 ab = 8 12
Chương III. Phương pháp tọa độ trong
mặt phẳng. 0916620899-0355334679
Tài liệu học tập Toán 10 GV. Lư Sĩ Pháp
Khi ab = 8 thì 2b + a = 8. Nên: b = 2;a = 4 ⇒ d : x + 2y − 4 = 0 . 1
Khi ab = −8 thì 2b + a = 8 − . Ta có: 2
b + 4b − 4 = 0 ⇔ b = 2 − ± 2 2 . Với b = 2
− + 2 2 ⇒ d : (1− 2 ) x + 2(1+ 2 ) y − 4 = 0 Với b = 2
− − 2 2 ⇒ d : (1+ 2 ) x + 2(1− 2 ) y + 4 = 0.
Bài 1.31. Trong mặt phẳng với hệ tọa độ Oxy, cho điểm A(2; –1) và đường thẳng d có phương trình 1
2x – y + 3 = 0. Lập phương trình đường thẳng (∆) qua A và tạo với d một góc α có cosα = . 10 HD Giải
Phương trình đường thẳng (∆) có dạng: (
a x –2) + b(y +1) = 0 ⇔ ax + by –2a + b = 0 2 2 (a + b ≠ 0) 2a b 1 Ta có: 2 2 cosα − = =
⇔ 7a − 8ab + b = 0 . Chọn a = 1 ⇒ b = 1 hoặc b = 7. 2 2 5(a + b ) 10
⇒ ∆ : x + y −1 = 0 và ∆ : x + 7y + 5 = 0 1 2
Bài 1.32. Trong mặt phẳng với hệ toạ độ Oxy , cho đường thẳng d : 2x − y − 2 = 0 và điểm I(1;1) . Lập
phương trình đường thẳng ∆ cách điểm I một khoảng bằng 10 và tạo với đường thẳng d một góc bằng 0 45 . HD Giải
Giả sử phương trình đường thẳng ∆ có dạng: ax + by + c = 0 2 2 (a + b ≠ 0). 2a − b 1 a = 3b Do 0 (d,∆) = 45 nên = ⇔ 2 2 a + b . 5 2 b = −3a 4 + c c = 6
Với a = 3b ⇒ ∆: 3x + y + c = 0 . Mặt khác d(I;∆) = 10 ⇔ = 10 ⇔ 10 c = 1 − 4 −2 + c c = −8 Với b = 3
− a ⇒ ∆: x − 3y + c = 0 . Mặt khác d(I;∆) = 10 ⇔ = 10 ⇔ 10 c = 12
Vậy các đường thẳng cần tìm: 3x + y + 6 = 0; 3x + y −14 = 0 ; x − 3y − 8 = 0; x − 3y +12 = 0 .
Bài 1.33. Trong mặt phẳng với hệ tọa độ Oxy , cho điểm M (0; 2) và hai đường thẳng d , d có phương 1 2
trình lần lượt là 3x + y + 2 = 0 và x − 3y + 4 = 0 . Gọi A là giao điểm của d và d . Viết phương trình 1 2
đường thẳng đi qua M, cắt 2 đường thẳng d và d lần lượt tại B , C ( B và C khác A ) sao cho 1 2 1 1 +
đạt giá trị nhỏ nhất. 2 2 AB AC HD Giải
A = d ∩ d ⇒ A( 1
− ;1) . Ta có d ⊥ d . Gọi ∆ là đường thẳng cần tìm. 1 2 1 2
H là hình chiếu vuông góc của A 1 1 1 1 trên ∆ . ta có: + = ≥ (không đổi) 2 2 2 2 AB AC AH AM 1 1 1 1 1 +
đạt giá trị nhỏ nhất khi và chỉ khi + =
khi và chỉ khi H ≡ M , hay ∆ là đường 2 2 AB AC 2 2 2 AB AC AM
thẳng đi qua M và vuông góc với AM. ⇒ Phương trình ∆: x + y − 2 = 0 .
Bài 1.34. Trong mặt phẳng với hệ tọa độ Oxy, cho đường thẳng d : x − 3y − 6 = 0 và điểm N(3;4). Tìm 15
tọa độ điểm M thuộc đường thẳng d sao cho tam giác OMN (O là gốc tọa độ) có diện tích bằng . 2 HD Giải
Ta có ON = (3;4) , ON = 5, Phương trình đường thẳng ON: 4x − 3y = 0 . Giả sử M(3m + 6;m)∈ d . 13
Chương III. Phương pháp tọa độ trong
mặt phẳng. 0916620899-0355334679
Tài liệu học tập Toán 10 GV. Lư Sĩ Pháp 1 2S Khi đó ta có S
= d(M,ON).ON ⇔ d(M,ON) O ∆ NM = = 3 ∆ONM 2 ON 4.(3m + 6) −3m −13 ⇔
= 3 ⇔ 9m + 24 = 15 ⇔ m = −1 hoặc m = 5 3 1 − 3 −13 Với m = 1 − ⇒ M(3; 1 − ) Với m = ⇒ M −7; 3 3
Bài 1.35. Trong mặt phẳng toạ độ Oxy, cho hai đường thẳng d : x + y − 3 = 0 , d : x + y − 9 = 0 và điểm 1 2
A(1; 4) . Tìm điểm B ∈ d ,C ∈ d sao cho tam giác 1 2
ABC vuông cân tại A. HD Giải Gọi B( ;
b 3 − b)∈ d , C( ;
c 9 − c)∈ d ⇒ AB = (b −1; 1
− − b) , AC = (c −1;5− c). 1 2 (
b −1)(c −1) − (b +1)(5 − c) = 0 ∆ A . B AC = 0
ABC vuông cân tại A ⇔ ⇔ (*) 2 2 2 2 AB = AC (
b −1) + (b +1) = (c −1) + (5 − c) (b +1)(5− c) b −1 = (1) c −1
Vì c = 1 không là nghiệm của (*) nên (*) ⇔ 2 2 (5 − c) 2 2 2 (b +1)
+ (b +1) = (c −1) + (5− c) (2) 2 (c −1) b = c − 2 Từ (2) ⇔ 2 2
(b +1) = (c −1) ⇔ . b = −c
Với b = c − 2 , thay vào (1) ta được c = 4, b = 2 ⇒ B(2;1), C(4;5) .
Với b = −c , thay vào (1) ta được c = 2, b = 2
− ⇒ B(−2;5), C(2;7).
Vậy: B(2;1), C(4;5) hoặc B(−2;5), C(2;7). 3
Bài 1.36. Trong mặt phẳng Oxy, cho tam giác ABC biết A(2; –3), B(3; –2), có diện tích bằng và trọng 2
tâm G thuộc đường thẳng ∆ : 3x – y –8 = 0 . Tìm tọa độ đỉnh C. HD Giải 5 5
Ta có: AB = 2 , trung điểm M ; − . Phương trình AB: x − y − 5 = 0 . 2 2 1 3 3 S = AB d . C
( , AB) = ⇒ d C ( , AB) = . ABC 2 2 2 1 t − ( t 3 − 8) − 5 1 = 1
Gọi G(t; t 3 − 8)∈ ∆ ⇒ d G ( , AB) = ⇒ = ⇔ t 2 2 2 t = 2
Với t = 1 ⇒ G(1; –5) ⇒ C(–2; –10)
Với t = 2 ⇒ G(2; –2) ⇒ C(1; –1)
Bài 1.37. Trong mặt phẳng với hệ toạ độ Oxy , cho đường thẳng d : x + 2y − 3 = 0 và hai điểm A( 1 − ;2) ,
B(2;1) . Tìm toạ độ điểm C thuộc đường thẳng d sao cho diện tích tam giác ABC bằng 2. HD Giải
Ta có AB = 10 , C( 2
− a + 3;a) ∈ d. Phương trình đường thẳng AB : x + 3y − 5 = 0 . 1 1 a − 2 a = 6 S 2 ∆ = ⇔ AB d . C ( , AB) = 2 ⇔ 10. = 2 ⇔ ABC 2 2 10 a = 2 −
Với a = 6 ta có C( 9 − ;6) Với a = 2 − ta có C(7; 2 − ) .
Bài 1.38. Trong mặt phẳng với hệ toạ độ Oxy, cho tam giác ABC có trung điểm cạnh AB là M( 1 − ;2) , tâm
đường tròn ngoại tiếp tam giác là I(2; 1
− ). Đường cao của tam giác kẻ từ A có phương trình
2x + y +1 = 0 . Tìm toạ độ đỉnh C. HD Giải
Phương trình đường thẳng AB qua M và nhận MI = (3;−3)làm VTPT: (AB) : x − y + 3 = 0 . 14
Chương III. Phương pháp tọa độ trong
mặt phẳng. 0916620899-0355334679
Tài liệu học tập Toán 10 GV. Lư Sĩ Pháp − + 3 = 0 4 5
Toạ độ điểm iA là nghiệm của hệ: x y ⇒ A − ; .
2x + y + 1 = 0 3 3 2 7 Với M( 1
− ;2) là trung điểm của AB nên B − ; . 3 3 2 x = − + 2t Đường thẳng 3
BC qua B và nhận n = (2;1) làm VTCP nên BC: t ( ∈ ℝ ) 7 y = + t 3 2 7
Giả sử C − + 2t; + t ∈(BC) . 3 3 2 2 2 2 8 10 8 10 t = 0 lo
( aïi vì C ≡ B) 14 47
Ta có: IB = IC ⇔ 2t − + t + = + ⇔ 4 . Vậy: C ; . 3 3 3 3 t = 15 15 5
Bài 1.39. Trong mặt phẳng với hệ toạ độ Oxy, cho tam giác ABC có A(2;1) . Đường cao BH có phương
trình x − 3y − 7 = 0 . Đường trung tuyến CM có phương trình x + y +1 = 0 . Xác định toạ độ các đỉnh B, C.
Tính diện tích tam giác ABC. HD Giải
AC qua A và vuông góc với đường cao BH ⇒ (AC) : x − 3y − 7 = 0 . − 3 − 7 = 0
Toạ độ điểm C thỏa mãn hệ: x y ⇒ C(4; 5 − ) . x + y + 1 = 0 2 + x 1+ y 2 + x 1+ y
Trung điểm M của AB có: B B x = ; y = . M ∈ C ( M) ⇒ B B + +1 = 0 . M M 2 2 2 2
x − 3y − 7 = 0
Toạ độ điểm B thỏa mãn hệ: 2 + x 1+ y ⇒ B( 2 − ; 3 − ) . B B + +1 = 0 2 2 − 3 − 7 = 0 14 7
Toạ độ điểm H thỏa mãn hệ: x y ; 3 ⇒ H − .
x + y − 7 = 0 5 5 8 10 1 1 8 10 Ta có: BH =
; AC = 2 10 ⇒ S AC B . H .2 10. 16 5 ∆ = = = (đvdt). ABC 2 2 5
Bài 1.40. Trong mặt phẳng với hệ toạ độ Oxy, cho tam giác ABC có A( 3
− ;6), trực tâm H(2;1) , trọng 4 7 tâm G ;
. Xác định toạ độ các đỉnh 3 3 B và C. HD Giải 2 7 1
Gọi I là trung điểm của BC. Ta có AG = AI ⇒ I ; 3 2 2
Đường thẳng BC qua I vuông góc với AH có phương trình: x − y − 3 = 0
Vì I là trung điểm của BC nên giả sử B(x ; y ) thì C(7 − x ;1− y ) và x − y − 3 = 0 . B B B B B B
H là trực tâm của tam giác ABC nên CH ⊥ AB ; CH = ( 5
− + x ; y ), AB = (x + 3; y − 6) B B B B x − y = 3 x = 1 x = 6 B B B B
CH.AB = 0 ⇔ ( ⇔ ∨ x
− 5)(x + 3) + (y − 6) = 0 y = −2 y = 3 B B B B B Vậy B(1; 2
− ),C (6;3) hoặc B(6;3),C (1; 2 − )
Bài 1.41. Trong mặt phẳng toạ độ với hệ toạ độ Oxy, cho ∆ABC với AB = 5, đỉnh C( 1 − ; 1 − ) , phương
trình cạnh AB : x + 2y − 3 = 0 và trọng tâm G của ∆ABC thuộc đường thẳng d : x + y − 2 = 0 . Xác định
tọa độ các đỉnh A, B của tam giác. HD Giải 15
Chương III. Phương pháp tọa độ trong
mặt phẳng. 0916620899-0355334679
Tài liệu học tập Toán 10 GV. Lư Sĩ Pháp
Gọi I(x; y) là trung điểm AB , G(x ; y ) là trọng tâm của ∆ABC G G 2x −1 x 2 = G 2 −1 2 −1 ⇒ x y CG = CI 3 ⇔
. G ∈ d : x + y − 2 = 0 nên có: x + y − 2 = 0 ⇔ + − 2 = 0 3 2y −1 G G 3 3 y = G 3
x + 2y − 3 = 0
Tọa độ điểm I thỏa mãn hệ: 2x −1 2y −1 ⇒ I(5; 1 − ) + − 2 = 0 3 3 2 2 2 2 AB 5
Gọi A(x ; y ) ⇒ IA = (x − 5) + (y +1) = = . A A A A 2 4
Hơn nữa A ∈ AB : x + 2y − 3 = 0 suy ra tọa độ điểm A thỏa mãn hệ:
x + 2y − 3 = 0 x = 4 = 6 x A A A A ( 2 2 5 ⇔ 1 hoặc 3 x − 5 + y + 1 = y = − y = − A ) ( A ) A 4 2 A 2 1 3 1 3
Vậy: A 4,− ,B6;−
hoặc B 4,− , A6;− . 2 2 2 2
CÁC BÀI TẬP LÀM TƯƠNG TỰ
Bài 1. Viết phương trình tổng quát của đường thẳng (∆) biết :
a) (∆) qua điểm A(2;4) và có VTPT n = (3;5)
b) (∆) qua điểm B(1;−2)và song song với (∆ ): x + 2y – 4 = 0 1
c) (∆) qua điểm C ( 2
− ;2)và vuông góc với (∆ ): x − y −5 = 0 2 2 d) (∆) qua E (3; 4
− ) và có hệ số góc k = 5
e) (∆) cắt trục Ox tại M (5;0) và cắt truc Oy tại N (0;−3)
Bài 2. Viết phương trình tham số , Phương trình tổng quát và phương trình chính tắc(nếu có) của đường
thẳng (∆) trong mỗi trường hợp sau:
a) (∆) qua M (1;−2) và có một vectơ chỉ phương u = (2; 1 − )
b) (∆) qua gốc toạ độ O và có một vectơ chỉ phương u = ( 3 − ;5)
c) (∆) qua N (3;2) và có một vectơ pháp tuyến n = (−3;7) d) (∆) qua P ( 1 − ; )
1 và vuông góc với đường thẳng có phương trình : 2x −3y +1 = 0
e) (∆) qua Q(2;0)và song song với đường thẳng có phương trình: 2x + y –5 = 0 f) (∆) qua K (3; 2
− )và có hệ số góc k = 2 −
g) (∆) qua hai điểm A(1;3),B(−2;3)
Bài 3. Viết phương trình tổng quát các đường cao của tam giác ABC biết A( 1
− ;2),B(2;−4),C(1;0).
Bài 4. Viết phương trình đường trung trực của đoạn thẳng AB:
a) Biết A(1;2),B(3;4). b) Biết A(2; ) 1 ,B( 6 − ;− ) 1 . c) Biết A(1; 2 − ),B(5;4).
Bài 5. Cho tam giác ABC có phương trình cạnh AB : 5x –3y + 2 = 0 và có phương trình hai đường cao: A ’
A : 4x –3y +1 = 0; B ’
B : 7x + 2y – 22 = 0 . Lập phương trình hai cạnh còn lại và đường cao CC’ của tam giác ABC .
Bài 6. Cho tam giác ABC có phương trình ba cạnh là: AB : x – y – 4 = 0,BC : 3x + 2y –7 = 0,
CA : x + 4y –19 = 0 . Lập phương trình tổng quát các đường cao của tam giác ABC . 16
Chương III. Phương pháp tọa độ trong
mặt phẳng. 0916620899-0355334679
Tài liệu học tập Toán 10 GV. Lư Sĩ Pháp
Bài 7. Cho tam giác ABC có trung điểm các cạnh AB,BC,CA lần lượt là M (−1;− )
1 , N (1;9),P(9; ) 1
a) Lập phương trình các đường trung trực của ba cạnh trong tam giác ABC .
b) Tìm tọa độ tâm đường tròn ngoại tiếp tam giác ABC .
Bài 8. Cho hai đường thẳng (d ) : 2x + y − 2 = 0;(d ) : x − y + 3 = 0 1 2
a) Tìm toạ độ giao điểm của (d ) và (d ) 1 2
b) Viết phương trình đường thẳng (d) đi qua N(2; 4) cắt (d ) và (d ) lần lượt tại 1 2
A và B sao cho N là
trung điểm của đoạn AB.
Bài 9. Xét vị trí tương đối của mỗi cặp đường thẳng sau và tìm giao điểm (Nếu có ) của chúng :
a) (∆ ) : 4x + y − 2 = 0 và (∆ ) : 2x − y + 5 = 0 1 2
b) (∆ ) : x − 2y + 7 = 0 và (∆ ) : 2x − 4y + 9 = 0 1 2
c) (∆ ) : 2x − y + 3 = 0 và (∆ ) : 2x − 2y + 3 2 = 0 1 2
d) (∆ ) : x − 3y + 4 = 0 và (∆ ) : 0,5x −1,5y + 4 = 0 1 2
Bài 10. Cho hình chữ nhật ABCD có A( 1
− ;3) , tâm đối xứng I ( 1 − ; 2
− ) và một trục đối xứng (d): y = 2x .
Tìm toạ độ các đỉnh B,C, D.
Bài 11. Biện luận vị trí tương đối hai đường thẳng sau theo tham số m
a) ∆ : 4x − my + 4 − m = 0;∆ : (2m + 6)x + y − 2m −1 = 0 1 2
b) ∆ : mx + y + 2 = 0;∆ : x + my + m +1 = 0 1 2
c) ∆ : 2mx + (m +1) y − 2 = 0;∆ : (m + 2)x + (2m −1)y − (m + 2) = 0 1 2
Bài 12. Viết phương trình tổng quát của các đường thẳng sau: x = 2 + 3t
x = −4 − 5t x = 1 − 2 +1 x = 3 a) b) c) d) y = 4 − t y = 6 + 2t y = t − y = 5 + 2t
Bài 13. Viết phương trình tham số của các đường thẳng sau:
a) 4x + y –5 = 0
b) −2x + y + 4 = 0 c) x –5 = 0 d) y – 7 = 0
Bài 14. Xét vị trí tương đối của các cặp đường thẳng sau và tìm toạ độ giao điểm của chúng( nếu có): x = 1+ t x = 1− t x − 3 y − 5
a) ∆ : 2x + y − 3 = 0;∆ : b) ∆ : ;∆ : = 1 2 1 2 y = 4 + 3t y = 1 − + 2t 3 6 − x = 2 − + t x = 4t ' x +1 y −1 x + 3 y − 2 c) ∆ : ;∆ : d) ∆ : = ;∆ : = 1 2 1 2 y = t −
y = 2 − t ' 2 1 − 4 − 2 x = 1+ t x = 1+ 2t '
Bài 15. Cho hai đường thẳng ∆ : ; ∆ : 1 2 y = 3 − + 2t y = 1+ t '
a) Tìm toạ độ giáo điểm I của (∆ ) và (∆ ) 1 2
b) Viết phương trình tham số và phương trình tổng quát của:
i) Đường thẳng (∆ ') đi qua I và vuông góc với (∆ ) . 1
ii) Đường thẳng (∆") đi qua I và vuông góc với (∆ ) 2 x = 2 − + 2t
Bài 16. Cho đường thẳng (∆) : và điểm A(4; ) 1 . y = 1+ t
a) Tìm toạ độ hình chiếu của điểm A xuống (∆) . b) Tìm điểm ’
A đối xứng của A qua (∆)
Bài 17. Cho tam giác ABC có A(6;2),B(1;4),C (3;− ) 1 .
a) Viết phương trình các cạnh của tam giác ABC .
b) Viết phương trình đường cao BH và trung tuyến BN của tam giác ABC .
Bài 18. Phương trình hai cạnh của một tam giác trong mpOxy là: 5x –2y + 6 = 0 và 4x + 7y –21 = 0 . Viết
phương trình cạnh thứ ba biết trực tâm của tam giác trùng với gốc toạ độ O.
Bài 19. Cho tam giác ABC với A(1;− ) 1 ,B(−2; ) 1 và C (3;5) .
a). Viết phương trình đường vuông góc AH kẻ từ A đến trung tuyến BK của tam giác ABC .
b). Tính diện tích tam giác ABK 17
Chương III. Phương pháp tọa độ trong
mặt phẳng. 0916620899-0355334679
Tài liệu học tập Toán 10 GV. Lư Sĩ Pháp x = 2 + t
Bài 20. Trong mpOxy cho A(3;0)và đường thẳng (∆): y = 3 + 2t
a) Tìm điểm B đối xứng của A qua (∆)
b) Viết phương trình đường thẳng (∆ ') là đối xứng của (∆) qua A.
Bài 21. Tính khoảng cách từ M (2;− )
1 đến các đường thẳng sau: x = 3 +12t x −1 y − 3
a) (∆ ) :3x + 4y + 8 = 0 b) (∆ ) : c) (∆ ) : = 1 2 3 y = 1+ 5t 2 4 −
Bài 22. Tính khoảng cách giữa hai đường thẳng sau:
a) (∆ ) : 2x + y −10 = 0 và (∆ ) : 4x + 2y −1 = 0 1 2
b) (∆ ) : −3x + y + 5 = 0 và (∆ ) : 3x – y +10 = 0 1 2
Bài 23. Tìm góc giữa hai đường thẳng sau:
a) (∆ ) : x + 2y + 4 = 0 và (∆ ) : 2x – y + 6 = 0 1 2
b) (∆ ) : 2x – y + 5 = 0 và (∆ ) : x –3y + 2 = 0 1 2
c) (∆ ) : 4x –2y + 5 = 0 và (∆ ) : x –3y +1 = 0 1 2
Bài 24. Viết phương trình đường thẳng (∆) trong mỗi trường hợp sau: a) Qua M ( 2
− ;0) và tạo với đường thẳng (∆ ): x +3y –3 = 0 một góc 450. 1 x = 5 + 6t b) Qua N ( 1
− ;2)và tạo với đường thẳng (∆ ): một góc 600. 2 y = 2 − − 4t
c) Qua P (2;5)và cách đều hai điểm A( 1 − ;2)và B(5;4). d) Qua Q(2; 2
− ) và cách điểm C(3; ) 1 một đoạn bằng 3.
Bài 25. Lập phương trình các đường phân giác của các góc giữa hai đường thẳng sau:
a) (∆ ) : 2x + 4y + 7 = 0 và (∆ ) : 5x + 3y + 7 = 0 1 2
b) (∆ ) : −3x + 4y + 8 = 0 và (∆ ) : x – y + 6 = 0 1 2
Bài 26. Tìm những điểm nằm trên đường thẳng (∆ ) : 3x + y –6 = 0 và có khoảng cách từ đó đến (∆ ) : 1 2
x + 2y – 2 = 0 bằng 5 .
Bài 27. Cho hình vuông có đỉnh A( 4
− ;5) và một đường chéo nằm trên đường thẳng có phương trình :
7x – y + 8 = 0.Lập phương trình các đường thẳng chứa các cạnh và đường chéo thứ hai của hình vuông.
Bài 28. Cho điểm A( 1
− ;3) và đường thẳng(d) : 4x –3y +8 = 0 . Tìm điểm M trên đường thẳng
(∆) : −x + 2y +1 = 0 sao cho AM song song với đường thẳng (d).
Bài 29. Cho điểm A(2;5)và B(4; )
1 . Tìm điểm C trên đường thẳng (∆) : x –4y + 6 = 0 sao cho tam giác
ABC cân tại C.
Bài 30. Cho điểm B (2;3) và đường thẳng (∆) :2x – y + 3 = 0. Tìm tọa độ điểm A là đối xứng của B qua đường thẳng (∆) .
Bài 31. Cho tam giác ABC với A(2;−4),B(0; 2
− )và trọng tâm G thuộc đường thẳng
(∆) : 3x – y + 1 = 0. Tìm toạ độ điểm C biết rằng tam giác có diện tích bằng 3.
Bài 32. Cho (∆) : 2x + y +1 = 0 và hai điểm A(0;3),B(1;5).
a) Tìm điểm M trên (∆) sao cho MA − MB lớn nhất
b) Tìm điểm N trên (∆) sao cho NA + NB nhỏ nhất
BÀI TẬP TRẮC NGHIỆM 18
Chương III. Phương pháp tọa độ trong
mặt phẳng. 0916620899-0355334679
Tài liệu học tập Toán 10 GV. Lư Sĩ Pháp Câu 1. Cho A
∆ BC có A(2;− ) 1 ;B(4; ) 5 ;C( 3
− ;2). Viết phương trình tổng quát của đường cao AH .
A. 7x + 3y −11 = 0.
B. 3x + 7y +1 = 0.
C. 7x + 3y +13 = 0. D. −3x + 7 y +13 = 0.
Câu 2. Cho hai điểm A( 2 − ; ) 3 ; B(4;− )
1 . viết phương trình trung trực đoạn AB.
A. 2x − 3y +1 = 0.
B. 2x + 3y − 5 = 0.
C. 3x − 2y −1 = 0.
D. x − y −1 = 0.
Câu 3. Cho tam giác ABC với A(2;− ) 1 ;B(4; ) 5 ;C( 3
− ;2) . Phương trình tổng quát của đường trung tuyến AM là
A. 7x + 3y −11 = 0.
B. 3x + 7y +1 = 0.
C. 7x + 3y +13 = 0. D. 7x + 3y − 4 = 0.
Câu 4. Mệnh đề nào sau đây đúng? Đường thẳng (d ) : x − 2y + 5 = 0 : 1
A. (d ) có hệ số góc k = .
B. (d ) cắt (d′) có phương trình: x − 2y = 0. 2 x = t
C. Đi qua A(1; 2 − ) .
D. Có phương trình tham số:
(t ∈R) . y = 2 − t
Câu 5. Cho tam giác ABC có C ( 1
− ;2) , đường cao BH : x − y + 2 = 0 , đường phân giác trong
AN : 2x − y + 5 = 0 . Tọa độ điểm A là 4 − 7 4 − 7 − 4 −7 4 7 A. A ; . B. A ; . C. A ; .
D. A ; . 3 3 3 3 3 3 3 3 x = − t
Câu 6. Giao điểm M của (d ) 1 2 :
và (d′) :3x − 2y −1= 0 là y = 3 − + 5t A. 1 M 0; . B. 1
M 0; − . C. 1
M − ; 0 . D. 11 M 2; − . 2 2 2 2
Câu 7. Cho hai đường thẳng (∆ :11x −12y +1= 0 và (∆ :12x +11y +9 = 0. Khi đó hai đường thẳng 2 ) 1 ) này A. Trùng nhau.
B. Song song với nhau.
C. Vuông góc nhau.
D. Cắt nhau nhưng không vuông góc.
Câu 8. Cho tam giác ABC có A( 1 − ; 2
− );B(0;2);C( 2 − ; )
1 . Đường trung tuyến BM có phương trình là:
A. 5x − 3y + 6 = 0.
B. 3x − 5y +10 = 0.
C. x − 3y + 6 = 0.
D. 3x − y − 2 = 0. x = + t Câu 9. Cho(d ) 2 3 :
. Điểm nào sau đây không thuộc (d )? y = 5 − 4t A. C( 1 − ;9). B. D(8;− ) 3 . C. A(5; ) 3 .
D. B(2;5).
Câu 10. Cho hai đường thẳng (d : mx + y = m +1 , d : x + my = 2 cắt nhau khi và chỉ khi : 1 ) ( 2)
A. m ≠ 2.
B. m ≠ 1 ± .
C. m ≠ 1.
D. m ≠ 1 − .
Câu 11. Cho tam giác ABC . Hỏi mệnh đề nào sau đây sai?
A. BC là một vecto pháp tuyến của đường cao AH.
B. BC là một vecto chỉ phương của đường thẳng BC.
C. Các đường thẳng AB,BC,CA đều có hệ số góc.
D. Đường trung trực của AB có AB là vecto pháp tuyến.
Câu 12. Cho hai đường thẳng (d : mx + y = m +1 , d : x + my = 2 song song nhau khi và chỉ khi 1 ) ( 2)
A. m = 1 ± .
B. m = 1.
C. m = 1 − .
D. m = 2.
Câu 13. Cho đường thẳng (d): 2x + 3y − 4 = 0 . Vectơ nào sau đây là vectơ pháp tuyến của (d)? 19
Chương III. Phương pháp tọa độ trong
mặt phẳng. 0916620899-0355334679
Tài liệu học tập Toán 10 GV. Lư Sĩ Pháp
A. n = −4;−6 . B. n = 2; 3 − . C. n = 2 − ;3 .
D. n = 3;2 . 1 ( ) 4 ( ) 3 ( ) 2 ( )
Câu 14. Gọi H là trực tâm của tam giác ABC . Phương trình các cạnh và đường cao của tam giác là:
AB : 7x − y + 4 = 0; BH :2x + y − 4 = 0; AH : x − y − 2 = 0 . Phương trình đường cao CH của tam giác ABC là
A. x + 7y − 2 = 0.
B. 7x − y = 0.
C. x − 7y − 2 = 0.
D. 7x + y − 2 = 0.
Câu 15. Cho đường thẳng (d ) đi qua điểm M (1; )
3 và có vecto chỉ phương a = (1; 2 − ) . Phương trình
nào sau đây không phải là phương trình của (d ) ? x −1 y − 3 x =1− t A. = .
B. 2x + y − 5 = 0.
C. y = −2x − 5. D. 1 − 2 y = 3 + 2t.
Câu 16. Viết phương trình tổng quát của đường thẳng đi qua điểm M ( 2; )1 và vuông góc với đường
thẳng có phương trình ( 2 + )1 x +( 2 − )1 y = 0.
A. −x + (3+ 2 2) y − 2 = 0.
B. x − (3+ 2 2) y +3+ 2 = 0.
C. (1− 2) x + ( 2 + )1 y +1= 0.
D. (1− 2) x +( 2 + )1 y +1− 2 2 = 0.
Câu 17. Phương trình tham số của đường thẳng (d) đi qua điểm M ( 2 − ; )
3 và vuông góc với đường thẳng
(d′):3x−4y +1= 0là x = 2 − + 3t x = 2 − + 3t x = 5 + 4t x = 2 − + 4t A. . B. . C. . D. . y = 3 − 4t y = 3 + 4t y = 6 − 3t y = 3 + 3t
Câu 18. Đường thẳng đi qua A( 1
− ;2), nhận n = (2;−4) làm véctơ pháo tuyến có phương trình là
A. x − 2y + 4 = 0.
B. x − 2y + 5 = 0
C. x − 2y − 4 = 0.
D. x + y + 4 = 0.
Câu 19. Cho tam giác ABC có A( 2 − ; ) 3 , B(1; 2 − ),C( 5
− ;4).Đường trung trực trung tuyến AM có phương trình tham số x = 2 x = 2 − − 4t x = 2 − t x = −2 A. . B. . C. . D. . 3 − 2t y = 3 − 2t
y = −2 + 3t y = 3 − 2t
Câu 20. Viết phương trình tổng quát của đường thẳng đi qua điểm I ( 1
− ;2) và vuông góc với đường
thẳng có phương trình 2x − y + 4 = 0
A. x − 2y + 5 = 0.
B. −x + 2y − 5 = 0.
C. x + 2y − 3 = 0.
D. x + 2y = 0.
Câu 21. Cho ∆ABC có A(4; 2
− ) . Đường cao BH : 2x + y − 4 = 0 và đường cao CK : x − y − 3 = 0 . Viết
phương trình đường cao kẻ từ đỉnh A
A. 4x − 3y − 22 = 0.
B. 4x + 5y − 6 = 0.
C. 4x − 5y − 26 = 0.
D. 4x + 3y −10 = 0.
Câu 22. Cho tam giác ABC có A(1; 2
− ) , đường cao CH : x − y +1 = 0 , đường phân giác trong
BN : 2x + y + 5 = 0 . Tọa độ điểm B là A. (−4;3). B. (−4; 3 − ). C. (4;3). D. (4;−3).
Câu 23. Mệnh đề nào dưới đây sai? Đường thẳng (d ) được xác định khi biết
A. Hai điểm phân biệt thuộc (d ) .
B. Hệ số góc và một điểm thuộc đường thẳng.
C. Một điểm thuộc (d ) và biết (d ) song song với một đường thẳng cho trước.
D. Một vectơ pháp tuyến hoặc một vectơ chỉ phương. 20
Chương III. Phương pháp tọa độ trong
mặt phẳng. 0916620899-0355334679
Tài liệu học tập Toán 10 GV. Lư Sĩ Pháp
Câu 24. Cho tam giác ABC có A( 4 − ; ) 1 B(2; 7 − )C(5; 6
− ) và đường thẳng (d ):3x + y +11 = 0 . Quan hệ
giữa (d ) và tam giác ABC là:
A. Đường Phân giác góc BAC.
B. Đường cao vẽ từ B.
C. Đường trung tuyến vẽ từ A.
D. Đường cao vẽ từ A.
Câu 25. Cho tam giác ABC biết trực tâm H (1;1) và phương trình cạnh AB : 5x − 2y + 6 = 0, phương trình
cạnh AC : 4x + 7 y − 21 = 0 . Phương trình cạnh BC là
A. 4x − 2y +1 = 0.
B. x − 2y +14 = 0.
C. x + 2y −14 = 0.
D. x − 2y −14 = 0. x = − t Câu 26. 7
Cho đường thẳng (d ) 2 3 :
và điểm A ;−2 . Điểm A∈(d ) ứng với giá trị nào của t? y = 1 − + 2t 2 1 3 1
A. t = − .
B. t = 2.
C. t = .
D. t = . 2 2 2
Câu 27. Cho hai điểm P(6; ) 1 và Q( 3 − ; 2
− ) và đường thẳng ∆ : 2x − y −1= 0. Tọa độ điểm M thuộc ∆
sao cho MP + MQ nhỏ nhất.
A. M (3;5). B. M (0; 1 − ).
C. M (2;3).
D. M (1;1).
Câu 28. Viết Phương trình đường thẳng đi qua điểm M (2; ) 3
− và cắt hai trục tọa độ tại hai điểm A và B
sao cho tam giác OAB vuông cân.
x + y −1 = 0 x + y +1 = 0
x + y −1 = 0 A. . B. . C. .
D. x + y +1 = 0.
x − y + 5 = 0
x − y − 5 = 0
x − y − 5 = 0
Câu 29. Cho đường thẳng (d ) : x − 2y +1 = 0 . Nếu đường thẳng (∆) đi qua M (1; ) 1 − và song song
với (d ) thì(∆) có phương trình là
A. x + 2y +1 = 0.
B. x − 2y + 5 = 0.
C. x − 2y + 3 = 0.
D. x − 2y − 3 = 0.
Câu 30. Cho ba điểm A(1; 2 − ),B(5; 4 − ),C( 1
− ;4). Đường cao AA′ của tam giác ABC có phương trình
A. 3x − 4y + 8 = 0.
B. 3x − 4y −11 = 0.
C. −6x + 8y +11 = 0.
D. 8x + 6y +13 = 0.
Câu 31. Cho ba điểm A(1; )
1 ;B(2;0);C(3;4). Viết phương trình đường thẳng đi qua Avà cách đều hai
điểm B,C .
A. 4x − y − 3 = 0;2x − 3y +1 = 0.
B. 4x − y − 3 = 0;2x + 3y +1 = 0.
C. 4x + y − 3 = 0;2x − 3y +1 = 0.
D. x − y = 0;2x − 3y +1 = 0. x = 1+ t
Câu 32. Cho hai điểm A( 1 − ;2), B(3; )
1 và đường thẳng ∆ :
. Tọa độ điểm C thuộc ∆ để tam y = 2 + t
giác ACB cân tại C là 7 13 13 7 7 13 7 13
A. − ; . B. ; . C. ; .
D. ;− . 6 6 6 6 6 6 6 6 x = + t
Câu 33. Cho (d ) 2 3 :
. Hỏi có bao nhiêu điểm M ∈(d ) cách A(9; )
1 một đoạn bằng 5? y = 3 + t. A. 3. B. 2. C. 1. D. 0.
Câu 34. Cho 4 điểm A( 3 − ; ) 1 , B( 9 − ;− ) 3 ,C ( 6 − ;0),D( 2
− ;4). Tọa độ giao điểm của 2 đường thẳng
AB và CD là A. (−9; 3 − ). B. (−9;3). C. (0;4). D. (−6;− ) 1 .
Câu 35. Đường thẳng (d ) có vecto pháp tuyến n = ( ;
a b) . Mệnh đề nào dưới đây sai? 21
Chương III. Phương pháp tọa độ trong
mặt phẳng. 0916620899-0355334679
Tài liệu học tập Toán 10 GV. Lư Sĩ Pháp A. u2 = (− ;
b a) là vecto chỉ phương của (d ) . B. ′ n = (k ;
a kb) k ∈ R là vecto pháp tuyến của (d ) . − C. ( b
d ) có hệ số góc k = (b ≠ 0) . D. u1 = ( ;
b −a) là vecto chỉ phương của (d ) . a
Câu 36. Cho hai điểm A(4;0), B(0;5) . Phương trình nào dưới đây không phải là phương trình của
đường thẳng AB? 5 − x − 4 x = 4 − 4t A. x y y y = x +15. B. + = 1. C. = . D.
(t∈ R). 4 4 5 −4 5 y = 5t x = −2 + 5t
Câu 37. Hai đường thẳng (d :
và (d : 4x +3y −18 = 0 cắt nhau tại điểm có tọa độ là 2 ) 1 ) y = 2t A. (1;2). B. (2; ) 1 . C. (2;3). D. (3;2).
Câu 38. Đường thẳng (∆) :3x − 2y − 7 = 0cắt đường thẳng nào dưới đây? A. (d : 3
− x + 2y −7 = 0.
B. (d :6x − 4y −14 = 0. 4 ) 3 )
C. (d :3x + 2y = 0.
D. (d :3x − 2y = 0. 2 ) 1 )
Câu 39. Cho đường thẳng (d ) :3x − 7 y +15 = 0. Mệnh đề nào dưới đây sai? 3
A. u = (7;3) là vecto chỉ phương của(d ) .
B. (d ) có hệ số góc k = . 7 C. ( 1
d ) không đi qua góc tọa độ.
D. (d )đi qua hai điểm M − ;2 và N (5;0) . 3
Câu 40. Với giá trị nào của tham số m thì hai đường thẳng dưới đây vuông góc 2 (
x = 1+ m +1 t
x = 2 − 3t ' ∆ : và (∆ : ? 2 ) 1 ) ( )
y = 2 − mt
y = 1− 4mt ' A. m = 2 ± 3.
B. m = ± 3. C. m = 3 ± . D. m = 1 ± .
Câu 41. Cho 4 điểm A(1;2), B(4;0),C(1;− ) 3 , D(7; 7
− ) . Vị trí tương đối của hai đường thẳng AB và CD là
A. Vuông góc nhau.
B. Cắt nhau nhưng không vuông góc.
C. Trùng nhau. D. Song song.
Câu 42. Cho đường thẳng (d ) : 4x − 3y + 5 = 0. Nếu đường thẳng (∆) đi qua góc tọa độ và vuông góc với
(d) thì (∆) có phương trình là
A. 3x + 4y = 0.
B. 4x − 3y = 0.
C. 4x + 3y = 0.
D. 3x − 4y = 0.
Câu 43. Phương trình đường thẳng đi qua hai điểm A( 2 − ;4);B( 6 − ; ) 1 là
A. 3x − 4y + 22 = 0.
B. 3x − 4y + 8 = 0.
C. 3x − 4y − 22 = 0.
D. 3x + 4y −10 = 0.
Câu 44.Cho hai điểm P(1;6) và Q( 3 − ; 4
− ) và đường thẳng ∆ : 2x − y −1= 0. Tọa độ điểm N thuộc ∆
sao cho NP − NQ lớn nhất là A. N(3;5). B. N( 1 − ; 3 − ).
C. N(1;1). D. N( 9 − ; 1 − 9).
Câu 45. Với giá trị nào của tham số m thì hai đường thẳng (∆ :3x + 4y −1= 0 và 1 ) (∆ ):(2m− ) 2
1 x + m y +1= 0 trùng nhau ? 2 A. m = 1 ± .
B. m = 2. C. Với mọi . m D. Không có . m
Câu 46. Cho phương trình: ax + by + c = 0 ( ) 1 với 2 2
a + b > 0 . Mệnh đề nào dướ đây sai? 22
Chương III. Phương pháp tọa độ trong
mặt phẳng. 0916620899-0355334679
Tài liệu học tập Toán 10 GV. Lư Sĩ Pháp
A. Với b = 0, ( )
1 là phương trình đường thẳng song song hoặc trùng với trục O . y
B. Điểm M x ; thuộc đường thẳng ( )
1 khi và chỉ khi ax + by + c ≠ 0 . 0 ( 0 0 y ) 0 0 C. ( )
1 là phương trình tổng quát của đường thẳng có vectơ pháp tuyến là n = ( ; a b) .
D. Với a = 0 ( )
1 là phương trình đường thẳng song song hoặc trùng với trục Ox.
Câu 47. Phương trình đường thẳng đi qua điểm M (5; ) 3
− và cắt hai trục tọa độ tại hai điểm A và B sao
cho M là trung điểm của AB là:
A. 5x − 3y + 34 = 0.
B. 3x − 5y − 30 = 0.
C. 3x + 5y − 30 = 0.
D. 5x − 3y − 34 = 0.
Câu 48. Đường thẳng dưới đây không song song với đường thẳng (d) : y = 2x −1?
A. −2x + y = 0.
B. 2x + y − 5 = 0.
C. 2x − y + 5 = 0.
D. 2x − y − 5 = 0.
Câu 49. Cho đường thẳng (d ) :3x + 5y −15 = 0 . Phương trình nào dưới đây không phải là một dạng khác của (d) ? 5 3 x = t x = 5 − t A. x y
y = − x + 3. B.
(t ∈ℝ). C. 3 (t ∈ ℝ).. D. + =1. 5 y = 5 5 3 y = t
Câu 50. Cho tam giác ABC với A(2; ) 3 ;B( 4 − ;5);C(6;− )
5 . M , N lần lượt là trung điểm của AB và
AC . Phương trình tham số của đường trung bình MN là x = 1 − + t x = −1+ 5t x = 4 + 5t x = 4 + t A. . B. . C. . D. . y = 4 − t y = 4 + 5t y = −1+ 5t y = −1+ t ĐÁPÁN
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25
D C D A C B C A D C C C A A C D A B D C B B D A D
26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50
A B B D B A C B A C A C C D B D A A D D B B B B A 23
Chương III. Phương pháp tọa độ trong
mặt phẳng. 0916620899-0355334679
Tài liệu học tập Toán 10 GV. Lư Sĩ Pháp
§2. PHƯƠNG TRÌNH ĐƯỜNG TRÒN
A. KIẾN THỨC CẦN NẮM
1. Một đường tròn được xác định khi biết tâm I(a; b) và bán kính R. Phương trình: y 2 2 Dạng 1: ( − ) + ( − ) 2 x a y b = R . R 2 2 Dạng 2: 2 2
x + y − 2ax − 2by + c = 0 , điều kiện a + b − c > 0 và b I 2 2
R = a + b − c .
Đặc biệt: Đường tròn tâm O, bán kính R: 2 2 2
x + y = R O a x
2. Điều kiện để đường thẳng ∆: Ax + By + C = 0 tiếp xúc với đường tròn (C) là:
Aa + Bb + C d (I,∆) = = R 2 2 A + B
3. Vị trí tương đối của đường thẳng d và đường tròn (C):
d(I , d) > R ⇔ d ∩ (C) = O
: d không có điểm chung với (C).
d(I , d) = R ⇔ d ∩ (C) = { } A
: d tiếp xúc với (C).
d(I , d) < R ⇔ d ∩ (C) = { ; A }
B : d cắt (C) tại hai điểm phân biệt.
4. Phương trình tiếp tuyến của đường tròn tại M(x0 ; y0) có dạng :
x x + y y − a(x + x) − b(y + y) + c = 0
x − a x − x + y − b y − y = 0 0 0 0 0 hoặc ( 0 )( 0 ) ( 0 )( 0) B. BÀI TẬP
ấn đề 1. Nhận dạng phương trình bậc hai là phương trình đường tròn. Tìm tâm và bán kính Vđường tròn Phương pháp :
1. Phương trình có dạng : 2 2
(x − a) + (y − b) = m,với m > 0 là phương trình đường tròn tâm I( ; a b), bán kính R = m .
2. Phương trình có dạng: 2 2
x + y − 2ax − 2by + c = 0 , với 2 2
a + b − c > 0 là trình đường tròn tâm I ( ; a b), 2 2
bán kính R = a + b − c .
Bài 2.1. Trong các phương trình sau, phương trình nào là phương trình đường tròn? Tìm tâm và bán kính của nó nếu có. a. 2 2
x + y − 6x + 8y +100 = 0 (1) b. 2 2
x + y + 4x − 6y −12 = 0 (2) c. 2 2
2x + 2y − 4x + 8y − 2 = 0 (3) d. 2 2
x + y − 2x − 2y − 2 = 0 (4) HD Giải −6 8
a. Phương trình (1) có dạng : 2 2
x + y − 2ax − 2by + c = 0 với a = = 3;b = = 4 − ,c = 100 −2 −2 Ta có: 2 2
a + b − c = 9 +16 −100 = 7
− 5 < 0 . Vậy (1) không phải là phương trình đường tròn.
b. Phương trình (2) có dạng : 2 2
x + y − 2ax − 2by + c = 0 với a = 2 − ;b = 3,c = 1 − 2 Ta có: 2 2
a + b − c = 4 + 9 −12 = 25 > 0 . Vậy (2) là phương trình đường tròn có tâm I( 2 − ;3), R = 5. c. Phương trình 2 2 2 2 2 2
2x + 2y − 4x + 8y − 2 = 0 ⇔ x + y − 2x + 4y −1 = 0 ⇔ (x −1) + (y + 2) = 6
Vậy (3) là phương trình đường tròn với tâm I (1; −2), R = 6. d. Phương trình 2 2 2 2
x + y − 2x − 2y − 2 = 0 ⇔ (x −1) + (y −1) = 4 24
Chương III. Phương pháp tọa độ trong
mặt phẳng. 0916620899-0355334679
Tài liệu học tập Toán 10 GV. Lư Sĩ Pháp
Vậy (4) là phương trình đường tròn với tâm I (1;1), R = 2.
Bài 2.2. Cho phương trình 2 2
x + y − 2mx + 4my + 6m −1 = 0 (1) . Với giá trị nào của tham số m thì (1) là
phương trình đường tròn? Tìm tâm và bán kính theo m. HD Giải
Phương trình (1) có dạng 2 2
x + y − 2ax − 2by + c = 0 với a = ; m b = 2
− m,c = 6m −1 2 2 2 2
Ta có: (1) là phương trình đường tròn ⇔ a + b − c > 0 ⇔ m + 4m − 6m + 1 > 0 1 m < 2
⇔ 5m − 6m +1 > 0 ⇔ 5 . m > 1 (1) có tâm I ( ;
m −2m),bán kính 2
R = 5m − 6m +1.
ấn đề 2. Lập phương trình đường tròn
VPhương pháp: Viết phương trình đường tròn (C), cần xác định tâm và bán kính của nó. taâm I( ; a b)
1. Đường tròn (C) : . Có phương trình : 2 2 2
(x − a) + (y − b) = R hay viết dưới dạng khai triển baùn kính R là 2 2
x + y − 2ax − 2by + c = 0 , với 2 2 2
c = a + b − R .
2. Các dạng thường gặp
Đường tròn (C) có tâm I( ;
a b) và đi qua điểm M(x ; y )
R = IM = (x − a) + (y − b) 0 0 . Ta có: 2 2 o 0 taâm I( ;
a b) laø trung ñieåm cuûa AB
Đường tròn (C) có đường kính AB . Suy ra (C) : baùn kính AB R = 2
Đường tròn (C) có tâm I và tiếp xúc với đường thẳng ∆ : ax + by + c = 0 tại điểm A . Ta có:
R = IA = d(I,∆)
Đường tròn (C) có tâm I và tiếp xúc với hai đường thẳng ∆ ∆
R = d(I,∆ ) = d(I,∆ ) 1 và 2 . Ta có 1 2
Đường tròn (C) qua ba điểm A,B,C . Ta gọi (C) có dạng 2 2
x + y − 2ax − 2by + c = 0 , lần lượt thay tọa
độ các điểm A,B,C vào ta được hệ phương trình ba ẩn , a , b .
c Sử dụng máy tính, tìm các hệ số , a , b c và
kết luận kết luận kết quả bài toán.
Bài 2.3. Lập phương trình đường tròn (C) trong các trường hợp sau: a. (C) có tâm I ( 2
− ;3) và đi qua điểm M(2; 3 − ). b. (C) có tâm I ( 1
− ;2) và tiếp túc với đường thẳng ∆ : x − 2y + 7 = 0.
c. (C) có đường kính AB với A(1;1), B(7;5). HD Giải a. Ta có : IM = (4; 6
− ) ⇒ IM = 16 + 36 = 52. taâm I(−2;3) Như vậy : (C) : có phương trình : 2 2
(x + 2) + (y − 3) = 52.
baùn kính R = IM = 52 −1− 2.2 + 7 2
b. Ta có : d(I , ∆) = = . 2 2 1 + ( 2 − ) 5 taâm I(−1;2) Như vậy : (C) : 2 + + − = baùn kính có phương trình : 2 2 4 (x 1) (y 2) . R = d(I,∆) = 5 5 c. Gọi I ( ;
x y) là trung điểm của AB ⇒ I(4;3) . Ta có : AB = (6;4) ⇒ AB = 2 13 taâm I(4;3) Như vậy : (C) : có phương trình : 2 2
(x − 4) + (y −3) = 13. baùn kính AB R = = 13 2 25
Chương III. Phương pháp tọa độ trong
mặt phẳng. 0916620899-0355334679
Tài liệu học tập Toán 10 GV. Lư Sĩ Pháp
Bài 2.4. Viết phương trình đường tròn (C) đi qua ba điểm A(1;2),B(5;2) và C(1; 3 − ) . HD Giải
Gọi đường tròn (C) có dạng : 2 2
x + y − 2ax − 2by + c = 0 . Ta có: 2 2 a = 3
A ∈(C) ⇔ 1 + 2 − 2 . a 1− 2 . b 2 + c = 0
2a + 4b − c = 5 2 2 1
B ∈ (C) ⇔ 5 + 2 − 2 . a 5 − 2 . b 2 + c = 0 ⇔ 1
0a + 4b − c = 29 ⇔ b = − 2 2 2
C ∈(C) ⇔ 1 + (−3) − 2 . a 1− 2 ( b 3 − ) + c = 0 2a
− 6b − c = 10 c = −1 Vậy (C): 2 2
x + y − 6x + y −1 = 0
Bài 2.5. Viết phương trình đường tròn tiếp xúc với các trục tọa độ và a. Đi qua A(2; 1 − )
b. Có tâm thuộc đường thẳng 3x − 5y − 8 = 0 HD Giải
Gọi đường tròn (C) có tâm I ( ;
a b) và bán kính R có phương trình dạng : 2 2 2
(x − a) + (y − b) = R (1)
Theo đề bài, ta có : d(I ,Ox) = d(I ,Oy) = R ⇔ a = b = R (2) Từ (1) và (2), ta có : 2 2 2
(x − a) + (y − b) = a và a = ±b a. Ta có : 2 2 2
A ∈(C) ⇔ (2 − a) + ( 1 − − b) = a
Với a = b , ta có : 2 2 2 2
(2 − a) + (−1− a) = a ⇔ a − 2a + 5 = 0 vô nghiệm
Với a = −b , ta có : 2 2 2 2
(2 − a) + (−1+ a) = a ⇔ a − 6a + 5 = 0 ⇔ a = 1 hoặc a = 5 + 2 2 a = 1 ⇒ b = 1
− , R = 1.(C) : (x −1) + (y +1) = 1 + 2 2 a = 5 ⇒ b = 5
− , R = 5.(C) : (x − 5) + (y + 5) = 25
b. Ta có: I ∈ ∆ : 3x − 5y − 8 = 0 ⇒ tọa độ điểm I thỏa mản: 3a − 5b − 8 = 0
Với a = b , ta có : 3a − 5a − 8 = 0 ⇔ a = −4 ⇒ b = 4 − , R = 4. Vậy 2 2
(C) : (x + 4) + (y + 4) = 16
Với a = −b , ta có : 3a + 5a − 8 = 0 ⇔ a = 1 ⇒ b = 1 − , R = 1. Vậy 2 2
(C) : (x −1) + (y +1) =1
Bài 2.6. Viết phương trình đường tròn tiếp xúc với trục hoành tại A(6;0) và đi qua điểm B(9;9). HD Giải
Gọi đường tròn (C) có tâm I ( ;
a b) và bán kính R có phương trình dạng : 2 2 2
(x − a) + (y − b) = R (1)
Theo đề bài, ta có : (C) tiếp xúc với trục hoành tại A(6; 0) nên a = 6, d(I ,Ox) = b = R Suy ra: 2 2 2
(C) : (x − 6) + (y − b) = b . Mặt khác : 2 2 2
B ∈(C) ⇔ (9 − 6) + (9 − b) = b ⇔ b = 5 ⇒ R = 5 Vậy 2 2
(C) : (x − 6) + (y − 5) = 25
Bài 2.7. Viết phương trình đường tròn đi qua A( 1
− ;0),B(1;2) và tiếp xúc với đường thẳng ∆ : x − y −1 = 0 HD Giải
Gọi đường tròn (C) có tâm I ( ;
a b) và bán kính R có phương trình dạng : 2 2 2
(x − a) + (y − b) = R (1) a − b −1
Ta có : (C) tiếp xúc với ∆ ⇔ d(I , ∆) = R ⇔ = R (2) 2 2 2 2 (
−1− a) + b = R
Ta lại có : A, B ∈(C) ⇔ (3) 2 2 2 (
1− a) + (2 − b) = R 2 2 2 (a − b −1) a = 0 ( 1 − − a) + b = a = 1 2 − b Từ (2) và (3), ta có : ⇔ ⇒ b = 1 2 2 2 2 (a − b −1)
b + (b − 2) = 2 2 2 (1
− a) + (2 − b) b = R = 2 2 Vậy : 2 2
(C) : x + (y −1) = 2 26
Chương III. Phương pháp tọa độ trong
mặt phẳng. 0916620899-0355334679
Tài liệu học tập Toán 10 GV. Lư Sĩ Pháp
Vấn đề 3. Lập phương trình tiếp tuyến của đường tròn y Phương pháp : M0
Loại 1. Phương trình tiếp tuyến tại tiếp điểm M b I
Gọi ∆ là tiếp tuyến của đường tròn (C) tại điểm M (x ; y ) 0 0 0
qua M (x ; y ) 0 0 0 Ta có : ∆ : có phương trình là O V TPT IM = (x − ; a y − b) x 0 0 0 a
(x −a x − x + y −b y− y = 0 0 )( 0 ) ( 0 )( 0)
Loại 2. Phương trình tiếp tuyến khi không biết tiếp điểm
Xác định tâm I và bán kính của (C).
Dựa vào các yếu tố viết phương trình đường thẳng ∆
Sử dụng điều kiện tiếp xúc : d(I , ∆) = R
Bài 2.8. Viết phương trình tiếp tuyến tại điểm M (4;2) C x − + y + = 0 thuộc đường tròn 2 2 ( ) : ( 1) ( 2) 25 HD Giải
Đường tròn (C) có tâm I(1;−2). Vậy phương trình tiếp tuyến với (C) tại M (4;2) 0 có dạng :
(x −a x − x + y −b y− y = 0 ⇔ (4−1)(x −4)+(2+2)(y −2) = 0 ⇔ 3x +4y−20 = 0 0 )( 0 ) ( 0 )( 0)
Bài 2.9. Lập phương trình tiếp tuyến với đường tròn 2 2
(C) : x + y − 4x − 2y = 0. Biết rằng tiếp tuyến đi
qua điểm A(3; −2). HD Giải
Đường tròn (C) có tâm I(2;1) và bán kính R = 5 .
Gọi ∆ là đường thẳng qua A và có hệ số góc k có phương trình dạng :
y + 2 = k(x − 3) ⇔ kx − y − 2 − 3k = 0 k = 2
2k −1− 2 − 3k ∆
là tiếp xúc với đường tròn (C) 2
⇔ d(I,∆) = R ⇔
= 5 ⇔ 4k − 6k − 4 = 0 ⇔ 1 2 k +1 k = − 2
Vậy có hai tiếp tuyến với (C) kẻ từ A : 2x − y − 8 = 0; x + 2y + 1 = 0
Bài 2.10. Lập phương trình tiếp tuyến ∆ với đường tròn 2 2
(C) : x + y − 4x + 6y + 3 = 0
a. Biết rằng ∆ song song với đường thẳng d : 3x − y + 2020 = 0
b. Biết rằng ∆ song song với đường thẳng d : 3x − y + 2019 = 0 HD Giải
Đường tròn (C) có tâm I(2; 3
− ) và bán kính R = 10 .
a. Ta có: ∆ / /d ⇒ ∆ : 3x − y + m = 0, m ≠ 2020 . 6 + 3+ m m = 1
∆ là tiếp xúc với đường tròn (C) ⇔ d(I,∆) = R ⇔ = 10 ⇔ 9 +1 m = 1 − 9
Vậy phương trình của ∆ : 3x − y +1 = 0 hoặc 3x − y −19 = 0
b. Ta có: ∆ ⊥ d ⇒ ∆ : x + 3y + m = 0 . 2 − 9 + m m = 3 −
∆ là tiếp xúc với đường tròn (C) ⇔ d(I,∆) = R ⇔ = 10 ⇔ 9 +1 m = 17
Vậy phương trình của ∆ : x + 3y − 3 = 0 hoặc x + y +17 = 0
Bài 2.11. Trong mặt phẳng với hệ toạ độ Oxy, gọi A, B là các giao điểm của đường thẳng (d):
2x – y – 5 = 0 và đường tròn (C’): 2 2
x + y − 20x + 50 = 0 . Hãy viết phương trình đường tròn (C) đi qua
ba điểm A, B, C(1; 1). HD Giải 27
Chương III. Phương pháp tọa độ trong
mặt phẳng. 0916620899-0355334679
Tài liệu học tập Toán 10 GV. Lư Sĩ Pháp
2x − y − 5 = 0 Giải hệ
. Tìm được A(3; 1), B(5; 5) 2 2
x + y − 20x + 50 = 0
Viết phương trình đường tròn (C) qua ba điểm A, B, C. Vậy (C): 2 2
x + y − 4x − 8 y +10 = 0
Bài 2.12. Trong mặt phẳng với hệ toạ độ Oxy, cho ba đường thẳng: d : 2x + y − 3 = 0 1 ,
d : 3x + 4y + 5 = 0 d : 4x + 3y + 2 = 0 d 2 , 3
. Viết phương trình đường tròn có tâm thuộc 1 và tiếp xúc với d d 2 và 3 . HD Giải
Gọi tâm đường tròn là I ( ;
t 3 − 2t)∈ d1 .
3t + 4(3− 2t) + 5
4t + 3(3− 2t)+ 2 t = 2
Khi đó: d(I ,d ) = d(I , d ) = 2 3 ⇔ 5 5 ⇔ t = 4 2 2 49 2 2 9
Vậy có 2 đường tròn thoả mãn: (x − 2) + (y +1) = (x 4) (y 5) 25 và − + + = 25.
Bài 2.13. Trong mặt phẳng với hệ toạ độ Oxy, cho hai đường thẳng ∆ : x + 3y + 8 = 0 , ∆ ' :3x − 4y +10 = 0
và điểm A(–2; 1). Viết phương trình đường tròn có tâm thuộc đường thẳng ∆ , đi qua điểm A và tiếp xúc
với đường thẳng ∆′. HD Giải
Gọi tâm đường tròn là: I (−3t − 8;t) ∈ ∆ . Ta có: d(I , ∆′) = IA 3( 3
− t − 8) − 4t +10 2 2 ⇔ = ( 3
− t − 8 + 2) + (t −1) ⇔ t = −3 ⇒ I(1;−3), R = 5 2 2 3 + 4
Vậy đường tròn cần tìm: 2 2
(x −1) + (y + 3) = 25 .
Bài 2.14. Trong mặt phẳng với hệ toạ độ Oxy, viết phương trình đường tròn đi qua A(2; 1 − ) và tiếp xúc
với các trục toạ độ. at Giải 2 2
Gọi phương trình đường tròn (C) cần tìm có dạng: ( − ) + ( − ) = 2 x a y b R
Ta có (C) tiếp xúc với Ox và Oy nên: a = b = R (x − 2 a) + (y + 2 a) = 2 a (1)
Nên phương trình đường tròn (C) có dạng:
và (C) qua A(2; 1 − ) (x − 2 a) + (y − 2 a) = 2 a (2)
Ta có: 1) a = 1; a = 5 2) ⇒ vô nghiệm.
Vậy có hai đường tròn thỏa mãn đề bài: 2 2
(x −1) + (y +1) = 1 và 2 2
(x − 5) + (y + 5) = 25.
Bài 2.15. Trong mặt phẳng với hệ tọa độ Oxy, cho đường thẳng d : 2x − y − 4 = 0 . Lập phương trình
đường tròn tiếp xúc với các trục tọa độ và có tâm ở trên đường thẳng d. HD Giải Gọi I ( ;
a 2a − 4) ∈ (d) là tâm đường tròn (C) cần tìm. Ta có đường tròn tiếp xúc với các trục tọa độ nên: 4
a = 2a − 4 ⇔ a = 4,a = 3 . 4 2 2 4 4 16 m =
x − + y + =
3 thì phương trình đường tròn (C) là: . 3 3 9
m = 4 thì phương trình đường tròn là (C): 2 2
(x − 4) + (y − 4) =16 .
Bài 2.16. Trong mặt phẳng với hệ tọa độ Oxy, cho điểm A(–1;1) và B(3;3), đường thẳng (∆):
3x –4y + 8 = 0. Lập phương trình đường tròn qua A, B và tiếp xúc với đường thẳng (∆). HD Giải
Tâm I của đường tròn nằm trên đường trung trực d của đoạn AB 28
Chương III. Phương pháp tọa độ trong
mặt phẳng. 0916620899-0355334679
Tài liệu học tập Toán 10 GV. Lư Sĩ Pháp
d qua M(1; 2) có VTPT là AB = (4;2)⇒ d: 2x + y – 4 = 0 ⇒ Tâm I ( ; a 4 – 2a) a = 3
Ta có IA = d(I,d) ⇔ a − = a2 − a + ⇔ a2 11 8 5 5 10 10 2 − 37a + 93 = 0 ⇔ 31 a = 2 2 2
Với a = 3 ⇒ I(3;–2), R = 5 ⇒ (C): ( x − 3) + (y + 2) = 25 31 31 65 2 31 2 4225 Với a = I ; 2 − 7 x − + y + 27 = 2 ⇒ 2 , R = 2 ⇒ (C): ( ) 2 4
Bài 2.17. Trong mặt phẳng với hệ toạ độ Oxy, cho đường tròn (C): 2 2
x + y − 2x − 4y − 5 = 0 và A(0; –1) ∈
(C). Tìm toạ độ các điểm B, C thuộc đường tròn (C) sao cho ∆ABC đều. HD Giải 3 7
Ta có: (C) có tâm I(1;2) và R= 10 . Gọi H là trung điểm BC. Suy ra AI = 2.IH ⇔ H ; 2 2 A
∆ BC đều ⇒ I là trọng tâm. Phương trình (BC): x + 3y −12 = 0
Vì B, C ∈ (C) nên tọa độ của B, C là các nghiệm của hệ phương trình: 2 2 2 2 x y 2x 4y 5 0 + − − − =
x + y − 2x − 4y − 5 = 0 ⇔
x + 3y −12 = 0
x = 12 − 3y 7 3 3 3 3 7 3 3 3 3 + − − +
Giải hệ PT trên ta được: B ; ;C ; hoặc 2 2 2 2 7 3 3 3 3 7 3 3 3 3 + − − + C ; ; B ; 2 2 2 2
Bài 2.18. Trong mặt phẳng tọa độ Oxy, cho đường tròn 2 2
(C) : x + y = 1, đường thẳng (d) : x + y + m = 0 .
Tìm m để (C) cắt (d) tại A và B sao cho diện tích tam giác ABO lớn nhất. HD Giải
Ta có: (C) có tâm O(0; 0) , bán kính R = 1. (d) cắt (C) tại A, B ⇔ d( ; O d) < 1 1 1 1 0 Khi đó: S = O .
A OB.sin AOB = .sin AOB ≤ . Dấu "=" xảy ra ⇔ AOB = 90 . OAB 2 2 2 1 Vậy S lón nhất ⇔ 0
AOB = 90 . Khi đó d(I; d) = ⇔ m = ±1. AOB 2
Bài 2.19. Trong mặt phẳng với hệ toạ độ Oxy, cho đường thẳng (d) : 2x + my +1− 2 = 0 và đường tròn có phương trình 2 2
(C) : x + y − 2x + 4y − 4 = 0 . Gọi I là tâm đường tròn (C) . Tìm m sao cho (d) cắt
(C) tại hai điểm phân biệt A và B. Với giá trị nào của m thì diện tích tam giác IAB lớn nhất và tính giá trị đó. HD Giải
Ta có: (C) có tâm I(1; –2) và bán kính R = 3. 2
(d) cắt (C) tại 2 điểm phân biệt A, B ⇔ d(I , d) < R ⇔
2 − 2m +1− 2 < 3 2 + m 2 2 2
⇔ 1 − 4m + 4m < 18 + 9m ⇔ m 5
+ 4m +17 > 0 ⇔ m ∈ ℝ 1 1 9 Ta có: S = I .
A IB sin AIB ≤ I . A IB = IAB 2 2 2 9 0 3 2 Vậy: S lớn nhất là
AIB = 90 ⇔ AB = R 2 = 3 2 ⇔ d(I,d) = IAB 2 khi 2 3 2 2 ⇔ 1− 2m = 2 + 2 m
⇔ 2m +16m + 32 = 0 ⇔ m = − 2 4 29
Chương III. Phương pháp tọa độ trong
mặt phẳng. 0916620899-0355334679
Tài liệu học tập Toán 10 GV. Lư Sĩ Pháp
Bài 2.20. Trong mặt phẳng với hệ trục tọa độOxy , cho đường tròn 2 2
(C) :(x + 4) + (y − 3) = 25 và đường
thẳng ∆ : 3x − 4y + 10 = 0 . Lập phương trình đường thẳng d biết d ⊥ (∆) và d cắt (C) tại A, B sao cho AB = 6. HD Giải
Ta có: (C) có tâm I(– 4; 3) và có bán kính R = 5. Gọi H là trung điểm AB, AH = 3. Do d ⊥ ∆ nên PT của
d có dạng: 4x + 3y + m = 0 . −16 + 9 + m m = 27 2 2 2 2
Ta có: d(I ,(∆ ))
AI − AH = 5 − 3 = 4 = 4⇔ 1 = IH = ⇔ 2 2 4 + 3 m = 1 − 3
Vậy d: 4x + 3y + 27 = 0 hoặc d: 4x + 3y −13 = 0 .
Bài 2.21. Trong mặt phẳng với hệ trục tọa độ Oxy, cho hai đường thẳng d1: x + y + 5 = 0, d2:
x + 2y – 7 = 0 và tam giác ABC có A(2; 3), trọng tâm là điểm G(2; 0), điểm B thuộc d1 và điểm C thuộc d2
. Viết phương trình đường tròn ngoại tiếp tam giác ABC. HD Giải
Do B ∈ d1 nên B(m; – m – 5), C ∈ d2 nên C(7 – 2n; n)
2 + m + 7 − 2n = 3.2 m = 1 −
Do G là trọng tâm ∆ABC nên 3 ⇔
⇒ B(–1; –4), C(5; 1)
− m − 5 + n = 3.0 n = 1 2 2 83 17 338
Vậy phương trình đường tròn ngoại tiếp ∆ABC: x + y − x + y − = 0 27 9 27
Bài 2.22. Trong mặt phẳng với hệ toạ độ Oxy, cho tam giác ABC có A(4;6) , phương trình các đường
thẳng chứađường cao và trung tuyến kẻ từ đỉnh C lần lượt là d x − y 1 : 2 +13 = 0 và d x − y 2 : 6
13 + 29 = 0 . Viết phương trình đường tròn ngoại tiếp tam giác ABC . HD Giải
Đường cao CH : 2x − y +13 = 0 , trung tuyến CM : 6x −13y + 29 = 0 ⇒ C( 7 − ; −1)
PT đường thẳng AB: x + 2y −16 = 0 . M = CM ∩ AB ⇒ M(6;5) ⇒ B(8; 4) . 2 2
Giả sử phương trình đường tròn (C) ngoại tiếp ∆ABC : x + y − 2ax − 2by + c = 0. 52 − a 8 −12b + c = 0 a = 4 −
Vì A, B, C ∈ (C) nên 8
0 − 16a − b
8 + c = 0 ⇔ b = 6 . 50 14a 2b c 0 + + + = c = 7 − 2 2 2
Vậy phương trình đường tròn: x + y − 4x + 6y − 72 = 0 .
Bài 2.23. Trong mặt phẳng toạ độ Oxy, cho tam giác ABC, có điểm A(2; 3), trọng tâm G(2; 0). Hai đỉnh B
và C lần lượt nằm trên hai đường thẳng d x + y 1 :
+ 5 = 0 và d x + y 2 :
2 – 7 = 0 . Viết phương trình đường
tròn có tâm C và tiếp xúc với đường thẳng BG. HD Giải Giả sử B( 5
− − b;b)∈ d ; C(7 − 2c;c)∈ d 1 2 . x + x + 2 = 6
Vì G là trọng tâm ∆ABC nên ta có hệ: B C
⇒ B(–1;–4) , C(5; 1). y + y + 3 = 0 B C 9
Phương trình BG: 4x – 3y – 8 = 0 . Bán kính R = d C ( ,BG) = 5 2 2 81
Vậy phương trình đường tròn: (x – 5) + (y –1) = 25
Bài 2.24. Trong mặt phẳng với hệ toạ độ Oxy, cho tam giác ABC có đỉnh A( 1 − ; 3
− ) , trọng tâm G(4; 2 − ) ,
trung trực của AB là d : 3x + 2y − 4 = 0 . Viết phương trình đường tròn ngoại tiếp tam giác ABC. HD Giải 3 13 3
Gọi M là trung điểm của BC ⇒ AM = AG ;− 2 ⇒ M . 2 2 30
Chương III. Phương pháp tọa độ trong
mặt phẳng. 0916620899-0355334679
Tài liệu học tập Toán 10 GV. Lư Sĩ Pháp
AB ⊥ d ⇒ AB nhận u = (2; 3 − ) : 2 − 3 − 7 = 0 d
làm VTPT ⇒ Phương trình AB x y .
Gọi N là trung điểm của AB ⇒ N = AB ∩ d ⇒ N(2; 1
− ) ⇒ B(5;1) ⇒ C(8; 4 − ). 2 2 2 2
Gọi đường tròn (C) ngoại tiếp ∆ABC có dạng: x + y + 2ax + 2by + c = 0 ( a + b − c > 0 ). 2 74
a + 6b − c = 10 a = 21 2 2 148 46 8 Khi đó ta có hệ: 1
0a + 2b + c = 2 − 6 ⇔ . Vậy: C ( ) : x + y − x + y + = 0 1 23 8 21 7 3 6a − b 8 + c = 8 − 0 b = − ;c = 7 3
Bài 2.25. Trong mặt phẳng toạ độ Oxy, cho ∆ ABC có phương trình cạnh AB: x + y –3 = 0 , phương trình 1
cạnh AC: 3x + y – 7 = 0 và trọng tâm G 2; 3. Viết phương trình đường tròn đi qua trực tâm H và hai
đỉnh B, C của tam giác ABC. HD Giải
A = AB ∩ AC ⇒ A(2;1) . Giả sử B(m;3 – m), C(n;7 – n 3 ). 1 2 + m + n = 6 m = 1 G 2; ⇔
3 là trọng tâm ∆ABC nên:
⇒ B(1; 2), C(3; –2) 1
+ 3 − m + 7 − n 3 = 1 n = 3 AH ⊥ BC
H là trực tâm ∆ABC ⇔ ⇔ H(10;5) . BH ⊥ AC 2 2 2 2
Gọi đường tròn (C) qua B, C, H có dạng: x + y + 2ax + 2by + c = 0 (a + b − c > 0)
2a + 4b + c = 5 − a = 6 − 2 2
Do B, C, H ∈ (C) ⇔ 6a − 4b + c = 1 − 3 ⇔ b = 2
− . Vậy (C): x + y –12x – 4y +15 = 0. 20a 10b c 125 + + = − c = 15
Bài 2.26. Trong mặt phẳng toạ độ Oxy, cho tam giác ABC vuông tại A. Đỉnh B(1; 1). Đường thẳng AC có
phương trình: 4x + 3y − 32 = 0 . Trên tia BC lấy điểm M sao cho BC B
. M = 75. Tìm đỉnh C biết bán kính 5 5
của đường tròn ngoại tiếp tam giác AMC bằng 2 . HD Giải
Đường thẳng (AB) qua B và vuông góc với (AC) ⇒ (AB) : 3x − 4y +1 = 0 ⇒ A(5;4) .
Gọi E là giao điểm của đường tròn ngoại tiếp của tam giác AMC với BA thì ta có: BA B . E = BM B
. C = 75 ( vì M nằm trên tia BC ) ⇒ E(13;10).
Vì ∆AEC vuông tại A nên CE là đường kính của đường tròn ngoại tiếp ∆AMC ⇒ EC = 5 5 . Do đó C là
giao của đường tròn tâm E bán kính r = 5 5 với đường thẳng AC.
4x + 3y − 32 = 0 x = 2; y = 8
Toạ độ của C thỏa mãn hệ ( ⇔ . x 2 −13) + (y 2 −10) = 125 x = 8; y = 0
Vậy: C(2;8) hoặc C(8; 0) .
Bài 2.27. Trong mặt phẳng với hệ trục tọa độ Oxy, cho đường thẳng d : x –3y – 4 = 0 và đường tròn 2 2
(C) : x + y –4y = 0 . Tìm M thuộc d và N thuộc (C) sao cho chúng đối xứng qua điểm A(3; 1). HD Giải
Ta có: M ∈ d ⇒ M (3b + 4;b). N đối xứng với M qua A nên N (2 − 3 ; b 2 − b) 2 2 6
Do N ∈ (C) nên (2 − 3b) + (2 − b) –4(2 − b) = 0 ⇔ b = 0 hoặc b = 5 38 6 8 4
Vậy M(4;0) và N(2;2) hoặc M ; , N − ; 5 5 5 5 31
Chương III. Phương pháp tọa độ trong
mặt phẳng. 0916620899-0355334679
Tài liệu học tập Toán 10 GV. Lư Sĩ Pháp
BÀI TẬP LÀM TƯƠNG TỰ
Bài 2.28. Xét xem các phương trình sau có phài là phương trình đường tròn không ? Nếu có hãy tìm tâm và bán kính của nó. a) 2 2
(x − 2) + ( y − 3) = 6 b) 2 2
(x + 4) + ( y + 5) = 36 c) 2 2
x + y − 6x − 4 y − 36 = 0 d) 2 2
x + y − 2x + 4 y − 4 = 0 e) 2 2
x + y + 4x − 2 y + 4 = 0 f) 2 2 x + y = 16
Bài 2.29. Lập phương trình đường tròn (C) trong các trường hợp sau: a) ( C ) có tâm I ( 2
− ;3)và đi qua M (2; 3 − ). b) ( C ) có tâm I ( 1
− ;2)và tiếp xúc đường thẳng: x − 2y + 7 = 0
c) ( C ) có đường kính là AB với A (2;− ) 1 và B(−4;5) .
d) ( C ) có tâm I (2;−3)và tiếp xúc với trục Ox . e) ( C ) có tâm I ( 1
− ;4)và tiếp xúc với trục Oy
f) ( C ) đi qua hai điểm A (1;2),B( 2
− ;4) và đi qua gốc toạ độ O.
Bài 2.30. Viết phương trình đường tròn ( C ):
a) đi qua A (2;3),B (−2; )
1 và có tâm nằm trên trục Ox . b) đi qua C (3; )
1 ,D (5;5)và có tâm nằm trên trục Oy .
c) qua điểm E (10;10) và tiếp xúc với trục Oy tại M (0;7) .
d) qua điểm F (9;9) và tiếp xúc với trục Ox tại N (6;0).
e) qua điểm P (−1;0),Q(1;2) và tiếp xúc với đường thẳng: x – y –1 = 0 .
f) qua điểm K (−2; )
1 và tiếp xúc với (d):3x –2y –6 = 0 tại S(0;−3) .
g) qua điểm G (1;3),L (0;− )
1 và có tâm nằm trên đường thẳng (d): x + 2y –10 = 0 .
Bài 2.31. Viết phương trình đường tròn đường kính AB trong các trường hợp sau:
a) A (9;−5) và B(0;5) b) A ( 2 − ;3) và B(8; 7 − )
c) A (7;−3) và B(1;7) d) A ( 3 − ;2) và B(7;−4)
e) A (2m +1;m) và B(2;3m)
Bài 2.32. Viết phương trình đường tròn ngoại tiếp tam giác ABC trong các trường hợp sau:
a) A (5;3),B(6;2) vàC (3;− ) 1
b) A (1;3),B(5;6) và C (7;0)
Bài 2.33. Viết phương trình đường tròn ( C ) tiếp xúc các trục toạ độ và qua điểm M (4;2).
Bài 2.34. Viết phương trình đường tròn ( C ) tiếp xúc các trục toạ độ và có tâm thuộc
đường thẳng : 4x –2y –8 = 0
Bài 2.35. Viết phương trình đường thẳng (∆) tiếp xúc với đường tròn ( C ) tại A∈(C) trong mỗi trường
hợp sau, rồi sau đó vẽ (∆) và ( C ) trên cùng hệ trục toạ độ a) (C): 2 2
x + y = 25 , A (3;4) . b) ( C ): 2 2
x + y = 80 , B ( 4 − ; 8 − ). c) ( C ): 2 2
x + y = 100 , C ( 8 − ;6). d) ( C ): 2 2
(x − 3) + ( y + 4) = 169 , D (8; 1 − 6).
Bài 2.36. Cho đường tròn ( C ): 2 2
x + y − 6x + 2 y + 6 = 0 và điểm A (1;3).
a) Chứng minh rằng điểm A nằm ngoài đường tròn
b) Viết phương trình tiếp tuyến của ( C ) kẻ từ A
Bài 2.37. Cho đường tròn ( C ): 2 2
x + y + 4x + 4 y −17 = 0 . Viết phương trình tiếp tuyến (∆) trong mỗi trường hợp sau:
a) (∆) tiếp xúc với ( C ) tại M (2; ) 1
b) (∆) vuông góc với đường thẳng (d): 3x – 4y +1 = 0 c) (∆) qua A (2;6) .
d) (∆) có hệ số góc bằng 1 32
Chương III. Phương pháp tọa độ trong
mặt phẳng. 0916620899-0355334679
Tài liệu học tập Toán 10 GV. Lư Sĩ Pháp
e) (∆) song song với đường phân giác thứ II của các góc toạ độ
Bài 2.38. Cho hai đường tròn: 2 2 2 2
(C ) : x + y − 6x + 5 = 0;(C ) : x + y −12x − 6 y + 44 = 0 . 1 2
a) Tìm tâm và bán kính của (C ) và (C ) 1 2
b) Viết phương trình tiếp tuyến chung của (C ) và (C ) 1 2
Bài 2.39. Cho hai đường tròn: 2 2 2 2
(C ) : x + y − 4x − 8y +11 = 0;(C ) : x + y − 2x − 2 y − 2 = 0 . 1 2
a) Xét vị trí tương đối của (C ) và (C ) 1 2
b) Viết phương trình tiếp tuyến chung của (C ) và (C ) 1 2
Bài 2.40. Viết phương trình đường tròn ( C ):
a) Có tâm nằm trên (d ) : 4x + 3y –2 = 0 và tiếp xúc với hai đường thẳng (d ) : x + y + 4 = 0 và 1
(d ) : 4x + 3y − 7 = 0 2
b) Qua M (2;3)và tiếp xúc với hai đường thẳng: (d ) : 3x − 4y +1 = 0 và (d ) : 7x − y + 4 = 0 1 2
Bài 2.41. Cho đường tròn x2 + y2 − 4x + 8y − 5 = 0 .
a) Tìm tọa độ tâm và bán kính của (C)
b) Viết phương trình tiếp tuyến với (C) đi qua điểm A (−1;0)
c) Viết phương trình tiếp tuyến với (C) vuông góc với đường thẳng 3x − 4y + 5 = 0 .
Bài 2.42. Viết phương trình đường tròn đi qua hai điểm A(−1;0),B(1;2) và tiếp xúc với đường thằng
x − y − 1 = 0 .
Bài 2.43. Cho đường tròn x2 + y2 − 2x + 6y + 5 = 0 và đường thẳng d : 2x + y −1 = 0. Viết phương trình
tiếp tuyến ∆ của (C), biết ∆ song song với d. Tìm tọa độ tiếp điểm.
BÀI TẬP TRẮC NGHIỆM
Câu 1. Cho tam giác ABC có A( 2
− ;4), B(5;5), C (6; 2
− ) . Đường tròn ngoại tiếp tam giác ABC có phương trình là:
A. (x − )2 + ( y − )2 2 1 = 20. B. 2 2
x + y − 4x − 2 y + 20 = 0. C. 2 2
x + y − 4x − 2 y − 20 = 0. D. 2 2
x + y − 2x − y + 20 = 0.
Câu 2. Tìm tọa độ tâm I của đường tròn đi qua ba điểm A(0;4) , B(2;4) , C (4;0) .
A. I (0;0) .
B. I (1;0) .
C. I (3;2) . D. I (1; ) 1 .
Câu 3. Đường tròn (C) 2 2
: x + y − 4x + 6 y −12 = 0 có tâm I và bán kính R lần lượt là: A. I ( 2 − ;3), R = 5. B. I (2; 3 − ), R = 5. C. I ( 2
− ;3), R = 25. D. I (2; 3 − ), R = 25.
Câu 4. Cho phương trình 2 2
x + y − 2mx − 4(m − 2) y + 6 − m = 0 ( )
1 . Tìm điều kiện của m để ( ) 1 là
phương trình đường tròn. A. 1 m ∈ − ; ∞ ∪(2;+∞).
B. m ∈ R. 3 C. m ∈(− ; ∞ ) 1 ∪ (2;+∞). D. m∈(− ; ∞ ] 1 ∪[2;+∞).
Câu 5. Đường tròn (C) có tâm I ( 2
− ;3) và đi qua M (2; 3
− ) có phương trình là: A. 2 2
x + y + 4x − 6 y − 57 = 0. B. 2 2
x + y + 4x − 6 y − 39 = 0. C. ( 2 2
x + )2 + ( y − )2 2 3 = 52.
D. (x − 2) + ( y + 3) = 52.
Câu 6. Đường tròn (C) có tâm I (2; 3
− ) và tiếp xúc với trục Oy có phương trình là: 33
Chương III. Phương pháp tọa độ trong
mặt phẳng. 0916620899-0355334679
Tài liệu học tập Toán 10 GV. Lư Sĩ Pháp A. ( 2 2
x − )2 + ( y + )2 2 3 = 9.
B. ( x + 2) + ( y – 3) = 4. C. ( 2 2 x + )2 + ( y )2 2 – 3 = 9.
D. (x − 2) + ( y + 3) = 4.
Câu 7. Đường tròn (C) đi qua điểm M (2; )
1 và tiếp xúc với hai trục tọa độ O ,
x Oy có phương trình là: A. ( 2 2
x + )2 + ( y − )2 1 1 = 1 hoặc (x + ) 5 +( y − ) 5 = 5. B. ( 2 2
x + )2 + ( y + )2 1 1
= 1 hoặc (x + 5) + ( y + 5) = 25. C. ( 2 2
x − 5)2 + ( y + 5)2 = 25 hoặc (x − 2) +( y − ) 1 = 25 D. ( 2 2
x − )2 + ( y − )2 1 1 = 1 hoặc (x− ) 5 +( y − ) 5 = 25.
Câu 8. Đường tròn (C) có tâm ( )
1 thuộc đường thẳng ∆ : x = 5 và tiếp xúc với hai đường thẳng
d : 3x – y + 3 = 0, d
: x – 3 y + 9 = 0 có phương trình là: 1 2 A. ( 2 2
x − )2 + ( y + )2 5 2
= 40 hoặc (x −5) + ( y + 8) =10.
B. (x − )2 + ( y + )2 5 2 = 40.
C. ( x − )2 + ( y − )2 5 8 =10. D. ( 2 2
x − )2 + ( y + )2 5 2
= 40 hoặc (x − 5) + ( y −8) =10.
Câu 9. Đường tròn đường kính AB với A(1; )
1 , B (7;5) có phương trình là: A. 2 2
x + y – 8x – 6 y – 12 = 0 . B. 2 2
x + y + 8x – 6 y – 12 = 0 . C. 2 2
x + y + 8x + 6 y +12 = 0 . D. 2 2
x + y – 8x – 6 y +12 = 0 .
Câu 10. Có bao nhiêu đường thẳng đi qua điểm N ( 2
− ;0) tiếp xúc với đường tròn
(C) (x − )2 + ( y + )2 : 2 3 = 4 ? A. Vô số. B. 0. C. 1. D. 2.
Câu 11. Trong các phương trình sau, phương trình nào không phải là phương trình của đường tròn? A. 2 2
x + y – 2 = 0. B. 2 2
x + y − y = 0. C. 2 2
x + y − x + y + 4 = 0. D. 2 2
x + y – 100 y +1 = 0.
Câu 12. Tìm bán kính R của đường tròn đi qua ba điểm A(0;4) , B (3;4) , C (3;0) .
A. R = 10 . B. 5 R = .
C. R = 5 .
D. R = 3 . 2
Câu 13. Viết phương trình tiếp tuyến ∆ của đường tròn (C) 2 2
: x + y − 4x − 4y + 4 = 0 , biết tiếp tuyến đi
qua điểm B (4;6) .
A. ∆ : x − 4 = 0 hoặc ∆ : y − 6 = 0.
B. ∆ : y − 6 = 0 hoặc ∆ :3x + 4y − 36 = 0 .
C. ∆ : x − 4 = 0 hoặc ∆ :3x − 4y +12 = 0 .
D. ∆ : x − 4 = 0 hoặc ∆ :3x + 4y −36 = 0 .
Câu 14. Viết phương trình tiếp tuyến của đường tròn (C) 2 2
: x + y + 4x + 4 y −17 = 0 , biết tiếp tuyến song
song với đường thẳng d : 3x − 4y − 2019 = 0 .
A. 3x – 4y + 23 = 0 hoặc 3x – 4y – 27 = 0.
B. 3x – 4y + 23 = 0 hoặc 3x – 4y + 27 = 0.
C. 3x – 4y − 23 = 0 hoặc 3x – 4y + 27 = 0.
D. 3x – 4y − 23 = 0 hoặc 3x – 4y – 27 = 0.
Câu 15. Đường tròn (C) có tâm I (2;3) và tiếp xúc với trục Ox có phương trình là: A. ( 2 2
x + )2 + ( y + )2 2 3 = 9.
B. ( x − 2) + ( y – 3) = 9. C. ( 2 2 x − )2 + ( y )2 2 – 3 = 4.
D. (x − 2) + ( y – 3) = 3.
Câu 16. Có bao nhiêu đường thẳng đi qua gốc tọa độ O và tiếp xúc với đường tròn (C) 2 2
: x + y − 2x + 4y −11 = 0 ? A. 0. B. 2. C. 1. D. 3.
Câu 17. Phương trình tiếp tuyến d của đường tròn (C) 2 2
: x + y − 3x − y = 0 tại điểm N (1; ) 1 − là: 34
Chương III. Phương pháp tọa độ trong
mặt phẳng. 0916620899-0355334679
Tài liệu học tập Toán 10 GV. Lư Sĩ Pháp
A. d : x − 3y − 4 = 0.
B. d : x + 3y + 2 = 0.
C. d : x + 3y − 2 = 0.
D. d : x − 3y + 4 = 0.
Câu 18. Cho phương trình 2 2
x + y − 2ax − 2by + c = 0 ( ) 1 . Điều kiện để ( )
1 là phương trình đường tròn là: A. 2 2
a + b > c . B. 2 2
a + b < c . C. 2 2
a − b < c . D. 2 2
a − b > c .
Câu 19. Trong các phương trình sau, phương trình nào là phương trình của một đường tròn? A. 2 2
x + y − 2x − 8y + 20 = 0. B. 2 2
x + 2 y − 4x − 8y +1 = 0. C. 2 2
x + y − 4x + 6 y −12 = 0. D. 2 2
4x + y −10x − 6 y − 2 = 0. Câu 20. Đườ 2 2
ng tròn (C ) : ( x − )
1 + ( y + 2) = 25 có dạng khai triển là: A. (C) 2 2
: x + y + 2x − 4 y + 30 = 0. B. (C) 2 2
: x + y − 2x + 4 y + 30 = 0. C. (C) 2 2
: x + y + 2x − 4 y − 20 = 0. D. (C) 2 2
: x + y − 2x + 4y − 20 = 0.
Câu 21. Tọa độ tâm I và bán kính R của đường tròn (C) 2 2
: x + y = 9 là:
A. I (0;0), R = 3. B. I (1; ) 1 , R = 3.
C. I (0;0), R = 9. D. I (1; ) 1 , R = 9.
Câu 22. Tâm của đường tròn (C) 2 2
: x + y −10x +1 = 0 cách trục Oy một khoảng bằng: A. 10. B. 5 . C. −5 . D. 0 . Câu 23. 2 2
Có bao nhiêu phương trình tiếp tuyến của đường tròn (C ) : ( x − 2) + ( y − ) 1 = 25, biết tiếp
tuyến song song với đường thẳng d : 4x + 3y + 2020 = 0? A. 1. B. 2. C. 3. D. 0.
Câu 24. Đường tròn (C) đi qua ba điểm A( 3 − ;− ) 1 , B ( 1 − ;3) và C ( 2
− ;2) có phương trình là:
A. (x − )2 + ( y + )2 2 1 = 20. B. 2 2
x + y + 2x − y − 20 = 0.
C. (x + )2 + ( y − )2 2 1 = 25. D. 2 2
x + y − 4x + 2 y − 20 = 0. Câu 25. 2 2
Viết phương trình tiếp tuyến của đường tròn (C ) : ( x − 2) + ( y + 4) = 25 , biết tiếp tuyến vuông
góc với đường thẳng d : 3x − 4 y + 5 = 0 .
A. 4x + 3y + 29 = 0.
B. 4x + 3y + 29 = 0 hoặc 4x + 3y – 21= 0.
C. 4x – 3y + 5 = 0 hoặc 4x – 3y – 45 = 0.
D. 4x + 3y + 5 = 0 hoặc 4x + 3y + 3 = 0.
Câu 26. Đường tròn đường kính AB với A(3;− ) 1 , B (1; 5
− ) có phương trình là: A. ( 2 2
x − )2 + ( y + )2 2 3 = 5.
B. ( x − 2) + ( y + 3) = 5. C. ( 2 2
x + )2 + ( y − )2 2 3 = 5. D. (x + )
1 + ( y + 2) = 17.
Câu 27. Đường tròn (C) 2 2
: x + y +12x −14y + 4 = 0 có dạng tổng quát là: A. ( 2 2
C ) ( x + )2 + ( y − )2 : 6 7 = 89.
B. (C) :( x + 6) + ( y − 7) = 89. C. ( 2 2
C ) ( x + )2 + ( y − )2 : 6 7 = 9.
D. (C) :(x + 6) + ( y − 7) = 81.
Câu 28. Tọa độ tâm I và bán kính R của đường tròn (C) x + ( y + )2 2 : 4 = 5 là:
A. I (0;−4), R = 5. B. I (0; 4 − ), R = 5.
C. I (0;4), R = 5.
D. I (0;4), R = 5.
Câu 29. Đường tròn (C) đi qua ba điểm O(0;0), A( ;
a 0), B(0;b) có phương trình là: A. 2 2
x + y − ax − by = 0. B. 2 2
x − y − ay + by = 0 . C. 2 2
x + y − 2ax − by = 0 . D. 2 2
x + y − ax − by + xy = 0 .
Câu 30. Đường tròn (C) có tâm I thuộc đường thẳng d : x +3y +8 = 0, đi qua điểm A(−2; ) 1 và tiếp
xúc với đường thẳng ∆ :3x − 4 y +10 = 0 . Phương trình của đường tròn (C) là: A. ( 2 2
x − )2 + ( y + )2 2 2 = 25 .
B. ( x + 5) + ( y + ) 1 = 16. C. ( 2 2
x + )2 + ( y + )2 2 2 = 9 . D. ( x − )
1 + ( y + 3) = 25 . 35
Chương III. Phương pháp tọa độ trong
mặt phẳng. 0916620899-0355334679
Tài liệu học tập Toán 10 GV. Lư Sĩ Pháp
Câu 31. Cho phương trình 2 2
x + y + mx + (m ) 2 2 2
–1 y + 2m = 0 ( )
1 . Tìm điều kiện của m để ( ) 1 là
phương trình đường tròn.
A. m > 1.
B. m = 1. C. 1 m < . D. 1 m ≤ . 2 2
Câu 32. Đường tròn (C) có tâm I thuộc đường thẳng d : x +3y −5 = 0, bán kính R = 2 2 và tiếp xúc
với đường thẳng ∆ : x − y −1 = 0 . Phương trình của đường tròn (C ) là: A. ( 2 2
x − )2 + ( y + )2 1 2 = 8 hoặc (x + )2 2 5 + y = 8. B. ( x + )
1 + ( y − 2) = 8 hoặc ( x − )2 2 5 + y = 8 . C. ( 2 2
x + )2 + ( y − )2 1 2 = 8 hoặc (x + )2 2 5 + y = 8. D. ( x − )
1 + ( y + 2) = 8 hoặc ( x − )2 2 5 + y = 8 . Câu 33. 2 2
Viết phương trình tiếp tuyến ∆ của đường tròn (C ) : ( x − )
1 + ( y + 2) = 8 , biết tiếp tuyến đi qua điểm A(5; 2 − ) .
A. ∆ : x − 5 = 0 .
B. ∆ : x + y −3 = 0 hoặc ∆ : x − y − 7 = 0.
C. ∆ : x − 5 = 0 hoặc ∆ : x + y −3 = 0 .
D. ∆ : y + 2 = 0 hoặc ∆ : x − y − 7 = 0.
Câu 34. Tọa độ tâm I và bán kính R của đường tròn (C) 2 2
: 2x + 2 y − 8x + 4 y −1 = 0 là: A. I ( ) 11 2;1 , R = . B. I ( 2 − ; ) 1 , R = 22. 2 C. I ( − ) 2 2; 1 , R = . D. I ( − ) 22 2; 1 , R = . 2 2
Câu 35. Đường tròn (C) có tâm I thuộc đường thẳng 2 2
x + y − 2ax − 2by + c = 0 ( ) 1 và tiếp xúc với
hai trục tọa độ có phương trình là: A. ( 2 2 2 2
x − )2 + ( y − )2 2 2
= 4 hoặc (x + 3) + ( y − 3) = 9. B. (x − 3) + ( y + 3) = 9. C. ( 2 2 2 2
x − )2 + ( y − )2 2 2
= 4 hoặc (x − 3) + ( y + 3) = 9. D. (x − 2) + ( y − 2) = 4 .
Câu 36. Đường tròn (C) đi qua hai điểm (
A 1; 2), B(3; 4) và tiếp xúc với đường thẳng ∆ : 3x + y − 3 = 0 .
Viết phương trình đường tròn (C) , biết tâm của (C ) có tọa độ là những số nguyên. A. 2 2
x + y − 6x – 4 y + 5 = 0. B. 2 2
x + y − 8x – 2 y −10 = 0. C. 2 2
x + y − 2x − 8y + 7 = 0. D. 2 2
x + y − 3x – 7 y +12 = 0.
Câu 37. Tọa độ tâm I và bán kính R của đường tròn (C) 2 2
: x + y − 4x + 2 y − 3 = 0 là: A. I ( 4
− ;2), R = 8. (C) B. I ( 2 − ; ) 1 , R = 8. C. I (2;− ) 1 , R = 2 2. D. I ( 2 − ; ) 1 , R = 2 2. Câu 38. 2 2
Phương trình tiếp tuyến d của đường tròn (C ) : ( x + 2) + ( y + 2) = 25 tại điểm M (2; ) 1 là:
A. d : 3x − 4y − 2 = 0.
B. d : 4x + 3y −11= 0.
C. d : −y +1 = 0.
D. d : 4x + 3y +14 = 0.
Câu 39. Đường tròn (C) đi qua ba điểm O(0;0) , A(8;0) và B(0;6) có phương trình là: A. ( 2 2
x + )2 + ( y + )2 4 3 = 5.
B. (x + 4) + ( y + 3) = 25. C. ( 2 2
x − )2 + ( y − )2 4 3 = 5.
D. (x − 4) + ( y − 3) = 25.
Câu 40. Đường tròn (C) đi qua hai điểm A(1; )
1 , B (5;3) và có tâm I thuộc trục hoành có phương trình là: A. (x − )2 2 4 + y = 10. B. (x − )2 2 4 + y = 10. C. (x + )2 2 4 + y = 10. D. (x + )2 2 4 + y = 10.
Câu 41. Cho phương trình 2 2
x + y − 2x + 2my + 10 = 0 ( )
1 . Có bao nhiêu giá trị m nguyên dương không vượt quá 10 để ( )
1 là phương trình của đường tròn? 36
Chương III. Phương pháp tọa độ trong
mặt phẳng. 0916620899-0355334679
Tài liệu học tập Toán 10 GV. Lư Sĩ Pháp A. Không có. B. 6 . C. 7 . D. 8 . Câu 42. 2 2
Tọa độ tâm I và bán kính R của đường tròn (C ) : ( x − )
1 + ( y + 3) = 16 là: A. I (1; 3 − ), R =16. B. I ( 1 − ;3), R =16. C. I ( 1 − ;3), R = 4. D. I (1; 3 − ), R = 4.
Câu 43. Cho tam giác ABC có A(1; 2 − ), B( 3 − ;0), C (2; 2
− ) . Tam giác ABC nội tiếp đường tròn có phương trình là: A. 2 2
x + y + 3x + 8 y +18 = 0. B. 2 2
x + y − 3x − 8 y −18 = 0. C. 2 2
x + y − 3x − 8 y +18 = 0. D. 2 2
x + y + 3x + 8 y −18 = 0.
Câu 44. Đường tròn (C) đi qua hai điểm A( 1 − ;2), B( 2
− ;3) và có tâm I thuộc đường thẳng
∆ :3x − y +10 = 0. Phương trình của đường tròn (C) là: A. ( 2 2
x − )2 + ( y + )2 3 1 = 5.
B. (x −3) + ( y + ) 1 = 5. C. ( 2 2
x + )2 + ( y − )2 3 1 = 5.
D. (x + 3) + ( y − ) 1 = 5. Câu 45. 2 2
Cho đường tròn (C ) : ( x − )
1 + ( y + 2) = 8 . Viết phương trình tiếp tuyến d của (C) tại điểm A(3; 4 − ) .
A. d : x − y − 7 = 0.
B. d : x − y + 7 = 0.
C. d : x + y +1= 0.
D. d : x − 2y −11= 0.
Câu 46. Cho đường tròn (C) 2 2
: x + y + 5x + 7 y − 3 = 0 . Tính khoảng cách từ tâm của (C ) đến trục Ox . A. 3,5 . B. 2,5. C. 5 . D. 7 .
Câu 47. Có bao nhiêu đường tròn (C) đi qua điểm M (2; ) 1
− và tiếp xúc với hai trục tọa độ O , x Oy ? A. 0. B. 1. C. 2. D. 3.
Câu 48. Có bao nhiêu phương trình tiếp tuyến của đường tròn (C) 2 2
: x + y + 4x − 2 y − 8 = 0 , biết tiếp
tuyến vuông góc với đường thẳng d : 2x − 3y + 2018 = 0 ? A. 2. B. 0. C. 1. D. 3.
Câu 49. Đường tròn (C) đi qua điểm A(1; 2
− ) và tiếp xúc với đường thẳng ∆ : x − y +1= 0 tại M (1;2) .
Phương trình của đường tròn (C ) là: A. (x − )2 2 3 + y = 8. B. 2 2
x + ( y − 3) = 8. C. ( x − )2 2 4 + y = 13. D. ( x − )2 2 6 + y = 29.
Câu 50. Tọa độ tâm I và bán kính R của đường tròn (C) (x + )2 2 : 1 + y = 8 là:
A. I (1;0), R = 2 2. B. I ( 1 − ;0), R = 8. C. I ( 1
− ;0), R = 64. D. I ( 1
− ;0), R = 2 2. Câu 51. 2 2
Cho đường tròn (C ) :( x − 3) + ( y + 3) = 1. Qua điểm M (4;− 3) có thể kẻ được bao nhiêu
đường thẳng tiếp xúc với đường tròn (C)? A. Vô số. B. 0. C. 1. D. 2. Câu 52. 2 2
Cho đường tròn (C ) : ( x + ) 1 + ( y − ) 1
= 25 và điểm M (9; 4
− ). Gọi ∆ là tiếp tuyến của (C),
biết ∆ đi qua M và không song song với các trục tọa độ. Khi đó khoảng cách từ điểm P (6;5) đến ∆ bằng: A. 3 . B. 3 . C. 4 . D. 5 . Câu 53. 2 2
Viết phương trình tiếp tuyến của đường tròn (C ) : ( x − 3) + ( y + ) 1
= 5, biết tiếp tuyến song
song với đường thẳng d : 2x + y + 7 = 0 .
A. 2x + y +1= 0 hoặc 2x + y −1= 0.
B. 2x + y = 0 hoặc 2x + y −10 = 0.
C. 2x + y +10 = 0 hoặc 2x + y −10 = 0.
D. 2x + y = 0 hoặc 2x + y +10 = 0.
Câu 54. Trong các phương trình sau, phương trình nào là phương trình của một đường tròn? 37
Chương III. Phương pháp tọa độ trong
mặt phẳng. 0916620899-0355334679
Tài liệu học tập Toán 10 GV. Lư Sĩ Pháp A. 2 2
x + y − x − y + 9 = 0 . B. 2 2
x + y − x = 0 . C. 2 2
x + y − 2xy −1 = 0. D. 2 2
x − y − 2x + 3y −1 = 0.
Câu 55. Cho phương trình 2 2
x + y − 2(m + )
1 x + 4 y −1 = 0 ( )
1 . Với giá trị nào của m để ( ) 1 là phương
trình đường tròn có bán kính nhỏ nhất? A. m = 1.
B. m = −2. C. m =2.
D. m = −1.
Câu 56. Tọa độ tâm I và bán kính R của đường tròn (C) 2 2
: x + y –10x −11 = 0 là: A. I ( 5 − ;0), R = 5. B. I (0; 5 − ), R = 6.
C. I (5;0), R = 36.
D. I (5;0), R = 6.
Câu 57. Trong các phương trình sau, phương trình nào là phương trình của một đường tròn? A. 2 2
x + y − 6x + 4 y +13 = 0. B. 2 2
2x + 2 y − 8x − 4 y − 6 = 0. C. 2 2
5x + 4 y + x − 4 y +1 = 0. D. 2 2
x + y + 2x − 4 y + 9 = 0.
Câu 58. Đường tròn (C) 2 2
: x + y − 6x + 2 y + 6 = 0 có tâm I và bán kính R lần lượt là:
A. I (0;0), R = 9.
B. I (0;0), R = 9. C. I (3;− ) 1 , R = 2.
D. I (0;0), R = 9.
Câu 59. Tọa độ tâm I và bán kính R của đường tròn (C) 2 2
: x + y – 5y = 0 là: A. 5 5
I 0; , R = . B. 5 5
I 0; − , R = . C. 5 5
I 0; − , R = . D. 5 5
I ;0, R = . 2 2 2 2 2 2 2 2
Câu 60. Đường tròn (C) đi qua hai điểm A(1; )
1 , B (3;5) và có tâm I thuộc trục tung có phương trình là:
A. x + ( y − )2 2 4 = 6.
B. x + ( y + )2 2 4 = 6. C. 2 2
x + y + 4 y + 6 = 0. D. 2 2
x + y − 8 y + 6 = 0.
Câu 61. Tọa độ tâm I và bán kính R của đường tròn (C) 2 2
:16x +16 y +16x − 8y −11 = 0 là: A. 1 1
I − ; , R = 1. B. I ( 2 − ;4), R =1. C. 1 1
I ; − , R = 1. D. I (2; ) 1 , R = 1. 2 4 2 4
Câu 62. Đường tròn có tâm I (1;2), bán kính R = 3 có phương trình là: A. 2 2
x + y − 2x + 4 y − 4 = 0. B. 2 2
x + y − 2x − 4 y − 4 = 0. C. 2 2
x + y + 2x + 4 y − 4 = 0. D. 2 2
x + y + 2x − 4 y − 4 = 0.
Câu 63. Đường tròn có tâm trùng với gốc tọa độ, bán kính R =1 có phương trình là:
A. ( x + )2 + ( y + )2 1 1 = 1.
B. x + ( y + )2 2 1 = 1. C. 2 2 2 2
x + y = 1. D. ( x − ) 1 + ( y − ) 1 = 1.
Câu 64. Đường tròn (C) có tâm I (−1;2) và tiếp xúc với đường thẳng ∆ : x – 2y + 7 = 0 có phương trình là: A. ( 2 2 4 x + )2 + ( y )2 4 1 – 2 = . B. ( x + )
1 + ( y – 2) = . 25 5 C. ( 2 2 x + )2 + ( y )2 2 1 – 2 = . D. (x + ) 1
+ ( y – 2) = 5. 5
Câu 65. Cho phương trình 2 2
x + y – 8x +10 y + m = 0 ( )
1 . Tìm điều kiện của m để ( ) 1 là phương trình
đường tròn có bán kính bằng 7 .
A. m = –8 .
B. m = – 4 .
C. m = 4 .
D. m = 8 .
Câu 66. Đường tròn (C) đi qua hai điểm A(–1; )
1 , B (3;3) và tiếp xúc với đường thẳng
d : 3x – 4y + 8 = 0 . Viết phương trình đường tròn (C ) , biết tâm của (C) có hoành độ nhỏ hơn 5. A. ( 2 2
x + )2 + ( y + )2 5 2 = 5.
B. (x − 5) + ( y − 2) = 25. C. ( 2 2
x − )2 + ( y + )2 3 2 = 25.
D. (x + 3) + ( y − 2) = 5.
Câu 67. Đường tròn (C) có tâm I (1; 5
− ) và đi qua O(0;0) có phương trình là: 38
Chương III. Phương pháp tọa độ trong
mặt phẳng. 0916620899-0355334679
Tài liệu học tập Toán 10 GV. Lư Sĩ Pháp A. ( 2 2
x + )2 + ( y − )2 1 5 = 26. B. (x − )
1 + ( y + 5) = 26. C. ( 2 2
x − )2 + ( y + )2 1 5 = 26. D. (x + )
1 + ( y − 5) = 26.
Câu 68. Đường tròn (C) có tâm I ( 2 − ; )
1 và tiếp xúc với đường thẳng ∆ : 3x – 4y + 5 = 0 có phương trình là: A. ( 2 2 x + )2 + ( y )2 2 – 1 = 4.
B. (x + 2) + ( y – ) 1 = 1. C. ( 2 2 x + )2 + ( y )2 1 2 –1 = .
D. (x − 2) + ( y + ) 1 = 1. 25
Câu 69. Đường tròn (C) có tâm I thuộc đường thẳng d : x + 2y − 2 = 0, bán kính R = 5 và tiếp xúc với
đường thẳng ∆ :3x − 4y −11 = 0 . Biết tâm I có hoành độ dương. Phương trình của đường tròn (C) là: A. ( 2 2
x − )2 + ( y + )2 2 2
= 25 hoặc (x + 8) + ( y −3) = 25 . B. ( 2 2
x + )2 + ( y − )2 2 2
= 25 hoặc (x −8) + ( y + 3) = 25 .
C. ( x − )2 + ( y + )2 8 3 = 25 .
D. ( x + )2 + ( y − )2 8 3 = 25 .
Câu 70. Viết phương trình tiếp tuyến của đường tròn (C) 2 2
: x + y − 4x − 4y + 4 = 0 , biết tiếp tuyến vuông góc với trục hoành.
A. x = 0 hoặc x − 4 = 0
B. y = 0.
C. x = 0 .
D. y = 0 hoặc y − 4 = 0 . ĐÁP ÁN
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25
C D B C B D D D D D C B C A B A B A C D A B A D B
26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50
B D A A D C B B D A C C B D A C D B C A A C A A D
51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75
D B B B D D C C A A A C C B A C B B C A 39
Chương III. Phương pháp tọa độ trong
mặt phẳng. 0916620899-0355334679
Tài liệu học tập Toán 10 GV. Lư Sĩ Pháp §3 ELÍP
A. KIẾN THỨC CẦN NẮM 1. Định nghĩa :
Cho hai điểm cố định F , F và một độ dài không đổi 2a lớn hơn F F . Elip là tập hợp các điểm M trong 1 2 1 2
mặt phẳng sao cho MF + MF = 2a . 1 2
Các điểm F , F gọi là các tiêu điểm của elip. Độ dài F F = 2c gọi là tiêu cự của elip. 1 2 1 2
2. Phương trình chính tắc của elip
Cho elip (E) có hai tiêu điểm F (−c;0), F ( ; c 0) . 1 2 y B 2 2 1 y M(x;y)
Ta có : M ∈ (E) ⇔ MF + MF = 2a ⇔ x + =1 (1) trong đó 1 2 2 2 a b -c 2 2 2 c
b = a − c , (a > b > 0). A1 O A2 F x 1 F2
Phương trình (1) được gọi là phương trình chính tắc của elip. B2
3. Hình dạng của elip 2 2 x y (E) : +
=1, a > b > 0 y 2 2 a b B1
Trục đối xứng O .
x Oy và có tâm đối xứng là gốc O. M1 M
Tiêu cự: F F = 2c 1 2
Độ dài trục lớn A A = 2a Độ dài trục nhỏ B B = 2b A1 O A2 F F x 1 2 1 2 1 2
Bốn đỉnh: đỉnh trên trục lớn A − ; a 0 , A ; a 0 M 1 (
) 2 ( ), đỉnh trên trục bé 3 M2
B 0; −b , B 0; b B 1 ( ) 2 ( ). 2 c
Bán kính qua tiêu điểm: MF = a + ex = a + x ; c 1 M M e = < a Tâm sai: 1; a c
MF = a − ex = a − x a 2 M M x = ± a Đường chuẩn: e
Khoảng cách giữa hai đường chuẩn: = 2 a d e
4. Điều kiện tiếp xúc 2 2 x y
Cho đường thẳng ∆ : Ax + By + C = 0 và elip (E) : + = 1. ∆ tiếp xúc với 2 2 2 2 2
(E) ⇔ A a + B b = C 2 2 a b B. BÀI TẬP
ấn đề 1. Xác định các thành phần của một elip khi biết phương trình chình tắc V của elip đó 2 2 Phương pháp: x y y Cho elip (E) : +
=1, a > b > 0 B1 b 2 2 a b
- Trục lớn của (E) nằm trên Ox , A A = 2a 1 2 -a -c c a
- Trục lớn của (E) nằm trên Oy , B B = 2b A1 O A F F 2 x 1 2 1 2
- Hai tiêu điểm F (− ; c 0), F ( ; c 0), với 2 2
c = a − b . Tiêu cự: F F = 2c 1 2 1 2 -b B2
- Bốn đỉnh A (−a;0), A (a : 0), B (0; −b), B (0;b) 1 2 1 2 c - Tâm sai e = < 1 a
- Phương trình các đường thẳng chứa các cạnh của hình chữ nhật cơ sở là x = ± ; a y = ±b 40
Chương III. Phương pháp tọa độ trong
mặt phẳng. 0916620899-0355334679
Tài liệu học tập Toán 10 GV. Lư Sĩ Pháp
Bài 3.1. Xác định độ dài các trục, tọa độ các tiêu điểm, tâm sai, tọa độ của các đỉnh và vẽ elip (E) có x2 y2 phương trình + =1 25 9 HD Giải x2 y2 c 4
Phương trình elip có dạng: + = 1. - Tâm sai: e = = a2 b2 a 5 a2 = 25 a = 5 - Hình vẽ Do đó: ⇔ . Ta có y b2 = 9 b = 3 B1 3 M
c = a2 − b2 = 4 Vậy (E) có: -5 -4 4 5 A A
- Trục lớn: A A = 2a = 10 1 F O F 2 x 1 2 1 2
- Trục nhỏ: B B = 2b = 6 1 2 -3 B
- Hai tiêu điểm: F (−4; 0), F (4; 0) 2 1 2 - Bốn đỉnh: A ( 5
− ;0); A (5;0);B (0;−3);B (0;3) 1 2 1 2 2 2 Bài 3.2. x y Cho elip (E) : +
=1. Viết phương trình đường tròn (C) có đường kính là F F với F và 100 36 1 2 1
F là hai tiêu điểm của (E). 2 HD Giải 2 2 x y
Phương trình (E) có dạng + = 1. Ta có: 2 2 2 2 2
a = 100, b = 36 ⇒ c = a − b = 64 ⇒ c = 8 2 2 a b
Khi đó: F (−8;0), F (8;0) . 1 2
Taâm O(0;0) laø trung ñieåm cuûa F F Đường tròn 1 2 (C) : có phương trình: 2 2 x + y = 64
Baùn kính R = c = 8
ấn đề 2. Lập phương trình chính tắc của một elip khi biết các thành phần đủ để xác định elip Vđó Phương pháp: y
- Từ các thành phần đã biết, áp dụng công thức liên quan ta tìm được B1 M(x;y)
phương trình chính tắc của elip. x2 y2 -c c
- Lập phương trình chính tắc của elip theo công thức: + = 1 A a2 b2 1 O A2 F x 1 F2
Lưu ý: a > b > 0 và 2 2 2
c = a − b B2
Bài 3.3. Lập phương trình chính tắc của elip (E), biết
a) Một đỉnh là A(0; -2) và một tiêu điểm F(1; 0) b) F ( 7 − ;0) − 1
là một tiêu điểm và (E) đi qua M( 2;12) 3
c) Tiêu cự bằng 6, tâm sai bằng 5
d) Phương trình các cạnh của hình chữ nhật cơ sở là x = 4 ± ; y = 3 ±
e) (E) đi qua hai điểm M (4; 3) và N (2 2;−3) HD Giải x2 y2
Elip (E) có phương trình chính tắc: + =
1 (a > b > 0) a2 b2
a) A(0; -2) là một đỉnh ⇒ b = 2 ; F(1; 0) là một tiêu điểm ⇒ c = 1 x2 y2
Ta có a2 = b2 + c2 = 5 . Phương trình của (E): + = 1 5 4 41
Chương III. Phương pháp tọa độ trong
mặt phẳng. 0916620899-0355334679
Tài liệu học tập Toán 10 GV. Lư Sĩ Pháp b) F ( 7 − ;0) (7;0) 1
là một tiêu điểm ⇒ tiêu điể thứ hai là F2
Ta có: M ∈(E) ⇒ 2a = MF + MF 2 2 2 2 = ( 7
− + 2) +12 + (7 + 2) +12 = 28 1 2 ⇒ a = 14 Ta lại có: F ( 7 − ;0) ⇒ = 2 2 2 = − = 147 1 là một tiêu điểm c 7 và b a c x2 y2
Vậy phương trình của (E): + = 1 196 147 c
c) Ta có c = ⇒ c =
e = ⇒ a = b2 = a2 − c2 2 6 3; 5, =16 a x2 y2
Vậy phương trình của (E): + = 1 25 16 x2 y2
d) Ta có a = 4, b = 3 nên phương trình của (E): + =1 16 9 16 3 + = 1 2 2 a2 a b = 20
e) (E) đi qua hai điểm M và N nên ta có: ⇔ 8 9 b2 = 15 + = 1 a2 b2 x2 y2
Vậy phương trình của (E): + = 1 20 15 2 2 Bài 3.4. x y
Tìm những điểm trên elip (E): + = 1 9 1 thỏa mãn
a) Có bán kính qua tiêu điểm trái bằng hai lần bán kính qua tiêu điểm phải
b) Nhìn hai tiêu điểm dưới một góc vuông 0
c) Nhìn hai tiêu điểm dưới góc 60 HD Giải x2 y2
Phương trình elip có dạng: + = 1. a2 b2 a2 = 9 a = 3 2 2 Do đó: ⇔
. Ta có c = a − b = 2 2 b2 = 1 b = 1
Elip (E) có hai tiêu điểm F (−2 2;0);F 2 2;0 1 2 ( ) a a2 3
a) Gọi M(x; y) ∈(E) là điểm cần tìm. Khi đó: MF = 2MF ⇔ a + ex = 2(a − ex) ⇔ x = = = 1 2 e 3 c 3 2 2 x2 2 7 7
Do điểm M ∈(E) ⇒ y = 1− = ⇒ y = ± 9 8 2 2 3 7 3 7
Vậy có hai điểm cần tìm: M ; ; M ;− 1 2 2 2 2 2 2 2 2 2
b) Gọi N (x; y) ∈ (E) là điểm cần tìm. Khi đó: F N = (x + 2 2;y 1 ),
F N = (x − 2 2;y 2
). Từ N nhìn hai tiêu điểm dưới một góc vuông nên ta có: F N F
. N = 0 ⇔ (x +2 2)(x −2 2)+ y2 = 0 ⇔ x2 + y2 −8 = 0 1 2 (1) x2 Và N ∈ E ⇒ + y2 ( ) = 1 9 (2) 42
Chương III. Phương pháp tọa độ trong
mặt phẳng. 0916620899-0355334679
Tài liệu học tập Toán 10 GV. Lư Sĩ Pháp 2 1 3 7 1
Giải (1) và (2), ta được: x2 63 = = ⇒ = ± = ± 8 và y x 8 và y 2 2 2 2 3 7 1
Vậy có bốn điểm cần tìm là ± ;± 2 2 2 2
c) Gọi P(x; y) ∈(E) là điểm cần tìm. Ta có: 2 1
F F2 = F P2 + F P2 − 2F P F . P 0 cos60 = + − 2 . − 2 . 1 2 1 2 1 2 (FP F P 1 2 ) FP F P FP F P 1 2 1 2 2 = 4a2 − 3F P F
. P = 4a2 −3(a + ex)(a − ex) = 4a2 − 3(a2 −e2x2 1 2 ) 2 2 2 = a + e 3 x 2 4 − . (4.8 − 9) 69 69 2 2 2 2
( c2 a2) a2 c
Như vậy: 4c = a + 3. x ⇒ x = = = ⇒ x = ± a2 c2 3 3.8 8 2 2 x2 x2 2 2 1 1 Mà P ∈(E) ⇒
+ y = 1⇒ y = 1− = ⇒ y = ± 9 9 24 2 6 69 1
Vậy có bốn điểm cần tìm là ± ;± 2 2 2 6
Bài 3.5. Cho elip (E): x2 + y2 9 25 = 225
a) Tìm tọa độ hai tiêu điểm F , F 1
2 và các đỉnh của (E)
b) Tìm điểm M ∈ (E) sao cho M nhìn F F 1 2 dưới một góc vuông HD Giải 2 2 x2 y2
(E): 9x + 25y = 225 ⇔ + = 1 25 9 a2 = 25 a = 5 2 2 2 Ta có: ⇔
. c = a − b = 16 ⇒ c = 4 b2 = 9 b = 3
Vậy (E) có hai tiêu điểm là: F (−4; 0), F (4; 0) ( 5
− ;0); (5;0); (0;−3); (0;3) 1 2
và có bốn đỉnh là A A B B 1 2 1 2
b) Gọi M(x; y) ∈(E) là điểm cần tìm, ta có: 175 2 2 x2 M ∈(E) = M ∈ (E)
9x + 25y = 225 16 ⇔ ⇔ ⇔ F MF 0 = 90 O M2 = c2
x2 + y2 = 16 81 y2 1 2 = 16 5 7 x = ± 4 5 7 9 ⇒
. Vậy có bốn điểm cần tìm là M ± ;± 9 4 4 y = ± 4
Bài 3.6. Cho elip (E): x2 + y2 4
9 = 36 và điểm M(1; 1). Viết phương trình đường thẳng (d) qua M và cắt
(E) tại hai điểm A và B sao cho M là trung điểm của AB. HD Giải
(E): x2 + y2 4 9 = 36 (1)
Phương trình đường thẳng (d) đi qua điểm M(1; 1) và có hệ số góc k. Ta có phương trình của (d):
y = k(x −1) +1 (2).
Thay (2) vào (1) ta được: 2 2 x2 + k x
− + = ⇔ ( k2 + ) x2 4 9 ( 1) 1 36 9 4 +1 k
8 (1− k) x + 9(1− k) −36 = 0(3)Ta có: (d) cắt (E) tại hai
điểm A và B thỏa mãn MA = MB khi và chỉ khi phương trình (3) có hai nghiệm x , x sao cho: A B 43
Chương III. Phương pháp tọa độ trong
mặt phẳng. 0916620899-0355334679
Tài liệu học tập Toán 10 GV. Lư Sĩ Pháp x + x −1 k 8 (1− k) 4 A B = x ⇔ = 1 ⇔ 1 k2 8 −1 k 8 = 1 k2 8 + 8 ⇔ k = − M 2 2(9k2 + 4) 9
Vậy phương trình của (d) là: 4x + 9y −13 = 0 2 2 Bài 3.7. x y
Trong mặt phẳng với hệ toạ độ Oxy, cho elip (E): + = 1 9 3
và điểm A(3; 0) . Tìm trên (E) các
điểm B, C sao cho B, C đối xứng qua trục Ox và ∆ABC là tam giác đều. HD Giải
Không mất tính tổng quát, giả sử B(x ; y ),C(x ; −y 0 0 0 0) với y0 > 0 . x2 y2 0 0 2 2 Ta có: + = 1 ⇔ x + 3y 0 0 = 9 = 2 ( ) : = ( ,( )) = 3 − 9 3 . BC
y0 và BC x x0 ⇒ d A BC x0
Do A ∈ Ox , B và C đối xứng qua Ox nên ∆ABC cân tại A 3 2 2
Suy ra: ∆ABC đều ⇔ d(A,(BC)) = BC 3 − = 3 3 = ( − 3) 2 ⇔ x y 0 0 ⇔ y x 0 0 2 2 x = 0 ⇒ x + (x 0 0 0 − 3) = 9 ⇔ . x 0 = 3
Với x0 = 0 ⇒ y0 = 3 ⇒ B(0; 3), C(0;− 3) .
Với x0 = 3 ⇒ y0 = 0 (loại).
Vậy: B(0; 3), C(0; − 3) .
BÀI TẬP LÀM TƯƠNG TỰ
Bài 3.8. Xác định độ dài trục lớn, trục nhỏ, tiêu cự, tâm sai, toạ độ các tiêu điểm, các đỉnh và vẽ hình của mỗi elip sau: 2 2 x y a) + =1 b) 2 2 4x +16 y = 1 c) 2 2 x + 4 y = 1 25 9 d) 2 2 4x + 5 y = 20 e) 2 2 x + 3y = 2 f) 2 2
mx + ny = 1;(n > m > 0, n ≠ m)
Bài 3.9. Lập phương trình chính tắc của elip (E) biết:
a) Độ dài trục lớn bằng 10 và tiêu cự bằng 6 3
b) Có một tiêu điểm (− 3;0) và điểm M 1; nằm trên elip 2
c) Có một đỉnh trên trục lớn là điểm (3; 0) và một tiêu điểm là( -2; 0 ) 3
d) Elip qua điểm M( 0; 1 ) và N 1; 2
Bài 3.10. Lập phương trình chính tắc của elip (E) trong các trường hợp sau : 3
a) Elip có tâm sai e =
và độ dài trục lớn bằng 6 3 1
b) Elip có tâm sai e = và tiêu cự bằng 8 2 2 c) Tiêu điểm F ( 6
− ;0) và tâm sai e = 1 3
d) Phương trình các cạnh hình chữ nhật cơ sở là: x = 4 ± , y = ±3
e) Elip đi qua hai điểm M (4; 3), N (2 2; 3 − )
Bài 3.11. Cho elip (E) : 2 2 9x + 25 y = 225
a) Tìm toạ độ hai tiêu điểm F ; F , tiêu cự, tâm sai và các đỉnh của (E) 1 2 44
Chương III. Phương pháp tọa độ trong
mặt phẳng. 0916620899-0355334679
Tài liệu học tập Toán 10 GV. Lư Sĩ Pháp
b) Viết phương trình hai đường chuẩn của (E) và tìm khoảng cách giữa hai đường chuẩn.
c) Tìm điểm M ∈ (E) sao cho M nhìn xuống F F dưới một góc vuông 1 2 2 2 Bài 3.12. x y Cho elip (E) : +
=1 có các tiêu điểm là F ; F . 25 16 1 2
a) Tìm điểm M trên (E) sao cho MF = 2MF
b) Tìm điểm M trên (E) sao cho 0 F MF = 90 1 2 1 2 2 2 Bài 3.13. x y Cho (E) : +
=1. Tìm các điểm M ∈(E) nhìn hai tiêu điểm một góc 1200 100 25 2 2 Bài 3.14. x y Cho (E): +
=1 với a > b > 0. Gọi M là điềm tuỳ ý trên (E) . Chứng minh rằng: 2 2 a b a) 2 2 2
MO + MF .MF = a + b
b) a ≤ OM ≤ b c) 2 2 2
(MF − MF ) = 4(OM − b ) 2 2 1 2 Bài 3.15. Cho 2 2
(E) : 9x +16 y = 144
a) Tìm tiêu điểm , tâm sai và độ dài các trục của (E)
b) Lấy điểm M tuỳ ý thuộc (E) . Chứng minh rằng: i) 2
MO + MF .MF là một hằng số ii) 3 ≤ OM ≤ 4 iii) 2 2
(MF − MF ) = 4(OM − 9) 2 2 1 2 Bài 3.16. Cho 2 2
(E) : 4x + 9 y = 36 .
a) Tìm toạ độ các tiêu điểm, các đỉnh, tâm sai và vẽ elip (E) .
b) Xác định m để đường thẳng (d) : y = x + m và (E) có điểm chung.
c) Viết phương trình đường thẳng (∆) đi qua M (1; ) 1 và cắt (E) tại ,
A B sao cho M là trung điểm đoạn thẳng A . B 2 2 Bài 3.17. x y Cho (E) : + =1 25 9
a) Tìm toạ độ các tiêu điểm, các đỉnh, tâm sai, viết phương trình hai đường chuẩn và vẽ elip (E) .
b) Cho M (4;m). Viết phương trình tiếp tuyến của (E) tại M khi m < 0.
c) Viết phương trình tiếp tuyến của (E) đi qua A(5; 2)
d) Viết phương trình tiếp tuyến của (E) song song với (d ) : 3x + 5 y +1 = 0 . 1
e) Viết phương trình tiếp tuyến của (E) vuông góc với (d ) : 3x + 5 y −1 = 0 . 2 2 2 2 2 Bài 3.18. x y x y Cho hai elip (E ) : + = 1 và (E ) : + =1. 1 16 1 2 9 4
a) Viết phương trình đường tròn đi qua các giao điểm của (E ) và (E ) 1 2
b) Viết phương trình tiếp tuyến chung của (E ) và (E ) 1 2 2 2 2 2 Bài 3.19. x y x y Cho hai elip (E ) : + =1 và (E ) : + =1. 1 5 4 2 4 5
a) Viết phương trình đường tròn đi qua các giao điểm của (E ) và (E ) 1 2
b) Viết phương trình tiếp tuyến chung của (E ) và (E ) 1 2 2 2 Bài 3.20. x y Cho elip (E): +
= 1có hai tiêu điểm (F ) và (F ) 25 16 1 2
a) Tìm tâm sai, toạ độ các đỉnh và viết phương trình hai đường chuẩn của (E) .
b) Cho điểm M(3; m) ∈ (E) . Viết phương trình tiếp tuyến của (E) khi m > 0. c) Cho ,
A B ∈ (E) sao cho AF + BF = 8 . Tính AF + BF 1 2 2 1 2 2 2 2 Bài 3.21. x y x y Cho hai elip (E ) : + =1 và (E ) : + =1. 1 16 1 2 9 4
a) Viết phương trình đường tròn đi qua các giao điểm của (E ) và (E ) 1 2
b) Viết phương trình tiếp tuyến chung của (E ) và (E ) 1 2 45
Chương III. Phương pháp tọa độ trong
mặt phẳng. 0916620899-0355334679
Tài liệu học tập Toán 10 GV. Lư Sĩ Pháp 2 2 Bài 3.22. x y Biết (E) : +
= 1 nhận các đường thẳng ∆ :3x − 2y − 20 = 0 và ∆ : x + 6y − 20 = 0 2 2 a b 1 2
làm tiếp tuyến. Viết phương trình chính tắc của (E) .
Bài 3.23. Lập phương trình chính tắc của (E) có tiêu điểm F (− 15;0) và tiếp xúc với đường thẳng 1
(d): x +4y –10 = 0 2 2 Bài 3.224. x y Cho elip (E): + = 1 M −2;1 25 16 và điểm
( ). Viết phương trình đường thẳng (d) qua M và cắt
(E) tại hai điểm A và B sao cho M là trung điểm của AB. 2 2 Bài 3.25 x y . Cho elip (E): + =1 ; 25 16
có các tiêu điểm là F F 1 2 .
a) Tìm điểm M trên (E) sao cho MF = 2MF = 90 1 2
b) Tìm điểm M trên (E) sao cho F MF 0 1 2 2 2 Bài 3.26 x y . Cho (E): + = 1 ∈( ) 100 25 . Tìm các điểm M
E nhìn hai tiêu điểm một góc 1200. 2 2 Bài 3.27. x y
Trong mặt phẳng với hệ toạ độ Oxy, cho elip (E): + = 1 100 25
. Tìm các điểm M ∈ (E) sao cho F MF 0 1 2 = 120 ( F , F E 1
2 là hai tiêu điểm của ( ) ). 2 2 Bài 3.28. x y
Trong mặt phẳng tọa độ Oxy , cho elip (E) : + = 1 25 9
và điểm M(1;1) . Viết phương trình
đường thẳng đi qua M và cắt elip tại hai điểm A, B sao cho M là trung điểm của AB . 2 2 Bài 3.29. x y Cho (E): +
=1. Tìm các điểm M ∈(E) nhìn hai tiêu điểm một góc 1200 100 25 46
Chương III. Phương pháp tọa độ trong
mặt phẳng. 0916620899-0355334679
Tài liệu học tập Toán 10 GV. Lư Sĩ Pháp
BÀI TẬP TRẮC NGHIỆM Câu 1. x y Cho elip ( E) 2 2 : +
=1 với a > b > 0. Gọi 2c là tiêu cự của (E). Mệnh đề nào dưới đây đúng? 2 2 a b A. 2 2 2
c = a + b . B. 2 2 2
b = a + c . C. 2 2 2
a = b + c .
D. c = a + . b Câu 2. Elip (E) 2 2
: 4x +16 y = 1 có độ dài trục lớn bằng: A. 1. B. 1 . C. 2. D. 4. 2
Câu 3. Elip (E) có độ dài trục lớn bằng 4 2 , các đỉnh trên trục nhỏ và các tiêu điểm của elip cùng nằm
trên một đường tròn. Độ dài trục nhỏ của ( E ) bằng: A. 8. B. 16. C. 2. D. 4.
Câu 4. Lập phương trình chính tắc của elip có độ dài trục lớn bằng 26 và tỉ số của tiêu cự với độ dài trục 12 lớn bằng . 13 2 2 2 2 2 2 2 2
A. x + y = x y x y x y 1. B. + =1. C. + =1. D. + =1. 26 25 169 25 52 25 169 5
Câu 5. Tìm phương trình chính tắc của elip có tiêu cự bằng 6 và trục lớn bằng 10. 2 2 2 2 2 2 2 2
A. x + y = x y x y x y 1. B. − =1. C. + =1. D. + =1. 100 81 25 16 25 16 25 9 Câu 6. x y Cho elip ( E) 2 2 : +
=1 và điểm M nằm trên (E). Nếu M có hoành độ bằng −13 thì 169 144
khoảng cách từ M đến hai tiêu điểm bằng: A. 10 và 6. B. 8 và 18. C. 13 ± 5 . D. 13 ± 10 . Câu 7. x y Elip ( E) 2 2 : +
=1. Tỉ số k của tiêu cự và độ dài trục bé của elip bằng: 16 8
A. k = 8 .
B. k = 1.
C. k = −1.
D. k = 8 .
Câu 8. Elip có độ dài trục nhỏ là 4 6 và có một tiêu điểm F (5;0) . Phương trình chính tắc của elip là: 2 2 2 2 2 2 2 2
A. x + y = x y x y x y 1. B. + =1. C. + =1. D. + =1. 29 24 121 96 101 96 49 24
Câu 9. Tìm phương trình chính tắc của elip, biết elip có tiêu cự bằng 6 và đi qua A(5;0) . 2 2 2 2 2 2 2 2 A. x y x y x y x y + =1. B. − =1. C. + =1. D. + =1. 100 81 25 16 25 16 25 9 Câu 10. x Elip ( E) 2 2 :
+ y = 4 có tổng độ dài trục lớn và trục bé bằng: 16 A. 40. B. 5. C. 10. D. 20. Câu 11. x y Cho ( E ) 2 2 : +
=1. Một đường thẳng đi qua điểm A(2;2) và song song với trục hoành cắt 20 16
(E) tại hai điểm phân biệt M và N . Tính độ dài MN . A. 3 5. B. 15 2. C. 2 15. D. 5 3. Câu 12. x y Elip ( E) 2 2 : +
=1 có một tiêu điểm là: 9 6 A. (− 3;0). B. (3;0). C. (0;3). D. (0 ; 6).
Câu 13. Elip có độ dài trục lớn là 10 và có một tiêu điểm F ( 3
− ;0) . Phương trình chính tắc của elip là: 2 2 2 2 2 2 2 2
A. x + y = x y x y x y 1. B. + =1. C. + =1. D. + =1. 100 81 25 16 25 9 100 16 47
Chương III. Phương pháp tọa độ trong
mặt phẳng. 0916620899-0355334679
Tài liệu học tập Toán 10 GV. Lư Sĩ Pháp
Câu 14. Elip có một tiêu điểm F ( 2
− ;0) và tích độ dài trục lớn với trục bé bằng 12 5 . Phương trình chính tắc của elip là: 2 2 2 2 2 2 2 2
A. x + y = x y x y x y 1. B. + =1. C. + =1. D. + =1. 45 16 36 20 144 5 9 5 Câu 15. 3
Elip có tổng độ dài hai trục bằng 18 và tỉ số của tiêu cự với độ dài trục lớn bằng . Phương trình 5
chính tắc của elip là: 2 2 2 2 2 2 2 2
A. x + y = x y x y x y 1. B. + =1. C. + =1. D. + =1. 9 4 5 4 25 9 25 16 Câu 16. x y Elip ( E) 2 2 : +
=1 có tiêu cự bằng: 9 4 A. 5. B. 10. C. 2 5. D. 5.
Câu 17. Phương trình của elip (E) có độ dài trục lớn bằng 8, độ dài trục nhỏ bằng 6 là: 2 2 2 2 A. x y x y 2 2
9x +16 y = 144. B. 2 2
9x +16 y = 1. C. + =1. D. + =1. 9 16 64 36
Câu 18. Elip (E) 2 2
: x + 5y = 25 có độ dài trục lớn bằng: A. 2. B. 5. C. 10. D. 1. Câu 19. x y Cho elip ( E) 2 2 : +
=1 và M là một điểm tùy ý trên (E). Mệnh đề nào dưới đây đúng? 16 9
A. 3 ≤ OM ≤ 4.
B. 4 ≤ OM ≤ 5.
C. OM ≥ 5.
D. OM ≤ 3.
Câu 20. Lập phương trình chính tắc của elip biết tỉ số giữa độ dài trục nhỏ và tiêu cự bằng 2 , tổng bình
phương độ dài trục lớn và tiêu cự bằng 64 . 2 2 2 2 2 2 2 2
A. x + y = x y x y x y 1. B. + =1. C. + =1. D. + =1. 8 4 12 8 8 12 12 4
Câu 21. Cho elip có phương trình 2 2
16x + 25y = 100 . Tính tổng khoảng cách từ điểm M thuộc elip có
hoành độ bằng 2 đến hai tiêu điểm. A. 4 3. B. 3. C. 2 2. D. 5 . Câu 22. Đườ x y
ng thẳng d : 3x + 4y −12 = 0 cắt elip ( E) 2 2 : +
=1 tại hai điểm phân biệt M và N . Khi 16 9
đó độ dài đoạn thẳng MN bằng: A. 4. B. 5. C. 25. D. 3.
Câu 23. Elip có một đỉnh là A(5;0) và có một tiêu điểm F −4;0 . Phương trình chính tắc của elip là: 1 ( ) 2 2 2 2 2 2
A. x + y = x y x y x y 1. B. + =1. C. + =1. D. + =1. 5 4 25 9 5 4 25 16 Câu 24. x y Elip ( E ) 2 2 : +
=1, với p > q > 0 có tiêu cự bằng: 2 2 p q A. 2 2
2 p − q .
B. p − q . C. 2 2
p − q .
D. p + q .
Câu 25. Lập phương trình chính tắc của elip biết độ dài trục lớn hơn độ dài trục nhỏ 4 đơn vị, độ dài trục
nhỏ hơn độ dài tiêu cự 4 đơn vị. 2 2 2 2 2 2 2 2
A. x + y = x y x y x y 1. B. + =1. C. + =1. D. + =1. 100 64 9 1 64 60 25 9 Câu 26. 5
Elip qua điểm M 2; và có một tiêu điểm F ( 2
− ;0). Phương trình chính tắc của elip là: 3 2 2 2 2 2 2 2 2
A. x + y = x y x y x y 1 . B. + =1. C. + =1. D. + =1. 25 9 9 5 9 4 25 16 48
Chương III. Phương pháp tọa độ trong
mặt phẳng. 0916620899-0355334679
Tài liệu học tập Toán 10 GV. Lư Sĩ Pháp Câu 27. 3
Một elip ( E) có khoảng cách giữa hai đỉnh kế tiếp nhau gấp lần tiêu cự của nó. Tỉ số e của 2
tiêu cự với độ dài trục lớn bằng: A. 2 e = . B. 2 e = . C. 3 e = . D. 5 e = . 5 5 5 5
Câu 28. Elip (E) có hai đỉnh trên trục nhỏ cùng với hai tiêu điểm tạo thành một hình vuông. Tỉ số e của
tiêu cự với độ dài trục lớn của ( E) bằng: A. 1 e = . B. 1 e = .
C. e = 1 .
D. e = 2 . 2 3 Câu 29. x y Cho elip ( E) 2 2 : +
=1. Khẳng định nào dưới đây là đúng? 2 2 a b
A. (E) không có tâm đối xứng.
B. (E) có đúng một tâm đối xứng.
C. (E) có hai tâm đối xứng.
D. (E) có vô số tâm đối xứng. Câu 30. 12
Elip đi qua các điểm M (0;3) và N 3;−
có phương trình chính tắc là: 5 2 2 2 2 2 2 2 2
A. x + y = x y x y x y 1. B. − =1. C. + =1. D. + =1. 9 25 25 9 16 9 25 9
Câu 31. Lập phương trình chính tắc của elip có độ dài trục nhỏ bằng 12 và tỉ số của tiêu cự với độ dài 4 trục lớn bằng . 5 2 2 2 2 2 2 2 2
A. x + y = x y x y x y 1. B. + =1. C. + =1. D. + =1. 100 36 25 36 64 36 36 25 Câu 32. 5
Tìm phương trình chính tắc của elip nếu nó đi qua điểm N 2; − và tỉ số của tiêu cự với độ 3 2 dài trục lớn bằng . 3 2 2 2 2 2 2 2 2
A. x + y = x y x y x y 1. B. + =1. C. + =1. D. + =1. 9 6 9 3 9 4 9 5
Câu 33. Elip (E) có độ dài trục bé bằng tiêu cự. Tỉ số e của tiêu cự với độ dài trục lớn của (E) bằng:
A. e = 1.
B. e = 2 . C. 1 e = . D. 1 e = . 2 3
Câu 34. Tìm phương trình chính tắc của elip, biết elip có tiêu cự bằng 2 3 và đi qua A(2; ) 1 . 2 2 2 2 2 2 2 2 A. x y x y x y x y + =1. B. + =1. C. + =1. D. + =1. 6 3 8 2 8 5 9 4
Câu 35. Phương trình chính tắc của elip có hai tiêu điểm F −2;0 , F 2;0 và đi qua điểm M (2;3) là: 1 ( ) 2 ( ) 2 2 2 2 2 2 2 2
A. x + y = x y x y x y 1. B. + =1. C. + =1. D. + =1. 16 12 16 9 16 4 16 8
Câu 36. Phương trình chính tắc của elip đi qua hai điểm A(7;0) và B(0;3) có dạng là 2 2 2 2 2 2 2 2
A. x + y = x y x y x y 1. B. + =1. C. + =1. D. + =1. 40 9 16 9 9 49 49 9 2 2 Câu 37. x y
Cho điểm M (2;3) nằm trên đường elip ( E) có phương trình chính tắc: + =1. Trong các 2 2 a b
điểm sau đây điểm nào không nằm trên (E): A. M 3;2 . B. M 2; 3 − . C. M 2 − ;−3 . D. M 2 − ;3 . 1 ( ) 3 ( ) 2 ( ) 4 ( ) 49
Chương III. Phương pháp tọa độ trong
mặt phẳng. 0916620899-0355334679
Tài liệu học tập Toán 10 GV. Lư Sĩ Pháp Câu 38. x y Cho elip ( E) 2 2 : +
=1. Khẳng định nào dưới đây là đúng? 2 2 a b
A. (E) không có trục đối xứng.
B. (E) có một trục đối xứng là trục hoành.
C. (E) có hai trục đối xứng là trục hoành và trục tung. D. (E) có vô số trục đối xứng. Câu 39. x y Elip ( E) 2 2 : +
=1 có độ dài trục lớn bằng: 25 9 A. 5. B. 10. C. 25. D. 50. Câu 40. x y Cho elip ( E) 2 2 : +
=1. Trong các khẳng định sau, khẳng định nào sai? 25 9 A. ( c 4
E ) có các tiêu điểm F 4
− ;0 và F 4;0 .
B. (E) có tỉ số = . 2 ( ) 1 ( ) a 5
C. (E) có đỉnh A −5;0 .
D. (E) có độ dài trục nhỏ bằng 3. 1 ( )
Câu 41. Một elip (E) có trục lớn dài gấp 3 lần trục nhỏ. Tỉ số e của tiêu cự với độ dài trục lớn bằng: A. 1 e = . B. 2 e = . C. 3 e = . D. 2 2 e = . 3 3 3 3
Câu 42. Cho elip (E) 2 2
: x + 4 y = 1. Khẳng định nào dưới đây là đúng?
A. Elip có tiêu cự bằng 3.
B. Elip có trục nhỏ bằng 2. C. 2
Elip có một tiêu điểm là F 0; .
D. Elip có trục lớn bằng 4. 3 Câu 43. x y Cho elip ( E) 2 2 : + =1. Hai điểm ,
A B là hai đỉnh của elip lần lượt nằm trên hai trục Ox , 25 9
Oy . Khi đó độ dài đoạn thẳng AB bằng: A. 5. B. 136. C. 34. D. 34.
Câu 44. Tìm phương trình chính tắc của elip nếu nó đi qua điểm A(2; 3) và tỉ số của độ dài trục lớn với 2 tiêu cự bằng . 3 2 2 2 2 2 2 2 2
A. x + y = x y x y x y 1. B. + =1. C. + =1. D. + =1. 3 4 4 16 16 4 4 3 Câu 45. x y Elip ( E) 2 2 : +
=1 có tiêu cự bằng: 25 16 A. 6. B. 9. C. 18. D. 3. Câu 46. x y Cho elip ( E) 2 2 : +
=1. Qua một tiêu điểm của (E) dựng đường thẳng song song với trục 100 36
Oy và cắt ( E) tại hai điểm M và N . Tính độ dài MN . A. 36 . B. 48 . C. 25 . D. 64 . 5 5 2 5
Câu 47. Tìm phương trình chính tắc của elip nếu trục lớn gấp đôi trục bé và có tiêu cự bằng 4 3 . 2 2 2 2 2 2 2 2 A. x y x y x y x y + =1. B. + =1. C. + =1. D. + =1. 24 16 16 4 36 9 36 24 Câu 48. x y Elip ( E) 2 2 : +
=1. Tỉ số f của độ dài trục lớn và tiêu cự của elip bằng: 9 4 A. 5 f = . B. 3 f = . C. 3 f = . D. 2 f = . 3 2 5 3 50
Chương III. Phương pháp tọa độ trong
mặt phẳng. 0916620899-0355334679
Tài liệu học tập Toán 10 GV. Lư Sĩ Pháp Câu 49. x y Elip ( E) 2 2 : +
=1 có một đỉnh nằm trên trục lớn là: 100 36 A. (−10;0) . B. (−100;0) . C. (0;10) . D. (100;0) . Câu 50. x y
Cặp điểm nào là các tiêu điểm của elip ( E) 2 2 : + =1? 5 4 A. F 0; 1 − và F 0;1 . B. F 2
− ;0 và F 2;0 2 ( ) 1 ( ) 2 ( ) 1 ( ) C. F 1
− ;0 và F 1;0 . D. F 3
− ;0 và F 3;0 . 2 ( ) 1 ( ) 2 ( ) 1 ( ) Câu 51. 3
Elip đi qua các điểm A(0; ) 1 và N 1;
có phương trình chính tắc là: 2 2 2 2 2 2 2 2 2
A. x + y = x y x y x y 1. B. + =1. C. + =1. D. + =1. 2 1 16 4 8 4 4 1 Câu 52. x y
Dây cung của elip ( E) 2 2 : +
=1 (0 < b < a) vuông góc với trục lớn tại tiêu điểm có độ dài 2 2 a b bằng: 2 2 2 2 A. a 2c 2b 2a . B. . C. . D. . c a a c Câu 53. x y Elip ( E) 2 2 : +
=1 có độ dài trục bé bằng: 100 64
A. 10.
B. 16. C. 20. D. 8.
Câu 54. Tìm phương trình chính tắc của elip, biết elip có tiêu cự bằng 8 và đi qua điểm M ( 15;− )1. 2 2 2 2 2 2 2 2
A. x + y = x y x y x y 1. B. + =1. C. + =1. D. + =1. 16 4 18 4 20 4 12 4
Câu 55. Cho elip có hai tiêu điểm F , F và có độ dài trục lớn bằng 2a . Mệnh đề nào dưới đây đúng? 1 2
A. 2a < F F .
B. 4a = F F .
C. 2a = F F .
D. 2a > F F . 1 2 1 2 1 2 1 2
Câu 56. Cho elip (E) 2 2
: 4x + 9 y = 36 . Tìm mệnh đề sai trong các mệnh đề sau:
A. (E) có trục lớn bằng 6.
B. (E) có trục nhỏ bằng 4. C. ( c 5
E ) có tiêu cự bằng 5.
D. (E) có tỉ số = . a 3 Câu 57. x y Elip ( E) 2 2 : +
=1 có một đỉnh nằm trên trục bé là: 16 12 A. (4;0) . B. (0;12) . C. (0;2 3). D. (4;0) .
Câu 58. Lập phương trình chính tắc của elip có độ dài trục lớn bằng 6 và tỉ số của tiêu cự với độ dài trục 1 lớn bằng . 3 2 2 2 2 2 2 2 2 A. x y x y x y x y + =1. B. + =1. C. + =1. D. + =1. 9 8 9 5 6 5 9 3
Câu 59. Tìm phương trình chính tắc của elip nếu nó đi qua điểm A(6;0) và tỉ số của tiêu cự với độ dài 1 trục lớn bằng . 2 2 2 2 2 2 2 2 2 A. x y x y x y x y + =1. B. + =1. C. + =1. D. + =1. 36 18 6 2 36 27 6 3
Câu 60. Elip có hai đỉnh là (−3;0); (3;0) và có hai tiêu điểm là ( 1
− ;0); (1;0). Phương trình chính tắc của elip là: 51
Chương III. Phương pháp tọa độ trong
mặt phẳng. 0916620899-0355334679
Tài liệu học tập Toán 10 GV. Lư Sĩ Pháp 2 2 2 2 2 2 2 2
A. x + y = x y x y x y 1. B. + =1. C. + =1. D. + =1. 8 9 9 8 1 9 9 1
Câu 61. Tìm phương trình chính tắc của elip nếu nó có trục lớn gấp đôi trục bé và đi qua điểm M (2; 2 − ). 2 2 2 2 2 2 2 2 A. x y x y x y x y + =1. B. + =1. C. + =1. D. + =1. 16 4 36 9 24 6 20 5 Câu 62. x y
Giá trị của m để đường thẳng ∆ : x − 2 y + m = 0 cắt elip ( E) 2 2 : +
=1 tại hai điểm phân biệt 4 1 là:
A. −2 2 < m < 2 2.
B. m > 2 2.
C. m < −2 2. D. m = 2 ± 2. Câu 63. x y Cho elip ( E) 2 2 : +
=1 và điểm M nằm trên (E). Nếu M có hoành độ bằng 1 thì khoảng 16 12
cách từ M đến hai tiêu điểm bằng: A. 9 4 ± 2 . B. 2 4 ± . C. 7 và . D. 3 và 5 . 2 2 2 Câu 64. 5
Elip có tổng độ dài hai trục bằng 10 và tỉ số của tiêu cự với độ dài trục lớn bằng . Phương 3
trình chính tắc của elip là: 2 2 2 2 2 2 2 2
A. x + y = x y x y x y 1. B. + =1. C. + =1. D. + =1. 9 4 5 4 25 9 25 16 Câu 65. x y Elip ( E) 2 2 : +
=1. Tỉ số e của tiêu cự và độ dài trục lớn của elip bằng: 16 9
A. e = 1. B. 7 e = . C. 3 e = . D. 5 e = . 4 4 4 ĐÁP ÁN
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25
C A D B C B B D C D C A B D D C A C A B D B B A A
26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50
B D A B D A D C A A D A C B D D A D C A B B C A C
51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75
D B B C D C C A C B D A C A B 52
Chương III. Phương pháp tọa độ trong
mặt phẳng. 0916620899-0355334679
Tài liệu học tập Toán 10 GV. Lư Sĩ Pháp ÔN TẬP CHƯƠNG III
PHƯƠNG PHÁP TỌA ĐỘ TRONG MẶT PHẲNG
Bài 1. Trong mặt phẳng với hệ tọa độ Oxy, cho hình chữ nhật ABCD có điểm C thuộc đường thẳng
d : 2x + y + 5 = 0 và điểm A (−4;8) . Gọi M là điểm đối xứng của B qua C, N là hình chiếu vuông góc của
B lên đường thẳng MD. Tìm tọa độ điểm B và C, biết rằng N (5;−4) . (ĐH.KA,A1.2013 – Chuẩn ) HD Giải
Do điểm C ∈ d ⇒ C ( ;t 2
− t − 5) . Gọi I là tâm của hình chữ nhật ABCD, suy ra I là A D t − 4 2 − t + 3
trung điểm của AC. Do đó: I ; . Tam giác 2 2
BDN vuông tại N nên IN
= IB. Suy ra IN = IA I N 2 2 t − 4 2 − t + 3 Do đó, ta có: 5 − + −4 − 2 2 B C M 2 2 t − 4 2 − t + 3 = 4 − − + 8 −
⇔ t = 1 . Vậy C (1;−7) 2 2
Do M đối xứng với B qua C nên CM = CB. Mà CB = AD và CM / / AD nên tứ giác ACMD là hình bình
hành. Suy ra AC // DM. Theo giả thiết, BN ⊥ DM , suy ra BN ⊥ AC và CB = CN. Vậy B là đối xứng của N qua AC.
Đường thẳng AC có phương trình: 3x + y + 4 = 0
Đường thẳng BN qua N và vuông góc với AC nên có phương trình: x − 3y −17 = 0
3a +17 + 5 a − 4
Do đó: B (3a +17;a) . Trung điểm BN thuộc AC nên: 3 + + 4 = 0 ⇔ a = 7 − 2 2 Vậy B (−4;−7)
Bài 2. Trong mặt phẳng với hệ tọa độ Oxy, cho đường thẳng ∆ : x − y = 0 . Đường tròn (C) có bán kính
R = 10 cắt ∆ tại hai điểm A và B sao cho AB = 4 2 . Tiếp tuyến của (C) tại A và B cắt nhau tại một
điểm thuộc tia Oy. Viết phương trình đường tròn (C). (ĐH.KA, A1.2013 – Nâng cao) HD Giải
Gọi M là giao điểm của tiếp tuyến tại A và B của (C), H là giao điểm của AB M
và IM. Khi đó M (0;t) với t ≥ 0. H là trung điếm của AB. Suy ra: B AB AH =
= 2 2 . Tam giác AMI vuông, ta có: 2 H I 1 1 1 = +
⇒ AM = 2 10 . Do đó 2 2
MH = AM − AH = 4 2 A 2 2 2 AH AM AI t
Mà MH = d (M,∆) =
nên t = 8 . Vậy M (0;8) 2
Đường thẳng IM qua M va vuông góc với ∆ nên có phương trình x + y − 8 = 0 x − y = 0
Do đó, tọa độ điểm H thỏa mãn hệ: ⇒ H (4;4)
x + y − 8 = 0 1 1 Ta có: 2 2
IH = IA − AH = 2 = HM nên IH = HM . Vậy I (5;3) 4 4 2 2
Vậy đường tròn (C) có phương trình: (x − 5) + (y −3) =10
Bài 3. Trong mặt phẳng với hệ tọa độ Oxy, cho hình thang cân ABCD có hai đường chéo vuông góc với 53
Chương III. Phương pháp tọa độ trong
mặt phẳng. 0916620899-0355334679
Tài liệu học tập Toán 10 GV. Lư Sĩ Pháp
nhau và AD = 3BC. Đường thẳng BD có phương trình x + 2y − 6 = 0 và tam giác ABD có trực tâm
H (−3;2) . Tìm tọa độ các điểm C và D. (ĐH.KB.2013 – Chuẩn) HD Giải
Gọi I là giao điểm của AC và BD suy ra IB = IC. Mà IB ⊥ IC nên tam giác B C
IBC vuông cân tại I Do đó: 0 ICB = 45
Mặt khác: BH ⊥ AD ⇒ BH ⊥ BC ⇒ H
∆ BC vuông cân tại B ⇒ I là I
trung điểm của đoạn thẳng H HC
Do CH ⊥ BD và trung điểm I của CH thuộc BD nên tọa độ điểm C
2(x + 3) − (y − 2) = 0 A D thỏa mãn hệ: x − 3 y + 2 ⇒ C ( 1 − ;6) + 2 − 6 = 0 2 2 IC IB BC 1 CH Ta có: = =
= ⇒ ID = 3IC . 2 2 10
CD = IC + ID = IC 10 = = 5 2 ID ID AD 3 2 2 2 t = 1
D ∈ BD ⇒ D (6 − 2 ;tt) và CD = 5 2 nên: (7 − 2t) + (t − 6) = 50 ⇔ t = 7 Vậy D (4; ) 1 hoặc D ( 8 − ;7)
Bài 4. Trong mặt phẳng với hệ tọa độ Oxy, cho tam giác ABC có chân đường cao hạ từ đỉnh A là 17 1 H ;−
, chân đường phân giác trong của góc
D 5;3 và trung điểm của cạnh M 0;1 . 5 5 A là ( ) AB là ( )
Tìm tọa độ điểm C. (ĐH.KB.2013 – Nâng cao) HD Giải
Ta có: H ∈ AH và AH ⊥ HD nên AH có phương trình: A
x + 2y − 3 = 0 . Do đó A (3− 2 ; a a)
Do M là trung điểm AB và tam giác ABH vuông nên MA = MH N 2 2 1 M
Suy ra: (3− 2a) + (a − )
1 = 13 ⇔ a = 3 hoặc a = − . Do A khác H 5 nên A( 3 − ;3) H D C B
Phương trình đường thẳng AD: y − 3 = 0 . Gọi N là điểm đối xứng của M qua AD. Suy ra N ∈ AC và tọa 1+ y − 3 = 0
độ điểm N thỏa mãn hệ: 2 ⇒ N (0;5) 1
.x + 0.(y −1) = 0
Đường thẳng AC có phương trình: 2x − 3y +15 = 0
Đường thẳng BC có phương trình: 2x − y − 7 = 0
2x − 3y +15 = 0
Tọa độ của điểm C thảo mãn hệ: ⇒ C (9;1 ) 1
2x − y − 7 = 0 9 3
Bài 5. Trong mặt phẳng với hệ tọa độ Oxy, cho tam giác ABC có điểm M − ; là trung điểm của 2 2
cạnh AB, điểm H ( 2
− ;4) và điểm I (−1; )
1 lần lượt là chân đường cao kẻ từ B và tâm đường tròn ngoại
tiếp tam giác ABC. Tìm tọa độ điểm C. (ĐH.KD.2013 – Chuẩn) HD Giải 7 1 Ta có: IM = − ;
. M ∈ AB và AB ⊥ IM nên đường thẳng x − y + = 2 2
AB có phương trình: 7 33 0 54
Chương III. Phương pháp tọa độ trong
mặt phẳng. 0916620899-0355334679
Tài liệu học tập Toán 10 GV. Lư Sĩ Pháp
A ∈ AB ⇒ A ( ;
a 7a + 33), do M là trung điểm của AB nên B(−a − 9; 7 − a − 30) Ta có: 2
HA ⊥ HA ⇔ H .
A HB = 0 ⇔ a + 9a + 20 = 0 ⇔ a = 4 − hoặc a = 5 B Với a = 4 − ⇒ A( 4 − ;5),B(−5; 2
− ). Ta có: BH ⊥ AC nên đường thẳng
AC: x + 2y − 6 = 0 Điểm M
C ∈ AC ⇒ C (6 − 2 ;
c c) . Mặt khác: IC = IA suy ra I
( − x)2 +(c− )2 7 2
1 = 25 ⇔ c =1 hoặc c = 5 − . Do C
C khác A nên C (4; ) 1 A H
Với a = 5 ⇒ A(−5;−2),B( 4
− ;5) . Ta có: BH ⊥ AC nên đường thẳng AC: 2x − y +8 = 0 2 2
Điểm C ∈ AC ⇒ C (t;2t + 8) . Mặt khác: IC = IA suy ra (t + )
1 + (2t + 7) = 25 ⇔ t = 1 − hoặc t = −5 .
Do C khác A nên C ( 1 − ;6) 2 2
Bài 6. Trong mặt phẳng với hệ tọa độ Oxy, cho đường tròn (C) : (x − ) 1 + (y − ) 1 = 4 và đường thẳng
∆ : y − 3 = 0 . Tam giác MNP có trực tâm trùng với tâm của (C), các điểm N và P thuộc ∆ , đỉnh M và
trung điểm của cạnh MN thuộc (C). Tìm tọa độ điểm P. (ĐH.KD.2013 – Nâng cao) HD Giải
Đường tròn (C) có tâm I (1; )
1 . Đường thẳng IM vuông góc với ∆ M
nên có phương trình: x = 1. Do đó M (1;a). Do M ∈(C) nên (a− )2 1 = 4 ⇔ a = 1 − hoặc a = 3 I K
Mà M ∉ ∆ ⇒ M (1;− ) 1
N ∈ ∆ ⇒ N ( ;
b 3) . Trung điểm của MN thuộc (C), suy ra: 2 b +1 P N −1 + (1− )2
1 = 4 ⇔ b = 5hoặc b = −3 2
Do đó: N (5;3) hoặc N ( 3
− ;3). P∈∆ ⇒ P( ;c3)
Khi N (5;3), từ MP ⊥ IN suy ra c = −1. Do đó: P( 1 − ;3) Khi N ( 3
− ;3), từ MP ⊥ IN suy ra c = 3. Do đó: P(3;3)
Bài 7. Trong mặt phẳng với hệ tọa độ Oxy, cho đường thẳng d : x + y − 3 = 0 , ∆ : x − y + 2 = 0 và điểm M ( 1
− ;3). Viết phương trình đường tròn đi qua M, có tâm thuộc d, cắt ∆ tại hai điểm A và B sao cho
AB = 3 2 (CĐ.KA,A1,B và D. 2013 – Chuẩn) HD Giải
Gọi (C) là đường tròn cần viết phương trình và I là tâm của (C). Do M AB 3 2
I ∈ d ⇒ I (t;3 − t). Gọi H là trung điểm của AB, suy ra AH = = 2 2 2t −1 I
và IH = d(I,∆) = . Do đó: 2 2 2
IA = IH + AH = 2t − 2t + 5 2
Từ IM = IA , ta có được: 2 2
2t + 2t +1 = 2t − 2t + 5 ⇔ t = 1 ⇒ I (1;2) A H B 2 2
Bán kính của đường tròn (C) là R = IM = 5 .Vậy phương trình của (C) : (x − ) 1 + (y −2) = 5
Bài 8. Trong mặt phẳng với hệ tọa độ Oxy, cho tam giác ABC vuông tại A(−3;2) và có trọng tâm là 55
Chương III. Phương pháp tọa độ trong
mặt phẳng. 0916620899-0355334679
Tài liệu học tập Toán 10 GV. Lư Sĩ Pháp 1 1 G ;
. Đường cao kẻ từ đỉnh P 2
− ;0 . Tìm tọa độ điểm 3 3
A của tam giác ABC đi qua điểm ( ) B và C.
(CĐ.KA,A1,B và D. 2013 – Nâng cao) HD Giải 3 1
Gọi M là trung điểm của BC. Suy ra AM = AG ⇒ M A 2; − 2 2
Đường thẳng BC qua M và vuông góc với AP, nên có phương trình:
x − 2y − 3 = 0 P G
Tam giác ABC vuông tại A nên B và C thuộc đường tròn tâm M, bán kính 5 5 B M C MA = 2
x − 2y − 3 = 0 x = 7, y = 2
Tọa độ điểm B và C là nghiệm của hệ: 2 ( ⇔ x − 2)2 1 125 + y + = x = 3 − , y = −3 2 4
Vậy: B (7;2),C (−3; 3 − ) hoặc B(−3; 3 − ),C (7;2)
Bài 9. Trong mặt phẳng với hệ tọa độ Oxy, cho hình vuông ABCD. Gọi M là trung điểm cạnh BC, N là 11 1
điểm trên cạnh CD sao cho CN = 2ND. Giả sử M ; và đường thẳng 2 2 AN có phương trình
2x − y −3 = 0. Tìm tọa độ điểm A. (ĐH.KA,A1.2012 – Chuẩn ) HD Giải
Gọi H là giao điểm của AN và BD. Kẻ đường thẳng qua H và song song với
AB, cắt AD và BC lần lượt tại P và Q. A B
Đặt HP = x . Suy ra PD = x, AP = 3x v aø HQ = 3x .
Ta có QC = x , nên MQ = x . M H Do đó A
∆ HP = ∆HMQ , suy ra AH ⊥ HM . P Q
Hơn nữa, ta cũng có AH = HM D N C 3 10
Do đó AM = 2MH = 2d(M,(AN)) =
. Ta có: A ∈ AN ⇒ A(t;2t − 3) 2 3 10 2 2 11 7 45 MA =
⇔ t − + 2t − = 2
⇔ t − 5t + 4 = 0 ⇔ t = 1 hoaëc t = 4 2 2 2 2 Vậy: A(1; 1 − ) hoặc A(4;5) .
Bài 10. Trong mặt phẳng với hệ tọa độ Oxy, cho đường tròn (C): 2 2 x + y = 8
Viết phương trình chính tắc của elip (E), biết rằng (E) có độ dài trục lớn bằng 8 và (E) cắt (C) tại bốn
điểm tạo thành bốn đỉnh của một hình vuông. (ĐH.KA, A1.2012 – Nâng cao) HD Giải 2 2 x y
Phương trình chính tắc của (E) có dạng: +
= 1, với a > b > 0 và 2a = 8 ⇒ a = 4 . 2 2 a b
Do (E) và (C) cùng nhận Ox và Oy làm trục đối xứng và các giao điểm là các đỉnh của một hình vuông
nên (E) và (C) có một giao điểm với tọa độ dạng A(t;t),t > 0 . 4 4 16 2 2
A ∈(C) ⇔ t + t = 8 ⇒ t = 2 . Nên A(2;2) và 2
A(2; 2)∈ (E) ⇔ + = 1 ⇔ b = 2 16 b 3 2 2 x y
Vậy phương trình chính tắc của (E) là: + = 1 4 16 3
Bài 11. Trong mặt phẳng với hệ tọa độ Oxy, cho các đường tròn 2 2
(C ) : x + y = 4, 1 56
Chương III. Phương pháp tọa độ trong
mặt phẳng. 0916620899-0355334679
Tài liệu học tập Toán 10 GV. Lư Sĩ Pháp 2 2
(C ) : x + y −12x +18 = 0 và đường thẳng d : x − y − 4 = 0 . Viết phương trình đường tròn có tâm thuộc 2
(C ) , tiếp xúc với
(C ) tại hai điểm phân biệt 2 d và cắt 1
A và B sao cho AB vuông góc với d. (ĐH.KB.2012 – Chuẩn) HD Giải
(C ) có tâm là gốc tọa độ 1
O. Gọi I là tâm đường tròn (C) cần viết phương trình.
Ta có AB ⊥ OI mà AB ⊥ d nênOI / /d , do đó OI có phương trình y = x
Mặt khác, I ∈(C ) , nên tọa độ của 2
I thỏa mãn hệ phương trình: y = x x = 3 ⇔ ⇒ I(3;3) 2 2
x + y −12x +18 = 0 y = 3
Do (C) tiếp xúc với d nên (C) có bán kính R = d(I,d) = 2 2 2 2
Vậy phương trình đường tròn (C): (x −3) + (y −3) = 8.
Bài 12. Trong mặt phẳng với hệ tọa độ Oxy, Cho hình thoi ABCD có AC = 2BD và đường tròn tiếp xúc
với các cạnh của hình thoi có phương trình 2 2
x + y = 4 . Viết phương trình chính tắc của elip (E) đi qua A,
B, C, D của hình thoi. Biết A thuộc Ox. (ĐH.KB. 2012 – Nâng cao) HD Giải 2 2 x y y Giả sử (E) : +
= 1(a > b > 0). 2 2 a b
Hình thoi ABCD có AC = 2BD và A, B, C, D thuộc (E). Suy ra OA B H = 2OB. a
Không mất tính tổng quát, ta có thể xem A(a;0) và B A 0; . Gọi 2 H C O x
là hình chiếu của O trên AB.
Suy ra OH là bán kính của đường tròn (C): 2 2 x + y = 4 D 1 1 1 1 1 4 Ta có: = = + = + . Suy ra 2 a = 20 , do đó 2 2 2 2 2 4 OH OA OB a a 2 2 2 x y
b = 5 . Vậy: (E) : + = 1 20 5
Bài 13. Trong mặt phẳng với hệ tọa độ Oxy, Cho hình chữ nhật ABCD. Các đường thẳng AC và AD lần 1
lượt có phương trình là x + 3y = 0 và x − y + 4 = 0 ; đường thẳng BD đi qua điểm M − ;1 . Tìm tọa độ 3
các đỉnh của hình chữ nhật ABCD. (ĐH.KD. 2012 – Chuẩn) HD Giải x + 3y = 0 A B
Tọa độ của điểm A thỏa mãn hệ: ⇒ ( A 3 − ;1) M
x − y + 4 = 0
Gọi N là điểm thuộc AC sao cho MN // AD. Suy ra MN có phương K ∆ I 4
trình là: x − y + = 0 . 3 N
Vì N thuộc AC, nên tọa độ của điểm N D C 4 x − y + = 0 1
thỏa mãn hệ phương trình: 3 ⇒ N −1; 3 x + 3y = 0
Đường trung trực ∆ của MN đi qua trung điểm của MN và vuông góc với AD,
nên có phương trình là: x + y = 0 .
Gọi I, K lần lượt là giao điểm của ∆ với AC và AD. Suy ra tọa độ của điểm I thỏa mãn hệ: 57
Chương III. Phương pháp tọa độ trong
mặt phẳng. 0916620899-0355334679
Tài liệu học tập Toán 10 GV. Lư Sĩ Pháp x + y = 0 x + y = 0
⇒ I(0;0) và tọa độ của điểm K thỏa mãn hệ: ⇒ K( 2 − ;2) x + 3y = 0
x − y + 4 = 0
Do đó, ta có: AC = 2AI ⇒ C(3; 1
− ); AD = 2AK ⇒ D( 1
− ;3) ; BC = AD ⇒ B(1; 3 − ) .
Bài 14. Trong mặt phẳng với hệ tọa độ Oxy, cho đường thẳng d : 2x − y + 3 = 0 . Viết phương trình đường
tròn có tâm thuộc d, cắt trục Ox tại A và B, cắt trục Oy tại C và D sao cho AB = CD = 2. (ĐH.KD. 2012 – Nâng cao) HD Giải
Gọi I là tâm của đường tròn (C) cần viết phương trình. Do I ∈ d ⇒ I( ;t2t + 3)
Ta có: AB = CD ⇔ d(I,Ox) = d(I,Oy) ⇔ t = 2t + 3 ⇔ t = −1 hoaëc t = 3 − Với t = 1 − ta được I( 1
− ;1) nên d(I,Ox) = 1. Suy ra, bán kính của (C) là 2 2 R = 1 +1 = 2 . Do đó 2 2
(C) : (x +1) + (y −1) = 2
Với t = −3 ta được I( 3 − ; 3
− ) nên d(I,Ox) = 3 . Suy ra, bán kính của (C) là 2 2 R = 3 +1 = 10 . Do đó 2 2
(C) : (x + 3) + (y + 3) = 10 .
Bài 15. Trong mặt phẳng với hệ tọa độ Oxy, cho đường tròn 2 2
(C) : x + y − 2x − 4y +1 = 0 và đường thẳng
d : 4x − 3y + m = 0 . Tìm m để d cắt (C) tại hai điểm A, B sao cho 0
AIB = 120 , với I là tâm của (C).
(CĐ.KA,A1,B và D. 2012 – Chuẩn) HD Giải
Đường tròn (C) có tâm I(1;2) và bán kính R = 2
Gọi H là hình chiếu của I trên d. Khi đó, ta có: 0 IH = I . A cos 60 = 1 m − 2 m = 7 Do đó: = 1 ⇔
. Vậy m = 7;m = 3
− là giá trị cần tìm. 5 m = 3 −
Bài 16. Trong mặt phẳng với hệ tọa độ Oxy, cho tam giác ABC. Các đường thẳng BC, BB’,B’C’ lần lượt
có phương trình là y − 2 = 0, x − y + 2 = 0, x − 3y + 2 = 0 ; với B’, C’ tương ứng là chân đường cao kẻ từ B,
C của tam giác ABC. Viết phương trình các đường thẳng AB, AC. (CĐ.KA,A1,B và D. 2012 – Nâng cao). HD Giải
x − y + 2 = 0 x = 2 −
Tọa độ điểm B’ là nghiệm của hệ: ⇔ ⇒ B '(−2;0)
x − 3y + 2 = 0 y = 0
Đường thẳng AC đi qua B’ và vuông góc với BB’ nên AC có phương trình: x + y + 2 = 0
x − y + 2 = 0 x = 0
Tọa độ điểm B là nghiệm của hệ: ⇔ ⇒ B (0;2) y − 2 = 0 y = 2 x + y + 2 = 0 x = −4
Tọa độ điểm C là nghiệm của hệ: ⇔ ⇒ C (−4;2) y − 2 = 0 y = 2 4 2
Ta có: C '∈ B 'C ' ⇒ C '(3t − 2;t) và BC ' ⊥ CC ' nên suy ra: C '− ; hoặc C'( 2 − ;0) 5 5 4 2 Nếu C ' − ; thì đường thẳng x − y + = 5 5
AB có phương trình: 2 2 0 4 2 Nếu C ' − ; thì đường thẳng x − y + = 5 5
AB có phương trình: 2 0
Bài 17. Trong mặt phẳng tọa độ Oxy, cho đường thẳng ∆ : x + y + 2 = 0 và đường tròn 2 2
(C) : x + y − 4x − 2y = 0. Gọi I là tâm của (C), M là điểm thuộc ∆ . Qua M kẻ các tiếp tuyến MA và MB
đến (C) (A và B là các tiếp điểm). Tìm tọa độ điểm M, biết tứ giác MAIB có điện tích bằng 10.(ĐH.KA.2011 – Chuẩn) HD Giải 58
Chương III. Phương pháp tọa độ trong
mặt phẳng. 0916620899-0355334679
Tài liệu học tập Toán 10 GV. Lư Sĩ Pháp
Đường tròn (C) có tâm I (2; )
1 , bán kính R = IA = 5 Tứ giác MAIB có 0
MAI = MBI = 90 và MA = MB. Suy ra S = I .
A MA ⇒ MA = 2 5 MAIB
Ta có: M ∈ ∆ ⇒ M (t;−t − 2) t = 2 A
M = ⇔ (t − )2 + (t + )2 I 5 2 3 = 25 2
⇔ 2t + 2t −12 = 0 ⇔ t = −3 I Vậy: M (2; 4 − ) hoặc M (−3; ) 1 B M Bài 18. x y
Trong mặt phẳng tọa độ Oxy, cho elip (E) 2 2 : +
= 1. Tìm tọa độ các điểm 4 1
A và B thuộc (E), có
hoảnh độ dương sao cho tam giác OAB cân tại O và có diện tích lớn nhất.(ĐH. KA. 2011 – Nâng cao) HD Giải y
Gọi A(x;y). Do A, B thuộc (E) có hoành độ dương và tam A
giác OAB cân tại O, nên: B (x;−y),x > 0 . Suy ra: 2
AB = 2 y = 4 − x
Gọi H là trung điểm của AB, ta có: OH ⊥ AB và OH = x . H O x 1 1 1 CoâSi Diện tích: 2 2 S
= OH.AB = x a − x = x − x ≤ OAB ( 2 4 ) 1 2 2 2 B
Dấu " = " xảy ra khi và chỉ khi: 2 2
x = 4 − x ⇔ x = 2 2 2 2 2 Vậy: A 2; và B 2; − hoặc A 2; − và B 2; 2 2 2 2
Bài 19. Trong mặt phẳng tọa độ Oxy, cho đường thẳng ∆ : x − y − 4 = 0 và d : 2x − y − 2 = 0 . Tìm tọa độ
điểm N thuộc đường thẳng d sao cho đường thẳng ON cắt đường thẳng ∆ tại điểm M thỏa mãn
OM.ON = 8 .(ĐH.KB.2011 – Chuẩn) HD Giải
Ta có: N ∈ d ⇒ N ( ;
a 2a − 2) và M ∈∆ ⇒ M ( ; b b − 4). d
O, M, N cùng thuộc một đường thẳng khi và chỉ khi: ∆ ( − ) = ( − ) ⇔ ( − ) 4 4 2 2 = 4 a a b b a a b a a ⇔ b = 2 − a M 2 2 N
Theo giả thiết: OM ON = ⇔ ( 2 . 8
5a − 8a + 4) = 4(a−2) O ( 5 − =
⇔ a − 6a)(5a −10a +8) 2 5a 6a 0 2 2 = 0 ⇔ 2
5a −10a + 8 = 0 6
a = 0 hoaëc a = 6 2 ⇔ 5 . Vậy: N (0; 2 − ) hoặc N ; . 5 5 ptvn 1
Bài 20. Trong mặt phẳng tọa độ Oxy, cho tam giác ABC có đỉnh B ;1 . Đường tròn nội tiếp tam giác 2
ABC tiếp xúc với các cạnh BC, CA, AB tương ứng tại các điểm D, E, F. Cho D (3; )
1 và đường thẳng EF
có phương trình y − 3 = 0 . Tìm tọa độ điểm A, biết A có tung độ dương. (ĐH. KB. 2011 – Nâng cao) HD Giải 59
Chương III. Phương pháp tọa độ trong
mặt phẳng. 0916620899-0355334679
Tài liệu học tập Toán 10 GV. Lư Sĩ Pháp 5 Ta có: BD = ;0 ⇒ BD / / EF ⇒
tam giác ABC cân tại A 2
Suy ra, đường thẳng AD vuông góc với EF, có phương trình: x − 3 = 0
Mặt khác, ta có: F ∈ EF ⇒ F ( ;t3) . 2 1 25 t = −1 A Ta lại có: 2
BF = BD ⇔ t − + 2 = ⇔ 2 4 t = 2 Với t = 1
− ⇒ F (−1;3). Suy ra đường thẳng BF có phương trình: F E
4x + 3y − 5 = 0 7
Khi đó, A là giao điểm của AD và BF ⇒ A3;− , không thỏa yêu 3 B C
cầu(A có tung độ dương). D
Với t = 2 ⇒ F (2;3) . Suy ra đường thẳng BF có phương trình:
4x − 3y +1 = 0 13
Khi đó, A là giao điểm của AD và BF ⇒ A3; , thỏa yêu cầu( 3
A có tung độ dương). 13 Vậy, có: A3; 3
Bài 21. Trong mặt phẳng tọa độ Oxy, cho tam giác ABC có đỉnh B (−4; )
1 , trọng tâm G (1; ) 1 và đường
thẳng chứa đường phân giác trong của góc A có phương trình x − y −1 = 0 . Tìm tọa độ điểm A và C. (ĐH. KD. 2011 – Chuẩn) HD Giải Gọi D B
( ;xy) là trung điểm của AC, ta có: d
x + 4 = 3(x −1) 7 BD = 3GD ⇔ ⇒ D ;1
y −1 = 3(y −1) 2 I G
Mặt khác: Gọi E (x;y)là điểm đối xứng của B qua phân giác trong d : x D E
− y −1 = 0 của góc A và I là trung điểm của EB. A
C Ta có: BE ⊥ d ⇒ BE : x + y+3= 0
x − 4 y +1
Ta lại có: I là trung điểm của EB ⇒ I ; và I ∈ d . 2 2 x + y + 3 = 0
Nên tọa độ điểm E là nghiệm của hệ: − 4 +1 ⇒ E x y (2; 5 − ) − −1 = 0 2 2
Đường thẳng AC qua D và E, có phương trình: 4x − y −13 = 0
x − y −1 = 0
Do đó, tọa độ của A là nghiệm của hệ:
⇒ A(4;3). Suy ra: C (3;− ) 1
4x − y −13 = 0
Bài 22. Trong mặt phẳng tọa độ Oxy, cho điểm A(1;0) và đường tròn 2 2
(C) : x + y − 2x + 4y − 5 = 0 . Viết
phương trình đường thẳng ∆ cắt (C) tại hai điểm M và N sao cho tam giác AMN vuông cân tại A. (ĐH. KD. 2011 – Nâng cao). HD Giải
Đường tròn (C) có tâm I (1;−2) và bán kính R = 10 .
Ta có: IM = IN và AM = AN ⇒ AI ⊥ MN , suy ra phương trình ∆ có dạng: y = m . 60
Chương III. Phương pháp tọa độ trong
mặt phẳng. 0916620899-0355334679
Tài liệu học tập Toán 10 GV. Lư Sĩ Pháp
Hoành độ điểm M, N là nghiệm phương trình: 2 2
x − 2x + m + 4m − 5 = 0 (1)
(1) có hai nghiệm phân biệt khi và chỉ khi: 2
m + 4m − 6 < 0 (*); khi đó:
M (x ;m ,N x ;m và Theo Vi ét, ta có: 2
x + x = 2; x .x = m + 4m − 5 1 ) ( 2 ) 1 2 1 2
Mặt khác: AM ⊥ AN ⇔ AM.AN = 0 ⇔ (x − ) 1 (x − ) 2
1 + m = 0 ⇔ x x − (x + x ) 2 2
+ m +1 = 0 ⇔ 2m + 4m − 6 = 0 1 2 1 2 1 2 m = 1 ⇔
(thỏa (*)). Vậy, phương trình ∆ : y = 1 hoặc y = 3 − . m = 3 −
Bài 23. Trong mặt phẳng tọa độ Oxy, cho đường thẳng d : x + y + 3 = 0 . Viết phương trình đường thẳng đi qua điểm A(2; 4
− ) và tạo với đường thẳng d một góc bẳng 0 45 .(CĐ. 2011 – Chuẩn) HD Giải
Gọi ∆ là đường thẳng qua A và có vectơ pháp tuyến n = ( ; a b) ∆
Phương trình đường thẳng ∆ : ( a x − 2) + ( b y + 4) = 0 , với 2 2 a + b ≠ 0
Đường thẳng d : x + y + 3 = 0 , có vectơ pháp tuyến n = (1;1) d a + b 2
Theo giả thiết: cos(d;∆) 0 2 2 = cos45 ⇔ =
⇔ a + b = a + b ⇔ ab = 0 2 2 2 2. a + b
Với a = 0 , ta có phương trình ∆ : y + 4 = 0
Với b = 0 , ta có phương trình ∆ : x − 2 = 0
Bài 24. Trong mặt phẳng tọa độ Oxy, cho tam giác ABC có phương trình các cạnh là
AB : x + 3y − 7 = 0, BC : 4x + 5y − 7 = 0,CA : 3x + 2y − 7 = 0 . Viết phương trình đường cao kẻ từ đỉnh A
của tam giác ABC. (CĐ. 2011 – Nâng cao). HD Giải
x + 3y − 7 = 0
Tọa độ điểm A thỏa mãn hệ phương trình: ⇒ A(1;2) 3
x + 2y − 7 = 0
Gọi AH là đường cao kẻ từ A, suy ra: AH ⊥ BC ⇒ AH có vectơ pháp tuyến n = (5; 4 − )
Vậy, phương trình đường cao AH : 5(x − )
1 − 4(y −2) = 0 ⇔ 5x − 4y +3 = 0
Bài 25. Trong mặt phẳng tọa độ Oxy, cho hai đường thẳng d : 3x + y = 0 và d : 3x − y = 0 . Gọi ( 1 2 T) là
đường tròn tiếp xúc với d tại d tại hai điểm 1 A, cắt 2
B và C sao cho tam giác ABC vuông tại B. Viết 3
phương trình của (T), biết tam giác ABC có diện tích bằng và điểm 2
A có hoành độ dương.(ĐH. KA. 2010 – Chuẩn) HD Giải 3. 3 −1.1 1
Ta có: d và d cắt nhau tại cos d ;d = = và tam giác 1 2 O, ( 1 2) OAB 3 +1. 3+1 2
vuông tại O, do đó: 0 0
AOB = 60 ⇒ BAC = 60 . 1 3 3 3 Ta lại có: 0 S = AB.AC sin 60 = OA OA = OA ABC ( 0 .sin 60 )( 0 .t an60 ) 2 2 4 8 3 4 Theo giả thiết: S = . Suy ra: 2 OA = ABC 2 3 3x + y = 0 3
Tọa độ A(x;y),x > 0, thỏa hệ: ⇒ A ; 1 4 − 2 2 x + y = 3 3 61
Chương III. Phương pháp tọa độ trong
mặt phẳng. 0916620899-0355334679
Tài liệu học tập Toán 10 GV. Lư Sĩ Pháp
Đường thẳng AC qua A và vuông góc với d , suy ra x − y − = 1
AC có phương trình: 3 3 4 0
3x − y = 0 −2
Tọa độ điểm C ( ;xy), thỏa hệ: ⇒ C ; 2 −
3x − 3y − 4 = 3 1 3 −
Đường tròn (T) có đường kính AC, suy ra tâm của (T) là I ;− và bán kính 2 3 2 2 2 1 3
R = IA = 1 . Vậy, phương trình (T): x + + y + = 1 2 3 2
Bài 26. Trong mặt phẳng tọa độ Oxy, cho tam giác ABC cân tại A có đỉnh A(6;6) ; đường thẳng đi qua
trung điểm của các cạnh AB và AC có phương trình: x + y − 4 = 0 . Tìm tọa độ điểm B và C, biết điểm E (1; 3
− ) nằm trên đường cao đi qua đỉnh C của tam giác đã cho (ĐH. KA.2010 – Nâng cao) HD Giải
Gọi H là trung điểm của BC, D là trung điểm của AH, ta có: AH ⊥ BC hay AH ⊥ d ⇒ AH : x − y = 0 .
x + y − 4 = 0
Do đó tọa độ D( ;
x y) thỏa mãn hệ:
⇒ D (2;2) ⇒ H ( 2 − ; 2 − ) x − y = 0
Đường thẳng BC đi qua H và song song với d, suy ra BC có phương trình: x + y + 4 = 0
Điểm B và C thuộc đường thẳng BC và B, C đối xứng với nhau qua H ( 2
− ;−2), do đó tọa độ B, C có dạng: B(t;−4 −t),C( 4 − − ;tt) A
Điểm E (1;−3)nằm trên đường cao đi qua đỉnh C của tam giác ABC, suy ra: D d A . B CE E
= 0 ⇔ (t − )( + t) +(− − t)(− −t) 2 6 5 10 3
= 0 ⇔ 2t +12t = 0 ⇔ t = 0 hoặc t = −6 B H C
Vậy, B(0;−4),C( 4
− ;0) hoặc B(−6;2),C(2; 6 − )
Bài 27. Trong mặt phẳng tọa độ Oxy, cho tam giác ABC vuông tại A, có đỉnh C (−4; ) 1 , phân giác trong
góc A có phương trình: x + y − 5 = 0. Viết phương trình đường thẳng BC, biết diện tích tam giác ABC
bằng 24 và đỉnh A có hoành độ dương.(ĐH. KB.2010 – Chuẩn) HD Giải
Gọi D là điểm đối xứng của C (−4; )
1 qua d : x + y − 5 = 0 , suy ra, CD có D
x − 4 y +1
phương trình: x − y + 5 = 0. Và I là trung điểm CD, nên I ; B 2 2 I
Do đó, tọa độ điểm D (x;y) thỏa mãn hệ: C A x − y + 5 = 0 −4 +1 ⇒ D x y (4;9) + − 5 = 0 2 2
Phương trình đường tròn, đườnh kính CD là (C): x + (y − )2 2 5 = 32
Điểm A thuộc đường tròn đường kính CD, nên A = (C) ∩ d x + y − 5 = 0
Do đó tọa độ A(x;y),x > 0 thỏa mãn hệ: + ( ⇒ A x y − 5)2 4;1 2 ( ) = 32 1
Suy ra: AC = 8 . Ta lại có: S
= 24 ⇔ AB.AC = 24 ⇔ AB = 6 ABC 2
Mặt khác: B thuộc AD: x − 4 = 0 , suy ra tọa độ điểm B (4;y) và có: AB = ( y − ) 2 0;
1 ⇒ AB = (y −1) 62
Chương III. Phương pháp tọa độ trong
mặt phẳng. 0916620899-0355334679
Tài liệu học tập Toán 10 GV. Lư Sĩ Pháp 2 y = 7 Do đó: (y − ) 1 = 36 ⇔ ⇒
B (4;7) hoaëc B(4; 5 − ) y = 5 −
d là phân giác trong của góc A, nên AB và AD cùng hướng, suy ra B (4;7)
Vậy, đường thẳng BC có phương trình: 3x − 4y +16 = 0 2 2 Bài 28. x y
Trong mặt phẳng tọa độ Oxy, cho điểm A(2; 3) và elip (E): + =1. Gọi F và F là tiêu 3 2 1 2
điểm của (E) ( F có hoành độ âm); AF với ( 1
M là giao điểm có tung độ dương của đường thẳng 1 E); N là
điểm đối xứng của F qua ANF .(ĐH. KB.2010 – 2
M. Viết phương trình đường tròn ngoại tiếp tam giác 2 Nâng cao) HD Giải 2 2 x y ( y E) : +
= 1⇒ F −1;0 ,F 1;0 N 1 ( ) 2 ( ) 3 2 A M x +1 y
Đường thẳng AF có phương trình: = . 1 3
M là giao điểm có tung 3 O F F 1 2 x
độ dương của đường thẳng AF với ( M ; x y , y > 0 1
E), nên tọa độ điểm ( ) 2 2 x y + = 1 3 2 2 3 2 3 thỏa mãn hệ: .Suy ra M 1;
⇒ MA = MF = x 2 +1 y = 3 3 3 3
Do N là điểm đối xứng của F qua
MF = MN , suy ra: MF = MN = MA 2 M nên 2 2
Do đó đường tròn (T) ngoại tiếp tam giác ANF là đường tròn tâm MF 2 M, bán kính 2 2 2 2 3 4
Vậy, phương trình (T): (x − ) 1 + y − = 3 3
Bài 29. Trong mặt phẳng tọa độ Oxy, cho tam giác ABC có đỉnh A(3;−7) , trực tâm là H (3;− ) 1 , tâm
đường tròn ngoại tiếp là I ( 2
− ;0). Xác định tọa độ điểm C, biết C có hoành độ dương. (ĐH. KD.2010 – Chuẩn) HD Giải
Đường tròn ngoại tiếp tam giác ABC có tâm I ( 2
− ;0) và bán kính IA nên có
phương trình: (x − )2 2 2 + y = 74.
Phương trình AH: x = 3 và BC ⊥ AH , suy ra phương trình BC có dạng: y = ( a a ≠ 7
− do BC không đi qua A)
Do đó hoành độ B, C thỏa mãn phương trình: (x − )2 2 2 2
2 + a = 74 ⇔ x + 4x + a − 70 = 0(1)
Phương trình (1) có hai nghiệm phân biệt, trong đó có ít nhất một nghiệm
dương khi và chỉ khi: a < 70
Do C có hoành độ dương, nên B ( 2 − − − a a) C( 2 2 74 ; , 2
− + 74 − a ;a)
Ta có: AC ⊥ BH ⇒ AC BH = ⇔ ( 2 − a − ) ( 2 . 0 74
5 . 74 − a + 5)+(a+7)(−1−a) = 0 2
⇔ a + 4a − 21 = 0 ⇔ x = 3 (thỏa mãn) hoặc x = 7 − (loại). Vậy: C (−2+ 65;3) 63
Chương III. Phương pháp tọa độ trong
mặt phẳng. 0916620899-0355334679
Tài liệu học tập Toán 10 GV. Lư Sĩ Pháp
Bài 30. Trong mặt phẳng tọa độ Oxy, cho điểm A(0;2) và ∆ là đường thẳng đi qua O. Gọi H là hình
chiếu vuông góc của A trên ∆ . Viết phương trình đường thẳng ∆ , biết khoảng cách từ H đến trục hoành
bằng AH. (ĐH. KD.2010 – Nâng cao). HD Giải y
Gọi tọa độ H là ( ;
a b), ta có: AH = a + (b − )2 2 2
2 và d (H;Ox) = b . Do đó: A ∆ a + (b − )2 2 2 2 = b H
Do H thuộc đường tròn đường kính OA, nên: a + (b − )2 2 1 = 1 O x
Do vậy, tọa độ điểm H thỏa mãn hệ: 2 2 a 4b 4 0 − + = a = 4b − 4 ⇔ 2 2 2
a + b − 2b = 0
4b − 4 + b − 2b = 0(1) b = −1+ 5 Giải(1): 2
b + 2b − 4 = 0 ⇔ . Với 2 b = 1
− − 5 ⇒ a = −8− 4 2 (khoâng thoûa) b = −1− 5 Suy ra: H 2
5 − 2; 5 −1 hoặc H −2 5 − 2; 5 −1
Vậy, phương trình đường thẳng ∆ : ( 5 − )1x −2 5 −2y = 0 hoặc ( 5 − )1x + 2 5 −2y = 0
Bài 31. Trong mặt phẳng tọa độ Oxy, Cho hình chữ nhật ACBD có điểm I (6;2) là giao điểm của hai
đường chéo AC và BD. Điểm M (1;5) thuộc đường thẳng AB và trung điểm E của CD thuộc đường thẳng
∆ : x + y − 5 = 0. Viết phương trình đường thẳng AB. (ĐH. KA.2009 – Chuẩn) HD Giải
Gọi N đối xứng với M qua I, suy ra N A M B
(11;− )1 và N thuộc đường thẳng CD
E ∈ ∆ ⇒ E (x;5− x),IE = (x − 6;3− x) và NE = (x −11;6 − x) I
E là trung điểm của CD ⇒ IE ⊥ NE ⇔ IE.NE = 0 D ( =
⇔ x − )(x − )+ ( − x)( − x) x 6 6 11 3 6 = 0 ⇔ E N C x = 7
Với x = 6 ⇒ IE = (0; 3
− ), đường thẳng AB qua điểm M và nhận vectơ IE
làm vectơ pháp tuyến. Vậy, phương trình AB: y − 5 = 0
Với x = 7 ⇒ IE = (1; 4
− ) , đường thẳng AB qua điểm M và nhận vectơ IE làm vectơ pháp tuyến. Vậy,
phương trình AB: x − 4y +19 = 0.
Bài 32. Trong mặt phẳng tọa độ Oxy, cho đường tròn 2 2
(C) : x + y + 4x + 4y + 6 = 0 và đường thẳng
∆ : x + my − 2m + 3 = 0, với m là tham số thực. Gọi I là tâm của đường tròn (C). Tìm m để ∆ cắt (C) tại
hai điểm phân biệt A và B sao cho diện tích tam giác IAB lớn nhất. (ĐH. KA.2009 – Nâng cao) HD Giải
Đường tròn (C) có tâm I ( 2 − ; 2
− ) và bán kính R = 2 1 1
Diên tích tam giác IAB: 2 S = I .
A IB sin AIB ≤ R = 1. ⊥ 2 2
S lớn nhất khi và chỉ khi IA IB m = 0
−2 − 2m − 2m R + 3 Khi đó, khoảng cách từ
I đến ∆ : d(I , ∆) = ⇔ = 1 ⇔ (1− 4m)2 2 = 1+ m ⇔ 8 2 2 1 + m m = 15 5
Bài 33. Trong mặt phẳng tọa độ Oxy, cho đường tròn (C) : (x − 2)2 2
+ y = và hai đường thẳng 4 64
Chương III. Phương pháp tọa độ trong
mặt phẳng. 0916620899-0355334679
Tài liệu học tập Toán 10 GV. Lư Sĩ Pháp
∆ : x − y = 0,∆ : x − 7y = 0 . Xác định tâm
(C ) ; biết (C ) tiếp xúc 1 2
K và tính bán kính của đường tròn 1 1
với các đường thẳng ∆ ,∆ và 1 2
K thuộc đường tròn (C)(ĐH.KB.2009 – Chuẩn) HD Giải a − b a − 7b Gọi K (a b) 2 2 5
; ;K ∈(C) ⇔ (a − 2) + b = (1); (C ) tiếp xúc ∆ ,∆ ⇔ = (2) 4 1 1 2 2 5 2 5 ( a 2 − 2) + b2 5 = b = −2a 4 (a 2 2) b2 − + = 4
5(a − b) = a − 7b 2 a2 5 − 20a +16 = 0 Từ (1) và (2), ta có: ⇔ ⇔ a b a 7b − − 2 2 5 a = 2b ( a 2) b = − + = 2 5 2 4 2 b2 5 − 40b +16 = 0
5(a − b) = 7b − a voâ nghieäm 8 8 4 a − b 2 2 a = ⇔ 5
. Vậy, K ; , bán kính của (C ) là R = = 1 1 5 5 2 5 4 b = 5
Bài 34. Trong mặt phẳng tọa độ Oxy, cho tam giác ABC cân tại A có đỉnh A( 1
− ;4) và hai đỉnh B, C
thuộc đường thẳng ∆ : x − y − 4 = 0 . Xác định tọa độ các điểm B và C, biết diện tích tam giác ABC bằng
18. (ĐH.KB.2009 – Nâng cao) HD Giải A
Gọi H là hình chiếu của A trên ∆ , suy ra H là trung điểm của BC.
Ta có: AH = d (A BC) 9 , =
. Diện tích tam giác ABC: 2 1 2 = . S S AH BC ⇒ BC = = 4 2 2 AH B H C 2 BC Tam giác 2 97
ABC cân tại A, nên có: AB = AC = AH + = 4 2 11 3 2 2 97 ( x = +1) + ( − 4) x = x y = Tọa độ điểm 2 2
B và C là nghiệm của hệ: 2 ⇔ hoặc . Vậy, 3 5
x − y − 4 = 0 y = y = − 2 2 11 3 3 5 3 5 11 3 B ; ,C ;−
hoặc B ;− ,C ; 2 2 2 2 2 2 2 2
Bài 35. Trong mặt phẳng tọa độ Oxy, cho tam giác ABC có M (2;0) là trung điểm của cạnh AB. Đường
trung tuyến và đường cao qua đỉnh A lần lượt có phương trình là 7x − 2y − 3 = 0 và 6x − y − 4 = 0 . Viết
phương trình đường thẳng AC. (ĐH.KD.2009 – Chuẩn) HD Giải 7x A − 2y − 3 = 0
Tọa độ điểm A thỏa hệ: ⇒ A(1;2)
6x − y − 4 = 0 M
M là trung điểm của AB, suy ra B (3; 2 − )
Đường thẳng BC qua B và vuông góc có AH, nên có phương trình: B H N C x + 6y + 9 = 0
Tọa độ trung điểm N của đoạn thẳng BC thỏa hệ: 65
Chương III. Phương pháp tọa độ trong
mặt phẳng. 0916620899-0355334679
Tài liệu học tập Toán 10 GV. Lư Sĩ Pháp
x + 6y + 9 = 0 3 ⇒ N 0;− 7
x − 2y − 3 = 0 2
Ta có: MN là đường trung bình của tam giác ABC nên ⇒ AC = 2MN = ( 4 − ;−3)
Vậy, phương trình đường thẳng AC: 3x − 4y + 5 = 0 3
Cách khác: Tìm được tọa độ điểm B (3; 2
− ) và N 0;− . Ta tìm được tọa độ điểm C( 3 − ;− ) 1 do 2 N là
trung điểm của BC. Viết được phương trình đường thẳng AC.
Bài 36. Trong mặt phẳng tọa độ Oxy, cho đường tròn 2 2
(C) : (x −1) + y = 1. Gọi I là tâm của (C). Xác
định tọa độ điểm M thuộc (C) sao cho 0
IMO = 30 (ĐH.KD.2009 – Nâng cao) HD Giải
Đường tròn (C) có tâm I (1;0) và bán kính R =1 Gọi điểm M ( ;
a b) . Do M ∈ C ⇒ (a − )2 2 ( )
1 + b =1; O ∈(C) ⇒ IO = IM = R = 1 và 0 IMO = 30 nên suy
ra tam giác IMO cân tại I và 0 IOM = 120 y M
Áp dụng định lí Co6sin, có: 2 2 2 0 2 2
OM = OI + IM − 2OI.IM.cos120 ⇔ a + b = 3 300 3 x O I ( − )2 2 1 + = 1 a = a b 2
Tọa độ điểm M là nghiệm của hệ: ⇔ . 2 2 a + b = 3 3 b = ± 2 3 3 Vậy: M ; ± 2 2
Bài 37. Trong mặt phẳng tọa độ Oxy, cho tam giác ABC có đỉnh C ( 1 − ; 2
− ), đường trung tuyến kẻ từ A và
đường cao kẻ từ B lần lượt có phương trình là 5x + y − 9 = 0 và x + 3y − 5 = 0 . Tìm tọa độ các đỉnh A và
B.(CĐ.2009 – Chuần). HD Giải
Đường thẳng AC qua điể C và vuông góc với BH: x + 3y − 5 = 0 nên A
có phương trình: 3x − y +1 = 0 . H
x − 3y +1 = 0
Tọa độ điểm A thỏa mãn hệ: ⇒ A(1;4)
5x + y − 9 = 0
Điểm B thuộc đường thẳng BH và trung điểm M của BC thuộc đường thẳng AM. B M
C Tọa độ điểm B thỏa mãn hệ:
x + 3y − 5 = 0
x −1 y − 2
⇒ B (5;0).Vậy: A(1;4) và B(5;0). 5 + − 9 = 0 2 2
Bài 38. Trong mặt phẳng tọa độ Oxy, cho đường thẳng ∆ : x − 2y − 3 = 0 và ∆ : x + y +1 = 0 . Tìm tọa độ 1 2 1
điểm M thuộc đường thẳng ∆ sao cho khoảng cách từ điểm ∆ bằng .(CĐ.2009 1
M đến đường thẳng 2 2 – Nâng cao). HD Giải
Ta có: M ∈ ∆ ⇒ M 2t + 3;t 1 ( ) 66
Chương III. Phương pháp tọa độ trong
mặt phẳng. 0916620899-0355334679
Tài liệu học tập Toán 10 GV. Lư Sĩ Pháp 2t + 3+ t +1
Khoảng cách từ M đến ∆ là: d (M,∆ = 2 ) 2 2 t = −1 1 3t + 4 1
Theo giả thiết, ta có: d (M, ∆ = ⇔ = ⇔ 2 ) 5 2 2 2 t = − 3 1 5 Vậy: M (1;− ) 1 hoặc M − ;− 3 3
Bài 39. Trong mặt phẳng với hệ tọa độ Oxy, hãy viết phương trình chính tắc của (E) biết rằng (E) có tâm 5 sai bằng
và hình chữ nhật cơ sở của ( 3
E) có chu vi bằng 20.(ĐH.CĐ KA.2008). HD Giải 2 2 x y
Gọi phương trình chính tắc của (E) là: +
= 1,a > b > 0 2 2 a b c 5 = a 2 a = 3 2 2 x y
Theo giả thiết, ta có: 2(2a + 2b) = 20 ⇔
. Vậy, phương trình chính tắc của (E) là: + = 1 b = 2 9 4 2 2 2
c = a − b
Bài 40. Trong mặt phẳng với hệ tọa độ Oxy, hãy xác định tọa độ đỉnh C của tam giác ABC, biết rằng hình
chiếu vuông góc của C trên đường thẳng AB là điểm H ( 1 − ;− )
1 , đường phân giác trong góc A có phương
trình: x − y + 2 = 0 và đường cao kẻ từ B có phương trình: 4x + 3y −1 = 0 . (ĐH.CĐKB.2008). HD Giải C
Kí hiệu: d : x − y + 2 = 0 và d : 4x + 3y −1 = 0 1 2 K
Gọi H '(x; y), khi đó H ' thuộc đường thẳng AC và I là hình chiếu của d H' 1 H ' lên d nên HH . 1
I là trung điểm của ' I
Đường thẳng HH ' qua H và vuông góc với d nên có phương trình: d2 1 x + y + 2 = 0 B H A
x + y + 2 = 0 . Tọa độ điểm I là nghiệm của hệ: ⇒ I (−2;0).
x − y + 2 = 0 Suy ra: H '( 3 − ; ) 1
Đường thẳng AC qua H ' và vuông góc với d nên có phương trình: 3x − 4y +13 = 0 2 3
x − 4y +13 = 0
Tọa độ điểm A là nghiệm của hệ: ⇒ A(5;7)
x − y + 2 = 0
Đường thẳng CH qua H và vuông góc với HA nên có phương trình: 3x + 4y + 7 = 0 3
x + 4y + 7 = 0 10 3
Tọa độ điểm C là nghiệm của hệ: ⇒ C − ; 3
x − 4y +13 = 0 3 4
Bài 41. Trong mặt phẳng với hệ tọa độ Oxy, cho parabol 2
(P) : y = 16x và điểm A(1;4). Hai điểm phân
biệt B, C (B và C khác A) di động trên (P) sao cho 0
BAC = 90 . Chứng minh rẳng đường thẳng BC luôn đi
qua một điểm cố định.(ĐH.CĐKD.2008) HD Giải 2 2 b c
Do B,C ∈(P), B khác C, B và C khác A nên B
;b,C ;c,( ,bc∉ℝ,b ≠ 4,c ≠ 4) 16 16 67
Chương III. Phương pháp tọa độ trong
mặt phẳng. 0916620899-0355334679
Tài liệu học tập Toán 10 GV. Lư Sĩ Pháp 2 2 b c Ta có: AB =
−1;b − 4, AC = −1;c − 4 . Góc 0 BAC = 90 nên: 16 16 2 2 . = 0 b ⇔ −1 c AB AC
−1 + (b − 4)(c − 4) = 0 ⇔ 272 + 4(b + c)+ bc = 0 (1) 16 16 2 c x − y − c
Phương trình đường thẳng 16 BC: =
⇔ 16x − b + c y + bc = 0 (2) 2 2 ( ) b c b − c − 16 16
Lấy (1) trừ (2), ta được: 272 −16x + (b + c)(4 + y) = 0 272 −16x = 0 x = 17
Để tìm điểm cố định đường thẳng BC đi qua, ta giải hệ: ⇔ y + 4 = 0 y = −4
Vậy, BC luôn đi qua điểm cố định M (17;−4)
Bài 42. Trong mặt phẳng với hệ tọa độ Oxy, tìm điểm A thuộc trục hoành và điểm B thuộc trục tung sao
cho A và B đối xứng với nhau qua đường thẳng d : x − 2y + 3 = 0 (CĐ.2008) HD Giải
Ta có: A ∈Ox,B ∈Oy ⇒ A ( ;
a 0),B(0;b), AB = (− ; a b) a b
Đường thẳng d có vectơ chỉ phương là u = (2; )
1 . Gọi I là trung điểm của AB ⇒ I ; 2 2 −2a + b = 0 A . B u = 0 a = 2
A, B đối xứng với nhau qua d khi và chỉ khi: ⇔ a ⇔ I ∈ d − b + 3 = 0 b = 4 2
Vậy: A(2;0),B(0;4)
Bài 43. Trong mặt phẳng với hệ tọa độ Oxy, cho tam giác ABC có A(0;2),B(−2; 2 − ) và C(4; 2 − ) . Gọi
H là chân đường cao kẻ từ B; M và N lần lượt là trung điểm của các cạnh AB và BC. Viết phương trình
đường tròn đi qua các điểm H, M, N.(ĐH.CĐKA.2007) HD Giải
Ta có: M và N lần lượt là trung điểm của các cạnh AB và BC nên M (−1;0),N (1;−2)
Gọi H (x;y). Ta có: AC = (4;−4) , phương trình đường thẳng AC : 4x + 4y −8 = 0 .
Đường cao BH qua B và vuông góc với AC nên có phương trình: 4x − 4y = 0 . 4x − 4y = 0
Tọa độ điểm H thỏa hệ: ⇒ H (1; ) 1
4x + 4y − 8 = 0
Gọi phương trình đường tròn (C) cần tìm có dạng: 2 2
x + y − 2ax − 2by + c = 0(1) 1 a = 2 2a + c = 1 − 1
Do M, N, H ∈(C) nên ta có: −2a + 4b + c = 5 − ⇔ b = − 2 2
− a − 2b + c = 2 − c = 2 − Vậy: 2 2
(C) : x + y − x + y − 2 = 0
Bài 44. Trong mặt phẳng với hệ tọa độ Oxy, cho điểm A(2;2) và các đường thẳng
d : x + y − 2 = 0,d : x + y − 8 = 0 . Tìm tọa độ các điểm
d và d sao cho tam giác 1 2
B và C lần lượt thuộc 1 2
ABC vuông cân tại A.(ĐH.CĐKB.2007) 68
Chương III. Phương pháp tọa độ trong
mặt phẳng. 0916620899-0355334679
Tài liệu học tập Toán 10 GV. Lư Sĩ Pháp HD Giải
Vì B ∈ d ,C ∈ d nên B ( ;
b 2 − b),C ( ;
c 8 − c). Từ giả thiết, ta có hệ: 1 2 −1 − 4 = 2 AB.AC = 0 − 4 − + 2 = 0 (b )(c bc b c ) ⇔ ⇔ 2 2 2 2 AB = AC
b − 2b = c − c 8 +18 (b− )1 −(c−4) =3 2 xy = 2 y = (x ≠ 0) x = 2 x = −2
Đặt x = b −1; y = c − 4 , ta có hệ: ⇔ x ⇔ hoặc 2 2
x − y = 3 y = 1 y = 1 4 2 −
x − 3x − 4 = 0 Vậy: B (3;− )
1 ,C (5;3) hoặc B( 1 − ;3),C(3;5) 2 2
Bài 45. Trong mặt phẳng với hệ tọa độ Oxy, cho đường tròn (C) :(x − )
1 + (y + 2) = 9 và đường thẳng
d : 3x − 4y + m = 0 . Tìm m để trên d có duy nhất một điểm P mà từ đó kẻ được hai tiếp tuyến PA, PB tới
(C) (A, B là các tiếp điểm) sao cho tam giác PAB đều.(ĐH.CĐKD.2007) HD Giải 2 2
Đường tròn (C) :(x − )
1 + (y + 2) = 9 , có tâm I (1; 2
− ) và bán kính R = 3 A
Tam giác PAB đều nên 0 0
APB = 60 ⇒ API = 30 ⇒ tam giác PAI là nửa tam I giác đều
Do đó: IP = 2IA = 2R = 6 hay P thuộc đường tròn P
(C') tâm I, bán kính R ' = 6 B d
Như vậy, trên d có duy nhất một điểm P thỏa mãn yêu cầu bài toán khi và chỉ m +11 m = 19
khi d tiếp xúc với (C') tại P ⇔ d(I,d) = R' ⇔ = 6 ⇔ 5 m = −41
Vậy, có hai giá trị m thỏa yêu cầu m = 19 và m = 4 − 1
Bài 46. Trong mặt phẳng với hệ tọa độ Oxy, cho các đường thẳng: d : x + y + 3 = 0 , d : x − y − 4 = 0 và 1 2
d : x − 2y = 0 . Tìm tọa độ điểm
d sao cho khoảng cách từ d bằng hai 3 M nằm trên 3
M đến đường thẳng 1
lần khoảng cách từ M đến đường thẳng d . (ĐH.CĐKA.2006) 2 HD Giải
Vì điểm M ∈ d ⇒ M 2 ; y y 3 ( ) 2y + y + 3 3y + 3 2y − y − 4 y − 4
Ta có: d (M,d = = ;d M,d = = 1 ) ( 2 2 2 ) 2 2 1 +1 2 1 + ( 1 − ) 2 3y + 3 y − 4 y = 1 − 1
Theo giả thiết, ta có: d (M,d = 2d M,d ⇔ = 2 ⇔ 1 ) ( 2) 2 2 y = 1 Vậy: M (−22; 1 − ) 1 hoặc M (2; ) 1
Bài 47. Trong mặt phẳng với hệ tọa độ Oxy, cho đường tròn (C) 2 2
: x + y − 2x − 6y + 6 = 0 và điểm M (−3; )
1 . Gọi T và T là các tiếp tuyến kẻ từ 1 2
M đến (C). Viết phương trình đường thẳng T T .(ĐH.CĐKB.2006) 1 2 HD Giải Cách 1. Đường tròn (C) 2 2
: x + y − 2x − 6y + 6 = 0 , có tâm I (1;3) và bán kính R = 2 . Ta có: MI = 2 5 > R nên
M nằm ngoài (C). T ∈(C) T ∈(C)
Nếu T (x ;y là tiếp điểm của tiếp tuyến kẻ từ ⇒ 0 0 )
M đến (C) thì: MT ⊥ IT MT.IT = 0 69
Chương III. Phương pháp tọa độ trong
mặt phẳng. 0916620899-0355334679
Tài liệu học tập Toán 10 GV. Lư Sĩ Pháp
Ta có: MT = (x + 3;y −1 ,IT = x −1;y −3 0 0 ) ( 0 0 ) 2 2 2 2
x + y − 2x − 6y + 6 = 0
x + y − 2x − 6y + 6 = 0 Do đó: 0 0 0 0 0 0 0 0 ( ⇔
⇒ 2x + y − 3 = 0 (1)
x + 3 x −1 + y −1 y − 3 = 0 x
+ y + 2x − 4y = 0 0 )( 0 ) ( 0 )( 0 ) 2 2 0 0 0 0 0 0
Vậy, tọa độ các tiếp điểm T và T của tiếp tuyến kẻ từ 1 2
M đến (C) đếu thỏa mãn đẳng thức (1). Do đó,
phương trình đường thẳng T T : 2x + y − 3 = 0 1 2 Cách 2.
Đường tròn (C) 2 2
: x + y − 2x − 6y + 6 = 0 , có tâm I (1;3) và bán kính R = 2 .
Ta có: MI = 2 5 > R nên M nằm ngoài (C). Do đó từ M kẻ được hai tiếp tuyến MT và MT đến đường 1 2 tròn (C).
Gọi k là hệ số góc của đường thẳng ∆ đi qua điểm M (−3; )
1 thì phương trình đường thẳng ∆ là:
y −1 = k(x + 3) ⇔ kx − y + 3k +1 = 0 . Để ∆ là tiếp tuyến của đường tròn (C) k = 0 ( k − d I , ) 2 1 2 2 R 1 2k 1 k 1 3k 4k 0 ⇔ ∆ = ⇔ = ⇔ − = + ⇔ − = ⇔ 4 2 k +1 k = 3
Với k = 0 , ta có phương trình tiếp tuyến ∆ : y −1 = 0 1 3
Với k = , ta có phương trình tiếp tuyến ∆ : 4x − 3y +15 = 0 4 2 3 21
Khi đó: T = ∆ ∩ (C) ⇒ T 1;1 ,T = ∆ ∩ (C) ⇒ T − ; 1 1 1 ( ) 2 2 2 5 5
Vậy, phương trình đường thẳng T T : 2x + y − 3 = 0 1 2
Bài 48. Trong mặt phẳng với hệ tọa độ Oxy, cho đường tròn (C) 2 2
: x + y − 2x − 2y +1 = 0 và đường
thẳng d : x − y + 3 = 0 . Tìm tọa độ điểm M nằm trên d sao cho đường tròn tâm M có bán kính gấp đôi bán
kính đường tròn (C), tiếp xúc ngoài với đường tròn (C). (ĐH.CĐKD.2006) HD Giải
Đường tròn (C) 2 2
: x + y − 2x − 2y +1 = 0 có tâm I (1; ) 1 và bán kính R = 1. A
Vì M ∈ d ⇒ M 2R R
(x;x +3). Đườn tròn tâm M, tiếp xúc ngoải với M I
đường tròn (C) tại A thì MI =MA + IA. Trong đó IA là bán kính
đường tròn (C) và MA là bán kính đường tròn tâm M. d
Theo giả thiết, ta có: MI = R + 2R = 3R = 3.1 = 3 2 2
Như vậy: MI = 3 ⇔ (x − )
1 + (x + 2) = 9 ⇔ x =1 hoặc x = 2 −
Vậy, có hai điểm M thỏa yêu cầu bài toán là: M 1; 4 , M 2 − ;1 1 ( ) 2 ( )
Bài 49. Trong mặt phẳng với hệ tọa độ Oxy, cho hai đường thẳng d : x − y = 0 và d : 2x + y −1 = 0 . Tìm 1 2
tọa độ các đỉnh của hình vuông ABCD biết rằng đỉnh A thuộc d , đỉnh d và các đỉnh 1 C thuộc 2 B, C thuộc
trục hoành.(ĐH.CĐKA.2005) HD Giải Vì điểm A y
∈d ⇒ A ;tt . Do C ; t −t 1 ( )
AC đối xứng với nhau qua BD nên ( ) A
Mà C ∈ d nên có: 2t − t −1 = 0 ⇔ t = 1⇒ C (1;− ) 1 , A(1; ) 1 2 I D
Gọi I là trung điểm của AC ⇒ I (1;0) . B x C 70
Chương III. Phương pháp tọa độ trong
mặt phẳng. 0916620899-0355334679
Tài liệu học tập Toán 10 GV. Lư Sĩ Pháp IB = IA = 1
Vì I là tâm hình vuông nên: ID = IA = 1 B ∈Ox B( ; b 0) b −1 = 1 b = 0,b = 2 Ta có: ⇔ ⇒ ⇔ D ∈Ox D(d; 0) d −1 = 1 d = 0, d = 2
Suy ra: B (0;0),D(2;0) hoặc B(2;0),D(0;0)
Vậy, bốn đỉnh hình vuông là: A(1; ) 1 ,C (1;− )
1 , B(0;0),D(2;0) hoặc A(1; ) 1 ,C (1;− )
1 , B(2;0),D(0;0)
Bài 50. Trong mặt phẳng với hệ tọa độ Oxy, cho hai điểm A(2;0),B(6;4) .Viết phương trình đường tròn
(C) tiếp xúc với trục hoành tại điểm A và khoảng cách từ tâm của (C) đến điểm B bằng 5.(ĐH.CĐKB.2005) HD Giải
Gọi tâm của (C) là I ( ;
a b) và bán kính của (C) là R
Đường tròn (C)tiếp xúc với trục hoành tại điểm A ⇒ a = 2 và b = R . Như vậy: I (2;b) 2 2
Theo giả thiết, ta có: IB = ⇔ ( − ) + ( − b) 2 5 6 2 4
= 25 ⇔ b − 8b + 7 = 0 ⇔ b = 1 hoặc b = 7 2 2
Với b = 1 ⇔ I (2; )
1 ,R = 1, ta có phương trình đường tròn: (C : x −2 + y −1 =1 1 ) ( ) ( ) 2 2
Với b = 7 ⇔ I (2;7),R = 7, ta có phương trình đường tròn: (C : x − 2 + y − 7 = 49 2 ) ( ) ( ) 2 2 Bài 51. x y
Trong mặt phẳng với hệ tọa độ Oxy, cho điểm C (2;0) và elip (E): + = 1. Tìm tọa độ các 4 1
điểm A, B thuộc (E), biết rằng hai điểm A, B đối xứng với nhau qua trục hoành và tam giác ABC là tam giác đều.(ĐH.CĐKD.2005) HD Giải
Giả sử A(x ;y . Do B x ; −y 0 0 )
A, B đối xứng nhau qua Ox nên ( 0 0) Ta có: 2 2
AB = 4y và AC = (x − 2 + y 0 )2 2 2 0 0 2 2 2 x y x
Vì A ∈(E) nên 0 0 2 0 (E) : + = 1⇒ y = 1− (1) 0 4 1 4
và tam giác ABC đều nên AB = AC 4y = (x − 2)2 2 2 + y (2) 0 0 0 2
Thay (1) vào (2), ta được: 2
7x −16x + 4 = 0 ⇔ x = 2 hoặc x = 0 0 0 0 7
Với x = 2 thay vào (1), ta có: y = 0 ⇒ A 2;0 ≡ C nên loại 0 ( ) 0 2 4 3
Với x = thay vào (1), ta có: y = ± 0 7 0 7 2 4 3 2 4 3 2 4 3 2 4 3 Vậy: A ; , B ; − hoặc A ;− , B ; 7 7 7 7 7 7 7 7
Bài 52. Trong mặt phẳng với hệ tọa độ Oxy, cho hai điểm A(0;2) và B(− 3;− )1 . Tìm tọa độ trực tâm
và tọa độ tâm đường tròn ngoại tiếp tam giác OAB.(ĐH.CĐKA. 2004) HD Giải
Gọi H (x;y)là trực tâm tam giác ABC.
Đường thẳng AH qua điểm H và vuông góc với OB nên có phương trình: 3x + y − 2 = 0
Đường thẳng BH qua điểm H và vuông góc với OA nên có phương trình: y +1 = 0 71
Chương III. Phương pháp tọa độ trong
mặt phẳng. 0916620899-0355334679
Tài liệu học tập Toán 10 GV. Lư Sĩ Pháp
Như vậy: H = AH ∩ BH ⇒ H ( 3;− )1 Gọi I ( ;
a b) là tâm đường tròn (C) ngoại tiếp tam giác OAB có dạng: 2 2
x + y − 2ax − 2by + c = 0 . Khi đó, 2 2 2 2 2 2
a + b = a + (b−2) IO = IA a = 1 ta có: 2 2 2
IA = IO = IB ⇔ ⇔ ⇔ ⇒ I − 3;1 2 2 2 2 ( ) 2 2 IO = IB + = ( + 3) +( + )1 b a b a b = − 3
Vậy,: H ( 3;− )1 và I (− 3; )1
Cách khác: Viết phương trình đường tròn (C) qua ba điểm A, B, C.
Bài 53. Trong mặt phẳng với hệ tọa độ Oxy, cho hai điểm A(1; )
1 ,B(4;−3). Tìm điểm C thuộc đường
thẳng x − 2y −1 = 0 sao cho khoảng cách từ điểm C đến đường thẳng AB bằng 6.(ĐH.CĐKB. 2004) HD Giải
Phương trình đường thẳng AB : 4x + 3y − 7 = 0
Gọi C ( ;xy). Theo giả thiết C ∈d : x − 2y −1= 0 , ta có: x − 2y −1 = 0 (1) 4x + 3y − 7
4x + 3y − 37 = 0 (2a)
Ta lại có: d (C, AB) = = 6 ⇔ 2 2 4 + 3
4x + 3y + 23 = 0 (2b) 43 27
Giải (1) với (2a), ta được C (7;3) . Giải (1) với (2b), ta được C − ;− 11 11 43 27
Vậy, có 2 điểm C thỏa yêu cầu bài toán: C (7;3) hoặc C − ;− . 11 11
Bài 54. Trong mặt phẳng với hệ tọa độ Oxy, cho tam giác ABC có các đỉnh A( 1
− ;0),B(4;0),C(0;m)
với m ≠ 0 . Tìm tọa độ trọng tâm G của tam giác ABC theo m. Xác định m để tam giác GAB vuông tại G.(ĐH.CĐKD. 2004) HD Giải x + x + x y + y + y m
Trọng tâm G của tam giác ABC có tọa độ: A B C x = =1; A B C y = = G 3 G 3 3 m m m Vậy G 1; . Ta có: GA = 2
− ;− ,GB = 3;− 3 3 3 2 m
Tam giác GBC vuông tại G ⇔ G . A GB = 0 ⇔ 6 − + = 0 ⇔ m = 3 ± 6 9
Bài 55. Trong mặt phẳng với hệ tọa độ Oxy, cho tam giác ABC có AB = AC, 0
BAC = 90 . Biết M (1;− ) 1 là 2
trung điểm cạnh BC và G ;0 là trọng tâm của tam giác 3
ABC. Tìm tọa độ các đỉnh A, B, C. (ĐH.CĐKB. 2003) HD Giải
Gọi A(x;y). Vì G là trọng tâm của tam giác ABC và M là trung điểm của BC nên:
MA = 3MG ⇔ (x −1; y + )
1 = (−1;3) ⇒ A(0;2)
Phương trình đường thẳng BC qua M và vuông góc với AM (Do tam giác ABC vuông cân tại A) nên có
phương trình: −x + 3y + 4 = 0 (1)
Nhận thấy: MA = MB = MC = 10 ⇒ tọa độ điểm B, C thảo mãn phương trình đường tròn tâm M, đường 2 2
kính MA: (x − ) 1 + (y + ) 1 =10 (2) 72
Chương III. Phương pháp tọa độ trong
mặt phẳng. 0916620899-0355334679
Tài liệu học tập Toán 10 GV. Lư Sĩ Pháp
−x + 3y + 4 = 0 x = 3y + 4 x = 4 x = −2
Từ (1) và (2) có hệ: ( ⇔ ⇔ hoặc x − y = 2 )2 1 + (y + )2 1 = 10 (y+ )2 1 = 1 y = 0 −
Vậy: B (4;0),C (−2; 2 − ) hoặc B(−2; 2 − ),C(0;4) . 2 2
Bài 56. Trong mặt phẳng với hệ tọa độ Oxy, cho đường tròn (C) : (x − )
1 + (y −2) = 4 và đường thẳng
d : x − y −1 = 0 . Viết phương trình đường tròn (C ') đối xứng với đường tròn (C) qua đường thẳng d.
Tìm tọa độ các giao điểm của (C) và (C').(ĐH.CĐKD. 2003) HD Giải
Đường tròn (C) có tâm I (1;2) và bán kính R = 2 . (C') đối xứng với đường tròn (C) qua đường thẳng
d nên (C ') có tâm I ' và bán kính R' = R = 2 .
Gọi H (x;y) là hình chiếu của I lên trên d, suy ra H là trung điểm của II ' . Ta có đường thẳng IH qua
điểm I và vuông góc với d nên có phương trình: x + y − 3 = 0 .
Khi đó: H = d ∩ IH ⇒ H (2; ) 1 ⇒ I '(3;0)
Vậy: (C ) (x − )2 2 ' : 3 + y = 4
Tọa độ các giao điểm của (C) và (C') là nghiệm của hệ phương trình: (x )2 1 (y 2)2 4 ( − + − = x − 3)2 2 2 + y = 4
2y − 4y = 0 x = 1 x = 3 ⇔ ⇔ ⇔ hoặc ( x − 3 y = 2 )2 2 + y = 4
x − y −1 = 0 x = y +1 y = 0
Vậy, (C) và (C') cắt nhau tại hai điểm: A(1;0),B(3;2).
Bài 57. Trong mặt phẳng với hệ tọa độ Oxy, xét tam giác ABC vuông tại A, phương trình đường thẳng
BC là 3x − y − 3 = 0 , các đỉnh A và B thuộc trục hoành và bán kính đường tròn nột tiếp bằng 2. Tìm
tọa độ trọng tâm G của tam giác ABC.(ĐH.CĐKA. 2002) HD Giải
Ta có: B thuộc trục Ox, nên B = Ox ∩ BC ⇒ B (1;0) . Đặt x = a ⇒ A( ;
a 0 và x = a ⇒ y = 3a − 3 . A ) C C
Vậy C ( ;a 3a− 3) 2 a +1 3 (a− )1
G (x ; y là trọng tâm của tam giác ABC nên G ; G G ) 3 3 1 3
Ta có: AB = a −1 , AC = 3 a −1 ,BC = 2 a −1 . Do đó: S △ = A . B AC = a − ABC ( )2 1 2 2 2S (a− )2 3 1 a −1 Ta có: r = = =
AB + AC + BC
3 a −1 + 3 a −1 3 +1 a 1 − a = 2 3 + 3 Và r = 2 ⇔
= 2 ⇔ a −1 = 2 3 + 2 ⇔ 3 +1 a = 2 − 3 −1 7 4 3 6 2 3 + + 4 3 1 6 2 3 − − − −
Với a = 2 3 + 3 ⇒ G ; . Với a = 2 − 3 −1⇒ G ; 3 3 3 3 1
Bài 58. Trong mặt phẳng với hệ tọa độ Oxy, cho hình chữ nhật ABCD có tâm I ;0 , phương trình 2
đường thẳng AB là x − 2y + 2 = 0 và AB = 2AD . Tìm tọa độ các đỉnh A,B,C, D biết rằng A có hoành độ 73
Chương III. Phương pháp tọa độ trong
mặt phẳng. 0916620899-0355334679
Tài liệu học tập Toán 10 GV. Lư Sĩ Pháp âm.(ĐH.CĐKB. 2002) HD Giải Cách 1.
Điểm A thuộc đường thẳng AB ⇒ A(2a − 2;a) (do A có hoành độ âm nên a <1)
I là trung điểm của AC ⇒ C (3 − 2 ; a −a)
BC qua C va vuông góc với AB ⇒ BC : 2x + y + 5a − 6 = 0
Do đó: B = AB ∩ BC ⇒ B(2 − 2 ;
a 2 − a), I là trung điểm của BD ⇒ D(2a −1;a − 2) a =
Ta có: AB = AD ⇔ ( − a)2 0 2 1 = 1 ⇔ a = 2(loaïi)
Với a = 0 ,ta có: A( 2
− ;0),B(2;2),C(3;0),D(−1;−2) Cách 2. 5 5
Khoảng cách từ I đến đường thẳng AB bằng
⇒ AD = 5 và IA = IB = 2 2
Do đó A, B là các giao điểm của AB với đường tròn tâm I và bán kính y B 5 R = . 2 H
x − 2y + 2 = 0 A I C
Vậy, tọa độ A, B là nghiệm của hệ: 2 O x 1 (do 2 25
x − + y = 2 4 D
x < 0 ) ⇒ A ( 2
− ;0),B(2;2) ⇒ C(3;0),D( 1 − ; 2 − ) A 2 2 Bài 59. x y
Trong mặt phẳng với hệ tọa độ Oxy, cho elip (E) : + = 1. Xét điểm 16 9
M chuyển động trên tia
Ox và điểm N chuyển động trên tia Oy sao cho đường thẳng MN luôn tiếp xúc với (E). Xác định tọa độ
điểm M, N để đoạn MN có độ dài nhỏ nhất. Tính giá trị nhỏ nhất đó. (ĐH.CĐKD. 2002) HD Giải Cách 1
Điểm M chuyển động trên tia Ox và điểm N chuyển động trên tia Oy ⇒ M ( ;
m 0),N (0;n) với
m > 0,n > 0 . x y
Đường thẳng MN có phương trình: + = 1. m n 2 2 1 1
Đường thẳng MN tiếp xúc với (E) khi và chi khi: 16 + 9 = 1 m n Theo BĐT Co6si, ta có: = + = ( + ) 2 2 2 2 2 2 2 16 9 +
= 25 +16 n + 9 m MN m n m n
≥ 25+ 2 16.9 = 47 ⇒ MN ≥ 7 2 2 2 2 m n m n 2 2 16n 9m = 2 2 m n m = 2 7 Đẳng thức xảy ra 2 2
⇔ m + n = 49 ⇔ n = 21
m > 0,n > 0
Vậy, M (2 7;0),N (0; 21) thì MN đạt giá trị nhỏ nhất và GTNN bằng 7. Cách 2 74
Chương III. Phương pháp tọa độ trong
mặt phẳng. 0916620899-0355334679
Tài liệu học tập Toán 10 GV. Lư Sĩ Pháp
Điểm M chuyển động trên tia Ox và điểm N chuyển động trên tia Oy ⇒ M ( ;
m 0),N (0;n) với
m > 0,n > 0 . x y
Đường thẳng MN có phương trình: + = 1. m n 2 2 1 1
Đường thẳng MN tiếp xúc với (E) khi và chi khi: 16 + 9 = 1 m n
Theo BĐT Bunhiacốpski, ta có: 2 2 2
MN = m + n = ( 2 2 m + n ) 16 9 4 3 + ≥ . m + . n = 49 ⇒ MN ≥ 7 2 2 m n m n 4 3 m : = n : m n m = 2 7 Đẳng thức xảy ra 2 2
⇔ m + n = 49 ⇔ n = 21
m > 0,n > 0
Vậy, M (2 7;0),N (0; 21) thì MN đạt giá trị nhỏ nhất và GTNN bằng 7.
Bài 60. Trong mặt phẳng với hệ tọa độ Oxy, cho điểm K(3 ; 2) và đường tròn 2 2
(C) : x + y − 2x − 4y +1 = 0 với tâm là I. Tìm tọa độ điểm M ∈(C) sao cho 0 IMK = 60 . HD Giải Ta có 2 2
(C) : (x −1) + (y − 2) = 4 . Suy ra tâm I(1 ; 2) và bán kính R = 2.
Nhận thấy IK = 2. Suy ra K ∈(C). Do M ∈(C) và 0
IMK = 60 . Suy ra I
∆ MK đều. Do đó yêu cầu bài toán ⇔ Tìm M ∈(C) sao cho KM = R = 2.
Gọi M(x , y ) và M(x , y )∈(C) 2 2
⇔ (x −1) + (y − 2) = 4 (1) 0 0 0 0 0 0 Ta lại có 2 2
KM = 2 ⇔ (x − 3) + (y − 2) = 4 (2) 0 0
Từ (1) và (2) suy ra M (2 ; 2+ 3) hoặc M (2 ; 2− 3)
Bài 61. Trong mặt phẳng với hệ tọa độ Oxy. Lập phương trình đường thẳng qua M (2; ) 1 và tạo với các
trục tọa độ một tam giác có diện tích bằng 4 . HD Giải
Gọi d là đường thẳng cần tìm và A( ;
a 0),B(0;b) là giao điểm của d với Ox, Oy. x y 2 1 1 1
Suy ra d : + = 1 . Theo giả thiết, ta có: M ∈ d ⇔ + = 1 và S = O . A OB = .
a b = 4 ⇔ ab = 8 a b a b 2 2 ab = 8 a = 4 ⇔
⇒ d : x + 2y − 4 = 0 1 2b + a = 8 b = 2 b = 2 − + 2 2 2 ab = 8 −
b + 4b − 4 = 0 ⇔ ⇔ b = 2 − − 2 2 2b + a = −8 a = 8 − − 2b
a = −8 − 2b Với b = 2
− + 2 2 ⇒ d : 1− 2 x + 2 1+ 2 y − 4 = 0 2 ( ) ( ) Với b = 2
− − 2 2 ⇒ d : 1+ 2 x + 2 1− 2 y − 4 = 0 3 ( ) ( )
Bài 62. Trong mặt phẳng với hệ tọa độ Oxy, cho các đường thẳng d : 3x + 2y − 4 = 0 , 1 75
Chương III. Phương pháp tọa độ trong
mặt phẳng. 0916620899-0355334679
Tài liệu học tập Toán 10 GV. Lư Sĩ Pháp
d : 5x − 2y + 9 = 0 .Viết phương trình đường tròn có tâm I ∈ d và tiếp xúc với d tại điểm A( 2 − ;5) . 2 2 1 HD Giải
Do đường tròn tiếp xúc với đường thẳng d tại A nên IA ⊥ d . 1 1
Vậy, đường thẳng IA có phương trình: 2x − 3y +19 = 0
5x − 2y + 9 = 0 x = 1
Khi đó tọa độ điểm I là nghiệm hệ : ⇔ ⇒ I (1;7)
2x − 3y +19 = 9 y = 7
Bán kính đường tròn R = IA = 13 . 2 2
Vậy phương trình đường tròn cần tìm là: (x − ) 1 + (y − 7) =13
Bài 63. Trong mặt phẳng với hệ tọa độ Oxy, cho tam giác ABC có phương trình đường cao AH và trung
tuyến AM lần lượt là: x − 2y −13 = 0 và 13x − 6y − 9 = 0 . Biết tâm đường tròn ngoại tiếp tam giác ABC là I (−5; )
1 . Tìm toạ độ các đỉnh A, B, C. HD Giải Toạ độ điểm A là nghiệm của hệ : A
x − 2y −13 = 0 x = 3 − ⇔ ⇒ A(−3; 8 − ) 1
3x − 6y − 9 = 0 y = 8 − I Ta có IM đi qua I ( 5 − ; )
1 và song song với AH .Phương trình IM là
x − 2y + 7 = 0 H M C B
x − 2y + 7 = 0 x = 3
Toạ độ điểm M là nghiệm của hệ ⇒ ⇒ M (3;5) 1
3x − 6y − 9 = 0 y = 5
Đường thẳng BC qua M và vuông góc với AH. Phương trình BC là 2x + y −11 = 0 b = 2 Gọi B( ;
b 11− 2b) . Ta có IB = IA 2 2 2
⇔ (b + 5) + (10 − 2b) = 85 ⇔ b − 6b + 8 = 0 ⇔ b = 4
Với b = 2 ⇒ B (2;7),C (4;3). Vớib = 4 ⇒ B(4;3),C (2;7) 2 2 Bài 64 x y
. Trong mặt phẳng với hệ tọa độ Oxy, cho elip (E) : +
= 1 và hai điểm A(4; 3 − ),B(−4;3). 16 9
Tìm toạ độ điểm C thuộc (E) sao cho diện tích tam giác ABC đạt giá trị lớn nhất. HD Giải 2 2 x y
Gọi C(x ; y )∈(E) . Ta có o 0 2 2 +
= 1 ⇔ 9x +16y = 144 (1) o 0 0 0 16 9
Phương trình đường thẳng AB là: 3x + 4y = 0 3x + 4y 0 0 1
d(C, AB) = , S = A .
B d(C, AB) 5 A ∆ BC 2
Do AB không đổi nên diện tích tam giác ABC lớn nhất khi d(C,AB) lớn nhất
Áp dụng BĐT Bunhiacopxki cho hai bộ số ta có 12 2 2 2 2
(3x + 4y ) ≤ 2(9x +16y ) = 2.144 ⇒ 3x + 4y ≤ 12 2 ⇒ d(C, AB) ≤ 0 0 0 o 0 0 5
(Dấu = xảy ra khi 3x = 4y ) 0 0
Vậy diện tích tam giác ABC lớn nhất khi và chỉ khi 3x = 4y 0 0 3 x = 2 2; = 2 2 y 0 0
9x +16y = 144 2
Kết hợp với (1) ta có hệ: 0 0 ⇔ 3 x 4y = 3 0 0 x = 2 − 2; y = − 0 0 2 76
Chương III. Phương pháp tọa độ trong
mặt phẳng. 0916620899-0355334679
Tài liệu học tập Toán 10 GV. Lư Sĩ Pháp 3 2 3 2 Vậy: C 2 2; hoặc C 2 − 2;− 2 2 2 2
Bài 65. Trong mặt phẳng với hệ tọa độ Oxy, cho đường tròn (C) : (x − )
1 + (y −2) = 4và đường thẳng
d : x − y + 7 = 0 . Tìm trên d điểm M mà từ đó có thể kẻ được hai tiếp tuyến MA, MB tới (C) (với A, B là
các tiếp điểm) sao cho độ dài đoạn AB nhỏ nhất. HD Giải
Đường tròn (C) có tâm I (1;2), bán kính R = 2 . Gọi H = IM ∩ AB thì H là trung điểm của AB. Ta có :
IA = IB, MB = MB ⇒ IM ⊥ AB 1 1 1 4 1 1
Tam giác vuông AMI, có : = + ⇔ = + (1) 2 2 2 2 2 2 2 AH AI AM AB R IM − R
Ta có : d (I,d) = 3 2 > R : d không cắt (C) nên M nằm ngoài (C) ⇒ IM > R
Do đó từ (1), ta có : Độ dài AB đạt GTNN ⇔ IM ngắn nhất ⇔ M là hình chiếu của I trên d
Đường thẳng ∆ qua I và vuông góc với d, nên có phương trình : x + y − 3 = 0
Khi đó : M = ∆ ∩ d ⇒ M ( 2 − ;5)
BÀI TẬP LÀM TƯƠNG TỰ 9 3
Bài 66. Trong mặt phẳng với hệ tọa độ Oxy, cho hình chữ nhật ABCD có diện tích bằng 12, tâm I ; 2 2
và trung điểm của cạnh AD là M (3;0) . Xác định tọa độ các đỉnh của hình chữ nhật ABCD.
Kết quả : A (2; )
1 ,B(5;4),C(7;2),D(4;− ) 1 1
Bài 67. Trong mặt phẳng với hệ tọa độ Oxy, cho đường tròn (C ) : (x − )2 2 1 + y = và 1 2
(C ) : (x −2)2 +(y −2)2 = 4. Viết phương trình đường thẳng tiếp xúc với (C và cắt đường tròn (C tại 2 ) 1 ) 2
các điểm M, N sao cho MN = 2 2
Kết quả : x + y − 2 = 0 hoặc 7x − y − 2 = 0
Bài 68. Trong mặt phẳng với hệ tọa độ Oxy, cho tam giác ABC cân tại A, có phương trình các cạnh x = t
AB : x + y +1 = 0 và BC :
5 2 ,t ∈ ℝ . Tìm phương trình cạnh AC biết nó đi qua điểm I (1; ) 1 . y = − + t 3 3
Kết quả : AC :17x + 7y − 24 = 0
Bài 69. Trong mặt phẳng với hệ tọa độ Oxy. Viết phương trình đường thẳng cách điểm A(1; ) 1 một
khoảng bằng 2 và cách điểm B (2;3) một khoảng bằng 4.
Kết quả : ∆ : y = −1 hoặc ∆ : 4x + 3y + 3 = 0
Bài 70. Trong mặt phẳng với hệ tọa độ Oxy, cho elip (E) có các tiêu điểm F 4
− ;0 , F 4;0 và độ dài 2 ( ) 1 ( ) 32
trục nhỏ bằng 6. Tìm điểm M thuộc (E) sao cho MF − MF = 1 2 5 9 9 9 9
Kết quả : M 4; , M 4;− , M −4; , M 4 − ;− 1 2 3 4 4 4 5 5
Bài 71. Trong mặt phẳng với hệ tọa độ Oxy. Viết phương trình đường tròn (C) đi qua điểm A(−1;4) và x 1− y
tiếp xúc với đường thẳng ∆ : =
tại điểm B (3;2) . 3 1 − 77
Chương III. Phương pháp tọa độ trong
mặt phẳng. 0916620899-0355334679
Tài liệu học tập Toán 10 GV. Lư Sĩ Pháp 2 2
Kết quả : (C) : (x − 2) + (y − 5) = 10
Bài 72. Trong mặt phẳng với hệ tọa độ Oxy, cho điểm M (1;2) và đường thẳng d : 2x − 6y + 5 = 0. Viết
phương trình đường thẳng d ' đi qua M và hợp với d một góc 0 45
Kết quả : d ' : 2x − y = 0 hoặc d ' : x + 2y − 5 = 0 11 9
Bài 73. Trong mặt phẳng với hệ tọa độ Oxy, cho tam giác ABC có đỉnh A(2; ) 1 , trực tâm H ; và 7 7 2 4 trọng tâm G ;
. Xác định tọa độ các đỉnh 3 3 B và C.
Kết quả : B (1;3),C ( 1
− ;0) hoặc B(−1;0),C(1;3)
Bài 74. Trong mặt phẳng với hệ tọa độ Oxy, cho hai điểm A(3;2),B(1;4). Viết phương trình đường tròn
(C) đi qua hai điểm A, B và tiếp xúc với trục Ox.
Kết quả : (C ) 2 2
: x + y − 2x − 4y +1 = 0,(C ) 2 2
: x + y −18x − 20y + 81 = 0 1 2
Bài 75. Trong mặt phẳng với hệ tọa độ Oxy, cho đường tròn (C) (x + )2 2 :
1 + y =1. Viết phương trình tiếp
tuyến ∆ của (C), biết góc giữa tiếp tuyến này với trục tung bằng 0 30 .
Kết quả : có bốn tiếp tuyến ∆ : 3x − y ± 2 + 3 = 0 , 3x + y ± 2 + 3 = 0
Bài 76. Trong mặt phẳng với hệ tọa độ Oxy, cho đường tròn (c) 2 2
: x + y −8x − 6y + 21 = 0 và đường
thẳng ∆ : x − y +1 = 0 . Viết phương trình đường tròn (C')đối xứng với đường tròn (C) qua đường thẳng ∆ . 2 2
Kết quả : (C ') : ( x − 2) + (y − 5) = 4
Bài 77. Trong mặt phẳng với hệ tọa độ Oxy, cho các đường thẳng d : x + y + 4 = 0 , d : x − y − 5 = 0 và 1 2
d : x − 3y = 0 . Tìm tọa độ điểm
d sao cho khoảng cách từ 3
M nằm trên đường thẳng 3
M đến đường thẳng
d bằng 3 lần khoảng cách từ d . 1 M đến 2 57 19 33 11
Kết quả : M ; , M ; 1 2 2 2 10 10
Bài 78. Trong mặt phẳng với hệ tọa độ Oxy, cho điểm M (3; )
1 và hai đường thẳng ∆ : x − y + 2 = 0 , 1
∆ : 2x + y + 2 = 0 . Viết phương trình đường thẳng ∆ ,∆ lần lượt 2
d đi qua điểm M và cắt hai đường thẳng 1 2
tại A và B sao cho M là trung điểm của đoạn thẳng AB.
Kết quả : d :17x − 5y − 46 = 0
Bài 79. Trong mặt phẳng với hệ tọa độ Oxy, cho elip (E) có tiêu điểm thứ nhất là (− 3;0) 4 33
và đi qua điểm M 1;
. Hãy xác định tọa độ các đỉnh của ( 5 E).
Kết quả : A 5
− ;0 , A 5;0 ,B 0;− 22 ,B 0; 22 1 ( ) 2 ( ) 1( ) 2( )
Bài 80. Trong mặt phẳng với hệ tọa độ Oxy, cho ba điểm A(10;5),B(15; 5
− ),D(−20;0)là ba đỉnh của
một hình thang cân ABCD. Tìm tọa độ điểm C, biết rằng CD // AB.
Kết quả : C (−7; 2 − 6)
Bài 81. Trong mặt phẳng với hệ tọa độ Oxy, cho hình bình hành có hai cạnh nằm trên hai đường thẳng
x + 3y − 6 = 0 và 2x − 5y −1 = 0 . Biết hình bình hành có tâm đối xứng là I (3;5) . Hãy viết phương trình
hai cạnh còn lại của hình bình hành đó.
Kết quả : x + 3y − 30 = 0 và 2x − 5y + 39 = 0 . 78
Chương III. Phương pháp tọa độ trong
mặt phẳng. 0916620899-0355334679
Tài liệu học tập Toán 10 GV. Lư Sĩ Pháp
Bài 82. Trong mặt phẳng với hệ tọa độ Oxy, cho hình bình hành có một đỉnh là (4;− ) 1 . Biết phương trình
các đường thẳng chứa hai cạnh là x − 3y = 0 và 2x + 5y + 6 = 0 . Tìm tọa độ ba đỉnh còn lại của hình bình hành đó. 9 3 17 20 18 6
Kết quả : ; , ;− , − ;− 11 11 11 11 11 11
Bài 83. Trong mặt phẳng với hệ tọa độ Oxy, cho đường thẳng ∆ : x − y + 2 = 0 . Tìm điểm M thuộc ∆
cách đều hai điểm E (0;4) và F (4; 9 − ) . 133 97
Kết quả : M − ;− 18 18
Bài 84. Trong mặt phẳng với hệ tọa độ Oxy, cho ba điểm A(3;0),B( 5
− ;4) và P(10;2) . Viết phương
trình đường thẳng đi qua P đồng thời cách đều A và B.
Kết quả : ∆ : x + 2y −14 = 0
Bài 85. Trong mặt phẳng với hệ tọa độ Oxy, cho hai đường thẳng ∆ : x + 2y − 3 = 0 và 1
∆ : 3x − y + 2 = 0 .Viết phương trình đường thẳng ∆ đi qua điểm P (3; )
1 và cắt ∆ , ∆ lần lượt ở 2 1 2 A, B
sao cho ∆ tạo với ∆ và ∆ một tam giác cân cạnh đáy là 1 2 AB.
Kết quả : ∆ : (1+ 2)(x −3)+ (y − ) 1 = 0 và /
∆ : (1− 2)(x −3)+(y − )1 = 0
Bài 86. Trong mặt phẳng với hệ tọa độ Oxy, cho một cạnh tam giác có trung điểm I ( 1 − ; ) 1 . Hai cạnh kia x = 2 − t
nằm trên các đường thẳng 2x + 6y + 3 = 0 và
. Lập phương trình đường thẳng chứa cạnh thứ ba y = t của tam giác. x = 1 − + 5t'
Kết quả : ,(t'∈ℝ) y = 1+ 3t ' x = −2t
Bài 87. Trong mặt phẳng với hệ tọa độ Oxy, cho hai đường thẳng ∆ : và y = 1+ t
x = −2 − t ' / ∆ :
. Viết phương trình đường thẳng đối xứng với / ∆ qua ∆ . y = t '
Kết quả : x + 7y − 22 = 0 x = 1+ t
Bài 88. Trong mặt phẳng với hệ tọa độ Oxy, cho hai điểm A( 1 − ;2),B(3; )
1 và đường thẳng ∆ : . y = 2 + t
Tìm tọa độ điểm C trên ∆ sao cho : a) Tam giác ABC cân
b) Tam giác ABC đều 30 30 + 2 30 30 − 2 7 13
Kết quả : a) C ; ,C ; ,C 1
− ;0 ,C 4;5 ,C ; 1 2 3 ( ) 4 ( ) 5 2 2 2 2 6 6
b) Không tồn tại điểm C trên ∆ sao cho tam giác ABC đều. x = 2 − − 2t
Bài 89. Trong mặt phẳng với hệ tọa độ Oxy, cho đường thẳng ∆ : và điểm M (3; ) 1 . y = 1+ 2t
a) Tìm tọa độ điểm A trên ∆ sao cho A cách M một khoảng bằng 13
b) Tìm tọa độ điểm B trên ∆ sao cho đoạn MB ngắn nhất. 1 3
Kết quả : a) A 0; 1 − , A 1; 2 −
b) B ≡ H ;− ( 1 ( ) 2 ( ) 2
2 H là hình chiếu M lên ∆ )
Bài 90. Trong mặt phẳng với hệ tọa độ Oxy, cho hai điểm P (1;6),Q(−3; 4 − ) và đường thẳng 79
Chương III. Phương pháp tọa độ trong
mặt phẳng. 0916620899-0355334679
Tài liệu học tập Toán 10 GV. Lư Sĩ Pháp
∆ : 2x − y −1 = 0
a) Tìm tọa độ điểm M trên ∆ sao cho MP + MQ nhỏ nhất
b) Tìm tọa độ điểm N trên ∆ sao cho NP − NQ lớn nhất.
Kết quả : a) M (0;− ) 1 b) N (−9;−19)
Bài 91. Trong mặt phẳng với hệ tọa độ Oxy, cho A( 1
− ;0),B(2;3),C(3; 6 − ) và đường thẳng
∆ : x − 2y − 3 = 0 . Tìm điểm M trên ∆ sao cho MA + MB + MC nhỏ nhất. 19 13
Kết quả : M ;− 15 15
Bài 92. Trong mặt phẳng với hệ tọa độ Oxy. Lập phương trình đường tròn có tâm nằm trên đường thẳng
∆ : 4x + 3y − 2 = 0 và tiêp xúc với hai đường thẳng d : x + y + 4 = 0 và d : 7x − y + 4 = 0 . 1 2 2 2 2 2
Kết quả : ( x − 2) + (y + 2) = 8 và ( x + 4) + (y − 6) = 18
BÀI TẬP TRẮC NGHIỆM
Câu 1. Cho đường tròn (C): 2 2
x + y + 6x − 2 y = 0 và đường thẳng (d) : x + 3y + 2 = 0. Phương trình tiếp
tuyến của (C) song song với (d) là
A. x + 3y ± 9 = 0.
B. x + 3y ±10 = 0.
C. x + 3y ±11 = 0.
D. x + 3y ± 5 = 0.
Câu 2. Cho đường tròn (C): 2 2
(x −1) + ( y − 2) = 5. Phương trình đường thẳng (d) đi qua M (6,2) và cắt (C) tại hai điểm ,
A B sao cho AB = 10 là
A. 3x − y = 0 và x +12y −12 = 0
B. x −3y = 0 và x + 3y +12 = 0
C. x −3y = 0 và x + 3y −12 = 0
D. 3x − y = 0 và x +12y +12 = 0 2
Câu 3. Elip có hai tiêu điểm nằm trên trục hoành, đối xứng O, (E) có tâm sai e = và đi qua điểm 3 5
M −2; . Phương trình chính tắc của (E) là 3 2 2 2 2 2 2 2 2 A. x y + =1. B. x y + =1. C. x y + =1. D. x y + =1. 9 4 9 5 16 12 9 6
Câu 4. Cho đường thẳng d : 4x –3y +13 = 0. Phương trình các đường phân giác của các góc tạo bởi (d) và trục Ox là
A. 4x –8y +13 = 0 và 4x + 2y +13 = 0.
B. x + 3y +13 = 0 và x –3y +13 = 0.
C. 3x + y +13 = 0 và 3x – y +13 = 0.
D. 4x + 4y +13 = 0 và 4x – y +13 = 0.
Câu 5. Trong các phương trình dưới đây, phương trình nào không phải là phương trình đường tròn ? A. 2 2
x + y − 8x + 4 y +16 = 0. B. 2 2
x + y + 2x − 4 y + 9 = 0. C. 2 2
x + y − 6x − 4 y −13 = 0. D. 2 2
2x + 2y − 8x − 4y − 6 = 0.
Câu 6. Cho hai đường thẳng d : 2x + y + 4 – m = 0 và d : m + 3 x + y –2m –1 = 0. d song song 2 ( ) 1 1
với d khi và chỉ khi 2 m bằng A. 1. B. −1. C. 2. D. 3.
Câu 7. Cho điểm I (1; )
1 và đường thẳng (d): x –2y + 2 = 0. Phương trình đường thẳng ( d ) đối xứng với 1
đường thẳng (d) qua I là
A. 2x – y +12 = 0.
B. x –2y +12 = 0.
C. 2x – y = 0.
D. x –2y = 0.
Câu 8. Cho đường tròn (C): 2 2
(x − 3) + (y +1) = 4 và điểm A(1;3).Phương trình tiếp tuyến (C) vẽ từ A là
A. x −1 = 0 và 3x − 4y +15 = 0.
B. x −1 = 0 và 3x + 4y +15 = 0.
C. x −1 = 0 và 3x + 4y −15 = 0.
D. x −1 = 0 và 3x − 4y −15 = 0.
Câu 9. Cho đường tròn (C): 2 2
x + y + 6x + 2 y +1 = 0 . Tiếp tuyến của (C) vuông góc với đường thẳng 80
Chương III. Phương pháp tọa độ trong
mặt phẳng. 0916620899-0355334679
Tài liệu học tập Toán 10 GV. Lư Sĩ Pháp
(d):4x +3y+2 = 0 có phương trình là A. 3
− x + 4y +10 = 0và 3
− x + 4y − 20 = 0. B. 3
− x + 4y +15 = 0 và 3
− x + 4y −5 = 0. C. 3
− x + 4y + 5 = 0 và 3
− x + 4y −15 = 0. D. 3
− x + 4y + 20 = 0 và 3
− x + 4y −10 = 0.
Câu 10. Cho đường thẳng (d) có phương trình tổng quát là: 4x + 5y –8 = 0. Phương trình tham số của (d) là: x = 2 + 5t x = 2 + 4t x = 2 + 5t x = 5 − t A. . B. . C. . D. . y = 4 − t y = 5t y = 4t y = 4t x = 1 − + t
Câu 11. Đường thẳng nào vuông góc với đường thẳng: ;(t ∈ ℝ) ? y = 1 − + 2t x +1 y +1 A. = .
B. 2x + y +1 = 0.
C. x + 2y +1 = 0.
D. 4x − 2y +1 = 0. 1 2
Câu 12. Đường tròn qua A (5;3) và tiếp xúc với đường thẳng: x +3y + 2 = 0 tại điểm B(1;− ) 1 có phương trình là A. 2 2
x + y − 4x − 4 y − 2 = 0. B. 2 2
x + y + 4x + 4 y + 2 = 0. C. 2 2
x + y − 4x − 4 y + 2 = 0. D. 2 2
x + y + 4x + 4 y − 2 = 0.
Câu 13. Cho điểm M (1;2)và đường thẳng (d) : 2x + y –5 = 0. Toạ độ của điểm M’đối xứng với điểm M qua (d) là: 3 9 12 A. M’(3; 5 − ).
B. M ' 0; . C. M’( 2 − ;6).
D. M ' ; . 2 5 5
Câu 14. Cho đường tròn (C): 2 2
x + y − 2x + 8y − 23 = 0 và điểm M (8; 3
− ).Chiều dài của tiếp tuyến xuất
phát từ M với (C) là 10 A. 10. B. 10. C. 2 10. D. . 2
Câu 15. Phương trình chính tắc của elip (E) có độ dài trục lớn bằng 12, trục nhỏ bằng 8 là: 2 2 x 2 2 2 2 2 2 2 A. y + =1. B. x y + =1. C. x y − =1. D. x y + =1. 16 36 12 8 36 16 36 16
Câu 16. Đường thẳng qua M (2; )
1 và nhận u = (1;−1) là vectơ chỉ phương có phương trình là:
A. x – y –1 = 0.
B. x – y + 5 = 0.
C. x + y –3 = 0.
D. x + y –1 = 0.
Câu 17. Cho hai đường thẳng ∆ : x + y −1 = 0 và ∆ : x − 3y + 3 = 0 . Phương trình đường thẳng ∆ đối 1 2 xứng với ∆ qua ∆ là 1 2
A. 7x + y +1 = 0.
B. x –7y +1 = 0.
C. x + 7y +1 = 0.
D. 7x – y +1 = 0.
Câu 18. Với giá trị nào của m thì phương trình dưới đây là phương trình của đường tròn 2 2
x + y − 2(m + 2)x + 4my +19m − 6 = 0 ?
A. m < −2 hoặc m > 1.
B. 1 < m < 2.
C. 1 ≤ m ≤ 2.
D. m < 1hoặc m > 2.
Câu 19. Đường thẳng nào không cắt đường thẳng 2x + 3y –1 = 0?
A. 2x –3y + 3 = 0.
B. 4x –6y –2 = 0.
C. 2x + 3y +1 = 0.
D. x –2y + 5 = 0.
Câu 20. Khoảng cách từ điểm O đến đường thẳng 4x –3y –5 = 0 bằng 1 A. −5. B. . C. 0. D. 1. 5
Câu 21. Cho A(2; ) 1 và B (3; 2
− ).Tập hợp những điểm M ( ;x y) sao cho 2 2
MA + MB = 30 là một đường tròn có phương trình A. 2 2
x + y −10x − 2 y −12 = 0 B. 2 2
x + y − 5x + y − 6 = 0 C. 2 2
x + y + 5x − y − 6 = 0 D. 2 2
x + y − 5x + y + 6 = 0 81
Chương III. Phương pháp tọa độ trong
mặt phẳng. 0916620899-0355334679
Tài liệu học tập Toán 10 GV. Lư Sĩ Pháp 2 2
Câu 22. Elip ( ) : x y E + =1 và đường tròn 2 2
(C) : x + y = 25 có bao nhiêu điểm chung? 25 16 A. 2. B. 4. C. 0. D. 1.
Câu 23. Cho tam giác ABC có toạ độ các đỉnh là A(1;2),B(3; )
1 và C (5;4).Phương trình nào dưới đây
là phương trình đường cao của tam giác vẽ từ A?
A. 5x –6y + 7 = 0.
B. 3x –2y + 5 = 0.
C. 2x + 3y –8 = 0.
D. 3x –2y –5 = 0.
Câu 24. Toạ độ điểm I là hình chiếu vuông góc của điểm M (1;4)trên đường thẳng (∆): x − 2y + 2 = 0 là: A. ( 2 − ;2). B. (2;2). C. (2; 2 − .) D. (3;0).
Câu 25. Đường tròn: 2 2
x + y + 2x + 4 y − 20 = 0 có tâm và bán kính là
A. I (1;2), R = 15. B. I (−1; 2 − ),R = 5. C. I (1; 2 − ),R = 5.
D. I (1;2),R = 5.
Câu 26. Cho đường thẳng (d) : 3
− x + y –3 = 0 và điểm N ( 2
− ;4).Toạ độ hình chiếu vuông góc N’ của
N trên (d) là: 2 21 1 33 1 11 A. ; . B. ; . C. ( 3 − ; 6 − ). D. − ; . 5 5 10 10 3 3
Câu 27. Đường thẳng nào dưới đây song song với đường thẳng: x –3y + 4 = 0? x = 1− 3t x = 1− 3t x = 1+ t x = 1− t A. . B. . C. . D. . y = 2 + t y = 2 − t y = 2 + 3t y = 2 + 3t 2
Câu 28. Phương trình chính tắc của (E) có tâm sai e =
và khoảng cách giữa hai đường chuẩn bằng 2 8 2 là: 2 2 2 2 2 2 2 2 A. x y + =1 B. x y + =1 C. x y + =1 D. x y + =1 16 12 16 8 16 9 16 4
Câu 29. Cho đường thẳng (∆) : 2x − 3y +1 = 0 . Phương trình đường thẳng (d) đi qua gốc toạ độ O và (d) //(∆) là:
A. 2x – y + 6 = 0.
B. 2x − 3y + 2 = 0.
C. 2x –3y = 0.
D. x –2y –6 = 0.
Câu 30. Cho đường thẳng d : 2x + y –2 = 0 và điểm M (6;5).Toạ độ điểm M’ đối xứng với M qua
đường thẳng d là: A. M’( 5 − ; 6 − ).
B. M’(−6;5). C. M’( 6 − ;− ) 1 . D. M’(5;6).
Câu 31. Cho hai đường thẳng song song ∆ : 5x − 7 y + 4 = 0 và ∆ : 5x − 7 y + 6 = 0 . Phương trình đường 1 2
thẳng song song và cách đều ∆ và ∆ là: 1 2
A. 5x –7y + 3 = 0.
B. 5x –7y + 5 = 0.
C. 5x –7y + 2 = 0.
D. 3x –7y − 3 = 0.
Câu 32. Khoảng cách từ điểm M (0;3) đến đường thẳng ∆ : xcosα + ysinα +3(2−sinα) = 0 bằng 3 A. 3sinα. B. . C. 6. D. 6. sinα + cosα 2
Câu 33. Đường thẳng qua N (3; 2
− )và có hệ số góc k = có phương trình là: 3
A. 2x –3y –12 = 0.
B. 3x –2y −13 = 0.
C. 2x –3y –9 = 0.
D. 2x + 3y = 0.
Câu 34. Cho đường tròn (C): 2 2
x + y − 4x − 2 y = 0 . Từ điểm A (3; 2
− ) có thể kẻ đến (C) 2 tiếp tuyến phân
biệt có phương trình là:
A. 2x − y −8 = 0 và x + 2y −1 = 0.
B. 2x − y + 8 = 0 và x + 2y +1 = 0.
C. 2x − y −8 = 0 và x + 2y +1 = 0.
D. 2x − y + 8 = 0và x + 2y −1 = 0.
Câu 35. Cho hai điểm A(6;2) và B( 2
− ;0).Phương trình đường tròn đường kính AB là A. 2 2
x + y + 4x + 2 y +12 = 0. B. 2 2
x + y − 4x − 2 y +12 = 0. 82
Chương III. Phương pháp tọa độ trong
mặt phẳng. 0916620899-0355334679
Tài liệu học tập Toán 10 GV. Lư Sĩ Pháp C. 2 2
x + y + 4x + 2 y −12 = 0. D. 2 2
x + y − 4x − 2 y −12 = 0.
Câu 36. Cho tam giác ABC có toạ độ các đỉnh là A(−1; )
1 ,B(4;7) và C(3; 2
− ), M là trung điểm đoạn thẳng A .
B Phương trình tham số của trung tuyến CM là: x = 3 + t x = 3 − t x = 3 + 3t x = 3 + t A. . B. . C. . D. . y = 2 − − 4t y = 4 + 2t y = 2 − + 4t y = 2 − + 4t
Câu 37. Cho hai đường thẳng ∆ : x − 3y + 5 = 0 và ∆ : 3x − y +15 = 0 . Phương trình hai đường phân giác 1 2
của góc tạo bởi hai đường thẳng trên là: x + y + 5 = 0 x + y + 5 = 0 A. .
B. x + y + 5 = 0.
C. x – y + 5 = 0. D. .
x − y + 5 = 0
x − y + 5 = 0
Câu 38. Cho tam giác ABC,biết A (1;3)và hai trung tuyến lần lượt có phương trình là:
x – 2y +1 = 0, y –1 = 0. Phương trình cạnh AB là
A. x + 2y + 7 = 0.
B. 2x + y + 7 = 0.
C. x + 2y –7 = 0.
D. 2x + y –7 = 0.
Câu 39. Cho M (2; )
1 . Đường thẳng (d) đi qua M cắt 2 trục toạ độ tại ,
A B sao cho M là trung điểm
AB có phương trình là:
A. x + 2y –2 = 0.
B. 2x + y –2 = 0.
C. 2x + y − 2 = 0.
D. x + 2y –4 = 0.
Câu 40. Cho hai đường thẳng d : x + y + 5 = 0 và d : y = −10.Số đo của góc giữa hai đường thẳng d và 1 2 1 d bằng 2 A. 0 88 57 '52". B. 0 1 13'8". C. 0 45 . D. 0 30 .
Câu 41. Đường thẳng qua P (1;−2)và nhận n = (−2;4) là vectơ pháp tuyến có phương trình là: A. 2
− x + 4y = 0.
B. x + 2y + 4 = 0.
C. x –2y –5 = 0.
D. x –2y + 4 = 0.
Câu 42. Phương trình nào là phương trình tham số của đường thẳng x – y + 3 = 0? x = 2 + t x = t x = t x = 3 A. . B. . C. . D. . y = 1+ t y = 3 − t y = 3 + t y = t
Câu 43. Cho hai điểm A (2;3) và B(4;7).Phương trình đường tròn đường kính AB là A. 2 2
x + y − 6x −10 y + 29 = 0. B. 2 2
x + y + 6x +10 y + 29 = 0. C. 2 2
x + y + 6x +10 y − 29 = 0. D. 2 2
x + y − 6x −10 y − 29 = 0.
Câu 44. Hai cạnh hình chữ nhật có phương trình: 3x –4y + 5 = 0,4x + 3y −12 = 0 và một đỉnh có toạ độ (3; 2
− ). Phương trình hai cạnh còn lại là:
A. 4x + 3y –6 = 0 và 3x –4y −17 = 0.
B. 4x + 3y –6 = 0 và 3x –4y +17 = 0.
C. 4x + 3y + 6 = 0 và 3x –4y +17 = 0.
D. 4x + 3y + 6 = 0 và 3x − 4y –17 = 0.
Câu 45. Đường thẳng đi qua điểm M (1;0)và song song với đường thẳng d : 4x + 2y +1= 0 có phương trình tổng quát là:
A. 4x + 2y + 3 = 0.
B. 2x + y + 4 = 0.
C. 2x + y − 2 = 0.
D. x –2y + 3 = 0. 2 2 Câu 46. Elip ( x y
E) có phương trình chính tắc +
=1. Điểm dưới đây là tiêu điểm của (E) ? 100 36 A. (10;0). B. (6;0). C. (4;0). D. ( 8 − ;0). x = 5 + t
Câu 47. Phương trình nào dưới đây là phương trình tổng quát của đường thẳng : ;(t ∈ ℝ) ? y = 9 − − 2t
A. x + 2y –2 = 0.
B. 2x + y –1 = 0.
C. 2x + 3y +1 = 0.
D. x + 2y + 2 = 0.
Câu 48. Cho hai điểm A(1; )
1 ,B(−3;3) và đường thẳng (d): x + y + 5 = 0.Điểm M thuộc đường thẳng (d)
và cách đều hai điểm A, B có toạ độ là A. ( 3 − ;2). B. ( 3 − ; 2 − ). C. (3; 2 − ). D. (3;2). 83
Chương III. Phương pháp tọa độ trong
mặt phẳng. 0916620899-0355334679
Tài liệu học tập Toán 10 GV. Lư Sĩ Pháp 1
Câu 49. Phương trình chính tắc của elip (E) qua điểm M 3;− và có một tiêu điểm F − 3;0 là: 1 ( ) 2 2 2 2 2 2 2 2 2 x 2 A. x y + =1. B. x y + =1. C. x y + =1. D. y + =1. 4 2 4 3 4 1 4 1
Câu 50. Cho tam giác ABC có đỉnh A( 1 − ;−3),G(4; 2
− ) là trọng tậm của tam giác ABC.Đường trung
trực của cạnh AB có phương trình: 3x + 2y –4 = 0.Toạ độ đỉnh C của tam giác ABC là: A. (8;4). B. ( 8 − ; 4 − ). C. (8; 4 − ). D. ( 8 − ;4).
Câu 51. Cho hai điểm A (5;6),B(−3;2).Phương trình chính tắc của đường thẳng AB là: x + 3 y − 2 x + 5 y + 6 x − 5 y − 6 x − 5 y − 6 A. = . B. = . C. = . D. = . 2 − 1 − 2 1 2 1 − 2 − 1
Câu 52. Cho đường thẳng (d ) : x + y −1 = 0 và (d ) : x − 3y + 3 = 0 . Gọi ( 1 2
d) là đường thẳng đối xứng với
d qua d . Phương trình đường thẳng ( 1 2 d) là:
A. 7x + y +1 = 0.
B. 7x + y –1 = 0.
C. 7x – y +1 = 0.
D. 7x – y –1 = 0.
Câu 53. Cho đường thẳng d : 3x + 5y + 2006 = 0. Mệnh đề nào dưới đây sai? 5
A. (d) có vectơ chỉ phương u = (5; 3 − ).
B. (d) có hệ số góc k = . 3
C. (d) song song với đường thẳng: 3x + 5y = 0.
D. (d) có vectơ pháp tuyến n = (3;5).
Câu 54. Phương trình chính tắc của elip (E) đi qua hai điểm M (4;− 3), N (2 2;3)là 2 2 2 2 2 2 2 2 A. x y + =1. B. x y + =1. C. x y + =1. D. x y + =1. 16 9 9 16 15 20 20 15
Câu 55. Đường thẳng ∆ : mx + y + 2 = 0 tiếp xúc với đường tròn (C): 2 2
x + y + 2x − 4 y + 4 = 0 khi m bằng 8 8 15 A. − . B. . C. . D. 0. 15 15 8
Câu 56. Cho tam giác ABC có phương trình hai đường cao là B ’
B : x + 3y −17 = 0,
CC’: 3x + 8y −12 = 0 và đỉnh A( 1 − ; 3
− ).Toạ độ đỉnh B là A. ( 2 − ;−5). B. (2; 5 − ). C. (2;5). D. ( 2 − ;5). 2 2
Câu 57. Với giá trị nào của m thì đường thẳng ∆ : x −
y + m = 0 tiếp xúc với đường tròn 2 2 2 2 x + y = 1? 2 A. m = .
B. m = 1.
C. m = 0. D. m = 2. 2 x = 5 + t
Câu 58. Phương trình nào dưới đây là phương trình tổng quát của đường thẳng ∆ : ;(t ∈ ℝ) ? y = 9 − − 2t
A. x + 2y +1 = 0.
B. 2x + y –1 = 0.
C. 2x + y –3 = 0.
D. x –2y = 0.
Câu 59. Cho tam giác ABC có A(1; ) 1 , đường cao B ’ B : 2
− x + y –8 = 0và đường cao
CC’: 2x + 3y –8 = 0. Đường cao A ’
A có phương trình là:
A. x + y + 2 = 0.
B. x + y –2 = 0.
C. x – y –2 = 0.
D. x – y + 2 = 0.
Câu 60. Phương trình đường tròn tâm I (1; 2
− ) và bán kính R = 2 là A. 2 2
x + y − 2x + 4 y +1 = 0. B. 2 2
x + y − 2x + 4 y − 6 = 0. C. 2 2
x + y − x + 2 y −1 = 0. D. 2 2
x + y − 2x + 4 y −1 = 0.
Câu 61. Đường tròn (C): 2 2
x + y − x + y −1 = 0 có tâm I và bán kính R là 1 1 6 1 1 6
A. I ;− , R = .
B. I − ; , R = . 2 2 2 2 2 2 84
Chương III. Phương pháp tọa độ trong
mặt phẳng. 0916620899-0355334679
Tài liệu học tập Toán 10 GV. Lư Sĩ Pháp C. I (1;− ) 1 , R = 6. D. I ( 1 − ;1), R =1.
Câu 62. Bán kính của đường tròn tâm I (0;−2)và tiếp xúc với đường thẳng d :3x –4y − 23 = 0 bằng 3 A. 5. B. 3. C. . D. 15. 5
Câu 63. Cho đường thẳng (d ) : x − 3y + 3 = 0 và (d ) : 3x − y −1 = 0 . Điểm M nằm trên trục hoành có 1 2
hoành độ dương và cách đều d và d có toạ độ là 1 2 1 A. (2;0). B. (3;0). C. (1;0). D. ;0. 2
Câu 64. Đường tròn tâm I (1, 2
− )tiếp xúc với đường thẳng (d):3x –4y −26 = 0có bán kính R bằng A. 5. B. 2. C. 4. D. 3.
Câu 65. Đường thẳng 2x + y –1 = 0 có vectơ pháp tuyến là:
A. n = (2;1).
B. n = (−1;2).
C. n = (2;−1).
D. n = (1;−1).
Câu 66. Cho hình thoi ABCD biết A( 1 − ;2),B(−2;− )
1 và D (2;3). Phương trình đường chéo AC là:
A. x + y –1 = 0.
B. x + y –3 = 0.
C. x – y + 3 = 0.
D. 2x + 3y –6 = 0.
Câu 67. Cho đường tròn (C): 2 2
x + y − 4x − 4 y − 8 = 0 và đường thẳng (d ) : x – y –1 = 0. Một tiếp tuyến
của (C) song song với (d) có phương trình là:
A. x − y + 3 − 2 = 0.
B. x − y + 4 2 = 0.
C. x − y − 3 + 3 2 = 0.
D. x – y + 6 = 0.
Câu 68. Một tam giác vuông cân có đỉnh góc vuông A (4;− )
1 ,cạnh huyền có phương trình:
3x – y + 5 = 0.Hai cạnh góc vuông có phương trình là
A. 2x + y + 6 = 0 và x –2y +1 = 0.
B. 3x + y –7 = 0 và x –3y +1 = 0.
C. x + 2y –6 = 0 và 2x – y + 7 = 0.
D. x − 2y –6 = 0 và 2x + y –7 = 0. 2 2
Câu 69. Cho elip (E): x y +
=1. Phương trình đường thẳng (d) đi qua M (1; )
1 và cắt ( E ) tại hai điểm 9 4 ,
A B sao cho M là trung điểm của đoạn thẳng AB là
A. 4x + 9y –13 = 0.
B. 4x – 9y –13 = 0.
C. 9x + 4y +13 = 0.
D. 9x – 4y −13 = 0.
Câu 70. Phương trình tổng quát của đường thẳng đi qua hai điểm A(2;− ) 1 và B(4; ) 1 là:
A. 2x + y −1 = 0.
B. x – y –3 = 0.
C. x + y + 2 = 0.
D. x + y –3 = 0.
Câu 71. Cho A(−2;5),B(2;3).Đường thẳng (d) : x –4y + 4 = 0 cắt AB tại điểm M có toạ độ là: A. (2; 4 − ). B. (4;2). C. ( 2 − ;4). D. ( 2 − ; 4 − ).
Câu 72. Cho hai đường thẳng song song ∆ : 5x − 7 y + 4 = 0 và ∆ : 5x − 7 y + 6 = 0 . Khoảng cách giữa 1 2
hai đường thẳng ∆ và ∆ là: 1 2 4 6 2 10 A. . B. . C. . D. . 74 74 74 74
Câu 73. Cho đường tròn (C): 2 2
x + y = 1. Đường thẳng qua M (1;2) và tiếp xúc với (C) có phương trình là
A. 3x + 4y = 0 và 3x − 4y +1 = 0
B. x −1 = 0 và 3x − 4y + 5 = 0
C. x +1 = 0 và 3x + 4y + 5 = 0
D. 3x + 4y + 5 = 0 và 3x + 4y − 5 = 0 Câu 74. Cho tam giác ABC có cạnh AB, AC lần lượt có phương trình là:
4x + y +15 = 0,2x + 5y + 3 = 0và trọng tâm G ( 2 − ;− )
1 .Toạ độ trung điểm M của cạnh BC là: A. (−1; 2 − ). B. (1; 2 − ). C. (1;2). D. (−1;2).
Câu 75. Đường thẳng nào vuông góc với đường thẳng: 4x – 3y +1 = 0? 85
Chương III. Phương pháp tọa độ trong
mặt phẳng. 0916620899-0355334679
Tài liệu học tập Toán 10 GV. Lư Sĩ Pháp x = 4 − t x = 8t x = 4t x = 4t A. . B. . C. . D. . y = 3 − −3t y = 3 − + t y = 3 − −3t y = 3 − + 3t
Câu 76. Đường trung trực của đoạn thẳng AB với A( 3 − ;2),B( 3
− ;3) có vectơ pháp tuyến là A. n = ( 1 − ;0).
B. n = (0;1). C. n = ( 3 − ;5). D. n = (6;5).
Câu 77. Phương trình tiếp tuyến của đường tròn 2 2
x + y = 5 tại điểm M (1;2) là
A. 2x + y –5 = 0.
B. x –2y –5 = 0.
C. x + 2y –5 = 0.
D. 2x – y + 5 = 0.
Câu 78. Cho đường tròn (C): 2 2
x + y − 4x − 2 y = 0 và đường thẳng ∆ : x + 2 y +1 = 0 . Khẳng định nào dưới đây đúng?
A. ∆ đi qua tâm của (C).
B. ∆ cắt (C) tại hai điểm.
C. ∆ tiếp xúc với (C).
D. ∆ không có điểm chung với (C).
Câu 79. Cho hai đường thẳng d : x + 2y + 4 = 0 và d : 2x − y + 6 = 0. Số đo của góc giữa hai đường 1 2
thẳng d và d bằng 1 2 A. 0 30 . B. 0 60 . C. 0 45 . D. 0 90 . x = 1 − + 2t
Câu 80. Vectơ pháp tuyến của đường thẳng có phương trình: ;(t ∈ ℝ) là: y = 3 − t
A. n = (1;2).
B. n = (−1;2).
C. n = (1; −2).
D. n = (2;−1).
Câu 81. Đường thẳng qua A(4;2) và tiếp xúc với đường tròn: 2 2
(x −1) + (y + 2) = 25 có phương trình là
A. 4x + 3y –20 = 0.
B. 3x + 4y –20 = 0.
C. 3x – 4y + 20 = 0.
D. 4x –3y + 20 = 0.
Câu 82. Cho hai đường thẳng ∆ : 2x − 4y − 3 = 0 và ∆ : 3x − y +17 = 0 . Góc giữa ∆ và ∆ bằng 1 2 1 2 π π 3π π A. . B. . C. . D. − . 4 2 4 4
Câu 83. Cho hai đường thẳng ∆ : mx + (m −1)y + 2m = 0 và ∆ : 2x + y −1 = 0 . Nếu ∆ song song với 1 2 1 ∆ thì 2 m có giá trị là:
A. m tuỳ ý.
B. m = 1.
C. m = −2. D. m = 2.
Câu 84. Cho điểm M (0;4) và đường tròn (C): 2 2
x + y − 8x − 6 y + 21 = 0 . Khẳng định nào dưới đây đúng?
A. M trùng với tâm cùa (C).
B. M nằm trên (C).
C. M nằm trong (C).
D. M nằm ngoài (C). 2 2
Câu 85. Một elip ( ) : x y E +
=1. Gọi 2c là tiêu cự của (E). Mệnh đề nào dưới đây đúng? 2 2 a b A. 2 2 2
b = a + c . B. 2 2 2
a = b + c .
C. c = a + . b D. 2 2 2
c = a + b .
Câu 86. Elip (E) có độ dài trục bé bằng tiêu cự. Tâm sai của (E) bằng 1 2 A. 1. B. 2. C. . D. . 3 2 x = 1 − + 3t
Câu 87. Cho đường thẳng (d) có phương trình tham số là:
;(t ∈ ℝ) . Phương trình tồng quát y = 2 − t của (d) là:
A. x + 3y –5 = 0.
B. x + 3y = 0.
C. 3x – y + 2 = 0.
D. 3x – y + 5 = 0.
Câu 88. Cho đường thẳng (∆) : 2x − 3y +1 = 0 . Phương trình đường thẳng (d) đi qua điểm M (1;2) và (d) //(∆) có là:
A. 2x − 3y + 4 = 0.
B. x + 2y –3 = 0.
C. 2x – y = 0.
D. 4x + 2y –6 = 0.
Câu 89. Phương trình đường tròn đi qua ba điểm A( 2
− ;4), B(5;5) và C (6; 2 − ) là A. 2 2
x + y − 2x − y +10 = 0 B. 2 2
x + y − 4x − 2 y + 20 = 0 C. 2 2
x + y − 4x − 2 y − 20 = 0 D. 2 2
x + y + 4x + 2 y + 20 = 0 86
Chương III. Phương pháp tọa độ trong
mặt phẳng. 0916620899-0355334679
Tài liệu học tập Toán 10 GV. Lư Sĩ Pháp
Câu 90. Cho đường thẳng (d ) : x + 3y −1 = 0 và (d ) : x − 3y − 5 = 0 . Phương trình đường thẳng (∆) đi 1 2
qua giao điểm của d và d đồng thời vuông góc với đường thẳng (d) : 2x – y + 7 = 0 là: 1 2
A. x + 3y –6 = 0.
B. 2x + 6y = 0.
C. 6x + y –2 = 0.
D. 3x + 6y –5 = 0.
Câu 91. Phương trình chính tắc của (E) đi qua điểm M ( 15;− )1và có tiêu cự bằng 8 là 2 2 2 2 2 2 2 2 A. x y + =1. B. x y + =1. C. x y + =1. D. x y + =1. 20 4 24 8 26 10 18 2
Câu 92. Cho elip (E): 2 2
9x +16y −144 = 0 và điểm M ( ;
x y) ∈ (E), F ,
là hai tiêu điểm. Biểu thức 1 2 F 2 OM + MF .
có giá trị không đổi và bằng 1 M 2 F A. 7. B. 9. C. 16. D. 25.
Câu 93. Đường thẳng ∆ : 4x + 3y + m = 0 tiếp xúc với đường tròn (C): 2 2
x + y = 1 khi và chỉ khi
A. m = 1.
B. m = 0.
C. m = 3. D. m = 5. x = 3− t
Câu 94. Đường thẳng nào dưới đây song song với đường thẳng : ;(t ∈ ℝ) ? y = 1 − + 2t x = 5 + t '
x = 5 − 2t ' x = 5 + 4t ' x = 5 + t ' A. . B. . C. . D. . y = 2 − t ' y = t ' y = 2t ' y = 2t '
Câu 95. Cho đường thẳng (∆) : x − 3y +1 = 0 . Phương trình đường thẳng (d) đi qua điểm A(1;0) và (d) ⊥ (∆) là
A. 2x – y +1 = 0.
B. x + 3y = 0.
C. 3x + y –3 = 0.
D. 3x + y + 5 = 0. ĐÁP ÁN
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25
B C B A B D D C D A D A D A D C D D C D B A C B B
26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50
B B B C C B D A C C A D C D C C C A A C D B B C C
51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75
A B B D C C B B B A A B A D A A B D A B B C B A C
76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100
A C C D A B A D D B D A A C D A D D A C 87
Chương III. Phương pháp tọa độ trong
mặt phẳng. 0916620899-0355334679




