Tài liệu Searching and Sorting | Học viện Nông nghiệp Việt Nam
Tài liệu này cung cấp một cái nhìn tổng quan về các thuật toán sắp xếp cơ bản, bao gồm Sắp xếp chèn, Sắp xếp lựa chọn, Sắp xếp nổi bọt, Sắp xếp rung, Sắp xếp đổi chỗ, Sắp xếp Shell, Sắp xếp Heap và Sắp xếp Quick. Nó giải thích các khái niệm và các bước triển khai cho mỗi thuật toán, cung cấp một hướng dẫn toàn diện để hiểu và áp dụng các kỹ thuật sắp xếp này.
Môn: Ứng dụng công nghệ thông tin chuyên ngành
Trường: Học viện Nông nghiệp Việt Nam
Thông tin:
Tác giả:
Tài liệu liên quan:
Preview text:
Searching and Sorting Nội dung
I/. Các giải thuật sắp xếp cơ bản:
II/. Các giải thuật sắp xếp cải tiến:
III/. Các giải thuật tìm kiếm: 1
Lưu ý: Các giải thuật có thể được trình bày khác nhau, tùy theo hướng xử lý (Top Down hoặc Bottom Up, hoặc cách chọn phần tử, chọn vị trí,..) và tùy theo tài liệu tham khảo.
I/. Các giải thuật sắp xếp cơ bản:
Giải thuật Sắp Xếp:
Trong khoa học máy tính, giải thuật sắp xếp là một giải thuật bố trí và xếp đặt các phần tử của
một danh sách (mảng) tuân theo một thứ tự (tăng hoặc giảm). Để minh họa và đơn giản hóa, người
ta thường sử dụng danh sách các phần tử cần sắp xếp là các số.
1/. Giải thuật Insertion Sort
A/. Ý tưởng:
Mọi dãy a[0] , a[1] ,..., a[n-1] luôn có (i-1) phần tử đầu tiên a[0] , a[1] ,... ,a[i-2] đã có thứ tự (1 ≤ i).
Ý tưởng chính: Tìm cách chèn phần tử a[i] vào vị trí thích hợp của đoạn đã được sắp để có dãy mới
a[0] , a[1] ,... ,a[i-1] trở nên có thứ tự.
Vị trí chèn này chính là pos thỏa : a[pos-1] a[i ]< a[pos] , với (1 pos i).
B/. Các bước tiến hành như sau :
Mô tả một cách đơn giản:
• Dãy ban đầu a[0] , a[1] ,..., a[n-1], xem như đã có đoạn gồm một phần tử a[0] đã được sắp.
• Thêm a[1] vào đoạn a[0] sẽ có đoạn a[0] a[1] được sắp
• Thêm a[2] vào đoạn a[0] a[1] để có đoạn a[0] a[1] a[2] được sắp
• Tiếp tục cho đến khi thêm xong a[n-1] vào đoạn a[0] a[1] ...a[n-1] sẽ có dãy a[0] a[1]….... A[n-1] được sắp.
input: dãy (a, n)
output: dãy (a, n) đã được sắp xếp • Bước 1: i = 2;
// giả sử có đoạn a[0] đã được sắp
• Bước 2: x = a[i]; Tìm vị trí pos thích hợp trong đoạn a[0]
đến a[i] để chèn x vào
• Bước 3: Dời chỗ các phần tử từ a[pos] đến a[i-1] sang
phải 1 vị trí để dành chổ cho x
• Bước 4: a[pos] = x; // có đoạn a[0]..a[i] đã được sắp • Bước 5: i = i+1; Nếu i n : Lặp lại Bước 2. Ngược lại : Dừng.
C/. Cài đặt:
Hàm hoán vị 2 phần tử trong mảng A 2
public static void InsertionSort(int A[], int n) { int x, pos;
for (int i=1; i{ x = A[i]; pos = i-1; //vị trí chèn
while (pos>=0 && A[pos] > x) { A[pos+1] = A[pos]; pos = pos-1; } A[pos+1] = x; } }
Xem file: Xem_Insertion Sort.MP4 Ví dụ: Bước i 57 19 24 12 9 13 45 25 3
2/. Giải thuật chọn trực tiếp _ Selection Sort
A/. Ý tưởng:
Dãy có thứ tự thì a[i]=min(a[i], a[i+1], …, a[n-1])
Ý tưởng của giải thuật chọn trực tiếp mô phỏng một trong những cách sắp xếp tự nhiên nhất thực tế
thường được sử dụng: Chọn phần tử nhỏ nhất trong n phần tử ban đầu, đưa phần tử này về vị trí
đúng là đầu dãy hiện hành, sau đó không quan tâm đến nó nữa, xem dãy hiện hành chỉ còn n-1
phần tử của dãy ban đầu, bắt đầu từ vị trí thứ 2, lặp lại quá trình trên cho dãy hiện hành chỉ còn 1
phần tử. Dãy ban đầu có n phần tử, vậy tóm tắt ý tưởng giải thuật là thực hiện n-1 lượt việc đưa
phần tử nhỏ nhất trong dãy hiện hành về vị trí đúng ở đầu dãy.
B/. Các bước tiến hành như sau :
input: dãy (a, n)
output: dãy (a, n) đã được sắp xếp
• Bước 1 : i = Vị trí đầu;
• Bước 2 : Tìm phần tử a[min] nhỏ nhất trong dãy hiện hành từ a[i] đến a[n-1]
• Bước 3 : Nếu min i: Hoán vị a[min] và a[i]
• Bước 4 : Nếu i chưa là Vị trí cuối » i = Vị trí kế(i); » Lặp lại Bước 2
Ngược lại: Dừng. //n phần tử đã nằm đúng vị trí.
C/. Cài đặt:
Hàm Selection Sort nhận vào một mảng chứa dãy số cần sắp xếp nội dung và tiến hành sắp xếp
ngay trên mảng đã nhập.
public static void SelectionSort(int A[], int n)
{ int i, j, vtmin, temp;
for (i = 0; i < n-1; i++) { vtmin = i;
for (j = i+1; j < n; j++)
{ if (A[j] < A[vtmin]) vtmin = j; } /* Swap(i, vtmin, A) */ temp = A[i]; A[i] = A[vtmin]; A[vtmin]= temp; } } 4
Xem file: Xem_Selection Sort.MP4 Ví dụ: i 57 19 24 12 9 13 45 25 5
3/. Giải thuật nổi bọt _ Bubble Sort
A/. Ý tưởng: dùng cách so sánh trực tiếp từng cặp số, có 2 cách: sắp xếp từ trên xuống (Top down)
hoặc sắp xếp từ dưới lên (Bottom up).
• Xuất phát từ đầu dãy, đổi chỗ các cặp phần tử kế cận để đưa phần tử nhỏ hơn trong cặp phần
tử đó về vị trí đúng ở đầu dãy hiện hành, sau đó sẽ không xét đến nó ở bước tiếp theo. (có
thể thực hiện ngược lại từ cuối đến đầu để đưa phần tử lớn hơn về cuối dãy hiện hành)
• Ở lần xử lý thứ i có vị trí đầu dãy là i
• Lặp lại xử lý trên cho đến khi không còn cặp phần tử nào để xét.
B/. Các bước tiến hành như sau :
input: dãy (a, n)
output: dãy (a, n) đã được sắp xếp
• Bước 1 : i = Vị trí đầu;
• Bước 2 : j = Vị trí cuối; //Duyệt từ cuối dãy ngược về vị trí i
– Trong khi (j > i) thực hiện:
• Nếu a[j]//đổi chỗ 2 phần tử kế cận
• j = Vị trí trước(j);
• Bước 3 : i = Vị trí kế(i);
// lần xử lý kế tiếp
– Nếu i = Vị trí cuối: Dừng. // Hết dãy.
– Ngược lại : Lặp lại Bước 2.
C/. Cài đặt:
Bubble sort (sắp xếp bằng cách đổi chỗ) 6
public static void BubbleSort(int A[] , int n) // sắp xếp từ dưới lên. { int i, j, temp;
for (i=0; ifor (j=n-1; j>i; j--) if(A[j]< A[j-1]) Swap(j, j-1, A); }
Xem file: Xem_Bubble Sort.MP4 (sắp xếp từ trên xuống) Ví dụ: i 57 19 24 12 9 13 45 25 7
4/. Giải thuật Shaker Sort
A/. Ý tưởng: Shaker Sort (giải thuật rung) là một cải tiến của Bubble Sort. Sau khi đưa phần
tử nhỏ nhất về đầu dãy, giải thuật sẽ giúp chúng ta đưa phần tử lớn nhất về cuối dãy. Do
đưa các phần tử về đúng vị trí ở cả hai đầu nên Shaker Sort sẽ giúp cải thiện thời gian sắp xếp dãy số.
B/. Giải thuật:
input: dãy (a, n)
output: dãy (a, n) đã được sắp xếp Bước 1:
Khởi tạo: l=0; r = n-1; // từ l(eft) đến r(ight) là đoạn cần được sắp xếp K= 0; n-1;
// ghi nhận lại vị trí l xảy ra hoán vị sau cùng để làm cơ sở thu hẹp đoạn l đến r Bước 2: Bước 2a: i = r;
// đẩy phần tử nhỏ nhất về đầu mảng Trong khi (i>l)
Nếu a[i] < a[i-1]: a[i]↔ a[i-1]; k=i;
// lưu lại nơi xảy ra hoán vị i = i-1; l = k;
//loại bớt phần tử đã có thứ tự ở đầu dãy Bước 2b: i=l;
// đẩy phần tử lớn về cuối mảng
Trong khi (iNếu a[i]>a[i+1]: a[i]↔ a[i+1]; k=i;
//lưu lại nơi xảy ra hoán vị i=i+1; r = k;
//loại bớt phần tử đã có thứ tự ở cuối dãy Bước 3:
Nếu l < r : lặp lại bước 2.
C/. Cài đặt:
public static void ShakerSort(int A[], int n)
{ int i, k, left, right;
k = 0; left = 0; right = n - 1; 8
while (left < right)
{ for (i = right; i > left; i--)
if (A[i] < A[i - 1]) { Swap(i, i-1, A); k = i;
// biến k dùng đánh dấu để bỏ qua đọan đã có thứ tự } left = k;
for (i = left; i < right; i++)
if (A[i] > A[i + 1]) { Swap(i, i+1, A); k = i; } right = k; } }
Xem file: Xem_SHAKERSORT.MP4 Ví dụ: Bước 57 19 24 12 9 13 45 25
5/. Giải thuật Interchange Sort
A/. Ý tưởng:
• Để sắp xếp một dãy số, ta có thể xét các nghịch thế có trong dãy và làm triệt tiêu dần chúng đi.
• Ý tưởng chính của giải thuật này là tìm các cặp nghịch thế và triệt tiêu chúng. Ta xuất phát
từ phần tử đầu tiên của dãy, tìm tất các các cặp nghịch thế chứa phần tử này, triệt tiêu chúng
bằng các hoán vị phần tử này với phần tử tương ứng trong cặp nghịch thế. Ta dễ nhận thấy
sau lần duyệt đầu tiên, phần tử đầu tiên chính là phần tử nhỏ nhất của dãy. Ta tiếp tục xử lý
với phần tử thứ hai, ta có được phần tử thứ hai chính là phần tử nhỏ thứ hai của dãy. Cứ như
vậy, sau khi xử lý với phần tử thứ (n -1) của dãy, ta được một dãy sắp .
B/. Các bước tiến hành như sau : 9
input: dãy (a, n)
output: dãy (a, n) đã được sắp xếp • Bước 1 : i = 0;
// bắt đầu từ đầu dãy • Bước 2 : j = i+1;
//tìm các cặp phần tử nghịch thế
a[j] < a[i], với j>i • Bước 3 : Trong khi j n thực hiện
• Nếu a[j]// đổi chỗ cặp phần tử này • j = j+1; • Bước 4 : i = i+1;
– Nếu i < n: Lặp lại Bước 2. – Ngược lại: Dừng.
C/. Cài đặt: Ví dụ: Bước 57 19 24 12 9 13 45 25 10
II/. Các giải thuật sắp xếp cải tiến:
1/. Giải thuật Shell Sort:
A/. Ý tưởng:
• Khởi tạo giá trị h (có nhiều cách khác nhau)
• Chia danh sách thành các danh sách con theo khoảng h
• Sử dụng Insertion Sort để sắp xếp các danh sách con
• Lặp lại liên tục việc giảm h đến khi danh sách hoàn thành với h = 1.
Yếu tố quyết định tính hiệu quả của một giải thuật là cách chọn khoảng cách h trong từng bước sắp
xếp. Giả sử quyết định sắp xếp k bước, các khoảng cách chọn phải thoả điều kiện: hi > hi+1 và hk = 1
Tuy nhiên đến nay vẫn chưa có tiêu chuẩn rõ ràng trong việc lựa chọn dãy giá trị khoảng cách tốt
nhất, một số khoảng h đã được Knuth đề nghị:
hi = ( hi-1 –1)/3 và hk =1, k= log3n-1 (h1=121, h2=40, h3=13, h4=4, h5=1) hay
hi = ( hi-1 –1)/2 và hk =1, k= log2-1 (h1=15, h2=7, h3=3, h4=1)
B/. Cài đặt:
Xem file Xem_ShellSort.MP4 Ví dụ: 11 Bước h 57 19 24 12 9 13 45 25
C/. Độ phức tạp giải thuật:
• Trường hợp xấu nhất: O(n log n)
• Trường hợp tốt nhất: O(n log n) 12
2/. Phương pháp Heap Sort:
A/. Ý tưởng:
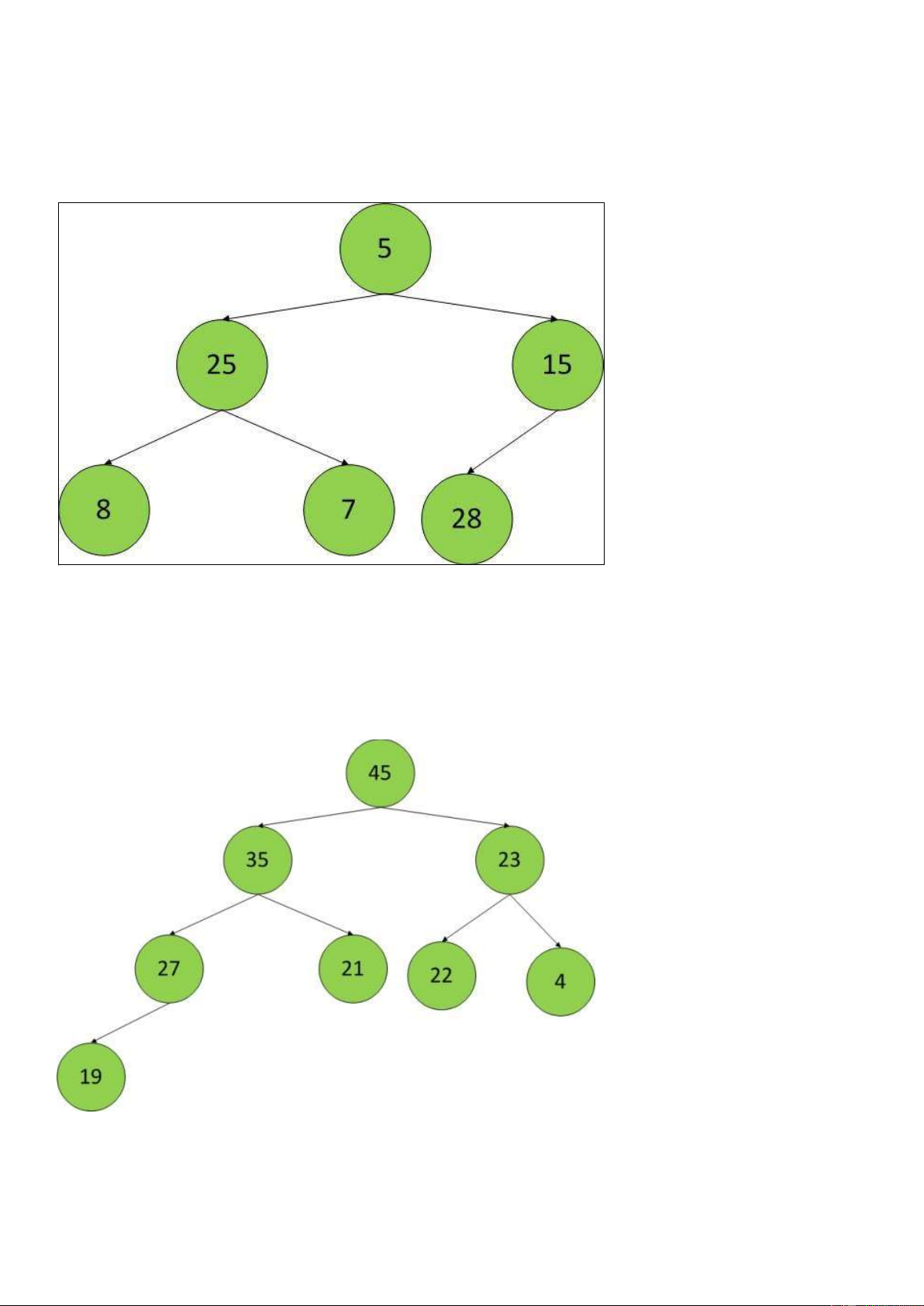
Định nghĩa Heap: hiểu sơ lược Heap là 1 cây nhị phân đầy đủ như hình sau: Vd:
Tính chất Heap: có 1 trong 2 tính chất sau:
+ Max Heap: Giá trị của mỗi node >= giá trị của các node con nó
=> Node lớn nhất là node gốc
+ Min Heap: Giá trị của mỗi node <= giá trị của các node con nó
=> Node nhỏ nhất là node gốc Vd: 13
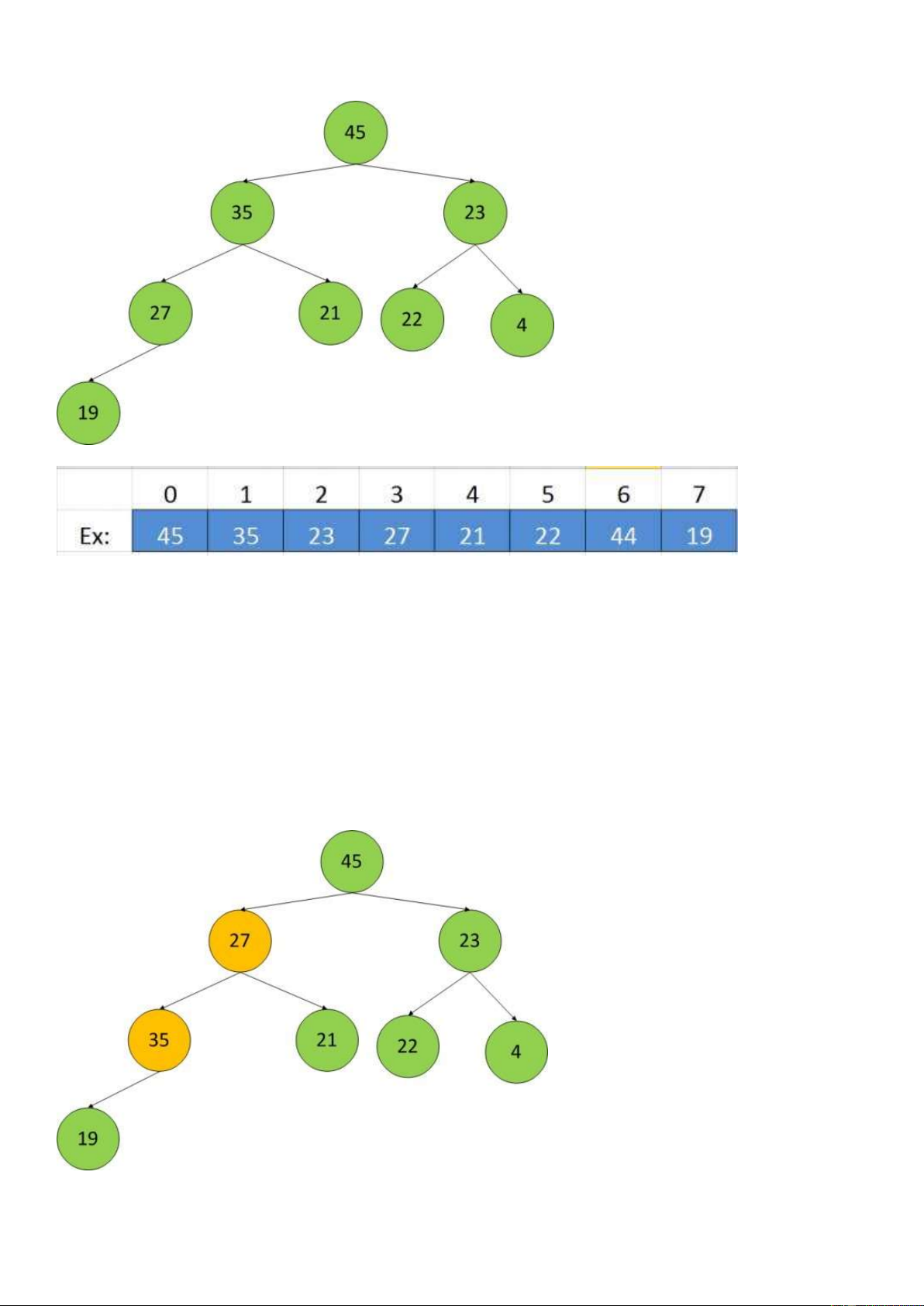
Biểu diễn Heap bằng mảng:
• Thứ tự lưu trữ trên mảng được thực hiện từ trái => phải
• Nếu ta biết được chỉ số của 1 phần tử trên mảng, ta sẽ dễ dàng xác định được chỉ số của node
cha và các node con của nó: o Node gốc ở chỉ số 0
o Node cha của node i có chỉ số (i – 1)/2
o Các node con của node i (nếu có) có chỉ số [2i + 1] và [2i + 2]
o Node cuối cùng có con trong 1 Heap có n phần tử là: [n/2 – 1]
Vd: Thử thực hiện Heapify theo Max Heap. Tức là node con của node đang xét mà lớn hơn node
cha thì thực hiện đổi chỗ. 14
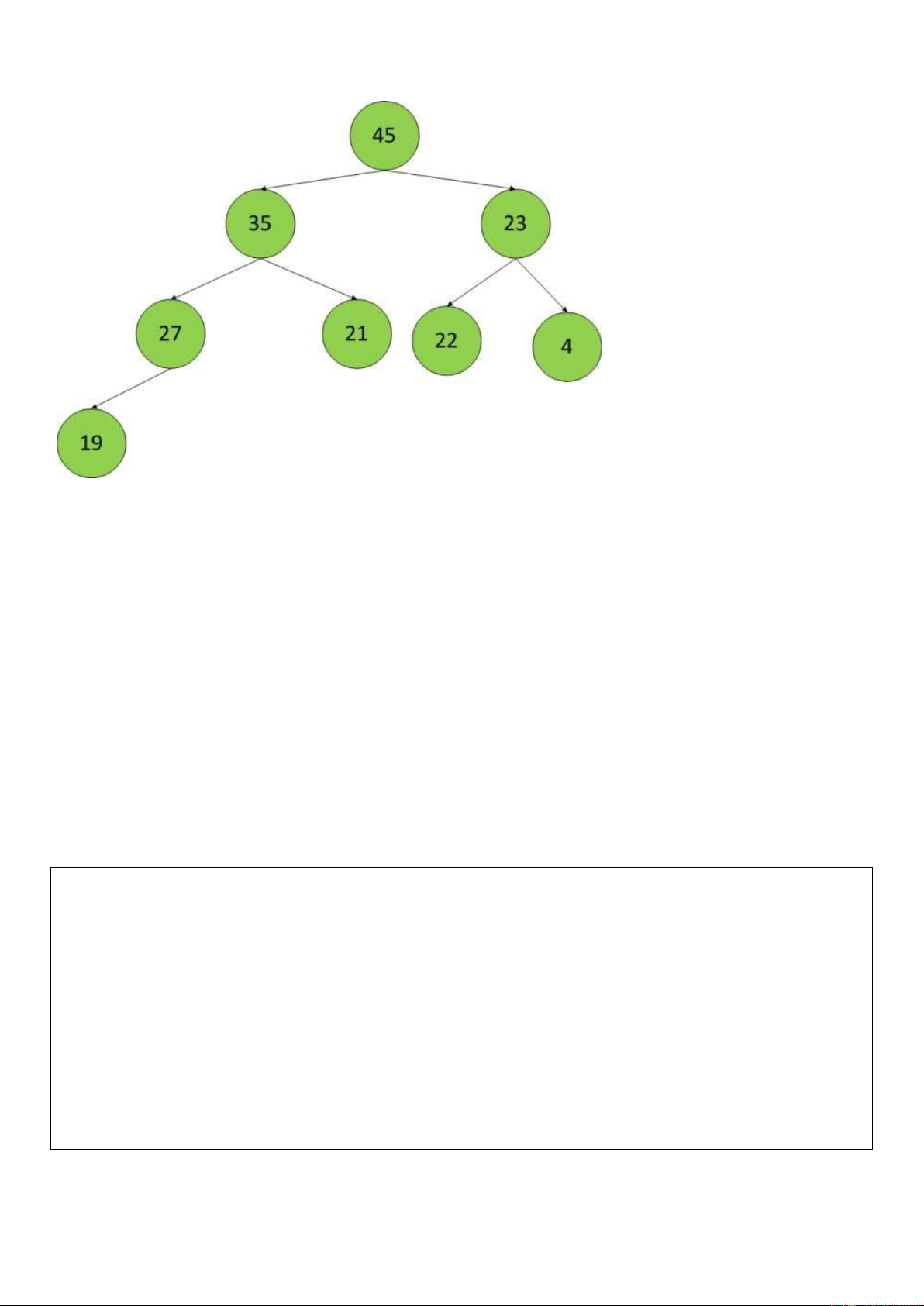
Ý tưởng giải thuật HeapSort
Bước 1: Xây dựng Heap
• Sử dụng thao tác Heapify để chuyển đổi mảng bình thường thành Heap
Bước 2: Sắp xếp
• Hoán vị phần tử cuối cùng của Heap với phần tử đầu tiên của Heap
• Loại bỏ phần tử cuối cùng
• Thực hiện thao tác Heapify để điều chỉnh phần tử đầu tiên
B/. Cài đặt: Cần viết 3 hàm sau:
Heapify: Tạo Heap từ mảng. 15
Bulid Heap: Thực hiện tạo các Heap
HeapSort: Thực hiện sắp xếp Heap
Xem file Xem_HeapSort.MP4 Ví dụ: Bước i 45 35 23 27 21 22 44 19 Ví dụ: Bước i 9 12 4 6 1 25 5 16
3/. Giải thuật Quick Sort:
A/. Ý tưởng:
• Giải thuật QuickSort sắp xếp dãy a[0], a[1] ..., a[n-1] dựa trên việc chọn 1 phần tử làm mốc
x (pivot) và phân hoạch dãy ban đầu thành 3 phần :
– Phần 1: Gồm các phần tử có giá trị không lớn hơn x
– Phần 2: Gồm các phần tử có giá trị bằng x
– Phần 3: Gồm các phần tử có giá trị không nhỏ hơn x
với x là giá trị của một phần tử tùy ý trong dãy ban đầu.
• Sau khi thực hiện phân hoạch, dãy ban đầu được phân thành 3 đoạn:
– 1. a[k] ≤ x , với k = 1 .. j
– 2. a[k ] = x , với k = j+1 .. i-1 – 3. a[k ] x , với k = i..n-1 Nhận xét:
• Về lý thuyết ta có thể chọn giá trị mốc x là một phần tử tùy ý trong dãy, nhưng để đơn giản,
phần tử có vị trí giữa thường được chọn, khi đó pivot = (left +right)/ 2.
• Giá trị mốc x (pivot) được chọn sẽ có tác động đến hiệu quả thực hiện giải thuật vì nó quyết
định số lần phân hoạch.
– Số lần phân hoạch sẽ ít nhất nếu ta chọn được x là phần tử có giá trị là trung bình các
phần tử, nhiều nhất nếu x là cực trị (lớn nhất / nhỏ nhất) của dãy.
– Tuy nhiên do chi phí xác định phần tử trung bình khá cao nên trong thực tế người ta
không chọn phần tử này mà chọn phần tử nằm chính giữa dãy làm mốc với hy vọng
nó có thể gần với giá trị trung bình.
B/. Các bước tiến hành như sau :
input: dãy con (a, left, right)
output: dãy con (a, left, right) được sắp tăng dần • Bước 1 :
Chọn tuỳ ý một phần tử a[k] trong dãy là giá trị mốc left<=k<=right X = a[k]; i=left, j=right; 17 • Bước 2 :
Phát hiện và hiệu chỉnh cặp phần tử a[i], a[j] nằm sai chỗ: ▪ Bước 2a :
Trong khi a[i] ▪ Bước 2b : Trong khi a[j]>x j--;
▪ Bước 2c : Nếu i• Bước 3: Sắp xếp đoạn 1: a[left].. a[j]
• Bước 4: Sắp xếp đoạn 3: a[i].. a[right]
C/. Cài đặt:
public static void QuickSort(int A[], int left, int right)
{ int i = left, j = right; int temp;
int pivot = A[(left + right) / 2]; // Phần tử pivot là phần tử giữa while (i <= j)
{ while (A[i] < pivot) i++;
while (A[j] > pivot) j--; if (i <= j)
{ /** hoán vị 2 phần tử **/ temp = A[i]; A[i] = A[j]; A[j] = temp; i++; j--; } } if (left < j) QuickSort(A, left, j); if (i < right)
QuickSort(A, i, right); }
Xem file Xem_QuickSort.MP4 (Pivot là phần tử đầu)
Ví dụ: Pivot là phần tử giữa Pivot Left Right 57 19 24 12 9 13 45 25 12 0 7 9 0 1 57 2 7 18 25 2 6 19 2 4 25 5 6
Ví dụ: Pivot là phần tử đầu Pivot Left Right 57 19 24 12 9 13 45 25 57 0 7 25 0 6 13 0 4 9 0 1 24 2 4 13 2 3 25 5 6
4/. Giải thuật Merge Sort: Sinh viên tìm hiểu và tự cài đặt
A/. Ý tưởng: Giải thuật Merge sort là giải thuật chia để trị (tương tự Quick Sort). Merge sort chia
dãy thành 2 nửa thành 2 dãy con, tiếp tục chia các dãy con thành 2 nửa,… cho đến khi chỉ còn 1
phần tử. Sau đó thực hiện trộn các dãy con có sắp xếp các phần tử theo đúng thứ tự của nó, tiếp tục
trộn cho đến khi trở lại thành 1 dãy, kết quả dãy đã được sắp xếp.
B/. Các bước tiến hành như sau :
input: dãy con (a, left, right)
output: dãy con (a, left, right) được sắp tăng dần 19
C/. Cài đặt: 20 21
5. Giải thuật Radix Sort:
Sinh viên tìm hiểu và tự cài đặt
Radix Sort: sắp xếp dựa trên cơ số. Có thể khái quát là sắp xếp theo hàng đơn vị trước,
sau đó đến hàng chục, hàng trăm,…
Lưu ý: Radix Sort chỉ xử lý dãy số nguyên >0.
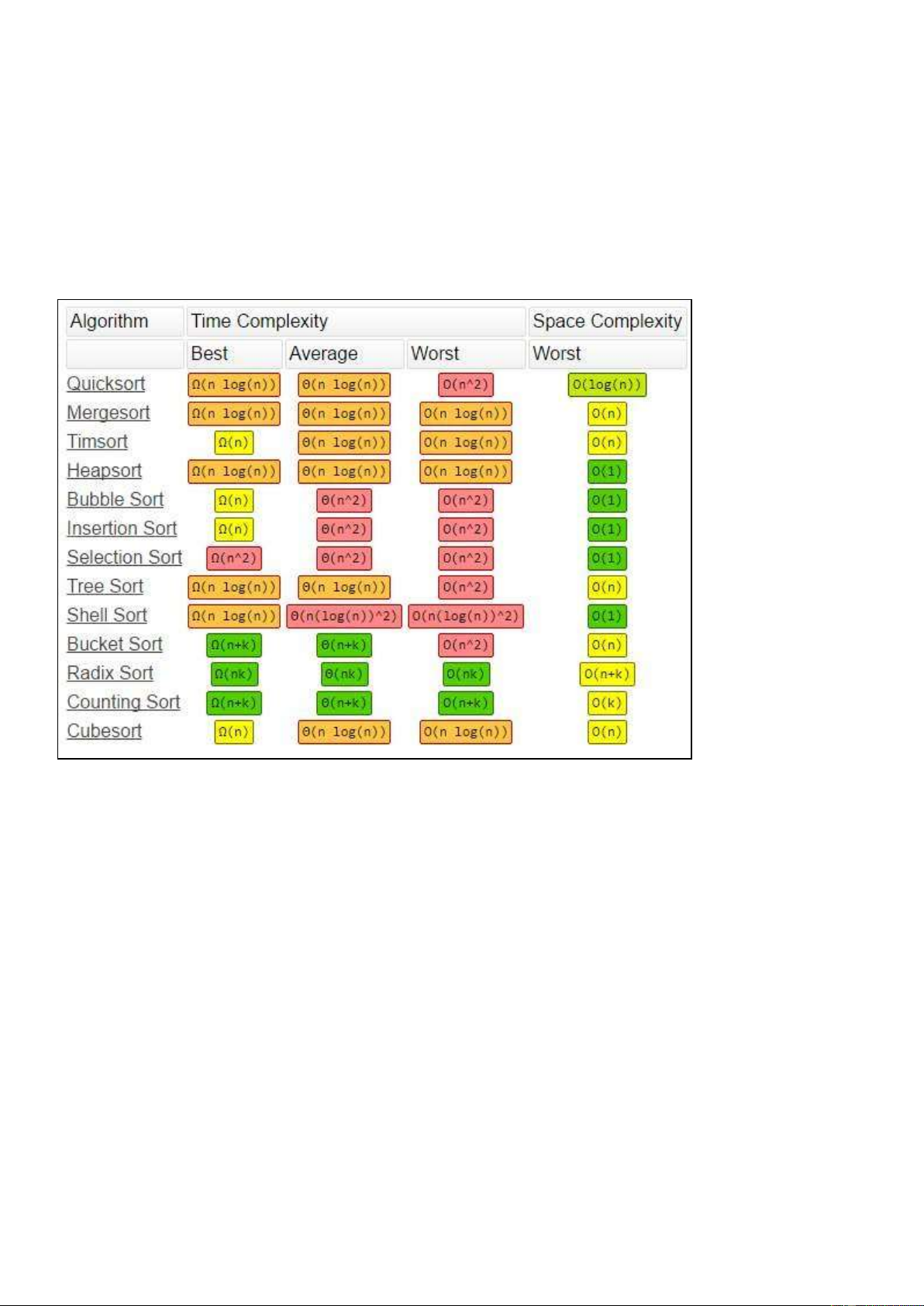
Đánh giá các phương pháp sắp xếp: (trong khuôn khổ giáo trình này, ngoài các giải thuật đã
giới thiệu còn nhiều giải thuật khác nữa)
• Phần lớn các giải thuật sắp xếp cơ bản dựa trên sự so sánh giá trị giữa các phần tử. Bắt đầu
từ nhóm các giải thuật cơ bản, đơn giản nhất. Đó là các giải thuật Selecttion Sort (chọn trực
tiếp), Insertion Sort (chèn trực tiếp), Bubble Sort (nổi bọt), Interchange Sort (đổi chỗ trực
tiếp). Các giải thuật này đều có một điểm chung là chi phí thực hiện tỷ lệ với n2.
• Tiếp theo, chúng ta khảo sát một số cải tiến của các giải thuật trên. Nếu như các giải thuật
Binary Insertion Sort (chèn nhị phân), Shaker Sort (rung); tuy chi phí có ít hơn các giải thuật
gốc nhưng chúng vẫn chỉ là các giải thuật thuộc nhóm có độ phức tạp O(n2), thì các giải
thuật Shell Sort (cải tiến của chèn trực tiếp), Heap Sort lại có độ phức tạp nhỏ hơn hẳn các
giải thuật gốc. Giải thuật Shell Sort có độ phức tạp O(nx) với 1có độ phức tạp O(n log2 n).
• Các giải thuật Merge Sort và Quick sort là những giải thuật thực hiện theo chiến lược chia để
trị. Cài đặt chúng tuy phức tạp hơn các giải thuật khác nhưng chi phí thực hiện lại thấp, cả
hai giải thuật đều có độ phức tạp O(n log2 n). Merge sort có nhược điểm là cần dùng thêm bộ
nhớ đệm. Giải thuật này sẽ phát huy tốt ưu điểm của mình hơn khi cài đặt trên các cấu trúc
dữ liệu khác phù hợp hơn như danh sách liên kết hay file.
• Giải thuật Quick Sort, như tên gọi của mình được đánh gía là giải thuật sắp xếp nhanh nhất
trong số các giải thuật sắp xếp dựa trên nền tảng so sánh giá trị của các phần tử. Tuy có chi
phí trong trường hợp xấu nhất là O(n2) nhưng trong kiểm nghiệm thực tế, giải thuật Quick
sort chạy nhanh hơn hai giải thuật cùng nhóm O(n log2 n) là Merge Sort và Heap Sort. Từ
giải thuật Quick Sort, ta cũng có thể xây dựng được một giải thuật hiệu quả tìm phần tử
trung vị (median) của một dãy số.
• Người ta cũng chứng minh được rằng O(n log2 n) là ngường chặn dưới của các giải thuật sắp
xếp dựa trên nền tảng so sánh giá trị của các phần tử. Để vượt qua ngưỡng này, ta cần phát
triển giải thuật mới theo hướng khác các giải thuật trên. Radix sort là một giải thuật như vậy. 22
Nó được phát triển dựa trên sự mô phỏng qui trình phân phối thư của những người đưa thư.
Giải thuật này đại diện cho nhóm các giải thuật sắp xếp có độ phức tạp tuyến tính. Tuy
nhiên, thường thì các giải thuật này không thích hợp cho việc cài đặt trên cấu trúc dữ liệu mảng một chiều.
• Trên thực tế dữ liệu cần thao tác có thể rất lớn do vậy không thông thường thì các dữ liệu
được lưu trên bộ nhớ thứ cấp, tức trên các đĩa từ. Việc thực hiện các thao tác sắp xếp trên các
dữ liệu này đòi hỏi phải có các phương pháp khác thích hợp.
III/. Các giải thuật tìm kiếm:
Tìm kiếm là một bài toán cơ bản, rất cần trong nhiều ứng dụng thực tế. Có nhiều dạng bài toán
tìm kiếm khác nhau như: tìm kiếm không có thông tin – tìm kiếm có thông tin; tìm kiếm trên
danh sách – tìm kiếm trên cây- tìm kiếm trên đồ thị; tìm kiếm đối kháng, …
Trong phạm vi môn học CTDL, ta quan tâm đến tìm kiếm trên danh sách với 2 phương pháp là
tìm kiếm tuyến tính và tìm kiếm nhị phân.
1/. Tìm kiếm tuyến tính _ Linear Search
A/. Ý tưởng
Tìm kiếm tuyến tính là một kỹ thuật tìm kiếm cơ bản và cổ điển. Giải thuật tiến hành so sánh giá trị
cần tìm (khóa) với phần tử thứ nhất, thứ hai,..., của dãy số cung cấp cho đến khi gặp được phần tử có khóa cần tìm.
B/. Các bước tiến hành:
Gọi x là giá trị cần tìm và a là mảng chứa dãy số dữ liệu. Các bước tiến hành như sau: 23 Bước 1: i=0;
Bước 2 : So sánh a[i] với x, có 2 khả năng :
a[i] = x: Tìm thấy. Dừng. a[i] != x: Sang bước 3.
Bước 3 : i = i + 1; //xét phần tử kế
Nếu i > n: hết mảng, không tìm thấy. Dừng
Ngược lại: lặp lại bước 2.
C/. Cài đặt
Hàm LinearSearch được cài đặt bên dưới sẽ nhận vào một mảng các số nguyên a và một giá trị cần
tìm x. Sau khi thực hiện xong hàm trả về vị trí đầu tiên tìm thấy giá trị x nếu tìm thấy x trong mảng
a và trả về giá trị -1 nếu x không có trong mảng.
Từ giải thuật trên, ta có thể sửa đổi để tìm phần tử = x cuối cùng, đếm số phần tử = x, …
D/. Đánh giá giải thuật
Có thể ước lượng độ phức tạp của giải thuật tìm kiếm qua số lượng các phép so sánh được tiến
hành để tìm ra x. Các trường hợp giải thuật tìm tuyến tính có thể có: Trường hợp Số lần so sánh Giải thích Tốt nhất 1
Phần tử đầu tiên có giá trị là x. Xấu nhất n
Phần tử cuối cùng có giá trị là x. Trung bình (n+1)/2
Giả sử xác xuất các phần tử trong mảng nhận giá trị x là như nhau.
Vậy giải thuật tìm kiếm tuyến tính có độ phức tạp O(n). 24
E/. Nhận xét
Giải thuật tìm kiếm tuyến tính không phụ thuộc vào thứ tự của các phần tử trong mảng. Do đó, đây
là phương pháp tổng quát nhất để tìm kiếm trên một dãy số bất kỳ.
Giải thuật có thể được cài đặt theo nhiều cách khác nhau như dùng for,…, và có thể cải tiến để đạt
giảm bớt các thao tác thừa và tốc độ thực hiện.
2/. Tìm nhị phân _ Binary Search
A/. Ý tưởng
Trường hợp dãy số đã cho là có thứ tự (giả sử thứ tự tăng), các phần tử trong dãy có quan hệ a[i-1]
≤ a[i] ≤ a[i+1], từ đó kết luận được nếu x > a[i] thì x chỉ có thể xuất hiện trong đoạn [a[i+1], a[n-1]]
của dãy, ngược lại nếu x < a[i] thì x chỉ có thể xuất hiện trong đoạn [a[0], a[i-1]] của dãy. Giải
thuật tìm nhị phân áp dụng cho dãy đã có thứ tự để tìm các giới hạn phạm vi tìm kiếm sau mỗi lần
so sánh x với một phần tử trong dãy.
Ý tưởng của giải thuật là tại mỗi bước tiến hành so sánh x với phần tử nằm ở giữa của dãy tìm kiếm
hiện hành, dựa vào kết quả so sánh này để quyết định giới hạn dãy tìm kiếm ở bước kế tiếp là nửa
trên hay nửa dưới của dãy tìm kiếm hiện hành.
B/. Các bước tiến hành:
Gọi x là giá trị cần tìm, a là mảng chứa các giá trị dữ liệu gồm n phần tử đã dược sắp xếp (có thứ
tự), left và right là chỉ số đầu và cuối của đoạn cần tìm, mid là chỉ số của phần tử nằm giữa của
đoạn cần tìm. Các bước tìm kiếm được tiến hành như sau:
Bước 1: Khởi đầu tìm kiếm trên tất cả các phần tử left = 0; right = n;
Bước 2: mid = (left+right)/2;
So sánh a[mid] với x, có 3 khả năng :
• a[mid] = x : Tìm thấy. Dừng
• a[mid] > x : Chuẩn bị tìm tiếp x trong dãy con a[left]..a[mid -1] : right = mid – 1;
• a[mid] < x: Chuẩn bị tìm tiếp x trong dãy con a[mid +1]..a[right] : left = mid + 1; Bước 3:
• Nếu left <= right : Dãy tìm kiếm hiện hành vẫn còn phần tử. Lặp lại bước 2.
• Ngược lại : Dãy tìm kiếm hiện hành hết phần tử. Dừng.
C/. Cài đặt
Tương tự như hàm LinearSearch, hàm BinarySearch cũng nhận vào một dãy n phần tử và một
giá trị cần tìm x. Ngoài ra, để BinarySearch thực hiện đúng thì dãy ban đầu phải có thứ tự tăng dần (hoặc giảm dần). 25
Hàm BinarySearch cũng chỉ đơn giản sử dụng một vòng lặp để duyệt qua các phần tử trong dãy.
Tuy nhiên, vòng lặp này sẽ không duyệt qua hết tất cả các phần tử như đối với tìm kiếm tuyến tính.
Tư tưởng cài đặt của hàm này cũng giống như đối với LinearSearch, nghĩa là khi kết thúc vòng lặp
cũng có 2 khả năng xảy ra:
- Chỉ số left vẫn còn bé hơn hoặc bằng chỉ số right. Điều này có nghĩa là đã có một phần tử
nào đó bằng với giá trị x cần tìm, cụ thể là giá trị của phần tử middle. Do đó, hàm sẽ trả về
giá trị nằm trong biến mid.
- Chỉ số left đã vượt qua chỉ số right, nghĩa là đã duyệt qua hết các phần tử trong dãy mà
không tìm thấy phần tử nào có giá trị bằng x. Do đó, hàm trả về giá trị -1.
D/. Đánh giá giải thuật
Trường hợp giải thuật tìm nhị phân ta có bảng phân tích sau: Trường hợp Số lần so sánh Giải thích Tốt nhất 1
Phần tử giữa của dãy có giá trị = x. Xấu nhất log2 n
Phần tử cần tìm x ở cuối dãy. Trung bình (log2 n) / 2
Giả sử xác xuất các phần tử trong mảng nhận giá trị x là như nhau. 26
Vậy giải thuật tìm kiếm nhị phân có độ phức tạp O(log2 n). 27