TÍCH PHÂN KÉP
1) Khái niệm tích phân kép, tính chất 2) Cách tính 3) Ứng dụng 3/30/2020
Tích phân kép và ứng dụng 1 1. Tích phân kép
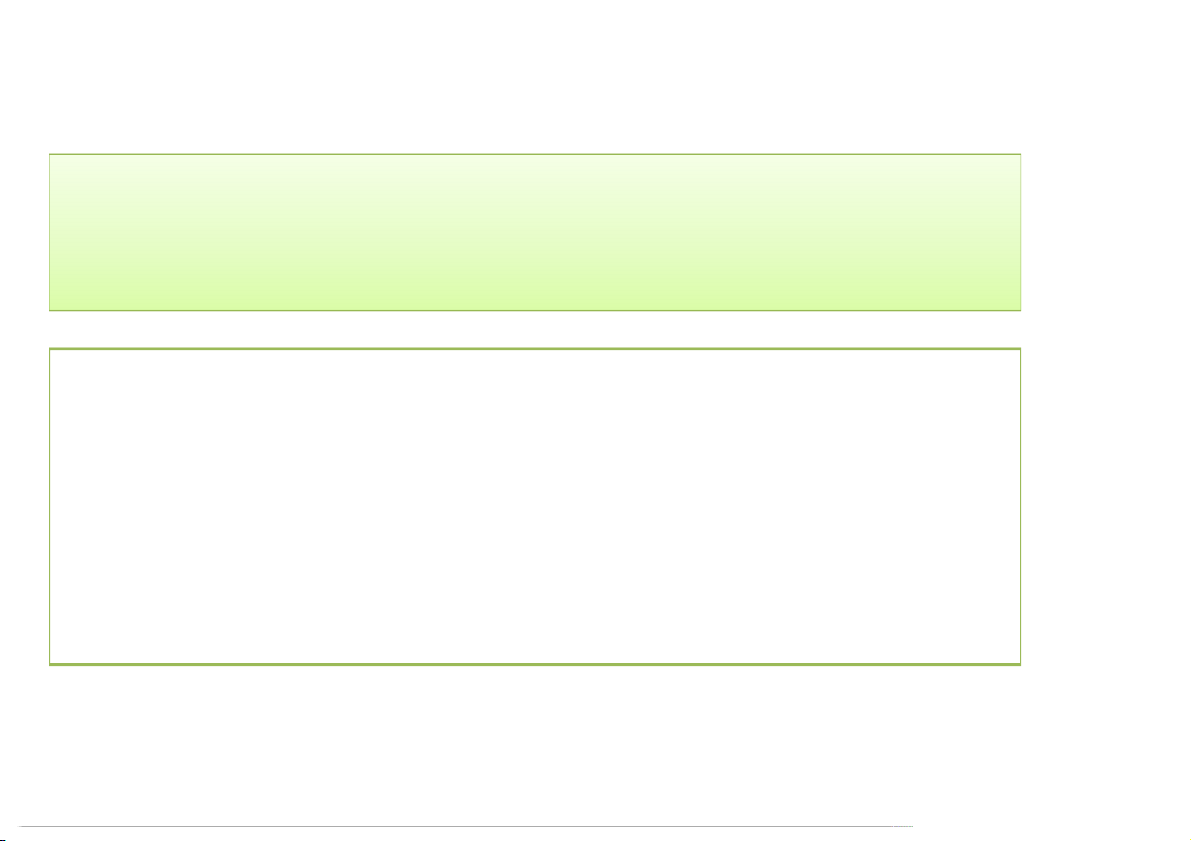
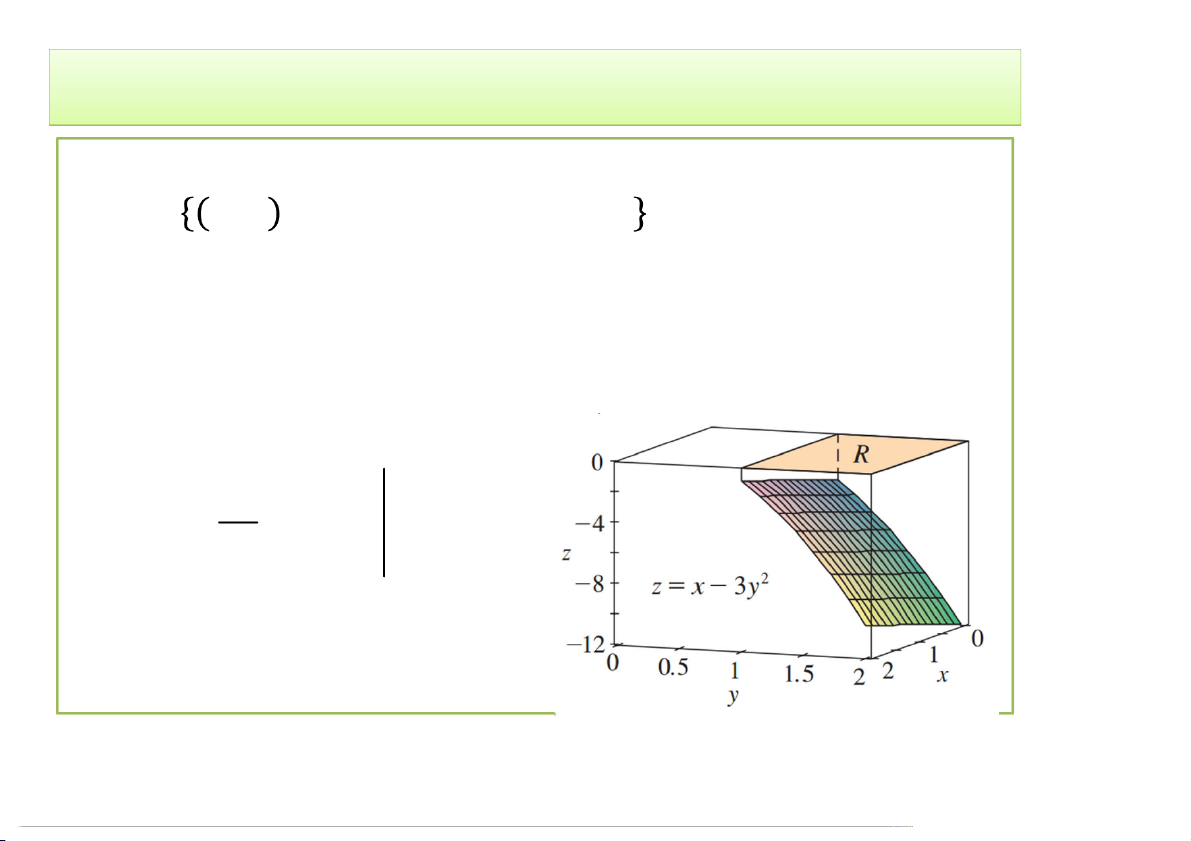
 Cho vật thể S xác định bởi:
 = , ,  ∈ |0 ≤  ≤  ,  , (, ) ∈ 
Tính thể tích vật thể S? 3/30/2020
Tích phân kép và ứng dụng 2 1. Tích phân kép
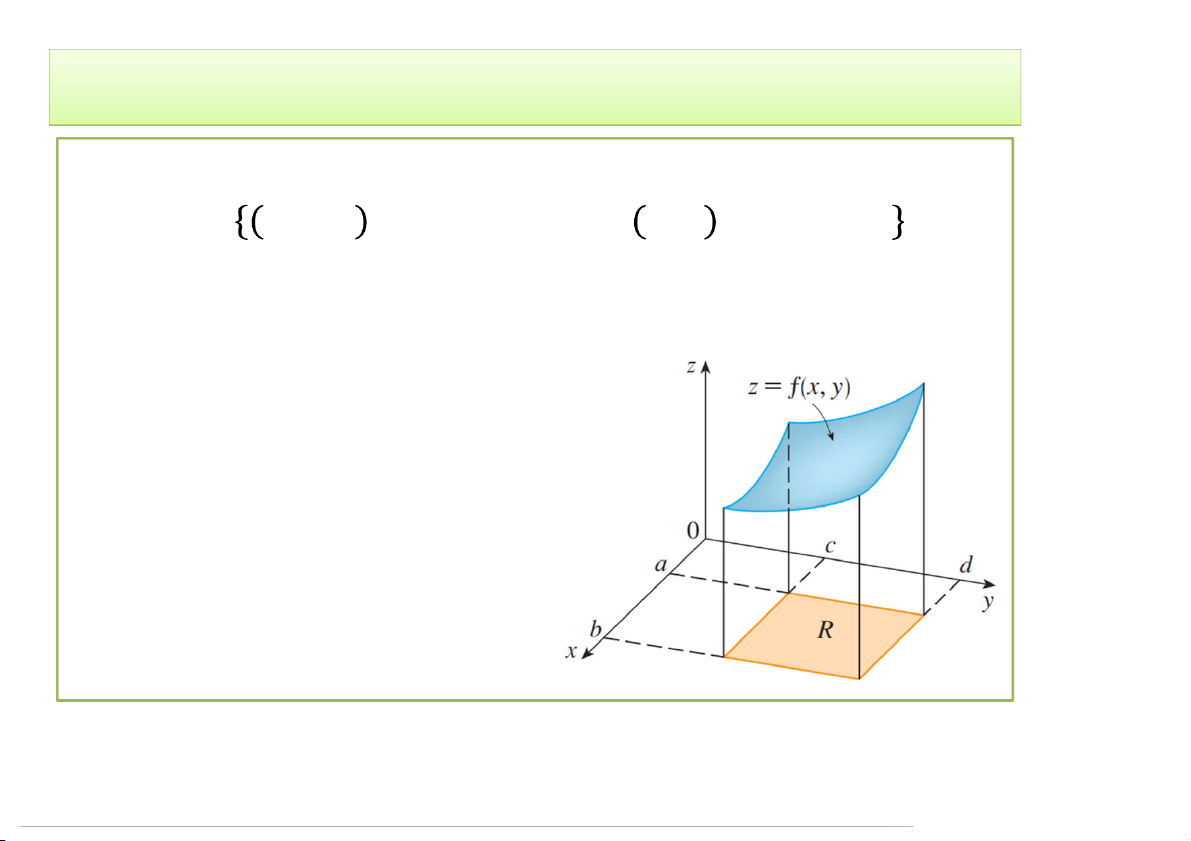
• Chia miền R thành các hình chữ nhật con ,:
R  x , x   y , y   x, y | x  x  x , y  y  y ij i 1  i  j 1  j     i 1 i j 1  j
Diện tích của các hcn con: ∆ = ∆ × ∆, Trong đó:
∆ =  ; ∆ = .   3/30/2020
Tích phân kép và ứng dụng 3 1. Tích phân kép
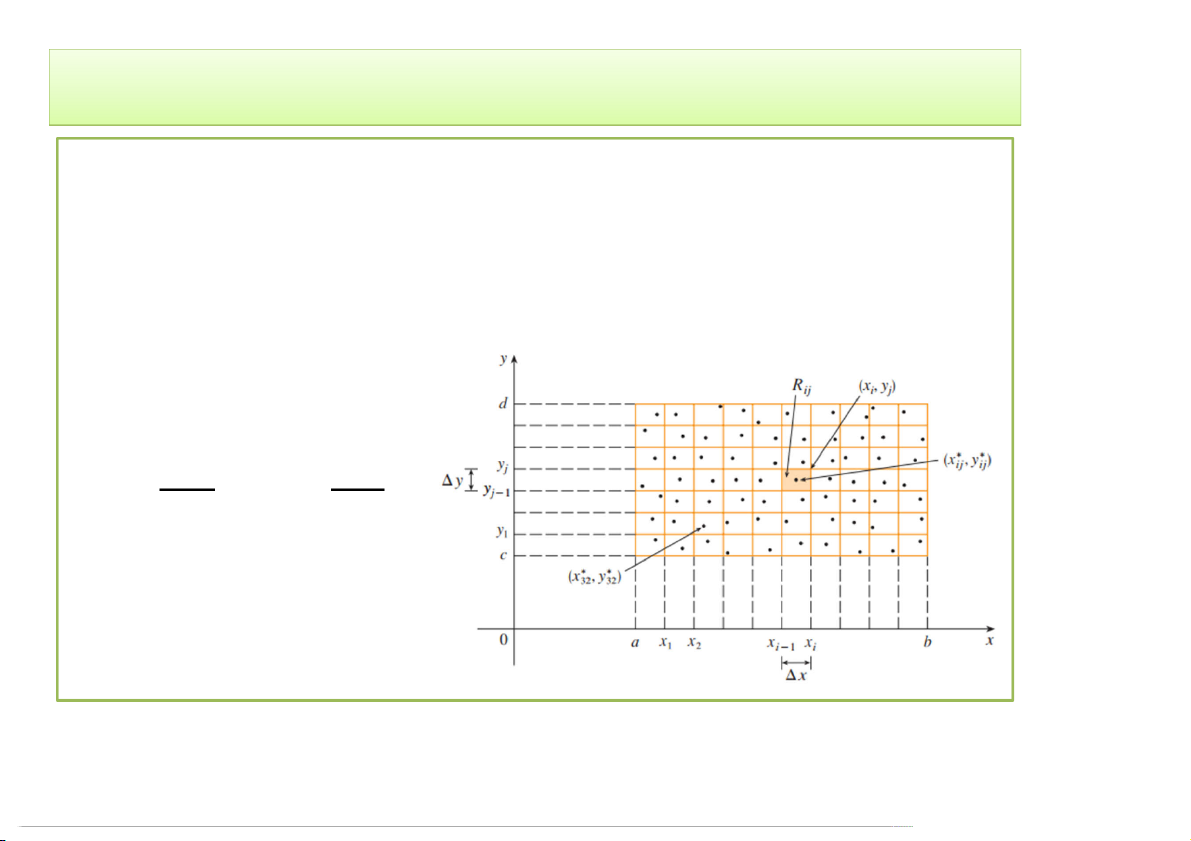
• Khi đó vật thể S ban đầu được chia thành mxn vật thể con  hình trụ: V  f x y A  S  * * , ij ij . ij m n
• Thể tích của S được xấp xỉ bằng: V  f x y  A S  * * , ij ij . i 1  j 1  3/30/2020
Tích phân kép và ứng dụng 4 1. Tích phân kép
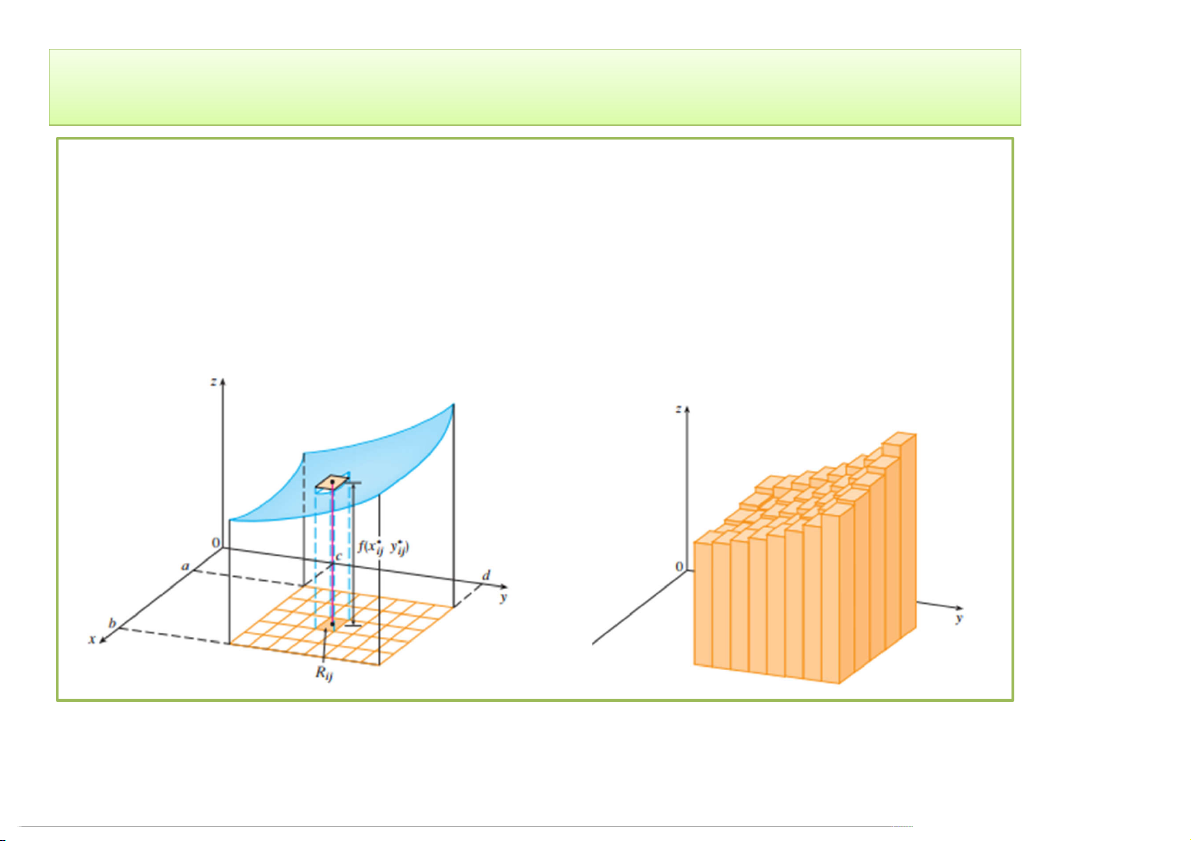
Khi m, n càng lớn. Độ chính xác của V càng cao. Do đó: m n V  lim  f  * * x , y A  ij ij . m,n i 1  j 1 
 Định nghĩa: Tích phân hai lớp của  trên một miền hình chữ nhật R là: m n f   ,x ydA lim f   * * x , y A ij ij  . m,n R i 1  j1
nếu giới hạn trên tồn tại. 3/30/2020
Tích phân kép và ứng dụng 5 1. Tích phân kép
• Hàm  ,  xác định trong một miền đóng, bị chặn D.
Tích phân kép của hàm  ,  trong miền D: f x, ydxdy D Miền lấy Hàm dưới dấu Yếu tố tích phân tích phân diện tích
Nếu tích phân trên tồn tại:  ,  khả tích trong miền D
 Nếu hs liên tục trong miền bị chặn, đóng D thì nó khả tích trong miền đấy. 3/30/2020
Tích phân kép và ứng dụng 6 1. Tích phân kép
• Nếu  ,  liên tục, không âm trên D, tích phân kép bằng
thể tích vật thể hình trụ: V  f   ,x ydS  f   ,x ydxdy D D
• Nếu  ,  = 1, ∀ ,  ∈ , tích phân kép bằng diện tích của miền D: S  dS  dxdy   D D 3/30/2020
Tích phân kép và ứng dụng 7 1. Tích phân kép 1)  f
 x, y  gx, ydxdy  f  x,ydxdy  g  x, ydxdy   D D D 2) kf  , x ydxdy  k f  , x ydxdy k  const    D D 3) f   ,x ydxdy  f   ,x ydxdy  f   ,x ydxdy D 1 D 2 D 4) f  ,
x y  g x, y,  , x y D : f  x, ydxdy  g  x, ydxdy D D 5) m  f  , x y  M,  , x y D : mS  f  , x ydxdy  MS D
6) x, y D : f  ,x y dxdy  f  x, yS D 3/30/2020
Tích phân kép và ứng dụng 8 2. Cách tính 2.1. Trong hệ Đề các
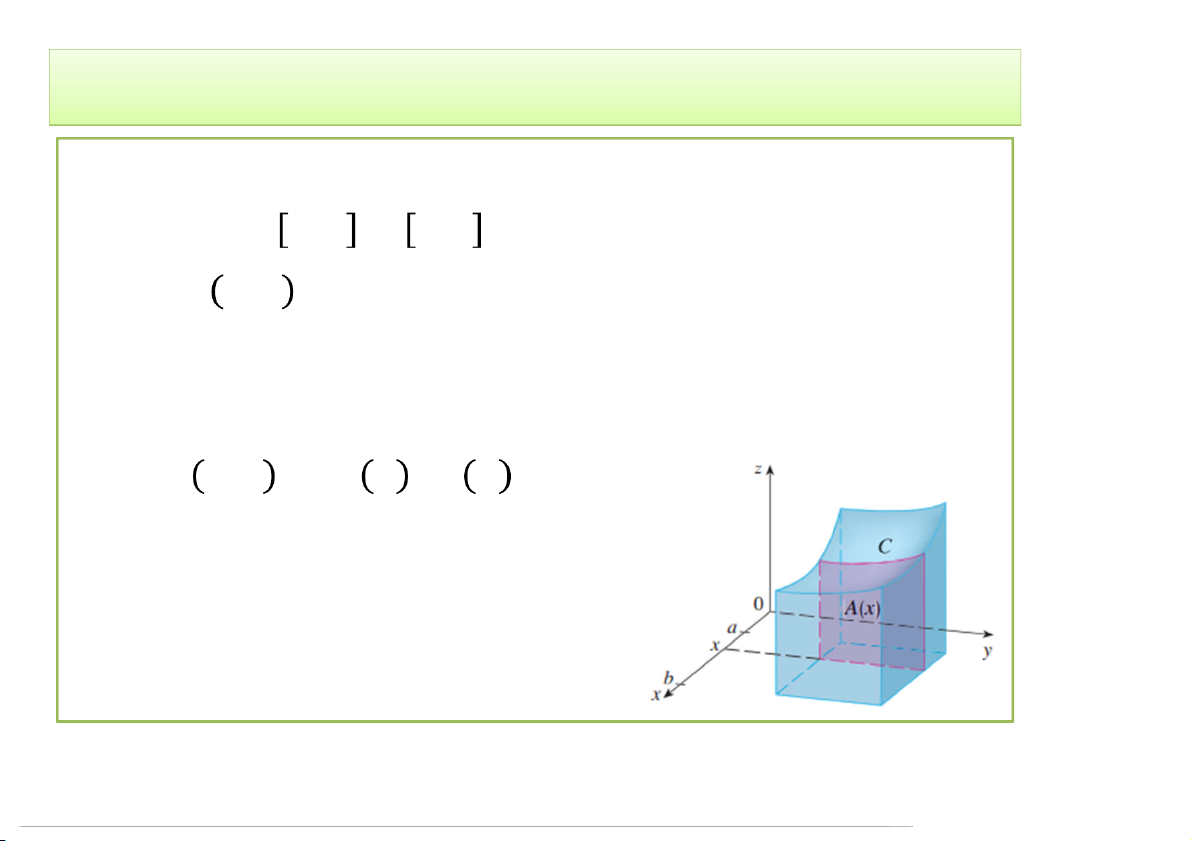
 TH1.  = ,  × , 
Nếu  ,  liên tục trên D thì: f   b d d b x, y dxdy  f x y dy dx  f x y dx dy     a   ,  c  c   ,  a  D
Nếu  ,  =   .   : f   b d , x y dxdy  f x d . x f y dy  1    2   a c D 3/30/2020
Tích phân kép và ứng dụng 9 2. Cách tính
 Ví dụ. Tính tích phân trong miền
 = ,  |0 ≤  ≤ 2, 1 ≤  ≤ 2 :  2 x  3y dS D I  x 3y  2 2 2 dS     2 x  3y dxdy 1 0 D x2  2  2  x  2 I    3xy d  y    1  2    x0   2 I    2 2  6y dy  12 1 3/30/2020
Tích phân kép và ứng dụng 10 2. Cách tính  Ví dụ 1. Tính dxdy I  , D  1,2  2  2  D  x y
Vì (, ) liên tục trên D nên: 2     2 2 1 2 1 I   dy dx    dx     x  y2 1 1 1 x  y   1     2 2  1 1  x 1 9 I   dx  ln  ln    1  x 1 x  2  x  2 8 1 3/30/2020
Tích phân kép và ứng dụng 11 2. Cách tính
 TH2. Miền lấy tích phân là miền bị chặn bất kỳ: D  
 x,y:a  x b,y x  y  y x 1   2   f   b y x , x y 2   dxdy  f x y dy dx   a   ,  1 y x    D 3/30/2020
Tích phân kép và ứng dụng 12 2. Cách tính Nếu D  
 ,x y: x y  x  x y ,c  y  d 1   2    f   d x y , x y 2   dxdy  f x y dx dy   c   ,  x y 1    D 3/30/2020
Tích phân kép và ứng dụng 13 2. Cách tính
• Ví dụ 2. Tính tích phân trong miền D giới hạn bởi các
đường  = 2,  = ,  = 1: 2 x I  dxdy 2  2y D
Cách 1. Coi  ∈ 1,2 ,  ≤  ≤   2 2 x   2  x  2 x x I  dy dx    dx 2    2  1 1/ x 1 y y    1/ x    9 I  2 4 3/30/2020
Tích phân kép và ứng dụng 14 2. Cách tính
• Cách 2. Coi  ∈ [ , 2]  2 2 1  2  2  2 x x  I  dx dy  dx dy 2     2   2  1/2 1/ y 1 y  y   y  9 I  2 4 3/30/2020
Tích phân kép và ứng dụng 15 2. Cách tính
 Ví dụ 3. Tính tích phân trong miền D giới hạn bởi các
parabol  = ,  = : x I  dxdy 3  y D Hướng dẫn:
Khi  ∈ [0,1] thì y thay đổi từ  đến : x 1  x x  dxdy  dy dx    2  0 x y  y D  3/30/2020
Tích phân kép và ứng dụng 16 2. Cách tính 1 1 x 3 I  x ln y dx   x ln xdx 2 3   TPSR loại II 0 x 0 2 1 3   1 3  1 1 2 2 I lim xln xdx lim  x ln x x           3 a0 a a0 2 2  2 4  a   3 2 3 3 I   lim a ln a   3 a0 4 8 8 ln L a 1/ a 1  Do: 2 lim a ln a 0. 2  lim  lim  lim a  0 3 a 0  a 0  1 a 0  a 0 2  / a 2  2 a 3/30/2020
Tích phân kép và ứng dụng 17 2. Cách tính
• 2.2. Đổi biến số trong tích phân kép
• Xét tích phân kép ∬  ,   , f(x,y) liên tục trên D. 
Thực hiện phép đổi biến số  =  ,  ,  =  ,  . f  x,ydxdy  f
 xu,v, yu,v J dudv D D ' D x, y ' ' x x u v J    Du,v 0 ' ' y y u v 3/30/2020
Tích phân kép và ứng dụng 18 2. Cách tính
• Ví dụ 4. Tính tích phân trong miền D giới hạn bởi các
đường  = −,  = − + 3,  = 2 − 1,  = 2 + 1: I  x  y dxdy 4   D • Đổi biến số:  u  v x  u   x  y  3 1/ 3 1  / 3 1     J    0 v  2x  y 2u  v   2 / 3 1/ 3 3 y   3 3 1 1 I  ududv  3 4   0 1 3  3/30/2020
Tích phân kép và ứng dụng 19
2.2. Đổi biến số trong tích phân kép
Trong phép biến đổi từ tọa độ x,y sang tọa độ cực: x  r cos y  r sin • Khi đó: cos r sin   r  0 sin r cos (trừ điểm (0,0)). 3/30/2020
Tích phân kép và ứng dụng 20
2.2. Đổi biến số trong tích phân kép  I  f   ,x ydxdy  f  r,  J drd D D' Nếu: D '     ,r  r  r 1   2   2 r I  f   r, rdr  d   1 r  3/30/2020
Tích phân kép và ứng dụng 21 2. Cách tính
• Ví dụ 5. Tính tích phân trong miền D giới hạn bởi đường tròn  +  = 2: I   2 2 x  y dxdy 5  D
• Đổi sang tọa độ cực x  r cos  ,    , 0  r  2cos y  r sin 2 2  /2 2cos 2 3 I  r rdrd  5    /2 0 2 3/30/2020
Tích phân kép và ứng dụng 22 3. Ứng dụng
 3.1. Tính diện tích của miền phẳng D trong Oxy S  dxdy D
 3.2. Tính thể tích của vật thể hình trụ:
Phía trên: mặt  = (, ), V  f   ,x ydxdy
Phía dưới: miền D trong Oxy D
3.3. Diện tích mặt S:  = (, ) chiếu lên miền D của Oxy: '2 '2 S  1 z  z dxdy  x y D 3/30/2020
Tích phân kép và ứng dụng 23 3. Ứng dụng
 Ví dụ 6. Tính diện tích của miền phẳng D giới hạn bởi các
đường thẳng  = 1,  = 0 và đường cong  = . Hướng dẫn: 1
Chiếu miền D lên trục Ox được I  6 4
đoạn [0,1]: biên dưới của D.
Khi  ∈ 0,1 , y biến thiên: 0 →  3 1 x 1   x I  dy dx  y dx 6      30 0 0 0    3/30/2020
Tích phân kép và ứng dụng 24 3. Ứng dụng
Ví dụ 7. Tính diện tích của miền phẳng D giới hạn bởi các
đường thẳng  = 0,  =  và đường tròn  +  = 2
• Chuyển sang tọa độ cực
Phương trình đường tròn: 2 r  2r cos  r  2cos   0   ; 0  r  2cos  4    /4 2cos 1 S  rdr   d     0  0  4 2 3/30/2020
Tích phân kép và ứng dụng 25 3. Ứng dụng
Ví dụ 8. Tính thể tích vật thể giới hạn bởi các mặt
 = 0,  = 0,  = 0,  = 4,  = 4 và mặt parabolid  =  +  + 1.
Miền D (hình chiếu của mặt Parabolid lên Oxy) là hình
vuông giới hạn bởi các đường thẳng:  = 0,  = 0,  = 0,  = 4,  = 4 . V  x y  4 4 2 2 1 dxdy     2 2 x y 1dx       dy 0  0   D 2 V 186 3 3/30/2020
Tích phân kép và ứng dụng 26 3. Ứng dụng
Ví dụ 9. Tìm thể tích vật thể T ở bên dưới mặt  =  + 
và bên trên miền D trong mặt phẳng xy giới hạn bởi các
đường  = 2,  =  3/30/2020
Tích phân kép và ứng dụng 27 3. Ứng dụng
Hình chiếu của vật thể Tlên mặt phẳng Oxylà miền D:
 = ,  |0 ≤  ≤ 2,  ≤  ≤ 2
Thể tích vật thể T bằng: 2 2 x 2 2 V  x  y dydx   2   0 x 2 x 3 2  y  2 V  x y  dx    0 3   2x 216 V  35 3/30/2020
Tích phân kép và ứng dụng 28 3. Ứng dụng
 Ví dụ 10. Tính diện tích mặt Paraboloid  =  +  nằm bên dưới mặt  = 9?
• Giao của mặt paraboid với mặt  = 9 là đường tròn:  +  = 9
Hình chiếu của paraboid cần tính lên Oxy
là D: hình tròn  +  ≤ 9 '2 '2 S  1 z  z dxdy  x y D 2 2 S  1 4x  4y dxdy D 3/30/2020
Tích phân kép và ứng dụng 29 3. Ứng dụng
• Chuyển sang tọa độ cực: x  r cos 
,0   2 ,0  r  3, J  r y  rsin  2 3 2 S  1 4r rdrd   0 0 1 3  2 .  1 4r 1/2 2 d  2 1 4r  0 8 1 2  2 . . .1 4r  3 3/2 2  37 37   1 8 3 0 6 3/30/2020
Tích phân kép và ứng dụng 30 Bài tập
• Đổi thứ tự lấy tích phân trong các tích phân sau 2 4 2 1) dx f x, y dy   1 1 1 y 4) dy f   x, ydx 2   2 x 0 2 y 3 2 y 2) dy f   x,ydx 2 x2 5) dx f x, y dy   2   0 0 1 x e ln x 3) dx f   x,ydy 2a 2ax 6) dx f x, y dy   2   1 0 0 2ax x 3/30/2020
Tích phân kép và ứng dụng 31 Bài tập
• Tính các tích phân sau: 2 /2 3) xsin ydydx   0 0 3 1 1)   1 4xydxdy 10 /2 5 1 0 4) cos ydxdy   /6 1 1 2 2)    3 2 2 4 x 9 x y dydx 6 2 1 8 0 1 5)   2x y dxdy 0 0 6)   2 3 4 6x y  5y dS, D  
 x, y| 0  x  3,0  y  1 D 7) cos
 x 2ydS, D   ,x y| 0  x  ,0  y  /  2 D 2 xy 8)
dS , D  x, y | 0  x  1,3  y  3  2     x 1 D 3/30/2020
Tích phân kép và ứng dụng 32 Baitập
• Tính các tích phân sau: 3 4 y 1)    x ydxdy y0 x 1  2)  2 2
cos x  sin y dxdy, D : 0  x  , 0  y  4 4 D dxdy 3)
, D : x  1, y  1,x  y  3   D  x y3 2 2 2 2 2 4) x  y dxdy, D :x  y  a D  2 2  x y  2 2 2 5) e dxdy, D :x  y  a . D 3/30/2020
Tích phân kép và ứng dụng 33 Bài tập
6)  x ydxdy, D :ABC |A1,1, B 4,1, C 4,4 D 2 7)
xdxdy, D : y  3x , y  6 3x D 2 2 1 8)
x y dxdy, D :x  2, y  x, y   x D 9) x e dxd ,
y D :x  0, y 1, y  2, x  ln y D 2 2
10) xdxdy, D :x  y  4x  2y  4.  . D 3/30/2020
Tích phân kép và ứng dụng 34 Bài tập
• Tính thể tích các vật thể giới hạn bởi các mặt:
1) 3x  2 y  z  12, x  0, x 1, y  2,  y  3 95 / 2 2 2
2) z  4  x  y ,z  0, x  1
 , x 1, y  0, y  2 12 2 2 x y 166 3)   z 1,z  0, x  1  , x 1, y  2,  y  2 4 9 27  1  216 2 2
4) z  x  y , D   x, y | 0  y  4, y  x  y  2  35 5) z  x , y  , x y  2
 Dgh:y  x-1, y  2 x 6; 36 2 2
6) z 1 x  y , y  x, y  3x,z  
 0,x  0, y  0,z  0 48   3/30/2020
Tích phân kép và ứng dụng 35 Bài tập
• Tính diện tích của các miền giới hạn bởi các đường sau: 1)
 0;  0; x  2; y  ex x y 2 2 2) y  1  ; y   ; x x  y  2  y 2 3) x  2; y  x  2 4)  x  y 2 2 2 2  2.a  2 2 x  y  5)  x  y 3 2 2 4 4  x  y 6)  x  y 2 2 2 3  2y 3/30/2020
Tích phân kép và ứng dụng 36 Bài tập
• Tính thể tích vật thể giới hạn bởi các mặt sau: 2 1) y  x ; y  1; x  y  z  4; z  4 4 / 5 2 2
2) z  y  x ; z  0; y  2 
3) x  2 y  z  2, x  2 , y x  0, z  0; 1/ 3 2 2 4) z  x  3y , x  0, y 1, y  , x z  0 5 / 6 2 2 2 2
5) z  4  x  y ; 2z  2  x  y 3 2 6) y  x ; z  0; y  z  2; 32 5 /15 2 2 2 2 2 2 3
7) x  y  z  R ; x  y  Rx; R 3 4/ 18 2 2 2 2
8) 2z  x  y ;x  y  1; 2 2 2   1 / 3 3/30/2020
Tích phân kép và ứng dụng 37 Bài tập
• Tính diện tích của các phần mặt cong sau:
1. Tính diện tích của phần mặt cầu +  +  =  nằm
trong hình trụ  +  = . 4  − 1 
2. Tính diện tích của phần mặt cầu +  +  =  nằm
trong hình trụ  +  =  + 
3. Tính diện tích phần mặt nón  =  +  nằm bên
trong hình trụ  +  = 2.  2
4. Tính diện tích mặt trụ  = 2 bị cắt bởi các mặt phẳng
 − 2 = 0,  = 2,  = 2 2. 13 3/30/2020
Tích phân kép và ứng dụng 38 Bài tập 3/30/2020
Tích phân kép và ứng dụng 39 Bài tập 3/30/2020
Tích phân kép và ứng dụng 40 Bài tập 3/30/2020
Tích phân kép và ứng dụng 41 Bài tập
In the first octant: góc phần tám thứ nhất. 3/30/2020
Tích phân kép và ứng dụng 42