Tài liệu Tính Tích phân bội - Giải tích 2 | Trường Đại học Công nghệ, Đại học Quốc gia Hà Nội

TÍNH TÍCH PHÂN BỘI
Tài liệu: Toán cao cấp tập 3 (NĐT – NXB GD)
Calculus – Jame Stewart, trang 990 - 1011 4/23/2020 Tích phân bội 1 1. Giới thiệu
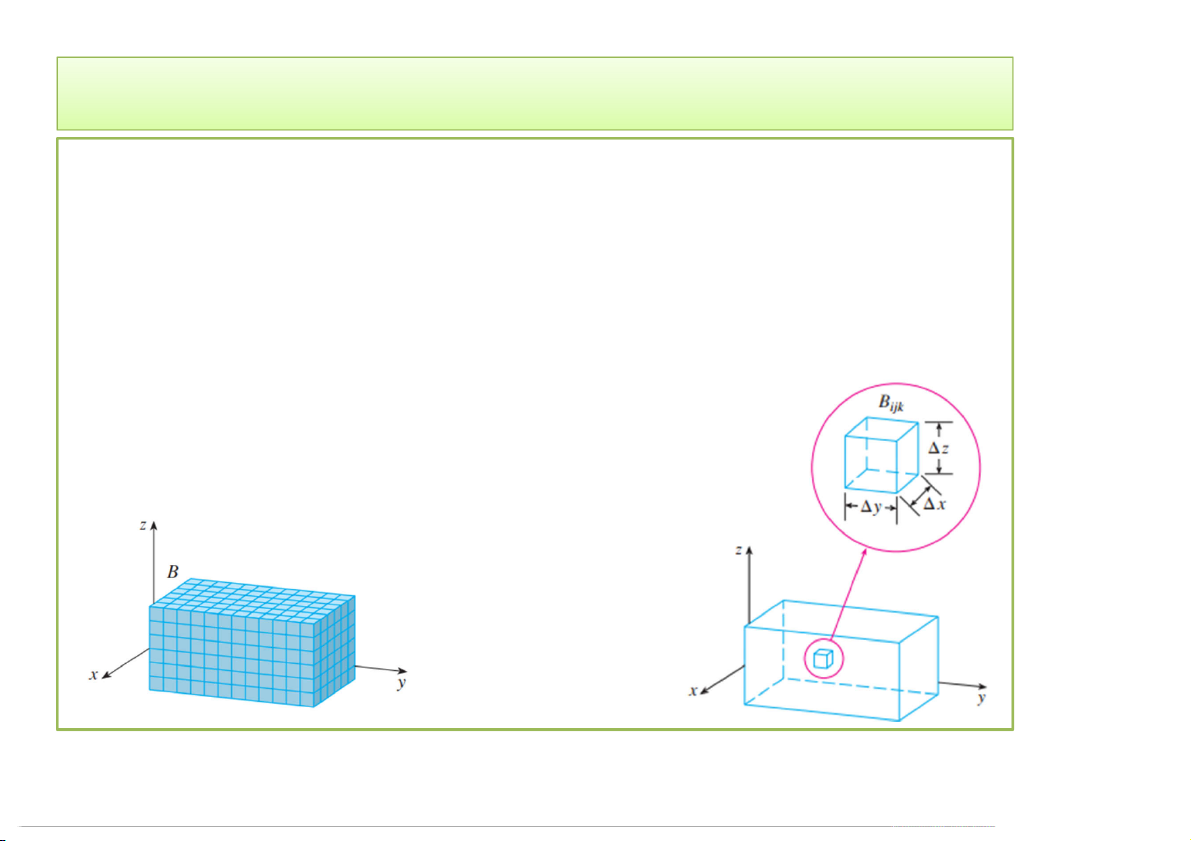
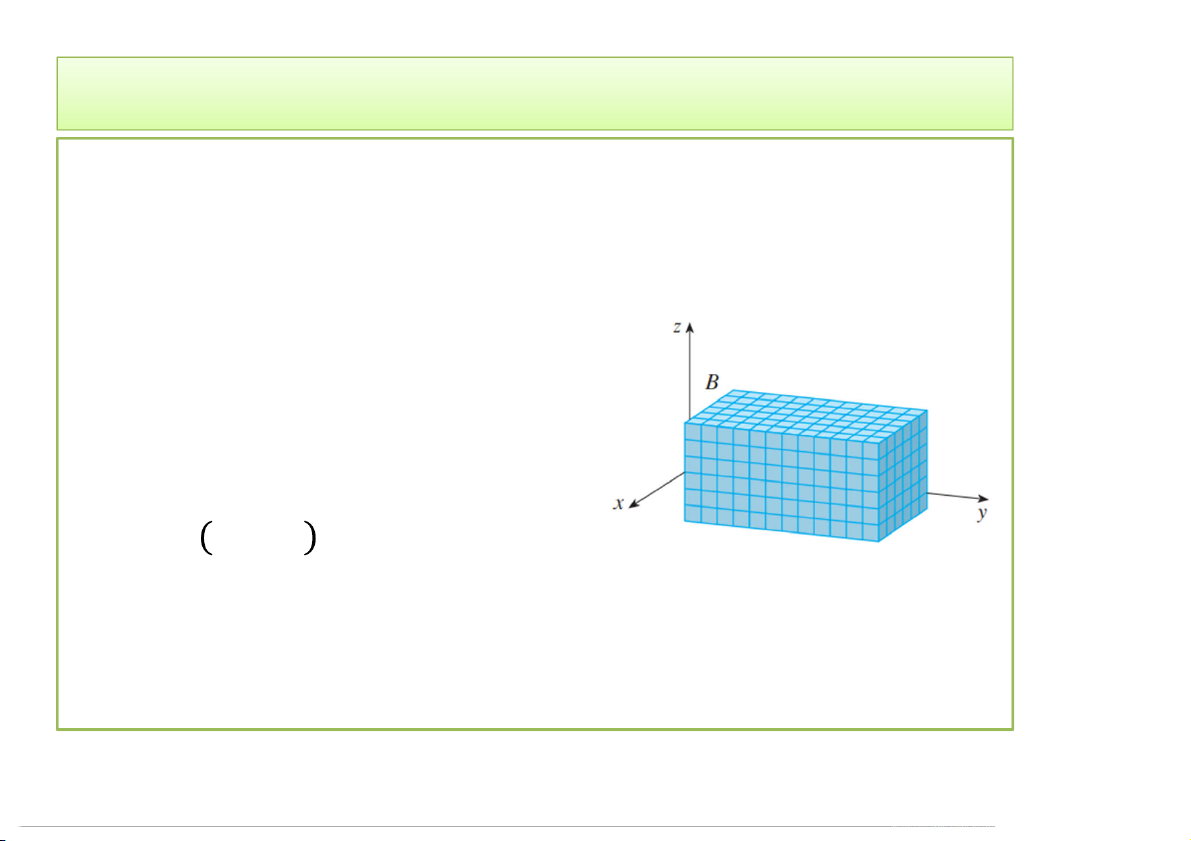
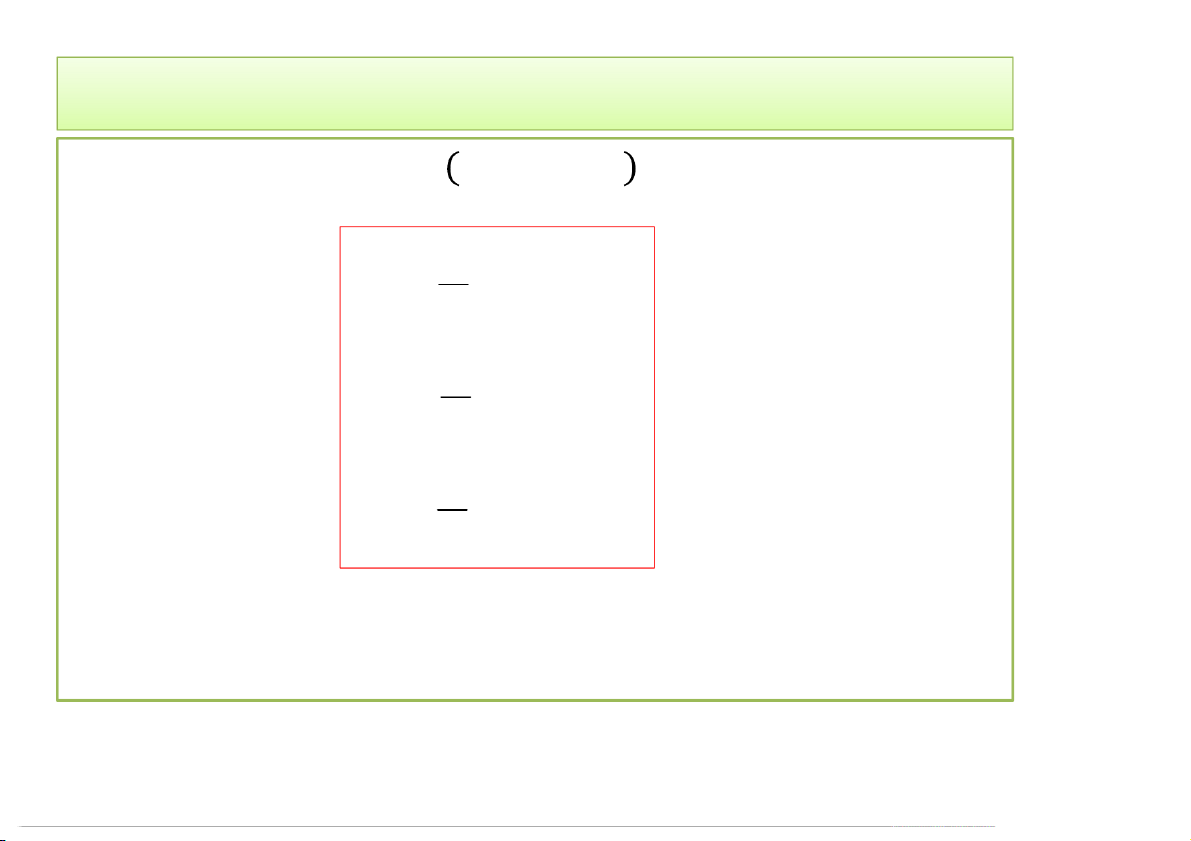
Định nghĩa: Tích phân bội của hàm f xác định trên hộp B là: l m n f
 x, y,zdV  lim f   * * * x , y , z V  ijk ijk ijk  m,n,l  i 1  j 1  k B 1 
nếu giới hạn trên tồn tại
Chú ý: Nếu f liên tục trên B thì ∃ TP. 4/23/2020 Tích phân bội 2 1. Giới thiệu
• Tích phân bội 3 của hàm số (, , ) trong miền V dạng: I  f , x y, z dV 1    V
• Nếu (, , ) là khối lượng riêng của vật thể V
⇒I1 là khối lượng của vật thể đó
• Nếu  , ,  = 1 thì ∭   : thể tích miền V
• Tích phân bội 3 có các tính chất tương tự tích phân kép. 4/23/2020 Tích phân bội 3 1. Giới thiệu  Trọng tâm vật thể
• Vật thể V trong Oxyz có khối lượng riêng tại M là
 , ,  , tọa độ trọng tậm của V:  1 x  x x y z dxdydz  G   , ,  m  V  1  y  y x y z dxdydz m     ,x ,yzdxdydz G   , ,  m  V V  1 z  z x y z dxdydz G   , ,  m  V 4/23/2020 Tích phân bội 4 1. Giới thiệu
• Nếu vật thể đồng chất  =  :  1 x  xdxdydz G  V V   1  y  ydxdydz G  V  V  1 z  zdxdydz G  V  V 4/23/2020 Tích phân bội 5 2. Cách tính 2.1. Trong hệ Đề-các
Có thể đưa tích phân bội 3 về ba tích phân đơn liên tiếp
TH1. Nếu hàm f liên tục trên 1 hình hộp đóng V= ,  × ,  × ,  : f   s d b x, y, z dV  f    x, y,zdxdydz r c a V (Định lý Fubini)
 Ví dụ. Tính tích phân sau trên miền
 = , ,  |0 ≤  ≤ 1, −1 ≤  ≤ 2, 0 ≤  ≤ 3 2 xyz dV V 4/23/2020 Tích phân bội 6 2. Cách tính 2.1. Trong hệ Đề-các 1 3 2 1 3 2   2 2  1 2 2  xyz dV  xyz dxdydz   x yz         dydz 0 1  0 0 1   2  V 0   2 2 2 2 2   3 2 yz 3 y z 3 3z 27  dydz    dz  dz      0 1  0 0 2  4  4 4 1    4/23/2020 Tích phân bội 7 2. Cách tính 2.1. Trong hệ Đề-các  TH2. Nếu
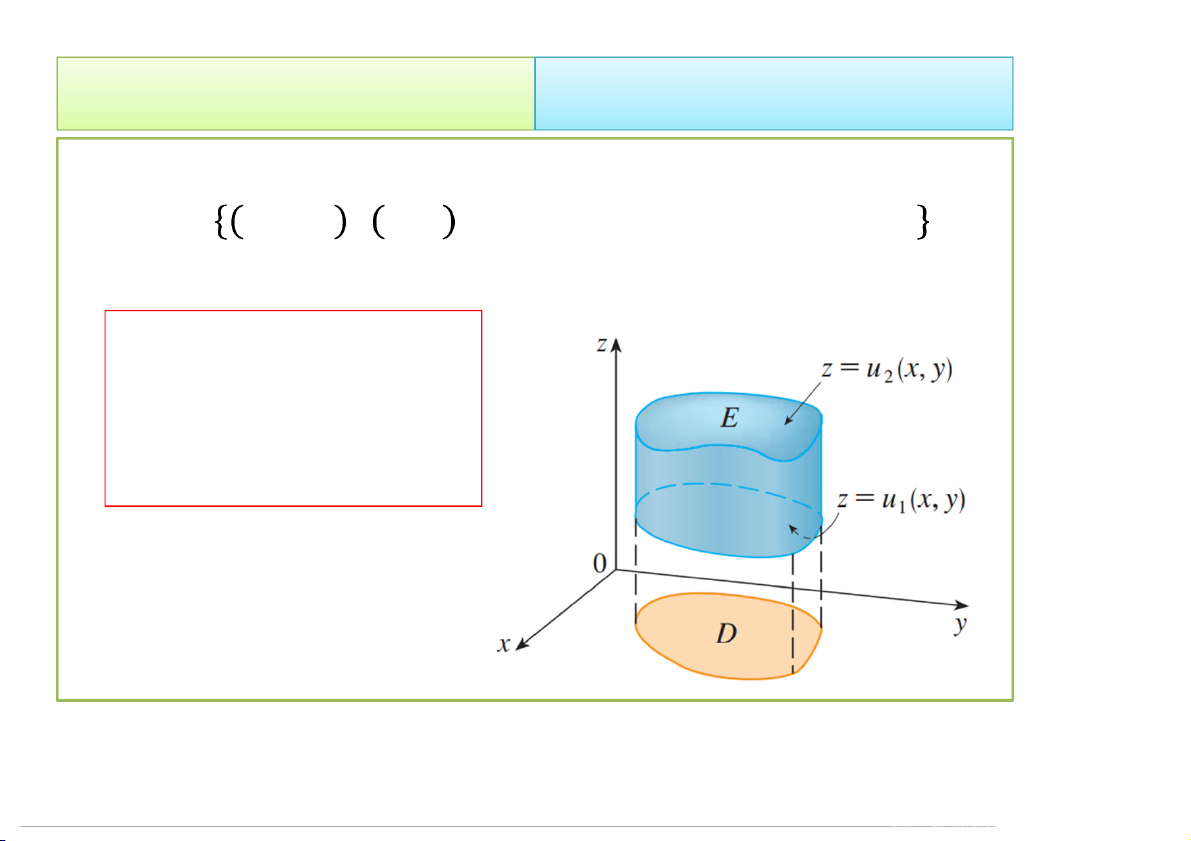
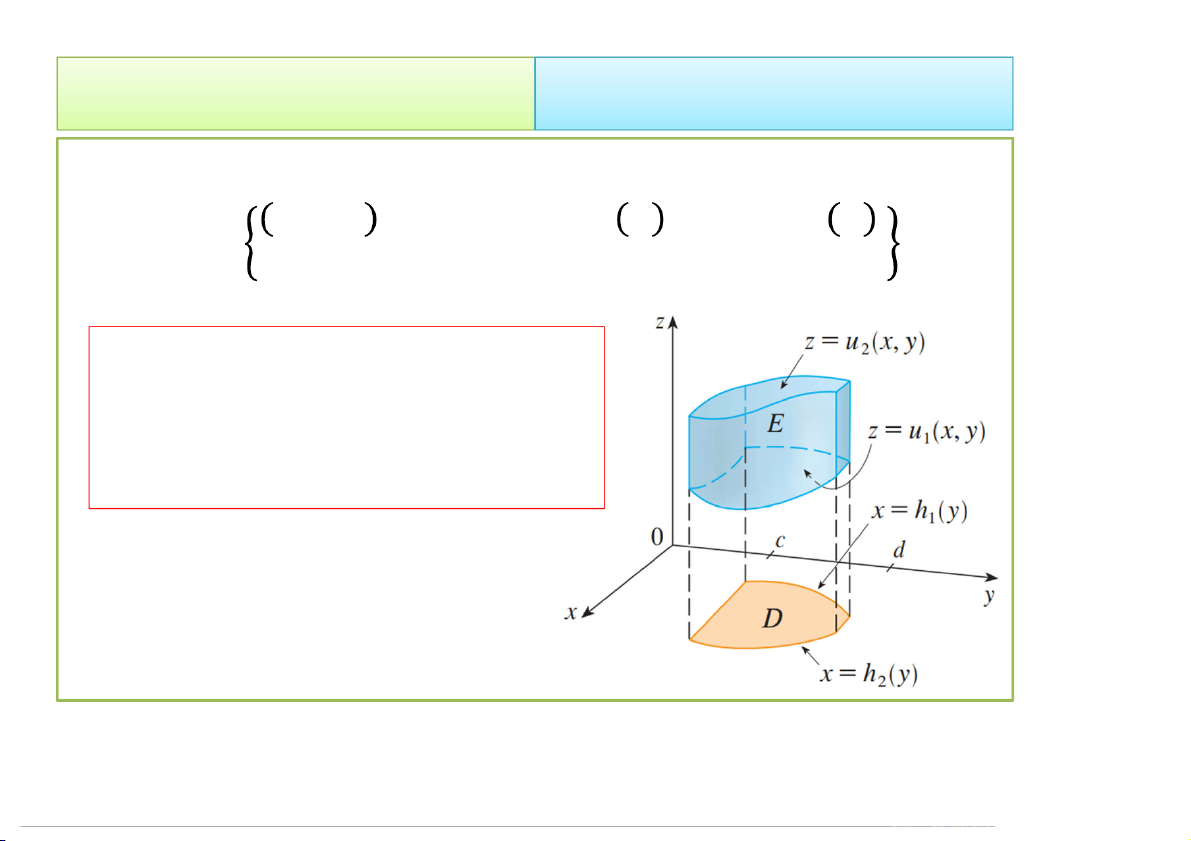
 = , ,  | ,  ∈ , (, ) ≤  ≤ (, ) f   ,x y,zdV E 2 u  f    ,x y,zdz  dA   1 u  D 4/23/2020 Tích phân bội 8 2. Cách tính 2.1. Trong hệ Đề-các  TH2.1. Nếu
 = , ,  | ≤  ≤ ,   ≤  ≤   ,
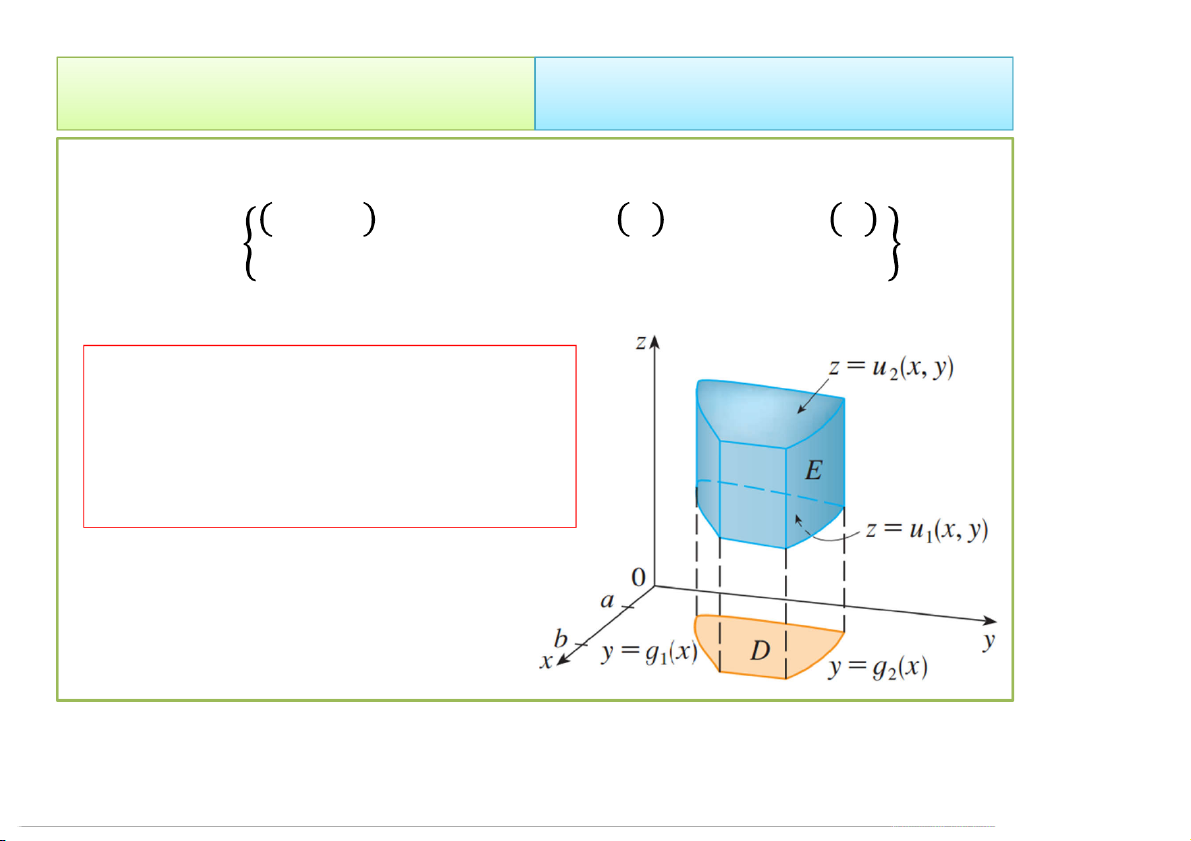
(, ) ≤  ≤ (, ) f  x, y,zdV E b g2 x 2 u  x, y  f     ,x y, zdzdydx a 1 g x 1 u x,y 4/23/2020 Tích phân bội 9 2. Cách tính 2.1. Trong hệ Đề-các  TH2.2. Nếu
 = , ,  | ≤  ≤ , ℎ  ≤  ≤ ℎ  ,
(, ) ≤  ≤ (, ) f   ,x ,y zdV E d 2 h  y u2x,y  f     ,x y, zdzdxdy c 1 h  y 1 u x, y  4/23/2020 Tích phân bội 10 2. Cách tính 2.1. Trong hệ Đề-các  TH3. Nếu E  
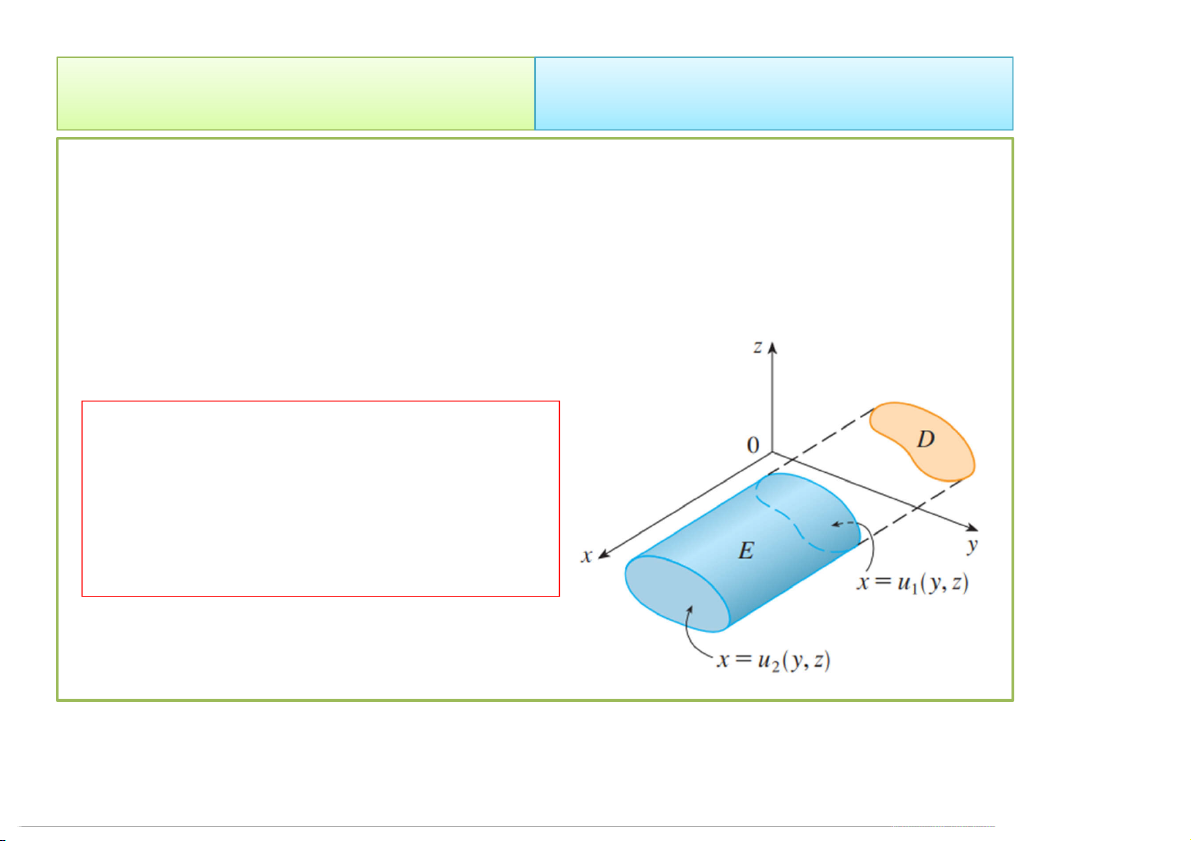
 x, y,z| y,zD,u y,z  x u y,z 1   2   • Khi đó: f   ,x y,zdV E 2 u  , y z  f    ,x y, zdx  dydz  u y ,   1 z   D 4/23/2020 Tích phân bội 11 2. Cách tính 2.1. Trong hệ Đề-các  TH4. Nếu E  
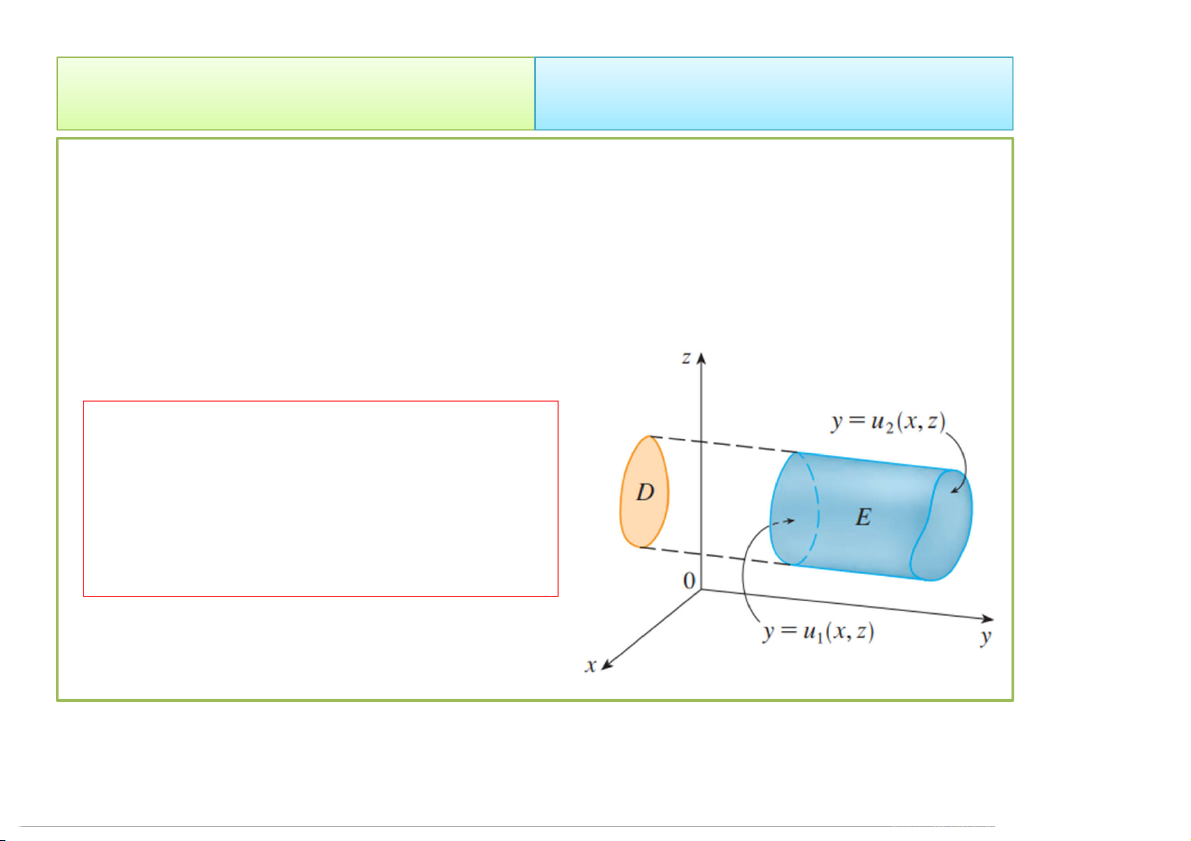
 x, y,z |x,zD,u x,z  y  u x,z 1   2   • Khi đó: f  x, y,zdV E 2 u  x,z  f    ,x y, zdy  dxdz  u x,   1 z   D 4/23/2020 Tích phân bội 12 2. Cách tính 2.1. Trong hệ Đề-các
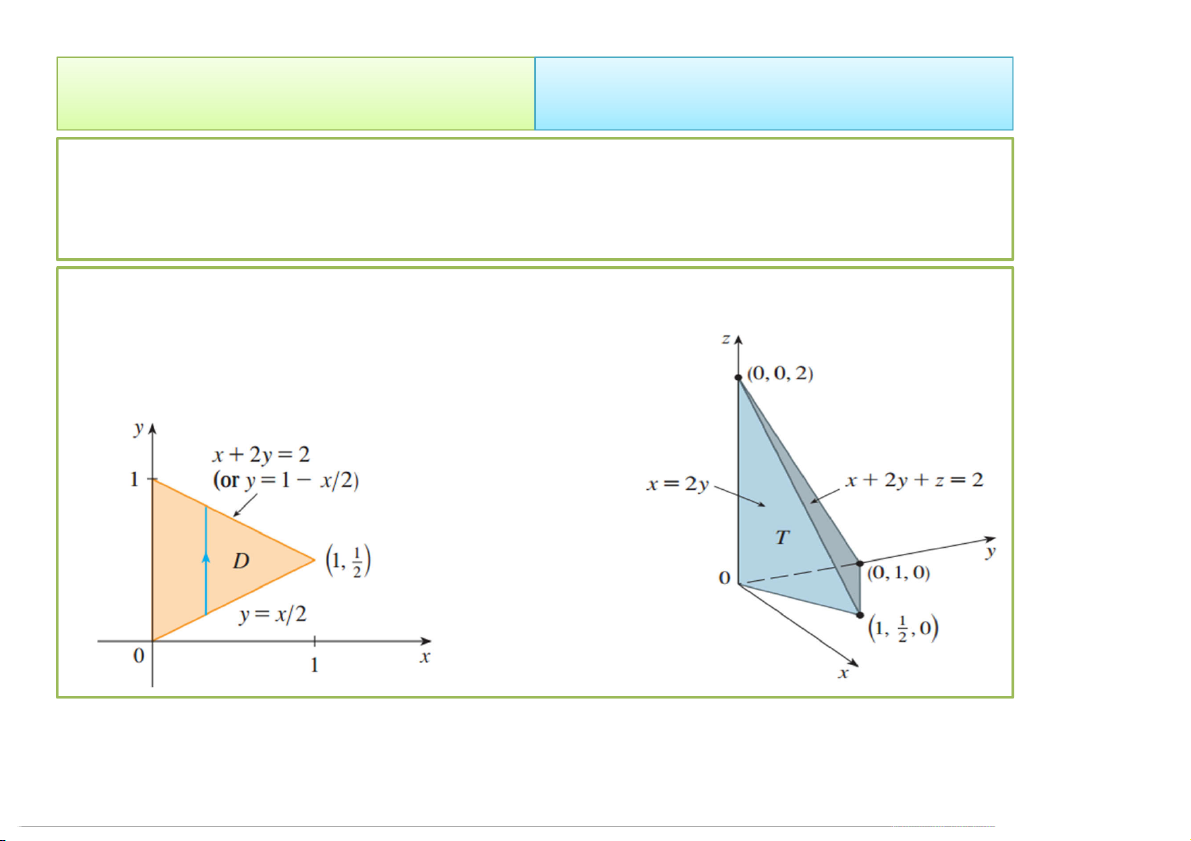
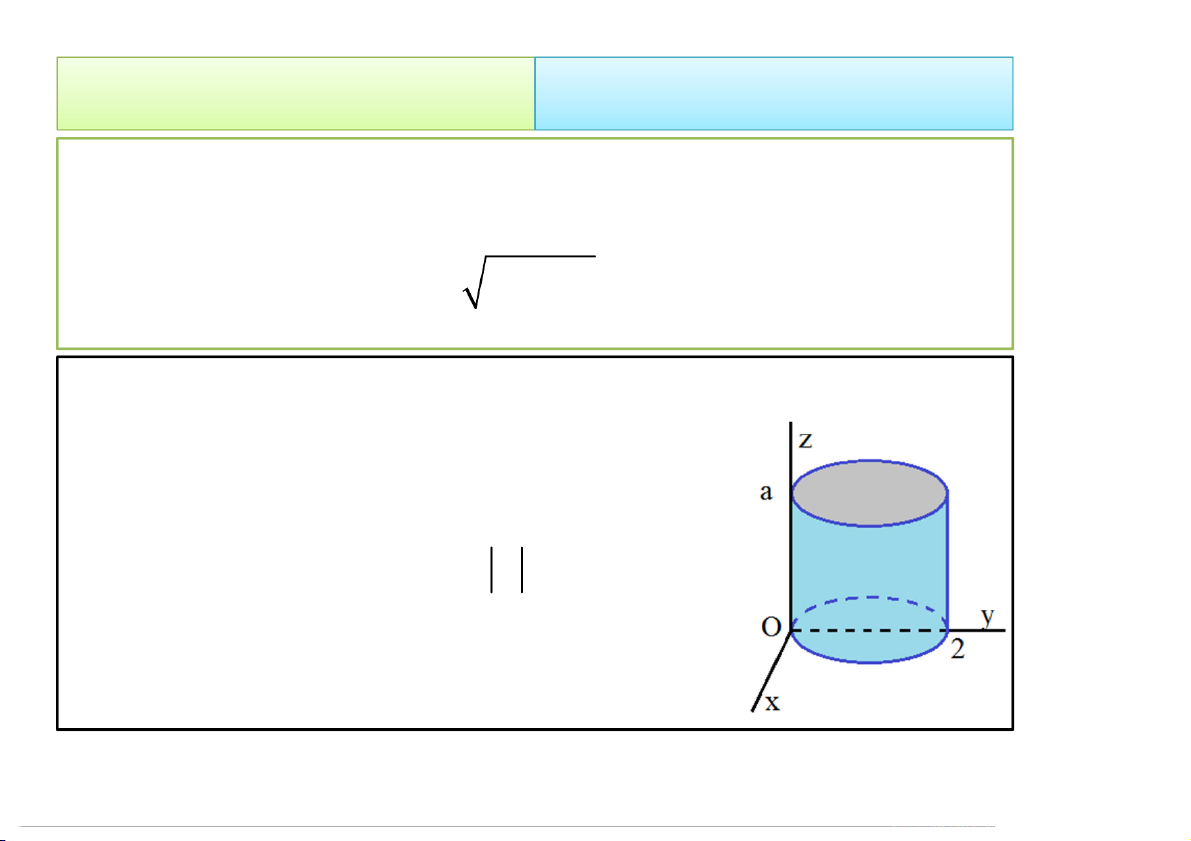
 Ví dụ 1. Sử dụng tích phân bội tính thể tích vật thể T được
giới hạn bởi các mặt  + 2 +  = 2,  = 2,  = 0,  = 0
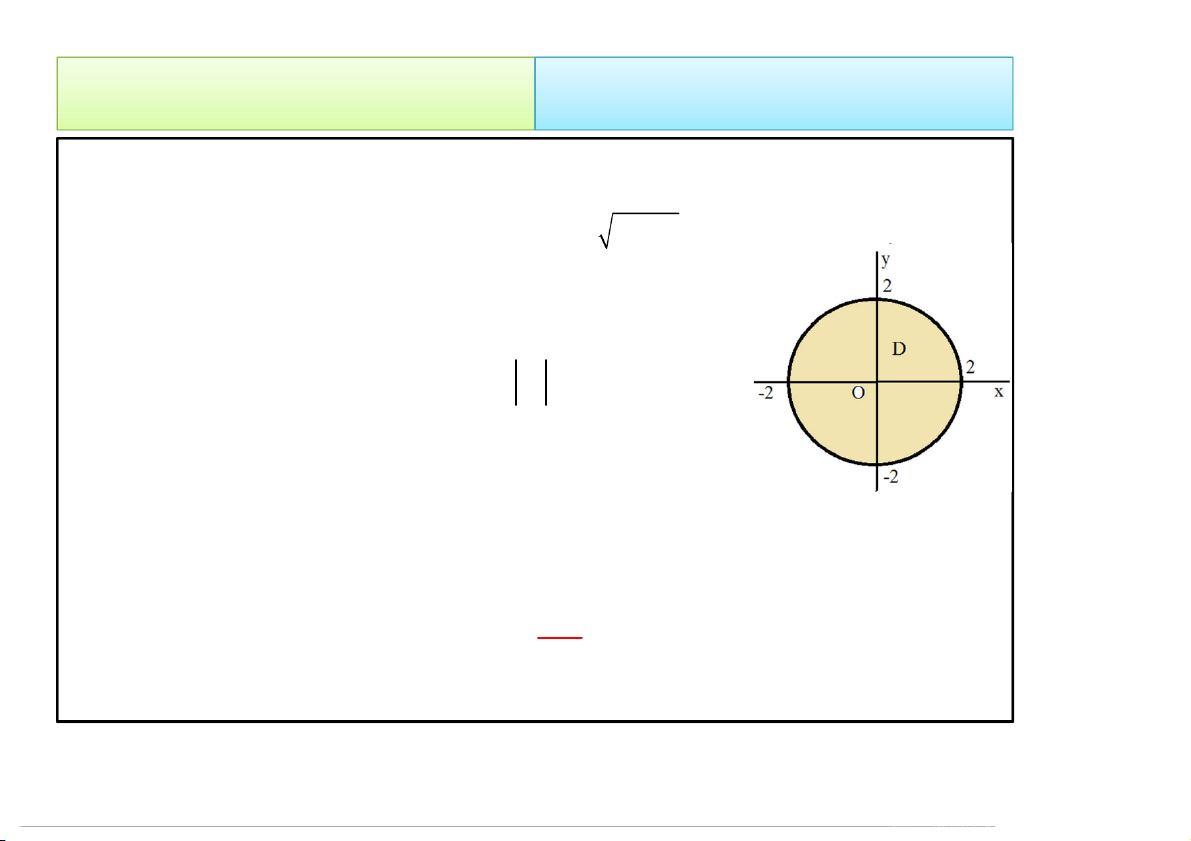
Hình chiếu của T lên Oxy là miền giới hạn bởi các đường:
 + 2 = 2,  = 2,  = 0. 4/23/2020 Tích phân bội 13 2. Cách tính 2.1. Trong hệ Đề-các • Thể tích vật thể T:    V T  1 1 x/2 2 x 2 y  dV  dzdydx     0 / x 2 0 T 1 1 x /2 2x2 y  z dydx   0 x/2 0   1 1x /2   1 2  x  2y dydx    0 x/2 3 4/23/2020 Tích phân bội 14 2. Cách tính • Ví dụ 2. Tính ∭  +  
, trong đó E là miền đóng
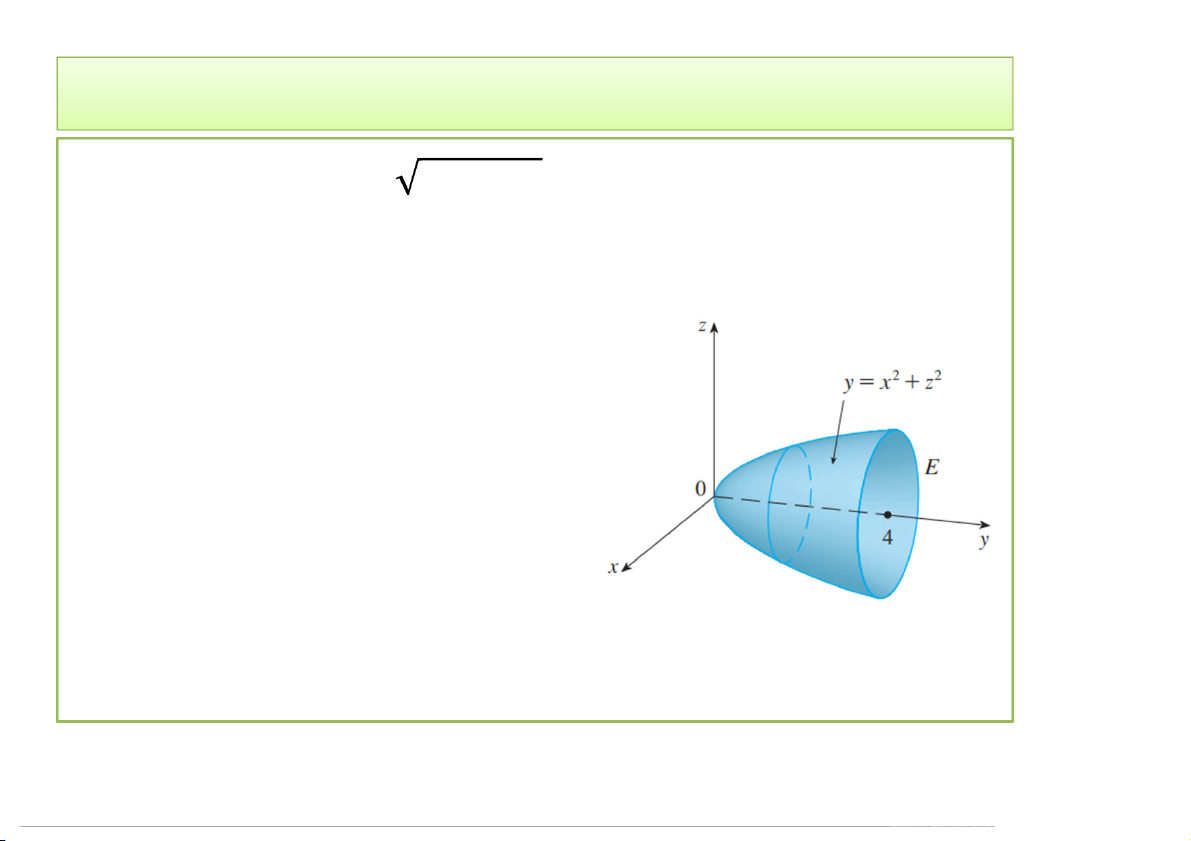
được giới hạn bởi mặt parabol  =  +  và mặt  = 4. 4/23/2020 Tích phân bội 15 2. Cách tính Ví dụ 2. Tính ∭  +  
, trong đó E là miền đóng
được giới hạn bởi mặt parabol  =  +  và mặt  = 4.
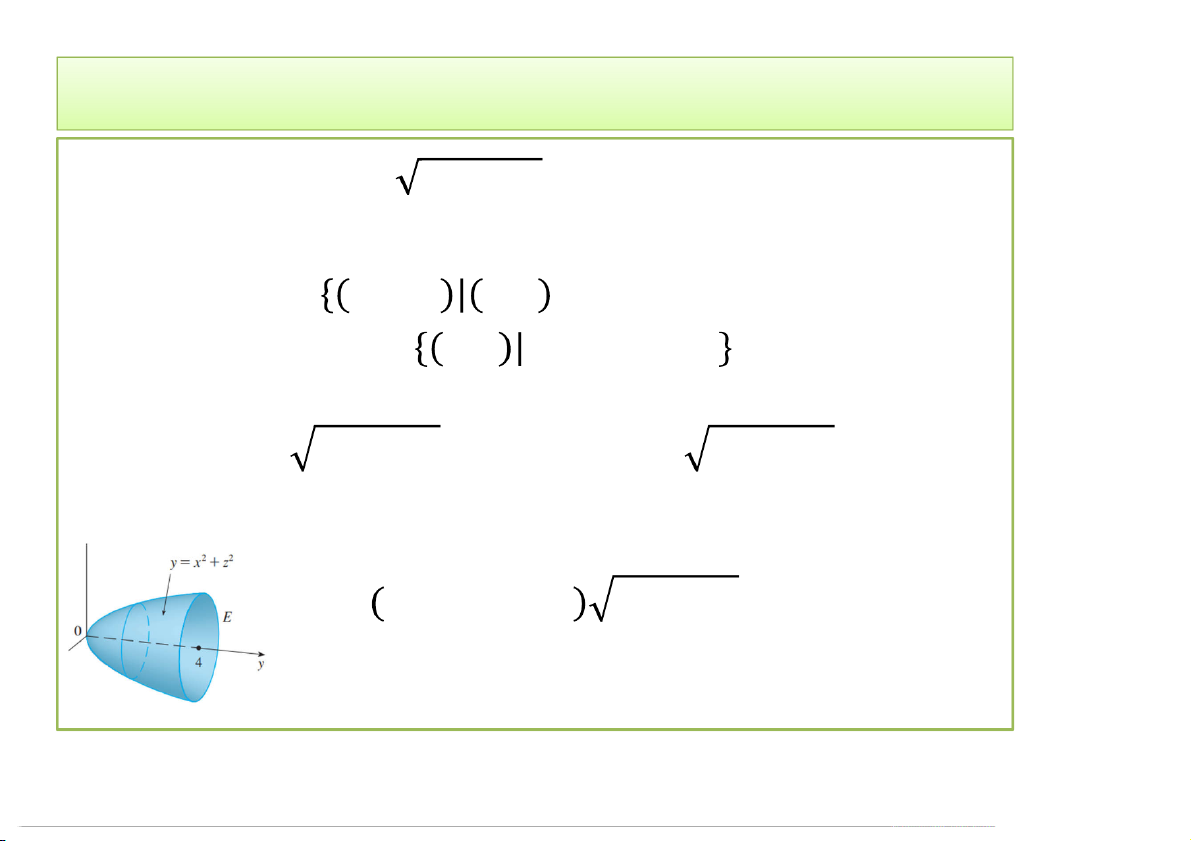
Giải: Miền  = , ,  ,  ∈ ,  +  ≤  ≤ 4}
 = ,   +  ≤ 4 
 =   +   =    +     
=  4 −  −   +   4/23/2020 Tích phân bội 16 2. Cách tính
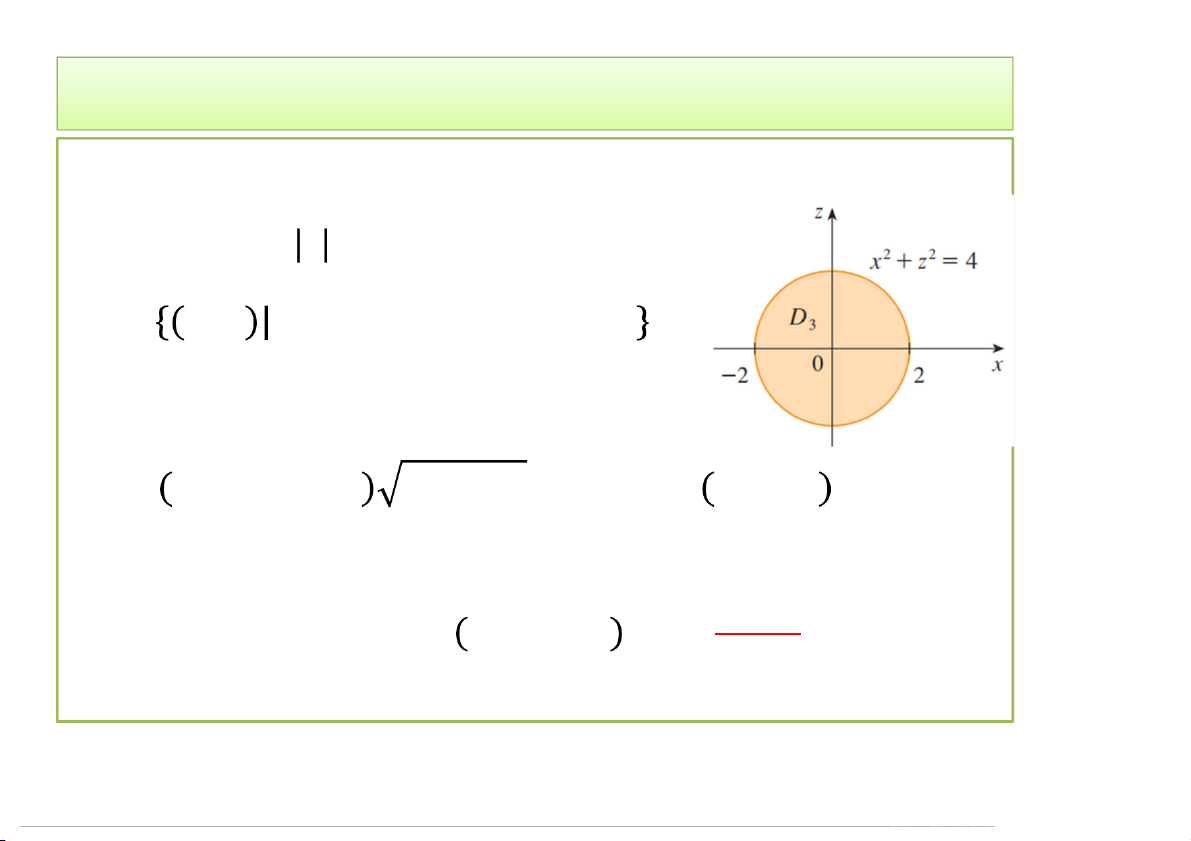
• Chuyển sang tọa độ cực trong mặt phẳng xOz  = . cos 
 = .sin ,  = ;
 = ,  0 ≤  ≤ 2, 0 ≤  ≤ 2 ;  
 4 −  −   +  =   4 −        128
=   .  4 −   = 15   4/23/2020 Tích phân bội 17 2. Cách tính 2.1. Trong hệ Đề-các
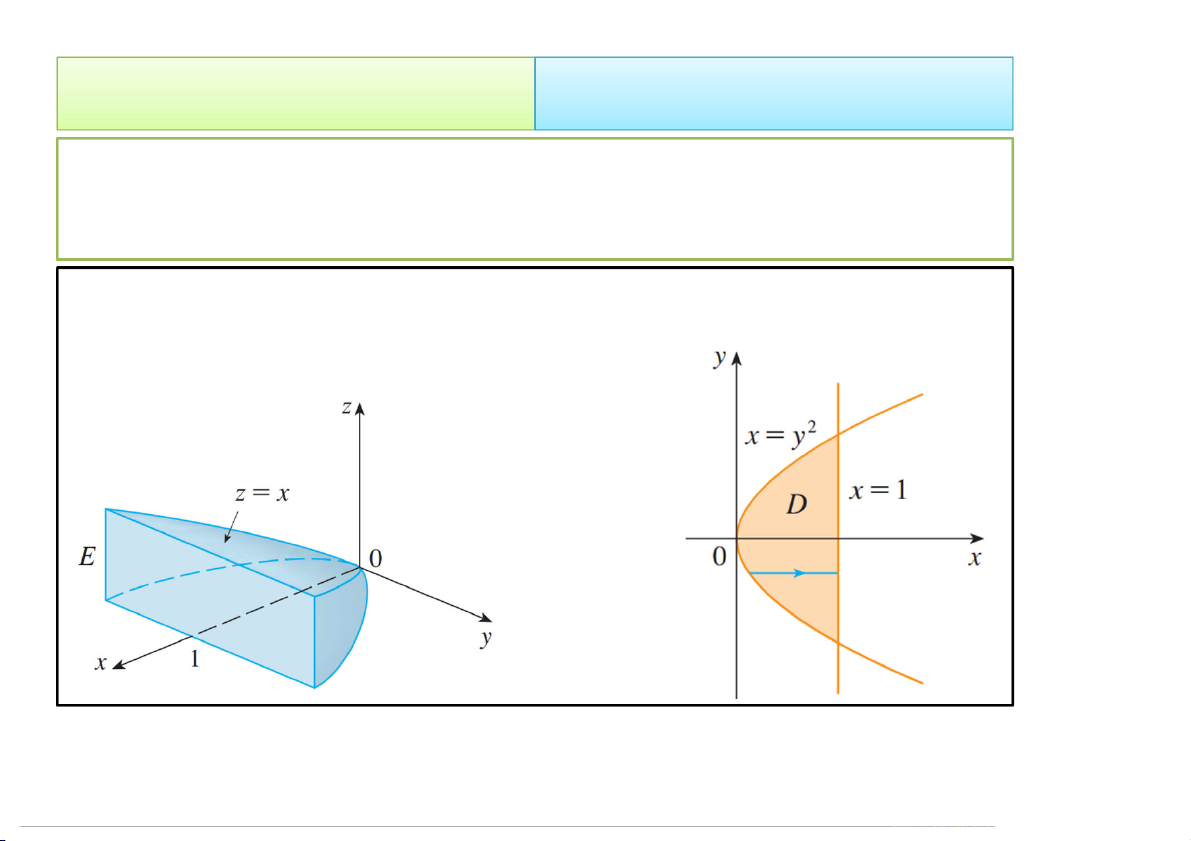
 Ví dụ 3. Tìm trọng tâm của vật thể giới hạn bởi các mặt:
 = ,  = ,  = 1à = 0,với mật độ khối .
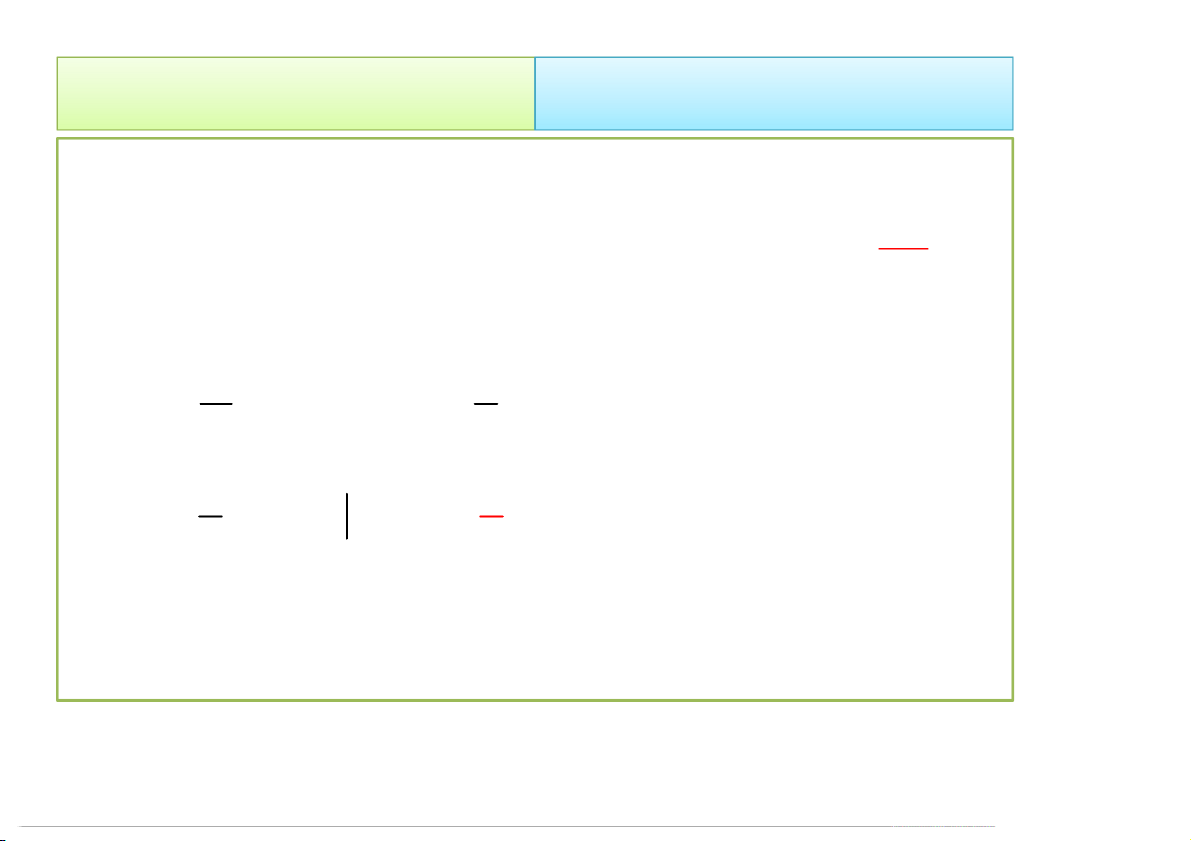
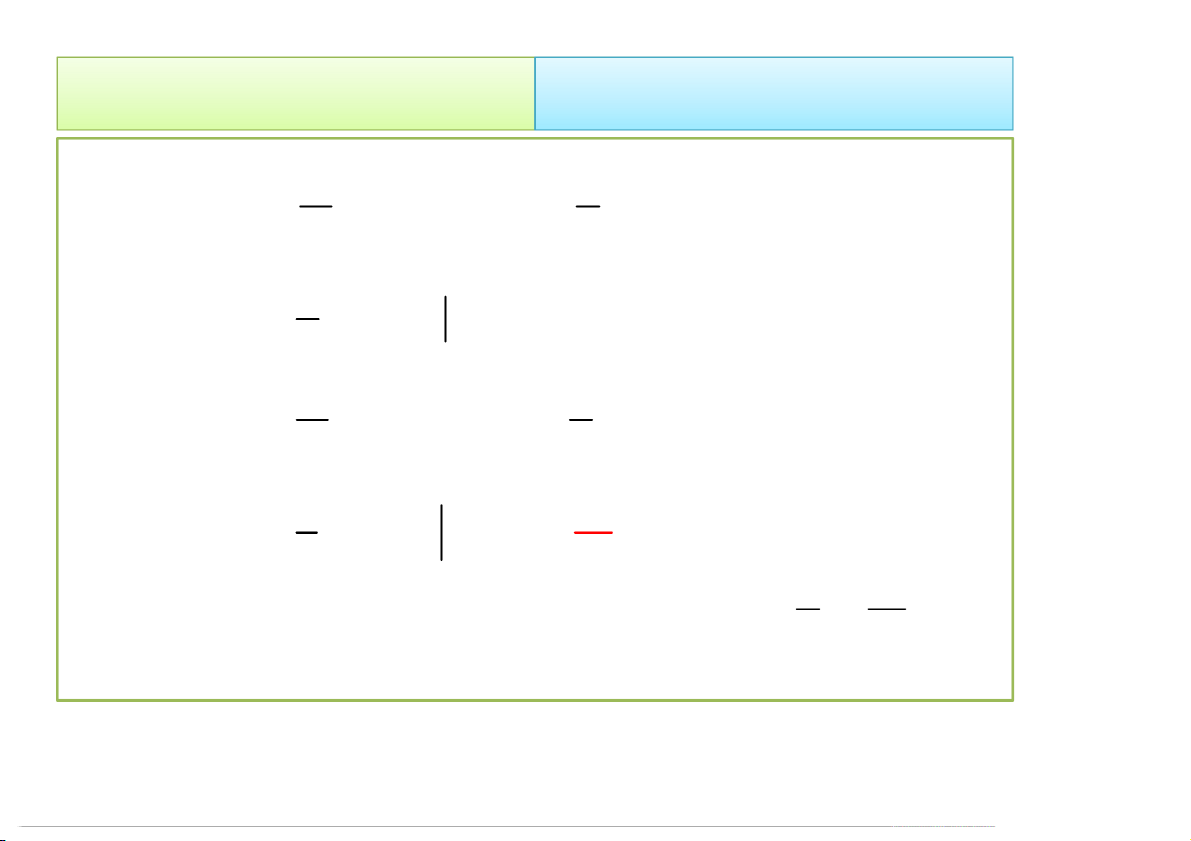
Miền D của vật thể E trên Oxy được giới hạn bởi các đường:  = ,  = 1 4/23/2020 Tích phân bội 18 2. Cách tính 2.1. Trong hệ Đề-các • Ta có: 1 1 x 1 1 4 m   dV  dzdxdy   xdxdy        2 2 1  y 0 1  y 5 E 1 1 1 5 x x  xdxdydz  xdzdxdy G    2 1 y 0 m 4 V 1 1 5 x 5  xz dxdy    2 0 1 4 y 7 4/23/2020 Tích phân bội 19 2. Cách tính 2.1. Trong hệ Đề-các 1 5 1 1 x y  ydxdydz  ydzdxdy G    2 1 y 0 m 4 V 5 1 1 x  yz dxdy  0   2  0 1 4 y 1 5 1 1 x z  zdxdydz  zdzdxdy G    2 1  y 0 m 4 V 5 1 1 x 5 2  z dxdy    2 1  y 0 8 14  
Vậy tọa độ trong tâm của vật thể E:  x y z 5 5 , ,  ,0,  7 14    4/23/2020 Tích phân bội 20 2. Cách tính 2.2 Đổi biến số 2.2. Đổi biến số Xét tính phân f  x, y,zdV V
Thực hiện phép đổi biến số:
f  x, y, z  gu,v,w x  xu, , v w   y  y u, , v w; D x y z x ' x ' x ' , , u v w J    z  z   ,u ,v w Du v  y' y' y' 0 , , u v w w z' z' z' u v w Khi đó: f  x, y,zdV  g  u,v,w J dudvdw V V ' 4/23/2020 Tích phân bội 21 2. Cách tính 2.2 Đổi biến số  Hệ tọa độ trụ
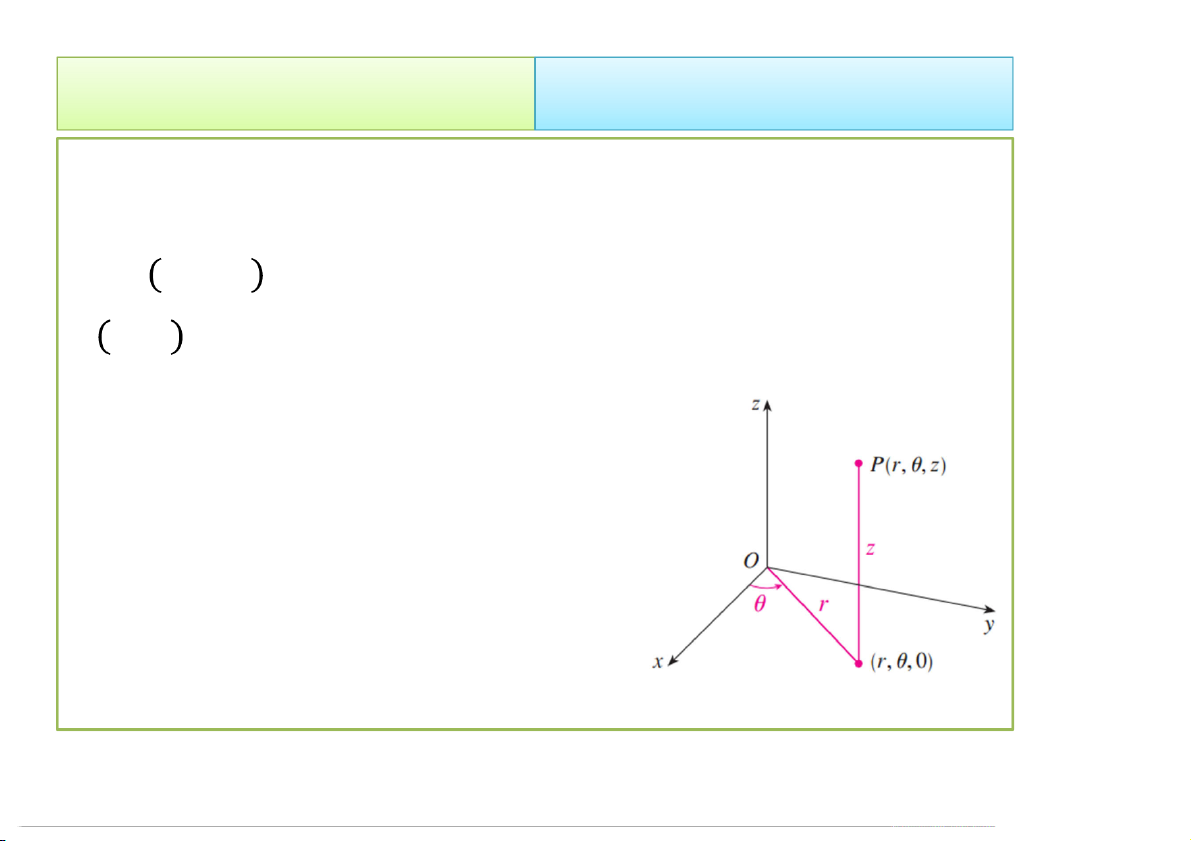
• Điểm P trong không gian ba chiều được biểu diễn bởi bộ 3
số , ,  , trong đó:
,  là tọa độ cực của điểm P’ (hình chiếu của P lên Oxy)
: khoảng cách từ P đến (Oxy)
• Mối liên hệ giữa tọa độ trụ và
tọa độ Đề-các: x  rcos   y  rsin z  z  P’ 4/23/2020 Tích phân bội 22 2. Cách tính 2.2 Đổi biến số
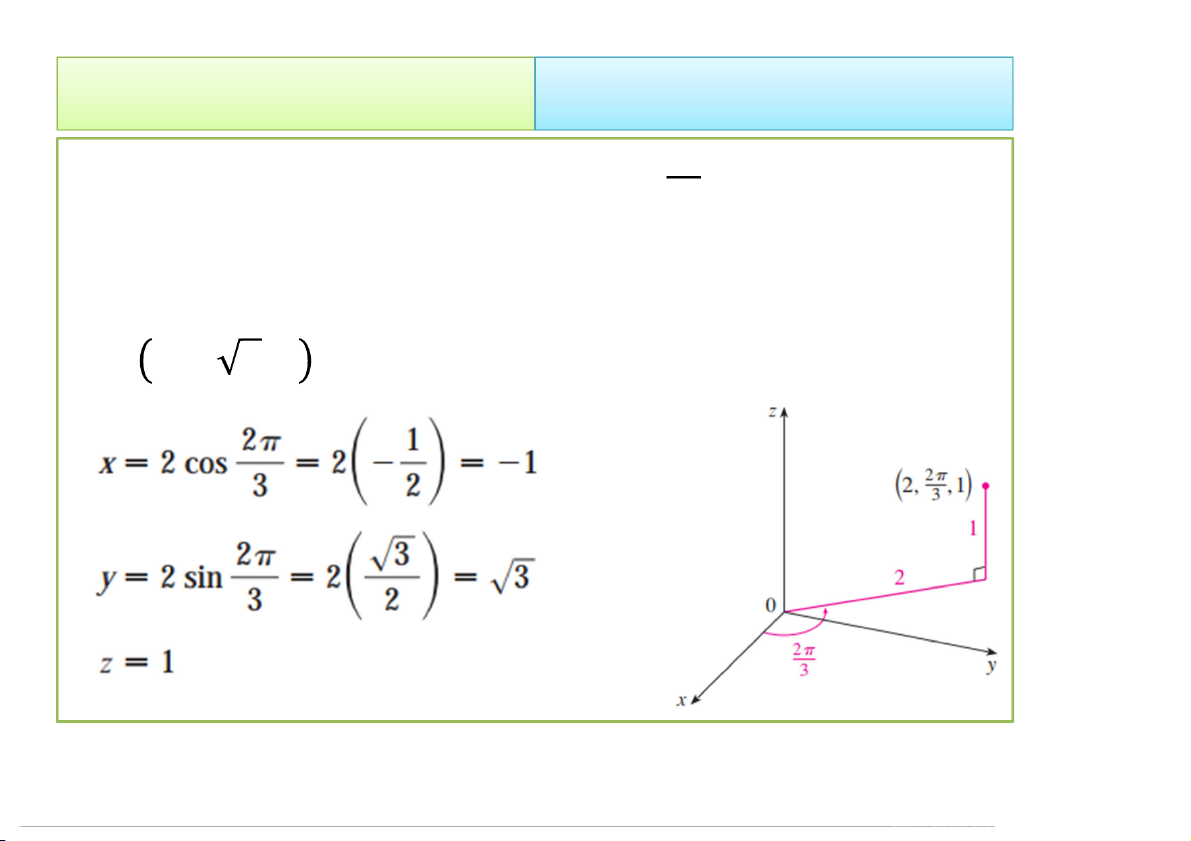
• Ví dụ 4. 1) Hãy biểu diễn điểm (2,  , 1) trong hệ tọa độ 
trụ và xác định tọa độ của nó trong hệ đề các Oxyz. Đáp án:
1)  −1, 3, 1 −  4/23/2020 Tích phân bội 23 2. Cách tính 2.2 Đổi biến số
2) Xác định tọa độ trụ của điểm N biết tọa độ của nó trong
hệ Đề các Oxyz là (3, −3, −7). Đáp án:
 =  +  = 3 + (−3)= 3 2  3 7
tan  =  = −3 = −1 →  = 4 + 2, ∈   = −7
Vậy tọa độ điểm N trong hệ tọa độ trụ: 7 −
 3 2, 4 ,−7 ℎặ  3 2, 4 ,−7 4/23/2020 Tích phân bội 24 2. Cách tính 2.2 Đổi biến số
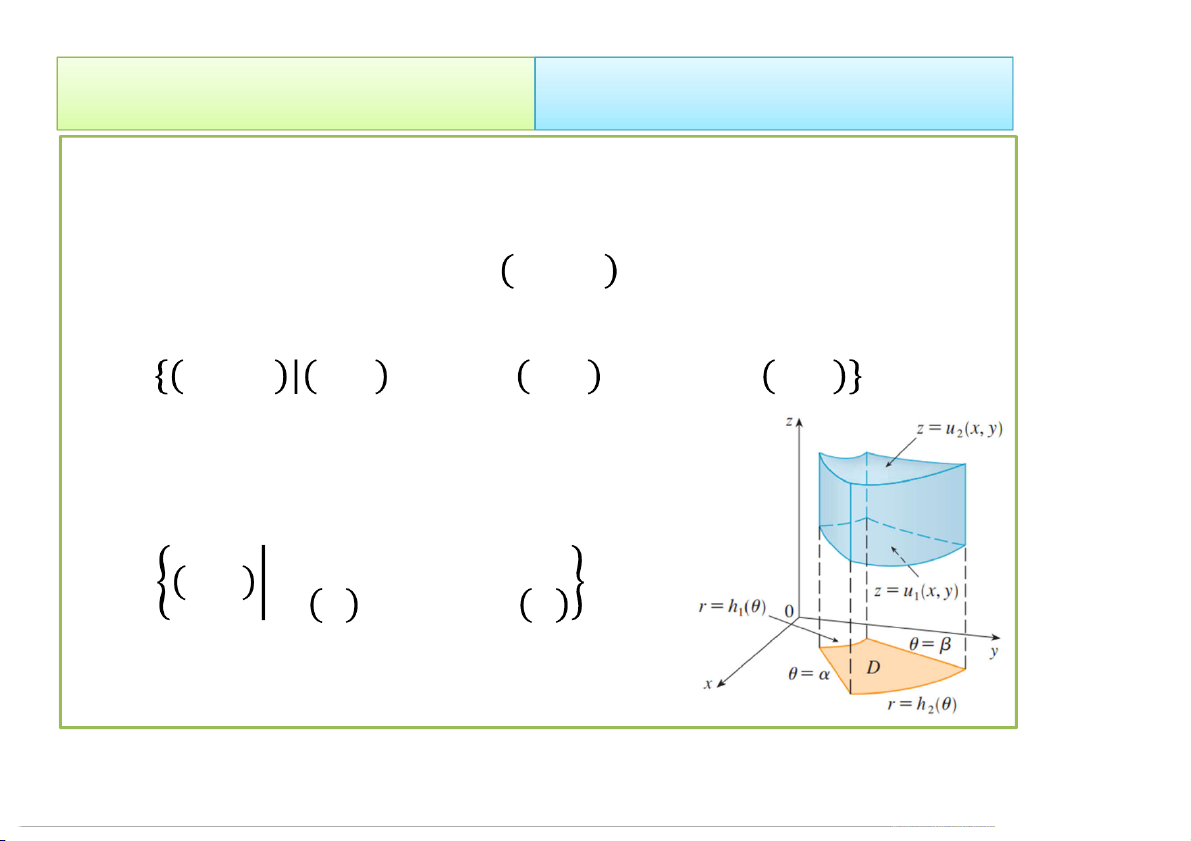
 Tính tích phân trong hệ tọa độ trụ  , ,   
 = , ,  ,  ∈ ,  ,  ≤  ≤  , 
• D: hình chiếu của E lên (Oxy) - biểu
diễn trong hệ tọa độ cực;  = ,   ≤  ≤ ,
ℎ  ≤  ≤ ℎ  4/23/2020 Tích phân bội 25 2. Cách tính 2.2 Đổi biến số • Đổi biến x  r cos cos rsin 0   y  r sin J  sin r cos 0  r z  z 0 0 1 
• Vậy, công thức tích phân bội ba trong hệ tọa độ trụ    f   h u r x, y,z  2   2  ,  dV  f    r,,zrdzdrd  1 h   1 u r ,  E 4/23/2020 26 Tích phân bội 2. Cách tính 2.2 Đổi biến số
 Ví dụ 5. Tính tích phân sau với E là miền giới hạn bởi các
mặt  =  + ,  = 2:  2 2 x  y dxdydz E
• Hình chiếu của E lên Oxy là miền
hình tròn D có phương trình:  +  ≤ 4 Do đó, ta có: 4/23/2020 Tích phân bội 27 2. Cách tính 2.2 Đổi biến số x y  2 2 2  2 2 dxdydz x y dz    dxdy   2 2    x y   E D
• Tọa độ trụ: x  rcos  y  rsin  J  r z  z    x  y  2 2 2 2 2 2 dxdydz  d dr r rdz    0 0 r V 2 2 3  r   2 r 16 drd   0 0 5 4/23/2020 Tích phân bội 28 2. Cách tính 2.2 Đổi biến số
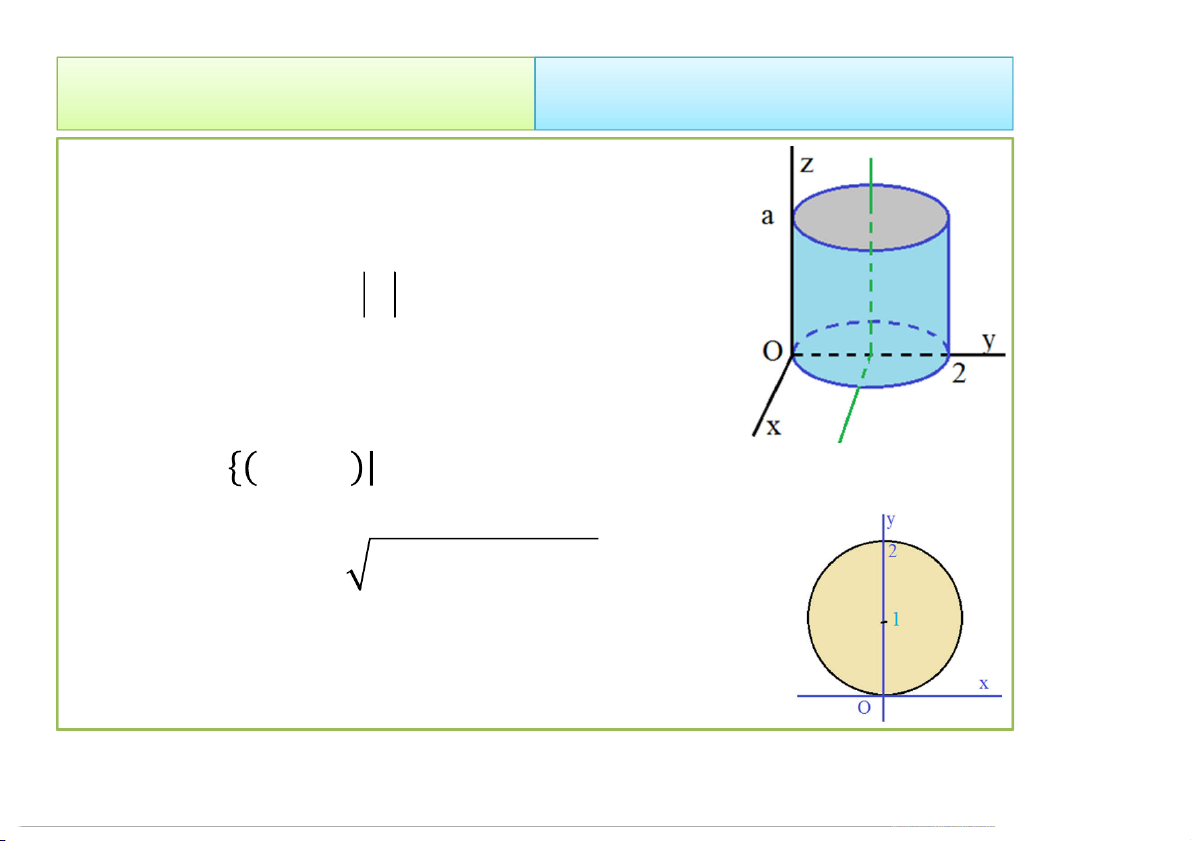
 Ví dụ 6. Tích tích phân sau với V là miền hình trụ giới hạn
bởi các mặt  +  = 2,  = 0,  = : 2 2 I  x  y .zdxdydz 6 V
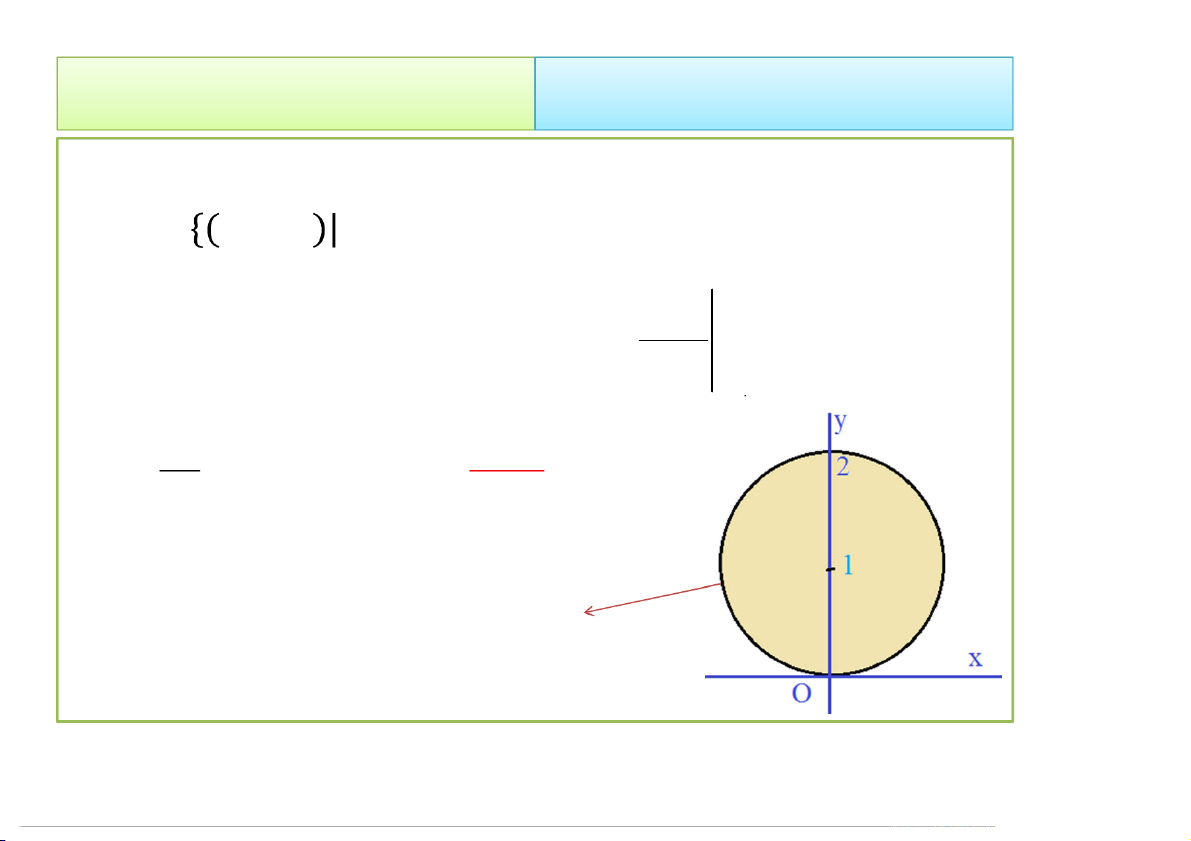
Hình chiếu của vật V lên Oxy là hình tròn D được bao bởi
đường tròn  +  = 2.
Tọa độ trụ: x  r cos  y  r sin  J  r z  z 
Pt đường tròn C:  = 2 sin  4/23/2020 Tích phân bội 29 2. Cách tính 2.2 Đổi biến số • Suy ra: •  =
, ,  0 ≤  ≤ , 0 ≤  ≤ 2 sin  , 0 ≤  ≤ } 2 2 a    2sin  a  2sin  r z 2 I  r zdzdrd    drd 6      0 0 0 0 0  2 0    2 a  2sin 2  16a 2 I  r drd  6   0 0 2 9 D C:  = 2 sin  4/23/2020 Tích phân bội 30 2. Cách tính 2.2 Đổi biến số
• Chú ý: Nếu sử dụng hệ tọa độ trụ suy rộng x  r cos 
y 1  r sin  J  r z  z  Pt đường tròn C:  = 2
 = , ,  0 ≤  ≤ 2, 0 ≤  ≤ 2, 0 ≤  ≤ } 2 2 a 2 I  r  2r sin 1rzdzdrd 6    0 0 0
- Hàm dưới dấu tích phân phức tạp, khó tính. 4/23/2020 Tích phân bội 31 2. Cách tính 2.2 Đổi biến số
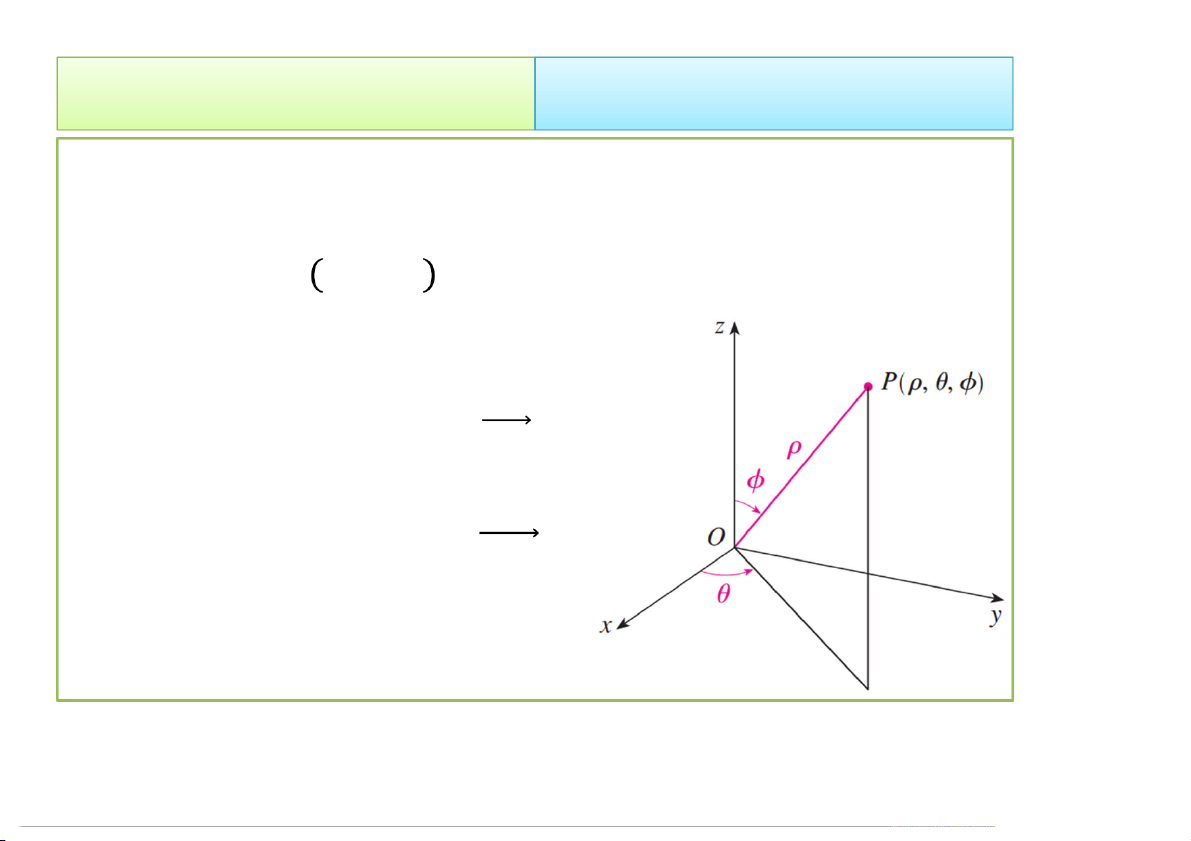
 Trong hệ tọa độ cầu
• Tọa độ cầu của điểm P trong không gian được xác định bởi
3 thành phần , ,  , trong đó:
ρlà khoảng cách từ O đến P,  ≥ 0
 là góc giữa trục Oz và , 0 ≤  ≤ 
 là góc giữa trục Ox và ′,
P’ là hình chiếu của P lên Oxy 4/23/2020 Tích phân bội 32 2. Cách tính 2.2 Đổi biến số
• Mối liên hệ giữa hệ Đề-các và hệ tọa độ cầu x   sin cos 2 2 2 2  x  y  z  
 y   sin sin ; f  ,x y,z  g,, z   cos 
sin cos  cos cos  sin sin 2 J  sin sin  cos sin
 sin  cos   sin  cos   sin 0 f
 x,y,zdxdydz  g
 , ,  2  sin d d d V V ' 4/23/2020 Tích phân bội 33 2. Cách tính 2.2 Đổi biến số
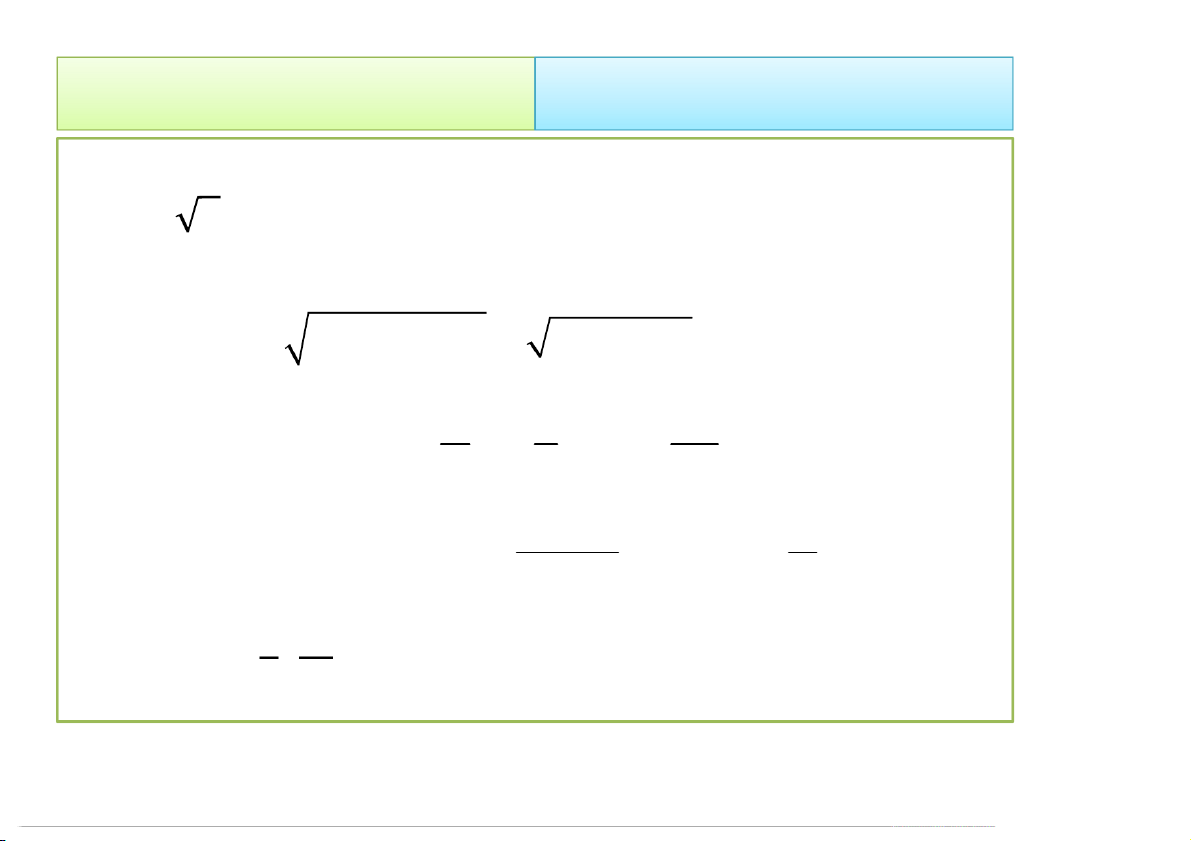
Ví dụ 7. Cho điểm M trong hệ Oxyz có tọa độ
(0, 2 3, −2). Tìm tọa độ của M trong hệ tọa độ cầu. Hướng dẫn: • Ta có: 2 2 2
  x  y  z  0 12  4  4 z 1 2
z   cos  cos        2 3 x x  sin cos  cos   0         ( y  0)  sin 2 • Vậy (4,  , )   4/23/2020 Tích phân bội 34 2. Cách tính 2.2 Đổi biến số
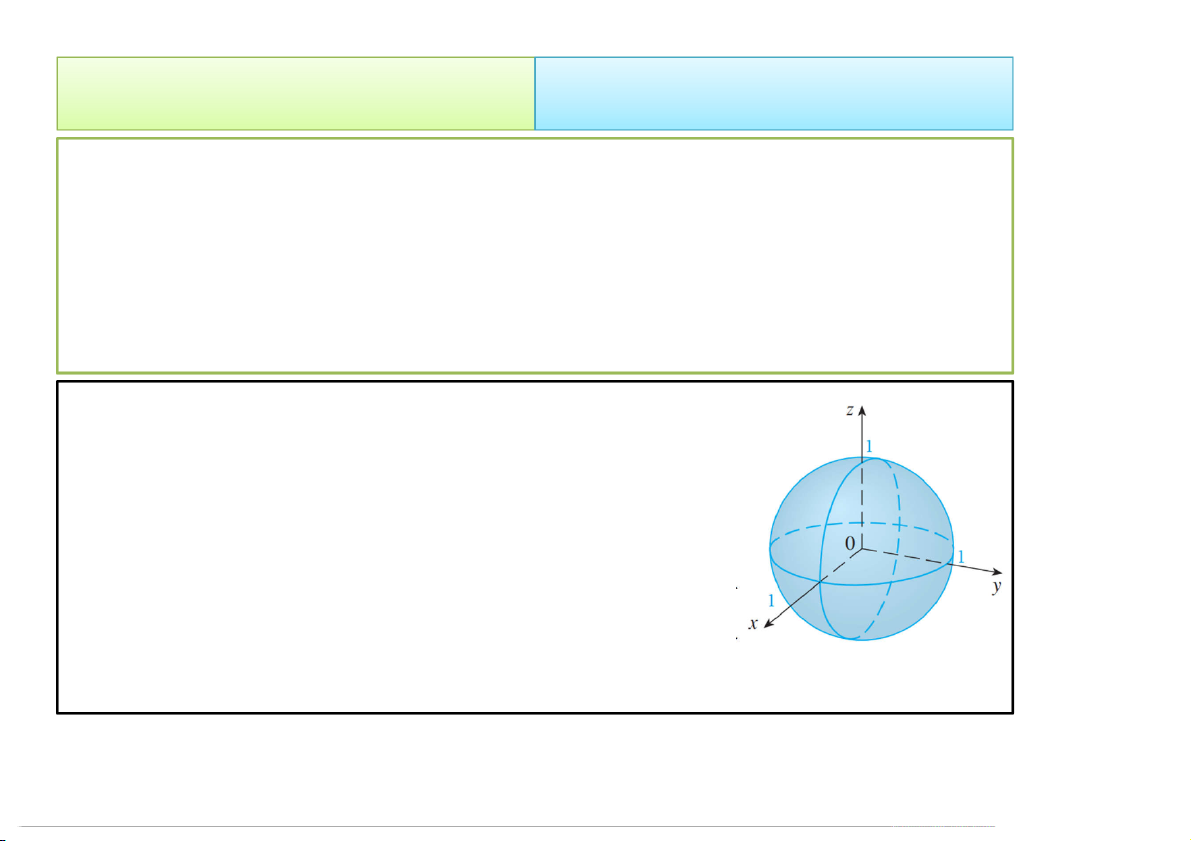
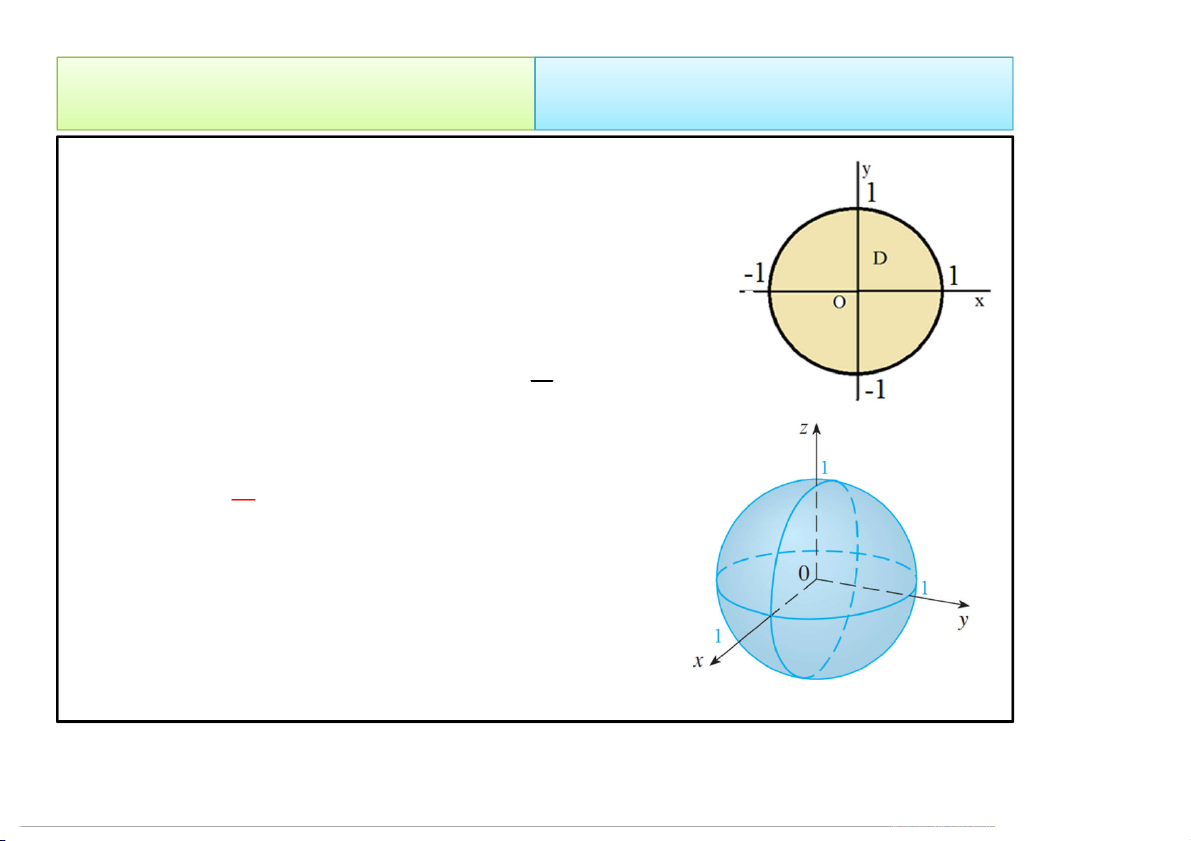
 Ví dụ 8. Tính tích phân sau với B là quả cầu đơn vị B    x y z 2 2 2 , , | x  y  z   1  x  y z 3/2 2 2 2 I  e dV 8 B
Sử dụng tọa độ cầu: x  rsin cos   y  rsin sin  Khi đó: z  r cos  B  
 r,, | 0  r 1,0   ,0   2 2 2 2 2 x  y  z  r 4/23/2020 Tích phân bội 35 2. Cách tính 2.2 Đổi biến số Nên 2  1 3 r 2 I  e .r sindrdd 8     0 0 0 2  1 1 3   sin r I d d e d     3r 8  0 0 0 3 4 I   e 1 8   3 4/23/2020 Tích phân bội 36 2. Cách tính 2.2 Đổi biến số
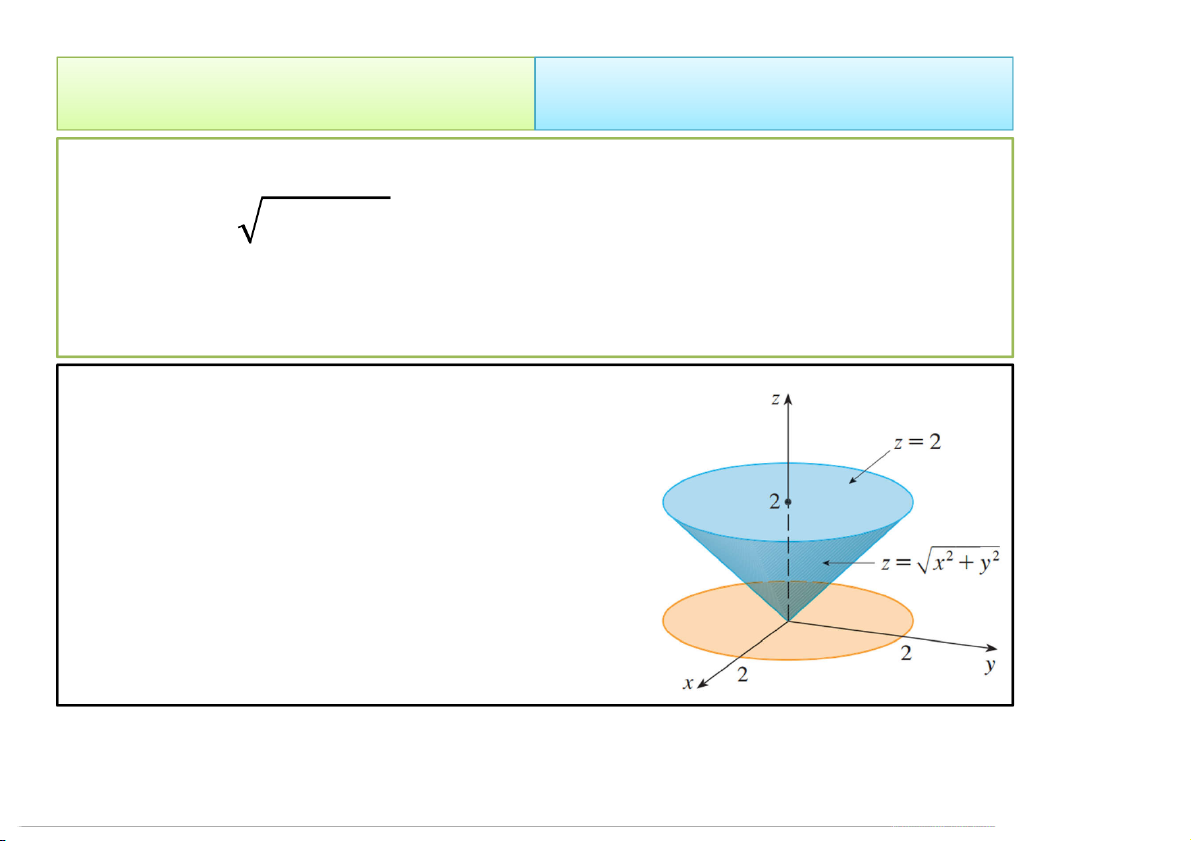
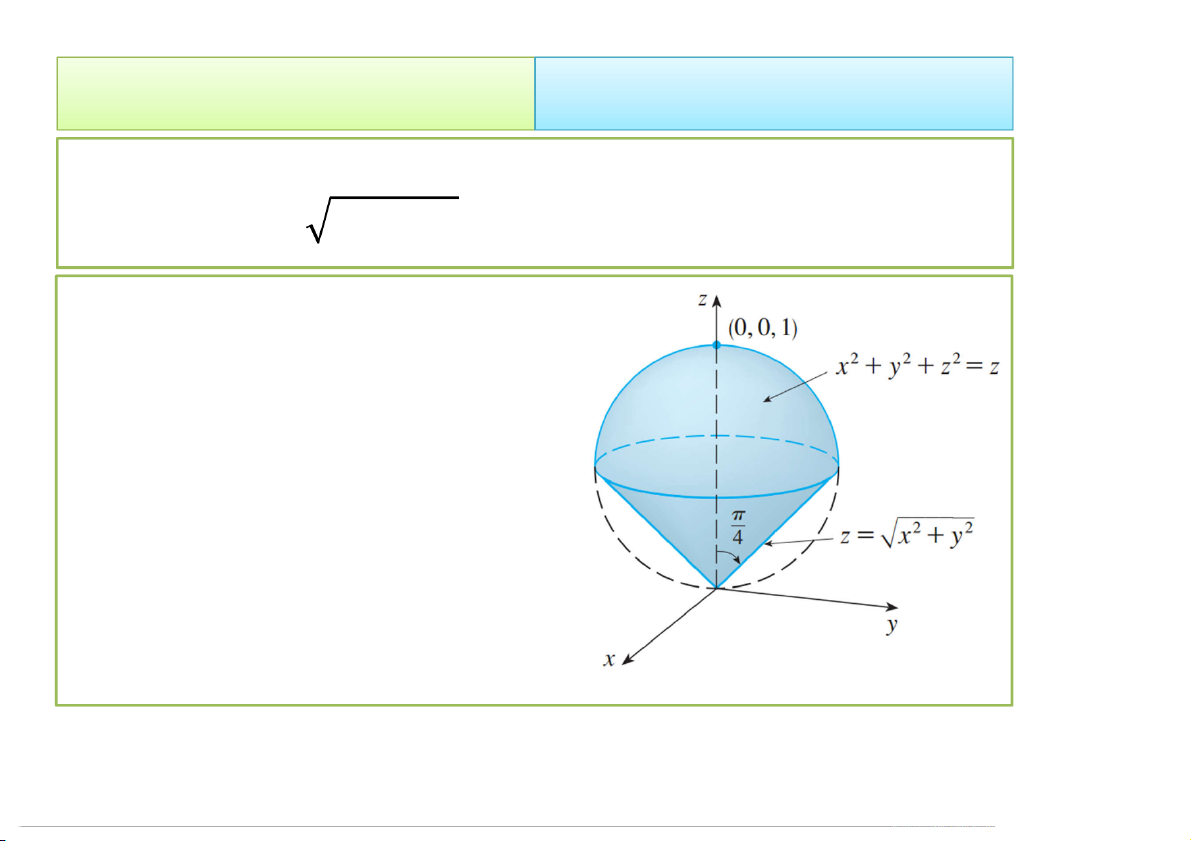
 Ví dụ 9. Dùng tọa độ cầu tính thể tích vật thể E nằm bên
trên mặt  =  +  và bên dưới mặt  +  +  =  Xét trong tọa độ cầu: x  r sin cos y  r sin sin z  r cos 2 J  r sin Phương trình mặt cầu: 2
r  r cos  r  cos 4/23/2020 Tích phân bội 37 2. Cách tính 2.2 Đổi biến số
• Phương trình mặt nón: 2 2 2 2 2 2
r cos  r sin  cos   r sin  sin   r sin     / 4
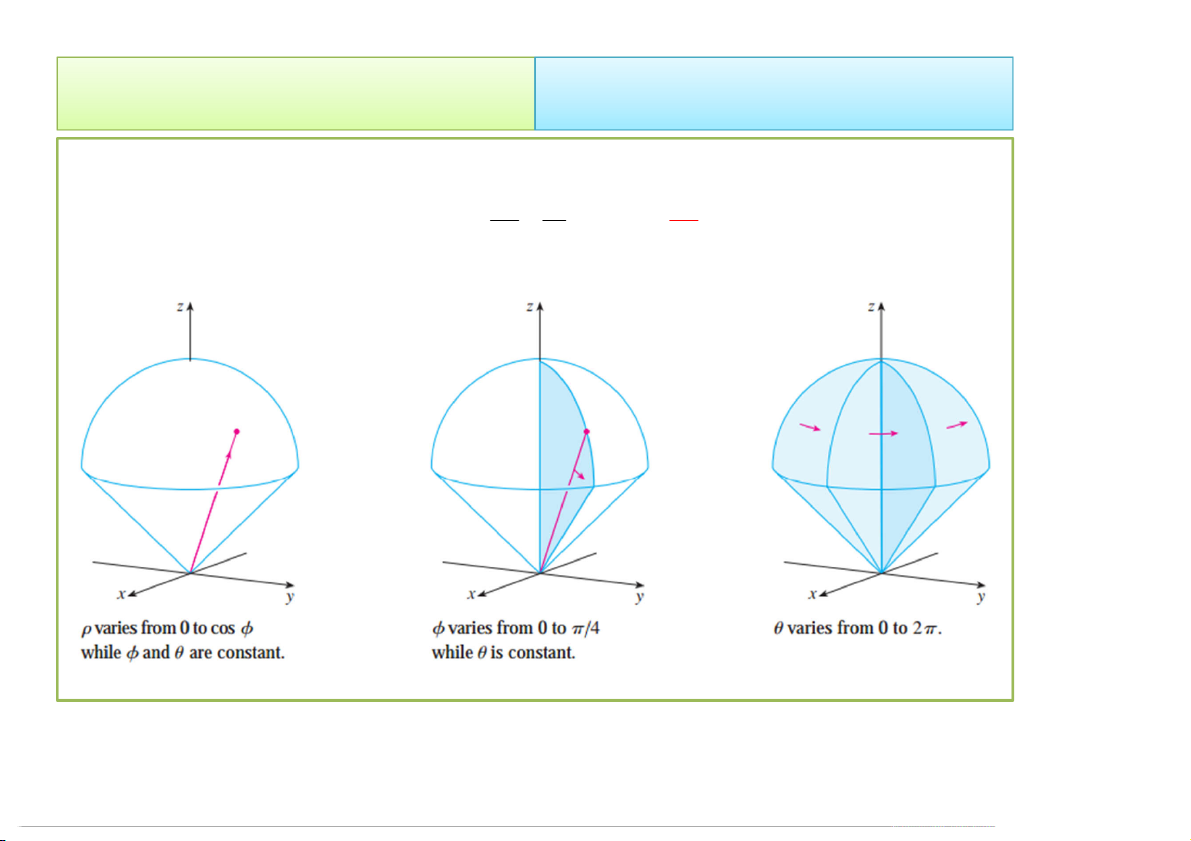
• Vật thể E trong tọa độ cầu được giới hạn bởi: E  
 r,, |0  r  cos, 0   / 4, 0   2 Thể tích vật thể:    V E 2 /4 cos 2  dxdydz  d d r sin dr     0 0 0 E   V E /4 1  /4 3 4 2 cos  sin d cos      0  0 3 6   4/23/2020 Tích phân bội 38 2. Cách tính 2.2 Đổi biến số • Vậy:   V  E  1   1   6  4    8 4/23/2020 Tích phân bội 39 Bài tập 1.
• Tính các tích phân sau: 1 z x z 1) 6xzdydxdz 1    0 0 0 1 2x y 2) 2xyzdzdydx 5 / 8    0 x 0 2 3 1 1x 3) y ze dzdydx 3  3e    0 0 0  /2 y x 4) cos    x  y  zdzdxdy 1  / 3 0 0 0 1 1x 1x y ) 5 xydzdydx 1/120    0 0 0 2 2 x  2 4x y /2 4 2 6)  dx dy xdz    0 0 0 3 4/23/2020 Tích phân bội 40 Bài tập 2.
1) Cho V là miền xác định bởi 0 ≤  ≤  ,  ≤  ≤ 2, 0 ≤ 
 ≤ 1 −  −  zdxdydz 43/3072 V
1) V là miền xác định bởi  ≥ 0,  ≥ 0,  ≥ 0,  +  +  ≤ 1. Tính: 1 )
a 1 x  y  zdxdydz 24 V b) xyz
 1 x  y  zdxdydz V 4/23/2020 Tích phân bội 41 Bài tập 3.
• Tính tích phân sau nếu V là miền giới hạn bởi các mặt
 +  +  = ,  = 0,  ≥ 0 xzdxdydz  0 V
• Tính tích phân sau nếu V là miền giới hạn bởi các mặt
 +  +  = 1,  = 0,  = 0,  = 0: 
x  y  z dxdydz  V
• Tính tích phân sau nếu V là miền hình nón tròn xoay giới
hạn bởi các mặt  +  = ,  = :  5 2 2 2  a x  y  z  3 dxdydz 10 V 4/23/2020 Tích phân bội 42 Bài tập 4.
• Tính thể tích các vật thể giới hạn bởi các mặt đã cho: 2
1) y  x , z  0, z  4, y  9 144 2 2
2) x  y  9, y  z  5, z 1 36 2 2 3) x  y  z , x 16 128
4) x  y  z  4, x  3, y  2, x  0, y  0, z  0 55 / 6 2 2 2 2 2 2
5) x  y  z  2z, x  y  z  81 2 2 6) 2  z  x  y , y  z  4 4 3  a 2 2 2 2 2 2
7) x  y  z  3a , x  y  2az 6 35 3 4/23/2020 Tích phân bội 43 Bài 5 4/23/2020 Tích phân bội 44 Bài 5
Solid tetrahedron: vật thể hình tứ diện 4/23/2020 Tích phân bội 45