1
TÓM T T M T S CÔNG TH C SỬ DỤNG TRONG H C PHẦN
NGUYÊN LÝ TH NG KÊ KINH T
Biên soạn: Võ Hải Thuỷ
Chương II. Phân tổ th ng kê
Tính chất của tiêu thức
a-Trường hợp đơn giản
b-Trường hợp phức tạp phân tổ
1.Tiêu thức định tính
Tiêu th c có ít biểu hiện, ng Tiêu th c có nhiều biểu hiện, ta ghép nhiều biểu hiện vào 1 tổ
v i m i biểu hiện ta l p 1 tổ
2.Tiêu thức định lượng
Tiêu th c có ít lư ng biến, ng Tiêu th c có nhiều lư ng biến, ta ghép nhiều lư ng biến vào 1 tổ tạo
v i m i lư ng biến ta l p 1 tổ
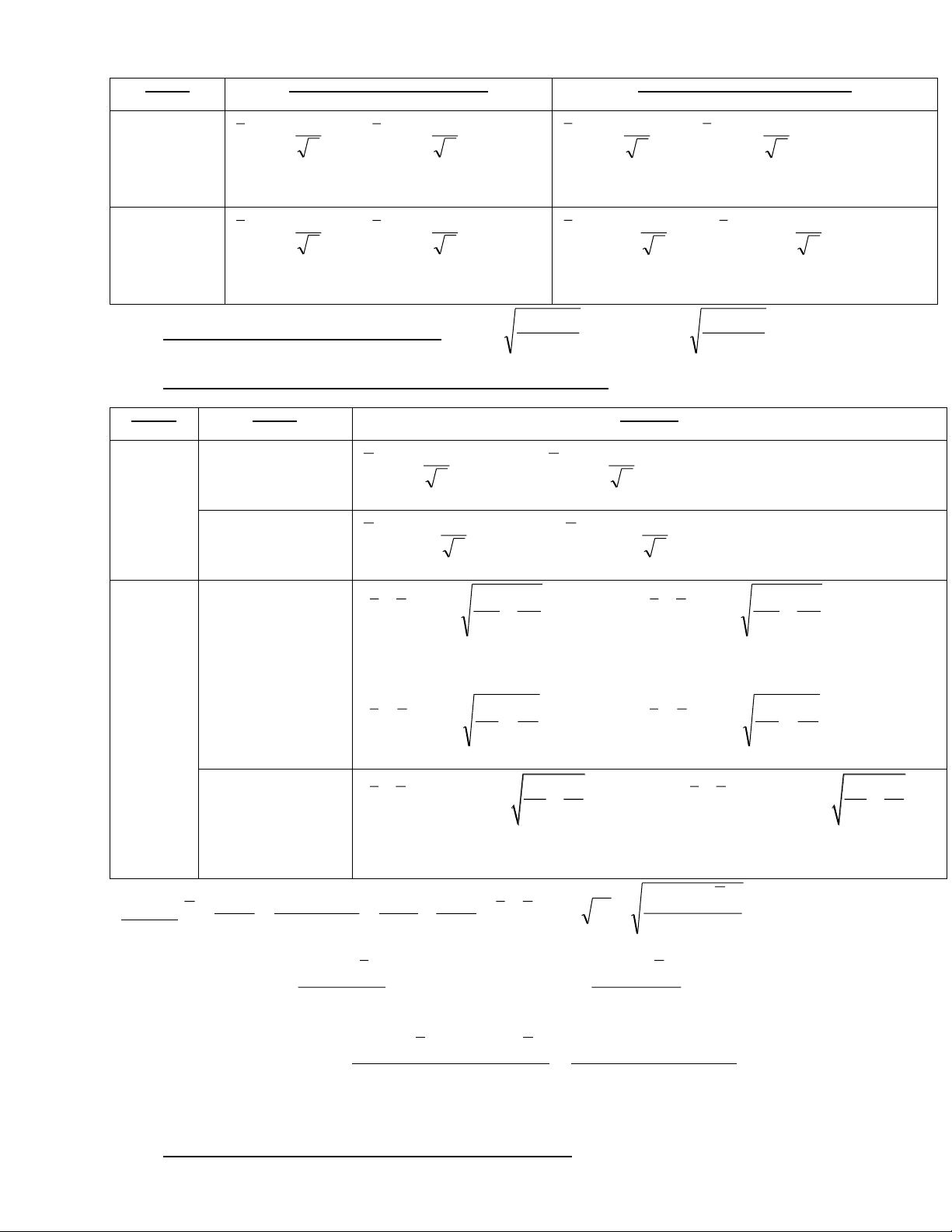
nên khoảng cách tổ. Nếu khoảng cách tổ đều, có 2 trường h p: X  X max
+Nếu lư ng biến liên tục : h min  k ( X
 X ) (k  ) 1 max min
+Nếu lư ng biến rời rạc : h  k 1/ 3 0,3333
Chú thích: k : s tổ - Thường tính k theo công th c TK kinh nghiệm: k  (2 ) n  (2 ) n
n: s đơn vị , h: khoảng cách tổ; x , x
: lư ng biến l n nhất và nh nhất của tiêu th c phân tổ max min
Chương IV : Cách tính các tham s dùng để phân tích dữ liệu th ng kê
1- Cách tính s y u v (Mode - M ): Có 2 trường h p: o
a-Nếu dữ liệu không có khoảng cách tổ
b-Nếu dữ liệu có khoảng cách tổ
-Tìm tổ có ch a M (tổ có tần s l n nhất) o
Dựa vào khái niệm để tính f f Mo  Mo 1  -Tính M : M x h o  Mo  o (min) Mo ( f f ) f f Mo Mo  ( Mo  )  1  Mo 1  Chú thích: h
: khoảng cách tổ của tổ ch a M ; x
: gi i hạn dư i của tổ ch a M ; f
: tần s của tổ ch a M ; M 0 0 M 0 M 0 0 (min) 0 f
: tần s của tổ đ ng trư c tổ có ch a M ; f
: tần s của tổ đ ng sau tổ có ch a M M 1  M  0 0 1 0 0 2
2- Cách tính s trung v (Median - M ): Có 2 trường h p: e
a)Nếu dữ liệu không phân tổ
b) Nếu dữ liệu có phân tổ a1-Nếu n lẻ:
b1-Nếu không có khoảng cách tổ : n 1 f 1  i 
M là lư ng biến đ ng ở vị trí th e
M là lư ng biến có tần s tích lũy bằng 2 e 2
b2-Nếu có khoảng cách tổ: a2-Nếu n chẵn: f 1  i 
-Tìm tổ có ch a M (tổ có tần s tích lũy bằng ) e n 2
M là s trung bình của 2 lư ng biến ở vị trí th e 2 f  n i  S và th ( + 1) Me 1  2 2
-Tính M : M  x  h e e Me(min) Me f Me Chú thích: h
: khoảng cách tổ của tổ ch a M ; x
: gi i hạn dư i của tổ ch a M ; f
: tần s của tổ ch a M M e e M e M e e (min) e S
: tần số tích lũy của tổ đ ng trư c tổ có ch a M M e 1 e
3-Cách tính s trung bình (mean, average). Có 2 trường h p: Tham số
a-Đối với dữ liệu không phân tổ
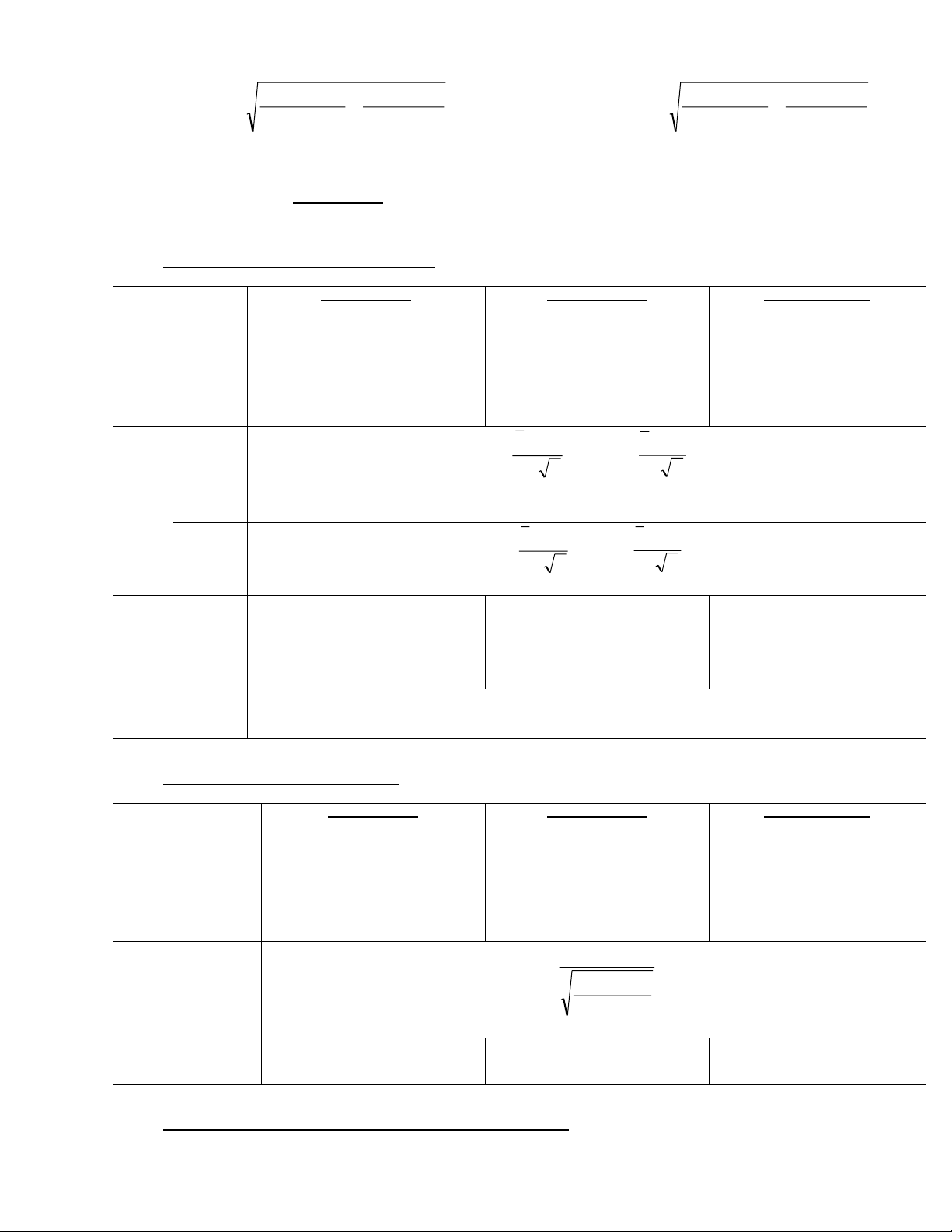
b-Đối với dữ liệu có phân tổ N k x  x f i i i Trung bình tổng i   1  i   1  thể N k fi i 1 n k x  x f i i i Trung bình m u x i   1 i  x  1 n k fi i 1
Chú thích: x : lư ng biến th i (i =1,2,3…) ; f : tần s của tổ th i (i =1,2,…,k); N: s đơn vị của tổng thể; n: s đơn vị của m u i i
4-Cách tính khoảng bi n thiên (Range ậ R): R  X  X max min
5- Cách tính khoảng t phân v (Interquartile Range) : ∆Q = Q3 ậ Q1
a)Nếu DL không phân tổ hay không có
b)Nếu dữ liệu có khoảng cách tổ khoảng cách tổ
Q1(tứ phân vị thứ nhất): Là lư ng biến ở f 1  i  n 1 -Tìm tổ có ch a Q1 (tổ có tần s tích lũy bằng ); vị trí th 4 4 f  i Q3  S
(tứ phân vị thứ ba): Là lư ng biến ở vị 1 Q 1  4   ( 3 n  ) 1 Q x h 1 Q ( 1 min) Q1 trí th f 1 Q 4 3 ( 3 f ) 1  i  -Tìm tổ có ch a Q3 (tổ có tần s TL bằng ) ; 4 3 f
 i SQ3 1 4 Q  x  h 3 Q ( 3 min) Q3 f Q3
5- Cách tính phương sai : Tham số
a-Đối với dữ liệu không phân tổ
b-Đối với dữ liệu có phân tổ Phương sai N k tổng thể (x   2 ) (x 2 ) .f i  i i 2 i    1 2 i    1 N k fi i 1 Phương sai m u n k hiệu chỉnh (  x (x x 2).f i  i  x)2 i 2 i 1 s   2 i  s  1 n 1 k f 1 i  i 1
4-Cách tính đ lệch chu n (Standard Deviation)
Đ lệch chu n c a tổng thể 2 2
:    Đ lệch chu n c a m u: s  s
Chương VI : Cách tính các tham s c a bi n ng u nhiên TRUNG BÌNH M U Tham số Cách tính Trung bình của trung bình  =  m u X Phương sai của trung 2    2 N n 2 bình m u  2
Đối với tổng thể vô hạn: 
Đối với tổng thể hữu hạn:   . X n X N 1 n Đ lệch chu n của trung  N  n  bình m u
 Đối với tổng thể vô hạn :  
 Đối với tổng thể hữu hạn:   . X n X N 1 n
Chương VII : Công th c khoảng tin c y cho các tham s c a tổng thể
1-Công th c khoảng tin c y cho trung bình tổng thể: 4 Cỡ mẫu
a-Nếu đã biết phương sai tổng thể :
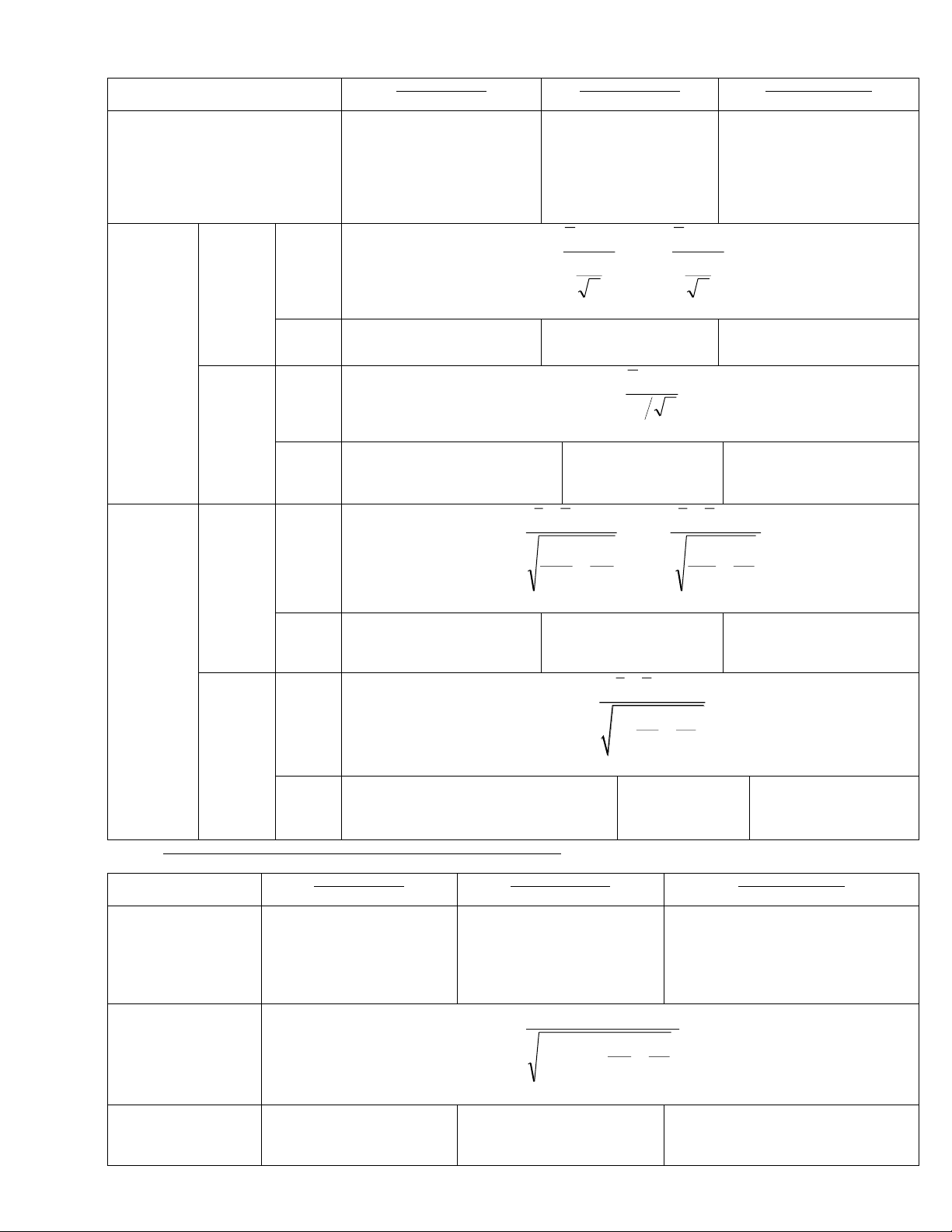
b-Nếu chưa biết phương sai tổng thể :   s s x  z    x  z   x z / 2  x z/2    / 2  / 2 L N n n n n n ≥ 30   s s x  z    x  t 
   x  t / 2  x z/2 n , 1 n , 1   / 2 NH n n / 2 n n n < 30 pˆ 1 (  pˆ) pˆ 1 (  pˆ)
2-Công th c khoảng tin c y cho tỷ lệ tổng thể: pˆ  z
 p  pˆ  z / 2  n / 2 n
3-Công th c khoảng tin c y cho khác biệt giữa 2 trung bình c a 2 tổng thể: T/c mẫu Cỡ mẫu Công th c L N(n ≥ 30) s s d  z d     d  z d   / 2 X Y  / 2 2 M U n n PH I H P NG C P NH s s d  t d 
     d t d    ( n , 1 X Y n , 1 / 2 n < 30) / 2 n n L N  2  2 2 2   ( x  y)  X z X Y 
( x  y)  z / 2  Y    X  Y  2 M U Đ C   / 2
( n ≥30, n ≥ 30) n n n n L P x y X Y X Y Ho c: 2 2 s2 s2 (x  y)  s s X z X Y 
(x  y)  z  / 2  Y    X  Y  n n / 2 n n X Y X Y NH 1 1 1 1
(x  y)  t .s   
 (x  y) t .s  (4) n n 2;      / 2    X Y X Y n n 2; / 2 X Y
( n <30, n < 30) n n n n x y X Y X Y d ( x  y ) x y     (di  d )2 s s  i i i i 2 Chú thích: d i      x  y ; d  d  n n n n n 1 ( x x ( y y i  )2 i  )2 Phương sai m 2 2 u th 1: s
Phương sai m u th 2: s Y   X  n nY 1 X  1 (x x y y s n s n i  )2  ( i  )2 2 ( x x  ) 1 2  ( y y  ) 1 Phương sai chung củ 2 a cả 2 m u : s     (n n n n X  ) 1  ( Y  ) 1 x  y  2
4-Công th c khoảng tin c y cho khác biệt giữa 2 tỷ lệ c a 2 tổng thể: 5 pˆ 1 ( pˆ ) pˆ 1 ( pˆ ) pˆ 1 (  pˆ ) pˆ 1 (  pˆ ) X  X Y  ( pˆ pˆ ) z p p X X Y Y
( pˆ  pˆ )  z  X  Y  /2  Y  X  Y  n n X Y / 2 n n X Y X Y
Chương VIII : Kiểm đ nh giả thuy t về các tham s c a tổng thể
1-Kiểm đ nh giả thuy t về trung bình tổng thể: Kiểm định 2 bên Kiểm định bên trái Kiểm định bên phải C p giả thuyết H :   
H :    hayH :   
H :    hayH :    0 0 0 0 0 0 0 0 0 0 H :    H :    H :    1 0 1 0 1 0 x   x   z 0  0 ho c z  Giá trị M u l n  / n s / n cần KĐ (n≥30) M u nh x   x   z 0  0 ho c t  (n<30)  / n s / n Miền bác b ( ,  z )  (z , )   ( ,   ) ( , )  z  / 2 / 2  z ho c: ( ,  t ) t   t n   n  ( , ) n   , 1 / 2 , 1 / 2 ho c: ( , t ) ho c: ( , ) n , 1  , 1 Quy tắc ra quyết H H đị
Nếu z (hay t) miền bác b thì bác b
, nếu z (hay t) miền bác b thì chấp nh n nh 0 0
2-Kiểm đ nh giả thuy t về tỷ lệ tổng thể: Kiểm định 2 bên Kiểm định bên trái Kiểm định bên phải C p giả thuyết
H : p  p
H : p  p hayH : p  p
H : p  p hayH : p  p 0 0 0 0 0 0 0 0 0 0
H : p  p
H : p  p
H : p  p 1 0 1 0 1 0
Giá trị cần kiểm định pˆ  p (m u l n) z 0  p 1 (  p ) 0 0 n Miền bác b ( ,  z )  (z , )   ( ,   ) ( , )  z  / 2 / 2  z
3-Kiểm đ nh giả thuy t về khác biệt giữa 2 trung bình c a 2 tổng thể: 6 Kiểm định 2 bên Kiểm định bên trái Kiểm định bên phải
H :     D
H :     D
H :     D 0 X Y 0 0 X Y 0 0 X Y 0 C p giả thuyết
H :     D
hayH :     D
hayH :     D 1 X Y 0 0 X Y 0 0 X Y 0
H :     D
H :     D 1 X Y 0 1 X Y 0 m u l n Giá trị d  D d  D cần KĐ z 0  0 hay z  2 M U  s d d PH I n  30 n n H P MBB ( ,  z )  (z , )   ( ,   ) ( , )  z  / 2 / 2  z T NG m u nh Giá trị d  D C P cần KĐ t 0  s n d n  30 MBB ( ,  t ) t ( ,  t ) (t , ) n   n  ( , ) n   , 1 / 2 , 1 / 2 n , 1  , 1 m u l n Giá trị
( x  y)  D
( x  y)  D cần KĐ z 0  0 hay z  2 2 2   s2 s2 X Y  X Y  M U n n n n n x  30 X Y X Y Đ C n y  30 MBB ( ,  z )  (z , )   ( ,   ) ( , )  z  / 2 / 2  z L P m u nh Giá trị
(x  y)  D cần KĐ 0 t  n 1 1 x  30 2 s (  ) n n X Y n y  30 MBB ( ,  t ) t ( ,  t ) (t , )
nxny    n nx ny   x ny   ( , ) nx ny    2, / 2 2, / 2 2, 2,
4-Kiểm đ nh giả thuy t về sự bằng nhau giữa 2 tỷ lệ c a 2 tổng thể: Kiểm định 2 bên Kiểm định bên trái Kiểm định bên phải H : p p H : p p H : p p X  Y  0 X  Y  0 X  Y  0 0 0 0 C p giả thuyết H : p p hayH : p p hayH : p p X  Y  0 X  Y  0 X  Y  0 1 0 0 H : p p H : p p X  Y  0 X  Y  0 1 1
Giá trị cần kiểm định ˆp  ˆp X Y z  (2 m u đ c l p, c m u 1 1 ˆp 1 (  ˆ l n) p)(  ) n n X Y Miền bác b ( ,  z )  (z , )   ( ,   ) ( , )  z  / 2 / 2  z Nha trang 2014 7