Tài liệu Vật lý đại cương I: Sai số thí nghiệm và phép đo

Học online tại: https://mapstudy.edu.vn
Tài liệu: VẬT LÝ ĐẠI CƯƠNG I SAI SỐ THÍ NGHIỆM
I. PHÂN LOẠI SAI SỐ
1. Sai số hệ thống
+) Khái niệm: Sai số hệ thống là những sai số thường có trị số và dấu không đổi, được lặp đi, lặp
lại trong tất cả các lần đo.
+) Nguyên nhân: thường do máy móc, dụng cụ chế tạo chưa chuẩn, đôi khi do tật của người đo. Sai
số này xuất hiện có quy luật, dễ tính toán và hiệu chỉnh.
2. Sai số ngẫu nhiên
+) Khái niệm: Là loại sai số làm cho kết quả đo thay đổi một cách ngẫu nhiên, khi lớn hơn khi nhỏ
hơn đại lượng cần đo.
+) Nguyên nhân: khó đoán chính xác, vì nhiều khi nó chỉ là những yếu tố rất nhỏ nhặt như gió, sức
cản không khí, điện áp không ổn định, ….
+) Không thể khử được sai số ngẫu nhiên, nhưng có thể giảm nhỏ giá trị của nó bằng cách thực hiện
phép đo nhiều lần trong cùng điều kiện để xác định giá trị trung bình của đại lượng cần đo.
3. Sai số dụng cụ:
+) Là sai số nằm ngay tại dụng cụ đo, không thể khắc phục được sai số này vì không có cái sản phẩm
nào hoàn hảo 100%. Tuy nhiên, có thể làm giảm sai số này bằng cách lựa chọn các thiết bị có độ
chính xác cao, có xuất sứ từ những nơi có uy tín.
+) Nếu thích đo chính xác tới đơn vị nhỏ hơn thì phải dùng những dụng cụ khác có độ chính xác
hơn, tức là có sai số dụng cụ nhỏ hơn ví dụ như thước kẹp để đo độ dài thay vì thước bình thường. 4. Sai số thô đại
+) Là sai số do sơ suất của người thực hiện phép đo gây ra. Loại sai số này rất dễ nhận ra vì giá trị
của nó thường rất ảo.
+) Khi thực hiện thí nghiệm mỗi nhóm nên lựa chọn một bạn mắt tinh để quan sát kết quả, một bạn
khéo tay để tiến hành thí nghiệm tránh sai số thô đại.
Thầy Phạm Ngọc Lam 1 Trường
Học online tại: https://mapstudy.edu.vn
II. PHÉP ĐO TRỰC TIẾP – GIÁN TIẾP 1. Phép đo trực tiếp:
+) Sử dụng dụng cụ đo trực tiếp được luôn kết quả cần đo. Tất nhiên, ai cũng mong muốn là đo đạc
cái gì cũng nên trực tiếp vì giảm càng nhiều bước đo trung gian thì sai số nó sẽ càng giảm. 2. Phép đo gián tiếp:
+) Trong phép đo gián tiếp một đại lượng cần đo sẽ được đo thông qua các đại lượng khác thường
là có thể xác định bằng các phép đo trực tiếp.
III. SAI SỐ CÁC PHÉP ĐO 1. Sai số tuyệt đối
+) Sai số tuyệt đối bằng tổng số học của sai số tuyệt đối trung bình của tất cả các lần đo và sai số của dụng cụ kèm theo.
+) Công thức cơ bản sẽ là: a  a (a) dc
+) Muốn xác định sai số tuyệt đối thì phải tìm được sai số tuyệt đối trung bình và sai số dụng cụ.
+) Ví dụ: Dùng thước đo chiều dài đo chiều dài chiếc điện thoại:
Bước 1: Tiến hành đo viết kết quả ra bảng Lần đo Chiều dài (mm) Sai số tuyệt đối 1 110 2 112 3 113 4 109
Bước 2: Sau khi có bảng số liệu chuẩn, ta chuyển sang bước tính giá trị trung bình của chiều dài theo công thức sau: L     L L L L 1 2 3
4  110  112  113  109  111(mm) 4 4
Trong đó L ,L ,L ,L là chiều dài của ứng với lần đo 1, 2, 3, 4. 1 2 3 4
L là chiều dài trung bình
Thầy Phạm Ngọc Lam Trường 2
Học online tại: https://mapstudy.edu.vn
Bước 3: Xác định sai số tuyệt đối trong mỗi lần đo bằng công thức
L  L  L i i
Cụ thể là: L  111110  1,L  111112  1,L  111113  2,L  111109  2 1 z 3 4
Bước 4: Xác định sai số tuyệt đối trung bình        L  L L L L 1 2 3
4  1 1 2  2  1,5(mm) 4 4
Bước 5: Xác định sai số dụng cụ rồi từ đó tính sai số tuyệt đối. Sai số dụng cụ sẽ được trình bày chi
tiết ở phần sau. Ở đây, do sử dụng thước có độ chia nhỏ nhất là 1mm nên ta có thể coi sai số dụng
cụ là 1mm. Sai số tuyệt đối lúc này sẽ được tính theo công thức:
L  L (L)  1,5 1  2,5(mm) dc
2. Sai số tương đối: L
+) Công thức: δ  L
Trong đó: ∆� là sai số tuyệt đối, � là giá trị trung bình đo được, � là sai số tương đối
+) Sai số tương đối đặc trưng cho độ chính xác của phép đo: phép đo có sai số tương đối lớn hơn,
thì độ chính xác của nó kém hơn và ngược lại.
3. Quy tắc xử lý sai số tuyệt đối và sai số tương đối
a/ Quy tắc 1: Làm tròn sao cho có tối đa hai chữ số có nghĩa:
+) Lỗi này rất nhiều bạn mắc phải. Lý do đơn giản là mọi người chưa hiểu được thế nào là chữ số có nghĩa.
Định nghĩa: chữ số có nghĩa là những chữ số (kể cả chữ số 0) tính từ trái sang phải kể từ chữ số khác không đầu tiên.
Ví dụ: Giả sử sai số tuyệt đối hoặc tương đối của một đại lượng A nào đó nhận một trong các giá trị sau:
0.023: 2 chữ số có nghĩa
0.00021: 2 chữ số có nghĩa
0.0230: 3 chữ số có nghĩa (mặc dù số thứ 3 bằng 0 nhưng đã viết vào kể từ sau chữ số khác 0 đầu
tiên nên phải tính) -> cần chỉnh sửa để loại bỏ bớt 1 đến 2 chữ số: 0.02 hoặc 0.023
1.23: 3 chữ số có nghĩa -> chỉnh làm tròn về 1.2
2.000: 4 chữ số có nghĩa -> chỉnh về 2.0 hoặc 2
Thầy Phạm Ngọc Lam 3 Trường
Downloaded by Nguyen Linh (vjt45@gmail.com)
Học online tại: https://mapstudy.edu.vn
b/ Quy tắc 2: Phần giảm bớt hoặc tăng thêm phải nhỏ hơn 1/10 giá trị gốc:
+) Quy tắc này đa phần mọi người đều không để ý và thường mặc định nếu lớn hơn hoặc bằng 5
thì làm tròn lên còn nhỏ hơn 5 thì làm tròn xuống. Nhìn chung là phần lớn kết quả áp dụng lập luận
trên đều không sai nhưng có một số trường hợp ngoại lệ nếu ta làm theo lập luận trên thì sẽ sai.
Ví dụ: Giả sử bạn thu được sai số tuyệt đối của một đại lượng A là 0.164. Quan sát đại lượng này
ta thấy có 3 chữ số có nghĩa -> sai qui tắc 1.
 Đối với trường hợp làm tròn thành 0.16 vì phần mất đi 0.004 <1/10.0,164 = 0.0164.
 Nếu chúng ta làm tròn thành 0.2 (nhìn thì có vẻ rất hợp lý vì đã đảm bảo quy tắc 1). Bây giờ
chúng ta hãy để ý phần thêm vào để thành 0.2 là 0.036 rõ ràng là lớn hơn 1/10 giá trị gốc là 0.0164 - sai qui tắc 2.
+) Tóm lại đối với sai số tuyệt đối của một đại lượng A trong ví dụ này ta chỉ được làm tròn tới 2 chữ số có nghĩa.
Chú ý: Sai số tương đối của hằng số thì không đóng góp vào sai số của của đại lượng đo, tóm lại cứ
thấy hằng số thì không cần để ý.
L  L (L)  L  (L) dc dc
c/ Quy tắc 3: Viết kết quả
+) Giá trị trung bình của đại lượng cần đo phải viết qui tròn đến chữ số có nghĩa cùng bậc thập phân
với chữ số có nghĩa cuối cùng của giá trị sai số tuyệt đối đã qui tròn => “Phẩy tương xứng – Mũ tương xứng”
• Phẩy tương xứng: sai số tuyệt đối lấy bao nhiêu số sau dấu phẩy thì giá trị trung bình cũng phải
lấy bấy nhiêu số sau dấu phẩy.
• Mũ tương xứng: nếu giá trị trung bình có dạng A×10n thì sai số tương đối cũng phải để ở dạng
B×10n. Không thể có chuyện bên này mũ n mà bên kia lại là mũ m
Chú ý: Phẩy tương xứng và mũ tương xứng phải thỏa mãn đồng thời vì đôi khi phẩy thì tương
xứng nhưng mũ không tương xứng -> kết quả sai.
Thầy Phạm Ngọc Lam Trường 4
Downloaded by Nguyen Linh (vjt45@gmail.com)
Học online tại: https://mapstudy.edu.vn
+) Ví dụ minh họa những lỗi liên quan tới qui tắc này mà các bạn thường gặp phải: Giá trị trung bình Sai số tuyệt đối CHỈNH SỬA GTTB  SSTĐ GTTB  SSTĐ 1482,5  10,6 1483  11 4,78.10−8  6,67.10−11 4,78XX.10−8  0,0067. 10−8 7,31.10−4  0,19.10−4  123434  1234 1234.102  12. 102 0,03243  0,0031 0,0324  0,0031 0,06421  0,00310 0,0642  0,0031
 Các bạn có thể chỉnh sửa theo cách khác miễn phải đúng các quy tắc đã nêu trên
4. Thiết lập công thức tính sai số
Ta cần thiết lập sai số của phép đo gián tiếp. Sai số của phép đo gián tiếp sẽ có sự đóng góp từ sai
số của các phép đo các đại lượng trung gian.
a/ Phương pháp 1: Vi phân riêng
Ưu điểm: đây là phương pháp thường dùng khi đại lượng F có dạng là một tổng hoặc hiệu của
các đại lượng đo trực tiếp x và y F F
Cơ sở lý thuyết: dựa vào công thức vi phân riêng phần: dF  dx 
dy . Ở đây ta chỉ xét hàm x y
đơn giản F = F(x,y), có những bài toán mà xuất hiện nhiều đại lượng thêm vào như z, g, h thì các
bạn cứ bổ sung thêm vào công thức trên thôi. Phương pháp này sẽ giúp ta tính sai số tuyệt đối
trước sai số tương đối
Các bước làm: F F
Bước 1: dF  dx  dy x y
Bước 2: d  Δ và thêm trị tuyệt đối vào các đạo hàm riêng phần (ở đây là F F và ) x y  
F  F x  F y x y
Thầy Phạm Ngọc Lam 5 Trường
Downloaded by Nguyen Linh (vjt45@gmail.com)
Học online tại: https://mapstudy.edu.vn F
Bước 3: Áp dụng mối liên hệ để tìm sai số tương đối   F
F chính là đạo hàm của hàm số F(x,y) theo x (chỉ cần coi các biến khác là hằng số và đạo hàm theo biến x x như bình thường)
b/ Phương pháp 2: Logarit hóa
Ưu điểm: đây là phương pháp thường dùng khi đại lượng F có dạng là một tích hoặc thương
của các đại lượng đo trực tiếp x và y  nếu có cả tổng (hiệu) – tích (thương) thì ta vẫn nên sử dụng phương pháp này.
Cơ sở lý thuyết: dựa vào quá trình ln hóa hai vế và vi phân toàn phần d(lnF) dF  tính sai số F
tương đối trước  sai số tuyệt đối Các bước làm:
Bước 1: ln F  ln F(x, y)
Bước 2: d(lnF)  dF  dlnF(x, y)   lnF(x, y)  lnF(x, y) dx  dy F x y
Bước 3: Rút gọn vế phải và góp các thành phần dx và dy lại  thu được dạng
dF  f(x, y)dx  g(x,y)dy F
Bước 4: thay d  ,F  F,x  x,y  y , lấy trị tuyệt đối của thành phần nhân với dx và dy  sai
số tương đối có dạng: dF  
 f (x, y) dx  g(x, y) dy  Sai số tuyệt đối F
Chú ý một số phép vi phân:
 d(x  y)  dx  dy
 d( f (x))  f '(x)dx
 d(uv)  udv  vdu u udv  vdu  d  v v2 f f  d( f (x, y))  dx  dy x y
 d(αf (x))  αd( f (x))
Thầy Phạm Ngọc Lam Trường 6
Downloaded by Nguyen Linh (vjt45@gmail.com)
Học online tại: https://mapstudy.edu.vn Chú ý:
- Sai số tuyệt đối và sai số tương đối luôn dương.
- Sai số tuyệt đối của một đại lượng cho trước phải cùng bậc và bằng 1 đơn vị. VD: thước L = 100
cm  sai số tuyệt đối 1 cm
- Sai số tuyệt đối và sai số tương đối không được quá 2 chữ số có nghĩa
- Hằng số không đóng góp vào sai số của đại lượng cần đo, không quan tâm đến hằng số khi thiết
lập công thức tính sai số của phép đo gián tiếp. Nếu công thức tính sai số tương đối hoặc tuyệt đối
mà lại thấy xuất hiện các đại lượng là hằng số thì có nghĩa là đã thiết lập sai. Ví dụ: a Xét hàm F 
 thương, hiệu  phương pháp 2 có lợi hơn (giả sử a, b >0, a – b > 0 vì ở đây ta a  b
quan tâm đến độ lớn của đại lượng F)
Bước 1: ln F  ln a  ln a  ln(a  b) a  b dF da d(a b  )
Bước 2: d(ln F)   d  F
lna  ln(a  b)  dlna  dln(a  b)   a a  b
Bước 3: d(lnF)  dF  da  da  db  b 1 da  db F
a a  b a  b a(a  b) a  b dF ba b
ba  ab Bước 4:      F
a(a  b) a  b a(a  b) 5. Sai số dụng cụ
+) Thước kẻ: sai số dụng cụ chính là độ chia nhỏ nhất, hoặc tùy thuộc vào độ chia mà ta có thể lấy
sai số đến ½; 1/5; 1/10 độ chia nhỏ nhất.
+) Banme, thước kẹp: sai số dụng cụ chính là độ chính xác.
+) Đồng hồ đo điện chỉ thị kim: (a)  .a dc max
• δ: cấp chính xác của vôn kế hoặc ampe kế (thường ghi trên mặt đồng hồ đo, ở góc dưới cùng bên
trái hoặc bên phải  giá trị thường gặp là 1.5%; 2%; 2.5% ).
• �max: thang đo lớn nhất (thang hiện đang sử dụng).
• ví dụ �max = 30A thì sai số dụng cụ sẽ bằng:
(a)  2.5% 30  0.75A dc
Thầy Phạm Ngọc Lam 7 Trường
Downloaded by Nguyen Linh (vjt45@gmail.com)
Học online tại: https://mapstudy.edu.vn
+) Hộp điện trở mẫu và điện dung mẫu: (a)  .a dc
• δ: cấp chính xác ứng với thang đo hiện thời (chú ý với hộp điện trở mẫu thì cấp chính xác thường là 0.2%)
• a: giá trị đo được (chú ý là không phải giá trị lớn nhất của thang đo  tức là nếu đo được giá trị
R bằng 10 ôm thì ΔR = 0,2%.10)
- Dụng cụ đo hiện số (cái này tính toán cũng hơi phức tạp một chút): (a)  .a  nα dc
+) Như vậy ta thấy có 4 đại lượng cần tìm để xác định sai số của đồng hồ đo hiện số:
δ: cấp chính xác của dụng cụ đo
n: phụ thuộc vào dụng cụ đo và thang đo (nhà sản xuất quy định)
a: giá trị hiển thị trên dụng cụ đo
α: độ phân giải. Các đồng hồ sử dụng trong thí nghiệm đều là loại 4 số (tức là 2000 digital). Với
thang đo 20V thì Umax là 19.99V, 200V thì Umax là 199.9V tương tự I cũng thế. Để tính độ phân
giải ta sẽ lấy thang đo lớn nhất chia cho 2000. U
α  max  19,99  0.01 2000 2000
(thực ra có thể lấy thẳng số thang đo chia cho 2000 vì cũng chả khác nhau là mấy).
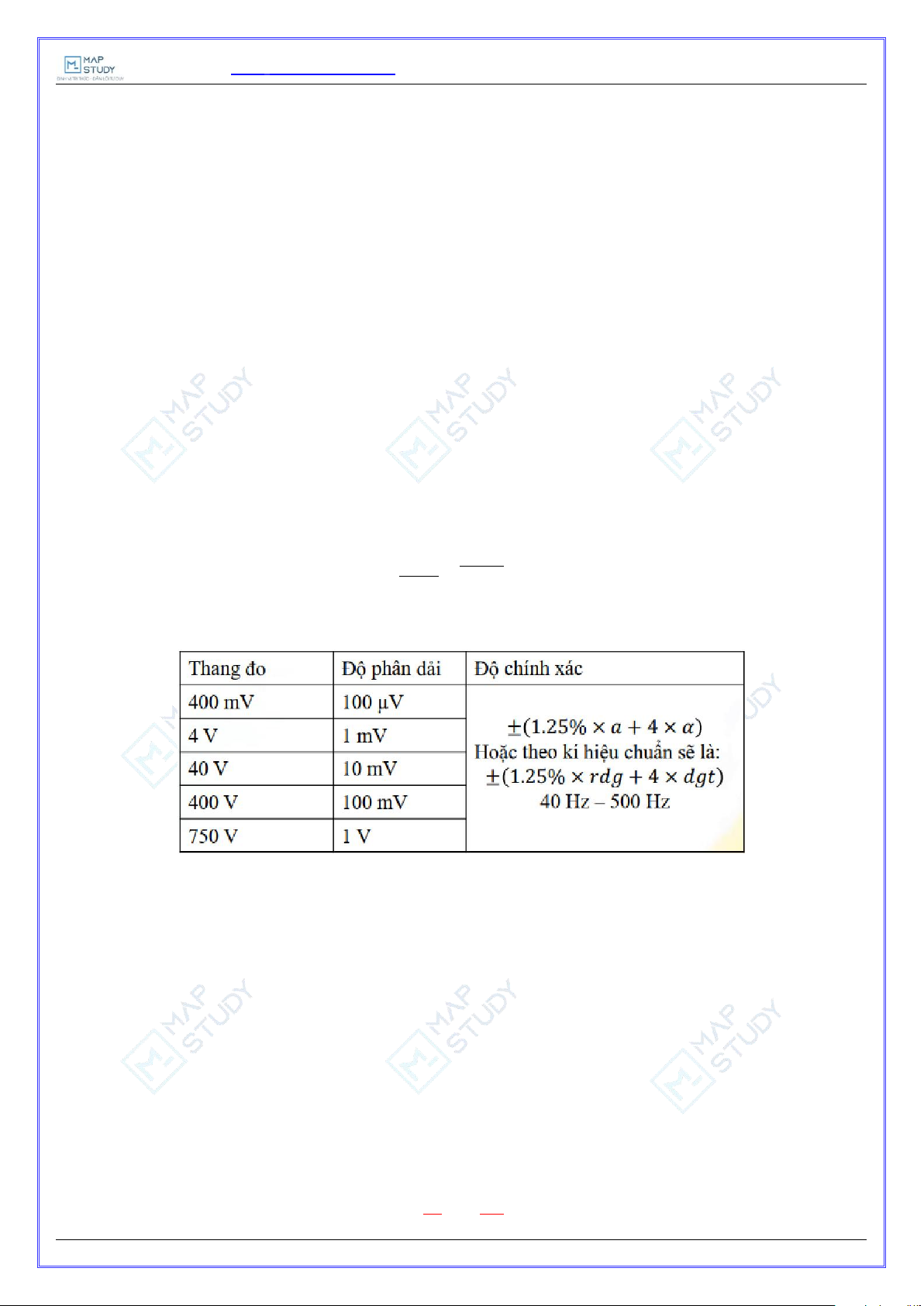
 Bảng trên chính là thông số kĩ thuật của đồng hồ ở chế độ đo điện áp xoay chiều (AC mode) đo
điện đa năng APPA 95 được cung cấp bởi nhà sản xuất. Kí hiệu rdg chính là giá trị hiển thị, dgt là
độ phân giải. Chúng ta để ý thấy có thông tin về 40-500 Hz, dải tần này có ý nghĩa là tần số điện áp
nằm trong dải này thì sẽ cho độ chính xác tính bằng công thức trên. Nếu nó vượt ngưỡng thì bó tay.
Do đó, khi đo đạc thì phải để ý tới giới hạn của dụng cụ đo. Ví dụ nếu ta để ở thang đo 4V, giá trị
đo được trên màn hình là: 3.458 V, độ phân giải ở thang này là 1 mV = 0.001 V. Khi đó độ chính xác
của phép đo này là: (1.25% 3.458  40.001)  0.047 HẾT
Thầy Phạm Ngọc Lam Trường 8
Downloaded by Nguyen Linh (vjt45@gmail.com)
Document Outline

• I.PHÂN LOẠI SAI SỐ
• 2.Sai số ngẫu nhiên
• 3.Sai số dụng cụ:
• 4.Sai số thô đại
• II.PHÉP ĐO TRỰC TIẾP – GIÁN TIẾP
• 2.Phép đo gián tiếp:
• III.SAI SỐ CÁC PHÉP ĐO
• 2.Sai số tương đối:
• 3.Quy tắc xử lý sai số tuyệt đối và sai số tương đối
• c/ Quy tắc 3: Viết kết quả
• 4.Thiết lập công thức tính sai số
• a/ Phương pháp 1: Vi phân riêng
• b/ Phương pháp 2: Logarit hóa
• Các bước làm:
• Chú ý một số phép vi phân:
• Ví dụ:
• 5.Sai số dụng cụ