Thời giá của tiền tệ và mô hình chiết khấu dòng tiền ( time value of money ) - Tài liệu tham khảo | Đại học Hoa Sen

Thời giá của tiền tệ và mô hình chiết khấu dòng tiền
( time value of money )
 Tình huống : Tiền giống chiều cao em bé : giá trị khác nhau ở nhũng thời gian khác nhau.
 Nếu muốn so sánh, tính toán tiền cần quy về cùng 1 thời điểm
 Một số khái niệm chủ yếu :
- giá trị hiện tại ( present value ) -
- giá trị tương lai ( future value ) - - lãi suất ( lãi đơn / –
- số kỳ tính lãi tính từ thời điểm mình đứng – n. Ví dụ : bạn đang đứng ở năm 0, muốn tính giá trị tiền từ năm
6 về năm 0 thì n = 6, nhưng nếu đứng ở năm 2 , muốn tính giá trị tiền từ năm 6 về năm 2 thì n = 6-2 =4
 Công thức lượng tiền đơn :
- Lãi đơn- simple interest ( chỉ được dùng khi đề nói tính lãi đơn ) : Tính lãi chỉ trên lượng tiền
gốc -> Tiền lãi của số tiền X không đổi qua thời gian. Ví dụ : gửi 100 tr vào ngân hàng với lãi
10%, số tiền lãi năm 1 là 10tr ( 10% của 100 tr ), lãi năm 2 vẫn là 10 triệu,năm 3 vẫn là 10 tr FV PV  1 ( nr  )
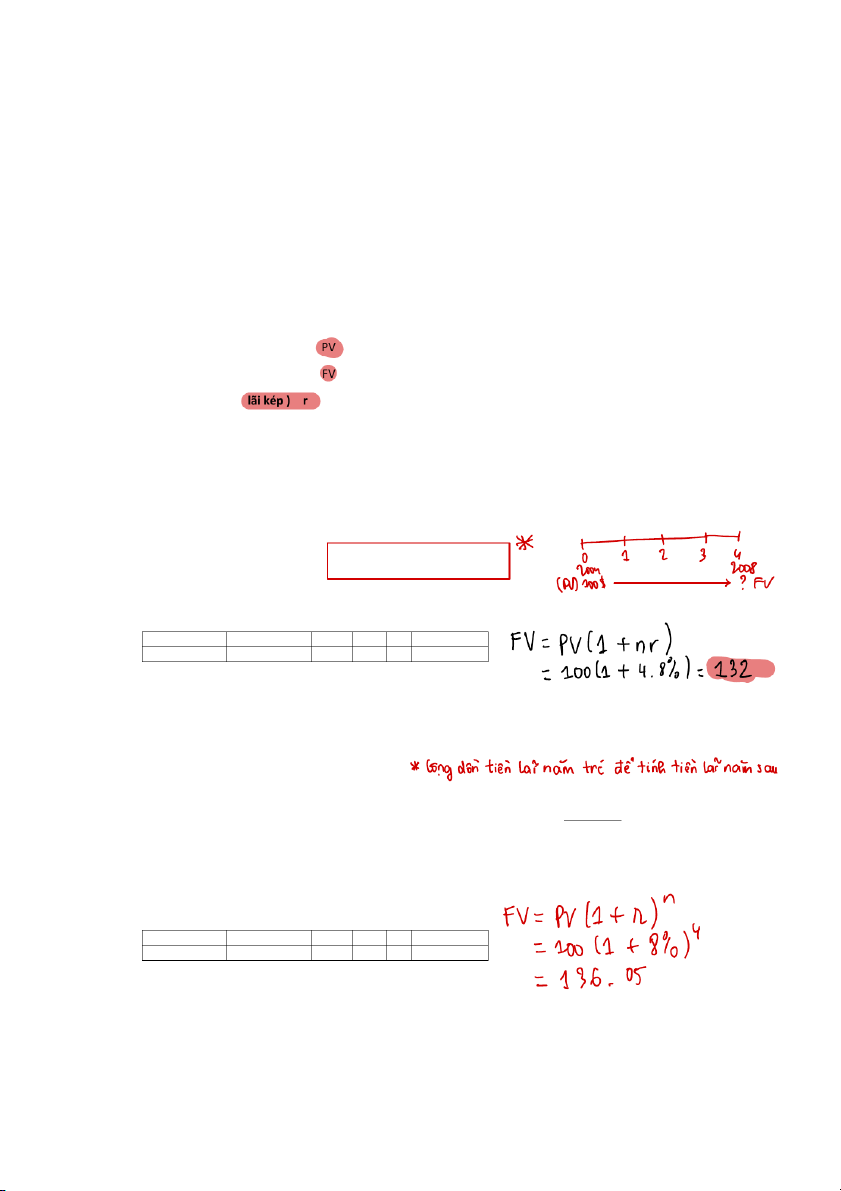
Bài tập mẫu : Gửi tiết kiệm 100 $ vào năm 2004 nhận lãi mỗi cuối năm , hỏi năm 2008 tài khoản tiết
kiệm có bao nhiêu tiền biết tài khoản được tính lãi đơn 8%/ năm ? Năm 0 1 2 3 4 Số tiền 100 ? ( Answer : 132 $ )
- Lãi kép-compund interest ( ở môn này đề mặc định là lãi kép ) : Lãi kỳ sau tính trên tiền
gốc + lãi kỳ trước gốc -
> Tiền lãi của số tiền X thay đổi theo thời gian. Ví dụ : gửi 100 tr vào
ngân hàng với lãi 10%, số tiền lãi năm 1 là 10tr ( 10% của 100 tr ), lãi năm 2 là 11 tr ( 10%
của 110 tr – 100 tr tiền gốc +10 tr lãi năm 1 ) ,năm 3 là 12,1 tr ( 10% của 121 tr – 100 tr tiền
gốc +10 tr lãi năm 1 + 11 tr lãi năm 2 ) - n FV PV r  1 (  ) FV PV hay  n r 1 (  )
Bài tập mẫu : Gửi tiết kiệm 100 $ vào năm 2004 nhận lãi mỗi cuối năm , hỏi năm 2008 tài khoản tiết
kiệm có bao nhiêu tiền biết tài khoản được tính lãi kép 8%/ năm ? Năm 0 1 2 3 4 Số tiền 100 ? ( Answer : 136,05 $ )
Bài tập mẫu : Năm 2000 ông A phải gửi vào tài khoản tiết kiệm bao nhiêu để sau 4 năm ông có 100$
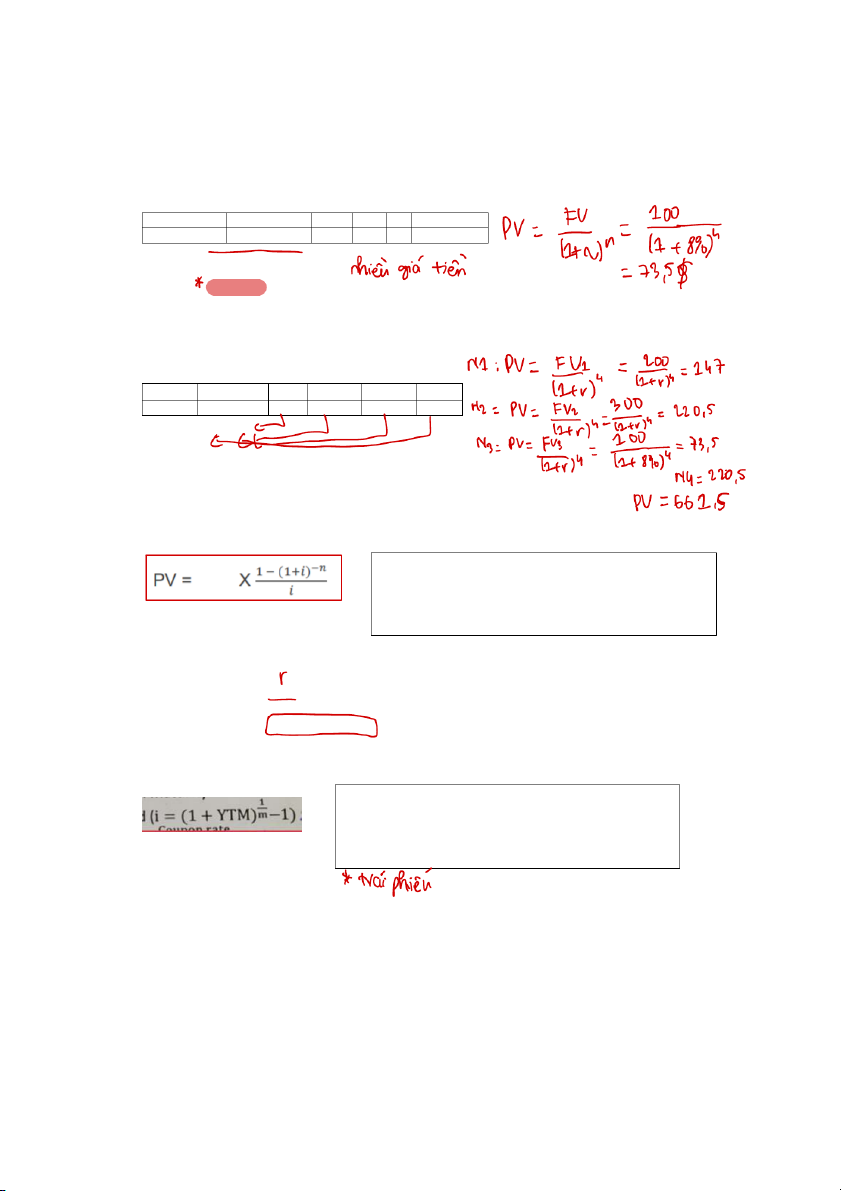
trong tài khoản tiết kiệm để đi du lịch ? Biết rằng tài khoản được tính lãi kép 8%/ năm ? Năm 0 1 2 3 4 Số tiền ? 100 ( Answer : 96,86 $ )
 Chuỗi dòng tiền – cashflow :
- Không đều ( số tiền nhận được ở mỗi kỳ không giống nhau ) : Ghép nhiều lần công thức
lượng tiền đơn - lãi kép
Bài tập mẫu : Bạn đang lập 1 dự án đầu tư với thông tin như sau : Năm 1 bạn sẽ n ậ h n được 200 $, năm 2
nhận được 300$, năm 3 nhận được 100$, năm 4 nhận được 300$. Tính giá trị những dòng tiền của dự án ở năm 0. Năm 0 1 2 3 4 Số tiền ? 200 300 100 300
- Đều ( số tiền nhận được ở mỗi kỳ không giống nhau ) :
- chuỗi dòng tiền đều vô hạn ( perpetuties ) - ( gần như ko có thật  ) - chỉ tính được PV PV = CF/r
Với : CF : số tiền nhận được mỗi kỳ
- chuỗi dòng tiền đều hữu hạn ( annuities ) : (phát sinh cuối kỳ - chỉ care đầu cuối kỳ nếu muốn thi trên 8 ) Với : CF
CF : số tiền nhận được mỗi kỳ
.i : lãi suất ( ý nghĩa giống r, khác ký hiệu )
**Lưu ý : thời gian của lãi suất và khoảng cách thời gian giữa các kỳ ( thời gian trả lãi,ghép lãi ) phải
giống nhau thì ghép vào công thức tính mới đúng, ví dụ như gửi ngân hàng trả lãi mỗi 6 tháng thì lãi suất
trong công thức phải là lãi suất mỗi 6 tháng, không được dùng lãi suất 1 năm.
Vậy nếu đề chỉ cho lãi 1 năm mà không cho lãi 6 tháng thì sao ? Thì dùng công thức này :
Với : .i : lãi suất theo thời gian trả lãi ( 6 tháng ) YTM : lãi suất 1 năm
m : số kỳ nhận tiền trong năm =12/số tháng nhận tiền
**Cách làm tổng quát :
1. Vẽ ra sơ đồ dòng tiền từ đề bài
2. Tìm công thức tương ứng để giải, nhớ : tính giá trị ở những năm đầu là PV, giá trị ở những năm cuối là FV
Bài tập : Viết bài giải hoàn chỉnh từ sơ đồ trên :
Định giá Trái phiếu :
Trái phiếu ở đây hiểu là 1 hợp đồng vay nợ, khi bạn mua 1 trái phiếu bạn như là ngân hàng cho
họ ( người phát hành trái phiếu ) vay tiền. và sẽ có 2 cách để họ thuyết phục bạn cho vay : Ví dụ ở đây cty/ nhà nướ
ếu 10 đồng ( nghĩa là họ c phát hành 1 trái phi
hỏi vay bạn 10 đồng ). Họ sẽ
có 2 cách “deal” khoảng nợ này với nhà đầu tư :
1/ Bán trái phiếu ( khoảng nợ ) này cho nhà đầu tư với giá 10 đồng trả lãi đều đặn trong 1
khoảng thời gian nhất định rồi trả khoản gốc 10 đồng vào 1 ngày nào đó trong tương lai ( ngày đáo hạn ). 2/ Hoặc h s
ọ ẽ bán khoảng vay đó v ng ) và h
ới giá 8 đồng ( mượn 8 đồ ứa trả ng trong 10 đồ
tương lai mà không trả thêm lãi
 Công thức : 1. ếu có hưở ỗi năm 1 lầ
Trái phiếu có kỳ hạn được hưởng lãi (nonzero coupon bond) là loại trái phiếu có xác định
thời hạn đáo hạn và ng ờ ư i mua được hưởn
g lãi suất qua từng thời kỳ nhất định.
Nhà đầu tư được hưởng lãi định kỳ, thường là hàng năm, theo lãi suất công bố (coupon
rate) trên mệnh giá trái phiếu và được hoàn lại vốn gốc bằng mệnh giá khi trái phiếu đáo hạn. English vocab in exercise : I: coupon .i: coupon rate
C : Face value ( khi đề không nói tới C, mặc định hiểu C là 1000 $ )
.n : coupon for n year ( n nghĩa là số kỳ đ ợ ư c hưởng lãi )
.rd : expected return, tất cả các loại lãi suất ko có tên là coupon rate
Bài tập mẫu :
Ví dụ 1: Giả sử một trái phiếu có mệnh giá là 1000 , được hưởng lãi suất là 10% kỳ hạn c a
ủ trái phiếu là
9 năm, nhà đầu tư đòi hỏi lãi suất là 12%/ năm. Giá của trái phiếu này khi mới phát hành, nhà đầu tư sẽ mua với giá nào?
Ví dụ 2: Trái phiếu trên đã thực hiện được 3 năm và nhà đầu tư đòi hỏi lãi suất là 12%/ năm. Giá của trái
phiếu này nhà đầu tư sẽ mua với giá nào?
1/ US treasury bond has a face value $1,000; 9% coupon rate and 25 years to maturity. Please
compute the bond price with YTM/interest rate = 10%/ year
2/ Us treasury bond has a 10%coupon rate and a $1,000 face value. Interest is paid semi-annually
and the bond has 20 years to maturity. If investors require 1 12% yield, what is the bond value?
Giải mẫu : Nhiệm vụ : giải V
í dụ 2 : ( Đáp án : 917,77 ) hoặc bài 1,2 : 2. ế hưở ỗ : lưu ý r,I,n ải đượ ớ ẩ
tháng, không được dùng giá trị của chuẩn 1 năm :
a. Tính 6 tháng từ 1 năm ( nếu cần ) :
( Với rd2 là lãi suất mỗi 6 tháng, rd là lãi suất mỗi 1 năm )
Công thức tính r 6 tháng :
Công thức tính I 6 tháng : I 6 tháng = I 1 năm /2 = C*i/2
Công thức tính n 6 tháng : lấy số năm được nhận lãi nhân đôi
b. Tính P bằng công thức như ở m c
ụ 3.1 với số liệu 6 tháng :
Ví dụ : Kho bạc phát hành trái phiếu có mệnh giá 10 triệu đồng, kỳ hạn 5 năm, lãi suất 10%, nửa
năm trả lãi 1 lần (paid semi-annual) và nhà đầu tư đòi hỏi tỷ suất lợi nhuận 12,36% khi mua trái
phiếu này. Giá trái phiếu sẽ là: 3. ếu không hưở Ở l ạ
o i trái phiếu này không có lãi nên không có I , công thức sẽ thành : Po = C x (1 + 𝑟𝑑)-n
Ví dụ: Giả sửa nhà nước phát hành trái phiếu không trả lãi có thời hạn 3 năm và mệnh giá là
100.000 đồng. Nếu lãi suất đòi hỏi của nhà đầu tư là 12%, giá bán của trái phiếu này là bao nhiêu? Định giá cổ phiếu
1. Định giá cổ phiếu ưu đãi (preferrence stock )
Cổ phiếu ưu đãi là loại cổ phiếu mà công ty phát hành cam kết trả tỷ lệ cổ tức cố định hàng năm
tính trên mệnh giá cổ phiếu và không có tuyên bố ngày đáo hạn.( Ngày không được nhận lãi nữa ) 𝐼𝑝 Công thức : Po = 𝑟𝑝
Trong đó: Ip: cổ tức hàng năm của cổ ph ế
i u ưu đãi, rp: lãi suất kỳ vọng của nhà đầu tư
Ví dụ: Giả sử công ty ABC phát hành cổ phiếu ưu đãi mệnh giá là 100.000 đồng, trả cổ tức là 9%
và nhà đầu tư muốn lãi suất đầu tư là 14%, giá cổ phiếu là:
Giải : Po = 100.000 x 9%/ 0.14 = 64.286 đồng
2. ĐỊNH GIÁ CỔ PHIẾU THƯỜNG : Trong đó:
A/ MÔ HÌNH CHIẾT KHẤU CỔ TỨC :
 Div: là cổ tức được chia ( dividend )
 r: là lợi nhuận mong đợi của nhà đầu tư,required return
 PH : giá cổ phiếu mà nhà đầu tư dự kiến bán lại vào thời điểm H
Ví dụ: Ông A mua cổ phiếu của công ty ABC, dự kiến cổ tức trong năm tới sẽ được chia là 1.500 đồng/ cổ
phiếu và giá của cổ phiếu vào thời điểm chia cổ tức (cuối năm) là 19.000 đồng/ cổ phiếu. Hỏi ông A có
thể mua cổ phiếu trên giá bao nhiêu? Biết rằng lãi suất kỳ vọng ông A mong đợi là 14%
Giải : Po = 1.500 + 19.000 × (1 + 14%) −1= 17.983 đồng
**Các trường hợp đặc biệt ( định gia qua nhiều năm ) : ổ ức đượ ổn đị ức là D1 = D2 =… = Dn = D
Đây là trường hợp đặc biệt, cách tính tương tự như đối với cổ ph ế i u ưu đãi: Po = D1/ r ốc độ tăng trưở ổ ức không đổ ỷ ệ
R = r : lợi nhuận mong đợi của nhà đầu tư,required return
.g : tỷ lệ tăng trưởng, growth rate
D1 : dividend, cổ tức được chia ở năm 1
**Lưu ý : D1 là cổ tức được chia ở thời điểm n = 1 ( chia ở tương lai : năm tới, sắp chia…. ), I0 l à cổ tức đã
được chia trong quá khứ
Ví dụ 1: Công ty XYZ vừa chia cổ tức là 20.000 đồng/ cổ phiếu. Cổ tức này được kỳ vọng tăng 5% trong
tương lai. Hỏi giá cổ phiếu là bao nhiêu nếu nhà đầu tư đòi hỏi lãi suất là 15%?
Ví dụ 2: Bà Lan đang xem xét việc mua một cửa hàng tạp hóa để kinh doanh. Doanh thu của cửa hàng
ước tính là 50 triệu đồng ỗ
m i năm. Tỷ suất lợi nhuận sau thuế trên doanh thu là 14% và bà lan mong
muốn rằng tỷ suất sinh lời l i bà Lan s à 16%/ năm. Hỏ
ẽ chấp nhận mua cửa hàng này với giá bao nhiêu? Giải ví dụ 2 :
Lợi nhuận sau thuế mỗi năm của cửa hàng: 50.000.000 x 14% = 7.000.000 đồng
■ Áp dụng mô hình tăng trưởng bằng 0 (tăng trưởng ổn định) ta có:
Po = = 7.000.000/ 16% = 43.750.000 đồng
■ Như vậy bà Lan chỉ có thể mua cửa hàng này với giá tối đa là 43,75 triệu đồng. Nếu bà Lan mua được
với giá thấp hơn thì vốn đầu tư sẽ sinh lợi trên 16%/ năm và ngược lại thì mức sinh lợi trên vốn đầu tư sẽ thấp hơn 16%/ năm. ốc độ tăng trưở ổ ức thay đổ
■ Giả sử công ty chia cổ tức theo hai giai đoạn tăng trưởng, ta có: Với : Dt = Dt-1 * ( 1+gt ) D : dividend, cổ tức
.g : growth rate, tốc độ tăng trưởng
Ví dụ: Giả sử một cổ phiếu trả cổ tức hiện tại Io = 200, tốc độ tăng trưởng cổ tức trong 5 năm tới là 10%
và 6% cho những năm tiếp theo đó, ngoài ra nhà đầu tư đòi hỏi lợi suất đầu tư là 14% ■ ă ưở ổ ế ậ ổ ế
■ Nếu một công ty chọn việc trả cổ tức thấp hơn, và tái đầu tư các khoản tiền, giá cổ phiếu có thể tăng
do cổ tức trong tương lai có thể cao hơn.
■ Lợi nhuận sau thuế gồm 2 phần:
– Phần thu nhập sau khi chi trả cổ tức
–Phần lợi nhuận giữ lại của công ty ( Plowback Ratio ) = 1-
Tốc độ tăng trưởng có thể được bắt nguồn từ việc áp dụng trở lại trên vốn chủ sở hữu tỷ lệ phần trăm
của lợi nhuận tái đầu tư vào hoạt động nên ta có công thức :
Ví dụ 1: Công ty chúng tôi dự báo sẽ trả cổ tức 5,00$ trong năm tới, đại diện cho 100% thu nhập của
mình. Điều này sẽ cung cấp cho các nhà đầu tư với 12% lợi nhuận kỳ vọng. DN quyết định để giữ lại 40%
lợi nhuận. ROE = 20%. Giá trị của các cổ phiếu trước và sau khi quyết định giữ lại (plowback) là gì ? GIải :
RISK & RETURN – LỢI NHUẬN VÀ RỦI RO : ** Phần trọng tâm : *
: Tính lợi nhuận kỳ vọng / lợi nhuận trung bình. Phương sai, độ lệch chuẩn của cổ phiếu/ trái phiếu
Calculate expected return, Variance, Covariance, standard deviation of stock/ bond
Cách làm : ( Cụ thể : Trang 2-4)
Tổng quát : Tính theo thứ tự :
1. lợi nhuận kỳ vọng / lợi nhuận trung bình 2. Square deviation 3. Phương sai 4. Độ lệch chuẩn
ạng 1.2 ( ít được hỏi hơn ) : Tính hệ số b ế
i n đổi ( coefficient of variation ), hiệp phương sai,
***Dạng 2 : Tính các thông số liên quan đến danh mục đầu tư ( portfolio ) như : a) lợi nhuận kỳ vọn ,
g tỷ suất sinh lời trong mỗi tình huốn , g Beta :
b) Variance, standard deviation :
Dạng 3 : Các vấn đề xung quanh công thức CAPM
Bài tập mẫu Dạng 1 : ( từ slide bài giảng, chú thích tiếng việt ở dưới )
Calculate expected return, Variance, Covariance, standard deviation of stock & bond below
Rate of return : tỷ suất lợi nhuận / tỷ suất
sinh lời trong mỗi scenario ( ký hiệu : r )
Scenario : Tình trạng nền kinh tế Probability : Xác suất
Stock/ bond : Cổ phiếu/ trái phiếu
Recession : suy thoái >< boom : Tăng trưởng
1. Lợi nhuận kỳ vọng / trung bình ( expected return ) - Công thức chung :
Tính cho cổ phiếu / trái phiếu nào thì lấy tất cả
tỷ suất lợi nhuận*xác suất của các scenario của nó cộng lại
-Cách ký hiệu : 2 trường hợp :
Đề cho bond và stock : E(rB )& E(rS)
Đề cho 2 stock A&B : E(rA ) & E(rB )
** Với trường hợp cho lợi nhuận qua các năm
của cổ phiếu, trái phiếu, có thể hiểu mỗi năm là
1 scenario với xác suất mỗi năm như nhau = 1/
tổng số năm đề cho lợi nhuận
Áp dụng : Tính lợi nhuận cho bond : ( kết quả ra 7% Là đúng hen ) E(rB ) =