Thuật toán tìm đường đi ngắn nhất Môn Công nghệ thông tin | Trường Cao đẳng công thương Việt Nam

lOMoAR cPSD| 58675420
Chương 5. Đường đi ngắn nhất trên đồ thị  Thuật toán Dijkstra:
- Tìm đường đi ngắn nhất từ đỉnh s đến các đỉnh còn lại trong đồ thị.
- Áp dụng cho đồ thị có trọng số không âm.
- Độ phức tạp là O(n2)
 Thuật toán Ford-Bellman:
- Tìm đường đi ngắn nhất từ đỉnh s đến các đỉnh còn lại của đồ thị.
- Áp dụng được cho đồ thị có trọng số không âm, hoặc có cả trọng số âm.
- Độ phức tạp là O(n3)  Thuật toán Floyd
- Tìm đường đi ngắn nhất giữa tất cả các cặp đỉnh trong đồ thị. - Độ phức tạp là
 Cho đồ thị vô O(n4)h
ướng, các trọng số không âm. Thuật toán nào, được sử
dụng để tìm đường đi ngắn nhất từ đỉnh s đến tất cả các đỉnh còn lại?
Thuật toán Ford – Bellman hoặc Thuật toán Dijkstra đều được
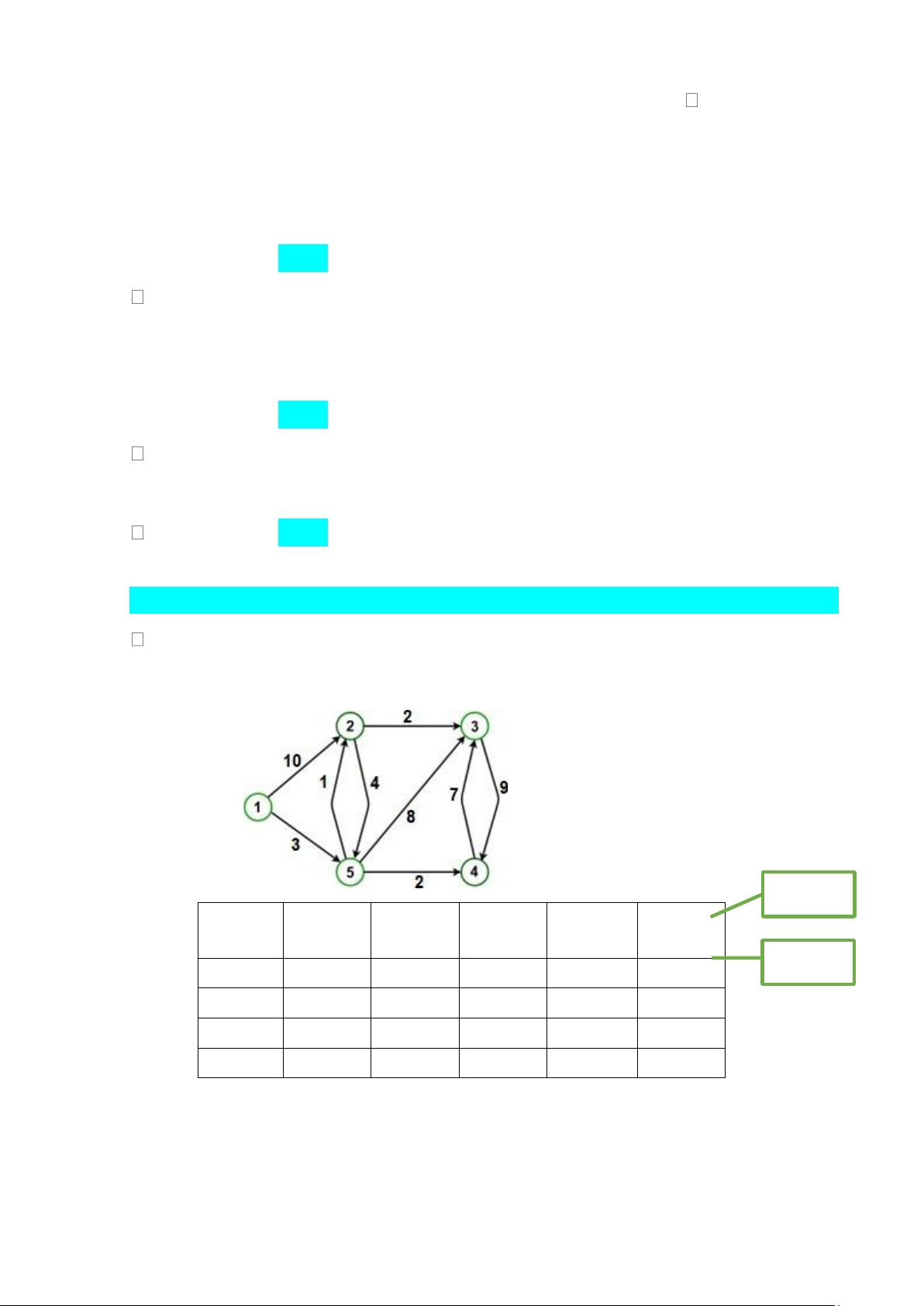
 Áp dụng thuật toán Dijkstra, tìm đường đi ngắn nhất từ đỉnh a đến tất cả các
đỉnh còn lại của đồ thị G dưới đây. Hãy điền vào chỗ dấu chấm hỏi của bảng H bằng đáp án đúng? Dòng 1 T Đỉnh 1 Đỉnh 2 Đỉnh 3 Đỉnh 4 Đỉnh 5 d[1], Truoc[1] d[2],
d[3], Truoc[3] d[4], Truoc[4] d[5], Truoc[5] Truoc[2] Dòng 2 ? ? ? ? ?
A. (0,1)* , (10,1) , (∞,1) , (∞,1) , (3,1) 1
B. (0,1)* , (4,5), (11,5), (5,5), (3,1)* lOMoAR cPSD| 58675420
C. (0,1)* , (4,5)* , (6,2) , (5,5) , (3,1)*
D. (0,1)* , (4,5)*, (6, 2), (5,5)* , (3,1)*
Giải: Nên chạy thuật toán để tìm đáp án đúng là B Lưu ý:
- Dòng 2 là dòng khởi tạo, có 1 dấu * : (0,1)* , (10,1) , (∞,1) , (∞,1) , (3,1) - Dòng 3 có 2 dấu *
- Tùy theo câu hỏi, nó sẽ yêu cầu điền dòng nào: dòng 2 hoặc 3 hoặc 4. Nếu
điềndòng 2 thì dễ. Còn dòng 3, 4, thì phải chạy thuật toán nên hơi căng.
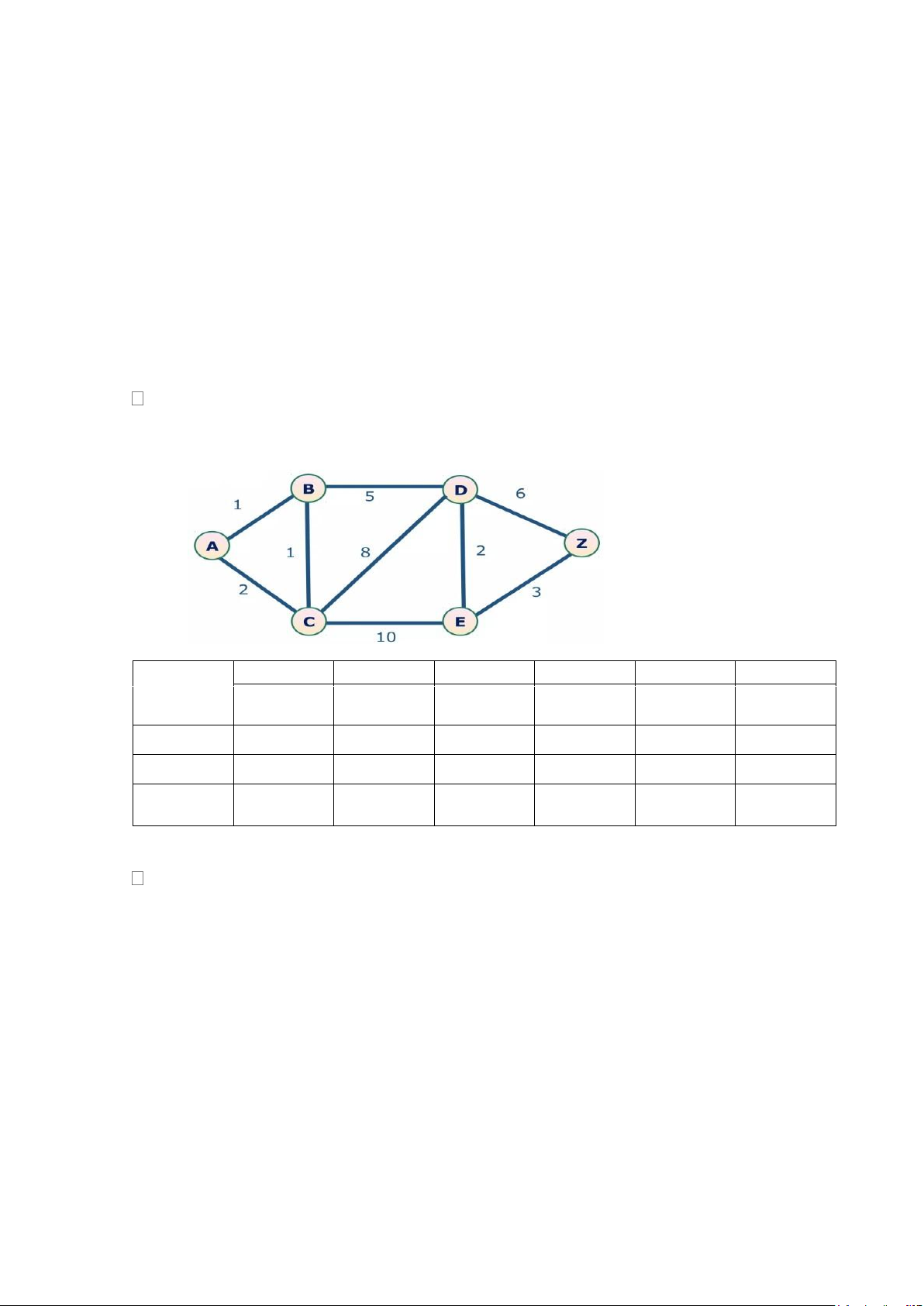
 Áp dụng thuật toán Dijkstra, tìm đường đi ngắn nhất từ đỉnh a đến tất cả các
đỉnh còn lại của đồ thị G dưới đây. Hãy điền vào chỗ dấu chấm hỏi của bảng H bằng đáp án đúng? Đỉnh a Đỉnh b Đỉnh c Đỉnh d Đỉnh e Đỉnh z T
(d[a], Truoc[a]) (d[b], Truoc[b] )(d[c], Truoc[c])
(d[d], (d[e], Truoc[e]) (d[z], Truoc[z]) Truoc[d]) ? ? ? ? ? ? Bảng H
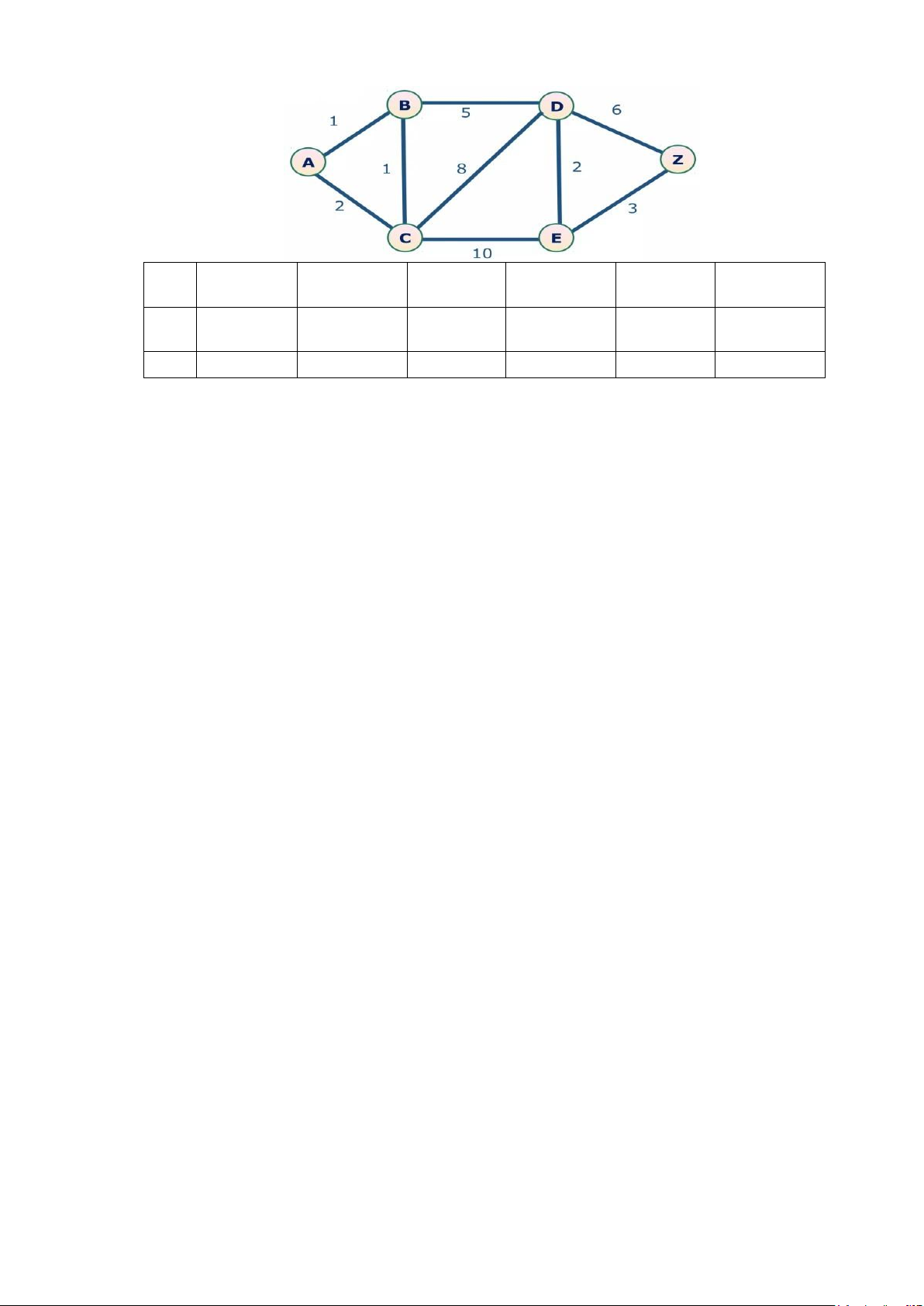
 Áp dụng thuật toán Ford - Bellman, tìm đường đi ngắn nhất từ đỉnh a đến tất cả
các đỉnh còn lại của đồ thị G như hình dưới đây. Hãy điền vào chỗ dấu chấm hỏi
của bảng H bằng đáp án đúng? 2 lOMoAR cPSD| 58675420 Bước Đỉnh a Đỉnh b Đỉnh c Đỉnh d Đỉnh e Đỉnh z
k (d[a], Truoc[a]) (d[b], Truoc[b]) (d[c], Truoc[c]) (d[d], Truoc[d]) (d[e], Truoc[e]) (d[z], Truoc[z]) Khởi tạo 1 ? ? ? ? ? ? Bảng H
Lưu ý: Nên chạy thuật toán để tìm đáp án (xem lại bài học) 3