








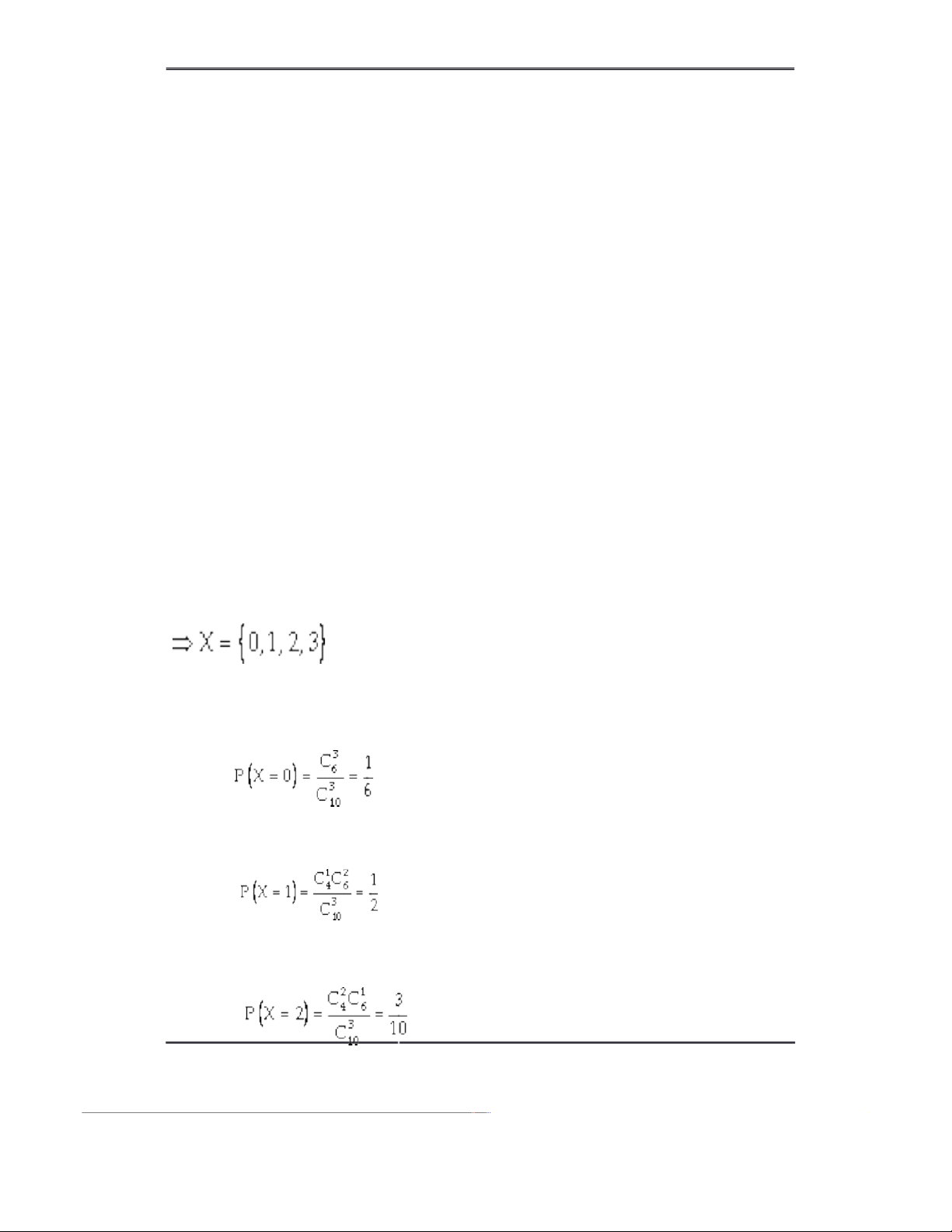




Preview text:
Bài Tiểu luận Lý thuyết xác suất – Thống kê toán – Nhóm 2 MỤC LỤC
LỜI MỞ ĐẦU ....................................................................................................... 2
PHẦN I: CƠ SỞ LÝ THUYẾT ........................................................................... 3
I, Khái quát chung về biến ngẫu nhiên ................................................................ 3
1. Khái niệm về biến ngẫu nhiên ............................................................................ 3
2. Phân loại ............................................................................................................. 4
II, Quy luật phân phối xác suất của biến ngẫu nhiên ......................................... 5
1. Bảng phân phối xác suất ..................................................................................... 5
2. Hàm mật độ xác suất ........................................................................................... 7
3. Đại lượng đặc trưng của biến ngẫu nhiên ............................................................ 8
PHẦN 2: BÀI TẬP VẬN DỤNG .......................................................................... 10
1, Ví dụ về biến ngẫu nhiên rời rạc ......................................................................... 10
2, Ví dụ về hàm mật độ xác suất ............................................................................. 11
3, Ví dụ về đại lượng đặc trưng của biến ngẫu nhiên .............................................. 12
LỜI KẾT ................................................................................................................ 14 Trang 1
Bài Tiểu luận Lý thuyết xác suất – Thống kê toán – Nhóm 2 LỜI MỞ ĐẦU
Trong chương trình đào tạo ngành ở hầu hết các trường Đại học, Cao đẳng, Trung
tâm GD; môn “Xác suất – Thống kê” thường có khối lượng 2 – 3 tín chỉ, thuộc khối
kiến thức giáo dục đại cương. Đây là môn học có lịch sử phát triển lâu đời, và là bộ môn
học nghiên cứu các hiện tượng ngẫu nhiên. Đặc biệt bộ môn này còn trang bị cho sinh viên
chúng ta một số vấn đề cơ sở của biến ngẫu nhiên để từ đó chúng ta có thể tiếp cận vào
việc nghiên cứu lý thuyết vận dụng vào nghiên cứu phương pháp thu thập xử lý thông tin
và làm bài tập, nhằm đưa ra những kết luận cần thiết.
Nhận biết được những ưu điểm của bộ môn “lý thuyết xác suất thống kê” để có thể am
hiểu và nhận thức ngày càng cao hơn về những ưu điểm đó. Qua hệ thống lý thuyết cùng
một số bài tập ví dụ thực tiễn, nhóm chúng tôi đã tiến hành nghiên cứu và phân tích sâu
hơn về đề tài: “Quy luật phân phối xác suất của biến ngẫu nhiên và bài tập vận dụng”
thông qua bộ môn “lý thuyết xác suất thống kê” nhằm tìm hiểu sâu hơn về bộ môn này.
Quá trình thực hiện đề tài được hoàn thành trong thời gian có hạn và quy mô thông tin
nhỏ, chủ yếu dựa vào sách giáo trình và bài tập “ Lý thuyết xác suất- thống kê toán”; vì
vậy, không thể tránh khỏi những sai sót, thiếu ví dụ và bài tập thực tiễn. Mong các bạn đọc
bỏ qua và góp ý cho nhóm chúng tôi để hoàn thiện bài tiểu luận này hơn nữa. Xin chân
thành cảm ơn giảng viên hướng dẫn Ths. Lê Thị Thanh Hoa đã giúp đỡ nhóm tôi hoàn
thành bài tiểu luận này! Trang 2
Bài Tiểu luận Lý thuyết xác suất – Thống kê toán – Nhóm 2
PHẦN I: CƠ SỞ LÝ THUYẾT
I, Khái quát chung về biến ngẫu nhiên
Khi tiến hành một phép thử ngẫu nhiên, các kết quả của phép thử thường là các đặc tính
định tính. Tuy nhiên trong nhiều phép thử mỗi một kết quả của phép thử thường được gán
tương ứng với một giá trị định lượng nào đó.
Chẳng hạn khi chơi các trò chơi ăn tiền, mỗi kết quả của một lần chơi được gán tương
ứng với một số tiền (đặc tính định lượng) mà người chơi được hay mất hoặc khi nhắm bắn
một phát đạn nào đó vào bia, mỗi kết quả của việc bắn tương ứng với điểm số (đặc tính
định lượng) mà xạ thủ đạt được. 1. Khái niệm
- Một biến cố được gọi là biến ngẫu nhiên nếu trong một kết quả của phép thử nó nhận
được một trong các giá trị có thể có của nó với các xác suất tương ứng.
- Ta thường dùng các chữ cái in hoa X, Y, Z... để chỉ các biến ngẫu nhiên và các chữ cái
thường x, y, z... hoặc xi, yi, ... để chỉ các giá trị cụ thể mà biến ngẫu nhiên đó nhận • Ví dụ 1
Gieo con xúc sắc xuống mặt bàn phẳng, đó là “phép thử”
Gọi X là số chấm xuất hiện.
Xuất hiện mặt 1 chấm ( X=1)
Xuất hiện mặt 4 chấm (X=4)
Xuất hiện mặt 6 chấm (X=6)
Vậy tập hợp gồm tất cả các giá trị có thể có của X là: {1; 2;...; 6} Trang 3
Bài Tiểu luận Lý thuyết xác suất – Thống kê toán – Nhóm 2 • Ví dụ 2
Với các biến cố về số mặt sấp khi gieo hai đồng xu, gọi X là số chấm khi gieo hai đồng xu Khi đó:
+ X là biến số có thể nhận các giá trị 0; 1; 2
+ Sau khi gieo hai đồng xu thì X nhận đúng một trong ba giá trị trên
Do đó X là biến ngẫu nhiên, X ={0; 1; 2}
2. Phân loại biến ngẫu nhiên
Dựa vào miền giá trị của biến ngẫu nhiên mà người ta phân thành hai loại chính đó là:
biến ngẫu nhiên rời rạc và biến ngẫu nhiên liên tục.
2.1. Biến ngẫu nhiên rời rạc a, Khái niệm
- Biến ngẫu nhiên rời rạc là biến ngẫu nhiên có các giá trị có thể có của nó lập nên một
tập hợp hữu hạn hoặc đếm được.
Với biến ngẫu nhiên rời rạc, ta có thể liệt kê được các giá trị có thể có của biến ngẫu
nhiên. Nếu biến ngẫu nhiên rời rạc X, nếu có n giá trị có thể có, các giá trị có thể có được
viết bằng chữ thường, chẳng hạn là x , x 1
2... x , khi đó có thể viết X= n { x , x 1 ... x 2 } n b, Ví dụ:
+ Số sản phẩm bị lỗi của một lô hàng.
+ Số cuộc điện thoại đến một tổng đài ở bưu điện trong một ngày.
2.2. Biến ngẫu nhiên liên tục a, Khái niệm
- Biến ngẫu nhiên liên tục là biến ngẫu nhiên có các giá trị có thể có của nó lấp đầy một
khoảng xác định trên số thực, thậm chí lấp đầy cả trục số thực. Tuy nhiên trên tập số thực,
chúng ta không thể liệt kê các số của nó. b,Ví dụ:
Tại một bến xe buýt cứ 15 phút lại có một chuyến xe. Một hành khách tới bến vào một thời điểm ngẫu nhiên.
Đặt T là thời gian hành khách đó phải chờ xe buýt, đơn vị là phút, thì:
• T là biến số, có thể nhận các giá trị bất kì thuộc nửa đoạn [0;15). Trang 4
Bài Tiểu luận Lý thuyết xác suất – Thống kê toán – Nhóm 2
• Với mỗi hành khách trong một lần đợi xe buýt thì thời gian chờ xe T nhận đúng một
giá trị trong khoảng trên.
Vậy T là biến ngẫu nhiên, có thể viết là T ∈ [0;15).
II. Quy luật phân phối của biến ngẫu nhiên.
* Luật phân phối xác suất của biến ngẫu nhiên là một biểu đồ, trong đó chỉ ra:
- Các giá trị có thể nhận được của biến ngẫu nhiên
- Xác suất tương ứng để biến ngẫu nhiên nhận các giá trị đó.
* Luật phân phối xác suất thường được thể hiện dưới hai hình thức: hàm mật độ xác suất
và hàm phân phối xác suất.
1. Bảng phân phối xác suất: a. Tóm tắt lý thuyết:
* Bảng phân phối xác suất dùng để mô tả quy luật phân phối của biến ngẫu nhiên rời rạc.
* Cho X là biến ngẫu nhiên rời rạc nhận các giá trị x1,x ,…,x 2
. Khi đó bảng phân phối xác n suất của X có dạng: XiX1X2 X … n PiP1P2 P … n
với Pi = P ( X = Xi ), I = 1,n Nếu X12 <…3
thì hàm phân phối xác suất củ n a X có dạng: { 0≤Pi≤1 n
∑ Pi=1(P1+P2+P3+…+Pn+1) i=1 b. Bài tập minh hoạ:
Bài 1: Một hộp đựng 12 viên phấn trong đó có 9 viên trắng và 3 viên đỏ. Lấy ngẫu
nhiên đồng thời 3 viên. Lập bảng phân phối xác suất cho số viên phấn đỏ trong 3 viên lấy ra. Giải
Gọi X là số viên phấn đỏ trong 3 viên lấy ra, X nhận các giá trị 0,3. C39 P(X=0)= = 21 C312 55 C 2 P(X=1)= 31XC9 =27 C 3 55 12 C 1 2XC9 3 27 P(X= 2)= = C 3 220 12 Trang 5
Bài Tiểu luận Lý thuyết xác suất – Thống kê toán – Nhóm 2 C3 P(X=3)= 3 = 1 C3 220 12
Bảng phân phối xác suất của X: X0123 21 27 27 1 P 55 55 220 220
Bài 2: Một lô thuốc lớn có tỷ lệ thuốc
hỏng là 10%. Lấy ngẫu nhiên 3 lọ để kiểm tra.
Gọi X là số lọ hỏng trong 3 lọ lấy ra. Lập bảng phân phối xác suất của X Giải
Vì lô thuốc lớn nên việc lấy đồng thời 3 lọ xem như lấy 3 lọ, mỗi lần 1 lọ có hoàn lại. Suy ra n=3, P=0.1
Vì X là số lọ hỏng trong 3 lọ lấy ra nên X nhận các giá trị 0,3. Ta có:
P(X=0)=C03(0.1 )0¿ =0.729 P(X=1) = C31 1 (0.1) (0.9)2=0.243
P(X=2) = C32(0.1)2(0.9)1=0.027
P(X=3) = C33(0.1)3 (0.9)0=0.001
Bảng phân phối xác suất của X: X0123 P 0.7290.2430.0270.001
Bài 3: Ba khẩu pháo cùng bắn vào một mục tiêu, mỗi khẩu bắn 1 viên với xác suất
trúng mục tiêu tương ứng là 0,7, 0,8 và 0,9. Lập bảng phân phối xác suất và tìm hàm
phân phối xác suất cho số viên đạn trúng mục tiêu của 3 khẩu pháo. Giải
Gọi X là số viên đạn trúng mục tiêu của 3 khẩu pháo, ta có X nhận các giá trị 0,3.
Gọi Ai là biến cố “khẩu thứ i bắn trúng mục tiêu”, i=1,3. Ta có:
P(A1) = 0.7 ; P(A2) = 0.8 ; P(A3) = 0.9
P(A1) = 0.3 ; P(A2) = 0.2 ; P(A3) = 0.1
Áp dụng công thức nhân xác suất với các biến cố độc lập, ta được:
P(X=0) = P(A1A2A3)=P(A1)P(A2)P(A3) = 0.3. 0.2 .0.1=0.006
P(X=1) = P(A1A2A3+ P(A1A2A3) + P(A1A2A3)
= P(A1A2A3)+ P(A1A2A3) +P (A1A2A3) Trang 6
Bài Tiểu luận Lý thuyết xác suất – Thống kê toán – Nhóm 2
= P(A1)P(A2)P(A3)+ P(A1)P(A2)P(A3) + P(A1)P(A2)P(A3) = 0.092 Tương tự ta có:
P(X=2) = P(A1A2A3) + P(A1A2A3) + P(A1A2A3) = 0.398 P(X=3) = P(A1A2A3) = 0.504
Bảng phân phối xác suất của X: X0123 p 0.0060.0920.3980.504
2. Hàm mật độ xác suất:
a, Định nghĩa hàm mật độ xác suất:
Cho biến ngẫu nhiên liên tục X có hàm phân phối xác suất F(x). Nếu tồn tại hàm số
f(x) sao cho: f(x) = F′(x) thì hàm số f(x) được gọi là hàm mật độ xác suất của biến ngẫu
nhiên X. Khái niệm hàm mật độ xác suất chỉ được dùng với biến ngẫu nhiên liên tục.
b, Tính chất hàm mật độ xác suất: * Tính chất 1:
f(x) thỏa mã điều kiện sau {f(x)≥0∀x +∞
∫ f (x)dx=1 −∞ * Tính chất 2: b
P (a<X<b )=∫ f (x)dx a b b
Ta có: P (a<X<b )=F (b)−F (a)=∫ F' (x)dx=∫ f (x)dx a a * Tính chất 3: x
Với mọi số thực a, ta có: F (x)=∫ f (x )dx −∞ Trang 7
Bài Tiểu luận Lý thuyết xác suất – Thống kê toán – Nhóm 2 x
Thật vậy, ta thấy: F (x)=P (X<x )=P (−∞<X<x )=∫ f (x)dx −∞
Công thức trên cho phép tìm hàm phân bố xác suất của biến ngẫu nhiên liên tục khi đã biết
hàm mật độ xác suất của nó.
3. Đại lượng đặc trưng của biến ngẫu nhiên
Khi nghiên cứu các đại lượng ngẫu nhiên, ta thường quan tâm đến các giá trị phản ánh đặc
trưng khái quát của biến ngẫu nhiên như: Giá trị trung bình, độ phân tán,… Trong phần
này, chúng ta sẽ nghiên cứu một số tham số quan trọng nhất. a, Kỳ vọng * Định nghĩa
Cho biến ngẫu nhiên X. kỳ vọng của X là một số, kí hiệu E(X) và xác định như sau:
- Nếu X là biến ngẫu nhiên rời rạc nhận các giá trị x1,x2,…, xn với xác suất tương ứng
p1,p2,…, pn thì:
E (X )=∑ xipi i
- Nếu X chỉ nhận hữu hạn giá trị x1,x2,…, xn với các xác suất tương ứng p1,p2,…, pn thì: n
E (X )=∑ xipi i=1
- Nếu X nhận giá trị liên tục thì: +∞
E (X )=∫ xf (x )dx −∞
Kỳ vọng là giá trị trung bình theo xác suất của các giá trị mà biến ngẫu nhiên X nhận.
Trong kinh tế, kỳ vọng đặc trưng cho năng suất trung bình của một phương án sản xuất, lợi
nhuận trung bình của một danh mục đầu tư, trọng lượng trung bình của một loại sản phẩm,
tuổi thọ trung bình của một chi tiết máy,...
Đơn vị của E(X) trùng với đơn vị của X.
* Các tính chất của kỳ vọng
Tự định nghĩa của kỳ vọng, ta có thể chứng minh được các tính chất sau:
- Tính chất 1: Kỳ vọng của hằng số bằng chính hằng số đó
E (C)=C với C là hằng số
- Tính chất 2: Có thể đưa hằng số ta ngoài kỳ vọng Trang 8
Bài Tiểu luận Lý thuyết xác suất – Thống kê toán – Nhóm 2
E (C. X )=C. E (X)
- Tính chất 3: Kỳ vọng của tổng các biến ngẫu nhiên bằng tổng các kỳ vọng của mỗi biến ngẫu nhiên thành phần:
E (X+Y )=E(X )+E(Y) Hệ quả:
E (X−Y )=E (X )−E(Y)
- Tính chất 4: Kỳ vọng của tích hai biến ngẫu nhiên độc lập bằng tích các kỳ vọng của chúng:
E (XY )=E (X ).E(Y)
- Tính chất 5: Cho g là một hàm nào đó và X là một biến ngẫu nhiên. Lúc đó ta có:
E (g (X ))=∑ g(xi)pi i b,Phương sai * Định nghĩa
Phương sai của biến ngẫu nhiên là X là kỳ vọng của bình phương độ chênh lệch giữa X và
E(X), thường được ký hiệu là V(X) hoặc Var(X)
V (X )=E(X−E (X ) 2=E¿¿ ) – ¿ * Tính chất
Từ tính chất kỳ vọng ta có:
- Nếu X là biến ngẫu nhiên rời rạc nhận các giá trị x1,x2,…, xn với xác suất tương ứng
p1,p2,…, pn thì:
E (X2 )=∑ xi2pi i
- Nếu X là biến ngẫu nhiên liên tục với hàm mật độ f(x) thì: +∞
E (X2 )=∫ x2f (x )dx −∞
Theo định nghĩa, phương sai của biến ngẫu nhiên X là trung bình của bình phương sai lệch
giữa các giá trị của biến ngẫu nhiên X và trung bình của nó. Do đó, phương sai đặc trưng
cho độ phân tán các giá trị của biến ngẫu nhiên xung quanh E(X) . Nếu V(X) lớn chứng tỏ
sự biến động của X lớn, nếu V(X) nhỏ thì X biến động ít, tương đối ổn định. Chẳng hạn, X
là biến ngẫu nhiên chỉ lượng mưa hàng năm ở một vùng, E(X) cho biết lượng mưa trung
bình hàng năm của vùng này, cho biết độ dao động của lượng mưa hàng năm xung quanh
giá trị trung bình đó. Nếu V(X) lớn thì lượng mưa ở vùng đó biến động thất thường, nếu
V(X) nhỏ thì lượng mưa ở vùng đó ổn định. Trong kinh tế, phương sai đặc trưng cho độ Trang 9
Bài Tiểu luận Lý thuyết xác suất – Thống kê toán – Nhóm 2
rủi ro các quyết định. Tùy từng bài toán, có thể cũng dùng nhiều danh từ khác để chỉ độ
phân tán các giá trị của đại lượng ngẫu nhiên tưng ứng như: độ dao động, độ biến động, độ
bấp bênh, độ phân tán, độ ổn định, độ đồng đều, độ chính xác...
Trong định nghĩa phương sai, thứ nguyên của V(X) không trùng với thứ nguyên của biến
ngẫu nhiên X, để đưa về cùng thứ nguyên với X ta phải lấy căn bậc hai của V(X). c, Độ lệch chuẩn
Căn bậc hai của phương sai được gọi là độ lệch chuẩn của biến ngẫu nhiên X, ký hiệu là:
σX= √V(X)
Từ đây người ta cũng có thể sử dụng 2
σX để thể hiện phương sai của biến ngẫu nhiên X.
Độ lệch chuẩn có cùng thứ nguyên với biến ngẫu nhiên X. Do đó đơn vị độ lệch chuẩn trùng đơn vị đo của X.
PHẦN 2: BÀI TẬP VẬN DỤNG
I.Ví dụ về biến ngẫu nhiên rời rạc ( bảng phân phối xác suất).
Một nhóm có 7 người, trong đó gồm có 4 nam và 3 nữ. Chọn ngẫu nhiên 3 người. Gọi X là số nữ được chọn.
Hãy lập bảng phân bố xác suất của X. Giải
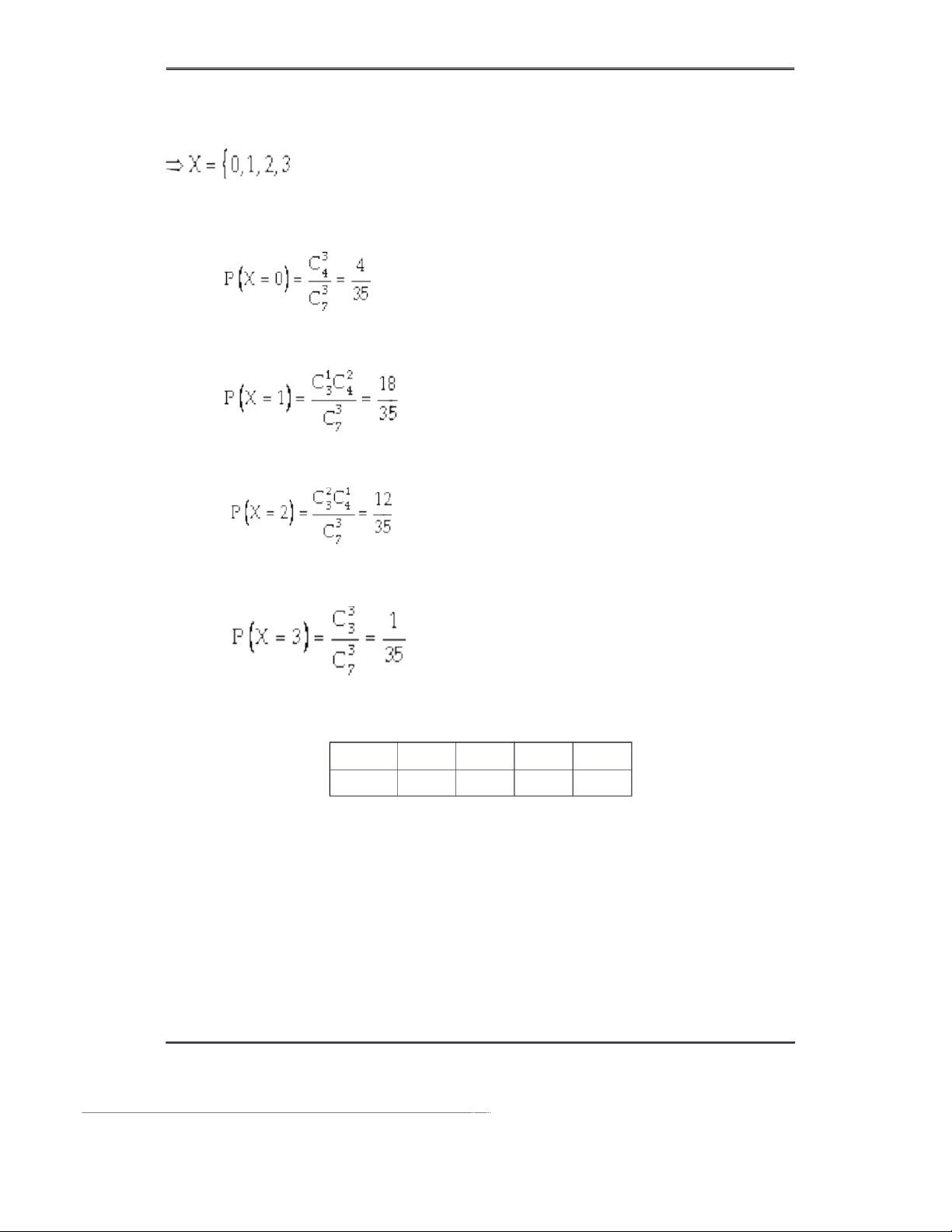
Gọi X là số nữ được chọn
Biến cố X=0 có nghĩa là 3 người được chọn đều nam. Vậy .
Biến cố X=1 có nghĩa là: chọn được 1 nữ và 2 nam. Vậy .
Biến cố X=2 có nghĩa là: chọn được 2 nữ và 1 nam. Vậy . Trang 10
Bài Tiểu luận Lý thuyết xác suất – Thống kê toán – Nhóm 2
Biến cố X=3 có nghĩa là chọn được 3 bạn đều nữ. Vậy .
Bảng phân phối xác suất của X: x 0 1 2 3 p 4/35 18/35 12/35 1/35
II. Ví dụ về hàm mật độ xác suất (biến ngẫu nhiên liên tục).
(3x−x3 )khi x∈ [0; √3]
Cho f(x) = {49 0khix∉ [0; √3]
Chứng minh f(x) là hàm mật độ xác suất? Giải:
Để f(x) là hàm mật độ xác suất thì: {f(x)≥0∀x +∞
∫ f (x)dx=1 −∞ Mặt khác: √3
∫ 4(3x−x3 )dx 9 0 √3 √3 4 4
¿∫ 3xdx−∫ 9x3dx 0 0 ¿23x2 |√3 x4 0−1 |√30 9 =1 Trang 11
Bài Tiểu luận Lý thuyết xác suất – Thống kê toán – Nhóm 2
III. Ví dụ về đại lượng đặc trưng của biến ngẫu nhiên
Một nhóm trẻ gồm 6 bé trai và 4 bé gái. Chọn ngẫu nhiên 3 bé. Gọi X là số bé gái trong 3 bé được chọn.
a). Lập bảng phân phối xác suất của biến X.
b). Tính kỳ vọng E( X) phương sai V( X). . Giải: Gọi X là số bé gái
Biến cố X=0 có nghĩa là trong 3 bé được chọn không có bé gái nào (chọn được cả 3 bé đều là bé trai). Vậy .
Biến cố X=1 có nghĩa là trong 3 bé được chọn, có 1 bé gái và 2 bé trai. Vậy .
Biến cố X=2 có nghĩa là trong 3 bé được chọn, có 2 bé gái và 1 bé trai. Vậy .
Biến cố X=3 có nghĩa là trong 3 bé được chọn đều là bé gái. Vậy .
Bảng phân phối xác suất của X: X 0 1 2 3 P 1/6 1/2 3/10 1/30 Trang 12
Bài Tiểu luận Lý thuyết xác suất – Thống kê toán – Nhóm 2 Kỳ vọng : Phương sai: Trang 13
Bài Tiểu luận Lý thuyết xác suất – Thống kê toán – Nhóm 2 LỜI KẾT
Qua quá trình thực hành và nghiên cứu đề tài, nhóm chúng tôi đã nhận thấy nhiều lợi
ích mà bộ môn “Lý thuyết xác suất - Thống kê toán” mang lại cho sinh viên chúng tôi
không những trong thời điểm hiện tại mà còn sau này khi giải quyết những vấn đề trong
cuộc sống. Với quỹ thời gian giới hạn và quy mô thông tin nhỏ nhóm chúng tôi có thể vẫn
chưa thể hoàn thành tiểu luận một cách hoàn chỉnh nhất, vì vậy mong cô thông cảm!
Nhóm chúng tôi mong nhận được sự nhận xét và đánh giá của cô cho cuốn tiểu luận của
chúng tôi hoàn chỉnh hơn.
Cuối cùng nhóm chúng tôi xin gửi lời cảm ơn đặc biệt tới Ths. Lê Thị Thanh Hoa đã tận
tình giảng dạy chúng tôi và giúp đỡ chúng tôi hoàn thành bài tiểu luận này.
Chúng tôi xin chân thành cảm ơn! Trang 14




