Tìm các khoảng đơn điệu của hàm số thông qua bảng biến thiên, đồ thị hàm số | Chuyên đề Toán 12

Chuyên đề Toán 12: Tìm các khoảng đơn điệu của hàm số thông qua
bảng biến thiên, đồ thị hàm số
A. Điều kiện để hàm số đơn điệu trên khoảng
Định lí (thừa nhận): Giả sử hàm số y = f (x) có đạo hàm trên khoảng K . Nếu f (x
¢ ) > 0, " x Î K thì hàm số đồng biến trên khoảng K . Nếu f (x
¢ ) < 0, " x Î K thì hàm số nghịch biến trên khoảng K . Nếu f (x
¢ ) = 0, " x Î K thì hàm số không đổi trên khoảng K .
B. Tìm khoảng đồng biến, nghịch biến của hàm số khi biết bảng biến thiên của hàm số Phương pháp giải
Bước 1. Tìm đạo hàm của hàm số y  f ux; y  f ux hx;. .
y '  u ' x. f 'u x; y '  u 'x. f 'u x  h'x
Bước 2. Từ bảng biến thiên xác định nghiệm phương trình f 'x  0 , nghiệm của
bất phương trình f 'x  0 và nghiệm của bất phương trình f 'x  0
Bước 3. Đánh giá các khoảng thỏa mãn y'  0; y'  0
Bước 4. Kết luận khoảng đồng biến, nghịch biến của hàm số
y  f  x; y  f u x; y  f u x  hx
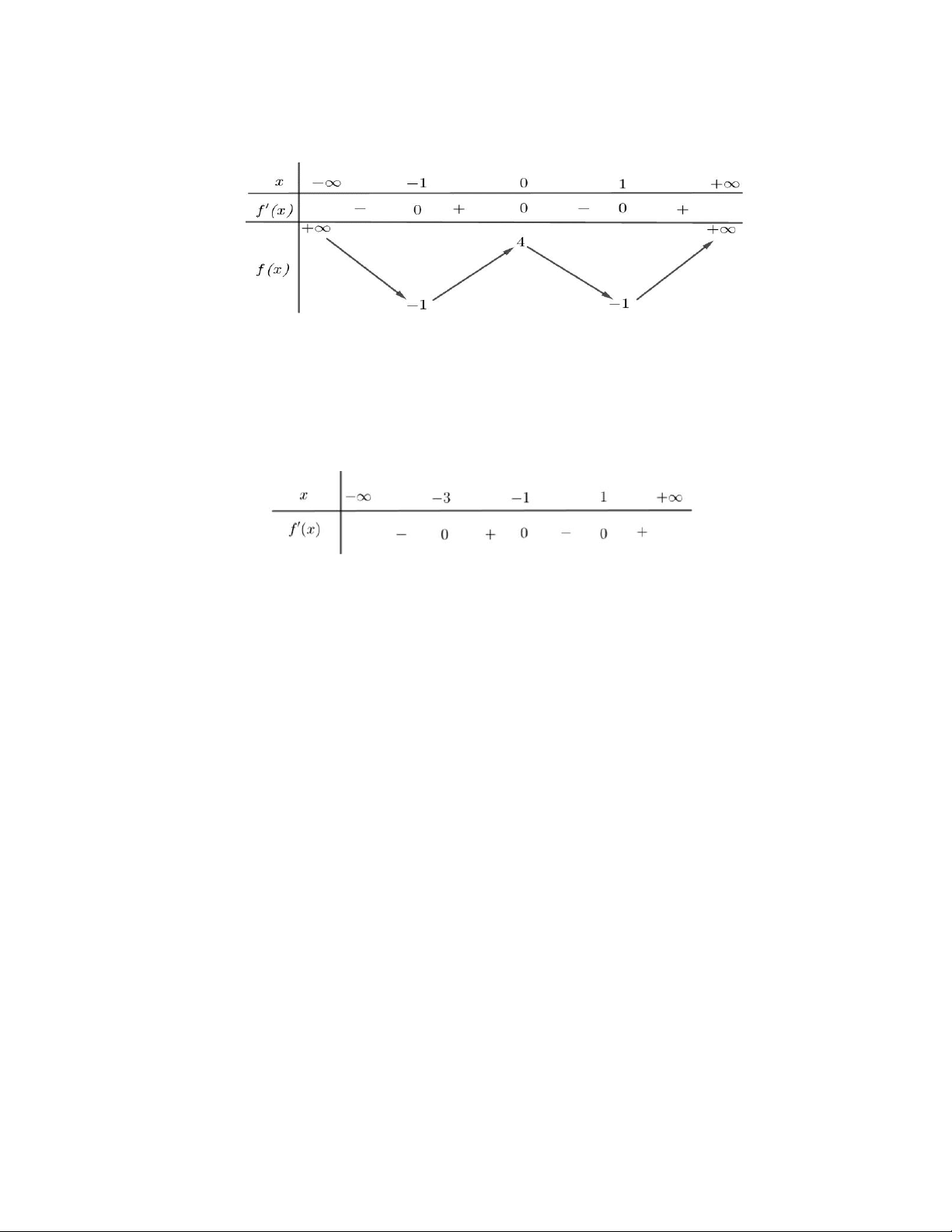
Ví dụ: Cho hàm số f x có bảng biến thiên như sau:
Hàm số đã cho đồng biến trên khoảng nào? Hướng dẫn giải
Hàm số đã cho đồng biến trên khoảng 1;0 và 1;
Ví dụ: Cho hàm số f x có bảng xét dấu f 'x như sau:
Hàm số y  f 2x  
1 nghịch biến trên khoảng nào dưới đây? A.  1  ;2 B.  2  ;0 C.  1  ;0 D. 0; Hướng dẫn giải Ta có: y'   f  2x   1 '  2 f '  2x  1  0 2x 1 3  x  2      1 2x 1 1       1   x  0
Vậy khoảng nghịch biến của hàm số y  f 2x   1 là:  1  ;0 Chọn đáp án C.
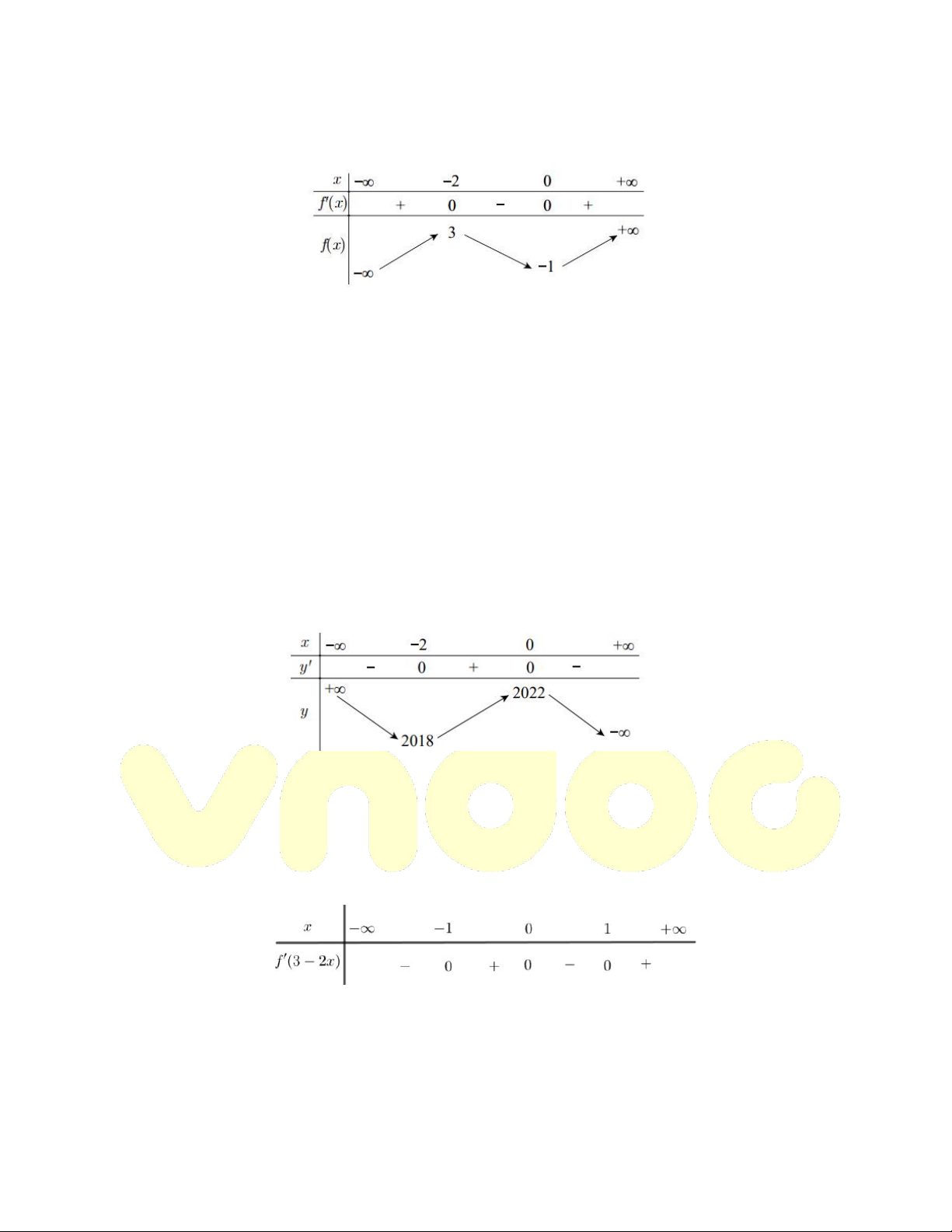
Ví dụ. Cho hàm số y  f x có bảng biến thiên như sau:
Hỏi hàm số y  2021 f x đồng biến trên khoảng nào? A. 1; B. 1;0 C.  ;  2 D. 0;2 Hướng dẫn giải
Hàm số y  2021 f x có y '   f 'x   
y    f x   f x  x 2 ' 0 ' 0 '  0  x  0
Từ bảng biến thiên của hàm số y  f x ta có bảng biến thiên của hàm số
y  2021 f  x
Dựa vào bảng biến thiên ta có hàm số y  2021 f x đồng biến trong khoảng 1;0 . Chọn đáp án B.
Ví dụ. Cho hàm số y  f 3 2x có bảng xét dấu như sau:
Hỏi hàm số y  f x nghịch biến trên các khoảng nào dưới đây? A. 3;5 B.  1  ;2 C. 1;3 5; Hướng dẫn giải Ta có:
y '  f '3 2x  2 f '3 2x f ' 
1  f '3  f '5  0
f 'x  k x 5x 3x   1
Xét x  3 y'  2  f ' 3    0  f ' 3    0
Bảng xét dấu y  f 'x là:
Căn cứ vào bảng xét dấu ta thấy
Hàm số y  f x nghịch biến trên khoảng 3;5 . Chọn đáp án A
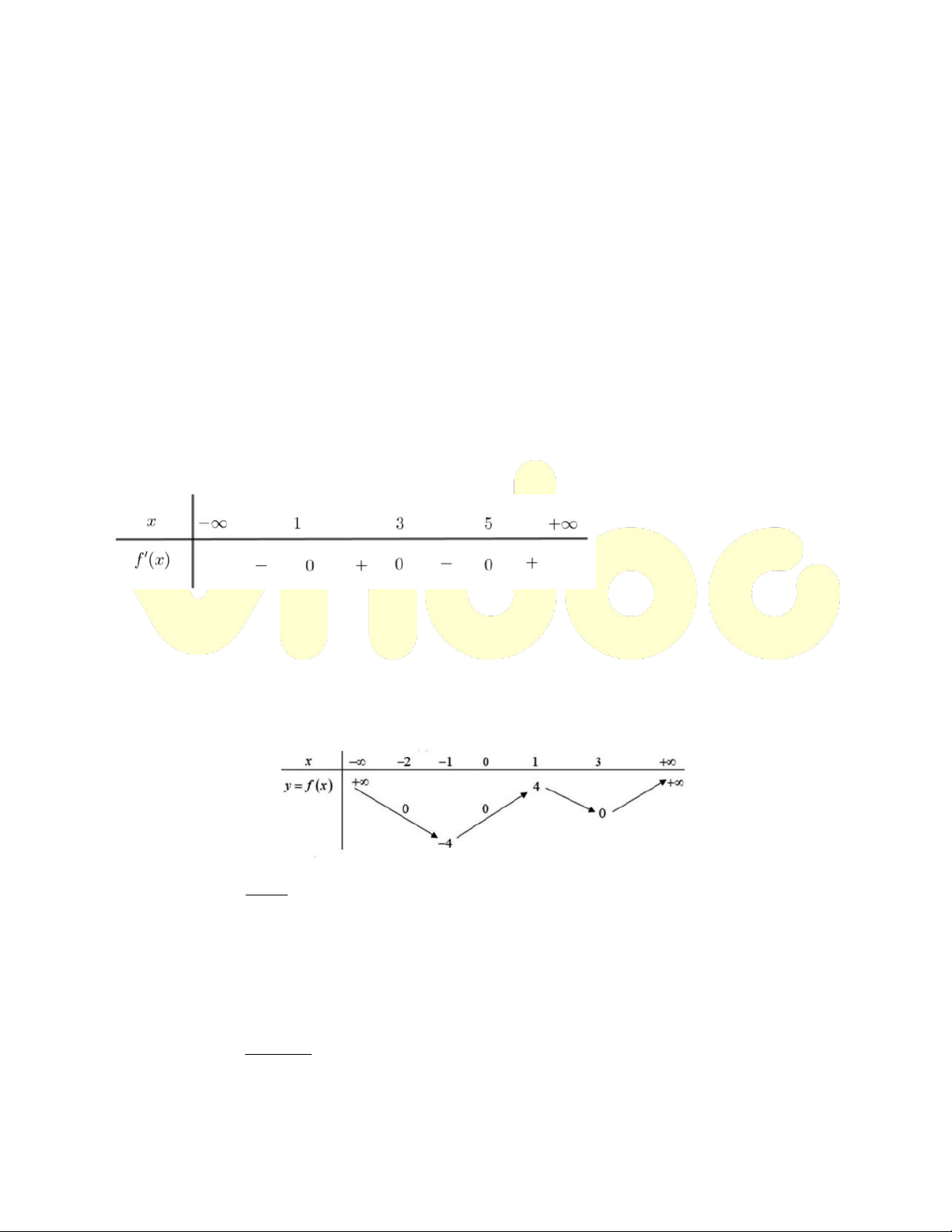
Ví dụ. Cho hàm số y  f x có bảng biến thiên như sau: Hàm số   1 g x 
đồng biến trên khoảng nào sau đây? f x A.  2  ;0 B. 3; C. 1;2 D.  ;    1 Hướng dẫn giải Ta có: f x g 'x '     0  f x 2           f x x 1 x 2 '  0              f   x 1 x 3 2 x 1 0    x    2  ;0;  3 1    x  3 Vậy hàm số   1 g x 
đồng biến trên các khoảng  ;  2  , 2  ;  1 ,1;3 f x Suy ra hàm số   1 g x 
đồng biến trên khoảng 1;2 . f x
C. Tìm khoảng đồng biến, nghịch biến của hàm số thông qua đồ thị của hàm số Phương pháp giải
Bước 1. Tìm đạo hàm của hàm số y  f ux; y'  u 'x. f 'ux
Bước 2. Từ đồ thị hàm số y  f x xác định được hàm số y  f x (hoặc nghiệm
phương trình f 'x  0 , nghiệm của bất phương trình f 'x  0 và nghiệm của
bất phương trình f 'x  0 ).
Bước 3. Đánh giá các khoảng thỏa mãn y'  0; y'  0
Bước 4. Kết luận khoảng đồng biến, nghịch biến của hàm số y  f x; y  f ux Nhận xét:
Nếu hàm số đồng biến trên K thì từ trái sang phải đồ thị đi lên.
Nếu hàm số nghịch biến trên K thì từ trái sang phải đồ thị đi xuống.
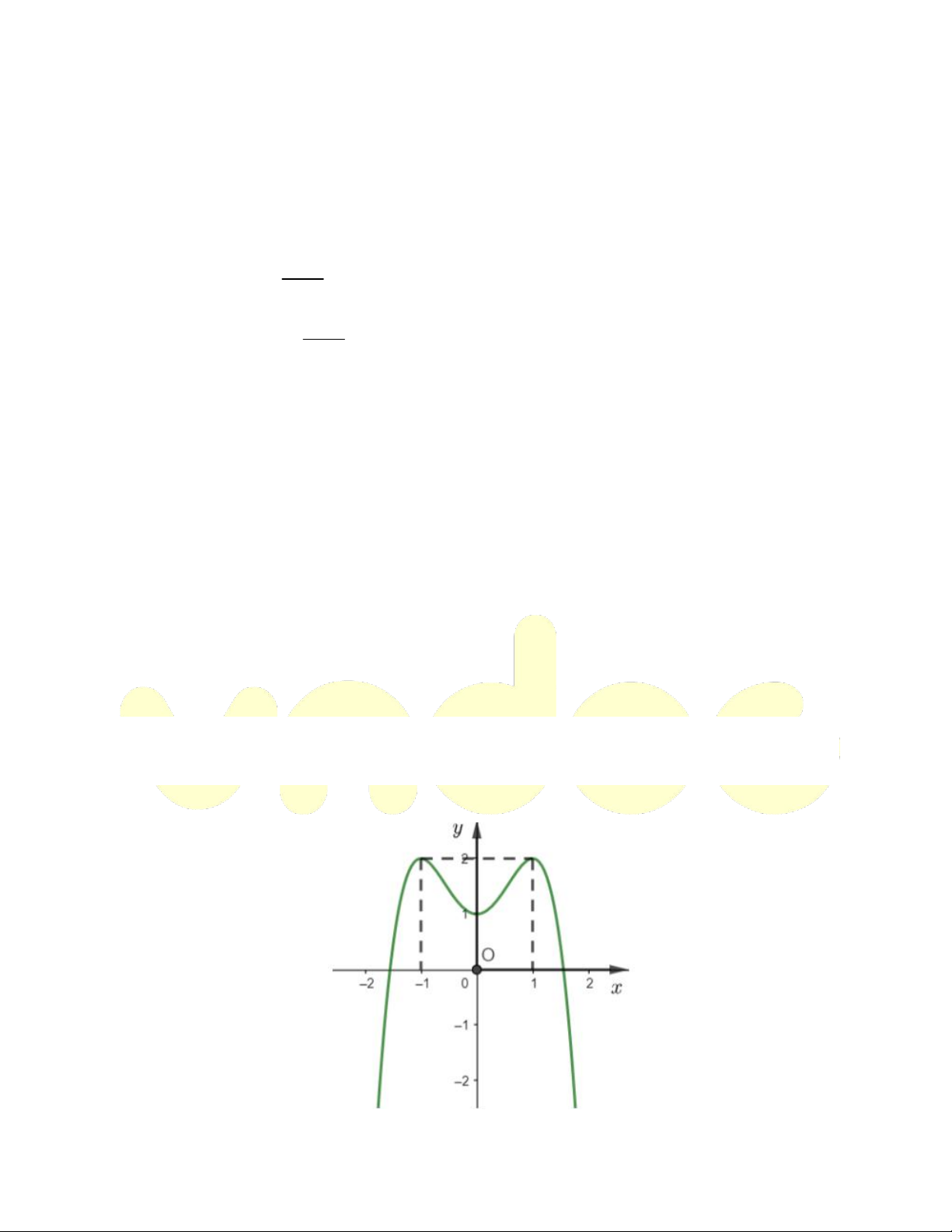
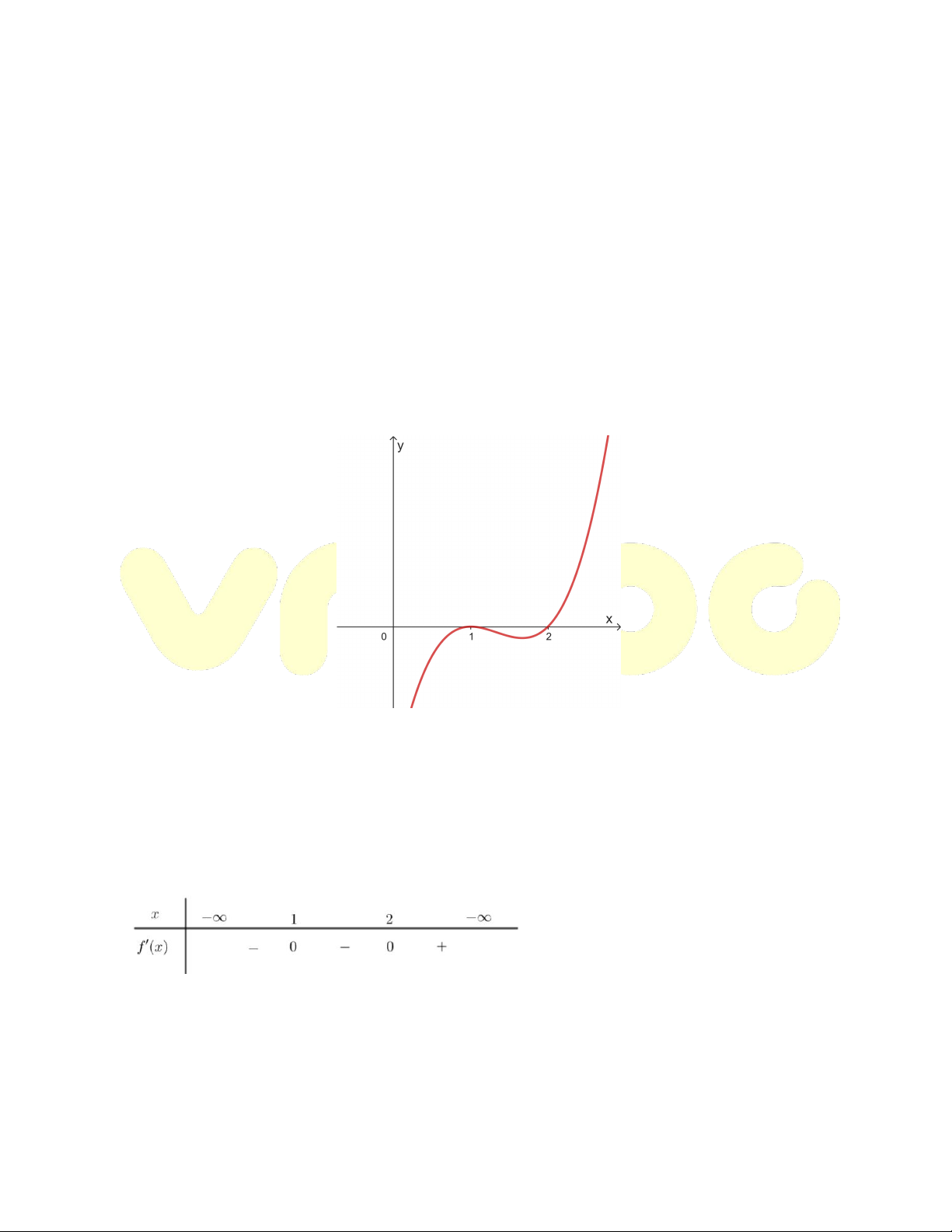
Ví dụ: Cho hàm số y  f x có đồ thị như hình vẽ như sau:
Hàm số đã cho đồng biến trên khoảng nào dưới đây? A. 1;  1 B. 0;  1 C. 1; D.  1  ;0 Hướng dẫn giải
Dựa vào đồ thị dễ dàng thấy hàm số đồng biến trên 0;  1 . Chọn đáp án B.
Ví dụ: Cho hình vẽ là đồ thị hàm số y  f 'x. Hỏi hàm số y  f x đồng biến
trên khoảng nào dưới đây? A. 2; B. 0;  1 và 1; C. 0;  1 D. 1;2 Hướng dẫn giải
Từ đồ thị y  f 'x ta có bảng xét dấu y  f 'x như sau:
Vậy hàm số đồng biến trên khoảng 0;  1 Chọn đáp C
Ví dụ. Cho hàm số y  f x có đồ thị như hình vẽ:
Hàm số y  f x nghịch biến trên khoảng nào dưới đây? A. 2;0 B. 0;2 C. 2;2 D. 2; Hướng dẫn giải
Từ đồ thị hàm số y  f x ta thấy hàm số đồng biến trên khoảng 0;2
 f 'x  0  0  x  2
Xét hàm số y  f x ta có: y '   f 'x
y '  0   f 'x  0  f 'x  0
 0  x  2  2  x  0
Suy ra hàm số y  f x nghịch biến trên khoảng 2;0 . Chọn đáp án A.
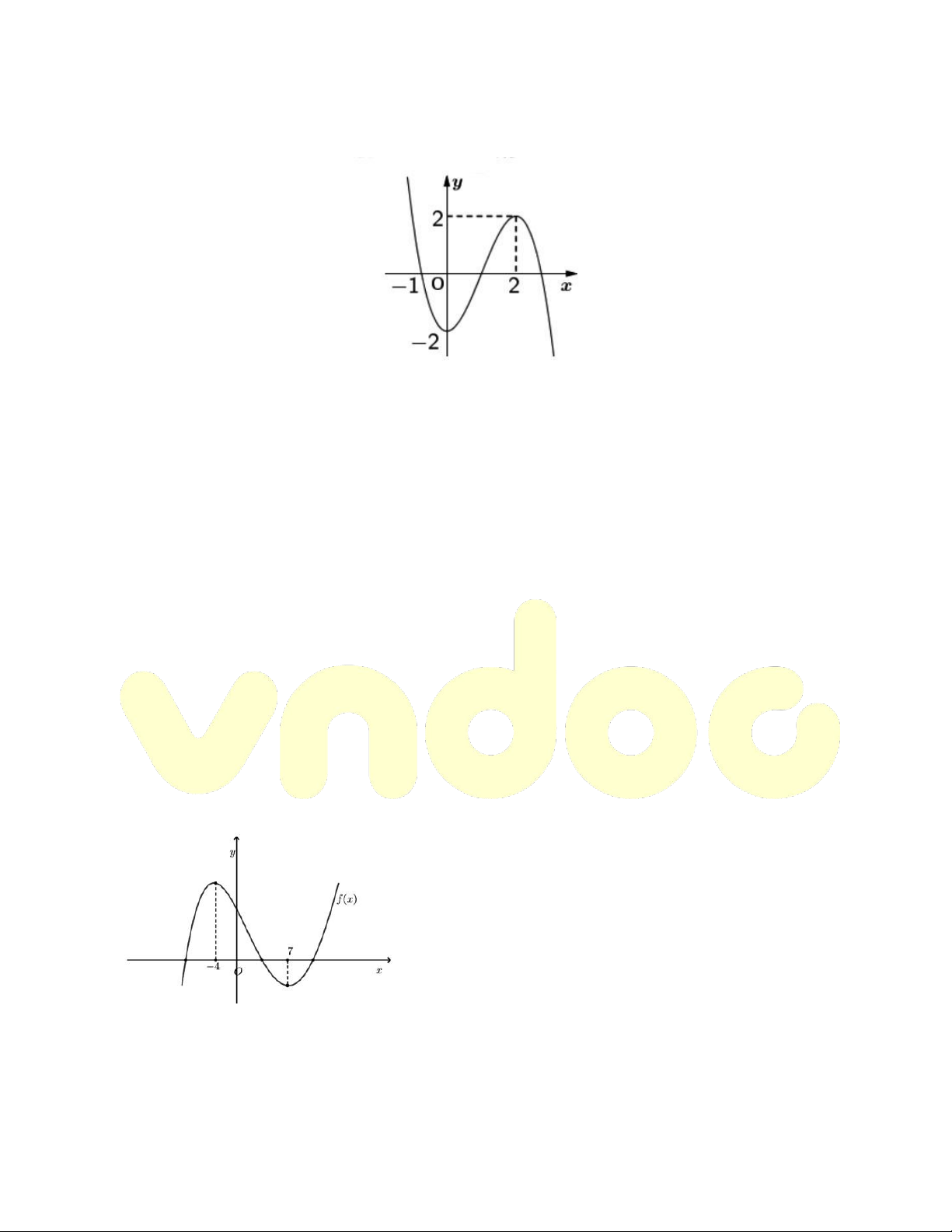
Ví dụ. Cho đồ thị hàm số y  f x như hình vẽ:
Hàm số g x  2 f x 2021 đồng biến trên khoảng: A.  ;  3   B.  4  ;7 C. 4; D. 8; Hướng dẫn giải
Ta có: g 'x  2 f 'x  0  f 'x  0  x ;  4  7;
Nên suy ra hàm số cũng đồng biến trên 8; . Chọn đáp án D
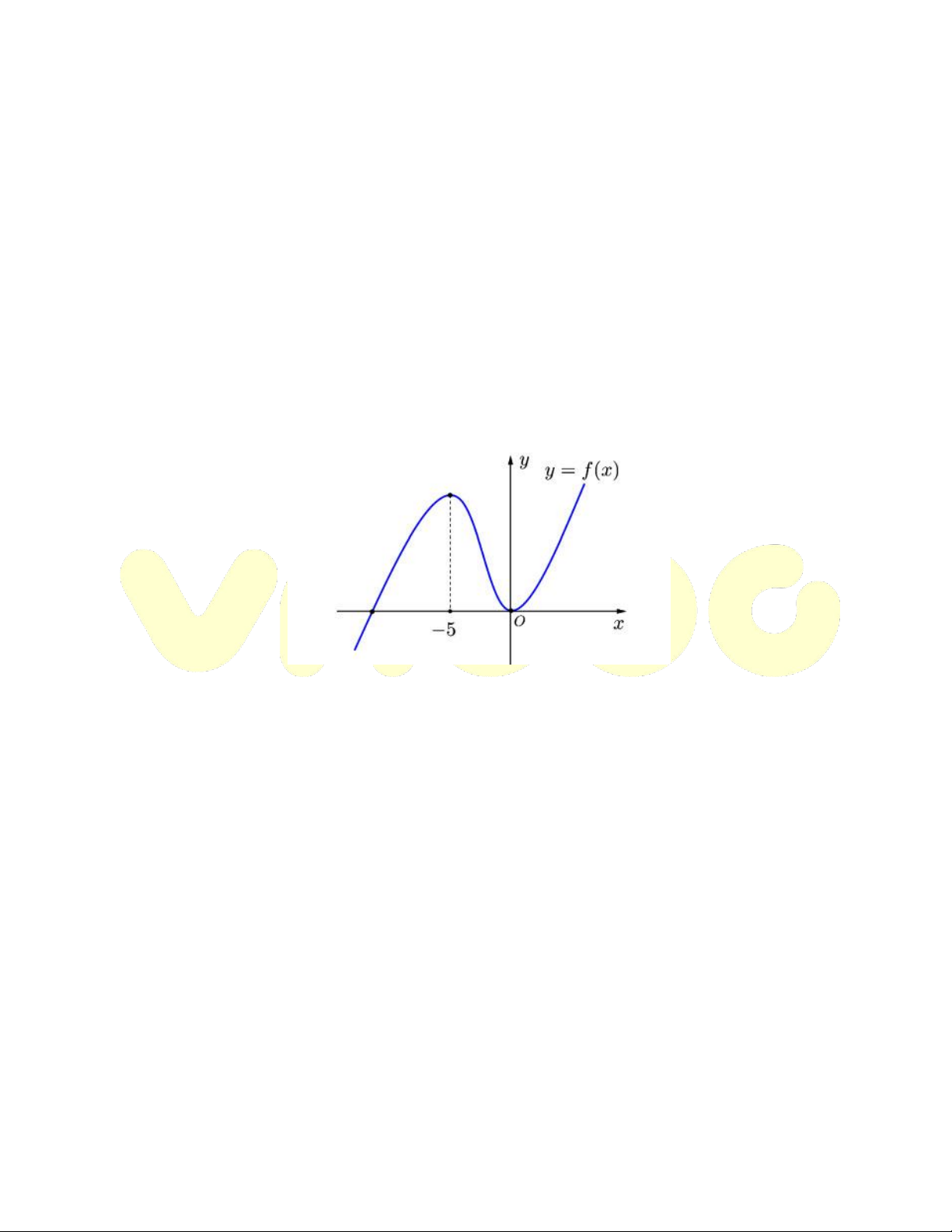
Ví dụ. Cho hàm số y  f x có đồ thị như hình vẽ:
Xác định khoảng đồng biến của hàm số g x  3
 f x  2? A.  ;  0 B.  ;  6 C. 5;0 D. 0; Hướng dẫn giải
Từ đồ thị hàm số y  f x ta có:    f  x x 5 '  0  
và f 'x  0  5   x  0 x  0
Ta có: g 'x  3  f 'x
Khi đó: g 'x  0  3
 f 'x  0  f 'x  0  5   x  0 x  
g 'x  0  3
 f 'x  0  f x 5 '  0  x  0
Vậy hàm số g x  3
 f x  2 đồng biến trên khoảng 5;0. Chọn đáp án C