Tìm cực trị của hàm số | Chuyên đề Toán 12

Chuyên đề Toán 12: Tìm cực trị của hàm số
A. Cực trị của hàm số
Giả sử hàm số y  f x xác định trên tập K và x  K . Ta nói: 0
 x là điểm cực tiểu của hàm số f nếu tồn tại một khoảng a;b sao cho 0
x  a;b sao cho a;b  K và f  x  f  x x
 a;bx . Khi đó f  x0  0 0  0  
được gọi là giá trị cực tiểu của hàm số f x .
 x là điểm cực đại của hàm số f nếu tồn tại một khoảng a;b sao cho 0
x  a;b sao cho a;b  K và f  x  f  x x
 a;bx . Khi đó f  x0  0 0  0  
được gọi là giá trị cực đại của hàm số f x .
+ Điểm cực đại và điểm cực tiểu chung là điểm cực trị.
+ Giá trị cực đại và giá trị cực tiểu gọi chung là cực trị.
+ Điểm cực đại và điểm cực tiểu được gọi chunh là điểm cực trị của hàm số và
điểm cực trị phải là một điểm trong tập hợp K .
+ Giá trị cực đại và giá trị cực tiểu được gọi chung là giá trị cực trị (hay cực trị) của hàm số.
+ Nếu x là điểm cực trị của hàm số thì điểm x ; f x
được gọi là điểm cực trị 0  0 0
của đồ thị hàm số f .
B. Quy tắc tìm cực trị cho bởi công thức Phương pháp 1
Bươc 1. Tìm tập xác định D của hàm số.
Bươc 2. Tinh đạo hàm y  f (x). Tìm các điểm x , (i  1,2,3,. ., )
n mà tại đó đạo hàm i
băng 0 hoăc không xác định.
Bươc 3. Săp xếp các điểm x theo thư tự tăng dân và lập bảng biến thiên. i
Bươc 4. Tư bảng biến thiên, suy ra các điểm cực trị (dựa vào nội dung định ly 1). Phương pháp 2
Bươc 1. Tìm tập xác định D của hàm số.
 Bươc 2. Tinh đạo hàm y  f (x). Giải phương trình f (x)  0 và ki hiêu
x , (i  1,2,3,. ., )
n là các nghiêm của nó. i
 Bươc 3. Tinh f  (x) và f  (x ). i
 Bươc 4. Dựa vào dâu của y (x ) suy ra tinh chât cực trị của điểm x : i i
+ Nếu f  (x )  0 thì hàm số đạt cực đại tại điểm x . i i
+ Nếu f  (x )  0 thì hàm số đạt cực tiểu tại điểm x . i i Ví dụ: Cho hàm số 4 2
y  x  2x 1. Xét các mênh đề sau đây:
1) Hàm số có 3 điểm cực trị
2) Hàm số đồng biến trên các khoảng (-1;0) và (1; +∞)
3) Hàm số có 1 điểm cực trị
4) Hàm số nghịch biến trên các khoảng (-∞; -1) và (0; 1)
Xét sự đúng sai của các mênh đề đã cho. Hương dẫn giải Ta có: 3
y '  4x  4x
 x  0  y  1 y ' 0  
  x  1 y  0 
x  1 y   0
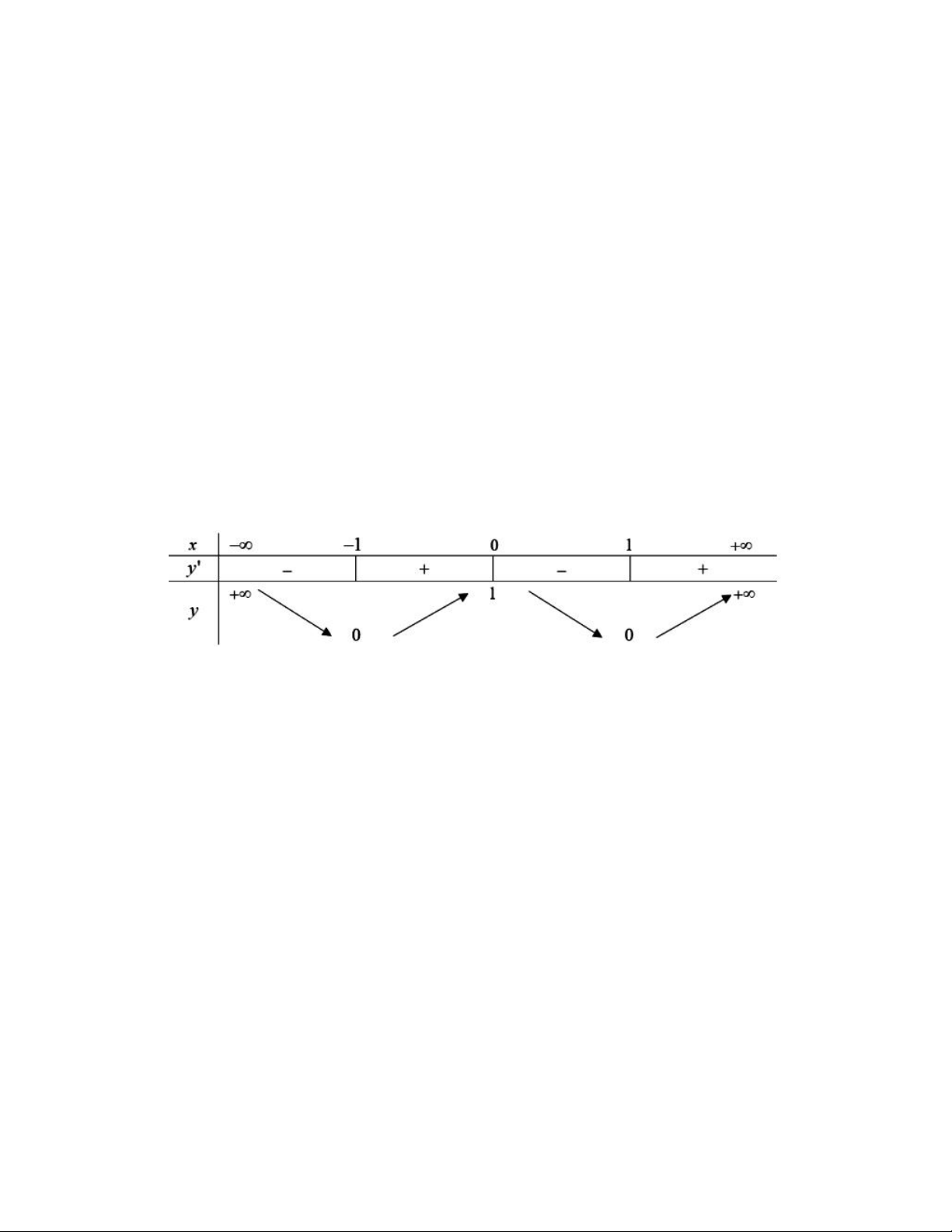
Ta có bảng xét dâu như sau:
Quan sát bảng xét dâu ta thây
Hàm số có 3 điểm cực trị
Hàm số đồng biến trên khoảng (-1; 0), (1; +∞) và nghịch biến trên khoảng (-∞; -1), (0; 1)
Vậy mênh đề 1, 2, 4 là các mênh đề đúng.
Ví dụ. Cho hàm số y = f(x) có đạo hàm trên là
f x  x  x  x  4 ' 2018 2019
2020 . Hàm số đã cho có bao nhiêu điểm cực trị? Hương dẫn giải
Tập xác định: D  x  2018
Ta có: f 'x   0  x   2019 x   2020
Ta có bảng xét dâu’(x) như sau:
Dựa vào bảng xét dây của f’(x) ta thây f’(x) đổi dâu qua hai điểm x = 2018, x =
2019 nên hàm số đã cho có hai điểm cực trị.
Ví dụ. Cho các hàm số sau: y x
 x  y   x  2 2 2 1; 2
1 ; y  2x 1 3 2 x ; y  . Có bao 2 x 1
nhiêu hàm số có đúng một điểm cực trị? Hương dẫn giải Ta có: 2
y  x 1 có y '  2x  y '  0  x  0 và y' đổi dâu khi x qua nghiêm đó nên hàm
số có đúng 1 điểm cực trị. x  0
y   x  2 2 2 1 có y ' 2 2 2x 1.4x y ' 0       1 
và y' đổi dâu khi x qua các x    2
nghiêm đó nên hàm số có 3 điểm cực trị. 
y   x   2 2x 1 3 2 3 2   10x 2
2 1 x  y '  2 x   3 3 3 x 3 x 1
 y '  0  x  ; y’ không xác định khi x  0 và y’ đổi dâu khi x qua 1 0; nên 5 5
hàm số có hai điểm cực trị. 2 x 1   '  x y y 
 0  x  1 và y’ đổi dâu khi x qua các nghiêm đó nên 2 x 1  2x  2 1
hàm số có hai điểm cực trị.
Vậy chỉ có một hàm số có đúng một cực trị.
Ví dụ. Viết phương trình đường thẳng AB sao cho A và B là hai điểm cực trị của đồ thị hàm số 3 2
y  x  3x  9x 1 ? Hương dẫn giải
Cách 1: Xét hàm số f x 3 2
 x  3x  9x 1
Ta có: f x  1 1 x   
. f ' x 8x    2  3 3 
Đồ thị hàm số f(x) có hai điểm cực trị A và B nên f’(A) = f’(B) = 0
y  f x   x  A  A  Suy ra 8 A 2 
 y  f x   x   B  B  8 B 2
Do đó phương trình đường thẳng AB là y = -8x – 2
Cách 2: Xét hàm số y  f x 3 2
 x  3x  9x 1 f 'x 2
 3x  6x 9  x  f 'x 3 2
 0  3x  6x 9  x  1
=> Tọa độ hai điểm cực trị của hàm số là A(3; -26) và B(-1; 6)  
Ta có: AB  4;32  u  1;8 
Phương trình đường thẳng AB đ qua B(-1; 6) nhận vecto u làm vecto chỉ phương
là x  1t  ;t   .
 y  6  8t
Ví dụ. Tìm số cực trị của các hàm số sau: 2 a. 2x  5 y  b. x  3  
d. y  sin x  ,x   ;  x y  1 x 1 4
c. f x  0 C  1 C x  2 2 C x  3 3
C x  . . 2019 2019 C x 3 2019 2019 2019 2019 2019
e. y  x   1  x   1 Hương dẫn giải a. 2x  5 y  x1
Tập xác định D   \   1 Ta có: 3 y'   0,x D x12
Do y’ không đổi dâu nên hàm số không có cực trị. 2 b. x  3 y  x1
Tập xác định D  \  1 2 x  2x  3
y '  x 21 x  1 2
y '  0  x  2x  3  0   x 3 8 y '   1  1   0 y '     x  3 1  y '  3 1 0
y  y    CD   1 2
  y  y   CT 3 3
Vậy hàm số có 2 cực trị.
c. f x  0 C  1 C x  2 2 C x  3 3
C x  . . 2019 2019 C x 2019 2019 2019 2019 2019 Ta có:
f x  C C x C x C x . .C x  1 x2019 0 1 2 2 3 3 2019 2019 2019 2019 2019 2019 2019
 f 'x  2019.1 x2018
f 'x  0  x  1
Vì x = -1 là nghiêm bội chẵn nên x = -1 không phải là điểm cực trị của hàm số. d. Xét hàm số x
y  f x  sin x  ; x   ;  4 Ta có: f x 1 '  cos x  4     x  x    ; 0 1   f 'x 1   2   0  cos x   4    
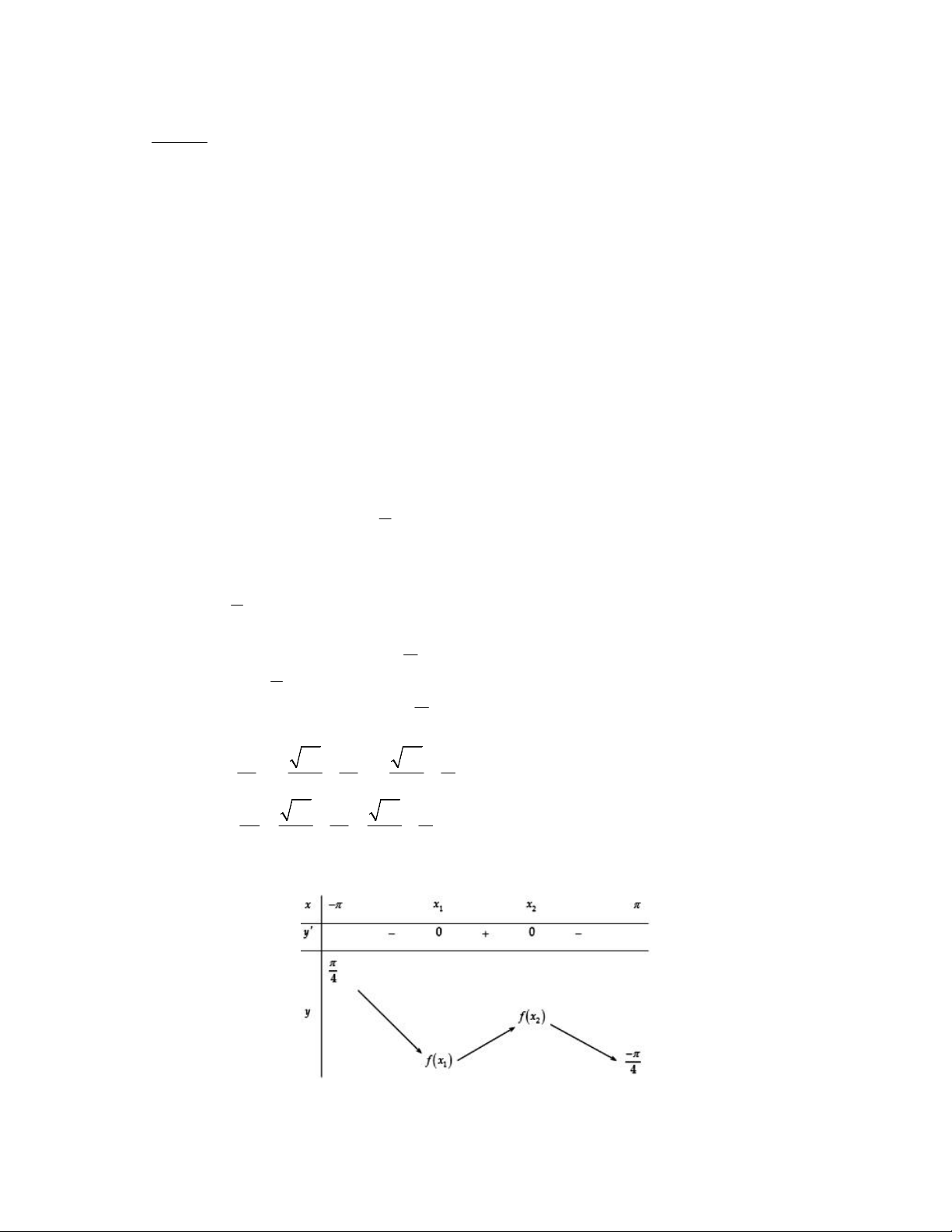
 x  x  0; 1     2  f  x 15 x 15 x sin x 0 1     1    1     1 4 4 4 4 8 f  x 15 x 15 x sin x 0 2     2   1    2 4 4 4 4 8 Ta có bảng biến thiên:
Dựa vào bảng biến thiên, ta thây hàm số có hai điểm cực trị và đồ thị hàm số căt
trục hoành tại hai điểm phân biêt khác x1; x2 => Hàm số x
y  sin x  ,x 
 ,  có 5 điểm cực trị. 4
e. Xét hàm số y  x  3 1 x   1 ta có đạo hàm
y   x  2  x     x  3   x  2 ' 3 1 1 1 1 4x  2
x  1 y  0 y ' 0     1 27
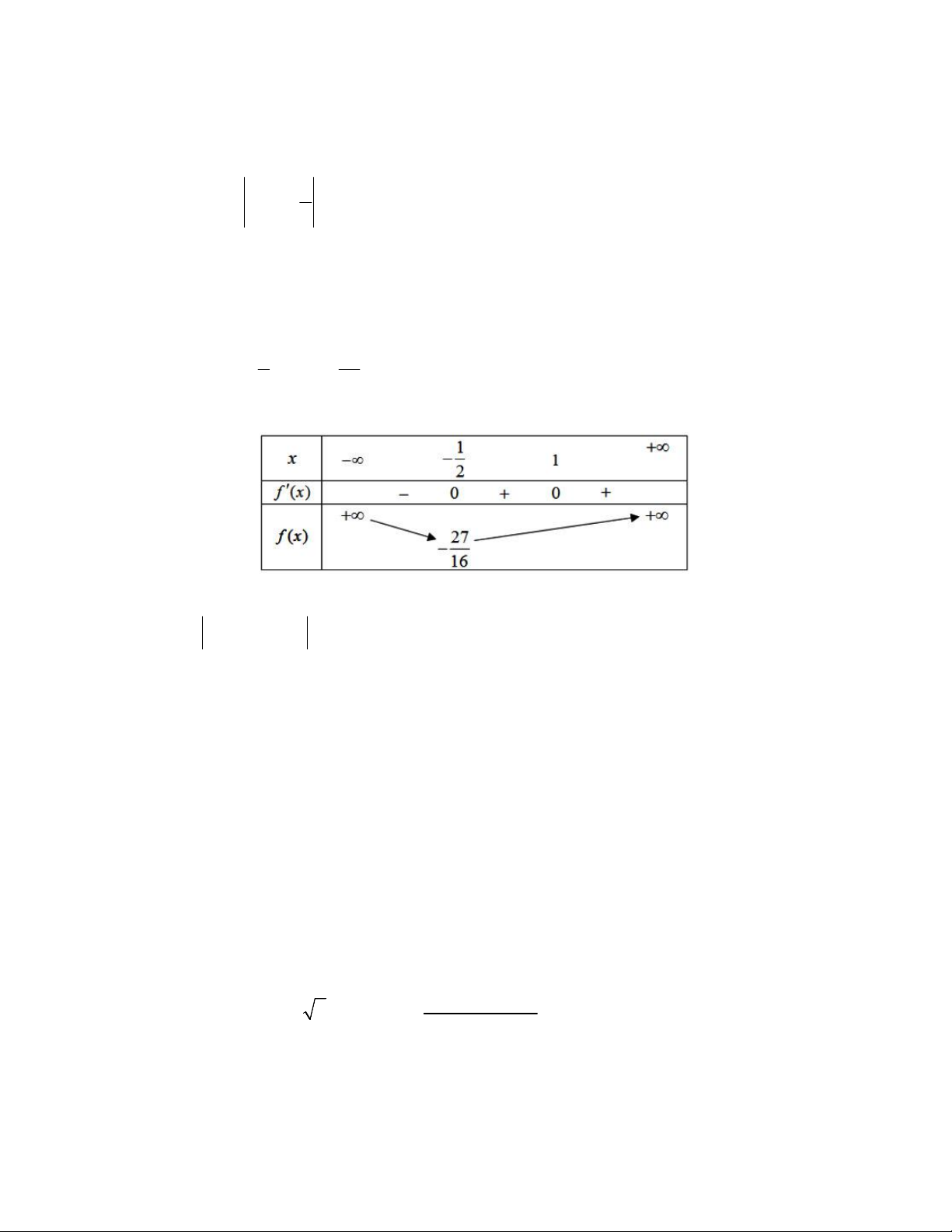
x    y    2 16 Ta có bảng biến thiên
Dựa vào bảng biến thiên của hàm số y  f x suy ra hàm số
y  f x  x  3 1 x   1 có ba cực trị.
Ví dụ. a. Gọi A, B, C là các điểm cực trị của đồ thị hàm số 4 2
y  x  2x  4 . Tinh
bán kinh của đường tròn nội tiếp tam giác ABC?
b. Cho hàm số y  4 x  2
2x 1có đồ thị (C). Biết răng đồ thị (C) có ba điểm cực trị
tạo thành ba đỉnh của tam giác ABC. Tinh diên tich tam giác ABC? Hương dẫn giải a. Ta có: f x 3 '  4x  4x   f x x 0 '
 0  x  1
=> Đồ thị hàm số y  4 x  2
2x 1có ba điểm cực trị là A(0; 4), B(1; 3), C(-1; 3) Tinh được AB  AC    2;  2;  BC AB AC BC p 2
Áp dụng công thưc tinh bán kinh đường tròn nội tiếp tam giác ABC ta có: S p AB p BC p AC ABC
       r    2 1 p P b. Ta có: y  3 ' 4x  4x  x  0
y'  0  x    1
Tọa độ các điểm cực trị của đồ thị hàm số là A0; 
1 ,B1;0,C1;0   AB  1;  1 , AC  1;  1    A . B AC  0
 AB AC   2
=> Tam giác ABC vuông cân tại A => 1 S  A . B AC  1 2
Ví dụ. Hàm số nào trong bốn hàm số được liêt kê dưới đây không có cực trị? A. 2x  3 y  . B. 4 y  x . C. 3
y  x  x .
D. y  x  2 . x  2 Hương dẫn giải + Hàm số 2x  3 y  x2
Tập xác định: D   ;  2   2  ; . Có 7 y '   0 x
  D  hàm số luôn đồng biến trên tưng khoảng xác định x  22
 Hàm số không có cực trị.