Tìm cực trị của hàm số khi biết bảng biến thiên, đồ thị hàm số | Chuyên đề Toán 12

Chuyên đề Toán 12: Tìm cực trị của hàm số khi biết
bảng biến thiên, đồ thị hàm số A. Cực trị hàm số
Giả sử hàm số y  f x xác định trên tập K và x  K . Ta nói: 0 
x là điểm cực tiểu của hàm số f nếu tồn tại một khoảng a;b sao 0
cho x  a;b sao cho a;b  K và f x  f x x
 a;bx . Khi đó f  x0  0 0  0  
được gọi là giá trị cực tiểu của hàm số f x . 
x là điểm cực đại của hàm số f nếu tồn tại một khoảng a;b sao 0
cho x  a;b sao cho a;b  K và f x  f x x
 a;bx . Khi đó f  x0  0 0  0  
được gọi là giá trị cực đại của hàm số f x .
+ Điểm cực đại và điểm cực tiểu chung là điểm cực trị.
+ Giá trị cực đại và giá trị cực tiểu gọi chung là cực trị.
+ Điểm cực đại và điểm cực tiểu được gọi chunh là điểm cực trị của hàm số và
điểm cực trị phải là một điểm trong tập hợp K .
+ Giá trị cực đại và giá trị cực tiểu được gọi chung là giá trị cực trị (hay cực trị) của hàm số.
+ Nếu x là điểm cực trị của hàm số thì điểm x ; f x
được gọi là điểm cực trị 0  0 0
của đồ thị hàm số f .
B. Định lí cực trị của hàm số
Điều kiện cần (định lí 1):
Nếu hàm số y = f (x) có đạo hàm trên khoảng ( ; a )
b và đạt cực đại (hoặc cực tiểu)
tại x thì f (x ¢ ) = 0. o o
Điều kiện đủ (định lí 2): Nếu f ( ) x
¢ đôi dâu tư âm sang dương khi x đi qua điểm x (theo chiêu tăng) thì o
hàm số y = f (x) đạt cực tiểu tại điểm x .o Nếu f ( ) x
¢ đôi dâu tư dương sang âm khi x đi qua điểm x (theo chiêu tăng) thì o
hàm số y = f (x) đạt cực đại tại điểm x .o
Định lí 3: Giả sử y = f (x) có đạo hàm câp 2 trong khoảng (x - ;
h x + h), vơi o o h > 0. Khi đó:
Nếu y (ⅱx ) = 0, y (x ) > 0 thì x là điểm cực tiểu. o o o
Nếu y (ⅱx ) = 0, y (x ) < 0 thì x là điểm cực đại. o o o
Ví dụ: Cho hàm số y  f x xác định trên \ 
0 và có bảng xét dâu đạo hàm
f 'x như sau:
Hàm số y  f x có bao nhiêu điểm cực trị? Hướng dẫn giải
Dựa vào bảng xét dâu đạo hàm ta thây hàm số y  f x có 1 điểm cực trị.
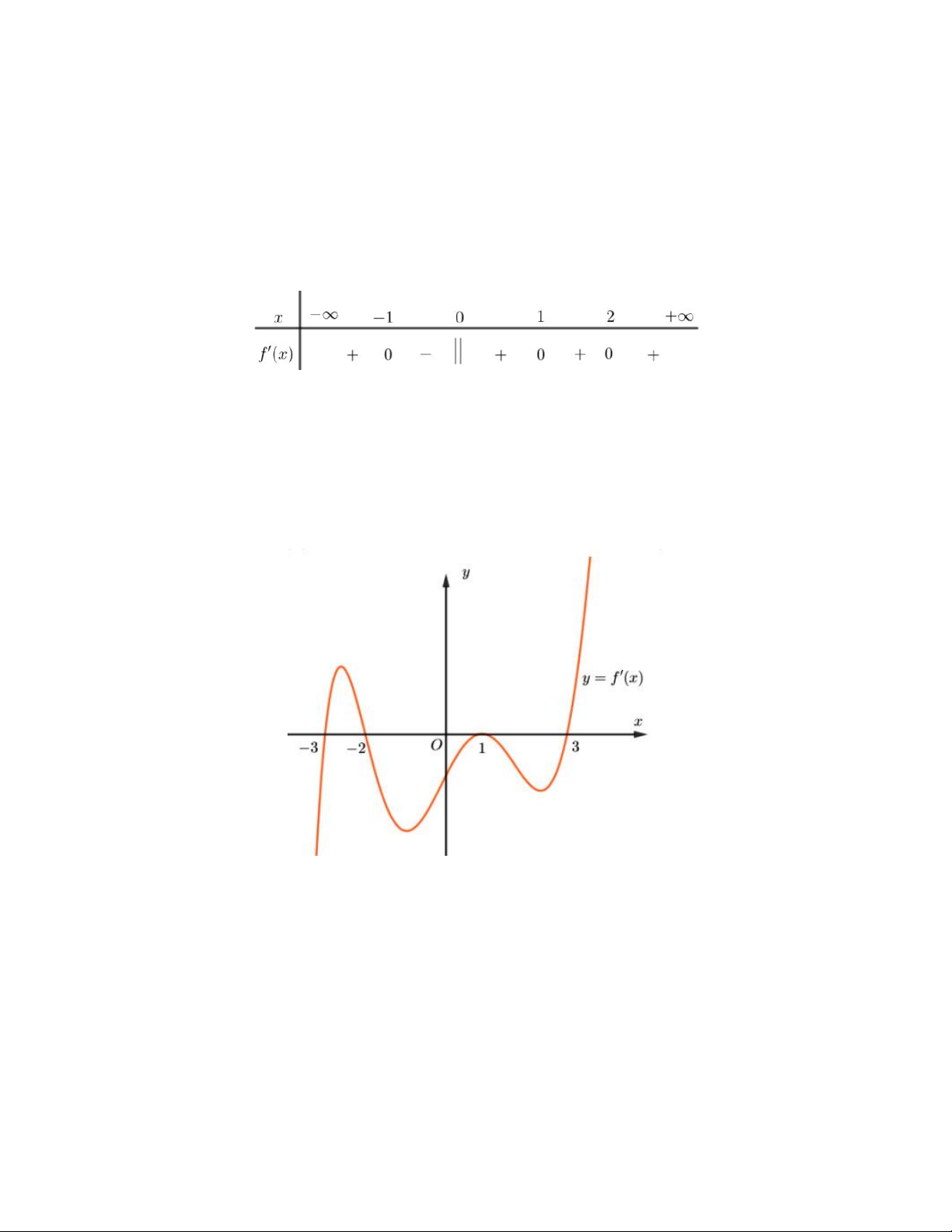
Ví dụ. Cho hàm số y  f x liên tục và có đạo hàm trên , biết y  f 'x có đồ thị như hình vẽ:
Xác định điểm cực đại của hàm số y  f x đã cho? Hướng dẫn giải x  3 x  2
Dựa vào đồ thị hàm số y  f 'x ta có: f 'x  0  x 1  x  3
Khi đó ta có bảng xét dâu f 'x như sau:
Dựa vào bảng xét dâu suy ra điểm cực đại của hàm số y  f x là x  2  .
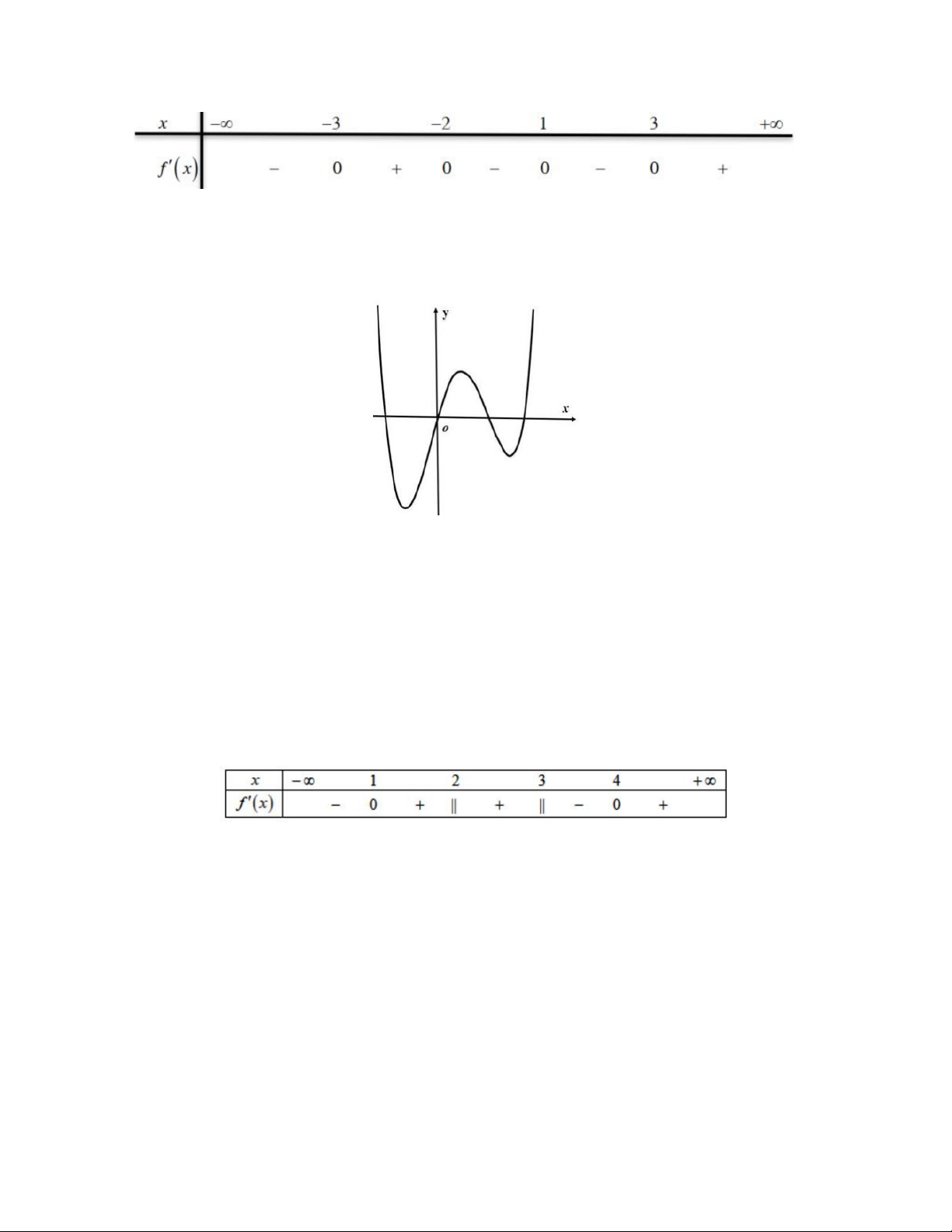
Ví dụ. Cho hàm số y  f x có đạo hàm trên
và hàm số y  f 'x có đồ thị như hình vẽ:
Tìm số điểm cực trị của hàm số y  f x ? Hướng dẫn giải
Tư đồ thị hàm số y  f 'x ta có đồ thị hàm số y  f 'x cắt trục hoành tại 4 điểm phân biệt.
Do đó phương trình f 'x  0 có bốn nghiệm phân biệt. Qua các nghiệm này
f 'x đêu đôi dâu nên số cực trị của hàm số y  f x là bốn cực trị.
Ví dụ. Cho hàm số f x liên tục trên
và có bảng xét dâu f 'x như sau:
Kết luận nào sau đây đúng?
A. Hàm số có hai điểm cực đại.
B. Hàm số có bốn điểm cực trị.
C. Hàm số có hai điểm cực trị.
D. Hàm số có hai điểm cực tiểu. Hướng dẫn giải
Dựa vào bảng xét dâu đạo hàm ta thây: hàm số đạt cực trị tại x 1; x  3; x  4 .
Tại x 1; x  4 ta thây f 'x đôi dâu tư âm sang dương nên hàm số đạt cực tiểu tại
x  1; x  4 .
Tại x  3 ta thây f 'x đôi dâu tư dương sang âm nên hàm số đạt cực đại tại x  3.
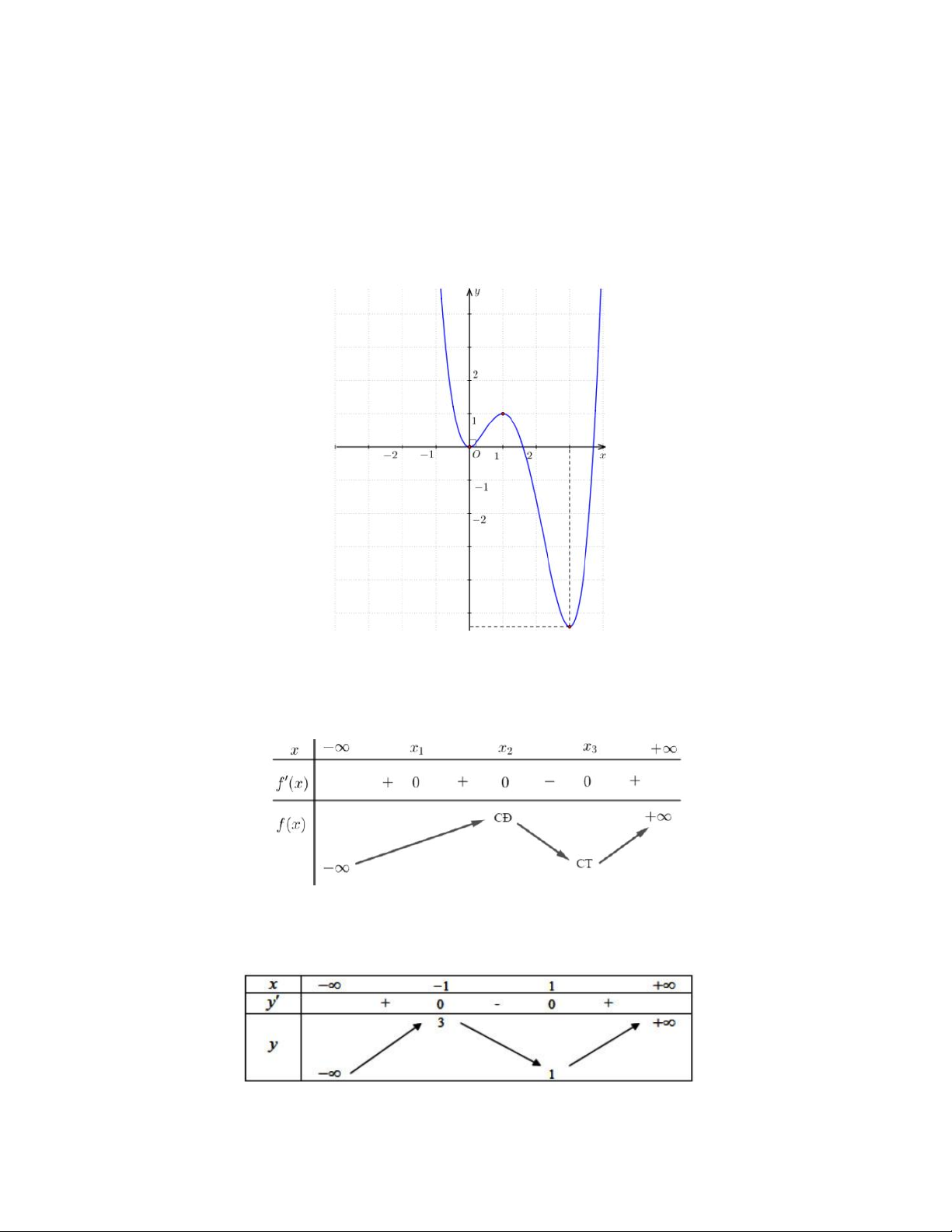
Ví dụ. Cho hàm số bậc năm y  f x và đồ thị hàm số y  f 'x trên biểu diễn bởi hình vẽ:
Em có nhận xét gì vê số điểm cực tiểu, số điểm cực đại của hàm số? Hướng dẫn giải
Tư đồ thị hàm số y  f 'x ta có bảng biến thiên của hàm số y  f x
Tư bảng biến thiên ta thây hàm số y  f x có 1 cực đại và 1 cực tiểu.
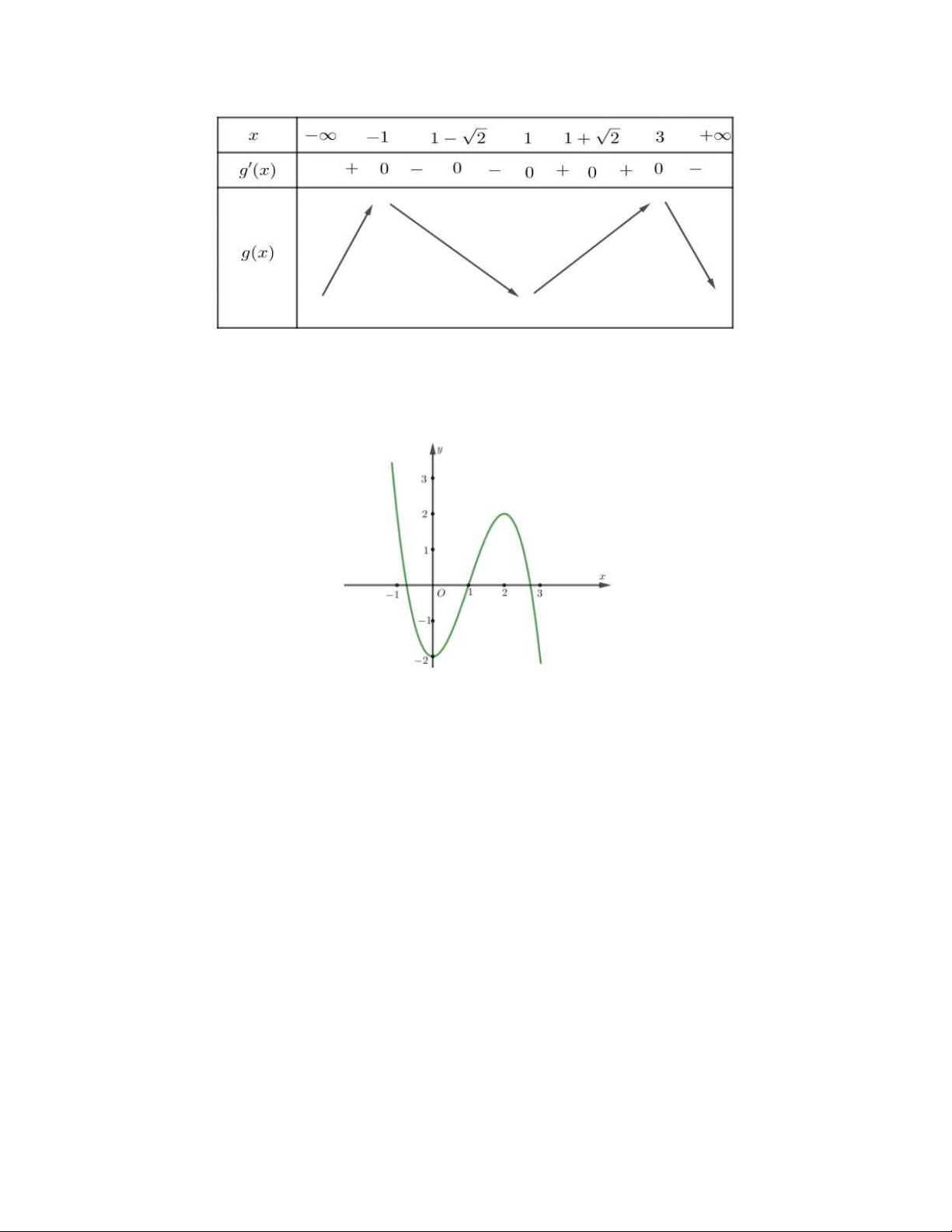
Ví dụ. Cho hàm số y  f x có bảng biến thiên như sau:
Tìm số điểm cực trị của hàm số g x  f x  2 ? Hướng dẫn giải
Số điểm cực trị của hàm số g x  f x  2  m  n
Vơi m là số điểm cực trị của hàm số y  f x  2  m  2
n là số nghiệm bội lẻ của phương trình f x  2  n  3
Suy ra số điểm cực trị của hàm số g x  f x  2  23  5
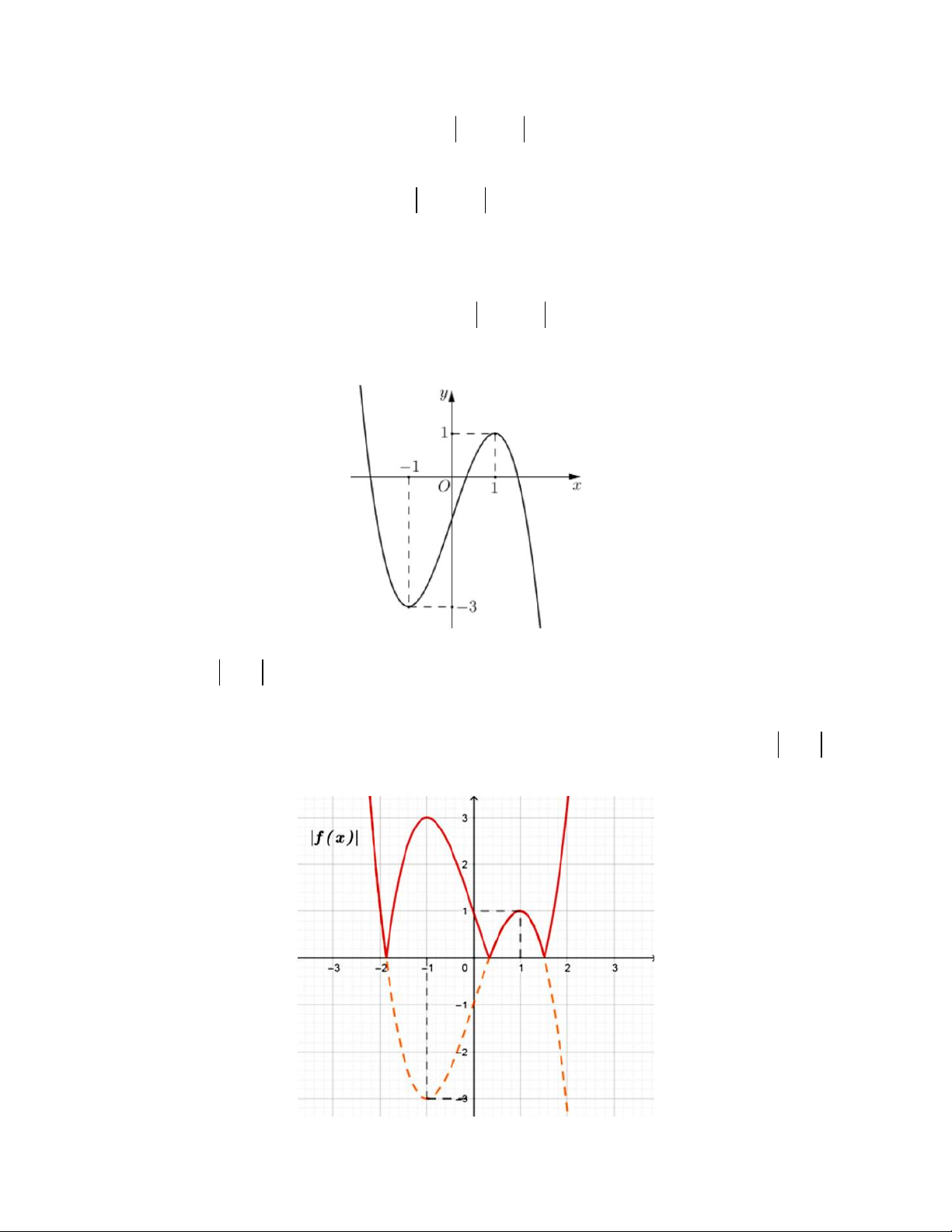
Ví dụ. Cho hàm số y  f x 3 2
 ax  bx  cx  d;a  0 có đồ thị như sau:
Hàm số y  f x có bao nhiêu điểm cực trị? Hướng dẫn giải
Tư đồ thị hàm số y  f x 3 2
 ax  bx  cx  d;a  0 suy ra đồ thị hàm số y  f x như hình vẽ:
Do đó hàm số y  f x có 5 điểm cực trị.
Ví dụ. Cho hàm số y  f x có đạo hàm trên
và có bảng xét dâu f 'x như sau:
Hỏi hàm số y  f  2x  2x có bao nhiêu điểm cực tiểu? Hướng dẫn giải
Đặt g x  f  2x  x  g x   x   f  2 2 ' 2 2 ' x  2x
Tư bảng xét dâu của hàm số f 'x có 2x  2  0
g ' x  0  g  x  f  2
x  2x   f '   2 x  2x   0 2
x  2x  2 x  1  2 
x  2x  1 x  1 2    2 x  2x  3 x  3   2x  2  0 x 1
g x    x   f  2 ' 0 2
2 ' x  2x  0 x 1 2x  2  0         f
  x  x 2 2 2 x 2x 3 ' 2  0     x  1 2x 2 0      2  
x  x   f '   2 3 2
x  2x  0  2
x  2x  2 x  1  2 x  1
x  2x  2  0    1 x  3 2
x  2x  3  0 1   x  3     x 1  x  1     x  1  x  3 2
x  2x  3  0   x  1 2
x  2x  2  0 Ta có bảng biến thiên
Tư bảng xét dâu ta suy ra hàm số y  f  2x  2x có 1 điểm cực tiểu.
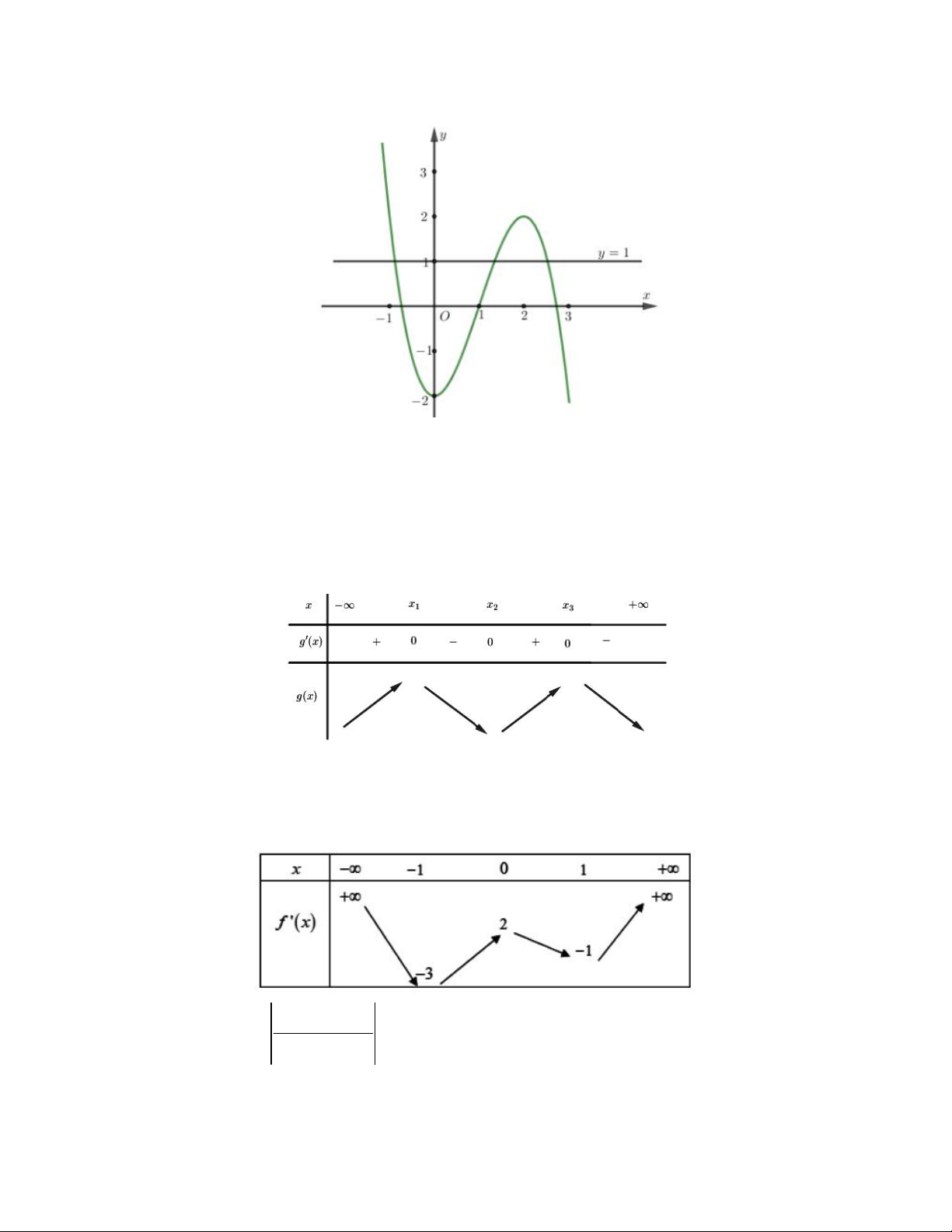
Ví dụ. Cho hàm số y  f x có đạo hàm trên . Biết rằng hàm số y  f 'x có đồ thị như sau:
Đặt g x  f x  x . Hỏi hàm số g x có bao nhiêu điểm cực trị? Hướng dẫn giải
Hàm số y  f x có đạo hàm trên
nên g x  f x  x cũng có đạo hàm trên
Ta có: g 'x  f 'x 1
 g ' x  0  f ' x 1
x  x  1;0 1   Dựa vào đồ thị 
f 'x ta có: f 'x 1  x  x  1;3 suy ra x ; x ; x là ba nghiệm 2   1 2 3
x  x  2;3  3  
phân biệt và x  x  x 1 2 3
Bảng biến thiên của hàm g x
Vậy hàm số g x  f x  x có 3 điểm cực trị.
Ví dụ. Cho hàm số f(x) liên tục trên
và có bảng biến thiên của đạo hàm như sau:   2 ln x 1 2 
Hàm số g x  f 
 có bao nhiêu điểm cực trị?  2    Hướng dẫn giải  2 ln x   1  2
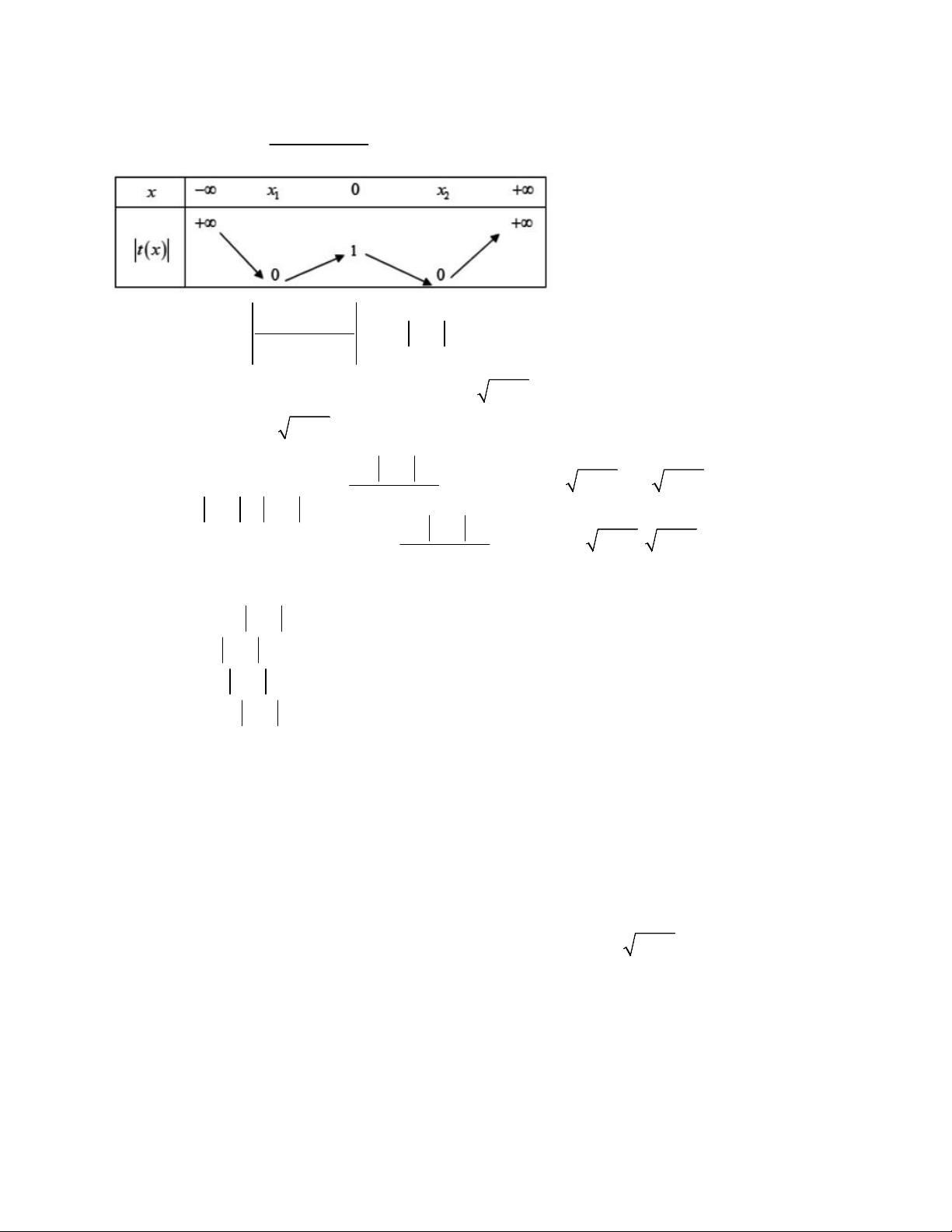
Xét hàm số t x 
, ta có bảng giá trị |t(x)| 2   2 ln x 1  2 
Ta có: g x  f 
  f t x    2   
Hàm số không có đạo hàm tại điểm 2 x   e 1 Tại mọi điểm 2
x   e 1 ta có:
 f ' t x .x  khi x    2  ;
  e 1  2e 1; 2 
g 'x  f ' t x .t x  ' x 1   f ' *
t x .x   khi x  2 2
 e 1; e 1 2   x 1  x  0 
t x  t ; t 1 1 1  1     g 'x  0 
 t  x  t ; 1 t  0 2 2  2    
 t x  t ; 0  t  1 3 3  3     
t x  t ; t 1 4  4  4   
Dựa vào bảng giá trị hàm |t| suy ra:
+ Phương trình (1), (2) vô nghiệm
+ Phương trình (3) có 4 nghiệm phân biệt khác 0
+ Phương trình (4) có hai nghiệm phân biệt khác 0 và khác các nghiệm của phương trình (3)
=> g’(x) = 0 có 7 nghiệm và qua các nghiệm này g’(x) đêu đôi dâu
Tư (*) ta thây g’(x) cũng đôi dâu khi x đi qua 2 điểm 2 x   e 1
Vậy hàm số g(x) có 9 điểm cực trị.