Tìm hiểu thuật toán K-Means Clustering | Bài báo cáo học phần Khai phá dữ liệu | Trường Đại học Phenikaa

TRƯỜNG ĐẠI HỌC PHENIKAA KHOA
CÔNG NGHỆ THÔNG TIN ⸎⸎⸎⸎⸎ BÀI TẬP LỚN
Đề tài: Tìm hiểu thuật toán K-Means Clustering
Học phần : Khai phá dữ liệu (N01)
Giảng viên : TS. Trịnh Thành
Sinh viên : Nguyễn Nam Hải - 21012056
Vi Đăng Quang - 21010583
Nguyễn Thanh Hải - 21011491
Hoàng Thế Cường - 21012482
HÀ NỘI, THÁNG 5 NĂM 2023 Mục lục
I. Giới thiệu ...................................................................................................... 3
II. Nội dung ..................................................................................................... 4
1. Phân cụm .................................................................................................. 4
2. Giới thiệu thuật toán xác định số cụm - Elbow ..................................... 4
2.1 Khởi tạo dữ liệu .................................................................................. 5
2.2 Tìm số cụm .......................................................................................... 6
3. Thuật toán K-Means ................................................................................ 7
3.1 .Khái niệm K-Means........................................................................... 7
3.2 Các bước của thuật toán K-Means Clustering ................................ 7
3.3 Phân tích toán học .............................................................................. 8
3.4 Thực nghiệm trong thuật toán ........................................................ 10
3. Đánh giá .................................................................................................. 13
III. Tổng kết ................................................................................................... 17
IV. Tài liệu tham khảo .................................................................................. 18 1
BẢNG PHÂN CÔNG CÔNG VIỆC Nguyễn Nam Hải
Code và viết báo cáo thuật toán K-Means, Tổng hợp báo cáo. Vi Đăng Quang
Code và viết báo cáo xác định số cụm Elbow Nguyễn Thanh Hải
Trình bày mở đầu và tổng kết, tổng hợp
báo cáo, làm slide thuyết trình. Hoàng Thế Cường
Tìm hiểu về ưu, nhược điểm K-Means.
Ứng dụng của K-Means trong thực tế. Danh sách hình ảnh Hình 1
Biểu đồ phân tán dữ liệu trong không gian 2 chiều Hình 2
Đồ thị hàm biến dạng của thuật toán K-Means Hình 3
Phương pháp tính khoảng cách Euclidean Hình 4
Phương pháp tính khoảng cách Square Euclidean Hình 5
Phương pháp tính khoảng cách Manhattan Hình 6
Chọn 3 điểm dữ liệu ngẫu nhiên Hình 7 Phân cụm lần 1 Hình 8 Phân cụm lần 2 Hình 9 Phân cụm lần 3 Hình 10 Phân cụm lần 4 Hình 11 Phân cụm lần 5 Hình 12
Image classification by using SVM and K-means Hình 13
Customer Segmentation using K-means Clustering Hình 14
Skin Cancer Classification Using K-Means ClusteringCustomer
Segmentation using K-means Clustering 2 I. Giới thiệu
Từ những năm đầu của thế kỉ XX, dưới sự phát triển bùng nổ của Internet và
cuộc cách mạng công nghiệp 4.0 đã thay đổi hoàn toàn cách các doanh nghiệp
vận hành thông qua các công nghệ. Khai phá dữ liệu đã trở thành một khía
cạnh quan trọng của các doanh nghiệp và ngành công nghiệp hiện đại, cho
phép các tổ chức đưa ra quyết định sáng suốt dựa trên những hiểu biết dựa trên dữ liệu.
Khai phá dữ liệu (Data mining) là quá trình phân loại, sắp xếp các tập hợp dữ
liệu lớn để xác định các mẫu và thiết lập các mối liên hệ nhằm giải quyết các
vấn đề nhờ phân tích dữ liệu.
Trong nội dung của đề tài này, chúng ta sẽ tập trung nghiên cứu các vấn đề liên
quan đến thuật toán K-Means (một trong những thuật toán phổ biến nhất trong
lĩnh vực phân cụm), mang lại rất nhiều hiệu quả trong cả nghiên cứu lý thuyết và ứng dụng thực tế. 3 II. Nội dung 1. Phân cụm
Phân cụm (Clustering) là kỹ thuật phân tích dữ liệu để tập hợp các phần tử dữ
liệu giống nhau vào một cụm. Các phần tử trong cùng một cụm thường có độ
tương đồng cao hơn so với các phần tử ở các cụm khác. Clustering là một trong
những nhiệm vụ chính trong khai phá dữ liệu thám hiểm và cũng là một kỹ
thuật được sử dụng trong phân tích dữ liệu thống kê.
Machine Learning ngày càng tiến bộ và mang đến nhiều giải pháp cho bài toán
Clustering. Trong số đó, có một số mô hình nổi bật như Gaussian Mixture
Model, Mean Shift, DBSCAN, K-Means, .v.v.
Trong bài toán phân cụm có 2 vấn đề lớn cần giải quyết: - Xác định số cụm
- Xác định đối tượng thuộc về 1 cụm cụ thể
2. Giới thiệu thuật toán xác định số cụm - Elbow
Trong thuật toán K-Means thì chúng ta cần phải xác định trước số cụm. Câu hỏi
đặt ra là đâu là số lượng cụm cần phân chia tốt nhất đối với một bộ dữ liệu cụ
thể? Phương pháp Elbow là một cách giúp ta lựa chọn được số lượng các cụm
phù hợp dựa vào đồ thị trực quan hoá bằng cách nhìn vào sự suy giảm của hàm
biến dạng và lựa chọn ra điểm khuỷ tay (elbow point). Để tìm hiểu phương pháp
Elbow, bên dưới chúng ta cùng thử nghiệm vẽ biểu đồ hàm biến dạng bằng
cách điều chỉnh số lượng cụm của thuật toán k-Means. 4
2.1 Khởi tạo dữ liệu
Trong thuật toán K-means, việc khởi tạo và làm sạch dữ liệu là một bước rất
quan trọng. Điều này được thực hiện bằng cách chọn ngẫu nhiên một số điểm
dữ liệu làm các tâm ban đầu cho các cụm. Các điểm dữ liệu khác sẽ được phân
vào các cụm tương ứng dựa trên khoảng cách đến các tâm này.
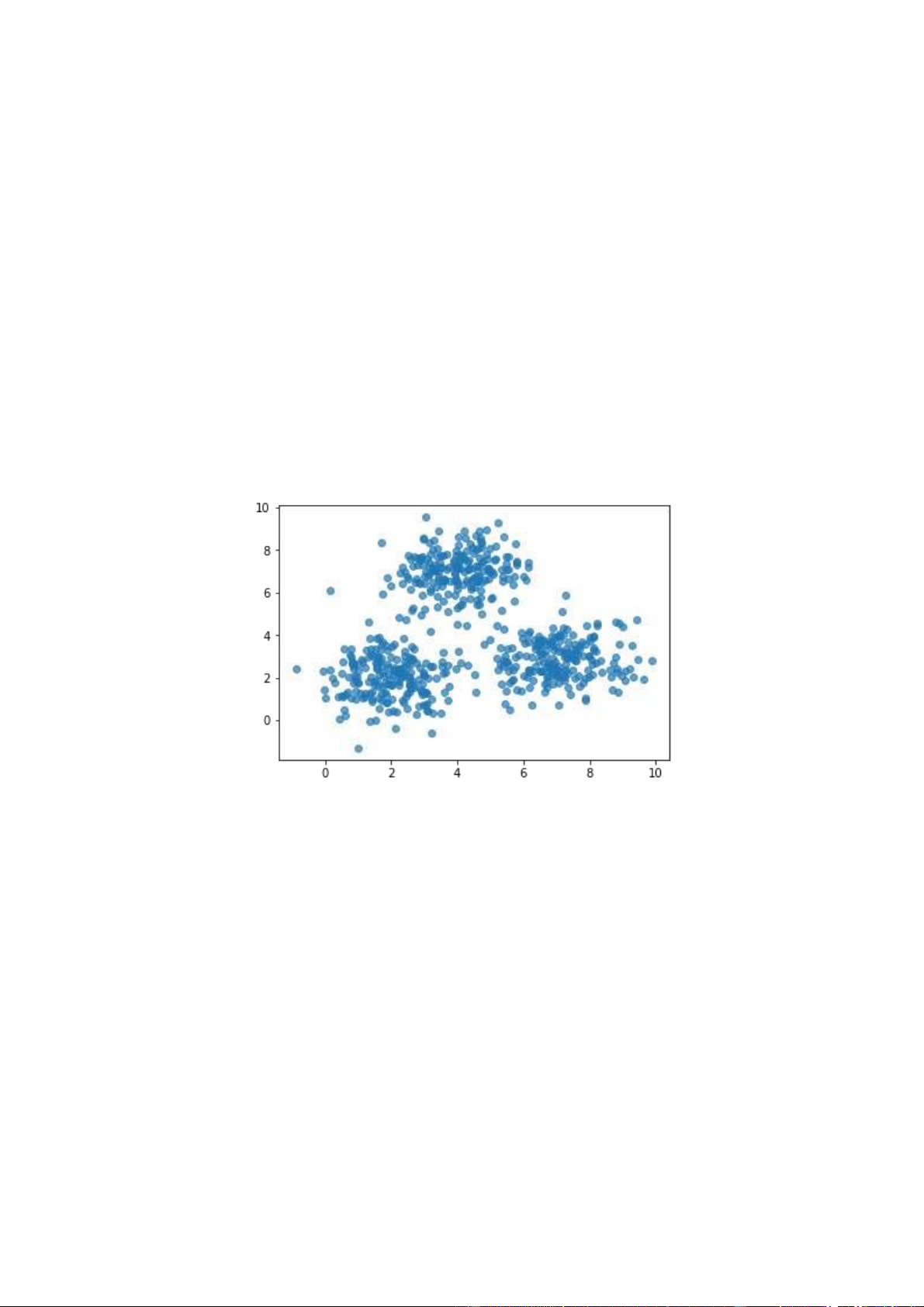
Trong trường hợp này, chúng tôi đã tạo ra 600 điểm ngẫu nhiên trong không gian 2 chiều.
Hình 1: Biểu đồ phân tán dữ liệu trong không gian 2 chiều 5 2.2 Tìm số cụm
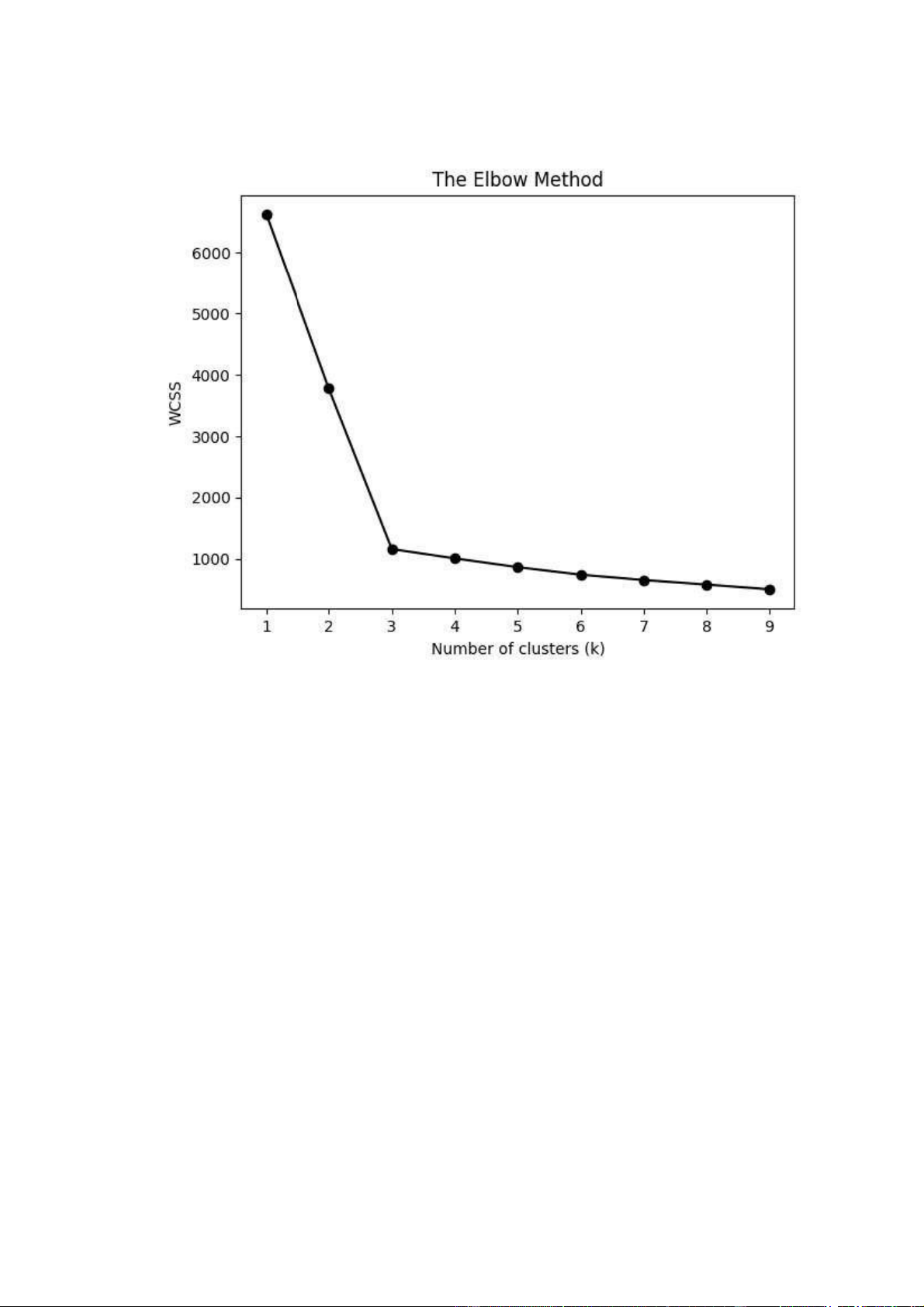
Hình 2: Đồ thị hàm biến dạng của thuật toán K-Means
Điểm khuỷ tay là điểm mà ở đó tốc độ suy giảm của hàm biến dạng sẽ thay đổi
nhiều nhất. Tức là kể từ sau vị trí này thì gia tăng thêm số lượng cụm cũng
không giúp hàm biến dạng giảm đáng kể. Nếu thuật toán phân chia theo số
lượng cụm tại vị trí này sẽ đạt được tính chất phân cụm một cách tổng quát nhất
mà không gặp các hiện tượng vị khớp (overfitting). Trong hình trên thì ta thấy
vị trí của điểm khuỷ tay chính là k=3 vì khi số lượng cụm lớn hơn 3 thì tốc độ
suy giảm của hàm biến dạng dường như không đáng kể so với trước đó.
Phương pháp Elbow là một phương pháp thường được sử dụng để lựa chọn số
lượng cụm phân chia hợp lý dựa trên biểu đồ, tuy nhiên có một số trường hợp
chúng ta sẽ không dễ dàng phát hiện vị trí của Elbow, đặc biệt là đối với những
bộ dữ liệu mà quy luật phân cụm không thực sự dễ dàng được phát hiện. Nhưng 6
nhìn chung thì phương pháp Elbow vẫn là một phương pháp tốt nhất được ứng
dụng trong việc tìm kiếm số lượng cụm cần phân chia.
3. Thuật toán K-Means
3.1 .Khái niệm K-Means
Phân cụm K-Means là một thuật toán Học máy không giám sát, thuật toán này
nhóm tập dữ liệu chưa được gắn nhãn thành các cụm khác nhau.
Học máy không giám sát là quá trình dạy máy tính sử dụng dữ liệu chưa được
gắn nhãn, chưa được phân loại và cho phép thuật toán hoạt động trên dữ liệu
đó mà không cần giám sát. Không có bất kỳ đào tạo dữ liệu nào trước đó, công
việc của học máy trong trường hợp này là sắp xếp dữ liệu chưa được sắp xếp
theo các điểm tương đồng, mẫu và biến thể.
Trong thuật toán K-means clustering, chúng ta không biết nhãn (label) của từng
điểm dữ liệu. Mục đích là làm thể nào để phân dữ liệu thành các cụm (cluster)
khác nhau sao cho dữ liệu trong cùng một cụm có tính chất giống nhau.
3.2 Các bước của thuật toán K-Means Clustering
Trong thuật toán k-Means mỗi cụm dữ liệu được đặc trưng bởi một tâm
(centroid). Tâm là điểm đại diện nhất cho một cụm và có giá trị bằng trung bình
của toàn bộ các điểm quan sát nằm trong cụm. Chúng ta sẽ dựa vào khoảng
cách từ mỗi điểm quan sát tới các tâm để xác định nhãn cho chúng trùng thuộc
về tâm gần nhất. Ban đầu thuật toán sẽ khởi tạo ngẫu nhiên một số lượng xác
định trước tâm cụm. Sau đó tiến hành xác định nhãn cho từng điểm dữ liệu và
tiếp tục cập nhật lại tâm cụm. Thuật toán sẽ dừng cho tới khi toàn bộ các điểm
dữ liệu được phân về đúng cụm hoặc số lượt cập nhật tâm chạm ngưỡng. 7
Đầu vào: Dữ liệu X và số lượng cluster cần tìm K.
Đầu ra: Các center M và label vector cho từng điểm dữ liệu Y.
1. Chọn K điểm bất kỳ làm các center ban đầu.
2. Phân mỗi điểm dữ liệu vào cluster có center gần nó nhất.
3. Nếu việc gán dữ liệu vào từng cluster ở bước 2 không thay đổi so với
vòng lặp trước nó thì ta dừng thuật toán.
4. Cập nhật center cho từng cluster bằng cách lấy trung bình cộng của tất
các các điểm dữ liệu đã được gán vào cluster đó sau bước 2. 5. Quay lại bước 2.
3.3 Phân tích toán học
Mục đích cuối cùng của thuật toán phân nhóm này là: từ dữ liệu đầu vào và số
lượng nhóm chúng ta muốn tìm, hãy chỉ ra tâm của mỗi nhóm và phân các điểm
dữ liệu vào các nhóm tương ứng.
Trong thuật toán K-means, độ đo khoảng cách được sử dụng để xác định độ
tương đồng giữa các phần tử và ảnh hưởng đến hình dạng của các cụm. Độ đo
khoảng cách được sử dụng phải đáp ứng được một số yêu cầu nhất định. Nó
phải là một hàm số phi tuyến, không âm và có tính đối xứng.
Có thể dùng nhiều phương pháp để đo khoảng cách như:
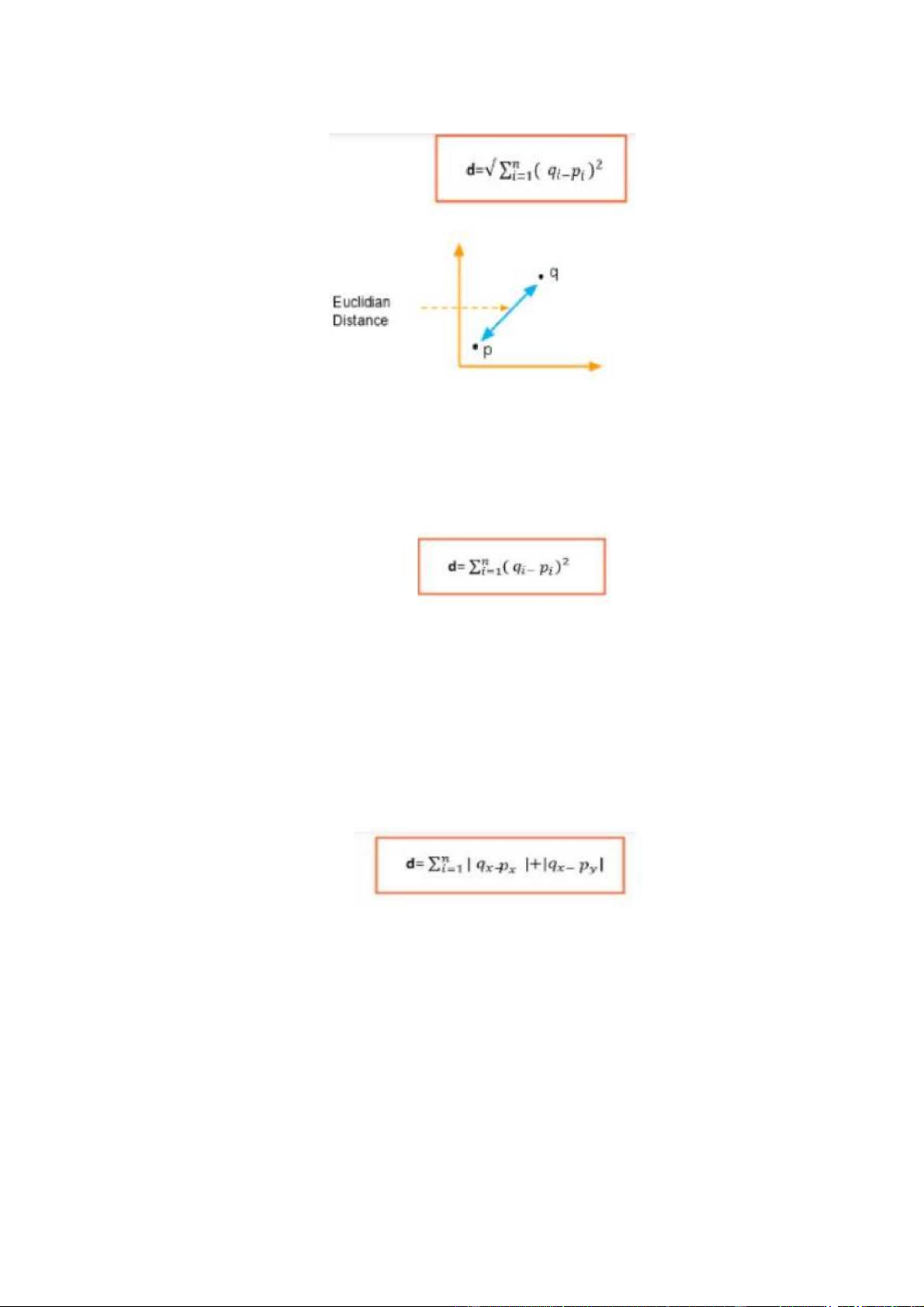
- Euclidean: Trường hợp phổ biến nhất là xác định khoảng cách giữa hai
điểm. Nếu chúng ta có điểm P và điểm Q, khoảng cách euclidean là một
đường thẳng bình thường. Đó là khoảng cách giữa hai điểm trong không gian Euclide. 8
Hình 3: Phương pháp tính khoảng cách Euclidean
- Squared Euclidean: Điều này giống với phép đo khoảng cách Euclidean
nhưng không lấy căn bậc hai ở cuối.
Hình 4: Phương pháp tính khoảng cách Square Euclidean
- Manhattan: Khoảng cách Manhattan là tổng đơn giản của các thành phần
ngang và dọc hoặc khoảng cách giữa hai điểm được đo dọc theo trục vuông góc.
Hình 5: Phương pháp tính khoảng cách Manhattan
Tùy thuộc vào độ đo khoảng cách được sử dụng, các cụm có thể có hình dạng
khác nhau. Do đó, lựa chọn độ đo khoảng cách phù hợp là rất quan trọng trong thuật toán. 9
3.4 Thực nghiệm trong thuật toán
3.4.1 Chọn K điểm bất kỳ làm các tâm ban đầu
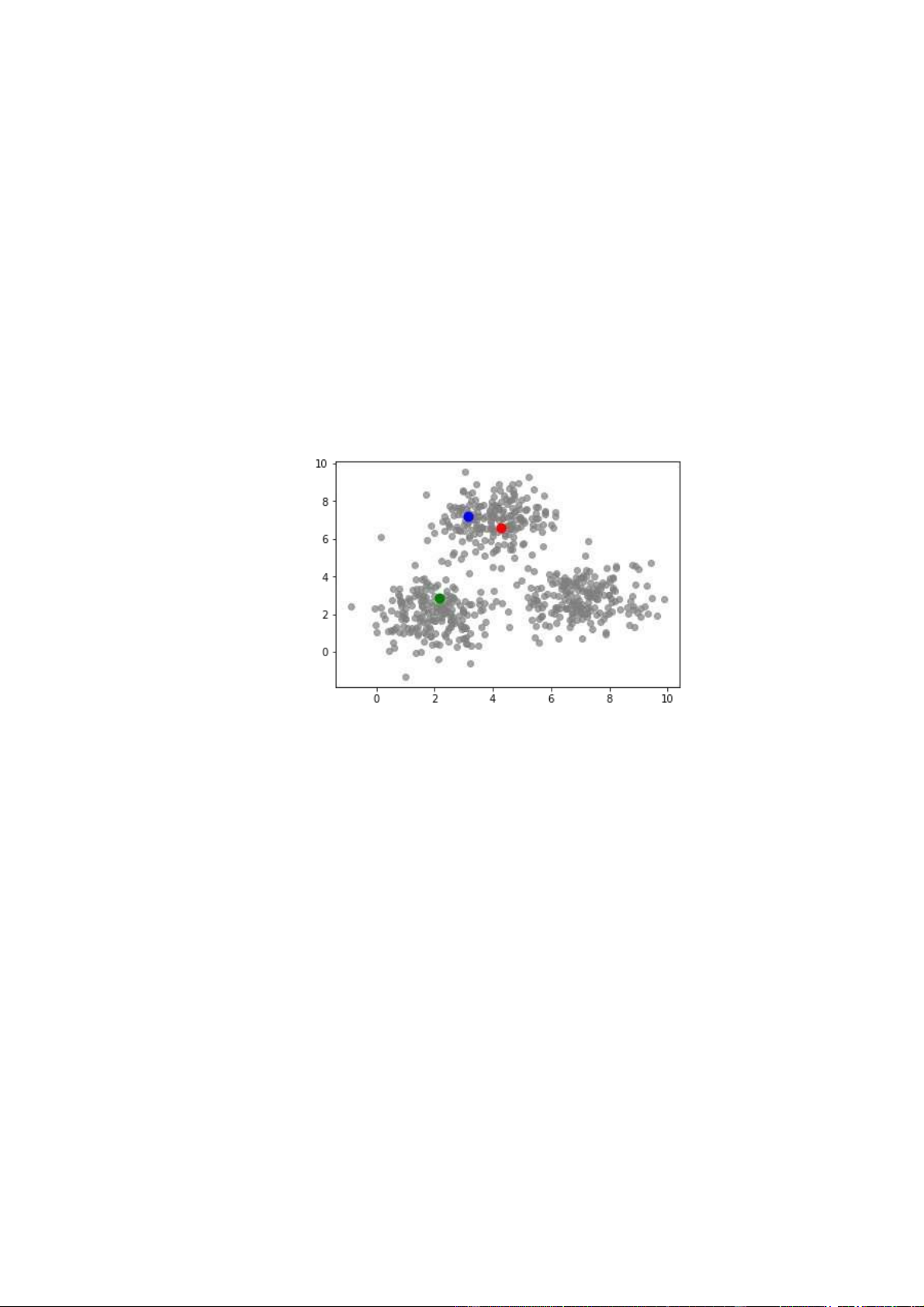
Bước đầu tiên trong phân cụm K-means là phân bổ trọng tâm một cách ngẫu
nhiên. Sau khi áp dụng Elbow, chúng ta tìm ra được số tâm phù hợp với bài
toán là K = 3. Ba điểm được gán là trọng tâm. Lưu ý rằng các điểm có thể ở bất
kỳ đâu vì chúng là các điểm ngẫu nhiên. Chúng được gọi là trọng tâm, nhưng
ban đầu, chúng nhất thiết không phải là điểm trung tâm của một tập dữ liệu nhất định.
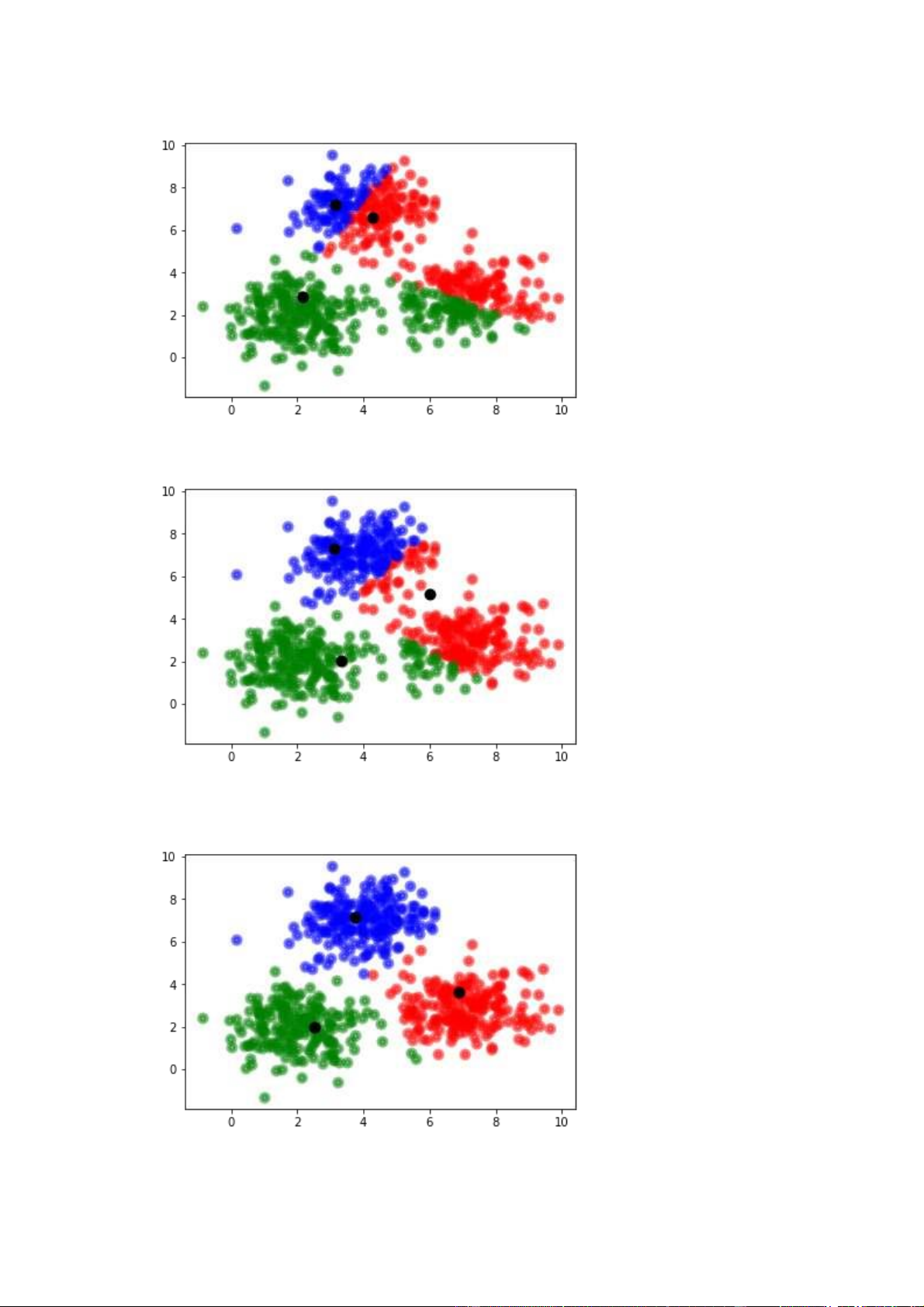
Hình 6: Chọn 3 điểm dữ liệu ngẫu nhiên
3.4.2 Phân mỗi điểm dữ liệu vào cụm có tâm gần nó nhất
Sau khi chọn được các tâm cụm, chúng ta tiến hành phân mỗi điểm dữ liệu vào
cụm có tâm gần nó nhất.
Đầu tiên, ta tính toán khoảng cách giữa các điểm dữ liệu và tâm, sau đó chúng
ta chọn cụm có tâm gần nhất với điểm dữ liệu để phân loại điểm đó vào cụm
đó. Việc phân loại này được thực hiện bằng cách gán nhãn cho từng điểm dữ
liệu, cho biết nó thuộc vào cụm nào. 10
Hình 7: Phân cụm lần 1
3.4.3 Cập nhật lại tâm và thực hiện lại bước 3.4.2
Hình 8: Phân cụm lần 2
Hình 9: Phân cụm lần 3 11
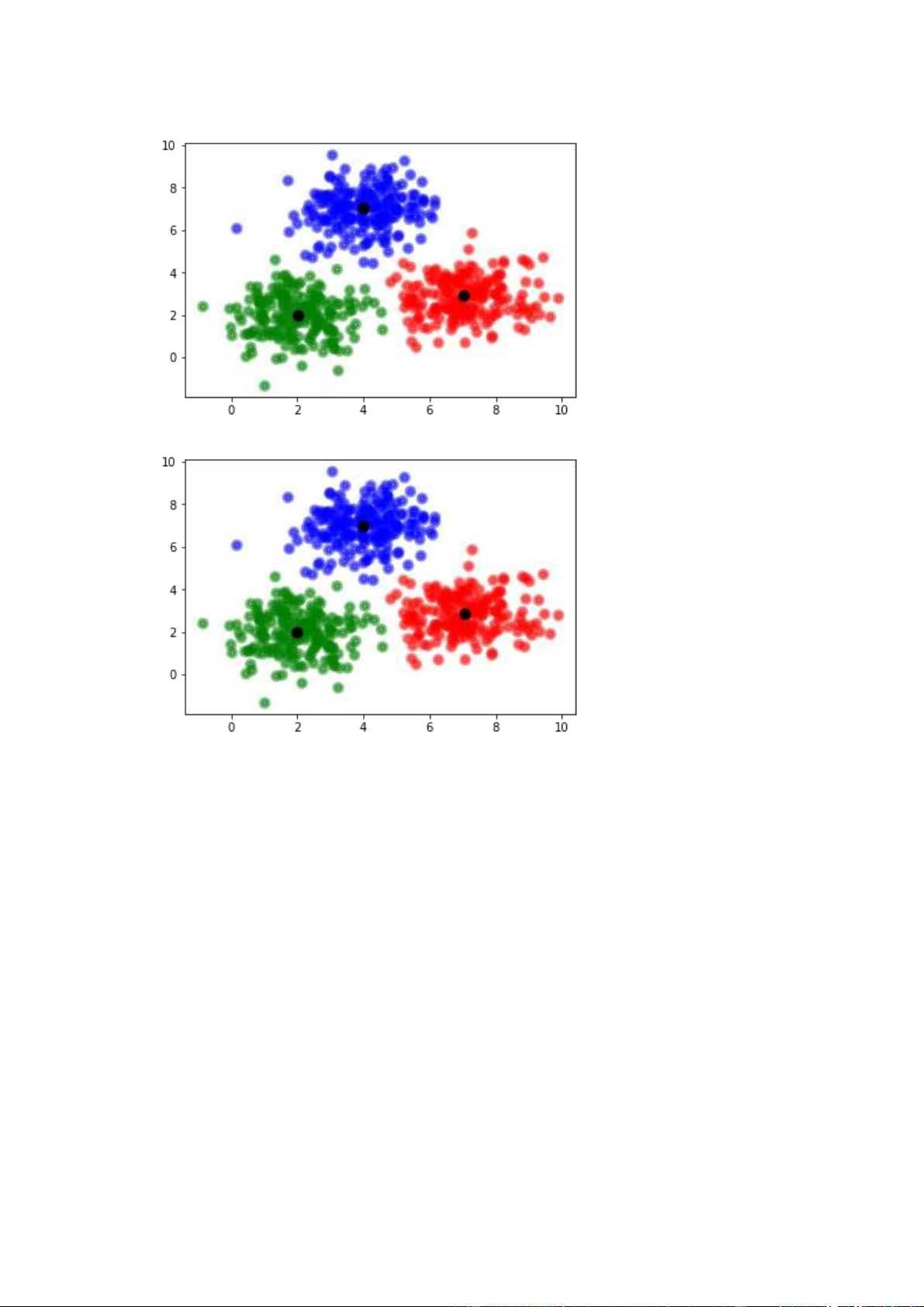
Hình 10: Phân cụm lần 4
Hình 11: Phân cụm lần 5
Khi các tâm của các cụm ổn định, nghĩa là chúng không thay đổi so với lần gần
nhất, có thể hiểu là thuật toán đã hội tụ và đạt được một giải pháp tối ưu.
Khi đó, thuật toán sẽ dừng lại và trả về kết quả. 12 3. Đánh giá
Những ưu điểm của thuật toán K-means:
¥ Tộc độ xử lý nhanh: K-means là một thuật toán phân cụm đơn giản với
tốc độ xử lý nhanh hơn so với mốt số thuật toán phân cụm khác như
hierarchical clustering, DBSCAN(Density-Based Spatial Clustering
of Application with Noise) hay spectral clustering trong một số
trường hợp. Nó có thể xử lý các tập dự liệu lớn và phân cụm nhanh chóng.
¥ Hiệu quả trong việc phân cụm dữ liệu: K-means có thể phân cụm dữ
liệu một cách hiệu quả với một số lượng cụm nhất định. Nó có thể xử
lý các tập dữ liệu phực tạp và phân cụm chúng thành các nhóm có
tính tương đồng với nhau.
¥ Dễ dàng triển khai: K-means là một thuật toán đơn giản và dễ triển
khai Nó có không yêu cầu nhiều thông số đầu vào và có thể được sử
dụng trong nhiều ứng dụng khác nhau.
¥ Dễ dàng hiểu và giải thích: Kết quả phân cụm của K-means rất dễ hiểu
và giải thích. Nó cho phép người dùng dễ dàng phân tích và hiểu rõ
hơn về dữ liệu mà họ đang làm việc
Tuy nhiên, thuật toán K-means cũng có những hạn chế riêng:
¥ Tâm của cụm sẽ bị ảnh hưởng bởi các điểm khởi tạo tâm cụm ngẫu nhiên
đầu tiên. Việc lấy tâm ngẫu nhiên sẽ có thể khiến các cụm không chính xác.
¥ Phải chỉ ra số lượng cluster trước khi thực hiện phân nhóm.
¥ Không thể xử lý tốt với các cụm có kích thước, mật độ và hình dạng khác nhau. 13
Thuật toán K-means có nhiều ứng dụng trong thực tế, nó có thể áp dụng trong
nhiều lĩnh vực khác nhau để tìm ra các nhóm và mẫu dữ liệu đáng chú ý để giúp
đưa ra những quyết định trong thực tế:
1. Phân tích hình ảnh, video: Image Classification Based on K-means and SVM
Thuật toán k-means clustering được sử dụng để phân đoạn ảnh, tức là
chia ảnh thành nhiều vùng khác nhau. Mục tiêu của việc phân đoạn ảnh
là thay đổi cách biểu diễn của ảnh thành một cái gì đó có ý nghĩa hơn và
dễ phân tích hơn. Nó thường được sử dụng để xác định vị trí của các đối
tượng và ranh giới trong ảnh.
Hình 12: Image classification by using SVM and K-means 14
2. Phân tích khách hàng: Trong giao dịch ngân hàng, việc phân loại dữ liệu
khách hàng là đặc biết quan trọng, thường được dựa vào đó để đưa ra các
chính sách chung cho toàn hệ thống hay là có những chính sách chăm sóc
đến từng khách hàng. Một vài cách phân lọa dựa trên hành vì người dùng
như: lịch sử thanh toán, hoạt động trên ứng dụng website hay trên các nền tảng ATM.
Hình 23: Customer Segmentation using K-means Clustering 15
3. Phân tích dữ liệu y tế: Chẩn đoán ung thư
Trong y tế, K-Means có thể được sử dụng để phân loại bệnh nhân theo các
tiêu chí khác nhau, ví dụ như phát hiện bệnh tật dựa vào triệu chứng, kết quả
xét nghiệm, v.v. Điều này có thể giúp cho việc chẩn đoán, điều trị và phòng ngừa bệnh tật,..
Hình 34: Skin Cancer Classification Using K-Means ClusteringCustomer Segmentation
using K-means Clustering 16 III. Tổng kết
Qua bài báo cáo, chúng ta đã tìm hiểu rõ hơn về cách thức vận hành, ý nghĩa và
những ứng dụng của thuật toán K-Means trong lĩnh vực Machine Learning nói
chung và bài toán phân cụm (Clustering) nói chung. K-Means là một thuật toán
hiệu quả và đơn giản để triển khai, nhưng là một công cụ mạnh mẽ cho các nhà
phân tích dữ liệu và được sử dụng rộng rãi trong các ứng dụng thực tế. Nó hoạt
động tốt với các tập dữ liệu lớn và cho phép phân tích định tính và định lượng
của dữ liệu. Tuy nhiên, nó cũng có một số hạn chế nhất định đòi hỏi người thực
hiện phải có kinh nghiệm và kĩ năng để có thể triển khai bài toán tối ưu nhất. 17
IV. Tài liệu tham khảo
[1] Prateek Majumder. “K-Means clustering with Mall Customer
Segmentation Data”. [Published On May 25, 2021]
https://www.analyticsvidhya.com/blog/2021/05
[2] International Journal of Technical Research and Applications e-ISSN:
2320-8163, www.ijtra.com Volume 5, Issue 1[Jan – Feb 2017], PP. 62-65.
“Skin Cancer Classification Using K-Means Clustering”.
https://www.ijtra.com/view/skin-cancer-classification-using-k- meansclustering.pdf
[3] Jakkrich Laosai and Kosin Chamnongthai. “Acute leukemia classification
by using SVM and K-Means clustering”.
Date Added to IEEE Xplore: 16 October 2014
https://ieeexplore.ieee.org/abstract/document/6925840
[4] Pham Dinh Khanh, DeepAI KhanhBlog. “Các bước trong thuật toán K-
Means Clustering ” [Post on 2021]
https://phamdinhkhanh.github.io/deepai-book/ch_ml/KMeans 18