



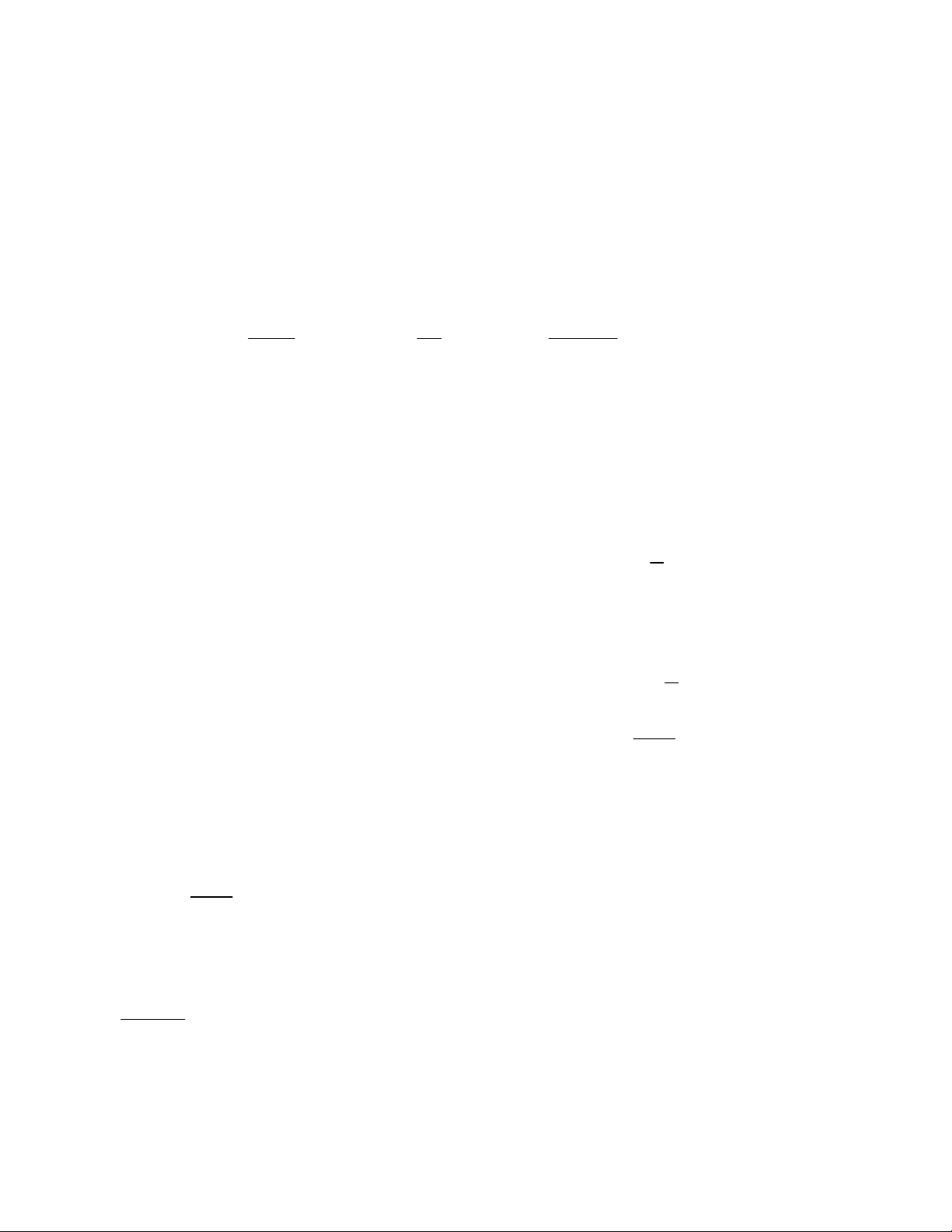



Preview text:
Chuyên đề Toán 12: Tìm tham số m để hàm số đồng biến
nghịch biến trên khoảng
A. Điều kiện đủ để hàm số đơn điệu
Giả sử hàm số y f x có đạo hàm trên khoảng K . Khi đó:
Nếu f 'x 0; x
K và f ' x 0 chỉ tại hữu hạn điểm thuộc K thì hàm số f x
đồng biến trên khoảng K .
Nếu f 'x 0; x
K và f ' x 0 chỉ tại hữu hạn điểm thuộc K thì hàm số f x
nghịch biến trên khoảng K .
B. Tìm tham số m để hàm số bậc ba đồng biến, nghịch biến trên khoảng Nhắc lại kiến thức
Xét tam thức bậc hai 2
y ax bx ;
c a 0 (đã học ở lớp 10) y x a 0 0 0 y x a 0 0; 0
Xét bài toán 1. Tìm điều kiện của tham số m để hàm số bậc ba đồng biến, nghịch biến trên . Phương pháp giải Cho hàm số bậc ba 3 2
y ax bx cx d;a 0 chứa tham số m Hàm số đồng biến trên a
y ' 0x 3 0 2
3ax 2bx c 0 x ' y 0 '
Hàm số nghịch biến trên a
y ' 0x 3 0 2
3ax 2bx c 0 x ' y 0 '
Chú ý: Trong trường hợp hệ số a chứa tham số m , ví dụ y m 3 2
1 x mx 2x 3
ta cần xét a 0 trước.
Số giá trị nguyên trên đoạn a;b bằng b a 1.
Ví dụ. Có bao nhiêu giá trị nguyên của tham số m để hàm số 3 2
y 2x 3mx 6mx 2 đồng biến trên ? Hướng dẫn giải Ta có: 2
y ' 6x 6mx 6m Hàm số đồng biến trên
y ' 0 x a 6 0 2
' m m y 9 36 0 ' 0 m 4
Kết hợp với m . Vậy có 5 giá trị nguyên của tham số m thỏa mãn yêu cầu đề bài. Ví dụ. Cho hàm số 3 2
y x mx 4m 9 x 5 với m là tham số. Có bao nhiêu giá
trị nguyên của m để hàm số nghịch biến trên khoảng ; ? Hướng dẫn giải Ta có: 2 y ' 3
x 2mx 4m 9
Hàm số nghịch biến trên khoảng ;
y ' 0 x a y 3 0 ' 9 m 3 2 ' m m y 3 4 9 0 ' Kết hợp với m
Suy ra có 7 giá trị của tham số m thỏa mãn yêu cầu đề bài.
Ví dụ. Gọi S là tập hợp các giá trị nguyên của tham số m để hàm số 3 x 2 y
mx 4x 3 luôn tăng trên
. Số phần tử của tập hợp S là bao nhiêu? 3 Hướng dẫn giải Ta có: 2
y ' x 2mx 4
Hàm số đồng biến trên y ' 0 x a y 1 0 ' 2 m 2 2 ' m y 4 0 '
Kết hợp với m m2;1;0;1; 2
Vậy số phần tử của tập hợp S là 5.
Ví dụ. Tìm tất cả các giá trị của tham số m để hàm số 1
y m 2 3
x m 2 2
x m 8 2
x m 1 luôn nghịch biến trên ? 3 Hướng dẫn giải
Với m 2 ta có y 1
0x 3 (hàm số này luôn nghịch biến trên tập số thực)
Với m 2 ta có y m 2 '
2 x 2m 2 x m 8
Hàm số nghịch biến trên y ' 0 x
a m y 2 0 ' 2 m 2 ' y 0 '
Kết hợp với m m2;1;0;1; 2
Vậy số phần tử của tập hợp S là 5.
Xét bài toán 2. Tìm điều kiện của tham số m để hàm số y f ;xm đồng biến
hoặc nghịch biến trên một khoảng (hoặc nửa khoảng, đoạn hoặc nửa đoạn). Phương pháp giải
Xét hàm số y f ;xm ta tính y ' f ' ;xm
Hàm số đồng biến trên D y ' 0 x D
Hàm số nghịch biến trên D y ' 0 x D
Cô lập tham số m và đưa bất phương trình y' 0; y' 0 về dạng m y' hoặc m y '. Sử dụng tính chất
Bất phương trình m y '; x
D m max f x D
Bất phương trình m y'; x
D m min f x D
Chú ý: Với hàm số 3 2
y ax bx cx d;a 0 liên tục trên tập số thực nên hàm số
đồng biến và nghịch biến trên khoảng a;b thì nó đồng biến trên đoạn a;b .
Lưu ý: Bất đẳng thức CauChy (AM – GM): Cho các số thực không âm a ;a ;a ;. .a 1 2 3 n thì ta có:
a a a . . n
a n a a a a n . . . . . 1 2 3 1 2 3 n
Dấu bằng xảy ra khi a a a . . a 1 2 3 n MaxF x 2 2 a b c
Với hàm số lượng giác F x asin x bcos x c thì . MinF x 2 2
a b c
Ví dụ. Tìm giá trị của tham số m để hàm số 1 3
y x m 2 1 x 2
m 2m x 3 3
nghịch biến trên khoảng 1; 1 ? Hướng dẫn giải Ta có: 2
y x m x 2 ' 2 1 m 2m Xét 2
y x m x 2 ' 0 2 1
m 2m 0 x m ; m x m 2
Hàm số luôn nghịch biến trong khoảng ; m m 2; m
Để hàm số nghịch biến trên khoảng (−1;1) thì 1; 1 ; m m 2 m 1 Nghĩa là m 1 1 m 2 1 1 m 1 . 1 m 2 Ví dụ. Cho hàm số 3 2
y x mx m . Tìm điều kiện cần và đủ của tham số m để
hàm số nghịch biến trên 0;2 . Hướng dẫn giải
Tập xác định D Ta có: 2
y ' 3x 2mx
Để hàm số đã cho nghịch biến trên 0;2 thì y ' 0; x 0;2 2
3x 2mx 0; x 0;2 2 3 2 2mx 3
x m x ; x 0;2 2 3 m min x 3 0;2 2
Vậy giá trị cần tìm là m 3 .
Ví dụ. Tìm tập hợp tất cả các giá trị thực của tham số m để hàm số 3 2
y x 3x 4 m x đồng biến trên khoảng 2; ? Hướng dẫn giải
Tập xác định D Ta có: 2
y ' 3x 6x 4 m
Hàm số đồng biến trên khoảng 2; y ' 0; x 2; 2
m 3x 6x 4; x 2;
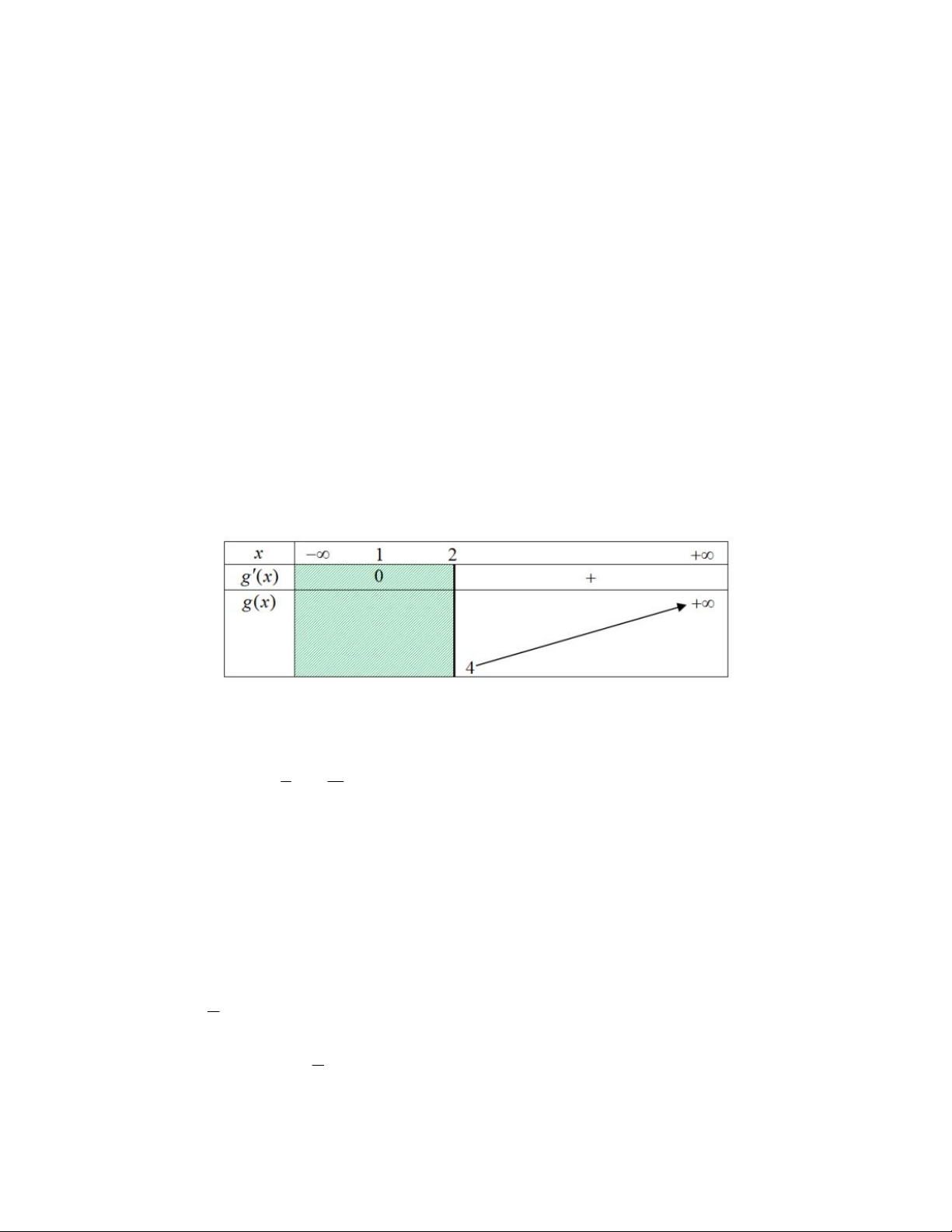
Xét hàm số g x 2
3x 6x 4 trên khoảng 2; .
Ta có: g 'x 6x 6; g 'x 0 x 1 Ta có bảng biến thiên
Dựa vào bảng biến thiên ta có: m g x;; x
2; m 4
Vậy m 4 thỏa mãn yêu cầu bài toán. Ví dụ. Hàm số 1 3 m 2
y x x x 6 đồng biến trên nửa khoảng 1; khi nào? 3 2 Hướng dẫn giải Ta có: 2
y ' x mx 1
Để hàm số đã cho đồng biến trên nửa khoảng 1; khi đó: y ' 0; x 1; 2
x mx 1 0; x 1; 1
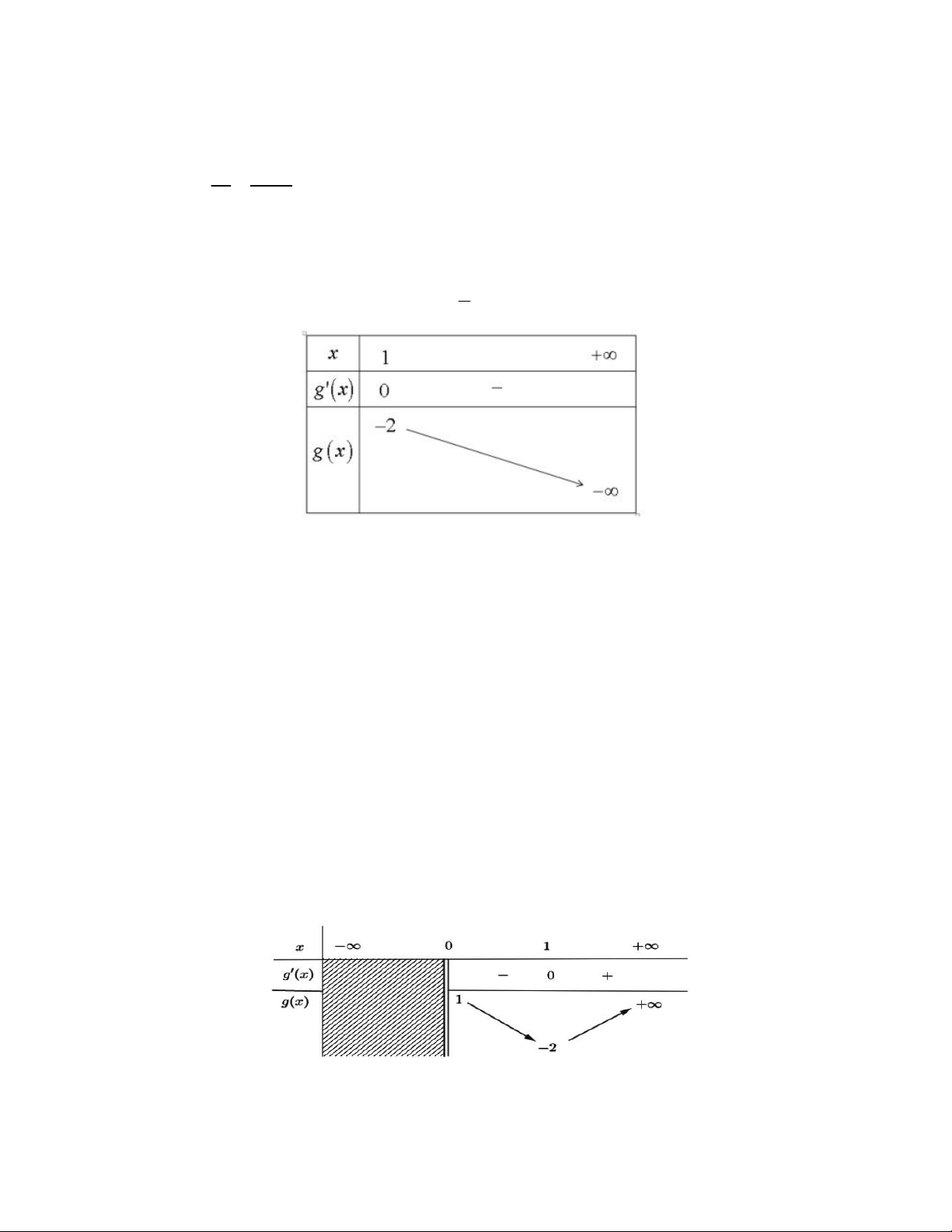
m x ; x 1; x Xét hàm số 1
g x x trên nửa khoảng 1; ta có: x 2 1 1 ' 1 x g x 2 2 x x g x x 1 '
0 x 1
Bảng biến thiên của hàm số 1
g x x trên nửa khoảng 1; là: x
Từ bảng biến thiên suy ra max g x g 1 2 1;
Vậy m g x; x
1; khi và chỉ khi m 2 .
Ví dụ. Xác định điều kiện của tham số m để hàm số
y f x 3 2
x 3x 2m
1 x 1 nghịch biến trên khoảng 0; ? Hướng dẫn giải
Tập xác định D Ta có: 2 y ' 3
x 6x 2m 1
Hàm số đã cho nghịch biến trên khoảng 0; y ' 0; x
0; khi và chỉ khi 2
2m 3x 6x 1; x 0;
Xét hàm số g x 2
3x 6x 1 trên 0; ta có bảng biến thiên như sau:
Dựa vào bảng biến thiên ta có:
min g x 2 0;
Do đó 2m min g x 2m 2 m 1 0;
Vậy m 1 thỏa mãn yêu cầu bài toán.
C. Tìm tham số m để hàm phân thức đồng biến, nghịch biến trên khoảng Xét hàm số ax b y . TXĐ d D ta có: ' ad bc y cx d c cx d 2
Nếu ad bc thì hàm số đã cho suy biến thành hàm hằng. Do đó:
Hàm số đồng biến trên mỗi khoảng xác định của nó ad bc 0 .
Hàm số nghịch biến trên mỗi khoảng xác định của nó ad bc 0 .
ad bc 0
Hàm số đồng biến trên miền D ;i j
y ' 0; x ;i j d ;i j c
ad bc 0
Hàm số nghịch biến trên miền D ;i j
y ' 0; x ;i j d ;i j c
Ví dụ. Xác định giá trị thực của tham số m để hàm số x 5 y đồng biến trên x m khoảng ;8 ? Hướng dẫn giải
Tập xác định D \ m Hàm số x 5 y
đồng biến trên khoảng ;8 x m
y ' 0; x ; 8
x m
m 5 0;x ; 8 2
x m m ;8 m 5 m 5 5 m 8 m 8 m 8
Vậy đáp án cần tìm là 5;8.
Ví dụ. Có tất cả bao nhiêu các giá trị nguyên của tham số m để hàm số 2x 4
y xm
đồng biến trên khoảng ;4 ? Hướng dẫn giải
Tập xác định D \ m Ta có: 2 4 ' m
y xm2
Hàm số đã cho đồng biến trên khoảng m m
;4 khi và chỉ khi 4 4 2m 4 0 m 2
Vì m m4; 3
Vậy có hai giá trị nguyên của tham số m thỏa mãn yêu cầu bài toán. 2 Ví dụ. Cho hàm số m x 5 y
với m là tham số. Gọi S là tập hợp các số nguyên 2mx 1
m2020;2020 để hàm số đã cho nghịch biến trên khoảng 3; . Xác định số
phần tử của tập hợp S ? Hướng dẫn giải
Xét m 0 y 5 là hàm hằng nên hàm số không nghịch biến. Vậy m 0 không thỏa mãn. Xét m 0 Tập xác định 1 1 D ; ; 2m 2m
Để hàm số nghịch biến trên khoảng 3; khi và chỉ khi 2 m 10m 2 y ' 0 mx 2 m 10m 0 2 1 6m 1 1 0 3 2m 2m 0 m 10 1 m 0 m 10 6 m 0 m Mà
nên m1;2;3;. .; 9 m 2020;2020
Vậy tập hợp S có tất cả 9 giá trị. 2
Ví dụ. Tìm tập hợp tất cả các giá trị của tham số m để hàm số x 8x 4 y 2
x 8x m
nghịch biến trên 1;0 ? Hướng dẫn giải Đặt 2
t x 8x Điều kiện xác định x 0 2
x 8x 0 x 8 Xét hàm 2
t x 8x; x 1;0 ta có: 2x 8 x 4 t ' 0; x 1 ;0 2 2 2 x 8x x 8x Ta có bảng biến thiên
Từ bảng biến thiên ta thấy hàm số 2
t x 8x nghịch biến trên khoảng 1;0 và t 0;3 Khi đó yêu cầu bài toán t 4 y đồng biến trên 0;3 t m
Điều kiện xác định D \ m Ta có: m 4 y ' ; x D t m2
Để hàm số đồng biến trên 0;3 thì m 4 0 y ' 0 m m 0 0;3 m 3 m 4 4 m 3
m 0 m 0 m 3
Vậy đáp án cần tìm là m4; 3 0; .
Ví dụ. Tìm tất cả các giá trị thực của tham số m để hàm số 2cot x 1 y đồng biến cot x m trên khoảng ; ? 4 2 Hướng dẫn giải
Điều kiện xác định cot x m 2 1 cot x m 2cot x 1 2 2 Ta có: sin x sin y '
cot x m2 1 2m 2 sin .
x cot x m2
Hàm số đồng biến trên khoảng ; khi và chỉ khi 4 2 1 2m 0 y ' 0 m m 1 0;1 m 0 m 1 m 1 ; 1 0; m 0 2
Vậy đáp án cần tìm là m 1 ; 1 0; . 2




