114 trang 3 lượt tải

Toàn tập khảo sát hàm số và ứng dụng môn Toán 12 THPT

6

Tài liệu gồm 114 trang, được biên soạn bởi thầy giáo Đặng Công Đức (Giang Sơn), tuyển chọn các bài tập trắc nghiệm (nhiều lựa chọn, đúng sai, trả lời ngắn) chủ đề khảo sát hàm số và ứng dụng môn Toán 12 THPT.

Chủ đề: Tài liệu chung 172 tài liệu

Môn: Toán 12 4.3 K tài liệu

Tác giả:

Profile

Linh Đan

2 tuần trước
Danh sách Quiz
/114
1
T
T
À
À
I
I
L
L
I
I
Ệ
Ệ
U
U
T
T
H
H
A
A
M
M
K
K
H
H
Ả
Ả
O
O
T
T
O
O
Á
Á
N
N
H
H
Ọ
Ọ
C
C
P
P
H
H
Ổ
Ổ
T
T
H
H
Ô
Ô
N
N
G
G
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
T
T
O
O
À
À
N
N
T
T
Ậ
Ậ
P
P
K
K
H
H
Ả
Ả
O
O
S
S
Á
Á
T
T
H
H
À
À
M
M
S
S
Ố
Ố
V
V
À
À
Ứ
Ứ
N
N
G
G
D
D
Ụ
Ụ
N
N
G
G
L
L
Ớ
Ớ
P
P
1
1
2
2
T
T
H
H
P
P
T
T
(
(
K
K
Ế
Ế
T
T
H
H
Ợ
Ợ
P
P
3
3
B
B
Ộ
Ộ
S
S
Á
Á
C
C
H
H
G
G
I
I
Á
Á
O
O
K
K
H
H
O
O
A
A
)
)
T
T
H
H
Â
Â
N
N
T
T
Ặ
Ặ
N
N
G
G
T
T
O
O
À
À
N
N
T
T
H
H
Ể
Ể
Q
Q
U
U
Ý
Ý
T
T
H
H
Ầ
Ầ
Y
Y
C
C
Ô
Ô
V
V
À
À
C
C
Á
Á
C
C
E
E
M
M
H
H
Ọ
Ọ
C
C
S
S
I
I
N
N
H
H
T
T
R
R
Ê
Ê
N
N
T
T
O
O
À
À
N
N
Q
Q
U
U
Ố
Ố
C
C
C
C
R
R
E
E
A
A
T
T
E
E
D
D
B
B
Y
Y
G
G
I
I
A
A
N
N
G
G
S
S
Ơ
Ơ
N
N
(
(
F
F
A
A
C
C
E
E
B
B
O
O
O
O
K
K
)
)
Đ
Đ
Á
Á
P
P
Á
Á
N
N
C
C
H
H
I
I
T
T
I
I
Ế
Ế
T
T
Q
Q
U
U
Ý
Ý
T
T
H
H
Ầ
Ầ
Y
Y
C
C
Ô
Ô
V
V
U
U
I
I
L
L
Ò
Ò
N
N
G
G
L
L
I
I
Ê
Ê
N
N
H
H
Ệ
Ệ
T
T
Á
Á
C
C
G
G
I
I
Ả
Ả
G
G
A
A
C
C
M
M
A
A
1
1
4
4
3
3
1
1
9
9
8
8
8
8
@
@
G
G
M
M
A
A
I
I
L
L
.
.
C
C
O
O
M
M
(
(
G
G
M
M
A
A
I
I
L
L
)
)
;
;
T
T
E
E
L
L
0
0
3
3
9
9
8
8
0
0
2
2
1
1
9
9
2
2
0
0
T
T
H
H
À
À
N
N
H
H
P
P
H
H
Ố
Ố
T
T
H
H
Á
Á
I
I
B
B
Ì
Ì
N
N
H
H
–
–
T
T
H
H
Á
Á
N
N
G
G
5
5
/
/
2
2
0
0
2
2
5
5
DUNG
LƯỢNG
NỘI DUNG BÀI TẬP
2
2 FILE
1 file 2 trang
T
T
R
R
Ắ
Ắ
C
C
N
N
G
G
H
H
I
I
Ệ
Ệ
M
M
A
A
B
B
C
C
D
D
C
C
Ơ
Ơ
B
B
Ả
Ả
N
N
C
C
Ự
Ự
C
C
T
T
R
R
Ị
Ị
2 FILE
1 file 2 trang
T
T
R
R
Ắ
Ắ
C
C
N
N
G
G
H
H
I
I
Ệ
Ệ
M
M
A
A
B
B
C
C
D
D
C
C
Ơ
Ơ
B
B
Ả
Ả
N
N
Đ
Đ
Ơ
Ơ
N
N
Đ
Đ
I
I
Ệ
Ệ
U
U
2 FILE
1 file 2 trang
T
T
R
R
Ắ
Ắ
C
C
N
N
G
G
H
H
I
I
Ệ
Ệ
M
M
A
A
B
B
C
C
D
D
C
C
Ơ
Ơ
B
B
Ả
Ả
N
N
T
T
I
I
Ệ
Ệ
M
M
C
C
Ậ
Ậ
N
N
2 FILE
1 file 4 trang
T
T
R
R
Ắ
Ắ
C
C
N
N
G
G
H
H
I
I
Ệ
Ệ
M
M
A
A
B
B
C
C
D
D
C
C
Ơ
Ơ
B
B
Ả
Ả
N
N
Đ
Đ
Ồ
Ồ
T
T
H
H
Ị
Ị
H
H
À
À
M
M
S
S
Ố
Ố
2 FILE
1 file 2 trang
T
T
R
R
Ắ
Ắ
C
C
N
N
G
G
H
H
I
I
Ệ
Ệ
M
M
A
A
B
B
C
C
D
D
C
C
Ơ
Ơ
B
B
Ả
Ả
N
N
G
G
T
T
L
L
N
N
,
,
G
G
T
T
N
N
N
N
2 FILE
1 file 2 trang
T
T
R
R
Ắ
Ắ
C
C
N
N
G
G
H
H
I
I
Ệ
Ệ
M
M
A
A
B
B
C
C
D
D
V
V
Ậ
Ậ
N
N
D
D
Ụ
Ụ
N
N
G
G
C
C
Ự
Ự
C
C
T
T
R
R
Ị
Ị
2 FILE
1 file 2 trang
T
T
R
R
Ắ
Ắ
C
C
N
N
G
G
H
H
I
I
Ệ
Ệ
M
M
A
A
B
B
C
C
D
D
V
V
Ậ
Ậ
N
N
D
D
Ụ
Ụ
N
N
G
G
Đ
Đ
Ơ
Ơ
N
N
Đ
Đ
I
I
Ệ
Ệ
U
U
2 FILE
1 file 2 trang
T
T
R
R
Ắ
Ắ
C
C
N
N
G
G
H
H
I
I
Ệ
Ệ
M
M
A
A
B
B
C
C
D
D
V
V
Ậ
Ậ
N
N
D
D
Ụ
Ụ
N
N
G
G
Đ
Đ
Ư
Ư
Ờ
Ờ
N
N
G
G
T
T
I
I
Ệ
Ệ
M
M
C
C
Ậ
Ậ
N
N
2 FILE
1 file 4 trang
T
T
R
R
Ắ
Ắ
C
C
N
N
G
G
H
H
I
I
Ệ
Ệ
M
M
A
A
B
B
C
C
D
D
V
V
Ậ
Ậ
N
N
D
D
Ụ
Ụ
N
N
G
G
Đ
Đ
Ồ
Ồ
T
T
H
H
Ị
Ị
H
H
À
À
M
M
S
S
Ố
Ố
1 FILE
1 file 2 trang
T
T
R
R
Ắ
Ắ
C
C
N
N
G
G
H
H
I
I
Ệ
Ệ
M
M
A
A
B
B
C
C
D
D
V
V
Ậ
Ậ
N
N
D
D
Ụ
Ụ
N
N
G
G
G
G
T
T
L
L
N
N
,
,
G
G
T
T
N
N
N
N
2 FILE
1 file 4 trang
T
T
R
R
Ắ
Ắ
C
C
N
N
G
G
H
H
I
I
Ệ
Ệ
M
M
A
A
B
B
C
C
D
D
V
V
Ậ
Ậ
N
N
D
D
Ụ
Ụ
N
N
G
G
Ứ
Ứ
N
N
G
G
D
D
Ụ
Ụ
N
N
G
G
T
T
H
H
Ự
Ự
C
C
T
T
Ế
Ế
1 file 4 trang
T
T
R
R
Ắ
Ắ
C
C
N
N
G
G
H
H
I
I
Ệ
Ệ
M
M
Đ
Đ
Ú
Ú
N
N
G
G
S
S
A
A
I
I
H
H
À
À
M
M
S
S
Ố
Ố
Đ
Đ
A
A
T
T
H
H
Ứ
Ứ
C
C
1 file 4 trang
T
T
R
R
Ắ
Ắ
C
C
N
N
G
G
H
H
I
I
Ệ
Ệ
M
M
Đ
Đ
Ú
Ú
N
N
G
G
S
S
A
A
I
I
H
H
À
À
M
M
S
S
Ố
Ố
P
P
H
H
Â
Â
N
N
T
T
H
H
Ứ
Ứ
C
C
H
H
Ữ
Ữ
U
U
T
T
Ỷ
Ỷ
1 file 4 trang
T
T
R
R
Ắ
Ắ
C
C
N
N
G
G
H
H
I
I
Ệ
Ệ
M
M
Đ
Đ
Ú
Ú
N
N
G
G
S
S
A
A
I
I
H
H
À
À
M
M
S
S
Ố
Ố
K
K
H
H
Á
Á
C
C
4 FILE
1 file 4 trang
T
T
R
R
Ắ
Ắ
C
C
N
N
G
G
H
H
I
I
Ệ
Ệ
M
M
Đ
Đ
Ú
Ú
N
N
G
G
S
S
A
A
I
I
Ứ
Ứ
N
N
G
G
D
D
Ụ
Ụ
N
N
G
G
T
T
H
H
Ự
Ự
C
C
T
T
Ế
Ế
1 FILE
1 file 2 trang
T
T
R
R
Ả
Ả
L
L
Ờ
Ờ
I
I
N
N
G
G
Ắ
Ắ
N
N
Ứ
Ứ
N
N
G
G
D
D
Ụ
Ụ
N
N
G
G
T
T
H
H
Ự
Ự
C
C
T
T
Ế
Ế
T
T
Í
Í
N
N
H
H
Đ
Đ
Ơ
Ơ
N
N
Đ
Đ
I
I
Ệ
Ệ
U
U
1 FILE
1 file 2 trang
T
T
R
R
Ả
Ả
L
L
Ờ
Ờ
I
I
N
N
G
G
Ắ
Ắ
N
N
Ứ
Ứ
N
N
G
G
D
D
Ụ
Ụ
N
N
G
G
T
T
H
H
Ự
Ự
C
C
T
T
Ế
Ế
Đ
Đ
Ư
Ư
Ờ
Ờ
N
N
G
G
T
T
I
I
Ệ
Ệ
M
M
C
C
Ậ
Ậ
N
N
6 FILE
1 file 4 trang
T
T
R
R
Ả
Ả
L
L
Ờ
Ờ
I
I
N
N
G
G
Ắ
Ắ
N
N
Ứ
Ứ
N
N
G
G
D
D
Ụ
Ụ
N
N
G
G
T
T
H
H
Ự
Ự
C
C
T
T
Ế
Ế
C
C
Ự
Ự
C
C
T
T
R
R
Ị
Ị
,
,
G
G
T
T
L
L
N
N
,
,
G
G
T
T
N
N
N
N
8 FILE
1 file 4 trang
L
L
U
U
Y
Y
Ệ
Ệ
N
N
T
T
Ậ
Ậ
P
P
C
C
H
H
U
U
N
N
G
G
K
K
H
H
Ả
Ả
O
O
S
S
Á
Á
T
T
H
H
À
À
M
M
S
S
Ố
Ố
V
V
À
À
Ứ
Ứ
N
N
G
G
D
D
Ụ
Ụ
N
N
G
G
3
KHẢO SÁT HÀM SỐ LỚP 12 THPT
CỰC TRỊ HÀM SỐ (CỰC ĐẠI, CỰC TIỂU)
LỚP BÀI TOÁN TRẮC NGHIỆM ABCD CƠ BẢN – PHẦN 1
____________________________________
Câu 1.Chohàmsố
f x
cóbảngxétdấucủa
f x
nhưhìnhvẽ
Hàmsốđãchođạtcựcđạitại
A.
3
x
. B.
1
x
. C.
1x
. D.
1
y
.
Câu 2.Tínhtổngcáccựctrịcủahàmsố
3
3 6y x x
.
A.1 B.2 C.0 D.4
Câu 3.Tìmsốcựctrịcủahàmsố
2
3
x x
y
.
A.3 B.1 C.2 D.3
Câu 4.Chohàmsố
cóđạohàm
3
1 4 ,f x x x x x
.Sốđiểmcựcđạicủahàmsốđãcho
là
A.
3
. B.
4
. C.
2
. D.
1
.
Câu 5.Chohàmsố
y f x
xácđịnhtrên
vàcóbảngxétdấucủađạohàmnhưsau.
Khiđósốđiểmcựctrịcủahàmsố
y f x
là
A.
3
.B.
2
C.
4
. D.
1
.
Câu 6.Hàmsố
2
8 19
y x x
đạtcựctrịtại
A.
2
x
B.
3
x
C.
1x
D.
4
x
Câu 7.Chohàmsố
f x
cóđạohàm
3
1 4 ,f x x x x x
.Sốđiểmcựcđạicủahàmsốđãcholà
A.
2
. B.
3
. C.
4
. D.
1
.
Câu 8.Tìmsốcựctrịcủahàmsố
2
log 2 1
y x
.
A.2 B.1 C.3 D.0
Câu 9.Hàmsố
y f x
cóđồthịnhưhìnhvẽ.Khẳngđịnhnàosauđâyđúng?
A.Đồthịhàmsốcóđiểmcựcđạilà
1; 1
. B.Đồthịhàmsốcóđiểmcựctiểulà
1; 1
.
C.Đồthịhàmsốcóđiểmcựctiểulà
1;3
. D.Đồthịhàmsốcóđiểmcựctiểulà
1;1
.
Câu 10.Tìmmộtđiểmcựctrịcủahàmsố
2
1
y x
.
A.
1y
. B.
0
x
.  C.
0
y
. D.
1x
.
Câu 11.Hàmsố
x
y e xe
đạtcựctrịtại
A.
3
x
. B.
1
x
. C.
1x
. D.
1
y
.
Câu 12.Chohàmsố
( )y f x
cóđạohàm
2
( ) ( 2)
f x x x
,
x
.Sốđiểmcựctrịcủahàmsốđãcholà
A.
0
. B.
3
. C.
2
. D.
1
.
Câu 13.Tìmmộtđiểmcựctrịnàođócủahàmsố
cosy x x
.
A.
0
x
B.
2
x
C.
2
x
D.
2
3
x
Câu 14.Chohàmsố
f x
cóđạohàm
3
1 2 ,f x x x x x
.Sốđiểmcựctrịcủahàmsốđãcholà
4
A.
1
. B.
3
. C.
5
. D.
2
.
Câu 15.Tìmđiểmcựctiểucủađồthịhàmsố
3 2
1
2 3 1
3
y x x x
.
A.
3;1
.  B.
3
x
.  C.
7
1;
3
. D.
1x
.
Câu 16.Hàmsốnàodướiđâykhôngcócựctrị?
A.
2
1
x
y
x
B.
2 2
1
x
y
x
C.
2
2 1y x x
D.
3
1y x x
Câu 17.Chohàmsố
y f x
cóbảngbiếnthiênnhưhìnhvẽdướiđây.
Giátrịcựcđạicủahàmsốđãcholà
A.
1y
. B.
0
x
.  C.
0
y
. D.
1x
.
Câu 18.Hàmsố
2
2 5
y x x
đạtcựctrịtại
A.
3
x
. B.
1
x
. C.
1x
. D.
1
y
.
Câu 19.Giátrịcựcđạicủahàmsố
3
3 2y x x
bằng
A.
0
.  B.
1
.  C.
4
. D.
1
.
Câu 20.Tìmsốđiểmcựctrịcủahàmsố
2
2
log 2x
f x x
.
A.
2
.  B.
3
.  C.
0
. D.
1
.
Câu 21.Giátrịcựctiểu
CT
y
củahàmsố
3 2
3 4
y x x
là:
A.
0
CT
y
. B.
3
CT
y
. C.
2
CT
y
. D.
4
CT
y
.
Câu 22.Tìm
m
đểhàmsố
3 2
2 1y x mx mx
đạtcựctiểutại
1
x
A.khôngtồntại
m
. B.
1
m
. C.
1
m
. D.
1;2
m
.
Câu 23.Đồthịhàmsố
4 2
1
y x x
cóbaonhiêuđiểmcựctrịcótungđộlàsốdương?
A.
3
. B.
1
. C.
2
. D.
0
.
Câu 24.Chohàmsố
y f x
cóbảngbiếnthiênnhưsau.
Giátrịcựcđạicủahàmsốlà
A.
2
y
. B.
1
y
. C.
5
y
. D.
0
y
.
Câu 25.Sốđiểmcựctrịcủađồthịhàmsố
4 2
2 2
y x x
là
A.
2
.  B.
3
.  C.
0
. D.
1
.
Câu 26.Hàmsố
2
6 10
y x x
đạtcựctrịtạiđiểm
A.
3
x
B.
3
x
C.
1x
D.
5
x
Câu 27.Hàmsố
2 3
1
x
y
x
cóbaonhiêuđiểmcựctrị?
A.
1
B.
3
C.
0
D.
2
Câu 28.Hàmsố
2
2 15
y x x
cógiátrịcựctiểubằng
A.
5
. B.
1
. C.
3
. D.
14
Câu 29.Điểmcựcđạicủađồthịhàmsố
3 2
6 9y x x x
cótổnghoànhđộvàtungđộbằng
A.
5
. B.
1
. C.
3
. D.
1
.
_________________________________
5
KHẢO SÁT HÀM SỐ LỚP 12 THPT
CỰC TRỊ HÀM SỐ (CỰC ĐẠI, CỰC TIỂU)
LỚP BÀI TOÁN TRẮC NGHIỆM ABCD CƠ BẢN – PHẦN 2
____________________________________
Câu 1.Chohàmsố
4 2
y ax bx c
(a,
b
,
c
)cóđồthịnhưhìnhvẽbên.
Sốđiểmcựctrịcủahàmsốđãcholà
A.
2
B.
3
C.
0
D.
1
Câu 2.Tìmgiátrịcựctiểu
CT
y
củahàmsố
3
3 4
y x x
.
A.
6
CT
y
B.
1
CT
y
C.
2
CT
y
D.
1
CT
y
Câu 3.Chohàmsố
f x
cóđạohàmtrên
vàcóbảngxétdấu
f x
nhưsau
Mệnhđềnàosauđâysai?
A.Hàmsố
y f x
đạtcựctrịtại
2
x
. B.Hàmsố
y f x
đạtcựcđạitại
1x
.
C.Hàmsố
y f x
đạtcựctiểutại
1
x
. D.Hàmsố
y f x
cóhaiđiểmcựctrị.
Câu 4.Gọi
1
x
làđiểmcựcđại,
2
x
làđiểmcựctiểucủahàmsố
3
3 2y x x
.Tính
1 2
2x x
.
A.
2
.  B.
1
.  C.
1
. D.
0
.
Câu 5.Hàmsố
2
x x
y e e
đạtcựctrịtạiđiểm
A.
3
x
. B.
ln 2
x
. C.
1
ln 2
2
x
. D.
1
x
.
Câu 6.Nếuhàmsố
f x
cóđạohàmlà
4
2 2
' 2 2 1
f x x x x x x
thìtổngcácđiểmcựctrịcủahàm
số
f x
bằng
A.
1
. B.
2
. C.
1
. D.
0
.
Câu 7.Chohàmsố
4 2
2
y x mx m
.Tìmtấtcảcácgiátrịthựccủa
m
đểhàmsốcó
3
cựctrị
A.
0
m
. B.
0
m
. C.
0
m
. D.
0
m
.
Câu 8.Hàmsố
cos siny x x
cócựctrịtại
0
x
.Giátrị
0
tan x
khiđóbằng
A.2 B.1 C.–1 D.0
Câu 9.Tìmgiátrịthựccủathamsố
m
đểhàmsố
3 2 2
1
4 3
3
y x mx m x
đạtcựcđạitại
3
x
.
A.
1
m
B.
7
m
C.
5
m
D.
1
m
Câu 10.Tìmsốđiểmcựctrịcủahàmsố
1 2x
y e
.
A.2 B.1 C.3 D.0
Câu 11.Chohàmsố
y f x
cóbảngbiếnthiênnhưsau
Giátrịcựcđạicủahàmsốđãchobằng
A.
1
. B.
2
. C.
0
. D.
5
.
6
Câu 12.Chohàmsố
y f x
cóđạohàmtrên
và
2
1 2 3
f x x x x
.Sốđiểmcựctrịcủahàm
sốđãcholà:
A.
3
B.
1
C.
0
D.
2
Câu 13.Chohàmsố
4 2
2 1
y x x
.Xétcácmệnhđềsauđây
Hàmsốcó3điểmcựctrị.
Hàmsốđồngbiếntrêncáckhoảng
1;0
;
1;

.
Hàmsốcó1điểmcựctrị.
Hàmsốnghịchbiếntrêncáckhoảng
; 1
;
0;1
.
Cóbaonhiêumệnhđềđúngtrongbốnmệnhđềtrên?
A.2. B.1. C.4. D.3.
Câu 14.Tìmsốcựctiểucủahàmsố
2
2y x x x
A.2 B.3 C.1 D.0
Câu 15.Tínhgiátrịcựctiểucủahàmsố
2
ln 2 10
y x x
.
A.3 B.
2ln3
C.
3ln 2
D.
2ln 2
Câu 16.Hàmsốnàotrongbốnhàmsốđượcliệtkêdướiđâykhôngcócựctrị?
A.
2 3
2
x
y
x
. B.
4
y x
. C.
3
y x x
. D.
2
y x
.
Câu 17.Hàmsố
2
5
3
x x
y
tạicựctrịtạiđiểm
A.
5
2
x
. B.
3
x
. C.
1x
. D.
1
x
.
Câu 18.Hàmsố
4 3 2
1 1 5
3 2019
4 3 2
y x x x x m
m
đạtcựctiểutạiđiểm:
A.
3
x
. B.
3
x
. C.
1x
. D.
1
x
.
Câu 19.Chohàmsố
( )f x
cóbàngbiếnthiênnhưsau:
Điểmcựcđạicủahàmsốđãcholà:
A.
3
x
.  B.
1x
.  C.
2
x
D.
2
x
.
Câu 20. Hàmsố
2
2
y x x
đạtcựcđạitạiđiểm
A.
1
x
. B.
1x
. C.
0
x
. D.
2
x
.
Câu 21.Cóbaonhiêusốthực
m
đểhàmsố
3 2 2
1
1 1
3
y x mx m m x
đạtcựcđạitại
1x
.
A.
0
B.
2
C.
1
D.
3
Câu 22.Hàmsố
3 2
1
3 1
3
y x x x
đạtcựctiểutạiđiểm
A.
1
x
. B.
1x
. C.
3
x
. D.
3
x
.
Câu 23.Tìmsốđiểmcựctrịcủahàmsố
4 2
2y x x
.
A.2. B.4. C.3. D.1.
Câu 24.Chohàmsố
f x
cóbảngbiếnthiênnhưsau:
Hàmsốđãchođạtcựcđạitại
A.
2
x
. B.
2
x
. C.
1x
. D.
1
x
.
7
KHẢO HÀM SỐ LỚP 12 THPT
TÍNH ĐƠN ĐIỆU CỦA HÀM SỐ (ĐỒNG BIẾN, NGHỊCH BIẾN)
LỚP BÀI TOÁN TRẮC NGHIỆM ABCD CƠ BẢN_PHẦN 1
_________________________________
Câu 1.Chohàmsố
f x
cóbảngbiếnthiênnhưsau:
Hàmsốđãchođồngbiếntrênkhoảngnàodướiđây?
A.
; 1
. B.
0;1
. C.
1;1
. D.
1;0
Câu 2.Hàmsốnàodướiđâyđồngbiếntrên
?
A.
1
2
x
y
x
. B.
2
2y x x
. C.
3 2
y x x x
. D.
4 2
3 2
y x x
.
Câu 3.Hàmsốnàodướiđâynghịchbiếntrên
A.
3
y x x
. B.
4 2
y x x
. C.
3
y x x
. D.
2
1
x
y
x
.
Câu 4.Hàmsốnàodướiđâyđồngbiếntrên
?
A.
4 2
y x x
. B.
3
y x x
. C.
1
2
x
y
x
. D.
3
y x x
.
Câu 5.Trongcáchàmsốsau,hàmsốnàoluônđồngbiếntrên
?
A.
2015
y
2016
x
B.
3
y
2016 2
x
C.
2x
y (0,1)
D.
2
(2016)
x
y
Câu 6.Chohàmsố
y f x
cóđạohàm
1f x x
vớimọi
x
.Hàmsốđãchonghịchbiếntrênkhoảng
nàodướiđây?
A.
1;

. B.
1;
. C.
; 1
. D.
;1

.
Câu 7.Hàmsốnàodướiđâyđồngbiếntrênkhoảng
;
?
A.
1
2
x
y
x
B.
3
y x x
C.
3
3y x x
D.
1
3
x
y
x
Câu 8.Hàmsốnàodướiđâyđồngbiếntrênkhoảng
;
 
?
A.
4 2
3y x x
. B.
2
1
x
y
x
. C.
3
3 3 2
y x x
. D.
3
2 5 1y x x
.
Câu 9.Hàmsốnàodướiđâyđồngbiếntrêntậpxácđịnhcủanó?
A.
1
π
x
y
B.
2
3
x
y
C.
3
x
y
D.
0,5
x
y
Câu 10.Hỏihàmsố
4
2 1
y x
đồngbiếntrênkhoảngnào?
A.
;0 .

B.
1
;
2

. C.
0;

. D.
1
;
2

.
Câu 11.Chohàmsố
y f x
xácđịnhvàliêntụctrên
,cóbảngđạohàm
f x
thỏamãn:
Hàmsố
( )y f x
nghịchbiếntrênkhoảngnàodướiđây
A.
1;3
. B.
1;1
. C.
2; 1
. D.
1;

.
Câu 12.Chohàmsố
3 2
2 1 y x x x
.Mệnhđềnàodướiđâyđúng?
A.Hàmsốnghịchbiếntrênkhoảng
1;

B.Hàmsốnghịchbiếntrênkhoảng
1
;1
3
8
C.Hàmsốnghịchbiếntrênkhoảng
1
;
3

D.Hàmsốđồngbiếntrênkhoảng
1
;1
3
Câu 13.Chohàmsố
4 2
2y x x
.Mệnhđềnàodướiđâyđúng?
A.Hàmsốnghịchbiếntrênkhoảng
 ; 2
B.Hàmsốđồngbiếntrênkhoảng
1;1
C.Hàmsốnghịchbiếntrênkhoảng
1;1
D.Hàmsốđồngbiếntrênkhoảng
 ; 2
Câu 14.Chohàmsố
2
2 1
y x
.Mệnhđềnàodướiđâyđúng?
A.Hàmsốđồngbiếntrênkhoảng
0;
B.Hàmsốđồngbiếntrênkhoảng
;0
C.Hàmsốnghịchbiếntrênkhoảng
0;
D.Hàmsốnghịchbiếntrênkhoảng
1;1
Câu 15.Chohàmsố
3
2
2019
3
x
y x x
A.Hàmsốđãchođồngbiếntrên
.
B.Hàmsốđãchonghịchbiếntrên
;1
.
C.Hàmsốđãchođồngbiếntrên
;1
vànghịchbiếntrên
1;

.
D.Hàmsốđãchođồngbiếntrên
1;

vànghịchbiếntrên
;1
.
Câu 16.Chođồthịhàmsố
y f x
liêntụctrên
vàcóđồthịnhưhìnhvẽbêndưới.
Khẳngđịnhnàosauđâylàđúng?
A.Hàmsốđồngbiếntrênkhoảng
1;3
. B.Hàmsốnghịchbiếntrênkhoảng
6;

.
C.Hàmsốđồngbiếntrênkhoảng
;3

. D.Hàmsốnghịchbiếntrênkhoảng
3;6
.
Câu 17.Hàmsốnàosauđâynghịchbiếntrên
?
A.
3
3 2y x x
. B.
4 2
2 2
y x x
.
C.
3 2
2 4 1y x x x
. D.
3 2
2 5 2y x x x
.
Câu 18.Hàmsố
2
2018
y x x
nghịchbiếntrênkhoảngnàotrongcáckhoảngsauđây?
A.
1010;2018
. B.
2018;

. C.
0;1009
. D.
1;2018
.
Câu 19.Hàmsố
3 2
3 4
y x x
đồngbiếntrêntậphợpnàotrongcáctậphợpđượcchodướiđây?
A.
2;
. B.
0;2
. C.
;0 2;

. D.
;0

.
Câu 20.Chohàm
2
6 5
y x x
.Mệnhđềnàosauđâylàđúng?
A.Hàmsốđồngbiếntrênkhoảng
5; .
B.Hàmsốđồngbiếntrênkhoảng
3; .
C.Hàmsốđồngbiếntrênkhoảng
;1 .

D.Hàmsốnghịchbiếntrênkhoảng
;3 .

Câu 21.Đườngcongởhìnhbênlàđồthịcủahàmsố
ax b
y
cx d
với
, , ,a b c d
làcácsốthực.Mệnhđềnàodưới
đâyđúng?
A.
0,y x
B.
0,y x
C.
0, 1y x
D.
0, 1y x
9
KHẢO HÀM SỐ LỚP 12 THPT
TÍNH ĐƠN ĐIỆU CỦA HÀM SỐ (ĐỒNG BIẾN, NGHỊCH BIẾN)
LỚP BÀI TOÁN TRẮC NGHIỆM ABCD CƠ BẢN_PHẦN 2
_________________________________
Câu 1.Chohàmsố
y f x
cóđạohàm
3
2
f x x x
,vớimọi
x
.Hàmsốđãchonghịchbiếntrên
khoảngnàodướiđây?
A.
1; 3
. B.
1; 0
. C.
0; 1
. D.
2; 0
.
Câu 2.Hàmsốnàosauđâyđồngbiếntrên
.
A.
1
.
1
x
y
x
B.
3 2
3 1
y x x
C.
x
y e
D.
2
2
y x
Câu 3.Chohàmsố
( )y f x
cóbảngxétdấuđạohàmnhưsau:
Hỏimệnhđềnàosai?
A.Hàmsốđãchođồngbiếntrênkhoảng
(2; ).

B.Hàmsốđãchođồngbiếntrênkhoảng
(3; ).
C.Hàmsốđãchođồngbiếntrênkhoảng
( ;1).

D.Hàmsốđãchonghịchbiếntrênkhoảng
(0;3).
Câu 4.Hàmsốnàodướiđâyđồngbiếntrên
?
A.
4 2
3 5
y x x
. B.
3
y x x
. C.
10
2
x
y
x
. D.
3
y x x
.
Câu 5.Hàmsố
3
3
y x x m
nghịchbiếntrênkhoảngnào?
A.
; 1
. B.
;
 
. C.
1;1
. D.
0;

.
Câu 6.Trongcáchàmsốsauhàmsốnàonghịchbiếntrên
?
A.
2
3
log
x
B.
3
log
y x
C.
e
4
x
y
D.
2
5
x
y
Câu 7.Chohàmsố
2
8 7 4
y x x
.Mệnhđềnàosauđâylàđúng?
A.Hàmsốđồngbiếntrênkhoảng
17; .
B.Hàmsốđồngbiếntrênkhoảng
3;

C.Hàmsốđồngbiếntrênkhoảng
;1 .

D.Hàmsốnghịchbiếntrênkhoảng
;3 .

Câu 8.Chohàmsố
y f x
cóbảngxétdấuđạohàmnhưsau:
Khoảngnghịchbiếncủahàmsố
y f x
là
A.
( ;3)
. B.
(1; )
. C.
(1;3)
. D.
( ;1)
.
Câu 9.Hàmsốnàosauđâyđồngbiếntrên
.
A.
1
.
1
x
y
x
B.
sin 2y x x
C.
6
x
y e x
D.
2
2
y x
Câu 10.Chohàmsố
3 2
3 1
y x x
,kếtluậnnàosauđâyvềtínhđơnđiệucủahàmsốlàđúngnhất:
A.Hàmsốđồngbiếntrênkhoảng
0;2
vànghịchbiếntrêncáckhoảng
;0

;
2;

;
B.Hàmsốđồngbiếntrênkhoảng
0;2
;
C.Hàmsốnghịchbiếntrênkhoảng
0;2
vàđồngbiếntrêncáckhoảng
;0

;
2;

;
D.Hàmsốnghịchbiếntrêncáckhoảng
;0

và
2;

.
Câu 11.Tìmhàmsốđồngbiếntrên
.
A.
3
x
f x
. B.
3
x
f x
. C.
1
3
x
f x
. D.
3
3
x
f x
.
Câu 12.Chohàmsố
( )y f x
cóđồthịnhưhìnhvẽ
10
Hàmsốđãchođồngbiếntrênkhoảngnào
A.
0;3
. B.
3;

. C.
;2

. D.
1;3
.
Câu 13.Hàmsốnàosauđâyđồngbiếntrên
.
A.
1
6
x
y
x
B.
cos 5 3y x x
C.
6
x
y e x
D.
2
2y x x
Câu 14.Chohàmsố
y f x
cóđạphàm
2
1
f x x
,
x
.Mệnhđềnàodướiđâyđúng?
A.Hàmsốnghịchbiếntrênkhoảng
;0

. B.Hàmsốnghịchbiếntrênkhoảng
1;

.
C.Hàmsốnghịchbiếntrênkhoảng
1;1
. D.Hàmsốđồngbiếntrênkhoảng
;

.
Câu 15.Chohàmsố
y f x
cóđạohàm
2
2, .
f x x x
Mệnhđềnàodướiđâylàđúng?
A.
1 1f f
. B.
1 1f f
. C.
1 1f f
. D.
1 1f f
.
Câu 16.Chohàmsố
y f x
cóđạohàmtrên
vàcóbảngxétdấuđạohàmnhưsau:
Trongcácmệnhđềsaumệnhđềnàođúng?
A.Hàmsố
f x
nghịchbiếntrên
;0

. B.Hàmsố
f x
đồngbiếntrên
1;3
.
C.Hàmsốđồngbiếntrên
1;1
. D.Hàmsốnghịchbiếntrên
; 2 2;
 
Câu 17.Chohàmsố
1
.
1
x
y
x
Khẳngđịnhnàosauđâylàđúng?
A.Hàmsốđãchonghịchbiếntrênkhoảng
;1
.
B.Hàmsốđãchođồngbiếntrênkhoảng
;1
vàkhoảng
1;

.
C.Hàmsốđãchođồngbiếntrênkhoảng
0;

.
D.Hàmsốđãchonghịchbiếntrêntập
\ 1
.
Câu 18.Chohàmsố
y f x
cóđạohàm
2
2f x x x
,
x
.Hàmsố
2
y f x
đồngbiếntrên
khoảng
A.
0;2
. B.
2;

. C.
; 2
. D.
2;0
.
Câu 19.Hàmsốnàodướiđâyđồngbiếntrênkhoảng
(0; )
?
A.
3
log
y x
. B.
6
logy x
. C.
3
log
e
y x
. D.
1
4
logy x
.
Câu 20.Chohàmsố
y f x
thỏamãn
2
5 4.
f x x x
Khẳngđịnhnàosauđâylàđúng?
A.Hàmsốđãchođồngbiếntrênkhoảng
;3
.
B.Hàmsốđãchonghịchbiếntrênkhoảng
2;3
.
C.Hàmsốđãchonghịchbiếntrênkhoảng
3;
.
D.Hàmsốđãchođồngbiếntrênkhoảng
1;4
.
Câu 21.Chohàmsố
( )y f x
cóđạohàm
1 3 ,f x x x x
.Hàmsốđãchonghịchbiếntrên
khoảngnàodướiđây?
A.
0;3
. B.
3;

. C.
;2

. D.
1;3
.
_________________________________
11
KHẢO SÁT HÀM SỐ LỚP 12 THPT
ĐƯỜNG TIỆM CẬN CỦA ĐỒ THỊ HÀM SỐ
LỚP BÀI TOÁN TRẮC NGHIỆM ABCD CƠ BẢN – PHẦN 1
______________________________________
Câu 1.Chohàmsố
( )y f x
có
lim ( ) 1
x
f x

và
lim ( ) 1
x
f x

.Khẳngđịnhnàosauđâylàkhẳngđịnhđúng?
A.Đồthịhàmsốđãchocóhaitiệmcậnnganglàcácđườngthẳng
1x
và
1
x
.
B.Đồthịhàmsốđãchokhôngcótiệmcậnngang.
C.Đồthịhàmsốđãchocóđúngmộttiệmcậnngang.
D.Đồthịhàmsốđãchocóhaitiệmcậnnganglàcácđườngthẳng
1y
và
1
y
.
Câu 2.Tiệmcậnngangcủađồthịhàmsố
2
1
x
y
x
là
A.
2
y
. B.
1y
. C.
1
x
. D.
2
x
.
Câu 3.Chohàmsố
y f x
cóbảngbiếnthiênnhưhìnhvẽdướiđây.Hỏiđồthịcủahàmsốđãchocóbao
nhiêuđườngtiệmcận?
A.
1
. B.
3
. C.
2
. D.
4
Câu 4.Tiệmcậnđứngcủađồthịhàmsố
1
3
x
y
x
là
A.
3
x
. B.
1
x
. C.
1x
. D.
3
x
.
Câu 5.Tìmđườngtiệmcậnxiêncủađồthịhàmsố
1
1
y x
x
.
A.
y x
B.
1y x
C.
2
y x
D.
3y x
Câu 6.Tiệmcậnngangcủađồthịhàmsố
2 1
1
x
y
x
là:
A.
1
2
y
. B.
1
y
. C.
1y
. D.
2
y
.
Câu 7.Hàmsố
y f x
xácđịnhtrên
\ 1
,liêntụctrênmỗikhoảngxácđịnhvàcóbảngbiếnthiên:
Khẳngđịnhnàodướiđâysai?
A.Đồthịhàmsốđãchocóhaitiệmcậnnganglà
1y
và
1
y
.
B.Đồthịhàmsốcótiệmcậnđứng
1
x
.
C.Đồthịhàmsốcó3đườngtiệmcận.
D.Đồthịhàmsốđãchocóhaitiệmcậnđứnglà
1x
và
1
x
.
Câu 8.Tìmđườngtiệmcậnxiêncủađồthịhàmsố
2
1
1
y x
x
.
A.
y x
B.
1y x
C.
2
y x
D.
3y x
Câu 9.Tiệmcậnđứngcủađồthịhàmsố
3 2
2
x
y
x
làtậphợptấtcảcácđiểmcóhoànhđộbằngbaonhiêu
A.
2
x
. B.
1
x
. C.
3
x
. D.
2
x
.
Câu 10.Tiệmcậnngangcủađồthịhàmsố
4 1
1
x
y
x
điquađiểmnàosauđây
A.
1;3
A
. B.
2;4
B
. C.
6;1
C
. D.
4;2
D
.
Câu 11.Chohàmsốcóbảngbiếnthiênnhưhìnhsau
12
Tổngsốđườngtiệmcậnngangvàtiệmcậnđứngcủađồthịhàmsố
y f x
là
A.
3
. B.
2
. C.
4
. D.
1
.
Câu 12.Tiệmcậnđứngcủađồthịhàmsố
2 1
1
x
y
x
làđườngthẳngcóphươngtrình
A.
2
x
. B.
1x
. C.
1
2
x
. D.
1
x
.
Câu 13.Tìmđườngtiệmcậnxiêncủađồthịhàmsố
5
3
3
y x
x
.
A.
y x
B.
1y x
C.
2
y x
D.
3y x
Câu 14.Tiệmcậnđứngcủađồthịhàmsố
1
2
x
y
x
làđườngthẳngcóphươngtrình
A.
1
x
. B.
2
x
. C.
2
x
. D.
1
x
.
Câu 15.Tiệmcậnngangcủađồthịhàmsố
2 1
2 4
x
y
x
làđườngthẳngcóphươngtrình
A.
2
y
. B.
2
x
. C.
1x
. D.
1y
.
Câu 16.Tìmđườngtiệmcậnxiêncủađồthịhàmsố
4
3
1
y x
x
.
A.
y x
B.
1y x
C.
2
y x
D.
3y x
Câu 17.Chohàmsố
y f x
cóbảngbiếnthiênnhưsau:
Tiệmcậnđứngcủađồthịhàmsốđãcholàđườngthẳngcóphươngtrình:
A.
1
x
. B.
1
y
. C.
2
y
. D.
2
x
.
Câu 18.Tiệmcậnngangcủađồthịhàmsố
3 1
1
x
y
x
là:
A.
1
3
y
. B.
3
y
. C.
1
y
. D.
1y
.
Câu 19.Chohàmsố
y f x
cóđồthị
C
và
lim


x
f x
,
lim 2

x
f x
.Sốtiệmcậnngangcủa
C
là
A.0. B.2. C.1. D.3.
Câu 20.Tiệmcậnxiêncủađồthìhàmsố
1
1
x
y x
x
làđườngthẳngcóphươngtrình:
A.
y x
B.
1y x
C.
2
y x
D.
3y x
Câu 21.Tiệmcậnđứngcủađồthịhàmsố
2 2
1
x
y
x
là
A.
2
x
. B.
1x
. C.
1
x
. D.
2
x
.
Câu 22.Tiệmcậnđứngcủađồthịhàmsố
2 2
1
x
y
x
là
A.
2
x
. B.
2
x
. C.
1.
x
D.
1
x
.
_________________________________
13
KHẢO SÁT HÀM SỐ LỚP 12 THPT
ĐƯỜNG TIỆM CẬN CỦA ĐỒ THỊ HÀM SỐ
LỚP BÀI TOÁN TRẮC NGHIỆM ABCD CƠ BẢN – PHẦN 2
______________________________________
Câu 1.Tiệm
cậnđứngcủađồthịhàmsố
1
2
x
y
x
làđườngthẳngcóphươngtrình
B.
2
x
. B.
1
x
. C.
2
x
. D.
1x
.
Câu 2.Chocáchàmsố
2
2 2 5 2 7 2 6
, , ,
1 1 1 1
x x x x
y y y y
x x x x
Cóbaonhiêuhàmsốmàđồthịcóđườngtiệmcậnđứngbằng
1
x
?
A.2 B.3 C.1 D.4
Câu 3.Chohàmsố
y f x
cóbảngbiếnthiênnhưsau:
Tổngsốtiệmcậnđứngvàtiệmcậnngangcủađồthịhàmsốđãcholà:
A.2. B.3. C.4. D.1.
Câu 4.Tìmgiátrị
m
đểđườngtiệmcậnđứngcủađồthịhàmsố
2 2
1
x
y
x
làđườngthẳng
1.
x
A.
2
m
. B.
1
m
. C.
1
m
. D.
2
m
.
Câu 5.Tiệmcậnđứngcủađồthịhàmsố
2 2
1
x
y
x
cáchtrụctungmộtkhoảnglớnhơn
A.2 B.1 C.
2
2
D.
7
2
Câu 6.Tiệmcậnđứngcủađồthịhàmsố
2 2
1
x
y
x
cắtđườngthẳngnàosauđây
A.
2
x
. B.
2
x
. C.
y x
D.
1
x
.
Câu 7.Chohàmsố
f x
cóbảngbiếnthiênnhưsau
Tổngsốtiệmcậnđứngvàtiệmcậnngangcủađồthịhàmsốđãcholà
A.
1
. B.
2
. C.
4
. D.
3
.
Câu 8.Đồthịhàmsốnàosauđâykhôngcóđườngtiệmcậnđứng
A.
2 2
1
x
y
x
B.
4 13
1
x
y
x
C.
14
3
1
y x
x
D.
2
1
1
y x
x
Câu 9.Chohàmsố
y f x
cóbảngbiếnthiênnhưsau:
Tổngsốtiệmcậnđứngvàtiệmcậnngangcủađồthịhàmsốđãcholà:
A.
4
. B.
1
. C.
3
. D.
2
.
14
Câu 10.Tìmgiátrị
m
đểđườngtiệmcậnđứngcủađồthịhàmsố
2 2
x
y
x m
làđườngthẳng
1
x
A.
2
m
. B.
1
m
. C.
1
m
. D.
2
m
.
Câu 11.Tiệmcậnngangcủađồthịhàmsố
4 13
1
x
y
x
điquađiểmnàosauđây
A.
1;3
A
. B.
2;4
B
. C.
6;1
C
. D.
4;2
D
.
Câu 12.Chohàmsố
y f x
cóbảngbiếnthiênnhưsau
Tổngsốđườngtiệmcậnngangvàđườngtiệmcậnđứngcủađồthịhàmsốđãcholà
A.
3
B.
2
C.
4
D.
1
Câu 13.Đườngtiệmcậnxiêncủađồthịhàmsố
14
3
1
y x
x
điquađiểmnàosauđây
A.
1;4
A
. B.
2;4
B
. C.
6;1
C
. D.
4;2
D
.
Câu 14.Tổngsốtiệmcậnđứngvàtiệmcậnngangcủađồthịhàmsố
2
2
5 4 1
1
x x
y
x
là
A.
0.
B.
1.
C.
2.
D.
3.
Câu 15.Tiệmcậnngangcủađồthịhàmsố
5 1
1
x
y
x
cáchtrụchoànhmộtkhoảngbằng
A.4 B.2 C.5 D.6
Câu 16.Chohàmsốcóbảngbiếnthiênnhưhìnhsau
Khoảngcáchgiữahaiđườngtiệmcậnngangđồthịhàmsố
y f x
là
A.
3
. B.
2
. C.
4
. D.5.
Câu 17.Đườngtiệmcậnxiêncủađồthịhàmsố
12
1
1
y x
x
cắtđườngthẳngnàosauđây
A.
y x
B.
2 1y x
C.
2
y x
D.
3y x
Câu 18.Đồthịcủahàmsốnàodướiđâycótiệmcậnđứng?
A.
2
3 2
1
x x
y
x
B.
2
2
1
x
y
x
C.
2
1
y x
D.
1
x
y
x
Câu 19.Tìmsốtiệmcậncủađồthịhàmsố
2
2
5 4
1
x x
y
x
.
A.
2
B.
3
C.
0
D.
1
Câu 20.Tìmsốtiệmcậnđứngcủađồthịhàmsố:
2
2
3 4
16
x x
y
x
A.
2
B.
3
C.
1
D.
0
Câu 21.Đườngtiệmcậnxiêncủađồthịhàmsố
5
3 1
1
y x
x
cóhệsốgócbằng
A.2 B.3 C.4 D.1
Câu 22.Đồthịhàmsố
2
2
4
x
y
x
cómấyđườngtiệmcận.
A.
3
B.
1
C.
2
D.
0
_________________________________
15
KHẢO SÁT HÀM SỐ LỚP 12 THPT
ĐỒ THỊ HÀM SỐ, BẢNG BIẾN THIÊN CỦA HÀM SỐ
LỚP BÀI TOÁN TRẮC NGHIỆM ABCD CƠ BẢN– PHẦN 1
________________________________________
Câu 1.Đồthịcủahàmsố
3 2
f x ax bx cx d
códạngnhưhìnhvẽ.Hệsốakhôngthểbằng
A.3 B.2 C.1 D.–4
Câu 2.Đồthịcủahàmsốnàodướiđâycódạngnhưđườngcongtrongdướiđây?
A.
4 2
2y x x
. B.
4 2
2y x x
. C.
3 2
3y x x
. D.
3 2
3y x x
.
Câu 3.Đồthịcủahàmsố
3 2
f x ax bx cx d
códạngnhưhìnhvẽ.Giátrị
0
f
bằng
A.1 B.0 C.2 D.4
Câu 4.Đồthịcủahàmsốnàodướiđâycódạngnhưđườngcongtronghìnhbên?
A.
1
1
x
y
x
. B.
2 1
1
x
y
x
. C.
2
2 1
x
y
x
D.
2
3 1
x
y
x
Câu 5.Đồthịcủahàmsốnàodướiđâycódạngnhưđườngcongtronghìnhbên?
16
A.
3
3 y x x
. B.
3
3 y x x
. C.
4 2
2
y x x
. D.
4 2
2
y x x
.
Câu 6.Đồthịhàmsốnàodướiđâycódạngnhưđườngcongtronghìnhbên?
A.
3 2
3 1
y x x
. B.
3 2
3 1
y x x
. C.
4 2
2 1
y x x
. D.
4 2
2 1
y x x
.
Câu 7.Hàmsốnàodướiđâycóbảngbiếnthiênnhưsau?
A.
3
3y x x
. B.
2
2y x x
. C.
3
3y x x
. D.
2
2y x x
.
Câu 8.Đồthịhàmsốnàodướiđâycódạngnhưđườngcongtronghìnhbên?
A.
4 2
2y x x
. B.
4 2
2 1
y x x
. C.
4 2
2y x x
. D.
3
3y x x
.
Câu 9.Đồthịcủahàmsốdướiđâycódạngnhưđườngcongbên?
A.
3
3 1y x x
. B.
4 2
2 1
y x x
. C.
4 2
2 1
y x x
. D.
3
3 1y x x
.
17
Câu 10.Đồthịcủahàmsố
3 2
f x ax bx cx d
códạngnhưhìnhvẽ.Giátrịdkhôngthểbằng
A.2 B.3 C.4 D.0
Câu 11.Đồthịcủahàmsốnàodướiđâycódạngnhưđườngcongtronghìnhbên?
A.
4 2
2y x x
. B.
3
3y x x
. C.
3
3y x x
. D.
4 2
2y x x
.
Câu 12.Đồthịcủahàmsốnàodướiđâycódạngnhưđườngcongtronghìnhbên
A.
1
1
x
y
x
. B.
2 1
1
x
y
x
. C.
2
3
1
x x
y
x
D.
2
3 1
x
y
x
Câu 13.Đườngcongởhìnhbênlàđồthịcủahàmsố
ax b
y
cx d
với
, , ,a b c d
làcácsốthực.
Tínhgiátrịbiểuthức
2d c
c
.
A.2 B.3 C.4 D.1
18
Câu 14.Đườngcongtronghìnhvẽbênlàđồthịcủahàmsốnàodướiđây?
A.
3 2
1
y x x
B.
4 2
2 1
y x x
C.
3 2
1
y x x
D.
4 2
2 1
y x x
Câu 15.Hàmsốnàodướiđâycóbảngbiếnthiênnhưsau?
A.
4 2
2y x x
. B.
3
3y x x
. C.
4 2
2y x x
. D.
3
3y x x
.
Câu 16.Đườngcongởhìnhbêndướilàđồthịcủamộttrongbốnhàmsốdướiđây.Hàmsốđólàhàmsốnào?
A.
3 2
3 1
y x x
B.
3 2
3 3
y x x
C.
4 2
2 1
y x x
D.
4 2
2 1
y x x
.
Câu 17.Đồthịhàmsốnàodướiđâycódạngnhưđườngcongtronghìnhvẽbên?
A.
3 2
3 2
y x x
. B.
4 2
2 2
y x x
. C.
3 2
3 2
y x x
. D.
4 2
2 2
y x x
.
Câu 18.Đườngcongởhìnhbênlàđồthịcủahàmsố
ax b
y
cx d
với
, , ,a b c d
làcácsốthực.Mệnhđềnàodưới
đâyđúng?
A.
0,y x
B.
0, 1y x
C.
0, 1y x
D.
0,y x
_________________________________
19
KHẢO SÁT HÀM SỐ LỚP 12 THPT
ĐỒ THỊ HÀM SỐ, BẢNG BIẾN THIÊN CỦA HÀM SỐ
LỚP BÀI TOÁN TRẮC NGHIỆM ABCD CƠ BẢN_ P2
________________________________________
Câu 1.Đồthịcủahàmsốnàodướiđâycódạngnhưđườngcongtrongdướiđây?
A.
4 2
2y x x
. B.
4 2
2y x x
. C.
3 2
3y x x
. D.
3 2
3y x x
.
Câu 2.Đườngcongtronghìnhbên làđồthịcủamộthàmsốtrongbốnhàmsốđượcliệtkêởbốnphương
án
, , ,A B C D
dướiđây.Hỏihàmsốđólàhàmsốnào?
A.
3
3 1y x x
B.
3
3 1y x x
C.
4 2
1
y x x
D.
2
1y x x
Câu 3.Đồthịcủahàmsốnàodướiđâycódạngnhưđườngcongtronghìnhvẽbên?
A.
1
1
x
y
x
. B.
2 1
1
x
y
x
. C.
2
1
x
y
x
D.
2
3
1
x
y
x
Câu 4.Đồthịcủahàmsốnàodướiđâycódạngnhưđườngcongtronghìnhvẽbên?
A.
3 2
3 3
y x x
. B.
33
23
xxy
. C.
32
24
xxy
.s D.
32
24
xxy
.
Câu 5.Đườngcongtronghìnhvẽbênlàđồthịcủahàmsốnàodướiđây?
20
A.
3 2
3 1
y x x
B.
3 2
3 1
y x x
C.
4 2
3 1
y x x
D.
4 2
3 1
y x x
Câu 6.Đườngcongởhìnhbênlàđồthịcủahàmsố
ax b
y
cx d
với
, , ,a b c d
làcácsốthực.Mệnhđềnàodưới
đâyđúng?
A.
y 0, 1x
B.
y 0, x 1
C.
y 0, x 2
D.
y 0, 2
Câu 7.Hìnhvẽsauđâylàđồthịcủamộttrongbốnhàmsốchoởcácđápán
, , ,A B C D
.Hỏiđólàhàmsốnào?
A.
3
2 1y x x
. B.
3 2
2 1
y x x
. C.
3
2 1y x x
. D.
3
2 1y x x
.
Câu 7.Hìnhvẽbêndướilàđồthịcủahàmsốnào
A.
1
1
x
y
x
. B.
2 1
1
x
y
x
. C.
2 3
1
x
y
x
. D.
2 5
1
x
y
x
.
Câu 8.Đồthịhàmsốsaucóđườngtiệmcậnxiênlà

Tài liệu khác của Toán 12

Preview text:


TÀI LIỆU THAM KHẢO TOÁN HỌC PHỔ THÔNG
______________________________________________________________
------------------------------------------------------------------------------------------
TOÀN TẬP KHẢO SÁT HÀM SỐ VÀ ỨNG DỤNG LỚP 12 THPT
(KẾT HỢP 3 BỘ SÁCH GIÁO KHOA)
THÂN TẶNG TOÀN THỂ QUÝ THẦY CÔ VÀ CÁC EM HỌC SINH TRÊN TOÀN QUỐC
CREATED BY GIANG SƠN (FACEBOOK)
ĐÁP ÁN CHI TIẾT QUÝ THẦY CÔ VUI LÒNG LIÊN HỆ TÁC GIẢ
GACMA1431988@GMAIL.COM (GMAIL); TEL 0398021920
THÀNH PHỐ THÁI BÌNH – THÁNG 5/2025 DUNG NỘI DUNG BÀI TẬP LƯỢNG 1 2 FILE
TRẮC NGHIỆM ABCD CƠ BẢN CỰC TRỊ 1 file 2 trang 2 FILE
TRẮC NGHIỆM ABCD CƠ BẢN ĐƠN ĐIỆU 1 file 2 trang 2 FILE
TRẮC NGHIỆM ABCD CƠ BẢN TIỆM CẬN 1 file 2 trang 2 FILE 1 file 4 trang
TRẮC NGHIỆM ABCD CƠ BẢN ĐỒ THỊ HÀM SỐ 2 FILE
TRẮC NGHIỆM ABCD CƠ BẢN GTLN, GTNN 1 file 2 trang 2 FILE
TRẮC NGHIỆM ABCD VẬN DỤNG CỰC TRỊ 1 file 2 trang 2 FILE
TRẮC NGHIỆM ABCD VẬN DỤNG ĐƠN ĐIỆU 1 file 2 trang 2 FILE
TRẮC NGHIỆM ABCD VẬN DỤNG ĐƯỜNG TIỆM CẬN 1 file 2 trang 2 FILE
TRẮC NGHIỆM ABCD VẬN DỤNG ĐỒ THỊ HÀM SỐ 1 file 4 trang 1 FILE
TRẮC NGHIỆM ABCD VẬN DỤNG GTLN, GTNN 1 file 2 trang 2 FILE
TRẮC NGHIỆM ABCD VẬN DỤNG ỨNG DỤNG THỰC TẾ 1 file 4 trang 1 file 4 trang
TRẮC NGHIỆM ĐÚNG SAI HÀM SỐ ĐA THỨC 1 file 4 trang
TRẮC NGHIỆM ĐÚNG SAI HÀM SỐ PHÂN THỨC HỮU TỶ 1 file 4 trang
TRẮC NGHIỆM ĐÚNG SAI HÀM SỐ KHÁC 4 FILE 1 file 4 trang
TRẮC NGHIỆM ĐÚNG SAI ỨNG DỤNG THỰC TẾ 1 FILE 1 file 2 trang
TRẢ LỜI NGẮN ỨNG DỤNG THỰC TẾ TÍNH ĐƠN ĐIỆU 1 FILE 1 file 2 trang
TRẢ LỜI NGẮN ỨNG DỤNG THỰC TẾ ĐƯỜNG TIỆM CẬN 6 FILE 1 file 4 trang
TRẢ LỜI NGẮN ỨNG DỤNG THỰC TẾ CỰC TRỊ, GTLN, GTNN 8 FILE 1 file 4 trang
LUYỆN TẬP CHUNG KHẢO SÁT HÀM SỐ VÀ ỨNG DỤNG 2
KHẢO SÁT HÀM SỐ LỚP 12 THPT
CỰC TRỊ HÀM SỐ (CỰC ĐẠI, CỰC TIỂU)
LỚP BÀI TOÁN TRẮC NGHIỆM ABCD CƠ BẢN – PHẦN 1
____________________________________
Câu 1. Cho hàm số f x có bảng xét dấu của f  x như hình vẽ
Hàm số đã cho đạt cực đại tại A. x  3  . B. x  1  . C. x  1. D. y  1.
Câu 2. Tính tổng các cực trị của hàm số 3
y x  3x  6 . A.1 B. 2 C. 0 D. 4 2
Câu 3. Tìm số cực trị của hàm số 3x x y   . A.3 B.1 C. 2 D. 3
Câu 4. Cho hàm số f x có đạo hàm f  x  xx   x  3 1 4 , x
   . Số điểm cực đại của hàm số đã cho là A. 3 . B. 4 . C. 2 . D. 1.
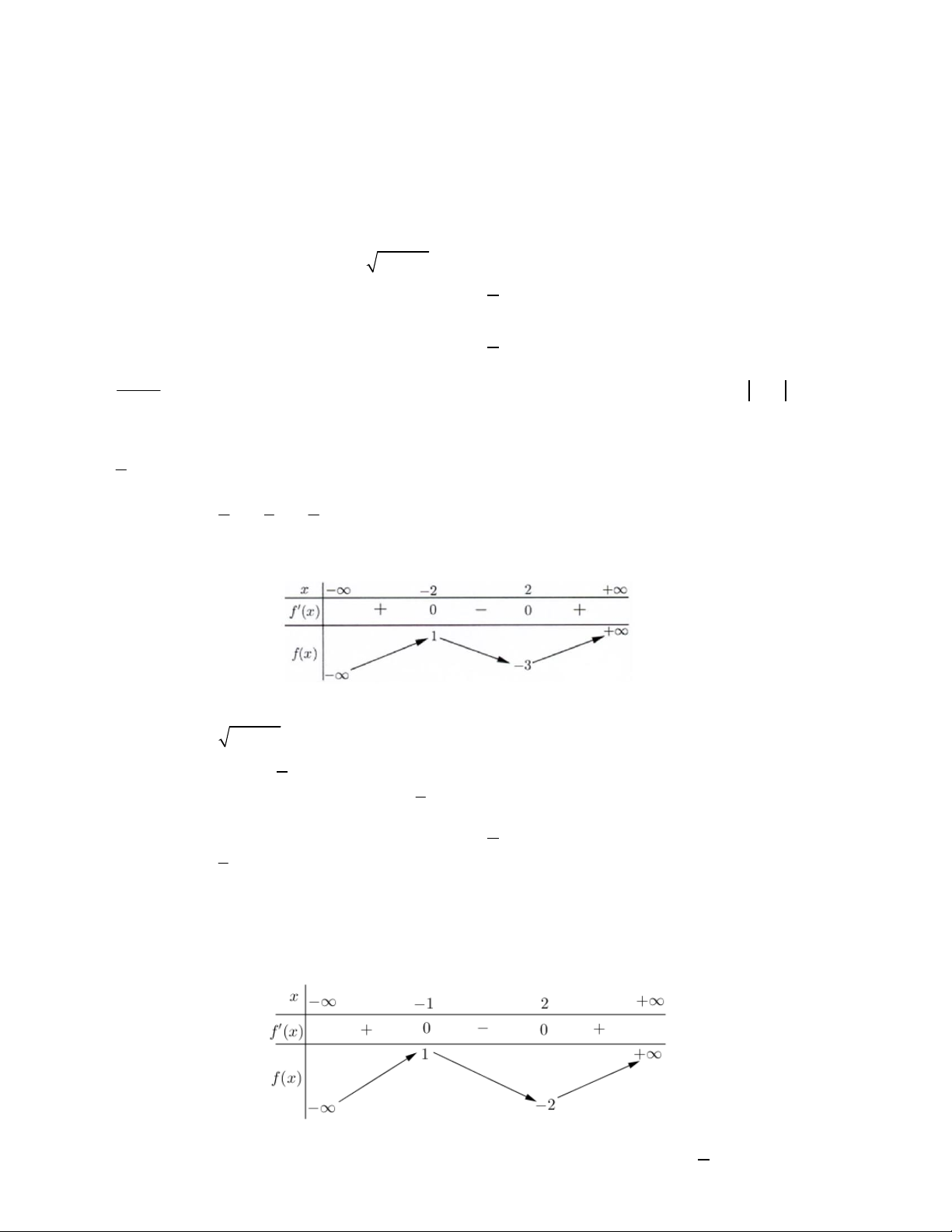
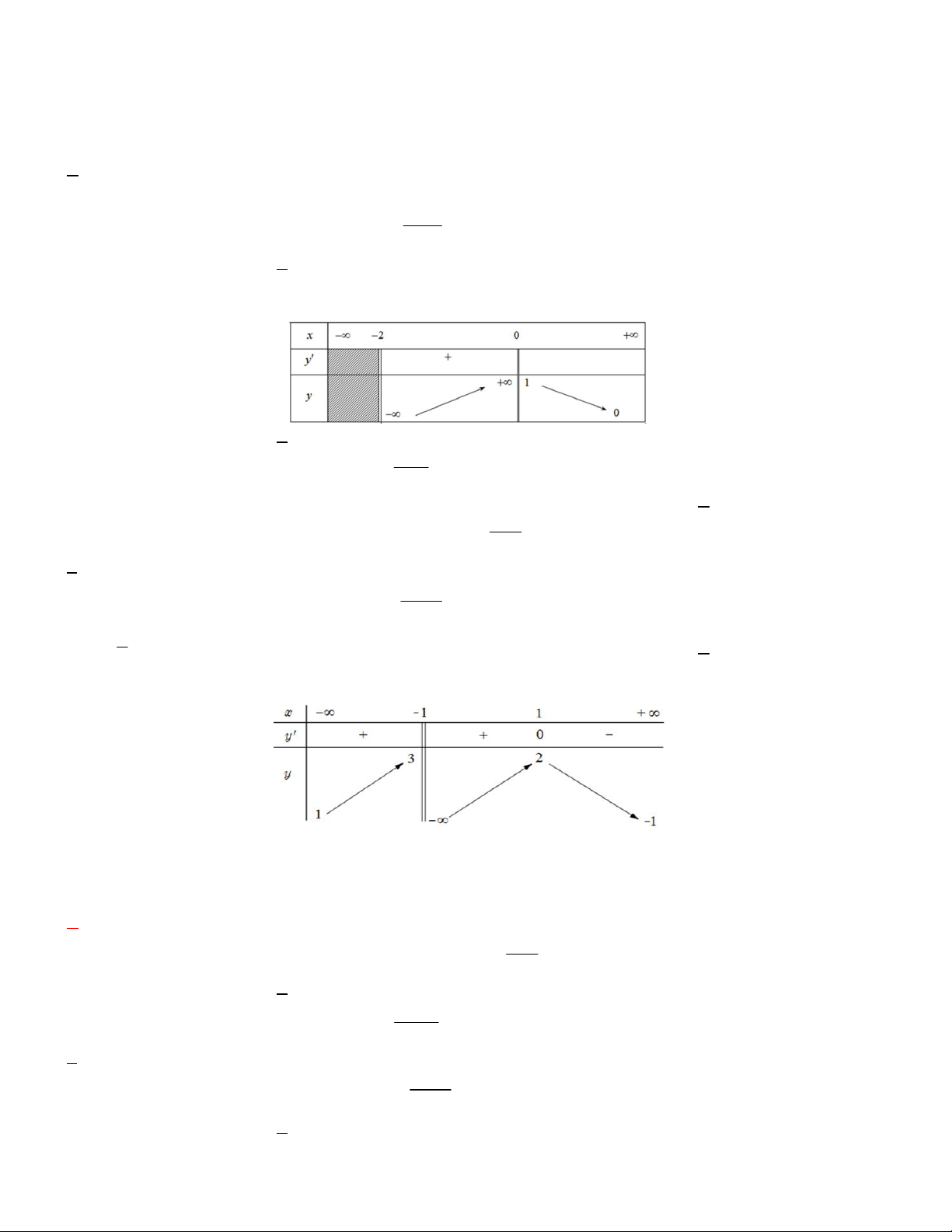
Câu 5. Cho hàm số y f x xác định trên  và có bảng xét dấu của đạo hàm như sau.
Khi đó số điểm cực trị của hàm số y f x là A. 3 . B. 2 C. 4 . D. 1. Câu 6. Hàm số 2 y
x  8x 19 đạt cực trị tại A. x  2 B. x  3 C. x  1 D. x  4 
Câu 7. Cho hàm số f x có đạo hàm f  x  x x   x  3 1
4 , x   . Số điểm cực đại của hàm số đã cho là A. 2 . B. 3 . C. 4 . D. 1.
Câu 8. Tìm số cực trị của hàm số y  log 2x 1 . 2   A.2 B. 1 C. 3 D. 0
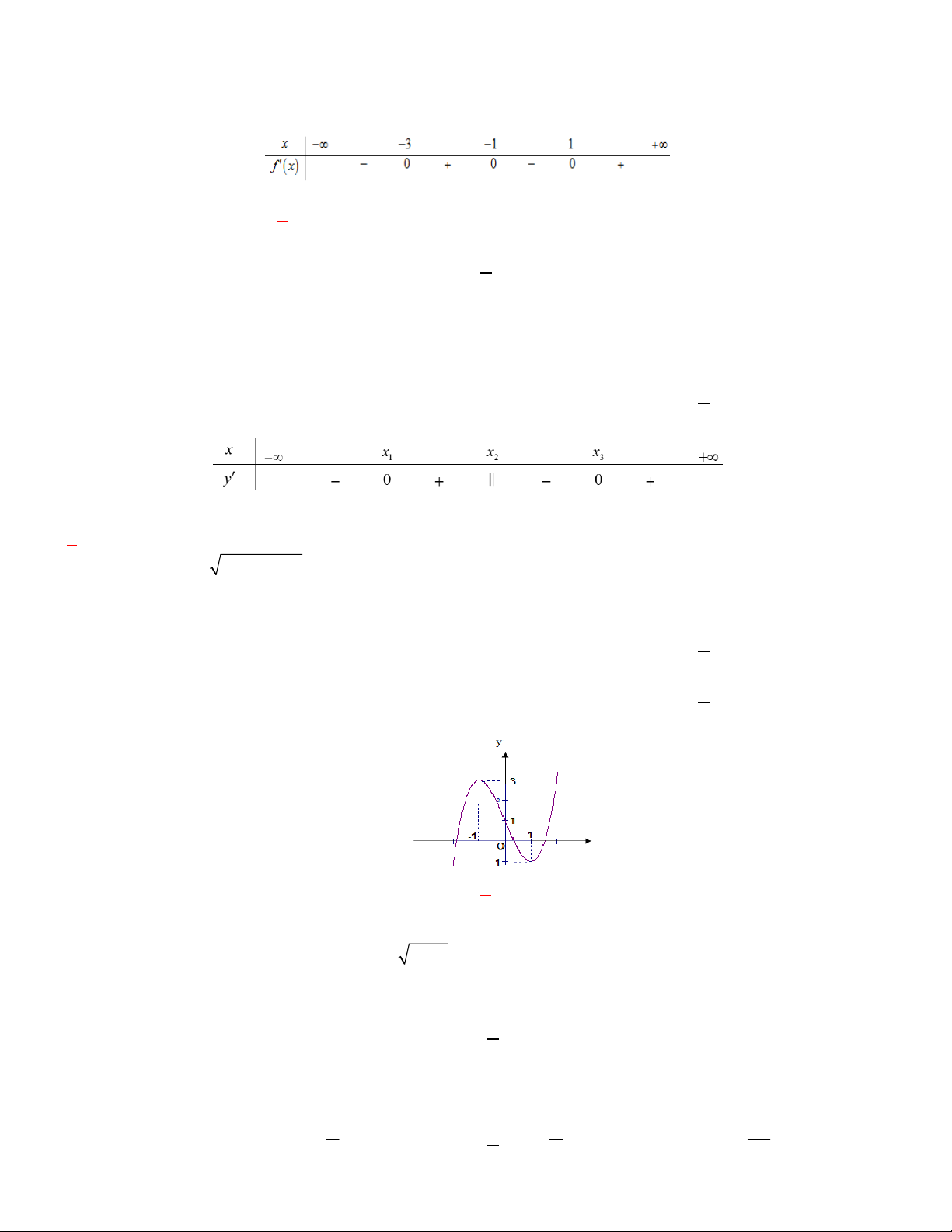
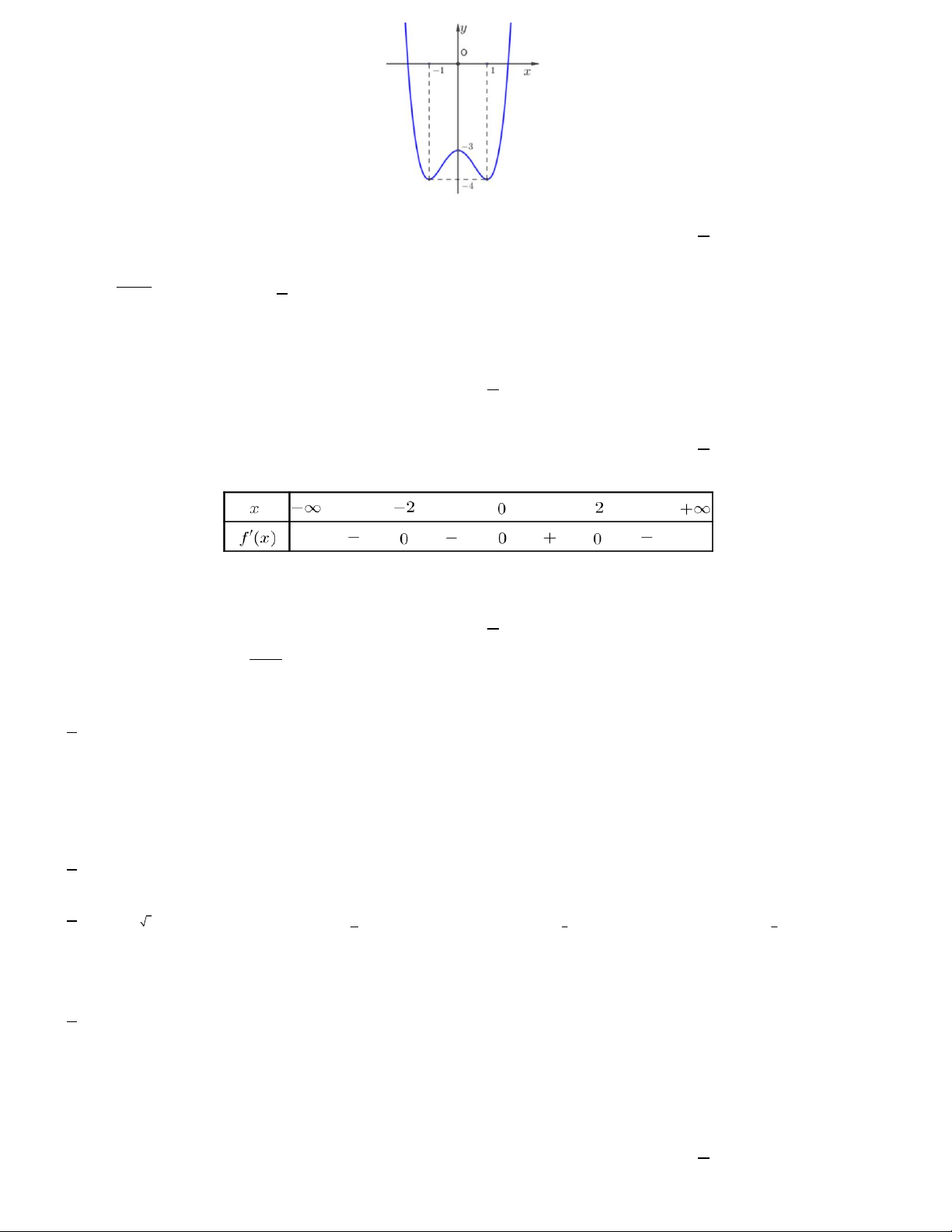
Câu 9. Hàm số y f x có đồ thị như hình vẽ. Khẳng định nào sau đây đúng?
A. Đồ thị hàm số có điểm cực đại là 1;  1  .
B. Đồ thị hàm số có điểm cực tiểu là 1;  1  .
C. Đồ thị hàm số có điểm cực tiểu là  1  ;3 .
D. Đồ thị hàm số có điểm cực tiểu là 1;  1 .
Câu 10. Tìm một điểm cực trị của hàm số 2 y  1 x . A. y  1. B. x  0 . C. y  0 . D. x  1. Câu 11. Hàm số x
y e xe đạt cực trị tại A. x  3  . B. x  1  . C. x  1. D. y  1.
Câu 12. Cho hàm số y f (x) có đạo hàm 2 f (
x)  x(x  2) , x   . Số điểm cực trị của hàm số đã cho là A. 0 . B. 3 . C. 2 . D. 1.
Câu 13. Tìm một điểm cực trị nào đó của hàm số y  cos x x .   2 A. x  0 B. x  C. x   D. x  2 2 3
Câu 14. Cho hàm số f x có đạo hàm f  x 3
x x  
1  x  2 ,x   . Số điểm cực trị của hàm số đã cho là 3 A. 1 . B. 3 . C. 5 . D. 2 . 1
Câu 15. Tìm điểm cực tiểu của đồ thị hàm số 3 2 y
x  2x  3x 1. 3  7  A. 3;  1 . B. x  3 . C. 1;   . D. x  1 .  3 
Câu 16. Hàm số nào dưới đây không có cực trị? 2 x 1 2x  2 A. y  B. y  C. 2
y x  2x 1 D. 3
y  x x 1 x x 1
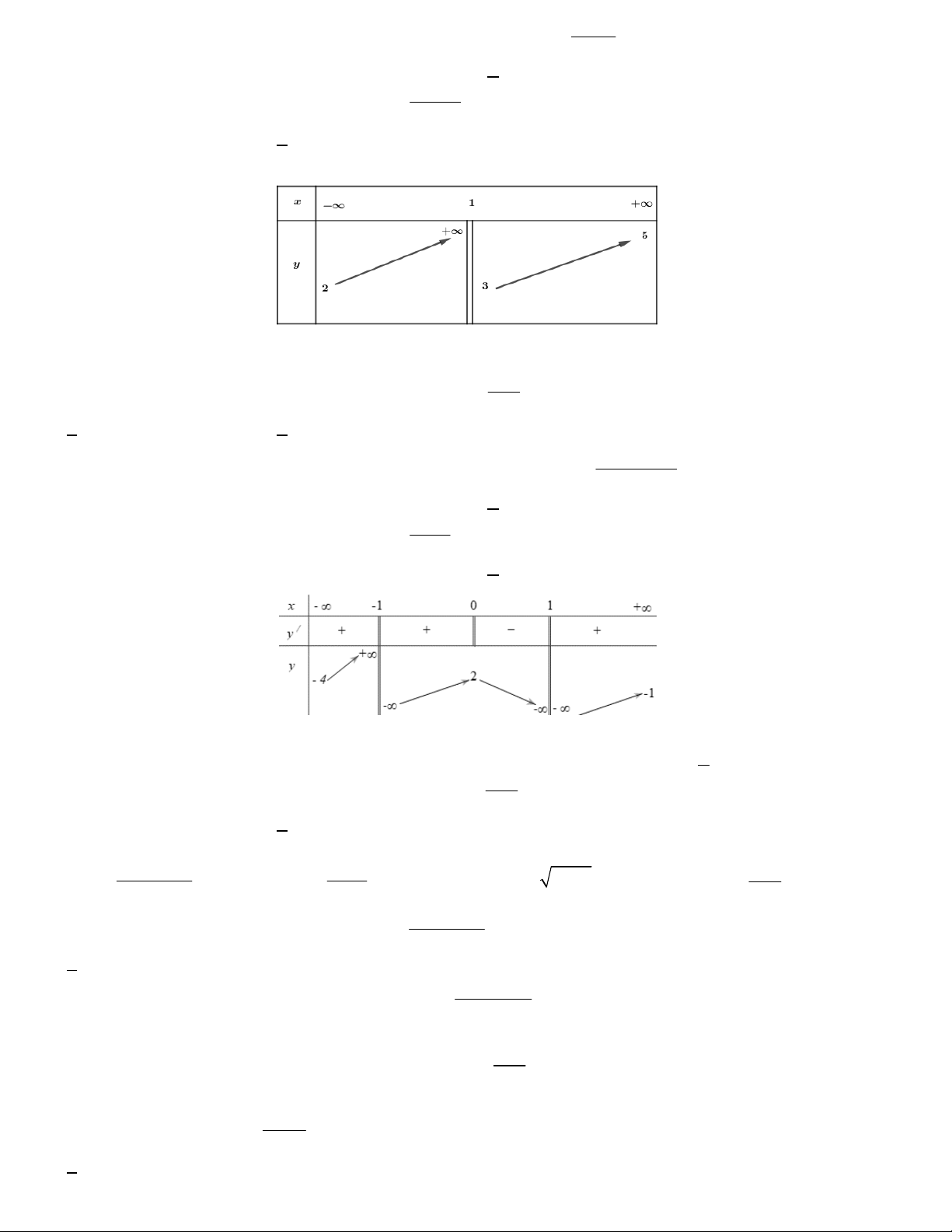
Câu 17. Cho hàm số y f x có bảng biến thiên như hình vẽ dưới đây.
Giá trị cực đại của hàm số đã cho là A. y  1. B. x  0 . C. y  0 . D. x  1. Câu 18. Hàm số 2 y
x  2x  5 đạt cực trị tại A. x  3  . B. x  1  . C. x  1. D. y  1.
Câu 19. Giá trị cực đại của hàm số 3
y x  3x  2 bằng A. 0 . B. 1. C. 4 . D. 1  .
Câu 20. Tìm số điểm cực trị của hàm số f x  log  2 x  2x . 2  A. 2 . B. 3 . C. 0 . D. 1.
Câu 21. Giá trị cực tiểu y của hàm số 3 2
y x  3x  4 là: CT A. y  0 . B. y  3 . C. y  2 . D. y  4 . CT CT CT CT
Câu 22. Tìm m để hàm số 3 2
y x  2mx mx  1 đạt cực tiểu tại x  1
A. không tồn tại m . B. m  1 . C. m  1 . D. m 1;  2 .
Câu 23. Đồ thị hàm số 4 2
y x x 1 có bao nhiêu điểm cực trị có tung độ là số dương? A. 3 . B. 1. C. 2 . D. 0 .
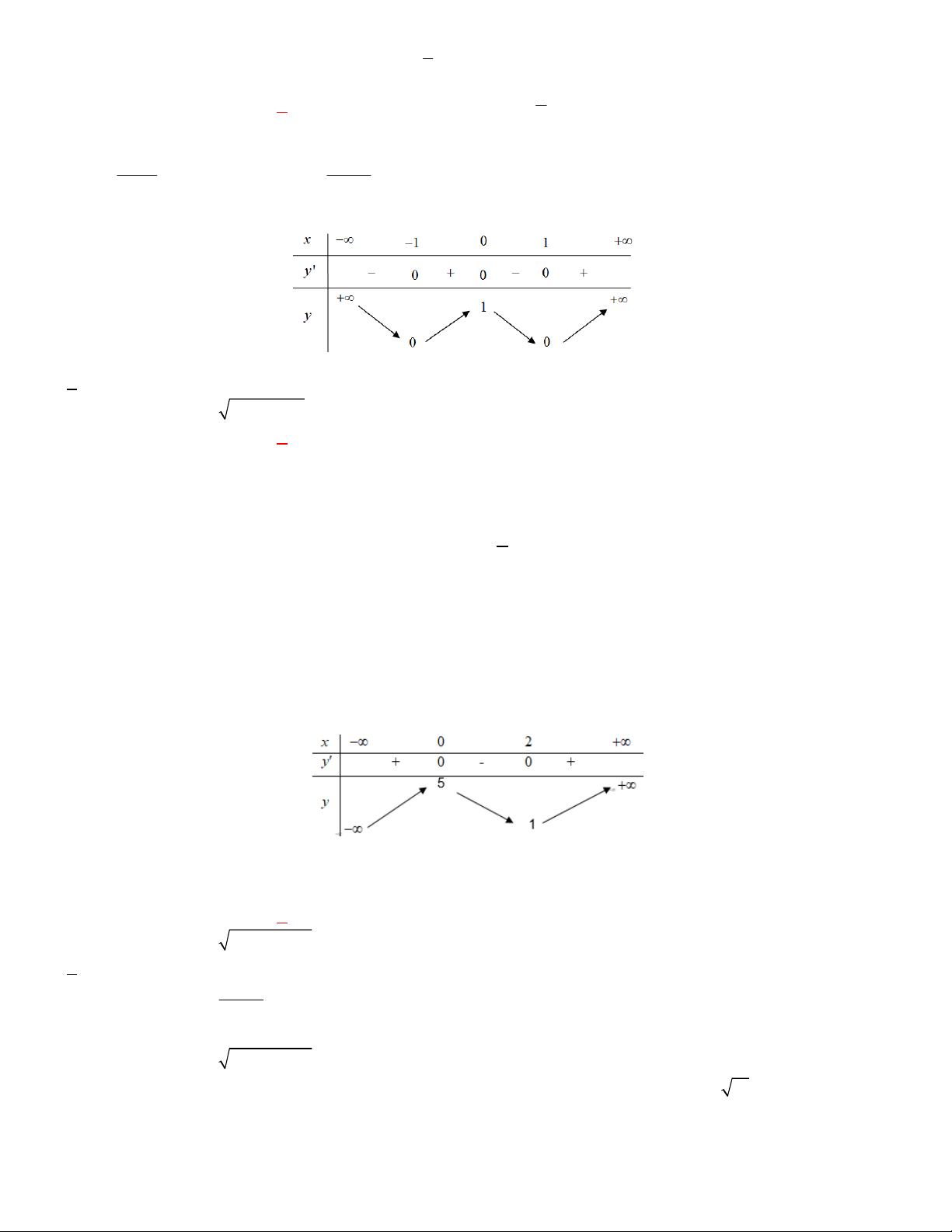
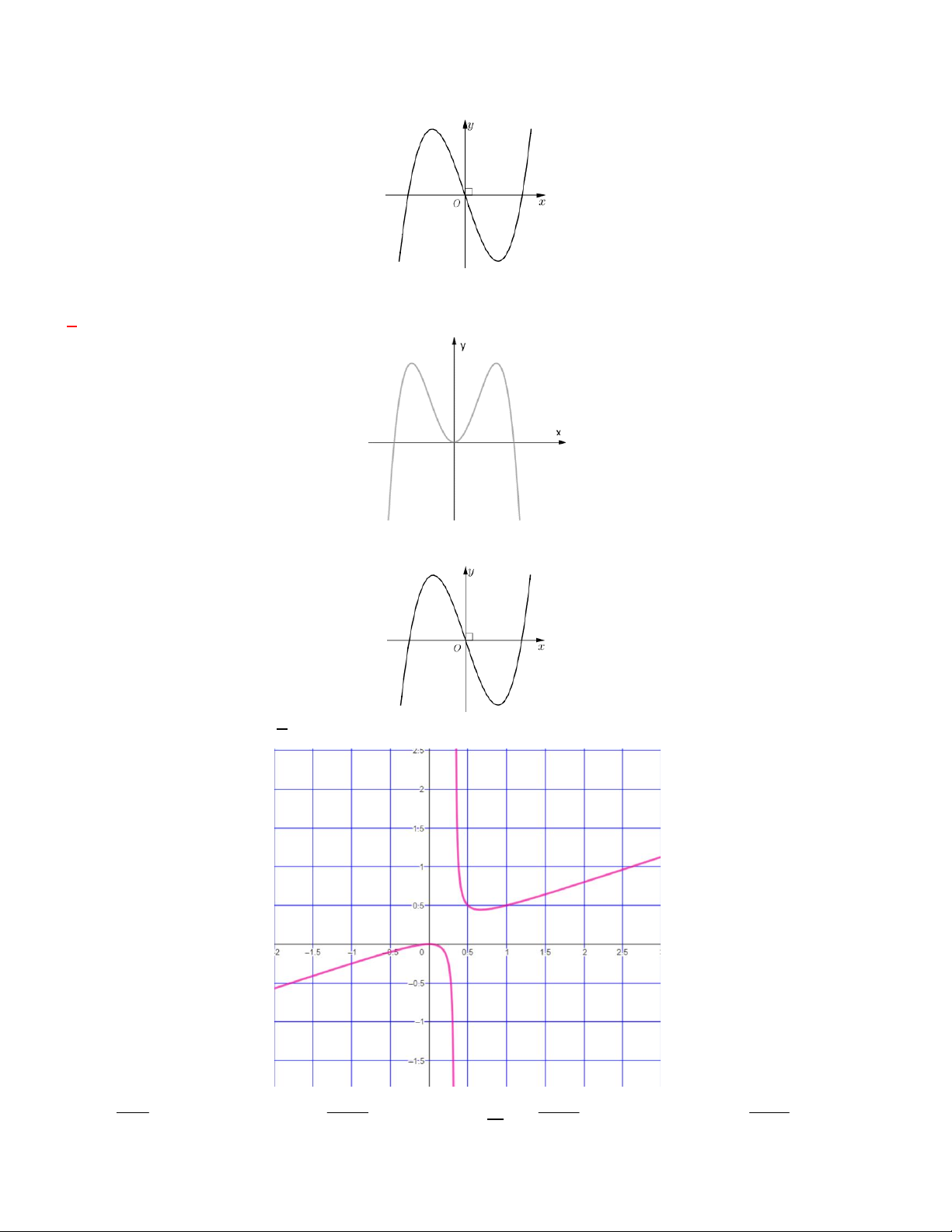
Câu 24. Cho hàm số y f x có bảng biến thiên như sau.
Giá trị cực đại của hàm số là A. y  2 . B. y  1  . C. y  5 . D. y  0.
Câu 25. Số điểm cực trị của đồ thị hàm số 4 2
y  x  2x  2 là A. 2 . B. 3 . C. 0 . D. 1. Câu 26. Hàm số 2 y
x  6x 10 đạt cực trị tại điểm A. x  3  B. x  3 C. x  1 D. x  5 2x  3
Câu 27. Hàm số y
có bao nhiêu điểm cực trị? x 1 A. 1 B. 3 C. 0 D. 2 Câu 28. Hàm số 2 y
x  2x 15 có giá trị cực tiểu bằng A. 5. B. 1 . C. 3. D. 14
Câu 29. Điểm cực đại của đồ thị hàm số 3 2
y x  6x  9x có tổng hoành độ và tung độ bằng A. 5 . B. 1 . C. 3 . D. 1.
_________________________________ 4
KHẢO SÁT HÀM SỐ LỚP 12 THPT
CỰC TRỊ HÀM SỐ (CỰC ĐẠI, CỰC TIỂU)
LỚP BÀI TOÁN TRẮC NGHIỆM ABCD CƠ BẢN – PHẦN 2
____________________________________ 4 2
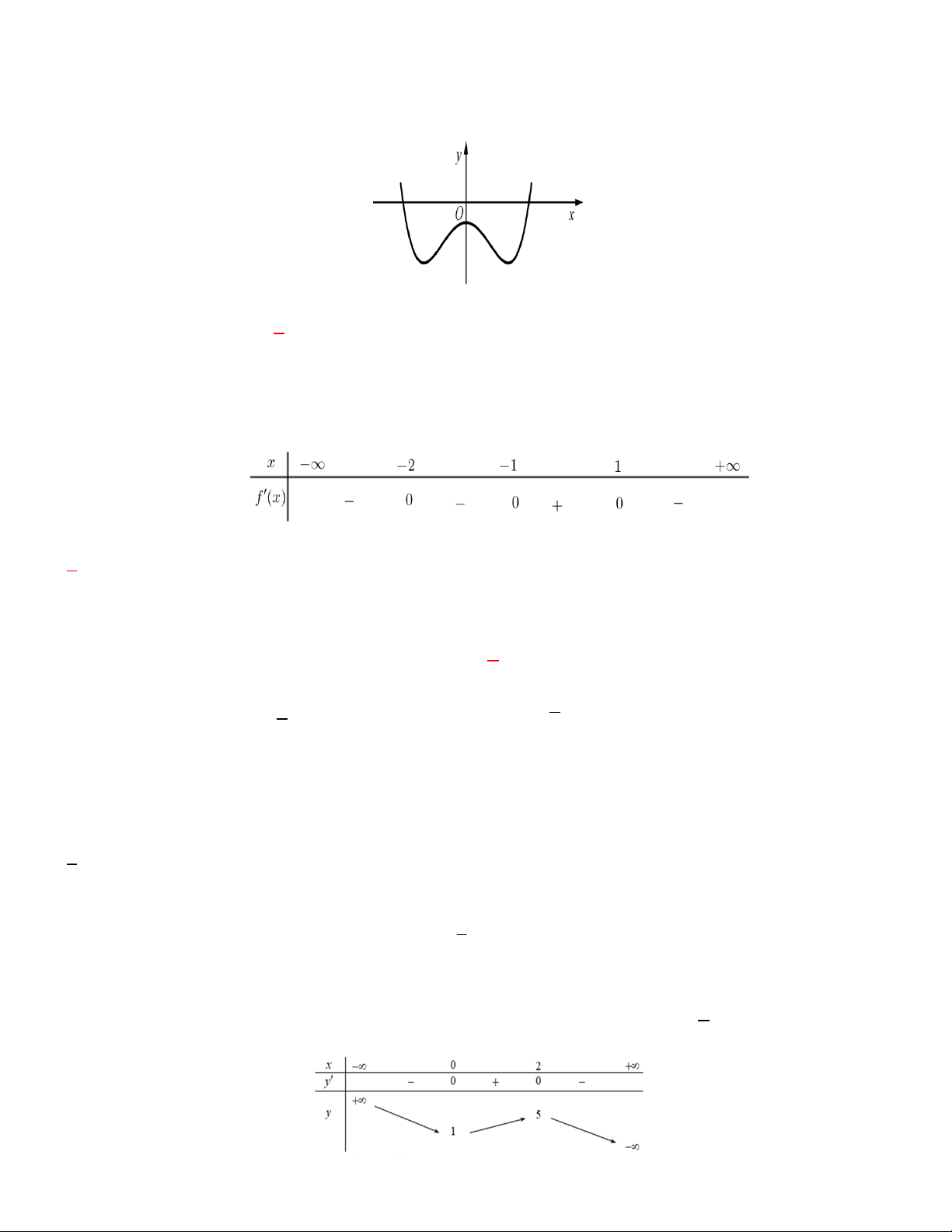
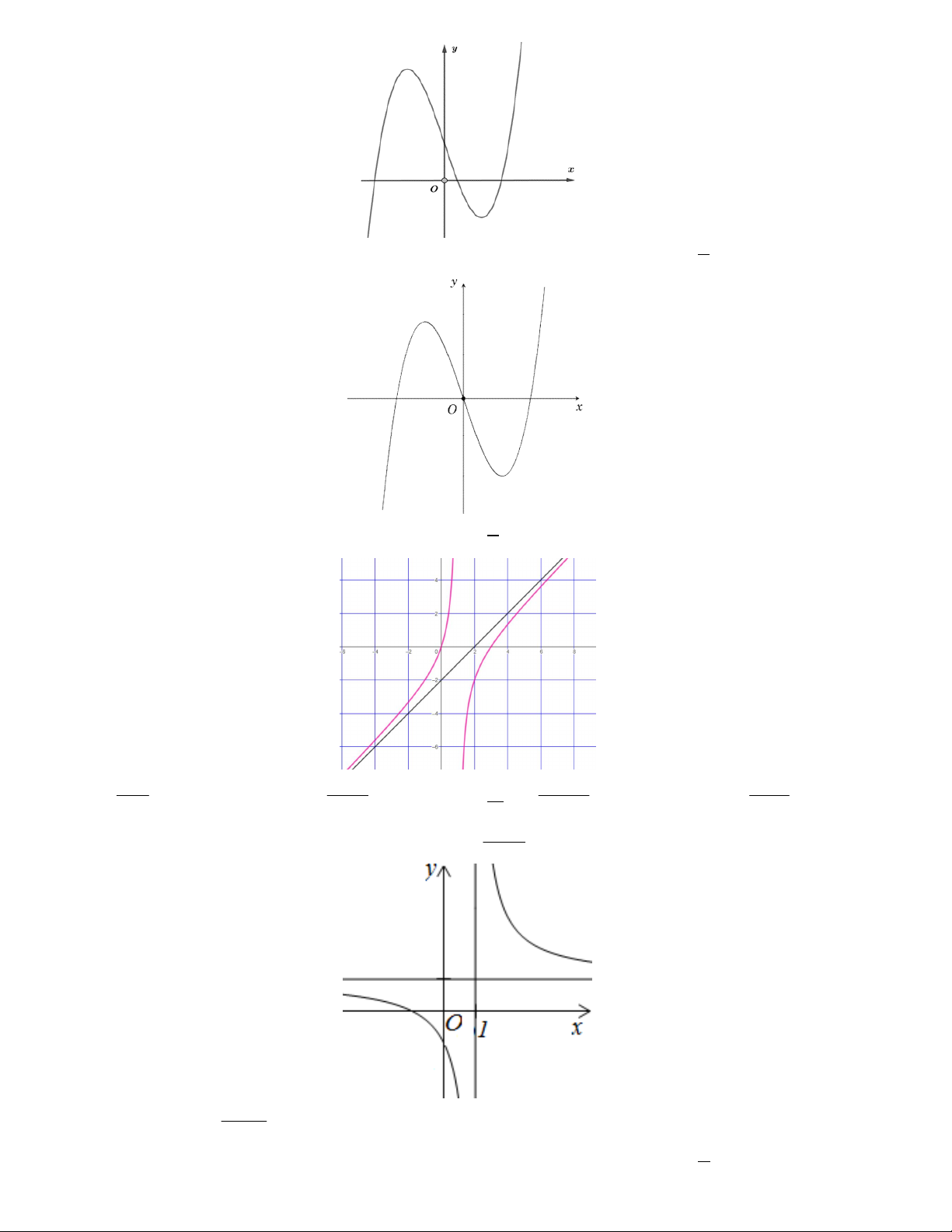
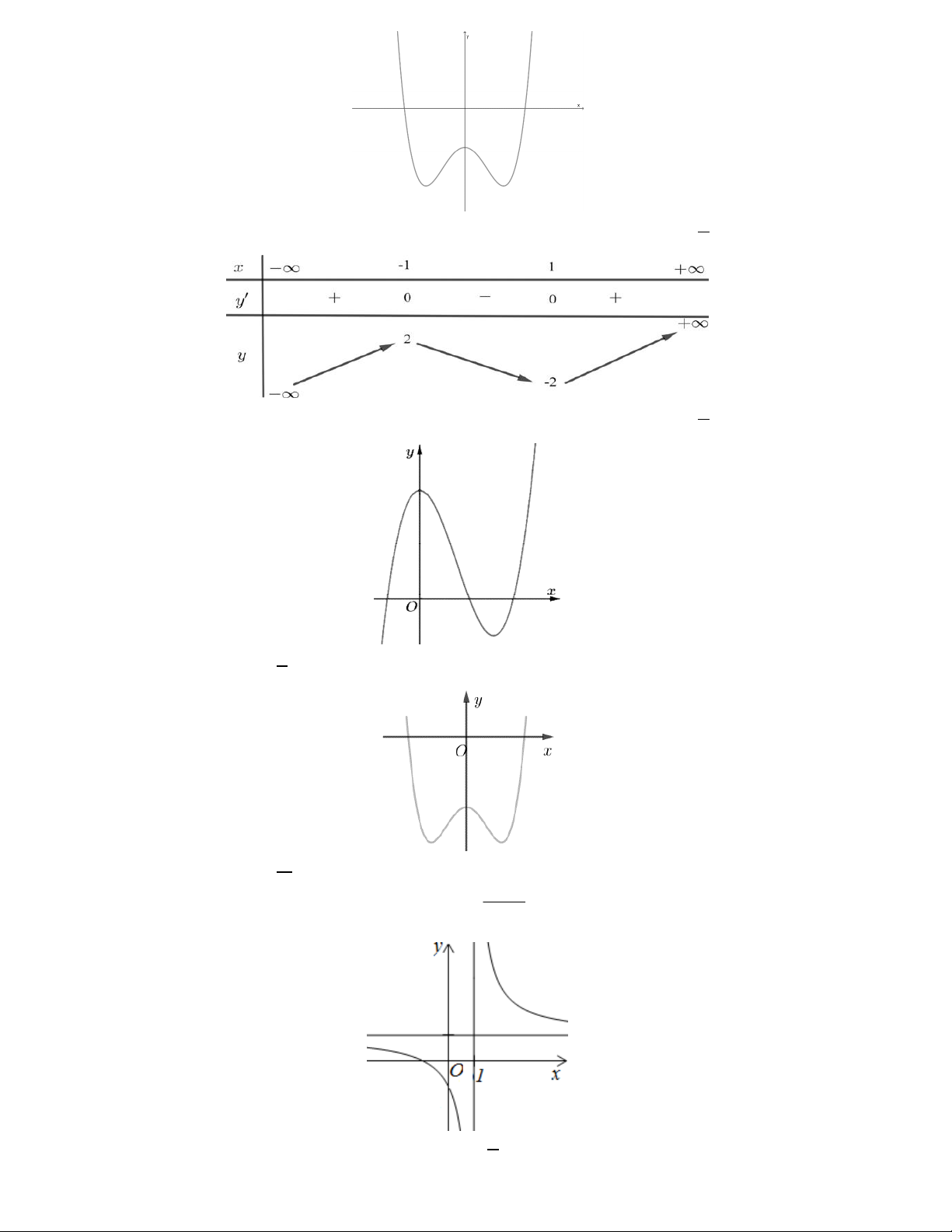
Câu 1. Cho hàm số y ax bx c (a, b, c   ) có đồ thị như hình vẽ bên.
Số điểm cực trị của hàm số đã cho là A. 2 B. 3 C. 0 D. 1
Câu 2. Tìm giá trị cực tiểu y của hàm số 3 y x  3x4 . CT A. y  6  B. y  1  C. y  2  D. y 1 CT CT CT CT
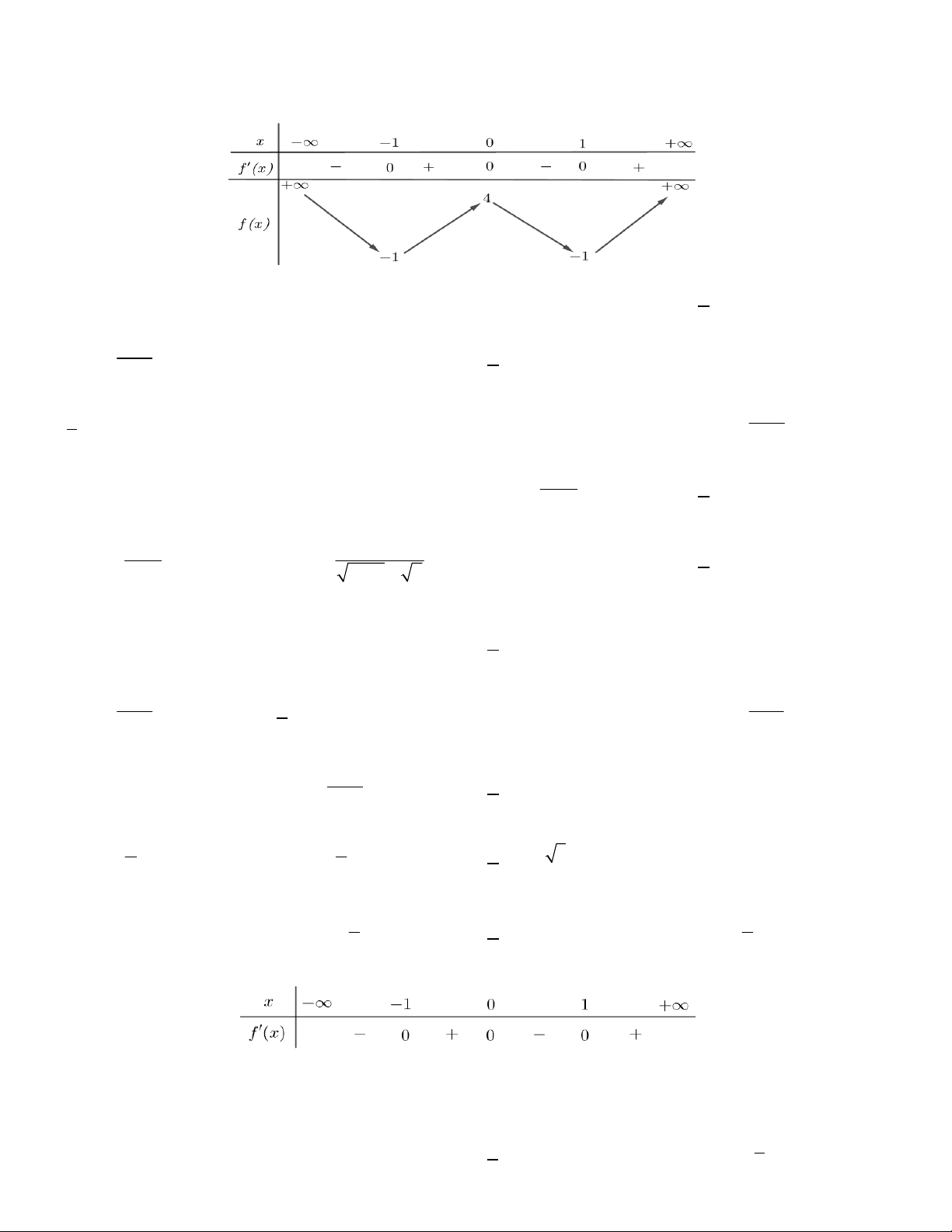
Câu 3. Cho hàm số f x có đạo hàm trên  và có bảng xét dấu f  x như sau
Mệnh đề nào sau đây sai?
A. Hàm số y f x đạt cực trị tại x  2  .
B. Hàm số y f x đạt cực đại tại x  1.
C. Hàm số y f x đạt cực tiểu tại x  1  .
D. Hàm số y f x có hai điểm cực trị.
Câu 4. Gọi x là điểm cực đại, x là điểm cực tiểu của hàm số 3
y  x  3x  2 . Tính x  2x . 1 2 1 2 A. 2 . B. 1. C. 1  . D. 0 . Câu 5. Hàm số 2 x x y e
e đạt cực trị tại điểm 1 A. x  3 . B. x   ln 2 . C. x   ln 2 . D. x  1  . 2
Câu 6. Nếu hàm số f  
x có đạo hàm là f x  x x  x x x  4 2 2 ' 2 2
1 thì tổng các điểm cực trị của hàm số f   x bằng A. 1  . B. 2 . C. 1. D. 0 . Câu 7. Cho hàm số 4 2
y x  2mx m . Tìm tất cả các giá trị thực của m để hàm số có 3 cực trị A. m  0 . B. m  0 . C. m  0 . D. m  0 .
Câu 8. Hàm số y  cos x  sin x có cực trị tại x . Giá trị tan x khi đó bằng 0 0 A.2 B. 1 C. – 1 D. 0 1
Câu 9. Tìm giá trị thực của tham số m để hàm số 3 2 y
x mx   2
m  4 x  3 đạt cực đại tại x  3. 3 A. m  1  B. m  7  C. m  5 D. m  1
Câu 10. Tìm số điểm cực trị của hàm số 1 2 x y e   . A.2 B. 1 C. 3 D. 0
Câu 11. Cho hàm số y f x có bảng biến thiên như sau
Giá trị cực đại của hàm số đã cho bằng A. 1. B. 2 . C. 0 . D. 5 . 5 2
Câu 12. Cho hàm số y f x có đạo hàm trên  và f  x   x  
1  x  2  x  3 . Số điểm cực trị của hàm số đã cho là: A. 3 B. 1 C. 0 D. 2 Câu 13. Cho hàm số 4 2
y x  2x  1. Xét các mệnh đề sau đây
 Hàm số có 3 điểm cực trị.
 Hàm số đồng biến trên các khoảng 1; 0 ; 1;  .
 Hàm số có 1 điểm cực trị.
 Hàm số nghịch biến trên các khoảng ;   1 ; 0  ;1 .
Có bao nhiêu mệnh đề đúng trong bốn mệnh đề trên? A. 2. B. 1. C. 4. D. 3.
Câu 14. Tìm số cực tiểu của hàm số 2
y x x  2x A.2 B. 3 C. 1 D. 0
Câu 15. Tính giá trị cực tiểu của hàm số y   2
ln x  2x 10 . A.3 B. 2 ln 3 C. 3ln 2 D. 2 ln 2
Câu 16. Hàm số nào trong bốn hàm số được liệt kê dưới đây không có cực trị? 2x  3 A. y  . B. 4 y x . C. 3
y  x x .
D. y x  2 . x  2 2 5 Câu 17. Hàm số 3x x y  
tại cực trị tại điểm 5 A. x  . B. x  3  . C. x  1. D. x  1  . 2 1 1 5 Câu 18. Hàm số 4 3 2 y x x
x  3x  2019m m   đạt cực tiểu tại điểm: 4 3 2 A. x  3 . B. x  3  . C. x  1. D. x  1  .
Câu 19. Cho hàm số f (x) có bàng biến thiên như sau:
Điểm cực đại của hàm số đã cho là: A. x  3 . B. x  1 . C. x  2 D. x  2 . Câu 20. Hàm số 2 y
2x x đạt cực đại tại điểm A. x  1  . B. x  1 . C. x  0 . D. x  2 . 1
Câu 21. Có bao nhiêu số thực m để hàm số 3 2 y
x mx   2 m m  
1 x 1 đạt cực đại tại x 1. 3 A. 0 B. 2 C. 1 D. 3 1 Câu 22. Hàm số 3 2 y
x x  3x  1 đạt cực tiểu tại điểm 3 A. x  1  . B. x  1 . C. x  3  . D. x  3 .
Câu 23. Tìm số điểm cực trị của hàm số 4 2
y x  2x . A. 2. B. 4. C. 3. D. 1.
Câu 24. Cho hàm số f x có bảng biến thiên như sau:
Hàm số đã cho đạt cực đại tại A. x  2  . B. x  2 . C. x  1 . D. x  1  . 6
KHẢO HÀM SỐ LỚP 12 THPT
TÍNH ĐƠN ĐIỆU CỦA HÀM SỐ (ĐỒNG BIẾN, NGHỊCH BIẾN)
LỚP BÀI TOÁN TRẮC NGHIỆM ABCD CƠ BẢN_PHẦN 1
_________________________________
Câu 1. Cho hàm số f x có bảng biến thiên như sau:
Hàm số đã cho đồng biến trên khoảng nào dưới đây? A.  ;    1 . B. 0  ;1 . C.  1   ;1 . D.  1  ; 0
Câu 2. Hàm số nào dưới đây đồng biến trên  ? x 1 A. y  . B. 2
y x  2x . C. 3 2
y x x x . D. 4 2
y x  3x  2 . x  2
Câu 3. Hàm số nào dưới đây nghịch biến trên  x  2 A. 3
y  x x . B. 4 2
y  x x . C. 3
y  x x . D. y  . x 1
Câu 4. Hàm số nào dưới đây đồng biến trên  ? x 1 A. 4 2
y x x . B. 3
y x x . C. y  . D. 3
y x x . x  2
Câu 5. Trong các hàm số sau, hàm số nào luôn đồng biến trên  ? x x  2015   3  A. y    B. y    C. 2 x y  (0,1) D. 2 (2016) x y   2016   2016  2 
Câu 6. Cho hàm số y f x  có đạo hàm f   x   x  1 với mọi x   . Hàm số đã cho nghịch biến trên khoảng nào dưới đây? A. 1; . B. 1;  . C. ;  1 . D.  ;  1 .
Câu 7. Hàm số nào dưới đây đồng biến trên khoảng  ;   ? x 1 x 1 A. y  B. 3
y x x C. 3
y  x  3x D. y x  2 x  3
Câu 8. Hàm số nào dưới đây đồng biến trên khoảng  ;   ? x  2 A. 4 2
y x  3x . B. y  . C. 3
y  3x  3x  2 . D. 3
y  2x  5x 1. x 1
Câu 9. Hàm số nào dưới đây đồng biến trên tập xác định của nó? x x  1   2  x x A. y    B. y    C. y   3 D. y  0,5  π   3 
Câu 10. Hỏi hàm số 4
y  2x 1 đồng biến trên khoảng nào?  1   1  A.  ;  0. B. ;    . C. 0;  . D.  ;    .  2   2 
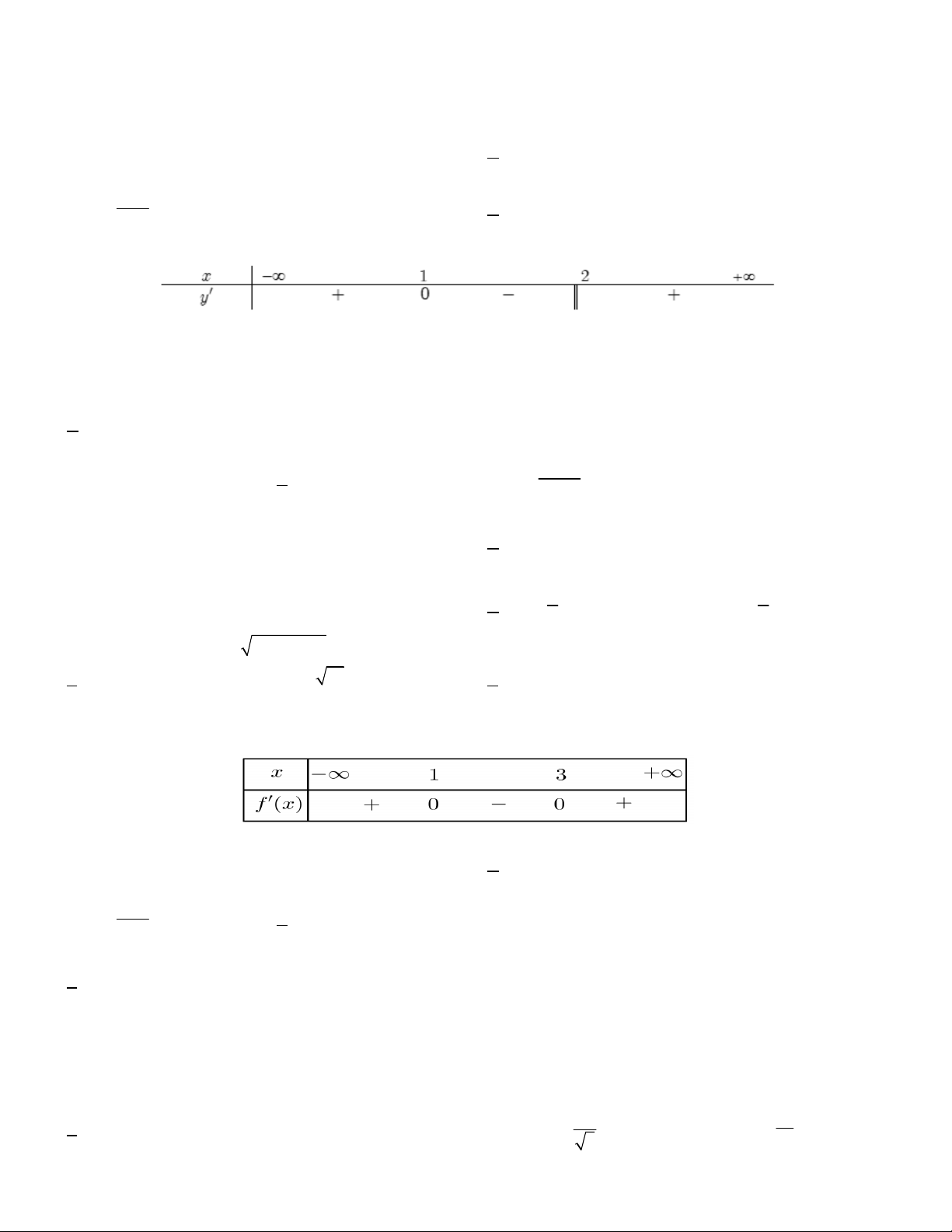
Câu 11. Cho hàm số y f x xác định và liên tục trên  , có bảng đạo hàm f  x thỏa mãn:
Hàm số y f (x) nghịch biến trên khoảng nào dưới đây A.  1  ;3 . B. 1  ;1 . C.  2  ;   1 . D. 1; . Câu 12. Cho hàm số 3 2
y x  2x x 1. Mệnh đề nào dưới đây đúng?  1 
A. Hàm số nghịch biến trên khoảng 1;
B. Hàm số nghịch biến trên khoảng ;1    3  7  1   1 
C. Hàm số nghịch biến trên khoảng ;   
D. Hàm số đồng biến trên khoảng ;1    3   3 
Câu 13. Cho hàm số y  4 x  2
2x . Mệnh đề nào dưới đây đúng?
A. Hàm số nghịch biến trên khoảng ;  2
B. Hàm số đồng biến trên khoảng 1;1
C. Hàm số nghịch biến trên khoảng 1;1
D. Hàm số đồng biến trên khoảng ;  2 Câu 14. Cho hàm số 2 y
2x  1 . Mệnh đề nào dưới đây đúng?
A. Hàm số đồng biến trên khoảng 0;  
B. Hàm số đồng biến trên khoảng ; 0
C. Hàm số nghịch biến trên khoảng 0;  
D. Hàm số nghịch biến trên khoảng 1;1 3 x Câu 15. Cho hàm số 2 y
x x  2019 3
A. Hàm số đã cho đồng biến trên  .
B. Hàm số đã cho nghịch biến trên  ;   1 .
C. Hàm số đã cho đồng biến trên  ;  
1 và nghịch biến trên 1; .
D. Hàm số đã cho đồng biến trên 1; và nghịch biến trên  ;   1 .
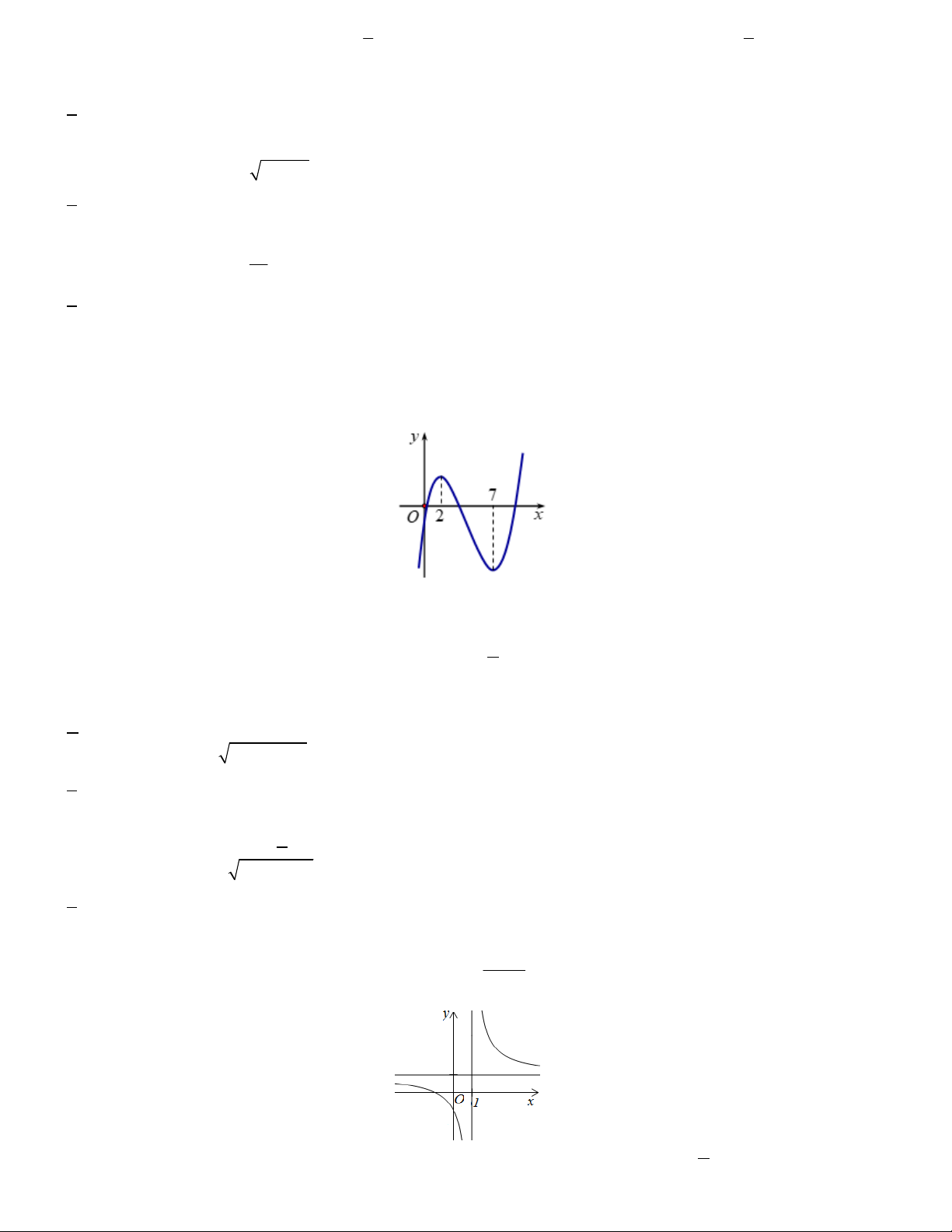
Câu 16. Cho đồ thị hàm số y f x liên tục trên  và có đồ thị như hình vẽ bên dưới.
Khẳng định nào sau đây là đúng ?
A. Hàm số đồng biến trên khoảng 1;3 .
B. Hàm số nghịch biến trên khoảng 6;  .
C. Hàm số đồng biến trên khoảng  ;  3 .
D. Hàm số nghịch biến trên khoảng 3;6 .
Câu 17. Hàm số nào sau đây nghịch biến trên  ? A. 3
y x  3x  2 . B. 4 2
y x  2x  2 . C. 3 2
y  x  2x  4x 1. D. 3 2
y  x  2x  5x  2 . Câu 18. Hàm số 2
y  2018x x nghịch biến trên khoảng nào trong các khoảng sau đây? A. 1010; 2018 . B. 2018;  . C. 0;1009 . D. 1; 2018 . Câu 19. Hàm số 3 2
y  x  3x  4 đồng biến trên tập hợp nào trong các tập hợp được cho dưới đây? A. 2;   . B. 0; 2 .
C. ;0  2;   . D. ;0 . Câu 20. Cho hàm 2 y
x  6x  5 . Mệnh đề nào sau đây là đúng?
A. Hàm số đồng biến trên khoảng 5; . B. Hàm số đồng biến trên khoảng 3; .
C. Hàm số đồng biến trên khoảng  ;  
1 . D. Hàm số nghịch biến trên khoảng  ;  3. ax b
Câu 21. Đường cong ở hình bên là đồ thị của hàm số y
với a,b,c,d là các số thực. Mệnh đề nào dưới cx d đây đúng ?
A. y  0,x  
B. y  0,x  
C. y  0,x  1
D. y  0,x  1 8
KHẢO HÀM SỐ LỚP 12 THPT
TÍNH ĐƠN ĐIỆU CỦA HÀM SỐ (ĐỒNG BIẾN, NGHỊCH BIẾN)
LỚP BÀI TOÁN TRẮC NGHIỆM ABCD CƠ BẢN_PHẦN 2
_________________________________
Câu 1. Cho hàm số y f x có đạo hàm f  x  x x  3
2 , với mọi x   . Hàm số đã cho nghịch biến trên khoảng nào dưới đây? A. 1; 3 . B.  1  ; 0 . C. 0;  1 . D.  2  ; 0 .
Câu 2. Hàm số nào sau đây đồng biến trên  . x 1 A. y  . B. 3 2
y  x  3x 1 C. x y e D. 2 y x  2 x 1
Câu 3. Cho hàm số y f (x) có bảng xét dấu đạo hàm như sau: Hỏi mệnh đề nào sai ?
A. Hàm số đã cho đồng biến trên khoảng (2; )  .
B. Hàm số đã cho đồng biến trên khoảng (3;  )  .
C. Hàm số đã cho đồng biến trên khoảng ( ;  1).
D. Hàm số đã cho nghịch biến trên khoảng (0;3).
Câu 4. Hàm số nào dưới đây đồng biến trên  ? x 10 A. 4 2
y x  3x  5 . B. 3
y x x . C. y  . D. 3
y x x . x  2 Câu 5. Hàm số 3
y x  3x m nghịch biến trên khoảng nào? A.  ;    1 . B. ; . C.  1  ;  1 . D. 0; .
Câu 6. Trong các hàm số sau hàm số nào nghịch biến trên  ? xx  e   2  A. 2 log x B. y   3 log x  C. y  D. y  3      4   5  Câu 7. Cho hàm số 2 y
x  8x  7  4 . Mệnh đề nào sau đây là đúng?
A. Hàm số đồng biến trên khoảng  17;.
B. Hàm số đồng biến trên khoảng 3; 
C. Hàm số đồng biến trên khoảng  ;   1 .
D. Hàm số nghịch biến trên khoảng  ;  3.
Câu 8. Cho hàm số y f x có bảng xét dấu đạo hàm như sau:
Khoảng nghịch biến của hàm số y f x là A. ( ;  3) . B. (1; ) . C. (1;3) . D. ( ;1  ) .
Câu 9. Hàm số nào sau đây đồng biến trên  . x 1 A. y  .
B. y  sin x  2x C. x
y e  6x D. 2 y x  2 x 1 Câu 10. Cho hàm số 3 2
y  x  3x 1, kết luận nào sau đây về tính đơn điệu của hàm số là đúng nhất:
A. Hàm số đồng biến trên khoảng 0; 2 và nghịch biến trên các khoảng ;0 ; 2;  ;
B. Hàm số đồng biến trên khoảng 0; 2 ;
C. Hàm số nghịch biến trên khoảng 0; 2 và đồng biến trên các khoảng  ;
 0 ; 2;  ;
D. Hàm số nghịch biến trên các khoảng ;0 và 2;  .
Câu 11. Tìm hàm số đồng biến trên  . x  1  3 A.   3x f x  . B.   3 x f x   .
C. f x    .
D. f x  .  3  3x
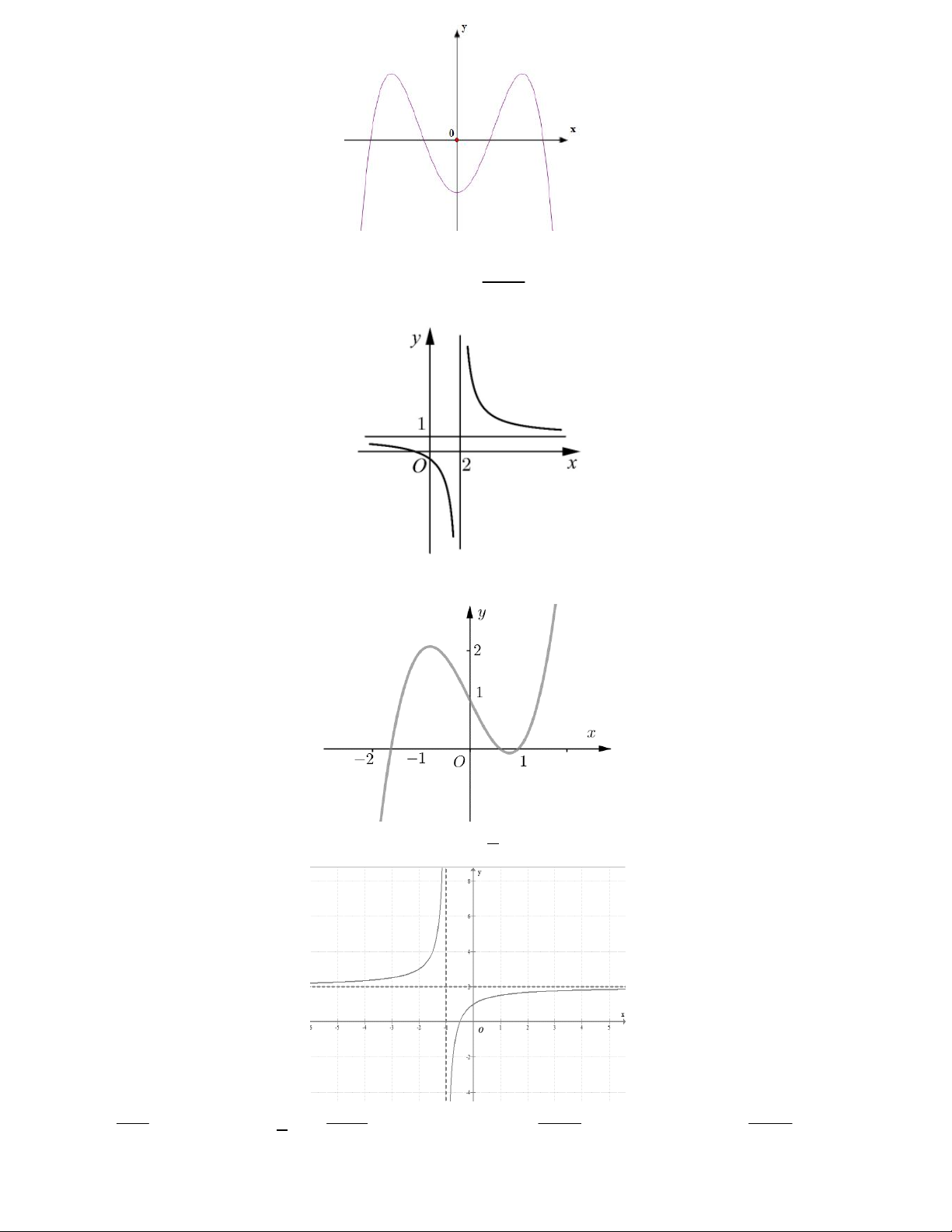
Câu 12. Cho hàm số y f (x) có đồ thị như hình vẽ 9
Hàm số đã cho đồng biến trên khoảng nào A. 0;3 . B. 3;  . C. ; 2 . D. 1;3 .
Câu 13. Hàm số nào sau đây đồng biến trên  . x 1 A. y
B. y  cos x  5x  3 C. x
y e  6x D. 2
y x  2x x  6
Câu 14. Cho hàm số y f x có đạp hàm f  x 2
x 1, x   . Mệnh đề nào dưới đây đúng ?
A. Hàm số nghịch biến trên khoảng  ;  0 .
B. Hàm số nghịch biến trên khoảng 1; .
C. Hàm số nghịch biến trên khoảng  1  ;  1 .
D. Hàm số đồng biến trên khoảng  ;   .
Câu 15. Cho hàm số y f x có đạo hàm f  x 2  x  2, x   .
 Mệnh đề nào dưới đây là đúng? A. f   1  f   1 . B. f   1  f   1 . C. f   1  f   1 . D. f   1  f   1 .
Câu 16. Cho hàm số y f x có đạo hàm trên  và có bảng xét dấu đạo hàm như sau:
Trong các mệnh đề sau mệnh đề nào đúng ?
A. Hàm số f x nghịch biến trên  ;  0 .
B. Hàm số f x đồng biến trên 1;3 .
C. Hàm số đồng biến trên 1  ;1 .
D. Hàm số nghịch biến trên  ;  2   2;  x 1
Câu 17. Cho hàm số y
. Khẳng định nào sau đây là đúng? x 1
A. Hàm số đã cho nghịch biến trên khoảng   ;1  .
B. Hàm số đã cho đồng biến trên khoảng  ;  
1 và khoảng 1; .
C. Hàm số đã cho đồng biến trên khoảng 0; .
D. Hàm số đã cho nghịch biến trên tập  \   1 .
Câu 18. Cho hàm số y f x có đạo hàm f  x 2
x  2x , x
   . Hàm số y  2
f x đồng biến trên khoảng A. 0; 2 . B. 2;  . C.  ;  2   . D.  2  ;0 .
Câu 19. Hàm số nào dưới đây đồng biến trên khoảng (0;  ) ? A. y  log x .
B. y  log x .
C. y  log x .
D. y  log x . 3  e 1 6 3 4
Câu 20. Cho hàm số y f x thỏa mãn f  x 2
x  5x  4. Khẳng định nào sau đây là đúng?
A. Hàm số đã cho đồng biến trên khoảng  ;  3 .
B. Hàm số đã cho nghịch biến trên khoảng 2;3 .
C. Hàm số đã cho nghịch biến trên khoảng 3;  .
D. Hàm số đã cho đồng biến trên khoảng 1; 4 .
Câu 21. Cho hàm số y f (x) có đạo hàm f  x   x  
1  x  3, x
   . Hàm số đã cho nghịch biến trên khoảng nào dưới đây? A. 0;3 . B. 3; . C. ; 2 . D. 1;3 .
_________________________________ 10
KHẢO SÁT HÀM SỐ LỚP 12 THPT
ĐƯỜNG TIỆM CẬN CỦA ĐỒ THỊ HÀM SỐ
LỚP BÀI TOÁN TRẮC NGHIỆM ABCD CƠ BẢN – PHẦN 1
______________________________________
Câu 1. Cho hàm số y f (x) có lim f (x)  1và lim f (x)  1 . Khẳng định nào sau đây là khẳng định đúng? x x
A. Đồ thị hàm số đã cho có hai tiệm cận ngang là các đường thẳng x  1 và x  1  .
B. Đồ thị hàm số đã cho không có tiệm cận ngang.
C. Đồ thị hàm số đã cho có đúng một tiệm cận ngang.
D. Đồ thị hàm số đã cho có hai tiệm cận ngang là các đường thẳng y  1 và y  1. x  2
Câu 2. Tiệm cận ngang của đồ thị hàm số y  là x 1 A. y  2  . B. y  1. C. x  1  . D. x  2 .
Câu 3. Cho hàm số y f x có bảng biến thiên như hình vẽ dưới đây. Hỏi đồ thị của hàm số đã cho có bao
nhiêu đường tiệm cận? A. 1. B. 3 . C. 2 . D. 4 x 1
Câu 4. Tiệm cận đứng của đồ thị hàm số y  là x  3 A. x  3  . B. x  1 . C. x  1 . D. x  3 . 1
Câu 5. Tìm đường tiệm cận xiên của đồ thị hàm số y x  . x 1 A. y x B. y x 1
C. y x  2
D. y x  3 2x 1
Câu 6. Tiệm cận ngang của đồ thị hàm số y  là: x 1 1 A. y  . B. y  1. C. y  1. D. y  2 . 2
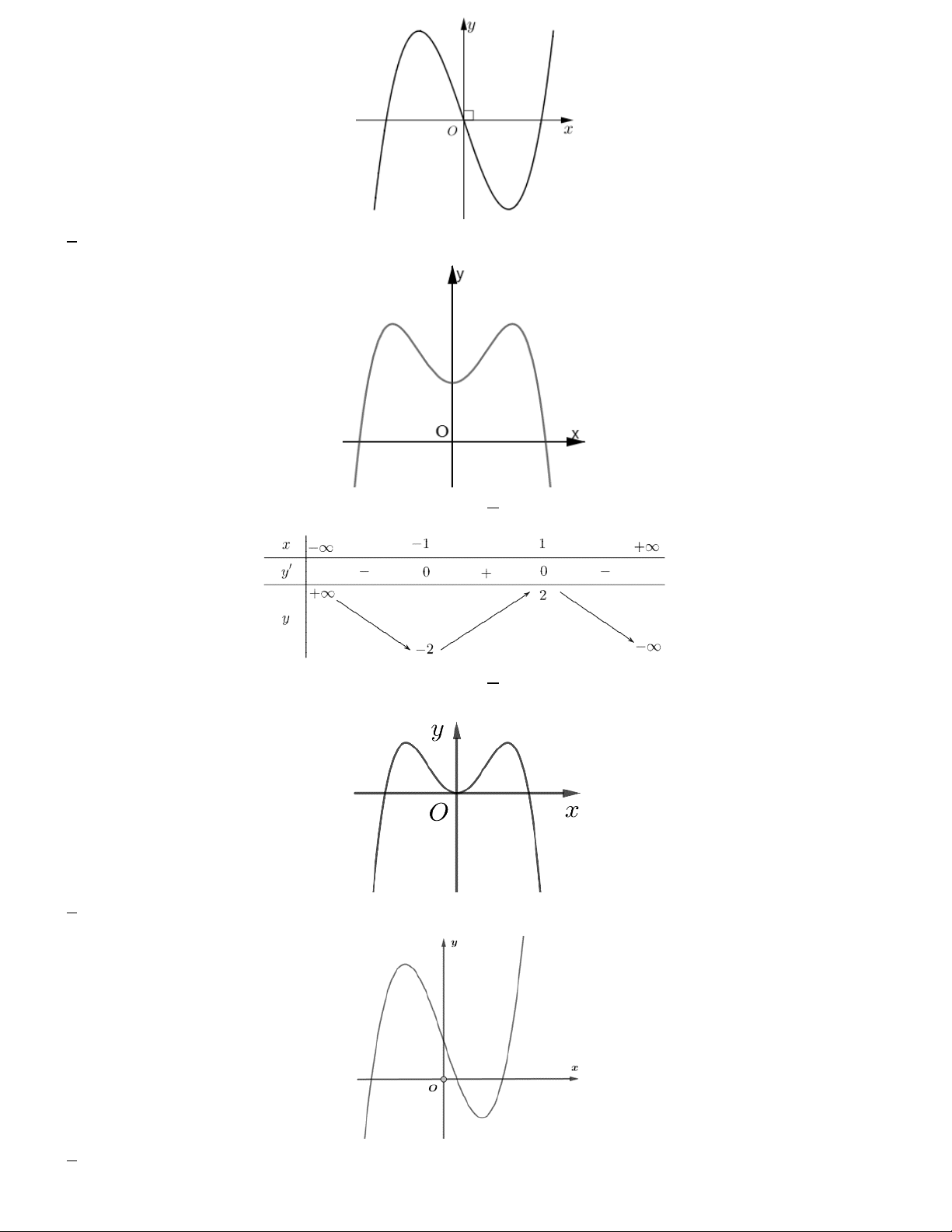
Câu 7. Hàm số y f x xác định trên  \   1 
, liên tục trên mỗi khoảng xác định và có bảng biến thiên:
Khẳng định nào dưới đây sai?
A. Đồ thị hàm số đã cho có hai tiệm cận ngang là y  1 và y  1.
B. Đồ thị hàm số có tiệm cận đứng x  1  .
C. Đồ thị hàm số có 3 đường tiệm cận.
D. Đồ thị hàm số đã cho có hai tiệm cận đứng là x  1 và x  1  . 2
Câu 8. Tìm đường tiệm cận xiên của đồ thị hàm số y x 1 . x 1 A. y x B. y x 1
C. y x  2
D. y x  3 3x  2
Câu 9. Tiệm cận đứng của đồ thị hàm số y
là tập hợp tất cả các điểm có hoành độ bằng bao nhiêu x  2 A. x  2 . B. x  1  . C. x  3 . D. x  2  . 4x 1
Câu 10. Tiệm cận ngang của đồ thị hàm số y
đi qua điểm nào sau đây x 1 A. A1;3 . B. B 2; 4 . C. C 6;  1 . D. D 4; 2 .
Câu 11. Cho hàm số có bảng biến thiên như hình sau 11
Tổng số đường tiệm cận ngang và tiệm cận đứng của đồ thị hàm số y f x là A. 3 . B. 2 . C. 4 . D. 1. 2x 1
Câu 12. Tiệm cận đứng của đồ thị hàm số y
là đường thẳng có phương trình x 1 1 A. x  2 . B. x  1. C. x   . D. x  1  . 2 5
Câu 13. Tìm đường tiệm cận xiên của đồ thị hàm số y x  3  . x  3 A. y x B. y x 1
C. y x  2
D. y x  3 x 1
Câu 14. Tiệm cận đứng của đồ thị hàm số y
là đường thẳng có phương trình x  2 A. x  1  . B. x  2 . C. x  2 . D. x  1 . 2x 1
Câu 15. Tiệm cận ngang của đồ thị hàm số y
là đường thẳng có phương trình 2x  4 A. y  2 . B. x  2  . C. x  1 . D. y  1. 4
Câu 16. Tìm đường tiệm cận xiên của đồ thị hàm số y x  3  . x 1 A. y x B. y x 1
C. y x  2
D. y x  3
Câu 17. Cho hàm số y f x  có bảng biến thiên như sau:
Tiệm cận đứng của đồ thị hàm số đã cho là đường thẳng có phương trình: A. x   1 . B. y  1  . C. y  2  . D. x   2 . 3x 1
Câu 18. Tiệm cận ngang của đồ thị hàm số y  là: x 1 1 A. y  . B. y  3 . C. y  1  . D. y  1. 3
Câu 19. Cho hàm số y f x có đồ thị C  và lim f x   , lim f x  2
 . Số tiệm cận ngang của C x x là A. 0. B. 2. C. 1. D. 3. x 1
Câu 20. Tiệm cận xiên của đồ thì hàm số y x
là đường thẳng có phương trình: x 1 A. y x B. y x 1
C. y x  2
D. y x  3 2x  2
Câu 21. Tiệm cận đứng của đồ thị hàm số y  là x 1 A. x  2  . B. x  1. C. x  1  . D. x  2 . 2x  2
Câu 22. Tiệm cận đứng của đồ thị hàm số y  là x 1 A. x  2 . B. x  2 . C. x  1. D. x  1 .
_________________________________ 12
KHẢO SÁT HÀM SỐ LỚP 12 THPT
ĐƯỜNG TIỆM CẬN CỦA ĐỒ THỊ HÀM SỐ
LỚP BÀI TOÁN TRẮC NGHIỆM ABCD CƠ BẢN – PHẦN 2
______________________________________ x 1
Câu 1. Tiệm cận đứng của đồ thị hàm số y
là đường thẳng có phương trình x  2 B. x  2 . B. x   1 . C. x   2 . D. x  1 . 2x  2 5x  2 7x  2 x  6
Câu 2. Cho các hàm số y  , y  , y  , y  2 x 1 x 1 x 1 x 1
Có bao nhiêu hàm số mà đồ thị có đường tiệm cận đứng bằng x  1  ? A.2 B. 3 C. 1 D. 4
Câu 3. Cho hàm số y f x có bảng biến thiên như sau:
Tổng số tiệm cận đứng và tiệm cận ngang của đồ thị hàm số đã cho là: A. 2. B. 3. C. 4. D. 1. 2x  2
Câu 4. Tìm giá trị m để đường tiệm cận đứng của đồ thị hàm số y
là đường thẳng x  1. x 1 A. m  2  . B. m  1. C. m  1. D. m  2 . 2x  2
Câu 5. Tiệm cận đứng của đồ thị hàm số y
cách trục tung một khoảng lớn hơn x 1 2 7 A.2 B. 1 C. D. 2 2 2x  2
Câu 6. Tiệm cận đứng của đồ thị hàm số y
cắt đường thẳng nào sau đây x 1 A. x  2 . B. x  2 . C. y x D. x  1 .
Câu 7. Cho hàm số f x có bảng biến thiên như sau
Tổng số tiệm cận đứng và tiệm cận ngang của đồ thị hàm số đã cho là A. 1. B. 2 . C. 4 . D. 3 .
Câu 8. Đồ thị hàm số nào sau đây không có đường tiệm cận đứng 2x  2 4x 13 14 1 A. y  B. y
C. y x  3  D. y x x 1 x 1 x 1 2 x 1
Câu 9. Cho hàm số y f x có bảng biến thiên như sau:
Tổng số tiệm cận đứng và tiệm cận ngang của đồ thị hàm số đã cho là: A. 4 . B. 1. C. 3 . D. 2 . 13 2x  2
Câu 10. Tìm giá trị m để đường tiệm cận đứng của đồ thị hàm số y
là đường thẳng x  1  x m A. m  2  . B. m  1. C. m  1. D. m  2 . 4x 13
Câu 11. Tiệm cận ngang của đồ thị hàm số y
đi qua điểm nào sau đây x 1 A. A1;3 . B. B 2; 4 . C. C 6;  1 . D. D 4; 2 .
Câu 12. Cho hàm số y f x có bảng biến thiên như sau
Tổng số đường tiệm cận ngang và đường tiệm cận đứng của đồ thị hàm số đã cho là A. 3 B. 2 C. 4 D. 1 14
Câu 13. Đường tiệm cận xiên của đồ thị hàm số y x  3 
đi qua điểm nào sau đây x 1 A. A1; 4 . B. B 2; 4 . C. C 6;  1 . D. D 4; 2 . 2 5x  4x 1
Câu 14. Tổng số tiệm cận đứng và tiệm cận ngang của đồ thị hàm số y  là 2 x 1 A. 0. B. 1. C. 2. D. 3. 5x 1
Câu 15. Tiệm cận ngang của đồ thị hàm số y
cách trục hoành một khoảng bằng x 1 A.4 B. 2 C. 5 D. 6
Câu 16. Cho hàm số có bảng biến thiên như hình sau
Khoảng cách giữa hai đường tiệm cận ngang đồ thị hàm số y f x là A. 3 . B. 2 . C. 4 . D.5. 12
Câu 17. Đường tiệm cận xiên của đồ thị hàm số y x 1
cắt đường thẳng nào sau đây x 1 A. y x
B. y  2x 1
C. y x  2
D. y x  3
Câu 18. Đồ thị của hàm số nào dưới đây có tiệm cận đứng? 2 x  3x  2 2 x x A. y  B. y  C. 2 y x 1 D. y x 1 2 x 1 x  1 2 x  5x  4
Câu 19. Tìm số tiệm cận của đồ thị hàm số y  . 2 x 1 A. 2 B. 3 C. 0 D. 1 2 x  3x  4
Câu 20. Tìm số tiệm cận đứng của đồ thị hàm số: y  2 x  16 A. 2 B. 3 C. 1 D. 0 5
Câu 21. Đường tiệm cận xiên của đồ thị hàm số y  3x 1 có hệ số góc bằng x 1 A.2 B. 3 C. 4 D. 1 x  2
Câu 22. Đồ thị hàm số y
có mấy đường tiệm cận. 2 x  4 A. 3 B. 1 C. 2 D. 0
_________________________________ 14
KHẢO SÁT HÀM SỐ LỚP 12 THPT
ĐỒ THỊ HÀM SỐ, BẢNG BIẾN THIÊN CỦA HÀM SỐ
LỚP BÀI TOÁN TRẮC NGHIỆM ABCD CƠ BẢN– PHẦN 1
________________________________________
Câu 1. Đồ thị của hàm số   3 2
f x ax bx cx d có dạng như hình vẽ. Hệ số a không thể bằng A.3 B. 2 C. 1 D. – 4
Câu 2. Đồ thị của hàm số nào dưới đây có dạng như đường cong trong dưới đây? A. 4 2
y  x  2x . B. 4 2
y x  2x . C. 3 2
y x  3x . D. 3 2
y  x  3x .
Câu 3. Đồ thị của hàm số   3 2
f x ax bx cx d có dạng như hình vẽ. Giá trị f 0 bằng A.1 B. 0 C. 2 D. 4
Câu 4. Đồ thị của hàm số nào dưới đây có dạng như đường cong trong hình bên? x 1 2x 1 2 x 2 x A. y  . B. y  . C. y  D. y x 1 x 1 2x 1 3x 1
Câu 5. Đồ thị của hàm số nào dưới đây có dạng như đường cong trong hình bên? 15 A. 3
y x  3x . B. 3
y  x  3x . C. 4 2
y x  2x . D. 4 2
y  x  2x .
Câu 6. Đồ thị hàm số nào dưới đây có dạng như đường cong trong hình bên? A. 3 2
y x  3x 1. B. 3 2
y  x  3x 1. C. 4 2
y  x  2x 1. D. 4 2
y x  2x 1.
Câu 7. Hàm số nào dưới đây có bảng biến thiên như sau? A. 3
y x  3x . B. 2
y x  2x . C. 3
y  x  3x . D. 2
y  x  2x .
Câu 8. Đồ thị hàm số nào dưới đây có dạng như đường cong trong hình bên? A. 4 2
y  x  2x . B. 4 2
y  x  2x 1. C. 4 2
y x  2x . D. 3
y x  3x .
Câu 9. Đồ thị của hàm số dưới đây có dạng như đường cong bên? A. 3
y x  3x 1. B. 4 2
y x  2x 1. C. 4 2
y  x  2x 1. D. 3
y  x  3x 1. 16
Câu 10. Đồ thị của hàm số   3 2
f x ax bx cx d có dạng như hình vẽ. Giá trị d không thể bằng A.2 B. 3 C. 4 D. 0
Câu 11. Đồ thị của hàm số nào dưới đây có dạng như đường cong trong hình bên? A. 4 2
y x  2x . B. 3
y  x  3x . C. 3
y x  3x . D. 4 2
y  x  2x .
Câu 12. Đồ thị của hàm số nào dưới đây có dạng như đường cong trong hình bên x 1 2x 1 2 x  3x 2 x A. y  . B. y  . C. y  D. y x 1 x 1 x 1 3x 1 ax b
Câu 13. Đường cong ở hình bên là đồ thị của hàm số y
với a, b, c, d là các số thực. cx d d  2c
Tính giá trị biểu thức . c A.2 B. 3 C. 4 D. 1 17
Câu 14. Đường cong trong hình vẽ bên là đồ thị của hàm số nào dưới đây? A. 3 2
y  x x 1 B. 4 2
y  x  2x 1 C. 3 2
y x x 1 D. 4 2
y x  2x 1
Câu 15. Hàm số nào dưới đây có bảng biến thiên như sau? A. 4 2
y x  2x . B. 3
y  x  3x . C. 4 2
y  x  2x . D. 3
y x  3x .
Câu 16. Đường cong ở hình bên dưới là đồ thị của một trong bốn hàm số dưới đây. Hàm số đó là hàm số nào? A. 3 2
y  x  3x 1 B. 3 2
y x  3x  3 C. 4 2
y  x  2x 1 D. 4 2
y x  2x 1.
Câu 17. Đồ thị hàm số nào dưới đây có dạng như đường cong trong hình vẽ bên? A. 3 2
y x  3x  2 . B. 4 2
y x  2x  2 . C. 3 2
y  x  3x  2 . D. 4 2
y  x  2x  2 . ax b
Câu 18. Đường cong ở hình bên là đồ thị của hàm số y
với a, b, c, d là các số thực. Mệnh đề nào dưới cx d đây đúng?
A. y  0,x   B. 
y  0,x  1 C. 
y  0,x  1
D. y  0,x  
_________________________________ 18
KHẢO SÁT HÀM SỐ LỚP 12 THPT
ĐỒ THỊ HÀM SỐ, BẢNG BIẾN THIÊN CỦA HÀM SỐ
LỚP BÀI TOÁN TRẮC NGHIỆM ABCD CƠ BẢN_ P2
________________________________________
Câu 1. Đồ thị của hàm số nào dưới đây có dạng như đường cong trong dưới đây? A. 4 2
y  x  2x . B. 4 2
y x  2x . C. 3 2
y x  3x . D. 3 2
y  x  3x .
Câu 2. Đường cong trong hình bên là đồ thị của một hàm số trong bốn hàm số được liệt kê ở bốn phương án ,
A B, C, D dưới đây. Hỏi hàm số đó là hàm số nào? A. 3
y x  3x 1 B. 3
y  x  3x 1 C. 4 2
y x x 1 D. 2
y  x x 1
Câu 3. Đồ thị của hàm số nào dưới đây có dạng như đường cong trong hình vẽ bên? 2 2 x 1 2x 1 x x  3 A. y  . B. y  . C. y  D. y x 1 x 1 x 1 x 1
Câu 4. Đồ thị của hàm số nào dưới đây có dạng như đường cong trong hình vẽ bên? A. 3 2
y x  3x  3 . B. 3
y  x  3 2 x  3 . C. 4 y x  2 2 x  3 .s D. 4
y  x  2 2 x  3 .
Câu 5. Đường cong trong hình vẽ bên là đồ thị của hàm số nào dưới đây? 19 A. 3 2
y x  3x 1 B. 3 2
y  x  3x 1 C. 4 2
y  x  3x 1 D. 4 2
y x  3x 1 ax b
Câu 6. Đường cong ở hình bên là đồ thị của hàm số y
với a,b,c,d là các số thực. Mệnh đề nào dưới cx d đây đúng? A.  y  0,x  1 B.  y  0,x  1 C.  y  0,x  2 D.  y  0,  2
Câu 7. Hình vẽ sau đây là đồ thị của một trong bốn hàm số cho ở các đáp án , A ,
B C, D . Hỏi đó là hàm số nào? A. 3
y x  2x  1 . B. 3 2
y x  2x 1. C. 3
y x  2x 1. D. 3
y  x  2x 1.
Câu 7. Hình vẽ bên dưới là đồ thị của hàm số nào x 1 2x 1 2x  3 2x  5 A. y  . B. y  . C. y  . D. y  . x 1 x 1 x 1 x 1
Câu 8. Đồ thị hàm số sau có đường tiệm cận xiên là 20

Tài liệu liên quan: