
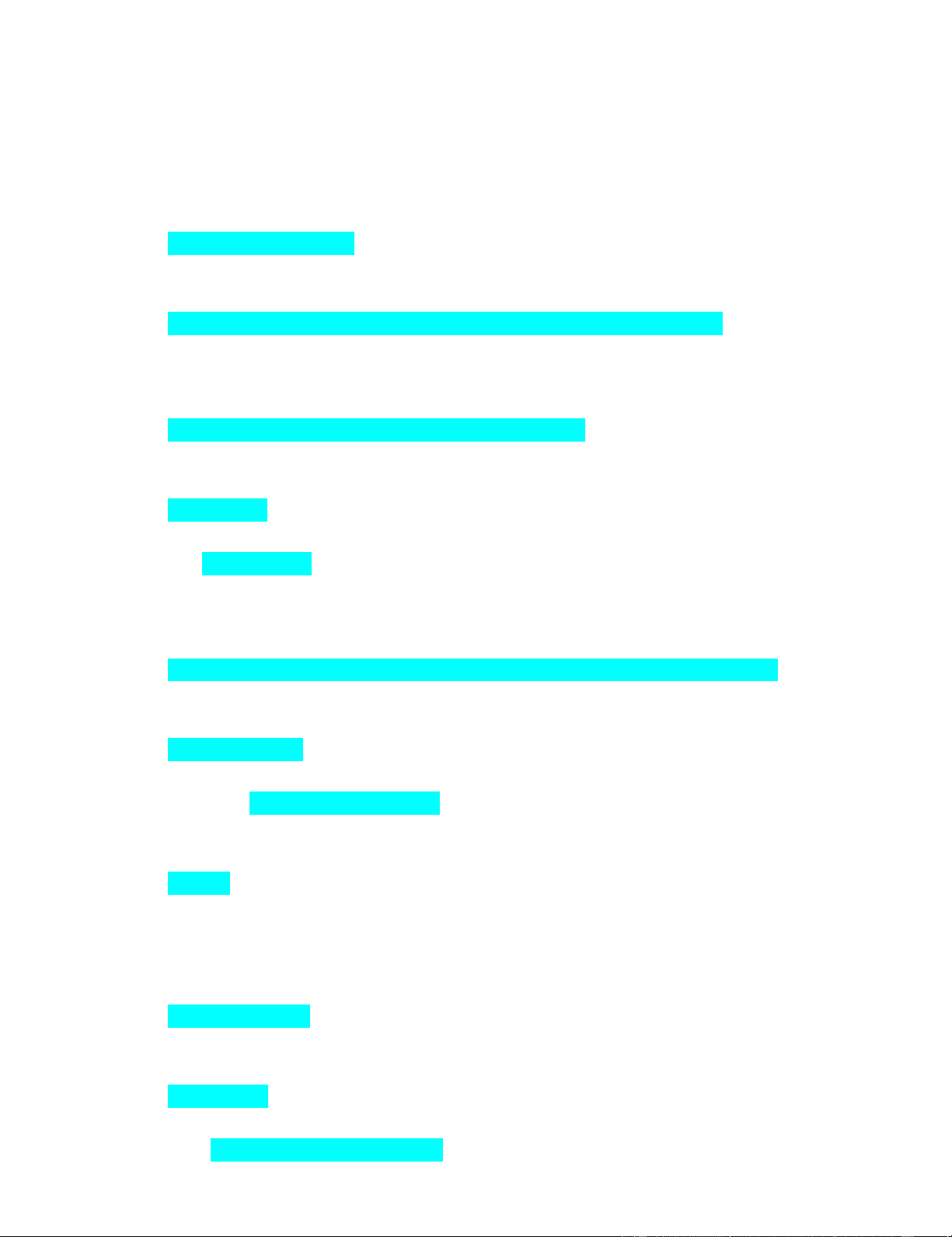



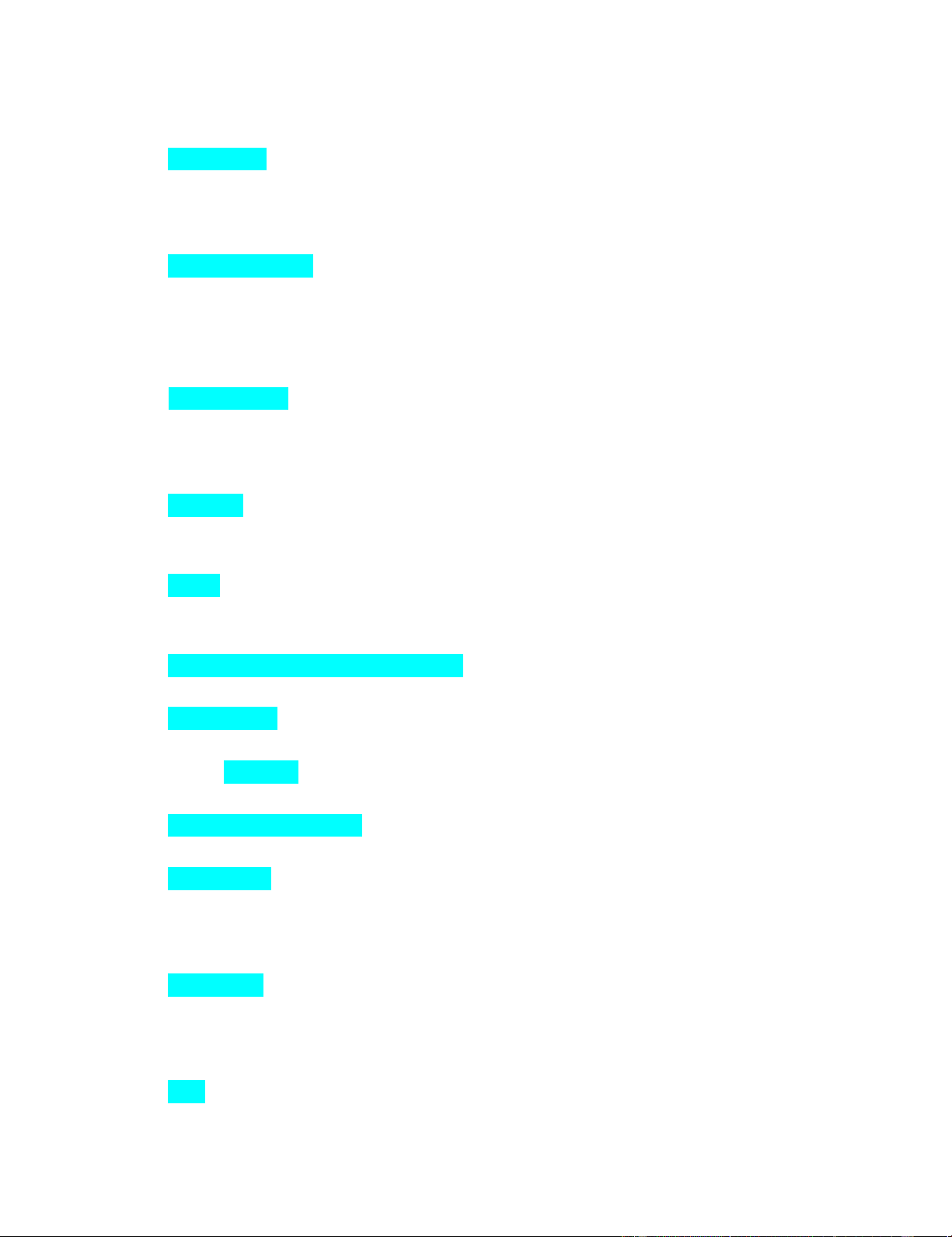
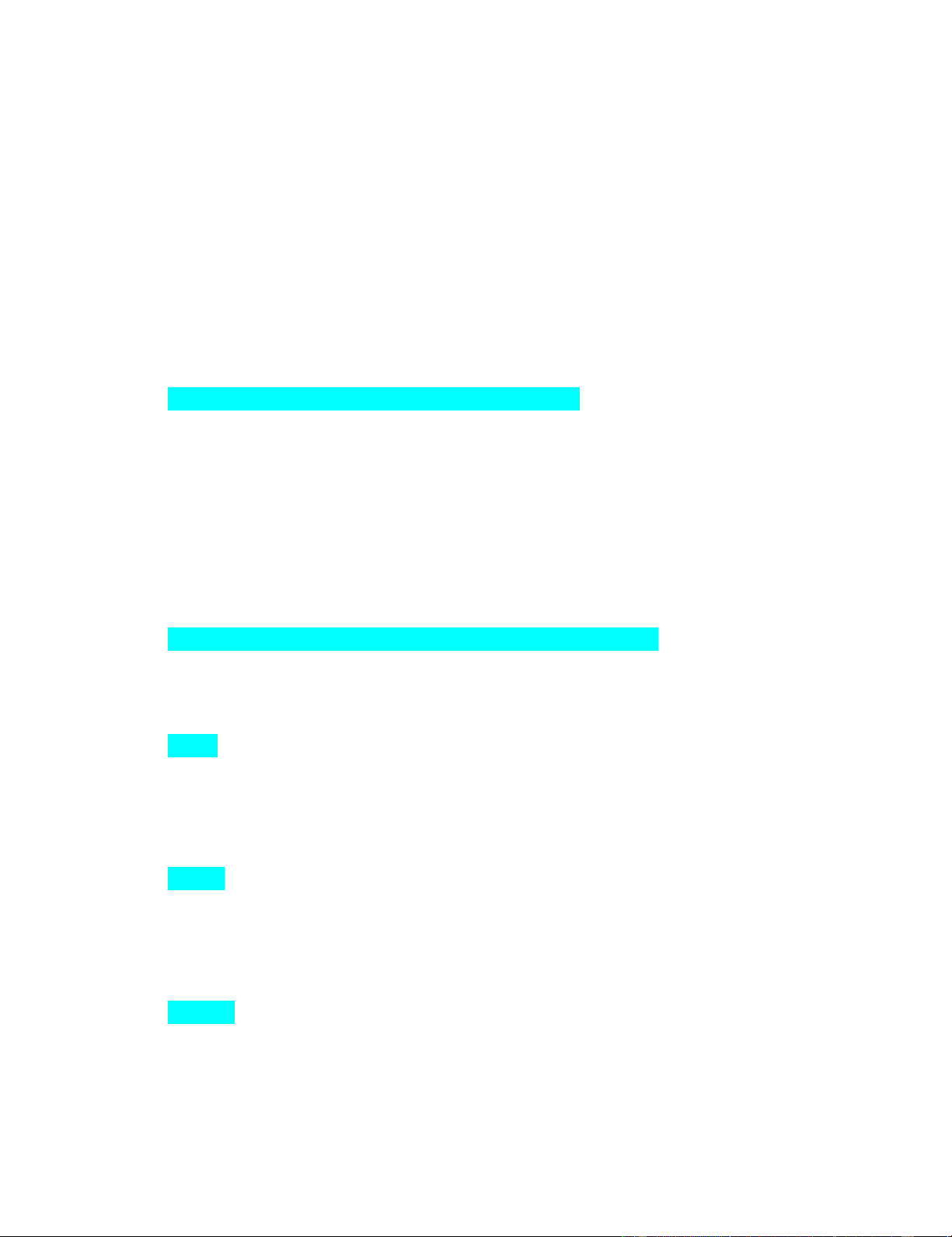


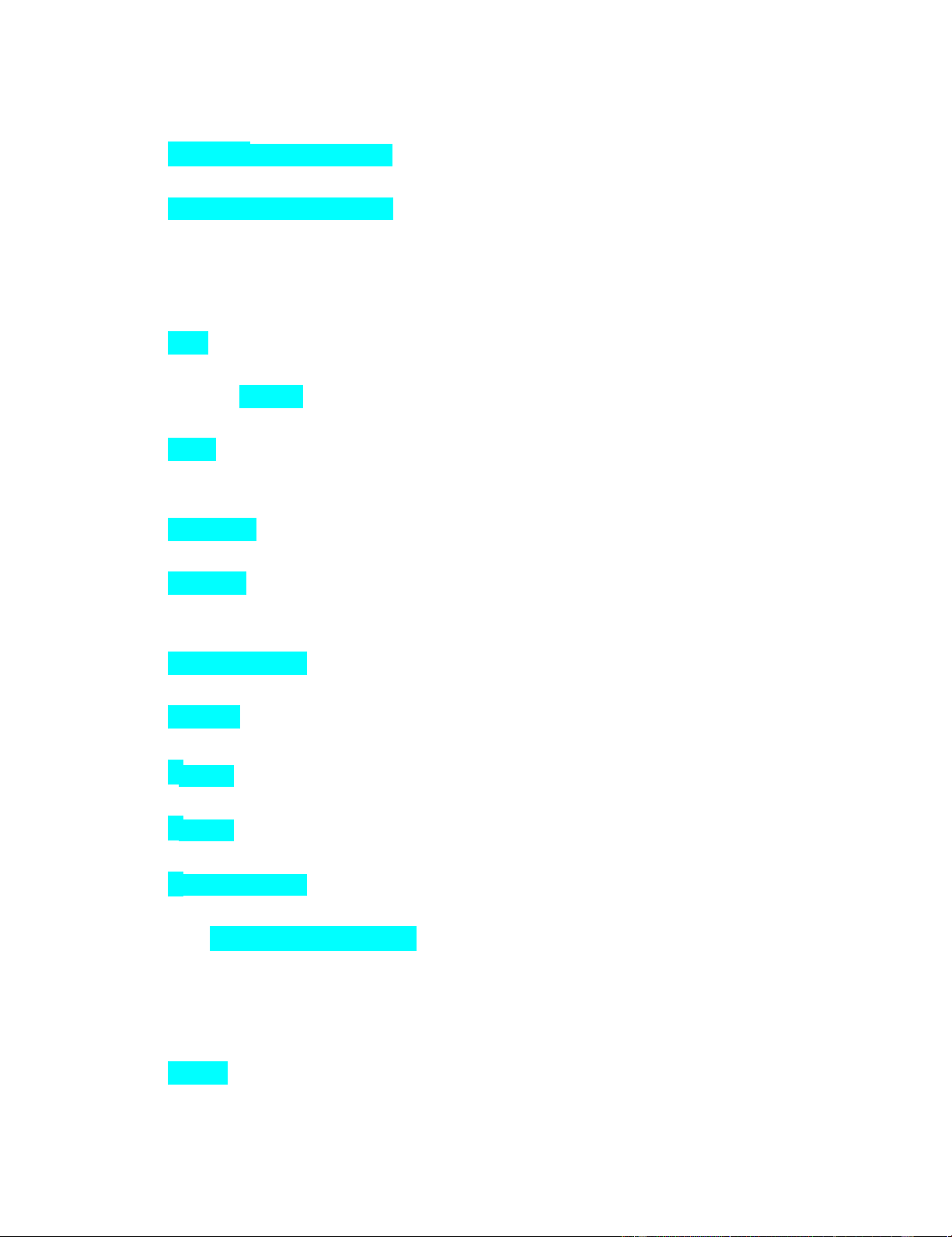



Preview text:
lOMoAR cPSD| 44744371 lOMoAR cPSD| 44744371
TOÁN ỨNG DỤNG TRONG KINH TẾ - TOÁN CAO CẤP – EG50
1. Bài toán QHTT: max{x=y}, v.đ.k x-y≤2-3x+2y≤-1 x≥0,y≥0 có phương án tối ưu (PATƯ) không? Không có PATƯ
2. Bài toán QHTT: max{x+y}, v.đ.k x+y≤3 0≤y≤1 x≥0 có mấy phương án tối ưu (PATƯ)? Có vô số PATƯ
3. Bài toán QHTT: max{6x+5y}, v.đ.k 2x+5y≤3-3x+8y≤-5 x≥0, y≥0 có mấy phương án tối ưu (PATƯ)? Không có PATƯ
4. Bài toán QHTT: min{2x+5y}, v.đ.k 5x+4y≥20 2x+5y≥10 x≥0, y≥0 có mấy
phương án tối ưu (PATƯ)? Có vô số PATƯ
5. Biết hàm chi phí cận biên của 1 công ty là: MC=3Q2-2Q+5, trong đó Q là lượng
sản phẩm đầu ra và chi phí cố định FC=100. Tìm hàm tổng chi phí TC. TC= Q3-Q2+5Q+100
6. Biết mức thu nhập Y là tổng hòa của 2 mức chi tiêu C và tiết kiệm S và C=0,05Y2
+ 0,2Y + 60. Tính khuynh hướng tiêu dùng biên MPC và khuynh hướng tiết kiện biên MPS tại Y=25. MPC=2,25; MPS=-1,52
7. Biết thặng dư của nhà sản xuất là 500 tại Q = a với hàm cung P=3+4Q. Tìm a. a=15,81
8. Chi phí cố định để sản xuất một loại sản phẩm là 84, còn chi phí biến đổi trên 1
đơn vị sản phẩm là 2+. Từ ý nghĩa của chi phí cận biên, hãy ước lượng sự thay đổi
của tổng chi phí khi lượng hàng Q tăng 2 đơn vị từ lượng ban đầu Q0=30 (đơn vị). Tăng 16 đơn vị
9. Cho A=(1 2 4), B= (5 6 7). Tính ABT ABT=(45)
10. Cho A= (1 -1; 2 1) B= (1 3; 1 2) Tính E=AB- BA. E= (-7 -1; -2 7)
11. Cho A= (111 112 123). Tìm A- 1 A-1 =11-1 1-21 -110
12. Cho biết khuynh hướng tiêu dùng biên MPC=0,6 + 0,15/3Y và mức tiêu dùng
C=95 khi thu nhập Y=125. Tìm hàm tiêu dùng C. C=0,6++0,225Y2/3 +14,375 lOMoAR cPSD| 44744371
13. Cho biết khuynh hướng tiết kiệm biên MPS=0,4 – 0,2/3Y và mức tiết kiệm S=40
khi thu nhập Y=64. Tìm hàm tiết kiệm S. S=0,4Y -0,3Y2/3 + 9,6
14. Cho các hàm cung, cầu Nếu gia tăng thêm 1 đươn vị từ giá cân bằng thì các lượng
hàng cung cà cầu thay đổi như thế nào?
Lượng cung tăng 0,06, lượng cầu giảm 0,05 so với lượng cân bằng 4
15. Cho các hàm cung, cầu P=+10 và P=-3+90.QSQD Nếu chính phủ đánh thuế
38USD trên một đơn vị sản phẩm, thì giá và lượng cân bằng thay đổi thế nào so
với khi chưa đánh thuế?
Giá P Tăng lên 28,5 USD, lượng Q giảm 9,5 đơn vị
16. Cho các hàm cung, cầu P=+2 +12, QS2QS P= - - 4 + 68. Tìm giá và lượng cân bằng QD2QD P= 36, Q= 4
17. Cho các hàm cung, cầu P= 2+ 15 và QS P= -3+70. Tìm giá và lượng cân bằng. QD P= 37, Q= 11
18. Cho các hàm cung, cầu P= + 10 + 40 và QS2QS P= + + 14+ 168.QD2QD Nếu gia
tăng thêm 1 đơn vị từ giá cân bằng thì các lượng hàng cung và cầu thay đổi như thế nào?
Lượng cung tăng 0,06, lượng cầu giảm 0,05 so với lượng cân bằng 4QSQD
19. Cho các ma trận A= (342 -101), B=(475 021). Tìm ma trận X làm thỏa mãn phương trình 2A + XT = 3B X=(62 136 11 1)
20. Cho các ma trận A= (132 01-1), B= (1-1 40 52) Tính 2A+3.BT 2A+3BT=(51819 -324)
21. Cho các ma trận A= (3 -2 4; 1 1 0; 0 5 6) B= (1 -5 8; 2 1 0; -4 3 1) C= (1 4 2; 0 7
5; -3 1 9) Biết D= (2A+3B)C. Tìm phần tử d23 d23=41
22. Cho các phương trình cung cầu QSt=Pt-1-38, QDt= -2Pt+142. Biết thị trường luôn
ở trạng thái cân bằng tại mọi thời điểm và giá khởi điểm năm đầu tiên P0=55. Hỏi
lượng cân bằng cung cầu tại năm t=10 thay đổi thế nào so với lượng cân bằng cung cầu năm đầu tiên? Giảm 9,99 đơn vị
23. Cho các phương trình cung, cầu =0,4-12QStPt-1= -0,8+60. Biết thị trường luôn ở
trạng thái cân bằng cung cầu P0 tại năm t=11.Qt 12,0098Q11
24. Cho hàm u= xz3/y+ ln(yz). Tính các đạo hàm riêng u”xy
u”yz u”xy= z3/y2 u”yz= -3xz2/y2 lOMoAR cPSD| 44744371
25. Cho hàm z= ln(x+ y-1). Tính z(1, e2). z(1, e2) = 1
26. Cho hàm z= ln( +). Tính E= xz’x và y .xz’y E= 0,5
27. Cho hàm z= ln(x2+e3y-16). Tính z(4, 2). z(4, 2)= 6
28. Cho hàm z= 2x+3y. Tìm minz thỏa mãn điều kiện x≥2, y≥1. Minz = 7
29. Cho hàm z= 4x+3y. Tìm maxz thỏa mãn điều kiện x ≥3, y ≥4. Không tồn tại maxz
30. Cho hàm z= + -3xy.x3y3 Tìm x, y để hàm z đạt được giá trị cực tiểu x=y=1
31. Cho hàm z= - 10xy + . Tính và tại điểm (2,3).x2y3y2zx’zy’
(2,3)= 78;zx’ (2,3)= 94zy’
32. Cho hàm z= x2y3 - 10xy + y2 . Với x=2, y=3, hãy ước lượng sự thay đổi của z khi
x tăng 0,2 còn y giảm 0,1. Tăng 6,2
33. Cho hàm cầu thỏa mãn 4P + 5Q = 120. Tìm giá trị lớn nhất và nhỏ nhất của giá P. Pmax= 30 khi Q= 0
34. Cho hàm cầu thỏa mãn phương trình 2Q+P=35 và hàm chi phí trung bình AC= + 7. Tìm hàn lợi nhuận 56Qπ =π-2+28Q-56Q2
35. Cho hàm cầu P=ln(2Q/3Q-1). Tính doanh thu cận biên tại Q= 7. MR= -0,41
36. Cho hàm cầu P = -Q2- 4Q + 68. Tính lượng cầu Q, biết giá P=40 Q= 3,66
37. Cho hàm cầu P= -Q2-4Q +96. Tính tỷ lệ phần trăm thay đổi về lượng cầu từ ý
nghĩa của độ co giãn, khi giá tăng 3% so với giá ban đầu P0=51 Giảm 2,19%
38. Cho hàm cầu P= -6Q+154. Tìm độ co giãn E của cầu theo giá, khi giá P=63.Q2 E= 0,45
39. Cho hàm cầu P= -Q + 3. Tính giá P, biết lượng cầu Q=10.17 P= 1,57
40. Cho hàm cầu P= 20-2Q và hàm tổng chi phí TC= Q3- 8Q2+ 20Q +2, trong đó P,
Q là giá và lượng sản phẩm được sản xuất. Tìm độ co giãn của lợi nhuận theo giá
ETC,P tại sản lượng Q làm cực đại lợi nhuận. ETC,P=0 lOMoAR cPSD| 44744371
41. Cho hàm cầu P= 100-Q. Từ ý nghĩa của doanh thu cận biên, hãy ước sự thay đổi
của tổng doanh thu TR khi lượng cầu tăng lên 2 đơn vị từ lượng cầu ban đầu Q0=60 TR giảm 40 đơn vị
42. Cho hàm cầu P= 120 – 5Q. Tìm doanh thu cận biên MR tại Q=10. MR= 20
43. Cho hàm cầu Q= , trong đó P là giá, Y là mức thu nhập. Tính Y2P, tại Y=2, P=5.∂Q∂Y∂Q∂P
(2,5)= 0,8; ∂Q∂Y (2,5)= -0,16∂Q∂P
44. Cho hàm chi phí trung bình AC= 2Q + 8 + . Từ ý nghĩa của chi phí cận biên, hãy
ước lượng sự thay đổi của tổng chi phí TC khi lượng hàng giảm đi 3 đơn vị từ
lượng ban đầu Q0=15. 15Q TC giảm 204 đơn vị
45. Cho hàm chi phí trung bình AC= 3Q+5+14/Q . Tìm chi phí cận biên MC tại Q=5. MC= 35
46. Cho hàm cung P= 5 +3Q . Tìm độ co giãn E của cung theo giá, khi giá tăng từ P1= 8 lên P2 = 10 E= 5,8
47. Cho hàm cung P = + 2Q + 12. Tính lượng cung Q, biết giá Q2 P=16 Q = 1,24
48. Cho hàm cung P = Q + 10. Tính lượng hàng Q, biết giá P=16 13 Q= 18
49. Cho hàm sản xuất Q= 5 + 3L, với vốn K= 160, lượng nhân công L=40. Tính các
sản phẩm cận biên MPK và MPL.KL MPK= 1,25; MPL= 8
50. Cho hàm sản xuất Q= 6 -0,2, trong đó L là lượng nhân công. Tìm lượng nhân công
L để tăng năng suất lao động trung bình cực đại.L2L3 L= 15
51. Cho hàm sản xuất Q= 10KL + 7L, với vốn K=90 và lượng nhân công L=40. Từ ý
nghĩa của đạo hàm riêng, hãy ước lượng sự thay đổi của sản lượng Q khi K tăng
lên 3 đơn vị, còn L giảm đi 2 đơn vị. Q giảm 19 đơn vị
52. Cho hàm sản xuất Q= 600 -5L, trong đó Q là sản lượng (số lượng đơn vị sản phẩm
của 1 loại hàng hóa), L là số nhân công. Tính sản lượng lao động biên L23 MPL tại L= 125. MPL = 75
53. Cho ma trận A= (3 7 2 5) và hàm số f(x)= x2-8x+1 Tính f(A). lOMoAR cPSD| 44744371 f(A)= 0
54. Cho ma trận A= (-1 -2 1-2a; a2+1 1 3; a+1 1 a+4) Tìm a để định thức det(A) của
ma trận A đạt giá trị nhỏ nhất. a=3/11
55. Cho ma trận A=7352 Tìm ma trận nghịch đảo .A- 1 = A-1-235-7
56. Cho ma trận A có nghịch đảo A-1, tìm ma trận X thỏa mãn hệ thức AX-2B=C, với
A=(6-427) , B=(1 1 -2 0), C = (1 3 4 -5). Chọn một câu trả lời: X= (21/50 3/10 -3/25 -4/5)
57. Cho mô hình thị trường 1 loại hàng hóa: = 5P-7QS = -3P+9QD = 0,125(-
)dPdtQDQS Tìm mức ổn định cân bằng P, ==Q của mô hình trên, biết giá khởi điểm P(0)=3. QSQD P=2 Q=3
58. Cho mô hình thị trường với các phương trình cung cầu = 0,4 – 24, QStPt-1 = -0,8
+ 120.QDtPt Biết thị trường luôn ở trạng thái cân bằng tại mọi thời điểm t và giá
khởi điểm =90, tìm mức ổn định cân bằng P, P0 ==Q của mô hình.QSQD P=120Q=24
59. Cho mô hình thu nhập quốc dân: = 0,5(C+I-Y)dYdt C= 0,7Y + 500 I= 0,2Y + 500
Biết mức thu nhập ban đầu Y(0)= 2000, tính mức chi tiêu C tại t=10. C= 3603,25
60. Cho mô hình thu nhập quốc dân của 2 thành phần: = +, = 2500YtCtltY0=
0,8+400CtYt-1= 0,1+300ltYt- 1 Tìm mức ổn định cân bằng Y= C+l của mô hình trên. Y=7000C=6000l=1000
61. Cho mô hình thu nhập quốc dân 2 thành phần tại năm t:Yt= Ct+It Ct= 0,7Yt-
1+400 It = 0,1Y1-1+100 Biết mức thu nhập ban đầu Y0= 3500, tính mức tiêu dùng ở năm thứ 15. C15= 2180,79
62. Cho mô hình thu nhập quốc dân tại năm t:= + YtCtlt = 0,7+550Ct5Yt-1 = 250lt
Biết mức thu nhập khởi điểm =480, tính sự thay đổi của mức thu nhập từ năm t=5 đến năm t=11. Y0 Tăng 530,589 đơn vị
63. Cho mô hình thu nhập quốc dân tại năm t:= + YtCtlt = 0,8+300CtYt-1 =
0,15+100ltYt-1 Biết mức thu nhập ban đầu = 5000, tính mức chi phí tại năm thứ 10. Y0lt =1016,39l10
64. Cho phương trình Yt= -Yt-1+8 với Y0=20. Tìm Y2021.
NGUYỄN ĐÌNH THUẤN – AHTM217 lOMoAR cPSD| 44744371 Y2021= -12
65. Cho thị trường hàng hóa C= 0,8Y + 60, I= -30π + 740 và thị trường tiền tệ
Ms=4000, MD= 0,15- 20π+3825. Xác định thu nhập quốc dân Y và lãi suất π với
giả thiết thị trường hàng hóa và thị trường tiền tệ đều ở trạng thái cân bằng. Y= 2500, π= 10%
66. Giá cổ phiếu trên thị trường chứng khoán của 1 công ty tăng 32% ở nửa đầu năm,
nhưng giảm 18% ở nửa cuối năm. Biết giá cổ phiếu này trong phiên giao dịch cuối
cùng ở cuối năm là 45.000 vnd. Xác định giá trị của cổ phiếu tại phiên giao dịch
đầu tiên ở thời điểm đầu năm. 41.574,28 vnd
67. Giá tất cả các loại hàng của 1 cửa hàng bán lẻ được giảm 20% vào đợt xả hàng
cuối năm. Trong đợt xả hàng của cửa hàng, một người mua được chiếc áo khoác
với giá 470 ngàn vnd. Tính giá bán của chiếc áo khoác trước khi xả hàng. 587.500đ
68. Giá của một mặt hàng trong năm tăng 8%, nhưng bị giảm 30% trong đợt xả hàng.
Tổng thể mặt hàng này bị giảm bao nhiêu phần trăm giá trị? 24,4%
69. Giải bài toán QHTT:max/min {6x+5y}, v.đ.kx-2y≥-2 3x+7y≤ 21 4x-y≤ 20 4x+5y≥-20 y≥ -5
max6x+5y=35,03 min6x+5y=-27,69
70. Giải phương trình dy/dt= -2y+150, với y(0)=90 y= 15e-2t+75
71. Giải phương trình Yt=Yt-1 +5 với điều kiện ban đầu Y0=3. Yt= 3+5t
72. Giải phương trình = 0,15+5, với =120.YtYt-1Y0 = 113,33(0,2+6,67Yt5)t
73. Giải phương trình = 5+12 với =18.YtYt-1Y0 = 21()-3Yt5t
74. Hàm cầu và hàm tổng chi phí TC được cho bởi công thức: 4P + Q – 16 =0 và TC=
4 + 2Q – 3Q2/10 + Q3/20 Tính tổng doanh thu cận biên MR và chi phí cận biên
MC tại lượng hàng Q làm cực đại lợi nhuận. MR=MC=2
75. Một chiếc xe hơi có giá trị xuất xưởng 1250 triệu vnd, sau 2 năm nó được bán lại
với giá 572 triệu vnd. Hỏi chiếc xe bị giảm giá trị bao nhiêu phần trăm so với giá khởi điểm? 54%
NGUYỄN ĐÌNH THUẤN – AHTM217 lOMoAR cPSD| 44744371
76. Một công ty khai thác than sở hữu 2 mỏ than A và B. Mỗi giờ chi phí khai thác tại
mỏ A là 50 USD, tại mỏ B là 40 USD. Than khai thác tại 2 mỏ được phân thành 3
loại với chất lượng khác nhau: tốt, trung bình và thấp. Năng suất khai thác 1 giờ
tại mỏ A là 0,75 tấn than chất lượng cao, 0,25 tấn chất lượng trung bình và 0,5 tấn
chất lượng thấp. Tải mỏ B năng suất mỗi giờ là 0,25 tấn chất lượng cao; 0,25 tấn
chất lượng trung bình và 1,5 tấn chất lượng thấp. Công ty có hợp đồng cung cấp
cho đối tác mỗi tuần 36 tấn than chất lượng cao, 24 tấn chất lượng trung bình và
72 tấn chất lượng thấp. Hãy lập kế hoạch số giờ khai thác than mỗi tuần tại 2 mỏ
để công ty chịu chi phí khai thác ở mức thấp nhất.
Mỗi tuần khai thác ở mỏ A 24 giờ, ở mức B 72 giờ
77. Một công ty sản xuất 2 loại sản phẩm A, B từ 4 loại đơn vị nguyên liệu I, II, III,
IV. Để sản xuất 1 đơn vị sản phẩm A cần 8 đơn vị nguyên liệu I, 5 đươn vị nguyên
liệu II và 1 đơn vị nguyên liệu IV. Để sản xuất 1 đơn vị sản phẩm B cần 3 đơn vị
nguyên liệu I, 4 đơn vị nguyên liệu II và 1 đơn vị nguyên liệu III. Tiền lãi thu
được khi bán 1 đươn vị sản phẩm A là 5 triệu vnd, khi bán 1 đơn vị sản phẩm B là
2 triệu vnd. Hãy xây dựng phương án sản xuất tối ưu sao cho tổng số tiền lãi thu
được là lớn nhất, biết dự trữ các đơn vị nguyên liệu của công ty từ I đến IV lần
lượt là 24; 20; 3 và 2,5 đơn vị
Sản xuất 2,12 đơn vị sản phẩm A và 2,35 đơn vị sản phẩm B
78. Một cửa hàng xe máy có doanh số bán hàng tăng 5% mỗi năm và cửa hàng cần
bán được từ 500 xe trở lên thì mới có lãi. Hiện nay doanh số cả năm là 400 xe. Hỏi
sau ít nhất bao nhiêu năm nữa cửa hàng mới đạt được mức lãi đầu tiên? 5 năm
79. Một doanh nghiệp có hàm sản xuất là Q= 3L+1+4 K-1, trong đó Q, L, K là ký hiệu
sản lượng, nhân công và lượng vốn tương ứng. Chi phí nhân công là 2 USD cho 1
đơn vị và chi phí vốn là 3 USD cho mỗi đơn vị. Sản phẩm được bán với giá 12
USD. Tìm lợi nhuận cực đại của doanh nghiệp. π= 353
80. Một doanh nghiệp sản xuất 2 loại sản phẩm G1, G2 bán ra thị trường với giá tương
ứng là 80 USD và 70 USD cho một đơn vị sản phẩm. Tổng chi phí để sản xuất 2
loại sản phẩm trên là TC= Q12+Q1+Q22 , trong đó Q1, Q2 là số lượng các đơn vị
sản phẩm G1, G2 . Tìm cực đại lợi nhuận π của doanh nghiệp. π= 2600
81. Một hãng sản xuất 2 loại sản phẩm A1, A2, với các hàm cầu là P1= 300- 2Q1, và
hàm tổng chi phí là TC= 5000+100Q với Q= Q1+Q2. Ở đây P1, Q1, P2, Q2 là giá
và lượng sản phẩm đối với các sản phẩm A1, A2 tương ứng. Tìm Q1, Q2 để hãng
đạt được lợi nhuận cực đại.
NGUYỄN ĐÌNH THUẤN – AHTM217 lOMoAR cPSD| 44744371 Q1=Q2=50
82. Một hãng sản xuất có doanh thu cận biên MR= 15 – 4Q, với Q là lượng sản phẩm
đầu ra. Tìm hàm tồn doanh thu TR. TR=15Q- 2Q2
83. Một lượng tiền gốc 12.000 triệu vnd được đầu tư với lãi suất 15% một năm, lãi
kép tính theo năm. Hỏi sau bao nhiêu năm, tổng lượng đầu tiên sẽ vượt mức 25.000 triệu vnd ? 6 năm
84. Một mô hình kinh tế vĩ mô được cho bởi hệ phương trình tuyến Ax=b-, với các ma
trận A= {1 -1 0 0 –a 1 0 0 0 0 1 –c K1 00 K2} x=(Y c l π), b-= (l*+G b d MS*)
Hãy xác định lãi suất π của nhu cầu đầu tư l= cπ + d, ở đây 00,
c<0, d>0, K1>0, K2<0, G*>0, MS*>0
π = Ms*(1-a) - K1(b+d+G*)/K2(1-a)+cK1
85. Một người đầu tư 700 triệu VND trong thời hạn 5 năm với lãi suất 8%/năm, lãi
kép tính theo năm. Tính tổng lượng đầu tư thu được của người đó sau 5 năm. 1028,53 triệu
86. Một người gửi tiền tiết kiệm 1000 USD vào đầu mỗi năm với lãi suất 10% 1 năm,
lãi kép tính theo năm. Hỏi sau bao nhiêu năm tổng lượng tiền tiết kiệm đầu tiền vượt mức 50.000 USD 16 năm
87. Một người gửi tiết kiệm 5000 USD vào tài khoản của 1 ngân hàng vào đầu mỗi
năm. Ngân hàng tính lãi suất tiết kiệm 4%, lãi được tính theo quý. Hỏi sau bao
nhiêu năm, lượng tiền tiết kiệm lần đầu tiên vượt mức 100.000 USD? 9 năm
88. Một người gửi tiết kiệm một lượng tiền gốc vào 2 ngân hàng X, Y trong vòng 3
năm. Nếu gửi ở ngân hàng X thì lãi suất là 6% 1 năm. Nếu gửi ở ngân hàng Y, thì
năm đầu lãi suất là 3% và 7% cho tất cả các năm tiếp theo, lãi kép tính theo năm
cho cả 2 ngân hàng. Người gửi nên lựa chọn phương án nào trong các phương án
sau, để tổng lượng tiền tiết kiệm được sau 3 năm từ lượng tiền gốc ban đầu là lớn nhất?
Gửi vào ngân hàng X cả 3 năm
89. Một nhà máy có chi phí cố định 300 USD mỗi tuần và chi phí biến đổi trên 1 đơn
vị hàng VC= 3Q-42. Tìm lượng hàng Q sao cho chi phí trung bình mỗi tuần của
nhà máy bị chịu ở mức thấp nhất. Q=10
90. Một xí nghiệp sản xuất 2 loại sản phẩm A, B, trong đó A vừa là sản phẩm dùng để
bán vừa là nguyên liệu để sản xuất ra sản phẩm B. Để sản xuất ra 2 loại sản phẩm
NGUYỄN ĐÌNH THUẤN – AHTM217 lOMoAR cPSD| 44744371
trên, xí nghiệp cần sử dụng 1 loại hoạt chất tinh chế làm chất xúc tác. Biết 1 đơn
vị sản phẩm A cần 0,4 đơn vị xsuc tác, 1 đơn vị sản phẩm B cần 0,3 đơn vị chất
xúc tác và 0,2 đơn vị sản phẩm A, lợi nhuận thu được khi bán 1 đơn vị sản phẩm
A là 15 triệu VND, giá bán 1 đơn vị sản phẩm A lời gấp đôi giá bán 1 đơn vị sản
phẩm B. Hãy xây dựng phương án sản xuất tối ưu sao cho tổng lợi nhuận mà xí
nghiệp thu được từ việc bán 2 loại sản phẩm trên là lớn nhất, trong điều kiện dây
chuyền sản xuất đồng bộ cả 2 loại sản phẩm trên theo tỷ lệ 3:2, ngoài ra tùy theo
độ ổn định của thị trường trong việc tiêu thụ các sản phẩm A, B mà nguồn dự trữ
các chất xúc tác của xí nghiệp luôn dao động trong khoảng từ 60 đến 90 đơn vị.
Sản xuất 156,12 đơn vị sản phẩm A và 91,84 đơn vị sản phẩm B
91. Mức thu nhập quốc dân của 1 quốc gia tại năm t được xác định bới Yt =
+150.Yt34Yt-1 Biết mức thu nhập tại năm đầu tiên vào khoảng 100 tỷ USD, hãy
xác định mức thu nhập quốc dân của quốc gia này 60 năm sau kể từ năm đầu tiên.
Thu nhập khoảng 600 tỷ USD
92. Sâu cuộc đấu giá một người mua được chiếc bình cổ với giá 1575 triệu VND.
Tính tỷ lệ phần trăm gia tăng của một chiếc bình, biết giá khởi điểm của nó khi
đấu giá là 500 triệu VND. Tăng 215%
93. Siêu thị X hiện tại có doanh thu 500 tỷ VND và được dự báo tăng 2,5% năm. Siêu
thị Y, đối thủ cạnh tranh của siêu thị X có doanh thu 350 tỷ VND, nhưng doanh
thu được dự báo tăng 4,5% năm. Hỏi sau ít nhất bao nhiêu năm nữa doanh thu của
siêu thị Y sẽ vượt mức doanh thu của siêu thị X? 19 năm
94. Tìm a để hệ phương trình : ax-3y+z=0 ay+3z=1 4y+5z=6 có nghiệm duy nhất. a ≠2,4 và a ≠ 0
95. Tìm ma trận X làm thỏa mãn hệ thức: 3(2 1 5 3)X=2X+(1 4 5
2)T x = (5/17 -29/17 -1/17 67/17)
96. Tìm max/min{8x+10y},v.đ.k 2x+y≤8x+2y≤7 4x+5y≥10 x≥0
0≤y≤3 max8x+10y=44 min8x+10y=20
97. Tìm max/min{6x+2y},v.đ.k x-y≥0 3x+y≥8 x+y≤8 x≥0 y≥0 max6x+2y=48 min6x+2y=16
98. Tìm max/min{2x+5y}, v.đ.k x+y≥9 2x+y≥10 x+3y≥15 x+2y≥14 0≤x≤30
0≤y≤40 max2x+5y=260 min2x+5y=29
99. Tìm max/min{3x-4y}, v.đ.k -2x+y≤12 x-y≤2 x+y≤27 x≥0 y≥0 max3x-4y=6 min3x-4y=-73
100.Tìm max/min{5x+y}, v.đ.k x-2y≤3 x-y≤4 x≥1
0≤y≤10 max5x+y=80 min5x+y=5
NGUYỄN ĐÌNH THUẤN – AHTM217 lOMoAR cPSD| 44744371
101.Tìm tập xác định E của hàm z= 1-x2 + 1-y2
E={(x,y)∣ -1≤x≤1, -1≤y≤1}
102.Tìm tập xác định E của hàm z= 4-x2 - ln(1-y2) E={(x,y)∣ -2≤x≤2, -1
103.Tính đến 31/12/2020 lượng công nhân của 1 xí nghiệp dệt may gia tăng 25% so
với 01/01/2020. Tính số công nhân của xí nghiệp tại thời điểm cuối năm
31/12/2020, biết thời điểm đầu năm 01/01/2020 số công nhân của xí nghiệp là 1240. 1550
104.Tính diện tích S của hình phẳng bị giới hạn bới các đường y=, y=.x2x3 S= 0,08
105.Tính diện tích S của hình phẳng bị giới hạn bởi các đường y= x2+1, x+y=3. S=4,5
106.Tính diện tích S của hình phẳng bị giới hạn bởi các đường y=0, y=x3+1/x, x=1, x=3. S = 21,099
107.Tính diện tích S của hình phẳng bị giới hạn bởi các đường y= , x=1, x=5, y=0.x2 S = 41,33
108.Tính giá trị hiện tại So của 1 dòng thu nhập liên tục ở mức không đổi 2500 USD
1 năm, nếu tỷ lệ chiết khấu là 5% và tiền được chi trả trong 5 năm. So = 11000 USD
109.Tính tích phân ∣= ∫01dx(2x+5)2x+53 ∣= 0,105
110. Tính ∣ = . ∫25dxx2-1 ∣ = 0,35
111. Tính ∣= dx∫10 2x2+2x+1/x+1 ∣ = 1,69
112. Tính tích phân ∣ = dx∫4×7 ∣ = - 0,67/x6 + C
113. Tính tích phân ∣= ∫(e5x + 1/2x-
1)dx ∣= 1/5 e5x + 1/2ln∣2x-1∣ + C
114. Tổng sản phẩm thu nhập quốc dân năm (GNP) của 1 nước là 75.250 triệu USD
được dự báo tăng 4,7% năm. Tổng dân số nước này là 152 triệu dân, dự báo tăng
2% năm. Hỏi sau ít nhất bao nhiêu năm, GNP trên đầu người nước này sẽ vượt 750 triệu USD? 16 năm
NGUYỄN ĐÌNH THUẤN – AHTM217 lOMoAR cPSD| 44744371
115. Vào đầu tháng, một khách hàng có 1 thẻ tín dụng nợ của công ty với mức 8400
USD. Vào giữa tháng người đó trả được x USD (x≤8400). Đến cuối tháng, công ty
gộp vào khoản nợ thêm 6% khoản dư nợ. Quá trình cứ thế tiếp tục cho các tháng
sau, khi người sử dụng thẻ tín dụng tiếp tục trả được x USD vào giữa tháng. Tìm
giá trị x để số tiền nợ có thể trả được hết sau đúng 2 năm. 1257,34 USD
116. Viết biểu thức hàm tiêu dùng C theo thu nhập Y, biết hàm tiết kiệm S= Y2+ 400Y+20 C = 20Y-400Y+20
117. Viết biểu thức hàm tiết kiệm S theo thu nhập Y, biết hàm tiêu dùng C = 0,9Y + 72 S=0,1Y-72
118. Với giá trị nào của m, hệ phương trình: 5x+4y+2z=26 x+3y+3z=27 x+2y+3z=5
không có nghiệm duy nhất? m = 2,5
119. Với một nền kinh tế khép kín không có sự can thiệp của chính phủ, với hàm tiêu
dùng C= 0,5Y + 70 và lượng đầu tư cố định theo kế hoạch ∣= 450. Tính lượng tiết kiệm thu được S. S= 450
120.Với một nền kinh tế khép kín không có sự can thiệp của chính phủ, với hàm tiêu
dùng C= 0,7Y +40 và lượng đầu tư theo kế hoạch cố định ∣= 300. Tính lượng tiêu dùng. C= 833,33
121.Xét một nền kinh tế khép kín không có sự can thiệp của chính phủ, với hàm tiêu
dùng C= 0,8Y + 50 và lượng đầu tư cố định theo kế hoạch ∣= 200. Tính mức thu nhập quốc dân Y. Y= 1250
NGUYỄN ĐÌNH THUẤN – AHTM217 lOMoAR cPSD| 44744371
NGUYỄN ĐÌNH THUẤN – AHTM217



