17 trang 6 lượt tải

Tóm tắt công thức Xác Suất Thống Kê I môn Xác suất thống kê| Trường Đại học Ngoại Thương

12

Tóm tắt công thức Xác Suất Thống Kê I môn Xác suất thống kê|Trường Đại học Ngoại Thương. Tài liệu giúp bạn tham khảo, ôn tập và đạt kết quả cao. Mời đọc đón xem!

Môn: Xác suất thống kê (FTU) 355 tài liệu

Trường: Trường Đại học Ngoại Thương 1.1 K tài liệu

Tác giả:

Profile

Lan Anh Trần

3 tuần trước
Tải xuống
Báo cáo
Danh sách Quiz
Tải xuống
/17
17:54, 27/01/2026
Tóm tắt công thức Xác Suất Thống Kê I - Tài liệu ôn tập - Studocu
- 1 - T—m t ắt công thức
- 1 - XSTK
T—m t t c™ng th c X‡c Su t - Th ng K•ắ ứ ấ ố
I. Ph ần X‡c Su t ấ
1. X‡c suất c n ổ điể
C™ng th c c ng x‡c su t: P(A+B)=P(A)+P(B)-P(AB). ứ ộ ấ
A1, A2,É, An xung kh c tắ ừng đôi
P(A +A +É+A )=P(A )+P(A1 2 n 1 2)+É+P(An).
Ta c—
o A, B xung kh cắ
P(A+B)=P(A)+P(B).
o A, B, C xung kh c tắ ừng đôi
P(A+B+C)=P(A)+P(B)+P(C).
o
( ) 1 ( )P A P A
 .
C™ng th c x‡c suứ ất có điều kiện: ( )
( / )
( )
P AB
P A B
P B
,
( )
( / )
( )
P AB
P B A
P A
.
C™ng th c nh‰n x‡c su t: P(AB)=P(A).P(B/A)=P(B).P(A/B). ứ ấ
A1, A2,É, An độc lập với nhau
P(A .A É.A )=P(A ).P(A1 2. n 1 2).É.P( An).
Ta c—
o A, B độc lập
P(AB)=P(A).P(B).
o A, B, C độc lập với nhau
P(A.B.C)=P(A).P(B).P(C).
C™ng th c Bernoulli: ứ ( ; ; )
k k n k
n
B k n p C p q
, v i p=P(A): x‡c suớ ất để biến cố A
xảy ra m i phŽp th vˆ q=1-p. ở ỗ ử
C™ng th c x‡c suứ ất đầy đủ - C™ng th c Bayes ứ
o Hệ bi n c gế ố ồm n ph n t Aầ ử 1, A ,É, A c g i lˆ m2 n đượ ọ ột phŽp ph‰n
hoạch c a ủ
1 2
. ; , 1,
...
i j
n
A A i j i j n
A A A


o C™ng th c x‡c suứ ất đầy đủ:
1 1 2 2
1
( ) ( ). ( / ) ( ). ( / ) ( ). ( / ) ... ( ). ( / )
n
i i n n
i
P B P A P B A P A P B A P A P B A P A P B A

o C™ng th c Bayes: ứ
( ). ( / )
( / ) ( )
i i
i
P A P B A
P A B P B
với 1 1 2 2
( ) ( ). ( / ) ( ). ( / ) ... ( ). ( / )
n n
P B P A P B A P A P B A P A P B A

2. Bi ến ng u nhi•n ẫ
a. Bi ến ng u nhi•n r i r c ẫ ờ ạ
Luật ph‰n ph i x‡c su t ố ấ
với
( ), 1, .
i i
p P X x i n

Ta c—:
1
1
n
i
i
p
vˆ
f(
{a f(X) b}=
i
i
a x b
P p


X x1 x2 É xn
P p p É p 1 2 n
17:54, 27/01/2026
Tóm tắt công thức Xác Suất Thống Kê I - Tài liệu ôn tập - Studocu
- 2 - T—m t ắt công thức
- 2 - XSTK
Hˆm ph‰n ph i x‡c su t ố ấ
( ) ( )
i
X i
x x
F x P X x p

Mode
0 0
ModX max{ : 1, }
i
x p p i n
Median
0,5
( ) 0,5
MedX ( ) 0,5
0,5
i e
i e
i
x x
e
e
ei
x x
p
P X x
xP X x p







Kỳ v ng ọ
1 1 2 2
1
( . ) . . ... .
n
i i n n
i
EX x p x p x p x p

1 1 2 2
1
( ( )) ( ( ). ) ( ). ( ). ... ( ).
n
i i n n
i
E X x p x p x p x p


Phương sai
2 2
( ) ( )VarX E X EX
với 2 2 2 2 2
1 1 2 2
1
( ) ( . ) . . ... .
n
i i n n
i
E X x p x p x p x p

b. Bi ến ng u nhi•n li•n t c. ẫ ụ
f(x) lˆ hˆm mật độ x‡c su t cấ ủa X ( ) 1



f x dx ,
{a X b} ( ).
b
a
P f x dx
Hˆm ph‰n ph i x‡c su t ố ấ
( ) ( ) ( )
x
X
F x P X x f t dt


Mode
0
ModX x
Hˆm mật độ x‡c su t f(x) c t c i t i x . ấ ủa X đạ ực đạ ạ 0
Median
1 1
( ) ( )
2 2
e
x
e X e
MedX x F x f x dx


.
Kỳ v ng ọ
EX . ( )x f x dx


.
( ( )) ( ). ( )E X x f x dx



17:54, 27/01/2026
Tóm tắt công thức Xác Suất Thống Kê I - Tài liệu ôn tập - Studocu
- 3 - T—m t ắt công thức
- 3 - XSTK
Phương sai
2 2
( ) ( )VarX E X EX v i ớ 2 2 EX . ( )x f x dx


.
c. T’nh chất
- ( ) , ( ) 0E C C Var C
, C lˆ một hằng số.
-2
( ) , ( )E kX kEX Var kX k VarX

-( )E aX bY aEX bEY

- N c lếu X, Y độ ập th“ 2 2
( ) . , ( )E XY EX EY Var aX bY a VarX b VarY

-( ) X VarX
: Độ lệch chuẩn c a X, c— c•ng th nguy•n v i X vˆ EX. ủ ứ ớ
3. Lu ật ph‰n ph i x‡c su t ố ấ
a. Ph‰n ph i Chu n ố ẩ
2
( ~ ( ; ))X N 
( )X 
, EX=ModX=MedX=
,
2
VarX
Hàm mđxs
2
2
( )
2
1
( , , ) 2
x
f x e
 

 Với
0, 1:


2
2
1
( ) 2
x
f x e
(Hˆm Gauss)
(a X b) ( ) ( )
b a
P
 


v i ớ
2
2
0
1
( ) 2
t
x
x e dt

(Hˆm Laplace)
C‡ch s d ng m‡y t’nh bử ụ ỏ túi để t’nh gi‡ trị hˆm Laplace, hˆm ph‰n ph i ố
x‡c su t c a ph‰n ph i chu n chu n t c ấ ủ ố ẩ ẩ ắ
T‡c v M‡y CASIO 570MS M‡y CASIO 570ES ụ
Khởi động g—i Th ng k• ModeÉ(t“m)ÉSD ModeÉ(t“m)ÉSTAT 1-Var ố
T’nh
2
2
0
1
( ) 2
t
x
x e dt

2
2
1
( ) 2

t
x
F x e dt
Shift 3 2 x ) =
Shift 3 1 x ) =
Shift 1 7 2 x ) =
Shift 1 7 1 x ) =
Tho‡t kh i g—i Thỏ ống k• Mode 1 Mode 1
Lưu ý:
( ) 0, 5 ( )F x x
b. Ph‰n ph i Poisson ố
( ~ ( ))X P
( )X 
, EX . odX=k -1 kVarX M

(X=k)=e ,
!
k
P k
k


17:54, 27/01/2026
Tóm tắt công thức Xác Suất Thống Kê I - Tài liệu ôn tập - Studocu
- 4 - T—m t ắt công thức
- 4 - XSTK
c. Ph‰n ph i Nhố ị th c ứ ( ~ ( ; ))X B n p
( ) {0..n}X  , EX=np, VarX=npq, ModX=k ( 1) 1 ( 1)n p k n p 
(X=k)=C . . , q p 0 ,
k k n k
n
P p q k n k

Nếu ( 30; 0,1 0,9; 5, 5) n p np nq th“
2
~ ( ; ) ( ; )X B n p N v i ớ
. ,n p npq 
1
(X=k) ( ), 0 ,
k
P f k n k



(a X<b) ( ) ( )
b a
P
 


Nếu ( 30, 5) n p np th“ ~ ( ; ) ( )
X B n p P v i ớ
np
(X=k) e ,
!
k
P k
k


Nếu ( 30, 0,9, 5) n p nq
(X=k) e ,
( )!
n k
P k
n k


v i ớ
nq
d. Ph‰n ph i Si•u b i ố ộ ( ~ ( ; ; ))
A
X H N N n
( ) {max{0; ( )}..min{n;N }}
A A
X n N N
EX=np, VarX=npq
1
N n
N
v i ớ
A
N
p
N
, q=1-p.
( 1)( 1) 2 ( 1)( 1) 2
1
2 2
A A
N n N n
ModX k k
N N
 
 

.
(X=k)= , ( )
A A
k n k
N N N
n
N
C C
P k X
C

Nếu 20
N
n
th“ ~ ( ; ; ) ( ; )
A
X H N N n B n p v i ớ
A
N
p
N
.
(X=k) C . . , ( ), 1
k k n k
n
P p q k X q p
 .
17:54, 27/01/2026
Tóm tắt công thức Xác Suất Thống Kê I - Tài liệu ôn tập - Studocu
- 5 - T—m t ắt công thức
- 5 - XSTK
X
Y
Sơ đồ t—m t t c‡c d ng ph‰n ph i x‡c su t th™ng ắ ạ ố ấ
dụng:
n
30, np<5
p0,1
=np
N>20n
p=
A
N
N
, q=1-p
n
30, np
5
, nq
5
0,1<p<0,9
1
( ) ( )
k
P X k f


( ) ( ) ( )
b a
P a X b





với ,np npq


Si•u bội: X~H(N;N ;n) A
.
( )
A A
k n k
N N N
n
N
C C
P X k C

Poisson: X~
()
P
( )
!
k
P X k e
k

Nhị th c: X~B(n;p) ứ
( ) . .
k k n k
n
P X k C p q

Chuẩn: X~
2
( ; )N

2
2
( )
2
1
( ; ; ) .
2
x
f x e
 

Chuẩn chu n t c: Y~ N(0;1) ẩ ắ
2
2
1
( ) .
2
y
f y e
17:54, 27/01/2026
Tóm tắt công thức Xác Suất Thống Kê I - Tài liệu ôn tập - Studocu
- 6 - T—m t ắt công thức
- 6 - XSTK
II. Phần Thống K•.
1. Lý thuy t mế ẫu.
a. C‡c c™ng th n. ức cơ bả
C‡c gi‡ trị đặ ẫ ẫ ẫc trưng M u ng u nhi•n M u cụ th ể
Gi‡ trị trung b“nh 1...
n
X X
X
n

1...
n
x x
x
n

Phương sai không hiệu chỉnh
2 2
21
( ) ... ( )
ö
n
X
X X X X
S
n
2 2
21
( ) ... ( )
ö
n
x
x x x x
s
n
Phương sai hiệu chỉnh
2 2
21
( ) ... ( )
1


n
X
X X X X
S
n
2 2
21
( ) ... ( )
1


n
x
x x x x
s
n
b. Để dễ xử lý ta viế ệt số li u c a m u c th i d ng t n sủ ẫ ụ ể dướ ạ ầ ố như sau:
Khi đó
C‡c gi‡ trị đặ ẫc trưng M u cụ th ể
Gi‡ trị trung b“nh 1 1 ...
k k
x n x n
x
n

Phương sai không hiệu chỉnh
2 2
21 1
( ) ... ( )
ö
k k
x
x x n x x n
s
n
Phương sai hiệu chỉnh
2 2
21 1
( ) ... ( )
1


k k
x
x x n x x n
s
n
c. C‡ch sử d ng m‡y t’nh b tœi t’nh c‡c gi‡ trụ ỏ để ị đặc trưng mẫu
- N u sế ố liệu thống k• thu th p theo mi n ậ ề [ ; )a b hay ( ; ]a b th“ ta s d ng gi‡ ử ụ
trị đại di n cho miệ ền đó là
2
a b
để t’nh to‡n.
T‡c v D˜ng CASIO MS D˜ng CASIO ES ụ
Bật chế độ nhậ ầp t n số Kh™ng c n ầ Shift Mode
4 1
Kh iở động g—i Th ng k• ModeÉ(t“m)ÉSD ModeÉ(t“m)ÉSTAT 1-Var ố
Nhập s liố ệu
1
x Shift ,
1
n M+
k
x Shift ,
k
n M+
Nếu 1
i
n th“ chỉ c n ầ
nhấn
i
x M+
X FREQ
1
x =
k
x =
1
n =
k
n =
i
x
1
x
2
x
É
k
x
i
n
1
n
2
n
É
k
n
17:54, 27/01/2026
Tóm tắt công thức Xác Suất Thống Kê I - Tài liệu ôn tập - Studocu
- 7 - T—m t ắt công thức
- 7 - XSTK
X—a mˆn h“nh hi n th AC AC ể ị
Xác định:
Kích thước mẫu (n)
Gi‡ trị trung b“nh
(
x
)
Độ lệch chuẩn kh™ng
hiệu chỉnh (
ö
x
s )
Độ lệch chuẩn hiệu
chỉnh (
x
s )
Shift 1 3 =
Shift 2 1 =
Shift 2 2 =
Shift 2 3 =
Shift 1 5 1 =
Shift 1 5 2 =
Shift 1 5 3 =
Shift 1 5 4 =
Tho‡t kh i g—i Thỏ ống k• Mode 1 Mode 1
2. Ước lượng kho ng. ả
a) Kho ảng tin c y cho gi‡ trậ ị trung b“nh.
Trường h p 1. (ợ
đ‹ biết)
Ước lượng đối xứng.
2 2 2
1
( ) . ; )
2
z z z x x
n



Ước lượng ch ch tr‡i. ệ
( ) 0,5 . ; )z z z x
n


Ước lượng ch ch phệ ải.
( ) 0,5 . )z z z x
n

 
Trường h p 2ợ . ( chưa biết, 30n
)
Ước lượng đối xứng.
2 2 2
1
( ) . ; )
2
s
z z z x x
n



Ước lượng ch ch tr‡i. ệ
( ) 0,5 . ; )
s
z z z x
n


Ước lượng ch ch phệ ải.
( ) 0,5 . )
s
z z z x
n

 
Trường h p 3ợ . ( chưa biết, n<30)
Ước lượng đối xứng.
( 1; ) ( 1; )
2 2
1 . ; )
2n n
s
t t x x
n


  
Ước lượng ch ch tr‡i. ệ
( 1; ) ( 1; )
1 . ; )
n n
s
t t x
n
 
 
17:54, 27/01/2026
Tóm tắt công thức Xác Suất Thống Kê I - Tài liệu ôn tập - Studocu
- 8 - T—m t ắt công thức
- 8 - XSTK
Ước lượng ch ch phệ ải.
( 1; ) ( 1; )
1 . ; )
n n
s
t t x
n
 
 
b) Kho ảng tin c y cho tậ ỉ l . ệ
Ước lượng đối xứng.
2 2 2
(1 )1
( ) . ; )
2
f f
z z z f f
n



Ước lượng ch ch tr‡i. ệ
(1 )
( ) 0,5 . ; )
f f
z z z f
n


Ước lượng ch ch phệ ải.
(1 )
( ) 0,5 . )
f f
z z z f
n


c) Kho ảng tin cậy cho phương sai.
Trường h p 1ợ . ( chưa biết)
- Nếu đề bài chưa cho s mà cho mẫ ểu cụ th th“ phải xác định s (b ng m‡y ằ
t’nh).
Ước lượng kh™ng ch ch. ệ
2
2
( 1; )
2
12
 n, 1
2
( 1;1 )
2
1 1 2

 n
2 2
2 1
( 1) ( 1)
( ; )


n s n s
Ước lượng ch ch tr‡i. ệ
2
2
1 ( 1;1 )
1
( 1)
1 (0; )
n
n s


Ước lượng ch ch phệ ải.
2
2
2 ( 1; )
2
( 1)
1 ( ; )
n
n s

Trường h p 2ợ . ( đ‹ biết)
- T’nh
2 2
1
( 1) .( )
k
i i
i
n s n x

Ước lượng kh™ng ch ch. ệ
2
2
( ; )
2
12
 n, 2
1
( ;1 )
2
1 1 2
 n
2 2
2 1
( 1) ( 1)
( ; )


n s n s
17:54, 27/01/2026
Tóm tắt công thức Xác Suất Thống Kê I - Tài liệu ôn tập - Studocu
- 9 - T—m t ắt công thức
- 9 - XSTK
Ước lượng ch ch tr‡i. ệ
2
2
1 ( ;1 )
1
( 1)
1 (0; )


n
n s
Ước lượng ch ch phệ ải.
2
2
2 ( ; )
2
( 1)
1 ( ; )

n
n s
3. Ki ểm định tham s . ố
a) Ki ểm định gi‡ trị trung b“nh.
ng h p 1Trườ ợ . ( đ‹ biết)
1 : , :
o o o
H H  
2 2
1
( ) , .
2
o
x
z z z n


- N u ế
2
z z
: B‡c b H , ch p nh n Hỏ o ấ ậ 1.
- N u ế
2
z z
: Ch p nh n H . ấ ậ o
1 : , :
o o o
H H  
( ) 0,5 , .
o
x
z z z n


- N u ế z z
 : B‡c b H , ch p nh n Hỏ o ấ ậ 1.
- N u ế z z
 : Ch p nh n H . ấ ậ o
1 : , :
o o o
H H  
( ) 0,5 , .
o
x
z z z n


- N u ế z z
: B‡c b H , ch p nh n Hỏ o ấ ậ 1.
- N u ế z z
: Ch p nh n H . ấ ậ o
ng h p 2Trườ ợ . (
chưa biết,
30n )
1 : , :
o o o
H H  
2 2
1
( ) , .
2
o
x
z z z n
s


- N u ế
2
z z
: B‡c b H , ch p nh n Hỏ o ấ ậ 1.
- N u ế
2
z z
: Ch p nh n H . ấ ậ o
1 : , :
o o o
H H  
( ) 0,5 , .
o
x
z z z n
s


17:54, 27/01/2026
Tóm tắt công thức Xác Suất Thống Kê I - Tài liệu ôn tập - Studocu
- 10 - T—m t ắt công thức
- 10 - XSTK
- N u ế z z
 : B‡c b H , ch p nh n Hỏ o ấ ậ 1.
- N u ế z z
 : Ch p nh n H . ấ ậ o
1 : , :
o o o
H H  
( ) 0,5 , .
o
x
z z z n
s


- N u ế z z
: B‡c b H , ch p nh n Hỏ o ấ ậ 1.
- N u ế z z
: Ch p nh n H . ấ ậ o
ng h p 3Trườ ợ . ( chưa biết, n<30)
1 : , :
o o o
H H  
( 1; )
2
, .
2
o
n
x
t t n
s


- N u ế
( 1; )
2
n
t t
: B‡c b H , ch p nh n Hỏ o ấ ậ 1.
- N u ế
( 1; )
2
n
t t
: Ch p nh n H . ấ ậ o
1 : , :
o o o
H H  
( 1; )
, .
o
n
x
t t n
s



- N u ế
( 1; )n
t t

 : B‡c b H , ch p nh n Hỏ o ấ ậ 1.
- N u ế
( 1; )n
t t

 : Ch p nh n H . ấ ậ o
1 : , :
o o o
H H  
( 1; )
, .
o
n
x
t t n
s



- N u ế
( 1; )n
t t

: B‡c b H , ch p nh n Hỏ o ấ ậ 1.
- N u ế
( 1; )n
t t

: Ch p nh n H . ấ ậ o
b) Ki ểm định tỉ lệ.
1 : , :
o o o
H p p H p p
2 2
1
( ) , , .
2(1 )
o
o o
f pk
z z f z n
np p


- N u ế
2
z z
: B‡c b H , ch p nh n Hỏ o ấ ậ 1.
- N u ế
2
z z
: Ch p nh n H . ấ ậ o
1 : , :
o o o
H p p H p p
( ) 0,5 , , .
(1 )
o
o o
f p
k
z z f z n
np p

17:54, 27/01/2026
Tóm tắt công thức Xác Suất Thống Kê I - Tài liệu ôn tập - Studocu
- 11 - T—m t ắt công thức
- 11 - XSTK
- N u ế z z
 : B‡c b H , ch p nh n Hỏ o ấ ậ 1.
- N u ế z z
 : Ch p nh n H . ấ ậ o
1 : , :
o o o
H p p H p p
( ) 0,5 , , .
(1 )
o
o o
f pk
z z f z n
np p

- N u ế z z
: B‡c b H , ch p nh n Hỏ o ấ ậ 1.
- N u ế z z
: Ch p nh n H . ấ ậ o
c) Ki ểm định phương sai.
Trường h p 1ợ . ( chưa biết)
- Nếu đề chưa cho s mà cho mẫu cụ thể th“ ph i s dả ử ụng máy tính để x‡c
định s.
2 2 2 2
1
: , :
o o o
H H
 
2 2
1
( 1;1 )
2
12n

   , 2 2
2
( 1; )
2
2n
  ,
2
2
2
( 1)
o
n s

- N u ế
2 2
2
2 2
1


: B‡c b H , ch p nh n Hỏ 0 ấ ậ 1.
- N u ế
2 2 2
1 2

: Ch p nh n H . ấ ậ o
2 2 2 2
1
: , :
o o o
H H

2 2
1 ( 1;1 )
1n

   ,
2
2
2
( 1)
o
n s

- N u ế
2 2
1
 : B‡c b H , ch p nh n Hỏ 0 ấ ậ 1.
- N u ế
2 2
1

: Ch p nh n H . ấ ậ o
2 2 2 2
1
: , :
o o o
H H
 
2 2
2 ( 1; )n
  ,
2
2
2
( 1)
o
n s

- N u ế
2 2
2

: B‡c b H , ch p nh n Hỏ 0 ấ ậ 1.
- N u ế
2 2
2
 : Ch p nh n H . ấ ậ o
4. Ki ểm định so s‡nh tham s . ố
a) Ki ểm định so s‡nh gi‡ trị trung b“nh.
Trường h p 1. (ợ
1 2
,
đ‹ biết)
1 2 1 1 2
: , :
o
H H  
1 2
2 2
2 2
1 2
1 2
1
( ) ,
2
x x
z z z
n n



17:54, 27/01/2026
Tóm tắt công thức Xác Suất Thống Kê I - Tài liệu ôn tập - Studocu
- 12 - T—m t ắt công thức
- 12 - XSTK
- N u ế
2
z z
: B‡c b H , ch p nh n Hỏ o ấ ậ 1.
- N u ế
2
z z
: Ch p nh n H . ấ ậ o
1 2 1 1 2
: , :
o
H H  
1 2
2 2
1 2
1 2
( ) 0,5 ,
x x
z z z
n n


- N u ế z z
 : B‡c b H , ch p nh n Hỏ o ấ ậ 1.
- N u ế z z
 : Ch p nh n H . ấ ậ o
1 2 1 1 2
: , :
o
H H  
1 2
2 2
1 2
1 2
( ) 0,5 ,
x x
z z z
n n


- N u ế z z
: B‡c b H , ch p nh n Hỏ o ấ ậ 1.
- N u ế z z
: Ch p nh n H . ấ ậ o
ng h p 2. (Trườ ợ
1 2
, chưa biết, 1 2 30n n )
1 2 1 1 2
: , :
o
H H  
1 2
2 2
2 2
1 2
1 2
1
( ) ,
2
x x
z z z
s s
n n


- N u ế
2
z z
: B‡c b H , ch p nh n Hỏ o ấ ậ 1.
- N u ế
2
z z
: Ch p nh n H . ấ ậ o
1 2 1 1 2
: , :
o
H H  
1 2
2 2
1 2
1 2
( ) 0,5 ,
x x
z z z
s s
n n

- N u ế
z z

: B‡c b H , ch p nh n Hỏ o ấ ậ 1.
- N u ế
z z

: Ch p nh n H . ấ ậ o
1 2 1 1 2
: , :
o
H H  
1 2
2 2
1 2
1 2
( ) 0,5 ,
x x
z z z
s s
n n

17:54, 27/01/2026
Tóm tắt công thức Xác Suất Thống Kê I - Tài liệu ôn tập - Studocu
- 13 - T—m t ắt công thức
- 13 - XSTK
- N u ế z z
: B‡c b H , ch p nh n Hỏ o ấ ậ 1.
- N u ế z z
: Ch p nh n H . ấ ậ o
Trường h p 3. (ợ
1 2
 chưa biết, 1 2, 30n n )
1 2 1 1 2
: , :
o
H H  
1 2
1 2
( 2; ) 2
2
1 2
,
2
1 1
( )
n n
x x
t t
s
n n


, v i ớ
2 2
2
1 1 2 2
1 2
( 1). ( 1).
2
n s n s
sn n


- N u ế
1 2
( 2; )
2
n n
t t

: B‡c b H , ch p nh n Hỏ o ấ ậ 1.
- N u ế
1 2
( 2; )
2
n n
t t

: Ch p nh n H . ấ ậ o
1 2 1 1 2
: , :
o
H H  
1 2
1 2
( 2; )
2
1 2
,
1 1
( )
n n
x x
t t
s
n n


, với
2 2
2
1 1 2 2
1 2
( 1). ( 1).
2
n s n s
sn n


- N u ế
1 2
( 2; )
2
n n
t t

 : B‡c b H , ch p nh n Hỏ o ấ ậ 1.
- N u ế
1 2
( 2; )
2
n n
t t

 : Ch p nh n H . ấ ậ o
1 2 1 1 2
: , :
o
H H  
1 2
1 2
( 2; )
2
1 2
,
1 1
( )
n n
x x
t t
s
n n


, v i ớ
2 2
2
1 1 2 2
1 2
( 1). ( 1).
2
n s n s
sn n


- N u ế
1 2
( 2; )
2
n n
t t

: B‡c b H , ch p nh n H . ỏ o ấ ậ 1
- N u ế
1 2
( 2; )
2
n n
t t

: Ch p nh n H . ấ ậ o
b) Ki ểm định so s‡nh tỉ lệ.
1 2 1 2
1 2
1 2 1 2
, ,
k k k k
f f f
n n n n

1 2 1 1 2
: , :
o
H p p H p p
1 2
2 2
1 2
1
( ) ,
2
1 1
(1 ).( )
f f
z z z
f f
n n



- N u ế
2
z z
: B‡c b H , ch p nh n H . ỏ o ấ ậ 1
- N u ế
2
z z
: Ch p nh n H ấ ậ o.
17:54, 27/01/2026
Tóm tắt công thức Xác Suất Thống Kê I - Tài liệu ôn tập - Studocu
- 14 - T—m t ắt công thức
- 14 - XSTK
1 2 1 1 2
: , :
o
H p p H p p
1 2
1 2
( ) 0,5 ,
1 1
(1 ).( )
f f
z z z
f f
n n


- N u ế z z
 : B‡c b H , ch p nh n H . ỏ o ấ ậ 1
- N u ế z z
 : Ch p nh n H . ấ ậ o
1 2 1 1 2
: , :
o
H p p H p p
1 2
1 2
( ) 0,5 ,
1 1
(1 ).( )
f f
z z z
f f
n n


- N u ế z z
: B‡c b H , ch p nh n H . ỏ o ấ ậ 1
- N u ế z z
: Ch p nh n H . ấ ậ o
c. Ki ểm định so sánh phương sai.
-
1 2
, chưa biết n•n t’nh s vˆ s t m1 2 ừ ẫ ửu (s dụng m‡y t’nh) nếu đề bài chưa
cho.
2 2 2 2
1 2 1 1 2
: , :
o
H H 
-
2
11 1 2 2 1 2
2
2
, ( 1; 1;1 ) , ( 1; 1; )
2 2
s
f f f n n f f n n
s


- Nếu
1
2
f f
f f
: B‡c b H , ch p nh n H . ỏ o ấ ậ 1
- Nếu
1 2
f f f
 : Ch p nhấ ận H . o
2 2 2 2
1 2 1 1 2
: , :
o
H H
 
-
2
11 1 2
2
2
, ( 1; 1;1 )
s
f f f n n
s

- Nếu
1
f f
: B‡c b H , ch p nh n H . ỏ o ấ ậ 1
- Nếu 1
f f
: Ch p nhấ ận H . o
2 2 2 2
1 2 1 1 2
: , :
o
H H 
-
2
12 1 2
2
2
, ( 1; 1; )
s
f f f n n
s

- Nếu
2
f f
: B‡c b H , ch p nh n H . ỏ o ấ ậ 1
- Nếu
2
f f
: Ch p nhấ ận H . o
5. H ệ số tương quan mẫu “nh h i quy tuy n t’nh m u. và phương tr ồ ế ẫ
17:54, 27/01/2026
Tóm tắt công thức Xác Suất Thống Kê I - Tài liệu ôn tập - Studocu
- 15 - T—m t ắt công thức
- 15 - XSTK
a. H sệ ố tương quan mẫu: 11 1
2 2 2 2
1 1 1 1
( ) ( )
nn n
i i i i
i i i
n n n n
i i i i
i i i i
n x y x y
r
n x x n y y





Phương tr“nh hồi quy tuy n t’nh m u: ế ẫ x
x
y A B
 v i ớ
1 1 1
2 2
1 1
( )
n n n
i i i i
i i i
n n
i i
i i
n x y x y
B
n x x




vˆ 1 1
.
n n
i i
i i
y B x
An


.
b. ng h p s d ng b ng t n s : Trong trườ ợ ử ụ ả ầ ố
Ta t’nh theo c™ng th c thu gứ ọn như sau:
Hệ số tương quan mẫu: 1 1 1
2 2 2 2
1 1 1 1
( ) ( )
k k k
i i i i i i i
i i i
k k k k
i i i i i i i i
i i i i
n n x y n x n y
r
n n x n x n n y n y





Phương tr“nh hồi quy tuy n t’nh m u: ế ẫ x
x
y A B
 v i ớ
1 1 1
2 2
1 1
( )
k k k
i i i i i i i
i i i
k k
i i i i
i i
n n x y n x n y
B
n n x n x




vˆ 1 1
.
k k
i i i i
i i
n y B n x
An


.
i
x
1
x
2
x
É
k
x
i
y
1
y
2
y
É
k
y
i
n
1
n
2
n
É
k
n
17:54, 27/01/2026
Tóm tắt công thức Xác Suất Thống Kê I - Tài liệu ôn tập - Studocu
- 16 - T—m t ắt công thức
- 16 - XSTK
c. S d ng m‡y t’nh bử ụ ỏ túi để t’nh h sệ ố tương quan mẫu và phương tr“nh h i quy ồ
tuyến t’nh mẫu:
T‡c v D˜ng CASIO MS D˜ng CASIO ES ụ
Bật chế độ nhậ ầp t n số Kh™ng c n ầ Shift Mode
4 1
Khởi động g—i H i quy ồ
tuyến t’nh
ModeÉ(t“m)ÉREG
Lin
ModeÉ(t“m)ÉSTAT
A+BX
Nhập s liố ệu
1
x ,
1
y Shift ,
1
n M+
k
x ,
k
y Shift ,
k
n M+
1
i
n
th“ chỉ c n nh n ầ ấ
i
x ,
i
y M+
X Y FREQ
1
x =
k
x =
1
y =
k
y =
1
n =
k
n =
X—a mˆn h“nh hi n th AC AC ể ị
X‡c định:
Hệ số tương quan
mẫu (r)
Hệ s hố ằng: A
Hệ số ẩn (x): B
Shift 2 3 = 
Shift 2 1 = 
Shift 2 2 = 
Shift 1 7 3 =
Shift 1 7 1 =
Shift 1 7 2 =
Tho‡t kh i g—i H i quy Mode 1 Mode 1 ỏ ồ
Lưu ý: M‡y ES n ‹ k’ch ho t ch nh p t n s phếu đ ạ ế độ ậ ầ ố ở ần Lý thuy t mế ẫu rồi th“
kh™ng c n k’ch ho t nầ ạ ữa.
ÉÉÉÉÉÉÉÉÉÉÉÉÉÉÉ.
17:54, 27/01/2026
Tóm tắt công thức Xác Suất Thống Kê I - Tài liệu ôn tập - Studocu

Tài liệu khác của Trường Đại học Ngoại Thương

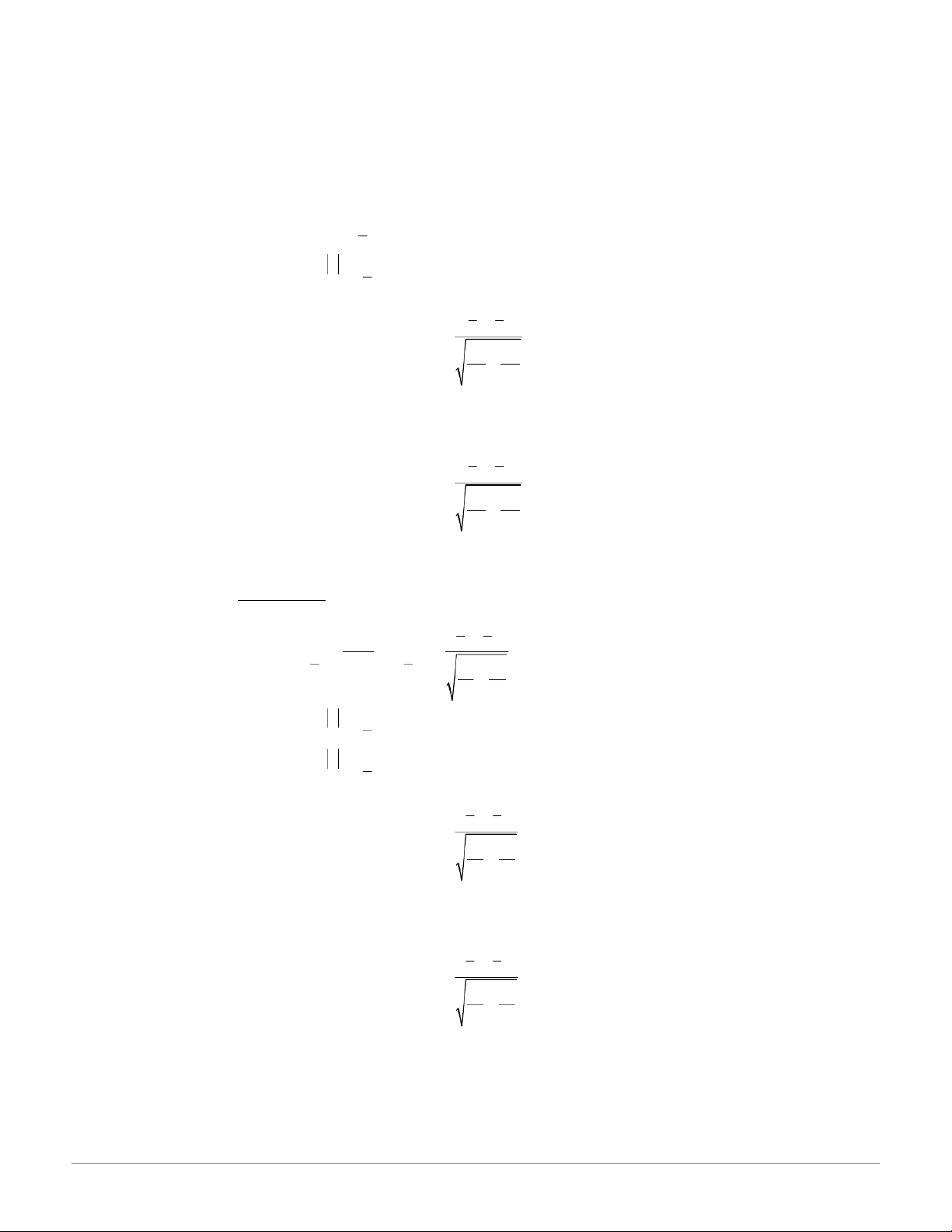
Preview text:

17:54, 27/01/2026
Tóm tắt công thức Xác Suất Thống Kê I - Tài liệu ôn tập - Studocu - 1 - T—m tắt công thức
T—m tắt c™ng thức X‡c Suất - Th ng K• ố I. Phần X‡c Suất 1. X‡c suất cổ điển
 C™ng thức cộng x‡c suất: P(A+B)=P(A)+P(B)-P(AB).
 A1, A2,É, An xung khắc từng đôi  P(A1+A2+É+An)=P(A1)+P(A2)+É+P(An).  Ta c—
o A, B xung khắc  P(A+B)=P(A)+P(B).
o A, B, C xung khắc từng đôi  P(A+B+C)=P(A)+P(B)+P(C).  .
o P(A) 1 P(A)
 C™ng thức x‡c suất có điều kiện:  P , (AB)  P . (AB) P( A / B) P(B / ) A P(B) P(A)
 C™ng thức nh‰n x‡c suất: P(AB)=P(A).P(B/A)=P(B).P(A/B).
 A1, A2,É, An độc lập với nhau  P(A1.A2.É.An)=P(A1).P(A2).É.P( An).  Ta c—
o A, B độc lập  P(AB)=P(A).P(B).
o A, B, C độc lập với nhau  P(A.B.C)=P(A).P(B).P(C).
 C™ng thức Bernoulli: ( ; ; ) , với p=P(A): x‡c suất để biến cố A B k n p C k pkq n k
xảy ra ở mỗi phŽp thử vˆ q=1-p. n
 C™ng thức x‡c suất đầy đủ - C™ng thức Bayes
o Hệ biến cố gồm n phần tử A1, A2,É, An được g i ọ lˆ một phŽp ph‰n      hoạch c a ủ   A .  A   i j;i, j 1,n i j  A A ... A
o C™ng thức x‡c suất đầy 1 đủ: 2 n       P(B )
n P(A ).P(B / A ) P(A ).P(B / A ) P(A ).P(B / A ) ... P(A ).P(B / A ) i i 1 1 2 2 n ni 1 o C™ng thức Bayes:
P(A ).P(B / A ) P(A / B ) P(B) i i i vớ  i   1 1 2 2 P(B)
P(A ).P(B / A ) P(A ).P(B / A ) ... P(A ).P(B / A ) 2. Biến ngẫu nhi•n n n
a. Biến ngẫu nhi•n rời rạc
 Luật ph‰n phối x‡c suất X x1 x2 É xn với  P p1 p2 É pn p P( X x ),i 1,n. i i Ta c—:  vˆ    n p 1 { P a f(X) b}= p ii  i 1 a f(x b i - 1 - XSTK 17:54, 27/01/2026
Tóm tắt công thức Xác Suất Thống Kê I - Tài liệu ôn tập - Studocu - 2 - T—m tắt công thức  Hˆm ph‰n ph i ố x‡c suất F ( )x   ( P X ) x pX i i x x  Mode ModX  x   p ma  x{ p i: 1, n } 0 0 i  Median  p 0,5   ( P X x  ) 0,5 i  MedX ( xP  X )  0,x  5 e i x ex p e     0, 5 eiixex  Kỳ vọng n  EX   ( .x ) p . x p . x p ... x . pi i 1 1 2 2 n n i 1  n  ( E (   ) X)   ( ( ). x p ) ( x ). p ( x ). p ... ( x ). pi i 1 1 2 2 n n i 1   Phương sai 2 2 VarX E  (X ) ( E ) X n v  ới E (X  2)  (x 2 . p ) x 2 . p 2 x p . 2 ...x p .  i i 1 1 2 2 n n i 1 
b. Biến ngẫu nhi•n li•n tục. 
 f(x) lˆ hˆm mật độ x‡c suất của X  ( ) 1  f x dx ,  b {a P X   b} f ( ). x dxa  Hˆm ph‰n ph i ố x‡c suất x F ( ) x   ( P X ) x f ( ) t dtX   Mode ModX x
Hˆm mật độ x‡c suất f(x) của X đạt cực đại tại x0. 0  Median 1 1 e x MedX x   F  ( x )  f ( ) x dxe X e 2 2 .   Kỳ vọng  EX x.f ( ) x dx .   ( E ( X  )) ( )
x . f ( )x dx   - 2 - XSTK 17:54, 27/01/2026
Tóm tắt công thức Xác Suất Thống Kê I - Tài liệu ôn tập - Studocu - 3 - T—m tắt công thức  Phương sai  2 2 VarX E  ( v X ới ) (2E2 ) X EX x . f ( ) x dx .  c. T’nh chất - E( ) C  , C Va ( r ) C 0 , C lˆ một hằng số. -2E( ) kX  , kEX ( ) Var kX k VarX -( ) E aX bY   aEX bEY
- Nếu X, Y độc lập th“ E( XY )  E
 X. ,EY ( Var aX ) bY a 2 2 VarX b VarY -( )  X VarX : Độ lệch chuẩn c a
ủ X, c— c•ng thứ nguy•n với X vˆ EX. 3. Luật ph‰n ph i ố x‡c suất a. Ph‰n phối Chuẩn 2 (X ~ N ( ;  ))  X ( )
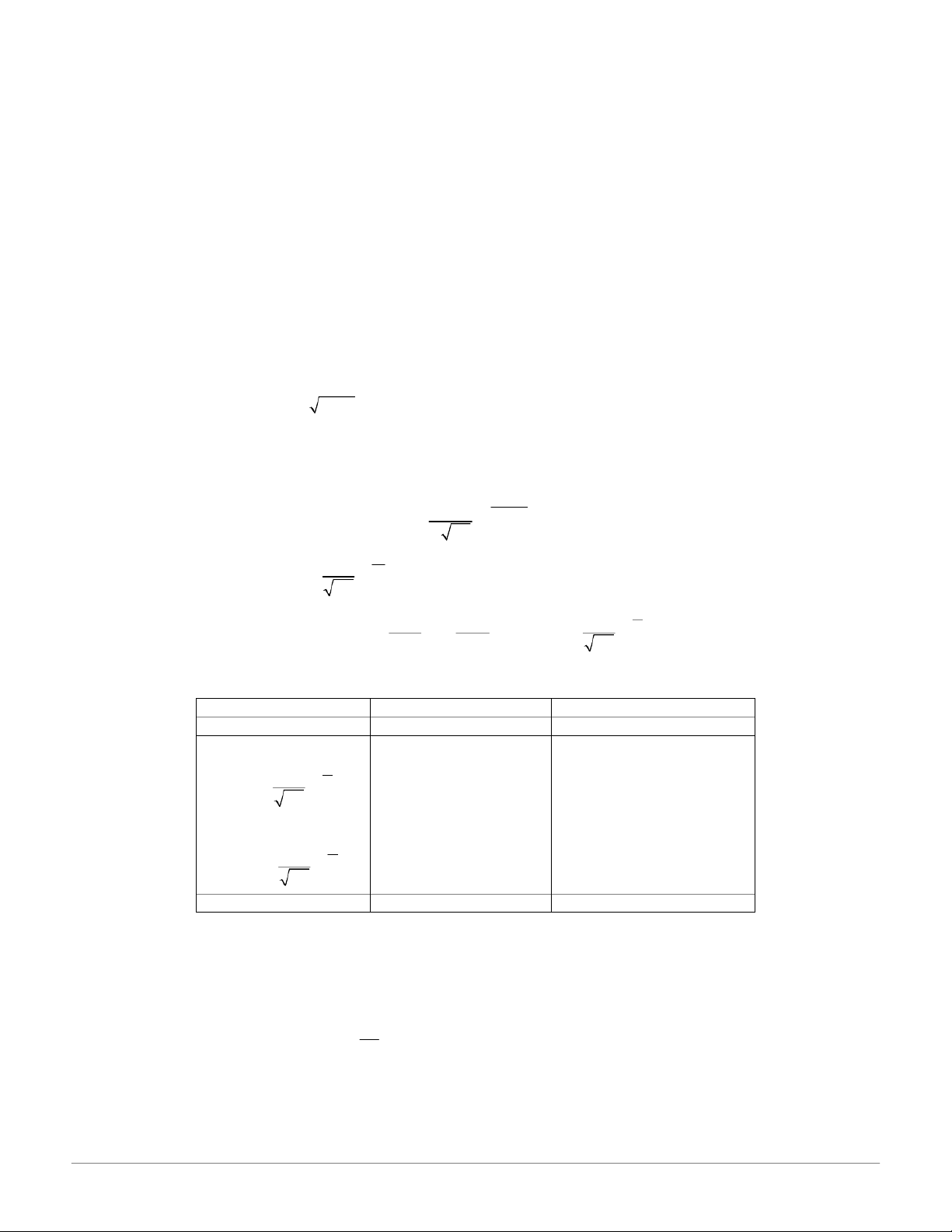
  , EX=ModX=MedX=  , 2 VarX   2 ( )x     1 2 Hàm mđxs 2
f (x, , )  2 e    Với  0  ,  1: 2 x 1  2 f (x)  2 (Hˆ e m Gauss)  2   x t   b a 1 ( P a  X   b)   ( ) ( ) với  2 ( ) x 2 e dt   (Hˆm Laplace)  0
 C‡ch sử dụng m‡y t’nh bỏ túi để t’nh gi‡ trị hˆm Laplace, hˆm ph‰n ph i ố
x‡c suất của ph‰n phối chuẩn chuẩn tắc T‡c vụ M‡y CASIO 570MS M‡y CASIO 570ES Khởi động g—i Th n ố g k• ModeÉ(t“m)ÉSD ModeÉ(t“m)ÉSTAT 1-Var T’nh 2 x t 1   2 ( ) x 2 e dt  Shift 3 2 x ) = Shift 1 7 2 x ) =  0 2 x t 1  2 F (x) 2 Shift 1 7 1 x ) =  e dt Shift 3 1 x ) =   Tho‡t kh i ỏ g—i Thống k• Mode 1 Mode 1
Lưu ý: F( ) x  0  ,  5 ( )x b. Ph‰n ph i ố Poisson ( X ~ P ( ))   X ( )    , E   X VarX M  . odX=k -1 k k    (X= Pk) k =e ,    k ! - 3 - XSTK 17:54, 27/01/2026
Tóm tắt công thức Xác Suất Thống Kê I - Tài liệu ôn tập - Studocu - 4 - T—m tắt công thức
c. Ph‰n phối Nhị thức (X ~ B( ; n ) p )  X ( )
 {0..n} , EX=np, VarX=npq, ModX=k (  1 n )p  1 k (n p 1)   (X= Pk)=C . . k k p , q q n k   p   0  k, n kn  Nếu (n  3  0
; 0,1 p 0,9;np n 5 q , 5) th“ 2 X ~ B( ; n ) p   ( N ; ) với  n. ,p  npq  1 k    
P(X=k)  f ( ), 0 k , n k   b a    P  (a  X   <  b) ( ) ( )   Nếu  ( 3 n 0  ,  p n 5 p ) th“ X ~ B( ; n ) p  (
P ) với  np k    (  X= P k) k e  ,  k!  Nếu ( 3 n 0,   0 p ,9, n 5 q ) n k    P  (X=k) k e  ,  với  nq ( ) n !k d. Ph‰n ph i ố Si•u b i
ộ (X ~ H (N ;N ; n )) AX (  ) {max{0  ; n  (N N )}..min{n;N }} A A   N n N EX=np, VarX=npq với A p , q=1-p. N 1 N      (N n 1)( 1) 2 N(n 1)( 1) 2 A A ModX k  1k . N N  2  2 k n k C C   N N NP(X=k)= A A , kX  ( )  n CNN N Nếu
 20 th“ X ~ H (N ;N ;n)  B v ( ớ ; ni ) p A p . n A N   
P(X=k) C .k p .k n k q   , k X ( ),q 1 p . n - 4 - XSTK 17:54, 27/01/2026
Tóm tắt công thức Xác Suất Thống Kê I - Tài liệu ôn tập - Studocu - 5 - T—m tắt công thức
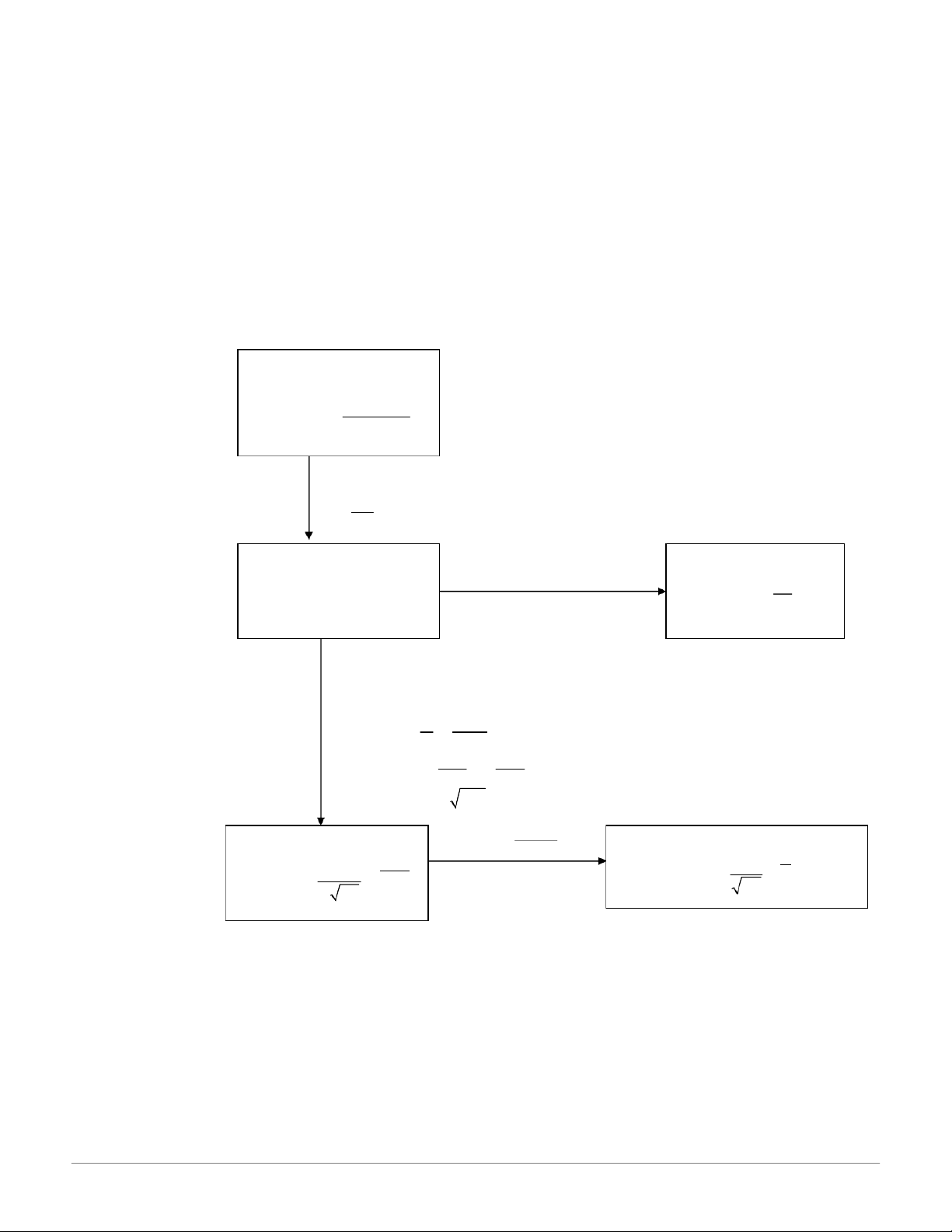
Sơ đồ t—m t t c‡c d ắ ng ph ạ ‰n ph i x ố ‡c su t th™ng ấ dụng:
Si•u bội: X~H(N;NA;n) k C . n k C   ( P ) N A A N N X kC n N N>20n N p= A , q=1-p N n30, np<5 p ứ 0,1 Nhị th c: X~B(n;p) Poisson: X~ P( )  =np kk k n k ( P ) X ke  ( P X k ) C . . p q   n k !
n30, np 5, nq  5 0,1

1 k   ( P X k  ) f ( )  b a    
P (a X  b  ) ( ) ( )  với 
  np,npq X   N Y  Chuẩn: X~ 2 ( ; )
Chuẩn chuẩn tắc: Y~ N(0;1)  2 2 y ( )  1 x  1  2 2 f (y )  .e 2 f (x ; ; )  .e    2 2 - 5 - XSTK 17:54, 27/01/2026
Tóm tắt công thức Xác Suất Thống Kê I - Tài liệu ôn tập - Studocu - 6 - T—m tắt công thức II. Phần Thống K•. 1. Lý thuyết mẫu.
a. C‡c c™ng thức cơ bản.
C‡c gi‡ trị đặc trưng
Mẫu ngẫu nhi•n
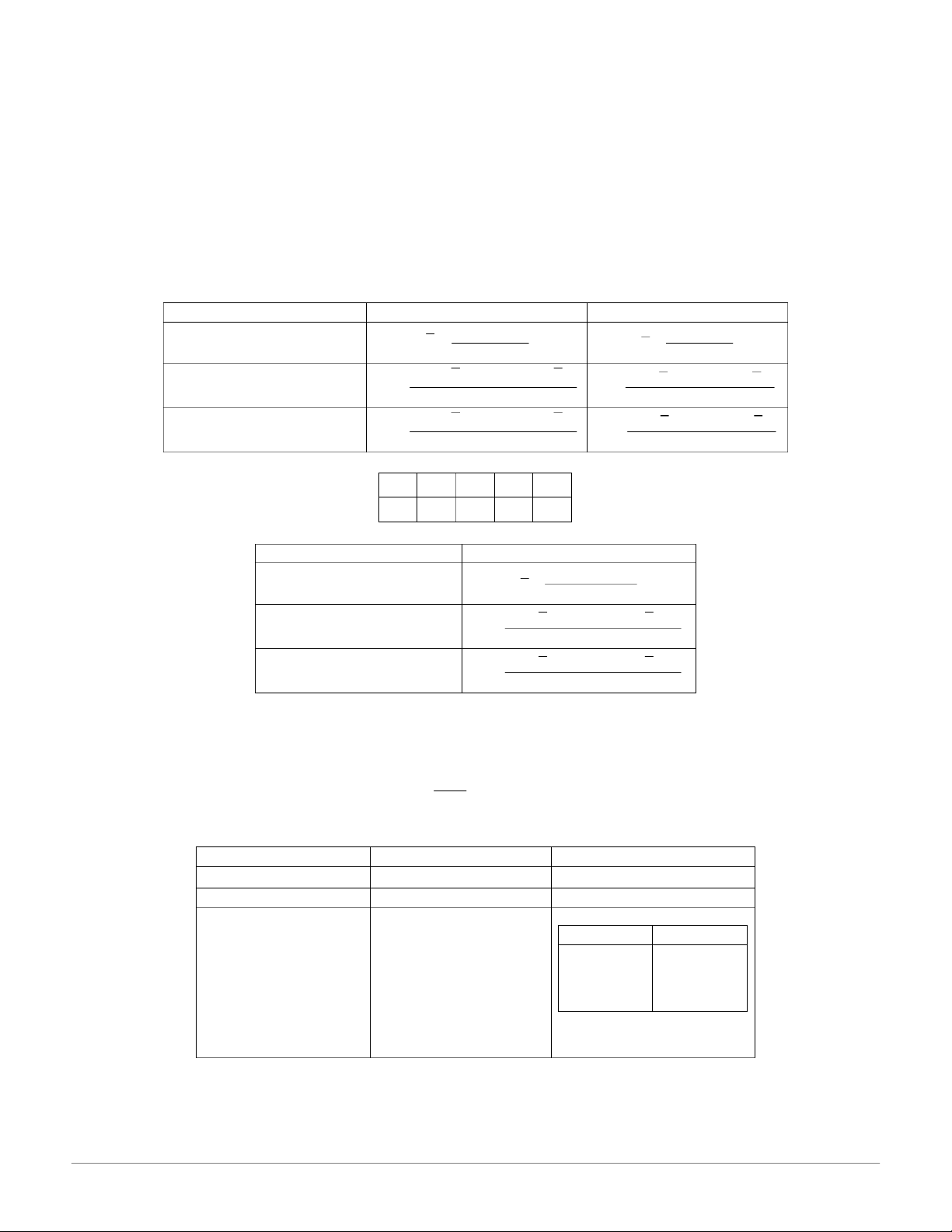
Mẫu cụ thể Gi‡ trị trung b“nh X1.. X.   x x 1... n X n x n n
Phương sai không hiệu chỉnh 2 2 ö  (X X ) ... ( X X ) 2 2 ö (x x ) ... (x x ) 21 21 Sn s n X n x n Phương sai hiệu chỉnh 2 2 (X X   ) ... ( X X ) 2 2 (x x  )  ... (x x ) 21 S  n 21 s  n X n 1 x n 1
b. Để dễ xử lý ta viết số liệu của mẫu c t
ụ hể dưới dạng tần số như sau: x x x É x i 1 2 k n n n É n i 1 2 k Khi đó
C‡c gi‡ trị đặc trưng
Mẫu cụ thể Gi‡ trị trung b“nh x n  x n 1 1 ... k k x n
Phương sai không hiệu chỉnh 2 2 ö    (x x )n ... (x x )n 21 1 s k k x n 2 2 (x    x)n ... (x x ) n Phương sai hiệu chỉnh 21 1 s  k k x n 1 c. C‡ch sử d ng m‡y t ụ
’nh bỏ tœi để t’nh c‡c gi‡ trị đặc trưng mẫu
- Nếu số liệu thống k• thu thập theo miền [ ; a ) b hay ( ; a ] b th“ ta sử d n ụ g gi‡ a b
trị đại diện cho miền đó là để t’nh to‡n. 2 T‡c vụ D˜ng CASIO MS D˜ng CASIO ES
Bật chế độ nhập tần số Kh™ng cần Shift Mode  4 1 Khởi động g—i Th n ố g k• ModeÉ(t“m)ÉSD ModeÉ(t“m)ÉSTAT 1-Var
x Shift , n M+ 1 1  X FREQ
x Shift , n M+ x = n = 1 1 k k Nhập số liệu  
Nếu n  1 th“ chỉ cần x = n = i k k nhấn x M+ i - 6 - XSTK 17:54, 27/01/2026
Tóm tắt công thức Xác Suất Thống Kê I - Tài liệu ôn tập - Studocu - 7 - T—m tắt công thức
X—a mˆn h“nh hiển thị AC AC Xác định:  Kích thước mẫu (n) Shift 1 3 = Shift 1 5 1 =  Gi‡ trị trung b“nh (x ) Shift 2 1 = Shift 1 5 2 =
 Độ lệch chuẩn kh™ng hiệu chỉnh ( ös ) Shift 2 2 = Shift 1 5 3 = x  Độ lệch chuẩn hiệu Shift 2 3 = Shift 1 5 4 = chỉnh (s ) x Tho‡t kh i ỏ g—i Thống k• Mode 1 Mode 1 2. Ước lượng khoảng.
a) Khoảng tin cậy cho gi‡ trị trung b“nh.
Trường hợp 1. ( đ‹ biết)
 Ước lượng đối xứng. 1         (  )z     z .z x ; x )  2  n 2 2 2
 Ước lượng chệch tr‡i.        (z ) 0    ,  5  z z . x ; )   n
 Ước lượng chệch phải.  ( z ) 0,  5   z
z    . x     )   n
Trường hợp 2. ( chưa biết, n  30)
 Ước lượng đối xứng. 1  s       (  )z     z .z x ; x )   2 n 2 2 2
 Ước lượng chệch tr‡i. s       (z ) 0    ,  5  z z . x ; )   n
 Ước lượng chệch phải. s ( z ) 0,  5   z
z    . x     )   n
Trường hợp 3. ( chưa biết, n<30)
 Ước lượng đối xứng.  s 1  t  t .   x x ;  )  2n n ( 1  ;  ) ( 1; ) n 2 2
 Ước lượng chệch tr‡i. s 1 t t 
.x ; ) ( n 1 n  ;  ) ( 1; ) n - 7 - XSTK 17:54, 27/01/2026
Tóm tắt công thức Xác Suất Thống Kê I - Tài liệu ôn tập - Studocu - 8 - T—m tắt công thức
 Ước lượng chệch phải. s 1 t t  x
.   ; ) ( n 1 n  ;  ) ( 1; ) n
b) Khoảng tin cậy cho tỉ lệ.
 Ước lượng đối xứng. 1  f (1 f )        (  )z     z .z f f ; )  2  n 2 2 2
 Ước lượng chệch tr‡i. f (1 f )      (z ) 0,5    z z . f ; )   n
 Ước lượng chệch phải. f (1 f )        (z ) 0,5    z z . f )   n
c) Khoảng tin cậy cho phương sai.
Trường hợp 1. (  chưa biết)
- Nếu đề bài chưa cho s mà cho mẫu cụ thể th“ phải xác định s (bằng m‡y t’nh).
 Ước lượng kh™ng chệch.   2 12    2 n, 
1 1 12   n  2 ( 1; ) ( 1;1  ) 2 2 2 2 ( 1) ( 1)  (  ;n s n s ) 2 1
 Ước lượng chệch tr‡i. 2    ( 1 n )s 2 1   (0; ) 1 ( 1 n;1 ) 1
 Ước lượng chệch phải. 2 2   ( 1) n s 1   (  ; ) 2 (n 1; )  2
Trường hợp 2. (  đ‹ biết) k - T’nh 2 2 ( 1 n )  s .(n x )  i i i 1 
 Ước lượng kh™ng chệch.   2 12
   n,
1  12  2 2  1 n  ( ; ) ( ;1  ) 2 2 2 2 ( 1) ( 1)  (  ;n s n s ) 2 1 - 8 - XSTK 17:54, 27/01/2026
Tóm tắt công thức Xác Suất Thống Kê I - Tài liệu ôn tập - Studocu - 9 - T—m tắt công thức
 Ước lượng chệch tr‡i. 2 2   ( 1 n )s 1   (0; ) 1 ( ;1 n ) 1
 Ước lượng chệch phải. 2  ( 1 n )s 2 1   ( ; ) 2 ( ; n )  2 3. Kiểm định tham s . ố
a) Kiểm định gi‡ trị trung b“nh.
Trường hợp 1. (  đ‹ biết)  1 H :
H   , :  o o o 1  x  ( ) z    , z z .o n   2  2 2
- Nếu z z  : B‡c bỏ Ho, chấp nhận H1. 2 - Nếu z z  : Chấp nhận Ho. 2  1 H :
H   , :  o o o x  (z ) 0   ,  5  , z z .o n   
- Nếu z z  : B‡c b H ỏ o, chấp nhận H1.
- Nếu z z  : Chấp nhận Ho.  1 H :
H   , :  o o o x  (z ) 0   ,  5  , z z .o n   
- Nếu z z  : B‡c bỏ Ho, chấp nhận H1.
- Nếu z z  : Chấp nhận Ho.
Trường hợp 2. (  chưa biết, n  30 )  1 H :
H   , :  o o o 1  x  ( ) z     , z z .o n  2  s 2 2
- Nếu z z  : B‡c bỏ Ho, chấp nhận H1. 2 - Nếu z z  : Chấp nhận Ho. 2  1 H :
H   , :  o o o x  (z ) 0   ,  5  , z z .o n   s - 9 - XSTK 17:54, 27/01/2026
Tóm tắt công thức Xác Suất Thống Kê I - Tài liệu ôn tập - Studocu - 10 - T—m tắt công thức
- Nếu z z  : B‡c b H ỏ o, chấp nhận H1.
- Nếu z z  : Chấp nhận Ho.  1 H :
H   , :  o o o x  (z ) 0   ,  5  , z z .o n   s
- Nếu z z  : B‡c bỏ Ho, chấp nhận H1.
- Nếu z z  : Chấp nhận Ho.
Trường hợp 3. (  chưa biết, n<30)  1 H :
H   , :  o o ox    t t  , . on 2  (n 1  ; ) s 2 - Nếu t t 
: B‡c bỏ Ho, chấp nhận H1. (n 1  ; )2 - Nếu t t: Ch  ấp nhận Ho. (n 1  ; )2  1 H :
H   , :  o o o x   t t  , . on ( n 1  ;  ) s
- Nếu t t : B‡c b H ỏ o, chấp nhận H ( n 1  ; ) 1.
- Nếu t t : Chấp nhận Ho. ( n 1  ; )  1 H :
H   , :  o o o x   t t  , . on ( n 1  ;  ) s
- Nếu t t: B‡c bỏ Ho, chấp nhận H (n 1  ; ) 1.
- Nếu t t: Chấp nhận Ho. (n 1  ; ) b) Kiểm định tỉ lệ.
 1 H : p p ,H  : p p o o o 1  k f p  ( ) z     , z f , o z . n  2(1 )  np p 2 2 o o
- Nếu z z  : B‡c bỏ Ho, chấp nhận H1. 2 - Nếu z z  : Chấp nhận Ho. 2
 1 H : p p ,H  : p p o o o k f p  (z  ) 0, 5     , z f , o z . n   np p (1 ) o o - 10 - XSTK 17:54, 27/01/2026
Tóm tắt công thức Xác Suất Thống Kê I - Tài liệu ôn tập - Studocu - 11 - T—m tắt công thức
- Nếu z z  : B‡c b H ỏ o, chấp nhận H1.
- Nếu z z  : Chấp nhận Ho.
 1 H : p p , H  : p p o o o k f p  (z  ) 0, 5     , z f , o z . n   np p (1 ) o o
- Nếu z z  : B‡c bỏ Ho, chấp nhận H1.
- Nếu z z  : Chấp nhận Ho.
c) Kiểm định phương sai.
Trường hợp 1. (  chưa biết)
- Nếu đề chưa cho s mà cho mẫu cụ thể th“ phải sử dụng máy tính để x‡c định s.  2 2 2 2 H : H    , : o o 1 o   2  2 2  ( 1 n )s 12  n   ,    , 2  1  2 2 2   ( 1;1  ) 2n ( 1  ; ) 2 2 2 o  2 2  - Nếu 2  : B‡c b H ỏ 0, chấp nhận H1. 2 2   1 - Nếu 2 2 2  ấ ậ 1 2 : Ch p nh n Ho.  2 2 2 2 H : H    , : o o 1 o 2 2 2  ( 1 n )s  1n   , 2   1 ( 1;1   ) 2 o - Nếu 2 2  : B‡c b H ỏ 0, chấp nhận H 1 1. - Nếu 2 2  ấ ậ 1 : Ch p nh n Ho.  2 2 2 2 H : H    , : o o 1 o 2 2 2   ( 1 n)s , 2   2 (n 1  ;  ) 2 o - Nếu 2 2  ỏ ấ ậ 2 : B‡c b H0, ch p nh n H1. - Nếu 2 2  : Chấp nhận Ho. 2
4. Kiểm định so s‡nh tham s . ố
a) Kiểm định so s‡nh gi‡ trị trung b“nh. Trường hợp 1. (  , đ 1 2 ‹ biết)  H : H   ,  :  o 1 2 1 1 2 1  x x 1 2 ( ) z    ,z z  2  2 2  2 2 1 2 n n 1 2 - 11 - XSTK 17:54, 27/01/2026
Tóm tắt công thức Xác Suất Thống Kê I - Tài liệu ôn tập - Studocu - 12 - T—m tắt công thức
- Nếu z z  : B‡c bỏ Ho, chấp nhận H1. 2 - Nếu z z  : Chấp nhận Ho. 2  H : H   , : o 1 2 1 1 2 x x 1 2 ( z ) 0   ,  5  ,z z   2 2  1 2 n n 1 2
- Nếu z z  : B‡c b H ỏ o, chấp nhận H1.
- Nếu z z  : Chấp nhận Ho.  H : H   ,  :  o 1 2 1 1 2 x x 1 2 ( z ) 0   ,  5  ,z z   2 2  1 2 n n 1 2
- Nếu z z  : B‡c bỏ Ho, chấp nhận H1.
- Nếu z z  : Chấp nhận Ho. Trường hợp 2. (  , chưa biết, n n   ) 1 2 1 2 30  H : H   ,  :  o 1 2 1 1 2 1  x x 1 2 ( ) z    ,z z  2  2 2 s s 2 2 1 2 n n 1 2
- Nếu z z  : B‡c bỏ Ho, chấp nhận H1. 2 - Nếu z z  : Chấp nhận Ho. 2  H : H   , : o 1 2 1 1 2 x x 1 2 ( z ) 0   ,  5  ,z z   2 2 s s 1 2 n n 1 2
- Nếu z z  : B‡c b H ỏ o, chấp nhận H1.
- Nếu z z  : Chấp nhận Ho.  H : H   ,  :  o 1 2 1 1 2 x x 1 2 ( z ) 0   ,  5  ,z z   2 2 s s 1 2 n n 1 2 - 12 - XSTK 17:54, 27/01/2026
Tóm tắt công thức Xác Suất Thống Kê I - Tài liệu ôn tập - Studocu - 13 - T—m tắt công thức
- Nếu z z  : B‡c bỏ Ho, chấp nhận H1.
- Nếu z z  : Chấp nhận Ho. Trường hợp 3. ( 
chưa biết, n n ) 1 2 1 2 , 30  H : H   ,  :  o 1 2 1 1 2  x x 2 2 ( 1 n).  ( s n 1).s 1 2   t t  , , với 2 1 1 2 2 sn n  2  (  1 n 2 n 2; ) 2 1 1 2 2 s ( )  1 2 n n 1 2
- Nếu t t: B‡c bỏ  Ho, chấp nhận H1. (  1 n 2 n 2; )2 - Nếu t t: Chấ  p nhận Ho. (  1 n 2 n 2; ) 2  H : H   , : o 1 2 1 1 2 x x 2 2 ( 1 n ).  s(n 1).s 1 2  t t ,  , với 2 1 1 2 2 sn n  (  1 n 2 n 2; ) 2 2 1 1 s ( )  1 2 n n 1 2
- Nếu t t : B‡c b  ỏ Ho, chấp nhận H1. (  1 n 2 n 2; )2
- Nếu t t : Chấ  p nhận Ho. (  1 n 2 n 2; )2  H : H   ,  :  o 1 2 1 1 2 x x 2 2 ( 1 n ).  s(n 1).s 1 2  t t ,  , với 2 1 1 2 2 sn n  ( 1 n 2 n  2; ) 2 2 1 1 s ( )  1 2 n n 1 2
- Nếu t t: B‡c bỏ  Ho, chấp nhận H1. ( 1 n 2 n 2; )2 - Nếu t t: Chấ  p nhận Ho. ( 1 n 2 n 2; )2
b) Kiểm định so s‡nh tỉ lệ. k k k k 1 2 1 2 f f    , , f 1 2 n n n n 1 2 1 2
H : p p ,H  : p p o 1 2 1 1 2 1  f f  1 2   ( )z   ,z z  2  1 1 2 2 f (1 f ) .(  ) n n 1 2
- Nếu z z  : B‡c bỏ Ho, chấp nhận H1. 2 - Nếu z z  : Chấp nhận Ho. 2 - 13 - XSTK 17:54, 27/01/2026
Tóm tắt công thức Xác Suất Thống Kê I - Tài liệu ôn tập - Studocu - 14 - T—m tắt công thức
H : p p ,H  : p p o 1 2 1 1 2 f f 1 2 ( z ) 0   ,  5  ,z z   1 1 f (1 f ) .(  ) n n 1 2
- Nếu z z  : B‡c b H ỏ o, chấp nhận H1.
- Nếu z z  : Chấp nhận Ho.
H : p p H,  : p p o 1 2 1 1 2 f f 1 2 ( z ) 0   ,  5  ,z z   1 1 f (1 f ) .(  ) n n 1 2
- Nếu z z  : B‡c bỏ Ho, chấp nhận H1.
- Nếu z z  : Chấp nhận Ho.
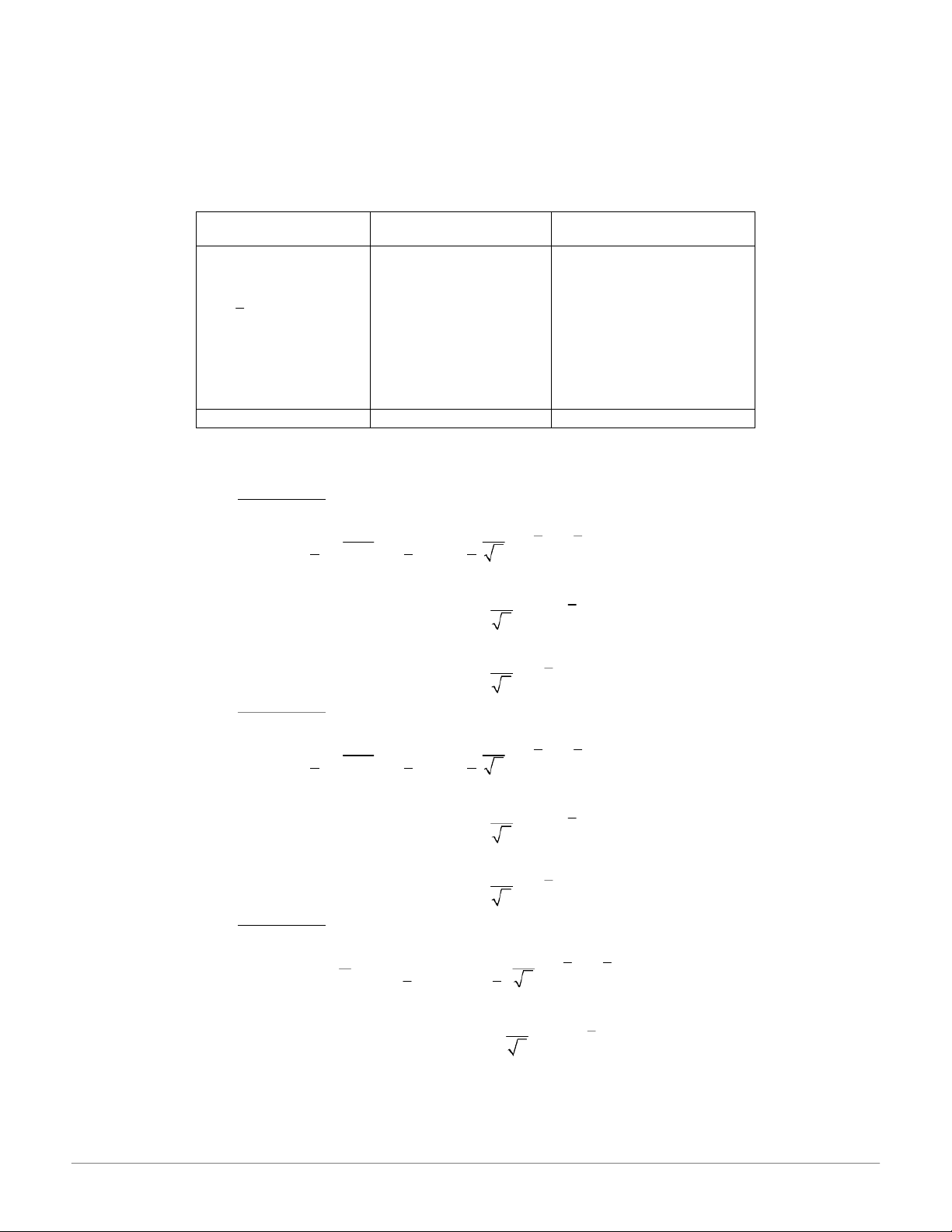
c. Kiểm định so sánh phương sai. - ,  
chưa biết n•n t’nh s1 vˆ s2 từ mẫu (sử dụng m‡y t’nh) nếu đề bài chưa 1 2 cho.  2 2 2 2 H : H    , : o 1 2 1 1 2 2 s  - 11 1 2 2 1 2 f   ,
 f f (n 1; 1 n ;1 ) , f ( f 1 n ; 1; ) n 2 s 2 2 2  f f - Nếu 1 : B‡c b H ỏ o, chấp nhận H1. f f 2 - Nếu f f  f : Chấp nhận Ho. 1 2  2 2 2 2 H : H    , : o 1 2 1 1 2 2 s - 11 1 2 f    ,
f f (n 1;n 1;1 ) 2 s2 - Nếu f f
: B‡c bỏ Ho, chấp nhận H1. 1
- Nếu 1 f f : Chấp nhận Ho.  2 2 2 2 H : H    , : o 1 2 1 1 2 2 s - 12 1 2 f  ,
f  f (n 1;n 1; )  2 s2 - Nếu f f : B‡c b H ỏ o, chấp nhận H1. 2 - Nếu f f : Chấp nhận Ho. 2
5. Hệ số tương quan mẫu và phương tr“nh hồi quy tuyến t’nh mẫu. - 14 - XSTK 17:54, 27/01/2026
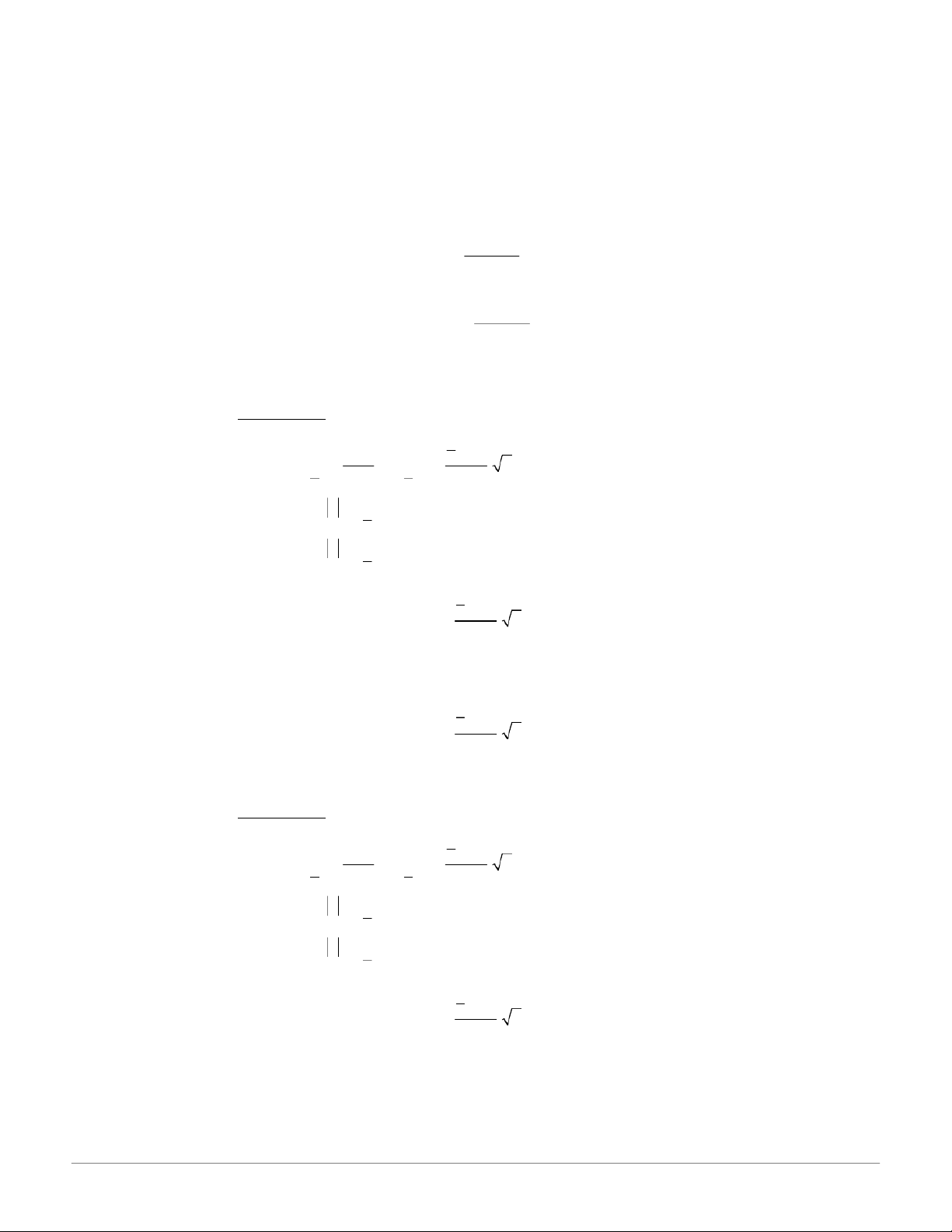
Tóm tắt công thức Xác Suất Thống Kê I - Tài liệu ôn tập - Studocu - 15 - T—m tắt công thức nn n n  x y    x y i i i i  
a. Hệ số tương quan mẫu: i i i r  11 1 n n n n 2 2 2 2 n x ()  x  n y ( )y i i i i i i 1  1 i 1 i 1
Phương tr“nh hồi quy tuyến t’nh mẫu: y  A  B với x x n n n n n n  x y    x y y B x  i i i i i i .  i 1  i i 1 1 B  vˆ i i 1 1 An   . n n 2 2 n x  ( )  x i i i i1  1
b. Trong trường hợp sử d ng ụ bảng tần số: x x x É x i 1 2 k y y y É y i 1 2 k n n n É n i 1 2 k
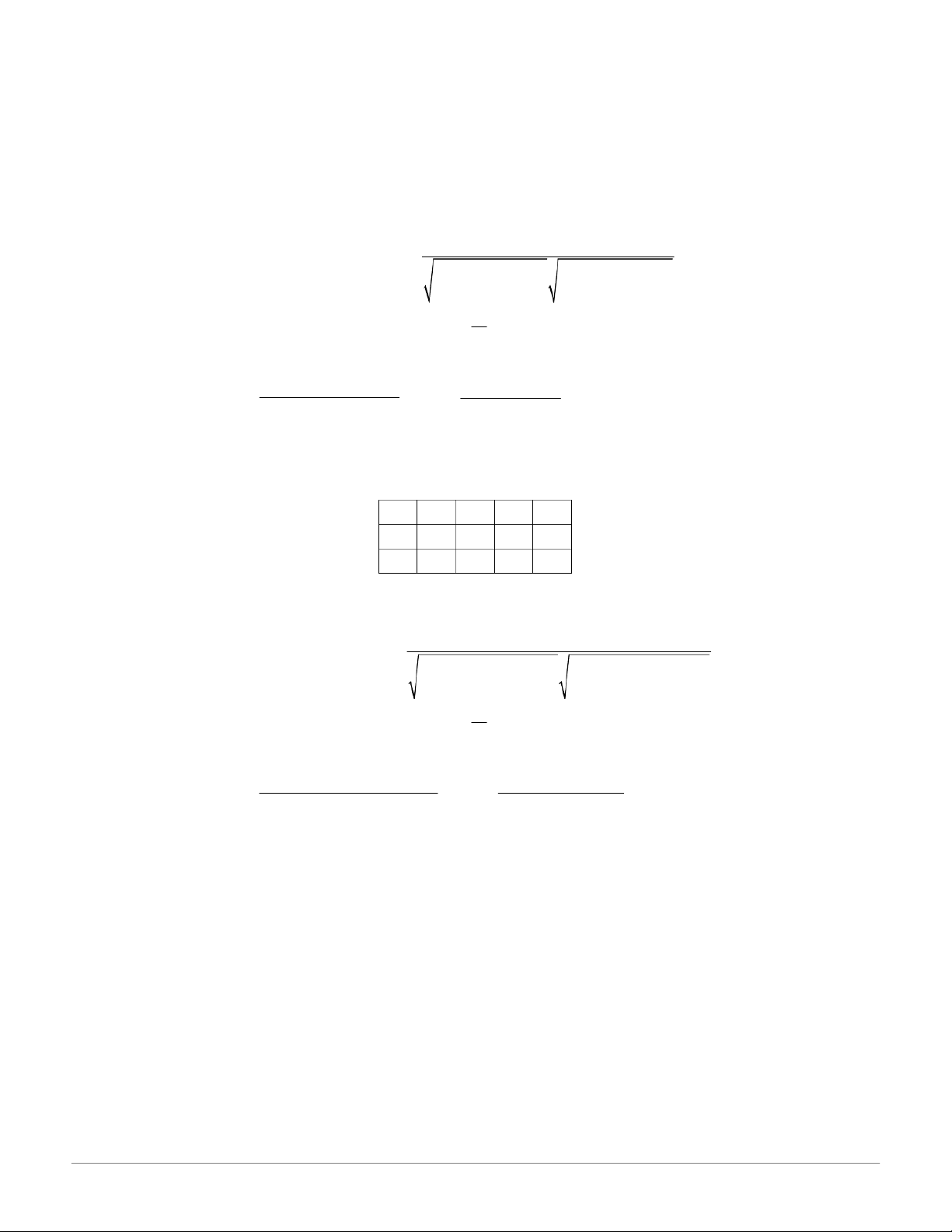
Ta t’nh theo c™ng thức thu gọn như sau: k k k n n x y  n x n y   iii i i i i   Hệ số tương quan mẫu: i i i r  1 1 1 k k k k 2 2 2 2 n  n x  ( )   nx n ( n y ) n y i i i i i i i i i i1  1 i 1 i 1
Phương tr“nh hồi quy tuyến t’nh mẫu: y  A  B với x x k k k k k n n x   y  nx n y n y   B n x i i i i i i i i i . i i  i 1  i i 1 1 B  vˆ i i 1 1 An  . k k 2 2 n n x  ( )  n x i i i i i i1  1 - 15 - XSTK 17:54, 27/01/2026
Tóm tắt công thức Xác Suất Thống Kê I - Tài liệu ôn tập - Studocu - 16 - T—m tắt công thức
c. Sử dụng m‡y t’nh bỏ túi để t’nh hệ số tương quan mẫu và phương tr“nh hồi quy tuyến t’nh mẫu: T‡c vụ D˜ng CASIO MS D˜ng CASIO ES
Bật chế độ nhập tần số Kh™ng cần Shift Mode  4 1
Khởi động g—i Hồi quy ModeÉ(t“m)ÉREG ModeÉ(t“m)ÉSTAT tuyến t’nh Lin A+BX
x , y Shift , n M+ 1 1 1 X Y FREQ 
x , y Shift , n M+ x = y = n = 1 1 1 Nhập s li ố ệu k k k   
n 1 th“ chỉ cần nhấn x = y = n = i k k k x , y M+ i i
X—a mˆn h“nh hiển thị AC AC X‡c định:  Hệ số tương quan Shift 2  3 = Shift 1 7 3 = mẫu (r)  Hệ s h ố ằng: A Shift 2  1 = Shift 1 7 1 =  Hệ số ẩn (x): B Shift 2  2 = Shift 1 7 2 = Tho‡t kh i ỏ g—i H i ồ quy Mode 1 Mode 1
Lưu ý: M‡y ES nếu đ‹ k’ch hoạt chế độ nhập tần số ở phần Lý thuyết mẫu rồi th“
kh™ng cần k’ch hoạt nữa.
ÉÉÉÉÉÉÉÉÉÉÉÉÉÉÉ. - 16 - XSTK 17:54, 27/01/2026
Tóm tắt công thức Xác Suất Thống Kê I - Tài liệu ôn tập - Studocu

Tài liệu liên quan: