TRƯỜNG ĐẠI HỌC QUỐC TẾ HỒNG BÀNG – KHOA KIẾN TRÚC M C L C Ch ng 1 : PH
NG PHÁP HÌNH CHI U TR C ĐO: ................................................................................... 3
I. KHÁI Ni M HÌNH CHI U TR C ĐO: ...................................................................................................... 3
II. CÁC LO I HÌNH CHI U TR C ĐO TH
NG DÙNG TRONG K THU T: ................................... 3 1.
Hình chi u tr c đo th ng góc đ u: ....................................................................................................... 4 2.
Hình chi u tr c đo th ng góc cân: ....................................................................................................... 4 3.
Hình chi u tr c đo xiên góc đ u: ......................................................................................................... 5 4.
Hình chi u tr c đo xiên góc cơn: ......................................................................................................... 6 III. PH
NG PHÁP V HÌNH CHI U TR C ĐO: (Chuy n t hình chi u th ng góc sang hình chi u tr c
đo) .................................................................................................................................................................... 7 1.
Hình chi u tr c đo c a một đi m: ........................................................................................................ 7 2. Hình chi u tr c đo c a đ
ng th ng, đa giác: ...................................................................................... 8 3.
Hình chi u tr c đo c a đa di n: ........................................................................................................... 8 4.
Hình chi u tr c đo c a m t cong ậ hình tr : ........................................................................................ 8 5.
ng d ng và các bài t p:...................................................................................................................... 9 Ch
ng 2 : PH I C NH M T TRANH PH NG TH NG Đ NG (PH I C NH 2 ĐI M T ): ................. 12 I. ĐI M ậ Đ
NG TH NG ậ M T PH NG: ............................................................................................ 12
1. H th ng m t ph ng hình chi u: ............................................................................................................ 12
2. Đồ th c c a một đi m: ........................................................................................................................... 13
3. Đ ng th ng: ......................................................................................................................................... 14
4. M t ph ng: ............................................................................................................................................ 18
II. V PH I C NH T HAI HÌNH CHI U TH NG GÓC: ...................................................................... 33
1. Bi u di n đi m: ...................................................................................................................................... 33
2. Bi u di n hình hộp chữ nh t: ................................................................................................................. 35
3. Ph ng pháp v ph i c nh dành cho ki n trúc: ..................................................................................... 37
4. Hình Chi u Ph i C nh Một S Chi Ti t Ki n Trúc: .............................................................................. 42
Ch ng 3 : PH I C NH M T TRANH NGHIÊNG (PH I C NH 3 ĐI M T ): ........................................ 44 I. TR
NG H P 1 (α<90°): ........................................................................................................................ 44 1.
H th ng các m t ph ng hình chi u: .................................................................................................. 44 2.
Cách xác định đ ng tầm mắt vƠ đi m t SẲ vƠ đồ th c c a đi m A (AẲ; AẲ2): ............................... 45 3.
Cách đ t độ cao cho đi m A: ............................................................................................................. 45 4.
Ph ng pháp dựng ph i c nh một hình hộp chữ nh t: ...................................................................... 46
Tài Liệu Học Tập: Môn HÌNH HỌC HỌA HÌNH 2 - Soạn: kts. Bùi Minh Huy Tước 1
TRƯỜNG ĐẠI HỌC QUỐC TẾ HỒNG BÀNG – KHOA KIẾN TRÚC II. TR
NG H P 2 (α > 90°): .................................................................................................................... 47 1.
H th ng các m t ph ng hình chi u: .................................................................................................. 47 2.
Cách xác định đ ng tầm mắt vƠ đi m t SẲ vƠ đồ th c c a đi m A (AẲ; AẲ2): ............................... 48 3.
Cách đ t độ cao cho đi m A: ............................................................................................................. 48 4.
Ph ng pháp dựng ph i c nh một hình hộp chữ nh t: ...................................................................... 49
Ch ng 4 : BÓNG TRểN CÁC HÌNH CHI U: ............................................................................................... 50
I. KHÁI NI M CHUNG: ............................................................................................................................... 50
1. Các định nghĩa: ...................................................................................................................................... 50
2. Các ph ng pháp v bóng th ng dùng: ............................................................................................... 50
II. BÓNG TRÊN HÌNH CHI U TR C ĐO: ................................................................................................ 52 1.
Bóng c a đo n th ng lên m t ph ng: ................................................................................................. 52 2.
Bóng c a đo n th ng lên m t cong: ................................................................................................... 52 3.
Bóng c a một s chi ti t ki n trúc: .................................................................................................... 53
III. BÓNG TRÊN HÌNH CHI U PH I C NH: ........................................................................................... 54 1.
Bi u di n nguồn sáng: ........................................................................................................................ 54 2.
Bóng c a một đi m: ........................................................................................................................... 55 3.
Bóng c a đo n th ng: ......................................................................................................................... 56 4.
Bóng c a hình ph ng: ........................................................................................................................ 60 5.
Bóng c a một s kh i hình học c b n: ............................................................................................. 61 6.
Ph i c nh và bóng c a một s chi ti t ki n trúc: ................................................................................ 63
IV. BÓNG TRÊN HÌNH CHI U PH I C NH M T TRANH NGHIÊNG: ............................................... 68
TÀI LI U THAM KH O ................................................................................................................................. 69
Tài Liệu Học Tập: Môn HÌNH HỌC HỌA HÌNH 2 - Soạn: kts. Bùi Minh Huy Tước 2
TRƯỜNG ĐẠI HỌC QUỐC TẾ HỒNG BÀNG – KHOA KIẾN TRÚC Ch ng 1 : PH
NG PHÁP HÌNH CHI U TR C ĐO:
I. KHÁI Ni M HÌNH CHI U TR C ĐO:
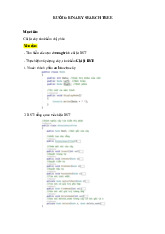
Trong không gian, ta gắn vào một h tr c tọa độ Đêcác vuông góc Oxyz. N u có một
đi m A, qua A v ch đ ng th ng song song v i tr c Oz, cắt m t ph ng Oxy t i đi m A1. Khi đó A1
đ c gọi là hình chi u th hai c a đi m A. Một m t ph ng qua đi m A và song song v i m t ph ng
Oyz cắt tr c Ox t i đi m Ax. Khi đó đ
ng gãy khúc OAxA1A gọi là đường gãy khúc tọa độ tự nhiên của A.
Chi u song song tất c các hình này lên m t ph ng hình chi u (P) theo h ng chi u s t ng ng ta có (hình v ): - Ta đ t:
p = OẲAẲx/OAx; q = AẲxAẲ1/AxA1; r = AẲAẲ1/AA1
Þ: là góc t o bởi h
ng chi u S và m t ph ng chi u (P). Khi đó:
p2 + q2 + r2 = 2 + cotg2Þ
II. CÁC LO I HÌNH CHI U TR C ĐO TH
NG DÙNG TRONG KỸ THU T:
Dựa vào các h s bi n d ng p,q,r và góc chi u Þ, trong k thu t ng i ta th ng sử d ng
các lo i hình chi u tr c đo sau:
• Hình chi u tr c đo th ng góc (v.góc) đ u: Þ = 900; p = q = r.
• Hình chi u tr c đo th ng góc cân: Þ = 900; p = r = 2q.
• Hình chi u tr c đo xiên góc cân: Þ >< 900; p = r = 2q.
• Hình chi u tr c đo xiên góc đ u: Þ >< 900; p = q = r.
Tài Liệu Học Tập: Môn HÌNH HỌC HỌA HÌNH 2 - Soạn: kts. Bùi Minh Huy Tước 3
TRƯỜNG ĐẠI HỌC QUỐC TẾ HỒNG BÀNG – KHOA KIẾN TRÚC
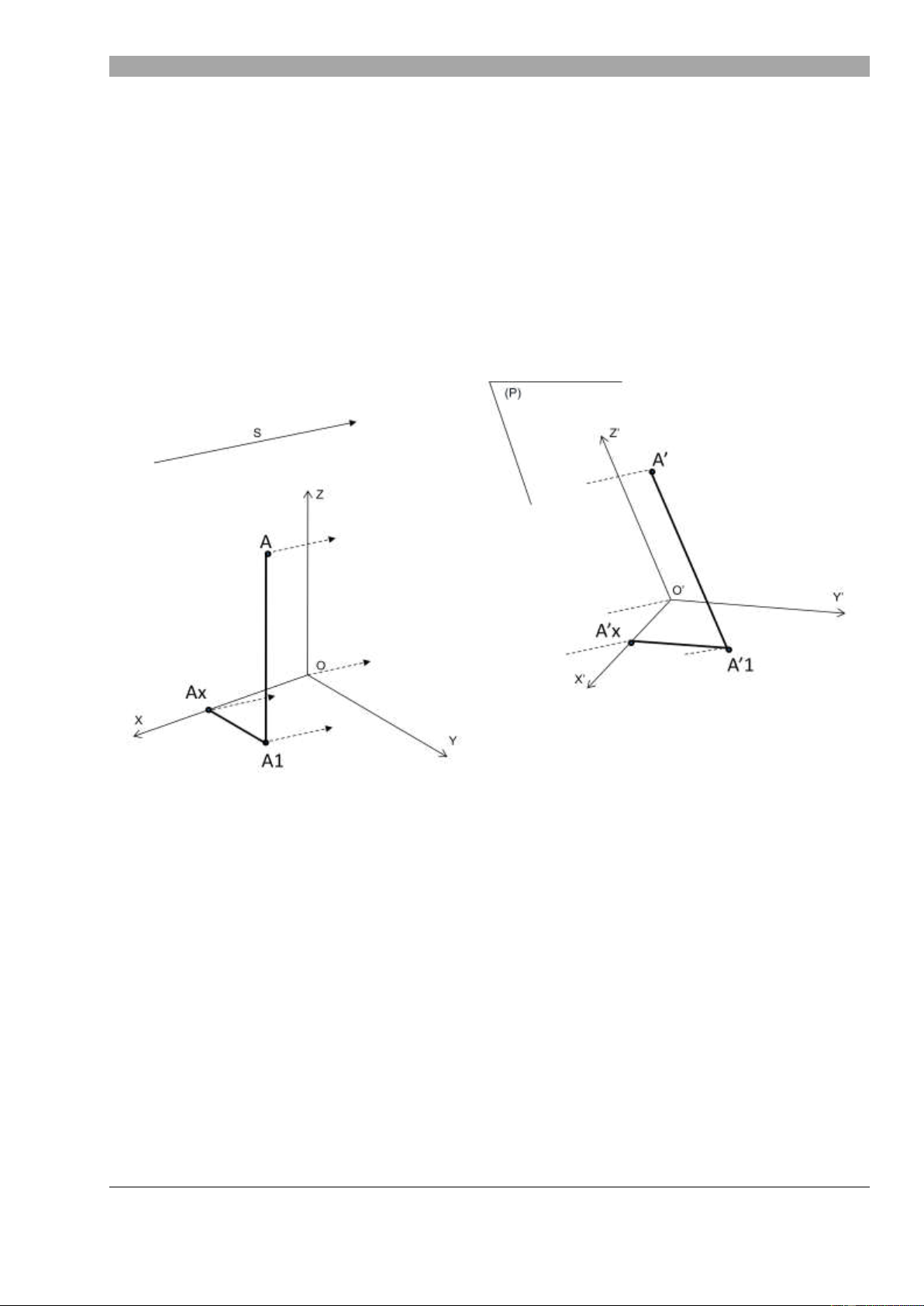
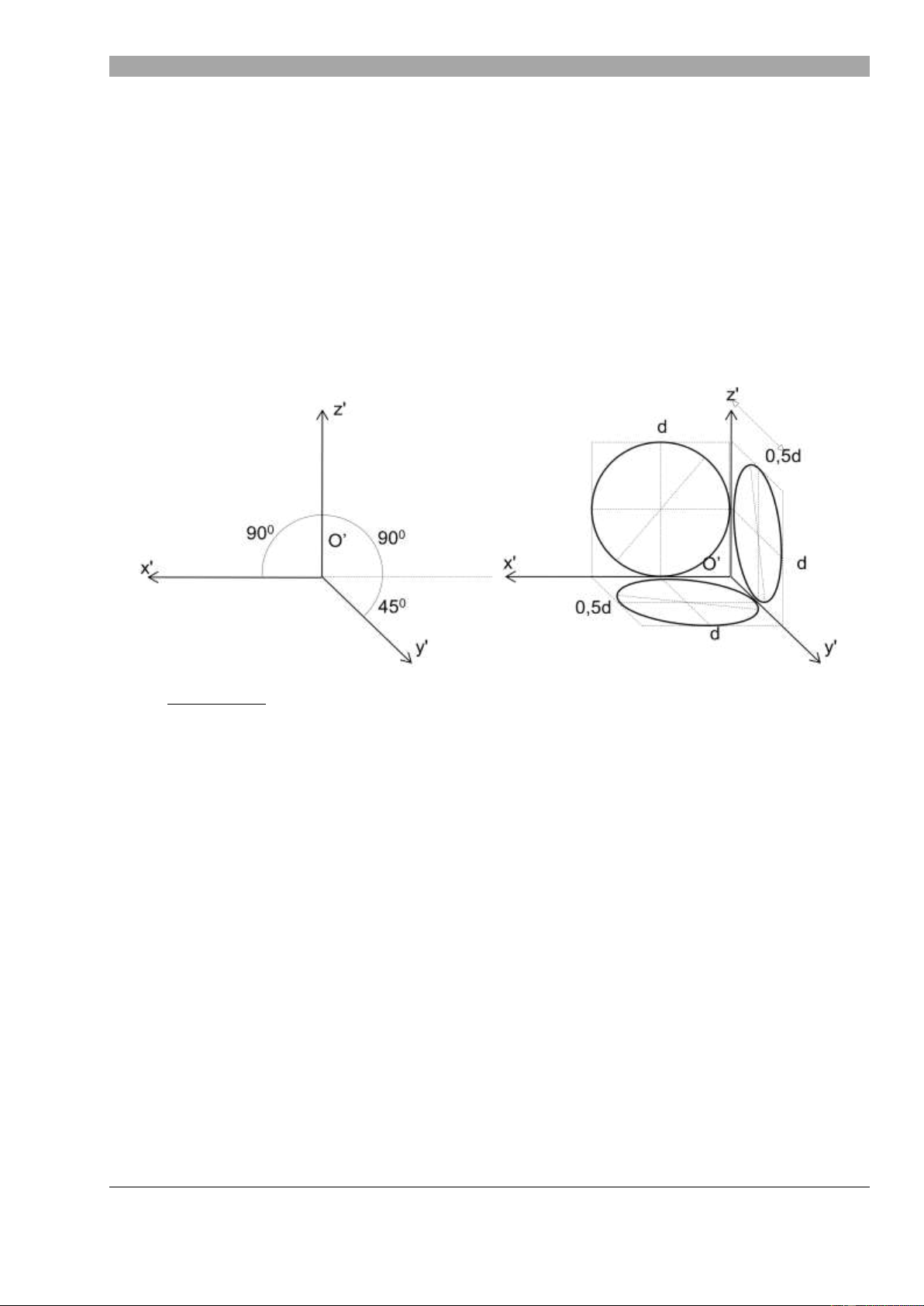
1. Hình chi u tr c đo th ng góc đ u: • Các tính chất:
- Tính chất 1: p = q = r = 0,82 (thực t sử d ng: p = q = r = 1).
- Tính chất 2: Góc giửa các tr c tọa độ tr c đo b ng nhau và b ng 1200
- Tính chất 3: Hình chi u tr c đo c a các đ
ng tròn thuộc (ho c song song v i) các m t ph ng
tọa độ là một ellip có:
 H ng c a đ ng kính dài c a ellip vuông góc v i tr c tr c đo không thuộc m t ph ng ch a đ ng tròn đó.
 Đ ng kính dài c a ellip = Đ ng kính d c a đ ng tròn khi h s bi n d ng (p = q = r =
0,82) và = 1,22d khi h s bi n d ng (p = q = r = 1).
 Đ ng kính ngắn c a ellip = 0,58d khi h s bi n d ng (p = q = r = 0,82) và = 0,7d khi h s bi n dàng (p = q = r = 1).
2. Hình chi u tr c đo th ng góc cân:
Tài Liệu Học Tập: Môn HÌNH HỌC HỌA HÌNH 2 - Soạn: kts. Bùi Minh Huy Tước 4
TRƯỜNG ĐẠI HỌC QUỐC TẾ HỒNG BÀNG – KHOA KIẾN TRÚC • Các tính chất:
- Tính chất 1: p = r = 2q = 2x0,47 (thực t sử d ng: p = r = 2q = 1).
- Tính chất 2: Góc giửa các tr c tọa độ tr c đo: (nh hình v ).
- Tính chất 3: Hình chi u tr c đo c a các đ
ng tròn thuộc (ho c song song v i) các m t ph ng
tọa độ là một ellip có:
 H ng c a đ ng kính dài c a ellip vuông góc v i tr c tr c đo không thuộc m t ph ng ch a đ ng tròn đó.
 N u đ ng tròn thuộc ho c song song v i m t ph ng Oxy hay m t ph ng Oyz thì:
Đk dƠi = d; Đk ngắn = d/3; (Đk dƠi = 1,06d; Đk ngắn = 0,35d )
 N u đ ng tròn thuộc ho c song song v i m t ph ng Ozx thì:
Đk dƠi = d; Đk ngắn = 0,88d; (Đk dƠi = 1,06d; Đk ngắn = 0,93d )
• Cách xác định tr c tọa độ tr c đo c a hình chi u tr c đo th ng góc cân:
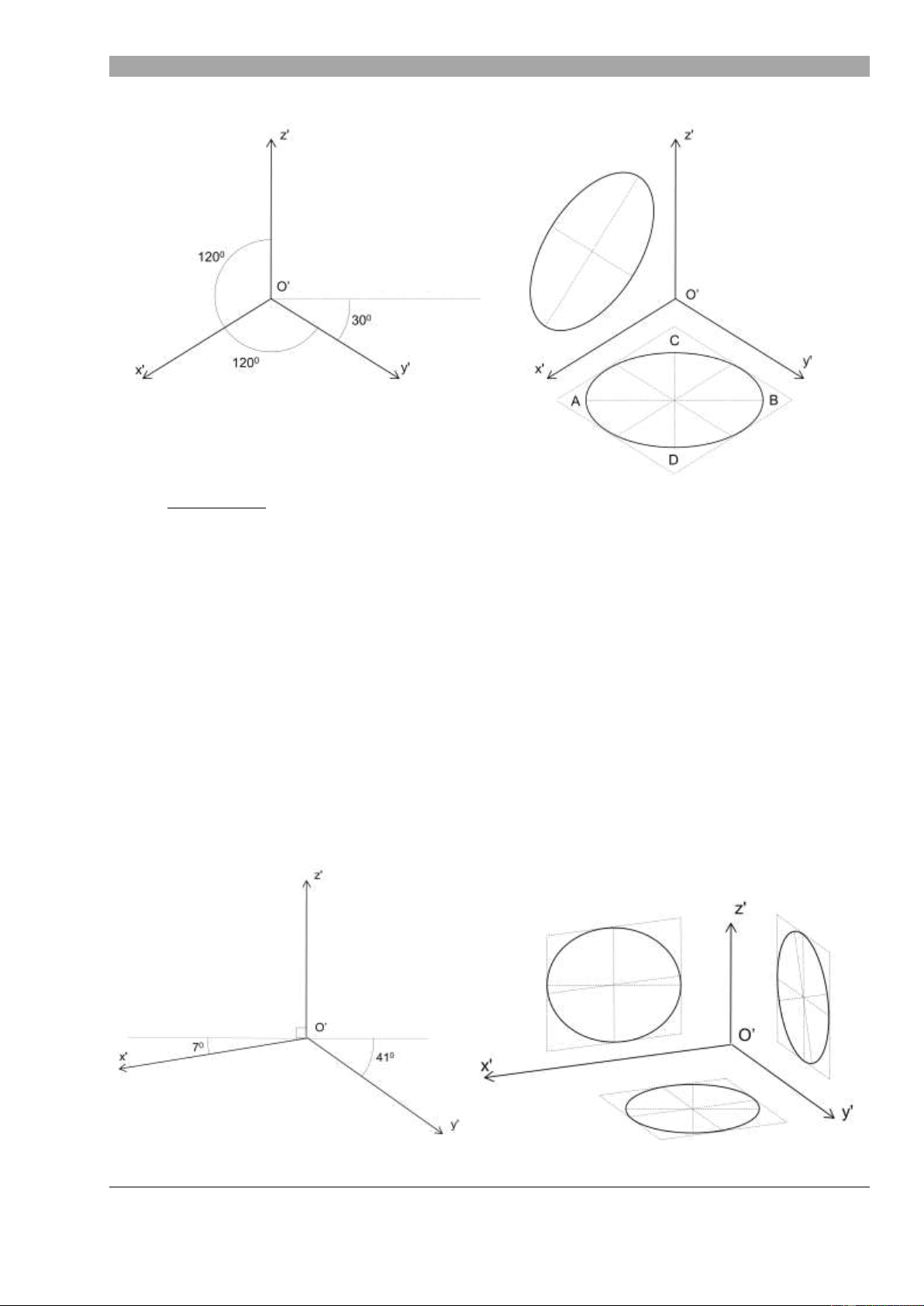
3. Hình chi u tr c đo xiên góc đ u: • Các tính chất:
- Tính chất 1: p = q = r = 0,82 (thực t sử d ng: p = q = r = 1).
Tài Liệu Học Tập: Môn HÌNH HỌC HỌA HÌNH 2 - Soạn: kts. Bùi Minh Huy Tước 5
TRƯỜNG ĐẠI HỌC QUỐC TẾ HỒNG BÀNG – KHOA KIẾN TRÚC
- Tính chất 2: Góc giửa tr c OẲx vƠ OẲz = 900 ; tr c OẲy vƠ OẲz = 1200
- Tính chất 3: Hình chi u tr c đo c a các đ ng tròn:
 Đ ng tròn thuộc m t ph ng Ozx có hình chi u lƠ đ ng tròn đ ng kính d.
 Đ ng tròn thuộc m t ph ng Oxy và Oyz có hình chi u là một hình eliip có: - H ng c a đ
ng kính dài ellip nghiêng v i tr c OẲx ho c OẲy (tùy theo đ ng tròn thuộc
m t ph ng Oxy hay Oyz) một góc là: 220 30Ẳ
- Đk dƠi = 1,3d; Đk ngắn = 0,54d.
4. Hình chi u tr c đo xiên góc cơn:
Đơy lƠ hình chi u tr c đo th ng đ c sử d ng nhất trong ki n trúc. • Các tính chất:
- Tính chất 1: p = r = 1; q = 0,5.
- Tính chất 2: Góc giửa tr c OẲx vƠ OẲz = 900 ; tr c OẲy vƠ OẲz = 1350
- Tính chất 3: Hình chi u tr c đo c a các đ ng tròn:
 Đ ng tròn thuộc m t ph ng Ozx có hình chi u lƠ đ ng tròn đ ng kính d.
 Đ ng tròn thuộc m t ph ng Oxy và Oyz có hình chi u là một hình eliip có: - H ng c a đ
ng kính dài ellip nghiêng v i tr c OẲx ho c OẲz (tùy theo đ ng tròn thuộc
m t ph ng Oxy hay Oyz) một góc là: 70 10Ẳ
- Đk dƠi = 1,06d; Đk ngắn = 0,35d.
Tài Liệu Học Tập: Môn HÌNH HỌC HỌA HÌNH 2 - Soạn: kts. Bùi Minh Huy Tước 6
TRƯỜNG ĐẠI HỌC QUỐC TẾ HỒNG BÀNG – KHOA KIẾN TRÚC III. PH
NG PHÁP V HÌNH CHI U TR C ĐO: (Chuy n t hình chi u th ng góc
sang hình chi u tr c đo)
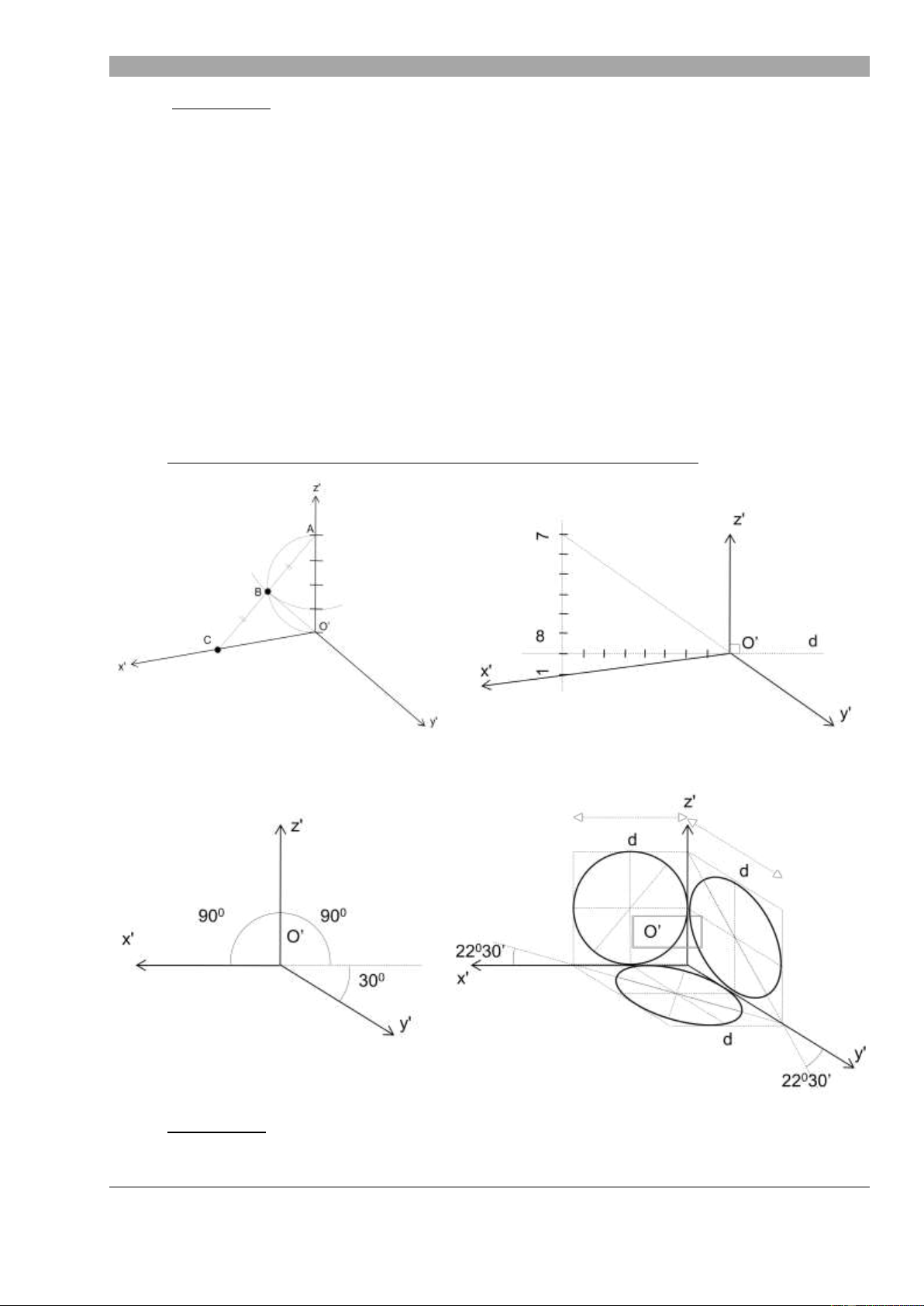
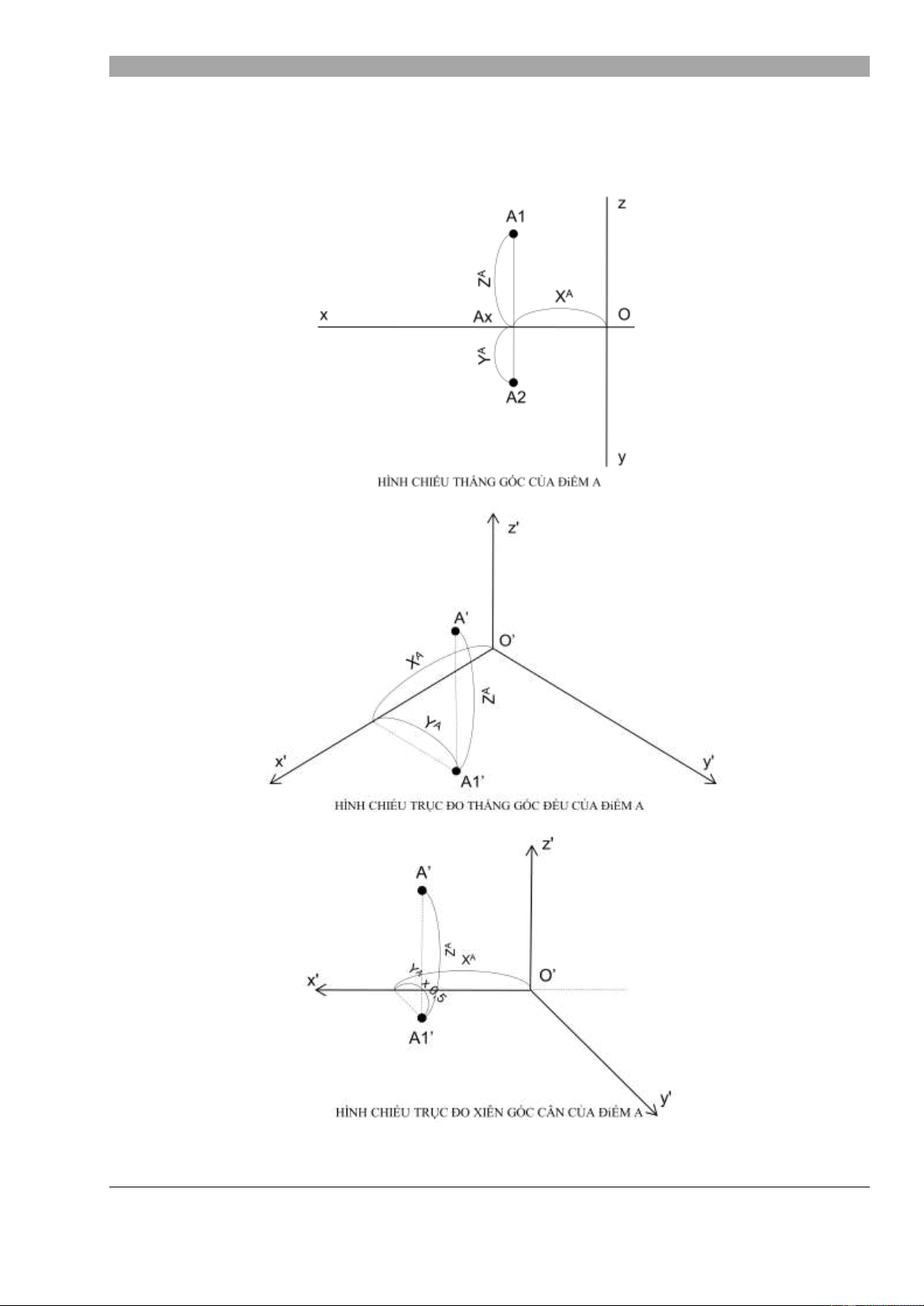
1. Hình chi u tr c đo c a một đi m:
Tài Liệu Học Tập: Môn HÌNH HỌC HỌA HÌNH 2 - Soạn: kts. Bùi Minh Huy Tước 7
TRƯỜNG ĐẠI HỌC QUỐC TẾ HỒNG BÀNG – KHOA KIẾN TRÚC
2. Hình chi u tr c đo c a đ ng th ng, đa giác: Một đ ng th ng đ
c xác định khi bi t hai đi m. Hình chi u tr c đo c a đ ng th ng cũng
đ c xác định khi bi t hình chi u tr c đo c a 2 đi m. T ng tự n u xác định hình chi u tr c đo c a
các đỉnh ta s xác định hình chi u tr c đo c a một đa giác.
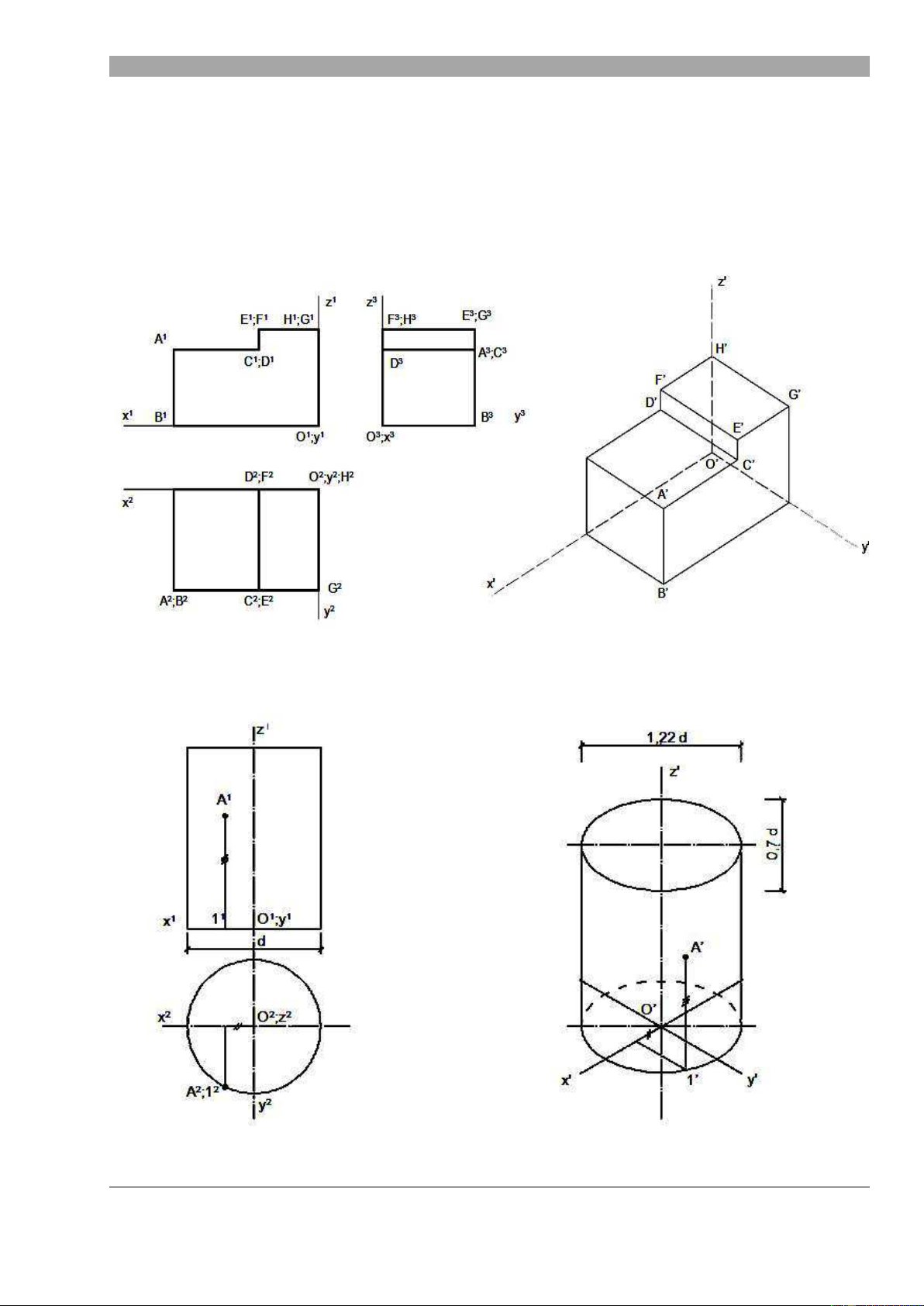
3. Hình chi u tr c đo c a đa di n:
4. Hình chi u tr c đo c a m t cong ậ hình tr :
Tài Liệu Học Tập: Môn HÌNH HỌC HỌA HÌNH 2 - Soạn: kts. Bùi Minh Huy Tước 8
TRƯỜNG ĐẠI HỌC QUỐC TẾ HỒNG BÀNG – KHOA KIẾN TRÚC 5.
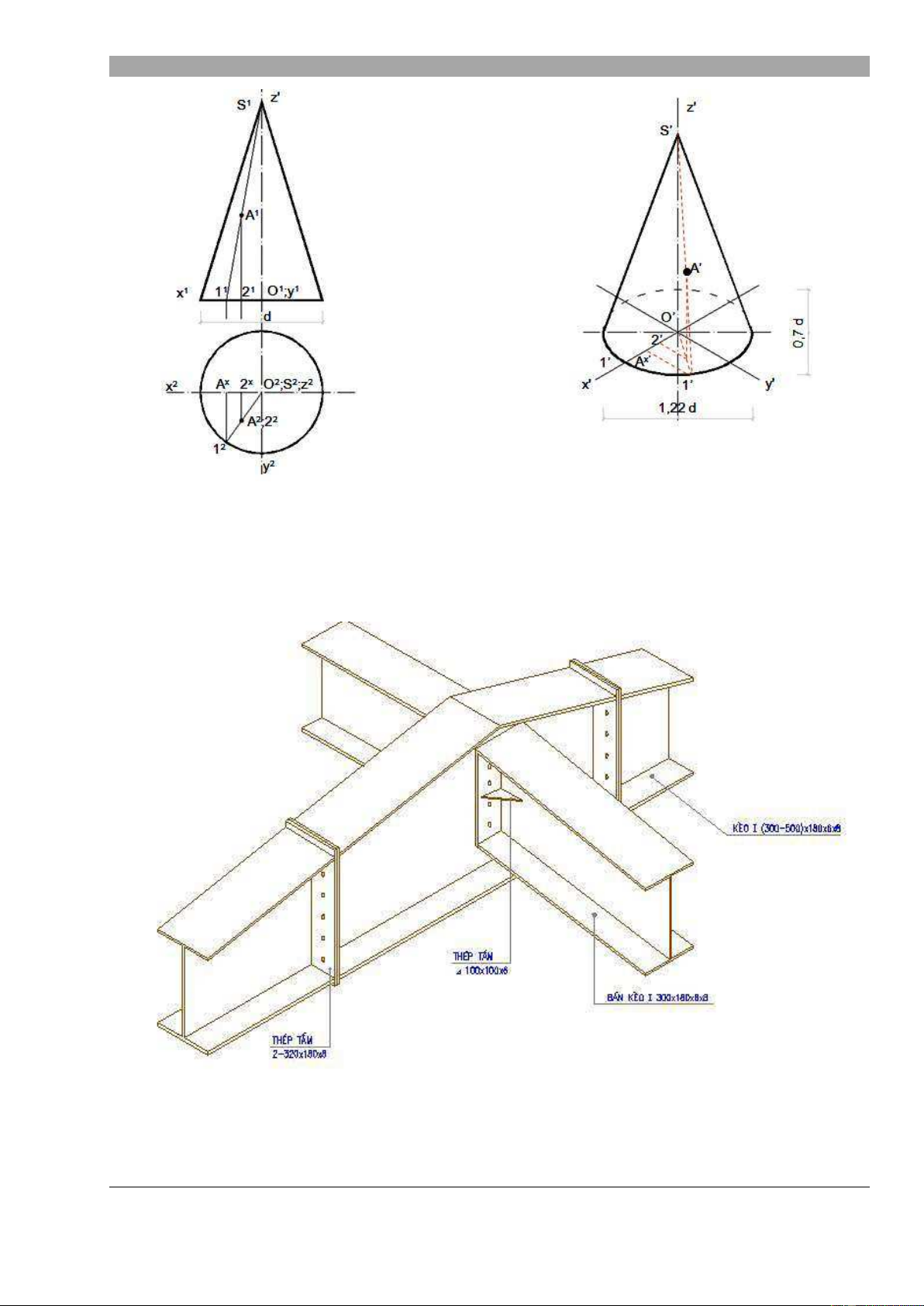
ng d ng và các bài t p:
Tài Liệu Học Tập: Môn HÌNH HỌC HỌA HÌNH 2 - Soạn: kts. Bùi Minh Huy Tước 9
TRƯỜNG ĐẠI HỌC QUỐC TẾ HỒNG BÀNG – KHOA KIẾN TRÚC
Tài Liệu Học Tập: Môn HÌNH HỌC HỌA HÌNH 2 - Soạn: kts. Bùi Minh Huy Tước 10
TRƯỜNG ĐẠI HỌC QUỐC TẾ HỒNG BÀNG – KHOA KIẾN TRÚC HÌNH CHI U PH I C NH Ph i c nh lƠ ph
ng pháp bi u di n v t th dựa trên phép chi u xuyên tâm. Hình bi u di n c a ph
ng pháp nƠy mô ph ng mắt ng i quan sát sự v t đ c chi u qua con ng i lên võng m c.
Cho nên ph ng pháp nƠy rất thông d ng trong ngành ki n trúc xây dựng và là
một công c không th thi u đ i v i ng
i làm công tác sáng tác, thi t k ki n trúc.Ngày nay những ch
ng trình mô ph ng không gian ba chi u rất m nh có th thi t l p nhanh chóng những b n
v ph i c nh rất đẹp. Tuy nhiên, trong ho t động sáng tác, công c chính v n là phác th o b ng tay và bi u di n ý t ởng d
i d ng hình chi u ph i c nh. Những giáo trình tr c đơy v ch ng trình
nƠy th ng n ng v lý thuy t hình học và h n ch rất nhi u khi ph i th hi n những công trình ki n
trúc gồm rất nhi u chi ti t ph c t p.
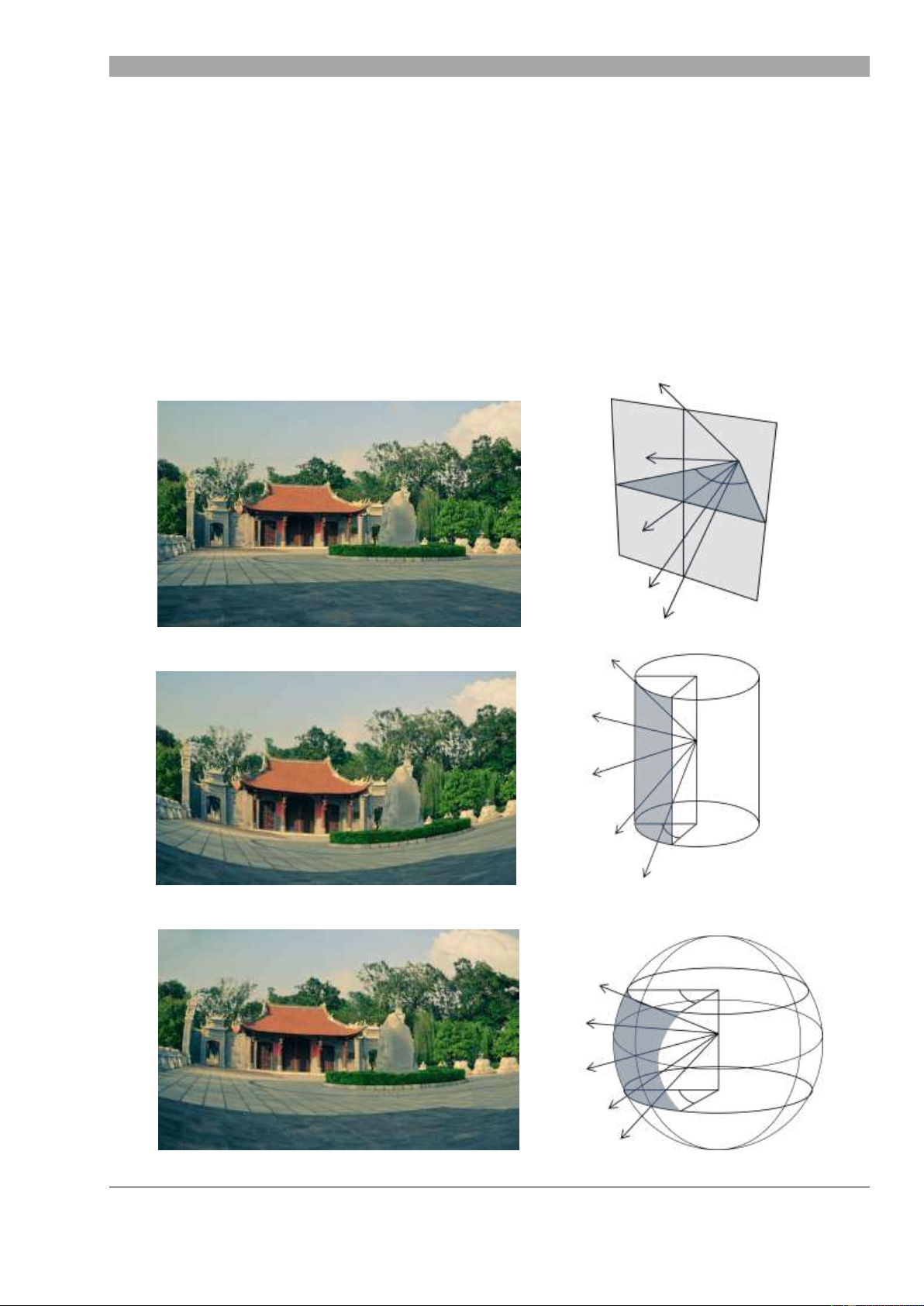
Dựa vào m t tranh mƠ ta có các ph
ng pháp hình chi u ph i c nh sau :
 Ph i c nh m t tranh ph ng: .
 Ph i c nh v i m t tranh là m t tr : .
 Ph i c nh v i m t tranh là m t cầu:
Tài Liệu Học Tập: Môn HÌNH HỌC HỌA HÌNH 2 - Soạn: kts. Bùi Minh Huy Tước 11
TRƯỜNG ĐẠI HỌC QUỐC TẾ HỒNG BÀNG – KHOA KIẾN TRÚC
Ch ng 2 : PH I C NH M T TRANH PH NG TH NG Đ NG (PH I C NH 2 ĐI M T ): I. ĐI M ậ Đ
NG TH NG ậ M T PH NG:
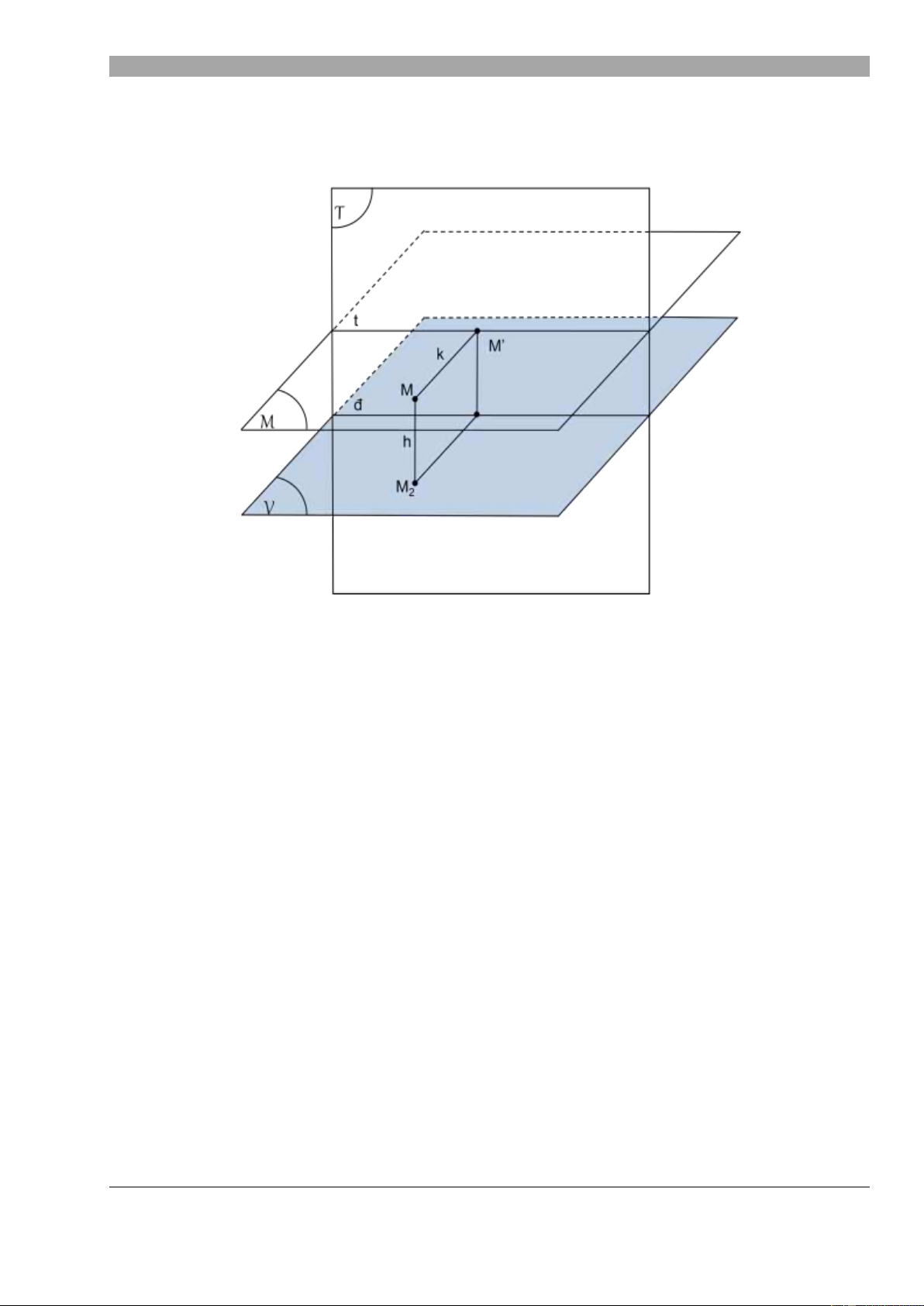
1. H th ng m t ph ng hình chi u: V : m t ph ng v t th T : m t tranh đ : đáy tranh M : đi m nhìn M2 : chơn đi m nhìn
MM2 = h : độ cao đi m nhìn M : m t ph ng tầm mắt t
: đ ng tầm mắt, đ ng chân tr i MẲ : đi m chính MMẲ : tia chính
MMẲ = k : kho ng cách chính
Trong không gian, chọn một m t ph ng n m ngang làm mặt phẳng vật thể V (n i đ t các v t
th ) và m t ph ng th ng đ ng làm mặt tranh T giao nhau thành một đ
ng th ng gọi là đáy tranh đ. Một đi m M đ
c gọi là điểm nhìn (mắt ng
i quan sát). Hình chi u b ng c a M lên m t ph ng V là M2 đ
c gọi là chân của điểm nhìn. MM2 = h gọi là độ cao điểm nhìn. M t ph ng tầm mắt M n m
ngang song song v i m t ph ng V đi qua đi m nhìn M. M t ph ng tầm mắt M cắt m t tranh T thành một đ
ng th ng gọi là đường tầm mắt t (ho c đ ng chân tr i). Đ ng th ng qua M, vuông góc v i m t tranh T đ
c gọi là tia chính. Tia chính cắt m t tranh t i đi m chính MẲ. MMẲ=
k đ c gọi là khoảng cách chính.
Tài Liệu Học Tập: Môn HÌNH HỌC HỌA HÌNH 2 - Soạn: kts. Bùi Minh Huy Tước 12
TRƯỜNG ĐẠI HỌC QUỐC TẾ HỒNG BÀNG – KHOA KIẾN TRÚC
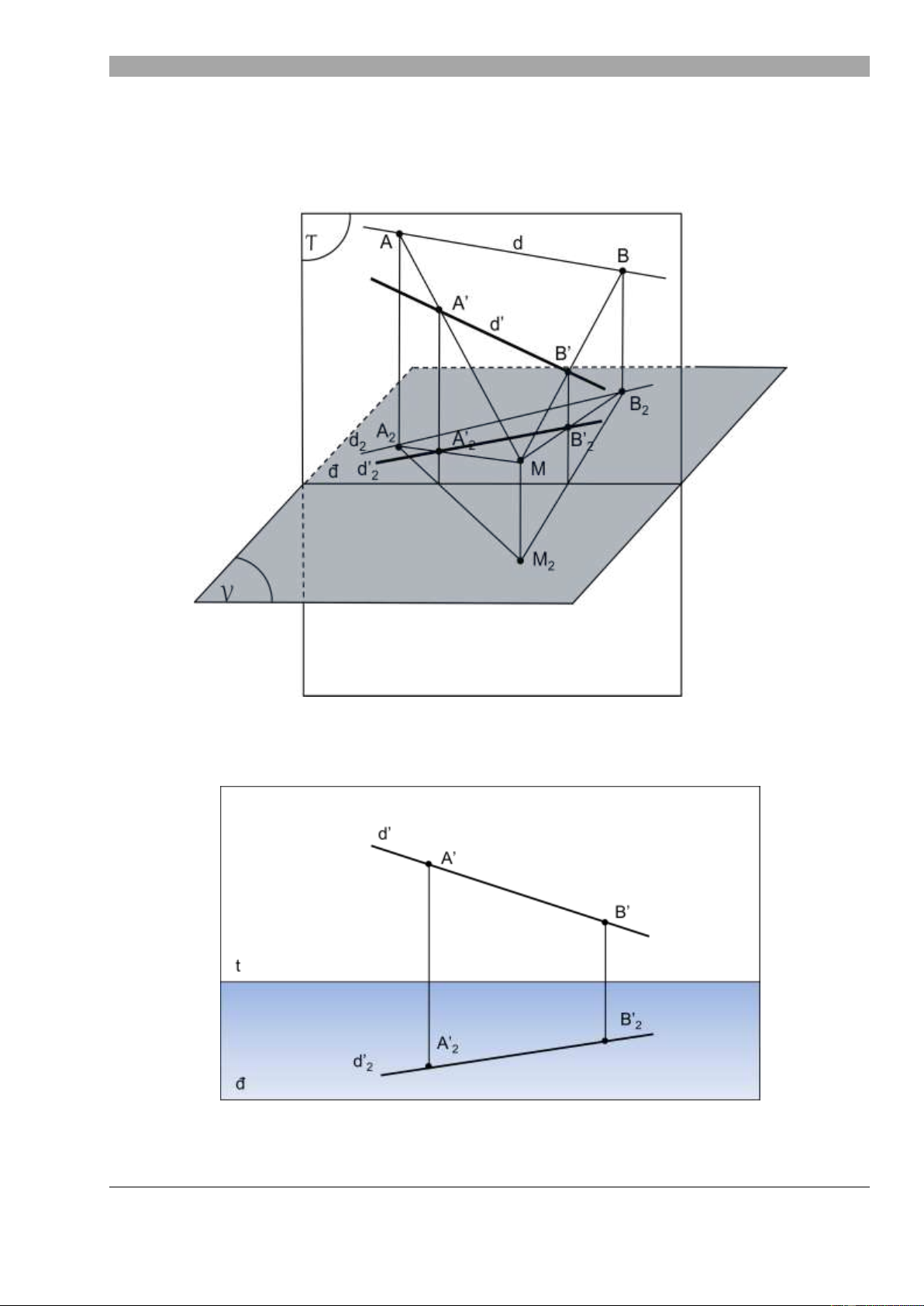
2. Đồ th c c a một đi m:
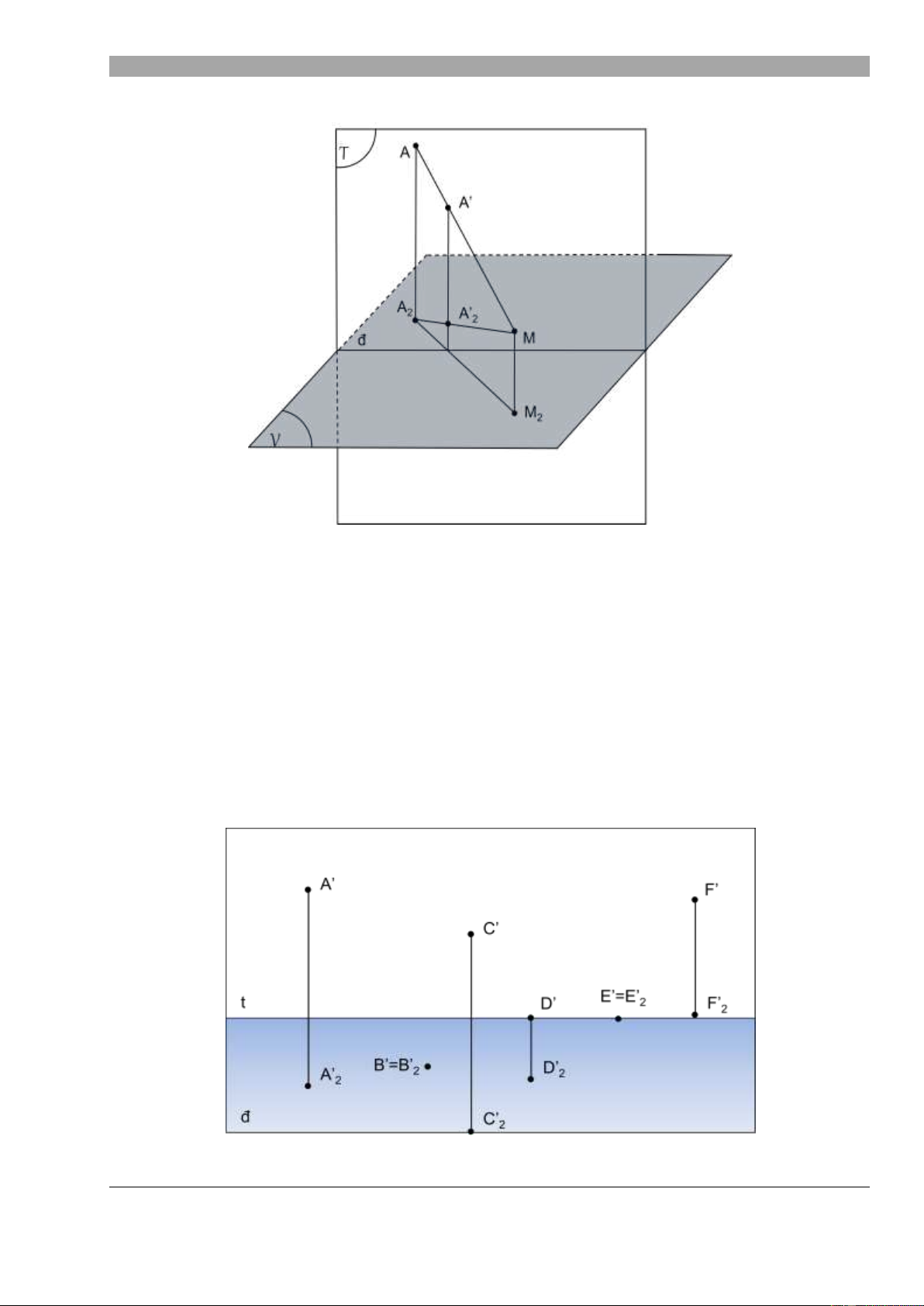
Gi sử có một đi m A bất kỳ. Chi u th ng góc đi m A lên m t ph ng v t th V ta đ c A2,
gọi là chân (ho c hình chi u b ng) c a đi m A. Chi u xuyên tâm M lần l t hai đi m A và A2 lên m t tranh T ta đ
c hai hình chi u AẲ (ph i c nh c a đi m A) vƠ AẲ2 (ph i c nh chân c a đi m A).
Ta thấy AẲAẲ2 luôn vuông góc v i đáy tranh đ. C p hình chi u ph i c nh AẲ và ph i c nh chơn AẲ2
gọi lƠ đồ th c c a đi m A. (đồ th c là hình v bi u di n tọa độ xác định c a một đi m)
Các đi m đ c bi t th ng g p khác: o Đi m B thuộc m t ph ng V o Đi m C thuộc m t tranh T
o Đi m D thuộc m t ph ng tầm mắt M
o Đi m E∞ thuộc m t ph ng v t th V o Đi m F∞ bất kỳ
Tài Liệu Học Tập: Môn HÌNH HỌC HỌA HÌNH 2 - Soạn: kts. Bùi Minh Huy Tước 13
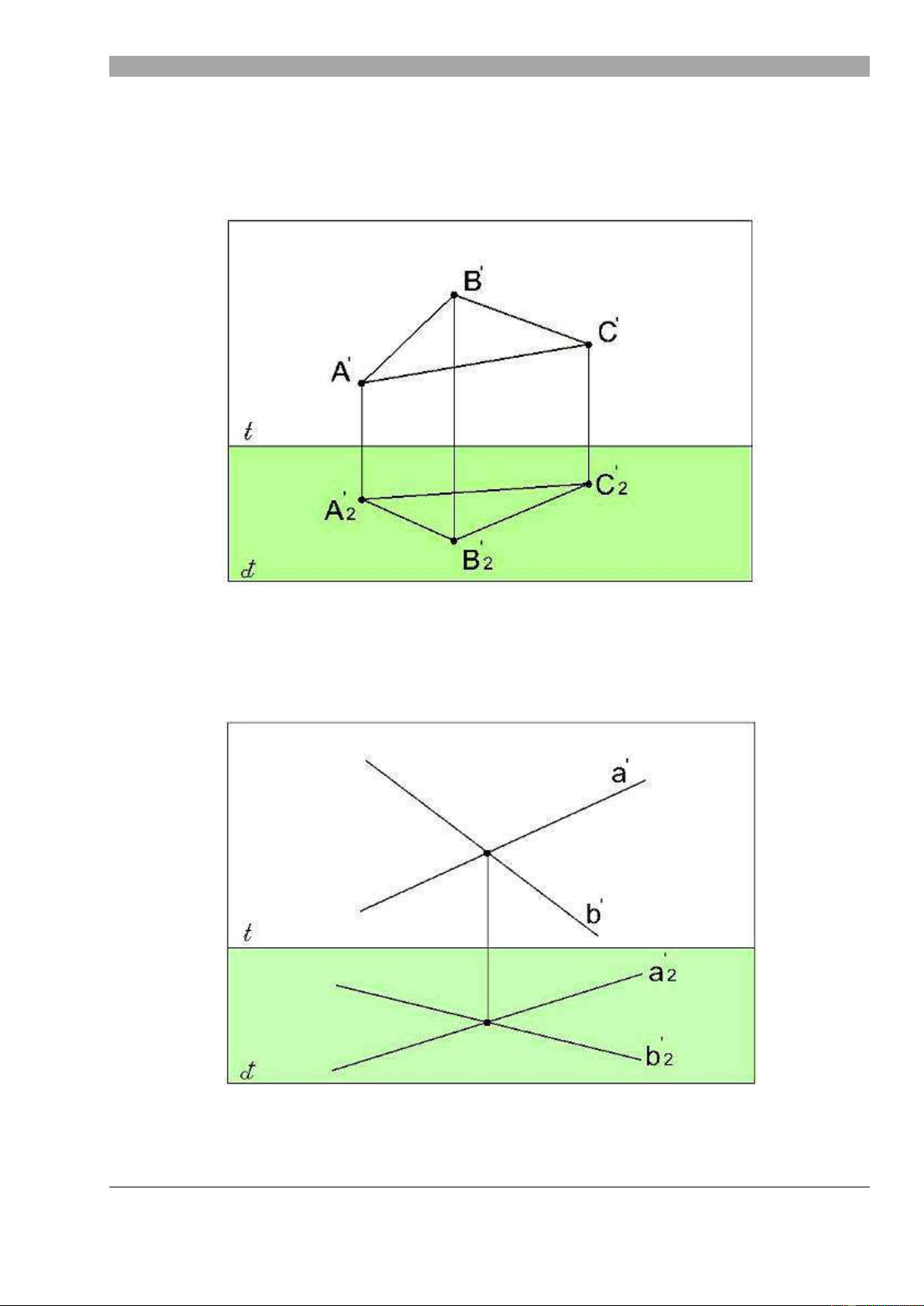
TRƯỜNG ĐẠI HỌC QUỐC TẾ HỒNG BÀNG – KHOA KIẾN TRÚC 3. Đ ng th ng:
Đ ng th ng đ c xác định qua hai đi m xác định. Hình v sau minh họa ph i c nh c a một
đ ng th ng qua hai đi m A và B.
Tài Liệu Học Tập: Môn HÌNH HỌC HỌA HÌNH 2 - Soạn: kts. Bùi Minh Huy Tước 14
TRƯỜNG ĐẠI HỌC QUỐC TẾ HỒNG BÀNG – KHOA KIẾN TRÚC
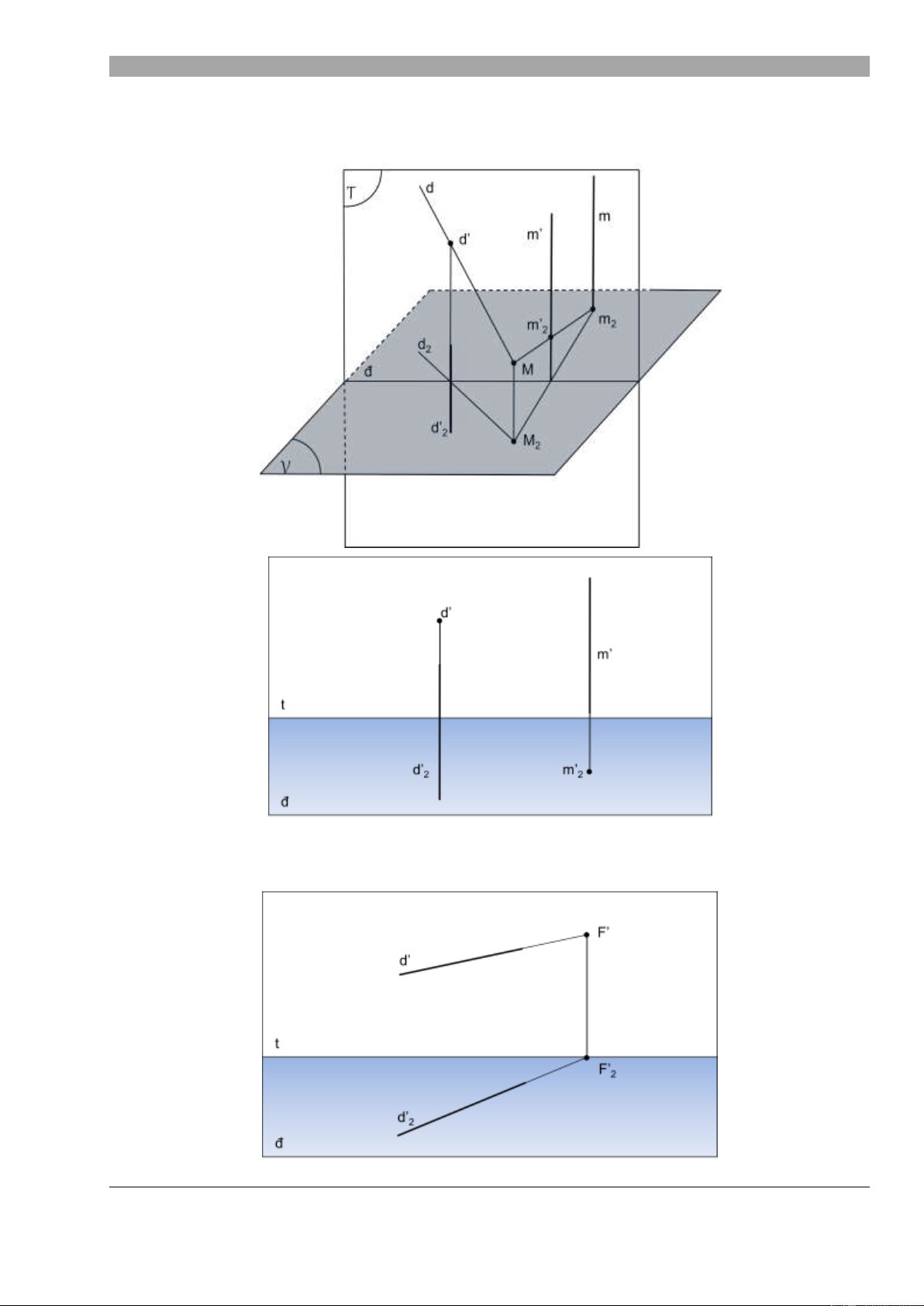
Các đ ng th ng đ c bi t:
o Đ ng th ng chi u b ng : (đ ng th ng m vuông góc v i m t ph ng v t th V )
o Đ ng th ng chi u ph i c nh : ( đ ng th ng d đi qua đi m nhìn M)
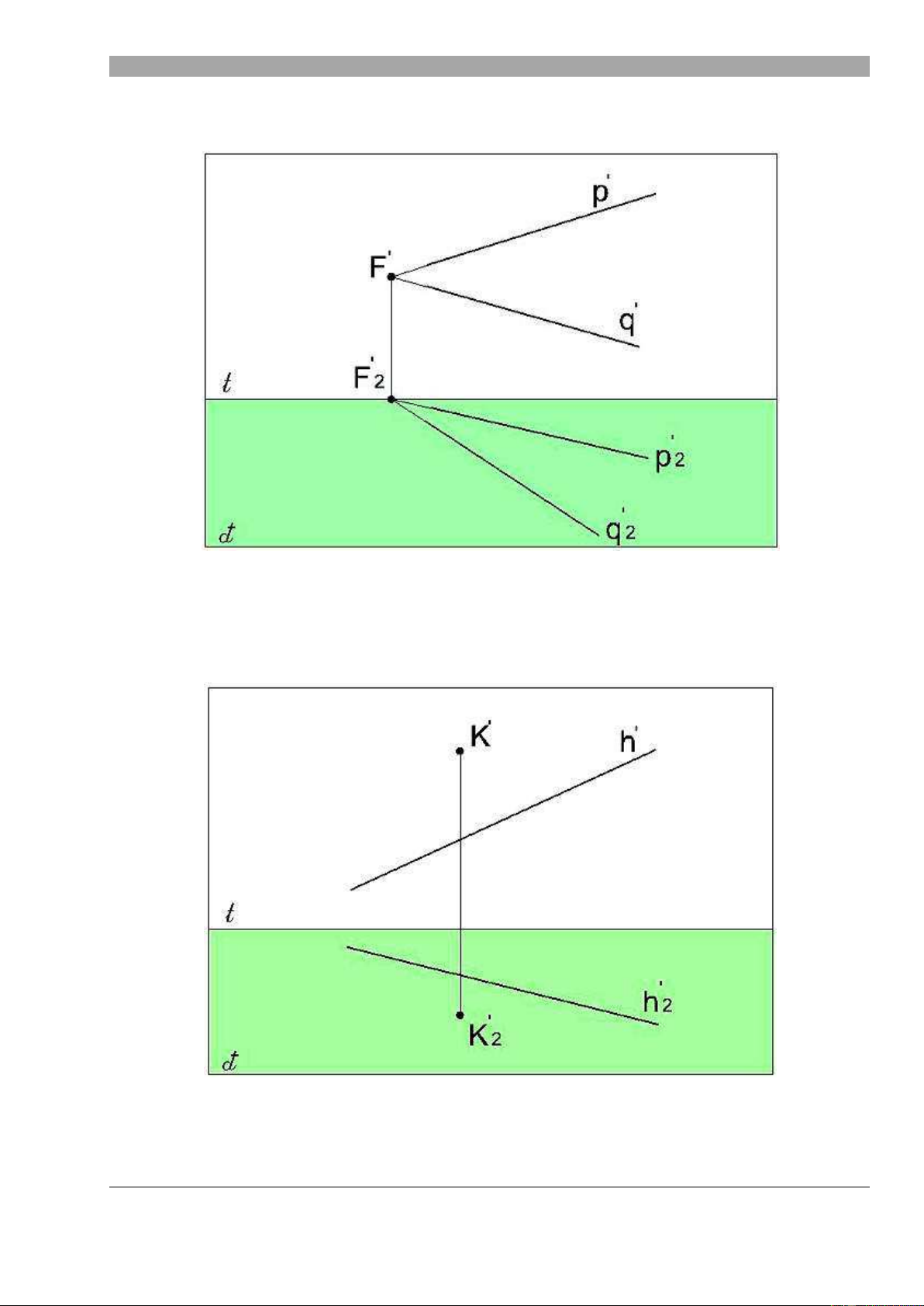
Đi m t c a một đ ng th ng: là ph i c nh đi m vô t n c a đ ng th ng. Hình v minh
họa cách xác định đi m t FẲ c a đ
ng th ng d ( ph i c nh chơn FẲ2 thuộc đ ng tầm mắt t).
Tài Liệu Học Tập: Môn HÌNH HỌC HỌA HÌNH 2 - Soạn: kts. Bùi Minh Huy Tước 15
TRƯỜNG ĐẠI HỌC QUỐC TẾ HỒNG BÀNG – KHOA KIẾN TRÚC
ụ nghĩa v m t hình học c a đi m t : các đ ng th ng song song v i nhau thì có chung
một đi m t . Đi m t c a một đ
ng th ng lƠ giao đi m c a m t tranh T v i một đ ng th ng đi qua
đi m nhìn M, v song song v i đ ng th ng đƣ cho.
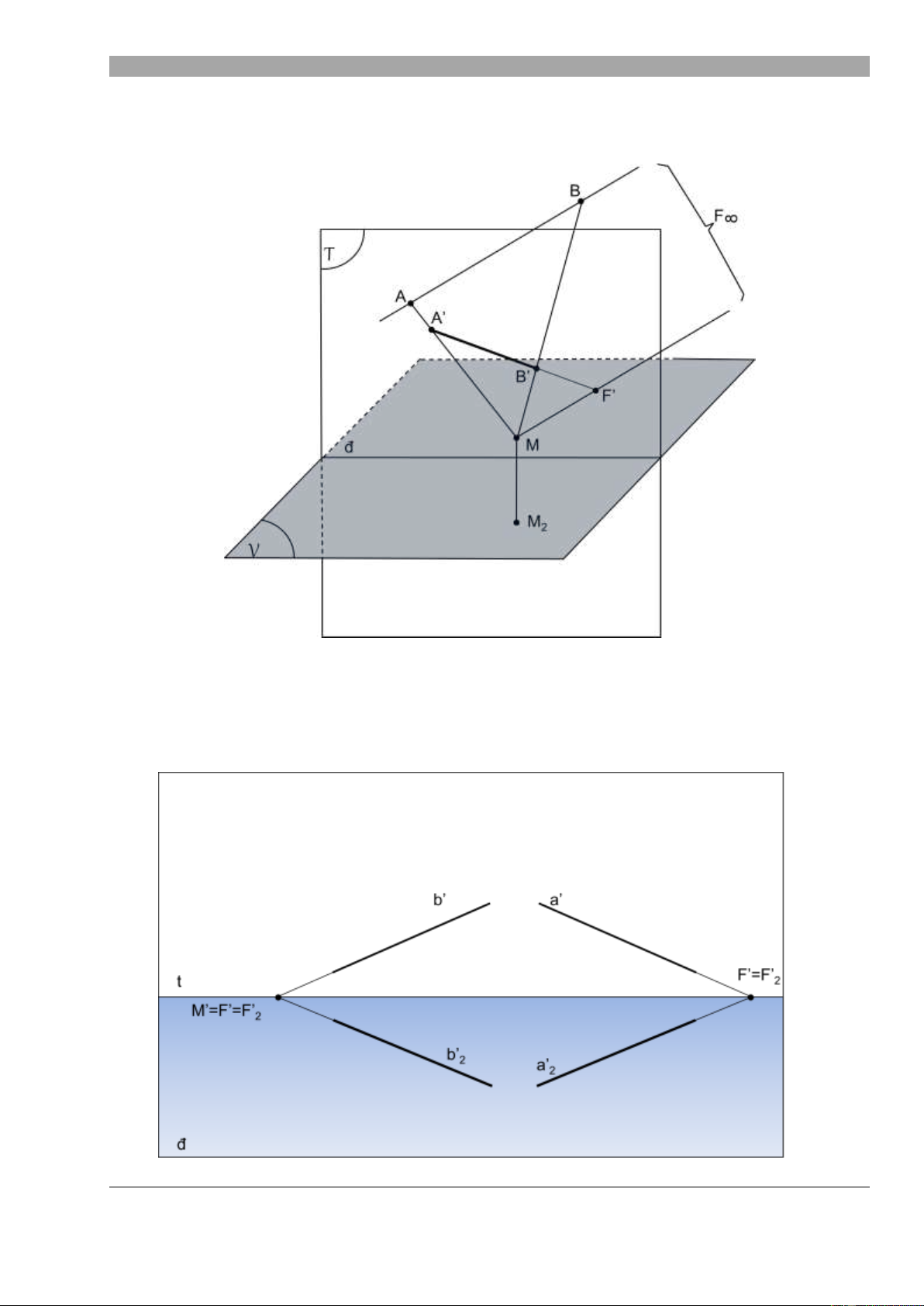
Đi m t c a một s đ ng th ng th ng g p:
o Đ ng th ng b ng a // V : đi m t thuộc đ ng tầm mắt t
o Đ ng th ng b vuông góc v i m t tranh T : đi m t trùng v i đi m chính MẲ
Tài Liệu Học Tập: Môn HÌNH HỌC HỌA HÌNH 2 - Soạn: kts. Bùi Minh Huy Tước 16
TRƯỜNG ĐẠI HỌC QUỐC TẾ HỒNG BÀNG – KHOA KIẾN TRÚC
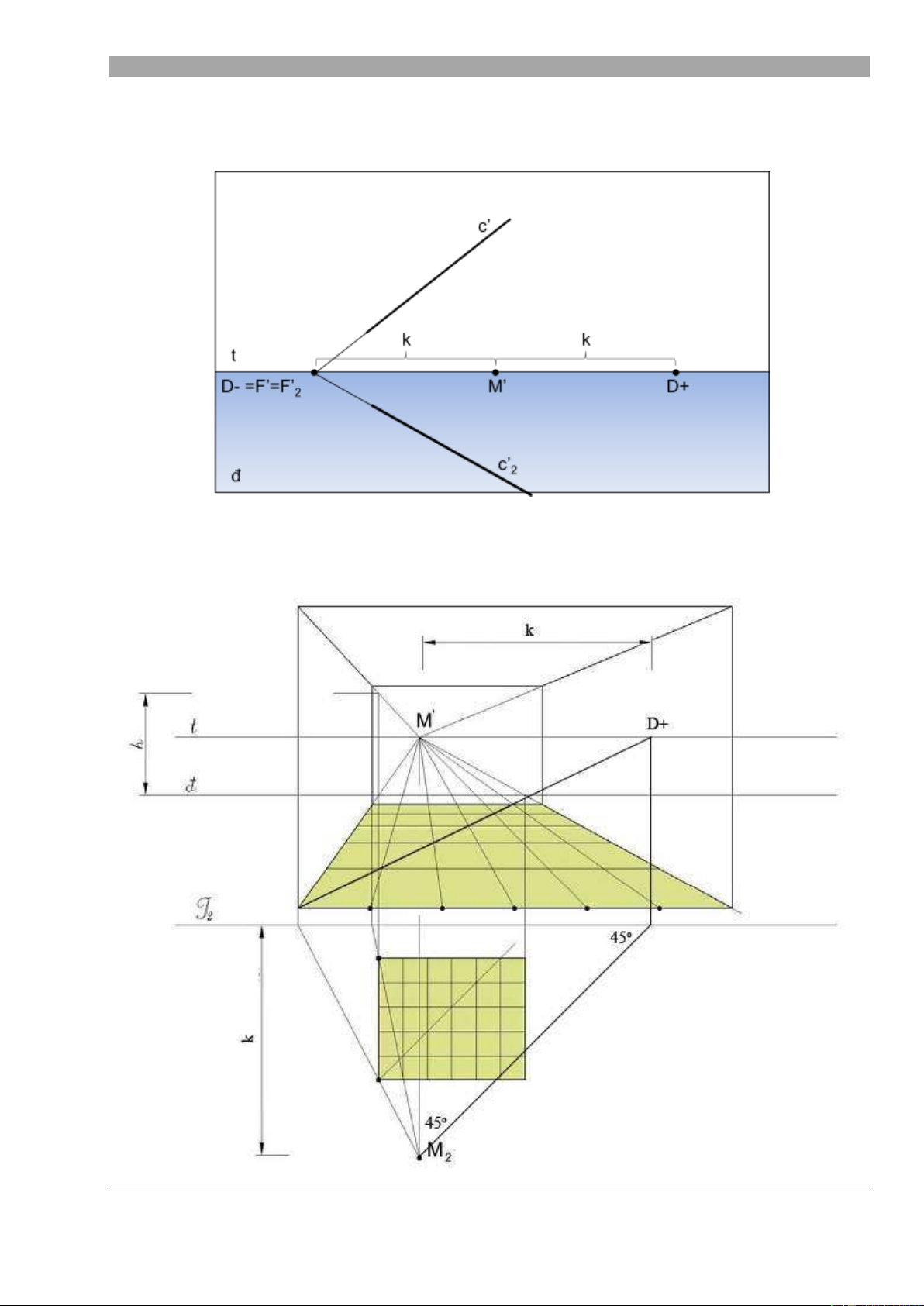
o Đ ng th ng b ng c t o v i m t tranh một góc 45° : đi m t thuộc đ ng tầm mắt và cách
đi m chính một kho ng cách b ng kho ng cách chính k. Đi m t này gọi là điểm cự ly (D- và D+)
Đi m cự ly th ng dùng đ xác định ô l i vuông m t b ng c a một căn phòng bi u di n theo ph
ng pháp ph i c nh một đi m t .
Tài Liệu Học Tập: Môn HÌNH HỌC HỌA HÌNH 2 - Soạn: kts. Bùi Minh Huy Tước 17
TRƯỜNG ĐẠI HỌC QUỐC TẾ HỒNG BÀNG – KHOA KIẾN TRÚC 4. M t ph ng: M t ph ng có th đ c bi u di n d i d ng sau : o M t ph ng đi qua ba đi m o M t ph ng qua hai đ ng th ng cắt nhau
Tài Liệu Học Tập: Môn HÌNH HỌC HỌA HÌNH 2 - Soạn: kts. Bùi Minh Huy Tước 18
TRƯỜNG ĐẠI HỌC QUỐC TẾ HỒNG BÀNG – KHOA KIẾN TRÚC o M t ph ng qua hai đ ng th ng song song
o M t ph ng qua một đi m và một đ ng th ng
Tài Liệu Học Tập: Môn HÌNH HỌC HỌA HÌNH 2 - Soạn: kts. Bùi Minh Huy Tước 19
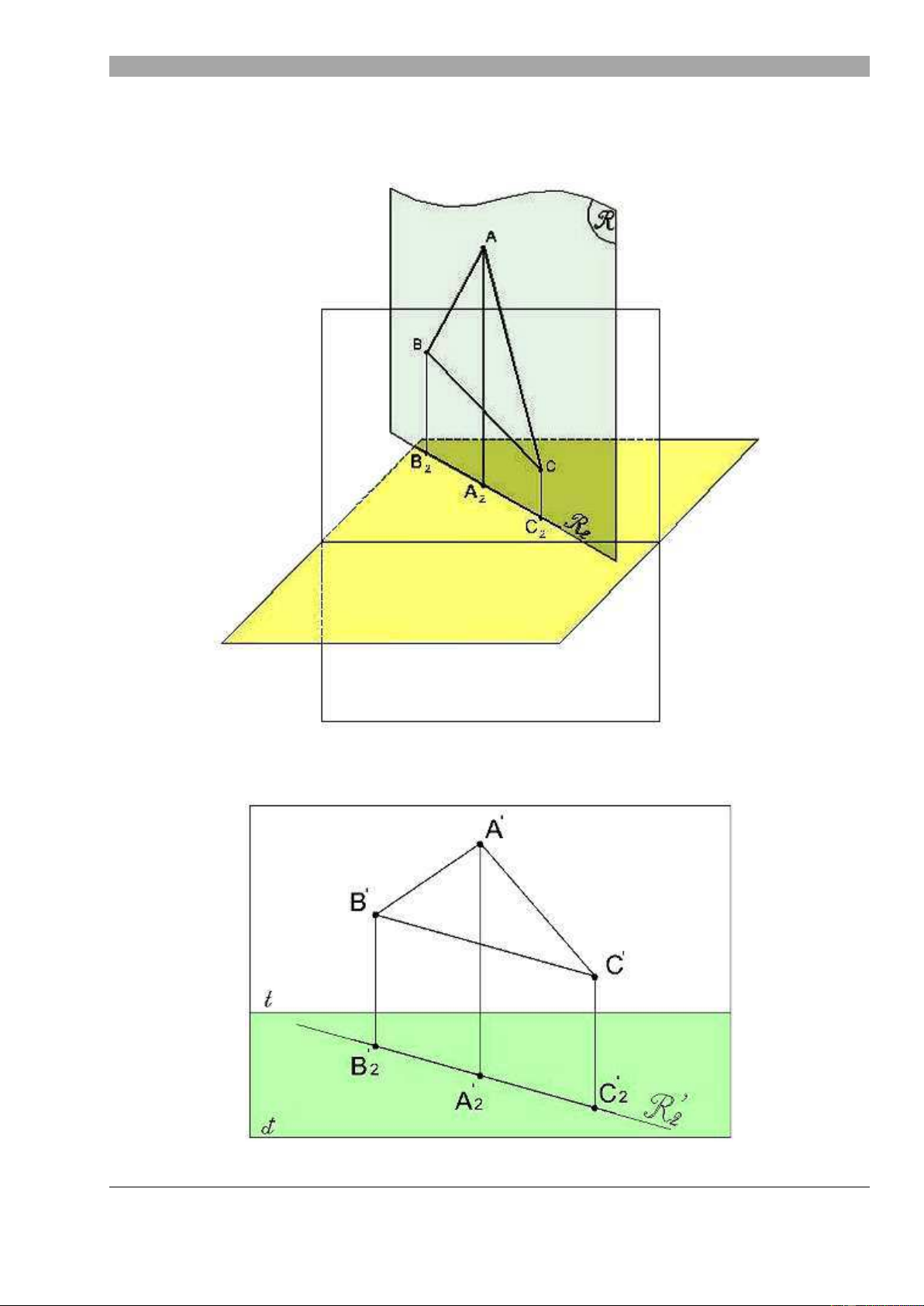
TRƯỜNG ĐẠI HỌC QUỐC TẾ HỒNG BÀNG – KHOA KIẾN TRÚC M t ph ng đ c bi t :
o M t ph ng chi u b ng vuông góc v i m t ph ng v t th (ABC) vuông góc v i V
Tài Liệu Học Tập: Môn HÌNH HỌC HỌA HÌNH 2 - Soạn: kts. Bùi Minh Huy Tước 20