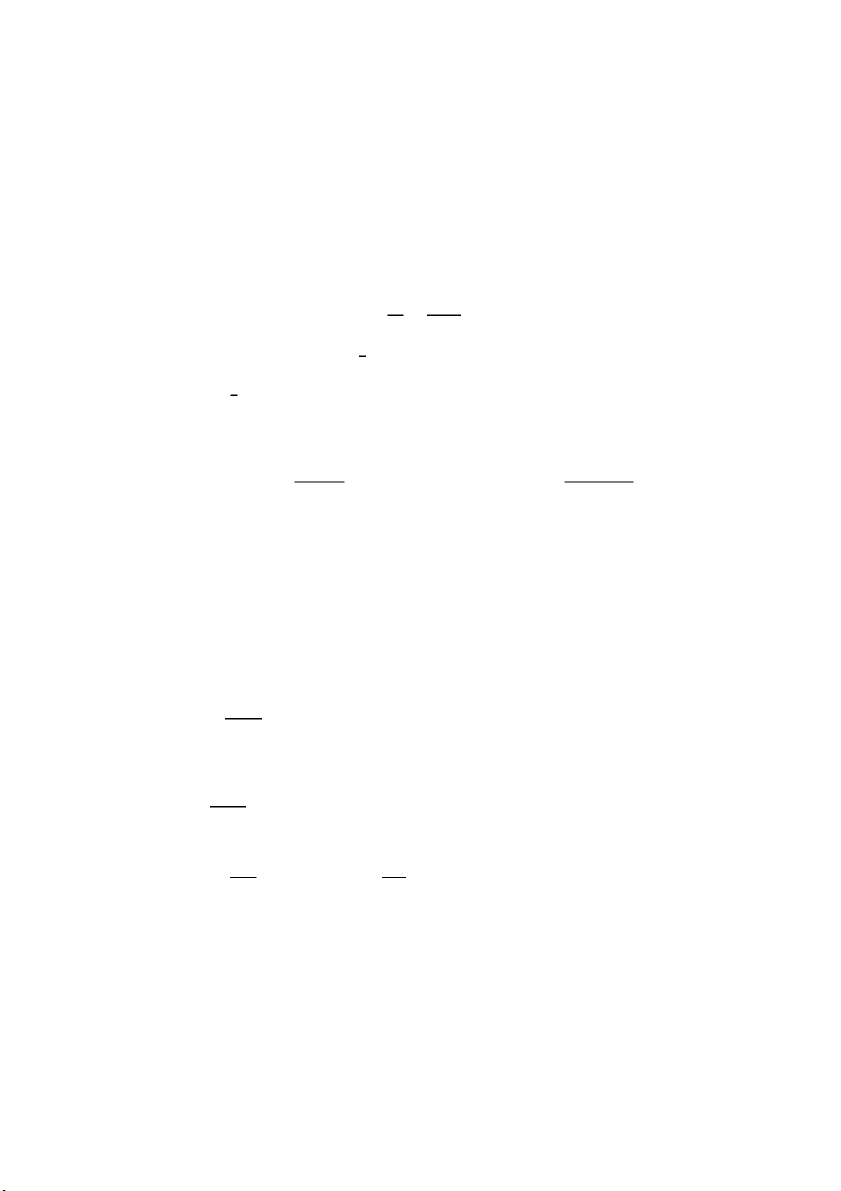













Preview text:
NGUYEN Dat Tien Sai số 𝐴: số đúng 𝑎: số gần đúng
- Sai số tuyệt đối: ∆= |𝐴 − 𝑎|
- Sai số tuyệt đối giới hạn: |𝐴 − 𝑎| < ∆𝑎
- Sai số tương đối giới hạn: 𝛿𝑎 = ∆ = |𝐴−𝑎| (%) |𝐴| |𝐴|
- Chữ số có nghĩa: Nếu ∆𝑎 ≤ 1. 10𝑠 thì 𝑎 ữ ố tin tưởng 2 𝑠 là ch s
Nếu ∆𝑎 ≥ 1. 10𝑠 thì 𝑎 ữ ố khả nghi 2 𝑠 là ch s
- Tính toán sai số viết sấp xỉ: 𝒏 𝜹𝒖(𝒙) 𝒏 𝜹𝒍𝒏𝒖(𝒙)
∆𝒖 = ∑ | 𝜹𝒙 |∆𝒙𝒊 𝜹𝒖 = ∑ | | ∆𝒙𝒊 𝒊 𝜹𝒙𝒊
Giải gần đúng 𝒇(𝒙) = 𝟎 ❖ Phương pháp chia đôi
Cho khoảng phân li nghiệm [𝑎𝑜; 𝑏𝑜]
[𝑎𝑛−1;𝑐𝑛−1] 𝑛ế𝑢 𝑓(𝑎𝑛−1)𝑓(𝑐𝑛−1) < 0
Đặt 𝐶𝑛 = 𝑎𝑛+𝑏𝑛 khi đó [𝑎𝑛; 𝑏 [𝑐 𝑓 𝑏 2
𝑛] = { 𝑛−1; 𝑏𝑛−1] 𝑛ế𝑢 𝑓(𝑐𝑛−1) ( 𝑛−1) < 0 𝑓(𝑐𝑛−1) = 0
Nếu chọn 𝑥𝑛 ∈ [𝑎𝑛; 𝑏𝑛] làm nghiệm gần đúng 𝑥 = 𝑥𝑛 thì 𝛼 = 𝑥𝑛 ± ∆𝑥𝑛 với
∆𝑥𝑛 = 𝑏𝑜−𝑎𝑜 2
Nhận xét: để đạt sai số cho trước 𝜀 ta cần:
∆𝑥 < 𝜀 → 𝑏−𝑎 ≤ 𝜀 → 𝑛 ≥ log 2𝑛+1 2 (𝑏−𝑎 ) − 1 𝜀 NGUYEN Dat Tien ❖ Phương pháp dây cung.
Điều kiện hội tụ: 𝑓′(𝑥), 𝑓′′(𝑥) tồn tại và không đổi dấu, chọn 𝑎 và 𝑑 sao cho
𝑓(𝑑). 𝑓′ (𝑥) > 0 ∀𝑥
Xây dựng dãy 𝑥𝑛 theo công thức truy hồi 𝒙𝒏+𝟏 = 𝒙𝒏 − 𝒇(𝒙𝒏)(𝒅−𝒙𝒏) 𝒇(𝒅)−𝒇(𝒙𝒏)
Chọn sai số: |𝒙𝒏𝒐 − 𝜶| = 𝑴𝟏−𝒎𝟏.|𝒙 𝒎
𝒏𝒐 − 𝒙𝒏−𝟏| < 𝜺 𝟏
Với 𝑀1 > |𝑓′(𝑥)| > 𝑚1 , ∀𝑥
❖ Phương pháp tiếp tuyến Điều kiện hội tụ:
- Hàm số 𝑓(𝑥) có đạo hàm cấp 1 và 2 tồn tại liên tục và không đổi dấu trên [𝑎, 𝑏]
- Chọn 𝑥𝑜 sao cho 𝑓(𝑥𝑜)𝑓′ (𝑥) > 0, ∀𝑥 ∈ [𝑎, 𝑏]
Xây dựng công thức lặp: 𝒙𝒏+𝟏 = 𝒙𝒏 − 𝒇(𝒙𝒏) 𝒇′(𝒙𝒏)
Sai số: |𝒙𝒏+𝟏 − 𝜶| ≤ 𝑴𝟐 (𝒙 𝟐𝒎
𝒏+𝟏 − 𝒙𝒏)𝟐 với 𝑀2 ≥ |𝑓′ (𝑥)| > 0, ∀𝑥 ∈ [𝑎, 𝑏] 𝟏
0 < 𝑚1 ≤ |𝑓′(𝑥)|,∀𝑥 ∈ [𝑎,𝑏]
❖ Phương pháp kết hợp
Kết hợp 2 phương pháp tiếp tuyến và dây cung. Đánh giá sai số:|𝑥 1 𝑛
− 𝛼| ≤ 1 |𝑥 − 𝑥 2 𝑛 𝑛2|
❖ Phương pháp lặp đơn
Biến đổi 𝑓(𝑥) = 0 → 𝑥 = 𝜑(𝑥) sao cho 𝜑(𝑥) có đạo hàm liên tục và
|𝜑′(𝑥) | ≤ 𝑞 ≤ 1 với mọi 𝑥 ∈ [𝑎, 𝑏], 𝑞 ∈ [0; 1] = 𝑐𝑜𝑛𝑠𝑡 gọi là hệ số co NGUYEN Dat Tien
Khi đó dãy lặp đơn 𝒙𝒏+𝟏 = 𝝋(𝒙𝒏) hội tụ.
Ta có: |𝒙𝒏 − 𝜶| ≤ 𝒒 |𝒙 𝟏−𝒒 𝒏 − 𝒙𝒏−𝟏|
|𝑥𝑛 − 𝛼| < 𝑞𝑛 |𝑥 1−𝑞 1 − 𝑥0|
Bài toán nội suy Lagrange
❖ Sai số của đa thức nội suy 𝒇𝒏+𝟏(𝒙)
𝒇(𝒙) − 𝑷(𝒙) = (𝒏+𝟏)!(𝒙−𝒙𝟎)(𝒙−𝒙𝟏)…(𝒙−𝒙𝒏) n (x − xi ) L ( ) x k = (x x) i =0 k − i i k
𝐿(𝑥) = 𝑦𝑜𝐿𝑜(𝑥) + 𝑦1𝐿1(𝑥) + ⋯ + 𝑦𝑛𝐿𝑛(𝑥)
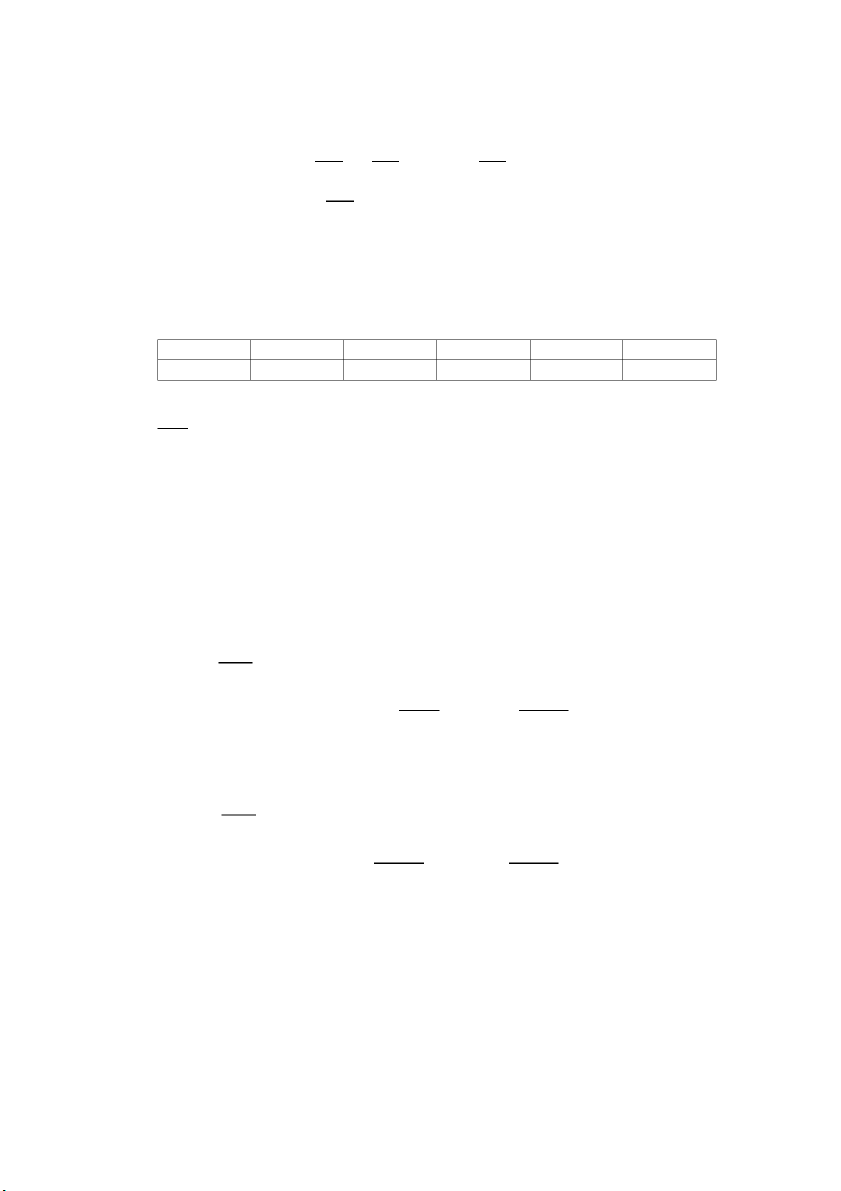
VD: Cho 𝑦 = sin (𝜋𝑥) và các mốc nội suy, 𝑥𝑜 = 0, 𝑥1 = 1,𝑥 6 2 = 1 , xây dựng đa
thức nội suy Lagrange ? tính giá trị gần đúng sin )(𝜋 và đánh giá 2sai số. 5 Giải Lập bảng (B): 𝑥 0 1 1 𝑦 0 1 1
Để thành lập đa thức nội suy ta dùng bảng sau: 𝑥 − 0 1 1 𝑥 0 − 0 − 12 1 1 1 1 1 1 − 6 − 0 𝑥 − 6 − 18 (𝑥 − 6) NGUYEN Dat Tien 1 1 1 1 1 1 𝑥 − 2 − 0 2 − 6 2 16 (𝑥 − 2) 1 1
Đa thức: 𝐿(𝑥) = 𝑥 (𝑥 − 2 6) (𝑥 − 12) [ 0𝑥 + + 1 1 12
− 118(𝑥−16) 16(𝑥−1 ] 2) = −3𝑥2 + 7𝑥 Ta có sin (𝜋) ≈ 2 𝐿 (1 ) = 0.58 5 5 Đánh giá sai số: 1 𝜋 𝑓(3)(𝜖)
|𝐿 (5) − sin(5)| = 3! (𝑥 −𝑥𝑜)(𝑥 −𝑥1)(𝑥 −𝑥2) 𝜋3 cos(𝜋𝜖)1 1 1 1 1 𝜋3 cos(𝜋𝜖) 𝜋3 =
3! ( 5 − 0) (5 − 6) (5 − 2) = 3000 ≤ 3000
Đa thức nội suy Newton Tỷ sai phân 𝑓[𝑥 0) ( 1)
𝑜; 𝑥1] = 𝑓(𝑥 −𝑓 𝑥 cấp 1 𝑥 ❖ 𝑜−𝑥1
Đa thức nội suy Newton tiến mốc bất kỳ.
𝑓(𝑥) = 𝑓(𝑥𝑜) + 𝑓[𝑥𝑜; 𝑥1](𝑥 − 𝑥𝑜) + 𝑓[𝑥𝑜; 𝑥1; 𝑥2](𝑥 − 𝑥𝑜)(𝑥 − 𝑥1) + ⋯
+ 𝑓[𝑥𝑜; 𝑥1; 𝑥2; … ; 𝑥𝑛](𝑥 − 𝑥𝑜)(𝑥 − 𝑥1) … (𝑥 − 𝑥𝑛−1)
+ 𝑓[𝑥; 𝑥𝑜; 𝑥1; 𝑥2; … ; 𝑥𝑛](𝑥 − 𝑥𝑜)(𝑥 − 𝑥1) … (𝑥 − 𝑥𝑛−1)(𝑥 − 𝑥𝑛)
Trong đó: 𝑅(𝑥) = 𝑓[𝑥; 𝑥𝑜; 𝑥1; 𝑥2; … ; 𝑥𝑛](𝑥 − 𝑥𝑜)(𝑥 − 𝑥1) … (𝑥 − 𝑥𝑛−1)(𝑥 − 𝑥𝑛)
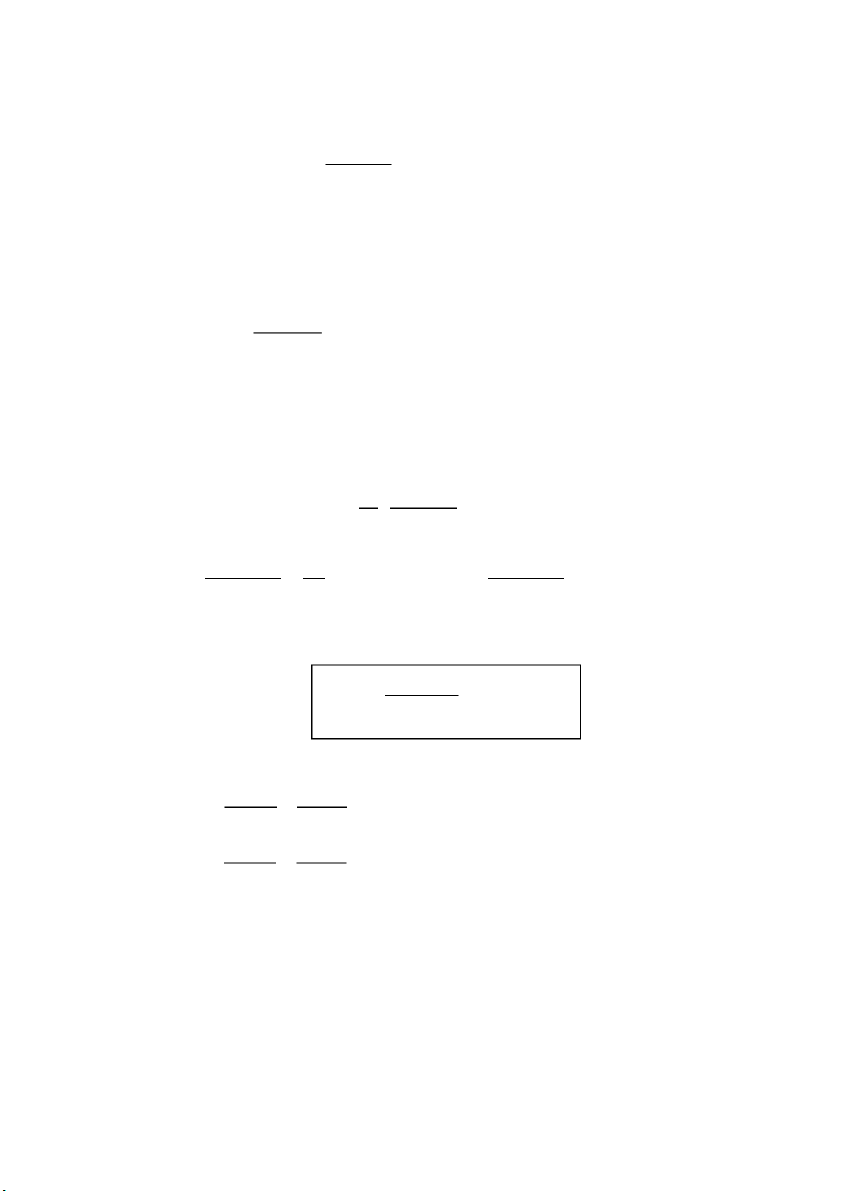
VD: cho bảng giá trị 𝑦 = 𝑓(𝑥) x 0 2 3 5 6 y 1 3 2 5 6
Lập đa thức nội suy Newton tiến. NGUYEN Dat Tien Giải Lập bảng tỉ sai phân x y TSP1 TSP2 TSP3 TSP4 0 1 1 -0.66667 0.3 -0.09167 2 3 -1 0.833333 -0.25 3 2 1.5 -0.16667 5 5 1 6 6
𝑁(𝑥) = 1 + 𝑥 − 0.66667x(x − 2) + 0.3x(x − 2)(𝑥 − 3)
− 0.09167x(x − 2)(𝑥 − 3)(𝑥 − 5)
❖ Đa thức nội suy Newton lùi mốc bất kỳ VD: Như trên Lập bảng tỉ sai phân x y TSP1 TSP2 TSP3 TSP4 0 1 1 -0.66667 0.3 -0.09167 2 3 -1 0.833333 -0.25 3 2 1.5 -0.16667 5 5 1 6 6
𝑁(𝑥) = 6 + (𝑥 − 6) − 0.16667(𝑥 − 6)(𝑥 − 5) − 0.25(𝑥 − 6)(𝑥 − 5)(x − 3)
− 0.09167(𝑥 − 6)(𝑥 − 5)(x − 3)(𝑥 − 2)
❖ Đa thức nội suy Newton tiến và lùi mốc cách đều
Sai phân ∆𝑦𝑜 = 𝑦1 − 𝑦𝑜 (sai phân cấp 1) Đặt 𝑡 = 𝑥−𝑥𝑜 ℎ Đa thức nội suy tiến : NGUYEN Dat Tien 2 3 𝑁 ∆ ∆ 𝑦 ∆ 𝑦 (𝑡) = 𝑦 𝑜𝑦 𝑜 𝑜
𝑜 + 1!𝑡 + 2!𝑡(𝑡 − 1) + 3!𝑡(𝑡 − 1)(𝑡 − 2) + ⋯ ∆𝑛𝑦
+ 𝑜𝑛!𝑡(𝑡 −1)(𝑡 −2)…(𝑡 −𝑛 +1)
VD: Lập công thức nội suy Newton tiến và lùi với mốc cách đều và đánh giá sai số,
áp dụng tính giá trị hàm số 𝑦 = 𝑠𝑖𝑛𝑥 tại 𝑥 = 12°. 𝑥 10 15 20 25 30 𝑦 0.1736 0.2588 0.3420 0.4226 0.5 Giải Ta có bảng sai phân: y SP1 SP2 SP3 Sp4 0.1736 0.0852 -0.002 -0.0006 0 0.2588 0.0832 -0.0026 -0.0006 0.342 0.0806 -0.0032 0.4226 0.0774 0.5
- Đa thức nội suy Newton tiến: Đặt 𝑡 = 𝑥−10 5 𝑁 0.002 0.0006
(𝑡) = 0.1736 + 0.0852t − 2! 𝑡(𝑡 −1)− 3! t(t− 1)(t− 2)
- Đa thức nội suy Newton lùi: Đặt 𝑢 = 𝑥−30 5 0.0032 0.0006
𝑁(𝑡) = 0.5 + 0.0774u − 2! 𝑢(𝑢 + 1)− 3! u(u+ 1)(u+ 2) NGUYEN Dat Tien
Phương pháp bình phương tối thiểu ❖ Bài toán
Cho bảng giá trị (B) như bài toán nội suy Đặt tổng: 𝑛
𝑆 = ∑(𝜑(𝑥𝑖) − 𝑦𝑖)2 với 𝑖 𝜑 =0
(𝑥) là một hàm số bất kỳ xác định trên [𝑥𝑜; 𝑥𝑛]
𝜀𝑖 = |𝑦𝑖 − 𝜑(𝑥𝑖)|
Sai số trung bình tối thiểu : 1 1 1 2 𝑆 2
𝜎 = [𝑛(𝜑(𝑥𝑖) − 𝑦𝑖)2] = (𝑛)
Tìm hàm số 𝜑(𝑥) = 𝑎𝑜𝑔𝑜(𝑥) + 𝑎1𝑔1(𝑥) + ⋯ + 𝑎𝑛𝑔𝑛(𝑥) với hàm 𝑔𝑖(𝑥) cho trước. 𝑛
𝑆 = ∑(𝜑(𝑥𝑖) − 𝑦𝑖)2 𝑛 𝑖=0
= ∑((𝑎𝑜𝑔𝑜(𝑥𝑖) + 𝑎1𝑔1(𝑥𝑖) + ⋯ + 𝑎𝑛𝑔𝑛(𝑥𝑖)) − 𝑦𝑖)2 Tổng S là n 𝑖=0
hỏ nhất khi bộ a là nghiệm của hệ ↔ 𝜕𝑆 = 0 𝜕𝑎𝑖 𝜕𝑆 = 0 𝜕𝑎0 𝜕𝑆 Ta có hệ: = 0 𝜕𝑎1… 𝜕𝑆 { Khi đó 𝝋(𝒙) = = 𝒂𝒐0 𝜕𝑎
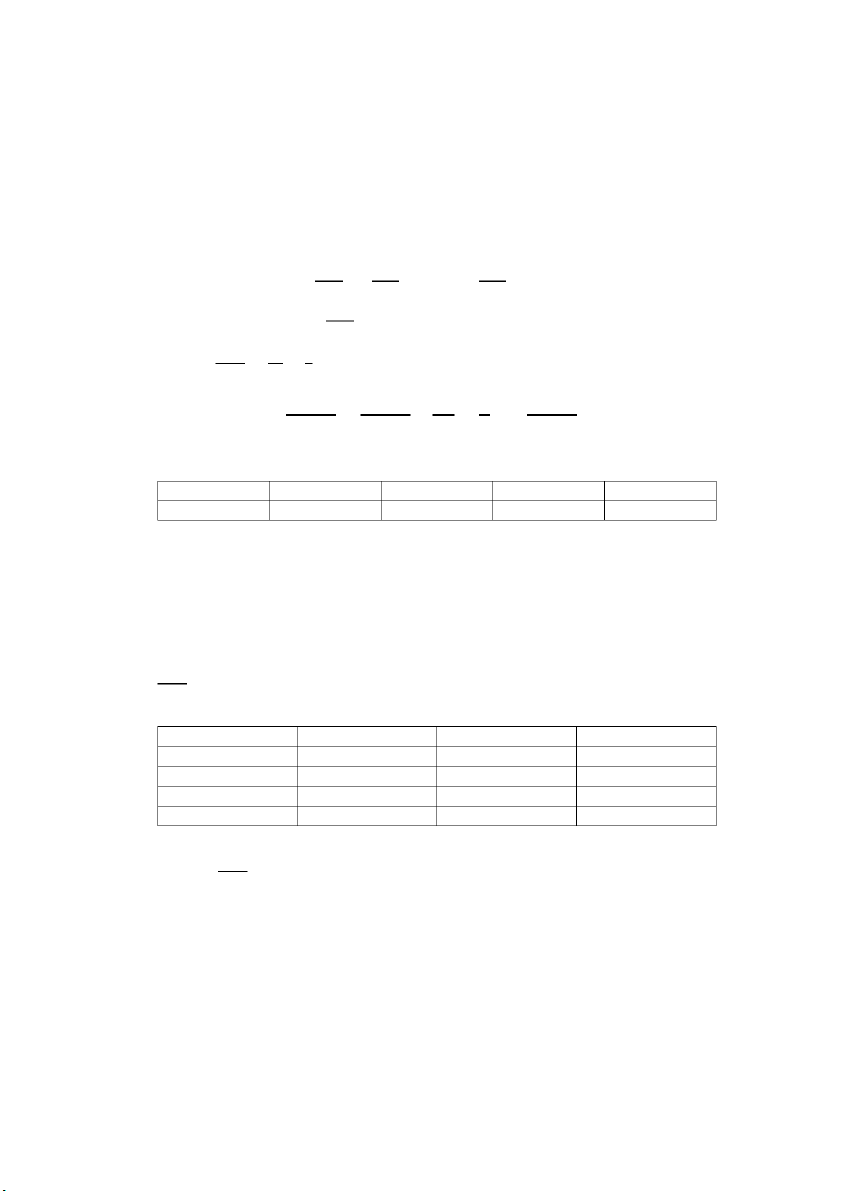
𝒈𝒐(𝒙) + 𝒂𝟏𝒈𝟏(𝒙) + ⋯ + 𝒂𝒏𝒈𝒏(𝒙) là lời giải. 𝑛 NGUYEN Dat Tien VD: cho bảng giá trị: x 1.5 1.6 1.8 1.9 2.1 y 2 3 5.5 7 10
Tìm hàm 𝜑(𝑥) = 𝑎𝑥3 + 𝑏𝑥2 + 𝑐𝑥 + 𝑑 khớp với bảng giá trị trên theo nghĩa bình phương tối thiểu? Giải
Tổng bình phương sai số: 4 𝑆 = ∑[𝑎𝑥3 2
𝑖 + 𝑏𝑥𝑖 + 𝑐𝑥𝑖 + 𝑑 − 𝑦𝑖]2 Tính đạo hàm 𝑖=0 𝜕𝑆 4 3 2 3
𝜕𝑎 = 2 ∑(𝑎𝑥𝑖 + 𝑏𝑥𝑖 + 𝑐𝑥𝑖 + 𝑑 − 𝑦𝑖)𝑥𝑖 𝑖=0 𝜕𝑆 4 3 2 2
𝜕𝑏 = 2 ∑(𝑎𝑥𝑖 + 𝑏𝑥𝑖 + 𝑐𝑥𝑖 + 𝑑 − 𝑦𝑖)𝑥𝑖 𝜕𝑆 4 𝑖=0 3 2
𝜕𝑐 = 2 ∑(𝑎𝑥𝑖 + 𝑏𝑥𝑖 + 𝑐𝑥𝑖 + 𝑑 − 𝑦𝑖)𝑥𝑖 𝜕𝑆 4 𝑖=0 3 2
𝜕𝑑 = 2 ∑(𝑎𝑥𝑖 + 𝑏𝑥𝑖 + 𝑐𝑥𝑖 + 𝑑 − 𝑦𝑖)
(∑ 𝑥6)𝑎 + (∑ 𝑥5) 𝑖=
𝑏 0+ (∑ 𝑥4)𝑐 + (∑ 𝑥3)𝑑 = (∑ 𝑥3𝑦)
(∑ 𝑥5)𝑎 + (∑ 𝑥4)𝑏 + (∑ 𝑥3)𝑐 + (∑ 𝑥2)𝑑 = (∑ 𝑥2𝑦)
Ta có hệ: (∑𝑥4)𝑎 + (∑𝑥3)𝑏 + (∑𝑥2)𝑐 + (∑𝑥)𝑑 = (∑𝑥𝑦) {
(∑ 𝑥3)𝑎 + (∑ 𝑥2)𝑏 + (∑ 𝑥1)𝑐 + 5𝑑 = (∑ 𝑦) NGUYEN Dat Tien Ta lập bảng: 𝑥6 𝑥5 𝑥4 𝑥3 𝑥2 𝑥 𝑦 𝑥𝑦 𝑥2𝑦 𝑥3𝑦 11.390625 7.59375 5.0625 3.375 2.25 1.5 2 3 4.5 6.75
16.777216 10.48576 6.5536 4.096 2.56 1.6 3 4.8 7.68 12.288
34.012224 18.89568 10.4976 5.832 3.24 1.8 5.5 9.9 17.82 32.076
47.045881 24.76099 13.0321 6.859 3.61 1.9 7 13.3 25.27 48.013
85.766121 40.84101 19.4481 9.261 4.41 2.1 10 21 44.1 92.61
194.992067 102.57719 54.5939 29.423 16.07 8.9 27.5 52 99.37 191.737 Hệ thành: 194.992067𝑎 + 102.5771 𝑏 9 + 54.593 𝑐 9 + 29.42 𝑑 3 = 191.737 {
102.57719𝑎 + 54.5939𝑏 + 29.423𝑐 + 16.07𝑑 = 99.37
54.5939𝑎 + 29.423𝑏 + 16.07𝑐 + 8.9𝑑 = 52 → ( 2𝑎9,.4 𝑏,23 𝑐,𝑎𝑑 + ) 1 =6.(07 2. 𝑏8 + 3; −5.𝑐 8.95 + 6; 5𝑑.6 = 4; 27.5 −3.35)
Tính gần đúng đạo hàm và tích phân
I. Tính gần đúng đạo hàm. ❖ Bài toán
Cho bảng (B) như bài toán nội suy
Tính gần đúng đạo hàm các cấp của hàm số 𝑦 = 𝑓(𝑥) ❖ Ý tưởng
Sử dụng đa thức nội suy bảng giá trị (B) 𝑓(𝑛+1)(𝜖) 𝑛
𝑓(𝑥) ≈ 𝑃(𝑥) + (𝑛 + 1)! × ∏(𝑥 − 𝑥𝑖)
𝑃(𝑥) là đa thức nội suy 𝑖=0 NGUYEN Dat Tien 𝑓(𝑛+1)(𝜖) 𝑛
(𝑛 + 1)! × ∏(𝑥 − 𝑥𝑖)= 𝑅(𝑥) 𝑖=0
𝑓′(𝑥) ≈ 𝑃′(𝑥) + 𝑅′(𝑥) lấy 𝑓′(𝑥) ≈ 𝑃′(𝑥)
Sai số |𝑓′(𝑥) − 𝑃′(𝑥)| ≤max |𝑅′(𝑥)| [𝑥𝑜;𝑥𝑛]
❖ Sử dụng đa thức nội suy Lagrange n (x − xi ) L ( ) x k = (x − x) i =0 k i i k
𝐿(𝑥) = 𝑦𝑜𝐿𝑜(𝑥) + 𝑦1𝐿1(𝑥) + ⋯+ 𝑦𝑛𝐿𝑛(𝑥)
Thì ta có 𝑓′(𝑥) ≈ 𝐿′(𝑥)
Để tính sai số ta tính 𝑅′(𝑥)|𝑥 = 𝑥 𝑘 𝑑 𝑓(𝑛+1)(𝜖) 𝑛
𝑟(𝑥) = 𝑑𝑥( (𝑛 + 1)! × ∏(𝑥 − 𝑥𝑖) 𝑖=0 𝑓(𝑛+1)(𝜖) 𝑑 𝑛 𝑓(𝑛+1)(𝜖) 𝑛 =
(𝑛 + 1)! × 𝑑𝑥 (∏(𝑥 − 𝑥𝑖) 𝑥=𝑥𝑘 ⇒
(𝑛 + 1)! × ∏(𝑥𝑘 − 𝑥𝑖) 𝑖=0 𝑖=0 𝑖≠𝑘 𝒇(𝒏+𝟏)(𝝐) 𝒏
→ 𝑹′(𝒙𝒌) = (𝒏+ 𝟏)! × ∏(𝒙𝒌 − 𝒙𝒊) 𝒊=𝟎
• Với trường hợp 𝑛 = 1: 𝒊≠𝒌 𝑦 𝑓(2)(𝜖) 𝑓′(𝑥 1 − 𝑦𝑜 𝑜) = 𝑥 + 1 − 𝑥𝑜 2! (𝑥𝑜 − 𝑥1) 𝑦 𝑓(2)(𝜖) 𝑓′(𝑥 1 − 𝑦𝑜 1) = 𝑥 + 1 − 𝑥𝑜 2! (𝑥1 − 𝑥𝑜)
• Với trường hợp 𝑛 = 2 mốc cách đều ℎ: NGUYEN Dat Tien −3𝑦 𝑓′(𝑥 𝑜+4𝑦1−𝑦2 𝑜) = 2ℎ 𝑦 𝑓′(𝑥 2 − 𝑦𝑜 1) = 2ℎ 𝑦 𝑓′(𝑥 𝑜−4𝑦1+3𝑦2 𝑜) = 2ℎ Sai số: 𝑓(3)(𝜖) 𝑓(3)(𝜖) × 2ℎ2
𝑅′(𝑥𝑜) = 3! (𝑥𝑜 −𝑥1)(𝑥𝑜 −𝑥2) = 3! −𝑓(3)(𝜖) × ℎ2 𝑅′(𝑥1) = 3! 𝑓(3)(𝜖) × 2ℎ2 𝑅′(𝑥1) = 3!
VD: Tính gần đúng đạo hàm của hàm số 𝑦 = 𝑒𝑥 tại 𝑥 = 1; 1.5; 2 và đánh giá sai số dựa vào bảng sau. 𝑥 1.5 2 2.5 𝑦 4.481 7.389 12.182 Giải
Áp dụng công thức Lagrange với 𝑛 = 2 mốc cách đều ℎ = 0.5: −3𝑦
−3 ∗ 4.481 + 4 ∗ 7.389 − 12.182 𝑓′(𝑥 𝑜+4𝑦1−𝑦2 𝑜) = 2ℎ , 𝑓′(1.5) = 2 ∗ 0.5 = 3.931 𝑦 12.182 − 4.481 𝑓′(𝑥 2 − 𝑦𝑜 1) = 2ℎ → 𝑓′(2) = 2 ∗ 0.5 = 7.701 𝑦
4.481 − 4 ∗ 7.389 + 3 ∗ 12.182 𝑓′(𝑥 𝑜−4𝑦1+3𝑦2 2) = 2ℎ → 𝑓′(2.5) = 2 ∗ 0.5 = 11.471 Sai số: | 𝑓(3)(𝜖)
𝑓′(1.5) − 𝑒1.5| ≤ 3! (𝑥𝑜 −𝑥1)(𝑥𝑜 −𝑥2) = 1.015 NGUYEN Dat Tien Còn lại tương tự.
❖ Sử dụng đa thức nội suy Newton
Đa thức nội suy tiến mốc cách đều. ∆ ∆ 2𝑦 ∆ 3𝑦 𝑁(𝑡) = 𝑦 𝑜𝑦 𝑜 𝑜
𝑜 + 1!𝑡 + 2!𝑡(𝑡 − 1) + 3!𝑡(𝑡 − 1)(𝑡 − 2) + ⋯ ∆𝑛𝑦
+ 𝑜𝑛!𝑡(𝑡 −1)(𝑡 −2)…(𝑡 −𝑛 +1)
Với 𝑡 = 𝑥−𝑥𝑜 → 𝑑𝑡 = 1 ℎ 𝑑𝑥 ℎ
𝑑𝑁(𝑡) 𝑑𝑁(𝑡) 𝑑𝑥 1 𝑑𝑁(𝑡) 𝑑𝑥 =
𝑑𝑥 × 𝑑𝑡 = ℎ × ( 𝑑𝑡 ) VD: cho bảng giá trị. x 50 55 60 65 y 1.6990 1.7404 1.7782 1.8129
1. Viết đa thức NS Newton tiến
2. Biểu thức của hàm số ở bảng trên 𝑦 = 𝑙𝑜𝑔𝑥. Tính gần đúng 𝑓′(50) và đánh giá sai số
3. Tính gần đúng 𝑓′ (50). Giải Bảng sai phân. y ∆𝑦 ∆2𝑦 ∆3𝑦 1.699 0.0414 -0.0036 0.0005 1.7404 0.0378 -0.0031 1.7782 0.0347 1.8129 Đặt 𝑡 = 𝑥−50 5 NGUYEN Dat Tien 0.0036 0.0005
𝑁(𝑡) = 1.699 + 0.0414t − 2! 𝑡(𝑡 − 1) + 3! 𝑡(𝑡 − 1)(𝑡 − 2) 𝑑𝑁( 𝑑𝑁( 𝑑𝑥 1 𝑑𝑁( 𝑁′(50) = 𝑡) 𝑡) 𝑡) 𝑑𝑥 =
𝑑𝑥 × 𝑑𝑡 = ℎ × ( 𝑑𝑡 ) 1 0.0036 0.0005
= ℎ(0.0414− 2! (2𝑡 − 1) + 3! (3𝑡2 − 6𝑡 + 2)) |𝑡=0 Đánh giá sai số: 𝑓(3)(𝜖)
|𝑁′(50) − 𝑓′(50)| ≤ 3! (50 − 55)(50 − 60) 2 𝑓(3)(𝜖) = −4
𝑥3𝑙𝑛10 ≤ 6.9487 × 10−8 → |𝑁′(50) − 𝑓′(50)| ≤ 3.47 × 10
II. Tính gần đúng tích phân xác định. ❖ Bài toán
Cho bảng giá trị hàm số 𝑦 = 𝑓(𝑥) trên đoạn [𝑎, 𝑏] với các mốc nội suy cách đều.
Trong đó 𝑥𝑜 = 𝑎, 𝑥𝑛 = 𝑏, ℎ = 𝑏−𝑎 𝑛 Tính gần đúng: 𝑏 𝐼 = ∫ 𝑓(𝑥)𝑑𝑥 ❖ Ý tưởng 𝑎
Xấp xỉ hàm số bởi đa thức nội suy sinh ra từ bảng. 𝑏
𝐼 = ∫ 𝑃𝑛(𝑥)𝑑𝑥 𝑎
Với 𝑃𝑛(𝑥) là đa thức nội suy NGUYEN Dat Tien
❖ Công thức Newton Côtes 𝑛 𝑛
𝐼 ≈ ∑ 𝑦𝑖𝐴𝑖 = (𝑏 − 𝑎) ∑ 𝑦𝑖𝐻𝑖 𝑖=0 𝑖=0
Với 𝐴𝑖 = (𝑏 − 𝑎)𝐻𝑖
Ta có 𝐻𝑖 dựa vào bảng dưới đây. Bảng Newton cotes n 𝐻 𝑜 𝐻1 𝐻2 𝐻3 𝐻4 𝐻5 𝐻6 𝐻7 𝐻8 𝑁 1 1 1 2 2 1 4 1 6 3 1 3 3 1 8 4 7 32 12 32 7 90 5 19 75 50 50 75 19 288 6 41 216 27 272 27 216 41 840 7
751 3577 1323 2989 2989 1323 3577 751 17280 8
989 5888 -928 10496 -4540 10496 -928 5888 989 28350 𝑯 𝒊 = 𝑯𝒊 𝑵
VD: Tính gần đúng tích phân: 1 1 𝐼 = ∫ 1+ 𝑥𝑑𝑥
Tính gần đúng I với 𝑛 = 6. 0 Giải
Lập bảng giá trị với các mốc nội suy cách đều (ℎ = 1 ). 6 x 0 1 2 3 4 5 1 y 1 6 3 2 3 6 1 5 NGUYEN Dat Tien Áp dụng Newton côtes:
𝐼 ≈ 𝑦𝑜𝐴𝑜 + 𝑦1𝐴1 + 𝑦2𝐴2 + 𝑦3𝐴3 + 𝑦4𝐴4 + 𝑦5𝐴5 + 𝑦6𝐴6 6
= (𝑏 − 𝑎) ∑ 𝑦𝑖𝐻𝑖 Tra bảng ta có: 𝑖=0 41 216 27 𝐻𝑜 = 𝐻1 = 𝐻2 = 272 27 216 𝐻3 = 𝐻4 = 𝐻5 = 41 𝐻6 = 𝐼 ≈ 0.693 ❖ Công thức hình thang 𝑏 ℎ
𝐼 = ∫ 𝑓(𝑥)𝑑𝑥 = 2[𝑦𝑜 +𝑦𝑛 +2(𝑦1 + 𝑦2 +⋯+ 𝑦𝑛−1)]± ∆ 𝑎 )
Với ∆= (𝑏−𝑎 𝑀2ℎ2 12
VD: Tính gần đúng tích phân: 1 1 𝐼 = ∫ 1+ 𝑥𝑑𝑥
Tính gần đúng I với 𝑛 = 6. 0 NGUYEN Dat Tien Giải Ta có bảng: x 0 1 2 3 4 5 1 6 6 6 6 6 y 1 6 3 2 3 6 1 7 4 3 5 11 2 1 1 1 1 6 3 2 3 6 𝐼 = ∫ 6
1 + 𝑥 𝑑𝑥 ≈ 2 [1 + 2 + 2 (7 + 4 + 3 + 5 + 11)] = 0.6948 0 Tính sai số:
𝑓′(𝑥) = − 1(1+𝑥)2 ,𝑓′ (𝑥) = 2 (1+𝑥)3 ≤ 2 = 𝑀2 2
∆= (𝑏−𝑎)𝑀2ℎ2= 1∗2∗1 6 = 0.00463 12 12 ❖ Công thức Simpson
Chia đoạn [𝑎; 𝑏] thành 2𝑛 đoạn bằng nhau có độ dài ℎ = 𝑏−𝑎 𝑏 2𝑛 𝐼 = ∫ 𝑓(𝑥)𝑑𝑥 ℎ 𝑎
𝐼 ≈ 3[𝑦𝑜 + 𝑦2𝑛 + 4(𝑦1 + 𝑦3 + ⋯+ 𝑦2𝑛−1) + 2(𝑦2 + 𝑦4 + ⋯+ 𝑦2𝑛−2)] )
Sai số: ∆= (𝑏−𝑎 𝑀4ℎ4 180
VD: Tính gần đúng tích phân: 1 1 𝐼 = ∫ 1 + 𝑥𝑑𝑥 0 NGUYEN Dat Tien
Tính gần đúng I với 𝑛 = 6. Giải Ta có bảng: x 0 1 2 3 4 5 1 6 6 6 6 6 y 1 6 3 2 3 6 1 7 4 3 5 11 2 ℎ = 1 6
Áp dụng công thức simpson ta có: 1 1 6 2 6 3 3
𝐼 ≈ 63 [1+ 2 +4(7 + 3 +11)+ 2(4 + 5)] = 0.693169 Sai số: 𝑓(4)(𝑥) = 4! 24 (1+𝑥)5 ≤ 4! = = 𝑀4 4 (𝑏 − 𝑎)𝑀 1 ∗ 24 ∗ 1 ∆= 4ℎ4 6 180 = 180 = 0.0001029
Giải gần đúng phương trình vi phân ❖ Bài toán côsi
Tìm một hàm số 𝑦 = 𝑓(𝑥) trên đoạn [𝑥𝑜; 𝑋] sao cho thoả mãn ràng buộc: {𝑦′ = 𝑓(𝑥, 𝑦) 𝑦(𝑥 𝑜) = 𝑎
❖ Phương pháp Euler
Xét bài toán cosi. Ta chia đoạn [𝑥𝑜; 𝑋] thành 𝑛 đoạn bằng nhau có độ dài ℎ 𝑦 (𝐸): { 𝑜 = 𝑎
𝑦𝑘+1 = 𝑦𝑘 + ℎ𝑓(𝑥𝑘; 𝑦𝑘) NGUYEN Dat Tien VD: { 𝑦′ = 𝑥𝑦 𝑦(𝑥 1 ≤ 𝑥 ≤ 1.2 ℎ = 0.1 𝑜) = 1 Giải
Đặt 𝑓(𝑥; 𝑦) = 𝑥𝑦; 𝑦𝑜 = 1; 𝑥𝑜 = 1; 𝑋 = 𝑥2 = 1.2; 𝑥1 = 1.1; ℎ = 0.1 Công thức Euler hiện: { 𝑦𝑜 = 1 𝑦 ới 𝑘 = 0; 1
𝑘+1 = 𝑦𝑘 + 0.1𝑥𝑘𝑦𝑘 v
Thay số ta được 𝑦𝑜 = 1; 𝑦1 = 1.1; 𝑦2 = 1.221
Vậy lời giải bài toán trên là: x 1 1.1 1.2 y 1 1.1 1.221
❖ Phương pháp Euler cải tiến 𝑦𝑜 = 𝑎 𝑦∗ ( ( = 𝑦 𝐸 𝑘+1
𝑘 + ℎ𝑓 𝑥𝑘; 𝑦𝑘) 2): { ℎ 𝑦𝑘+1 = 𝑦𝑘 + [
2 𝑓(𝑥𝑘;𝑦𝑘) + 𝑓(𝑥𝑘+1; 𝑦𝑘+1 ∗ )] VD: { 𝑦′ = 𝑥𝑦 𝑦(𝑥 1 ≤ 𝑥 ≤ 1.2 ℎ = 0.1 𝑜) = 1 Giải
Đặt 𝑓(𝑥; 𝑦) = 𝑥𝑦; 𝑦𝑜 = 1; 𝑥𝑜 = 1; 𝑋 = 𝑥2 = 1.2; 𝑥1 = 1.1; ℎ = 0.1
Công thức Euler cải tiến : 𝑦𝑜 = 1 {
𝑦∗𝑘+1 = 𝑦𝑘 + 0.1𝑥𝑘𝑦𝑘
𝑦𝑘+1 = 𝑦𝑘 + 0.05[𝑥𝑘𝑦𝑘 + 𝑥𝑘+1𝑦𝑘+1 ∗ ] ↔ 𝑦 { 𝑜 = 1
𝑦𝑘+1 = 𝑦𝑘 + 0.05[𝑥𝑘𝑦𝑘 + 𝑥𝑘+1(𝑦𝑘 + 0.1𝑥𝑘𝑦𝑘)]
Thay số ta có 𝑦𝑜 = 1; 𝑦1 = 1.1105; 𝑦2 = 1.2455368 NGUYEN Dat Tien ❖ Phương pháp RK
𝑦𝑖+1 = 𝑦𝑖 + ∆𝑦𝑖
∆𝑦𝑖 = 𝑃𝑟1𝐾1(ℎ) + 𝑃𝑟2𝐾2(ℎ) + 𝑃𝑟3𝐾3(ℎ) …
𝐾1(ℎ) = ℎ𝑓(𝑥𝑖; 𝑦𝑖)
𝐾𝑙(ℎ) = ℎ𝑓(𝑥𝑖 + 𝛼𝑙ℎ; 𝑦𝑖 + 𝛽𝑙1𝐾1ℎ)
Những phần trên không cần nhớ chỉ cần nhớ công thức sau đây. - Với 𝒓 = 𝟏 - Với 𝒓 = 𝟐
𝑦𝑖+1 = 𝑦𝑖 + ∆𝑦𝑖
𝑦𝑖+1 = 𝑦𝑖 + ∆𝑦𝑖 với ∆𝑦𝑖 = 𝐾1
với ∆𝑦𝑖 = 1 𝐾1 + 1 𝐾2 𝐾 2 2
1 = ℎ𝑓(𝑥𝑖; 𝑦𝑖)
𝐾1 = ℎ𝑓(𝑥𝑖; 𝑦𝑖)
𝐾2 = ℎ𝑓(𝑥𝑖 + ℎ; 𝑦 + 𝐾 𝑖 1) - Với 𝒓 = 𝟑 - Với 𝒓 = 𝟒
𝑦𝑖+1 = 𝑦𝑖 + ∆𝑦𝑖
𝑦𝑖+1 = 𝑦𝑖 + ∆𝑦𝑖 với ∆𝑦𝑖 = 1 (𝐾 với ∆𝑦 (𝐾 6 1 + 4𝐾2 + 𝐾2)
𝑖 = 16 1 + 2𝐾2 + 2𝐾1 + 𝐾2)
𝐾1 = ℎ𝑓(𝑥𝑖; 𝑦𝑖)
𝐾1 = ℎ𝑓(𝑥𝑖; 𝑦𝑖)
𝐾2 = ℎ𝑓 (𝑥𝑖 + ℎ2;𝑦𝑖 + 𝐾1 𝐾 2 )
2 = ℎ𝑓 (𝑥𝑖 + ℎ2 ;𝑦𝑖 + 𝐾12)
𝐾3 = ℎ𝑓(𝑥𝑖 + ℎ; 𝑦 − 𝐾 + 2𝐾 𝑖 1 2)
𝐾3 = ℎ𝑓 (𝑥𝑖 + ℎ ;𝑦 2 𝑖 + 𝐾2 2 )
𝐾4 = ℎ𝑓(𝑥𝑖 + ℎ; 𝑦 + 𝐾 𝑖 3)
VD: giải bài toán cô si {𝑦′ = 𝑥 + 𝑦 𝑦(0) = 1 với ℎ=0.1 0≤𝑥≤0.5
Giải gần đúng bằng phương pháp RK3? Giải
Ta đặt 𝑓(𝑥; 𝑦) = 𝑥 + 𝑦; 𝑦𝑜 = 1; 𝑥𝑜 = 0; 𝑥5 = 0.5; 𝑥1 = 0.1; 𝑥2 = 0.2
𝑥3 = 0.3;𝑥4 = 0.4; ℎ = 0.1 Ta có công thức RK3: NGUYEN Dat Tien 𝑦𝑜 = 1 {
𝑦𝑖+1 = 𝑦𝑖 + ∆𝑦𝑖 ∆𝑦𝑖 = 1 (𝐾 6 1 + 4𝐾2 + 𝐾3)
𝐾1=ℎ(𝑥𝑖+𝑦𝑖)=0.1(𝑥𝑖+𝑦𝑖) với 𝐾2=ℎ[(𝑥𝑖+ℎ 𝑦 2)+(𝑦𝑖+𝐾1
2 )]=0.1[(𝑥𝑖+0.05)+( 𝑖+0.1(𝑥 +𝑦 ) 𝑖 𝑖 2 )]
𝐾3=ℎ[(𝑥𝑖+ℎ)+(𝑦 −𝐾 +2𝐾 )]=0.1[ 𝑖 1 2
(𝑥𝑖+ℎ)+(𝑦 −𝐾 +2𝐾 )] 𝑖 1 2
Thay số vào công thức trên ta nhận được
𝒊 = 𝟎 𝑦1 = 𝑦0 + 1 (𝐾 6 1 + 4𝐾2 + 𝐾3) 𝐾1 = 0.1(0 + 1) = 0.1 𝐾 0 + 1
2 = 0.1 [(0 + 0.05) + (1 + 0.1( ) 2 )] = 0.11
𝐾3 = 0.1[(0 + 0.1) + (1 − 0.1 + 2 × 0.11)] = 0.122
Do đó 𝑦1 = 𝑦0 + 1 (𝐾
(0.1 + 4 × 0.11 + 0.122) = 1.1103 6 1 + 4𝐾2 + 𝐾3) = 1 + 16
Tương tự với 𝑖 = 1,4
VD: giải gần đúng bài toán dưới đây bằng phương pháp euler với ℎ = 0.1
{𝑦′ = 𝑥𝑦(𝑥 + 𝑦′) 𝑣ớ𝑖 𝑥𝜖[0.1; 0.2]
𝑦(0.1) = 1.1; 𝑦′(0.1) = 0.5 Giải
Đặt 𝑓(𝑥, 𝑦, 𝑦′) = 𝑥𝑦(𝑥 + 𝑦′);
ℎ = 0.1; 𝑎𝑜 = 1.1; 𝑎1 = 0.5; 𝑥𝑜 = 0.1; 𝑥1 = 0.2
Đưa về hệ phương trình vi phân
𝑦′(𝑥) = 𝑦1(𝑥) = 𝑓1
𝑦′1(𝑥) = 𝑥𝑦(𝑥 + 𝑦′) = 𝑓2
Và 𝑎𝑜 = 1.1; 𝑎1 = 0.5 NGUYEN Dat Tien 𝑌 = 𝑦 ( 𝑎𝑜 = 𝐹 𝑦 ) 𝑌′ = ( 𝑦′ ) 𝐴 = ( ) → { 𝑌′ 1 𝑦 𝑎 1′) 𝐹 = (𝑓1 𝑓2 1 𝑌(0.1) = 𝐴
Áp dụng phương pháp euler với ℎ = 0.1 𝑌 (0.1) = 𝐴
{𝑌𝑘+1 = 𝑌𝑘 +ℎ𝐹(𝑥𝑘,𝑦𝑘,𝑦 1𝑘)
𝑦(0.1) = 1.1; 𝑦1(0.1) = 0.5 → {
𝑦𝑘+1 = 𝑦𝑘 + ℎ𝑦𝑘1 𝑦𝑘+1 𝑘 𝑘 𝑘 1
= 𝑦1 + ℎ𝑥 𝑦𝑘(𝑥 + 𝑦1 𝑘) Với 𝑘 = 0
𝑦(0.1) = 1.1;𝑦1(0.1) = 0.5 {
𝑦1 = 𝑦0 + ℎ𝑦01 = 1.15 𝑦1 0 0 0
1 = 𝑦1 + ℎ𝑥 𝑦0(𝑥 + 𝑦10) = 0.5+ 0.1× 0.1×1.1 × (0.1+ 0.5) = 0.5066
Vậy 𝑦(0.2) = 1.15; 𝑦′(0.2) = 0.5066




