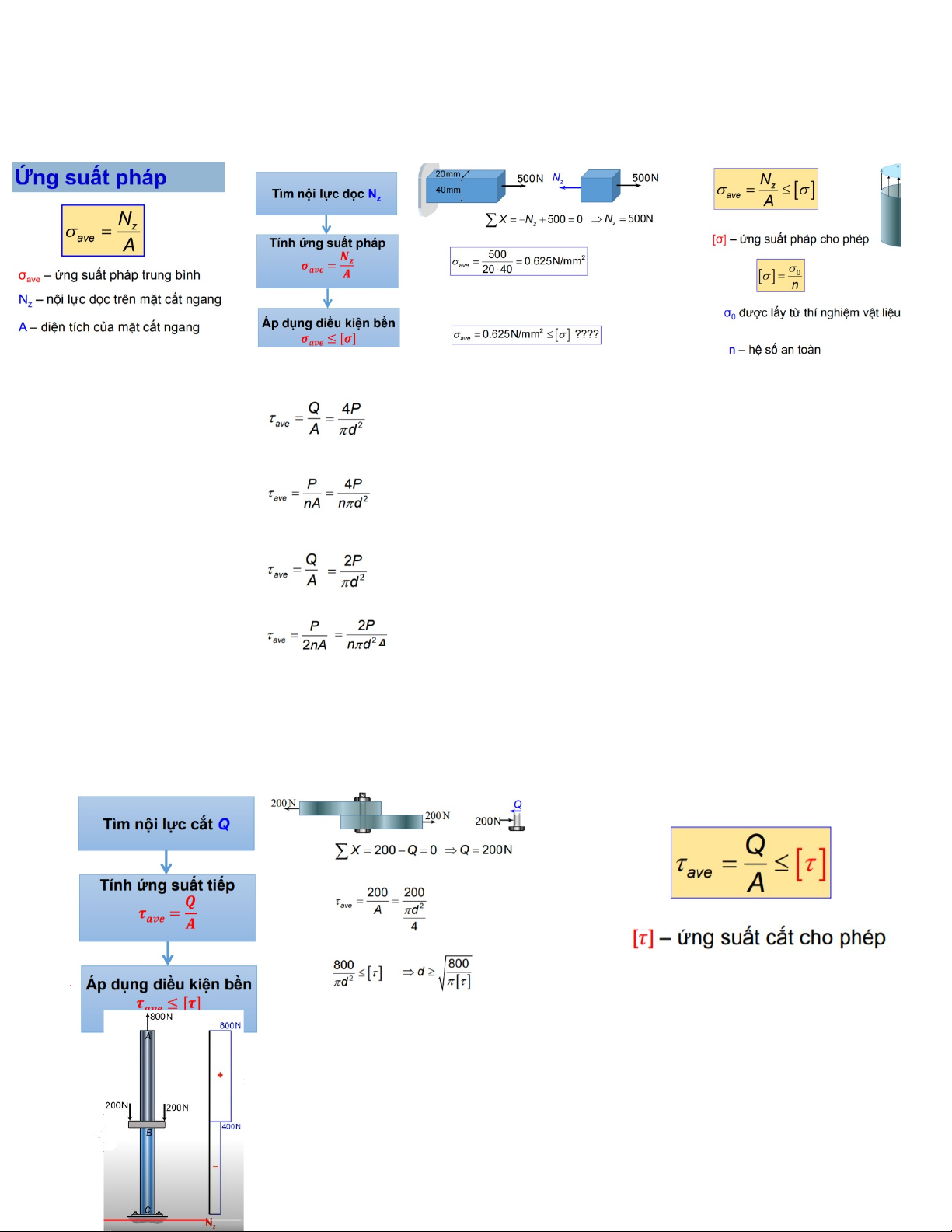
TỔNG HỢP CÔNG THỨC SỨC BỀN VẬT LIỆU CHƯƠNG 1: - Ứng suất pháp
- Các bước tính ứng suất pháp
- Điều kiện bền ứng suất pháp - Ứng suất cắt + Cắt đơn 1 bulong
Với P là lực cắt, d là đường kính bulong + Cắt đơn n bulong
+ Cắt đôi 1 bu long + Cắt đôi n bu long
- Các bước tính ứng suất cắt
- Điều kiện bền ứng suất cắt Chương 2
- Vẽ biểu đồ lực dọc
- Lực hướng ra khỏi mặt cắt ngang là dương (+)
- Lực hướng vào trong mặt cắt ngang là âm (-) n ∆ L=∑ ( Sn ) i=1 EA i
Trong đó: Sn(i) là diện tích biểu đồ lực dọc (Nz x L)
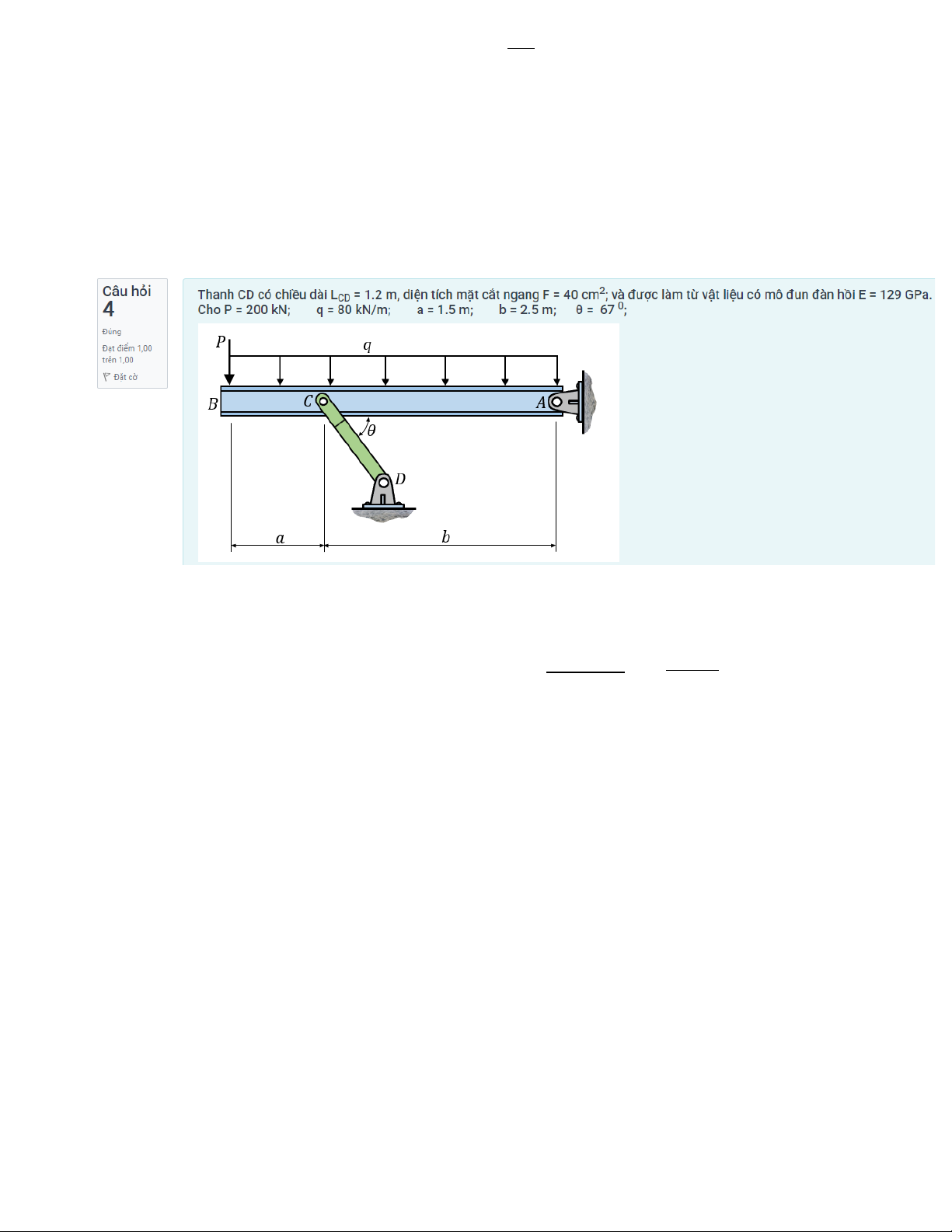
Tính đoạn BC trước rồi biến dạng dài của đoạn AC bằng đoạn AB + BC - Tính chuyển vị
Các bước chuyển vị tại điểm C (yC)
Điểm cần xét chuyển vị nằm trên thanh có biến dạng m ∆ L Tính∑ M m NDC × LDC DC
A=0= ¿ N DC∆ L yC= DC= EF sin ⁡(θ)
Nếu góc theta bằng 90 => sin(theta) = 1
Chuyển vị tại điểm B (yB)
Bước 1: Bỏ hết tải trọng.
Bước 2: Đặt lực bằng 1 tại điểm cần xét chuyển vị Tính∑ M k k
A=0= ¿ N DC yB= N DC × ∆ LDC
Tính chuyển vị ngang tại B m ∆ L Tính∑ M m N BC× LBC
BC Tính chuyển vị thẳng đứng
A=0= ¿ N BC∑ F x=0=¿ x A∑ F y=0=¿ y A∆ L x BC= EF B= sinθ tại D Bỏ hết tải trọng Đặt lực bằng 1 tại D Tính∑ M k k
A=0= ¿ N BC yD = N BC ×∆ LBC
Giải bài toán siêu tĩnh bằng phương pháp lực n k k δ × N z
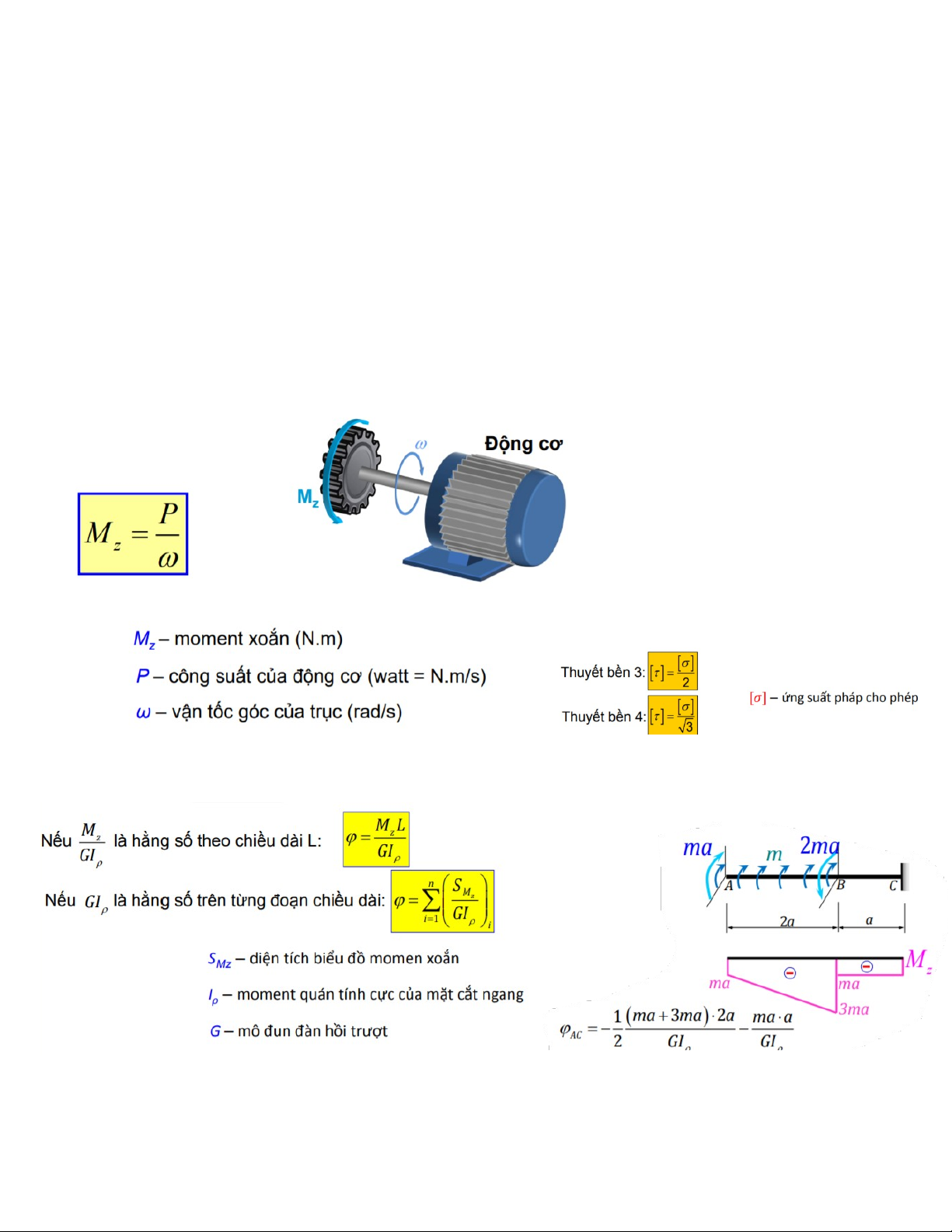
11 X1+ ∆1 p=0δ (Nz 11=∑ × L) i=1 EA i n m × N k ∆ (Nz z 1p=∑ × L) i=1 EA i ỨNG SUẤT CỦA THANH CHỊU XOẮN Tính biến dạng Bài toán siêu tĩnh
Bỏ liên kết – đặt moment xoắn theo chiều ngược kim đồng hồ
Vẽ biểu đồ trạng tháng “m” và trạng thái “k”
Tính góc xoắn theo M và Mc φ M MA
A= φAC+ φAC= 0 => Mc => M A => mm xoắn đoạn AB => mm xoắn đoạn BC