Tổng hợp đề thi cuối kì học phần Giải tích 1 | Đại học Bách Khoa Hà Nội

Tổng hợp đề thi cuối kì học phần Giải tích 1 | Đại học Bách Khoa Hà Nội. Tài liệu được biên soạn giúp các bạn tham khảo, củng cố kiến thức, ôn tập và đạt kết quả cao kết thúc học phần. Mời các bạn đọc đón xem!

44 22 lượt tải Tải xuống
Chia sẻ Báo cáo tài liệu

Môn: Giải tích 1

Trường: Đại học Bách Khoa Hà Nội

Thông tin:

43 trang 6 tháng trước

Tác giả:

Profile Thùy Dương
ĐỀ 4 VIỆN TOÁN ỨNG DỤNG VÀ TIN HỌC
ĐỀ THI CUỐI KÌ MÔN GIẢI TÍCH 1 – Học kì 20193
Mã HP: MI1112, Nhóm ngành 2, Thời gian: 90 phút
Chú ý: Thí sinh không được sử dụng tài liệu và giám thị phải ký xác nhận số đề vào bài thi
Câu 1: Tìm a để hàm số liên tục trên tập xác định :
2
3,
( )
4 1,
x x a
f x
x x a
Câu 2: Tính nguyên hàm
4
sin
dx
x
Câu 3: Tính giới hạn
3
lim ln
x
x
e x

Câu 4: Tính tích phân suy rộng
0
x
xe dx

Câu 5: Cho hàm số
cos
2
0
( ) (1 tan )
x
f x t dt
. Tính
'( / 2)
f
Câu 6: Cho hàm số
2 , 2
( )
(2 )(3 ), 2
x x
f x
x x x
. Tính
f
Câu 7: Tính giới hạn sau:
0
2
arctan
lim
2
x
x
tdt
x x

Câu 8: Cho hàm số
2
( )
x
f x e
. Tính
(997)
(0)
f
Câu 9: Cho hai hàm số
( )
x
f x x e
và
1
( )
2 1
x
g x
x
. Tính
1 1 1
( )(0)
f g g f
Cho Câu 10 :
( )f x
là hàm liên tục trên [0 ;1]. Tính
1
0
( )
( ) (1 )
f x
dx
f x f x
4
ĐỀ 5 VIỆN TOÁN ỨNG DỤNG VÀ TIN HỌC
ĐỀ THI CUỐI KÌ MÔN GIẢI TÍCH 1 – Học kì 20193
Mã HP: MI1112, Nhóm ngành 2, Thời gian: 90 phút
Chú ý: Thí sinh không được sử dụng tài liệu và giám thị phải ký xác nhận số đề vào bài thi
Câu 1: So sánh hai vô cùng bé sau khi
0x
:
( ) sinf x x x
và
2
( ) ln(1 )g x x
Câu 2: Tính giới hạn
sin
0
lim
x
x
x
Câu 3: Cho
2
ln(1 )
, 0
( )
| |
0, 0
x
x
f x
x
x
. Tính
'(0 ).
f
Câu 4: Tính tích phân
2
0
2
4
dx
x
Câu 5: Tìm tiệm cận của đồ thị hàm số
2
1
x
y
x
Câu 6: Tính tích phân suy rộng sau:
2
0
2 2
dx
x x
Câu 7: Tính giới hạn sau:
2 2
0
0
arcsin arcsin
lim
x
y
x y y x
x y
Câu 8: Tính tích phân kép:
2 2
D
x y dxdy
với
2 2 2
( , ) : 1, 0, 0
D x y x y x y
Câu 9: Cho
2 2
u x y
. Tính
2 2
2 2
.
u u
x y
Câu 10: Cho
3
( ) sin( )f x x
. Tính
(10)
(0)
f
5
ĐỀ 1 VIỆN TOÁN ỨNG DỤNG VÀ TIN HỌC
ĐỀ THI CUỐI KÌ MÔN GIẢI TÍCH 1 – Học kì 20191
Mã HP: MI1111, Nhóm ngành 1, Thời gian: 90 phút
Chú ý: Thí sinh không được sử dụng tài liệu và giám thị phải ký xác nhận số đề vào bài thi
Câu 1: Tìm
1
0
ln(1 )
)lim
x
x
x
a
x
3
6 2
( , ) (0;0)
lim
2 3
x y
x y
x y
Câu 2: Tính gần đúng nhờ vi phân
2 2
2, 02 3, 04 3
A
Câu 3: Chứng minh rằng:
2
cos 1 , 0
2
x
x x
Câu 4: Tính thể tích khối tròn xoay khi quay hình giới hạn bởi các đường
2
3y x x
và
0y
quanh trục
Oy
một vòng
Câu 5: Tính
1
2
2
2 3 | 1 |
x x dx
Câu 6: Hàm số
3
( )f x x x
có hàm ngược là
( )y g x
. Tính
'(2).
g
Câu 7: Tính
2 2
2 2
3z z z
P
x x
x y
với
2 2 3
1
( )
z
x y
Câu 8: Không khí được bơm vào một quả bóng bay hình cầu với tốc độ
3
100 /cm s
.Tính tốc độ tăng lên của
bán kính quả bóng khi bán kính quả bóng bằng 50cm.
Câu 9. Tính
2
0
cot
xdx
Thang điểm : Câu 1: 2 điểm . Các câu còn lại mỗi câu 1 điểm
6
ĐỀ 2 VIỆN TOÁN ỨNG DỤNG VÀ TIN HỌC
ĐỀ THI CUỐI KÌ MÔN GIẢI TÍCH 1 – Học kì 20191
Mã HP: MI1111, Nhóm ngành 1, Thời gian: 90 phút
Chú ý: Thí sinh không được sử dụng tài liệu và giám thị phải ký xác nhận số đề vào bài thi
Câu 1: Tìm
1
0
1
)lim
x
x
x
e
a
x
4
2 8
( , ) (0;0)
lim
4 3
x y
xy
x y
Câu 2: Tính gần đúng nhờ vi phân
2 2
4, 03 2, 02 5
A
Câu 3: Chứng minh rằng:
2
1 , 0
2
x
x
e x x
Câu 4: Tính thể tích khối tròn xoay khi quay hình giới hạn bởi các đường
2
4y x x
và
0y
quanh trục
Oy
một vòng
Câu 5: Tính
1
2
2
4 3 | 1 |
x x dx
Câu 6: Hàm số
5
( )f x x x
có hàm ngược là
( )y g x
. Tính
'(2).
g
Câu 7: Tính
2 2
2 2
5z z z
P
y y
x y
với
2 2 5
1
( )
z
x y
Câu 8: Không khí được bơm vào một quả bóng bay hình cầu với tốc độ
3
200 /cm s
.Tính tốc độ tăng lên của
bán kính quả bóng khi bán kính quả bóng bằng 60cm.
Câu 9. Tính
2
0
tan
xdx
Thang điểm : Câu 1: 2 điểm . Các câu còn lại mỗi câu 1 điểm
7
ĐỀ 3 VIỆN TOÁN ỨNG DỤNG VÀ TIN HỌC
ĐỀ THI CUỐI KÌ MÔN GIẢI TÍCH 1 – Học kì 20191
Mã HP: MI1111, Nhóm ngành 1, Thời gian: 90 phút
Chú ý: Thí sinh không được sử dụng tài liệu và giám thị phải ký xác nhận số đề vào bài thi
Câu 1. Tính )lim
sin
x
x
a
x
2
2 2
( , ) (1;0)
2 ln
) lim
( 1)
x y
y x
b
x y
Câu 2: Phương trình
3 5
3 5 0
x xy y
xác định hàm ẩn
( )y y x
. Tính
'(1)y
Câu 3: Tính đạo hàm của hàm số
2
2
arctan , 1
1
x
y x
x
Câu 4: Tìm khai triển Maclaurin của
ln(1 2 )y x
đến
3
x
Câu 5: Tìm các tiệm cận của đồ thị hàm số
1
x
x
y
e
Câu 6: Tính
) tan(2 )a x dx
2
0
)
( 3)( 1)
dx
b
x x x

Câu 7: Quay đường
3 2 2
3
4
x y
quanh trục
Ox
một vòng. Tính diện tích mặt tròn xoay được sinh ra.
Câu 8: Tìm cực trị của hàm số
3 3 2
( )z x y x y
Thang điểm: Câu 1: 2 điểm . Câu 6: 2 điểm.
Các câu còn lại mỗi câu 1 điểm.
8
ĐỀ 4 VIỆN TOÁN ỨNG DỤNG VÀ TIN HỌC
ĐỀ THI CUỐI KÌ MÔN GIẢI TÍCH 1 – Học kì 20191
Mã HP: MI1111, Nhóm ngành 1, Thời gian: 90 phút
Chú ý: Thí sinh không được sử dụng tài liệu và giám thị phải ký xác nhận số đề vào bài thi
Câu 1. Tính
2
2
)lim
cos
x
x
a
x
3
2 2
( , ) (1;0)
2 ln
) lim
( 1)
x y
x y
b
x y
Câu 2: Phương trình
4 3 5
3 3 8 0
x xy y
xác định hàm ẩn
( )y y x
. Tính
'(1)y
Câu 3: Tính đạo hàm của hàm số
2
2
arcsin , 1
1
x
y x
x
Câu 4: Tìm khai triển Maclaurin của
ln(1 3 )y x
đến
3
x
Câu 5: Tìm các tiệm cận của đồ thị hàm số
2 1
x
x
y
e
Câu 6: Tính
) cot(3 )a x dx
2
0
)
( 4)( 1)
dx
b
x x x

Câu 7: Quay đường
3 2 2
3
9
x y
quanh trục
Ox
một vòng. Tính diện tích mặt tròn xoay được sinh ra.
Câu 8: Tìm cực trị của hàm số
3 3 2
( )z x y x y
Thang điểm: Câu 1: 2 điểm . Câu 6: 2 điểm.
Các câu còn lại mỗi câu 1 điểm.
9
ĐỀ 5 VIỆN TOÁN ỨNG DỤNG VÀ TIN HỌC
ĐỀ THI CUỐI KÌ MÔN GIẢI TÍCH 1 – Học kì 20191
Mã HP: MI1112, Nhóm ngành 2, Thời gian: 90 phút
Chú ý: Thí sinh không được sử dụng tài liệu và giám thị phải ký xác nhận số đề vào bài thi
Câu 1: Tìm giới hạn
2
0
2 1
lim
1
x
x
x
e
Câu 2: Cho hàm số
( )y f x
xác định bởi
3
2 4
2 3
x t t
y t t
.Tính
'( ), ''( )f x f x
Câu 3: Tìm cực trị của hàm số
2
3
( 3)
y x x
Câu 4: Chứng mình rằng với mọi
ta có
2 2
ln 1
2
x x
Câu 5: Tìm giới hạn
6 6 6
7
1 2 ...
lim
n
n
n

Câu 6: Tính các tích phân sau
3
/2
0
sin
)
sin cos
xdx
a
x x
3
2
) arccot 3 .b xdx
Câu 7: Tính tích phân suy rộng:
4
1
(3 2)
dx
x x

Câu 8: Tính diện tích mặt tròn xoay tạo bởi đường tròn
2 2
( 2) 1
x y
quay quanh trục Ox
Câu 9: Cho hàm số :
3
arctan 3 0
( )
sin 0
x
x x khi x
f x
ae b x khi x
Tìm a và b để hàm số
( )f x
khả vi tại
10
ĐỀ 6 VIỆN TOÁN ỨNG DỤNG VÀ TIN HỌC
ĐỀ THI CUỐI KÌ MÔN GIẢI TÍCH 1 – Học kì 20191
Mã HP: MI1112, Nhóm ngành 2, Thời gian: 90 phút
Chú ý: Thí sinh không được sử dụng tài liệu và giám thị phải ký xác nhận số đề vào bài thi
Câu 1: Tìm giới hạn
3
0
1 3
lim
1
x
x
x
e
Câu 2: Cho hàm số
( )y f x
xác định bởi
3
5
3
5
x t t
y t t
.Tính
'( ), ''( )f x f x
Câu 3: Tìm cực trị của hàm số
2
3
( 3)
y x x
Câu 4: Chứng mình rằng với mọi
1x
ta có
1 2
ln
1 1
x
x x
Câu 5: Tìm giới hạn
5 5 5
6
1 2 ...
lim
n
n
n

Câu 6: Tính các tích phân sau
3
/2
0
cos
)
sin cos
xdx
a
x x
2
1
) arctan 2 .b xdx
Câu 7: Tính tích phân suy rộng:
4
1
(2 1)
dx
x x

Câu 8: Tính diện tích mặt tròn xoay tạo bởi đường tròn
2 2
( 2) 1
x y
quay quanh trục Ox
Câu 9: Cho hàm số :
sin 2 0
( )
2 arctan 0
x
x x khi x
f x
a b x khi x
Tìm a và b để hàm số
( )f x
khả vi tại
11
ĐỀ 7 VIỆN TOÁN ỨNG DỤNG VÀ TIN HỌC
ĐỀ THI CUỐI KÌ MÔN GIẢI TÍCH 1 – Học kì 20191
Mã HP: MI1113, Nhóm ngành 3, Thời gian: 90 phút
Chú ý: Thí sinh không được sử dụng tài liệu và giám thị phải ký xác nhận số đề vào bài thi
Câu 1: Tính
cos
lim
sin 1
x
x x
x x

Câu 2: Dùng vi phân tính gần đúng
3
7, 988
Câu 3: Tính hoặc xét sự phân kỳ
1
x
e xdx

Câu 4; Tính
3
0
sin(2 )
x
e x dx
Câu 5: Cho
2
xy
z e
. Tính
2
d z
Câu 6: Tìm giá trị lớn nhất, bé nhất của hàm số
2 2
3 4z x y
trong miền đóng
2 2
1
4 3
x y
Câu 7: Tính
2 2
1
D
x y dxdy
, ở đó
2 2
: 1
D x y
,
0, 0x y
Câu 8: Tìm các tiệm cận của đồ thị hàm số
3 3
1 2
,
8 8
t
x y
t t
Câu 9: Tính
/2
18
/2
| |
arcsin
1 sin
1
x
x
xdx
e
Câu 10. Tính
' ( ; )
x
z x y
,biết
,
arccot , 0
0 0
y
x
z
x
x
12
ĐỀ 8 VIỆN TOÁN ỨNG DỤNG VÀ TIN HỌC
ĐỀ THI CUỐI KÌ MÔN GIẢI TÍCH 1 – Học kì 20191
Mã HP: MI1113, Nhóm ngành 3, Thời gian: 90 phút
Chú ý: Thí sinh không được sử dụng tài liệu và giám thị phải ký xác nhận số đề vào bài thi
Câu 1: Tính
cos
lim
sin 1
x
x x
x x

Câu 2: Dùng vi phân tính gần đúng
3
8, 012
Câu 3: Tính hoặc xét sự phân kỳ
1
x
e xdx

Câu 4; Tính
3
0
cos(2 )
x
e x dx
Câu 5: Cho
2
x y
z e
. Tính
2
d z
Câu 6: Tìm giá trị lớn nhất, bé nhất của hàm số
2 2
4 3z x y
trong miền đóng
2 2
1
3 4
x y
Câu 7: Tính
2 2
1
D
x y dxdy
, ở đó
2 2
: 1
D x y
,
0, 0x y
Câu 8: Tìm các tiệm cận của đồ thị hàm số
3 3
1 2
,
8 8
t
x y
t t
Câu 9: Tính
/2
18
/2
| |
arcsin
1 sin
1
x
x
xdx
e
Câu 10. Tính
' ( ; )
x
z x y
,biết
,
arccot , 0
0 0
y
x
z
x
x
13
ĐỀ 1 VIỆN TOÁN ỨNG DỤNG VÀ TIN HỌC
ĐỀ THI CUỐI KÌ MÔN GIẢI TÍCH 1 – Học kì 20181
Mã HP: MI1111, Nhóm ngành 1, Thời gian: 90 phút
Chú ý: Thí sinh không được sử dụng tài liệu và giám thị phải ký xác nhận số đề vào bài thi
Câu 1. Tính giới hạn
x
x x
x x

sin
lim
arctan
Câu 2. Cho
f x
x x
2
1
( )
2 1
Tính đạo hàm cấp cao
f x
50
( )
Câu 3. Tính tích phân
x dx
5
2
0
9
Câu 4. Tính tích phân
x x
dx
x x
2
0
3 sin 4 cos
4 sin 3 cos
Câu 5. Tính giới hạn
in
x y
x
x y
3
2 2
( , ) (0,0)
s
lim
sin sin
Câu 6. Chỉ số Shannon đo lường mức độ đa dạng của một hệ sinh thái, trong trường hợp hai loài, được xác định
theo công thức:
H x x y y ln ln
ở đó x, y là tỉ lệ các loài, thỏa mãn
x y
x y
0, 0
1
Tìm giá trị lớn nhất của H.
Câu 7
. Chứng minh rằng cosx 1
x x
x
2 4
- , 0,
2 24 2
Câu 8. Cho
z f x y ( , )
là hàm số ẩn xác định bởi phương trình
z
y
z xe 0
. Ứng dụng vi phân, tính gần
đúng
f
(0,02;0,99)
Câu 9. Tính
n
n
n
n n

1 (2 1)!
lim
( 1)!
Câu 10. Xét sự hội tụ, phân kì của tích phân suy rộng
x
dx
x x

0
ln(1 2 )
14
ĐỀ 2 VIỆN TOÁN ỨNG DỤNG VÀ TIN HỌC
ĐỀ THI CUỐI KÌ MÔN GIẢI TÍCH 1 – Học kì 20181
Mã HP: MI1111, Nhóm ngành 1, Thời gian: 90 phút
Chú ý: Thí sinh không được sử dụng tài liệu và giám thị phải ký xác nhận số đề vào bài thi
Câu 1. Tính giới hạn
cos
lim
arccot
x
x x
x x

Câu 2. Cho
2
1
( )
2 1
f x
x x
Tính đạo hàm cấp cao
f x
50
( )
Câu 3. Tính tích phân
5
2
0
16x dx
Câu 4. Tính tích phân
2
0
5 sin 6 cos
6 sin 5 cos
x x
dx
x x
Câu 5. Tính giới hạn
in
3
2 2
( , ) (0,0)
s
lim
sin sin
x y
y
x y
Câu 6. Chỉ số Shannon đo lường mức độ đa dạng của một hệ sinh thái, trong trường hợp hai loài, được xác định
theo công thức:
H x x y y ln ln
ở đó x, y là tỉ lệ các loài, thỏa mãn
x y
x y
0, 0
1
Tìm giá trị lớn nhất của H.
Câu 7. Chứng minh rằng
3 5
sin - , 0,
6 120 2
x x
x x x
Câu 8. Cho
z f x y ( , )
là hàm số ẩn xác định bởi phương trình
0
z
y
z ye
. Ứng dụng vi phân, tính gần
đúng
(0,99;0, 02)
f
Câu 9. Tính
1 (2 )!
lim
!
n
n
n
n n

Câu 10. Xét sự hội tụ, phân kì của tích phân suy rộng
0
ln(1 3 )
x
dx
x x

15
ĐỀ 3 VIỆN TOÁN ỨNG DỤNG VÀ TIN HỌC
ĐỀ THI CUỐI KÌ MÔN GIẢI TÍCH 1 – Học kì 20181
Mã HP: MI1111, Nhóm ngành 1, Thời gian: 90 phút
Chú ý: Thí sinh không được sử dụng tài liệu và giám thị phải ký xác nhận số đề vào bài thi
Câu 1. (1 đ). Tính giới hạn
x
x
x x
1
0
lim(cos sin )
Câu 2. (1 đ). Tìm tiệm cận xiên của đồ thị hàm số
ary x c x cot
Câu 3. (1 đ). Tính tích phân
xdx
4
3
0
tan
Câu 4. (1 đ). Tính tích phân
x x dx
1
2
0
ln( 1)
Câu 5. (1 đ). Tìm các cực trị của hàm số
z x y x y
2 2
4( )
Câu 6. (2 đ). Cho hàm số
x
y neu y
f x y
y
neu y
2
arctan , 0
( , )
0, 0
a) Xét tính liên tục của
f x y( , )
tại điểm
A
(1,0)
b) Tính
y
f
'
(1, 0)
Câu 7. (1 đ). Cho
0<x,y<
2
Chứng minh
(tanx+tany)
x y
tan
2 2
Câu 8. (1 đ). Tính tích phân
x
x x
dx
2
2
sin
1 3
Câu 9. (1đ) Xét sự hội tụ, phân kì của tích phân suy rộng
xdx
x x x

0
arctan
1 cos
16
ĐỀ 4 VIỆN TOÁN ỨNG DỤNG VÀ TIN HỌC
ĐỀ THI CUỐI KÌ MÔN GIẢI TÍCH 1 – Học kì 20181
Mã HP: MI1111, Nhóm ngành 1, Thời gian: 90 phút
Chú ý: Thí sinh không được sử dụng tài liệu và giám thị phải ký xác nhận số đề vào bài thi
Câu 1. (1 đ). Tính giới hạn
x
x
x x
1
0
lim(cos sin )
Câu 2. (1 đ). Tìm tiệm cận xiên của đồ thị hàm số
arctany x x
Câu 3. (1 đ). Tính tích phân
xdx
4
4
0
tan
Câu 4. (1 đ). Tính tích phân
x x dx
1
2
0
ln( 1)
Câu 5. (1 đ). Tìm các cực trị của hàm số
z x y x
2 2
4(y )
Câu 6. (2 đ). Cho hàm số
y
x neu x
f x y
x
neu x
2
arctan , 0
( , )
0, 0
a) Xét tính liên tục của
f x y( , )
tại điểm
B(0,1)
b) Tính
y
f
'
(0,1)
Câu 7. (1 đ). Cho
0<x,y<
2
Chứng minh
+coty)
x y x
cot
cot
2 2
Câu 8. (1 đ). Tính tích phân
x
x x
dx
2
2
sin
1 2
Câu 9. (1đ) Xét sự hội tụ, phân kì của tích phân suy rộng
xdx
x x x x

0
arctan
sin
17
ĐỀ 5 VIỆN TOÁN ỨNG DỤNG VÀ TIN HỌC
ĐỀ THI CUỐI KÌ MÔN GIẢI TÍCH 1 – Học kì 20181
Mã HP: MI1112, Nhóm ngành 2, Thời gian: 90 phút
Chú ý: Thí sinh không được sử dụng tài liệu và giám thị phải ký xác nhận số đề vào bài thi
Câu 1. Tìm a để hàm số sau liên tục tại điểm = 1 x
a x khi x
f x
x khi x
3
1
( )
arccos 0 1
Câu 2. Tìm hàm ngược của hàm số
x x
y
2 2
Câu 3. Cho hai hàm số
f x x g x x x
3 2
( ) ; ( ) , 1 3
Tìm số
c
( 1;3)
sao cho
f c f f
g c g g
'( ) (3) ( 1)
'( ) (3) ( 1)
Điều này có mâu thuẫn với định lý Cauchy không? Giải thích?
Câu 4. Cho hai hàm số f(x), g(x):
R R
thỏa mãn
f x g x( ) ( )
với mọi . Chứng minh rằng nếu x
f x( )
là
hàm đơn điệu tăng thì
f f x g g x( ( )) ( ( ))
Câu 5.
Tính tích phân
x
dx
x x

2
0
3 1
( 1)( 1)
Câu 6. Tính giới hạn
x
x
x
x
3
0
1 1 2 sin
lim ln
1 sin 2
Câu 7. Tính độ dài cung y x x
ln(cos ), 0
3
Câu 8. Tìm tiệm cận xiên của đường cong
t t
x y
t
t
3 2
3
;
1
1
Câu 9. Tính giới hạn
x
n
n
n n n n

2 2 2 2 2
1 1 2 1
lim ....
1
4 1 4 2 4 ( 1)
Câu 10. Cho hàm số f(x) lồi, khả tích trên đoạn
a b
,
.CMR:
1 ( ) ( )
( )
2
b
a
f a f b
f x dx
b a
18
ĐỀ 6 VIỆN TOÁN ỨNG DỤNG VÀ TIN HỌC
ĐỀ THI CUỐI KÌ MÔN GIẢI TÍCH 1 – Học kì 20181
Mã HP: MI1112, Nhóm ngành 2, Thời gian: 90 phút
Chú ý: Thí sinh không được sử dụng tài liệu và giám thị phải ký xác nhận số đề vào bài thi
Câu 1. Tìm a để hàm số sau liên tục tại điểm = 1 x
3
1
( )
arccos 0 1
a x khi x
f x
x khi x
Câu 2. Tìm hàm ngược của hàm số
3 3
x x
y
Câu 3. Cho hai hàm số
3 2
( ) ; ( ) , 3 1
f x x g x x x
Tìm số
( 3;1)
c
sao cho
'( ) (1) ( 3)
'( ) (1) ( 3)
f c f f
g c g g
Điều này có mâu thuẫn với định lý Cauchy không? Giải thích?
Câu 4. Cho hai hàm số f(x), g(x):
R R
thỏa mãn
f x g x( ) ( )
với mọi . Chứng minh rằng nếu x
f x( )
là
hàm đơn điệu tăng thì
f f x g g x( ( )) ( ( ))
Câu 5. Tính tích phân
2
0
3
( 1)( 1)
x
dx
x x

Câu 6. Tính giới hạn
3
0
1 1 2 sin
lim ln
1 sin 2
x
x
x
x
Câu 7. Tính độ dài cung ln(sin ),
6 2
y x x
Câu 8. Tìm tiệm cận xiên của đường cong
2 3
3
3
;
1
1
t t
x y
t
t
Câu 9. Tính giới hạn
2 2 2 2 2
1 1 2 1
lim ....
1
4 1 4 2 4 ( 1)
x
n
n
n n n n

Câu 10. Cho hàm số f(x) lõm, khả tích trên đoạn
a b
,
.CMR:
1 ( ) ( )
( )
2
b
a
f a f b
f x dx
b a
19
PHẦN 1: TỔNG HỢP ĐỀ THI CUỐI KỲ CÁC NĂM
ĐỀ 7 VIỆN TOÁN ỨNG DỤNG VÀ TIN HỌC
ĐỀ THI CUỐI KÌ MÔN GIẢI TÍCH 1 – Học kì 20181
Mã HP: MI1113, Nhóm ngành 3, Thời gian: 90 phút
Chú ý: Thí sinh không được sử dụng tài liệu và giám thị phải ký xác nhận số đề vào bài thi
Câu 1. Tính
x
dx
x x
2
3 2
Câu 2
. Xét sự hội tụ, phân kì của tích phân suy rộng
dx
x x x
3
1
1 1
Câu 3.
Tính thể tích vật tròn xoay tạo bởi elip:
x y
2 2
1
4 9
quay quanh trục O . x
Câu 4. Tính
x
x x
x
2
0
cos - cos 4
lim
Câu 5. Tìm và phân loại điểm gián đoạn của hàm số
x
y
x x x
3 2
2 2
Câu 6. Cho hàm số
z x y x y xy
3 2 2 2
3 2
. Tính
dz
(1,1)
Câu 7. Tìm cực trị của hàm số
z xy x y x y
( )(2 3 );
là tham số thực
Câu 8. Tính tích phân kép
D
x y dxdy
( ) ;
với
x y
D
x y x
2 2
1 4
:
3
.
Câu 9. Tồn tại hay không hàm số sao cho f
f f f
(1) ( 1), (0) 0
và
f x
''(x) 0 ( 2,2)
Câu 10. Cho hàm số
z x x y x y x y
2 2 2 2 2018 2 2 2019
sin( ) ( ) 100( )
.
Chứng minh
z z
x xy zy
y x
2
20
PHẦN 1: TỔNG HỢP ĐỀ THI CUỐI KỲ CÁC NĂM
ĐỀ 8 VIỆN TOÁN ỨNG DỤNG VÀ TIN HỌC
ĐỀ THI CUỐI KÌ MÔN GIẢI TÍCH 1 – Học kì 20181
Mã HP: MI1113, Nhóm ngành 3, Thời gian: 90 phút
Chú ý: Thí sinh không được sử dụng tài liệu và giám thị phải ký xác nhận số đề vào bài thi
Câu 1. Tính
x
dx
x x
2
5 6
Câu 2
. Xét sự hội tụ, phân kì của tích phân suy rộng
dx
x x x
3
1
1 1
Câu 3.
Tính thể tích vật tròn xoay tạo bởi elip:
x y
2 2
1
9 4
quay quanh trục Ox.
Câu 4. Tính
x
x x
x
2
0
cos 4 - cos
lim
Câu 5. Tìm và phân loại điểm gián đoạn của hàm số
x
y
x x x
3 2
2 2
Câu 6. Cho hàm số
z x y x y xy
2 3 2 2
3 2
. Tính
dz
(1,1)
Câu 7
. Tìm cực trị của hàm số ; là tham số thực = + − − − 2 + 3
( )( )
Câu 8. Tính tích phân kép
D
x y dxdy
( ) ;
với
x y
D
x
y x
2 2
1 4
:
3
.
Câu 9. Tồn tại hay không hàm số sao cho f
f f f
(1) ( 1), (0) 0
và
f x x
''( ) 0 ( 2, 2)
Câu 10. Cho hàm số
z x x y x y x y
2 2 2 2 2018 2 2 2019
sin( ) ( ) 100( )
Chứng minh
z z
x xy zy
y x
2
21
PHẦN 1: TỔNG HỢP ĐỀ THI CUỐI KỲ CÁC NĂM
ĐỀ 1 VIỆN TOÁN ỨNG DỤNG VÀ TIN HỌC
ĐỀ THI CUỐI KÌ MÔN GIẢI TÍCH 1 – Học kì 20173
Mã HP: MI1111, Nhóm ngành 1, Thời gian: 90 phút
Chú ý: Thí sinh không được sử dụng tài liệu và giám thị phải ký xác nhận số đề vào bài thi
Câu 1. Tính giới hạn
x
x
tanx
0
lim(1 cos )
Câu 2. Cho
f x
x
1
( )
1
Tính đạo hàm cấp cao
f x
50
( )
Câu 3. Tính các tiệm cận của đồ thị hàm số
x x
y
x
2
2
arctan
1
Câu 4. Tính tích phân
x
dx
3
0
arccos
2
Câu 5. Tính diện tích mặt tròn xoay tạo bởi khi quay đường cong
y x
x
2
4
1 1
quanh trục Ox một vòng.
Câu 6. Cho hàm số ar
y
z c
x
cot
. Tính các vi phân
dz d z
2
,
Câu 7. Tìm các cực trị của hàm số
y y
z xe x e
3 3
3
Câu 8. Tính giới hạn
x y
x
x y
3
2 2
( , ) (0,0)
lim
Câu 9. Tính giới hạn
x
x
t dt
x

3
0
2
(arctan )
lim
3
Câu 10. Xét sự hội tụ, phân kì của tích phân suy rộng
x x
dx
x

3 10
0
sin
22
PHẦN 1: TỔNG HỢP ĐỀ THI CUỐI KỲ CÁC NĂM
ĐỀ 2 VIỆN TOÁN ỨNG DỤNG VÀ TIN HỌC
ĐỀ THI CUỐI KÌ MÔN GIẢI TÍCH 1 – Học kì 20173
Mã HP: MI1111, Nhóm ngành 1, Thời gian: 90 phút
Chú ý: Thí sinh không được sử dụng tài liệu và giám thị phải ký xác nhận số đề vào bài thi
Câu 1. Tính giới hạn
x
x
sinx
0
lim(1 cos )
Câu 2. Cho
f x x ( ) 1
Tính đạo hàm cấp cao
f x
50
( )
Câu 3. Tính các tiệm cận của đồ thị hàm số
x x
y
x
2
2
arccot
1
Câu 4. Tính tích phân
x
dx
3
0
arcsin
2
Câu 5. Tính diện tích mặt tròn xoay tạo bởi khi quay đường cong
y x
x
2
9
2 2
quanh trục Ox một vòng.
Câu 6. Cho hàm số
x
z
y
arctan
. Tính các vi phân
dz d z
2
,
Câu 7. Tìm các cực trị của hàm số
x x
z ye y e
3 3
3
Câu 8. Tính giới hạn
x y
x
x y
5
4 4
( , ) (0,0)
lim
Câu 9. Tính giới hạn
x
x
t dt
x

4
0
2
(arctan )
lim
2
Câu 10. Xét sự hội tụ, phân kì của tích phân suy rộng
x x
dx
x

7
0
sin
23
PHẦN 1: TỔNG HỢP ĐỀ THI CUỐI KỲ CÁC NĂM
ĐỀ 3 VIỆN TOÁN ỨNG DỤNG VÀ TIN HỌC
ĐỀ THI CUỐI KÌ MÔN GIẢI TÍCH 1 – Học kì 20173
Mã HP: MI1112, Nhóm ngành 2, Thời gian: 90 phút
Chú ý: Thí sinh không được sử dụng tài liệu và giám thị phải ký xác nhận số đề vào bài thi
Câu 1. (2đ) Tính các giới hạn:
a)
x o
x x
x
2
ln(1 )
lim
b)
osx
x
x
x
e c
0
ln(1 2 tan )
lim
Câu 2. (1đ) Tìm và phân loại điểm gián đoạn của hàm số
x
y e
1
arctan( )
Câu 3.
(1đ). Cho
x
f x
x
1
( ) ln
2
. Tính vi phân cấp cao
d f x
(10)
( )
Câu 4. (1đ). Tìm tiệm cận xiên của đồ thị hàm số
ary x c x cot
Câu 5. (1đ). Tính tích phân
inx osx
c
dx
x
2
s
sin
Câu 6. (1đ). Tính tích phân ar
c xdx
1
0
cot
Câu 7. (1đ). Tính độ dài của cung [
x x
y e e x
1
( ), 0, ln 2]
2
Câu 8. (1đ). Chứng minh rằng x x
arctan arccot
2
với mọi ∈ℝ
Câu 9. (1đ). Xét sự hội tụ, phân kì của tích phân suy rộng
xdx
x x

3
0
sin
24
PHẦN 1: TỔNG HỢP ĐỀ THI CUỐI KỲ CÁC NĂM
ĐỀ 4 VIỆN TOÁN ỨNG DỤNG VÀ TIN HỌC
ĐỀ THI CUỐI KÌ MÔN GIẢI TÍCH 1 – Học kì 20173
Mã HP: MI1112, Nhóm ngành 2, Thời gian: 90 phút
Chú ý: Thí sinh không được sử dụng tài liệu và giám thị phải ký xác nhận số đề vào bài thi
Câu 1. (2đ) Tính các giới hạn:
a)
x o
x x
x
3
arctan
lim
b)
osx
x
x
x
e c
0
ln(1 3 sin )
lim
Câu 2. (1đ) Tìm và phân loại điểm gián đoạn của hàm số
x
y e
1
arccot( )
Câu 3.
(1đ). Cho
x
f x
x
2
( ) ln
1
. Tính vi phân cấp cao
d f x
(10)
( )
Câu 4. (1đ). Tìm tiệm cận xiên của đồ thị hàm số
y x x arctan
Câu 5. (1đ). Tính tích phân
inx osx
c
dx
x
2
s
cos
Câu 6. (1đ). Tính tích phân
xdx
1
0
arctan
Câu 7. (1đ). Tính độ dài của cung
x
y x x
2
1
ln , 1,2
2 2
Câu 8. (1đ). Chứng minh rằng x x
arcsin arccos
2
với mọi
x
1,1
Câu 9. (1đ). Xét sự hội tụ, phân kì của tích phân suy rộng
xdx
x x

4
0
sin
25
PHẦN 1: TỔNG HỢP ĐỀ THI CUỐI KỲ CÁC NĂM
ĐỀ 5 VIỆN TOÁN ỨNG DỤNG VÀ TIN HỌC
ĐỀ THI CUỐI KÌ MÔN GIẢI TÍCH 1 – Học kì 20173
Mã HP: MI1113, Nhóm ngành 3, Thời gian: 90 phút
Chú ý: Thí sinh không được sử dụng tài liệu và giám thị phải ký xác nhận số đề vào bài thi
Câu 1. (1đ). Xét tính chẵn, lẻ của hàm số
x
y
x
2
2
arcsin
1
Câu 2
. (1 đ) Tính giới hạn
x
x
x
x
1
2
0
lim( 2 )
Câu 3. (1đ). Tính số thực α sao cho hàm số
x y x ay
( , ) ln( )
thỏa mãn phương trình
x y
x y
2 2 2
2 2
4 4 0
Câu 4. (1đ). Viết khai triển Maclaurin đến bậc 5 của hàm số
x
y
x
2
1
Câu 5. (1đ). Tính tích phân kép
D
x y dxdy
2 2
4 ;
trong đó là miền D
x y x
2 2
4, 0
Câu 6. (1đ). Tính tích phân xác định
xdx
3
1
arctan .
Câu 7. (1đ). Sử dụng vi phân toàn phần tính gần đúng:
e
0,02 2
3
4 1,95
Câu 8. (1đ). Tính giới hạn của dãy số
n
n
a
1 2
...
2! 3! (n 1)!
Câu 9. (1đ). Xét tính liên tục đều trên
0,1
của hàm số
os2x
c
f x
x
2
1
( )
Câu 10. (1đ) Xét sự hội tụ của tích phân
x
dx
x x

3
0
arctan
( ln(1 ))
26
PHẦN 1: TỔNG HỢP ĐỀ THI CUỐI KỲ CÁC NĂM
ĐỀ 6 VIỆN TOÁN ỨNG DỤNG VÀ TIN HỌC
ĐỀ THI CUỐI KÌ MÔN GIẢI TÍCH 1 – Học kì 20173
Mã HP: MI1113, Nhóm ngành 3, Thời gian: 90 phút
Chú ý: Thí sinh không được sử dụng tài liệu và giám thị phải ký xác nhận số đề vào bài thi
Câu 1. (1đ). Xét tính chẵn, lẻ của hàm số
x
y
x
2
2
arctan
1
Câu 2
. (1 đ) Tính giới hạn
x
x
x
x

1
2
lim( 2 )
Câu 3. (1đ). Tính số thực α sao cho hàm số
x y x ay
( , ) ln( )
thỏa mãn phương trình
x yx y
2 2 2
2 2
4 4 0
Câu 4. (1đ). Viết khai triển Maclaurin đến bậc 5 của hàm số
x
y
x
2
1
Câu 5. (1đ). Tính tích phân kép
D
x y dxdy
2 2
4 ;
trong đó là miền D
x y y
2 2
4, 0
Câu 6. (1đ). Tính tích phân xác định
xdx
3
1
arccot .
Câu 7. (1đ). Sử dụng vi phân toàn phần tính gần đúng:
e
0,02 2
3
4 2, 05
Câu 8. (1đ). Tính giới hạn của dãy số
n
n
a
1 2
...
2! 3! (n 1)!
.
Câu 9. (1đ). Xét tính liên tục đều trên
0,1
của hàm số
ln(1+x)
f x
x
( )
Câu 10. (1đ) Xét sự hội tụ của tích phân
inx
x
dx
x

3
0
arctan
( s )
27
PHẦN 1: TỔNG HỢP ĐỀ THI CUỐI KỲ CÁC NĂM
ĐỀ 1 VIỆN TOÁN ỨNG DỤNG VÀ TIN HỌC
ĐỀ THI CUỐI KÌ MÔN GIẢI TÍCH 1 – Học kì 20172
Mã HP: MI1111, Nhóm ngành 1, Thời gian: 90 phút
Chú ý: Thí sinh không được sử dụng tài liệu và giám thị phải ký xác nhận số đề vào bài thi
Câu 1. Tìm miền xác định của hàm
y x arccos(2 sin2 )
Câu 2. Tìm f(x) biết
x x x
f e e e
1
( )
2
Câu 3. Tìm
x
lim sin(ln(2 x 1)) sin(ln(2 x))
Câu 4. Cho hàm số
y y x ( )
xác định bởi
x t t
y t t
3
4 2
2
9
3
4
. Tính
y y
'(x), ''(x)
Câu 5.
Xét sự hội tụ phân kỳ của tích phân
x
dx
x

5
ln( 2)
Câu 6. Tìm giới hạn
n
n n n
n n n n

2 2 2 2 2 2
lim ...
1 2
Câu 7. Dùng vi phân toàn phần của hàm số để tính giá trị gần đúng của biểu thức
A
3 2
3
(1, 04) (2, 03) 3
Câu 8. Tìm cực trị của hàm số
x y
z x y e
2 2
2 2 ( )
2 3
Câu 9. Tính
x y
z z
' '
,
của hàm số
x
y
xy
z t tdt
2
cos 2
Câu 10. Tính tích phân
inx
dx
x
3
1 s
sin
28
PHẦN 1: TỔNG HỢP ĐỀ THI CUỐI KỲ CÁC NĂM
ĐỀ 2 VIỆN TOÁN ỨNG DỤNG VÀ TIN HỌC
ĐỀ THI CUỐI KÌ MÔN GIẢI TÍCH 1 – Học kì 20172
Mã HP: MI1111, Nhóm ngành 1, Thời gian: 90 phút
Chú ý: Thí sinh không được sử dụng tài liệu và giám thị phải ký xác nhận số đề vào bài thi
Chú ý: Thí sinh không được sử dụng tài liệu và giám thị phải ký xác nhận số đề vào bài thi
Câu 1. Tìm miền xác định của hàm
y x arcsin(2cos2 )
Câu 2. Tìm f(x) biết
x x x
f e e e
1
( )
2
Câu 3. Tìm
x
x x

lim sin(ln(3 1)) sin(ln(3 ))
Câu 4. Cho hàm số
y y x ( )
xác định bởi
x t t
y t t
3
4 2
3
15 15
4 2
. Tính
y x y x'( ), ''( )
Câu 5.
Xét sự hội tụ phân kỳ của tích phân
x
dx
x

5
ln( 2)
Câu 6. Tìm giới hạn
n
n n n
n n n n

2 2 2 2 2 2
lim ...
3 1 3 2 3
Câu 7. Dùng vi phân toàn phần của hàm số để tính giá trị gần đúng của biểu thức
A
2 3
4
(3, 04) (2, 02) 1
Câu 8. Tìm cực trị của hàm số
x y
z x y e
2 2
2 2
2 3
Câu 9. Tính
x y
z z
' '
,
của hàm số
x
y
xy
z t t
2
sin 2 dt
Câu 10. Tính tích phân
osx
cos
c
dx
x
3
1
29
PHẦN 1: TỔNG HỢP ĐỀ THI CUỐI KỲ CÁC NĂM
ĐỀ 1 VIỆN TOÁN ỨNG DỤNG VÀ TIN HỌC
ĐỀ THI CUỐI KÌ MÔN GIẢI TÍCH 1 – Học kì 20171
Mã HP: MI1111, Nhóm ngành 1, Thời gian: 90 phút
Chú ý: Thí sinh không được sử dụng tài liệu và giám thị phải ký xác nhận số đề vào bài thi
Câu 1. (2 điểm). Tìm các giới hạn sau
a)
x o
x
x
1 4 1
lim
ln(1 3 )
b)
inx
x
e x
1
s
0
lim ln( 2 )
Câu 2. (1 điểm). Tìm các tiệm cận của đồ thị hàm số
x
y
x
2
2
3
Câu 3. (1 điểm). Tính tích phân
x xdx
( 2)ln
Câu 4
. (1 điểm). Cho miền được giới hạn bởi các đường =sin , 0≤ ≤ ∕ 2 , =
( )
, 0 ≤≤1 ,=0
( )
và
x
/ 2
. Tìm để khối tròn xoay sinh ra khi quay miền quanh đường thẳng =
có thể tích nhỏ nhất?
Câu 5.
(1 điểm). Tính tích phân suy rộng
x
dx
x

2
2
0
(arctan )
1
Câu 6. (1 điểm). Cho
f
là hàm số khả vi đến cấp hai trên . Chứng minh rằng hàm số ℝ
w x t f x t ( , ) ( 3 )
thỏa mãn phương trình truyền sóng
w w
t x
2 2
2 2
9
Câu 7. ) (1 điểm Tìm cực trị của hàm số
z x xy x y y
3 2
2 7 6 4
Câu 8. (1 điểm). Hàm số
f x y x y
4 2
3
( , )
có khả vi tại điểm (0,0) không? Tại sao
Câu 9. (1 điểm). Cho
f
liên tục trên
a b
,
và thỏa mãn
b
a
f x dx
( ) 0
. Chứng minh rằng tồn tại
c a b( , )
sao cho
c
a
f x dx f
( ) 2017 (c)
30
PHẦN 1: TỔNG HỢP ĐỀ THI CUỐI KỲ CÁC NĂM
ĐỀ 3 VIỆN TOÁN ỨNG DỤNG VÀ TIN HỌC
ĐỀ THI CUỐI KÌ MÔN GIẢI TÍCH 1 – Học kì 20171
Mã HP: MI1111, Nhóm ngành 1, Thời gian: 90 phút
Câu 1. (2 điểm). Tìm các giới hạn sau
a)
x
x o
e
x
1
lim
arctan(2 )
b)
x
y
x y
2 2
1
3
( , ) (0,0)
lim 1 3 x )
Câu 2. (1 điểm). Tìm để hàm số sau liên tục trên ℝ
(
)
=
+ 1 ế  ≥
3 + 5 ế  <
Câu 3. (1 điểm). Tính cực trị của hàm số
f x x x
3
( ) 2ln
Câu 4. (1 điểm). Tìm các tiệm cận của đồ thị hàm số arf x x c
x
2
( ) cot
Câu 5. (1 điểm). Tính tích phân suy rộng
x
dx
x
2
3 2
1
Câu 6. (1 điểm). Chứng minh rằng hàm số
cos(2x+3)
t
e
16
u(x, t)
thỏa mãn phương trình truyền nhiệt
u u
t
x
2
2
4
Câu 7. ) (1 điểm Tìm cực trị của hàm số
z x xy x y y
4 2
2 4 4 1
Câu 8. (1 điểm). Xét sự hội tụ của tích phân suy rộng
2 2
0
1
x
dx
e x
Câu 9. (1 điểm). Cho hàm số
f x( )
khả vi liên tục đến cấp hai trên
a b
,
và
f a f b
( ) ( ) 0
. Chứng minh
rằng
b b b
a a a
f x dx f x dx f x dx
2
2 2 2
'( ) ( ) ''( )
31
PHẦN 1: TỔNG HỢP ĐỀ THI CUỐI KỲ CÁC NĂM
ĐỀ 4 VIỆN TOÁN ỨNG DỤNG VÀ TIN HỌC
ĐỀ THI CUỐI KÌ MÔN GIẢI TÍCH 1 – Học kì 20171
Mã HP: MI1111, Nhóm ngành 1, Thời gian: 90 phút
Chú ý: Thí sinh không được sử dụng tài liệu và giám thị phải ký xác nhận số đề vào bài thi
Câu 1. (2 điểm). Tìm các giới hạn sau
a)
x
x o
e
x
1
lim
arctan(3 )
b)
x
y
x y
y
2 2
1
3
( , ) (0,0)
lim 1 4 )
Câu 2. (1 điểm). Tìm để hàm số sau liên tục trên ℝ
(
)
=
+ 2 ế  <
7 − 4 ế ≥
Câu 3. (1 điểm). Tính cực trị của hàm số
f x x x
3
( ) 4 ln
Câu 4. (1 điểm). Tìm các tiệm cận của đồ thị hàm số arf x x c
x
3
( ) cot
Câu 5. (1 điểm). Tính tích phân suy rộng
x
dx
x
2
1 4
1
Câu 6. (1 điểm). Chứng minh rằng hàm số
sin(2x+1)
t
e
36
u(x, t)
thỏa mãn phương trình truyền nhiệt
u u
t
x
2
2
9
Câu 7. ) (1 điểm Tìm cực trị của hàm số
z x xy x y y
2 4
2 6 6 1
Câu 8. (1 điểm). Xét sự hội tụ của tích phân suy rộng
x
dx
e x
2 2
0
1
Câu 9. (1 điểm). Cho hàm số
f x( )
khả vi liên tục đến cấp hai trên
a b
,
và
f a f b
( ) ( ) 0
. Chứng minh
rằng
b b b
a a a
f x dx f x dx f x dx
2
2 2 2
'( ) ( ) ''( )
32
PHẦN 1: TỔNG HỢP ĐỀ THI CUỐI KỲ CÁC NĂM
ĐỀ 5 VIỆN TOÁN ỨNG DỤNG VÀ TIN HỌC
ĐỀ THI CUỐI KÌ MÔN GIẢI TÍCH 1 – Học kì 20171
Mã HP: MI1112, Nhóm ngành 2, Thời gian: 90 phút
Chú ý: Thí sinh không được sử dụng tài liệu và giám thị phải ký xác nhận số đề vào bài thi
Câu 1. (1đ). Cho bảng giá trị của hai hàm số
f x( )
và
g x( )
như sau
x 1 2 3 4 5 6 7 8 9
f x( )
2 3 1 4 6 9 5 7 8
g x( )
9 7 6 2 1 3 4 5 8
Hãy xác định giá trị
(
∘ 3
)( )
Câu 2. (1 đ) Tính giới hạn
os( x)
x
x x x
c
2
1
( 3 2) sin( 1)
lim
1
Câu 3. (1đ). Tìm và phân loại các điểm gián đoạn của hàm số
x
y
e
1/
1
1
Câu 4. (1đ). Cho hàm số
x
f x t dt
2
0
( ) sin( )
. Tính f
'( )
Câu 5. (1đ). Tìm khai triên Maclaurin của hàm số
y x
2 2
đến
x
3
Câu 6. (1đ). Tính giới hạn
x
x x
0
1 1
lim
arcsin
Câu 7. (1đ). Tính tích phân suy rộng
dx
x x

3
1
( 1)( 2)
(1đ). Tính tích phân Câu 8. cos(
x dx
1
0
arctan )
.
Câu 9. (1đ). Tìm số nghiệm của phương trình
x
x
2 4
Câu 10. (1đ) Xác định dấu của tích phân
dx
x
2
0
sinx
33
PHẦN 1: TỔNG HỢP ĐỀ THI CUỐI KỲ CÁC NĂM
ĐỀ 6 VIỆN TOÁN ỨNG DỤNG VÀ TIN HỌC
ĐỀ THI CUỐI KÌ MÔN GIẢI TÍCH 1 – Học kì 20171
Mã HP: MI1112, Nhóm ngành 2, Thời gian: 90 phút
Chú ý: Thí sinh không được sử dụng tài liệu và giám thị phải ký xác nhận số đề vào bài thi
Câu 1. (1đ). Cho bảng giá trị của hai hàm số
f x( )
và
g x( )
như sau
x 1 2 3 4 5 6 7 8 9
f x( )
2 3 1 4 6 9 5 7 8
g x( )
9 7 6 2 1 3 4 5 8
Hãy xác định giá trị
(
∘ 5
)( )
Câu 2. (1 đ) Tính giới hạn
os( x)
x
x x x
c
2
1
( 3 2)sin( 1)
lim
1
Câu 3. (1đ). Tìm và phân loại các điểm gián đoạn của hàm số
x
y
1/
1
2 1
Câu 4. (1đ). Cho hàm số cos
x
f x t dt
2
0
( ) ( )
. Tính f
'( )
Câu 5. (1đ). Tìm khai triên Maclaurin của hàm số
y x 2 2
đến
x
3
Câu 6. (1đ). Tính giới hạn
x
x x
0
1 1
lim
arctan
Câu 7. (1đ). Tính tích phân suy rộng
dx

3
1
(x 1)(x 2)
(1đ). Tính tích phân Câu 8. cos(
x dx
0
1
arctan )
.
Câu 9. (1đ). Tìm số nghiệm của phương trình
x
x
1
10
Câu 10. (1đ) Xác định dấu của tích phân
dx
x
0
2
sinx
34
PHẦN 1: TỔNG HỢP ĐỀ THI CUỐI KỲ CÁC NĂM
ĐỀ 8 VIỆN TOÁN ỨNG DỤNG VÀ TIN HỌC
ĐỀ THI CUỐI KÌ MÔN GIẢI TÍCH 1 – Học kì 20171
Mã HP: MI1113, Nhóm ngành 4, Thời gian: 90 phút
Chú ý: Thí sinh không được sử dụng tài liệu và giám thị phải ký xác nhận số đề vào bài thi
Câu 1. (1đ). Tính giới hạn
x
x
2
0
ln(cosx)
lim
tan
Câu 2. (1 đ) So sánh cấp vô cùng bé sau đây khi
x 0
x x x x x
4 5 4
( ) , ( ) ln(1 3 arctan( ))
Câu 3. (1đ). Điểm
x
là điểm gián đoạn loại gì của hàm số
=
1

+ 1
Câu 4. (1đ). Tính tích phân
dx
x
2
2
3
( 3) 1
.
Câu 5.
(1đ). Xét sự hội tụ của tích phân suy rộng
dx
x x

3 2
0
3 1
Câu 6. (1đ). Ứng dụng vi phân, tính gần đúng
2 2
3, 97 3, 03
Câu 7. (1đ). Tìm các cực trị của hàm số
z x y
2 2
2
với điều kiện
x y
2 2
1
(1đ). Tính tích phân kép Câu 8.
D
dxdy
(2 x y)
. Với là miền thỏa mãn D
x y
2 2
2
Câu 9. (1đ). Cho
xy
neu x y
f x y
x y
neu x y
2 2
, ( , ) (0;0)
( , )
2
0 ( , ) (0;0)
Chứng minh rằng các đạo hàm riêng
x y
f f
' '
(0; 0) (0; 0) 0
nhưng hàm số
f x y( , )
không liên tục tại điểm
(0,0)
Câu 10. (1đ) Cho
y x
2
cos( )
. Tính đạo hàm cấp cao
y
(8)
(0)
35
PHẦN 1: TỔNG HỢP ĐỀ THI CUỐI KỲ CÁC NĂM
ĐỀ 2 VIỆN TOÁN ỨNG DỤNG VÀ TIN HỌC
ĐỀ THI CUỐI KÌ MÔN GIẢI TÍCH 1 – Học kì 20161
Mã HP: MI1111, Nhóm ngành 1, Thời gian: 90 phút
Chú ý: Thí sinh không được sử dụng tài liệu và giám thị phải ký xác nhận số đề vào bài thi
Câu 1. Tính các số thực thỏa mãn ,
3
5
0
(1 sin ) 1
lim
x
x
ax
Câu 2. Tính
f
'(1)
với
()=

,ℎ ∈(−∞; 1)
0,ℎ ∈[1; +∞
)
Câu 3. Tìm khai triển Maclaurin của
osf x xc x( )
đến
x
5
Câu 4. Tính
2
cos
sin(2 ) .
x
e x dx
.
Câu 5. Tính độ dài của đường cong
x
y x
x
4
2
1
, 1;2
8
4
Câu 6. Xét sự hội tụ, phân kì của tích phân suy rộng
x dx
x x

3
0
(3 2)
4
Câu 7. Tính
5
4 2
( , ) (0;0)
lim
x y
y
x y
Tìm giá trị lớn nhất, nhỏ nhất của Câu 8.
2 2
2 3 13 18z x y xy x y
trong miền
OAB
, ở đó
O A B
(0;0), (7;0), (0;7)
Câu 9. Hàm số
z z u v ( ; )
khả vi trên ℝ
, có
u v
z z
' '
(1;1) 3, (1;1) 4
. Đặt
f x x
3 2
( ) z(x ; )
, tính
f
'(1)
Câu 10. Một chiếc xe cứu hộ xuất phát từ góc của một hồ nước hình chữ nhật có các cạnh dài 2000m và rộng
600m. Xe vừa có thể đi trên bờ hồ và đi trên mặt nước với vận tốc tương ứng là 20m/s và 12m/s. Tính thời gian
ít nhất để xe đi đến giao điểm hai đường chéo của hồ.
36
PHẦN 1: TỔNG HỢP ĐỀ THI CUỐI KỲ CÁC NĂM
ĐỀ 3 VIỆN TOÁN ỨNG DỤNG VÀ TIN HỌC
ĐỀ THI CUỐI KÌ MÔN GIẢI TÍCH 1 – Học kì 20161
Mã HP: MI1111, Nhóm ngành 1, Thời gian: 90 phút
Chú ý: Thí sinh không được sử dụng tài liệu và giám thị phải ký xác nhận số đề vào bài thi
Câu 1. Tìm và phân loại điểm gián đoạn của hàm số
3
1
\ 0; 9; 9
2 log | |
3 0; 9; 9
khi x
x
y
khi x
R
Câu 2. Tính
5 5
15
0
sin( )
lim
sin
x
x x
x
Câu 3. Cho ba số thực thỏa mãn a, b, c
a b c 0
. Chứng minh phương trình
ax bx c
5 4
6 5 0
có ít
nhất một nghiệm thuộc (0;1)
Câu 4. Tính
3
8
1
x
dx
x
.
Câu 5. Tính diện tích mặt tròn xoay được tạo ra khi quay đường
y x x
2
4
,
x
1;2
quanh trục Ox một
vòng.
Câu 6. Xét sự hội tụ, phân kì của tích phân suy rộng
osx
xdx
c
1
0
x
1
Câu 7. Tìm cực trị của hàm số
3
3
1 3y
z y
x
x
Câu 8. Tính đạo hàm riêng
y
z
'
(x; y)
của hàm số
x
x = 0
y
z
x
, 0
arctan
0
khi
khi,
Câu 9. Tìm hàm số
z x y( ; )
thỏa mãn
' ' 2
2 , 2 , (x; y)
x y
z x y z y x
R
.
Câu 10. Một sân bóng đá có biên ngang dài 69m, cầu môn rộng 7m. Bóng nằm trên biên dọc, cách biên ngang
x(m). Tính góc sút bóng vào cầu môn theo , tìm để góc sút lớn nhất x x
.
37
PHẦN 1: TỔNG HỢP ĐỀ THI CUỐI KỲ CÁC NĂM
ĐỀ 5 VIỆN TOÁN ỨNG DỤNG VÀ TIN HỌC
ĐỀ THI CUỐI KÌ MÔN GIẢI TÍCH 1 – Học kì 20161
Mã HP: MI1112, Nhóm ngành 2, Thời gian: 90 phút
Chú ý: Thí sinh không được sử dụng tài liệu và giám thị phải ký xác nhận số đề vào bài thi
Câu 1. Cho hàm số
z x y x y
2 2
ln( 3 ),( ; ) (0;0)
. Tính
x y
A x y
' '
. z . z
Câu 2. Tính
x x

x
lim 2arctan(2 )
Câu 3. Xét tính lồi, lõm của đồ thị hàm số
x
y x e
( 1)
.
Câu 4. Tính
dx
x x
5cos 12sin 13
.
Câu 5. Tính diện tích hình phẳng giới hạn bởi đường cong cho hệ tọa độ cực
r
5 2 cos
Câu 6
. Xét sự hội tụ, phân kì của tích phân suy rộng
inx osx
c dx
x

2
0
(s 2 )
1
Câu 7. Tìm điểm gián đoạn của hàm số
2
6
( ) lim ,
2
n
n
f x x
x

R
Câu 8. Tìm cực trị của hàm số
xy
z
x y
4 3
12
Câu 9. Phương trình
x y xy
3 3
3 13 0
xác định hàm ẩn
y y x ( )
. Viết phương trình tiếp tuyến của đồ
thị hàm ẩn này tại điểm
A
( 1; 2)
Câu 10. Gập một tấm tôn hình chữ nhật rộng 30cm, dài 3m thành một cái máng nước. Gấp theo chiều dài mỗi
bên tấm tôn 10cm, tính góc gập θ để thể tích của máng lớn nhất.
38
PHẦN 3: SƯU TẦM ĐÁP ÁN MỘT SÓ ĐỀ KHÁC CỦA VIỆN TOÁN ỨNG DỤNG
ĐỀ 1-20193
Câu 1
(1đ)
+)
3 4
5 cos 5 sin 5
5 5
y x x x
+)
3 2
sin 5 sin 5
5 5
y x T
.
Câu 2
(2đ)
+)
3 32 2
0 cos 1
;
0
sin cos cos 1
x
f x
x x x
.
+)
2
0
0
3 32 2
1
2
lim
6
cos cos 1
x
x
x
f x f x
x x x
.
+)
2
2
4
ln 2 2
2
x
I x x x x dx
x x
.
+)
2
1 2 1
ln 2 2 7 arctan
2
7
x
I x x x x C
.
Câu 3
(1đ)
+)
0
0
8
0 lim 0
x
x
f x f x x
x
là đbt +)
1
0
8
dx
x
HT, do đó I HT.
Câu 4
(1đ)
+)
4 4
2
2 4 2
0
x x
x
x y x
. +)
02
; 0;0
0 lim ; 0
x
x y
x z x y

.
Câu 5
(1đ)
+)
1
2
1
0; 0
0
0;1
0
0; 1
x
y
M
z
M
z
M
+)
1
M
không là điểm cực trị,
min
0; 1 1
y
.
Câu 6
(1đ)
+)
f x
liên tục
0, 1
x
. +)
x
là đgđ loại 2,
0
x
là đgđ loại 1.
Câu 7
(1đ)
+)
0;1 0;1 0;1 ; 0;1 1
x y
dx z dx z dy z
.
+)
0;1 2; 0;1 1 0;1 2
x y
z z dx dx dy
.
Câu 8
(1đ)
+)
1 1 1
2
2 2
0 0 0
1 1 1
VT f x dx dx f x dx
+)
2
1 1 1 1 1
2
2 2 2
0 0 0 0 0
1 1f x dx f x dx dx f x dx VT f x dx
Câu 9
(1đ)
+)
1 1
2 3 2 3
1
1 1
2 2
1 2 3 3 1 3 3 1
3 3
I x x f x dx x f x dx I
+)
1
3
1
1
1 3
3 3 4
I
t x I f t dt I
.
Ghi chú:- Mỗi dấu +) cho 0,5 điểm
- Sinh viên giải cách khác đúng vẫn được điểm.
101
ĐỀ 4-20193
Câu 1.
+ Giới hạn trái của hàm số tại bằng 4 – 1, giới hạn phải bằng a a a
2
+ 3
+ Để hàm số liên tục, ta cần có
2
a
.
Câu 2.
+ Đặt
cott x
, tích phân trở thành
2
1t dt
+ Tích phân cần tìm bằng
3
1
cot cot
3
x x C
.
Câu 3.
+
3
3
ln
lim ln lim
x
x
x x
x
e x
e
 
đủ điều kiện để áp dụng quy tắc Lhospital.
+
3 3
1 /ln
lim lim 0
3
x
x x
xx
e e x
 
.
Câu 4.
+
0 0
0x
x x x
x
xe dx xe e dx

 
.
+
0
1
x
x
x
e

.
Câu 5.
+
2
1 tan cos sinf x x x
+
/ 2 1
f
.
Câu 6.
+ Đạo hàm trái và phải của hàm số đều bằng 1.
+
2 1
f
.
Câu 7.
+
2
0
2
arctan
arctan
lim lim 2
1
2
x x
tdt
x
x x
x
x x
 
+
2
arctan
lim 2
1 2
x
x
x x
x

.
Câu 8.
+ Trong khai triển Maclaurin của hàm số chỉ có các số hạng chứa
2n
x
+ Suy ra
997
0 0
f
.
Câu 9.
+
1
0 1; 1 0
f f
(do
f
là đơn ánh).
+
1 1
1 2; 2 1
g g
; suy ra kết quả cần tìm bằng 0.
Câu 10.
+
1/2
1
0 1/2
1 1
f x f x
I dx dx
f x f x f x f x
1/2 1/2
0 0
1
1 1
f x f x
dx dx
f x f x f x f x
đặt
1
t x
ở TP thứ 2
+ Kết quả cần tìm bằng ½.
102
ĐỀ 4-20173
Câu 1
0,5 đ
0,5 đ
0,5 đ
0,5 đ
2
3 2
0 0
1
1
arctan x
1
lim lim
3
x x
x
x
x x
(L’Hospital)
2
2 2
0
x 1
lim
3
3 (1 )
x
x x
ln(1 3 sin ) 3 sin 3x x x
khi
0x
osx=( osx) x1) (1
x x
e c e c
(Ngắt bỏ VCB bậc cao)
osx
0
ln(1 3 tan )
lim 3
x
x
x
e c
Câu 2
0,5 đ
0,5 đ
TXĐ =
\ 0 ,
0
lim 0
x
y
0
lim 0
2
x
y x
là điểm gián đoạn loại I
Câu 3
0,5 đ
0,5 đ
(9)
9 9
(10)
10 10
( 1) 9! ( 1) 9 !1 1 1 1
'( ) ( )
2 1 2 1
( 2) ( 1)
f x f x
x x x x
x x
(10) (10) 10 10
10 10
9! 9!
( ) ( )dx ( 2 1)
2 1
d f x f x dx x x
x x
Câu 4
0,5 đ
0,5 đ
lim 1
x
y
x

lim( ) , lim( )
2 2 2
x x
y x y x y x
 
là TCX của đường cong.
Câu 5
0,5 đ
0,5 đ
sinx x
cosx x
cos
1 2 1 1
2 2
1 sin 1 1 sin
; ln
2 1 sin
1 sin
d x
I dx dx I I I C
x x
x
cosx x cosxcos
2 22
cos 1 1 1 sin 1
ln
2 1 sin
d x
I C I C
x
Câu 6
0,5 đ
0,5 đ
1
2
0
arctan ( 1)t x I td t
1
1
2
0
0
( 1)arctan 1
2
I t t dt
Câu 7
0,5 đ
0,5 đ
2 2 2
2
1 1 1 1 1 1
'( ) (x ) 1 '( ) 1 (x 2 ) (x )
2 4 4
f x f x
x x
x
2 2
2
1 1
1 1 3 ln 2
1 ( '( )) ( )
2 4 2
I f x dx x dx
x
Câu 8
0,5 đ
0,5 đ
arccosx f'(x)=0, x f(x)=c( ) arcsin 1,1f x x
(hằng số)
arccosx= , x
(0) arcsin 1,1
2 2
f x
Câu 9
0,5 đ
0,5 đ
inx inx inx
1
1 24 4 4
0 0 1
s s s
,I I
x x x x x x
 
inx
1
4
0
s
lim 1
x
I
x x
inx
4 4 4
1
s 1
0 , 1,
dx
x
x x x x

hội tụ → I
2
hội tụ tuyệt đối → I
2
hội tụ
inx
4
0
s
x x

hội tụ.
115
ĐỀ 6-20173
Câu 1
+) TXĐ =
,
2
2
( ) arctan
1
x
y x
x
+)
2
2
arctan ( )
1
x
y x
x
do arctanx là hàm lẻ, y làm lẻ.
Câu 2 +)
2
ln( 2 )
ln lim
x
x
x
I
x

+)
2
2 2 ln 2
lim ln2. 2
2
x
x
x
x
I
x

Câu 3
+)
2
' ' '' '' ''
2 2 2
1 1
, , , ,
( ) ( ) ( )
x y xx yx yy
a a a
x ay x ay
x ay x ay x ay
+)
2
'' '' ''
2 2 2
1 4 4 1
4 4 0
2
( ) ( ) ( )
xx yx yy
a a
a
x ay x ay x ay
Câu 4
+)
1
2 4
2 4
2
1 1 3
(1 ) 1 0( )
2 1! 2 2 2 !
x x
y x x x x
+)
3
5 5
3
0( )
2 8
x
x x x
Câu 5
+) Đặt
cos , sin , ' : 0 2,0x y D
+)
2
2 3
2 2
2
0 0
0
1 8
4 . (4 )
3 3
I d d
Câu 6
+)
3 3 3
3
1
1 1 1
arccot arccot ( 1) ( 1)arccot
2
dx
xdx xd x x x
x
+)
3
1
4 2 3 1
6 4 6
x
Hoặc đổi biến. +) Đặt
3
2 2
1
( ) , arccotud( 1)x u dx d u I u
+)
3
3 3
2
1 1
1
4 2
(u 1) arccotu 3 1
6 4 6
du u
Câu 7
+) Chọn
2
3
0 0
( , ) 4 ; 0, 2, 0, 02, 0,05
x
f x y e y x y x y
+)
2 2
' 2 ' 2
3 3
4 2
(4 ) , (4 )
3 3
x x x
x y
y
f e e y f e y
nên
0,02 23
4 1 2.2 1
4 1, 95 2 .0, 02. .0, 05. 2, 01
3 4 3 4
e
Câu 8
+)
1 1 1 1 1 1
1 ... 1
2! 2! 3! n! (n 1)! (n 1)!
n
a
+)
lim 1
n
n
a

Câu 9
+) Xét hàm
( ) ( ), 0 1,g x f x x
và
0
ln(1 )
(0) lim 1
x
x
g
x
+) g(x) liên tục trên
0,1
nên liên tục đều trên
0,1
, suy ra f(x) liên tục đều trên
0,1
Câu 10
+)
inx inx
1 1
3 3
0 0 1 0
arctan arctan 1
, 0 : ,
2 2( s ) ( s )
x x
dx x
x
x x
 
hội tụ
+)
inx
3
3
1
2
arctan
: ,
( s )
x
x
x
x


hội tụ. Tích phân ban đầu hội tụ.
116
ĐỀ 4-20171
Câu 1: . a) +)
0 0
1 1
lim lim
3
arctan 3
x x
x x
e e
x
x
+)
0
1 1
lim
3
arctan 3
x
x
e
x
b) +)
3
, 0 ;0
2 2
2 2
ln 1 4
1
lim
3
, 0;0
lim 1 4
x y
y
x y
x y
x y
y e
+)
3
3
, 0;0 , 0;02 2 2 2
ln 1 4
4
lim lim 0
x y x y
y
y
x y x y
. Giới hạn bằng 1
Câu 2 +) Hàm
f
liên tục tại mọi điểm
x a
+)
2
lim 2, lim 7 4 .
x a x a
f x a f x a
Hàm liên tục tại
2
: 2 7 4 .x a a a
Suy ra
hoac a=-5
2
4 5 0, 1a a a
Câu 3: +) TXĐ
khi x=
3
2
3
4 4 3 4
0, 3 , 0
3
x
x f x x f
x x
+) Cực đại:
3
min
4 4 4 4
, ln
3 3 3 3
x f
Câu 4: +)
khong co tiem can dung. lim
0
3
lim 0 lim arccot
2
x x x
y
f x
x x
 
+)
2
0 0
3
arccot3
1 9
3
2
lim lim arccot lim lim 3
2 2 1
x x t t
t
t
y x x
x t
 
Tiệm cận xiên:
3
2
y x
Câu 5: +)
2 2 2
1 4 1 4
1 1 1
x x
dx dx dx
x x x
+)
2
2
1 4
arcsin 4 1
1
x
dx x x C
x
Câu 6: +)
36
36 sin 2 1
t
t
u e x
+)
Suy ra
36 36
2 cos 2 1 , 4 sin 2 1 . 9
t t
x xx t xx
u e x u e x u u
Câu 7: +) TXĐ
Diem toi han
2
3
1 2,3
2 2 6 0
1 1
. 3; 0 , 3 ;
2 6 4 0
2 2
x
y
z x y
R M M
z x y
+)
T¹i M
2 2
1
2, 2, 12 . 3; 0 : 4 0,
xx xy yy
z z z y B AC
  
không phải điểm cực trị
Tại
M cuc tieu z
2
2,3 min 2,3
1 1 33
3 ; : 8 0,
4
2 2
B AC z M
Câu 8. +)
3
2
3 2 3
1 1
0
x
x x
e
e x e
+)
3
2
0
x
e
hội tụ, nên TPSR hội tụ
Câu 9. +)
2b b b b
a a a a
b
f dx f x df x f x f x f x f x dx f x f x dx
a
 
[ ]
2
2
2 2 2
)( '( ) ) ( ) ''( ) ( ) ''( )
b b b b
a a a a
f x dx f x f x dx f x dx f x dx
117
ĐỀ 6-20171
Câu 1
+)
5 1g
+)
Tu bang suy ra1 2. 5 5 2f f g f g
Câu 2
+)
0
1 sin
1; lim
1 cos
t
t t t
Dat t x L
t
+)
2L
Câu 3 +) Điểm 0 là điểm gián đoạn
+) Giới hạn trái bằng -1; giới hạn phải bằng 0. Gián đoạn loại 1
Câu 4
+)
2
cosf x x
+)
1f
Câu 5
+)
1
2
2 1y x
+)
2 3
2 1 ...
2 8 16
x x x
y
Câu 6
+)
2
0
arctan
lim
x
x x
L
x
+)
0Lhospital L
Câu 7
+)
3
1 1 1
3 1 2
dx
x x

+)
1 5
ln
3 3
Câu 8
+)
2
1
cos arctan
1
x
x
+)
0
2
2
1
0
ln 1 ln 1 2 ln 1 2
1
1
x
dx
x x
x
x
Câu 9
+)
1
1
10
. 0
10 ln 10 1
x
x
f x x
f x
f x
có 1 nghiệm duy nhất
+) Lập bảng biến thiên của hàm số
f x
. Dễ thấy
1 0f
. Suy ra phương trình có đúng 2 nghiệm
Câu
10
+) Tương tự đề 5
+) Tích phân mang dấu dương
118
ĐỀ 8-20171
Câu 1
inx
cosx
nx/cos x
2 2
0 0
s
ln cosx 1
lim lim
2
tan 2
x x
x ta
Câu 2
4
( )x x
4 4
( ) 3 arctan( ) 3x x x
là VCB cùng bậc với
( )x
Câu 3
0 0
lim 0, lim 1 0
x x
y y
là điểm gián đoạn loại I
lim 0, lim 1
x x
y y
là điểm gián đoạn loại I
Câu 4
2
2
3
l n ( 3) (x 3) 1 ln(1 2)I x
Câu 5
1
1 2
3 2 3 2 3 2
0 0 1
3 1 3 1 3 1
dx dx dx
I I I
x x x x x x
 
3
3 2
2
1 1
3 1x x
x
khi
x 
nên I
2
hội tụ → tích phân đã cho hội tụ.
Câu 6
Chọn hàm số
2 2
0 0
( , ) , 4, 3, 0, 03, 0, 03f x y x y x y x y
2 2 ' '
4 3
3, 97 3,03 (4, 3) (4, 3) (4, 3) 5 .( 0, 03) .(0, 03) 4,994
5 5
x y
f f x f x
Câu 7
Đặt
2 2 2 2
( , ) (2 ) ( 1)x y x y x y
. Hệ PT
'
'
( )
' 2 2
0
4 2 0
0 2 2 0
0 1
x
y
x x
y y
x y
Bốn điểm tới hạn là
(1, 0),( 1, 0),(0, 1),(0, 1)
Cực đại
( 1, 0) 2f
. Cực tiểu
(0, 1) 1f
Câu 8
2 2
0 0
( 2 ) (2 cos rsin ) dr 0
D
I x y dxdy d r

Câu 9
' '
0 0
f(0 x, 0) f(0, 0 )
(0, 0) lim 0, (0, 0) lim 0
x y
x y
y
f f
x y
Cho
( , ) (0, 0)x y
theo phương của đường thẳng
2
( , )
1 2
k
y kx f x kx
k
( , ) (0,0)
lim ( , )
x y
f x y
Hàm số không liên tục tại 0.
Câu
10
cosx os
2 2(2 )
2
0 0
( 1) c ( ) ( 1)
(2 )! (2 )!
n n
n n
n n
x x
x
n n
 
(8)
2 (8 )
(0) 1 8 !
( 1) . (0) 1680
8 ! 4 ! 4 !
f
f
119
ĐỀ 2-20172
1.
*)
1 1
1 2 cos 2 1 cos 2
2 2
x x
*)
2
2 ,
3 3 6 2 3 2
k k
k x k x k
2.
*) Đặt
2
1
( ) ln( 1)
2
x x
t e e x t t
*) Vậy
2
ln( 1)
2
1
( ) ,
1
x x
f x e x
x x
3.
*)
ln(3 1) ln(3 ) ln(3 1) ln(3 )
2 sin
2 2
x x x x
A cos
*)
cos(...) 0khi x
1
ln(1 )
3
2 sin
2
x
4.
*)
3
2
'( ) 15 15
'( ) 5
'( )
3 3
y t t t
y x t
x t
t
*)
2
' 5
''( )
3 3
dy
y x
dx
t
5.
*)
ln( 2) 1x
x x
Mà
3
1
dx
x

phân kỳ * nên
3
ln( 2)x
dx
x

phân kỳ
6.
*)
2
1
1 1
.
3
n
n
i
S
n
i
n
1
1
2
0
0
1
arctan
3
3 3 6 3
dx x
x
7.
*) Xét
2 3
4
0 0
( , ) 1; 3, 0, 04, 2, 0, 02f x y x y x x y y
thì
' '
0 0 0 0 0 0 0 0
( , y ) ( , y ) ( , y ) x ( , y )
x y
A f x x y f x f x f x y
*)
2
4
' '
0 0
2 3 3 2 3 3
4 4
2 3
( , ) 16 2;f ;f
4 ( 1) 4 ( 1)
x y
x y
f x y
x y x y
2
' '
0 0 0 0
3 3
2.3 3 3.2 3
( , ) ; ( , )
16 84.2 4.2
x y
f x y f x y
3 3
2 .0, 04 .0, 02 2, 015
16 8
A
8.
*)
2 2
2 2
( )
'
'
( )
2 2 0
0
(0, 0)
0
2 3 0
x y
x
x y
y
x e
z
M
z
y e
*)
'' '' ''
( ) 6, ( ) 0,C ( ) 8
xx xy yy
A z M B z M z M
2
min
48 0
(M) Z (0,0) 1
6 0
B AC
z
A
9.
*) Đặt
sin2tdt
2
, ,
v
u
x
u xy v z t
y
khi đó
*
2u.y+v 2v.
' ' ' ' ' 2 2
1
. . v . sin . sin
x u x v x
z z u z u
y
(2xy).y+ (2
2
2
1
( ) .sin . sin ).
x x
xy
y y y
2u.x+v 2v.(-
' ' ' ' ' 2 2
2
. . v .sin .sin )
y u y v y
x
z z u z u
y
(2xy).x+ (2
2
2
2
( ) . sin . sin ).( )
x x x
xy
y y
y
10
*)
2 3
tan
cos
dx dx
I x J
cos x x
Trong đó:
x)
2 2 2 2 2 2
(sin
(1 sin ) (1 ) (1 ) (1 )
d dt dt
J
x t t t
1 1 1
( ln 1 ln 1 ) , sin
4 1 1
t t C t x
t t
120
| 1/43
| | Tải xuống

Có thể bạn quan tâm:

Preview text:

ĐỀ 4 VIỆN TOÁN ỨNG DỤNG VÀ TIN HỌC
ĐỀ THI CUỐI KÌ MÔN GIẢI TÍCH 1 – Học kì 20193
Mã HP: MI1112, Nhóm ngành 2, Thời gian: 90 phút
Chú ý: Thí sinh không được sử dụng tài liệu và giám thị phải ký xác nhận số đề vào bài thi 2 x  3, x   a
Câu 1: Tìm a để hàm số liên tục trên tập xác định : f ( ) x   4x  1, x  a  dx Câu 2: Tính nguyên hàm  4 sin x Câu 3: Tính giới hạn  3 lim x e ln x x 0
Câu 4: Tính tích phân suy rộng x xe dx   cos x Câu 5: Cho hàm số 2 f (x)  (1  tan t )dt  . Tính f '( / 2) 0 2   , x x   2 Câu 6: Cho hàm số f ( ) x   . Tính f '(2) (2  ) x (3  ) x , x  2  x arctantdt 
Câu 7: Tính giới hạn sau: 0 lim x 2 x  2x 2 Câu 8: Cho hàm số ( ) x f x  e . Tính (997) f (0) x  1 Câu 9: Cho hai hàm số ( ) x f x  x  e và g(x)  . Tính 2x 1 1 1 1 ( f  g  g  f)(0) 1 f (x) Câu 10 : Cho f ( )
x là hàm liên tục trên [0 ;1]. Tính dx 0 f (x) f (1 x) 4
ĐỀ 5 VIỆN TOÁN ỨNG DỤNG VÀ TIN HỌC
ĐỀ THI CUỐI KÌ MÔN GIẢI TÍCH 1 – Học kì 20193
Mã HP: MI1112, Nhóm ngành 2, Thời gian: 90 phút
Chú ý: Thí sinh không được sử dụng tài liệu và giám thị phải ký xác nhận số đề vào bài thi
Câu 1: So sánh hai vô cùng bé sau khi x  0 : f ( ) x  x sin x và 2 g( ) x  ln(1 x ) Câu 2: Tính giới hạn sin lim x x x 0  2  ln(1  x )  , x  0 Câu 3: Cho f ( ) x    | x | . Tính f '(0 ). 0, x  0  2 dx Câu 4: Tính tích phân  0 2 x  4 x
Câu 5: Tìm tiệm cận của đồ thị hàm số y  2 x  1  dx
Câu 6: Tính tích phân suy rộng sau:  2 0 x  2x  2 xarcsin y  y arcsin x
Câu 7: Tính giới hạn sau: lim 2 2 x 0  x  y y0
Câu 8: Tính tích phân kép: 2 2 x y dxdy  với D   2 2 2 ( , x )
y   : x  y  1, x  0, y   0 D 2 2  u  u Câu 9: Cho 2 2 u  x  y . Tính  . 2 2 x y Câu 10: Cho 3 f ( ) x  sin(x ). Tính (10) f (0) 5
ĐỀ 1 VIỆN TOÁN ỨNG DỤNG VÀ TIN HỌC
ĐỀ THI CUỐI KÌ MÔN GIẢI TÍCH 1 – Học kì 20191
Mã HP: MI1111, Nhóm ngành 1, Thời gian: 90 phút
Chú ý: Thí sinh không được sử dụng tài liệu và giám thị phải ký xác nhận số đề vào bài thi 1  ln(1  ) x x  3 x y Câu 1: Tìm a) lim   lim x 0  x   6 2 ( , x y) (  0;0) 2 x  3 y
Câu 2: Tính gần đúng nhờ vi phân 2 2 A  2, 02  3, 04  3 2 x
Câu 3: Chứng minh rằng: cos x  1 ,x  0 2
Câu 4: Tính thể tích khối tròn xoay khi quay hình giới hạn bởi các đường 2
y  x  3x và y  0 quanh trục Oy một vòng 1   Câu 5: Tính 2 2
 2x  3 | 1  x | dx      Câu 6: Hàm số 3 f ( )
x  x  x có hàm ngược là y  ( g ) x . Tính g '(2). 2 2  z  z 3 z  1 Câu 7: Tính P    với z  2 2 x  y  x x  2 2 3 (x  y )
Câu 8: Không khí được bơm vào một quả bóng bay hình cầu với tốc độ 3
100cm / s .Tính tốc độ tăng lên của
bán kính quả bóng khi bán kính quả bóng bằng 50cm.  Câu 9. Tính 2 cot xdx  0
Thang điểm : Câu 1: 2 điểm . Các câu còn lại mỗi câu 1 điểm 6
ĐỀ 2 VIỆN TOÁN ỨNG DỤNG VÀ TIN HỌC
ĐỀ THI CUỐI KÌ MÔN GIẢI TÍCH 1 – Học kì 20191
Mã HP: MI1111, Nhóm ngành 1, Thời gian: 90 phút
Chú ý: Thí sinh không được sử dụng tài liệu và giám thị phải ký xác nhận số đề vào bài thi 1 x  e  1 x  4 xy Câu 1: Tìm a) lim   lim x 0  x   2 8 (x,y ) (  0;0) 4 x  3 y
Câu 2: Tính gần đúng nhờ vi phân 2 2 A  4, 03  2, 02  5 2 Câu 3: Chứng minh rằng: x x e  1 x  ,x  0 2
Câu 4: Tính thể tích khối tròn xoay khi quay hình giới hạn bởi các đường 2
y  x  4x và y  0 quanh trục Oy một vòng 1    Câu 5: Tính 2 2
 4  3x  | 1  x | d  x      Câu 6: Hàm số 5 f ( )
x  x  x có hàm ngược là y  ( g ) x . Tính g '(2). 2 2  z  z 5 z  1 Câu 7: Tính P    với z  2 2 x  y  y y  2 2 5 (x  y )
Câu 8: Không khí được bơm vào một quả bóng bay hình cầu với tốc độ 3
200cm / s .Tính tốc độ tăng lên của
bán kính quả bóng khi bán kính quả bóng bằng 60cm.  Câu 9. Tính 2 tan xdx  0
Thang điểm : Câu 1: 2 điểm . Các câu còn lại mỗi câu 1 điểm 7
ĐỀ 3 VIỆN TOÁN ỨNG DỤNG VÀ TIN HỌC
ĐỀ THI CUỐI KÌ MÔN GIẢI TÍCH 1 – Học kì 20191
Mã HP: MI1111, Nhóm ngành 1, Thời gian: 90 phút
Chú ý: Thí sinh không được sử dụng tài liệu và giám thị phải ký xác nhận số đề vào bài thi x   2 2 y ln x Câu 1. Tính a)lim ) b lim x   sin x 2 2 ( , x y) (  1;0) (x  1)  y Câu 2: Phương trình 3 5
x  3xy  y  5  0 xác định hàm ẩn y  ( y ) x . Tính y '(1)  2x 
Câu 3: Tính đạo hàm của hàm số y  arctan , x     1 2  1  x 
Câu 4: Tìm khai triển Maclaurin của y  ln(1  2 ) x đến 3 x x
Câu 5: Tìm các tiệm cận của đồ thị hàm số y  x e  1  dx Câu 6: Tính a) tan(2x)dx  ) b  2 0 ( x  3)( x  x  1) Câu 7: Quay đường 3 2 2 3
x  y  4 quanh trục Ox một vòng. Tính diện tích mặt tròn xoay được sinh ra.
Câu 8: Tìm cực trị của hàm số 3 3 2 z  x  y  (x  y)
Thang điểm: Câu 1: 2 điểm . Câu 6: 2 điểm.
Các câu còn lại mỗi câu 1 điểm. 8
ĐỀ 4 VIỆN TOÁN ỨNG DỤNG VÀ TIN HỌC
ĐỀ THI CUỐI KÌ MÔN GIẢI TÍCH 1 – Học kì 20191
Mã HP: MI1111, Nhóm ngành 1, Thời gian: 90 phút
Chú ý: Thí sinh không được sử dụng tài liệu và giám thị phải ký xác nhận số đề vào bài thi 2x   3 2 x ln y Câu 1. Tính a) lim ) b lim 2 2  x   cos x ( , x y) (1;0) x  ( y  1) 2 Câu 2: Phương trình 4 3 5
x  3xy  3y  8  0 xác định hàm ẩn y  ( y x). Tính y '(1)  2x 
Câu 3: Tính đạo hàm của hàm số y  arcsin , x    1 2  1  x 
Câu 4: Tìm khai triển Maclaurin của y  ln(1  3 ) x đến 3 x x
Câu 5: Tìm các tiệm cận của đồ thị hàm số y  2 x e  1  dx Câu 6: Tính a) cot(3x)dx  ) b  2 0 ( x  4)( x  x  1) Câu 7: Quay đường 3 2 3 2
x  y  9 quanh trục Ox một vòng. Tính diện tích mặt tròn xoay được sinh ra.
Câu 8: Tìm cực trị của hàm số 3 3 2 z  x  y  (x  y)
Thang điểm: Câu 1: 2 điểm . Câu 6: 2 điểm.
Các câu còn lại mỗi câu 1 điểm. 9
ĐỀ 5 VIỆN TOÁN ỨNG DỤNG VÀ TIN HỌC
ĐỀ THI CUỐI KÌ MÔN GIẢI TÍCH 1 – Học kì 20191
Mã HP: MI1112, Nhóm ngành 2, Thời gian: 90 phút
Chú ý: Thí sinh không được sử dụng tài liệu và giám thị phải ký xác nhận số đề vào bài thi  2 1  Câu 1:Tìm giới hạn lim    2 0 x x  e  1 x  3 x  t   t
Câu 2: Cho hàm số y  f ( ) x xác định bởi  .Tính f '( ) x , f ' ( ) x 2 4 y  2t  3t 
Câu 3: Tìm cực trị của hàm số 3 2 y  ( x x  3)  2  2
Câu 4: Chứng mình rằng với mọi x  0 ta có ln 1     x 2  x   6 6 6  1  2  ...  n 
Câu 5: Tìm giới hạn lim  7 n  n 
Câu 6: Tính các tích phân sau 3 /  2 sin xdx 3 a) ) b arccot 3  xd . x  0 sin x cos x 2  dx
Câu 7: Tính tích phân suy rộng:  4 1 ( x 3x  2)
Câu 8: Tính diện tích mặt tròn xoay tạo bởi đường tròn 2 2
x  (y  2)  1 quay quanh trục Ox  x arctan 3x khi x  0 Câu 9: Cho hàm số : f ( ) x   3 x ae  bsin x khi x  0 
Tìm a và b để hàm số f ( ) x khả vi tại x  0 10
ĐỀ 6 VIỆN TOÁN ỨNG DỤNG VÀ TIN HỌC
ĐỀ THI CUỐI KÌ MÔN GIẢI TÍCH 1 – Học kì 20191
Mã HP: MI1112, Nhóm ngành 2, Thời gian: 90 phút
Chú ý: Thí sinh không được sử dụng tài liệu và giám thị phải ký xác nhận số đề vào bài thi  1 3  Câu 1:Tìm giới hạn lim    3 0 x x  x e  1 3  x  3t  t
Câu 2: Cho hàm số y  f ( ) x xác định bởi  .Tính f '( ) x , f ' ( ) x 5 y  5t  t 
Câu 3: Tìm cực trị của hàm số 3 2 y  x ( x  3)  x 1  2
Câu 4: Chứng mình rằng với mọi x  1 ta có ln    x  1 x  1   5 5 5  1  2  ...  n 
Câu 5: Tìm giới hạn lim  6 n  n 
Câu 6: Tính các tích phân sau 3 /  2 cos xdx 2 a) ) b arctan 2  xd . x  0 sin x cos x 1  dx
Câu 7: Tính tích phân suy rộng:  4 1 ( x 2x  1)
Câu 8: Tính diện tích mặt tròn xoay tạo bởi đường tròn 2 2
x  (y  2)  1 quay quanh trục Ox  x sin 2 x khi x   0 Câu 9: Cho hàm số : f ( ) x   x a2  b arctan x khi x   0 
Tìm a và b để hàm số f ( ) x khả vi tại x  0 11
ĐỀ 7 VIỆN TOÁN ỨNG DỤNG VÀ TIN HỌC
ĐỀ THI CUỐI KÌ MÔN GIẢI TÍCH 1 – Học kì 20191
Mã HP: MI1113, Nhóm ngành 3, Thời gian: 90 phút
Chú ý: Thí sinh không được sử dụng tài liệu và giám thị phải ký xác nhận số đề vào bài thi cos x  x Câu 1: Tính lim x x  sin x  1
Câu 2: Dùng vi phân tính gần đúng 3 7, 988 
Câu 3: Tính hoặc xét sự phân kỳ  x e xdx  1  Câu 4; Tính 3 x e sin(2x)dx  0 2 Câu 5: Cho xy z  e . Tính 2 d z 2 2 x y
Câu 6: Tìm giá trị lớn nhất, bé nhất của hàm số 2 2
z  3x  4 y trong miền đóng   1 4 3 Câu 7: Tính 2 2 1  x  y dxdy  , ở đó 2 2
D : x  y  1, x  0, y  0 D 1 2t
Câu 8: Tìm các tiệm cận của đồ thị hàm số x  , y  3 3 t  8 t  8   /  2 arcsin x Câu 9: Tính 18 1   sin xdx    /2   | |  1 x  e   y ar  ccot , x  0
Câu 10. Tính z ' (x; y ),biết z  x  x 0  , x  0  12
ĐỀ 8 VIỆN TOÁN ỨNG DỤNG VÀ TIN HỌC
ĐỀ THI CUỐI KÌ MÔN GIẢI TÍCH 1 – Học kì 20191
Mã HP: MI1113, Nhóm ngành 3, Thời gian: 90 phút
Chú ý: Thí sinh không được sử dụng tài liệu và giám thị phải ký xác nhận số đề vào bài thi cos x  x Câu 1: Tính lim x x  sin x  1
Câu 2: Dùng vi phân tính gần đúng 3 8, 012 
Câu 3: Tính hoặc xét sự phân kỳ x e xdx  1  Câu 4; Tính 3x e cos(2x)dx  0 2 Câu 5: Cho x y z  e . Tính 2 d z 2 2 x y
Câu 6: Tìm giá trị lớn nhất, bé nhất của hàm số 2 2
z  4x  3y trong miền đóng   1 3 4 Câu 7: Tính 2 2 1  x  y dxdy  , ở đó 2 2
D : x  y  1 ,x  0, y  0 D 1 2t
Câu 8: Tìm các tiệm cận của đồ thị hàm số x  , y  3 3 8  t 8  t   /  2 arcsin x Câu 9: Tính 18 1   sin xdx    /2   | |  1 x  e   y ar  ccot , x  0
Câu 10. Tính z ' (x; y ),biết z  x  x 0  , x  0  13
ĐỀ 1 VIỆN TOÁN ỨNG DỤNG VÀ TIN HỌC
ĐỀ THI CUỐI KÌ MÔN GIẢI TÍCH 1 – Học kì 20181
Mã HP: MI1111, Nhóm ngành 1, Thời gian: 90 phút
Chú ý: Thí sinh không được sử dụng tài liệu và giám thị phải ký xác nhận số đề vào bài thi x  sin x Câu 1. Tính giới hạn lim x x  arctan x 1 Câu 2. Cho f x ( ) 
Tính đạo hàm cấp cao f 50(x) x2  2x  1 5 Câu 3. Tính tích phân x2 9 dx  0  2 3 sin x  4 cos x Câu 4. Tính tích phân dx  4 sin x  3 cos x 0 s in 3x Câu 5. Tính giới hạn lim x y  2 sin x  2 ( , ) (0,0) sin y
Câu 6. Chỉ số Shannon đo lường mức độ đa dạng của một hệ sinh thái, trong trường hợp hai loài, được xác định
theo công thức: H  x ln x  y ln y x  0, y   0
ở đó x, y là tỉ lệ các loài, thỏa mãn  x  y   1
Tìm giá trị lớn nhất của H. x2 x4  
Câu 7. Chứng minh rằng cosx  1-  , x   0,  2 24  2  z
Câu 8. Cho z  f (x, y)là hàm số ẩn xác định bởi phương trình y
z  xe  0 . Ứng dụng vi phân, tính gần đúng f (0, 02;0,99)  1 (2n  1)! Câu 9. Tính lim  n  n   n n (  1)!   
Câu 10. Xét sự hội tụ, phân kì của tích phân suy rộng  ln(1  2x) dx 0 x x 14
ĐỀ 2 VIỆN TOÁN ỨNG DỤNG VÀ TIN HỌC
ĐỀ THI CUỐI KÌ MÔN GIẢI TÍCH 1 – Học kì 20181
Mã HP: MI1111, Nhóm ngành 1, Thời gian: 90 phút
Chú ý: Thí sinh không được sử dụng tài liệu và giám thị phải ký xác nhận số đề vào bài thi x  cos x Câu 1. Tính giới hạn lim x x  arccot x 1 Câu 2. Cho f (x) 
Tính đạo hàm cấp cao f 50(x) 2 x  2x  1 5 Câu 3. Tính tích phân 2 x  16 dx  0  2 5 sin x  6 cos x Câu 4. Tính tích phân dx  6 sin x  5 cos x 0 s in 3y Câu 5. Tính giới hạn lim 2 2 ( , x y) (  0,0) sin x  sin y
Câu 6. Chỉ số Shannon đo lường mức độ đa dạng của một hệ sinh thái, trong trường hợp hai loài, được xác định
theo công thức: H  x ln x  y ln y x  0, y   0
ở đó x, y là tỉ lệ các loài, thỏa mãn  x  y   1
Tìm giá trị lớn nhất của H. 3 5 x x  
Câu 7. Chứng minh rằng sin x  x -  , x    0,  6 120  2  z
Câu 8. Cho z  f (x, y)là hàm số ẩn xác định bởi phương trình y
z  ye  0 . Ứng dụng vi phân, tính gần đúng f (0,99; 0, 02)  1 (2 ) n !  Câu 9. Tính lim n   n   n n !   
Câu 10. Xét sự hội tụ, phân kì của tích phân suy rộng  ln(1 3x) dx  0 x x 15
ĐỀ 3 VIỆN TOÁN ỨNG DỤNG VÀ TIN HỌC
ĐỀ THI CUỐI KÌ MÔN GIẢI TÍCH 1 – Học kì 20181
Mã HP: MI1111, Nhóm ngành 1, Thời gian: 90 phút
Chú ý: Thí sinh không được sử dụng tài liệu và giám thị phải ký xác nhận số đề vào bài thi 1
Câu 1. (1 đ). Tính giới hạn x lim(cos x  sin x) x 0
Câu 2. (1 đ). Tìm tiệm cận xiên của đồ thị hàm số y  a x rc cot x  4
Câu 3. (1 đ). Tính tích phân 3 tan xdx  0 1
Câu 4. (1 đ). Tính tích phân ln(x2  x  1 d ) x  0
Câu 5. (1 đ). Tìm các cực trị của hàm số z  x  y  x 2  y 2 4( )   x 2
 yarctan   , neu y 
Câu 6. (2 đ). Cho hàm số f x y  0 ( , )  y   0, neu y   0
a) Xét tính liên tục của f (x, y)tại điểm A(1,0) b) Tính f '(1, 0) y x  y (tanx+tany) Câu 7. (1 đ). Cho 0 2 2 2  2 x sin x
Câu 8. (1 đ). Tính tích phân dx  x 1  3  2
Câu 9. (1đ) Xét sự hội tụ, phân kì của tích phân suy rộng  arctan xdx  0 x x  1  cos x 16
ĐỀ 4 VIỆN TOÁN ỨNG DỤNG VÀ TIN HỌC
ĐỀ THI CUỐI KÌ MÔN GIẢI TÍCH 1 – Học kì 20181
Mã HP: MI1111, Nhóm ngành 1, Thời gian: 90 phút
Chú ý: Thí sinh không được sử dụng tài liệu và giám thị phải ký xác nhận số đề vào bài thi 1
Câu 1. (1 đ). Tính giới hạn x lim(cos x  sin x) x0
Câu 2. (1 đ). Tìm tiệm cận xiên của đồ thị hàm số y  arc x tanx  4
Câu 3. (1 đ). Tính tích phân 4 tan xdx  0 1
Câu 4. (1 đ). Tính tích phân ln(x2  x  1 d ) x  0
Câu 5. (1 đ). Tìm các cực trị của hàm số z   x  y 2  x 2 4(y )   y 2  xarctan   , ne u x 
Câu 6. (2 đ). Cho hàm số f x y  0 ( , )  x   0, neu x   0
a) Xét tính liên tục của f (x, y)tại điểm B(0,1) b) Tính f '(0,1) y x  y x+coty) Câu 7. (1 đ). Cho 0 cot cot 2 2 2  2 x sin x
Câu 8. (1 đ). Tính tích phân dx  x 1  2  2
Câu 9. (1đ) Xét sự hội tụ, phân kì của tích phân suy rộng  arctan xdx  0 x x  x  sinx 17
ĐỀ 5 VIỆN TOÁN ỨNG DỤNG VÀ TIN HỌC
ĐỀ THI CUỐI KÌ MÔN GIẢI TÍCH 1 – Học kì 20181
Mã HP: MI1112, Nhóm ngành 2, Thời gian: 90 phút
Chú ý: Thí sinh không được sử dụng tài liệu và giám thị phải ký xác nhận số đề vào bài thi
Câu 1. Tìm a để hàm số sau liên tục tại điểm x = 1 3 a  x khi x 1 f( x)   arccos x khi 0  x   1
Câu 2. Tìm hàm ngược của hàm số x x y   2  2
Câu 3. Cho hai hàm số f x  x3 g x  x2 ( ) ; ( ) , 1  x  3 f '(c) f (3) f  ( 1) Tìm số c   ( 1; 3)sao cho  g '(c) g(3)  g  ( 1)
Điều này có mâu thuẫn với định lý Cauchy không? Giải thích?
Câu 4. Cho hai hàm số f(x), g(x): R  R thỏa mãn f (x)  g(x) với mọi x. Chứng minh rằng nếu f (x) là
hàm đơn điệu tăng thì f ( f (x))  g(g(x))  3 x 1 Câu 5. Tính tích phân dx  x (  1) x2 (  0 1) 1  1  2 sinx  Câu 6. Tính giới hạn lim ln 3   x0 x 1  sin 2 x   
Câu 7. Tính độ dài cung y  ln(cos x), 0  x  3
Câu 8. Tìm tiệm cận xiên của đường cong t3 t2 x  ; y  1 t 3 1  t Câu 9. Tính giới hạn  1 1 2 n       1 lim .... 
x n  1 4n2  1 4 n2  2 2 4 n2  (n 2    1) 
Câu 10. Cho hàm số f(x) lồi, khả tích trên đoạn a, b   .CMR: b 1 f (a) f (b) f( ) x dx   b  a a 2 18
ĐỀ 6 VIỆN TOÁN ỨNG DỤNG VÀ TIN HỌC
ĐỀ THI CUỐI KÌ MÔN GIẢI TÍCH 1 – Học kì 20181
Mã HP: MI1112, Nhóm ngành 2, Thời gian: 90 phút
Chú ý: Thí sinh không được sử dụng tài liệu và giám thị phải ký xác nhận số đề vào bài thi
Câu 1. Tìm a để hàm số sau liên tục tại điểm x = 1  3  a  x khi x  1 f( ) x   arccos x khi 0  x  1 
Câu 2. Tìm hàm ngược của hàm số 3x 3 x y    Câu 3. Cho hai hàm số 3 2 f( ) x  x ; ( g ) x  x , 3   x  1 f '( ) c ( f 1)  f( 3  ) Tìm số c ( 3  ;1)sao cho  g '( ) c ( g 1)  ( g 3  )
Điều này có mâu thuẫn với định lý Cauchy không? Giải thích?
Câu 4. Cho hai hàm số f(x), g(x): R  R thỏa mãn f (x)  g(x) với mọi x. Chứng minh rằng nếu f (x) là
hàm đơn điệu tăng thì f ( f (x))  g(g(x))  x  3 Câu 5. Tính tích phân dx  2 x  x  0 ( 1)( 1) 1  1  2 sin x  Câu 6. Tính giới hạn lim ln   3 x0 x 1   sin 2x   
Câu 7. Tính độ dài cung y  ln(sin ), x  x  6 2
Câu 8. Tìm tiệm cận xiên của đường cong 2 3 t 3t x  ; y  3 1 t 1 t Câu 9. Tính giới hạn   1 1 2 n 1 lim    ....   x n   2 2 2 2 2 1 4n  1 4n  2 4n  (n  1)   
Câu 10. Cho hàm số f(x) lõm, khả tích trên đoạn a, b    .CMR: b 1 f (a) f (b) f( ) x dx   b  a a 2 19
PHẦN 1: TỔNG HỢP ĐỀ THI CUỐI KỲ CÁC NĂM
ĐỀ 7 VIỆN TOÁN ỨNG DỤNG VÀ TIN HỌC
ĐỀ THI CUỐI KÌ MÔN GIẢI TÍCH 1 – Học kì 20181
Mã HP: MI1113, Nhóm ngành 3, Thời gian: 90 phút
Chú ý: Thí sinh không được sử dụng tài liệu và giám thị phải ký xác nhận số đề vào bài thi x Câu 1. Tính dx  x2  3x  2  dx
Câu 2. Xét sự hội tụ, phân kì của tích phân suy rộng x3 1  x  1  x  1 x2 y2
Câu 3. Tính thể tích vật tròn xoay tạo bởi elip:   1 quay quanh trục Ox. 4 9 cos x - cos 4 x Câu 4. Tính lim x x2 0 x
Câu 5. Tìm và phân loại điểm gián đoạn của hàm số y  x3  x2 2  x  2
Câu 6. Cho hàm số z  x3 y2  x2 y2  3 xy  2 . Tính dz(1,1)
Câu 7. Tìm cực trị của hàm số z  xy  
(  x  y)(2x  3y);là tham số thực   x 2  y 2 1   4
Câu 8. Tính tích phân kép x  y dxdy  ( ) ; với D :  . x  y  3x D 
Câu 9. Tồn tại hay không hàm số f sao cho f (1)   f 
( 1), f (0)  0 và f ' (x)   0 x  ( 2,2) Câu 10. Cho hàm số z  x 
x2  y2  x2  y2 2018  x2  y2 2019 sin( ) ( ) 100( )    . 2 z z Chứng minh x  xy  zy y x 20
PHẦN 1: TỔNG HỢP ĐỀ THI CUỐI KỲ CÁC NĂM
ĐỀ 8 VIỆN TOÁN ỨNG DỤNG VÀ TIN HỌC
ĐỀ THI CUỐI KÌ MÔN GIẢI TÍCH 1 – Học kì 20181
Mã HP: MI1113, Nhóm ngành 3, Thời gian: 90 phút
Chú ý: Thí sinh không được sử dụng tài liệu và giám thị phải ký xác nhận số đề vào bài thi x Câu 1. Tính dx  x2  x 5  6  dx
Câu 2. Xét sự hội tụ, phân kì của tích phân suy rộng x3 1  x  1  x  1 x2 y2
Câu 3. Tính thể tích vật tròn xoay tạo bởi elip:   1 quay quanh trục Ox. 9 4 cos 4 x- cos x Câu 4. Tính lim x x2 0 x
Câu 5. Tìm và phân loại điểm gián đoạn của hàm số y  x3  x2 2  x  2
Câu 6. Cho hàm số z  x2 y3  x2 y2  3xy  2 . Tính dz(1,1)
Câu 7. Tìm cực trị của hàm số  =  + (− −  − )(2 + 3);  là tham số thực   x 2  y 2 1  4 
Câu 8. Tính tích phân kép x  y dxdy  ( ) ; với D :  x .  y  x D   3
Câu 9. Tồn tại hay không hàm số f sao cho f (1)   f 
( 1), f (0)  0 và f ' ( x)   0 x  ( 2, 2) Câu 10. Cho hàm số z  x 
x2  y2  x2  y2 2018  x2  y2 2019 sin( ) ( ) 100( )    z z Chứng minh x2  xy  zy y x 21
PHẦN 1: TỔNG HỢP ĐỀ THI CUỐI KỲ CÁC NĂM
ĐỀ 1 VIỆN TOÁN ỨNG DỤNG VÀ TIN HỌC
ĐỀ THI CUỐI KÌ MÔN GIẢI TÍCH 1 – Học kì 20173
Mã HP: MI1111, Nhóm ngành 1, Thời gian: 90 phút
Chú ý: Thí sinh không được sử dụng tài liệu và giám thị phải ký xác nhận số đề vào bài thi
Câu 1. Tính giới hạn lim(1  cos x tanx ) x0 1 Câu 2. Cho f x ( ) 
Tính đạo hàm cấp cao f 50(x) 1  x x2 arctan x
Câu 3. Tính các tiệm cận của đồ thị hàm số y  1 x2 3 x
Câu 4. Tính tích phân arccos dx  2 0 y   x2 4
Câu 5. Tính diện tích mặt tròn xoay tạo bởi khi quay đường cong  quanh trục Ox một vòng. 1  x   1 y
Câu 6. Cho hàm số z  arccot . Tính các vi phân dz d z 2 , x
Câu 7. Tìm các cực trị của hàm số y 3 3y z  x 3 e  x  e x3 Câu 8. Tính giới hạn lim x y  x2  y2 ( , ) (0,0) x (arctan t) dt  3 Câu 9. Tính giới hạn 0 lim x 3  x 2
Câu 10. Xét sự hội tụ, phân kì của tích phân suy rộng  x sin x dx  3 x10 0 22
PHẦN 1: TỔNG HỢP ĐỀ THI CUỐI KỲ CÁC NĂM
ĐỀ 2 VIỆN TOÁN ỨNG DỤNG VÀ TIN HỌC
ĐỀ THI CUỐI KÌ MÔN GIẢI TÍCH 1 – Học kì 20173
Mã HP: MI1111, Nhóm ngành 1, Thời gian: 90 phút
Chú ý: Thí sinh không được sử dụng tài liệu và giám thị phải ký xác nhận số đề vào bài thi
Câu 1. Tính giới hạn lim(1  cos x sinx ) x0
Câu 2. Cho f (x)  1  x Tính đạo hàm cấp cao f 50(x) x2 arccot x
Câu 3. Tính các tiệm cận của đồ thị hàm số y  1  x2 3 x
Câu 4. Tính tích phân arcsin dx  2 0 y   x2 9
Câu 5. Tính diện tích mặt tròn xoay tạo bởi khi quay đường cong  quanh trục Ox một vòng. 2  x   2 x
Câu 6. Cho hàm số z  arctan . Tính các vi phân dz d z 2 , y
Câu 7. Tìm các cực trị của hàm số x 3 3 x z  3ye  y  e x5 Câu 8. Tính giới hạn lim x y  x4  y4 ( , ) (0,0) x (arctan t) dt  4 Câu 9. Tính giới hạn 0 lim x 2  x2
Câu 10. Xét sự hội tụ, phân kì của tích phân suy rộng  x  sin x dx  x7 0 23
PHẦN 1: TỔNG HỢP ĐỀ THI CUỐI KỲ CÁC NĂM
ĐỀ 3 VIỆN TOÁN ỨNG DỤNG VÀ TIN HỌC
ĐỀ THI CUỐI KÌ MÔN GIẢI TÍCH 1 – Học kì 20173
Mã HP: MI1112, Nhóm ngành 2, Thời gian: 90 phút
Chú ý: Thí sinh không được sử dụng tài liệu và giám thị phải ký xác nhận số đề vào bài thi
Câu 1. (2đ) Tính các giới hạn: ln(1  x)  x ln(1  2 tan x) a) lim b) lim x o x2 x x0 e  o c sx
Câu 2. (1đ) Tìm và phân loại điểm gián đoạn của hàm số x y  1 arctan( e ) x  1
Câu 3. (1đ). Cho f( x)  ln
. Tính vi phân cấp cao d(10) f x ( ) x  2
Câu 4. (1đ). Tìm tiệm cận xiên của đồ thị hàm số y  x  arc cot x s inx  o c sx
Câu 5. (1đ). Tính tích phân dx  2 sin x 1
Câu 6. (1đ). Tính tích phân arc cot xdx  0 1
Câu 7. (1đ). Tính độ dài của cung x  x y  e ( e ),x [0, ln 2] 2
Câu 8. (1đ). Chứng minh rằng arctan x arccot x    với mọi  ∈ ℝ 2
Câu 9. (1đ). Xét sự hội tụ, phân kì của tích phân suy rộng  sin xdx  x  x3 0 24
PHẦN 1: TỔNG HỢP ĐỀ THI CUỐI KỲ CÁC NĂM
ĐỀ 4 VIỆN TOÁN ỨNG DỤNG VÀ TIN HỌC
ĐỀ THI CUỐI KÌ MÔN GIẢI TÍCH 1 – Học kì 20173
Mã HP: MI1112, Nhóm ngành 2, Thời gian: 90 phút
Chú ý: Thí sinh không được sử dụng tài liệu và giám thị phải ký xác nhận số đề vào bài thi
Câu 1. (2đ) Tính các giới hạn: arctan x  x ln(1  3 sin x) a) lim b) lim x o x3 x x0 e cosx
Câu 2. (1đ) Tìm và phân loại điểm gián đoạn của hàm số x y  1 arccot(e ) x  2
Câu 3. (1đ). Cho f( x)  ln
. Tính vi phân cấp cao d(10) f x ( ) x  1
Câu 4. (1đ). Tìm tiệm cận xiên của đồ thị hàm số y  x  arctan x s inx  o c sx
Câu 5. (1đ). Tính tích phân dx  2 cos x 1
Câu 6. (1đ). Tính tích phân arctan xdx  0  x2 1 
Câu 7. (1đ). Tính độ dài của cung y    ln x , x  1,2   2  2 
Câu 8. (1đ). Chứng minh rằng arcsin x arccos x   
với mọi x   1,  1 2  
Câu 9. (1đ). Xét sự hội tụ, phân kì của tích phân suy rộng  sin xdx  x  x4 0 25
PHẦN 1: TỔNG HỢP ĐỀ THI CUỐI KỲ CÁC NĂM
ĐỀ 5 VIỆN TOÁN ỨNG DỤNG VÀ TIN HỌC
ĐỀ THI CUỐI KÌ MÔN GIẢI TÍCH 1 – Học kì 20173
Mã HP: MI1113, Nhóm ngành 3, Thời gian: 90 phút
Chú ý: Thí sinh không được sử dụng tài liệu và giám thị phải ký xác nhận số đề vào bài thi 2 x
Câu 1. (1đ). Xét tính chẵn, lẻ của hàm số y  arcsin 1  x2 1
Câu 2. (1 đ) Tính giới hạn 2 x x lim(x  2 ) x0
Câu 3. (1đ). Tính số thực α sao cho hàm số ( x, y)  ln( x  ay) thỏa mãn phương trình   2   2   2  4  4  0 x2 xy y2 x
Câu 4. (1đ). Viết khai triển Maclaurin đến bậc 5 của hàm số y   x2 1
Câu 5. (1đ). Tính tích phân kép  x  y dxdy  2 2 4
; trong đó D là miền x2  y 2  4, x  0 D 3
Câu 6. (1đ). Tính tích phân xác định arctan xdx  . 1
Câu 7. (1đ). Sử dụng vi phân toàn phần tính gần đúng: 3 e0,02 4  2 1, 95
Câu 8. (1đ). Tính giới hạn của dãy số 1 2 n a   ...  n 2 ! 3! (n 1)!
Câu 9. (1đ). Xét tính liên tục đều trên 0,  1 của hàm số 1  cos2x f x ( )  x2
Câu 10. (1đ) Xét sự hội tụ của tích phân  arctan x dx  ( x  ln(1  x 3 0 )) 26
PHẦN 1: TỔNG HỢP ĐỀ THI CUỐI KỲ CÁC NĂM
ĐỀ 6 VIỆN TOÁN ỨNG DỤNG VÀ TIN HỌC
ĐỀ THI CUỐI KÌ MÔN GIẢI TÍCH 1 – Học kì 20173
Mã HP: MI1113, Nhóm ngành 3, Thời gian: 90 phút
Chú ý: Thí sinh không được sử dụng tài liệu và giám thị phải ký xác nhận số đề vào bài thi 2 x
Câu 1. (1đ). Xét tính chẵn, lẻ của hàm số y  arctan 1  x2 1
Câu 2. (1 đ) Tính giới hạn 2 x x lim( x  2 ) x
Câu 3. (1đ). Tính số thực α sao cho hàm số ( x, y)  ln( x  ay) thỏa mãn phương trình 2 2 2  4  4  0 x  2 x  y  y  2 x
Câu 4. (1đ). Viết khai triển Maclaurin đến bậc 5 của hàm số y   x2 1
Câu 5. (1đ). Tính tích phân kép  x  y dxdy  2 2 4
; trong đó D là miền x2  y 2  4, y  0 D 3
Câu 6. (1đ). Tính tích phân xác định arccot xdx  . 1
Câu 7. (1đ). Sử dụng vi phân toàn phần tính gần đúng: 3 4 e0,02  2 2, 05
Câu 8. (1đ). Tính giới hạn của dãy số 1 2 n a    ...  . n 2 ! 3! (n  1)!
Câu 9. (1đ). Xét tính liên tục đều trên 0,  1 của hàm số ln(1+x) f x ( )  x
Câu 10. (1đ) Xét sự hội tụ của tích phân  arctan x dx  (x  s inx 3 0 ) 27
PHẦN 1: TỔNG HỢP ĐỀ THI CUỐI KỲ CÁC NĂM
ĐỀ 1 VIỆN TOÁN ỨNG DỤNG VÀ TIN HỌC
ĐỀ THI CUỐI KÌ MÔN GIẢI TÍCH 1 – Học kì 20172
Mã HP: MI1111, Nhóm ngành 1, Thời gian: 90 phút
Chú ý: Thí sinh không được sử dụng tài liệu và giám thị phải ký xác nhận số đề vào bài thi
Câu 1. Tìm miền xác định của hàm y  arccos(2 sin2x)  1  Câu 2. Tìm f(x) biết x  x x f e (  e )    e  2 
Câu 3. Tìm lim sin(ln(2  x 1)) sin(ln(2 x)    ) x x  t3  t  2
Câu 4. Cho hàm số y  y(x)xác định bởi  9 . Tính y '(x), y ' (x)  y  t4  3t2  4  ln(x  2)
Câu 5. Xét sự hội tụ phân kỳ của tích phân dx  x 5  n n n  Câu 6. Tìm giới hạn lim   ...  2 2 2 2 2 2  n  n  1 n  2 n  n 
Câu 7. Dùng vi phân toàn phần của hàm số để tính giá trị gần đúng của biểu thức A  3 3 (1, 04)  2 (2, 03)  3
Câu 8. Tìm cực trị của hàm số x y z x y e     2 2 2 2 ( ) 2 3 x Câu 9. Tính z' z' , của hàm số y z  t tdt  2 cos2 x y xy 1  s inx Câu 10. Tính tích phân dx  3 sin x 28
PHẦN 1: TỔNG HỢP ĐỀ THI CUỐI KỲ CÁC NĂM
ĐỀ 2 VIỆN TOÁN ỨNG DỤNG VÀ TIN HỌC
ĐỀ THI CUỐI KÌ MÔN GIẢI TÍCH 1 – Học kì 20172
Mã HP: MI1111, Nhóm ngành 1, Thời gian: 90 phút
Chú ý: Thí sinh không được sử dụng tài liệu và giám thị phải ký xác nhận số đề vào bài thi
Chú ý: Thí sinh không được sử dụng tài liệu và giám thị phải ký xác nhận số đề vào bài thi
Câu 1. Tìm miền xác định của hàm y  arcsin(2 cos2x)  1  Câu 2. Tìm f(x) biết x  x  x f e (  e )  e    2  Câu 3. Tìm lim sin(ln( x 3  1)) sin(ln( x 3 )  ) x   x  t3  t  3
Câu 4. Cho hàm số y  y(x)xác định bởi  . Tính y '(x), y ' (x) y  15 t4  15  t2  4 2  ln(x  2)
Câu 5. Xét sự hội tụ phân kỳ của tích phân dx  x 5  n n n  Câu 6. Tìm giới hạn lim   ...   2 2 2 2 2 2  n n 3  1 n 3  2 n 3   n 
Câu 7. Dùng vi phân toàn phần của hàm số để tính giá trị gần đúng của biểu thức A  4 2 (3, 04)  3 (2, 02)  1
Câu 8. Tìm cực trị của hàm số x y z x y e     2 2 2 2 2 3 x y Câu 9. Tính z' z' , của hàm số z  t t  2 sin2 dt x y xy 1  cosx Câu 10. Tính tích phân dx  cos3x 29
PHẦN 1: TỔNG HỢP ĐỀ THI CUỐI KỲ CÁC NĂM
ĐỀ 1 VIỆN TOÁN ỨNG DỤNG VÀ TIN HỌC
ĐỀ THI CUỐI KÌ MÔN GIẢI TÍCH 1 – Học kì 20171
Mã HP: MI1111, Nhóm ngành 1, Thời gian: 90 phút
Chú ý: Thí sinh không được sử dụng tài liệu và giám thị phải ký xác nhận số đề vào bài thi
Câu 1. (2 điểm). Tìm các giới hạn sau 1  4x  1 1 a) lim b) s inx lim ln e (  2x  ) x o ln(1  3x) x0   x  2
Câu 2. (1 điểm). Tìm các tiệm cận của đồ thị hàm số y  x2  3
Câu 3. (1 điểm). Tính tích phân x  xdx ( 2)ln
Câu 4. (1 điểm). Cho miền  được giới hạn bởi các đường  = sin  , (0 ≤  ≤  ∕ 2),  =
, (0 ≤  ≤ 1),  = 0 và x   / 2. Tìm  để khối tròn xoay sinh ra khi quay miền  quanh đường thẳng  =
có thể tích nhỏ nhất?  (arctan x 2 )
Câu 5. (1 điểm). Tính tích phân suy rộng dx  x2  1 0
Câu 6. (1 điểm). Cho f là hàm số khả vi đến cấp hai trên ℝ. Chứng minh rằng hàm số w(x,t)  f (x  t 3 ) 2w 2w
thỏa mãn phương trình truyền sóng  9 t  2 x  2
Câu 7. (1 điểm) Tìm cực trị của hàm số z  x3  xy  x y  y2 2 7 6  4
Câu 8. (1 điểm). Hàm số f x y  3 ( , )
x4  y2 có khả vi tại điểm (0,0) không? Tại sao b
Câu 9. (1 điểm). Cho f liên tục trên a, b    và thỏa mãn f x dx   ( )
0. Chứng minh rằng tồn tại c  a ( ,b) a c sao cho f x dx  f  ( ) 2017 (c) a 30
PHẦN 1: TỔNG HỢP ĐỀ THI CUỐI KỲ CÁC NĂM
ĐỀ 3 VIỆN TOÁN ỨNG DỤNG VÀ TIN HỌC
ĐỀ THI CUỐI KÌ MÔN GIẢI TÍCH 1 – Học kì 20171
Mã HP: MI1111, Nhóm ngành 1, Thời gian: 90 phút
Câu 1. (2 điểm). Tìm các giới hạn sau x e  1 1 a) lim b) lim 1  3 3 x ) x2 y2 x o arctan(2x) ( x, y)(0,0)  
Câu 2. (1 điểm). Tìm  để hàm số sau liên tục trên ℝ
() =  + 1 ế  ≥ 
3 + 5 ế  < 
Câu 3. (1 điểm). Tính cực trị của hàm số f x  x 3 ( ) 2lnx 2
Câu 4. (1 điểm). Tìm các tiệm cận của đồ thị hàm số f (x)  a x rc cot x 3  2x
Câu 5. (1 điểm). Tính tích phân suy rộng dx  1  x2
Câu 6. (1 điểm). Chứng minh rằng hàm số t e  16 u(x, t)
cos(2x+3)thỏa mãn phương trình truyền nhiệt u  2u  4 t x2
Câu 7. (1 điểm) Tìm cực trị của hàm số z  x4  xy  x y  y2 2 4 4  1  1
Câu 8. (1 điểm). Xét sự hội tụ của tích phân suy rộng dx  2 x 2 0 e  x
Câu 9. (1 điểm). Cho hàm số f (x) khả vi liên tục đến cấp hai trên a, b  
 và f(a)  f(b)  0 . Chứng minh rằng 2 b b b  2  2 2
  f '(x) dx    f (x) dx  f ' (x) dx             a  a a 31
PHẦN 1: TỔNG HỢP ĐỀ THI CUỐI KỲ CÁC NĂM
ĐỀ 4 VIỆN TOÁN ỨNG DỤNG VÀ TIN HỌC
ĐỀ THI CUỐI KÌ MÔN GIẢI TÍCH 1 – Học kì 20171
Mã HP: MI1111, Nhóm ngành 1, Thời gian: 90 phút
Chú ý: Thí sinh không được sử dụng tài liệu và giám thị phải ký xác nhận số đề vào bài thi
Câu 1. (2 điểm). Tìm các giới hạn sau x e  1 1 a) lim b) lim 1  3 4 )x2 y y  2 x o arctan(3x) ( x, y)(0,0)  
Câu 2. (1 điểm). Tìm  để hàm số sau liên tục trênℝ
() =  + 2 ế  < 
7 − 4 ế  ≥ 
Câu 3. (1 điểm). Tính cực trị của hàm số f x  x  x 3 ( ) 4 ln 3
Câu 4. (1 điểm). Tìm các tiệm cận của đồ thị hàm số f (x)  a x rc cot x 1  4x
Câu 5. (1 điểm). Tính tích phân suy rộng dx  1  x2
Câu 6. (1 điểm). Chứng minh rằng hàm số t e  36 u(x, t)
sin(2x+1) thỏa mãn phương trình truyền nhiệt u  2 u  9 t x  2
Câu 7. (1 điểm) Tìm cực trị của hàm số z  x2  xy  x  y  y4 2 6 6  1  1
Câu 8. (1 điểm). Xét sự hội tụ của tích phân suy rộng dx  2 x e  x2 0
Câu 9. (1 điểm). Cho hàm số f (x) khả vi liên tục đến cấp hai trên a, b  
 và f(a)  f(b)  0 . Chứng minh rằng b 2 b b  2  2 2
  f '(x) dx    f (x) dx  f ' (x) dx             a  a a 32
PHẦN 1: TỔNG HỢP ĐỀ THI CUỐI KỲ CÁC NĂM
ĐỀ 5 VIỆN TOÁN ỨNG DỤNG VÀ TIN HỌC
ĐỀ THI CUỐI KÌ MÔN GIẢI TÍCH 1 – Học kì 20171
Mã HP: MI1112, Nhóm ngành 2, Thời gian: 90 phút
Chú ý: Thí sinh không được sử dụng tài liệu và giám thị phải ký xác nhận số đề vào bài thi
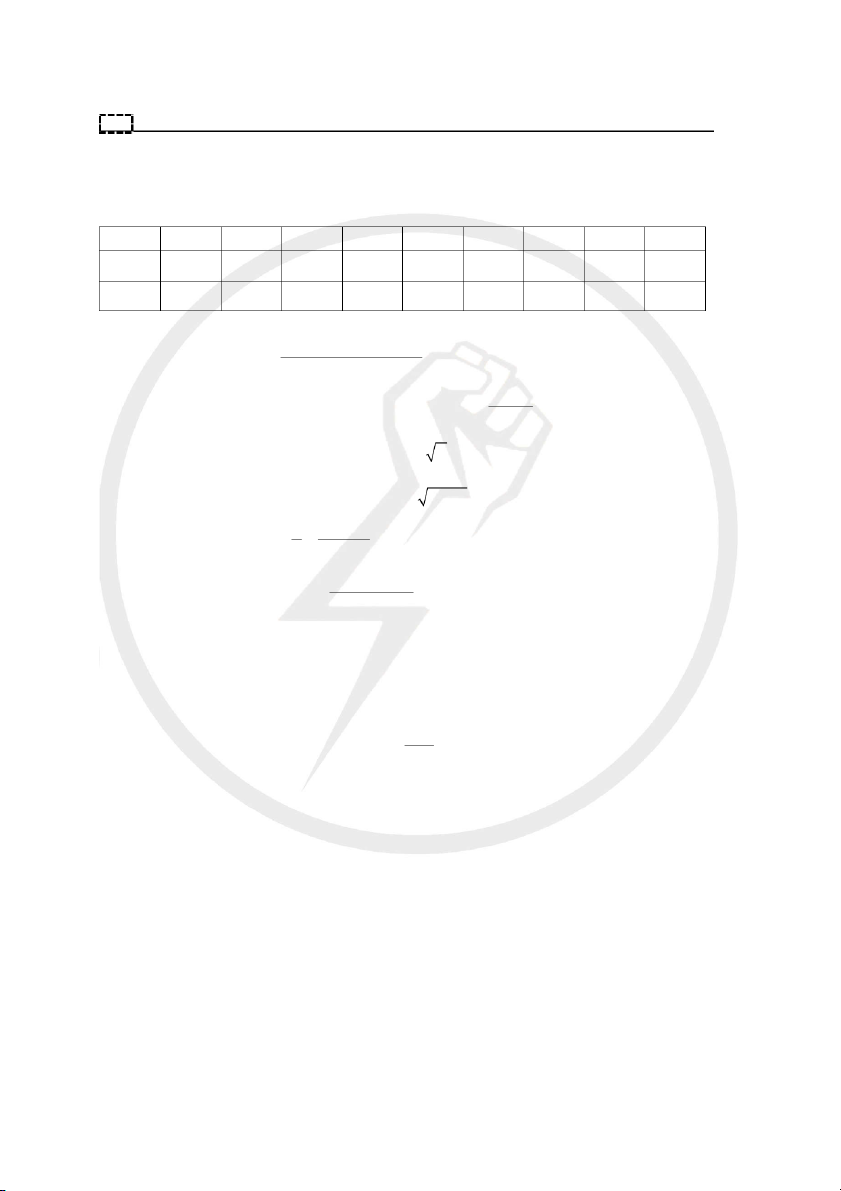
Câu 1. (1đ). Cho bảng giá trị của hai hàm số f (x) và g(x) như sau x 1 2 3 4 5 6 7 8 9 f (x) 2 3 1 4 6 9 5 7 8 g(x) 9 7 6 2 1 3 4 5 8
Hãy xác định giá trị ( ∘ )(3)
(x2  3 x  2) sin(x  1)
Câu 2. (1 đ) Tính giới hạn lim x1 1  o c s(x) 1
Câu 3. (1đ). Tìm và phân loại các điểm gián đoạn của hàm số y  1/x e  1 x
Câu 4. (1đ). Cho hàm số f x ( )  sin t ( d ) t  2 . Tính f '(  ) 0
Câu 5. (1đ). Tìm khai triên Maclaurin của hàm số y  2 2 x đến x3  1 1 
Câu 6. (1đ). Tính giới hạn lim    x0  x arcsin x   1
Câu 7. (1đ). Tính tích phân suy rộng dx  x (  1) x (  2) 3 1
Câu 8. (1đ). Tính tích phân cos(arctan x)dx  . 0
Câu 9. (1đ). Tìm số nghiệm của phương trình x 2  4x
Câu 10. (1đ) Xác định dấu của tích phân  2 sin d x x  x 0 33
PHẦN 1: TỔNG HỢP ĐỀ THI CUỐI KỲ CÁC NĂM
ĐỀ 6 VIỆN TOÁN ỨNG DỤNG VÀ TIN HỌC
ĐỀ THI CUỐI KÌ MÔN GIẢI TÍCH 1 – Học kì 20171
Mã HP: MI1112, Nhóm ngành 2, Thời gian: 90 phút
Chú ý: Thí sinh không được sử dụng tài liệu và giám thị phải ký xác nhận số đề vào bài thi
Câu 1. (1đ). Cho bảng giá trị của hai hàm số f (x) và g(x) như sau x 1 2 3 4 5 6 7 8 9 f (x) 2 3 1 4 6 9 5 7 8 g(x) 9 7 6 2 1 3 4 5 8
Hãy xác định giá trị ( ∘ )(5)
(x2  3 x  2) sin(x  1)
Câu 2. (1 đ) Tính giới hạn lim x1 1  o c s(x) 1
Câu 3. (1đ). Tìm và phân loại các điểm gián đoạn của hàm số y  1 x / 2  1 x
Câu 4. (1đ). Cho hàm số f x ( )  cos t ( d ) t  2 . Tính f '(  ) 0
Câu 5. (1đ). Tìm khai triên Maclaurin của hàm số y  2  2x đến x3  1 1 
Câu 6. (1đ). Tính giới hạn lim    x0 x arctan x    1
Câu 7. (1đ). Tính tích phân suy rộng dx  (  x 1)(  x 2) 3 0
Câu 8. (1đ). Tính tích phân cos(arctan x d ) x  . 1
Câu 9. (1đ). Tìm số nghiệm của phương trình x1 10  x
Câu 10. (1đ) Xác định dấu của tích phân 0 sinxdx  x 2 34
PHẦN 1: TỔNG HỢP ĐỀ THI CUỐI KỲ CÁC NĂM
ĐỀ 8 VIỆN TOÁN ỨNG DỤNG VÀ TIN HỌC
ĐỀ THI CUỐI KÌ MÔN GIẢI TÍCH 1 – Học kì 20171
Mã HP: MI1113, Nhóm ngành 4, Thời gian: 90 phút
Chú ý: Thí sinh không được sử dụng tài liệu và giám thị phải ký xác nhận số đề vào bài thi ln(cosx)
Câu 1. (1đ). Tính giới hạn lim x 2 0 tan x
Câu 2. (1 đ) So sánh cấp vô cùng bé sau đây khi x  0  x  x4  x5  x   x4 ( ) , ( ) ln(1 3 arctan( ))
Câu 3. (1đ). Điểm x   là điểm gián đoạn loại gì của hàm số 1  =  + 1 2 dx
Câu 4. (1đ). Tính tích phân  . 2 3 (x  3)  1  dx
Câu 5. (1đ). Xét sự hội tụ của tích phân suy rộng  x3  x2 0 3  1
Câu 6. (1đ). Ứng dụng vi phân, tính gần đúng 2  2 3, 97 3, 03
Câu 7. (1đ). Tìm các cực trị của hàm số z  x 2  y 2 2
với điều kiện x2  y2  1
Câu 8. (1đ). Tính tích phân kép  dxdy  (2x y)
. Với D là miền thỏa mãn x2  y2  2 D  xy  , neu( x, y)  (0; 0)
Câu 9. (1đ). Cho f( x, y)  x2  2 y2 0 neu(x, y)   (0; 0)
Chứng minh rằng các đạo hàm riêng f '  f ' (0; 0)
(0; 0)  0 nhưng hàm số f (x, y) không liên tục tại điểm x y (0,0) Câu 10. (1đ) Cho y  x2
cos( ). Tính đạo hàm cấp cao y(8) (0) 35
PHẦN 1: TỔNG HỢP ĐỀ THI CUỐI KỲ CÁC NĂM
ĐỀ 2 VIỆN TOÁN ỨNG DỤNG VÀ TIN HỌC
ĐỀ THI CUỐI KÌ MÔN GIẢI TÍCH 1 – Học kì 20161
Mã HP: MI1111, Nhóm ngành 1, Thời gian: 90 phút
Chú ý: Thí sinh không được sử dụng tài liệu và giám thị phải ký xác nhận số đề vào bài thi 5 3 (1  sin ) x  1
Câu 1. Tính các số thực ,  thỏa mãn lim x 0 ax 
Câu 2. Tính f '(1)với () =  
 , ℎ  ∈ (−∞; 1) 0, ℎ  ∈ [1; +∞)
Câu 3. Tìm khai triển Maclaurin của f (x)  x o c sx đến x5 2 Câu 4. Tính cos x e sin(2x)dx.  . x4 1
Câu 5. Tính độ dài của đường cong y   ,x  1;  2 8 x2   4  (3x  2)dx
Câu 6. Xét sự hội tụ, phân kì của tích phân suy rộng  x3  x  0 4 5 y Câu 7. Tính lim 4 2 (x,y ) (  0;0) x  y
Câu 8. Tìm giá trị lớn nhất, nhỏ nhất của 2 2
z  x 2y 3xy 13x 18 y trong miền OAB , ở đó O(0;0), A(7;0), B(0;7) Câu 9. Hàm số z  z u
( ;v) khả vi trên ℝ, có z'  z' (1;1)
3, (1;1)  4 . Đặt f x  3 x 2 ( ) z(x ; ), tính f '(1) u v
Câu 10. Một chiếc xe cứu hộ xuất phát từ góc của một hồ nước hình chữ nhật có các cạnh dài 2000m và rộng
600m. Xe vừa có thể đi trên bờ hồ và đi trên mặt nước với vận tốc tương ứng là 20m/s và 12m/s. Tính thời gian
ít nhất để xe đi đến giao điểm hai đường chéo của hồ. 36
PHẦN 1: TỔNG HỢP ĐỀ THI CUỐI KỲ CÁC NĂM
ĐỀ 3 VIỆN TOÁN ỨNG DỤNG VÀ TIN HỌC
ĐỀ THI CUỐI KÌ MÔN GIẢI TÍCH 1 – Học kì 20161
Mã HP: MI1111, Nhóm ngành 1, Thời gian: 90 phút
Chú ý: Thí sinh không được sử dụng tài liệu và giám thị phải ký xác nhận số đề vào bài thi  1 khi x  R \ 0;  9;  9
Câu 1. Tìm và phân loại điểm gián đoạn của hàm số y  2  log | x | 3 3 khi x   0;9; 9 5 5 x  x Câu 2. Tính sin( ) lim 15 x0 sin x
Câu 3. Cho ba số thực a, b, c thỏa mãn a  b  c  0 . Chứng minh phương trình ax5  bx 4 6 5  c  0 có ít
nhất một nghiệm thuộc (0;1) 3 x Câu 4. Tính dx  . 8 1  x
Câu 5. Tính diện tích mặt tròn xoay được tạo ra khi quay đường y  x  x2 4 , x  1;2    quanh trục Ox một vòng. 1 x xdx
Câu 6. Xét sự hội tụ, phân kì của tích phân suy rộng  1  cosx 0 1 3y
Câu 7. Tìm cực trị của hàm số 3 z   y  3 x x  y arctan ,khi x  0
Câu 8. Tính đạo hàm riêng z' (x; y) của hàm số z   x y 0, khi x = 0 
Câu 9. Tìm hàm số z(x; y)thỏa mãn ' ' 2
z  2x  y, z  2 y  , x (x; y)  R . x y
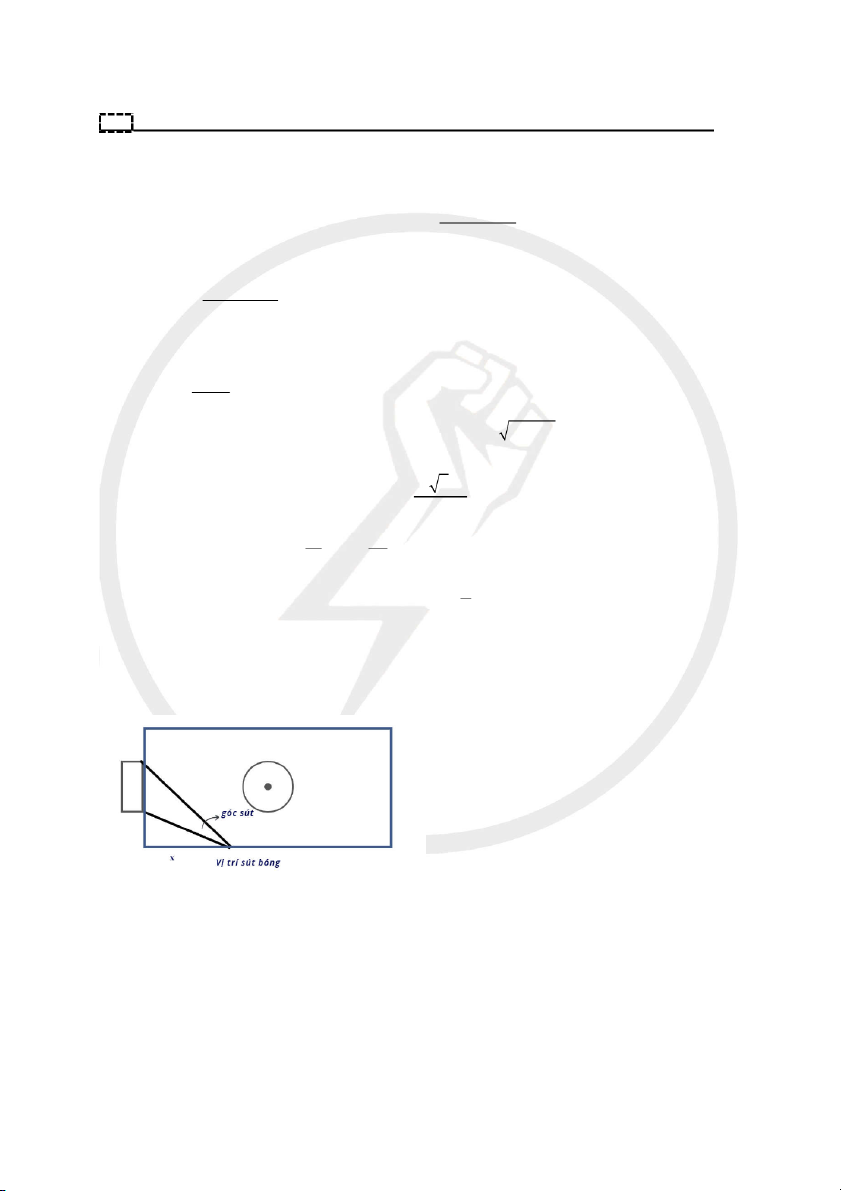
Câu 10. Một sân bóng đá có biên ngang dài 69m, cầu môn rộng 7m. Bóng nằm trên biên dọc, cách biên ngang
x(m). Tính góc sút bóng vào cầu môn theo x, tìm x để góc sút lớn nhất . 37
PHẦN 1: TỔNG HỢP ĐỀ THI CUỐI KỲ CÁC NĂM
ĐỀ 5 VIỆN TOÁN ỨNG DỤNG VÀ TIN HỌC
ĐỀ THI CUỐI KÌ MÔN GIẢI TÍCH 1 – Học kì 20161
Mã HP: MI1112, Nhóm ngành 2, Thời gian: 90 phút
Chú ý: Thí sinh không được sử dụng tài liệu và giám thị phải ký xác nhận số đề vào bài thi Câu 1. Cho hàm số z  x2  y2 ln(
3 ),(x; y)  (0;0) . Tính A  x '  y ' . z . z x y Câu 2. Tính lim x    2arctan(2x) x   
Câu 3. Xét tính lồi, lõm của đồ thị hàm số x y  ( x 1)e . dx Câu 4. Tính  . 5 cos x 12 sin x  13
Câu 5. Tính diện tích hình phẳng giới hạn bởi đường cong cho hệ tọa độ cực r  5  2 cos  (sinx  2 o c sx)dx
Câu 6. Xét sự hội tụ, phân kì của tích phân suy rộng  x2  1 0 6
Câu 7. Tìm điểm gián đoạn của hàm số f ( ) x  lim , x  R 2  2 n n  x 4 3 xy
Câu 8. Tìm cực trị của hàm số z    x y 12
Câu 9. Phương trình x3  y3  3 xy  13  0 xác định hàm ẩn y  y(x). Viết phương trình tiếp tuyến của đồ
thị hàm ẩn này tại điểm A  ( 1; 2)
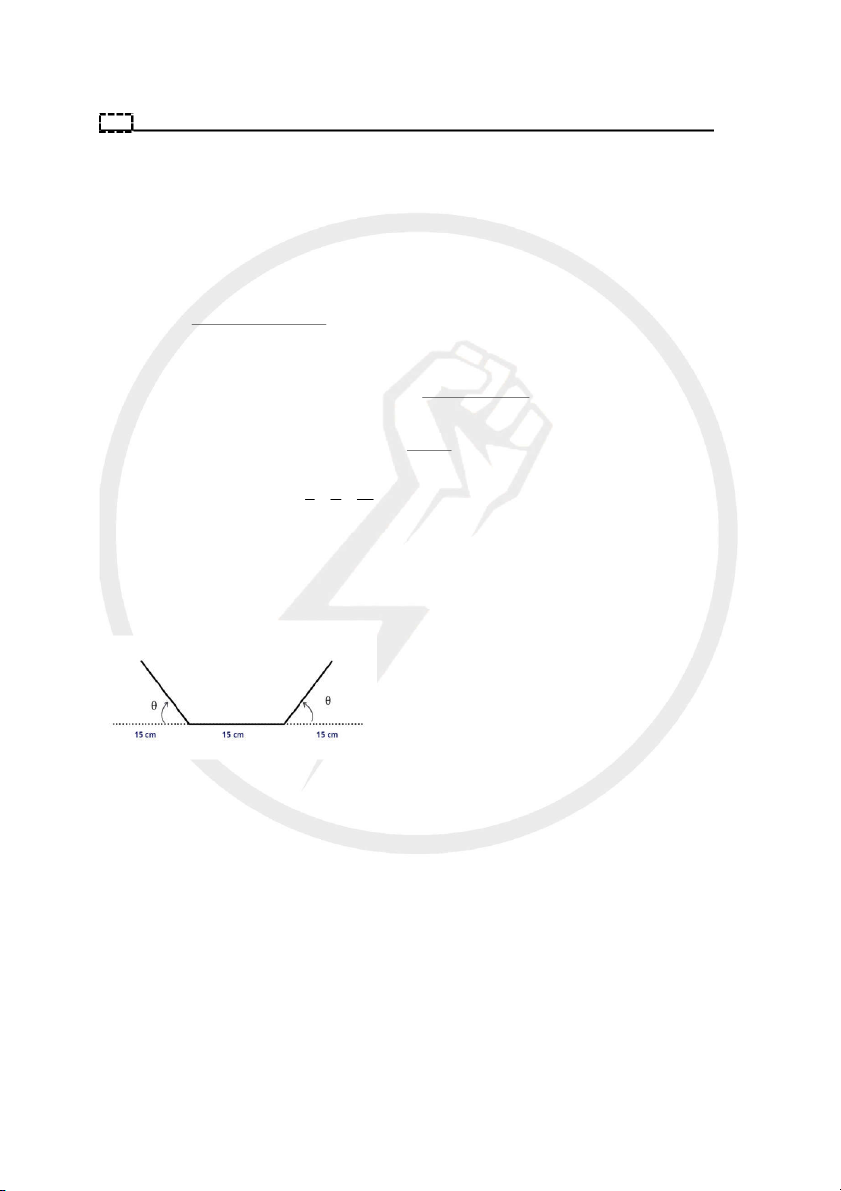
Câu 10. Gập một tấm tôn hình chữ nhật rộng 30cm, dài 3m thành một cái máng nước. Gấp theo chiều dài mỗi
bên tấm tôn 10cm, tính góc gập θ để thể tích của máng lớn nhất. 38
PHẦN 3: SƯU TẦM ĐÁP ÁN MỘT SÓ ĐỀ KHÁC CỦA VIỆN TOÁN ỨNG DỤNG ĐỀ 1-20193 3 4 
+) y  5 cos 5x  sin 5x x     Câu 1 5 5  (1đ)  +) 3    y   x   2 sin 5 sin 5  T  . 5 5 0 cos x  1 +) ; f x  . 2 0 sin x 3 2 3 cos x  cos x  1 2 x x0 1 +) f x  2   lim f x   . Câu 2 2  x  3 2 3 x  x     x 0 6 cos cos 1 (2đ)  +) x I  x ln  4 2 x  x  2  2x  dx  . 2 x  x  2    +) 1 I   x    x 2 x  x   2 1 ln 2  2x 7 arctan  C .  2 7 Câu 3  x 0  1 +)  8 f x  8 0   lim f     là đbt +) dx  HT, do đó I HT.  x  x 0 (1đ) x 0 x  0 x Câu 4 4 4 x x +) 2 0    x . +) 2 x 0 x   0  lim z  x; y  0 . (1đ) 2 4 2 x  y x  ;x y   0;  0 M 0; 0 1   Câu 5 z  0  +) x   M 0;1
+) M không là điểm cực trị, y 0;1  1 . min   2   (1đ) z  0  1 y  M 0; 1   1   
Câu 6 +) f x liên tục x  0, 1 .
+) x  1 là đgđ loại 2, x  0 là đgđ loại 1. (1đ)       Câu 7 +) dx 0;1 z 0;1 dx z 0;1 d ; y z 0;1 1. x y (1đ) +) z 0; 
1  2; z 0;1  1  dx 0;  1  2dx  dy . x y 1 1 1 2     +) VT  2    1  f   x 2
 dx   1dx   1  f    xdx    Câu 8  0   0  0 (1đ) 2 1 1 1 1 1           2 +)  f  x 2 dx    f  x 2 dx   1dx    f 
  x dx  VT 2  1   f  x dx             0   0   0   0   0  1 1 2 2 +)  2 I 1 x 2 x f   3x    dx    3 3   2 1  x f 
 3x dx  3 3  1 I1 Câu 9 3 3 1 1 (1đ) 1 1 I 3 +) 3  t  x  I  f t dt   I   . 1   3 3 4 1
Ghi chú:- Mỗi dấu +) cho 0,5 điểm
- Sinh viên giải cách khác đúng vẫn được điểm. 101 ĐỀ 4-20193
+ Giới hạn trái của hàm số tại a bằng 4a – 1, giới hạn phải bằng a2 + 3 Câu 1.
+ Để hàm số liên tục, ta cần có a  2 .
+ Đặt t  cot x , tích phân trở thành   2t  1dt Câu 2. 1
+ Tích phân cần tìm bằng 3  cot x  cot x  C . 3 x     x ln + 3 lim e ln x  lim
  đủ điều kiện để áp dụng quy tắc Lhospital. 3 x x  x  e   Câu 3. ln x 1 / x + lim  lim  0 . 3x 3 x  x e  3e x 0 0 x 0  + x x x xe dx  xe  e dx   . x Câu 4.   x 0 + x   e  1  . x + f   x   2 1  tan  cos  x   sin  x Câu 5. + f  / 2  1  .
+ Đạo hàm trái và phải của hàm số đều bằng 1. Câu 6. + f 2  1.  arctan tdt  + arctan x 0 2 lim  lim x  2 x Câu 7. x  2 x  x   1 x 2 x + arctan x 2  lim x  2x  . x  x  1 2
+ Trong khai triển Maclaurin của hàm số chỉ có các số hạng chứa 2n x Câu 8. + Suy ra  99 7 f  0  0. +  f    1 0 1; f
1  0 (do f là đơn ánh). Câu 9. + 1 g   1 1 2; g 
 2  1; suy ra kết quả cần tìm bằng 0. 1/2 f   1 x f  x + I  dx  dx   f x  f  x f x  f  x 0   1  1/2   1  1/2 f x 1/2 f 1   x Câu 10.  dx  dx       0 f x f 1 x 0 f  x f 1 x
đặt t  1  x ở TP thứ 2
+ Kết quả cần tìm bằng ½. 102 ĐỀ 4-20173 Câu 1 1  0,5 đ 1 2 arctan x  x 1  lim  lim x (L’Hospital) x 0  3 x 0  2 x 3 x 0,5 đ 2  x 1  lim   2 2 x0 3x (1  x ) 3 0,5 đ 0,5 đ ln(1  3 sin )
x  3 sin x  3x khi x  0 ln(1  3 tan ) x  osx=( x x e c e  1)  (1  o
c sx)  x (Ngắt bỏ VCB bậc cao)  lim  3 0 x x e  cosx Câu 2   0,5 đ TXĐ =  \  0 , lim y 0 lim y 
 x  0 là điểm gián đoạn loại I   x0 x0 2 0,5 đ Câu 3 (9) 9 9 1 1  1 1  ( 1  ) 9! ( 1  ) 9 ! 0,5 đ (10) f '(x)    f (x)       10 10 x  2 x  1 x  2 x  1 (x  2) (x  1)   0,5 đ   (10) (10) 10  9 ! 9 !  10  d f (x )  f (x ) dx    dx (x  2 x  1)    x  210 x   10 1   Câu 4 y 0,5 đ lim  1 x x 0,5 đ    lim (y  x)  , lim (y  x)    y  x  là TCX của đường cong. x 2 x 2 2 Câu 5 1 sinx d sin x 1 1 sin x 0,5 đ I  dx  dx  I  I ; I    ln  C    cosx cos2 1 2 1 2 x 1 sin x 2 1  sin x 1 0,5 đ d cos x 1 1 1  sin x 1 I     C  I   ln   C  2 cos2x cosx 2 2 1  sin x cosx Câu 6 1 2 0,5 đ t  x  I  arctan td(t  1)  0 1 0,5 đ 1  2 I  ( t  1) arctan t  dt   1  0 2 0 Câu 7 1 1 2 1 2 1 1 1 2           0,5 đ f '(x) (x ) 1 f '( ) x 1 (x 2 ) (x ) 2 2 x 4 x 4 x 2 2 1 1 3 ln 2 0,5 đ 2 I  1  ( f '( ) x ) dx  ( x  )dx     2 x 4 2 1 1 Câu 8 f ( )
x  arcsin x  arccosx  f'(x)=0,x   1
 ,1  f(x)=c(hằng số) 0,5 đ 0,5 đ   f (0)   arcsin x  arccosx= , x    1  ,1   2 2
Câu 9  sinx 1 sinx  sinx s 0,5 đ    I  I ,    inx lim  1  I   4 4 4 1 2 x  x x  x x  x  4 1 x0 x  x 0 0 1   0,5 đ s inx 1 dx s 0   , x
  1,  hội tụ → I2 hội tụ tuyệt đối → I2 hội tụ  inx  hội tụ. 4 4 4 x  x x x 4 x  x 1 0 115 ĐỀ 6-20173 2 +) TXĐ = x  , y (x )  arctan 2 1 x Câu 1 +) 2x   arctan   ( y )
x do arctanx là hàm lẻ, y làm lẻ. 2 1  x 2 x x  x x  Câu 2 +) ln( 2 ) 2 2 ln 2 ln I  lim +)  lim  ln 2.I  2 x x  2 x  2x x 2   +) 1 a 1 a a ' ' ' ' '   ,  ,  ,  ,  x y xx 2 yx 2 yy 2 x  ay x  ay (x  ay) (x  ay) (x  ay) Câu 3 2 1  4a 4a 1 +) ' ' '   4  4     0  a   xx yx yy 2 2 2 (x  ) ay ( x  ) ay (x  ) ay 2 1 2 4   1 x  1   3  x  3 x 3 Câu 4 +) 2 2 4 y  ( x 1  x )  x 1         0(x ) 5 5  +)  x   x  0( x ) 2 1! 2 2 2 !        2 8
+) Đặt x   cos, y   sin , D ' : 0    2, 0     Câu 5 2  2 3 1 8 +) 2 2 2 I 
d   4   d  . (4   )    3 3 0 0 0 3 3 3 3 dx
+) arccot xdx  arccot xd (x  1)  (x  1)arccot x     1 1 1 1 2 x 3    +)  4  2  x   3 1 6 4 1 6 Câu 6 3
Hoặc đổi biến. +) Đặt 2 2
x  u  dx  d(u) , I  arccotud(u  1)  1 3 3 3 4 2  +) 2  (u  1)arccotu  du    u   3  1  1 1 6 4 6 1 +) Chọn 3 x 2 f ( , x y)  4e  y ; x  0, y  2, x
  0, 02, y  0, 05 0 0 2 2   ' 4 y x x 2 ' 2 x 2 Câu 7 +) 3 3 f  e (4e  y ) , f  (4e  y ) nên x 3 y 3 3 0,02 2 4 1 2.2 1 4e
 1, 95  2  .0, 02.  .0, 05.  2, 01 3 4 3 4 1 1 1 1 1 1 Câu 8 +) a  1    ...    1  +) lim a  1 n 2 ! 2 ! 3 ! n! (n 1)! (n 1)! n n  x +) Xét hàm ln(1 ) g(x)  f ( )
x , 0  x  1, và g(0)  lim  1 Câu 9 x0 x
+) g(x) liên tục trên 0,1 
 nên liên tục đều trên 0  ,1 
, suy ra f(x) liên tục đều trên 0,1  1  1 +) arctan x  arctan x 1 dx   , x  0 :  ,     hội tụ (x  s inx 3 ) ( x  s inx 3 0 0 1 ) 2 2x 0 Câu 10 arctan +) x   x   : 
,  hội tụ. Tích phân ban đầu hội tụ. (x  s inx 3 3 ) 1 2 x 116 ĐỀ 4-20171 x x   x  Câu 1: . a) +) e 1 e 1 e 1 1 lim  lim +) lim  x0   arctan 3  x 0 x 0 x 3 x arctan 3x 3 ln1 4  y 3 1 lim x y  b) +) lim  y   e  x y   3 1 4 x y x y , 0;0   ,  0;0 2 2 2 2     ln  3 1  4 y  3 4 +) y li    m lim 0 . Giới hạn bằng 1 x,y 0;  0 2 2 x,y0;0 2 2 x  y x  y
Câu 2 +) Hàm f liên tục tại mọi điểm x  a +)     Hàm liên tục tại 2      f x a : a 2 7 4 . a  x  2 lim a 2, lim  f  x  7 4a . x a x a Suy ra 2 a  4a  5  0, a  1 hoac a=-5 3 4 4  3x 4
Câu 3: +) TXĐ x  0, f  x 2   3 x  , f   0 khi x=3 x x 3   +) Cực đại: 4 4 4 4 3 x  , f  ln    min 3 3  3  3 Câu 4: +) y  f x    x   3 lim 0 khong co tiem can dung. lim lim arccot 0 x x x  x 2 3  arccot 3t     2 1      9 3 t  +) 2 lim  y  x   lim  arccot   x  lim  lim   3 x x t 0  t 0 2 x 2 t  1      Tiệm cận xiên: y  x  3 2  Câu 5: +) 1 4 x 1 4 x dx  dx  dx    2 2 2 1  x 1  x 1  x 1 4x +) 2
dx  arcsinx  4 1 x  C  2 1 x Câu 6: +)  36 u  3  6 t e sin x  t 2 1 +)  36t u e x u e      x  u  u x   36 2 cos 2 1 , 4 t sin xx 2 1. Suy ra 9 t xx
z  2x  2y  6  0    x 1 1 Câu 7: +) TXĐ 2 R .Diem toi han   M 3; 0 , M  3  ;  3 1   2,3 z  2x  6  4y  0  y   2 2  +) 2
z  2, z  2, z  12 y . T¹i M 3; 0 : B  AC  4  0, không phải điểm cực trị xx xy yy 1   2  1 1  33 Tại M 2 3   ;   : B  AC  8   0, cuc tieu z  z M   2,3 min  2,3  4  2 2  3  1 1  x 3 x  Câu 8. +) 2 0    e +) 2 e 
hội tụ, nên TPSR hội tụ 3 x 2 3 x e  x e 0 b 2 b b b b Câu 9. +) f   dx  f     
xdf x  f x f x  f
 x f xdx   f
 x f  xdx a a a a a 2 b b b b 2  [   f x ]2 2 2 )( '( ) d ) x    f( ) x f ''( ) x dx    f ( ) x dx  f ' ( ) x  dx     a a a a   117 ĐỀ 6-20171 Câu 1 +) g 5  1 +) f   1  2
. Tu bang suy ra  f  g 5  f g 5  2 Câu 2 t  1 t sint +)L  2
+) Dat t  x  1; L  lim t0 1  cos t  Câu 3
+) Điểm 0 là điểm gián đoạn
+) Giới hạn trái bằng -1; giới hạn phải bằng 0. Gián đoạn loại 1 Câu 4 +) f  x 2  cos x +) f      1 Câu 5 +) y    x12 2 1 2 3   +) x x x y  2 1    ...  2 8 16    Câu 6    +) Lhospital L  0 +) arctan x x L  lim   2 x 0   x  Câu 7  1  1 1  1 5 +)    dx  +) ln 3 x   1 x  2 3 3 3  Câu 8 +)  x  1 cos arctan  2 1  x 0 dx x  0 +)  ln   2 x  1  x
  ln 1  2  ln 1  2 2      x  1   1 1 x Câu 9 f   x 1 x  10   x +)   có 1 nghiệm duy nhất f  x  . f x 0 x 1    10 ln 10  1
+) Lập bảng biến thiên của hàm số f x . Dễ thấy f 1   0 . Suy ra phương trình có đúng 2 nghiệm Câu +) Tương tự đề 5 10
+) Tích phân mang dấu dương 118 ĐỀ 8-20171 Câu 1 s inx ln cosx cosx 1 lim  lim   2 x  tan x x  2tanx/cos2 0 0 x 2 Câu 2 4 ( ) x  x 4 4 là VCB cùng bậc với (  ) x  3 arctan(x )  3x  (x) Câu 3
lim y  0, lim y  1  0 là điểm gián đoạn loại I x 0 x 0  
lim y  0, lim y  1   là điểm gián đoạn loại I   x x Câu 4 2  2 I  l n (x  3) (x 3)  1  ln(1 2) 3  Câu 5  1  dx dx dx I     I  I    1 2 3 2 3 2 3 2 0 x  3x  1 0 x  3x  1 1 x  3x  1 1 1 
khi x  nên I2 hội tụ → tích phân đã cho hội tụ. 3 3 2 x  3x  1 2 x Câu 6 Chọn hàm số 2 2 f ( , x ) y 
x  y , x  4, y  3, x  0  , 03, y   0, 03 0 0 2 2 ' ' 4 3
3, 97  3, 03  f (4, 3) f (4, 3)x  f (4, 3) x
  5  .(0, 03) .(0, 03)  4,994 x y 5 5 Câu 7 '    0 4  x  2x  0 x   Đặt 2 2 2 2  ( ,
x y)  (2x  y )   (x  y  1). Hệ PT '  
 0  2y  2y  0 ( y)  '  2 2   0 x  y  1    
Bốn điểm tới hạn là (1, 0),(1, 0),(0,1),(0, 1  )
Cực đại f (1, 0)  2 . Cực tiểu f (0, 1  )  1 Câu 8 2 2 I  (x  2 ) y dxdy  d
(2r cos  rsin ) dr  0    D 0 0 Câu 9    y  ' f(0 x, 0) ' f(0, 0 ) f (0, 0)  lim  0, f (0, 0)  lim  0 x  0 y x y 0 x   y  Cho k ( ,
x y)  (0, 0) theo phương của đường thẳng y  kx  f ( , x k ) x  2 1  2k lim f ( , x )
y  Hàm số không liên tục tại 0. ( , x y) (  0,0) Câu  2n  2(2n) x x 10 cosx  (  1  )n  c os 2 ( x )  (  1  )n  n  n n 0 (2 )! n 0 (2 )! (8) f (0) 2 1 (8) 8 !   (1) .  f (0)   1680 8 ! 4 ! 4 ! 119 ĐỀ 2-20172 *) 1 1
 1 2 cos 2x  1    cos 2x  1. 2 2     *) 2 k k   k  2 x   k     x   , k   3 3 6 2 3 2 2. *) Đặt 1 x x 2  x x  1 t 
(e  e )  x  ln(t  t  1) *) Vậy 2 ln( 1) f ( ) x  e  , x   2 2 x  x  1 1 3.     ln(1  ) *) ln(3x 1) ln(3x ) ln(3x 1) ln(3x ) x A  2 sin cos *) 3  2 sin cos(...)  0khi x   2 2 2 3 4.  *) y '(t) 15t 15t dy ' 5 y '(x )    5t *) y ' (x )   2 x'( ) t 3t  3 2 dx 3t  3    5.  1 ln(x 2) *) ln(x 2) 1  Mà dx  phân kỳ * nên dx  phân kỳ x x x x 3 3 1 1 n 1 1 dx 1 x  6. *) S   .    arctan   n 2 n 2 3  i 1   i  0 x 3 3 6 3 3  0   n   *) Xét 4 2 3 f ( , x y)  x  y  1; x  3, x   0, 04, y  2, y   0, 02 0 0 thì ' ' A  ( f x   ,x y   ) y  ( f x, y )  f ( x, y ) x   f ( x, y ) y  0 0 0 0 x 0 0 y 0 0 7. 2 x y *) 4 2 3 ' ' f (x , y )  16  2; f  ; f  0 0 x 2 3 3 y 2 3 3 4 4 4 ( x  y 1) 4 ( x  y  1) 2 3 3 ' 2.3 3 ' 3.2 3 f (x , y )   ; f (x , y )    A  2  .0, 04  .0, 02  2, 015 x 0 0 3 y 0 0 3 4.2 16 4.2 8 16 8 2 2 '  (x y )       0 2x 2 e z  0  *) x       M(0, 0)*) ' ' ' A  z ( ) M  6, B  z ( ) M  0,C  z ( ) M  8 2 2 ' ( x    y ) z 0  xx xy yy     y 2 y 3 e 0 8.    2  B  AC  48   0   ( z M)  Z (0, 0)  1 min A  6  0  v x *) Đặt u  xy v  z  t s 2 , , in2tdt  khi đó y u 2 9.   * ' ' ' ' ' 2 x x 1 z  z u  z  u 2u.y+v2 2v. 1 . . v . sin . sin 2  (x )
y . sin (2xy).y+   . sin (2 ). x u x v x y y y y   2 x   ' ' ' ' ' 2 x x x
z  z .u  z . v  u . sin 2u.x+v2. sin 2v.(- ) 2
 (xy ) . sin (2xy).x+   . sin(2 ).( ) y u y v y 2 y 2 y y y   *) dx dx I     tan x  J   2 3 cos x cos x d (sin x) dt dt 10 J       2 2 2 2 2 2 (1  sin x ) (1  t ) (1 t ) (1  t ) Trong đó: 1 1 1  ( 
 ln 1 t  ln 1 t ) C, t  sin x 4 1  t 1  t 120