Tổng hợp đề thi cuối kì môn Xử lý tín hiệu| Môn Xử lý tín hiệu| Trường Đại học Bách Khoa Hà Nội

EE2000 Tín hiệu và hệ thống Điểm thi:
Trường Đại học Bách Khoa Hà Nội
Thi cuối kỳ 20171 (2017-2018) Viện Điện Thời gian thi: 90 phút
Bộ môn Điều khiển tự động Ngày thi: 08/01/2018 Đề số 1 Họ tên SV: Chữ ký CB chấm thi: Chữ ký CB coi thi: Mã số SV: Số thứ tự:
Lưu ý: Sinh viên làm bài vào 3 mặt giấy này.Nếu trình bày vào mặt giấy thứ 4 sẽ bị trừ một nửa số điểm của
phần trình bày đó.Chỉ được sử dụng quyển bài tập có dấu đỏ của Bộ môn và máy tính không lập trình được.
(Sinh viên tắt điện thoại di động. Không sử dụng bút phủ, bút tẩy).
PHẦN A: TÍN HIỆU VÀ HỆ THỐNG LIÊN TỤC
Bài 1 (Đáp ứng của hệ thống)
Cho hệ thống LTI nhân quả có hàm truyền: 10 H (s)  2 s 10s 100
a) (1đ) Hãy vẽ sơ đồ điểm cực của hệ. Hãy xác định các giá trị n
 và  . Hệ có ổn định không? Tại sao?
b) (2đ) Hãy tìm biểu thức đáp ứng bước nhảy s(t) của hệ. Vẽ phác s(t) . 1 j t
c) (1đ) Theo tính chất hàm riêng của hệ LTI, chúng ta đã biết rằng với tín hiệu vào 0
x (t) e   thì tín hiệu j t ra 0
y(t) H (jw )e  
trong đó H (jw ) là đáp ứng tần số của hệ. 0
Hãy tìm đáp ứng của hệ (ở trạng thái xác lập) với tín hiệu vào x (t)  cos(10t)u(t ) .(Lưu ý: u(t) là ký
hiệu tín hiệu bước nhảy đơn vị).
Bài 2 (Trích mẫu tín hiệu)
(2đ) Giả sử trong quá trình trích mẫu tín hiệu, ta thu được tín hiệu x (t) s
từ tín hiệu x (t) . Biết rằng 
x (t)  x (t)p(t) s với p(t) 
 (t  nT ) 
là hàm trích mẫu với chu kỳ trích mẫu T  2 3 giây. n 
Hãy vẽ phổ biên độ X (j) s của x (t) s
khi biết phổ biên độ X (j) của x (t) có đồ thị như hình dưới đây.
Xác định xem có xảy ra hiện tượng trùng phổ hay không. X ( j ) 2 -2 -1 0 1 2  2
PHẦN B: TÍN HIỆU VÀ HỆ THỐNG KHÔNG LIÊN TỤC
Bài 3 (Tích chập không liên tục) n
(2đ) Hãy tính tích chập x[n ] [
v n] trong đó x[n]  u[n] và v[n]  2(0.8) u[n] . (Lưu ý: u[n] là ký hiệu tín
hiệu bước nhảy đơn vị).
Bài 4 (Phép biến đổi Z ngược)
(2đ) Hãy tìm đáp ứng xung h[n] cho hệ thống nhân quả có hàm truyền z (z 1) H (z )  2
z  0.5z  0.5
Vẽ h[n] với 5 giá trị đầu tiên của n . 3 4
EE2000 Tín hiệu và hệ thống Điểm thi:
Trường Đại học Bách Khoa Hà Nội
Thi cuối kỳ 20171 (2017-2018) Viện Điện Thời gian thi: 90 phút
Bộ môn Điều khiển tự động Ngày thi: 08/01/2018 Đề số 2 Họ tên SV: Chữ ký CB chấm thi: Chữ ký CB coi thi: Mã số SV: Số thứ tự:
Lưu ý: Sinh viên làm bài vào 3 mặt giấy này.Nếu trình bày vào mặt giấy thứ 4 sẽ bị trừ một nửa số điểm của
phần trình bày đó. Chỉ được sử dụng quyển bài tập có dấu đỏ của Bộ môn và máy tính không lập trình được.
(Sinh viên tắt điện thoại di động. Không sử dụng bút phủ, bút tẩy).
PHẦN A: TÍN HIỆU VÀ HỆ THỐNG LIÊN TỤC
Bài 1 (Đáp ứng của hệ thống)
Cho hệ thống LTI nhân quả có hàm truyền: 1 H (s)  2 s  4s 16
a) (1đ) Hãy vẽ sơ đồ điểm cực của hệ. Hãy xác định các giá trị n
 và  . Hệ có ổn định không? Tại sao?
b) (2đ) Hãy tìm biểu thức đáp ứng bước nhảy s(t) của hệ. Vẽ phác s(t) . 1 j t
c) (1đ) Theo tính chất hàm riêng của hệ LTI, chúng ta đã biết rằng với tín hiệu vào 0
x (t) e   thì tín hiệu j t ra 0
y(t) H (jw )e  
trong đó H (jw ) là đáp ứng tần số của hệ. 0
Hãy tìm đáp ứng của hệ (ở trạng thái xác lập) với tín hiệu vào x (t)  sin(4t)u(t) .(Lưu ý: u(t) là ký hiệu
tín hiệu bước nhảy đơn vị).
Bài 2 (Trích mẫu tín hiệu)
(2đ) Giả sử trong quá trình trích mẫu tín hiệu, ta thu được tín hiệu x (t) s
từ tín hiệu x (t) . Biết rằng 
x (t)  x (t)p(t) s với p(t) 
 (t  nT ) 
là hàm trích mẫu với chu kỳ trích mẫu T   4 giây. n 
Hãy vẽ phổ biên độ X (j) s của x (t) s
khi biết phổ biên độ X (j) của x (t) có đồ thị như hình dưới đây.
Xác định xem có xảy ra hiện tượng trùng phổ hay không. X ( j ) 2 -2 -1 0 1 2  2
PHẦN B: TÍN HIỆU VÀ HỆ THỐNG KHÔNG LIÊN TỤC
Bài 3 (Tích chập không liên tục) n
(2đ) Hãy tính tích chập x[n ] [
v n] trong đó x[n]  u[n 1] và v[n]  2(0.5) u[n] . (Lưu ý: u[n] là ký hiệu
tín hiệu bước nhảy đơn vị).
Bài 4 (Phép biến đổi Z ngược)
(2đ) Hãy tìm đáp ứng xung h[n] cho hệ thống nhân quả có hàm truyền 2 z 1 H (z)  2 z 1.5z 1
Vẽ h[n] với 5 giá trị đầu tiên của n . 3 4 Cán bộ ĐỀ phụ trách HP BCN bộ môn THI CUỐI KỲ 20191 duyệt Trường ĐHBKHN
Học phần: Tín hiệu & Hệ thống Phạm Văn Trường
Mã học phần: EE2000 Viện Điện Đặng Văn Mỹ Bm. ĐKTĐ
Thời gian làm bài: 90 phút Ngày thi: 15/01/2020 Đỗ Thị Tú Anh Đề số 2 Điểm
Chữ ký CB chấm thi CB coi thi 1 CB coi thi 2
Họ tên SV: …………………………………………. Mã số SV: ……………………… Số thứ tự: ……………
Lưu ý: Đề thi gồm 4 bài. Sinh viên làm bài trực tiếp vào 4 mặt giấy này. Chỉ được sử dụng 1 quyển slide bài
giảng và 1 máy tính không lập trình được.
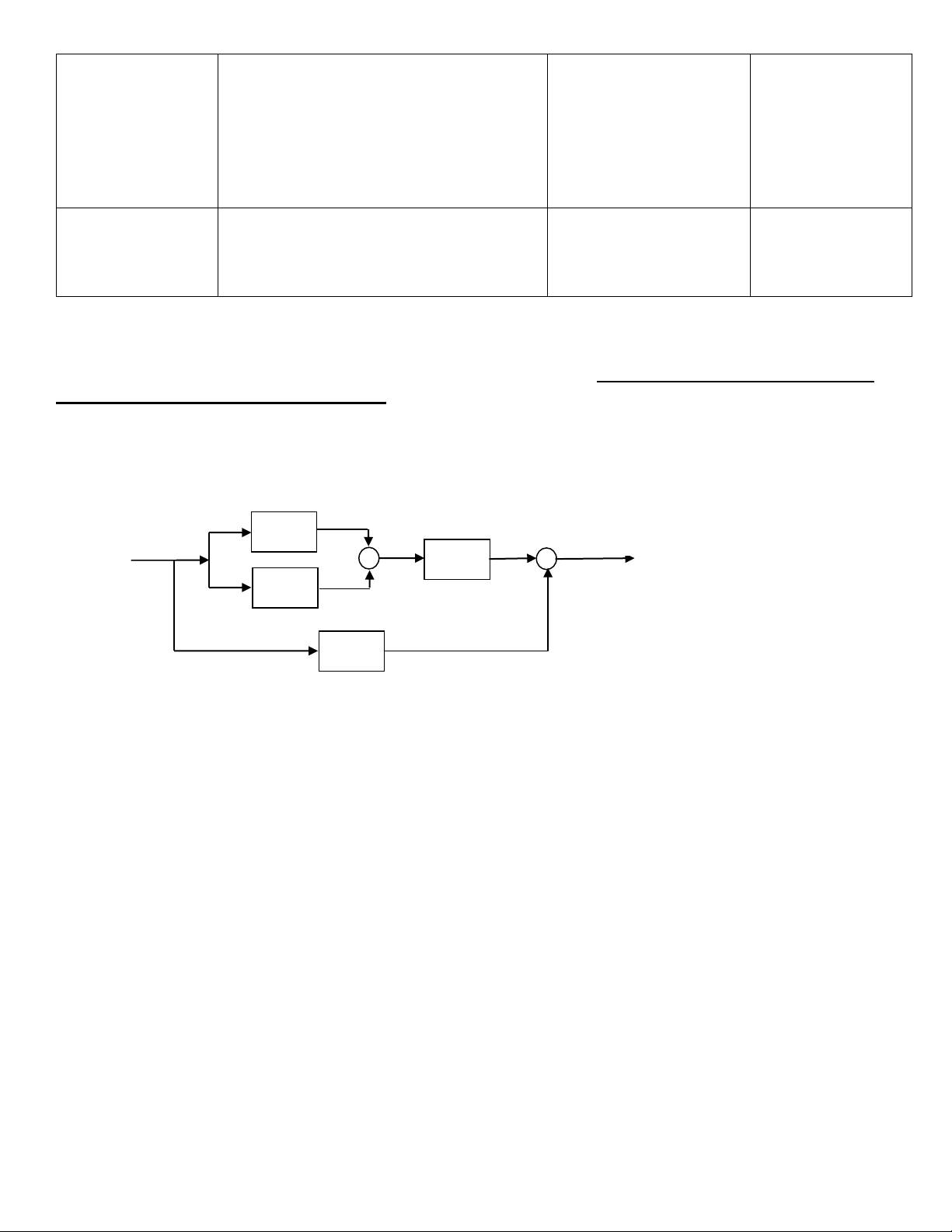
Bài 1 (Ghép nối hệ thống)
Xét hệ ghép nối của bốn hệ LTI như được biểu diễn bằng sơ đồ khối trên Hình 1. h1(t) x(t) + + y(t) h3(t) _ + h2(t) h4(t) Hình 1.
a) (1đ) Hãy tìm đáp ứng xung h (t ) của cả hệ thống thông qua h (t) , h (t) , h (t ) và h (t) . Giải thích. 1 2 3 4
………………………………………………………………………………………………………………
………………………………………………………………………………………………………………
………………………………………………………………………………………………………………
………………………………………………………………………………………………………………
………………………………………………………………………………………………………………
………………………………………………………………………………………………………………
………………………………………………………………………………………………………………
………………………………………………………………………………………………………………
………………………………………………………………………………………………………………
……………………………………………………………………………………………………………… at −
b) (1đ) Giả thiết rằng h (t) = u(t − 3) −u(t), h (t) = u(t), h (t) =  (t + 3) và h (t) = e
u(t). Hãy tìm h(t). 1 2 3 4
………………………………………………………………………………………………………………
………………………………………………………………………………………………………………
………………………………………………………………………………………………………………
……………………………………………………………………………………………………………… 1
………………………………………………………………………………………………………………
………………………………………………………………………………………………………………
Bài 2 (Phép biến đổi Fourier và lọc tín hiệu)
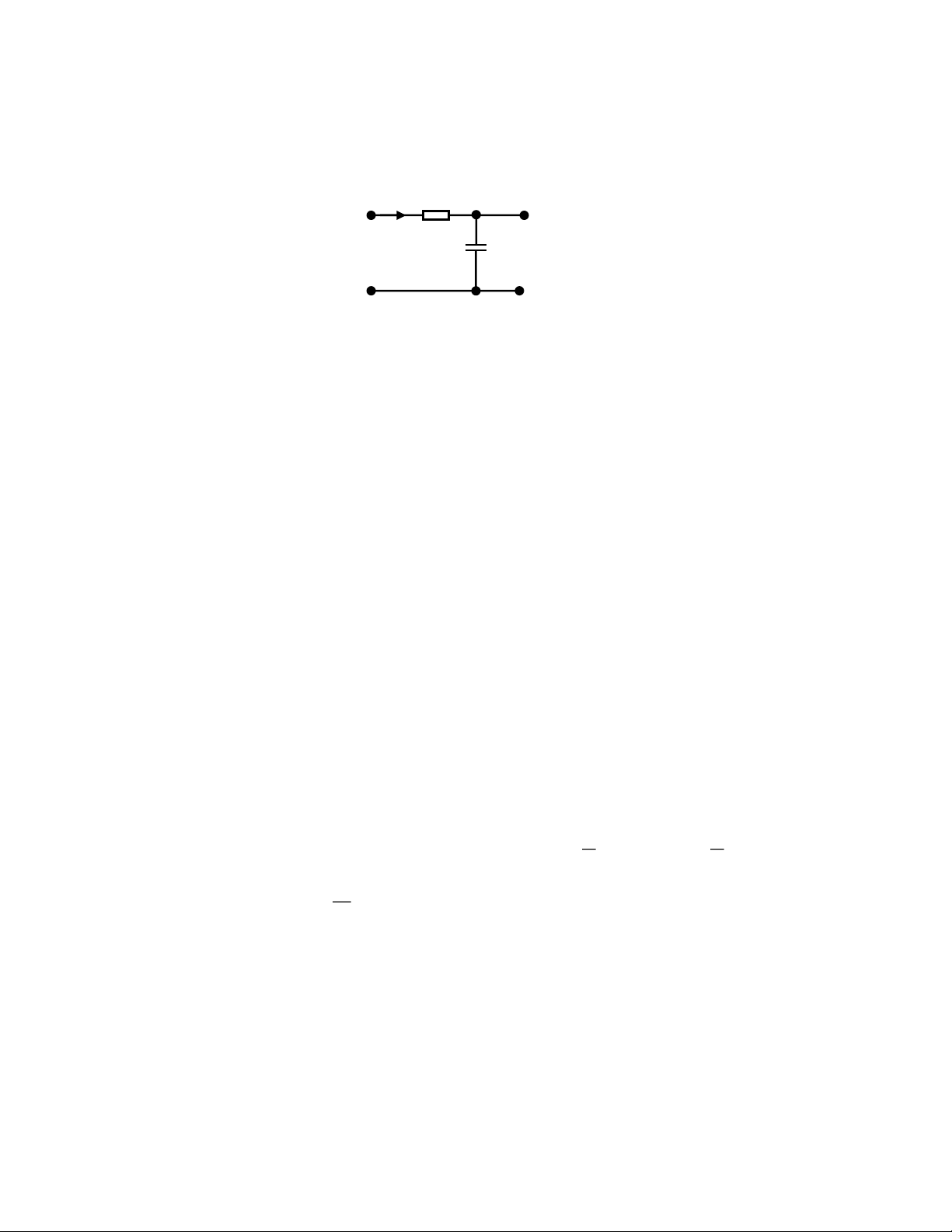
Xét một bộ lọc gồm hai phần tử RC mắc nối tiếp như được biểu diễn trên Hình 2. Giả sử tín hiệu vào x (t )
là điện áp cấp cho mạch điện, tín hiệu ra y (t) là điện áp trên hai đầu của tụ điện. i(t) R C x(t) y(t) Hình 2.
a) (2đ) Tìm biểu thức và vẽ đáp ứng biên độ-tần số | H () | của bộ lọc? Đây là bộ lọc loại gì? Hãy xác
định tần số ngưỡng wc của bộ lọc theo R và C.
………………………………………………………………………………………………………………
………………………………………………………………………………………………………………
………………………………………………………………………………………………………………
………………………………………………………………………………………………………………
………………………………………………………………………………………………………………
………………………………………………………………………………………………………………
………………………………………………………………………………………………………………
………………………………………………………………………………………………………………
………………………………………………………………………………………………………………
………………………………………………………………………………………………………………
………………………………………………………………………………………………………………
………………………………………………………………………………………………………………
………………………………………………………………………………………………………………
………………………………………………………………………………………………………………
………………………………………………………………………………………………………………      
(1đ) Giả sử với tín hiệu vào bộ lọc có dạng x (t) = 5cos 2t + + cos 16t +     , ta nhận được tín     b) 4 3   
hiệu ra là y (t )  4 cos 2 t + . 
 Dựa vào | H () | , hãy xác định giá trị các thông số R và C của bộ  10  lọc.
………………………………………………………………………………………………………………
………………………………………………………………………………………………………………
………………………………………………………………………………………………………………
………………………………………………………………………………………………………………
………………………………………………………………………………………………………………
………………………………………………………………………………………………………………
……………………………………………………………………………………………………………… 2
………………………………………………………………………………………………………………
………………………………………………………………………………………………………………
………………………………………………………………………………………………………………
………………………………………………………………………………………………………………
………………………………………………………………………………………………………………
………………………………………………………………………………………………………………
………………………………………………………………………………………………………………
………………………………………………………………………………………………………………
(1đ) Giả sử điện áp đầu ra được lấy trên hai đầu điện trở, bộ lọc trong trường hợp này là bộ lọc loại gì? Tại sao?
………………………………………………………………………………………………………………
………………………………………………………………………………………………………………
………………………………………………………………………………………………………………
………………………………………………………………………………………………………………
………………………………………………………………………………………………………………
………………………………………………………………………………………………………………
………………………………………………………………………………………………………………
………………………………………………………………………………………………………………
………………………………………………………………………………………………………………
…………………………………………………………………………………………………………….
Bài 3 (Phép biến đổi Laplace và hàm truyền)
Quan hệ giữa đầu vào x (t ) và đầu ra y (t ) của một hệ thống bậc 2 được biểu diễn bằng phương trình sau: 2 d y (t ) dy (t ) dx t + 8 + 12y t = − 3x t 2 ( ) ( ) ( ) dt dt dt
Giả sử y (0) = y(0) = 0 , x(0) = 0.
a) (1đ) Xác định hàm truyền H (s) của hệ thống?
………………………………………………………………………………………………………………
………………………………………………………………………………………………………………
………………………………………………………………………………………………………………
………………………………………………………………………………………………………………
………………………………………………………………………………………………………………
………………………………………………………………………………………………………………
………………………………………………………………………………………………………………
………………………………………………………………………………………………………………
b) (1) Hãy xác định và vẽ điểm cực (x) và điểm không (o) của hệ thống nên mặt phẳng phức s . Hệ thống
trên có ổn định không? Tại sao?
………………………………………………………………………………………………………………
………………………………………………………………………………………………………………
………………………………………………………………………………………………………………
……………………………………………………………………………………………………………… 3
………………………………………………………………………………………………………………
………………………………………………………………………………………………………………
c) (1đ) Tìm đáp ứng đầu ra của hệ thống khi tín hiệu đầu vào của hệ thống là x (t ) = u (t ).
………………………………………………………………………………………………………………
………………………………………………………………………………………………………………
………………………………………………………………………………………………………………
………………………………………………………………………………………………………………
………………………………………………………………………………………………………………
………………………………………………………………………………………………………………
………………………………………………………………………………………………………………
………………………………………………………………………………………………………………
………………………………………………………………………………………………………………
………………………………………………………………………………………………………………
………………………………………………………………………………………………………………
………………………………………………………………………………………………………………
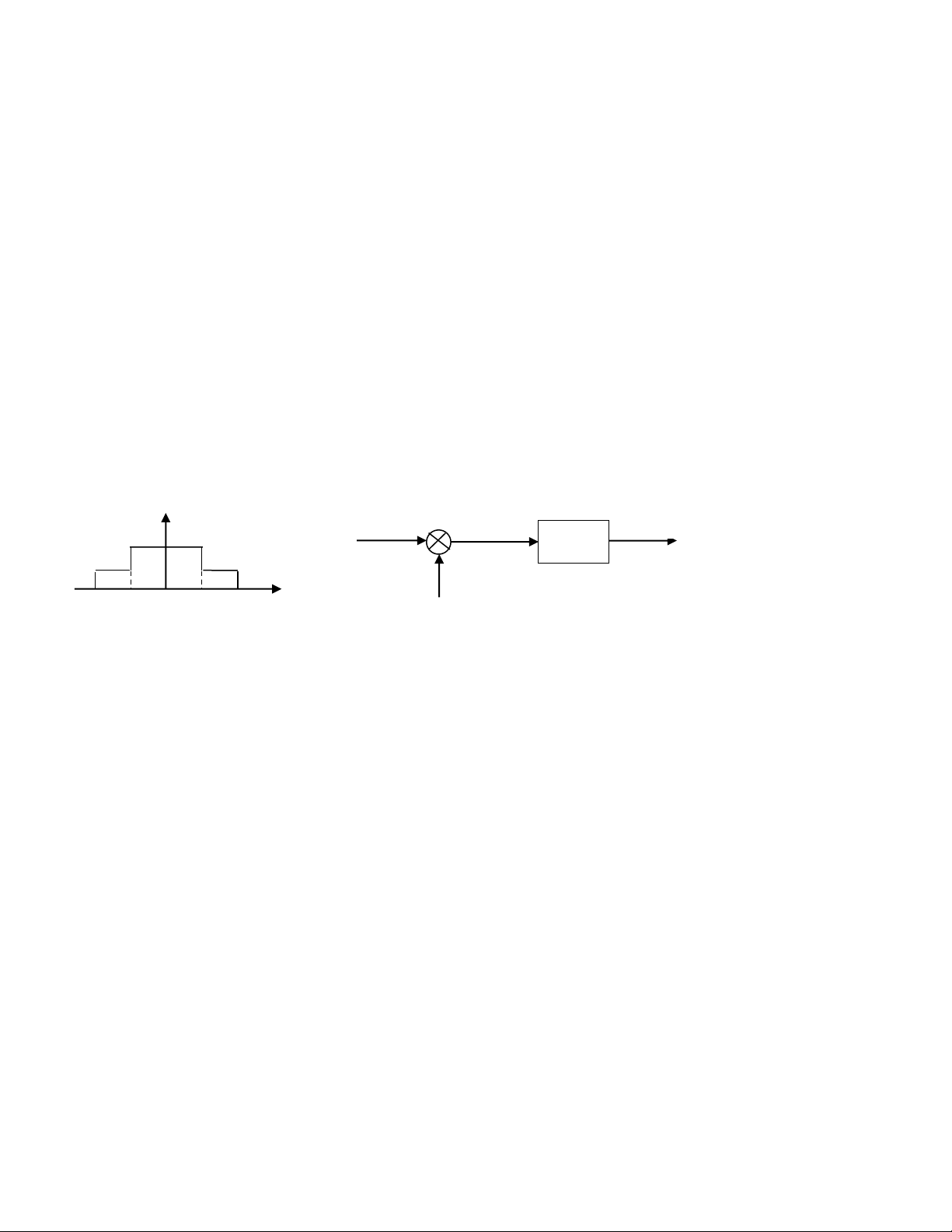
Bài 4 (Lấy mẫu tín hiệu)
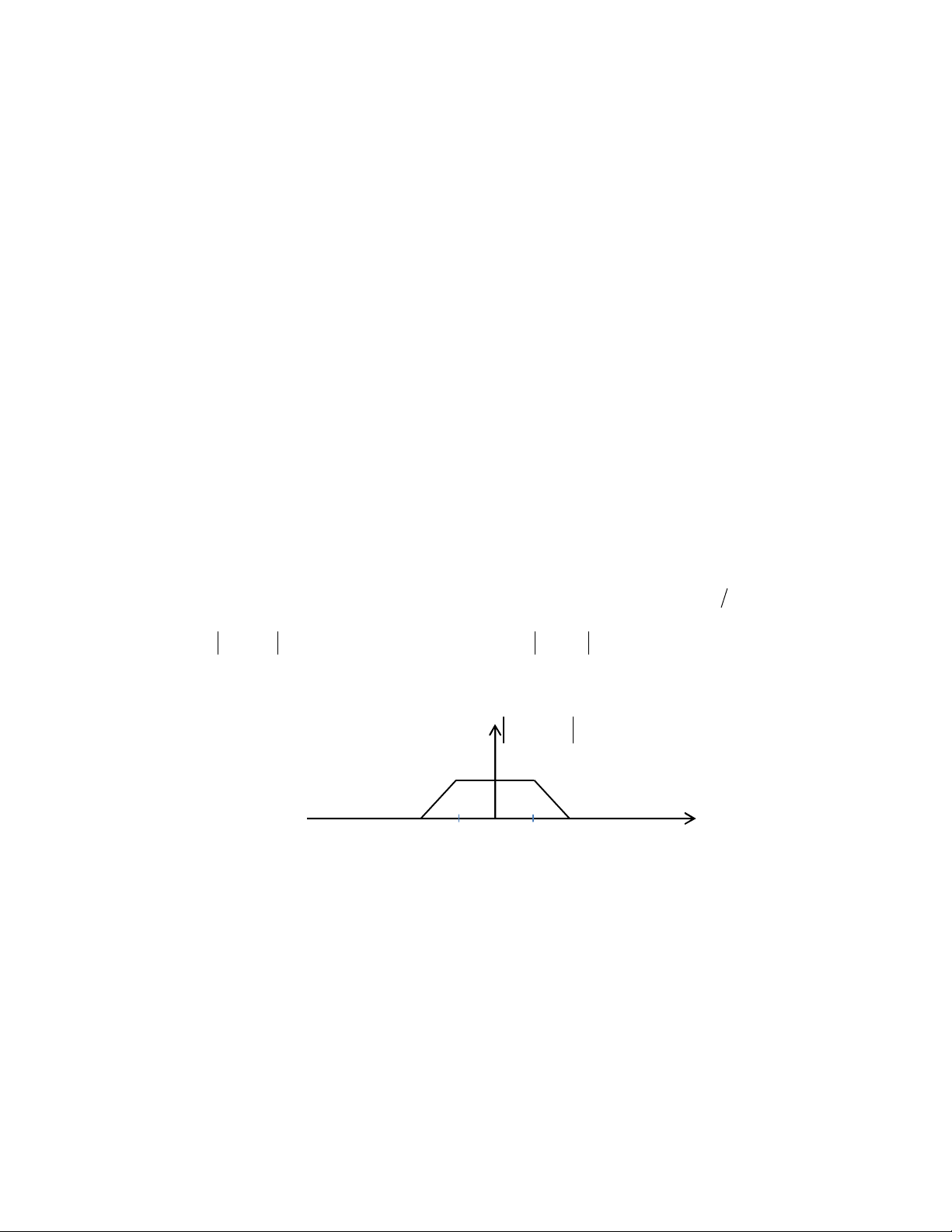
Sơ đồ khối của việc lấy mẫu tín hiệu x (t ) và phổ của nó được cho trên Hình 3. X(ω) x(t) x y(t) s(t) H(ω) ω ω -ωx 0 x 
s(t) =T   (t −nT ) s s Hình 3. n=−
(1đ) Hãy vẽ phổ của x (t)  =  T s
để tìm điều kiện cho tần số lấy mẫu 2 / s
s để không xảy ra hiện tượng
chồng phổ. Giải thích làm thế nào x (t ) có thể được khôi phục từ x (t) s .
………………………………………………………………………………………………………………
………………………………………………………………………………………………………………
………………………………………………………………………………………………………………
………………………………………………………………………………………………………………
………………………………………………………………………………………………………………
………………………………………………………………………………………………………………
………………………………………………………………………………………………………………
………………………………………………………………………………………………………………
………………………………………………………………………………………………………………
………………………………………………………………………………………………………………
………………………………………………………………………………………………………………
………………………………………………………………………………………………………………
………………………………………………………………………………………………………………
………………………………………………………………………………………………………………
……………………………………………………………………………………………………………… 4
……………………………………………………………………………………………………................
........................................................................................................................................................................ 5 Cán bộ ĐỀ phụ trách HP BCN bộ môn THI CUỐI KỲ 20181 duyệt Trường ĐHBKHN
Học phần: Tín hiệu & Hệ thống Phạm Văn Trường
Mã học phần: EE2000 Viện Điện Đào Phương Nam Bm. ĐKTĐ
Thời gian làm bài: 90 phút Ngày thi: 07/01/2019 Đỗ Thị Tú Anh Đề số 1 Điểm
Chữ ký CB chấm thi CB coi thi 1 CB coi thi 2
Họ tên SV: …………………………………………. Mã số SV: ……………………… Số thứ tự: ……………
Lưu ý: Sinh viên làm bài trực tiếp vào 4 mặt giấy này. Chỉ được sử dụng 1 quyển slide bài giảng, 1 vở ghi bài
viết tay, và 1 máy tính không lập trình được.
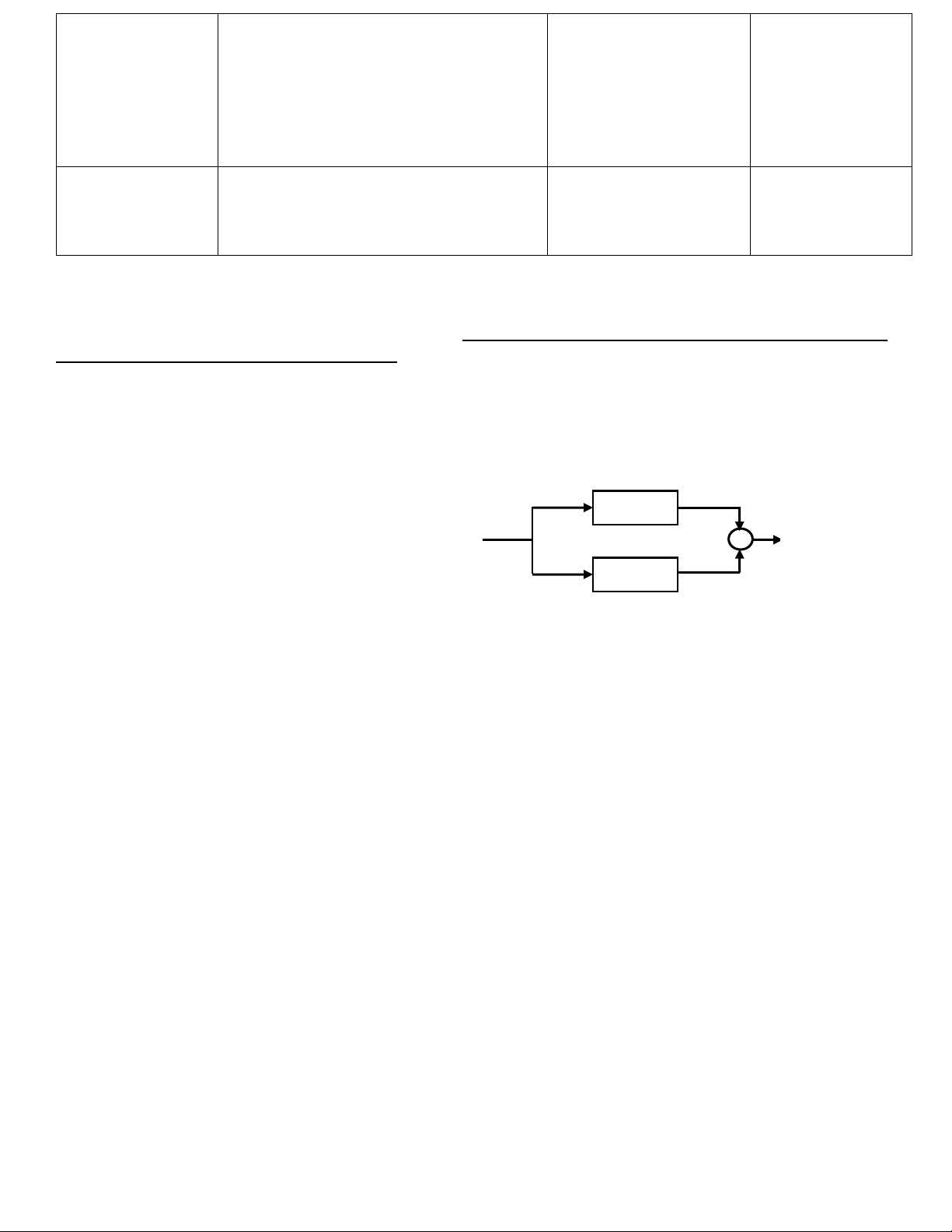
Bài 1 (Đáp ứng xung và tích chập) (5đ)
Xét hai hệ thống tuyến tính bất biến (hệ LTI) được ghép song song với nhau như Hình 1 dưới đây.
Biết rằng quan hệ vào-ra của hai hệ được cho bởi: t y (t) y 1 (t) = x( )d ,  1 Hệ 1 t − 1 t 1 − y x (t) y t (t) = x( )d.  ( ) + 2 t −2 Hệ 2 y (t)
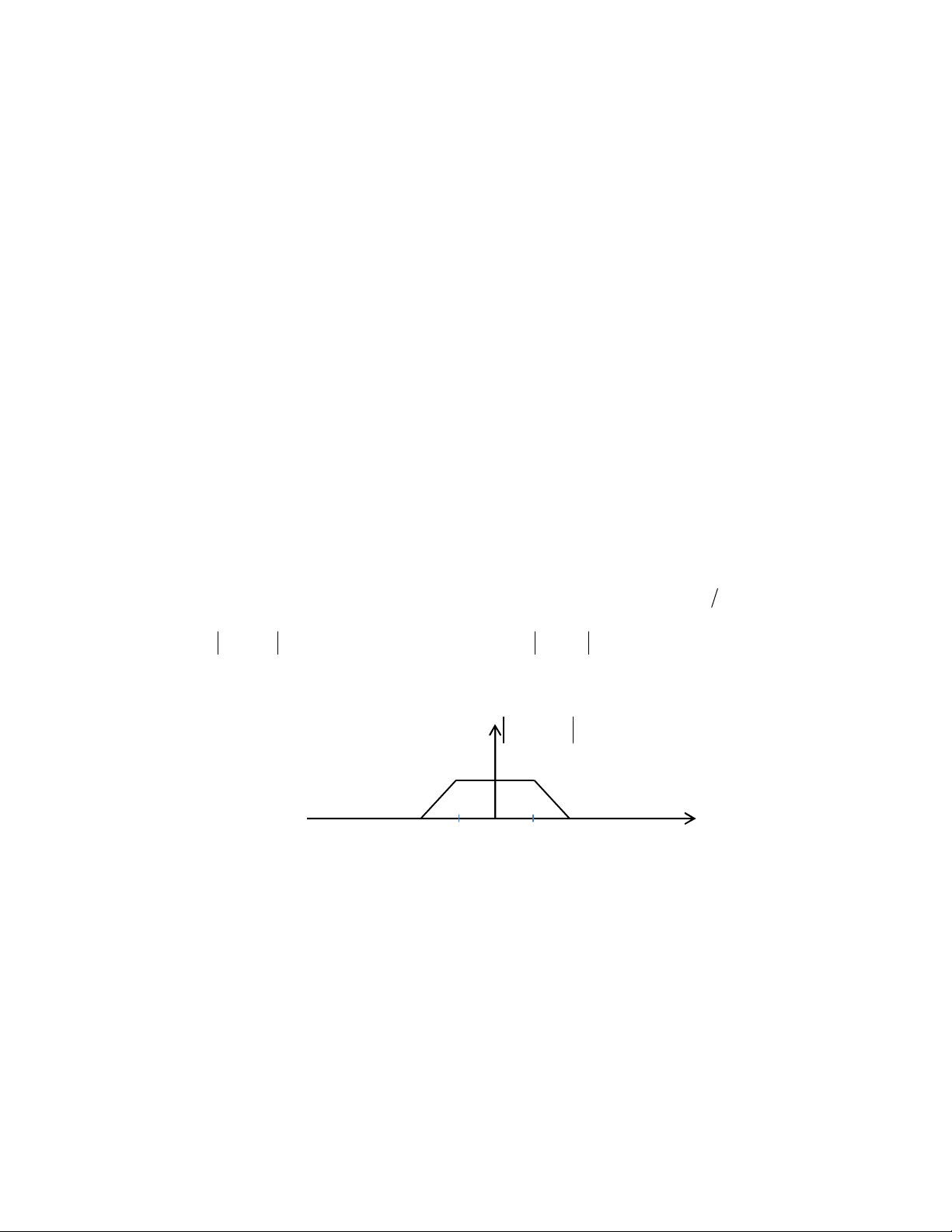
Giả thiết tín hiệu vào là: 2 x(t) = (
− t − 2)u(t) −u(t −2). Hình 1.
a) (1đ) Các đáp ứng xung h (t) và h (t) của hai hệ thống con là gì? 1 2 t t 2 [Gợi ý: Sử dụng  ( )d =1 
với bất kỳ t  0  t , hoặc sử dụng
 ( )d = u(t)  .] t 1 2 − 1
b) (1đ) Đáp ứng xung h (t ) của cả hệ thống là gì?
c) (1đ) Cả hệ thống có nhân quả không? có ổn định không? Hãy giải thích. 1
d) (1đ) Hãy vẽ x (t ) và h (t ) .
e) (1đ) Hãy tính và vẽ tín hiệu ra y(t ) của cả hệ thống.
Bài 2 (Phép biến đổi Fourier và lọc tín hiệu) (2đ)
a) (1đ) Hãy tính và vẽ phổ X () của tín hiệu tuần hoàn x (t ) có biểu thức như sau:
[Lưu ý: Nếu X () là hàm thực thì chỉ cần vẽ một đồ thị của X () theo  .]
x (t) = 2cos(t) + 5cos(3t − ) . 2
b) (1đ) Giả sử x (t ) được cho qua một bộ lọc lý tưởng sao cho ở đầu ra của bộ lọc ta thu được
y(t) = 2 cos(t) . Hãy vẽ đáp ứng biên độ -tần số H () của bộ lọc và tìm điều kiện của tần số ngưỡng c của
bộ lọc. Đó là loại bộ lọc gì?
Bài 3 (Phép biến đổi Laplace và hàm truyền) (3đ)
Cho một hệ thống bậc hai có quan hệ vào-ra được cho bởi phương trình vi phân: 2 d y(t) dy(t) − 4
+16y(t) = x(t). 2 dt dt
a) (1đ) Hãy tìm hàm truyền H (s) của hệ thống.
b) (2đ) Hãy tìm tín hiệu ra y(t ) của hệ thống với tín hiệu vào dạng bước nhảy đơn vị x (t) = u(t). Vẽ phác y(t) . 3 4 Cán bộ ĐỀ phụ trách HP BCN bộ môn THI CUỐI KỲ 20181 duyệt Trường ĐHBKHN
Học phần: Tín hiệu & Hệ thống Phạm Văn Trường
Mã học phần: EE2000 Viện Điện Đào Phương Nam Bm. ĐKTĐ
Thời gian làm bài: 90 phút Ngày thi: 07/01/2019 Đỗ Thị Tú Anh Đề số 2 Điểm
Chữ ký CB chấm thi CB coi thi 1 CB coi thi 2
Họ tên SV: …………………………………………. Mã số SV: ……………………… Số thứ tự: ……………
Lưu ý: Sinh viên làm bài trực tiếp vào 4 mặt giấy này. Chỉ được sử dụng 1 quyển slide bài giảng, 1 vở ghi bài
viết tay, và 1 máy tính không lập trình được.
Bài 1 (Đáp ứng xung và tích chập) (5đ)
Xét hai hệ thống tuyến tính bất biến (hệ LTI) được ghép song song với nhau như Hình 1 dưới đây.
Biết rằng quan hệ vào-ra của hai hệ được cho bởi: t y (t) y (t) = x ( )d ,  1 1 Hệ 1 t − 1 t 1 − y x t y t (t) = x ( )d.  ( ) ( ) + 2 t −3 Hệ 2 y (t)
Giả thiết tín hiệu vào là: 2 x(t) = (
− t −3)u(t) −u(t −3). Hình 1.
a) (1đ) Các đáp ứng xung h (t) và h (t) của hai hệ thống con là gì? 1 2 t t 2 [Gợi ý: Sử dụng  ( )d =1 
với bất kỳ t  0  t , hoặc sử dụng
 ( )d = u(t)  .] t 1 2 − 1
b) (1đ) Đáp ứng xung h (t ) của cả hệ thống là gì?
c) (1đ) Cả hệ thống có nhân quả không? có ổn định không? Hãy giải thích. 1
d) (1đ) Hãy vẽ x (t ) và h (t ) .
e) (1đ) Hãy tính và vẽ tín hiệu ra y(t ) của cả hệ thống.
Bài 2 (Phép biến đổi Fourier và lọc tín hiệu) (2đ)
a) (1đ) Hãy tính và vẽ phổ X () của tín hiệu tuần hoàn x (t ) có biểu thức như sau:
[Lưu ý: Nếu X () là hàm thực thì chỉ cần vẽ một đồ thị của X () theo  .]
x (t) = cos(2t) + 4cos(6t − ) . 2
b) (1đ) Giả sử x (t ) được cho qua một bộ lọc lý tưởng sao cho ở đầu ra của bộ lọc ta thu được
y(t) = cos(2t) . Hãy vẽ đáp ứng biên độ -tần số H () của bộ lọc và tìm điều kiện của tần số ngưỡng c của
bộ lọc. Đó là loại bộ lọc gì?
Bài 3 (Phép biến đổi Laplace và hàm truyền) (3đ)
Cho một hệ thống bậc hai có quan hệ vào-ra được cho bởi phương trình vi phân: 2 d y(t) dy(t) +10
+100y(t) =10x(t). 2 dt dt
a) (1đ) Hãy tìm hàm truyền H (s) của hệ thống.
b) (2đ) Hãy tìm tín hiệu ra y(t ) của hệ thống với tín hiệu vào dạng bước nhảy đơn vị x (t) = u(t). Vẽ phác y(t) . 3