Tổng hợp kiến thức Toán rời rạc và Thuật toán môn Toán rời rạc | Đại học Kinh tế Quốc Dân

lOMoAR cPSD| 58569740 Đ
ề cương t ổ ng h ợ p ki ế n th ứ c Toán rời rạc
Khoa Toán Kinh Tế - Bộ môn Toán cơ bản Mã học phần: TOCB1107 lOMoAR cPSD| 58569740 Chương 1
Cơ sở logic – Tập hợp
Bài 1: Logic – Mệnh đề I. Mệnh đề
- Mệnh đề là một khẳng định và chỉ có 2 kết quả: hoặc đúng hoặc sai.
- Mệnh đề P là đúng thì P nhận giá trị là 1, ký hiệu P=1.
- Mệnh đề P là sai thì P nhận giá trị là 2, ký hiệu P=0.
- Bảng giá trị chân lý của P: P P 0 1 1 Hoặc 0
1. Các phép toán của mệnh đề
1.1. Phép phủ định của mệnh đề
- Phủ định của mệnh đề P là một mệnh đề, đọc “ không phải A” và ký hiệu 𝑃 P 𝑃 0 1 1 0 1.2. Phép hội-AND
-Hội hai mệnh đề P và Q là mệnh
đề, đọc “P và Q”, ký hiệu P∧Q P Q P∧Q 0 0 0 0 1 0 lOMoAR cPSD| 58569740 1 0 0 1 1 1
- Hội hai mệnh đề chỉ đúng khi cả hai cùng đúng. 1.3. Phép tuyển-OR
- Tuyển hai mệnh đề P và Q là mệnh đề, đọc “P hoặc Q”, ký hiệu P∨Q P Q P∨Q 0 0 0 0 1 1 1 0 1 1 1 1
- Tuyển của hai mệnh đề chỉ sai khi cả hai cùng sai. 1.4. Phép kéo theo
- Mệnh đề P kéo theo mệnh đề Q, ký hiệu P→Q P Q P→Q 0 0 1 0 1 1 1 0 0 1 1 1
- Mệnh đề P→Q chỉ sai khi P đúng và Q sai.
- Ta nói “Q là điều kiện cần của P” và “P là điều kiện đủ của Q”
1.5. Phép tuyển loại - XOR
- Mệnh đề tuyển loại của A và B được kí hiệu là A⊕B P Q P⨁Q 0 0 0 0 1 1 1 0 1 1 1 0 lOMoAR cPSD| 58569740
- Mệnh đề này chỉ đúng khi A và B không cùng đúng hoặc cùng sai.
1.6. Phép tương đương
- Mệnh đề P tương đương mệnh đề Q, ký hiệu P↔Q P Q P↔Q 0 0 1 0 1 0 1 0 0 1 1 1
- Mệnh đề P↔Q chỉ đúng khi P và Q cùng đúng và cùng sai.
- A tương đương B là một mệnh đề nhận giá trị đúng khi cả hai mệnh đề P→Q và Q→P
đều đúng. Do đó, để chứng minh P⇔Q ta đi xét hai mệnh đề P→Q và Q→P
- Nhận xét: P↔Q tương đương logic với 𝑃⨁𝑄
- Tương đương logic là hai mệnh đề phức hợp có cùng bảng giá trị chân lý
2. Các quy luật logic
1. Phủ định của phủ định: : A = A
2. Tính chất giao hoán: A ∧ B ⇔ B ∧ A A ∨ B ⇔ B ∨ A
3. Tính chất kết hợp:
(A ∧ B) ∨ C ⇔ (A ∨ C) ∧ (B ∨ C)
(A ∨ B) ∧ C ⇔ (A ∧ C) ∨ (B ∧ C)
4. Tính chất phân phối:
(A ∧ B) ∧ C ⇔ A ∧ (B ∧ C)
(A ∨ B) ∨ C ⇔ A ∨ (B ∨ C)
5. Tính chất của phép kéo theo: A → B ⇔ A ∨ B lOMoAR cPSD| 58569740 A → B ⇔ B → A
6. Tính chất của phép tương đương:
A ↔ B ⇔ (A → B) ∧ (B → A)
7. Tính lũy đẳng: A ∧ A ⇔ A A ∨ A ⇔ A
8. Tính bắc cầu:
((A → B) ∧ (B → C)) → (A → C) ⇔ T
9. Luật De Morgan: A ∨ B ⇔ A ∧ B A ∧ B ⇔ A ∨ 𝐵 10.
Đẳng thức với T và F: A ∧ F ⇔ F A ∧ T ⇔ A A ∨ T ⇔ T A ∨ F ⇔ A
A ∧ A ⇔ F (𝐿𝑢ậ𝑡 𝑚â𝑢 𝑡h𝑢ẫ𝑛)
A ∨ A ⇔ T (𝐿𝑢ậ𝑡 𝑏à𝑖 𝑡𝑟𝑢𝑛𝑔)
[A ∧ (A → B)] → B ⇔ T (𝑄𝑢𝑦 𝑡ắ𝑐 𝑡𝑎𝑚 đ𝑜ạ𝑛 𝑙𝑢ậ𝑛)
2. Vị từ và lượng từ
- Một phát biểu P(x) đối với biến x∈D được gọi là hàm mệnh đề hoặc một vị từ nếu với
mỗi giá trị cụ thể x∈D thì P(x) là một mệnh đề.3
- D gọi là miền xác định của P(x)
VD: 𝑃(𝑥) = 𝑥2 > 9, 𝑥 ∈ 𝑍
Mệnh đề trên được phát biểu là "Số nguyên x thỏa mãn 𝑥2 > 9"
Với số nguyên x thỏa mãn −3 ≤ 𝑥 ≤ 3 thì mệnh đề P(x) sai
Với số nguyên x thỏa mãn 𝑥 < −3 hoặc 𝑥 > 3 thì mệnh đề P(x) đúng
Lượng từ phổ biến (với mọi) và lượng từ tồn tại
- Cho vị từ P(x) xác định trên miền M , ta có thể phát biểu các mệnh đề ở các dạng sau : lOMoAR cPSD| 58569740
+ "Với mọi x∈M có tính chất P(x)". Khi đó, mệnh đề này được quy ước và kí hiệu như sau: ∀𝑥 ∈ 𝑀, 𝑃(𝑥)
* Kí hiệu ∀ được gọi là lượng từ phổ biến hay lượng từ toàn thể, hoặc lượng từ với mọi
+ "Tồn tại x∈M có tính chất P(x)". Khi đó, mệnh đề này được quy ước và kí hiệu như sau: ∃𝑥 ∈ 𝑀, 𝑃(𝑥)
* Kí hiệu ∃ gọi là lượng từ tồn tại
* Mệnh đề "Tồn tại duy nhất một phần tử x của X có tính chất P(x)" được viết như sau: 𝑀, 𝑃(𝑥)
-Phép phủ định của lượng từ phổ biến và lượng từ tồn tại được cho bởi công thức:
3. Phép toán với các xâu bit
- Một bit là một kí tự 0 hoặc 1 (binary digit - kí tự nhị phân).
- Xâu bit (Xâu nhị phân): Là dãy gồm một hoặc nhiều bit (là dãy chỉ gồm số 0 và 1). Chiều
dài của xâu là số các bit trong xâu đó.
- Thông tin trên máy tính thường được biểu diễn bằng cách dùng các xâu bit. - Các phép
toán với xâu bit : OR, AND, XOR Bài 2: Tập hợp 1. Khái niệm
- Tập hợp không được định nghĩa, mà chỉ được mô tả như là sự tụ tập của một lớp các đối
tượng nào đó. Mỗi đối tượng của tập hợp gọi là phần tử của tập hợp đó. lOMoAR cPSD| 58569740
- Kí hiệu tập hợp bởi các chữ cái in, chẳng hạn A, B, C, X, Y, …
- Khi mô tả một tập hợp, ta thường sử dụng cách liệt kê tất cả các phần tử hoặc nêu tính
chất đặc trưng của tập hợp để phân biệt phần tử bất kì thuộc tập hợp hoặc không thuộc tập hợp đó.
- Một tập hợp có hữu hạn phần tử được gọi là tập hữu hạn. Tập hợp có vố số phần tử
được gọi là tập vô hạn.
- Cho tập hợp hữu hạn A. Số phần tử trong tập A được gọi là lực lượng (hay gọi là bản số)
của tập A. Kí hiệu là |𝐴|.
- Tập rỗng là tập hợp không chứa phần tử nào, kí hiệu .
- Tập con: Ta nói tập hợp A là tập con của tập B nếu và chỉ nếu mọi phần tử của tập A đều
thuộc tập B. Kí hiệu: 𝐴 𝐵
- Tập hợp bằng nhau: Ta nói tập hợp A bằng tập hợp B nếu tập A là tập con của B và 𝐴 𝐵
ngược lại. Ta kí hiệu: 𝐴 = 𝐵 ⇔ { 𝐵 𝐴 2. Các phép toán
2.1. Phép toán đối với tập hợp
- Phép hợp: Hợp của hai tập hợp A và B là tập hợp gồm tất cả các phần tử thuộc A hoặc thuộc B. Kí hiệu: A B
- Phép giao: Giao của hai tập hợp A và B là một tập hợp gồm tất cả các phần tử chung của A và B. Kí hiệu 𝐴 .
+ Hai tập hợp A và B được gọi là rời nhau nếu 𝐴 .
- Phép hiệu: Hiệu của tập hợp A với tập hợp B là một tập hợp, kí hiệu 𝐴\𝐵 (hoặc 𝐴 − 𝐵),
gồm tất cả các phần tử thuộc tập hợp A nhưng không thuộc tập hợp B
+ Khi 𝐵 𝐴 thì hiệu của tập hợp A với tập hợp B được gọi là phần bù của tập hợp B trong
tập hợp A. Kí hiệu phần bù của tập hợp B trong tập hợp A là: 𝐶𝐴𝐵 hay 𝐵
- Hiệu đối xứng: Hiệu đối xứng của hai tập hợp A và B là hợp của tập 𝐴\𝐵 và 𝐵\𝐴. Kí hiệu: 𝐴
- Tích Đề-các: Tích Đề-các của tập hợp A với B là một tập hợp được ký hiệu và xác định như sau: 𝐴 × 𝐵 𝐴, 𝑏 . lOMoAR cPSD| 58569740 + Đặc biệt 𝐴 × 𝐴
+ 𝑋 × 𝑌 𝑌 × 𝑋 hay tích đề các không có tính chất giao hoán 2.2. Tính chất
Cho X,Y,Z là các tập con của tập U. Khi đó ta có : X Y thì X Y = Y, X ∩ Y = X Luật đồng nhất: X = X, X ∩ = Luật lũy đẳng: X ∪ X = X, X ∩ X = X Luật giao hoán:
X ∪ Y = Y ∪ X, X ∩ Y = Y ∩ X Luật kết hợp:
(X ∪ Y) ∪ Z = X ∪ (Y ∪ Z) (X
∩ Y) ∩ Z = X ∩ (Y ∩ Z) Luật phân phối:
X ∩ (Y ∪ Z) = (X ∩ Y) ∪ (X ∩ Z) X ∪ (Y ∩ Z) = (X ∪ Y) ∩ (X ∪ Z) Luật nuốt:
X ∩ (X ∪ Y) = X X ∪ (X ∩ Y) = X Công thức Demorgan
𝐴\(𝐵 ∩ 𝐶) = (𝐴\𝐵) ∪ (𝐴\𝐶)
𝐴\(𝐵 ∪ 𝐶) = (𝐴\𝐵) ∩ (𝐴\𝐶) Tổng quan: X\ (𝑋\𝐴𝑖) X\ (𝑋\𝐴𝑖)
3. Biểu diễn tập hợp trên máy tính lOMoAR cPSD| 58569740
- Tập vũ trụ : Tập hợp lớn/tập hợp cha của máy tính, dùng để so sánh và đối chiếu với các
tập hợp con khi cần sử dụng các phép tính, phép biến đổi với tập hợp.
-Các tập hợp trên máy tính thường được lưu trữ dưới dạng sắp xếp có thứ tự (tăng dần
hoặc giảm dần) của các phần tử của tập vũ trụ - Quy trình biểu diễn tập hợp trong máy tính:
+ Cho tập vũ trụ U là tập hữu hạn (có kích thước hợp lí để không vượt quá bộ nhớ máy tính)
+ Sắp xếp các phần tử của tập U theo thứ tự tăng dần/giảm dần
+ Biểu diễn tập A là con của U bằng một xâu bit có chiều dài n
* Bit thứ 𝑎𝑖 sẽ mang giá trị 1 nếu phần tử thứ i tương ứng thuộc U
* Bit thứ 𝑎𝑖 sẽ mang giá trị 0 nếu phần thử thứ i tương ứng không thuộc U
Bài 3: Ánh xạ và quan hệ hai ngôi 1. Ánh xạ 1.1. Ánh xạ
Khái niệm: Cho X và Y là hai tập hợp khác rỗng. Ánh xạ từ tập X vào Y là một quy tắc đặt
tương ứng mỗi phần tử x ∈ X với một phần tử y ∈ Y
𝑋 × 𝑌 ⊇ 𝑓 = {(𝑥, 𝑦)|𝑚ỗ𝑖 𝑥 ∈ 𝑋, ∃! 𝑦 ∈ 𝑌} Ký hiệu: 𝒇: 𝑿 ⟶ 𝒀 𝒙 ↦ 𝒚 = 𝒇(𝒙) Trong đó: X là tập nguồn Y là tập đích
Y gọi là ảnh của x qua ánh xạ f lOMoAR cPSD| 58569740
X được gọi là tạo ảnh của Y
Cho tập 𝑿 ≠ ∅, ánh xạ từ X đến chính nó gọi là ánh xạ đồng nhất trên X. Kí hiệu là: 𝑰𝒅𝑿
1.2. Tập ảnh-Tập nghịch ảnh
Cho ánh xạ 𝑓: 𝑋 ⟶ 𝑌. Với mỗi tập con 𝐴 ⊂ 𝑋, 𝐴 ≠ ∅ , tập con của Y gồm các phần tử là
ảnh của x∈A qua ánh xạ f, kí hiệu là f(A) được gọi là tập ảnh của A qua f. Khi đó:
𝑓(𝐴) = {𝑓(𝑥)|𝑥 ∈ 𝐴} Chú ý: + + 𝒀 + 𝑨, 𝒚 + 𝑁ế𝑢 𝑨
Cho ánh xạ 𝑓: 𝑋 ⟶ 𝑌. Với mỗi tập con 𝐵 𝑌, tập con của 𝑋 gồm các phần tử x có ảnh 𝑓
𝐵, kí hiệu là 𝑓 (B), được gọi là tập nghịch ảnh của tập B. 𝑓 Chú ý: + 𝑿 + ⇔ 𝒇 𝑩
1.3. Tính chất của tập ảnh và tập nghịch ảnh
Cho ánh xạ 𝑓: 𝑋 ⟶ 𝑌, khi đó: 𝑓 𝐴,𝐵 𝑋 𝑓 𝐴, 𝐵 𝑋 𝑓 𝐴, 𝐵 𝑌 𝑓 𝐴, 𝐵 𝑌 𝑓 𝐴,𝐵 𝑌
𝑁ế𝑢 𝑓 𝑙à đơ𝑛 á𝑛 𝐴,𝐵 𝑋 lOMoAR cPSD| 58569740
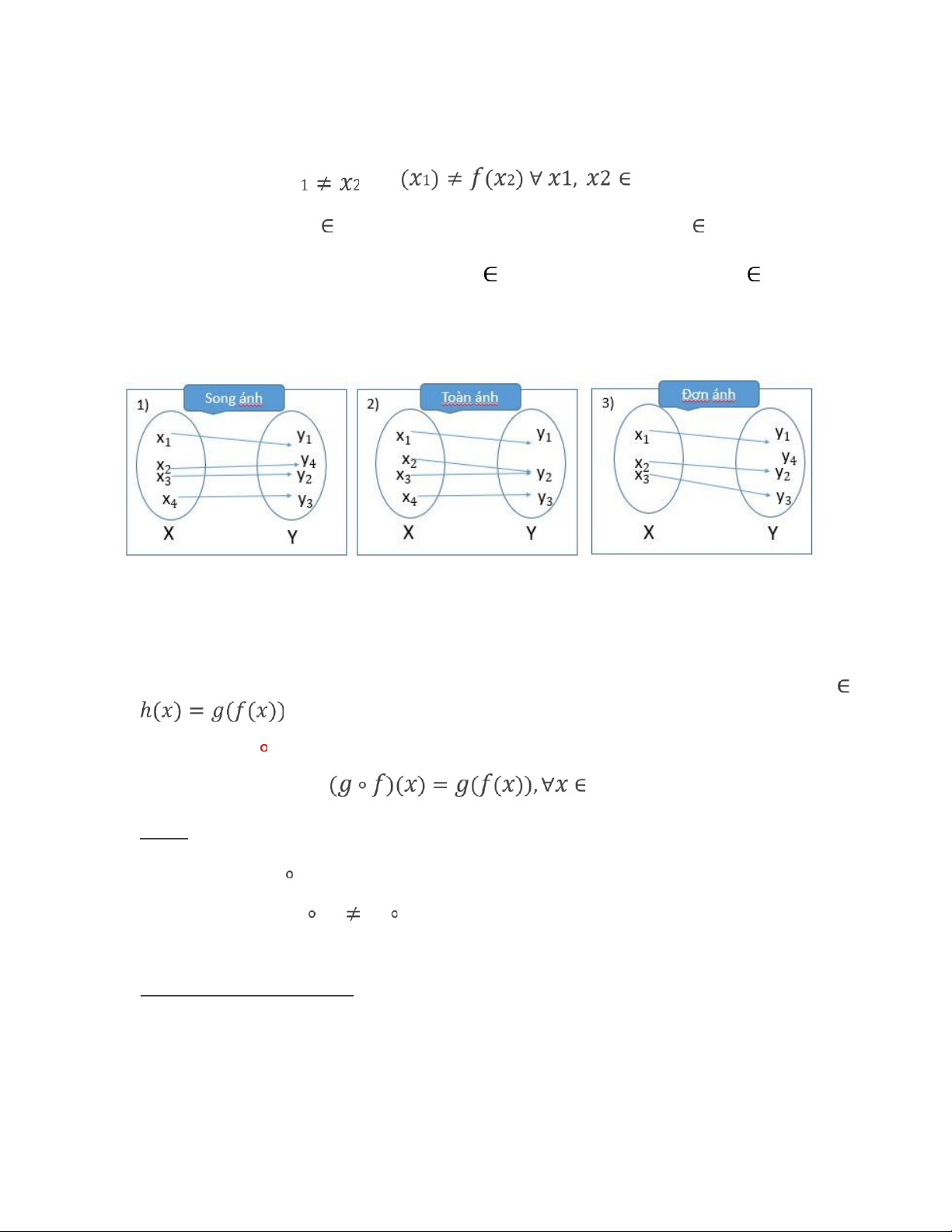
2. Đơn ánh - Toàn ánh - Song ánh
Ánh xạ f được gọi là đơn ánh nếu: 𝑥 ⇒ 𝑓 𝑋
Tức là, mỗi 𝑦 𝑌 chỉ là ảnh của duy nhất một phần tử 𝑥 𝑋
Ánh xạ f được gọi là toàn ánh nếu với mỗi 𝑦 𝑌 đều tồn tại ít nhất một 𝑥 𝑋 sao cho 𝑦
= 𝑓(𝑥). Nghĩa là ảnh của tập nguồn bằng chính tập đích.
Ánh xạ f được gọi là song ánh nếu nó đồng thời là đơn ánh và toàn ánh.
3. Tích ánh xạ - Ánh xạ ngược 3.1. Tích ánh xạ
Cho hai ánh xạ 𝑓: 𝑋 ⟶ 𝑌 và 𝑔: 𝑌 ⟶ 𝑍 . Ánh xạ ℎ: 𝑋 ⟶ 𝑍 là một quy tắc biến mỗi 𝑥 𝑋 thành
. Ánh xạ h được gọi là tích hợp thành của hai ánh xạ
𝑓 và 𝑔. Kí hiệu bởi 𝑔 𝑓 hoặc 𝑔𝑓. Khi đó: 𝑋 Lưu ý:
- Ánh xạ 𝑔 𝑓 chỉ thực hiện được khi tập đích của f là tập nguồn của g. - Ánh xạ 𝑔 𝑓 𝑓
𝑔 , nghĩa là tích hai ánh xạ không có tính chất giao hoán.
Tính chất tích hai ánh xạ:
- Hợp thành của hai đơn ánh là một đơn ánh
- Hợp thành của hai toàn ánh là một toàn ánh
- Hợp thành của hai song ánh là một song ánh lOMoAR cPSD| 58569740
3.2. Ánh xạ ngược
Cho ánh xạ 𝑓: 𝑋 ⟶ 𝑌 , nếu tồn tại ánh xạ 𝑔: 𝑌 ⟶ 𝑋 thỏa mãn 𝑥 𝑣à 𝑦
thì g được coi là ánh xạ ngược của f, kí hiệu là 𝑓 Tính chất:
- Ánh xạ f có ánh xạ ngược 𝑓−1 khi và chỉ khi f là song ánh - 𝐼𝑑𝑌 - 𝐼𝑑𝑋 Lưu ý: 𝑓
Nếu ánh xạ f là hàm số thì ánh xạ ngược 𝑓 được tìm bằng cách xét phương trình []với
ẩn x. Tiến hành giải phương trình tìm nghiệm x theo y. Đó là ánh xạ ngược cần tìm.
4. Quan hệ hai ngôi
Cho 2 tập A, B. Một quan hệ hai ngôi từ A đến B là một tập con của tích Descartes 𝐴 × 𝐵
Cho S là một quan hệ 2 ngôi từ A đến B, hay 𝐴 × 𝐵 . Giả sử 𝑎 𝐴, 𝑏 : +) Nếu
𝑆 thì ta nói a có quan hệ S với b. Kí hiệu: 𝑎𝑆𝑏 +) Nếu
𝑆 thì ta nói a không quan hệ S với b. Kí hiệu: 𝑎𝑆𝑏
Cho X là một tập hợp khác rỗng và S là quan hệ 2 ngôi trong X
𝑋 × 𝑋). Khi đó, S được
gọi là một quan hệ tương đương trong X khi và chỉ khi S thỏa mãn các tính chất sau: - Tính phản xạ: : 𝑎𝑆𝑎
- Tính đối xứng: 𝑎, 𝑏
: Nếu 𝑎𝑆𝑏 thì 𝑏𝑆𝑎
- Tính bắc cầu: 𝑎, 𝑏, 𝑐
: Nếu 𝑎𝑆𝑏 và 𝑏𝑆𝑐 thì 𝑎𝑆𝑐. lOMoAR cPSD| 58569740 Chương 2 Thuật toán Bài 1: Thuật toán 1. Định nghĩa
Thuật toán là tập hợp hữu hạn các lệnh chính xác để thực hiện tính toán hoặc để giải một bài toán. Ví dụ:
Mô tả thuật toán tìm phần tử lớn nhất trong một dãy hữu hạn các số nguyên
− B1: Đặt giá trị cực đại tạm thời bằng số nguyên đứng đầu dãy
− B2: So sánh số nguyên tiếp sau với giá trị cực đại tạm thời. Nếu nó lớn hơn thì đặt
giá trị cực đại tạm thời bằng số nguyên tố đó
− B3: Lặp lại B2 cho đến khi so sánh hết các số trong dãy
− B4: Dừng thuật toán khi hết nguyên trong dãy để so sánh. Cực đại tạm thời sẽ là số nguyên lớn nhất 2. Tính chất
− Đầu vào(Input): Một thuật toán có các giá trị đầu vào từ một tập đã được chỉ rõ
− Đầu ra(Output): Từ mỗi tập các giá trị đầu vào, thuật toán sẽ tạo ra các giá trị đầu ra.
Các giá trị đầu ra chính là nghiệm của bài toán.
− Tính xác định: Các bước của một thuật toán phải được xác định rõ ràng
− Tính đúng đắn: thuật toán phải tạo ra các giá trị đầu ra đúng đắn với giá trị đầu vào
− Tính hữu hạn: Một thuật toán cần phải tạo ra các giá trị đầu ra mong muốn sau một
số hữu hạn bước (nhưng có thể rất lớn) đối với mọi tập đầu vào. lOMoAR cPSD| 58569740
− Tính hiệu quả: Mỗi bước của thuật toán cần phải thực hiện được một cách chính xác
và trong một khoảng thời gian hữu hạn
− Tính tổng quan: Thủ tục cần phải áp dụng được cho mọi bài toán có dạng mong
muốn, chứ không chỉ cho một tập đặc biệt các giá trị đầu vào.
3. Thuật toán tìm kiếm
3.1. Tìm kiếm tuyến tính Giả code
procedure linearSeach(x,a1,a2,….,an) i:=1
while (i<=n and x <> ai) if i<=n then location:=i else location:=0
Ví dụ: Do dãy gồm Tài, Thắng, Minh, Hiệp, Hoàn, Nhất. Tìm Hà có trong dãy không? Bài làm i=1;n=6 x = Hà
a1=Tài => 1<=6 và Tài <> Hà => T => i=i+1=2
a2=Thắng => 2<=6 và Thắng <> Hà => T =>
i=i+1=3 a3=Minh => 3<=6 và Minh <> Hà => T =>
i=i+1=4 a4=Hiệp => 4<=6 và Hiệp <> Hà => T =>
i=i+1=5 a5=Hoàn => 5<=6 và Hoàn <> Hà => T =>
i=i+1=6 a6=Nhất => 6<=6 và Nhất <> Hà => T =>
i=i+1=7 a7=…=> 7<=6 và => F => i=7 Location := 0 Hà không có trong dãy
3.2. Tìm kiếm nhị phân
Danh sách đã được sắp xếp theo một trình tự nhất định lOMoAR cPSD| 58569740
procedure binarySearch(x,a1,a2,a3,...an):
i:= 1 {i là điểm nút bên trái của khoảng tìm kiếm(điểm bắt đầu)}
j:=n {j là diêm nút bên phái của khoảng tim kiêm (điểm kết
thúc)} while (i if( x> am) then I := m+1 else j := m end if x=ai then location := 1 else location := 0
Bài 2: Độ phức tạp của thuật toán (chưa xong)
Độ phức tạp thời gian của một thuật toán có thể được biểu diễn qua số phép toán
đươc dùng bởi thuật toán đó có giá trị đầu vào có kích thước xác định
Các phép toán được dùng do độ phức tạp thời gian có thể là phép so sánh các sô nguyên,
các phép cộng trừ nhân chia các số nguyên hoặc bất kỳ phép toán sơ cấp nào.
Ví dụ 1: Thuật toán tìm giá trị lớn nhất của tập hợp n phần tử
2n-1 phép so sánh => 2n - 1 là 𝛩(𝑛) => độ phức tạp thời gian của thuật toán tìm giá trị lớn nhất là 𝛩(𝑛)
Ví dụ 2: thuật toán tìm kiếm tuyến tính
2n+1 phép so sánh => Θ(n) => Trường hợp xấu nhất sẽ sử dụng O(n) phép so sánh
Ví dụ 3: Thuật toán tìm kiếm nhị phân
N=2𝑘 phần tử với k là 1 số nguyên k âm k = log(n) (nếu bảng có n phần tử mà n này không
phải lũy thừa của 2 thì 2𝑘 i và j là vị trí của số hạng đầu tiên và cuối cùng: phép so sánh này giúp mình kiểm tra xem
cái bảng các phần tử đang được xét có nhiều hơn 1 phần tử hay không lOMoAR cPSD| 58569740
Nếu ilớn hơn giá trị ở giữa của bảng hay không Có 2 phép so sánh
Bảng liệt kê có 2𝑘 phần tử thì sau 2 phép so sánh mình sẽ còn xet bảng 2𝑘−1
Có 2 phép so sánh tiếp thì 2𝑘−2 cho đến khi bảng liệt kê còn có 21 = 2 phần tử sử dụng
tiếp 2 phép so sánh cho đến khi còn 1 phần tử, một phép so sánh để biết không còn phần
tử nào nữa, 1 phép so sánh cho biết số hạng đó có phải là 𝑥𝑘 Cần nhiều nhất 2k+2 phép
so sánh từ bằng 2𝑘 phần tử
Mà 𝑘 = 𝑙𝑜𝑔(𝑛) => 2𝑙𝑜𝑔(𝑛) + 2 phép so sánh => 𝛩(𝑙𝑜𝑔𝑛)
Bài 3: Thuật toán về các số nguyên và nhân hai ma trận
1. Biểu diễn số nguyên 1.1. Định lý 1
Cho b là một số nguyên dương lớn hơn 1. Khi đó nếu n là số nguyên dương thì nó có thể
đươc biểu diễn duy nhất dưới dạng: 𝑛 𝑎𝑘𝑏𝑘 𝑎 trong đó 𝑎𝑖 𝑏 với mọi 𝑖 , … , 𝑘 và 𝑎𝑘 .
 Khai chiển cơ số 𝑏 của n
1.2. Khai chiển nhị phân
Ví dụ: Số (101011111)2 được biểu diễn theo cơ số thập phân là:
(101011111)2 = 1.28+0.27+1.26+0.25+1.24+1.23+1.22+1.2+1= 351
1.3. Khai chiển bát phân (cơ số 8) Ví dụ:
Số (245)8 biểu diễn theo cơ số 10 là: 2.82 + 4.81 + 5 = 165 lOMoAR cPSD| 58569740 1.4. Đổi cơ số
Ví dụ: Khai triển theo cơ số 8 của số (12467)10 Chia 12467 cho 8 ta được: 12467 = 8.1558 + 3 a0 1558 = 8.194 + 6 a1 194 = 8.24 + 2 a2 24 = 8.3 + 0 a3 3 = 8.0 + 3 a4 (12345)10 = (30263)8
2. Thuật toán của phép toán đối với số nguyên
2.1. Tổng hai số nguyên
Tổng hai số nguyên được tính bằng cách cộng liên tiếp các cặp bit và khi cần phải cộng cả số nhớ nữa
Ví dụ: Sử dụng phép cộng trong hệ nhị phân hãy tìm tổng của hai số nguyên 125 và 38
125 = (1111101)2 và 28 = (100110)2 +1111101 100110 10100011 Thuật toán:
Procedure cộng (a, b: positive integers)
{Khai triển nhị phân của a và b tương ứng là lOMoAR cPSD| 58569740
(an-1an-2…a1a0)2 và (bn-1bn-2…b0)2} c: =0 for j: = 0 to n - 1 𝑎𝑗+𝑏𝑗+𝑐 begin 𝑑: = [ ] ; 2 sj: = aj + bj + c - 2d; c: = d; end sn: = c
{khai triển nhị phân của tổng là (𝑠𝑛𝑠𝑛−1 … 𝑠1𝑠0)2}
2.2. Nhân hai số nguyên
Khai triển nhị phân của b=(bn-1bn-2…b1b0)2 n−1 n−1 ab = a bj 2 j =
a(bj 2 j ). j=0 j=0
Trước hết, ta thấy rằng abj=a nếu bj=1 và abj=0 nếu bj=0.
Mỗi lần ta nhân một số hạng với 2 là ta dịch khai triển nhị phân của nó một chỗ về
phía trái bằng cách thêm một số không vào cuối khai triển nhị phân của nó.
Do đó, ta có thể nhận được (abj)2j bằng cách dịch khai triển nhị phân của abj đi j chỗ về
phía trái, tức là thêm j số không vào cuối khai triển nhị phân của nó.
Cuối cùng, ta sẽ nhận được tích ab bằng cách cộng n số nguyên abj.2j với j=0, 1, ..., n-1.
Ví dụ : Tìm tích của a = (110)2 và b = (101)2. Ta có:
ab0.20 = (110)2.1.20 = (110)2,
ab1.21 = (110)2.0.21 = (0000)2, ab2.22 = (110)2.1.22 = (11000)2. lOMoAR cPSD| 58569740
Để tìm tích, hãy cộng (110)2, (0000)2 và (11000)2. ab= (11110)2.
Thuật toán: Nhân hai số nguyên procedure nhân (a,b:
positive integers) for j := 0 to n-1 begin
if bj = 1 then cj := a được dịch đi j chỗ else cj := 0 end
{c0, c1,..., cn-1 là các tích riêng
phần} p := 0 for j := 0 to n-1 p := p + cj
{p là giá trị của tích ab}
3. Thuật toán nhân hai ma trận
Cho hai ma trận 𝐴 = [𝑎𝑖𝑗]𝑚×𝑛 và 𝐵 = [𝑏𝑗𝑘]𝑛×𝑝. Tích của ma trận A với ma trận B là một ma trận:
𝐶 = 𝐴𝐵 = [𝑐𝑖𝑘]𝑚×𝑝
trong đó, 𝑐𝑖𝑘 được xác định bởi công thức
𝑐𝑖𝑘 = 𝑎𝑖1𝑏1𝑘 + 𝑎𝑖2𝑏2𝑘 + ⋯ + 𝑎𝑖𝑛𝑏𝑛𝑘
Với mọi 𝑖 = 1, … , 𝑚 và 𝑘 = 1, … , 𝑝.
Thuật toán: Thuật toán nhân ma trận
Procedure nhân_ma_trận (A,B:ma trận) for i := 1 to m do begin lOMoAR cPSD| 58569740 for 𝑗 : = 1 to p do begin 𝑐𝑖𝑗 = 0; for 𝑞 : = 1 to n
𝑐𝑖𝑗 ≔ 𝑐𝑖𝑗 + 𝑎𝑖𝑞𝑏𝑞𝑗; end
end {c = [cij] là tích của A và B} Bài 4: Quy t ắc
Quy nạp toán học thường được sử dụng để chứng minh mệnh đề dạng ∀ 𝒏 ∈
ℕ, 𝒏 ≥ 𝒏𝟎: 𝑷(𝒏),
Chứng minh một bài toán bằng phương pháp quy nạp có ba bước sau:
− B1 - Bước cơ sở: Ta chỉ ra 𝑃(𝑛0) đúng với 𝑛0là một số nguyên không âm đặc biệt nào đó.
− B2 - Giả thiết quy nạp: Giả sử k là một số nguyên sao cho 𝑘 ≥ 𝑛0và P(k) đúng. −
B3 - Bước quy nạp: Ta cần chứng minh P(k+1) cũng đúng.
Hai dạng của nguyên lý quy nạp toán học: Dạng thứ nhất
Cho P(n) là một mệnh đề hay tính chất nào đó chứa số nguyên không âm n và đặt 𝑛0là số
nguyên không âm cố định.
− B1: Chỉ ra 𝑃(𝑛0) đúng (tức là P(n) đúng với 𝑛 = 𝑛0).
− B2: Khi với k là một số nguyên sao cho 𝑘 ≥ 𝑛0và P(k) đúng thì cần chứng minh P(k+1)
là đúng. Khi đó P(n) đúng với mọi số nguyên 𝑛 ≥ 𝑛0. Dạng thứ hai
Cho P(n) là một mệnh đề phụ thuộc vào số nguyên không âm n và 𝑛0 là một số nguyên
không âm cố định.
− B1: Chỉ ra 𝑃(𝑛0) đúng
− B2: Nếu 𝑃(𝑛0), 𝑃(𝑛0 + 1),… , 𝑃(𝑘) đúng với mọi số nguyên 𝑘 thì suy ra 𝑃(𝑘 +
1) đúng. Do đó, 𝑃(𝑛) đúng với mọi 𝑛 .