Tổng hợp lý thuyết môn Xác suất thống kê| Trường Đại học Ngoại Thương

Xác su t ấ
Xác suất có điều kiện
Cho hai biến cố A và B. Xác suất của biến cố A được tính trong điều kiện biến cố B đã xảy ra rồi gọi là xác suất có điều kiện
của A với điều kiện B, kí hiệu là P(A B) , và được xác định như sau P(AB) . P(A B)  (P(B) 0) P(B)
Công thức xác suất đầy đủ , ,. .,
các biến cố và B là một biến cố bất kỳ. Khi đó n A A A 1 2  P(B) 
P(A )P(B A ) n  i  i          1 i | | . . |
 P A P B A  P A P B A   P A P B A 1 1 2 2 n n
Công thức Bayer
Cho , ,. ., là một nhóm đầy đủ các biến cố và B là một biến cố bất kỳ. Khi đó n A A A 1 2 ( ) ( ) ( ) ( ) ( ) P A  P  B A P A P B A P A B P B  P A P B A i i (i ) ( i ) in i i 1 i
Biến ngẫu nhiên
Biến ngẫu nhiên rời rạc
Cho biến ngẫu nhiên rời rạc X nhận các giá trị x ,x ,. ., với các xác suất tương ứng PX  x p i  . i i ( 1,2, 1 2 xn
Bảng phân phối xác suất của biến ngẫu nhiên rời rạc X có dạng X x1 x2 …. xn P p1 p2 …. pn Tính chất: 0 1  p  i 1.  n  p  i 1 i 1  ít ra
2. P( )a X b    p i a x  b i n 3.    i i i 1  n 4.   2    i 1 
Biến ngẫu nhiên liên tục Cÿung có t he r a F( X)
Cho X là một biến ngẫu nhiên liên tục với hàm mật độ xác suất f x . Tính chất: i)     ii)     b
iii) Pa  X b Pa 
X b  P a  X b    P  a X b  f x dx    a x iv) F x  f t   dt  hàm phân phôi   v) E X  x f (x)dx   máy tính là đÿc  vi) V X   x
 EX f 2 (x)dx 
MỘT SỐ QUY LUẬT XÁC SUẤT THÔNG DỤNG
Phân phối xác suất của biến ngẫu nhiên rời rạc t ra
Phân phối Phân phối không-một Phân phối nhị thức
Phân phối Poisson
Phân phối siêu bội Định
- X chỉ nhận hai giá trị 0 - X là số lần sự kiện A - X là số lần xảy ra một - Xét tập hợp N phần tử, nghĩa và 1.
xảy ra trong n phép thử hiện tượng nào đó trong có M phần tử tính chất A. - X . giống nhau.
một đơn vị thời gian nhất Lấy ngẫu nhiên n phần
+ p: xác suất xuất hiện giá - X định.
tử. X là số phần tử có tính trị 1 + n: số phép thử - X chất A.
+ p: xác suất xảy ra sự +  : trung bình số hiện - X  M ,n kiện A tượng xảy ra trong khoảng thời gian đang xét
Công thức E  Xp V X pq    P(X k ) k C p (k1 ) n k p     k  ( ) k n C .kC M N M  n  P X k C  (  X )pq P( ) X k , e n k ! N
i) E X  np
i) E(X ) np
E X  V  ( X )  N n ii) V X  n  p (1 p )
ii) V ( )X  n  . pq N 1
Phân phối chuẩn ra
Biến ngẫu nhiên X được gọi là có phân phối chuẩn với tham số  và  2(  0) , kí hiệu:  2 X nếu hàm mật độ có dạng: 2 ( )x  f x  1, 2 2  e  x R  2    Nếu  2 X thì biến ngẫu nhiên    Nếu  2 X thì     tra bang    
Tích phân Laplace (Tra bảng phụ lục 2) 2 x x t    x 1 2  ( )tdt 2 e dt  . 0 0 Tính chất: i)   x x    ii) x x 5  :( ) 0,5
ƯỚC LƯỢNG – KIỂM ĐỊNH
Ước lượng điểm đ - Trung bình m 1 ẫu: n x x . trung binh mau i n i 1 - Phương sai: bam may 2
+ Phương sai chưa hiệu chỉnh:  x x phuong sai tong the i  ni 1 2 n 1
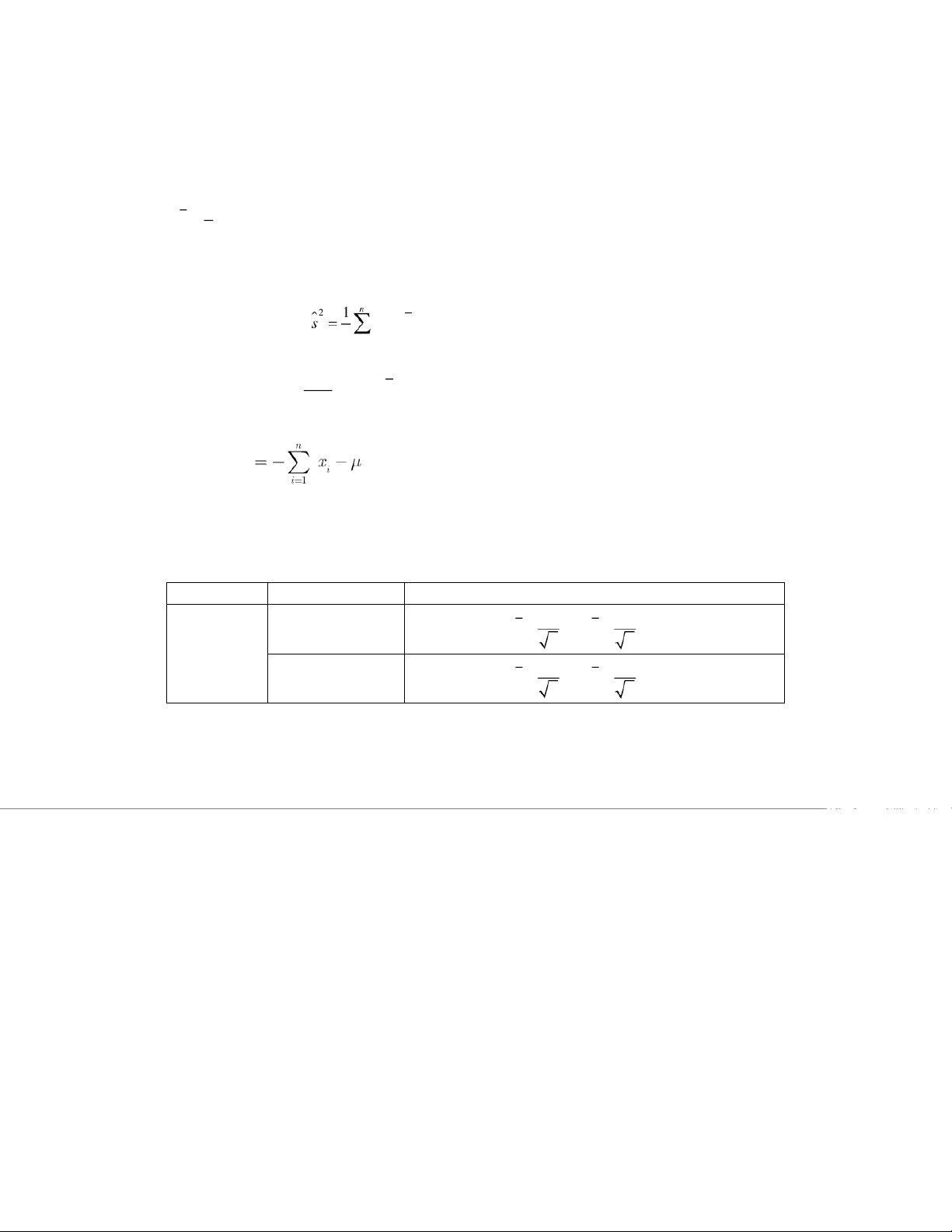
+ Phương sai hiệu chỉnh: 2
s   x x i  n 1 i 1 2 1 + Phương sai mẫu: 2 * s n - Tỷ lệ mẫu f
Ước lượng khoảng quan trong
Bài toán Đặc điểm mẫu
Khoảng ước lượng với độ tin cậy 1  n 30 và  đã   x   z x ; z Ước lượng biết /2 /2  n n
trung bình  n 30 và  chưa  s s x   z x ; z bi ết /2 /2  n n n 30 , pp chuẩn   x   z x ; z và  đã biết /2 /2  n n n 30 , pp chuẩn  s s x  t n  ( 1);x t n ( 1) và  chưa biết /2 /2  n n Ước lượng  f f1 1  f f   t  f  z f ; z ỉ lệ mẫu p n 100 /2 /2  n n   *2 *2  ns ns Ước lượng  đã biết  ; 2 2    ( ) n n ( ) phương sai /2 1 /2  2 2 2   
 n s1 1 n s   chưa biết  ; 2 2    /2  ( 1 n )n 1 /2( 1) Kiểm định Kiểm định H :  H  :  H  :  0 0 0 0 0 0 v ề trung    H :  H :   H :   bình 1 0 1 0 1 0 n 30 và     W X        đã biết 0 W : X  G   n G z 0:  G    n G z 0 W : X  G   n G  z         2  n 30 và  X     X         chưa biết 0 W : G   Sz n G
W z  G    0: n G 0 W : X G     n G z    S S  2    n 30, pp     W X       chuẩn và  0 W : X  G   n G z 0:  G    n G z 0 W : X  G   n G  z        đã biết  2  n 30, pp        X   chuẩn và  0 W 1 XG n  G   n :t  W 1 X  G  
St 0n: n G   t W 1  G   0: n G      n         S  S chưa biết 2  Kiểm H :  H  :  H  :  0 0 0 0 0 0
định về tỷ H :      1   0  1 H :  0  1 H :  0 lệ Khin p  05   Fp n     F p n   Fp n 0/2 0 0 và W : G  G  z W : G  G  z
W : G  G z  p (1 p )      p (1 p )  p (1 p )  n     p (  1 5 0 0 0 0 0 0 0) Kiểm định  0 H 0:  H  :  H  :  0 0 0 0 v ề phương    H :  H :  H :  sai 1 0 1 0 1 0  chưa biết 22  ( 1 n ) 22  ( 1 n ) : S  S G G          (n 1) W= G :G  (n  1) 21   22  2  ( 1 n )S   02 W ( 1)  0 W  G  :G    (n  1) 2 1 2
 hoac G       0  n   2  đã biết 2  ( )X  2   ( )X   2   ( )X  i 2 G  :G  i 2 W= G  :G  i 2 W  G  :G  (n  )  ( n )  (n)  21 2 1 W    2    02  0   0   2
hoac G  (n)   2