Top 30 câu trắc nghiệm ôn tập các phép toán trên tập hợp (giải chi tiết)
Top 30 câu trắc nghiệm ôn tập các phép toán trên tập hợp (giải chi tiết) theo chương trình chuẩn. Tài liệu được biên soạn dưới dạng file pdf gồm 3 trang chứa nhiều thông tin hay và bổ ích giúp bạn dễ dàng tham khảo và ôn tập đạt kết quả cao. Mời bạn đọc đón xem!
Chủ đề: Chương 2: Bất phương trình và hệ bất phương trình bậc nhất hai ẩn (KNTT)
Môn: Toán 10
Thông tin:
Tác giả:
Thông tin :
Chủ đề:
Chương 2: Bất phương trình và hệ bất phương trình bậc nhất hai ẩn (KNTT)
Môn:
Tác giả:
Tài liệu liên quan:
Preview text:
TRẮC NGHIỆM ÔN TẬP CÁC PHÉP TOÁN TRÊN TẬP HỢP
Câu 1: Cho X 7; 2;8; 4;9;1 2 ;Y 1;3;7;
4 . Tập nào sau đây bằng tập X Y ?
A. 1; 2;3; 4;8;9;7;1 2 . B. 2;8;9 ;12 . C. 4; 7 . D. 1; 3 .
Câu 2: Cho tập hợp A 1; 2;3; 4;
5 . Tìm số tập hợp X sao cho A \ X 1;3;
5 và X \ A 6; 7 . A. 1 B. 2 C. 3 D. 4
Câu 3: Cho tập hợp A 2; 4;6;
9 , B 1; 2;3;
4 . Tập nào sau đây bằng tập A \ B ? A. 1; 2;3; 5 B. 1; 2;3; 4;6; 9 C. 6; 9 D.
Câu 4: Cho A 0;1; 2;3;
4 , B 2;3; 4;5;
6 . Tập hợp A \ B bằng: A. 0 . B. 0; 1 . C. 1; 2 . D. 1; 5 .
Câu 5: Cho A ; 2 , B 3;
,C 0;4 . Khi đó tập A BC là: A. 3; 4 . B. ; 2 3; . C. 3; 4 . D. ; 2 3; .
Câu 6: Cho hai tập hợp A 2
;7, B 1;9. Tìm A B . A. 1;7
B. 2;9 C. 2 ;1 D. 7;9
Câu 7: Cho A 1
;5, B 2;7 . Tìm A \ B .
A. 1; 2 B. 2;5
C. 1; 7 D. 1; 2
Câu 8: Cho hai tập hợp X ,Y thỏa mãn X Y 7
;15 và X Y 1
;2. Xác định số phần tử là số nguyên của X . A. 2 . B. 5 . C. 3. D. 4 .
Câu 9: Cho hai tập hợp A 3
;3 và B 0;
. Tìm A B .
A. A B 3; .
B. A B 3; .
C. A B 3 ;0.
D. A B 0;3 .
Câu 10: Xác định phần bù của tập hợp ;2 trong ;4 . A. 2 ;4 .
B. 2; 4 .
C. 2; 4 . D. 2; 4 .
Câu 11: Xác định phần bù của tập hợp ; 1 010; 0 trong .
A. 10;10 . B. 10 ;10 0 . C. 1
0;00;10 . D. 1 0;00;10 .
Câu 12: Cho hai tập A 0;5; B 2 ; a 3a 1 , a 1
. Với giá trị nào của a thì A B . 5 5 a a 2 1 5 2 1 5 A. B. a . C. . D. a . 1 3 2 1 3 2 a a 3 3
Câu 13: Cho A x R x m
25 ; B x R x 20
20 . Có bao nhiêu giá trị nguyên m thỏa A B A. 3987 . B. 3988 . C. 3989 . D. 2020.
Câu 14: Cho 2 tập hợp A m 2; m 5 và B 0; 4 . Tìm tất cả các giá trị thực của tham số m để B A . A. m 1 . B. 1
m 2 . C. 1
m 2 . D. m 2 .
Câu 15: Cho hai tập hợp A 2
;3 và B ;
m m 5 . Tìm tất cả các giá trị thực của tham số m để
A B . A. 7 m 2 . B. 2
m 3. C. 2
m 3. D. 7 m 3.
Câu 16: Cho hai tập hợp A 4
;3 và B m 7;m. Tìm giá trị thực của tham số m để B A .
A. m 3 .
B. m 3 .
C. m 3 . D. m 3 .
Câu 17: Cho hai tập hợp A
;m và B 3m 1;3m
3 . Tìm tất cả các giá trị thực của tham số m
để A C B . 1 1 1 1 A. m . B. m . C. m . D. m . 2 2 2 2
Câu 18: Một lớp có 30 học sinh, trong đó mỗi học sinh giỏi ít nhất một trong hai môn Hóa và Văn, biết
rằng có 15 bạn học giỏi môn Hóa, 20 bạn học giỏi môn Văn. Hỏi lớp đó có bao nhiêu học sinh giỏi cả hai môn A. 25 . B. 20 . C. 10 . D. 5 .
Câu 19: Trong số 45 học sinh của lớp 10A có 15 bạn được xếp loại học lực giỏi, 20 bạn được xếp loại
hạnh kiểm tốt, trong đó có 10 bạn vừa được học sinh giỏi vừa được hạnh kiểm tốt. Khi đó lớp 10 A có
bao nhiêu bạn được khen thưởng, biết rằng muốn được khen thưởng bạn đó phải có học lực giỏi hay hạnh kiểm tốt. A. 25 . B. 20 . C. 35 . D. 40 .
Câu 20: Trong số 45 học sinh của lớp 10A có 15 bạn được xếp loại học lực giỏi, 20 bạn được xếp loại
hạnh kiểm tốt, trong đó có 10 bạn vừa được học sinh giỏi vừa được hạnh kiểm tốt. Khi đó lớp 10 A có
bao nhiêu bạn chưa được xếp loại học lực giỏi và chưa có hạnh kiểm tốt. A. 25 . B. 20 . C. 35 . D. 40 .
Câu 21: Trong kì thi học sinh giỏi cấp trường, lớp 10 A có 17 bạn được xếp công nhận học sinh giỏi
Văn, 25 bạn học sinh giỏi Toán. Tìm số học sinh giỏi cả Văn và Toán biết lớp 10 A có 45 học sinh và có
13 học sinh không đạt học sinh giỏi. A. 10 . B. 32 . C. 30 . D. 15.
Câu 22: Trong kì thi học sinh giỏi cấp trường, lớp 10 A có 17 bạn được xếp công nhận học sinh giỏi
Văn, 25 bạn học sinh giỏi Toán. Tìm số học sinh giỏi cả Văn và Toán biết lớp 10 A có 45 học sinh và có
10 học sinh không đạt học sinh giỏi. A. 7 . B. 32 . C. 12 . D. 15.
Câu 23: Một lớp có 40 học sinh, trong đó mỗi học sinh giỏi ít nhất một trong hai môn Hóa và Văn, biết
rằng có 25 bạn học giỏi môn Hóa, 30 bạn học giỏi môn Văn. Có bao nhiêu học sinh giỏi cả hai môn? A. 25 . B. 20 . C. 10 . D. 15 .
Câu 24: Trong số 50 học sinh của lớp 10 A có 15 bạn được xếp loại học lực giỏi, 25 bạn được xếp loại
hạnh kiểm tốt, trong đó có 10 bạn vừa được học sinh giỏi vừa được hạnh kiểm tốt. Khi đó lớp 10 A có
bao nhiêu bạn được khen thưởng, biết rằng muốn được khen thưởng bạn đó phải có học lực giỏi hay hạnh kiểm tốt. A. 25 . B. 20 . C. 35 . D. 30 .
Câu 25: Đội tuyển thi đá cầu và đấu cờ vua của Trường Lý Tự Trọng có 22em , trong đó có 15 em thi đá
cầu và 12 em thi đấu cờ vua. Hỏi có bao nhiêu em trong đội tuyển thi đấu cả hai môn ? A. 8 . B. 7 . C. 10 . D. 5 .
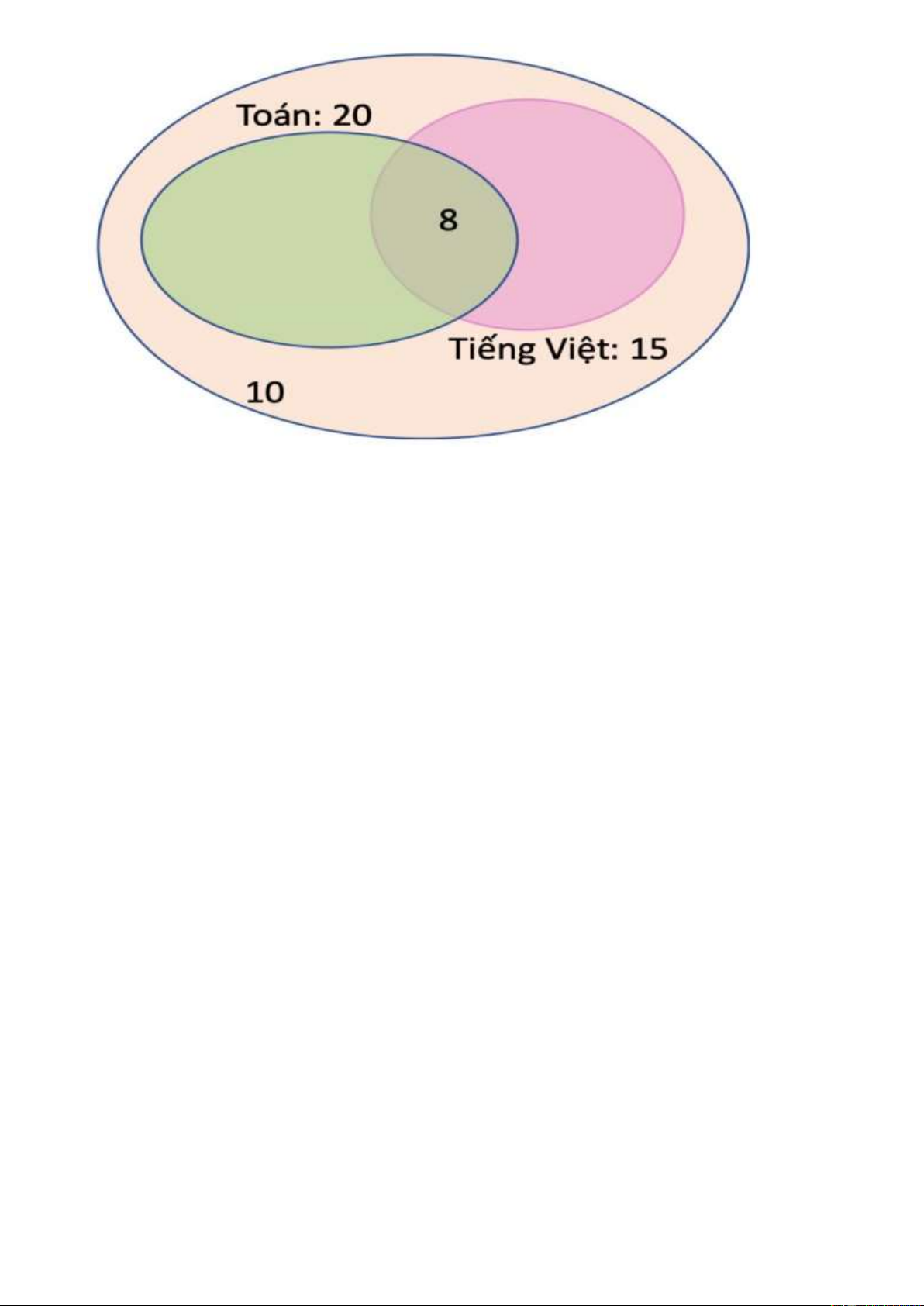
Câu 26: Lớp 10A của trường Phạm Văn Đồng có 15 bạn thích môn tiếng Việt, 20 bạn thích môn Toán.
Trong số các bạn thích Tiếng Việt hoặc thích Toán có 8 bạn thích cả hai môn Tiếng Việt và Toán. Trong
lớp vẫn còn có 10 bạn không thích môn nào (trong hai môn Tiếng Việt và Toán). Hỏi lớp 10A của trường
Phạm Văn Đồng có bao nhiêu bạn tất cả?
Số bạn thích Toán nhưng không thích Tiếng việt: 20 - 8 = 12 (bạn)
Số bạn thích Tiếng việt nhưng không thích Toán: 15 8 7 (bạn)
Số học sinh của cả lớp là: 12 7 8 10 37 (bạn) A. 7 . B. 12 . C. 37 . D. 35 .
------ HẾT ------