

































































Preview text:
KIỂM TRA ĐỊNH KỲ HỌC KÌ 2 1 MÔN TOÁN LỚP 12 30 ĐỀ ÔN THI HỌC KÌ 2 MÔN TOÁN 12 NĂM HỌC 2020-2021 2020 - 2021 30 ĐỀ
30 ĐỀ ÔN THI HKII-LỚP 12
30 ĐỀ ÔN THI HỌC KÌ 2-LỚP 12 NĂM HỌC 2020-2021
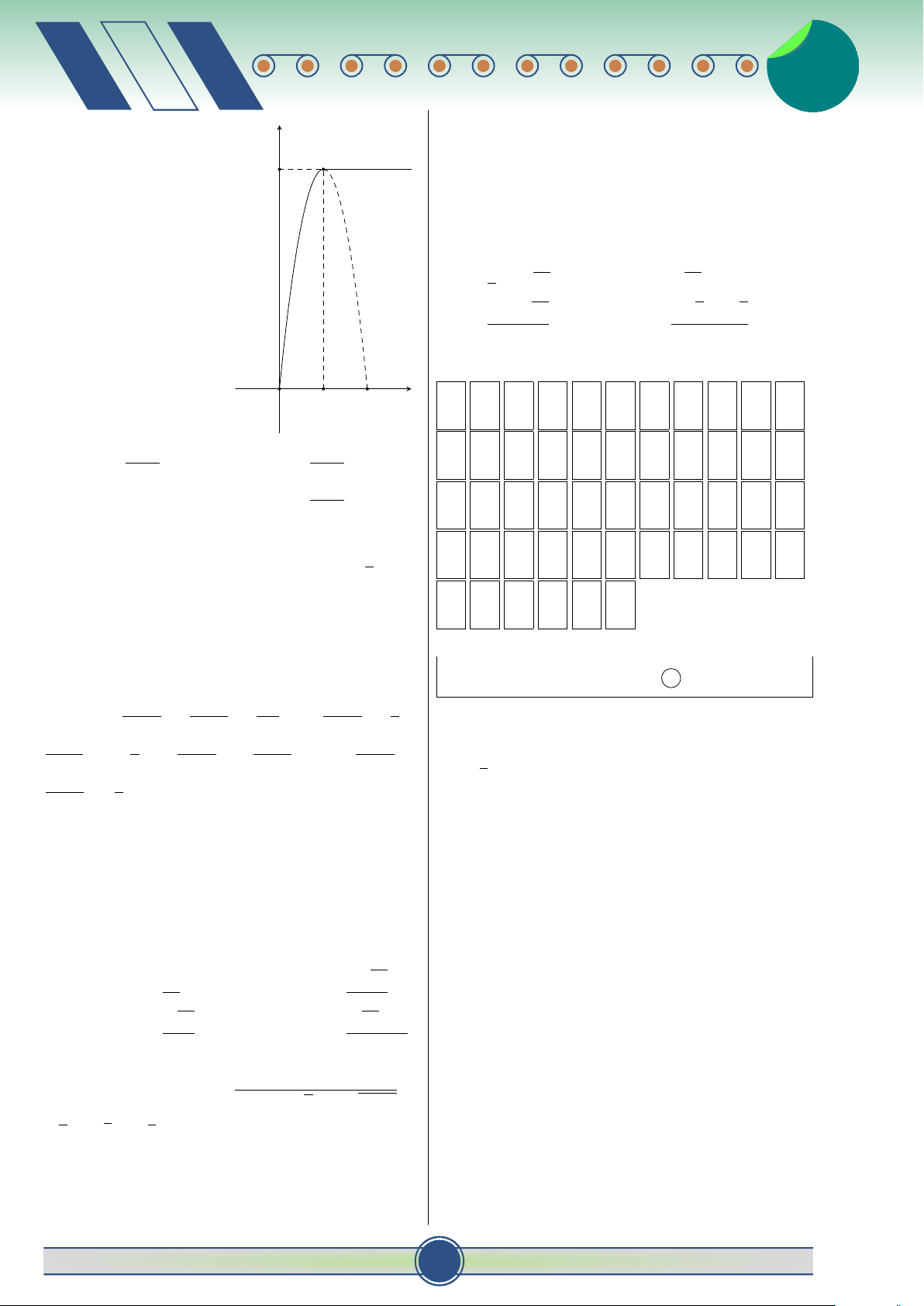
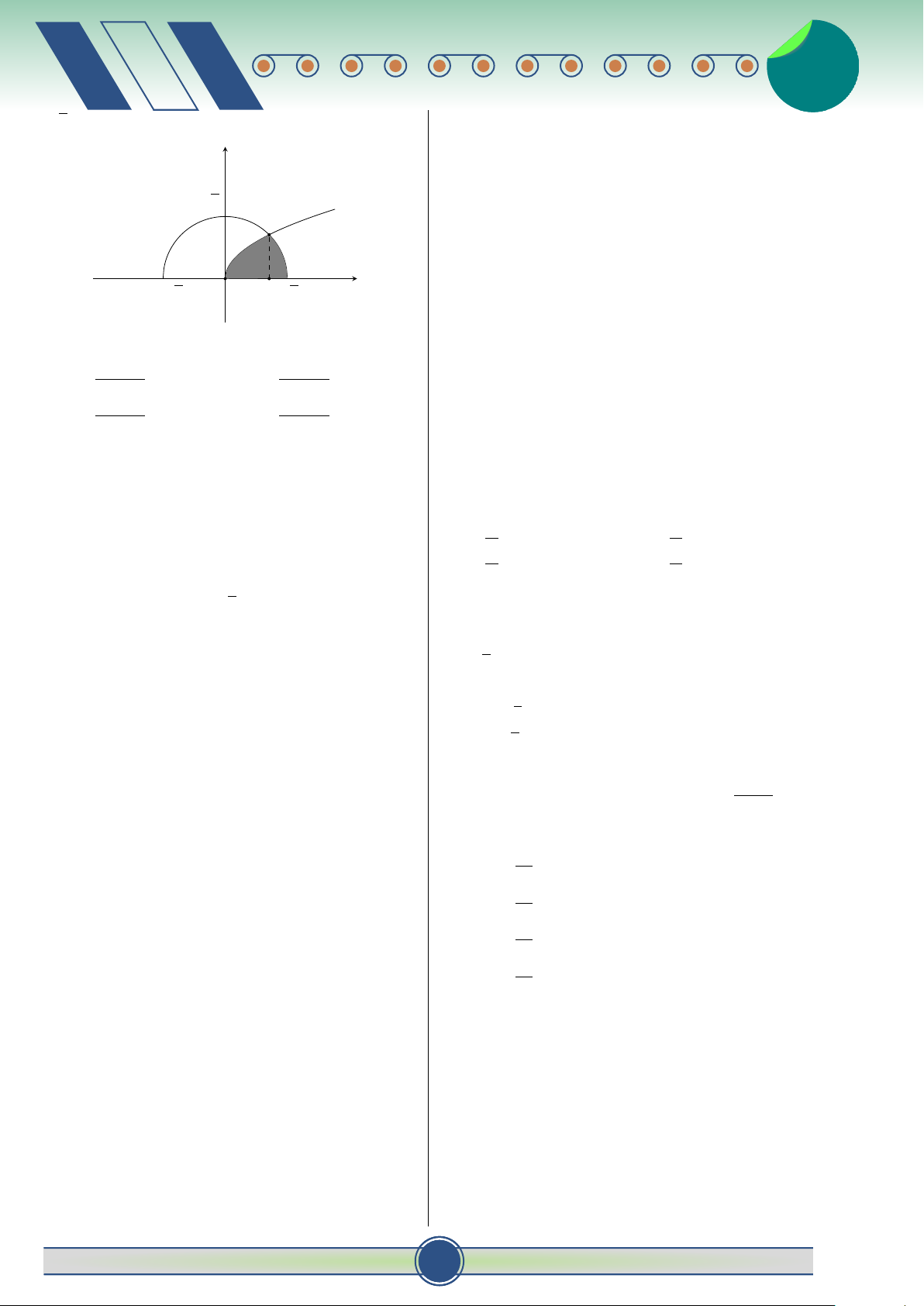
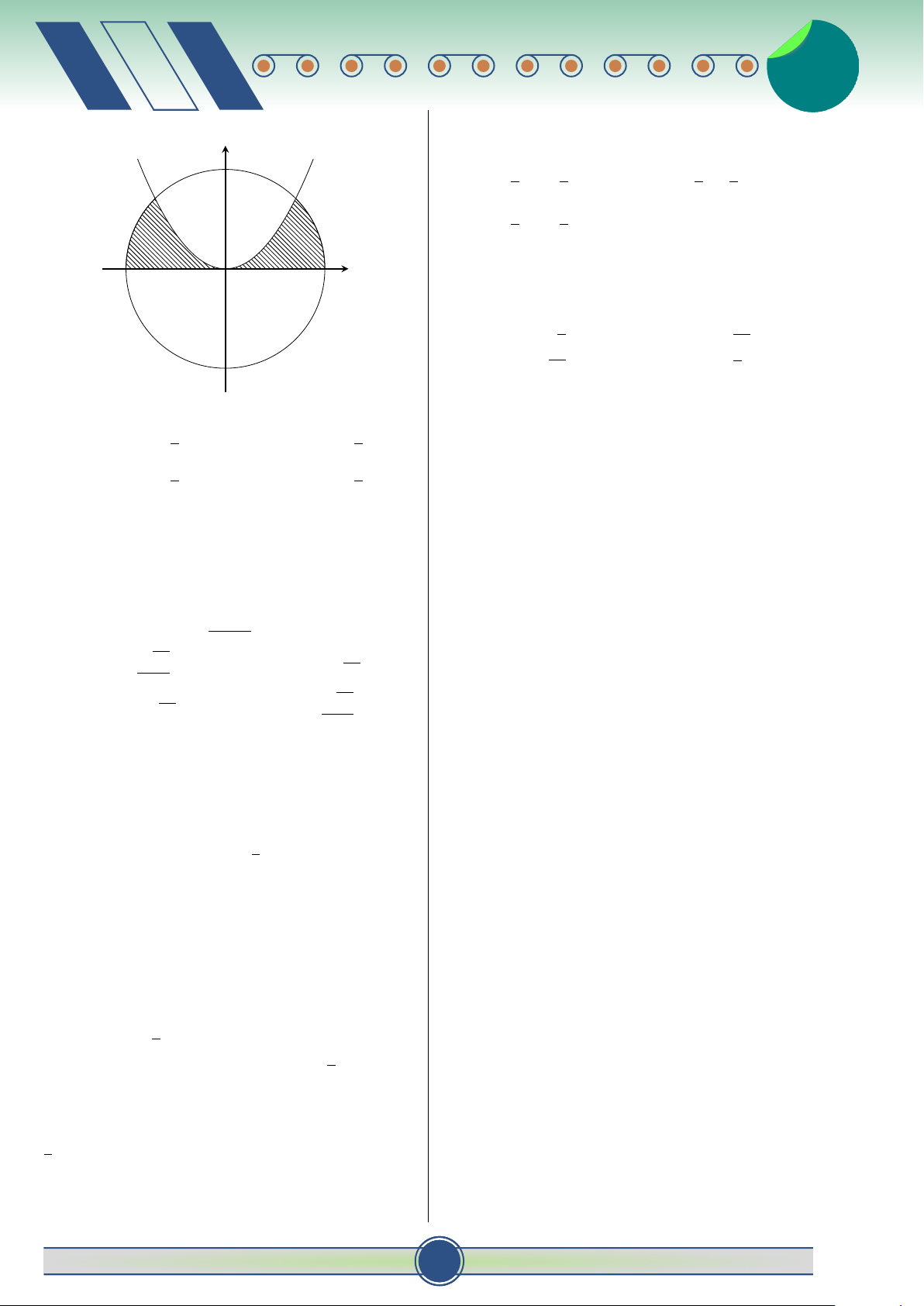
Câu 6. Cho hình phẳng (H) được giới hạn bởi các ĐỀ ÔN SỐ 1
đường x = 0, x = π, y = 0 và y = − cos x. Tính thể
Câu 1. Trong không gian Oxyz, các véc tơ đơn tích V của khối tròn xoay tạo thành khi quay (H) #» #»
vị trên các trục Ox, Oy, Oz lần lượt là i , j , xung quanh trục Ox được tính theo công thức: #» π
k , cho điểm M (3; −4; 12)? Mệnh đề nào sau đây Z A. V = π cos2 xdx . đúng?# » #» #» #» 0
A. OM = 3 i − 4 j + 12 k . π # » #» #» #» Z
B. OM = 3 i + 4 j + 12 k . B. V = π (− cos x) dx. # » #» #» #»
C. OM = −3 i − 4 j + 12 k . 0 # » #» #» #» π Z
D. OM = −3 i + 4 j − 12 k . C. V = π |cos x| dx .
Câu 2. Trong không gian Oxyz , đường thẳng đi 0 π Z
qua điểm A (3; 1; 2) và vuông góc với mặt phẳng D. V = cos2 xdx.
x + y + 3z + 5 = 0 có phương trình là: 0 x − 3 y − 1 z − 2 A. = = .
Câu 7. Trong không gian Oxyz, viết phương trình 1 1 3 x + 1 y + 1 z + 3
đường thẳng đi qua điểm A (1; 2; 3) và có vectơ chỉ B. = = . 3 1 2 #» phương u = (2; −1; −2). x − 1 y − 1 z − 3 C. = = . x − 2 y + 1 z + 2 3 1 2 A. = = . x + 3 y + 1 z + 2 1 2 3 D. = = . x + 1 y + 2 z + 3 1 1 3 B. = = . 2 −1 −2
Câu 3. Trong không gian với hệ tọa độ Oxyz , một x + 2 y − 1 z − 2 x y z C. = = .
vectơ pháp tuyến của mặt phẳng + + = 1 2 3 −5 1 −2 x − 1 y − 2 z − 3 1 là D. = = . #» 2 −1 −2
A. n = (−2; −10; 20). #»
Câu 8. Nghiệm phức có phần ảo dương của
B. n = (−5; 1; −2) . #»
phương trình z2 − 2z + 5 = 0 là: C. n = (2; −10; 5). A. 1 + 2i. B. −1 + 2i. #» 1 1 D. n = − ; −1; − . C. −1 − 2i. D. 1 − 2i. 5 2
Câu 4. Họ nguyên hàm của hàm số f (x) = 3x2 − Câu 9. Cho các số phức z1 = 3 + 4i, z2 = 5 − 2i 2x + 3 là
. Tìm số phức liên hợp ¯z của số phức z = 2z1 + A. x3 − x2 + C . 3z2 B. x3 − x2 + 3x + C. A. ¯z = 8 − 2i. B. ¯z = 8 + 2i. . C. 6x − 2 + C. C. ¯z = 21 − 2i. D. ¯z = 21 + 2i. .
D. 3x3 − 2x2 + 3x + C.
Câu 10. Phần thực của số phức (2 − i) (1 + 2i) Z là: Câu 5. e−2x+1dx bằng A. 0. B. 5. C. 3. . D. 4. 1 A. −2e−2x+1 + C. B. e−2x+1 + C . 2
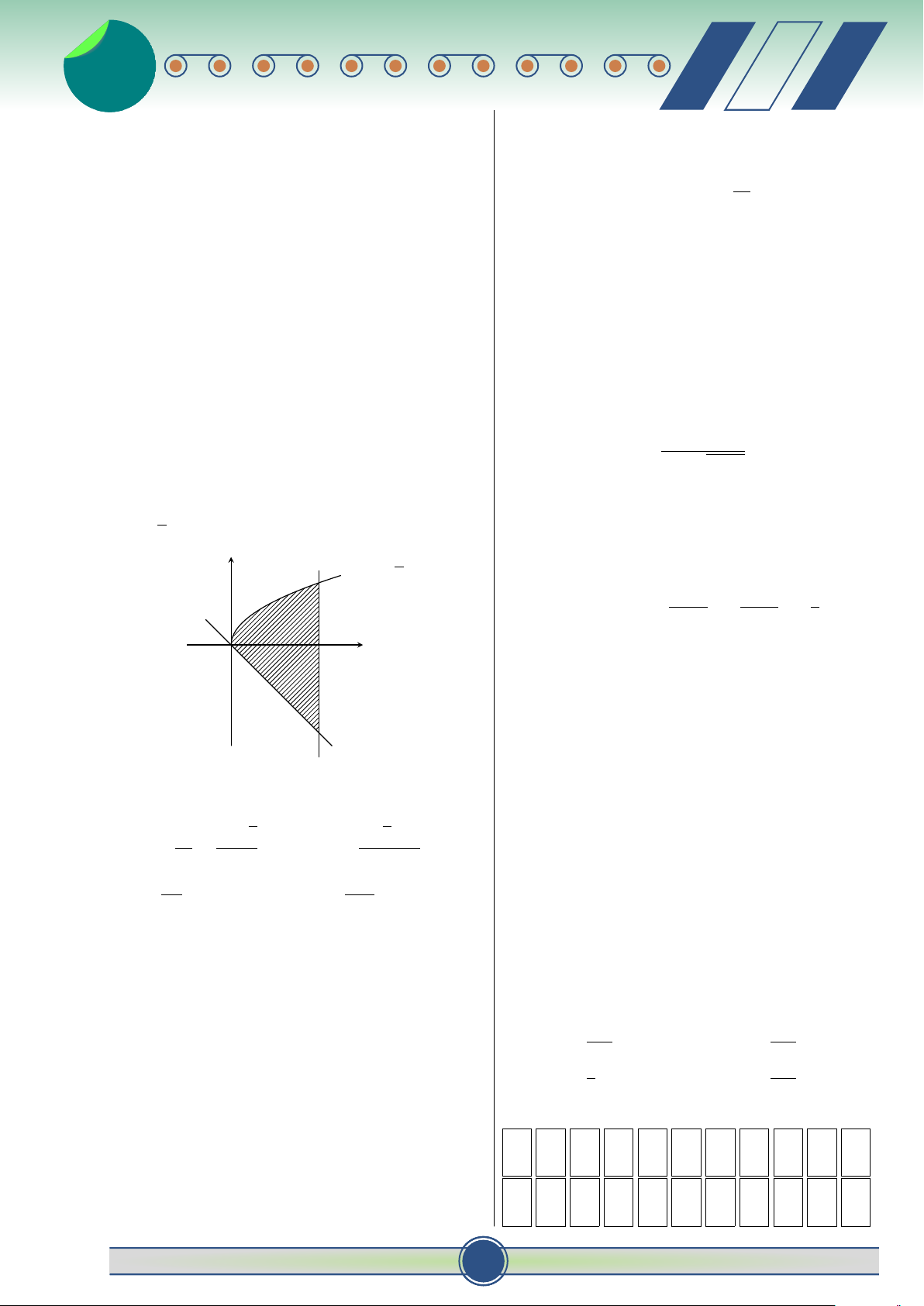
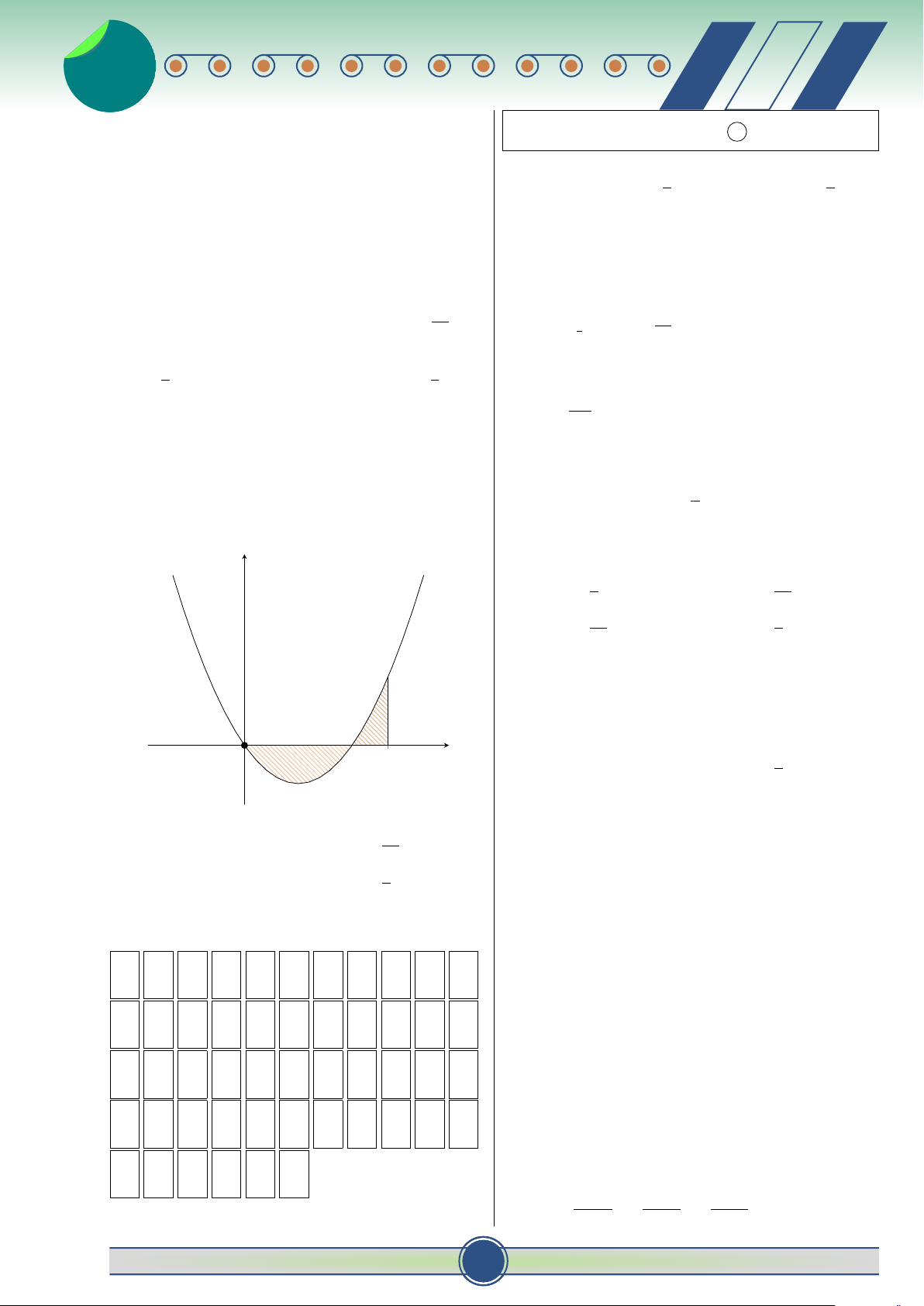
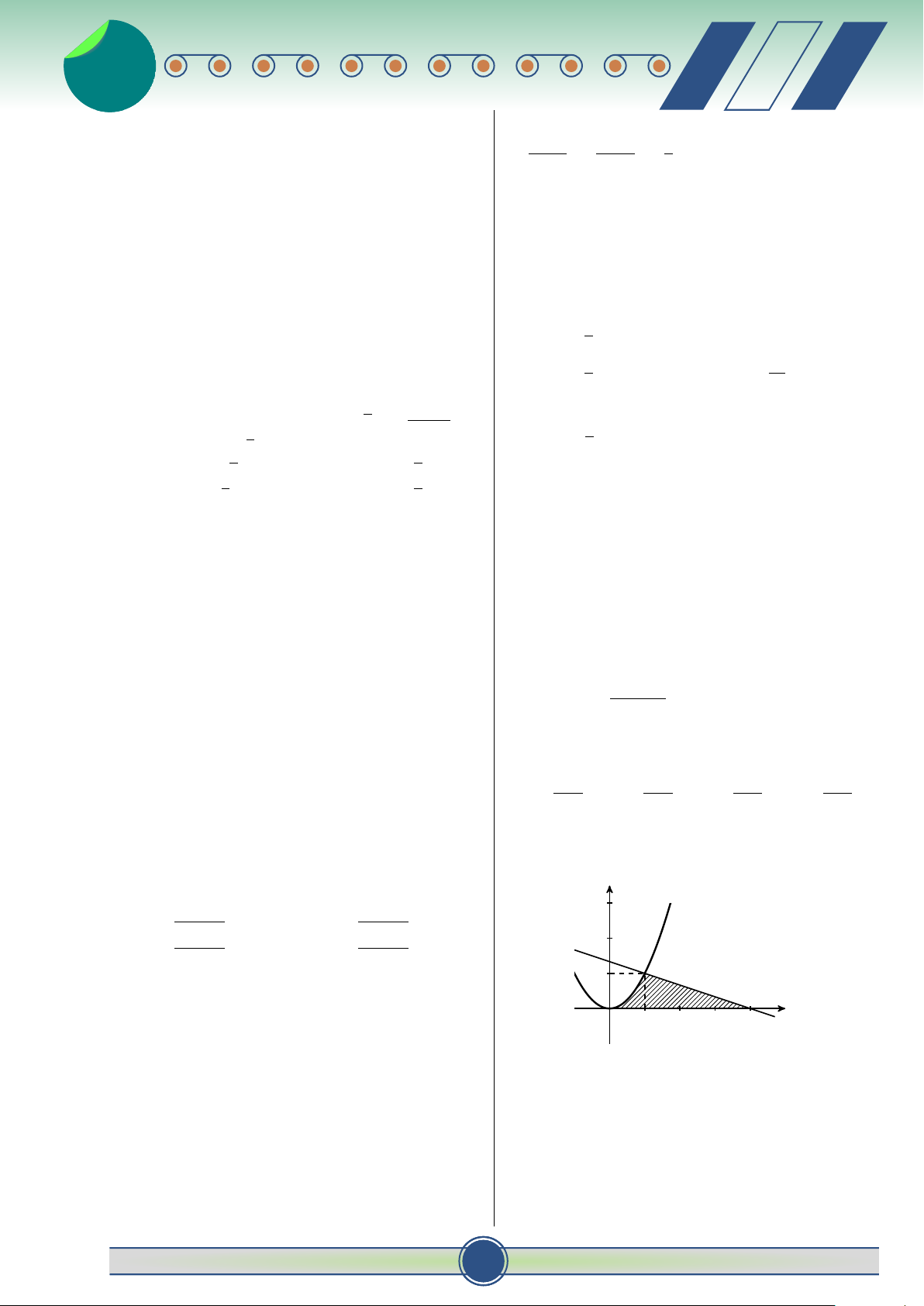
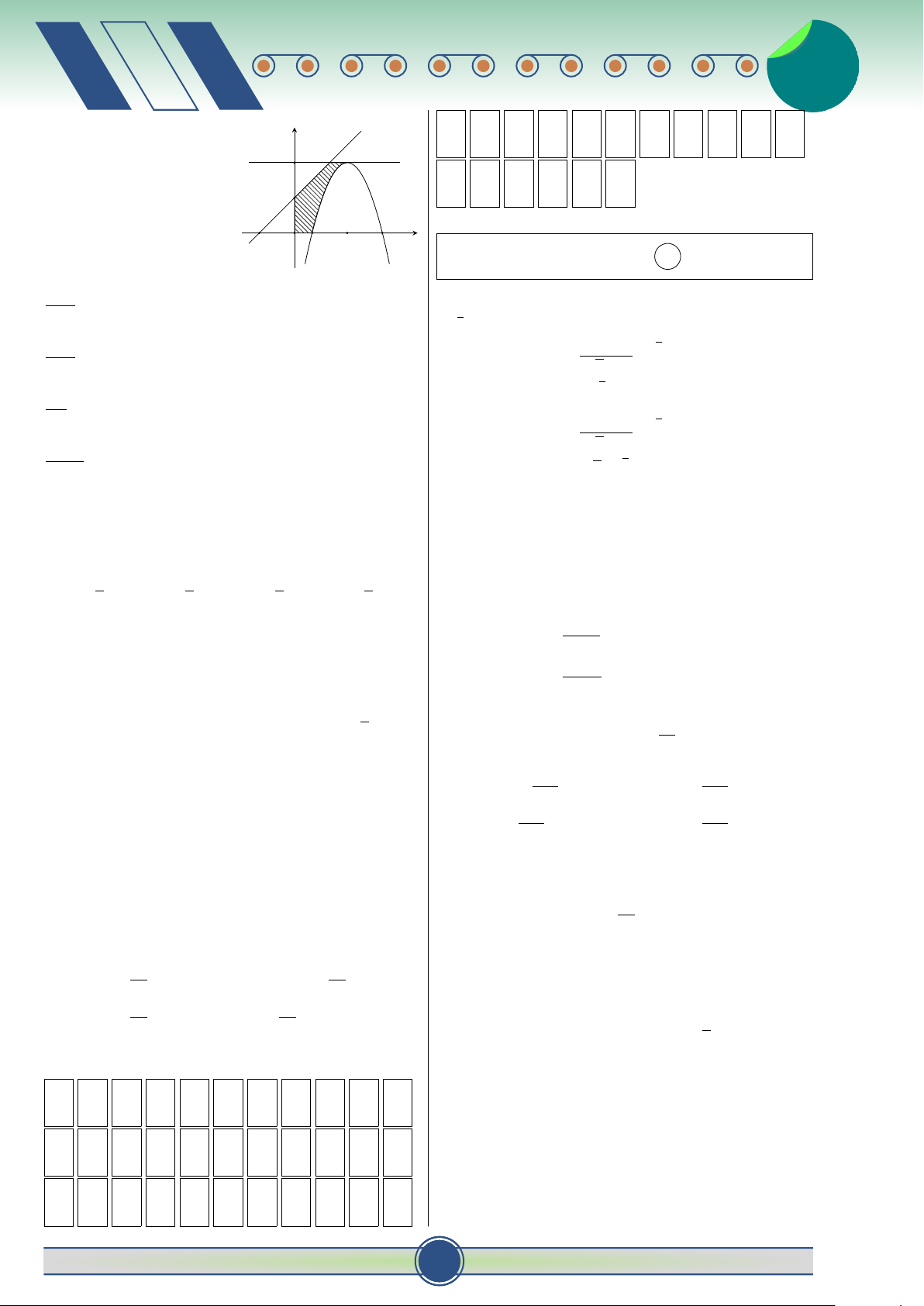
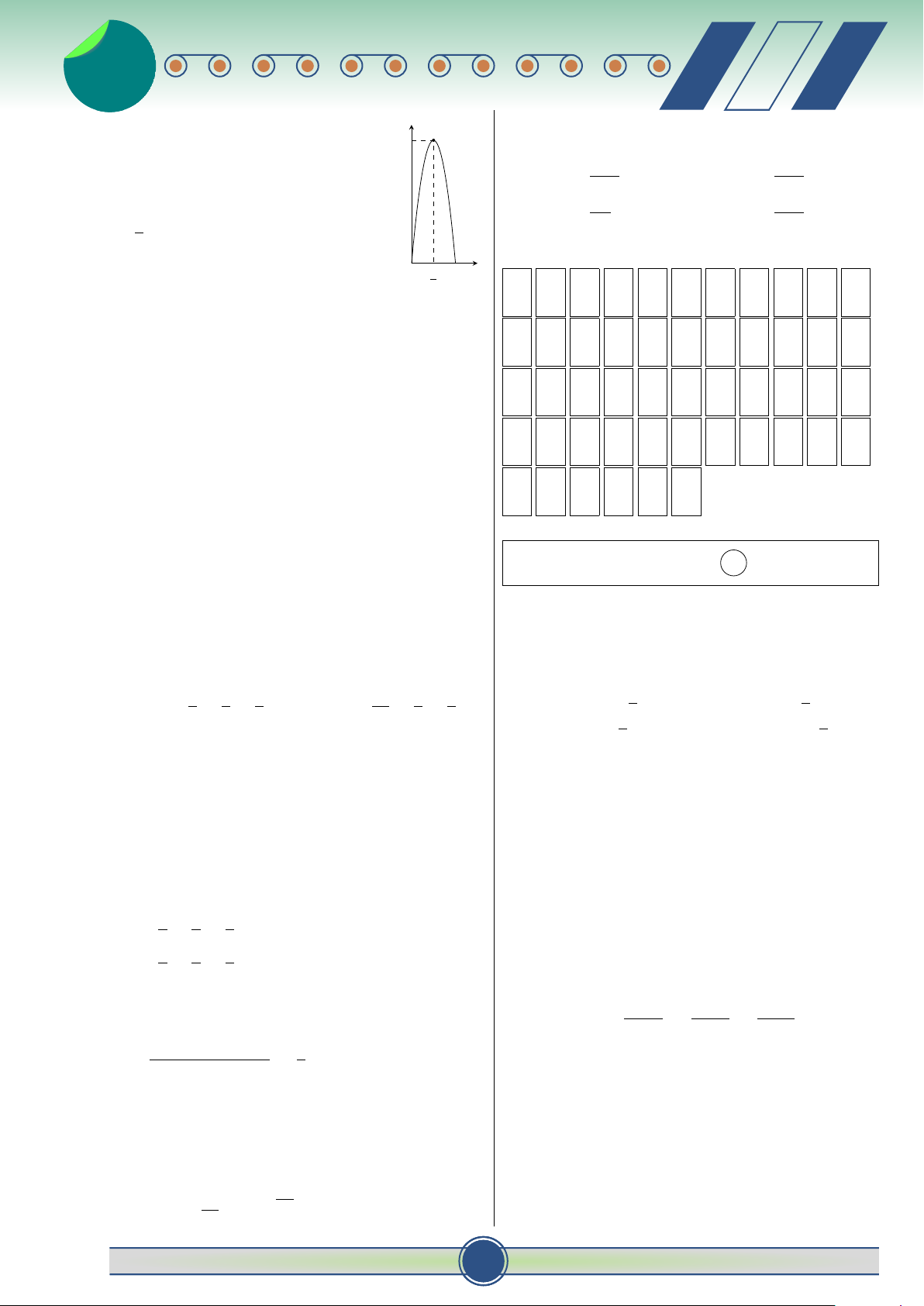
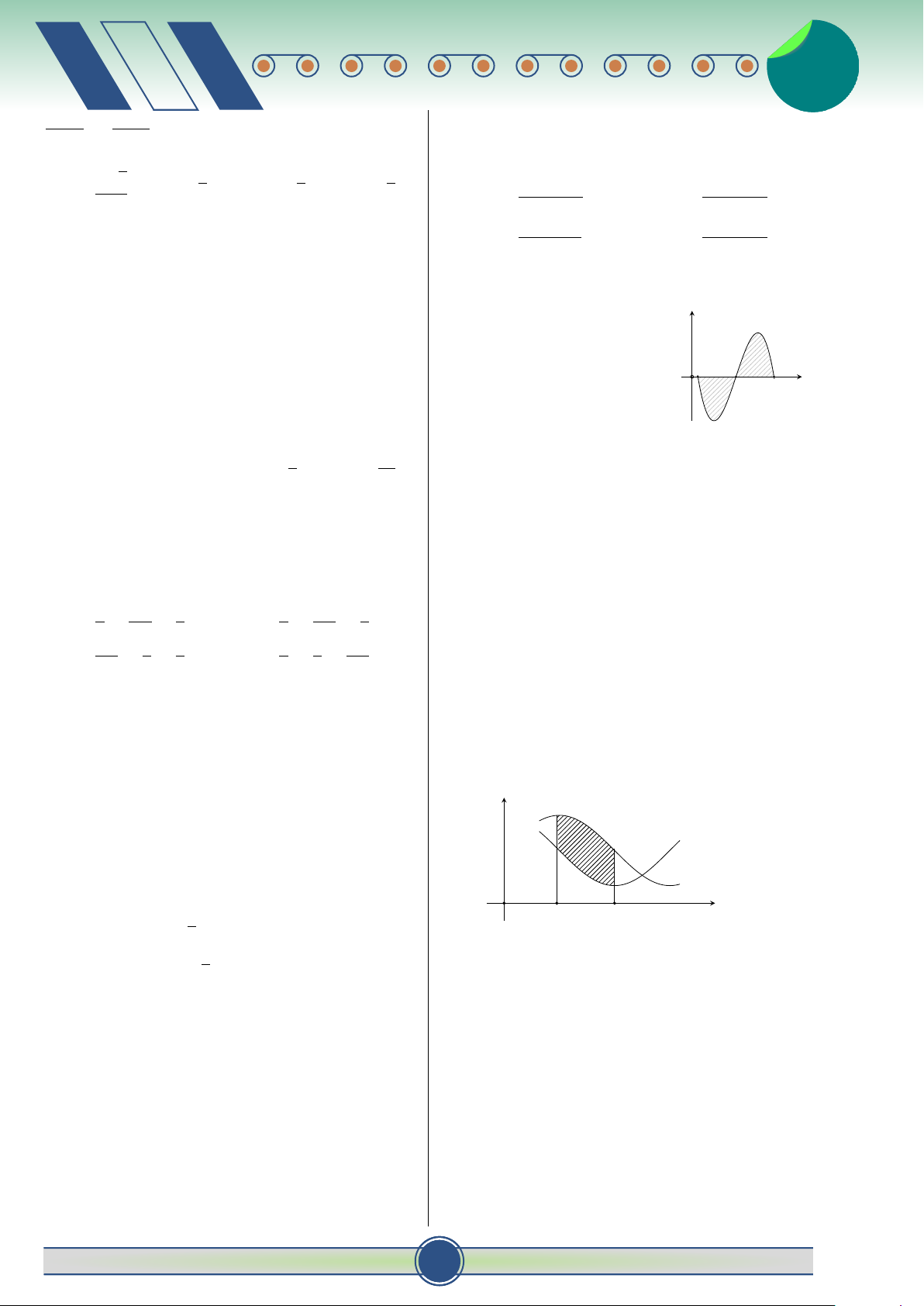
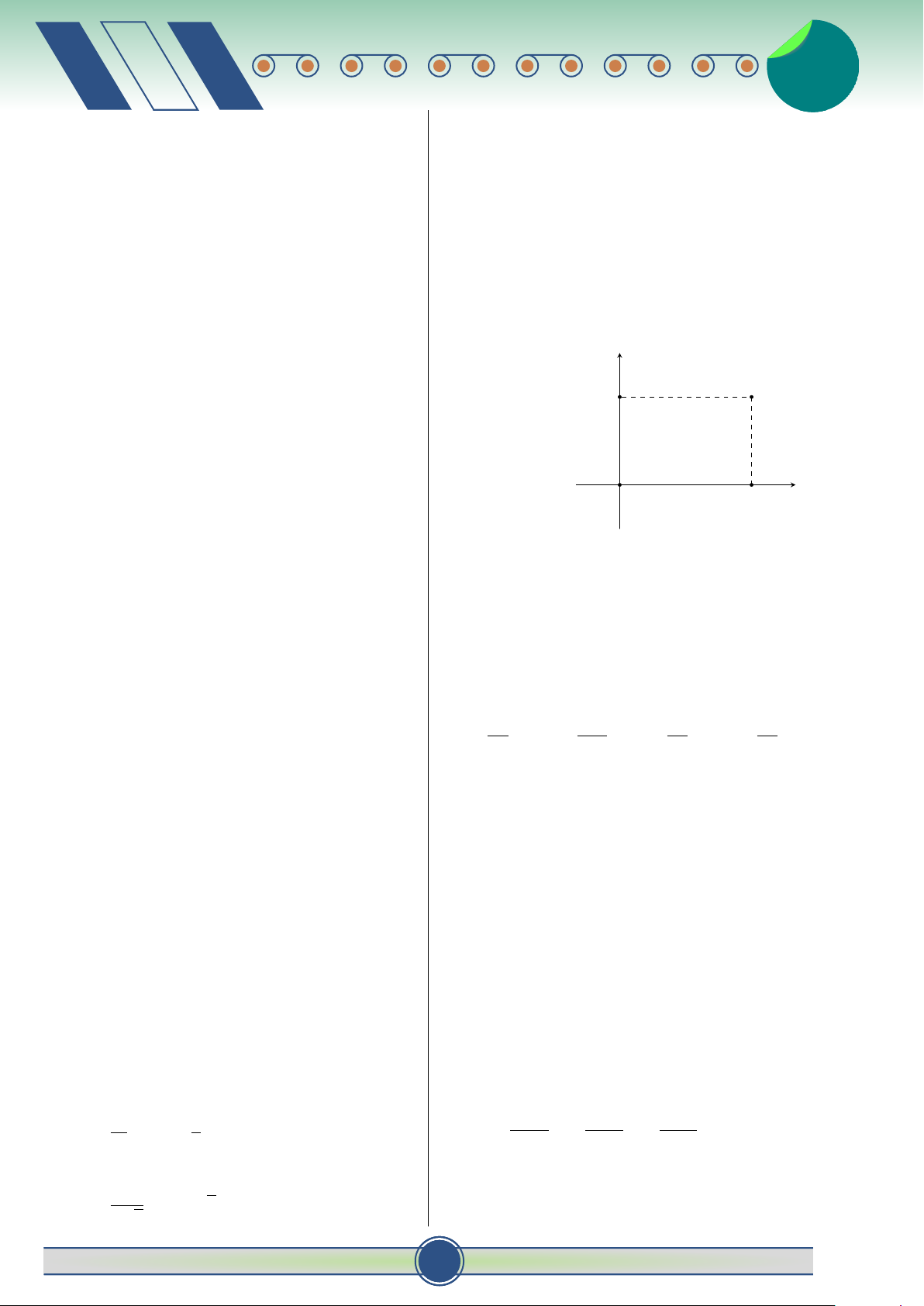
Câu 11. Cho hàm số y = f (x) liên tục trên đoạn 1 C. − e−2x+1 + C. D. e−2x+1 + C.
[a; b]. Công thức tính diện tích S của hình phẳng 2 ♂ 30 đề ôn thi t HKII-12 2 v 2
Những nẻo đường phù sa 2021 30 ĐỀ - ĐỀ
30 ĐỀ ÔN THI HKII-LỚP 12 2020
giới hạn bởi đồ thị hàm số y = f (x), trục hoành và Câu 17. Trong không gian Oxyz, cho điểm #»
hai đường thẳng x = a, x = b là:
A (1; −4; −3) và n = (−2; 5; 2). Phương trình mặt b b #» Z Z
phẳng (P) đi qua điểm A và nhận n = (−2; 5; 2) A. S = π f 2(x)dx. B. S = f (x)dx. làm vectơ pháp tuyến là: a a b b
A. −2x + 5y + 2z + 28 = 0. Z Z C. S = f (x)dx . D. S = | f (x)| dx.
B. −2x + 5y + 2z − 28 = 0 . a a
C. x − 4y − 3z + 28 = 0 . 5 + 15i
D. x − 4y − 3z − 28 = 0.
Câu 12. Số phức z = có phần thực là: 3 + 4i A. 3. B. 1. C. −3. D. −1. 7 Z √
Câu 18. Tính tích phân I = x + 2dx bằng
Câu 13. Cho hai hàm số y = f (x), y = g(x) liên 2
tục trên đoạn [a, b]. Công thức tính diện tích hình 38 670 A. I = . B. I = . 3 3
phẳng giới hạn bởi hai đồ thị của hai hàm số trên C. I = 19. D. I = 38.
với các đường thẳng x = a, x = b là b
Câu 19. Trong không gian Oxyz, cho đường thẳng Z x − 1 y + 1 z − 2 A. | f (x) − g(x)| dx . d : = = . Đường thẳng đi qua −1 2 −1 a
điểm M (2 ; 1 ; −1) và song song với đường thẳng b Z B. d có phương trình là [ f (x) − g(x)] dx . x + 2 y + 1 z − 1 a A. = = . b b −1 2 −1 Z Z x y − 5 z + 3 C. | f (x)dx| − |g(x)| dx. B. = = . 1 −2 1 a a x + 1 y − 2 z + 1 b C. = = . Z 2 1 −1 D. [ f (x) − g(x)] dx. x − 2 y − 1 z + 1 D. = = . a 1 −1 2
Câu 14. Cho hàm số y = f (x) liên tục trên [1; 9] , Câu 20. Diện tích S của hình phẳng giới hạn bởi 9 5 Z Z
các đường y = e2x, y = 0, x = 0, x = 2 được thoã mãn f (x)dx = 7 và f (x)dx = 3. Tính giá ea − b biểu diễn bởi
với a, b, c ∈ Z. Tính P = 1 4 c 4 9 a + 3b − c. Z Z trị biểu thức P = f (x)dx + f (x)dx. A. P = −1. B. P = 3. 1 5 C. P = 5. D. P = 6. A. P = 3 . B. P = 4 . 4 + 6i C. P = 10 . D. P = 2 .
Câu 21. Số phức liên hợp ¯z của số phức z = 1 − i là
Câu 15. Trong không gian Oxyz cho điểm A. ¯z = −1 − 5i. B. ¯z = −2 + 10i.
A (2; 3; 5). Tọa độ điểm A0 là hình chiếu vuông C. ¯z = −1 + 5i. D. ¯z = −2 − 10i. góc của A lên trục Oy. A. A0 (2; 0; 0) . B. A0 (0; 3; 0) .
Câu 22. Trong không gian với hệ tọa độ Oxyz, cho C. A0 (2; 0; 5) . D. A0 (0; 3; 5) .
mặt cầu (S) có tâm I (1; 2; 1) và cắt mặt phẳng
(P) : 2x − y + 2z + 7 = 0 theo một đường tròn có
Câu 16. Gọi z1; z2 là hai nghiệm của phương trình đường kính bằng 8. Phương trình mặt cầu là
2z2 + 10z + 13 = 0, trong đó z1 có phần ảo dương.
A. (x − 1)2 + (y − 2)2 + (z − 1)2 = 81. Số phức 2z1 + 4z2 bằng
B. (x − 1)2 + (y − 2)2 + (z − 1)2 = 5 . A. 1 − 15i . B. −15 − i .
C. (x + 1)2 + (y + 2)2 + (z + 1)2 = 9 . C. −15 + i . D. −1 − 15i .
D. (x − 1)2 + (y − 2)2 + (z − 1)2 = 25. ♂ 30 đề ôn thi t HKII-12 3 v 3
Những nẻo đường phù sa 2020 - 2021 30 ĐỀ
30 ĐỀ ÔN THI HKII-LỚP 12
Câu 23. Tìm nguyên hàm F(x) của f (x) = tan2 x Câu 29. Diện tích của hình phẳng giới hạn bởi đồ π
biết phương trình F(x) = 0 có một nghiệm .
thị hàm số y = x2 − 4 và các đường thẳng y = 0, 4 π A. F(x) = tan x − x + − 1 . x = −1, x = 5 bằng 4 65 49 A. 36. B. 18. C. . D. . B. F(x) = tan x − 1 . 3 3
C. F(x) = tan x − x − π − 1 .
Câu 30. Trong không gian Oxyz , cho ba điểm 4 tan x
A (0; 0; 1), B (0; 2; 0), C (3; 0; 0). Gọi H (x; y; z) là D. F(x) = 2 − 4. cos2 x
trực tâm của tam giác ABC. Giá trị của x + 2y + z
Câu 24. Trong không gian Oxyz, cho hai đường bằng x − 2 y − 4 z x − 3 y + 1 thẳng = = và = = 66 36 74 12 1 1 −2 2 −1 A. . B. . C. . D. . 49 29 49 7
z + 2 . Gọi M là trung điểm của đoạn vuông góc −1
Câu 31. Trong không gian Oxyz, cho mặt phẳng
chung của hai đường thẳng trên. Tính độ dài đoạn (P): 3x + 4y − 12z + 5 = 0 và điểm A (2; 4; −1). thẳng OM. √
Trên mặt phẳng (P) lấy điểm M. Gọi B là điểm sao # » # » 14 √ A. OM = . B. OM = 5 .
cho AB = 3AM. Tính khoảng cách d từ B đến mặt 2 √ √ phẳng (P). C. OM = 2 35 . D. OM = 35 . 30 A. d = 6. B. d = .
Câu 25. Gọi S là diện tích hình phẳng giới hạn bởi 13 66 12
các đường y = −3x, y = 0, x = 0, x = 4 . Mệnh đề C. d = . D. . 13 7 nào sau đây đúng Câu 32. không gian Oxyz, cho bốn điểm 4 4 Z Z
A (0; 1; −1), B (1; 1; 2), C (1; −1; 0) và D (0; 0; 1). A. S = (−3x) dx. B. S = π 3xdx .
Mặt phẳng (α) song song với mặt phẳng (BCD) và 0 0 4 4
chia khối tứ diện ABCD thành hai khối đa diện sao Z Z C. S = 3xdx. D. S = π 32xdx.
cho tỉ số thể tích của khối đa diện có chứa điểm A 1 0 0
và khối tứ diện ABCD bằng . Viết phương trình 27
Câu 26. Cho hai số phức z1 = −1 + 2i, z2 = 1 + 2i. mặt phẳng (α). Tính T = |z1|2 + |z2|2 √ A. y + z − 4 = 0 . B. y − z − 1 = 0. A. 2 5 . B. 10.
C. T = 4. D. T = 7. C. −y + z − 4 = 0. D. 3x − 3z − 4 = 0.
Câu 27. Trong không gian Oxyz, cho mặt phẳng Câu 33. Cho hình phẳng (H) giới hạn bởi các
(P) có phương trình 2x − 6y − 4z + 7 = 0 và ba 1 đường y = √ , y = 0, x = 0, x = 1. Tính
điểm A (2; 4; −1) , B (1; 4; −1) , C (2; 4; 3). Gọi S là 2x + 1
thể tích V của khối tròn xoay sinh ra khi cho hình
điểm thuộc mặt phẳng (P) sao cho SA = SB = SC. phẳng (H) quay quanh trục hoành. Tính l = SA + SB √ √ 1 A. V = ln 3. A. l = 117. B. l = 37 . π ln 3. B. V = √ √ 2 π C. l = 53. D. l = 101. C. V = π ln 2 . D. V = ln 3. 2
Câu 28. Trong không gian Oxyz, tọa độ tâm I và 1 Z x2ex a − be
bán kính R của mặt cầu (S) : x2 + y2 + z2 − 4x + Câu 34. Biết dx = với a là số (x + 2)2 a 2y + 2z − 3 = 0 là 0
nguyên tố. Tính S = 2a2 + b
A. I (2; −1; −1) và R = 9. A. S = 99 . B. S = 19.
B. I (−2; 1; 1) và R = 3. C. S = 9. D. S = 241 .
C. I (2; −1; −1) và R = 3.
D. I (−2; 1; 1) và R = 9.
Câu 35. Trong không gian với hệ trục tọa độ Oxyz,
cho mặt cầu (S) : x2 + y2 + z2 + 2z − 24 = 0 và ♂ 30 đề ôn thi t HKII-12 4 v 4
Những nẻo đường phù sa 2021 30 ĐỀ - ĐỀ
30 ĐỀ ÔN THI HKII-LỚP 12 2020
điểm K(3; 0; 3). Viết phương trình mặt phẳng chứa C. m = −10. D. m = 14.
tất cả các tiếp tuyến kẻ từ K đến mặt cầu (S).
Câu 42. Trên tập số phức, phương trình z2 − 6z +
A. 2x + 2y + z − 4 = 0.
20192020 + 9 = 0 có một nghiệm là
B. 6x + 6y + 3z − 8 = 0 . A. z = 3 − 20192020i. B. z = 3 + 20192020 . C. 3x + 4z − 21 = 0. C. z = 3 − 20191010i. D. z = 3 + 20191010.
D. 6x + 6y + 3z − 3 = 0 . #»
Câu 36. Trong không gian Oxyz biết vector n = Câu 43. Tính môđun |z| của số phức z =
(a; b; c) là vector pháp tuyến của mặt phẳng đi (2 + i) (1 + i)2 + 1
qua điểm A (2; 1; 5) và chứa trục Ox. Khi đó tính A. |z| = 17. B. |z| = 3 . √ √ b k = . C. |z| = 17. D. |z| = 15. c 1 A. k = 5. B. k = − .
Câu 44. Tính diện tích hình phẳng giới hạn bởi 5 1
đồ thị hàm sốy = x3 − x và đồ thị hàm số y = C. k = −5. D. k = . 5 x − x2. c 9
Câu 37. Cho phương trình x2 − 4x + = 0 có hai A. S = 13. B. S = . d 4
nghiệm phức. Gọi A, B là hai điểm biểu diễn của 81 37 C. S = . D. S = . 12 12
hai nghiệm đó trên mặt phẳng Oxy. Biết tam giác OAB đều, tính P = c + 2d.
Câu 45. Trong không gian Oxyz, viết phương A. P = 18. B. P = −10.
trình đường thẳng ∆ đi qua hai điểm A (1; 4; 4) và C. P = −14 . D. P = 22. B (−1; 0; 2). x + 1 y z + 2 Câu 38. Choz A. = = .
1 và z2 là hai nghiệm phức của 2 4 −2
phương trình z2 − 2z + 5 = 0, biết z x y − 2 z − 3 1 − z2 có B. = = . 1 2 1
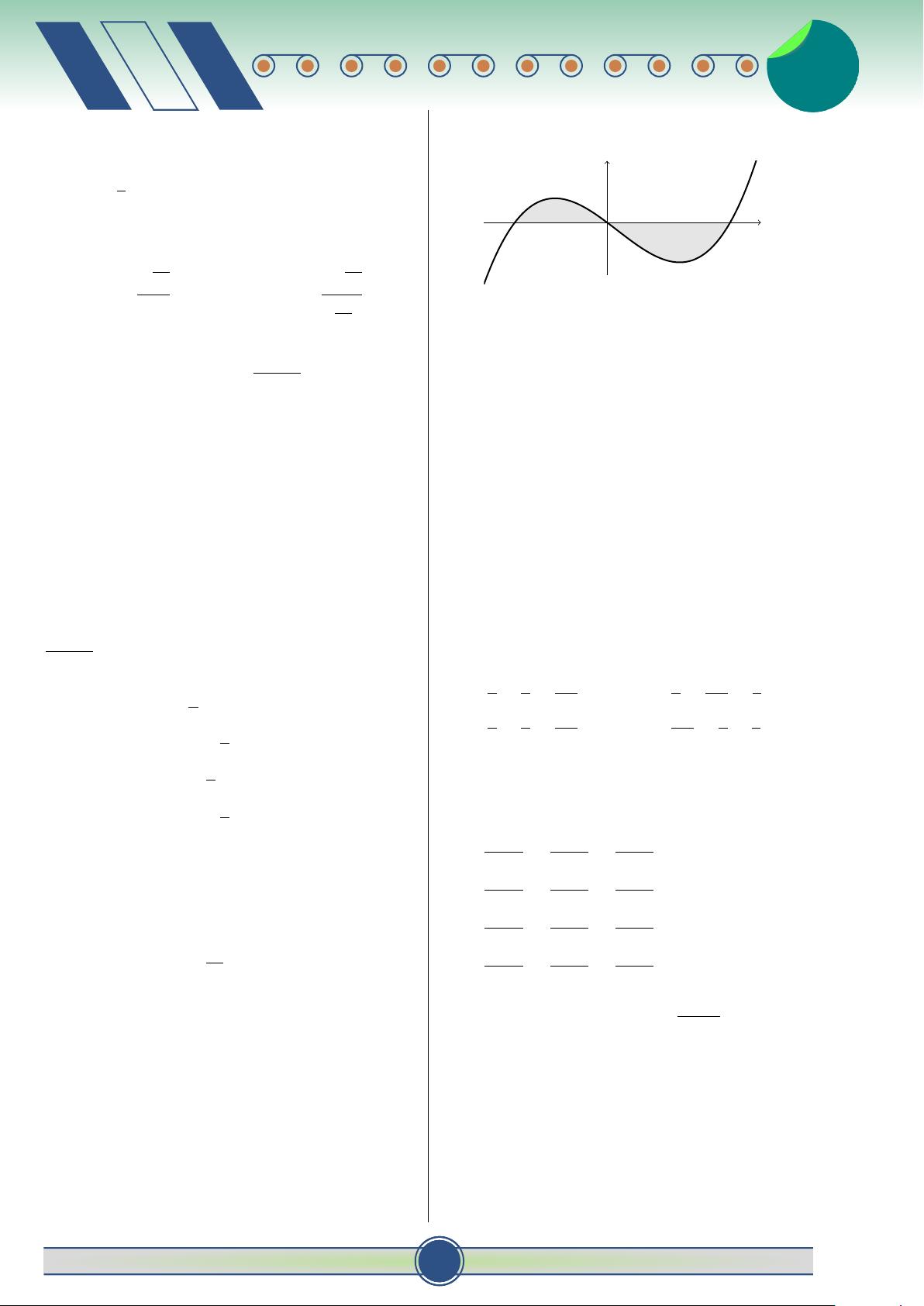
phần ảo là số thực âm. Tìm phần ảo của số phức x + 1 y z + 2 C. = = . w = 2z2 − z2. − − − 1 2 2 4 2 x − 1 y − 4 z − 4 A. −12. B. −3. C. 3. D. 12. D. = = . 2 2 2 π 4
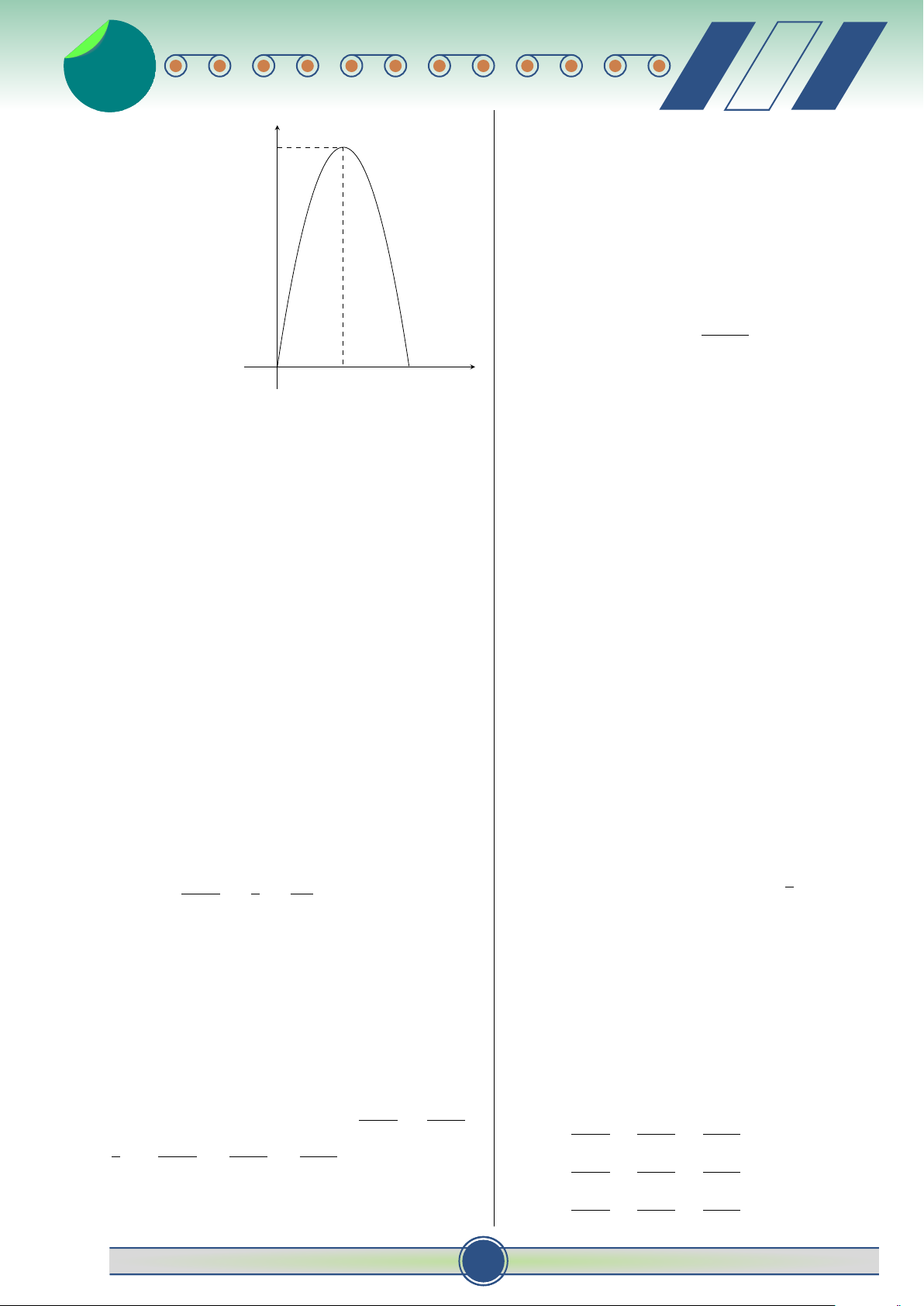
Câu 46. Cho hai hàm số y = g(x) và y = f (x) liên Z Câu 39. Biết I = tan2 x + 2 tan8 x dx
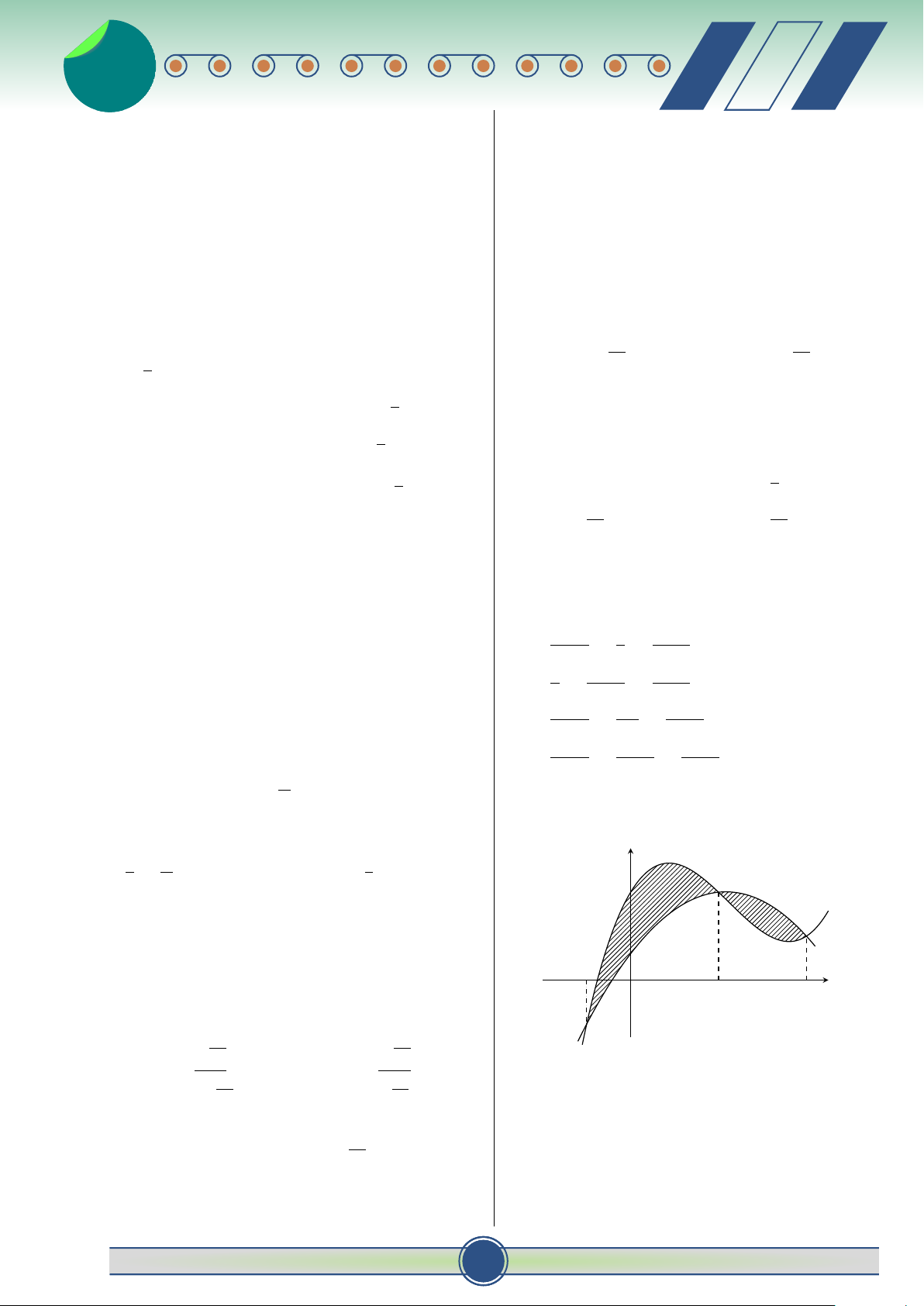
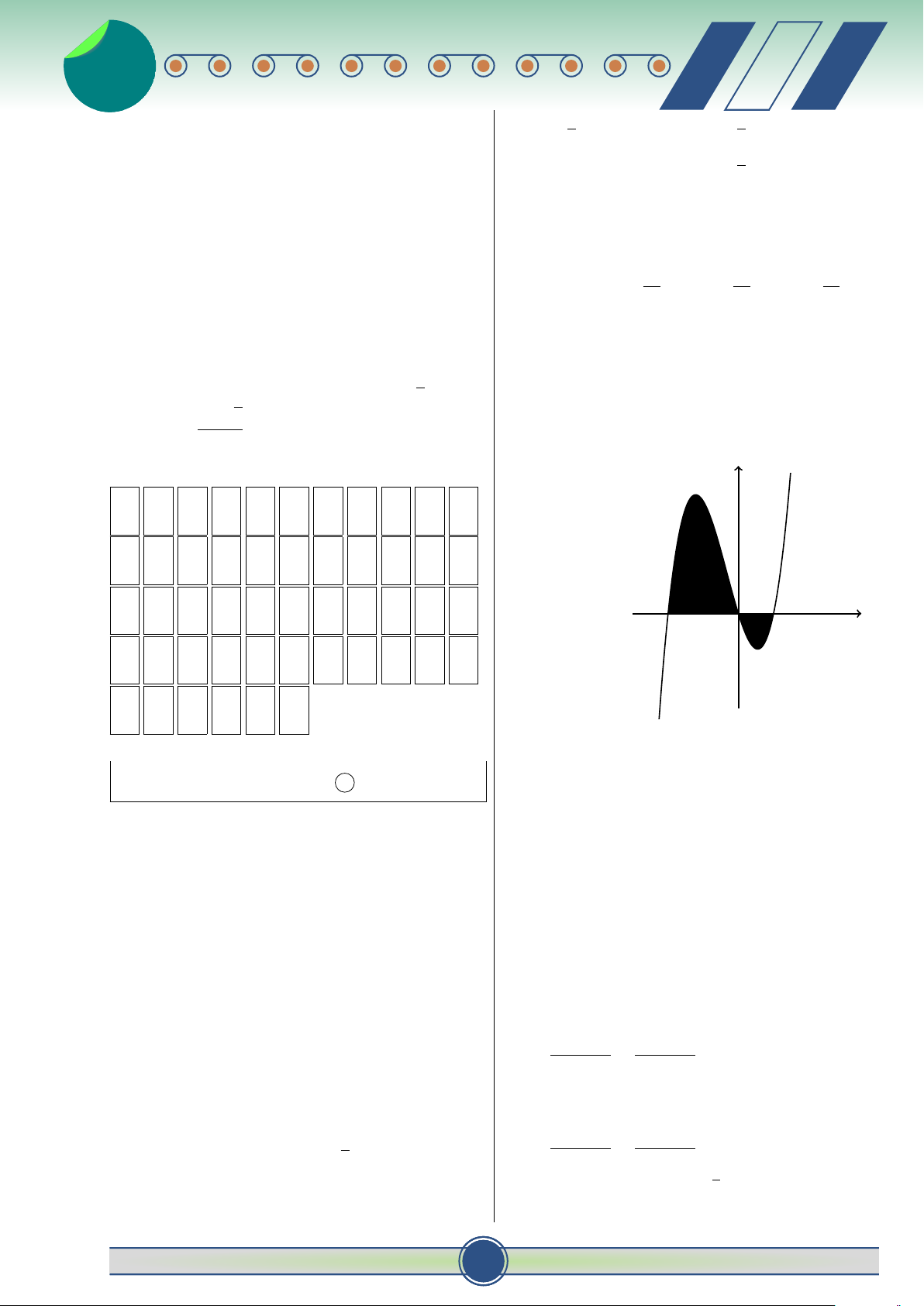
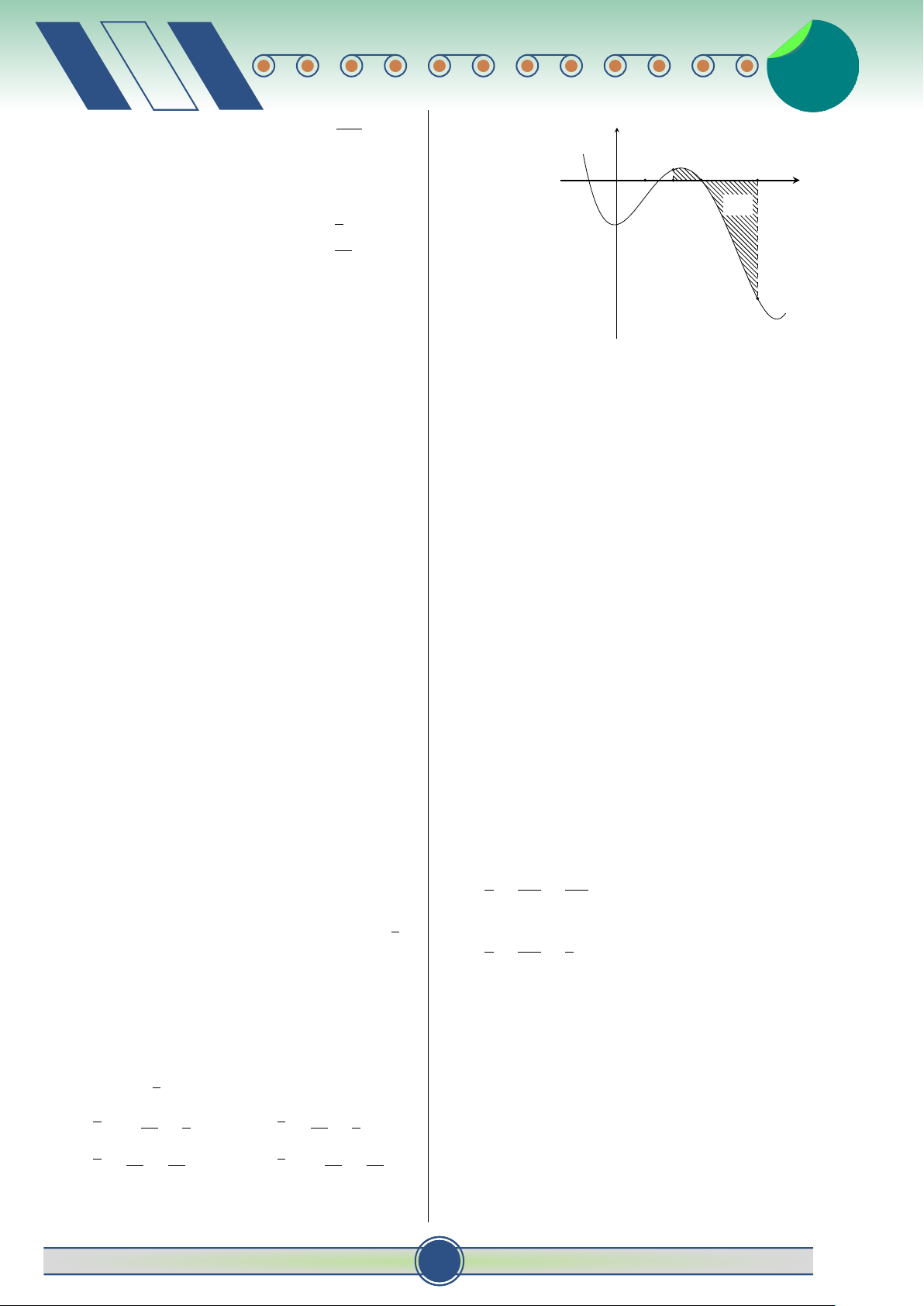
= tục trên đoạn [a; c] có đồ thị như hình vẽ. 0 y a a − π +
với a, b ∈ N, phân số tối giản. Tính b c b T = a + b + c A. T = 167. B. T = 62 . C. T = 156. D. T = 159. a Câu 40. Trong không gian Oxyz, tính x O b c diện tích S của tam giác ABC, biết
A (2; 0; 0) , B (0; 3; 0) , C (0; 0; 4) √ √ 61 61 A. S = . B. S = .
Diện tích S của hình phẳng giới hạn bởi đồ thị hai 3 √ 2 √ C. S = 2 61 . D. S = 61.
hàm số trên được tính theo công thức: b c Z Z
Câu 41. Gọi z là số phức có mô đun nhỏ nhất thỏa A. S = [g(x) − f (x)] dx + [ f (x) − g(x)] dx. √
mãn điều kiện |z − 2 − 8i| = 17. Biết z = a + bi a b c
với a, b ∈ R, tính m = 2a2 − 3b. Z B. S = [ f (x) − g(x)] dx. A. m = −18. B. m = 54 . a ♂ 30 đề ôn thi t HKII-12 5 v 5
Những nẻo đường phù sa 2020 - 2021 30 ĐỀ
30 ĐỀ ÔN THI HKII-LỚP 12 c Z
24. 25. 26. 27. 28. 29. 30. 31. 32. 33. 34. C. S = [ f (x) − g(x)] dx . B C B C C A D A B D B a b c
35. 36. 37. 38. 39. 40. 41. 42. 43. 44. 45. Z Z D. S = [ f (x) − g(x)] dx − [ f (x) − g(x)] dx. C C D A C D C C C D B a b 46. 47. 49. 50. e D D D C Z 2 ln x + 3
Câu 47. Cho tích phân I = dx. Nếu x 1 đặt t = ln x thì ĐỀ ÔN SỐ 2 1 Z A. I = (2 ln t + 3)dt. PHẦN TRẮC NGHIỆM 0
Câu 1. Trong không gian Oxyz, cho đường thẳng e Z ∆ #» đi qua M ( a = B. I = (
0; 2; −3) và có véc tơ chỉ phương 2t + 3)dt.
(4; −3; 1). Phương trình tham số của đường thẳng 1 1 ∆ là Z C. I = ( 2t)dt . x = 4t x = 4t 0 A. y = −2 − 3t . B. y = −2 − 3t . 1 Z D. I = (2t + 3)dt. z = 3 + t z = 3 − t 0 x = −4t x = 4 4 Z a C. y = 2 + 3t . D. y = −3 + 2t . Câu 48. Biết x ln(x2 + 1)dx = ln a − c, trong b z = −3 − t z = 1 − 3t 0
đó a, b là các số nguyên tố, c là số nguyên dương. Câu 2. Mặt phẳng (P) tiếp xúc với mặt cầu (S) : Tính T = a + b + c.
(x − 1)2 + (y + 3)2 + (z − 2)2 = 49 tại điểm A. T = 11. B. T = 27.
M (7; −1; 5) có phương trình là C. T = 35. D. T = 23.
A. 6x + 2y + 3z − 55 = 0 . 2 Z 2x − 3 2
B. 6x + 2y + 3z + 55 = 0. Câu 49. Biết dx = a ln + b với a, b là x + 1 3
C. 3x + y + z − 22 = 0 . 1
hai số hữu tỉ. Khi đó b2 − 2a bằng D. 3x + y + z + 22 = 0. A. 17. B. 33. C. 6 . D. −6 .
Câu 3. Cho x, y là các số thực. Số phức z =
i (1 + xi + y + 2i) bằng 0 khi
Câu 50. Gọi D là hình phẳng giới hạn bởi đồ thị A. x = −1; y = −2. B. x = 0; y = 0 .
hàm số y = x ln x, trục hoành và đường thẳng C. x = −2; y = −1. D. x = 2; y = 1.
x = e. Thể tích khối tròn xoay được tạo thành
khi quay D quanh trục hoành được viết dưới dạng Câu 4. Cho hai số phức z = x − yi và w = 2i + 3x, π
b.e3 − 2 với a, b là hai số nguyên. Tính giá trị (x, y ∈ R) . Biết z = w. Giá trị của x và y lần lượt a biểu thức T = a − b2. là A. T = −9. B. T = −1 . A. 2 và −3. B. −2 và 0. C. T = 2. D. T = −12. C. 0 và 2 . D. 0 và −2. Z 3 x Z 2
BẢNG ĐÁP ÁN THAM KHẢO Câu 5. Nếu √ dx = f (t)dt, với 0 1 + 1 + x 1 √ 1. 2. 3. 4. 5. 6. 7. 8. 9. 10. 11. t =
1 + x thì f (t) là hàm số nào trong các hàm A A C B C A D A C D D số dưới đây?
12. 13. 14. 15. 16. 17. 18. 20. 21. 22. 23. A. f (t) = t2 − t. B. f (t) = 2t2 + 2t. A A B B B A A A A D A C. f (t) = t2 + 2 . D. f (t) = 2t2 − 2t. ♂ 30 đề ôn thi t HKII-12 6 v 6
Những nẻo đường phù sa 2021 30 ĐỀ - ĐỀ
30 ĐỀ ÔN THI HKII-LỚP 12 2020 Câu 6. Trong không gian Oxyz, cho điểm A. I = 60. B. I = 240.
M (1 ; 2 ; 0) và mặt phẳng (α) : x + 2y − 2 + 1 = 0. C. I = 56. D. I = 120.
Khoảng cách từ M đến (α) là
Câu 15. Trong không gian với hệ tọa độ Oxyz , cho A. 1. B. 3. C. 2. D. 4.
mặt cầu (S): x2 + y2 + z2 + 6x − 4y + 2z − 2 = 0.
Câu 7. Tìm các căn bậc hai của −6? √ √
Tọa độ tâm I và bán kính R của mặt cầu (S) là A. − 6i . B. ± 6i. √
A. I (−3; 2; −1) và R = 4. C. ±6i. D. 6i.
B. I (−3; 2; −1) và R = 16.
Câu 8. Tính diện tích hình phẳng giới hạn bởi các
C. I (3; −2; 1) và R = 4 .
đường y = −x2 + 4x − 3, x = 0 , x = 3, Ox.
D. I (3; −2; 1) và R = 16. 8 4 4 8 A. − . B. − . C. . D. .
Câu 16. Phương trình đường thẳng ∆ đi qua điểm 3 3 3 3 x
A (3; 2; 1) và song song với đường thẳng d : =
Câu 9. Vị trí tương đối của hai mặt phẳng (α) : 2 y z + 3 3x + 2y − z + 1 = 0 và ( 0
α ) : 3x + y + 11z − 1 = 0 = là 4 1 là x = 3 − 2t x = 2 + 3t
A. Vuông góc với nhau. A. y = 2 − 4t . B. y = 4 + 2t . B. Trùng nhau. z = 1 − t z = 1 + t
C. Cắt nhau nhưng không vuông góc với nhau. x = 2t x = 3 + 2t D. Song song. C. y = 4t . D. y = 2 − 4t .
Câu 10. Trên mặt phẳng tọa độ Oxy, cho hai điểm z = 3 + t z = 1 + t
A (4 ; 0), B (0 ; −3) và điểm C thỏa mãn điều kiện # » # » # »
OC = OA + OB. Khi đó số phức được biểu diễn Câu 17. Biết F(x) là nguyên hàm của hàm số bởi điểm C là 1 f (x) =
và F(2) = 1. Khi đó F(3) bằng bao x − 1 A. −3 − 4i. B. 4 + 3i . nhiêu? C. 4 − 3i. D. −3 + 4i. 3 A. ln . B. ln 2 + 1. 2
Câu 11. Cho số phức z = 6 + 7i. Điểm M biểu diễn 1 C. ln 2. D. .
cho số phức ¯z trên mặt phẳng Oxy là 2 A. M (−6; −7) . B. M (6; −7). 5 Z 1 Câu 18. Biết rằng dx = ln a. Giá trị của a C. M (6; 7i). D. M (6; 7). 2x − 1 1
Câu 12. Trong tập số phức, phương trình z2 − là: 2z + 5 = 0 có nghiệm là A. 81. B. 27 . C. 3. D. 9. A. z = −1 ± 2i. B. z = 2 ± 2i.
Câu 19. Gọi V là thể tích khối tròn xoay do hình C. z = −2 ± 2i . D. z = 1 ± 2i.
phẳng giới hạn bởi các đường thẳng sau quay
Câu 13. Phát biểu nào sau đây là đúng?
quanh trục hoành y = sin x, y = 0, x = 0, x = Z A.
x sin xdx = x cos x + sin x + C.
12π. Mệnh đề nào dưới đây đúng? 12π Z Z B.
x sin xdx = −x cos x + sin x + C. A. V = π (sin x)2 dx . Z C.
x sin xdx = −x cos x − sin x + C. 0 12π Z Z D.
x sin xdx = x cos x − sin x + C. B. V = π sin xdx . 0 2 12π Z Z
Câu 14. Tính tích phân I = (x + 2)3 dx . C. V = 2 π (sin x)2 dx . 0 0 ♂ 30 đề ôn thi t HKII-12 7 v 7
Những nẻo đường phù sa 2020 - 2021 30 ĐỀ
30 ĐỀ ÔN THI HKII-LỚP 12 12π 5 Z Z dx D. V = 2 π sin xdx. Câu 25. Giả sử = a ln 5 + b ln 3 + c ln 2. x2 − x 0 3 π
Tính giá trị biểu thức S = −2a + b + 3c2. 2 A. S = 3. B. S = 6. Z cos x 4 Câu 20. Cho dx = a ln + C. S = −2. D. S = 0. (sin x)2 − 5 sin x + 6 c 0
b, với a, b là các số hữu tỉ, c > 0. Tính tổng S = Câu 26. Cặp hàm số nào sau đây có tính chất a + b + c.
“Có một hàm số là nguyên hàm của hàm số còn A. S = 3 . B. S = 4. lại”?. 1 C. S = 0. D. S = 1. A. tan x2 và . B. s in2x và sin2 x. cos2 x2 e2 C. ex và e−x. D. s in2x và cos2 x. Z (1 − ln x)2
Câu 21. Tích phân I = dx có giá trị x
Câu 27. Cho hàm số y = f (x) có đạo hàm trên e là
đoạn [−2; 1] và f (−2) = 3, f (1) = 7. Tính I = 4 5 1 13 1 A. . B. . C. . D. . Z 3 3 3 3 f 0(x)dx.
Câu 22. Diện tích hình phẳng giới hạn bởi các −2 1 7 đường y =
x2 và y = x xác định bởi công thức A. I = . B. I = −4. 2 3 2 C. I = 10 . D. I = 4. Z A. S = x2 − 2x dx . #» #»
Câu 28. Cho m = (1; 0; −1) , n = (0; 1; 1). Kết 0 2 luận nào sai? Z 1 B. S = #» #» x2 − x dx.
A. Góc của m và n là 30◦. 2 #» #» 0
B. [m, n ] = (1; −1; 1). 2 #» #» Z 1 2 C. m. n = −1. . C. S = x2 − x dx . 2 #» #»
D. m và n không cùng phương. 0 2 Z 1
Câu 29. Trong không gian với hệ trục Oxyz, cho D. S = x2 − x dx. 2
ba điểm A (0; −2; −1) , B (−2; −4; 3), C (1; 3; −1). 0 # » # » # »
Tìm điểm M ∈ (Oxy) sao cho MA + MB + 3MC
Câu 23. Cho hàm số y = f (x) liên tục trên đoạn
đạt giá trị nhỏ nhất.
[a ; b]. Mệnh đề nào dưới đây là sai? 1 3 1 3 b a A. − ; ; 0 . B. ; ; 0 . Z Z 5 5 5 5 A. f (x)dx = − f (x)dx. 3 4 1 3 a b C. ; ; 0 . D. ; − ; 0 . 5 5 5 5 b Z B. kdx = k (a − b).
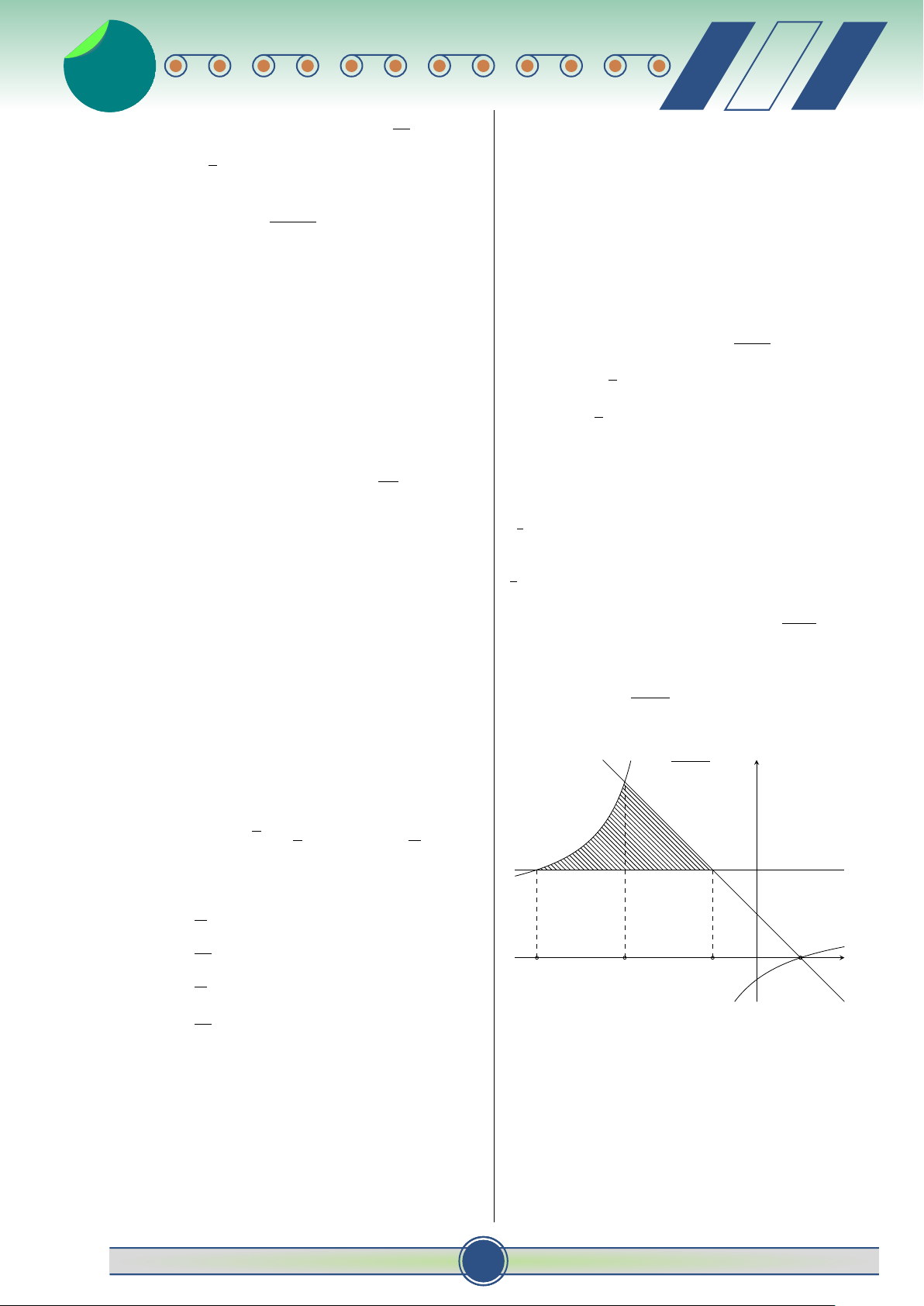
Câu 30. Cho (H) là hình phẳng giới hạn bởi đồ thị √ a các hàm số (P) : y = x , y = 0, y = 2 − x. (hình b c b Z Z Z vẽ) C. f (x)dx = f (x)dx + f (x)dx, ∀c ∈ y a a c (a; b). 2 √ b b y = x Z Z D. f (x)dx = f (t)dt. a a Z 1 Câu 24. Biết (x + 3) e−3x+1dx = − e−3x+1 (3x + n) + m x O 2 y = 2 − x
C, với m, n ∈ Z. Khi đó tổng S = m + n bằng A. 10. B. 1. C. 9 . D. 19. Diện tích của (H) là ♂ 30 đề ôn thi t HKII-12 8 v 8
Những nẻo đường phù sa 2021 30 ĐỀ - ĐỀ
30 ĐỀ ÔN THI HKII-LỚP 12 √ √ 2020 4 2 − 1 8 2 + 3
Câu 37. Một ôtô đang chạy với vận tốc 54km/h thì A. . B. . 3 6 7 5
tăng tốc chuyển động nhanh dần đều với gia tốc C. . D. . 6 6
a(t) = 3t − 8 (m/s2) trong đó t là khoảng thời gian
Câu 31. Trong không gian Oxyz, phương trình tính bằng giây. Quãng đường mà ôtô đi được sau
mặt cầu (S) tiếp xúc với hai mặt phẳng song song 10 giây kể từ lúc bắt đầu tăng tốc là
(P) : x − 2y + 2z + 6 = 0 và (Q) : x − 2y + 2z − A. 540(m). B. 150(m).
10 = 0 có tâm trên trục Oy là C. 250(m). D. 246(m). 55
A. x2 + y2 + z2 + 2y − = 0. 9
Câu 38. Cho hàm bậc hai y = f (x) có đồ thị như
B. x2 + y2 + z2 + 2y − 60 = 0. hình dưới đây.
C. x2 + y2 + z2 − 2y + 55 = 0. y 55 1
D. x2 + y2 + z2 − 2y − = 0. 9
Câu 32. Tính diện tích hình phẳng giới hạn bởi x O 1
(C) : y = x4 − 2x2 + 1 và trục hoành. 8 16 A. S = . B. S = . 15 15
Tính thể tích khối tròn xoay tạo thành khi quay 15 15 C. S = . D. S = . 8 16
hình phẳng giới hạn bởi đồ thị hàm số y = f (x), Câu 33. Trong không gian Oxyz, cho
tứ trục hoành quanh trục Ox. diện 4 12 16 16 ABCD có A (3 ; −2 ; 1), B (−4 ; 0 ; 3), π π π π A. . B. . C. . D. . 3 15 15 5
C (1 ; 4 ; −3), D (2 ; 3 ; 5) ˙Phương trình mặt phẳng Câu 39. Trong không gian với hệ tọa độ Oxyz, cho
chứa AC và song song với BD là
mặt phẳng (P) : x + 2y + z − 4 = 0 và đường
A. 12x − 10y + 21z − 35 = 0. x + 1 y z + 2 thẳng d : = = . Đường thẳng ∆ nằm
B. 12x + 10y − 21z + 35 = 0 . 2 1 3
C. 12x + 10y + 21z + 35 = 0 .
trong mặt phẳng (P) đồng thời cắt và vuông góc
D. 12x − 10y − 21z − 35 = 0.
với đường thẳng d có phương trình là x − 1 y − 1 z − 1 A. ∆ : = = .
Câu 34. Cho hàm số f (x) liên tục trên R, biết 5 −1 3 π x − 1 y + 1 z − 1 B. ∆ : = = . 4 1 5 −1 2 Z Z x2. f (x) x − 1 y + 1 z − 1 f (tan x) dx = 4 và dx = 2. Tính C. ∆ : = = . x2 + 1 5 −1 −3 0 0 x − 1 y − 1 z − 1 1 D. ∆ : = = . Z 5 −1 −3 I = f (x)dx.
Câu 40. Cho số phức z thỏa mãn |z| = 2 và 0 A. 6. B. 1. C. 0. D. 2. z2 + 1
= 4. Tính |z + z| + |z − z|. √ √
Câu 35. Cho số phức z = x + yi (x, y ∈ R) có A. 3 + 7. B. 3 + 2 2. √
môđun nhỏ nhất thỏa mãn điều kiện |z − 4 − 2i| = C. 7 + 3. D. 16. |z − 2|. Tính P = x2 + y2. PHẦN TỰ LUẬN A. 10. B. 16 . C. 8. D. 32. Z 1
Câu 1. Tính tích phân (2x + 1)5 dx. 0
Câu 36. Trong không gian với hệ tọa độ Oxyz, cho Câu 2. Tìm phần thực, phần ảo, số phức liên hợp
mặt cầu (S) : x2 + y2 + z2 + 4x − 2y + 6z − 11 = 0 và tính môđun của số phức z = (2 − 4i) (5 + 2i) +
và mặt phẳng (P) : x − 2y + 2z + 1 = 0. Gọi (C) là 4 − 5i
đường tròn giao tuyến của (P) và (S). Tính chu vi 2 + i của đường tròn (C).
Câu 3. Trong không gian với hệ tọa độ Oxyz, A. 10π. B. 4π. C. 6π . D. 8π.
cho tam giác ABC với A (1; −3;4), B (−2; −5; −7), ♂ 30 đề ôn thi t HKII-12 9 v 9
Những nẻo đường phù sa 2020 - 2021 30 ĐỀ
30 ĐỀ ÔN THI HKII-LỚP 12
C (6; −3; −1). Viết phương trình đường trung A. x = 3, y = 1. B. x = −1, y = 3.
tuyến AM cuả tam giác ABC. C. x = 1, y = 3. D. x = 3, y = −1.
BẢNG ĐÁP ÁN THAM KHẢO
Câu 6. Nguyên hàm của hàm số y = xexlà Z 1. 2. 3. 4. 5. 6. 7. 8. 9. 10. 11. A. xexdx = xex + C. C A C D D C B D A C B Z B. xexdx = (x − 1) ex + C.
12. 13. 14. 15. 16. 17. 18. 19. 20. 21. 22. Z D B A A A B C A B C B C. xexdx = (x + 1) ex + C. Z
23. 24. 25. 26. 27. 28. 29. 30. 31. 32. 33. D. xexdx = x2ex + C. B D B B D A B C A B D 34. 35. 36. 37. 38. 39. 40.
Câu 7. Trong không gian với hệ tọa độ Oxyz, viết A C D C C D A
phương trình mặt phẳng trung trực của đoạn AB
biết A (2; 1; 4), B (−1; −3; −5) .
A. −3x − 4y − 9z + 5 = 0. ĐỀ ÔN SỐ 3
B. −3x − 4y − 9z + 7 = 0.
Câu 1. Trong không gian với hệ trục tọa độ Oxyz, C. 3x + 4y + 9z = 0.
phương trình của mặt phẳng đi qua ba điểm
D. 3x + 4y + 9z + 7 = 0.
A (1; 1; 1) ,B (2; 4; 5) , C (4; 1; 2) là:
Câu 8. Số phức liên hợp của số phức z =
A. 3x − 11y + 9z − 1 = 0. √ 2 3 − 2i là
B. 3x + 11y − 9z − 5 = 0. √ √ A. ¯z = 1 + 4 3i. B. ¯z = −1 − 4 3i.
C. 3x + 3y − z − 5 = 0. √ √ C. ¯z = 1 − 4 3i. D. ¯z = −1 + 4 3i. D. 9x + y − 10z = 0. π Z 2 5 Z Z
Câu 9. Giá trị của I = (2 cos x − sin 2x) dx Câu 2. Cho f (x)dx = −3, f (x)dx = 7. Khi 0 0 0 là 5 Z A. I = 1. B. I = −1. đó f (x)dx bằng: C. I = 0. D. I = 2. 2 A. 10. B. 4. C. 7. D. 3.
Câu 10. Rút gọn biểu thức M = i2018 + i2019 ta
Câu 3. Giải phương trình z2 − 2z + 3 = 0 trên tập được
số phức ta được các nghiệm: A. M = −1 − i. B. M = −1 + i. √ √
A. z1 = 1 + 2i; z2 = 1 − 2i. C. M = 1 − i. D. M = 1 + i. √ √
B. z1 = −1 + 2i; z2 = −1 − 2i. √ √
Câu 11. Nguyên hàm của hàm số y = x cos x là
C. z1 = −2 + 2i; z2 = −2 − 2i. √ √
A. x cos x − sin x + C. B. x sin x + cos x + C.
D. z1 = 2 + 2i; z2 = 2 − 2i.
C. x cos x + sin x + C. D. x sin x − cos x + C.
Câu 4. Trong không gian với hệ trục tọa độ Oxyz, Câu 12. Diện tích hình phẳng giới hạn bởi các đồ
cho mặt cầu có phương trình: (S √ m) : x2 + y2 + z2 −
thị hàm số: y = x 3 1 − x, y = 0, x = 1, x = 9 là
4mx + 4y + 2mz + m2 + 4m = 0, (Sm)là mặt cầu có 467 568 A. S = . B. S = .
bán kính nhỏ nhất khi m là: 9 11 468 468 A. m = 0. B. m = −1. C. S = . D. S = . 1 3 11 7 C. m = . D. m = − . 2 2
Câu 13. Hai điểm biểu diễn số phức z = 1 + i và
Câu 5. Cho 2 số phức: z =
(2x + 1) + z0 = −1 + i đối xứng nhau qua
(3y − 2) i, z0 = (x + 2) + (y + 4) i. Tìm các số thực A. Trục tung. B. Điểm E (1; 1). x, y để z = z0. C. Trục hoành. D. Gốc O. ♂ 30 đề ôn thi t HKII-12 10 v 10
Những nẻo đường phù sa 2021 30 ĐỀ - ĐỀ
30 ĐỀ ÔN THI HKII-LỚP 12 2020 2 1 Z x2 + x + 1 Z Câu 14. Biết
dx = a + ln b. Khi đó Câu 22. Giá trị của (2x + 2) exdx. x + 1 1 0 a + b bằng A. 2e. B. 4e. C. e. D. 3e. A. 2. B. 4. C. 0. D. 3.
Câu 23. Trong không gian với hệ toạ độ Oxyz, cho
Câu 15. Trong không gian với hệ tọa độ Oxyz, điểm M (3; 6; −2) và mặt cầu (S) : x2 + y2 + z2 −
bán kính của mặt cầu đi qua bốn điểm O (0; 0; 0), 6x − 4y + 2z − 3 = 0. Phương trình của mặt phẳng
A (4; 0; 0), B (0; 4; 0), C (0; 0; 4) là
tiếp xúc với mặt cầu (S) tại M là: √ √ A. R = 2 3. B. R = 4 3. A. y − 4z − 14 = 0. B. 4x − z − 14 = 0. √ √ C. R = 3. D. R = 3 3. C. 4x − y − 6 = 0 . D. 4y − z − 26 = 0.
Câu 16. Trong không gian với hệ tọa độ Oxyz, Câu 24. Diện tích S của hình phẳng giới hạn bởi #» #» #»
cho các vecto a (3; 1; 2), b (1; 2; m), c (5; 1; 7). đồ thị hai hàm số y = x2 − 2x và y = x là #» h #» #»i 9 13
Để c = a , b khi giá trị của mlà: A. S = . B. S = . 4 2 A. m = 0. B. m = −1. 9 13 C. S = . D. S = . C. m = 1. D. m = 2. 2 4 3
Câu 25. Để hàm số F(x) = (a sin x + b cos x) ex Z Câu 17. Cho
(x − 3) f 0(x)dx = 12 và f (0) = 3. là một nguyên hàm của hàm số f (x) = 0
(3 sin x − 2 cos x) ex thì giá trị a + b là: 3 Z A. a + b = 3. B. a + b = 2. Khi đó giá trị của f (x)dx là: C. a + b = −3 . D. a + b = −2. 0 A. −21. B. 12. C. −3. D. 9.
Câu 26. Trong không gian với hệ tọa độ Oxyz,
Câu 18. Cho số phức z1 = 2 + 6i và z2 = 5 − 8i. phương trình của đường thẳng d đi qua điểm
Mô đun của số phức w = z1z2 là:
A (1; −2; 3) và B (3; 0; 0) là √ √ A. |w| = 2 890. B. |w| = 2 610. x = 1 + 2t x = 1 + 2t √ √ C. |w| = 2 980. D. |w| = 2 601. A. d : y = −2 + 2t . B. d : y = −2 + 2t . 3 z = 3 + 3t z = 3 − 3t Z Câu 19. Cho
f x2 dx = 3, khi đó giá trị x = 3 + t x = 2 + t 0 9 C. d : y = −2t . D. d : y = 2 − 2t . Z của f (x)dxlà: z = 3t z = −3 + 3t 0 A. 3. B. 9. C. 12. D. 6. 1 Z a Câu 27. Biết ln (2x + 1) dx = ln 3 − c với a,b,c
Câu 20. Trong không gian với hệ trục toạ độ b 0
Oxyz, phương trình nặt cầu có đường kính ABvới là các số nguyên dương. Mệnh đề đúng là A (4; 3; 7), B (2; 1; 3) là: A. a + b = c. B. a + b = 2c. .
A. (x − 3)2 + (y + 1)2 + (z − 5)2 = 9. C. a − b = c. D. a − b = 2c.
B. (x + 3)2 + (y − 1)2 + (z + 5)2 = 9.
Câu 28. Thể tích khối tròn xoay tạo thành khi quay
C. (x − 1)2 + (y + 2)2 + (z − 2)2 = 36.
hình phẳng giới hạn bởi các đường y = x2,x = y2
D. (x + 1)2 + (y − 2)2 + (z + 2)2 = 36. xung quanh trục Ox là. Z 4x − 3 3 10π Câu 21. Biết dx = ln |x − a| + A. V = . B. V = . 2x2 − 3x − 2 10 3
b ln |cx + 1| + C. Khi đó a + b − c bằng: 3π 10 C. V = . D. V = . 10 3 A. 5. B. −2. C. 1. D. −3. ♂ 30 đề ôn thi t HKII-12 11 v 11
Những nẻo đường phù sa 2020 - 2021 30 ĐỀ
30 ĐỀ ÔN THI HKII-LỚP 12
Câu 29. Diện tích S của hình phẳng giới hạn bởi A. ln |cos x| + C. B. sin x + C .
đồ thị hàm số y = 4 − x2 và trục hoành là C. ln |sin x| + C. D. tan x + C. 22 33 A. S = . B. S = . 3 2
Câu 37. Nguyên hàm của hàm số y = tan2 x là 23 32 C. S = . D. S = . A. tan x + x + C . B. tan x − x + C. 2 3 C. − tan x − x + C. D. − tan x + x + C.
Câu 30. Trong không gian với hệ tọa độ Oxyz, x − 1
Câu 38. Trong không gian với hệ tọa độ Oxyz, tâm
cho điểm M (5; 3; 2) và đường thẳng d : = 1
và bán kính của mặt cầu (S) : x2 + y2 + z2 + 4x − y + 3 z + 2 =
. Tọa độ điểm H là hình chiếu vuông 2y + 6z + 5 = 0 là 2 3
góc của điểm M trên d là
A. I (−4 ; 2 ; −6) , R = 5. A. H (1; −3; −2). B. H (2; −1; 1) .
B. I (2 ; −1 ; 3) , R = 3. C. H (3; 1; 4). D. H (4; 3; 7).
C. I (4 ; −2 ; 6) , R = 5.
D. I (−2 ; 1 ; −3) , R = 3.
Câu 31. Tập hợp các điểm biểu diễn các số phức z π
thỏa mãn |z + i − 1| = |z − 2i| là: Z √
Câu 39. Giá trị của 1 + cos 2xdx là A. Một elip.
B. Một đường tròn. 0 √ √ C. Một Parabol.
D. Một đường thẳng. A. 0 . B. 2 2. C. 3 2 . D. 1.
Câu 32. Trong không gian với hệ tọa độ Oxyz, cho Câu 40. Trong không gian với hệ tọa độ Oxyz, x + 2 y
điểm A (3; −3; 5) và đường thẳng d : =
= cho 3 điểm A (0 ; 0 ; 3), B (1 ; 1 ; 3); C (0 ; 1 ; 1). 1 3 z − 3
Khoảng cách từ gốc tọa độ O đến mặt phẳng
. Phương trình của đường thẳng qua A và 4 (ABC) bằng: song song với d là: A. 4. B. 2. C. 3. D. 1. x = 3 + t x = −3 + t
Câu 41. Trong không gian với hệ tọa độ Oxyz, cho A. y = −3 + 3t . B. y = 3 + 3t .
điểm A (2; −1; 0) và mặt phẳng (P) : x − 2y + z + z = 5 + 4t z = −5 + 4t
2 = 0. Gọi I là hình chiếu vuông góc của A lên mặt x = 1 + 3t x = 1 − 3t
phẳng (P). Phương trình của mặt cầu có tâm I và C. y = 3 − 3t . D. y = 3 + 3t . đi qua A là: z = 4 + 5t z = 4 − 5t
A. (x + 1)2 + (y + 1)2 + (z + 1)2 = 6. m + 3i
B. (x − 1)2 + (y − 1)2 + (z + 1)2 = 6.
Câu 33. Cho số phức z = , m ∈ R. Số phức 1 − i
C. (x + 1)2 + (y − 1)2 + (z + 1)2 = 6.
w = z2 có |w| = 9 khi các giá trị của m là:
D. (x + 1)2 + (y + 1)2 + (z − 1)2 = 6. A. m = ±1. B. m = ±3.
Câu 42. Với số phức z tùy ý, cho các mệnh đề C. m = ±2. D. m = ±4.
|−z| = |z|, |z| = |z|, |z + z| = 0, |z| > 0. Số mệnh
Câu 34. Diện tích hình phẳng giới hạn bởi các đồ đề đúng là: √ thị hàm số y = x, y = x − 2, y = −x là: A. 3. B. 4. C. 1. D. 2. 13 11 A. S = . B. S = . 3 3
Câu 43. Cho hình phẳng giới hạn bởi các đường 13 11 4 C. S = . D. S = . y =
, y = 0,x = 0,x = 2 quay xung quanh 2 2 4 − x
trục Ox. Thể tích khối tròn xoay tạo thành là:
Câu 35. Cho số phức z thỏa mãn |z + i − 1| = A. V = 4. . B. V = 4π.
|z − 2i|. Giá trị nhỏ nhất của |z| là: √ √ √ C. V = 9. D. V = 9 2 √ 3 π. A. 2. B. . C. 2 2. D. . 2 2
Câu 44. Số phức z thỏa mãn z + 2z = (1 + 5i)2có
Câu 36. Nguyên hàm của hàm số y = cot x là: phần ảo là: ♂ 30 đề ôn thi t HKII-12 12 v 12
Những nẻo đường phù sa 2021 30 ĐỀ - ĐỀ
30 ĐỀ ÔN THI HKII-LỚP 12 2020 A. −8. B. −10. C. −8i. D. −10i.
23. 24. 25. 26. 27. 28. 29. 30. 31. 32. 33. 16 D C D B C C D C D A B Z dx
Câu 45. Giá trị của √ √ là :
34. 35. 36. 37. 38. 39. 40. 41. 42. 43. 44. x + 9 − x 0 A B C B D B D B D B B A. 4. B. 12. C. 9. D. 15. 45. 46. 47. 48. 49. 50.
Câu 46. Trong không gian với hệ tọa độ Oxyz B A A D C C
phương trình nào sau đây là phương trình của một mặt cầu? ĐỀ ÔN SỐ 4
A. 2x2 + 2y2 + 2z2 − 2x + 5y + 6z − 2019 = 0.
B. 2x2 + 2y2 + 2z2 + 2x + 5y + 6z + 2019 = 0.
Câu 1. Trong không gian với hệ tọa độ Oxyz,
C. x2 + y2 + z2 + 4x − 2yz − 1 = 0.
phương trình mặt phẳng qua A (−1; 1; −2) và có
D. x2 + y2 + z2 + 4x − 2xy + 6z + 5 = 0. #»
véctơ pháp tuyến n = (1; −2; −2) là: √
Câu 47. Cho số phức z biết z = 2 − 2 3i. Khẳng
A. −x + y − 2z − 1 = 0.
định nào sau đây là khẳng định sai?
B. x − 2y − 2z − 1 = 0. √ A. z2 = 64. B. ¯z = 2 + 2 3i.
C. x − 2y − 2z + 7 = 0. √ 2 C. z = 3 − 1 . D. |z| = 4.
D. −x + y − 2z + 1 = 0.
Câu 48. Thể tích khối tròn xoay tạo thành khi quay Câu 2. Trong không gian với hệ tọa độ Oxyz, điểm
hình phẳng giới hạn bởi các đường y = x2 − 4x + 4, M (−2; 1; −1) thuộc mặt phẳng nào sau đây:
y = 0, x = 0, x = 3 xung quanh trục Ox là
A. x + 2y − z − 1 = 0. 29 33 A. V = . B. V = . B. −2x + y − z = 0. 4 5 29π 33π
C. 2x − y − z + 6 = 0. C. V = . D. V = . 4 5
D. −2x + y − z − 4 = 0.
Câu 49. Số phức z biết z = (7 − 2i) (1 + 5i)2 có Câu 3. Tìm môđun của số phức z = 3 − 2i. phần ảo là √ A. |z| = 13. B. |z| = 5. A. √ 118i. B. −148. C. |z| = 13. D. |z| = 5. C. 118. D. −148i.
Câu 4. Tìm nguyên hàm của hàm số f (x) = 4x3 +
Câu 50. Trong không gian với hệ tọa độ Oxyz, 2x là:
cho hai mặt phẳng (P) : 2x + y − z − 8 = 0 và Z 4 A. f (x)dx = x4 + x2 + C.
(Q) : 3x + 4y − z − 11 = 0. Gọi d là giao tuyến của 3 Z B. f (x)dx = 12x2 + 2 + C.
(P) và, phương trình của đường thẳng d là Z x = 1 + 3t x = 3 + 3t C. f (x)dx = x4 + x2 + C. A. y = 1 − t . B. y = t . Z D. f (x)dx = 12x2 + x2 + C. z = 5 + 5t z = −2 + 5t
Câu 5. Trong không gian với hệ tọa độ Oxyz, cho x = 3 − 3t x = 3t
A (−1; 2; −3) và bán kính B (−3; −1; 1). Tọa độ của C. y = t . D. y = 1 + t . # » véc tơ AB là # » # » z = −2 − 5t z = −7 + 5t A. AB = (2; 3; −4).
B. AB = (−2; −3; 4). # » # »
BẢNG ĐÁP ÁN THAM KHẢO C. AB = (4; −3; 4).
D. AB = (−4; 1; −2). 1. 2. 3. 4. 5. 6. 7. 8. 9. 10. 11.
Câu 6. Trong không gian với hệ tọa độ Oxyz, mặt B A A C C B D D C A B
cầu có tâm A(–1; 2; 3) và bán kính R=6 có phương
12. 13. 14. 15. 16. 17. 18. 19. 20. 21. 22. trình D A D A B C A D A C A
A. (x + 1)2 + (y − 2)2 + (z − 3)2 = 36. ♂ 30 đề ôn thi t HKII-12 13 v 13
Những nẻo đường phù sa 2020 - 2021 30 ĐỀ
30 ĐỀ ÔN THI HKII-LỚP 12 #»
B. (x + 1)2 + (y − 2)2 + (z + 3)2 = 36. C. a = (−2 ; 3 ; 1). #»
C. (x − 1)2 + (y + 2)2 + (z + 3)2 = 36.
D. a = (2 ; − 3 ; −1).
D. (x + 1)2 + (y − 2)2 + (z − 3)2 = 6.
Câu 14. Mệnh đề nào sau đây đúng? Z 1 3 Z Z A. sin xdx = cos x + C. Câu 7. Cho f (x)dx = 3 và f (x)dx = −2. Z 1 1 0 1 B. dx = − + C (x 6= 0). x x2 3 Z Z Tính f (x)dx. C. cos xdx = sin x + C. Z 0 D. axdx = ax + C (0 < a 6= 1). A. 5. B. –1. C. 1. D. –5.
Câu 15. Cho các hàm số f (x) và g(x) liên tục trên
Câu 8. Trong mặt phẳng phức Oxy, điểm M biểu R diễn cho số phức z = . Tìm mệnh đề sai. 3 − 5i có tọa độ b b b Z Z Z A. (−5; 3). B. (3; −5i). A. [ f (x) − g(x)] dx = f (x)dx − g(x)dx. C. (−5i; 3). D. (3; −5). a a a c b b
Câu 9. Trong không gian với hệ tọa độ Oxyz, tọa Z Z Z B. f (x)dx + f (x)dx = f (x)dx.
độ tâm I và bán kính R của mặt cầu (S): x2 + y2 + a c a
z2 − 2x + 6y − 4z − 2 = 0 lần lượt là b a √ Z Z C. f (x)dx = − f (x)dx.
A. I (−1; 3; −2), R = 2 3. a b
B. I (1; −3; 2), R = 4.√ b b b Z Z Z
C. I (1; −3; 2), R = 2 3. D. f (x).g(x)dx = f (x)dx. g(x)dx.
D. I (−1; 3; −2), R = 4. a a a
Câu 10. Số phức liên hợp của số phức z
= Câu 16. Trong không gian Oxyz, cho đường thẳng (3 + i) (2 − 3i) là x = 1 − t A. z = 6 + 7i. B. z = 6 − 7i. d :
y = −2 + 3t . Tọa độ một véctơ chỉ phương C. z = 9 + 7i. D. z = 9 − 7i. z = 3 + t của d là
Câu 11. Cho các hàm số f (x), g(x) liên tục trên tập A. (−1 ; 3 ; 1). B. (−1 ; 3 ; 0).
xác định. Mệnh đề nào sau đây sai? Z Z C. (−1 ; −2 ; 3). D. (1 ; −2 ; 3). A. k f (x)dx = k f (x)dx, k khác 0. Z
Câu 17. Tìm số phức z thỏa mãn (2 − 3i) z − B. f 0(x)dx = f (x) + C. (9 − 2i) = (1 + i) z. Z f (x)dx 13 16 Z f (x) A. 1 − 2i. B. + i. C. dx = . 5 5 g(x) Z g(x)dx C. 1 + 2i. D. −1 − 2i. Z Z Z D. [ f (x) − g(x)]dx = f (x)dx − g(x)dx.
Câu 18. Trong không gian với hệ tọa độ Oxyz, cho
mặt phẳng (P) : x + y − 2z + 4 = 0 và đường 2 Z x = 3 + t
Câu 12. Tính tích phân I = (2x − 1) dx. thẳng d : y = 1 + t
(t ∈ R). Tìm khẳng định 1 5 A. I = 2. B. I = 1. C. I = 3. D. I = . z = −1 + t 6 đúng. #» #»
Câu 13. Trong không gian Oxyz, cho a = −2 i + #» #»
A. d và (P) cắt nhau nhưng không vuông góc #»
3 j + k . Tọa độ của a là: với nhau. #» #» #» #»
A. a = −2 i ; 3 j ; 1 k .
B. d và (P) vuông góc với nhau. #» B. a = (−2 ; 3 ; 0).
C. d và (P) song song nhau. ♂ 30 đề ôn thi t HKII-12 14 v 14
Những nẻo đường phù sa 2021 30 ĐỀ - ĐỀ
30 ĐỀ ÔN THI HKII-LỚP 12 2020 D. d nằm trong (P). π π 1 1 Z B. T = (x + 1) sin 2x 4 4 − sin 2xdx.
Câu 19. Trong không gian với hệ tọa độ Oxyz, 2 2 0 0
mặt cầu (S) có tâm I (−1; 2; 1) và tiếp xúc với mặt π π Z
phẳng (P) : x − 2y − 2z − 2 = 0 có phương trình
C. T = −2 (x + 1) sin 2x 4 4 + 2 sin 2xdx. 0 là 0 π π
A. (x − 1)2 + (y + 2)2 + (z + 1)2 = 9. Z
D. T = − (x + 1) sin 2x 4 4 + sin 2xdx.
B. (x + 1)2 + (y − 2)2 + (z − 1)2 = 3. 0 0
C. (x + 1)2 + (y − 2)2 + (z − 1)2 = 9.
Câu 25. Trong không gian với hệ tọa độ Oxyz, cho
D. (x + 1)2 + (y − 2)2 + (z + 1)2 = 3.
A (1; 1; 2), B (2; −1; 1) và C (3; 2; −3). Tìm tọa độ
Câu 20. Trong không gian với hệ tọa độ Oxyz, điểm D để ABCD là hình bình hành.
phương trình mặt cầu có tâm I (1; −2; 3) và đi qua A. (4; 2; −4). B. (0; −2; 6).
điểm A (−1; 2; 1) có phương trình C. (2; 4; −2). D. (4; 0; −4).
A. x2 + y2 + z2 + 2x − 4y + 6z − 10 = 0.
Câu 26. Tìm tất cả các giá trị thực x, y sao cho
B. x2 + y2 + z2 − 2x + 4y − 6z − 10 = 0.
2x − (3 − y) i = y + 4 + (x + 2y − 2) i, trong đó i
C. x2 + y2 + z2 − 2x + 4y + 2z + 18 = 0. là đơn vị ảo.
D. x2 + y2 + z2 + 2x − 4y − 2z − 18 = 0. A. x = 1, y = −2. B. x = −1, y = 2.
Câu 21. Cho số phức z thỏa mãn phương trình 17 6 17 6 C. x = , y = . D. x = − , y = − .
z + 3z = (3 − 2i)2 (2 + i) là 7 7 7 7 11 19 11 19
Câu 27. Tìm một nguyên hàm F(x) của hàm số A. z = + i. B. z = − i. 2 2 2 2
f (x) = 2x biết F(0) = 2 bằng: C. z = 11 − 19i. D. z = 11 + 19i. 2x 1 a A. F(x) = + 2 + . Z ln 2 ln 2
Câu 22. Tìm a (a > 0) biết (2x − 3) dx = 4. 2x 1 B. F(x) = + 2 − . 0 ln 2 ln 2 A. a = 4. B. a = 2. C. F(x) = 2x + 1. C. a = 1. D. a = −1. D. F(x) = 2x + 2.
Câu 23. Trong không gian với hệ trục tọa độ Oxyz Câu 28. Trong không gian Oxyz, phương trình
cho điểm M (−2; 3; −1), N (−1; 2; 3) , P (2; −1; 1). đường thẳng đi qua M (2 ; −1 ; 1) và vuông góc với
Phương trình đường thẳng d đi qua M và song mặt phẳng (P) : 2x − y + 3z + 1 = 0 là:
song ới đường thẳng NP là x − 2 y + 1 z − 3 A. = = . . x = − 1 + 3t x = 2 + 3t 2 −1 1 x + 2 y − 1 z + 1 A. y = 2 − 3t . B. y = −1 − 3t . B. = = . 2 −1 3 x + 2 y − 1 z + 3 z = 3 − 2t z = 1 − 2t C. = = . . 2 −1 1 x = 3 − 2t x = −2 + 3t x − 2 y + 1 z − 1 D. = = . C. y = −3 + 3t . D. y = 3 − 3t . 2 −1 3 Câu 29. Kí hiệu z
1, z2 là nghiệm của phương trình z = −2 − t z = −1 − 2t
z2 + 2z + 5 = 0. Trong đó z2 có phần ảo âm. Tính π Z T = 2z1 − 3z2.
Câu 24. Cho tích phân T = 4 (x + 1) cos 2xdx. 0 A. −1 − 10i. B. 1 + 10i. (u = x + 1 C. 1. D. 4 + 16i. Nếu đặt thì ta được dv = cos 2xdx
Câu 30. Tìm họ nguyên hàm của hàm số f (x) = π π Z e2x+1. A. T = (x + 1) sin 2x 4 4 − sin 2xdx. Z 1 0 A. f (x)dx = e2x+1 + C. 0 2 ♂ 30 đề ôn thi t HKII-12 15 v 15
Những nẻo đường phù sa 2020 - 2021 30 ĐỀ
30 ĐỀ ÔN THI HKII-LỚP 12 Z 20 22 B. f (x)dx = e2x+1 + C. C. S = . D. S = . 3 3 Z C. f (x)dx = 2e2x+1 + C. Z
Câu 37. Cho hình phẳng D giới hạn bởi đường D. f (x)dx = ex2+x + C. √ cong y =
ln x, trục hoành và đường thẳng x = 3. Z 1
Khối tròn xoay tạo thành khi quay D quanh trục Câu 31. Cho I =
x2p1 − x3dx. Nếu đặt t = √ 0
hoành có thể tích bằng bao nhiêu? 1 − x3 thì ta được 2 3 Z 1 3 Z 1
A. (3 ln 3 − 2) π. B. π. A. I = t2dt. B. I = − t2dt. 3 2 0 2 0
C. (3 ln 3 − 3) π.
D. (3 ln 3 + 2) π. 2 Z 1 2 Z 1 C. I = − t2dt. D. I = t2dt. 3 0 3 0
Câu 38. Gọi M là điểm biểu diễn số phức
Câu 32. Cho hình phẳng D giới hạn bởi đường z1 = a + a2 − 2a + 2 i (với a là số thực thay 1 cong y =
x2 − x, trục hoành và các đường thẳng đổi) và N là điểm biểu diễn số phức z 2 2 biết
x = 1, x = 4. Khối tròn xoay tạo thành khi quay D |z2 − 2 − i| = |z2 − 6 + i|. Tìm độ dài ngắn nhất
quanh trục hoành có thể tích bằng: của đoạnMN. √ 42π 4π 128π √ A. . B. 3 6 5 π. C. . D. . 5 15 25 A. 2 5. B. . C. 1. D. 5. 5
Câu 33. Trong không gian với hệ tọa độ Oxyz, cho
hai điểm A (−2; 3; −1), B (1; −2; −3) và mặt phẳng Câu 39. Cho hình phẳng D giới hạn bởi các đường
(P) : 3x − 2y + z + 9 = 0. Mặt phẳng (α) chứa hai y = ex, y = 1, x = 2. Tính thể tích khối tròn xoay
điểm A, B và vuông góc với (P) có phương trình tạo thành khi cho D quay quanh Ox. là π A. e4 − 1. 2
A. x + y − z − 2 = 0. π 5π B. e4 − .
B. 3x − 2y + z + 13 = 0. 2 2 1 7 C. x + y − z + 2 = 0. C. π e4 − 2e2 + . 2 2
D. x − 5y − 2z + 19 = 0. D. π e2 − 3.
Câu 34. Cho hàm số f (x) có f 0(x) và f 00(x) liên
tục trên R. Biết f 0(2) = 4 và f 0 (−1) = −2, tính Câu 40. Trong không gian hệ trục toạ độ Oxyz, 2
đường vuông góc chung của hai đường thẳng chéo Z f 00(x)dx x − 2 y − 3 z + 4 x + 1 nhau d1 : = = và d2 : = −1 2 3 −5 3 A. −8. B. −6. C. 2. D. 6. y − 4 z − 4 = có phương trình −2 −1
Câu 35. Trong không gian với hệ tọa độ Oxyz, cho x y z − 1 A. = = .
hai điểm A (2; −3; −1), B (4; −1; 3). Phương trình 1 1 1 x − 2 y + 2 z − 3
mặt phẳng trung trực của đoạn thẳng AB là B. = = . 2 2 2
A. x + y + 2z − 9 = 0. x y − 2 z − 3 C. = = . − B. x + y + 2z + 3 = 0. 2 3 1 x − 2 y − 2 z − 3 = =
C. x + y + 2z − 3 = 0. D. . 2 3 4
D. 2x + 2y + 4z − 3 = 0.
Câu 41. Trong không gian hệ trục toạ độ Oxyz,
Câu 36. Tính diện tích S của hình phẳng giới hạn cho hai mặt phẳng (P) : x + y + z − 3 = 0 và
bởi đồ thị các hàm số y = x2 − 2x, x = 1, x = 4 và (Q) : x + 2y − z + 5 = 0. Tìm phương trình đường trục hoành.
thẳng d là giao tuyến của hai mặt phẳng (P) và 16 A. S = 6. B. S = . (Q) 3 ♂ 30 đề ôn thi t HKII-12 16 v 16
Những nẻo đường phù sa 2021 30 ĐỀ - ĐỀ
30 ĐỀ ÔN THI HKII-LỚP 12 2020 4 2 x = −1 − 3t Z Z f (x)dx = 6. Tính I = x f 0 (2x) dx. y = 2t x = 1 − 3t 0 0 y = 1 + 2t 13 A. 10. B. 2. C. . D. 5. A. d : quad . B. d : z = 1 + t . 2
Câu 46. Trong không gian với hệ tọa độ Oxyz, z = 4 − t
cho ba điểm A (1; −2; 3), B (3; 2; −1), C (0; 2; 1) và mặt phẳng (P)
: x + y − 2z − 6 = 0. Gọi
M (a; b; c) là điểm thuộc mặt phẳng (P) sao cho x = −1 − 3t x = −1 − 3t # » # » # »
MA + MB + 2MC đạt giá trị nhỏ nhất. Tính S = y = 2t y = −2t a + b + c. quad C. d : . D. d : quad . A. S = 3. B. S = 4. z = 4 + t C. S = −3. D. S = 0. z = 4 + t 1 Z 1 √ Câu 47. Cho I = dx = a + b ln 2 + 2 + x + 3 −2
c ln 3 (a, b, c ∈ Q). Tính S = a + b + c.
Câu 42. Cho hình phẳng D giới hạn bỏi các đường √ A. S = −1. B. S = 2. y =
x, y = −x, x = 2 (phần tô đậm trong hình). C. S = −1. D. S = −2. y √ y = x
Câu 48. Trong không gian với hệ trục tọa độ Oxyz, x − 1 y + 1 z cho đường thẳng d : = = và mặt 2 1 2
phẳng (P) : x − y + 2z + 3 = 0. Gọi M(a; b; c) là x O 2
giao điểm của d và (P). Tình S = a2 + b2 + c2. A. S = 15. B. S = 9. C. S = 42.. D. S = −7. y = −x
Câu 49. Trong không gian với hệ tọa độ Oxy,
cho điểm A (−4; 2; −1) và đường thẳng d :
Khối tròn xoay tạo thành khi D quay quanh trục x = −1 + t
hoành có thể tích bằng bao nhiêu? √ √ ! !
y = 3 − t . Gọi A0 (a; b; c) là điểm đối xứng với 14 16 2 4 2 + 6 A. + π. B. π. 3 5 3 z = t 2π 17π A qua d. Tính P = a + b + c C. . D. . 3 6 A. P = −2. B. P = −1. Câu 43. Gọi z =
a + bi (a, b ∈ R) thỏa mãn C. P = 1. D. P = 5.
¯z (1 + i) = 3 − i. Tính a − 2b
Câu 50. Tính diện tích S của hình phẳng giới hạn A. 6. B. −2. C. 5. D. −3.
bởi đồ thị các hàm số y = x2 − 2x − 2 và y = x + 2.
Câu 44. Tập hợp các điểm biểu diễn cho số phức 125 145 A. S = . B. S = . 6 6
z thỏa mãn |z + 1 − 2i| = | ¯z − 2 + i| là một đường 5 265 C. S = . D. S = . thẳng có phương trình 6 6 A. x + 3y = 0. B. 3x − y = 0.
BẢNG ĐÁP ÁN THAM KHẢO C. x − y = 0. D. x + y = 0. 1. 2. 3. 4. 5. 6. 7. 8. 9. 10. 11. B A A C B B C D B C C
Câu 45. Cho hàm số y = f (x) liên tục và có
12. 13. 14. 15. 16. 17. 18. 19. 20. 21. 22.
đạo hàm f 0(x) liên tục trên R thỏa f (4) = 8 và A C C D A C C C B A A ♂ 30 đề ôn thi t HKII-12 17 v 17
Những nẻo đường phù sa 2020 - 2021 30 ĐỀ
30 ĐỀ ÔN THI HKII-LỚP 12
23. 24. 25. 26. 28. 29. 30. 31. 32. 33. 34.
A. x − 2y + 2z + 6 = 0. D B C A B B A D A A D
B. x − 2y + 2z + 8 = 0.
35. 37. 38. 39. 40. 41. 42. 43. 44. 45. 46.
C. x − 2y + 2z − 6 = 0. D A B B A D C D B C A
D. x + 2y + 2z − 6 = 0. 47. 48. 49. 50.
Câu 7. Trong không gian Oxyz, viết phương trình D B D A
mặt phẳng lần lượt cắt ba trục tọa độ Ox, Oy, Oz
tại các điểm A(2; 0; 0), B(0; 3; 0), C(0; 0; 4). ĐỀ ÔN SỐ 5 x y z x y z A. + + = 0. B. + + = 1. 2 3 4 3 2 4 #» #» x y z x y z
Câu 1. Trong không gian Oxyz, véc-tơ v = 2 i + C. + + = 1. D. + + = 1. #» #» 2 3 4 4 3 2
5 j − k có tọa độ bằng bao nhiêu?
Câu 8. Cho số thực a > 0, a 6= 1. Khẳng định nào 5 1 A. (−2; −5; 1). B. 1; ; − . dưới đây đúng? 2 2 Z 2 5 1 A. ax dx = ax ln a + C. C. ; ; − . D. (2; 5; −1). 3 3 3 Z ax+1 B. ax dx = + C.
Câu 2. Trong không gian Oxyz, véc-tơ nào sau đây x + 1 Z ax
là véc-tơ pháp tuyến của mặt phẳng (P) : 3x − z + C. ax dx = + C. log a 1 = 0? Z ax #» #» D. ax dx = + C. A. n 1 = (3; −1; 1). B. n 2 = (3; −1; 0). ln a #» #» C. n 3 = (3; 0; −1). D. n 4 = (0; 3; −1).
Câu 9. Viết công thức tính thể tích V của khối tròn
Câu 3. Mô-đun của số phức w = a + 2i với a ∈ R xoay được tạo ra khi quay hình thang cong được bằng bao nhiêu?
giới hạn bởi đồ thị hàm số y = f (x), trục Ox, hai √ √ A. |w| = a + 2. B. |w| = a2 − 4.
đường thẳng x = a, x = b (a < b), xung quanh √ C. |w| = a2 + 4. D. |w| = a2 + 4. trục Ox. b b Z Z
Câu 4. Cho hàm số f (x) = sin 3x. Khẳng định nào A. V = 2 π f (x) dx. B. V = f 2(x) dx. sau đây đúng? a a b b Z 1 Z Z A. f (x) dx = cos 3x + C. 3 C. V = π
| f (x)| dx. D. V = π f 2(x) dx. Z 1 B. f (x) dx = − cos 3x + C. a a 3
Câu 10. Trong không gian Oxyz, tính khoảng cách Z C. f (x) dx = 3 cos 3x + C.
d từ điểm M(−1; 2; 3) đến mặt phẳng (P) : 2x − Z D. f (x) dx = −3 cos 3x + C. 6y + 3z + 1 = 0. 6 4 A. d = . B. d = .
Câu 5. Trong không gian Oxyz, cho đường thẳng 7 7 4 6 x = 1 + 5t C. d = . D. d = . 49 49 d : y = 2t
. Điểm nào dưới đây không thuộc Câu 11. Cho hàm số f (x) có đạo hàm liên tục z = −3 + t
trên đoạn [0; 2], f (0) = 1; f (2) = 5. Tích phân 2 đường thẳng d? Z
f 0(x) dx có giá trị bằng bao nhiêu? A. M(−4; −2; −4). B. N(1; 0; −3). 0 C. P(6; 2; 2). D. Q(51; 20; 7). A. 1. B. 4. C. 6. D. 2. √ 2
Câu 6. Trong không gian Oxyz, phương trình mặt Câu 12. Cho số phức z = 2 + 3i . Tổng phần
phẳng đi qua điểm M(−4; 2; 1) và có véc-tơ pháp thực và phần ảo của số phức z bằng bao nhiêu? #» √ √
tuyến n = (1; −2; 2) là phương trình nào dưới A. 2 + 3. B. 6 2 + 11. √ đây? C. 6 2 − 7. D. 11. ♂ 30 đề ôn thi t HKII-12 18 v 18
Những nẻo đường phù sa 2021 30 ĐỀ - ĐỀ
30 ĐỀ ÔN THI HKII-LỚP 12 2020
Câu 13. Trong không gian Oxyz, cho tam giác Câu 18. Cho x > 0. Tìm hàm số f (x) biết rằng Z
ABC có A(1; 2; 3), B(2; −3; 1) và C(3; 1; 2). Tìm tọa 1 f (x) dx = + ln x + C. x
độ trọng tâm G của tam giác ABC. 1 1 A. f (x) = ln x + . B. f (x) = ln x − . A. G(2; 0; 2). B. G(3; 0; 3). x x2 1 1 1 1 C. G(3; 2; 1). D. G(6; 0; 6). C. f (x) = + . D. f (x) = − + . x2 x x2 x
Câu 14. Trong không gian Oxyz, viết phương Câu 19. Gọi z1, z2 là hai nghiệm phức của phương
trình mặt cầu tâm I(1; 1; 0) và đi qua điểm trình z2 + 3z + 5 = 0. Tìm phần thực, phần ảo của √ A(1; 1; 5). số phức w = z √ √ 1z2 + (z1 + z2)i.
A. (x − 1)2 + (y − 1)2 + (z − 5)2 = 5.
A. Phần thực bằng 5, phần ảo bằng 3.
B. (x + 1)2 + (y + 1)2 + z2 = 5. √
B. Phần thực bằng 3, phần ảo bằng 5.
C. (x − 1)2 + (y − 1)2 + (z − 5)2 = 5.
C. Phần thực bằng −5, phần ảo bằng 3.
D. (x − 1)2 + (y − 1)2 + z2 = 5.
D. Phần thực bằng 5, phần ảo bằng −3.
Câu 15. Trong mặt phẳng tọa độ Oxy, số phức Câu 20. Trong không gian Oxyz, cho mặt phẳng
z = (2 − 3i) − (3 + i) được biểu diễn bởi điểm nào (P) : 2x + 2y − z − 1 = 0 và mặt cầu (S) : x2 + y2 + sau đây?
z2 − 2x − 4y + 6z + 5 = 0. Khẳng định nào sau đây A. M(−1; −4). B. N(1; −4). đúng? C. P(1; 4). D. Q(−1; 4).
A. (P) đi qua tâm của mặt cầu (S).
B. (P) cắt mặt cầu (S).
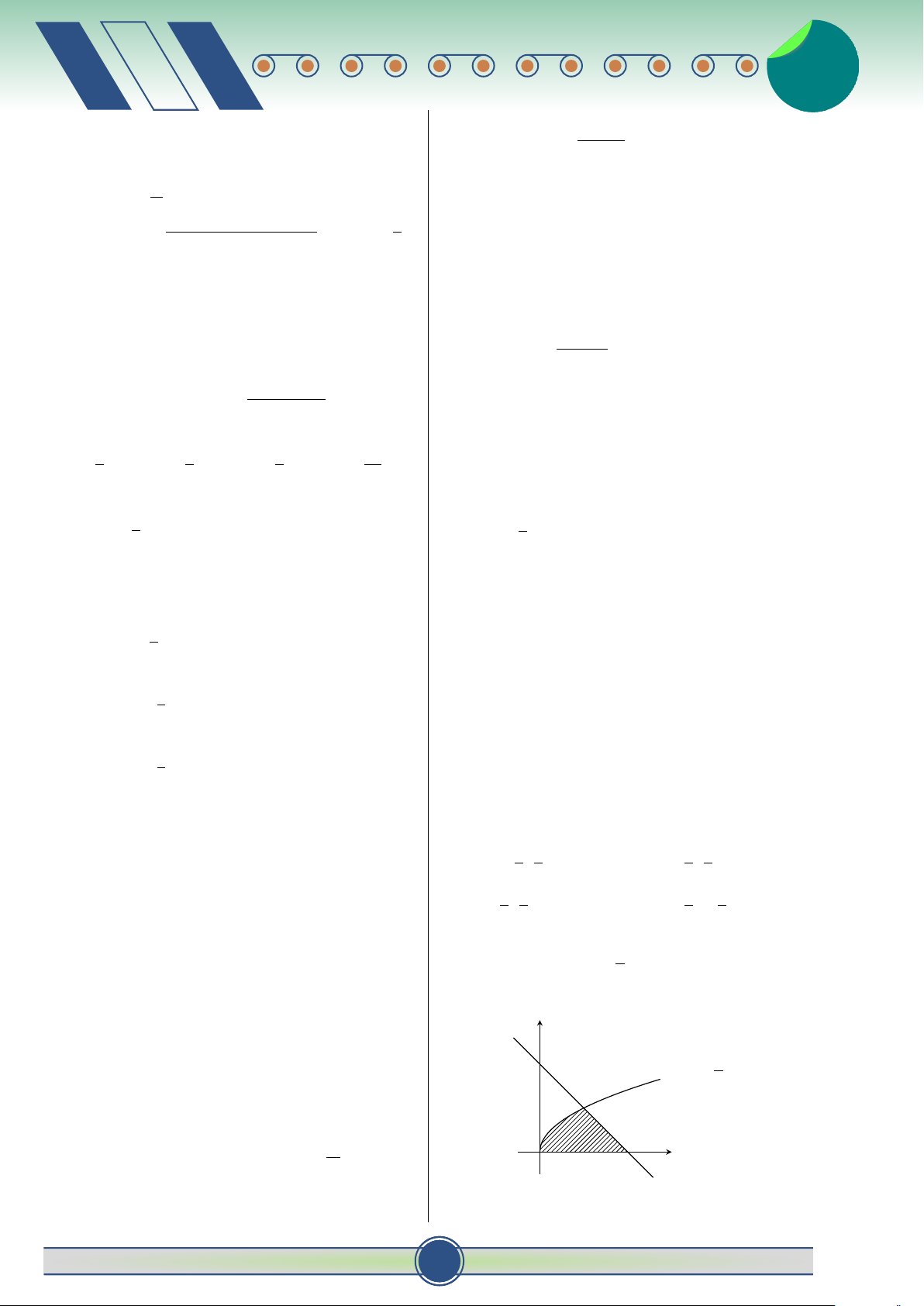
Câu 16. Trong mặt phẳng tọa độ Oxy, cho hình bình hành
C. (P) tiếp xúc với mặt cầu (S).
OABC có tọa độ điểm A(3; 1), C(−1; 2) (như hình vẽ bên).
D. (P) không cắt mặt cầu (S). y B
Câu 21. Cho phương trình z2 + mz + n = 0 với
m, n ∈ R có một nghiệm là z = 1 + i. Tìm mô-đun C(−1; 2) của số phức w = m + ni. √ A. 2 2. B. 4. C. 8. D. 16. A(3; 1)
Câu 22. Cho hàm số y = f (x) liên tục trên R và x
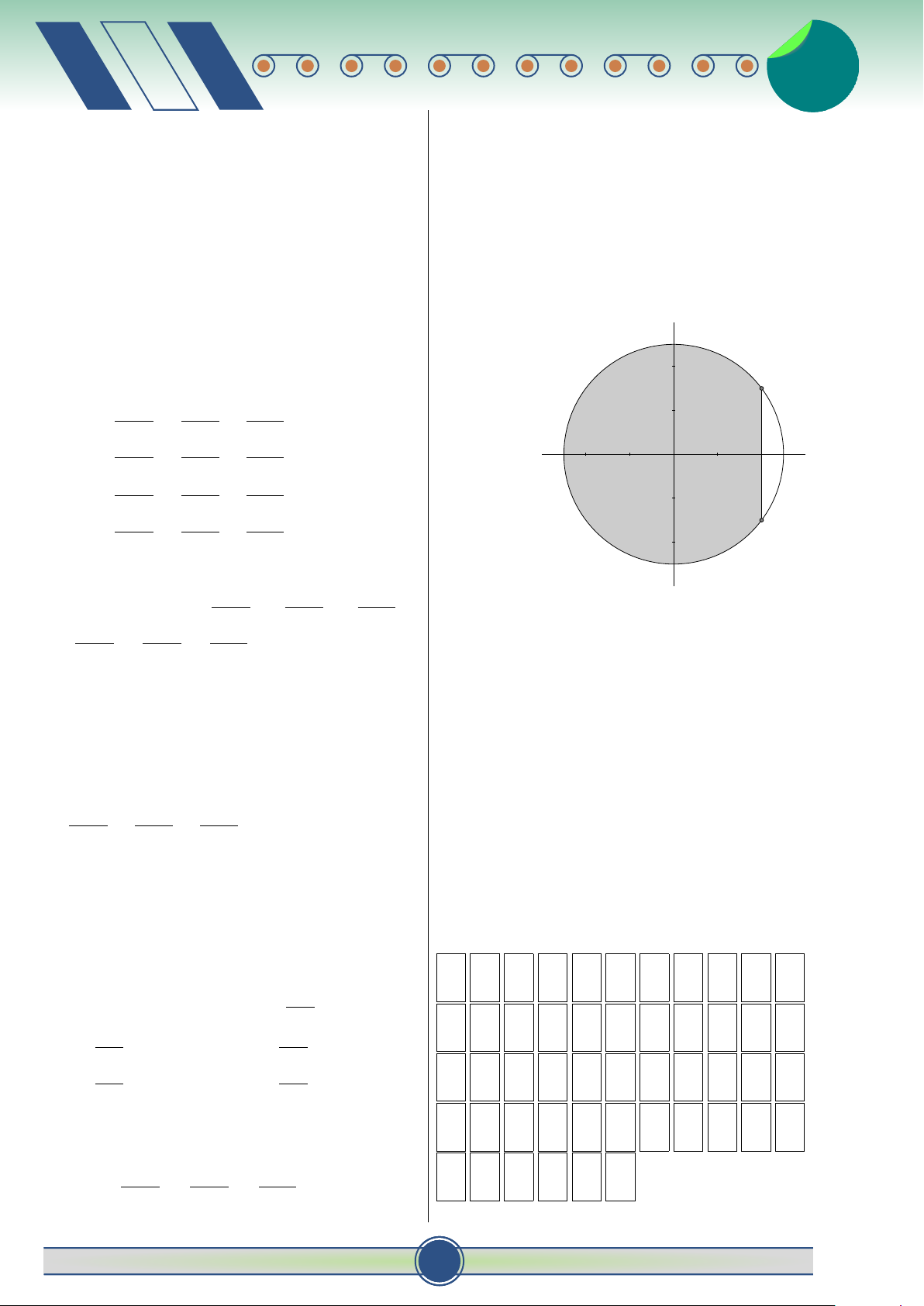
có đồ thị (C) cắt trục Ox tại ba điểm có hoành độ O
a, b, c với c ∈ (a; b) như hình bên. y
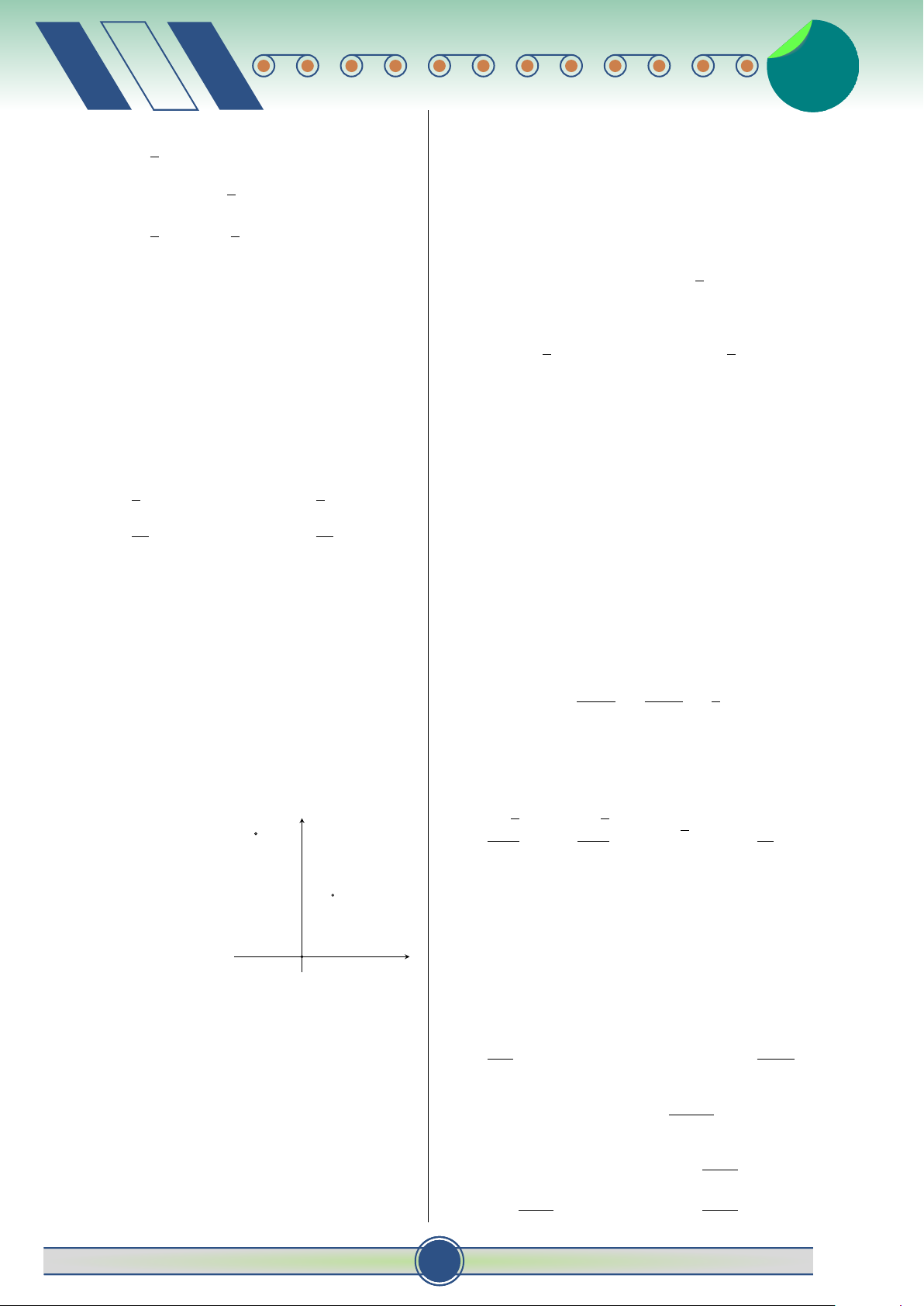
Số phức nào sau đây có điểm biểu diễn là điểm B? A. w1 = −2 + 3i. B. w2 = 2 + 3i. C. w3 = 4 − i. D. w4 = −4 + i. c a b x
Câu 17. Trong không gian Oxyz, viết phương O
trình chính tắc của đường thẳng qua điểm
E(1; 2; −3) và F(3; −1; 1). c b x − 1 y − 2 z + 3 Z Z A. = = . Đặt m = f (x) dx, n = f (x) dx. Diện tích của 3 −1 1 x − 3 y + 1 z − 1 a c B. = = .
hình phẳng giới hạn bởi đồ thị (C) và trục hoành 2 −3 4 x − 3 y + 1 z − 1
(phần tô đậm) bằng bao nhiêu? C. = = . 1 2 −3 A. m + n. B. −m − n. x + 1 y + 2 z − 3 D. = = . 2 −3 4 C. m − n. D. n − m. ♂ 30 đề ôn thi t HKII-12 19 v 19
Những nẻo đường phù sa 2020 - 2021 30 ĐỀ
30 ĐỀ ÔN THI HKII-LỚP 12
Câu 23. Trong không gian Oxyz, biết mặt phẳng Biết tập hợp các điểm biểu y
(P) : 3x − 2y + 2z − 5 = 0 và mặt phẳng (Q) : 4x + diễn số phức z = x + yi là 2
5y − z + 1 = 0 cắt nhau theo giao tuyến là đường nửa hình tròn tâm O(0; 0)
thẳng d. Véc-tơ nào dưới đây là véc-tơ chỉ phương bán kính R = 2 (phần tô x của đường thẳng d?
đậm, kể cả đường giới hạn) #» O 1 2 A. v như hình bên. Trong các 1 = (3; −2; 2). #» B. v
khẳng định sau, khẳng định 2 = (−8; −11; 23). #» C. v nào đúng? 3 = (4; 5; −1). √ #» D. v A. x ≥ 0 và |z| = 2. B. y ≥ 0 và |z| = 2. 4 = (8; −11; −23).
C. x ≥ 0 và |z| ≤ 2.
D. y ≥ 0 và |z| ≤ 2.
Câu 24. Gọi F(x) là nguyên hàm của hàm số Câu 29. Trong không gian Oxyz, cho hai điểm
f (x) = 4x − 1 thỏa mãn F(0) = −1. Đồ thị của A(−1; 2; 4), B(−1; 1; 2). Tính độ dài đoạn thẳng
hai hàm số y = f (x) và y = F(x) có bao nhiêu AB. điểm chung? √ A. AB = 5. B. AB = 5. √ A. Không có. B. 1. C. AB = 3. D. AB = 3. C. 2. D. Vô số. 1 Z
Câu 30. Tính tích phân I = (2x + 1)ex dx bằng
Câu 25. Trong không gian Oxyz, cho đường thẳng 0 x + 1 y z − 5 d : = =
và mặt phẳng (P) : 3x − phương pháp tích phân từng phần, đặt u = 2x + 1 1 −3 −1 và
3y + 2z + 6 = 0. Trong các khẳng định dưới đây,
dv = ex dx. Kết quả nào sau đây đúng? 1 1
khẳng định nào đúng? Z A. I = (2x + 1)ex − ex dx.
A. d cắt và không vuông góc với (P). 0 0
B. d vuông góc với (P). 1 1 Z B. I = (2x + 1)ex − 2 ex dx.
C. d song song với (P). 0 0 D. d chứa trong (P). 1 1 Z C. I = (2x + 1)ex + 2 ex dx. e √ Z 1 + ln x 0
Câu 26. Cho tích phân I = dx. Đổi 0 x 1 1 Z 1 √ D. I = (2x + 1)ex − e2x dx. biến t =
1 + ln x ta được kết quả nào sau 0 0 đây? √ √
Câu 31. Cho hai số thực x, y thỏa mãn x(3 + 2i) + 2 2 Z Z
y(1 − 4i) = 1 + 24i. Tính giá trị x + y. A. I = t2 dt. B. I = 2 t2 dt. A. x + y = 4. B. x + y = 3. 1 1√ 2 2 C. x + y = 2. D. x + y = −3. Z Z C. I = 2 t2 dt. D. I = 2 t dt.
Câu 32. Trong không gian Oxyz, cho đường thẳng 1 1 x = 2t
Câu 27. Trong không gian Oxyz, cho hai véc-tơ d : y = −t
(t ∈ R) và mặt phẳng (P) : x − #» #» #» #»
a = (1; 2; 3), b = (1; m − 1; m) thỏa mãn a · b = z = −1 + t
1. Giá trị m bằng bao nhiêu?
2y − 2z + 5 = 0. Tìm tọa độ điểm H thuộc đường 1 5 A. m = . B. m = .
thẳng d, biết rằng khoảng cách từ điểm H đến mặt 5 2 2 2 phẳng (P) bằng C. m = − . D. m = . 3. 5 5 A. H(0; 0; −1). B. H(−2; 1; −2). Câu 28. C. H(2; −1; 0). D. H(4; −2; 1). ♂ 30 đề ôn thi t HKII-12 20 v 20
Những nẻo đường phù sa 2021 30 ĐỀ - ĐỀ
30 ĐỀ ÔN THI HKII-LỚP 12 2020
Câu 33. Tính diện tích S của hình phẳng giới hạn 1 Z f (x) dx.
bởi đồ thị hàm số y = x3 − 3x và trục Ox. 9 9 0 A. S = . B. S = . 1 1 4 8 Z Z 9 11 A. f (x) dx = 1. B. f (x) dx = 4. C. S = . D. S = . 2 4 0 0
Câu 34. Trong không gian Oxyz, gọi H là hình 1 1 Z Z C. f (x) dx = 2. D. f (x) dx = 8.
chiếu vuông góc của điểm M(2; 0; 1) trên đường x − 1 y z − 2 0 0 thẳng d : = = . Tìm tọa độ điểm 1 2 1
Câu 40. Trong không gian Oxyz, cho điểm H. x − 1 y + 1 A. H(2; 2; 3). B. H(0; −2; 1).
M(2; 1; 0) và đường thẳng d : = = 2 1 z C. H(1; 0; 2). D. H(−1; −4; 0).
. Viết phương trình đường thẳng đi qua điểm −1
Câu 35. Trong mặt phẳng tọa độ Oxy, gọi M(x; y) M và song song với đường thẳng d. x + 2 y + 1 z
là điểm biểu diễn số phức z = x + yi (x, y ∈ R) A. = = . 2 1 −1
thỏa mãn |z + 1 − 2i| = |z|. Biết rằng tập hợp các x − 2 y − 1 z B. = = .
điểm M là một đường thẳng, tìm phương trình 4 2 −2 x − 2 y − 1 z đường thẳng đó. C. = = . 2 1 1 A. 2x + 4y + 5 = 0. B. 2x − 4y + 5 = 0. x − 2 y − 1 z D. = = . C. 2x − 4y + 3 = 0. D. 2x − y + 1 = 0. 4 4 2 1
Câu 41. Cho số phức z = x + yi (x, y ∈ R) thỏa Z x − 5
Câu 36. Biết tích phân I =
dx = a − ln b mãn z + 2i ( ¯z) = 3(1 + i). Tính giá trị của biểu thức x + 1 0 P = 4x + 5y.
với a, b là các số nguyên. Mệnh đề nào sau đây A. P = 12. B. P = 8. đúng? C. P = 9. D. P = 21. A. a + b = −63. B. ab = −64. C. a + b = 65. D. ab = 65.
Câu 42. Tính thể tích V của khối tròn xoay tạo
thành khi cho hình phẳng giới hạn bởi đồ thị hàm
Câu 37. Trong không gian Oxyz, cho tứ diện √ số y =
x, đường thẳng x = 4, trục Ox quay
ABCD có tọa độ các đỉnh là A(0; 2; 0), B(2; 0; 0), C(0; 0; 2) quanh trục Ox.
và D(0; −2; 0). Số đo góc giữa hai đường thẳng AB A. V = 8π. B. V = 4π. và CD bằng bao nhiêu? C. V = 16 2 π. D. V = 8π . A. 30◦. B. 45◦. C. 60◦. D. 90◦.
Câu 38. Phần thực và phần ảo của số phức z = Câu 43. Cho hàm số y = f (x) > 0, ∀x ∈ [1; 2] và √3 + i
có đạo hàm liên tục trên [1; 2]. Biết f (2) = 20 và
lần lượt bằng bao nhiêu? 2 1 − i √ √ Z f 0(x) A. 3 − 1 và 3 + 1.
dx = ln 2. Tính giá trị của f (1). √ √ f (x) 3 − 1 3 + 1 1 B. và . A. f (1) = 10. B. f (1) = 20. √ 2 2 3 − 1 √ C. f (1) = −10. D. f (1) = 0. C. và 3 + 1. 2 √ √ 3 + 1
Câu 44. Cho tập X = {1; 3; 5; 7; 9}. Có bao nhiêu D. 3 − 1 và . 2
số phức z = x + yi có phần thực, phần ảo đều
Câu 39. Cho hàm số f (x) liên tục trên R và thỏa thuộc X và có tổng x + y ≤ 10? π 2 A. 20. B. 10. C. 15. D. 24. Z mãn
sin x · f (cos x) dx = 4. Tính tích phân Câu 45. 0 ♂ 30 đề ôn thi t HKII-12 21 v 21
Những nẻo đường phù sa 2020 - 2021 30 ĐỀ
30 ĐỀ ÔN THI HKII-LỚP 12 Một ô tô bắt đầu v
Câu 50. Trong không gian Oxyz, cho hai mặt cầu chuyển động với vận
(S1), (S2) có phương trình lần lượt là (x − 2)2 + tốc v(t) = at2 + bt với 50
(y − 1)2 + (z − 1)2 = 16 và (x − 2)2 + (y − 1)2 + t tính bằng giây và v
(z − 5)2 = 4. Gọi (P) là mặt phẳng thay đổi tiếp tính bằng mét/giây
xúc với cả hai mặt cầu (S1), (S2). Tính khoảng cách (m/s). Sau 10 giây thì
lớn nhất từ gốc tọa độ O đến mặt phẳng (P). √ √ ô tô đạt vận tốc cao 9 A. − 15. B. 15. 2 √ nhất √ √ v = 50 m/s và 9 + 15 8 3 + 5
giữ nguyên vận tốc đó, C. . D. . 2 2
có đồ thị vận tốc như
BẢNG ĐÁP ÁN THAM KHẢO hình bên. Tính quãng t 1. 2. 3. 4. 5. 6. 7. 8. 9. 10. 11.
đường s ô tô đi được 0 10 D C C B C A C D D B B trong 20 giây đầu. 2500 2600
12. 13. 14. 15. 16. 17. 18. 19. 20. 21. 22. A. s = m. B. s = m. 3 3 C A D A B B D D B A C 2000 C. s = 800 m. D. s = m.
23. 24. 25. 26. 27. 28. 29. 30. 31. 32. 33. 3 D C A B D C B B D C C
Câu 46. Trong không gian Oxyz, cho bốn điểm
34. 35. 36. 37. 38. 39. 40. 41. 42. 43. 44. 1
A(2; 0; 0), B(0; 3; 0), C(0; 0; 3) và D 1; 1; . Có C B C C B B B C A A C 2
tất cả bao nhiêu mặt phẳng phân biệt đi qua ba 45. 46. 47. 48. 49. 50.
trong năm điểm O, A, B, C, D? A C D B C C A. 5. B. 6. C. 7. D. 10.
Câu 47. Trong không gian Oxyz, cho bốn đường ĐỀ ÔN SỐ 6 x − 1 y − 2 z x − 2 y thẳng d1 : = = , d = = 1 2 −2 2 : 2 2
Câu 1. Trong mặt phẳng tọa độ Oxy, tập hợp các z − 1 x y + 2 z − 4 x − 4 , d = = và d
= điểm biểu diễn số phức z thỏa mãn điều kiện −1 3 : 2 4 −4 4 : 2 y − 2 z z2 + (z)2 = 0 là =
. Có bao nhiêu đường thẳng cắt cả bốn 1 1
A. Trục hoành và trục tung. đường thẳng đã cho?
B. Đường phân giác của góc phần tư thứ nhất A. Không có. B. 1. và thứ ba. C. 2. D. Vô số. C. Trục hoành.
Câu 48. Xét các số phức z, w thỏa mãn |z − 1 −
D. Các đường phân giác của góc tạo bởi hai trục
3i| ≤ |z + 2i| và |w + 1 + 3i| ≤ |w − 2i|. Tính giá trị tọa độ.
nhỏ nhất của biểu thức P = |z − w|. √
Câu 2. Tìm nguyên hàm của hàm số y = sin(x − 3 3 26 A. min P = . B. min P = . 1). 13 √ 13 √ Z 26 13 + 1 A.
sin(x − 1) dx = − cos(x − 1) + C. C. min P = . D. min P = . 4 2 Z B.
sin(x − 1) dx = cos(x − 1) + C. 2 Z 4 Z
Câu 49. Biết tích phân √ √ dx = C.
sin(x − 1) dx = (x − 1) cos(x − 1) + C. (x + 4) x + x x + 4 Z 1 √ √ √ D.
sin(x − 1) dx = (1 − x) cos(x − 1) + C. a + b −
c − d (với a, b, c, d là các số nguyên
dương). Tính giá trị T = a + b + c + d.
Câu 3. Cho số phức z = 2 − i. Mệnh đề nào dưới A. T = 48. B. T = 46. đây đúng? C. T = 54. D. T = 52.
A. Phần thực bằng 2. ♂ 30 đề ôn thi t HKII-12 22 v 22
Những nẻo đường phù sa 2021 30 ĐỀ - ĐỀ
30 ĐỀ ÔN THI HKII-LỚP 12 2020
B. Phần thực bằng −1. 1 Z B. I = − t(t + 1)2 dt.
C. Phần thực bằng 1. 0
D. Phần ảo bằng 2. 1 Z C. I = t(t − 1)2 dt.
Câu 4. Trong không gian với hệ tọa độ Oxyz, cho 0
mặt cầu (S) có phương trình x2 + y2 + z2 − 2x − 1 Z
6y + 4z − 2 = 0. Tìm tọa độ tâm I và tính bán kính D. I = t(t + 1)2 dt. R của (S). 0
A. Tâm I(−1; −3; 2) và bán kính R = 4. √
Câu 9. Trong mặt phẳng tọa độ Oxy, tập hợp các
B. Tâm I(1; 3; −2) và bán kính R = 2 3.
điểm biểu diễn các số phức z thỏa mãn điều kiện
C. Tâm I(1; 3; −2) và bán kính R = 4. z = 3 là
D. Tâm I(−1; −3; 2) và bán kính R = 16. z − 1 9 9
A. Đường tròn x2 + y2 − x − = 0.
Câu 5. Một người lái xe ô tô đang chạy với vận tốc 4 8 9 9
20 m/s thì người lái xe phát hiện có hàng rào ngăn
B. Đường tròn x2 + y2 − x + = 0. 4 8
đường ở phía trước cách 45 m (tính từ vị trí đầu 9 9
C. Đường tròn x2 + y2 + x + = 0. 4 8
xe đến hàng rào) vì vậy, người lái xe đạp phanh. 9
D. Đường tròn tâm I 0; và bán kính R =
Từ thời điểm đó xe chuyển động chậm dần đều 8
với vận tốc v(t) = −5t + 20 (m/s), trong đó t là 1 . 8
khoảng thời gian tính bằng giây, kể từ lúc bắt đầu
đạp phanh. Hỏi từ lúc đạp phanh đến khi dừng Câu 10. Cho hình trụ (T) có chiều cao h, độ dài
hẳn, xe ô tô còn cách hàng rào ngăn cách bao nhiêu đường sinh l, bán kính đáy r. Ký hiệu Sxq là diện
mét (tính từ vị trí đầu xe đến hàng rào)?
tích xung quanh của (T). Công thức nào sau đây là đúng? A. 5 m. B. 6 m. C. 4 m. D. 3 m. A. Sxq = 2πrl. B. Sxq = πrh.
Câu 6. Trong không gian với hệ tọa độ Oxyz, cho C. Sxq = πrl. D. Sxq = 2πr2h.
hai điểm A(−3; 2; 2); B(−5; 3; 7) và mặt phẳng Câu 11. Trong không gian với hệ tọa độ Oxyz, cho
(P) : x + y + z = 0. Điểm M(a; b; c) thuộc (P) # » # » #» #»
hai vec-tơ a = (0; 1; 3); b = (−2; 3; 1). Tìm tọa độ
sao cho |2MA − MB| có giá trị nhỏ nhất. Tính #» #» #» #»
của vec-tơ x biết x = 3 a + 2 b . T = 2a + b − c. #» #» A. x = (−2; 4; 4). B. x = (4; −3; 7). A. T = −1. B. T = −3. #» #» C. x = (−4; 9; 11). D. x = (−1; 9; 11). C. T = 4. D. T = 3. Câu 12. Gọi z
Câu 7. Tính diện tích S của hình phẳng giới hạn
1, z2 là hai nghiệm phức của phương 1
trình z2 − 4z + 10 = 0. Khi đó giá trị của P =
bởi các đường y = ln x, x = e, x = và trục e z1 + z2 − z1 · z2 là hoành. 1 2 A. P = 14. B. P = −14. A. S = 1 − (đvdt). B. S = 2 − (đvdt). e e C. P = −6. D. P = 6. 2 1 C. S = 2 + (đvdt). D. S = 1 + (đvdt). 5 e e Z dx Câu 13. Nếu
= ln c với c ∈ Q thì giá trị −1 2x − 1 Z 1 Câu 8. Cho I =
x(x − 1)2 dx khi đặt t = −x ta của c bằng 0 có A. 9. B. 3. C. 6. D. 81. 1 Z
Câu 14. Trong không gian với hệ tọa độ Oxyz, A. I = − t(t − 1)2 dt.
cho ba điểm A(2; −1; 2); B(3; 1; −1); C(2; 0; 2).Viết 0 ♂ 30 đề ôn thi t HKII-12 23 v 23
Những nẻo đường phù sa 2020 - 2021 30 ĐỀ
30 ĐỀ ÔN THI HKII-LỚP 12
phương trình mặt phẳng ( b c b α) đi qua ba điểm Z Z Z B. f (x) dx = f (x) dx + f (x) dx với c ∈ A, B, C. a a c
A. (α) : 3x + z − 8 = 0. [a; b].
B. (α) : 3x + z + 8 = 0. b a Z Z
C. (α) : 5x − z − 8 = 0. C. f (x) dx = f (x) dx.
D. (α) : 2x − y + 2z − 8 = 0. a b b Z
Câu 15. Trong các khẳng định sau, khẳng định D.
k dx = k(b − a), ∀k ∈ R. a nào đúng? b b b
Câu 20. Tìm số các số phức thỏa mãn điều kiện Z Z Z A. f1(x) · f2(x) dx = f1(x) dx · f2(x) dx. z2 + 2z = 0. a a a A. 0. B. 4. C. 1. D. 2. 1 Z B. dx = 1.
Câu 21. Trong không gian với hệ tọa độ Oxyz, cho −1
hai điểm A(2; 2; −1); B(−4; 2; −9). Viết phương
C. Nếu f (x) liên tục và không âm trên [a; b] thì b
trình mặt cầu đường kính AB. Z f (x) dx ≥ 0.
A. (x + 3)2 + y2 + (z + 4)2 = 5. a
B. (x + 1)2 + (y − 2)2 + (z + 5)2 = 25. a Z D. Nếu
f (x) dx = 0, a > 0 thì f (x) là hàm số
C. (x + 6)2 + y2 + (z + 8)2 = 5. 0
D. (x + 1)2 + (y − 2)2 + (z + 5)2 = 5. lẻ.
Câu 22. Gọi S là tập nghiệm của phương trình
Câu 16. Trong mặt phẳng tọa độ Oxy, tọa độ điểm z2 + z + 1 = 0 trên tập số phức. Số tập con của
M biểu diễn số phức z = 4 − i là S là A. M(4; 1). B. M(−4; 1). A. 2. B. 1. C. 0. D. 4. C. M(4; −1). D. M(−4; −1).
Câu 23. Trong không gian với hệ tọa độ Oxyz, cho
điểm A(3; 2; 1). Tính khoảng cách từ A đến trục
Câu 17. Trong mặt phẳng tọa độ Oxy, tập hợp Oy.
các điểm biểu diễn các số phức z thỏa mãn điều √ |z + 2 − i| = 2 là A. 2. B. 10. C. 3. D. 10.
A. đường tròn (x + 2)2 + (y − 1)2 = 4.
Câu 24. Tìm nguyên hàm của hàm số y = x3. Z
B. đường tròn tâm I(2; −1) và bán kính R = 2. A. x3 dx = 3x4 + C.
C. đường thẳng x − y − 2 = 0. Z 1 B. x3 x4 + C.
D. đường thẳng x + y − 2 = 0. dx = 4 Z C. x3 dx = 4x4 + C.
Câu 18. Cho số phức z = 2 − 3i. Số phức liên hợp Z 1 z của số phức z là D. x3 dx = x4 + C. 3 A. z = −3 + 2i. B. z = 2 + 3i.
Câu 25. Giải phương trình z2 + 2z + 2 = 0 trên tập C. z = −2 + 3i. D. z = −2 − 3i.
hợp số phức, ta có tập nghiệm S là
A. S = {1 − i; 1 + i}.
Câu 19. Cho hàm số f (x) liên tục trên [a; b]. Hãy
B. S = {1 − i; −1 + i}.
chọn mệnh đề sai dưới đây. b a
C. S = {−1 − i; −1 + i}. Z Z A. f (x) dx = − f (x) dx.
D. S = {−1 − i; 1 + i}. a b ♂ 30 đề ôn thi t HKII-12 24 v 24
Những nẻo đường phù sa 2021 30 ĐỀ - ĐỀ
30 ĐỀ ÔN THI HKII-LỚP 12 2020
Câu 26. Cho hàm số f (x) có đạo hàm liên tục trên A. D(4; 3; −2). B. D(8; −3; 4). 1 Z C. D(−4; −3; 2). D. D(−2; 1; 0). đoạn [0; 1], biết rằng f 0(x)dx = 17 và f (0) = 5. 0
Câu 34. Trong không gian với hệ tọa độ Oxyz, cho Tìm f (1).
mặt cầu (S) có tâm I(−1; 2; −5) cắt mặt phẳng A. f (1) = −12. B. f (1) = 12.
(P) : 2x − 2y − z + 10 = 0 theo giao tuyến là đường √ C. f (1) = 22. D. f (1) = −22.
tròn có chu vi 2π 3. Viết phương trình của mặt
Câu 27. Thu gọn số phức z = i + (2 − 4i) − (3 − cầu (S). 2i), ta được:
A. (x + 1)2 + (y − 2)2 + (z + 5)2 = 25. A. z = −1 − i. B. z = 1 − i.
B. x2 + y2 + z2 + 2x − 4y + 10z + 18 = 0. C. z = −1 − 2i. D. z = 1 + i.
C. x2 + y2 + z2 + 2x − 4y + 10z + 12 = 0.
D. (x + 1)2 + (y − 2)2 + (z + 5)2 = 16.
Câu 28. Gọi z1, z2 là hai nghiệm của phương trình
z2 − 4z + 5 = 0. Tính giá trị của P = |z
Câu 35. Tìm nguyên hàm của hàm số y = xex. 1|2 + Z |z A. xexdx = xex + C. 2|2. Z A. P = 5. B. P = 6. B. xexdx = xex − ex + C. C. P = 9. D. P = 10. Z C. xexdx = ex + C.
Câu 29. Biết f (x) là hàm số liên tục trên R và Z D. xexdx = xex + ex + C. π π 2 4 Z Z f (x)dx = 4. Tính [ f (2x) − sin x] dx.
Câu 36. Trong không gian với hệ tọa độ Oxyz, viết 0 0 √ √
phương trình mặt cầu (S) có tâm I(1; 2; −3) biết 2 2 A. 2 + . B. 2 − .
rằng mặt cầu (S) đi qua điểm A(1; 0; 4). 2 √ 2 √ 2 2
A. (x + 1)2 + (y + 2)2 + (z − 3)2 = 53. C. 3 − . D. 1 + . √ 2 2
B. (x + 1)2 + (y + 2)2 + (z − 3)2 = 53. √
Câu 30. Tìm nguyên hàm của hàm số y =
C. (x − 1)2 + (y − 2)2 + (z + 3)2 = 53. cos(3x − 2).
D. (x − 1)2 + (y − 2)2 + (z + 3)2 = 53. Z 1 A.
cos(3x − 2)dx = − sin(3x − 2) + C. 3
Câu 37. Trong không gian với hệ tọa độ Oxyz, cho Z 1 x − 2 y − 1 z + 1 B.
cos(3x − 2)dx = − sin(3x − 2) + C. đường thẳng d : = = và điểm 2 3 −1 1 Z 1
A(1; 2; 3). Tìm tọa độ điểm H là hình chiếu vuông C. cos(3x − 2)dx = sin(3x − 2) + C. 2
góc của điểm A trên đường thẳng d. Z 1 D. cos(3x − 2)dx = sin(3x − 2) + C. A. H(3; 1; −5). B. H(−3; 0; 5). 3 C. H(3; 0; −5). D. H(2; 1; −1).
Câu 31. Tính bán kính R của mặt cầu ngoại tiếp
hình lập phương có cạnh bằng 2a.
Câu 38. Trong không gian với hệ tọa độ Oxyz, cho √3 √ √
mặt cầu (S) : (x + 3)2 + (y − 1)2 + (z + 1)2 = 3 và A. a . B. a. C. 2 3a. D. a 3. 3
mặt phẳng (α) : (m − 4)x + 3y − 3mz + 2m − 8 = 0.
Câu 32. Cho số phức z thỏa mãn (2 + i)z + Với giá trị nào của m thì (α) tiếp xúc với (S)?
2(1 + 2i) = 7 + 8i. Tính mô-đun của số phức A. m = 1. B √ . m = −1. √ 1 + i −7 + 33 −7 ± 33 w = z + 1 − 2i. C. m = . D. m = . √ 2 2 A. 7. B. 7. C. 25. D. 4.
Câu 39. Trong không gian với hệ tọa độ Oxyz, cho
Câu 33. Trong không gian với hệ tọa độ Oxyz, cho mặt phẳng (P) : 2x − 3y + 2z − 15 = 0 và điểm
ba điểm A(1; 2; −1), B(3; −1; 2), C(6; 0; 1). Tìm tọa M(1; 2; −3). Viết phương trình mặt phẳng (Q) qua
độ điểm D để tứ giác ABCD là hình bình hành. M và song song với (P). ♂ 30 đề ôn thi t HKII-12 25 v 25
Những nẻo đường phù sa 2020 - 2021 30 ĐỀ
30 ĐỀ ÔN THI HKII-LỚP 12
A. (Q) : 2x − 3y + 2z − 10 = 0.
Câu 45. Trong không gian với hệ tọa độ Oxyz, cho
B. (Q) : x + 2y − 3z − 10 = 0. x − 1 y + 1 z − 2 đường thẳng d : = = . Véc-tơ 5 −2 3
C. (Q) : 2x − 3y + 2z + 10 = 0.
nào là một véc-tơ chỉ phương của d?
D. (Q) : x + 2y − 3z + 10 = 0. #» #» A. u = (1; −1; 2). B. u = (−1; 1; −2). #» #» C. u = (5; −2; 3). D. u = (5; 2; −3).
Câu 40. Trong không gian với hệ tọa độ Oxyz, cho
mặt phẳng (P) : 3x + 2y − z + 2 = 0. Véc-tơ nào Câu 46. Trong không gian với hệ tọa độ Oxyz, cho
dưới đây là một véc-tơ pháp tuyến của mặt phẳng x = 2 − 2t (P)? đường thẳng d :
y = 1 + 3t Phương trình nào #» #» A. n = (3; 2; 1). B. n = (3; 1; −2). z = 3t. #» #» C. n = (3; 2; −1). D. n = (2; −1; 2).
sau đây là phương trình chính tắc của d? x − 2 y − 1 z A. = = .
Câu 41. Cho hàm số y = f (x) liên tục và không −2 3 3 x + 2 y + 1 z
đổi dấu trên đoạn [a; b]. Viết công thức tính diện B. = = . 2 −1 −3
tích hình thang cong giới hạn bởi đồ thị hàm số y =
C. x − 2 = y − 1 = z.
f (x), trục hoành và hai đường thẳng x = a, x = b x − 2 y − 1 z D. = = . với a < b. 2 3 −3 b b Z Z
Câu 47. Trong không gian với hệ tọa độ Oxyz, A. S = f (x)dx. B. S = π | f (x)| dx.
cho mặt phẳng (P) : 2x − y + z + 3 = 0 và điểm a a b b
A(1; −2; 1). Viết phương trình đường thẳng d đi Z Z C. S = f 2(x)dx. D. S = | f (x)| dx.
qua A và vuông góc với (P). a a x = 1 + 2t x = 1 + 2t
Câu 42. Trong không gian với hệ tọa độ Oxyz, cho A. d : y = −2 − t . B. d : y = −2 − 4t .
hai điểm A(2; −1; 1), B(1; 2; 4). Viết phương trình z = 1 + t z = 1 + 3t
mặt phẳng (P) đi qua A và vuông góc với đường x = 2 + t x = 1 + 2t thẳng AB. C. d : y = −1 − 2t . D. d : y = −2 − t .
A. (P) : − x + 3y + 3z − 2 = 0. z = 1 + t z = 1 + 3t
B. (P) : x − 3y − 3z − 2 = 0.
C. (P) : 2x − y + z + 2 = 0.
Câu 48. Trong mặt phẳng tọa độ Oxy, tập hợp
D. (P) : 2x − y + z − 2 = 0.
điểm biểu diễn số phức z có phần thực bằng 3 là
đường thẳng có phương trình
Câu 43. Cho số phức z thỏa mãn (1 + 2i)z = 8 + i. A. x = −3. B. x = 1.
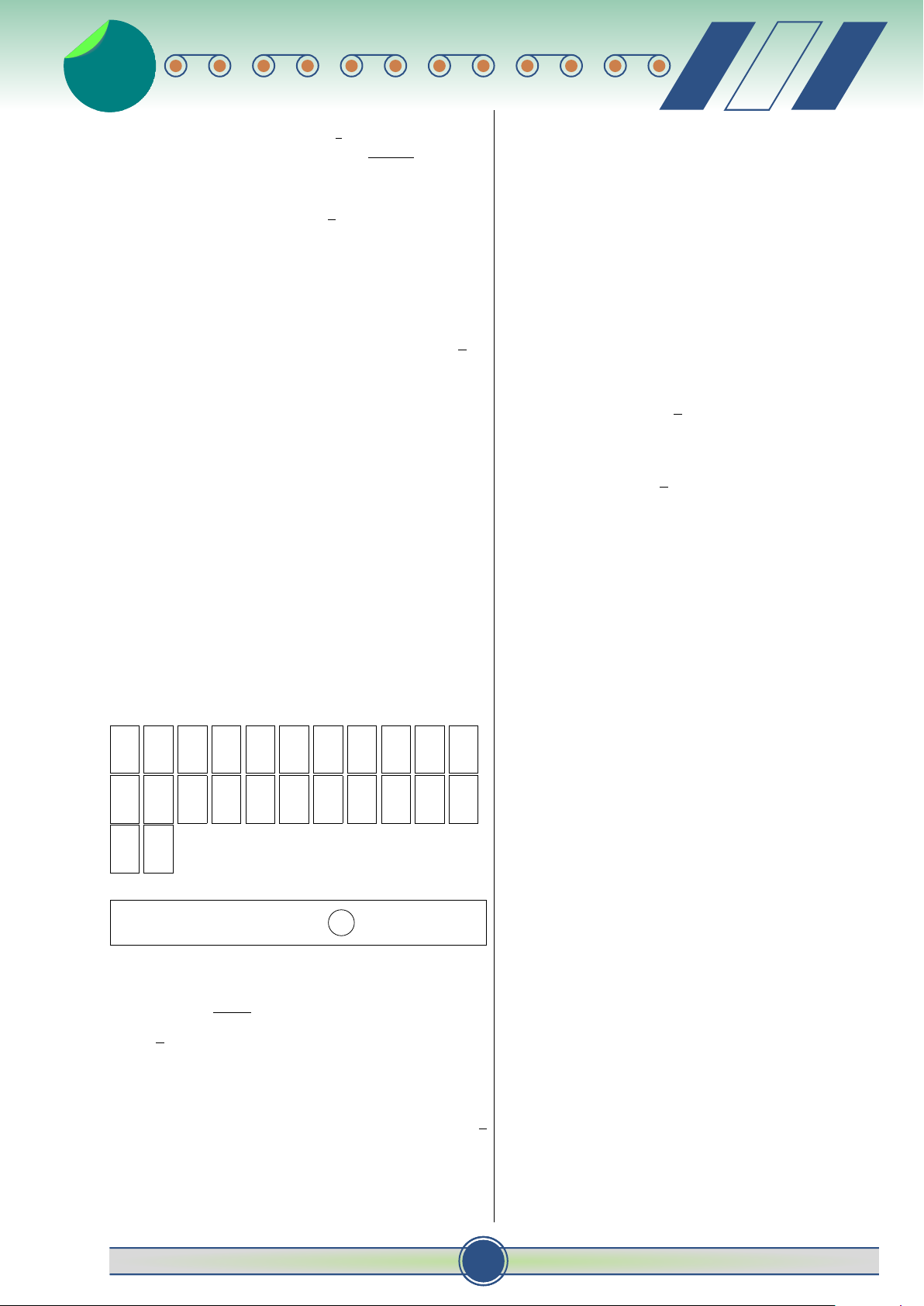
Số phức liên hợp ¯z của z là C. x = −1. D. x = 3. A. ¯z = −2 − 3i. B. ¯z = −2 + 3i. Câu 49. C. ¯z = 2 + 3i. D. ¯z = 2 − 3i. Cho đồ thị hàm y
Câu 44. Trong không gian với hệ tọa độ Oxyz, số y = f (x) (như
cho hai điểm A(9; −3; 5), B(a; b; c). Gọi M, N, P lần hình vẽ). Diện
lượt là giao điểm của đường thẳng AB với các mặt tích S của hình O 3
phẳng tọa độ Oxy, Oxz, Oyz. Biết M, N, P nằm trên phẳng (phần tô −2 x
đoạn thẳng AB sao cho AM = MN = NP = PB. đậm trong hình Tính tổng T = a + b + c. dưới) là A. T = 21. B. T = −15. −2 3 Z Z C. T = 13. D. T = 14. A. S = f (x)dx + f (x)dx. 0 0 ♂ 30 đề ôn thi t HKII-12 26 v 26
Những nẻo đường phù sa 2021 30 ĐỀ - ĐỀ
30 ĐỀ ÔN THI HKII-LỚP 12 2020 3 1 1 Z A. − sin 4x + C. B. sin 4x + C. B. S = f (x)dx. 4 4 1 −2 C. sin 4x + C. D. sin x + C. 0 0 4 Z Z C. S = f (x)dx + f (x)dx.
Câu 5. Diện tích hình phẳng giới hạn bởi đồ thị −2 3
hàm số y = −x2 + 4, trục hoành và các đường 0 3 Z Z thẳng x = 0, x = 3 là D. S = f (x)dx + f (x)dx. 23 25 32 A. 3. B. . C. . D. . −2 0 3 3 3
Câu 50. Một khối nón có diện tích toàn phần bằng Câu 6. Gọi z1 và z2 là các nghiệm phức của
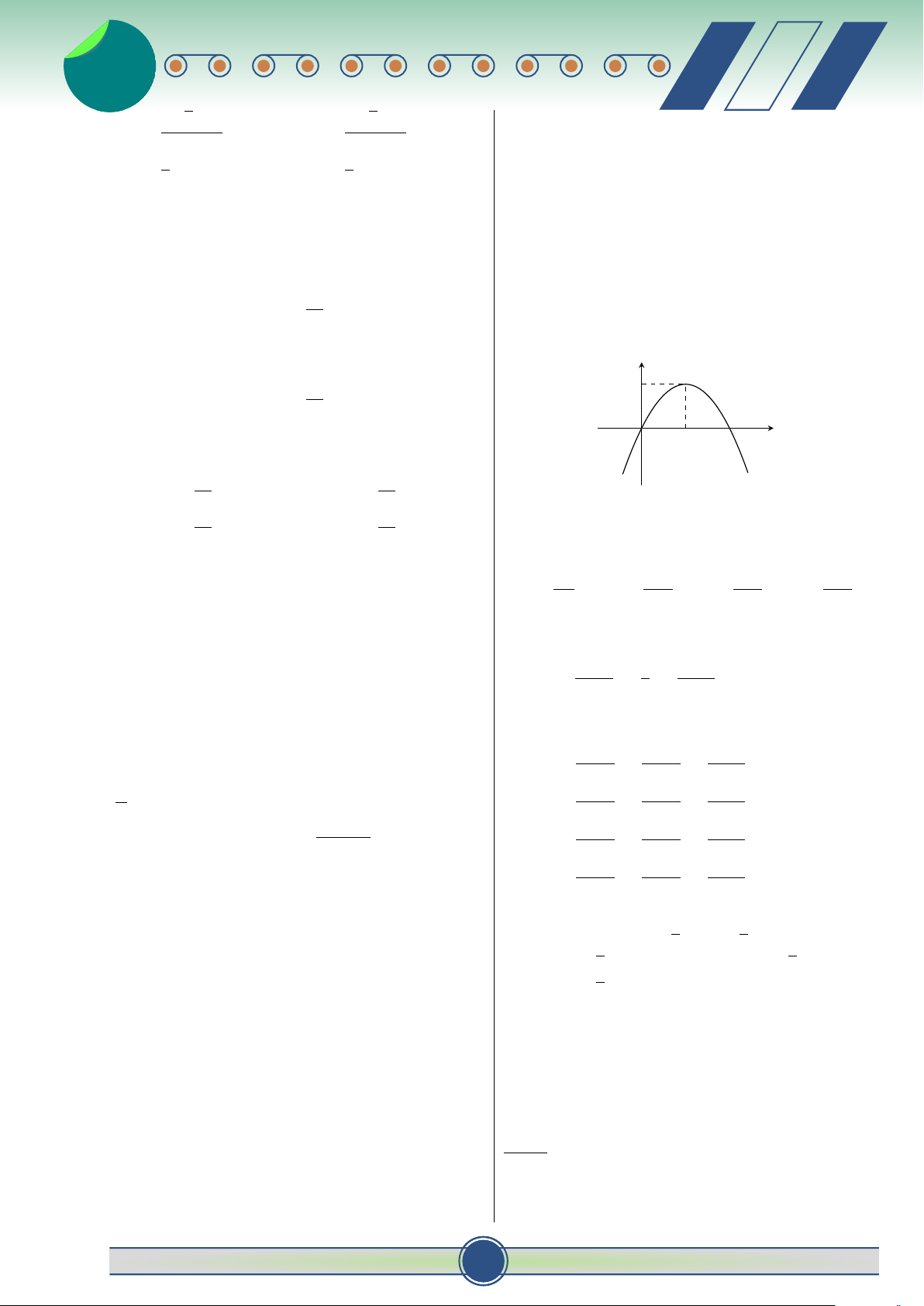
10π và diện tích xung quanh bằng 6π. Tính thể tích phương trình z2 − 2z + 5 = 0. Giá trị của biểu thức V của khối nón đó. z4 + z4 bằng √ 1 2 A. V = 12π. B. V = 4π 5. √ A. 14. B. −7. C. −14. D. 7. 4π 5 C. V = . D. V = 4π. 3 Câu 7.
BẢNG ĐÁP ÁN THAM KHẢO Diện tích của y hình phẳng 1. 2. 3. 4. 5. 6. 7. 8. 9. 10. 11. giới hạn bởi D A A C A C B D B A C đồ thị hàm
12. 13. 14. 15. 16. 17. 18. 19. 20. 21. 22. số y = f (x) C B A C C A B C B B D
23. 24. 25. 26. 27. 28. 29. 30. 31. 32. 33. và trục hoành B B C C A D D D D D A (phần tô đậm −2 O 1 x
34. 35. 36. 37. 38. 39. 40. 41. 42. 43. 44. trong hình vẽ) B B D D A C C D B C B là 45. 46. 47. 48. 49. 50. C A A D A C 0 1 Z Z A. f (x) dx − f (x) dx. − ĐỀ ÔN SỐ 2 0 7 0 1 Z Z B. f (x) dx + f (x) dx.
Câu 1. Gọi a, b lần lượt là phần thực và phần ảo −2 0
của số phức z = −3 + 2i. Giá trị của a + 2b bằng 1 0 Z Z A. 1. B. −1. C. −4. D. −7. C. f (x) dx − f (x) dx. 0 −2
Câu 2. Diện tích hình phẳng giới hạn bởi đồ thị 1 Z
hàm số y = x2 − 2x và y = −x2 + 4x là D. f (x) dx. A. 34. B. 18. C. 17. D. 9. −2
Câu 3. Biết f (x) là hàm số liên tục trên R, a là Câu 8. Họ các nguyên hàm của hàm số y = x(x + a Z 1)5 là
số thực thỏa mãn 0 < a < π và f (x) dx = (x + 1)7 (x + 1)6 A. + + C. 0 7 6 π π Z Z
B. 6(x + 1)5 + 5(x + 1)4 + C. f (x) dx = 1. Tính f (x) dx.
C. 6(x + 1)5 − 5(x + 1)4 + C. a 0 1 (x + 1)7 (x + 1)6 A. 0. B. 2. C. . D. 1. D. − + C. 2 7 6
Câu 4. Họ các nguyên hàm của hàm số y = cos 4x Câu 9. Số phức z thỏa mãn z = −3 − 2i là là A. z = 3 + 2i. B. z = −3 − 2i. ♂ 30 đề ôn thi t HKII-12 27 v 27
Những nẻo đường phù sa 2020 - 2021 30 ĐỀ
30 ĐỀ ÔN THI HKII-LỚP 12 √ C. z = −3 + 2i. D. z = 3 − 2i. C. I(2; −6; 8), R = 103.
D. I(1; −3; 4), R = 25.
Câu 10. Trong không gian Oxyz, đường thẳng đi
qua hai điểm M(−1; 0; 0) và N(0; 1; 2) có phương Câu 17. Nguyên hàm F(x) của hàm số f (x) = trình là π sin x − cos x thỏa mãn F = 0 là x y + 1 z − 2 √ 4 A. = = . 1 1 2 2 x − 1 y z
A. − cos x − sin x + . B. = = . 2 √ 1 1 2
B. − cos x − sin x − 2. x y − 1 z + 2 C. = = . C. cos x − sin x. 1 1 2 √ x + 1 y z
D. − cos x − sin x + 2. D. = = . 1 1 2 b
Câu 18. Xét (H) là hình phẳng giới hạn bởi đồ thị Z
Câu 11. Tất cả các giá trị của b thỏa mãn
(2x − hàm số y = 2x + 1, trục hoành, trục tung và đường 1
thẳng x = a (a > 0). Giá trị của a sao cho thể tích 6) dx = 0 là
của khối tròn xoay tạo thành khi quay (H) quanh
A. b = −5 hoặc b = 5.
trục hoành bằng 57π là
B. b = −1 hoặc b = 1.
A. a = 3. B. a = 5. C. a = 4. D. a = 2.
C. b = −3 hoặc b = 3. D. b = 1 hoặc b = 5.
Câu 19. Xét vật thể (T ) nằm giữa hai mặt phẳng #»
x = −1 và x = 1. Biết rằng thiết diện của vật thể
Câu 12. Trong không gian Oxyz cho các vectơ a = #» #»
cắt bởi mặt phẳng vuông góc với trục Ox tại điểm
(1; −1; 2), b = (3; 0; −1), c = (−2; 5; 1). Tọa độ #» #» #»
có hoành độ x (−1 ≤ x ≤ 1) là một hình vuông có của vectơ u = a + b − #» c là √ #» #»
cạnh 2 1 − x2. Thể tích vật thể (T ) bằng A. u = (−6; 6; 0). B. u = (6; −6; 0). 16π 16 8 #» #» A. . B. . C. π. D. . C. u = (6; 0; −6). D. u = (0; 6; −6). 3 3 3
Câu 13. Trong không gian Oxyz, cho hai mặt Câu 20. Thể tích của khối tròn xoay được tạo
phẳng (P) : 2x + 4y + 3z − 5 = 0 và (Q) : mx − thành khi quay hình phẳng giới hạn bởi đồ thị của
ny − 6z + 2 − 0. Giá trị của m, n sao cho (P) k (Q) hàm số y = x2 − x và trục hoành quanh trục hoành là là π π π π A. m = 4; n = −8. B. m = n = 4. A. . B. . C. . D. . 5 3 30 15 C. m = −4; n = 8. D. m = n = −4.
Câu 21. Trong mặt phẳng tọa độ Oxy, cho M, N, P
Câu 14. Hàm số f (x) thỏa mãn f 0(x) = xex là
lần lượt là điểm biểu diễn của các số phức 2 + ex+1 A. (x − 1)ex + C. B. x2 + + C.
3i, 1 − 2i và −3 + i. Tìm tọa độ của điểm Q sao cho x + 1
tứ giác MNPQ là hình bình hành. C. x2ex + C. D. (x + 1)ex + C. A. Q(0; 2. B. Q(6; 0).
Câu 15. Trong không gian Oxyz, một véc-tơ pháp x y z C. Q(−2; 6). D. Q(−4; −4. tuyến của mặt phẳng + + = 1 là −2 −1 3 #» #»
Câu 22. Trong không gian Oxyz, mặt cầu tâm A. n = (3; 6; −2). B. n = (2; −1; 3). #» #»
I(1; 2; 3) và đi qua điểm A(1; 1; 2) có phương trình
C. n = (−3; −6; −2). D. n = (−2; −1; −3). là √
Câu 16. Trong không gian Oxyz, cho mặt cầu (S):
A. (x − 1)2 + (y − 2)2 + (z − 3)2 = 2. √
x2 + y2 + z2 − 2x + 6y − 8z + 1 = 0. Tâm và bán
B. (x − 1)2 + (y − 1)2 + (z − 2)2 = 2.
kính của (S) lần lượt là
C. (x − 1)2 + (y − 1)2 + (z − 2)2 = 2.
A. I(−1; 3; −4), R = 5.
D. (x − 1)2 + (y − 2)2 + (z − 3)2 = 2.
B. I(1; −3; 4), R = 5. ♂ 30 đề ôn thi t HKII-12 28 v 28
Những nẻo đường phù sa 2021 30 ĐỀ - ĐỀ
30 ĐỀ ÔN THI HKII-LỚP 12 2020
Câu 23. Trong mặt phẳng tọa độ Oxy, tập Câu 30. Phương trình bậc hai nào dưới đây nhận
hợp điểm biểu diễn số phức z thỏa mãn
hai số phức 2 − 3i và 2 + 3i làm nghiệm ?
|z − i| = |2 − 3i − z| là A. z2 + 4z + 13 = 0. B. z2 + 4z + 3 = 0.
A. Đường thẳng x − 2y − 3 = 0. C. z2 − 4z + 13 = 0. D. z2 − 4z + 3 = 0.
B. Đường thẳng x + 2y + 1 = 0.
Câu 31. Trong không gian Oxyz, cho mặt phẳng
C. Đường tròn x2 + y2 = 2.
(P) : 2x + 2y − z − 7 = 0 và mặt cầu (S) : x2 + y2 +
D. Đường tròn x2 + y2 = 4.
z2 − 2x + 4y − 6z − 11 = 0. Mặt phẳng song song e Z 3 ln x + 1
với (P) và cắt (S) theo giao tuyến là một đường
Câu 24. Cho tích phân I = dx. Nếu x
tròn có chu vi bằng 6π có phương trình là 1 đặt t = ln x thì
A. 2x + 2y − z − 19 = 0. 1 e
B. 2x + 2y − z + 17 = 0. Z 3t + 1 Z 3t + 1 A. I = dt. B. I = dt. et t
C. 2x + 2y − z − 17 = 0. 0 1 e 1
D. 2x + 2y − z + 7 = 0. Z Z C. I = (3t + 1) dt. D. I = (3t + 1) dt.
Câu 32. Trong không gian Oxyz, giá trị dương của 1 0
m sao cho mặt phẳng (Oxy) tiếp xúc với mặt cầu
Câu 25. Trong không gian Oxyz, đường thẳng đi (x − 3)2 + y2 + (z − 2)2 = m2 + 1 là√
qua điểm M(1; −2; 3) và vuông góc với mặt phẳng A. m = 5. B. m = 3. √
x + y − 2z + 3 = 0 có phương trình là C. m = 3. D. m = 5. x = 1 − t x = 1 + t
Câu 33. Xét hàm số f (x) xác định trên R \ {−2; 2} A. y = 1 + 2t . B. y = 2 + t . 4 và thỏa mãn f 0(x) = , f (−3) + f (3) = z = −2 − 3t z = 3 − 2t x2 − 4
f (−1) + f (1) = 2. Giá trị của biểu thức f (−4) + x = 1 + t x = 1 + t f (0) + f (4) bằng C. y = −2 + t . D. y = 1 − 2t . A. 4. B. 1. C. 2. D. 3. z = 3 − 2t z = −2 + 3t
Câu 34. Trong không gian Oxyz, cho mặt phẳng
Câu 26. Cho số phức z thỏa mãn (2 + i)z = 9 − 8i. (P) : x + y + 2z − 5 = 0 và các điểm A(1; 2; 3),
Mô-đun của số phức w = z + 1 + i bằng
B(−1, 1, −2), C(3, 3, 2). Gọi M(x0, y0, z0) là điểm A. 3. B. 5. C. 6. D. 4.
thuộc mặt phẳng (P) sao cho MA = MB = MC.
Câu 27. Cho x, y là các số thực thỏa mãn (2x − Giá trị của x0 + y0 + z0 bằng
1) + (y + 1)i = 1 + 2i. Giá trị của biểu thức x2 + A. 6. B. 4. C. 7. D. 5. 2xy + y2 bằng √
Câu 35. Cho số phức z thỏa mãn |z − 3 − 4i| = 5. A. 2. B. 0. C. 1. D. 4.
Gọi M và m lần lượt là giá trị lớn nhất và giá trị nhỏ
Câu 28. Đặt S là diện tích của hình phẳng giới nhất của biểu thức P = |z + 2|2 − |z − i|2. Môđun x2 − 2x
của số phức w = M + mi là
hạn bởi đồ thị hàm số y = , đường thẳng √ √ x − 1 A. |w| = 3 137. B. |w| = 1258.
y = x − 1 và các đường thẳng x = m, x = 2m √ √ C. |w| = 2 309. D. |w| = 2 314.
(m > 1). Giá trị của m sao cho S = ln 3 là e A. m = 5. B. m = 4. Z 2 ln x + 3 a Câu 36. Biết dx = + b với a, b ∈ Z. C. m = 2. D. m = 3. x2 e 1 Giá trị của a + b bằng
Câu 29. Mô-đun của số phức z = 3 + 4i bằng √ A. −2. B. −8. C. 2. D. 8. A. 1. B. 7. C. 5. D. 7. ♂ 30 đề ôn thi t HKII-12 29 v 29
Những nẻo đường phù sa 2020 - 2021 30 ĐỀ
30 ĐỀ ÔN THI HKII-LỚP 12
Câu 37. Trong không gian Oxyz, cho mặt phẳng A. a = −2, b = −1. B. a = 3, b = 2. (P) : x − 2y + z − 4 = 0 và đường thẳng C. a = −3, b = −1. D. a = 3, b = 1. x − m y + 2m z d : = = . Nếu giao điểm của d 1 3 2
Câu 43. Một vật trượt không vận tốc đầu xuất
và (P) thuộc mặt phẳng (Oyz) thì giá trị của m phát từ đỉnh của mặt ván phẳng nằm nghiêng (như bằng
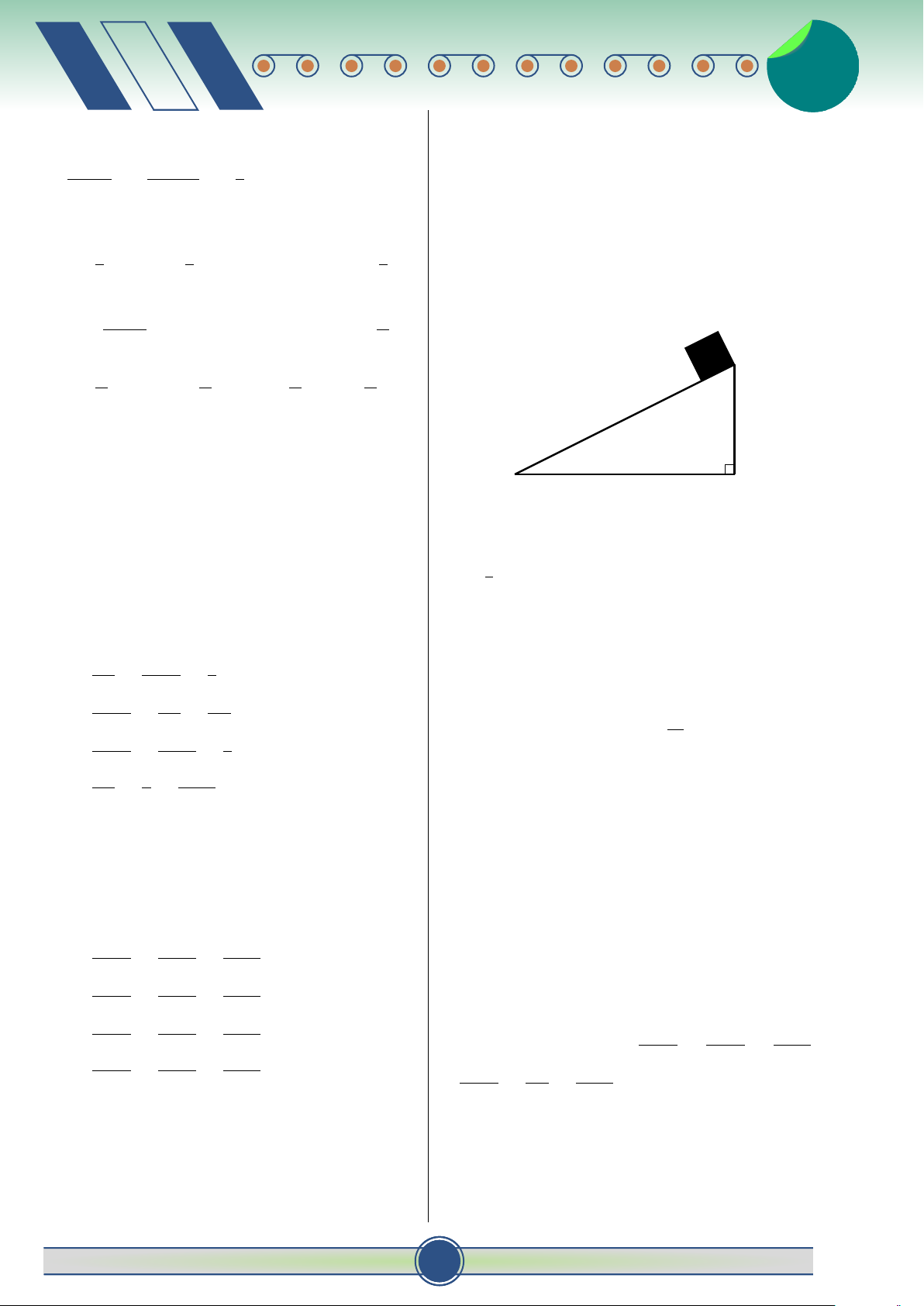
hình vẽ). Biết gia tốc của chuyển động là 5 m/s2 và 4 1 1 A. . B. . C. 1. D. − .
sau 1, 2 giây thì vật đến chân của mặt ván. Độ dài 5 2 2 của mặt ván là
Câu 38. Biết F(x) là nguyên hàm của hàm số 1 π f (x) = + m thoả mãn F(0) = 0 và F = cos2 x 4 2. Giá trị của m bằng 4 4 π A. . B. − . C. − π . D. . π π 4 4
Câu 39. Cho số phức z thoả mãn z − 4 = (1 +
i)|z| − (4 + 3z)i. Môđun của số phức z bằng A. 2. B. 1. C. 16. D. 4.
Câu 40. Trong không gian Oxyz, cho điểm
A. 3, 6 m. B. 3, 2 m. C. 3 m. D. 2, 8 m. x = 4 + 3t
M(0; 2; 0) và đường thẳng d :
y = 2 + t . Câu 44. Cho số phức z = a + bi thỏa mãn z(1 +
2i)2 + z = −20 + 4i. Giá trị của a2 − b2 bằng z = −1 + t A. 16. B. 1. C. 5. D. 7.
Đường thẳng đi qua M, cắt và vuông góc với d có phương trình là
Câu 45. Cho hàm số f (x) thỏa mãn [ f 0(x)]2 + x y − 2 z A. = = .
f (x) · f ”(x) = 2x2 − x + 1, ∀x ∈ R và f (0) = −1 1 2 x − 1 y z
f 0(0) = 3. Giá trị của [ f (1)]2 bằng B. = = . 1 −1 −2 19 A. 28. B. 22. C. . D. 10. x − 1 y − 1 z 2 C. = = . 1 1 2 x y z − 1
Câu 46. Một xe mô tô đang chạy với vận tốc 20 D. = = . −1 1 2
m/s thì người lái xe nhìn thấy một chướng ngại
Câu 41. Trong không gian Oxyz, cho mặt cầu vật nên đạp phanh. Từ thời điểm đó, mô tô chuyển
(S) : x2 + y2 + z2 + 2x − 4y − 2z − 10 = 0 và điểm động chậm dần đều với vận tốc v(t) = 20 − 5t
M(1; 1; −1). Giả sử đường thẳng d đi qua M và cắt m/s, trong đó t là thời gian (tính bằng giây) kể từ
(S) tại hai điểm P, Q sao cho độ dài đoạn thẳng lúc đạp phanh. Quãng đường mà mô tô đi được từ
PQ lớn nhất. Phương trình của d là
khi người lái xe đạp phanh đến lúc mô tô dừng lại x + 1 y + 1 z − 1 A. = = . là 2 −1 −2 x − 1 y − 1 z + 1 A. 20 m. B. 80 m. C. 60 m. D. 40 m. B. = = . 2 1 −2 x − 1 y − 1 z + 1
Câu 47. Trong không gian Oxyz, mặt phẳng chứa C. = = . x − 1 y + 2 z − 4 2 1 2
hai đường thẳng cắt nhau = = x − 1 y − 1 z + 1 −2 1 3 D. = = . x + 1 y z + 2 2 −1 −2 và = = có phương trình là 1 −1 3
Câu 42. Trong không gian Oxyz, cho hai đường A. − 2x − y + 9z − 36 = 0. x = 2 + at x = 2 + 3t0 B. 2x − y − z = 0. thẳng d : y = 1 − bt và d0 : y = 3 − t0 . Giá trị C. 6x + 9y + z + 8 = 0. z = 2 − t z = t0
D. 6x + 9y + z − 8 = 0.
của a và b sao cho d và d0 song song với nhau là ♂ 30 đề ôn thi t HKII-12 30 v 30
Những nẻo đường phù sa 2021 30 ĐỀ - ĐỀ
30 ĐỀ ÔN THI HKII-LỚP 12 2020
Câu 48. Trong không gian với Oxyz, cho các véc- #» #» #» ĐỀ ÔN SỐ 8
tơ a = (−5; 3; −1), b = (1; 2; 1) và c = (m; 3; −1) #» #» #»
Giá trị của m sao cho a = [ b , c ]
Câu 1. Phương trình nào sau đây nhận hai số √ √ A. m = −1. B. m = −2. phức z1 = 1 + 2i và z2 = 1 − 2i làm C. m = 1. D. m = 2. nghiệm? A. z2 − 2z + 3 = 0. B. z2 − 2z − 3 = 0.
Câu 49. Biết diện tích hình phẳng giới hạn bởi đồ C. z2 + 2z + 3 = 0. D. z2 + 2z − 3 = 0.
thị của hàm số y = x2 − 2x + 3, trục hoành và các 20
Câu 2. Mệnh đề nào dưới đây đúng?
đường thẳng x = 1, x = m(m > 1) bằng . Giá Z √ 3 x A. e 2 dx = 2 ex + C. trị của m bằng Z 5 3 A. . B. 2. C. 3. D. . B. sin 2x dx = −2 cos 2x + C. 2 2 Z dx C. = ln x + C.
Câu 50. Cho hàm số y = x2 − mx (0 < m < 4) có x Z
đồ thị (C). Gọi S1 + S2 là diện tích của hình phẳng D. 2x dx = 2x · ln 2 + C.
giới hạn bởi (C), trục hoành, trục tung và đường Câu 3. Cho hình phẳng (H) giới hạn bởi các đồ
thẳng x = 4 (phần tô đậm trong hình vẽ bên dưới). √ thị của các hàm số y =
x, y = 2 − x và trục tung.
Giá trị của m sao cho S1 = S2 là
Tính thể tích V của khối tròn xoay tạo thành khi y quay (H) quanh Ox. (C) 5 11 A. V = . B. V = π. 6 6 11 5 C. V = . D. V = π. 6 6
Câu 4. Trong không gian tọa độ Oxyz, cho hai
mặt phẳng (P) : (m − 1)x + y − 2z + m = 0 và
(Q) : 2x − z + 3 = 0. Tìm m để (P) vuông góc với S x 2 (Q). O S1 4 3 A. m = 0. B. m = . 2 C. m = 5. D. m = −1. 10
Câu 5. Thể tích V của khối tròn xoay tạo thành khi A. m = 3. B. m = . 3
cho hình phẳng giới hạn bởi các đường y = f (x), 8 C. m = 2. D. m = .
y = 0, x = a, x = b (a < b) quay quanh Ox được 3
tính bởi công thức nào dưới đây?
BẢNG ĐÁP ÁN THAM KHẢO b Z A. V = ( f (x))2 dx. 1. 2. 3. 4. 5. 6. 7. 8. 9. 10. 11. a A D B B B C A D C D D b Z
12. 13. 14. 15. 16. 17. 18. 19. 20. 21. 22. B. V = | f (x)| dx. B C A A B D A B C C D a b
23. 24. 25. 26. 27. 28. 29. 30. 31. 32. 33. Z C. V = π ( f (x))2 dx. A D C B D C C C B B D a
34. 35. 36. 37. 38. 39. 40. 41. 42. 43. 44. b Z D B A B A A A D C A D D. V = π | f (x)| dx. 45. 46. 47. 48. 49. 50. a
Câu 6. Trong không gian tọa độ Oxyz, cho đường A D C D C D x − 1 y + 1 z − 2 thẳng d : = = . Véc-tơ nào dưới 2 −1 −3 ♂ 30 đề ôn thi t HKII-12 31 v 31
Những nẻo đường phù sa 2020 - 2021 30 ĐỀ
30 ĐỀ ÔN THI HKII-LỚP 12
đây không phải là một véc-tơ chỉ phương của C. F(−1) = 10 + ln 5. đường thẳng d?
D. F(−1) = 10 − ln 5. #» #» A. a (2; 1; 3). B. b (2; −1; −3). #» #»
Câu 14. Trong không gian tọa độ Oxyz, điểm nào C. c (−2; 1; 3). D. d (6; −3; −9).
sau đây là hình chiếu của điểm M(2; 1; −3) lên mặt
Câu 7. Tính diện tích S của hình phẳng giới hạn phẳng Oxz?
bởi đồ thị hai hàm số y = x2 − 4 và y = −x2 − A. M1(2; 1; 0). B. M2(0; 1; 0). 2x. C. M3(0; 1; −3). D. M1(2; 0; −3). A. S = 9. B. S = −99.
Câu 15. Tính diện tích S của hình phẳng giới hạn C. S = 3. D. S = 9π.
bởi đồ thị hàm số y = tan2 x, trục hoành, trục tung π π 2 và đường thẳng x = . Z Câu 8. Biết 8x(3x + cos x) dx = a 3 4 π + bπ + c, 2 0
A. S = π − π .
B. S = 1 − π . 4 4
với a, b, c là các số nguyên. Tính S = a2 + b2 + 2 π π ac. C. S = 1 + . D. S = π + . 4 4 A. S = 9. B. S = 25.
Câu 16. Trong không gian tọa độ Oxyz, tính thể C. S = −25. D. S = −9.
tích V của vật thể nằm giữa hai mặt phẳng x = 0
Câu 9. Tìm phần thực và phần ảo của số phức ¯z, và x = π, biết rằng thiết diện của vật thể khi cắt biết z = −i(4i + 3).
bởi mặt phẳng vuông góc với trục Ox tại điểm có
A. Phần thực bằng 4, phần ảo bằng 3.
hoành độ x (0 ≤ x ≤ π) là một tam giác đều cạnh √
B. Phần thực bằng 4, phần ảo bằng −3. bằng 2 sin x. √ √
C. Phần thực bằng 4, phần ảo bằng 3i. A. V = 2 3. B. V = 2 3π. 3 3 2
D. Phần thực bằng 4, phần ảo bằng −3i. C. V = π. D. V = π . 2 2
Câu 10. Cho số phức z thỏa mãn các điều kiện Câu 17. Cho số phức z = 2 + i. Tìm tọa độ điểm
|z − 2| = | ¯z| và (z − 3)( ¯z + 1 − 4i) ∈ R. Tìm phần biểu diễn của số phức liên hợp của số phức z. ảo của số phức z. A. (−2; −1). B. (−2; 1). A. −2. B. −1. C. 2. D. 1. C. (2; 1). D. (2; −1).
Câu 11. Cho các số phức z
Câu 18. Cho hình phẳng (H) giới hạn bởi các 1, z2 thỏa mãn |z1 − 1 + π đường y = 2i| = 1 và |z cos x, y = 0, x = 0, x = . Tính thể 2 − 2 + i| = | ¯ z2 + i|. Tìm giá trị nhỏ 4 nhất P
tích V của khối tròn xoay tạo thành khi quay (H)
min của biểu thức P = |z1 − z2|. √ √ A. P quanh trục Ox. min = 2 − 1. B. Pmin = 2 + 1. √ 1 1 2 C. P 2 π min = 0. D. Pmin = 1. A. V = π + π. B. V = . 8 4 2 √
Câu 12. Cho số phức z thỏa mãn (1 + 2i)z − 5 = π 1 2 C. V = + . D. V = .
3i. Tìm số phức liên hợp của số phức z. 8 4 2 11 7 11 7 3 A. ¯z = − i. B. ¯z = + i. Z 2x − 3 a 3 5 5 5 5 Câu 19. Cho √ dx = − + c ln , với 11 7 11 7 1 + x + 1 b 2 C. ¯z = − − i. D. ¯z = − + i. 0 5 5 5 5
a, b, c là các số nguyên dương. Tính giá trị của biểu
Câu 13. Cho F(x) là một nguyên hàm của hàm số thức P = a + b + c. 4 1 f (x) = trên khoảng −∞; thỏa mãn A. P = 17. B. P = 12. 1 − 4x 4 F(0) = 10. Tính F(−1). C. P = 15. D. P = 1.
A. F(−1) = 10 − 4 ln 5.
Câu 20. Trong mặt phẳng phức, biết số phức z có
B. F(−1) = 10 + 4 ln 5.
điểm biểu diễn nằm trong góc phần tư (I). Hỏi ♂ 30 đề ôn thi t HKII-12 32 v 32
Những nẻo đường phù sa 2021 30 ĐỀ - ĐỀ
30 ĐỀ ÔN THI HKII-LỚP 12 2020 1
điểm biểu diễn của số phức w = nằm trong góc Cho hàm số y iz phần tư nào? y = f (x) có đồ thị như hình vẽ. A. (I). B. (I I). C. (I I I). D. (IV). −2 Gọi S là diện tích x O 1
Câu 21. Trong không gian tọa độ Oxyz, cho hai hình phẳng giới hạn x =2 − 2t bởi đồ thị hàm số x − 2 y = f (x) và trục đường thẳng (d1) : y = 3 và (d2) : = 1 hoành (phần gạch z =t chéo trong hình). y − 1 z =
. Khẳng định nào sau đây đúng? −1 2 Khẳng định nào sau A. (d đây đúng? 1) và (d2) cắt nhau. 0 1 B. (d Z Z
1) và (d2) song song với nhau. A. S = f (x) dx + f (x) dx.
C. (d1) và (d2) chéo nhau và vuông góc với −2 0 nhau. 0 1 Z Z D. (d B. S = f (x) f (x)
1) và (d2) chéo nhau và không vuông góc dx − dx. với nhau. −2 0 1 Z C. S = f (x) dx.
Câu 22. Cho số phức z thỏa mãn (1 + i)z + 2 ¯z = −2
3 − 2i. Tính mô-đun của số phức z. 0 1 Z Z 1 √ 53 A. |z| = 106. B. |z| = . D. S = − f (x) dx + f (x) dx. 2 2 41 1 √ −2 0 C. |z| = . D. |z| = 2. 8 4 Câu 27.
Một cốc rượu có hình dạng
Câu 23. Trong không gian tọa độ Oxyz, cho mặt 8 cm
tròn xoay với chiều cao (của
cầu (S) : x2 + y2 + z2 − 4x + 2y − 6z − 11 = 0. Tính phần đựng rượu) bằng 10
bán kính R của mặt cầu. √ cm và đường kính miệng cm A. R = 3. B. R = 25. 10 cốc bằng 8 cm (tham khảo C. R = 3. D. R = 5.
hình mô phỏng ở bên). Biết
thiết diện dọc (bổ dọc cốc
Câu 24. Tìm nguyên hàm của hàm số f (x) = thành hai phần bằng nhau) e3x 1 − 3e−5x . là một parabol. Tính dung Z 1 3 A. f (x) dx = e3x + e−2x + C. 3 2 tích V Z 1 3
của chiếc cốc (làm tròn đến hai chữ số thập phân, B. f (x) dx = e3x − e−2x + C. 3 2
coi thể tích thành cốc là không đáng kể). Z C.
f (x) dx = e3x − 3e−2x + C. A. V ≈ 320 cm3. B. V ≈ 1005,31 cm3. Z D. f (x) dx = 3e3x + 6e−2x + C. C. V ≈ 251,33 cm3. D. V ≈ 502,65 cm3.
Câu 28. Trong mặt phẳng phức, gọi M, N là điểm
Câu 25. Gọi z1, z2 là các nghiệm phức của phương biểu diễn của các số phức là nghiệm của phương
trình z2 − 2z + 5 = 0. Tính F = |z1| + |z2|. √
trình z2 − 4z + 9 = 0. Tính độ dài đoạn thẳng A. F = 2 5. B. F = 6. MN. C. F = 10. D. F = 3. A. MN = 4. B. MN = 5.√ C. MN = 20. D. MN = 2 5. Câu 26. ♂ 30 đề ôn thi t HKII-12 33 v 33
Những nẻo đường phù sa 2020 - 2021 30 ĐỀ
30 ĐỀ ÔN THI HKII-LỚP 12
Câu 29. Trong không gian Oxyz, vật thể B giới hạn 4 4 C. sin α = .
D. sin α = − . 9 9
bởi hai mặt phẳng x = a và x = b (a < b). Gọi S(t)
là diện tích thiết diện của vật khi cắt bởi mặt phẳng
x = t (a ≤ t ≤ b). Giả sử S(t) là hàm số liên tục Câu 34. Trong không gian tọa độ Oxyz, cho điểm
trên đoạn [a; b]. Thể tích V của vật thể B tính theo x − 1 y + 2
A(1; 0; 0) và đường thẳng d : = =
công thức nào dưới đây? 2 1 z − 1 b
. Viết phương trình mặt phẳng (P) chứa điểm Z A. V = S(x) dx. 2 A và đường thẳng d. a b Z
A. (P) : 5x + 2y + 4z − 5 = 0. B. V = π (S(x))2 dx.
B. (P) : 2x + y + 2z − 1 = 0. a b
C. (P) : 2x + 2y + z − 2 = 0. Z C. V = π S(x) dx.
D. (P) : 5x − 2y − 4z − 5 = 0. a b Z D. V = (S(x))2 dx. a
Câu 35. Cho các hàm số f (x), g(x) liên tục trên
Câu 30. Xét trên khoảng (0; +∞), hàm số nào dưới đoạn [a; b]. Khẳng định nào sau đây sai?
đây không phải là một nguyên hàm của hàm số b b b Z Z Z x2 − 1 f (x) = ? A. ( f (x) · g(x)) dx = f (x) dx · g(x) dx. x2 a a a x2 − x + 1 b b A. F1(x) = . Z Z x B. ( f (x) + g(x)) dx = f (x) dx + x2 + 1 B. F a a 2(x) = . x b x2 + 2x + 1 Z C. F g(x) dx. 3(x) = . x a x2 − 1 a D. F4(x) = . Z x C. f (x) dx = 0.
Câu 31. Cho z là một số phức mà (z + 1 − 2i)( ¯z + a b a
3) là một số thực. Tìm giá trị nhỏ nhất P Z Z 0 của biểu D. f (x) dx = − f (x) dx. thức P = |z − 3 + 2i|. √ a b √ 3 2 A. P0 = 4 2. B. P0 = . √ 2 C. P0 = 2. D. P0 = 0.
Câu 36. Trong không gian tọa độ Oxyz, cho đường
Câu 32. Cho số phức z = a + bi (a, b ∈ R). Mệnh x − 1 y + 1 z − 2 thẳng ∆ : = = và mặt phẳng −
đề nào dưới đây luôn đúng? 2 1 3
(α) : 4x − 2y − 6z + 5 = 0. Khẳng định nào sau đây A. z − ¯z = 2a. B. z ¯z = a2 − b2. đúng? C. z + ¯z = 2bi. D. |z2| = |z|2.
A. ∆ song song với (α).
Câu 33. Trong không gian tọa độ Oxyz, cho đường x − 1 y + 1 z − 2
B. ∆ nằm trên (α). thẳng ∆ : = = và mặt phẳng −2 2 −1
C. ∆ vuông góc với (α).
(P) : 2x − y − 2z + 1 = 0. Gọi α là góc giữa đường
D. ∆ cắt và không vuông góc với (α).
thẳng ∆ và mặt phẳng (P). Khẳng định nào sau đây đúng? 4 4 A. cos α = .
B. cos α = − . Câu 37. 9 9 ♂ 30 đề ôn thi t HKII-12 34 v 34
Những nẻo đường phù sa 2021 30 ĐỀ - ĐỀ
30 ĐỀ ÔN THI HKII-LỚP 12 2020 Một người v x =1 + t, x =1 − 2t, I chạy bộ trong 2 5 A. d0 : y =1 − 2t, B. d0 : y =1 + 2t, giờ, với vận tốc z = − 2t. z =t. v = v(t) (t tính x = 1 + t, x =1 + t, theo giờ, v tính C. d0 : y =1 + 2t, D. d0 : y =1 − 4t, theo km/h). Biết rằng đồ thị z = − 2t. z =2t. của v = v(t) là
Câu 41. Tính diện tích S của hình phẳng giới hạn một parabol có 2x − 1 bởi đường cong (C) : y = , đường tiệm cận x − 1 trục đối xứng
ngang của (C) và các đường thẳng x = 2, x = song song với O 1 t 3. trục tung và có A. S = ln 2. B. S = 2 + ln 2. đỉnh là điểm C. S = 1 + ln 2. D. S = − ln 2. I(1; 5) (tham
Câu 42. Trong không gian tọa độ Oxyz, tìm tọa độ khảo hình vẽ
điểm M0 đối xứng với điểm M(1; 4; −2) qua đường bên).
Tính quãng đường người đó chạy được trong 1 giờ x =1 + 2t,
30 phút đầu tiên kể từ lúc chạy (làm tròn đến hàng thẳng (d) : y = − 1 − t, phần trăm). z =2t. A. 2,11 km. B. 6,67 km. A. M0(−1; 0; −2).
B. M0(−3; −4; −2). C. 5,63 km. D. 3,33 km. C. M0(3; −2; 2). D. M0(5; −8; 6).
Câu 38. Trong không gian tọa độ Oxyz, cho mặt Câu 43. Giả sử phương trình z2 + az + b = 0 (với
phẳng (α) đi qua hai điểm A(1; −1; 2), B(3; 0; −1) a, b ∈ R) nhận z1 = 1 − i làm nghiệm. Tìm nghiệm
và vuông góc với mặt phẳng (β) : x − y + 2z + 1 = z2 còn lại.
0. Véc-tơ nào dưới đây là một véc-tơ pháp tuyến A. z2 = −1 − i. B. z2 = 1 − i. của (α)? C. z2 = −1 + i. D. z2 = 1 + i. # » # » A. n1(1; 7; 3). B. n2(1; −7; 3).
Câu 44. Một vật bắt đầu chuyển động thẳng đều # » # » C. n3(−1; −7; 3). D. n4(1; −1; 3).
với vận tốc v0 (m/s), sau 6 giây chuyển động thì
Câu 39. Trong không gian tọa độ Oxyz, cho đường phát hiện có chướng ngại vật nên bắt đầu giảm tốc x − 1 y z 5 thẳng d : = =
và hai điểm A(2; 1; 0), độ với vận tốc chuyển động v(t) = − t + a (m/s) 2 1 −2 2
B(−2; 3; 2). Viết phương trình mặt cầu (S) có tâm cho đến lúc dừng hẳn. Tìm v0, biết trong toàn bộ
thuộc d và đi qua hai điểm A, B.
quá trình, vật di chuyển được 80 m.
A. (S) : (x + 1)2 + (y + 1)2 + (z − 2)2 = 17. A. v0 = 10 m/s. B. v0 = 5 m/s.
B. (S) : (x − 1)2 + (y − 1)2 + (z + 2)2 = 17. C. v0 = 12 m/s. D. v0 = 8 m/s.
C. (S) : (x − 3)2 + (y − 1)2 + (z + 2)2 = 5.
Câu 45. Trong không gian tọa độ Oxyz, viết
D. (S) : (x + 3)2 + (y + 1)2 + (z − 2)2 = 33.
phương trình chính tắc của đường thẳng d đi qua
A(1; 2; −1) và vuông góc với mặt phẳng (P) : x +
Câu 40. Trong không gian tọa độ Oxyz, điểm x − 1 y + 1 2y − 3z + 1 = 0.
A(1; 1; 0) và hai đường thẳng d : = = x + 1 y + 2 z − 1 2 1 A. d : = = . z x − 1 y − 1 z + 1 1 −2 −3 , ∆ : = = . Viết phương trình 2 1 2 −1 x + 1 y + 2 z − 1 B. d : = = .
đường thẳng d0 đi qua điểm A, vuông góc với d và 1 2 −3 x − 1 y − 2 z + 1 cắt ∆. C. d : = = . 1 2 3 ♂ 30 đề ôn thi t HKII-12 35 v 35
Những nẻo đường phù sa 2020 - 2021 30 ĐỀ
30 ĐỀ ÔN THI HKII-LỚP 12 x − 1 y − 2 z + 1 D. d : = = .
34. 35. 36. 37. 38. 39. 40. 41. 42. 43. 44. −1 −2 3 D A C C A A C A B D A
Câu 46. Trong không gian tọa độ Oxyz, mặt 45. 46. 47. 48. 49. 50.
phẳng (α) đi qua M(1; −3; 8) và chắn trên tia Oz D A D B C A
một đoạn thẳng dài gấp đôi các đoạn thẳng mà nó
chắn trên các tia Ox và Oy. Giả sử (P) : ax + by +
cz + d = 0, với a, b, c, d là các số nguyên và d 6= 0. ĐỀ ÔN SỐ 9 a + b + c Tính S = . d π 2 5 5 Z √ A. S = − . B. S = .
Câu 1. Cho tích phân I = 2 + cos x · sin x dx. 4 4 C. S = 3. D. S = −3. 0
Nếu đặt t = 2 + cos x thì kết quả nào sau đây
Câu 47. Mặt phẳng (P) : ax + by + cz + 2 = 0 đúng?
(a, b, c là các số nguyên không đồng thời bằng 0) 2 3 Z √ Z √ x − 1 y z A. I = t dt. B. I = t dt. chứa đường thẳng d : = = và cắt mặt 1 −2 2 3 2
cầu (S) : x2 + y2 + z2 − 2x + 4y + 6z − 11 = 0 theo 2 π 2 Z √ Z √
một đường tròn có bán kính nhỏ nhất. Tính giá trị C. I = 2 t dt. D. I = t dt.
của biểu thức M = a + b + c. 3 0 A. M = −5. B. M = −43.
Câu 2. Trong không gian Oxyz, cho mặt phẳng C. M = 5. D. M = 43. (P) : 3x + 5y − z − 2 = 0 và đường thẳng x − 12 y − 9 z − 1 = =
Câu 48. Tìm phần ảo của số phức z = 3 − 2i. d : . Tọa độ giao điểm M 4 3 1 của d và (P) là A. Imz = −2i. B. Imz = −2. A. M(0; 0; −2). B. M(0; 2; 0). C. Imz = 2. D. Imz = 3. C. M(4; 3; −1). D. M(1; 0; 1).
Câu 49. Tính diện tích S của hình phẳng giới hạn √
Câu 3. Hàm số f (x) = x x + 1 có một nguyên
bởi đồ thị (C) : y = x3 − 3x2 và tiếp tuyến của (C) hàm là F(x). Nếu F(0) = 2 thì F(3) bằng
tại điểm có hoành độ bằng −1. 116 146 886 5 81 A. . B. . C. . D. 3. A. S = . B. S = . 15 15 105 4 4 43 C. S = 108. D. S = .
Câu 4. Hàm số F(x) = ex2 là nguyên hàm của 2 hàm số nào sau đây?
Câu 50. Cho số phức z thỏa mãn |z − 3| = 1. A. f (x) = x2ex2 + 3. B. f (x) = 2x2ex2 + C.
Biết rằng tập hợp các điểm biểu diễn của số phức √ C. f (x) = 2xex2. D. f (x) = xex2. w = (1 −
3i)z + 1 − 2i là một đường tròn. Tính Câu 5. Trong không gian Oxyz, cho mặt cầu
bán kính r của đường tròn đó.
(S) : x2 + y2 + z2 − 2x + 2y − 2z − 1 = 0. Tâm và A. r = 2. B. r = 1. √
bán kính của mặt cầu (S) là C. r = 4. D. r = 2. √ A. I(2; −2; 2), R = 11. √
BẢNG ĐÁP ÁN THAM KHẢO
B. I(−2; 2; −2), R = 13.
C. I(1; −1; 1), R = 2. 1. 2. 3. 4. 5. 6. 7. 8. 9. 10. 11. √ D. I(1; −1; 1), R = 2. A A B A C A A A A A A
12. 13. 14. 15. 16. 17. 18. 19. 20. 21. 22. 1 Z B D D B A D A A C C A
Câu 6. Giá trị của tích phân πxex dx bằng
23. 24. 25. 26. 27. 28. 29. 30. 31. 32. 33. 0 π 1 D A A B C D A D A D C A. π. B. πe. C. . D. . 3 3 ♂ 30 đề ôn thi t HKII-12 36 v 36
Những nẻo đường phù sa 2021 30 ĐỀ - ĐỀ
30 ĐỀ ÔN THI HKII-LỚP 12 2020
Câu 7. Trong không gian Oxyz, cho bốn điểm Câu 16. Trong không gian Oxyz, cho các véctơ #» #» #»
M(2; −3; 5), N(4; 7; −9), E(3; 2; 1), F(1; −8; 12). Bộ
a = (3; −2; 1), b = (−1; 1; −2), c = (2; 1; −3), #»
ba điểm nào sau đây thẳng hàng?
u = (11; −6; 5). Mệnh đề nào dưới đây đúng? #» #» #» #» A. M, N, E. B. M, E, F.
A. u = 3 a − 2 b + c . #» #» #» #» C. N, E, F. D. M, N, F. B. u = 2 a + 3 b + c . #» #» #» #»
C. u = 2 a − 3 b + c .
Câu 8. Trong không gian Oxyz, cho ba điểm #» #» #» #»
D. u = 3 a − 2 b − 2 c .
A(0; 0; 6), B(0; 4; 0), C(−2; 0; 0). Gọi I(a; b; c) là tâm a
của mặt cầu ngoại tiếp tứ diện OABC với O là gốc Z x2 + 2x + 2
Câu 17. Cho số a dương thỏa mãn dx =
tọa độ. Giá trị của a + b + c bằng x + 1 0 A. 8. B. 2. C. 4. D. 6.
a2 + a + ln3. Giá trị của a là 2
Câu 9. Trong các số phức z thỏa mãn |z| = |z − A. 1. B. 2. C. 3. D. 4.
1 + 2i|, số phức có môđun nhỏ nhất là
Câu 18. Cho hai số phức z 3 1 1 = 1 + 3i, z2 = 3 − 4i. A. z = 1 + i. B. z = + i. 4 2
Môđun của số phức w = z1 + z2 bằng √ √ C. z = 3 + i. D. z = 5. A. 17. B. 15. C. 17. D. 15.
Câu 10. Cho số thực x, y thỏa mãn 2x + y + (2y − Câu 19. Cho hàm số y = f (x) liên tục và
x)i = x − 2y + 3 + (y + 2x + 1)i. Khi đó giá trị của 4 2 Z Z M = x2 + 4xy − y2 bằng
f (x) dx = 12. Khi đó giá trị của f (2x) dx 0 0 A. −1. B. 1. C. 0. D. −2. là
Câu 11. Nguyên hàm của hàm số y = e−3x+1 A. 3. B. 24. C. 12. D. 6. là
Câu 20. Trong không gian Oxyz, phương trình 1 1 A. e−3x+1 + C. B. − e−3x+1 + C.
của đường thẳng d đi qua điểm A(1; 2; −5) và 3 3 C. 3e−3x+1 + C. D. −3e−3x+1 + C.
vuông góc với mặt phẳng (P) : 2x + 3y − 4z + 5 = 0 là
Câu 12. Trong không gian Oxyz, mặt phẳng đi x = 2 + t x = 1 + 2t
qua 3 điểm A(2; 3; 5), B(3; 2; 4) và C(4; 1; 2) có A. y = 3 + 2t . B. y = 2 + 3t . phương trình là z = −4 − 5t z = −5 + 4t A. x + y + 5 = 0. B. x + y − 5 = 0. x = 1 + 2t x = 2 + t C. y − z + 2 = 0. D. 2x + y − 7 = 0. C. y = 2 + 3t . D. y = 3 + 2t .
Câu 13. Số phức liên hợp của số phức z = z = −5 − 4t z = 4 + 5t √ 3 1 − 3i là 1 1 − i Z dx A. 4 + 4i. B. 4 − 4i. Câu 21. Biết = a ln 5 + b ln 4 + x2 + 7x + 12 C. −4 − 4i. D. −4 + 4i. 0
c ln 3 với a, b, c là các số nguyên. Mệnh đề nào dưới π 2 đây đúng? Z
Câu 14. Giá trị của sin x cos2 x dx là A. a + 3b + 5c = 0.
B. a − 3b + 5c = −1. 0 10 C. a + b + c = −2. D. a − b + c = 2. π 1 1 A. . B. . C. − . D. . 3 3 3 3
Câu 22. Trong không gian Oxyz, phương trình
Câu 15. Nếu môđun của số phức z bằng r (r > 0) nào dưới đây là phương trình mặt cầu?
thì môđun của số phức (1 − i)2z bằng
A. x2 + y2 − z2 + 4x − 2y + 6z + 5 = 0. √ A. 2r. B. 4r. C. r. D. r 2.
B. x2 + y2 + z2 + 4x − 2y + 6z + 15 = 0. ♂ 30 đề ôn thi t HKII-12 37 v 37
Những nẻo đường phù sa 2020 - 2021 30 ĐỀ
30 ĐỀ ÔN THI HKII-LỚP 12
C. x2 + y2 + z2 + 4x − 2y + z − 1 = 0.
C. 6x + 8y + z − 5 = 0.
D. x2 + y2 + z2 − 2x + 2xy + 6z − 5 = 0.
D. 6x − 8y + z + 11 = 0. Z Câu 23. Để tính x ln(2 + x) dx theo phương 5 Z Câu 29. Cho f (x) dx = 10. Khi đó
pháp tính nguyên hàm từng phần, ta đặt 2 (u = x 2 A. . Z dv = ln(2 + x) dx [2 − 4 f (x)] dx bằng (u = x 5 ln(2 + x) B. . A. 32. B. 34. C. 42. D. 46. dv = dx
Câu 30. Trong không gian Oxyz, cho mặt cầu (S) (u = ln(2 + x) C. .
có tâm I(−1; 4; 2) và tiếp xúc mặt phẳng (P) : − dv = dx
2x + 2y + z + 15 = 0. Khi đó phương trình của (u = ln(2 + x) D. . mặt cầu (S) là dv = x dx
A. (x − 1)2 + (y + 4)2 + (z + 2)2 = 9.
Câu 24. Cho A, B, C lần lượt là các điểm biểu diễn
B. (x − 1)2 + (y + 4)2 + (z + 2)2 = 81. 1
của các số phức 4 − 3i, (1 + 2i)i và . Số phức có
C. (x + 1)2 + (y − 4)2 + (z − 2)2 = 9. i
D. (x + 1)2 + (y − 4)2 + (z − 2)2 = 81.
điểm biểu diễn D sao cho tứ giác ABCD là hình bình hành là
Câu 31. Diện tích S của hình phẳng giới hạn bởi A. −6 − 4i. B. −6 + 3i.
đồ thị hàm số y = x3 − 1, đường thẳng x = 2, trục C. 6 − 5i. D. 4 − 2i. tung và trục hoành là 9
Câu 25. Thể tích khối tròn xoay tạo thành khi quay A. S = . B. S = 4. x 2
hình phẳng giới hạn bởi các đường y = xe 2 , y = 0, 7 C. S = 2. D. S = .
x = 0, x = 1 xung quanh trục Ox là 2 3
A. V = π(e − 2). B. V = e − 2. Z 9π Câu 32. Biết
ln(x2 − x) dx = a ln 3 − b với a, b C. V = . D. V = 2 π e. 4 2
là các số nguyên. Khi đó a − b bằng
Câu 26. Môđun của số phức z = (2 − 3i)(1 + i)4 A. 1. B. 2. C. 0. D. −1. là √ A. |z| = −8 + 12i. B. |z| = 13.
Câu 33. Rút gọn biểu thức M = (1 − i)2018 ta √ √ C. |z| = 4 13. D. |z| = 31. được
Câu 27. Thể tích khối tròn xoay tạo thành khi quay A. M = 21009. B. M = −21009.
hình phẳng giới hạn bởi đường cong y = sin x, C. M = 21009i. D. M = −21009i.
trục hoành và hai đường thẳng x = 0, x = π xung Câu 34. Trong không gian Oxyz, cho bốn điểm quanh trục Ox là
A(0; 1; 1), B(−1; 0; 2), C(−1; 1; 0) và D(2; 1; −2). A. V = 2 2 π. B. V = 2π .
Thể tích khối tứ diện ABCD bằng 2 π π C. V = . D. V = . 5 5 6 3 2 2 A. . B. . C. . D. . 6 3 5 2
Câu 28. Trong không gian Oxyz, phương trình x + 1 2x4 + 3
của mặt phẳng chứa hai đường thẳng d
Câu 35. Họ nguyên hàm của f (x) = là 1 : = 3 x2 y − 1 z − 3 x y − 1 z + 3 2x3 2x3 = và d = = là A. − 3 ln |x| + C. B. + 3 ln x + C. 2 −2 2 : 1 1 2 3 3 2x3 3 2x3 3 A. 6x + 2y + z + 1 = 0. C. − + C. D. + + C. 3 x 3 x
B. 6x − 2y + 2z + 2 = 0. ♂ 30 đề ôn thi t HKII-12 38 v 38
Những nẻo đường phù sa 2021 30 ĐỀ - ĐỀ
30 ĐỀ ÔN THI HKII-LỚP 12 2020 π 2
Câu 43. Trong không gian Oxyz, cho điểm Z
Câu 36. Để tính tích phân
esin x cos x dx ta chọn M(1; 4; 2) và mặt phẳng (P) : x + y + z − 1 = 0. 0
Tọa độ hình chiếu H của điểm M trên mặt phẳng
cách đặt nào sau đây cho phù hợp? (P) là A. Đặt t = ecos x. B. Đặt t = ex. A. H(2; 2; −3). B. H(−1; −2; 4). C. Đặt t = cos x. D. Đặt t = sin x. C. H(−1; 2; 0). D. H(2; 5; 3).
Câu 37. Trong không gian Oxyz, cho mặt phẳng Câu 44. Tập hợp các điểm biểu diễn số phức z thỏa
(P) : 2x − 2y − z + 9 = 0 và mặt cầu (S) : (x − 3)2 + mãn 2|z − i| = |z − z + 2i| là
(y + 2)2 + (z − 1)2 = 100. Mặt phẳng (P) cắt mặt
A. Một đường thẳng.
B. Một đường tròn.
cầu (S) theo một đường tròn (C). Tọa độ tâm K và C. Một parabol. D. Một điểm.
bán kính r của đường tròn (C) là
A. K(3; −2; 1), r = 10.
Câu 45. Trong không gian Oxyz, cho hai đường x − 1 y − 2 z x − 1
B. K(−1; 2; 3), r = 8. thẳng d1 : = = , d = −1 2 3 2 : 1
C. K(1; −2; 3), r = 8. y − 3 z − 1 =
. Mệnh đề nào sau đây đúng? D. K(1; 2; 3), r = 6. −2 1 A. d1 cắt d2.
Câu 38. Diện tích S của hình phẳng giới hạn bởi
B. d1 và d2 chéo nhau.
đồ thị hàm số y = x3 − x và y = x − x2 là C. d1 trùng d2. 9 4 A. S = . B. S = . D. d 4 3 1 và d2 song song. 7 37 C. S = . D. S = . i
Câu 46. Cho số phức z, biết z = . Phần 3 12 2 − i + 1 + i
Câu 39. Để hàm số F(x) = mx3 + (3m + 2)x2 − ảo của số phức z2 là 5 5 5 5
4x + 3 là một nguyên hàm của hàm số f (x) = A. . B. i. C. − . D. − i. 2 2 2 2
3x2 + 10x − 4 thì giá trị của m là
Câu 47. Diện tích S của hình phẳng giới hạn bởi A. m = −1. B. m = 2. √ đồ thị hàm số y =
x, trục hoành và đường thẳng C. m = 0. D. m = 1. y = x − 2 bằng 16 10
Câu 40. Giải phương trình z2 − 4z + 5 = 0 trên tập A. S = . B. S = . 3 3
số phức ta được các nghiệm 17 C. S = 2. D. S = .
A. −2 + i, −2 − i. B. 2 + i, 2 − i. 2 C. 4 + i, 4 − i.
D. −4 + i, −4 − i.
Câu 48. Cho số phức z thỏa mãn |z − 3 + 3i| = 2.
Giá trị lớn nhất của |z − i| bằng
Câu 41. Trong không gian Oxyz, cho mặt cầu A. 7. B. 9. C. 6. D. 8.
(S) : x2 + y2 + z2 − 4x + 8y − 2mz + 6m = 0. Biết Câu 49. Cho hình phẳng giới hạn bởi các đường
đường kính của (S) bằng 12, tìm m. √ " y =
x − 1, y = 0 và x = 4 quay xung quanh trục m = −2 "m = 2 A. . B. .
Ox. Thể tích khối tròn xoay tạo thành bằng m = 8 m = −8 2π 7π A. V = . B. V = . "m = −2 "m = 2 3 6 C. . D. . 5π 7 m = 4 m = −4 C. V = . D. V = . 6 6
Câu 42. Diện tích S của hình phẳng giới hạn bởi Câu 50. Cho số phức z thỏa mãn z + 2z = 12 − 2i.
đồ thị hàm số y = x3 − 4x, trục hoành và hai Phần thực a và phần ảo b của z là
đường thẳng x = −2, x = 4 là A. a = 4, b = 2i. B. a = 4, b = 2. A. S = 22. B. S = 36. C. a = 4, b = −2. D. a = 4, b = −2i. C. S = 44. D. S = 8.
BẢNG ĐÁP ÁN THAM KHẢO ♂ 30 đề ôn thi t HKII-12 39 v 39
Những nẻo đường phù sa 2020 - 2021 30 ĐỀ
30 ĐỀ ÔN THI HKII-LỚP 12 1. 2. 3. 4. 5. 6. 7. 8. 9. 10. 11. #» 29 35 1 C. u = − ; ; − . B A B C C A D C B A B 12 12 2 #» 29 19 1
12. 13. 14. 15. 16. 17. 18. 19. 20. 21. 22. D. u = − ; − ; − . 12 12 2 B D D A C B A D C A C
23. 24. 25. 26. 27. 28. 29. 30. 31. 32. 33.
Câu 4. Họ nguyên hàm của hàm số f (x) = sin 2x D C A C D D B D D A D là
34. 35. 36. 37. 38. 39. 40. 41. 42. 43. 44. A. − cos 2x + C. B. cos 2x + C. A C D B D D B A C C C C. − cos2 x + C. D. − sin2 x + C. 45. 46. 47. 48. 49. 50.
Câu 5. Trong không gian với hệ tọa độ Oxyz, cho B A B A B B #»
điểm A(−3; 4; −2) và n = (−2; 3; −4). Phương #»
trình mặt phẳng (P) đi qua điểm A và nhận n làm véc-tơ pháp tuyến là ĐỀ ÔN SỐ 10
A. −3x + 4y − 2z + 26 = 0.
B. −2x + 3y − 4z + 29 = 0.
Câu 1. Trong không gian với hệ tọa độ Oxyz, mặt
C. 2x − 3y + 4z + 29 = 0.
cầu (S) tâm I(2; 3; −6) và bán kính R = 4 có
D. 2x − 3y + 4z + 26 = 0. phương trình là
A. (x + 2)2 + (y + 3)2 + (z − 6)2 = 4.
Câu 6. Cho hình phẳng (H) giới hạn bởi đồ thị
B. (x − 2)2 + (y − 3)2 + (z + 6)2 = 4.
hàm số y = 3x2 + 2x + 1 và các đường thẳng
C. (x − 2)2 + (y − 3)2 + (z + 6)2 = 16.
y = 0, x = −1, x = 1. Tính diện tích S của hình
D. (x + 2)2 + (y + 3)2 + (z − 6)2 = 16. phẳng (H).
A. S = 5. B. S = 0. C. S = 2. D. S = 4.
Câu 2. Cho hàm số y = f (x) liên tục trên đoạn
[a; b]. Gọi (H) là hình thang cong giới hạn bởi đồ Câu 7. Tính mô-đun của số phức z = (2 − i)(1 +
thị hàm số y = f (x), trục Ox và hai đường thẳng i)2 + 1.
x = a, x = b. Thể tích V của khối tròn xoay tạo A. |z| = 4. B. |z| = 5. √
thành khi quay (H) quanh trục Ox được tính theo C. |z| = 2 5. D. |z| = 25. công thức
Câu 8. Cho hình phẳng (H) giới hạn bởi đồ thị b Z 1 A. V = 2 π f 2(x) dx. hàm số y =
và các đường thẳng y = 0, x = x + 1 a
0, x = 2. Tính thể tích V của khối tròn xoay sinh ra b Z
khi cho hình phẳng (H) quay quanh trục Ox. B. V = π f 2(x) dx. 2 a A. V = . B. V = ln 3. 3 b Z 2π C. V = f 2(x) dx. C. V = π ln 3. D. V = . 3 a
Câu 9. Trong không gian với hệ tọa độ Oxyz, cho b Z D. V =
hai điểm A(−2; 7; 3) và B(4; 1; 5). Tính độ dài đoạn π | f (x)| dx. a thẳng AB. √
Câu 3. Trong không gian với hệ tọa độ Oxyz, cho A. AB = 6 2. B. AB = 76. #» #» √
a = (−5; 2; 3) và b = (1; −3; 2). Tìm tọa độ của C. AB = 2. D. AB = 2 19. #» 1 #» 3 #» véc-tơ u = a − b .
Câu 10. Cho hàm số f (x) có đạo hàm liên tục trên 3 4 #» 11 35 5
đoạn [1; 3] và thỏa mãn f (1) = 2 và f (3) = 9. Tính A. u = − ; ; . 12 12 2 3 Z #» 11 19 5 I = f 0(x) dx. B. u = − ; − ; . 12 12 2 1 ♂ 30 đề ôn thi t HKII-12 40 v 40
Những nẻo đường phù sa 2021 30 ĐỀ - ĐỀ
30 ĐỀ ÔN THI HKII-LỚP 12 2020 A. I = 11. B. I = 7. C. M = 106. D. M = 8. C. I = 2. D. I = 18. √
Câu 18. Tập nghiệm S của phương trình ( 2 − √ √ √ √
Câu 11. Trong không gian với hệ tọa độ Oxyz, cho i 3)z + i 2 =
3 + 2i 2 trên tập số phức là
ba điểm A(1; 3; 2), B(2; −1; 5), C(3; 2; −1). Tìm tọa A. S = {i}. B. S = {−5i}.
độ điểm D sao cho tứ giác ABCD là hình bình C. S = {5i}. D. S = {−12 − 5i}. hành.
Câu 19. Trong không gian với hệ tọa độ Oxyz, A. D(2; 6; 8). B. D(0; 0; 8).
cho hình hộp ABCD.A0B0C0D0, với A(−3; 0; 0), C. D(2; 6; −4). D. D(4; −2; 4).
B(0; 2; 0), D(0; 0; 1) và A0(1; 2; 3). Tìm tọa độ điểm
Câu 12. Trong không gian với hệ tọa độ Oxyz, cho C0.
mặt phẳng (P) có phương trình −2x + 3y − 5z + A. C0(10; 4; 4). B. C0(−13; 4; 4).
5 = 0. Mặt phẳng (P) có một véc-tơ pháp tuyến C. C0(13; 4; 4). D. C0(7; 4; 4). là #» #»
Câu 20. Cho số phức z = a + bi (a, b ∈ R) thỏa A. n = (−2; −3; 5). B. n = (−2; 3; 5). #» #»
mãn 7a + 4 + 2bi = −10 + (6 − 5a)i. Tính P = C. n = (2; −3; 5). D. n = (2; 3; 5). (a + b)|z|. √
Câu 13. Họ nguyên hàm của hàm số f (x) = −e−x √ 72 2 A. P = 12 17. B. P = . là √ 49 −4 29 √ A. −e−x + C. B. −ex + C. C. P = . D. P = 24 17. 7 C. e−x + C. D. ex + C. 8 Z
Câu 14. Tập hợp các điểm trong mặt phẳng tọa độ Câu 21. Cho f (x + 1) dx = 10. Tính J =
biểu diễn các số phức z thỏa mãn |z + 4 − 8i| = 3 √ 1 Z
2 5 là đường tròn có phương trình f (5x + 4) dx.
A. (x − 4)2 + (y + 8)2 = 20. √ 0
B. (x + 4)2 + (y − 8)2 = 2 5. A. J = 4. B. J = 10. √
C. (x − 4)2 + (y + 8)2 = 2 5. C. J = 32. D. J = 2.
D. (x + 4)2 + (y − 8)2 = 20.
Câu 22. Trong không gian với hệ tọa độ Oxyz, cho c c
mặt phẳng (P) có phương trình x − 2y − 2z − 5 = 0 Z Z Câu 15. Cho f (x) dx = 17 và
f (x) dx = −11 và mặt cầu (S) có phương trình (x − 1)2 + (y + a b
2)2 + (z + 3)2 = 4. Tìm phương trình mặt phẳng b Z với
song song với mặt phẳng (P) và đồng thời tiếp xúc a < b < c. Tính I = f (x) dx. với mặt cầu (S). a A. I = −6. B. I = 6.
A. x − 2y − 2z + 1 = 0. C. I = 28. D. I = −28.
B. −x + 2y + 2z + 5 = 0. e Z
C. x − 2y − 2z − 23 = 0. Câu 16. Tính I = x ln x dx.
D. −x + 2y + 2z + 17 = 0. 1 1 1 A. I = . B. I = (e2 − 2).
Câu 23. Trong không gian với hệ tọa độ Oxyz, cho 2 2 1
điểm I(3; 4; −5) và mặt phẳng (P) có phương trình C. I = 2. D. I = (e2 + 1). 4
2x + 6y − 3z + 4 = 0. Phương trình mặt cầu (S) có 2
tâm I và tiếp xúc với mặt phẳng (P) là Z 1 … a Câu 17. Giả sử dx = ln với a, b ∈ 361 2x + 1 b
A. (x − 3)2 + (y − 4)2 + (z + 5)2 = . 1 49
N∗ và a, b < 10. Tính M = a + b2.
B. (x − 3)2 + (y − 4)2 + (z + 5)2 = 49. A. M = 28. B. M = 14.
C. (x + 3)2 + (y + 4)2 + (z − 5)2 = 49. ♂ 30 đề ôn thi t HKII-12 41 v 41
Những nẻo đường phù sa 2020 - 2021 30 ĐỀ
30 ĐỀ ÔN THI HKII-LỚP 12 361
D. (x + 3)2 + (y + 4)2 + (z − 5)2 = . Cho hàm số y 49 y = f (x) liên b
Câu 24. Cho hai số phức z tục trên đoạn 1 = 1 − i, z2 = 2 + 3i. O x 1 a c
Tính mô-đun của số phức z = z [a; b] có đồ thị 1 + z2. (H) √ A. |z| = 1. B. |z| = 5. như hình bên √ C. |z| = 5. D. |z| = 13. và c ∈ [a; b]. Gọi S là diện
Câu 25. Cho hàm số f (x) có đạo hàm liên tục trên tích của hình 1 phẳng (H) Z đoạn [−1; 1], thỏa mãn
f 0(x) dx = 5 và f (−1) = giới hạn bởi −1 đồ thị hàm số 4. Tìm f (1). y = f (x) và A. f (1) = −1. B. f (1) = 1. các C. f (1) = 9. D. f (1) = −9.
đường thẳng y = 0, x = a, x = b. Mệnh đề nào sau đây sai?
Câu 26. Trong không gian với hệ tọa độ Oxyz, cho c b Z Z
hai mặt phẳng (P), (Q) lần lượt có phương trình A. S = f (x) dx + f (x) dx.
là x + y − z = 0, x − 2y + 3z = 4 và cho điểm a c c b
M(1; −2; 5). Tìm phương trình mặt phẳng ( Z Z α) đi B. S = f (x) dx − f (x) dx.
qua điểm M và đồng thời vuông góc với hai mặt a c phẳng (P), (Q). b Z C. S = | f (x)| dx.
A. 5x + 2y − z + 14 = 0. a
B. x − 4y − 3z + 6 = 0. c c Z Z
C. x − 4y − 3z − 6 = 0. D. S = f (x) dx + f (x) dx.
D. 5x + 2y − z + 4 = 0. a b
Câu 31. Trong không gian với hệ tọa độ Oxyz,
Câu 27. Cho số phức z thỏa mãn (1 + i)z = 11 − cho ba điểm A(0; 6; 0), B(0; 0; −2) và C(−3; 0; 0).
3i. Điểm M biểu diễn số phức z trong mặt phẳng Phương trình mặt phẳng (P) đi qua ba điểm A, B, tọa độ là C là A. M(4; −7). B. M(14; −14).
A. −2x + y − 3z + 6 = 0. x y z C. M(8; −14). D. M(7; −7). B. + + = 1. 6 −2 −3
C. 2x − y + 3z + 6 = 0.
Câu 28. Tìm số phức z thỏa mãn z − (2 + 3i)z = x y z D. + + = 1. 1 − 9i. 3 −6 2 A. z = −2 + i. B. z = −2 − i.
Câu 32. Trong không gian với hệ tọa độ Oxyz, cho C. z = 2 − i. D. z = 2 + i.
ba điểm A(1; 3; 2), B(2; −1; 5) và C(3; 2; −1). Gọi #» h # » # »i # »
n = AB, AC là tích có hướng của hai véc-tơ AB # »
Câu 29. Cho số phức z thỏa (3 + 2i)z = 7 + 5i. Số #»
và AC. Tìm tọa độ véc-tơ n .
phức liên hợp z của số phức z là #» #» A. n = (15; 9; 7). B. n = (9; 3; −9). 31 1 31 1 #» #» A. z = − + i. B. z = − i. C. n = (3; −9; 9). D. n = (9; 7; 15). 5 5 5 5 31 1 31 1 C. z = − i. D. z = − + i.
Câu 33. Cho hình phẳng (H) giới hạn bởi đồ thị 13 13 13 13
hàm số y = (x − 1)3(x − 2) và trục hoành. Tính Câu 30.
diện tích S của hình phẳng (H). ♂ 30 đề ôn thi t HKII-12 42 v 42
Những nẻo đường phù sa 2021 30 ĐỀ - ĐỀ
30 ĐỀ ÔN THI HKII-LỚP 12 2020 1 A. S = 0,05. B. S = − .
Câu 40. Cho hình phẳng (H) giới hạn bởi đồ thị 20 1
hàm số y = x2 và đường thẳng y = mx với m 6= 0. C. S = − . D. S = 0,5. 5
Hỏi có bao nhiêu số nguyên dương m để diện tích 4
hình phẳng (H) là số nhỏ hơn 20? Z 2x + 1 Câu 34. Biết I = dx = a ln 2 + b ln 3 + x2 + x A. 4. B. 6. C. 3. D. 5. 2
c ln 5, với a, b, c là các số nguyên. Tính P = 2a + Câu 41. Trong không gian với hệ tọa độ Oxyz, cho 3b + 4c.
mặt phẳng (P) đi qua điểm A(1; −3; 2) và chứa #» A. P = −3. B. P = 3.
trục Oz. Gọi n = (a; b; c) là một véc-tơ pháp tuyến b + c C. P = 9. D. P = 1.
của mặt phẳng (P). Tính M = . a
Câu 35. Cho hình phẳng (H) giới hạn bởi đồ thị 1 A. M = − . B. M = 3. 3
hàm số y = sin x và các đường thẳng y = 0, x = 0, 1 C. M = . D. M = −3.
x = π. Tính diện tích S của hình phẳng (H). 3 A. S = 2. B. S = 1.
Câu 42. Cho hàm số f (x) liên tục trên đoạn 2 π 3 C. S = 0. D. S = . Z 2 [2; 3] thỏa mãn f (x) dx = 2018. Tính I =
Câu 36. Trong không gian với hệ tọa độ Oxyz, cho 2 √
hai điểm A(1; 6; −7) và B(3; 2; 1). Phương trình 3 Z
mặt phẳng trung trực của đoạn thẳng AB là x f (x2) dx. √
A. x − 2y + 4z + 2 = 0. 2 A. I = 20182. B. I = 1009.
B. x − 2y − 3z − 1 = 0. √ C. I = 4036. D. I = 2018.
C. x − 2y + 3z + 17 = 0.
D. x − 2y + 4z + 18 = 0.
Câu 43. Cho hình phẳng (H) giới hạn bởi đồ thị x − 1
Câu 37. Cho số phức z = a + bi (a, b ∈ R) thỏa của hàm số y =
và hai đường thẳng y = 2, x + 2
mãn (−2 + 2i)z = 10 + 6i. Tính P = a + b.
y = −x + 1 (phần tô đậm trong hình vẽ). A. P = 3. B. P = 5. x − 1 y y = C. P = −3. D. P = −5. x + 2
Câu 38. Cho hình phẳng (H) giới hạn bởi đồ thị √ x π các hàm số y = x cos , y = 0, x = , x = π. 2 2 y = 2
Tính thể tích V của khối tròn xoay sinh ra khi cho
hình phẳng (H) quay quanh trục Ox. π A. V = (3 2 y = −x + 1 π + 4π − 8). 6π B. V = (3 2
π − 4π − 8). 16 −5 −3 −1 O x π 1 C. V = (3 2 π + 4π − 8). 81 D. V = (3 2
π − 4π − 8).
Tính diện tích S của hình phẳng (H). 16
Câu 39. Trong không gian với hệ tọa độ Oxyz, cho A. S = 8 + 3 ln 3. B. S = 8 − 3 ln 3. #» #» #»
hai véc-tơ m = (4; 3; 1), n = (0; 0; 1). Gọi p là véc- C. S = 3 ln 3. D. S = −4 + 3 ln 3. #» #»
tơ cùng hướng với véc-tơ [m, n ] (tích có hướng của Câu 44. Trong không gian với hệ tọa độ Oxyz, cho #» #»
hai véc-tơ m và n ). Biết | #»
p | = 15, tìm tọa độ véc-tơ mặt phẳng (P) có phương trình 3x − 6y − 4z + #»p.
36 = 0. Gọi A, B, C lần lượt là giao điểm của mặt #» #» A. p = (9; −12; 0). B. p = (45; −60; 0).
phẳng (P) với các trục tọa độ Ox, Oy, Oz. Tính thể #» #» C. p = (0; 9; −12). D. p = (0; 45; −60).
tích V của khối chóp O.ABC. ♂ 30 đề ôn thi t HKII-12 43 v 43
Những nẻo đường phù sa 2020 - 2021 30 ĐỀ
30 ĐỀ ÔN THI HKII-LỚP 12 A. V = 216. B. V = 108.
Câu 50. Trong không gian với hệ tọa độ Oxyz, cho C. V = 117. D. V = 234.
ba điểm A(1; −3; 2), B(−2; −1; 5) và C(3; 2; −1).
Gọi (P) là mặt phẳng qua A và trực tâm của tam
Câu 45. Cho hàm số f (x) liên tục trên đoạn [−1; 1] giác ABC, đồng thời vuông góc với mặt phẳng
và f (x) 6= 0 với mọi x ∈ [−1; 1]. Đặt g(x) = f (x) + f (−x)
(ABC). Tìm phương trình mặt phẳng (P).
, với mọi x ∈ [−1; 1]. Mệnh đề nào f (x) · f (−x)
A. 5x + 3y + 4z − 22 = 0. sau đây đúng?
B. 5x + 3y + 4z − 4 = 0. 1 1 Z Z
C. 5x + 3y − 6z + 16 = 0. A. g(x) dx = −2 g(x) dx.
D. 5x + 3y − 6z − 8 = 0. −1 0 1 Z
BẢNG ĐÁP ÁN THAM KHẢO B. g(x) dx = 0. −1 1. 2. 3. 4. 5. 6. 7. 8. 9. 10. 11. 1 1 C B C C D D B D D B C Z Z C. g(x) dx = 2 g(x) dx.
12. 13. 14. 15. 16. 17. 18. 19. 20. 21. 22. −1 0 C C D C D B A D D D D 1 Z
23. 24. 25. 26. 27. 28. 29. 30. 31. 32. 33. D. g(x) dx = 0. B D C B A C C A C A A 0
34. 35. 36. 37. 38. 39. 40. 41. 42. 43. 44.
Câu 46. Cho hình phẳng (H) giới hạn bởi đồ thị √ B A D D B A A C B C B các hàm số y = x2 và y = x. Tính thể tích V 45. 46. 47. 48. 49. 50.
của khối tròn xoay sinh ra khi cho hình phẳng (H) C D B D D C quay quanh trục Ox. 9π 3 A. V = . B. V = . 70 10 9 3 ĐỀ ÔN SỐ 11 π C. V = . D. V = . 70 10 −2 − 3i
I. PHẦN TRẮC NGHIỆM
Câu 47. Cho số phức z thỏa mãn z + 1 = 3 − 2i
Câu 1. Điểm biểu diễn của các số phức z = 7 + bi
2. Giá trị lớn nhất của mô-đun số phức z là √ √
với b ∈ R nằm trên đường thẳng có phương trình A. 3. B. 3. C. 2. D. 2. là
Câu 48. Trong không gian với hệ trục tọa độ Oxyz, A. y = x + 7. B. y = 7.
cho ba điểm M(m; 0; 0), N(0; n; 0) và P(0; 0; p), với C. x = 7. D. y = x. 1 1
m, n, p là các số dương thay đổi thỏa mãn +
+ Câu 2. Với các số phức z thỏa mãn |z − 2 + i| = 4, m n 1
tập hợp điểm biểu diễn các số phức z là một đường
= 3. Mặt phẳng (MNP) luôn đi qua điểm p
tròn. Tìm bán kính R của đường tròn đó. 1 1 1 A. H − ; − ; − . B. G(1; 1; 1). A. R = 8. B. R = 16. 3 3 3 1 1 1 C. R = 2. D. R = 4. C. F(3; 3; 3). D. E ; ; . 3 3 3
Câu 3. Trong mặt phẳng với hệ tọa độ Oxy, cho
Câu 49 (2D3G2-4). Cho hàm số f (x) có đạo hàm các điểm A(4; 0), B(1; 4) và C(1; −1). Gọi G là
liên tục trên đoạn [0; 1] thỏa mãn f (1) = 5, trọng tâm của tam giác ABC. Biết rằng G là điểm 1 1 Z Z
biểu diễn số phức z. Mệnh đề nào sau đây là f (x) dx = 12. Tính J = x f 0(x) dx. đúng? 0 0 3 3 A. J = −17. B. J = 17. A. z = 3 − i. B. z = 3 + i. 2 2 C. J = 7. D. J = −7. C. z = 2 − i. D. z = 2 + i. ♂ 30 đề ôn thi t HKII-12 44 v 44
Những nẻo đường phù sa 2021 30 ĐỀ - ĐỀ
30 ĐỀ ÔN THI HKII-LỚP 12 2020
Câu 4. Cho ba số phức z 1 1, z2, z3 phân biệt thỏa Z
Câu 10. Biết rằng tích phân (2x + 1)ex dx = a +
mãn |z1| = |z2| = |z3| = 3 và z1 + z2 = z3. 0
Biết z1, z2, z3 lần lượt được biểu diễn bởi các điểm be với a, b ∈ Z. Tích ab bằng
A, B, C trên mặt phẳng phức. Tính góc ’ ACB. A. 1. B. −1. C. −15. D. 20. A. 150◦. B. 90◦. C. 120◦. D. 45◦.
Câu 5. Tìm nguyên hàm của hàm số f (x) = Câu 11. Trong không gian Oxyz cho điểm xex.
H(1; 2; 3). Viết phương trình mặt phẳng (P) đi Z
qua điểm H và cắt các trục tọa độ tại ba điểm phân A. f (x) dx = (x + 1)ex + C.
biệt A, B, C sao cho H là trực tâm của tam giác Z B. f (x) dx = (x − 1)ex + C. ABC. Z y z C. f (x) dx = xex + C. A. (P) : x + + = 1. 2 3 Z D. f (x) dx = x2ex + C.
B. (P) : x + 2y + 3z − 14 = 0.
C. (P) : x + y + z − 6 = 0.
Câu 6. Trong không gian Oxyz, cho hai mặt phẳng x y z D. (P) : + + = 1.
(P) : x + my + (m − 1)z + 1 = 0 và (Q) : x + y + 3 6 9
2z = 0. Tập hợp tất cả các giá trị m để hai mặt Câu 12. Người ta làm một chiếc phao bơi như
phẳng này không song song là
hình vẽ (với bề mặt có được bằng cách quay A. (0; +∞).
B. R \ {−1; 1; 2}.
đường tròn (C ) quanh trục d). Biết rằng OI = C. (−∞; 3). D. R.
30 cm, R = 5 cm. Tính thể tích V của chiếc phao.
Câu 7. Trong không gian Oxyz, cho ba điểm R
A(1; −2; 3), B(4; 2; 3), C(3; 4; 3). Gọi S1, S2, S3 là I
các mặt cầu có tâm A, B, C và bán kính lần
lượt là 3, 2, 3. Hỏi có bao nhiêu mặt phẳng qua (C ) 14 2 điểm I ; ; 3
và tiếp xúc với cả ba mặt cầu 5 5 (S1), (S2), (S3)? A. 2. B. 7. C. 0. D. 1. d O 9 0 Z Z Câu 8. Giả sử f (x) dx = 37 và g(x) dx = 16. A. V = 1500 2 cm3. B. V = 9000 2 cm3. 0 9 π π 9 C. V = 1500 Z π cm3.
D. V = 9000π cm3. Khi đó, I = [2 f (x) + 3g(x)] dx bằng 2 0 Z √ p A. 122. B. 26. C. 143. D. 58. Câu 13. Cho I = x 4 − x2 dx và t = 4 − x2. 1
Câu 9. Cho các số phức z1 = 3i, z2 = −1 − 3i Khẳng định nào sau đây sai? √
và z3 = m − 2i. Tập giá trị của tham số m để số √ t2 3 phức z A. I = 3. B. I = .
3 có mô-đun nhỏ nhất trong 3 số phức đã 2 0 √ cho là √ 3 3 Z h √ √ i t3 A. − 5; 5 . C. I = t2 dt. D. I = . 3 √ √ 0 B. − 5; 5 . 0 √ √ C. {− 5; 5}.
Câu 14. Cho (H) là hình phẳng giới hạn bởi √ √ √ D. −∞; − 5 ∪ 5; +∞.
đường cong có phương trình y = x, nửa đường √ tròn có phương trình y = 2 − x2 (với 0 ≤ x ≤ ♂ 30 đề ôn thi t HKII-12 45 v 45
Những nẻo đường phù sa 2020 - 2021 30 ĐỀ
30 ĐỀ ÔN THI HKII-LỚP 12
√2) và trục hoành (phần tô đậm trong hình vẽ). 3 0 Z Z y A. f (x) dx = 4. B. f (x) dx = 2. −3 3 √ 3 3 Z Z 2 C. f (x) dx = −2. D. f (x) dx = 2. 0 −3
Câu 19. Trong không gian với hệ tọa độ Oxyz, √ √
điểm nào dưới đây thuộc trục Oy? − O x 2 1 2 A. N(2; 0; 0). B. Q(0; 3; 2). C. P(2; 0; 3). D. M(0; −3; 0). Diện tích của (H) bằng 3π + 2 4π + 2 A. . B. .
Câu 20. Cho số phức z = 3 − 5i. Gọi a, b lần lượt 12 12 3π + 1 4π + 1
là phần thực và phần ảo của z. Tính S = a + b. C. . D. . 12 6 A. S = −8. B. S = 8. Z C. S = 2. D. S = −2. Câu 15. Biết
f (u) du = F(u) + C. Mệnh đề nào dưới đây đúng?
Câu 21. Cho số phức z1 = 1 + 2i, z2 = 3 − i. Tìm Z A.
f (2x − 1) dx = 2F(2x − 1) + C.
số phức liên hợp của số phức w = z1 + z2. Z A. w = 4 − i. B. w = 4 + i. B.
f (2x − 1) dx = 2F(x) − 1 + C. C. w = −4 + i. D. w = −4 − i. Z 1 C. f (2x − 1) dx = F(2x − 1) + C. 2
Câu 22. Cho z là một số thuần ảo khác 0. Mệnh đề Z D.
f (2x − 1) dx = F(2x − 1) + C. nào sau đây đúng? A. z là số thực.
Câu 16. Trong không gian với hệ trục tọa độ Oxyz,
B. Phần ảo của z bằng 0.
cho hai điểm A(1; −2; 3) và B(5; 4; 7). Phương trình C. z = z.
mặt cầu nhận AB làm đường kính là D. z + z = 0.
A. (x − 6)2 + (y − 2)2 + (z − 10)2 = 17. 2
B. (x − 1)2 + (y + 2)2 + (z − 3)2 = 17. Z x
Câu 23. Tính tích phân I = x2 + dx
C. (x − 3)2 + (y − 1)2 + (z − 5)2 = 17. x + 1 1
D. (x − 5)2 + (y − 4)2 + (z − 7)2 = 17. có giá trị là 10 A. I = + ln 2 − ln 3.
Câu 17. Trong không gian Oxyz, cho hai mặt 3 10
phẳng (P) : x − y − z + 6 = 0 và (Q) : 2x + 3y − B. I = + ln 2 + ln 3. 3
2z + 1 = 0. Gọi (S) là mặt cầu có tâm thuộc 10 C. I = − ln 2 + ln 3.
(Q) và cắt (P) theo giao tuyến là đường tròn tâm 3 10
E(−1; 2; 3), bán kính r = 8. Phương trình mặt cầu D. I = − ln 2 − ln 3. 3 (S) là
Câu 24. Cho hàm số f (x) liên tục trên đoạn [a; b].
A. x2 + (y + 1)2 + (z + 2)2 = 64.
Diện tích hình phẳng giới hạn bởi đường cong y =
B. x2 + (y − 1)2 + (z − 2)2 = 67.
f (x), trục hoành, các đường thẳng x = a, x = b
C. x2 + (y − 1)2 + (z + 2)2 = 3. là
D. x2 + (y + 1)2 + (z − 2)2 = 64. a b Z Z A. f (x) dx. B. f (x) dx.
Câu 18. Cho f (x) là hàm số chẵn trên R thỏa mãn b a 0 b b Z Z Z
f (x) dx = 2. Chọn mệnh đề đúng. C. | f (x)| dx. D. − f (x) dx. −3 a a ♂ 30 đề ôn thi t HKII-12 46 v 46
Những nẻo đường phù sa 2021 30 ĐỀ - ĐỀ
30 ĐỀ ÔN THI HKII-LỚP 12 2020
Câu 25. Khẳng định nào sau đây đúng?
Câu 30. Trong không gian với hệ tọa độ Oxyz, 2 2 Z Z
phương trình mặt phẳng (Oxz) là A. f (x) dx = − [ f (x) + f (−x)] dx. A. x = 0. B. x + z = 0. −2 0 2 2 C. z = 0. D. y = 0. Z Z B. f (x) dx = −2 f (x) dx.
Câu 31. Tìm hàm số F(x) biết F0(x) = sin 2x và −2 0 π 2 2 F = 1. Z Z 2 C. 2 f (x) dx = 2 f (x) dx. 1 3 A. F(x) = cos 2x + . −2 −2 2 2 2 2
B. F(x) = 2x − π + 1. Z Z D. f (x) dx = 2 f (x) dx. 1 1
C. F(x) = − cos 2x + . −2 0 2 2 D. F(x) = − cos 2x.
Câu 26. Tìm nguyên hàm của hàm số f (x) = 5x.
Câu 32. Trong không gian với hệ tọa độ Oxyz, Z A. f (x) dx = 5x ln 5 + C.
cho mặt cầu (S) có tâm I(3; 2; −1) và đi qua điểm Z
A(2; 1; 2). Mặt phẳng nào dưới đây tiếp xúc với (S) B. f (x) dx = 5x + C. tại A? Z 5x C. f (x) dx = + C.
A. x + y − 3z − 8 = 0. B. x + y − 3z + 3 = 0. ln x Z 5x
C. x + y + 3z − 9 = 0. D. x − y − 3z + 3 = 0. D. f (x) dx = + C. ln 5 Câu 33.
Câu 27. Trong không gian với hệ tọa độ Oxyz, cho Cho đồ thị hàm số y
mặt phẳng (P) : 2x + 3y + 4z − 5 = 0 và điểm y = f(x) như hình
A(1; −3; 1). Tính khoảng cách d từ điểm A đến mặt 0 Z phẳng (P). vẽ và f (x) dx = a, 8 8 −2 A. d = . B. d = . −2 9 29 O 3 x 3 8 3 Z C. d = √ . D. d = √ . f (x) dx = b. Tính 29 29 0
Câu 28. Hàm số nào dưới đây là nguyên hàm của diện tích của phần 1 hàm số f (x) = ? được gạch chéo theo 1 − x a 1 , b.
A. F(x) = − ln |4 − 4x| + 3. a + b 4 A. . B. a − b. C. b − a. D. a + b. 2
B. F(x) = − ln |1 − x| + 4.
Câu 34. Trong không gian với hệ tọa độ Oxyz, cho
C. F(x) = ln |1 − x| + 2. 1
A(1; 2; 3), B(−2; 4; 4), C(4; 0; 5). Gọi G là trọng tâm D. F(x) = ln(x2 − 2x + 1) + 5. 2
của tam giác ABC. M là điểm nằm trên mặt phẳng
Câu 29. Trong không gian với hệ trục tọa độ Oxyz, (Oxy) sao cho độ dài đoạn thẳng GM ngắn nhất. gọi (
Tính độ dài đoạn thẳng GM.
α) là mặt phẳng cắt ba trục tọa độ tại ba điểm √
A(4; 0; 0), B(0; −2; 0) và C(0; 0; 6). Phương trình A. GM = 4. B. GM = 5. √ của ( C. GM = 1. D. GM = 2. α) là x y z A. + + = 0. 4 −2 6
Câu 35. Tính diện tích S của hình phẳng giới hạn x y z B. + + = 1.
bởi đồ thị các hàm số y = |x| và y = x2 − 2. 2 −1 3 x y z 20 11 C. + + = 1. A. S = . B. S = . 4 −2 6 3 2 13
D. 3x − 6y + 2z − 1 = 0. C. S = 3. D. S = . 3 ♂ 30 đề ôn thi t HKII-12 47 v 47
Những nẻo đường phù sa 2020 - 2021 30 ĐỀ
30 ĐỀ ÔN THI HKII-LỚP 12 a 1 Z Z
Câu 36. Giá trị nào của a để
(3x2 + 2) dx = Câu 1. Tính tích phân I = x(1 + x)2 dx. 0 0 a3 + 2?
Câu 2. Tìm số phức z thỏa mãn |z| = 2 và z là số A. 1. B. 2. C. 0. D. 3. thuần ảo.
Câu 37. Trong không gian với hệ tọa độ Oxyz, cho Câu 3. Trong không gian với hệ tọa độ Oxyz, cho
A(1; −1; 0), B(0; 2; 0) và C(2; 1; 3). Tọa độ điểm M I(2; 1; 1) và mặt phẳng (P) : 2x + y + 2z + 2 = 0. # » # » # » #»
thỏa mãn MA − MB + MC = 0 là
Viết phương trình mặt phẳng qua điểm I và song A. M = (3; 2; −3). B. M = (3; −2; 3). song với mặt phẳng (P). C. M = (3; −2; −3). D. M = (3; 2; 3).
BẢNG ĐÁP ÁN THAM KHẢO 1. 2. 3. 4. 5. 6. 7. 8. 9. 10. 11.
Câu 38. Một ô tô đang đi với vận tốc lớn hơn C D D C B D D B B A B
72 km/h, phía trước là đoạn đường chỉ cho phép
12. 13. 14. 15. 16. 17. 18. 19. 20. 21. 22.
chạy với tốc độ tối đa là 72 km/h, vì thế người A B A C C B A D D A D
lái xe đạp phanh để ô tô chuyển động chậm dần
23. 24. 25. 26. 27. 28. 29. 30. 31. 32. 33.
đều với vận tốc v(t) = 30 − 2t (m/s), trong đó t A C C D C B C D C B B
là khoảng thời gian tính bằng giây kể từ lúc bắt 34. 35. 36. 37. 38. 39. 40.
đầu đạp phanh. Hỏi từ lúc bắt đầu đạp phanh đến A A A B D C A
lúc đạt tốc độ 72 km/h, ô tô đã di chuyển quãng đường là bao nhiêu mét? ĐỀ ÔN SỐ 12 A. 100 m. B. 150 m. C. 175 m. D. 125 m.
Câu 1. Cho hai số phức z = a + bi và z0 = a0 + b0i z
(z0 6= 0, a, a0, b, b0 ∈ R). Số phức có phần thực
Câu 39. Thể tích khối tròn xoay sinh ra khi quay z0 là
hình phẳng giới hạn bởi đồ thị các hàm số y = aa0 + bb0 2bb0 A. . B. .
x2 − 2x, y = 0, x = −1, x = 2 quanh trục Ox a2 + b2 a02 + b02 aa0 + bb0 a + a0 bằng C. . D. . a02 + b02 a2 + b2 16π 17π 18π 5π A. . B. . C. . D. . 5 5 5 18
Câu 2. Họ nguyên hàm của hàm số y = 2x(1 + 3x3) là
Câu 40. Thể tích của khối tròn xoay sinh ra khi
A. F(x) = x2(x + x3) + C.
cho hình phẳng giới hạn bởi parabol (P) : y = x2
B. F(x) = 2x(x + x3) + C.
và đường thẳng d : y = x xoay quanh trục Ox
C. F(x) = x2(1 + 3x2) + C. bằng 6x3 1 1 D. F(x) = x2 1 + + C. Z Z A. 5 π x2 dx − π x4 dx.
Câu 3. Trong không gian với hệ tọa độ Oxyz, hình 0 0 1 1
chiếu của điểm M(1; −3; −5) trên mặt phẳng Oxy Z Z B. π x2 dx + π x4 dx. có tọa độ là 0 0 A. (1; −3; 5). B. (1; −3; 2). 1 Z 2 C. C. (1; −3; 0). D. (1; −3; 1). π x2 − x dx. 0
Câu 4. Cho F(x) và f 0(x) lần lượt là một nguyên 1 Z
hàm và đạo hàm của hàm số f (x). Khẳng định nào D. π x2 − x dx. sau đây là sai? 0 b A. R f (x) II. PHẦN TỰ LUẬN dx = F(a) − F(b). a ♂ 30 đề ôn thi t HKII-12 48 v 48
Những nẻo đường phù sa 2021 30 ĐỀ - ĐỀ
30 ĐỀ ÔN THI HKII-LỚP 12 2020 a c c x − 2 y + 1 z Z Z Z B. = = . B. f (x) dx = f (x) dx + f (x) dx. −1 −1 1 x − 2 y − 1 z b a b C. = = . b −1 1 1 Z x + 2 y + 1 z C. dx = b − a. D. = = . −1 1 1 a b
Câu 11. Nếu F(x) + C là một nguyên hàm của Z D. f 0(x) dx = f (b) − f (a). x − 3 hàm số f (x) = và F(0) = 0 thì hằng a x2 + 2x − 3 số C bằng
Câu 5. Cho hình phẳng (S) được giới hạn bởi 3 2 x2 A. ln 3. B. − ln 3. đồ thị các hàm số (P 2 3 1) : y = x2, (P2) : y = , 4 2 3 2 8 C. ln 3. D. − ln 3. (H 3 2 1) : y = , (H . Diện tích hình phẳng x 2) : y = x
Câu 12. Tập nghiệm của bất phương trình 2x+1 > (S) bằng 0 là A. 8 ln 2. B. 12 ln 2. A. x ∈ R. B. x > −1. C. 6 ln 2. D. 4 ln 2. C. x > 1. D. x > 0.
Câu 6. Biết ax < ay ⇔ x > y. Khi đó, khẳng định Câu 13. Trong không gian với hệ tọa độ Oxyz, đúng về a là #» #» #»
cho ba véc-tơ a = (−1; 1; 0), b = (1; 1; 0), c = A. a > 0. B. 0 < a < 1.
(1; 1; 1). Trong các khẳng định sau, khẳng định nào C. a ∈ R. D. a > 1. là sai? #» #»
Câu 7. Tập hợp các giá trị của m để bất phương #» A. b ⊥ #» c . B. a ⊥ b . √ √ √ √ trình 2x + 2 +
6 − 2x ≥ m có nghiệm là C. | #» a | = √ √ 2. D. | #» c | = 3. A. 2 2 ≤ m ≤ 4. B. 0 ≤ m ≤ 2 2.
Câu 14. Cho z1 = 1 + 2i, z2 = 2 − 3i. Khi đó C. m ≥ 4. D. m ≤ 4. w = z1 − 2z2 bằng
Câu 8. Trong không gian với hệ tọa độ Oxyz, A. w = 5 + 8i. B. w = −3 + 8i. √
cho bốn điểm A(0; 2; 0), B(2; 0; 0), C(0; 0; 2) và C. w = 3 − i. D. w = −3 − 4i.
D(0; −2; 0). Số đo góc giữa hai mặt phẳng (ABC) Câu 15. Trong không gian với hệ tọa độ Oxyz, cho và (ACD) bằng
(P) : 3x − 4y + 2z + 4 = 0 và điểm A(1; −2; 3). Tính A. 45◦. B. 30◦. C. 60◦. D. 90◦.
khoảng cách từ A đến (P). √
Câu 9. Trong không gian với hệ tọa độ Oxyz, cho 5 5 21 5 A. . B. √ . C. √ . D. . 3 9
ba điểm A(a; 0; 0), B(0; b; 0), C(0; 0; c), trong đó 29 29 1 2 3
Câu 16. Trong không gian với hệ tọa độ Oxyz, mặt
a > 0, b > 0, c > 0 và + + = 7. Biết mặt a b c
phẳng (P) đi qua điểm G(1; 1; 1) và vuông góc với
phẳng (ABC) tiếp xúc với mặt cầu (S) : (x − 1)2 + đường thẳng OG có phương trình là 72 (y − 2)2 + (z − 3)2 =
. Thể tích của khối tứ diện 7 A. x + y + z − 3 = 0. B. x − y + z = 0. OABC là
C. x + y − z − 3 = 0. D. x + y + z = 0. 5 3 1 2 A. . B. . C. . D. . 6 8 6 9
Câu 17. Biết tập nghiệm của bất phương trình
Câu 10. Trong không gian với hệ tọa độ Oxyz, log ( (
2 3x − 2) > log2 6 − 5x) là (a; b). Khi đó, giá x = 2 − t trị của ab bằng đường thẳng d :
y = 1 + t , t ∈ R. Phương trình 6 12 A. 1. B. . C. . D. +∞. 5 5 z = t
Câu 18. Trong không gian với hệ tọa độ Oxyz,
chính tắc của đường thẳng d là
đường thẳng đi qua M(1; 2; 3) và song song với x + 2 y − 1 z A. = = .
trục Oy có phương trình là 1 1 1 ♂ 30 đề ôn thi t HKII-12 49 v 49
Những nẻo đường phù sa 2020 - 2021 30 ĐỀ
30 ĐỀ ÔN THI HKII-LỚP 12 x = 1 + t x = 1
Câu 25. Trong không gian với hệ tọa độ Oxyz, A. y = 2 , t ∈ R. B. y = 2 + t , t ∈ R.
cho tứ diện ABCD với A(−1; −2; 4), B(−4; −2; 0),
C(3; −2; 1), D(1; 1; 1). Đường cao của tứ diện kẻ từ z = 3 z = 3 đỉnh D bằng x = 1 x = 1 − t 1 A. . B. 1. C. 2. D. 3. C. y = 2 , t ∈ R. D. y = 2 + t , t ∈ R. 2 z = 3 + t z = 3 − t
Câu 26. Hình phẳng giới hạn bởi các đồ thị y = x, y = x2 có diện tích bằng
Câu 19. Họ nguyên hàm của hàm số y = (1 + 1 1 1 sin x)2 là A. . B. . C. . D. 1. 2 6 3 2 1 A. F(x) = x − 2 cos x − sin 2x + C.
Câu 27. Trong không gian với hệ tọa độ Oxyz, cho 3 4 3 1
mặt phẳng (P) : x − 3y + 2z + 1 = 0 và (Q) : (2m − B. F(x) = x − 2 cos x + sin 2x + C. 2 4
1)x + m(1 − 2m)y + (2m − 4)z + 14 = 0 với m là 3 1 C. F(x) = x + 2 cos x − sin 2x + C.
tham số thực. Tổng các giá trị của m để (P) và (Q) 2 4 3 1 vuông góc nhau bằng D. F(x) = x − 2 cos x − sin 2x + C. 2 4 7 5 3 1 A. − . B. − . C. − . D. − .
Câu 20. Cho số phức z = a + bi. Khi đó phần ảo 2 2 2 2 của số phức z2 bằng
Câu 28. Diện tích hình phẳng giới hạn bởi đồ thị A. b. B. a.
(P) của hàm số y = x2 − 2x + 2, tiếp tuyến của (P) C. 2ab. D. a2 − b2.
tại điểm M(3; 5) và trục Oy bằng A. 9. B. 27. C. 12. D. 4.
Câu 21. Cho số phức z = a + bi, (a, b ∈ R) thỏa |z|2 2(z + i) a
Câu 29. Trong không gian với hệ tọa độ Oxyz, cho mãn + 2iz + = 0. Khi đó bằng z 1 − i b
mặt cầu (S) : (x − 1)2 + (y − 2)2 + (z + 1)2 = 9 và 3 3 A. 5. B. − . C. . D. −5.
điểm A(3; 4; 0) thuộc (S). Phương trình mặt phẳng 5 5 Câu 22. Gọi z
tiếp diện của (S) tại A là
1, z2 là hai nghiệm của phương trình
z2 − 4z + 5 = 0. Khi đó, phần thực của w = z2 + z2 A. x + y + z − 7 = 0. 1 2 bằng
B. 2x − 2y + z + 2 = 0. A. 6. B. 8. C. 16. D. 0.
C. 2x + 2y + z − 14 = 0.
D. 2x − 2y − z + 2 = 0.
Câu 23. Trong không gian với hệ tọa độ Oxyz cho hai điểm A(
Câu 30. Cho hai số phức z = m +
2; 1; −1) và B(0; 3; 1) và mặt phẳng 3i và z0 =
(P) : x + y − z + 3 = 0. Điểm M thuộc (P) thỏa 2 − (m + 1)i. Tích các giá trị của m để zz0 là số thực # » # » mãn là
2MA − MB nhỏ nhất có hoành độ bằng A. A. 4. B. 1. C. −1. D. −4. 6. B. −6. C. 10. D. 12.
Câu 31. Cho hình phẳng (S) giới hạn bởi đồ thị
Câu 24. Trong không gian với hệ tọa độ Oxyz, √ x = 1 − t các hàm số y =
x, y = −x và x = 4. Quay hình
phẳng (S) quanh trục Ox ta được khối tròn xoay cho hai đường thẳng d : y = t , t ∈ R và có thể tích bằng z = −t 43π 38π 40π 41π A. . B. . C. . D. . x = 2t0 2 3 3 3
Câu 32. Trong không gian với hệ tọa độ Oxyz, cho d0 :
y = −1 + t0 , t0 ∈ R. Khoảng cách giữa hai
ba điểm A(−3; 4; 2), B(−5; 6; 2), C(−4; 6; −1). Tọa z = t0 # » # » # »
độ điểm D thỏa mãn AD = 2AB + 3AC là đường thẳng d và d0 là 1 √ √ 1 A. (10; 17; −7). B. (−10; −17; 7). A. √ . B. 7. C. 14. D. √ . 14 7 C. (10; −17; 7). D. (−10; 14; −7). ♂ 30 đề ôn thi t HKII-12 50 v 50
Những nẻo đường phù sa 2021 30 ĐỀ - ĐỀ
30 ĐỀ ÔN THI HKII-LỚP 12 2020 1 x − 1 y − 2 z − 3 Z ea − 1 d0 : = =
. Vị trí tương đối của d
Câu 33. Giá trị của e3x dx = (a, b là các −3 1 2 b và d0 là 0
số nguyên). Khi đó khẳng định đúng là A. song song. B. trùng nhau. A. a < b. B. a = b. C. chéo nhau. D. cắt nhau. C. a > b. D. a = −b.
Câu 42. Trong không gian với hệ tọa độ Oxyz,
Câu 34. Trong không gian với hệ tọa độ Oxyz, mặt cho hai điểm A(0; 1; 1), B(1; 2; 1) và đường thẳng
phẳng (P) : 2x − 3y + 5z = 0 có véc-tơ pháp tuyến x y + 1 z − 2 d : = = . Hoành độ của điểm M − − là 1 1 2
thuộc d sao cho diện tích tam giác MAB có giá trị A. (2; 3; 5). B. (−2; −3; −5).
nhỏ nhất có giá trị bằng C. (2; −3; 5). D. (5; −3; 2). A. 2. B. 0. C. −1. D. 1. √
Câu 35. Với x, y là hai số thực thỏa mãn x(3 + 2 3 √ Z 3 aπ a
5i) + y(1 − 2i)3 = 9 + 14i. Giá trị của 2x − 3y Câu 43. Biết rằng √ dx = với là x x2 − 3 b b bằng 2 205 172 353 94
phân số tối giản. Kết quả a + b bằng A. . B. . C. . D. . 109 61 61 109 A. 1. B. 5. C. 3. D. 7.
Câu 36. Biết phương trình z2 + mz + n = 0 (với Câu 44. Diện tích hình phẳng giới hạn bởi các đồ
m, n là tham số thực) có một nghiệm là z = 1 + i. thị y = x2 − 3x + 2, y = x − 1, x = 0, x = 2
Mô-đun của số phức w = m + ni bằng √ √ bằng A. 6. B. 8. C. 3 2. D. 2 2. 2 4 8 2 3 A. 2. B. . C. . D. . Z Z 3 3 3 Câu 37. Nếu f (x) dx = 3,
f (x) dx = 4 thì Câu 45. Cho hai số phức z1, z2 thỏa mãn |iz1 + 1 2 √ 1 3 2| = và z Z 2
2 = iz1. Giá trị nhỏ nhất của biểu f (x) dx bằng thức |z1 − z2| bằng 1 1 1 A. 7. B. 12. C. −1. D. 2. A. 2 + √ . B. 2 − √ . 2 2 √ √
Câu 38. Trong không gian với hê tọa độ Oxyz, cho 1 1 C. 2 − √ . D. 2 + √ .
điểm A(1; 2; 3). Khoảng cách từ A đến trục Oy 2 2 bằng
Câu 46. Khi quay hình phẳng giới hạn bởi y = √ √ A. 10. B. 10. C. 3. D. 2.
1 − x2 quanh trục Ox ta được một khối tròn xoay có thể tích bằng
Câu 39. Tập nghiệm của bất phương trình 4 3 3 2 π π π π log x − x < A. . B. . C. . D. . 2 1 + log 1 log9 1 có dạng S = 3 4 2 3 9 1 ; b
với a, b là những số nguyên. Mối liên hệ Câu 47. Tập nghiệm của bất phương trình a giữa ( a và b là log2 2x + 1) ≤ 1 là 1 1 A. a = b. B. a = 2b. A. −∞; . B. − ; +∞ . 2 2 C. a + b = 1. D. a = −b. 1 1 1 C. − ; . D. −∞; .
Câu 40. Phần thực của số phức z = 3 + 2i bằng 2 2 2 √ A. 13. B. 2. C. 3. D. 5.
Câu 48. Trong không gian với hệ tọa độ Oxyz, x − 1
Câu 41. Trong không gian với hệ tọa độ Oxyz, véc-tơ chỉ phương của đường thẳng d : = 5 x = −1 + 3t y − 2 z + 3 = là −8 7 cho hai đường thẳng d : y = −t , t ∈ R và #» #» A. u = (1; 2; −3). B. u = (−1; −2; 3). #» #» z = 1 − 2t C. u = (5; −8; 7). D. u = (−5; −8; 7). ♂ 30 đề ôn thi t HKII-12 51 v 51
Những nẻo đường phù sa 2020 - 2021 30 ĐỀ
30 ĐỀ ÔN THI HKII-LỚP 12
Câu 49. Khẳng định nào sau đây là sai?
Câu 3. Trong không gian Oxyz, phương trình mặt Z A. sin x dx = − cos x + C.
phẳng (P) đi qua điểm M(−2; 3; 1) và vuông góc Z
với hai mặt phẳng (Q) : x − 3y + 2z − 1 = 0; B.
sin x dx = sin x − π + C. 2
(R) : 2x + y − z − 1 = 0 là Z π C. sin x dx = − sin x + + C. 2
A. −2x + 3y + z − 10 = 0. Z D. sin x dx = sin x + C.
B. x − 3y + 2z − 1 = 0.
C. x + 5y + 7z − 20 = 0.
Câu 50. Trong không gian với hệ tọa độ Oxyz cho
D. x + 5y + 7z + 20 = 0. x = t đường thẳng ∆ :
y = 8 + 4t , t ∈ R và mặt phẳng Câu 4. Gọi x, y là hai số thực thỏa x(3 − 5i) −
y(2 − i)2 = 4 − 2i. Tính M = 2x − y. z = 3 + 2t A. M = 1. B. M = 2.
(P) : x + y + z = 7. Phương trình đường thẳng d là C. M = −2. D. M = 0.
hình chiếu vuông góc của ∆ trên (P) là √ 2 x = − 8 + 4t x = −8 − 4t Z 1
Câu 5. Để tính tích phân dx, ta đặt A. y = 15 − 5t . B. y = 5 − 5t . 2 + x2 0 z = t z = t
A. t = 2 + x2 ⇒ dt = 2x dx. x = − 8 − 4t x = 8 + 4t
B. x = 2 tan t ⇒ dx = 2(1 + tan2 t) dt. √ √ C. C. t = 2 tan x ⇒ dx = 2(1 + tan2 x) dt. y = 15 − 5t . D. y = 15 − 5t . √ √ D. x = 2 tan t ⇒ dx = 2(1 + tan2 t) dt. z = t z = t
Câu 6. Gọi z1 và z2 là hai nghiệm phức của
BẢNG ĐÁP ÁN THAM KHẢO
phương trình z2 + 4z + 29 = 0. Tính giá trị biểu 1. 2. 3. 4. 5. 6. 7. 8. 9. 10. 11. thức |z1|4 + |z2|4. C D C A D B D C D C D A. 1682. B. 58. C. 841. D. 1282.
12. 13. 14. 15. 16. 17. 18. 19. 20. 21. 22. A A B C A B B D C C A
Câu 7. Cho số phức z thỏa mãn |z + 1 − i| = |z −
23. 24. 25. 26. 27. 28. 29. 30. 31. 32. 33.
1 + 2i|. Tập hợp các điểm biểu diễn các số phức z B A D B D A C B A D B
trên mặt phẳng tọa độ là một đường thẳng. Viết
34. 35. 36. 37. 38. 39. 40. 41. 42. 43. 44.
phương trình đường thẳng đó. C C D A B A C A B D A A. 4x + 6y − 3 = 0. B. 4x − 6y + 3 = 0. 45. 46. 47. 48. 49. 50. C. 4x − 6y − 3 = 0. D. 4x + 6y + 3 = 0. B A C C D A Câu 8. Trong không gian Oxyz, cho điểm
A(1; 4; 3). Viết phương trình mặt cầu (S) có tâm A ĐỀ ÔN SỐ 13
và cắt trục Ox tại hai điểm B, C sao cho BC = 6.
A. (S) : (x − 1)2 + (y − 4)2 + (z − 3)2 = 19.
I. PHẦN TRẮC NGHIỆM
B. (S) : (x − 1)2 + (y − 4)2 + (z − 3)2 = 28.
Câu 1. Tìm m để hàm số y = x3 − 3x2 + mx − 1 có
C. (S) : (x − 1)2 + (y − 4)2 + (z − 3)2 = 26.
hai điểm cực trị x1, x2 thỏa x2 + x2 = 6. 1 2
D. (S) : (x − 1)2 + (y − 4)2 + (z − 3)2 = 34. A. m = −1. B. m = −3.
Câu 9. Trong không gian Oxyz, cho mặt cầu C. m = 3. D. m = 1.
(S) : x2 + y2 + z2 − 4x − 2z − 4 = 0 và mặt phẳng Z
Câu 2. Tìm nguyên hàm I = sin4 x cos x dx.
(P) : 2x + y − 2z + 61 = 0. Điểm M thay đổi trên sin5 x cos5 x
(S), điểm N thay đổi trên (P). Độ dài nhỏ nhất của A. + C. B. + C. 5 5 MN bằng sin5 x cos5 x C. − + C. D. − + C. A. 24. B. 21. C. 3. D. 18. 5 5 ♂ 30 đề ôn thi t HKII-12 52 v 52
Những nẻo đường phù sa 2021 30 ĐỀ - ĐỀ
30 ĐỀ ÔN THI HKII-LỚP 12 2020 m Z
B. x2 + y2 + (z − 4)2 = 14.
Câu 10. Cho tích phân I = (t − 2) dt. Với giá trị
C. x2 + y2 + (z − 4)2 = 16. 0 nào của m thì I = −2?
D. x2 + y2 + (z − 4)2 = 6. A. m = 1. B. m = −2.
Câu 19. Trong không gian Oxyz, cho hai điểm C. m = 2. D. m = −1.
A(1; 2; 3), B(−3; 0; 5). Phương trình mặt cầu (S)
Câu 11. Trong không gian Oxyz, cho ba điểm đường kính AB là
A(3; 1; −2), B(5; 3; −1), C(2, 3, −4). Tọa độ trực
A. (x + 1)2 + (y − 1)2 + (z − 4)2 = 6. tâm H của 4ABC là
B. (x − 1)2 + (y + 1)2 + (z − 4)2 = 14. A. H(7; 6; −3). B. H(3; 1; −2).
C. (x − 1)2 + (y + 1)2 + (z − 4)2 = 26. C. H(4; 2; −2). D. H(1; −2; 2).
D. (x + 1)2 + (y − 1)2 + (z − 4)2 = 24.
Câu 12. Trong không gian Oxyz, cho điểm Câu 20. Trong không gian Oxyz, cho hai mặt
M(1; 1; 0) và mặt phẳng (P) : x + y − 2z + 4 = 0. phẳng (P) : x − y + z − 7 = 0, (Q) : 3x + 2y − 12z +
Tìm tọa độ của điểm N đối xứng với M qua mặt 5 = 0. Phương trình mặt phẳng (R) đi qua gốc phẳng (P).
tọa độ O và vuông góc với hai mặt phẳng nói trên A. N(−1; −1; 4). B. N(0; 0; 2). là C. N(−2; −2; 2). D. N(1; 1; 4). A. x + 3y + z = 0. B. 2x + 3y + z = 0. C. x + 2y + z = 0. D. 3x + 2y + z = 0.
Câu 13. Cho số phức z = 2 − 3i. Tìm mô-đun của Câu 21. Tìm m để đồ thị hàm số y = x4 − 2x2 + m số phức w = 2z + (1 + i)z. √
cắt trục hoành tại 4 điểm phân biêt. A. |w| = 10. B. |w| = 4. √ √ A. 0 ≤ m < 1. B. −1 ≤ m < 0. C. |w| = 15. D. |w| = 2 2. C. −1 < m < 0. D. 0 < m < 1.
Câu 14. Diện tích hình phẳng giới hạn bởi đồ thị Câu 22. Diện tích hình phẳng giới hạn bởi các đồ
các hàm số y = sin x; y = 0; x = 0 và x = 2π là
thị các hàm số y = x4 − x + 2 và y = x2 − x + 2 A. 0. B. 2. C. 4. D. 1. là.
Câu 15. Tìm m để giá trị nhỏ nhất của hàm số 4 2 4 A. − . B. . C. 0. D. . 15 15 15
y = x3 − 3mx2 + 6 trên đoạn [0; 3] bằng 2. 3 3 31 Z Z A. m = 2. B. m = . f (x) [ f (x) − 27 Câu 23. Cho dx = −5; 2g(x)] dx = 3 C. m = 1. D. m > . 1 1 2 3 Z
Câu 16. Cho hai số phức z 9. Tính I = g(x) dx. 1; z2 thỏa mãn z1, z2 6= 0; 1 1 2 z 1 z 1 1 + z2 6= 0 và = + . Tính . A. I = 14. B. I = −14. z1 + z2 z1 z2 z2 √ √ 2 2 3 √ C. I = 7. D. I = −7. A. . B. √ . C. . D. 2 3. 2 9 3 2 Z
Câu 24. Cho hàm số f (x) có f (x) dx = 9. Tính
Câu 17. Tìm số giao điểm n của hai đồ thị 0
(C1) : y = x4 − 3x2 + 2 và (C2) : y = x2 − 2. 3 Z
A. n = 1. B. n = 4. C. n = 2. D. n = 0. f (3x) dx. 0
Câu 18. Trong không gian Oxyz, cho hai điểm 3 3 Z Z
A(1; 2; 3), B(−2; 1; 5). Phương trình mặt cầu (S) đi A. f (3x) dx = −3. B. f (3x) dx = 3.
qua A, B và tâm thuộc trục Oz có phương trình 0 0 3 3 là Z Z C. f (3x) dx = 27. D. f (3x) dx = 1.
A. x2 + y2 + (z − 4)2 = 9. 0 0 ♂ 30 đề ôn thi t HKII-12 53 v 53
Những nẻo đường phù sa 2020 - 2021 30 ĐỀ
30 ĐỀ ÔN THI HKII-LỚP 12
Câu 25. Trong không gian Oxyz, cho hai điểm
2) Viết phương trình mặt cầu (S) ngoại cầu tứ
A(−2; 3; −1), B(1; −2; −3) và (P) : 3x − 2y + z − diện ABCD.
9 = 0. Viết phương trình mặt phẳng (Q) chứa hai
BẢNG ĐÁP ÁN THAM KHẢO
điểm A, B và vuông góc với (P). 1. 2. 3. 4. 5. 6. 7. 8. 9. 10. 11.
A. x − 5y − 2z + 19 = 0. B A C C D A C D D C B
B. x + y − z − 2 = 0.
12. 13. 14. 15. 16. 17. 18. 19. 20. 21. 22. C. x + y − z + 2 = 0. A A C C A C D A B D D
D. 3x − 2y + z + 13 = 0.
23. 24. 25. 26. 27. 28. 29. 30.
Câu 26. Với các số phức z thỏa mãn |(1 + i)z + 1 − D B B D A C B D √ 7i| =
2, hãy tìm giá trị lớn nhất của |z|. A. max |z| = 3. B. max |z| = 4. ĐỀ ÔN SỐ 14 C. max |z| = 7. D. max |z| = 6.
I. PHẦN TRẮC NGHIỆM
Câu 27. Thể tích khối tròn xoay sinh ra khi cho
Câu 1. Cho số phức z = hình phẳng 2 − 3i. Tìm mô-đun của
(H) giới hạn bởi các đường y = sin x; 13 y = 0;x = 0;x = 2 số phức w = ¯z + .
π xoay quanh trục Ox là √ z √ √ 2 π π π A. 2 A. 10. B. 2 5. C. 4. D. 2 13. π . B. . C. . D. . 2 4 2
Câu 2. Trong không gian với hệ tọa độ Oxyz, cho
Câu 28. Trong không gian Oxyz, cho ba điểm mặt cầu (S): x2 + y2 − 2x + 4y − 6z − 11 = 0. Tìm
A(1; 2; 0), B(5; 3; −1), C(2; 3; −4). Tọa độ tâm K của tọa độ tâm I và bán kính R của (S).
đường tròn nội tiếp 4ABC là √ 3 1 8 8 5 A. I (1; −2; 3) , R = 3. A. K 3; , − . B. K ; ; . 5 2 3 3 3
B. I (1; −2; 3) , R = 5.√ 8 8 5 7 5 C. K ; ; − . D. K ; 3; − .
C. I (−1; 2; −3) , R = 3. 3 3 3 2 3
D. I (−1; 2; −3) , R = 5.
Câu 29. Thể tích khối tròn xoay sinh ra khi cho Z π Câu 3. Tính 4 sin 2x + dx, kết quả nào sau
hình phẳng (H) giới hạn bởi các đường y = 3 √ đây là đúng?
x x; y = 0; x = 0; x = 1 xoay quanh trục Ox là π 1 π 2π π A. −2 cos 2x + + C. A. . B. . C. . D. . 3 4 4 5 2 1 π B. − cos 2x + + C.
Câu 30. Trong không gian Oxyz, tính khoảng cách 2 3 x − 1 y + 2 z − 4 π C. − + C. giữa đường thẳng 4 cos 2x + d : = = và 3 2 −4 3 π trục Ox. D. 2 cos 2x + + C. 3 A. 1. B. 4. C. 3. D. 2.
Câu 4. Trong không gian với hệ tọa độ Oxyz, cho II. PHẦN TỰ LUẬN
(α) là mặt phẳng đi qua điểm M (1; −2; 4) và có 1 #»
véc-tơ pháp tuyến n = (2; 3; 5). Phương trình mặt Z Câu 1. Tính I = x(1 − x)14 dx. phẳng (α) là 0
A. 2x + 3y + 5z − 16 = 0. π 2
B. x − 2y + 4z − 16 = 0. Z Câu 2. Tính I = x sin 2x dx.
C. 2x + 3y + 5z + 16 = 0. 0 D. x − 2y + 4z = 0.
Câu 3. Trong không gian Oxyz, cho tứ diện ABCD 1 2
với A(8; 8; 0); B(0; 8; 8); C(8; 0; 8); D(8; 8; 8). Z
Câu 5. Tìm số thực a thỏa cos (πx) dx = 2a + 1.
1) Viết phương trình mặt phẳng (ACD). 0 ♂ 30 đề ôn thi t HKII-12 54 v 54
Những nẻo đường phù sa 2021 30 ĐỀ - ĐỀ
30 ĐỀ ÔN THI HKII-LỚP 12 2020 π + 1 1 − π A. a = . B. a = .
D. x − 4y + 2z − 8 = 0. 2 2 π + 1 1 − π C. . D. a = .
Câu 11. Gọi z0 là nghiệm phức có phần ảo âm của 2π 2π
phương trình 2z2 − 2z + 13 = 0. Trên mặt phẳng
Câu 6. Trong không gian với hệ tọa độ Oxyz, tọa độ, điểm nào dưới đây là điểm biểu diễn của
cho bốn điểm A (1; 0; 0) , B (0; −2; 0) , C (0; 0; 3) và số phức w = iz0?
D (1; −2; 3). Gọi M, N lần lượt là trung điểm của 5 1 5 1 A. M ; . B. N ; − .
AB và CD. Tìm tọa độ của trung điểm G của 4 4 4 4 MN. 5 1 5 1 C. P ; − . D. Q ; . 1 2 1 2 3 2 2 2 2 A. G ; − ; 1 . B. G ; − ; . 3 3 4 4 4
Câu 12. Trong không gian với hệ tọa độ Oxyz, cho 2 4 1 3 C. G ; − ; 2 . D. G ; −1; .
d là đường thẳng đi qua điểm M (1; 2; 3) và vuông 3 3 2 2
góc với mặt phẳng (P) : 4x + 3y − 7z + 2 = 0.
Câu 7. Trong không gian với hệ tọa độ Oxyz, cho Phương trình tham số của d là
∆ là đường thẳng đi qua điểm M (2; 0; −1) và có #» x = −1 + 4t x = 1 + 4t
véc-tơ chỉ phương u = (4; −6; 2). Phương trình A. y = −2 + 3t . B. y = 2 + 3t . chính tắc của ∆ là x + 2 y z − 1 z = −3 − 7t z = 3 − 7t A. = = . 4 −6 2 x + x = x = − 2 y z − 1 1 + 3t 1 + 4t B. = = . 2 −3 1 C. y = 2 − 4t . D. y = −2 − 3t . x − 2 y z + 1 C. = = . z = z = − 2 −3 1 3 − 7t 3 − 7t x − 4 y + 6 z − 2 D. = = .
Câu 13. Trong không gian với hệ tọa độ Oxyz, cho 2 −3 1
(Q) là mặt phẳng đi qua gốc tọa độ và vuông góc a Z √ x = −13 + 2t
Câu 8. Tìm số a > 0 thỏa ex dx = 2(e − 1). với đường thẳng d :
y = −16 + t . Phương trình 0 1 A. a = 1. B. a = . z = −2t 2 C. a = 2. D. a = 4. mặt phẳng (Q) là A. 2x + y − 2z = 0. B. 2x + y = 0.
Câu 9. Trong không gian với hệ tọa độ Oxyz, cho x + 3 y + 2 z − 6 C. 2x − y + 2z = 0. D. 2x − y − 2z = 0. hai đường thẳng d : = = và 2 3 4 2 4 Z Z x = 5 + t Câu 14. Cho f (u) du = 4 và f (v) dv = 18. d0 :
y = −1 − 4t . Tìm tọa độ giao điểm I của d 1 1 4 Z 3 z = 20 + t Tính tích phân I = f (x) − dx. x và d0. 2 A. I (−3; −2; 6). B. I (5; −1; 20). A. I = 22 − 3 ln 2. B. I = 14 + 3 ln 2. C. I (3; 7; 18). D. I (13; −33; 28). C. I = 14 − 3 ln 2. D. I = 22 + 3 ln 2.
Câu 15. Trong không gian với hệ tọa độ Oxyz, cho
Câu 10. Trong không gian với hệ tọa độ (
Oxyz, cho (P) là mặt phẳng đi qua ba điểm
γ) là mặt phẳng đi qua điểm M (3; −1; −5) đồng
thời vuông góc với hai mặt phẳng (
I (8; 0; 0) , J (0; −2; 0), K (0; 0; 4). Phương trình của α) : 3x − 2y + 2z + 7 = 0, ( mặt phẳng (P) là
β) : 5x − 4y + 3z + 1 = 0. Phương x y z trình của (γ) là A. + + = 0. 8 −2 4 x y z
A. 2x + y − 2z − 15 = 0. B. + + = 1. 4 −1 2
B. 2x + y − 2z + 15 = 0. C. x − 4y + 2z = 0. C. x + y + z + 3 = 0. ♂ 30 đề ôn thi t HKII-12 55 v 55
Những nẻo đường phù sa 2020 - 2021 30 ĐỀ
30 ĐỀ ÔN THI HKII-LỚP 12 D. x + 2y + z = 0. x = 0 x = 0 C. y = 3 + t . D. y = 3t .
Câu 16. Tìm nguyên hàm F(x) của hàm số f (x) = z = 4 + t z = 4t (ex − 1)2.
A. F(x) = 2ex (ex − 1).
Câu 22. Cho hình phẳng giới hạn bởi các đường √ 1 y =
x và y = x quay quanh trục hoành. Tính thể B. F(x) = e2x − 2ex + x + C. 2
tích V của khối tròn xoay tạo thành.
C. F(x) = e2x − 2ex + x + C. 3π π A. V = . B. V = .
D. F(x) = 2e2x − 2ex + C. 5 6 2π C. V = π. D. V = .
Câu 17. Trong không gian với hệ tọa độ Oxyz, 3
Câu 23. Trong không gian với hệ tọa độ Oxyz, cho
cho d là giao tuyến của mặt phẳng (Oyz) với mặt mặt cầu (S): (x −5)2 +(y−1)2 +(z−3)2 = 36 và
phẳng (P) : 6x − 3y + 2z − 6 = 0. Phương trình của mặt phẳng (P): x +2y +2z +5 = 0 tiếp xúc nhau. d là x = 0
Tìm tiếp điểm H của (S) và (P). x − 1 y z A. H (1; −1; −2). B. H (−3; −1; 0). A. = = . B. y = −2 − 2t . 6 −3 2 C. H (−3; 0; −1). D. H (3; −3; −1). z = 3 + 3t
Câu 24. Cho hàm số f (x) có đạo hàm liên tục x = 0 x = 0 2 Z f (x) C. y = 2t . D. y = −2 + 2t .
trên [1; 2], có f (2) = 14 và dx = 6. Tính x z = 3 + 3t z = 3 − 3t 1 2 Z 2x − 1 I = f 0(x) ln x dx.
Câu 18. Trên đồ thị (C) của hàm số y = 5x + 2 1
có bao nhiêu điểm M mà tiếp tuyến của (C) tại M A. I = 14 ln 2 − 6. B. I = 7 ln 2 − 6.
song song với đường thẳng d : 9x − 4y − 2 = 0? C. I = 7 ln 2 − 6. D. I = 14 ln 2 + 6. A. 0. B. 1. C. 2. D. 4.
Câu 25. Trong không gian với hệ tọa độ Oxyz, cho x − 3 y − 3 z đường thẳng d : = = , mặt phẳng
Câu 19. Tìm số phức liên hợp của số phức z = 1 3 2 13
(P) : x + y − z + 3 = 0 và điểm A (1; 2; −1). Đường . 12 + 5i
thẳng ∆ đi qua A, song song với mặt phẳng (P) và 13 12 5 A. z = . B. z = − i.
cắt d có phương trình là 12 − 5i 13 13 13 13 13 13 x = 1 + t x = 1 − t C. z = + i. D. z = − i. 12 5 12 5 A. y = 2 + 2t . B. y = 2 − 2t .
Câu 20. Tính diện tích S của hình phẳng giới hạn z = −1 + t z = −1 + t √
bởi đồ thị hàm số y = x x + 1 và trục hoành. x = 1 + t x = 1 + t 2 4 A. S = . B. . C. y = 2 − 2t . D. y = 2 − 2t . 15 15 1 z = −1 − t z = −1 + t C. S = . D. S = 1. 2
Câu 26. Trong không gian với hệ tọa độ Oxyz, cho
Câu 21. Trong không gian với hệ tọa độ Oxyz, cho x − 2 y + 1 z + 3 hai đường thẳng d1 : = = và
∆ là đường thẳng đi qua gốc tọa độ, vuông góc 1 2 2 x − 1 y − 1 z + 1 x − 1 d = = . Gọi M, N lần lượt là
với trục hoành và cắt đường thẳng d : = 2 : 1 2 2 1 y −
các điểm di động trên d 2 z − 1
1, d2. Tính giá trị nhỏ nhất = . Phương trình ∆ là −1 −3 của độ dài đoạn MN. √ x y z x y z √ 4 2 4 √ A. = = . B. = = . A. 4 2. B. . C. . D. 2 3. 2 −1 1 1 −2 1 3 3 ♂ 30 đề ôn thi t HKII-12 56 v 56
Những nẻo đường phù sa 2021 30 ĐỀ - ĐỀ
30 ĐỀ ÔN THI HKII-LỚP 12 2020
Câu 27. Trong không gian với hệ trục tọa độ Oxyz, Câu 4. Tính mô-đun của số phức z, biết
cho ba điểm A (1; 1; 0) , B (1; −2; 4) , C (13; 1; 0) và d (1 − 2i) z − (3 + 4i) z = 2 − 24i.
là đường thẳng mà mọi điểm của d luôn cách đều
BẢNG ĐÁP ÁN THAM KHẢO
A, B, C. Phương trình đường thẳng d là 1. 2. 3. 4. 5. 6. 7. 8. 9. 10. 11. x = 7 x = 7 D B A A D D C C C D D 1 A. y = − + 4t . B. y = 1 − 8t .
12. 13. 14. 15. 16. 17. 18. 19. 20. 21. 22. 2 B A C A B C B A B D B z = −6t z = 2 + 3t
23. 24. 25. 26. 27. 28. 29. 30. x = 1 x = 5 D A C B A C D D 1 C. y = − − 24t . D. y = 48t . 2 4 ĐỀ ÔN SỐ 15 z = + 36t z = 2 − 18t 3
Câu 28. Có tất cả bao nhiêu số phức z thỏa Câu 1. Trong không gian Oxyz, cho hai điểm √
|z + 3 − i| = 2 2 và z2 thuần ảo?
A(−1; 2; 2) và B(3; −2; −4). Khi đó mặt phẳng A. 1. B. 2. C. 3. D. 4.
trung trực của đoạn thẳng AB có phương trình là
Câu 29. Trong không gian với hệ trục tọa độ Oxyz,
A. 2x − 2y − 3z − 5 = 0. x = 0
B. 2x − 2y − 3z = 0. cho đường thẳng d : y = t , biết rằng d và
C. 2x − 2y + 3z + 1 = 0. z = 2 − t
D. 2x + 2y − 3z − 5 = 0.
trục Ox chéo nhau. Lập phương trình đường 5
vuông góc chung của d và trục Ox. Z 1
Câu 2. Biết tích phân dx = ln a. Tìm giá x = 1 x = 0 2x − 1 1 A. y = t . B. y = 2t . trị của a. A. 27. B. 9. C. 81. D. 3. z = t z = t x = 0 x = 0
Câu 3. Cho hai số phức z1 = 2 + i, z2 = 4 − 3i. Khi đó z C. y = 2 − t . D. y = t . 1 · z2 có phần ảo bằng A. 11. B. 2. C. −11. D. −2. z = t z = t
Câu 4. Trong không gian Oxyz, cho điểm A thỏa
Câu 30. Trong không gian với hệ trục tọa độ Oxyz, # » #» #» #»
mãn OA = 2 i − 3 j + 7 k . Khi đó tọa độ điểm A
cho ba điểm A (1; 1; 3) , B (−1; 3; 2) , C (−1; 2; 3). là
Hỏi có bao nhiêu mặt phẳng cách đều cả ba điểm A. (−2; 3; 7). B. (2; −3; 7). A, B, C. C. (−3; 2; 7). D. (2; 7; −3). A. 1. B. 2. C. 5. D. Vô số.
Câu 5. Cho hai hàm số y = f (x), y = g(x) liên II. PHẦN TỰ LUẬN
tục trên đoạn [a; b] và có đồ thị lần lượt là (C1), 1 Z p (C
Câu 1. Tính tích phân I = x x2 + 3 dx.
2). Công thức tính diện tích hình phẳng giới hạn
bởi (C1), (C2) và hai đường thẳng x = a, x = b 0 là 2 b b Z dx Z Z
Câu 2. Tính tích phân K = . A. S = f (x) g(x) x2 + x dx − dx. 1 a a b
Câu 3. Tính diện tích hình phẳng giới hạn bởi đồ Z B. S = [ f (x) − g(x)] dx.
thị hàm số y = x · ex và đường thẳng y = x · e. a ♂ 30 đề ôn thi t HKII-12 57 v 57
Những nẻo đường phù sa 2020 - 2021 30 ĐỀ
30 ĐỀ ÔN THI HKII-LỚP 12 b Z C. z = 4 − 5i. D. z = −4 − 5i. C. S = | f (x) − g(x)| dx.
Câu 12. Trong không gian Oxyz, góc giữa hai véc- a b #» #»
tơ u = (1; 1; −2) và v = (−2; 1; 1) bằng Z D. S = [ f (x) − g(x)] dx. A. 150◦. B. 45◦. C. 60◦. D. 120◦. a
Câu 13. Tìm các số thực x, y thỏa mãn (x + y) +
Câu 6. Số phức z = 12 − 3i có phần thực và phần (2x − y)i = 3 − 6i. ảo lần lượt bằng A. x = −1; y = −4. B. y = −1; x = 4. A. −12 và 3. B. 12 và 3. C. x = −1; y = 4. D. x = 1; y = −4. C. −3 và 12. D. 12 và −3.
Câu 14. Trong không gian Oxyz, véc-tơ nào sau
Câu 7. Cho hai số phức z1, z2 là các nghiệm của đây là một véc-tơ pháp tuyến của mặt phẳng
phương trình z2 − 6z + 13 = 0. Khi đó |z1| + |z2| (β) : 3x + 2y − 7z = 0? bằng √ √ √ √ #» A. v = (−7; 2; 3). A. 3 2. B. 2 3. C. 13. D. 2 13. #» B. a = (−3; −2; 7). #»
Câu 8. Trong không gian Oxyz, đường thẳng ∆ đi
C. b = (−3; −2; −7).
qua điểm E(−2; 7; 1) và vuông góc với mặt phẳng #» D. n = (3; 2; 7).
(α) : x − 7y + 3z + 1 = 0 có phương trình tham số #»
Câu 15. Trong không gian Oxyz, cho véc-tơ u thỏa là #» #» #» #» #» x = − 2 + t x = −2 + t
u = −4 i + 5 j + 6 k . Khi đó véc-tơ u có tọa độ là A. y = 7 + 7t . B. y = 7 − 7t . A. (−4; 5; 6). B. (4; −5; −6). z = 1 + 3t z = 1 − 3t C. (5; −4; 6). D. (−4; 6; 5). x = − 2 − t x = −2 + t
Câu 16. Tìm nguyên hàm của hàm số f (x) = x2 − C. y = 7 − 7t . D. y = 7 − 7t . 2x. z = 1 + 3t z = 1 + 3t Z x3 2x A. f (x) dx = + + C. 3 ln 2
Câu 9. Trong không gian Oxyz, đường thẳng Z 2x #» B. f (x) dx = 2x − + C.
đi qua điểm M(2; −1; 3) và nhận véc-tơ u = ln 2 Z x3 2x
(−5; 3; 4) làm véc-tơ chỉ phương có phương trình C. f (x) dx = − + C. 3 ln 2 chính tắc là Z x + 5 y − 3 z − 4 D. f (x) dx = 2x − 2x ln 2 + C. A. = = . 2 −1 3 x − 2 y + 1 z − 3
Câu 17. Trong không gian Oxyz, gọi H là hình B. = = . −5 3 4
chiếu của điểm A (−1; −1; −4) lên đường thẳng x − 2 y + 1 z − 3 x − 1 y + 1 z C. = = . ∆ : = =
. Khi đó hoành độ điểm H −5 −3 4 1 1 −2 x + 2 y − 1 z + 3 là D. = = . −5 3 4 A. 1. B. 2. C. 0. D. −2. #»
Câu 10. Trong không gian Oxyz, hai véc-tơ u = #»
Câu 18. Trên tập hợp số phức, khẳng định nào sau
(1; 2; −3) và v = (m − 1; 2m; 3) vuông góc với đây sai? nhau khi và chỉ khi
A. Phương trình z2 + 1 = 0 vô nghiệm. A. m = 1. B. m = −1.
B. Phương trình z3 + 8 = 0 có 3 nghiệm phân C. m = 2. D. m = −2. biệt.
Câu 11. Tìm số phức z thỏa mãn (3 − 2i)z − 2 =
C. Phương trình z2 − 4z + 5 = 0 có hai nghiệm z + 18i. phân biệt. A. z = −4 + 5i. B. z = 4 + 5i.
D. z2 = −4 ⇔ z = 2i hoặc z = −2i. ♂ 30 đề ôn thi t HKII-12 58 v 58
Những nẻo đường phù sa 2021 30 ĐỀ - ĐỀ
30 ĐỀ ÔN THI HKII-LỚP 12 2020
Câu 19. Cho số phức z thỏa mãn |z| + z + 5i = 25. Câu 27. Trong không gian Oxyz, cho đường thẳng Khi đó mô-đun z bằng ∆ x − 1 y + 4 z : = =
. Véc-tơ nào sau đây là một −5 2 1 A. 12. B. 10. C. 11. D. 13.
véc-tơ chỉ phương của ∆. #» #» A. a = (−5; 2; 1). B. b = (1; 2; −5).
Câu 20. Xét số phức z thỏa mãn |z + 1 − 3i| = 5. #» #» C. n = (5; 2; 1). D. v = (5; −2; 1).
Khi đó, tập hợp điểm biểu diễn số phức z là đường Z tròn có Câu 28. Xét I =
x3(3x4 + 5)6 dx. Bằng cách đặt
A. tâm I (1; −3), bán kính R = 25.
u = 3x4 + 5, khẳng định nào sau đây đúng?
B. tâm I (−1; 3), bán kính R = 25. 1 Z Z A. I = u6 du. B. I = u6 du.
C. tâm I (−1; 3), bán kính R = 5. 4 1 Z 1 Z
D. tâm I (1; −3), bán kính R = 5. C. I = u6 du. D. I = u6 du. 3 12 1 + 3i
Câu 21. Cho số phức thỏa mãn z =
.Tìm Câu 29. Cho số phức z = a + bi (a, b ∈ R) thỏa 1 − i mô-đun của w = iz + z.
mãn 3z − 2z − 6 + 10i = 0. Tính a − b. √ √ A. |w| = 2 2. B. |w| = 4 2. A. 8. B. −8. C. −4. D. 4. √ √ C. |w| = 2. D. |w| = 3 2.
Câu 30. Gọi A, B, C là các điểm trong mặt phẳng
Câu 22. Trong không gian Oxyz, cho mặt cầu Oxy theo thứ tự biểu diễn các số phức 2 + 3i, 3 + i,
(S) : x2 + y2 + z2 − 2x + 4y − 6z + 5 = 0 có bán 1 + 2i. Trọng tâm G của tam giác ABC biểu diễn số kính bằng phức z. Tìm z. A. 5. B. 3. C. 4. D. 9. A. z = 1 + i. B. z = 1 − i. C. z = 2 − 2i. D. z = 2 + 2i.
Câu 23. Trong không gian Oxyz, cho mặt cầu
có tâm I(−1; 3; 0) và tiếp xúc với mặt phẳng Câu 31. Cho hình phẳng (H) giới hạn bởi đồ thị √
(α) : 2x + y − 2z + 14 = 0. Khi đó mặt cầu có hàm số y =
4x − x2 và trục hoành. Tính thể tích phương trình là
vật thể tròn xoay tạo thành khi quay hình phẳng
A. (x − 1)2 + (y + 3)2 + z2 = 25. (H) quanh trục Ox.
B. (x + 1)2 + (y − 3)2 + z2 = 5. 34π 31π 32π 35π A. . B. . C. . D. . 3 3 3 3
C. (x − 1)2 + (y + 3)2 + z2 = 5.
D. (x + 1)2 + (y − 3)2 + z2 = 25.
Câu 32. Xét hình phẳng (H) giới hạn bởi các
đường như hình vẽ (phần gạch sọc).
Câu 24. Mô-đun của số phức z = m − 2i (m ∈ R) y là 3 √ √ (C1) : y = f (x) A. m2 − 2. B. m2 + 2. √ √ 2 C. m2 − 4. D. m2 + 4. 1 (C2) : y = g(x)
Câu 25. Trong mặt phẳng Oxy, điểm biểu diễn số x phức z = −3 + 4i là O 1 2 3 4 A. M(3; −4). B. M(−3; −4).
Diện tích hình phẳng (H) được tính theo công C. M(−3; 4). D. M(3; 4). thức 1 1 4 Z Z Z Câu 26. Tính P = e1−x dx. A. S = f (x) dx + g(x) dx. 0 0 1 A. P = e − 1. B. P = 1. 4 Z C. P = 1 − e. D. P = −1. B. S = [ f (x) − g(x)] dx. 0 ♂ 30 đề ôn thi t HKII-12 59 v 59
Những nẻo đường phù sa 2020 - 2021 30 ĐỀ
30 ĐỀ ÔN THI HKII-LỚP 12 1 4 1 Z Z Z x C. S = f (x) dx − g(x) dx. Câu 40. Tích phân dx bằng cos2 x 0 1 0 4 1 1 Z Z D. S = | f (x) − g(x)| dx. A. − (x tan x) − tan x dx. 0 0 0 1
Câu 33. Trong không gian Oxyz, phương trình 1 Z B. (x tan x) − tan x dx.
x2 + y2 + z2 − 2mx + 6y + 4mz + 6m2 − 4m + 12 = 0 0
0 là phương trình mặt cầu khi và chỉ khi 1 1 Z A. 1 ≤ m ≤ 3.
B. −3 < m < −1. C. (−x tan x) + tan x dx. 0 C. −1 < m < 3. D. 1 < m < 3. 0 1 1 3 5 Z Z Z D. (x tan x) + tan x dx. Câu 34. Cho f (x) dx = 2 và f (x) dx = 7. 0 0 1 1 5
Câu 41. Trong các số phức z thoả mãn điều kiện Z Tính I = f (x) dx.
|z + 1 − 2i| = |z − i|, tìm số phức z có mô-đun nhỏ 3 nhất. A. z = 1 + i. B. I = 9. A. z = −1 + i. B. z = −1 − i. C. I = −5. D. I = 5. C. z = 1 − i. D. z = 1 + i.
Câu 35. Tính diện tích hình phẳng giới hạn bởi Câu 42. Cho hình phẳng (H) giới hạn bởi các
đường thẳng y = 2x + 1 và đồ thị hàm số y = đường y = x2, y = 2x. Thể tích của khối tròn x2 − x + 3.
xoay được tạo thành khi quay (H) quanh trục Ox 1 1 1 1 A. . B. . C. − . D. . 8 7 6 6 bằng 64π 32π 16π 21π
Câu 36. Tính diện tích S của hình phẳng giới hạn A. . B. . C. . D. . 15 15 15 15 1 bởi các đường y =
, trục hoành và hai Câu 43. Tìm F(x) là một nguyên hàm của hàm số 2x + 3
đường thẳng x = −1, x = 2.
f (x) = 3x2 + ex − 1, biết F(0) = 2. 1 A. S = 2 ln 7. B. S = ln 7.
A. F(x) = 6x + ex − x − 1. 2√ 1 − π 2 B. F(x) = x3 + x + 1. C. S = ln 7. D. S = ln 7. ex 6 3
C. F(x) = x3 + ex − x + 1. π 2
D. F(x) = x3 + ex − x − 1. Z Câu 37. Tính I = ecos x sin x dx. e √ Z 1 + 3 ln x 0
Câu 44. Cho tích phân I = dx và A. I = e − 1. B. I = −e − 1. x 1 √ C. I = −e + 1. D. I = e + 1. đặt t =
1 + 3 ln x. Khẳng định nào sau đây đúng?
Câu 38. Trong không gian Oxyz, cho tam giác 2 2 Z Z
ABC có A(−2; 3; 1), B(4; 2; −1), C(5; −2; 0). Biết 2 2 A. I = t dt. B. I = t2 dt.
D(a; b; c) là điểm sao cho ABCD là hình bình hành, 3 3 1 1 khi đó 2a + b + c bằng 2 e 1 Z 2 Z C. I = t2 dt. D. I = t2 dt. A. 0. B. 1. C. −1. D. 2. 3 3 e 1 1 Z em + 1 Câu 39. Cho x ln x dx =
với m, n ∈ N∗. Câu 45. Họ nguyên hàm của hàm số f (x) = n 1 1 là Khi đó tổng m + n bằng x2 + x − 2 Z x + 2 A. 5. B. 6. C. 4. D. 3. A. f (x) dx = ln + C. x − 1 ♂ 30 đề ôn thi t HKII-12 60 v 60
Những nẻo đường phù sa 2021 30 ĐỀ - ĐỀ
30 ĐỀ ÔN THI HKII-LỚP 12 2020 Z 1 x + 2 B. f (x) dx = ln 1. 2. 3. 4. 5. 6. 7. 8. 9. 10. 11. + C. 3 x − 1 A D D B C D D D B C A Z x − 1 C. f (x) dx = ln + C.
12. 13. 14. 15. 16. 17. 18. 19. 20. 21. 22. x + 2 Z 1 x − 1 D C B A C B A D C D B D. f (x) dx = ln + C. 3 x + 2
23. 24. 25. 26. 27. 28. 29. 30. 31. 32. 33.
Câu 46. Trong không gian với hệ tọa độ Oxyz, cho D D C A A D A D C A D
tam giác ABC có A(1; 1; 1), đường trung tuyến kẻ
34. 35. 36. 37. 38. 39. 40. 41. 42. 43. 44.
từ B và đường cao kẻ từ C lần lượt có phương trình D D B A C B B A A C B x − 8 y + 7 z − 5 x − 7 y + 1 z − 3 45. 46. 47. 48. 49. 50. = = , = = . 10 −9 5 2 5 −1 D A A C C B
Biết B (a; b; c), khi đó a + b + c bằng A. 0. B. 1. C. −2. D. 2. ĐỀ ÔN SỐ 16 b Z Câu 47. Biết
(2x + 1) dx = 1. Khẳng định nào
I. PHẦN TRẮC NGHIỆM a sau đây đúng?
Câu 1. Trong không gian Oxyz, cho vật thể (H)
A. b2 − a2 = a − b + 1.
giới hạn bởi hai mặt phẳng có phương trình x = a
B. b2 − a2 = b − a + 1.
và x = b (a < b). Gọi f (x) là diện tích thiết diện
C. b2 − a2 = b − a − 1.
của (H) bị cắt bởi mặt phẳng vuông góc với trục
D. b2 − a2 = a − b − 1.
Ox tại điểm có hoành độ là x, với a ≤ x ≤ b. Biết
Câu 48. Tìm họ nguyên hàm của hàm số f (x) = hàm số y = f (x) liên tục trên đoạn [a; b], khi đó thể x
tích V của vật thể (H) được cho bởi công thức sin 2x. Z 1 1 b A. x sin 2x dx = − x cos 2x − sin 2x + C. Z 2 4 A. V = π ( f (x))2 dx. Z 1 1 B. x sin 2x dx = x cos 2x − sin 2x + C. a 2 4 b Z Z 1 1 C. x sin 2x dx = − x cos 2x + sin 2x + C. B. V = π f (x) dx. 2 4 a Z 1 1 D. x sin 2x dx = x cos 2x + sin 2x + C. b 2 4 Z C. V = f (x) dx. π 3 √ a Z π 3 1 b Câu 49. Biết I = x cos x dx = − với a, b Z a b D. V = f 2(x) dx. 0 a
là các số nguyên tố. Tính S = a + b.
Câu 2. Trong không gian Oxyz, cho hai điểm A. S = 4. B. S = −4.
A(2; −1; 4) và B(−1; 3; 2). Đường thẳng AB có một C. S = 8. D. S = 5. véc-tơ chỉ phương là
Câu 50. Trong không gian Oxyz, mặt phẳng đi #» #» A. m(1; −4; 2). B. u (1; 2; 2).
qua điểm M(1; 2; −3) và vuông góc với hai mặt #» #» C. v (−3; 4; −2). D. n (1; 2; 6).
phẳng (α) : 2x − y + 4 = 0, (β) : 3y − z + 5 = 0 Câu 3. Trong không gian Oxyz, cho ba điểm có phương trình là
A(1; 0; 0), B(0; −1; 0) và C(0; 0; 2). Khoảng cách từ
A. −x + 2y + 6z + 15 = 0.
gốc tọa độ đến mặt phẳng (ABC) bằng
B. x + 2y + 6z + 13 = 0. 2 A. . B. 2.
C. x + 2y − 6z − 23 = 0. 3√ √
D. x − 2y + 6z + 21 = 0. 2 7 2 11 C. . D. . 7 11
BẢNG ĐÁP ÁN THAM KHẢO Câu 4. ♂ 30 đề ôn thi t HKII-12 61 v 61
Những nẻo đường phù sa 2020 - 2021 30 ĐỀ
30 ĐỀ ÔN THI HKII-LỚP 12 Điểm M trong hình vẽ y b a c Z Z Z C. f (x) f (x) f (x) bên là điểm biểu diễn dx = dx + dx. a c b
của số phức z. Số phức −4 x b c c Z Z Z liên hợp của iz là O D. f (x) dx = f (x) dx + f (x) dx. − a a 2 b M
Câu 11. Họ nguyên hàm của hàm số f (x) = 5x A. 2 + 4i. B. −4 + 2i. là C. −4 − 2i. D. 2 − 4i. A. 5x+1 + C. B. 5ln 5 + C.
Câu 5. Trong không gian Oxyz, cho đường thẳng 5x+1 5x C. + C. D. + C. x − 3 y + 1 z − 1 x + 1 ln 5 d : = = và điểm M(1; 2; −3). 2 1 2
Câu 12. Cho số phức z thỏa mãn iz = 7 + 4i. Mô-
Gọi H(a; b; c) là hình chiếu vuông góc của M trên đun của z bằng √
d. Giá trị của a + b + c bằng 65 A. 65. B. . A. 4. B. −2. C. 2. D. 0. 3 √ √ 5 65 Câu 6. Gọi z C. 65. D. .
1 và z2 là các nghiệm phức của 3 1 1
phương trình z2 + z + i = 0, giá trị của
Câu 13. Trong không gian Oxyz, cho hai đường + z1 z2 x y − 1 z − 3 x − 1 bằng thẳng d1 : = = và d2 : = √ 1 1 3 1 A. −i. B. 1. C. 2. D. i. y − 2 z − 4 = . Mặt phẳng chứa d 2 5 1 và song song
Câu 7. Cho các số thực x và y thỏa mãn x+2+yi=- với d2 có phương trình là
2+5i. Giá trị của x + y bằng
A. x + 2y − z − 1 = 0. B. x − y − 2z + 7 = 0. C. x + A. −1. B. 1. C. 5. D. 9.
2y − z + 1 = 0. D. x − y − 2z − 7 − 0.
Câu 14. Số phức nào dưới đây là số thuần ảo?
Câu 8. Trong không gian Oxyz, cho mặt cầu √ A. z = 2. B. z = −1 + i.
(S) : x2 + y2 + z2 − 2x + 4y + 6z + 10 = 0 và mặt √ √ C. z = 2i. D. z = 2 + i.
phẳng (P) : 2x − y + 2z − 4 = 0. Mệnh đề nào sau đây đúng?
Câu 15. Trong không gian Oxyz, mặt phẳng
A. (P) cắt và không đi qua tâm của (S).
(P) : 3x + 4y + 5z + 8 = 0 và đường thẳng d là
B. (P) tiếp xúc với (S).
giao tuyến của hai mặt phẳng (α) : x − 2y + 1 = 0,
C. (P) không có điểm chung với (S).
(β) : x − 2z − 3 = 0. Góc giữa d và (P) bằng
D. (P) đi qua tâm của (S). A. 45◦. B. 90◦. C. 30◦. D. 60◦.
Câu 16. Trong không gian Oxyz, cho mặt cầu
Câu 9. Cho hai số phức z1 = 2 − 7i và z2 = −4 + i. (S): x2 + y2 + z2 − 2x + 6y − 6 = 0. Bán kính của
Điểm biểu diễn số phức z1 + z2 trên mặt phẳng tọa (S) bằng
độ là điểm nào dưới đây? √ A. 46. B. 16. C. 2. D. 4. A. Q(−2; −6). B. P(−5; −3). √ C. N(6; −8). D. M(3; −11).
Câu 17. Biết z1 = −1 + 2i là một nghiệm phức
của phương trình z2 + 2z + m = 0 (m là tham số
Câu 10. Cho hàm số y = f (x) liên tục trên [a; b] và thực) và z2 là nghiệm còn lại của phương trình. Giá
c ∈ [a; b]. Mệnh đề nào sau đây đúng? trị của |z b a b 1 − z2| bằng √ √ Z Z Z A. f (x) dx = f (x) dx + f (x) dx. A. 2 2. B. 2. C. 3. D. 3 3. a c c
Câu 18. Trong không gian Oxyz, cho điểm b c c Z Z Z M( B. f (x) dx = f (x) dx + f (x) dx.
4; −2; 7). Hình chiếu vuông góc của điểm M a a trên trục Ox là điểm b ♂ 30 đề ôn thi t HKII-12 62 v 62
Những nẻo đường phù sa 2021 30 ĐỀ - ĐỀ
30 ĐỀ ÔN THI HKII-LỚP 12 2020 A. H(0; −2; 7). B. S(4; −2; 0).
thời cách đều hai điểm A, B. Khi đó giá trị của C. R(0; 0; 7). D. K(4; 0; 0). a + b + c bằng A. −4. B. 0. C. 1. D. 4.
Câu 19. Cho hàm số f (x) xác định trên R thỏa
mãn f 0(x) = (x + 1)2, ∀x ∈ R và f (0) = 1. Giá Câu 24. Trong không gian Oxyz, cho mặt cầu
trị của biểu thức f (−1) + f (1) bằng
(S) : x2 + y2 + z2 = 16 cắt mặt phẳng (Oxy) theo 10
giao tuyến là đường tròn (C). Một hình nón có A. 4. B. . C. 2. D. 20. 3
đỉnh I(0; 0; 3) và đáy là hình tròn (C) có đường 2 sinh bằng bao nhiêu? Z 1 1 √ Câu 20. Cho + dx = a ln 2 + b ln 3 x x + 2 A. 5. B. 3. C. 4. D. 7. 1
với a, b là các số nguyên. Giá trị biểu thức a + 4b Câu 25. bằng Trên mặt phẳng tọa y A. −5. B. 7. C. −1. D. 2. độ, đường thẳng d trong hình vẽ bên là 2
Câu 21. Cho hàm số f (x) liên tục trên R và thỏa tập hợp các điểm biểu ln 2 2 d Z Z 2x + f (x) mãn f (ex) dx = 4. Khi đó dx diễn số phức z. Khi x đó |z| có giá trị nhỏ x 0 1 bằng nhất bằng O 1 A. 4. B. 6. C. 8. D. 2. A. 5 .
Câu 22. Cho hàm y = f (x) có đạo hàm liên tục 5√ B.
trên [1; 3]. Gọi (H) là hình phẳng giới hạn bởi đồ 2 5.
thị hàm số y = f 0(x) và đường thẳng y = x (phần 5 C.
gạch chéo trong hình vẽ bên). √ y 5. √ D. y = f 0(x) 5 y = x . 2 2 √ Z 1 + x2 √ Câu 26. Biết √ √ dx = a 2 + b với 2x + x x + x 1
a, b là các số nguyên. Giá trị của a + 2b bằng A. 6. B. −2. C. −1. D. 0.
Câu 27. Một ô tô đang chạy với vận tốc 10 m/s thì O x 1 2 3
người lái đạp phanh, từ thời điểm đó, ô tô chuyển
động chậm dần đều với vận tốc v(t) = −5t + 10 Diện tích hình (H) bằng
m/s. Hỏi từ lúc đạp phanh đến khi dừng hẳn, ô tô
A. 2 f (2) − f (1) − f (3) + 1.
còn di chuyển bao nhiêu mét?
B. f (3) − f (1) − 4. A. 20 m. B. 2 m.
C. 0,2 m. D. 10 m.
C. 2 f (3) − f (2) − f (1) + 1.
Câu 28. Cho hàm số f (x) có đạo hàm liên tục trên D. f (1) − f (3) + 4. 1 Z
[−1; 1] và thỏa mãn f (1) = 7, x f (x) dx = 1. Khi
Câu 23. Trong không gian Oxyz, cho đường thẳng 0 x − 1 y z 1 d : = = và hai điểm A(2; 1; 0), Z 2 1 −2 đó x2 f 0(x) dx bằng
B(−2; 3; 2). Gọi M(a; b; c) là điểm thuộc d và đồng 0 ♂ 30 đề ôn thi t HKII-12 63 v 63
Những nẻo đường phù sa 2020 - 2021 30 ĐỀ
30 ĐỀ ÔN THI HKII-LỚP 12 A. 6. B. 8. C. 5. D. 9.
12. 13. 14. 15. 16. 17. 18. 19. 20. 21. 22. C C C D D A D A C B A
Câu 29. Cho số phức z = a + bi (a, b là số thực)
23. 24. 25. 26. 27. 28. 29. 30.
thỏa mãn z + |z| − z = 5 − 8i. Giá trị của biểu thức B A B B D C B D a2 + b bằng A. −1. B. 5. C. −7. D. 12. ĐỀ ÔN SỐ 17
Câu 30. Cho số phức z = a + bi (a, b là số nguyên)
thỏa mãn (1 − 3i)z là số thực và |z − 2 + 5i| = 1. 3
Câu 1. Tìm phần ảo của số phức z = . Giá trị của a + b bằng i A. −1. B. 1. C. −3. D. 3. A. 4. B. 10. C. 12. D. 8.
Câu 2. Trong không gian Oxyz, cho mặt phẳng II. PHẦN TỰ LUẬN
(P) : x − 2y + 5z − 4 = 0. Điểm nào sau đây thuộc
Câu 1. Cho hàm số y = f (x) có đạo hàm liên tục mặt phẳng (P)?
trên đoạn [1; 3] thảo f (1) = 4, f (3) = −2. Tính tích A. A(0; 0; 4). B. B(−1; 2; 3). 3 Z phân G = f 0(x) + 1 dx. C. C(1; −2; 5). D. D(−5; −2; 1). 1
Câu 3. Tập nghiệm của phương trình x2 + 9 = 0 1
trên tập hợp số phức là tập hợp nào sau đây? Z 2x − 3
Câu 2. Tính tích phân K = dx. x + 1 A. ∅. B. {−3; 3}. 0 C. {0; 3}. D. {−3i, 3i}.
Câu 3. Tính diện tích S của hình phẳng giới hạn Câu 4. Trong không gian Oxyz, cho đường thẳng
bởi hai đường y = x2 + 3x và y = 4. x − 2 y + 1 z − 3 d : = = . Véc-tơ nào sau đây là − −
Câu 4. Cho hình phẳng (D) được giới hạn bởi các 1 3 2
một véc-tơ chỉ phương của d?
đường x = 0, x = 1, trục hoành và đường cong #» #» A. u = (1; 3; −2). B. u = (−1; 3; 2).
y = x2 + 1. Tính thể tích V của khối tròn xoay tạo #» #» C. u = (2; −1; 3). D. u = (−2; 1; −3).
thành khi quay (D) xung quanh trục Ox.
Câu 5. Họ nguyên hàm của hàm số f (x) = sin x
Câu 5. Trong không gian Oxyz, cho đường thẳng là ∆ x − 1 y z + 3 : = =
. Gọi H là hình chiếu của A. sin x + C. B. cos x + C. −2 2 −1
gốc tọa độ O trên ∆. Tính độ dài đoạn OH. C. − sin x + C. D. − cos x + C.
Câu 6. Trong không gian Oxyz, gọi
Câu 6. Trong không gian Oxyz, cho mặt cầu α là góc giữa
mặt phẳng (P) : x − y + 3 = 0 và đường thẳng (S) : (x + 1)2 + y2 + (z − 3)2 = 4. Tìm tâm I và x − 1 y z + 3 d : = = . Tính sin
bán kính r của mặt cầu (S). α. 2 3 −2
A. I(1; 0; −3), r = 4.
B. I(−1; 0; 3), r = 2.
Câu 7. Trong không gian Oxyz, viết phương trình
C. I(−1; 0; 3), r = 4.
D. I(1; 0; −3), r = 2.
mặt cầu đường kính AB với A(1; −3; 4), B(3; 3; 2).
Câu 7. Điểm biểu diễn của số phức z = 2 − 3i trên
Câu 8. Trong không gian Oxyz, cho tam giác ABC mặt phẳng Oxy là điểm nào sau đây?
với A(2; 0; 0), B(0; 1; 0), C(0; 0; 5). Viết phương A. (−2; 3). B. (−3; 2).
trình tham số đường cao của tam giác ABC đi qua C. (2; 3). D. (2; −3). đỉnh A.
Câu 8. Họ nguyên hàm của hàm số f (x) = ex là
BẢNG ĐÁP ÁN THAM KHẢO biểu thức nào sau đây? A. ln |x| + C. B. −ex + C. 1. 2. 3. 4. 5. 6. 7. 8. 9. 10. 11. 1 C C A A B B B B A D D C. ex + C. D. + C. x ♂ 30 đề ôn thi t HKII-12 64 v 64
Những nẻo đường phù sa 2021 30 ĐỀ - ĐỀ
30 ĐỀ ÔN THI HKII-LỚP 12 2020 2 Z
Câu 17. Cho hàm số f (x) liên tục trên đoạn Câu 9. Tính I = 6x2 dx.
[0; 2017] và có một nguyên hàm là F(x) = 2x + −1 2017 A. I = 18. B. I = 22. Z 2018. Tính f (x) dx. C. I = 26. D. I = 14. 0 A. I = 6052. B. I = 4068289.
Câu 10. Trong không gian Oxyz, cho mặt phẳng C. I = 8138589. D. I = 4034.
(P) : 4x − y − 3z + 7 = 0. Véc-tơ nào dưới đây là
một véc-tơ pháp tuyến của (P)?
Câu 18. Gọi z1, z2 là các nghiệm phức của phương #» #» A. n = (4; −1; 3). B. n = (−4; −1; 3).
trình 5z2 − 7z + 11 = 0. Tính T = |z1 − z2|. √ #» #» 3 19 171 C. n = (4; −3; 7). D. n = (4; −1; −3). A. . B. . 5 25 2 7 11
Câu 11. Số phức liên hợp của số phức z = là C. . D. . 1 + i 5 5
số phức nào trong các số phức dưới đây?
Câu 19. Trong không gian Oxyz, cho hai điểm −2 −2 A. . B. 1 − i. C. . D. 1 + i.
M(1; 0; −2) và N(4; 3; 0). Tính độ dài đoạn thẳng 1 − i 1 + i MN.
Câu 12. Trong không gian Oxyz, cho hai điểm √ # » A. MN = 14.
A(2; −1; 3) và B(3; 1; 2). Tọa độ AB là bộ số nào B. MN = (3; 3; 2). sau đây? √ C. N M = 22. A. (1; 0; −1). B. (1; −2; −1).
D. N M = (−3; −3; −2). C. (1; 2; −1). D. (−1; −2; 1).
Câu 20. Trong không gian Oxyz, cho đường thẳng
Câu 13. Họ nguyên hàm của hàm số f (x) = 2x + x − 1 y − 3 z + 4 d : = = . Phương trình nào dưới
1 là họ hàm số nào sau đây? 1 −2 1
đây là phương trình của đường thẳng đi qua điểm A. x2 + x + C. B. x2 + 1 + C.
M(1; −3; 6) và song song với d? C. 2x2 + 1 + C. D. 4x2 + x + C. x − 1 y + 3 z − 6 A. = = . 1 1 3 −4 Z Câu 14. Tính I = ex dx. x − 1 y + 3 z + 4 B. = = . 1 −3 6 0 x + 1 y − 3 z + 6 A. I = e2 − e. B. I = e − 1. C. = = . 1 −2 1 C. I = 1 − e. D. I = e. x − 1 y + 3 z − 6 D. = = . 5 1 −2 1 Z 1 Câu 15. Biết dx = ln a. Tính a.
Câu 21. Trong không gian Oxyz, cho hai véc-tơ 2x − 1 #» #» #» 1
u = (1; −3; 4) và v = (1; 3; 0). Tính u · #» v . A. a = 8. B. a = 3. A. (1; −3; 4). B. −8. C. a = 9. D. a = 81. C. −5. D. (1; −9; 0).
Câu 16. Trong không gian Oxyz, cho mặt phẳng Câu 22. Cho số phức z = 2 + bi. Tính z · ¯z. √
(α) : 2x − y + 3z + 4 = 0 và điểm A(2; −1; 2). Mặt A. z · ¯z = 4 + b2. B. z · ¯z = 4 − b2.
phẳng qua A song song với trục Oy và vuông góc C. z · ¯z = −b. D. z · ¯z = 4 + b2.
với (α) có phương trình là phương trình nào dưới Câu 23. Diện tích hình phẳng giới hạn bởi đồ thị đây?
hàm số y = x3 − 3x + 2 và đường thẳng y = x + 2
A. −3x − 2z + 10 = 0. bằng bao nhiêu? B. 3y − 2z − 2 = 0. A. 12. B. 0. C. 8. D. 6. C. 3x − 2z − 2 = 0. 4 Z √ D. 3x − 2y − 8 = 0. Câu 24. Tính I = x2 + 3 x dx. 1 ♂ 30 đề ôn thi t HKII-12 65 v 65
Những nẻo đường phù sa 2020 - 2021 30 ĐỀ
30 ĐỀ ÔN THI HKII-LỚP 12 √ A. I = 34. B. I = 36.
C. (x − 1)2 + (y + 1)2 + (z − 2)2 = 2 2. C. I = 35. D. I = 37.
D. (x − 3)2 + (y + 1)2 + (z − 4)2 = 8. 5 2018 Z Z Z 1 Câu 25. Cho f (x) dx = a và
f (x) dx = Câu 31. Xác định f (x) biết f (x) dx = + ex + x 1 1 C. 2018 1 Z A. f (x) = ln |x| + ex. B. f (x) = + ex. b. Khi đó,
f (x) dx bằng biểu thức nào dưới x2 1 5 C. f (x) = − + ex. D. f (x) = ln x + ex. đây? x2 A. b − a. B. −a − b.
Câu 32. Gọi S là diện tích hình phẳng giới hạn bởi C. a − b. D. a + b.
các đường y = x2 và y = 2 − x2. Đẳng thức nào
Câu 26. Trong không gian Oxyz, cho A(1; −2; 1) sau đây đúng? 1
và B(0; 1; 3). Phương trình đường thẳng đi qua hai Z A. S = 2 1 − x2 dx. điểm A, B là x + 1 y − 3 z − 2 0 A. = = . 1 −1 −2 1 Z x y − 1 z − 3 B. S = 2 1 − x2 dx. B. = = . −1 3 2 −1 x + 1 y − 2 z + 1 1 C. = = . Z −1 3 2 C. S = 2 x2 − 1 dx. x y − 1 z − 3 D. = = . 0 1 −2 1 1 Z
Câu 27. Cho số phức z có điểm biểu diễn trong D. S = 2 x2 − 1 dx.
mặt phẳng tọa độ Oxy là điểm M(−1; 5). Tính mô- −1 đun của z.
Câu 33. Tổng phần thực và phần ảo của số phức √ A. |z| = 26. B. |z| = 4. 1 + 5i √ z = bằng 2i C. |z| = 2. D. |z| = 24. A. 3. B. −2. C. 2. D. −3.
Câu 28. Họ nguyên hàm của hàm số f (x) = Câu 34. Trong không gian Oxyz, cho mặt phẳng 4x ln x là
(α) : 3x − 2y + 4z + 4 = 0 và điểm M(4; −1; 2). A. x2 (2 ln x + 1) + C.
Phương trình nào sau đây là phương trình đường
B. 4x2 (2 ln x − 1) + C.
thẳng qua M và vuông góc với mặt phẳng (α)?
C. x2 (2 ln x − 1) + C. x + 3 y − 2 z + 4 A. = = .
D. x2 (8 ln x − 16) + C. 4 −1 2 x + 4 y − 1 z + 2 Z Z B. = = . Câu 29. Đặt A = cos2 x dx, B = sin2 x dx. 3 −2 4 x − 4 y + 1 z − 2 Xác định A − B. C. = = . 1 3 −2 4
A. A − B = − · sin 2x + C. x − 3 y + 2 z − 4 2 D. = = . 4 −1 2
B. A − B = − cos 2x + C.
C. A − B = −2 cos 2x + C.
Câu 35. Trong không gian Oxyz, mặt phẳng đi 1
điểm M(1; 2; 3) và song song với mặt phẳng x + D. A − B = · sin 2x + C. 2
2y − 3z + 1 = 0 có phương trình là
Câu 30. Trong không gian Oxyz, phương trình
A. x + 2y − 3z + 2 = 0.
mặt cầu có tâm I(3; −1; 4) và đi qua điểm
B. x + 2y − 3z + 5 = 0. M(1; −1; 2) là
C. x + 2y − 3z + 4 = 0.
A. (x − 3)2 + (y + 1)2 + (z − 4)2 = 4.
D. x + 2y − 3z + 3 = 0.
B. (x + 3)2 + (y − 1)2 + (z + 4)2 = 8. ♂ 30 đề ôn thi t HKII-12 66 v 66
Những nẻo đường phù sa 2021 30 ĐỀ - ĐỀ
30 ĐỀ ÔN THI HKII-LỚP 12 2020 e Z ln x ae + b
Câu 42. Cho số phức z có điểm biểu diễn trong Câu 36. Cho dx = . Tìm S = a + x2 e
mặt phẳng tọa độ Oxy là điểm M(1; −2). Tính mô- 1 b.
đun của số phức w = i ¯z − z2. A. S = −1. B. S = −3. √ √ A. 6. B. 26. C. 26. D. 6. C. S = 1. D. S = 3.
Câu 37. Họ nguyên hàm của hàm số f (x) = 98 là
Câu 43. Trong không gian Oxyz, cho hai mặt (2x + 1)50
phẳng (P) : 7x + 3ky + mz + 2 = 0 và (Q) : kx − 1 2 A. − + C. B. − + C. my + z + (
5 = 0. Khi giao tuyến của (P) và (Q) 2x + 1)49 (2x + 1)49 1 2
vuông góc với mặt phẳng (α) : x − y − 2z − 5 = 0 C. + C. D. + C. 51(2x + 1)51 (2x + 1)51 hãy tính T = m2 + k2.
Câu 38. Gọi z1, z2, z3, z4 là các nghiệm phức của A. T = 10. B. T = 2.
phương trình z4 + z2 − 6 = 0. Tính T = z2 + z2 + 1 2 C. T = 8. D. T = 18. z2 + z2. 3 4 A. T = 2. B. T = 14. C. T = 4. D. T = −2.
Câu 44. Trong không gian Oxyz, cho đường thẳng x − 1 y + 3 z − 5
Câu 39. Các điểm biểu diễn số phức z thỏa mãn d : = = . Viết phương trình mặt 2 −1 3
z · ¯z + 3 (z − ¯z) = 5 + 12i thuộc đường nào trong cầu có tâm I(5; 1; −1) và tiếp xúc với d.
các đường cho bởi phương trình sau đây? A. y = 2x2. B. (x − 1)2 + y2 = 5.
A. (x − 5)2 + (y − 1)2 + (z + 1)2 = 56. C. y = 2x. D. y = −2x.
B. (x − 5)2 + (y − 1)2 + (z + 1)2 = 54. √
C. (x − 5)2 + (y − 1)2 + (z + 1)2 = 56.
Câu 40. Trong không gian Oxyz, cho mặt cầu
D. (x − 5)2 + (y − 1)2 + (z + 1)2 = 110.
(S) có tâm I(1; 0; −5), bán kính r = 4 và điểm
M(1; 3; −1). Các đường thẳng qua M tiếp xúc với
(S) tại các tiếp điểm thuộc đường tròn có bán kính Câu 45. Gọi (H) là hình phẳng giới hạn bởi các R bằng bao nhiêu? √
đường y = x2 − 3x, y = 0. Tính thể tích khối tròn 12 3 5 A. R = . B. R = .
xoay được tạo thành khi quay hình (H) quanh trục 5 5 5 hoành. C. R = 3. D. R = . 2 81π 85π 81 41π A. . B. . C. . D. .
Câu 41. Trong không gian Oxyz, cho hai đường 10 10 10 10 x − 1 y + 1 z − 3 thẳng d1 : = = và 2 3 −5 x = −1 + t
Câu 46. Tập hợp các điểm biểu diễn số phức z d2 :
y = 4 + 3t . Tìm phương trình mặt phẳng trong mặt phẳng tọa độ Oxy là đường thẳng có √ z = 1 + t phương trình
3x − y − 2018 = 0. Tìm giá trị nhỏ √ chứa đường thẳng d
nhất của P = z − 2 3 + 2i.
1 và song song với đường thẳng d √ √ 2. 1005 2 1013 3
A. 18x + 7y + 3z + 20 = 0. A. min P = . B. min P = . 2 3
B. 18x − 7y + 3z + 34 = 0. C. min P = 1013. D. min P = 1005.
C. 18x + 7y + 3z − 20 = 0.
D. 18x − 7y + 3z − 34 = 0. Câu 47. ♂ 30 đề ôn thi t HKII-12 67 v 67
Những nẻo đường phù sa 2020 - 2021 30 ĐỀ
30 ĐỀ ÔN THI HKII-LỚP 12 Tính thể tích của khối y
34. 35. 36. 37. 38. 39. 40. 41. 42. 43. 44. tròn xoay được tạo C C A A D A A D B A B 4 thành khi quay hình 45. 46. 47. 48. 49. 50. phẳng (H) (phần tô 2 A D B A D D
màu đen trong hình bên) 5 −2 O 1 3 x quanh trục Ox. ĐỀ ÔN SỐ 18 A. 61π .
Câu 1. Tìm nguyên hàm của hàm số f (x) = 15 √ B. x 5. 88 Z √ π 1 . A. f (x)dx = √ x 5−1 + C. 5 5 − 1 C. Z √5+1 8π B. f (x)dx = x + C. . 5 Z 1 √5+1 D. C. f (x)dx = √ x + C. 424π 5 + 1 . Z √ √ 15 D. f (x)dx = 5x 5−1 + C.
Câu 48. Cho hàm số f (x) liên tục trên [0; 1] thỏa 1
Câu 2. Trong các khẳng định sau, khẳng định nào Z
mãn 3x f (x2) − f (x) = 9x3 − 1. Tính f (x) dx. sai? Z 0 A. 0dx = C. 5 5 1 1 A. . B. . C. . D. . Z 2 4 4 8 B. dx = x + C.
Câu 49. Trong không gian Oxyz, cho mặt cầu (S) Z 1 C. xedx = xe+1 + C.
có phương trình x2 + y2 + z2 − 2x + 2y + 1 = 0. e + 1 Z 5x+1
Viết phương trình (P) đi qua hai điểm A(0; −1; 1) D. 5xdx = + C. x + 1
và B(1; −2; 1) đồng thời cắt mặt cầu (S) theo giao √ 2 Z 1
tuyến là một đường tròn có chu vi bằng 2π.
Câu 3. Tính tích phân I = dx. x6
A. x + y + 3z − 2 = 0, x + y − 5z + 6 = 0. 1 31 31
B. x + y + 3z − 2 = 0, x + y + z = 0. A. I = − . B. I = . 125 125
C. x + y − 3z + 4 = 0, x + y − z + 2 = 0. 31 24 C. I = . D. I = .
D. x + y + 1 = 0, x + y + 4z − 3 = 0. 160 125
Câu 4. Cho hàm số f (x) liên tục trên đoạn
Câu 50. Trong không gian Oxyz, cho mặt cầu [−5;3] và F(x) là một nguyên hàm của f(x), biết
(S) : x2 + y2 + z2 − 2x − 4y − 4z − 7 = 0. Gọi 15 F(−5) = 3, F(3) = . Tính tích phân I =
M(a; b; c) là điểm thuộc (S) sao cho 2a + 3b + 6c 7 3
đạt giá trị lớn nhất. Tính a + b + c. Z 81 12 [7 f (x) − x] dx. A. T = . B. T = − . 7 7 −5 11 79 A. I = 2. B. I = 11. C. T = . D. . 7 7 7 C. I = 19. D. I = . 2
BẢNG ĐÁP ÁN THAM KHẢO 1 Z 1. 2. 3. 4. 5. 6. 7. 8. 9. 10. 11.
Câu 5. Tính tích phân (4x + 3)exdx C D D B D B D C A D D 0 A. I = 3e + 1. B. I = 3e − 1.
12. 13. 14. 15. 16. 17. 18. 19. 20. 21. 22. C. I = −3e − 1. D. I = 1 − 3e. C A B B C D A C D B D
23. 24. 25. 26. 27. 28. 29. 30. 31. 32. 33.
Câu 6. Một vật chuyển động với gia tốc a(t) = C C A B A C D D C B C
6t2 + 2t (m/s2). Vận tốc ban đầu của vật là 2 (m/s). ♂ 30 đề ôn thi t HKII-12 68 v 68
Những nẻo đường phù sa 2021 30 ĐỀ - ĐỀ
30 ĐỀ ÔN THI HKII-LỚP 12 2020
Hỏi vận tốc của vật là bao nhiêu sau khi chuyển Câu 11. Một bác thợ xây bơm nước vào bể chứa
động với gia tốc đó được 2 giây?
nước. Gọi h(t) là thể tích nước bơm được sau t A. 29 m/s. B. 22 m/s.
giây. Cho h0(t) = 6at2 + 2bt và ban đầu bể không C. 18 m/s. D. 20 m/s.
có nước. Sau 3 giây thì thể tích nước trong bể là π
90 m3, sau 6 giây thì thể tích nước trong bể là 504 1 4 Z Z
m3. Tính thể tích nước trong bể sau khi bơm được Câu 7. Cho f (x)dx = 16. Tính I = f (sin 2x) · 9 giây. 0 0 cos 2xdx. A. 1458 m3. B. 1458 m3. A. I = 5. B. I = 9. C. 1458 m3. D. 1458 m3. C. I = 8. D. I = 10.
Câu 12. Cho (H) là hình phẳng giới hạn bởi
Câu 8. Hình phẳng giới hạn bởi các đường x = đường cong (C) : y = −x2 + 4x và đường thẳng
−3, x = 1, y = 0, y = x2 − x có diện tích được tính d : y = x. Tính thể tích V của vật thể tròn xoay do theo công thức
hình phẳng (H) quay quanh trục hoành. 1 81π 81π A. V = . B. V = . Z A. S = x2 − x dx. 10 5 108π 108π − C. V = . D. V = . 3 5 10 0 1 Z Z B. S = x2 − x dx − x2 − x dx.
Câu 13. Tính diện tích hình phẳng được giới hạn − bởi hai đồ thị (C 3 0
1) : y = x2 + 2x và (C2) : y = 0 1 x3. Z Z C. S = x2 − x dx + x2 − x dx. 83 15 A. S = . B. S = . − 12 4 3 0 37 9 1 C. S = . D. S = . Z 12 12 D. S = x2 − x dx.
Câu 14. Thể tích khối tròn xoay khi quay hình 0
phẳng (S) giới hạn bởi các đường y = 4 − x2, y = 0
Câu 9. Cho hình phẳng (H) giới hạn bởi các πa √
quanh trục Ox có kết quả có dạng với a, b là các đường y = x3 và y = x. Khối tròn xoay tạo ra b a
khi (H) quay quanh trục Ox có thể tích là số nguyên dương và
là phân số tối giản. Khi đó b 1
giá trị của a − 30b bằng Z A. V = π x6 − x dx. A. 62. B. 26. C. 82. D. 28. 0 1
Câu 15. Trong mặt phẳng tọa độ Oxy, cho hình Z √ B. V = π x3 − x dx.
thang ABCD với A(−2; 3), B(3; 6), C(3; 0), D(−2; 0). 0
Quay hình thang ABCD xung quanh trục Ox 1 Z √
thì thể tích khối tròn xoay tạo thành bằng bao C. V = π x − x3 dx. nhiêu? 0 1 A. 72π. B. 74π. C. 76π. D. 105π. Z D. V = π x − x6 dx.
Câu 16. Cho số phức z thỏa mãn (1 + 2i)z = 6 − 0
3i. Tìm phần thực của z. 4 9 Z x2 + 2x + 2 b Câu 10. Biết I = dx = a + 2 ln với A. 3. B. −3i. C. 0. D. . x + 2 2 5 2
Câu 17. Cho hai số phức z = 6 + 5i và z0 = 5 −
a, b là các số nguyên. Tính S = a − 2b.
4i + z. Tìm mô-đun của số phức w = z · z0. A. S = 2. B. S = 10. A. |w| = 612. B. |w| = 61. C. S = 5. D. S = 0. √ √ C. |w| = 61 2. D. |w| = 6 2. ♂ 30 đề ôn thi t HKII-12 69 v 69
Những nẻo đường phù sa 2020 - 2021 30 ĐỀ
30 ĐỀ ÔN THI HKII-LỚP 12
Câu 18. Tìm tất cả các giá trị thực của tham số m Câu 26. Cho số phức z có số phức liên hợp là z. m + 2i để số phức z = có phần thực dương.
Gọi M và M0 tương ứng, lần lượt là điểm biểu diễn m − 2i "
hình học của z và z. Hãy chọn mệnh đề đúng. m < −2 A. m > 2. B. .
A. M và M0 đối xứng qua trục thực. m > 2
B. M và M0 trùng nhau. C. −2 < m < 2. D. m < −2.
C. M và M0 đối xứng qua gốc tọa độ.
Câu 19. Cho số phức z có |z| = 9. Tập hợp các
D. M và M0 đối xứng qua trục ảo.
điểm M trong mặt phẳng tọa độ Oxy biểu diễn số Câu 27. Kí hiệu z
phức w = ¯z + 5i là một đường tròn. Tính bán kính
1, z2, z3, z4 là 4 nghiệm phức của
phương trình z4 − 5z2 − 36 = 0. Tính tổng T = đường tròn đó. 9 √ |z1| + |z2| + |z3| + |z4|. A. 9. B. . C. 3. D. 9 2. 5 A. T = 6. B. T = −4. √
Câu 20. Gọi z1 và z2 là hai nghiệm của phương C. T = 10. D. T = 6 + 2 3.
trình z2 − 2z + 7 = 0. Biết z1 − z2 có phần ảo Câu 28. Tìm số phức z thỏa mãn zi + z = 4 −
là số thực âm. Tìm phần thực của số phức w = 4i. 2z2 − z2. 1 2√ √ A. z = 4 − 4i. B. z = 3 − 4i. A. 6 6. B. −6 6. C. z = 3 + 4i. D. z = 4 + 4i. C. 5. D. −5.
Câu 29. Cho phương trình z2 + bz + c = 0 với
Câu 21. Tìm điểm M biểu diễn số phức z = i − b, c ∈ R. Xác định b và c nếu phương trình nhận 2.
z = 1 − 3i làm một nghiệm. A. M = (1; −2). B. M = (2; 1). A. b = −2, c = 10. B. b = 6, c = 10. C. M = (2; −1). D. M = (−2; 1). C. b = −6, c = −10. D. b = −6, c = 10.
Câu 22. Kí hiệu z1, z2 là các nghiệm phức của Câu 30. Trong mặt phẳng tọa độ, hãy tìm số phức
phương trình z2 − 6z + 10 = 0 (z1 có phần ảo là z có môđun nhỏ nhất, biết rằng số phức z thỏa mãn
số âm). Tìm số phức liên hợp của số phức w = √
điều kiện |z − 2 − 4i| = 5. 3z2 − 2z2 + 1. 1 2 A. z = −1 − 2i. B. z = 1 − 2i. A. w = 9 + 30i. B. w = 9 − 30i. C. z = −1 + 2i. D. z = 1 + 2i. C. w = 9 − 10i. D. w = 30 − 9i.
Câu 31. Trong không gian với hệ tọa độ Oxyz, cho
Câu 23. Tìm môđun của số phức w = (1 + z)z biết mặt cầu (S) : (x − 9)2 + (y − 1)2 + (z − 1)2 = 25.
rằng số phức z thỏa mãn biểu thức (3 + 2i)z + (2 − Tìm tâm I và tính bán kính R của (S). i)2 = 4 + i. √
A. I(9; 1; 1) và R = 5. A. |w| = 2. B. |w| = 10. √ √
B. I(9; −1; −1) và R = 5. C. |w| = 8. D. |w| = 2.
C. I(9; 1; 1) và R = 25.
Câu 24. Tìm số phức z thỏa mãn (2 + 3i)(z − 2) +
D. I(9; 1; −1) và R = 25. 13 − 13i = 0.
Câu 32. Trong không gian với hệ tọa độ Oxyz, cho A. z = 3 − 5i. B. z = 5 + 3i.
điểm A(2; 2; 1) và mặt phẳng (P) : x + 2y − 2z − C. z = 3 + 5i. D. z = 5 − 3i.
1 = 0. Viết phương trình mặt cầu tâm A và tiếp 3 + i
Câu 25. Cho số phức z =
với x ∈ R. Tổng xúc với mặt phẳng (P). x + i
phần thực và phần ảo của z là
A. (x − 2)2 + (y + 2)2 + (z + 1)2 = 3. 2x − 4 4x + 2
B. (x − 2)2 + (y − 2)2 + (z − 1)2 = 1. A. . B. . 2 2
C. (x + 2)2 + (y − 2)2 + (z − 1)2 = 1. 4x − 2 2x + 6 C. . D. . x2 + 1 x2 + 1
D. (x − 2)2 + (y + 2)2 + (z − 1)2 = 1. ♂ 30 đề ôn thi t HKII-12 70 v 70
Những nẻo đường phù sa 2021 30 ĐỀ - ĐỀ
30 ĐỀ ÔN THI HKII-LỚP 12 2020
Câu 33. Trong không gian với hệ tọa độ Oxyz, cho Câu 39. Trong không gian với hệ tọa độ Oxyz,
hai điểm A(1; 2; 3) và B(−1; 4; 1). Phương trình cho ba điểm A(3; 0; −1), B(1; −1; 3), C(0; 1; 3).
mặt cầu đường kính AB là
Viết phương trình mặt phẳng đi qua ba điểm
A. x2 + (y − 3)2 + (z − 2)2 = 3. A, B, C.
B. (x − 1)2 + (y − 2)2 + (z − 3)2 = 12.
A. 8x + 4y + 5z − 19 = 0.
C. (x + 1)2 + (y − 4)2 + (z − 1)2 = 12.
B. 10x + 3y + z − 19 = 0.
D. x2 + (y − 3)2 + (z − 2)2 = 12.
C. 2x − y + z − 3 = 0.
D. 10x − 3y − z − 21 = 0.
Câu 34. Trong không gian với hệ tọa độ Oxyz,
cho mặt cầu S(I; R) có tâm I(1; 1; 3) và bán kính Câu 40. Trong không gian với hệ tọa độ Oxyz, mặt √ R =
10. Hỏi có bao nhiêu giao điểm giữa mặt phẳng (P) cắt ba trục Ox, Oy, Oz tại A, B, C, trực
cầu (S) với các trục Ox, Oy, Oz?
tâm tam giác ABC là H(4; 5; 6). Phương trình mặt A. 1. B. 2. C. 4. D. 6. phẳng (P) là
A. 4x + 5y + 6z − 77 = 0.
Câu 35. Cho phương trình x2 + y2 + z2 − 2mx −
B. 4x + 5y + 6z + 14 = 0.
2(m + 2)y − 2(m + 3)z + 16m + 13 = 0. Tìm tất x y z C. + + = 1.
cả các giá trị thực của m để phương trình trên là 4 5 6 x y z
phương trình của một mặt cầu. D. + + = 0. 4 5 6
A. m < 0 hay m > 2.
Câu 41. Trong không gian với hệ tọa độ Oxyz,
B. m ≤ −2 hay m ≥ 0.
cho các điểm A(2; 3; 4), B(4; 6; 2), C(3; 0; 6). Gọi G
C. m < −2 hay m > 0.
là trọng tâm tam giác ABC. Biết điểm M nằm trên D. m ≤ 0 hay m ≥ 2.
mặt phẳng (Oxy) sao cho độ dài đoạn thẳng GM
nhỏ nhất. Tính độ dài đoạn thẳng GM.
Câu 36. Trong không gian với hệ tọa độ Oxyz, √
viết phương trình mặt cầu A. GM = (S) đi qua A(−1; 2; 0), 4. B. GM = 5. √ C. GM =
B(−2; 1; 1) và có tâm nằm trên trục Oz. 3. D. GM = 5 2.
A. x2 + y2 + z2 − z − 5 = 0.
Câu 42. Trong không gian với hệ tọa độ Oxyz, cho
B. x2 + y2 + z2 + 5 = 0. x = 4 − t
C. x2 + y2 + z2 − x − 5 = 0.
điểm A(1; 1; 1) và đường thẳng (d) : y = 1 − t .
D. x2 + y2 + z2 − y − 5 = 0. z = 1 + t
Câu 37. Trong không gian với hệ tọa độ Oxyz, cho Tìm tọa độ hình chiếu A0 của A trên (d). mặt phẳng ( A. A0(2; 3; 0). B. A0(−2; 3; 0).
α) : y − 2z + 4 = 0. véc-tơ nào dưới
đây là véc-tơ pháp tuyến của ( C. A0(3; 0; 2). D. A0(−3; 0; −2). α)? # » # » A. n2 = (1; −2; 0). B. n1 = (0; 1; −2).
Câu 43. Trong không gian với hệ tọa độ Oxyz, # » # » C. n3 = (1; 0; −2). D. n4 = (1; −2; 4).
cho hai mặt phẳng (P) : 3x − my − z + 7 = 0,
(Q) : 6x + 5y − 2z − 4 = 0. Xác định m để hai
Câu 38. Trong không gian với hệ tọa độ Oxyz, cho mặt phẳng (P) và (Q) song song với nhau.
hai điểm A(2; 1; −1) và B(1; 0; 1) và mặt phẳng 5
(P) : x + 2y − z + 0. Viết phương trình mặt phẳng A. m = 4. B. m = − . 2
(Q) qua A, B và vuông góc với (P). 5 C. m = −30. D. m = . 2
A. (Q) : 2x − y + 3 = 0.
Câu 44. Trong không gian với hệ tọa độ Oxyz, cho
B. (Q) : 3x − y + z − 4 = 0. x = 1 + mt
C. (Q) : −x + y + z = 0. hai đường thẳng d : y = t (t ∈ R) và
D. (Q) : 3x − y + z = 0. z = −1 + 2t ♂ 30 đề ôn thi t HKII-12 71 v 71
Những nẻo đường phù sa 2020 - 2021 30 ĐỀ
30 ĐỀ ÔN THI HKII-LỚP 12 x = 1 − t0 x = 3 − 6t x = 5 + 6t d0 :
y = 2 + 2t0 (t0 ∈ R). Giá trị của m để hai A. y = 11 − 9t . B. y = 11 − 9t . z = 3 − t0 z = 0 z = 0
đường thẳng d và d0 cắt nhau là x = 5 − 6t x = 5 − 6t A. m = −1. B. m = 1. C. y = 11 + 9t . D. y = 11 − 9t . C. m = 0. D. m = 2. z = 0 z = 0
Câu 45. Trong không gian với hệ tọa độ Oxyz, cho Câu 50.
điểm M(2; 3; 4) và mặt phẳng (P) : 2x + 3y − 7z + Một người
1 = 0. Viết phương trình đường thẳng d đi qua M có mảnh 4 A và vuông góc với (P). đất hình x − 2 y − 3 z + 7 tròn có 2 A. d : = = . 2 3 4 bán kính 5 x − 2 y − 3 z − 4 B. d : = = . m. Người 2 3 −7 −4 −2 2 4 x + 2 y + 3 z − 7 này tính C. d : = = . − 2 3 4 2 x + trồng cây 2 y + 3 z + 4 D. d : = = . B 2 3 −7 trên mảnh −4 đất đó,
Câu 46. Trong không gian với hệ tọa độ Oxyz, cho x − 1 y − 2 z − 3 biết mỗi hai đường thẳng d : = = và 3 4 5 mét vuông x − 4 y − 6 z − 8 d0 : = =
. Mệnh đề nào sau đây trồng cây 6 8 10 là đúng? thu hoạch
A. d vuông góc với d0. B. d song song với d0. được 100 C. d trùng với d0. D. d và d0 chéo nhau. nghìn.
Tuy nhiên, cần có khoảng trống để dựng chòi và đồ
Câu 47. Trong không gian với hệ tọa độ Oxyz, cho dùng nên người này căng sợi dây 6 m vào hai đầu
mặt phẳng (P) : x + y − z − 1 = 0 và đường thẳng mút dây nằm trên đường tròn xung quanh mảnh x − 1 y − 2 z − 3 d : = =
. Tìm giao điểm M của d đất. Hỏi người này thu hoạch được bao nhiêu 2 1 2 và (P).
tiền? (Tính theo đơn vị nghìn đồng và bỏ số thập phân). A. M(3; −3; −5). B. M(3; 3; −5). A. 3722. B. 7445. C. 7446. D. 3723. C. M(3; 3; 5). D. M(−3; −3; −5).
BẢNG ĐÁP ÁN THAM KHẢO
Câu 48. Trong không gian với hệ tọa độ Oxyz, cho 1. 2. 3. 4. 5. 6. 7. 8. 9. 10. 11.
A(1; 3; −2) và B(3; 5; −12). Đường thẳng AB cắt BN C D C A A B C B D D A
mặt phẳng Oyz tại N. Tính tỉ số . AN
12. 13. 14. 15. 16. 17. 18. 19. 20. 21. 22. BN BN A. = 4. B. = 2. C C A D C C B A D D A AN AN BN BN
23. 24. 25. 26. 27. 28. 29. 30. 31. 32. 33. C. = 5. D. = 3. AN AN B C C A C D A D A B A
34. 35. 36. 37. 38. 39. 40. 41. 42. 43. 44.
Câu 49. Trong không gian với hệ tọa độ Oxyz, viết C A A B B A A A C B C
phương trình hình chiếu vuông góc của đường 45. 46. 47. 48. 49. 50. x + 1 y − 2 z + 3 thẳng d : = = trên mặt phẳng 2 3 1 B C C D D B tọa độ Oxy. ♂ 30 đề ôn thi t HKII-12 72 v 72
Những nẻo đường phù sa 2021 30 ĐỀ - ĐỀ
30 ĐỀ ÔN THI HKII-LỚP 12 2020 x = 1 + 4t x = 1 + t ĐỀ ÔN SỐ 19 C. y = 4 + 3t . D. y = 2 + 4t . z = 7 + t z = −2 + 7t
I. PHẦN TRẮC NGHIỆM
Câu 7. Cho A (1; 2; 3), mặt phẳng (P) : x + y + z −
Câu 1. Cho số phức z = 3 − 2i. Tìm điểm biểu 2 = 0. Mặt phẳng (Q) song song với mặt phẳng
diễn của số phức w = z + i · z. √
(P) và (Q) cách điểm A một khoảng bằng 3 3. A. M (5; −5). B. M (1; −5).
Phương trình mặt phẳng (Q) là C. M (1; 1). D. M (5; 1).
A. x + y + z + 3 = 0 và x + y + z − 3 = 0.
Câu 2. Họ nguyên hàm của hàm số f (x) = cos 3x
B. x + y + z + 3 = 0 và x + y + z + 15 = 0. là
C. x + y + z + 3 = 0 và x + y + z − 15 = 0. 1 1 A. − · sin 3x + C. B. · sin 3x + C.
D. x + y + z + 3 = 0 và x + y − z − 15 = 0. 3 3 C. 3 sin 3x + C. D. −3 sin 3x + C. Câu 8. 2 Điểm M trong hình vẽ y Z ea − 1 Câu 3. Biết e3xdx =
. Tìm khẳng định bên là điểm biểu diễn b 0
của số phức z. Tìm phần O 3 x
đúng trong các khẳng định sau?
thực và phần ảo của số A. a + b = 10. B. a = b. phức z. C. a = 2b. D. a < b. 4 M
Câu 4. Công thức nguyên hàm nào sau đây không
A. Phần thực là −4 và phần ảo là 3. đúng? Z 1
B. Phần thực là 3 và phần ảo là −4i. A. dx = tan x + C. cos2 x
C. Phần thực là 3 và phần ảo là −4. Z ax B. axdx = + C (0 < a 6= 1).
D. Phần thực là −4 và phần ảo là 3i. ln a Z xα+1 b C. xαdx = + C (α 6= −1). Z α + 1 Câu 9. Biết
f (x)dx = 10, F(x) là một nguyên Z 1 D. dx = ln x + C. a x
hàm của f (x) và F(a) = −3. Tính F(b).
Câu 5. Trong không gian với hệ trục tọa độ Oxyz, A. F(b) = 13. B. F(b) = 10. x − 1 y + 1 z − 5 cho đường thẳng d : = = và mặt C. F(b) = 16. D. F(b) = 7. 2 −3 4
phẳng (P) : x − 3y + 2z − 5 = 0. Mệnh đề nào sau Câu 10. Tìm số phức liên hợp của số phức z = đây đúng? i(3i + 1).
A. d cắt và không vuông góc với (P). A. z = 3 − i. B. z = −3 − i.
B. d vuông góc với (P). C. z = −3 + i. D. z = 3 + i.
C. d song song với (P).
Câu 11. Biết F(x) là một nguyên hàm của hàm số D. d nằm trong (P). 4 y = f (x) = và F(0)=2. Tìm F(2). 1 + 2x
Câu 6. Phương trình tham số của đường thẳng đi A. 4 ln 5 + 2. B. 5 (1 + ln 2).
qua điểm A (1; 4; 7) và vuông góc với mặt phẳng C. 2 ln 5 + 4. D. 2(1 + ln 5).
(P) : x + 2y − 2z − 3 = 0 là
Câu 12. Diện tích hình phẳng được giới hạn bởi x = 1 + 2t x = −4 + t
đồ thị của hàm số y = x2, trục hoành và hai đường A. y = 4 + 4t . B. y = 3 + 2t . thẳng x = −1, x = 3 là 1 28 8 28 z = 7 − 4t z = −1 − 2t A. . B. . C. . D. . 3 3 3 9 ♂ 30 đề ôn thi t HKII-12 73 v 73
Những nẻo đường phù sa 2020 - 2021 30 ĐỀ
30 ĐỀ ÔN THI HKII-LỚP 12
Câu 13. Gọi z1 và z2 lần lượt là nghiệm của Câu 20. Cho đồ thị hàm số y = f (x). Diện tích
phương trình: z2 − 2z + 5 = 0. Tính P = |z1| + hình phẳng (phần tô đậm trong hình) là y |z2|. √ A. 2 5. B. 10. C. 3. D. 6. O x
Câu 14. Tính mô-đun của số phức thoả mãn: −3 4 z (2 − i) + 13i = 1. √ √ 34 5 34 A. |z| = . B. |z| = . 3 √ 2 C. |z| = 34. D. |z| = 34. 4 Z 1 A. S = f (x)dx. Z 2dx
Câu 15. Tích phân I = = ln a. Giá trị −3 3 − 2x −3 4 0 Z Z của a bằng B. S = f (x)dx + f (x)dx. A. 0 0 3. B. 2. C. 4. D. 1. 1 4 3 Z Z Z C. S = f (x)dx + f (x)dx. Câu 16. Biết f (x)dx = 12. Tính I = −3 1 0 0 4 1 Z Z Z D. S = f (x)dx − f (x)dx. f (3x) dx. −3 0 0 A. 4. B. 6. C. 36. D. 3.
Câu 21. Trong không gian với hệ trục tọa độ Oxyz,
Câu 17. F(x) là nguyên hàm của hàm số f (x) = cho ba điểm A(−2; 0; 0), B(0; 3; 0) và C(0; 0; 2). 3x + 4
Phương trình nào dưới đây là phương trình của
, (x 6= 0), biết rằng F(1) = 1. F(x) là biểu x2 mặt phẳng (ABC)? thức nào sau đây x y z x y z 4 A. + + = 1. B. + + = 1. A. F(x) = 2x + − 5. 3 2 −2 2 −2 3 x x y z x y z 4 C. + + = 1. D. + + = 1. B. F(x) = 3 ln |x| − + 5. 2 3 −2 −2 3 2 x 4
Câu 22. Phương trình nào sau đây là chính tắc C. F(x) = F(3x − + 3. x
của đường thẳng đi qua hai điểm A (1; 2; −3) và 4 D. F(x) = 3 ln |x| − + 3. x B (3; −1; 1)? x − 1 y − 2 z + 3
Câu 18. Trong hệ tọa độ Oxyz, cho hai điểm A. = = . 3 −1 1
A(2; −3; −1), B(4; −1; 2). Phương trình mặt phẳng x − 3 y + 1 z − 1 B. = = .
trung trực của đoạn thẳng AB là 1 2 −3 x − 1 y − 2 z + 3
A. 2x + 2y + 3z + 1 = 0. C. = = . 2 −3 4 15 B. x + y + z − 4x − 4y − 6z + = 0. 1 2 3 D. = = . 2 2 −3 4
C. 4x + 4y + 6z − 7 = 0. 3 + 4i D. x + y − z = 0.
Câu 23. Tìm số phức z biết z = i2019 A. z = 4 − 3i. B. z = −4 + 3i.
Câu 19. Trong không gian với hệ trục tọa độ Oxyz, x = 2 + 2t C. z = 3 − 4i. D. z = 3 + 4i. cho đường thẳng d : y = −3t
(t ∈ R). Véc- Câu 24. Trong không gian với hệ tọa độ Oxyz, cho z = −3 + 5t
mặt phẳng (P) : x − 2z + 3 = 0. Véc-tơ nào dưới
tơ nào dưới đây là véc-tơ chỉ phương của d?
đây là một véc-tơ pháp tuyến của (P)? #» #» #» #» A. u = (2; 0; −3). B. u = (2; −3; 5). A. n = (1; −2; 0). B. n = (1; 0; −2). #» #» #» #» C. u = (2; 3; −5). D. u = (2; 0; 5) . C. n = (3; −2; 1). D. n = (1; −2; 3). ♂ 30 đề ôn thi t HKII-12 74 v 74
Những nẻo đường phù sa 2021 30 ĐỀ - ĐỀ
30 ĐỀ ÔN THI HKII-LỚP 12 2020 II. PHẦN TỰ LUẬN
Câu 3. Tìm nguyên hàm của hàm số f (x) = 3x2 − √7 1. Z Z
Câu 25. Tính tích phân I = x 3 p1 + x2dx. A. f (x) dx = x3 + x + C. 0 Z B. f (x) π dx = x3 + C. 4 Z Z
Câu 26. Tính tích phân I = (3 − 2x) cos 2xdx. C. f (x) dx = x3 − x + C. 0 Z D. f (x) dx = 6x + C.
Câu 27. Giải phương trình (1 + i)z + (4 − 7i) = 8 − 4i.
Câu 4. Tìm họ nguyên hàm của hàm số f (x) =
Câu 28. Tìm số phức z thỏa mãn (3 + i) z + cos 2x.Z (1 + 2i) z = 3 − 4i. A. cos 2x dx = 2 sin 2x + C. Z 1
Câu 29. Trong không gian với hệ tọa độ Oxyz, B. cos 2x dx = − sin 2x + C. 2
cho mặt phẳng (P) : 2x − y + 2z + 4 = 0 và điểm Z C. cos 2x dx = −2 sin 2x + C. M (2; 1; 1). Z 1 D. cos 2x dx = sin 2x + C.
1) Viết phương trình đường thẳng 2 d đi qua M
và vuông góc với mặt phẳng (P).
Câu 5. Viết công thức tính thể tích V của khối tròn
xoay được tạo ra khi quay hình phẳng giới hạn bởi
2) Tìm hình chiếu vuông góc của điểm M trên đồ thị hàm số liên tục y = f (x), trục Ox và hai mặt phẳng (P).
đường thẳng x = a, x = b (a < b), xung quanh trục Ox.
3) Viết phương trình mặt cầu (S) tâm M và tiếp b b xúc với mặt phẳng Z Z (P). A. V = | f (x)| dx. B. V = f 2(x) dx. a a
BẢNG ĐÁP ÁN THAM KHẢO b b Z Z 1. 2. 3. 4. 5. 6. 7. 8. 9. 10. 11. C. V = π
f 2(x) dx. D. V = π f (x) dx. C B C D A A C C D B D a a
12. 13. 14. 15. 16. 17. 18. 19. 20. 21. 22.
Câu 6. Trong không gian với hệ tọa độ Oxyz, cho B A D A A B C B D D C
mặt phẳng (P) : 2x − y + 3z − 2 = 0. Điểm nào 23. 24. dưới đây thuộc (P)? B B A. P(1; 1; 0). B. M(1; 0; 1). C. N(0; 1; 1). D. Q(1; 1; 1). ĐỀ ÔN SỐ 20
Câu 7. Cho các hàm số f (x), g(x) liên tục trên tập
xác định. Mệnh đề nào sau đây là sai?
Câu 1. Cho số phức z = a + bi, (a, b ∈ R). Mệnh Z Z A. k f (x) dx = k f (x) dx, (k 6= 0).
đề nào sau đây sai? √ Z Z Z A. |z| = a + b là mô-đun của z. B. f (x) · g(x) dx = f (x) dx · g(x) dx. Z Z
B. z = a − bi là số phức liên hợp của z. C. [ f (x) + g(x)] dx = f (x) dx +
C. a là phần thực của z. Z g(x) dx.
D. b là phần ảo của z. Z D.
f 0(x) dx = f (x) + C, (C ∈ R).
Câu 2. Cho số phức z = 2 + i. Số phức liên hợp z
có phần thực, phần ảo lần lượt là
Câu 8. Trong không gian với hệ tọa độ Oxyz, cho A. 2 và 1. B. −2 và −1.
mặt phẳng (P) : 4x + 3z − 5 = 0. Tính khoảng cách C. −2 và 1. D. 2 và −1.
d từ điểm M(1; −1; 2) đến mặt phẳng (P). ♂ 30 đề ôn thi t HKII-12 75 v 75
Những nẻo đường phù sa 2020 - 2021 30 ĐỀ
30 ĐỀ ÔN THI HKII-LỚP 12 4 A. d = . B. d = 1.
A(1; −2; 3). Mặt phẳng qua A và vuông góc với 5 7 1
đường thẳng (d) có phương trình là C. d = . D. d = . 5 5
A. x − y + 2z − 9 = 0.
Câu 9. Trong không gian với hệ tọa độ Oxyz,
B. x − 2y + 3z − 14 = 0.
phương trình nào dưới đây là phương trình của
C. x − y + 2z + 9 = 0.
mặt phẳng đi qua điểm M(1; 2 − 1) và có một véc-
D. x − 2y + 3z − 9 = 0. #»
tơ pháp tuyến n = (2; 0; −3)?
Câu 17. Tính diện tích S của hình phẳng giới hạn A. 2x − 3z − 5 = 0. B. 2x − 3z + 5 = 0.
bởi đồ thị các hàm số y = 3x2, y = 2x + 5, x = −1
C. x + 2y − z − 6 = 0. D. x + 2y − z − 5 = 0. và x = 2.
Câu 10. Trong không gian với hệ tọa độ Oxyz, cho 256 269 A. S = . B. S = . 27 27
mặt cầu (S) : (x − 2)2 + y2 + (z + 1)2 = 4. Tọa độ C. S = 9. D. S = 27.
tâm I của mặt cầu (S) là
Câu 18. Cho số phức z, biết số phức liên hợp z = A. I(2; 1 − 1). B. I(2; 0; −1).
(1 − 2i)(1 + i)3. Điểm biểu diễn z trên mặt phẳng C. I(−2; 0; 1). D. I(−2; 1; 1).
phức Oxy là điểm nào dưới đây? Z 1
Câu 11. Tính tích phân I = 3x dx. A. P(6; −2). B. M(2; 6). 0 2 3 C. Q(6; 2). D. N(2; −6). A. I = . B. I = . ln 3 ln 3 9
Câu 19. Trong không gian với hệ tọa độ Oxyz, cho C. I = . D. I = 2 ln 3. 5
hai điểm A(3; 2; 0), B(1; 0 : −4). Mặt cầu nhận AB
Câu 12. Trong không gian với hệ tọa độ Oxyz, cho làm đường kính có phương trình là
điểm A(−2; 3; 1). Hình chiếu vuông góc của điểm
A. x2 + y2 + z2 − 4x − 2y + 4z − 15 = 0.
A lên trục Ox có tọa độ là
B. x2 + y2 + z2 + 4x + 2y − 4z − 15 = 0. A. (2; 0; 0). B. (0; −3; −1).
C. x2 + y2 + z2 − 4x − 2y + 4z + 3 = 0. C. (−2; 0; 0). D. (0; 3; 1).
D. x2 + y2 + z2 + 4x + 2y − 4z + 3 = 0.
Câu 13. Cho các hàm số f (x) và F(x) liên tục trên Z 1
Câu 20. Tính tích phân I = (2x + 1)ex dx bằng Z 1 R 0
thỏa F0(x) = f (x), ∀x ∈ R. Tính
f (x) dx biết cách đặt u = 2x + 1, dv = ex dx. Mệnh đề nào 0 F(0) = 2, F(1) = 5. dưới đây đúng? Z 1 Z 1 1 Z 1 A. f (x) dx = −3. B. f (x) dx = 7. A. I = (2x + 1)ex − 2 ex dx. 0 0 0 0 Z 1 Z 1 1 Z 1 C. f (x) dx = 1. D. f (x) dx = 3. B. I = (2x + 1)ex + e2x dx. 0 0 0 0
Câu 14. Tính mô-đun của số phức z biết z = 1 Z 1 C. I = (2x + 1)ex − e2x dx. 1 + 7i . 0 0 3 − 4i 1 Z 1 √ D. I = (2x + 1)ex + 2 ex dx. A. |z| = 25 2. B. |z| = 0. 0 √ 0 C. |z| = 2. D. |z| = 2. Z 3
Câu 21. Cho tích phân I = f (x) dx = 8. Tính 1
Câu 15. Trong không gian với hệ tọa độ Oxyz, cho Z 12 x x y + 2 z + 4 tích phân I = f dx đường thẳng (d) : = = . Một véc-tơ 4 4 3 −1 1 A. I = 12. B. I = 2.
chỉ phương của đường thẳng (d) có tọa độ là C. I = 32. D. I = 3. A. (0; −2; −4). B. (0; 2; 4).
Câu 22. Tìm tất cả các giá trị thực x, y sao cho: C. (3; −1; 1). D. (3; −1; 0).
x − 1 − yi = y + (2x − 5)i.
Câu 16. Trong không gian với hệ tọa độ Oxyz, cho A. x = 3, y = 2. B. x = 2, y = 1. x + 2 y − 2 z + 3 đường thẳng (d) : = = và điểm 1 −1 2 C. x = −2, y = −1. D. x = −2, y = 9. ♂ 30 đề ôn thi t HKII-12 76 v 76
Những nẻo đường phù sa 2021 30 ĐỀ - ĐỀ
30 ĐỀ ÔN THI HKII-LỚP 12 2020
Câu 23. Trong không gian với hệ tọa độ Oxyz, cho 4 4 A. P = − . B. P = . #» #» 9 9
a = (1; −1; 3), b = (2; 0; −1). Tìm tọa độ véc-tơ 9 9 #» #» #» C. P = . D. P = − . u = 2 a − 3 b . 4 4 #» #» A. u = (4; 2; −9). B. u = (−4; −2; 9).
Câu 29. Trong không gian với hệ tọa độ Oxyz, cho #» #» C. u = (1; 3; −11). D. u = (−4; −5; 9). x = 3 − t đường thẳng (d) (t ∈ R). Phương
Câu 24. Hàm số nào sau đây không là một nguyên : y = −1 + 2t √
hàm của f (x) = 3 x trên (0; +∞)? z = −3t √ 3 3 x4
trình nào dưới đây là phương trình chính tắc của A. F1(x) = + 1. 4√ đường thẳng (d)? 3x 3 x x − 3 y + 1 z B. F3(x) = + 3. A. = = . 4 −1 2 −3 3 4 C. F x + 3 y − 1 z 4(x) = x 3 + 4. 4 B. = = . √ −1 2 −3 3 4 x3 x + 1 y − 2 z − 3 D. F2(x) = + 2. C. = = . 4 3 −1 −3 x − 3 y + 1 z − 3
Câu 25. Cho hình phẳng D giới hạn bởi đường D. = = . −1 2 −3
cong y = sin x, trục hoành và các đường thẳng Câu 30. Trong không gian với hệ tọa độ Oxyz, mặt π x = 0,x =
. Khối tròn xoay tạo thành khi D 6
cầu tâm I(3; −1; 0), bán kính R = 5 có phương
quay quanh trục hoành có thể tích V bằng bao trình là nhiêu? √ !
A. (x + 3)2 + (y − 1)2 + z2 = 5. π π 3 A. V = − .
B. (x − 3)2 + (y + 1)2 + z2 = 5. 4 3 2 1
C. (x − 3)2 + (y + 1)2 + z2 = 25. √ B. V = 2 − 3 . 2
D. (x + 3)2 + (y − 1)2 + z2 = 25. π √ C. V = 2 − 3 . 2 √
Câu 31. Tìm họ nguyên hàm của hàm số f (x) = ! 1 π 3 D. V = − . x(x + 1)2016. 4 3 2 Z (x + 1)2018 (x + 1)2017 A. f (x) dx = − + C.
Câu 26. Trong không gian với hệ tọa độ Oxyz, 2018 2017 Z B.
f (x) dx = 2018(x + 1)2018 + 2017(x +
phương trình nào dưới đây là phương trình của một mặt cầu? 1)2017 + C.
A. x2 + y2 + z2 − 2x + 4y + 3z + 8 = 0. Z (x + 1)2018 (x + 1)2017 C. f (x) dx = + + C.
B. x2 + y2 + z2 − 2x + 4y + 3z + 7 = 0. 2018 2017 Z D.
f (x) dx = 2018(x + 1)2018 − 2017(x +
C. x2 + y2 − 2x + 4y − 1 = 0.
D. x2 + z2 − 2x + 6z − 2 = 0. 1)2017 + C. Z 2 Z 2
Câu 32. Trong không gian với hệ tọa độ Oxyz, cho Câu 27. Cho biết f (x) dx = 3 và g(x) dx = 0 0 x = 1 − t Z 2 −2. Tính tích phân I =
[2x + f (x) − đường thẳng (d) :
y = −1 + 2t (t ∈ R). Đường 0 2g(x)] dx. z = 2 − t A. I = 18. B. I = 5.
thẳng đi qua điểm M(0; 1; −1) và song song với C. I = 11. D. I = 3.
đường thẳng (d) có phương trình là x y − 1 z + 1 Câu 28. Kí hiệu z A. = = .
1, z2 là hai nghiệm phức của 1 −2 1 1
phương trình 2z2 − 4z + 9 = 0. Tính P = + x + 1 y − 2 z + 1 = = z B. . 1 1 −1 2 1 x y + 1 z − 1 . C. = = . z2 −1 2 −1 ♂ 30 đề ôn thi t HKII-12 77 v 77
Những nẻo đường phù sa 2020 - 2021 30 ĐỀ
30 ĐỀ ÔN THI HKII-LỚP 12 x − 1 y + 2 z − 1 7 D. = = . C. S = −3. D. S = . 1 −1 2 3
Câu 33. Trong không gian với hệ tọa độ Oxyz, cho Câu 40. Trong không gian với hệ tọa độ Oxyz, cho #» #»
u = (2; −1; 1), v = (0; −3; −m). Tìm số thực m mặt cầu (S) : x2 + y2 + z2 + 4x − 2y − 4 = 0 và #»
sao cho tích vô hướng u · #» v = 1.
điểm A(1; 1; 0) thuộc (S). Mặt phẳng tiếp xúc với A. m = 4. B. m = 2.
(S) tại A có phương trình là C. m = 3. D. m = −2. A. x + y = 1 = 0. B. x + 1 = 0.
Câu 34. Cho hàm số f (x) = 2x + ex. Tìm một C. x + y − 2 = 0. D. x − 1 = 0.
nguyên hàm F(x) của hàm số f (x) thỏa mãn Câu 41. Trong không gian với hệ tọa độ Oxyz, F(0) = 0.
cho mặt phẳng (P) : x − my + z − 1 = 0 (m ∈
A. F(x) = x2 + ex − 1.
R), mặt phẳng (Q) chứa trục Ox và đi qua điểm B. F(x) = x2 + ex.
A(1; −3; 1). Tìm số thực m để hai mặt phẳng (P), C. F(x) = ex − 1. (Q) vuông góc. D. F(x) = x2 + ex + 1. 1 A. m = −3. B. m = − . 3
Câu 35. Tìm tất cả các số phức z thỏa 2z − 3(1 + 1 C. m = . D. m = 3. i) = iz + 7 − 3i. 3 √ √ 8 4 Z e A. z = − i. B. z = 4 − 2i. 3 + ln x a − b 3 5 5 Câu 42. Cho dx = với a, b x 3 8 4 1 C. z = + i. D. z = 4 + 2i.
là các số nguyên. Mệnh đề nào dưới đây là 5 5 đúng?
Câu 36. Cho F(x) là một nguyên hàm của hàm số A. a − 2b = 12. B. ab = 24. 2x2 − 2x − 1 f (x) = thỏa mãn F(0) = −1. Tính x − 1 C. a − b = 10. D. a + b = 10. F(−1).
Câu 43. Trong không gian với hệ tọa độ Oxyz, A. F(−1) = − ln 2.
cho bốn điểm A(1; 0; 3), B(2; −1; 1), C(−1; 3; −4),
B. F(−1) = −2 + ln 2.
D(2; 6; 0) tạo thành một hình tứ diện. Gọi M, N lần C. F(−1) = ln 2.
lượt là trung điểm các đoạn thẳng AB, CD. Tìm tọa D. F(−1) = 2 + ln 2.
độ trung điểm G của đoạn MN.
Câu 37. Tập hợp điểm biểu diễn số phức z thỏa A. G(4; 8; 0). B. G(2; 4; 0).
mãn |z + 1| = |1 − i − 2z| là đường tròn (C). Tính 4 8 C. G ; ; 0 . D. G(1; 2; 0).
bán kính R của đường tròn (C). 3 3 10 √ A. R = . B. R = 2 3.
Câu 44. Trong không gian với hệ tọa độ Oxyz, cho 9 √ x + 1 y + 4 z 7 10 đường thẳng (∆) : = = và điểm C. R = . D. R = . 1 2 1 3 3
A(2; 0; 1). Hình chiếu vuông góc của A trên (∆) là π Z 4 sin2 x điểm nào dưới đây?
Câu 38. Tính tích phân I = dx bằng 0 cos4x A. Q(2; 2; 3). B. M(−1; 4; −4).
cách đặt u = tan x, mệnh đề nào dưới đây C. N(0; −2; 1). D. P(1; 0; 2). đúng? π Z 4 Z 1 1
Câu 45. Tính diện tích S của hình phẳng giới hạn A. I = u2 du. B. I = du. 0 0 u2
bởi đồ thị các hàm số y = 2x − 2, y = 0 và Z 1 Z 1 C. I = − u2 du. D. I = u2 du. x = 2. 0 0 2 + 2 ln 2 3 − 4 ln 2 A. S = . B. S = .
Câu 39. Số phức z = a + bi (a, b ∈ R) thỏa mãn ln 2 ln 2 3 + 4 ln 2 2 − 2 ln 2
z + 1 + 3i − |z|i = 0. Tính S = a − 3b. C. S = . D. S = . ln 2 ln 2 7 A. S = − . B. S = 3. Câu 46. 3 ♂ 30 đề ôn thi t HKII-12 78 v 78
Những nẻo đường phù sa 2021 30 ĐỀ - ĐỀ
30 ĐỀ ÔN THI HKII-LỚP 12 2020
Một người chạy trong thời gian 1 v I
khi quay D quanh trục hoành có thể tích V bằng
giờ, vận tốc v (km/h) phụ thuộc 8 bao nhiêu? 28π 12π
thời gian t (h) có đồ thị làm một A. V = . B. V = . 5 5
phần của đường parabol với đỉnh 4π 36π C. V = . D. V = . 1 I ; 8 và trục đối xứng song 3 35 2
BẢNG ĐÁP ÁN THAM KHẢO
song với trục tung như hình vẽ. O 1 1 t
Tính quãng đường S người đó chạy 2 1. 2. 3. 4. 5. 6. 7. 8. 9. 10. 11.
được trong khoảng thời gian 45 A D C D C C B B A B A
12. 13. 14. 15. 16. 17. 18. 19. 20. 21. 22.
phút, kể từ khi bắt đầu chạy. C D C C A B D C A C B A.
23. 24. 25. 26. 27. 28. 29. 30. 31. 32. 33. S = 5,3 km. B D A B C B A C A A B B.
34. 35. 36. 37. 38. 39. 40. 41. 42. 43. 44. S = 4,5 km. A D A D D B D D C D D C. 45. 46. 47. 48. 49. 50. S = 4 km. D B A D C B D. S = 2,3 km. ĐỀ ÔN SỐ 21
Câu 47. Trong không gian với hệ tọa độ Oxyz, cho
mặt cầu (S) : (x − 1)2 = (y + 2)2 + z2 = 4 có tâm Câu 1. Gọi z1 là nghiệm phức có phần ảo âm của
I và mặt phẳng (P) : 2x − y + 2z + 2 = 0. Tìm tọa phương trình z2 + 2z + 3 = 0. Trên mặt phẳng tọa
độ điểm M thuộc (P) sao cho đoạn thẳng I M ngắn độ, điểm nào sau đây là điểm biểu diễn số phức nhất. 1 4 4 11 8 2 z1? √ √ A. − ; − ; − . B. − ; − ; − . 3 3 3 9 9 9 A. P(−1; − 2i). B. Q(−1; 2i). √ √ C. (1; −2; 2). D. (1; −2; −3). C. N(−1; 2). D. M(−1; − 2).
Câu 48. Trong không gian với hệ tọa độ Oxyz, cho Câu 2. Trong không gian với hệ tọa độ Oxyz, mặt
điểm M(3; 2; 1). Mặt phẳng (P) qua M và cắt các #»
phẳng (α) đi qua điểm M(1; 2; −3) và nhận n =
trục Ox, Oy, Oz lần lượt tại A, B, C sao cho M là (1; −2; 3) làm véc-tơ pháp tuyến có phương trình
trực tâm tam giác ABC. Phương trình mặt phẳng là (P) là
A. x − 2y − 3z + 6 = 0. A. x + y + z − 6 = 0.
B. x − 2y − 3z − 6 = 0. x y z B. + + = 0.
C. x − 2y + 3z − 12 = 0. 3 2 1 x y z C. + + = 1.
D. x − 2y + 3z + 12 = 0. 3 2 1
D. 3x + 2y + z − 14 = 0.
Câu 3. Trong không gian với hệ tọa độ Oxyz, cho x − 3 y + 2 z + 1 đường thẳng d: = = . Điểm nào
Câu 49. Cho số phức z = a + bi, (a, b ∈ R) thỏa 2 −1 4 |z − 3 + 4i| + 1 1
sau đây không thuộc đường thẳng d? mãn = và mô-đun |z| lớn nhất. 3|z − 3 + 4i| − 3 2 A. M(1; −1; −3). B. N(3; −2; −1). Tính tổng S = a + b. C. P(1; −1; −5). D. Q(5; −3; 3). A. S = 2. B. S = −1.
Câu 4. Trong không gian với hệ tọa độ Oxyz, cho C. S = −2. D. S = 1.
hai điểm E(1; −2; 4), F(1; −2; −3). Gọi M là điểm
Câu 50. Cho hình phẳng D giới hạn bởi đồ thị các thuộc mặt phẳng (Oxy) sao cho tổng ME + MF có x2 √ hàm số y = , y =
2x. Khối tròn xoay tạo thành giá trị nhỏ nhất. Tìm tọa độ điểm M. 2 ♂ 30 đề ôn thi t HKII-12 79 v 79
Những nẻo đường phù sa 2020 - 2021 30 ĐỀ
30 ĐỀ ÔN THI HKII-LỚP 12 A. M(−1; 2; 0). B. M(−1; −2; 0). π 4 Z C. M(1; −2; 0). D. M(1; 2; 0).
Câu 11. Tính tích phân sin x dx. 1 0 √ √ Z
Câu 5. Tính tích phân I = 2ex dx. 2 − 2 2 A. I = . B. I = . 2 √ 2 √ 0 2 2 + 2 A. I = e2 − 2e. B. I = 2e. C. I = − . D. I = . 2 2 C. I = 2e + 2. D. I = 2e − 2.
Câu 12. Trong không gian với hệ tọa độ Oxyz, cho
Câu 6. Cho hàm số f (x) thỏa mãn f 0(x) = 3 + x − 2 y + 1 z − 1 đường thẳng d : = = . Phương
2 sin x và f (0) = 3. Mệnh đề nào dưới đây 2 −1 −1
trình tham số của đường thẳng d là đúng? x = 2 − 2t
A. f (x) = 3x − 2 cos x + 5.
B. f (x) = 3x + 2 cos x + 3. A. y = 1 − t , (t ∈ R).
C. f (x) = 3x − 2 cos x + 3. z = −1 − t
D. f (x) = 3x + 2 cos x + 5. x = 2 + 2t
Câu 7. Cho số phức z = a + bi (a, b ∈ R) thỏa mãn B.
y = −1 − t , (t ∈ R).
(1 + 2i)z + i ¯z = 7 + 5i. Tính S = 4a + 3b. z = 1 − t A. S = 7. B. S = 24. x = 2 + 2t C. S = −7. D. S = 0. C.
y = −1 − t , (t ∈ R).
Câu 8. Tìm nguyên hàm của hàm số f (x) = 3x. z = −1 + t Z A. 3x dx = 3x + C. x = 2 + 2t Z 3x D.
y = −1 − t , (t ∈ R). B. 3x dx = + C. ln 3 Z z = −1 − t C. 3x dx = 3x ln 3 + C. Z 3x+1
Câu 13. Cho hàm số f (x) có đạo hàm liên tục trên D. 3x dx = + C. x + 1
đoạn [0; 1] thỏa mãn 3 f (x) + x f 0(x) = x2018, với 1 3 Z Z 1 m Câu 9. Biết dx = ln
(với m, n là những mọi x ∈ [0; 1]. Tính I = f (x) dx. x + 1 n 0 2 m 1 1 số thực dương và
tối giản), khi đó, tổng m + n A. I = . B. I = . n 2018 · 2021 2019 · 2020 bằng 1 1 C. I = . D. I = . A. 12. B. 7. C. 1. D. 5. 2019 · 2021 2018 · 2019
Câu 14. Cho hàm số f (x) liên tục trên đoạn [a; b].
Câu 10. Trong không gian hệ tọa độ Oxyz, cho Diện tích S của hình phẳng giới hạn bởi đồ thị
phương trình x2 + y2 + z2 − 2x − 4y − 6z − 11 = 0. hàm số y = f(x), trục hoành và hai đường thẳng
Viết phương trình mặt phẳng (α), biết (α) song x = a,x = b(a < b) được tính bằng công thức
song với (P) : 2x + y − 2z + 11 = 0 và cắt mặt b
cầu (S) theo tiết diện là một đường tròn có chu vi Z A. S = | f (x)| dx. bằng 8π. a
A. 2x + y − 2x − 11 = 0. b Z
B. 2x − y − 2z − 7 = 0. B. S = π | f (x)| dx. a
C. 2x + y − 2z − 5 = 0. b Z
D. 2x + y − 2z − 7 = 0. C. S = f 2(x) dx. a ♂ 30 đề ôn thi t HKII-12 80 v 80
Những nẻo đường phù sa 2021 30 ĐỀ - ĐỀ
30 ĐỀ ÔN THI HKII-LỚP 12 2020 b Z
Câu 22. Trong không gian với hệ tọa độ Oxyz, D. S = π f 2(x) dx.
cho hai mặt phẳng (P) : x + 2y − 2z + 3 = 0 và a
(Q) : x + 2y − 2z − 1 = 0. Khoảng cách giữa hai
Câu 15. Cho hàm số f (x) liên tục trên R và a là số mặt phẳng (P) và (Q) là
dương. Trong các khẳng định sau, khẳng định nào 4 2 4 4 A. . B. . C. . D. − . đúng? 9 3 3 3 a a Z Z
Câu 23. Cho số phức z = −3 − 2i. Tổng phần thực A. f (x) dx = 0. B. f (x) dx = a2.
và phần ảo của số phức z bằng a a a a A. −1. B. −i. C. −5. D. −5i. Z Z C. f (x) dx = 2a. D. f (x) dx = 1.
Câu 24. Diện tích hình phẳng giới hạn bởi hai đồ a a
thị hàm số y = x2 − x và y = x bằng
Câu 16. Trong không gian với hệ tọa độ Oxyz, cho 8 4 4 2
điểm M(2; −1; 2). Tính độ dài đoạn thẳng OM. A. . B. − . C. . D. . √ 3 3 3 3 A. OM = 5. B. OM = 9. √ 4 − 3i
Câu 25. Số phức z = có phần thực là C. OM = 3. D. OM = 3. i A. 3. B. −3. C. −4. D. 4. Z Câu 17. Biết
f (x) dx = −x2 + 2x + C. Tính Câu 26. Cho hàm số f(x) có đạo hàm và liên tục Z f (−x) dx.
trên R thỏa mãn f (x3 + 2x − 2) = 3x − 1. Tính 10 A. x2 + 2x + C0. B. −x2 + 2x + C0. Z I = f (x) dx. C. −x2 − 2x + C0. D. x2 − 2x + C0. 1 135 125 105 75
Câu 18. Trong không gian với hệ tọa độ Oxyz, cho A. . B. . C. . D. . 4 4 4 4
mặt cầu (S) có phương trình (x + 4)2 + (y − 3)2 + Câu 27. Trong các mệnh đề sau, mệnh đề nào
(z + 1)2 = 9. Tọa độ tâm I của mặt cầu (S) là đúng? A. I(4; −3; 1). B. I(−4; 3; 1). Z A. sin x dx = cos x + C. C. I(−4; 3; −1). D. I(4; 3; 1). Z 1 1 B. dx = − + C.
Câu 19. Cho số phức z thỏa mãn (1 + 2i)z = 4 − x x2 Z
3i + 2z. Số phức liên hợp của số phức z là C. ex dx = ex + C. A. ¯z = 2 + i. B. ¯z = −2 + i. Z 1 D. ln x dx = + C. C. ¯z = −2 − i. D. ¯z = 2 − i. x
Câu 28. Trong không gian với hệ tọa độ Oxyz, tìm
Câu 20. Biết phương trình z2 + 2z + m = 0 (m ∈ #» #» #» #» #»
tọa độ u biết u = 2 i − 3 j + 5 k .
R) có một nghiệm phức z1 = −1 + 3i và z2 là #» #» A. u = (5; −3; 2). B. u = (2; −3; 5).
nghiệm phức còn lại. Số phức z1 + 2z2 là #» #» C. u = (2; 5; −3). D. u = (−3; 5; 2). A. −3 + 3i. B. −3 + 9i. C. −3 − 3i. D. −3 + 9i.
Câu 29. Cho số phức z = a + bi, (a, b ∈ R). Tính
mô-đun của số phức ¯z. √
Câu 21. Vật thể B giới hạn bởi mặt phẳng có A. | ¯z| = a2 + b2. B. | ¯z| = a2 + b2. phương trình √
x = 0 và x = 2. Cắt vật thể B với mặt √ C. | ¯z| = a2 − b2. D. | ¯z| = a + b.
phẳng vuông góc với trục Ox tại điểm có hoành độ bằng
Câu 30. Trong không gian với hệ tọa độ Oxyz, mặt
x, (0 ≤ x ≤ 2) ta được thiết diện có diện tích bằng cầu tâm I(
x2(2 − x). Thể tích của vật thể B là
2; −1; 3) tiếp xúc với mặt phẳng (Oxy) 2 2 có phương trình là A. V = π. B. V = . 3 3
A. (x − 2)2 + (y + 1)2 + (z − 3)2 = 9. 4 4 C. V = . D. V = π.
B. (x − 2)2 + (y + 1)2 + (z − 2)2 = 4. 3 3 ♂ 30 đề ôn thi t HKII-12 81 v 81
Những nẻo đường phù sa 2020 - 2021 30 ĐỀ
30 ĐỀ ÔN THI HKII-LỚP 12
C. (x − 2)2 + (y + 1)2 + (z − 3)2 = 2. x = 3 − t
D. (x − 2)2 + (y + 1)2 + (z − 3)2 = 3. B.
y = −8 + 5t , (t ∈ R). Z z = 5 − 4t Câu 31. Biết
f (x) dx = F(x) + C. Trong các x = 1 + t
khẳng định sau, khẳng định nào đúng? C. , (t ∈ R). b y = 2 − 5t Z A. f (x) dx = F(b) + F(a). z = −3 − 2t a x = 2 + t b Z B. f (x) dx = F(b) · F(a). D.
y = −3 + 5t , (t ∈ R). a z = 1 + 4t b Z C. f (x) dx = F(a) − F(b). x = 1 + t a y = 2 − 5t , (t ∈ R). b Z D. f (x) dx = F(b) − F(a). z = −3 − 2t a
Câu 35. Trong không gian với hệ tọa độ Oxyz
Câu 32. Trong không gian với hệ tọa độ Oxyz, cho cho các điểm A(1; −2; 1), B(2; 1; 3) và mặt phẳng
hai điểm M(2; −1; 2) và N(2; 1; 4). Viết phương (P) : x − y + 2z − 3 = 0. Tìm tọa độ giao điểm H
trình mặt phẳng trung trực của đoạn thẳng của đường thẳng AB và mặt phẳng (P) là MN. A. H(0; −5; −1). B. H(1; −5; −1). A. 3x + y − 1 = 0. B. y + z − 3 = 0. C. H(4; 1; 0). D. H(5; 0; −1). C. x − 3y − 1 = 0. D. 2x + y − 2z = 0. Z 1
Câu 36. Tính nguyên hàm A = dx bằng x ln x Câu 33.
cách đặt t = ln x. Mệnh đề nào dưới dây đúng? Z Z 1 Cho (H) là hình y A. A = dt. B. A = dt. t2 phẳng giới hạn Z Z 1 1 C. A = t dt. D. A = dt. bởi parabol t √3 1 y = x2 và Z 2 x − Câu 37. Biết rằng
xe2x dx = ae2 + b với (a, b ∈ nửa elip có 2 O 2 0 phương trình Q). Tính P = a + b. 1 √ 1 y =
4 − x2 (với −2 ≤ x ≤ 2) và trục hoành A. P = . B. P = 0. 2 2
(phần tô đậm trong hình vẽ). Gọi S là diện tích 1 √ C. P = . D. P = 1. aπ + b 3 4 của, biết S =
(với a, b, c, ∈ R). Tính c
Câu 38. Tính thể tích V của khối tròn xoay được P = a + b + c.
sinh ra khi xoay hình phẳng giới hạn bởi các đường A. P = 9. B. P = 12. √ y =
2x, y = 0 và hai đường thẳng x = 1, x = 2 C. P = 15. D. P = 17. quanh trục Ox.
Câu 34. Trong không gian với hệ tọa độ Oxyz, A. V = 3. B. V = π.
đường thẳng đi qua hai điểm A(1; 2; −3) và C. V = 1. D. V = 3π.
B(2; −3; 1) có phương trình tham số là
Câu 39. Trong không gian với hệ tọa độ Oxyz, cho x = 1 + t
m, n là hai số thực dương thỏa mãn m + 2n = 1. A.
y = 2 − 5t , (t ∈ R).
Gọi A, B, C lần lượt là giao điểm của mặt phẳng z = 2 + 4t
(P) : mx + ny + mnz − mn = 0 với các trục tọa độ ♂ 30 đề ôn thi t HKII-12 82 v 82
Những nẻo đường phù sa 2021 30 ĐỀ - ĐỀ
30 ĐỀ ÔN THI HKII-LỚP 12 2020
Ox, Oy, Oz. Khi mặt cầu ngoại tiếp tứ diện OABC x + 2 y − 1 z + 2 C. ∆ : = = . −1 2 −1
có bán kính nhỏ nhất thì 2m + n có giá trị bằng x − 1 y + 2 z − 1 3 4 2 D. ∆ : = = . A. . B. . C. . D. 1. 2 −1 2 5 5 5 Câu 40.
Câu 45. Phần ảo của số phức z = 2 − 3i là Điểm M trong hình y A. 2. B. 3. C. 3i. D. −3. vẽ bên là điểm biểu
Câu 46. Trong không gian với hệ trục tọa độ Oxyz, diễn số phức z. Tìm x + 2 y − 1 z 1 cho đường thẳng ∆ : = = và điểm phần thực và phần 2 2 −1 x O
I(2; 1; −1). Mặt cầu tâm I tiếp xúc với đường thẳng ảo của số phức.
∆ cắt trục Ox tại hai điểm A, B. Tính độ dài đoạn −2 AB. M √ A. AB = 2 6. B. AB = 24. √
A. Phần thực là 1 và phần ảo là −2i. C. AB = 4. D. AB = 6.
B. Phần thực là −2 và phần ảo là 1.
Câu 47. Trong không gian với hệ trục tọa độ Oxyz,
C. Phần thực là −2 và phần ảo là i.
cho mặt phẳng (P) : x + y − 2z + 3 = 0. Một véc-tơ
D. Phần thực là 1 và phần ảo là −2.
pháp tuyến của mặt phẳng (P) là
Câu 41. Tìm nguyên hàm của hàm số f (x) = #» #» 2x + A. n = (1; 1 − 2). B. n = (0; 0; −2). #» #» 1. C. n = (1; −2; 1). D. n = (−2; 1; 1). Z x2 A. (2x + 1) dx = + x + C. 2
Câu 48. Trong không gian với hệ trục tọa độ Oxyz, Z B. (2x + 1) dx = x2 + x + C.
mặt cầu (S) : (x + 2)2 + (y − 1)2 + z2 = 4 có tâm I Z và bán kính R bằng C. (2x + 1) dx = 2x2 + 1 + C.
A. I(2; −1; 0), R = 4.
B. I(2; −1; 0), R = 2. Z D. (2x + 1) dx = x2 + C.
C. I(−2; 1; 0), R = 2.
D. I(−2; 1; 0), R = 4.
Câu 42. Một ô tô đang chạy với vận tốc 54 km/h Câu 49. Trong không gian với hệ trục tọa độ Oxyz,
thì tăng tốc chuyển động nhanh dần đều với gia điểm nào sau đây thuộc mặt phẳng x − 3y + 2z +
tốc a(t) = 3t − 8 (m/s2) trong đó t là khoảng thời 1 = 0?
gian tính bằng giây. Quãng đường mà ô tô đi được A. N(0; 1; 1). B. Q(2; 0; −1).
sau 10s kể từ lúc tăng tốc là C. M(3; 1; 0). D. P(1; 1; 1). A. 150 m. B. 250 m.
Câu 50. Trong không gian với hệ trục tọa độ Oxyz, C. 246 m. D. 540 m. x = 3 + t
Câu 43. Xét số phức z = a + bi (a, b ∈ R, b > 0) cho đường thẳng ∆ :
y = −1 − t , (t ∈ R), điểm
thỏa mãn |z| = 1. Tính P = 2a + 4b2 khi |z3 − z + 2| z = −2 + t
đạt giá trị nhỏ nhất. √
M(1; 2; −1) và mặt cầu (S) : x2 + y2 + z2 − 4x + A. P = 4. B. P = 2 − 2. √
10y + 14z + 64 = 0. Gọi ∆0 là đường thẳng đi qua C. P = 2. D. P = 2 + 2.
M cắt đường thẳng ∆ tại A, cắt mặt cầu tại B sao
Câu 44. Trong không gian với hệ tọa độ Oxyz, AM 1 #» cho =
và B có hoành độ là số nguyên. Mặt
đường thẳng ∆ đi qua A(2; −1; 2) và nhận u = AB 3
phẳng trung trực của đoạn AB có phương trình
(−1; 2; −1) làm véc-tơ chỉ phương có phương trình là chính tắc là x − 2 y + 1 z − 2
A. 2x + 4y − 4z − 19 = 0. A. ∆ : = = . −1 2 −1
B. 3x − 6y − 6z − 62 = 0. x + 1 y − 2 z + 1 B. ∆ : = = . 2 −1 2
C. 2x − 4y − 4z − 43 = 0. ♂ 30 đề ôn thi t HKII-12 83 v 83
Những nẻo đường phù sa 2020 - 2021 30 ĐỀ
30 ĐỀ ÔN THI HKII-LỚP 12
D. 3x + 6y − 6z − 31 = 0.
Câu 6. Họ các nguyên hàm của hàm số y = x sin x
BẢNG ĐÁP ÁN THAM KHẢO là A. −x cos x + C. 1. 2. 3. 4. 5. 6. 7. 8. 9. 10. 11.
B. −x cos x + sin x + C. D D A C D A D B B D A
12. 13. 14. 15. 16. 17. 18. 19. 20. 21. 22.
C. −x sin x + cos x + C. x B C A A D A C B C C C D. x2 sin + C. 2
23. 24. 25. 26. 27. 28. 29. 30. 31. 32. 33.
Câu 7. Diện tích hình phẳng giới hạn bởi các C C B A C B B A D B A
đường x = 0; x = π và đồ thị y = sin x; y = cos x
34. 35. 36. 37. 38. 39. 40. 41. 42. 43. 44.
được tính bởi biểu thức B A D A D B D B B C A Z π A. S = sin xdx. 45. 46. 47. 48. 49. 50. 0 Z π D A A C A C B. S = (sin x − cos x) dx. 0 Z π C. S = |cos x| dx. ĐỀ ÔN SỐ 22 0 Z π D. S = |sin x − cos x| dx. Z 1 2 0 Câu 1. Tích phân dx = ln a. Giá trị của 0 3 − 2x
Câu 8. Trong không gian với hệ tọa độ Oxyz cho a bằng:
hai mặt phẳng (P) : 2x + y − z − 3 = 0 và (Q) : A. 3. B. 2. C. 4. D. 1.
x + y + z − 1 = 0. Phương trình chính tắc đường Z 1 √ Câu 2. Cho tích phân
3 1 − xdx, với cách đặt thẳng giao tuyến của hai mặt phẳng (P) và (Q) √ 0
t = 3 1 − x thì tích phân đã cho bằng với tích phân là x + 1 y − 2 z − 1 nào sau đây? A. = = . −2 −3 1 Z 1 Z 1 x y − 2 z + 1 A. 3 t2dt. B. 3 tdt. B. = = . 0 0 2 −3 1 Z 1 Z 1 x − 1 y + 2 z + 1 C. 3 t3dt. D. 3 t4dt. C. = = . 0 0 2 3 1 x y + 2 z − 1
Câu 3. Trong không gian với hệ trục tọa độ Oxyz, D. = = . 2 −3 −1
cho ba điểm A(1; −2; 1), B(−1; 3; 3), C(2; −4; 2). Câu 9. Trong không gian với hệ tọa độ Oxyz, tọa
Phương trình mặt phẳng (ABC) là
độ hình chiếu vuông góc của điểm A(2; −1; 0) lên A. 4y + 2z − 3 = 0. B. 2y + z − 3 = 0.
mặt phẳng (P) : 3x − 2y + z + 6 = 0 là C. 3x + 2y + 1 = 0. D. 9x + 4y − z = 0. A. (1; 1; 1). B. (−1; 1; −1).
Câu 4. Cho f (x) là hàm số liên tục trên [a; b] thỏa C. (3; −2; 1). D. (5; −3; 1). Z b Z b mãn f (x)dx = 7. Tính I = f (a + b − a a
Câu 10. Trong không gian với hệ tọa độ Oxyz, cho x)dx
hai điểm B(1; 2; −3) và C(7; 4; −2). Nếu điểm E A. I = a + b + 7. B. I = a + b − 7. # » # »
thỏa mãn đẳng thức CE = 2EB thì tọa độ điểm C. I = 7 − a − b. D. I = 7. E là 8 8 8
Câu 5. Gọi (H) là hình phẳng giới hạn bởi các A. ; 3; − . B. 3; 3; − . π 3 3 3
đường y = tan x; Ox; x = 0; x = . Quay (H) 4 8 8 1 C. 3; ; − . D. 1; 2; .
quanh trục Ox ta được khối tròn xoay có thể tích 3 3 3 bằng π 2 Z A. 4 π − π . B. 1 − π . Câu 11. Tích phân 2 sin2 x dx bằng 4 4 0 2 √ √ 2 π π 2 π 2 C. 2 π . D. − π. A. − . B. + . 4 4 2 4 2 ♂ 30 đề ôn thi t HKII-12 84 v 84
Những nẻo đường phù sa 2021 30 ĐỀ - ĐỀ
30 ĐỀ ÔN THI HKII-LỚP 12 √ √ 2020 2 2 x = 4 + t x = 1 + 4t C. − π + . D. − π − . 4 2 4 2 C. y = 3 + 2t . D. y = 2 + 3t .
Câu 12. Họ các nguyên hàm của hàm số y = 102x z = −7 + 3t z = 3 − 7t là 10x
Câu 17. Một nguyên hàm của hàm số y = A. + C. B. 102x2 ln 10 + C. 2 ln 10 cos 5x cos x là 102x 102x 1 1 1 C. + C. D. + C. A. sin 6x + sin 4x . 2 ln 10 ln 10 2 6 4 1 1 1 B. cos 6x + cos 4x .
Câu 13. Trong không gian với hệ tọa độ Oxyz, cho 2 6 4 mặt phẳng ( 1 sin 6x sin 4x
α) đi qua điểm A(2; −1; 5) và vuông C. − + . góc với hai mặt phẳng 2 6 4
(P) : 3x − 2y + z + 7 = 0 và 1
(Q) : 5x − 4y + 3z + 1 = 0. Phương trình của mặt D. sin 5x sin x. 5 phẳng (α) là
Câu 18. Trong không gian với hệ tọa độ Oxyz, #» #» #»
A. x + 2y + z − 5 = 0.
cho ba véc-tơ a = (−1; 1; 0), b = (1; 1; 0), c =
B. 2x + 4y + 2z + 10 = 0.
(1; 1; 1). Trong các mệnh đề sau, mệnh đề nào
C. x + 2y − z + 5 = 0. đúng?#» #»
D. 2x − 4y − 2z − 10 = 0. A. a . c = 1. #» #»
B. a và b cùng phương.
Câu 14. Trong mặt phẳng phức, gọi A, B, C lần #» #» 2 C. cos b , c = √ .
lượt là các điểm biểu diễn của các số phức z1 = 6 #» #» #» #» (1 − i)(2 + i), z D. a + b + c = 0 .
2 = 1 + 3i, z3 = −1 − 3i. Tam giác ABC là Z 2 Câu 19. Tích phân K = (2x − 1) ln xdx
A. Một tam giác vuông cân. 1 bằng
B. Một tam giác cân (không đều). 1 1 A. K = 2 ln 2 − . B. K = .
C. Một tam giác vuông (không cân). 2 2 1
D. Một tam giác đều. C. K = 3 ln 2. D. K = 3 ln 2 + . 2
Câu 15. Trong không gian với hệ tọa độ Oxyz, Câu 20. Cho số phức z có phần ảo âm và thỏa
phương trình đường thẳng đi qua hai điểm mãn z2 − 3z + 5 = 0. Tìm mô-đun của số phức √
A(1; 1; 2) và B(2; −1; 0) là ω = 2z − 3 + 14. √ √ x − 1 y − 1 z − 2 A. 24. B. 17. C. 4. D. 5. A. = = . 3 2 2 x − 2 y + 1 z
Câu 21. Cho hàm số f (x) = a sin πx + b thỏa mãn B. = = . Z 1 −1 2 2 f (1) = 2 và
f (x)dx = 4 thì a, b nhận giá trị x y − 3 z − 4 0 C. = = . đúng là 1 −2 −2 x + 1 y + 1 z + 2 A. a = 2 D. = = . π, b = 3.
B. a = π, b = 2. 1 −2 −2
C. a = π, b = 0.
D. a = 2π, b = 2.
Câu 16. Trong không gian với hệ tọa độ Oxyz, cho Câu 22. Trong không gian với hệ tọa độ Oxyz, cho
đường thẳng d đi qua điểm A(1; 2; 3) và vuông góc mặt cầu (S) có tâm I(1; 3; −2), biết diện tích mặt
với mặt phẳng (α) : 4x + 3y − 7z + 1 = 0. Phương cầu bằng 100π. Khi đó phương trình mặt cầu (S) trình tham số của d là là x = 1 + 3t x = −1 + 4t
A. x2 + y2 + z2 − 2x − 6y + 4z − 86 = 0. A. y = 2 + 4t . B. y = −2 + 3t .
B. x2 + y2 + z2 − 2x − 6y + 4z + 4 = 0. z = 3 − 7t z = −3 − 7t
C. x2 + y2 + z2 − 2x − 6y + 4z + 9 = 0. ♂ 30 đề ôn thi t HKII-12 85 v 85
Những nẻo đường phù sa 2020 - 2021 30 ĐỀ
30 ĐỀ ÔN THI HKII-LỚP 12
D. x2 + y2 + z2 − 2x − 6y + 4z − 11 = 0.
Câu 29. Trong không gian với hệ tọa độ Oxyz, cho x − 7 y − 3 z − 9
Câu 23. Trong không gian với hệ tọa độ Oxyz, cho hai đường thẳng d1 : = = và 1 2 −1 x = 1 + 2t x − 3 y − 1 z − 1 d = = . Phương trình đường 2 : −7 2 3 đường thẳng d1 :
y = 2 + 3t và đường thẳng thẳng vuông góc chung của d1 và d2 là: z = 3 + 4t x − 7 y − 3 z − 9 A. = = . 2 1 −4 x = 3 + 4t0 x − 7 y − 3 z − 9 B. = = . d2 :
y = 5 + 6t0 . Trong các mệnh đề sau, mệnh 2 −1 4 x − 7 y − 3 z − 9 z = 7 + 8t0 C. = = . 2 1 4 đề nào đúng x − 3 y − 1 z − 1 D. = = . − A. d 1 2 4 1 k d2. B. d 1 1 và d2 chéo nhau.
Câu 30. Điểm biểu diễn của số phức z = 2 − 3i C. d1 ≡ d2. là D. d 2 3 1 ⊥ d2. A. ; . B. (4; −1). 13 13
Câu 24. Trong không gian với hệ tọa độ Oxyz, cho C. (2; −3). D. (3; −2).
mặt cầu (S) : x2 + y2 + z2 − 2x − 4y − 6z = 0 và Câu 31. Gọi (H) là hình phẳng giới hạn bởi các
ba điểm O(0; 0; 0), A(1; 2; 3), B(2; −1; −1). Trong đường: y = sin x; Ox; x = 0; x = π. Quay (H)
số ba điểm trên số điểm nằm trên mặt cầu là
quanh trục Ox ta được khối tròn xoay có thể tích A. 2. B. 0. C. 3. D. 1. là 2
Câu 25. Trong không gian với hệ tọa độ Oxyz, cho π π A. 2 π . B. 2π. C. . D. . 2 2 6 − 4t
Câu 32. Trong không gian với hệ tọa độ Oxyz,
điểm A(1; 1; 1) và đường thẳng d :
−2 − t (t ∈ khoảng các từ điểm A(1; −2; −1) đến mặt phẳng −1 + 2t
(P) : 2x − y + 2z − 5 = 0 là R √
). Hình chiếu của A trên d có tọa độ là 11 1 A. (−2; 3; 1). B. (2; −3; 1). A. . B. 1. C. 3. D. . 3 3 C. (2; 3; 1). D. (2; −3; −1). π Z
Câu 33. Cho tích phân I = 2 esin2 x sin x cos3 xdx.
Câu 26. Vận tốc chuyển động của một vật là 0
v(t) = 3t2 + 5 m/s. Quãng đường vật di chuyển Nếu đổi biến số t = sin2 x thì Z 1
được từ giây thứ 4 đến giây thứ 10 là A. I = 2 et (1 − t) dt. 0 A. 252 m. B. 36 m. 1 Z 1 B. I = et (1 − t) dt. C. 1200 m. D. 966 m. 2 0 1 Z 1 Z t C. I = etdt + tetdt .
Câu 27. Trong không gian với hệ tọa độ Oxyz, tọa 2 0 0 x − 12 Z 1 Z t
độ giao điểm M của đường thẳng d : = D. I = 2 etdt + tetdt . 4 y − 9 z − 1 0 0 =
và mặt phẳng (P) : 3x + 5y − z − 3 1
Câu 34. Phương trình chính tắc của đường thẳng 2 = 0 là:
d đi qua điểm M(2; 0; −1) có véc-tơ chỉ phương A. (12; 9; 1). B. (1; 1; 6). #»a(4; −6;2) là C. (0; 0; −2). D. (1; 0; 1). x − 2 y z + 1 A. = = . 2 −3 1
Câu 28. Tính diện tích hình phẳng (H) giới hạn x + 2 y z − 1 = =
bởi các đường y = x3 − B. . 4x, Ox, x = −3, x = 4. 4 6 2 201 119 x + 2 y z − 1 A. 36. B. 44. C. . D. . C. = = . 4 4 2 −3 1 ♂ 30 đề ôn thi t HKII-12 86 v 86
Những nẻo đường phù sa 2021 30 ĐỀ - ĐỀ
30 ĐỀ ÔN THI HKII-LỚP 12 2020 x − 4 y + 6 z − 2 D. = = . A. A(−2; 6; 4). B. A(2; −6; −4). 2 −3 1 C. A(−1; 3; 2). D. A(−1; −3; 2).
Câu 35. Phương trình z2 + |z| = 0 có mấy nghiệm trong tập số phức?
Câu 43. Diện tích hình phẳng giới hạn bởi y = − A. Có 2 nghiệm. B. Có 3 nghiệm.
x2 + 5x + 6, Ox, x = 0, x = 2 là 56 52 55 58 C. Có 1 nghiệm. D. Có 4 nghiệm. A. . B. . C. . D. . 3 3 3 3
Câu 36. Trong không gian với hệ tọa độ Oxyz, cho Câu 44. Cho hai hàm số f (x) và g(x) liên tục trên
mặt phẳng (P) có phương trình (P) : −x + 3z − [a; b] và thỏa mãn 0 < g(x) < f (x), ∀x ∈ [a; b]. Gọi 2 = 0. Tìm đáp án đúng
V là thể tích của khối tròn xoay sinh ra khi quay A. (P) k Oy. B. (P) k xOz.
quanh Ox hình phẳng (H) giới hạn bởi các đường: C. (P) ⊃ Oy. D. (P) k Ox.
y = f (x), y = g(x), x = a, x = b. Khi đó V được
tính bởi công thức nào sau đây? Z 2 Câu 37. Cho f x2 + 1 xdx = 2. Khi đó Z b 1 A. V = | f (x) − g(x)| dx. Z 5 a f (x)dx bằng Z b h i 2 B. V = π f 2(x) − g2(x) dx. A. 2. B. 4. C. −1. D. 1. a Z b 2
Câu 38. Trong không gian với hệ tọa độ Oxyz, cho C. V = π [ f (x) − g(x)] dx . a
hai điểm A(−1; 0; 1), B(−2; 1; 1). Phương trình mặt Z b D. π [ f (x) − g(x)]2 dx.
trung trực của đoạn AB là a A. x − y + 2 = 0. B. x − y + 1 = 0.
Câu 45. Cho số phức z = a + a2i với a ∈ R. Khi C. −x + y + 2 = 0. D. x − y − 2 = 0.
đó điểm biểu diễn của số phức liên hợp của z nằm
Câu 39. Với giá trị nào của m > 0 thì diện tích trên đường nào?
của hình phẳng giới hạn bởi hai đồ thị y = x2 và
A. Đường thẳng y = −x + 1. 4
B. Đường thẳng y = 2x. y = mx bằng ? 3 C. Parabol y = x2. A. m = 1. B. m = 4. D. Parabol y = −x2. C. m = 2. D. m = 3.
Câu 46. Diện tích của hình phẳng (H) giới hạn bởi
Câu 40. Nghiệm của phương trình 2z2 + 3z + 4 = (C) : y = 3x4 − 4x2 + 5; Ox; x = 1; x = 2 là 0 trên tập số phức là √ √ 212 214 213 43 −3 + 23i 3 − 23i A. . B. . C. . D. . A. z1 = ; z . 15 15 15 3 4 2 = √ 4√ 3 + 23i −3 − 23i
Câu 47. Nguyên hàm của hàm số f (x) = B. z1 = ; z . 1 + cos 4x 4 2 = √ 4 √ là −3 + 23i −3 − 23i 2 C. z x 1 x 1 1 = ; z . 4 2 = √ √ 4 A. + sin 2x + C. B. + sin 4x + C. 2 8 2 2 3 + 23i 3 − 23i D. z x 1 x 1 1 = ; z . 4 2 = 4 C. + sin 4x + C. D. + sin 4x + C. 2 8 2 4
Câu 41. Cho ba điểm A(2; 1; 4), B(−2; 2; −6), # » # »
Câu 48. Trong không gian với hệ tọa độ Oxyz cho
C(6; 0; −1). Tích AB.AC bằng x = 1 − 3t A. −67. B. 65. C. 33. D. 67. đường thẳng d : y = 2t và mặt phẳng
Câu 42. Trong không gian với hệ tọa độ Oxyz, cho z = −2 − mt
mặt cầu có phương trình là (S) : x2 + y2 + z2 − (P) : 2x − y − 2z − 6 = 0. Giá trị của m để d ⊂ (P)
2x + 6y + 4z = 0. Biết OA (O là gốc tọa độ) là là
đường kính của mặt cầu (S). Tọa độ của điểm A A. m = 4. B. m = −4. là C. m = 2. D. m = −2. ♂ 30 đề ôn thi t HKII-12 87 v 87
Những nẻo đường phù sa 2020 - 2021 30 ĐỀ
30 ĐỀ ÔN THI HKII-LỚP 12 π Z Z A.
(ex + 2 sin x) dx = ex − cos2 x + C.
Câu 49. Tích phân I = 4 cos 2xdx bằng Z 0 1 B.
(ex + 2 sin x) dx = ex + sin2 x + C. A. −2. B. −1. C. 1. D. . Z 2 C.
(ex + 2 sin x) dx = ex − 2 cos x + C.
Câu 50. Trong không gian với hệ tọa độ Oxyz, mặt Z
cầu (S) : x2 + y2 + z2 − 2x + 4y − 6z − 2 = 0 có tâm D.
(ex + 2 sin x) dx = ex + 2 cos x + C. I và bán kính R là
Câu 4. Tìm nguyên hàm của hàm số f (x) = x2 +
A. I(−1; 2; −3), R = 4. √ x − 2. B. I(2; −4; 6), R = 58. Z x3 x2 A. f (x)dx = + − 2 + C.
C. I(1; −2; 3), R = 4. 3 2 √ Z x3 x2
D. I(−2; 4; −6), R = 58. B. f (x)dx = + + C. 3 2 Z
BẢNG ĐÁP ÁN THAM KHẢO C. f (x)dx = 2x + 1 + C. Z 1. 2. 3. 4. 5. 6. 7. 8. 9. 10. 11. x3 x2 D. f (x)dx = + − 2x + C. 3 2 A C D D B B D B B C A Z
12. 13. 14. 15. 16. 17. 18. 19. 20. 21. 22. Câu 5. Tính x(x2 + 7)15dx. C A A B D A C A D B D Z 1 16 A. x(x2 + 7)15dx = x2 + 7 + C.
23. 24. 25. 26. 27. 28. 29. 30. 31. 32. 33. 2 Z 1 16 C D B D C C C A D B B B. x(x2 + 7)15dx = x2 + 7 + C. 32
34. 35. 36. 37. 38. 39. 40. 41. 42. 43. 44. Z 1 16 C. x(x2 + 7)15dx = − x2 + 7 + C. A B A B A C C C B D B 32 Z 1 16 45. 46. 47. 48. 49. 50. D. x(x2 + 7)15dx = x2 + 7 + C. 16 D B C A D C
Câu 6. Cho F(x) = x2 là một nguyên hàm của
hàm số f (x)e2x. Tìm nguyên hàm của hàm số ĐỀ ÔN SỐ 23 f 0(x)e2x. Z A. f 0(x)e2xdx = 2x2 − 2x + C.
I. PHẦN TRẮC NGHIỆM Z B. f 0(x)e2xdx = −x2 + 2x + C.
Câu 1. Tìm nguyên hàm của hàm số f (x) = Z 10x. C. f 0(x)e2xdx = −2x2 + 2x + C. Z 10x Z A. 10xdx = + C. D. f 0(x)e2xdx = −x2 + x + C. ln 10 Z B. 10xdx = 10x ln 10 + C. 1 Z 6a Z
Câu 7. Tính tích phân I = dx, a hằng C. 10xdx = 10x+1 + C. 3x + 1 0 Z 10x+1 số. D. 10xdx = + C. x + 1 A. I = 4a ln 4. B. I = 6a ln 2.
Câu 2. Mệnh đề nào sau đây đúng? C. I = 3a ln 2. D. I = 2a ln 4. Z 1 A. dx = ln x2 + C. 2 2 x2 Z Z Z Câu 8. Cho f (x)dx = 2, g(x)dx = −1. Tính B. cos xdx = sin x + C. −1 −1 Z 1 2 C. dx = cot x + C. Z sin2 x I = [x + 2 f (x) − 3g(x)] dx. Z D. e2xdx = 2ex + C. −1 17 7 A. I = . B. I = .
Câu 3. Tìm nguyên hàm của hàm số f (x) = ex + 2 2 5 11 2 sin x. C. I = . D. I = . 2 2 ♂ 30 đề ôn thi t HKII-12 88 v 88
Những nẻo đường phù sa 2021 30 ĐỀ - ĐỀ
30 ĐỀ ÔN THI HKII-LỚP 12 2020 2 Z x2 Cho đồ thị hàm số y Câu 9. Biết
dx = a + ln b (a, b ∈ Z). Gọi x + 1 y = f (x). Diện tích S 0
S = 2a + b, giá trị của S thuộc khoảng nào sau của hình phẳng thuộc đây? phần tô đậm trong −3 4 A. (4; 6). B. (8; 10). hình vẽ bên là O x C. (2; 4). D. (6; 8). 2 Z Câu 10. Cho
f (2x) dx = 8. Tính tích phân I = 0 4 Z Z A. S = f (x)dx − f (x)dx. 0 4 −3 0 Z f (x)dx. 0 4 Z Z B. S = f (x)dx + f (x)dx. 0 A. I = 8. B. I = 32. −3 0 −3 4 C. I = 4. D. I = 16. Z Z C. S = f (x)dx + f (x)dx. 2 Z p 0 0 Câu 11. Cho I = 2x x2 − 1dx và u = x2 − 1. 4 Z 1 D. S = f (x)dx.
Mệnh đề nào dưới đây sai? −3 2 Z √ 2 √ A. I = udu. B. I = 27.
Câu 16. Diện tích S của hình phẳng giới hạn bởi 3 1 1 đồ thị hàm số y = , y = 1 và đường thẳng 3 2x − 1 Z √ 2 3 C. I = udu. D. I = 3 2 . x = 2 là 3 1 0 A. S = 1 + ln 3. B. S = 1 − ln 3. 2 1 1 π Z C. S = ln 3. D. S = + ln 3.
Câu 12. Tính tích phân I = (2x + 1) sin xdx. 2 2 0
Câu 17. Cho hình phẳng D giới hạn bởi đường A. I = 2π + 1. B. I = 2π + 2.
cong y = 1 − x2 và trục Ox. Khối tròn xoay tạo C. I = 2π. D. I = −2π.
thành khi quay D quanh trục hoành có thể tích V
Câu 13. Cho hàm số f (x) là hàm có đạo hàm trên bằng bao nhiêu? 4 16 16 Z π [1; 4], biết
f (x)dx = 20 và f (4) = 16; f (1) = 7. A. V = . B. V = . 15 15 4 4 1 π C. V = . D. V = . 4 3 3 Z Tính I = x · f 0(x)dx.
Câu 18. Thể tích V của khối tròn xoay do hình 1 √ A. I = 57. B. I = 67.
phẳng giới hạn bởi các đường y = x x2 + 1, trục C. I = 37. D. I = 47.
hoành và đường thẳng x = 1 khi quay quanh trục Ox là
Câu 14. Diện tích S của hình phẳng giới hạn bởi 9 8π A. V = . B. V = .
đường cong y = −x3 + 3x2 − 2, trục hoành và hai 15 15 8 9π
đường thẳng x = 0, x = 2 là C. V = . D. V = . 15 15 7 A. S = . B. S = 4. 2 x2 3 5
Câu 19. Cho Parabol (P):y = và đường tròn C. S = . D. S = . 2 2 2
(C) : x2 + y2 = 8. Gọi (H) là phần hình phẳng giới Câu 15.
hạn bởi (P), (C) và trục hoành (phần tô đậm như ♂ 30 đề ôn thi t HKII-12 89 v 89
Những nẻo đường phù sa 2020 - 2021 30 ĐỀ
30 ĐỀ ÔN THI HKII-LỚP 12 hình vẽ bên).
Câu 26. Trong không gian Oxyz, cho A(1; 5; −2); B(2; 1; 1). y
Tọa độ trung điểm I của đoạn thẳng AB là 3 1 3 1 A. I ; 3; − . B. I ; 3; . 2 2 2 2 3 1 C. I ; 2; − . D. I (3; 6; −1). 2 2 x
Câu 27. Trong không gian với hệ tọa độ Oxyz, cho O
điểm A(2; 2; 1); B(0; −1; 2). Tính độ dài đoạn thẳng AB. √ √ A. AB = 2 3. B. AB = 14. √ √ C. AB = 13. D. AB = 6.
Tính diện tích S của hình phẳng (H).
Câu 28. Trong không gian với hệ tọa độ Oxyz, cho 1 2
ba điểm M(2; 3; 1), N(3; 1; 1) và P(1; m − 1; 2). Tìm A. S = 2π + . B. S = 2π − . 3 3 m để MN ⊥ NP. 4 4 C. S = 2π − . D. S = 2π + . 3 3 A. m = −4. B. m = 2.
Câu 20. Cho số phức z = (2 − 3i)(3 − 4i). Điểm C. m = 1. D. m = 0.
biểu diễn số phức z là
Câu 29. Trong không gian Oxyz, cho mặt cầu (S) A. M (6; 17). B. M (17; 6).
có phương trình x2 + y2 + z2 − 2x − 4y + 6z − 2 = C. M (−17; −6). D. M (−6; −17).
0. Tìm tọa độ tâm I và bán kính R của mặt cầu 2 − 3i
Câu 21. Số phức z = có mô-đun bằng (S). √ 1 + i 26 √
A. I(1; 2; −3) và R = 4. A. |z| = . B. |z| = 3 26. 3 √
B. I(−1; −2; 3) và R = 4. √ 26 C. |z| = 2 26. D. |z| = .
C. I(1; 2; −3) và R = 16. 2
D. I(−1; −2; 3) và R = 16.
Câu 22. Rút gọn biểu thức P = i2000 + i2021. A. P = 1 + i. B. P = 1 − i.
Câu 30. Trong không gian Oxyz, viết phương C. P = −1 + i. D. P = −1 − i.
trình mặt cầu (S) đi qua hai điểm A(1; 1; 1);
B(0; 0; 1) và có tâm nằm trên trục Ox.
Câu 23. Cho số phức z = a + bi (a, b ∈ R) thỏa
A. (x + 1)2 + y2 + z2 = 4.
mãn điều kiện (1 + i)z + 2z = 4 − 3i. Tính P =
B. (x − 1)2 + y2 + z2 = 2. a + b.
C. (x + 1)2 + y2 + z2 = 2. A. P = 3. B. P = 10.
D. (x − 1)2 + y2 + z2 = 4. C. P = 7. D. P = 5. Câu 24. Gọi z
Câu 31. Trong không gian với hệ tọa độ Oxyz,
1 và z2 lần lượt là nghiệm của
phươngtrình: z2 − 2z + 5 = 0. Tính P = |z
phương trình nào dưới đây là phương trình mặt 1|2 + |z
phẳng đi qua điểm M(1; 2; −3)và có một véc-tơ 2|2. √ #» A. P = 2 5. B. P = 20.
pháp tuyến n = (1; −2; 3)? √ C. P = 10. D. P = 5.
A. x − 2y − 3z + 6 = 0.
B. x − 2y + 3z − 12 = 0.
Câu 25. Cho z = 2 + 3i là một số phức. Hãy tìm
C. x − 2y − 3z − 6 = 0.
một phương trình bậc hai với hệ số thực nhận z và
D. x − 2y + 3z + 12 = 0. z làm nghiệm. A. z2 + 4z + 13 = 0. B. z2 − 4z + 12 = 0.
Câu 32. Trong không gian với hệ tọa độ Oxyz, cho C. z2 + 4z + 12 = 0. D. z2 − 4z + 13 = 0.
mặt phẳng P : 3x − 4y + 5z − 2 = 0. Véc-tơ nào ♂ 30 đề ôn thi t HKII-12 90 v 90
Những nẻo đường phù sa 2021 30 ĐỀ - ĐỀ
30 ĐỀ ÔN THI HKII-LỚP 12 2020
dưới đây là một véc-tơ pháp tuyến của mặt phẳng x = 2 + 2t P? D. y = −3t , t ∈ R. #» #» A. n = (3; −5; −2). B. n = (−4; 5; −2). #» #» z = −1 + t C. n = (3; −4; 5). D. n = (3; −4; 2).
Câu 38. Trong không gian với hệ tọa độ Oxyz, cho
Câu 33. Trong không gian với hệ trục toạ độ Oxyz, x − 4 y − 5 z − 6 đường thẳng d : = = . Điểm nào cho mặt phẳng ( 2 3 4
α) : 2x − 3y − z − 1 = 0. Điểm nào
dưới đây thuộc đường thẳng d?
dưới đây không thuộc mặt phẳng (α)? A. M (2; 2; 2). B. M (2; 2; 4). A. M (−2; 1; −8). B. N (4; 2; 1). C. M (2; 3; 4). D. M (2; 2; 10). C. P (3; 1; 3). D. Q (1; 2; −5).
Câu 39. Trong không gian với hệ tọa độ Oxyz,
Câu 34. Trong không gian với hệ tọa độ Oxyz, cho x − 1
cho đường thẳng d có phương trình =
mặt phẳng (P) : x − 2y + z − 5 = 0. Điểm nào dưới 3 y + 2 z − 3
đây thuộc mặt phẳng (P)? =
. Điểm nào sau đây không thuộc 2 −4 A. P(0; 0; −5). B. N(−5; 0; 0). đường thẳng d? C. Q(2; −1; 5). D. M(1; 1; 6). A. Q (−2; −4; 7). B. P (7; 2; 1).
Câu 35. Trong không gian với hệ tọa độ Oxyz, cho C. M (1; −2; 3). D. N (4; 0; −1).
mặt phẳng (P) : 3x + 4y + 2z + 4 = 0 và điểm Câu 40. Trong không gian với hệ tọa độ Oxyz, cho
A (1; −2; 3). Tính khoảng cách d từ A đến mặt đường thẳng ∆ đi qua điểm A (1; 2; 3) và vuông phẳng (P).
góc với mặt phẳng 4x + 3y − 7z + 1 = 0. Phương 5 5 A. d = √ . B. d = .
trình tham số của đường thẳng ∆ là 29 29 √ x = 1 + 3t 5 5 C. d = . D. d = . 9 3 A. y = 2 − 4t , t ∈ R.
Câu 36. Trong không gian với hệ tọa độ Oxyz, cho z = 3 − 7t
hai điểm A(1; 1; 0) và B(0; 1; 2). Véc-tơ nào dưới x = −1 + 8t
đây là một véc-tơ chỉ phương của đường thẳng B.
y = −2 + 6t , t ∈ R. AB? #» #» z = −3 − 14t A. a = (−1; 0; −2). B. b = (−1; 0; 2). #» #» x = 1 + 4t C. c = (1; 2; 2). D. d = (−1; 1; 2). C. y = 2 + 3t , t ∈ R.
Câu 37. Cho đường thẳng ∆ đi qua điểm #» z = 3 − 7t
M (2; 0; −1) và có véc-tơ chỉ phương a = x = −1 + 4t
(4; −6; 2). Phương trình tham số của đường thẳng ∆ là D.
y = −2 + 3t , t ∈ R. x = −2 + 2t z = −3 − 7t A. y = −3t , t ∈ R. II. PHẦN TỰ LUẬN z = 1 + t π 2 Z x = −2 + 4t
Câu 41. Tính tích phân I = x sin xdx. B. y = −6t , t ∈ R. 0
Câu 42. Trong không gian Oxyz, viết phương z = 1 + 2t
trình mặt phẳng (P) đi qua A(0; −2; 1) và vuông x = 4 + 2t x − 1 y − 2 z − 3
góc với đường thẳng d : = = . C. y = −3t , t ∈ R. 2 3 −4 z = 2 + t
BẢNG ĐÁP ÁN THAM KHẢO ♂ 30 đề ôn thi t HKII-12 91 v 91
Những nẻo đường phù sa 2020 - 2021 30 ĐỀ
30 ĐỀ ÔN THI HKII-LỚP 12 1. 2. 3. 4. 5. 6. 7. 8. 9. 10. 11.
Câu 6. Cho số phức z thỏa mãn |z − 2i| = |z + 2|. A B C D B C D A C D A
Tính giá trị nhỏ nhất của biểu thức P = |z + 2i| +
12. 13. 14. 15. 16. 17. 18. 19. 20. 21. 22. |z − 5 + 9i|. √ √ √ √ B C D A B A B C D D A A. 70. B. 4 5. C. 74. D. 3 10.
23. 24. 25. 26. 27. 28. 29. 30. 31. 32. 33.
Câu 7. Trong không gian Oxyz, cho ba điểm B A D A B C A B D C C 34. 35. 36. 37. 38. 39. 40.
A(0; 1; 1), B(1; −2; 3), C(4; 1; 0), phương trình mặt D A B D A B C phẳng (ABC) là A. x + 3y + 4z + 7 = 0.
B. x + 3y + 4z − 7 = 0. ĐỀ ÔN SỐ 24
C. 3x + y + 4z − 5 = 0.
D. 4x + y + 3z − 4 = 0.
I. PHẦN TRẮC NGHIỆM
Câu 8. Trong không gian Oxyz, cho mặt cầu (S)
Câu 1. Tính diện tích S của hình phẳng giới hạn tâm I nằm trên mặt phẳng (Oxy) đi qua ba điểm
bởi đồ thị hai hàm số y = x2 − 4 và y = x + 2.
A(1; 2; −4), B(1; −3; 1), C(2; 2; 3). Tìm tọa độ điểm 125 √ A. S = . B. S = 10 3. 6 I. 125 25 C. S = − . D. S = . A. I(2; −1; 0). B. I(0; 0; 1). 6 6 C. I(0; 0; −2). D. I(−2; 1; 0). Câu 2.
Trong mặt phẳng tọa độ Oxy, y
Câu 9. Cho hình lập phương ABCD.A0B0C0D0
cho đường tròn (C) : (x − 5
cạnh bằng 1. Gọi M là điểm trên mặt phẳng I
3)2 + (y − 4)2 = 1. Tính thể 4 B C
(A0BD) sao cho CM2 + C0 M2 + B0 M2 đạt giá trị 3
tích của khối tròn xoay thu nhỏ nhất. √Tính BM.√ √ 2 2 6 3 2 3 2
được khi quay hình phẳng A. . B. . C. . D. . 1 9 9 9 9
giới hạn bởi đường tròn (C) A D x
Câu 10. Tìm hai số thực x, y thỏa mãn 2 + (5 − quanh trục hoành. O 1 2 3 4 y)i = (x − 1) + 5i. A. 5 2 2 π . B. 9π . (x = 3 (x = 6 C. 8 2 2 π . D. 6π . A. . B. . m y = 0 y = 3 Z Câu 3. Tìm m biết (2x + 5) dx = 6. (x = −6 (x = −3 C. . D. . 0 y = 3 y = 0 A. m = −1, m = 6. B. m = 1, m = 6. C. m = −1, m = −6. D. m = 1, m = −6. 2 Z Câu 11. Cho I =
x(x − 1)5 dx và u = x − 1.
Câu 4. Tìm phần thực và ảo của số phức z = 1 3 − i 2 + i + .
Khẳng định nào sau đây là khẳng định sai? 1 + i i 1
A. Phần thực bằng 2; phần ảo bằng −4i. Z A. I = (u + 1)u5du.
B. Phần thực bằng 2; phần ảo bằng −4. 0
C. Phần thực bằng 2; phần ảo bằng 4i. 2 Z
D. Phần thực bằng −2; phần ảo bằng 4. B. I = x(1 − x)5 dx. 1
Câu 5. Tìm số phức z thỏa mãn (3 + i)z + (1 + u6 u5 1 C. I = + . 2i)z = 3 − 4i. 6 5 0 A. z = 2 + 5i. B. z = 2 + 3i. 13 D. I = . 42 C. z = −1 + 5i. D. z = −2 + 3i. ♂ 30 đề ôn thi t HKII-12 92 v 92
Những nẻo đường phù sa 2021 30 ĐỀ - ĐỀ
30 ĐỀ ÔN THI HKII-LỚP 12 2020
Câu 12. Cho số phức z = 1 + i. Tính mô-đun của Câu 18. Tìm tất cả các nghiệm phức có phần ảo âm z + 2i số phức w = .
của phương trình (z2 + 9)(z2 − z + 1) = 0. z − 1 √ √ A. z = −3i. A. |w| = 2. B. |w| = 3. √3 C. |w| = 1. D. |w| = 2. B. z = −3i; z = i. 2 √ Z Câu 13. Tính F(x) = x cos 2x dx. 1 3 C. z = −3i; z = − i. 2 2 √ 1 1 A. F(x) = x sin 2x + cos 2x + C. 1 3 2 2 D. z = −2i; z = − i. 1 1 2 2 B. F(x) = x sin 2x + cos 2x + C. 2 4
Câu 19. Trong không gian Oxyz, cho hai điểm x2 sin 2x C. F(x) = + C.
A(−1; 2; 6), B(5; −4; 2), đường thẳng AB cắt mặt 4 # » # »
phẳng (Oxz) tại M và MA = k · MB. Tính k. D. F(x) = sin 2x + C. 1 1 A. k = − . B. k = . 2 2
Câu 14. Trong không gian Oxyz, cho điểm C. k = 2. D. k = −2. x = −1
Câu 20. Trong mặt phẳng Oxy, cho điểm A là
A(0; 1; 1) và hai đường thẳng d1 : y = −1 + t
điểm biểu diễn số phức z = 1 + 2i, B là điểm thuộc z = t
đường thẳng y = 2 sao cho tam giác OAB cân tại x − 1 y − 2 z và d2 : = =
. Gọi d là đường thẳng O. Điểm B là điểm biểu diễn của số phức nào trong 3 1 1
đi qua điểm A, cắt đường thẳng d
các số phức dưới đây? 1 và vuông góc với đường thẳng d A. −3 + 2i. B. −1 + 2i.
2. Đường thẳng d đi qua điểm
nào trong các điểm dưới đây? C. 3 + 2i. D. 1 − 2i. A. N(2; 1 − 5). B. Q(3; 2; 5).
Câu 21. Một học sinh đang điều khiển xe đạp điện C. P(−2; −3; 11). D. M(1; 0; −1).
chuyển động thẳng đều với vận tốc a m/s. Khi
Câu 15. Cho hàm số y = f (x) xác định và liên tục phát hiện có chướng ngại vật phía trước học sinh
trên đoạn [a; b]. Diện tích S của hình phẳng giới đó thực hiện phanh xe. Sau khi phanh, xe chuyển
hạn bởi đồ thị hàm số y = f (x), trục hoành và các động chậm dần đều với vận tốc v(t) = a − 2t
đường thẳng x = a, x = b, (a < b) được tính theo m/s. Tìm giá trị lớn nhất của a để quãng đường xe công thức.
đạp điện đi được sau khi phanh không vượt quá 9 b b m. Z Z A. S = f (x) dx. B. S = | f (x)| dx.
A. a = 7. B. a = 4. C. a = 5. D. a = 6. a a 1 1 Z Z b b 1 π 1 + x4 Z Z Câu 22. Biết dx = và dx = C. S = − f (x) dx. D. S = f 2(x) dx. x2 + 1 4 1 + x6 0 0 a a a a
π với a, b ∈ Z và tối giản. Tính a + b. b b
Câu 16. Tìm điểm cực đại của hàm số f (x) = A. 3. B. 4. C. 7. D. 5. e2x Z ln t dt.
Câu 23. Trong không gian Oxyz, cho mặt cầu ex
(S) : (x − 3)2 + (y + 2)2 + (z + 1)2 = 25 và mặt A. ln 2.
B. − ln 4. C. 0. D. ln 4.
phẳng (P) : 4x + 3z − 34 = 0. Có bao nhiêu mặt
Câu 17. Cho hàm số f (x) có đạo hàm cấp hai trên phẳng song song với (P) và tiếp xúc (S)?
đoạn [2; 4] và f 0(2) = 1, f 0(4) = 5. Tính I = A. 0. B. 1.
C. Vô số. D. 2. 4 3 Z Z f 00(x) dx. Câu 24. Biết I =
ln(x3 − 3x + 2) dx = a ln 5 + 2 2 A. I = 3. B. I = 4. C. I = 2. D. I = 1.
b ln 2 + c với a, b, c ∈ Q. Tính tổng S = a + b + c. ♂ 30 đề ôn thi t HKII-12 93 v 93
Những nẻo đường phù sa 2020 - 2021 30 ĐỀ
30 ĐỀ ÔN THI HKII-LỚP 12 √ √ A. S = 2. B. S = −3. a b A. 3 a + b = 7. B. + = 7. 9 4 C. S = −2. D. S = 3. C. a − b = 11. D. a + b < 22. Câu 25.
Câu 29. Trong không Oxyz, cho đường thẳng Người ta cắt hai x = 1 + t hình cầu có bán d :
y = 2 − 2t . Véc-tơ nào trong các véc-tơ sau kính lần lượt là z = 3 R = 13 cm và √
đây là một véc-tơ chỉ phương của đường thẳng r = 41 cm để làm d. hồ lô đựng rượu #» #» A. v = (1; 2; 3). B. a = (1; −2; 3). như hình vẽ bên. #» #» C. b = (−2; 4; 6). D. u = (1; −2; 0). Biết đường tròn 1 Z giao của hình cầu 2x + 3 Câu 30. Biết I = dx = a ln 2 + b, (a, b ∈ 2 − x có bán kính r0 = 5 0 cm và nút đựng
Q). Khi đó a + 2b bằng rượu là một hình A. 0. B. 2. C. 3. D. 7. trụ có bán kính đáy √
Câu 31. Trong không gian Oxyz, cho đường thẳng bằng 5 cm, chiều x − 1 y + 2 z d : = − . Mặt phẳng (P) chứa − − cao bằng 4 cm. Giả 1 1 2
đường thẳng d và tạo với trục tung góc lớn nhất. sử độ dày vỏ hồ lô
Biết rằng phương trình (P) có dạng là ax + by + không đáng kể.
cz + 9 = 0. Tính tổng a + b + c.
Hỏi hồ lô đựng được bao nhiêu lít rượu? (kết quả A. 9. B. 5. C. 3. D. 4.
làm trong đến một chữ số thập phân sau dấu phẩy).
Câu 32. Cho hình trụ có bán kính đáy bằng 5 cm A. 9,5 lít. B. 8,2 lít.
chiều cao bằng 4 cm. Tính thể tích của khối trụ C. 10,2 lít. D. 11,4 lít. A. 90π cm3. B. 100π cm3. C. 92π cm3. D. 96π cm3.
Câu 26. Cho hình lập phương ABCD.A0B0C0D0
cạnh a và một hình trụ có hai đáy nội tiếp hình Câu 33. Cho số phức z = 4 − 3i. Điểm biểu diễn
vuông ABCD và A0B0C0D0. Tỉ số diện tích xung của z trên mặt phẳng phức là
quanh của hình trụ và diện tích toàn phần của hình A. M(4; 3). B. M(−4; 3). lập phương bằng C. M(4; −3). D. M(−3; 4). π 1 π A. . B. . C. π. D. .
Câu 34. Viết phương trình mặt cầu (S) có tâm 6 2 2
I(−1; 1; −2) và đi qua điểm A(2; ; 1; 2).
Câu 27. Gọi z1, z2 lần lượt là hai nghiệm của
A. (S) : (x − 1)2 + (y + 1)2 + (z − 2)2 = 5.
phương trình 2z2 − 2z + 5 = 0. Tính A = |z1| +
B. (S) : (x − 2)2 + (y − 1)2 + (z − 2)2 = 25. |z2|. √
C. (S) : (x + 1)2 + (y − 1)2 + (z + 2)2 = 25. 10 √ √ A. . B. 2 5. C. 1. D. 10.
D. (S) : x2 + y2 + z2 + 2x − 2y + 4z + 1 = 0. 2 1
Câu 35. Tìm nguyên hàm của hàm số f (x) = Z 1 1 1 a Câu 28. Biết − dx = ln 2x3 − 9. 2x + 1 3x + 1 6 b Z 1 0 A. f (x) dx = x4 − 9x + C. a 2
trong đó a, b nguyên dương và là phân số tối Z b B. f (x) dx = x4 − 9x + C.
giản. Khẳng định nào sau đây là khẳng định Z 1 sai? C. f (x) dx = x4 + C. 2 ♂ 30 đề ôn thi t HKII-12 94 v 94
Những nẻo đường phù sa 2021 30 ĐỀ - ĐỀ
30 ĐỀ ÔN THI HKII-LỚP 12 Z 2020 D. f (x) dx = 4x3 + 9x + C.
24y − 8z + 35 = 0. Tìm giá trị nhỏ nhất của biểu
thức P = |2x − y + 2z + 5|.
Câu 36. Trong không gian Oxyz, cho mặt cầu
(S) : x2 + y2 + z2 − 2x − 4y + 4z − m = 0 (m là
BẢNG ĐÁP ÁN THAM KHẢO
tham số ). Biết mặt cầu có bán kính bằng 5. Tìm 1. 2. 3. 4. 5. 6. 7. 8. 9. 10. 11. m. A C D B A D B D A A C A. m = 25. B. m = 11.
12. 13. 14. 15. 16. 17. 18. 19. 20. 21. 22. C. m = 16. D. m = −16. A B D B B B C A B D B
Câu 37. Cho khối nón (N) có thể tích V = 12
23. 24. 25. 26. 27. 28. 29. 30. 31. 32. 33. π
cm3 và chiều cao h = 4 cm. Tính diện tích xung B C C A D D D C D B C 34. 35. 36. 37. 38. 39. 40. quanh của khối nón (N). C A C C A A A A. 30π cm2. B. 12π cm2. C. 15π cm2. D. 45π cm2. 4m Câu 38. Cho f (x) = + sin2 x. Gọi F(x) là một ĐỀ ÔN SỐ 25 π
nguyên hàm của hàm số f (x). Tìm m để F(0) = 1 π π
Câu 1. Trong không gian với hệ trục tọa độ Oxyz, và F = . 4 8
cho mặt phẳng (P) : x − y + 2z + 1 = 0 và đường 3 3 A. m = − . B. m = . x − 1 y z + 1 4 4 thẳng d : = = . Tính góc giữa đường 4 4 1 2 −1 C. m = − . D. m = .
thẳng d và mặt phẳng (P). 3 3 A. 60◦. B. 120◦. C. 150◦. D. 30◦.
Câu 39. Cho khối nón tròn xoay đỉnh S có đường
cao h = 20 cm, bán kính đáy r = 25 cm. Một mặt Câu 2. Trong không gian với hệ tọa độ Oxyz, cho
phẳng (P) đi qua S và có khoảng cách đến tâm O x + 1 y − 2 z đường thẳng d : = = , véc-tơ nào 1 3 −2
của đáy là 12 cm. Thiết diện của (P) với khối nón là dưới đây là véc-tơ chỉ phương của đường thẳng
tam giác SAB, với A, B thuộc đường tròn đáy. Tính d?
diện tích S4SAB của tam giác SAB. #» #» A. u = (−1; −3; 2). B. u = (1; 3; 2).
A. S4SAB = 400 cm2. B. S4SAB = 300 cm2. #» #» C. u = (1; −3; −2). D. u = (−1; 3; −2).
C. S4SAB = 600 cm2. D. S4SAB = 500 cm2.
Câu 3. Trong không gian với hệ tọa độ Oxyz,
Câu 40. Mệnh đề nào sau đây đúng? Z
cho hai điểm A(2; 3; −1), B(1; 2; 4). Phương trình A. cot x dx = ln | sin x| + C.
đường thẳng nào được cho dưới đây không phải Z B. sin x dx = cos x + C.
là phương trình đường thẳng AB? x + 2 y + 3 z − 1 Z 1 1 A. = = . C. dx = . 1 1 −5 x2 x Z x = 2 − t D. cos x dx = − sin x + C. B. y = 3 − t . II. PHẦN TỰ LUẬN z = −1 + 5t
Câu 41 (HK2 (2017-2018), THPT LÊ QUÝ ĐÔN, HÀ NỘI). x = 1 − t
[Trần Hòa, dự án EX9][2D3B2-1] Tính tích phân 1 C. y = 2 − t . Z x I = dx. z = 4 + 5t (x + 1)5 0 x − 1 y − 2 z − 4 D. = = .
Câu 42 (HK2 (2017-2018), THPT LÊ QUÝ ĐÔN, HÀ NỘI). 1 1 −5
[Trần Hòa, dự án EX9][2H3K4-2] Cho các số thực Câu 4. Trong không gian với hệ tọa độ Oxyz, x − 1
x, y, z thỏa mãn hệ thức 4x2 + 4y2 + 4z2 − 8x − cho điểm A(2; 1; 1) và đường thẳng d : = 1 ♂ 30 đề ôn thi t HKII-12 95 v 95
Những nẻo đường phù sa 2020 - 2021 30 ĐỀ
30 ĐỀ ÔN THI HKII-LỚP 12 y − 2 z − 3 2 =
. Tính khoảng cách từ A đến đường Z 2 −2
Câu 11. Tính tích phân I = 22018xdx. thẳng d.√ 0 3 5 √ √ √ A. . B. 5. C. 2 5. D. 3 5. 24036 − 1 24036 − 1 2 A. I = . B. I = . ln 2 2018
Câu 5. Trong không gian với hệ tọa độ Oxyz, cho 24036 24036 − 1 C. I = . D. I = .
các điểm A(1; 0; 3), B(2; 3; −4),C(−3; 1; 2). Tìm tọa 2018 ln 2 2018 ln 2
độ điểm D sao cho tứ giác ABCD là hình bình Câu 12. hành.
Kí hiệu S là diện tích hình y A. D(−2; 4; −5). B. D(4; 2; 9).
phẳng giới hạn bởi đồ thị C. D(6; 2; −3). D. (−4; −2; 9). hàm số y = f (x), trục a
hoành, đường thẳng x = a, O c x b
Câu 6. Trong không gian với hệ tọa độ Oxyz, cho x = b (như hình bên). Hỏi y = f (x)
hai điểm M(2; 1; −2), N(4; −5; 1). Tìm độ dài đoạn khẳng định nào dưới đây là thẳng MN. √ √ khẳng định đúng? A. 49. B. 7. C. 7. D. 41. c b Z Z A. S = f (x)dx + f (x)dx.
Câu 7. Trong không gian với hệ tọa độ Oxyz, cho a c
ba điểm A(1; 0; 0), B(0; −2; 0),C(0; 0; 3). Phương c b Z Z
trình nào dưới đây là phương trình mặt phẳng B. S = f (x)d + f (x)dx. (ABC)? a c x y z x y z c b A. + + = 1. B. + + = 1. Z Z 3 −2 1 1 −2 3 C. S = − f (x)dx + f (x)dx. x y z x y z C. + + = 1. D. + + = 1. a c −2 1 3 3 1 −2 b Z
Câu 8. Cho biết F(x) là nguyên hàm của hàm số D. S = f (x)dx. Z a f (x). Tìm I = [2 f (x) + 1]dx.
Câu 13. Cho hai hàm số y = f A. I = 2F(x) + 1 + C. 1(x) và y = f2(x)
liên tục trên đoạn [a; b] và có đồ thị như hình bên. B. I = 2xF(x) + 1 + C. y C. I = 2xF(x) + x + C. y = f D. I = 2F(x) + x + C. 2(x)
Câu 9. Tìm nguyên hàm của hàm số f (x) = y = f1(x) cos 2x. Z 1 O a x b A. f (x)dx = sin 2x + C. 2 Z 1
Gọi S là hình phẳng giới hạn bởi hai đồ thị trên và B. f (x)dx = − sin 2x + C. 2
các đường thẳng x = a; x = b. Thể tích V của vật Z C. f (x)dx = 2 sin 2x + C.
thể tròn xoay tạo thành khi S quay quanh trục Ox Z D. f (x)dx = −2 sin 2x + C.
được tính bởi công thức nào sau đây? b Z 5 7 A. V = π [ f 2 Z Z 1 (x) − f 2 2 (x)]dx. Câu 10. Nếu f (x)dx = 3 và f (x)dx = 9 thì a b 2 5 Z 7 B. V = π [ f1(x) − f2(x)]dx. Z f (x)dx bằng bao nhiêu? a b 2 Z A. 3. B. 6. C. 12. D. −6. C. V = [ f 21(x) − f 22(x)]dx. a ♂ 30 đề ôn thi t HKII-12 96 v 96
Những nẻo đường phù sa 2021 30 ĐỀ - ĐỀ
30 ĐỀ ÔN THI HKII-LỚP 12 2020 b x − 1 y + 3 z − 4 Z B. ∆ : = = . D. V = π [ f1(x) − f2(x)]2dx. −1 −1 −2 x − 1 y + 3 z − 4 a C. ∆ : = = . 1 1 −2 π 2 x − 1 y + 3 z − 4 Z D. ∆ : = = . Câu 14. Cho I = sin2 x cos xdx và u = sin x. 1 −1 2 0
Câu 22. Trong không gian với hệ tọa độ Oxyz,
Mệnh đề nào dưới đây đúng?
cho mặt cầu (S) : x2 + y2 + z2 = 1 và mặt phẳng 1 1 Z Z
(P) : x + 2y − 2z + 1 = 0. Tìm bán kính r đường A. I = u2du. B. I = 2 udu.
tròn giao tuyến của (S) và (P). 0 0 √ 0 1 1 2 2 Z Z A. r = . B. r = . C. I = − u2du. D. I = − u2du. √ 3 3 2 1 −1 0 C. . D. . 2 2
Câu 15. Tính mô-đun của số phức z = 4 − 3i. √
Câu 23. Trong không gian với hệ tọa độ Oxyz, A. |z| = 7. B. |z| = 7.
cho hai mặt phẳng (α) : x − 2y − 2z + 4 = 0 và C. |z| = 5. D. |z| = 25.
(β) : − x + 2y + 2z − 7 = 0. Tính khoảng cách giữa
Câu 16. Gọi M là điểm biểu diễn của số phức z hai mặt phẳng (α) và (β)
trong mặt phẳng tọa độ, N là điểm đối xứng của A. 3. B. −1. C. 0. D. 1.
M qua Oy (M, N không thuộc các trục tọa độ). Số Câu 24. Trong không gian với hệ tọa độ Oxyz, cho
phức ω có điểm biểu diễn lên mặt phẳng tọa độ là điểm I(0; 2; 3). Viết phương trình mặt cầu (S) tâm
N. Mệnh đề nào sau đây đúng? I tiếp xúc với trục Oy. A. ω = −z. B. ω = − ¯z.
A. x2 + (y + 2)2 + (z + 3)2 = 2. C. ω = ¯z.
D. |ω| > |z|.
B. x2 + (y + 2)2 + (z + 3)2 = 3.
Câu 17. Tính S = 1 + i + i2 + · · · + i2017 + i2018.
C. x2 + (y − 2)2 + (z − 3)2 = 4. A. S = −i. B. S = 1 + i.
D. x2 + (y − 2)2 + (z − 3)2 = 9. C. S = 1 − i. D. S = i.
Câu 25. Trong không gian với hệ tọa độ Oxyz, cho
Câu 18. Tính mô-đun của số phức nghịch đảo của ba điểm A(−2; 3; 1), B(2; 1; 0), C(−3; −1; 1). Tìm số phức z = (1 − 2i)2.
tất cả các điểm D sao cho ABCD là hình thang có 1 1 √ 1 đáy AD và S A. √ . B. . C. 5. D. . ABCD = 3S4ABC. 5 25 5 " D(−8; −7; 1) A. D(8; 7; −1). B. .
Câu 19. Phương trình z2 + 3z + 9 = 0 có hai D(12; 1; −3) nghiệm phức z "
1, z2. Tính S = z1z2 + z1 + z2. D(8; 7; −1) A. −6. B. 6. C. 12. D. −12. C. . D. D(−12; −1; 3). D(−12; −1; 3)
Câu 20. Cho số phức z thỏa (1 + i)z = 3 − i. Tìm Câu 26. Tìm nguyên hàm F(x) của hàm số f (x) = phần ảo của z. 2 6x + sin 3x, biết F(0) = . A. −2i. B. 2i. C. 2. D. −2. 3 cos 3x 2 A. F(x) = 3x2 − + .
Câu 21. Trong không gian với hệ tọa độ Oxyz, 3 3 x + 2 cos 3x − cho điểm B. F(x) =
M(1; −3; 4), đường thẳng d : = 3x2 − 1. 3 3 y − 5 z − 2 cos 3x + = và mặt phẳng ( C. V = F(x) = P) : 2x + z − 2 = 0. 3x2 + 1. −5 −1 3 cos 3x
Viết phương trình đường thẳng ∆ qua M vuông D. F(x) = 3x2 − + 1. 3
góc với d và song song với (P).
Câu 27. Tìm nguyên hàm F(x) của hàm số f (x) = x − 1 y + 3 z − 4 A. ∆ : = = . 1 −1 −2 x · e2x. ♂ 30 đề ôn thi t HKII-12 97 v 97
Những nẻo đường phù sa 2020 - 2021 30 ĐỀ
30 ĐỀ ÔN THI HKII-LỚP 12
A. F(x) = 2e2x (x − 2) + C.
và không thẳng hàng). Mệnh đề nào sau đây 1 B. F(x) = e2x (x − 2) + C. đúng? 2 1 A. |z1 + z2| = 2OI. C. F(x) = 2e2x x − + C. 2 B. |z1 + z2| = OI. 1 1 C. |z D. F(x) = e2x x − + C. 1 − z2| = OM + ON. 2 2
D. |z1 − z2| = 2(OM + ON).
Câu 28. Biết f (x) là hàm liên tục trên R và Câu 34. Cho số phức z thỏa 2z + 3z = 10 + i. Tính 9 5 Z Z
f (x) dx = 9. Khi đó tính I = f (3x − 6) dx. |z|. 0 2 A. |z| = 1. B. |z| = 3. √ √ A. I = 27. B. I = 3. C. |z| = 3. D. |z| = 5. C. I = 24. D. I = 0.
Câu 35. Cho a, b là các số thực thỏa phương trình
Câu 29. Cho hình phẳng (H) giới hạn bởi đồ thị z2 + az + b = 0 có nghiệm 3 − 2i, tính S = a + b.
y = 2x − x2 và trục hoành. Tính thể tích V vật thể A. S = 19. B. S = −7.
tròn xoay sinh ra khi cho (H) quay quanh Ox. C. S = 7. D. S = −19. 4 4 A. V = . B. V = π. 3 3
Câu 36. Trong không gian với hệ tọa độ Oxyz, 16 16 C. V = π. D. V = .
cho hình hộp ABCD.A0B0C0D0. Biết tọa độ các 15 15
đỉnh A(−3; 2; 1), C(4; 2; 0), B0(−2; 1; 1), D0(3; 5; 4).
Câu 30. Một ô tô đang chạy với vận tốc 10 m/s Tìm tọa độ điểm A0 của hình hộp.
thì người lái xe đạp phanh, từ thời điểm đó ô tô A. A0(−3; 3; 3).
B. A0(−3; −3; −3).
chuyển động chậm dần đều với vận tốc v(t) = C. A0(−3; 3; 1). D. A0(−3; −3; 3).
−5t + 10 (m/ s) trong đó t là khoảng thời gian
tính bằng giây kể từ lúc đạp phanh. Hỏi từ lúc đạp Câu 37. Trong không gian với hệ tọa độ Oxyz, cho x − 3 y − 3 z
phanh đến khi dừng hẳn ô tô còn di chuyển được đường thẳng (d) : = = , mặt phẳng 1 3 2 bao nhiêu mét?
(P) : x + y − z + 3 = 0 và điểm A(1; 2; −1). Cho
A. 0.2 m. B. 2 m. C. 10 m. D. 20 m.
đường thẳng (∆) đi qua A, cắt (d) và song song Câu 31.
với mặt phẳng (P). Tính khoảng cách từ gốc tọa Cho số phức z có y độ O đến (∆). √ √ N 2 3 4 3 √ 16 điểm biểu diễn trên A. . B. . C. 3. D. . 3 3 3 mặt phẳng tọa độ là
Câu 38. Trong không gian với hệ tọa độ Oxyz,
M, biết z2 có điểm biểu M
cho mặt cầu (S) : x2 + y2 + z2 − 2x + 2z − 7 = 0 diễn là N như hình vẽ.
và điểm A(1; 3; 3). Qua A vẽ tiếp tuyến AT của Mệnh đề nào sau đây
mặt cầu (T là tiếp điểm), tập hợp các tiếp điểm đúng? x O
T là đường tròn khép kín (C). Tính diện tích A. |z| < 1. B. 1 < |z| < 3.
hình phẳng giới hạn bởi (C) (phần bên trong mặt C. 3 < |z| < 5. D. |z| > 5. cầu).
Câu 32. Tìm số thực m sao cho m2 − 1 + (m + 1)i 144 144π A. . B. 16π. C. 4π. D. . là số ảo. 25 25 2 A. m = 0. B. m = 1. Z x2018
Câu 39. Tính tích phân I = dx. C. m = ±1. D. m = −1. ex + 1 −2
Câu 33. Gọi M, N lần lượt là các điểm biểu diễn 22020 A. I = 0. B. I = . của z 2019
1, z2 trong mặt phẳng phức, I là trung điểm 22019 22018
MN, O là gốc tọa độ (3 điểm O, M, N phân biệt C. I = . D. I = . 2019 2018 ♂ 30 đề ôn thi t HKII-12 98 v 98
Những nẻo đường phù sa 2021 30 ĐỀ - ĐỀ
30 ĐỀ ÔN THI HKII-LỚP 12 2020 1 Z x3 + 3x
Câu 47. Trong không gian với hệ tọa độ Oxyz, cho Câu 40. Biết dx = a + b ln 2 + c ln 3 x − 1 y − 1 z − 1 x2 + 3x + 2 3 đường thẳng (d1) : = = , 0 2 1 −2
với a, b, c là các số hữu tỉ, tính S = 2a + b2 + c2. x − 3 y + 1 z − 2 x − 4 (d2) : = = , (d3) : = A. S = 515. B. S = 164. 1 2 2 2 y − 4 z − 1 C. S = = 436. D. S = −9.
. Mặt cầu bán kính nhỏ nhất −2 1
tâm I(a; b; c), tiếp xúc với ba đường thẳng
Câu 41. Số điểm cực trị của hàm số f (x) = (d x3+1
1) , (d2) , (d3). Tính S = a + 2b + 3c. Z p 2017 t2 + 12 − 4 dt là. A. S = 10. B. S = 11. 1 C. S = 12. D. S = 13. A. 1. B. 3. C. 2. D. 0.
Câu 48. Cho hàm số f (x) có đạo hàm trên R thỏa
Câu 42. Biết phương trình z2 + 2017 · 2018z + 1
(x + 2) f (x) + (x + 1) f 0(x) = ex và f (0) = . Tính 2
22018 = 0 có hai nghiệm z1, z2. Tính S = |z1| + f (2). |z e e 2| A. f (2) = . B. f (2) = . 3 6 A. 22018. B. 22019. C. 21009. D. 21010. e2 e2 C. f (2) = . D. f (2) = .
Câu 43. Cho số phức z = a + bi (a, b ∈ R, a > 0) 3 6 √
Câu 49. Cho đồ thị (C) : y = f (x) = x. Gọi (H)
thỏa zz − 12|z| + (z − z) = 13 − 10i. Tính S = là hình phẳng giới hạn bởi (C), đường thẳng x = 9, a + b. Ox. A. S = −17. B. S = 5. y C. S = 7. D. S = 17. M
Câu 44. Tập hợp các điểm biểu diễn số phức z = x + yi với x, y ∈ R thỏa mãn (12 − 5i)z + 17 + 7i O A = 13 có phương trình nào x z − 2 − i sau đây?
Cho điểm M thuộc (C), A(9; 0). Gọi V1 là thể tích
A. (d) : 6x + 4y − 3 = 0.
khối tròn xoay khi quay (H) quanh Ox, V2 là thể
B. (d) : x + 2y − 1 = 0.
tích khối tròn xoay khi cho tam giác AOM quay
C. (C) : x2 + y2 − 2x + 2y + 1 = 0.
quanh Ox. Biết V1 = 2V2. Tính diện tích S phần
D. (C) : x2 + y2 − 4x + 2y + 4 = 0.
hình phẳng giới hạn bởi (C), OM (hình vẽ không
Câu 45. Tìm tổng các giá trị số thực a sao cho thể hiện chính xác điểm M). √ 27 3
phương trình z2 + 3z + a2 − 2a = 0 có nghiệm A. S = 3. B. S = . √ 16 phức z0 thỏa |z0| = 2. 3 3 4 C. S = . D. S = . A. 0. B. 2. C. 6. D. 4. 2 3
Câu 50. Cho số phức z thỏa mãn |z| = 1. Gọi m, M
Câu 46. Trong không gian với hệ tọa độ Oxyz,
5 4 8 lần lượt là giá trị lớn nhất, giá trị nhỏ nhất của
cho bốn điểm A(1; 0; 0), B(3; 2; 1), C − ; ; 3 3 3
P = z5 + z3 + 6z − z4 + 1. Tính M − m
và M thay đổi sao cho hình chiếu của M lên mặt A. M − m = 1. B. M − m = 3.
phẳng (ABC) nằm trong tam giác ABC và các mặt C. M − m = 6. D. M − m = 12.
phẳng (MAB), (MBC), (MCA) hợp với mặt phẳng
BẢNG ĐÁP ÁN THAM KHẢO
(ABC) các góc bằng nhau. Tính giá trị nhỏ nhất của 1. 2. 3. 4. 5. 6. 7. 8. 9. 10. 11. OM. √ √ D A A B D B B D A C D 26 5 √ 28 A. . B. . C. 3. D. .
12. 13. 14. 15. 16. 17. 18. 19. 20. 21. 22. 3 3 3 C A A C B D D B D C B ♂ 30 đề ôn thi t HKII-12 99 v 99
Những nẻo đường phù sa 2020 - 2021 30 ĐỀ
30 ĐỀ ÔN THI HKII-LỚP 12
23. 24. 25. 26. 27. 28. 29. 30. 31. 32. 33. a Z Câu 7. Tính I = 48 (sin x)2 dx theo a. D D D D D B C C B C A 0
34. 35. 36. 37. 38. 39. 40. 41. 42. 43. 44.
A. I = 24a − 12 sin 2a. D C A B D C A C D C A
B. I = 24(1 − cos 2a). 45. 46. 47. 48. 49. 50. C. I = 16(sin a)3. D A B D B A
D. I = 24(1 − sin 2a). Câu 8. Tính theo a tích phân I = a ĐỀ ÔN SỐ 26 Z 24 sin x cos x dx. 0
Câu 1. Họ các nguyên hàm của hàm số f (x) = A. I = 12 cos 2a. B. I = 12 sin 2a. 48 sin 2x là C. I = 12(sin a)2. D. I = 24 sin 2a. A. 24 cos 2x + C. B. 96 cos 2x + C. a Z Câu 9. Cho I = 18 x sin x dx và J = C. −96 cos 2x + C. D. −24 cos 2x + C. 0 6 a
Câu 2. Tìm hàm số f (x) thỏa mãn f 0(x) = Z 3 − 2x 18
cos x dx với a ∈ R. Khẳng định nào sau đây và f (2) = 0. 0
A. f (x) = −3 ln |3 − 2x|. đúng?
B. f (x) = 2 ln |3 − 2x|. A. I = 18a cos a + J.
B. I = −18a cos a − J.
C. f (x) = −2 ln |3 − 2x|.
C. I = −18a cos a + J. D. I = 18a cos a − J.
D. f (x) = 3 ln |3 − 2x|. a Z Câu 10. Cho I = ln 36 · x · 3x dx và J =
Câu 3. Cho F(x) là một nguyên hàm của hàm số 0 a
f (x) = 8(1 − 2x)3. Tính I = F(1) − F(0). Z 6
3x dx, với a ∈ R. Khẳng định nào sau đây A. I = 2. B. I = −2. 0 C. I = 0. D. I = −16. đúng? A. I = −6a · 3a + J.
B. I = −6a · 3a − J.
Câu 4. Cho F(x) là một nguyên hàm của hàm số C. I = 6a · 3a + J. D. I = 6a · 3a − J.
f (x) = 3x ln 9 thỏa mãn F(0) = 2. Tính F(1). a Z A. F(1) = 12 · ln2 3. B. F(1) = 3. Câu 11. Cho I = 8
ecos 2x sin 2x dx, với a ∈ R. C. F(1) = 6. D. F(1) = 4. 0
Mệnh đề nào sau đây đúng?
Câu 5. Để tìm nguyên hàm của hàm số f (x) = A. I = 4 e + ecos 2a.
12x ln x, ta đặt u = ln x và dv = 12x dx. Tính B. I = 4 e − ecos 2a. du. 1 1
C. I = 4 −e + ecos 2a. A. du = . B. du = dx. x x
D. I = −4 e + ecos 2a. 1 C. du = 12x dx. D. du = dv. a x Z x Câu 12. Cho I = 56 dx, với a ∈ R. a 1 + x2 Z 0 Câu 6. Tính I = ln 28 2x dx theo a.
Khẳng định nào sau đây đúng? 0 A. I = 28 ln(1 + a). B. I = 28 ln(1 + a2). A. I = 8 · 2a. C. I = 14 ln(1 + a2). D. I = 56 ln(1 + a2). 2a B. I = 2 ln 28 · − 1 . a + 1
Câu 13. Gọi S là diện tích hình phẳng giới hạn bởi √
C. I = a · ln 28 · 2a.
các đường y = 6 x, y = 0, x = 1 và x = 9. Tính D. I = 8 · (2a − 1). S. ♂ 30 đề ôn thi t HKII-12 100 v 100
Những nẻo đường phù sa 2021 30 ĐỀ - ĐỀ
30 ĐỀ ÔN THI HKII-LỚP 12 2020 A. S = 234. B. S = 104. A. N(0; 0; −1). B. M(−10; 15; −1). C. S = 208. D. S = 52. C. E(1; 0; −4). D. F(−1; −2; −6).
Câu 14. Gọi V là thể tích của khối tròn xoay sinh Câu 21. Trong không gian Oxyz, cho mặt phẳng
ra khi quay quanh trục hoành hình phẳng giới (P) : 2x − 2z + 1 = 0. Véc-tơ nào dưới đây là một
hạn bởi các đường y = sin x, y = 0, x = 0 và véc-tơ pháp tuyến của (P)? #» #» x = 12π. A. n = (2; −2; 1). B. v = (2; −2; 0). 12π #» #» Z C. m = (1; 0; −1). D. u = (2; 0; 2). A. V = π (sin x)2 dx. 0
Câu 22. Trong không gian Oxyz, viết phương 12π Z
trình của mặt cầu có tâm I(−1; 0; 0) và bán kính B. V = 2 π (sin x)2 dx. R = 9. 0 12π
A. (x + 1)2 + y2 + z2 = 3. Z C. V = 2 π sin x dx.
B. (x + 1)2 + y2 + z2 = 81. 0
C. (x − 1)2 + y2 + z2 = 3. 12π Z
D. (x + 1)2 + y2 + z2 = 9. D. V = π sin x dx. 0
Câu 23. Trong không gian Oxyz, phương trình
Câu 15. Tìm số phức z có điểm biểu diễn là nào dưới đây là phương trình mặt cầu? (−2; 9).
A. x2 + y2 + z2 − x + 1 = 0. A. z = −2i + 9i. B. z = −2i + 9.
B. x2 + y2 + z2 − 6x + 9 = 0. C. z = −2x + 9yi. D. z = −2 + 9i.
C. x2 + y2 + z2 + 9 = 0.
D. x2 + y2 + z2 − 2 = 0.
Câu 16. Tìm phần thực a và phần ảo b của số phức z = (−2 + 3i)(−9 − 10i).
Câu 24. Trong không gian Oxyz, viết phương A. a = 48 và b = 7.
trình của mặt phẳng (P) đi qua điểm M(−3; −2; 3) B. a = −48 và b = 7.
và vuông góc với trục Ox.
C. a = −48 và b = −7. A. (P) : x + 3 = 0. D. a = 48 và b = −7. B. (P) : x + y + 5 = 0.
C. (P) : y + z − 1 = 0.
Câu 17. Tìm số phức liên hợp của số phức z thỏa D. (P) : x − 3 = 0. (−7 + 6i)z = 1 − 2i. 19 8 19 8 A. z = − + i. B. z = − − i.
Câu 25. Trong không gian Oxyz, phương trình 85 85 85 85 19 8 19 8
nào dưới đây là phương trình của mặt phẳng đi C. z = − i. D. z = + i. 85 85 85 85
qua điểm E(1; 2; 3) và song song với mặt phẳng
Câu 18. Tìm mô-đun của số phức z = (−6 + Oxy? 8i)2. A. z − 3 = 0. B. x + y − 3 = 0. √ √ A. |z| = 4 527. B. |z| = 2 7. C. x + y + z − 6 = 0. D. z + 3 = 0. C. |z| = 100. D. |z| = 10.
Câu 26. Trong không gian Oxyz, cho ba mặt
Câu 19. Tìm số phức z có phần ảo dương thỏa phẳng (P), (Q), (R) lần lượt có phương trình là z2 − 2z + 10 = 0.
x − 4z + 8 = 0, 2x − 8z = 0, y = 0. Mệnh đề nào A. z = 1 + 3i. B. z = −1 + 3i. dưới đây đúng? C. z = 2 + 6i. D. z = −2 + 6i. A. (P) ≡ (Q). B. (P) cắt (Q).
Câu 20. Trong không gian Oxyz, cho mặt phẳng C. (Q) k (R). D. (R) cắt (P).
(P) : 3x + 2y − z + 1 = 0. Điểm nào dưới đây thuộc Câu 27. Trong không gian Oxyz, hãy tính p và q (P)?
lần lượt là khoảng cách từ điểm M(5; −2; 0) đến ♂ 30 đề ôn thi t HKII-12 101 v 101
Những nẻo đường phù sa 2020 - 2021 30 ĐỀ
30 ĐỀ ÔN THI HKII-LỚP 12
mặt phẳng (Oxz) và mặt phẳng (P) : 3x − 4z + 5 =
B. (P) : x − y − 1 = 0. 0. C. (P) : y − 1 = 0. A. p = 2 và q = 3. B. p = 2 và q = 4. D. (P) : y + 1 = 0. C. p = −2 và q = 4. D. p = 5 và q = 4.
Câu 34. Trong không gian Oxyz, cho ba điểm
Câu 28. Trong không gian Oxyz, cho điểm M(0; 1; 0), N(2; 0; 0), P(0; 0; −3). Phương trình nào
M(1; −2; 3). Tìm tọa độ điểm H là hình chiếu dưới đây là phương trình mặt phẳng (MNP)? x y z x y z
vuông góc của điểm M trên mặt phẳng (Oxz). A. + + = 1. B. + + = 0. 2 1 −3 2 1 −3 A. H(0; 0; 3). B. H(1; 0; 0). x y z x y z C. + + = 1. D. + + = 0. C. H(1; 0; 3). D. H(0; −2; 0). 1 2 −3 1 2 −3
Câu 35. Tìm tập nghiệm S của bất phương trình
Câu 29. Trong không gian Oxyz, hãy viết phương 25x−5 − 5x ≤ 0.
trình của đường thẳng d đi qua điểm M(−1; 0; 0) A. S = (0; 10]. B. S = (∞; 10].
và vuông góc với mặt phẳng (P) : x + 2y − z + 1 = C. S = (−∞; 10). D. S = (0; 10). 0. x + 1 y z A. d : = = .
Câu 36. Tìm tập nghiệm của bất phương trình 1 2 −1 x − 1 y z log x + 8 log x ≤ 10. B. d : = = . 6 36 1 2 −1 A. S = (0; 36]. B. S = (−∞; 36]. x + 1 y z C. d : = = . C. S = (−∞; 36). D. S = [0; 36]. 1 2 1 x − 1 y z D. d : = = .
Câu 37. Cho số phức z = a + bi với a, b ∈ R 1 2 1
thỏa z + 2i + 1 = |z|(1 + i) và |z| > 1. Tính
Câu 30. Trong không gian Oxyz, hãy viết phương P = a − b.
trình của đường thẳng d đi qua hai điểm A. P = −3. B. P = 3. M(0; −2; 0), N(1; −3; 1). x y − 2 z x y − 2 z C. P = −1. D. P = 1. A. d : = = . B. d : = = . 1 −1 1 1 1 1 x y + 2 z x y + 2 z
Câu 38. Tìm các số phức z thỏa 2iz + 3z = 5. C. d : = = . D. d : = = . 1 −1 1 1 1 1 A. z = −3 − 2i. B. z = 3 − 2i.
Câu 31. Trong không gian Oxyz, cho hai đường C. z = −3 + 2i. D. z = 3 + 2i. x
thẳng d1 và d2 lần lượt có phương trình là = 1
Câu 39. Trong không gian Oxyz, viết phương y + 1 z x − 1 y z = và = =
. Mệnh đề nào dưới trình mặt cầu (S) có tâm I(0; −5; 0) biết (S) tiếp −2 1 −2 1 1 đây đúng?
xúc với mặt phẳng (P) : x + 2y − 2z + 16 = 0. A. d1 k d2. B. d1 cắt d2.
A. (S) : x2 + (y + 5)2 + z2 = 2. C. d1 trùng với d2. D. d1 chéo d2.
B. (S) : x2 + (y + 5)2 + z2 = 4.
C. (S) : x2 + (y − 5)2 + z2 = 2.
Câu 32. Trong không gian Oxyz, hãy viết phương
D. (S) : x2 + (y − 5)2 + z2 = 4.
trình đường thẳng d đi qua điểm M(0; −9; 0) và x y + 2 z
song song với đường thẳng ∆ : = = .
Câu 40. Trong không gian Oxyz, viết phương 1 −2 1 x y − 9 z x y + 9 z
trình mặt phẳng (P) biết (P) đi qua hai điểm A. d : = = . B. d : = = . 1 −2 1 1 −2 1
M(0; −1; 0), N(−1; 1; 1) và vuông góc với mặt x y − 9 z x y + 9 z C. d : = = . D. d : = = . phẳng (Oxz). 1 2 1 1 2 1
A. (P) : x + z + 1 = 0. B. (P) : x − z = 0.
Câu 33. Trong không gian Oxyz, hãy viết phương C. (P) : z = 0. D. (P) : x + z = 0.
trình của mặt phẳng (P) đi qua điểm M(0; −1; 0)
và vuông góc với đường thẳng OM.
Câu 41. Trong không gian Oxyz, cho mặt phẳng x A. (P) : x + y + 1 = 0.
(P) : 2x + y + z + 3 = 0 và đường thẳng d : = 2 ♂ 30 đề ôn thi t HKII-12 102 v 102
Những nẻo đường phù sa 2021 30 ĐỀ - ĐỀ
30 ĐỀ ÔN THI HKII-LỚP 12 2020 y z + 2 =
, với m 6= 0. Tìm m để d song song C. m ≈ 39505476. D. m ≈ 33935125. 1 m (P).
Câu 49. Cho hình lập phương MNPQ.M0 N0P0Q0 A. m = 5. B. m = −5. có E, F, G lần lượt là trung điểm của C. m = 1. D. m = −1.
NN0, PQ, M0Q0 Tính góc giữa hai đường thẳng
Câu 42. Viết phương trình tiếp tuyến của đồ thị EG và P0F.
hàm số y = x + ln x tại điểm M(1; 1). A. 45◦. B. 30◦. C. 90◦. D. 60◦. A. y = 2x − 1. B. y = 2x + 1.
Câu 50. Cho hình hộp chữ nhật MNPQ.M0 N0P0Q0 C. y = 2x − 2. D. y = 1.
có MN = 6, MQ = 8, MP0 = 26. Tính diện tích
Câu 43. Tìm tập nghiệm S của bất phương trình toàn phần S của hình trụ có hai đường tròn đáy 2(log x)2 − x + 9 3 log9 1 ≤ 0.
là hai đường tròn ngoại tiếp hai hình chữ nhật A. S = [3; 9]. B. S = [−3; 9]. MNPQ và M0 N0P0Q0. C. S = (3; 9). D. S = (3; 9]. A. S = 145π. B. S = 250π.
Câu 44. Tìm tập nghiệm S của bất phương trình C. S = 265π. D. S = 290π. 16x − 5 · 4x + 4 ≤ 0.
BẢNG ĐÁP ÁN THAM KHẢO A. S = (0; 1). B. S = [1; 4]. C. S = (1; 4). D. S = [0; 1]. 1. 2. 3. 4. 5. 6. 7. 8. 9. 10. 11. D A C C B D A C C D B
Câu 45. Tính diện tích S của hình phẳng giới hạn
12. 13. 14. 15. 16. 17. 18. 19. 20. 21. 22.
bởi hai đường y = 6x2 và y = 6x. B B A D D B C A D C B A. S = 1. B. S = 2. 1 1
23. 24. 25. 26. 27. 28. 29. 30. 31. 32. 33. C. S = . D. S = . 2 3 D A A D B C A C D B D
Câu 46. Có bao nhiêu giá trị nguyên của tham số
34. 35. 36. 37. 38. 39. 40. 41. 42. 43. 44. √ m để phương trình 3
pm + 3 3 m + 3 sin x = sin x có A B A D D B D B A A D nghiệm thực. 45. 46. 47. 48. 49. 50. A. 7. B. 3. C. 5. D. 2. A C D D C D
Câu 47. Cho hình chóp S.MNPQ có đáy là hình
vuông cạnh bằng 1, SM vuông góc với đáy và ĐỀ ÔN SỐ 27
SM = 2. Tính khoảng cách h giữa hai đường thẳng SN và MP.
I. PHẦN TRẮC NGHIỆM A. h = 1. B. h = 2. 1 2
Câu 1. Trong không gian với hệ trục tọa độ Oxyz, C. h = . D. h = . 3 3 x = 1
Câu 48. Ông N vay ngân hàng 100 triệu đồng với cho đường thẳng d :
y = 2 + 3t (t ∈ R). Đường
lãi suất 0,9%/tháng và thỏa thuận việc hoàn nợ z = 5 − t
theo cách: lần hoàn nợ thứ nhất sau ngày vay đúng thẳng d đi qua điểm nào dưới đây?
một tháng, hai lần hoàn nợ liên tiếp cách nhau A. M1(1; 5; 4).
B. M2(−1; −2; −5).
đúng một tháng; số tiền hoàn nợ m của mỗi lần là C. M3(0; 3; −1). D. M4(1; 2; −5).
như nhau và trả hết nợ sau 3 tháng kể từ ngày vay,
lãi suất của ngân hàng không thay đổi trong thời Câu 2. Cho số phức z = 2 + 5i. Tìm số phức
gian trên. Tìm gần đúng số tiền hoàn nợ m (đồng), w = iz + z.
làm tròn đến chữ số hàng đơn vị. A. w = −3 − 3i. B. w = 3 + 7i. A. m ≈ 33935120. B. m ≈ 39505475. C. w = −7 − 7i. D. w = 7 − 3i. ♂ 30 đề ôn thi t HKII-12 103 v 103
Những nẻo đường phù sa 2020 - 2021 30 ĐỀ
30 ĐỀ ÔN THI HKII-LỚP 12 Z
Câu 3. Trong không gian với hệ trục tọa độ Oxyz, D.
ax dx = ax · ln a + C (a > 0, a 6= 1).
cho mặt cầu (S) : (x + 1)2 + (y − 2)2 + (z − 1)2 = 9. Câu 9. Trong không gian với hệ trục tọa độ Oxyz,
Tìm tọa độ tâm I và tính bán kính R của mặt cầu cho mặt phẳng (P): − 3x + 2z − 1 = 0. Véc-tơ (S).
nào dưới đây là véc-tơ pháp tuyến của mặt phẳng
A. I(−1; 2; 1) và R = 3. (P)?
B. I(−1; 2; 1) và R = 9. #» #» A. n = (6; 0; −2). B. n = (−3; 2; 0).
C. I(1; −2; −1) và R = 3. #» #» C. n = (−6; 0; 4). D. n = (−3; 0; −2).
D. I(1; −2; −1) và R = 9. Câu 10.
Câu 4. Trong không gian với hệ trục tọa độ Oxyz, #» #» #» #» #» Điểm A trong y
cho véc-tơ u = 2 i + 3 j − 5 k . Tọa độ véc-tơ u hình vẽ biểu là #» #» diễn cho số 2 A A. u = (2; −3; −5). B. u = (−2; −3; 5). #» #» phức z. Tìm C. u = (−2; 3; −5). D. u = (2; 3; −5). phần thực và
Câu 5. Trong không gian với hệ trục tọa độ Oxyz, phần ảo của số x
cho hai điểm A(1; 1; 0) và B(0; 1; 2). Véc-tơ nào phức z. O 3
dưới đây là véc-tơ chỉ phương của đường thẳng
A. Phần thực là 3, phần ảo là −2i. AB? #» #»
B. Phần thực là 3, phần ảo là 2. A. a = (−1; 0; −2). B. b = (−1; 0; 2). #» #»
C. Phần thực là 3, phần ảo là −2. C. c = (1; 2; 2). D. d = (−1; 1; 2).
D. Phần thực là 3, phần ảo là 2i.
Câu 6. Cho hàm số f (x) xác định và liên tục trên 5 7
Câu 11. Tính thể tích vật thể tạo thành khi quay Z Z R thỏa f (x) dx = 3 và
f (x) dx = 9. Tính hình phẳng (H) quanh trục Ox, biết (H) được giới 2 5
hạn bởi các đường y = 4x2 − 1, y = 0. 7 8π 16π 4π 2π Z A. . B. . C. . D. . I = f (x) dx. 15 15 15 15 2
Câu 12. Có bao nhiêu số thực a thỏa mãn đẳng A. I = −6. B. I = 12. 2 Z C. I = 3. D. I = 6. thức tích phân x3 dx = 2?
Câu 7. Cho hàm số y = f (x) xác định và liên tục a A. 1. B. 4. C. 3. D. 2.
trên đoạn [a; b]. Diện tích hình phẳng giới hạn bởi Câu 13. Trong không gian với hệ trục tọa độ Oxyz,
đồ thị hàm số y = f (x), đường thẳng x = a, x = b cho hai mặt phẳng (P): x + 2y − z + 3 = 0 và
và trục Ox được tính bởi công thức b b
(Q) : x − 4y + (m − 1)z + 1 = 0, với m là tham số. Z Z A. S =
Tìm tất cả các giá trị của tham số thực m để mặt f (x) dx. B. S = | f (x)| dx. a a
phẳng (P) vuông góc với mặt phẳng (Q). b a Z Z A. m = −3. B. m = −6. C. S = f (x) dx. D. S = | f (x)| dx. C. m = 2. D. m = 1. a b
Câu 8. Khẳng định nào sau đây là khẳng định Câu 14. Trong không gian với hệ trục tọa độ Oxyz, sai?
cho hai điểm A(1; −2; −3), B(−1; 4; 1) và đường Z 1 1 x + 2 y − 2 z + 3 A. dx = − + C. thẳng d : = = . Phương trình x2 x 1 −1 2 Z B. cos x dx = sin x + C.
nào dưới đây là phương trình của đường thẳng đi
qua trung điểm đoạn thẳng AB và song song với Z 1 √ C. √ dx = x + C. 2 x d? ♂ 30 đề ôn thi t HKII-12 104 v 104
Những nẻo đường phù sa 2021 30 ĐỀ - ĐỀ
30 ĐỀ ÔN THI HKII-LỚP 12 2020 x y − 1 z + 1 A. = = .
Câu 21. Trong không gian với hệ trục tọa độ Oxyz, 1 −1 2 x y − 2 z + 2 x = t B. = = . 1 −1 2 cho đường thẳng d :
y = −1 (t ∈ R) và hai mặt x y − 1 z + 1 C. = = . 1 1 2 z = −t x y + 1 z − 1 D. = = .
phẳng (P) : x + 2y + 2z + 3 = 0, (Q) : x + 2y + 2z + 1 −1 2
7 = 0. Mặt cầu (S) có tâm I(a; b; c) thuộc đường
Câu 15. Biết rằng phương trình z2 + bz + c = thẳng d và (S) tiếp xúc với hai mặt phẳng (P) và
0 (b, c ∈ R) có một nghiệm phức là z1 = 1 + 2i. (Q). Khi đó a + b + c bằng Khi đó A. 1. B. −1. C. 2. D. −2. A. b + c = 2. B. b + c = 3. C. b + c = 0. D. b + c = 7.
Câu 22. Trên mặt phẳng tọa độ, tập hợp điểm biểu
diễn số phức z thỏa mãn điều kiện |z + 2 − 5i| = 6
Câu 16. Trong không gian với hệ trục tọa độ Oxyz, là đường tròn có tâm I và bán kính R lần lượt là
tìm tất cả các giá trị m để phương trình x2 + y2 +
A. I(−2; 5) và R = 36.
z2 − 2x − 2y − 4z + m = 0 là phương trình của một
B. I(−2; 5) và R = 6. mặt cầu.
C. I(2; −5) và R = 36. A. m > 6. B. m ≤ 6.
D. I(2; −5) và R = 6. C. m < 6. D. m ≥ 6. Câu 23.
Câu 17. Trong không gian với hệ trục tọa độ Oxyz, Cho hàm bậc hai y = y
cho điểm M(1; 2; −1). Gọi H là điểm đối xứng với
f (x) có đồ thị như hình 1
M qua trục Ox. Tọa độ điểm H là
vẽ bên. Tính thể tích khối A. H(−1; −2; 1). B. H(1; −2; −1). tròn xoay tạo thành khi x O 1 C. H(1; −2; 1). D. H(1; 2; 1). quay hình phẳng giới
Câu 18. Biết rằng F(x) là một nguyên hàm của hạn bởi đồ thị hàm số 1
hàm số f (x) = sin(1 − 2x) và thỏa mãn F = y = f (x) và Ox quanh 2 trục Ox.
1. Mệnh đề nào sau đây là đúng? 4π 4π
A. F(x) = cos(1 − 2x). A. . B. . 3 5
B. F(x) = cos(1 − 2x) + 1. 16π 16π C. . D. . 1 3 15 5
C. F(x) = − cos(1 − 2x) + . 2 2
Câu 24. Biết hàm số F(x) = ax3 + (a + b)x2 + 1 1 D. F(x) = cos(1 − 2x) + .
(2a − b + c)x + 1 là một nguyên hàm của hàm số 2 2
f (x) = 3x2 + 6x + 2. Tổng a + b + c là
Câu 19. Trong không gian với hệ trục tọa độ Oxyz, A. 5. B. 3. C. 4. D. 2.
cho mặt phẳng (P) : 3x + 4y + 2z + 4 = 0 và điểm
A(1; −2; 3). Tính khoảng cách d từ A đến mặt Câu 25. Trong không gian với hệ trục tọa độ Oxyz, phẳng (P). √
cho mặt phẳng (P) : 6x − 2y + z − 35 = 0 và điểm 5 5 A. d = . B. d = .
A(−1; 3; 6). Gọi A0 là điểm đối xứng của A qua 3 9 5 5 (P). Tính OA0. C. d = . D. d = √ . √ √ 29 29 A. OA0 = 5 3. B. OA0 = 3 26. √ √
Câu 20. Tính diện tích hình phẳng giới hạn bởi C. OA0 = 46. D. OA0 = 186.
đồ thị hàm số y = x3 − x và đồ thị hàm số y = Câu 26. Trong không gian với hệ trục tọa độ Oxyz, x − x2.
cho tứ diện ABCD với A(−3; 1; −1), B(1; 2; m), 9 37 81 A. . B. 13. C. . D. .
C(0; 2; −1), D(4; 3; 0). Tìm tất cả các giá trị thực của 4 12 12 ♂ 30 đề ôn thi t HKII-12 105 v 105
Những nẻo đường phù sa 2020 - 2021 30 ĐỀ
30 ĐỀ ÔN THI HKII-LỚP 12
m để thể tích khối tứ diện ABCD bằng 10. hình vẽ. y A. m = ±30. B. m = ±120. C. m = ±20. D. m = ±60.
Câu 27. Trong không gian với hệ trục tọa độ Oxyz, x − 12 y − 9 z − 1 cho đường thẳng d : = = và 4 3 1 O
mặt phẳng (P) : 3x + 5y − z − 2 = 0. Gọi ∆ là hình a x b c
chiếu vuông góc của d lên (P). Phương trình tham số của ∆ là
Mệnh đề nào dưới đây là đúng? x = −62t
A. f (c) > f (b) > f (a). A. y = 25t (t ∈ R).
B. f (b) > f (a) > f (c).
C. f (a) > f (c) > f (b). z = 2 − 61t
D. f (c) > f (a) > f (b). x = −8t B. y = 7t (t ∈ R). II. PHẦN TỰ LUẬN
Câu 1. Tìm nguyên hàm F(x) của hàm số f (x) = z = −2 + 11t
(2x + 1)(x − 2), biết F(1) = 2. x = 62t e C. y = −25t (t ∈ R). Z
Câu 2. Tính tích phân I = x · ln x dx. z = −2 + 61t 1 x = −8t
Câu 3. Tìm số phức z thỏa mãn z( 2i − 3) − 8iz = D. y = 7t (t ∈ R). −16 − 15i. z = 2 + 11t
Câu 4. Tìm tập hợp các điểm biểu diễn của số
phức z thỏa mãn |z − 2 − i| = |z + 2i|.
Câu 28. Cho số phức z = x + iy (x, y ∈ R) thỏa
BẢNG ĐÁP ÁN THAM KHẢO
mãn |z2 + 1| = |(z + i)(z + 2)|. Khi z có mô-
đun nhỏ nhất hãy tính giá trị của biểu thức P = 1. 2. 3. 4. 5. 6. 7. 8. 9. 10. 11. x2 + 2y. A A A D B B B D C B A 6 4
12. 13. 14. 15. 16. 17. 18. 19. 20. 21. 22. A. P = . B. P = − . 25 25 D B A B C C D D C B B 4 6 C. P = . D. P = − .
23. 24. 25. 26. 27. 28. 29. 30. 25 25 C A D D C D D D
Câu 29. Trong không gian với hệ trục tọa độ Oxyz,
cho mặt cầu (S) : x2 + y2 + z2 − 2x − 3 = 0 và ba ĐỀ ÔN SỐ 28
điểm A(−1; −3; 1), B(0; −7; 0), C(−2; −1; 1). Gọi
D(a; b; c) thuộc (S) sao cho thể tích tứ diện ABCD Câu 1. Cho hàm số y = f(x) liên tục và có đạo
đạt giá trị lớn nhất. Tính tổng P = a + b + c.
hàm trên [a; b] và có một nguyên hàm là hàm số 1 A. P = . B. P = 1.
F(x) trên [a; b] , a < c < b. Khẳng định nào sau đây 3 5 là sai? C. P = 5. D. P = . 3 b a Z Z A. f (x) dx = − f (x) dx.
Câu 30. Cho hàm số y = f (x) có đồ thị y = f 0(x) a b Z
cắt trục Ox tại ba điểm có hoành độ a < b < c như B. f 0(x) dx = f (x) + C. ♂ 30 đề ôn thi t HKII-12 106 v 106
Những nẻo đường phù sa 2021 30 ĐỀ - ĐỀ
30 ĐỀ ÔN THI HKII-LỚP 12 2020 b c c 3 3 Z Z Z D. g(x) = (x + 3) 2 + C. C. f (x) dx = f (x) dx + f (x) dx. 2 a a b
Câu 7. Trong không gian với hệ tọa độ Oxyz, cho b Z
mặt phẳng (α) : 2x + y − 3z + 1 = 0. Véc-tơ nào sau D. f (x) dx = F(b) − F(a).
đây là véc-tơ pháp tuyến của mặt phẳng (α)? a #» #» A. n = (1; 2; 3).
B. n = (−2; −1; −3). 2 #» #» Z C. n = (2; 1; −3). D. n = (−2; 1; −3).
Câu 2. Cho hàm số f (x) thỏa mãn f (x) dx = Z −1 Câu 8. Tìm F(x) = cos x dx. 3 3 Z Z A. sin x + C. B. cos x + C. 5; f (x) dx = −2. Tính f (x) dx. C. − cos x + C. D. − sin x + C. 2 −1 A. 7. B. −7. C. 3. D. −3.
Câu 9. Khẳng định nào sau đây đúng? Z
Câu 3. Trong không gian với hệ tọa độ Oxyz, cho A. 2x dx = 2xln2 + C. Z hai mặt phẳng ( 1
α) : x + 2y + 4z − 1 = 0; (β) : 2x + B. ln x dx = + C. x
3y − 2z + 5 = 0. Chọn khẳng định đúng. Z C. ex dx = −ex + C.
A. (α) ⊥ (β). Z x4
B. (α) , (β) chéo nhau. D. x3 dx = + C. 4
C. (α) k (β). 4 D. ( Z √ α) ≡ (β). Câu 10. Tính I = x2 + 3 x dx.
Câu 4. Khẳng định nào sau đây đúng? 1 A. 5,3. B. 35. C. 3,5. D. 53. b b b Z Z A. u dv = (uv) − v du.
Câu 11. Phần thực của số phức z = (a + i)(1 − i) a a a là b b b Z Z B. v dv = (uv) A. −a + 1. B. a − 1. − v du. a a a C. a + 1. D. a2 + 1. b b b Z Z
Câu 12. Trong không gian với hệ tọa độ Oxyz, tính C. u dv = (uv) − u du.
bán kính mặt cầu tâm I (1; 0; 0) và tiếp xúc với mặt a a a b b b
phẳng (P) : x − 2y + 2z + 2 = 0. Z Z D. u dx = (uv) − v dx. A. R = 3. B. R = 5. √ a a a C. R = 2. D. R = 1.
Câu 5. Điểm nào sau đây thuộc đường thẳng 1
Câu 13. Cho z = 1 + 3i. Tính . x = 1 + t z 1 3 1 3 ∆ : y = 2 − t (t ∈ R)? A. + i. B. i − . 10 10 10 10 1 3 1 3 z = t C. − i. D. − − i. 10 10 10 10 A. M (0; −3; −1). B. M (3; 0; 2).
Câu 14. Trong không gian với hệ tọa độ Oxyz, tính C. M (2; 3; 1). D. M (6; −3; 2).
độ dài đoạn AB với A (1; −1; 0), B (2; 0; −2). √ √
Câu 6. Hàm số f (x) = x + 3 là một nguyên hàm A. AB = 2. B. AB = 2. √
của hàm số nào bên dưới? C. AB = 6. D. AB = 6. 2 3 A. g(x) = (x + 3) 2 + C. 3
Câu 15. Trong không gian với hệ tọa độ Oxyz, 1 B. g(x) = √ .
viết phương trình mặt phẳng (P) qua điểm 2 x + 3 #» −1
M (x0; y0; z0) và nhận n (A; B; C) làm véc-tơ pháp C. g(x) = √ . x + 3 tuyến. ♂ 30 đề ôn thi t HKII-12 107 v 107
Những nẻo đường phù sa 2020 - 2021 30 ĐỀ
30 ĐỀ ÔN THI HKII-LỚP 12
A. A(x − x0) + B(y − y0) + C(z − z0) = 0.
Câu 23. Mô-đun của số phức z = a − 2i là √ √
B. A(x + x0) + B(y + y0) + C(z + z0) = 0. A. |z| = a2 + 4. B. |z| = a2 − 4. √
C. A(x − x0) + B(y − y0) + C(z − z0) = 1. C. |z| = z + 2. D. |z| = a + 2.
D. A(x + x0) + B(y + y0) + C(z + z0) = 1.
Câu 24. Tìm phần thực và phần ảo của số phức
Câu 16. Tính thể tích khối tròn xoay do hình z = 5 − 4i.
phẳng giới hạn bởi các đường y = cos x, y = 0, x =
A. Phần thực là 5, phần ảo là 4i.
0, x = π quay xung quanh Ox.
B. Phần thực là 5, phần ảo là −4i. 2 π A. 0. B. 2π. C. . D. 2.
C. Phần thực là 5, phần ảo là −4. 2
D. Phần thực là 5, phần ảo là 4.
Câu 17. Số phức liên hợp của số phức z = 7i + 2 là
Câu 25. Trong không gian với hệ tọa độ Oxyz, A. z = 7i − 2. B. z = 2 − 7i.
tính tọa độ trọng tâm G của tam giác ABC với C. z = −2 − 7i. D. z = 2 + 7i.
A(1; −1; 0), B(2; 0; −2), C(0; −2; −4) là
Câu 18. Trong không gian với hệ tọa độ Oxyz, cho A. G (1; −1; −2). B. G (1; −1; 2). # » #» #» #»
OA = i − 2 j + 3 k . Tìm tọa độ điểm A.
C. G (−1; −1; −2). D. G (−1; 1; 2).
A. A (−1; −2; −3). B. A (1; 2; 3).
Câu 26. %[HK2 (2017-2018), THPT Tân Hiệp, Kiên C. A (1; −2; 3). D. A (2; −4; 6).
Giang]Trong không gian với hệ tọa độ Oxyz,
Câu 19. Trong không gian với hệ tọa độ Oxyz, x = −1 + 3t
véc-tơ nào là véc-tơ chỉ phương của đường thẳng cho đường thẳng ∆ : y = 1 + t (t ∈ R) và hai x − 1 y z + 1 d : = = . z = 3t 2 1 3 #» #» 1 2
điểm A(5; 0; 2), B(2; −5; 3). Tìm điểm M thuộc ∆ A. u = (2; 1; −3). B. u = 1; ; . 2 3 sao cho 4ABM vuông tại A. #» 1 3 #» C. u = 1; ; . D. u = (−4; −2; 6). A. M(2; 2; 3). B. M(5; 3; 6). 2 2 C. M(−4; 0; −3). D. M(−7; −1; −6).
Câu 20. Gọi z1, z2 là hai nghiệm của phương trình
z2 + 3z + 3 = 0 trên tập C. Tính T = |z
Câu 27. Trong không gian với hệ tọa độ Oxyz, cho 1| + |z2|. √ √ √ A. 2 3. B. 2 5. C. 6. D. 3 2.
khối cầu (S) : (x − 1)2 + (y − 2)2 + (z + 1)2 = 25,
mặt phẳng (P) có phương trình x + 2y − 2z + 5 = 0
Câu 21. Trong không gian với hệ tọa độ Oxyz. Tìm cắt khối cầu (S) thành 2 phần. Tính thể tích của
tâm I và tính bán kính R của mặt cầu (S) : x2 + phần không chứa tâm của mặt cầu (S).
y2 + z2 − 2x − 4y + 2z + 2 = 0. 25π 25π 14π 16π A. . B. . C. . D. .
A. I (−1; −2; 1) , R = 2. √ 3 6 3 3
B. I (1; 2; −1) , R = 2 2. √
Câu 28. Trong không gian với hệ tọa độ Oxyz, cho
C. I (−1; −2; 1) , R = 2 2.
2 điểm A(−2; 1; 3), B(3; −2; 4), đường thẳng ∆ :
D. I (1; 2; −1) , R = 2. x − 1 y − 6 z + 1 = =
và mặt phẳng (P) : 41x − 2 11 −4 1 Z x
6y + 54z + 49 = 0. Đường thẳng (d) đi qua B, cắt
Câu 22. Đặt t = x + 1. Khi đó dx = (x + 1)2
đường thẳng ∆ và mặt phẳng (P) lần lượt tại C và 0 2
D sao cho thể tích của 2 tứ diện ABCO và OACD Z
f (t) dt. Hàm số f (t) là hàm số nào dưới đây
bằng nhau, biết (d) có một véc-tơ chỉ phương là #» 1 u = (4; b; c). Tính b + c. t − 2 1 A. f (t) = . B. f (t) = ln |t| + . A. b + c = 11. B. b + c = 6. t2 t 1 1 1 1 C. b + c = 9. D. b + c = 4. C. f (t) = − . D. f (t) = + . t t2 t t2 ♂ 30 đề ôn thi t HKII-12 108 v 108
Những nẻo đường phù sa 2021 30 ĐỀ - ĐỀ
30 ĐỀ ÔN THI HKII-LỚP 12 2020 a c a c Z sin3 x, với và
là phân số tối giản và a, b, c, d là Câu 29. Biết xex dx = 1. Tìm a. d b d
các số nguyên dương. Tính T = a + b + c + d. 0
A. a = 1. B. a = 5. C. a = 2. D. a = 3. A. Đáp án khác. B. T = 11.
Câu 30. Trong không gian với hệ tọa độ Oxyz, cho C. T = 10. D. T = 9.
3 điểm A(2; 3; 0), B(0; −4; 1), C(3; 1; 1). Mặt cầu đi Câu 36. Trong không gian với hệ tọa độ Oxyz,
qua ba điểm A, B, C và có tâm I thuộc mặt phẳng cho tứ giác ABCD có A(8; 6; −7), B(2; −1; 4),
(Oxz), biết I(a; b; c). Tính tổng T = a + b + c. C(0; −3; 0), D(−8; −2; 9) và đường thẳng A. T = 3. B. T = −3. ∆ x + 2 y − 1 z − 3 : = = . Mặt phẳng (P) chứa C. T = −1. D. T = 2. 2 1 −2
đường thẳng ∆ và cắt tứ diện ABCD thành 2 phần π 4 Z 5 + 5 cos2 x + 6 sin 2x
có thể tích bằng nhau, biết (P) có một véc-tơ pháp Câu 31. Biết dx = #» (2 sin x + 3 cos x)2
tuyến là n = (7; b; c). Tính b + c. 0 aπ + b A. 8. B. 11. C. 13. D. 9.
với a, b và c là các số nguyên dương √ c √ Z 1 + tan x a b Câu 37. Đặt t = 1 + tan x thì dx và và
là các phân số tối giản. Tính tổng cos2 x c c
trở thành nguyên hàm nào? T = a + b + c. Z Z t2 A. T = A. 79. B. T = 36. 2t dt. B. dt. Z Z C. T = 63. D. T = 69. C. dt. D. 2t2 dt.
Câu 32. Trong không gian với hệ tọa độ Oxyz. Câu 38. Cho số phức z thỏa mãn |z| = 5 và
Phương trình mặt phẳng đi qua điểm A(1; 2; 0) và |z + 3| = |z + 3 − 10i|. Tìm số phức w = z − 4 + x + 1 y z chứa đường thẳng d : = = có một véc- 3i. 2 3 1 #»
tơ pháp tuyến là n (1; a; b). Tính a + b. A. w = −1 + 7i. B. w = −3 + 8i. A. a + b = 2. B. a + b = 0. C. w = 1 + 3i. D. w = −4 + 8i. C. a + b = −3. D. a + b = 3.
Câu 39. Trên tập số phức, tích 4 nghiệm của
Câu 33. Cho số phức z = a + bi, (a, b ∈ R) thỏa phương trình x x2 − 1 (x + 2) = 24 bằng
mãn (1 + i)z + 2z = 3 + 2i. Tính S = a + b. A. −24. B. −12. C. 12. D. 24. 1 A. S = − . B. S = 1. π √ 2 6 Z 1 a 3 + b 1
Câu 40. Biết tích phân dx = C. S = . D. S = −1. 1 + sin x c 2 0
Câu 34. Trong không gian với hệ tọa độ Oxyz, cho với a, b, c là các số nguyên. Tính tổng T = a + b + x = 1 + t c. đường thẳng d A. T = 7. B. T = 11. 1 :
y = 2 − t (t ∈ R) và đường C. T = 5. D. T = 12. z = 3t x = 2s
Câu 41. Trong không gian với hệ tọa độ Oxyz, thẳng d cho mặt phẳng ( 2 :
y = 1 − 2s (s ∈ R). Chọn khẳng định α) : x + y − 2z + 1 = 0
đi qua điểm M(1; −2; 0) và cắt đường thẳng z = 6s đúng. x = 11 + 2t A. d d
(t ∈ R) tại N. Tính độ dài đoạn 1, d2 chéo nhau. B. d1, d2 cắt nhau. : y = 2t C. d 1 k d2. D. d1 ≡ d2. z = −4t MN.
Câu 35. Một nguyên hàm của hàm số f (x) = √ √ √ √ a A. 7 6. B. 3 11. C. 10. D. 4 5.
sin2 x · cos3 x có dạng là F(x) = − sin5 x + b ♂ 30 đề ôn thi t HKII-12 109 v 109
Những nẻo đường phù sa 2020 - 2021 30 ĐỀ
30 ĐỀ ÔN THI HKII-LỚP 12
Câu 42. Trong không gian với hệ tọa độ Oxyz, cho Câu 49. Trong không gian với hệ tọa độ Oxyz,
A(2; 3; −1) ,B(−1; 1; 1), C(1; m − 1; 2). Tìm m để x = 3 + t tam giác ABC vuông tại B. cho 2 đường thẳng ∆1 : y = 1 + t (t ∈ R); A. m = 1. B. m = 0. z = 1 + 2t C. m = 2. D. m = −3. ∆ x + 2 y − 2 z 2 : = = và điểm M(0; 3; 0). 2 5 −1
Câu 43. Cho số phức z1 = a − 2i, z2 = 1 + bi. Tìm Đường thẳng d đi qua M, cắt ∆1 và vuông góc với
phần ảo của số phức z, biết z #» 1z + z2z = 1 + i.
∆2 có một véc-tơ chỉ phương là u = (4; a; b). Tính a + b − 1 A. . T = a + b (a + 1)2 + (b − 2)2 a − b + 3 A. T = −2. B. T = 4. B. . (a + 1)2 + (b − 2)2 C. T = −4. D. T = 2. b − a − 3 C. . (a + 1)2 + (b − 2)2 Câu 50. 1 − a − b D. . Diện y (a + 1)2 + (b − 2)2 h(x) f (x) tích hình 3 phẳng Z 1 Câu 44. Biết dx = m ln 10 + n ln 7 3x + 1 (phần 2
(m, n ∈ Q). Tính m − n. gạch 2 2 chéo) giới g(x) A. 1. B. . C. − . D. 0. 3 3 hạn bởi
Câu 45. Diện tích hình phẳng giới hạn bởi hai đồ thị O a x b c
đường y = x3 − x; y = 3x bằng 3 hàm A. 0. B. 8. C. 16. D. 24. số f (x), g(x), h(x)
Câu 46. Cho số phức z thỏa mãn điều kiện như hình √
|z − 1 − 2i| + |z − 3| = 7 + 3i. Tìm giá trị nhỏ bên, bằng
nhất của P = |z − 2 − i|. √ kết quả A. P = 2. B. P = 2. √ nào sau C. P = 3. D. P = 3. đây. Z 1 c Câu 47. Biết + x5 dx = a ln |x| + bx6 + C Z 2x A. S = | f (x) − g(x)| dx +
với (a, b ∈ Q, C ∈ R). Tính a2 + b? a c 7 7 5 Z A. . B. . C. 9. D. . | 6 13 12 g(x) − h(x)| dx. b
Câu 48. Trong không gian với hệ tọa độ Oxyz, cho b Z
mặt phẳng (P) : x + 2y − 5z − 3 = 0 và hai điểm B. S = [ f (x) − g(x)] dx +
A(3; 1; 1), B(4; 2; 3). Gọi (Q) là mặt phẳng qua AB a c
và vuông góc với (P). Phương trình nào là phương Z [g(x) − h(x)] dx.
trình của mặt phẳng (Q). b
A. 9x − 7y − z + 19 = 0. b Z
B. −9x + 7y + z − 19 = 0. C. S = [ f (x) − g(x)] dx −
C. −9x − 7y + z − 19 = 0. a c Z
D. 9x − 7y − z − 19 = 0. [g(x) − h(x)] dx. b ♂ 30 đề ôn thi t HKII-12 110 v 110
Những nẻo đường phù sa 2021 30 ĐỀ - ĐỀ
30 ĐỀ ÔN THI HKII-LỚP 12 2020 c 1 Z Z D. S = [ f (x) + h(x) − g(x)] dx.
Câu 5. Tìm tham số m để I = ex(x + m) dx = a 0 e.
BẢNG ĐÁP ÁN THAM KHẢO A. m = 0. B. m = 1. √ 1. 2. 3. 4. 5. 6. 7. 8. 9. 10. 11. C. m = e. D. m = e. C C A A B B C A D B C
Câu 6. Trong không gian với hệ trục tọa độ Oxyz,
12. 13. 14. 15. 16. 17. 18. 19. 20. 21. 22.
mặt phẳng (P) cắt ba trục Ox, Oy, Oz lần lượt tại A, D C D A C B C C A D C
B, C; trực tâm tam giác ABC là H(1; 2; 3). Phương
23. 24. 25. 26. 27. 28. 29. 30. 31. 32. 33.
trình của mặt phẳng (P) là A C A A C D A C A B D
A. x + 2y + 3z − 14 = 0.
34. 35. 36. 37. 38. 39. 40. 41. 42. 43. 44.
B. x + 2y + 3z + 14 = 0. C C C D D A C D B C B x y z C. + + = 1. 45. 46. 47. 48. 49. 50. 1 2 3 x y z B B D D D C D. + + = 0. 1 2 3 2 Z x dx Câu 7. Biết I = = a ln 2 + ĐỀ ÔN SỐ 29 (x + 1)(2x + 1) 1
b ln 3 + c ln 5. Tính S = a + b + c.
Câu 1. Cho số phức z = −4 − 6i. Gọi M là điểm A. S = 1. B. S = 0.
biểu diễn số phức z. Tung độ của điểm M là C. S = −1. D. S = 2. A. 4. B. −6. C. 6. D. −4.
Câu 8. Cho hàm số y = f (x) có đạo hàm trên
đoạn [−2; 1] và f (−2) = 3, f (1) = 7. Tính I =
Câu 2. Tìm nguyên hàm của hàm số f (x) = 1 Z sin 3x. f 0(x) dx. Z A. f (x) dx = 3 cos 3x + C. −2 Z 1 A. I = 10. B. I = −4. B. f (x) dx = cos 3x + C. 7 3 C. I = . D. I = 4. Z 1 3 C. f (x) dx = − cos 3x + C. √ 3
Câu 9. Cho số phức z = 7 − i 5. Phần thực và Z D. f (x) dx = −3 cos 3x + C.
phần ảo của số phức z lần lượt là √ √ A. 7 và 5. B. −7 và 5. 2 √ √ Z ln x b Câu 3. Biết dx =
+ a ln 2 (với a là số thực, C. 7 và i 5. D. 7 và − 5. x2 c 1
Câu 10. Cho các số phức z thỏa mãn |z| = 12. b
b, c là các số nguyên dương và
là phân số tối Biết rằng tập hợp các điểm biểu diễn các số phức c
giản). Tính giá trị của T = 2a + 3b + c.
w = (8 − 6i)z + 2i là một đường tròn. Tính bán A. T = 5. B. T = 4.
kính r của đường tròn đó. C. T = −6. D. T = 6. A. r = 120. B. r = 122. √ C. r = 12. D. r = 24 7.
Câu 4. Trong không gian với hệ trục tọa độ Oxyz,
cho hai điểm M(−2; 6; 1) và M0(a; b; c) đối xứng Câu 11. Trong không gian với hệ tọa độ #» #» #» # » #» #»
nhau qua mặt phẳng (Oyz). Tính S = 7a − 2b +
O; i ; j ; k , cho véc-tơ OM = j − k . Tìm tọa 2017c − 1. độ điểm M. A. S = 2017. B. S = 2042. A. M(0; 1; −1). B. M(1; 1; −1). C. S = 0. D. S = 2018. C. M(1; −1). D. M(1; −1; 0). ♂ 30 đề ôn thi t HKII-12 111 v 111
Những nẻo đường phù sa 2020 - 2021 30 ĐỀ
30 ĐỀ ÔN THI HKII-LỚP 12
Câu 12. Số phức z = (1 + 2i)(2 − 3i) bằng
C. Mỗi số thực a được coi là một số phức với A. 8 − i. B. 8. phần ảo bằng 0. C. 8 + i. D. −4 + i.
D. Số 0 không phải là số ảo.
Câu 13. Mệnh đề nào trong các mệnh đề sau là Câu 18. Cho hàm số f (x) liên tục trên R và 1 3 mệnh đề sai? Z Z Z x2 có f (x) dx = 2; f (x) dx = 6. Tính I = A. x ln x dx = x2 ln x − + C. 2 0 0 Z 1 B. ln x dx = x ln x − x + C. Z f (|2x − 1|) dx. Z x2 x2 C. x ln x dx = ln x − + C. −1 2 4 2 3 A. I = 6. B. I =
. C. I = 4. D. I = . Z x2 D. 2x ln x dx = x2 ln x − + C. 3 2 2 4 4 Z Z
Câu 14. Trong không gian với hệ tọa độ Oxyz, Câu 19. Cho f (x) dx = 10 và g(x) dx = 5.
cho mặt phẳng (P) : 2x − 2y − z + 3 = 0 và điểm 2 2 4
M(1; −2; 13). Tính khoảng cách d từ M đến (P). Z 4 7 Tính I = [3 f (x) − 5g(x)] dx. A. d = . B. d = . 3 3 2 10 A. I = 5. B. I = −5. C. d = . D. d = 4. 3 C. I = 10. D. I = 15. 1 Z
Câu 20. Tìm phần ảo của số phức z thỏa mãn Câu 15. Cho f (4x) dx = 4. Tính I = z + 2z = (2 − i)3(1 − i). 0 4 A. −9. B. 9. C. 13. D. −13. Z f (x) dx.
Câu 21. Trong không gian với hệ tọa độ Oxyz. Mặt 0 A. I = 1. B. I = 8.
cầu tâm I(1; 3; 2), bán kính R = 4 có phương C. I = 4. D. I = 16. trình
A. (x − 1)2 + (y − 3)2 + (z − 2)2 = 8.
Câu 16. Thể tích của khối tròn xoay khi cho hình
B. (x − 1) + (y − 3) + (z − 2) = 16.
phẳng giới hạn bởi parabol (P) : y = x2 và đường
C. (x − 1)2 + (y − 3)2 + (z − 2)2 = 16.
thẳng d : y = x xoay quanh trục Ox bằng
D. (x − 1)2 + (y − 3)2 + (z − 2)2 = 4. 1 1 Z Z A. π x2 dx − π x4 dx.
Câu 22. Cho hai số phức z1 = m + 3i, z2 = 2 − 0 0
(m + 1)i, với m ∈ R. Tìm các giá trị của m để 1 1 Z Z w = z B. π x2 dx + π x4 dx. 1 · z2 là số thực.
A. m = 1 hoặc m = −2. 0 0 1
B. m = 2 hoặc m = −1. Z 2 C. π x2 − x dx.
C. m = 2 hoặc m = −3. 0
D. m = −2 hoặc m = −3. 1 Z D. π x2 − x dx. Câu 23. Cho A(
2; 1; −1), B(3; 0; 1), C(2; −1; 3), 0
điểm D nằm trên trục Oy và thể tích tứ diện ABCD
Câu 17. Trong các mệnh đề sau, mệnh đề nào bằng 5. Tọa độ điểm D là sai? A. (0; 8; 0).
A. Số phức z = a + bi, a, b ∈ R được gọi là số
B. (0; −7; 0) hoặc (0; 8; 0).
thuần ảo (hay số ảo) khi a = 0.
C. (0; 7; 0) hoặc (0; −8; 0).
B. Số i được gọi là đơn vị ảo. D. (0; −7; 0). ♂ 30 đề ôn thi t HKII-12 112 v 112
Những nẻo đường phù sa 2021 30 ĐỀ - ĐỀ
30 ĐỀ ÔN THI HKII-LỚP 12 2020 b b b a Z Z Z Z Câu 24. Giả sử f (x) dx = 2, f (x) dx = 3 với A. f (x) dx = − f (x) dx. a c a b c b b Z Z Z a < b < c thì f (x) dx bằng B. [ f (x) + g(x)] dx = f (x) dx + a a a A. 5. B. 1. C. −2. D. −1. b 2 + i Z
Câu 25. Số phức z = bằng g(x) dx. 4 + 3i 11 2 11 2 a A. − i. B. + i. b b 25 25 5 5 Z Z 11 2 11 2 C. k f (x) dx = k f (x) dx. C. + i. D. − i. 25 25 5 5 a a b b a Z Z Z x + 1 D. x f (x) dx = x f (x) dx. Câu 26. Cho
dx = e, a > 1. Khi đó, giá trị x a a 1 của a là
Câu 31. Trong không gian với hệ trục tọa độ Oxyz, e 2 2 #» #» A. . B. . C. . D. e.
cho u = (−2; 3; 0), v = (2; −2; 1). Độ dài của véc- 2 1 − e e − 1 #» #» #» tơ w = u − 2 v là
Câu 27. Diện tích S của hình phẳng giới hạn bởi √ √ √ √ A. 3 7. B. 83. C. 89. D. 3 17.
đồ thị các hàm số y = f (x) và hàm số y = g(x)
liên tục trên [a; b] và hai đường thẳng x = a; x = b Câu 32. Tính diện tích hình phẳng giới hạn bởi là
(P) : y = x2 − 4x + 3 và trục Ox. b Z 4 4 2 4 A. S = | f (x) − g(x)| dx. A. π. B. . C. . D. − . 3 3 3 3 a
Câu 33. Trong không gian với hệ tọa độ Oxyz b Z B. S =
cho M(2; 3; −1), N(−2; −1; 3). Tìm tọa độ điểm E π ( f (x) − g(x)) dx. a
thuộc trục hoành sao cho tam giác MNE vuông tại b Z M. C. S = ( f (x) − g(x)) dx. A. (−2; 0; 0). B. (0; 6; 0). a b C. (6; 0; 0). D. (4; 0; 0). Z D. S = ( f (x) + g(x)) dx.
Câu 34. Trong không gian với hệ trục toạ độ Oxyz, a Câu 28. Gọi z
cho mặt phẳng (α) : 2x − 3y − z − 1 = 0. Điểm nào
1, z2 là các nghiệm của phương trình
z2 + 4z + 5 = 0. Đặt w = (1 + z
dưới đây không thuộc mặt phẳng (α)? 1)100 + (1 + z2)100. Khi đó A. Q(1; 2; −5). B. P(3; 1; 3). A. w = 250i. B. w = −251. C. M(−2; 1; −8). D. N(4; 2; 1). C. w = 251. D. w = −250i.
Câu 35. Biết F(x) là một nguyên hàm của hàm số √3 1 1 Z √ f (x) = và F(2) = 3 + ln 3. Tính F(3). p 2 Câu 29. Biết I = x x2 + 1 dx = a − b , 2x − 1 2 3 1 1 A. F(3) = ln 5 + 5.
với a, b là các số nguyên dương. Mệnh đề nào sau 2 1 B. F(3) = ln 5 + 3. đây đúng? 2 A. a = 2b. B. a = 3b.
C. F(3) = −2 ln 5 + 5. C. a < b. D. a = b. D. F(3) = 2 ln 5 + 3.
Câu 30. Cho hai hàm số f (x), g(x) liên tục trên Câu 36. Trong không gian Oxyz, cho tam giác
đoạn [a; b] và số thực k tùy ý khác 0. Trong các ABC, biết A(1; 1; 1), B(5; 1; −2), C(7; 9; 1). Tính độ
khẳng định sau, khẳng định nào sai?
dài đường phân giác trong AD của góc A. ♂ 30 đề ôn thi t HKII-12 113 v 113
Những nẻo đường phù sa 2020 - 2021 30 ĐỀ
30 ĐỀ ÔN THI HKII-LỚP 12 √ 3 74 √
Câu 42. Trong không gian với hệ trục toạ độ Oxyz, A. . B. 2 74. 2 √
cho mặt phẳng (P) đi qua gốc toạ độ và nhận √ 2 74 C. 3 74. D. . #»
n = (3; 2; 1) là véctơ pháp tuyến. Phương trình 3 của mặt phẳng (P) là
Câu 37. Cho hai điểm A(3; 3; 1), B(0; 2; 1) và mặt
A. 3x + 2y + z − 14 = 0.
phẳng (α) : x + y + z − 7 = 0. Đường thẳng d B. 3x + 2y + z = 0.
nằm trong (α) sao cho mọi điểm thuộc d cách đều C. 3x + 2y + z + 2 = 0.
2 điểm A, B có phương trình là D. x + 2y + 3z = 0. x = t x = t A. y = 7 − 3t . B. y = 7 + 3t . z
Câu 43. Số phức z thỏa + (2 − 3i) = 5 − 2i. 4 − 3i z = 2t z = 2t Mô-đun của z bằng √ √ x = −t x = 2t A. |z| = 10 2. B. |z| = 10. √ C. y = 7 − 3t . D. y = 7 − 3t . C. |z| = 250. D. |z| = 5 10. z = 2t z = t
Câu 44. Trong không gian với hệ trục tọa độ Oxyz,
Câu 38. Tìm độ dài đường kính của mặt cầu (S) có cho mặt phẳng (P) : 2x − y − z + 3 = 0, và đường x + 1 y − 1 z
phương trình x2 + y2 + z2 − 2y + 4z + 2 = 0. thẳng ∆ : = =
. Xét vị trí tương đối √ √ 1 −2 2 A. 2 3. B. 2. C. 1. D. 3. của (P) và ∆.
Câu 39. Trong không gian với hệ tọa độ Oxyz, cho
A. (P) và ∆ chéo nhau. mặt phẳng ( B. (P) song song ∆.
α) cắt các trục tọa độ tại A, B, C.
Biết trọng tâm của tam giác ABC là G(−1; −3; 2). C. (P) chứa ∆. Mặt phẳng ( D. (P) cắt ∆.
α) song song với mặt phẳng nào sau đây?
Câu 45. Trong không gian với hệ tọa độ Oxyz cho
A. 6x − 2y + 3z − 1 = 0.
đường thẳng ∆ đi qua điểm M(2; 0; −1) và có véc-
B. 6x + 2y − 3z + 18 = 0. #»
tơ chỉ phương a = (4; −6; 2). Phương trình tham
C. 6x + 2y + 3z − 18 = 0.
số của đường thẳng ∆ là
D. 6x + 2y − 3z − 1 = 0. x = − 2 + 4t x = −2 + 2t
Câu 40. Trong không gian với hệ tọa độ Oxyz, cho A. y = −6t . B. y = −3t . #»
véc-tơ n = (2; −4; 6). Trong các mặt phẳng có z = 1 + 2t. z = 1 + t.
phương trình sau đây, mặt phẳng nào nhận véc-tơ x = 2 + 2t x = 4 + 2t #» n làm véc-tơ pháp tuyến? C. y = −3t . D. y = −3t .
A. 2x + 6y − 4z + 1 = 0. z = −1 + t. z = 2 + t. B. x − 2y + 3 = 0.
C. 3x − 6y + 9z − 1 = 0.
Câu 46. Trong không gian với hệ tọa độ Oxyz,
D. 2x − 4y + 6z + 5 = 0. x = 3 + 2t cho đường thẳng d :
y = 5 − 3mt và mặt phẳng π 4 Z z = −1 + t. Câu 41. Giả sử I =
sin 3x sin 2x dx = (a + (P): 4x − 4y + 2z − 5 = 0. Giá trị nào của m để 0 √2
đường thẳng d vuông góc với mặt phẳng (P). b)
. Khi đó, giá trị S = a + b là 2 3 2 A. m = . B. m = . 1 3 2 3 A. S = − . B. S = . 6 5 5 5 C. m = − . D. m = . 3 3 6 6 C. S = − . D. S = . 10 10 ♂ 30 đề ôn thi t HKII-12 114 v 114
Những nẻo đường phù sa 2021 30 ĐỀ - ĐỀ
30 ĐỀ ÔN THI HKII-LỚP 12 2020
Câu 47. Cho hai điểm A(5; 1; 3), H(3; −3; −1). Tọa
độ của điểm A0 đối xứng với A qua H là A. (−1; 7; 5). B. (1; 7; 5). C. (1; −7; −5). D. (1; −7; 5).
Câu 48. Trong mặt phẳng tọa độ Oxy, cho
hình thang ABCD với A (−1; 2), B (5; 5), C (5; 0),
D (−1; 0). Quay hình thang ABCD xung quanh
trục Ox thì thể tích khối tròn xoay tạo thành bằng bao nhiêu? A. 78. B. 18π. C. 78π. D. 74π. π 2 Z Câu 49. Cho I = sin2 x cos x dx và u = sin x. 0
Mệnh đề nào dưới đây đúng? 0 1 Z Z A. I = − u2 du. B. I = u2 du. −1 0 1 1 Z Z C. I = − u2 du. D. I = 2 u du. 0 0
Câu 50. Trong không gian với hệ trục tọa độ Oxyz, #» #» #»
cho các vectơ a = (1; −2; 0), b = (−1; 1; 2), c = #» 1 3 (4; 0; 6) và u = −2; ; . Khẳng định nào sau 2 2
đây là khẳng định đúng? #» 1 #» 3 #» 1 #» A. u = a + b − c . 2 2 4 #» 1 #» 3 #» 1 #» B. u = − a + b − c . 2 2 4 #» 1 #» 3 #» 1 #» C. u = a + b + c . 2 2 4 #» 1 #» 3 #» 1 #» D. u = a − b − c . 2 2 4
BẢNG ĐÁP ÁN THAM KHẢO 1. 2. 3. 4. 5. 6. 7. 8. 9. 10. 11. C C B D B A B D A A A
12. 13. 14. 15. 16. 17. 18. 19. 20. 21. 22. C A A D A D C A C C C
23. 24. 25. 26. 27. 28. 29. 30. 31. 32. 33. B D A D A B A D C B C
34. 35. 36. 37. 38. 39. 40. 41. 42. 43. 44. B B D A A D D B B D D 45. 46. 47. 48. 49. 50. C B C C B A ♂ 30 đề ôn thi t HKII-12 115 v 115
Những nẻo đường phù sa