Total probability and bayes' theorem overview môn Xác suất thống kê| Trường Đại học Ngoại Thương

Total Probability and 35.4   Introduction
When the ideas of probability are applied to engineering (and many other areas) there are occasions
when we need to calculate conditional probabilities other than those already known. For example, if
production runs of ball bearings involve say, four machines, we might know the probability that any
given machine produces faulty ball bearings. If we are inspecting the total output prior to distribution
to users, we might need to know the probability that a faulty ball bearing came from a particular
machine. Even though we do not address the area of statistics known as Bayesian Statistics here, it
is worth noting that Bayes’ theorem is the basis of this branch of the subject. ' $
•understand the ideas of sets and subsets. Prerequisites
•understand the concepts of probability and events. &
Before starting this Section you should . . .
•understand the addition and multiplication ' % $
laws and the concept of conditional probability.
•understand the term ‘partition of a sample space’ Learning Outcomes
•understand the special case of Bayes’
theorem arising when a sample space is
On completion you should be able to . . .
partitioned by a set and its complement & %
•be able to apply Bayes’ theorem to solve
basic engineering related problems 44 HELM (2008):
Workbook 35: Sets and Probability ®
1. The theorem of total probability
Toestablishthisresultwestartwiththedefinitionofapartitionofasamplespace.
A partition of a sample space
ThecollectionofeventsA1, A2,...Anissaidtopartition asamplespaceSif (a)A1∪A2∪ ··· ∪ An=S (b)Ai∩Aj=∅foralli, j (c)Ai6=∅foralli
Inessence,apartitionisacollectionofnon-empty,non-overlappingsubsetsofasamplespacewhose
unionisthesamplespaceitself. ThedefinitionisillustratedbyFigure10. S A4 A1 A3 A5 A6 A2 Figure 10
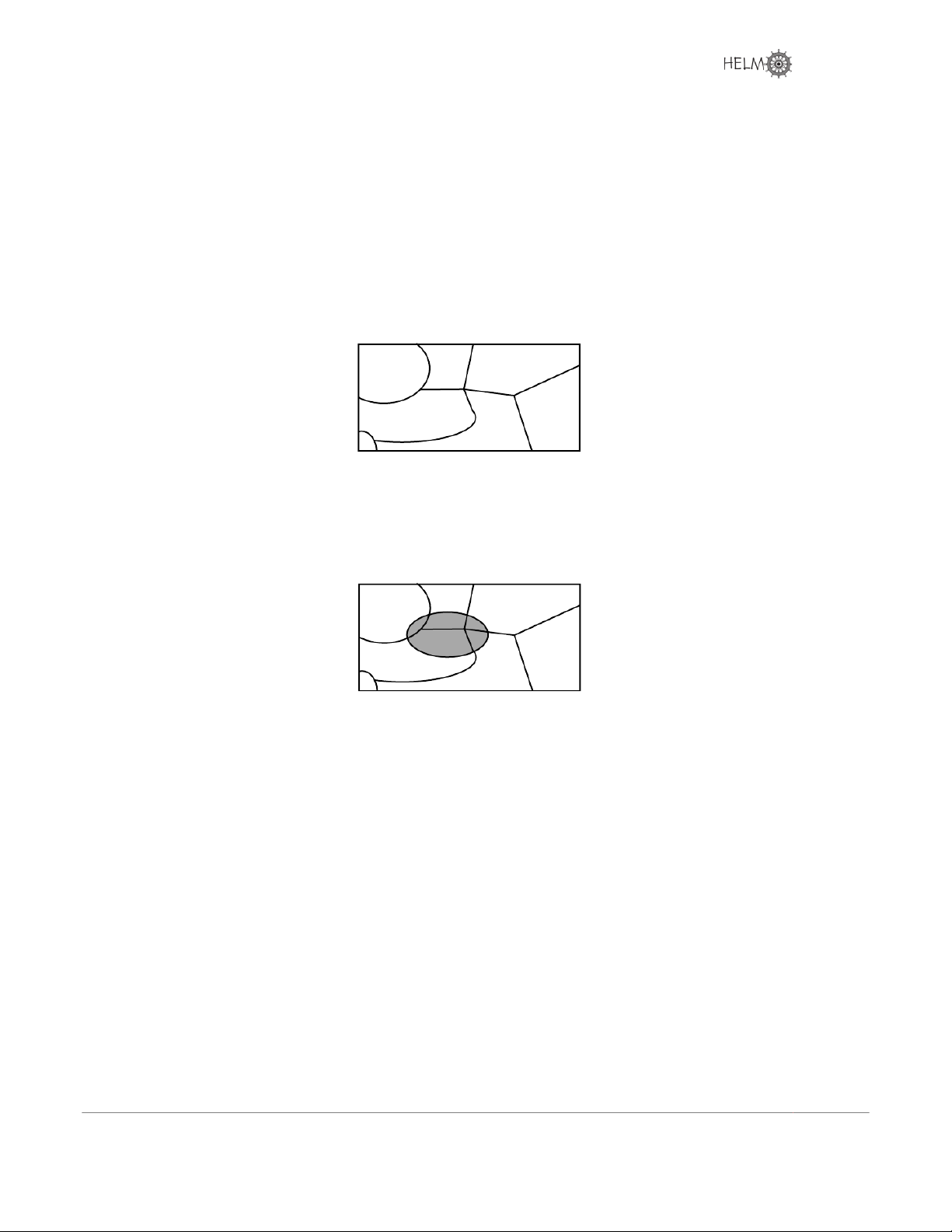
IfBisanyeventwithinSthenwecanexpressBastheunionofsubsets:
B= (B∩A1)∪(B∩A2)∪ ··· ∪ (B∩An)
ThedefinitionisillustratedinFigure11inwhichaneventBinSisrepresentedbytheshadedregion. S A A 4 1 A3 B A5 A6 A2 Figure 11
Thebracketedevents(B∩A1),(B∩A2). . . (B∩An)aremutuallyexclusive(ifoneoccursthennone
oftheotherscanoccur)andso,usingtheadditionlawofprobabilityformutuallyexclusiveevents:
P(B) = P(B∩A1) + P(B∩A2) + ··· +P(B∩An)
Eachoftheprobabilitiesontheright-handsidemaybeexpressedintermsofconditionalprobabilities:
P(B∩Ai) = P(B|Ai)P(Ai)foralli
UsingtheseintheexpressionforP(B),above,gives:
P(B) = P(B|A1)P(A1) + P(B|A2)P(A2) + ··· +P(B|An)P(An) n X = P(B|Ai)P(Ai) i=1
ThisisthetheoremofTotalProbability. Arelatedtheoremwithmanyapplicationsinstatisticscan
bededucedfromthis,knownasBayes’theorem. HELM (2008): 45
Section 35.4: Total Probability and Bayes’ Theorem 2. Bayes’ theorem
Weagainconsidertheconditionalprobabilitystatement: P(A|B) = P(A P ∩ ( B B))=P(A∩B)
P(B|A1)P(A1) + P(B|A2)P(A2) + ··· +P(B|An)P(An)
inwhichwehaveusedthetheoremofTotalProbabilitytoreplaceP(B).Now
P(A∩B) = P(B∩A) = P(B|A)×P(A)
Substitutingthisintheexpressionfor P(A|B)weimmediatelyobtaintheresult P(A|B) = P(B|A)×P(A)
P(B|A1)P(A1) + P(B|A2)P(A2) + ··· +P(B|An)P(An)
Thisistrueforany eventAandso,replacingAbyAigivestheresult,knownasBayes’theoremas P(Ai|B) = P(B|Ai)×P(Ai)
P(B|A1)P(A1) + P(B|A2)P(A2) + ··· +P(B|An)P(An) 3. Special cases
InthecasewhereweconsiderAtobeaneventinasamplespaceS(thesamplespaceispartitioned
byAandA0)wecanstatesimplifiedversionsofthetheoremofTotalProbabilityandBayestheorem asshownbelow.
The theorem of total probability: special case
ThisspecialcaseenablesustofindtheprobabilitythataneventBoccurstakingintoaccountthe
factthatanothereventAmayormaynothaveoccurred. Thetheorembecomes
P(B) = P(B|A)×P(A) + P(B|A0)×P(A0)
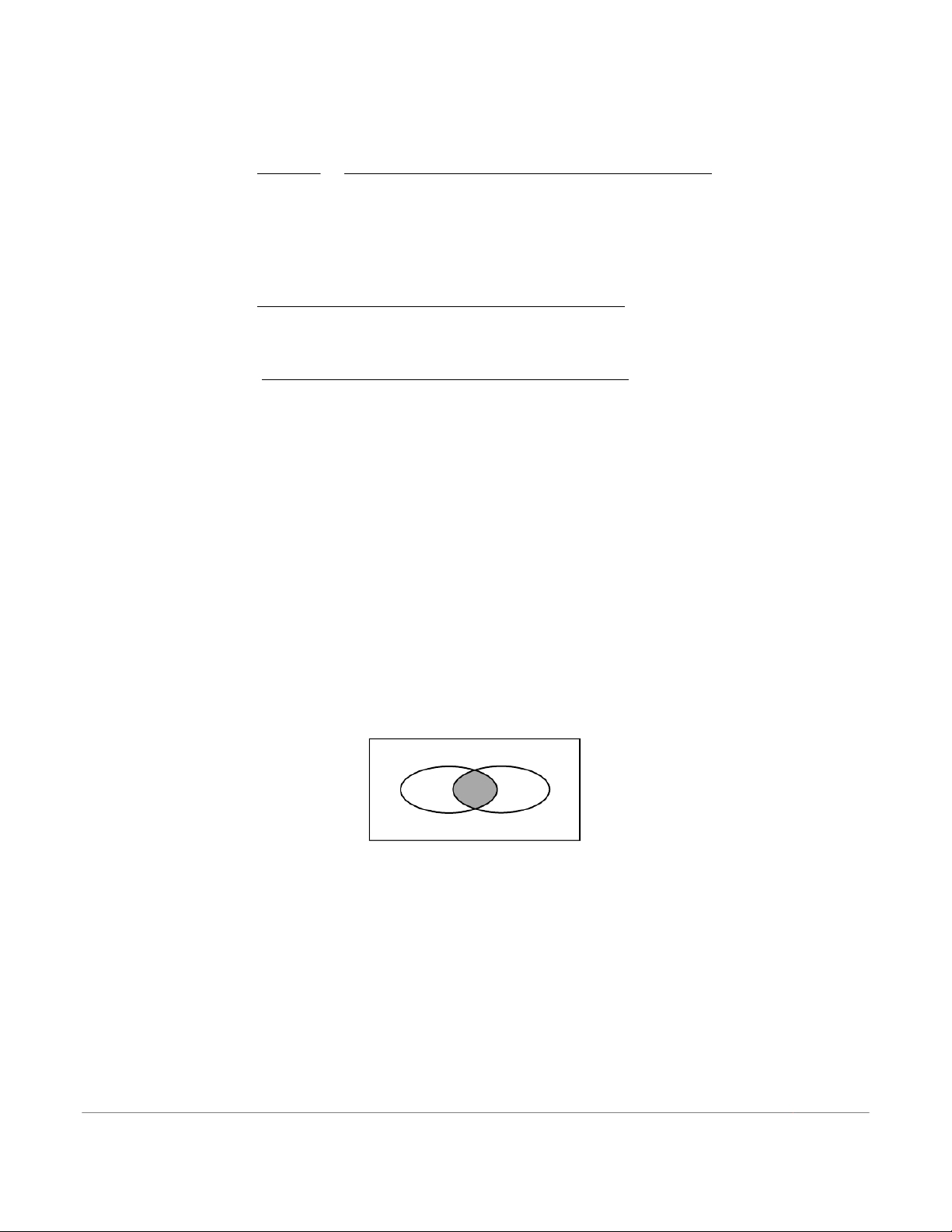
Theresultiseasilyseenbyconsideringthegeneralresultalreadyderivedoritmaybederiveddirectly asfollows. ConsiderFigure12: AB A∩B!A∩BB∩A! S Figure 12
ItiseasytoseethattheeventBconsistsoftheunionofthe(disjoint)eventsA∩BandB∩A0so
thatwemaywriteBastheunionofthesedisjointevents. Wehave B= (A∩B)∪(B∩A0)
SincetheeventsA∩BandB∩A0aredisjoint,theymustbeindependentandso P(B) = P(A∩B) + P(B∩A0) 46 HELM (2008):
Workbook 35: Sets and Probability ®
Usingtheconditionalprobabilityresultswealreadyhavewemaywrite P(B) = P(A∩B) + P(B∩A0) =P(B∩A) + P(B∩A0) =P(B|A)×P(A) + P(B|A0)×P(A0) Theresultwehavederivedis
P(B) = P(B|A)×P(A) + P(B|A0)×P(A0)
Bayes’ theorem: special case
ThisresultisobtainedbysupposingthatthesamplespaceSispartitionedbyeventAandits complementA0togive: P(A|B) = P(B|A)×P(A) P(B|A)×P(A) + P(B|A0)×P(A0) Example 13
Atacertainuniversity,4%ofmenare over6feettalland1%ofwomenareover
6feettall. Thetotalstudentpopulationisdividedintheratio3:2infavourof
women. Ifastudentisselectedatrandomfromamongallthoseoversixfeettall,
whatistheprobabilitythatthestudentisawoman? Solution
LetM={StudentisMale},F={StudentisFemale}.
NotethatMandFpartitionthesamplespaceofstudents. LetT={Studentisover6feettall}.
WeknowthatP(M) = 2/5,P(F) = 3/5,P(T|M) = 4/100 andP(T|F) = 1/100.
Werequire P(F|T). UsingBayes’theoremwehave: P(F|T) = P(T|F)P(F) P(T|F)P(F) + P(T|M)P(M) 1100 ×3 = 5 11 00 ×35+4 100 ×2 5 =3 11 HELM (2008): 47
Section 35.4: Total Probability and Bayes’ Theorem Example 14
Afactory productionlineismanufacturingboltsusingthreemachines, A,Band
C. Ofthetotaloutput,machineAisresponsiblefor25%,machineBfor35%and
machineCforthe rest. Itisknownfrompreviousexperiencewiththemachines
that5%oftheoutputfrommachineAisdefective,4%frommachineBand2%
frommachineC. Aboltischosenatrandomfromtheproductionlineandfound
tobedefective. Whatistheprobabilitythatitcamefrom
(a)machineA(b)machineB(c)machineC? Solution Let D={boltisdefective}, A={boltisfrommachineA}, B={boltisfrommachineB}, C={boltisfrommachineC}.
WeknowthatP(A) = 0.25,P(B) = 0.35 andP(C) = 0.4. Also
P(D|A) = 0.05,P(D|B) = 0.04,P(D|C) = 0.02.
AstatementofBayes’theoremforthreeeventsA, B andCis P(A|D) = P(D|A)P(A)
P(D|A)P(A) + P(D|B)P(B) + P(D|C)P(C) =0.05 ×0.25
0.05 ×0.25 + 0.04 ×0.35 + 0.02 ×0.4 = 0.362 Similarly P(B|D) = 0.04 ×0.35
0.05 ×0.25 + 0.04 ×0.35 + 0.02 ×0.4 = 0.406 P(C|D) = 0.02 ×0.4
0.05 ×0.25 + 0.04 ×0.35 + 0.02 ×0.4 = 0.232 48 HELM (2008):
Workbook 35: Sets and Probability ® Task
Anengineeringcompanyadvertisesajobinthreenewspapers, A, B andC.It
isknownthatthesepapersattractundergraduateengineeringreadershipsinthe
proportions2:3:1. Theprobabilitiesthatanengineeringundergraduateseesand
repliestothejobadvertisementinthesepapersare0.002, 0.001and0.005respec-
tively. Assumethattheundergraduateseesonlyonejobadvertisement.
(a) Iftheengineeringcompanyreceivesonlyonereplytoitadvertisements,
calculatetheprobabilitythattheapplicanthasseenthejobadvertised inplaceA. (i)A, (ii)B, (iii)C.
(b) Ifthecompanyreceivestworeplies,whatistheprobabilitythatboth
applicantssawthejobadvertisedinpaperA? Your solution HELM (2008): 49
Section 35.4: Total Probability and Bayes’ Theorem Answer Let A={PersonisareaderofpaperA}, B={PersonisareaderofpaperB}, C={PersonisareaderofpaperC}, R={Readerappliesforthejob}. Wehave theprobabilities (a) P(A) = 1/3P(R|A) = 0.002 P(B) = 1/2P(R|B) = 0.001 P(C) = 1/6P(R|C) = 0.005 P(A|R) = P(R|A)P(A) P + (R P( |A R| )P B ( ) A P( )B) + P(R|C)P(C)=1 3 Similarly P(B|R) = 14andP(C|R) = 5 12
(b)Now,assumingthattherepliesandreadershipsareindependent
P(BothapplicantsreadpaperA) = P(A|R)×P(A|R) =1 3×1 3 =1 9 50 HELM (2008):
Workbook 35: Sets and Probability ® Exercises
1. Obtainthesamplespaceofanexperimentthatconsistsofafaircoinbeingtossedfourtimes. Considerthefollowingevents:
Aistheevent‘allfourresultsarethesame.’
Bistheevent‘exactlyoneHeadoccurs.’
Cistheevent‘atleasttwoHeadsoccur.’
ShowthatP(A) + P(B) + P(C) = 17
16 andexplainwhyP(A) + P(B) + P(C)>1.
2. Thetablebelowshowthenumberofcompleteyearsagroupofpeoplehavebeenworkingin theircurrentemployment.
YearsofEmployment NumberofPeople 0or1year 15 2or3years 12 4or5years 9 6or8years 6 8to11years 6 12yearsandover 2
Whatistheprobabilitythatapersonfromthegroup,selected atrandom; (a) isinthemodalgroup
(b) hasbeenworkingthereforlessthan4years
(c) hasbeenworkingthereforatleast8years.
3. ItisafactthatifAandBareindependenteventsthenitisalsotruethatA0andB0are
independentevents. IfAandBareindependenteventssuchthattheprobabilitythatthey
bothoccursimultaneouslyis 1 8andtheprobabilitythatneitherofthemwilloccuris 3 8,find:
(a) theprobabilitythateventAwilloccur
(b) theprobabilitythateventBwilloccur.
4. IfAandBaretwoeventsassociatedwithanexperimentandP(A) = 0.4,
P(A∪B) = 0.7andP(B) = p,find:
(a) thechoiceofpforwhichAandBaremutuallyexclusive
(b) thechoiceofpforwhichAandBareindependent.
5. Theprobabilitythateachrelayclosesinthecircuitshownbelowisp. Assumingthateachrelay
functionsindependentlyoftheothers,findtheprobability thatcurrentcanflowfromLtoR. AB LR CD HELM (2008): 51
Section 35.4: Total Probability and Bayes’ Theorem
6. Fromabatchof100itemsofwhich20aredefective,exactlytwoitemsarechosen,oneata
time,withoutreplacement. Calculatetheprobabilitiesthat:
(a) thefirstitemchosenisdefective
(b) bothitemschosenaredefective
(c) theseconditemchosenisdefective.
7. Agaragemechanickeepsaboxofgoodspringstouseasreplacementsoncustomerscars. The
boxcontains5springs. Acolleague,thinkingthatthespringsareforscrap,tossesthreefaulty
springsintothe box. Themechanicpickstwospringsoutoftheboxwhileservicingacar. Find theprobabilitythat:
(a)thefirstspringdrawn isfaulty
(b)thesecondspringdrawnisfaulty.
8. Twocoinsaretossed. FindtheconditionalprobabilitythattwoHeadswilloccurgiventhatat leastoneoccurs.
9. MachinesAandBproduce10%and90%respectivelyoftheproductionofacomponent
intendedforthemotorindustry. Fromexperience,itisknownthattheprobabilitythatmachine
Aproducesadefectivecomponentis0.01whiletheprobabilitythatmachineBproducesa
defectivecomponentis0.05. Ifacomponentisselectedatrandomfromaday’sproduction
andisfoundtobedefective,findtheprobabilitythatitwasmadeby (a)machineA(b)machineB. Answers
1.P(A) = 216,P(B) = 416,P(C) = 116,P(A) + P(B) + P(C) = 17 16
A,BandCarenotmutuallyexclusivesinceevents AandChaveoutcomesincommon. This
isthereasonwhyP(A) + P(B) + P(C) = 1716;weareaddingtheprobabilitiescorresponding tocommonoutcomesmorethanonce.
2. (a) P(personfallsinthemodalgroup)=15 50
(b) P(personhasbeenworkingforlessthan4years)=27 50
(c) P(personhasbeenworkingformorethan8years)=8 50
3.P(A)×P(B) = 1 8and(1 −P(A)) ×(1 −P(B)) = 3 8 Treattheseequationsasxy =1
8and(1 −x)(1 −y) = 3 8andsolvetoget: P(A) = 1 2(or1 4)andP(B) = 1 4(or1 2)
4. (a)P(A∪B) = P(A) + P(B)so0.7 = 0.4 + pimplyingp= 0.3
(b)P(A∪B) = P(A) + P(B)−P(A)×P(B)so0.7 = 0.4 + p−0.4×pimplyingp= 0.5. 52 HELM (2008):
Workbook 35: Sets and Probability ® Answers
5.P((A∩B)∪(C∩D)) = P(A∩B) + P(C∩D)−P(A∩B∩C∩D) =p2+p2−p4 = 2p2−p4
6.LetA={firstitemchosenisdefective},B={seconditemchosenisdefective} (a)P(A) = 20 100 =1 5
(b)P(A∩B) = P(A|B)P(A) = 1999 ×20 100 =19 495
(c)P(B) = P(B|A)P(A) + P(B|A0)P(A0) = 199 ×20 100 +20 99 ×80 100 =198 90 =1 5
7.LetA={firstspringchosenisfaulty},B={secondspringchosenisfaulty} (a)P(A) = 3 8
(b)P(B) = P(B|A)P(A) + P(B|A0)P(A0) = 27×3 8+3 7×5 8=2156 =3 8
8.LetA={atleastoneHeadoccurs},B={twoHeadsoccur} 12×1 P(B) = P( P A ( ∩ A B ∪ ) B =P(A)×P(B) 2 =1 P(A) + P(B)−P(A)×P(B)= 12+12−1 2×1 3 2
9.LetA={itemfrommachineA},B={itemfrommachineB},D={itemisdefective}.
Weknowthat: P(A) = 0.1,P(B) = 0.9,P(D|A) = 0.01,P(D|B) = 0.05. (a) P(A|D) = P(D|A)P(A) P(D|A)P(A) + P(D|B)P(B) =0.01 ×0.1 0.01 ×0.1 + 0.05 ×0.9 = 0.02 (b) SimilarlyP(B|D) = 0.98 HELM (2008): 53
Section 35.4: Total Probability and Bayes’ Theorem