




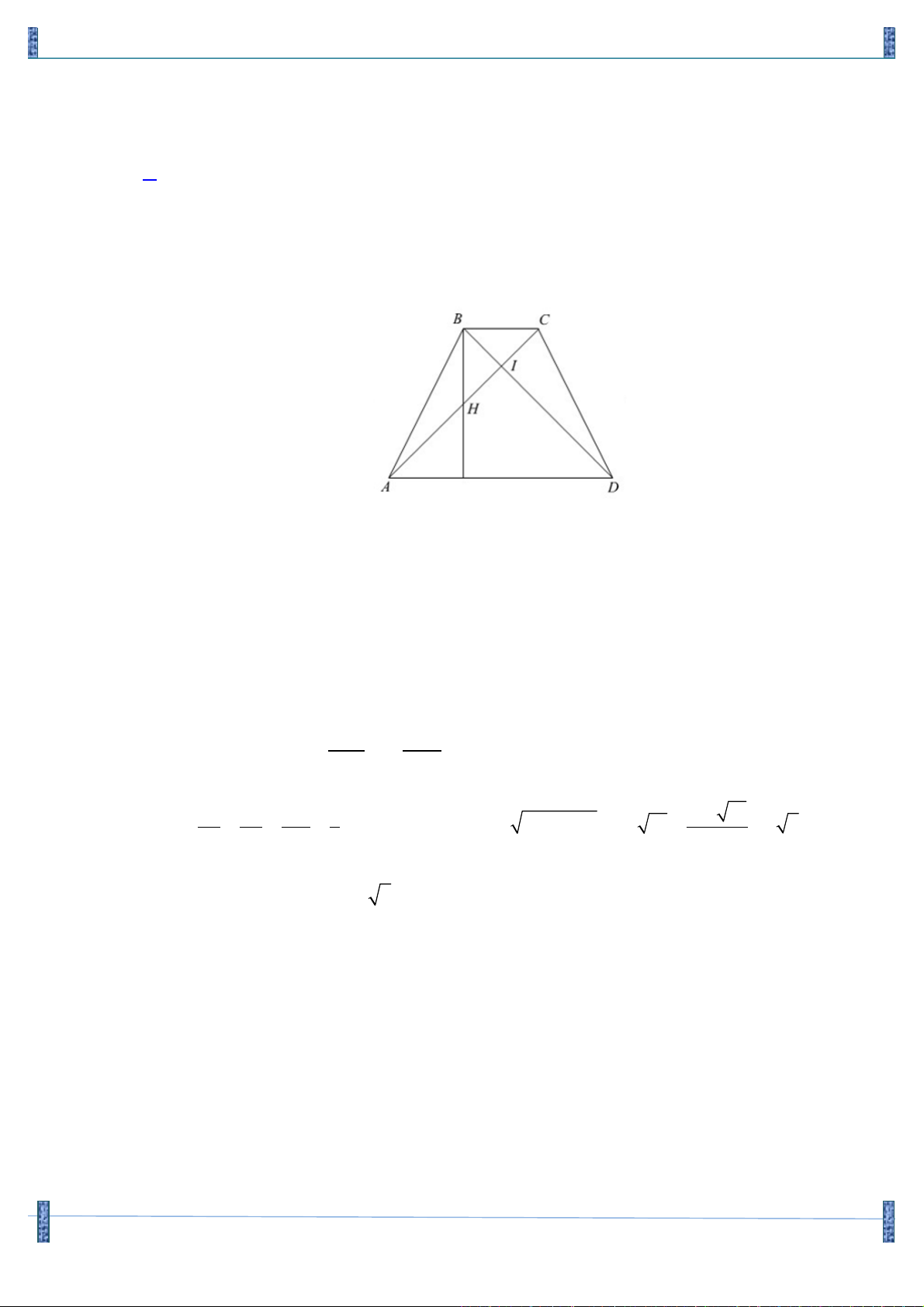
























































Preview text:
File làm chuyên đề HÌNH GIẢI TÍCH OXY QUA CÁC THI 3 CHUNG BGD Group FB: Strong Team TOÁN VD–VDC
TRẮC NGHIỆM HÌNH GIẢI TÍCH OXY ĐỀ
CHÍNH THỨC VÀ DỰ BN QUA CÁC KỲ THI HỌC
CỦA BGD TỪ 2002 ĐẾN 2016
Hãy tham gia group để cùng học và cùng làm- Nhóm chỉ dành cho các Gv, Sv toán! 1
File làm chuyên đề HÌNH GIẢI TÍCH OXY QUA CÁC THI 3 CHUNG BGD Group FB: Strong Team TOÁN VD–VDC
Email: nguyentuanblog1010@gmail.com
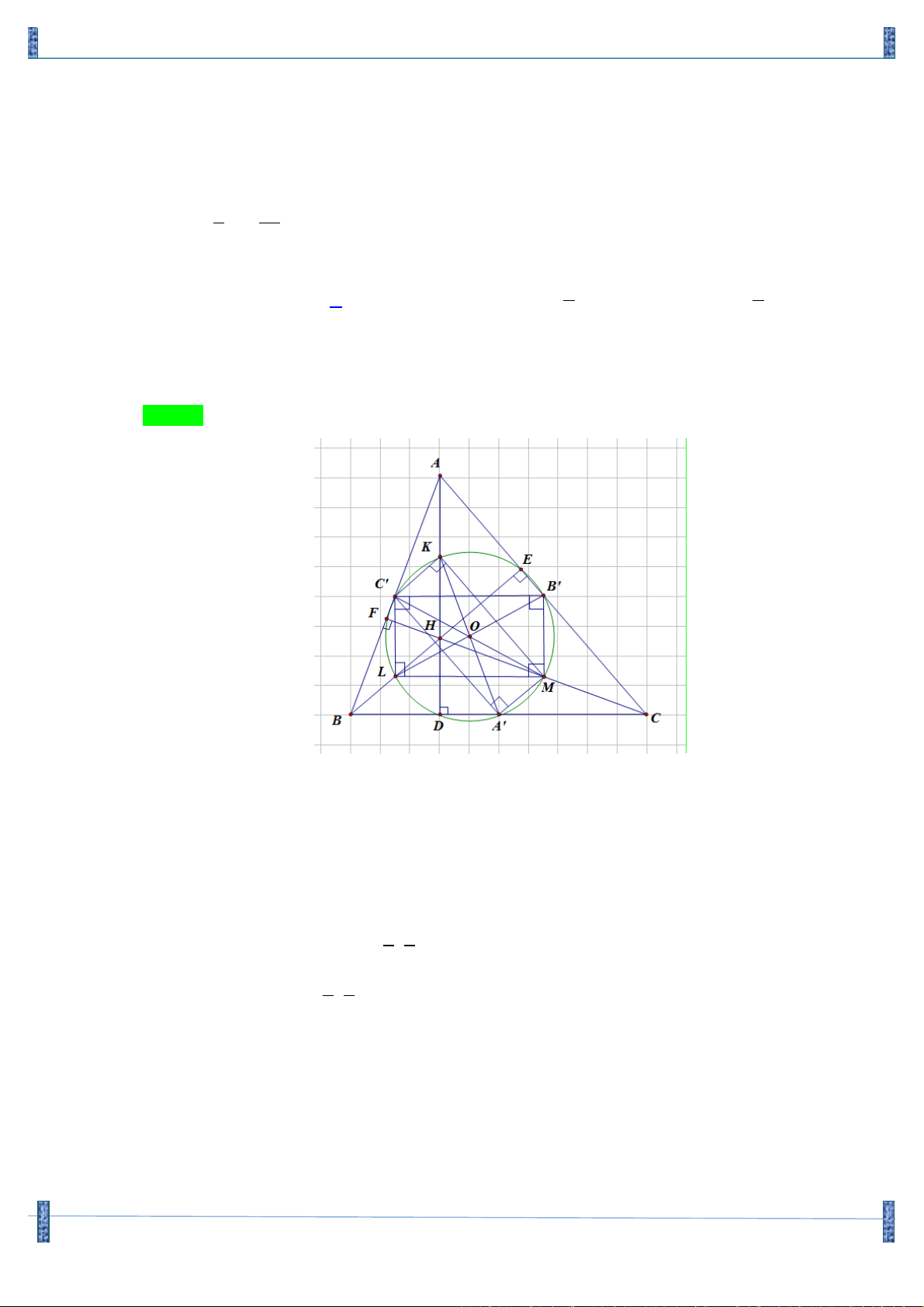
Câu 1. Trong mặt phẳng với hệ tọa độ vuông góc Oxy cho hình thoi ABCD có 0 BAD = 0 6 , D( ; a b)
với b > a > 0 . Trên các cạnh AB, BC lấy các điểm M , N sao cho MB + NB = AB . Biết
P( 3;1) thuộc đường thẳng DN và đường phân giác của góc MDN có phương trình là
d : x - y 3 + 6 = 0.Tính giá trị của biểu thức T = 3a - b ? A. 6 . B. 7 . C. 8 . D. 9 . Lời giải
Tác giả: Phạm Chí Tuân Facebook. Tuân Chí Phạm Chọn C D P Q A C N M B
Å Cách 1: Từ đề bài ta có các tam giác ,
ABD CBD là các tam giác đều, AM = BN và BM = CN . Xét AD D M và BD D
N có: DAM = DBN, AD = BD và AM = BN nên AD D M = BD D N Þ ADM = BDN ( ) 1 . Xét BM D D và C
D ND có: DBM = DCN,CD = BD và CN = BM nên BM D D = C D ND Þ NDC = MDB(2) Từ ( ) 1 và (2) ta có 0 MDN = 60 .
Å Cách 2: Xét (Q ta có: A ® ;
B B ® C nên M ® N . Do đó tam giác DMN đều. 0 D,60 )
Gọi Q là điểm đối xứng của P qua đường phân giác của góc MDN . 3 - 3 + 6
Khi đó ta có: DP = PQ = 2d (P,d ) = 2. = 6 1+ ( 3)2 æ 2 t + 6 ö 2 æ t + 6 - 3 ö ét = 3+ 3 Gọi D t; Îd ç ÷ . Ta có: 2 DP = (t - 3) +ç ÷ = 36 Þ ê . è 3 ø ç 3 ÷ è ø êët = 6 - + 3
Hãy tham gia group để cùng học và cùng làm- Nhóm chỉ dành cho các Gv, Sv toán! 2
File làm chuyên đề HÌNH GIẢI TÍCH OXY QUA CÁC THI 3 CHUNG BGD Group FB: Strong Team TOÁN VD–VDC
Vậy D (3+ 3;1+ 3 3) hoặc D(-6 + 3; )
1 . Theo giả thuyết ta nhận ìï = + D ( + + ) a 3 3 3
3;1 3 3 Þ íbïî =1+3 3
Ta có giá trị của biểu thức T = 3a - b = 8 .
Email: thinhvanlamha@gmail.com
Câu 2. Trong mặt phẳng với hệ tọa độ Oxy , cho tam giác ABC cân tại B với A(1;- ) 1 , C (3;5). Định
B nằm trên đường thẳng d : 2x - y = 0 . Phương trình các đường thẳng AB, BC lần lượt là
d : ax + by - 24 = 0, d : cx + dy + 8 = 0. Tính giá trị biểu thức P = . a . b . c d . 1 2 A. P = 975 . B. P = 5681. C. P = 3059 . D. P = 5083. Lời giải
Họ và tên tác giả: Nguyễn Văn Thịnh Tên FB: Thịnh Nguyễn Văn Chọn B Cách 1:
Gọi I là trung điểm AC Þ I (2;2).
Đường thẳng D đi qua I và vuông góc với AC có phương trình: x + 3y -8 = 0 (D). æ 8 16 ö
Tam giác ABC cân tại B nên ta có B ÎD Þ B = D Ç d Þ B ; ç ÷ . è 7 7 ø x -1 y +1
Phương trình đường thẳng AB : =
Û 23x - y - 24 = 0. 8 16 -1 +1 7 7 x - 3 y - 5
Phương trình đường thẳng BC : =
Û 19x -13y + 8 = 0. 8 16 - 3 - 5 7 7
Vậy a = 23,b = 1 - ,c =19,d = 13 - Þ P = . a . b . c d = 5681.
Hãy tham gia group để cùng học và cùng làm- Nhóm chỉ dành cho các Gv, Sv toán! 3
File làm chuyên đề HÌNH GIẢI TÍCH OXY QUA CÁC THI 3 CHUNG BGD Group FB: Strong Team TOÁN VD–VDC Cách 2: Gọi B( ;2 a a)Îd .
Tam giác ABC cân tại B nên ta có AB = CB Þ (a - )2 +( a + )2 = (a - )2 +( a - )2 1 2 1 3 2 5 8 Û æ 8 16 ö a = . Suy ra B ; ç ÷. 7 è 7 7 ø x -1 y +1
Phương trình đường thẳng AB : =
Û 23x - y - 24 = 0. 8 16 -1 +1 7 7 x - 3 y - 5
Phương trình đường thẳng BC : =
Û 19x -13y + 8 = 0. 8 16 - 3 - 5 7 7
Vậy a = 23,b = 1 - ,c =19,d = 13 - Þ P = . a . b . c d = 5681.
Email: thinhvanlamha@gmail.com
Câu 3. Trong mặt phẳng với hệ tọa độ Oxy , cho tam giác ABC cân tại B với A(1;- ) 1 , C (3;5). Định
B nằm trên đường thẳng d : 2x - y = 0 . Phương trình các đường thẳng AB, BC lần lượt là
d : ax + by - 24 = 0, d : cx + dy + 8 = 0. Tính giá trị biểu thức P = . a . b . c d . 1 2 A. P = 975 . B. P = 5681. C. P = 3059 . D. P = 5083. Lời giải
Họ và tên tác giả: Nguyễn Văn Thịnh Tên FB: Thịnh Nguyễn Văn Chọn B Cách 1:
Gọi I là trung điểm AC Þ I (2;2).
Đường thẳng D đi qua I và vuông góc với AC có phương trình: x + 3y -8 = 0 (D).
Hãy tham gia group để cùng học và cùng làm- Nhóm chỉ dành cho các Gv, Sv toán! 4
File làm chuyên đề HÌNH GIẢI TÍCH OXY QUA CÁC THI 3 CHUNG BGD Group FB: Strong Team TOÁN VD–VDC æ 8 16 ö
Tam giác ABC cân tại B nên ta có B ÎD Þ B = D Ç d Þ B ; ç ÷ . è 7 7 ø x -1 y +1
Phương trình đường thẳng AB : =
Û 23x - y - 24 = 0. 8 16 -1 +1 7 7 x - 3 y - 5
Phương trình đường thẳng BC : =
Û 19x -13y + 8 = 0. 8 16 - 3 - 5 7 7
Vậy a = 23,b = 1 - ,c =19,d = 13 - Þ P = . a . b . c d = 5681. Cách 2: Gọi B( ;2 a a)Îd .
Tam giác ABC cân tại B nên ta có AB = CB Þ (a - )2 +( a + )2 = (a - )2 +( a - )2 1 2 1 3 2 5 8 Û æ 8 16 ö a = . Suy ra B ; ç ÷. 7 è 7 7 ø x -1 y +1
Phương trình đường thẳng AB : =
Û 23x - y - 24 = 0. 8 16 -1 +1 7 7 x - 3 y - 5
Phương trình đường thẳng BC : =
Û 19x -13y + 8 = 0. 8 16 - 3 - 5 7 7
Vậy a = 23,b = 1 - ,c =19,d = 13 - Þ P = . a . b . c d = 5681.
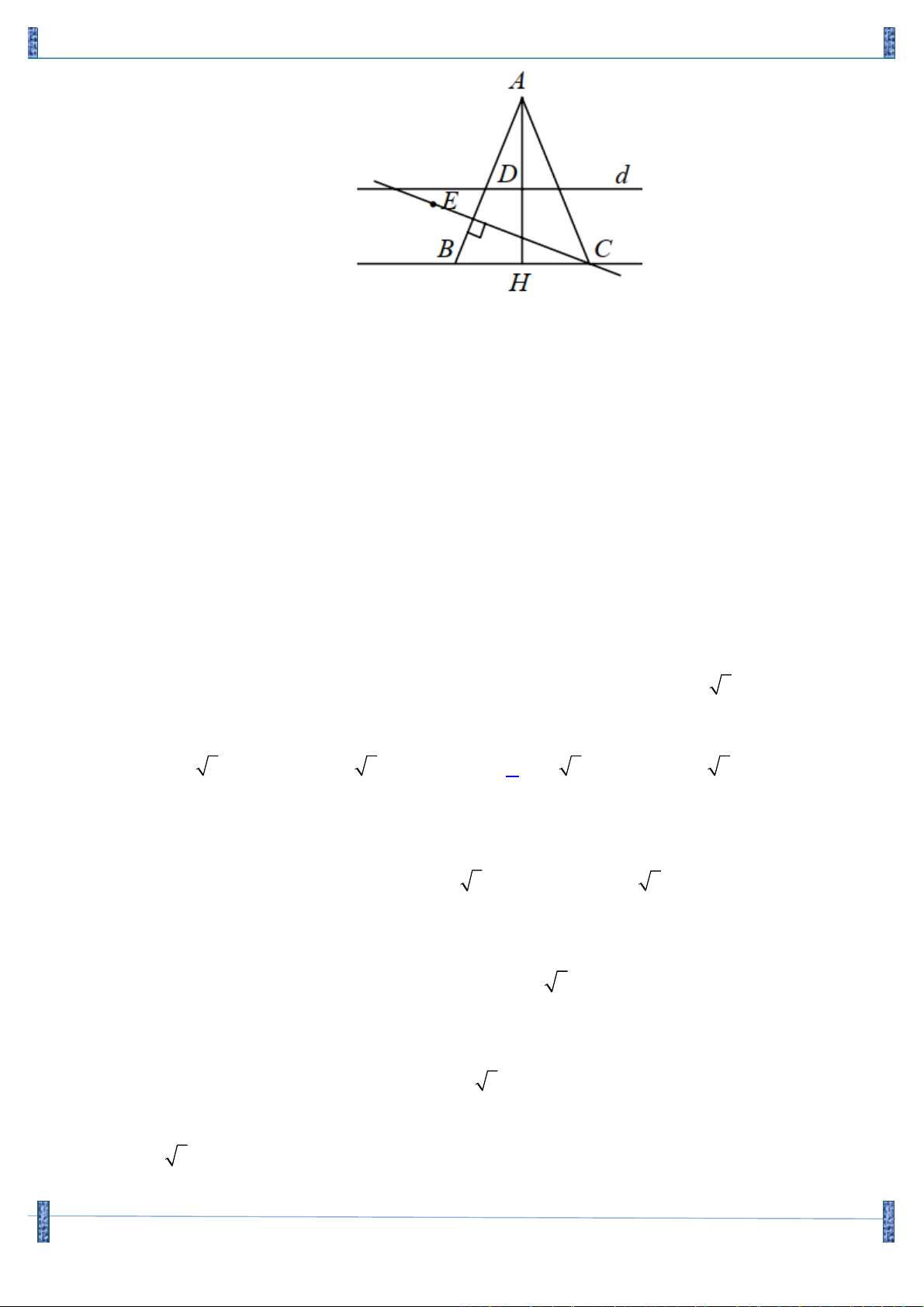
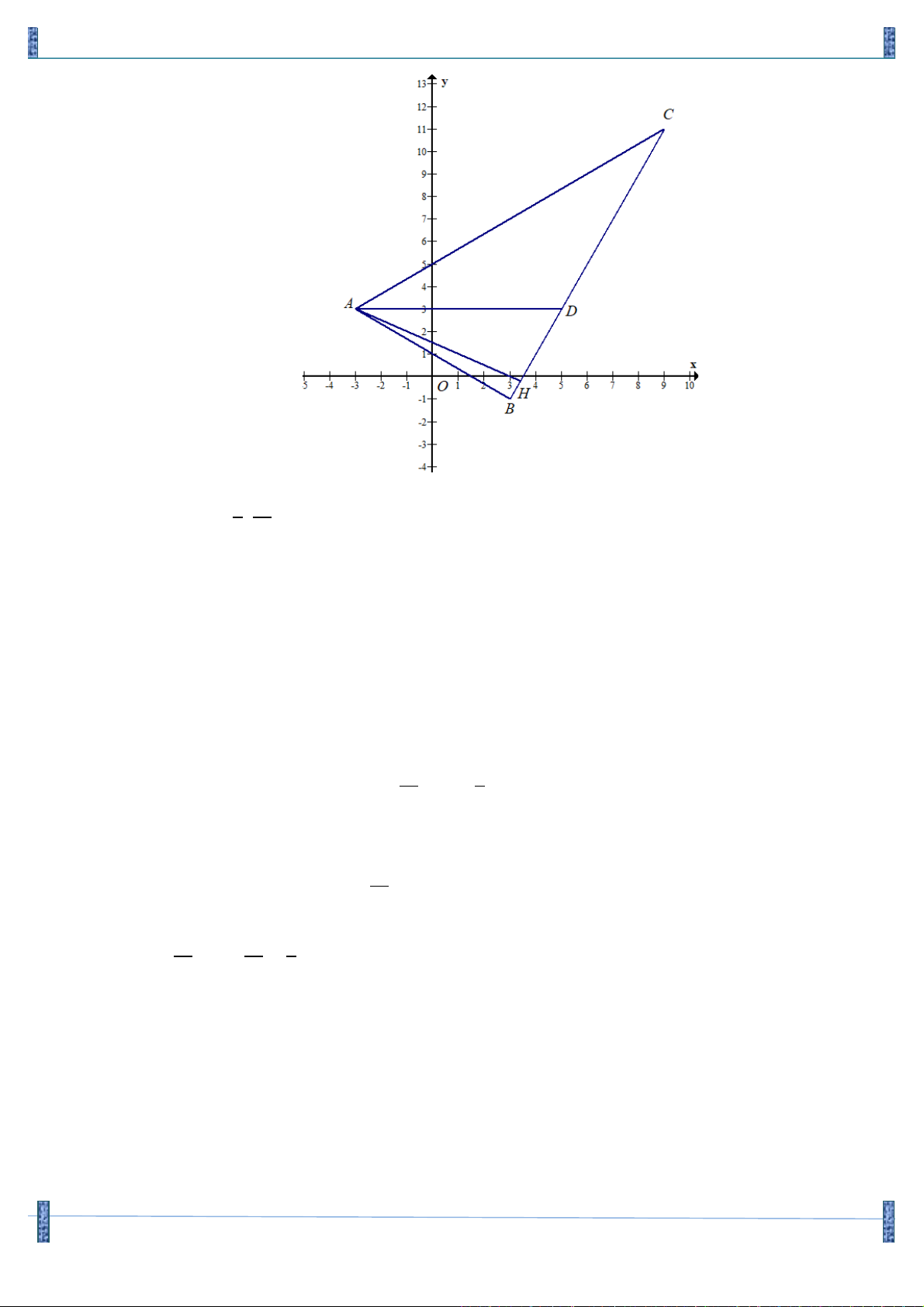
Câu 4. (Đề ĐH Khối A năm 2010, Tân Độc Trong mặt phẳng toạ độ Oxy , cho tam giác ABC cân tại
A biết đỉnh A(6;6). Đường thẳng d đi qua trung điểm các cạnh AB, AC có phương trình
x + y - 4 = 0. Biết điềm E (1;- )
3 thuộc đường cao đi qua đỉnh C của tam giác ABC . Giả sử
C (x ; y và x > 0 . Khẳng định nào sau đây đúng? C C ) C A. 3 x + y = 2. B. 2 y - 2x = 2 . C. OC = 10 . D. 2
3x + 2y > 0 . C C C C C C Lời giải Chọn A
Hãy tham gia group để cùng học và cùng làm- Nhóm chỉ dành cho các Gv, Sv toán! 5
File làm chuyên đề HÌNH GIẢI TÍCH OXY QUA CÁC THI 3 CHUNG BGD Group FB: Strong Team TOÁN VD–VDC
AH ^ d Þ phương trình đường thẳng AH : x - y = 0.
Gọi H , D lần lượt là trung điểm của BC, AH . Toạ độ D là nghiệm của hệ: ìx + y - 4 = 0 í
Û x = y = 2. Vậy D(2;2) Þ H ( 2; - 2 - ). îx - y = 0
BC / /d Þ BC có phương trình: x + y + 4 = 0 .
C Î BC Þ C (t;-t - 4) với t > 0 . Do H là trung điểm BC nên suy ra B( t - - 4;t). !!!" !!!" Ta có 2 .
AB CE = 0 Û t + 2t -8 = 0 Þ t = 2 (do t > 0 ).
Vậy C (2;- 6). Ta chọn A.
Câu 5. (ĐỀ KHỐI A -2004) Trong mặt phẳng Oxy, cho hai điểm (0
A ; 2) và B(- 3; 1) - . Tìm tọa độ
trực tâm H và tọa độ tâm đường tròn ngoại tiếp I của tam giác OAB. Phương trình đường thẳng HI là:
A. x - 3y = 0
B. 3x - y = 0
C. x + 3y = 0
D. 3x + y = 0 Lời giải
GV: Nguyễn Thị Mai; facebook: mainguyen !!"
+ Đường thẳng qua O, vuông góc với (
BA 3;3) có phương trình 3x + 3y = 0. !!"
Đường thẳng qua B, vuông góc với (0
OA ;2) có phương trình y = 1 - .
Giải hệ phương trình trên ta được trực tâm H ( 3;- ) 1
+ Đường trung trực cạnh OA có phương trình y = 1.
Đường trung trực cạnh OB có phương trình 3x + y + 2 = 0.
Giải hệ phương trình trên ta được tâm đường tròn ngoại tiếp I của tam giác OAB là I (- 3 );1
Hãy tham gia group để cùng học và cùng làm- Nhóm chỉ dành cho các Gv, Sv toán! 6
File làm chuyên đề HÌNH GIẢI TÍCH OXY QUA CÁC THI 3 CHUNG BGD Group FB: Strong Team TOÁN VD–VDC !!" + HI( 2 - 3;2) !
VTPT đường thẳng HI là n = (1; 3)
Phương trình đường thẳng HI là x + 3y = 0.
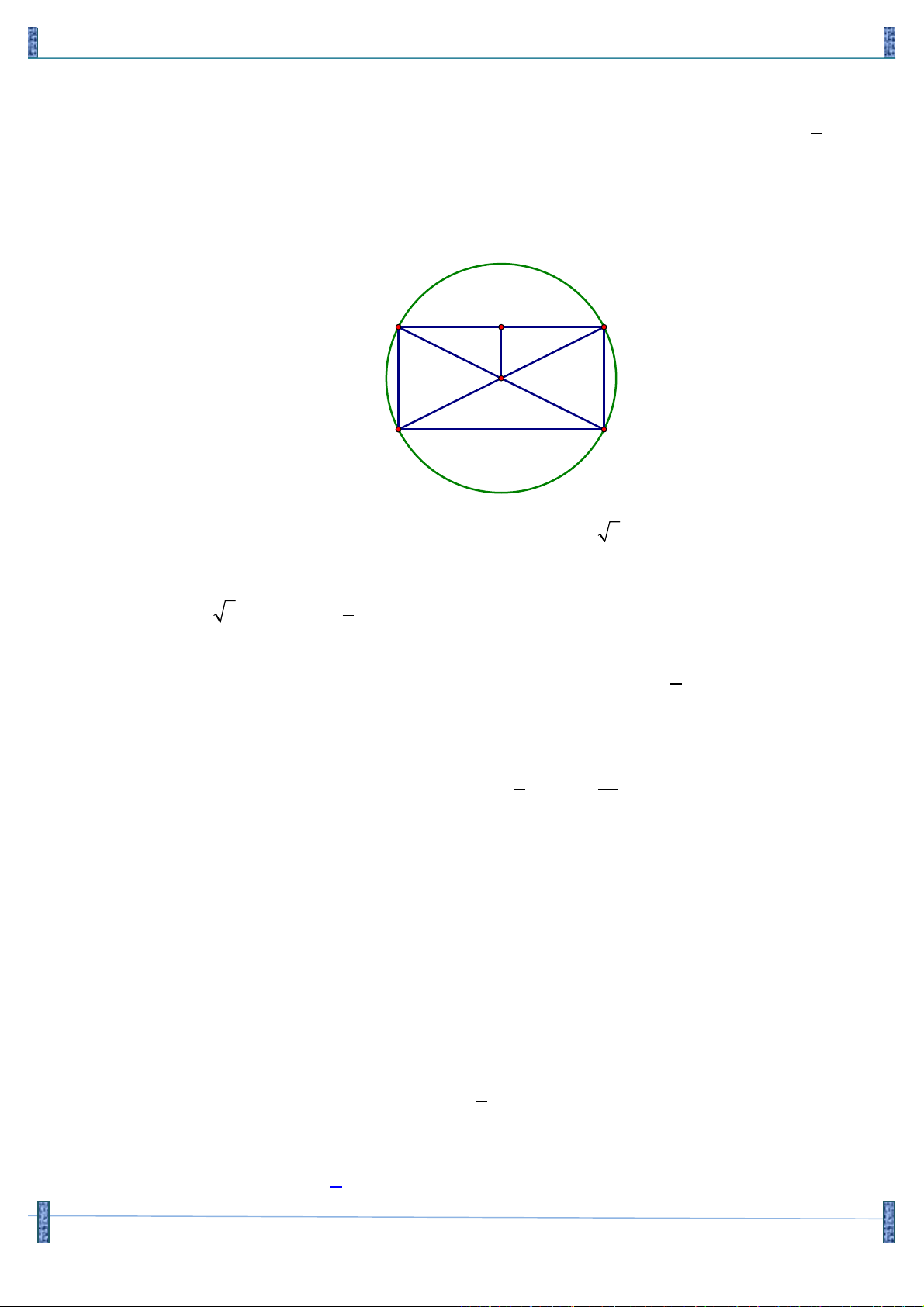
Câu 6. Cho hình chữ nhật ABCD , với I (6;2) là giao điểm của hai đường chéo. M thuộc đoạn thẳng
AB với M (1;5). Trung điểm E của đường thẳng CD nằm trên đường thẳng x + y - 5 = 0.
Phương trình dường thẳng AB là:
A. y - 5 = 0 và x + 4y - 21 = 0 B. x + 4y - 21 = 0
C. x + y - 6 = 0 và x - 4y +19 = 0
D. x - 4y +19 = 0 và y - 5 = 0 Lời giải
trAnght145@gmAil.Com fb: Trang Nguyen
Lấy M’ đối xứng qua I Þ M 'ÎCD
I là trung điểm MM’ nên M’(11; ) 1 -
Theo giả thiết E là trung điểm CDÞ IE ^ CD . Tam giác IEM’ vuông
Gọi E ÎD : x + y - 5 = 0 : E( ; a 5 - a) !!" !!!!" Ta có . IE M 'E = 0 !!"
IE = (a - 6;3- a) Với !!!!!"
M ' E = (a -11;6 - a) !!" !!!!" éa = 6
IE.M 'E = 0 Û êëa =7 A M B I D C E M' !!"
Phương trình AB qua A nhận IE làm vtpt !!"
Th1 a=6 Þ IE = (0;1): phương trình AB: y-1=0 !!"
Th1 a=7 Þ IE = (1; -4): phương trình AB: x-4y+19=0 Đáp án D
Hãy tham gia group để cùng học và cùng làm- Nhóm chỉ dành cho các Gv, Sv toán! 7
File làm chuyên đề HÌNH GIẢI TÍCH OXY QUA CÁC THI 3 CHUNG BGD Group FB: Strong Team TOÁN VD–VDC
Chú ý: đến đoạn tìm vec tơ pháp tuyến của AB là có thể chọn đáp án. æ 1 ö
Câu 7. (B 2002) Trong mặt phẳng với hệ tọa độ Oxy, cho hình chữ nhật ABCD có tâm I ç ;0÷ , è 2 ø
phương trình đường thẳng AB là x - 2y + 2 = 0 và AB = 2AD . Tìm tọa độ các đỉnh , A B, , C D
biết điểm A có hoành độ âm. Lời giải H A B I D C
Khoảng cách từ I đến đường thẳng AB là IH = d (I AB) = 5 ; 2
Þ AD = 5 và IA = IB = 5 . 2 æ 5 ö Suy ra ,
A B là các giao điểm của đường thẳng AB với đường tròn ç I; ÷ . Do đó, tọa độ các è 2 ø éìx = - ìx - y + = 2 2 2 0 êí ï y 0 2 êî = điểm ,
A B là nghiệm của hệ phương trình: í Û æ 1 ö 2 25 ê x - + y = ï ìx = ç ÷ 2 4 ê 2 è î ø í êëîy = 2
Ycbt Þ A(-2;0), B(2;2)
Vì I là trung điểm của AC Þ C(3;0) !!!" !!!"
Và AB = DC Þ D(-1;-2).
Email: slowrock321@gmail.com
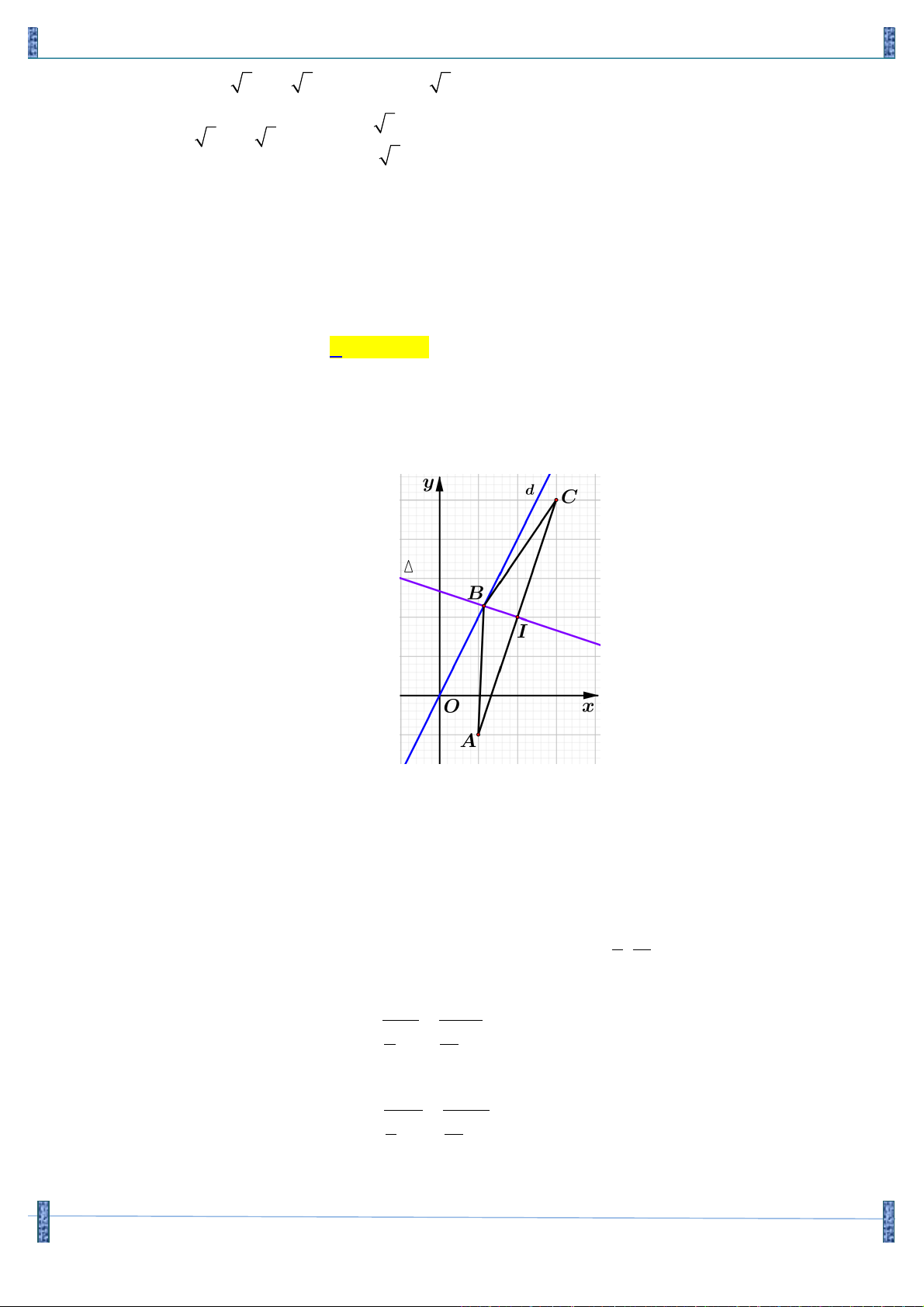
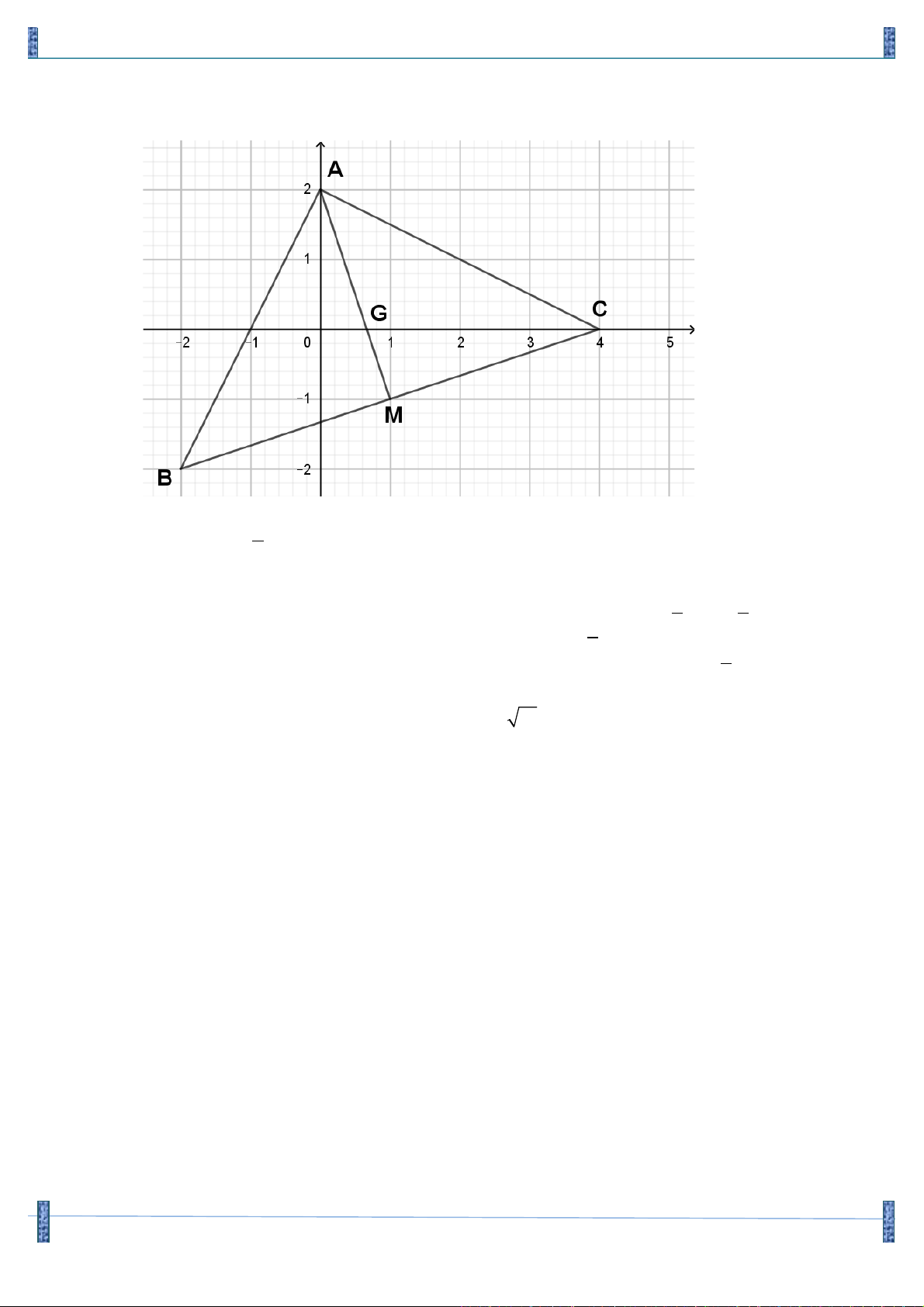
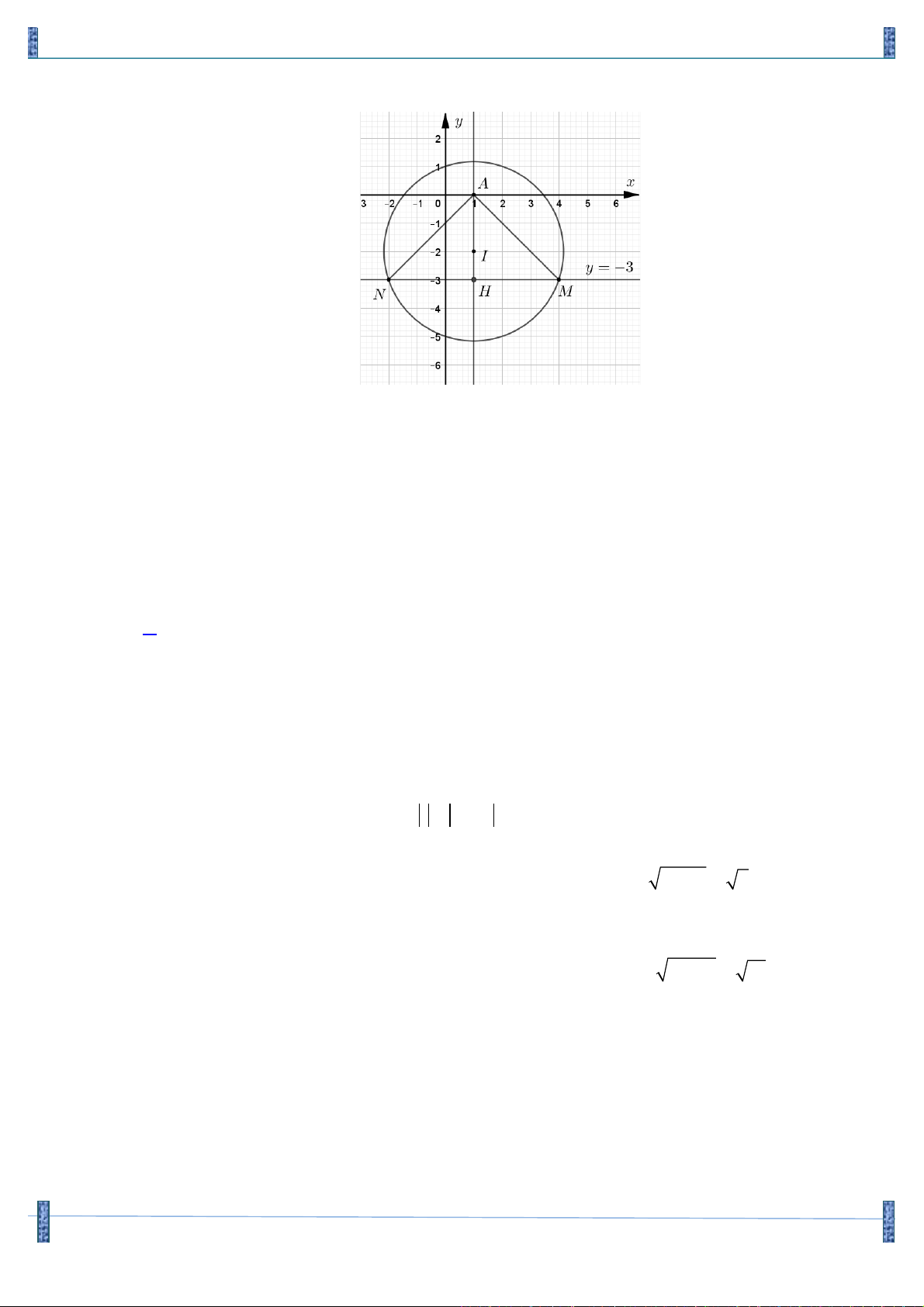
Câu 8. (B - 2003) Trong mặt phẳng với hệ tọa độ Oxy cho AB
D C có AB = AC , 90o BAC = . Biết æ 2 ö M (1,- )
1 là trung điểm cạnh BC và G ,0 ç ÷ là trọng tâm AB
D C . Khi đó, A(x , y A A ) , è 3 ø
B(x , y ),(x < 0). Tính 2
T = 2019x + y + 2x - 3y B B B A A B B A. 3 . B. 4 . C. 5 . D. 6 . Lời giải
Hãy tham gia group để cùng học và cùng làm- Nhóm chỉ dành cho các Gv, Sv toán! 8
File làm chuyên đề HÌNH GIẢI TÍCH OXY QUA CÁC THI 3 CHUNG BGD Group FB: Strong Team TOÁN VD–VDC
Họ và tên tác giả: Đỗ Minh Đăng Tên FB: Johnson Do Chọn B !!!" æ 2 ö !!!!" Ta có: AG =
- x ,-y ; AM = ç ÷ (1- x , 1 - - y ) è 3 A A A A ø ì2 2 - x = - x !!!" !!!!" ï A (1 A) ï
+G là trọng tâm AB
D C và AM là trung tuyến suy ra: 2 3 3 AG = AM Û í 3 2 ï-y = - - y A ( 1 A) ïî 3 ìx = 0 !!!!" A Û í
Þ A(0,2) Þ AM = (1, 3 - ) Þ AM = 10 . y = 2 î A + AB
D C vuông tại A nên AB
D C nội tiếp đường tròn (C) tâm M, bán kính AM.
Þ (C) (x - )2 +( y + )2 : 1 1 =10
+ BC qua M và vuông góc AM Þ (BC): x -1-3( y + )
1 = 0 Û x = 3y + 4 (
ìï x - )2 +( y + )2 1 1 = 10
+ Ta có: (C) Ç(BC) = { , B }
C . Suy ra tọa độ B, C là nghiệm hệ: í ïîx = 3y + 4 éìx = 4 ( êí
ìï 3y +3)2 +( y + )2 1 = 10 ( ìï y + )2 1 =1 êîy = 0 Û í Û í Û Þ B( 2, - 2 - ) ( vì x < 0 ) ï B îx = 3y + 4 ïîx = 3y + 4 êìx = 2 - êí êëîy = 2 - Vậy 2
T = 2019x + y + 2x - 3y = 4 A A B B
Hãy tham gia group để cùng học và cùng làm- Nhóm chỉ dành cho các Gv, Sv toán! 9
File làm chuyên đề HÌNH GIẢI TÍCH OXY QUA CÁC THI 3 CHUNG BGD Group FB: Strong Team TOÁN VD–VDC
Câu 9. (B-2013-1) Trong mặt phẳng với hệ tọa độ Oxy, cho hình thang cân ABCD có hai đường chéo
vuông góc với nhau và AD = 3BC. Đường thẳng BD có phương trình x + 2y – 6 = 0 và tam
giác ABD có trực tâm là H ( 3;
- 2). Tìm tọa độ các đỉnh C và . D A. C ( 1 - ;6), D(4; ) 1 và C ( 1 - ;6),D( 8 - ;7).
B. C (1;6), D( 4 - ; )
1 và C (1;6),D( 8 - ;7).
C. C(1;6),D( 4 - ; )
1 và C(1;6),D(8;7). D. C( 1 - ;6),D(4;- ) 1 và C( 1 - ;6),D(8; 7 - ). Lời giải
Tác giả: Nguyễn Đắc Tuấn - Facebook: Đỗ Đại Học
Gọi I là giao điểm của AC và BD Þ IB = IC.
Mà IB ^ IC nên I
D BC vuông cân tại 0 I Þ ICB = 45 .
BH ^ AD Þ BH ^ BC Þ H
D BC vuông cân tại B Þ I là trung điểm của đoạn thẳng HC.
Do CH ^ BD và trung điểm I của CH thuộc BD nên tọa độ điểm C thỏa mãn hệ
ì2(x + 3) -( y - 2) = 0 ï ìx = 1 - í x -3 æ y + 2 Û ö í Þ C ( 1 - ;6). + 2 - 6 = 0 ï ç ÷ îy = 6 î 2 è 2 ø IC IB BC 1 CH Ta có: = = = Þ ID = 3IC 2 2 10
Þ CD = IC + ID = IC 10 = = 5 2. ID ID AD 3 2 ét =
Ta có: D(6 - 2t;t) và CD = 5 2 suy ra ( - t)2 + (t - )2 1 7 2 6 = 50 Û êët =7. Do đó: D(4; ) 1 hoặc D( 8; - 7).
Câu 10. [A-2006] Trong mặt phẳng với hệ tọa độ Oxy, cho các đường thẳng lần lượt có phương trình:
d : x + y + 3 = 0, d : x - y - 4 = 0, d : x - 2y = 0. Tìm toạ độ điểm M nằm trên đường 1 2 3
thẳng d3 sao cho khoảng cách từ M đến đường thẳng d1 bằng hai lần khoảng cách từ M đến đường thẳng d2. Lời giải
Do M Î d nên M (2 ; y y) 3
Hãy tham gia group để cùng học và cùng làm- Nhóm chỉ dành cho các Gv, Sv toán! 10
File làm chuyên đề HÌNH GIẢI TÍCH OXY QUA CÁC THI 3 CHUNG BGD Group FB: Strong Team TOÁN VD–VDC 2y + y + 3 3y + 3
Ta có d (M ,d = = 1 ) 2 2 1 +1 2 - - - d ( 2y y 4 y 4 M ,d = = 2 ) + (- )2 2 2 1 1 3y + 3 y - 4
é3y + 3 = 2( y - 4) é = - d ( y 11
M ,d = 2d M ,d Û = 2 Û ê Û 1 ) ( 2 ) ê 2 2 ê3y + 3 = 2 ë (4- y) ëy =1 Với y = 11 - Þ M 22 - ; 11 - 1 ( )
Với y =1Þ M 2;1 2 ( )
Câu 11. Trong mặt phẳng tọa độ Oxy , cho tam giác ABC vuông tại A , có đỉnh C ( 4 - ) ;1 , phân giác
trong góc A có phương trình x + y - 5 = 0. Viết phương trình đường thẳng BC , biết diện tích
tam giác ABC bằng 24 và đỉnh A có hoành độ dương. Trắc nghiệm hoá:
Trong mặt phẳng tọa độ Oxy , cho tam giác ABC vuông tại A , có đỉnh C ( 4 - ) ;1 , phân giác
trong góc A có phương trình x + y - 5 = 0. Biết diện tích tam giác ABC bằng 24 và đỉnh A có
hoành độ dương. Giả sử B(x ; y , tính giá trị biểu thức T = x + y . 0 0 ) 0 0 A. T = 1 - B. T = 11 C. T = 5 D. T = 3 - Lời giải
Họ và tên tác giả: Nguyễn Hồng Hạnh Tên FB: Nguyễn Hồng Hạnh Chọn B
Gọi D là điểm đối xứng của C ( 4 - )
;1 qua d : x + y - 5 = 0, suy ra toạ độ D( ; x y) thoả mãn: (
ì x + 4) -( y - ) 1 = 0 ï í Þ D x - y + (4;9 4 1 ) ï + - 5 = 0 î 2 2
Điểm A thuộc đường tròn đường kính CD , nên toạ độ A( ; x y) thoả mãn:
Hãy tham gia group để cùng học và cùng làm- Nhóm chỉ dành cho các Gv, Sv toán! 11
File làm chuyên đề HÌNH GIẢI TÍCH OXY QUA CÁC THI 3 CHUNG BGD Group FB: Strong Team TOÁN VD–VDC ìx + y - 5 = 0 ï 2S í
Þ A 4;1 (do x > 0 )Þ = 8 ABC AC Þ AB = = 6 2 ( ) 2 ïx + î ( y -5) = 32 AC
B thuộc đường thẳng AD :x = 4, suy ra toạ độ B(4; y thoả mãn ( y -1 = 36. Þ B(4;7); 0 )2 0 ) B(4;-5). !!!" !!!"
Do d là phân giác trong góc A nên AB , AD cùng hướng, suy ra B(4;7). Vậy T =11.
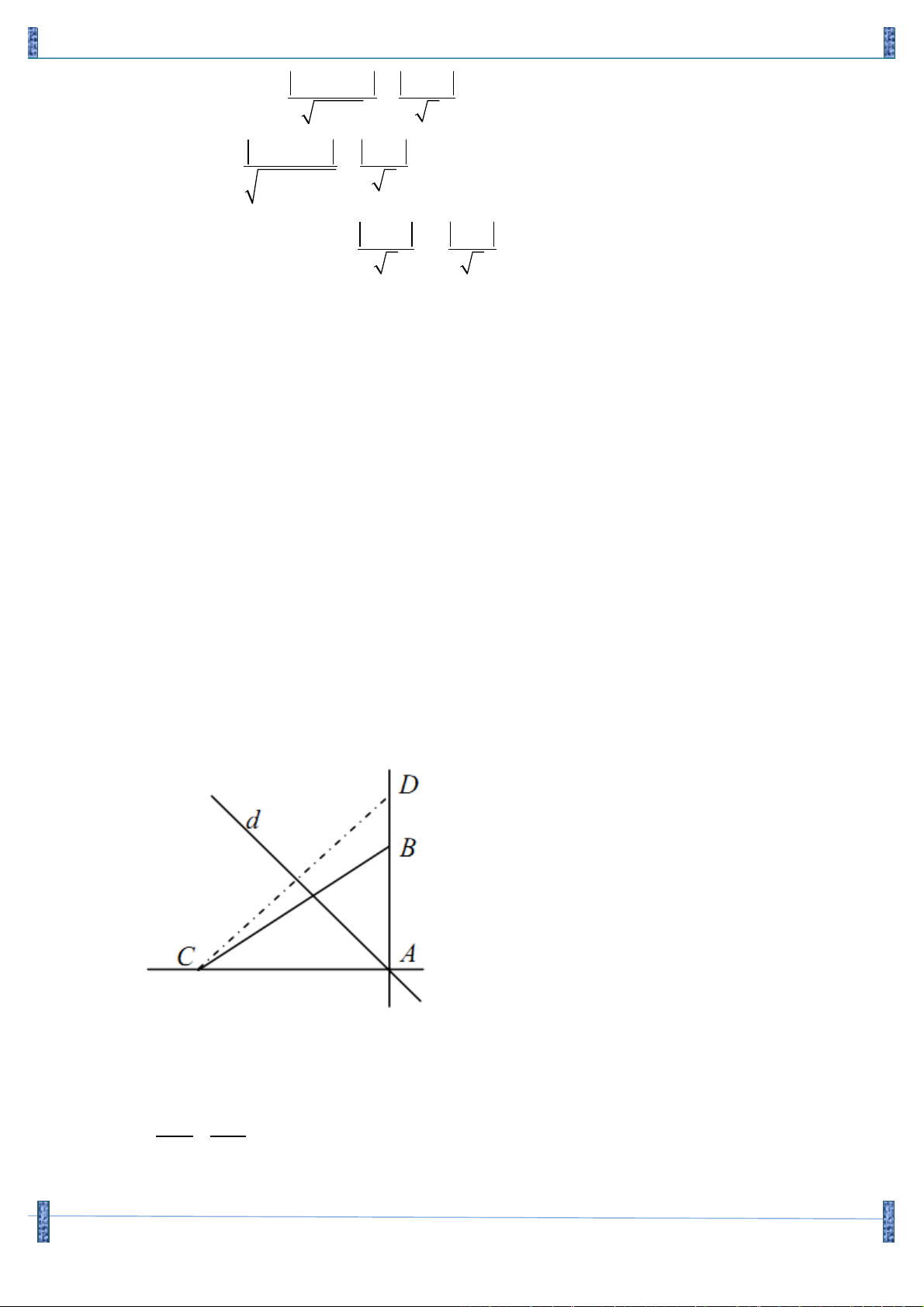
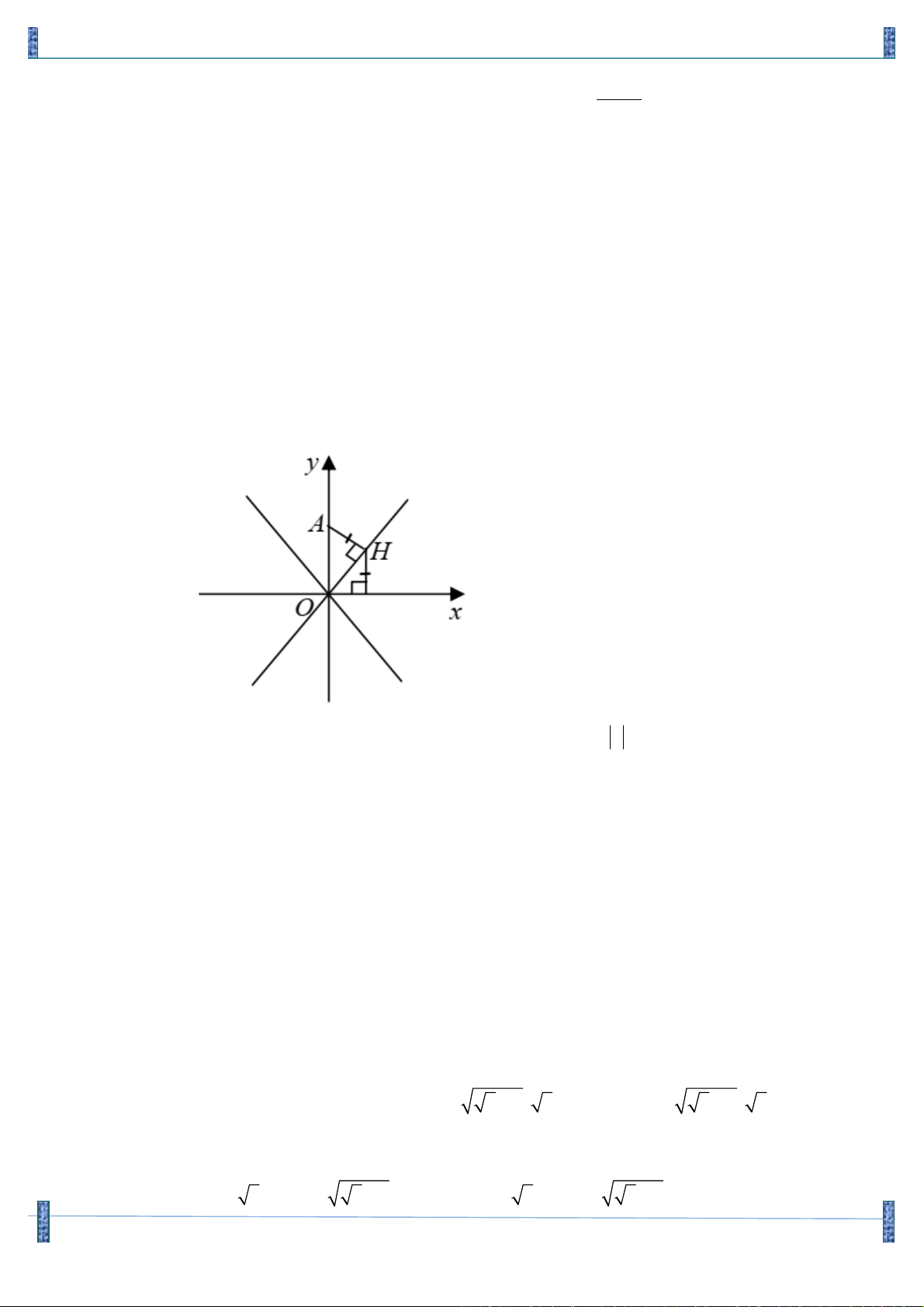
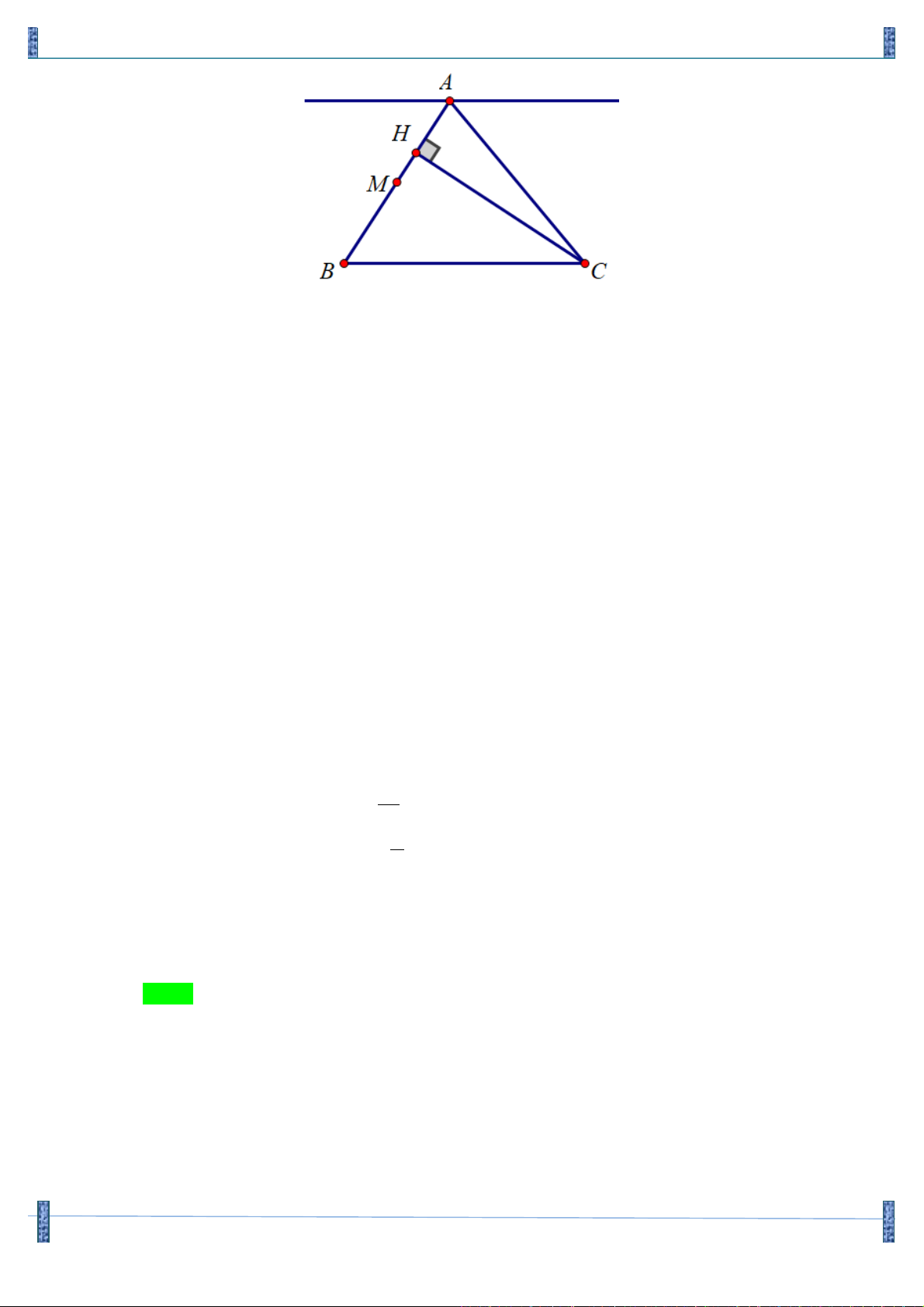
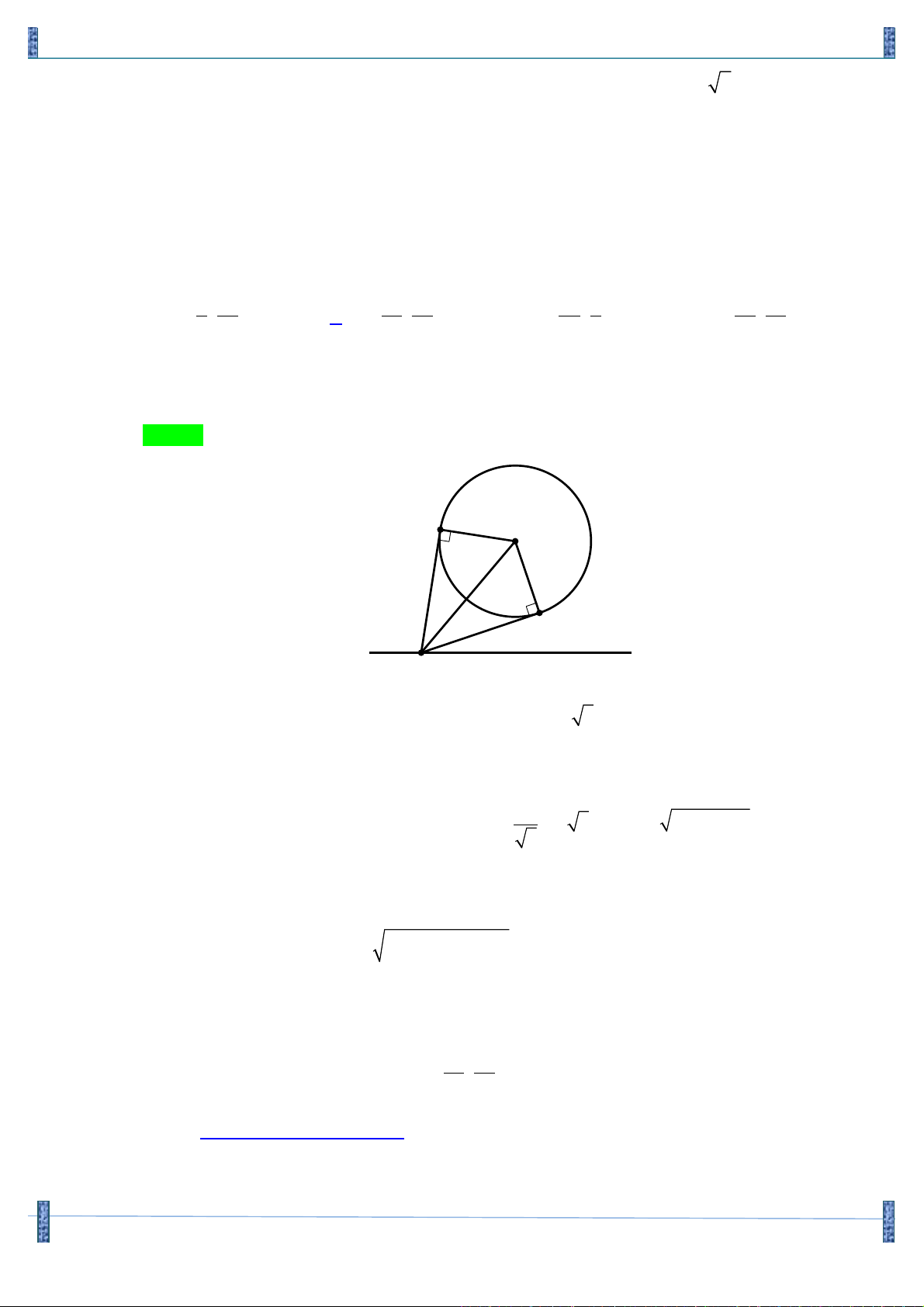
Câu 12. Trong mặt phẳng tọa độ Oxy , cho điểm A(0;2) và D là đường thẳng đi qua O . Gọi H là hình
chiếu vuông góc của A trên D . Viết phương trình đường thẳng D , biết khoảng cách từ H đến
trục hoành bằng AH . Lời giải
Họ và tên: Vũ Ngọc Tân Tên FB: Vũ Ngọc Tân Gọi H ( ; a b), ta có: 2 2 2
AH = a + (b - 2) và d(H,Ox) = b . Theo giả thiết thì 2 2 2 2 2
d(H,Ox) = AH Û d (H,Ox) = AH Û a + (b - 2) = b 2
Û a - 4b + 4 = 0 (1)
Phương trình đường tròn (C) có đường kính OA là: 2 2
x + (y -1) =1 mà 0 AHO = 90 nên H Î(C)
Khi đó ta có: a + (b - )2 2 2 2
1 =1Û a + b - 2b = 0 (2) 2
ìïa - 4b + 4 = 0 Từ ( )
1 &(2) ta được hệ phương trình: í . 2 2
ïîa +b - 2b = 0
Giải hệ phương trình ta được: H(2
5 - 2; 5 -1) hoặc H( 2 - 5 - 2; 5 -1)
Vậy có hai đường thẳng D thỏa mãn là D : 5 -1 x - 2 5 - 2y = 0 hoặc D : 5 -1 x + 2 5 - 2y = 0 1 ( ) 1 ( )
Hãy tham gia group để cùng học và cùng làm- Nhóm chỉ dành cho các Gv, Sv toán! 12
File làm chuyên đề HÌNH GIẢI TÍCH OXY QUA CÁC THI 3 CHUNG BGD Group FB: Strong Team TOÁN VD–VDC
Email: vungoctan131@gmail.com
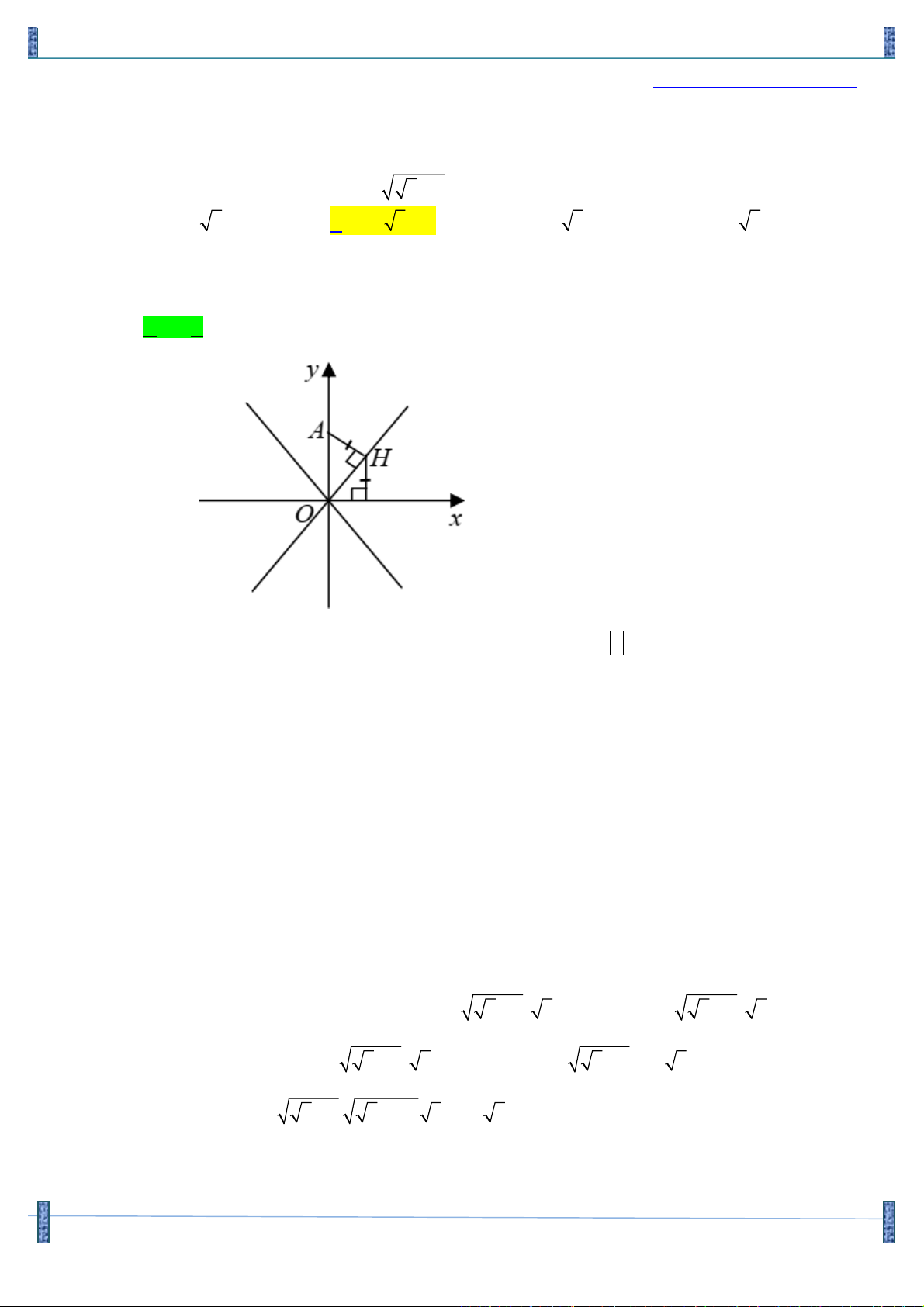
Câu 13. Trong mặt phẳng tọa độ Oxy , cho điểm A(0;2) và D là đường thẳng đi qua O . Gọi H là hình
chiếu vuông góc của A trên D . Tọa độ điểm H ( ;
a b)và khoảng cách từ H đến trục hoành
bằng AH và a > 0. Tính T = . a 5 + 2 + b. A. T = 5 - 2. B. T = 5 +1. C. T = 5 -1. D. T = 5. Lời giải
Họ và tên: Vũ Ngọc Tân Tên FB: Vũ Ngọc Tân Chọn B Gọi H ( ; a b), ta có: 2 2 2
AH = a + (b - 2) và d(H,Ox) = b . Theo giả thiết thì 2 2 2 2 2
d(H,Ox) = AH Û d (H,Ox) = AH Û a + (b - 2) = b 2
Û a - 4b + 4 = 0 (1)
Phương trình đường tròn (C) có đường kính OA là: 2 2
x + (y -1) =1 mà 0 AHO = 90 nên H Î(C)
Khi đó ta có: a + (b - )2 2 2 2
1 =1Û a + b - 2b = 0 (2) 2
ìïa - 4b + 4 = 0 Từ ( )
1 &(2) ta được hệ phương trình: í . 2 2
ïîa +b - 2b = 0
Giải hệ phương trình ta được: H(2
5 - 2; 5 -1) hoặc H( 2 - 5 - 2; 5 -1)
Vì a > 0 nên H(2
5 - 2; 5 -1). Khi đó a = 2 5 - 2;b = 5 -1 Vậy T = 2 5 - 2. 5 + 2 + 5 -1= 5 +1.
Họ tên: Trương Văn Quắng, Email: quangtv.c3kl@gmail.com
Hãy tham gia group để cùng học và cùng làm- Nhóm chỉ dành cho các Gv, Sv toán! 13
File làm chuyên đề HÌNH GIẢI TÍCH OXY QUA CÁC THI 3 CHUNG BGD Group FB: Strong Team TOÁN VD–VDC æ 1 ö
Câu 14. Trong mặt phẳng Oxy, cho tam giác ABC có đỉnh B ;1 ç
÷. Đường tròn nội tiếp tam giác ABC è 2 ø
tiếp xúc với các cạnh BC,CA, AB tương ứng tại các điểm D, E, F . Cho D(3; ) 1 và đường
thẳng EF có phương trình y - 3 = 0 . Tìm tọa độ đỉnh A , biết A có hoành độ dương. Lời giải !!!" æ 5 ö Ta có BD = ;0 Þ BD / EF ç ÷
, suy ra tam giác ABC cân tại A; è 2 ø
Þ Đường thẳng AD vuông góc với EF, có phương trình là x - 3 = 0 . 2 æ 1 ö 25 ét = -1
F có tọa độ dạng F (t ) ;3 , ta có: 2
BF = BD Û t - + 2 = Û ç ÷ . è 2 ø 4 ê ët = 2 + Với t = 1 - Þ F ( 1
- ;3) ; suy ra đương thẳng BF có phương trình : 4x + 3y - 5 = 0. æ 7 - ö
A là giao điểm của AD và BF Þ A 3; ç
÷ (không thỏa mãn yêu cầu (A có tung độ dương). è 3 ø
+ với t = 2 Þ F (2;3); Suy ra phương trình BF : 4x - 3y +1 = 0. æ 13 ö Þ A 3; ç ÷, thỏa mãn yêu cầu. è 3 ø æ 13 ö Vậy A 3; ç ÷ . è 3 ø
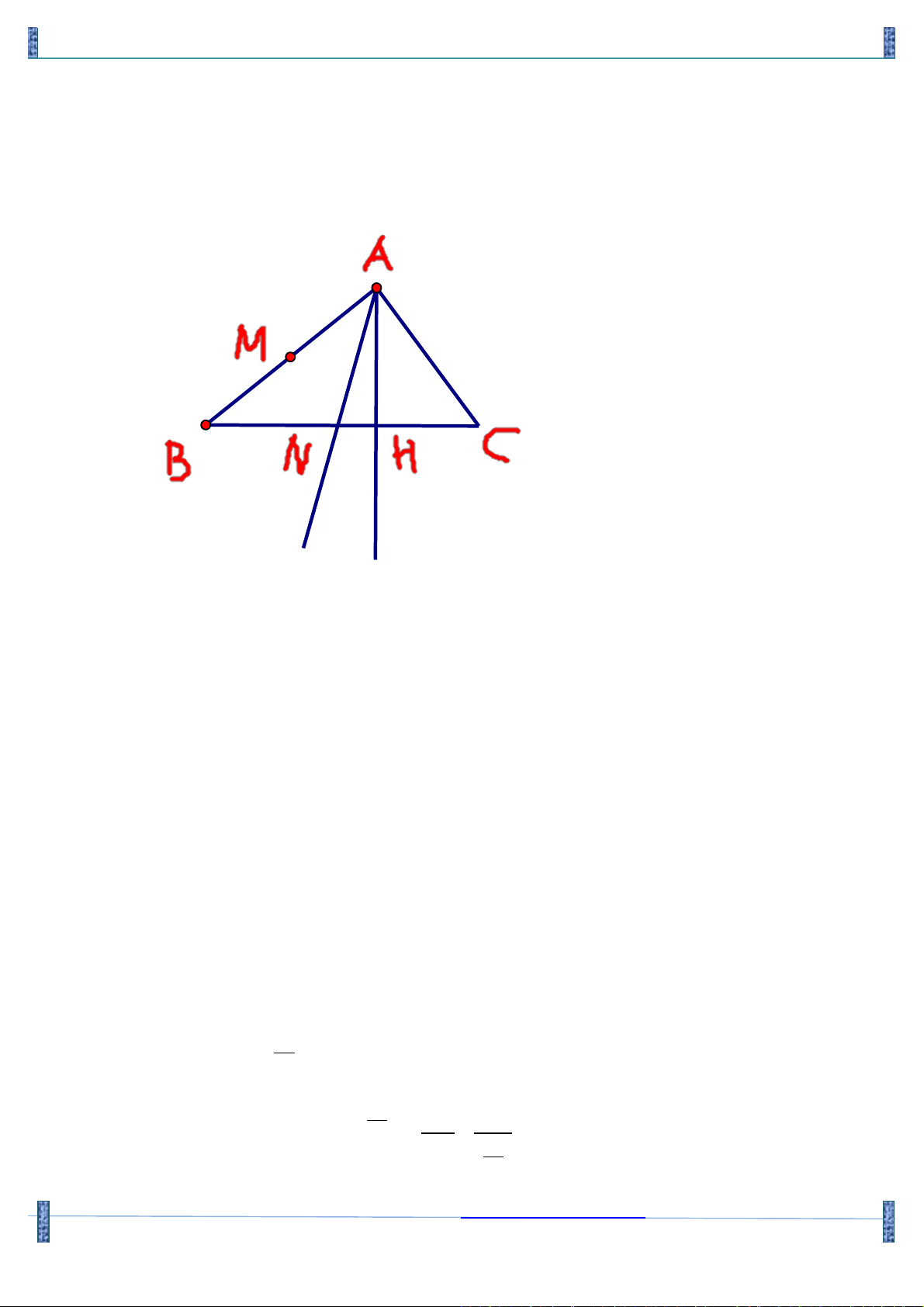
Câu 15. Trong mặt phẳng với hệ tọa độ Oxy , cho tam giác ABC có chân đường cao hạ từ đỉnh A là æ17 1 ö H ;- ç
÷ , chân đường phân giác trong của góc A là D(5;3) và trung điểm của cạnh AB là è 5 5 ø M (0; )
1 . Tung độ của điểm C là A. 9 . B. 9 - . C. 11. D. 11 - . Lời giải
GV: Bùi Thị Lợi, Email: builoiyka@gmail.com, Facebook: LoiBui Chọn C
Hãy tham gia group để cùng học và cùng làm- Nhóm chỉ dành cho các Gv, Sv toán! 14
File làm chuyên đề HÌNH GIẢI TÍCH OXY QUA CÁC THI 3 CHUNG BGD Group FB: Strong Team TOÁN VD–VDC !!!" æ 8 16 ö Ta có HD ; ç
÷ là véc tơ chỉ phương của đường thẳng BC . è 5 5 ø !
Do đó, đường thẳng BC đi qua D và có véc tơ pháp tuyến n(2;- )
1 nên có phương trình là
2(x -5) -( y -3) = 0 Û 2x - y - 7 = 0.
B thuộc đường thẳng BC nên B( ;2
b b - 7); M là trung điểm của AB nên A(- ;9 b - 2b) .
Tam giác ABH vuông tại H và có M là trung điểm của AB nên MA = MB = MH 2 2 æ17 ö æ 1 ö 2 2
MH = MB Û b + (2b -8)2 2 = + - -1 ç ÷ ç ÷ è 5 ø è 5 ø éb = 3 2
Û 5b - 32b + 51 = 0 ê Û 17 . êb = ë 5 17 æ17 1 ö b = Þ B ;- ç
÷ (loại vì B trùng với H ). 5 è 5 5 ø b = 3 Þ B(3;- ) 1 ; A( 3; - 3). !!!"
AD(8;0) nên phương trình của AD là y - 3 = 0.
Gọi N là điểm đối xứng của M qua AD thì N thuộc đường thẳng AC .
Phương trình MN : x = 0 ; MN Ç AD = I Þ I (0; )
3 ; I là trung điểm của MN Þ N (0;5).
Hãy tham gia group để cùng học và cùng làm- Nhóm chỉ dành cho các Gv, Sv toán! 15
File làm chuyên đề HÌNH GIẢI TÍCH OXY QUA CÁC THI 3 CHUNG BGD Group FB: Strong Team TOÁN VD–VDC x - 0 y - 5 Phương trình AC : =
Û 2x - 3y +15 = 0. 3 - - 0 3- 5
C là giao điểm của AC và BC nên tọa độ C là nghiệm của hệ ì2x - y = 7 ìx = 9 í Û í Þ C (9;1 ) 1 . î2x - 3y = 15 - îy =11
Vậy tung độ của điểm C là 11.
Email: nghianguyennhan78@gmail.com
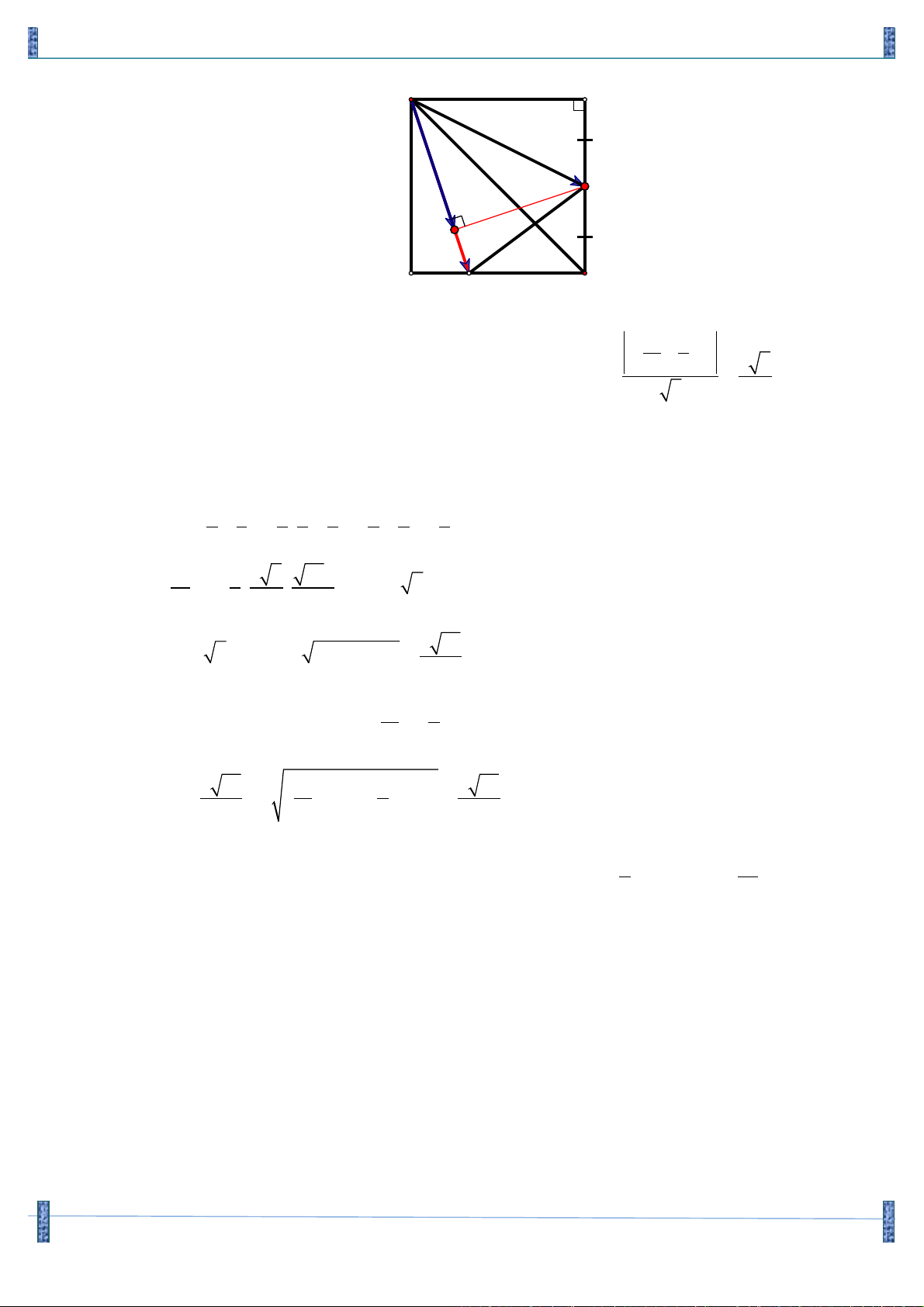
Câu 16. (KA _ 2014)Trong mặt phẳng với hệ trục tọa độ Oxy, cho hình vuông ABCD có điểm M là
trung điểm của đoạn AB và N là điểm thuộc đoạn AC sao cho AN = 3NC . Viết phương trình
đường thẳng CD, biết M (1;2), N (2;- ) 1 ..
A. 3x + 4y -15 = 0; y + 2 = 0 .
B. 3x - 4y -15 = 0; y + 2 = 0
C. 3x - 4y +15 = 0; y + 2 = 0 .
D. 3x + 4y -15 = 0; y - 2 = 0 Hướng dẫn giải
Họ và tên tác giả: Nguyễn Thị Thanh Thảo Tên FB: Nguyễn Thanh Thảo Chọn B D I C N A M B +) Ta có MN = 10 .
Gọi a là độ dài cạnh của hình vuông ABCD, vậy a > 0. a 3AC 3a 2 2 5a
Ta có AM = và AN = = nên 2 2 2
MN = AM + AN - 2AM.AN. o c sMAN = . 2 4 2 8 2 5a Do đó: =10 Þ a = 4. 8
Hãy tham gia group để cùng học và cùng làm- Nhóm chỉ dành cho các Gv, Sv toán! 16
File làm chuyên đề HÌNH GIẢI TÍCH OXY QUA CÁC THI 3 CHUNG BGD Group FB: Strong Team TOÁN VD–VDC BD
+) Gọi I là trung điểm của CD. Ta có IM = AD = 4 và IN = = 2 nên ta có hệ phương 4 ( ì x - ï )2 +( y - )2 éx =1, y = 2 1 2 = 16 - trình: ê í Û 17 6 . ( ïî )2 ( )2 êx = ; 2 1 2 y x y = - - + + = ë 5 5 !!!"
+) Với x = 1, y = 2 - có I (1; 2 - ) và IM = (0;4). !!!"
Đường thẳng CD đi qua I và có véc tơ pháp tuyến IM nên có phương trình là y + 2 = 0. 17 6 æ17 6 ö !!!" æ 12 16 ö +) Với x = ; y = - có I ; - ç ÷ và IM = - ; ç ÷. 5 5 è 5 5 ø è 5 5 ø !!!"
Đường thẳng CD đi qua I và có véc tơ pháp tuyến IM nên có phương trình là 3x - 4y -15 = 0 .
Email: cunconsieuquay1408@gmail.com
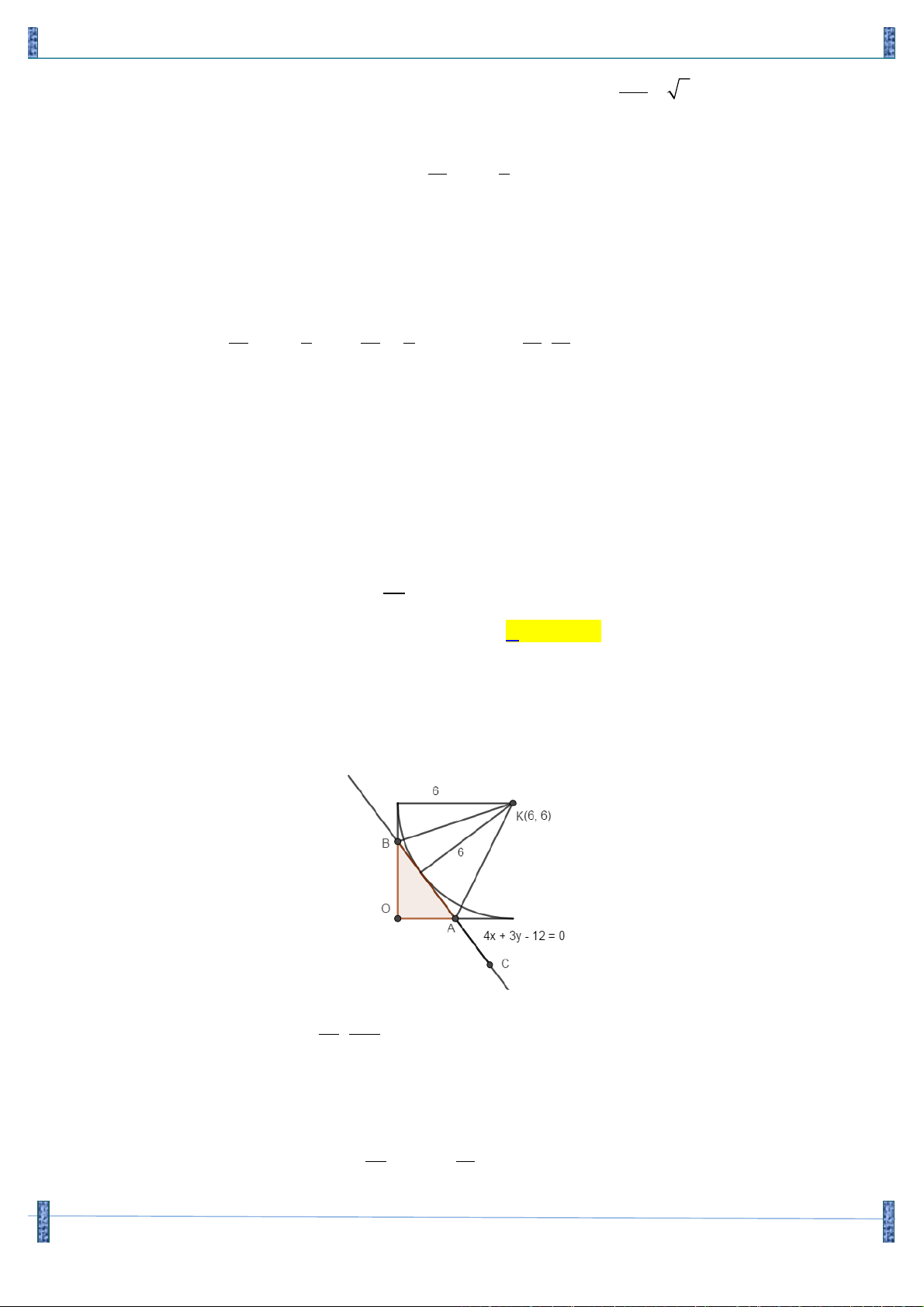
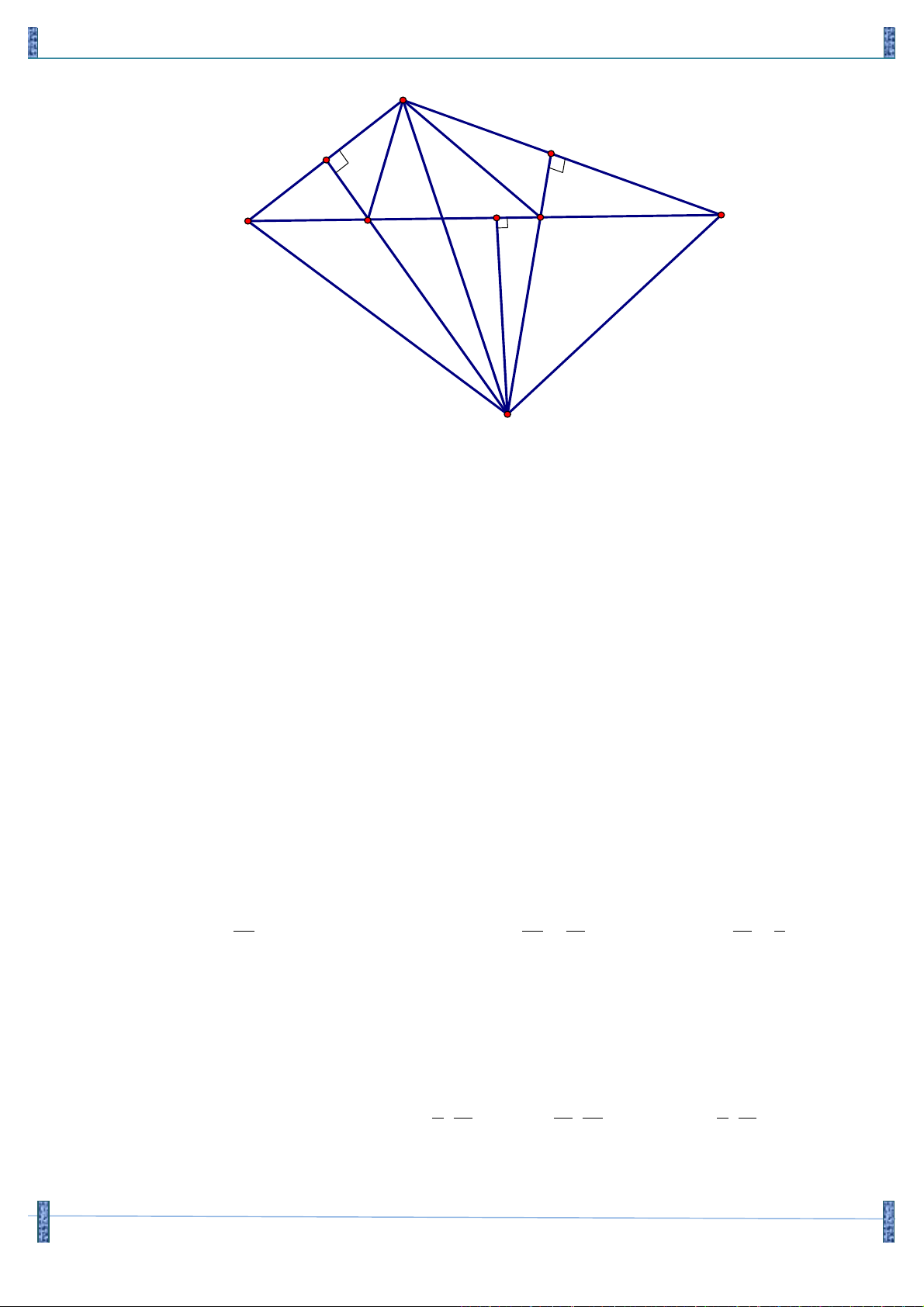
Câu 17. Trong mặt phẳng với hệ tọa độ Oxy , cho tam giác OAB có các đỉnh (
A a, b) và B(c,d) thuộc
đường thẳng D : 4x + 3y -12 = 0 và điểm K (6;6) là tâm đường tròn bàng tiếp góc O . Gọi C
là điểm nằm trên D sao cho AC = AO và các điểm C, B nằm khác phía nhau so với điểm A 24
Biết điểm C có hoành độ bằng
. T = 2018d - 2019a . 5 A. T = 2016 B. T = 2014 C. T = 2015 D. T = 2017 Lời giải
Họ và tên tác giả: Nguyễn Thị Thanh Mai Tên Fb: Thanh Mai Nguyen Chọn C æ - ö * C Î(D) 24 12
: 4x + 3y -12 = 0 Þ C ; ç ÷ è 5 5 ø * Giả sử A( ; a b) 2 2 æ ö æ ö
+ Vì OA = AC nên ta có 2 2 24 12
a + b = a - + b + ç ÷ ç ÷ è 5 ø è 5 ø
Hãy tham gia group để cùng học và cùng làm- Nhóm chỉ dành cho các Gv, Sv toán! 17
File làm chuyên đề HÌNH GIẢI TÍCH OXY QUA CÁC THI 3 CHUNG BGD Group FB: Strong Team TOÁN VD–VDC Û 2 - a + b + 6 = 0
+ AÎ(D) nên: 4a + 3b -12 = 0 ì 2 - a + b + 6 = 0 ìa = 3 + Vậy có hệ: í Þ í Þ A(3;0)
î4a + 3b -12 = 0 b î = 0
* Bán kính đường tròn bàng tiếp góc O bằng: + -
R = d (K D) 4.6 3.6 12 ; = = 6 5 *Giả sử B ( ;
c d ) (d ¹ 0)thì phương trình đường thẳng (OB) là: dx - cy = 0 (D') ì + - = ìï BÎ(D) 4c 3d 12 0 ï + Ta có íïî ( Û í d - c d K,(D')) 6 6 = 6 = 6 ï 2 2 î d + c ì4c + 3d =12 ìc = 0 Û í Û í
(do d ¹ 0 ) Þ B(0;4) î cd = 0 îd = 4
Vậy T = 2018.4 - 2019.3 = 2015 nên chọn C.
Email: trandongphong.c3lehongphong@lamdong.edu.vn.
Câu 18. (Bài 62- A2012-DB2) Trong mặt phẳng tọa độ Oxy , cho điểm M (1;- ) 1 và hai đường thẳng
có phương trình (d : x - y -1= 0, d : 2x + y -5 = 0 . Gọi A là giao điểm của hai đường 1 ) ( 2)
thẳng trên. Biết rằng có hai đường thẳng (d ) đi qua M cắt hai đường thẳng trên lần lượt tại
hai điểm B,C sao cho ABC là tam giác có BC = 3AB có dạng: ax + y + b = 0 và
cx + y + d = 0 , giá trị của T = a + b + c + d A. T = 5 . B. T = 6 . C. T = 2 . D. T = 0 . Lời giải
Họ và tên tác giả: Trần Đông Phong, FB: Phong Do Chọn C
Hãy tham gia group để cùng học và cùng làm- Nhóm chỉ dành cho các Gv, Sv toán! 18
File làm chuyên đề HÌNH GIẢI TÍCH OXY QUA CÁC THI 3 CHUNG BGD Group FB: Strong Team TOÁN VD–VDC Tọa độ A(2; ) 1 1 3
Gọi a là góc giữa hai đường thẳng (d và (d , cosa = Þ sina = 2 ) 1 ) 10 10 AB BC 1
Xét tam giác ABC ta có: = Þ sin C = sin C sin A 10 1 3
Gọi b là góc giữa hai đường thẳng (d ) và (d , suy ra: sin b = Þ cos b = ( ) 1 1 ) 10 10 !
Giả sử (d ) có vec tơ pháp tuyến là n( ; a b) 3 2a + b 3 éa = b Từ ( ) 1 ta có: 2 2 cos b = Û =
Û a -8ab + b = 0 Û ê 2 2 10 a + b 5 10 ëa = 7b !
Với a = b một vec tơ pháp tuyến n = (1 )
;1 Þ d : x + y = 0 !
Với a = 7b một vec tơ pháp tuyến n(7 )
;1 Þ d : 7x + y - 6 = 0
Vậy: T = 1+ 0 + 7 - 6 = 2 3
Câu 19. Cho tam giác ABC có diện tích bằng . Gọi a,b,clần lượt là độ dài các cạnh BC,CA, ABvà 2
h ;h ;h tương ứng là đường cao kẻ từ các đỉnh ,
A B,C của tam giác. Khi đó giá trị nhỏ nhất a b c æ 1 1 1 öæ 1 1 1 ö của biểu thức P = + + ç ÷ç + + ÷ là: è a b c ø h h h è a b c ø 3 A. B. 3 C. 6 D. 9 2 Lời giải
Họ và tên tác giả: Nguyễn Thị Thanh Thương, Tên FB:Nguyễn Thương Chọn B
Hãy tham gia group để cùng học và cùng làm- Nhóm chỉ dành cho các Gv, Sv toán! 19
File làm chuyên đề HÌNH GIẢI TÍCH OXY QUA CÁC THI 3 CHUNG BGD Group FB: Strong Team TOÁN VD–VDC 3
Vì tam giác có diện tích là nên . a h = . b h = . c h = 3. 2 a b c 3 3 3
Từ đó suy ra: h = ;h = ;h = thay vào biểu thức a b c a b c æ 1 1 1 öæ 1 1 1 ö 1 æ 1 1 1 ö P = + + ç ÷ç + + ÷ = + + . ç
÷ (a + b + c) è a b c ø h h h 3 è ø è a b c ø a b c
Do a,b,c là các số dương nên áp dụng bất đẳng thức Cauchy ta được: 1 1 1 1 3 + + ³ 3 và 3
a + b + c ³ 3 abc a b c abc 1 æ 1 1 1 ö 1 1 Vậy nên: P = + + . ç
÷ (a + b + c) 3 3 ³ .3.
.3. abc = 3 Þ P ³ 3 3 è a b c ø 3 abc
Vậy MinP = 3 Û a = b = c hay tam giác ABC đều.
Câu 20. (D2003 DB1) Trong mặt phẳng với hệ tọa độ Oxy, cho đường thẳng d : x - 7y +10 = 0 . Viết
phương trình đường tròn có tâm thuộc đường thẳng D : 2x + y = 0 và tiếp xúc với đường thẳng d tại A(4; 2). Lời giải
Gọi I là tâm của đường tròn.
Vì đường tròn tiếp xúc với d tại A nên IA ^ d tại A Þ IA : 7x + y - 30 = 0
Ta có: I là giao điểm của đường thẳng D và đường thẳng IA Þ I(6; -12) Bán kính R = IA =10 2
Vậy phương trình đường tròn là: ( - )2 +( + )2 x 6 y 12 = 200.
Gmail: phan.hien.k54a@gmail.com
Câu 21. (D2004 DB 1) Trong mặt phẳng với hệ tọa độ Oxy , cho tam giác ABC vuông ở A . Biết æ 7 ö ( A 1 - ;4), B(1; 4)
- , đường thẳng BC đi qua điểm K ; 2 ç ÷. Biết điểm C( ;
a b) . Phát biểu nào è 3 ø sau đây đúng ?
A. b > a . B. 2 a + 2 b =16. C. b Î(1;3). D. 2 b - a = 6. Lời giải
Họ và tên tác giả: Phan Thị Hiền Tên FB: Phan Hiền Chọn A
Hãy tham gia group để cùng học và cùng làm- Nhóm chỉ dành cho các Gv, Sv toán! 20
File làm chuyên đề HÌNH GIẢI TÍCH OXY QUA CÁC THI 3 CHUNG BGD Group FB: Strong Team TOÁN VD–VDC B (1; -4) A (-1; 4) C K (7/3; 2) !!!" !" +) Có AB = (2; 8
- ) . Đường thẳng AC đi qua điểm ( A 1 - ;4), nhận n = (1; 4 - ) làm một vectơ 1
pháp tuyến nên AC :1(x +1) - 4(y - 4) = 0
Û x - 4y +17 = 0 !!!" æ 4 ö !!" +) BK = ;6 ç
÷. Đường thẳng BC đi qua B(1; 4) - , nhận n = 9; 2
- làm một vectơ pháp tuyến 2 ( ) è 3 ø
nên BC : 9(x -1) - 2(y + 4) = 0
Û 9x - 2y -17 = 0 +) { }
C = AC ! BC nên tọa độ điểm C là nghiệm của hệ phương trình : ìx - 4y +17 = 0 ìx - 4y = 1 - 7 ìx = 3 í Û í Û í 9
î x - 2y -17 = 0 9 î x - 2y =17 îy = 5 Vậy C(3;5) .
Email: tranhanhvxhd1@gmail.com
Câu 22. Trong mặt phẳng với hệ tọa độ (Oxy) cho điểm A(2;3) và hai đường thẳng d ;d có phương 1 2
trình lần lượt là d : x + y + 5 = 0; d : x + 2y - 7 = 0 . Gọi B(x ; y Îd ;C(x ; y )Îd sao cho 1 1 ) 1 2 1 2 2 2
tam giác ABC nhận điểm G(2;0) là trọng tâm. Tính giá trị của biểu thức T = x x + y y . 1 2 1 2 A. T = 21 - . B. T = -9 . C. T = 9 . D. T = 12 . Lời giải
Họ và tên tác giả: Trần Hạnh Tên FB: Trần Hạnh Chọn B
Hãy tham gia group để cùng học và cùng làm- Nhóm chỉ dành cho các Gv, Sv toán! 21
File làm chuyên đề HÌNH GIẢI TÍCH OXY QUA CÁC THI 3 CHUNG BGD Group FB: Strong Team TOÁN VD–VDC Vì B(x ;y Îd Þ B( 5
- - y ;y );C(x ;y )Îd Þ C(7 -2y ;y ) 1 1 ) 1 1 1 2 2 2 2 2
Vì tam giác ABC nhận điểm G(2;0) là trọng tâm nên ì2 + ( 5 - - y ) + (7 - 2y ) = 6 ìy + 2y = 2 - ìy = 4 - ìx = 1 - 1 2 1 2 1 1 í Û í Û í Þ í Þ T = 9 - 3+ y + y = 0 y + y = 3 - y =1 x = 5 î 1 2 î 1 2 î 2 î 2
Gmail: nvanphu1981@gmail.com
Câu 23. Trong hệ trục Oxy , cho tam giác ABC có đỉnh A thuộc đường thẳng d : x - 4y - 2 = 0, cạnh
BC song song với d. Phương trình đường cao BH : x + y + 3 = 0và trung điểm của cạnh AC là
M (1;1). Tìm tọa độ trọng tâm G của tam giác ABC. 2 2 2 2 A. G( ; 1 - ) B. G(- ; 1 - ) C. G( ;1) D. G(- ;1) 3 3 3 3 Lời giải
Họ và tên: Nguyễn Văn Phú Tên fb: Nguyễn Văn Phú
Hãy tham gia group để cùng học và cùng làm- Nhóm chỉ dành cho các Gv, Sv toán! 22
File làm chuyên đề HÌNH GIẢI TÍCH OXY QUA CÁC THI 3 CHUNG BGD Group FB: Strong Team TOÁN VD–VDC
d: x - 4y - 2 = 0 A H M(1;1) B
BH: x + y + 3 = 0 C ìM Î AC +) í Þ AC : y = . x îBH ^ AC ì 2 x = - ìx - 4y - 2 = 0 ïï +) 3 2 2 ( A ;
x y) = AC Ç d nên ( ;
x y) là nghiệm hệ: í Û í Þ ( A - ;- ). îy = x 2 3 3 ïy = - ïî 3 8 8
+) Vì M (1;1) là trung điểm của cạnh AC nên C( ; ). 3 3 æ 8 ö æ 8 ö
+) Cạnh BC song song với d và đi qua B nên phương trình BC : x - - 4 y - = 0 ç ÷ ç ÷ è 3 ø è 3 ø
hay d : x - 4y - 8 = 0. ìx - 4y -8 = 0 ìx = 4 - +) B( ;
x y) = BC Ç BH nên ( ;
x y) là nghiệm hệ: í Û í Þ B( 4 - ;1). îx + y + 3 = 0 îy =1 2
+) Vậy trọng tâm G(- ;1). 3
Facebook: Đàm Anh – Email: damanhsphn@gmail.com
Câu 24. (B2006 – DB2) Trong mặt phẳng với hệ tọa độ Oxy , cho tam giác ABC với đỉnh A(2; ) 1 , gọi
m là đường cao qua đỉnh B có phương trình là x - 3y - 7 - 0 và n là đường trung tuyến qua
đỉnh C có phương trình là x + y +1 = 0 . Giả sử B(x ; y ,C x ; y , tính 1 1 ) ( 2 2 )
P = x + y + x + y ? 1 1 2 2 A. P = 6 - . B. P = 4 - . C. P = 3 - . D. P = 5 - . Lời giải
Hãy tham gia group để cùng học và cùng làm- Nhóm chỉ dành cho các Gv, Sv toán! 23
File làm chuyên đề HÌNH GIẢI TÍCH OXY QUA CÁC THI 3 CHUNG BGD Group FB: Strong Team TOÁN VD–VDC m A n D B C
+ Lập phương trình đường thẳng AC .
Do đường thẳng AC vuông góc với m nên phương trình đường thẳng AC có dạng:
3x + y + c = 0. Ta có A(2; )
1 Î AC Þ 3.2 +1+ c = 0 Û c = 7
- Þ AC : 3x + y - 7 = 0
Lại có C = AC Ç n nên tọa độ điểm C thỏa mãn hệ phương trình: 3 ì x + y - 7 = 0 ìx = 4 í Û í Þ C (4; 5 - ) îx + y +1 = 0 îy = 5 -
+ Có B Î m nên tọa độ điểm B có dạng B(3b + 7;b). Gọi D là trung điểm của đoạn AB , suy æ 3b + 9 b +1ö ra D ; ç ÷. è 2 2 ø æ 3b + 9 b +1ö 3b + 9 b +1 Mà D ; Î n Þ + +1 = 0 Û b = 3 - Þ B( 2 - ; 3 - ç ÷ ) è 2 2 ø 2 2
Vậy P = 4 - 5 - 2 - 3 = 6
- . Chọn đáp án A.
Email: hakhanhuyen229@gmail.com
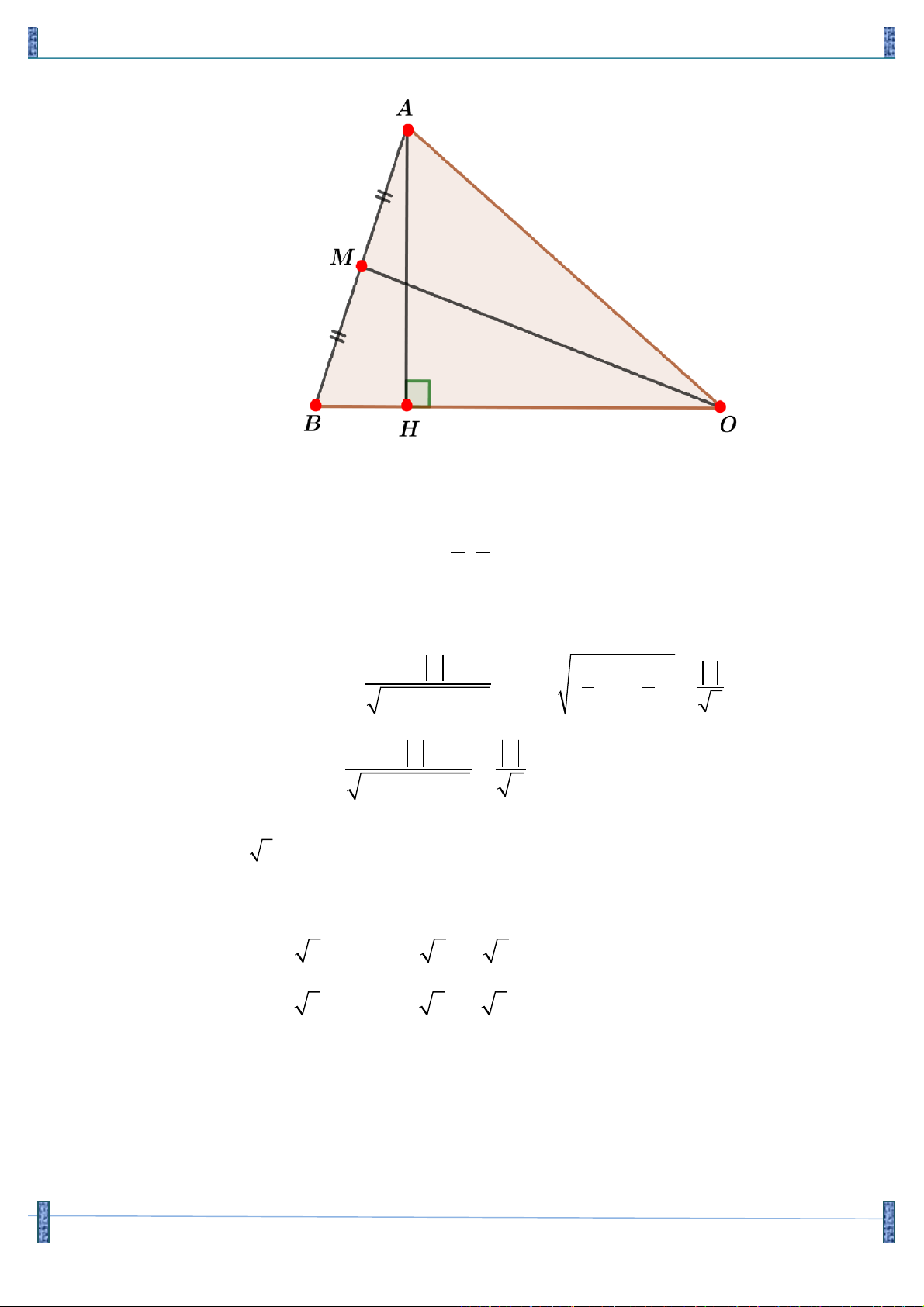
Câu 25. Trong mặt phẳng tọa độ Oxy, cho điểm A (0; -2). Điểm B thuộc đường thẳng d: x – y + 2 = 0
sao cho đường cao AH và đường trung tuyến OM của tam giác OAB có độ dài bằng nhau. Tính
tổng hoành độ của tất cả các điểm B thỏa mãn đề bài. A. 2 B. - 2. C. 0. D. – 4. Lời giải
Họ và tên tác giả: Hà Khánh Huyền Tên FB: Hà Khánh Huyền Chọn B
Hãy tham gia group để cùng học và cùng làm- Nhóm chỉ dành cho các Gv, Sv toán! 24
File làm chuyên đề HÌNH GIẢI TÍCH OXY QUA CÁC THI 3 CHUNG BGD Group FB: Strong Team TOÁN VD–VDC
B Îd : x - y + 2 = 0 Þ B ( ; a a + 2). a a
M là trung điểm của AB Þ M ( ; ). 2 2 !!!"
OB = (a;a + 2) nên phương trình đường thẳng BO: (a+2) x – ay = 0. 2 a 2 2 AH = d( , A BO) = ; æ a ö æ a ö a OM = + = . 2 ç ÷ ç ÷ 2a + 4a + 4 è 2 ø è 2 ø 2 2 a a AH = OM Û = 2 4 3 2
Û 8a = 2a + 4a + 4a 2 2a + 4a + 4 2 éa = 0 Û êëa= 1-± 3
+ a = 0 Þ B(0; 2) + a = 1 - + 3 Þ B( 1 - + 3;1+ 3) + a = 1 - - 3 Þ B( 1 - - 3;1- 3)
Vậy tổng hoành độ của tất cả điểm B thỏa mãn yêu cầu bài toán là – 2.
Câu 26. ( D2010 DB2-1) Trong mặt phẳng Oxy, cho tam giác ABC có đỉnh A(0;3), trực tâm H (0; ) 1
và trung điểm M (1;0) của BC. Tìm tọa độ điểm B của tam giác ABC biết B có hoành độ âm. A. B(0; ) 1 - B. B( 1 - ;0) C. B(0;3) D. B(3;0) Lời giải
Hãy tham gia group để cùng học và cùng làm- Nhóm chỉ dành cho các Gv, Sv toán! 25
File làm chuyên đề HÌNH GIẢI TÍCH OXY QUA CÁC THI 3 CHUNG BGD Group FB: Strong Team TOÁN VD–VDC Chọn B !!!"
BC đi qua M (1;0), nhận HA(0;2) làm véc tơ pháp tuyến nên BC có phương trình:
0.(x-1) + 2( y -0) = 0 Û y = 0 Gọi B( ;0
b )ÎBC (b < 0), M (1;0) là trung điểm BC nên C(2- ; b 0) !!!" ( !!!" HB ; b - ) 1 , AC (2 - ; b 3 - ) !!!" !!!"
HB AC = Û b( -b) 2 . 0 2
+ 3 = 0 Û b - 2b - 3 = 0 Û b = 1 - ( dob < 0) Vậy Chọn B
Email: duongquanghung.duke@gmail.com
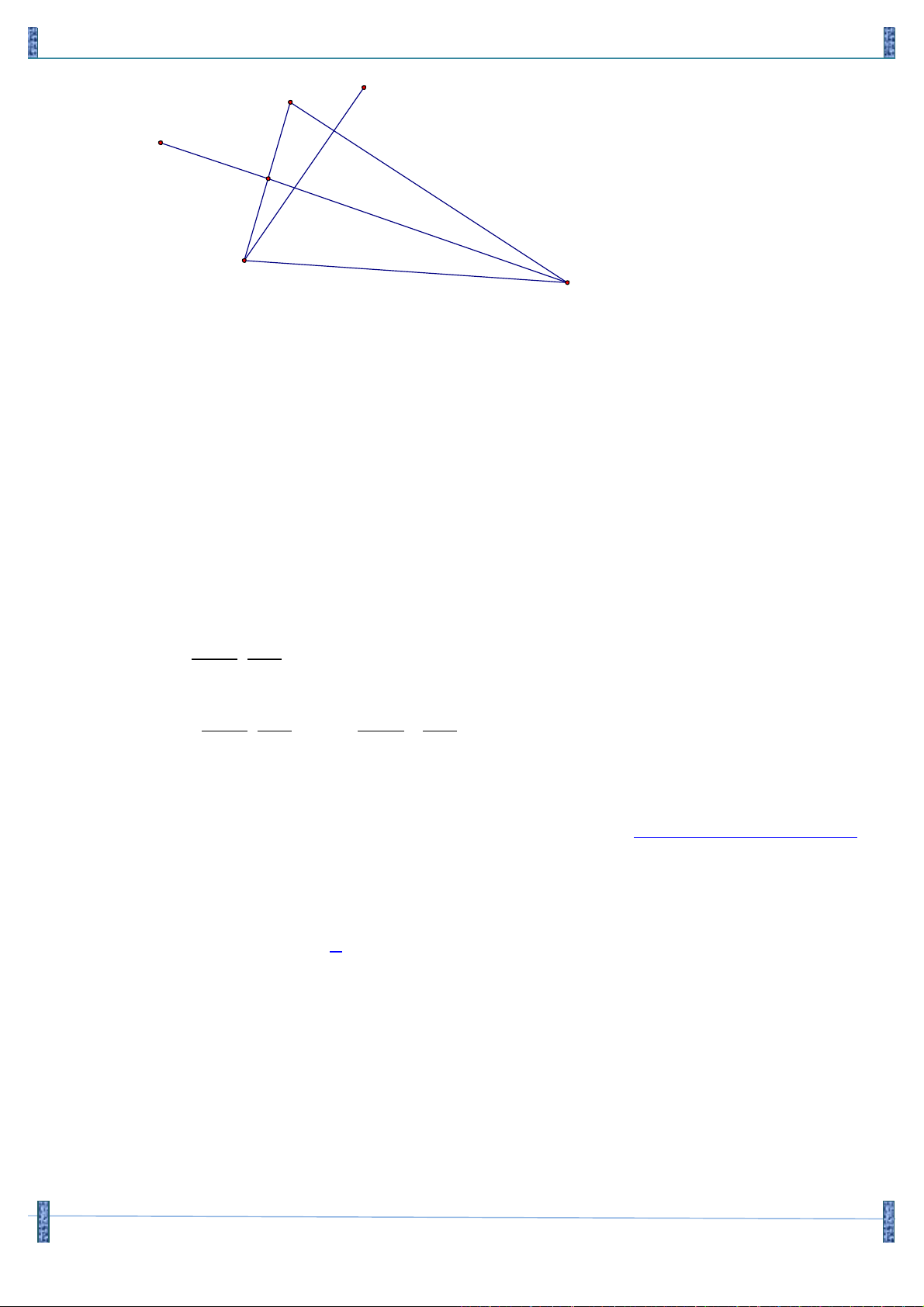
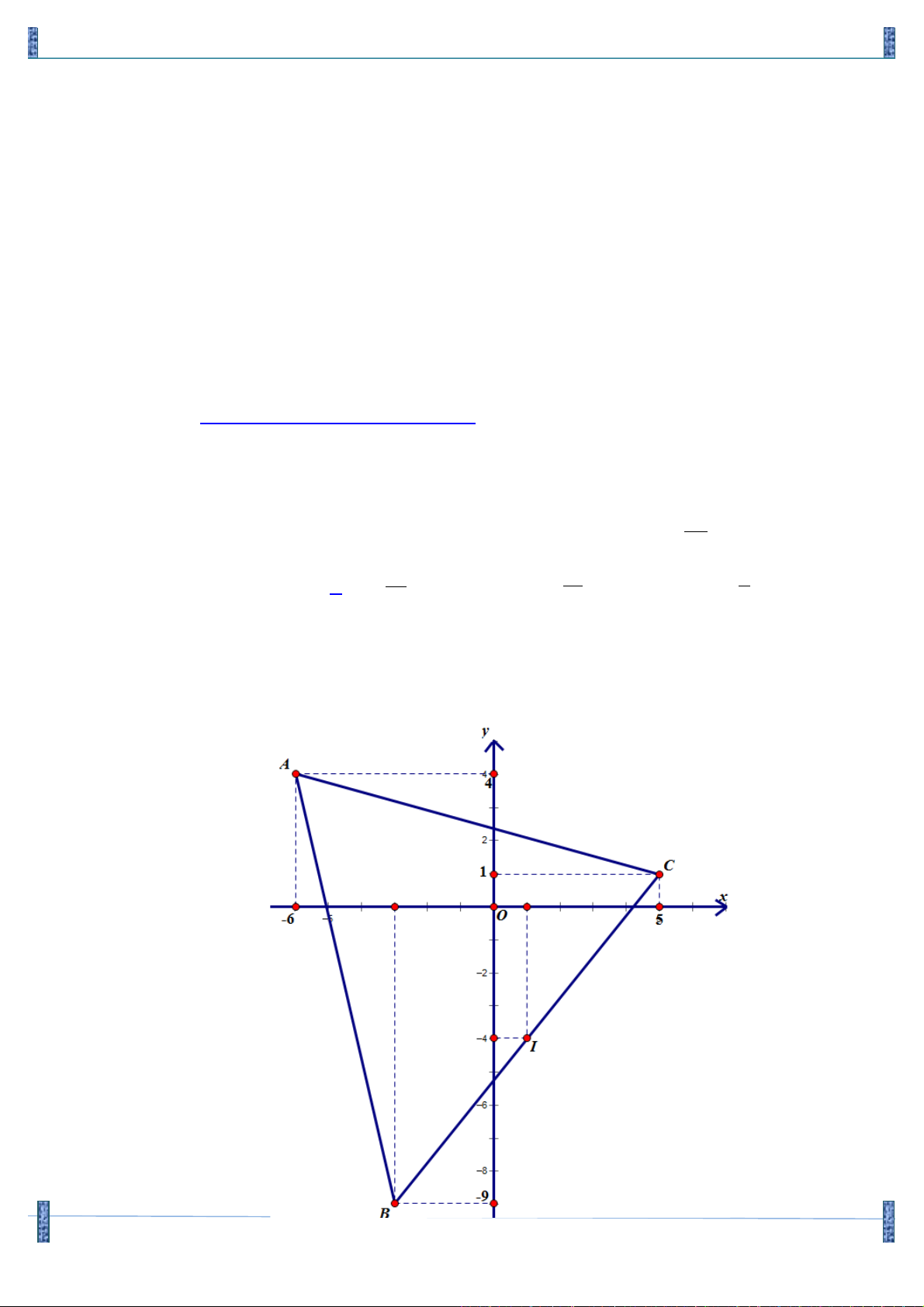
Câu 27. Trong mặt phẳng Oxy , cho bốn điểm A( 6; - 4); B( 3; - 9 - ); C (5; ) 1 và I (1; 4 - ). Giả sử đường
thẳng d : ax + by + c = 0 ( a,b la hai số nguyên dương và nguyên tố cùng nhau) đi qua điểm I . b c
và chia tam giác ABC thành hai phần có diện tích bằng nhau. Tính T = . a 35 15 2 A. T = 6 . B. T = . C. T = . D. T = . 2 2 3 Lời giải
Họ và tên người giải: Đàm Văn Thượng Tên FB:Thượng Đàm Chọn B
Hãy tham gia group để cùng học và cùng làm- Nhóm chỉ dành cho các Gv, Sv toán! 26
File làm chuyên đề HÌNH GIẢI TÍCH OXY QUA CÁC THI 3 CHUNG BGD Group FB: Strong Team TOÁN VD–VDC
Phương trình đường thẳng AB : 13x + 3y + 66 = 0, AB = 178 .
Phương trình đường thẳng AC : 3x +11y - 26 = 0, AC = 130 .
Phương trình đường thẳng BC : 10x - 8y - 42 = 0. 67
Ta thấy điểm I nằm trên cạnh BC và S = S = . IA D B IA D C 2
Do đó, đường thẳng d là đường thẳng AI :8x + 7 y + 20 = 0. . b c 35 Vậy T = = . a 2
Câu 28. (A2007 DB2) Trong mặt phẳng Oxy, cho tam giác ABC có trọng tâm G(-2; 0). Biết phương
trình các cạnh AB và AC lần lượt là: 4x + y +14 = 0 & 2x + 5y - 2 = 0. Tìm tọa độ các điểm A, B, C của tam giác ABC
A. A(-4; 2), B(0; -14), C(1; 0)
B. A(-4; 2), B(-3; -2), C(1; 0)
C. A(-4; 2), B(0; -14), C( 6; -2)
D. A(-3;-2), B(-4; 2), C(6; -2) Lời giải
Ta thấy A là giao điểm của AB và AC nên tọa độ A là nghiệm của hệ ì4x + y +14 = 0 ìx = 4 - í Û í Do đó điểm A(-4; 2)
î2x + 5y - 2 = 0 îy = 2 2 - 2c
Tọa độ hóa 2 điểm B và C. Giả sử B( b; -4b-14) là điểm nằm trên AB và C( ; c ) là điểm 5
nằm trên AC. Vì G là trọng tâm tam giác ABC nên ta có hệ phương trình ì 4 - + b + c = 6 - ï b ì + c = 2 - b ì = 3 - Þ B( 3 - ; 2 - ) í 2 - 2c Û í Û í 4 - b -14 + 2 + = 0 10 ï î b + c = 29 - îc = 1Þ C(1;0) î 5
Vậy A(-4; 2), B(-3; -2), C(1; 0).
Câu 29. (D2011-2)
Đề gốc. Trong mặt phẳng tọa độ Oxy , cho tam giác ABC có đỉnh B( 4 - )
;1 , trọng tâm G (1 ) ;1
và đường thẳng chứa phân giác trong của góc A có phương trình x - y -1 = 0. Tìm tọa độ các
đỉnh A và C . Trắc nghiệm hóa.
Trong mặt phẳng tọa độ Oxy , cho tam giác ABC có đỉnh B( 4 - )
;1 , trọng tâm G (1 ) ;1 và
đường thẳng chứa phân giác trong của góc A có phương trình x - y -1 = 0. Giả sử A(x ; y , 1 1 )
C (x ; y . Tính 2 2 2 2
T = x + x + y + y . 2 2 ) 1 2 1 2 A. 35. B. 34. C. 36. D. 37. Lời giải
Hãy tham gia group để cùng học và cùng làm- Nhóm chỉ dành cho các Gv, Sv toán! 27
File làm chuyên đề HÌNH GIẢI TÍCH OXY QUA CÁC THI 3 CHUNG BGD Group FB: Strong Team TOÁN VD–VDC !!!!" !!!!" æ 7 ö
Gọi M là trung điểm AC thì BM = 3GM nên M ;1 ç ÷. è 2 ø
Gọi B¢ là điểmm đối xứng của B qua phân giác trong d : x - y -1 = 0 của góc A .
Ta có BB¢ vuông góc với d và trung điểm I của BB¢ thuộc d nên tọa độ B¢ thỏa: 1
ì (x + 4) +1( y - ) 1 = 0 ï ìx + y + 3 = 0 í x - 4 y +1 Û í Û B¢(2; 5 - ). ï - -1 = 0 îx - y - 7 = 0 î 2 2
Đường thẳng AC đi qua B¢ và M có phương trình 4x - y -13 = 0. ìx - y -1 = 0
Tọa độ A thỏa í Û A(4; ) 3 . Suy ra C (3;- ) 1 . î4x - y -13 = 0 Vậy T = 35 .
Câu 30. (B-2005-DB2) Trong mặt phẳng với hệ tọa độ Oxy, cho tam giác ABC cân đỉnh A , trọng tâm 4 1
G( ; ). Phương trình đường thẳng BC
x - y - = và phương trình đường thẳng BG là 3 3 là 2 4 0
7x - 4y -8 = 0. Gọi đỉnh A(x ;y ), B(x ;y ) x y x y A A B B . Tính tổng 2 2 2 2 + + + A A B B A. 13. B. 1. C. 4 . D. 25 . Lời giải Chọn A A E G B H C ìx - 2y - 4 = 0 ìx = 0
Tọa độ B là nghiệm hệ phương trình í Û í Þ 0 B( ; 2 - ) î7x - 4y - 8 = 0 îy = 2 -
Gọi H là trung điểm của BC suy ra AH ^ BC . æ 4 1 ö
Phương trình AH có dạng 2x + y + c = 0 do G ; Î ç
÷ AH nên C = -3 Þ AG : 2x + y - 3 = 0 è 3 3 ø
H là giao diểm của BC, AG nên tọa độ H là nghiệm hệ phương trình ìx - 2y - 4 = 0 ìx = 2 í Û í Þ H(2; 1 - ) î2x + y - 3 = 0 îy = 1 - !!!" !!!"
Do G là trọng tâm nên AG = 2GH Þ (0 A ;3)
Hãy tham gia group để cùng học và cùng làm- Nhóm chỉ dành cho các Gv, Sv toán! 28
File làm chuyên đề HÌNH GIẢI TÍCH OXY QUA CÁC THI 3 CHUNG BGD Group FB: Strong Team TOÁN VD–VDC Vậy 2 2 2 2 x + y + x + y =13. A A B B
Câu 31. Trong mặt phẳng tọa độ Oxy cho tam giác ABC vuông tại A, đường cao AH với H (5;3), đường
phân giác trong góc AD: x - 7y + 6 = 0. Biết K ( 10
- ;3) nằm trên trung tuyến AM . Tìm tọa độ
các đỉnh của tam giác ABC. A K K' D B H C M
Ta có ACB = BAH ( do cùng phụ với góc B), mà AM=MB=MC nên MAC = ACM , suy ra
BAH = MAC . Suy ra AD cũng là phân giác góc HDM .
Gọi K’ là điểm đối xứng với K qua AD thì K thuộc AH. KK’: 7x + y + 67 = 0 KK 'Ç AD = I æ 19 - 1 - ö Þ I ; ç ÷ Þ K '( 9 - ; 4 - ). è 2 2 ø
AH: x - 2y +1 = 0, AH Ç AD = A Þ A(1; ) 1 æ13 Þ ö
BC : 2x + y -13 = 0 . AM đi qua A và K nên AM : 2x +11y -13 = 0. Vậy M ;0 ç ÷. è 2 ø éb = 9
Vì B thuộc BC nên B( ;1 b 3- 2b). Do 2
MA = MB Þ 5b - 65b +180 = 0 Þ êëb = 4 Vậy B(9; 5
- ),C(4;5) hoặc B(4;5),C(9; 5 - )
Email: nguyenminhduc.hl@gmail.com
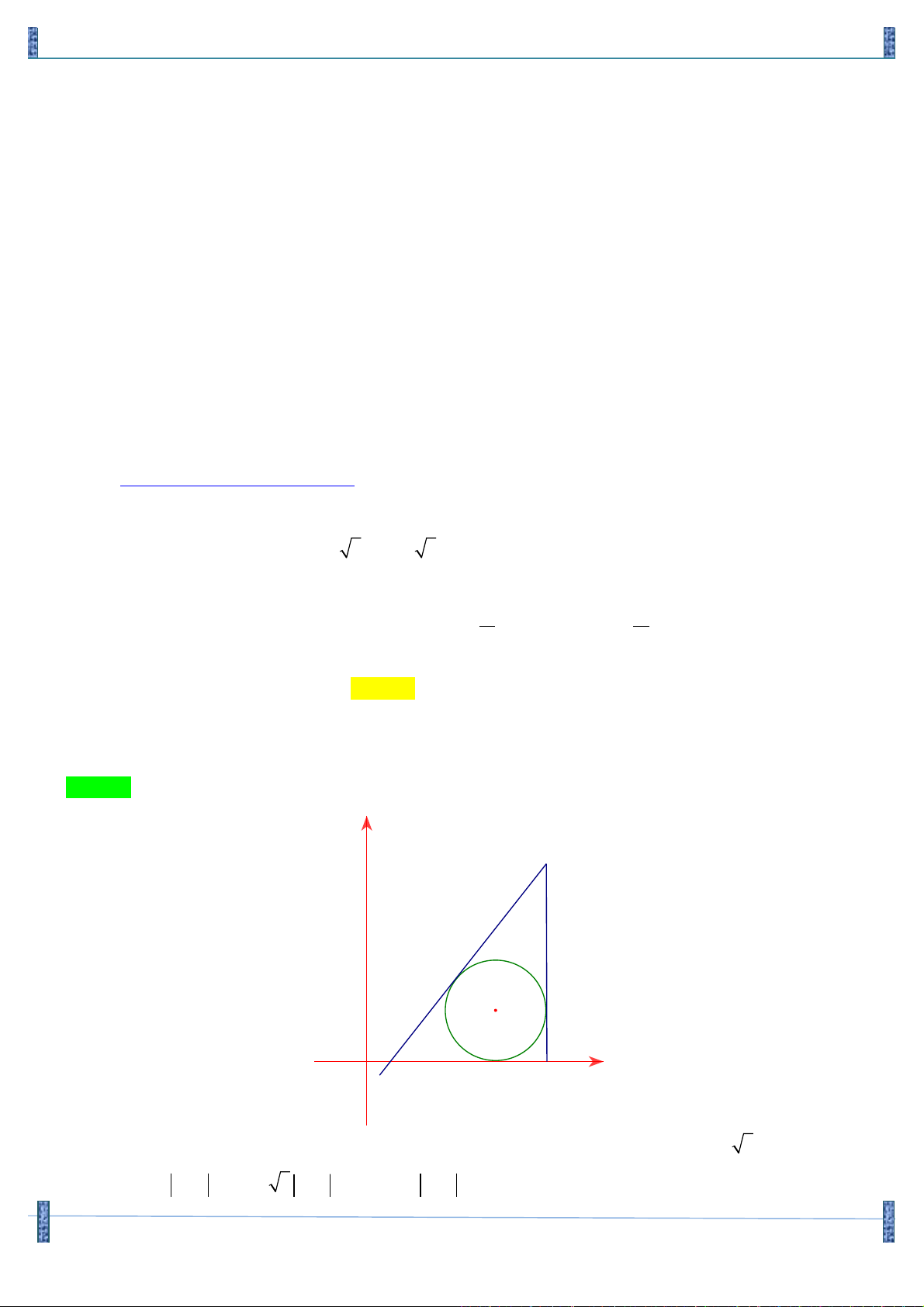
Câu 32. (DB1 D 2007) Trong mặt phẳng tọa độ Oxy , cho điểm (
A 2;1). Lấy điểm B thuộc trục Ox có
hoành độ không âm và điểm C thuộc trục Oy có tung độ không âm sao cho tam giác ABC
vuông tại A . Biết rằng khi điểm B có hoành độ là b và điểm C có tung độ là c thì tam giác
ABC có diện tích lớn nhất. Tính S = b + c . 5 A. S = 5. B. S = 4 . C. S = . D. S = 2 . 2 Lời giải
Họ và tên tác giả: Nguyễn Minh Đức Tên FB: Duc Minh
Hãy tham gia group để cùng học và cùng làm- Nhóm chỉ dành cho các Gv, Sv toán! 29
File làm chuyên đề HÌNH GIẢI TÍCH OXY QUA CÁC THI 3 CHUNG BGD Group FB: Strong Team TOÁN VD–VDC Giả sử B( ;
x 0), C(0; y) với x ³ 0, y ³ 0. !!!" !!!"
Ta có AB = (x - 2; 1 - ), AC = ( 2 - ; y -1) !!!" !!!"
Vì tam giác ABC vuông tại A nên . AB AC = 0 Û 2(
- x - 2) - (y -1) = 0 Û y = 2 - x + 5 5
Do x ³ 0, y ³ 0 nên suy ra 0 £ x £ . 2
Diện tích tam giác ABC là 1 1 S = A . B AC = x - + + y - (*) ABC D ( 2)2 1 4 ( )2 1 2 2 Thay y = 2
- x + 5 vào (*) ta được: 1 S = x - + + x - = x - + = x - x + ABC D ( 2)2 1 4 4( 2)2 ( 2)2 2 1 4 5 2 5 Xét hàm số 2
f (x) = x - 4x + 5 với 0 £ x £ 2 Bảng biến thiên x 5 0 2 2 f (x) 5 5 4 1
Từ bảng biến thiên suy ra: Tam giác ABC có diện tích lớn nhất là 5 khi x = 0
Do đó b = 0, c = 5 Þ S = 5.
Email: lamdienan@gmail.com
Câu 33. (B2011-1) Trong mặt phẳng tọa độ oxy , cho hai đường thẳng D : x- y - 4 = 0 và
d : 2x - y - 2 = 0 . Gọi N ( ;
m n),m > 0 là điểm thuộc đường thẳng d sao cho đường thẳng
ON cắt đường thẳng D tại điểm M thỏa mãn OM .ON = 8. Tính S = m + n? 8 6 4 A. S = . B. S = 2. - C. S = . D. S = . 5 5 5 Lời giải
Họ và tên tác giả: Lâm Điền An Tên FB: Lâm Điền An Chọn A
Hãy tham gia group để cùng học và cùng làm- Nhóm chỉ dành cho các Gv, Sv toán! 30
File làm chuyên đề HÌNH GIẢI TÍCH OXY QUA CÁC THI 3 CHUNG BGD Group FB: Strong Team TOÁN VD–VDC N d
Œ , M ŒD có tọa độ lần lượt là N ( ;2 a a- ) 2 , M ( ; b b- ) 4 .
Ba điểm O, N, M thẳng hàng khi và chỉ khi
( - )=( a- )b € b( - a) 4a a b 4 2 2 2 = 4a € b = . 2- a ⎛ 4a 8a−8⎞ ⇒ B⎜⎜ ; ⎟⎟
⎝⎜2− a 2− a ⎠⎟⎟.
ON = a +( a- )2 2 2 2 2 2 = 5a - 8a +4 ; ⎛ 2 2 4a ⎞ ⎛8a−8⎞
80a2 −128a + 64 16 5 ( a2−8a+4) OM 2 = ⎜⎜ ⎟⎟ +⎜⎜ ⎟⎟ = = . ⎝⎜2− a⎠⎟⎟ ⎝⎜ 2− a ⎠⎟⎟ a2 −4a + 4 a2 −4a + 4 ⎡ ⎤ ⎢ ( )⎥ OM.ON = 8 ⇒ 5
( a2−8a+4) 16 5a2−8a+4 ⎢ ⎥ = 64 ⇔ 5
( a2−8a+4)2 =(2a−4)2 ⎢ ⎥ ⎢ (a−2)2 ⎣ ⎦⎥ ⇔ 5
( a2−8a+4−2a+4) 5(a2−8a+4+2a−4)=0⇔ 5(a2−10a+8) 5(a2−6a)=0 ⎡a = 0 ⎢ 6 ⎛6 2⎞ 8
⇔ 5a2 −6a = 0 ⇔ ⎢ ⎟ 6 m>0 ⎯ →
⎯ a = ⇒ N ⎜⎜ ; ⎟ . ⎢a = 5
⎝⎜5 5⎠⎟⎟⇒ S = m+ n = 5 ⎣⎢ 5
Email: nguyentuanblog1010@gmail.com
Câu 34. (Đề A2002) Trong mặt phẳng với hệ tọa độ Oxy , xét tam giác ABC vuông tại A , phương
trình đường thẳng BC là 3x - y - 3 = 0, các đỉnh ,
A B thuộc trục hoành và bán kính đường
tròn nội tiếp tam giác bằng 2. Gọi G(x ; y với x > 0 là trọng tâm của tam giác ABC . Biết 0 0 ) 0 m m
rằng giá trị của biểu thức T = 2y - x bằng với , m n +
Î! và là phân số tối giản. Khi đó 0 0 n n
kết luận nào dưới dây là đúng?
A. 3m - 4n = 5
B. m > n
C. m < n +1 D. . m n < 12 . Lời giải
Phạm Chí Tuân Fb: Tuân Chí Phạm Chọn B
Hãy tham gia group để cùng học và cùng làm- Nhóm chỉ dành cho các Gv, Sv toán! 31
File làm chuyên đề HÌNH GIẢI TÍCH OXY QUA CÁC THI 3 CHUNG BGD Group FB: Strong Team TOÁN VD–VDC y C B x A O
Ta có B = BC ÇOx Þ B(1;0), AÎOx Þ A( ;0
a ). Lại có AC ^ AB và
C Î BC Þ C ( ; a 3 (a - ) 1 ).
Lại có: AB = a -1 , AC = 3 a -1 và BC = 2 a -1 . ì x + x + x A B C x = ï G ï 3 æ 2a +1 3(a - ) 1 ö
Vì G là trọng tâm của tam giác ABC nên ta có í ,G ç ; ÷ y + y + y ç 3 3 ÷ ï A B C y = è ø G ïî 3 2a +1 1 Do x > 0 Û > 0 Û a > - . 0 3 2 2S 1 Theo bài ta có ABC r = Û 2. .A .
B AC = 2 AB + BC + CA ABC ( )
AB + BC + CA 2 1 a>- 2 Û (a - )2 3 1 = 2 3 ( 3 + )
1 a -1 Û a -1 = 2( 3 + ) 1 Þ a = 2 3 + 3 ì 7 + 4 3 ïx = 0 æ 7 + 4 3 6 + 2 3 ö ï 5 Vậy 3 G ç ; ÷ Þ í ç
Þ T = 2y - x = Þ m = 5 > n = 3. 3 3 ÷ 0 0 è ø ï 6 + 2 3 3 y = 0 ïî 3
Email: damanhsphn@gmail.com
Câu 35. Trong mặt phẳng với hệ tọa độ Oxy , cho tam giác ABC với đỉnh A(2; )
1 , gọi m là đường
cao qua đỉnh B có phương trình là x - 3y - 7 - 0 và n là đường trung tuyến qua đỉnh C có
phương trình là x + y +1 = 0. Giả sử B(x ; y ,C x ; y , tính P = x + y + x + y ? 1 1 ) ( 2 2 ) 1 1 2 2 A. P = 6 - . B. P = 4 - . C. P = 3 - . D. P = 5 - . Lời giải
Họ và tên tác giả: Đàm Thị Lan Anh Tên FB: Đàm Anh Chọn A
Hãy tham gia group để cùng học và cùng làm- Nhóm chỉ dành cho các Gv, Sv toán! 32
File làm chuyên đề HÌNH GIẢI TÍCH OXY QUA CÁC THI 3 CHUNG BGD Group FB: Strong Team TOÁN VD–VDC m A n D B C
+ Lập phương trình đường thẳng AC .
Do đường thẳng AC vuông góc với m nên phương trình đường thẳng AC có dạng:
3x + y + c = 0. Ta có A(2; )
1 Î AC Þ 3.2 +1+ c = 0 Û c = 7
- Þ AC : 3x + y - 7 = 0
Lại có C = AC Ç n nên tọa độ điểm C thỏa mãn hệ phương trình: 3 ì x + y - 7 = 0 ìx = 4 í Û í Þ C (4; 5 - ) îx + y +1 = 0 îy = 5 -
+ Có B Î m nên tọa độ điểm B có dạng B(3b + 7;b). Gọi D là trung điểm của đoạn AB , suy æ 3b + 9 b +1ö ra D ; ç ÷. è 2 2 ø æ 3b + 9 b +1ö 3b + 9 b +1 Mà D ; Î n Þ + +1 = 0 Û b = 3 - Þ B( 2 - ; 3 - ç ÷ ) è 2 2 ø 2 2
Vậy P = 4 - 5 - 2 - 3 = 6
- . Chọn đáp án A.
Email: Thuylieu.sptoan@gmail.com
Câu 36. (ĐH 2007D–db2) Trong mặt phẳng với hệ tọa độ Oxy, cho các điểm A(0; 1), B(2; –1) và các đường thẳng d
m - x + m - y + - m = 1 : ( 1) ( 2) 2 0, d
- m x + m - y + m 2 :(2 ) ( 1) 3 -5 = 0. Gọi P là
giao điểm của d1 và d2. Biết rằng có hai giá trị m1 và m2 sao cho PA + PB lớn nhất. Tính 2 m + 2 1 2 m A. 10 B. 3 C. 4 D. 5 Lời giải Chọn D
Dễ thấy A Î d ;BÎ 1 2 d và d ^ 1 2
d nên DAPB vuông tại P Þ P nằm trên đường tròn đường kính AB. Ta có PA + 2 P £ 2 PA + 2 PB = 2 AB = 2 ( B) 2( ) 2 2(2 2) = 16.
Þ PA + P B £ 4 .
Dấu bằng xẩy ra khi và chỉ khi PA = P B Û P là trung điểm của cung .
Hãy tham gia group để cùng học và cùng làm- Nhóm chỉ dành cho các Gv, Sv toán! 33
File làm chuyên đề HÌNH GIẢI TÍCH OXY QUA CÁC THI 3 CHUNG BGD Group FB: Strong Team TOÁN VD–VDC
Vậy GTLN của PA + PB bằng 4 khi P là trung điểm của cung .
Do đó P nằm trên đường thẳng (d) đi qua trung điểm I(1; 0) của đoạn AB và vuông góc với AB AB và IP = = 2 . 2
Phương trình đường thẳng (d) là y = x - 1 .Vì P Î d nên tọa độ P(p; p-1) do đó é 2 p = 2
IP = 2 Û 2(p -1) = 2 Û ê . ë p = 0
Vậy P(2; 1) hay P(0; -1). Do đó m 2 2
1= 1 và m2 = 2. Tức m + m = 1 2 5.
Câu 37. Trong mặt phẳng với hệ tọa độ Oxy, cho tam giác ABC có trực tâm H , phương trình đường
thẳng AH là 3x - y + 3 = 0 , trung điểm của cạnh BC là M (3;0) . Gọi E và F lần lượt là
chân đường cao hạ từ B và C đến AC và AB , phương trình đường thẳng EF là
x - 3y + 7 = 0. Biết A( ;
a b)và A có hoành độ dương, tính tổng a + b . A. 7 + 2 2 B. 2 - + 2 C. 7 + 4 2 D. 3+ 2 Lời giải Chọn C A H I E I E F J H F A J B D M C B D M C
Gọi I là trung điểm của AH . Tứ giác AEHF nội tiếp và bốn điểm B, C, E, F cùng thuộc
một đường tròn nên IM ^ EF .
- Ta chứng minh: IEF = ABE (cùng phụ góc A hoặc cùng phụ góc EHF ) Ta có
BFHD nÈi ti’ p Þ ABE = ü
FDH ïýÞ FDH = HDE Þ DH là phân giác trong góc FDE.
DHEC nÈi ti’ p Þ FCE = HDEï þ
Tương tự Þ H là tâm đường tròn nội tiếp DFDE .
Hãy tham gia group để cùng học và cùng làm- Nhóm chỉ dành cho các Gv, Sv toán! 34
File làm chuyên đề HÌNH GIẢI TÍCH OXY QUA CÁC THI 3 CHUNG BGD Group FB: Strong Team TOÁN VD–VDC
Lại có : DMFC cân tại MFC c©n tπi M BMF 2.BCF
2.BAD (cÔng phÙ ABC)ü D Þ = = ï ï
Mµ AFHE nÈi ti’ p Þ FEH = FAH ý Þ DEF = BMF ï mµ DEH = BCF ï þ
Suy ra M thuộc đường tròn ngoại tiếp DEDF . Mặt khác :
DAHE vu´ ng, c„ EI lµ trung tuy’n Þ HIE = ü 2.HAEïý
DAHF vu´ ng, c„ FI lµ trung tuy’n Þ HIF = 2.HAFïþ
+ Þ FIE = 2(HAE + HAF) ! = 2.A ! Û °
180 - 2.IEF = 2.A ! Þ IEF = ° 90 - A = ABE
ABE = FDH = 1 FDE = 1 FME = IME - Và 2 2
Þ MEI = 90° Þ MFI = MEI = 90°
Do đó tứ giác MEIF nội tiếp đường tròn đường kính IM , tâm là trung điểm J của IM .
Đường thẳng IM qua M , vuông góc với EF nên có phương trình 3x + y - 9 = 0.
Lại có I = AH Ç IM nên I (1;6).
Đường tròn đường kính IM có tâm J (2; )
3 và bán kính r = JM = 10 nên có pt: (x- )2 +(y - )2 2 3 =10 ìx - 3y + 7 = 0 ï ìx = 5 ìx = 1 -
Tọa độ điểm E thỏa mãn í Û í Ú ( í ï x - 2 î
)2 +( y -3)2 =10 îy = 4 îy = 2
Suy ra E (5;4) hoặc E( 1 - ;2). Gọi A( ;3 a a + ) 3 Î AH
Ta có IA = IE Û (a - )2 +( a - )2 1 3 3 = 20 Û a =1± 2
Theo ycbt suy ra A(1+ 2;6 + 3 2)
Email: toan.anlac2012@gmail.com
Câu 38. Trong mặt phẳng toạ độ Oxy , cho hình vuông ABCD có đỉnh D( 1 - ; 1
- ). Gọi N là trung điểm
cạnh AB và M là điểm trên cạnh AD sao cho 2.S =11.S
. Biết điểm B có toạ độ NBCM CMD
nguyên, điểm B nằm trên đường thẳng d : 3x - y + 2 = 0 và (CM ) : 2x - 9y + 3 = 0.
Khẳng định nào sau đây là sai? 65 A. MN = . B. BD = 2 10 .
C. d(B,Ox) = 4.
D. d(B,Oy) =1. 2 Lời giải
Họ và tên tác giả: Bồ Văn Hậu Tên FB: Bồ Văn Hậu
Hãy tham gia group để cùng học và cùng làm- Nhóm chỉ dành cho các Gv, Sv toán! 35
File làm chuyên đề HÌNH GIẢI TÍCH OXY QUA CÁC THI 3 CHUNG BGD Group FB: Strong Team TOÁN VD–VDC · Đặt: AD = ;
a MD = x , với a > 0,0 < x < a 1 a 1 · Khi đó: S = 1 a ; x S = (a - x) ; 2 S = a CMD 2 MBC 2 2 MBC 2 1 a 1 1 a Nên 2 2.S =11.S
Û 2( (a - x) + a ) =11. ax Û x = NBCM CMD 2 2 2 2 4 10 1 1 85 5 · Ta có: d( , D (CM )) = suy ra + = Þ x = 85 2 2 x 16x 100 2
( Đến đây ta kiểm tra được khẳng định A, B đúng rồi )
· Ta có: B Î d Þ B( ;
b 3b + 2),b Î! é b =1
· Mà d (B, (CM )) 4.d(D, (CM )) 25b 15 40 ê = Û - - = Û 11 êb = - ë 5 Hay B(1;5)
Email: vanthoindh@gmail.com
Câu 39. Trong mặt phẳng với hệ tọa độ Oxy, cho hình chữ nhật ABCD có điểm C thuộc đường thẳng
d:2x+y+5=0 và A(-4;8). Gọi M là điểm đối xứng của B qua C, N là hình chiếu vuông góc của
B trên đường thẳng MD. Tìm tọa độ các điểm B và C, biết N(5;-4) Lời giải
Họ và tên tác giả: Trần Thị Phương Uyên Tên FB: Uyentran
Do C thuộc d nên C(t;-2t-5). Gọi I là tâm của hình chữ nhật ABCD, suy ra I là trung điểm của AC.
Hãy tham gia group để cùng học và cùng làm- Nhóm chỉ dành cho các Gv, Sv toán! 36
File làm chuyên đề HÌNH GIẢI TÍCH OXY QUA CÁC THI 3 CHUNG BGD Group FB: Strong Team TOÁN VD–VDC t - 4 2 - t + 3 Do đó I( ( ; ) . 2 2
Tam giác BDN vuông tại N nên IN = IB. Suy ra IN = IA. Do đó ta có phương trình 2 2 2 2 æ t - 4ö æ 2 - t + 3ö æ t - 4ö æ 2 - t + 3ö 5 - + 4 - - = -4 - + 8 - ç ÷ ç ÷ ç ÷ ç ÷ Û è t=1.Suy ra C(1;-7) 2 ø è 2 ø è 2 ø è 2 ø
Do M đối xứng với B qua C nên CM=CB. Mà CB=AD và CM//AD nên tứ giác ACMD là hình bình hành.Suy ra AC//DM
Theo giả thiết BN ^ DM, suy ra BN ^ AC và CB=CN. Vậy B là điểm đối xứng với N qua AC
Đường thẳng AC có phương trình: 3x+y+4=0
Đường thẳng BN qua N và vuông góc với AC nên có phương trình x-3y-17=0 Do đó B(3a+17;a) 3a +17 + 5 a - 4
Trung điểm của BN thuộc AC nên 3( )+
+ 4 = 0 Û a=-7. Vậy B(-4;-7) 2 2
Email: toan.anlac2012@gmail.com
Câu 40. Trong mặt phẳng với hệ toạ độ Oxy , cho hình thoi ABCD có tâm I(2;1) và AC = 2.BD . Điểm 1
M (0; ) thuộc đường thẳng AB , điểm N (0;7) thuộc đường thẳng CD và điểm B có hoành 3
độ dương. Khẳng định nào sau đây là sai? 3 A. BN = 65.
B. 2.AB + OB = 6 2 . C. S = . D. S = 3. OIB 2 BIN Lời giải
Họ và tên tác giả: Bồ Văn Hậu Tên FB: Bồ Văn Hậu Chọn D
Gọi N ' là điểm đối xứng của N qua I Þ N '(4; 5
- ) và N 'Î(AB)
Phương trình đường thẳng AB : 4x + 3y -1 = 0.
Hãy tham gia group để cùng học và cùng làm- Nhóm chỉ dành cho các Gv, Sv toán! 37
File làm chuyên đề HÌNH GIẢI TÍCH OXY QUA CÁC THI 3 CHUNG BGD Group FB: Strong Team TOÁN VD–VDC 4.2 + 3.1-1
Gọi H chân đường cao kẻ từ I của tam giác IAB Þ IH = d(I,(AB)) = = 2 2 2 4 + 3 . Đặt IB = ,(
x x > 0). Vì AC = 2.BD Þ IA = 2.IB = 2x 1 1 1 1 1 1 Ta có: + = Û + = Þ x = 5 2 2 2 2 2 IA IB IH x 4x 4 1- 4b
Khi đó: B Î(AB) Þ B( ; b ), với b > 0 3 2 é b =1 æ1- 4b ö Mà 2 2 2 IB 5 (b 2) 1 5 25b 20b 5 0 ê = Û - + - = Û - - = Û ç ÷ 1 è 3 ø êb = - ë 5 Suy ra B(1; -1)
Email: Tanbaobg@gmail.com
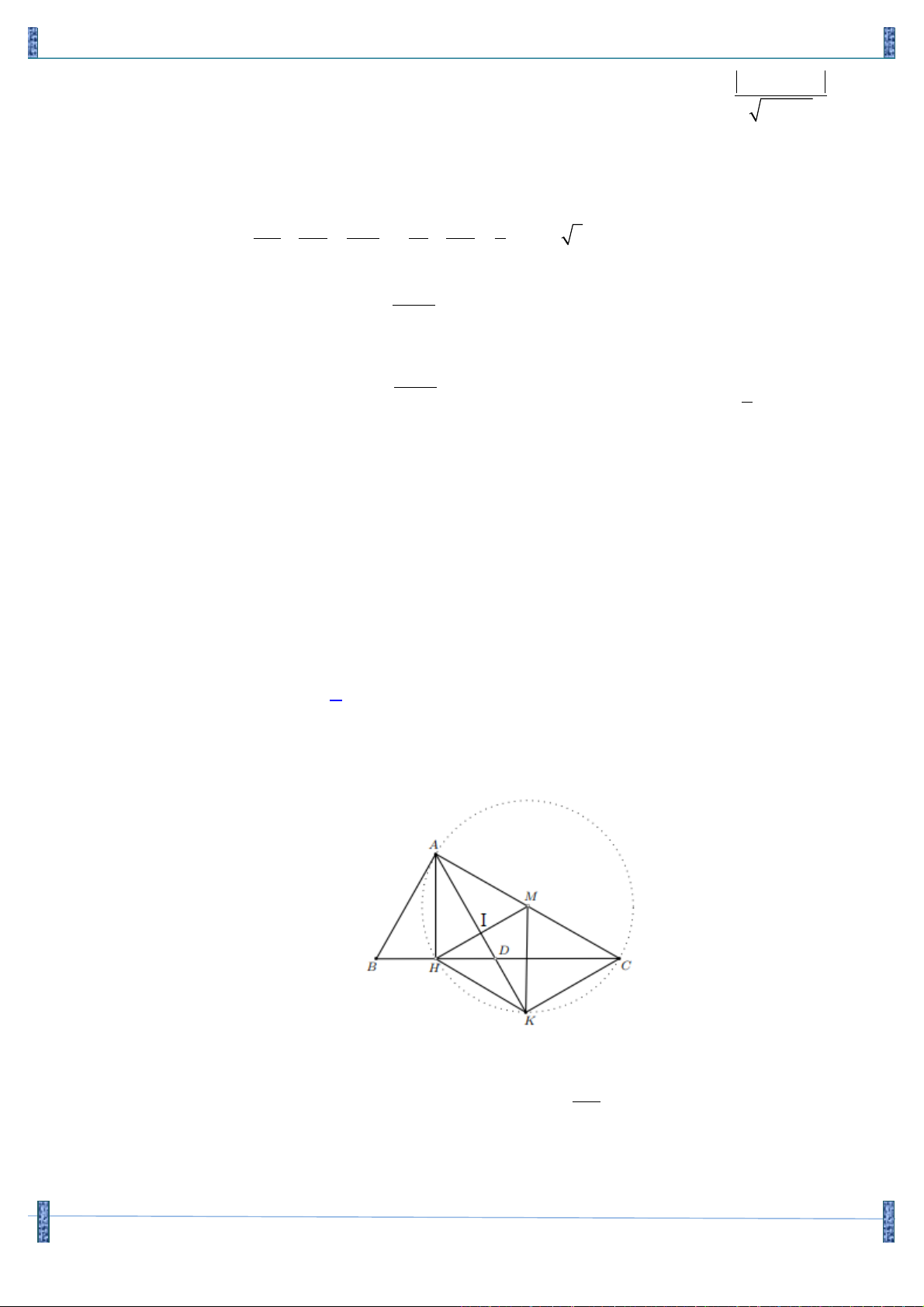
Câu 41. (Đề Thi Quốc Gia-2015) Trong mặt phẳng với hệ tọa độ Oxy, cho tam giác ABC vuông tại
A. Gọi H là hình chiếu vuông góc của A trên cạnh BC; D là điểm đối xứng của B qua H; K
là hình chiếu vuông góc của C trên đường thẳng AD. Giả sử H ( 5; - 5 - ), K (9; 3 - ) và trung
điểm của cạnh AC thuộc đường thẳng x - y +10 = 0.Giả sử điểm A có tọa độ là A( ; a b). Tính 2 a + b ? A. 2 a + b = 10 - . B. 2 a + b = 10. C. 2 a + b = 2 - . D. 2 a + b = 354. Lời giải
Tên FB: Đỗ Tấn Bảo Chọn B AC
Gọi M là trung điểm của AC. Ta có MH = MK =
, nên M thuộc đường trung trực 2 của HK.
Đường trung trực của HK có phương trình 7x + y -10 = 0 .
Hãy tham gia group để cùng học và cùng làm- Nhóm chỉ dành cho các Gv, Sv toán! 38
File làm chuyên đề HÌNH GIẢI TÍCH OXY QUA CÁC THI 3 CHUNG BGD Group FB: Strong Team TOÁN VD–VDC ì7x + y -10 = 0
Suy ra tọa độ của điểm M thỏa mãn hệ phương trình í . Suy ra M (0;10). îx - y +10 = 0
Ta có HKA = HCA = HAB = HAD nên tam giác HAK cân tại H, suy ra HA = HK .
Mà MA = HK nên A và K đối xứng qua MH .
Ta lại có đường thẳng MH có phương trình là 3x - y +10 = 0.
Gọi hình chiếu lên đường thẳng HM của điểm K là I (t;3t +10) với t Î ! . ìa = 15 -
Từ IK ^ HM suy ra I ( 3 - ) ;1 . Do đó A( 15 - ;5). Suy ra 2 í Þ a + b =10. b î = 5
Phân tích các phương án nhiễu.
Phương án A học sinh tính a + b = 10 - .
Phương án C học sinh “rút gọn” thành A( 1 - ;3).
Phương án D học sinh giải tìm điểm M (0; 1 - 0).
Email:tuandel2009@gmail.com
Facebook:Trần Minh Tuấn
Câu 42. Trong mặt phẳng với hệ tọa độ Oxy,cho tam giác ABC có Điểm M(2;0) là trung điểm cạnh
AB.Đường trung tuyến và đường cao qua đỉnh A lần lượt có phương trình là 7x-2y-3=0 và 6x-
y-4=0.Viết phương trình đường thẳng AC. A.-3x+4y+5=0 B.3x-4y+5=0 C.4x-3y+5=0 D.-4x+3y+5=0 Lời giải AN:7x-2y-3=0 AH:6x-y-4=0
Hãy tham gia group để cùng học và cùng làm- Nhóm chỉ dành cho các Gv, Sv toán! 39
File làm chuyên đề HÌNH GIẢI TÍCH OXY QUA CÁC THI 3 CHUNG BGD Group FB: Strong Team TOÁN VD–VDC
Tọa độ A là nghiệm hệ phương trình
ìAN : 7x - 2y -3 = 0 í Þ A(1;2)
îAH : 6x - y - 4 = 0
ìx + x = 2x 1 ì + x = 4 Do M là trung điểm BC A B M í B Û í Û B(3; 2 - )
y + y = 2y î 2 + y = 0 A B M î B !
Lập phương trình BC vuông góc AH có nBC (1;6) ! ìïnBC(1;6) Phương trình BC í
Þ BC :1(x - 3) + 6(y + 2) = 0 Û x + 6y + 9 = 0 ïîB(3; 2 - )
ìBC : x + 6y + 9 = 0 Tọa độ N í àN(0;-3/2)
îAN : 7x - 2y -3 = 0 Phương trình AC: !!!" !!!!" 3 - u = MN = ( 2 - ; ) AC 2 ì!!!" 3 - u ï = ( 2 - ; ) x - y - AC 1 2 Phương trình AC: í 2 Þ =
Û 3x - 4y + 5 = 0 2 - 3 - ïî ( A 1; 2) 2
Email:tuandel2009@gmail.com
Facebook:Trần Minh Tuấn
Câu 43. Trong mặt phẳng với hệ tọa độ Oxy,cho tam giác ABC có Điểm M(2;0) là trung điểm cạnh
AB.Đường trung tuyến và đường cao qua đỉnh A lần lượt có phương trình là 7x-2y-3=0 và 6x-
y-4=0.Viết phương trình đường thẳng AC.
Hãy tham gia group để cùng học và cùng làm- Nhóm chỉ dành cho các Gv, Sv toán! 40
File làm chuyên đề HÌNH GIẢI TÍCH OXY QUA CÁC THI 3 CHUNG BGD Group FB: Strong Team TOÁN VD–VDC A. -3x+4y+5=0 B. 3x-4y+5=0 C. 4x-3y+5=0 D. -4x+3y+5=0 Lời giải AN:7x-2y-3=0 AH:6x-y-4=0
Tọa độ A là nghiệm hệ phương trình
ìAN : 7x - 2y -3 = 0 í Þ A(1;2)
îAH : 6x - y - 4 = 0
ìx + x = 2x 1 ì + x = 4 Do M là trung điểm BC A B M í B Û í Û B(3; 2 - )
y + y = 2y î 2 + y = 0 A B M î B !
Lập phương trình BC vuông góc AH có nBC (1;6) ! ìïnBC(1;6) Phương trình BC í
Þ BC :1(x - 3) + 6(y + 2) = 0 Û x + 6y + 9 = 0 ïîB(3; 2 - )
ìBC : x + 6y + 9 = 0 Tọa độ N í àN(0;-3/2)
îAN : 7x - 2y -3 = 0 Phương trình AC: !!!" !!!!" 3 - u = MN = ( 2 - ; ) AC 2 ì!!!" 3 - u ï = ( 2 - ; ) x - y - AC 1 2 Phương trình AC: í 2 Þ =
Û 3x - 4y + 5 = 0 2 - 3 - ïî ( A 1; 2) 2
Soạn trắc nghiệm: Vũ Huỳnh Đức, Email: vutoanpvd@gmail.com
Hãy tham gia group để cùng học và cùng làm- Nhóm chỉ dành cho các Gv, Sv toán! 41
File làm chuyên đề HÌNH GIẢI TÍCH OXY QUA CÁC THI 3 CHUNG BGD Group FB: Strong Team TOÁN VD–VDC
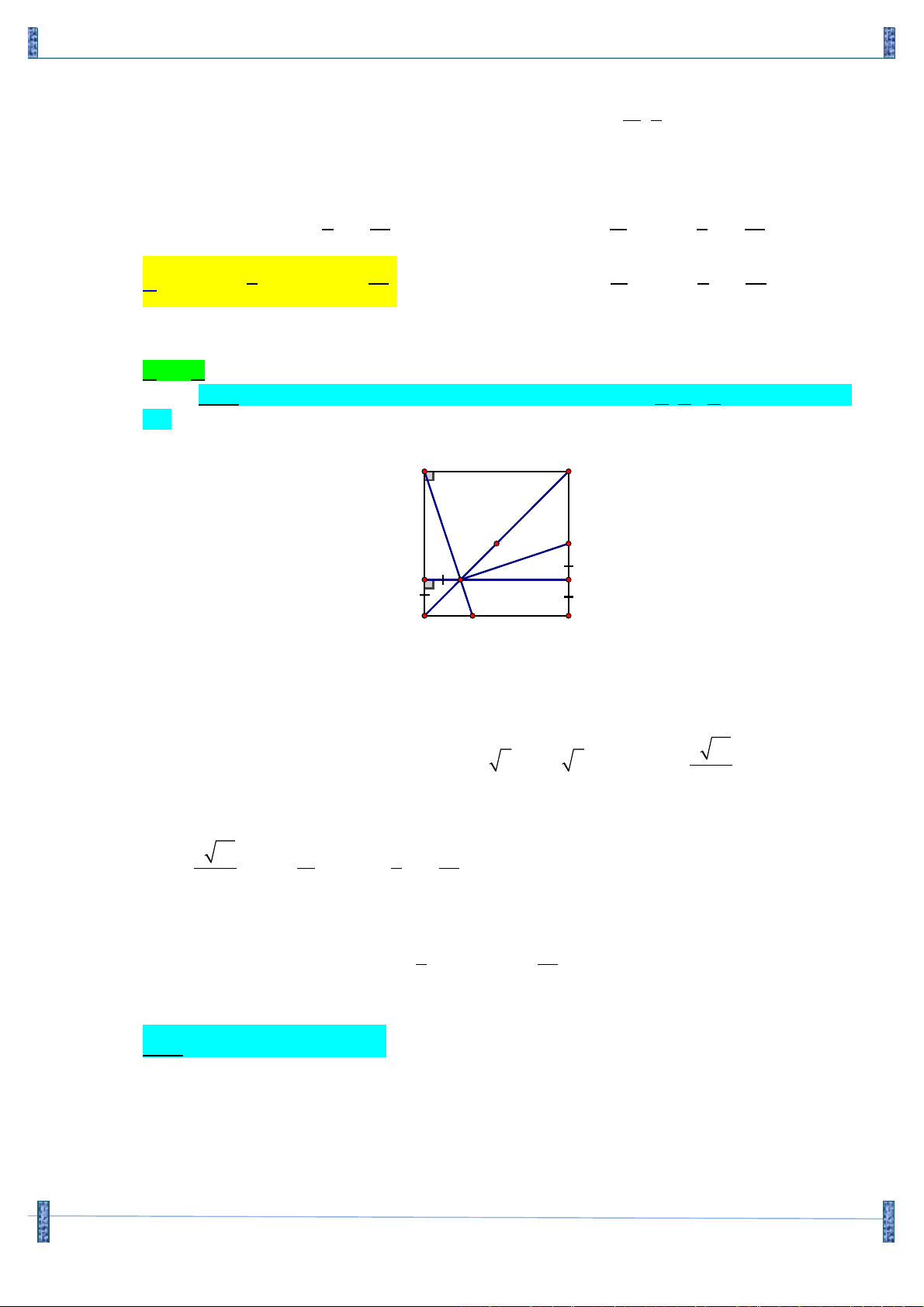
Câu 44. Trong mặt phẳng với hệ tọa độ Oxy, cho hình vuông ABCD . Gọi M là trung điểm của cạnh
BC, N là điểm trên cạnh CD sao cho CN = 2ND. Giả sử æ11 1 ö
M ç ; ÷và đường thẳng AN có è 2 2 ø
phương trình 2x - y - 3 = 0. Hỏi điểm A nằm trên đường tròn nào trong các đường tròn sau đây? 2 2
A. C ) : (x - 4) + ( 5 y - )2 2 45 ( 11 1 65 1 = . B. ( 2 C ) : (x - + y - = 2 ) ( 2) . 4 16 4 2 2 2 C. C ) : ( 9
x - ) +( y - )2 65 ( 11 1 25 3 1 = . D. ( 4 C ) : (x - + y - = 2 ) ( 2) . 2 4 2 Lời giải Chọn C
CÁCH 1: (Đáp án đề thi tuyển sinh Đại học năm 2012-Khối A, A1- Bộ giáo dục và đào tạo) A B M x x P x H 3x Q x D N C
Gọi H là giao điểm của AN và BD . Kẻ đường thẳng qua H và song song với AB , cắt AD
và BC lần lượt tại P và Q . Đặt HP = x . Suy ra PD = x, AP = 3x và HQ = 3x.
Ta có QC = x nên MQ = x . Do đó DAHP = DMH ,
Q suy ra AH ^ M . Q 3 10
Hơn nữa, ta cũng có AH = MH. Do đó AM = 2MH = 2d(M,(AN)) = . 2 AÎ AN Þ (t A ;2t-3). 3 10 æ 11ö2 æ 7 ö2 45 ét 1 2 = AM = Û t - + 2t - =
Û t - 5t + 4 = 0 Û ç ÷ ç ÷ ê . 2 è 2 ø è 2 ø 2 ët = 4 Þ A(1;- ) 1 hoặc A(4; ) 5 . 2
Vậy A thuộc đường tròn C ) : ( 9
x - ) +( y - )2 65 ( 3 1 = . 2 4
Họ và tên tác giả: Vũ Huỳnh Đức. Tên facebook: Huỳnh Đức.
CÁCH 2 (Khai thác góc MAN )
Hãy tham gia group để cùng học và cùng làm- Nhóm chỉ dành cho các Gv, Sv toán! 42
File làm chuyên đề HÌNH GIẢI TÍCH OXY QUA CÁC THI 3 CHUNG BGD Group FB: Strong Team TOÁN VD–VDC A B M D N C
+ Đặt AB = a , ta tính được = 5 = 5 , a AM a MN , AN = 10a 2 6 3 5 2 a + 10 2 a - 25 2 a 2 2 2 + AM + AN - = MN = 4 9 36 cosMAN = 2 ( ) 1 2AM.AN 5 10 2 2. . a a 2 3 !!!!" æ11 7 ö + A Î AN Þ (
A ;t2t - 3),AM = ç - ;t - 2t÷ è 2 2 ø
+ Gọi !u = (1;2)là vec tơ chỉ phương của đường thẳng AM. !!!!" "
Vì MAN < 90o nên cosMAN = cos(AM,u) (2). !!!!" " !!!!" AM.u Từ (1) và (2) ta có = 2 Û ( " AM u) = 2 Û = 2 cosMAN cos , " 2 2 AM. u 2 25 -5t 2 é 2 t = 1 Û = Û 2
10t - 50t + 40 = 0 Û ê . æ11 ö2 æ 7 ö2 2 ët = 4 ç
- t ÷ + ç - 2t÷ . 5 è 2 ø è 2 ø 2 2 Vậy A(1;- )
1 hoặc A(4;5) nên A thuộc đường tròn æ 9 ö 65 (C ): x y 1 . 3 ç - ÷ + ( - ) = è 2 ø 4
*CÁCH 3 (Khai thác khoảng cách d(M; AN) )
Hãy tham gia group để cùng học và cùng làm- Nhóm chỉ dành cho các Gv, Sv toán! 43
File làm chuyên đề HÌNH GIẢI TÍCH OXY QUA CÁC THI 3 CHUNG BGD Group FB: Strong Team TOÁN VD–VDC A B M H D N C 11 - 1 2. - 3 ! 2 2
Gọi H là hình chiếu của M trên AN thì MH = d (M AN ) = = 3 5 , 5 2
! Đặt AB = a , vì M, N lần lượt nằm trên các cạnh BC, CD nên S = S + S + S + S ABCD ADN NCM MBA AMN Û 2 a = 1 1 a a + 1 2 1 a a + 1 1 a a + 1 . . . . MH.AM 2 3 2 3 2 2 2 2 Û 5 2 = 1 3 5 10 . . a a Û a = 3 2 12 2 2 3 !AB = Þ AM = 2 AB + 2 BM = 3 10 3 2 2 !!!!" æ11 7 ö #A Î AN Þ (
A ;t2t - 3),AM = ç - ;t - 2t÷ è 2 2 ø 2 2 é 3 10 æ11 ö æ 7 ö 3 10 t =1 !AM =
Û ç -t÷ +ç -2t÷ =
Û 2t - 5t + 4 = 0 Û ê 2 è 2 ø è 2 ø 2 ët = 4 2 2 Vậy A(1;- )
1 hoặc A(4;5) nên A thuộc đường tròn æ 9 ö 65 (C ): x y 1 . 3 ç - ÷ + ( - ) = è 2 ø 4
Hãy tham gia group để cùng học và cùng làm- Nhóm chỉ dành cho các Gv, Sv toán! 44
File làm chuyên đề HÌNH GIẢI TÍCH OXY QUA CÁC THI 3 CHUNG BGD Group FB: Strong Team TOÁN VD–VDC
*CÁCH 4 ((Khai thác góc MAN và khoảng cách d(M; AN)). A B 45o M H B' D N C 2 AM + 2 AN - 2 ! = MN = 2 cosMAN Þ MAN = 45o 2AM.AN 2 11 - 1 2. - 3 ! 2 2
Gọi H là hình chiếu của M trên AN thì MH = d (M AN ) = = 3 5 , 5 2
! DAMN vuông cân tại H Þ AM = MH Þ AM = 3 10 2 2 !!!!" æ11 7 ö #A Î AN Þ (
A ;t2t - 3),AM = ç - ;t - 2t÷ è 2 2 ø 2 2 é 3 10 æ11 ö æ 7 ö 3 10 t =1 !AM =
Û ç -t÷ +ç -2t÷ =
Û 2t - 5t + 4 = 0 Û ê . 2 è 2 ø è 2 ø 2 ët = 4 Vậy A(1;- )
1 hoặc A(4;5) nên A thuộc đường tròn A B æ 9 ö2 2 65 (C ): x y 1 . 3 ç - ÷ + ( - ) = è 2 ø 4
CÁCH 5 (Sử dụng hai tam giác đồng dạng và khoảng cách
d(M; AN)) H M
Gọi E là giao điểm của hai đường thẳng AN và BC . Ta có: D N C
! DEHMˇ DEBA Þ AB MH = AE ME Þ AE 2 10 AB= .MH= .d(M,AN) = 3 2 ME 5
- Việc tìm tọa độ của A tương tự như Cách 3.
*)CÁCH 6 ( Sử dụng vectơ - Xác định vị trí của điểm H trên đoạn thẳng AN )
Hãy tham gia group để cùng học và cùng làm- Nhóm chỉ dành cho các Gv, Sv toán! 45 E
File làm chuyên đề HÌNH GIẢI TÍCH OXY QUA CÁC THI 3 CHUNG BGD Group FB: Strong Team TOÁN VD–VDC A B 45o 45o 45o M H D N C
- Gọi H là hình chiếu của M trên AN , ta chứng minh ba điểm B, D, H thẳng hàng !!!" !!!" !!!" !!!" !!!" !!!!" !!!" !!!"
Giả sử AH = x AN thì x æ x ö æ 1 ö
AH = DC - xD ,
A MH=ç -1÷DC + ç - x ÷DA . 3 è 3 ø è 2 ø !!!" !!!!" !!!" !!!!" # AH ^ Û AH = Û x = 3 MH .MH 0 4 !!!" !!!" !!!" !!!" !!!" !!!" !!!" !!!" # DH = 1 DA + 1
DC, DB = DA + DC Þ DB = 4DH Þ H thuộc đoạn . DB 4 4
! àABMH nội tiếp Þ = = = 45o MAH MBH MBD
Þ DMAH vuông cân tại H Þ AM = HM = d M AN = 3 10 2 2 ( ; ) . 2
Đến đây, việc tìm tọa độ của A tương tự như cách 3 *)CÁCH 7 2 AM + 2 AN - 2 = MN = 2 cosMAN Þ MAN = 45o 2AM.AN 2
Gọi H là giao điểm của AN và DB . Ta có = = 45o MAN HBM Þ àABMH nội tiếp Þ = 90o AHM
Þ DMAH vuông cân tại H. Þ AM = HM = d M AN = 3 10 2 2 ( ; ) 2
Đến đây, việc tìm tọa độ của A tương tự như cách 3.
Hãy tham gia group để cùng học và cùng làm- Nhóm chỉ dành cho các Gv, Sv toán! 46
File làm chuyên đề HÌNH GIẢI TÍCH OXY QUA CÁC THI 3 CHUNG BGD Group FB: Strong Team TOÁN VD–VDC A A B B 45o 45o I I M M H E H F D N C D N C *)CÁCH 8
- Gọi H là hình chiếu của M trên AN thì MH : 2x+4y-13=0,
H = AN Ç MH Þ 5 H( ;2) 2 !!!" !!!" !!!" !!!"
- Bằng công cụ vectơ như cách 6, ta tìm được AH = 3 AN vả DB = 4DH . 4
- Gọi E, F theo thứ tự là giao điểm của đường thẳng MH với AC, AD . Ta có: !!!" !!!!" #DHDFˇ D HF HD 1 1 æ 3 5 ö HBM Þ =
= Þ HF = - HM Þ F ç ; ÷ HM HB 3 3 è 2 2 ø !D ˇ E Þ EM = MC EMC FA = 3 Þ EM = 3 FM=EH EF FA 5 8
Þ E là trung điểm của MH æ 5 ö Þ E ç 4; ÷. è 4 ø
! Î AN Þ A t t - AE = 2
t - t + 545 AF = 2 t - t + 65 A ( ;2 3), 5 25 , 5 25 , 16 2
! àABCD là hình vuông Þ AC = AD Û 8 6 2 AE= 2. .AF 5 5 ét =1 Û 2 t - t + 545 = 2 t - t + 65 4 5 25 3 2 5 25 Û 2
10t - 50t + 40 = 0 Û . 16 2 ê ët = 4 2 2 Vậy A(1;- )
1 hoặc A(4;5) nên A thuộc đường tròn æ 9 ö 65 (C ): x y 1 . 3 ç - ÷ + ( - ) = è 2 ø 4
*) Nhận xét: Với cách giải này, ta có thể tìm được tọa độ của các điểm B, C, D dễ dàng sau khi
tìm được tọa độ của A. *)CÁCH 9
Hãy tham gia group để cùng học và cùng làm- Nhóm chỉ dành cho các Gv, Sv toán! 47
File làm chuyên đề HÌNH GIẢI TÍCH OXY QUA CÁC THI 3 CHUNG BGD Group FB: Strong Team TOÁN VD–VDC A B M I K D N C P
Gọi K là giao điểm của hai đường thẳng AN và BD .
! K nằm trên đường trung trực của AC nên KA = KC (1) !D ˇ D Þ KD = DN KDN KBA
= 1 Þ KD = 1 KB Þ KD = 1 KI Þ K là trung điểm của DI. KB AB 3 3 2 ìIM / /DC ! í Þ KM = KC(2)
îK laø trung ñieåm cuûa ID
! Từ (1) và (2) suy ra tam giác KMA cân tại K. (3) ! A Î AN Þ (
A ;t2t -3)
! Gọi P là giao điểm của AM và DC thì AP=2AM, DP=2AD
! àABCD là hình vuông Þ 2 = 2 + 2 AP AD DP 2 2 2 æ ö2
Û AP = AD Û AP =
AN.cosNAD Û AP = 3 5 5ç ÷ AN è ø 2 Û AM = 3 4 2
. AK Û AM = 2AK (4) 2 3
! Từ (3) và (4) suy ra tam giác KMA vuông cân tại K. Do đó AM = AK Û AM = KM Û AM =
d M AN Û AM = 3 10 2 2 2 ( ; ) . 2 *)CÁCH 10 M B C I N H A D F
Hãy tham gia group để cùng học và cùng làm- Nhóm chỉ dành cho các Gv, Sv toán! 48
File làm chuyên đề HÌNH GIẢI TÍCH OXY QUA CÁC THI 3 CHUNG BGD Group FB: Strong Team TOÁN VD–VDC
- Bước 1: Gọi H là hình chiếu của M trên AN, lập luận tương tự như Cách 6 ta được H thuộc đoạn BD.
- Bước 2: Tìm tọa độ của H. Đây chính là dạng của Đề thi Đại học khối A, A1 năm 2014. Đến
đây, chúng ta có nhiều cách giải.)
(-Trích đề thi tuyển sinh Đại học năm 2014- khối A, A1 - Bộ giáo dục và đào tạo:
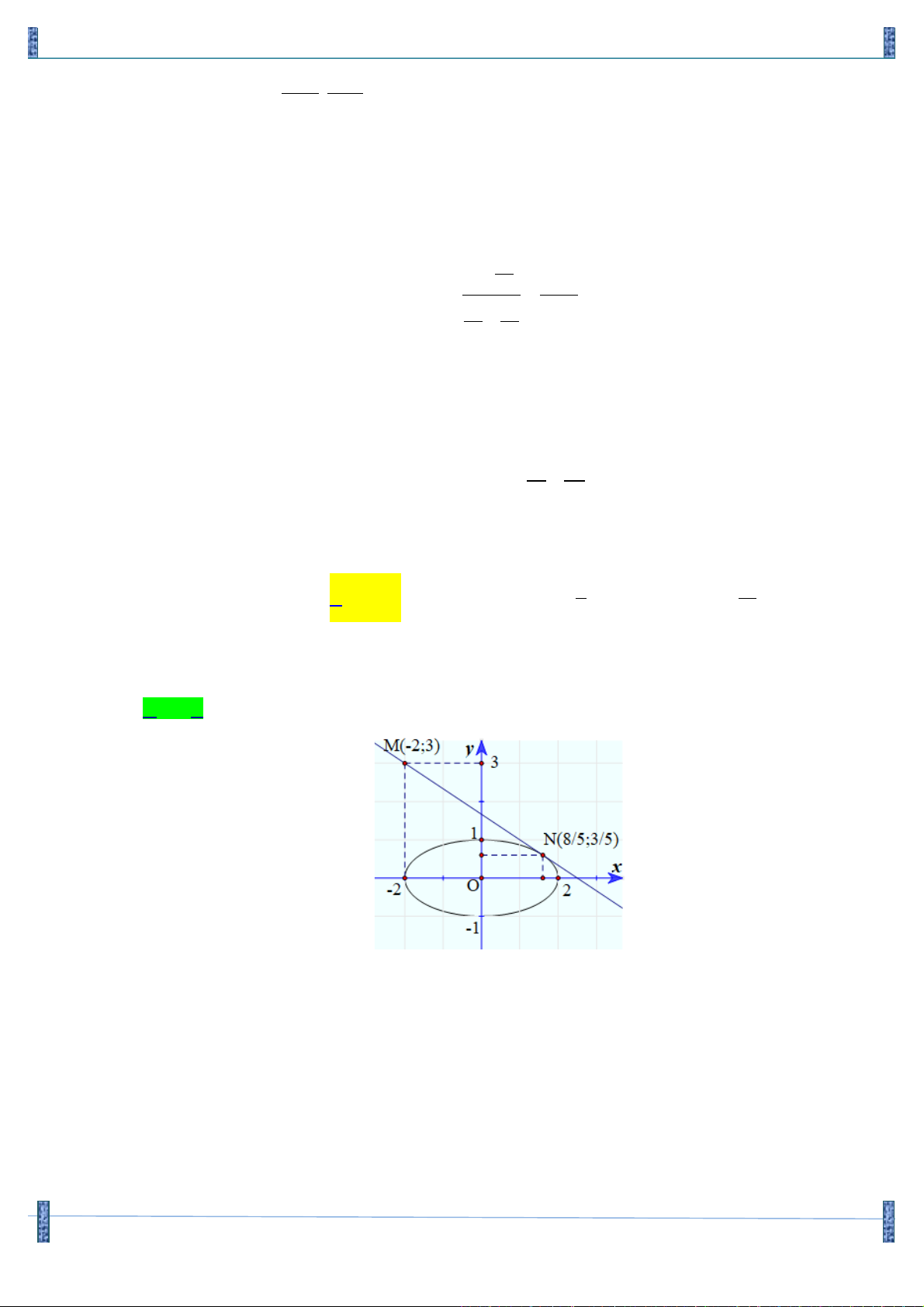
Trong mặt phẳng với hệ tọa độ Oxy, cho hình vuông ABCD có điểm M là trung điểm của đoạn
AB và N là điểm thuộc đoạn AC sao cho AN=3NC. Viết phương trình đường thẳng CD, biết rằng M(1;2) và N(2;-1) ) A M B I N D C
-Từ cách 2 trở đi là do cá nhân tôi tự nghĩ ra. Xin cam đoan rằng không lấy của bất kì một ai.
Câu 45. Trong mặt phẳng với hệ trục tọa độ Oxy, cho hai điểm A(1; 1), B(4; -3). Tìm điểm C thuộc
đường thẳng x – 2y – 1 = 0 sao cho khoảng cách từ C đến đường thẳng AB bằng 6. Lời giải
Phương trình đường thẳng AB là: 4x + 3y – 7 = 0
Điểm C thuộc đường thẳng x – 2y – 1 = 0 nên tọa độ điểm C có dạng C(2a + 1; a)
Từ giả thiết khoảng cách từ C đến đường thẳng AB bằng 6, ta có phương trình
4 2 + 1 + 3 − 7 = 3
= 6 ↔ 11 − 3 = 30 ↔ 27 5 = − 11 æ 43 - 27 ö
Vậy có 2 điểm C thỏa mãn bài toán là C(7; 3) và C ;- ç ÷ è 11 11 ø
Nguồn: (D2004) Trong mặt phẳng với hệ trục tọa độ Oxy, cho hai điểm A(1; 1), B(4; -3). Có
một điểm C(a; b) thuộc đường thẳng x – 2y – 1 = 0 với a > 0, sao cho khoảng cách từ C đến
đường thẳng AB bằng 6. Tổng của a + b là: A. 10 B. 2 C. -1 D. 5
Email: minhduc486@gmail.com
Câu 46. (A2010 – DB2) Trong mặt phẳng với hệ trục tọa độ Oxy cho tam giác ABC có đỉnh A nằm trên
đường thẳng d : 2x - 3y +14 = 0, cạnh BC song song với d , đường cao CH có phương trình:
x - 2y -1 = 0. Biết trung điểm của cạnh AB là M ( 3;
- 0). Xác định tọa độ các đỉnh , A B,C. Lời giải
Hãy tham gia group để cùng học và cùng làm- Nhóm chỉ dành cho các Gv, Sv toán! 49
File làm chuyên đề HÌNH GIẢI TÍCH OXY QUA CÁC THI 3 CHUNG BGD Group FB: Strong Team TOÁN VD–VDC
Đường thẳng AB qua điểm M ( 3;
- 0) và vuông góc với CH : x - 2y -1= 0 nên có phương trình
AB : 2x + y + 6 = 0. ìAÎ AB ì2x + y + 6 = 0 ìx = 4 - Ta có: í suy ra í Û í vậy A( 4; - 2). îAÎ d
î2x - 3y +14 = 0 îy = 2 Do M ( 3;
- 0) là trung điểm AB nên suy ra B( 2; - 2 - ).
Đường thẳng BC qua B( 2; - 2
- ) và song song với d : 2x -3y +14 = 0 nên có phương trình
BC : 2x - 3y - 2 = 0. C ì Î BC
ì2x - 3y - 2 = 0 ìx =1 Ta có: í suy ra í Û í vậy C (1;0). C î ÎCH îx - 2y -1 = 0 îy = 0
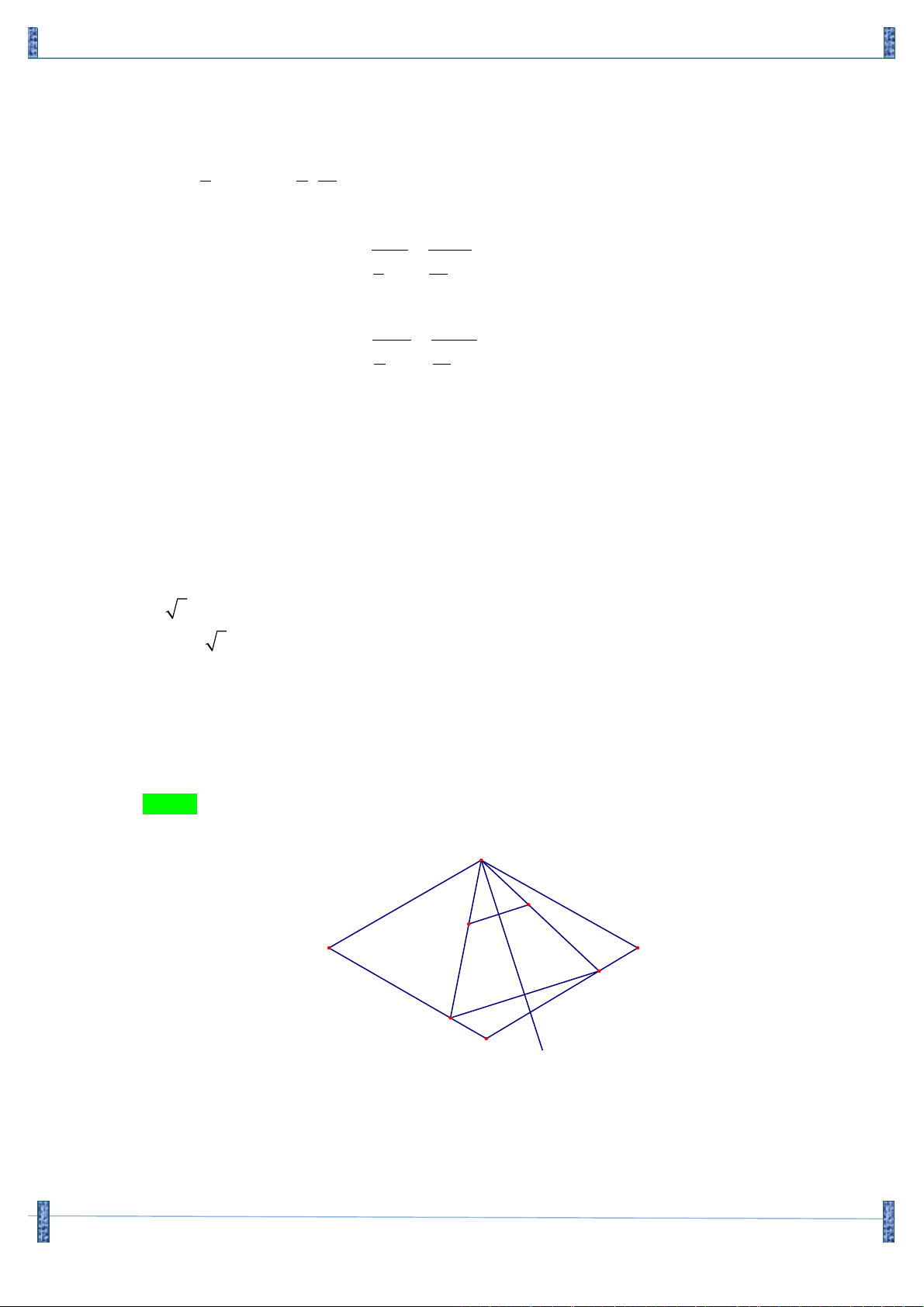
Câu 47. Câu 106: Trong mặt phẳng với hệ tọa độ Oxy , cho tam giác OAB có các đỉnh A và B thuộc
đường thẳng D : 4x + 3y -12 = 0 và điểm K (6; 6) là tâm đường tròn bàng tiếp góc O . Gọi C
là điểm nằm trên D sao cho AC = AO và các điểm C , B nằm khác phía nhau so với điểm A . 24
Biết điểm C có hoành độ bằng
. Tính tổng x + x + y + y 5 A B A B A. 6 . B. 7 . C. 8 . D. 9 . Lời giải
Họ và tên: Huỳnh Thanh Tịnh
Tên FB: huynhthanhtinh Chọn B
Hãy tham gia group để cùng học và cùng làm- Nhóm chỉ dành cho các Gv, Sv toán! 50
File làm chuyên đề HÌNH GIẢI TÍCH OXY QUA CÁC THI 3 CHUNG BGD Group FB: Strong Team TOÁN VD–VDC O F E H C D B A K
● Trên D , lấy điểm D sao cho BD = BO và D , A nằm khác phía nhau so với B . Gọi E là
giao điểm của các đường thẳng KA và OC ; gọi F là giao điểm của các đường thẳng KB và OD .
Vì K là tâm đường tròn bàng tiếp góc O của O
D AB nên KE là phân giác của góc OAC . Mà O
D AC là tam giác cân tại A nên suy ra KE cũng là đường trung trực của OC . Do đó E
là trung điểm của OC và KC = KO . Xét tương tự đối với KF , ta cũng có E là trung điểm của
OC và KD = KO . Suy ra CKD D
cân tại K . Do đó, hạ KH ^ D , ta có H là trung điểm của CD . ● Như vậy:
+ A là giao của D và đường trung trực d1 của đoạn thẳng OC ; (1)
+ B là giao của D và đường trung trực d2 của đoạn thẳng OD , với D là điểm đối xứng của
C qua H và H là hình chiếu vuông góc của K trên D . æ 24 ö æ 24 12 ö æ12 6 ö C ; y ç C ; - E ; - 0 ÷ ç ÷ ç ÷ ● Vì è 5
ø thuộc đường thẳng D nên è 5 5 ø. Từ đó suy ra è 5 5 ø và
đường thẳng OC có phương trình x + 2y = 0 . Do đó phương trình d : 2x - y - 6 = 0 1 , từ đó suy A(3;0) ra . K (6; 6)
● Gọi d là đường thẳng đi qua
và vuông góc với D , ta có phương trình của æ 6 12 ö æ 12 36 ö æ 6 18 ö H ; D - ; F - ;
d : 3x - 4y + 6 = 0 ç ÷ ç ÷ ç ÷ . Từ đây, suy ra
è 5 5 ø và è 5 5 ø . Do đó è 5 5 ø và đường
Hãy tham gia group để cùng học và cùng làm- Nhóm chỉ dành cho các Gv, Sv toán! 51
File làm chuyên đề HÌNH GIẢI TÍCH OXY QUA CÁC THI 3 CHUNG BGD Group FB: Strong Team TOÁN VD–VDC
thẳng OD có phương trình 3x + y = 0 . Suy ra phương trình d : x - 3y +12 = 0 2 , từ đó suy ra B(0;4).
Email: thinhvanlamha@gmail.com
Câu 48. Trong mặt phẳng với hệ tọa độ Oxy , cho tam giác ABC cân tại B với A(1;- )
1 , C (3;5). Định B
nằm trên đường thẳng d : 2x - y = 0 . Phương trình các đường thẳng AB, BC lần lượt là
d : ax + by - 24 = 0, d : cx + dy + 8 = 0. Tính giá trị biểu thức P = . a . b . c d . 1 2 A. P = 975 . B. P = 5681. C. P = 3059 . D. P = 5083 . Lời giải
Họ và tên tác giả: Nguyễn Văn Thịnh
Tên FB: Thịnh Nguyễn Văn Chọn B Cách 1:
Gọi I là trung điểm AC Þ I (2;2).
Đường thẳng D đi qua I và vuông góc với AC có phương trình: x + 3y -8 = 0 (D). æ 8 16 ö
Tam giác ABC cân tại B nên ta có B ÎD Þ B = D Ç d Þ B ; ç ÷ . è 7 7 ø x -1 y +1
Phương trình đường thẳng AB : =
Û 23x - y - 24 = 0. 8 16 -1 +1 7 7 x - 3 y - 5
Phương trình đường thẳng BC : =
Û 19x -13y + 8 = 0. 8 16 - 3 - 5 7 7
Vậy a = 23,b = 1 - ,c =19,d = 13 - Þ P = . a . b . c d = 5681. Cách 2:
Hãy tham gia group để cùng học và cùng làm- Nhóm chỉ dành cho các Gv, Sv toán! 52
File làm chuyên đề HÌNH GIẢI TÍCH OXY QUA CÁC THI 3 CHUNG BGD Group FB: Strong Team TOÁN VD–VDC Gọi B( ;2 a a)Îd .
Tam giác ABC cân tại B nên ta có AB = CB Þ (a - )2 +( a + )2 = (a - )2 + ( a - )2 1 2 1 3 2 5 8 Û æ 8 16 ö a = . Suy ra B ; ç ÷. 7 è 7 7 ø x -1 y +1
Phương trình đường thẳng AB : =
Û 23x - y - 24 = 0. 8 16 -1 +1 7 7 x - 3 y - 5
Phương trình đường thẳng BC : =
Û 19x -13y + 8 = 0. 8 16 - 3 - 5 7 7
Vậy a = 23,b = 1 - ,c =19,d = 13 - Þ P = . a . b . c d = 5681.
Email: nguyentuanblog1010@gmail.com
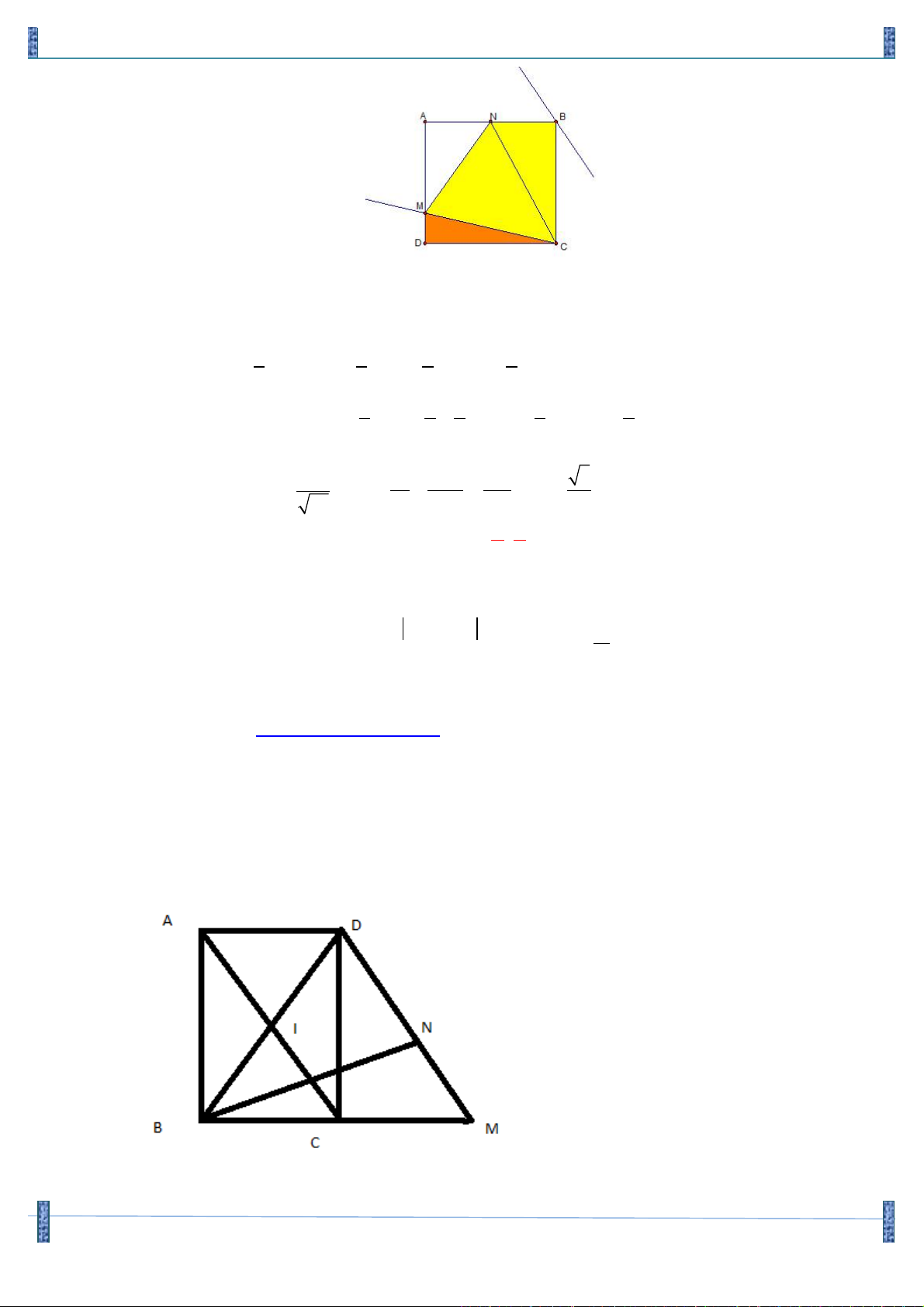
Câu 49. Trong mặt phẳng với hệ tọa độ vuông góc Oxy cho hình thoi ABCD có 0 BAD = 0 6 , D( ; a b)
với b > a > 0 . Trên các cạnh AB, BC lấy các điểm M , N sao cho MB + NB = AB . Biết
P( 3;1) thuộc đường thẳng DN và đường phân giác của góc MDN có phương trình là
d : x - y 3 + 6 = 0.Tính giá trị của biểu thức T = 3a - b ? A. 6 . B. 7 . C.8 . D. 9 .
Tác giả: Phạm Chí Tuân.
Facebook. Tuân Chí Phạm Hướng dẫn giải. Chọn C. D P Q A C N M B
Å Cách 1: Từ đề bài ta có các tam giác ,
ABD CBD là các tam giác đều, AM = BN và BM = CN . Xét AD D M và BD D
N có: DAM = DBN, AD = BD và AM = BN nên AD D M = BD D N Þ ADM = BDN ( ) 1 .
Hãy tham gia group để cùng học và cùng làm- Nhóm chỉ dành cho các Gv, Sv toán! 53
File làm chuyên đề HÌNH GIẢI TÍCH OXY QUA CÁC THI 3 CHUNG BGD Group FB: Strong Team TOÁN VD–VDC Xét BM D D và C
D ND có: DBM = DCN,CD = BD và CN = BM nên BM D D = C D ND Þ NDC = MDB(2) ( ) 1 (2) 0 Từ và ta có MDN = 60 . Q Å 0
Cách 2: Xét (D,60 ) ta có : A ® ;
B B ® C nên M ® N . Do đó tam giác DMN đều.
Gọi Q là điểm đối xứng của P qua đường phân giác của góc MDN . 3 - 3 + 6
DP = PQ = 2d (P,d ) = 2. = 6 1+ ( 3)2 Khi đó ta có : 2 æ t + 6 ö 2 æ t + 6 - 3 ö ét = 3+ 3 D t; Îd 2 DP = (t - 3) ç ÷ + ç ÷ = 36 Þ ê . ç 3 ÷ Gọi è 3 ø . Ta có : è ø êët = 6 - + 3 D (3+ 3;1+ 3 3) D (-6 + 3; ) 1 Vậy hoặc
. Theo giả thuyết ta nhận ìï = + D ( + + ) a 3 3 3
3;1 3 3 Þ íbïî=1+3 3
Ta có giá trị của biểu thức T = 3a - b = 8 .
Hãy tham gia group để cùng học và cùng làm- Nhóm chỉ dành cho các Gv, Sv toán! 54
File làm chuyên đề HÌNH GIẢI TÍCH OXY QUA CÁC THI 3 CHUNG BGD Group FB: Strong Team TOÁN VD–VDC
Email: Lenguyet150682@gmail.com Chủ đề: Hình giải tích Oxy, Faceboook: NguyệtLê
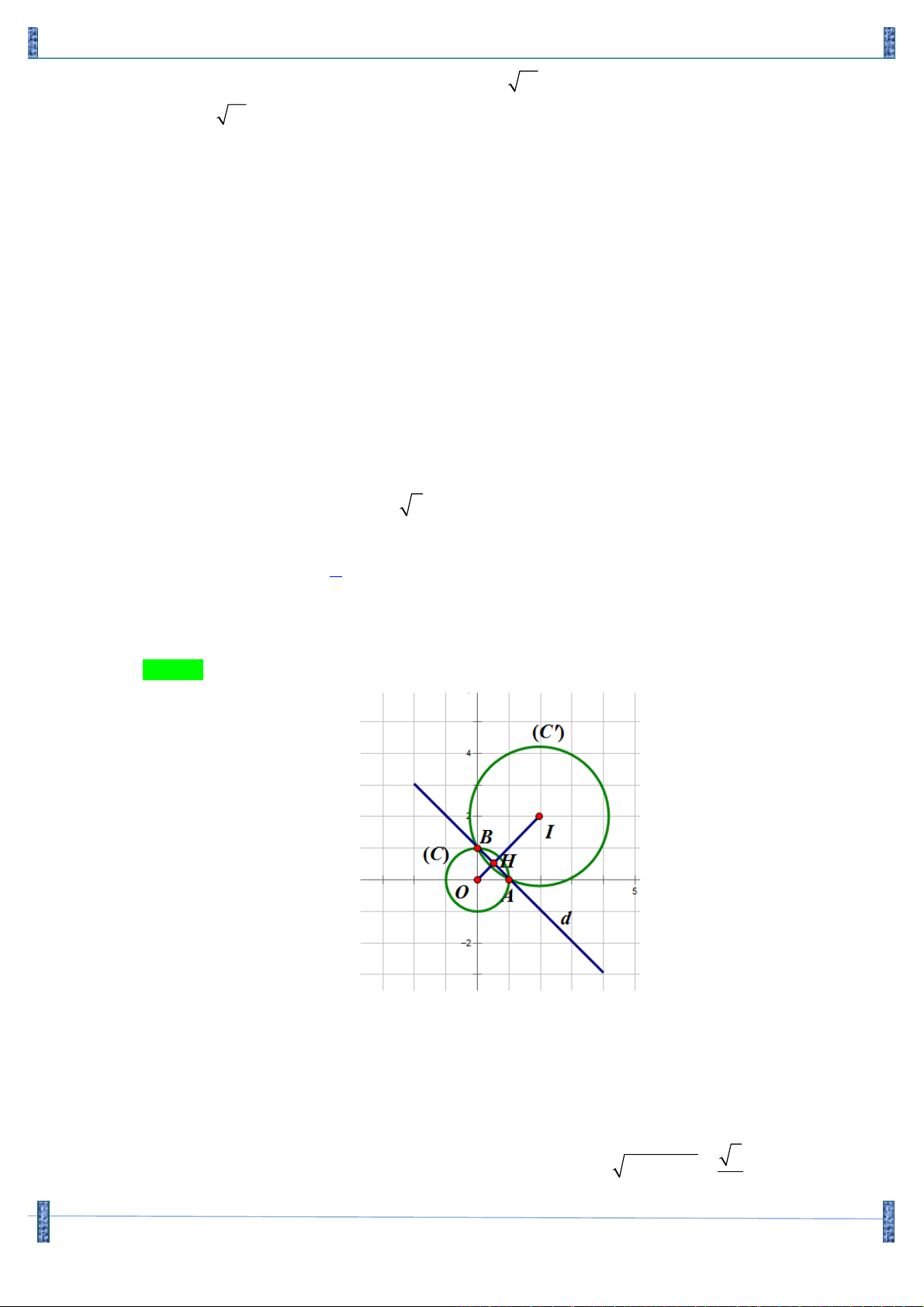
Câu 1. Trong hệ trục vuông góc Oxy , cho đường tròn 2 2
(c ) : x + y = 9 có tâm là I bán kính R và 1 1 1 đường tròn 2 2
(C ) : x + y - 2x - 2y - 23 = 0. Gọi (T) là tập hợp các điểm điểm M(x;y) sao 1 cho 2 2 2 2
MI - MI = R - R . Giả sử K(a;b) là điểm nằm trên (T ) sao cho khoảng cách từ 1 2 1 2
K đến I bằng 5. Khi đó 1 A. 2 2 a - b !3. B. 2 2
a - b chỉ có hai ước dương. C. 2 2 a - b = 0.
D. 3a + 4b = 0 . Lời giải Chọn B
I (0;0);R = 3;I (1;1);R = 5. 1 1 2 2 2 2 2 2 2 2 2 2
MI - MI = R - R € (x - 0) + (y- 0) - (x - 1) - (y - 1) = 9 - 25 1 2 1 2
€ x + y + 7 = 0.
Suy ra (T) là đường thẳng có phương trình x + y + 7 = 0. Gọi K(a;b) (
Œ T) là điểm thỏa 2 IK = 25. Ta có a ⎧ 2 ⎪ +(7 −a)2 = 25 a ⎡ = −4;b = −3 ⎨⎪ ⇔ ⎢ b = 7 −a ⎢ . ⎩⎪⎪
a = −3;b = −4 ⎣ Suy ra 2 2 a - b = 7 ± . Hình Giải Tích Oxy
Email: hoathptsontay@gmail.com
Câu 2. Trong mặt phẳng tọa độ Oxy , cho đường thẳng d : x - y +1- 2 = 0 và điểm A( 1 - ; ) 1 . Đường
tròn (C) đi qua A , gốc tọa độ O và tiếp xúc với đường thẳng d . Khi đó đường tròn (C) có tâm I ( ;
a b) thì tích ab bằng
Hãy tham gia group để cùng học và cùng làm- Nhóm chỉ dành cho các Gv, Sv toán! 55
File làm chuyên đề HÌNH GIẢI TÍCH OXY QUA CÁC THI 3 CHUNG BGD Group FB: Strong Team TOÁN VD–VDC A. 1 - . B. 0 . C. 1. D. 2 . Lời giải
Họ và tên tác giả: Nguyễn Thị Hoa, Tên FB: Hoa Nguyen Chọn B Cách 1:
Gọi D là đường trung trực của OA .
Theo bài ra ta có IA = I O = d (I,d )(= R) .
IA = I O Þ I Î D .
OA ^ d Þ D//d và R = d ( , D d ). æ 1 1 !!!" D ö
đi qua trung điểm J - ; ç
÷ của OA , véctơ pháp tuyến OA( 1 - )
;1 nên có phương trình là è 2 2 ø x - y +1 = 0 . 1 1 - - +1- 2
R = d (D d ) = d ( J d ) 2 2 , ; = =1. 2
I Î D và OI = R = 1, nên có tối đa hai điểm I .
Mà D cắt Ox,Oy lần lượt tại I 0;1 , I 1 - ;0 . 2 ( ) 1 ( )
Nên tâm của (C) là I (0; ) 1 hoặc I ( 1 - ;0) Khi đó ab = 0 .
Cách 2: Sử dụng phương trình tổng quát của đường tròn để viết phương trình đường trung trực:
Giả sử đường tròn (C) có phương trình: 2 2
x + y - ax - by + c = ( 2 2 2 2
0 a + b - c > 0). O ì Î ï (C) ìc = 0 ìc = 0 í Û í Û í Þ I ( ; a a + ) 1 . ïAÎ î
(C) î2a - 2b + c = 2 - b î = a +1
Hãy tham gia group để cùng học và cùng làm- Nhóm chỉ dành cho các Gv, Sv toán! 56
File làm chuyên đề HÌNH GIẢI TÍCH OXY QUA CÁC THI 3 CHUNG BGD Group FB: Strong Team TOÁN VD–VDC
d tiếp xúc với (C) khi và chỉ khi d (I;d ) = IO a - (a + ) 1 +1- 2 Û = a + (a + )2 2 2 2
1 Û1 = 2a + 2a +1 Û 2a + 2a = 0 2 éa = 0(Þ b = ) 1 Û ê (thỏa mãn). êa = 1 - ë (Þ b = 0) Khi đó ab = 0 .
Cách 3: Tác giả Lưu Thêm
Gọi D là đường trung trực của OA . æ 1 1 !!!" D ö
đi qua trung điểm J - ; ç
÷ của OA , véctơ pháp tuyến OA( 1 - )
;1 nên có phương trình là è 2 2 ø x - y +1 = 0 .
+) IA = I O Û I ÎD Û I ( ; a a + ) 1 . a - a +1 +1- 2 2 ( )
+) I O = d (I,d ) 2 Û a + (a + ) 2 2 1 =
Û 2a + 2a +1 =1Û 2a + 2a = 0 2 éa = 0(Þ b = ) 1 Û ê (thỏa mãn). êa = 1 - ë (Þ b = 0) Khi đó ab = 0 .
Email: thanhtam14@gmail.com
Câu 3. Trong mặt phẳng với hệ tọa độ Oxy cho đường tròn (C) 2 2
: x + y - 4x - 6y -12 = 0. Gọi I là
tâm và R là bán kính của (C). Gọi M ( ;
a b) (a > 0) thuộc đường thẳng d : 2x - y + 3 = 0 sao
cho MI = 2R . Tính tổng 2 2 a + b . 333 A. 15. B. 137 . C. P = . D. P = 136. 5 Lời giải
Họ và tên tác giả: A2005-DB2 Tên FB: Thanh Tâm Chọn B
(C) có tâm I (2;3), bán kính R = 5.
M Îd : 2x - y + 3 = 0 Þ M (t;2t +3) !!!"
IM = (t - 2;2t)
Hãy tham gia group để cùng học và cùng làm- Nhóm chỉ dành cho các Gv, Sv toán! 57
File làm chuyên đề HÌNH GIẢI TÍCH OXY QUA CÁC THI 3 CHUNG BGD Group FB: Strong Team TOÁN VD–VDC
ét = 4 Þ M (4;1 ) 1
IM = R Û (t - )2 + ( t)2 2 2 2 =10 2
Û 5t - 4t - 96 = 0 ê Û ê 24 æ 24 33 ö t = - Þ M - ;- ç ÷ êë 5 è 5 5 ø
Do đó: a = 4;b =11 và 2 2 a + b =137.
Email: nguyentinh050690@gmail.com
Câu 4. Trong mặt phẳng với hệ tọa độ Oxy, cho đường tròn (C) 2 2
: x + y - 2x - 2y +1= 0 và đường
thẳng d : x - y + 3 = 0. Điểm M ( ;
a b), a > 0 thuộc d sao cho đường tròn tâm M có bán kính
gấp đôi đường tròn (C), tiếp xúc ngoài với đường tròn (C). Tính tổng 2 2
T = a + b . A. 5. B. 20 C. 17 D. 16 Lời giải Họ
Tên: Nguyễn Tình Tên FB: Gia Sư Toàn Tâm
Đường tròn (C) có tâm I (1; ) 1 và bán kính R = 1. 1
Điểm M Îd Þ b = a + 3 Þ M ( ; a a + ) 3
Đường tròn tâm M tiếp xúc ngoài với đường tròn (C) nên: éa =
IM = R + 2R Û IM = 9 Û (a - )2 1 + (a + 2)2 1 2 = 9 Û Þ M ê (1;4) ëa = 2( - L) 2 2
Þ a =1;b = 3 Þ a + b =10 Chọn C.
Câu 5. (A2007) Trong mặt phẳng tọa độ Oxy , cho tam giác ABC có A(0;2),B( 2 - ; 2 - ),C(4; 2 - ). Gọi
H là chân đường vuông góc kẻ từ B ; M và N lần lượt là trung điểm của các cạnh AB và
BC . Phương trình đường tròn đi qua các điểm H ,M ,N . A. 2 2
x + y - x - y - 2 = 0 B. 2 2
x + y - x + y - 2 = 0 C. 2 2
x + y + x - y + 2 = 0 D. 2 2
x + y - x + 2y = 0 Lời giải Chọn B
Hãy tham gia group để cùng học và cùng làm- Nhóm chỉ dành cho các Gv, Sv toán! 58
File làm chuyên đề HÌNH GIẢI TÍCH OXY QUA CÁC THI 3 CHUNG BGD Group FB: Strong Team TOÁN VD–VDC A H M B C N
Có M là trung điểm của AB nên M ( 1 - ;0)
N là trung điểm của BC nên N (1; 2 - )
Phương trình đường thẳng AC : x+y -2=0 !!!"
Vì BH ^ AC nên phương trình đường thẳng BH qua B và nhận AC = (4; 4 - ) làm VTPT BH : x - y = 0 ìx - y = 0 ìx =1
Suy ra H là tọa độ giao điểm của BH và AC : í Û í Þ H (1; ) 1 îx + y - 2 = 0 îy =1
Giả sử phương trình đường tròn có dạng (C) : 2 2
x + y - 2ax - 2by + c = 0
Vì 3 điểm H ,M ,N cùng thuộc (C) nên ta có: ì 1 a = 2 2 1 1 2a 2b c 0 ï ì + - - + = 2 ï ï(ïí- )2 ï 1 - 1 + 2a + c = 0 Û b í = 2 ï ï 1 ï + î ( 2 - )2 2
- 2a + 4b + c = 0 ïc = 2 - ïî
Vậy phương trình đường tròn: 2 2
x + y - x + y - 2 = 0
Câu 6. Trong mặt phẳng với hệ tọa độ Oxy , cho đường tròn (C): (x- )2 +(y + )2 1 2 = 9 và đường
thẳng d :3x - 4y + m = 0. Tìm m để trên d có duy nhất một điểm P mà từ đó kẻ được hai
tiếp tuyến PA , PB với (C) ( A , B là các tiếp điểm) sao cho tam giác PAB đều. ém =19 ém = -19 A. m = 19 . B. m = 41 - . C. ê . D. ê . ëm = 41 - ëm = 41 Lời giải
Giáo viên: Phạm Quốc Toàn, Email: phamquoctoan87@gmail.com
Hãy tham gia group để cùng học và cùng làm- Nhóm chỉ dành cho các Gv, Sv toán! 59
File làm chuyên đề HÌNH GIẢI TÍCH OXY QUA CÁC THI 3 CHUNG BGD Group FB: Strong Team TOÁN VD–VDC Chọn C
Đường tròn (C) có tâm I (1;- )
2 và bán kính R = 3 .
Tam giác PAB đều nên góc APB ! = 60! ⇒ API ! = 30!. IA IA 3
Xét tam giác vuông IAP , ta có sin API ! = ⇒ IP = = 6 . IP sin API ! = 1 2
Vậy P thuộc đường tròn tâm I bán kính bằng 6 .
Để trên d có duy nhất một điểm P thỏa mãn điều kiện đề bài thì d pahir tiếp xúc với đường 3.1−4. − ( 2)+ m
tròn tâm I , bán kính bằng 6 ⇔ d(I,d)= 6 ⇔ = 6 32 + − ( 4)2 ⎡m =19
⇔ m+11 = 30 ⇔ ⎢⎢ . m = −41 ⎣
Mail: anduynguyen2903@gmail.com
Câu 7. Trong mặt phẳng với hệ tọa độ Oxy, cho đường tròn 2 2
(C):(x- 1) + y =1. Gọi I là tâm của (C).
Điểm M(a;b) thuôc (C)sao cho IMO
! =300. Tính a- 3 b . A. 0 B. 3 C. 3 - D. - 3 Lời giải
Face: Nguyễn Thị Duy An Chọn A Do M(a;b) ∈ (C) ⇔ 2 2
(a- 1) +b =1. Mà O ∈ (C) ⇒ IO = IM =1
Tam giác IMO có OIM ! =1200 nên 2 2 2 0 2 2
OM = IO + IM - 2 . IO IM.co 1
s 20 € a + b = 3 ⎧⎪⎪ 3 ⎧ a ⎪ ⎪ = ⎪
Tọa độ điểm M là nghiệm của hệ: ( ⎪ a−1)2 + b2 =1 ⎪ 2 ⎨ ⇔ ⎨ a2 + b2 = 3 ⎩⎪⎪ ⎪b⎪ 3 ⎪ = ± ⎪ ⎩⎪ 2
Hãy tham gia group để cùng học và cùng làm- Nhóm chỉ dành cho các Gv, Sv toán! 60
File làm chuyên đề HÌNH GIẢI TÍCH OXY QUA CÁC THI 3 CHUNG BGD Group FB: Strong Team TOÁN VD–VDC 3 3
Vậy: a - 3 b = - 3 = 0 2 2
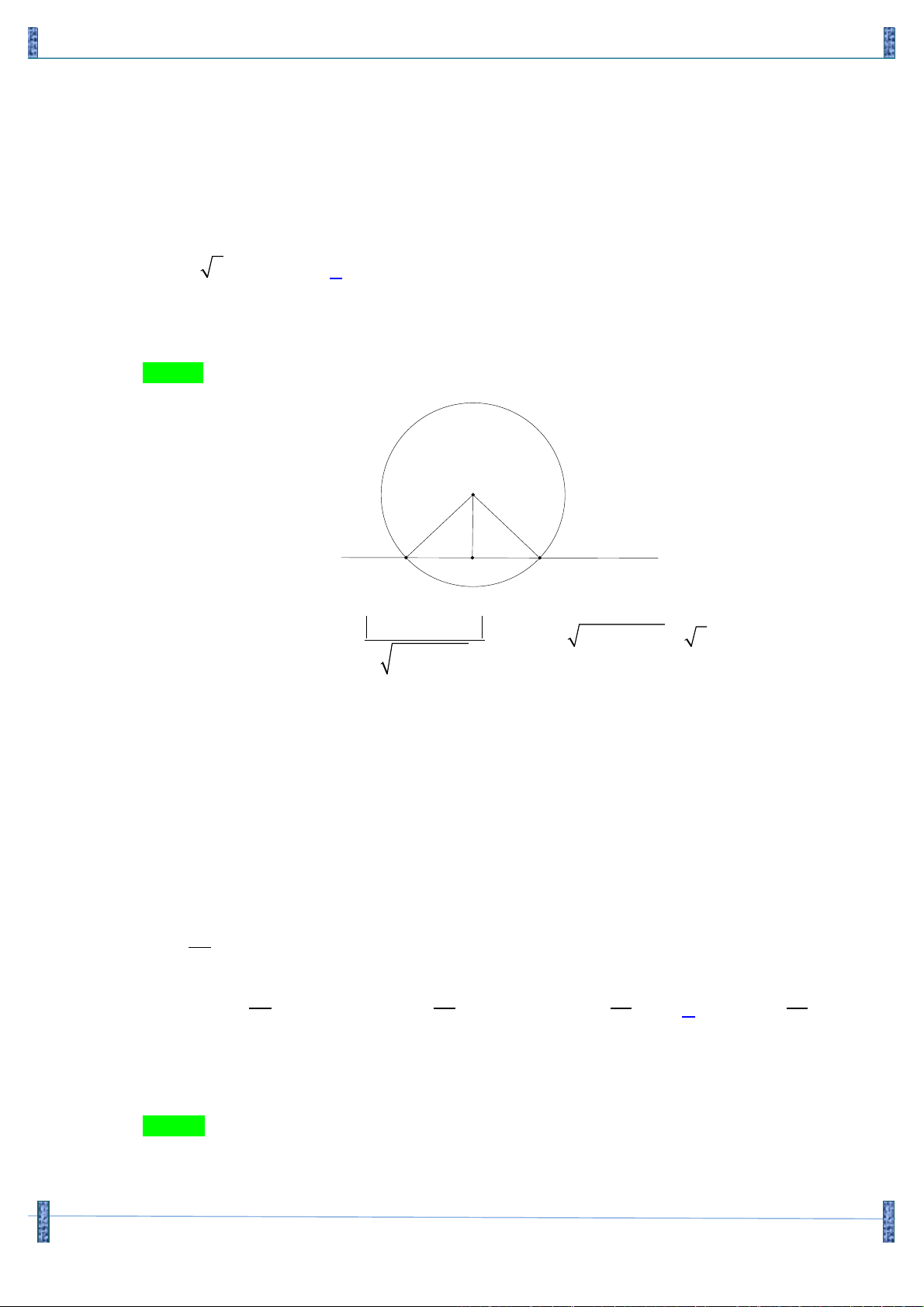
Câu 8. Trong mặt phẳng tọa độ Oxy , cho đường thẳng d : 3x + y = 0 và d : 3x - y = 0. Gọi (T ) là 1 2
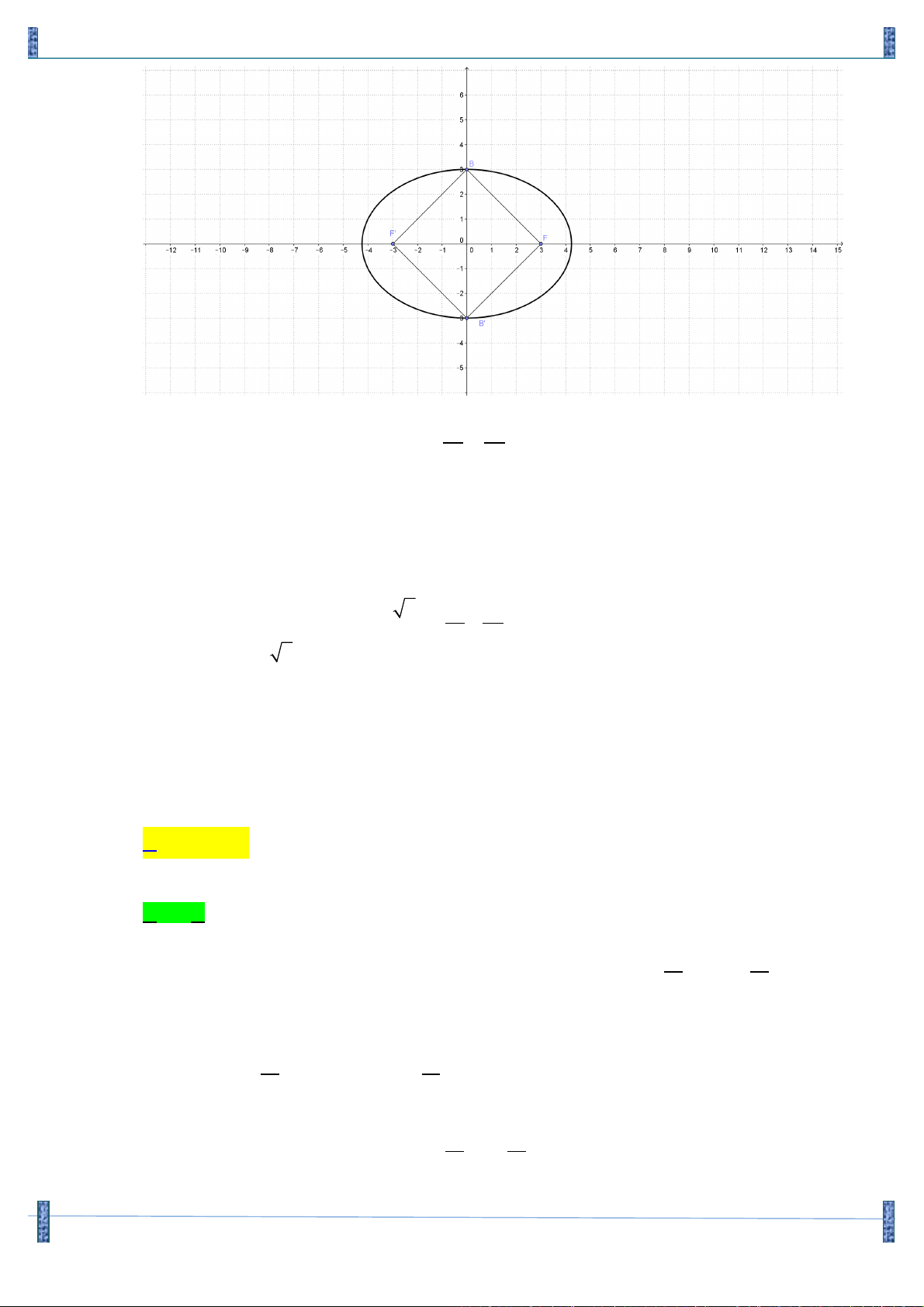
đường tròn tiếp xúc với d tại A , cắt d tại B và C sao cho tam giác ABC vuông tại B . Biết 1 2 3 AB D
C có diện tích bằng
và điểm A có x > 0. Khi đó phương trình của (T ) là 2 A 2 2 æ 1 ö æ 3 ö 2 2 æ 1 ö æ 3 ö A. x + + y + =1 ç ÷ ç ÷ . B. x + + y + = 4 ç ÷ ç ÷ . è 2 3 ø è 2 ø è 2 3 ø è 2 ø 2 2 æ 1 ö æ 3 ö 2 2 æ 1 ö æ 3 ö C. x - + y - =1 ç ÷ ç ÷ . D. x - + y - = 4 ç ÷ ç ÷ . è 2 3 ø è 2 ø è 2 3 ø è 2 ø Lời giải Chọn A 3. 3 -1.1 1
Ta nhận thấy d và d cắt nhau tại O có cos(d ,d = = và O D AB vuông tại 1 2 ) 1 2 3+1. 3 +1 2 B, do đó 0 0
OBA = 60 Þ BAC = 60 (tính chất góc tạo bởi tiếp tuyến và dây cung). 1 3 3 3 Ta có 0 S = A . B AC.sin 60 = OA OA = OA ABC ( 0 .sin 60 ).( 0 .tan 60 ) 2 2 4 8 3 4 Theo giả thiết 2 S = Þ OA = . ABC 2 3 ì 3x + y = 0 ï æ 1 ö Tọa độ ( A ;
x y) với x > 0 , thỏa mãn hệ: í Þ A ; 1 4 - ç ÷ 2 2 ïx + y = è 3 ø î 3
Đường thẳng AC qua A và vuông góc với d nên có phương trình 3x - 3y - 4 = 0 . 1
Hãy tham gia group để cùng học và cùng làm- Nhóm chỉ dành cho các Gv, Sv toán! 61
File làm chuyên đề HÌNH GIẢI TÍCH OXY QUA CÁC THI 3 CHUNG BGD Group FB: Strong Team TOÁN VD–VDC ìï 3x - y = 0 æ 2 - ö Tọa độ C ( ;
x y) thỏa mãn hệ í Þ C ; 2 - ç ÷
ïî 3x -3y - 4 = 0 è 3 ø æ 1 3 ö
Đường tròn (T ) có đường kính AC nên tâm của (T) là I - ;- ç ÷ và bán kính è 2 3 2 ø IA = 1. 2 2 æ 1 ö æ 3 ö
Phương trình của (T ) là: x + + y + =1 ç ÷ ç ÷ . è 2 3 ø è 2 ø
Mail: tieplen@gmail.com
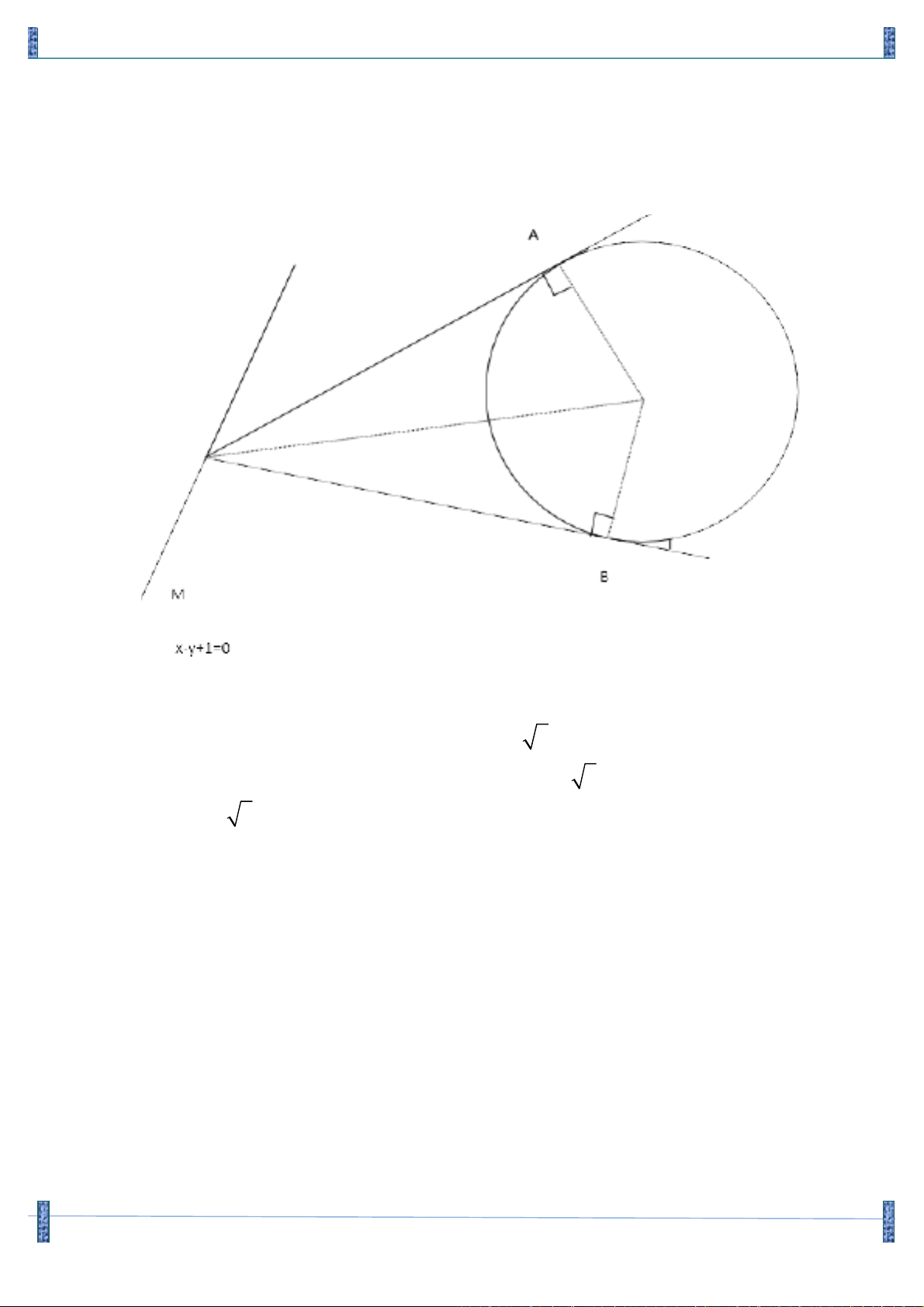
Câu 9. (D2011-1) Trong mặt phẳng tọa độ Oxy , cho A(1;0) và đường tròn 2 2
(C) : x + y - 2x + 4y -5 = 0. Viết phương trình đường thẳng D cắt (C) tại hai điểm M và N sao cho AM D
N vuông cân tại A . Lời giải
Đường tròn (C) có tâm I (1; 2
- ) và bán kính R = 10 !!"
Ta có IA = (0;2) Þ IA = 2 < R Þ A nằm phía trong (C).
Gọi H là trung điểm MN , đặt: AH = a,(0 < a < 2 + 10) . Do AM D
N vuông cân tại A Þ H , ,
A I thẳng hàng và NH = HA = a (1).
Ta có NAM = 90° nên H không thuộc đoạn AI . + Trường hợp 1: 2 2 2
IH = IA+ AH = 2 + a Þ NH = R - IH = a - - 4a + 6 (2). !!" !!!" Từ (1) và (2) 2
Þ a + 2a - 3 = 0 Þ a =1Þ IA = 2AH Þ H = (1;1)
Khi đó phương trình D là: y = 1.
+ Trường hợp 2: IH = AH - IA = a - 2 !!" 2 !!!"
Tương tự ta có: a = 3 Þ IA = - AH Þ H = (1; 3 - ) 3
Hãy tham gia group để cùng học và cùng làm- Nhóm chỉ dành cho các Gv, Sv toán! 62
File làm chuyên đề HÌNH GIẢI TÍCH OXY QUA CÁC THI 3 CHUNG BGD Group FB: Strong Team TOÁN VD–VDC
Khi đó phương trình D là: y = -3.
Câu 10. (D2012-2) Trong mặt phẳng với hệ trục tọa độ Oxy , cho đường thẳng d : 2x - y + 3 = 0 . Viết
phương trình đường tròn có tâm thuộc d , cắt trục Ox tại A và B , cắt trục Oy tại C và D sao
cho AB = CD = 2 .
A. (C) (x + )2 +( y - )2 : 1 1 = 2.
B. (C) (x - )2 +( y + )2 : 3 3 =10.
C. (C) (x + )2 +( y + )2 : 3
3 =10.hoặc (C) (x + )2 +( y - )2 : 1 1 = 2.
D. (C) (x + )2 +( y - )2 : 1
1 = 2.hoặc (C) (x + )2 +( y + )2 : 3 3 =10. Lời giải
Gọi I là tâm của đường tròn (C)cần viết phương trình.
Do I Îd Þ I (t;2t + ) 3 . é = -
AB = CD Û d (I Ox) t 1 ,
= d(I,Oy) Û t = 2t + 3 Û êët = 3- Với t = 1 - Þ I ( 1 - ; )
1 nên d (I,Ox) =1. Suy ra bán kính của (C)là 2 2 1 +1 = 2 . Do đó
(C) (x+ )2 +(y - )2 : 1 1 = 2. Với t = 3 - Þ I ( 3
- ;3)nên d (I,Ox) = 3. Suy ra bán kính của (C)là 2 2 3 +1 = 10. Do đó
(C) (x+ )2 +(y + )2 : 3 3 =10.
Câu 11. (QG 2016-2) Trong mặt phẳng với hệ toạ độ Oxy , cho tứ giác ABCD nội tiếp đường tròn
đường kính BD . Gọi M , N lần lượt là hình chiếu vuông góc của A trên các đường thẳng
BD, BD và P là giao điểm của hai đường thẳng MN, AC . Biết đường thẳng AC có phương
trình x - y -1 = 0, M (0;4), N (2;2) và hoành độ điểm A nhỏ hơn 2. Tìm toạ độ các điểm
P, A và B .
Hãy tham gia group để cùng học và cùng làm- Nhóm chỉ dành cho các Gv, Sv toán! 63
File làm chuyên đề HÌNH GIẢI TÍCH OXY QUA CÁC THI 3 CHUNG BGD Group FB: Strong Team TOÁN VD–VDC Lời giải
Phương trình MN : x + y - 4 = 0. ìx + y - 4 = 0 æ 5 3 ö
Toạ độ P là nghiệm của hệ í Þ P ; . îx y 1 0 ç ÷ - - = è 2 2 ø
Vì AM song song với DC và các điểm ,
A B, M , N cùng thuộc một đường tròn nên ta có
PAM = PCD = ABD = AMP .
Suy ra PA = PM .
Vì AÎ AC : x - y -1 = 0 nên A( ; a a - ) 1 ,a < 2. Ta có: 2 2 2 2 æ 5 ö æ 5 ö æ 5 ö æ 5 ö éa = 0 a - + a - = + Û Þ A(0;- ç ÷ ç ÷ ç ÷ ç ÷ ê ) 1 . è 2 ø è 2 ø è 2 ø è 2 ø ëa = 5
Đường thẳng BD đi qua N và vuông góc với AN nên có phương trình là 2x + 3y -10 = 0.
Đường thẳng BC đi qua M và vuông góc với AM nên có phương trình là y - 4 = 0.
ì2x + 3y -10 = 0
Toạ độ B là nghiệm của hệ í Þ B( 1 - ;4). îy - 4 = 0
Email: Phamhaiduong29@gmail.com
Câu 12. [A2004 DB1] Trong mặt phẳng với hệ tọa độ Oxy cho đường thẳng d :x - y +1- 2 = 0 và điểm A( 1 - ; )
1 . Khi đó có hai phương trình đường tròn đi qua A , gốc tọa độ O và tiếp xúc với
đường thẳng d có tâm lần lượt là I, K . Tìm độ dài IK . A. 3 . B. 2 . C. 2 . D. 1. Lời giải
Họ và tên tác giả:Phạm Hải Dương Tên FB: Duong Pham
Hãy tham gia group để cùng học và cùng làm- Nhóm chỉ dành cho các Gv, Sv toán! 64
File làm chuyên đề HÌNH GIẢI TÍCH OXY QUA CÁC THI 3 CHUNG BGD Group FB: Strong Team TOÁN VD–VDC Chọn B Gọi I ( ;
a b) là tâm đường tròn. Ta có: ( ì a + )2 1 + (b - )2 2 2 1 = a + b 1 2 2 ( ) ìIA = IO ï ï ï í Û í IO = d ïî ( 2 2 2 I (d )) a - b +1- 2 2 2 ïa +b = (2) ïî 2 ( ) éa = 0,b =1
1 Û b = a +1 thế vào (2) được: a + (a + )2 2 2
1 =1 Û 2a + 2a = 0 Û êëa =1,b =0 Suy ra IK = 2
Email: Phamhaiduong29@gmail.com
Câu 13. [A2004 DB1] Trong mặt phẳng với hệ tọa độ Oxy cho đường thẳng d :x - y +1- 2 = 0 và điểm A( 1 - ; )
1 . Khi đó có hai phương trình đường tròn đi qua A , gốc tọa độ O và tiếp xúc với
đường thẳng d có tâm lần lượt là I, K . Tìm độ dài IK . A. 3 . B. 2 . C. 2 . D. 1. Lời giải
Họ và tên tác giả:Phạm Hải Dương Tên FB: Duong Pham Chọn B Gọi I ( ;
a b) là tâm đường tròn. Ta có: ( ì a + )2 1 + (b - )2 2 2 1 = a + b 1 2 2 ( ) ìIA = IO ï ï ï í Û í IO = d ïî ( 2 2 2 I (d )) a - b +1- 2 2 2 ïa +b = (2) ïî 2 ( ) éa = 0,b =1
1 Û b = a +1 thế vào (2) được: a + (a + )2 2 2
1 =1 Û 2a + 2a = 0 Û êëa =1,b =0 Suy ra IK = 2.
Email: honghacma@gmail.com
Câu 14. (B2005-DB1) Trong mặt phẳng với hệ tọa độ Oxy cho hai điểm A(0; 5), B(2; 3). Viết phương
trình đường tròn đi qua hai điểm A, B và có bán kính R bằng 10 A. 2 2
(x+1) + (y - 2) =10 và 2 2
(x - 3) + (y - 6) =10 B. 2 2
(x-1) + (y + 2) =10 và 2 2
(x - 3) + (y - 6) =10 C. 2 2
(x-1) + ( y + 2) = 10 và 2 2
(x + 3) + ( y + 6) = 10 D. 2 2
(x+1) + (y - 2) =10 và 2 2
(x + 3) + (y + 6) =10 Lời giải
Hãy tham gia group để cùng học và cùng làm- Nhóm chỉ dành cho các Gv, Sv toán! 65
File làm chuyên đề HÌNH GIẢI TÍCH OXY QUA CÁC THI 3 CHUNG BGD Group FB: Strong Team TOÁN VD–VDC
Gọi I(a; b) là tâm của đường tròn. Ta có IA=IB= 10 2 2 ìïIA = 10
ìïa + (5-b) =10 Û í Û í 2 2 2 2 ïîIA = IB
ïîa + (5-b) = (2 - a) + (3- ) b 2 2 ìa +(5 - b) =10 ìa = b - 3 Û í Û í 2 2 î4a - 4b = 12 -
î(b - 3) + (5 - b) =10 éìa = 1 - ìa = b - 3 êí ìa = b - 3 ï b êî = 2 Û í Û íéb = 2 Û 2 î2b 16b 24 0 ê - + = ïê ìa = 3 îëb = 6 êí ê b ëî = 6
Vậy phương trình đường tròn là: 2 2
(x+1) + (y - 2) =10 hoặc: 2 2
(x - 3) + (y - 6) =10
Email: honganh161079@gmail.com
Câu 15. Trong mặt phẳng Oxy, cho đường tròn (C): x2 + y2 = 1. Đường tròn (C’) tâm I(2; 2) cắt (C) tại
hai điểm A, B sao cho AB = 2 . Nếu viết phương trình đường thẳng AB dưới dạng
x + ay + b = 0, ,
a bÎ R,b > 0 thì 2 + 2 a b bằng: A. 4. B. 2. C. 1. D. 5. Lời giải
Họ và tên tác giả: Đỗ Thị Hồng Anh Tên FB: Hong Anh Chọn B
Đường tròn (C) có tâm O(0; 0), bán kính R = 1. !!" OI = (2;2)
Đường thẳng AB vuông góc với OI nên phương trình có dạng: x + y + C = 0.
Gọi H là trung điểm AB. Tính được: d O = = 2 R - 2 2 ( ;AB) OH BH = . 2
Hãy tham gia group để cùng học và cùng làm- Nhóm chỉ dành cho các Gv, Sv toán! 66
File làm chuyên đề HÌNH GIẢI TÍCH OXY QUA CÁC THI 3 CHUNG BGD Group FB: Strong Team TOÁN VD–VDC
Từ đó suy ra C = ±1. Do đó phương trình đường thẳng AB cần tìm là x + y +1 = 0.
Email: ngbdai@gmail.com
Câu 16. Trong mặt phẳng với hệ tọa độ Oxy , cho I ( 1
- ;3). Phương trình đường tròn tâm I và cắt
đường thẳng 3x - 4y +10 = 0 tại hai điểm ,
A B sao cho AIB 120° = có dạng 2 2
x + y + ax + by + c = 0. Khi đó T = a + b + c bằng? A. P = 2 . B. P = 4 . C. P = 2 . D. P = 6 . Lời giải
Họ và tên tác giả: Nguyễn Bá Đại Tên FB: Dai NB Chọn B I d A H B 3( 1 - ) - 4.3 +10
Ta có IH = d (I,d ) = = 1 2 2
Þ R = IH + AH = 2 3 + ( 4 - )2 2
Phương trình đường tròn là: (x + )2 +( y - )2 1 3 = 2 hay 2 2
x + y + 2x - 6y + 8 = 0
Vậy T = a + b + c = 4 .
Email: thsphanmanhtruong@gmail.com
Câu 17. Trong mặt phẳng tọa độ Oxy , cho tam giác OAB có các đỉnh ,
A B thuộc đường thẳng
D : 4x + 3y - 12 = 0 và điểm K(6;6) là tâm đường tròn bàng tiếp góc O . Gọi C là điểm
trên đường thẳng D , sao cho AC = AO và C với B khác phía so với A. Biết hoành độ của 24 C là . Gọi ( A x ;y ); (
B x ;y ). Tìm x + x . 15 1 1 2 2 1 2 48 36 12 51
A. x + x = .
B. x + x = .
C. x + x = .
D. x + x = . 1 2 13 1 2 13 1 2 13 1 2 13 Lời giải
Bài 114-B2012-DB1, Phan Mạnh Trường Tên FB: Phan Mạnh Trường Chọn D
Hãy tham gia group để cùng học và cùng làm- Nhóm chỉ dành cho các Gv, Sv toán! 67
File làm chuyên đề HÌNH GIẢI TÍCH OXY QUA CÁC THI 3 CHUNG BGD Group FB: Strong Team TOÁN VD–VDC O A1 24 12 C( ;- ) 5 5 A B :4x+3y-12=0 K(6;6) 24 12 Ta tìm được C(
; - ), phương trình đường phân giác OK : x - y = 0. 5 5
Tham số hóa đường thẳng D , ta gọi điểm (3
A t;4 - 4t). Khi đó: 2 2 24 2 32 2 2 2
AC = AO Û (3t - ) + (4t -
) = 9t + (4 - 4t) Û t = 1 Þ ( A 3;1). 5 5
Gọi A đối xứng với A qua đường OK là đường phân giác của góc phần tư thứ nhất, nên ta 1
tìm được A (1; 3), theo tính chất đường phân giác thì A nằm trên đường thẳng OB . Khi đó 1 1
đường thẳng OB có phương trình: y = 3x . ìï3x - y = 0
Do B = OB Ç D , suy ra tọa độ B là nghiệm của hệ phương trình: í4x + 3y -12 = 0 ïî 12 36 51
Giải hệ ta tìm được: B( ;
). Do đó: x + x = . Chọn đáp án D. 13 13 1 2 13
Email: Samnk.thptnhuthanh@gmail.com
Câu 18. (DỰ bị khối A năm 2002): Trong mặt phẳng tọa độ Oxy, cho đường thẳng
(d) : x - y +1= 0 và đường tròn 2 2
(C) : x + y + 2x - 4y = 0. Giả sử điểm M (x ; y 1 1 )
thuộc đường thẳng (d ) mà qua đó kẻ được hai đường thẳng tiếp xúc với đường tròn (C )tại A
và B sao cho góc AMB bằng 600. Tính 2 2
S = x + y , biết x > 0 1 1 1 A. S = 25 B. S = 13 C. S = 5 D. S = 16
Hãy tham gia group để cùng học và cùng làm- Nhóm chỉ dành cho các Gv, Sv toán! 68
File làm chuyên đề HÌNH GIẢI TÍCH OXY QUA CÁC THI 3 CHUNG BGD Group FB: Strong Team TOÁN VD–VDC Lời giải
Họ và tên tác giả: Nguyễn Khắc Sâm Tên FB: Nguyễn Khắc Sâm Chọn A
Đường tròn (C) có tâm I ( 1
- ;2), bán kính R = 5 . Theo giả thiết ta có góc 0 0
MAB = 60 Þ AMI = 30 Þ MI = 2AI = 2R = 2 5 . Vậy M thuộc đường tròn tâm I 2 2
bán kính 2 5 có phương trình: ( x + )
1 + ( y - 2) = 20. Do M Î(d) nên toạ độ M thoả ìx - y +1 = 0 ï
mãn hệ phương trình: íïî(x+ )2
1 + ( y - 2)2 = 20 éx = 3; y = 4.
Giả hệ phương trình trên ta được : êëx = 3; - y = 2.
Vì x > 0 nên M (3;4). Vậy S=25. 1
facebook: Thuy Tong gmail: tongthuyqn@gmail.com
Câu 19. (A2005 – DB1) Trong mặt phẳng với hệ tọa độ Oxy cho đường tròn (C : 1 ) 2 2
x + y -12x - 4y + 36 = 0. Viết phương trình đường tròn (C tiếp xúc với hai trục tọa độ Ox 2 )
, Oy đồng thời tiếp xúc ngoài với đường tròn (C1)
Hãy tham gia group để cùng học và cùng làm- Nhóm chỉ dành cho các Gv, Sv toán! 69
File làm chuyên đề HÌNH GIẢI TÍCH OXY QUA CÁC THI 3 CHUNG BGD Group FB: Strong Team TOÁN VD–VDC Lời giải (C : 2 2
x + y -12x - 4y + 36 = 0 Û (x - )2 +( y - )2 6
2 = 4, có tâm I 6;2 , bán kính R = 2 . 1 ( ) 1 ) 1
Gọi đường tròn (C có tâm I ;
a b , bán kính R . 2 ( ) 2 ) 2 éb = a
Vì (C tiếp xúc với hai trục tọa độ Ox , Oy Û . 2 ) ê ëb = -a
TH1: b = a , I ; a a 2 ( )
Đường tròn (C tiếp xúc ngoài với đường tròn (C Û I I = R + R 1 ) 2 ) 1 2 1 2
Û (a - )2 + (a - )2 6
2 = a + 2 Û (a - )2 + (a - )2 6 2 = ( a + 2)2 ( ) * éa =18 +) 2 2 2 a ³ 0 : ( )
* Û (a -6) +(a - 2) = (a + 2) 2
Û a - 20a + 36 = 0 Û ê (TM ). ëa = 2 2 2
· a = 18 , phương trình đường tròn (C : (x -18) + ( y -18) = 324. 2 ) 2 2
· a = 2 , phương trình đường tròn (C : (x - 2) + ( y - 2) = 4. 2 ) +) 2 2 2 a < 0 : ( )
* Û (a -6) +(a - 2) = (-a + 2) Û (a - )2
6 = 0 Û a = 6(KTM )
TH2: b = -a : I ; a -a 2 ( )
Đường tròn (C tiếp xúc ngoài với đường tròn (C Û I I = R + R 1 ) 2 ) 1 2 1 2
Û (a - )2 + (-a - )2 6 2 = ( a + 2)2 ( ) ** +) 2 2 2 a ³ 0 , ( )
** Û (a -6) +( a
- - 2) = (a + 2) Û (a - )2
6 = 0 Û a = 6(TM )
Phương trình đường tròn (C : (x - )2 +( y + )2 6 6 = 36. 2 ) +) 2 2 2 a < 0 : ( )
** Û (a -6) +( a - - 2) = (-a + 2) 2
Û a - 4a + 36 = 0(vô nghiệm).
Vậy có ba đường tròn (C thỏa mãn yêu cầu bài toán: (x - )2 +( y - )2 18 18 = 324; 2 ) (x- )2 +(y - )2 2
2 = 4; (x - )2 +( y + )2 6 6 = 36.
Email: Lenguyet150682@gmail.com Chủ đề: Hình giải tích Oxy Faceboook: NguyệtLê
Câu 20. Trong hệ trục vuông góc Oxy , cho đường tròn 2 2
(c ) : x + y = 9 có tâm là I bán kính R và 1 1 1 đường tròn 2 2
(C ) : x + y - 2x - 2y - 23 = 0. Gọi (T) tập hợp các điểm điểm M(x;y) sao 1 cho 2 2 2 2
MI - MI = R - R . Giả sử K(a;b) là điểm nằm trên (T ) sao cho khoảng cách từ 1 2 1 2
K đến I bằng 5. Khi đó 1 A. 2 2 a - b !3. B. 2 2
a - b chỉ có hai ước dương. C. 2 2 a - b = 0.
D. 3a + 4b = 0 . Lời giải Chọn B
Hãy tham gia group để cùng học và cùng làm- Nhóm chỉ dành cho các Gv, Sv toán! 70
File làm chuyên đề HÌNH GIẢI TÍCH OXY QUA CÁC THI 3 CHUNG BGD Group FB: Strong Team TOÁN VD–VDC
I (0;0);R = 3;I (1;1);R = 5. 1 1 2 2 2 2 2 2 2 2 2 2
MI - MI = R - R € (x - 0) + (y- 0) - (x - 1) - (y - 1) = 9 - 25 1 2 1 2
€ x + y + 7 = 0.
Suy ra (T) là đường thẳng có phương trình x + y + 7 = 0. Gọi K(a;b) (
Œ T) là điểm thỏa 2 IK = 25. Ta có 2 2 Ï a Ô + (7 - a) = 25 a È = - 4;b = - 3 Ô Í Ì € . b = 7 - a a Í Ô = - 3;b = - 4 Ô Í Ó Î Suy ra 2 2 a - b = 7 ± . Hình Giải Tích Oxy
Mail: dogiachuyen@gmail.com
Câu 21. (D2010-1) Trong mặt phẳng tọa độ Oxy , cho tam giác ABC có đỉnh A(3; - 7) , trực tâm H (3; - )
1 , tâm đường tròn ngoại tiếp là I ( 2; - 0). Biết C ( ;
a b) và C có hoành độ dương. Đặt 2 2
P = a - b . Chọn khẳng định đúng trong các khẳng định sau? A. P Î( 10 - ;5). B. P Î(5;18). C. PÎ(18; 25). D. PÎ(25;35) Lời giải
Họ tên: Đỗ Gia Chuyên Facebook: Chuyên Đỗ Gia Chọn D
Hãy tham gia group để cùng học và cùng làm- Nhóm chỉ dành cho các Gv, Sv toán! 71
File làm chuyên đề HÌNH GIẢI TÍCH OXY QUA CÁC THI 3 CHUNG BGD Group FB: Strong Team TOÁN VD–VDC A I H B M C D
Đường tròn ngoại tiếp AB
D C có tâm I ( 2;
- 0) , bán kính IA = 74 nên có phương trình: (x+ )2 2 2 + y = 74.
Kẻ đường kính AD ; gọi M là trung điểm BC .
Khi đó, BHCD là hình bình hành, suy ra M là trung điểm HD . !!!" 1 !!!"
Trong tam giác AHD có IM là đường trung bình trong tam giác Þ IM = AH Þ M ( 2; - 3). 2 !!!"
Đường thẳng BC qua M , nhận AH = (0; 6) là véc tơ pháp tuyến nên có dạng: y - 3 = 0. ( ìï x + )2 2 2 + y = 74 ìïx = 2 - ± 65
Tọa độ C là nghiệm của hệ phương trình í Û í ïîy = 3 ïîy = 3
Do C có hoành độ dương nên C ( 2
- + 65; 3), suy ra P = (- + )2 2 2 65 -3 = 58 - 4 65 . Vậy P Î(25; 35).
Email: phamquynhanhbaby56@gmail.com
Câu 22. (DB2/D2010/BGD) Trong mặt phẳng với hệ tọa độ Oxy cho tam giác ABC cân tại B có
tung độ B khác - 3 ; đỉnh A(3;- )
3 và đường tròn nội tiếp tam giác ABC có phương trình x 2 - + y2 ( 1)
= 9. Phương trình đường thẳng BC là
A. 5x +12y + 21 = 0.
B. 12x + 5y + 27 = 0 . C. 5x -12y - 31 = 0 . D. 12x - 5y - 3 = 0. Lời giải
Họ và tên tác giả: Nguyễn Thị Thỏa Facebook: Nguyễn Thị Thỏa Chọn C
Hãy tham gia group để cùng học và cùng làm- Nhóm chỉ dành cho các Gv, Sv toán! 72
File làm chuyên đề HÌNH GIẢI TÍCH OXY QUA CÁC THI 3 CHUNG BGD Group FB: Strong Team TOÁN VD–VDC
Đường tròn nội tiếp tam giác ABC có tâm I (1; ) 0 và bán B kính R = 3 .
Giả sử đường thẳng AC có dạng a x ( - 3) +b y
( + 3) = 0 với a2 +b2 π 0 - a 2 + b 3 Khi đó ta có ( d = R € = 3 I AC ; ) a2 + b2 I € - a + b =
a2 +b2 € a2 2 3 3 5 - 1 a 2 b = 0 a È = 0 A C Í € H Í . a 12 = b 5 ÍÎ
Với a = 0 thì chọn b = 1 ta có phương trình là y + 3 = 0.
Với 12a = 5b thì ta chọn a = 5;b = 12 nên có phương trình là x 5 + 1 y 2 + 21 = 0 .
Vì AB và AC đều tiếp xúc với đường tròn nội tiếp và giả thiết tung độ điểm B khác - 3 .
nên đường thẳng AB có phương trình là x 5 + 1 y
2 + 21 = 0 thì đường thẳng AC có phương trình y + 3 = 0.
Gọi H là hình chiếu của I lên AC ta có ABC cân tại B nên H là trung điểm của AC .
Ta có H(1;- 3) suy ra C (- 1;- )
3 và phương trình BH là x = 1. ⎧⎪ x ⎧⎪ = 1 x = 1 ⎪ ⎛ 13⎞
Tọa độ điểm B là nghiệm của hệ ⎨⎪ ⇔ ⎨⎪ ⇒ B 1 ⎜⎜ ;− ⎟⎟ 5x +12y + 21 = 0 13 ⎜ ⎟ ⎩⎪⎪ y ⎪⎪ = − ⎝⎜ 6 ⎠⎟ ⎩⎪ 6 !! "!⎛ 5⎞ !" Ta có BC −
⎜⎜ 2;− ⎟⎟⎟ nên vec tơ pháp tuyến của BC là n(5;- 1 ) 2 ⎝⎜ 6⎠⎟
Phương trình đường thẳng BC là x 5 - 1 y 2 - 31 = 0.
Email: dacgiap@gmail.com
Câu 23. Cho đường (C) 2 2
: x + y - 2x + 4y + 2 = 0. Tính tổng bình phương bán kính các đường tròn tâm M (5 )
;1 cắt đường tròn (C) tại các điểm ,
A B sao cho AB = 3 . A. 16. B. 46 . C. 56 . D. 59 . Lời giải Chọn C
Hãy tham gia group để cùng học và cùng làm- Nhóm chỉ dành cho các Gv, Sv toán! 73
File làm chuyên đề HÌNH GIẢI TÍCH OXY QUA CÁC THI 3 CHUNG BGD Group FB: Strong Team TOÁN VD–VDC
Phương trình đường tròn (C) 2 2
: x + y - 2x + 4y + 2 = 0 có tâm I (1; 2 - ), R = 3.
Đường tròn (C ') tâm M cắt đường tròn (C) tại ,
A B nên AB ^ IM tại trung điểm H của AB 3
đoạn AB . Ta có AH = BH = = . 2 2
Có 2 vị trí cho AB đối xứng qua tâm I .
Gọi A¢B¢ là vị trí thứ 2 của AB .
Gọi H ¢ là trung điểm của A¢B¢ . 2 æ 3 ö 3 Ta có: 2 2
IH¢ = IH = IA - AH = 3- ç ÷ = ç 2 ÷ 2 è ø
Ta có: MI = ( - )2 + ( + )2 5 1 1 2 = 5 3 7
Và MH = MI - HI = 5 - = 2 2 3 13
MH¢ = MI + H I¢ = 5 + = . 2 2 3 49 52 Ta có: 2 2 2 2
R = MA = AH + MH = + = =13. 1 4 4 4 3 169 172 2 2 2 2
R = MA¢ = A H ¢ ¢ + MH¢ = + = = 43. 2 4 4 4
Hãy tham gia group để cùng học và cùng làm- Nhóm chỉ dành cho các Gv, Sv toán! 74
File làm chuyên đề HÌNH GIẢI TÍCH OXY QUA CÁC THI 3 CHUNG BGD Group FB: Strong Team TOÁN VD–VDC
Vậy tổng bình phương bán kính các đường tròn là 56 .
Email: vanphu.mc@gmail.com
Câu 24. Trong mặt phẳng Oxy cho có phương trình các đường thẳng AB, AC lần lượt là 3x-y+8=0 và
x+y-4=0. Đường tròn đi qua trung điểm các đoạn thẳng HA,HB,HC có phương trình là: 1 25 2 2 x + ( y - ) = , trong đó H ( ;
a b) là trực tâm tam giác ABC và x < 5. Tính giá trị của biểu 2 4 C
thức P = a + b . 1 1 A. P = 2 - . B. P = 2 . C. P = . D. P = - . 2 2 Lời giải
Họ và tên tác giả: Nguyễn Văn Phu Tên FB: Nguyễn Văn Phu Chọn B
* Chứng minh được 9 điểm A', B ',C ', D, E, F, K, ,
L M cùng thuộc một đường tròn (Đường tròn Euler).
* A = AB Ç AC Þ ( A 1 - ;5)
* Gọi E,B’ lần lượt là chân đường cao kẻ từ B và trung điểm của AC é 3 5
B '(2;2), E( ; ) Þ C(5; 1 - ) (L) ê 2 2
EB ' = AC Ç (C) Þ ê 3 5
êB'( ; ),E(2;2) Þ C(4;0) êë 2 2
* Đường thẳng BH qua E và vuông góc với AC có PT x-y=0
* Đường thẳng CH qua C và vuông góc với AB có PT x+3y-4=0.
Điểm H = BH ÇCH Þ H (1;1) Þ a =1;b = 1Þ P = 2
Hãy tham gia group để cùng học và cùng làm- Nhóm chỉ dành cho các Gv, Sv toán! 75
File làm chuyên đề HÌNH GIẢI TÍCH OXY QUA CÁC THI 3 CHUNG BGD Group FB: Strong Team TOÁN VD–VDC
Câu 25. Trong mặt phẳng tọa độ Oxy, cho đương tròn (C) (x - )2 + ( y - )2 : 1
2 = 4 và các đường thẳng
(d : mx + y - m-1= 0, (d : x - my + m-1= 0. Tìm các giá trị của tham số m để mỗi đường 2 ) 1 )
thẳng d , d cắt (C)tại 2 điểm phân biệt sao cho 4 điểm đó lập thành 1 tứ giác có diện tích lớn 1 2
nhất. Khi đó tổng của tất cả các giá trị tham số m là: A. 0 B. 1 C. 2 D. 3 Lời giải
Họ và tên tác giả: Phùng Thị Thu Hằng Tên FB: Phùng Hằng Chọn A
Đường tròn (C)có tâm và bán kính là: I (1;2), R = 2 1 m
Ta có: h = d I,d =
< R = 2, h = d I,d = < R = 2 1 ( 1) 2 ( 2 ) 2 2 m +1 m +1
Suy ra với mọi m mỗi đường thẳng d , d luôn cắt đường tròn (C) tại 2 điểm phân biệt. 1 2
Gọi d cắt (C) tại A, B, d cắt (C) tại C, D khi đó: 1 2 2 2 2 1 4m + 3 m 3m + 4 2 2 2 2
AB = 2 R - h = 2 4 - = 2
, CD = 2 R - h = 2 4 - = 2 1 2 2 2 2 2 m +1 m +1 m +1 m +1 Xét hệ phương trình:
ìmx + y - m -1 = 0
ìy = m +1- mx ï
ìy = m +1- mx ìx = 1 í Û í Û í Û í
îx - my + m -1 = 0 ïx - m î
(m +1- mx) + m -1= 0 îx =1 îy = 1
Suy ra d , d cắt nhau tại M (1; )
1 , IM = 1 < R = 2 nên điểm I nằm trong đường tròn. 1 2 Mặt khác: ( 2 4m + 3)( 2 3m + 4 1 ) 2 2 4m + 3 + 3m + 4
d ^ d Þ AB ^ CD Þ S = A . B CD = 2. £ = 1 1 2 ACBD 2 2 2 m +1 m +1 Vậy (S ) 2 2 2 max
=1 Û 4m + 3 = 3m + 4 Û m = 1 Û m = 1 ± ABCD
Trần Chí Thanh, chithanhlvl@gmail.com
Câu 26. (KA2004) Trong mặt phẳng với hệ tọa độ Oxy cho hai điểm A(0;2) , B(- 3;- ) 1 . Tìm tọa độ
trực tâm H và tọa độ tâm I của đường tròn ngoại tiếp tam giác OAB .
Từ bài toán này ta có hai câu trắc nghiệm như sau:
Câu 27. Trong mặt phẳng với hệ tọa độ Oxy cho hai điểm A(0;2) , B(- 3;- )
1 . Tìm tọa độ trực tâm
H của tam giác OAB . A. H ( 3;- ) 1 . B. H (- 3;- ) 1 . C. H (1;- 3). D. H (1; 3). Lời giải
Hãy tham gia group để cùng học và cùng làm- Nhóm chỉ dành cho các Gv, Sv toán! 76
File làm chuyên đề HÌNH GIẢI TÍCH OXY QUA CÁC THI 3 CHUNG BGD Group FB: Strong Team TOÁN VD–VDC Chọn A !!!"
+ Đường thẳng qua O, vuông góc với BA = (- 3; 3
- ) là d : 3x+3y = 0 1 !!!"
+ Đường thẳng qua B , vuông góc với OA = (0;2) là d : y = 1 - 2
+ Khi đó H = d Ç d Þ H ( 3;- ) 1 . 1 2
Câu 28. Trong mặt phẳng với hệ tọa độ Oxy cho hai điểm A(0;2) , B(- 3;- )
1 . Tìm tọa độ tâm I của
đường tròn ngoại tiếp tam giác OAB . A. I ( 3; ) 1 . B. I (- 3; ) 1 . C. I (- 3;- ) 1 . D. I (1;- 3). Lời giải Chọn B
+ Đường trung trực của cạnh AB là d : 3x + 3y = 0 1
+ Đường trung trực của cạnh OA là d : y =1 3
+ Khi đó I = d Ç d Þ I (- 3; ) 1 1 3
Câu 29. (KB2004) Trong mặt phẳng với hệ tọa độ Oxy cho hai điểm A(1; ) 1 , B(4;- ) 3 . Tìm điểm C
thuộc đường thẳng x - 2y -1 = 0 sao cho khoảng cách từ C đến đường thẳng AB bằng 6 .
Từ bài toán này ta có hai câu trắc nghiệm như sau:
Câu 30. Trong mặt phẳng với hệ tọa độ Oxy cho hai điểm A(1; ) 1 , B(4;- )
3 . Tìm điểm C thuộc đường
thẳng x - 2y -1 = 0 sao cho khoảng cách từ C đến đường thẳng AB bằng 6 , biết rằng hoành
độ của điểm C là một số thực âm. æ 43 27 ö æ 27 43 ö A. C ( 7; - - ) 3 . B. C ( 3; - 7 - ). C. C - ;- ç ÷. D. C - ;- ç ÷. è 11 11 ø è 11 11 ø Lời giải Chọn C x -1 y -1
+ Đường thẳng AB có phương trình là =
Û 4x + 3y - 7 = 0 3 4 -
+ Ta có điểm C thuộc đường thẳng x - 2y -1 = 0 (1) và + -
é4x + 3y - 37 = 0(2a) d (C AB) 4x 3y 7 , = 6 Û = 6 Û ê 2 2 4 + 3
ê4x + 3y + 23 = 0 ë (2b) æ 43 27 ö
+ Có hai điểm C thỏa đề: từ (1) và (2a) Þ C 7;3 ; từ (1) và (2b) Þ C - ;- 1 ( ) 2 ç ÷ è 11 11 ø
Hãy tham gia group để cùng học và cùng làm- Nhóm chỉ dành cho các Gv, Sv toán! 77
File làm chuyên đề HÌNH GIẢI TÍCH OXY QUA CÁC THI 3 CHUNG BGD Group FB: Strong Team TOÁN VD–VDC æ 43 27 ö
+ Vì x < 0 nên chọn C - ;- . C ç ÷ è 11 11 ø
Câu 31. Trong mặt phẳng với hệ tọa độ Oxy cho hai điểm A(1; ) 1 , B(4;- )
3 . Tìm điểm C thuộc đường
thẳng x - 2y -1 = 0 sao cho khoảng cách từ C đến đường thẳng AB bằng 6 , biết rằng tung độ
của điểm C là một số nguyên. A. C ( 7; - - ) 3 . B. C ( 3; - 7 - ). C. C (3;7). D. C (7;3). Lời giải Chọn D x -1 y -1
+ Đường thẳng AB có phương trình là =
Û 4x + 3y - 7 = 0 3 4 -
+ Ta có điểm C thuộc đường thẳng x - 2y -1 = 0 (1) và + -
é4x + 3y - 37 = 0(2a) d (C AB) 4x 3y 7 , = 6 Û = 6 Û ê 2 2 4 + 3
ê4x + 3y + 23 = 0 ë (2b) æ 43 27 ö
+ Có hai điểm C thỏa đề: từ (1) và (2a) Þ C 7;3 ; từ (1) và (2b) Þ C - ;- 1 ( ) 2 ç ÷ è 11 11 ø
+ Vì y Î! nên chọn C (7;3). C
Facebook: Duy Hùng. Email: Duyhungprudential@gmail.com, Đại học khối A -2009 -2
Câu 32. Trong mặt phẳng với hệ tọa độ Oxy, cho đường tròn (C) 2 2
: x + y + 4x + 4y + 6 = 0 và đường
thẳng D : x + my - 2m + 3 = 0 , với m là tham số thực. Gọi I là tâm đường tròn (C).Tìm tổng các
giá trị m để D cắt (C) tại hai điểm phân biệt A và B sao cho diện tích tam giác IAB lớn nhất 15 8 16 17 A. B. C. D. 8 15 7 6 Lời giải Chọn B
Ta có (C) có tâm I ( 2; - 2 - ) . Bán kính R = 2 1 1
Diện tích tam giác IAB là: 2 S = I . A I .
B sin AIB £ R =1. Diện tích S lớn nhất khi và chỉ khi 2 2 IA ^ IB R 2 - - 2m - 2m + 3
Khi đó,khoảng cách từ I đến D : d (I,D) = =1 Û =1 2 2 1+ m
Hãy tham gia group để cùng học và cùng làm- Nhóm chỉ dành cho các Gv, Sv toán! 78
File làm chuyên đề HÌNH GIẢI TÍCH OXY QUA CÁC THI 3 CHUNG BGD Group FB: Strong Team TOÁN VD–VDC é m = 0 (1 4m)2 2 1 m ê Û - = + Û 8 . êm = ë 15 Giachuan85@gmail.com
Câu 33. (D 2003) Trong mặt phẳng với hệ tọa độ Đềcac vuông góc Oxy cho đường tròn ( ) ( - )2 +( - )2 C : x 1
y 2 = 4 , và đường thẳng d
: x - y -1 = 0 . Viết phương trình đường tròn
(C')đối xứng với đường tròn (C)qua đường thẳng d . Tìm tọa độ các giao điểm của(C) và (C'). Lời giải Từ ( ) ( - )2 +( - )2 C : x 1
y 2 = 4 suy ra (C) có tâm I (1;2) và bán kính R = 2 . !
Đường thẳng d có véctơ pháp tuyến là n (1;- )
1 . Do đó đường thẳng D đi qua I (1;2) và x -1 y - 2
vuông góc với d có phương trình: =
Û x + y - 3 = 0. 1 1 -
Tọ độ giao điểm H của d và D là nghiệm của hệ phương trình: ìx - y -1 = 0 ìx = 2 í Û í Þ H (2 ) ;1 . îx + y - 3 = 0 îy =1
ìx = 2x - x = 3
Gọi J là điểm đối xứng với I (1;2) qua d . Khi đó J H I í
Þ J (3;0). Vì (C')đối
y = 2y - y = 0 î J H I
xứng với (C) qua d nên (C') có tâm là J (3;0) và bán kính R = 2 . Do đó (C') có phương trình 2 2
(x - 3) + y = 4.
Tọa độ giao điểm của (C) và (C') là nghiệm của hệ phương trình ( ìï x - )2 1 + ( y - 2)2 = 4 ìx - y -1 = 0 ìy = x -1 éx =1, y = 0 í Û í Û í Û 2 2 2 ê 2 2
ïî(x -3) + y = 4
î(x - 3) + y = 4 î2x -8x + 6 = 0 ëx = 3, y = 2
Vậy tọa độ giao điểm của (C) và (C') là A(1;0) và B(3;2).
Câu 34. Trong mặt phẳng với hệ tọa độ Đềcac vuông góc Oxy cho đường tròn ( ) ( - )2 +( - )2 C : x 1
y 2 = 4 , và đường thẳng d
: x - y -1 = 0 . Đường tròn (C') đối xứng với
đường tròn (C)qua đường thẳng d có tâm ( ;
a b). Tính tổng a + b ? A. 3 - . B. 3 . C. 2 . D. 4 - . Lời giải Chọn B
Hãy tham gia group để cùng học và cùng làm- Nhóm chỉ dành cho các Gv, Sv toán! 79
File làm chuyên đề HÌNH GIẢI TÍCH OXY QUA CÁC THI 3 CHUNG BGD Group FB: Strong Team TOÁN VD–VDC Từ ( ) ( - )2 +( - )2 C : x 1
y 2 = 4 suy ra (C) có tâm I (1;2) và bán kính R = 2 . !
Đường thẳng d có véctơ pháp tuyến là n (1;- )
1 . Do đó đường thẳng D đi qua I (1;2) và x -1 y - 2
vuông góc với d có phương trình: =
Û x + y - 3 = 0. 1 1 -
Tọ độ giao điểm H của d và D là nghiệm của hệ phương trình: ìx - y -1 = 0 ìx = 2 í Û í Þ H (2 ) ;1 . îx + y - 3 = 0 îy =1
ìx = 2x - x = 3
Gọi J là điểm đối xứng với I (1;2) qua d . Khi đó J H I í
Þ J (3;0). Vì (C')đối
y = 2y - y = 0 î J H I
xứng với (C)qua d nên (C') có tâm là J (3;0)
Câu 35. Trong mặt phẳng với hệ tọa độ Đề các vuông góc Oxy cho đường tròn ( ) ( - )2 +( - )2 C : x 1
y 2 = 4 , và đường thẳng d
: x - y -1 = 0 . Đường tròn (C') đối xứng với
đường tròn (C)qua đường thẳng d , gọi các giao điểm của(C) và (C') là A và B. Tính
độ dài đoạn AB .
A. AB = 3 2 .
B. AB = 2 2 .
C. AB = 2 5 .
D. AB = 2 . Lời giải Chọn B Từ ( ) ( - )2 +( - )2 C : x 1
y 2 = 4 suy ra (C) có tâm I (1;2) và bán kính R = 2 . !
Đường thẳng d có véctơ pháp tuyến là n (1;- )
1 . Do đó đường thẳng D đi qua I (1;2) và x -1 y - 2
vuông góc với d có phương trình: =
Û x + y - 3 = 0. 1 1 -
Tọ độ giao điểm H của d và D là nghiệm của hệ phương trình: ìx - y -1 = 0 ìx = 2 í Û í Þ H (2 ) ;1 . îx + y - 3 = 0 îy =1
ìx = 2x - x = 3
Gọi J là điểm đối xứng với I (1;2) qua d . Khi đó J H I í
Þ J (3;0). Vì (C') đối
y = 2y - y = 0 î J H I
xứng với (C) qua d nên (C') có tâm là J (3;0) và bán kính R = 2 . Do đó (C') có phương trình 2 2
(x - 3) + y = 4.
Tọa độ giao điểm của (C) và (C') là nghiệm của hệ phương trình ( ìï x - )2 1 + ( y - 2)2 = 4 ìx - y -1 = 0 ìy = x -1 éx =1, y = 0 í Û í Û í Û 2 2 2 ê 2 2
ïî(x -3) + y = 4
î(x - 3) + y = 4 î2x -8x + 6 = 0 ëx = 3, y = 2
Hãy tham gia group để cùng học và cùng làm- Nhóm chỉ dành cho các Gv, Sv toán! 80
File làm chuyên đề HÌNH GIẢI TÍCH OXY QUA CÁC THI 3 CHUNG BGD Group FB: Strong Team TOÁN VD–VDC
Vậy tọa độ giao điểm của (C) và (C') là A(1;0) và B(3;2) suy ra AB = 2 2 .
Email: lehongphivts@gmail.com
Câu 36. [Câu 33-Khối A 2011-VI.a.1] Trong mặt phẳng tọa độ Oxy , cho đường thẳng D : x + y + 2 = 0
và đường tròn (C) 2 2
: x + y - 4x - 2y = 0 . Gọi I là tâm của (C), M là điểm thuộc D . Qua M
kẻ các tiếp tuyến MA , MB đến (C) ( A và B là các tiếp điểm). Biết rằng có hai vị trí M , M 1 2
của M sao cho tứ giác MAIB có diện tích bằng 10 . Tìm tọa độ trung điểm K của M M ? 1 2 æ 1 5 - ö æ 1 - 3 - ö æ 5 - 1 ö æ 3 - 1 - ö A. K ; ç ÷. B. K ; ç ÷ . C. K ; ç ÷. D. K ; ç ÷. è 2 2 ø è 2 2 ø è 2 2 ø è 2 2 ø Lời giải
Trắc nghiệm hóa: Lê Hồng Phi Tên FB: Lê Hồng Phi Chọn B A I B
x+y+2=0 M
Đường tròn (C) có tâm I (2; )
1 và bán kính IA = 5 . Tứ giác MAIB có 0
MAI = MBI = 90 và MA = MB nên 10 2 2 S = 2S = M . A IA Þ MA =
= 2 5 Þ IM = MA + IA = 5. MAIB MAI 5
Do M Î D nên M (t; t - - 2). Như thế, ét =
IM = 5 Û (t - 2)2 + (t + 3)2 2 2
= 5 Û 2t + 2t -12 = 0 Û êët = 3. -
Suy ra, M 2;- 4 và M 3; - 1 . 2 ( ) 1 ( ) æ 1 - 3 - ö
Vậy tọa độ trung điểm K là K ; ç ÷ . è 2 2 ø
Email: pvbinh161187@gmail.com
Hãy tham gia group để cùng học và cùng làm- Nhóm chỉ dành cho các Gv, Sv toán! 81
File làm chuyên đề HÌNH GIẢI TÍCH OXY QUA CÁC THI 3 CHUNG BGD Group FB: Strong Team TOÁN VD–VDC ⎛ 9 3⎞
Câu 37. (D2013-1) Trong mặt phẳng với hệ tọa độ Oxy , cho tam giác ABC có điểm M − ⎜⎜ ; ⎟⎟ ⎝⎜ 2 2⎠⎟⎟ là
trung điểm của cạnh AB , điểm H (- 2; ) 4 và điểm I (- 1; )
1 lần lượt là chân đường cao kẻ từ
B và tâm đường tròn ngoại tiếp tam giác ABC . Biết điểm C( ;
m n) với m < 0 , giá trị
P = 3m + n là A. P = 6 . B. P = 3. C. P = 0 . D. P = 4 . Lời giải Chọn B B M I C A H !!" ⎛ 7 1⎞ Ta có IM = − ⎜⎜ ; ⎟⎟ ⎝⎜ 2 2⎠⎟⎟.
Vì M ŒAB và AB ^ IM nên đường thẳng AB có phương trình 7x- y +33 = 0.
Vì A ŒAB nên ( A ;7 a a +3 )
3 . Do M là trung điểm của AB nên B(- a- 9;- 7a- 3 ) 0 . !!!" !!!" Ta có 2 HA ^ HB fi .
HA HB = 0 fi a +9a +20 = 0 fi a = - 4 hoặc a = - 5.
Với a = - 4 suy ra A(- 4; ) 5 , B(- 5;- )
2 . Ta có BH ^ AC nên đường thẳng AC có phương
trình x + 2y - 6 = 0. Do đó C(6- 2 ;
c c). Từ IC = IA suy ra ( - c)2 +(c- )2 7 2 1 = 25. Do đó
c =1 hoặc c = 5. Do C khác A , suy ra C(4; )
1 (không thỏa mãn đề bài).
Với a = - 5 suy ra A(- 5;- ) 2 , B(- 4; )
5 . Ta có BH ^ AC nên đường thẳng AC có phương
trình 2x- y +8 = 0. Do đó C(t;2t + )
8 . Từ IC = IA suy ra (t + )2 +( t + )2 1 2 7 = 25. Do đó
t = - 1 hoặc t = - 5 . Do C khác A , suy ra C(- 1; ) 6 (thỏa mãn đề bài).
Vậy m = - 1;n = 6 nên P = 3 .
Email: thuyhung8587@gmail.com
Hãy tham gia group để cùng học và cùng làm- Nhóm chỉ dành cho các Gv, Sv toán! 82
File làm chuyên đề HÌNH GIẢI TÍCH OXY QUA CÁC THI 3 CHUNG BGD Group FB: Strong Team TOÁN VD–VDC
Câu 38. Trong mặt phẳng với hệ tọa độ Oxy , cho tam giác ABC có chân đường phân giác trong của
góc A là điểm D(1;- )
1 . Đường thẳng AB có phương trình 3x + 2y - 9 = 0, tiếp tuyến tại A
của đường tròn ngoại tiếp tam giác ABC có phương trình x + 2y - 7 = 0. Phương trình đường
thẳng BC có dạng x + ay + b = 0 . Khi đó 2018a - 2019b bằng bao nhiêu? A. 2018 . B. 2019 . C. 2020 . D. 2021. Lời giải
Họ và tên tác giả: Cấn Việt Hưng Tên FB: Viet Hung Chọn D Δ A C E B D
+) Gọi D là tiếp tuyến của đường tròn ngoại tiếp !ABC tại A . +) Ta có A( ;
x y) = AD ÇD nên tọa độ của A là nghiệm của hệ phương trình: 3
ì x + 2y - 9 = 0 ìx =1 í Û í Þ A(1;3). îx + 2y - 7 = 0 îy = 3 !!!" +) Có AD = (0; 4
- ) không là VTPT của D Þ AD và D không vuông góc với nhau
Þ D và BC không song song với nhau.
+) Gọi E = D Ç BC ( Và giả sử EB < EC ).
+) Ta có EAB = ACB và BAD = DAC
Suy ra EAD = EAB + BAD = ACB + DAC = ADE Þ!EAD cân tại E .
+) Gọi I là trung điểm của AD Þ I (1; )
1 ,gọi d đường trung trực của AD Þ phương trình
của d là: y -1 = 0. ìx + 2y - 7 = 0 ìx = 5
+) E = d Ç D nên tọa độ của E thỏa mãn hệ phương trình: í Û í Þ E (5; ) 1 îy -1 = 0 îy =1 . !!!"
+) Đường thẳng BC đi qua E (5; )
1 và nhận véctơ DE = (4;2) làm véctơ chỉ phương nên có !
véctơ pháp tuyến là n = (1; 2
- ) Þ phương trình của BC :(x -5) - 2(y -1) = 0 Û x- 2 y-3 = 0.
Hãy tham gia group để cùng học và cùng làm- Nhóm chỉ dành cho các Gv, Sv toán! 83
File làm chuyên đề HÌNH GIẢI TÍCH OXY QUA CÁC THI 3 CHUNG BGD Group FB: Strong Team TOÁN VD–VDC ìa = 2 - Þ í
Þ 2018a - 2019b = 2021. b î = 3 - Hoàng Trâm
Câu 39. Trong mặt phẳng tọa độ Oxy, cho điểm (4
A ;3). Đường thẳng (d) : x- y - 2 = 0 và
(d '): x + y - 4 = 0 cắt nhau tại M . Tìm tọa độ các điểm B ( Œ d) và C (
Œ d ') sao cho A là tâm
đường tròn ngoại tiếp tam giác MBC. Lời giải
B ∈ (d) : x− y−2 = 0 ⇒ B(x ;x −2). B B
C ∈ (d ') : x + y−4 = 0 ⇒ C(x ;4− x ). C C
Ta thấy: d ^ d ' nên D MBC vuông tại M .
Do đó: A là trung điểm của đoạn BC. ⎧⎪x ⎪ + x = 2.4
⎧⎪ + x =8 ⎧⎪ = 6 Suy ra: B c ⎨ ⇔ xB c ⇔ xB
⇒ B(6;4),C(2;2)
x −2+ 4− x = 2.3 ⎨ ⎨ ⎩⎪⎪ x − x = 4 x = 2 B C ⎩⎪⎪ B C ⎩⎪⎪ C
Email: nguyentuanblog1010@gmail.com
Câu 40. (Đề A2002): Trong mặt phẳng với hệ tọa độ Oxy , xét tam giác ABC vuông tại A , phương
trình đường thẳng BC là 3x - y - 3 = 0, các đỉnh ,
A B thuộc trục hoành và bán kính đường
tròn nội tiếp tam giác bằng 2. Gọi G(x ; y với x > 0 là trọng tâm của tam giác ABC . Biết 0 0 ) 0 m m
rằng giá trị của biểu thức T = 2y - x bằng với , m n +
Î! và là phân số tối giản. Khi đó 0 0 n n
kết luận nào dưới dây là đúng ?
A. 3m - 4n = 5
B. m > n
C. m < n +1 D. . m n < 12 .
Chỉnh sửa đề thành đề trắc nghiệm : Phạm Chí Tuân Fb: Tuân Chí Phạm Lời giải Chọn B. y C B x A O
Ta có B = BC ÇOx Þ B(1;0), AÎOx Þ A( ;0
a ). Lại có AC ^ AB và C Î BC Þ C ( ; a 3 (a - ) 1 ).
Lại có: AB = a -1 , AC = 3 a -1 và BC = 2 a -1 .
Hãy tham gia group để cùng học và cùng làm- Nhóm chỉ dành cho các Gv, Sv toán! 84
File làm chuyên đề HÌNH GIẢI TÍCH OXY QUA CÁC THI 3 CHUNG BGD Group FB: Strong Team TOÁN VD–VDC ì x + x + x A B C x = ï G ï 3 æ 2a +1 3(a - ) 1 ö
Vì G là trọng tâm của tam giác ABC nên ta có í ,G ç ; ÷ y + y + y ç 3 3 ÷ ï A B C y = è ø G ïî 3 2a +1 1 Do x > 0 Û > 0 Û a > - . 0 3 2 2S 1 Theo bài ta có ABC r = Û 2. .A .
B AC = 2 AB + BC + CA ABC ( )
AB + BC + CA 2 1 a>- 2 Û (a - )2 3 1 = 2 3 ( 3 + )
1 a -1 Û a -1 = 2( 3 + ) 1 Þ a = 2 3 + 3 ì 7 + 4 3 ïx = 0 æ 7 + 4 3 6 + 2 3 ö ï 5 Vậy 3 G ç ; ÷ Þ í ç
Þ T = 2y - x = Þ m = 5 > n = 3. 3 3 ÷ 0 0 è ø ï 6 + 2 3 3 y = 0 ïî 3
Hãy tham gia group để cùng học và cùng làm- Nhóm chỉ dành cho các Gv, Sv toán! 85
File làm chuyên đề HÌNH GIẢI TÍCH OXY QUA CÁC THI 3 CHUNG BGD Group FB: Strong Team TOÁN VD–VDC
Email: lienquocnl@gmail.com facebook: Phuonglien Le
Câu 1. (KA- 2012-2) Cho đường tròn 𝐶 : 𝑥( + 𝑦( = 8 và elip 𝐸 có độ dài trục lớn bằng 8. Đường
tròn 𝐶 và elip 𝐸 cắt nhau tại 4 điểm tạo thành một hình vuông. Khi đó phương trình chính
tắc của elip 𝐸 là: 2 2 2 2 2 2 2 A. 3 2 + = 1 B. + = 1 C. + = 1 D. + = 1 16 16 16 16 64 16 4 4 3 15 3 Lời giải Chọn B 2 2
Phương trình chính tắc của elip có dạng. + = 1 với >
> 0 và 2 = 8 suy 2 2 ra = 4. Do và đều nhận các trục ,
làm trục đối xứng và cắt nhau tại 4 điểm là đỉnh của
một hình vuông nên có một điểm chung 0; 0
à 0 = 0 ớ 0 > 0 ∈ ⇔ 2 2 0 + 0 = 8 ⇒ 0 = 2. 2; 2 ∈
⇔. 4 + 4 = 1 ⇔ 2 = 16 42 2 3 2 2
Suy ra phương trình chính tắc của là: + = 1. nên chọn B. 16 16 3
Gmail: huuquoc88@gmail.com x y
Câu 2. (A – 2011 (NC)) Trong mặt phẳng toạn đọ Oxy, cho elip (E) 2 2 : + = 1. A, B là 2 điểm có 4 1
hoành độ dương thuộc (E) sao cho tam giác OAB cân và có diện tích lớn nhất. Khi đó tọa độ trung điểm của AB là A. (1;2) B. ( 2;0) C. (- 2; ) 0 D. (2 2;0) Lời giải
Gọi A(x;y). Vì A, B thuộc (E) có hoành độ dương và tam giác OAB cân tại O nên
B ( x;-y), x > 0
Hãy tham gia group để cùng học và cùng làm- Nhóm chỉ dành cho các Gv, Sv toán! 86
File làm chuyên đề HÌNH GIẢI TÍCH OXY QUA CÁC THI 3 CHUNG BGD Group FB: Strong Team TOÁN VD–VDC Khi đó ta có: 2 AB = 2 y = 4 - x
Gọi H là trung điểm AB, Ta có: OH ^ A , B OH = x Suy ra: 1 1 1 2 2 S = O . H AB = .x. 4 - x = x - x £ OA D B ( 2 4 ) 1 2 2 2 Dấu " = " xảy ra 2 2
Û x = 4- x Þ x = 2
Vậy tọa độ trung điểm của AB là H ( 2;0)
Họ tên: Võ Hữu Quốc fb: Hữu Quốc
Email: trichinhsp@gmail.com 2 2 x y
Câu 3. Trong mặt phẳng Oxy, cho điểm C (2;0)và elip (E) : +
=1.Tìm các điểm A,B thuộc 4 1
(E), biết rằng 2 điểm A,B đối xứng nhau qua trục hoành và tam giác ABC là tam giác đều. Khi
đó diện tích S của tam giác ABC là kết quả nào dưới đây: 4 3 16 3 48 3 16 A. S = . B. S = . C. S = . D. S = . 7 49 49 49 Lời giải
Họ và tên tác giả: Nguyễn Trí Chính Tên FB: Nguyễn Trí Chính Chọn C Gọi A( ;
x y). Do A, B đối xứng nhau qua Ox nên B( ;
x -y) và Ox là đường trung trực của BC
Có C (2;0)ÎOx. Suy ra CA = CB = (x - )2 2
2 + y , Có AB = 2 y 2 2 x y 1 Có A( ; x y)Î(E) 2 : + =1Þ y = ( 2 4 - x ) 4 1 4 AB
D C đều Û AB = AC = BC Û y = (x - )2 2 2 4 2 + y Û 3y = (x - 2)2 1 2 2 ; y = ( 2 4 - x ) 4 3
Û (4- x ) = (x - 2)2 2 4
éx = 2; y = 0(º C) 2
Û 7x -16x + 4 = 0 ê Û ê 2 4 3 x = ; y = ± êë 7 7 æ 2 4 3 ö æ 2 4 3 ö æ 2 4 3 ö æ 2 4 3 ö Vậy Aç ; ÷ ç và Bç ;- ÷ hay Aç ;- ÷, Bç ; ÷ 7 7 ÷ ç ÷ ç ÷ ç ÷ è ø 7 7 è ø 7 7 è ø 7 7 è ø
Hãy tham gia group để cùng học và cùng làm- Nhóm chỉ dành cho các Gv, Sv toán! 87
File làm chuyên đề HÌNH GIẢI TÍCH OXY QUA CÁC THI 3 CHUNG BGD Group FB: Strong Team TOÁN VD–VDC 8 3 2 AB . 3 48 3 Khi đó AB = , dt ( ABC) = = 7 4 49
Email: pandahoa@gmail.com
Câu 4. (D2008) Trong mặt phẳng với hệ tọa độ Oxy , cho parabol (P) 2
: y =16x và điểm A(1;4) . Hai
điểm phân biệt B , C ( B và C khác A ) đi động trên (P) sao cho góc o BAC = 90 . Đường
thẳng BC luôn đi qua một điểm cố định I . Tọa độ I là: A. I (17;- 4). B. I ( 17 - ;- 4). C. I (17;4). D. I ( 17 - ;4). Lời giải
Họ và tên tác giả: Nguyễn Phú Hòa Tên FB: Nguyễn Phú Hòa Chọn A 2 æ b ö 2 æ c ö
Do hai điểm phân biệt B , C thuộc (P) ( B và C khác A ) nên B ; ç b÷, C ; ç c ÷, b ¹ 4 , è16 ø è16 ø c ¹ 4 . 2 !!!" æ b ö 2 !!!" æ c ö
Khi đó: AB = ç -1;b - 4÷, AC = ç -1;c - 4÷. è16 ø è16 ø !!!" !!!" 2 2 æ b öæ c ö Theo đề: o BAC = 90 Þ .
AB AC = 0 Û ç -1÷ç -1÷ +(b - 4)(c - 4) = 0 è16 øè16 ø ( æ + + ö
Û b - )(c - ) b 4 c 4 4 4 . +1 = 0 ç ÷ è 16 16 ø éb = 4 ê Û c = 4 ê
Û bc + 4(b +c)+16.17 = 0 ( ) 1 . êbc + 4 ë (b +c)+ 272 = 0 2 c x - y - c
Mặt khác, phương trình đường thẳng 16 BC : =
Û16x -(b +c) y +bc = 0(2). 2 2 b c b - c - 16 16 Từ ( )
1 và (2) suy ra BC luôn đi qua một điểm cố định I (17;- 4).
Email: vukieuoanh2405@gmail.com 2 2 x y
Câu 5. (B2003-DB1) Trong mặt phẳng tọa độ Oxy cho Elip (E) : +
=1.Gọi (d ; d là các 1 ) ( 2 ) 9 4
tiếp tuyến của (E) đi qua điểm N (1;- )
3 . Tổng tung độ các tiếp điểm là: -216 72 17 - 29 A. .. B. .. C. . D. . 85 85 5 17
Hãy tham gia group để cùng học và cùng làm- Nhóm chỉ dành cho các Gv, Sv toán! 88
File làm chuyên đề HÌNH GIẢI TÍCH OXY QUA CÁC THI 3 CHUNG BGD Group FB: Strong Team TOÁN VD–VDC Lời giải
Họ và tên tác giả: Vũ Kiều Oanh Tên FB: Rio Vũ Vũ Chọn A 2 2 ( ) x y E : + =1. 9 4 . x x . y y
Phương trình tiếp tuyến của elip (E) tại điểm M (x ; y Î E là: 0 0 + =1. 0 0 ) ( ) 9 4
Vì tiếp tuyến của (E) đi qua điểm N (1;- ) 3 nên ta có: 1.x 3 - .y 0 ( ) 0 + =1 9 4 27 Û x = y + 9 0 0 4
(học sinh có thể rút y theo x nhưng vì yêu cầu tìm tổng các tung độ của các tiếp điểm 0 0
nên việc rút x theo y sẽ thuận tiện tính tổng các nghiệm nhanh hơn dựa vào định lí Vi-et). 0 0 2 2 x y
Mà M (x ; y Î E 0 0 Þ + =1. 0 0 ) ( ) 9 4 2 1 æ 27 ö 1 2 Þ y + 9 + y = 1 ç 0 ÷ 0 9 è 4 ø 4 81 27 1 2 2 Û y +
y + 9 + y -1 = 0 0 0 0 16 2 4 85 27 2 Û y + y + 8 = 0 0 0 16 2 é 8 - y = ê 0 5 Û ê . 16 - ê y = 0 êë 17
(hoặc dựa vào định lí Vi-et để tính tổng mà không cần tính rõ 2 nghiệm) -216
Tổng các tung độ của các tiếp điểm là . 85 Đáp án A. 2 2 x y
Câu 6. Trong mặt phẳng tọa độ Oxy cho Elip (E) : +
=1 và đường thẳng (d mx - y - = . m ) : 1 0 9 4
Hãy tham gia group để cùng học và cùng làm- Nhóm chỉ dành cho các Gv, Sv toán! 89
File làm chuyên đề HÌNH GIẢI TÍCH OXY QUA CÁC THI 3 CHUNG BGD Group FB: Strong Team TOÁN VD–VDC
Số giá trị nguyên dương của m không vượt quá 2019 để (d cắt (E) tại hai điểm phân biệt là: m ) A. 2019 . B. 2018 . C. 2020 . D. 2017 . Lời giải Chọn A
Xét elip (E) có a = 3;b = 2. 1 Ta có: d ( ; O d = . m ) 2 m +1 Vì 2
m +1 ³1Þ 0 < d ( ;
O d ) £1Þ d ( ; O d
< b < a nên (d luôn cắt (E) tại hai điểm phân biệt với m ) m m ) m " Î ! . Mà 1 £ m £ 2019 .
Nên có 2019 giá trị nguyên của m thỏa mã yêu cầu bài toán.
Câu 7. (DỰ BN 2_KHỐI D_2003) Trong mặt phẳng với hệ tọa độ Oxy, cho parabol (P) 2 : x = y và !!!" !!"
điểm I (0;2). Tìm tọa độ hai điểm M , N thuộc (P) sao cho IM = 4IN. Lời giải Gọi N ( 2
n ;n)Î(P) !!" !!!" Khi đó IN = ( 2
n ;n - 2). Gọi M ( ;
x y) thì IM = ( ; x y - 2) 2 2 !!!" !!" ìï x = 4n ì x = 4n
Từ giải thiết: IM = 4IN Þ í Þí Þ M ( 2 4n ;4n - 6) ïy - = î (n- ) . 2 4 2 îy = 4n - 6 én = 3
Vì M Î(P) Þ 4n = (4n - 6)2 2 Þ êën=1 ìï N (1 ) ;1 ìï N (9;3) Vậy í hoặc í ïM î (4; 2 - ) ïM î (36;6) TRẮC NGHIỆM HÓA
Câu 8. DỰ BN 2_KHỐI D_2003 Trong mặt phẳng với hệ tọa độ Oxy, cho parabol (P) 2 : x = y và !!!" !!"
điểm I (0;2). Gọi M và N là hai điểm thuộc (P) sao cho IM = 4IN.Tổng các hoành độ của
M và N chia hết cho số nào dưới đây? A. 5 B. 2 C. 6 D. 4 Lời giải Chọn A
Email: Levietthuong38@gmail.com
Hãy tham gia group để cùng học và cùng làm- Nhóm chỉ dành cho các Gv, Sv toán! 90
File làm chuyên đề HÌNH GIẢI TÍCH OXY QUA CÁC THI 3 CHUNG BGD Group FB: Strong Team TOÁN VD–VDC 2 2 x y
Câu 9. Trong mặt phẳng với hệ tọa độ Oxy , cho elip (E): +
=1. Viết phương trình hypebol (H) 12 2
có hai đường tiệm cận là y = 2
± x và có hai tiêu điểm là hai tiêu điểm của elip (E). Lời giải
Elip (E) có hai tiêu điểm 1 F (- 10;0), 2 F ( 10;0) 2 2 x y
Giả sử phương trình (H) là - =1 2 2 a b
Tiêu điểm của (H) lần lượt là F ( ;0 c -
), F '( ;c0),( 2 2 2
c = a + b ) b
Phương trình hai đường tiệm cần là y = ± x a ìc = 10 ï Theo bài rat a có íb ï = 2 îa 2 2 2 2 2
ìïa + b =10 ìïa + b =10 ìïa = 2 Û í Þ í Þ í 2 2 2 b ïî = 2a b ïî - 4a = 0 b ïî = 8 2 2 x y
Vậy phương trình (H) cần tìm là - =1 2 8
Người gửi: Lương Văn Huy – Mail:Luongvanhuydhsphn@gmail.com
Email: letai868686@gmail.com
Câu 10. Trong mặt phẳng với hệ tọa độ Oxy, biết elip (E) có độ dài trục lớn bằng 4 2 , các đỉnh trên
trục nhỏ và các tiêu điểm của (E) cùng nằm trên một đường tròn.Giả sử phương trình chính tắc 2 2 x y của elip (E) có dạng +
=1. Tính giá trị biểu thức P = a 2 +b 2 2 a b A. P = 6 . B. P = 4 . C. P = 8 . D. P = 4 2 . Lời giải
Họ và tên tác giả: lê ngọc tài Tên FB: lê Tài
Hãy tham gia group để cùng học và cùng làm- Nhóm chỉ dành cho các Gv, Sv toán! 91
File làm chuyên đề HÌNH GIẢI TÍCH OXY QUA CÁC THI 3 CHUNG BGD Group FB: Strong Team TOÁN VD–VDC 2 2 x y
Phương trình chính tắc của (E) có dạng +
=1 với a>b>0. Đỉnh thuộc trục nhỏ là B(0;b), 2 2 a b
B’(0;-b) và tiểu điểm là F(c;0); F’(-c;0).
Vì tứ giác FBF’B’ hai đường chéo vuông góc cắt nhau tại trung điểm lên là hình thoi đồng thời
nội tiếp lên tứ giác FBF’B’ là hình vuông Þ 2 2 2 2
2BF = F ' F Û b = c Û b = c. 2 2 2
ìa = b + c 2 2 ï ìïa = 2 2 x y Vậy ta có b í = c Þ í Þ +
= 1là phương trình chính tắc của (E). b ï ïî = c = 2 8 4 îa = 2 2 Chọn: A.
Câu 11. (D2008) Trong mặt phẳng với hệ tọa độ Oxy , cho parabol (P) 2
: y =16x và điểm A(1;4) . Hai
điểm phân biệt B , C ( B và C khác A ) đi động trên (P) sao cho góc o BAC = 90 . Đường
thẳng BC luôn đi qua một điểm cố định I . Tọa độ I là: A. I (17;- 4). B. I ( 17 - ;- 4). C. I (17;4). D. I ( 17 - ;4). Lời giải Chọn A 2 æ b ö 2 æ c ö
Do hai điểm phân biệt B , C thuộc (P) ( B và C khác A ) nên B ;b ç ÷, C ;c ç ÷, b ¹ 4 , è16 ø è16 ø c ¹ 4 . 2 !!!" æ b ö 2 !!!" æ c ö
Khi đó: AB = ç -1;b - 4÷, AC = ç -1;c - 4÷. è16 ø è16 ø !!!" !!!" 2 2 æ b öæ c ö Theo đề: o BAC = 90 Þ .
AB AC = 0 Û ç -1÷ç -1÷ +(b - 4)(c - 4) = 0 è16 øè16 ø
Hãy tham gia group để cùng học và cùng làm- Nhóm chỉ dành cho các Gv, Sv toán! 92
File làm chuyên đề HÌNH GIẢI TÍCH OXY QUA CÁC THI 3 CHUNG BGD Group FB: Strong Team TOÁN VD–VDC ( æ + + ö
Û b - )(c - ) b 4 c 4 4 4 . +1 = 0 ç ÷ è 16 16 ø éb = 4 ê Û c = 4 ê
Û bc + 4(b +c)+16.17 = 0 ( ) 1 . êbc + 4 ë (b +c)+ 272 = 0 2 c x - y - c
Mặt khác, phương trình đường thẳng 16 BC : =
Û16x -(b +c) y +bc = 0(2). 2 2 b c b - c - 16 16 Từ ( )
1 và (2) suy ra BC luôn đi qua một điểm cố định I (17;- 4).
Email: tranthanhsonndc@gmail.com 2 2 x y
Câu 12. Trong mặt phẳng với hệ tọa độ Oxy cho elip (E) : +
=1. Gọi (d ) là đường thẳng đi qua 4 1 M ( 2;
- 3), tiếp xúc với (E) tại N (x ; y không trùng với đỉnh của (E). Khi đó giá trị của 0 0 )
biểu thức T = x + 4y bằng 0 0 4 11 A. T = 1. B. T = 4 .
C. T = - . D. T = . 5 5
Họ và tên tác giả: Trần Thanh Sơn Tên FB: Trần Thanh Sơn Lời giải Chọn B
Gọi (d ): ax +by + c = 0, ( 2 2
a + b ¹ 0). Ta có (d ) tiếp xúc với (E) 2 2 2
Û 4a + b = c . Lại có M ( 2; - ) 3 Î(d ) Þ 2
- a + 3b + c = 0 . 2 2 2
ì4a + b = c éb = 0 Do đó ta được hệ 2 í
Þ 8b -12ab = 0 Û ê . î 2
- a + 3b = c - ë2b = 3a
Với b = 0 không thỏa. ìa = 2
Với 3a = 2b chọn í
Þ (d): 2x +3y -5 = 0. b î = 3
Hãy tham gia group để cùng học và cùng làm- Nhóm chỉ dành cho các Gv, Sv toán! 93
File làm chuyên đề HÌNH GIẢI TÍCH OXY QUA CÁC THI 3 CHUNG BGD Group FB: Strong Team TOÁN VD–VDC xx yy
Mặt khác, tiếp tuyến của (E) tại N (x ; y : 0 0 +
=1. Tiếp tuyến này trùng với (d ) suy 0 0 ) 4 1 ì 8 x = x 4y 4 - ï 0 ï ra 0 0 Þ = = 5 æ 8 3 ö Û í Þ N ; . 2 3 5 - 3 ç ÷ ï è 5 5 ø y = 0 ïî 5 8 12
Vậy T = x + 4y = + = 4. 0 0 5 5
Đề khối A năm 2008_thuytoanqx2@gmail.com
Câu 13. Trong mặt phẳng với hệ trục tọa độ vuông góc Oxy,elip (E) có phương trình: 2 2 x y + = 5
1 (0 < b < a) có tâm sai e =
.Các đường thẳng x = ±a ; y = ±b tạo thành một hình 2 2 a b 3
chữ nhật có chu vi bằng 20. Gọi F , F là hai tiêu điểm của (E). M , N là hai điểm thuộc (E) 1 2
sao cho MF + NF = 4.Tính giá trị biểu thức T = MF + NF 1 2 2 1 A. T = 4 B. T = 8 C. T = 2 D. T = 4 5 - 4 Lời giải
Tác giả:lê thị thúy Tên FB: ThúyLê Chọn B ì c 5 ï = a 3 ïï ìa = 3
Từ giả thiết ta có hệ phương trình í2(2a + 2b) = 20.Giải hệ phương trình ta tìm được í ï b î = 2 2 2 2 c = a - b ï ïî
MF + MF = 2a = 6
Với " M , N thuộc (E) ta có 1 2
suy ra T = MF + NF =12- (MF + NF )
NF + NF = 2a = 6 2 1 1 2 1 2 =8
Email: thuoanh2207@gmail.com
Câu 14. Trong mặt phẳng với hệ tọa độ Oxy, cho hình thoi ABCD có AC = 2BD và đường tròn tiếp xúc
với các cạnh của hình thoi có phương trình 2 2
x + y = 4. Phương trình chính tắc của elip (E) đi
qua các đỉnh A, B, C, D của hình thoi, biết A thuộc Ox. Tổng bình phương độ dài trục lớn và trục nhỏ của (E) là: A. 100 B. 90 C. 80 D. 120 Lời giải
Họ và tên: Nguyễn Thị Thu Oanh - Tên FB: Thu oanh
Hãy tham gia group để cùng học và cùng làm- Nhóm chỉ dành cho các Gv, Sv toán! 94
File làm chuyên đề HÌNH GIẢI TÍCH OXY QUA CÁC THI 3 CHUNG BGD Group FB: Strong Team TOÁN VD–VDC
Ta có AC = 2BD nên OC = 2OB. Trong tam giác OBC: 1 1 1 1 1 1 + = € +
= € OB = 5,OC = 2 5 2 2 2 2 OB OC 4 OB 4OB 4
Nên độ dài trục lớn là 4 5 , độ dài trục nhỏ 2 5 . 2 2
Vậy (4 5) +(2 5) =100. Chọn A.
Cách hỏi 2: Giả sử hoành độ điểm A, C lần lượt là x1, x2. Tung độ điểm B, D lần lượt là y1, y2. Tính x1. x2 + y1. y2 A. -25 B. -24 C. -22 D. -26
Email: ngocsonnguyen82@gmail.com
Câu 15. (Bài 88-D2006 DB2) Trong mặt phẳng với hệ tọa độ Oxy , phương trình chính tắc của elip 2 2 ( ) x y E : +
=1, biết (E) có độ dài trục lớn bằng 4 2 , các đỉnh trên trục nhỏ và các tiêu 2 2 a b
điểm của (E) cùng nằm trên một đường tròn khí đó tỉ số 2 2 a + b bằng A. 12. B. 10 . C. 16 . D. 48 Lời giải
Họ và tên tác giả: Nguyễn Ngọc Sơn Tên FB: Ngoc Son Nguyen Chọn A
+ Vì độ dài trục lớn của (E) bằng 4 2 nên ta có: 2a = 4 2 Û a = 2 2
+Vì các đỉnh trên trục nhỏ và các tiêu điểm của (E) cùng nằm trên một đường tròn nên b = c
+ ADCT: b + c = a Û b = ( )2 2 2 2 2 2
2 2 Û b = 2 (do b > 0 ) + 2 2 a + b = 12. 2 2 x y
Câu 16. [Khối D-2005] Trong mặt phẳng tọa độ Oxy , cho điểm C (2;0) và elip (E) : + =1. Các 4 1 điểm ,
A B thuộc (E)và ,
A B đối xứng qua trục hoành đồng thời tam giác ABC là tam giác
đều. Gọi S, P, R, r lần lượt là diện tích, chu vì, bán kính đường tròn ngoại tiếp, bán kính đường
tròn nội tiếp tam giác ABC . Mệnh đề nào sau đây là sai?
Hãy tham gia group để cùng học và cùng làm- Nhóm chỉ dành cho các Gv, Sv toán! 95
File làm chuyên đề HÌNH GIẢI TÍCH OXY QUA CÁC THI 3 CHUNG BGD Group FB: Strong Team TOÁN VD–VDC S P S S R A. < 1. B. > 4. C. <1. D. = . 3 3 P P 2 Lời giải Chọn B Gọi A( ; a b) Vì ,
A B đối xứng với nhau qua trục hoành suy ra B( ; a b - ) 2 2 2 a b a
Có A(a b)Î(E) 2 ; Û + =1Û b =1- ( )1 4 1 4
Tam giác ABC cân tại C nên tam giác đều AB = AC Û b = (a - )2 2 2 4 2 + b (2) Từ ( ) 1 ,(2)ta có hệ éì 2 a = ì 2 êï é ï 7 a = ê êï í é æ 2 4 3 ö æ 2 4 3 7 ö ï ê 2 4 3 ì ê ï í = êAç ; ÷; B ç ; a - ÷ 2 b b ï = 1- ê 48 ê ç ï 7 7 ÷ ç 7 7 ÷ 2 ï î 7 ê è ø è ø í 4 Û b = Û ê Û êï ê î . ê ï ì æ ö æ ö b = î (a - ) 49 2 2 2 2 + ê = ê 2 4 3 2 4 3 4 2 b a ê êì = ï Aç ;- ÷; B ç ; a 2 ï 7 ÷ ê ç 7 7 ÷ ç 7 7 ÷ í (l) ê ê í ë è ø è ø b ëî = 0 ê 4 3 b ï = - êï ëî 7 8 3 12 48 3 24 3 2 4 Khi đó AB =
;d (C; AB) = suy ra S = ; P = ;r = ; R = . 7 7 49 7 7 7 Vậy chọn đáp án B. Facebook: Dangquang
Mail: Dangvanquanggb1@gmail.com
Email: chitoannd@gmail.com
Câu 17. Trong mặt phẳng với hệ tọa độ Đề các vuông góc Oxy, cho elip có phương trình: 2 2 ( ) x y E : +
=1. Xét điểm M chuyển động trên tia Ox và điểm N chuyển động trên tia Oy sao 16 9
cho đường thẳng MN luôn tiếp xúc với (E). Xác định tọa độ của M, N để đoạn MN có độ dài
nhỏ nhất. Tính giá trị nhỏ nhất đó. Lời giải
Họ và tên tác giả: Nguyễn Văn Chí Tên FB: Nguyễn Văn Chí Giả sử M ( ;0
m ), N (0;n) với m > 0;n > 0là hai điểm chuyển động trên hai tia Ox, Oy. x y
Phương trình của đường thẳng MN : + -1 = 0. m n 2 2 æ 1 ö æ 1 ö
Đường thẳng tiếp xúc với (E) khi và chỉ khi 16 + 9 = 1 ç ÷ ç ÷ . è m ø è n ø
Hãy tham gia group để cùng học và cùng làm- Nhóm chỉ dành cho các Gv, Sv toán! 96
File làm chuyên đề HÌNH GIẢI TÍCH OXY QUA CÁC THI 3 CHUNG BGD Group FB: Strong Team TOÁN VD–VDC æ 16 9 ö
Áp dụng bất đẳng thức CôSi ta có: 2 2 2
MN = m + n = ( 2 2 m + n ) + ç 2 2 ÷ è m n ø 2 2 n m = 25 +16 + 9
³ 25 + 2 16.9 = 49 Þ MN ³ 7 . 2 2 m n 2 2 16 ì n 9m = ï 2 2 m n ì ï ì M ï ïm = ï (2 7;0 2 7 )
Đẳng thức xảy ra khi và chỉ khi: 2 2
ím + n = 49 Û í ¾¾ ®í . ï ïîn = 21 ïN m > n > î (0; 21 0, 0 ) ï ïî
Câu 18. Trong mặt phẳng với hệ tọa độ Đề các vuông góc Oxy, cho elip có phương trình: 2 2 ( ) x y E : +
=1. Xét điểm M chuyển động trên tia Ox và điểm N chuyển động trên tia Oy sao 16 9
cho đường thẳng MN luôn tiếp xúc với (E). Biết rằng khi tọa độ của M, N thỏa mãn đoạn MN
có độ dài nhỏ nhất. Tính giá trị nhỏ nhất đó thuộc khoảng? A. (6;9) . B. ( 21;2 7 ). C. (46;48). D. (48;50). Lời giải Chọn A
Câu 19. Trong mặt phẳng với hệ tọa độ Đề các vuông góc Oxy, cho elip có phương trình: 2 2 ( ) x y E : +
=1. Xét điểm M chuyển động trên tia Ox và điểm N chuyển động trên tia Oy sao 16 9
cho đường thẳng MN luôn tiếp xúc với (E). Biết rằng khi tọa độ của M, N thỏa mãn đoạn MN
có độ dài nhỏ nhất. Tính giá trị của biểu thức T = 2018x + 2019 3y . M M A. T =10093 7 . B. T = 2021 - 7 . C. T =10039 7 . D. T = 2021 7 . Lời giải Chọn A
Email: nguyendangdungpc@gmail.com 2 2 x y
Câu 20. Trong mặt phẳng tọa độ Oxy , cho điểm A(2; 3) và elip(E): + =1. Gọi F ,F là các tiêu 3 2 1 2
điểm của (E), ( F có hoành độ âm), M là giao điểm có tung độ dương của đường thẳng AF 1 1
với (E), N là điểm đối xứng với F qua M . Bán kính đường tròn ngoại tiếp tam giác ANF có 2 2 độ dài là. 2 3 A. 1. B. . C. 2 . D. 3 . 3 Lời giải 2 2 (E) x y 2 2 2 : +
=1Þ c = a -b = 3- 2 =1. Do đó F ( 1 - ;0), F (1;0) 3 2 1 2
Hãy tham gia group để cùng học và cùng làm- Nhóm chỉ dành cho các Gv, Sv toán! 97
File làm chuyên đề HÌNH GIẢI TÍCH OXY QUA CÁC THI 3 CHUNG BGD Group FB: Strong Team TOÁN VD–VDC
Đường thẳng AF có phương trình x - y 3 +1 = 0 1
M là giao điểm có tung độ dương của đường thẳng AF với (E) 1 ì 2 2 x y ï + = 1 æ 2 ö
Giải hệ phương trình í 3 2 Þ M 1; ç ÷ ï è 3 ø îx - y 3 +1 = 0 æ ö !!!" æ ö N 4 1
là điểm đối xứng với F qua M suy ra N 1; và NA = 1; - 2 ç ÷ ç ÷ è 3 ø è 3 ø !!!" !!!" !!!"
Mà F A = 1; 3 Þ NA.F A = 0 Þ DANF 2 ( ) 2
2 vuông tại A nên đường tròn ngoại tiếp tam giác
này có đường kính là F2N suy ra bán kính của đường tròn ngoại tiếp tam giác ANF là 2 2 3 R = 3
Họ và tên tác giả: Nguyễn Đăng Dũng Tên FB: Dũng Nguyễn Đăng
Email: manhluonghl4@gmail.com 2 2 x y
Câu 21. Trong mặt phẳng với hệ tọa độ Oxy cho elip (E) : +
=1. Biết rằng có hai tiếp tuyến của 8 4
(E) song song với đường thẳng d : x + 2y -1= 0. Khi đó khoảng cách giữa hai tiếp tuyến đó bằng: 8 3 8 2 8 6 A. 8 . B. . C. . D. . 3 3 3 Lời giải
Họ và tên tác giả: Nguyễn Văn Mạnh Tên FB: Nguyễn Văn Mạnh Chọn B
Gọi D là tiếp tuyến cần tìm, do D / /d : x + 2y -1 = 0 Þpt x + m
D : x + 2y + m = 0 Û pt D : y = - 2 ( với m ¹ 1
- ). Xét phương trình hoành độ giao điểm của (E) và D : x (x + m)2 2 2 2 +
=1 Û 2x + 2mx + m -8 = 0 (*). D là tiếp tuyến với (E) € pt (*) có nghiệm 8 8 kép ém = 4 2 Û D¢ = m - 2( 2 m -8) 2 = 0 Û16 - m = 0 Û ê ( thỏa mãn m ¹ 1 - ). ëm = 4 -
Với m = 4 ta được tiếp tuyến D : x + 2y + 4 = 0 1
Hãy tham gia group để cùng học và cùng làm- Nhóm chỉ dành cho các Gv, Sv toán! 98
File làm chuyên đề HÌNH GIẢI TÍCH OXY QUA CÁC THI 3 CHUNG BGD Group FB: Strong Team TOÁN VD–VDC Với m = 4
- ta được tiếp tuyến D : x + 2y - 4 = 0 2 4 - ( 4 - ) 8 8 3
Khi đó khoảng cách giữa hai tiếp tuyến là d (D ;D = = = Þ chọn B. 1 2 ) 1+ 2 3 3 ĐỀ DỰ BỊ KHỐI D 2005 2 2 x y
Câu 22. Trong mặt phẳng với hệ tọa độ Oxy cho elip (E) : +
=1. Viết phương trình tiếp tuyến d của 64 9
(E) , biết d cắt hai trục tọa độ Ox , Oy lần lượt tại A, B sao cho OA = 2 . OB 2304 3200 1152 288 A. B. C. D. 25 729 25 25 Lời Giải:
Gọi M (x ; y là tiếp điểm của tiếp tuyến d với (E). 0 0 ) x .x y .y 9 - x 9
Phương trình tiếp tuyến d có dạng 0 0 0 + =1 Û y = .x +
( y ¹ 0 vì d cắt 2 trục tọa độ). 64 9 64y y 0 0 0 1
Theo đề, d cắt hai trục ;
Ox Oy tại A, B sao cho OA = 2OB nên d có hệ số góc bằng ± 2 32 Do đó suy ra x = ±
y . Thay vào pt (E) tìm được 4 điểm M là: 0 0 9 æ 9 32 ö æ 9 3 - 2 ö æ 9 - 32 ö æ 9 - 3 - 2 ö ; ; ; ; ; ; ; ç ÷ ç ÷ ç ÷ ç ÷
è 5 5 ø è 5 5 ø è 5 5 ø è 5 5 ø
Các điểm này tạo thành 2 cặp điểm đối xứng qua gốc tọa độ nên tạo thành hcn có diện tích bằng æ 9 ö æ 32 ö 1152 .2 . .2 = ç ÷ ç ÷ è 5 ø è 5 ø 25
Hãy tham gia group để cùng học và cùng làm- Nhóm chỉ dành cho các Gv, Sv toán! 99




