Trắc nghiệm - Phần lý thuyết & bài tập môn Toán rời rạc | Đại học Kinh tế Thành phố Hồ Chí Minh

Logic
1. Suy diễn nào dưới đây đúng:
b.nếu “a + 4 = 2+ b” thì “a = b - 2” c.nếu = 0 thì “b + c = 0” can bc .
2. những mệnh đề nào sau đây là đúng: b.NOT p -> (p -> q) d.q -> (p -> q)
3. những mệnh đề nào sau đây là đúng: c.(p AND (p -> q)) -> q
d.(NOT q AND (p -> q)) -> NOT p
4. bảng chân trị của 2 mệnh đề p -> q và NOT(q) + p là:
b.có cùng số giá trị đúng S
d.có cùng số giá trị đúng Đ
5. những mệnh đề nào dưới đây là đúng:
c. nếu n là số nguyên lẻ thì 2n là số nguyên chẵn d. nếu 3 = 5 thì 3 = 0
6. bảng chân trị của hai mệnh đề pq và p + NOT(q) là :
b.có đúng hai dòng giống nhau
c.có ít nhất một dòng giống nhau
7. những mệnh đề nào dưới đây là sai:
a.”(3=5) hay ( 2 là số chẵn)” và “4 là số lẻ”
d.”(3 = 5) và (2 là số chẵn)” hay “ 4 là số lẻ”
8. tâp các mệnh đề có các phép toán sau: a.NOT b.AND d.Kéo theo 9.
mệnh đề “n lẻ suy ra 2n lẻ” sai , vì 2n lẻ là mệnh đề sai. Lập luận này là một:
b.ngụy biện( lập luận sai)
10. Mệnh đề nào dưới đây, bảng chân trị có 3 trường hợp đúng và 1 trường hợp saia.p OR q b. p -> NOT q d.p -> (p AND q)
11.bảng chân trị của hai mệnh đề NOT(p -> q) và p NOT(q) là; c. giống nhau hoàn toàn
d.có cùng số giá trị đúng Đ
12. mệnh đề “ n lẻ suy ra 2n chẵn” đúng, vì 2n chẵn là mệnh đề đúng.Lập luận này là môt….
a.chứng minh tầm thường
13.suy diễn nào dưới đây là đúng:
d.có p nhưng không có r, áp dụng luật pq -> r, ta không có q
14.Mênh đề “n lẻ thì n + 1 chẵn” là đúng vì: giả sử n + 1 lẻ, n + 1 = 2k + 1, suy ra n = 2k
suy ra n là chẵn. lập luận này là một: a.chứng minh gián tiếp
15. bảng chân trị của 2 mệnh đề p -> q và NOT(q) + p là:
b.có cùng số giá trị đúng S
c.có cùng số giá trị đúng Đ
16. suy diễn nào dưới đây là đúng;
b.không có q, áp dụng luật p -> q, ta cũng không có p
d.có p, áp dụng luật p -> q, ta có q
17. mệnh đề “n lẻ thì n + 1 là chẵn” đúng, vì giả sử n + 1 chẵn, n + 1 = 2k suy ra n =
2k , suy ra n lẻ. Lập luận này là một: a.ngụy biện( lập luận sai)
18.bảng chân trị của mệnh đề (pq + r)(q -> r) có mấy dòng( không tính dòng tiêu đề) a.8 Số nguyên
1.Phương trình đồng dự X = a mod 5 = b mod 7 có dạng x = (a.m+ b.n) mod 35: (m,n ở đây là) a. (21. 15) b.(-14, 15) d. (21.-20) 2.24 ^ 4 mod 11 là a. 5 3.(7 + 5)/(4 + 3) mod 11 là a. 8
4.Có bao nhiêu số nguyên là nghịch đảo theo cơ số 4 của 21 ? c. Có vô số
5. Phương trình đồng dự X = a mod 3 = b mod 7 Có dạng x = (a,m + b.n) mod 21: (m,n) ở đây là a. (7.-6) b.(-14, 15)
6. Phương trình đồng dư X = a mod 4 = b mod 5 có dạng x = (a.m + b.n) mod 20: (m,n ) ở đây là C. (5,-4)
7. Có bao nhiêu số nguyên n, -2 < n <3 là nghịch đảo theo cơ số 4 của 11 ? a. Có duy nhất d. Không quá một
8. USCLN(3,5) = 3m + 5n theo Định lý Bezout; (m, n) ở đây là C.(-3, 2)
9.Cho biết số n có biểu diễn cơ số 10 là 34; vậy biểu diễn cơ số 2 của n là a. 100010
10.USCLN(4, 9) = 4m + 9n theo Định lý Bezout; (m, n) ở đây là b.(- 2.1) d. (7.-3) 11. 7x3 mod 11 là d. 10
12. Cho biết số n có biểu diễn cơ số 3 là 21; vậy biểu diễn cƠ Số 4 của n làd. 13
13. Cho biết số nguyên n có biểu diễn cơ số 3 là 212; vậy biểu diễn cơ số 9 của n làd. 25
14. Có bao nhiêu số nguyên là nghịch đảo theo cơ số 4 của 20 ? c. Không có 15. 7/3 mod 11 là a. 6
17. Có bao nhiêu số nguyên n, -2 < n < 4 là nghịch đảo theo Cơ số 4 của 15 ?a. Có hai
18. Phương trình đồng dư x = a mod 3 = b mod 5 có dạng x = (a.m + b.n) mod 15; (m, n) ở đây là a. (10,6) C.(-5,6) 19. 2* 10 mod 4 là d.0
20. Nghịch đảo theo cơ số 4 của 127 là 3 và 7
21. Cho biết số n có biểu diễn cơ số 2 là 10111; vậy biểu diễn cơ số 10 của n là C.23
22. Cho biết số n có biểu diễn cƠ Số 9 là 36; vậy biểu diễn cơ số 3 của n làd. 1020 Quan hệ
1.Quan hệ tương đương R có tính chất: (xRy = yRx) suy ra x = y (xRy và yRz) suy ra xRz xRy suy ra yRx
2.Quan hệ thứ tự R có tính chất: (xRy và yRz) suy ra xRz xRx với mọi x 3.Quan hệ thứ tự là: Hai ngôi Trên cùng 1 tập
4.Bài toán vẽ biểu đồ Hasse được phát biểu trong : quan hệ thứ tự
5. Bài toán bắc cầu là bài toán phát biểu trong: quan hệ thứ tự quan hệ tương đương
6.Quan hệ chia hết trên số nguyên có tính chất:
phản xứng, phản xạ, bắc cầu, đối xứng
7. Quan hệ cùng quốc tịch có tính chất :
, phản xạ, bắc cầu, đối xứng
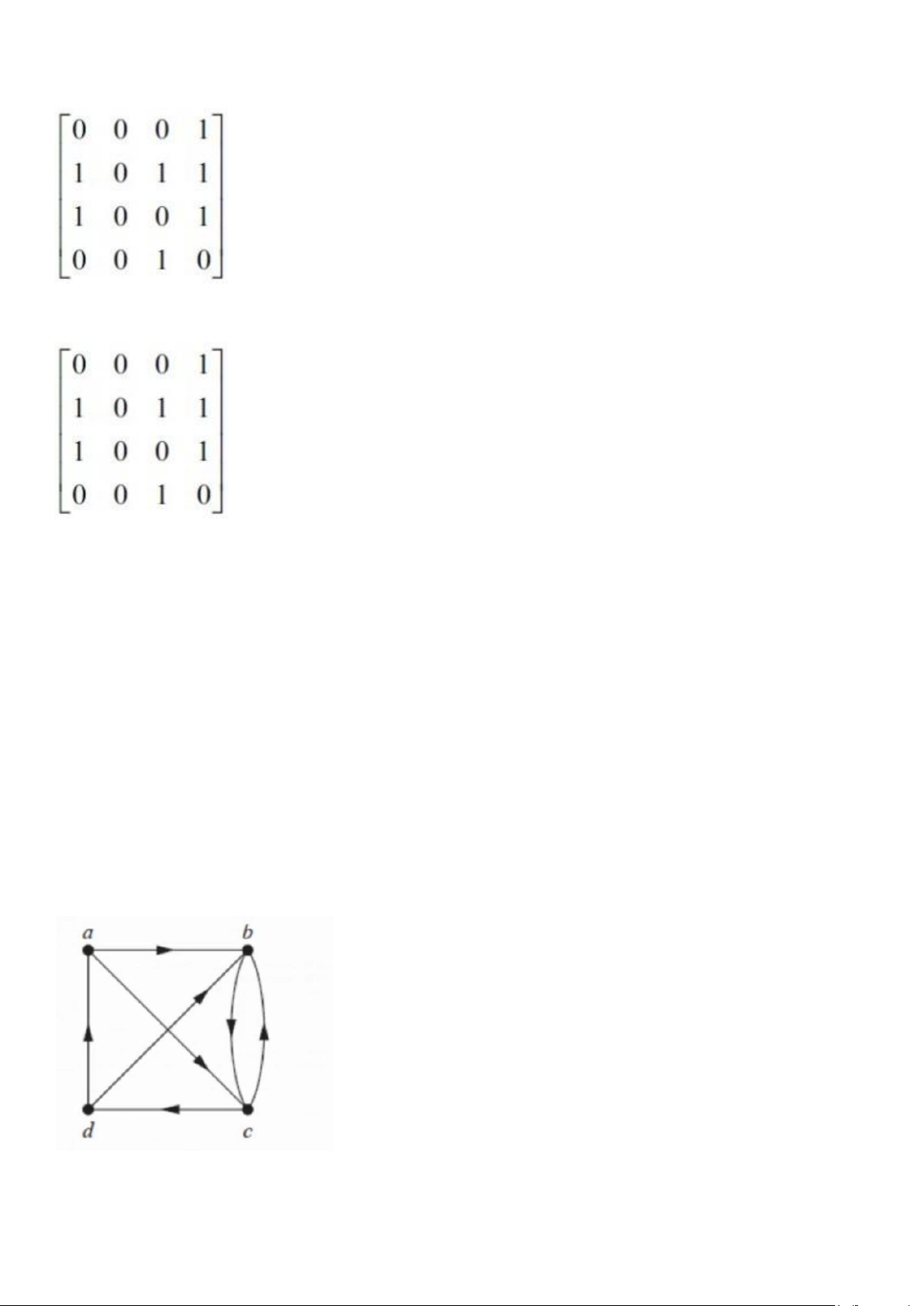
8. Cho hai quan hệ R[X,Y] và S[Y,Z] có biểu diễn ma trận theo thứ tự:
Gọi U = SoR[X,Z]. Hãy cho biết: •
Dòng thứ nhất biểu diễn ma trận U có mấy số 1 : 4 •
Dòng thứ hai biểu diễn ma trận U có mấy số 1 : 3 •
Cột thứ ba biểu diễn ma trận U có mấy số 1 : 3
9.R là một quan hệ trên X={3,4,6,12} với xRy được hiểu là “x<= y”. Từ biểu diễn đồ thị
Hasse của E, bao đóng bắc cầu của nó sẽ phải vẽ thêm bao nhiêu mũi tên nữa ( nếu xRy, ta vẽ 1 mũi từ x đến y) 3
10.R là một quan hệ trên X={3,4,6,12} với xRy được hiểu là “x là bội của y”. Từ biểu diễn
đồ thị Hasse của E, bao đóng bắc cầu của nó sẽ phải vẽ thêm bao nhiêu mũi tên nữa ( nếu
xRy, ta vẽ 1 mũi từ x đến y) 1
11.R là một quan hệ trên X={3,4,6,12} với xRy được hiểu là “x <= y”. Từ biểu diễn đồ thị
Hasse của R có bao nhiêu mũi tên ( nếu xRy, ta vẽ 1 mũi từ x đến y) 3
12. R là một quan hệ trên X={3,4,6,12} với xRy được hiểu là “x là ước của y”. Từ biểu diễn
đồ thị Hasse của R có bao nhiêu mũi tên ( nếu xRy, ta vẽ 1 mũi từ x đến y) 3
13.Tập X={3,4,6,9,12} với xRy được hiểu là “x là bội của y”. Từ biểu diễn đồ thị Hasse của
R có bao nhiêu mũi tên ( nếu xRy, ta vẽ 1 mũi từ x đến y) 4
14.Tập X={2.3.4.6.12} với xRy được hiểu là “x là bội của y”. Từ biểu diễn đồ thị Hasse của
E, bao đóng bắc cầu của nó sẽ phải vẽ thêm bao nhiêu mũi tên nữa ( nếu xRy, ta vẽ 1 mũi từ x đến y) 2
15.Tập X={2.3.4.6.12} với xRy được hiểu là “x là ước của y”. Từ biểu diễn đồ thị Hasse
của E, bao đóng bắc cầu của nó sẽ phải vẽ thêm bao nhiêu mũi tên nữa ( nếu xRy, ta vẽ 1 mũi từ x đến y) 2
16.Tập X={2,3,4,6,12} với xRy được hiểu là “x là bội của y”. Từ biểu diễn đồ thị Hasse của
nó thì có bao nhiêu mũi tên ( nếu xRy, ta vẽ 1 mũi từ x đến y) 5
17.Cho X={a,b,c} gọi P là tập con của X. Quan hệ xRy được xác định nghĩa trên P “x là tập
con của y”. Từ biểu diễn đồ thị Hasse của R thì có bao nhiêu mũi tên nữa ( nếu xRy, ta vẽ 1 mũi từ x đến y) 12
18.Áp dụng thuật toán Warrshall tại đỉnh 3 của quan hệ biểu diễn ma trận dưới đây số cạnh sẽ được bổ sung là: 2
19.Áp dụng thuật toán Warrshall tại đỉnh 4 của quan hệ biểu diễn ma trận dưới đây số cạnh sẽ được bổ sung là: 2 Đồ thị
1.Cho một đồ thị có hướng liên thông mạnh G, khi ấy nếu G có chu trình hamilton thì
a. Tổng bậc vào bằng tổng bậc ra
2.Cho một đồ thị có hướng liên thông mạnh G, khi ấy nếu G có chu trình Euler thì
a.Tất cả các đỉnh đều cân bằng( bậc vào bằng ra) (chu trình euler chỉ xảy ra khi bậc chẵn)
b.Tổng vào = tổng ra ( liên thông mạnh)
3.Một đồ thị vô hướng liên thông mạnh G, khi ấy nếu G có chu trình Euler nếu
a.không có đỉnh bậc lẻ (euler) b.Tổng bậc phải chẵn
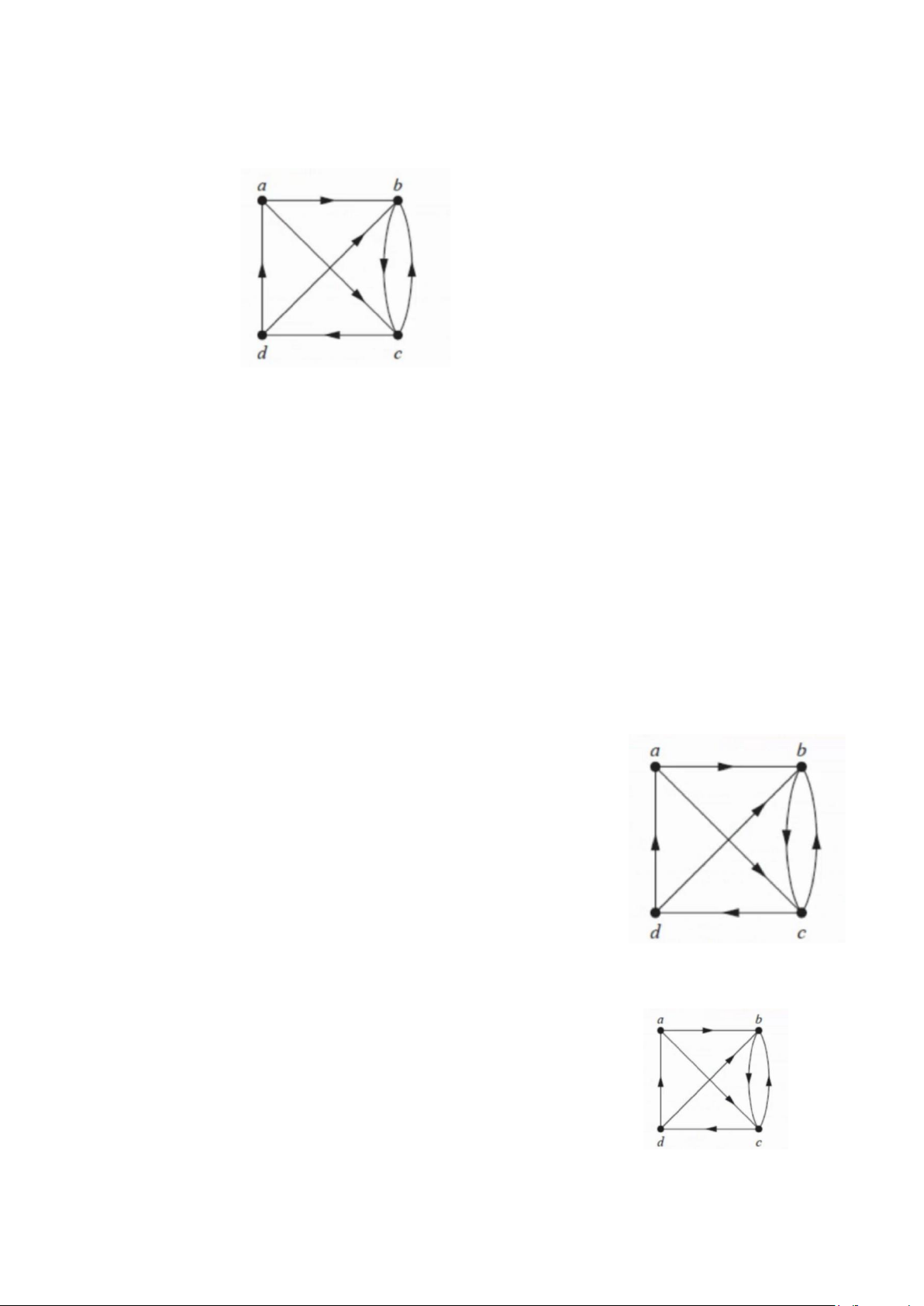
4. Đồ thị dưới đây nếu bỏ đi tất cả các cung nối giữa b và c sẽ a. liên thông yếu b.liên thông không mạnh
5. Một đồ thị vô hướng có chu trình Euler thì
Không có đỉnh bậc lẻ vì mỗi bậc đều chẵn (định nghĩa chu trình euler)
ð Tổng bậc phải chẵn ð Liên thông
6.Đồ thị dưới đây là:
a.Liên thông mạnh vì đỉnh nào cũng có vào có ra
b.Liên thông mạnh nên cũng liên thông yếu
7.Một đồ thị vô hướng có đường Euler( Không phải chu trình thì)
a.Có đúng 2 đỉnh bậc lẻ ( định nghĩa đường đi không phải chu trình) b.Tổng bậc phải chẵn
8.Một đồ thị có hướng có đường Hamilton thì:
a.Có không quá một đỉnh không có cung vào
b.Có không quá một đỉnh không có cung ra
9.Đỉnh nào sau đêy bị gỡ bỏ sẽ làm đồ thị không liên thông mạnh: a. Bỏ d và c
10.Cung nào sau đây bị gỡ bỏ sẽ làm đồ thị không liên thông mạnh: a.Bỏ dc và bc
11.Một đồ thị có hướng có chu trình Euler thì: a.Liên thông mạnh
b.Tại mỗi đỉnh bậc vào bằng bậc ra
c.Tổng bậc vào bằng tổng bậc ra
12.Đường đi ngắn nhất: Tà đạo đi người ae. Đại số Bool
1.Phát biểu nào dưới đây là ĐÚNG?
c.Cây là một đồ thị vô hướng.
d.Cây là một đồ thị liên thông.
2.Phát biểu nào dưới đây là SAI?
a.Một đồ thị liên thông là một cây.
c.Một đồ thị đơn không có chu trình là một cây.
3.Phát biểu nào dưới đây là ĐÚNG?
b.Một cây có 4 đỉnh sẽ có 3 cạnh.
d.Một cây có 8 cạnh sẽ có 9 đỉnh.
4.Phát biểu nào dưới đây là ĐÚNG?
a.Cây khung, nếu có, của đồ thị có 10 đỉnh thì cũng có 10 đỉnh.
d.Cây khung, nếu có, của đồ thị có 10 đỉnh sẽ có 9 cạnh.
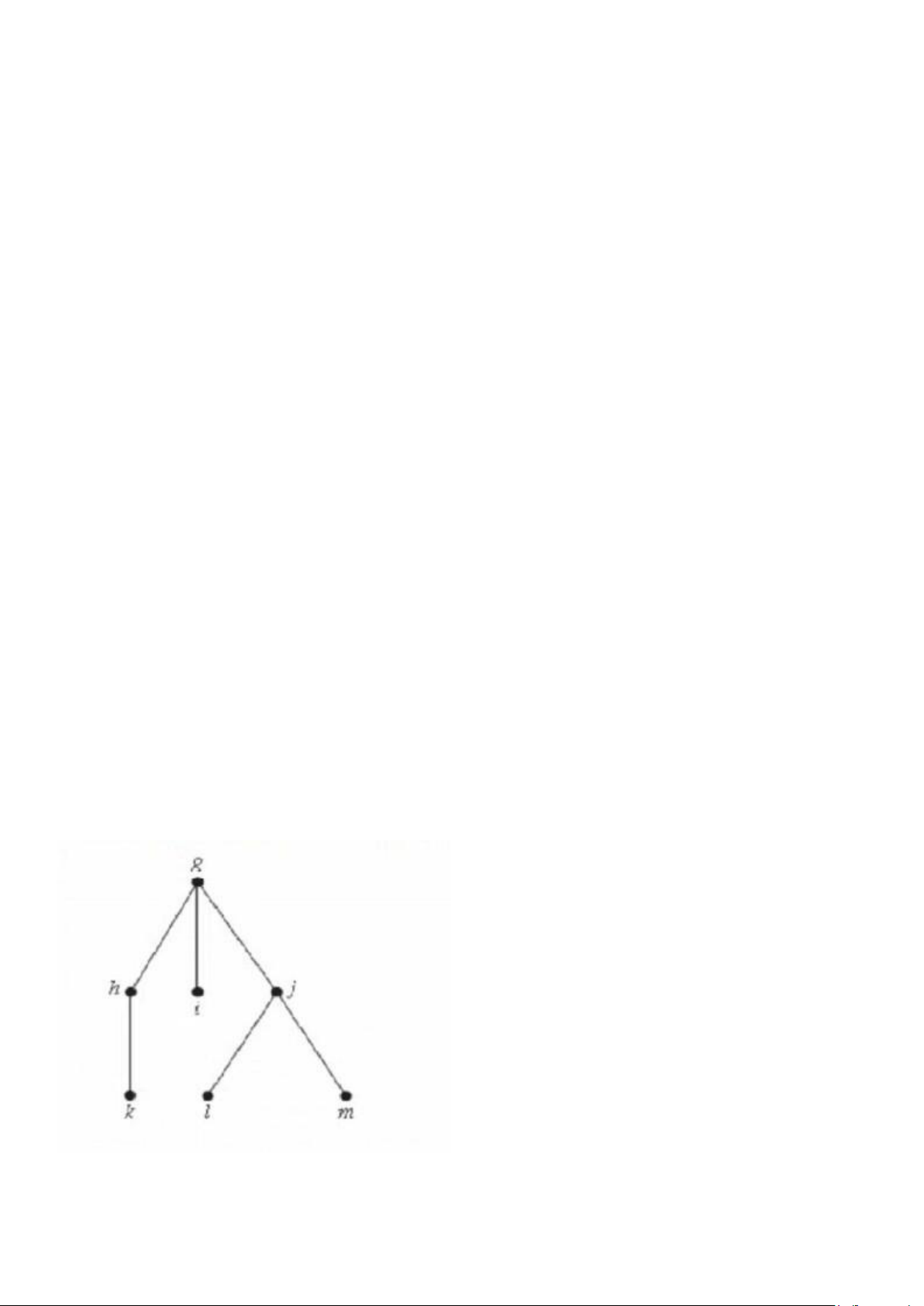
5.Thứ tự các đỉnh khi duyệt cây sau theo các phương pháp:
TIỀN THỨ TỰ: g,h,k,i,j,l,m
TRUNG THỨ TỰ: k,h,g,i,l,j,m HẬU THỨ TỰ: k,h,i,l,m,j,g
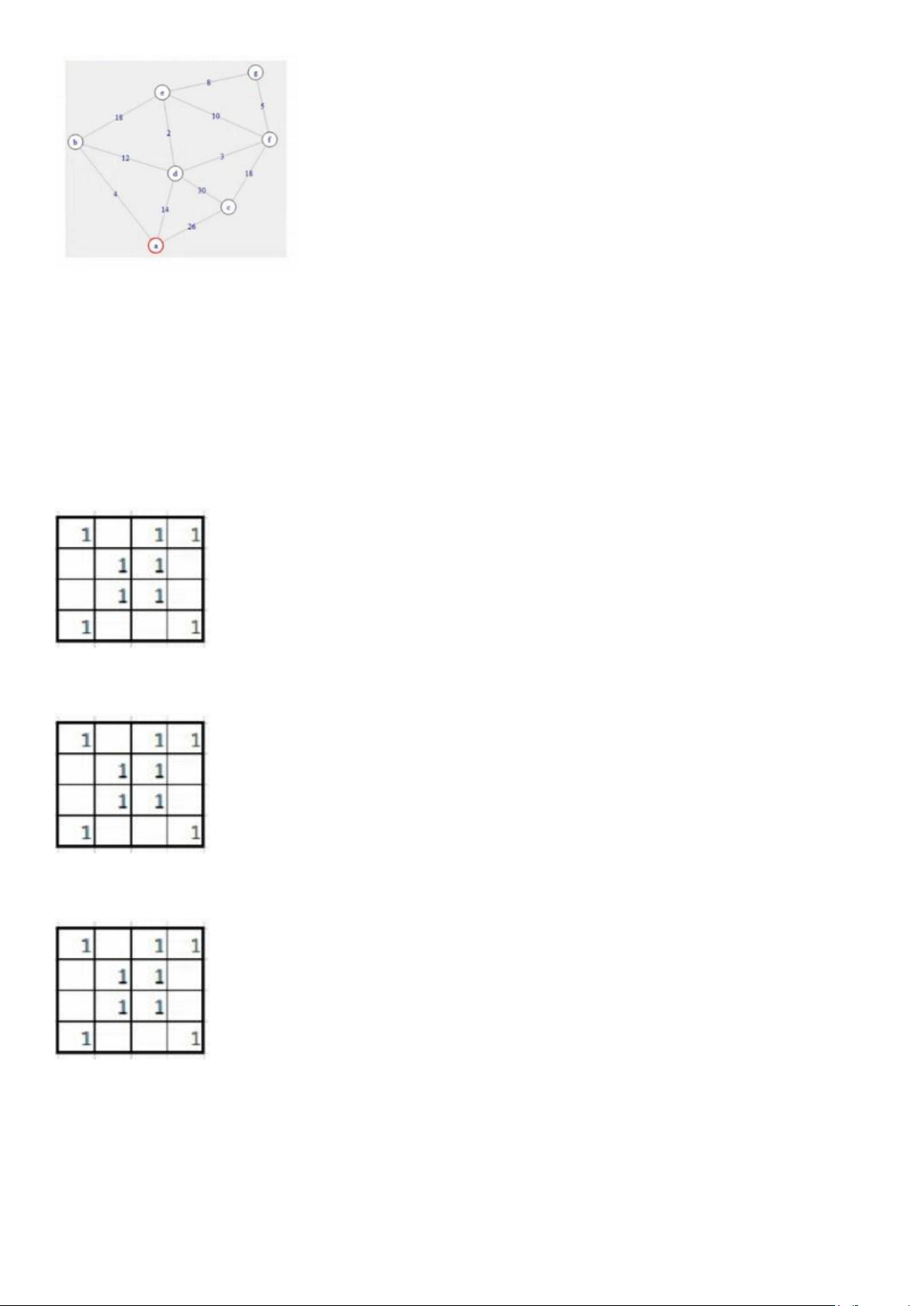
6. Thứ tự 4 cạnh đầu tiên được chọn khi áp dụng thuật toán: Kruskal: de, df, ba và fg.
Prim: . đỉnh a : ab, bd, de và df.
. đỉnh c : cf, df, ed và fg.
. đỉnh e : de, df, fg và bd.
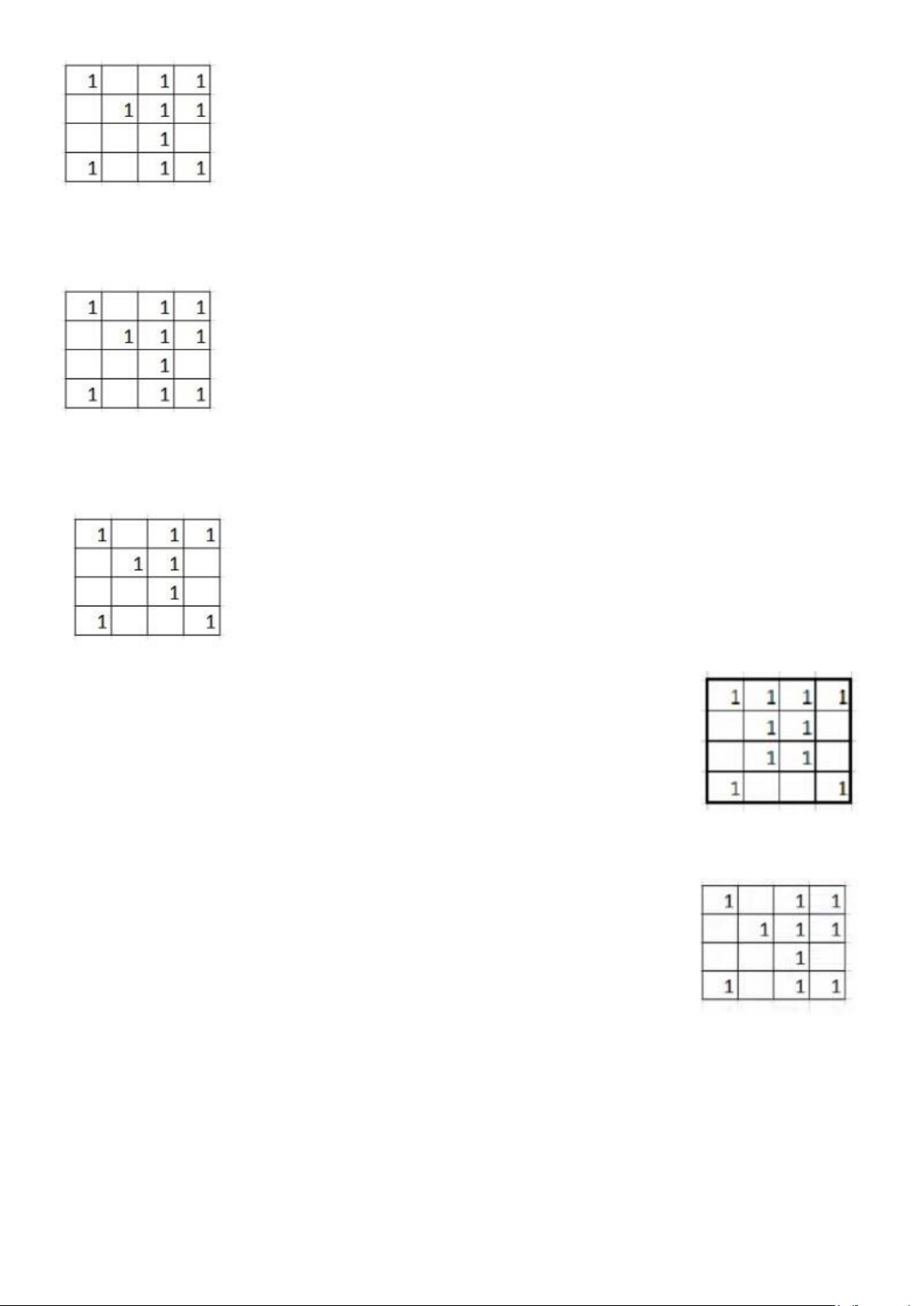
7. Với bản đồ Karnaugh dưới đây, đa thức Bool tối tiểu có mấy tế bào? b.3
8.. Số tế bào có 4 ô gồm toàn số 1 trong bản đồ Karnaugh dưới đây là: a.2
9. Số tế bào có 2 ô gồm toàn số 1 trong bản đồ Karnaugh dưới đây là: c.8
10. Đa thức tối tiểu thu được từ bản đồ Karnaugh dưới đây được xây dựng từ bao nhiêu tế
bào có 2 ô gồm toàn số 1? c.1
11. Đa thức tối tiểu thu được từ bản đồ Karnaugh dưới đây được xây dựng từ bao nhiêu tế
bào có 4 ô gồm toàn số 1? b.4
12. Đa thức Bool tối tiểu trong bản đồ Karnaugh dưới đây được xây dựng từ bao nhiêu tế bào? d.4
13. Số tế bào có 4 ô gồm toàn số 1 trong bản đồ Karnaugh dưới đây là: a.4
14. Số tế bào có 4 ô gồm toàn số 1 trong bản đồ Karnaugh dưới đây là: a.4