Trắc nghiệm và tự luận chủ đề đường tiệm cận của đồ thị hàm số
Tài liệu gồm 133 trang, được biên soạn bởi thầy giáo Trương Ngọc Vỹ, phân dạng và tuyển tập các bài tập trắc nghiệm và tự luận chủ đề đường tiệm cận của đồ thị hàm số môn Toán 12 chương trình mới (Cánh Diều, Chân Trời Sáng Tạo, Kết Nối Tri Thức Với Cuộc Sống).
Chủ đề: Tài liệu chung 172 tài liệu
Môn: Toán 12 4.3 K tài liệu
Tác giả:
Preview text:
Đại số 12 - Chương 1 - Ứng dụng ĐH để khảo sát và vẽ ĐTHS - Trắc nghiệm và tự luận 4 phần Dùng chung 3 bộ sách BÀI 3
ĐƯỜNG TIỆM CẬN CỦA ĐỒ THỊ HÀM SỐ
1. Đường tiệm cận đứng
Đường thẳng x x được gọi là đường tiệm cận đứng (hay tiệm cận đứng) của đồ thị hàm số 0
y f x nếu ít nhất một trong các điều kiện sau được thỏa mãn:
lim f x xx 0
lim f x xx 0
lim f x x 0 x
lim f x x 0 x
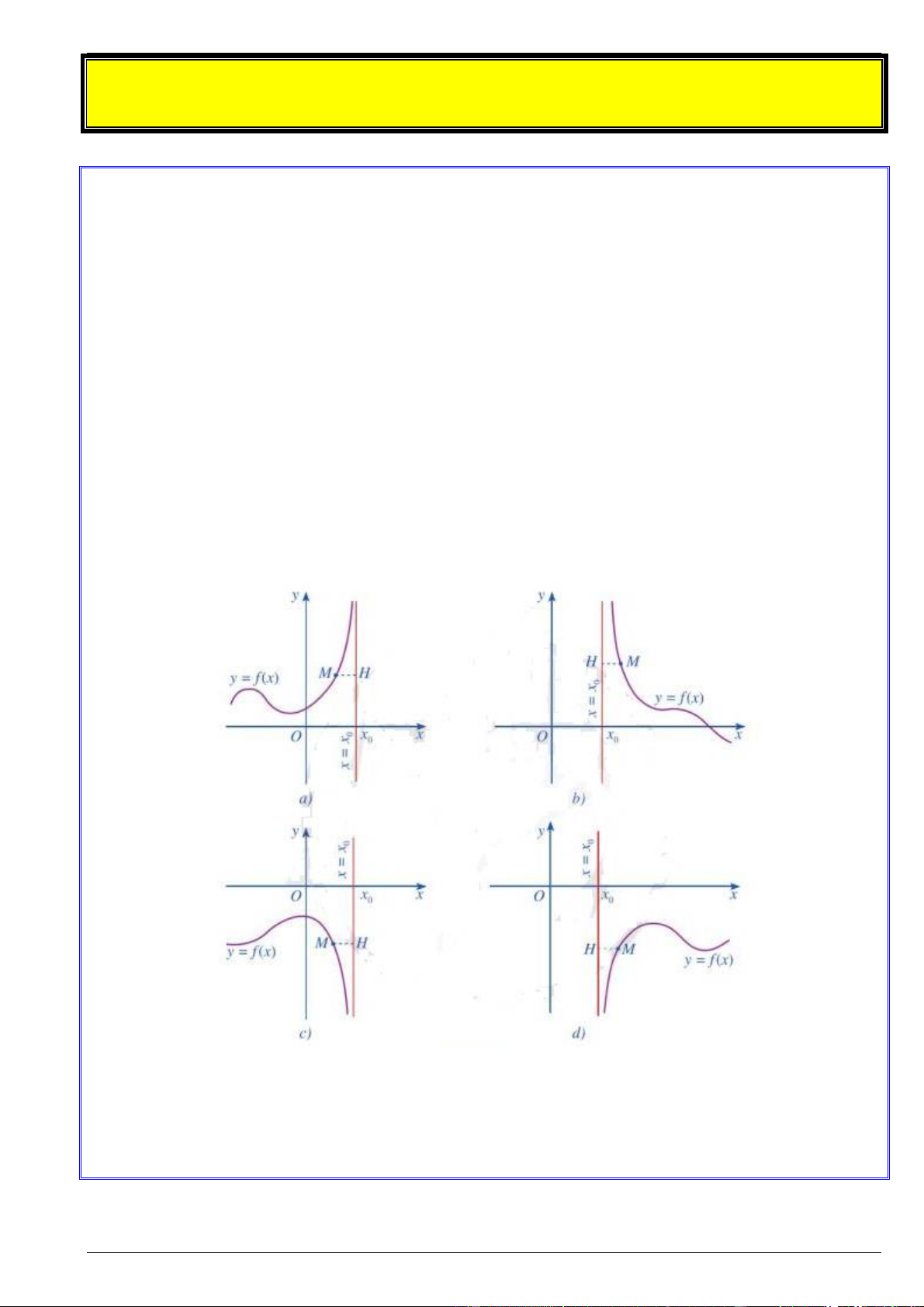
Nhận xét: Giả sử đường thẳng x x là tiệm cận đứng của đồ thị hàm số y f x . Lấy điểm M ; x y 0
thuộc đồ thị hàm số. Gọi MH là khoảng cách từ điểm M đến đường thẳng x x . Khi đó, độ dài MH 0 tiến tới 0 khi x x
(hình a, c ) hay khi x x (hình , b d ) 0 0
2. Đường tiệm cận ngang
Đường thẳng y y được gọi là đường tiệm cận ngang (hay tiệm cận ngang) của đồ thị hàm số 0
y f x nếu: lim f x y hoặc lim f x y . 0 0 x x
https://www.facebook.com/truongngocvy8/ T r an g
1 Trương Ngọc Vỹ - Nha Trang
Đại số 12 - Chương 1 - Ứng dụng ĐH để khảo sát và vẽ ĐTHS - Trắc nghiệm và tự luận 4 phần Dùng chung 3 bộ sách
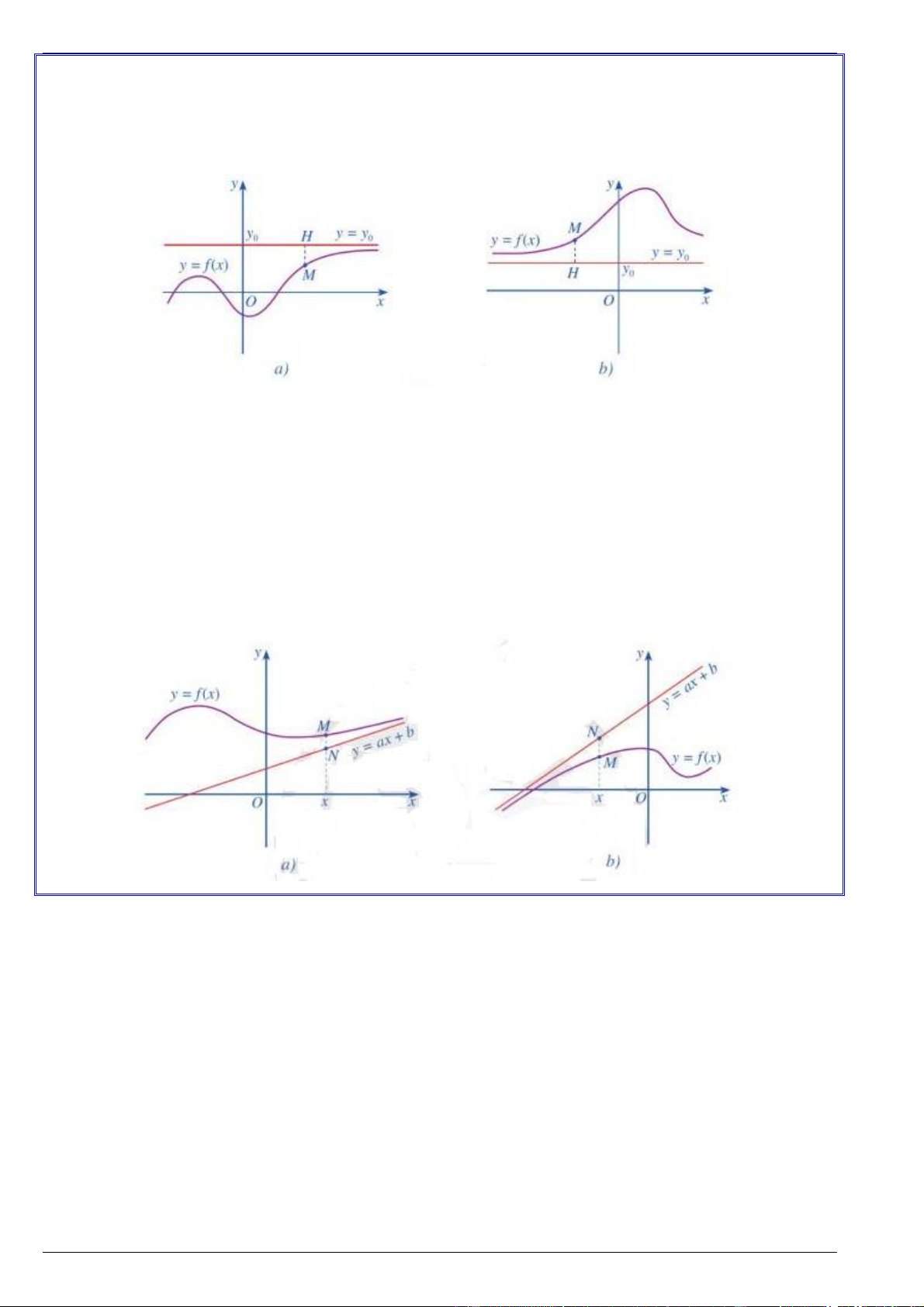
Nhận xét: Giả sử đường thẳng y y là tiệm cận ngang của đồ thị hàm số y f x . Lấy điểm 0 M ;
x y thuộc đồ thị hàm số. Gọi MH là khoảng cách từ điểm M đến đường thẳng y y . Khi đó, độ 0
dài MH tiến tới 0 khi x (hình a ) hay khi x (hình b )
3. Đường tiệm cận xiên
Đường thẳng y ax b a 0 được gọi là đường tiệm cận xiên (hay tiệm cận xiên) của đồ thị
hàm số y f x nếu: lim f x ax b 0
hoặc lim f x ax b 0 . x x
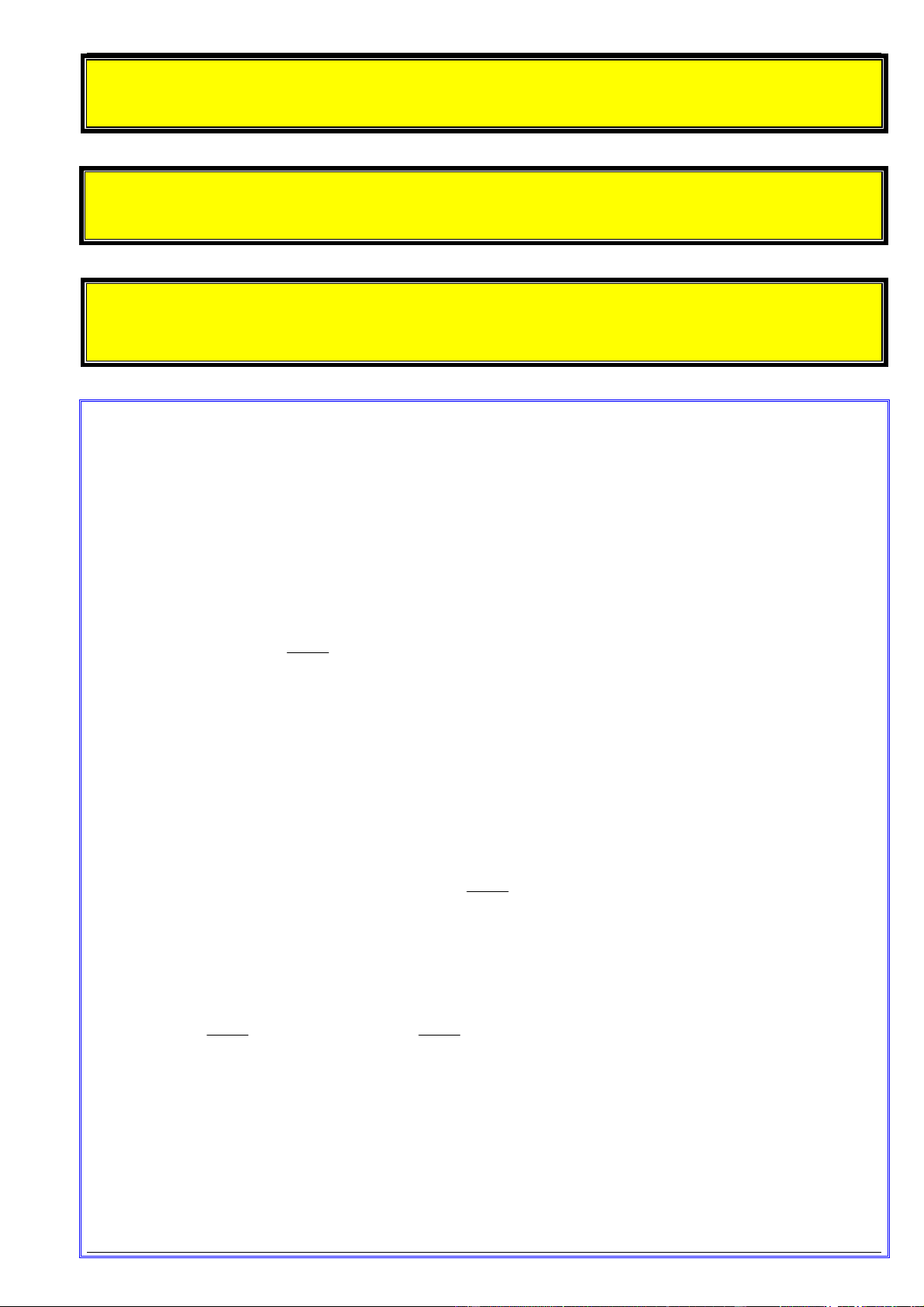
Nhận xét: Giả sử đường thẳng y ax b a 0 là tiệm cận xiên của đồ thị hàm số y f x . Lấy điểm
M thuộc đồ thị hàm số y f x và điểm N thuộc đường thẳng y ax b có cùng hoành độ x . Khi
đó, độ dài MN tiến tới 0 khi x (hình a ) hay khi x (hình b )
https://www.facebook.com/truongngocvy8/ T r an g
2 Trương Ngọc Vỹ - Nha Trang
Đại số 12 - Chương 1 - Ứng dụng ĐH để khảo sát và vẽ ĐTHS - Trắc nghiệm và tự luận 4 phần Dùng chung 3 bộ sách CHỦ ĐỀ 1
XÁC ĐỊNH ĐƯỜNG TIỆM CẬN CỦA ĐỒ THỊ HÀM SỐ PHẦN A
TỰ LUẬN PHÂN DẠNG DẠNG 1
TÌM ĐƯỜNG TIỆM CẬN CỦA ĐỒ THỊ HÀM SỐ y f x KHI BIẾT HÀM SỐ y f x
I . Phương pháp tìm đường tiệm cận của đồ thị hàm số
Để tìm tiệm cận của đồ thị hàm số y f x ta thực hiện các bước sau:
Bước 1: Tìm miền xác định (tập xác định) của hàm số y f x
Bước 2: Tìm giới hạn của f x khi x tiến đến biên của miền xác định.
Bước 3: Từ các giới hạn và định nghĩa tiệm cận suy ra phương trình các đường tiệm cận. Chú ý: P x
Trường hợp y f x
là hàm số phân thức hữu tỷ. Q x
+ Nếu Q x 0 có nghiệm x thì đồ thị có tiệm cận đứng x x ( x là điểm tại đó hàm số không 0 0 0
xác định x x là tiệm cận đứng). 0
+ Nếu bậc P x bậc Q x thì đồ thị có tiệm cận ngang.
+ Nếu bậc P x bậc Q x 1 thì đồ thị có tiệm cận xiên. P x Q x 0
+ Số tiệm cận đứng của hàm số phân thức y
là số nghiệm của hệ: Q x
P x 0
+ Đồ thị có tiệm cận ngang thì không có tiệm cận xiên và ngược lại.
Để xác định các hệ số ,
a b trong phương trình của đường tiệm cận xiên, ta có thể áp dụng các công f x f x a lim a lim thức: x x hoặc x x . b
lim f x ax
b lim f x ax x x
Thông thường, ta tìm cận xiên bằng cách chia đa thức, lấy phần nguyên là tiệm cận xiên do lim (phần x dư) = 0.
Hàm đa thức không có các đường tiệm cận.
https://www.facebook.com/truongngocvy8/ T r an g
3 Trương Ngọc Vỹ - Nha Trang
Đại số 12 - Chương 1 - Ứng dụng ĐH để khảo sát và vẽ ĐTHS - Trắc nghiệm và tự luận 4 phần Dùng chung 3 bộ sách
II. Kỹ năng dùng Casio
1. Giới hạn của hàm số tại một điểm
lim f x thì nhập f x và CALC 9 x a 10 . x a
lim f x thì nhập f x và CALC 9 x a 10 . x a
lim f x thì nhập f x và CALC 9 x a 10 hoặc 9 x a 10 . xa
2. Giới hạn của hàm số tại vô cực
lim f x thì nhập f x và CALC 9 x 10 . x
lim f x thì nhập f x và CALC 9 x 10 . x Bài 1.
Tìm các đường tiệm cận đứng, tiệm cận ngang của các đồ thị hàm số sau: 2x 2024 x 2025 a) y b) y c) y x 2025 3x 2 2024 x Bài 2.
Tìm các đường tiệm cận đứng, tiệm cận ngang của các đồ thị hàm số sau: 2025x 2 x 2 2x 5x 1 a) y b) y c) y 2 x 9 2 1 x 2 x 5x 4 Bài 3.
Tìm các đường tiệm cận đứng, tiệm cận ngang của các đồ thị hàm số sau: x 1 5 x 2 x 3x 2 a) y b) y c) y 2 x 1 2 x 25 2 x 8x 7 Bài 4.
Tìm các đường tiệm cận đứng, tiệm cận xiên của các đồ thị hàm số sau: 1 2 x x 2 x
a) y x 2025 b) y c) y x 3 x x 2 2 x 3x 4 Bài 5.
Tìm các đường tiệm cận đứng, tiệm cận ngang của các đồ thị hàm số sau: 1 2 x 2 x 2x 1
a) y 2x 1 b) y c) y x 2 1 x x 2 Bài 6.
Tìm các đường tiệm cận đứng, tiệm cận ngang của các đồ thị hàm số sau: 2 x 4 x 3 2x 2 x 4x 3 a) y b) y c) y x 1 2 x 1 2 x 7 4
https://www.facebook.com/truongngocvy8/ T r an g
4 Trương Ngọc Vỹ - Nha Trang
Đại số 12 - Chương 1 - Ứng dụng ĐH để khảo sát và vẽ ĐTHS - Trắc nghiệm và tự luận 4 phần Dùng chung 3 bộ sách DẠNG 2
TÌM TIỆM CẬN KHI BIẾT ĐỒ THỊ HOẶC BẢNG BIẾN THIÊN CỦA HÀM SỐ y f x Phương pháp
Bước 1: Dựa vào bảng biến thiên và đồ thị để tìm tập xác định của hàm số.
Bước 2: Quan sát bảng biến thiên và đồ thị để suy ra giới hạn khi x đến một bên của miền xác định.
Bước 3: Kết luận. Bài 1.
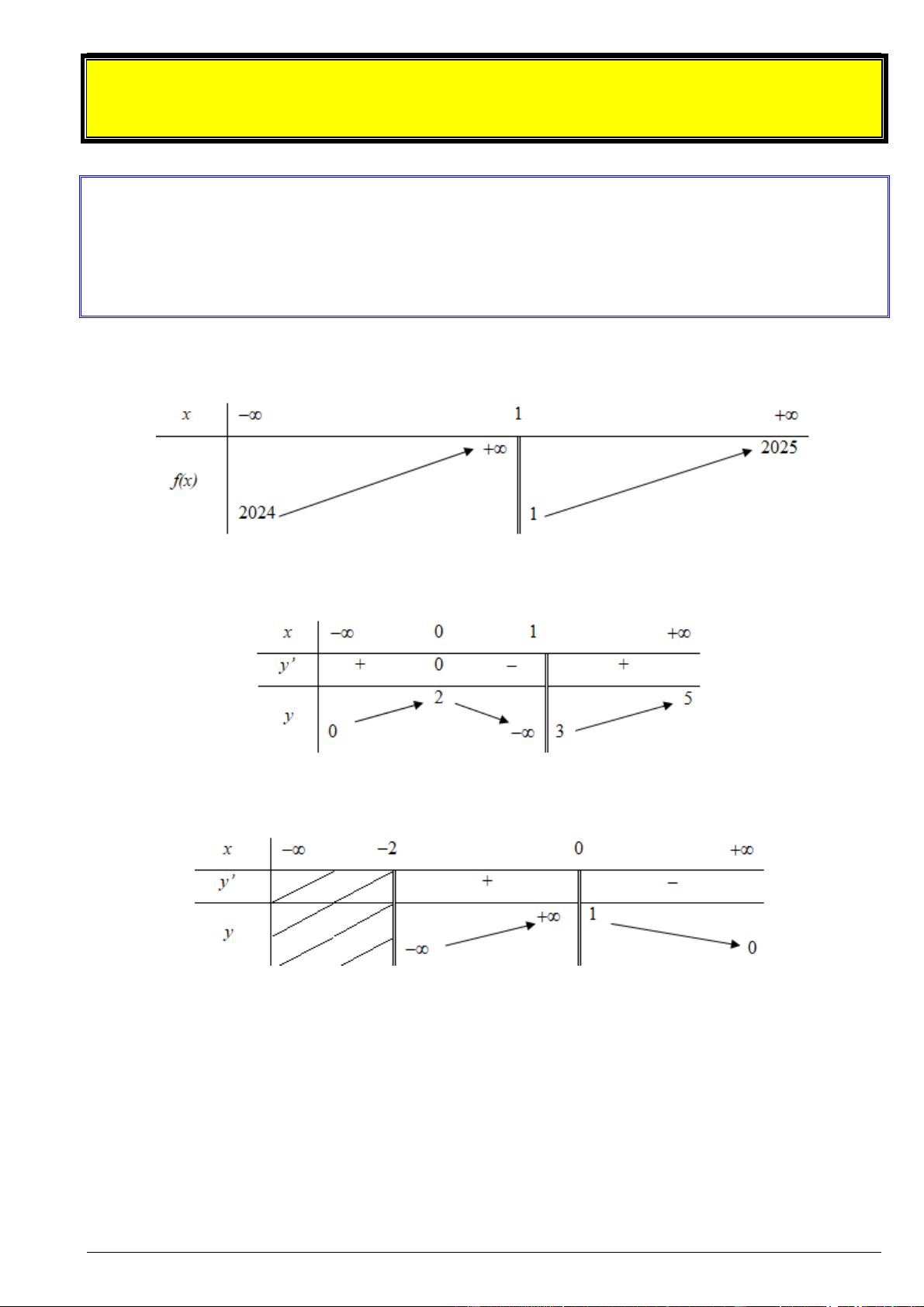
Cho hàm số y f x có bảng biến thiên như sau:
Tìm tiệm cận ngang và tiệm cận đứng của đồ thị hàm số đã cho. Bài 2.
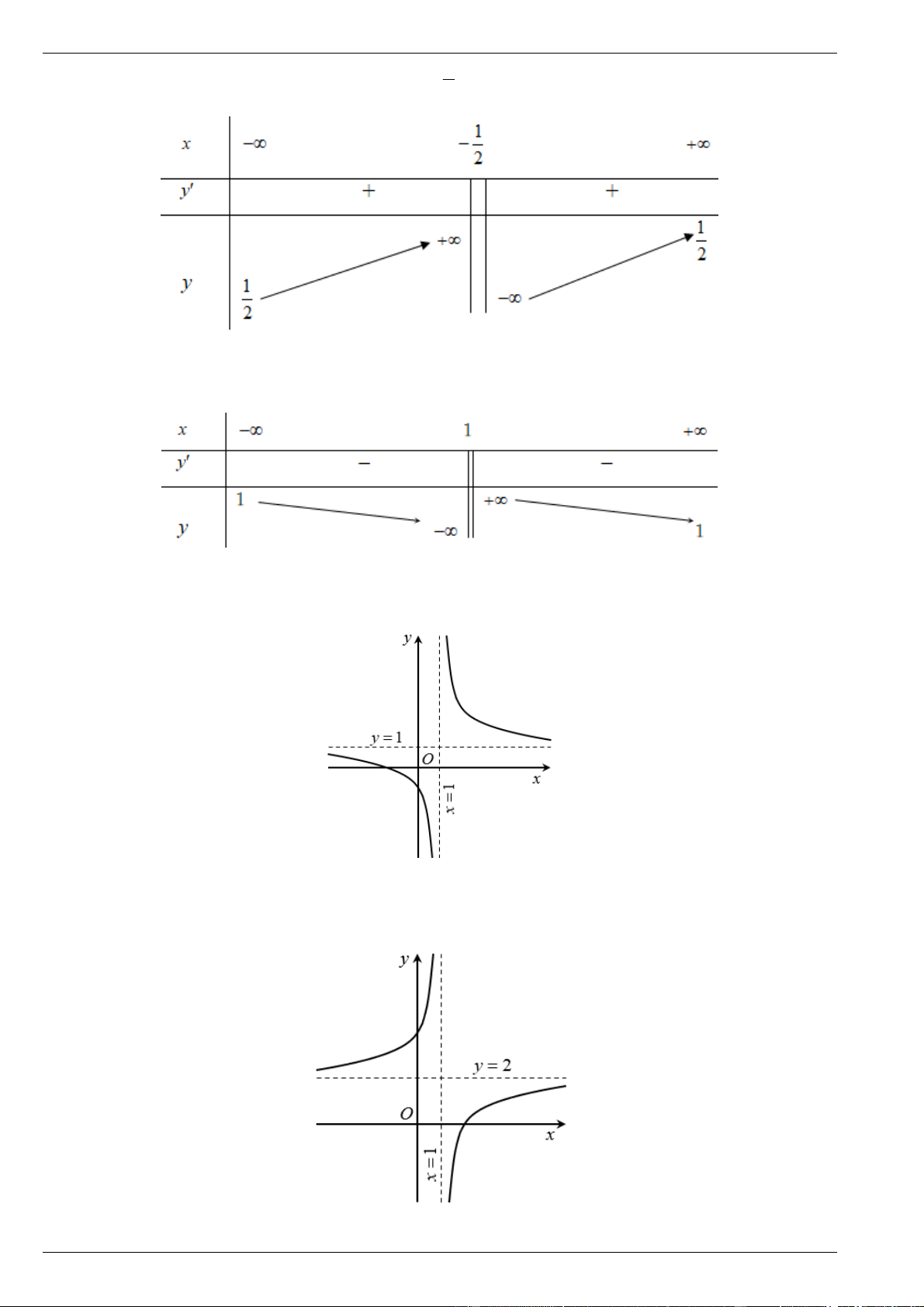
Cho hàm số y f x có bảng biến thiên như sau:
Tìm tiệm cận ngang và tiệm cận đứng của đồ thị hàm số đã cho. Bài 3.
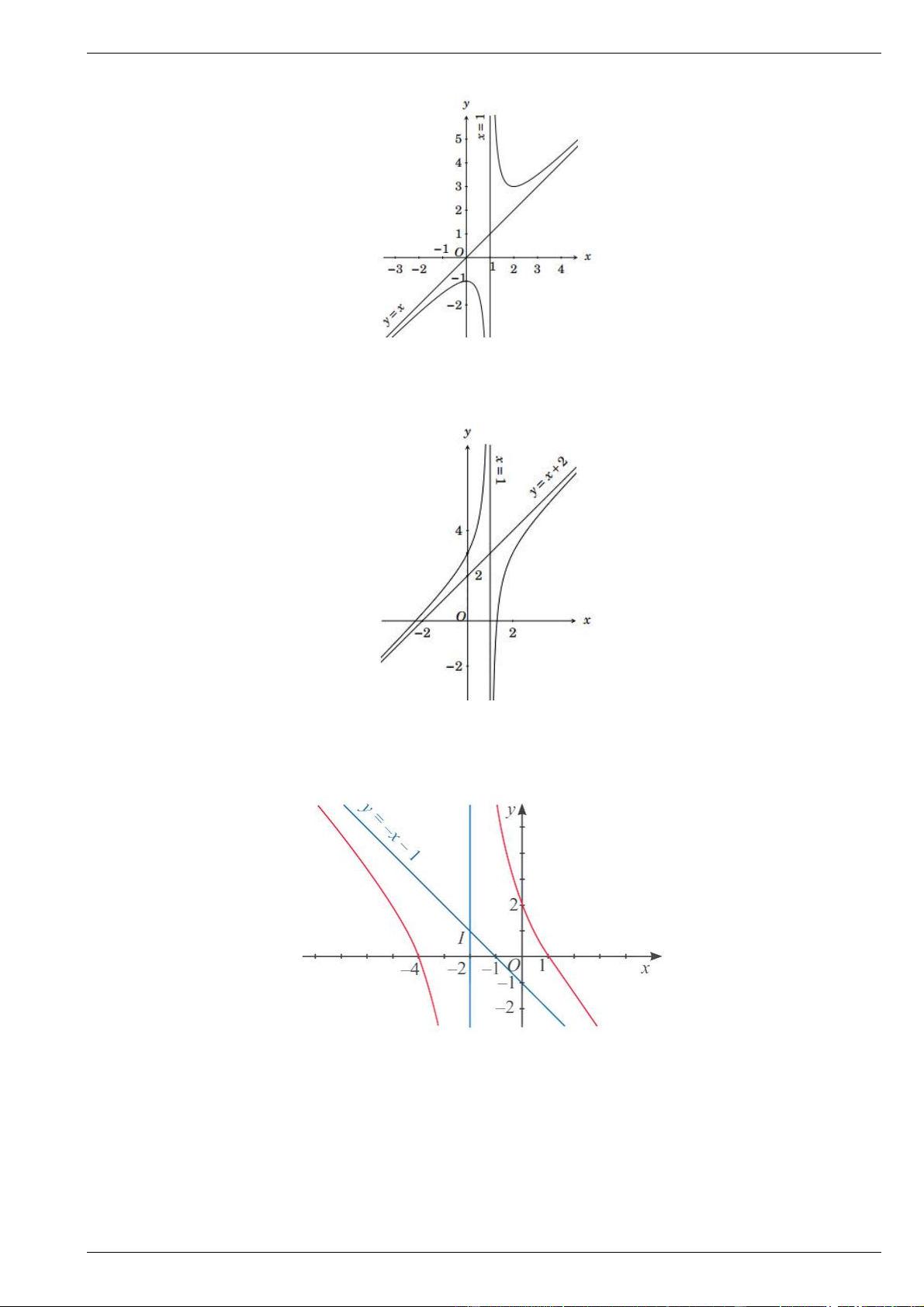
Cho hàm số y f x xác định trên khoảng 2
; và có bảng biến thiên như hình vẽ
Tìm tiệm cận ngang và tiệm cận đứng của đồ thị hàm số đã cho.
https://www.facebook.com/truongngocvy8/ T r an g
5 Trương Ngọc Vỹ - Nha Trang
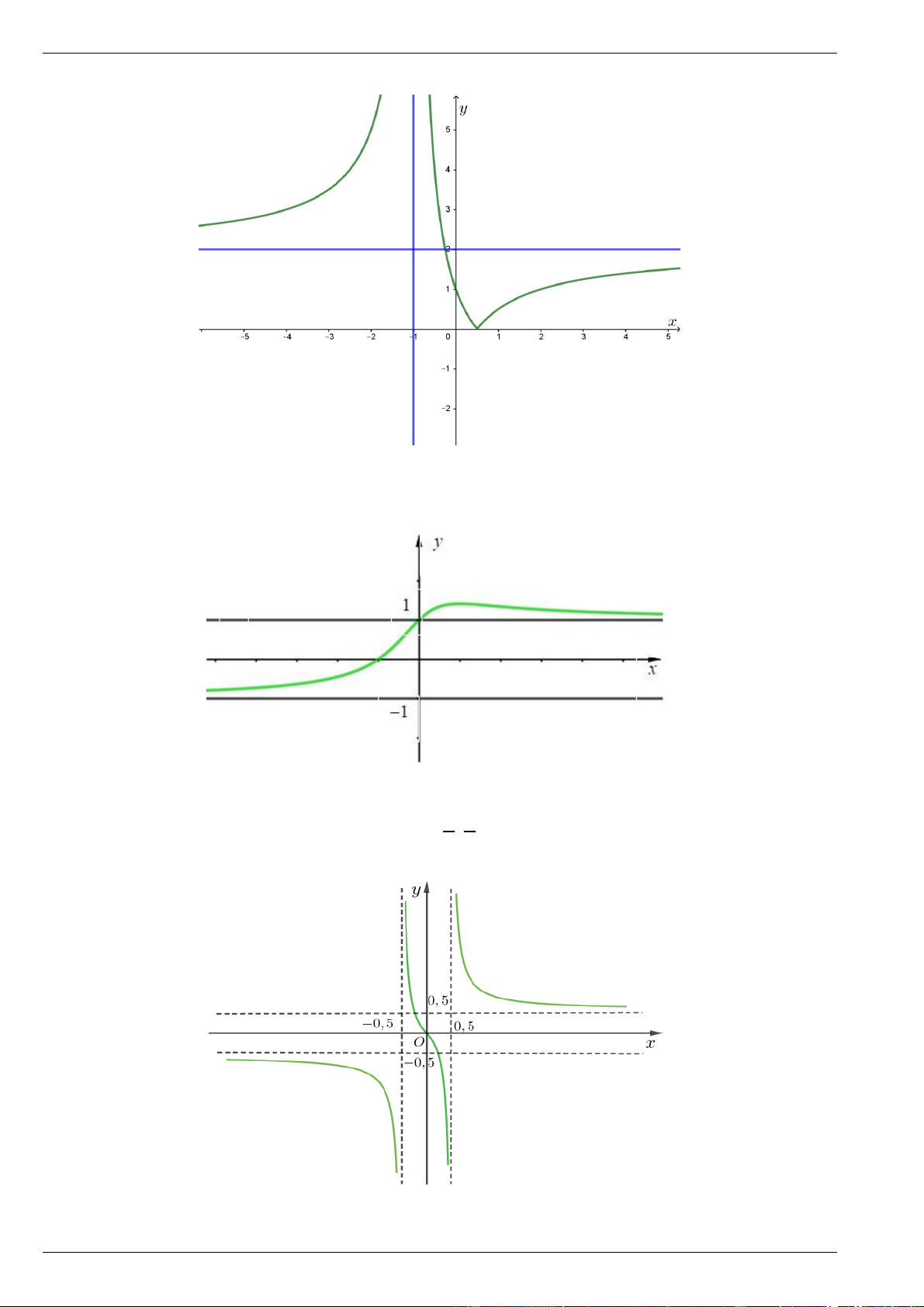
Đại số 12 - Chương 1 - Ứng dụng ĐH để khảo sát và vẽ ĐTHS - Trắc nghiệm và tự luận 4 phần Dùng chung 3 bộ sách 1 Bài 4.
Cho hàm số y f x xác định trên \ và có bảng biến thiên như hình vẽ 2
Tìm tiệm cận ngang và tiệm cận đứng của đồ thị hàm số đã cho. Bài 5.
Cho hàm số y f x xác định trên \
1 và có bảng biến thiên như hình vẽ
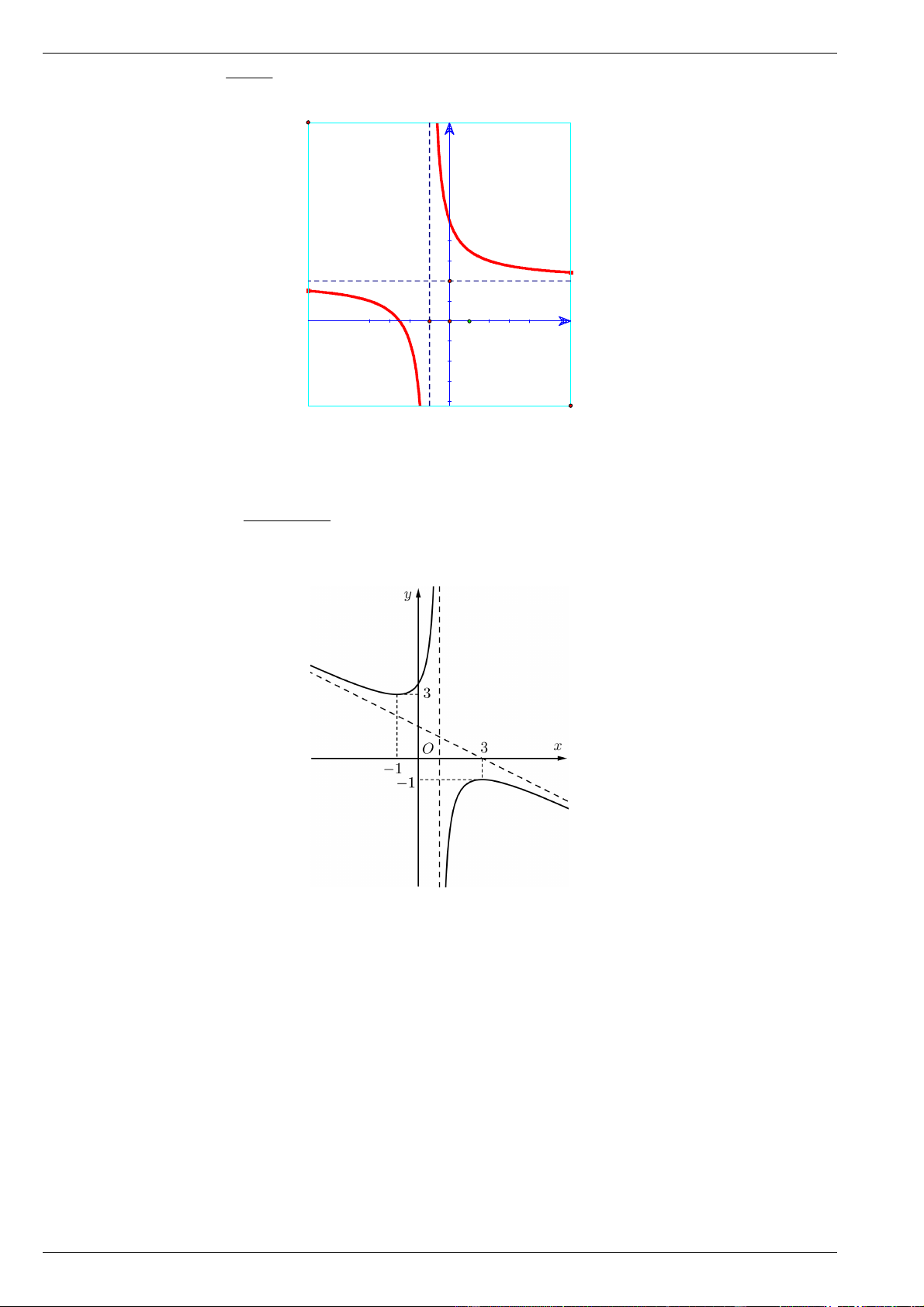
Tìm tiệm cận ngang và tiệm cận đứng của đồ thị hàm số đã cho. Bài 6.
Cho hàm số y f x xác định trên \
1 và có đồ thị như hình vẽ
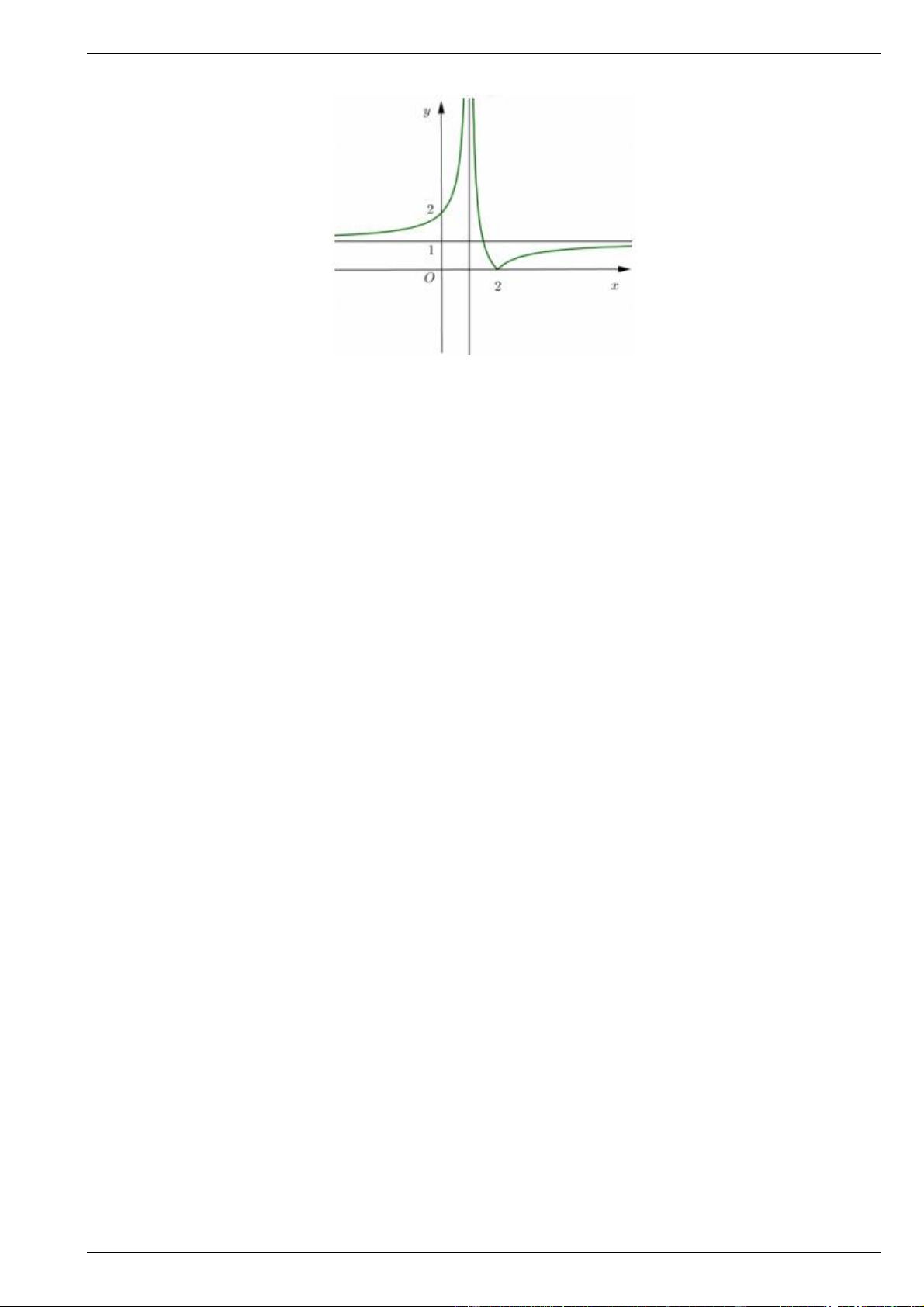
Tìm tiệm cận ngang và tiệm cận đứng của đồ thị hàm số đã cho. Bài 7.
Cho hàm số y f x xác định trên \
1 và có đồ thị như hình vẽ
Tìm tiệm cận ngang và tiệm cận đứng của đồ thị hàm số đã cho.
https://www.facebook.com/truongngocvy8/ T r an g
6 Trương Ngọc Vỹ - Nha Trang
Đại số 12 - Chương 1 - Ứng dụng ĐH để khảo sát và vẽ ĐTHS - Trắc nghiệm và tự luận 4 phần Dùng chung 3 bộ sách Bài 8.
Cho hàm số y f x xác định trên \
1 và có đồ thị như hình vẽ
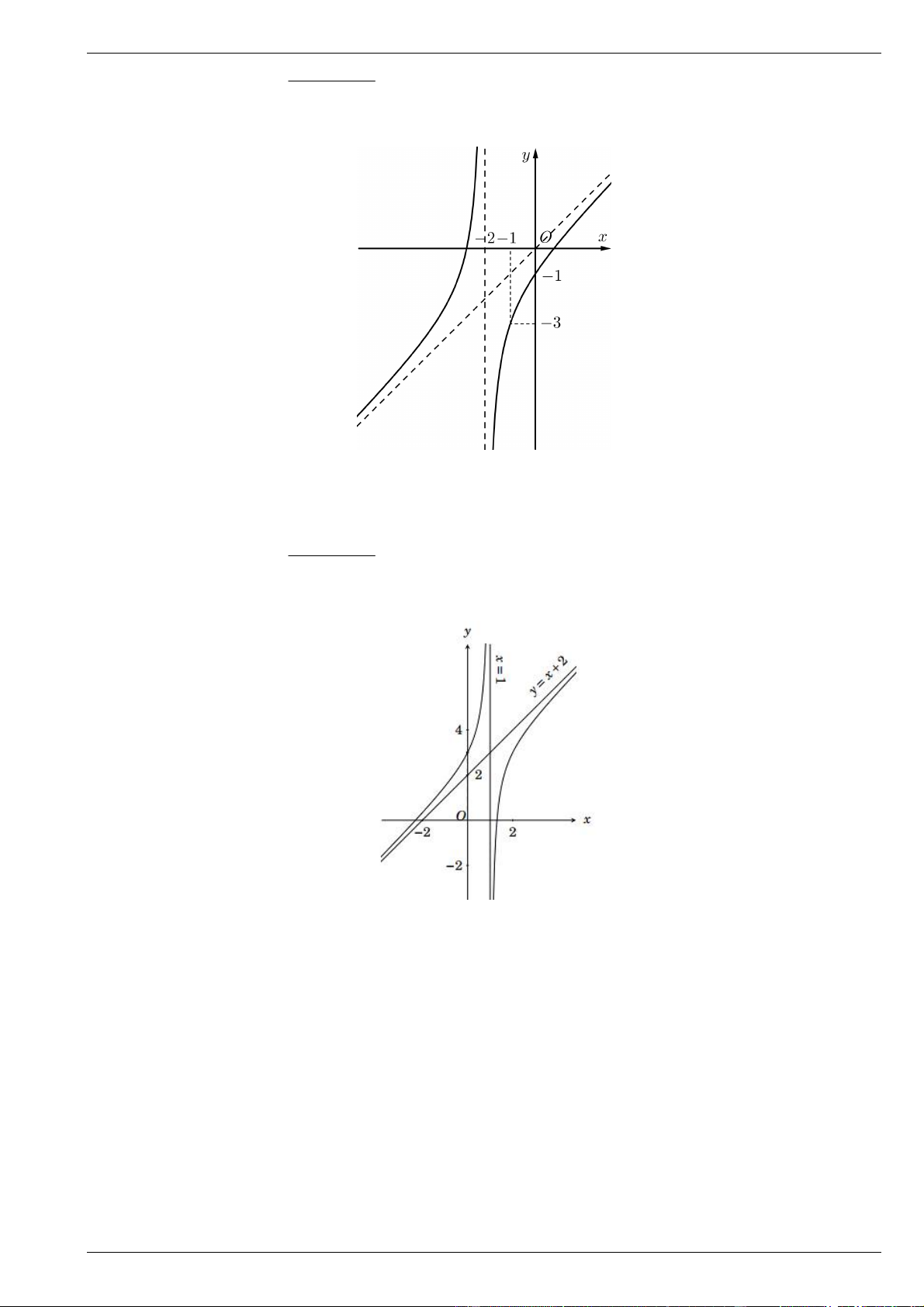
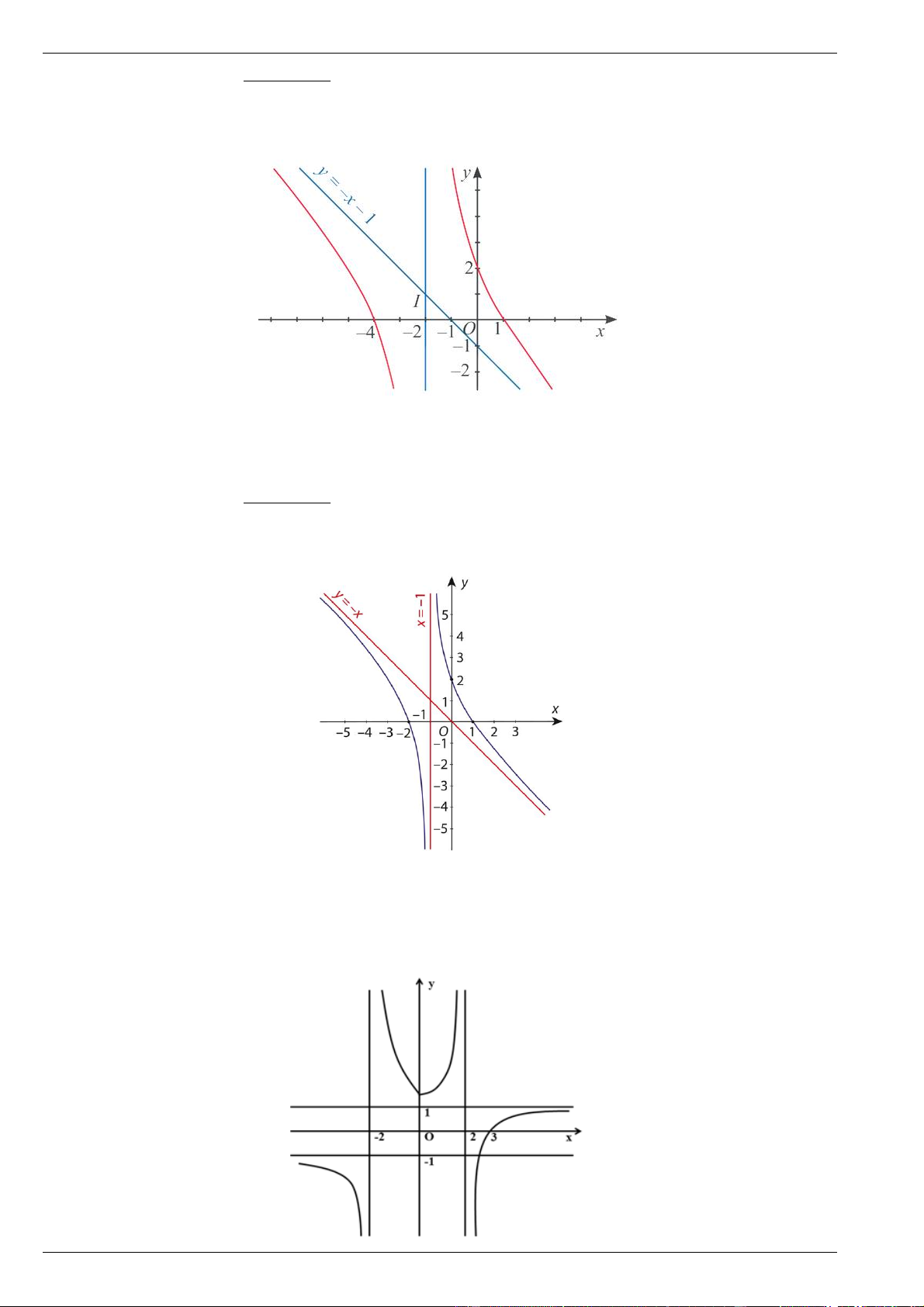
Tìm tiệm cận đứng và tiệm cận xiên của đồ thị hàm số đã cho. Bài 9.
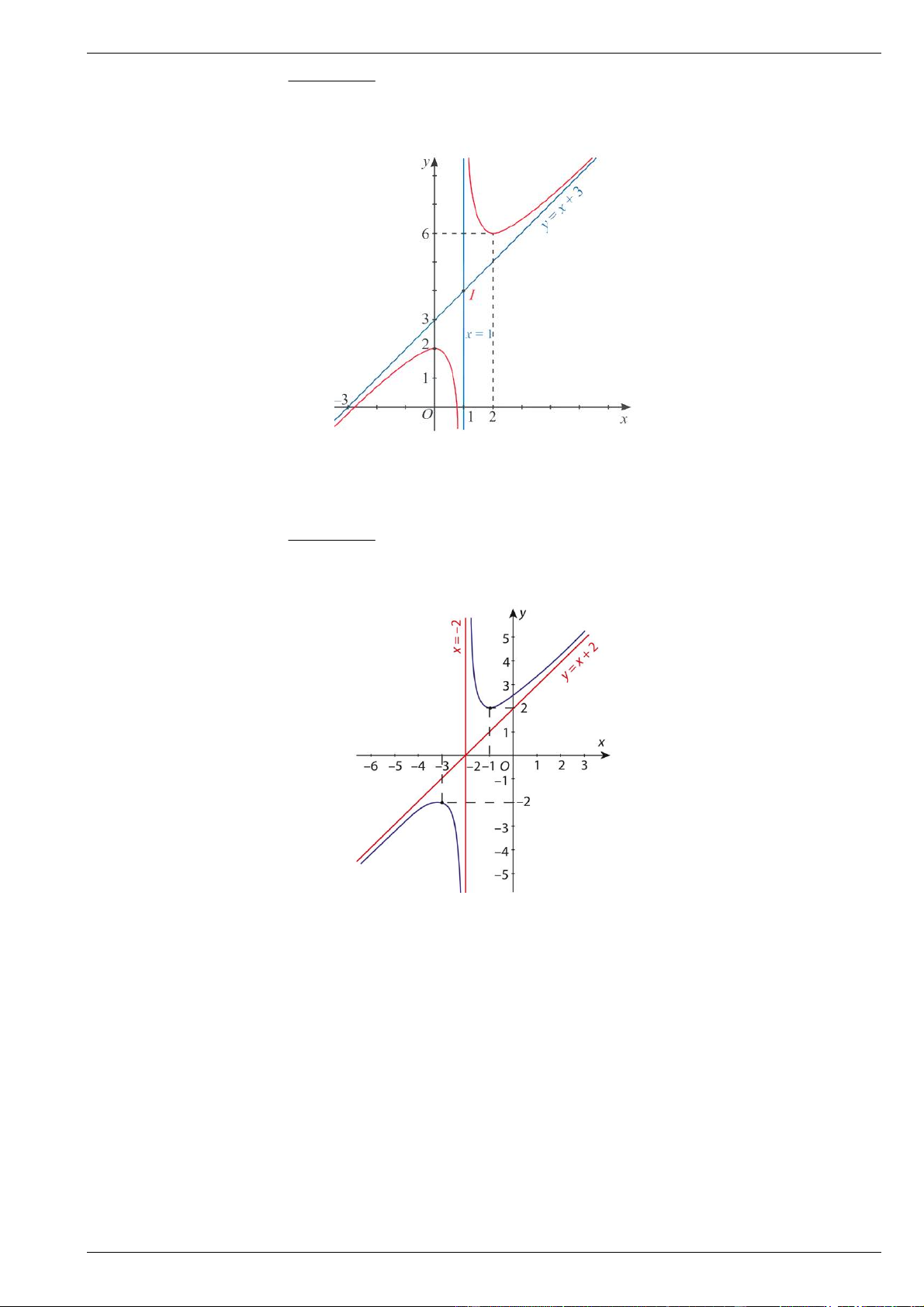
Cho hàm số y f x xác định trên \
1 và có đồ thị như hình vẽ
Tìm tiệm cận đứng và tiệm cận xiên của đồ thị hàm số đã cho.
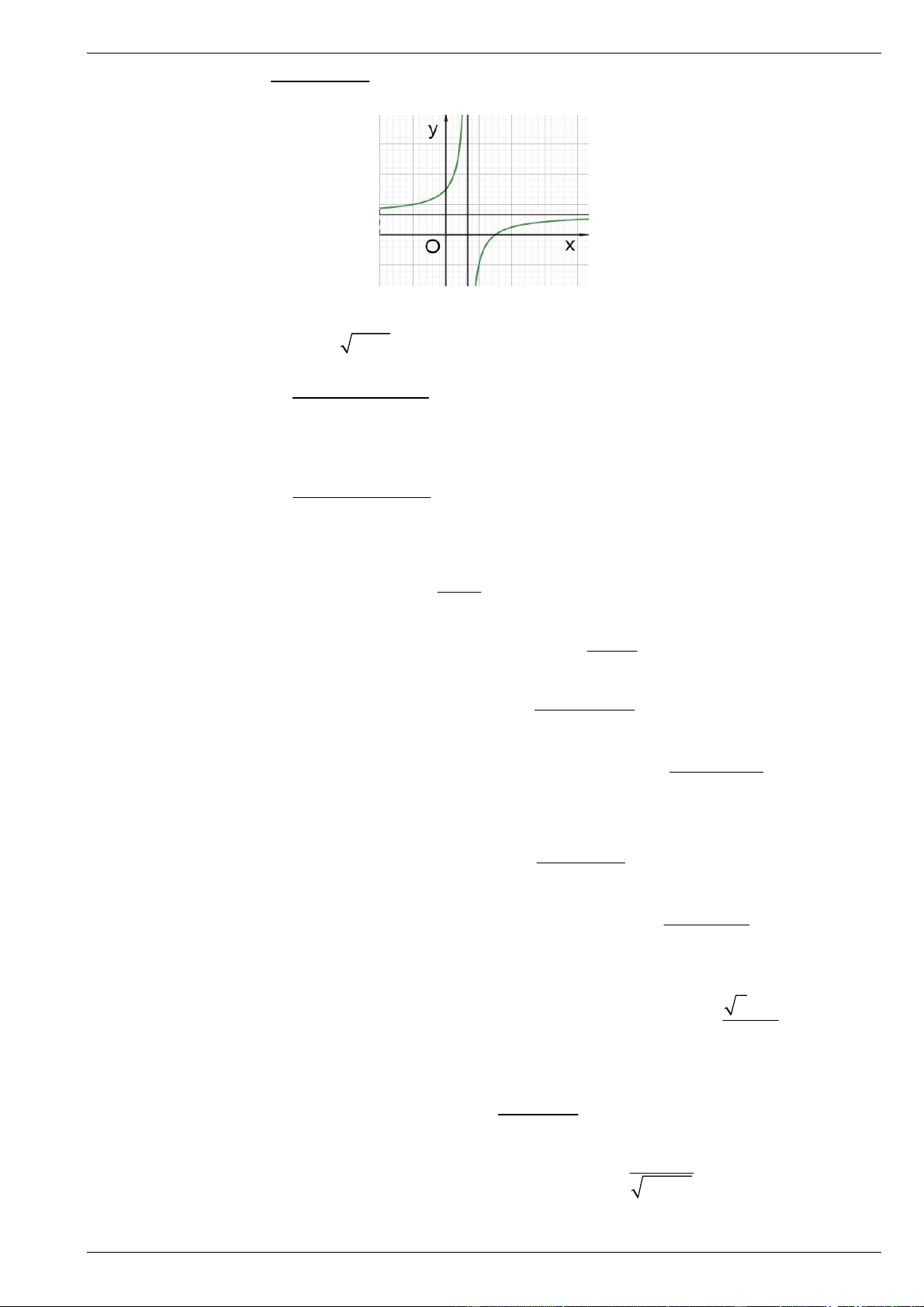
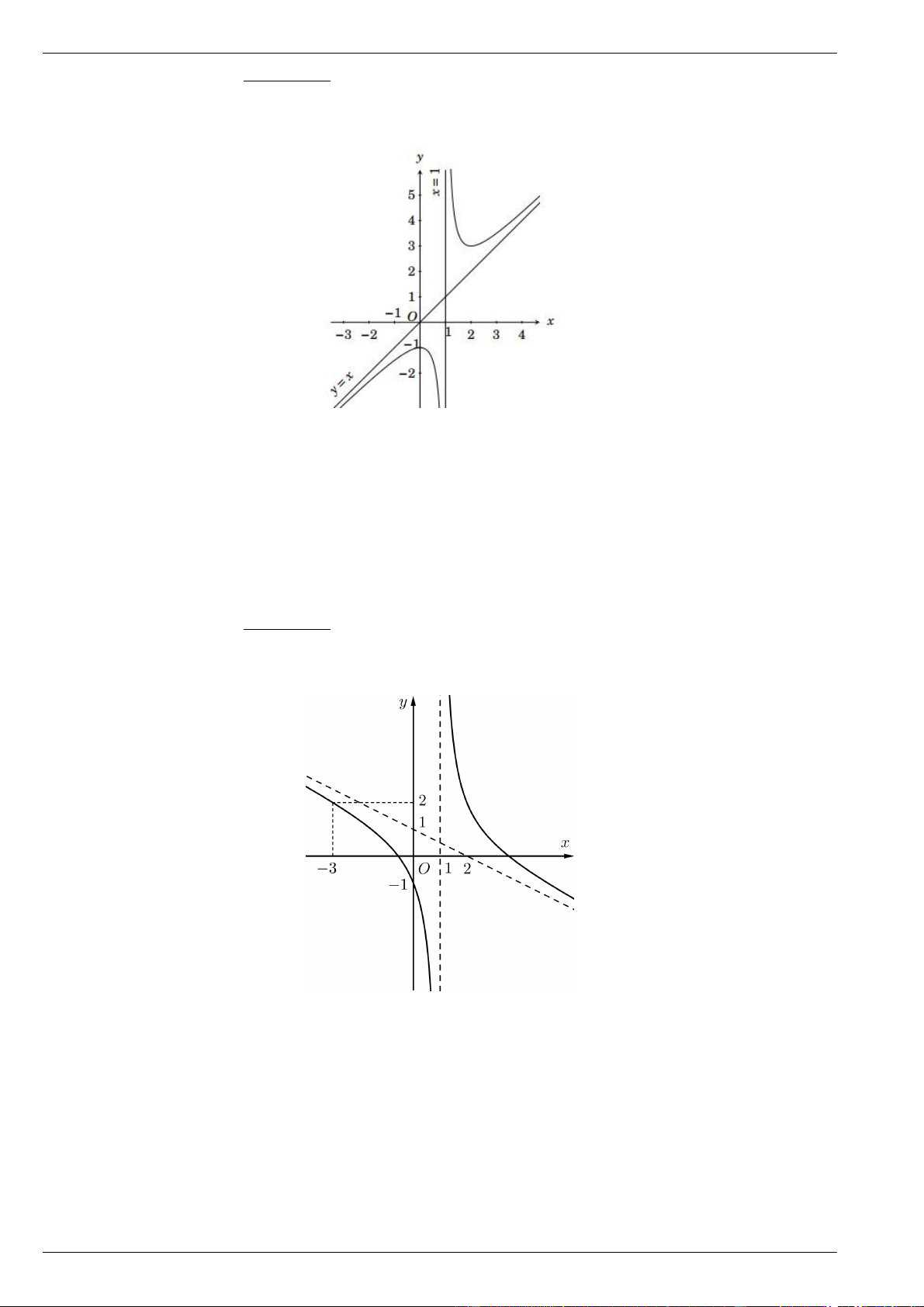
Bài 10. Cho hàm số y f x xác định trên \ 2
và có đồ thị như hình vẽ
Tìm tiệm cận đứng và tiệm cận xiên của đồ thị hàm số đã cho.
https://www.facebook.com/truongngocvy8/ T r an g
7 Trương Ngọc Vỹ - Nha Trang
Đại số 12 - Chương 1 - Ứng dụng ĐH để khảo sát và vẽ ĐTHS - Trắc nghiệm và tự luận 4 phần Dùng chung 3 bộ sách
Bài 11. Cho hàm số y f x xác định trên \ 1
và có đồ thị như hình vẽ
Tìm tiệm cận ngang và tiệm cận đứng của đồ thị hàm số đã cho.
Bài 12. Cho hàm số y f x xác định trên và có đồ thị như hình vẽ
Tìm tiệm cận ngang và tiệm cận đứng của đồ thị hàm số đã cho. 1 1
Bài 13. Cho hàm số y f x xác định trên \ ; và có đồ thị như hình vẽ 2 2
Tìm tiệm cận ngang và tiệm cận đứng của đồ thị hàm số đã cho.
https://www.facebook.com/truongngocvy8/ T r an g
8 Trương Ngọc Vỹ - Nha Trang
Đại số 12 - Chương 1 - Ứng dụng ĐH để khảo sát và vẽ ĐTHS - Trắc nghiệm và tự luận 4 phần Dùng chung 3 bộ sách
Bài 14. Cho hàm số y f x xác định trên \
1 và có đồ thị như hình vẽ
Tìm tiệm cận ngang và tiệm cận đứng của đồ thị hàm số đã cho.
https://www.facebook.com/truongngocvy8/ T r an g
9 Trương Ngọc Vỹ - Nha Trang
Đại số 12 - Chương 1 - Ứng dụng ĐH để khảo sát và vẽ ĐTHS - Trắc nghiệm và tự luận 4 phần Dùng chung 3 bộ sách DẠNG 3
ỨNG DỤNG THỰC TIỄN Bài 1.
Số lượng sản phẩm bán được của một công ty trong t (tháng) được tính theo công thức 1800
S t 1000 , trong đó t 1. t 2
a) Xem y S t là một hàm số xác định trên nửa khoảng 1; , hãy tìm tiệm cận ngang của đồ thị hàm số đó.
b) Nêu nhận xét về số lượng sản phẩm bán được của công ty đó trong t (tháng) khi t đủ lớn. 15t Bài 2.
Nồng độ oxygen trong hồ theo thời gian t cho bởi công thức y t 5
với y được tính 2 9t 1
theo mg / l và t được tính theo giờ, t 0 . Tìm các đường tiệm cận của đồ thị hàm số y y t . Từ đó,
có nhận xét gì về nồng độ oxygen trong hồ khi thời gian t trở nên rất lớn? Bài 3.
Một công ty sản xuất đồ gia dụng ước tính chi phí để sản xuất x (sản phẩm) là C x 2x 50 C x
(triệu đồng). Khi đó f x
là chi phí sản xuất trung bình cho mỗi sản phẩm. Chứng tỏ rằng hàm x
số f x giảm và lim f x 2 . Tính chất này nói lên điều gì? x Bài 4.
Một mảnh vườn hình chữ nhật có diện tích bằng 2
144m . Biết độ dài một cạnh của mảnh vườn là x (m).
a) Viết biểu thức tính chu vi P x (mét) của mảnh vườn.
b) Tìm các tiệm cận của đồ thị hàm số P x .
https://www.facebook.com/truongngocvy8/ T r an g
10 Trương Ngọc Vỹ - Nha Trang
Đại số 12 - Chương 1 - Ứng dụng ĐH để khảo sát và vẽ ĐTHS - Trắc nghiệm và tự luận 4 phần Dùng chung 3 bộ sách DẠNG 4
TIỆM CẬN CỦA HÀM SỐ y f x CÓ CHỨA THAM SỐ
Một số dạng toán thường gặp: ax b
Dạng 1: Biện luận số tiệm cận đứng của đồ thị hàm số y với c 0 . cx d
Đồ thị hàm số có tiệm cận đứng khi ad bc 0 . 2
ax bx c
Dạng 2: Biện luận số tiệm cận đứng của đồ thị hàm số y với a 0 . x x0
- Đồ thị hàm số có một tiệm cận đứng khi g x 2
ax bx c 0 không có nghiệm
x x g x 0 . 0 0
- Đồ thị hàm số không có tiệm cận đứng khi g x 2
ax bx c 0 có nghiệm x x g x 0 . 0 0
- Đồ thị hàm số có tiệm cận xiên khi a 0 .
- Đồ thị hàm số không có tiệm cận xiên khi a 0 . x x
Dạng 3: Biện luận số tiệm cận đứng của đồ thị hàm số 0 y với a 0 . 2
ax bx c
- Đồ thị hàm số có hai tiệm cận đứng khi g x 2
ax bx c 0 có hai nghiệm phân biệt khác 0 x . 0 g x 0 0
- Đồ thị hàm số có một tiệm cận đứng khi g x 2
ax bx c 0 có nghiệm kép 0 .
- Đồ thị hàm số không có tiệm cận đứng khi g x 2
ax bx c 0 vô nghiệm 0 . 2
ax bx c
Dạng 4: Biện luận số tiệm cận đứng của đồ thị hàm số y
với a 0, x x . x x x x 1 2 1 2
- Đồ thị hàm số có hai tiệm cận đứng khi phương trình g x 2
ax bx c 0 không nhận x , x là 1 2 g x 0 1 nghiệm . g x 0 2
- Đồ thị hàm số có một tiệm cận đứng khi phương trình g x 2
ax bx c 0 có nghiệm x x 1 g x 0 1
hoặc x x
(Chú ý hai điều kiện này không đồng thời xảy ra). 2 g x 0 2
- Đồ thị hàm số không có tiệm cận đứng khi g x 2
ax bx c 0 nhận x x và x x là nghiệm 1 2 g x 0 1 . g x 0 2
https://www.facebook.com/truongngocvy8/ T r an g
11 Trương Ngọc Vỹ - Nha Trang
Đại số 12 - Chương 1 - Ứng dụng ĐH để khảo sát và vẽ ĐTHS - Trắc nghiệm và tự luận 4 phần Dùng chung 3 bộ sách f x
Dạng 5: Biện luận số tiệm cận ngang của đồ thị hàm số y . g x
Đồ thị hàm số có tiệm cận ngang bậc của mẫu số lớn hơn hoặc bằng bậc của tử số và phải tồn tại các
giới hạn lim y hoặc lim y . x x
Bài 1. Hàm số y f x liên tục trên các khoảng xác định và có bảng biến thiên như hình vẽ dưới đây
Tìm m để đồ thị hàm số có tiệm cận đứng x x và tiệm cận ngang y y sao cho x y 30 . o o o o
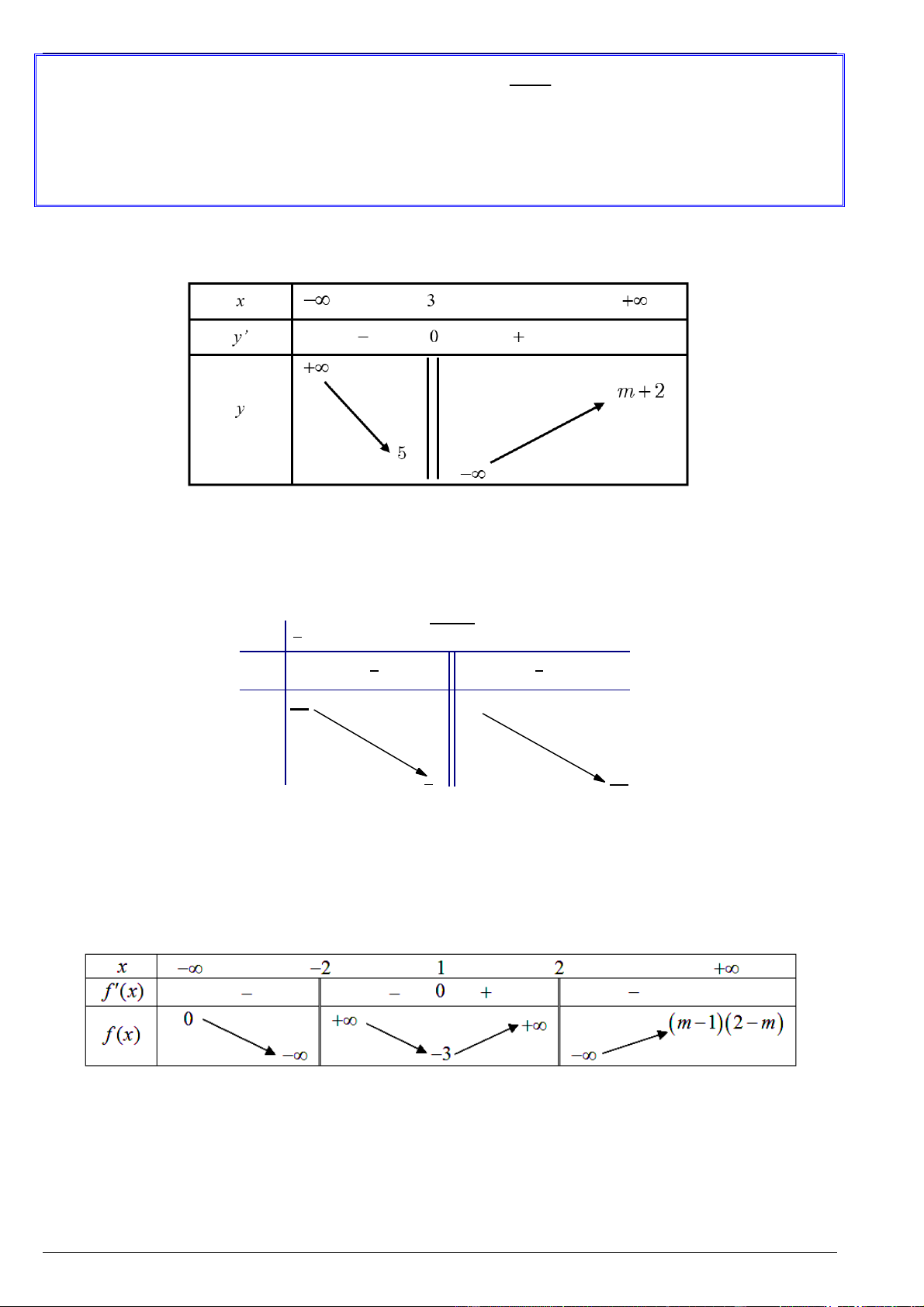
Bài 2. Cho hàm số y f x có bảng biến thiên như hình vẽ. 2-2m x ∞ n +∞ y' m +∞ y n m ∞ n
Tìm tham số m và n để đồ thị hàm số nhận đường thẳng x 2 , y 2 lần lượt là tiệm cận đứng và tiệm cận ngang.
Bài 3. Cho hàm số y f x có bảng biến thiên sau:
Tìm tổng số các giá trị nguyên dương của tham số m 10;10 để đồ thị hàm số y f x có tổng số
đường tiệm cận đứng và đường tiệm cận ngang là 4 .
https://www.facebook.com/truongngocvy8/ T r an g
12 Trương Ngọc Vỹ - Nha Trang
Đại số 12 - Chương 1 - Ứng dụng ĐH để khảo sát và vẽ ĐTHS - Trắc nghiệm và tự luận 4 phần Dùng chung 3 bộ sách 2m 1 x 3
Bài 4. Cho hàm số y
có đồ thị như hình dưới đây x m
Có bao nhiêu giá trị nguyên của tham số m để tâm đối xứng của đồ thị hàm số nằm trong đường tròn
tâm gốc tọa độ O bán kính bằng 2026 ? a 3b 2 x bx 1 Bài 5. Cho hàm số y . Tìm ,
a b để đồ thị hàm số có x 2 là tiệm cận đứng và 2
x ax a
y 1 là tiệm cận ngang. a 2b 2 x bx 1 Bài 6. Cho hàm số y . Tìm ,
a b để đồ thị hàm số có x 1 là tiệm cận đứng và 2
x x b
y 0 là tiệm cận ngang. 3x 1 Bài 7.
Tìm tham số m để đồ thị hàm số y
có đường tiệm cận đứng là x 5. x m mx 2 Bài 8.
Tìm tất cả các giá trị của tham số m để đồ thị hàm số y có tiệm cận đứng. x 1 2x 1 Bài 9.
Tìm tập hợp các giá trị thực của m để hàm số y
có đúng một đường tiệm cận. 2 4x 4mx 1 2
2x 3x m
Bài 10. Tìm tất cả các giá trị thực của tham số m sao cho đồ thị hàm số y không có tiệm x m cận đứng. x 1
Bài 11. Tìm tất cả giá trị thực của m để đồ thị hàm số y
có đúng một tiệm cận đứng. 2
x mx m 2 x x 2
Bài 12. Tìm tất cả các giá trị của tham số thực m để đồ thị hàm số y có hai tiệm cận 2
x 2x m đứng. x m
Bài 13. Tìm tập hợp tất cả các giá trị thực của tham số m để đồ thị hàm số y có đúng hai x 1 đường tiệm cận. 2 x m
Bài 14. Tìm tất cả các giá trị m để đồ thị hàm số y
có đúng một tiệm cận đứng. 2 x 3x 2 x 4
Bài 15. Tìm tất cả các giá trị thực của tham số m để đồ thị hàm số y có 3 tiệm cận 2 x m
https://www.facebook.com/truongngocvy8/ T r an g
13 Trương Ngọc Vỹ - Nha Trang
Đại số 12 - Chương 1 - Ứng dụng ĐH để khảo sát và vẽ ĐTHS - Trắc nghiệm và tự luận 4 phần Dùng chung 3 bộ sách 2 m 2 1 x x 2
Bài 16. Tìm các giá trị thực của tham số m sao cho đồ thị hàm số y có đúng một x 1 tiệm cận ngang. Bài 17. Cho hàm số 2 y
mx 2x x . Tìm các giá trị của m để đồ thị hàm số có đường tiệm cận ngang.
Bài 18. Tìm giá trị của tham số m sao cho đồ thị hàm số 2
y 2x mx x 1 1 có tiệm cận ngang.
https://www.facebook.com/truongngocvy8/ T r an g
14 Trương Ngọc Vỹ - Nha Trang
Đại số 12 - Chương 1 - Ứng dụng ĐH để khảo sát và vẽ ĐTHS - Trắc nghiệm và tự luận 4 phần Dùng chung 3 bộ sách PHẦN B
TRẮC NGHIỆM GỒM BA PHẦN
PHẦN I. Câu trắc nghiệm nhiều phương án lựa chọn. Mỗi câu hỏi thí sinh chỉ chọn một phương án. ax b
Câu 1. Cho hàm số y
(c 0, ad bc 0) có đồ thị như hình vẽ. cx d
Đồ thị hàm số đã cho có đường tiệm cận đứng bằng: A. x 1 . B. x 1 . C. x 0 . D. y 1 . ax b
Câu 2. Cho hàm số y
(c 0, ad bc 0) có đồ thị như hình vẽ. cx d
Đồ thị hàm số đã cho có đường tiệm cận ngang bằng: A. x 2 . B. x 1 . C. y 1. D. y 2 .
https://www.facebook.com/truongngocvy8/ T r an g
15 Trương Ngọc Vỹ - Nha Trang
Đại số 12 - Chương 1 - Ứng dụng ĐH để khảo sát và vẽ ĐTHS - Trắc nghiệm và tự luận 4 phần Dùng chung 3 bộ sách ax b
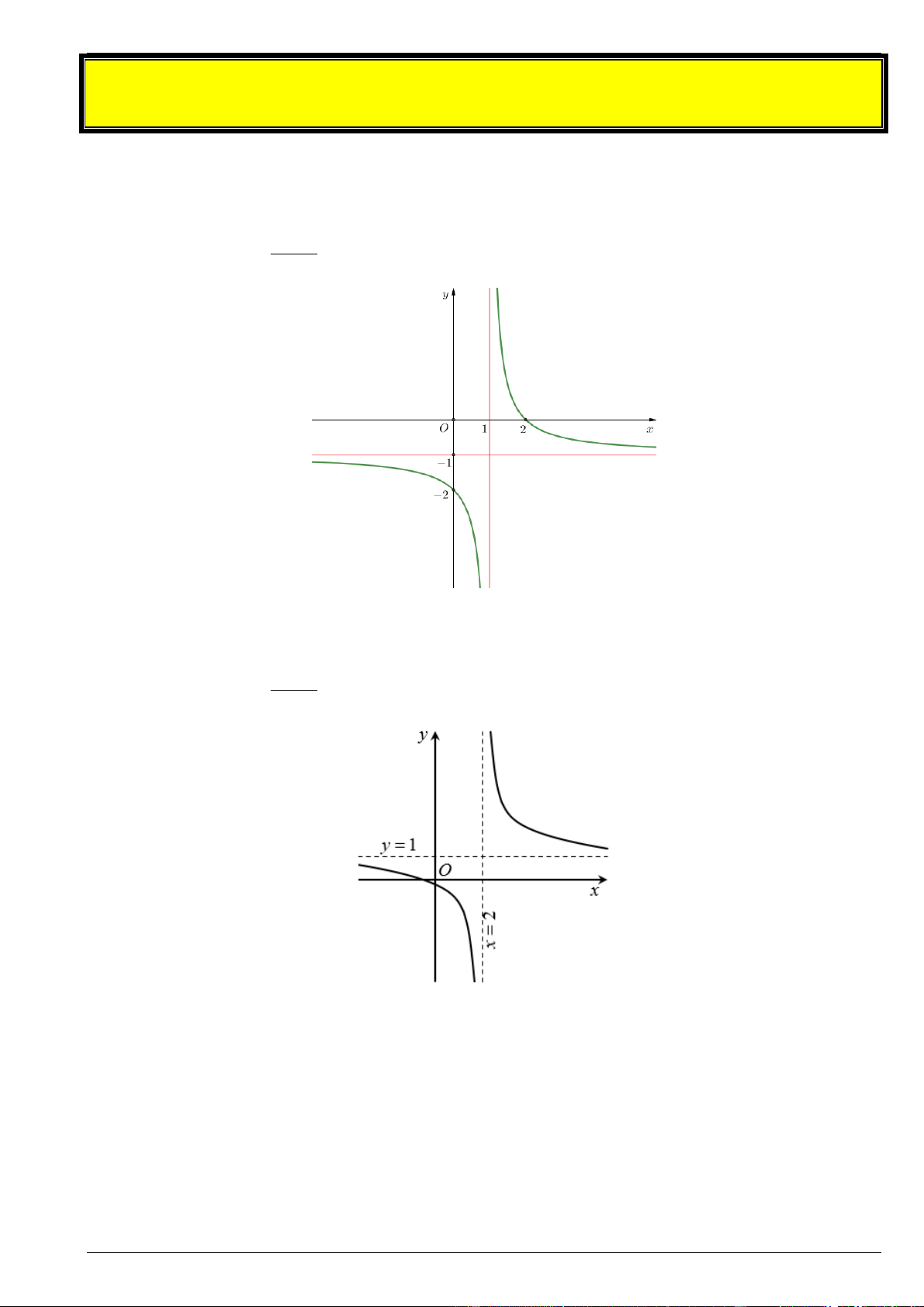
Câu 3. Cho hàm số y
(c 0, ad bc 0) có đồ thị như hình vẽ. cx d y 2 x -2 -1 0 1
Đồ thị hàm số đã cho có đường tiệm cận ngang bằng: A. x 1 . B. x 2 . C. y 1 . D. y 2 . 2
ax bx c
Câu 4. Cho hàm số y
(a 0, m 0) với a, b, c, m, n là các số thực và có đồ thị là (C) có mx n dạng như hình vẽ sau.
Đồ thị hàm số đã cho có bao nhiêu đường tiệm cận? A. 4 . B. 2 . C. 1. D. 3 .
https://www.facebook.com/truongngocvy8/ T r an g
16 Trương Ngọc Vỹ - Nha Trang
Đại số 12 - Chương 1 - Ứng dụng ĐH để khảo sát và vẽ ĐTHS - Trắc nghiệm và tự luận 4 phần Dùng chung 3 bộ sách 2
ax bx c
Câu 5. Cho hàm số y
(a 0, m 0) với a, b, c, m, n là các số thực và có đồ thị là (C) có mx n dạng như hình vẽ sau.
Đồ thị hàm số đã cho có đường tiệm cận đứng bằng: A. x 2 . B. x 1 . C. y 2 . D. y 1 . 2
ax bx c
Câu 6. Cho hàm số y
(a 0, m 0) với a, b, c, m, n là các số thực và có đồ thị là (C) có mx n dạng như hình vẽ sau.
Khẳng định nào sau đây sai?
A. Đồ thị hàm số (C) có tiệm cận đứng là đường thẳng x 1
B. Đồ thị hàm số (C) có tiệm cận xiên là đường thẳng y x 2
C. Đồ thị hàm số (C) có tiệm cận ngang là đường thẳng y 0
D. Giao điểm của tiệm cận đứng và tiệm cận xiên có tọa độ 1;3 .
https://www.facebook.com/truongngocvy8/ T r an g
17 Trương Ngọc Vỹ - Nha Trang
Đại số 12 - Chương 1 - Ứng dụng ĐH để khảo sát và vẽ ĐTHS - Trắc nghiệm và tự luận 4 phần Dùng chung 3 bộ sách 2
ax bx c
Câu 7. Cho hàm số y
(a 0, m 0) với a, b, c, m, n là các số thực và có đồ thị là (C) có mx n dạng như hình vẽ sau.
Khẳng định nào sau đây đúng?
A. Đồ thị hàm số (C) có tiệm cận đứng là đường thẳng x 0
B. Đồ thị hàm số (C) có tiệm cận xiên là đường thẳng y 1
C. Đồ thị hàm số (C) có tiệm cận ngang là đường thẳng y x
D. Giao điểm của tiệm cận đứng và tiệm cận xiên có tọa độ 1; 1 . 2
ax bx c
Câu 8. Cho hàm số y
(a 0, m 0) với a, b, c, m, n là các số thực và có đồ thị là (C) có mx n dạng như hình vẽ sau.
Đồ thị hàm số đã cho có đường tiệm cận đứng bằng: A. x 2 . B. x 1 . C. x 1 . D. x 2 .
https://www.facebook.com/truongngocvy8/ T r an g
18 Trương Ngọc Vỹ - Nha Trang
Đại số 12 - Chương 1 - Ứng dụng ĐH để khảo sát và vẽ ĐTHS - Trắc nghiệm và tự luận 4 phần Dùng chung 3 bộ sách 2
ax bx c
Câu 9. Cho hàm số y
(a 0, m 0) với a, b, c, m, n là các số thực và có đồ thị là (C) có mx n dạng như hình vẽ sau.
Đồ thị hàm số đã cho có đường tiệm cận xiên bằng: A. x 1 . B. x 1 .
C. y x 3 .
D. y x 3 . 2
ax bx c
Câu 10. Cho hàm số y
(a 0, m 0) với a, b, c, m, n là các số thực và có đồ thị là (C) có mx n dạng như hình vẽ sau.
Đồ thị hàm số đã cho có đường tiệm cận xiên bằng:
A. y x 2 . B. x 2 .
C. y 2 .
D. y x 2 .
https://www.facebook.com/truongngocvy8/ T r an g
19 Trương Ngọc Vỹ - Nha Trang
Đại số 12 - Chương 1 - Ứng dụng ĐH để khảo sát và vẽ ĐTHS - Trắc nghiệm và tự luận 4 phần Dùng chung 3 bộ sách 2
ax bx c
Câu 11. Cho hàm số y
(a 0, m 0) với a, b, c, m, n là các số thực và có đồ thị là (C) có mx n dạng như hình vẽ sau.
Đồ thị hàm số đã cho có đường tiệm cận xiên bằng:
A. y x 1 . B. x 2 .
C. y 2 .
D. y x 1 . 2
ax bx c
Câu 12. Cho hàm số y
(a 0, m 0) với a, b, c, m, n là các số thực và có đồ thị là (C) có mx n dạng như hình vẽ sau.
Đồ thị hàm số đã cho có đường tiệm cận xiên bằng:
A. y x . B. x 1 . C. y 1.
D. y x .
Câu 13. Cho hàm số y f x có đồ thị như hình vẽ.
https://www.facebook.com/truongngocvy8/ T r an g
20 Trương Ngọc Vỹ - Nha Trang