234 trang 4 lượt tải

Trắc nghiệm và tự luận chủ đề tích phân

7

Tài liệu gồm 234 trang, được biên soạn bởi thầy giáo Trương Ngọc Vỹ, phân dạng và tuyển tập các bài tập trắc nghiệm và tự luận chủ đề tích phân môn Toán 12 chương trình mới (Cánh Diều, Chân Trời Sáng Tạo, Kết Nối Tri Thức Với Cuộc Sống).

Chủ đề: Tài liệu chung 176 tài liệu

Môn: Toán 12 4.3 K tài liệu

Tác giả:

Profile

Linh Đan

3 tuần trước
Danh sách Quiz
/234
Đại số 12 - Chương 4 – Nguyên hàm. Tích phân - Trắc nghiệm và tự luận 4 phần có lời giải Dùng chung 3 bộ sách
https://www.facebook.com/truongngocvy8/ Trương Ngọc Vỹ 0978 333 093
Trang 1
BÀI 2
TÍCH PHÂN
1. Khái niệm tích phân
a. Diện tích hình thang cong
Nếu hàm số
f x
liên tục và không âm trên đoạn
;
a b
thì diện tích
S
của hình thang cong giới hạn
bởi đồ thị
, trục hoành và hai đường thẳng ,
x a x b
được tính bởi:
S F b F a
trong đó
F x
là một nguyên hàm của
f x
trên đoạn
;
a b
.
b. Khái niệm tích phân
Cho hàm số
f x
liên tục trên đoạn
;
a b
. Nếu
F x
là nguyên hàm của hàm số
f x
trên đoạn
;
a b
thì hiệu số
F b F a
được gọi là tích phân từ
a
đến
b
của hàm số
f x
, kí hiệu
b
a
f x dx
Chú ý:
Hiệu số
F b F a
còn được kí hiệu là
b
a
F x
.
Vậy
b
b
a
a
f x dx F x F b F a
Ta gọi
b
a
là dấu tích phân,
a
là cận dưới,
b
là cận trên,
f x dx
là biểu thức dưới dấu tích phân và
f x
là hàm số dưới dấu tích phân.
Quy ước:
;
a b a
a a b
f x dx f x dx f x dx
Tích phân của hàm số
f
từ
a
đến
b
chỉ phụ thuộc vào
f
và các cận
,
a b
mà không phụ thuộc vào
biến
x
hay
t
, nghĩa là
b b
a a
f x dx f t dt
.
Đại số 12 - Chương 4 – Nguyên hàm. Tích phân - Trắc nghiệm và tự luận 4 phần có lời giải Dùng chung 3 bộ sách
https://www.facebook.com/truongngocvy8/ Trương Ngọc Vỹ 0978 333 093
Trang 2
Ý nghĩa hình học của tích phân
Nếu hàm số
f x
liên tục và không âm trên đoạn
;
a b
thì
b
a
f x dx
là diện tích
S
của hình thang
cong giới hạn bởi đồ thị
, trục hoành và hai đường thẳng ,
x a x b
.
b
a
S f x dx
Nhận xét:
Nếu hàm số
f x
có đạo hàm
'
f x
và
'
f x
liên tục trên đoạn
;
a b
thì
'
b
a
f b f a f x dx
.
Cho hàm số
f x
liên tục trên đoạn
;
a b
. Khi đó
1
b
a
f x dx
b a
được gọi là giá trị trung bình của
hàm số
f x
trên đoạn
;
a b
.
Đạo hàm của quãng đường di chuyển của vật theo thời gian bằng tốc độ của chuyển động tại mọi
thời điểm:
( ) '( )
v t s t
. Do đó, nếu biết tốc độ
( )
v t
tại mọi thời điểm
;
t a b
thì tính được quãng đường
di chuyển trong khoảng thời gian từ
a
đến
b
theo công thức:
( )
b
a
s s b s a v t dt
2. Tính chất của tích phân
Cho hai hàm số
,
f x g x
liên tục trên đoạn
;
a b
. Khi đó:
Tính chất 1:
b b
a a
kf x dx k f x dx
, với
k
là hằng số.
Tính chất 2:
b b b
a a a
f x g x dx f x dx g x dx
b b b
a a a
f x g x dx f x dx g x dx
Tính chất 3:
b c b
a a c
f x dx f x dx f x dx
với
;
c a b
.
Đại số 12 - Chương 4 – Nguyên hàm. Tích phân - Trắc nghiệm và tự luận 4 phần có lời giải Dùng chung 3 bộ sách
https://www.facebook.com/truongngocvy8/ Trương Ngọc Vỹ 0978 333 093
Trang 3
PHẦN A
TỰ LUẬN PHÂN DẠNG TOÁN
DẠNG 1
TÍNH TÍCH PHÂN SỬ DỤNG BẢNG NGUYÊN HÀM SƠ CẤP
Chú ý : Dùng công thức sau làm trắc nghiệm cho nhanh
1
1 1
1
n n
dx C
x n x
1
1
n
n
ax b
ax b dx C
a n
1
ax b ax b
e dx e C
a
1
0 1
ln
x
x
a
a dx C a
a
Nguyên hàm của một hàm số sơ cấp
Nguyên hàm của hàm số lũy thừa
0
dx C
Cxdx
1
1
1
x
x dx C
Nguyên hàm của hàm số
1
y
x
0ln
xCx
x
dx
Nguyên hàm của hàm số lượng giác
Cxxdx
sincos
Cxxdx
cossin
Cxdx
x
tan
cos
1
2
Cxdx
x
cot
sin
1
2
Nguyên hàm của hàm số mũ
Cedxe
xx
10
ln
aC
a
a
dxa
x
x
Đại số 12 - Chương 4 – Nguyên hàm. Tích phân - Trắc nghiệm và tự luận 4 phần có lời giải Dùng chung 3 bộ sách
https://www.facebook.com/truongngocvy8/ Trương Ngọc Vỹ 0978 333 093
Trang
4
Bài 1. Tính các tích phân sau đây:
a)
3
0
2
3 +202
d
4
x
x
b)
1
3 2
0
4 3 2 d
x x x
c)
4
2
1
d
1
x
x x
d)
2
1
1
d
x
x
x
e)
2
3
2
1
2 2025
d
x
x x
x
f)
2
2
1
d
1
x
x
x
Bài 2. Tính các tích phân sau đây:
a)
3
2024
1
d
x x
b)
3
2
3
1
d
x x
c)
8
3
1
d
x x
d)
1
7
d
3
e
x
x
e)
2
3
1
1
d
x
x
f)
4
1
1
d
2
x
x
Bài 3. Tính các tích phân sau đây:
a)
4
1
2 2
dx
x x
b)
4
3
0
1 1
x x dx
c)
2
2
34
1
x x
dx
x
d)
1
2 3
2
3
( 1)
x
dx
x
e)
4
3
1
1
x
dx
x
f)
2
3
8
3 2
1
1x
dx
x
Bài 4. Tính các tích phân sau đây:
a)
3
0
sin d
x x
b)
4
2
0
d
1
cos
x
x
c)
2
0
3sin 2024
d
x
x
d)
4
2 2
6
1 1
d
cos sin
x
x x
e)
4
0
cos2
cos
d
1 tan
x
x
x x
f)
2
2
0
sin
1 cos
d
x
x
x
Bài 5. Tính các tích phân sau đây:
a)
1
2 1
0
2 3 d
.
x x
x
b)
1
0
2.3 5 d
x x
e x
c)
2
3 1
2
1
1
4 2.3
x
x dx
x
d)
2
1
1
0
2
x
x
e
dx
e
e)
2
1
3
0
2024 1
x
x
dx
e
f)
2
2
2
3
1
2025
2024
x
x
e
e dx
x
Bài 6. Tính các tích phân sau đây:
a)
1
1 2 1
0
5 .7
x x
dx
b)
1
2
0
x
x e dx
c)
2
3 2
6
1
sin
x dx
x
d)
3
2
2
6
sin
1
x
x dx
x
e)
3
0
sin sin cos
2 2 2
x x x
dx
f)
2
1
1
2
2 1
x
x
dx
e
Đại số 12 - Chương 4 – Nguyên hàm. Tích phân - Trắc nghiệm và tự luận 4 phần có lời giải Dùng chung 3 bộ sách
https://www.facebook.com/truongngocvy8/ Trương Ngọc Vỹ 0978 333 093
Trang 5
DẠNG 2
TÍCH PHÂN HÀM ẨN BIẾN ĐỔI CƠ BẢN
. .
b b
a a
k f x dx k f x dx
b b b
a a a
f x g x dx f x dx g x dx
b c b
a a c
f x dx f x dx f x dx
Bài 1. Cho hàm số
f x
liên tục trên
và thỏa mãn:
a)
0
6
( ) 1
f x dx
. Tính tích phân
6
0
2025 ( )
f x dx
b)
2
0
4
f x dx
. Tính tích phân
2
0
2 1)
f x dx
c)
7
2
d 3
f x x
và
7
1
d 3
f x x
. Tính tích phân
2
1
d
f x x
.
Bài 2. Cho hàm số
f x
liên tục trên
và thỏa mãn:
a)
1
0
2 3
f x x dx
. Tính tích phân
1
0
d
f x x
b)
3
1
2 3 10
f x x dx
. Tính tích phân
3
1
f x dx
.
c)
2
0
d 4
f x x
. Tính tích phân
2
0
2 sin d
f x x x
.
Bài 3. Cho hàm số
y f x
liên tục trên
và thỏa mãn:
a)
11
6
d 8
f x x
,
6
2
d 3
f x x
. Tính giá trị của biểu thức
2 11
6 6
d d
P f x x f x x
.
b)
8
1
d 9
f x x
,
12
4
d 3
f x x
,
8
4
d 5
f x x
. Tính
12
1
d
I f x x
.
Bài 4. Cho
,
f x g x
là hai hàm liên tục trên
, thỏa mãn:
a)
5
2
3
f x dx
và
5
2
2
g x dx
. Tính
5
2
f x g x dx
Đại số 12 - Chương 4 – Nguyên hàm. Tích phân - Trắc nghiệm và tự luận 4 phần có lời giải Dùng chung 3 bộ sách
https://www.facebook.com/truongngocvy8/ Trương Ngọc Vỹ 0978 333 093
Trang
6
b)
1
0
3
f x dx
và
1
0
4
g x dx
. Tính
0
1
f x g x dx
.
c)
4
1
6
f x dx
và
4
1
5
g x dx
. Tính
4
1
1 1
3 5
f x g x dx
Bài 5. Cho
,
f x g x
là hai hàm liên tục trên
, thỏa mãn:
a)
3
2
3
f x dx
và
2
3
1
g x dx
. Tính
3
2
2
f x g x dx
b)
3
1
2024
f x dx
và
1
3
1
g x dx
. Tính
3
1
1
3
2024
f x g x dx
c)
2
1
d 3
f x x
và
1
2
d 2
g x x
. Tính
2
1
1
3 d
2
f x g x x
Bài 6. Cho
3
0
d 2024
f x x
và
3
0
d 2025
g x x
. Tính các tích phân sau:
a)
3
0
d
f x g x x
b)
0
3
1
d
5
g x x
c)
3
0
1
3 d
2
f x g x x
d)
3
2
0
1
3 d
2024
f x x x
e)
0
3 2
3
d
g x x x
f)
3
3 1
0
1
d
4
x
f x g x e x
Bài 7. Cho
,
f x g x
là hai hàm liên tục trên đoạn
1;3
thoả:
3
1
3 d 10
f x g x x
,
3
1
2 d 6
f x g x x
. Tính
3
1
d
I f x g x x
.
Đại số 12 - Chương 4 – Nguyên hàm. Tích phân - Trắc nghiệm và tự luận 4 phần có lời giải Dùng chung 3 bộ sách
https://www.facebook.com/truongngocvy8/ Trương Ngọc Vỹ 0978 333 093
Trang
7
DẠNG 3
TÍCH PHÂN HÀM TRỊ TUYỆT ĐỐI
Tính tích phân:
b
a
I f x dx
Phương pháp
Bước 1. Xét dấu
f x
trên đoạn
;
a b
.
Bước 2. Dựa vào bảng xét dấu trên đoạn
;
a b
để khử
f x
. Sau đó sử dụng các phương pháp tính tích
phân đã học đê tính
.
b
a
I f x dx
Bài 1. Tính tích phân
3
2
3
1
I x dx
.
Bài 2. Tính tích phân
2
1
2
3
2 d
I x x x x
.
Bài 3. Tính tích phân
2
1
3
3 2 d
I x x x
.
Bài 4. Tính tích phân
2
4 2
2
3 4 d
I x x x
.
Bài 5. Tính tích phân
2
3
0
3
2 d
I x x x x
.
Bài 6. Tính tích phân
5
1
2 2 1
d
x
I x
x
.
Bài 7. Tính tích phân
5
3
2 2 d
I x x x
.
Bài 8. Tính tích phân
2
1
1 2 d
I x x x x
.
Bài 9. Tính tích phân
6
2
2
8 16
I x x dx
.
Bài 10. Tính tích phân
1
2
2
4 6 9
I x x dx
.
Bài 11. Tính tích phân
2
0
1 cos2
I xdx
.
Bài 12. Tính tích phân
2
0
1 cos2
I xdx
.
Đại số 12 - Chương 4 – Nguyên hàm. Tích phân - Trắc nghiệm và tự luận 4 phần có lời giải Dùng chung 3 bộ sách
https://www.facebook.com/truongngocvy8/ Trương Ngọc Vỹ 0978 333 093
Trang 8
DẠNG 4
TÍCH PHÂN HÀM NHIỀU CÔNG THỨC
Dạng 1: Cho hàm số
khi
khi
g x x c
f x
h x x c
liên tục trên
D
. Tính
d
b
a
f x x
, với
;
c a b
.
Phương pháp giải:
Bước 1: Kiểm tra hàm số
f x
có liên tục tại
x c
hay không (kiến thức hàm số liên tục tại một
điểm lớp 11)
Tức là kiểm tra
lim lim lim lim
x b x b x b x b
f x f x f b g x h x f b
Bước 2: Tách cận:
d d d
b c b
a a c
f x x g x x h x x
.
Bước 3: Tính tích phân
d
c
a
g x x
và
d
b
c
h x x
bằng các phương pháp đã học.
Dạng 2: Cho hàm số
; khi
;
; khi
g x m x c
f x m
h x m x c
liên tục trên
D
và
m
là tham số. Tính
; d
b
a
f x m x
, với
;
c a b
.
Phương pháp giải:
Bước 1: Kiểm tra hàm số
f x
có liên tục tại
x c
hay không.
Tức là kiểm tra:
lim ; lim ; l m ;im ; li
x b x b x b x b
x m x m f b g h f b
x m x m
Chú ý: Bước này tìm tham số
m
.
Bước 2: Tách cận:
; d ; d ; d
b c b
a a c
f x m x g x m x h x m x
.
Bước 3: Tính tích phân
; d
c
a
g x m x
và
; d
b
c
x m x
bằng các phương pháp đã học.
Đại số 12 - Chương 4 – Nguyên hàm. Tích phân - Trắc nghiệm và tự luận 4 phần có lời giải Dùng chung 3 bộ sách
https://www.facebook.com/truongngocvy8/ Trương Ngọc Vỹ 0978 333 093
Trang 9
Bài 1. Cho
khi
k
1
1 1
hi
1
2
x
f x
x x
. Tính tích phân
2
1
d
I f x x
Bài 2. Cho hàm số
2
1 khi 0
khi 0
x
x x
f x
e x
. Tính tích phân
2
1
d
I f x x
.
Bài 3. Cho hàm số
2
3 2 khi 1
5 2 khi 1
x x m x
f x
x x
(
m
là tham số thực). Biết rằng
f x
có nguyên
hàm trên
là
F x
thỏa mãn
2 10
F
, khi đó tính
3
F .
Bài 4. Cho số thực
a
và
f x
liên tục trên
thỏa mãn
2
2 0
0
x khi x
f x
a x x khi x
. Tính tích
phân
1
1
f x dx
.
Bài 5. Cho hàm số
3
2 3
e khi
1
0
i
0
kh
x
x
f
x
x
x x
m
(với
m
tham số). Biết hàm số
f x
liên tục trên
và tích phân
1
1
d .
b
f x x a e
c
với
*
, , ;
a
a b c
b
tối giản (
2,718281...
e
.). Tính giá trị biểu thức
a b c m
.
Bài 6. Cho hàm số
2
2 3 khi 0
.
2 3 khi 0
x x
f x
x x x
Giả sử
F
là nguyên hàm của
f
trên
thỏa mãn
3 0
F
. Tính giá trị của
2 1 3 2
F F
.
Bài 7. Cho hàm số
y f x
có nguyên hàm trên
là
2
1
3
2
5 khi 1
4 khi 1
x x C x
F x
x x C x
. Tính tích phân
2
0
d
f x x
Bài 8. Cho hàm số
2
3 2 1 khi 0
1 2 khi 0
x x x
f x
x x
. Giả sử
F
là 1 nguyên hàm của
f
trên
thỏa
mãn
2020 1 2021 2 2022
F F
. Tính giá trị của
1
F
.
Bài 9. Cho hàm số
2
3 2 khi 1
3 2 4 khi 1
x x
f x
x x x
. Giả sử
F x
là nguyên hàm của
f x
trên
thỏa mãn
2 4
F
. Giá trị của
2 4 3
F F
bằng bao nhiêu?
Bài 10. Cho hàm số
2
4 4 9 khi 0
4 tan khi 0
x x x
f x
a x x
, đồng thời
4
4
50
d
3
I f x x
. Tính
a
.
Đại số 12 - Chương 4 – Nguyên hàm. Tích phân - Trắc nghiệm và tự luận 4 phần có lời giải Dùng chung 3 bộ sách
https://www.facebook.com/truongngocvy8/ Trương Ngọc Vỹ 0978 333 093
Trang 10
Bài 11. Cho hàm số
2
sin 2 khi 0
2cos khi 0
x x
f x
x x
. Giả sử
F
là nguyên hàm của
f
trên
thỏa
mãn
3
F
. Tính giá trị của
2
6 6 4
F F F
.
Bài 12. Cho hàm số
2
3 khi 0
sin 2 cos khi 0
x a x
f x
x x b x
liên tục và có nguyên hàm
F
liên tục trên
thỏa mãn
2 10
2
F F
với
,
a b
là tham số thực. Giá trị
1
6
d
4
m
f x x
, với
m
là một số thực.
Khi đó
2
m
bằng bao nhiêu?
Đại số 12 - Chương 4 – Nguyên hàm. Tích phân - Trắc nghiệm và tự luận 4 phần có lời giải Dùng chung 3 bộ sách
https://www.facebook.com/truongngocvy8/ Trương Ngọc Vỹ 0978 333 093
Trang 11
DẠNG 5
TÍCH PHÂN HÀM ẨN BIẾN ĐỔI PHỨC TẠP
I. Cần nhớ các công thức đạo hàm của hàm hợp
f '( x)dx f ( x ) C
'
'
ln
f x
f x
f x
'
2
'
1
f x
f x f x
'
1
1
'
1
nn
n f
f x
f x
x
'
. ' .
n
n f x f f xx
'
'
2 f
f
x
f x
x
'
' . . ' .
f x g x f x g x f x g x
'
2
' . . '
f x g x f x g x f x
g x g x
II. Các dạng hàm ẩn thường gặp
1. Hàm ẩn có dạng:
f x f x p x
Phương pháp giải:
f x f x p x
2
2
x
f x
p
2
2
d
p x x
f x
2. Hàm ẩn có dạng:
f x p x f x
Phương pháp giải:
Chia hai vế với
f x
ta đựơc
f x
p x
f x
Suy ra
d d ln | | d
f x
x p x x f x p x x
f x
Từ đây ta dễ dàng tính được
f x
Đại số 12 - Chương 4 – Nguyên hàm. Tích phân - Trắc nghiệm và tự luận 4 phần có lời giải Dùng chung 3 bộ sách
https://www.facebook.com/truongngocvy8/ Trương Ngọc Vỹ 0978 333 093
Trang 12
3. Hàm ẩn có dạng:
n
f x p x f x
Phương pháp giải:
n
f x p x f x
Chia hai vế với
n
f x
ta được
n
f x
p x
f x
Suy ra
1
1
n
n
f x
f x
dx p x dx p x dx
n
f x
4. Hàm ẩn có dạng:
u x f x u x f x h x
Phương pháp giải:
Dễ dàng thấy rằng
u x f x u x f x u x f x
Do dó
u x f x u x f x h x u x f x h x
Suy ra
d
u x f x h x x
Từ đây ta dễ dàng tính được
f x
5. Hàm ẩn có dạng:
A x f x B x f x h x
1
Ý tưởng giải:
Ta cần nhân thêm một lượng
u x
vào
1
để tạo thành
' .
u x f x u x f x u x h x
và
lúc này:
'
'
' .
.
.
.
.
u x f x u x f x u x h x
u x f x u x h x
u x f x dx u x h x dx
u x f x u x h x dx
u x h x dx
f x
u x
Cách tìm
u x
u x
được chọn sao cho :
u A
u B
x x
x x
( )
.
( )
. . ln .
A x
dx
B x
u A
x
u A A
dx dx u dx u x e
u B u B
xx x x x
xBx x x x
Tóm lại phương pháp giải:
A x f x B x f x h x
1
như sau:
Đại số 12 - Chương 4 – Nguyên hàm. Tích phân - Trắc nghiệm và tự luận 4 phần có lời giải Dùng chung 3 bộ sách
https://www.facebook.com/truongngocvy8/ Trương Ngọc Vỹ 0978 333 093
Trang 13
+ Bước 1: Tìm
u x
:
.
A
dx
B
x
x
u x e
+ Bước 2: Nhân
u x
vào
1
.
u x h x dx
f x
u x
Hai dạng đặc biệt của
1
f x f x h x
Phương pháp giải:
Nhân hai vế với
x
e
ta được
( )
x x x x x
e f x e f x e h x e f x e h x
Suy ra
d
x x
e f x e h x x
Từ đây ta dễ dàng tính được
( )
f x
( ) ( ) ( )
f x f x h x
Phương pháp giải:
Nhân hai vế với
x
e
ta được
( ) ( ) ( ) ( ) ( )
x x x x x
e f x e f x e h x e f x e h x
Suy ra
( ) ( )d
x x
e f x e h x x
Từ đây ta dễ dàng tính được
( )
f x
Bài 1. Cho hàm số
0
f x
, liên tục trên đoạn
1;2
và thỏa mãn
1
(1)
3
f
;
2 2
. ( ) ( )
x f x f x
với
1;2
x . Tính tích phân
2
2
1
2 1 ( )
I x f x dx
Bài 2. Cho hàm số
( )
f x
đồng biến, có đạo hàm trên đoạn
1;4
và thoả mãn
2
2 . ( ) ( )
x x f x f x
với
1;4
x . Biết
3
(1)
2
f
, tính
4
1
( )
I f x dx
Bài 3. Cho hàm số
có đạo hàm liên tục trên
và thỏa mãn điều kiện
3 4
6
27 1 0,x f x f x x
và
1 0
f
. Tính
3
2
( )
I f x dx
Bài 4. Cho hàm số
f x
thỏa mãn
e ,
x
f x f x x
và
0 2
f
. Tính
2
1
e
x
f x
I dx
x
.
Bài 5. Cho hai hàm
f x
và
g x
có đạo hàm trên
1;4
, thỏa mãn
1 1 4
f g
g x xf x
f x xg x
với mọi
1;4
x . Tính tích phân
4
1
I f x g x dx
.
Đại số 12 - Chương 4 – Nguyên hàm. Tích phân - Trắc nghiệm và tự luận 4 phần có lời giải Dùng chung 3 bộ sách
https://www.facebook.com/truongngocvy8/ Trương Ngọc Vỹ 0978 333 093
Trang 14
Bài 6. Cho hàm số
f x
xác định và liên tục trên
\ 0
thỏa mãn
2 2 '
2 1 1
x f x x f x xf x
, với mọi
\ 0
x
đồng thời thỏa
1 2
f
. Tính
2
1
d
f x x
Bài 7. Cho hàm số
f x
có đạo hàm liên tục trên
,
0 0, ' 0 0
f f
và thỏa mãn hệ thức
2 2
. ' 18 3 ' 6 1 ;f x f x x x x f x x f x
. Biết
1
2
0
1 , ,
f x
x e dx ae b a b
. Giá
trị của
a b
bằng bao nhiêu?
Bài 8. Cho hàm số
( )
y f x
xác định và có đạo hàm
f x
liên tục trên
[1;3]
;
0, 1;3 ;
f x x
2 4
2
1 1
f x f x x f x
và
1 1
f
. Biết rằng
3
d ln3 ,
e
f x x a b a b
, giá trị của
2
a b
bằng bao nhiêu?
Bài 9. Cho hàm số
có đạo hàm liên tục trên
0;1
thỏa mãn
2018
3
f x xf x x
,
0;1
x . Tìm giá trị nhỏ nhất của
1
0
d
f x x
.
Đại số 12 - Chương 4 – Nguyên hàm. Tích phân - Trắc nghiệm và tự luận 4 phần có lời giải Dùng chung 3 bộ sách
https://www.facebook.com/truongngocvy8/ Trương Ngọc Vỹ 0978 333 093
Trang 15
PHẦN B
TRẮC NGHIỆM VÀ TỰ LUẬN TỔNG HỢP GỒM BỐN PHẦN
PHẦN I. Câu trắc nghiệm nhiều phương án lựa chọn. Mỗi câu hỏi thí sinh chỉ chọn một phương
án.
Câu 1. Cho hàm số
liên tục trên
;
a b
. Các mệnh đề sau, mệnh đề nào sai?
A.
2024 d 0
a
a
f x x
B.
d d
b a
a b
f x x f x x
C.
1 1
d d
2025 2025
b b
a a
f x x f x x
D.
d d
b a
a b
f x x f x x
Câu 2. Cho hàm số
liên tục trên
và , ,a b c
thỏa mãn
a b c
. Các mệnh đề sau đây,
mệnh đề nào đúng?
A.
d d d
c b c
a a b
f x x f x x f x x
B.
d d d
c b c
a a b
f x x f x x f x x
C.
d d d
c b c
a a b
f x x f x x f x x
D.
d d d
c b b
a a c
f x x f x x f x x
Câu 3. Cho
f x
,
( )
g x
là hai hàm số liên tục trên
. Các mệnh đề sau đây, mệnh đề nào sai?
A.
( )d ( )d
b b
a a
f x x f y y
B.
( ) ( ) d ( )d ( )d .
b b b
a a a
f x g x x f x x g x x
C.
( )d ( )d
b b
a a
kf x x k f t t
D.
( ) ( ) d ( )d ( )d .
b b b
a a a
f x g x x f x x g x x
Câu 4. Các mệnh đề sau đây, mệnh đề nào sai?
A.
2024
2024
d 4048
x
.
B.
1 2 1 2
. d d . d
b b b
a a a
f x f x x f x x f x x
.
C. Cho hàm số
f x
liên tục trên đoạn
;
a b
. Khi đó
1
b
a
f x dx
b a
được gọi là giá trị trung bình
của hàm số
f x
trên đoạn
;
a b
.
D. Nếu hàm số
f x
có đạo hàm
'
f x
và
'
f x
liên tục trên đoạn
;
a b
thì
'
b
a
f b f a f x dx
.
Đại số 12 - Chương 4 – Nguyên hàm. Tích phân - Trắc nghiệm và tự luận 4 phần có lời giải Dùng chung 3 bộ sách
https://www.facebook.com/truongngocvy8/ Trương Ngọc Vỹ 0978 333 093
Trang 16
Câu 5. Cho hàm
f x
là hàm liên tục trên đoạn
;
a b
với
a b
và
F x
là một nguyên hàm của
hàm
f x
trên
;
a b
.
Cho các mệnh đề sau đây, mệnh đề nào đúng?
A.
b
a
kf x dx k F b F a
B.
a
b
f x dx F b F a
C. Diện tích S của hình phẳng giới hạn bởi đường thẳng ;
x a x b
; đồ thị của hàm số
và
trục hoành được tính theo công thức
S F b F a
D.
2 3 2 3
b
b
a
a
f x dx F x
Câu 6. Nếu
3
0
d 3
f x x
thì
3
0
4 d
f x x
bằng
A.
3
. B.
12
. C.
36
. D.
4
.
Câu 7. Cho
2
0
1
( )
2025
f x dx
. Tính
2
0
2025 ( ) .
I f x dx
A.
2
I
B.
1
2025
I C.
1
I
D.
2025
I
Câu 8. Nếu
5
0
d 5
f x x
thì
0
5
5 d
f x x
bằng
A.
1
. B.
1
. C.
25
. D.
25
.
Câu 9. Nếu
4
1
( )dx 5
f x
và
4
1
( )dx 4
g x
thì
4
1
( ) ( ) dx
f x g x
bằng
A.
1
. B.
9
. C. 1 . D. 9.
Câu 10. Nếu
4
1
( ) 3
f x dx
và
4
1
( ) 2
g x dx
thì
4
1
( ) ( )
f x g x dx
bằng
A.
1
. B.
5
. C. 5 . D. 1 .
Câu 11. Cho
1
0
d 2
f x x
và
1
0
d 5
g x x
, khi
1
0
2 d
f x g x x
bằng
A.
8
B.
1
C.
3
D.
12
Câu 12. Giả sử
9
0
d 7
f x x
và
0
9
d 1
g x x
. Khi đó
9
0
2 3 d
I f x g x x
bằng
A.
11
I
. B.
17
I
. C.
23
I
. D.
8
I
.
Câu 13. Nếu
4
1
d 2
f x x
và
4
1
d 3
g x x
. Khi đó
4
1
d
f x g x x
bằng
Đại số 12 - Chương 4 – Nguyên hàm. Tích phân - Trắc nghiệm và tự luận 4 phần có lời giải Dùng chung 3 bộ sách
https://www.facebook.com/truongngocvy8/ Trương Ngọc Vỹ 0978 333 093
Trang
17
A.
5
. B.
6
. C.
1
. D.
1
.
Câu 14. Nếu
3
0
d 6
f x x
thì
3
0
1
2 d
3
f x x
bằng bao nhiêu?
A.
8
. B.
5
. C.
9
. D.
6
.
Câu 15. Nếu
2
0
5
f x dx
thì
2
0
2 1
f x dx
bằng:
A. 8 . B. 9 . C. 10 . D. 12 .
Câu 16. Nếu
2
0
3
f x dx
thì
2
0
2 2024
f x dx
bằng:
A.
4040
. B.
4042
. C.
4044
. D.
4046
.
Câu 17. Cho
2
0
d 5
f x x
. Tính
2
0
2sin d 5
I f x x x
.
A.
7
I
B. 5
2
I
C.
3
I
D.
5I
Câu 18. Cho
2
1
4 2 1
f x x dx
. Khi đó
2
1
f x dx
bằng:
A.
1
. B.
3
. C.
3
. D.
1
.
Câu 19. Cho
1
0
1
f x dx
, tích phân
1
2
0
2 3
f x x dx
bằng
A.
1
. B.
0
. C.
3
. D.
1
.
Câu 20. Cho
2
1
d 2
f x x
và
2
1
d 1
g x x
. Tính
2
1
2 3 d
I x f x g x x
.
A.
17
2
I
B.
5
2
I
C.
7
2
I
D.
11
2
I
Câu 21. Cho
2
0
d 3
f x x
,
2
0
d 1
g x x
thì
2
0
5 d
f x g x x x
bằng:
A.
12
. B.
0
. C.
8
. D.
10
Câu 22. Cho
5
0
d 2
f x x
. Tích phân
5
2
0
4 3 d
f x x x
bằng
A.
140
. B.
130
. C.
120
. D.
133
.
Câu 23. Cho
2
1
4 2 1
f x x dx
. Khi đó
2
1
f x dx
bằng:
A.
1
. B.
3
. C.
3
. D.
1
.
Câu 24. Cho
2
2
d 1
f x x
,
4
2
d 4
f t t
. Tính
4
2
d
f y y
.
A.
5
I
. B.
3
I
. C.
3
I
. D.
5
I
.
Đại số 12 - Chương 4 – Nguyên hàm. Tích phân - Trắc nghiệm và tự luận 4 phần có lời giải Dùng chung 3 bộ sách
https://www.facebook.com/truongngocvy8/ Trương Ngọc Vỹ 0978 333 093
Trang 18
Câu 25. Cho hàm số
f x
liên tục trên
R
và có
2 4
0 2
( )d 9; ( )d 4.
f x x f x x
Tính
4
0
( )d .
I f x x
A.
5
I
. B.
36
I
. C.
9
4
I
. D.
13
I
.
Câu 26. Cho hàm số
f x
liên tục trên
và
4
0
d 10
f x x
,
4
3
d 4
f x x
. Tích phân
3
0
d
f x x
bằng
A.
4
. B.
7
. C.
3
. D.
6
.
Câu 27. Cho hàm số
f x
liên tục trên đoạn
0;10
và
10
0
7
f x dx
;
6
2
3
f x dx
. Tính
2 10
0 6
P f x dx f x dx
.
A.
4
P
B.
10
P
C.
7
P
D.
4
P
Câu 28. Cho hàm số
f x
liên tục trên đoạn [0; 6] thỏa mãn
6
0
10
f x dx
và
4
2
6
f x dx
. Tính giá
trị của biểu thức
2 6
0 4
P f x dx f x dx
.
A.
4
P
. B.
16
P
. C.
8
P
. D.
10
P
.
Câu 29. Tính tích phân
2
0
(2 1)
I x dx
A.
5
I
. B.
6
I
. C.
2
I
. D.
4
I
.
Câu 30. Tích phân
1
0
3 1 3 d
x x x
bằng
A.
12
. B.
9
. C.
5
. D.
6
.
Câu 31. Tính tích phân
2
1
1 1
e
I dx
x x
A.
1
I
e
B.
1
1
I
e
C.
1
I
D.
I e
Câu 32. Biết
3
1
2
ln ,
x
dx a b c
x
với
, , , 9.
a b c c
Tính tổng
.
S a b c
A.
7
S
. B.
5
S
. C.
8
S
. D.
6
S
.
Câu 33. Kết quả tích phân
1
0
5 d
x
I x
bằng
A.
5
ln5
I
. B.
4ln5
I
. C.
5ln5
I
. D.
4
ln5
I
.
Câu 34. Tích phân
1
3
0
e d
x
x
bằng
Đại số 12 - Chương 4 – Nguyên hàm. Tích phân - Trắc nghiệm và tự luận 4 phần có lời giải Dùng chung 3 bộ sách
https://www.facebook.com/truongngocvy8/ Trương Ngọc Vỹ 0978 333 093
Trang 19
A.
3
1
e
2
. B.
e 1
. C.
3
e 1
3
. D.
3
e 1
.
Câu 35. Tích phân
1
3 1
0
d
x
e x
bằng
A.
4
1
3
e e
B.
3
e e
C.
4
1
3
e e
D.
4
e e
Câu 36. Biết
1
0
2
x
x
e e
dx b
a
,a b
. Khi đó giá trị của
P a b
là
A.
3
P
B.
1
P
C.
1
P
D.
3
P
Câu 37. Giá trị của
1
2
0
4
2
x
x
e
I dx
e
bằng
A.
2 3
I e
0. B.
1
3
2
I e
. C.
3
I e
. D.
2 3
I e
.
Câu 38. Biết
2
2
1
1 . ln2
x
x
e
e dx e a e b
x
,a b
. Khi đó giá trị của
.
a b
P
a b
là
A.
3
P
B.
1
P
C.
1
P
D.
2
P
Câu 39. Biết
1
2 1 3
0
1 1
x x
x
e e
I dx b
e a
,a b
. Khi đó giá trị của
.
a b
P
a b
là
A.
4
1
P e
B.
4
2
1
e
P
e
C.
4
4
1
e
P
e
D.
4
4
1
e
P
e
Câu 40. Giá trị của
2
0
sin
xdx
bằng
A. 0. B. 1. C. -1. D.
2
.
Câu 41. Biết
2
2
3
3
2sin 3cos
2
a b
x x x dx
c
, ,a b c
. Khi đó giá trị của
2 3
P a b c
là
A.
45
P
B.
60
P
C.
65
P
D.
70
P
Câu 42. Biết
3
2
4
3tan 3xdx a b
c
, ,a b c
. Khi đó giá trị của
P a b c
là
A.
6
P
B.
4
P
C.
4
P
D.
6
P
Câu 43. Biết
4
2
6
2cot 5 3
x dx b c
a
, ,a b c
. Khi đó giá trị của
P a b c
là
A.
6
P
B.
4
P
C.
4
P
D.
6
P
Đại số 12 - Chương 4 – Nguyên hàm. Tích phân - Trắc nghiệm và tự luận 4 phần có lời giải Dùng chung 3 bộ sách
https://www.facebook.com/truongngocvy8/ Trương Ngọc Vỹ 0978 333 093
Trang 20
Câu 44. Biết
2
2 2
0
sin cos
4 4
x x a
dx
c b
với ,a b
và
a
b
là phân số tối giản. Khi đó giá trị của
P a b c
là
A.
17
P
B.
16
P
C.
32
P
D.
49
P
Câu 45. Giá trị của
2
0
1 cos2
I xdx
bằng
A.
3
. B.
4 2
. C.
2 3
. D.
2
.
Câu 46. Tính tích phân
2
0
2
I x dx
.
A.
2
I
. B.
4
I
. C.
2
I
. D.
0
I
.
Câu 47. Tính
2
1
2 1 d
x x
A.
1
2
. B.
2
. C.
5
2
. D.
13
2
.
Câu 48. Tính
2
0
2 2 d .
I x x
A.
0.
B.
2.
C.
1.
D.
3.
Câu 49. Tính
2
2
0
2 1d
x x x
A.
1
2
. B.
2
. C.
5
2
. D.
1
.
Câu 50. Tính
3
0
2 4 d .
I x x x
A.
16
.
3
B.
2.
C.
16
.
3
D.
4
.
3
Câu 51. Tính tích phân
8
2
0
6 d
x x x
.
A.
64
3
. B.
64
3
. C.
152
3
. D.
152
3
.
Câu 52. Biết
3
2
1
3 2 d ,
a
I x x x
b
với
*
, ,
a
a b
b
tối giản. Tính
T a b
A.
12.
B.
14.
C.
11.
D.
4.
Câu 53. Tính tích phân
2
3
0
I x x dx
.

Tài liệu khác của Toán 12

Preview text:

Đại số 12 - Chương 4 – Nguyên hàm. Tích phân - Trắc nghiệm và tự luận 4 phần có lời giải Dùng chung 3 bộ sách BÀI 2 TÍCH PHÂN
1. Khái niệm tích phân
a. Diện tích hình thang cong
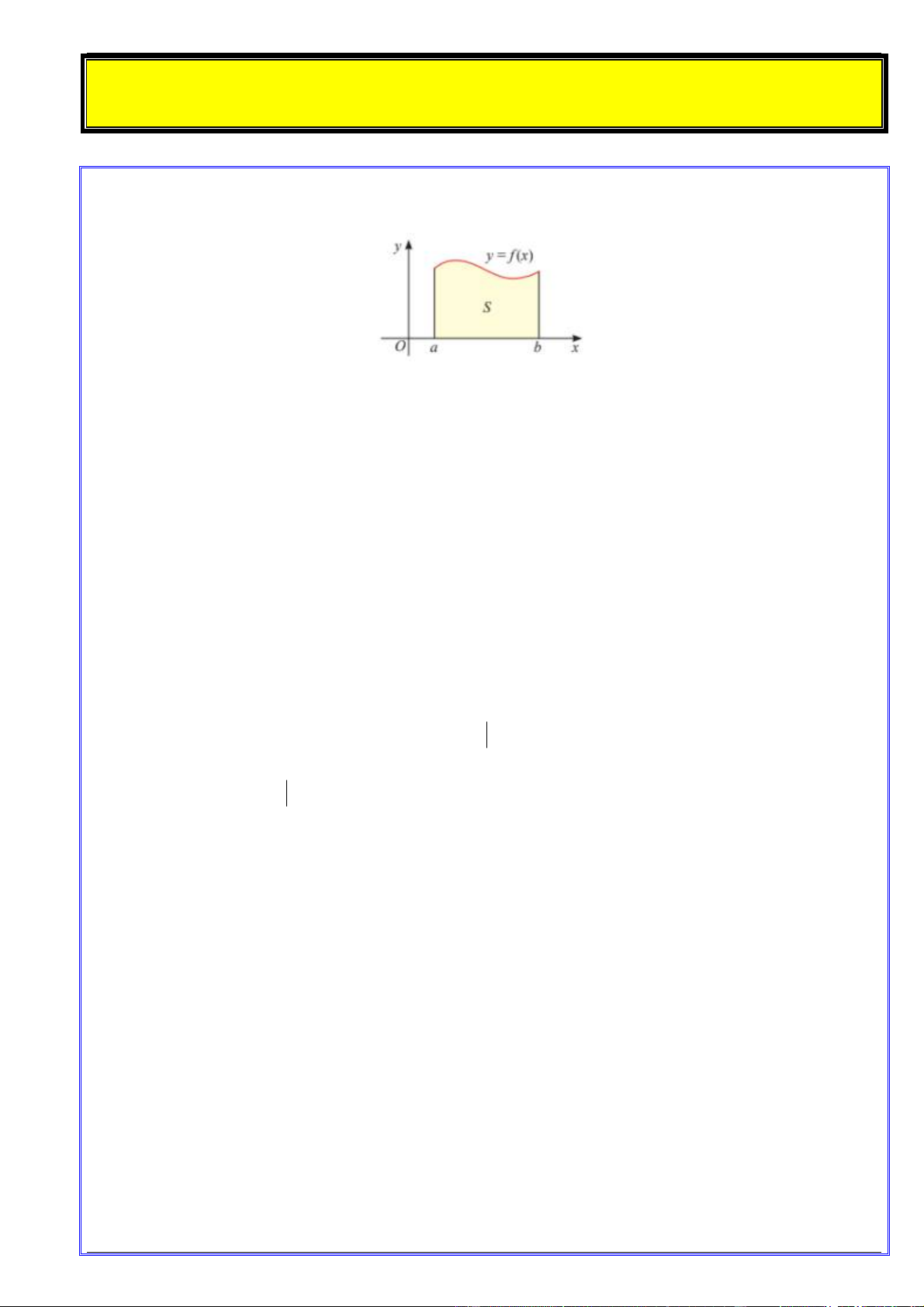
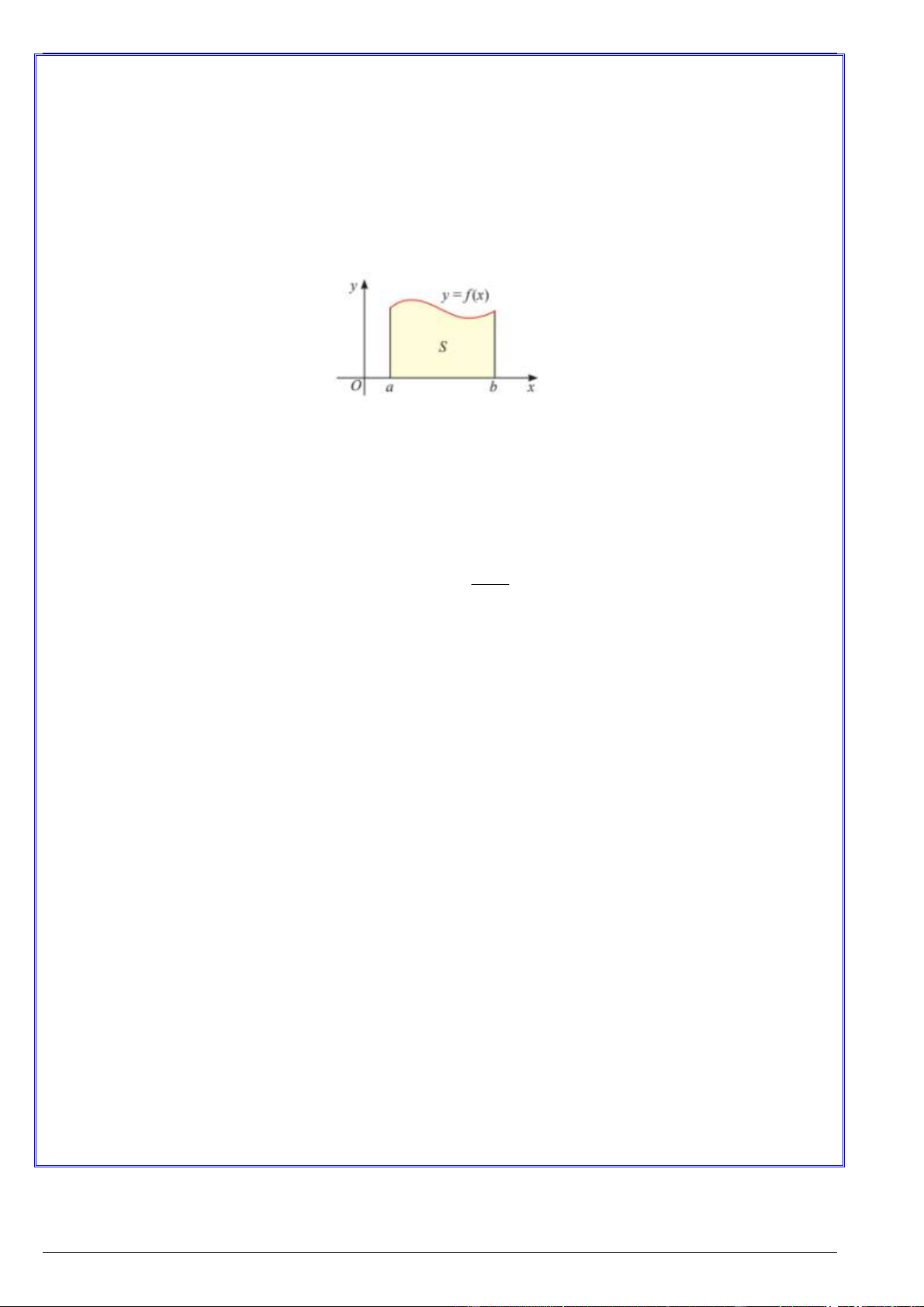
Nếu hàm số f x liên tục và không âm trên đoạn a;b thì diện tích S của hình thang cong giới hạn
bởi đồ thị y f x , trục hoành và hai đường thẳng x  ,
a x b được tính bởi:
S F b  F a
trong đó F x là một nguyên hàm của f x trên đoạn a;b .
b. Khái niệm tích phân
Cho hàm số f x liên tục trên đoạn a;b . Nếu F x là nguyên hàm của hàm số f x trên đoạn b
a;b thì hiệu số F b  F a được gọi là tích phân từ a đến b của hàm số f x , kí hiệu f xdxa Chú ý:
 Hiệu số F b  F a còn được kí hiệu là F xb . a b b Vậy
f xdx F x  F b  F a  a a b
 Ta gọi  là dấu tích phân, a là cận dưới, b là cận trên, f xdx là biểu thức dưới dấu tích phân và a
f x là hàm số dưới dấu tích phân. a b a  Quy ước:
f xd ;
x f xdx   f xdx    a a b
 Tích phân của hàm số f từ a đến b chỉ phụ thuộc vào f và các cận ,
a b mà không phụ thuộc vào b b
biến x hay t , nghĩa là
f xdx f t dt   . a a
https://www.facebook.com/truongngocvy8/ T r an g
1 Trương Ngọc Vỹ 0978 333 093
Đại số 12 - Chương 4 – Nguyên hàm. Tích phân - Trắc nghiệm và tự luận 4 phần có lời giải Dùng chung 3 bộ sách
Ý nghĩa hình học của tích phân b
Nếu hàm số f x liên tục và không âm trên đoạn a;b thì f xdx
là diện tích S của hình thang a
cong giới hạn bởi đồ thị y f x , trục hoành và hai đường thẳng x  , a x b . b S
f xdxa Nhận xét:
 Nếu hàm số f x có đạo hàm f ' x và f ' x liên tục trên đoạn a;b thì b
f b  f a  f ' xdx  . a 1 b
 Cho hàm số f x liên tục trên đoạn a;b . Khi đó
f xdx
được gọi là giá trị trung bình của b a a
hàm số f x trên đoạn a;b .
 Đạo hàm của quãng đường di chuyển của vật theo thời gian bằng tốc độ của chuyển động tại mọi
thời điểm: v(t)  s '(t) . Do đó, nếu biết tốc độ v(t) tại mọi thời điểm t a;b thì tính được quãng đường b
di chuyển trong khoảng thời gian từ a đến b theo công thức: s s b  s a  v(t)dta
2. Tính chất của tích phân
Cho hai hàm số f x , g x liên tục trên đoạn a;b . Khi đó: b b
Tính chất 1: kf xdx k f xdx  
, với k là hằng số. a a b b b
Tính chất 2:f x  g x dx f xdx g xdx      a a a b b b
f x  g x dx f xdx g xdx      a a a b c b
Tính chất 3: f xdx f xdx f xdx   
với c a;b . a a c
https://www.facebook.com/truongngocvy8/ T r an g
2 Trương Ngọc Vỹ 0978 333 093
Đại số 12 - Chương 4 – Nguyên hàm. Tích phân - Trắc nghiệm và tự luận 4 phần có lời giải Dùng chung 3 bộ sách PHẦN A
TỰ LUẬN PHÂN DẠNG TOÁN DẠNG 1
TÍNH TÍCH PHÂN SỬ DỤNG BẢNG NGUYÊN HÀM SƠ CẤP
Nguyên hàm của một hàm số sơ cấp 0dx C
dx x C
Nguyên hàm của hàm số lũy thừa1  x x dx
C    1  1 1 dx
Nguyên hàm của hàm số y
 ln x C   0  x x x cos xdx x C  sin sin xdx   x C  cos
Nguyên hàm của hàm số lượng giác 1 dx x C  tan cos 2 x 1 dx   x C  cot sin 2 x
e x dx e x C
Nguyên hàm của hàm số mũ x a a x dx   C 0    1  a ln a
Chú ý : Dùng công thức sau làm trắc nghiệm cho nhanh n 1 1 n 1 ax b  dx    C
 ax bdx   C nxn   n 1 1 x a n 1   a   x 1 x axb 1  axb e dx eC   a dx
C 0  a   1  a ln a
https://www.facebook.com/truongngocvy8/ T r an g
3 Trương Ngọc Vỹ 0978 333 093
Đại số 12 - Chương 4 – Nguyên hàm. Tích phân - Trắc nghiệm và tự luận 4 phần có lời giải Dùng chung 3 bộ sách Bài 1.
Tính các tích phân sau đây: 3 1 4 a)  2 3x +2024dx b)   3 2
4x  3x  2dx c)  x   1  x   1 dx  0 0 2 2 x 1 2 3
2x x  2025  x  2 2 1 d) dx  e) dx  f) d xx 2 x x 1 1 1 Bài 2.
Tính các tích phân sau đây: 3 3 2 8 a) 2024 x dx  b) 3 x dx  c) 3 xdx  1 1 1 e 7 2 1 4 1 d) dx  e) dx  f) d  x 3x 3 x 2 x 1 1 1 Bài 3.
Tính các tích phân sau đây: 2 4 4 2 4 3  x x  
a)  x  2 x  2dx b)  x   1  3 x   1dx c)   dx   x  1 0 1   1  2 3 (x  1) 4 3 x 1  x  2 3 8 1 d) dx  e) dx dx 2  f)  x x 3 2 3 1 1 x Bài 4.
Tính các tích phân sau đây: 3 4 1 2 a) sin d x x  b) dx
c) 3sin x  2024 dx 2  cos x 0 0 0 4  1 1  4 cos 2x 2 2 sin x d)  dx   e) dx dx 2 2   f)   cos x sin x cos x 1 tan x 1 cos x 0    0 6 Bài 5.
Tính các tích phân sau đây: 1 1 2   1  a)  2x x 1 2 3 .   dx
b) 2.3x 5 x e dx c) 3 1 4  2.3x xdx  2   x  0 0 1  x e  22 1 2024x  2 1 1 2 2 e   x 2025 x d) dx  e) dx 2 e 2024  dx x 1  f)    e  3x e 3 x 0 0 1   Bài 6.
Tính các tích phân sau đây: 1 1 2  1  a) x 1  2 x 1 5 .7  dx  b)   x2 x edx c) sin x dx   3 2 0 0 x  6 3 2  sin x  3 x x x x  2  d) 2 x 1 dx  1  e) sin sin  cos dx f) 2 1 dx 2       x   x 2  2 2  e    0 1 6
https://www.facebook.com/truongngocvy8/ T r an g
4 Trương Ngọc Vỹ 0978 333 093
Đại số 12 - Chương 4 – Nguyên hàm. Tích phân - Trắc nghiệm và tự luận 4 phần có lời giải Dùng chung 3 bộ sách DẠNG 2
TÍCH PHÂN HÀM ẨN BIẾN ĐỔI CƠ BẢN b b
k. f xdx k. f xdx   a a b b b
  f x  g x dx f xdx g xdx      a a a b c b
f xdx f xdx f xdx    a a c Bài 1.
Cho hàm số f x liên tục trên  và thỏa mãn: 0 6 a)
f (x)dx  1 
. Tính tích phân 2025 f (x)dx  6 0 2 2 b)
f xdx  4 
. Tính tích phân 2 f x 1) dx    0 0 7 7 2
c) f x dx  3   và
f xdx  3  . Tính tích phân
f x dx  . 2 1 1 Bài 2.
Cho hàm số f x liên tục trên  và thỏa mãn: 1 1
a)  f x  2x dx  3    . Tính tích phân
f xdx  0 0 3 3
b)  f x  2x  3 dx  10    . Tính tích phân
f xdx  . 1 1 2 2 c)
f xdx  4 
. Tính tích phân 2 f x  sin x d  x    . 0 0 Bài 3.
Cho hàm số y f x liên tục trên  và thỏa mãn: 11 6 2 11 a)
f xdx  8 
, f xdx  3 
. Tính giá trị của biểu thức P
f xdx f xdx   . 6  2 6  6 8 12 8 12 b)
f x dx  9  ,
f x dx  3  ,
f x dx  5  . Tính I
f x dx  . 1 4 4 1 Bài 4.
Cho f x, g x là hai hàm liên tục trên  , thỏa mãn: 5 5 5 a)
f xdx  3 
và g xdx  2  
. Tính  f x  g x dx    2 2 2
https://www.facebook.com/truongngocvy8/ T r an g
5 Trương Ngọc Vỹ 0978 333 093
Đại số 12 - Chương 4 – Nguyên hàm. Tích phân - Trắc nghiệm và tự luận 4 phần có lời giải Dùng chung 3 bộ sách 1 1 0 b)
f xdx  3 
và g xdx  4  
. Tính  f x  g x dx    . 0 0 1 4 4 4 1 1  c)
f xdx  6 
và g xdx  5   . Tính
f x  g xdx   3 5    1 1 1 Bài 5.
Cho f x, g x là hai hàm liên tục trên  , thỏa mãn: 3 2 3 a)
f xdx  3 
và g xdx  1 
. Tính  f x  2g xdx     2 3 2 3 1 3  1  b)
f xdx  2024 
và g xdx  1  . Tính
f x  3g xdx   2024    1 3 1 2 1 2  1  c)
f xdx  3 
và g xdx  2   . Tính
3 f x  g x dx   2    1 2 1 3 3 Bài 6. Cho
f x dx  2024 
và g x dx  2025  . Tính các tích phân sau: 0 0 3 0 1
a)  f x  g x dx    b)
g x dx  5 0 3 3 3  1   1  c)
f x  3g x dx  2  d)
f x  3x dx  2       2024  0 0 0 3 1 
e) g x 3 2 x   dx  f)
f x  g x 3x 1  e  dx    4    3 0 3 Bài 7.
Cho f x, g x là hai hàm liên tục trên đoạn 1; 
3 thoả:  f x  3g x d  x  10    , 1 3 3
2 f x  g x d  x  6   
. Tính I   f x  g x d  x    . 1 1
https://www.facebook.com/truongngocvy8/ T r an g
6 Trương Ngọc Vỹ 0978 333 093
Đại số 12 - Chương 4 – Nguyên hàm. Tích phân - Trắc nghiệm và tự luận 4 phần có lời giải Dùng chung 3 bộ sách DẠNG 3
TÍCH PHÂN HÀM TRỊ TUYỆT ĐỐI b
Tính tích phân: I
f xdxa Phương pháp
Bước 1. Xét dấu f x trên đoạn a;b .
Bước 2. Dựa vào bảng xét dấu trên đoạn a;b để khử f x . Sau đó sử dụng các phương pháp tính tích b
phân đã học đê tính I
f x .dxa 3 Bài 1. Tính tích phân 2 I x 1 dx  . 3 1 Bài 2. Tính tích phân 3 2 I
x x  2x dx  . 2 2 Bài 3. Tính tích phân 3 I
x  3x  2 dx  . 1 2 Bài 4. Tính tích phân 4 2 I
x  3x  4 dx  . 2 3 Bài 5. Tính tích phân 3 2 I
x  2x xdx  . 0 5 2 x  2 1 Bài 6. Tính tích phân I  dx  . x 1 5 Bài 7.
Tính tích phân I    x  2  x  2 dx . 3  2 Bài 8.
Tính tích phân I   x  1 x x  2 dx . 1 6 Bài 9. Tính tích phân 2 I
x  8x 16dx  . 2 1
Bài 10. Tính tích phân 2 I
4x  6x  9dx  . 2 2
Bài 11. Tính tích phân I  1 cos 2xdx  . 0 2
Bài 12. Tính tích phân I  1 cos 2xdx  . 0
https://www.facebook.com/truongngocvy8/ T r an g
7 Trương Ngọc Vỹ 0978 333 093
Đại số 12 - Chương 4 – Nguyên hàm. Tích phân - Trắc nghiệm và tự luận 4 phần có lời giải Dùng chung 3 bộ sách DẠNG 4
TÍCH PHÂN HÀM NHIỀU CÔNG THỨC g b   x khi x c
Dạng 1: Cho hàm số f x  
liên tục trên D . Tính
f x dx
, với c a;b . h   x khi x ca Phương pháp giải:
Bước 1: Kiểm tra hàm số f x có liên tục tại x c hay không (kiến thức hàm số liên tục tại một điểm lớp 11)
Tức là kiểm tra lim f x  lim f x  f b  lim g x  lim hx  f bx bx bx bx b     b c b
Bước 2: Tách cận:
f x dx g x dx h x dx    . a a c c b
Bước 3: Tính tích phân g x dx
và h x dx
bằng các phương pháp đã học. a cg   ; x m khi x c
Dạng 2: Cho hàm số f  ; x m  
liên tục trên D và m là tham số. Tính h   ; x m khi x cb f  ; x m dx
, với c a;b . a Phương pháp giải:
Bước 1: Kiểm tra hàm số f x có liên tục tại x c hay không.
Tức là kiểm tra: lim  ; x m  lim  ;
x m  f b  lim g  ; x m  l m i h  ;
x m  f bx bx bx bx b    
Chú ý: Bước này tìm tham số m . b c b
Bước 2: Tách cận: f  ;
x m dx g  ;
x m dx h  ; x m dx    . a a c c b
Bước 3: Tính tích phân g  ; x m dx  và  ; x m dx
bằng các phương pháp đã học. a c
https://www.facebook.com/truongngocvy8/ T r an g
8 Trương Ngọc Vỹ 0978 333 093
Đại số 12 - Chương 4 – Nguyên hàm. Tích phân - Trắc nghiệm và tự luận 4 phần có lời giải Dùng chung 3 bộ sách 1  khi x  1 2 Bài 1.
Cho f x  
. Tính tích phân I
f x dx
2x  1 khi x  1  1
x  1 khi x  0 2 Bài 2.
Cho hàm số f x  
. Tính tích phân I
f xdx  . 2 x e khi x  0  1  2
3x  2x m khi x  1 Bài 3.
Cho hàm số f x  
( m là tham số thực). Biết rằng f x có nguyên 5  2x khi x  1 
hàm trên  là F x thỏa mãn F 2  10 , khi đó tính F 3 . 2x khi x  0  Bài 4.
Cho số thực a và f x liên tục trên  thỏa mãn f x   . Tính tích a   2
x x khi x  0  1 phân
f xdx  . 1 ex m khi x  0  Bài 5.
Cho hàm số f x  
(với m tham số). Biết hàm số f x liên tục trên x  x  3 2 3 1 k i h x  0  1  b a và tích phân
f x dx  . a e   với * , a , b c   ;
tối giản ( e  2, 718281... .). Tính giá trị biểu thức c b 1
a b c m . 2x 3  khi x  0 Bài 6.
Cho hàm số f x  
. Giả sử F là nguyên hàm của f trên  thỏa mãn 2
x  2x  3 khi x  0 
F 3  0 . Tính giá trị của 2F   1  3F 2 . 2 
x  5x C khi x  1 Bài 7. Cho hàm số 1
y f x có nguyên hàm trên  là F x   . Tính tích phân 3
x  4x C khi x  1  2 2
f x dx  0 2
3x  2x  1 khi x  0 Bài 8.
Cho hàm số f x  
. Giả sử F là 1 nguyên hàm của f trên  thỏa 1  2x khi x  0  mãn 2020F  
1  2021F 2  2022 . Tính giá trị của F   1 . 3   2x khi x  1 Bài 9.
Cho hàm số f x  
. Giả sử F x là nguyên hàm của f x trên  2
3x  2x  4 khi x  1 
thỏa mãn F 2  4 . Giá trị của F 2  4F 3 bằng bao nhiêu?  4
4x  4x  9 khi x  0 50
Bài 10. Cho hàm số f x   , đồng thời I
f xdx   . Tính a . 2 4a  tan x khi x  0  3  4
https://www.facebook.com/truongngocvy8/ T r an g
9 Trương Ngọc Vỹ 0978 333 093
Đại số 12 - Chương 4 – Nguyên hàm. Tích phân - Trắc nghiệm và tự luận 4 phần có lời giải Dùng chung 3 bộ sách sin x  2 khi x  0
Bài 11. Cho hàm số f x  
. Giả sử F là nguyên hàm của f trên  thỏa 2 2 cos x khi x  0          mãn F  
. Tính giá trị của F   2FF       .  3   6   6   4  2 3  x a khi x  0
Bài 12. Cho hàm số f x  
liên tục và có nguyên hàm F liên tục trên 
sin 2x  cos x b khi x  0  1  m
thỏa mãn F 2  F   10   với ,
a b là tham số thực. Giá trị
f xdx  
, với m là một số thực.  2  4  6
Khi đó 2m bằng bao nhiêu?
https://www.facebook.com/truongngocvy8/ T r an g
10 Trương Ngọc Vỹ 0978 333 093
Đại số 12 - Chương 4 – Nguyên hàm. Tích phân - Trắc nghiệm và tự luận 4 phần có lời giải Dùng chung 3 bộ sách DẠNG 5
TÍCH PHÂN HÀM ẨN BIẾN ĐỔI PHỨC TẠP
I. Cần nhớ các công thức đạo hàm của hàm hợp
f '( x )dx f ( x ) C f ' x 
 ln  f x ' f x   ' f ' x  1       2 f xf x   ' f ' x  1       n f x  
n    f xn 1 1       ' n  .
n f ' x. f x  f x     f x ' ' 
2 f x  f x  
f xg x  f xg x   f xg x ' ' . . ' .    '
f ' x.g x  f x.g ' x
f x     2 g xg x  
II. Các dạng hàm ẩn thường gặp
1. Hàm ẩn có dạng: f  x  f x  p x Phương pháp giải: 2 
f x  2 f x 
f x  f x  p x   p    x  
p x dx  2   2
2. Hàm ẩn có dạng: f  x  p x f x Phương pháp giải: f   x
Chia hai vế với f x ta đựơc  p xf xf   x Suy ra dx
p x dx  ln | f x | p x dx    f x
Từ đây ta dễ dàng tính được f x
https://www.facebook.com/truongngocvy8/ T r an g
11 Trương Ngọc Vỹ 0978 333 093
Đại số 12 - Chương 4 – Nguyên hàm. Tích phân - Trắc nghiệm và tự luận 4 phần có lời giải Dùng chung 3 bộ sách
3. Hàm ẩn có dạng:          n f x p x f x    Phương pháp giải:
        n f x p x f x    f   x
Chia hai vế với    n f x    ta được  p x n  
f x   n 1  f   x
f x   Suy ra dx p x dx   p x dxn        f x n 1   
4. Hàm ẩn có dạng: u xf  x  u xf x  h x Phương pháp giải:
Dễ dàng thấy rằng u xf  x  u xf x  u xf x   
Do dó u xf  x  u xf x  hx  u xf x  h x  
Suy ra u xf x  h xdx
Từ đây ta dễ dàng tính được f x
5. Hàm ẩn có dạng: A xf x  B xf  x  h x   1 Ý tưởng giải:
 Ta cần nhân thêm một lượng u x vào  
1 để tạo thành u ' xf x  u xf  x  u x.h x  và lúc này:
u ' xf x  u xf  x  u x.h x
 u xf x '
  u x.h x  
 u xf x '
dx u x.h xdx    
u xf x  u x.h xdx
u x.hxdx
f x  u x
 Cách tìm u xu  
  x  Ax
u x được chọn sao cho :  u
  x  B x  u xAxu xAxAxA( x).dx     dx dx u x 
dx u xB( x) . . ln .  e    u xB xu xB xB x
Tóm lại phương pháp giải: A xf x  B xf  x  h x   1 như sau:
https://www.facebook.com/truongngocvy8/ T r an g
12 Trương Ngọc Vỹ 0978 333 093
Đại số 12 - Chương 4 – Nguyên hàm. Tích phân - Trắc nghiệm và tự luận 4 phần có lời giải Dùng chung 3 bộ sách
Ax.dx
+ Bước 1: Tìm u x : u xBx  e
u x.hxdx
+ Bước 2: Nhân u x vào  
1  f x  u x
Hai dạng đặc biệt của   1
f  x  f x  h x Phương pháp giải:  Nhân hai vế với x
e ta được x    x     x     x      x e f x e f x e h x e
f x   e h(x)   Suy ra x    x e
f x e h x dx
Từ đây ta dễ dàng tính được f (x)
f  (x)  f (x)  h(x) Phương pháp giải:  Nhân hai vế với x
e ta được x   ( )  x   ( )  x   ( )  x    ( )  x e f x e f x e h x e f x   eh(x)   Suy ra x  ( )  x e f x e  ( h x)dx
Từ đây ta dễ dàng tính được f (x) 1 Bài 1.
Cho hàm số f x  0 , liên tục trên đoạn 1;2 và thỏa mãn f (1)  ; 2 2 x . f (
x)  f (x) với 3 2 2 x
 1;2 . Tính tích phân I  2x   1 f (x)dx  1 Bài 2.
Cho hàm số f (x) đồng biến, có đạo hàm trên đoạn 1;4 và thoả mãn x x f x   f x 2 2 . ( ) ( ) 3 4 với x
 1;4 . Biết f (1)  , tính I f (x)dx  2 1 Bài 3.
Cho hàm số y f x có đạo hàm liên tục trên  và thỏa mãn điều kiện 3
x f   x 3    f x 4 6 27 1  0 , x        và f   1  0 . Tính I f (x)dx  2 2  ex f x Bài 4.
Cho hàm số f x thỏa mãn       ex f x f x , x
   và f 0  2 . Tính I dx  . x 1  f   1  g   1  4  Bài 5.
Cho hai hàm f x và g x có đạo hàm trên 1; 
4 , thỏa mãn  g x  xf  x với mọi
f x  xgx  4
x 1; 4 . Tính tích phân I   f x  g x dx    . 1
https://www.facebook.com/truongngocvy8/ T r an g
13 Trương Ngọc Vỹ 0978 333 093
Đại số 12 - Chương 4 – Nguyên hàm. Tích phân - Trắc nghiệm và tự luận 4 phần có lời giải Dùng chung 3 bộ sách Bài 6. Cho hàm số f x xác định và liên tục trên  \   0 thỏa mãn 2 2 2
x f x   x   f x ' 2 1
xf x 1 , với mọi x   \  
0 đồng thời thỏa f   1  2 . Tính
f xdx  1 Bài 7.
Cho hàm số f x có đạo hàm liên tục trên  , f 0  0, f '0  0 và thỏa mãn hệ thức 1
f xf x 2  x   2 . ' 18
3x xf ' x  6x  
1 f x;  . Biết  x   f x 2 1 e dx ae  ,
b a,b     . Giá 0
trị của a b bằng bao nhiêu? Bài 8.
Cho hàm số y f (x) xác định và có đạo hàm f   x liên tục trên [1;3] ; f x   0,x 1;  3 ; 3
f  x   f x 2    x  2 1
1  f x 4      và f   1  1. Biết rằng
f x dx a ln 3  b a, b     , giá trị của e 2
a b bằng bao nhiêu? Bài 9.
Cho hàm số y f x có đạo hàm liên tục trên 0  ;1 thỏa mãn      2018 3 f x xf x x , 1 x  0 
;1 . Tìm giá trị nhỏ nhất của
f x dx  . 0
https://www.facebook.com/truongngocvy8/ T r an g
14 Trương Ngọc Vỹ 0978 333 093
Đại số 12 - Chương 4 – Nguyên hàm. Tích phân - Trắc nghiệm và tự luận 4 phần có lời giải Dùng chung 3 bộ sách PHẦN B
TRẮC NGHIỆM VÀ TỰ LUẬN TỔNG HỢP GỒM BỐN PHẦN
PHẦN I. Câu trắc nghiệm nhiều phương án lựa chọn. Mỗi câu hỏi thí sinh chỉ chọn một phương án.
Câu 1. Cho hàm số y f x liên tục trên a;b. Các mệnh đề sau, mệnh đề nào sai? a b a
A. 2024 f x dx  0  B.
f x dx   f x dx   a a b b 1 1 b b a C.
f x dx
f x d  x   D.
f x dx f x dx   2025 2025 a a a b
Câu 2. Cho hàm số y f x liên tục trên  và , a ,
b c   thỏa mãn a b c . Các mệnh đề sau đây, mệnh đề nào đúng? c b c c b c A.
f x dx f x dx f x dx    B.
f x dx f x dx f x dx    a a b a a b c b c c b b C.
f x dx f x dx f x dx    D.
f x dx f x dx f x dx    a a b a a c
Câu 3. Cho f x , g(x) là hai hàm số liên tục trên  . Các mệnh đề sau đây, mệnh đề nào sai? b b b b b A.
f (x)dx f ( y)dy  
B. f (x)  g(x) dx f (x)dx g(x)d . x    a a a a a b b b b b C.
kf ( x)dx k f (t)dt  
D. f (x)g(x) dx f (x)dx g(x)d . x    a a a a a Câu 4.
Các mệnh đề sau đây, mệnh đề nào sai? 2024 A. dx  4048  . 2024 b b b B. f x . f x dx f x d . x f x dx 1   2   1   2      . a a a 1 b
C. Cho hàm số f x liên tục trên đoạn a;b . Khi đó
f xdx
được gọi là giá trị trung bình b a a
của hàm số f x trên đoạn a;b .
D. Nếu hàm số f x có đạo hàm f ' x và f ' x liên tục trên đoạn a;b thì b
f b  f a  f ' xdx  . a
https://www.facebook.com/truongngocvy8/ T r an g
15 Trương Ngọc Vỹ 0978 333 093
Đại số 12 - Chương 4 – Nguyên hàm. Tích phân - Trắc nghiệm và tự luận 4 phần có lời giải Dùng chung 3 bộ sách
Câu 5. Cho hàm f x là hàm liên tục trên đoạn  ;
a b với a b và F x là một nguyên hàm của
hàm f x trên  ; a b .
Cho các mệnh đề sau đây, mệnh đề nào đúng? b
A. kf xdx k F b  F a    a a B.
f xdx F b  F a   b
C. Diện tích S của hình phẳng giới hạn bởi đường thẳng x a; x b ; đồ thị của hàm số y f x và
trục hoành được tính theo công thức S F b  F a b b D.
f 2x  3 dx F 2x  3  a a 3 3 Câu 6. Nếu
f xdx  3 
thì 4 f xdx  bằng 0 0 A. 3 . B. 12 . C. 36 . D. 4 . 2 1 2 Câu 7. Cho
f (x)dx  
. Tính I  2025 f (x)d . x 2025 0 0 1
A. I  2 B. I
C. I  1 D. I  2025 2025 5 0 Câu 8. Nếu
f x dx  5 
thì 5 f x dx  bằng 0 5 A. 1. B. 1  . C. 25 . D. 2  5 . 4 4 4 Câu 9. Nếu f (x)dx  5 
và g(x)dx  4  
thì  f (x)  g(x)dx  bằng 1 1 1 A. 1  . B. 9  . C. 1 . D. 9. 4 4 4 Câu 10. Nếu
f (x)dx  3  và
g(x)dx  2   thì
f (x)  g(x)dx  bằng 1 1 1 A. 1  . B. 5  . C. 5 . D. 1 . 1 1 1 Câu 11. Cho
f xdx  2 
và g x dx  5 
, khi  f x  2g x dx    bằng 0 0 0 A. 8  B. 1 C. 3  D. 1 2 9 0 9 Câu 12. Giả sử
f xdx  7 
và g xdx  1 
. Khi đó I  2 f x  3g x dx    bằng 0 9 0 A. I  11. B. I  17 . C. I  23 . D. I  8 . 4 4 4 Câu 13. Nếu
f xdx  2 
và g xdx  3 
. Khi đó  f x  g x dx    bằng 1 1 1
https://www.facebook.com/truongngocvy8/ T r an g
16 Trương Ngọc Vỹ 0978 333 093
Đại số 12 - Chương 4 – Nguyên hàm. Tích phân - Trắc nghiệm và tự luận 4 phần có lời giải Dùng chung 3 bộ sách A. 5 . B. 6 . C. 1. D. 1  . 3 3 1  Câu 14. Nếu
f xdx  6  thì
f x  2 dx   bằng bao nhiêu? 3    0 0 A. 8 . B. 5 . C. 9 . D. 6 . 2 2 Câu 15. Nếu
f xdx  5 
thì 2 f x 1 dx     bằng: 0 0 A. 8 . B. 9 . C. 10 . D. 12 . 2 2 Câu 16. Nếu
f xdx  3 
thì 2 f x  2024 dx     bằng: 0 0 A. 4040 . B. 4042 . C. 4044 . D. 4046 . 2 2 Câu 17. Cho
f x dx  5 
. Tính I   f x  2sin x dx  5    . 0 0
A. I  7 B. I  5 
C. I  3
D. I  5  2 2 2
Câu 18. Cho 4 f x  2xdx  1    . Khi đó
f xdx  bằng: 1 1 A. 1 . B. 3  . C. 3 . D. 1  . 1 1 Câu 19. Cho
f xdx  1 
, tích phân 2 f x 2
 3x dx bằng 0 0 A. 1. B. 0 . C. 3 . D. 1 . 2 2 2 Câu 20. Cho
f x dx  2  và
g x dx  1  . Tính I
x  2 f x  3g x dx    . 1  1  1  17 5 7 11 A. I B. I C. I D. I 2 2 2 2 2 2 2 Câu 21. Cho
f x dx  3 
, g x dx  1  
thì  f x  5g x  x dx    bằng: 0 0 0 A. 12 . B. 0 . C. 8 . D. 10 5 5 Câu 22. Cho
f x dx  2 
. Tích phân 4 f x 2  3x  dx    bằng 0 0 A. 140 . B. 130 . C. 120 . D. 133 . 2 2
Câu 23. Cho 4 f x  2xdx  1    . Khi đó
f xdx  bằng: 1 1 A. 1 . B. 3  . C. 3 . D. 1  . 2 4 4 Câu 24. Cho
f x dx  1  ,
f t  dt  4  . Tính
f y dy  . 2 2 2 A. I  5 . B. I  3 . C. I  3 . D. I  5 .
https://www.facebook.com/truongngocvy8/ T r an g
17 Trương Ngọc Vỹ 0978 333 093
Đại số 12 - Chương 4 – Nguyên hàm. Tích phân - Trắc nghiệm và tự luận 4 phần có lời giải Dùng chung 3 bộ sách 2 4 4
Câu 25. Cho hàm số f x liên tục trên R và có f (x)dx  9; f (x)dx  4.   Tính I f (x)d . x  0 2 0 9 A. I  5 . B. I  36 . C. I  . D. I  13 . 4 4 4 3
Câu 26. Cho hàm số f x liên tục trên  và f x dx  10  ,
f x dx  4  . Tích phân
f x dx  bằng 0 3 0 A. 4 . B. 7 . C. 3 . D. 6 . 10 6
Câu 27. Cho hàm số f x liên tục trên đoạn 0;10 và
f xdx  7  ;
f xdx  3  . Tính 0 2 2 10 P
f xdx
f xdx   . 0 6 A. P  4 B. P  10 C. P  7 D. P  4  6 4
Câu 28. Cho hàm số f x liên tục trên đoạn [0; 6] thỏa mãn f xdx  10  và
f xdx  6  . Tính giá 0 2 2 6
trị của biểu thức P
f xdx f xdx   . 0 4
A. P  4 . B. P  16 . C. P  8 . D. P  10 . 2
Câu 29. Tính tích phân I  (2x 1)dx  0 A. I  5 . B. I  6 . C. I  2 . D. I  4 . 1
Câu 30. Tích phân 3x  
1  x  3 dx  bằng 0 A. 12 . B. 9 . C. 5 . D. 6 . e  1 1 
Câu 31. Tính tích phân I   dx  2   x x  1 1 1 A. I B. I   1
C. I  1
D. I e e e 3 x  2 Câu 32. Biết
dx a b ln c, 
với a, b, c  , c  9. Tính tổng S a b  . c x 1 A. S  7 . B. S  5 . C. S  8 . D. S  6 . 1
Câu 33. Kết quả tích phân  5x I dx  bằng 0 5 4 A. I  .
B. I  4 ln 5 .
C. I  5 ln 5 . D. I  . ln 5 ln 5 1 Câu 34. Tích phân 3 e xdx  bằng 0
https://www.facebook.com/truongngocvy8/ T r an g
18 Trương Ngọc Vỹ 0978 333 093
Đại số 12 - Chương 4 – Nguyên hàm. Tích phân - Trắc nghiệm và tự luận 4 phần có lời giải Dùng chung 3 bộ sách 1 3 e 1 A. 3 e  . B. e  1 . C. . D. 3 e 1 . 2 3 1 Câu 35. Tích phân 3x 1 e  dx  bằng 0 1 1 A.  4
e e B. 3 e e C.  4
e e D. 4 e e 3 3 1 x e e Câu 36. Biết dx   b
a, b   . Khi đó giá trị của P a b là 2x a 0 A. P  3 B. P  1 C. P  1 D. P  3 1 2 x e  4
Câu 37. Giá trị của I dx  bằng x e  2 0 1
A. I  2 e  3 0. B. I  e  3 .
C. I e  3 .
D. I  2 e  3 . 2 2  xea b Câu 38. Biết x 2 e 1 dx e  . a e b ln 2   
a, b   . Khi đó giá trị của P  là x . a b 1   A. P  3 B. P  1 C. P  1 D. P  2 1 2 x 1  3  x ee 1 1 a b
Câu 39. Biết I dx   b
a,b   . Khi đó giá trị của P  là x e a . a b 0 4 e 1 4 e 1 4 1 e A. 4 P e 1 B. P C. P D. P  2 e 4 e 4 e 2
Câu 40. Giá trị của sin xdx  bằng 0 A. 0. B. 1. C. -1. D. . 2 2 2 a b 3
Câu 41. Biết 2sin x  3cos x xdx   
a, b, c   . Khi đó giá trị của P a  2b  3c là 2 c 3 A. P  45 B. P  60 C. P  65 D. P  70 3 Câu 42. Biết 2
3 tan xdx a 3  b  
a, b, c   . Khi đó giá trị của P a b c là c 4 A. P  6 B. P  4 C. P  4 D. P  6 4 Câu 43. Biết   2
2 cot x  5 dx
b 3  c a, b, c   . Khi đó giá trị của P a b c là a 6 A. P  6 B. P  4 C. P  4 D. P  6
https://www.facebook.com/truongngocvy8/ T r an g
19 Trương Ngọc Vỹ 0978 333 093
Đại số 12 - Chương 4 – Nguyên hàm. Tích phân - Trắc nghiệm và tự luận 4 phần có lời giải Dùng chung 3 bộ sách 2 x x a a Câu 44. Biết 2 2 sin cos dx    với , a b   và
là phân số tối giản. Khi đó giá trị của 4 4 c b b 0
P a b c là A. P  17 B. P  16 C. P  32 D. P  49 2
Câu 45. Giá trị của I  1 cos 2xdx  bằng 0 A. 3 . B. 4 2 . C. 2 3 . D. . 2 2
Câu 46. Tính tích phân I x  2 dx  . 0 A. I  2  . B. I  4 . C. I  2 . D. I  0 . 2 Câu 47. Tính 2x  1 dx  1 1 5 13 A. . B. 2 . C. . D. . 2 2 2 2
Câu 48. Tính I  2x  2 d . x  0 A. 0. B. 2. C. 1. D. 3. 2 Câu 49. Tính 2
x  2x  1dx  0 1 5 A. . B. 2 . C. . D. 1. 2 2 3
Câu 50. Tính I
x 2x  4d . x  0 16 16 4 A. . B. 2. C. . D. . 3 3 3 8
Câu 51. Tính tích phân 2
x  6x dx  . 0 64 64 152 152 A. . B. . C. . D. . 3 3 3 3 3 a a Câu 52. Biết 2 I
x  3x  2 dx  ,  với * , a b   ,
tối giản. Tính T a b b b 1 A. 12. B. 14. C. 11. D. 4. 2
Câu 53. Tính tích phân 3 I x x dx  . 0
https://www.facebook.com/truongngocvy8/ T r an g
20 Trương Ngọc Vỹ 0978 333 093

Tài liệu liên quan: