Trình bày dữ liệu thống kê môn Xác suất thống kê| Trường Đại học Ngoại Thương

BÀI 2
TRÌNH BÀY DỮ LIỆU THỐNG KÊ 1. Dữ liệu thống kê
–Khái niệm: Dữ liệu thống kê là các sự kiện, con số được thu thập, phân tích và tổng
kết để trình bày, giải thích hiện tượng nghiên cứu. –Phân loại:
Dữ liệu định tính: Là các nhãn hoặc tên gọi để nhận dạng và đặc trưng cho mỗi phần
tử. Sử dụng thang đo chỉ danh hoặc thang đo thứ tự.
Dữ liệu định lượng: Là các con số biểu diễn giá trị của một đại lượng nào đó. Sử
dụng thang đo khoảng hoặc thang đo tỷ lệ. 2. Phân tổ dữ liệu
–Khái niệm: Phân tổ dữ liệu là căn cứ vào các đặc trưng của dữ liệu để phân chia dữ
liệu vào các tổ có tính chất khác nhau. –
Phân tổ theo tiêu thức thuộc tính –
Phân tổ theo tiêu thức số lượng Số tổ k=( 2×n)1/3
Khoảng cách tổ ( max  min )  (  h) 1 max  hmin x x x x k   k k Phân tổ mở 3.
Phương pháp trình bày dữ liệu –
Sử dụng bảng biểu thống kê –
Sử dụng biểu đồ, đồ thị thống kê –
Sử dụng bản đồ thống kê – Sử dụng sơ đồ nhánh/lá – Một số lưu ý:
Lựa chọn biểu đồ, đồ thị phù hợp với nội dung, tính chất của dữ liệu cần diễn đạt
Xác định qui mô (kích thước) phù hợp
Thống nhất các thang đo tỷ lệ, tỷ lệ xích
Các số liệu phải được ghi chú rõ ràng, đầy đủ
Sử dụng ký hiệu, màu sắc nhất quán Bài 3 THỐNG KÊ MÔ TẢ
1. Số tuyệt đối và số tương đối
– Số tuyệt đối: Là giá trị biểu hiện quy mô, khối lượng của hiện tượng nghiên cứu
trong điều kiện thời gian và địa điểm cụ thể.
– Số tương đối: Là giá trị biểu hiện quan hệ so sánh giữa hai mức độ của hiện tượng nghiên cứu. y1 t y0
2. Các đại lượng đo lường mức độ tập trung – Số trung bình (Mean) Trung bình tổng thể N xk 1 1 
 i f xii i i  N N Trung bình mẫu n k x f x 1 1   i i i x i i n n
– Số trung vị (Median): Là số nằm giữa tập dữ liệu khi các giá trị quan sát trong tập dữ liệu được sắp xếp. (n  ) 1 Me 2
Trường hợp số quan sát là số chẵn thì trung vị là giá trị trung bình của 2 quan sát ở giữa. n n 2   2  2  Me  2
– Số yếu vị (Mode): Là giá trị của tiêu thức thường gặp nhất trong tổng thể hoặc mẫu -
Giá trị quan sát có tần số xuất hiện nhiều nhất. Ký hiệu Mo
– Số phân vị (Percentiles): Phân vị p là giá trị có ít nhất p% phần tử của tập dữ liệu có
giá trị nhỏ hơn hoặc bằng giá trị này và có ít nhất (100 – p)% phần tử của tập dữ liệu
có giá trị lớn hơn hoặc bằng giá trị này.
– Số tứ phân (Quartiles): Là các số phân vị cụ thể, chia tập dữ liệu ra làm 4 phần, được gọi tên là:
Q1 = Số tứ phân thứ nhất = P25% = (n+1)/4
Q2 = Số tứ phân thứ hai
= P50% = 2(n+1)/4 = (n+1)/2 Q3 = Số tứ phân thứ ba = P75% = 3(n+1)/4
• Trường hợp (n+1) không chia hết cho 4, cần tính giá trị cộng thêm
3. Các đại lượng đo lường mức độ phân tán
– Khoảng biến thiên (Range): R = xmax - xmin
– Khoảng biến thiên nội tứ phân (Interquartile Range): IQR = Q3 – Q1
– Độ lệch tuyệt đối trung bình: Là trung bình cộng của các độ lệch tuyệt đối giữa các
giá trị biến và giá trị trung bình của các biến đó. n k ∑ ∑ ¯ |xi−¯x|
|xi−¯x|fi d i=1 i=1 = n= k ∑ fi i=1
– Phương sai (Variance): Là trung bình cộng của bình phương các độ lệch giữa giá trị
biến và trung bình cộng của các biến đó.
Phương sai của tổng thể: N k (x 2  ) (x 2 ) f i   i  i 2 i 1 i   1  k N  fi i1 n k (x  x 2) (x x 2 ) f i  i i 2 i 1 i  1 k  sˆ n  fi i1 Phương sai mẫu:
Phương sai mẫu hiệu chỉnh:
– Độ lệch chuẩn (Standard Deviation): Là căn bậc hai của phương sai. Độ lệch chuẩn
và phương sai được sử dụng phổ biến để đo lường sự biến thiên
Độ lệch chuẩn tổng thể
Độ lệch chuẩn mẫu
– Hệ số biến thiên (Coefficient of variation): Là tỷ số giữa độ lệch chuẩn và giá trị trung bình.
Hệ số biến thiên tổng thể
Hệ số biến thiên mẫu  V  s v  x Bài 4
ĐIỀU TRA CHỌN MẪU
1. Điều tra chọn mẫu
–Khái niệm: Là phương pháp điều tra không toàn bộ, chỉ lựa chọn một số đơn vị từ
tổng thể để điều tra, sử dụng kết quả để suy luận cho toàn bộ tổng thể.
–Ưu điểm: Tiết kiệm chi phí và thời gian, đáp ứng tính cấp thiết; có thể đảm bảo tính
chính xác nếu tuân thủ quy tắc
–Nhược điểm: Không đáp ứng được khi cần nghiên cứu toàn bộ tổng thể; kết quả suy
luận từ mẫu bao giờ cũng có sai số đại diện
–Ứng dụng khi: Không có điều kiện điều tra toàn bộ khi tổng thể; khi cần tổng hợp
kết quả nhanh; khi điều tra có thể phá hủy mẫu; khi cần so sánh các hiện tượng với
nhau mà chưa có thông tin cụ thể
2. Các phương pháp chọn mẫu
– Phương pháp chọn mẫu ngẫu nhiên:
Chọn mẫu ngẫu nhiên đơn giản (Simple Random Sampling)
Chọn mẫu hệ thống (System Sampling)
Chọn mẫu phân tổ (Stratified Random Sampling)
Chọn mẫu cụm (Cluster Sampling)
– Phương pháp chọn mẫu không ngẫu nhiên Chọn mẫu thuận lợi
Chọn mẫu có chủ đích
Chọn mẫu theo chỉ tiêu
Chọn mẫu theo p.p “ném bóng tuyết”
3. Sai số trong điều tra chọn mẫu
– Sai số trong điều tra chọn mẫu bao gồm: Sai số do chọn mẫu và các sai số khác (do
trả lời, ghi chép, giá trị khuyết thiếu, đo lường …). Với mỗi mẫu được chọn từ tổng
thể sẽ có một giá trị sai số cụ thể được gọi là sai số trung bình chọn mẫu.
– Cách tính sai số trong điều tra chọn mẫu
Chọn mẫu để ước lượng giá trị trung bình của tổng thể, sai số tính theo công thức:  2     x n n
Chọn mẫu để ước lượng giá trị tỷ lệ của tổng thể, sai số tính theo công thức: p 1 (  p)   p n
4. Phạm vi sai số trong điều tra chọn mẫu
– Phạm vi sai số  trong chọn mẫu để ước lượng giá trị trung bình t ổng thể tính theo công thức:   z    2 z x x  2 n
– Phạm vi sai số  trong chọn mẫu để ước lượng giá trị tỷ lệ tổng thể tính theo công thức: p 1 (  p) p z p  z 2 2 n – Trong đó:
: Là mức độ sai số
z : Là hệ số tin cậy được xác định thông qua bảng tra cứu (hoặc sử dụng hàm NORMSINV trong Excel)
5. Xác định kích thước mẫu
– Kích thước mẫu liên quan đến các yếu tố: Phương pháp chọn mẫu sử dụng, phạm vi sai số
có thể chấp nhận được, độ tin cậy mong muốn, độ lệch tiêu chuẩn của tổng thể, kinh phí, nhân lực, …
– Chọn mẫu để ước lượng giá trị trung bình của tổng thể 2 2 z   2 n  2  x
– Chọn mẫu để ước lượng giá trị tỷ lệ của tổng thể 2 1
( z 2)p  p n   2  p
Chú ý: Trong trường hợp không biết p thì p(1-p)  0.25 Bài 5
ƯỚC LƯỢNG THAM SỐ THỐNG KÊ 1. Mở đầu
– Ước lượng: Là một phương pháp suy luận các tham số tổng thể từ dữ liệu mẫu – Phân loại:
Ước lượng điểm: Là một giá trị duy nhất đại diện cho tham số tổng thể
Ước lượng khoảng: Là khoảng giá trị bao quanh giá trị tham số tổng thể (được
xác định bằng cận trên, cận dưới) và gọi là khoảng tin cậy
– Thống kê toán học đã chứng minh E(x)   ( E) p  P E(s2 )   2
– Do đó, với mẫu cụ thể ta có ước lượng điểm: x   p P 2 2 s  
2. Ước lượng giá trị trung bình tổng thể
– Trường hợp mẫu lớn (n >=30): Ước lượng khoảng tin cậy (1-) của số trung bình
tổng thể tính theo công thức:  x z   2 n
Chú ý: Nếu không biết  thì sử dụng đại lượng xấp xỉ s
– Trường hợp mẫu nhỏ (n < 30)
• Nếu biết độ lệch chuẩn tổng thể (), xác định như trường hợp mẫu lớn.
• Nếu chưa biết độ lệch chuẩn tổng thể (), xác định theo công thức: s x,1 n2t    n
Chú ý: Giá trị t tuân theo phân phối Student với bậc tự do df = n-1 và xác định bằng bảng
tra cứu (hoặc dùng hàm TINV trong Excel)
3. Ước lượng giá trị tỷ lệ của tổng thể
– Được sử dụng khi cần quan tâm tới tỷ lệ các phần tử có đặc trưng nào đó trong tổng thể.
–Ước lượng khoảng tin cậy (1- ) của giá trị tỷ lệ tổng thể xác định theo công thức: 1 ( p ) z p  p 
4. Ước lượng một bên của tham số tổng thể  2 n
– Sử dụng khi chỉ cần quan tâm đến giới hạn dưới hoặc giới hạn trên.
– Khi đó chỉ cần thay z/2 bằng z trong công thức tính ước lượng Bài 6
KIỂM ĐỊNH GIẢ THUYẾT THỐNG KÊ 1. Khái niệm
– Giả thuyết thống kê: Là một phát biểu về tham số tổng thể (có thể đúng hoặc sai)
– Kiểm định giả thuyết: Là việc tìm ra kết luận để bác bỏ hoặc không bác bỏ giả thuyết
– Giả thuyết không (H ): Là một phát biểu về tham số tổng thể, thường bị nghi ngờ;
được cho là đúng cho tới khi nó được chứng minh là sai.
– Giả thuyết thay thế, đối thuyết (H ): Là phát biểu ngược với giả thuyết không; được
cho là đúng nếu giả thuyết không bị bác bỏ.
2. Các trường hợp kiểm định – Giả sử
  : là một tham số tổng thể (trung bình, tỷ lệ …)
 0 : là một giá trị cụ thể
H0 , H1: là giả thuyết không và giả thuyết thay thế
– Trường hợp kiểm định 2 bên H0:
H0:  = 0
H1:  ≠ 0
– Trường hợp kiểm định 1 bên
H0:  ≥ 0hoặc H0:  ≤ 0 H1:  < 
H1:  > 0
3. Tiêu chuẩn kiểm định (giá trị kiểm định)
– Khái niệm: Là một giá trị thống kê (ký hiệu là z) được tính từ các đại lượng mẫu. Sử
dụng để ra quyết định bác bỏ hoặc chấp nhận giả thuyết H0 4. Miền bác bỏ
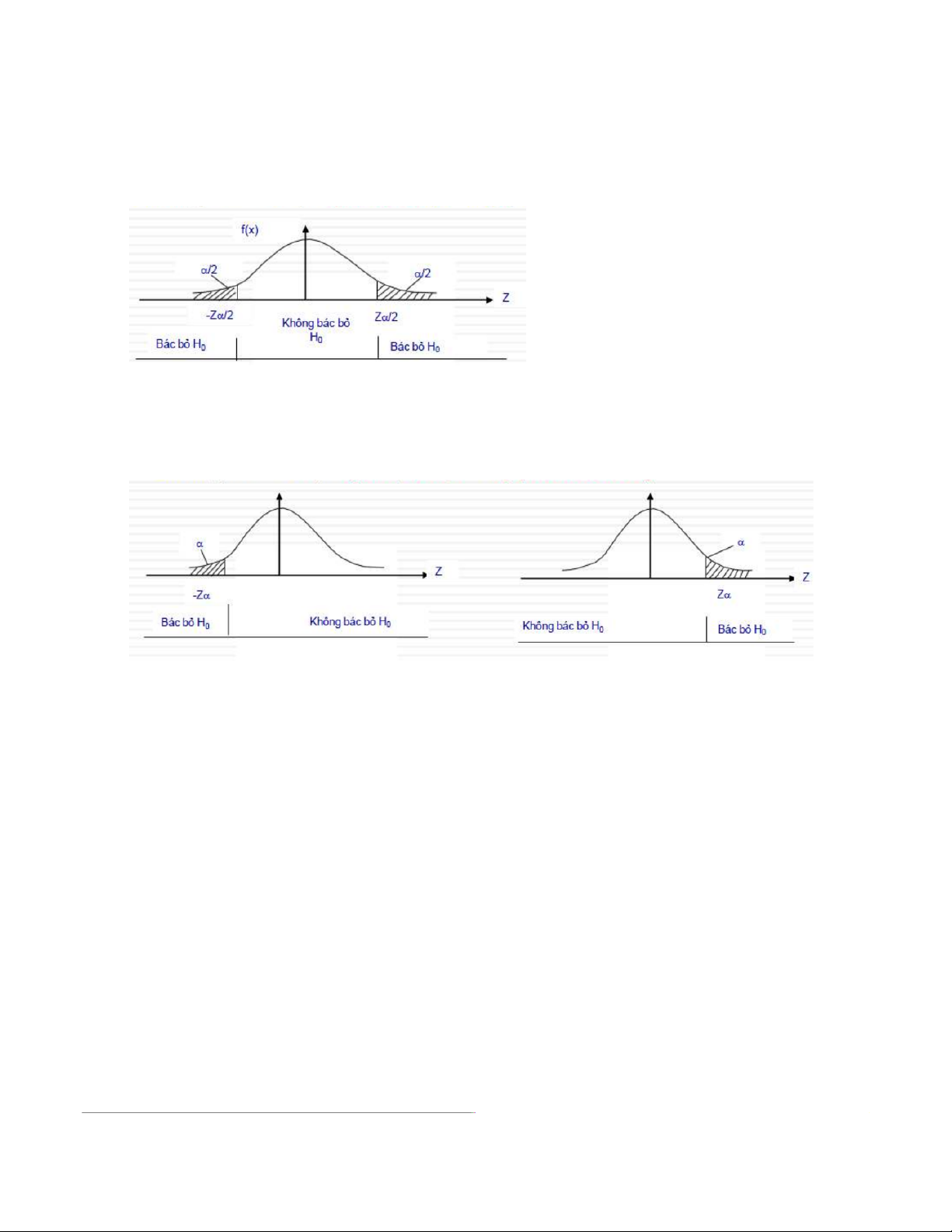
– Miền bác bỏ trong kiểm định 2 bên
– Miền bác bỏ trong kiểm định 1 bên
5. Sai lầm loại I và sai lầm loại II
– Khi tiến hành kiểm định giả thuyết, có thể mắc phải 1 trong 2 sai lầm:
Sai lầm loại I là bác bỏ giả thuyết H0 khi H0 đúng
Sai lầm loại II là không bác bỏ giả thuyết H0 khi H0 sai
Chú ý: Bác bỏ giả thuyết có thể mắc sai lầm loại I, không bác bỏ giả thuyết có thể mắc sai lầm loại II
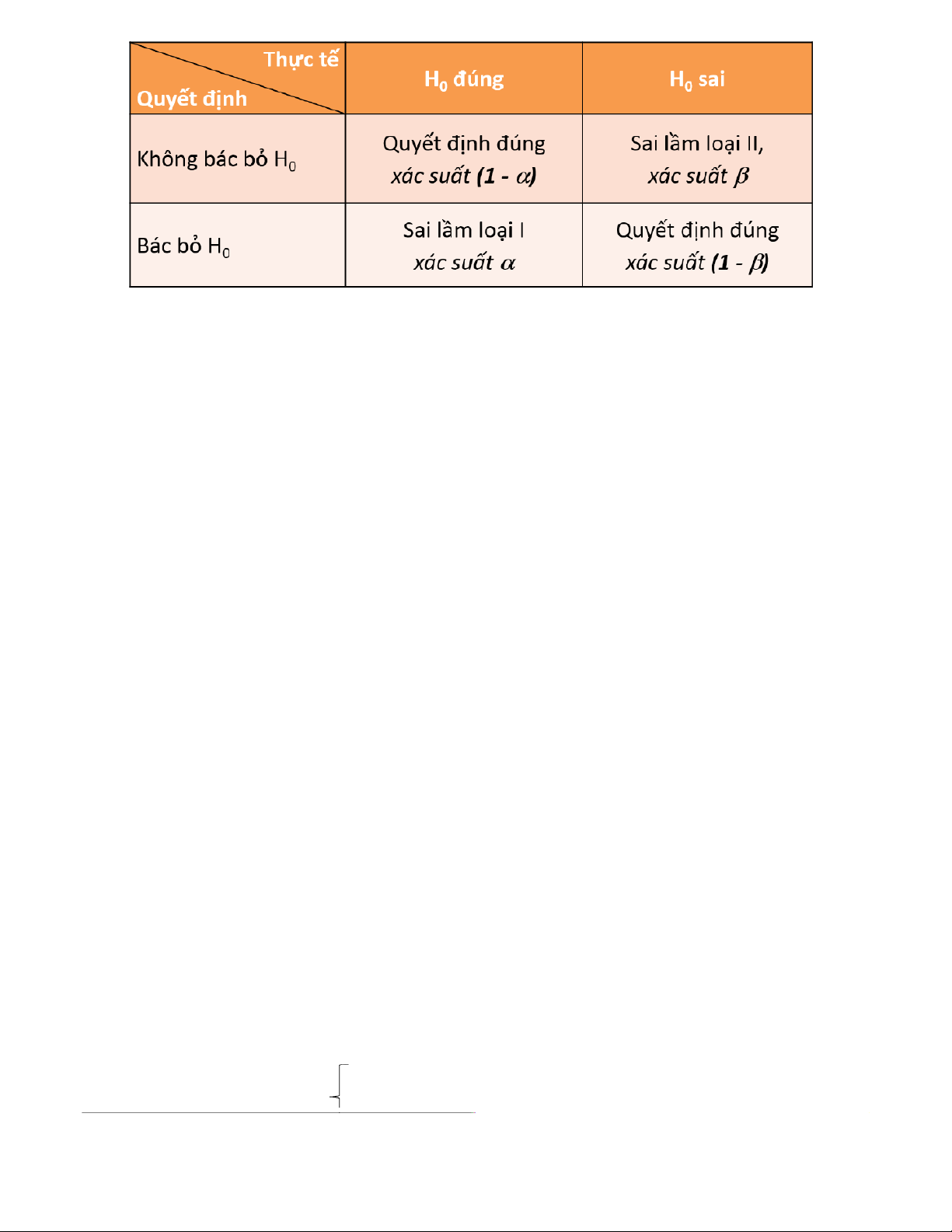
– Bảng tóm tắt sai lầm loại I và loại II
6. Mức ý nghĩa và năng lực kiểm định
– Giả sử  là xác suất của sai lầm loại I, khi đó  gọi là mức ý nghĩa của kiểm định
– Giả sử  là xác suất của sai lầm loại II, khi đó (1-) gọi là năng lực của kiểm định
Chú ý:  càng nhỏ thì  càng lớn
7. Giá trị p-value
– Giá trị p-value là mức ý nghĩa nhỏ nhất được tính từ giá trị kiểm định z, dùng để bác
bỏ giả thuyết H0.
– Nếu p-value < , bác bỏ giả thuyết H0
Chú ý: p-value được tính bằng cách tra bảng z hoặc sử dụng hàm NORMSDIST trong Excel
8. Các bước kiểm định giả thuyết thống kê
Bước 1: Xác định kiểu kiểm định và thiết lập các giả thuyết H0 và H1
Bước 2: Xác định tiêu chuẩn kiểm định (giá trị kiểm định)
Bước 3: Xác định miền bác bỏ giả thuyết H0
Bước 4: Kết luận bác bỏ hay không bác bỏ giả thuyết H0
(bằng cách sử dụng giá trị z hoặc p-value và các quy tắc bác bỏ)
9. Kiểm định giả thuyết về giá trị trung bình tổng thể
a - Trường hợp mẫu lớn (n>=30)
– Xác định kiểu kiểm định và thiết lập các giả thiết:
Kiểm định 2 bên: H0:  = 0
H1:  ≠ 0
Kiểm định 1 bên: H0:  ≤ 0hoặc H0:  ≥ 0
H1:  > 0
H1:  < 0
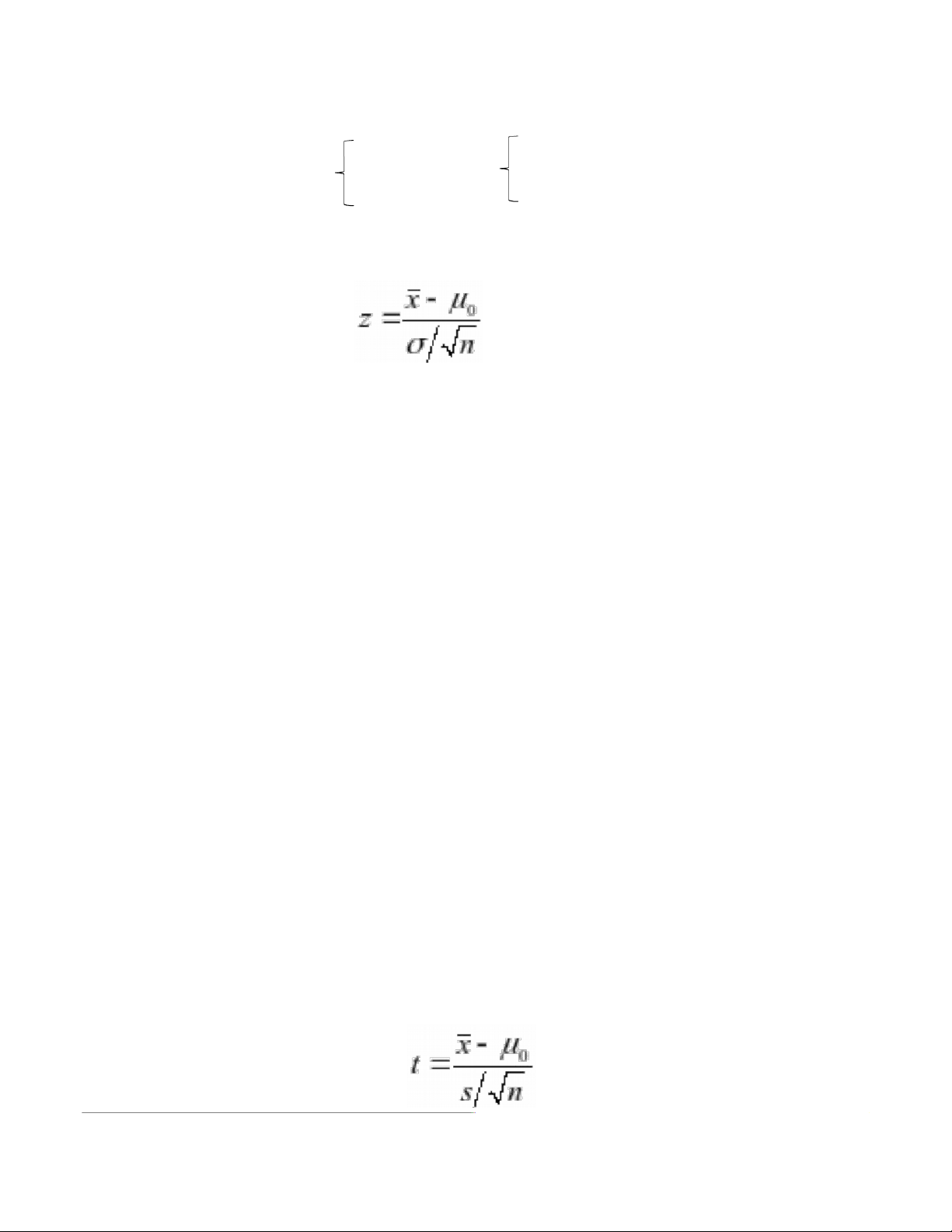
– Xác định tiêu chuẩn kiểm định: x   z 0  n
Chú ý: Nếu không biết  thì có thể thay bằng s
– Xác định miền bác bỏ giả thiết H0: Kiểm định 2 bên
z < -z/2 hoặc z > z/2 Kiểm định 1 bên
z > z trường hợp H1:  > 0
z < -z trường hợp H1:  < 0 –Kết luận:
Sử dụng giá trị tới hạn: Bác bỏ H0 nếu z nằm trong miền bác bỏ
Sử dụng p-value: Bác bỏ H0 nếu p-value < 
b - Trường hợp mẫu nhỏ (n<30)
– Khi cỡ mẫu nhỏ và biết độ lệch chuẩn tổng thể  :
Thực hiện kiểm định như mẫu lớn
– Khi cỡ mẫu nhỏ và không biết độ lệch chuẩn tổng thể  :
Giá trị kiểm định được xác định bằng công thức: x   t0 s n
Miền bác bỏ xác định theo tdf, /2
Các bước còn lại thực hiện như mẫu lớn
10. Kiểm định giả thuyết về giá trị tỷ lệ tổng thể
– Xác định kiểu kiểm định và thiết lập các giả thiết: Kiểm định 2 bên: H0: P = p0 H1: P ≠ p0 Kiểm định 1 bên: H0: P ≤ p0 hoặc H0: P ≥ p0 H1: P > p0 H1: P < p0
– Xác định tiêu chuẩn kiểm định: p  p 1 ( z) 0  p  p n 0 0
– Xác định miền bác bỏ: Kiểm định 2 bên:
z < -z/2 hoặc z > z/2 Kiểm định 1 bên: z > z trường hợp H1: P > p0 z < -z trường hợp H1: P < p0 – Kết luận:
Sử dụng giá trị tới hạn: Bác bỏ H0 nếu z nằm trong miền bác bỏ
Sử dụng p-value: Bác bỏ H0 nếu p-value < 