Tứ giác nội tiếp là gì? Tính chất và dấu hiệu nhận biết tứ giác nội tiếp Toán lớp 9
Tứ giác nội tiếp là gì? Tính chất và dấu hiệu nhận biết tứ giác nội tiếp Toán lớp 9. Bài viết dưới đây của
Luật Minh Khuê sẽ giúp bạn tìm hiểu một số vấn đề liên quan đến tứ giác nội tiếp. Kính mời quý bạn đọc tham khảo.
1. Tứ giác nội tiếp là gì?
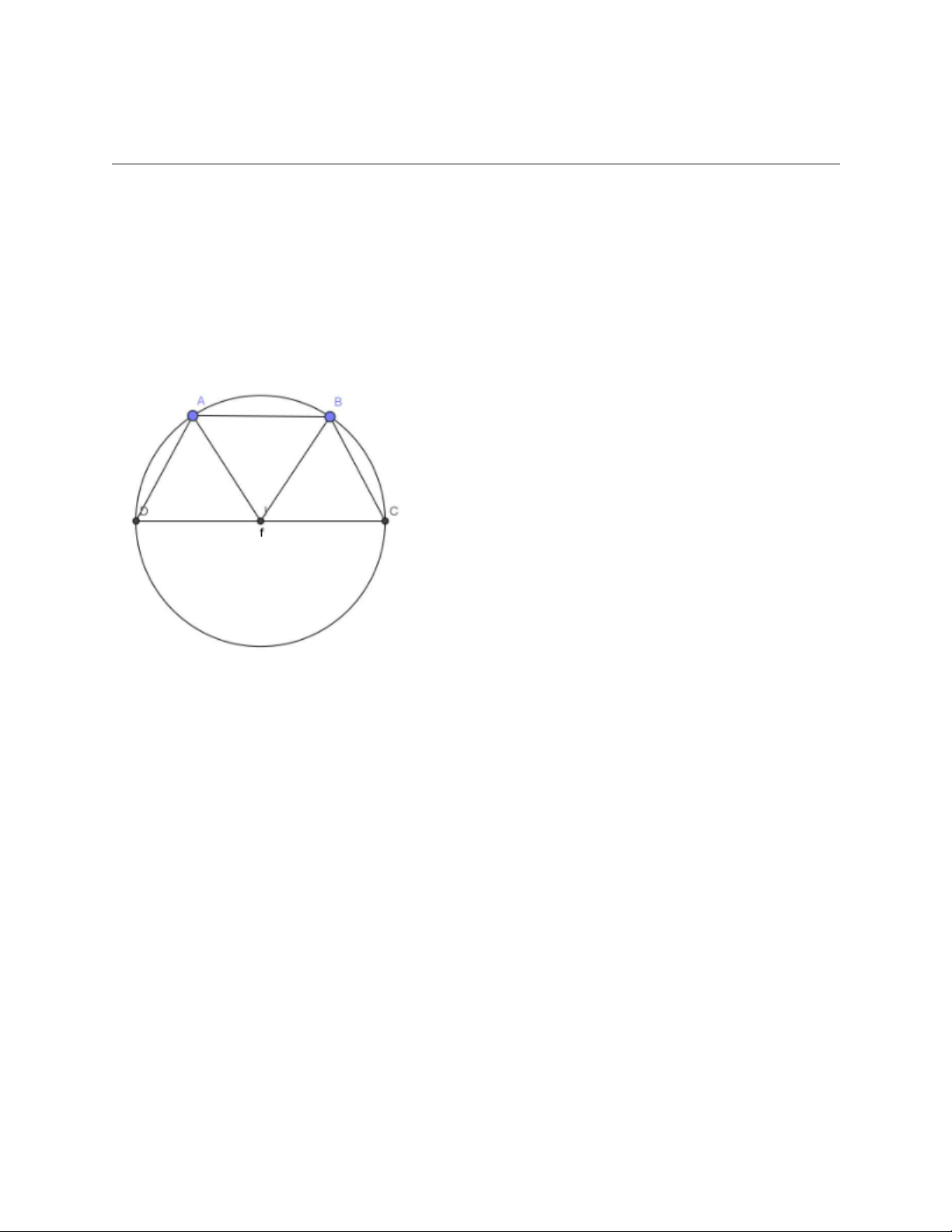
Tứ giác nội tiếp đường tròn là tứ giác có bốn đỉnh nằm trên đường tròn đó.
Đường tròn đó được gọi là đường tròn ngoại tiếp tứ giác.
Trong hình trên, tứ giác ABCD nội tiếp (I) và (I) ngoại tiếp tứ giác ABCD.
2. Tính chất của tứ giác nội tiếp
• Một tứ giác nội tiếp, tổng số đo hai góc đối diện bằng 180°
• Nếu một tứ giác có tổng số đo hai góc đối diện bằng 180° thì tứ giác đó nội tiếp được đường tròn.
3. Dấu hiệu nhận biết tứ giác nội tiếp
• Tứ giác có tổng hai góc đối bằng 180°
• Tứ giác có góc ngoài tại một đỉnh bằng góc trong của đỉnh đối diện
• Tứ giác có 4 đỉnh cách đều một điểm cố định (mà ta có thể xác định được). Điểm đó là tâm của
đường tròn ngoại tiếp tứ giác.
• Tứ giác có hai đỉnh kề nhau cùng nhìn cạnh chứa hai đỉnh còn lại dưới một góc a
* Lưu ý: Trong các hình đã học thì hình chữ nhật, hình vuông, hình thang cân nội tiếp được đường tròn.
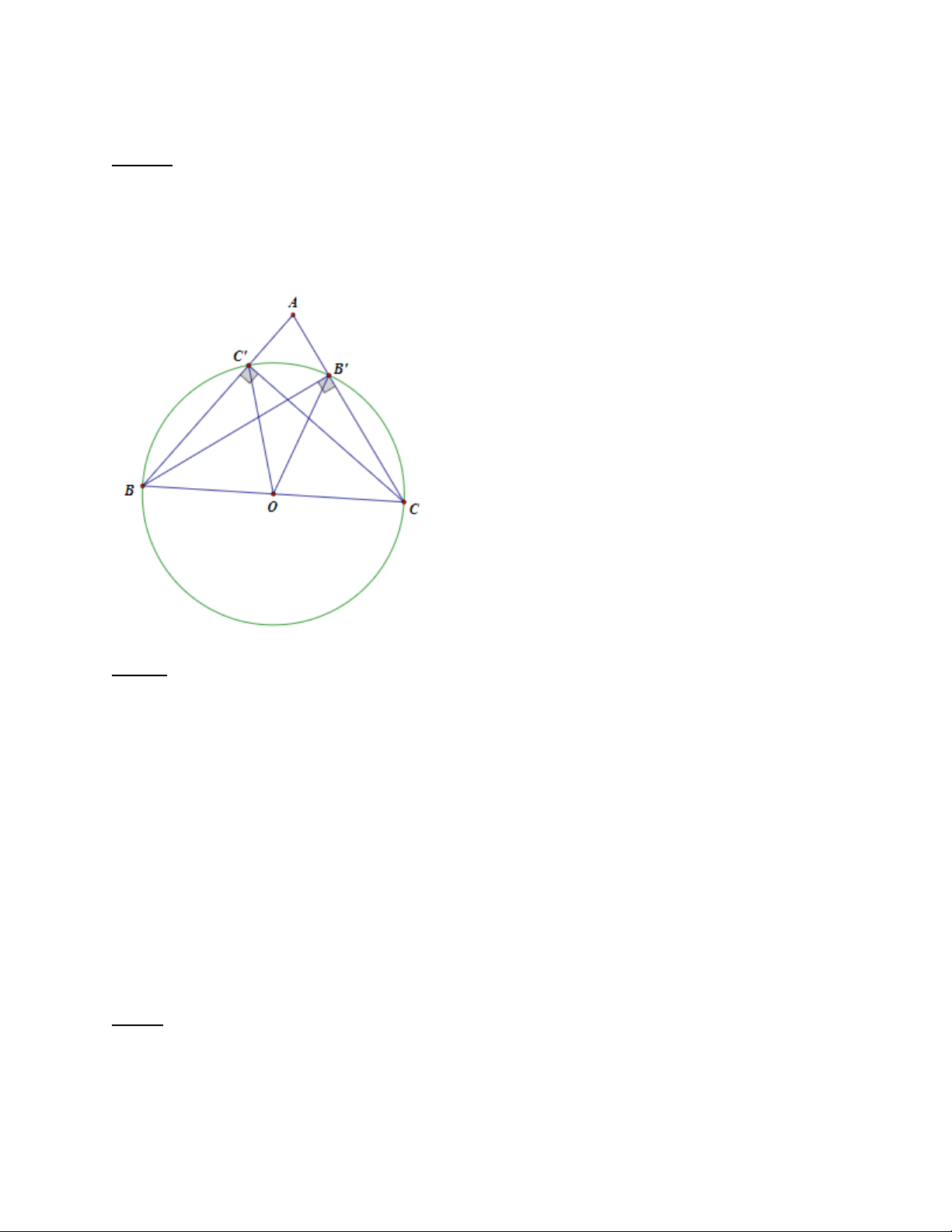
Ví dụ: Cho tam giác ABC, hai đường cao BB', CC'. Chứng minh tứ giác BCB'C' nội tiếp. Đáp án
Cách 1. Chứng minh bốn điểm cách đều một điểm
Gọi O là trung điểm của BC.
Xét tam giác BB'C = 90° (giả thiết)
OB' la đường trung tuyến ứng với cạnh huyền
=> OB' = OB = OC = r (1)
Xét tam giác BC'C có: góc BC'C = 90 (gt)
tương tự trên => OC' = OB = OC = r (2)
Từ (1) và (2) => B, C', B', C € (O,r)
=> Tứ giác BC'B'C nội tiếp đường tròn
Cách 2. Tứ giác có hai đỉnh kề nhau cùng nhìn cạnh chứa hai đỉnh còn lại dưới một góc bằn nhau là tứ giác nội tiếp
Ta có: BB' vuông góc AC (gt) => góc BB'C = 90°
CC' vuông góc Ab (gt) => góc BC'C = 90°
=> B', C' cùng nhìn cạnh BC dưới một góc vuông
=> B', C' nằm trên đường tròn đường kính BC
Hay tứ giác BC'B'C nội tiếp đường tròn đường kình BC
4. Bài tập về tứ giác nội tiếp
4.1. Dạng 1. Chứng minh tứ giác nội tiếp
Phương pháp giải: Để chứng minh tứ giác nội tiếp, ta có thể sử dụng một trong các cách sau:
- Cách 1. Chứng minh tứ giác có tổng hai góc đối bằng 180°
- Cách 2. Chứng minh tứ giác có hai đỉnh kề nhau cùng nhìn cạnh chứa hai đỉnh còn lại dưới một góc a
- Cách 3. Chứng inh tứ giác có góc ngoài tại một đỉnh bằng góc trong của đỉnh đối diện
- Cách 4. Tìm được một điểm cách đều bốn đỉnh của tứ giác
Bài 1. Cho tam giác ABC nhọn, đường cao BM và CN cắt nhau tại H. Chứng minh các tứ giác AMHN và
BNMC là những tứ giác nội tiếp. Đáp án
Xét tứ giác AMHN có:
góc AMH + góc ANH = 90° + 90° + 180° => tứ giác AMHN nội tiếp (điều phải chứng minh)
Xét tứ giác BNMC có:
góc BNC = góc BMC = 90° => tứ giác BNMC nội tiếp (điều phải chứng minh)
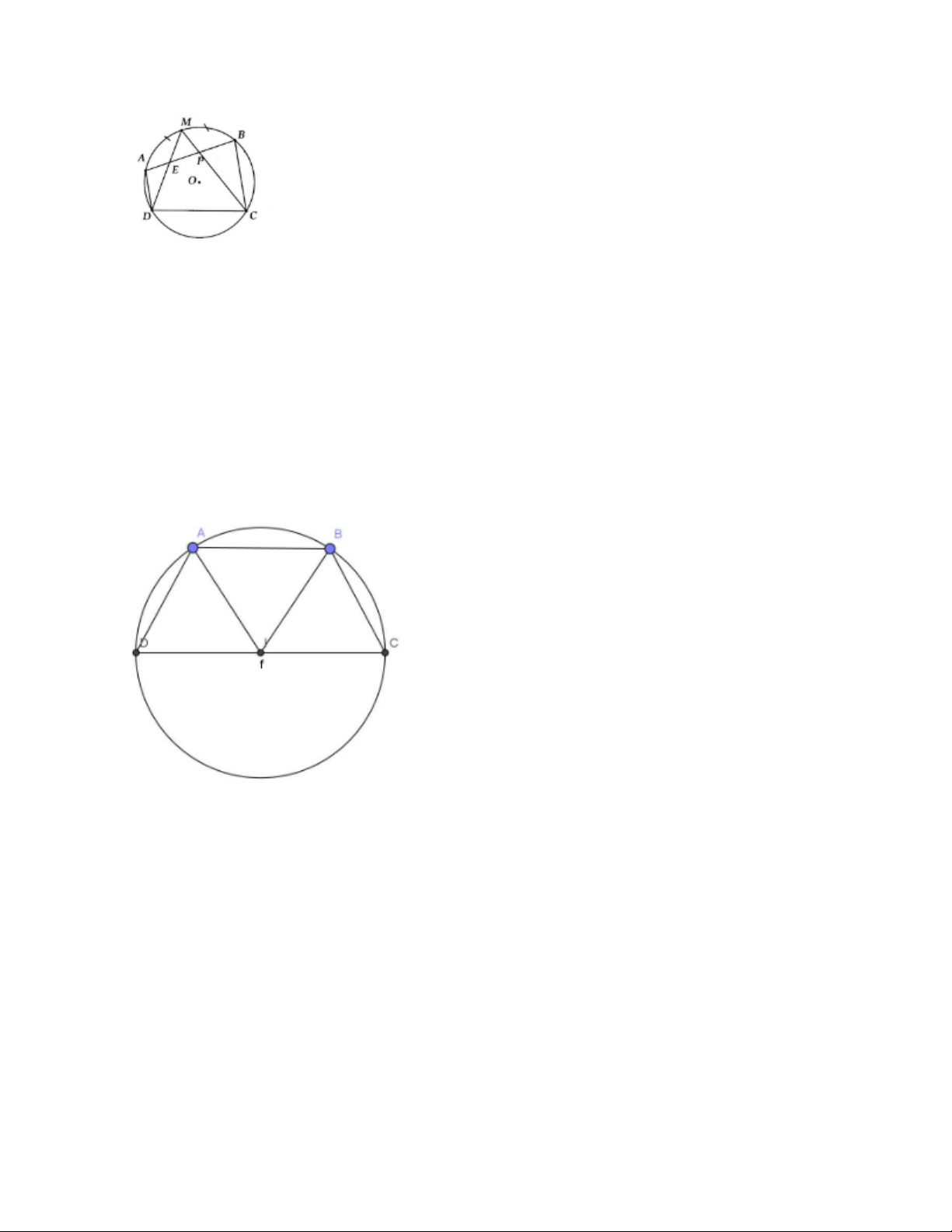
Bài 2. Cho tứ giác ABCD nội tiếp (O), M là điểm chính giữa của cung AB. Nối M với D, M với C cắt AB
lần lượt ở E và P. Chứng minh PEDC là tứ giác nội tiếp. Đáp án
Ta có: góc AED = 1/2 (sđ cung AD + sđ cung MB)
= 1/2 sđ cung DM = góc MCD
=> góc DEP + góc PCD = 180°
=> tứ giác PECD nội tiếp
Bài 3. Cho hình thang ABCD (AB//CD, AB < CD) có góc C = góc D = 60°, CD = 2AD. Chứng minh: bốn
điểm A, B, C, D cùng thuộc một đường tròn Đáp án
Gọi I là trung điểm của CD
Ta có: IC = AB và IC // AB => ICBA là hình bình hành => BC = AI (1)
Tương tự, AD = IB (2)
ABCD là hình thang có góc C = góc D = 60° nên ABCD là hình thang cân (3)
Từ (1) và (2) (3) ta có hai tam giác ICb; IAD đều hay IA = IB = IC = ID hay bốn điểm A, B, C, D cùng thuộc một đường tròn.
Bài 4. Cho tam giác ABC nhọn nội tiếp đường tròn (O). M là điểm thuộc đường tròn, vẽ MH vuông góc
với BC tại H, vẽ MI vuông góc với AC. Chứng minh MIHC là tứ giác nội tiếp. Đáp án
Ta có: góc MIC = góc CHM = 90°
=> tứ giác MIHC nội tiếp (hai đỉnh kề nhau cùng nhìn cạnh chứa hai đỉnh còn lại dưới một góc vuông)
Bài 5. Cho nửa đường tròn tâm O, đường kính AB = 2R và tia tiếp tuyến Ax cùng phía với nửa đường
tròn đối ới AB. Từ điểm M trên à kẻ tiếp tuyến thứ hai MC với nửa đường tròn (C là tiếp điểm). AC cắt
OM tại E; MB cắt nửa đường tròn (O) tại D (D#B)
a. Chứng minh: AMCO và AMDE là các tứ giác nội tiếp đường tròn
b. Chứng minh MBCD là tứ giác nội tiếp Đáp án
Vì MA, MC là tiếp tuyến nên góc MAO = góc MCO = 90° Tứ giác AMCO có
góc MAo + góc MCO = 180°
=> tứ giác AMCO là tứ giác nội tiếp đường tròn đường kính MO
Ta có: góc ABD = 90 (góc nội tiếp chắn nửa đường tròn) => góc ADM = 90 (1) Lại có: OA = OC = R
MA = MC (tính chất tiếp tuyến)
=> OM là đường trung trực của AC
=> góc AEM = 90 (2)
Từ (1) và (2) => góc ADM = góc AEM =90
Tứ giác AMDE có hai đỉnh A, E kề nhau cùng nhìn cạnh MA dưới một góc không đổi.
Vậy tứ giác AMDE nội tiếp đường tròn đường kính MA.
4.2. Dạng 2. Sử dụng tứ giác nội tiếp để chứng minh các góc bằng nhau, các đoạn thẳng bằng nhau, các
đường thẳng song song hoặc đồng quy, các tam giác đồng dạng...
Phương pháp giải: sử dụng tính chất của tứ giác nội tiếp
Bài 1. Cho đường tròn (O), đường kính AB. Gọi H là điểm nằm giữa O và B. Kẻ dây CD vuống góc với
AB tại H. Trên cung nhỏ AC lấy điểm E, kẻ CK vuông góc với AE tại K. Đường thẳng DE cắt CK tại F. Chứng minh:
a. tứ giác AKCH là tứ giác nội tiếp b. AD2 = AH . AB
c. Tam giác ACE là tam giác cân Đáp án
a. Có góc AKC + góc CHA = 180
=> tứ giác AKCH là tứ giác nội tiếp (DHNB)
b. Tam giác ADB vuông tại D, có đường cao DH => AD2 = AH . AB
c. Góc EAC = góc EDC = 1/2 sđ EC, góc EAC = góc KHC (tứ giác AKCH nội tiếp)
=> góc EDC = góc KHC => DF // HK (H là trung điểm DC nên K là trung điểm FC) => ĐPCM
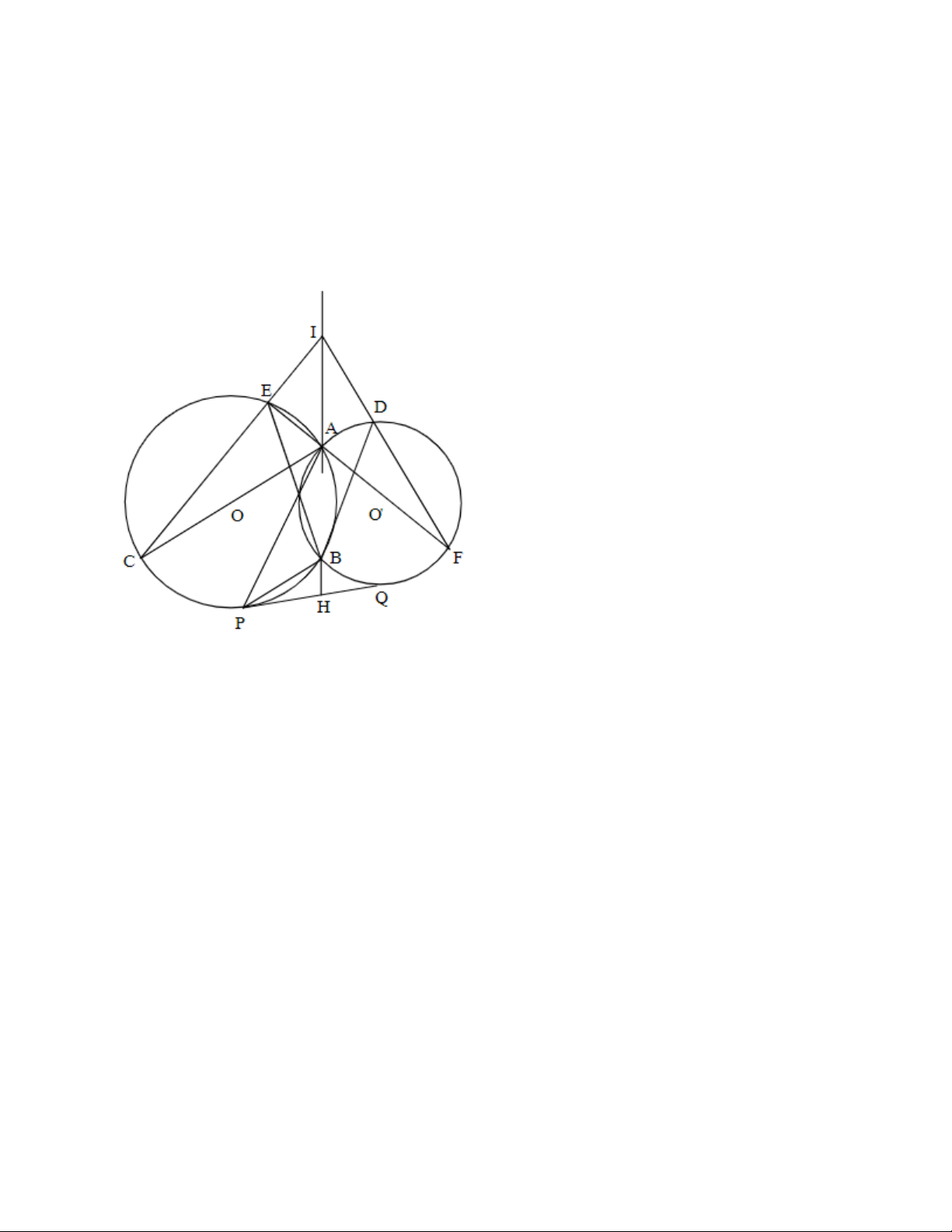
Bài 2. Cho hai đường tròn (O) và (O') cắt nhau tại hai điểm A và B phân biệt. Đường thẳng OA cắt (O),
(O') lần lượt tại điểm thứ hai C và D. Đường thẳng O'A cắt (O), (O') lần lượt tại điểm thứ hai E, F.
a. Chứng minh ba đường thẳng AB, CE và DF đồng quy tại một điểm I
b. Chứng minh tứ giác BEIF nội tiếp được trong một đường tròn Đáp án
a. Ta có: góc ABC = 90° (góc nội tiếp chắn nửa đường tròn)
góc ABF = 90° (gó nội tiếp chắn nửa đường tròn) nên B, C, F thẳng hàng.
AB, CE và DF la ba đường cao của tam giác ACF nên chúng đồng quy.
b. Do góc IEF = góc IBM = 90° => tứ giác BEIF nội tiếp đường tròn
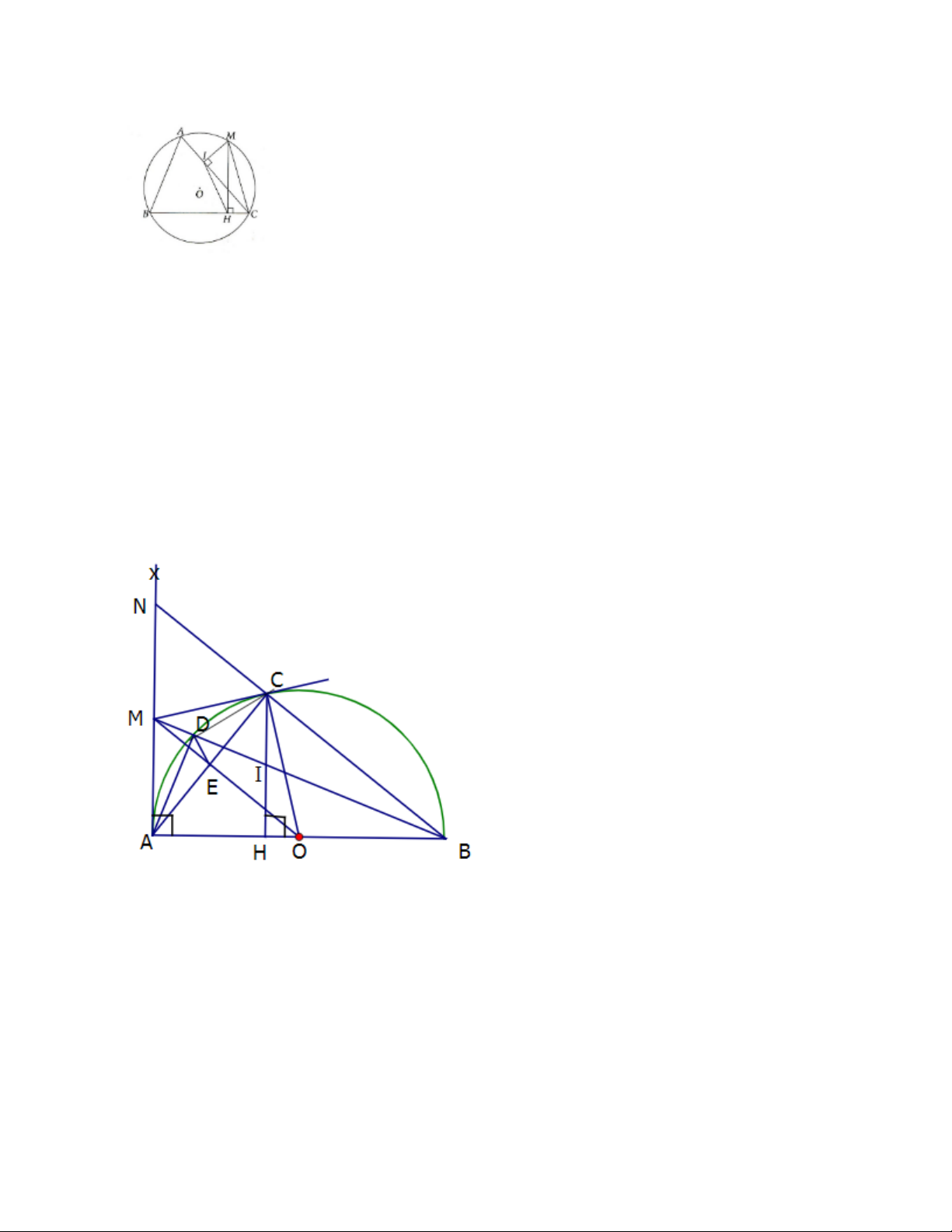
Bài 3. Cho nửa đường tròn tâm O, đường kính AB. Lấy điểm M thuộc đoạn thẳng OA, điểm N thuộc
nửa đường tròn (O). Từ A và B vẽ các tiếp tuyến Ax và By. Đường thẳng qua N và vuông góc với NM
cắt Ax, By thứ tự tại C và D.
a. Chứng minh: ACNM và BDNM là các tứ giác nội tiếp đường tròn
b. Chứng minh: Tam giác ANB đồng dạng với tam giác CMD. Từ đó suy ra IMKN là tứ giác nội tiếp. Đáp án
a. Ta có: tứ giác ACNM có:
góc MNC = 90° (tính chất tiếp tuyến)
=> góc MNC + góc MAC = 180° => tứ giác ACNM là tứ giác nội tiếp đường tròn đường kính MC.
Tương tự, tứ giác BDNM nội tiếp dường tròn đường kính MD
b. Tam giác ANB và tam giác CMD có:
góc ABN = góc CDM (do tứ giác BDNM nội tiếp)
góc BAN = góc DCM (do tứ giác ACNM nội tiếp)
=> tam giác ANB đồng dạng tam giác CMD (g.g)
c. Tam giác ANB đồng dạng tam giác CMD => góc CMD = góc ANB = 90° (do góc ANB là góc nội tiếp chắn
nửa đường tròn (O))
=> góc IMK = góc INK = 90° => góc INK + góc IMK = 180°
Vậy tứ giác IMKN là tứ giác nội tiếp đường tròn đường kính IK
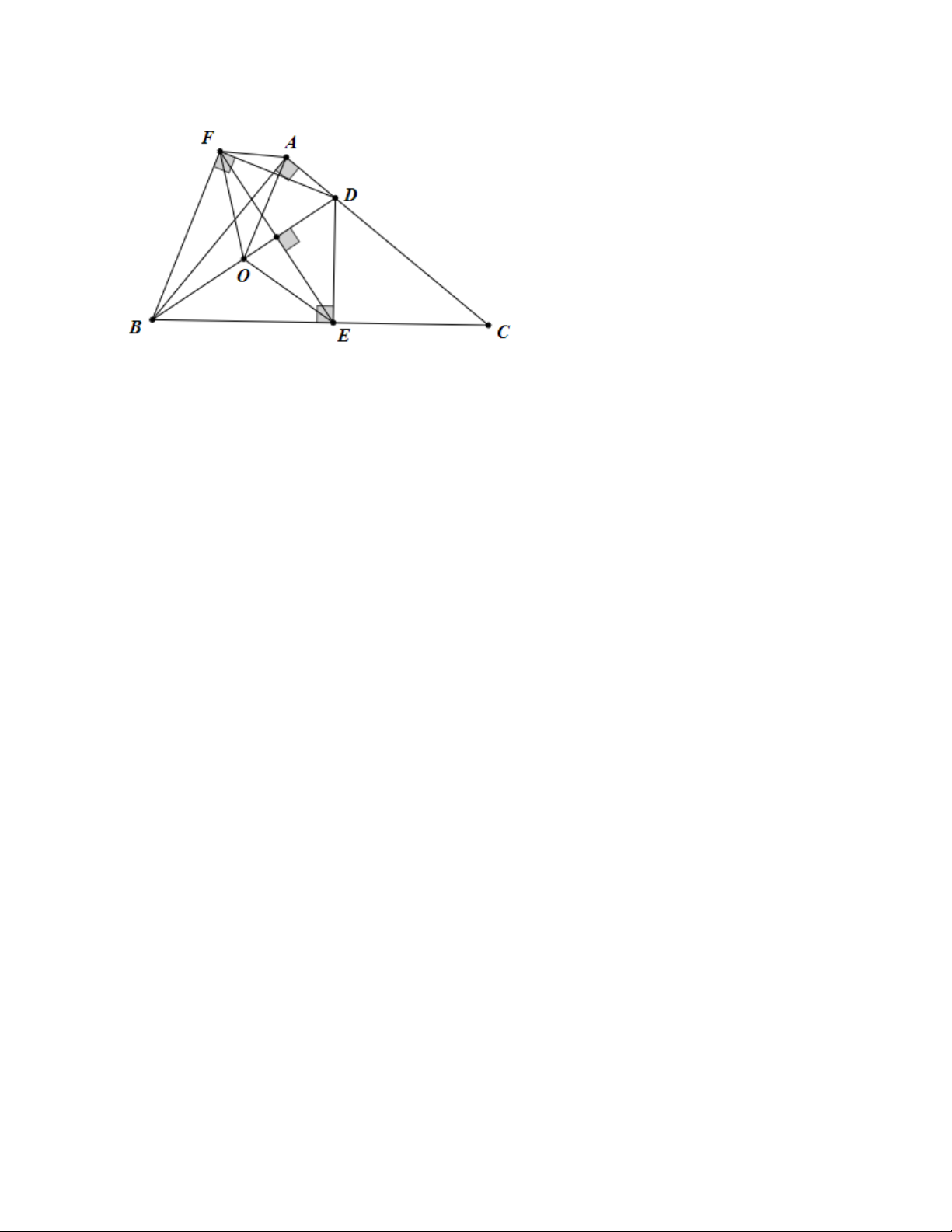
Bài 4. Cho tam giác ABC vuông tại A. Trên AC lấy điểm D. Hình chiếu của D lên BC là E, điểm đối xứng
của E qua BD là F. Chứng minh 5 điểm A, B, E, D, F cùng nằm trên một đường tròn. Xác định tâm O của đường tròn đó Đáp án
Do DE vuông góc với BC => góc DBE = 90°
Vì E và F đối xứng với nhau qua BD nên BD là đường tring trực của đoạn thẳng EF => BF=BE, DF = DE
Tam giác BFD = tam giác BED (ccc) => góc BFD = góc BED = 90°
Gọi O là trung điểm của BD
Xét tam giác vuông ABD vuông tại A có AO là trung tuyế nên AO = 1/2 BD = OB = OD (1)
Tam giác vuông BDE vuông tại E có OE là trung tuyến nên EO = 1/2 BD = OB = OD (2)
Tam giác vuông BFD vuông tại F có OF là tng tuyến nên FO = 1/2 BD = OB = OD (3)
Từ (1), (2) và (3) => OA = OB = OD = OE = OF
Vậy 5 điểm A, B, E, D, F cùng nằm trên một đường tròn tâm O với O là trung điểm của BC