XÁC SUẤT TRONG MỘT SỐ TRÒ CHƠI VÀ THÍ NGHIỆM ĐƠN GIẢN

XÁC SUẤT TRONG MỘT SỐ TRÒ CHƠI VÀ THÍ NGHIỆM ĐƠN GIẢN

Bài 1

Một hộp có 5 chiếc thẻ cùng loại, mỗi thẻ được ghi một trong các số 1, 2, 3, 4, 5; hai thẻ khác nhau thì ghi hai số khác nhau.

Rút ngẫu nhiên một chiếc thẻ trong hộp.

a) Nêu những kết quả có thể xảy ra đối với số xuất hiện trên thẻ được rút ra.

b) Số xuất hiện trên thẻ được rút ra có phải là phần tử của tập hợp {1; 2; 3; 4; 5} hay không?

c) Viết tập hợp các kết quả có thể xảy ra đối với số xuất hiện trên thẻ được rút ra.

d) Nêu hai điều cần chú ý trong mô hình xác suất của trò chơi trên.

Bài 2

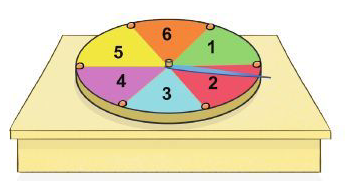
Lớp 6B tổ chức trò chơi “Vòng tròn lí thú”, trong đó chiếc đĩa hình tròn được chia thành sáu phần bằng nhau và được đánh số lần lượt từ I đến 6, chiếc kim được giữ cố định như trong hình bên.

Quay chiếc đĩa 1 lần

a) Nêu những kết quả có thể xảy ra đối với số ở hình quạt mà chiếc kim chỉ vào khi đĩa dừng lại.

b) Số ở hình quạt mà chiếc kim chỉ vào khi đĩa dừng lại có phải là phần tử của tập hợp {1; 2; 3; 4; 5; 6} hay không?

c) Viết tập hợp các kết quả có thể xảy ra đối với số ở hình quạt mà chiếc kim chỉ vào khi đĩa dừng lại.

d) Nêu hai điều cần chú ý trong mô hình xác suất của trò chơi trên

Bài 3

Trả lời các câu hỏi sau:

a) Nếu tung một đồng xu 22 lần liên tiếp; có 13 lần xuất hiện mặt N thì xác suất thực nghiệm xuất hiện mặt N bằng bao nhiêu?

b) Nếu tung một đồng xu 25 lần liên tiếp; có 11 lần xuất hiện mặt S thì xác suất thực nghiệm xuất hiện mặt S bằng bao nhiêu?

c) Nếu tung một đồng xu 30 lần liên tiếp; có 14 lần xuất hiện mặt N thì xác suất thực nghiệm xuất hiện mặt S bằng bao nhiêu?

Bài 4

Gieo một xúc xắc 10 lần liên tiếp, bạn Cường có kết quả như sau:

a) Hãy kiểm đếm số lần xuất hiện mặt 1 chấm và số lần xuất hiện mặt 6 chấm sau 10 lần gieo. Xác suất thực nghiệm xuất hiện

b) Tính xác suất thực nghiệm xuất hiện mặt 1 chấm.

c) Tính xác suất thực nghiệm xuất hiện mặt 6 chấm.

Bài 5. Gieo một con xúc sắc 4 mặt 50 lần và quan số ghi trên đỉnh của con xúc sắc, ta được kết quả như sau:

Hãy tính xác suất thực nghiệm để:

a) Gieo được mặt số 4

b) Gieo được mặt có số chẵn

BÀI TẬP VỀ NHÀ

Bài 1

Tung một đồng xu 20 lần liên tiếp. Hãy ghi kết quả thống kê theo mẫu sau:

Tính xác suất thực nghiệm:

a) Xuất hiện mặt N;

b) Xuất hiện mặt S;

Bài 2. Một hộp có 10 chiếc thẻ cùng loại, mỗi thẻ được ghi một trong các số 1, 2, 3, ..., 10; hai thẻ khác nhau thì ghi hai số khác nhau.

Rút ngẫu nhiên một chiếc thẻ từ trong hộp, ghi lại số của thẻ rút được và bỏ lại thẻ đó vào hộp. Sau 25 lần rút thẻ liên tiếp, hãy ghi kết quả thống kê theo mẫu sau:

Tính xác suất thực nghiệm:

a) Xuất hiện số 1;

b) Xuất hiện số 5;

c) Xuất hiện số 10.

Bài 3

Quan sát xúc xắc ở hình bên.

Mỗi xúc xắc có sáu mặt, số chấm ở mỗi mặt là một trong các số nguyên dương 1; 2; 3; 4; 5; 6.

Gieo xúc xắc một lần.

a) Nêu những kết quả có thể xảy ra đối với mặt xuất hiện của xúc xắc.

b) Mặt xuất hiện của xúc xắc có phải là phần tử của tập hợp {mặt I chấm; mặt 2 chấm; mặt 3 chấm; mặt 4 chấm; mặt 5 chấm; mặt 6 chấm} hay không?

c) Viết tập hợp các kết quả có thể xảy ra đối với mặt xuất hiện của xúc xắc.

d) Nêu hai điều cần chú ý trong mô hình xác suất của trò chơi trên.

Bài 4. Một hộp có 5 quả bóng, trong đó có 1 quả bóng xanh, 1 quả bóng đỏ, 1 quả bóng vàng, 1 quả bóng nâu và 1 quả bóng tím; các quả bóng có kích thước và khối lượng như nhau. Lấy ngẫu nhiên một quả bóng trong hộp.

a) Nêu những kết quả có thể xảy ra đối với màu của quả bóng được lấy ra.

b) Màu của quả bóng được lấy ra có phải là phần tử của tập hợp {màu xanh; màu đỏ; màu vàng; màu nâu; màu tím} hay không?

c) Viết tập hợp các kết quả có thể xảy ra đối với màu của quả bóng được lấy ra.

d) Nêu hai điều cần chú ý trong mô hình xác suất của trò chơi trên.

Bài 5

a) Nếu gieo một xúc xắc 11 lần liên tiếp, có 5 lần xuất hiện mặt 2 chấm thì xác suất thực nghiệm xuất hiện mặt 2 chấm bằng bao nhiêu?

b) Nếu gieo một xúc xắc 14 lần liên tiếp, có 3 lần xuất hiện mặt 6 chấm thì xác suất thực nghiệm xuất hiện mặt 6 chấm bằng bao nhiêu?

Bài 6. Trong hộp có một số bút xanh và một số bút đỏ. Lấy ngẫu nhiên 1 bút từ hộp, xem màu rồi trả lại. Lặp lại hoạt động trên 50 lần, ta được kết quả như sau:

a) Tính xác suất thực nghiệm của sự kiện lấy được bút xanh

b) Em hãy dự đoán xem trong hộp loại bút nào có nhiều hơn.

Bài 7. Tổng hợp kết quả xét nghiệm bệnh viêm gan ở một phòng khám trong một năm, ta được bảng sau:

Hãy tính xác suất thực hiện của sự kiện một ca xét nghiệm có kết quả dương tính

a) theo từng quý trong năm

b) sau lần lượt từng quý tính từ đầu năm