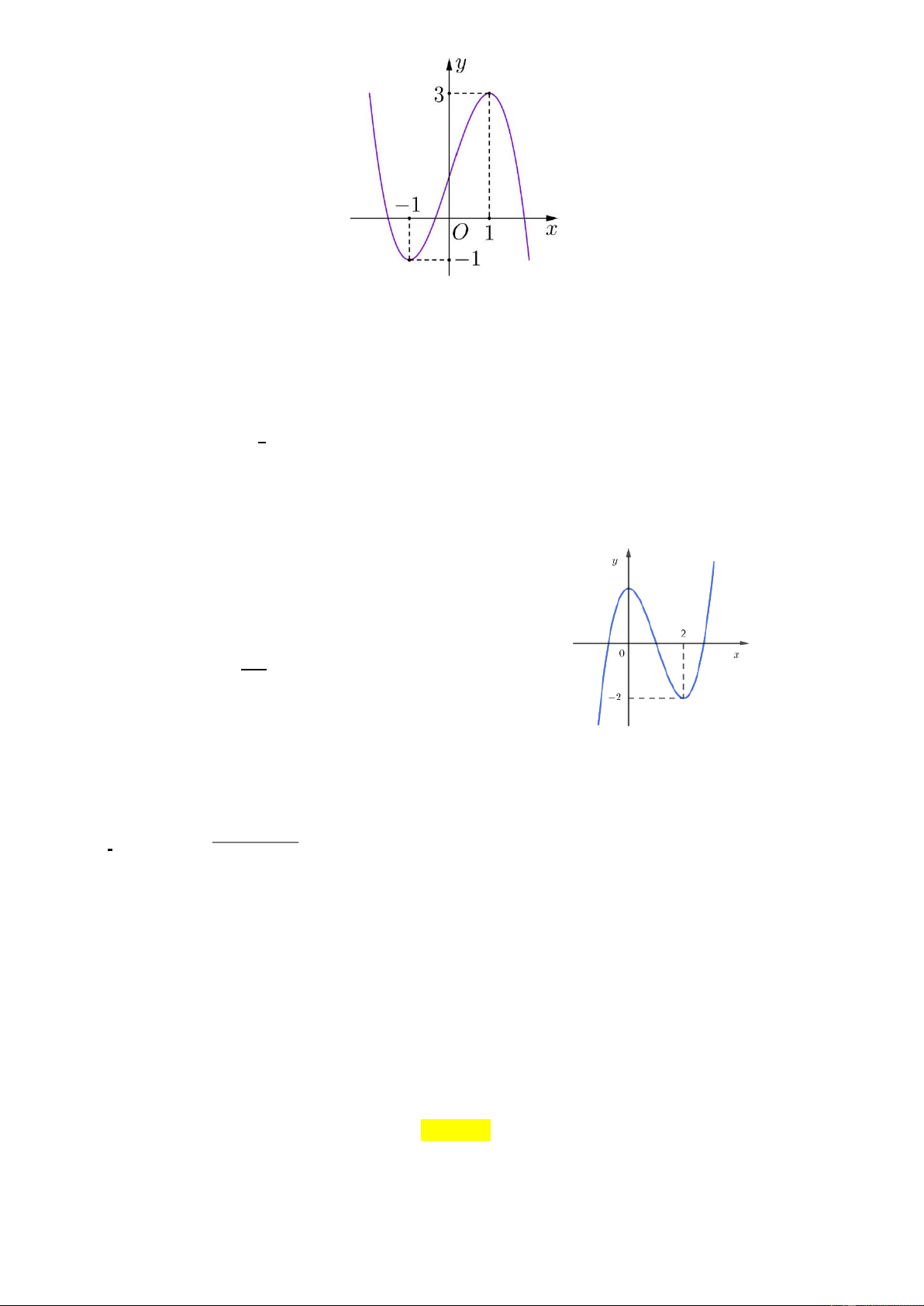


Preview text:
ĐỀ 1
ĐỀ ÔN TẬP GIỮA HỌC KỲ I NĂM HỌC 2025-2026
MÔN: TOÁN 12-CHÂN TRỜI SÁNG TẠO
Phần I. Câu trắc nghiệm nhiều phương án lực chọn. Học sinh trả lới từ câu 1 đến câu 12.Mỗi câu hỏi thí
sinh chỉ chọn một phương án.
Câu 1: Hàm số nào dưới đây đồng biến trên ? x +1 A. y = . B. 3 y = x + 2 . x x − 2 C. 3 2
y = x − x − . x D. 3 2
y = x + 3x + 2.
Câu 2: Cho hàm số y = f (x) có đồ thị như hình bên
Hàm số y = f (x) đạ t cực đại tại điểm: A. x = 3 B. x = 0 C. x = 2 D. x = 1
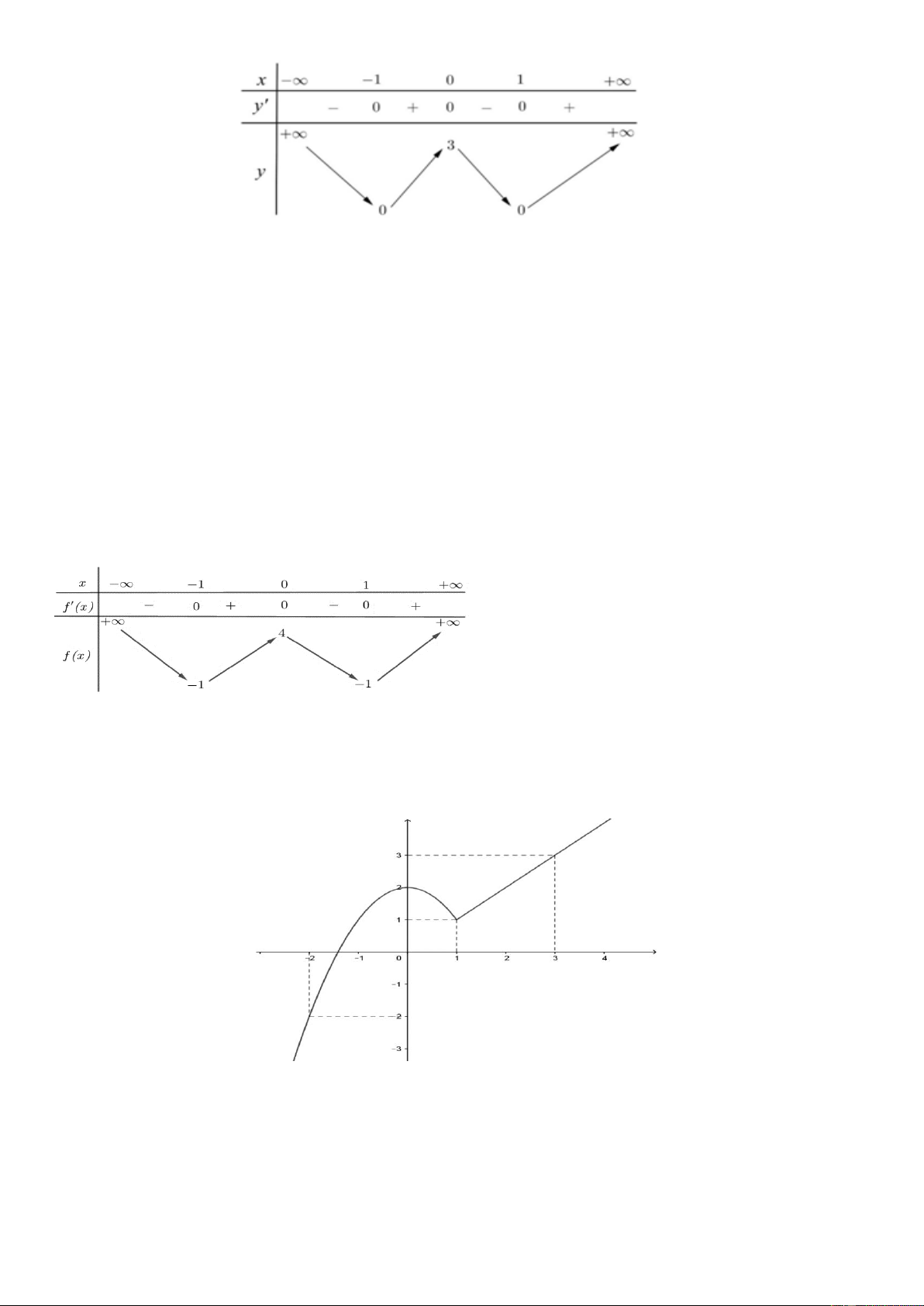
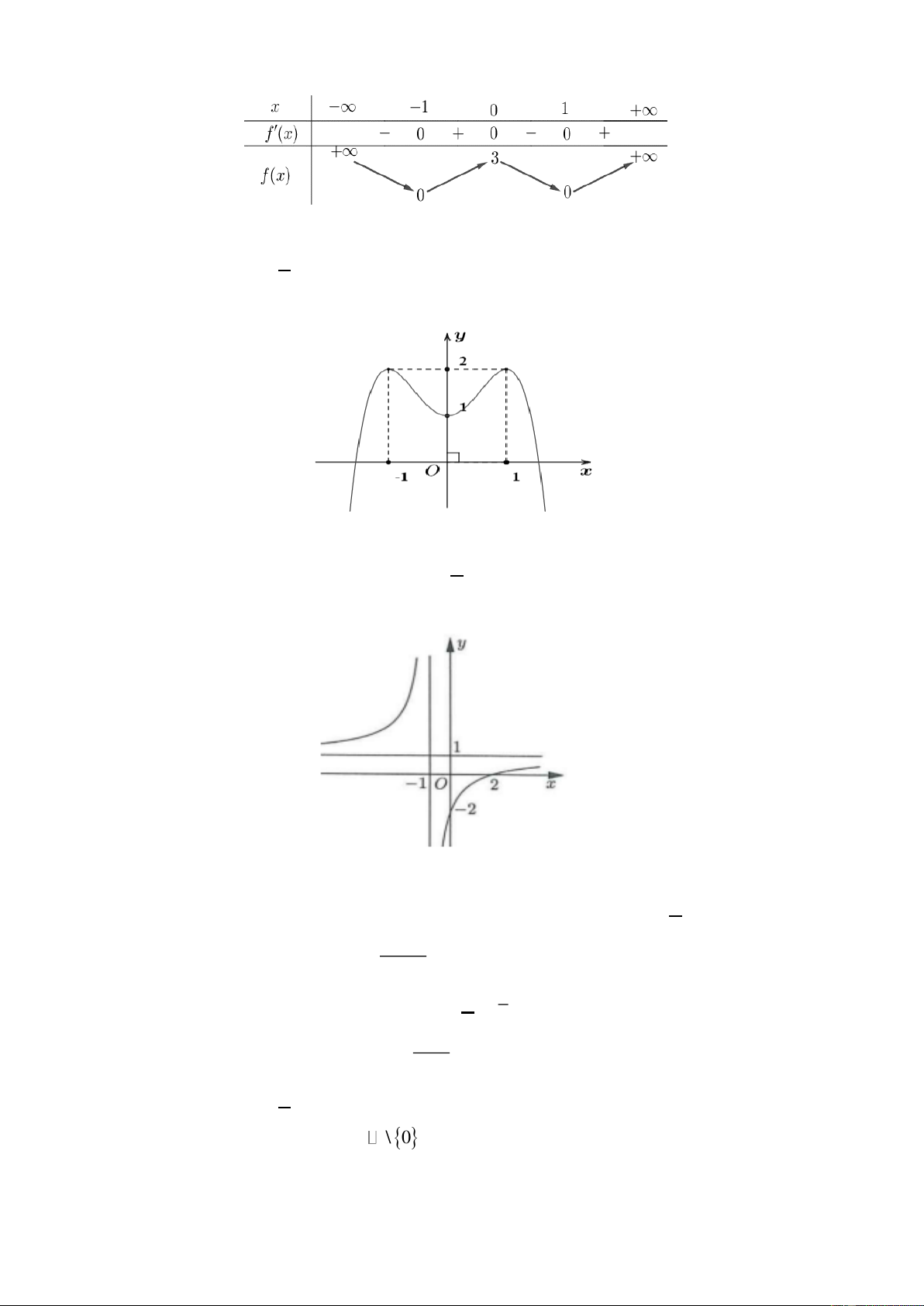
Câu 3: Cho hàm số f ( x) có bảng biến thiên như sau:
Hàm số đã cho đồng biến trên khoảng nào dưới đây? A. ( 1 − ;0) . B. (− ; − ) 1 . C. ( 1 − ; ) 1 . D. (0 ) ;1 .
Câu 4: Gọi m và M lần lượt là giá trị nhỏ nhất và giá trị lớn nhất của hàm số 3 2
y = x − x − x + 2 trên đoạn
0 ; 2. Tính m + M ? A. 4. B. 3. C. 6. D. 5.
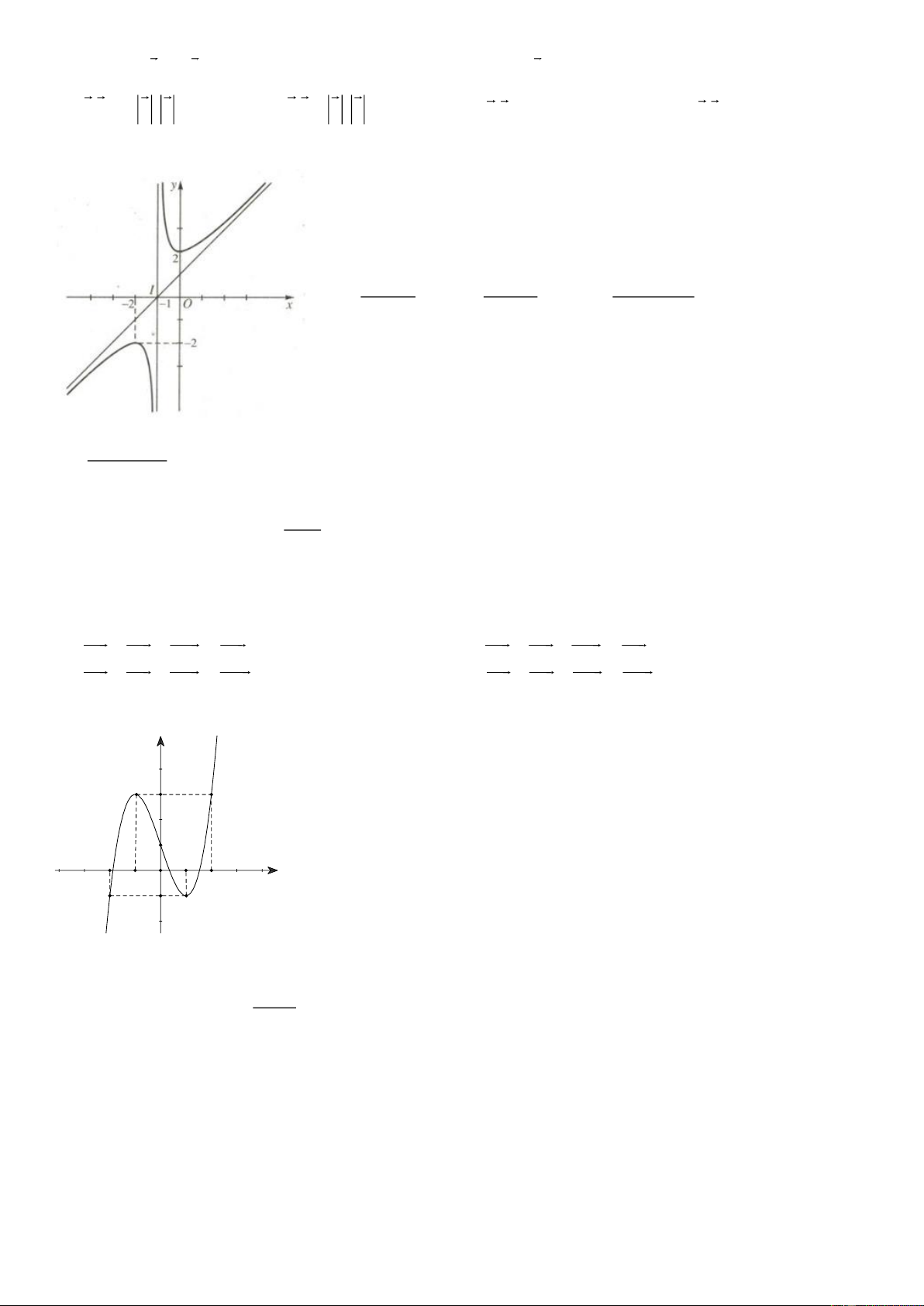
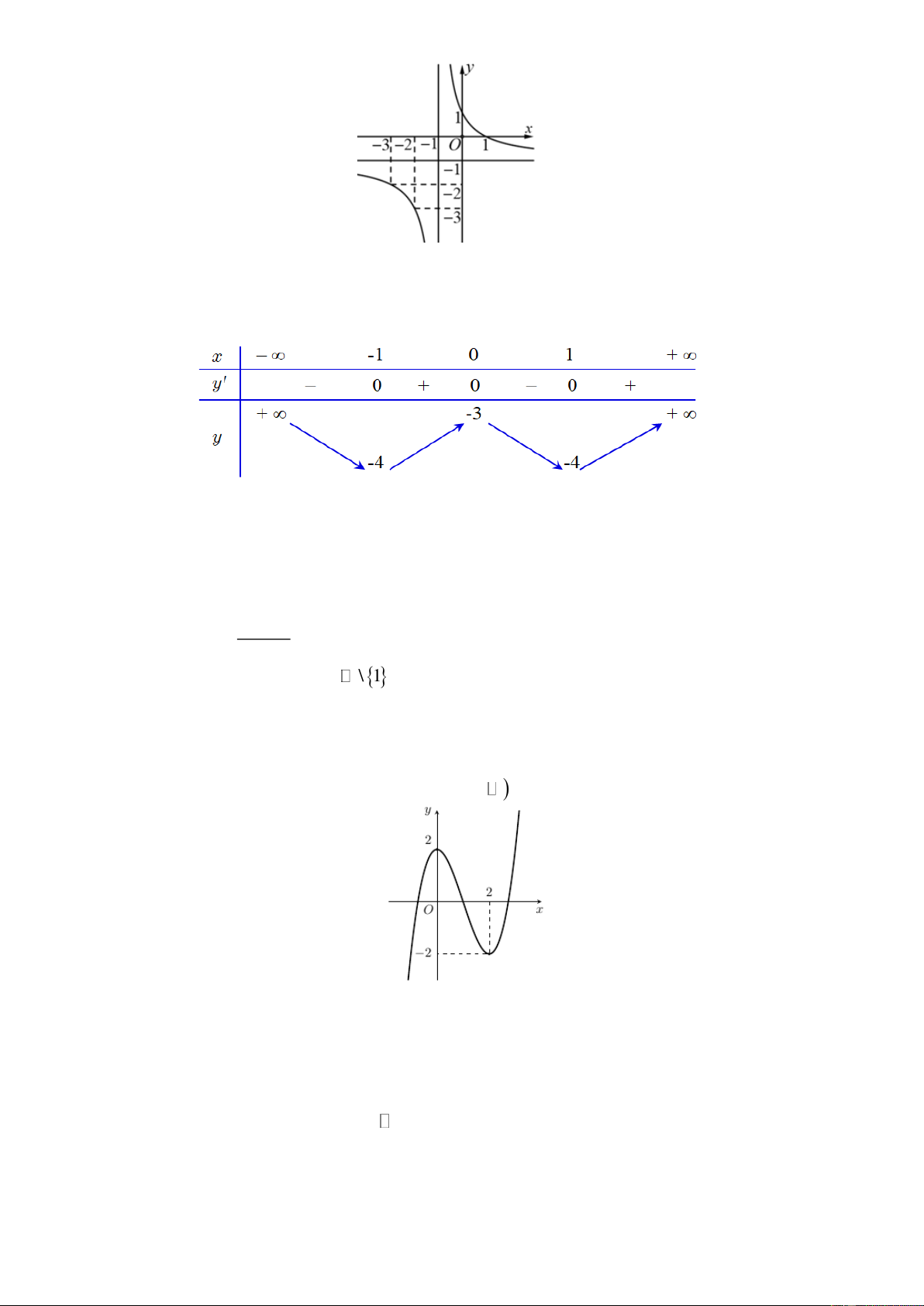
Câu 5: Hàm số nào dưới đây có đồ thị là đường cong trong hình bên? x +1 −x −1 −x +1 x −1 A. y = . B. y = . C. y = . D. y = . x −1 x −1 x +1 x +1 Trang 1
Câu 6: Cho hàm số f ( x) xác định trên
và có bảng xét dấu của hàm số f '( x) như sau
Số điểm cực trị của hàm số đã cho là A. 2. B. 3. C. 1. D. 4.
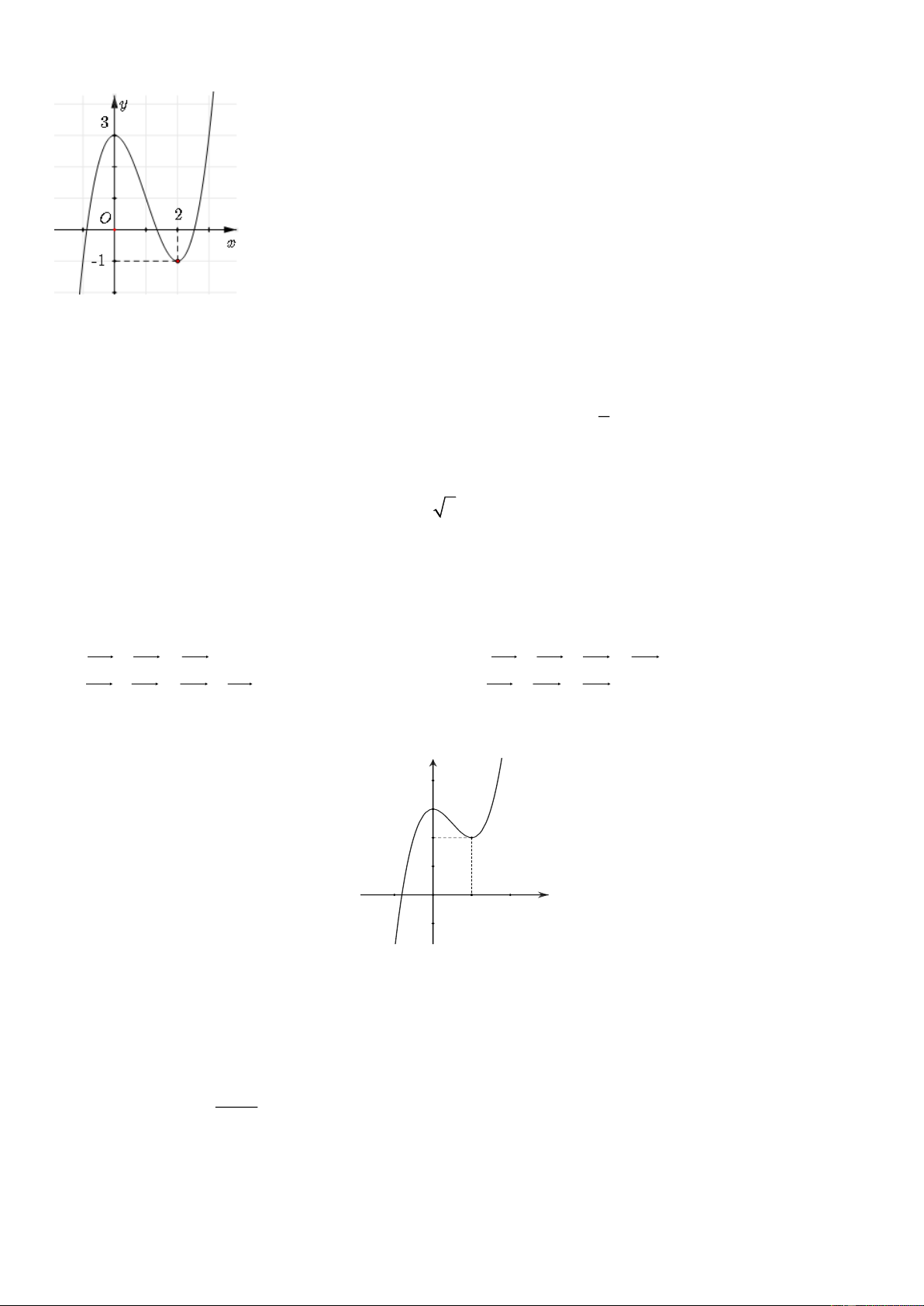
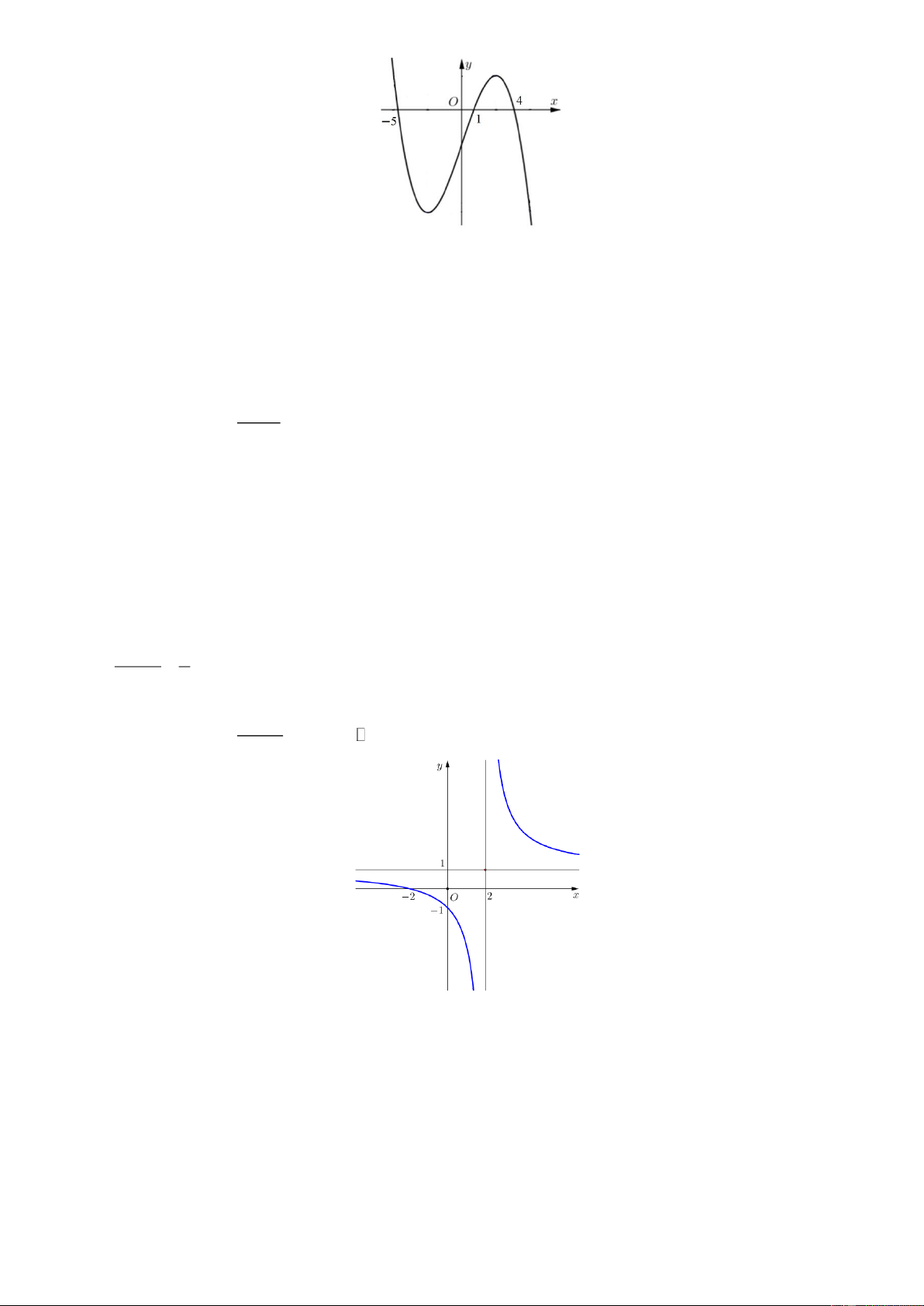
Câu 7: Cho hàm số bậc ba y = f ( x) có đồ thị là đường cong trong hình bên dưới.
Điểm cực tiểu của đồ thị hàm số đã cho có tọa độ là A. (1; − ) 1 . B. (1;3) . C. ( 1 − ;− ) 1 . D. (3; ) 1 . 2x +1
Câu 8: Tiệm cận đứng của đồ thị hàm số y = là: 2x −1 1 1 A. x = . B. x = 1 . C. y = . D. y = 1. 2 2 𝑥2−𝑥+2
Câu 9: Hàm số 𝑦 = có tiệm cận xiên 𝑥+1 A. 𝑦 = 𝑥 − 3 B. 𝑦 = 2𝑥 − 2 C. 𝑦 = 𝑥 − 2 D. 𝑦 = 2𝑥 + 2
Câu 10: Cho hàm số y = f (x) liên tục trên
và có đạo hàm f ( x) = (2x + )
1 (5x − 5) . Hàm số đã cho
nghịch biến trên khoảng nào dưới đây? 1 1 A. − ; + . B. − ;1 . C. (− ; 2 − ) . D. ( ) ;1 − . 2 2 Câu 11: Cho hàm số 3
y = x − 3x + 2 . Mệnh đề nào dưới đây đúng?
A. Hàm số đồng biến trên khoảng ( 1 − ; ) 1 .
B. Hàm số nghịch biến trên khoảng (1; + ) .
C. Hàm số nghịch biến trên khoảng (−;− ) 1 .
D. Hàm số nghịch biến trên khoảng ( 1 − ; ) 1 .
Câu 12: Đồ thị của hàm số nào dưới đây có dạng như đường cong trong hình dưới? Trang 2 A. 3
y = −x + 3x +1. B. 3
y = x − 3x +1. C. 3 2
y = x − 2x + 6 . D. 2
y = −x + 2x + 5 .
-----------------------------------------------
Phần II. Câu trắc nghiệm đúng sai. Học sinh trả lời từ câu 1 đến câu 3.Trong mỗi ý a), b), c), d) ở mỗi
câu, học sinh chọn đúng hoặc sai. 1
Câu 1: Cho hàm số 𝑦 = − 𝑥3 + 𝑥2 − 𝑥 + 1 3
a). Hàm số nghịch biến trên R.
b). Hàm số đồng biến trên R.
c). Hàm số có 2 điểm cực trị.
d). Hàm số không có cực trị.
Câu 2: Cho đồ thị hàm số y=f(x) có đồ thị như hình bên
a) Hàm số đạt cực đại tại x=0
b) Hàm số có hai điểm cực trị
c) Hàm số đạt cực tiểu tại x=−2
d) Hàm số có giá trị cực tiểu bằng 2 𝑥+3
Câu 3: Cho hàm số 𝑦 = 𝑥+2
a) Hàm số không có cực trị
b) Hàm số có tiệm cận đứng là y = 1
c) Hàm số nghịch biến trên R
d) Hàm số có tiệm cận ngang y = 1
Phần III. Câu trắc nghiệm trả lời ngắn. Học sinh trả lời từ câu 1 đến câu 4. 2 3x − 2x +1
Câu 1: Hàm số y =
có bao nhiêu đường tiệm cận ? 2 x − 3x + 2 3
Câu 2: Hàm số : y = x − 3x + 2 nghịch biến trên khoảng ( ; a b) = + . Tính T 2a 4b .
Câu 3: Gọi M và n lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của hàm số 3 2
y = x − 3x − 9x + 35 trên đoạn 4 − ;4 Tính 2M +3n . .
Câu 4: Xí nghiệp A sản xuất độc quyền một loại sản phẩm. Biết rằng hàm tổng chi phí sản xuất là 3 2
TC = x − 77x +1000x + 40000 và hàm doanh thu là 2 TR = 2
− x +1312x , với x là số sản phẩm.
Lợi nhuận của xí nghiệp A được xác định bằng hàm số f ( x) = TR −TC , cực đại lợi nhuận của
xí nghiệp A khi đó đạt bao nhiêu sản phẩm? ---Hết---- ĐÁP ÁN
Phần I. Câu trắc nghiệm nhiều phương án lực chọn. (Mỗi câu học sinh được 0,25 điểm. Tùy từng môn
điểm cho mỗi câu khác nhau) Trang 3 Câu 1. B Câu 2. C Câu 3. A Câu 4. D Câu 5. B Câu 6. D Câu 7. C Câu 8. A Câu 9. C Câu 10. B Câu 11. D Câu 12. A
Phần II. Câu trắc nghiệm đúng sai.
Điểm tối da của một câu hỏi là 1 điểm.
- Học sinh chỉ lựa chọn chính xác 01 ý trong 1 câu hỏi được 0,1 điểm.
- Học sinh chỉ lựa chọn chính xác 02 ý trong 1 câu hỏi được 0,25 điểm.
- Học sinh chỉ lựa chọn chính xác 03 ý trong 1 câu hỏi được 0,5 điểm.
- Học sinh chỉ lựa chọn chính xác 04 ý trong 1 câu hỏi được 1 điểm. Câu Lệnh hỏi a) Đ b) S 1 c) S d) Đ 2 a) Đ b) Đ c) S d) S 3 a) Đ b) S c) S d) Đ
Phần III. Câu trắc nghiệm trả lời ngắn. Mỗi câu trả lời đúng học sinh được 1 điểm (tuỳ từng môn). Câu 1 3 2 2 3 -43 4 52 ---Hết---- ĐỀ 2
ĐỀ ÔN TẬP GIỮA HỌC KỲ I NĂM HỌC 2025-2026
MÔN: TOÁN 12-CHÂN TRỜI SÁNG TẠO
PHÀN I. Câu trắc nghiệm nhiều phương án lựa chọn. Thí sinh trả lời từ câu 1 đến câu 12. Mỗi câu
hỏi thí sinh chỉ chọn một phương án. Trang 4
Câu 1. Cho a và b là hai vectơ cùng hướng và đều khác vectơ 0 . Mệnh đề nào sau đây đúng? A. .
a b = − a . b . B. .
a b = a . b . C. . a b = 0 . D. . a b = 1 − .
Câu 2. Đường cong trong hình là đồ thị của hàm số nào dưới đây? 2 x − 2x 2 x + 3x 2 x + 2x + 2 A. y = . B. y = . C. y = D. x +1 x − 2 x +1 2 x − 2x − 3 y = . x − 2 x − 2
Câu 3. Đồ thị của hàm số y =
có đường tiệm cận đứng là: A. x = 1.
− B. y = −1. C. y = 1. D. x =1. x +1
Câu 4. Cho hình hộp ABC . D A B C D
với tâm O . Hãy chỉ ra khẳng định đúng trong các khẳng định sau đây:
A. AB + BC + CC = AC .
B. AB + BC + CC = BC .
C. AB + BC + CC = AC ' .
D. AB + BC + CC = BC ' .
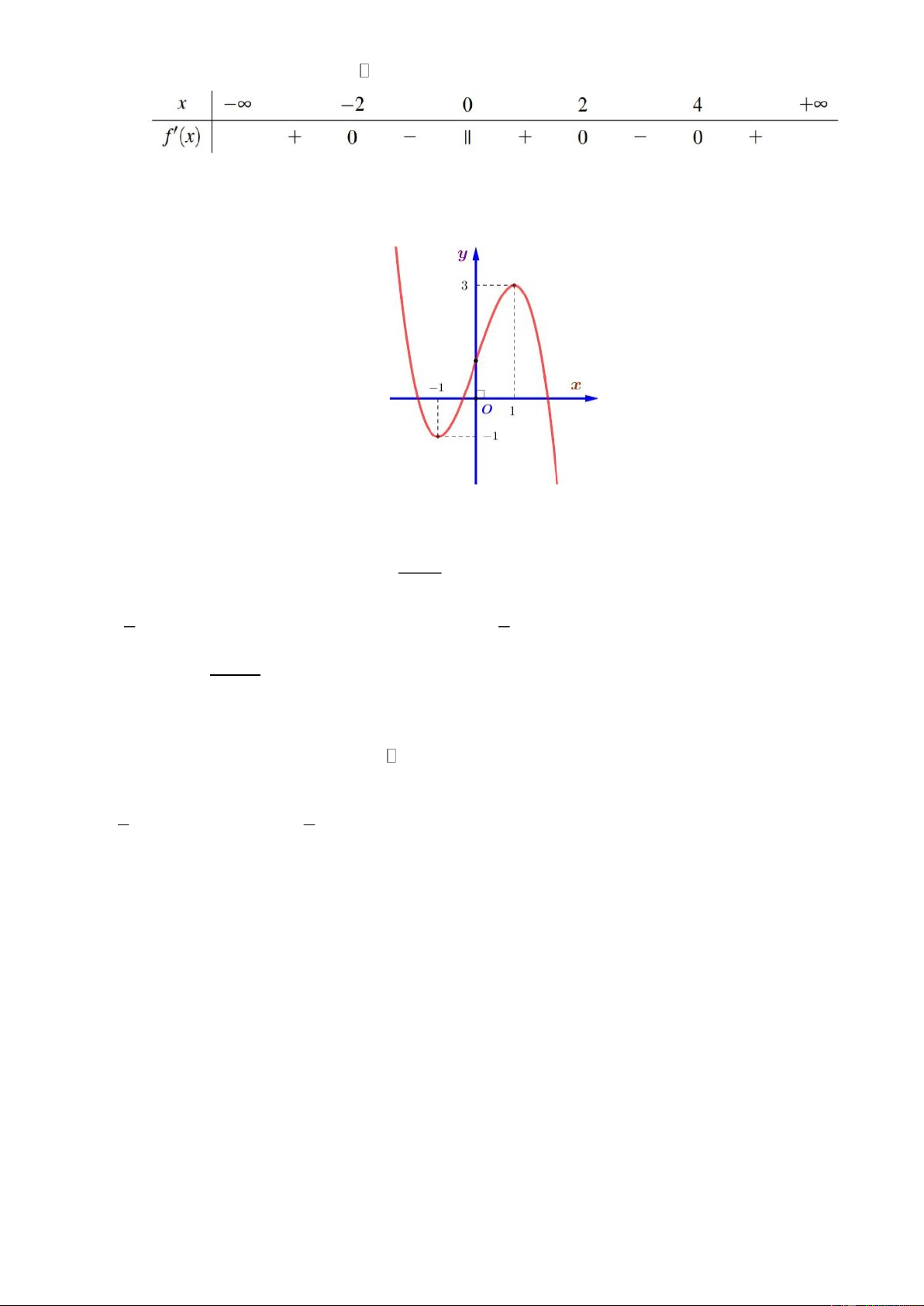
Câu 5. Đường cong cho trong hình bên là đồ thị của hàm số nào trong các hàm số dưới đậy? y 3 1 x 1 -2 -1 O 2 -1 A. 3
y = −x + 3x +1. B. 3
y = −x + 2x −1 . C. 3
y = x − 3x +1. D. 3
y = 2x − 6x +1 . 1+ 2x
Câu 6. Đồ thị hàm số y =
có đường tiệm cận ngang là:A. y = 1. B. x =1. C. x = 2 .D. y = 2 x −1
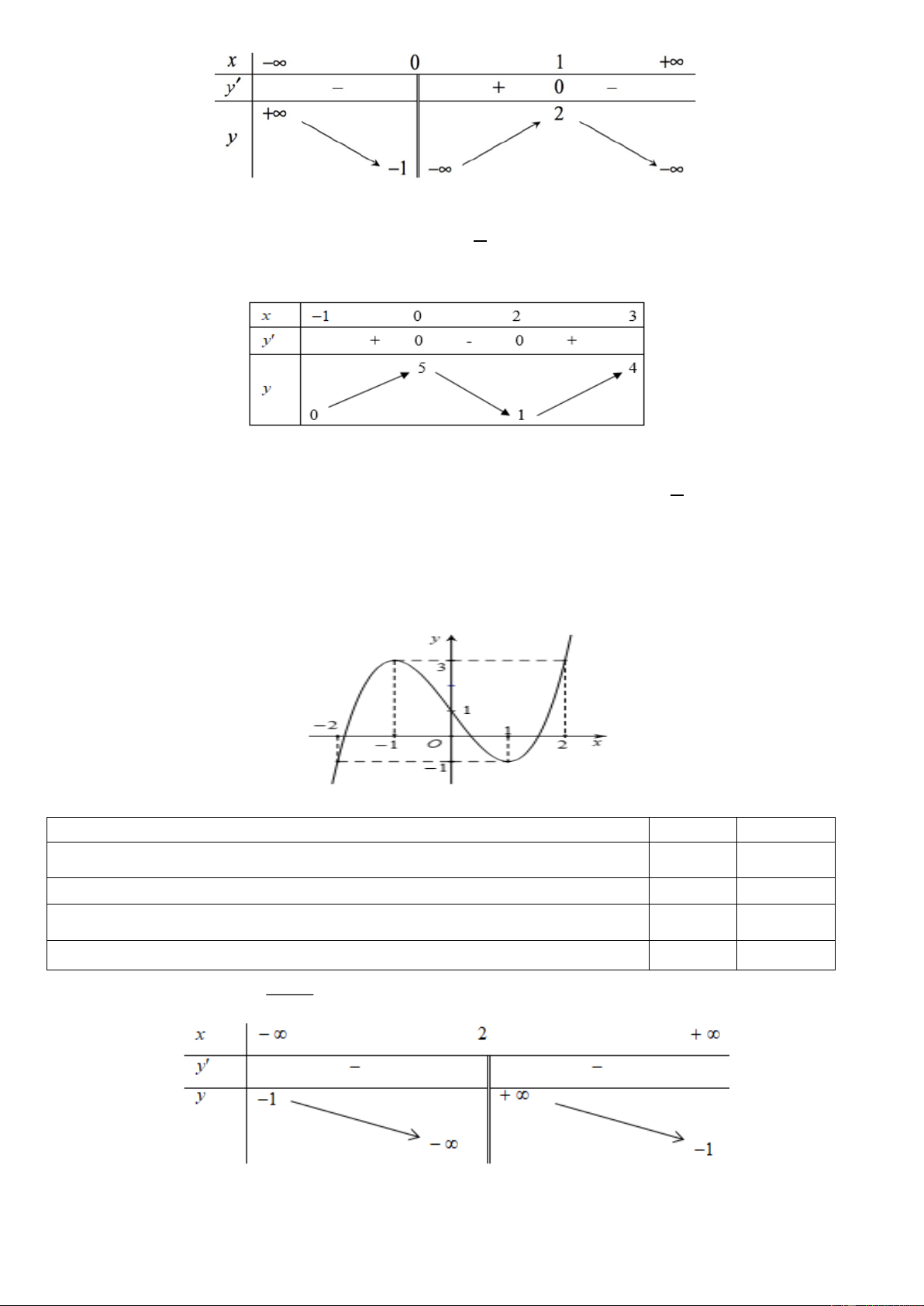
Câu 7. Cho hàm số y = f ( x) có bảng biến thiên như sau Trang 5
Cho biết giá trị nhỏ nhất của hàm số trên đoạn 1 − ; 1 là bao nhiêu?
A. min f ( x) = 1 min f ( x) = 0 min f ( x) = 1 − min f ( x) = 3 − B. C. D. 1;1 −1; 1 − 1;1 −1; 1
Câu 8. Độ giảm huyết áp của một bệnh nhân được cho bởi công thức G (x) 2
= 0,025x (30 − x) . Trong đó
x là liều lượng thuốc được tiêm cho bệnh nhân (đơn vị miligam). Tính liều lượng thuốc cần tiêm cho bệnh
nhân để huyết áp giảm nhiều nhất.
A. 15 mg. B. 30 mg. C. 20 mg. D. 25 mg. Câu 9. Hàm số 3 2
y = −x + 3x đồng biến trên khoảng nào dưới đây? A. (0;2) B. ( ;0 − ) . C. (0;4) . D. (2;+) .
Câu 10. Cho hàm số f ( x) có bảng biến thiên như sau:
Hàm số đã cho đồng biến trên khoảng nào dưới đây? A. (−1; ) 1 . B. (− ; − ) 1 . C. (0 ) ;1 . D. (−1; 0) .
Câu 11. Cho hàm số y = f ( x) có đồ thị như hình dưới đây:
Tìm giá trị lớn nhất và nhỏ nhất của hàm số f ( x) trên đoạn 2 − , 3 ? min f ( x) max f ( x) min f ( x) max f ( x) A. = 1 = 3 = −2 = 4 và . và . − B. 2, 3 2 − , 3 −2, 3 −2, 3 min f ( x) max f ( x) min f ( x) max f ( x) C. = −2 = 3 = −2 = 2 và . và . − D. 2, 3 2 − , 3 −2, 3 −2, 3 Trang 6 Câu 12. Cho hàm số 3 2
y = ax + bx + cx + d có đồ thị là đường cong trong hình bên dưới.
Điểm cực đại của hàm số đã cho là A. x = 1
− . B. x = 2 .
C. x = 0 . D. x = 3.
PHẦN II. Câu trắc nghiệm đúng sai. Thí sinh trả lời từ câu 13 đến câu 16. Trong mỗi ý a), b), c), d) ở
mỗi câu, thí sinh chọn đúng hoặc sai. 1
Câu 13. Cho chuyển động thẳng xác định bởi phương trình S (t ) 4 2
= − t + 3t − 2t − 4 , trong đó t tính 4
bằng giây (s) và S tính bằng mét (m) .
(a) Vận tốc lớn nhất của chuyển động bằng 2 − + 4 2 (m/s) .
(b) Vận tốc của chuyển động đạt giá trị lớn nhất khi t = 2.
(c) Gia tốc của chuyển động được xác định bởi a (t ) 2 = 3 − t + 6 .
(d) Vận tốc của chuyển động được xác định bởi v (t ) 3 = t − + 6t − 2 .
Câu 14. Cho tứ diện ABCD . Khẳng định dưới đây đúng hay sai?
(a) AB + BC = AC .
(b) AB + BC + CD = AD .
(c) AB + CD = AD + CB
(d) AB + AD = AC .
Câu 15. Cho hàm số y = f ( x) có đồ thị như hình vẽ bên. y 3 2 1 -1 O 1 x -1
(a) Hàm số đồng biến trên khoảng ( ;3 − ) và (1;+)
(b) Hàm số đồng biến trên khoảng ( ; − 0) và (1;+).
(c) Hàm số nghịch biến trên khoảng (0 ) ;1 .
(d) Hàm số đạt cực trị tại các điểm x = 0 và x = 1. 1
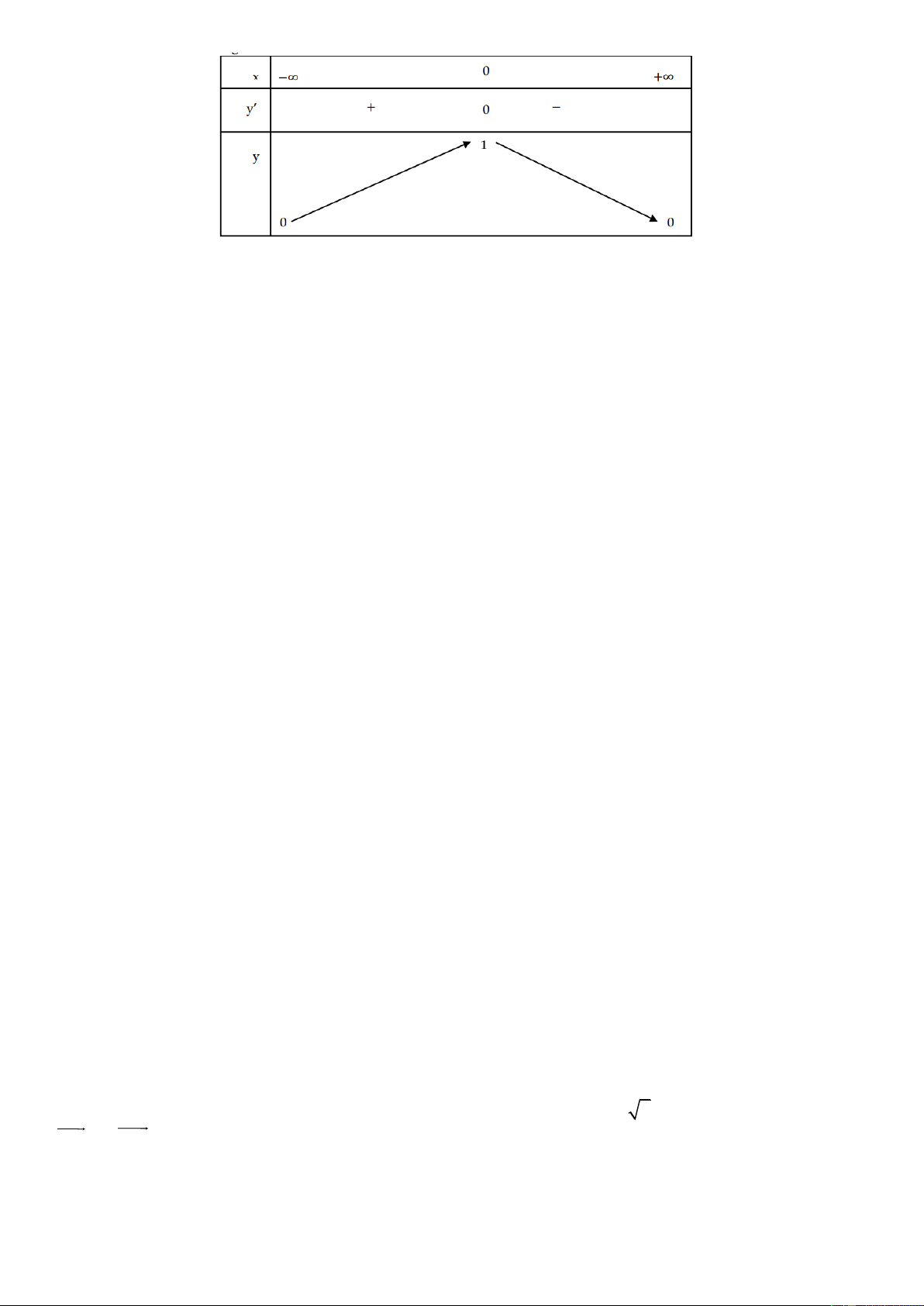
Câu 16. Hàm số y =
có bảng biến thiên như hình vẽ. 2 x +1 Trang 7
Xét trên tập xác định của hàm số.
(a) Hàm số có một điểm cực trị.
(b) Hàm số có giá trị lớn nhất bằng 1 và giá trị nhỏ nhất bằng 0.
(c) Hàm số có giá trị lớn nhất bằng 0.
(d) Không tồn tại giá trị lớn nhất và giá trị nhỏ nhất của hàm số.
PHẦN III. . Câu trả lời ngắn. Thí sinh trả lời vào phiếu làm bài từ câu 17 đến câu 18.
Câu 17. Một bể chứa 5 000 lít nước tinh khiết. Người ta bơm vào bể đó nước muối có nồng độ 30 gam
muối cho mỗi lít nước với tốc độ 25 lít/phút. Gọi f (t) là hàm số biểu diễn nồng độ muối trong bể sau t
phút (tính bằng tỉ số của khối lượng muối trong bể và thể tích nước trong bể, đơn vị: gam/lít). Biết tiệm cận
ngang của hàm số f (t) là đường thẳng y = . m Tìm . m
Trả lời ……………
Câu 18. Một công ty sản xuất dụng cụ thể thao nhận được một đơn đặt hàng sản xuất 8000 quả bóng
tennis. Công ty này sở hữu một số máy móc, mỗi máy có thể sản xuất 30 quả bóng trong một giờ. Chi phí
thiết lập các máy này là 200 nghìn đồng cho mỗi máy. Khi được thiết lập, hoạt động sản xuất sẽ hoàn toàn
diễn ra tự động dưới sự giám sát. Số tiền phải trả cho người giám sát là 192 nghìn đồng một giờ. Số máy
móc công ty nên sử dụng là bao nhiêu để chi phí hoạt động là thấp nhất?
PHẦN IV. TỰ LUẬN Thí sinh trình bày tư luận vào phiếu làm bài từ câu 19 đến câu 22 .
Câu 19 . Cho hàm số x y = e ( 2
x − 3) , tìm giá trị lớn nhất của hàm số đã cho trên đoạn 5 − ;− 2
Câu 20. Một công ty bất động sản có 50 căn hộ cho thuê. Biết rằng nếu cho thuê mỗi căn hộ với giá
2.000.000 đồng một tháng thì mọi căn hộ đều có người thuê và cứ mỗi lần tăng giá cho thuê, mỗi căn hộ
thêm 50.000 đồng một tháng thì có thêm một căn hộ bị bỏ trống. Công ty đã tìm ra phương án cho thuê đạt
lợi nhuận lớn nhất. Hỏi thu nhập cao nhất công ty có thể đạt được trong một tháng là bao nhiêu?
Câu 21 .Để thiết kế một chiếc bể cá hình hộp chữ nhật có chiều cao là 60 cm, thể tích là 96 000 cm3, người
thợ dùng loại kính để sử dụng làm mặt bên có giá thành 70 000 đồng/m2 và loại kính để làm mặt đáy có giá
thành là 100 000 đồng/m2. Chi phí thấp nhất để hoàn thành bể cá là bao nhiêu nghìn đồng?
Câu 22. Cho hình lăng trụ tam giác đều ABC.AB C
có AB = a và AA = a 2 . Số đo góc giữa hai vectơ
AB và BC bằng bao nhiêu độ?
------ HẾT ------ Trang 8 ĐÁP ÁN
Phần đáp án câu trắc nghiệm:
Tổng câu trắc nghiệm: 18. 1 B 2 C 3 A 4 C 5 C 6 D 7 B 8 C 9 A 10 D 11 C 12 C 13 ĐSDĐ 14 Đ ĐĐS 15 S Đ Đ Đ 16 ĐSSS 17 30 18 16
PHẦN IV. TỰ LUẬN CÂU NỘI DUNG THANG ĐIỂM Câu 19 Cho hàm số x y = e ( 2
x − 3) , tìm giá trị lớn nhất của hàm số đã cho trên đoạn 5 − ;− 2 . Ta có x y = e ( 2 x + 2x − 3) . 0,25 Trên khoảng ( 5 − ; 2
− ) , y = 0 x = 3 − . y (− ) 22 6 1 5 = ; y 3 − = ; y 2 − = . 5 ( ) 3 ( ) 2 e e e 6 0,25 Do đó, max y = − − 3 5; 2 e Trang 9 Câu
. Một công ty bất động sản có 50 căn hộ cho thuê. Biết rằng nếu cho thuê mỗi 20.
căn hộ với giá 2.000.000 đồng một tháng thì mọi căn hộ đều có người thuê
và cứ mỗi lần tăng giá cho thuê, mỗi căn hộ thêm 50.000 đồng một tháng
thì có thêm một căn hộ bị bỏ trống. Công ty đã tìm ra phương án cho thuê
đạt lợi nhuận lớn nhất. Hỏi thu nhập cao nhất công ty có thể đạt được trong một tháng là bao nhiêu? Lời giải: Ở
tháng thu nhập của công ty cao nhất, gọi số căn hộ bị bỏ trống là x thì số
tiền thuê mỗi phòng là 2.000.000 + 50.000x , khi đó số tiền thu được là
f ( x) = (2.000.000 + 50.000x)(50 − x) 2 = 5
− 0.000x + 500.000x +100.000.000 .
Ta cần tìm x (0;50) để f ( x) lớn nhất. 0,25
Ta có f ( x) = 1
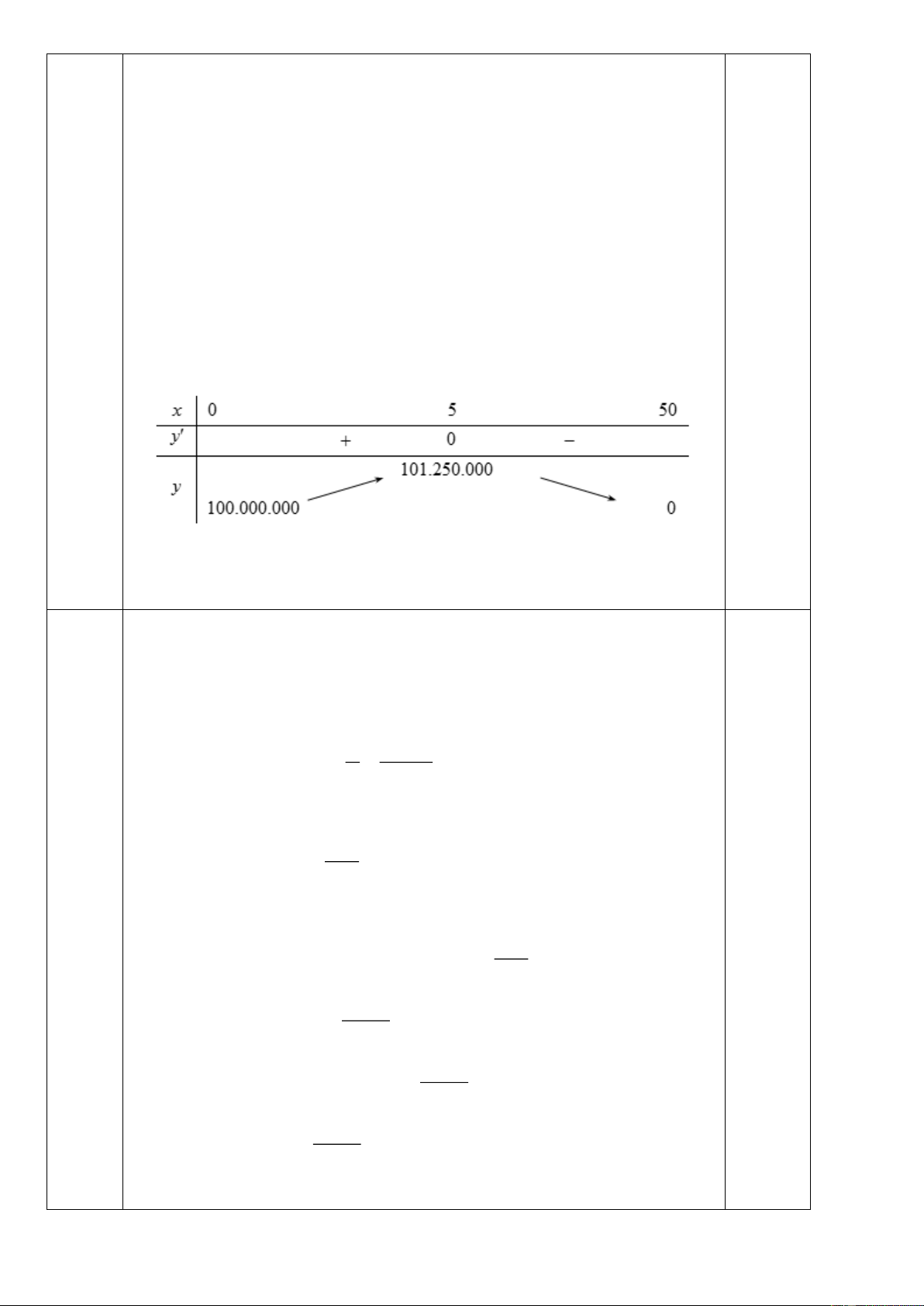
− 00.000x + 500.000 , f (x) = 0 x = 5 Bảng biến thiên
Vậy mỗi tháng lợi nhuận cao nhất thu được của công ty là 101.250.000
Câu 21 Để thiết kế một chiếc bể cá hình hộp chữ nhật có chiều cao là 60 cm, thể tích .
là 96 000 cm3, người thợ dùng loại kính để sử dụng làm mặt bên có giá thành
70 000 đồng/m2 và loại kính để làm mặt đáy có giá thành là 100 000 đồng/m2.
Chi phí thấp nhất để hoàn thành bể cá là bao nhiêu nghìn đồng?
Hướng dẫn giải V 96 000
Diện tích của đáy bể là: S = = = 1600 cm2 = 0,16 m2. h 60
Gọi chiều dài đáy của bể là x (m, x 0 ). 0,16
Chiều rộng đáy của bể là (m). x Chi phí để hoàn thành bể cá là: F ( x) 0,16
= 0,16100000 + 20,6 x 70000 + 20,6 70000 x 13440 0,25 =16000 + 84000x + (đồng). x
Xét hàm số F ( x) 13440 =16000 + 84000x +
với x (0; + ) . x 13440
Ta có: F( x) = 84000 −
. Trên khoảng (0; +) , F( x) = 0 x = 0, 4 . 2 x Trang 10
Bảng biến thiên của hàm số F ( x) trên khoảng (0; +) như sau: x 0 0, 4 + F( x) – 0 + + + F ( x) 83200 Căn cứ
vào bảng biến thiên, ta thấy min F ( x) = F (0, 4) = 83200 ( . 0;+) 0,25
Vậy chi phí thấp nhất để hoàn thành bể cá là 83200 đồng = 83, 2 nghìn đồng. Câu
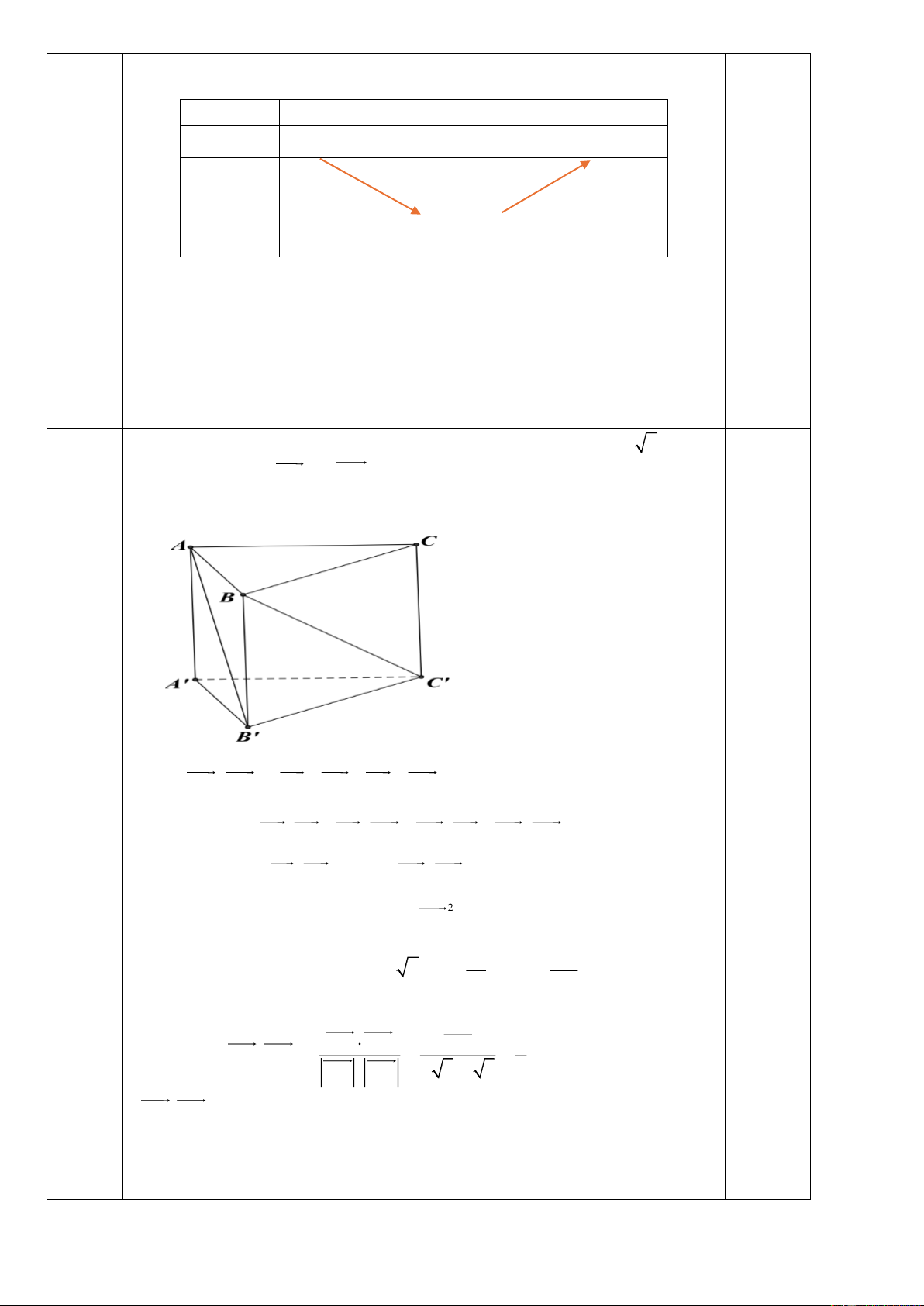
Cho hình lăng trụ tam giác đều ABC.AB C
có AB = a và AA = a 2 . Số đo 22.
góc giữa hai vectơ AB và BC bằng bao nhiêu độ?
. Hướng dẫn giải
Ta có: AB BC = ( AB + BB)(BC + CC)
= AB BC + ABCC+ BB BC + BBCC
= −BA BC + 0 + 0+ BB BB 2
= −BA BC cos ABC + BB a 3a
= −a a cos60 + (a 2) 2 2 2 2 = − + 2a = . 2 2 2 3a Khi đó, ( AB BC) AB BC 1 2 cos , = = = . Suy ra AB BC a 3 a 3 2
(AB ,BC)=60 0,25 . Trang 11 0,25 ĐỀ 3
ĐỀ ÔN TẬP GIỮA HỌC KỲ I NĂM HỌC 2025-2026
MÔN: TOÁN 12-CHÂN TRỜI SÁNG TẠO
PHẦN I. (3 điểm) Câu trắc nghiệm nhiều phương án lựa chọn. Thí sinh trả lời từ câu 1 đến câu 12.
Mỗi câu hỏi thí sinh chỉ chọn một phuơng án.
Câu 1. Cho hàm số f ( x) có đạo hàm f ( x) = x ( x + )2 ' 2 , x
. Số điểm cực trị của hàm số đã cho là A. 3 . B. 1. C. 2 . D. 0 .
Câu 2. Hàm số nào trong các hàm số sau đây có đồ thị như hình vẽ bên? y 3 1 1 x -1 O -1 A. 3 2
y = x − 3x +1. B. 3
y = −x + 3x +1. C. 2
y = x + 3x +1 . D. 3
y = x − 3x +1 .
Câu 3. Cho hàm số y = f ( x) có bảng biến thiên như sau
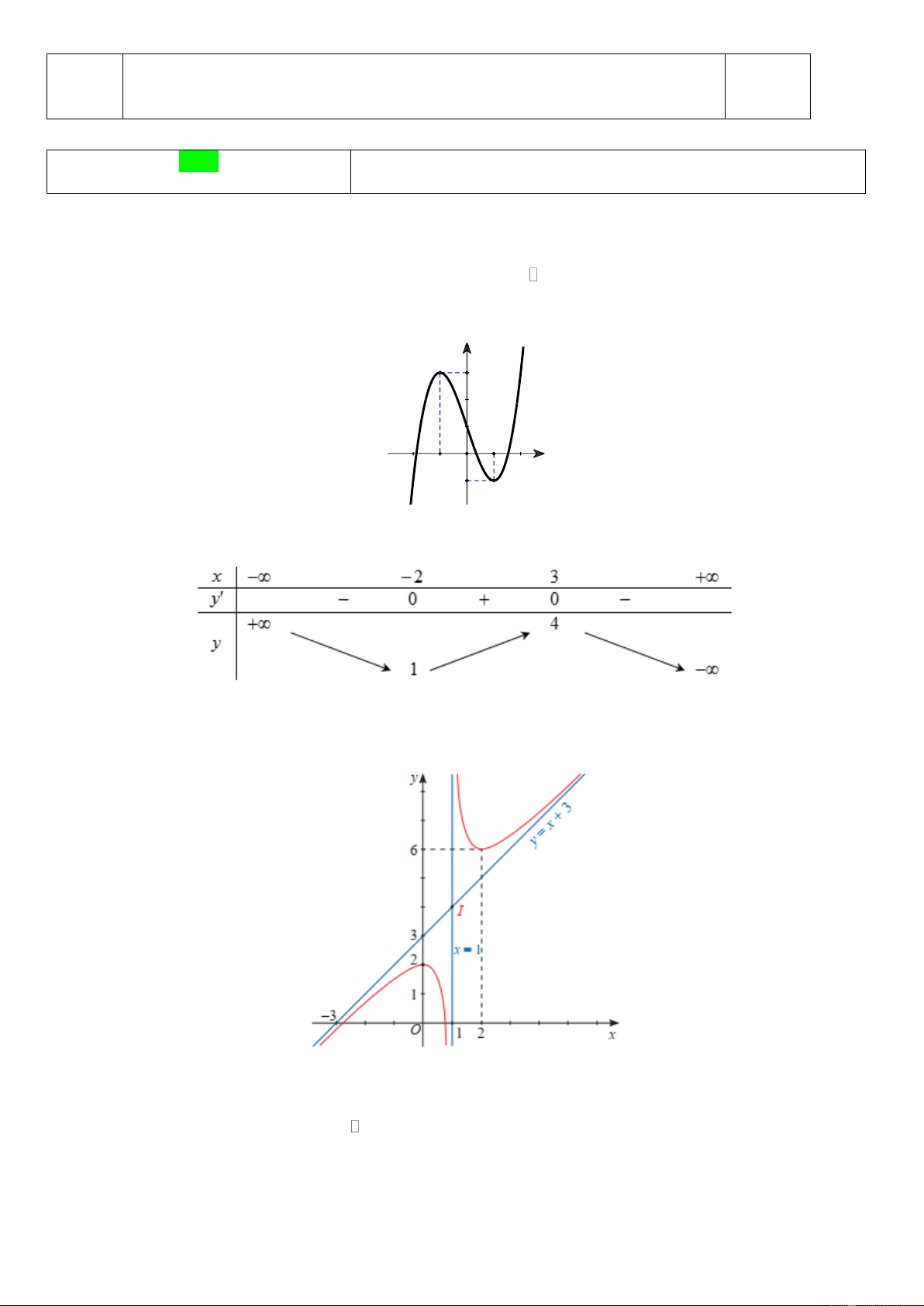
Hàm số đã cho đồng biến trên khoảng nào dưới đây? A. (− ; − 2). B. (3; + ) . C. ( 2; − + ). D. ( 2 − ;3) .
Câu 4. Cho hàm số y = f (x) có đồ thị như hình vẽ.
Tâm đối xứng của đồ thị hàm số y = f (x) là
A. I (0;3) .
B. I (1;6) .
C. I (2;6).
D. I (1;4) .
Câu 5. Cho hàm số f ( x) liên tục trên và có bảng xét dấu của f ( x) như sau: Trang 12
Số điểm cực đại của hàm số đã cho là A. 4 . B. 2 . C. 1. D. 3 . 2 x − 3x − 4
Câu 6. Tìm số tiệm cận đứng của đồ thị hàm số y = . 2 x −16 A. 1. B. 0 . C. 2 . D. 3 .
Câu 7. Giá trị lớn nhất của hàm số f ( x) 4 2
= −x +12x +1 trên đoạn 1 − ;2 bằng A. 37 . B. 33 . C. 1. D. 12 .
Câu 8. Trong các hàm số sau, đồ thị hàm số nào có đường tiệm cận xiên? 2 x − 2x + 3 2x −1 1 A. y = . B. y = . C. y = . D. 3 2
y = x − 3x + 2 . x −1 x +1 x
Câu 9. Cho hàm số y = f ( x) liên tục trên đoạn 1 − ;
3 và có đồ thị như hình vẽ bên. Gọi M và m lần
lượt là giá trị lớn nhất và nhỏ nhất của hàm số đã cho trên đoạn 1 − ;
3 . Giá trị của M − m bằng A. 5. B. 1. C. 4. D. 0.
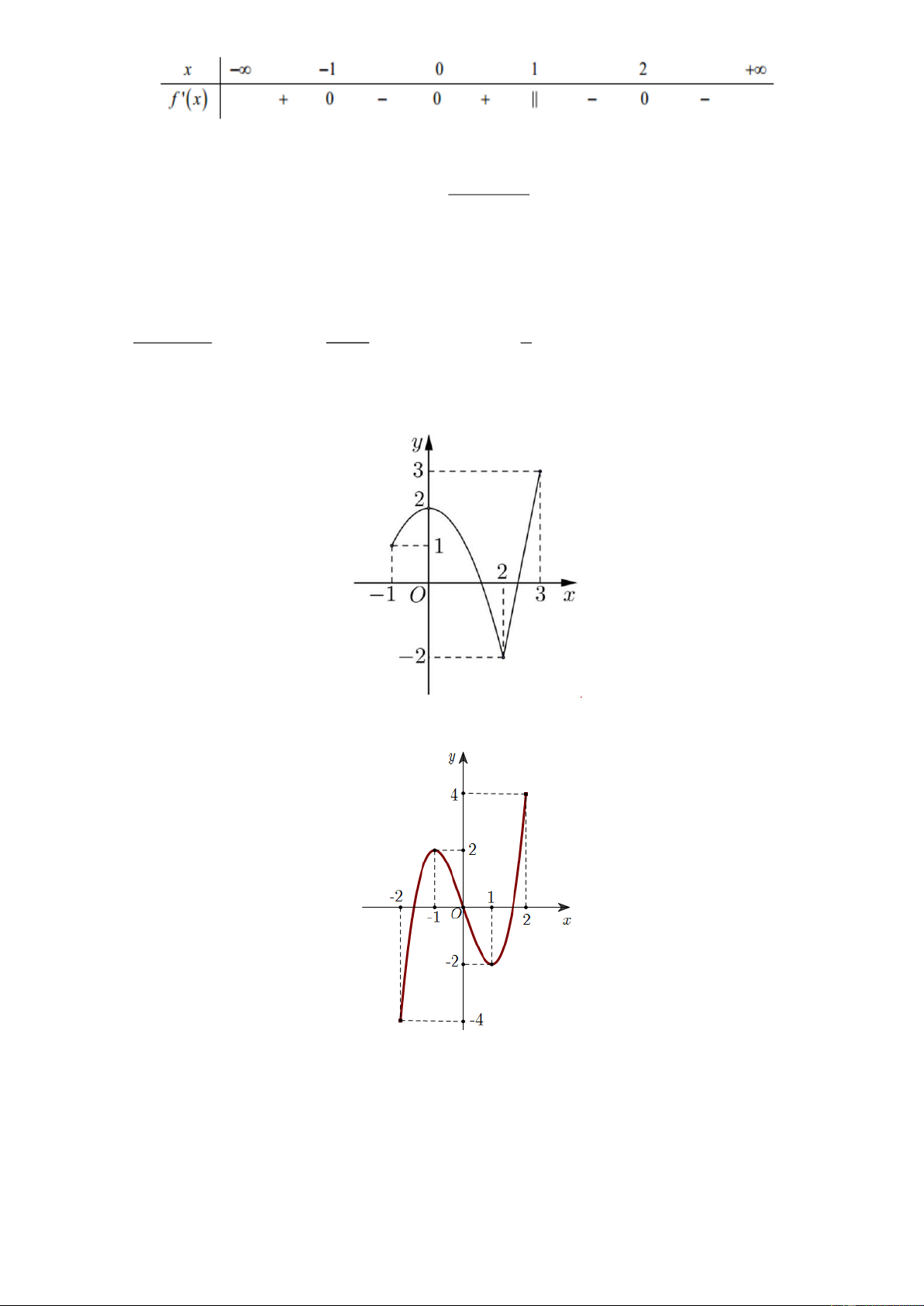
Câu 10. Cho hàm số y = f ( x) xác định và liên tục trên đoạn 2
− ;2 và có đồ thị như hình vẽ
Điểm cực tiểu của đồ thị hàm số y = f ( x) là
A. x = 1 .
B. M (1; − 2) . C. M ( 2 − ;− 4). D. x = 2 − .
Câu 11. Cho hàm số y = f (x) có đồ thị như hình vẽ Trang 13
Đường tiệm cận ngang của đồ thị hàm số y = f (x) là A. y = 1. −
B. x = −1.
C. y = 1. D. x = 1.
Câu 12. Cho hàm số y = f ( x) có bảng biến thiên như sau:
Hàm số f ( x) đạt cực đại tại điểm A. y = 3 − .
B. x = 0 . C. (0; − 3) . D. x = 3 − .
PHẦN II. (4 điểm). Câu trắc nghiệm đúng sai. Thí sinh trả lời từ câu 1 đến câu 4. Trong mỗi ý a, b, c,
d ở mỗi câu, thí sinh chọn đúng hoặc sai. 2 x − 8x
Câu 1. Cho hàm số y = . x +1
a) Tập xác định của hàm số là D = \ 1 .
b) Đồ thị hàm số có tiệm cận đứng là đường thẳng x = 1 , tiệm cận ngang là đường thẳng y = 1.
c) Tiệm cận xiên là đường thẳng y = x − 9 .
d) Tổng của giá trị cực đại và giá trị cực tiểu của hàm số f ( x) bằng 20 − .
Câu 2. Cho đồ thị hàm số 3 2
y = ax + bx + cx + 2 (a, , b c
) có đồ thị là đường cong như hình vẽ
a) Hàm số nghịch biến trên khoảng (0; 2) và (4; +).
b) Hàm số đạt cực tiểu tại x = 2.
c) min y + max y = 0. x 0;2 x 1 − ;2
d) Giá trị f (a − b + c) = 18.
Câu 3. Cho hàm số y = f ( x) liên tục trên
. Hàm số y = f ( x) có đồ thị như hình vẽ dưới đây Trang 14
a) Hàm số y = f ( x) đồng biến trên khoảng ( 2 − ;− ) 1 .
b) Hàm số y = f ( x) nghịch biến trên khoảng (1; 4) .
c) Hàm số y = f ( x) đạt cực đại tại x = 5 − .
d) GTLN của hàm số y = f ( x) trên đoạn 1;5 là f (4) . 1− 2x
Câu 4. Cho hàm số y = . x +1
a) Đường tiệm cận ngang của đồ thị hàm số đã cho là y = 1.
b) Đường tiệm cận đứng của đồ thị hàm số đã cho là x = 1 − .
c) Tâm đối xứng của đồ thị hàm số là I ( 1 − ; 2 − ) .
d) Hình chữ nhật giới hạn bởi hai đường tiệm cận của đồ thị hàm số và hai trục tọa độ có diện tích bằng 1.
PHẦN III. (3 điểm). Câu trắc nghiệm trả lời ngắn. Thí sinh trả lời từ câu 1 đến câu 6.
Câu 1. Giả sử chi phí tiền xăng C (đồng) phụ thuộc tốc độ trung bình v (km / h) theo công thức: C (v) 16000 5 =
+ v (0 v 120) . Hỏi tài xế xe tải lái xe với tốc độ trung bình là bao nhiêu để tiết kiệm v 2 tiền xăng nhất? ax + 2
Câu 2. Cho hàm số y =
(a, ,b c ) có đồ thị như hình vẽ. Tính 2 2 a + b − 3 . c bx + c
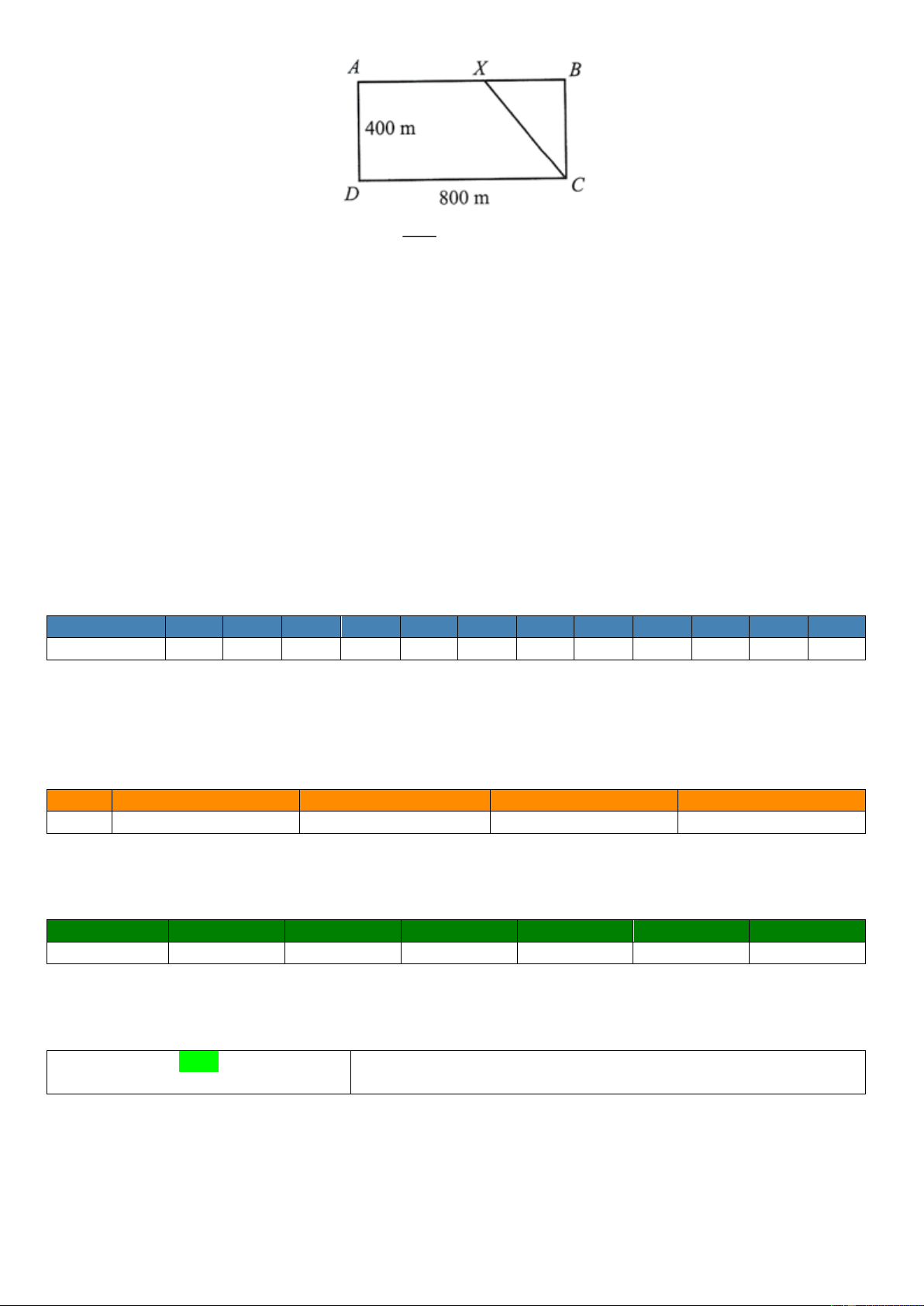
Câu 3. Một vận động viên thể thao hai môn phối hợp luyện tập với một bể bơi hình chữ nhật rộng 400 m ,
dài 800 m . Vận động viên chạy phối hợp với bơi như sau: Xuất phát từ điểm A , chạy đến điểm X và bơi
từ điểm X đến điểm C (như hình vẽ). Hỏi nên chọn điểm X cách A gần bằng bao nhiêu mét để vận
động viên đến C nhanh nhất (làm tròn kết quả đến hàng đơn vị)? Biết rằng vận tốc chạy là 30 km / h , vận
tốc bơi là 6 km / h Trang 15
Câu 4. Cho đồ thị hàm số f ( x) 8 = 5x −1+
có tâm đối xứng là I ( ;
a b) . Giá trị của biểu thức x −1
P = a + 3b bằng bao nhiêu?
Câu 5. Ông Nam cần xây dựng một bể chứa nước có dạng hình hộp chữ nhật không có nắp đậy để phụ vụ
cho việc tưới cây trong vườn. Do các điều kiện về diện tích vườn, ông Nam cần bể có thể tích là 3 36 m ,
đáy bể có chiều dài gấp đôi chiều rộng và chiều rộng không quá 4 m , biết rằng chi phí vật liệu xây dựng
mỗi mét vuông diện tích bề mặt là như nhau. Hỏi chiều cao bể nước bằng bao nhiêu để tổng chi phí vật liệu là nhỏ nhất?
Câu 6. Trong 5 giây đầu tiên, một chất điểm chuyển động theo phương trình s (t ) 3 2
= t − 6t +14t +1 trong
đó t tính bằng giây và s tính bằng mét. Gọi (a;b) là khoảng thời gian của 5 giây đầu tiên vận tốc tức thời
của chất điểm tăng lên. Tính giá trị 2 2
P = b − a .
---------------HẾT------------------ ĐÁP ÁN
PHẦN I: Trắc nghiệm nhiều lựa chọn
- Mỗi câu đúng được 0,25 điểm. Mã đề 1 2 3 4 5 6 7 8 9 10 11 12 411 B D D D B A B A A B A B
PHẦN II: Trắc nghiệm đúng sai
- Điểm tối đa mỗi câu là 1 điểm.
- Đúng 1 câu được 0,1 điểm; đúng 2 câu được 0,25 điểm; đúng 3 câu được 0,5 điểm; đúng 4 câu được 1 điểm. Mã đề Câu 1 Câu 2 Câu 3 Câu 4 411
a)S - b)S - c)Đ - d)Đ
a)S - b)Đ - c)Đ - d)Đ
a)S - b)S - c)Đ - d)Đ
a)S - b)Đ - c)Đ - d)S
PHẦN III: Trắc nghiệm trả lời ngắn
- Mỗi câu đúng được 0,5 điểm. Mã đề Câu 1 Câu 2 Câu 3 Câu 4 Câu 5 Câu 6 411 80 8 718 13 2 21
---------------HẾT--------------- ĐỀ 4
ĐỀ ÔN TẬP GIỮA HỌC KỲ I NĂM HỌC 2025-2026
MÔN: TOÁN 12-CHÂN TRỜI SÁNG TẠO
PHẦN I. Câu trắc nghiệm nhiều phương án lựa chọn. Thí sinh trả lời từ câu 1 đến câu 12. Mỗi câu hỏi
thí sinh chỉ chọn một phương án.
Câu 1. Cho hàm số f ( x) liên tục trên ¡ và có bảng xét dấu của f ( x) như sau: Trang 16
Số điểm cực trị của hàm số đã cho là A. 4 . B. 1. C. 2 . D. 3 .
Câu 2. Cho hàm số y = f ( x) có đồ thị như hình vẽ dưới đây. Mệnh đề nào sau đây là đúng?
A. Hàm số đồng biến trên ( 1 − ;3) .
C. Hàm số đồng biến trên (0;3) .
B. Hàm số nghịch biến trên (1; +) . D. Hàm số nghịch biến trên ( ;0 − ).
Câu 3: Cho hàm số y = f ( x) bảng biến thiên sau. Mệnh đề nào sau đây là sai?
A. Hàm số đạt cực đại tại x = 0 . C. Hàm số có giá trị cực tiểu bằng 2 − .
B. Hàm số có giá trị cực đại bằng 3 . D. Hàm số có một điểm cực đại.
Câu 4. Hàm số nào sau đây đồng biến trên ? A. 3
y = 2x − 3 B. 3 2
y = x + 2x − 7x C. 2
y = x + x +10 D. 3 2
y = −2x + x − 4x
Câu 5. Cho hàm số y = f ( x) liên tục trên đoạn 1 − ;
3 và có đồ thị như hình vẽ?
Tìm giá trị lớn nhất của hàm số y = f ( x) trên đoạn 1 − ; 3 . A. 3 . B. 1. C. 2 . D. 2 − . Trang 17
Câu 6. Cho hàm số y = f ( x) có bảng biến thiên như sau
Hàm số đã cho nghịch biến trên khoảng nào dưới đây? A. ( 1 − ) ;1 . B. (− ; − ) 1 . C. (1;+). D. ( ; − 0).
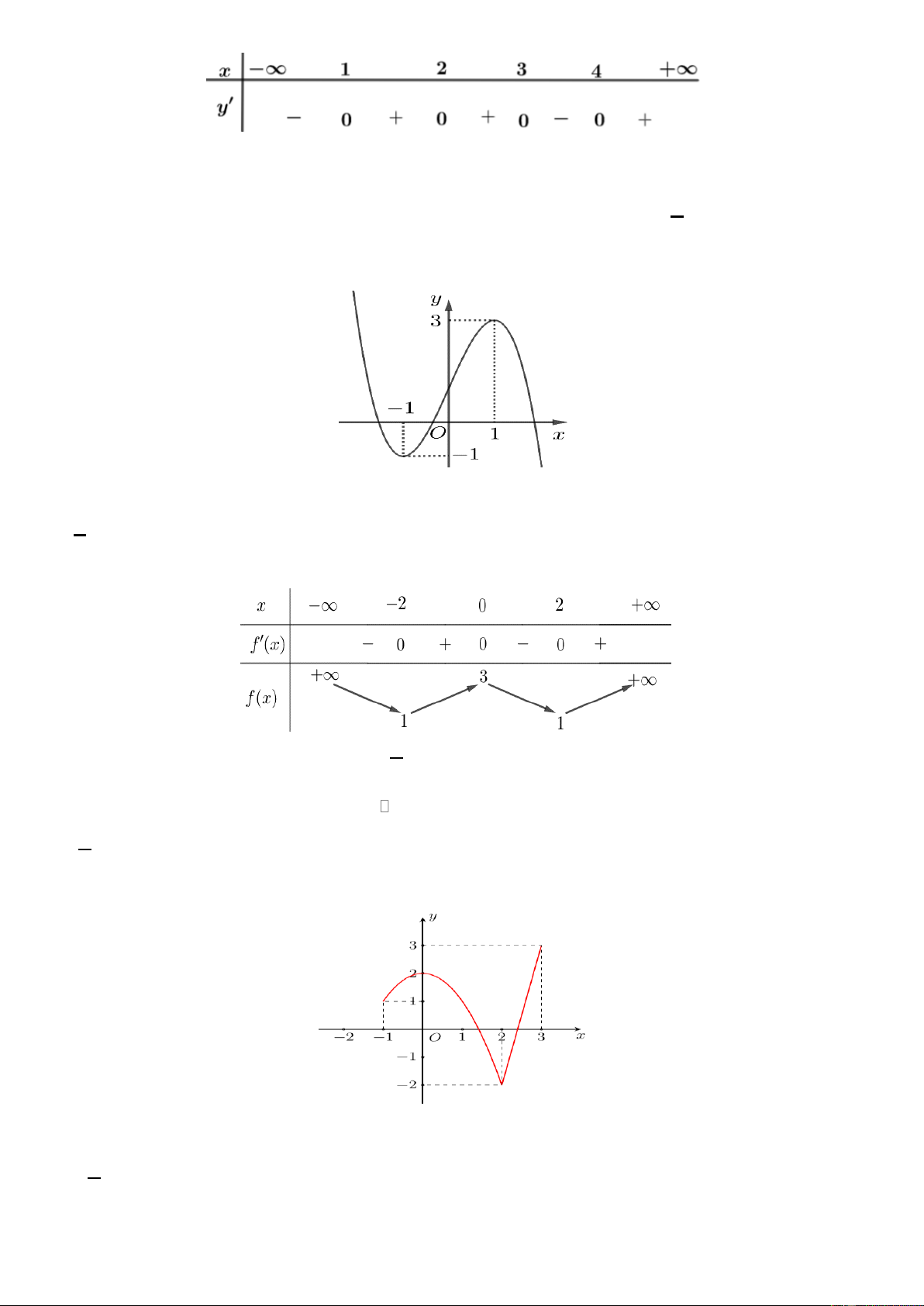
Câu 7. Cho hàm số y = f (x) có đồ thị là đường cong trong hình bên.
Giá trị cực tiểu của hàm số đã cho bằng A. 2 − . B. 0 . C. 1. D. 2 .
Câu 8. Cho hàm số y = f ( x) có đồ thị như hình vẽ.
Đồ thị hàm số đã cho có đường tiệm cận đứng là : A. x = 1 . B. y = 1 − . C. x = 2 . D. x = 1 − 2x + 7
Câu 9. Giá trị lớn nhất của hàm số f (x) = trên đoạn 1 − ;2 bằng x − 3 5 A. 1 − . B. 11 − . C. − . D. 2 . 4 4 − x
Câu 10. Tiệm cận ngang của đồ thị hàm số y =
là đường thẳng có phương trình: x + 5 A. y = 4 . B. y = 1 − . C. y = 5 − . D. x = 5 − .
Câu 11. Cho hàm số f ( x) xác định trên \
0 , liên tục trên các khoảng xác định và có bảng biến thiên như sau : Trang 18
Tổng số tiệm cận ngang của đồ thị hàm số đã cho là: A. 2. B. 3. C. 0 . D. 1.
Câu 12. Cho hàm số y = f (x) xác định trên 1 − ;
3 và có bảng biến thiên như hình vẽ:
Khẳng định nào sau đây là đúng?
A. max f (x) = 4 .
B. min f ( x) = 1 − .
C. max f ( x) = 0 .
D. min f ( x) = 0. 1 − ;3 1 − ; 3 1 − ; 3 1 − ; 3
PHẦN II. Câu trắc nghiệm đúng sai. Thí sinh trả lời từ câu 1 đến câu 4. Trong mỗi ý a), b), c), d) ở mỗi
câu, thí sinh chọn đúng hoặc sai.
Câu 1. Cho hàm số y = f (x) 3 2
= ax + bx + cx + d, (a 0) có đồ thị trong hình dưới đây.
Xét tính đúng, sai của các mệnh đề sau Mệnh đề Đúng Sai
a) Hàm số đồng biến trên khoảng (1;2) . Đ
b) Hàm số đạt cực tiểu tại x = 1 − . S
c) Giá trị lớn nhất của hàm số đã cho trên đoạn 1 − ;2 bằng 3. Đ
d) Đồ thị hàm số cắt trục hoành tại 3 điểm phân biệt. Đ − + Câu 2. x
Cho hàm số f ( x) 3 =
có bảng biến thiên như sau: x − 2 Trang 19
Xét tính đúng, sai của các mệnh đề sau Mệnh đề Đúng Sai
a) Hàm số f ( x) luôn đồng biến trên từng khoảng xác định. S
b) Hàm số f ( x) không có giá trị nhỏ nhất trên khoảng ( ; − 2) . Đ
c) Đồ thị hàm số có đường tiệm cận ngang là y = 1 − . Đ
d) Hàm số f ( x) nghịch biến trên khoảng( 1 − ;+). S x + x +
Câu 3. Cho hàm số y = f (x) 2 3 6 4 = = x +1+
có đồ thị (C ) . x + 2 x + 2
Xét tính đúng, sai của các mệnh đề sau Mệnh đề Đúng Sai
a) Tập xác định của hàm số f ( x) là D = \ − 2 . Đ
b) Đồ thị hàm số có đường tiệm cận đứng là x = −1. S
c) Đồ thị của hàm số đã cho đi qua điểm ( 1; − 4) . Đ
d) Đường thẳng y = x + 2 là đường tiệm cận xiên của (C ) . S
Câu 4. Anh Nam có một mảnh đất rộng và muốn dành ra một khu đất hình chữ nhật có diện tích 2
800 m để trồng vài loại cây mới. Anh dự kiến rào quanh ba cạnh
của khu đất hình chữ nhật này bằng lưới thép với giá 25.000 đồng /m. Cạnh còn
lại (chiều dài) của khu đất hình chữ nhật này sẽ tận dụng bức tường có sẵn (Hình
vẽ). Do điều kiện địa lí, chiều rộng khu đất không vượt quá 30 m. Gọi x( ) m là
chiều rộng của khu đất hình chữ nhật cần rào.
Xét tính đúng, sai của các mệnh đề sau Mệnh đề Đúng Sai
a) Theo giả thiết thì điều kiện của x là 0 x 30 Đ
b) Chiều dài của khu đất là 800 − 2x ( m) . S
c) Tổng chiều dài lưới thép rào quanh khu đất là 800
L(x) = x + ( m) . S x
d) Chi phí rào khu đất hình chữ nhật thấp nhất là 2000000 đồng. Đ
PHẦN III. Câu trắc nghiệm trả lời ngắn. Thí sinh trả lời từ câu 1 đến câu 6. 1
Câu 1. Một chất điểm chuyển động theo quy luật 4 3 2 s(t) =
t − t + 6t − 7 với t 0 (tính theo đơn vị giây) 4
là khoảng thời gian tính từ lúc vật bắt đầu chuyển động và s(t) (tính theo đơn vị mét) là quãng đường vật
chuyển động được trong thời gian t (giây). Hỏi vận tốc của chất điểm tại thời điểm 3 giây tính theo đơn vị m / s ? Trang 20




