30 Đề Thi HSG Toán 9 Cấp Tỉnh Năm 2025-2026 Có Lời Giải Chi Tiết

UBND TỈNH HẢI DƯƠNG KỲ THI CHỌN HỌC SINH GIỎI TỈNH LỚP 9
SỞ GIÁO DỤC VÀ ĐÀO TẠO MÔN THI: TOÁN
Thời gian làm bài: 150 phút, không kể thời gian ĐỀ CHÍNH THỨC giao đề
(Đề thi gồm 05 câu, 01 trang) Câu 1. (2,0 điểm)   2 2 x − y x − y x + y
1. Rút gọn biểu thức A =  + .  với x > y > 0. 2 2 + + −  2 2 x y x y
x − y − x + y x − y  
2. Cho a, b, c là các số thực khác 0 thỏa mãn: 1 1 1
| a + b + c − 2020 | + 2020(ab + bc + ca) − abc = 0 . Tính P = + + . 2021 2021 2021 a b c Câu 2. (2,0 điểm) 2 3x −17x + 27 1
1. Giải phương trình : = 4x − 9 2 x − 2 −1  y 1 9 1+ + =  2  x xy x
2. Giải hệ phương trình:  4 y  2 x + xy − 4 =  x Câu 3. (2,0 điểm)
1. Tìm các số nguyên x, y thỏa mãn đẳng thức: 2x2 + y2 + 3xy + 3x + 2y + 3 = 0.
2. Cho a, b, c là các số nguyên thỏa mãn : (a - b)(b - c)(c - a) = a + b + c.
Chứng minh a + b + c chia hết cho 27. Câu 4. (3,0 điểm)
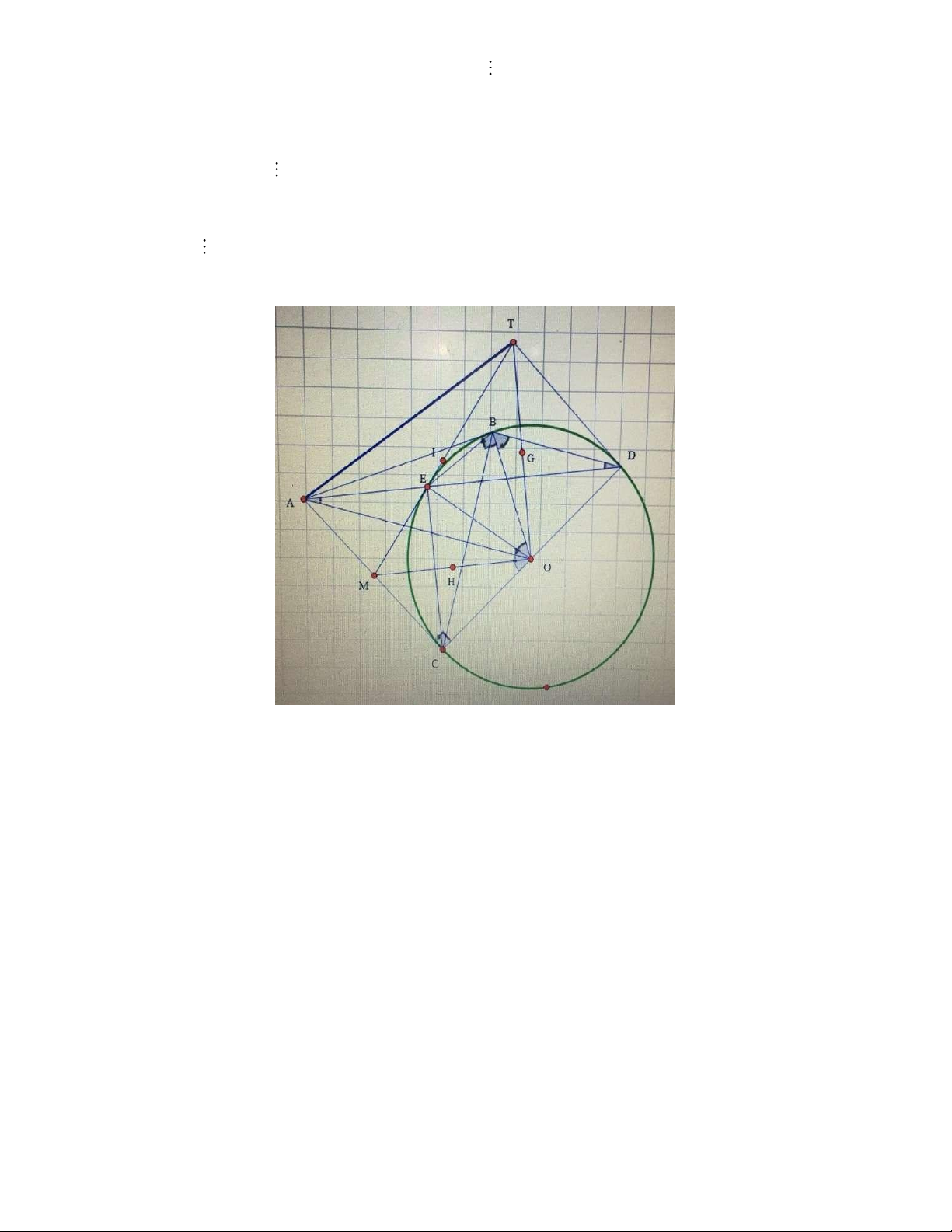
1. Cho đường tròn (O; R) và một điểm A nằm ngoài đường tròn (O; R). Qua A lần lượt kẻ
các tiếp tuyến AB, AC đến với đường tròn (O; R) (B, C là các tiếp điểm). Lấy điểm D
thuộc đường tròn (O; R) sao cho BD song song với AO, đường thẳng AD cắt đường tròn
(O; R) tại điểm thứ hai là E. Gọi M là trung điểm của AC.
a) Chứng minh ME là tiếp tuyến của đường tròn (O; R).
b) Từ D kẻ tiếp tuyến với đường tròn (O; R), tiếp tuyến này cắt ME tại T. Gọi r1, r2,
r3 lần lượt là bán kính các đường tròn nội tiếp của ΔOME, ΔOTE, ΔOMT. Chứng minh
khi A thay đổi thì r1 + r2 + r3 luôn không đổi.
2. Cho tam giác ABC có ba góc nhon. Chứng minh sin2A + sin2B + sin2C > 2.
Câu 5. (1,0 điểm) Cho x, y, z là các số thực dương thỏa mãn: 2xy + 5yz + 6zx = 18xyz. 16xy 25yz 81zx
Tìm giá trị nhỏ nhất của biểu thức: P = + + .
y + 2x 4z + y x + 4z
…………………….. HẾT …………………………. Trang 1
ĐÁP ÁN THAM KHẢO – HẢI DƯƠNG Câu 1. 1) Ta có: 2 2  x − y x − y  x + y P =  + .   2 2
x + y + x − y
x − y ( x + y − x − y )   x − y 2 2  x − y x − y  x + y =  + .   2 2
x + y + x − y
x + y − x − y   x − y 2 2
x − y ( x + y − x − y ) + x − y ( x + y + x − y ) x + y = . 2 2 2 2
( x + y ) − ( x − y ) x − y 2 2
x − y.2 x + y x + y = .
(x + y) − (x − y)
x + y. x − y 2 2 2.(x + y ) = 2y 2 2 x + y = y
2) Có | a + b + c − 2020 | + 2020(ab + bc + ca) − abc = 0
Mà | a + b + c − 2020 | 0, 2020(ab + bc + ca) − abc  0
a + b + c − 2020 = 0 Do đó: 
2020(ab + bc + ca) − abc = 0 Ta có:
| a + b + c − 2020 | + 2020(ab + bc + ca) − abc = 0
| a + b + c − 2020 | 0, 2020(ab + bc + ca) − abc  0
a + b + c − 2020 = 0 
2020(ab + bc + ca) − abc = 0
(a + b + c)(ab + bc + ca) − abc = 0 2 2 2 2 2 2
 a b + b a + b c + c b + a c + c a + 3abc − abc = 0 2 2 2 2 2 2
 a b + b a + b c + c b + a c + c a + abc + abc = 0 2  (a b 2 2 2 2 2
+ b a + b c + abc) + (c b + a c + c a + abc) = 0 2 2
 b(a + ab + bc + ca) + c(bc + a + ca + ab) = 0 2
 (b + c)(a + ab + bc + ca) = 0
 (a + b)(b + c)(c + a) = 0 b = −c   a = −b  a = −c 
Trong 3 số a, b, c có hai số đối nhau Trang 2
Không làm mất tính tổng quát, giả sử b = −c  a + b + c = a = 2020 1 1 1 1 1 1 1 Vậy: P = + + = + + = 2021 2021 2021 2021 2021 2021 2021 a b c 2020 b b − 2020 Câu 2.
1) Điều kiện xác định: 9 x  , x  2 4 Cách 1: 2 3x −17x + 27 1 = 4x − 9 2 x − 2 −1
(4x − 9)(2 x − 2 +1) 2
 3x −17x + 27 = 4(x − 2) −1 2
 3x −17x + 27 = 2 x − 2 +1 Ta có: 2
 3x −17x + 26 = 2 x − 2 2 2 2
 (3x −17x + 26) = (2 x − 2) 2 2
 (x − 3) (9x − 48x + 76) = 0 x = 3   2
9x − 48x + 76 = 0 KL: Vì 2
9x − 48x + 76 = 0 (vô nghiệm) nên x=3 là nghiệm của phương trình. Cách 2: 2 3x −17x + 27 1 = 4x − 9 2 x − 2 −1 2
3x − 6x −11x + 22 + 5 1  = 4(x − 2) −1 2 x − 2 −1
3(x − 2) −11(x − 2) + 5 1  = 4(x − 2) −1 2 x − 2 −1
Đặt x − 2 = t ( t  0 ) 2  x = t − 2 2 2 2
3(t + 2).t −11t + 5 1  = 2 4t −1 2t −1 2 2 2
3(t + 2).t −11t + 5 1  = 1 (t   ) (2t −1)(2t +1) 2t −1 2 4 2 2
 3t + 6t −11t + 5 = 2t +1 4 2
 3t − 5t − 2t + 4 = 0 3 2
 (t −1)(3t + 3t − 2t − 4) = 0 t = 1   3 2
3t + 3t − 2t − 4 = 0  t =1
Với t = 1  x = 3 KL: x=3 Trang 3
2) Điều kiện: x, y  0 1 9 𝑥 + 𝑦 + = (1) Hệ tương đương: { 𝑦 𝑥 4 4𝑦 𝑥 + 𝑦 − = (2) 𝑥 𝑥2
Lấy (1) trừ (2) ta được: 1 4 9 4y 4y 5 1 x = y 2 2 + = − 
− + = 0  x − 5xy + 4y = 0  (x − 4y)(x − y) = 0  2 2 y x x x x x y  x = 4y 8
Với x = y , thay vào (1) ta được: 2x −
= 0  x = y = 2  x 5 1
Với x = 4 y , thay vào (1) ta được: 5y −
= 0  y =   x = 2  4y 2 1 1 Vậy ( ; x y) = (2;2) = ( 2 − ; 2 − ) = (2; ) = ( 2 − ;− ) 2 2 Câu 3. 1) Cách 1: 2 2 2 2
2x + y + 3xy + 3x + 2y + 2 = 0  2x + 2xy + 2x + xy + y + y + x + y +1 = −1
 (x + y +1)(2x + y +1) = 1 −
x + y +1 =1 x = 2  
2x + y +1 = 1 − y = 4 −   x y 1 1  + + = − x = −2  
2x + y +1=1 y = 2 KL: (x;y)=(2;-4)=(-2;2) Cách 2: 2 2 2 2
2x + y + 3xy + 3x + 2 y + 2 = 0  y + (3x +12) y + 2x + 3x + 2 = 0 2  = x − 4
Để phương trình có nghiệm nguyên thi 2
 = x − 4 là số chính phương, ta đặt: 2
n − 4 = k ( k  ) 2
 (n − 2)(n + 2) = k Ta có bảng sau: x + k 1 4 -4 -1 2 -2 x - k 4 1 -1 -4 2 -2 x -5/2 (loại) 5/2 (loại) -5/2 (loại) 5/2 (loại) 2 -2 y -4 2 KL: (x;y)=(2;-4)=(-2;2) 2)
TH1: Nếu a, b, c có cùng số dư khi chia cho 3 a − b 3 b
 − c 3  a + b + c 3.3.3 = 27 c − a 3  Trang 4
TH2: Nếu a, b, c khác số dư khi chia cho 3  a + b + c 3
Mà (a − b)(b − c)(c − a) không chia hết cho 3 (vô lí)
Trong 3 số a, b, c tồn tại ít nhất 2 số có cùng số dư khi chia cho 3
Tổng a+b+c không chia hết cho 3 (1)
 (a − b)(b − c)(c − a) 3 (Mâu thuẫn với (1))  Loại TH1 đúng
Vậy a + b + c 27 Câu 4. 1)
a)Vì BD//AO  OBD = BOA (1)
Có AOC = BOA (2)
Từ (1) và (2) suy ra: AOC = OBD (3)
Lại có: ABC = AOC (4) (cung chắn cung AC)
Từ (3), (4) suy ra: OBD = ABC Mặt khác: 0 0
ABC + CBO = 90  OBD + CBO = 90
Suy ra tam giác CBD vuông tại B
Do đó CD là đường kính của (O) 0
 CED = 90  A  EC vuông tại C
Có M là trung điểm của AC nên EM=MC
Dễ dàng chứng minh MEO  = MCO (c.g.c) 0
 MEO = MCO = 90  ME là tiếp tuyến của (O). b) Đang cập nhật….. Trang 5 2) Ta có: 1− os c 2A 1− os c 2B 2 2 2 2
sin A + sin B + sin C = + +1− os c C 2 2 cos2A+cos2B 2 2 = 2 − − os c C = 2 − os c (A+B).cos(A-B)- os c C 2 2 = 2 + os
c C.cos(A-B)-cos C = 2 + os c C.cos(A-B)-cosC = 2 + os
c C.cos(A-B) + cos(A+B) = 2 + 2cos . A cos . B cos C
Vì tam giác có ba góc nhọn nên cosA, cosB, cosC đều có giá trị dương nên os . A cos . B cos C > 0. Do đó: 2 + 2 cos . A cos .
B cos C đpcm Câu 5. a b c ( + + )2 2 2 2 a b c Ta chứng minh: + +  k q n k + q + n Ấp dụng B.C.S: a b c
(a +b + c)2 2 2 2 + +  k q n k + q + n  a b c  ( ) ( ) ( )  
 ( k )2 ( q )2 ( r )2  + + + +
 (a + b + c)2 2 2 2  k q n    a b c
(a +b + c)2 2 2 2  + +  k q r k + q + n a b r a + b + c Dấu “=” xảy ra  = = = k q r k + q + n Áp dụng: 2 2 2 16xy 25yz 81zx 4 5 9 P = + + . = + +
y + 2x 4z + y x + 4z 1 2 4 1 1 4 + + + x y y z z x 2 2 (4 + 5 + 9) 18 P  = = 18 5 6 2
5yz + 6xz + 2xy + + x y z xyz 1 2 + = 4   1 x y x =   2  4 1 
 MinP = 18   + = 5  y =1 y z  z =1 1 4   + = 9   z x
SỞ GIÁO DỤC VÀ ĐÀO TẠO
KỲ THI HỌC SINH GIỎI LỚP 9 CẤP THÀNH PHỐ Trang 6
THÀNH PHỐ HỒ CHÍ MINH
KHÓA THI NGÀY 17.3.2021 Môn thi: TOÁN
ĐỀ THI CHÍNH THỨC
Thời gian làm bài: 120 phút
(Đề thi gồm 01 trang)
(Không kể thời gian phát đề)
Bài 1. (3 điểm)
Cho hai số a, b thỏa mãn điều kiện a-b=1
Tính giá trị của biểu thức: 4 3 2 2 3 2 4
P = a − 4ab + 3a b − a b − 3a b + b
Bài 2. (3 điểm) Giải phương trình: 2 2
x (2 − x) = 3(1− x) − 5
Bài 3. (4 điểm)
Cho tam giác ABC vuông tại A có đường phân giác trong BD ( D  AC ). Đường tròn (BCD) cắt
cạnh AB tại E. Chứng minh AE+AB=BC.
Bài 4. (3 điểm)
Cho bốn số thực a, b, c, d thỏa điều kiện 2 2 2 2
a + b + c + d = 4 . Chứng minh bất đẳng thức:
(a + 2)(b + 2)  cd
Bài 5. (4 điểm)
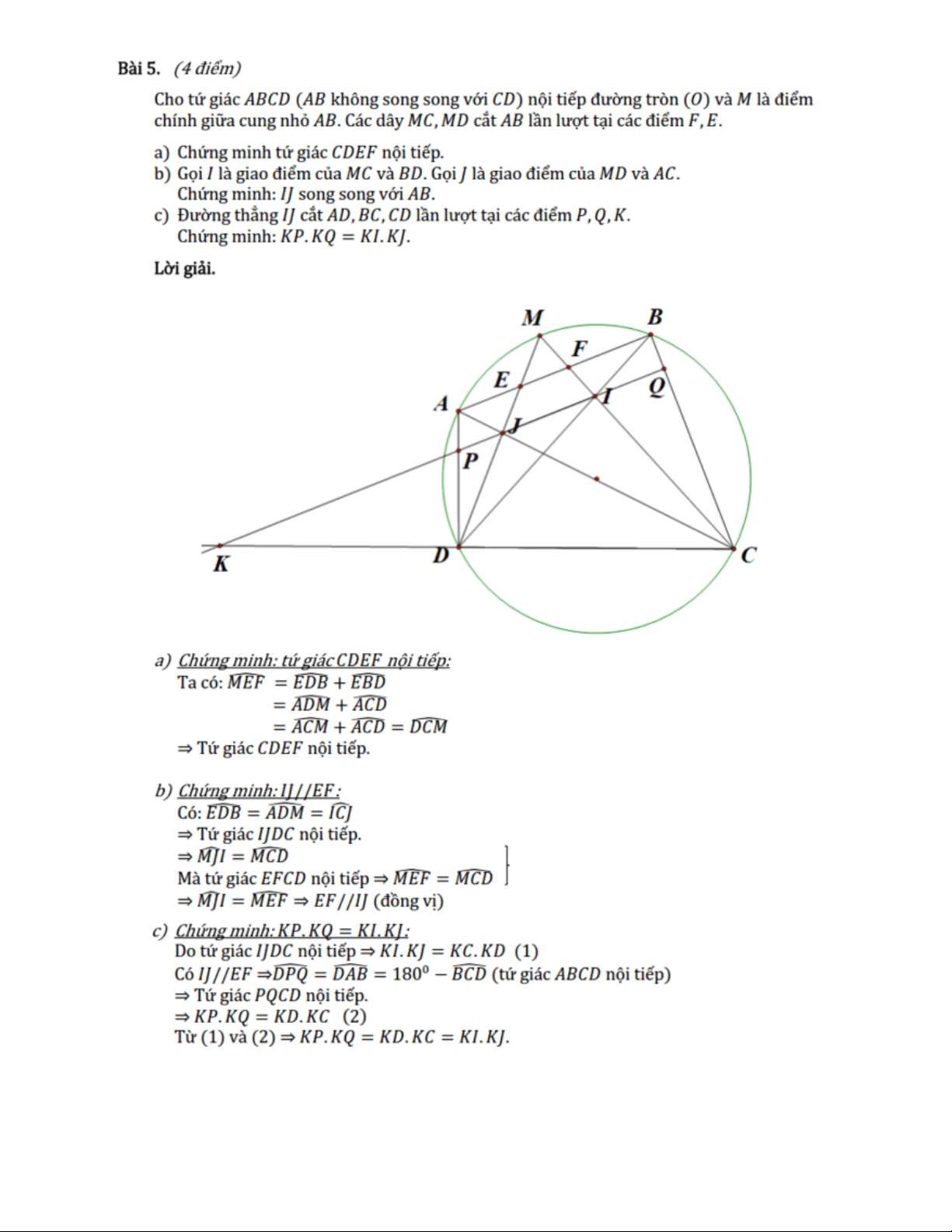
Cho tứ giác ABCD (AB không song song với CD) nội tiếp đường tròn (O) và M là điểm chính
giữa của cung nhỏ AB. Các dây MC, MD cắt AB lần lượt tại các điểm F, E.
a) Chứng minh tứ giác CDEF nội tiếp.
b) Gọi I là giao điểm của MC và MD. Gọi J là giao điểm của MD và AC.
Chứng minh: IJ song song với AB.
c) Đường thẳng IJ cắt AD, BC, CD lần lượt tại các điểm P, Q, K. Chứng minh: KP.KQ=KI.KJ
Bài 6. (3 điểm) Cho phương trình 2
x +ax+b=0 (1) với a, b là các tham số nguyên. Giả sử phương trình (1) có một nghiệm là 2 − 3 . a) Tìm a, b.
b) Chứng minh rằng A = ( + )2021 2021 2 3 + (2 − 3)
là một số nguyên và A chia hết cho 4. HẾT Trang 7
ĐÁP ÁN THAM KHẢO – HỒ CHÍ MINH (2020 – 2021) Trang 8 Trang 9 Trang 10 Trang 11
SỞ GIÁO DỤC VÀ ĐÀO TẠO
KỲ THI CHỌN HỌC SINH GIỎI THCS CẤP TỈNH HƯNG YÊN
NĂM HỌC 2020 – 2021 Môn thi: Toán ĐỀ CHÍNH THỨC
Thời gian làm bài: 150 phút, không kể thời gian giao đề Câu 1. (4,0 điểm) 2 2021 (2x − 6x + 3) 3 + 5
a) Tính giá trị của biểu thức 2 2020
B = (10x − 30x +11) + khi x = 5 4 3
x − 3x + x −1 2
b) Tìm các cặp số nguyên (x;y) thỏa mãn 2
x − (2y + 3)x − y +1 = 0 Câu 2. (4,0 điểm) a) Giải phương trình 2
x − x − 4 = 2 x −1(1− x)
b) Trên mặt phẳng tọa độ Oxy, cho hai điểm M, N là hai điểm phân biệt di động lần lượt trên
trục hoành và trục tung sao cho đường thẳng MN luôn đi qua điểm cố định I(1;2). Tìm giá 1 1
trị nhỏ nhất của biểu thức P = + . 2 2 OM ON Câu 3. (4,0 điểm) 3 3 x + y = 65
a) Giải hệ phương trình  2 2
x y + xy = 20
b) Một nhóm học sinh được giao sắp xếp 810 quyển sách vào tủ ở thư viện trong một thời
gian nhất định. Khi bắt đầu làm việc, nhóm được bổ sung thêm học sinh nên mỗi giờ
nhóm sắp xếp nhiều hơn dự định 110 quyển sách. Vì vậy không những hoàn thành trước
dự định 1 giờ 30 phút mà còn vượt mức được giao 60 quyển sách. Hỏi số quyển sách mỗi
giờ nhóm dự định sắp xếp là bao nhiêu? Câu 4. (2,0 điểm)
Cho tam giác ABC có ba góc nhọn. Chứng minh rằng: A .
B sin C + BC.sin A + .
CA sin B = (AB + BC + )
CA (sin A + sin B + sin C) Câu 5. (4,0 điểm)
Cho đường tròn (O;R) có hai đường kính AB và CD vuông góc với nhau. Lấy E là điểm bất kỳ
nằm trên cung nhỏ AD (E không trùng với A và D). Đường thẳng EC cắt OA tại M, đường thẳng EB cắt OD tại N.
a) Chứng minh rằng: AM.ED= 2 .OM.AE OM ON
b) Xác định vị trí của điểm E để tổng +
đạt giá trị nhỏ nhất AM DN Câu 6. (2,0 điểm) 3
Cho các số dương a, b, c thỏa mãn điều kiện a + b + c  . Tìm giá trị nhỏ nhất của biểu thức: 2 1 1 1 1 1 1
P = (3 + + )(3 + + )(3 + + ) . a b b c c a
…………HẾT…………
Thí sinh không được sử dụng tài liệu và máy tính cầm tay.
Cán bộ coi thi không giải thích gì thêm. Trang 12
ĐÁP ÁN THAM KHẢO – HƯNG YÊN (2020 – 2021) Câu 1. 3 + 5 a) Ta có: 2 2 x =
 (2x − 3) = 5  x − 3x +1 = 0 2 Lại có: 2 2
10x − 30x +11 = 10(x − 3x +1) +1 = 1 2 2
2x − 6x + 3 = 2(x − 3x +1) +1 = 1 5 4 3 3 2
x − 3x + x −1 = x (x − 3x +1) −1 = 1 − Suy ra: B=0 b) Ta có: 2 2
x − (2y + 3)x − y +1 = 0  x − 3x +1 = y(2x +1) (1)
Vì x  nên 2x +1  0 , do vậy: 2 x − 3x +1 x 7 11 (1)  y =  y = − + 2x +1 2 4 4(2x +1) 11
 4y = (2x − 7) + (2) 2x +1
Vì x, y là các số nguyên nên 4y và 2x-7 cũng là số nguyên.
Do vậy, từ (2) suy ra 11 (2x +1)  2x +1Ư(11)  2x +1 11 − ,1 , − 1−  11  x  6 − , 1 − ,0,  5 Thay x  6 − , 1 − ,0, 
5 vào phương trình (1) ta được: ( ;x y) = ( 6 − ; 5 − );( 1 − ; 5 − );(0;1);(5;1  ) (thỏa mãn (x;y) nguyên) Vậy ( ; x y) = (  6 − ; 5 − );( 1 − ; 5 − );(0;1);(5;1  ) . Câu 2.
a. Điều kiện x  1 Ta có: 2
x − x − 4 = 2 x −1(1− x) 2
 x + 2x x −1 + x −1− 2(x + x −1) − 3 = 0 2
 (x + x −1) − 2(x + x −1) − 3 = 0
Đặt x + x −1 = y (Điều kiện y  1) Suy ra 2
y − 2 y − 3 = 0 . Giải ra ta được y=-1, y=3 Với y=-1 (loại) Trang 13 Với y=3. Thay số ta có: x + x −1 = 3
 x −1 = 3 − x 1   x  3   2
x −1 = 9 − 6x + x 1   x  3
 x = 2,x =5  x = 2
Kết luận: Phương trình có nghiệm x=2
b. Đặt m = x , n = y , ,
m n  0; m  1; n  2 (1). m n
Gọi đường thẳng đi qua 3 điểm M, I, N có dạng y = ax+b , a  0 am + b = 0   a + b = 2 b  = n  1 2
 2m + n = mn  + = 1(2) m n 1 2  1 1  2 1 2 2 1 = ( + ) = 5 + − ( − )  2 2  m n  m n  m n 1 1 1 1 1 1 5( + )  P = +  2 2 2 2 m n m n 5 2 1 Đẳng thức xảy ra khi
= . Kết hợp (2) suy ra: m=5, n=2,5 (thỏa mãn (1)) m n 1
Vậy giá trị nhỏ nhất của P là . 5 Câu 3. 3 3 x + y = 65
a) Hệ phương trình tương đương:  2 2 3
 x y + 3xy = 60 Suy ra: 3 3 2 2
x + y + 3x y + 3xy = 125  x + y = 5 Dễ dàng suy ra: xy=4 x + y = 5 x = 4 x =1 Suy ra:    hoặc  xy = 4 y =1 y = 4
Vậy hệ phương trình có 2 nghiệm: (4;1), (1;4) Trang 14
b) Gọi số quyển sách mỗi giờ nhóm dự định sắp xếp là: x quyển ( * x  N )
Số quyển sách mỗi giờ thực tế sắp xếp là: x+110 (quyển) 810
Thời gian dự định để sắp xếp 810 quyển sách là: (h) x
Tổng số quyển sách đã được sắp xếp trong thực tế là: 810+60=870 (quyển) 870
Thời gian thực tế để sắp xếp 870 quyển sách là: (h) x +110
Do công việc hoàn thành trước dự định 1 giờ 30 phút nên ta có phương trình: 810 870 − =1,5 x x +110
Suy ra: x=180 (thỏa mãn) hoặc x=-330 (loại).
Vậy số quyển sách mỗi giờ nhóm dự đinh sắp xếp là180 quyển. Câu 4. A H C B
Kẻ đường cao AH của tam giác ABC. Ta có: AB AB . AB AC . AB AC.BC . AB AC.BC = = = = sin C AH AH AH.BC 2SABC AC A . B AC.BC Đặt
= k (k>0)  AB = k sin C 2SABC
Tương tự, suy ra: AC = k sin ;
B BC = k sin A
AB sin C + BC sin A + CAsin B 2 2 2
= k sin C + k sin A + k sin B
= k(sin A + sin B + sin C) Lại có: Trang 15 (AB + BC + )
CA (sin A + sin B + sin C)
= (k sin A + k sin B + k sin C)(sin A + sin B + sin C)
= k (sin A + sin B + sin C) Từ đó suy ra:
AB sin C + BC sin A + CAsin B = (AB + BC + )
CA (sin A + sin B + sin C) Câu 5. C O M A B N E D
a) Xét  COM và  CED, ta có: 0
COM = CED = 90 , ECD chung. CO OM  C  OM C  ED  = (1) CE ED
Do AB, CD là 2 đường kính vuông góc với nhau nên: 0 CEA = CAB = 45
Xét AMC và ECA có: 0
CEA = CAB = 45 , ACE chung. AC AM  A  MC EAC  = . CE AE
Mà AC = 2CO (Do ACO vuông cân tại O) AM 2CO 2OM Kết hợp với (1) suy ra: = = AE CE ED
 AM.ED = 2OM.AE (ĐPCM)
b) Tương tự câu a), ta có: ED 2OM = EA 2ON (2), = (3) AE AM DE DN Trang 16 OM ON 1
Nhân theo về của (2) và (3), suy ra: . = AM DN 2 OM ON OM ON Ta có: +  2 . = 2 AM DN AM DN OM ON ED EA
Dấu “=” xảy ra khi và chỉ khi: =  =
 ED = EA , E là điểm chính giữa cung AM DN 2EA 2ED nhỏ AD. OM ON GTNN của +
là 2 , đạt khi E là điểm chính giữa cung nhỏ AD. AM DN
Vậy E là điểm chính giữa cung nhỏ AD (thỏa mãn bài toán). 1 1 1 1 1 1
Câu 6. Đặt + = ; x
+ = y; + = z  x, y, z  0 . a b b c c a
Do đó: P = (3 + x)(3 + y)(3 + z) = 27 + 3(xy + yz + zx) + 9(x + y + z) + xyz
Áp dụng bất đẳng thức Cauchy ta có: 3 3 3
P  27 + 9 (xyz) + 27 xyz + xyz (*) 1 1 1 1 1 1 8
Mà: xyz = ( + )( + )( + )  a b b c c a abc 3 1 8 Mặt khác: 3 3
 a + b + c  3 abc   abc   64  xyz  64 2 2 abc
Từ (*) suy ra: P  343 1
Dấu “=” xảy ra khi và chỉ khi: a = b = c = 2 1
Vậy MinP=343, dấu “=” xảy ra khi a = b = c = . 2 Trang 17
SỞ GIÁO DỤC VÀ ĐÀO TẠO
ĐỀ THI CHỌN HỌC SINH GIỎI KHÁNH HÒA NĂM HỌC 2020 - 2021 Môn: Toán – Lớp: 9 ĐỀ CHÍNH THỨC
Thời gian làm bài: 150 phút Ngày: 3/12/2020
(Đề thi gồm: 01 trang)
Câu 1. (4,0 điểm) a) Rút gọn 3
A = 3 − 2 2 − 7 + 5 2 .
b) Cho các số thực x, y, z thỏa mãn x + y + z = 3 và 2 2 2
x + y + z = xy + yz + zx . Tính giá trị của biểu thức 2020 2020 2020 B = x + y + z + xyz .
Câu 2. (4,0 điểm) a) Cho đa thức 2
f (x) = x + bx + c biết rằng f (x) chia cho x + 4 dư 3, chia cho x −1 dư 8. Tìm b,c .
( 2x − x− )( 2x − x− ) 2 3 3 3 + x b) Giải phương trình: = 0 . x +1
Câu 3. (5,0 điểm) a + b 2 2 ( )2
a) Chứng minh rằng a + b 
 2ab với mọi số thực a,b . 2
b) Cho các số thực dương a,b, c thỏa mãn điều kiện abc = 1. Tìm giá trị lớn nhất của biểu thức 1 1 1 P = + + . 2 2 2 2 2 2
a + 2b + 3 b + 2c + 3 c + 2a + 3 Câu 4. (5,0 điểm)
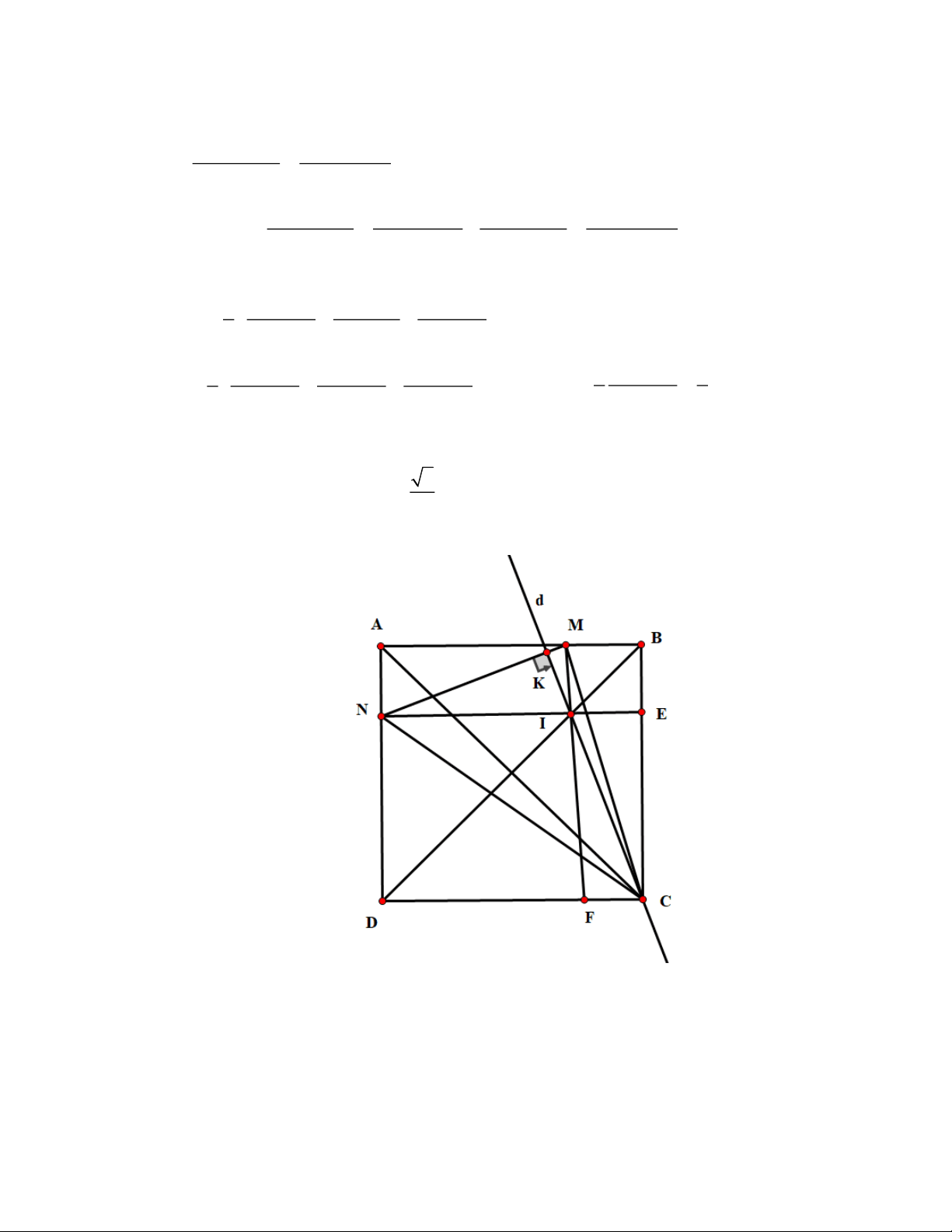
Cho hình vuông ABCD . Điểm I thay đổi trên đường chéo BD (điểm I khác B và D ). Gọi
M , N theo thứ tự là chân đường vuông góc kẻ từ I đến AB và AD .
a) Chứng minh rằng IM + IN không đổi.
b) Đường thẳng d đi qua I và vuông góc với MN . Chứng minh đường thẳng d luôn đi qua một điểm cố định.
c) Xác định vị trí điểm I để tam giác CMN có diện tích nhỏ nhất.
Câu 5. (3,5 diểm) 2 a b +1 a +1
a) Tìm tất cả các cặp số nguyên dương (a,b) sao cho: và là các số nguyên. a +1 b −1
b) Trên bản đồ có 2021 đồng xu. Hai bạn An và Bình thực hiện một số trò chơi bằng cách đi lần
lượt như sau: mỗi người, đến lượt của mình sẽ lấy đi một số các đồng xu sao cho nó là ước của số
các đồng xu hiện có trên bàn. Người lấy đồng xu lượt cuối cùng là thua. Nếu An đi trước, Bình sẽ
dùng chiến thuật như thế nào để chiến thắng? -----HẾT------ Trang 18
ĐÁP ÁN THAM KHẢO – KHÁNH HÒA (2020 – 2021) Câu 1. a) Ta có 3
A = 3 − 2 2 − 7 + 5 2 = ( − )2 − ( + )3 3 2 1 2 1 = 2 −1 − ( 2 + ) 1 = 2 −
x + y + z = xy + yz + zx  (x − y)2 + ( y − z)2 + (z − x)2 2 2 2 = 0 b)
 x = y = z
Mà x + y + z = 3 nên x = y = z = 1 do đó 2020 2020 2020 B = 1 +1 +1 +1 = 4 Câu 2.
a) Số dư của đa thức f (x) cho ( x − a) là f (a) ta có 2  f ( 4 − ) = 3 (  4
− ) − 4b + c = 3 b  = 4      2  f (1) = 8 1
 + b + c = 8 c = 3
Vậy b = 4;c = 3 b) ĐKXĐ: x  −1 Ta có ( 2 x − x − )( 2 x − x − ) 2 3 3 3 + x = 0 4 3 2
 x − 4x − 2x +12x + 9 = 0
 (x −3)(x + ) 2 1  = 0  x = 3(TM )  x = 1 − (TM ) Vậy x  1 − ;  3 Câu 3. a + b 2 2 ( )2 a) a + b 
 2ab với mọi số thực a,b 2 (a +b)2 Xét a + b   (a −b)2 2 2
 0 đúng với mọi số thực a,b (1) 2
(a +b)2  ab (a−b)2 2
 0 đúng với mọi số thực a,b (2) 2 a + b 2 2 ( )2
Từ (1) và ( 2) ta có a + b   2ab 2 Trang 19
b) Áp dụng bất đẳng thức Cô-si ta có 2 2
a + b  2ab và 2 b +1  2 . b Suy ra 2 2
a + 2b + 3  2(ab + b +1) và ta có 1 1  2 2
a + 2b + 3 2(ab + b +1) 1 1 1 1 Tương tự  ;  2 2
b + 2c + 3 2(bc + c +1) 2 2
c + 2a + 3 2(ac + a +1)
Đặt vế trái của BĐT cần chứng minh là A , ta có 1  1 1 1  A  + +  
2  ab + b +1 bc + c +1 ac + a +1 1  1 ab b  1 ab + b +1 1 = + + ( vì abc = 1)   = =
2  ab + b +1 b +1+ ab 1+ ab + b  2 ab + b +1 2
Đẵng thức xảy ra khi và chỉ khi a = b = c = 1 2
Vậy giá trị lớn nhất của P là
khi a = b = c = 1 2 Câu 4.
a) Kéo dài MI cắt DC tại F ; Kéo dài NI cắt BC tại E
Xét tứ giác MIEB có 0
B = M = E = 90 nên tứ giác MIEB là hình chữ nhật
Mà BI là đường phân giác nên hình chữ nhật MIEB là hình vuông
Tương tự tứ giác NDFI là hình vuông Trang 20